README.md

1914. 循环轮转矩阵

English Version

题目描述

给你一个大小为 m x n 的整数矩阵 grid​​​ ，其中 m 和 n 都是 偶数 ；另给你一个整数 k 。

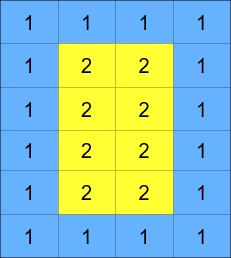
矩阵由若干层组成，如下图所示，每种颜色代表一层：

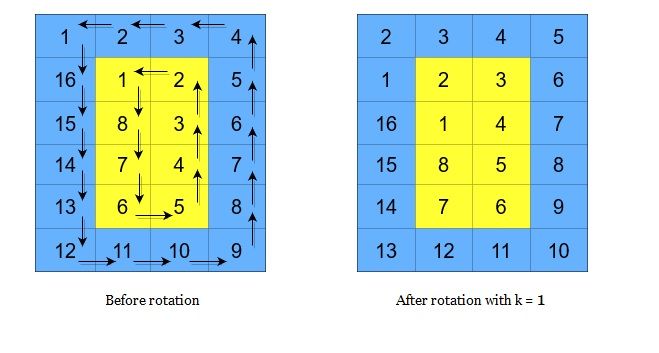
矩阵的循环轮转是通过分别循环轮转矩阵中的每一层完成的。在对某一层进行一次循环旋转操作时，层中的每一个元素将会取代其 逆时针 方向的相邻元素。轮转示例如下：

返回执行 k 次循环轮转操作后的矩阵。

 

示例 1：

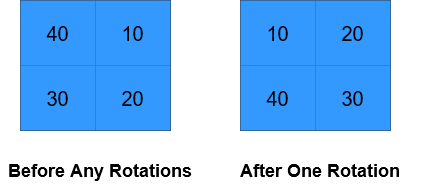
输入：grid = [[40,10],[30,20]], k = 1
输出：[[10,20],[40,30]]
解释：上图展示了矩阵在执行循环轮转操作时每一步的状态。

示例 2：

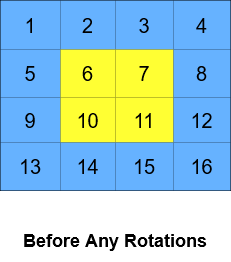
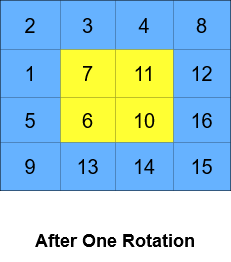
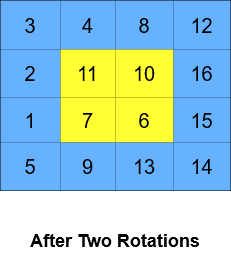
输入：grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2
输出：[[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]]
解释：上图展示了矩阵在执行循环轮转操作时每一步的状态。

 

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 50
• m 和 n 都是 偶数
• 1 <= grid[i][j] <= 5000
• 1 <= k <= 109

解法

Python3

class Solution:
    def rotateGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
        def rotate(grid, s1, e1, s2, e2, k):
            t = []
            for j in range(e2, e1, -1):
                t.append(grid[s1][j])
            for i in range(s1, s2):
                t.append(grid[i][e1])
            for j in range(e1, e2):
                t.append(grid[s2][j])
            for i in range(s2, s1, -1):
                t.append(grid[i][e2])
            k %= len(t)
            t = t[-k:] +t[:-k]
            k = 0
            for j in range(e2, e1, -1):
                grid[s1][j] = t[k]
                k += 1
            for i in range(s1, s2):
                grid[i][e1] = t[k]
                k += 1
            for j in range(e1, e2):
                grid[s2][j] = t[k]
                k += 1
            for i in range(s2, s1, -1):
                grid[i][e2] = t[k]
                k += 1
        
        m, n = len(grid), len(grid[0])
        s1 = e1 = 0
        s2, e2 = m - 1, n - 1
        while s1 <= s2 and e1 <= e2:
            rotate(grid, s1, e1, s2, e2, k)
            s1 += 1
            e1 += 1
            s2 -= 1
            e2 -= 1
        return grid

Java

class Solution {
    public int[][] rotateGrid(int[][] grid, int k) {
        int m = grid.length, n = grid[0].length;
        int s1 = 0, e1 = 0;
        int s2 = m - 1, e2 = n - 1;
        while (s1 <= s2 && e1 <= e2) {
            rotate(grid, s1++, e1++, s2--, e2--, k);
        }
        return grid;
    }

    private void rotate(int[][] grid, int s1, int e1, int s2, int e2, int k) {
        List<Integer> t = new ArrayList<>();
        for (int j = e2; j > e1; --j) {
            t.add(grid[s1][j]);
        }
        for (int i = s1; i < s2; ++i) {
            t.add(grid[i][e1]);
        }
        for (int j = e1; j < e2; ++j) {
            t.add(grid[s2][j]);
        }
        for (int i = s2; i > s1; --i) {
            t.add(grid[i][e2]);
        }
        int n = t.size();
        k %= n;
        if (k == 0) {
            return;
        }
        k = n - k;
        for (int j = e2; j > e1; --j) {
            grid[s1][j] = t.get(k);
            k = (k + 1) % n;
        }
        for (int i = s1; i < s2; ++i) {
            grid[i][e1] = t.get(k);
            k = (k + 1) % n;
        }
        for (int j = e1; j < e2; ++j) {
            grid[s2][j] = t.get(k);
            k = (k + 1) % n;
        }
        for (int i = s2; i > s1; --i) {
            grid[i][e2] = t.get(k);
            k = (k + 1) % n;
        }
    }
}

...