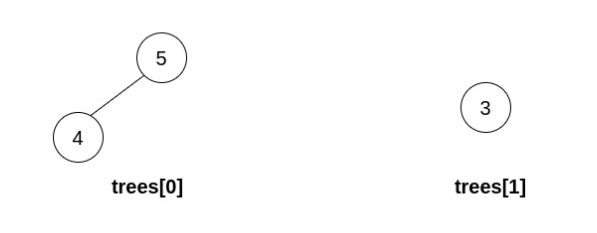README.md

1932. 合并多棵二叉搜索树

English Version

题目描述

给你 n 个 二叉搜索树的根节点 ，存储在数组 trees 中（下标从 0 开始），对应 n 棵不同的二叉搜索树。trees 中的每棵二叉搜索树 最多有 3 个节点 ，且不存在值相同的两个根节点。在一步操作中，将会完成下述步骤：

• 选择两个 不同的 下标 i 和 j ，要求满足在 trees[i] 中的某个 叶节点 的值等于 trees[j] 的 根节点的值 。
• 用 trees[j] 替换 trees[i] 中的那个叶节点。
• 从 trees 中移除 trees[j] 。

如果在执行 n - 1 次操作后，能形成一棵有效的二叉搜索树，则返回结果二叉树的 根节点 ；如果无法构造一棵有效的二叉搜索树，返回 null 。

二叉搜索树是一种二叉树，且树中每个节点均满足下述属性：

• 任意节点的左子树中的值都 严格小于 此节点的值。
• 任意节点的右子树中的值都 严格大于 此节点的值。

叶节点是不含子节点的节点。

 

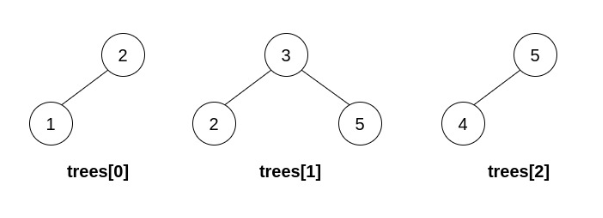
示例 1：

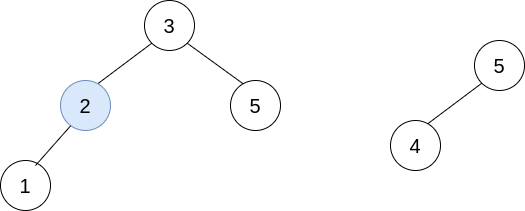
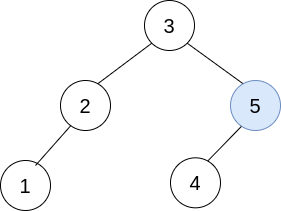
输入：trees = [[2,1],[3,2,5],[5,4]]
输出：[3,2,5,1,null,4]
解释：
第一步操作中，选出 i=1 和 j=0 ，并将 trees[0] 合并到 trees[1] 中。
删除 trees[0] ，trees = [[3,2,5,1],[5,4]] 。

在第二步操作中，选出 i=0 和 j=1 ，将 trees[1] 合并到 trees[0] 中。
删除 trees[1] ，trees = [[3,2,5,1,null,4]] 。

结果树如上图所示，为一棵有效的二叉搜索树，所以返回该树的根节点。

示例 2：

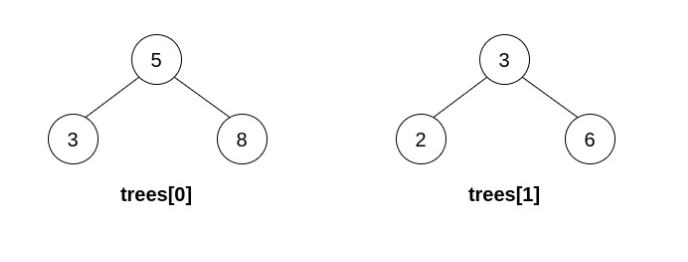
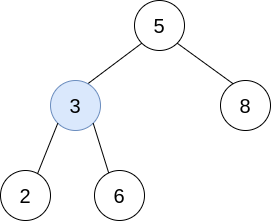
输入：trees = [[5,3,8],[3,2,6]]
输出：[]
解释：
选出 i=0 和 j=1 ，然后将 trees[1] 合并到 trees[0] 中。
删除 trees[1] ，trees = [[5,3,8,2,6]] 。

结果树如上图所示。仅能执行一次有效的操作，但结果树不是一棵有效的二叉搜索树，所以返回 null 。

示例 3：

输入：trees = [[5,4],[3]]
输出：[]
解释：无法执行任何操作。

示例 4：

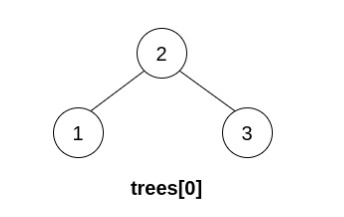
输入：trees = [[2,1,3]]
输出：[2,1,3]
解释：trees 中只有一棵树，且这棵树已经是一棵有效的二叉搜索树，所以返回该树的根节点。

 

提示：

• n == trees.length
• 1 <= n <= 5 * 104
• 每棵树中节点数目在范围 [1, 3] 内。
• trees 中不存在两棵树根节点值相同的情况。
• 输入中的所有树都是 有效的二叉树搜索树 。
• 1 <= TreeNode.val <= 5 * 104.

解法

Python3

Java

...