Function:
The main program file responsible for reading data, running the BSM and Heston models, calculating the error rates, and visualizing the results.
Dependencies:
Depends on the BSM_Model and Heston_Model classes to calculate option prices.Depends on the pandas and matplotlib libraries for data processing and visualization.
Key Components:
- Data reading and preprocessing.
- Running the BSM and Heston models, calculating error rates.
- Visualizing the variation of error rates over time and comparing the average error rates of the two models.
Function:
Uses the simulated annealing algorithm to find the optimal parameters for the Heston model, minimizing the mean squared error between market prices and model prices.
Dependencies:
Depends on the Heston_Model class to calculate option prices.Depends on the pandas library for data processing.
Key Components:
random_rangefunction: Randomly adjusts parameters within a specified range.NGclass: Implements the core logic of the simulated annealing algorithm.NGHestonclass: Inherits from theNGclass, specifically for optimizing parameters of the Heston model.SV_SAclass: Encapsulates the specific implementation of the simulated annealing algorithm.getBestParafunction: Reads data and invokes the simulated annealing algorithm to find the optimal parameters.
Function:
Defines the Heston model class for calculating option prices.
Dependencies:
Depends on the numpy and scipy.integrate libraries for mathematical computations.
Key Components:
Heston_Modelclass: Contains the initialization method and the core method for calculating option prices.characteristic_functionmethod: Calculates the characteristic function.integral_functionmethod: Computes the integral part.P_Valuemethod: Calculates the p-value.Call_Valuemethod: Computes the price of call options.
Function:
Defines the BSM model class for calculating option prices.
Dependencies:
Depends on the scipy.stats and numpy libraries for mathematical computations.
Key Components:
BSM_Modelclass: Contains the initialization method and the core method for calculating option prices.d1andd2methods: Calculate the intermediate variables d1 and d2.pricemethod: Computes the price of call or put options.
Mutual Dependencies:
main.pydepends onBSM_Model.pyandHeston_Model.pyto calculate option prices.-bestpara.pydepends onHeston_Model.pyto calculate option prices and optimizes the Heston model's parameters using the simulated annealing algorithm.
The BSM model only requires the parameters of the options themselves and can be directly called from BSM_Model.py.
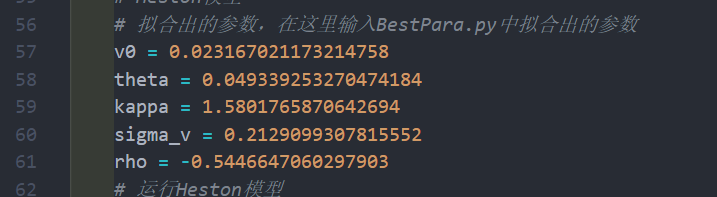
For the Heston model, in addition to the option parameters, fitting parameters are also needed, which can be obtained from bestpara.py. First, run bestpara.py to obtain the optimized parameters (i.e., the current historical optimal solution), and then run main.py for testing and plotting.
The data consists of the SHFE50 ETF option data from2016 to2020. Here, data from June12,2020, to September12,2020, is used to train the fitting parameters, while data from September12,2020, to December12,2020, serves as the testing data.
The paper link reports that results are obtained after over10,000 iterations. In my case, I ran160 iterations, and generally, the more iterations, the better the theoretical performance.
- A line chart showing the variation of average error rates over time for the BSM and Heston models.
- A bar chart comparing the overall average error rates of the BSM and Heston models.
The bestpara.py file is organized into several key components to implement the simulated annealing algorithm for optimizing parameters of the Heston model. Below is a detailed breakdown:
Define Auxiliary Functions:
random_range(x, a, b): - This function introduces a random perturbation to a given parameterxwhile ensuring the new value remains within the bounds[a, b].
Define the Simulated Annealing Class: NG
This class implements the core logic of the simulated annealing algorithm.
__init__(self, func, x0): - Initializes the simulated annealing parameters, including the initial solutionx0, the target functionfunc, and temperature-related parameters.T_change(self): - Defines the temperature decrement function to manage how the temperature decreases over iterations.save_xy(self)andsave_best_xy(self): - Functions to save the current solution and the best (optimal) solution encountered during the algorithm's execution.__p_delta(self, alpha): - Calculates the probability of accepting a new solution based on its improvement over the current solution.__find_solver(self, func, f0): - Implements binary search to find the root of the function used within the optimization process.find_alpha(self): - Searches for a probability factor,alpha, to adjust the acceptance probability of new solutions.get_x_new(self): - Generates a new candidate solution based on the current solution.judge(self): - Determines whether to accept the new solution based on the acceptance probability.get_history_best_xy(self): - Retrieves the historical best solution found so far.plot_best(self): - Plots the changes in the optimal value over the iterations for visualization.count_times_delta_smaller(self): - Counts the number of consecutive times the absolute difference between new and old function values is below a specified threshold.condition_end(self): - Checks if the termination conditions are satisfied, which can include limits on iterations or convergence criteria.run_T(self): - Performs the annealing process at a specific temperature over multiple iterations.accept_best_xf(self): - At the end of each temperature cycle, probabilistically accepts the new solution as the best if conditions are met.run(self): - Orchestrates the overall running of the simulated annealing process.
Define NGHeston Class Inheriting from NG
This class is specifically designed for optimizing parameters in the Heston model.
__init__(self, func, x0): - Initializes parameters in the same way as the parent class but can include specific temperature parameters relevant to the Heston model.get_x_new(self): - Generates new solutions, enforcing constraints on Heston model parameters to ensure they are within acceptable ranges.
Define SV_SA ClassThis class encapsulates the implementation of the simulated annealing algorithm for the specific objective of minimizing errors in option pricing.
__init__(self, data, v0, kappa, theta, sigma, rho): - Initializes the class with input data and the initial parameters for the Heston model.error_mean_percent(self, init_params): - Computes the mean percentage error of option pricing using the Heston model with given initial parameters.error_mean(self, init_params): - Calculates the mean squared error for option pricing under the Heston model.test_error_mean(self, multiple_parmas): - Tests and computes the mean squared errors for multiple sets of initial parameters.test_option_price(self, multiple_parmas): - Computes option prices for multiple sets of parameter values using the model.sa(self): - Executes the simulated annealing algorithm to find the optimal parameters for minimizing the mean squared error.
Define Main Function: getBestPara()
- Reads option data and selects specific dates and types of data needed for analysis.
- Instantiates the
SV_SAclass and begins the training process to find the best parameters for the Heston model. - Returns the optimal solution found.
Involvement of Complex FunctionsIn bestpara.py, several complex functions are utilized for error computation, probability determination, and parameter adjustment within the simulated annealing framework. Their interplay enables effective optimization, facilitating the search for the best-fitting parameters for the Heston pricing model under varying market conditions.
def run(self):
while self.T > self.T_min:
self.run_T() # 循环在该温度下的求解
self.xf_best_T[self.T] = [
self.get_history_best_xy()
] # 记录在每一个温度下的最优解
self.T_change() # 温度继续下降
self.accept_best_xf() # 当每个温度下的循环结束时,有一定概率将当前接受的新解替换为历史最优解
if self.condition_end() == True: # 如果满足终止条件,终止该温度循环
breakThe run function is the core loop of the simulated annealing algorithm. It seeks the optimal solution by continually lowering the temperature. The specific steps are as follows:
- Temperature Loop: Enter the loop when the current temperature T is greater than the minimum temperature T_min.
- Solve at Current Temperature: Call the run_T function to solve at the current temperature.
- Record Optimal Solution: Record the optimal solution at the current temperature in the xf_best_T dictionary.
- Decrease Temperature: Call the T_change function to lower the temperature.
- Accept Optimal Solution: Call the accept_best_xf function to probabilistically replace the current newly accepted solution with the historical optimal solution.
- Termination Condition: If the termination condition is met (calling the condition_end function), exit the loop.
def run_T(self):
for time_ in range(self.times_max):
self.time_ = time_
self.x_new = self.get_x_new() # 获得新解
self.f_new = self.func(self.x_new) # 获得新的函数值
self.save_xy() # 将新解和函数值记录下来
self.delta = self.f_new - self.f # 计算函数值的变化值
self.judge() # 判断是否接受新解
self.times_cycle += 1 # 统计循环次数
self.delta_best = np.abs(
self.f - self.f_last
) # 上次函数值与这次函数值的差值绝对值
self.count_times_delta_smaller() # 统计新旧函数值之差的绝对值连续小于此值的次数
if self.condition_end() == True: # 如果满足终止条件,终止该温度循环
print(
"满足终止条件:接受新解后的函数值变化连续小于{}达到次数".format(
self.delta_min
)
)
break
print(
"当前历史最优解{}:{}".format(self.f_best, self.x_best)
) # 展示当前最优值
print("当前接受的新解{}:{}".format(self.f, self.x)) # 展示当前接受的新解
print("当前新解{}:{}".format(self.f_new, self.x_new)) # 展示当前新产生的解
print("当前温度为{}".format(self.T)) # 展示当前温度The run_T function performs iterative solving at a specific temperature. The specific steps are as follows:
- Number of Iterations: Loop for times_max iterations at each temperature.
- Obtain New Solution: Call the get_x_new function to generate a new solution x_new.
- Calculate New Function Value: Use the objective function func to calculate the new function value f_new.
- Record New Solution and Function Value: Call the save_xy function to record the new solution and its function value.
- Calculate Change in Function Value: Calculate the change delta between the new and old function values.
- Determine Whether to Accept New Solution: Call the judge function to decide whether to accept the new solution.
- Count Iterations: Increment the iteration count times_cycle.
- Calculate Function Value Difference: Compute the absolute difference delta_best between the last function value and the current function value.
- Count Difference Occurrences: Call the count_times_delta_smaller function to count the number of times the absolute difference between the new and old function values is continuously less than a certain threshold.
- Termination Condition: If the termination condition is met (by calling the condition_end function), exit the loop.
- Print Information: Print the current optimal solution, the accepted new solution, the newly generated solution, and the current temperature.
def judge(self):
if self.delta < 0: # 如果函数值变动幅度小于0,则接受新解
self.x = self.x_new
self.f_last = self.f # 在最优解函数值更新之前将其记录下来
self.f = self.f_new
self.save_best_xy() # 记录每次循环接受的新解
self.get_history_best_xy() # 更新历史最优解
self.times_stay = 0 # 由于未接受新解,将连续未接受新解的次数归零
print(
"由于函数值变小新接受解{}:{}".format(self.f, self.x)
) # 展示当前接受的新解
else:
p = np.exp(-self.delta / (self.T * self.alpha)) # 接受新解的概率
p_ = np.random.random() # 判断标准概率
if p > p_: # 如果概率足够大,接受新解
self.x = self.x_new
self.f_last = self.f # 在接受的新解更新之前将其记录下来
self.f = self.f_new
self.save_best_xy() # 记录每次循环接受的新解
self.get_history_best_xy() # 更新历史最优解
print(
"由于概率{}大于{},新接受解{}:{}".format(p, p_, self.f, self.x)
) # 展示当前接受的新解
self.times_p += 1 # 统计因为概率而接受新解的次数
self.times_stay = 0 # 由于未接受新解,将连续未接受新解的次数归零
else:
if self.time_ == 0:
self.f_last = self.f # 在接受的新解更新之前将其记录下来
self.times_stay += 1 # 连续接受新解次数加1
print("连续未接受新解{}次".format(self.times_stay))The judge function is used to determine whether to accept the new solution x_new. The specific steps are as follows:
- Function Value Decreases: If the new function value f_new is less than the current function value f, then the new solution is accepted directly.
- Update the current solution x and function value f. - Record the optimal solution.
- Update the historical optimal solution.
- Reset the count of consecutive rejections times_stay to zero.
- Print the information about the accepted new solution.
- Function Value Increases: If the new function value f_new is greater than the current function value f, then determine whether to accept the new solution based on probability.
- Calculate the probability p of accepting the new solution.
- Generate a random probability p_. _
- If p is greater than p, then accept the new solution.
- Update the current solution x and function value f.
- Record the optimal solution.
- Update the historical optimal solution.
- Print the information about the accepted new solution.
- Increment the count of accepted new solutions due to probability times_p.
- Reset the count of consecutive rejections times_stay to zero.
- If p is less than p_, then do not accept the new solution.
- If this is the first iteration, record the current function value f as f_last.
- Increment the count of consecutive rejections times_stay.
- Print the count of rejections of the new solution.
def get_history_best_xy(self):
x_array = list(
np.array(list(self.xf_best_all.values()),dtype=object)[:, 0]
) # 从历史所有的最优x和f中获得所有的x
f_array = list(
np.array(list(self.xf_best_all.values()),dtype=object)[:, 1]
) # 从历史所有的最优x和f中获得所有的f
self.f_best = min(f_array) # 从每阶段最优的f中获得最优的f
self.x_best = x_array[f_array.index(self.f_best)] # 利用最优f反推最优x
return self.x_best, self.f_bestThe get_history_best_xy function is used to retrieve the historical optimal solution. The specific steps are as follows:
- Retrieve All Historical Optimal Solutions: Extract all x and f from the xf_best_all dictionary.
- Find the Optimal Function Value: Identify the minimum function value f_best from all the f values.
- Locate the Corresponding Optimal Solution: Find the corresponding x_best that matches the optimal function value f_best.
- Return the Optimal Solution: Return the optimal solution x_best and the optimal function value f_best.
** Functions:**
Can be used for user's own remodeling in order to allow users to get the data they need from databases (Tushare), etc. for research or applications.
It might take you some time to run the main.py as the Simulated Annealing Algorithm is time-consuming because of the condition of .the computer hardware. Also, the Simulated annealing algorithms usually require a higher number of iterations, but due to computer hardware condition, I iterated fewer times, which may have had some effect on the results.