diff --git a/generation/2d_diffusion_autoencoder/2d_diffusion_autoencoder_tutorial.ipynb b/generation/2d_diffusion_autoencoder/2d_diffusion_autoencoder_tutorial.ipynb
new file mode 100644
index 000000000..30a098fe9
--- /dev/null
+++ b/generation/2d_diffusion_autoencoder/2d_diffusion_autoencoder_tutorial.ipynb
@@ -0,0 +1,883 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "id": "1d4911a3-a66f-4c2f-8a4d-170cd178ed5c",
+ "metadata": {},
+ "source": [
+ "Copyright (c) MONAI Consortium \n",
+ "Licensed under the Apache License, Version 2.0 (the \"License\"); \n",
+ "you may not use this file except in compliance with the License. \n",
+ "You may obtain a copy of the License at \n",
+ " http://www.apache.org/licenses/LICENSE-2.0 \n",
+ "Unless required by applicable law or agreed to in writing, software \n",
+ "distributed under the License is distributed on an \"AS IS\" BASIS, \n",
+ "WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. \n",
+ "See the License for the specific language governing permissions and \n",
+ "limitations under the License."
+ ]
+ },
+ {
+ "attachments": {},
+ "cell_type": "markdown",
+ "id": "63d95da6",
+ "metadata": {},
+ "source": [
+ "# Diffusion Autoencoder Tutorial with Image Manipulation\n",
+ "\n",
+ "This tutorial illustrates how to use MONAI Generative Models for training a 2D Diffusion Autoencoder model [1].\n",
+ "\n",
+ "In summary, the tutorial will cover the following:\n",
+ "1. Training a 2D diffusion model and semantic encoder with a ResNet18 backbone;\n",
+ "2. Evaluate the learned latent space by applying a Logistic Regression classifier and manipulating images with using the direction learned by the classifier.\n",
+ "\n",
+ "We will us the 2D MRI slices from 3D BraTS volumes [2].\n",
+ "\n",
+ "\n",
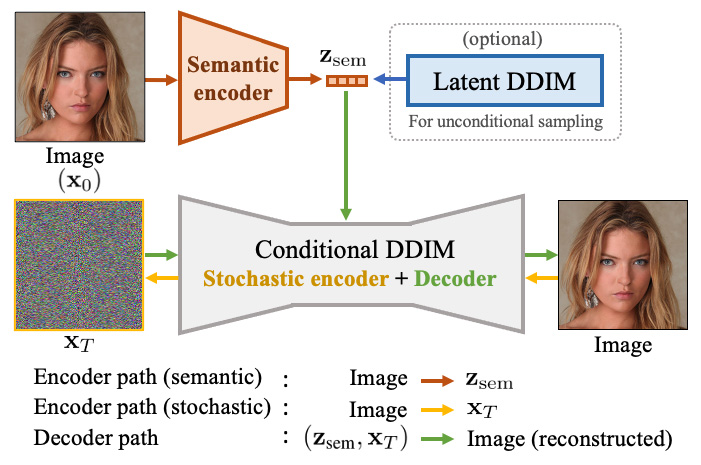
+ "During inference, the model encodes the image to latent space which is used as conditioning for the U-Net=based diffusion model. [1] trains a latent diffusion model for being able to generate unconditional images, which we do not do in this tutorial. Here, we are interested in checking wether the latent space contains classification information or not and if can be used to manipulate the images.\n",
+ "\n",
+ "[1] Preechakul et al. [Diffusion Autoencoders: Toward a Meaningful and Decodable Representation](https://arxiv.org/abs/2111.15640). CVPR 2022
\n",
+ "[2] Menze, B. H., Jakab, A., Bauer, S., Kalpathy-Cramer, J., Farahani, K., Kirby, J., Burren, Y., Porz, N., Slotboom, J., Wiest, R., Lanczi, L., Gerstner, E., Weber, M.-A., Arbel, T., Avants, B. B., Ayache, N., Buendia, P., Collins, D. L., Cordier, N., … van Leemput, K. (2015). The Multimodal Brain Tumor Image Segmentation Benchmark (BRATS). IEEE Transactions on Medical Imaging, 34(10), 1993–2024. https://doi.org/10.1109/TMI.2014.2377694\n",
+ "\n",
+ "\n",
+ "\n",
+ "In this tutorial, then, we train an image encoder and DDPM jointly, so that the generative process is always guided by the latent representation of the encoder. The latent space can then be manipulated in the direction of specific clusters (e.g. anomaly, healthy) using logistic regression, forcing the DDPM sample to lean more towards a specific phenotype conveyed by the latent space.\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "2838db54-6fff-4655-8341-f0c89921ed62",
+ "metadata": {},
+ "source": [
+ "## Setup environment "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "id": "0425c5fb-0fa7-4bd5-b435-2c6a6a50a99d",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "\n",
+ "\u001b[1m[\u001b[0m\u001b[34;49mnotice\u001b[0m\u001b[1;39;49m]\u001b[0m\u001b[39;49m A new release of pip is available: \u001b[0m\u001b[31;49m24.1.2\u001b[0m\u001b[39;49m -> \u001b[0m\u001b[32;49m24.3.1\u001b[0m\n",
+ "\u001b[1m[\u001b[0m\u001b[34;49mnotice\u001b[0m\u001b[1;39;49m]\u001b[0m\u001b[39;49m To update, run: \u001b[0m\u001b[32;49mpip install --upgrade pip\u001b[0m\n"
+ ]
+ }
+ ],
+ "source": [
+ "!python -c \"import monai\" || pip install -q \"monai-weekly[tqdm]\"\n",
+ "!python -c \"import matplotlib\" || pip install -q matplotlib\n",
+ "!pip install -q scikit-learn\n",
+ "%matplotlib inline"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "6b766027",
+ "metadata": {},
+ "source": [
+ "## Setup imports"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "972ed3f3",
+ "metadata": {
+ "collapsed": false,
+ "jupyter": {
+ "outputs_hidden": false
+ },
+ "lines_to_next_cell": 2
+ },
+ "outputs": [],
+ "source": [
+ "import os\n",
+ "import tempfile\n",
+ "import time\n",
+ "import matplotlib.pyplot as plt\n",
+ "import numpy as np\n",
+ "import torch\n",
+ "import torch.nn.functional as F\n",
+ "import torchvision\n",
+ "from monai import transforms\n",
+ "from monai.apps import DecathlonDataset\n",
+ "from monai.config import print_config\n",
+ "from monai.data import DataLoader\n",
+ "from monai.utils import set_determinism\n",
+ "from sklearn.linear_model import LogisticRegression\n",
+ "\n",
+ "from monai.inferers import DiffusionInferer\n",
+ "from monai.networks.nets.diffusion_model_unet import DiffusionModelUNet\n",
+ "from monai.networks.schedulers.ddim import DDIMScheduler\n",
+ "\n",
+ "torch.multiprocessing.set_sharing_strategy(\"file_system\")\n",
+ "\n",
+ "print_config()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "7d4ff515",
+ "metadata": {},
+ "source": [
+ "## Setup data directory"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "8b4323e7",
+ "metadata": {
+ "collapsed": false,
+ "jupyter": {
+ "outputs_hidden": false
+ }
+ },
+ "outputs": [],
+ "source": [
+ "directory = os.environ.get(\"MONAI_DATA_DIRECTORY\")\n",
+ "root_dir = tempfile.mkdtemp() if directory is None else directory"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "99175d50",
+ "metadata": {},
+ "source": [
+ "## Set deterministic training for reproducibility"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "34ea510f",
+ "metadata": {
+ "collapsed": false,
+ "jupyter": {
+ "outputs_hidden": false
+ }
+ },
+ "outputs": [],
+ "source": [
+ "set_determinism(42)"
+ ]
+ },
+ {
+ "attachments": {},
+ "cell_type": "markdown",
+ "id": "c3f70dd1-236a-47ff-a244-575729ad92ba",
+ "metadata": {},
+ "source": [
+ "## Setup BRATS Dataset - Transforms for extracting 2D slices from 3D volumes\n",
+ "\n",
+ "We now download the BraTS dataset and extract the 2D slices from the 3D volumes. The `slice_label` is used to indicate whether the slice contains an anomaly or not."
+ ]
+ },
+ {
+ "attachments": {},
+ "cell_type": "markdown",
+ "id": "6986f55c",
+ "metadata": {},
+ "source": [
+ "Here we use transforms to augment the training dataset, as usual:\n",
+ "\n",
+ "1. `LoadImaged` loads the brain images from files.\n",
+ "2. `EnsureChannelFirstd` ensures the original data to construct \"channel first\" shape.\n",
+ "3. The first `Lambdad` transform chooses the first channel of the image, which is the Flair image.\n",
+ "4. `Spacingd` resamples the image to the specified voxel spacing, we use 3,3,2 mm.\n",
+ "5. `CenterSpatialCropd`: we crop the 3D images to a specific size\n",
+ "6. `ScaleIntensityRangePercentilesd` Apply range scaling to a numpy array based on the intensity distribution of the input. Transform is very common with MRI images.\n",
+ "7. `RandSpatialCropd` randomly crop out a 2D patch from the 3D image.\n",
+ "6. The last `Lambdad` transform obtains `slice_label` by summing up the label to have a single scalar value (healthy `=1` or not `=2` )."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "c68d2d91-9a0b-4ac1-ae49-f4a64edbd82a",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "channel = 0 # 0 = Flair\n",
+ "assert channel in [0, 1, 2, 3], \"Choose a valid channel\"\n",
+ "\n",
+ "train_transforms = transforms.Compose(\n",
+ " [\n",
+ " transforms.LoadImaged(keys=[\"image\", \"label\"]),\n",
+ " transforms.EnsureChannelFirstd(keys=[\"image\", \"label\"]),\n",
+ " transforms.Lambdad(keys=[\"image\"], func=lambda x: x[channel, None, :, :, :]),\n",
+ " transforms.EnsureTyped(keys=[\"image\", \"label\"]),\n",
+ " transforms.Orientationd(keys=[\"image\", \"label\"], axcodes=\"RAS\"),\n",
+ " transforms.Spacingd(keys=[\"image\", \"label\"], pixdim=(3.0, 3.0, 2.0), mode=(\"bilinear\", \"nearest\")),\n",
+ " transforms.CenterSpatialCropd(keys=[\"image\", \"label\"], roi_size=(64, 64, 44)),\n",
+ " transforms.ScaleIntensityRangePercentilesd(keys=\"image\", lower=0, upper=99.5, b_min=0, b_max=1),\n",
+ " transforms.RandSpatialCropd(keys=[\"image\", \"label\"], roi_size=(64, 64, 1), random_size=False),\n",
+ " transforms.Lambdad(keys=[\"image\", \"label\"], func=lambda x: x.squeeze(-1)),\n",
+ " transforms.CopyItemsd(keys=[\"label\"], times=1, names=[\"slice_label\"]),\n",
+ " transforms.Lambdad(keys=[\"slice_label\"], func=lambda x: 1.0 if x.sum() > 0 else 0.0),\n",
+ " ]\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "9d378ac6",
+ "metadata": {},
+ "source": [
+ "### Load Training and Validation Datasets"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "f5bb1c17-60d6-4a76-aef7-adf615a7675c",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Parameters\n",
+ "batch_size = 12"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "da1927b0",
+ "metadata": {
+ "collapsed": false,
+ "jupyter": {
+ "outputs_hidden": false
+ }
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Loading dataset: 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 388/388 [01:57<00:00, 3.30it/s]"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Length of training data: 388\n",
+ "Train image shape torch.Size([1, 64, 64])\n"
+ ]
+ },
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "\n"
+ ]
+ }
+ ],
+ "source": [
+ "train_ds = DecathlonDataset(\n",
+ " root_dir=root_dir,\n",
+ " task=\"Task01_BrainTumour\",\n",
+ " section=\"training\",\n",
+ " cache_rate=1.0, # you may need a few Gb of RAM... Set to 0 otherwise\n",
+ " num_workers=4,\n",
+ " download=True, # Set download to True if the dataset hasnt been downloaded yet\n",
+ " seed=0,\n",
+ " transform=train_transforms,\n",
+ ")\n",
+ "print(f\"Length of training data: {len(train_ds)}\")\n",
+ "print(f'Train image shape {train_ds[0][\"image\"].shape}')"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "id": "5e39c256",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Loading dataset: 100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 96/96 [00:29<00:00, 3.22it/s]"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Length of training data: 96\n",
+ "Validation Image shape torch.Size([1, 64, 64])\n"
+ ]
+ },
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "\n"
+ ]
+ }
+ ],
+ "source": [
+ "val_ds = DecathlonDataset(\n",
+ " root_dir=root_dir,\n",
+ " task=\"Task01_BrainTumour\",\n",
+ " section=\"validation\",\n",
+ " cache_rate=1, # you may need a few Gb of RAM... Set to 0 otherwise\n",
+ " num_workers=4,\n",
+ " download=True, # Set download to True if the dataset hasnt been downloaded yet\n",
+ " seed=0,\n",
+ " transform=train_transforms,\n",
+ ")\n",
+ "print(f\"Length of training data: {len(val_ds)}\")\n",
+ "print(f'Validation Image shape {val_ds[0][\"image\"].shape}')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "33f7af0d-c0e0-4d42-ad53-775b72d3a694",
+ "metadata": {},
+ "source": [
+ "We create the dataloaders:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "id": "b1f94e74-dfae-4c50-bf16-d791c589732a",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "train_loader = DataLoader(\n",
+ " train_ds, batch_size=batch_size, shuffle=True, num_workers=4, drop_last=True, persistent_workers=True\n",
+ ")\n",
+ "val_loader = DataLoader(\n",
+ " val_ds, batch_size=batch_size, shuffle=False, num_workers=4, drop_last=True, persistent_workers=True\n",
+ ")"
+ ]
+ },
+ {
+ "attachments": {},
+ "cell_type": "markdown",
+ "id": "08428bc6",
+ "metadata": {},
+ "source": [
+ "## Define network, scheduler, optimizer, and inferer\n",
+ "\n",
+ "At this step, we instantiate the MONAI components to create a DDIM, the U-Net with conditioning, the noise scheduler, and the inferer used for training and sampling. We are using\n",
+ "the deterministic DDIM scheduler containing 1000 timesteps, and a 2D U-Net with attention mechanisms.\n",
+ "\n",
+ "The `attention` mechanism is essential for ensuring good conditioning and images manipulation here.\n",
+ "\n",
+ "The `embedding_dimension` parameter controls the dimension of the latent dimension learned by the semantic encoder.\n"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "id": "bee5913e",
+ "metadata": {
+ "collapsed": false,
+ "jupyter": {
+ "outputs_hidden": false
+ },
+ "lines_to_next_cell": 2
+ },
+ "outputs": [],
+ "source": [
+ "class DiffusionAE(torch.nn.Module):\n",
+ " def __init__(self, embedding_dimension=64):\n",
+ " super().__init__()\n",
+ " self.unet = DiffusionModelUNet(\n",
+ " spatial_dims=2,\n",
+ " in_channels=1,\n",
+ " out_channels=1,\n",
+ " channels=(64, 128, 256),\n",
+ " attention_levels=(False, False, True),\n",
+ " num_res_blocks=1,\n",
+ " num_head_channels=[64, 128, 256],\n",
+ " with_conditioning=True,\n",
+ " cross_attention_dim=1,\n",
+ " )\n",
+ " self.semantic_encoder = torchvision.models.resnet18()\n",
+ " self.semantic_encoder.conv1 = torch.nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3, bias=False)\n",
+ " self.semantic_encoder.fc = torch.nn.Linear(512, embedding_dimension)\n",
+ "\n",
+ " def forward(self, xt, x_cond, t):\n",
+ " latent = self.semantic_encoder(x_cond)\n",
+ " noise_pred = self.unet(x=xt, timesteps=t, context=latent.unsqueeze(2))\n",
+ " return noise_pred, latent\n",
+ "\n",
+ "\n",
+ "device = \"cuda\" if torch.cuda.is_available() else \"cpu\"\n",
+ "model = DiffusionAE(embedding_dimension=512).to(device)\n",
+ "scheduler = DDIMScheduler(num_train_timesteps=1000)\n",
+ "optimizer = torch.optim.Adam(params=model.parameters(), lr=1e-5)\n",
+ "inferer = DiffusionInferer(scheduler)"
+ ]
+ },
+ {
+ "attachments": {},
+ "cell_type": "markdown",
+ "id": "f815ff34",
+ "metadata": {},
+ "source": [
+ "## Training the diffusion model and the semantic encoder"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "id": "9a4fc901",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Iteration 0/1000 - train Loss 0.9465\n",
+ "Iteration 0 - Interval Loss 0.3134, Interval Loss Val 0.9484\n",
+ "Iteration 50/1000 - train Loss 0.0050\n",
+ "Iteration 100/1000 - train Loss 0.0565\n",
+ "Iteration 100 - Interval Loss 3.7005, Interval Loss Val 0.0101\n",
+ "Iteration 150/1000 - train Loss 0.0092\n",
+ "Iteration 200/1000 - train Loss 0.0124\n",
+ "Iteration 200 - Interval Loss 0.5862, Interval Loss Val 0.0161\n",
+ "Iteration 250/1000 - train Loss 0.0138\n",
+ "Iteration 300/1000 - train Loss 0.0226\n",
+ "Iteration 300 - Interval Loss 0.5498, Interval Loss Val 0.0215\n",
+ "Iteration 350/1000 - train Loss 0.0175\n",
+ "Iteration 400/1000 - train Loss 0.0308\n",
+ "Iteration 400 - Interval Loss 0.5473, Interval Loss Val 0.0150\n",
+ "Iteration 450/1000 - train Loss 0.0021\n",
+ "Iteration 500/1000 - train Loss 0.0102\n",
+ "Iteration 500 - Interval Loss 0.5300, Interval Loss Val 0.0249\n",
+ "Iteration 550/1000 - train Loss 0.0159\n",
+ "Iteration 600/1000 - train Loss 0.0838\n",
+ "Iteration 600 - Interval Loss 0.5258, Interval Loss Val 0.0223\n",
+ "Iteration 650/1000 - train Loss 0.0290\n",
+ "Iteration 700/1000 - train Loss 0.0062\n",
+ "Iteration 700 - Interval Loss 0.5236, Interval Loss Val 0.0262\n",
+ "Iteration 750/1000 - train Loss 0.0294\n",
+ "Iteration 800/1000 - train Loss 0.0064\n",
+ "Iteration 800 - Interval Loss 0.5162, Interval Loss Val 0.0124\n",
+ "Iteration 850/1000 - train Loss 0.0097\n",
+ "Iteration 900/1000 - train Loss 0.0135\n",
+ "Iteration 900 - Interval Loss 0.5090, Interval Loss Val 0.0178\n",
+ "Iteration 950/1000 - train Loss 0.0021\n",
+ "train diffusion completed, total time: 2672.74955368042.\n"
+ ]
+ }
+ ],
+ "source": [
+ "max_epochs = (\n",
+ " 1000 # training for longer (1e4 ~ 3h) helps a lot with reconstruction quality, even if the loss is already low\n",
+ ")\n",
+ "val_interval = 100\n",
+ "print_interval = 50\n",
+ "iter_loss_list, val_iter_loss_list = [], []\n",
+ "iter_loss = 0\n",
+ "\n",
+ "total_start = time.time()\n",
+ "\n",
+ "for epoch in range(max_epochs):\n",
+ " for step, batch in enumerate(train_loader):\n",
+ " model.train()\n",
+ " optimizer.zero_grad(set_to_none=True)\n",
+ " images = batch[\"image\"].to(device)\n",
+ " noise = torch.randn_like(images).to(device)\n",
+ " # Create timesteps\n",
+ " timesteps = torch.randint(0, inferer.scheduler.num_train_timesteps, (batch_size,)).to(device).long()\n",
+ " # Get model prediction\n",
+ " # cross attention expects shape [batch size, sequence length, channels], \n",
+ " #we are use channels = latent dimension and sequence length = 1\n",
+ " latent = model.semantic_encoder(images)\n",
+ " noise_pred = inferer(\n",
+ " inputs=images, diffusion_model=model.unet, noise=noise, timesteps=timesteps, condition=latent.unsqueeze(2)\n",
+ " )\n",
+ " loss = F.mse_loss(noise_pred.float(), noise.float())\n",
+ "\n",
+ " loss.backward()\n",
+ " optimizer.step()\n",
+ "\n",
+ " iter_loss += loss.item()\n",
+ " if epoch % print_interval == 0 and step == len(train_loader) - 1:\n",
+ " print(f\"Iteration {epoch}/{max_epochs} - train Loss {loss.item():.4f}\" + \"\\r\")\n",
+ "\n",
+ " if epoch % val_interval == 0:\n",
+ " model.eval()\n",
+ " val_iter_loss = 0\n",
+ " for _, val_batch in enumerate(val_loader):\n",
+ " with torch.no_grad():\n",
+ " images = val_batch[\"image\"].to(device)\n",
+ " timesteps = torch.randint(0, inferer.scheduler.num_train_timesteps, (batch_size,)).to(device).long()\n",
+ " noise = torch.randn_like(images).to(device)\n",
+ " latent = model.semantic_encoder(images)\n",
+ " noise_pred = inferer(\n",
+ " inputs=images,\n",
+ " diffusion_model=model.unet,\n",
+ " noise=noise,\n",
+ " timesteps=timesteps,\n",
+ " condition=latent.unsqueeze(2),\n",
+ " )\n",
+ " val_loss = F.mse_loss(noise_pred.float(), noise.float())\n",
+ "\n",
+ " val_iter_loss += val_loss.item()\n",
+ " iter_loss_list.append(iter_loss / val_interval)\n",
+ " val_iter_loss_list.append(val_iter_loss / len(val_loader))\n",
+ " iter_loss = 0\n",
+ " print(\n",
+ " f\"Iteration {epoch} - Interval Loss {iter_loss_list[-1]:.4f}, \n",
+ " Interval Loss Val {val_iter_loss_list[-1]:.4f}\"\n",
+ " )\n",
+ "\n",
+ "total_time = time.time() - total_start\n",
+ "\n",
+ "print(f\"train diffusion completed, total time: {total_time}.\")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "8e00670a-a807-4570-ba74-5453b1e3f841",
+ "metadata": {},
+ "source": [
+ "We plot the learning curves:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "id": "cdbd04f4-f212-43b0-b2a3-5376bda07c84",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAkEAAAHZCAYAAACB2e8eAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjkuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8hTgPZAAAACXBIWXMAAA9hAAAPYQGoP6dpAACDNUlEQVR4nO3dd3hT5dsH8G+SNukulA5aKC2jlL23yFAUEAuItaCIgCjqK7gXKDIUcaK4QWUpOCjwY4ksWQKyURmlLbSsDrrobtom5/0jzSG7K22S5vu5rlxNznnOOXdGm7vPlAiCIICIiIjIyUhtHQARERGRLTAJIiIiIqfEJIiIiIicEpMgIiIickpMgoiIiMgpMQkiIiIip8QkiIiIiJwSkyAiIiJySkyCiIiIyCkxCSKHNWTIEEgkEgwZMsTWoRDV2L59+yCRSCCRSLBv3z6z5c6ePYtHH30UoaGhkMvl4jFnzpzRK7dt2zYMHz4c/v7+kMlkkEgkaNSoUZ0+h+oIDw+HRCLBlClTbB0K6ajr96Wqn/P6xiTIDuh+OObNm2frcMhOXLhwAfPnz8egQYMQGhoKd3d3eHl5ISwsDFFRUVi8eDHS0tJsHaZTmTdvnvi7qntTKBQIDAxEREQE7rvvPrz99ts4cOCA1a578uRJ9OnTB2vWrMH169dRVlZmstzXX3+N+++/Hzt37kRWVhbUarXVYiBjU6ZM0fscPP7441U6bs2aNXrHhYeH122gZJaLrQMgIn3Z2dl44YUXsGbNGpNfYoWFhbh69Sq2bt2K119/HU888QQWLlwIPz8/G0RLAFBaWoqMjAxkZGQgMTER27dvxzvvvIP27dtj/vz5eOihh2p1/lmzZqG4uBg+Pj54//330atXL7i7uwMA2rRpAwAoKirC7NmzAQDt2rXDu+++i9atW8PFxQUymax2T5CqZP369fj666/h5uZmsdyPP/5YTxFRZZgEkcOypypVa7l8+TJGjhyJ+Ph4AEBgYCAeeeQRDBo0CMHBwZBIJEhJScG+ffuwfv163LhxA99++y2GDx+OsWPH2jZ4J7N8+XL07t0bACAIAnJzc5GRkYETJ05g69at+Pfff3HhwgXExMRg2rRpWLZsGaRS48r3IUOGwNI61mVlZdi/fz8AYPr06XjmmWdMljtx4gRyc3MBAB9//DFGjRpV26dYJ5KTk20dQp1wc3NDXl4eNm3ahPHjx5stl5aWht27d4vHlJSU1FeIZAKTICI7UVRUhKioKDEBmjZtGj799FN4e3sblX3ggQfw0Ucf4dtvv8Wbb75Z36ESgJYtW6JTp05G2x944AEsXLgQW7ZsweOPP47MzEz88MMP8PPzw4cffljt62RmZqK0tBQA0LZtW7Plbty4Id63VI7qxujRo/Hbb7/hxx9/tJgErV27FiqVCiEhIWjdujUOHjxYj1GSIfYJIrITs2bNwvnz5wEATzzxBL7//nuTCZCWXC7Hc889h7///huhoaH1FSZVUVRUFA4fPiy+hx999BFOnTpV7fMolUrxvqura63LUd147LHHAAA7duzAzZs3zZbTNoVNnDjRZM0g1S++Aw3I3r17MXnyZLRq1QoeHh7w8fFB586d8eqrryIlJcXisWfPnsW7776L4cOHo3nz5lAoFPDy8kJERAQmT56Mv//+2+Lxuh1GASA3NxfvvPMOunfvjkaNGkEikWDlypUmy5aUlOCjjz5Cjx494O3tDW9vb/Tp0wdffvklysvLzV7T0uiw5ORk8Rra6+7atQtRUVFo2rQpFAoFWrZsiWeeeQbXr1+3+NwAICsrC6+99hoiIyPh7u6OoKAg3HPPPdi4cSMAYOXKleL1alLdn5GRge+++w4AEBwcjM8++6zKx3bs2BE9e/bU21bVkXOG74Uhww77f/75Jx566CGEhobC1dUV4eHhKCoqgre3NyQSCSZOnFhpvEeOHBHP+/XXX5ssk5aWhjfffBO9evWCn58fFAoFQkNDERMTIzYlmKNSqbBy5UoMHz4cTZs2hVwuh6+vLyIiInD33XfjvffeE5PNuhYREYH3339ffKx7X8vcqBnte9OyZUtx29SpU/U61M6bN098r6dOnSqWa9mypV457XmrM0KnssEaKSkpeOONN9CjRw/4+vrC1dUVQUFB6Ny5Mx5++GGsXLkSeXl5RsdVdRTSli1bEB0dLf49atKkCfr374/3338fBQUFZo8z/F1Uq9VYtmwZBgwYgMaNG8PT0xNdunTBwoULUVRUZDGG6hg+fDgCAgJQXl6OX375xWSZs2fPiqP5Jk2aVOVzJycn48UXX0THjh3h7e0NDw8PRERE4KmnnsJ///1XpXNs374d9913HwICAuDh4YG2bdvipZde0qtBrIpTp07h6aefRmRkJLy8vODp6YnIyEg888wzYi22QxHI5vbu3SsAEAAIc+fOrfbxxcXFwoQJE8RzmLp5enoKmzdvrvT6lm5vvPGG2Rjmzp0rlouPjxfCw8ONjl+xYoVR2bS0NKFbt25mrxkVFSWoVCqT1xw8eLAAQBg8eLDRvqSkJL3rvvHGG2avERAQIJw/f97sc/v333+FoKAgs8dPnz5dWLFihfg4KSnJ7LnM+fzzz8Xj58yZU+3jDVl6bXTpvhem6H4uZ8+ebfTcw8LCBEEQhEcffVT8nBUUFFi85rPPPisAEFxcXISMjAyj/T/99JPg6elp8bM4bdo0oayszOjY/Px84c4776z0s/zggw9ajNEc3ddr7969VTqmsLBQaNSokQBA8PDwEEpLS/X26/7+6Z5T91rmbnPnzhXfa0s37XnNXcsUS3+TDhw4IPj4+FR63S1bthgdGxYWJgAQJk+ebPK6xcXFwgMPPGDxvCEhIcLp06dNHq/7u3ju3Dnh7rvvNnuePn36VPp5tWTy5Ml6vz/PPfecAEDo1auXyfKvvvqqAEDo2rWrIAi3f0+1v0emrFq1SlAoFGafg0wmE9577z2Lcb744osW//4dP3680vdFpVIJL774oiCRSMyey8XFRVi6dKnJ46vz2atPTILsQG2SILVaLYwaNUovafjxxx+FQ4cOCUeOHBGWLFkitGjRQgAgyOVy4fjx40bn2LVrl+Dp6SnExMQI3377rbBv3z7h1KlTwh9//CF88skn4i8HAGH58uUm49D9g92lSxfB1dVVmDlzprBr1y7hxIkTws8//ywcPnzYqOyAAQMEuVwuPPfcc8KuXbuEkydPCmvXrhXat28vlvn2229NXrOqSdCAAQPEcmvXrhVOnDgh7N69W3jsscfEMv369TN5jZycHCEkJEQsN2nSJGH79u3CiRMnhF9++UXo37+/AEDo27dvrZKgBx98UDz+77//rvbxhqydBHXu3Fn8uXz5cuHYsWPC/v37hSVLlgiCIAjbt28Xy65Zs8bs9crKyoTAwEABgDBq1Cij/b/++qv4R7ZVq1bC4sWLhT/++EM4efKksH79euG+++4Tr/Piiy8aHf/yyy+L+++//37h559/Fg4dOiScPHlS2L59u/Dee+8JAwYMEKKjoy2+LlV5varzh1w3bsP319yXQ3p6uvDff/8JO3bsEPe/++67wn///Sfe0tPThcuXLwv//fef8O6774rlduzYoVdO+0VvjSSopKRE/J3w9vYWXnvtNWH79u3CyZMnhSNHjghr164VZsyYITRr1qxGSVBMTIx47a5duwqrV68Wjh8/LuzYsUOYOnWq+Pnw8/MTrl+/bnS8bhI0YMAAQSqVCpMnTxa2bdsmnDx5Uti4caP4ewtY/ueuMoZJ0PHjx8XHFy5c0CurUqmEZs2aCQCEjz/+WBCEypOgrVu3is/Xy8tLmDt3rnDw4EHhyJEjwieffCL4+/uL1/v6669NnuPTTz/VSx6/+OIL4ejRo8L+/fuF1157TZDL5UJ4eLgQEBBg8X35v//7P/E8gwYNEpYvXy7s27dPOHbsmPDdd98JHTt2FPdv2rTJ6HgmQWRWbZKgZcuWCQAEV1dXYfv27SbLZGdnix/QO+64w2h/RkaGkJOTY/YaSqVSuOeee8Rf1vLycqMyul8OUqlU2LFjh9nz6ZZ1dXU1+QuRlZUl1r506dLF5HmqmgQBEJ588klBrVYblXviiSfEMqdOnTLa/8ILL4j7P/vsM6P95eXlwpgxY/SuVZMkqE2bNuJrV1JSUu3jDVk7CQIg3H333WZjqyy50dJNltauXau3LyMjQ/D19RUACI8//rjJmh5BEMQaKalUKsTFxentCw0NFQBUmuRkZWVZ3G9OTZOgt956Szxu9erVevsq+3IwrNU0pyq1kdZIgvbs2SPuM5XkaJWVlQm5ublG2y0lQVu3btX7vCmVSqMy2r95AISYmBij/bqvAwDhxx9/NCpTUlIidOrUSQAgNGnSxOxnrTKGSZAgCOI/cLNnz9Yru2vXLgHQ1NykpqYKgmA5CSotLRWTTS8vL5M1X8nJyUJwcLAAaGoZDWtW09PTBQ8PD/Ea2uvq2rNnj+Di4iI+D1Pvy86dO8X933//vcnXori4WLjrrrvEaxm+pvaaBLFPkAMTBAEffPABAOC5557DiBEjTJZr3LgxPvroIwDAoUOHkJCQoLff39/f4oyycrlcPP7KlStGM9QamjJlCu69994qPYeZM2ea7Lfi5+cn9nH477//xKG/NREcHIwvvvjCZL+XV155RbxvOEpDqVSK/Yl69+6N559/3uh4mUyGpUuXVjovSGWysrIAAL6+vlAoFLU6V12QSqX4/vvvzcbm4uIijojRTtRnypo1awAAXl5eGDNmjN6+b775Brm5uWjWrBm+/vpruLiYHrw6f/58NGvWDGq1GqtXr9bbp5088s4777T4fOp7TqUmTZqI93Nycur12tamO0HnoEGDzJZzcXGBj49Ptc791VdfAdB07F6xYgXkcrlRmSeffBLDhg0DAGzYsAGpqalmzzdu3Dg8+uijRtsVCgVmzJgBQPO7Z80+Ytq+PmvWrNGb+kDbIXrYsGFo2rRppefZuHGj2JfzrbfeQrdu3YzKhIWFiX+bi4qKsGLFCr39q1atEvs9ffLJJyave9ddd+HJJ5+0GIu2L9uDDz6IadOmmSzj5uaGL7/8EoDme2Lv3r0Wz2kvmAQ5sPPnz+PSpUsAgOjoaItldf9YHTlyxGJZpVKJq1ev4vz58zh79izOnj2r98v8zz//WDy+Kp1jq1JW29lXEAQkJSVV+ZyGoqOjzX55azv3AZo5enSdOHECt27dAgCTf0i1goKCMHz48BrHBwD5+fkAAE9Pz1qdp67ccccdlc5qq30vy8rK8NtvvxntLy4uxv/+9z8AwNixY+Hh4aG3f/PmzQCA+++/32Ii6OLigv79+wMw/iwHBwcDAH799VerdnqtLe1nDLj9Xjsq7WsMwOhLtzbKy8vF+ZDuvfdeiyMetV/a5eXlFjt4V+XvC2D8u18bEydOhEQiwZUrV8R/rIqKirBhwwYAVe8QrR0AUNlM1A899BB8fX31jjE8R+PGjY3+6dBl6fx5eXnia1zZ90z79u3h7+8PoPLvGXvBJMiBnThxQrzfv39/k9P5a2+6f4RNLbVQWFiIRYsWoWvXrvD09ERYWBg6duyIzp07o3PnzujevbtYNjMz02JcXbp0qfJzaNeundl9uv+t1+aLw9I1AM0fCFPXOHv2rHjfcPSVoV69etUwOg3tMOrCwsJanaeuVOU97du3L1q3bg3gdo2Prs2bN4ujegy/nFQqlVjDuHTpUoufZYlEgtjYWADGn+XJkycDAA4fPoyWLVtixowZ2LhxIzIyMqr3hK1M97NV3doRezNw4EC0atUKAPDCCy+gT58+WLRoEQ4dOiTOZ1QTly9fFhPXvn37Wiyru1/399RQffx9MdSiRQuxdltb+7NhwwYUFBTAy8sLDzzwQJXOo31eLVu2REBAgNlycrlc/Pts+FpoR451797dbM0qAHTr1s1krRsAnD59Wpy5/uGHH670d1P7/eAoS/owCXJgluaisMTwP+Tk5GR07twZs2fPxr///guVSmXx+OLiYov7tUlFVRjWBujSnUOjsphqeg3d6xheQ7fZwtIfoarsr4y2uSQ3N1dvvhd7UdX3VJvcHD582GiqAG1iFBgYKDZnaGVnZ1ucDsEcw8/ynDlz8Pjjj0MikeDmzZv46quvMG7cOAQGBqJTp06YO3cu0tPTq32d2tL9x8HRlzdxdXXFli1b0L59ewDA8ePHMXv2bAwcOBCNGjXCiBEjxAkBqyM7O1u8HxgYaLGsbrOO7nGG6uPviyna2p5169ahpKRETIYefPDBSv8eaWmfV2WvBXD79TB8Lap6DhcXF7OfS2t9z9grzhjtwHR/cbds2VLlRfgMfyEmTZqEpKQkca6RCRMmoH379ggICBBXq1ar1eL6Q7pNY6ZwnaLq69q1KxITE6FWq3HmzJlK/xOub1V9TydOnIgFCxZAEAT8/PPPmDVrFgDNH+MdO3YAAMaPH2/0X6nuZ/mJJ54w2f/KFMP/Xl1dXfHDDz/g5Zdfxs8//4w///wTJ06cQGlpKc6dO4dz585h8eLF+Omnnyw2D1jb6dOnxfuRkZH1dt260qFDB/z333/YsmULtmzZggMHDiAxMRHFxcXYsWMHduzYgcWLF+P333+v0pe4IXPzVjmK6OhoPPvss8jNzcWyZcuwZ88eANWbG0jLGq9Fbc6h+7u5dOlSDBgwoErHVeefYVtiEuTAdDtbNmrUyOQU/pWJi4vDX3/9BQCYPXs23n33XZPlLP231VDp/hJnZGRYXIqgts0tgwcPxvr16wEA27Ztq3USpP0vt7JVxK3d/Na2bVv06tULJ06cwNq1a8UkKDY2VmwqMdVPQ/e/UEEQavRZ1tWhQwe88847eOedd1BSUoK//voLa9euxerVq1FQUICHH34Yly5d0uvfUleKiopw+PBhAJq+QaY6uNYX3doPS5+NqnwuZDIZxo4dK65Zl5qaij/++ANfffUVTp48iZMnT+Kpp54SJxStjO5noLLaOt2mFnusWfP29sbYsWPx888/4/XXX4dKpULz5s0xdOjQKp9D+7yqUnOpfT0MX4vGjRsjLS2t0nOUl5eb/Ruv+z3j4eFR699Ne8PmMAem20/n0KFDNTrHuXPnxPuW1rvR7X/kLDp27CjeP3nypMWytX19JkyYIK4K/v3339c6OdH2MapsJFJdzPCqTXLOnj2Lf//9F8DtprDWrVubTPDkcrn4etf0s2yOm5sbhg0bhuXLl4sjaYqLi7F161arXsecFStWiKMb77//fot9M+qa7jIslj4bNflcBAcHY+rUqThy5Ah69OgBANi6dWulzeda2pnuAeDo0aMWyx47dky8b69fytpaH+0CqdVdJkP7vJKSkiz+k1VWVibWNBq+Fp07dwYAnDlzxmJz8z///GO2P1e3bt3EmiRr/27aAyZBDqxHjx5o3rw5AGDZsmU1Wo1Y9xfD0hfvt99+W/0AHVyvXr3EURc//fST2XLp6eliU09NBQQEiCNeUlNT8cILL1T52PPnzxsladqlFuLj4812+szMzMSuXbtqFrAFEyZMEJvP1qxZg+vXr4ujZCyN1hk9ejQATe1kbV9Pc+6++27xfmUd/K0hISFBrA0DgDfeeKPOr2mJbpO5pcT9559/rvE1XF1dMXjwYACavy/aEZaVcXFxEY/btWuXxeVsvv/+e/GYypaGsRXtCDeFQgGFQlHtpjBtvzlBECyOwouNjRWTbMO+dtrH2dnZ2LJli9lzLF++3Oy+gIAA9OvXD4Bm8VdbDzKwNiZBDkwqlWL27NkANCMrHnvsMYudavPy8sR5HLQiIiLE+9o5cQx988032LRpU+0DdjBubm7ioojHjx/HkiVLjMqo1Wo89dRTNUpADb333ntiZ9Pvv/8eTz75pMU1ksrKyvDll1+ib9++uHbtmt4+7ZdJaWkpvvjiC5PHPvHEE1X+L706mjZtirvuuguA5st07dq1Yj8yS0nQ888/L45inDp1ql4tpSnbtm0Ta5qA23/oLfVZ27lzp3hfd02uurB161YMGDBATEJnzZqFrl271uk1K9O4cWNxpN+KFStMNoH89ddfJj/rWgcPHkRiYqLZ/aWlpeJQdy8vr2oNGnj22WfFc0ybNg1lZWVGZZYvXy6+j+PGjauXJs2akMlkuHr1KkpKSlBSUqJXs1wVY8eORUhICABg4cKFJtcIu3btmjjXmYeHh976cYBmtKS2hvmll14y2Sy2f/9+LFu2zGIsb731FgDNd0h0dLTFxFapVOKrr76yyt/E+sA+QXbmzJkzZpMRXXfddRdatGiBp59+Grt27cLGjRuxbt06nDp1Ck899RT69OkDX19f5OXlIS4uDvv27cPmzZvh5uYmThIGaJrUOnXqhLNnz2Lp0qXIycnBpEmTEBwcjOvXr+Onn35CbGws7rjjjgZZFVqZefPmYd26dUhLS8MLL7yAkydPYuLEiQgICEBiYiKWLFmCw4cPo0+fPmIVfU07IXp6emLr1q0YOXIk4uPj8f3332Pz5s2YOHEiBg8ejODgYAiCgNTUVBw4cADr16/H1atXTZ5r1KhRCAsLw5UrVzBnzhxkZmZi3LhxcHNzw7lz5/D555/j9OnT6NevX6WL49bExIkTsWvXLly7dg2LFi0CoKlZs9SvKigoCKtWrUJ0dDRSU1PRq1cvTJkyBSNHjkTz5s1RVlaG69ev49ixY4iNjcXly5exZcsW8Us9Ly8Po0ePRnh4OMaNG4e+ffsiLCwMLi4uSE1NxZYtW8QahGbNmuH++++v1XNMSkoS50QRBAF5eXnIyMjAiRMnsGXLFr0Ebfr06Vi4cGGtrmctzz77LJ566imkp6fjzjvvxJw5cxAZGYns7Gxs27YNX3/9NXr16iX2YzK0Z88evPPOO7jzzjsxatQodOnSBQEBASguLkZ8fDy+/fZbnDp1CgAwbdq0ajX/jRo1Cg899BDWrVuHnTt3ol+/fnjppZfQrl075OTk4JdffhFrLfz8/LB48eLavyB2Si6XY9myZYiKikJeXh7uuOMOvPrqq7j77rshk8lw+PBhvP/+++LorY8//lj8PGoFBQXhnXfewSuvvILk5GT07NkTs2bNQp8+fVBSUoLff/8dn376KZo1a4aioiKztTz33Xcfnn/+eSxZsgQHDhxA+/bt8fTTT2PgwIFo0qQJCgsLkZiYiIMHD2LDhg3IyckRp6uwe7aZqJp0VXUBU93bxo0bxeNLS0uFZ555xuLCdtpby5Ytja5/+vRpoXHjxmaP6dy5s5CSkmJ2Gn1BqHz5hZqUrWya9eosoGpJZWsZnTlzRlxXx9RtypQpwg8//CA+TktLs3i9ymRlZQmTJk0SpFJppe+nq6ur8Nxzzwm3bt0yOs/BgwfNLkQqk8mEJUuWVGsB1erIy8sT3N3d9a756aefVunYzZs3C35+fpU+d6lUKvz555/icYZLpZi7BQcHCydOnKjW89GqyqKmurcOHToI69evt3jO+lw2QxA0a1iNHTvW4u97amqq2fe+qq/BmDFjhKKiIqPr1+cCqpZeh+r8jTDH1LIZ1VGVBVRXrlxZ6wVUtQu7mrr5+/sLx44dq/R9UavVwvz58/WW2DB38/T0NHrvuWwG1RlXV1d8/fXX+OeffzBz5kx07twZvr6+kMlk8PX1Rbdu3TBt2jTExsbiwoULRsd369YNZ86cwdNPP42wsDC4urrCz88Pffr0wccff4xjx47ZbZVzfejatSvOnz+Pl19+GREREVAoFPD398fQoUOxdu1arFixAnl5eWJ5bT+imvLz88Pq1atx9uxZzJ07FwMHDkSzZs2gUCjg4eGBFi1aICoqCp9++imuX7+OJUuWmLzmwIEDcfLkSUyaNAkhISFwdXVFcHAwHnzwQRw4cADPPfdcreK0xNvbG1FRUeJjmUyGCRMmVOnYqKgoJCUl4eOPP8Zdd92FoKAguLq6wt3dHS1btsT999+PxYsXIzk5WW+0TVhYGI4dO4Z58+bh3nvvRWRkJBo1agQXFxf4+/tj0KBB+OijjxAXF1fp5JfV5erqiiZNmqBVq1YYOXIk5syZg4MHD+LcuXMYN26cVa9VW1KpFLGxsfjqq6/Qu3dveHp6wtPTE126dMHChQtx9OhRi8s6vPLKK1i/fj2eeeYZ9OvXDy1atICbmxvc3NwQHh6OmJgYbN26Ff/73//EppjqcHNzw4YNG7B582aMGzcOISEhkMvlaNy4Mfr27YtFixbh4sWLNh1lV58mT56MuLg4PP/882jfvj08PT3h7u6O1q1b48knn8Tp06f1+p2ZsmTJEmzbtg3Dhw+Hn58f3Nzc0KZNGzz33HM4ffo0evfuXWkcEokEb7/9NuLj4/Haa6+hV69e8PPzg0wmg7e3Nzp06ICJEydi1apVSE1NrdF7bwsSQahk0hciqtQTTzyBH374Ac2bNzfqn0NERPaJNUFEtVRcXCx2HNeOoiAiIvvHJIioEpcuXTI74kilUuGZZ54Rh1s7TGdAIiJicxhRZaZMmYJjx45hwoQJ6Nu3LwIDA1FcXIx///0X3333nTgSZtiwYdi5c6fDT/lPROQsOESeqAouXLiAuXPnmt1/xx134JdffmECRETkQFgTRFSJixcvYv369di9ezeSk5ORkZGBsrIyNGnSBL169cL48eMxYcKEak2JT0REtsckiIiIiJwSm8MsUKvVSElJgbe3N5s5iIiIHIQgCMjPz0dISIjFWnomQRakpKQgNDTU1mEQERFRDVy7dk1caNwUJkEWeHt7A9C8iD4+PjaOhoiIiKoiLy8PoaGh4ve4OUyCLNA2gfn4+DAJIiIicjCVdWXhcBYiIiJySkyCiIiIyCkxCSIiIiKnxCSIiIiInBKTICIiInJKTIKIiIjIKXGIPBERWaRSqVBWVmbrMMiJyWQyuLq6Wv28TIKIiMgkQRCQlpaG3NxccJlJsjWFQgF/f3+rztvHJIiIiEzKzc3FrVu3EBAQAE9PT66hSDYhCALKysqQm5uLGzduAIDVEiEmQUREZEQQBNy8eRM+Pj7w9/e3dTjk5Nzd3eHt7Y3r168jMzPTakkQO0YTEZERlUoFlUrFJYPIbkgkEvj6+kKpVFqtjxqTICIiMlJeXg4AcHFhgwHZD23naJVKZZXzMQmiGku8WYANp66jqLTc1qEQUR1hPyCyJ9b+PDLFpxopKVNhwrIjyCwoRVxaPmbf197WIREREVULa4KoRuLT85FZUAoAOJiQaeNoiIiIqo9JENVIQnqBeP/SzQKUqdQ2jIaIqGGQSCQYMmSIrcNwGkyCqEYSM24nQaUqNZIzC20YDRGR9UgkkmrdyHGxTxDViG5NEABcSMtHRJC3jaIhIrKeuXPnGm377LPPkJuba3KfNV24cAEeHh51eg26jUkQ1cilDP0k6GJaHtA1xEbREBFZz7x584y2rVy5Erm5uSb3WVO7du3q9Pykj81hVG0lZSpcydJv/rqYlm+jaIiIbCM5ORkSiQRTpkzBhQsX8MADD6BJkyaQSCRITk4GAGzcuBEPP/ww2rRpAw8PD/j6+uLOO+/E+vXrTZ7TVJ+gKVOmQCKRICkpCZ9//jnatWsHhUKBsLAwzJ8/H2o1+2TWFGuCqNqSMguhNlhLMY5JEBE5qcTERPTr1w+dO3fGlClTkJWVBblcDgCYNWsW5HI5Bg4ciODgYGRkZGDz5s2Ijo7G559/jpkzZ1b5Oq+++ir279+P+++/H8OHD8f//vc/zJs3D6WlpVi4cGFdPb0GjUkQVVvizQKjbddzipFfUgZvN1cbREREZDuHDh3C22+/jfnz5xvt+/3339GqVSu9bQUFBRgwYADmzJmDadOmVbkP0KlTp/Dvv/8iODgYADBnzhxERETgiy++wNy5c8XEi6qOSRBVW4JOEhTgrUBGvhKAZu6gnmF+tgqLiOpJ1Bd/ib/39irAW4EtMwfWy7WaNm2KN9980+Q+wwQIALy8vDBlyhS8/PLLOH78OAYPHlyl68yZM0dMgADA398fY8aMwapVq3Dx4kV07ty5Zk/AiTEJomq7pJMEjeocjJWHkwFomsSYBBE1fBn5SqTlldg6DLvRtWtXs7UwN2/exPvvv4/t27fjypUrKC4u1tufkpJS5ev07NnTaFvz5s0BALdu3ap6wCRiEkTVlnBT0/9HLpPi3g5BYhLEztFEziHAW2HrECpVnzEGBQWZ3J6dnY3evXvj6tWruOOOOzBs2DA0atQIMpkMZ86cwaZNm6BUVr1GzcfHx2ibdoFbay0o6myYBFG1lKvUSKqYGLGlvyc6hNz+pYxLZRJE5Azqq5nJUZibMPGHH37A1atX8c477+Ctt97S2/f+++9j06ZN9REeWWCXQ+TPnTuHhx56CK1atYKHhwf8/f0xaNAgbNmypdJjV65caXZWz7S0tHqIvmG7kl2EMpVmaFibIC808pAjyEfzH1dcWh4EQbB0OBGR07h06RIAYMyYMUb7Dh48WN/hkAl2WRN05coV5OfnY/LkyQgJCUFRURHWr1+P0aNHY+nSpZg+fXql51iwYAFatmypt61Ro0Z1FLHz0J0puk2AFwAgsqkP0vMykFdSjrS8EgT7utsqPCIiuxEWFgYA+Ouvv/Q6La9duxa///67rcIiHXaZBN13332477779LbNmDEDPXv2xOLFi6uUBI0cORK9evWqqxCdlu5M0RFBmiSofVNvHIjPAKDpHM0kiIgImDRpEj744APMnDkTe/fuRVhYGP755x/s2bMH48aNw4YNG2wdotOzy+YwU2QyGUJDQ6vVAz4/P5+dxawsIf12v5+IQM1aYZFNb68Zxs7RREQazZs3x/79+3H33Xdj9+7dWLp0KUpLS7Fz505ERUXZOjyCndYEaRUWFqK4uBi5ubnYvHkztm/fjvHjx1fp2KFDh6KgoAByuRzDhw/HJ598goiIiDqOuOHTrh4vlQDh/poJvnSToLjUPJvERURUl7TLYOgKDw+vtB9k165dsWPHDpP7pkyZYrTN1PlWrlyJlStXmjzHvHnz6nw9s4bMrpOgl19+GUuXLgUASKVSjBs3Dl9++aXFYzw8PDBlyhQMHToUPj4+OHnyJBYvXowBAwbg1KlTCA0NNXusUqnUG66Yl8cvdF1qtSDOFh3exBMKFxkAoE2gF2RSCVRqgctnEBGRw7DrJOiFF15AdHQ0UlJS8Ntvv0GlUqG0tNTiMTExMYiJiREfjx07FsOHD8egQYOwcOFCfPvtt2aPXbRokclpz0njxq1ilJRpFuprHeglble4yNDK3xMJNwtwKaMAZSo1XGUO09JKREROyq6/qdq1a4dhw4bhsccew9atW1FQUICoqKhqD8MeOHAg+vbti927d1ssN2vWLOTm5oq3a9eu1Sb8Bkd3zbAInSQIuN0kVqYSxHmEiIiI7JldJ0GGoqOjcfz4ccTHx1f72NDQUGRnZ1sso1Ao4OPjo3ej27QzRQO3R4ZptdPpF3SB/YKIiMgBOFQSpF1zJTc3t9rHXr58GQEBAdYOyano1gS1CfDW2xfZ9HbCyBFiRETkCOwyCbp586bRtrKyMqxevRru7u7o0KEDACA1NRVxcXEoKysTy2VkZBgd+/vvv+PkyZMYMWJE3QXtBHRXj28d6Km3rx2HyRMRkYOxy47RTz31FPLy8jBo0CA0a9YMaWlpWLNmDeLi4vDJJ5/Ay0vTFDNr1iysWrUKSUlJCA8PBwAMGDAA3bt3R69eveDr64tTp05h+fLlCA0NxezZs234rBybIAhIrJgtulkjd3jI9T86zRu7w0vhggJlOUeIERGRQ7DLJGj8+PH44Ycf8M033yArKwve3t7o2bMnPvjgA4wePbrSY7dt24adO3eiqKgIwcHBePLJJzF37lyzK/1S5W7mK5GvLAdg3B8I0Cwg2DbIC6eu3sKNW8XIKymDj5trfYdJRERUZXaZBE2YMAETJkyotJypCaTeffddvPvuu3UUmfPSXTPMcGSYVmRTH5y6egsAEJ+Wj17hfvURGhERUY3YZZ8gsj+JOiPD2phJgtoH68wczSYxIiKyc0yCqEp0O0W3CfQ2WSYyiJ2jiYjIcTAJoirRT4JM1wS10xkmH5fGuYKIiMi+MQmiKrlUkQQFeivg6266w7Ovhyua+rgB0DSHVXdmbyIiovrEJIgqlV1YiqxCzZpt5mqBtLTLZ+SXlCM1t6TOYyMicjQrV66ERCIxGtgTHh4uTvdSm/NY07x58yCRSLBv3746u4YtMQmiSllaM8xQu2D2CyIix/bII49AIpHg559/tlguLy8PHh4eaNSokbiigaPZt28fJBIJ5s2bZ+tQbIJJEFVKd82wNkGmO0Vr6c4czRFiROSIpk2bBgBYvny5xXI///wziouL8fDDD8Pd3b3W192zZw/27NlT6/NY04wZM3DhwgX06dPH1qHUCbucJ4jsi+4cQW0CKmkOC2LnaCJybHfddRdatmyJP//8E1evXkWLFi1MltMmSdqkqbZat25tlfNYk7+/P/z9/W0dRp1hTRBV6lKGTnOYidmidbUO9IRMKgHA5jAickwSiQRTp06FWq3GihUrTJY5d+4cjh07hi5duiAiIgIffPABBg8ejJCQEMjlcoSEhOCxxx7DpUuXqnxdc32CsrOz8fTTTyMoKAgeHh7o3bs3Nm7caPY8y5cvx5gxYxAeHg43Nzf4+flh+PDh2Lt3r165efPmYejQoQCA+fPnQyKRiLfk5GSxjLk+QVu2bMHQoUPh6+sLd3d3dO3aFYsXL0Z5ebleueTkZEgkEkyZMgWJiYl44IEH0LhxY3h6emLYsGH4559/qvwaWRtrgqhS2pqgRh6uaOIpt1hW4SJD6wBPxKcX4FJGAcpUarjKmGsTkWOZMmUK5s2bh5UrV+Ltt9+GRCLR269NjqZNm4YLFy7g7bffxtChQ/HAAw/A09MTcXFxWLt2LbZt24ZTp04hLCysRnEUFRVhyJAh+O+//9C/f38MHjwY165dw/jx43HvvfeaPObZZ59F165dMWzYMAQEBODGjRv43//+h2HDhmHDhg0YM2YMAGDIkCFITk7GqlWrMHjwYAwZMkQ8R6NGjSzGtXjxYrz88svw8/PDI488Ak9PT2zevBkvv/wyDh48iA0bNhi9ZsnJyejXrx86duyIxx9/HJcuXcKmTZswdOhQXLhwwTZLWwlkVm5urgBAyM3NtXUoNpNXXCqEvb5VCHt9qxD9zaEqHTNj7SnxmLjUvDqOkIjqQnFxsXD+/HmhuLjY1qHYzIgRIwQAwu7du/W2l5WVCUFBQYJCoRCysrKEW7duCVlZWUbH//nnn4JUKhWeeOIJve0rVqwQAAgrVqzQ2x4WFiaEhYXpbZs7d64AQHjyySf1tv/xxx8CAJPnuXz5slEsKSkpQkhIiBAREaG3fe/evQIAYe7cuSZegdvX37t3r7gtMTFRcHFxEQIDA4WrV6+K20tKSoSBAwcKAITVq1eL25OSksRY33//fb3zv/XWWwIAYdGiRSavb6iqn8uqfn+zJogsSqzCTNGG2jX1xpaK2s24tDxx2DwRNQy/vXccRXmltg7DIg8fOWJm967VOaZNm4Y//vgDy5cvx9133y1u37p1K9LT0xETEwM/P/NrJA4dOhQdO3bE7t27axzD6tWrIZfLsWDBAr3tw4cPx913322yI3XLli2NtgUHB+PBBx/EF198gStXrtS4ZgoA1q5di/Lycrz88ssIDQ0VtysUCnzwwQe44447sHLlSkyaNMkorldffVVv27Rp0/Duu+/i+PHjNY6nNpgEkUWJVZgp2pDu8hlxafkYY/WoiMiWivJKUXhLaesw6tyYMWMQEBCAjRs3Ijc3F76+vgBMd4jet28fPvvsMxw9ehSZmZl6/WLkcsvdCMzJy8tDUlISOnTogKZNmxrtv/POO00mQZcvX8aiRYvw559/4saNG1Aq9d+rlJSUWiVBp0+fBgC95jOt/v37w83NDWfOnDHa161bN0il+t0jmjdvDgC4detWjeOpDSZBZFF15gjS4lxBRA2bh0/NvtTrkzVidHV1xaRJk7B48WKsXbsWzzzzDNLS0rB9+3a0aNECw4YNAwCsW7cO48ePh5eXF4YPH47w8HB4eHiIExleuXKlRtfPy9OMsA0MDDS531QfmsTERPTp0wd5eXkYOnQooqKi4OPjA6lUin379mH//v1GSVFN4zJ1fYlEgqCgINy4ccNon4+Pj9E2FxdNGqJSqWoVU00xCSKLqrJmmKFmjdzhrXBBvrKcSRBRA1TbZiZHMm3aNCxevBg//PADnnnmGfz4448oLy/H1KlTxVqNefPmwc3NDSdPnkRERITe8b/88kuNr61NGm7evGlyf3p6utG2Tz/9FDk5Ofjxxx/x6KOP6u17+umnsX///hrHYxhXenq6UY2SIAhIT083mfDYIw7bIYu0NUGechmCfd2qdIxEIkHbin5AN24VI7e4rM7iIyKqSx06dEC/fv1w8uRJ/Pvvv1ixYoU4hF7r0qVLaN++vVEClJqaisuXL9f42j4+PmjZsiUSExORlpZmtP/gwYNG27RD8rUjwLQEQcChQ4eMystkMgDVq4np3r07AJgcNn/06FGUlJSgW7duVT6fLTEJIrNKylS4llMEQDNTtOFwR0t0O0PHp7M2iIgcl7bvz//93//hwoULGDZsmF4NSFhYGBITE/VqZkpKSvDMM8+grKx2/wROmjQJpaWlePvtt/W279y502R/IG1cf/31l972999/H2fPnjUqr+3Yfe3atSrH9Mgjj8DFxQWLFy9GSkqKuL20tBSvv/46AM0UA46AzWFk1qWMAmgXgq9spmhD7Q2Wz+gdbn4EBRGRPRs/fjxeeOEFsSbFcIbomTNnYubMmejevTuio6NRXl6OXbt2QRAEdO3atVaTAb722mvYsGEDvvvuO5w7dw6DBg3CtWvX8Ntvv2HUqFHYtm2bXvmnn34aK1aswIMPPoiYmBg0adIEf//9N06dOmWyfLt27RASEoJffvkFCoUCzZs3h0QiwcyZM8WO4IZat26NDz74AC+//DK6dOmCmJgYeHp6YsuWLbh48SLGjBlj1BRnr1gTRGbpdYquZKZoQ5FNb7cHX+TyGUTkwLy9vRETEwNAU3MyduxYvf3PPvssvv32W/j5+eG7777Dxo0bMXjwYBw5cqTSSQcr4+npif3792P69OlISEjAZ599hri4OPz666+Ijo42Kt+9e3fs3LkTPXr0wIYNG7B8+XI0atQIhw4dQq9evYzKy2QybNiwAf369cPPP/+Mt99+G3PmzEFOTo7FuF566SVs2rQJnTp1wk8//YQvvvgCcrkcn3zyCWJjY6vVcmBLEkHQ/q9PhvLy8uDr64vc3FyH6eRlTR/vuIgv9yYCAL5/rBeGdaj6bJ65RWXoumAnAKB3eGOse3pAncRIRHWjpKQESUlJaNmyJdzcqtYfkKiuVfVzWdXvb9YEkVm1qQny9XAVO1LHpeWDuTYREdkbJkFkVsJNTYdmuYsUzRt7VPt4befo/JJypOSWWDU2IiKi2mISRCaVlqtxJUszMqx1gJe4Mnx1tGO/ICIismNMgsikK1mFKFdrmrCqOlO0oXYGI8SIiIjsCZMgMqkmM0Ub0p0rKC6VSRAREdkXJkFkUk3WDDPUOsALLhXNaFw+g4iI7A2TIDLJGjVBchcpWldMsngpowCl5WqrxEZE9YcjO8meWPvzyCSITNLWBLlIJQhr4lnj82ibxMrVAi5nFlRSmojshXZ17/LychtHQnSbdhkS7ZpntcUkiIyo1AIuZWgSlnB/T8hdav4xYb8gIsckk8kgk8mQl8eRnWQfBEFAbm4uFAoFXF1drXJOrh1GRq5lF4lNV9VdM8wQR4gROSaJRILAwECkpqZCoVDA09PTYZZCoIZFEASUlZUhNzcXBQUFaNasmdXOzSSIjNRmpmhD7YI5VxCRo/L19UVxcTEyMzORkZFh63DIySkUCjRr1syqy1gxCSIj1ugUrRXi6wZvNxfkl5RzhBiRg5FIJAgODkZgYKDYF4PIFmQymdWawHTZZRJ07tw5zJs3DydPnkRaWho8PDzQoUMHvPrqq4iKiqr0+Fu3buG1117Dxo0bUVRUhD59+uCTTz5Bjx496iF6x5doxSRIIpEgMsgbJ67kICW3BLnFZfB1t/4HmYjqjrZ/EFFDY5cdo69cuYL8/HxMnjwZS5YswZw5cwAAo0ePxrJlyyweq1arMWrUKKxduxYzZszAhx9+iJs3b2LIkCFISEioj/AdXmLFmmESCcQh7rWh2zmatUFERGQvJIKDTAKhUqnQs2dPlJSUIC4uzmy53377DePHj8e6desQHR0NAMjIyEDbtm0xcuRIrF27tsrXzMvLg6+vL3Jzc63aBmnPBEFAp7k7UFiqQgs/Dxx4bWitz/njkWTM2XQOAPDOmI6Y1D+81uckIiIyp6rf33ZZE2SKTCZDaGgobt26ZbFcbGwsgoKCMG7cOHFbQEAAYmJisGnTJiiVyjqO1LGl5pagsFQFoOYzRRvS7RzNEWJERGQv7DoJKiwsRGZmJi5duoRPP/0U27dvx913323xmNOnT6NHjx6QSvWfWp8+fVBUVIT4+Pi6DNnhWbNTtFbbIDaHERGR/bHLjtFaL7/8MpYuXQoAkEqlGDduHL788kuLx6SmpmLQoEFG24ODgwEAKSkp6Ny5s8ljlUqlXk2RM04SZs1O0Vq+7q4I8XVDSm4JLqblQxAEzjdCREQ2Z9c1QS+88AJ27dqFVatWYeTIkVCpVCgtLbV4THFxMRQKhdF2Nzc3cb85ixYtgq+vr3gLDQ2t3RNwQNpO0QAQoVODU1vaztH5ynLcuGX+PSAiIqovdp0EtWvXDsOGDcNjjz2GrVu3oqCgAFFRURYXUHN3dzfZ76ekpETcb86sWbOQm5sr3q5du1b7J+FgdGuCWgfUfM0wQ/qTJrJJjIiIbM+ukyBD0dHROH78uMV+PcHBwUhNTTXart0WEhJi9liFQgEfHx+9mzMRBAHx6ZokKNjXDd5u1pvPh8tnEBGRvXGoJEjblJWbm2u2TLdu3XDq1Cmo1Wq97UePHoWHhwfatm1bpzE6ssyCUuQWa2aFtVZ/IK1IJkFERGRn7DIJunnzptG2srIyrF69Gu7u7ujQoQMATe1OXFyc3nTu0dHRSE9Px4YNG8RtmZmZWLduHaKiokz2FyKNuugUrdXK3wsuUk1naK4hRkRE9sAuR4c99dRTyMvLw6BBg9CsWTOkpaVhzZo1iIuLwyeffAIvL80X9KxZs7Bq1SokJSUhPDwcgCYJ6tevH6ZOnYrz58/D398fX3/9NVQqFebPn2/DZ2X/dDtFWzsJkrtI0SbQC3Fp+bicUYjScjXkLnaZgxMRkZOwyyRo/Pjx+OGHH/DNN98gKysL3t7e6NmzJz744AOMHj3a4rEymQy///47Xn31VXz++ecoLi5G7969sXLlSkRGRtbTM3BMeqvHB1pvZJhWZFNvxKXlo1wt4FJGAdoHO1efKyIisi8Os2yGLTjbshmPfPc3Dl/KAgCcnnMPGnvKrXr+r/cl4sM/LgIAPh3fFQ90b27V8xMREQENcNkMqnva2aKbeMqtngABHCFGRET2hUkQAQByi8qQka+ZX8na/YG02jXlXEFERGQ/mAQRACAxo+46RWtp5h7SdENjEkRERLbGJIgAGHaKrpskSCKRiE1iqbklyC0qq+QIIiKiusMkiAAACek6SZAV1wwzpD9pIucLIiIi22ESRABud4oG6q45DAAidfsFpbNJjIiIbIdJEAG43Rzm7eaCQO+6m1W7PUeIERGRnWASRChUluPGLc26bG0CvSCRSOrsWm11kiB2jiYiIltiEkS4nFEo3q+rTtFaPm6uaNbIHYAmCeJcnUREZCtMgggJOmuG1cVyGYa0naMLlOW4nlNc59cjIiIyhUkQ1VunaK12bBIjIiI7wCSI9OYIqo8kSHeYPEeIERGRrTAJIjEJcneVif116pLu8hkXUjlXEBER2QaTICenLFfhSpamY3TrQE9IpXU3MkyrVYAnXGWa67A5jIiIbIVJkJNLyiyEumKAVpuAum8KAwBXmRStK651ObMQynJVvVyXiIhIF5MgJ6e3ZlgdLpdhSNs5WqUWcOlmYSWliYiIrI9JkJPTXTOsPjpFa+kvn8F+QUREVP+YBDm5+h4ZpqU7TD4ulf2CiIio/jEJcnLaJMhVJkGYn0e9XbddMNcQIyIi22IS5MTKVWpcztQkQS39PeEiq7+PQ1MfN/i4uQDgCDEiIrINJkFO7Gp2EcpUmqFh9bFchi6JRCLOF5SWV4JbRaX1en0iIiImQU6svpfLMKQ7czSbxIiIqL4xCXJituoUrRXJNcSIiMiGmAQ5Mf05guo/CWrPztFERGRDTIKcWMJNTeIhlWg6Rte3tkG6NUGcK4iIiOoXkyAnpdaZqTmsiScULrJ6j8HbzVVcsPViWj7U2vU7iIiI6gGTICd141Yxiss0a3bZoj+QlnbSxMJSFW7cKrZZHERE5HyYBDkpW3eK1uKkiUREZCtMgpyUXqdoGyZBemuIsV8QERHVIyZBTkrbKRqwj+YwgDVBRERUv5gEOSndmqDWAbZLglr6e8JVJgHAJIiIiOqXXSZBx48fx4wZM9CxY0d4enqiRYsWiImJQXx8fKXHrly5EhKJxOQtLS2tHqK3f4IgiLNFN2vkDk+Fi81icZVJ0aZiyY6kzEIoy1U2i4WIiJyL7b79LPjggw9w6NAhPPTQQ+jSpQvS0tLw5ZdfokePHvj777/RqVOnSs+xYMECtGzZUm9bo0aN6ihix3IzX4n8knIAtm0K02rX1BsXUvOgUgtIvFmAjiG+tg6JiIicgF0mQS+99BLWrl0LuVwubhs/fjw6d+6M999/Hz/99FOl5xg5ciR69epVl2E6LHvpFK1luHwGkyAiIqoPdtkcNmDAAL0ECAAiIiLQsWNHXLhwocrnyc/Ph0rF5hVDCen20SlaiwupEhGRLdhlEmSKIAhIT0+Hv79/lcoPHToUPj4+8PDwwOjRo5GQkFDHETqOxAzbrhlmqL3OMHkmQUREVF/ssjnMlDVr1uDGjRtYsGCBxXIeHh6YMmWKmASdPHkSixcvxoABA3Dq1CmEhoaaPVapVEKpVIqP8/Ia5rw1Cek6EyUGeFsoWT+CfBTwdXdFbnEZ5woiIqJ6IxEEwe4XbIqLi0Pfvn3RsWNHHDx4EDJZ9da5+uuvvzBo0CBMnz4d3377rdly8+bNw/z584225+bmwsfHx8QRjqnXu7uQWVCKAG8Fjr85zNbhAABilh7BsaRsAMDpOfegsae8kiOIiIhMy8vLg6+vb6Xf33bfHJaWloZRo0bB19cXsbGx1U6AAGDgwIHo27cvdu/ebbHcrFmzkJubK96uXbtW07DtVnZhKTILSgHYR6doLU6aSERE9c2um8Nyc3MxcuRI3Lp1CwcPHkRISEiNzxUaGoqLFy9aLKNQKKBQKGp8DUdgL2uGGdIfIZaH/q2b2DAaIiJyBnabBJWUlCAqKgrx8fHYvXs3OnToUKvzXb58GQEBAVaKznHZ2/B4rXa6a4ilsyaIiIjqnl02h6lUKowfPx5HjhzBunXr0L9/f5PlUlNTERcXh7KyMnFbRkaGUbnff/8dJ0+exIgRI+osZkehu2ZYaztKgjhMnoiI6ptd1gS9/PLL2Lx5M6KiopCdnW00OeKjjz4KQNOHZ9WqVUhKSkJ4eDgAzRxD3bt3R69eveDr64tTp05h+fLlCA0NxezZs+v7qdgd/Zog248M0/JSuKB5Y3dczynGxbR8qNUCpFKJrcMiIqIGzC6ToDNnzgAAtmzZgi1bthjt1yZBpowfPx7btm3Dzp07UVRUhODgYDz55JOYO3cugoKC6ipkh6FNghp5uMLfy75GYLVr6o3rOcUoKlXhek4xWjTxsHVIRETUgDnEEHlbqeoQO0eRX1KGzvN2AgB6hTVG7DMDbByRvo93XMSXexMBAMsm9cS9HZvaOCIiInJEDWaIPFnPpYxC8b49zBRtyHANMSIiorrEJMiJ6K4Z1jrA/pIgvbmCOEKMiIjqGJMgJ6K/Zpj9dIrWCvf3hFym+UjGpXL5DCIiqltMgpxIYrp9zhGk5SqTihM4JmcVoaRMZeOIiIioIWMS5EQSKkaGecplCPZ1s3E0pmmbxFRqQW84PxERkbUxCXISJWUqXMspAqBZLkMisc85eNg5moiI6guTICdxKaMA2skQ7GmmaEP6M0ezXxAREdUdJkFOwl5nijaku4YYl88gIqK6xCTISdjr6vGGgnwUaOThCoDNYUREVLeYBDmJBDsfGaYlkUgQWTF8/2a+EtmFpTaOiIiIGiomQU5CO0eQ3EWKUD/7XpOrHfsFERFRPWAS5ATKVGokZ2qWzGjl7wmZna/OHqnTL4hNYkREVFeYBDmBK1mFKFdrhobZ40zRhtoFc5g8ERHVPSZBTkC3P1AbO1wzzFDbIN3mMCZBRERUN5gEOYEE3eHxdrh6vCEvhQtC/dwBAPHp+VBX1GIRERFZE5MgJ6A/R5D9J0EAEBmk6RdUVHp7pmsiIiJrYhLkBLQ1QTKpBGFNPG0cTdW0D2aTGBER1S0mQQ2cSi3gcsXw+PAmHpC7OMZbzjXEiIiorjnGNyLV2PWcIijL1QDse6ZoQ+2YBBERUR1jEtTAOcqaYYbCm3iKtVYXOGEiERHVASZBDZyjjQzTcpFJxU7cyZmFKClT2TgiIiJqaJgENXC6cwS1doA5gnRp+wWpBf0aLSIiImtgEtTAadcMk0gcLwnSX0OM/YKIiMi6mAQ1YIIg4FJFDUrzxu5wl8tsHFH16K4hFpfKfkFERGRdTIIasLS8EhQoywE4VqdoLb0RYumsCSIiIutiEtSA6a0Z5kDD47UCvRVo7OEKgM1hRERkfUyCGjDdkWGOmARJJBKxc3RGvhLZhaU2joiIiBoSJkENmCOuGWaonW6/IM4XREREVsQkqAFLvHm7Cam1gyZBustnxKWySYyIiKyHSVADJQiC2BzW1McNPm6uNo6oZrh8BhER1RUmQQ1UVmEpbhWVAXDM/kBabYN0aoI4QoyIiKyISVAD5egjw7Q8FS5o4ecBAIhPy4daLdg4IiIiaihqlQSpVCrk5eWhvLxcb3txcTHmz5+PBx54AC+++CJSUlKqdd7jx49jxowZ6NixIzw9PdGiRQvExMQgPj6+SsffunUL06dPR0BAADw9PTF06FCcOnWqWjE4Ou1M0YBjrRlmirZfUHGZClezi2wcDRERNRS1SoIWLFiAxo0b48iRI+I2QRAwZMgQLFiwAJs2bcLnn3+O/v37Iycnp8rn/eCDD7B+/XrcfffdWLJkCaZPn44DBw6gR48eOHv2rMVj1Wo1Ro0ahbVr12LGjBn48MMPcfPmTQwZMgQJCQk1fq6OJlGn6aiNgy2XYag9l88gIqI6UKskaM+ePWjatCnuvPNOcduWLVtw/PhxRERE4LPPPsO9996L69ev47vvvqvyeV966SVcuXIFn3/+OZ544gm89dZbOHjwIMrLy/H+++9bPDY2NhaHDx/GypUrMXfuXDz77LPYt28fZDIZ5s6dW+Pn6mj0a4Icb7ZoXbrLZ7BzNBERWUutkqCkpCS0a9dOb9umTZsgkUiwZs0aPPfcc9iyZQsCAgIQGxtb5fMOGDAAcrlcb1tERAQ6duyICxcuWDw2NjYWQUFBGDdunLgtICAAMTEx2LRpE5RKZZXjcGTaPkF+nnL4ecorKW3fIvWWz+BcQUREZB21SoKysrLQtGlTvW2HDh1Cs2bN0LNnTwCAi4sL+vXrh6tXr9bmUhAEAenp6fD397dY7vTp0+jRowekUv2n1qdPHxQVFVW5X5Ejyy0uw818TbLnyJ2itcKbeEDuonk/OVcQERFZS62SIBcXFxQWFoqPc3JykJCQgDvuuEOvnLe3N3Jzc2tzKaxZswY3btzA+PHjLZZLTU1FcHCw0XbtNkudtJVKJfLy8vRujqghzBSty0UmRduKzt3JWYUoKVPZOCIiImoIapUEtWrVCn///TfUajUAYOvWrRAEAQMHDtQrd/PmTQQEBNT4OnFxcXj22WfRv39/TJ482WLZ4uJiKBQKo+1ubm7ifnMWLVoEX19f8RYaGlrjmG1Jd6bohlATBACRQZp+QWpBf/g/ERFRTdUqCRo9ejRu3ryJMWPGYMmSJXj99dchk8kQFRUllhEEAadPn0bLli1rdI20tDSMGjUKvr6+iI2NhUwms1je3d3dZL+fkpIScb85s2bNQm5urni7du1ajWK2Nf2aIMfuFK3VTm+EmGPW0BERkX1xqc3Br732GjZt2oRt27Zh27ZtAIA33ngDLVq0EMv89ddfyMzMNKodqorc3FyMHDkSt27dwsGDBxESElLpMcHBwUhNTTXart1m6RwKhcJkLZKjcfTV402J5DB5IiKyslolQT4+Pjh27BhiY2ORnp6O3r17Y/DgwXplsrKy8Pzzz1fal8dQSUkJoqKiEB8fj927d6NDhw5VOq5bt244ePAg1Gq1Xufoo0ePwsPDA23btq1WHI5IWxPkrXBBkI/jJ3UA1xAjIiLrq1USBGialyZNmmR2/9ixYzF27NhqnVOlUmH8+PE4cuQINm3ahP79+5ssl5qaitzcXLRu3RqurpoFQqOjoxEbG4sNGzYgOjoaAJCZmYl169YhKiqqQdT0WFJUWo7rOZp+T60DvSCRSGwckXUEeCvg5ylHdmEpa4KIiMgqap0EWZKbmwsfH59qfxG//PLL2Lx5M6KiopCdnY2ffvpJb/+jjz4KQNOHZ9WqVUhKSkJ4eDgATRLUr18/TJ06FefPn4e/vz++/vprqFQqzJ8/3yrPy55dunl7tF5DGBmmJZFIEBnkjSOXs5BZoERWgRJNvBp2QktERHWrVknQ2bNn8eeff2LEiBF6zUx79+7F448/jqtXr8LPzw8fffQRpkyZUuXznjlzBoBm9uktW7YY7dcmQabIZDL8/vvvePXVV/H555+juLgYvXv3xsqVKxEZGVnlGBxVYsbtWhJHXzPMUGRTTRIEaJrEBrRhEkRERDVXq9Fhn3/+OV566SW9EVdZWVkYO3Ysrly5AkEQkJWVhSeeeAKnT5+u8nn37dsHQRDM3rRWrlwJQRDEWiCtxo0b4/vvv0dmZiYKCwuxb98+9OrVqzZP1WE0lNXjTdHtF3SBTWJERFRLtUqCDh06hI4dO+rNp/Pjjz8iPz8fTz31FG7duoXVq1dDrVbjiy++qHWwVLmGODxeq12w7hpiHCZPRES1U6skKD09XW84PADs2rULMpkM7777Lnx8fPDoo4+ie/fueivNU93RJkFurlI0a2R+TiRH1DbIC9ruZRwhRkREtVWrJCgvLw++vr56244ePYpu3bqhSZMm4raIiAjcuHGjNpeiKlCWq5CcpekY3TrAC1JpwxgZpuUhd0ELPw8AQHx6AVRqoZIjiIiIzKtVEuTj46OX3Fy4cAHZ2dkYMGCAUdmGMlTbniVnFkGbFzSkkWG6IoM0TXzFZSpczS6ycTREROTIapUEdevWDYcPH0ZiYiIA4IcffoBEIjGaMDEpKcnkoqZkXQkNcM0wQ+wXRERE1lKrJOipp55CWVkZevbsie7du+PTTz9FYGAgRo0aJZbJz8/HmTNn0KlTp1oHS5Yl6i2X0bA6RWu14/IZRERkJbVKgh566CHMmzcP5eXl+OeffxAWFoZ169bpzcr822+/oayszKh2iKyvIa4ZZiiSy2cQEZGV1HrG6LfffhtvvPEG8vLy4O/vb7T/nnvuwenTp9G6devaXooqkVgxR5CrTIKwJh42jqZuhDfxhMJFCmW5mjVBRERUK7WqCdKSy+UmEyAAaNGiBbp27Qovr4ZZM2EvylVqJGVqRoa19PeEq8wqb63dkUklaFvROTo5qxDFpSobR0RERI7KamuHlZaW4uTJk+JosWbNmqFnz56Qy+XWugRZcDW7CKUqNYCG2xSmFdnUG//dyIUgaDqDd2neyNYhERGRA6p1ElReXo758+fjiy++QH6+fvOEt7c3nnvuObz99ttwcanTtVqdnjN0itYy7BzNJIiIiGqiVpmJWq3G6NGjsWPHDgiCgMaNG6Nly5YANMPic3JysHDhQpw8eRJbtmyBVNowm2jsgTN0itZi52giIrKGWmUl33//Pf744w+EhYUhNjYWWVlZOHHiBE6cOIGsrCysX78eYWFh+OOPP/DDDz9YK2YyQX/NMOdJguI4VxAREdVQrZKg1atXw93dHX/++SfGjRtntP+BBx7Anj17oFAosGrVqtpciiqhTYKkEk3H6IYswEuBJp6avmasCSIiopqqVRJ09uxZDBkyBOHh4WbLtGzZEnfddRfOnj1bm0uRBWq1ICZBLfw84OYqs3FEdUsikYi1QZkFpcgsUNo4IiIickS1SoKUSqXRAqqmeHt7Q6nkF1VdScktRnGZZqh4Q+8UrcV+QUREVFu1SoJCQ0Nx5MgRqFTm52pRqVT4+++/0bx589pciixwpk7RWrojxC6ksl8QERFVX62SoOHDh+Pq1at4/vnnUVZWZrS/tLQUzz33HK5evYqRI0fW5lJkwSUn6hSt1a6p7kKqrAkiIqLqq9UQ+TfeeANr167FN998g02bNmHChAniEPnLly/j119/RUpKCvz8/PD6669bJWAylpDufDVBbYO8IZEAggBcTGcSRERE1VerJKhZs2b4448/8NBDD+Hq1atYvHix3n5BENCiRQusX78ezZo1q1WgZF7CzdtJQGsnSYLc5TKE+XkgOasI8en5UKkFyKQSW4dFREQOpNbTOPfu3Rvx8fFYt24d9u3bp7dsxpAhQ/DQQw/h/PnzOHDgAAYNGlTrgEmfINweGdaskTu8FM4zM3dkU28kZxWhpEyNK1mFaBXgHAkgERFZh1W+MeVyOSZOnIiJEyea3P/MM8/g+PHjKC8vt8blSEdGvhJ5JZrX1VlqgbTaNfXBjnPpADT9gpgEERFRddTbOhaCINTXpZyKM80UbchwDTEiIqLq4GJeDs4Zh8drca4gIiKqDSZBDk63U7Sz1QSFNfGEm6vmI8w1xIiIqLqYBDm4RCeuCZJJJYiomCH7SnYRikrZ54yIiKqOSZCD0yZB/l4KNPKQ2zia+qftFyQI+vMlERERVYZJkAPLKSxFZkEpAOdrCtNivyAiIqqpag2RX716dY0ukpGRUaPjyLLEDOdtCtPSXT6DI8SIiKg6qpUETZkyBRJJ9WflFQShRseRZbrNPxFBzpkEReoNk2fnaCIiqrpqJUEtWrRgMmNHnLlTtFaAtwL+XnJkFpSyOYyIiKqlWklQcnJyHYWhr6CgAB999BGOHj2KY8eOIScnBytWrMCUKVMqPXblypWYOnWqyX2pqalo2rSplaO1Hd3h8c6aBAGa2qDMxCxkFZYiI1+JAG+FrUMiIiIHYJcLTWVmZmLBggVo0aIFunbtin379lX7HAsWLBBXtNdq1KiRdQK0E5cqaoJ83V0R4OW8X/yRQT44lJgFQNM5mkkQERFVhV0mQcHBwWKtzYkTJ9C7d+9qn2PkyJHo1atXHURnH/JLypCSWwJAUwvkzM2U7Qz6BQ2M8LdhNERE5Cjscoi8QqGwSrNVfn4+VCqVFSKyP5cyCsX7zjo8XqtdMNcQIyKi6rPLJMgahg4dCh8fH3h4eGD06NFISEiwdUhWxU7Rt0UEekNbEcbO0UREVFV22RxWGx4eHpgyZYqYBJ08eRKLFy/GgAEDcOrUKYSGhpo9VqlUQqlUio/z8ux3yDU7Rd/mLpchvIknkjILEZ+eD5VagEzqvM2DRERUNQ2uJigmJgYrVqzAY489hrFjx+Kdd97Bjh07kJWVhYULF1o8dtGiRfD19RVvlhImW7t0U3eOIG8LJZ1DZMVroCxXIzmrsJLSREREDTAJMmXgwIHo27cvdu/ebbHcrFmzkJubK96uXbtWTxFWX0JFEuQhlyHE183G0diebr8gNokREVFVOEUSBAChoaHIzs62WEahUMDHx0fvZo9KylS4ml0EgCPDtPRHiDEJIiKiyjlNEnT58mUEBATYOgyruJxRCEHQ3G8T4Nz9gbQiddYQu8jlM4iIqAocOglKTU1FXFwcysrKxG2mFmv9/fffcfLkSYwYMaI+w6szep2inXTNMEMt/Dzg5qr5OLM5jIiIqsJuR4d9+eWXuHXrFlJSUgAAW7ZswfXr1wEAM2fOhK+vL2bNmoVVq1YhKSkJ4eHhAIABAwage/fu6NWrF3x9fXHq1CksX74coaGhmD17tq2ejlXpdYoOZKdoAJBJJWgb5I1/r+fiSnYRikrL4SG32483ERHZAbv9lvj4449x5coV8fGGDRuwYcMGAMCjjz4KX19fk8eNHz8e27Ztw86dO1FUVITg4GA8+eSTmDt3LoKCguol9rqWwDmCTGrXVJMECQIQn16AbqGNbB0SERHZMYkgaHuXkKG8vDz4+voiNzfXrjpJ37N4PxJuFkDuIsX5+cPhInPoVk2r+eGvJLyz9TwA4IMHO2N87xY2joiIiGyhqt/f/PZ0MGUqNZIyNfPgtPL3ZAKkgyPEiIioOvgN6mCuZBWiXK2pvGNTmL5I3SQolUkQERFZxiTIwSSyU7RZ/l4K+HspAAAX0/PBll4iIrKESZCDSUhnp2hLtE1i2YWlyChQVlKaiIicGZMgB5OYobtmGJMgQ7pNYpwviIiILGES5GC0NUEyqQThTTxtHI39Yb8gIiKqKiZBDkSlFnCpoiYorIkH5C58+wy111k+gyPEiIjIEn6LOpAbOcVQlqsBcM0wcyKCvCCtWE/2YjrXECMiIvOYBDkQ3TXD2B/INDdXmdhMmJBeAJWaI8SIiMg0JkEOhMPjq0bbL0hZrkZyVqGNoyEiInvFJMiBcM2wqmmn2y+InaOJiMgMJkEORJsESSRAa/YJMkt/mDz7BRERkWlMghyEIAi4VJEENWvkDne5zMYR2S+uIUZERFXBJMhBpOWVoEBZDgCIYFOYRS38PODuqkkSL6YzCSIiItOYBDkIvU7RQewUbYlUKkHbitFzV7KKUFiRPBIREeliEuQg9NYMY3+gSul2jo5nbRAREZnAJMhB6I0M4xxBleIaYkREVBkmQQ7iEofHVws7RxMRUWWYBDkI7WzRQT4K+Li52jga+6e3kCqHyRMRkQlMghxAVoESOUVlADhTdFU18VIgwFsBQNMcJghcPoOIiPQxCXIAnCm6ZrRNYjlFZcjIV9o4GiIisjdMghxAIpOgGokMYr8gIiIyj0mQA2ASVDPsF0RERJYwCXIA2k7RAGeLro72wToLqbImiIiIDDAJcgDamiA/TzmaeClsHI3jaBPoBalEc59zBRERkSEmQXYur6QM6XmaTr2cKbp63FxlCPf3BKDpXF6uUts4IiIisidMguxcImeKrhXtCLHScjWSs4psHA0REdkTJkF2LpFrhtWK7hpi7BxNRES6mATZOb1O0awJqjauIUZEROYwCbJzHB5fO1xDjIiIzGESZOe0s0V7KVzQ1MfNxtE4ntDGHvCQywCwJoiIiPQxCbJjRaXluHGrGICmFkgikdg4IscjlUoQUTFz9NXsIhQoy20cERER2Qu7TIIKCgowd+5cjBgxAn5+fpBIJFi5cmWVj7916xamT5+OgIAAeHp6YujQoTh16lTdBVxHLmcUQrvuJ5vCaq69TpNYfDprg4iISMMuk6DMzEwsWLAAFy5cQNeuXat1rFqtxqhRo7B27VrMmDEDH374IW7evIkhQ4YgISGhjiKuG5wp2jrYOZqIiExxsXUApgQHByM1NRVNmzbFiRMn0Lt37yofGxsbi8OHD2PdunWIjo4GAMTExKBt27aYO3cu1q5dW1dhWx07RVsHkyAiIjLFLmuCFAoFmjZtWqNjY2NjERQUhHHjxonbAgICEBMTg02bNkGpVForzDqXoDNHUESgt4WSZInuXEEXUjlXEBERadhlElQbp0+fRo8ePSCV6j+1Pn36oKioCPHx8TaKrPoSMzRJkJurFM0au9s4Gsfl5ylHoLdmzbWL6fkQtB2tiIjIqTW4JCg1NRXBwcFG27XbUlJSzB6rVCqRl5end7MVZbkKVyqWeWjl7wWZlCPDakPbJHarqAw38x2nNpCIiOpOg0uCiouLoVAYr7Tu5uYm7jdn0aJF8PX1FW+hoaF1FmdlkjOLoFJraiw4U3TtcdJEIiIy1OCSIHd3d5P9fkpKSsT95syaNQu5ubni7dq1a3UWZ2X0OkVzzbBai9TpF3SRa4gRERHsdHRYbWhHlhnSbgsJCTF7rEKhMFmLZG2CICDzWgECWpjv7Mw1w6xLryYolTVBRETUAGuCunXrhlOnTkGtVuttP3r0KDw8PNC2bVsbRaaRk1aIrV/+g9/eO47UxFtmy+kPj+fIsNpqE3i7XxWbw4iICHDwJCg1NRVxcXEoKysTt0VHRyM9PR0bNmwQt2VmZmLdunWIioqql5oeS27E38LVc9kAgAO/xkOtNj1SSZsEuUglCGviUW/xNVRurjKEV7yOiRkFKFepKzmCiIgaOrttDvvyyy9x69YtcTTXli1bcP36dQDAzJkz4evri1mzZmHVqlVISkpCeHg4AE0S1K9fP0ydOhXnz5+Hv78/vv76a6hUKsyfP99WT0fUYWAIzh64gazrBci8VoALh1LQ8c5memXKVWpczigEALT094SrzKFzVbvRrqkPLmUUorRcjeSsQtawERE5ObtNgj7++GNcuXJFfLxhwwaxdufRRx+Fr6+vyeNkMhl+//13vPrqq/j8889RXFyM3r17Y+XKlYiMjKyX2C2RSiUYNL4tNn6iWcvs7/9dRusegXDzdBXLXMspRmlFTQVniraeyKbe2Pafpm/YhdR8JkFERE7ObqsYkpOTIQiCyZu21mflypV6j7UaN26M77//HpmZmSgsLMS+ffvQq1ev+n8SZoRENEJE7yAAQElhGY5tSdLbn5DONcPqQjsun0FERDrsNglq6AaMaw0XueblP7v/OrJu3O4IrZ0pGgBaMwmyGt3lM9g5moiImATZiFdjN/QcGQ4AEATg4K/x4nIOiVwzrE40b+wOD7kMAHAxnXMFERE5OyZBNtRtWCh8/DUzWd+Iv4VLpzIA3K4JkkqAVgGeNouvoZFKJWgbpEkqr2UXo0BZbuOIiIjIlpgE2ZCLqwwDY27PW3QoNgHKknJxeHyonwfcXGW2Cq9Bah/MfkFERKTBJMjGwjs3QYuOfgCAghwlDm6+hKJSFQB2iq4LkUFMgoiISINJkI1JJBIMfCgC0orZjOP3p8BXpbnPTtHWxzXEiIhIi0mQHWjc1BNd7tasWC+oBAwp0cwZxE7R1sfV5ImISItJkJ3ofV843H3kAIC2ZTKElUnZHFYHGnvKEeSjWTolLi1fHJFHRETOh0mQnZC7u2DAA63Fx3cVu6Il1wyrE9omsdziMqTnKW0cDRER2QqTIDvStk8Q0l01y2X4q6VIOpJu44gaJv0mMfYLIiJyVkyC7EhmUSl2KkohQNNEc2zLZRTlldo4qoaHI8SIiAhgEmRXEtMLkOYi4D+5Zoh8aYkKf2+6ZOOoGp52wewcTURETILsinam6INuZZC4at6aC4dTkZ7MJhtrahPoBVnFlARMgoiInBeTIDuSULFmWJEUCB3UVLNRu66YmqOYrEXhIkNLf81yJJduFqBMpbZxREREZAtMguxIws3btRIDhoejcVPN6LD0pDxcPJpmq7AapMiKztGlKjWSMwttHA0REdkCkyA7knhT82Xs7yVHEx833KmzrtjhjZdQWswFP62lnU7n6AtsEiMickpMguzEraJSZBZo5qxpUzFJYmgHP7TqFgAAKM4rxfHfk20VXoPTLpjLZxAROTsmQXZCu3I8cDsJAoA7ottA5qJ5m/7dcw05aWy6sQbduYI4TJ6IyDkxCbITCTpJkO6aYT7+7uh+bwsAgFot4K/fErjUgxU0a+QOT7kMAEeIERE5KyZBdkI7MgyA0ZphPUaEwauxZr2rq+ezkfxfVr3G1hBJpRK0ragNup5TjPySMhtHRERE9Y1JkJ3QzhEE6DeHAYCrXIY7oiPEx3/9Fo/yMlW9xdZQtWt6u19QfDprg4iInA2TIDuRWPEl7OPmggBvhdH+1j0C0KxtIwBAXmYJzuy+Vp/hNUj6a4gxCSIicjZMguxAgbIcKbklADS1QBKJxKiMRCLBnePbQrvr5PZkFOSU1GeYDU4kO0cTETk1JkF24JKZTtGGmjTzQqfBzQEA5aVqHN7AdcVqgzVBRETOjUmQHdAdHh8R5GWhJNAnqiXcPF0BAAnH05GScKsuQ2vQGnnI0dTHDQAQl5rHUXdERE6GSZAd0B0e3zrQchLk5umKvmNaiY8P/BoPNdcVqzFtk1heSTnS8ti8SETkTJgE2YFEnTXDDIfHm9JhYAj8QzXlsq4X4PxfKXUWW0PHJjEiIufFJMgOaJvD3F1lCPF1r7S8VCrBoPG31xX7e9MllBRynpuaYOdoIiLn5WLrAJxdSZkKV7OLAGhGhkmlxiPDTAlu0wht+wQh/lg6lIXlOLb5MgY9HFmXoTZIunMFfbPvErb/lwofd1f4Vtx07xvefNxd4a1wqfJ7RkRE9oVJkI0lZRZC26WnKk1huvo/0AaX/8lEuVKFswduoMOdIfBvbn50GRlrHegJhYsUynI1covL8M/13GodL5UA3m6mEyTTiZOLeN/bzRUyJlBERDbDJMjGqtMp2pBXYwV6jQzD3/+7DEEADv6agLEvdTc5zxCZpnCRYd7ojvjuwGVkFZYir6QM1RkkphaA3OIy5BZXvzlSIgG8FC4Wa5os7WMCRURUO0yCbCwxvXqdog11u7sFzh9KRV5GMVISbiHx5E1E9AqyZogN3sN9WuDhPrcXqc1XliOvIrGxdMsz+JlbXIbqDNQTBCC/pBz5JeW4nlNc7bi1CZQmWaq4X1G7JJFoJtiUQJNsSVCxDRXbDbZJpZqyMNwuuX0fOueT6p67IunWLat3fr04NI+lEv3zactKde7LXaRQuMigcJVCob3vIoWb6+372v1ymZTNkkRUbXabBCmVSrz99tv48ccfkZOTgy5duuDdd9/FPffcY/G4efPmYf78+UbbFQoFSkrsbwi0pTXDqkLmKsWdD0Vg29f/AgAOr09EeGd/uCpkVovRmUilErG2JbSaxwqCgAJluclESf9WbnK/qppTHRQoy1GgLMeNW9VPoBoiuawiWdJJkuQuUihctQmT6aRKoZdUVV7eVBKmcJGyBpbIAdltEjRlyhTExsbihRdeQEREBFauXIn77rsPe/fuxcCBAys9/ptvvoGX1+2kQiazz6RAu3q8XCZFCz+PGp0jrHMTtOjYBFfPZaEgR4lTO66g7+hWlR9IViWRSODtpunr07xx9Y4VBAGFpSpNQlRUhrySyhIp/X1lKs4VVapSo1SlRr7SNteXuxgnV3KZFC4ySUUtmaYGTFrxU/+xRKxh027T2y/VltfZD5gpU8VzSgzOKbVc3lSNoH4No+YxdGsctdt1ysJwn8E5YFhraXAOk+eHbny6NYvG55ZKABepFFKp5qdMCsikUsgqXkO9fRIJZDKJ5qdUc9O+btQw2GUSdOzYMfzyyy/46KOP8MorrwAAHnvsMXTq1AmvvfYaDh8+XOk5oqOj4e/vX9eh1kqZSo3krEIAQKsAT7jIajZjgUQiwZ0xEfh5QTbUKgGnd15Fu/7B8A2ofLg92QeJRAIvhQu8FC5o1qh675sgCCgu0yRQ+SXlUAsCBEHT3Kau6OAkCIAAQdwmVGxDxTYBmqZAQacsBE2fJ0GnjCAee/saJrfrnEctQJyNWz+O28fBYLtaEFCmUkNZroayTA1luUpzv1xV8Vhnm95+4zIlZWqrvEeVKS1Xo7RcjXyU18v1yHZkUv3ESO9maruFstokWa9sReLlIpVAKjX4WVFWu83c9aQGZcT7OkmfeF8K4xh0zietiFPvvKbiMEgYteXtmV0mQbGxsZDJZJg+fbq4zc3NDdOmTcPs2bNx7do1hIZabqwQBAF5eXnw9va226z9SlaR+B98dTtFG2oU5IGud4fi9M6rUJWrcSg2Afc908UaYZKdk0gk8JC7wEPugmBfW0djfwRBQJlK0E+UyjT3S8qMt1U52SpTVWm/WhDExI4rszQMKrUAFQRAZetIHIPpZKwiuZJKMG1gSzw5yDatF3aZBJ0+fRpt27aFj4+P3vY+ffoAAM6cOVNpEtSqVSsUFBTA09MTY8eOxSeffIKgIMsdhpVKJZTK23XpeXl5NXwGVVPdmaIr0+u+cFz8Ow1FeaVI+icTV89noUWHJrU+L5Ejk0gkkLtIIHeRwtYTSGhrygwTI83j27Vmap1teuXV5ssLEKBW1+CcgqDZr4bZ8rq1i7o1f7o1eLq1f9rH0Kl1FHTvw3TtoOE5dF+zSs9vLg6D47XPp1wtQK3W/6kSjLepBQHlKs0+lVr/ZngecZ+JsrrbnE25uqKK14zCUtvVntplEpSamorg4GCj7dptKSnml4lo3LgxZsyYgf79+0OhUODgwYP46quvcOzYMZw4ccIosdK1aNEik52q64ruwqk16RRtSO7mggHjWmP3ygsAgL9+S8D4txpD5sKJwYnsgXZknhT2WTtNdU+bYOolRxVJVrlaDbUaettUajVUaoj7ytVqvWO129SCAJUaBvtuJ2kqnYTNXLKmNiijTQINkzm12X2oiPd2XKqK5F03DsME0cfN1Wbvh10mQcXFxVAoFEbb3dzcxP3mPP/883qPH3zwQfTp0wcTJ07E119/jTfeeMPssbNmzcJLL70kPs7Ly6u0xqk2dOcIigi0zv+obfs0xdkDN5B2OQ85aUX4b991dBvWwirnJiKi2pFIJJBJwHm+7IRdVhG4u7vrNUtpaYe4u7tXr+PoI488gqZNm2L37t0WyykUCvj4+Ojd6pK2JkgqAcL9azYyzJBEKsGd49tC+4/msa1JKMy10XAZIiIiO2aXSVBwcDBSU1ONtmu3hYSEVPucoaGhyM7OrnVs1qJSC2ISFN7EEwoX6w3hDwzzQYcBmqbDshIV/t502WrnJiIiaijsMgnq1q0b4uPjjTomHz16VNxfHYIgIDk5GQEBAdYKsdZu5BRDWa4ZumuN/kCG+o5pDbm7prUz7nAq0pPqtpM3ERGRo7HLJCg6OhoqlQrLli0TtymVSqxYsQJ9+/YV++lcvXoVcXFxesdmZGQYne+bb75BRkYGRowYUbeBV0Nixu2RYXWRBHn4yNEnqqX4+MCv8RCccFQCERGROXbZMbpv37546KGHMGvWLNy8eRNt2rTBqlWrkJycjB9++EEs99hjj2H//v3iUEsACAsLw/jx49G5c2e4ubnhr7/+wi+//IJu3brhqaeessXTMUk7UzQARARZPwkCgE6Dm+H8XynITinEzeQ8xP2dhvYDjEfdEREROSO7TIIAYPXq1ZgzZ47e2mFbt27FoEGDLB43ceJEHD58GOvXr0dJSQnCwsLw2muv4c0334SHh3U6H1uD3vD4gLqZvUQmk2JgTAQ2f3YGAHDkf5fQqnsAFO52+7YTERHVG4mgW41CevLy8uDr64vc3FyrjxQb+9UhnLl2CwBwfsFweMjrLjH5Y+l/uHRa00zYdVgoBkZH1Nm1iIiIbK2q39922SeooRMEAZcqaoKaN3av0wQIAAY82AYyV81b/d+f15GdWlin1yMiInIETIJsID1PiXylZprwuugUbcjH3x097tVMmKhWC/hrXQJYAUhERM6OSZANJFh5zbCq6D48DF5+mlm4r53PRtI/mfVyXSIiInvFJMgGrL1mWFW4ymW448HbfYEOxSagvIxLIBMRkfNiEmQDCXpJUP2ta926RwCaRTYGAORlluDMrmv1dm0iIiJ7wyTIBmxREwRoFu67MyYCkoqF+07+kYz87JJ6uz4REZE9YRJkA9okKNBbAV9313q9dpNmXug8uBkAoLxUjSMbEuv1+kRERPaCSVA9yypQIruwFEDdzRRdmd73t4Sblyb5SjhxEzfic2wSBxERkS0xCapn+jNF2yYJcvN0Rb8xrcTHB39NgFqltkksREREtsIkqJ75erjikb4t0KelH7o0b2SzONrfEYKAFppO2Vk3CnDuYIrNYiEiIrIFLpthQV0um2EPUhNvYcPHpwAACg8XPLqgv9hMRkRE5Ki4bAZVKrhNI7TtGwQAUBaV4+jmyzaOiIiIqP4wCXJyAx5oA1eFDABw7uANZFzLr+QIIiKihoFJkJPzbKRAr/vCAQCCABz8NZ7rihERkVNgEkToelcofAPdAQCpiblIPHHTxhERERHVPSZBBJmrFAMf0llXbH0iSkvKbRgRERFR3WMSRACA8M7+COvcBABQeEuJU39csXFEREREdYtJEIkGRkdAKtOsK3Z691XkZhTZOCIiIqK6wySIRI2CPNBtWCgAQF0u4K91XFeMiIgaLiZBpKfnyHB4+MoBAMn/ZuLKuSwbR0RERFQ3mASRHrmbCwaMayM+/uu3BKjKua4YERE1PEyCyEjbPkFo2soXAHArvQj/7r1u44iIiIisj0kQGZFIJBg0oS2g6SON49uSUJirtG1QREREVsYkiEwKaOGNDgNDAABlJSr8vfGSjSMiIiKyLiZBZFa/0a2g8HABAMT9nYa0y7k2joiIiMh6mASRWe7ecvSJaik+PvhrPAQ11xUjIqKGgUkQWdRpUDP4hXgCAG5eyceFI6k2joiIiMg6mASRRVKZFHeObys+/vt/l6AsKrNhRERERNbBJIgq1TyyMVr3CAQAFOeX4fi2ZNsGREREZAVMgqhKBjzYGi6umo/Lf3uvIzul0MYRERER1Q6TIKoSnybu6DEiDACgVgs4+Fs8BIGdpImIyHHZbRKkVCrx+uuvIyQkBO7u7ujbty927dpVpWNv3LiBmJgYNGrUCD4+PhgzZgwuX75cxxE3fN3vaQFvPzcAwPW4HCSdybRxRERERDVnt0nQlClTsHjxYkycOBFLliyBTCbDfffdh7/++svicQUFBRg6dCj279+P2bNnY/78+Th9+jQGDx6MrCwuBlobLnIZ7nhIZ12x2ASUl6psGBEREVHNSQQ7bNM4duwY+vbti48++givvPIKAKCkpASdOnVCYGAgDh8+bPbYDz/8EK+//jqOHTuG3r17AwDi4uLQqVMnvPbaa3jvvfeqHEdeXh58fX2Rm5sLHx+f2j2pBkIQBGxecgbX43IAAH2iWqL3qJaVHGW/BEEABEAtCBDUAgQBBj8FCGpU/DS9Xa2uOIfOz6ocZ+p6mnMIUFsoo3cOE+eTSACJVAKJVAKpVAKJRAKJFLcfSyViGfGxFJBKpZpyEv3tEqkEUolEPKemrPa8Fh5XbJPqnOf2uSDur857pVZV3NQC1Cr17ccqzfNXVWwT1DplteV0t6mNj1WrNMfrH1txvNr42oJKe4z2eINyqtufDUgq3peK56t92hKp7mPN+wLDchLJ7fJ6j82Uh+axdp/581aUQ0W5ivvaa0Ci3VxxR6j4nAGA9vMoaH5C5772Mwnof3ZRcaygrrgvltc+Nn+s9mvq9ufe4BiDx9A9FhX7Ko6VSCWQySSQuUohlUkhc5FC5iLR3HeVQCaTQqq3TQqZTFKxTapzrKTi2Ir7rtKKYyu26953qbhvsE27XVrN3wV7oP9+1+5vp7u3HB4+cqvGV9Xvb7tMgl577TUsXrwY2dnZesEvWrQIs2fPxtWrVxEaGmry2D59+gDQJFK6hg8fjkuXLiExMbHKcTAJMi0rpQC/vnscglqAi6sUPUaEGX/A1YJxYlFxUwsAxP06+/QSCP1j1WrjXyi12ric9hdLr6zOL5xhLPb36XcuugmbJkG6/ViT1AgVyYaa7xU1XBIYJFA6SZc2Gau4r0mcpJBIYPB31/CfKej/zavOP2YG23T/ZkOt+acRVvx9rIt/pqv6/e1i1atayenTp9G2bVujwLUJzpkzZ0wmQWq1Gv/++y8ef/xxo319+vTBzp07kZ+fD29v77oJ3Ek0CfFClyHN8c+f11BepsaxLUm2DokclCAAgkoAVA0vw9HWhom1KNB8gYg1E4BVv0gaIrH2TKJTu6WtyQTE1/d2zZdEPEb/2Nv3xVq/cjVU5QLU5Wqoym2cZAuoiAcog/N1MbDla2+XSVBqaiqCg4ONtmu3paSkmDwuOzsbSqWy0mMjIyNNHq9UKqFU3l4tPS8vr9qxO4ve94fj0umbKMixweryEug0z8B8s4xRs9DtJhjDJpvb57ndHASJBFIpKn7qHg8Tx1Vl++39uueFBPrNVhbPp/0Dr3+s7k/92i7j2jW9pjbtY20tmup2WbVeLZ3B44r/DvUf69fsGda86TUTirV7FbV6etfVbJNKJZDKKm4V9yXSiv+KZRJIdLZLZVK9clLp7W2SinPIdI7XO7fMeJumyUQqHmt4Tv3j9bdp46pq84bYfKN5UNHcVJE0VWwXl6vRLadthtKW02k2Mnws6PznrtuEZfhY91zaJiltU5dhMqL9PAL6n03DMiYfS3Wa+KQ65zNIZOqTWn07IVKVa2oftfdV5WqoyzXNpeL9irLahEqtW1ZlcFy52sSx+tdQq9RQlamhUt2OQ60SxG01XrJIApN/W/T/bujUwlbl75CFsjX52xnQwnYVE3aZBBUXF0OhUBhtd3NzE/ebOw5AjY4FNM1t8+fPr3a8zkjh4YqY2b2RnpSn6fIg0UkqDPucGPQBMZes6PVDMfil0juvg7WdE1kiJgaaR5qNMhsG5KSkUgmkchlc5Pb54otJWkViBKDS5IJ/Lytnl0mQu7u7Xo2MVklJibjf3HEAanQsAMyaNQsvvfSS+DgvL89s3yPSdGYL7+Jv6zCIiBo8MUkDAPNfY1RNdpkEBQcH48aNG0bbU1M1i3eGhISYPM7Pzw8KhUIsV51jAU0NkqlaJCIiImp47HKeoG7duiE+Pt6oT87Ro0fF/aZIpVJ07twZJ06cMNp39OhRtGrVip2iiYiICICdJkHR0dFQqVRYtmyZuE2pVGLFihXo27ev2ER19epVxMXFGR17/PhxvUTo4sWL+PPPP/HQQw/VzxMgIiIiu2eX8wQBQExMDDZu3IgXX3wRbdq0wapVq3Ds2DHs2bMHgwYNAgAMGTIE+/fv11vDKj8/H927d0d+fj5eeeUVuLq6YvHixVCpVDhz5gwCAgKqHAPnCSIiInI8Dj1PEACsXr0ac+bMwY8//oicnBx06dIFW7duFRMgc7y9vbFv3z68+OKLePfdd6FWqzFkyBB8+umn1UqAiIiIqGGz25oge8CaICIiIsdT1e9vu+wTRERERFTXmAQRERGRU2ISRERERE6JSRARERE5JSZBRERE5JSYBBEREZFTYhJERERETsluJ0u0B9oplAzXMCMiIiL7pf3ermwqRCZBFuTn5wOAuFYZEREROY78/Hz4+vqa3c8Zoy1Qq9VISUmBt7c3JBKJ1c6bl5eH0NBQXLt2jTNR2wG+H/aH74l94fthX/h+VE4QBOTn5yMkJARSqfmeP6wJskAqlaJ58+Z1dn4fHx9+gO0I3w/7w/fEvvD9sC98PyyzVAOkxY7RRERE5JSYBBEREZFTYhJkAwqFAnPnzoVCobB1KAS+H/aI74l94fthX/h+WA87RhMREZFTYk0QEREROSUmQUREROSUmAQRERGRU2ISRERERE6JSVA9UiqVeP311xESEgJ3d3f07dsXu3btsnVYTun48eOYMWMGOnbsCE9PT7Ro0QIxMTGIj4+3dWhUYeHChZBIJOjUqZOtQ3Fqp06dwujRo+Hn5wcPDw906tQJn3/+ua3DckoJCQmYMGECmjdvDg8PD7Rr1w4LFixAUVGRrUNzWBwdVo8efvhhxMbG4oUXXkBERARWrlyJ48ePY+/evRg4cKCtw3Mq0dHROHToEB566CF06dIFaWlp+PLLL1FQUIC///6bX7w2dv36dURGRkIikSA8PBxnz561dUhOaefOnYiKikL37t0xfvx4eHl54dKlS1Cr1fjwww9tHZ5TuXbtGrp06QJfX188/fTT8PPzw5EjR7By5UqMHj0amzZtsnWIDolJUD05duwY+vbti48++givvPIKAKCkpASdOnVCYGAgDh8+bOMIncvhw4fRq1cvyOVycVtCQgI6d+6M6Oho/PTTTzaMjiZMmICMjAyoVCpkZmYyCbKBvLw8tG3bFgMGDEBsbKzF9Zeo7r333nt48803cfbsWXTs2FHcPnnyZKxevRrZ2dlo3LixDSN0TPxU15PY2FjIZDJMnz5d3Obm5oZp06bhyJEjuHbtmg2jcz4DBgzQS4AAICIiAh07dsSFCxdsFBUBwIEDBxAbG4vPPvvM1qE4tbVr1yI9PR0LFy6EVCpFYWEh1Gq1rcNyWnl5eQCAoKAgve3BwcGQSqVGf8+oapgE1ZPTp0+jbdu2Rovd9enTBwBw5swZG0RFugRBQHp6Ovz9/W0ditNSqVSYOXMmnnjiCXTu3NnW4Ti13bt3w8fHBzdu3EBkZCS8vLzg4+ODZ555BiUlJbYOz+kMGTIEADBt2jScOXMG165dw6+//opvvvkGzz33HDw9PW0boINiElRPUlNTERwcbLRduy0lJaW+QyIDa9aswY0bNzB+/Hhbh+K0vv32W1y5cgXvvPOOrUNxegkJCSgvL8eYMWMwfPhwrF+/Ho8//ji+/fZbTJ061dbhOZ0RI0bgnXfewa5du9C9e3e0aNECEyZMwMyZM/Hpp5/aOjyH5WLrAJxFcXGxyXVe3NzcxP1kO3FxcXj22WfRv39/TJ482dbhOKWsrCy8/fbbmDNnDgICAmwdjtMrKChAUVERnn76aXE02Lhx41BaWoqlS5diwYIFiIiIsHGUziU8PByDBg3Cgw8+iCZNmmDbtm1477330LRpU8yYMcPW4TkkJkH1xN3dHUql0mi7tlrZ3d29vkOiCmlpaRg1ahR8fX3FvltU/9566y34+flh5syZtg6FcPtv0sMPP6y3/ZFHHsHSpUtx5MgRJkH16JdffsH06dMRHx+P5s2bA9AkpWq1Gq+//joefvhhNGnSxMZROh42h9WT4OBgpKamGm3XbgsJCanvkAhAbm4uRo4ciVu3buGPP/7g+2AjCQkJWLZsGZ577jmkpKQgOTkZycnJKCkpQVlZGZKTk5GdnW3rMJ2K9nfBsCNuYGAgACAnJ6feY3JmX3/9Nbp37y4mQFqjR49GUVERTp8+baPIHBuToHrSrVs3xMfHiz38tY4ePSrup/pVUlKCqKgoxMfHY+vWrejQoYOtQ3JaN27cgFqtxnPPPYeWLVuKt6NHjyI+Ph4tW7bEggULbB2mU+nZsycAzXujS9t/kU2W9Ss9PR0qlcpoe1lZGQCgvLy8vkNqEJgE1ZPo6GioVCosW7ZM3KZUKrFixQr07dsXoaGhNozO+ahUKowfPx5HjhzBunXr0L9/f1uH5NQ6deqEjRs3Gt06duyIFi1aYOPGjZg2bZqtw3QqMTExAIAffvhBb/v3338PFxcXcbQS1Y+2bdvi9OnTRrPa//zzz5BKpejSpYuNInNsnCyxHsXExGDjxo148cUX0aZNG6xatQrHjh3Dnj17MGjQIFuH51ReeOEFLFmyBFFRUeIfe12PPvqoDaIiQ0OGDOFkiTY0bdo0LF++HDExMRg8eDD27duHdevWYdasWXjvvfdsHZ5TOXDgAO666y40adIEM2bMQJMmTbB161Zs374dTzzxBL777jtbh+iQmATVo5KSEsyZMwc//fQTcnJy0KVLF7zzzjsYPny4rUNzOkOGDMH+/fvN7uevhX1gEmRbZWVleO+997BixQqkpKQgLCwMzz77LF544QVbh+aUjh07hnnz5uH06dPIyspCy5YtMXnyZLz22mtwceE4p5pgEkREREROiX2CiIiIyCkxCSIiIiKnxCSIiIiInBKTICIiInJKTIKIiIjIKTEJIiIiIqfEJIiIiIicEpMgIiIickpMgoioWsLDwyGRSLBy5Upbh1LnVq5cCYlEgilTptg6FCKqA0yCiKjWHDFZSE5OhkQiQXh4uK1DISIb4WIjRERmPPDAA+jXrx98fX1tHQoR1QEmQUREZvj6+jIBImrA2BxGRLUSHh6OqVOnAgBWrVoFiUQi3oYMGWJUPjY2FiNGjEBAQADkcjmaNWuGRx99FOfPnzcqq9tkpVKpsHjxYnTv3h1eXl6QSCRiufPnz2Pu3Lm444470KxZM8jlcjRp0gTDhg3Db7/9ZnTeKVOmoGXLlgCAK1eu6MWse97KmvmOHTuGmJgYhISEQC6XIzAwEFFRUdi1a5fJ8lOmTBH7UyUlJWHSpElo2rQpFAoFWrdujbfeegtKpdLoOLVajWXLluGOO+5Ao0aN4OrqisDAQHTt2hUzZ85EcnKyyesRkWWsCSKiWomOjsbff/+NQ4cOoXXr1hg4cKC4r127duL98vJyTJw4Eb/99hsUCgV69uyJZs2aIT4+HmvWrMGGDRuwYcMGjBgxwugagiBg3Lhx+OOPP3DnnXeiffv2OHfunLh/8eLF+OGHH9CuXTt07twZjRo1wtWrV7F3717s2bMHf//9NxYvXiyWHzhwIAoKCrB+/Xp4enoiOjq62s/7u+++w9NPPw21Wo3u3btjyJAhuHLlCrZu3YqtW7di3rx5mDt3rsljz5w5g+effx6NGzfG4MGDkZ2djUOHDmHhwoU4d+4cNm7cqFf+iSeewIoVK+Dm5oaBAwciICAA2dnZuHz5Mr788kvcfffd7NtEVBMCEVE1hIWFCQCEFStWiNtWrFghABAmT55s9rjZs2cLAIS+ffsKly9f1tu3bt06QSaTCY0bNxZycnLE7UlJSQIAAYDQvHlz4eLFiybPvW/fPuHSpUtG2+Pi4oTmzZsLAISjR4/q7dOeOywszGzM5p7Xv//+K7i4uAgSiURYvXq13r7ff/9dkMvlAgBh586devsmT54sPp8333xTKC8vF/f9999/gqenpwBAOHz4sLj9ypUr4vNPTU01ivH8+fPClStXzD4HIjKPzWFEVOeys7Px6aefws3NDevXrxeborSio6Px1FNPIScnBz/99JPJc7z33nto27atyX2DBw9Gq1atjLZHRkZizpw5ADTNcNayZMkSlJeX44EHHsCkSZP09o0cORLTp08HAHz00Ucmj+/ZsyfeeecdyGQycVunTp3Ec+3evVvcnp6eDgDo0aMHmjZtanSu9u3bo0WLFrV7QkROikkQEdW5vXv3ori4WOyzY4q2/9Dhw4dN7n/wwQctXqOgoADr1q3D7NmzMX36dEyZMgVTpkzB+vXrAQAXL16s+RMwsG/fPgAw21do2rRpAICDBw9CpVIZ7b///vv1+h5ptW/fHgBw48YNcVu7du3g7e2N33//HQsXLkRSUlItoyciLfYJIqI6d/nyZQDAnj17TH7568rIyDDaFhgYCA8PD7PHbNmyBVOnTkVWVpbZMnl5eVWMtnLaJMWwRkurdevWAICSkhJkZWUhMDBQb7+5mhsfHx/xOC1vb2+sWLECU6dOxVtvvYW33noLwcHB6NevH0aMGIFHHnkEXl5etX5ORM6ISRAR1Tm1Wg0AaNOmDe644w6LZXU7U2u5u7ubLX/jxg2MHz8excXFeO211zBx4kSEh4fDy8sLUqkUO3fuxPDhwyEIQu2ehBVJpdWrhH/wwQcxbNgwbN68GQcPHsShQ4ewceNGbNy4EW+//TZ27dqFzp0711G0RA0XkyAiqnOhoaEANH10rL3cxpYtW1BcXIwHHngAH3zwgdH+hIQEq14PAJo1a4ZLly7h8uXL6NSpk9F+bc2Xm5sb/Pz8rHJNX19fTJo0Sew3dO3aNcycORObNm3CjBkzsH//fqtch8iZsE8QEdWaXC4HoBkGb8rdd98NuVyOffv24ebNm1a9dnZ2NgAgLCzMaJ8gCFi7dq3J4yqL2RJt/yVzCd3y5csBAHfeeSdcXOrmf83Q0FDMnz8fgGbIPRFVH5MgIqq15s2bA4DJCQ8BICgoCDNnzkRhYSGioqLw33//GZVRKpXYvHkz4uLiqnVtbWfi2NhYpKamittVKhXefvttsx2ttZM1pqWliYlUVT3//PNwcXHB//73P6PRbDt37sTSpUsBAK+88kq1zmvK6dOn8euvv6K4uNho35YtWwCYTgCJqHJsDiOiWuvXrx9CQkJw+vRp9OjRA507d4arqysiIyPx6quvAgDef/99pKamYu3atejWrRu6du2KVq1awcXFBdevX8eZM2dQWFiI7du3m+wXZE5UVBR69uyJkydPom3bthg8eDA8PT1x9OhRpKSk4PXXXzfZTObq6orRo0cjNjYW3bp1w8CBA8XO199//73Fa3bu3BlfffUVnnnmGUyaNAmffvop2rVrhytXruDw4cMQBAHz5s3DvffeW41X0bQrV65gwoQJcHd3R48ePRAaGory8nL8999/uHjxIuRyOT788MNaX4fIGTEJIqJak8vl2LFjB958800cOXIE//zzD9RqNQYPHiwmQS4uLlizZg0effRRfP/99zh69CjOnj0LT09PBAcHIyoqCqNHj8agQYOqdW0XFxfs27cPixYtwvr167Fnzx74+PhgwIABWL9+PfLz800mQQCwdOlSNGnSBNu3b0dsbCzKysoAVJ4EAcD06dPRtWtXfPzxx/jrr7/w77//wtfXF/fddx+ef/553HPPPdV6Hub069cP77//Pg4cOIALFy7g9OnTcHFxQfPmzfHss89i5syZiIyMtMq1iJyNRLCnIRNERERE9YR9goiIiMgpMQkiIiIip8QkiIiIiJwSkyAiIiJySkyCiIiIyCkxCSIiIiKnxCSIiIiInBKTICIiInJKTIKIiIjIKTEJIiIiIqfEJIiIiIicEpMgIiIickpMgoiIiMgp/T9LMHxJ3AkyIgAAAABJRU5ErkJggg==",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.title(\"Learning Curves Diffusion Model\", fontsize=20)\n",
+ "plt.plot(list(range(len(iter_loss_list))), iter_loss_list, color=\"C0\", linewidth=2.0, label=\"Train\")\n",
+ "plt.plot(list(range(len(iter_loss_list))), val_iter_loss_list, color=\"C4\", linewidth=2.0, label=\"Validation\")\n",
+ "plt.yticks(fontsize=12)\n",
+ "plt.xticks(fontsize=12)\n",
+ "plt.xlabel(\"Iterations\", fontsize=16)\n",
+ "plt.ylabel(\"Loss\", fontsize=16)\n",
+ "plt.legend(prop={\"size\": 14})\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "attachments": {},
+ "cell_type": "markdown",
+ "id": "fd2b79a4",
+ "metadata": {},
+ "source": [
+ "# Evaluation\n",
+ "## Generate synthetic data\n",
+ "\n",
+ "We use the semantic encoder to get a latent space from the validation dataset. We then use the diffusion model to generate synthetic data from the latent space."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 17,
+ "id": "73a9517a",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 100/100 [00:02<00:00, 42.10it/s]\n"
+ ]
+ }
+ ],
+ "source": [
+ "scheduler.set_timesteps(num_inference_steps=100)\n",
+ "batch = next(iter(val_loader))\n",
+ "images = batch[\"image\"].to(device)\n",
+ "noise = torch.randn_like(images).to(device)\n",
+ "latent = model.semantic_encoder(images)\n",
+ "reconstruction = inferer.sample(\n",
+ " input_noise=noise,\n",
+ " diffusion_model=model.unet,\n",
+ " scheduler=scheduler,\n",
+ " save_intermediates=False,\n",
+ " conditioning=latent.unsqueeze(2),\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 18,
+ "id": "425d60cc",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "(-0.5, 529.5, 133.5, -0.5)"
+ ]
+ },
+ "execution_count": 18,
+ "metadata": {},
+ "output_type": "execute_result"
+ },
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABJ4AAAE5CAYAAADRMuobAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjkuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8hTgPZAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9WY9c2ZXliS8zc7fZfHaSzkFBSimlstWq7MxONaoLhUbVN/h/2Ab6oYF+aqD7oQrVmSVBUkYqFIqJo882m7nZ/4H4HVt3+zXGoCDdSZ4FOJw0v3ans88e1t5nn8pyuVwqIyMjIyMjIyMjIyMjIyMjIyPjR0b1pm8gIyMjIyMjIyMjIyMjIyMjI+PDRCaeMjIyMjIyMjIyMjIyMjIyMjLeCjLxlJGRkZGRkZGRkZGRkZGRkZHxVpCJp4yMjIyMjIyMjIyMjIyMjIyMt4JMPGVkZGRkZGRkZGRkZGRkZGRkvBVk4ikjIyMjIyMjIyMjIyMjIyMj460gE08ZGRkZGRkZGRkZGRkZGRkZGW8FmXjKyMjIyMjIyMjIyMjIyMjIyHgr2PiuB1Yqlbd5HxkZGRkZGRkZGRkZGRkZGRkZ7xGWy+W3HpMrnjIyMjIyMjIyMjIyMjIyMjIy3goy8ZSRkZGRkZGRkZGRkZGRkZGR8VaQiaeMjIyMjIyMjIyMjIyMjIyMjLeC79zjKaLZbKper/+Y95LxAWM+n2s0GqX1n5VKRa1WSxsbP1gEMz4yTKdTjcfj9P9qtapWq6VarXaDd5XxPmE8Hms6nab/12o1tVotVas5B5Px7VgulxqPx5rNZumzzc1NNZvN3Acz4zthsVhoNBrp6uoqfdZoNNRoNG7wrjLeJ1xdXWk0GmmxWKTPckyW8X0wm800Ho9zTJbxgxFjsu+KHyxh9Xpd7Xb7h3494yPDZDIpKDkpO1sZ3x+u5CqViprNpjY3N2/wjjLeJ1xdXV0jntrtdiaeMr4TlsulZrNZgXja2NhQu93OxFPGd8LV1ZUmk0mBeNrc3Mz+dMZ3BqSBo9FoqNVq3dAdZbxvICYD+NOZvMz4PvghxFP2tjMyMjIyMjIyMjIyMjIyMjIy3goy8ZSRkZGRkZGRkZGRkZGRkZGR8VaQiaeMjIyMjIyMjIyMjIyMjIyMjLeCTDxlZGRkZGRkZGRkZGRkZGRkZLwVZOIpIyMjIyMjIyMjIyMjIyMjI+OtIBNPGRkZGRkZGRkZGRkZGRkZGRlvBZl4ysjIyMjIyMjIyMjIyMjIyMh4K8jEU0ZGRkZGRkZGRkZGRkZGRkbGW0EmnjIyMjIyMjIyMjIyMjIyMjIy3goy8ZSRkZGRkZGRkZGRkZGRkZGR8VaQiaeMjIyMjIyMjIyMjIyMjIyMjLeCTDxlZGRkZGRkZGRkZGRkZGRkZLwVZOIpIyMjIyMjIyMjIyMjIyMjI+OtIBNPGRkZGRkZGRkZGRkZGRkZGRlvBZl4ysjIyMjIyMjIyMjIyMjIyMh4K8jEU0ZGRkZGRkZGRkZGRkZGRkbGW0EmnjIyMjIyMjIyMjIyMjIyMjIy3go2bvoGMjIyMjIyMr4dtVpNm5ubqlarWiwWkqRqdX3+iGPisfxeLBZaLpeFn6urKy2Xy7f5GBkZGRkZGRkZGR8ZMvGUkZGRkZHxHmB/f19/93d/90biqVarqVqtajabaTqdajab6eLiQpK0s7Ojer2uer2uWq2mfr+vfr+v6XSq0Wik8XisV69eaT6fv/Nny8jIyMjIyMjI+HCRiaeMjIyMjIxbiGq1moil5XKpVqulvb091et1XV1dSXpNNFUqFUlSpVJJ35nNZhoOh5pMJqmCaX9/X81mM5FPZ2dn2tjY0GQyUa1Wu3bNMng1VK6MysjIyMjIyHjfgR+FXxP/n/HjIBNPGRkZGRkZtwzValU//elPde/ePc3nc83nc7VarbQcrtFoFAiiRqOhjY2NRD4Nh0ONRiNJr5fUVSoVNZtNdTodbW5uamNjQ61WS9PpVJubm2kZ32w209XVlZrNpqrVqqbTaaqAqlarms/nmkwmms/nGo1GqfIqIyMjIyMjI+N9Q7Va1cbGa0oEn6ZSqahSqejq6iol+jL+emTiKSMjIyMj4wZARm3d3w4PD/Wzn/1M0+lU4/FYkpITBFmEk9RoNNRoNJKzNJ/P0/kXi4VqtZo2NjYSQVWtVlWv1wsEVqVS0dbWlpbLpTqdjmq1mobDoabTqarVqiqViiaTSSKkuKeMjIyMjIyMjPcRTjzR59J7YZb5arkS6ochE08ZGRkZGRnvGPfv39cnn3xS+rflcqlKpaIHDx6o1WppY2NDm5ubGo/HGg6H2tzcTM4QVU5XV1caj8eq1Wqq1WqaTqeaTCa6urpSr9fT5uamut2uWq1W6gM1n8+1WCzU7/d1cXGhWq2mTz75RJVKRY1GQ5L0/PlzXV5eqtFoqF6v6+LiQv1+X5LUarW0WCzSdTLeH2xsbKjZbGpjY0PdblfL5VLHx8elZGKz2VS3203ko1RchhCXJkB8jkYjLZdL1et1VatVDQYDTSaTd/SEGRkZGRkfKtbZos3NTTUaDS0WC02nU9VqNe3s7CS/abFYJFu2XC7T/2OLAewWFeJ+ncViofF4rK+//rrQziDj25GJp4yMjIyMjHeM+/fv6z/+x/9YyKRRvUTGjb9tbm6mSidIHq9ioqfTZDJRvV7XxsaGZrNZIhG2trbUaDTU6XTUbreT0wV5NZlMNJlM1Ol09PjxYzUajbSkj6bjnU5HnU4nLcWrVCrqdDq6urpKn2W8P4BwajabunfvniRpMBiUEk+NRkN3795NfcBYzlmr1Qry4D+TyUTHx8daLBbqdrva2NhIyzQzMjIyMjJ+KNzW8H926a3X6+p2uymxVq/XdXR0pFarlewVybfFYpF8F9+wpVarpaTf9va2Op1OwW+aTqc6OzvTq1evNJ1OJeUKqO+KTDxlZGRkvANgyMis0FPHm0MT7FP2W61W01IojB7/JuvCdyQVKhIk6ezsTBcXF9rY2FC9XtdyudRkMtFisdBgMCiQBRsbG+lePEjMxvSvx8bGhh48eKBer5dIo8PDw0LmTVpl7Jx4ilk9D/JxnlwecKo8k7exsaGNjY30GT2b/O8QSxBXXL/dbmtra0vdblftdjtdYzwe6+XLl5rP56nKqtFoqFarJZIsy9DtAePqZCZzfj6fa7lcpioo10nValWtVusasbS5uVmQPWkVDJAllpQy0MvlUs1mU9PpNJGVGRkZGRkZkgp2hZYA8/k82QpPtkmrBB1+LPas0Wio2WxqNptpNpulDVQ4h38nXt+PGQ6HqlQqGo/Hqtfr6Rj8qOFwmGzmdDpN32OZHr4dCRvsKsd4/8yPCZl4ysjIyHgH2Nzc1P7+vjY3N9Vut1Wr1bS9vZ3IKJanTCaTVI1Qr9e1u7urer1eaABNBcx8PtfV1VXKuEBWgd/97nf64x//qF6vp729Pc1mM52fn2swGOirr75KxrdSqaher6vVamlzc1PNZlOj0UivXr3KlSw/Aur1un7zm9/oyZMnGo/Hmk6nyamC+FkulylDhxMT+zhBGjl5yZjzPc/iQSyxi91isdBsNkvBP9/vdDra399Xq9VKWT7Osb29rVqtlqql9vf39ZOf/ETPnz/X06dPNZ1O05ItzjEejzUej9Xv93OFyy0ABGK3202fQUbWajWNx+NEDOG4b25uJkccGXPC04ksZE5SgQw9ODiQpNQnbDweq1KpaDAYZOIpIyMjIyOBJMfm5qYODg7U6XTU7/fV7/cT2YO/Ikmj0Sj5zFdXV+p2u+p2u8kmeZ/L0Wik0WiUyB+W3GEDPVkym81SCwEIJiqBScjxPfzxy8vL5FdJSn8j6YtdpS3CcrnU2dlZJp4yMjIyMr4/IJEIxgjEyGxg4Nrttur1ura2tlI5cLPZLGRhWFfulSf+OdUlXpFAxUE0qu12W4eHh6lHC6QF5ADGeD6fF4JIztVoNFL1ildYZXw3UKZNtZD3ZvJqJpcTiMRYDSWtSsA9m8b32fkO8okKFicQYqYP0gvSkb5OXm3l5AN9E2huDnnGd3DeeEZ2zNvc3NT29raurq50cnKSSYe3DPSH64lOp6Nmsynp9VhBHiFTHEOGmM84n+sblwvgy/D8Gsjx5uZm6gkGaY7cI79Zt2RkZGR8XPBlbd1uV41GQ1tbW+p0Otf8DiqM8Ddms1nyt8uIJ5JoZSC550ldVgXg83IO/Hr/jS9O0g+fxwkvgO/l/jnP7n0SPwYbmImnjIyMjL8SjUZD//RP/6Sjo6MU4FHmS6+d6XSq8/NzVSoV3b9/X61WKwWHEECQAFdXVxoMBprP53r16pUkaW9vT51OR/P5PBlI/5FeZ2qWy6X6/b6m06n29vZ0586dZEB9Gd3R0ZGGw6H+/Oc/6+Tk5NozbW5uam9vT8vlMt3LeDz+KDM0PxTdblf/y//yv2hvb0+7u7tpGSWZNWnlkFCNNJ/PNRgMkiMD+Yij1el0CsukcGKGw6EuLi7UaDQScUW1EmQiThHOVqvVUrPZVLPZVLvdLtyPE6h8Z2trq9BLyjOPOIA0IcexGo/Hunv3rv79v//3Go/H+j//z/8zyXTG20G9XteDBw9SBRPjsrm5mZrO1+v11O8L0mh7e7sghzj7kfwsI56k1TIECG6+i7zt7+9rZ2dH3W5X5+fnacndZDLR5eVlrq7MyMjI+MjQarX05MkTtVqttNx/Z2dHrVYr+baxRcB8PtfZ2Zmm02nq27S9va1er5eIIWwZvSohk/wH36dararZbOrq6kqXl5eazWbJD2s0GppMJtra2tLOzk4iv66urpKvXa/XNR6PdXFxoeFwWNgRz0kpSek5KpVKOg+Jl4/BBmbiKSMjI+N7gl0zCMzb7ba2t7dTdUuj0UjVJ7PZTJubm5pMJmmpCUufyLRQrUJ2h6oDqmDijxtQabUmPRJRlCVTYUIV03w+V6/XS9dzosC3lfVME/fomRm/VsbrgJ+qksVikfom0SOH98W/gY8zY8vnfgwEgpNJjD3y5v2ZvA+Pny9Wr7F8qkymYi8piAcq9yAtqLDiWsgWjh0760Fe+XNxPUm5L9QPABlZ0Gw2UwUbY+cZWojLWOXoOieOiy/hjfJbVp3HZxzvOzAyTyCocMohYH0+ZGRkZGR8OPCqfcgX/CQqw30pt/dVwkeCKCJxslgski/r7QtIgHiCzyvM8cWxi54Y5De2zFsRsBpgNpslm8bKBr7nPaMcZX5X7OUZj/2QkImnjIyMjO8JKjiq1apGo5Gq1aqOjo5StsW3upeU1nZ3Op1EEtBXhWoAqphooNjr9VJjRZZPsYQKAghDTKUT2RIaQksro+dkBdvLtlotdbvdtO35crlUr9fT7u5uMoos/ZrNZvrmm2/SenuaI5btgvWx4smTJ/rHf/xHLZfLNL5XV1c6OzsrLEVyJ2O5XKaeAlQq4XQhEyx3bDQaevjwYeG79Pmir1Kz2Sz0FkA+pFWDaW9qiXxEB4fvtNttNRqNQvaR/j3/6T/9J00mEz19+jRVwyHTyFuz2dTW1pbG47FqtZr+83/+zwWCDRmmEufFixf6//6//y9lBzO+HQcHB3r8+HEaa3pyOVnEe47kqLQa6yibceMDPpeUxjpuS82xLCmQVNj8gHtzfUcG++rqShcXF5pMJjo7O8u6JSMjI+MDw87Ojvb391Wr1VJi6s6dO4Wl3/hQMaEhrZaSb21tFXwgGpI78MN7vZ6klR2jqtcTePjRkE/46/jS+Ol8p1qtJqKMBHO1WtVkMkn35Alb7Kz74b5DLJ9x3+4bfkjIxFNGRkbGtyA27e71ejo6OlKtVtPl5aUkpUyIB2De48T73/jyJXqhQPJAWtGbB6PkQWHM2ngmiOuyZM8raADnl1ZkBCD75EQXSwYvLi7SvXPNWClTBq/2+RABybK1taUHDx6kpW+TyUSnp6fJySFTV7aTHe8TefAdyCSl5W/tdvsascW5GWuvbHG54NqMIcSmV71wT75TTKyoQZa3t7eTbAyHQ52fn2symaSMI+QF5eQbGxu6c+dOWu7psgtxNp/P0w4ysfLrY66CYYzKlrg1m01tb28nMlh6Pa99i2knjrx3nFQkhvz8XHPd3I3L8ByexY2AkCxbKow8+lLSD1VvZGR8SHjTMlzwpn42P+Y892rLeH5PoMSeOxk/LqJvIb1OxHY6nZTQgnxyH2M6nRYqrjmX/7BTM3YCP8ztiveojHIZ/+9V3l75hJw4KYYMcW8k+fDxsGVObOGf+Tzxii2/J/f1vcL4Q/CjM/GUkZGR8QZUq1X9+te/1uPHjyUpVQW1Wq1UueRGhWwHwb8TDnt7e1osFrq8vNR4PC7sIEbAGAM/lvRBfkEYcG+QFFybgJLqGSelnNjCyGMADw8Ptbu7W1jz7uTIYrHQ7u6uJpOJnj17puPj47TenR3wlstlylr5Ep1KpaLRaKThcPiuhu2doVKp6MmTJ3r06JHu3LmTPiPwJxt2cXGhwWCg3d3dQjWbpEQSQibFJVFeSeLVbbPZTK9evUr9C6gk8R5NZSXk0+lUg8EgyQTNxZGF+Xyui4uL1CeMvgtUMvkufGTkFovXu8DQ34AeUMiSpEIvA77H+XAij46O9J//838ukGlUwXzzzTcfbX+oRqOhJ0+eFOYmTii9m6RyR9XJ5zf1ZkI/ACdF0TmepeWYeJ54br7D2Hvzcr8Gx0JQLhYLnZ6e6vz8/Md6jRkZGW8BtVotVX1jJ/gcoMtns1nqjcP8Z6n4j4FKpZJ6yWEDvfrk8vJSlUpFjx49UqfT0eeff/7R2pW3jY2NDf3kJz9Ru93WaDTSdDrV9vZ2Ip4YI/eBY6VPJGrKSCRPknKOSHJ6Fa6TUjExwwoFP7fD/Wqqx/F76ZXpVbzs7Mt1vGfqbDZLBFyj0Ug7XpOYOT8/13Q6Tf78cDhMfvT7SpZm4ikjIyNjDTB09+/f169//etrjf9wZLxaBULADR1b17fbbS0WC11cXBQCOW/i62va+Tv3IqkQpPE5QbtXvfiuUZ7RI+Pi6+dZ2kc1ChUnMfuytbWVjO1oNEqG8vz8PAWHzWYzkSUQC5VKJTV4fN+zNQ7k4/DwUH/zN3+T3pu06pcD+QipxHJMSYmQjGPsPRDKCEAnE/v9vgaDQaGnj2f7fBtfvo8zFPs2+fVGo5Emk4n29vZSxZNX3iEH3jeB4AFZ29zcVK/XS6SoV18xb7i+b028u7ubqnfm87levHih4XCos7OzUnLjQ4U7v5AxNIwHEH6+XLYsyx/PVwZ0x7pqPEkFwsnH4k3ndhnmPJ7ddplGFnDAadjq+FjG/31DmQzksfrwgd3Y2dnR4eFhYUmS6yqWI5Gswy+QrhPmfy3a7bZ2dnaSXcHmUVlbq9V09+5dbW9v69WrVzo+Pi58P8vtXw/8j729PW1vbxcSrvRxajabhXF3/9WJlTJfxf+GLLnNkq6PI75KTN7wNxIf3pqC80T7ynW8Sh3S1ZO9LBmEYNvY2EgJavq5kvzb2dlJO15jDyeTiSaTSWqUzvx5X5GJp4yMjIwSbGxs6OHDh9rZ2dHOzs61LeAxXjs7O1osFhoMBomModollnR7sE31SQz23GBSHRCJomgQIbFiJYG0CgbICPE3CIP9/X01Gg31er1rxFck2jB8W1tbifBiBxLeA6TEYDDQbDZLBIZviwsx9z5jc3NTv/jFL7S/v6/79++nRpdxK10cEjK8h4eHBadHWgXx9BTwMcNRodKFHk04cdLriqlGo6FGo6HlcqnRaFRwjli+5Nfa2NhI/cPYPtiXV7LFsRNAOFDILg7W8+fPdXFxoUqlUiiZh/Ty8nWpSDQgu07iutz5MrB79+6p0+no5OREL168eO9l6E3odrva29tLwRtLYpmDkgq7IcZKRvSI6xPeuWeFpRUJFB12X1aLXCMjEOWMbRkx7gQrQQgOPc/gY7ixsaHt7e3C+N+5c0edTid9fzAY6NmzZ3l3zVuEZrOpnZ2dQmUuODk5uUYcZnw4qNfrun//vrrdrg4PD9XtdlMAHpMm7GxJz0gqYzc3NzUYDHR+fp58hh9Dt3N+NjJAT9Hjjiqof/iHf9BvfvMbXV5e6vz8XMfHx/rTn/70Ueww9mOD3XLZ+Y33v7GxkXqH4jd6kpN37cm3uEzcewZ6kozPvZ9SWYKV87sf7T4YvyMZyn042cNn6LtYkeX2Ulpt2kNbAUlJDnkPzIXNzc1EyJG4pFoM2+n+0vvmT2fiKSMjI6MEGxsbevz4sY6OjtJOXNGRgni6urrS8+fPNZlMdHh4qHa7Xag+wvhgKGK236ujopGDuPB15mX9eAg6K5VKIRCVVgRGNNKSUjYqlhPHJTpUrVxdXanX66VsIt979OhRMqqz2UwvX77UaDTSy5cvNZlMUhUDTuf7jlqtpl/+8pf6+c9/fq3azR2OjY2NlKUaDodpGaYTjZCRBNi+nO7q6irtoujo9/uphJvsYaPR0Hg8TkRfWbUKcrC5uZmWP5J9835iBA4QTzhjVFXxjIvFQi9evNDJyYmOjo7U6XSSfOP4Q2RJ16tonGzi/xBn9EDjXHfv3tXR0ZH+9Kc/6cWLF295hG8W3W5XDx48SGPrTjbONaX8yIpvUsB7dTnjHfu8piIAJxfyVFLKyLqOoW+Yg/tijJ3E5P98l4DC9Ry6i8pLaUVyt9tt3b17Nznux8fHevXqVSaebhEajYbu3LmTAibGCtI7E08fLur1uh4/fqzd3d00h1ki7gkWdBa76g4GAy2Xy7QT8MnJSfIfqA7+oXBSAiLE9QX9eNCff//3f6+f//zn+uabb/T111/rj3/8oz7//PNMPP0AsHNtvV7X9vZ22tm2Vqtpa2sr/durvGPyhM8lFVpEAP+3k0qz2Sz5RJISAerHeO+v6B+DmHTFVjk8aeOV/U5CRYKMxCvy12q10jmYN/zmPWEPB4NB8tPwsamC8t2m3wd8dMQTSwZwiur1esokx7I+d+qkoqAiZLGqAKFwxZrx/oNdwMj0S9e3JndHOy4zciBnMUN8eXlZUJpsQT6ZTFJT54y3j0ajocPDw7S7GxUcHiTFgIlKD7I7sSmuZ1kwRBwznU4LQbyTMq5z3FGKshADvDKyIR7ry8K8hDkSUFzbvxOzRNJqSSDP1mq1VK1WNRwOE2nnmSv6UL1vOrLRaOjBgwfq9XqpHNpLrmN2jR5dOzs7KSijv5LDycbodPn4xEabyB8VTwTs8/k8LaeL5MNgMEjjQmYOUnE6nWpjY0P37t1L9+vjho0bj8eJXGR5HJnN8Xis6XSaqp24Xy9X9+fk3CzH88wmiKX2Hyq63a7a7ba2t7cLuwP6+4s7EnoVWnzHTtx5pZH7MsgQMoi+8+UPXkEVnfeoPzzL7I6333Os+MP2US0KYsBRqVRSVQW9zTJuBu12W91uV71eT1tbW6pWq4mkZty3trauBXFk7tnG3Mfbg77xeKzz8/P3zkZ8yGCX0mq1mnrT9Hq9ZCuY/3FcXd9ISlXTVHH6zmM/hn6n4iYmQSRpe3s7+Vrn5+f66quvJEnD4VDT6VTtdls/+9nPNBgM9PTp0w8iUfa2QcVOp9NJfb7YZc5jHX67f+ztKXwpdqwk8nNIRb+a/7t/5L6vVwehg0gCOieA3PoSUXSaV+xiI+Oxfj/+WUwcu01kNQD9VZ0s8+otNnQhGYgPR88ofsf3dNvw0RFPKEomSa/X08OHD9MaYM/aDQaDa9v5IqDeQJdsbrVa1eXlpc7OztIyCF92cZsFIePN2Nzc1E9+8pO0fWd0ygkOqUqgyXPsi+IVEfRiQRl+9tlnBeJpa2tLT548SU2JM/H0btBqtfT3f//32t3d1dbWVhrTWPLLtuX87OzsSFIytrGqAPhyBHrioI8I/PmOVwK4QYkERwzU473G7A5LoDCAGGB0WgxOOT/Nq3HQnHSNBpsG7DwPMkwWynd6e5/QarX0m9/8RgcHB2nMXCe400HGarl83XSdd3F6elrog+GJC3dOIGPcwfH+AzgjVEu1Wq0CgTQYDApjQrXZ6emp+v1+gYxYLpcaDod6/vy5Go2G7t+/r06nk4gsr5SZz+d6+fKl/p//5/+RJP30pz/VwcFBcjJfvXqlFy9eqF6v68mTJwUy022m20R2xpNU0IteMv8mcvRDQKVSSUs3fbkK4+ekomeHCbJiFZSkgg6iya6TxFQFSNeTIsgHzrpXq7kMIpOMqX/fydFIpEJqepWbpMJuQl6phU09PDzUaDTSs2fP3jv98SEBH6XZbGpvb0+z2UzffPNN8nHq9boODw91cHAgSYngvri4UL1e197eXoFc9Q0Frq6u9PLlS/X7/Vzddouwvb2tn/70p4mAoo+fL9eNVdmuq7BhbGZycnKi8/NzbWxsaH9/X9VqVc+fP/+r5zU7p3nCBr+n1WppNpvpxYsXqSfh559/rl6vp+3tbW1tbek//If/kCp5M/H07aA/Ubvd1sHBQYE0IhkqFds8+I/7OYyXEzZOSJclriIZBLgWpAyV4ufn5+r3+2q1WoVG5/jvfh4Sad6TCnIIW+uJRxArs7CPMXm2ubmpbrebSFzv8ckzY2MPDw91eHiYeh9COI3HY33xxRfvRaz4QRJPLuy+mw/OGYJFMy8Mn7Om0mr9pYPj1vVwgbGUpP39/VLlyUQja5xx+4ASkl4rLqoJKKv0wJ7AwI0tyx3i7guRgPByTaonQLfbTcss2AUrZga5F3q1ZHx/+C5u9DoigycpLUHy8YpZF//t1VAsS4kBHYgk5rpjIrmx7h7i99ZlDj2AjOfxZVDx3qLc+0/8O7qy1WqlQILeDV4x8T7DA3ypSAr6/yFaWHa27h3Ez8qqAmICAyfFq+XonyCp0FOAit9ut3tt+1+c8u3t7dSbAaICIoseTxChZKjb7baazWZyxsoay4J1zxGDFeYbxKY7YVQlTiYTXV5e3npH69tQqVRSppPKAZx19zPceY1zh3L76HNEki5WbvpvrlF2fzGzHOd+zDr72MXzuO7h2thKjuc3lXu+qyK6+UMlIG8jXEYZd6o40SUQkvg+zOF1tsoTNz72/JtAD//mTcnb2C8GQvN91w03CSdsiKHwjfiJ1U2RLHB/weFVH17pslgsEvH81ywhIskbe/xIKz/cl69TyevJoPl8nuKAXF15HcTCGxsbaXMT35iGd+nL8z0h6kmFCKomJb1Rh0Sfoczn4Dokeql24nP+5r6vF6H4PSEjLud+Xzyn+9ZOunny1ZfeeX9Wt43x2T1BjG6EmId7oEJr3bu9aXyQxJO0Mmg0zj04OCiw35JSTwQnC6SVcKBYQZkS9cm0XC7V7XZT5vHhw4fXghLpdTXMdDrV06dP9Ze//CVXQt1C7O7u6le/+pWk1+MFqUjA5Y1VURhuPNlFyjPG3kwxKqJaraZHjx5JKu76U6vV1O129eTJE0m6ppi8guFDb7b7tnBwcKCf//zn6nQ62t/f1+bmZuq1Q7YV59rH2MtuPfOBIaDseDwep+17vcojGpZITnA+32LWl2+y7IlMj1RceuPOllcjYIxY7uDyzHM4ielBL8bZqz69r4tnstCtZDbZzYb7G41GOj09fdvD+6NjuXy9HS5ktMsAiHZGWpE+HnzH6pDo6NBsnHfKuHNOyKLNzc2002ClUknVd9Jr/fXs2TNJSttHHx0dqdls6vLyMjU9H4/H6vV6evLkier1unZ3dwsB5fn5uZ4/f54SONVqVX/7t3+bGp+zvLJWq6nf76vf71/rS8U9Syrs/IiT2ul00jvGBvtcGA6HGo/H2t/f1+HhoZ4/f65//ud/vpXO1fcB+n93dzf5FpGYgZzheNcb0+k0VbB5mT7foarNnWyvlorLYtz5lopLGPz/ZYQof4vn4G9e+eSyT4DHeSCZLi4u9OrVq7QFNxXrg8FAX3/99Y8/GBmlYLON3d3dNAYEUIvFQqPRSIvFQu12W8vlMul/Xx6O7Hn/w0iWumxRPTEej7+1r1e73dadO3e0WCxSL73z8/P3XjfcNIhp9vf3UzxFUrTb7V4jnWKVC3YLv8Z7+XhygWpOekjSG+yHVrsNh0Odn5+r1WqlgBx/nHvZ2dlJPhR2vd/vF2zO0dGRptOp/vKXv6jf7/9o7/VDQKVS0e7ubtqJjSp6KuipkO90OimJBSGMHBAXxU0JvDrW7QTXdf/WE/hlZDe+8mQyST6EV/5SoYld5De+HTLORixOxO7s7Fxr4eN6j9/49lSnE1NMJpN0Lt5RWfKZz6iUZ/6w8gKyieXJPOdtLG75oIgnBARn3FnYVqt1rYIJoQIxixiDCQ86veQfBSsVGU/vB8T3+S731ul0Cp34YwVCxrsFFUYoBlduZdlV/u7VMH6sZ3X8PDjfnuVzcsDPL62q7yLxxHkJgqUVofG+7XRwU2g0Gtra2kr9KigFX1cxxOdOPkrFBoTRESvLXETjGUt1/dz83a/v9xPH2e+DH19e4+f0+3cCzRGv558j+060Rj1YrVYL1aAu15XKqhn6bQYEC6XQUvkWu1FPOFEZbYp0vSdA/HusJiNb5/aHDJgv/4zkA84/WUkybhCQ0mv9R1WDVyFgW3GwcLyYL4wxf282m8npjFm3KNf+uetRyJL4Hb8PHLD3FYwJdseJPieoOda/tw5uF5jPUrl+4nh3wuP9lVVYxWonjo3Xdvh4lj1PDCL8b34tZHE2m6ndbqeKvrwc68eBb2Tgu6Wi/7yyoWwMfZxcN/n4xuWT8RwEnZJSr8B2u126xTr/pzqK8xLQZvxwYDtYHUIfS4LfGEO57wJi1SOI485yK0iLv6a6yMksiNF19+ly6YQoMluWPMlYvUPkwxvKeyzufkS0QWX6gvNGH+ZNNm+dHgFOIMUl4fgR/HgfU/c/PLkb5dxjd3QUNikWn0RfGX8qEm/+nfje+b5Xly6Xy1QcQXXebV0i+kERT61WKzU4PTw8TIpRUmJipeKEkYoNeaWVo1+mrGJvBD/WszoeePn3EY5ms6nHjx/rwYMHOjs70+eff556cmTy6eZwdHSkn/zkJ4XqN28sLRXJRScNyKSUKU+AgvG1yhwTFU+srCkjpLgXbzpHyfDTp08LPaMyysHuUT6feddkJbxqAMeYncMYAxwW1w1kJNzJdlKav0EouPF1oyLpWmWSVzp5VU1ZkN5oNNJyQsiA8/PzAoExm80K2REntJxgLyNZkF8n7fjBQB4cHKRAERnd2NhIDTwHg8FbHee/FgcHB/r3//7fF9bhRwcbJ4Zn94oPz+7yf5cfxzryqd/v68WLF6k8m/GUlJpNAnpwbG1t6fDwMC2ToJkrOwexRA5ym/F14nBjY0MPHjzQwcFBwYkjc8wyGGT+3r172trakvR6O3WC1kg6RefTS9/9/fF/gkvPcL7PqNfr+uSTTxLZx1JG6frcckRiiuyyB0x8h+oPZJM5StWj6zSf104ic1ysvvJjIkmOPEgqVL+w/MV7wpAo8SCDhBwVF+hYMsYs7xyPx/rd7373we9y+K5wdHSkX/7yl5rNZrq8vFS1+rpBuLcNmM/n6W+SUlUDlU/u32B7PPtOUAY5hK5Bt1Dl1m63df/+fS0WCx0dHSW7i13EbkEw9Hq9RGCQ+c8+0F+HZrOp7e1tbW9vp+oO333LUVZp4vOaY/gbFdybm5vJtrGUNtrX7wvGH93oPgr34RUsECPoT/fL0bEZK7iPi5+Av+w7W5JYdN8VkkcqJkqq1WoqGqFHKL6zV06SqGQzEvRJ1CXcZ71eTxVPtVot9cHEj2o2m2q1Wtrf35f02mZyXul15Tn+jC8J5b6Xy6UuLy8L/TMpePGKL+yzE1L4cN6cP75njisj1CqVSvKrG42Grq6ukl9NFd9tw3vttUVGlGZy7AjjAX7MNCPkZZUIjjK2/k0MbMx+g5j1wfnD4cPpdwfPg5eMHx9l5GC73S4sUymrLkF2ojFdRzZGJx6FWFa1EEtJ31TJIq22aidb7g58bHDt58gytVpi4ktqGRMfz6hnpOs9kuKabI7xpWeSrjk1TkY40Qj8mvEe/Ptlx7us4txBFvhz8j3u12U7Zqc4L5/5dfjMl945WesbMkynU9VqtRTQnJycXFtSeNtklEa5rVar4DxHXR0rVeK//f/rbEmZbWE8fOmvLxX3ee12iO2NfYmcN6emwoElMoxDJECpGnYb5ku+nLhgCSLLTF22YoIn6ld/r+gvZInz8qw4bU5OvQ9w4hifxas5eE9vqtjwZ/V34vPeHV2IHh9TP5cTRdyDBwRR78TAY13CzL8Xn18qOvKSrhFSTmZ7BU6lUkm7J73vBORtAME3TYKpmK7Vatrd3dXGxutdBCGMmJNOQpbpsygn0vWeJzGoJ1sPMY6+IxikTQZBJMtV2OyBc0Nwuo5+X3TEbQB226tkvcJVKlb4+rvHXpXpFreRTu748msntn5Irxr3zUCMA71QwO93nU1mCfHHLkPuV/q8Z77FBDy2OSbsJRV8YSee2N3Vl+aid0hCYNuivvFrYAeRMe7Nk1mtVitV9KFj3BehqAC4b+L+CZtk9Pv9NHdiZaDLDvcWK8N4Z2Xv3c/h9plxgE/A37qNeG+tdbVa1dHRUdrunN4S3kTcAycXIj+HfxaVoR8Tz+UkkqRrRjgKSCwxd6Hodrv62c9+lnqrIPiz2UzPnz/X2dnZj/jmMsDm5qZ++tOfpl2nlsuler3eNRLIM70uG2Vlxi5TGFuUSqxGcWfZsy3uxOGURYfNr+kVWU5sPHnyJDXT84Dm/PxcJycnH7XxrFar+h//x/9RP/vZz1IWryxjX0YkomcgUujnRRaG8WYeM6bAAyjGyw1ZrIxxQ4rMxcq4GNy5I+DLeMrIM1D2rO44xM94Ds808W79HNwjxpt31Gw21e12NZ/PdXBwoNFopOFwqMlkohcvXtzanmX+/J6B8+bOODMQI/5eo8PuDlyZ84FDs1gsUmVjtVpNugp4FRRySSUNFb++hMXtJbpGWuklDwZjtaeT6MwT3gmZSKoOvIrO310kHOi/4HPBtz5mPiHPm5ub2tvb029+8xudn5/rj3/8Y6Hi6zaj0Wjo3r17aQvluISaOY1sSeVkJLrGAzN3kCuVSloa5cdOp1NVKpXC8mxQRqp7dteDNP/cHWvXb5JSNWe1Wk0ySWLEWw24znWn3u+J+59MJvr00091eXmpk5OTH3uIPipUKhU9evRIR0dH2tjY0MuXLwtVqWwiEAleb+hN/xuvVpSUlgbzW1JhUx9+OP9isUjVDpDkkq7ZREAlA0Qu+mljY0M/+9nPNJvNru1klfHdUKlU1O12tbe3p06nU1jiDNwndT2EjMQdM524cR00Go1S43J8sidPnujq6kr/+q//+r3meKXyus8hlb6uP/A/iMGc3PJ+PMRpp6enms/n2t7eVrfb1enp6a2sInlXwO6zsQAblcQG2ehuSel9OzGJrveEKJXR+C5ehe0/nOv8/PzapgOMG1VQ+OCARLNXtEWCaHt7O9leSCt0HzLiCcBKpZISSOzk7MvnXL/xPiCmIlHGs/FcfNerhiNRjx+Gn8gqh9uakLmdd/UtwMnZ2dnR3bt31ev10jb365jxqHh8oGNw5ax3xDrW3Vn9GNhFdtLPRTC2t7eXPlssFqnh6/n5+bX7uI3B2PsGFM7BwYH29/cLmWL+zpIZSQVjFRl6h2f0OY+TBi4PZRl//x6/o+KKQYI76SieWq2WDPpwOCz0k/KKBj/PxwLew927d/XLX/6yEGRJxSqWsnXXnoVHjqSVw41cYKSk6yR3lDc+cwLAyULPwsXssR9T9qzu3JfpkkiyO5gDsZLC79ErM1xu4/3E+69Wq2nZVLPZ1GQy0dnZmYbDoYbD4a1ZOhPJPAc2hyoA/x17HriMxfHD4fEddSqV1XIjr9wlIKN6ifMy33Hi3JnzknfPKON08RyMj5MLbg+90sVlgX9znzhOvIuy7F3UY7xHJxtwvqgEdnmjwrnb7arT6eizzz77EUf97QGHc3t7OzmHPjecaInzyI+LcunjKq30B4EVx+HYMv5+bAwacbYjCY6+cd8GOEHA3yGneV6fG56c8/O7HvasNkTsZDLR06dPc2LuByImGXZ2dvTo0SNdXFzo5OSkUHWEvET/F/+VAI/PJF2zG75UnKU2LsdOoNLA2s8bEyXcN/Lh8u8B5XL5utE5SY1IGnxMvs8PQb1ev7abIeMW5zr62RN3Xl0Z9YKkQn8aSAeqaw8PD7VYLPTll19+7/tmqbnfkyf6JF2zzW4HkSuajZPooZolPsfHANfP7Xa70A8SsjcmRf17vGdsnBMz2COW63kTbfdRGSd8i42NjUQsA8aOTTeWy2VKynmLAm8PEeM65Nf1DjqRVgWevCO5h0/rxBuy5y0xuAf0avzxFQDuW7mt553ESjwn4W8j3jviaWPjdRf5drutvb09dbvdQvM3JkCZkZJWzRJxXqRiFraMcIpOOJ95htoFxs/l5y9TVmVEFoZZku7du6dOp5O2kx2Px7q4uFhLgGV8O5rNph4+fKhOp5N6nnhA49UGBAnL5fKaYvMxRm6cvOQcUQ7cCEfHi+PciLtMunKJBBbfjbJB7wXubWdnp/Cd6XSq4+PjW9uI7sdErVbT0dGRtre3tbe3p1qtlgwJ8LlMwCRdr3p0MsiDY5ehSMQ4EelkOBVAZXrDCSgfN3f6YtYEkPlh/NFZMROFLPr/XZbQR3Fp12w2S/Miyp2TDV4d6BVa8XnXEWQ3icPDQz1+/LjQQ41n8erEuERSUqr+8YDIiR0vj5auJzAYEycPAPdA+Tm9CuLyUJyS+M7RaXHXE8/KcR2XLZxDabXdtVd88V0a0a7bcjveC05bDBKk1eYKTpg5WRcbHd9WdLvdtHOmz6OoG/gcG+Q6gL9JxS2nneSUigS6f999FHeM/V6iTSnLnHrwGZ1i4NlanwPoVsgIvybHUCGDPoJIiJXGGd8fzWZTT548KSzx3NnZSZVw3i9MUtox0eccY+pjtFwuU9UiVU1uezyo9IoASQX7hNxQAYGMoRPoY8KxroOxpYvFqvcLOpSdEyWlJNzl5WUpMZ6xqkjysXS5kJTeM+SkVFwVEu2ef84PQTvV4x6QY9++L+ibA9Hu+pX7gfTi7+PxWIPBIFVjeqK50+kkezadTvXy5ctbkxx7V6hUVkv8IVwgoHzzGD/eyRzgVdlsQkIs1m63U3Ii+h5uG9FDy+Uy7ViPH+J+Mce4/HEOfke5dt/H/RASeYvForADr6RCQp97oZcUCTTsPLqL3UFjzMG1PPZzOeYeuRdPLNIrmjnJ+WNsepN474inarWqg4MD9Xq9tL1urAiQVg6ZBzXOuPoAu7IELugxm8d33AlG2D1rG++pjDzgmTw4IENTq9XSVuTj8ThtD3p5eflW3u3HgmazqZ/+9KepdDgGVQTfBJjeCNqVVPyRrlcvoSzKqh6kIvlUVlnDd8syRjFYiUFLBI4884ZjB4OBzs7OPhri6cGDB7p79652d3cLmS2p2ADaMzPS9WDZnRLO4c6KfycSUIy566BqddV817HOUDjRvY544nz8uDzzvL6jnPdXkVbBAE4AgZ/DMzN8h9+LxSIRA7xT5kGUdydKblNgub+/r7//+79P900jW/S2Z+1wmHAAyJBJr5eXeJ8dJ51joqTMQfbfLoM4W1tbW6nsO+qaskyz9Hp5G8Em98L9ohshjtzhabfbhdJ5npdnYszLdCNZxJgpxxGNlU1SkfB0QILFHWtvKzqdju7fvy9pRdrFZawxmSVdT1Y4yPp6o/poY7yiCbtRZsv8O1wn2id3zp005Vj/Dj9OFPo9RR3mAYovE18ul4Wmxhyf8cPQaDT085//XHt7e4mcYfmipEIAeXV1pbOzM11dXV1bVhOX8l9dXaWmtrS/cHlBZvz8rgu86Tzf8d6VTowiT5HId7LKe8LUarWUqOb44XCowWCQiac3gJ1Oy5Lq6C96f2HjXKczT7Fb6D3mMRUoNDFnGRPH/tDdKiGqsVNOlsWKFnB1daXhcJgCetdfECyHh4dJrl++fHkrAvl3BXxAKlcheTudTlo27rE18MqlSqWSdAhjXq/Xr+2QWxbXOHEkrfxVYrnRaKTRaFT4PoQpiH69dL0Vjj+vy4iTqMSJg8GgkETxzV5Go1Fh05co8+iwsqq8mJjyqk6fU15sQ3EKqwbm83mqSI2x503ivSGems2m7ty5o1arlRq8eqWKVKwI8M9BdMajcDu7GJlWd9IQfg9EIJ3ckYsse3SY/Dhfx879c6yvo18ulzo6OkpNW1Gqt0WgbiN2dnbSbgWw48iPEw5ly9ncsXanx53ksgldRgjEio+oWNxI813P5klFkjQGC/49D2xdppHRqGjv3btXINYuLi7em34p3wc4vdvb2ynDRcVRWaY+Gr34vj2zx9In340Dhc9vd56l4jI6/l9WOeP/9mqWb4MHgmX37s8aszxOdPiuoH6fkbTgvDGzE68dZd3vJ2ZUbxoxyAFl9kVaOTG+TFEqT2JE/VA2rpGUxu5xTfr3rCOouScCMeTQmwR7YgbiCecSfenVDoxtp9MpVD0RgJQ9a1l1Dc/A3PJAhsCgUqkUsonu/BGkxKqt2wYapdIrRyonlH3uoD98/D2I8vnqvdaiD1RGKsXsZ9l8c9mN1QF8JxLF0dbxf+47LsXAUZZWGV4nIXg2vt/v99MuQZks+OvgSy3j8k7mo/ctjGPtOt6rDNi90snyaE+5btQV0ca6nEaSkt+NRkO9Xi/5yNhb9IeT1q1WS91ut5BY3N/f12w208XFhebzeWGHyduuV94WNjY2tLe3l5ouO3nolSPYj1h9Jl33ZUC0Zz627gv7WN+5c0fNZlMnJye6uLj4Ts8wHo/V7/evVVxxTmmlT33pV6za8eobnqusBcOHDMYSEpLll1Qwlq38cR2AL8FviCfOhy5y3eOV+NJ1/ymeHyKIxKCPeyRBXZdFUkpaJVyjvLgc8V3XnQ6eDUIufhdSrOy80vUiA3/uOK8icYU/4DrT+1TdNF/w3hBPnU5Hv/rVr1LGolqtpgoOV1axZwFwQeZY4P+OCopzuZPjJNQ64XDWF2cwntcVbtlOQi5gTK5Op6Pd3V0NBgN99tlnhWasGeU4OjrSr3/9a0krZ5kKDLJ9lI/6u/TMq495LAONjrzLBMdE57zMuYrOl8uMf5dz890YXLhS80CEY6I8dzqd5MijuP/85z9/sMTT9va2Dg4OCoGMl6Ni0DwY9gDKdYsHZvRsOTw8VK/XSxlkMh/z+Txt04ryd9LSHfloIPm730tZsOiyW0bs8H2XBYy+/x25IQPdbrcLOhengWVkHE/WhXlStkTHn83vhbl323QZTpePg2efOMb1BfpaKpLQIDpUvkyqjCSMJHRZIsSTHT7nsS8su5zP5xoMBoWmnD4GBIM4mHfu3FGv1yvoMu6ZpSsQUM+ePUs9MOJ9uq3mnXkg6vdKVS/XpWzcq17IZkNe3Cay0lGpvO6f8+DBg4LD6vIjFeWEsaSKjGW4jBlZXCekIAzdd3DZkK5XK7yp3QB6iooRH0dpNX7eqJXn8/8vl8tC2b/btfF4rLOzsyRLTlK7jvFMbqPR0ObmZmFpZ8b3Az4QS1QZV+wBSQUqT7wnidtG/Az8XeyrywDHQ/Y44SWt/CTu6026zatQ0IdUorhNw5+OzX273a62t7c1mUzU7/e1WCzU7XY1Ho/1b//2b7q6utLOzo56vZ5evnz5URNPn3zyiXZ2dhJR52MvvR43KuS8ElFaVXS4PpFWti5WO0rFxvXoEWTjyZMnWi6X+u1vf/udiafhcKjT01O12+20LMrjKfd3kbF6vZ52dBwMBols4Xmi7H0swJ+h91qj0dD29nbqxYVcRJvBXKdSku+ge6RV1VK0QSTHor/oyS/va4l+mUwmyU+QVKhwdH/Ne0+6Py5dT4657+W+lR/LefmbbzDjdlFarZ7xZyzjBvx98A7K7CvPTgUquhudji+/rt/mu8atJ57YkYd1oLxwEJlAUOa8++dkQ+I5OE8MiOJx8bMoHGXXxmi6IY2ZHL9vJ8FcMHknLK1gHel4PC6sJf2YUam83mq53W5fW9fvQbsrA3fQo+LxYClm/OJ1I4vOsZ4J4NgoU/F8Zef277mjFs/j5ZyVSqWwHNSBIkd5U5K+s7PzwWT92A2s2+0mY+BjHJe9xKyD64RINpDtY8vhWI7rRnBzc7NAFpYZMh/bCNcFrhPK5nw8D3ISiVQ/NiLqJ0kpCCUA9axNlPt1ZADP7P0bnODx9es3bSipDHJ54d1FeyQVdYSPL/93B8oJwhhcSderVqJN8M/iki2/Jvfgy7H8Gg6XX78vnm00GqXd5ba2tgrPgZPuO5V5kFFma/0dMO5knb26iuvH4JLP6V03GAxuxbJhHGOWA5aNi4+9VNzlkn+7LPnSJWSizN7439f9v8xPcZ3h9+b3XVYNGgPMmJGNQRrOcLW6avbqwYsf59f13iJlcy/juwPdytz0QB85KCMeQQx4nDj3ZXVOIpTBdWJMonEdqbgc3f/msudzB5kjaF4ul4UeQlTyuB3zHrAfuw/tKy1ms1lp9RJEcUyMlgXSruOir70uZorngfjw3pLrwBi77EKscl6IV6964jm9d3CMBT82vYOedv0LeVTmSzhBRLzqvd18vGez2bX36T5WmU3CH3FbFP1Hj/Wjn+sEmctdJMCjrx/tt+tLt3Fuv5GpMhuN3XMfO9r1GC9G/88JLI9ry4i9yWTyg3um/Zi49cRTp9PR0dGRtra2UjkdL9uVlxs4/i9dD6gioeDGFwGKBqwsCx8NU2Q9ywIwL1F3hzwqZb//OLHd+aJKZTweazab6YsvvtDp6Wlh6d7Himq1qp/97Gf65JNPtFy+zrgyyaXichjIALbARA7I9qEYvSeUj1d0fGKwyfXiMdJ1Zhs5XEc6xF4n8Twe0HqWslqtpl1dfKkOz4DTx8+jR4909+5dffXVV/riiy/eeyes3W7rN7/5jXZ2dnRwcFB4P2QJcKR9/Bg3d6hR6ATEvV4vNS7FKPNOmb+QelxvsVgkZy4aLH6vI6LcGCKL63bPk1bOoaRrjdT9O25cPTOzWLxukO3LzejrwbzgeTgP+i5WpPp7pOJssVgkco7KM0r8vcfLTWE2m+ny8rLgePOeGF/m9rctO/LPvdKMeedVK5IKvQPm83laVuLn8gQKMhb7bKDTvNkvzwaB40su3dFkZylk+8WLF/r000/VbDb14MEDtVot3b17N5Xfb2xs6OTkRKPRqDSzHZeKRiKVSiuX/2q1mhwm5NF78G1ubuoXv/iFRqORfve7392Knc6q1df9KHd2dgp91ZAJr/pwO+LOsFfCVSoVtVotLZerjQxcNzhhiE7wQMsDK28UzPcdjLVnnJFx3wIa+HIDxsOfNy4Z55k3Nze1s7NzTR54D37P3DdbbTu5kPH9gAxRTYYt8uWOVA8wf0mueCAzGAx0cnKier2emgM7oegyWZYYdVsmrVYKIDMcx/n4f6xWmM1mKRh2cprr08+RZ6GZ8WLxuuqdXjNck8rQjxW1Wi31zoPk5/16UO4tQKTrG6AA/GipqOv42zr7jk2i0rrb7erhw4c6OTn51v5KvV5Pd+7c0WQySbYIXcLyLpY+M97oHa+qpFrT48D33R/+vmC+oHvxQ7BHZRVC+MSNRkO7u7upLxxzDBsWK2g9/vZzSitfwWMW96ewD1ToeQLMfdEywtp9KfeJ191TjNn9Nz+xotivgw+wsbGhyWSSdK33fY3LAZFfX/aO/uP3crlMSyDxq3nPl5eXt6Kn3a0lnhgg+kjEZQtlx7qTH0mhqAzXMexl8GxNNJpl54jkUfxeVLSRRfX798kR74kAjudrt9vJuJdljj42sKuFB1fxPTqDXhbYu2Jz+JiUKch1WWjO74ovKhbOXTbu8b5dIfoc8EonD1zKnsPPyfE4cBAAEHPvqzxVKpXUBDEuXePvZWP6pvPF7K43+C2TCVBGOkcykmt8n+dbd8/fZ8zedL9lgaGTGn7f8X6+7Vlc3zNve71eas5408QTy4GczIUI5v6jkxJ/4nFOcsf5j2ygz/lpNBqpmXSr1Vorr2X2wv+GgybpmhMS9aCPJ/fFuLszXmbH4vXje3J7XUamORHsmWv/4d3hYJVl5t8lCMjoaQGJA/w9crz/Rjeskx/gSbM3+SH+vRiQl41TmSz5fF/X/8LHw6/Bedc98zqbXHbv3MtgMNBwOLxxB/p9A9V3BIyeJXc48ek9tr6LXYw/cb5H2UG2pOsJOul6YPeme/CA1GXV5b1M5ss+/xgB4cQudiSIPKZxnVs2V8t8zBjPfNsYxnN7Vd537a80m81SawPO5b10l8vVElIvCuAZCe75nEQ0Nv9jISbdN/OKokiKlH0HxPFnPCPxJBWrmMrOGXWJf9cTmMQwrrfe5Ce537HOPsVYC1+o7H6j3PvvaDO/DTEWdbsqrchcZJbEEuPkPluZf/6ucWuJJ7Jm29vbunfvXqoi8PJ6d0j5oe/DeDwuOHheqi8Vyz2jg4ZguYEkE8/1yypayhw9/oYxdMFDiZZNUt9mOAaoUdDJTD98+FB3797V06dP9ezZs0LFwccIf2dODJQd4xlaabUkRVLK6sTgzZVJVL5e5cLxPnbek4P7cqNc5ty7svKAn3uLLD3Olit5zs11fPmdX597unfvnrrdrk5PT/X555+/t46+ZxekVWbVg3if37wHrwKJSwd8uUe1uloDz3epLvKMBNnlwWCQqs8gMgis0RfrDEQZgR0JiDLHjPuMsuqVU+u+TymvO2LRsLpsOBm1rqJLWjUU9h4cLKs+PDzUN998o3/+539eS+K+Czx79kzn5+dqNpva3d1Vs9nU/v5+IasUK+HKiCjAd4BXOhHg0YPp+fPnOjs7U7/f18XFRZK7/f19/cf/+B/V7XZT5hDn0G0Yes31zmLxeut07KTvvFJGMLC8YTQaqd/vq9fr6R//8R9TzzJ3aKiScCcIGeDeuJe4vJX7LJN7iD4vE/cl0mWVVTeFzc1NPXr0KFXIeuC7XK4qaQmkcOC9MokKlEii4aTHzQqk8qXY0vVNV1w+om3zwN99mvl8rtFolI7FvrhejdfhXYBKpZJklQDB/RtfzonsOnmFbJ2fn+vPf/5z2vo847tje3tbv/71r1Mly/n5+bUAmjGhwfR0OtXTp08LKwMAOtH9jdhoGlkgkYWsMxeurl7vmjedTlOVFH1jPDBFR3rQVRYUev89lx/8PHYdHQ6Hac64baYHzcdYTdftdvU//A//gzqdjvb29lSv19OuXehxelYynq7T45g4yfBtQA+UEYDuQ32XeGa5XOqzzz7TV199pYcPH+rx48eprxeVw8vlMo0zCQISPNibarWqfr+v2Wymb775RpJSn6Lz8/MPPrZyX5fd7LyhePQn49hTxUNVD+/ZK4K84trJH+CxG0kclszGGIdeUpPJRN1uV8PhUM+ePUurVtxHirEMFVPce5RdfzZ8dul64s6XzsVVTvyfZ6aHo58XrmEdscl94HO6X0+bAyr46IuI7XSdty5h9S5wa4knMjPNZjM1E48DEbMYZQrLsyTrMhrrDEx06FC87ryVwcmCeC6/D1fYXoXhDD3P4I4q33UDvFwu07tqtVpqNBppOcJNs5vvEu74RKIoOubrsjbutLzpvZXJnR+/Tt4iiRQDrTJ2nuNhsb/tftbNh/icZZVx/p5wLNwYf1fjfxvgAVIkWMqIFsY8yoYHVXweyWnA9yG2fPcwyCgcHOZ0WXakzIkrQ/w8Bgd+jTd9P5JY8ZzxWDfOjhh8Sqvmj/GaUZ/xf4L2y8vL5GTcFIlOGTRN+HmWMuKvbA66DPG7jIyTVsQTlU79fj8RT2dnZwVihuUHfKeskbvfE//2ZE1czuQEjtsiv19K6H2JDtdwEtvlAOfR78X1CDJaVp3MO/PlWq4/ow7DgYzJoHcFAjLfgtzv1+cM72YdgVw2F11efIy+i71Z9zevPIvvzJMh3DPwcVunq6LueVMVsdvDqGN9eejZ2dm39njJWIH512q10vblBCQgVh35kky3mzHzHpdbRX3D3xhL1/nIjusNEIOjdedfl9gom0P+d3xjD97KEnj+vQ8dtA7A/oKoc3zJWbR9Dg/eo8+1DvGcPwTL5TJtKb+3t1foRSatdi1z+V+ndzifk+axCOJDhb+LWO0krZ8XbvudPPYETPwb1/Pf7kf4XGee+n24rET/IOoX4gLkgHN6iwO+/6Z4zJ8VRJ+JpKD7On4s78XjFJ8vfny8lidpFotFakfEPbDpiu9yx7PfZJLu1hJPR0dH+pu/+ZsU7C6Xy0Jj1BhYeR8Mhwt5FBYEz9d+esaP7/O7rGqkTNi5ZhTeWPEEUGplihnnuUwhxmszaQ4PD9VsNnV+fq6vv/76O5dJfwjY3NzUL3/5S+3s7Ghra6uQVWYMJRUq1/jcx6bMAY9KExY+NruUrrPgDsawbDeHeM0yx8oVWQzCyo5zJY0s8LwoOa8IrFQqKePIVuX1el3NZlOXl5f67LPP3hunv9Pp6MGDB6kvDuv1eR88NxkRMmG+BMENTzS66J7lcqlXr14VnBWveKKp38XFhabTacrwOjksSXt7e3r48GEqF5aUCKoyxM89s+LyEYN8R8zK+HyJ8DXwBJRRD7nTEfVqDGLinAOQx0dHR/oP/+E/6PT0VL/97W9vtNF9p9PRL37xi7RhgfcUgVwkK+c62itE+Kxsrs7nc/X7fU0mE52enmo0Gunk5ERnZ2cpS0u2r1ar6Q9/+IPa7XbaZILeSJKuBQbuUHE95IDsJZUA5+fnurq6StVM/X4/JTSolJrP59rc3NTR0VHK0i2Xy7SFNeNMlpR78rlVRvBK5cvpPeO5XC4TeUvlAhULi8VCDx480N27d/X111/r5OTkLUjCm+HOrld38H/voyOtnt1tfbPZTDbCHWLOj93h7/x2+YpOMxVE8XySCtlb13O8a/efvMqTa7HE0QN3xpr7w5fzTS/cN3EdIa12h0RPI1tUs2d8dxwdHenv/u7vUhXiaDRKy5BikIgM1Wq1ZA+3t7d1dfW6J9/5+bm2t7cTCY/e8J0nfbwjvJpfei3/+/v7BZl1+UTOuJfj42PNZrPUY8aXXjn5vFgsdHFxofl8nrZ+R575qdfr2traUrfb1U9/+lMNh0OdnZ1pPB6rUnmdeEO3f0wyt1gsUjVhtVpN+gh5YbMExqssScac5t2VBdKc37/n9kpaJQOpZKHy8rvixYsXaTfMbreb5H8ymejk5ETL5bLQzoX7iAmdbrebbPTJycl74wP/NfBYxRuEO/nmqwH4Dj/4x6PRKH0HvYBfim0pK6woszPL5etKKrc1+BTffPONXrx4oZOTEz179qxAkqInOp1OoWKL63Eej8d9gxSpuEO9k+mA73rM7j4AthQSk2rz7e1t7ezsqNlsamtrK+lakpDOPcTYjXOjr7D1fAefGVm+c+eOptOpTk5Obow8vbXEU6/X0/379wsl3gwijr1nDfm3B9tlQbkHY17aznc5H3DB9Cx3JBbKyCCuF5VuDOo8EIjElDuw35YF8CoVMr7ehOxjQLVa1eHhoe7cuZPeXVQOPoljFQ/HukzFTIiPkSuiddk54MEH9xqPWXesf84zxAqceN3I0Lsi9KZ3fh5f+uXOBWWd9Xpdf/nLX77jaNw86vW69vb21Ol0knGbzWYFMkBaKeVY8RQJAqm4jMzlBGOFPOCwUk48mUwS8XR5eVn47Ybt/v3715zcMoKnTF+Ukdfxc1/+6eBZ3tQPw/VnrGRYZ4idBIn35vcdEwOVyuutuank/MMf/qCbAM9br9d1cHCQlgJ6sOPb4npvCP9+JAbK3j+Eymg0SsHhaDQqlJtTAXZ8fKx+v5/mLE6hnzvKgQf5nv2K5AXPJK0qvrrdrnq9XiIAarVaInQ9o0z5OA4Xy3q8UbHL7rfBbR+kBYGhn4Nz7uzsSNKNkE7xXuKSa+m63nebgf6Qri/v5btOaPm4xeWbcf76WEcyLNqp6PA7ynyddTrHybGyqjc/NsoEOtHJRn4+JhLgx0Cv19Mnn3yi+Xyuk5OTQqUk4+k6DOIGmWo2m2kJMM24IX28UhK7tC7R6WSEtNrIoNlsqlarpSrOCHwSAtnxeJx2vkT2ff6wTA9CutvtqlarFTZrQL6azaYkpWXU9A9D599kZcC7Qtl8ZIxIdDC2kgq6Zt04M6djXFUW47gtLdN3vrvpt8VB8b76/b76/b62trbSUk+e7fLyMsWM0krn+n2ju7D5Z2dnuri4+JY3+mHAfRfIZF9i5/GBVN6OxAmjGPtI5T62XzvG8YyNyw0J3ouLC718+VLPnz/XX/7yF1Wr1ZSwY4dDJ8TdFrs/71VSbrvd9vpumP6s6ChP8GBv+ZxjIFKJT6gm91US6EtP5K7zu/GPmKvILM/pBOJNbsBya4kngLKRilv0uvC9yQmJJYEeGHnQ6AwiiJPjTYE+n7lQ+OT0Y8qcPJyr2OwxZs+/7V35T71e187OjsbjccpifwwOG46TVyg5YePvkt9xbW9kw11u+I4Tke6kO3HhMsv3yvpySMW1wU6qcj4nuvibK3LPRCNLPFvc3jw+UyQjFotFymByXMxsvA+gT1yr1ZKkFBgvFq93TiOTF+e+VCTv/L0wfrx/HxOOkZQqMiAS3OF1UoH7mc/n+uqrrzQcDrW5uZl2CGPXPK9oKSNAo9MmlS8jdpKL7/t3IDiikZZU0LnIWNQpXkHqcsy8LCO//P0ul6seY2Rs5vN5qp7BCL8rHB0d6ec//7l6vV6qdIoJASdsmSs4Aa6/49zhM941pNZwOJS0cmpoBu79U9wR7vf7KZPXbrfVbrcLOgFERwvZwZ5SAUAfMpw5X9ZHJYTrNuTCl+fgWAHGNla2cD/cXxxb/7/fM+8DOdne3i44up7BftdwMmddQgNEf8CrKqVVRbekwvhHQKjHICDqfJ9/3KfPR8/O+nH4KNgEghBkg+vEJvxUCfAsrj9iYOo6BZmiDxnOOH2BMr47qLr1hBO6AftDssltvVfCLRYL7e/va7FYpIpoZIwqXgK8smW10sqP5rwch1zg/yKXfiy90VgK1u121Ww2NR6PdXFxka5HJaqkVD0wHA6TDywpbV5Rq9U0Go3SfTWbTT169Ej37t1LhMXp6ameP3/+jkbqZrC1taV79+6p1+up3W4nHS6p0H9yOp0m2ZGu+w5eAEAywuc735FWetETfuuSJshat9tNut939UZOKpVKuub5+fm1HnCc23cxXiwWadmpJw3Ra+gbel3dZNX1TYAxooep79TsCYoyPxJC2XcEl663d3BfxY9BHtzXjjHKfD7XxcWFxuOxXr58mYhBbA4JD3adxo5xbZc/J6RBjPud7ELe+Bt/J2nPsdiu4+NjTadTnZ+fp1UQyNTp6alarZaePn1a0L1liVp/B+hw7LiPBYlbr9pcLpfq9/t68eLFjcnyrSWeXOicNfS/u9OyDl7RIOma4EbiKgZqsbIEEiwGVn68B4BxEpU9p2cg+T/OFyyzn7/smcsmP1tg1mq1xOx/DHAHpFpd7bwU379PYpSaB9ZljLt/D0fJlyXEANoDAWnVJNGVksskY+8Bu7RSch7Yxkx6vM9ICpTJOuXrGGLuq6wCLy5xfR9Qq9XSlq6M13A4LGQQmGM+7k7wAAxgJByp8IhEJ8sPptOpBoNBIaMC6YThxAD1+319/fXXyVA2m0198skn6nQ6BYKL+4oOIHIYqxj8O/7bHQfO700c485pOGEebPrcKiOjXJe/ibTk3UXSlnfDfb3r3WQODw/1D//wDwUdzXzxDJhvMx//74jvw3UEQRtVQjj9BFPMez6rVqu6uLjQcvl6p696va7d3d3CMlInmWJA6IQI6HQ612Ty8vIy3We3203bUbu88y42NjZSMAt5UUY6rnOoysgnjvWyed6RN/RnjtOo+CYQ51mEk7A+t1zuvVTeAz6vbsPpjRtEuG3x+Rl1tx8XK7KwmZGQchLMl8BBMLqs+TVjxrbMvjiJwTMvFgu9evVKx8fHf82QfPRAZ3ugx3JNfBKW6/I3ryQiaGm32wWiErmdzWa6vLxMc859hTKSOVbpYVewj+4PIXdUqVC9BPE8HA5TBSaV/shrp9ORJJ2dnaUKyOVyqf39/fQ3lm7y/Z2dHdVqNZ2cnOj09FSz2UwvXrwo9d8/FHS7XT1+/DgtqXYd7HreNz0o8419fkcdwvuLpLnLgRPjTtK77anX62q1WqnPYL/fV7VaLfQjhTBy4imSBp7kJQHI8/jSbc5HAuZjgvuFrHjw5Me6GCl+Z2trKy3JRSY8RpKu72bH2ON3Rx9yuVymcTs+Ptbl5aVOTk50eXmpwWCg0WiUZM+Xa6LjPI4CkST198BzuZ/quo2/eYIYW0rV+OnpqQaDgU5OTgqkD5XrjUZDvV5PzWZTh4eHqeVG9PuBzzdptTwd/73b7Wp3dzcdzwoyEgc3hVtHPLlQUfa7TrlJxcaV65x8R8z2+zXj8TH4j/dX9p0yoS27Pz/Oq67ijwdx6xzZ6FCiyD2rMxwO085F7zpwe9fgPcfKC3+vwDPJkWTwANFJJT/Gle86AjMqJu+nBJyUWFd1h6zHYN+vg4L1eyy7Z6mo6CE3cRi9FN/fQ7PZ1JMnT9Tv9/Xs2bNbn/1xJ5oKLhxsdthw0pZ3UtbwkH+7YYxyUhY012o1tdttzWazZCi9Z4JXI/D++RsOPZVTEBGx6gWZin3wvivpw7tyfepG1ZfLuEzGCqioq/w7ZED9PTtw/r2U2+cOO5a+64oHfzaei4As2id/NgIlAHEUA3B3cplvVD4dHR2p2WxqOp0W1vo7SUjvEir4vO8cxzFm6wgdvzbPQaaM/29tbaV+Ushb/A6VWTybO3ZO1npwCcpI7TJ58sxnnJs+34+OjjSfz3V2dqbj4+O3HjjiYLPrTySVfC7xvj0Y4hlcv0d7gGOJ7HnyjHfqAX8kBV0ncD4/1u8jjhuIY8+8XS5fE9NOMI5GowJp4OcryyxDbPk7uO025rahWq2m6hXmyMHBQdLBvvwb4tZ3m3L7RqDtBKTLF58tl8vCsfwQxPNvT9x6EtVtDr/jNX05nVfTbGxsaGtrq6Dn/BrVajUFvny/1WoVlh1zvMv9xsaGOp2O9vf3U9Xd2dnZB53A9XkXYx1svfu67v9IxQr9eJ4yQr6M+I6+cNRXTkIwRq5TqOxrNBppxQfk+OnpaYE4dTsZfTvu34n9jw1OPEWypswGe1IMkscr6N/0DmPM69eM+sHHA7+j2WwWdkKN9gy5IVHMfeEvuB1zf8PlOdqs6MvGhG+Zrxd9rXXHeYInzqPIJfi9VCqVRBByP+5nUsl5k/J8K4knhITGZV7xE52xKPhunKLTVkYqSSvh8oEoI4PKArdYReIToiy48sDUncUyptWNuVclrFujynfcMScwgelct4b+Q4G/p/F4fC3480DWlQnjgCKKY1GGyPZHxSAVnR+vjuA4aWX8PDvEPcZswLqABdLJAwxn56Oxj/dM3xiIDLadxRCg1La2tvSrX/0qba3+PgQFGCOaqd67dy9lO2Ng5gHUcrm8tszXjykLnBkDgDFrNBoaDoepAorlUAQBBFxOgEL+nZycFGTSAwVKmSkhhrBw8gZw3/H+3EGsVCqJ5KD8V1LqG0cfDIw8zy1dJzWQJY5luYxUDF65D+Yf79B1a7VaTT09BoPBtXn9thEJvLIyaO4TWUGGfGlSGWnA+/ax2draUqXyOnt2dHSkb775Rl9++aWWy2VaUhUdJzJl0iqjy7xFrtxZk3RtCa60Kj2nUSX/39/f1/7+fro2JCA2p1arpRJz5Jlr85w+ntKqoriMQHL77Q6tVwpJ16t1GJvHjx/rzp07+sMf/vBOKmbq9boePXpUWGLp+gVd4O9OWpG6HtB7UIy8lPkD/h7KbJZf2xMkXpLvvhL3QMaUseSarle8dB+yE6eeytKvvvpq7VyN9xod6Ywfhlqtpr/5m7/RJ598ck1G0OuM1XL5uidao9EoLHOTVn1+oq/s/qv76xDj2DR0vTfyjlVzkbDgM6+GiP6SB23YVppGI9vYenTgwcFBwa74MmAPePGjJKVqDews1RQfMgHBmLvNYLy9Wt97HPI93j0+qict/Hf0P328/Txl+s4JR0mpKvvq6vWScJJ7s9ksVUXRCHwymejp06d/1bv52IAt9mRnJJ6AE074oSyxwyYiX5yb3/gHEIeLxeJaA3CXj0hAsqzeCZdYZIJcoafwndZVpgPiAbfJ+FUeZ60D88FJ/+iH8ywcU6vV0nvCj+IazEtPUHP/vDN8bidY6Sd1enp643rs1hJPZdnMdeSPg8F0oXSBBWXC4o6iO8ZvEshIPPlglg2sn5v/+7/dUS27dyceyljdsvNISkJYllX+kBCzv14BFN+VkwmuBMsIQEfZ36IclN2XG3Gu699zMsmdu7JrlxEITp7EIKLsufiezy0/rytvn5NllS+3Gdx3o9FIcyCSvW8au5jx4ZxOWPO+vQIoGpZKpZKWUlFyTNk45/WAFf1RJp9OHpNJ4pyxIoSxikR4NOKA6ip23ijTx2Xvq4zQ9Mwl9+rPEXVrJHggOSSlHRYjwfW2MZlMdHZ2VnC6vFxbur77qG+K0Wg0VK1Wk2NVJnNxfAFL9ra2tnTnzp2UtapUKhqNRgUHhD5mTtB45c269+bXjIHecrlMpeOQ0y4z0d56xVGUW3Sxj7HLTNTTnumMjm48NsqcpILD+67gYxcJGx8rJwE5FoeyjJCJz+26Ic4719lcG73gVUzx3H6fXu0aCWy3Uy7Hrl98CeB3na8fY2D3tlA2H6TrfSmllQx5IgHyEHLKk79+Dc5PUoqlIW9ajlWpFDdggJAt88/fFNRFPyX6fugpbCXHYCsJ7LiG3zP3xHshSP1QQUDOWK+LQcp0adn4lNm2mCSPf3efCfmIfnX0Y9wP4zsQ+2W+Rcb3g89BJwX973Gs498jYiWtE8SuG0igMv+Yn8xNH3vOF68T/Qxp5RdwzpjA5779J7bYwc9x3cZv7hM/ejwe6/LyMpH+JGzK7Kr7bmVAN/sKBB8TxqOMe3BS0OPDm8Ct06S8TM/kxoFFkKJD40x5zOzGjJ4Lr58zKjs3gGRzpPKtoSOis+iCH5d2xSDQswxuBCqVSso6RKwLapbLZWqs9r6QBX8NcJq9d4+XL7oi8qyOK7CyAMIRjWWZLMZzuFKL55BWCmsdeeljx+fxuh6IeHY6BoIovkhkuTNGpUIknb4Ly39bwDujHH+5XKb11z4mPm8i8VGtVpOhQpb43DMobPGKXnFCB7m7c+eOZrOZnj17ptlspm63q263q+FwmHbSicRTLB3mWmT33BmjSgqwIxxLoGJlxXK5yuZ4KTD3KylVUxFQuE5l7qCznShiaSOEC8G1X5tn9eCA8YIshzyhifa7Jp7Oz8/16aefpgx4s9nUgwcPClt5E6TNZrPUd+TFixfa2NjQ/fv3Va/X1e/30zN7oMPzRnvC+6rVanrw4IEePHig8Xic3sOnn36aehmR5WJbaPqgILPex8R1gJMI0qqCwInBw8PDdD7sD5lot21+fprA87dK5XU2jmcss7/RfnmgExuTun71AFpa9Qiiautd9nrCxrhjvFgs0jz0ZyBAYmzwC8iK+jPxHa8EYG545Rv34M4y53F5i0AvsAT45ORE/X4/6Q2pGEAyflwPG8P9DwaDVA2X8e6B/oB4YQ6io1y3eN8wdC56+/LyUpK0vb19jXhxgrJer+uTTz5RrVZLGzDgb8aelW4j0BEcS/KEe+I7ZT49cy0GsNKKjGKpp1fiuY1DR6D33K+BuJ/P56mC4H3weX4IxuOxTk5O1Ol0ru38xvjhBzi5HfWJJ5rcd4TAQ2bcx5KKCTVWaUgru+irAdBt2BP0HUvAqQguWxqV8f3g1TPSapMCr4hzH8CXrbmNjvbcSSzmMD4R87CM+PUNLvDFuXZMgvjSWuwbScNOp5OWxHNu+lry/UpltYEG/osTYPgVnqBBvvG5aHT+9ddfp40xfG7wLnifVFd6wpDn83vyH38f6HY2TPD7bbfbabWCj+lN4NYRT46omBAuD5gjYwjKgmo/3h26sgHme64gy4iiMqInEgvxmZzM8iDThStmJv268fPokMfrSauMMUL4bRU67zMimShdrxAqO3bdcd/2nmLVUjy3O0ZS+RJMjnuTY7POiDoJG8nVb8s4+zXL5DtWXlGyedt7hTlZ4nNg3fxx/VJGOvqSgxhsg0gQx4wh8kgTQQ8k47bNHthFlFV+eKYDg8zfrq6uUlNuJ574vpPdTmi68ffy6nVZz0hqudPpZJW/82/TQ37tuBT1XcKztZB1TrZ4Lz6Cvfiuop6IpA+fM599Pnq2j6UFvV6vUAFGsLi5uZl+vylLH2WIMY/jgVz48hgnpvx5oq5xuxkdUq/UAb70Mr53//6658D5wonknbwLeKBLMPtdwHhz/1H3Stf9jTLEsfDPfV6+CR6sMT7fZg+jHF9dXRWSh5DwH6q/cRvBsgrPisdx/bbkEbahTCc40Bvef/BN8hb1R/TX1vm8XjEZrx91E+fzY/h79NW8Oia+D/RU2RLfDwnoLl+OGJPr7ietW80hlds2t/9vWibvfhj/j7bA5cZlwZM4nrDP+OEo81HwM6MfGu1dtEMcF8fF5cr9yOh7lumH6NNzPASOJ1H5W6PRSOQLZLv/3WXdSU/OxXPje2GzfW4sl0tdXFxoMBikFhtefRlJOd4D9+7v0t9XmT9Xxk8AbyUTibmbxK0jntz5io5U7KvhmZR1Bo6AMS6F8PN7xpTreHbEy845r/fliefiGp7dBwhX7Ovg5a0Ycr92zIRzLj+/OxNxuQRr7AlaqJj4EIGjUGYA1wWuHEs236tI3hTslpEVUrEnkxtqH3MnHX3s3+SARSPs631RvJF4io6WGwyvqvHr+PP5tc/Pz/Xb3/5Wg8Hg2la1twm7u7t69OhR6pUjqZChwYCUlax6gEfARKaYxuQYCGk1d2NPLHewpeI8ZVvqs7MzjcfjtAPlfP56a1Wfw+syKugFstVcb7FYaDAY6OrqSpeXl6XVE65PWY7k2R2MvVdLYaQ9G42eg0wj00PFCd9tNBq6vLzUcDhM2UpptfNiXJbBc1Sr1ZSpKSO83gXa7bbu3LmTgo/lcqmTk5NEGNJnotFopCWKtVpNd+/evebMRAIrjk38HXus1Go17e7uamdnR0dHR5pOp/rXf/3X9G6RUXZH4R4iMeSkQqx2c/tVrVbTrmLYw93dXd29e1fS9eoalrBwLnce3X6X2Xlv4kr1IAROJCr5PnP46upK/X5fs9ksbVV8fHysi4sLvXjx4q3KBxiPx/rqq6/UaDT0+PHja7vROlHvuoa5RjbU9UWZoy4Ve16h851Q4Jocy7uLNh/Si/dOb5x6va7t7e1rVSVRZiO57PeCXplOpzo9PU09dTLeLhaLhZ4/f67JZKJHjx7p/v37Go1Gury81HK5TEstPDEhrWQSsCTNdRZgvLFLUrHHCxUzbhc5P7KInYl6EV8GWUVHeJ86/u7/LvOn41K7SqWSkjwcQ9/TuHSG80tKNuhDxWAw0FdffaXt7e3Ux5FKTHQ5ugYfiOXX0iqp4nEHqw3QQ9gPfBKPZxaLhbrdrnZ2dpIfLpWvHGCs3J4gV/P5PDW0Rpdl/HBgXz2WZR6x5N9jTv+JiSUncfipVquFSmCHV/L6bt4ewxOnc3+NRkNbW1vJ36DqaLFYVR3fvXtX+/v71/xNEtVUSC6Xq9UATiDRQ4wm9q6HpJUOc97AE7ruwzC32OyIvmROspNI8w2gWMrnhK770WA4HKY4bbl8XQFFb9mbTATdSuIpOpaOKKBlAuuC/kMyFO5AeeaZz7kvr2iIQuxl7THL4s6ZO4nRgePzdZmesnfh5+czfwYm8oe6Lei6LJ6/Gx+vb0OZ4SrLxvjfXF78+n4ffn0/Lt4bcrbuWf2c8bvrSFmX3+9imF2OCexuM+kkrXakwVl0p6iMWPOqAwfvCOXvVTfuZLlu4BpvGl8nfbw6ZjweJ+NRtizNCQM3vugISoa9qjEuY+OeqEzwDJMTkP6ZOxI+x9bpMhzVmAF3mYvkw7oqz2/LzL9t4BzxHFEOWGoirRxjSrH93n2elslg/DfHRDvDfbCsoNPpJH0OcQkpRqPKeM6oJ8oIP8YH8gsHy3e7w+FfR3b7tfz5OTYGFTHR4z9cDxly20glJg7heDxOzuK7SrBAuvJsUR94UB8TSPzfs7PxOxHriNh1fsG3fd8dYfRPmd+xDlzDl2EgSzc5fz82LJevdwJk8w+CI2QTHVJWUVdWyfBdZCDO8eiDgOjTR33nvr8n6/xY973dbq+LFyJh5rYqNjn37zmh8aZlqh8C0LnsoCqtEgGuzwl4IfrcVjjKdAtjRBLPK6pYXhnbiJS983X+M/6M+zQ+dt/V380oIlbLlPnIZURTJJwgBj3BRDzqhEksrPDP+Nznpxdm4Bdtbm6mzVF8vvN9990d7uPy3Jwf34oEFzvD+cYw8Xoug/4c0f5Lq1VJcTmr33fZ2MRjfM5Q8c0zkCilHcFN4dYRTwzeYDDQ8fGxms2mut1uCpQklQpodGyjspSuB5w48h6IS0rZVg/4CCyoLIDNxylHwMr6N8WJGydCnFTcM/cI2+lsr8OVegxSAEredz36UMkn3rP3u/FMmCNOPoJtN1xONKA8OdblxGUuVhbwfV8y4xlpvhPHzR1C/47vEsF3YrDi8h+rHtzhQllHhzEq0TJG/bYCsgAihs8YX2llEMuWnvq7xCGLSwhivzCW9UUHJ1ZLSiudtbW1pXa7nXa786osMnYuf7GSL/Yo8woTjA1Bx3A4TM9GRohzRDIJ4sR3JcGgu7NARVMkSyUVKqT87z5ffAmOEwrNZlOtVkuz2UzD4TAtYboJ0HPC5zH37+9bKmYIea+eaa9WX+8YORqN1Gq10k590vXya+YfOssTCE4yP3z4UIeHhzo7O0tr+xeL10sn6DPllTEQn9w3PT08weH2hIaY/JAd5942Nzd1eHiYbCM/Pl98DvAsvqMj90sPL56dAIfjzs7OUjWfB6hOflE5VK2+3umPJu/vEv7+3D/wKhKf6/7Oo613ooBqQohQHEh6ebmuj73sPGPMPUI0+DIVt0Fl9gVC3J8p2otOp6NKpaLt7e3UP+Z92AH1Q8ByuUx94C4uLvTpp58mO9Dr9VI1nuvpSBQgn+12O8kgslKtVlMlgNsN7CzEuy/bdDhZ4T1T+e2kkgeCnrzAJ18uVxVLkeiVin1nor+EPaVqx+dAtVpN1avgY5DfwWCgP/zhD9rc3NTOzk7qa0hVKYHsYDAo7KiL7+M7A5b5u/P5XCcnJ0mHu32h4gO5azabOjo6SnoMnVYWX2HTarWaxuNxoR8QuzYOh0OdnJxk8ul7YDQaJR85+jyMQ6xaBJCMkpK+GA6HhZ0Ku92uDg4OCj4Wc5Rm3L7MX1o1wr+6uko7JUOu0AKhXq8n36perxd2av7ss8/0/PnzJGOsBCqLu5Crdrtd8H37/X7BV3F9w/fLiLPIARCjdLtdtVqtVNnPvHK5dtn3c3sM4vfP3Do5OdFoNNL5+XmqzvdExE3g1hFPDCKNcyuVSnKMYzDvg7iOjClj5REKFxZXRu4oerARz8933CDHElB3tl2Y3/T83BO/fUK7M+/3SyD8pneK0xgV94cEz37BUntQGEnISPa4Io2BtP9258jH1TP1wFnoGOD5eZ00BU6K+H06uVCW/YtyVMbkOyIZyrspU3LvAzzzFbMLMajyoA/4MRhblpL58ZyfMa5WqykQjvrGwf9x7Ji/jCuy65U1TpIzVsiSn5dxpsEzwSSGJjaVddnku/wdYsHJWP7ux5TJvJO4vAd0JcEwOov7hsj3pRI3vSzYx5bn5P4imelkgQc7ThRi32iiybvhd9l7dPl0+atUKur1eup2u4VtzPmhb4c7NE5m+DhSZk4ZNmPkBCYVRcPhMJFWLMOkYWUMAN1O8kySrlURjkajVEkZiVWOPT8/1/n5ebovAqFKpZJ2GuR63Neb+ly9LfgY+W/eJe/cj3Wd7XIR7VbMlKJvvJy/rDmzB/J8HvWJy7jfG9crs4vcA7oIUsDnf7QtGW8Pruv7/b6k1dgxZ+IOdvgSHOvBTzy36wSOifLCTyScQQz+ffk4+rLMT/X/l/lNTnT7s7zpGcuArfUEnX+37Jk+BMxmMx0fHxc2FfCKoegrEegTVzCGMX6SVjJI/zGvIoHMwg5tbW2p2+3qzp076bt+L65T+bvrMLdv2FlP3GR8N2CfIY7cf4jEsPvM/GY+Qy6y6QS23TeuwHdgbOkjOx6P00YV+E79fj/5Nx5/O0cQd8NDJ56fn2s4HGp7ezs103cfmPvh//ijklI7Bfw48G1xfRnQnd5rykk87p3NY/BlymKWONf4HB6l3+/r7OysQNi/qZr6bePWEU/g9PRU8/lc9+7d087OTsEIusJZZwB8EkSlE4Uk/t/75kRD5wGjCzn3QSURARPX5zsevLlxjssZIvgOTmZ8D36MT0IMAQHD2dmZhsPhB9tvYT6f649//KO+/PLL9PyHh4e6d+9eIYCOWd8YWHpvC8Y5Okse/Pn7llYKbN133KH3neT8t3S9dNIDOnfSXE5jWScy6cFIlO03EXB+L++L4XaygGf1ceRZCP7KlsEsl8tC1Y50fTtfzrdcFpfyxXfpOiJ+V1LKGF5dXanVamk+n2swGJQ679xDGcnoO8cw76nY8uoaDBsGmkDYM5gYKQ8CYpn05eWlJpNJoW8TusWXcyyXS33zzTf67LPPVK/X1e12Ja3K+clYEYB4oICjcdM96aJjJa3mEXPMdyTzTKzrbJwtiBoneaIzXabrXe/4fORdeXNznDvflcodR8acazAWTpYhC2yXPhqNdHFxkezJ2dmZvvrqKy2Xy9Rfg/eBXJHRZAks1+X9bWxspGAjEi/+7re3t1MlAnLmQYmTI/QhWSwW+uKLL348QfgWzGYzPX36VI1GQ/v7++p0Omn+O5nGO/eyd6+g4xje2Ww20+npaXLEGRvIYd8NiHfnehD/wmWW5F7ZLjrx37GS1oNyrokt5Vm2trZujPzLWGF7e1tHR0fq9Xra3t5WrVYr9PlwQknStQpf5nFZsFOtVgu9TrAHvhy3TL4hdlzXxATQZDLR5eWlarVaqr5Cfuk/eHZ2plevXqXqCYJTSSloc7+HZAwyH33BV69eaTAYaDQaaTweJ9s5m810584dTSYTnZyc3Lg9etugkoSlRIzNzs6ODg8P0y6q+BHui0LOuR9EMuzhw4dpydJkMknvGvvjifuyJCkoI8hJEjLu7XZbL1++1IsXL1IlbMb3w3K51OXlpf74xz+q1+vpk08+udbvzH3rarV6bYdm34yIZCuJIeJlr35cLBapl5LvxOlL67A7MSbxuHdzc1P37t0r+DXec4778r6+7htzfmzuxcVFqiyP1X2R/OLd+W+p2Bd1f39fW1tbqdm5PwO6GJ9uOBwWdCWYz+eFZX8eh56dneny8jI9n9vymyTPb603cHFxoYuLi4IzhUPjjelADAo86ItBoZMDHrxF4obrrsv6RVICQzqZTDSdTlO2icBuuVwWHG6+Q9kbpYheceUTITpvsVoAZcux3AvHYsRve3+evwbz+bw0yNjf3y+w2bxL3mGZcxKbqvKDMnI5inLC55GMitltz6p5EAg8+OB+4znKsoBejePNfskqlGUpouNQRjK9L8STpILhgIxxR4h56WMUgywn66SVAy5dd9bjuHA+JyYjONYrhzwrHY2tkzKRqMDRqtVqqfEhP8vl66ayrrO8Wahnhqhe8WO5hvffWSwWOj8/1+npacpSQk7hZLrz+OrVK/3lL39RvV7X7u5uYX6cn58Xll05eUJgs66i810jBuXVarXQt4Jml+6UeJYWuXO7AMqc9ThH3cl2Ytrfm6/nh+hDnspITODBILqC+9za2lKv10uZ6fPzcz179kyXl5f68ssvNR6P1e12U2NaAjyyetvb26rX6zo4OEj35Es5+Ldn2LGHLC3jndPDie95Bg9ZppT+iy++eKdVCldXVzo+PlatVlOv1ytscBBJNSq2XDd7hRA+A0sBYon8zs6OWq1WYblLDKZd/2EHIHU9AVVWtcf3Xc9F3ycmulwfcd/rKksy3g22trb0+PFjNRqN1Fzcq2m9isl3p3P/A7KKMfZATVJaeu7Lp91Guhy4n+K+d/SVZrOZLi4uCoEg12RZ1nw+19nZWcGGYivislW/73XLVs7OzvTy5cvUTHhra0v7+/uSXm9aMh6PdX5+/kETT558pUqFz9vttra3t9PuYNG3KSMCPIlx9+7dAsHHWFDZ7DLF98uSfX6vrv85lnt79uxZ2gwk4/uBd8ZmQjs7O7p//35Knjm8rQkJDc5BZRK2CjKXWEtSIjhjEQZyiK3knFFvuK/K/0nauF/Phj6cj9iYGBqfGHmlJxIV2RcXF4UeZdyDt1ZAr7l+lYrxHD7z4eFhSh7RWiJ+nzHAp/LimNFolDaTuLi4KPAC3m4GXXcbyNdbSzyB8/Nz/eEPf1Cv19PDhw9LnWcnj/i3E0IIh1RkxgEZaR9MqVhS68rUBVu6Xp5HlhvmPvbX8N8Ekqyh9mANuDManUq/P7+OE2cQTsPh8EbL624KTGCcdt43jLfvUIARdAbes9PA5cTHn/eOTDFGBIOsF3a4nEV58yCUa7m8Y6RRop7tIcjwDDu7G8Yyds5HFtSN+XK5alZ6GypPvgsuLi702WefJQXfaDR079695Hh7kIdD7GSgB2GSklOEs+t/w1Cy5tuNHGOAQ0X1gxMK0orQ8oDAHfoyOOHJdZHRuOzKq59wImNlJ+vNcQxiVVRZRqjX6yVdRxUTMuQkQqVS0e7urh4+fJgqcDxIYakY79WJHLKu9IW4CTiRy7xzeWFOOskjqTBHGRsqdiBGPEPHjxOHkA9eOYWNcT2EbJONG4/Hev78uer1us7OzlLfg0ajod3dXbXb7VJiHZl1WaLCjeCzWn3dx+fRo0eaTCba3t4u6BbO48s6mTvdbjc5T15px3M4scmzulPJub3Kxn/z77js7yYQs//RrmO3eVfcL02hp9NpYQdI9ALVch74Efh7uX60LdgT7sVtXln2uCwZ4aQov7FBPLOPZw74bh4XFxf6/PPPkz3EFrn98B19X7x4keRjY2NDOzs71xI1fIcgkySxy7tU3C260WikJbMOjnFbxfIedCHkM3MIf2q5XGpvby9VPzmcMJFWulda+cwstWm1WunYarWqw8PDwlIg3sfH5EOTQEJHOWkddXIMrkFZEtMTbE4u0J8Jn2M2mxXiKLe1ZdVQ+NrT6TTFOzfR4+9DhROS2Plo45i72BPXBU5ER7/WyRaPcbhGrbZqd+HkFOdzP6pM//j9ezIev44EIn4F/jE+HERZs9nUbDbT5eVlunf3kSMBBWnlsR3Vmr1eL7USchtKPME9cw0n33nvzWZTe3t7ms/naWdsv1a8l/Pz89Se4KZw64mnk5MTnZ6e6vDwMFWtuEBKxdI670/hyjBOAp88CEscUBf6SPa40nNnL65b9cDAs0WuMKNiRnmWOeB+LT++LFj2wJQldu8DafBjw0szcdxxYChDfP78ufr9ftr6nXFiYjvhw28PKAl0dnZ2CgqZsWaHJbL8ntX2sXRFCFCKMZjw7B2sPY3yOC9zg8wCMh/XCgMyAPzm36enp/rqq69uvETzu+L09LTghEKQ7OzsaGtrK+144fPb35WDjA2VgmTxGTeW/ZycnCSDW6vVCs0RZ7PX29w/ePAgBeeRSKYqoayMuOydk6HBIZaKy6UgT/kNedbv9wtkPNejXw/BycbGRnpv/OZz7r/Vaml/fz858Mvlagtanye1Wk2Hh4fJ6G5tbUlakRpssYwenkwmqRcE5cKvXr36ESXkuyPaGWllT9wBXywWyQmQVgQKc51/TyYT9fv9QsWTO+Cz2Sxl5UajUSJ2tre3r1XEeIm3V6mNRqO0hTr3vbm5qUePHqnX62l3d1e9Xq/QZwnb6YQppLMv0eK6LG2RVg29nYDzCl3XXdgp35gDp4t35k19fW56lYa/u/ibv/vcuAm4L+EBK+9juVwWmpZWq9VU1g/ZSrDu+gmH1W0HTjNyFpesxASdO/9U4EX74k4vujLqx0gyOalYZmMy3j3Oz891cXGR/t9sNvXzn/88bWwBwYPcDYfDpMsgqCBAJRV6yJ2cnKjdbif97jpRWgV+NI++vLxMtplgjnmCnHMM8sb1CQ7Rcfjb+/v7mk6nqdKw3W6n83jlBLYakqPRaGhvb0/NZlN37txJ5AZLdO7fv6/z83O9fPky2dTbUDHwLoBexp90/9GTIp4YcH0U/x3jL3oGoocgMdGHrBzBt5CKPVypoovxGYmqy8vLZAMzfhxALMWKdE9wMM/cT0FOGDMSsWV2m/97AsV9CS8KwNfEl/C4LSZGXPbQISSw+A73RSKI+2k0Gmq329ra2ko+3GAwSOegOgpCnxjy6ur1Kqbj4+PCigt02c7OTipEcF9lPp8XdNdyuUzJQq/WxM7H+cHcJJ7Fxzs/P9ef/vQnSTe7euXWE0+QOe7MABcygFKKwXtUfL4EwidOmVHB8HEeP6eTGWXwc5aRThzj/y5jat8Ezh8zMV7t1ev1Uu+NjyljIxV3pfIflIX0mpjAuXElF5dW+Vj5+EA84Uj5Dmcuc14xw7jFCpoymYnVdR4Mu6wTtLoz54rKn4floDgXLmsQTpAPvk34+4A4VpPJRK9evUo9GzxrW5bN9/fPDwQf7wwnFR3lDrIbBgyQ94uKZf4YR4wq2Zyrq9V2rcDlzoNqnC6IJxw7r3qKyys8GxJJdn9+qinQdTgQLofuQDgxz2e1Wi0t6/NnkVb975yQQ+fS/+Hw8FDT6VRnZ2fvdEfOfr+vL7/8Uo1GI+kJn0M4MlT8eKXWcvm6PwLvjv+zuwtVBqzR5z1SVg3xhA7zACzaMHQcWWNIaAJEJyBwnLyMnb95s3tkSVo5lJ7159mYB4yvJz1cRmKQwGdOOvl3Ijkc7X2Ezyd35Or1eiGZ8y7AWPtYIeME2e54OyE3GAwKzj29GxgL91P4nifC4n2UPTNBhKRryQjXFXFMGDPgROVisSgss6Sf5Ie6g+77gigDVB1Np9PUX8SDNQgGP3Y4HKa5zZgz1pHcxRZdXV2l5rkuV8xjdBpg3joRy3xBhqjodJvqGzVAcmFDXQ+h07gPKjA9qUKShXN4gke63rfzQwSyQGALMY1vcnp6mnZldV8m6ncH48/SPRJzEIFeMYlPFWM0P2+8nt+328abDLA/NMzn85Rgpc+XEzvSypeN5I+0SthhJ7DR/MYnIIFRFlczj2PVs/sGkRBz3wNZxqf3OFAqXz0EILkgNt0mk7jp9/tJX5CIPT8/L+hgqtVJsnJvnqxEb3JPnU6n4F+5bxTfM5WgcVfK6XSqbrdbSMrRp/Vd4tYTTyzhoHeEB8ieBfQAqcwpKyNbvIoFRzBWIMR/I8y+LIZydVfW7uSvM1TRwfb79CyR7xpFMMk9x+AuOogIX2zo9zGB/iIoLGn17pmAvV4vBdXOsrsifJNidaWG4fPsH9cHOG3ufHEsDhvyTJWKpFRuzm8nESqViobDYaoMYUnLvXv31Ol00nMjj4PBQJ999pk2Nzf1ySefJCVXq9VSMHz37l0dHR1psVjo3/7t3972UL01TCYT/eEPf0gO8MHBwbWsjROUjCtEDv0MptNp6jnhmWBIFek1iUk5LjoFeYm7i0nFahAyJASfXoniS9cYe4yWV/CRzXXSKTrerpM8W+nLntBjGCzIVQdByHK5LKzRx3hKq2zXxsZGmgeRSKVaJ1ZPQOT0ej3du3dPw+FQ//zP/6yTk5O3JSrX8PTpU718+VL7+/v61a9+VWgEidH2HlTtdjuVNI/HY718+bIQmBGIdzoddbtdjcdjHR8fS3o9vyuVSnrPNLglEGSJlbQiCzwwwCbh/LRarcKuMARcbN7hiRquS08isolOYtIIlj4HVAHSyPvRo0epMgu4jpKKPYGc/HCCwwmQSIi60+Vw54vsJYQ57/ld9jdcLBZ6+vSpnj9/ru3t7bRlMraGeYJsMJ7D4VCnp6eSVk4285ZlTd6Hy5c2up/iPkIZKXV1dZUISfQby1O8oWuZ/ePe+O1B+WAwSDYIB/xD7iv5PmI2m+nLL7/U5uamfvWrX2lvby/pCQ9uIHw+//xzSUokDWOPT1m27Obs7KwQoOLzOCG1u7urzc3Na74PS+LwdWazmc7Pz1PbCGwCDa7p44JserLH/XrXlz5vpJXe8F6IVDDv7Oyo3+/r9PS0kFT5kEE1WbfbTWOwWLzux/iv//qv2traUrvdVqvVSssVfWVJjLlIfD9//lzD4TARn94SAPhOqbHRPe+e2A5dh01hbFl54qRCxl+H0WikTz/9NPVoQlfE6ua4XM0JJ0jpuCTS7Y20Imek683jIZqp0PfkMH4k14R85l7w3TgfSboyXeA94haL1z0nh8OhBoOBnj17lnxtv++41N3j8njM8fFxWmkA0QSZ60v7aGfhbWB8aTQ/cTdZ5yrw8+7evav5fK779+9rPp/r97//fSaeAANHPxD6h3i2LQ7m94ETBwhGPE8sIeQz7iNWTaD4nGWVVhUt69j36Gj7sWR0nCjxdflSsUO9lyv6u8S4x7LDjwll2REnC92QOdMd36kvx4zkpFcaRcT37sc4weXHOgnGteP1/doefBGMcn4/DiUUq28gNHx7dM6ztbWVtlJ/37J+VHXhxLgjynNH8lhaOTdO+GDEIkHjWQbvieRy4fLh44/ewBg7wSxdJ74jIpkU5dOfsSyLJCkFxj4fuB73x5IrzlVGrJfJuMuy6x0cRnce/f7omVSmg98VIGti3yWywbwXDPzFxUV6X75EhUooeo6RSJGUnCFKqb3vIEtUkKsoR9HB8Z4C/LAjlDvxrnNwwKTrGWUcM5cFnB96BXhlgt+XV9U5nMwoS8CU2SfPaAK3zzFJRFKIe3jXciMVd/Ra10cJYP+RK4cnyDivb0vN96NNiYg2D/1PoO7HRXvFe/Rjyq6BA/y+2YiPCS5rzHHvNUbQHvV1TLbRZ8wDT47HHnpFHnqRgLHs3FRdeoNfYoFqtZp6OxGo+f1Ev8n1krSagy73fs/cL4Qb53W7yXN7IudDg5N07rvwfgiCvdJ5HRgPD34hDyQVxshJcK9i+zZEu+E/H+L43BTQG7T2gHTxcWI83Yf0uJl5479B1C8e60b77r5wPBb/FHhVLom/smSKP0P8ibaVa8VkbpmfEmWRY7wHnZP2/i7K5oD74GX3yv36Si38ina7nfxYSLl3jVtLPFH6eufOHf36179OjCTLLmIWVCo2eY2VIJ5t5f9uECP5s1yuSv2cgPKS8pjp8wDAnXEqI6hA4T484CoL3vx+/d5idRdZIkpYPYPspBgBiDfT/hjga45dUTl4vz75GcfoOJVVz7mD5aXdjI0TW1zbl1bwG7mjzJsxomIJp8iDX+SM8+3s7KhWq2l3dzfJ23A4LFRj1Wqv1yLfv3+/sAQQ2aICBcJyb29P//iP/6izszP99//+3ws7K70PaLVa+sd//Edtb29fc2idzPW5C9yQ+HIrCAXkYXt7O1VHUX3ieofx9PN51QcNC09OTpKcVatVbW9vXwsuvSQXHeDZFEg2elpAXni1HI4des4NqPeMcmeDjHW32y04E2WOAO/Wg28+j8u5OE8kTtkBjyWO0aF4lyBjX61W0zbxNLUlQ//s2TP9y7/8i3Z3d/W3f/u3qlarOjg40Gw20zfffKPhcKhPPvlE9+7dS449faxqtVpaEs17pArBCWInBF1nkY37+uuv9W//9m9JN/R6Pf3N3/xNIVAjWESnOYERm7H2ej11u90kk1TTQTw1m00dHh6m43gusnPRMfX3GUlIfiN/65IFTmhGX4D3MhwONRqNClnBdWTJ20a329W9e/cKZB86h3uiYrDT6SRdgs/z6tWrFJRVKhVdXFyo3+/rzp07qZqEChHIyWjfI2nEuFWr1VRV55nhzc3NJH9SMUMc/S70R6VS0dbWlu7cuaP5fJ4q5D7W/pK3HU4w+JJP3+QGfe2BDr8h07FDbu/u3LlzzXfCp7h3756kon5zfdbtdgubsCyXS+3s7BSIDuY8PUzKZJ7ncPsorfrERIIC3wfi1/1B9Ae9IufzeerF96GhWq2q2+2q1+sV/IvFYqFut6udnZ20jCfGMFE3uL98dXWVCgl2d3cLS737/b7Oz8/Vbrd17969wgZN62IkYjl8FCpnsMcfU5zzLuC+8fPnzwt94xhrSGH0CP6qk0fIjh/rvWmjD74OHBPblUBce5Xl8fGxxuOxTk9PC5tMcSwxkVeSx6XAjUYjJX3wbb1gQbreT7qsQhKdORgMClWgfG+xWKQVC66D447InqCKSe1qddWsHP+n2WymXSXpgeZJg3eFW008eRmtZ9djOdybMogxm+pBX1Rm0QghCE5exb4Mfm0nk7wqAiefrST5znchnsruzQM5fx/r3oO/KyZUdgKLeBMh9ab3yjE+higVaUWGuhzxHeAsuGfrpPItrrlG2TPAantWz5daOUmAIoqkmDuWAOLUd314H4DCpjGgb21OcMzzlmVVIkFUlk2QlDLFTliXGc8oS/zfSR134LmOk4L+3RhMejDrz0HJOsuvIHUwXtVqtbC8Bqc8LrdB7+Hk+Xvm/X3bfOG+IxlVRjB4IH1T2UvuAaLOyV53vhl3lqj5Frm879lspna7XegVhdzUajVtbW0VgjW+43aM9+O/JaWydYihSqWSyFFK43GKvPLG9YEnbVyGIRZ4H3zGHOJZ3eFaR/C4PY7BSrTX8RkdHqjG68Vs5Lp+Ee8KyEd0wKXrvf3QWe7Iu3Prjnx8VxGeEHO4reA4lh274xrnahncn8ERh9yeTCYFnyfjdsN1A/KHD+s6w6t/nSR2H4beIt6/h+8id5A2UR+hG9cR0+4Hu2+1zo8rOwf35Ofj/66X/B6iX/ahwe1aWfKAcfXK2TL9EsdKWvm57p+id7wCg6QZeuNNuiPq/7IYLuPHgye+vMm3tNpwwBNZyIYnGN1/9uKOuDqgbOzfJFfxOMYfAhLfiP6aVC1i33wlBDLqSWnXMdF+Rz+c39GHiXEh9xp7sLrNdY7AC2a+LbZw+L1D1Pv4vGvcWuLp7t27+ulPf1ra8R2sc44gjPiedL3ZGEFVdL75d5lQ+7+jA0+GBrLMA7q47tIrtqTrhJcbulhh5Q41WUrWyDKhvFoiVlrs7++r3W7r6dOnH03DTxxslyHesTtZntWK8uYBp1etRPITJj1m112hSEXCcB25FD9DQUVFy/3Sx4U+RTDm/kzcC2NPZRMOIDLrpanxWu8TdnZ29Ld/+7cpe+cBKO+UZ41Oro+vO+F8n+N9nrkMeR8XNzLSau0773MwGOibb75Ja7uBE4mxoaKvrWcckdlIPpaV5XqFFJ95ny+aUruOcWdjPB6r0+kkMi+Sqm4sMXwEE8gq98D7iEQtJNhgMNCf/vQn9fv9d7498t27d/WLX/xCrVYrVTg5iQM5J0lbW1t6/Pixer1eyrbTKLrT6STSj0a9OD/0KJGKZeHIE++eseFd+rK5r776Sl988YWurq50eHiY7rPdbqelLXHLc6lINnvg6JVV/ntrayvJGn3qqLjl/uMueFKxui+SqH4f/v9oE8ucUmSFJcCcg/dFleJyuby2jfu7AksTyggywLO5zkAOWG6Kb9PpdBLpiTOK3kfnk22O/oWTB+gN7/EQkxXYTua9J724bw8caEDr5MA6YizjZsF8xJekcsgTHR6I+Vjyb8YdWWRVAr6QV0lJK5uGbElKSRDf5jxWnPMbuTs5OVG/379Wkcn9ItcedOGDOdnkPVMrlVVvO+yn777GfKJ/1YeWwG21Wnr8+LGazWbagRmfoCzJgt2O9tt1l4Nkp7SqeMX33Nvb0+HhYdJLLjPuS2BbpOLySica4sYqGT8OSI75bpDME0/y8LknoxwxeReJJ+n6cjYQSScnbvjN+HtPOPqfcp8QqFTwbW5upoon3yBIWsmqXwN5jPFg5Ax4Vv4fE8vOVbChDLtg45P5O+MdOPx8Tk7Fd0RSyKu6bgK3lnhie1YfsDLnhcFG+cTBd+c6OsEE/gRDXCsyjOuuyXcrlUrKKBOIkeF2w+nXjllhN4T+nDE7GiejZwpiZol75TyS0rrqmyive9eIQZNUfH9epVE2Ho43ZY4ZY5/griTiefjtlWpOYpZd378fZcLP5/LG+V25RBKFEnsvswdl7+JNme/biHq9rnv37hWWGZXJgxPB68YAGfAsm+sVd4b4/psMjcvmbDbTxcVFoVGqH+P3wLW8YsGrZpbLZao4gHSI10VOnSjjc3e4cdTp5YNMYbx9t0gQdRrvwUle5ooHBbFai+9CcFxcXOj8/PydO5KU/vtyRXS7OyDSa3nr9XqpMSRzjb4kPt7Sanx9qYm0SjhEQi/Khduqfr+vly9fpkAMwgVHA+fOq4ejXPjvqD/5N4SWV/kRwJLMcYfLKxec6I0ok1GXn3hcPNbllbHhncXdSt81XN+DMhKfz5hf6HRfmiopJblcd6En/LlZDuBz169FwCAVbaPLdPRf3OmXirtsVqvVtNQlHp9xe+Dz2cfbZcnHLX4W/+YVLMgaOizaXE/Acs6YwENPxEpsv2fIXN9KPBJLkNzeiiD6MNH3cR8O+LuRlPrbfGhgGSGtF9zO0ETcx8kT8FJ5NWuEV5Yw9iS9vEl8mY9WRnqX6a1olzN+HEAc+o/vmub919yvWecfeguB6G94BSK/4w/HMD8hnUajkfr9fvIb0RVekIHOgoDyvnIxaeP34VyEP5fLrPvS2FlJhSXBZfGFLwF+U6XwOptapp9jzOv+U4wv3hVuLfvgWRFXIC4IwI/BieJlxkDaHTVXlu7U+eB4md3m5mZqvkvm2JfR0RCPRq5lQlPmSPv/v4sSdWPgitcFPAJiyndJ+pBRrVb15MkT3blzR71eL2XmIzkQ2epYEh7Hhs8joly64+SstSutWOlEcO7jj6L0z90BklZL+yAVo9zFdb6c1+/JFbc7bFz74uJCX3/9deqZ8r4Acs2XlMQS07LgLcqJB3FsVw94j7FXEp/5uHmwv1wu9fLlSw0GAx0fH6f3PhgMChkgmgjH6+GsYeB5PifEnFwFkVhzvYc+QaaobuG3f8ezRmRr3BmIgUT8G7+Xy2WpTFUqlbR87PT0VM+fP1e/33/n8sfOqtFeSKt3RpZVWu3wxlh0Op2C48P3ILB4dy5/npzgmvwdhwny59NPP9XZ2ZlevnyZdAhbXe/s7KTdo9wJ9Aw+P9gZ7oXrIR+TyST1zMCG8MxeeeVL77z3AueDRHGZYL54Lz7smd8bf6NkHtlfLBbp/XIsSw6pBL5Jm0e1Gcmh+Gy8Iy+Bx59x/c8z+DHuz7hcSuUV064fYsWvj2kkluLuUD6H0TH4RL1eL2WZcwB4+1Cv1/XJJ5+o0+loZ2enME+Zv+4bMX+i3eQ70ioxs7Ozk3S6k0fSyh7iX3AONkNwWfXvRGJ1sVhoa2srrS5AlmNFADvUvYmI8C3L/Tc7QDP/mJs3VSXwroDu9ko2bzQurRLibqOcfHZfE/j4+t/YwQ5d6L6Xk4VuOyMBdXV1lSrQsFNOemb8ONjY2EjEZKfTSf1MSWD4KiLpeuFHJKyd5C1LjLhMuSxFe+ZEMz7j2dmZ5vN5aiSODHP/9BrzXk5cz30ggG3DH+x2u8mvcztMf2p8HW+jcXp6qtlsliomeR++wy1+Nd+HBHN97LEj7yO+s3gsgCD0mORd41YTT2Rm4/KoKLzAX6IrPxztsmtEksf/FgUfhx4CCucfQUOwWWIRJ1Jkbv3z+FkkncqcxugEuIBF5cxzkqn50Nc+VyoV3blzR7/4xS80Ho9T2TfkjLRimCEV+Qw48SmtxqnM+YqEkGeLnRz0+/PfwGXEA7Ky41DcTkT6tV2x+/EuD95QWlpl/zAiOBuXl5f6y1/+8t4RlihenxuRYPIxj06uzznmoztA0soJ80ozL9X3d+9YLl8v/Xn16lVhu3saF8bANFZtEHT7Mhuu4RUzZbrD74Hx9wzL1dVVgWjnexyDc8d9UHnp8uvLrXh/PiYODG9Z1ms4HKatrG9iW3YSCwRgkajk2XBWqDZzx5peT9gh7AkyBJnmTeSj0+42jUzdZDLRs2fP9PXXXxeWmrEzULfbTb8hTmN1AzLiS1y4R9cXkD0sZ8CeSKulncgcVQjSSgfybK5rXV7ifeF4uZ7jh8bVTmRBprHTDs4eAUmsJn6XYD5Lq1YAvrSAZ/d35WROrMp2J9l/u0y6Lojy5FUHXvlaRkhK5TtJxsCTzxqNhjqdTlrmkEmn24fNzU3dv39f29vbBR8GefClU+gGbEKUBeSSOUq1Z7/fv1bZSYDpc3G5XBZI+ehjuU1wPYFO80pL12XYq1qtVtiUyGMEqbz6f7F4vXT38vIyyTPHut7+0ICu8SSFNzXGhrjMgKiHXLdJRV/KyXbOjf6J4+O+l9sGj2+wv77MjnNE3znjh4Ex7XQ6aQk/Ma8n5dxu4I/E80REmVoul4XzMuYet8a4mOtDPnp7CJfj3d1d9Xo9bW1tqdvtlt4b13E7ydxAx/Fdb2+zXC5TtTmk0Xg81vn5eSLXqcbyTcC8x9NisUgte/i7P68nejym8zHyCveoPz3muynbfGuJJ5QQiskNjnS9OaBn7HwwolEpI33iy2egfG062WnWgBJcxADVA30EMq4JjcsoyhhMZ3B9SR3fZ3I5e1k2KVHIdM+nk/2Htja9DATx0mqJYawk8EAvLpFzoulNkzQqUicuuKaPc6z6cERlGrN/8fMyAsuVijtxbvgJEr1iIRIyVDrx8z4HELFiyPs1xHfnhLUHbbyvWApLUIhhaTabhZL02OsAp5Z5SWDsZbgE97XaaqcN77lAVpJAIMrF9zUqbpR4R+gUD2aRE69AiYSsB9ExgI2ErVdykOnxHQF5v2VVhu8Kbms8wPH3cnJyopOTk5QJdOKtjAjwJvL+XuMyhPiefXOI3//+9xoOh3r58qWGw6F6vZ7u3Lmj7e1tbW9vq9VqJbLSNwXgPiLBh+zE6hp3xvhxktEdnUiAE0j48kR/vrL78WDByU0IT+wf10F2qMZy3Y4eQ/+/fPnyrcjIt8HfGcRbmb2Wrmd6/ViO8WSCO/n+f1Dm45QRRrwrzjWfz9PyGtd77oP5uZANr5a9d++eJpOJTk5OSpcmeRKv1Wrp6upKJycn71VV7fsK1z+SUq8n38kp7u4WZYtA3+3QdDpNfV6ovGw0GgUSuN/vS7peLcw9xaSxk9Dcj/deon9JWauAsirbaPPdD/B5gL6v1Woaj8d68eKF5vO5ut2uWq2WLi8vPzhZdT3sutx9Q5/zfMZ3QdQVkfR3nzQmc9zPiMRC1D8e77nfGxMpGT8cLhMkpd3eRn3h4+XzL45FJDml8iXcZd/1uU6S6fLyMvnUcfMXerzu7e0lvUTSal2C3/0jaeVrcCzP7rrH54y/H9owbG5uajKZqNlsFt5hXJnixFHZcnd/N3H++fn8Xp2D8NY80S9/27i1xBMlcpTBSassftlOS7EqyskcFCUoU1jAAwpKCGEuERzPCEVFS6DGsrarq6vUoJfSYwYcgYpElt+7bwuKkJJ1R2C9bC46g5QCQjix/ev7TCJ8V+BIkf0nGw4qlUoqY2SM3IGKFRoYwTihpZUSXNcjyR23SC565sYNJvBsAN+NCjCy3wRiy+UyNULmmig13o+klKV0EmFjY0Onp6f6t3/7t1LH4X2BB/PS9bLU6GA56exj44EVnzn5TP8hshVO/nil2GKxSBmQy8vLVKmC7kC/kWHe3d1Vu93W3t5eGqf4TO5kl+mCsuyIZ3wxrtwD3xsOh4V36M4nhAPOBmQm7yQey487gy5zBOXNZjNlL2MG9ibg9sUJeyeUXrx4oS+//FKHh4eJ5OAdYL+kVUaOpRvT6VT1el1bW1uF9+WVULESodFoaDgc6l/+5V90fn6ui4sLXV1d6eHDh7p///61HQyxRywVAS7/Ln8QT7HJLueIMsY5nHzydwVh5u+sTHaRJ7+n4XCo5XKZyAnK6AmEcO7c3kIIs4SGpe/rSvrfBbDDVEcvFq8rstyBjMRTtDmufyGqnaj1Kg8/X0xelM0jrskYspQS4hun3s/l5+d5eMb5fK5er6cnT55oOp3q008/LX0vjUYjLQfd39/XfD6/keW0HxuwA/g8kLqXl5daLlc9Ar3SRVqRz2CxWCTfiSo95I8mxIeHh9rZ2dHZ2ZmOj481HA7TXHXiSSpWfiLXkOa+8QW+XAycYqLZibUy4oxn8nnI83JtvntxcaGnT5+qUqno4cOHacfRD0lW3R+KFdBug/nNs3tFZ4T7smU+ZIzBPNDG/kVdw3e415jgx2a7n5zxw+FJKvwWaRXv+IofT1p5XI7v5zLgJIv3uSwbs0i2SKtVKdPpVP1+X+fn5+r3+0l+G42Gdnd3Va/Xtbe3l2J57hW/5k0EqqSCTLH8lvkRG6jj03LOq6urRH5tb28XNnQiHveK//izbtWM32/06dfFqR7HuF/rsc67wK0lntxBla4rL4TQBxuUBfkO/ywe44w7yhQB9goDL5svG+TomMelM54h5P8eUPI8ZIi8eTjC4grYgzfg1VFUPN3kcoN3DXeu1jkm8b35vyOhw+QsU06RgIyf+d/KJrt/x2U5njMety4YJ4gouzfvd+LBohOeXqL6PpNOBPpOXsR3KV3XAx5cSytjQoYkvnv+5pnSsjkpKQVpVD25MQAQTo1GIy2XctlFDt0Qr3PqIlx+/cflrkzWI2ngc8OvVUbI+28n5MqIdnceh8OhXr16ldbr3wT8uRl/1wmVSkW9Xk+Hh4dqNpsajUaFvmLMr16vl6pHRqNRsi2VSkX9fj9VfZRlibEf0+lUx8fHuri4SIkIr+yRlGTKK09wfKTrhCvfdYLMq6w8WRIrc7g2AarrEtcdbvf8+lG/RH3G39328dsDUoLkSqWSSCq+TwBycXFxY+SlO5C813UEHDYLRL3M+dzp9HcYM7J+bmSWf/PjFdlOdKKrvOKJ7zqx6PfE883nq90wu92uDg4O0jNxTQhSKkpw0tF3Gxsbaal8xl8PArFOp1NYHiup0DrC5cznrfux/N39Zen1Dq38fz6f6+7du2npbaPR0OXlZcEvjRWUXmWAD8f/JaUqJ44ts7Hf5vfHa/hnVHOQ4B2NRhoMBmm5XqVSSVUVHxLpBMriENcZ0mrny3WVyMiK66Co56Kf69/x4/ib2zhf2o8u8go4PvNxXAdsBgkBr/T16uSPHW4vov/ghJG/67iSx+0d/yYh5DZx3fX5DaFIguT8/DzZKa9gZPwkpTlLMg3b4zomjnOURWTUfZwy2XCdxbvyXlL0HOb+OT87JzcaDW1vb18rcol+Az9xHsZ37HMnJt79+d4Vbi3x5I5pmSMeJ0FUlG86r//bMyIeBHmZHssnYs8TJoBXHsVmwlJxxykUmy+T49oxa1ypVFIpszvd7vBFZ5HPJaWmZoPBIPWRidU0HzI8oCcT2+12C0bU30kZWSgVWWXGsQw402UTmv8jL+sCdq4XA/cYdHOMzxE/JlZacP/SawV8cXGhdrut/f39wnMSoFKV8W3z6baDzKjPbV+2EoN7glfvTeHGxskBz+pUKpXCbnQ43xjUeN3Ly0udnZ2lbDE/VBvs7u7qyZMnaamLG/C47KbMQSzL9LmzwP/jM/qSLz+G68Vg2auX+MwNnMs4x/p9cT2yTxcXF6l5+8bGhl69eqVPP/00ZchvCow9/fuoGkWujo6OdHh4qJOTE7148SLtcErSYmNjI+12+vnnn+vly5fpGHoANBoN3bt3LwV+Pr7sJHd6eqr/+l//ayIul8tVNRCVSjTTxtHh2t4glmDf3z/fj9tQD4fDRHLFii++59sqOxh3qUg4Skr34ssJo332BAx6nP5OvgukZzYhAJG/fr+vi4sLDQaDGyWenJyjMpAKEWy9VzR7/wx8CKqkGG8IRr9OrP4GUaY4lmQE9gtyioqOs7OzQvUHWWafA8gRveak1zro1atXqlaraX4wnt6Hheuy3TUbtdAr4+nTp5l4+pHQ6/X0P/1P/1Oh1yVj3263tbW1pel0mnSwBzzVajVVMbmPKr2en4PBQNPpVCcnJ0le2u22fvazn2l3d1d3795VvV7XycmJ6vW6+v2+vvjiixR8US1MxRyyyTxm2S1kFclgr1iQVoS4E7ExNsDGuX5Cdk9OTjQYDDQYDDSfz3V5eZmeiWNfvHixNuh8n8G7e9OqDv4Wq+jdP0DP4X+7rDBWTjJxbT9nJJ7cN6Fan9+sLCE+urq60mAwSDby2555b29P+/v7KV6SXuvS6XSqV69efXDj/H3hsaakgs9GzIod8bkWe1a63ojf4WddHzn3JVkF9PXXX6e+xd4nyf1cSGN8cnb6ZWdYt8vAfVovEIjLeeO98V2PLahol15XhnF/kKIk0K6urnRwcKCf//znaamypGvEZ0wG45u6PvJx4p7d33JCynXgu8KtJZ6+Dc7+fdfjQQz4gQenkXzy8rzI7roijY5dDNIWi4UajUahdI/jywg0N46u3J11dsXv2WFKpzGgH1O1k1RePVTWC0C6npF2eYlK6LteG0Ww7p07OeXH+P+/Tb4jEcuz4ED4PXBPyDUGg+ssFgtdXFyk4HOxWDUPfp8R5z7P7BlV/hbJqFgFxHHR6XRny8fOHXdIsHUkCsEejQ+9qee6zK4/V3TUfmiQHckpJ0m/C/x4/7c7Lq7HOE5SIl18jKh4uA3On+vemE2qVIqNWKUi+ebyg/En47Yue4xcQTRRmk2wiKPmxBHf83vjum96plhB68mOdQkLJ6/KbHIMJvgs/i4jnXyu4qDFiitIr1arlRxK+q9AoB0fH+vFixc6Ozu7UfvnfoD/jvoGJ9T9AY55U2Z43Xznc/+uX/9Nx7sDG/0Z5qo77XEMvbIRx9fl0glpEncEK2SkIWd5V5wb8usmCen3DbVaLbUeIDmBvMU56NXibteklQ6L44lv4To8/g1/ml5QZVl9EHVD1C8un/zdfzv83B6wOeGOTPnyl1iRte78Hwq+TbdEH4l5HquiQNQbZaRCvIZfFz1ETAPJ1O/3UxIfXxXCE9mNSS7XQX5++pBxP36vnU6n0FP3YwfzNcZK7hNJ5RtSSKudpaMfEIliR5Q/X80DgePFA4w7iRySLLVaLSXqoq6Iq6q4bll8EOdIjPP9PvHv/O/4Te12O8kpvePcBvr9+PfjnPIqP5JZJKbi8lP4AF8F9a5x64mnyHRKRWXkA+IDXOYI+Xed9PEmwQR/Gxsb6nQ66na7arfb2t7eTs4Txon13ePxOAUQvqSnbNtVMksxmxOVOYLkWVDfJtSVO4bTs8GDwUDn5+d69uxZIYv6IRvMiHq9rna7nZ57sVikLbjp++HO0XK5vFbqi5GrVCpJKXgj6LIgykkfN34EDvwwbs6Q+3VdqcelFsCXXbIOn4wkzTijMmo2m4XdbLjmdDrV7373O52cnKTPv61M+bYDR9u3t/dyVyefosMrrZQ8DmpZ0FZGFsdKDrJ0X3zxhUajUVonHjOz9+/f17/7d/8ufR5lEXilW5mOI2gt059OYjs8iIjLNF3+vJIwvq/ofDgRXiZHBNjo3p2dHUlKBB1VE7ehV4MTZ96zSFrZlW63WwigeFc+RiwnbDabunv3bqpa4T1IK7uHbfr000/1u9/9TpPJRKPRSNJK7nq9Xsrc8Tlyz3bjTg45kcEz0COJa1OBEpuIIpNeAeZzIpZxcx/83QNJJ1P8md1xpd/X2dmZzs/P0446VB5ub2/r6OhInU5HR0dHajabqbqLKqfPPvtM//v//r+nZes3AXS+B0a8K+9r45WV/DCHpNWYe+WUVEyK8J6jLZKuz8dIVDp56fcUK6orldcVnm7Poh/jcuHnxzZ5QClJOzs7heABncM8oUoKP2wymeizzz5Lfegyvh3Yfyee3FbF3h+8bxKv/M0rt5GxdrstSep2uwUfxjfEqNVeL43tdrvJX6EqVFKq1uQ+PYjkWvFevNKSZ0KG3Wa7TuYeeE6WME8mk7RsR1ofPH/I8KA2+rjM81iBiOyUxV1ePR19muiDxiQN3yEOOj091eXlpS4uLnR6enrNbyMOKkuUtFot3bt3r1D5y2/sJ705OdfV1ZV2d3c1Ho/15Zdfpqb4Hxt8Pm1tbSUb7PbcExDrSB3//E0Ep/uW0dYtFotEDg+Hw6T/3Ud2G4SsoifYmV5atRrhO2WcAtd08sbtnvMGrkt9pVK/30/P6/YdHefPjz/mvWT9GI9ZWfJKf1mWMR8cHKjX6yWylsrA0Wik4+Pj9H/u7V3j1hJPrM307HFEFFoX6jex6A4PtuKPVz55Hw2cZf7u33kT6RUNqAs3zhn37tfByHr22rM3fn4EfjgcFioFbjpouwmUKTbes2doUGoxIJOKLDfvMTLj6zI1cYzLZNIDQUdZBYBUrICL14ssuN+fnw+DC8vOvdGT40MyrlTMVCqVwq44EWXZlkgy+bv1KpcY1HugH/tkucPuDjOGsNPpqNfrSVJqDu/3wrXjGH8fRGc6OplvcgjKrhnvxc8fHZDvcm+825jpvimUyUzU8egQdyZ4F64/OBabEqtFYpAEaUW1U+zxExt6k01zsjQ6hmWBhcsoeoGMYiT93F5yXqm8Z5qTEq5vK5XiltpgnY4keeIJAwIIGnY3Go1EMvNeKpXXTZMJUt4lCMj9HTixEp+Z77g9ijrIHeWol9bNEbdR0R6VVbqU6RonpeK9RPlZN4b+2+d41EfeU4hj2ckRXY7ehOzwvoUZbwbjFasHpeKOuOv8FOQm+qSuD1z/ucwC5i4JIWyzn9evK13vsxKXjrpsxiRLnB/YYtcJJJJ92Tvf8Qb+N2mL3jYglSAIYwKMY+K/I+G8zj94k64q+77bI5LvbGLg/bViUUCZLuAYbIWTBVFPA1/N0mg0Cr12Pza4D+uVrnF8y+Jw/zu/Xb9/l2t7JTaEjhduxPt0f8t1V4yVom1aFyOsmwNl33f/Ryom3VwnkVh0/etL0OP7i5/597yFD3OF9zOdTjUajdKSQyeebsJu3lri6eXLl/rDH/6g3d1dPXr06BrjiVGLRikyrNFhBmRx3CGP/S+cbHJ2V3rNni+Xy8Q4xqDTSz1hPkej0bVG4Z5p8ntgVxHulXvwSinvTbRYLFLp3MuXL1Ol08eoIAHKyceGdbN8jsPDBKQfSLvd1u7ubkFZnJycaLlcpm3tXfaio+Zy6AGHdJ3Vx+Dh1PhuC648JaWgliU3nU4nySLXosKJSi2MKyWWnJ/7ZHtj5PNDwunpqf7f//f/1fb2tn7zm9+kZRv+XlHMlGL7PC8j8xgvdgzjeN8BqFqtJieJHj6j0SiV+Trht1gstLOzk3Z38h1D3IhBTnlWxg2q/w04MeDVV/48kTx3uOH0oDkac58DTizwnv1ZpGIQ4UEDcwJ92G63de/evZSpuangkncTnyc6XovFotA/xZ+Ze9/b20v9nmgqjl7y91+pVPTixYtUuUrWjEqjnZ2d5GxTQbdcLrW7u6u9vT1Jq54cVPn5jxNDyMV4PNarV6/SLma+FNwJLewUssVx2EknveJYc18xWEG+nIxDhtyRqlQqqR8NJK3PB85D1vCmbGC1WtWDBw+0s7OjWq2Wqm29jB79i/wjY5EU8KWcklLTbqo/eEfoMEmF94Cv4j6F+0yx+rtMF0RHnnuKvghLqlyPun7yrLTrXB9DjnUZwammAm5jY0P/8//8P6tareq//bf/pmfPnv3II/jhYbFY7Xbb7/cLASQ+kO+Y6Es/kBnm1NXVVaFhrtuZjY0NPXz4UFtbW6m3F5UKkpLt/MlPfqLFYpF2i3769KlOTk50fn6us7OzNF+Qb2QmVnHiO/kSVam4rNnnFjoVu4pcOana7/fV7/fV7Xb15MkTDQaD5Fd/qLi8vNR/+S//Rd1uV//u3/07bW9vlxKRktI7k8r7NTmBLpW3Mojwz5HV2Wym58+fp149yBA7wVLFcu/ePUnSf//v/12vXr26dm5iMfwKVkQ4iem+ldvGer2uX/ziF5pOp/rLX/5Sev6PAcPhUL/73e/Ubrf185//XNvb2+lvzDX/zfj7plxlPnUZ3H4x/0ejUfJNypIN7jf4ZxsbG6ln4NbWVlrJhJ3iXvCnYoFBjMVj4oQY0gkvt9fxmah6dv+xbP74vTnpXZasQoePx2N99dVX6Z7Q1fxg76mSuomY79YST+PxWKenpynTANYxfv73smPdseH/UbnEH4c7UTjW/DsGe/HeIEAi8eQNFAm0IJzKqrzcIXPnFIEiYwOr+SFnZr4LUFox0HLF6BkWCIjhcFhYAsV7Z4kMTlOEnwul4kF5zBwBD+4J6hl/luBIxS1reTZkkevgPKHcpFVmGkbcvwPirkUfCiaTiZ4/f57mnGfQvIS3zLGKpIIHRp6t4Dh3wH1MMZBkdhlfl4ednR3duXMnBWaR1IhGqWycyrI/brjikkAnZF3vRbLejSnvoSwTg8zHz2IGqEx/R6eUd+PN3L/NUXmX8GeKz+fv1+c+z01jS/R1HGvXO5CWkMYeVDlB7Vl6Sam5Nv0N0AGeTPH7llbyAcnDnHF5dpJq3XisO+bbdGYce+C2jr9BpqHHIknhtvEmdVqr1UoNm93BW/fu3LEsm8dO5Mxms5Qki5Uefg6c86hP1r0X1wnRkY6/SZjExErMKMfn8f87iS2t5NCJaycccJZrtZoODg4KBEkMGDKKcIIfm09T7ehXSirYK8bI5xQJF9cj6Jnt7W3t7e1dOz8kKEHgcrnUzs6ONjY20k6v7CDn98113TeOZHa0QXwe/fTZbKbLy8tEQpTpCqoCCFLX+W8fEmimTR9BSddkwuHJ0/hunHz6rog6ArvGEnN8KQhrKrNoHyGpsLuww+UiLmnmWaK9cv1F77KnT59+5+f50DCfz6/1mfT5FRMn7rchDzH2ANH/Aegrqt58l9V4XCRrvGij2WymiujYUDzaNvRMjAH5N75pmf4B+EGcwxMubjPjtaN+czItzg/gSSCKDjz2cI6BFVTRJ3mXuLXE03Q61cXFhXq9XsGYuOMtFZVJmYJzhfltARNBP1lXyoB9EpXBAwyO4d8MMCwtAhGP4/8EIv1+v/CcTDx6brhzjbF+9uxZ2inrQyMQvi8Wi4W+/PJLnZ6e6ujoSA8fPpRUDOrm87m+/PJLTafTxIbXajVtb2+r0WikQI5JTVN4MnfemBIjSTaG3iqQOWVMdVQoXuEUe0hxnC+/8qWgBLEuyygcngOFS0aaDNDm5qZ2dnZS9vxDxGAw0H/5L/9FnU5Hn3zyiba3t9PY0GMiVn94MOSVH8iCpJRJgSBxYzSZTNRut1Oz8Ol0qrOzs+RYe6kwVWtu0OISpig7HIMuWEdWR0IEODHgwaI7i3zfA3nPROL0SavqFDdmPj94hkggSKstsvnBKaCC8yabCLNcMy4N4r3wb377nHVZik4OwZc7v8gE5OhwONTFxYVms1k6Brl9+fJlYQwHg4E2NzfV6/WSHPF+3dFxAsr1Wezp5IE/8sUzTyaTdO5arZZ6PniTc3cE0UM+5uvspqSkR/kb2W2qTSHSSRSgy9lBpl6vpwDlpoLF5XKpp0+f6vT0VPv7+6mHke+YCTyol1ZLN2PPSv8uDiSVrT6XHK5H0GNO0HG9MqIoBtuxYktSWr7iy1KQAf/MSQoHcuYEGeO7WCwKSyp7vV7a+twrBn/5y1/qZz/7mf74xz/q888//95j9bFgc3Mz7f4Iycx4EHi7DsN38KBJUup/6gGn9Jpoffz4sTqdjvb39wtbljNf0SXValUHBweqVF4nbarVqu7fv6/d3V11Op3k17AbJdUIfh9OknqSA8T/+054kJcxmKPSCeKl3+/ryy+/vNHqyXcN5q5XjcYqD2mV4CCuYbzXJRmkYr9IH8cYWBM/XV1dpY0j6I9Jfx/0xsbGhk5PT7WxsaGDgwMdHR0VzrtYLNKu5Cyb8wQvdgKfOSY+uN/b0GvyNuDq6ir5ZVtbW+m9xgS/E73IkvuZbtsiaeTxTYy/GVO+4zEUgJzEHzg8PEzzH5+O+Mcrk/xavkw4cg9RF8UK75i08eeUim0ROHeZ/uJccYWTPzff73Q66VmWy9e7Z19eXibitlKpFHgNv/93iVsbZeL4+q5aPmDS9fJO6fpLLGNR/YW7o8U1EGAGOjK38fz+eVn21R1k36rT76esWsHhAudrmwkaCGo/1hLQiOVyqVevXunVq1dqNpt6+PDhNUd6uVzq5ORE/X5fd+/eTZMXJRozaDjXjEFUsIvF6+blcXK78okMugdeHnBKKgSkrsBdVp1Vd3JEKjYe94yxKzuCM6q4IjnxoWAymehPf/qTGo2G9vf3Uwk5TktslBgNGu8wZiUIuinb9myOE3zdblez2SzttgWZ4DoG4jsa5EiegzIyqWz8kGuXaSe4/LMYZLrMchxk+ng8vuYsOMFQVsWzTj87acUyj2q1mt6V67x3DeY7AbAHZ+4ElBF8vGdJqdzcx5PvxQDI9Qxr8VkSwN8uLi4SEVCr1VJ1E8vuXD+5LuD+qJYiuDs+Pi5k51x3xSourz6g+ggHjnvByfSlDMDfUexpgIPv16NqwqucPAtKBQcVMQRAN0mkLxYLnZ2dqVJ5vTTwzp07KQnFs5WRPT5vCPzjMltpRU5B1HrfPun6Ut2yBBo6Lc5j/ubgOPRG3LSCiiM/T1xOTuLD5YtgLy4xxgdzEpXkD+OKDnr06JF6vZ5OTk4y8fQGbGy83jSn0WgkMt2DtpjwcvJZWskfO0cyfuiVer2uhw8fJqLA/SPshutJb3fBb18h0O/3Ewntld1+T2WJoggPJFutVmrCy3dcV47H40KfS5bLf2xw4sd9FOafE8RUoPgyc4f73u7XQGj5NV1e0B9Uq/B9Eq30s8Xfbzab+qd/+qe0vBMfjpUDZaSkX9+JA5cnfxc3EajfNiwWi7QU35MKUjE54f6C+xIeg/jmF9J1u8Xf4hJ1J1y8rQx+Cedut9tp0xH6dC2Xy0LVlK+sivF+rJRzMpN3wXExHvTEi/t5TjZh2+LzRYIzxoweGyLHrLrAT0WP0hMt2vebkuVbSzzxQkajkZ49e6Zms5l6JZSRTTFzWsYagnVOVmQTIRH4P45P2WQpC95i4IZwRKIpEhTr3kfMQrCd6NnZWSK2Mq4Dp8od2n6/n9hudoXyTA2KAGYcdjqWZ/qYwzhLxZ0HvIrG+07xf6pfCN7coNMXhN5OZHmk1Xpkep9AhvD9Xq+XlJwrycvLSw0GAzUaDfV6PU0mEz179kzD4TDtbPWhguCVXXVQ4DFAjcGwb09KoIQzw/jhREXHiTlO6b43bI5EJHCjEMkblyec8VhNE42m6yKXcZfhaIjKsiIexEanlGd3h7EMvIuoW6vVasqIn56eajAY6OXLlzeeYTw+PtZvf/tb7ezs6Be/+EXSC+6EUtJcr9fVarXSd3FSCNR9LnqGkPPwf5IJOE78zftqYE8gWAgGIVUjich3XJ4mk0naGSY263Snm/NxLYggngGiMD4LshrJJH92r4CSlJqBS0rNxNnRFceKd4+T22q1dOfOnUQAVyoV/bf/9t/05z//Wf/6r/9648FCDNCl8tJ66XrFD9+XVnopZlJd73wf5zLqi7h0xmXBnWGX41ix60SaZ6DRo/5/PxeVMcAr6NAVTk5BVhH0QPxnXMfdu3f105/+VHfu3NHe3p4qlYouLy8lKRGIHghKxY13kI9IDLATGGPeaDQ0HA5Vq9WSPoIgcP+pzH8GnGd7ezvJFD6v2zruEeLZAy6X6+VyqcFgkHxknp3KTtc7V1dXadeui4uLD2qjle+LSMww5nHFCQQi/tFkMknzfF3CifOjy6VVz6iYXAfMd3bt9l6dfgy22e2Nk13x//EHXeO66+rqSs+fPy8UD3zMYE4xr6fTqTqdTtpR1nV72e9odzin27OyvxHzdDqd1BKAz6VVRSOrGPBVPLlMRZD70RGu79yXdZscybFIlEUCzuHVmzwfPRrdhjEXiDf8XlzGPS51HwAdJ72uiHc/5CZ9oltrpTFug8FAT58+LTQDc2ed324QHXHA34ToSLnDjGPExHKHed11I5senX4XnBiolRFoklKGdzQa6cWLF6kHyPu+7f3bhLPTVC2dnJwksqfdbifZQpZQGmTAFotFWj6HwsJQeTYXhQI5gazyN3fynHgiW+RrjyEXWc7EfJjP56kZJ4beFTbKCxbflzFVq1Wdnp7qm2++SSXt4/FYn3766UfTF4zlb+4UeYaCd+bBO2vDGVcMBWQg23vjtHiwxrz39eluwMqCxTjvI4kQsySuP5xY9woc7suJ0qiPIEm8uoZzch/oXCeeuBaf+z25E8H7IYCmoqPVaqVrzOdzHR8f6+nTp7q4uLgVxNPx8bE++eQT/fKXv0xj7WCrWqoJfLzcrkhFUjAuRaRqhOqAjY0N9Xq9pD9wztExEKmbm5u6d++etre31el0CvK3zrmSXjsmVJTFCrx435BcnU5HOzs7aSz5mxMVkQSXVAgcXTdG2YJwlKTDw0PVarW0k1Gv1yuQHujWdrutR48eJZJuNpvp97//vf6P/+P/uNHMHnDCuowcdj+G8fJ54mPhJEH0Q9ZdOzr1/jefn4wRNoh79vsFXlHgCTHXETHQe1MAir3lHpzM5F4hb6l8Yg4gl05sZaxwdHSk/+1/+9/UbrfTMnPf6dGXwPjGAJGMwi4y5p1OR7u7u2ms6/V6Infu37+vXq+nfr+v5XLV3J4ErrTytSNp2mq1tLOzo9FolHShV9h5lRPLSKiK8ft2wvLy8jJVL1HtwNJiaUVK0HZgsVhk4in4CV6Nz7wmuGf+4xe5voixj/snyJL3v0WG2u124Riq0ajiKNMnTmCRWGw0GtdsIs/j/prrLnQZFTVPnz7V+fn5jduS24DF4vVmViTCB4OB7ty5o06nU0ouQUx6giMmuED0V9wvxSagByi2wAeicTh9/9wfdR8L/RYrzblfT7r5b6+sjg3T/f7LSFt/J+4TYTuxtV7djMz7+3K9hv/MfPSKQ54d3Yyf1+/3b9ynvrXEE6A6RVLqXeQ7vq0TmphBcYXC9xg0HGGfFO7keAbSyQU3cM4g+rWphEBgXYCk4pId7pXvcY98F4YXAaK3Uy7/fDP6/b6+/vrrgkPv/SR86UZ0znG63vR+owLgvD65CUzLiFCu6YaZgIBKLGSu2+2m5WHIrWeZyxSKZ4xxwqhsqtfraSnPxyBDi8VCX331lWazmfb395PT7OSTVL6eO1YweSYB58azuhgUN6RugFwfOWL2xLNHbhCpsiH4hhiImRcnuPwHeXfjyvkjSeLnQt5cBv38/s74bmz8W6Zzl8tVBQ4Bwk0usQP+zmNJN70tkAXIYq8CknRtPJjfsYeP/2Y8vX+CE0++DIGKJ5wu4NVonqzh/qmoajQaidz2+5NW9pDjvArF7VaUJQfHLhar5cgQCFFeIdsg1fxvnmXl89FolEhhMvJR9m8aPo9idRI/ntGM9sO/7+PHZ+vIIa4XxyXKm5Ps8fxuX/jc/aIyuC11m+oJN984w+E6KOou/u/VY/R1efDgQdrlMKOIs7Mz/eEPf0gVgVdXV3r16pXm87kODg7Ssjl+mEdlKwx8bqGjPOGFvwThxDVd58fgjnkNoQDwgV1uY2Dqy1UkJeJCWu3SyPNgo/F5HMiyV9R8rJjP56kKngowT0T5UiYntaVVlS9Lvtf5zz7+2DXsqdspbMZkMklkx5uaIqNHvQLOfRO3U3EZIXCyg+fxe864vhHGeDzWxcVFSgThA7mtjoTwusqbaKf4brPZ1NXVVer/Vqms2oXgL7gOivfrxLr3uUQXeGJZUiGec0SdGOXV34s/ezxPGVfhxL4nlJ20ihVh8d5c1jme1grrvvcuceuJp8lkohcvXmg0Gml/fz85ne5MeQWKBzL8jd8MiBtXd7Cjow3TSEaFPjiU9seMbRmoUCJjwzrLKIwEjDjnXJvvnJ+f6+TkRMPhUMfHx2srvDKu48WLF6n3Fazwo0ePUoYMUmc6naY+Je4kUQmFUnB5QWmNRqPUP6GMSOr3+7q8vEyZPD7nPGWVVLVaLVXY0cCZZo6DwaDgoLlMudMvrZwvnC12jDw9PU1bUL9padSHhNlspv/6X/+rNjY29L/+r/9r2lVHKjoVcckGRI8TTxAll5eXqtVqKVPa7XZTtZmTwjGQjMGlA13gTpPrr9lspvPzcx0fH6eGsciyf9eDN56RsY7XdsLT79HviewzpIH33YjvkP/jAPr7i5kmgtHLy0udnJzo7OwsLYe4LToOGSC7tFi87uEzHA5TH4HRaKTLy0s1Go20NNwz9NVqNWV1pRUpB8HiFQabm5uJSPIsrhNP6LONjQ3duXNHW1tbKXvGO3V5cHlaLBZqtVprd1JFlhg3ZIk+PU60A47h3rgWTiO6h2U6Lq8c22g0Us89Kg9OTk60WCz06tUrTSYTtVot9Xq9JIsQUNjm2+BcRcRKI5eBSmW1nJDGylLRRrgTG+FjG30e6XWg6E2CfZ5zP36PHpjxnXht5NrtHPLpJCfjCxmPrXU9AsHg9+1VCx7cepVlrfa6v9jPfvYz/epXv9L/9X/9X3/tMH2Q+PLLL/XNN98Uxg9S6D/9p/+UeuLwfr0/m5M/0Saw1I6KMw/qnz59qlqtlpb4sfkBVUZOhj5//lwXFxd6/vy5zs7OdP/+fT148CD5354EJnD0ihY29pBeJ6i/+uorXV1dpWpRZAVdeXFxkSrZ0VV8/+XLl7eiKuAmMZ1O9fvf/14bGxv69a9/rfv376f57TYceCzDmLGigPYT0e9AFkmgDQYDnZ2dpTkNlsuljo+PdXl5qbOzs7TUbR2ZRUuDnZ2dwpIsqdjDF/+tLDHnSUP39zKuAxtxcXGh4XCoZrOZ2pfs7OwU/EkIH96/x+Hul7hdcdIJucCG3bt3L9kcX53kZGEEMR4JNGQV/84TpPgS3EOZnxSTPl5o4r1B8QWl68UAlcpql2zuJRaV8B49Voxw/e73zDNHsv2mcOuJJ4RxPp/r4uIiVR1dXV0VduFa52j+UGUR2UucJKobyhx6qdjThyx/WZWDM6TSahczjoeo6vf7Gg6H6TeE1MdsFL8vXJFIrycuDQlZuuFj6IbRA37ghogfglFfquTfoyKG/jDch5NNXLtMPlBOZVkClBU7XxHEeuaYe3b58wzyxwJ3OqSVI7JOT/i7ckPI3/w4snCQMQSSKH8nBPy8ZWSNG6RI6rhxjtle5E+63jtGKm9UHsklnAF0mD+vlwTHrIs/Cw5o2bsqux8M/mAwSKX0TtDcBpAQ4L3HqjAPjqUimUug5GRgdLy8eozG9Dj4EDU4xU4g4tTE6iPuAdnjvqNzwndj7w4nFnw5lfeh41jgts4rKHh/Ua+V6TlJqWrLM5leVQqRQvUCjYidvLtNum0ymajf76feE1K5P1BG8HAsv8uypn4e/060XV6BtO78/HYb4c53mZ103yWek+siX/E4lwu3STFAdUTZJ9hst9t68OCBBoNBXhZjiNlz4PrI37f7sS4HMZlCq4dut5uW3wKOgVTAx/Vdqrgmyd3lcpmSNlS8Rn27rvrEZXXdrpbx/rmfSqWSevO9KWj9WOB+0uXlpU5PT9VoNApL1txHcZmJyYiyKos3+TwOkh6+yca3zekyHRpJe/e5o1/lP3wP+9tsNj+q3Q2/CyBJaAnSarVSUp+KJ47zWMR9oLL4xG14tCX+223Pm5K5nlRxn4u+XZ6oi8t53d9Z5//7KiV+vGWH+9Vl9+i21X1EJ5A8iSNdb7geV0rxbOjS2+JP33riCYxGI3322Wfa3NzUgwcP1O12defOndRIlcGIDo0j/t0dKATDBxhBlFbLKi4uLq45bhAPMIssW9jd3S1cmyCRJoYeQHqwAns8Ho9TJgih+RjJgh8bk8lE33zzjVqtVupz5Az0eDwuNJyODrY7alQA0Kya8mxKPvne1taW9vb2NBwOdXl5Wais8jW9sRkr98S6eQJ0zw7XajWdn5/r6dOn2t7e1k9+8hNVq9UkZxhKXyKTobS9LvM8lvRLq21gXem7IfW5y5JgKqBQ/nzPySkQnSjky42TO0v8HUN/586dAtnIEgMqZfzaGOZIXOAcoEeHw6HOzs7UaDTSNvbSa90EAd5ut1NfpkhmxiAWx4T35fOH93t2dqbxeKyvv/46VXYSiNyW4HEymej58+cp88bzeabf+5eMx+P0/qUVMedVltgeKmHJenU6HXU6nQJRiTxEQhHnnPNIxQpfMm/VajU1YHYHxqvP3MlCP3mgGOEVWsimy4DrH3qrkLV0mYM8gEyiQTjO1507d3RwcJDk5uXLl3r69GnSh+PxWL1eT71eTz/5yU8SUXUbsFy+3nHp7OxMBwcHevz4caHM3/sqsbTaA21JhXnsGWGfy/7eo54ioPd7ioQX3/M5yrXdTjnp4N/xuRoDBbK+7sdwTZf95XLVU5FG9jHQxR6SBd/c3NSLFy+0ubmphw8f6v/3//v/6be//a3+7//7/84B4ndAbNvgeogkL0vhmMPdbleLxetKpS+//FI/+clP9Pjx41T5iS2azWY6OzvTxcVF6q1Ir9TZbKaTk5O0I/PLly+1vb2tg4MDjUYjff3117q8vEx2zHvQ4Uu77fGE3tHRUdJ9bn9YzuWyiwzRdJ3+chmvdcef//xnffnll3ry5Ik++eST9DcCXE8GeMIBv2o0GqXKRun6sn0nHqbTaerTdXV1pfPzc00mEx0fH3+nKjRkttlsJv0a9Zi0sj1e4YIMeXsTaRU37uzsqNvt6tWrVx917y8H+noymejg4EBPnjxJVf/u+0DCkPB3O+G2Aj8AnwJfxG2fk+ixIo2x9ASL+8/Sa7uFbprP52k1kVdVPXz4MBUKxIRQJLLxv9CN7CDnPndcPsyGRPQWpvo7JmV4J/hj/k64r8Vikaq2OO/5+XlKxrEz6OXlZSm5exN4b4gnXi5Z8Url9dIhd9Sk4vpGhwt7ZCqBBw/xuwxWmSODU+frSgk8yzKRfj8uBBALTFD6nLDuOTtRPw5wSKrVanrHGE3vHRENJYrLFR1/L6uciZlmr0zh7/FcZYgVA87sx0w4pJQTDGSK6A11WwKymwZVCIxNrOBxuO6IwVrM1CNDzFnPoPr4RazLCno1gH9OZtfJL3egkGNptZTNg9SYQQbRcfQKkij3sTLCn6Msq+jPRiZzNpul3g3oPe+ldFsA8XZ1dZUC6bLGkji1TjLynmIW1p0pvhcrk3iPLnf+7pExPyaC47z/BTrOrxWrHbxyMyZuov1y/RlJbhwz76vomcPojDpZJyll2p3sl1aOH73qIC+ig3jTQP/ipEMMOcnj91yWIOPf/v7KCMEy3eLn8fccrxMdbM8uu4xEfbjOv4rncT/GA8N19xwRdRDfGw6HKUH3Jj2eUcRyuUwV9cAz/+gLKgIgSd3OEGh5osV/XCe4jnL5RX4glPBbSMK478Vvt4vRVnrA6zrW217483Kffo2M1++C8Y07/UrF3nBSkdzBJkVEsjxW3DlR6FvBfxe/NZITsdo/wuW0TH9xP1km1sN9PMY/Vsr7T0yoxDGIc9yv4wQTx/hvP2+0ZXH8kQ/309fZ3W97fteDzBXXW44yPiC+x/gc/hPfW3xuaeVvkHT0hM9tkOX3hngC8/k8ZQ/H47G2trZ0eHiog4ODa6VwUnnDXBADJnfm3Mnix4MJFJozj5yjVqulBs6VSiUNugdTzrxz/tlslnbeePr0acrMeGlwxo+H2WymTz/9NC3rcEeIce10OvrJT36SSCgPpmPg6bKGswXZdHV1lTI/u7u7KUs/nU51fHys+Xyu+/fvq9FoFBw4QCWD78jg16QBJNVc9IdaLpf68ssvdXZ2luR0PB5/9PK0WCz0z//8z/rzn/+sv/3bv9U//MM/lGbi6vV6WvIEYTkajdRoNNLOeLHKhDJdr1zypbnSShfF8lk3zMhj7H3Cvz3LyP35zlBcv1KppP4JZE7cMLONq+shlglT4elb0LZardQbCGee++RZ+I0DEokrCINnz55pNBrpyy+/VL/fL6y3v23o9/v613/9V21tbemf/umftL29ncbNA+hqddXHyfXJzs5OQZZ4Zx5UOYHtjpA7cd4bKJLbHIOj7cvz5vO5vvrqq8I21A8fPtT9+/cTkUZlC5VbTozQa4VjIQypVIKYm06nunv3rvb391Owenl5qT/96U+qVCr65JNPUjaRd8WOkL41uz83MostpX8Ez8U22/Sc2d/fL/QJuS24uLjQH//4R/V6PT169CiRje5LeEbXK8mcoInVau60epDljq/LVfRz3Efyd++EfHSi3T65PeI3xCZBPeMM8ennQY9WKpVCNSHnQl+wdLnZbKZzzGYzffHFF3r16pV++9vf6o9//ONH36Pnu2I+n+v3v/+9/vznP+vx48d6+PChvvnmG3322WcFHYSeOjw8TJWYVN3SX+mLL75Qu91OVbhxSRLNoX35FJn5TqeTkr6TySQlXJEJD7rQT04wRAJcei03l5eXSW6oBDg7O1O329X+/r4mk0nqB/Xll19KUq5mWQN0LfqKajEnjwA6hso5dAnVzd7rFmDXaFJNe5VIFL4Ji8VCp6enms/nqcdTGTHuFaK0v3D/v1Z73Rjb7R6V2N/1Xj42nJ+f6/PPP9fu7m7yJSIxRMKlTDd7hS7fwT8ghooxe0xc4N96ciaSM/iyyCNtDaRV0st7lHlfpkiQQsrjyw6Hw2Qzd3Z2tLu7m2TJ4fyB37uvsuLe3cekQo/7wT9ghQ4ye3V1pXq9nlYo3Daf+r0jnsiEVKvVZCBoIOfLo/x4d7j8c4dn69/EJHKsG9Q4wRBOAjGIhKic4z2SEcXoDofDtd/J+OuxWHz7drmz2Sw1ui2rRIjyJl2vBPDPUBZeARCXH3gwEB0/rhtlmfJi5kel8rpnwXL5urH5+fn5X/WuPjQsl0udnZ3p7OxMh4eHaa4yzq7cI2kym82SQ+XnczLHCYSyLIoHfh5EumHz453AkK73aikLKr2SguUUGPeyiha/b94BZc9cj++7MXSd5/cW78/fFfqRcuDz8/Nb7/DjCPN82BscBpxXT2A4EYBT5E0j3YlBzmI1o1S0Y26rXL4icepEFtejqoz/QxRJq2bisZqGZ8OOOcngjWF9aUS73U7Lj0nCXF5eFuQryqpXhMZnc3nnNw4hldBeDeU7Ct4mkH2ETCrzM3zsyuZPzH66nYiVU+sQSct1meMyB57vlu0c5LpTWgUTsQo0jg1j7Top6hZ0BnPO9WW/39dsNtPz58/11VdfvfHZM1ZYLBYpKXVwcKD5/PWOcC9fvrzmw2xsbGh7ezv5GYwXSbnLy0vN5/PUbDwSqpBVklJyFlKBne/4P8R9vIdoU1ymosx7hRPkAUtPvI1CJhO+G/BDsf1lOicmDDwRxWe+9DvaAWnVS5GVH9+nQh8CezQapWVMLhfEbZ4k9nt1v8WTh5ISIZpRDlYQkDwvs7/uR/p4lxWNuGx5tb7/LfrXLmvRB43+Kf+OMTtkFz6Jw6+L3kFfEbezCgvd6MleP4//2/33WNXkCSlp1f/Jnwc7S6IR4k9SgSy+LXjviCeA08x6zW+++Ua7u7t6+PBhoYu8O0IxOPSgvkyo48SJAuHOmgcF7mxLKvTlwVknC3x2dpbK9CCeqI7JlU43j9FopD//+c9qNBo6PDxMOzbgbPl68KgEpVWPIAwZsugl5F6VQiYpKilKj6lWQDHSL8b7/FD59Oc//zkZg4z1+PzzzzUej3VwcKC/+7u/u9asGXiWD8cZuF6JAVOlstoZER1Drx3gVR9l4BxkfpABSPiY5QEQBvV6XUdHR0k3SUpG0UlVyFT0lVdz8Q5w7pwA8WvH+4gE3Gg00osXL9Tv9/XFF1+krZLfFywWr5cADAYDdTqdZOydLKjX66n/IFgul6niw6ujkAt3dKPTxPel6yXgOHJci+CRsXSnhj4VVB08e/ZMn3/+ue7cuaOf//znBSfn/Pxc0+lUJycnGo1Gunfvnu7evZuqHAjkuN5kMkn9L9gtk2sjdyyJox8iug4Syck713fMOfTtZDLRxcVFCk4qlYoODw+1u7ubyDT6nd1GYFeazWZ6p9JKx7itcDLGKwilYsPW6Li6/ilLqMVManRYuZ91BF4MFpwUjUkZT9a5nogkaoTLvOtPZAj9trOzU9jZLOP746uvvtLFxYX6/f5av5PsPfaRcaEn3+bmpobDYeoPiG/iFUrIC9UC0uvKy2q1qn/5l3/RV199leY585h/+znwudiQwoFsoWvZcQuCiR5St3FJ923EcrnU8+fPNRgMUpyFf4AuZ867L+HJK+yKb3nPONL7D/mhV833RbVaTTue4scATw7FxBn/dkIf3ckO5tEfzChiMpno7OxM9Xo99eqi4tXJEn/P2P51vg7xuS+DjYSMdL1XlFSsvuUYqbg5gf8QkxOHL5fLQh9e5Nyrl9wm7e/v6+DgIPW5azabarfb1+6FZ5BW/TnZXAH9ig/p94ud99VTELjoWCrG//KXv+j58+e3stpJes+JJ9hnjM5sNtPBwUHqpu/VAZBLznQ668rE8ACpzJGLGT2/H37HoM0b2KGIp9OpLi4u9OLFi1SCnEmm24fZbKZXr16pXq+nrb3ZtYGxhgCQdC0wQK6QR69EkYqEBZl7doRw8gInCzlml5hut5u2/MRQNhoNTadTvXr16lYHX7cFx8fHOj4+1uPHj/XTn/40VaW5YwIwQp6BiFkKJ6E9i884YlQ8K+wEZaz6cKco7mJBvxjIj0haYqQajYZarVZa3sCxfjz/9yqTaLS5Xw8iYzVKzHD+/9l709/IliO9O2qvYlVxa/Z6+17duRrJksaz2B7DBmzA8B9uwB/eDwNjbI+hGUEaSXfv2wt31r6/H4hf8jnBPFXFrZvszgcgSFadkydPZmRkxJORkdSVe9F9JHV8aKuI9KOuiqmMQBBo2LPZBYEcI6h1bvKRPegNPx9xrV+BJppSSQSex9YDVpTfvHljX3/9tY3HY3v27Flw5sfjsb169cp6vZ69fv3azs7O7K/+6q+s2WwG3aSJNCmP6LXT01M7Ozszs3MZ4bANjFLC3JUY8Qs+6DttY0+66up2q9WydrsdooXvM5mJflbiSUlexpDqGO1noHlM9F6/IkoZHrr1V6NT8khOs6yser3HZ54c0/rEnAR9FuXnjRMWenRcoVOTc3g9LBYXEcB5UH0UW7zViFqI4o2NjQwhqYuzjONyuRyIQzOzk5OTMBfhBCrByjhBN6BzfBSLkgi9Xi+QXGYWTpxNWB9Ei5mZPX36NJOTULfPqv3iCWfIbWwWrmE7Vb1ez0T75i3ELQMHPPE8s+xWYuyoPB2kdh8Lftety6cEbCL1d3U+8vJgZpk5zc89amsqCanzo59rdM7wfrovX6E6jMMOkGnsuVKpZI1GI5MOgDLL5bLt7OyEwAR8MiVflV/QuZH0HRykYHYRueT9Cea+6XQaggrU3kSuDw8Pw+LffcSDJZ5iODs7CyffbWxsWKVSse3t7cy2GAaAKko10DwLymBREsvs4hhD3SaDMDLoyH/R6XTCyixCNhqNbsTsJ7xfzGazsMcbx023dqLMMIowanAMmGz1HpSIKthyuRxYcCWedAJVMkOTepqdh7u/fv06OIIJ6+Pk5MT+6Z/+yba3t+03v/mNNZtNM7s4bVDz2wA1YryBnQf9Tkkcs6xThq7he4xx9BbkFd8tFotwEpx3XLVu1N+Ta94xVKKLOnFMNY4/Wzz1vTwJAzlxfHwcTqd59+5d2Gr60DCZTOybb76xN2/e2ObmptVqNXv69Knt7u6Ga+hXJdw8Kch1StZ5qMOu85HZZUddSUwlOdXYok4YUi9evAhzJZEGbFvSiKL5/Dx3xnfffRf6HBKTSCryynFKC9sKR6ORNRoN29raCmH4euCBNzC1HTCqNCq02+2G3C3VajWsNBKR+g//8A/2008/2XfffXe7HX8HmM1m9vr16zCuzMz29vZse3s7XKP2hbdP1HnXiEvuy1tEQzew7W9zc9PMsgdYxODHuBr3zG/6vdZJSTR1RPhbZVXfAZmtVCrWbrfD56qXf//735uZ2evXr6/dFwnLMZvNMotZxWIxnOCMfoNQHg6Hdnh4aJ1OJ9g8enITdsvZ2ZktFgv79ttvrVgshuhjMwvz2dHR0SX58fKC00XUG3MSThrHiifcHN1u17799lur1WohzyGRRERAqZ3iF+V1EVX9K3Z6dDqdMAddJxotj4jQ79Bz+GZ5Ucbco78TluPs7Mz+/Oc/W7PZDHlrmZ+I/Nf2Vt/czKK+j/rX3ubmXh80Aih3NBplno1PRsQRfpeZhTQlPlILHYcNRC5MdI6epmh2QY4TQYVfSCAC70o5mjdYbSKiQ1logzegPN7p3bt3ZnbuB95nfFTEU7fbtV6vF5jzer1uX331VdgOoathsdV8BNvnVYqtMHOtJvg1y67osK/87du3YWsAOZwe2ir/p47ZbBaSM5tZ2MtL2DAKlYgkJk1dsUe5aPhlzPnSrROetVem38zCtk0UaqfTsVevXiXS6RqAeGLbkW5fwkkjFFajMyC29QjVdaDkBP0HNCJTV28x4skTxrHx/LBlV/Wdd+aUeFKnUAkvjV7iM9rBzAJp3mg0MkScWXbPvpmFxM8//fST/fGPf7TxePygk/+yjRWHvV6vW6PRsGfPnmVW5vnRFV/gSSO/cgfyiAA12jSMG53CZ3o0Mc8jApOIhM8++8zevXtnf/rTn6zX69m7d++iq5IcfY7hBZlYrVbt17/+tbXbbdvc3LR2ux3GSa/Xs06nY41GwzY3NzP57SCOcA7VkMIY29raypAq3W7XDg4OwqJOq9Wyzz//3Pb29uzJkyc2nU7tf/2v/2X/9E//tPY4/JCYTCb2008/hf8LhUKIDvMrwdrXGnavkZVm2e1peo9+psQThE6pVArbFGOOWyz6SIGcIYNm2RMZ/TZKylDiyexicdA7kOVyOSShhlwl+TDbxB5Cnz9UzOdzOzg4CBGM9Xrdms1m0A/+AADkiLmIhRLG+Wg0srdv39p4PA4EAPYU+qDb7dr+/n5Gj6LL2JoF8cShArVaLRC3HEJ0n1f/HxqIfGq1WoF8JJKIrf9KPtFHmtJE9QrO/HA4tNPT07C4cJ1FKR/ppvOwRosyT3c6HRsMBhn7nO1hMRIqYTW63a79+c9/DgceNZvNML/4pONm2UUMXTij39AvugCjh6aozx0D15G+hjpgu3viabFYBB+NrWp6WI8m9NYgF3KK+Z0tRITzHOrLXIlsQmD5RSbuZWx0Oh3rdDqZdmOsXNUH+VD4qIgnsyyrbmZ2cHAQVl00TJh9wCrMeeVpJ+pWlMVikTnVR7dRaFjc6elpSKSb9pQ/bGhUiUY96VYQ5EsnLQztXq8XtqAgJ2yz5HqcsphjrgSAOh5E0vV6vQfr0N8H0L9//OMfbX9/3/b29sIWgNhWFzVsMFQ0usSTPWoUmVlGV2muIFZX/GqQWfa0C56JU6eTl9ZVHUDAPd5p1ev8VhpCqUmkWCgUMkTcbDYLETI6cRK+7Mt/qKD+RDh2u107OzvLrPT6rU7c5//X3BM4bz5yzhtq9L/OT2rEsM2P7Zsawo1sIT+lUsna7ba9ePHCJpNJOHUT2WGOw9EjmokkmvyNQYd8bmxshITiEJRci6GlBj6Gv5K6/jh3DEHaijwKxWLRfvjhhyCXD1m+Op2OvXnzJrxbXn6RmJPl4fWTWXbLAZ+zehuLCuEaJYG0DnymW6iYl9CHOhY8yeoJ1xjBpdseNLcTpwBj0Ce8H0AkmVmwg+hvXbSg/4vFYiCjdJssvyGfmQvRP5VKxVqt1iUyFdIcAh0nkIgnTt08OjoKC74Jtwsi1tTeaLfbma1pngDS6GoW5tFvnGKI83wdULaS1zrf6hZPPUVciQjdhse8hN2TsB6I7tnf37d+v5/Juaz2UZ6dE/PH9V6/SMFny+wlrYOZBZ8cHYQ8Ao2oYu7Z2NgIkduQabVaLUMW6UKgboP3sqhzouaV9ek00JuqJykXLkHt7YcwD350xJPZxWk74/HYvv3224wQk/9pb28vGNG6qmiWXYVTqPGH4bO/v2+dTidMcAo/CB6CQCQsx2KxsLOzs0woo5eTSqVif/EXf2EbGxuXVlhOTk7s4ODgkmLULQmHh4d2fHx85bp5xZdwPXQ6Hfv//r//zxqNhv23//bf7LPPPjOzC+LJkzi6kq/AWIFM0Ogosws9NRwOQ14vVoP9Fimz7BYDdBFbM8n1RA4f78zpPnm/IqOTsRqHmodBV436/b6dnZ0FMgCwQv3NN9+ECV23CX5soeqQlMPh0A4ODqzValmr1cpsWzKzkPTf5+KhnbXPlUjAkfNOuTp4XKeGPUT4aDSyTqeTMbg8+YCh8+TJE3v69Gnm/ZCT7777zk5OTkIUAjk0CC+nDAyzarVqu7u7tlgsQkRUuVwO3z158iREPig5ofMrRinG4PHxcdieh0yxkrq9vW2z2cz+6Z/+KRyX/lCxWCxsf3/fDg4O7PHjx/bFF19cGqMKNXgh5DyxRKSBPkMjuwuFQkjGe3R0FPRZTP+oYatyydylC25mFn5TB0+ieVLM7PLpQxCzZhfEKUQG9leyrd4vyuVyiHTRpLiqZzS6QfUT84QSyeRxUpIRp47oP7XVi8WitVqtkFOl3W5ncm0iHyTZTTbR7WM0GmW2tpZKJfvss89CtJnOcfSrygERHDrONbHzdeG3ZTI/QTaNRiM7OjoKybA9oZRnpyQZuhqIDCfIgy345G7T+cLMMraJ97+xeX0icrWHdL5SUks/V11E1CUn/SIbi8Uic9iH2cWJv1tbW/bixYvMAprKhbeHlRwiSkrHgEZyqX/BIi/kGHa3BiUoUQ8eyjz4URJPZvlkDx3V7/ft5OQkbJOKRT7pyhwChjBpqCYJyR5ivpKEq2MVq8zqDSsrmmdHwzk9ONWMJOMJHwYo/WKxGLYW0OePHj0KuZ+Y0CAN9EADjUgyy56skWfY6Gox9cApI6pJT4jB2dctOSqb3tlU6MpxHjRiC+eP7cz8VsMBAgWjgffnc/3/YwHt2u/37ejoyEqlUsj1pGMYclkjniaTSYgw8Tm5gN+2qKtpeQ67GmIYeton1EflxJMI/F4sFiFSiagGnEycT6KPlJTVSEw13nSMcJ1uN+Zz5A19CRmixh5tRe6Dt2/fhtxPDxm0w3A4tE6nY6VSKUSVsLXJLNuH2md8x99ECPG5XofcsUU3pju8PtJ6xsgpsyyxaWYZMkvBZ+uQ0ioXGOA+LULC3WOxOI/0h6SEKPJOoSbk1TyAw+HQTk5OMo6epixg+4u3k5Anf+oshJOeCk1OJ138SLhdxOzg4XBo3W7XRqNR0PeafkKdbt1ShV1wUz+KxaBisRi2S6mjTu5Tfif9cXeAdGHXD7pBDxbxtodZNsG72eWdBp7E5B6zC7vIQyNlKUOJL12EYZ4l4toTRdxHPfyJe2qP8w7YOJCq6ErsKF1IpG1YdCOIhkVqjXh6KESTx0dLPOWBTnv37p0dHR2Z2UWSXYSg1Wpl8pYgdMPhMCQ6VCNZ/09ImEwm9urVq0tGuVm+YpzPz5P3snKc8OExHo/t//7f/5sJff37v/97++yzz4Ihwwlti8XC9vb2gmOM08+kBDmlkQs+gomtU+qsmV04cWwjIr8GyQjNzpMV6gTKb500NfxciSsfDqyGYafTCZFZ0+nUfvzxx5D8s9/vZ5KtQ6rU63VrtVrhPTiGOc+BfehYLBb2008/2du3b+1v/uZv7Je//GUmAkRX0XSr9rt37+y7776zdrttn3/+eQjpJ6oIogoZ8uRQHsHIs5nLNIqN034wuiEElPjxslAqlUJ/aqi7yu3m5qYVi8WwdQFiktVEohLYTqrOIit5EE3qQDIG2u221et1e/TokW1uboYE44vFwr7//ns7Ozuz//f//l9ISvsxgEUtxmu9Xrdf/epX1mg0giGr+a/MsocI6Amr5NbS7bWFQiEQhyQl1S1rjGddgTW7kEMvM0Ta6eqtbjFmG3oscosyYkSaRnQhK4eHh+kAjQ+ExWJhP/zwQyY3GdC+pe9+/etf28uXL4NcnJ6e2m9/+9tASNRqNfv3//7fhxOpy+WyHR4ehshwyG4zC9uC2UpHst39/f3gBJ6dndmf/vSnlEv1PWOxWNjBwUHwqwqFgjWbzUsRwPyNDoP8HgwG1u12MzrsqpjNzg9rKBaL9vTpU9ve3rajo6MgSxoRc5PnJKyP8Xhs//qv/2qVSsX+7b/9t8F+NsseSGEWz/mnBzJh2w4GAzO7iCZX0mY8HgeCS79jntTk9ppfkvLq9bp98cUXVq1Wg42CPVMsFjPkD4sgi8Ui8AaQ58zNLNQOBoOQP5Po783NzXBSXr1eDylT8CvIowlZTxqBh24/f3LEkw/5RRBhJ5kclXXHgcDxSysoCcugRvpVkOTqfoHVWYWuorIigR7RbUBKLimUbNLPNATY36N5UvwqjYbx4tx5gkfv0W16ukrEqrVZNg8Ceekw8nWi5jpd1WHVWrf1aV0+VhDGT/JHQrF15SsW2aGRcH4Lp1k2lNxjWUQb4HlKOORB50UzyxBfOAi6OscqYuxzjajTRPeqG5Enze8yGo0yck3Z1Wo1OKWQpRpVChH6MTma2g6AvGoQh+TWMsvfIuKj4jQSk36iz/McsTy58VsN/HN9BDnPULIMMtav4jJmiIyAWIC0TJHBHw6M21UoFosZp61cLlu/38/kUyHiDtKTRNM4dJDfjHsOJICkRiZ0Gx9RNwnvD7pIAjQXmLcBdLzTt3kLs1epA1Hho9EoyFHKAffhsFgsQkQtJAx94e2kPDtYbWTdyq0R3Xqt2iGA8tUG56dWq4VrIJ+QW59cHLnF9uWUTxZ3tA7oLeYv2gF597lfOUVYf7PA8jHlh/7kiCcP79ARWeCNOL0uISHh08Tbt2/tf//v/x0mlkqlYpubm1YqlcJEwWSoEQM+l1zM8WMVx6/Q4LTrxIPTxWSI42+WzXGAs8ZKEKdvaGQTW5VIAD0ajQKB8v333wdCYD6fh9PJvHHAdjq/ylwsFh/81qer4Ntvv7XDw0P74osv7L/8l/9yyehWJ2pzc9OeP39ujUbDGo2GFQoXJyNitOico+SN2QVRTbmeVNQElKwC+hMI/Xby8Xhs7969C5EIZmZHR0c2GAzs6dOntrGxYbVazZrN5iUCdTqdWqPRCCd36kl18/k8rNbhXLAtjnccj8fW7/fDqVSNRsNevnxptVotbKs6PT21n376yX788Uf7+uuvM2TZx+5ojsdj+/Of/5whe549e2a7u7uB4DOLb+f1RI8mnzfLT+gdK8PrMN0yoXKu+ol66bOUnNQoTT0q2m9RZhv74eHhtY9bT3h/WCwWIc+S2QXJpATFeDy2f/mXf8nMkbEtV+hN5jp1AHmWd0wTPizIpxTDursBroPF4jy/IKclJtLpw2M+n9vXX39tr169Cp/t7OzYF198EQ4GULtF5wki+slnSj7l2Wx2KdekHlqi+sH/T+7VVqsVInWJNCfCijm12WyGHQDYLb1eL0Rnm5ltb28H22VjYyOceKzRV9jHEPGkZyBCCjso9vtjSlHxyRNPZpcN+Y+pgxMSEm4P/X7fDg8PwwRXrVbDqXesTLBagqPko0D8So5uJdFVEnW2NFpFCYXJZBK2uykR4Lfe6I+PhGLvONEr/M8JjEyurAZ5x5OVJBzHT1l/9no96/V6trGxEbZX0l9+9Q0SkFNRzLLRKcuixLS82BYlnuEjd9VR91F3/K9bsliFU2eRbeledvlOSTMiFEajUYgWZosWeXp4vq4WshKK8cbJVOPx2Lrdrp2entrR0dEn5VDM53PrdrvhfwxZdayUfAQ+Wi6mh/yCmrarRijF9BjjX+/V7Xpatm6l8MSlkojI3Hg8zmwn5J09eZFwP7FYLMJ22zzM5/NLB/Msg+qdT2n8P0TEojbfF8iLk3A/sFgsgn0EisWi9fv9kIbALLuQoXavRu7roRXYDnmnwqmO0DkPG4WFMo3OYxuw2lhqD2m+JRa8iNBUW5lITL9TgXqxIMi8rTmj1M7/2PRcIp4SEhIS1kS327UffvjBHj16ZL/4xS9sNBrZv/zLv4TE8OVy2X7zm9/YZ599lnGsdPIETKyVSiUYSXqcr4brKonAxKrRB965ZJVFJ14iprrdrs3n87AaeHh4aIPBwFqtljUaDTs+Pra3b9+GfeZmFpLDai4NT2p8bJPjTfDu3Tv7H//jfwSnnPwGRKcUCuf5dYiWw8Bh1avf79tsNguJeXVVH8fdG2pqsFEmOZUo9/j42KbTaehrlTEITOQGgqhUKtloNLJarRZydW1sbGRkDueC7XC6XRNjjC02nGjFO2OMPXv2zH72s5/ZeDy2w8NDm06nITfH7373Ozs4OLDBYBBOokk4j0bTPFCtVsueP3+e0RFK6LGCqxEhMZIImdAoPWRJt0H6yCrKUXmMrd7WarVAuJLagFMy2YZ1dnYWthYqPIGa8OkhkU4JCQ8f3W43RPHqdv1isWjPnz8PJ9ayLd9v0SWnEvlOY4txZhZyMTEH+cU6b6sTcdnpdEKEFYfpTKdTq1ar9vz5c6tUKra1tWWFQsFOTk7CgSAHBwf2008/hTkUe5k5j6he5lPINJ1fP2b9loinhISEhDVBqCzJAKfTqf30008hEqFcLtvLly/txYsXZnb5RKhYtFO5XA4TXSw3lE/Iq9tmtByF3xIDGaGO3enpqY1Go0A8jUYjazQatr+/b69evQqrNBxrTcTFx76l6TbQ7XbtD3/4Q/ifhJU7OzsZZx5CD0AmQUSSwyd2eor2e4yQ8tEp5AsYDAbB8Ve5rFQqVqlUQl9z1Dnb7tiu6U8j8s+GONXt6xhzGGbkJ+KY69lsZq1Wy7788ks7PT21k5OTkK9lPB7bN998kwnRT4hHk0ynU3vy5EkY+6pzvLwo4eQjllTn8D+EpPZ9LJeGyoOeaIXxD+nIijOywXZK8lkQdZmQoPiYHbKEhE8JPjUD0c6VSsUePXpkZhfzCXMDBI3uKNCDT3S7N2WaXeRqYgFWI2n9wq0eHMQuh9PT00zi8Ha7bc1m0168eJHJz3l8fGwnJyeBpCKHFO/GdmNfV92N8LEjEU8JCQkJV8Tp6an97ne/uxTOPZ/P7ZtvvrHT01NrNpvhWFZWOnC22VfO3nRCfHHWIAJYocGRV6KAlSDdaoezD7n07t07Ozw8DPlzvMNpdnGSB3vYWRnSCZE96Wl7y/UwnU7tD3/4g7158yYYSU+fPrXPPvsscx2kDaHnbNXjO42Y8yHZse18egod+cjYLql5wjTptIa3K5AxzSUEmQkZRWJX6tHtdkNUzvHxcYa4Qs5//vOf24sXL6xardrp6am9efPG/vCHP4QIQHI7JazGcDi0H3/8MbNy/PjxY6vX65eMWs0fxucqL14OdOwr4ajlYIBrXg0zy2wL5odcPicnJzYajQIhqVuAExISEhI+HbBY8erVKzs5OQkn4nKCpdmFPcPCLbYL2+B0wQ2yaGNjIyx+sEVOT2alLCKdWCgjfQZzGWkCvv/+eyuXy/b69WsrFAohV+pkMskcsKNRxxr5q1G7nwrhBBLxlJCQkHBFdLtd+9d//ddLn8/nc/vuu+/s+++/t62tLdve3g55oKrVakhAWCgUQi4oiCe2nLDvWydTyvZb5waDQZjkcPqIahoOh/bmzRv77rvvrN/vh6gsolKo29bWltVqNTs8PLxEPPHcj+m0sA+B6XRqf/rTnzKf/d3f/V0gnug/HP5Go5E5LRGySo0fDDS/zVH/5h5IrFarFfpTTwszs3C6K5EtHsipJijXxPdE7c3n82AMHh4e2uvXr204HNrp6Wkm3xXv97Of/cz+43/8j/b69Wv7+uuv7d27d/bHP/4xydw1MBwOM8fcVyoVazabIWJNiUv63ke9+RxRPk+T/44VZAx9TSqOrOhWA4gnVn4hxpGPhISEhIRPD7r17M2bN1YoFGx3d9d2dnbCKcssoGkkP/byYDAIOZZ0gcPMrNFoZKJ1B4NBOPBEdxpMp1M7PT3NnLKLDU+E1nA4tP39/Ux5zG3VajWTZ0rzO3ES76eORDwlJCQk3DLYPtLtdsOJdxwlXS6X7fj42CqVSthKxYSrOZ1qtdqlo+v1yNnhcGhnZ2eZkzxYZWEP+cHBQdgy5XPysOIzmUysVCqFY69TpMH7wdHRkf3ud78zMwt5oJ48eRLIHRJZzmazsDXOJ4g3u5yQnNU8DCAfxo3hAzmk5JFulYO0QkY1eacmx1Ty4eTkxAaDQVj56/V6dnJyYqVSKaw4ciIZhuE///M/h+v29/ft4OAgERC3hPl8HiKKNH8EeqVer9tsNgvRkOifdrttjUYjXKeHBhDthFGuZJVuOUAO0TWQU7PZLHMikOa7SEhISEhIMLMwz3Q6nWCrEi1UrVZDGgC/bZ/DSbCtzSzMQZw+3ev1Qt5J3dLNNcxJi8Uis1OBdAlE52qOJj00hfp+atvo1kEinhISEhLuAKyomF2QAz43k8fGxoZtb28Hp5BQ4WKxaM1mM5OIvN/v2+np6aUJTqGElp4+tVgsQgTUYDAIUVV+G17C3eHHH3/MRKe0Wi379a9/bZubm/b8+fNwMl6/37dmsxkSVcaMGN0WRW6cZrMZEoj7U1WUXIKQxHCC9FLDLiYPMcPr9evXdnBwYAcHB3ZychLqubu7a3/9139tk8nEvv32W+t0OkH+f/rppwyhqgRJws0wm83s9evX0e9arZY9efLEptOpvXnzJpO09dmzZyEikm165KVg++fBwYGNx2N79OiRtVqtIGdgPB6HZPZmF6QoiVg5uCDpnISEhISEGPxJeGYW5o5Xr16FxTEWYCuVirXbbdve3g72sh6mg71LOgqitc0uopOYszRCt16v287Ojj179szq9bptb2/bYrEIC21v3rwJhw+Rm9LnQ01z3DkS8ZSQkJBwB8jb/rQMEEpsuzO7iEwh5w0JFtlOF8uHggNPyLFOphopoys3Ce8XmgvH7JwwOjk5CQSAJh6nzzU3EokqfcJojWTSXD309XQ6DeSS5oHSkHOfC4jvlCzlhERORqT+3W435FHQ+p+cnITnK3GWZO9ukde+5MxgC57muoC8xDjXI6whntiuyWk/Psk4Rr6SiGzn9Nv+EhISEhISPGK2s190Y+HVzDLzTaVSseFwGBZayYuqeVD14BbuZW4ikpsDPIj4rlar4TPKOT4+Dlv9uC8RTXEk4ikhISHhnsAfF+t/K4ngTzYzs7C3nJWcVqtl9XrdhsNhiHDySJPj/cBoNLI///nPmUikr776yp4+fWpmFhx28no9efIkEEgqFxoeznY5IqWQL8gpzbej+aPMLuROw9dJgk8+hR9//NHOzs7sz3/+c4Zw8qRCp9Ox3/3udyHqJeHDYzQa2du3by9FSi4WCzs5ObHT09NLxKYCQpKDBzxW5YZKSEhISEi4Cdjyz0IHc9a7d+9CwnAW3XQ7OXbNsgVibJXhcGiFQsFevXqV2VbOPRqJzkJumuPykYinhISEhHuCq2wz0mgVfxqZnjaV9pg/DGBAgWKxaN1u15rNZlhBIy8OiTLNLBwHTF4BMwtH/iohgLwsFotAbGkOMSU4yVXASXX8r9d2u107PT21Tqdj3W435EWIkQ2QXgn3B8tIwKtsdUyRSwkJCQkJHwp5tq3mPdXclprEfFW5em/C7SARTwkJCQkPEOo4Qhr4SZb95yns9+FhsVjYTz/9ZAcHB5kkz4vFwh49emR7e3uZZOBHR0d2fHxsjx49skePHlmpVAqnirEFb29vLxMVVS6XwzUQWOVy2YbDoX333Xd2enoarj04OLDDw0Mzy2634nda5UtISEhISEi4D9CoW2wTUhUkW+XDIRFPCQkJCQ8Q6+SQWmdVJ+F+gpMLh8Phpe8qlYoNBoNw8iHHA/f7/ZBUU7dgEvlEhBxkpNk5SamRUawGnp6ehgThZmYHBwf29u3bO3vfhISEhISEhITbgreNU+T/h0cinhISEhISEh4QOp2O/cM//EM48bBUKtnOzo41m82QgJzk8+SDKpfLYSscW/b4abfb9ujRI+v3+/bmzRvrdDr2zTff2MnJSXhmjABLSEhISEhISEhIWAeJeEpISEhISHhAGI1G9uOPP4b/S6WS/fKXvwy5n6bTqU0mE+t0OraxsRHIKfJ+cSpit9u1TqdjZmbb29s2HA5tf3/fzs7O7OjoKBxbnJCQkJCQkJCQkHATJOIpISEhISHhAWM+n9u7d+9CxNLGxkaIeqpUKvanP/0p5IgiJ9N0OrXxeGyj0cgajYZ9/fXX4VjgvC1+CQkJCQkJCQkJCddBIp4SEhISEhIeMBaLhR0eHobk3wkJCQkJCQkJCQn3CcXVlyQkJCQkJCQkJCQkJCQkJCQkJFwdiXhKSEhISEhISEhISEhISEhISLgTJOIpISEhISEhISEhISEhISEhIeFOkIinhISEhISEhISEhISEhISEhIQ7QSKeEhISEhISEhISEhISEhISEhLuBIl4SkhISEhISEhISEhISEhISEi4EyTiKSEhISEhISEhISEhISEhISHhTpCIp4SEhISEhISEhISEhISEhISEO0EinhISEhISEhISEhISEhISEhIS7gSJeEpISEhISEhISEhISEhISEhIuBMk4ikhISEhISEhISEhISEhISEh4U6QiKeEhISEhISEhISEhISEhISEhDtBIp4SEhISEhISEhISEhISEhISEu4E5eveOJ1ObTQa3WZdEj5iTCYTWywWlz5LSFgX0+k08/9isbDJZGLz+fwD1SjhoWE2m2X+n8/nNhqNrFhMazAJq7FYLC7pm9lsZqPRyAqFwgeqVcJDwnw+v2QLJXs64SqYzWZRezrNYwnrwvtfi8XCxuPxJblKSMiD98nWRWGxppR5oyoZWQlXhRe1JEMJV0WSoYSbIDbdJRlKuAqSDCXcFEmGEm6KZAsl3BRJhhJuCi9D61BK1yaeEhISEhISEhISEhISEhISEhI+XaxDKaW4zISEhISEhISEhISEhISEhISEO8G1czwVCoUUBZWwNhaLRTSsM8lQwrpIMpRwU8TygSE/SY4SViGmg8xsaW6VxWJxJdmifL3Hf6Z18J/dphxf9TnXqUPeu/kyYnXh8+vW5ab3ck3eKm/eO6wzj63q83W2613lmpv2p7al1i+v39Z5dt5z1x1TWj51WtVXsfZep76xa66ylWnZWPNlJFso4aZIMpRwUyzTp8twbeKp0WhYvV6/7u0Jnxgmk4l1u93MpNxsNq1arX7gmiU8FIxGI+v1euH/YrForVbLSqWSmd0+cXATp+Q+4SqO7zrXvq92uQ2n0GMwGNhwOAz/l8tlazabucSBOg/XeV6MPLgJrlveVZxXf98yx/EqdVnmTN0V8uofq0vMCI/lL+j3+zYej8NntVrNWq1W+B7jvVAo2HQ6tfl8bsViMSNj3mCLOerqBECYouti5XrHP9YW/l19OxSLRSsUCjafz0MSbH0O/xcKBatUKlYsFm02m2WuXea86Hc8ZzabZT6nbcrlshWLxVAX2qFQKIR24Ln+mVoXbZ/YO/t60b7aHopYP/E83wfcT9vRVr1eL3PQQaPRsGazmSFIOJCFMujzUqkU2l2TuxYKBatWqxliQtuO9ymVSpfedT6fW7lcDmXT7si5b59YP06nUysWi1ar1axYLNp4PLbZbBbeuVQqWblcDu3BwQ5mZtVqNbSR1rtYLFqlUsn0Ne+j7er7BnBttVq1Uqlkk8kkJFD2/U8duHY8Htt0Og3X6rNpQx0v/hr6gTIYL/pMlQt+m53rlFKpZKPRKPQx15fLZZtOp9bpdDJ9u7GxYbVazRIS1sF4PLZer5fRY61WK4y3hIRVGA6H1u/3r3zftYmncrl8ScmtY8jeNW7b0H/ouCtj/yp9HVsFMzOrVCppokxYG/5EMpwfJsr3RQQl4imfELrtaIvbJp6UMKAMHI5lzvqqd/vQxNMqfXwbxNN13n9VHe4aecSTkhHLolBixJMSl2bnTmitVstcjzxNJhObzWbBoVeog6rl86OkiSeeIB4gC/Q9lpGoPlrC9wkONY4wxBCEhTrW9XrdisWiTafTQC54sievDvxAnsTetVKpWKlUCuSFkmCriCetC9fG3tkThbQP76okjbZdrA2po8oY71UqlQI5Q3vqfFYul63RaIQ6UHcth7YolUpWKpUunSikpA/vT7/oNZVKJdNeEESVSiXIE+SGtoe+a6y9ec+NjY1AXs1mszAGyuVyIF+oI+1Yr9dDG0HA8K61Wi1DRnGN9k0e+UQb1+t1q1QqYeyqHNMu1KFarVq5XLZyuRxIKq0X/UWfKPHkiVTkYbFYBEJLnwnxBPlHm9frdSuXy5fGTKlUskqlYpPJxHq9XuYdYj5ZQkIMjBtdyMWeTjKUsC6ue6rdtYmnGO4D0XMf6nCfsKo9rutEX6WdU58k3BWWrfDfFMvIhmXRA/cNV6nXOteu0ya3gWXPydMpsb5YFrETc6SWlX3VOq1LxuVdcxVCJy8yIw95cus/v61+vepCRawuNylXr837fd1yuR5DDMfU7DLR4ckpBU4sDmUeQaTRKRA4EBpalj7Xv5OP4DCzTHQFP1pPJYjG43Gm/not44HyfWSIOt3rtKuvr48k8u+m77+sPfR/1QE+Os2/p74j1yjBpeXzznn10uv0N+8IUQRZo3WCjID49PpMo4hUlrQvKpWKVavVQJrMZjMbjUahvXmGRtdpJJNfEOI6ItZ4Zowo0ugKfSeN5qJ8fvt+1ugoHQ9mFsibxeI8gkz7QklcjQQbjUaXyGX6GmKI8T0ej5cSyFoH3kGJN0iqSqWSkSEl3jY2NjL1WEbsJiSsA6+jEhLeJ26VeFKss0J8Xx21hIRPBR/DOLzL+sfa56G3F7gpYfa+ZCdWz9hz8wypVYSSX71fRmwtQx6Bs6qsZW24rC7XaftVbbEKeX2uq/u+/Js8c13SLkY6KKHA8zUCIVbPZXVc9b1GRKiT7h1SnE8vdzHEtot5J15JBE8u6DvGSCwcX5xjnHhIgxgxSzuwFUyjufw7xcgOHGr9flmb8tsTKL7cvD6NlZknF0po6Xdanl5Lm5nZpa1iWheNYMp7T+6jT2hXJTHpM+SMetTrdSsUCoFc0baJvafWm+ie0WgUiBSVYyWdkAu2gBHR5LfwIVO8E2Sj17NKyvhrNGrLy4DvD9pM+4D6awSYbxv/fmbnaSEmk0mI0PLP0bE7nU7D++uP9jntwpY7JWF5DuOBSLvRaGSz2czq9XogBRXXjTRISLhN+Dlxlb3yPsiu9/Wc+/bsdXHTOt7GO94K8ZRn+K265zbgDeHbdoZuWt5Nnbu7xn2tV8L7wcfQ/3dFgHwMbbMMH9v73eaccp3yY5ERy8rLuy+PwLkK1p13rtJmV6nLVfvipotUedEG/v4YibwOQbiqfj5ySMtTR1qf4YkLdayXRTZ4ggvkRdz4+ug7qROsn+s7aZSLtoNuv1Kiz9dLwedKMChp5YkmX1/uUXImRsDFiKFl5LInafRzrQ/PjEH7W7c/KiHCdrzYvVyrZEehUMhs1fS5rsjp5LcQQ1YRoaPvrNvHzLJyE8tBpPLh2wwyiu/YLuYJUv4vl8s2m80yuaPMLBPV5Z8NaDvd5qY5xvw4Uuj33EfdfJ8rwebHKzlJlexia2KsPCVoPdlMe+i2S36znVIjo2izxeIib1RCwoeEl8FVCzPvAx9yXDyEMXnTOt7GO95axNP7YPpiK3b8vkty6Lrle+M39ox1yr7O8+874ZWQcBt4H4o+b/ypg3jdMlbdY/Z+x/BV6rlMXy77/qp4H++/6r3XrUOsnBiJlDdfrhu1sW69fbmxeq267rrPvA3ktdF1x5L/X8evfrZu+5tZJrGyRg5peT7JsydGcGT9liF/DWXGIqt8hEmMBPJj0+dt0vbQaCutv+YcUsKJcnyklMJHgmlbe5JHf/R+dfr9s6gDTnseScdzfH19G/C/T8Adq5t/R93+SNQK5eTJNSSG9jF/a+4l3pFy2RpGvjqNWKM+lUrFxuOxnZ6eZvJRKcGiZIeSbPou2t6eHCGKZzabWaPRyPQ39SJpOWQM7aPRTz7Si7Yzs0u5qPwWOq7XPtRIO72X72h/bQNPAmtkn5JrREaxXU5laD6f22AwsNlsFhKGa3nIEuVpTiolOCeTifX7/cw481FQCQkfG96nrZHw/nBrxNP7cADzVivvWjDv0oFap+zrPj8N2ISPHe9DxvOecZVnX6eeH2L83sYzP3W9c1dz0jJSy193XbyPBaTYM2PIq8dNxtJdvBtOvT5DbZO8PvMRRPqdwhND/ro8uVhmb+g9eX3uiSFPGHlyhnK1vsATAcv6QwmiZfmR8hYgIUeUOMi737+LLyt2jSaSjvWNEn/+MyUVY23ty49B31NJQK0zhJqW7ZO2K9GSJ4cxQjJW75gMQURNp9NM5BV/K5nj3x1CxxOovq8g4fife/2BI1pHHXearFzh82mpXOiPJ7e0/rQxJGCMAI4917+L/462/RC6OiHhfeJTtyU/VtwK8fQhld86httVy7hpeeus+N81YeYN09jnq5CiphIeApJ8frq4LT26qox1dKE6ArHrl81Vq+ZQ7xAvu2bVZ3nP9qRG7PNlz1/XEVqnv/IilK7ynHWfteo+H8XgyyyXy7axsZFJyqzEgNnl09cWi0VIzo1jqtcoiCLBoVZiJQafW0ojqfLeM5Ybh2foiWWr2spHdamzr+XG7uFzjfjxiav1Ou6NkWNml+XXv39etJSvCySCEicadUId6RuiibT/fc6kmC7gVDfdUqXQSBzqVqvVMqf++XryzMXifMuXmVmj0cjVJ/yPLEISEUnl+0tzKPn25j2Gw6GNx+PwPyezQdjqdj5klYik2WwWornoC+pBPqrY6X5sQfR5lSDBKI920bpTJ94V+VX5iEWIcR05n6gDpxUqSUbZegKevluMqERPcKLhYDCwhISEu0WKurp93Fly8YT7g+uujKQVlYSEhPuM+24QXJUouk/4GPV/3jtd5T2XXesjFWL970keLXMZqbfs+f4zJX2UZPB5a7TO/jkxIjXv+bF6LnuvmxrzniSNleuJ0mVt7L/jf7aXecLB999tjnG/pTH2DPqRBN8ahRO7XkkTJRVjchXbxuXLjtUvtoVSSVj/v4/u0b+VSCR6yV8T2/7p39WPRyXutAz9LPbDe2mdfVt68k0JUn1vvd8TqJBr/vnaZhCU933uS0j4GJDG2e3jXhJP75thXGc1+ypYp5z3Lcw3XflNrG9CQsJDxrr6K8955u88EkAdrmWIfb/McV3HeV11zbJ3X/e7GAmxyqnPI0m0na46r1yXJLqNOTDvffzR8rF2gPjRbU5mdsnJ53p1lmO5mGJ1jEVkcZ8mA/dlaFJjX4Y6x5Ad1EufSZ1j9/NsHH2fFNzXlc8hCpRIiG1XUzKCXD4+2bpGIvn2oe5EwRBFRJTQsi1yRGj5PqAc3395OZ6I+tGIGZ6rebY0gqnT6WRICX0PH7lE1JySG7y/1l+vZQspkU+0HeQH9aCPta+JJKpWq1apVDJ9Q5JurvF6BFQqFWu32zafz63X64W66Ul39LWWQQ4p4PM6EZ2oydApg0hEbRe+I4+T3lMsnp/yR7/5Z/GObHEcj8eZnHCTycQGg4GVSiWr1WpWLBZD+cgQbU65Kb9TQsLNcR/92vtYp9vGvSSePhbclgB9CoKYkJCQ8DHiQ+vvhzh35DmiN8Fd9YOPjPBREnwGfEROXj2XEXz62U3q7cuMleuJV70vRsTkRemsqm+sHusQuVeF1jtWvidllKzK65tYhIs+z/8fg08KT3mQHrGTByGEIESWyXgewePfBYIsj6DTrZfrnK6mhFVepI4vQ9/Fb/GMjTO/xTJGEueRwcvq72VF3we58H2vJCXtFXs//97+77y8aAkJCbeHD22ffYq4l8TTh4oGWrYCe93V2ZtimZG3zn3vM4orISEh4SFiHed2Hcd5mfO5jg5dVg8cmTwHPVaXmyLmeGk9l71zrF6+3sscYP0dm8+uQ0jEHMCrtF0eUaRRCdomvr+W2RYxsiJGCihwaomEwGHVMnCUtS19xITvQ3Wa9QQ5nhWDj/jxn8Uca/3O97HvayUhNK+Pvp8mq/bvqNu99OS7QqGQObFN66lJ46kHkVM8G2JI8whBShCdohFDsVxb4/HYer1eJlG9RtCYWSZ/EPWkTN7FR2ZpXqBlMs2JfXp/jFAjAqxWq2XyS+l1tI1GaOlzlLzSd9NxQ3TPdDq1w8PDzL3kThoMBjadTkO9eWahULgUbQSor0Yn0jYaYUY/cmKeRtEpkaaRUHm51ag3kVREs9Gfi8XCarVakMPZbGa9Xi/0NTJRrVZtsViE6KrbJmQTEj413Ee/9j7W6bbx3omnD0Xg3ASfmoJ/iH2UkHBXeF8rIvdx5eW263Qf33Ed5BEGMcLlpuWuuv4m89FVdPv7mPfWic5Yde9N66ltsir6IQ84vHmEmX52FVBuLDdTXr1WRXvo93nEFPf4a2PvkReVkUeI+jqsIid9eZ6U8/VfRtBqHfTavO90CxvkR2y7oydoNBJH6xsjncwskFPlcjma50eJQMrldx5JxPeQobHtmrG2jJWjZIrvtxhxGvtfP/dJ3H3yfcqez+chYT/v6sk1T3hp3WKEp76DtiFtpRFmvo1i5KgSUcueo32nWydVfnkGSdA1rxN10rxeCQkJCQ8N9zLi6b7BGycf+7MfomOY8OnirsfH+xoP93Hc3Xad7uM7mq1HOqxyuJfdn3etLzeP4NLfy65d9V2MXMh73jp95QmNdcpZFcUTu2cZQeWviT03r2/0Hu+g+mvy6oqTGXPaY/XW/DRmlonW0GeqY+odYD0NTB1f6mJml3Ic+WgbJbT0FC1tEx/FEWtfvT4WZaRtp0SKolC4vKVKv/NjhIiWWHSNJwG8XGj+I5+Ti/pr+Rrxpe+ibVgoFDJJvrmWqBff/v79a7WabW5uXiJEFouF9Xq9zOecZgdRpbLrc0iRV0jbwie3J98S70tEjn7m7+X0PW1zJXCoSx6RR/sSueZPdCSiJ0bOEBVUrVatVquFumibEpnFZ5A1mmOMyCn6czKZ2Hg8tkajEaKodAvjYnERtaQnGPp298SkjnOvG5QM1O/q9bpVq9VLEXyJbEpISHjouDbxdFsOxG05jffJ+bztyeG+OmsJCQnvFx+KAP8UsIwg4f9Vbb8OiaKfrTNXrEMWXaWOy3DduWvd+67yvnr9Vd5pWXtfpR7rlo3jGMv3ovf5U7xiBI5GfZhlI57435fniSnNDROTHSWrsiAgHAABAABJREFU2ArmT+TS+mky9HUIvNh1q/rPv7Ovq76jb0szC9vbYu3uy8WZn0wmmagSbTvIKcgVTbquxI2WD7FB+UqcxOqjKJfL1mg0Mom9SeA9Go1sOp1atVoNiashlJQ08eTHKiJc+xcShS2HROTkEapE3ni599vn/LsTvQOhMxwOM9fQpprY3T8fgq9er1ulUrHhcGjj8TjTj9wLgaRkL89Q4mk6ndpgMLD5fG61Ws3MsnmjeB8lnmgHT/zRZp5IVfKM/+lj+pzvKZ/+JgIqEU8JHwsemi37Iev70NpqFa5NPN224fYxNeptv8t12uchtOdDqGPC/UYyxBLuCuqcgVVEyIde/Ljp89e9/yrE2VXG6HXKzSOVlr1LjKC4iS5ZRbzEIn30Wv1cyQ0IkFiCZaJF9P5lxJASIfztcyVpXX29/DYv/65+u5CvL/CJumNt50kwT3zkXav1zGsD8i0pGaHvps/QiBP/HCUb9F7fjvSf9oEH9YpFCBFdQwQMhI2/xxNDvizfNz5CiTxCs9nMptNp5mTAGJHmI5KUBOT/UqkUCCitg+Yo8nmlFJrzSk/NUxLKzDL9pH2kn/lyIc40Ko0yGReQPhB7AMIyJpc+txP3QZjpiXiMbx9V5+Wb77TshISHjIfm/33I+j60tlqFG2+185PbXeI6q5/+3mX337T+NyHQVhnR1y37Jm2WkPBQ8LGR13n4FN7xrnAdYiFGFOjf6xAly3Twqv5cd369qvzflGiJlZdXl1XPUXJhVdmrylz2+U0Xb7xT679bRXx45J1aRVk+ysbsggDAab4KGemJJ1+HVfIV2/Kk9onmE9IfM8s421qfmL3DT6wdPanjt2h5YoV7VC607ZQM0mgdAPHin6N10bJ8Li5frm9/vc7nT6L+bCcjescnvS4UCoGc4R6+V+LCt7tu/YPYKpfLIcpL3ylGVvK/365I+fV6PUPcaAJ8TbRdKBTCu3nCs1QqhQgkPoeIG4/HoS4QONzn+1GJKG3D6XQaSDyIPfqBiCiIPi1fTxPUdldSLkYk8vlsNrN6vW71ej1EmXFNoXCRoN7LsxJlCQkJCQ8RHzzH01UM4Js4XauM29vATeuX9/nH6lTfpuOT8GliHacpIeE2EIt6MFufWLnps6/y/ao54yr1WYf80ufddPFl3c/9s1a906o2uW4/xQgqHw0UKz8vusGTLxpV4aNbPBGSR8IsI7j02th167SJkjD63Fg0jkLf0ZcVg2+rvOv9u3nkJfmOPUeft0z++Z1HTvl6KXS7VaFQCP9rfYnE0S2SvnzqwRYtJc70Gn4gPSBEzCyz3Y/nKEHF8yuVyqVIIA8lUXULX16b+pxYfKbX0C56Qp3mbdJ2iPUT10PuQFrxm3pSPiSTL0ffAbKKPlGCVbd4MkaVkPX96MenEmXUNyEhIeGh4sY5ntY1Mq+6onnd+tz0mnXxPiOJ3sczUmRUwkNFktmEmyIWpbPOfHVXiybL9PFVoqD8db6+nqi4SpnL6nwVsiJ27VVIj2Vl+zJ437x3jS30XGVu9KSTRsp4skOJJ5/nBmdWj1T3ZIvmXlJiis+8wxuDkg5eXigvllfKlwFZQvRL3jV5hA711HbxEUAxQitv25+2j9/ytCxZc6xeHuTl8TJKfX2kGu0CYRPb/jWZTGw4HGbyH0H+bGxsWKlUsn6/b+Px2JrNpm1sbATyZDabhVxJyFqz2bRqtRpyA/ntY0qWaE4qM7PxeGyDwSBTX6J/eLdGo2H1et0Gg0EmOkfBO2q/5iWQpx2n06mNx+MQHUXbKAk2Go0yuaUmk4lNJpMQQaR94duZNiKReKlUso2Njcy45x0Hg0FoBx+px29kiugpTiX0CdQ9Mc/ztHwl/3RbYalUstFoZIPBICSWzyMwExISEu47EnWeYGa3v/UiISEh4SFi3Qib23zWdYiW216wuerizTLCaB2sikC6Sl2uUvaqNr6tPlbnMLZQ58mUVfWMzdF583bs/b2s5UVBad21bJ//yD8rj3hYp0553+fhKu3o71n2jp4gWEVa6meUp+X6z/IIA32mRgWZWSAf9N68E+O0LE9K+ut4hkYM+S2R+jx999lsliGAtI18P/jteDGyz8tZTNY82ah94skzffaydo6R0D4nkz7Ty0ds66QvR+vK90qK6j2xNvB1TVvtEhISHjLeW3JxnURuw7C7rXKui/uw2rDuSux1jLmEhIeGD60TEh42rhPpkuccrSOHOFyrCBRf3qqy140g8uXkkRjqRMfKXOf5eXVYhyxYVudV5a/CdforL0rGl7dYLIIz7BMRx6KcYsetq+OpdYiRJrE6aJvgJBOVEYs24j7NhaPbh2JtptEzer+2A99rLh8lM7Q9lPSIvauWD3g3zVvkt/3FIs6UPND29VFJWpY/qc1Hyvi+4H21DWNEQ6VSCVvYNGm35l7iXXyUkUYkmVmIgvLb7YheAhBIWl6hcB5lpfLO9jbapd/v23Q6tUqlEk7YI1JL60n5o9EoXKttp+1bKBTCNfpsLwuNRsMKhfOIpMlkYpVKxRqNhplZJncUEUTad8g+kU66pbFWq1mxWLThcJiRe6KMtB1oUyK+6DvdTjgajTLyzBioVCpWq9UyWxq9ftd2JSKKSLt+v5/Ip4SEGyBm5yW8P6SIp4SEhI8CiXRKuA4+pOGRR+b4lW6FOsCriCIcIRwlEgfHtkwtI24e8iJPHkGjuC3SOi8iZlV9lpF63khet66eeFJydFkUSawMiAV/vyKP8MqT1VhbxZ4fu37ZPb4+efBjjXvWIXZj18TIwHX62tfBQ4kxJS3z+kEJQ09Y8r3POeXfX6N2lARSUi92upq2QYwo9CStXrtYXGz7U+JN6xJrx9hWNd/OShjG3tlf46/zYznmuPo+VCLV98Gqemh99D2Tk5yQcDMkP+HD470TT7fV6Ul41m+D2zKqExISbgex8XgVo3IdZzrhaljm/OfhJiRNLKKFLSmNRsMqlYptbm6G1Xy+Hw6HNplM7Pj4+FJuHi270WjY5uam1et129nZsdlsZl9//bX1+/0QRUGeGHWuWNXPky8fiaDXxj5bp028PPuomqtgGVmRVx/vKK9DFvj7tR81306eg0m53mHVY+71lDJ/jzqi6rxzjebImc1mwannszwnWsmiUqlk9XrdNjY2bHd318wsmodGozJms1k4cYzImNPT08wz/btoPTyhoe1KHRkn/jQw7Qttzxjx4J16T/AolAjRU958f8beTQkEf6+/noghxjnP9mQM41YjkYia0sTY3D+dTm00GmVkgHq0Wq3Qb5oDKUZw8Q7VajUQkZrgO0b+tFotq9VqNhwObTAYXGpLMwvPI3JLo/M41U/zWAEijTTfmcoF0VNEH5XLZavX60GGdLshJ9ch76PRKLSvtrO2nUaq0baeKCM5up40iM4lism3d6/Xy4wLxiEYj8chr1RCwqeCq9gD69of17XzEq6PFPF0A9wGoXOVMhKBlJDw8WGVc5znBCfyaT3cpt68CSHiof2o23EKhfOtFtVq1TY2NqzVaoVnT6fTkGy22+2aWTbfi9arUqnYxsaG1Wo129zctNlsZrVazUajkZXLZatWqzYej4Mz5ZMO+/e9LVmLRYXc9jM+FNYhL2PjOY/s8k6sJ6rWIbN8xIqPfokRUFoWstJsNq1QKFzKA6QnqCFTbFcyO3eS+/1+JoIllhfHJwP39VpGFvr2yhvz/nNPDuaRSUq25l2jRFZePfOilPy1SoLpdiyez48mc6dPtA2V/OBaiBDqof2mz9f7/bsrAeNPndO2MrNAHilJEmtfH13ln8V1PA+9qYSeb3/Vq/xfLpdDXfR6ytVrIIg8UabEE+V6Atm3B+9IP/iT7/SdPaFUq9XC9f6dEhI+Nty2vRGDbotN21bfL258qt2njJghdNV2ucr112nz1E8JHzseohEWM7z939758qcxrXJgPB5aG90Wrkrsr0MWrGMU5V1D7g4iEVg1N7swhnZ3d61Wq1m73bZGo2Hj8djG47GVy2VrtVq2ublpn3/+uZld5BkZjUYhssWfrMWK/5MnT2xnZydsxdFy9Sjy6XRqJycn4VQ1jUKItU9sK811VhlvW0bXNV6XGbreqY5978cm5J3fKhmLyvAkjJ7IpWSg3q9EgDq13GNmGSLBn65WKJznDiLahfI4Up4oKa3reDwOZKaZhRw7SpRwj+anmc/ngXggOmR/f98ODg7C6WXVatU2NzdtPp/bwcFBJjonlsBZyQjeWduDNvLROv4a/leSBPA+RH5pHiyNFKxUKlEC0D8/1tdehjSXj+aD0h+ebWYhGmg8HmfkwtfFzC69A9ehCzRPFnmmkEXIxuFwaIvFwur1ulWr1UxkUr1eD3XRZw8Gg3Afz0evaL9pAm0laXg3r9eUHGMLsSctlRyFsKEuIO9ddTz5ZOvkSKMsJYxi0Y7co3mgkH2fTF7ll+8pG/g2Tkj4mHAb9usq++Ply5f2/Plze/v2rX333XdLx9M6NmHC+rjViCedzK97/4dwjm7juTFn8UPivtQjIeEu8T6U/03G0jorN6sIJF3VpR5+1XodJJ0QRywCQv9f5/6r9INGGHC/OiTlcjkcmd5oNIKDNxwOg/OysbFhz58/t1KpZGdnZzaZTKzX69lkMgkJiok0wZkqFAq2vb1tZmbdbtcGg0F4V6Kr+H8ymVi32w3EmDro3rn1ESn3xSC7ST1ifbrKMMUZNruIUPKRIvqZj57R6AclO3xEW4xY0SgTJTVx9guFQmZrEU5vq9UKW7MKhfNtRiRYxrnlO+pRq9XMzEKSYyXdeH61Wg3PwIE2M6vX61apVKzf79vBwUHQaxBP0+nUjo6OzCybuwdSAH3oiU4lqZQI832k7RbrQ03OzbiBjPFtz7vr+3t5yeu32LN1u1yM4EVm2GKlkTm6GKFzBW1Be8b0v0ZDIS/0mxLOs9ksEJJKtlG+bt3VtmBbGFGcXp7pZ0++0MboLo3M1Lrru8fK1rZdLBaXEnrriXhKQOk49YnjfYSVPp/y9R79X8uk/5T8VRlhS/RkMgkkr46HhISHhqvaS9yjv0GMc8grW68pFAq2t7dnX375pU2nU/v+++9vdTwlomo5bvVUu5s6NQ/ZKfrQdY85lcnRTPjYcdfyfdPJYrFY2NbWlr18+TKs7KsDEHMiIRn29/etUCjY559/bhsbG8HIHgwGNhgMgjE9Go3s4ODAptNpyA/CMyAqiGxZhwRLOuNqiLVp7DP6pNVq2dbWViCIWNXXiJNGoxGcP5wO+pV8LCcnJ8ER1dV+HFONnOFHPyMfDPUg98l4PLZSqWQ7OzsZ54rTr4iu8g7QumPlpgtU65YXI8mWIa8+V9EBOLAaqQNxofmIzLLklP6vcqBbepTIoF+0bupgl0qlQBBBBDQajUDy4NDWarUM4UIfk1MGmZ3NZiGyrtFoZPI6mVmItKPO5CeiHYhIIapua2vLPv/885C0XEkj8pKRJ0oj7TRCRttOySa9VtvMt5WSD96h94SWypLex+eeWNTn8Bn3xRK5Mw4Xi4UNBoNMOUqQ8D/vhk6H2PNla9/qc8yyEXEKImtoD20HJWbQAfqd1oFy2YqpcrK5uWlm2a16njBFlikbmUJeIGYnk0km4kvbTIlWzQOlhJwnrWgjzaGkbUgbebKXMZtHGOq7aLtrnzDOmcfR7bSjJ5kTEh4a1iGGYmi1Wra7u5uJQIyVyRyAnXJ6empmFhb39ATKfr9vjUbDvvrqq3C9LgTyDOyeXq9nZ2dna9U37/0SAXXPczzdlXK9a6V9k/KvY5R7Qb4NZ/mqdcgrJ02OCXeN9yFj15XlxWJh29vb9td//ddWr9et3W5nEryq0asryycnJ/bP//zPViqV7O///u/t0aNHIQrh5OTETk9PQ2TB6empzefnxyx3Oh0zu5hk6/W61et16/f7uUmjY/9/auN2VUTCVbAqomFra8seP35sm5ubtrOzY/1+3969e2eLxSI4VRpBw6r/ZDLJOHnHx8dmlj2uWyMTzC7ILu+oQjwRuQApCglWLBZtb28vYyyxZYYEwT6BMe8ZI0TWIef03nXnoJjD71c2V9XjNkCbauSE9onfqmN2mXhSsoPoESUKuUadZi1T+1qjmc7Ozmw6nVqz2Qz6gIT1ONpEovR6PRsOh9ZqtUJ0UrVatV6vZwcHB1Yul63dbmeMeORASVGIAL+9aTqdWq1Ws62tLWu1WkHuhsOhvX371mazWchpdnBwEAgr6qknhOlvyD0l+pR40jaj3XwUk24VpE0hBChDy9W+9jpTiaYY4eVBW45Go0Cw8K6qD7SP0QlKVOq2LK2v3g+BQdt6qNzRlvV6PbyLboFTwkVlUgkWZAUCvVwu29bWls1mMzs9PbXZbBaSiqPrlHRS4lujAclfp7mYPLlLfSFaAcS89i0/OLYQn/puGlGn45x29lF62u+0E8/3fa/txrZp3frIdmzqkZDwMSJvzm+32/azn/3MKpWK1Wq1DMnudfxkMrHBYGCdTifoDRbzOLilWCxar9ezer1uP//5z20ymdjZ2ZkVCgXb2NjILBYNBgMbj8f29u1b63Q6N7IjYgEifP6pkFK3Qjzd9gomeF/OT+w5N3G+blLv23hnv9L7Iepwm+UkJNwHLBtT5XLZPv/885CAl+sXi4U9fvzY2u12WGlR51pX6NWBxHFUZxaHA6cRo79cLtvPfvYzGw6HdnJyksnzwzOPj49tOBwGw16hRJhfkfXG+ceKGAkSm9fWaQO9vlqt2uPHjzNb61qtVnA0tD80ogNnnh+cMbMLhxQHh8gDJZg0Ea1GZ/AOeXM2TqYSKRrJwClROKaNRiPzv277iW1FyWtDHw2i1+a1eV4569gjngyIIc8uuAo8iajGLOPal6vtmfdcdXjpF069wvkl0qTVatl0OrV6vW61Wi0Y3epsA6KkYlEqevqZj7yIEZvUU+WBk8lwpCENyP+kybGbzWYmybMSqvSP6k3VW55o4vpYX8ZkTIkjT4bmyWRsfoj1Wx7ZQ3QLbaBkCvKjcwULD5Aa+kzduqVbBXmO9pvmI/ORdZSnW7tVv8TaX0kr1QP63ug0rtGTNSGqlGSEwKKePJN6Qcr4OunfOp9B2jF2tG/0lD4llbT+Si6pfozJHFF+2i48L+9UOt0yqItSfl5OSHiIQP+j0znBt1gsBtKc+YDx2263gw5CX4A8fVWtVm13d9fm83kgq9h14BcmzCyMVbOsLcH1rVbLHj9+HIgtP+eY5efxy8On6CffmHh6H85IzCl4n8+7z8ir63Xa6K4IxIQExU1I0VhZt1neOs+LTXi1Ws3+03/6T/bFF19cchT8lhS2nvicGZpotFKp2M7OToaIwCjf3NwMkzTG+IsXL2w6ndrx8XFYVVYn/rvvvrOzs7NM3h+MclaC+JlMJmGViFXxWHJjs49bV1x1Bcq3RaFQsGazaf/u3/07a7VagfxTgomtTVyPE0R023A4DJFOyIgaTrPZzDqdjvX7fdvc3LxkOOGQ+lX7POeM1T7d8gJqtZrVajWbTCbhORBREArdbjezRQqoI6qf6XjS6AwAWXed9l92TR6pc9t6iXEIceIJZoxonp1HRvs6auQHUUg7OzuBiMTAJjLELEsmqZGskTWtViuQ5zwHUujp06c2m82s1+tliEnecTweZ05MVCceAvX09NSKxaJtbm7a1tZWyCVWKBQyWwNxPCCzxuOxdbvdTP4nJUBikShKHOg9MRJ0GfkU2+ao1/h7ln2nOYkU0+k0bJ+GkNOtZYVCITNX8KNkI7IEOcPzNIoL4snMgh6hf3TrrycXiazi3Wu1Wph7eCaEFvcqeaqEEDKFjtA6Qoxq/iMORuBdtc+QX2QnpoOVpFKiczQahdx2yAjkqG7/oy66SIBeHY1G4b1j2+hKpVIYT+h/FnpUJ/hINZ9nSrf2xXRzQsJDAGOx0WhYu9224XBop6entrGxYT//+c+tXC5bt9u12Wxm7XY7s91bdYVuB9Zydb4sFovWbDat3W5noqM0QtVHHauOUZIYPVCtVm1nZ8e63a69fv06ENhajm7RvU77rPJnPoZxf2Pi6arG+XWfYXZ7Db7KuHwf73RbuG3H72N2JBPuBx6SjHldsLW1FXLfqHNNMmicO3UOgRryuoLJd4pKpRIinnyCYeqlky1RDM1mM7NVgYmalRoSUMdy8/BOuuK7DrGd58w/pH6OQdtn1btwypNuW5rP57axsRFyb9G2agThVOCAqIMXc1x1tVu3lfjoAOrsV8253suPAkfKQwkTfiCg1GDC8GJ84CTp6VTUCfKAz/U74Ff773Juvg6hqgaqwo8RbXOz+HYZf02sLJVHyAL9Hv2jW3+U7KSMGInsyZm8NlfDXcke3x6UqRFO+j5c66M6lTwxs+CoQ4oiS7FoGn0n317r2H4eV5U7HX/rPteTjT5S0RNoep/+9sm2VQ+oTvFypoRQ3vcqH9QDvUUdtI28LGmZ1BfS0kfW6vyqBKBZdpuafh6TV5Urf4+eLqryo++q2/3y+lDbLiaHmnNRy9T7Y/XXer8P3XdXWFeXvo93e0i+3ccM9Dzbrjc2NsJ8pRGPXnY8IeTLjPWt6lJfltnFNm3KWAbKqlar1mw2AwmmddK8hMC/CzoMu1D180O3m9fBtYmnmONx13ifHfIpdL7HVY3tq95zk+clJMTwPmRIJ7Rf//rX9t//+38PSQt1stje3s4QAwBHSSc6VknU+cNAxUlrNBrBWFXDPOYUsCq7vb2dCfknEfnz589tb2/P9vf37R//8R9tMBhkEkSrExmLVuE5sTpo+3iHz7fjfcQ6hmjeu/D53t6ePX361DY3N213dzfkC5hOp7a/v58h88g3Ql9rclwMEp/fg88I8Sb5s9lFsl3kBKJLCUvdDhIzsvhsMpnYycmJmVnYHqryrE4Yp+tpAmYwGo1sNBrZeDy2Xq9n4/HYTk9PrVAo2ObmZuY0LiLtKH82m2WOPGf8sLroI4Q81pGzmEEb+3+dshaLReb0P0/yUI4mxvZEgD5L2zJGICrJ12g0QkQFpxRCfuuWO3XQVSZ8HhpIH/LxUBclDqkjdUK3KfHEVgice7aEEcGn5KxGb+GMIAeLxSLoQZLy93o9e/XqVSbqI0YMqKOu5KwnKpT08UmkY9fo+PFyUihcEMm6COH1ha8rc4KWD6mrUTeUodFk6HAleXWMatJuT2rptUThVqvVkNOJe2J5nGgPn4+Md/SRWupUMl7a7baZnUd4og90OyV15F7kbTabhRxk+v5E6FKGbm2n74nII2KUeZB21xNGeT/dyqeyrltMScpfrVYz47vX64U2pl2B6gPVBcibjj+VPyWu7hPWIXY9mRa796bk0DKS8KrkUyKqro9YP6iu3N7ett3d3dAnjGugc44fJ0oYeftDr/XRR55k1s+0bnkgipGUBFqW3ofO5RAP3d5HztW3b9/a6elpiJxcteCrdXvIcnmvk4snJHwMWMa2J9xfsLKhhh5bRHTFXZ2W2Aqv314RW5mNPdtHsfB3zHDjc4xzfSYOYKPRsOFwmDlRbT6fBweBKBW2zZhd5K3wTptG6Si0rTT/xccG2hUSiaTNtVotONn1et1Go5H1er2MQxgLy/ay4B1mzQ+iCb1xRPLamXI1SirPuPJEBNDyvfPDD0RHrHzuhYSo1+vhpMXpdBraUIkXbS/egfKJnPEO6l0gFi2xDtTB0TJixvE6zpoSIionPheTkh3r1E/7CF2lz9BoJE8u6Tv4CDVfvsqJlzEfUcLffjsdDj3GPH+v04ZXaWu9Z1WZeZ/5/laycJ1nm9klp4rfSvAsiwT0ddF5yjvfqxx1/dFnLyMS9H7+jpF+vg6+DCVb/efqVCqJ6dsgVj5103lSZU91mdfRsXJ1rJhl50ol71SfxXSL1kXroWTTQ7Ef2SJutjohuo9svS6W6etVRIj/rYSql92Eq4N0AWzVJVE45K3Z5XHqf/u5xiy7EOLH0TK9uKofYzoZHeqjFv04RT+xcMAPeo98rZxorPdoPfPs6YdMQN2IeFqn49aZ7BM+TTzEAXMdxIyUdQzlhPVwE/3iJyv9vFKp2C9+8Qvb3d21jY0Nq1ar9uzZs8yKq9+esFgsQqQHWLYao0aoGuKeoNA6qsGvBmyhUAirJm/fvrVer2fNZtMajYbVajVrtVpWq9Ws2WyG3CpquHOiVbfbDVEvAKP60aNHVq/X7dtvv7U3b95k6oVz+PjxYysUCvbu3btwNPh9wDLnatn3MSwW5/l7fvGLX9ijR49CP/Z6Pev3+4EgKRbPk3UrSUeET7fbDacTKmFolnXUi8ViWBEj9wtlQAqpk6Kf+xW0mCNYKp0fSd7v983MbGNjI1xDYmkilHiPWq12iRhV2cXRarfb1m63bTKZ2ObmphUKhZBz4ezszEaj0aWk0hhlSphxT7PZtFqtZq9evbJvv/32Up9on+aN7bx71u13D96VtuQ6Hb8xBz1WX29smlk4aIATeQqFC5JYSSd0QaPRyEQMecIT2SHaYz6/OKreR8ZpFI13HP02KaCEpJcNZFW3UZGDyutI3YKJsc94ePToUYii09Me2VqsDoAnQGP9h3PsnRs/VlTveuKF99FtIp40yVvNhrymbfS9NdqHd8QhJiqNPqVs+l7zNo1GowwR4POn1Wq1zLgvFC4idLyOJIqJ8mLOuF/8oJ603WQysdPTU1ssFhl9ou3sD1ng81KpZN1uN0SQVqvVkJuQMUBbLhaLsIBEHjKtix8nkLe0P/m3eH8/jlm8oTzksVar2Xw+DznRSJaPfVCr1TI5ZdDt8/nc6vV6pg6Autz3HE/04c7Ojr148cLMLuTBR+Wh8weDgZ2enoaI3eu+n/aRfqbf8T/tS58zXtBf4/HYDg8PbT6fBxkl/2JCPmJzbrFYtJcvX9qjR48yOtJHrurCWgyxuVMPX8kjrvR+nef0Hn77iMIYseS/R27QBSysjcdj63Q6mXkSf+L58+f25MkT63a71ul0bDKZhBxzjBFy0L1798663W50ceM+64IYbu1Uu/dBLiUS6xzrGNTrlpPa82a4q0H/kNnshww1PqvVaggF3tzctHq9HvZ1qzGtqy0YsjrJqBNlFp9QtZ/9pKiIyYVfiWXLwWAwCM4EhjZ5qDheXVdyG42G9Xq9sHVCy8fJ3dnZsY2NDdvf37/kcOB0YaDd1+0AtwFN6ry9vW39fj9sFyEigy0u2g5KJqkRzmo4cqNOp7YlRnpeNJnKpdkFkaW63q8Ia9kYTl6veaLTb/dQx1oNNORO24KEoThZtGUsgoK/kSmSXx8dHV06aSpPV8bmuXX16rrzI/WOtbtek0dc5X1GmUSFYYRCGKFrICTQXWZZksPXQ4kMvVZ1j5IQXLNOu6iRrmSiAj2pZJ0n2s0ukjhr+0L6F4tF63Q6GVmL1dETBbH65ulVP1Z0HPhrlLxQ0k3Ly4OOJ7Xv/DjT5+iPd6jziDE/ZvVe+gK50n70/afXeJJO30mJIvSARm+ST46tKEq8ejKW5+mJoEQLUC66V+WXd/QkrZavz/FOJmRSjKBUuVCyn3fw8q9jAl1Ke2r76QKC9tk6W3E+JHx0Xr1et83NTTO7yB1IsniN4OOdIPiUmL4q1iGeeDbzruZnZCHE58hbN5o04QLa7hx0sbm5mRkDsbGRBz+fcY/qIa/jvG7Pi5jSOsdsBq9j/XfIim7NNbsg6TV9AuMbvUddIDS1HZjziaTX53su4L7qBY9rE09eUefhNgfpfR/w74t5vK12uO/ted8Rc+RuUo7ZasXx0BTMfUes7dvttv3t3/6tbW5uWrvdtlqtZhsbG5dySpAbQg1j4CM4NCrFLGt08WxWbdRA1jrGJkfvfGAYPXr0KOTSwXnj1CQMKN6F8h89ehRWaEajUZjkWLWdz+ch8mJjY8N+8Ytf2KtXr+zrr78O943HY3v37p0Vi8VgrGvbfkgsq8O6YxCC7pe//KU1m02rVqvW6XRsPB5nknLP5/MQQeSdeXI6VSoV29vbyziGlKF5XdQB8qv5Wv9er2ej0ciazaa1Wq1g8JhdRDNQnn7H83Z2djKGjZ5SRV+SG4Vy+FHizJ+iBSGHUcW1rPyrY4rRxjZQPVVxOp3a6empdbtdMzP77LPPbDgc2snJSWZLhOrlvMWVdeRy2X15WGU0U0+NYvEEQLvdDuNMoy+UtCsWi5nIABwm+tbXRR08Be3sDX7aG2dbv/N5i2Krw5ThdaJGPvkk+T6aju0Yqj/JobO1tWWDwcBOTk4CKR6LvlrWJzH9yThT2abtvL3rnRb0ttqB/to88Gw9sQngqCsB7duc9/Zbahm/kLb63j5iEZlUIgACgLlOjzjXk1NxjCBfyuWyvXz50lqtVmiL0Whkg8HAOp2OvX792orFon3++edWrVbDyarkAEMPdLtd29/fv0Te6PjxW9x1TuY+IoE1f6EnarlHIxaIBPQn6tHOlUol5Cvz2/4gh6mzyjxtrwcwmJ2f9sX9jG2dDxiT9812p09evnwZIlvNssfTa3/peGCMI0NEfUwmk3BK71XqoRG/CvSm5pHTrcrcjy7ERnry5EmYz5kT35ev99AQI0/JPYrt0Ov1MoSqzsUxEtgj1u46z3u9HCOcVtXf/46lEgDoQ6IUWSQivcXGxkYY15TB/I4dhm4gZYPZxXhBlvf29sIuC/JgdjqdSzZPXhvdJ9xJjqd1CKmPDeu+68eksD6l/vXIW1FZB8vGh3eA8+TlfchRntN23+BXH68LNZa++uor297eDsajroSZXezF9m2kK7a6zQJnMy+0Vx0/dQgUGk3C9/p8LbvZbIZ7MHbH43HmFCzdwuLfQR2x2ez8GHQ9nafVagXH8scffwzlQ1JRTp6cfqg54qpjJta35XLZXrx4YZubm3Z4eGj9fj+TH4u+zzOgkB2O8sbB01Ux3bqlfU5EkpllSCozC/mkIJmUeNEcA9yrTjp14T2VjKBuOGS6XcdHKCj5g7OlR5grYaZtxlhhjDUajYzByPYSHMhSqWTb29vW7Xbt7Owst1+vK1/XWUzT/uY6Xy8d5zhl/iSxer1uW1tbIf8FbUj70K5KVLANT8lLX1f0EOSUEohezhaLRdjGpUS4j3bzUTUevJs/KVFJMCU5cFaU0NTj6tVx1NVj7xQsI5K9zqWftAwlerWcvPmZe+gbHQNXXaT1kR7MM4xfiFmtB9fQ3mz74Hucer1Gt7rwfHXYdeGEedBHM6peQu9AUD158sR2d3dDPU9PT+3k5CRsGSaiuNFohLxv3W7XRqNRmG8Xi4UdHx9fIv6UeMobZ/xG7vW3LgSpLPMukGAsEOiCk45h9BXJ+LXP/XY4/1yz7PYzXVRA3+l8AAF834gnlYHt7W17/Phx+E5JNXXilWDwpPJ0OrVarWbD4dBOT0+vXB/6z8/B6A4lB3wUXkwnbG1t2Ww2s36/f0kOPxZf7jYQ84nYOdButwOhMhwOw7jR+SW2EHAVH8Rfuw7RtC783KC6QuUKXaGLM7oohF3HoSyDwSAs9JKSgWtqtZqZXdhqbNXV/JadTufW3vF94k6Ip/ukFO8ascH2KRJvnxLoV/KX+HBos8tJ6NTYMIuHe/rV2rOzMzs4OMiVsWXG9W3gocnvVck/vzqwu7tr/+bf/Bvb3Ny0zc3NENqK4cff3mmPRQzguPjrmDBiTgYONXWK9amPWlCnBznzq06VSiWsNBNFoM6dOkm8oxptWkeehVw/f/7cfvOb34RVSkiC8Xhs+/v7uTmePpRsrfPcPINHj/7l1LVutxtWxc2yuWGUpFwsFiGawP+oQ0OeEJUdZAljRh0cJXuIRJvP53Z2dhZOlFPHCSee6CjIJJxB1VOUz/0aPYexrvlSlGjS9uA9IFq0vTSiS5123glyijoQPWV2kYft5cuXNhwO7d27d1dOOO51gH4WQ9641Pf1ZejYUaIXEoj/t7e3Q+4Hv7KKTGoovpmFVWRIKD9OuU+JPXQFpFWM9PbyS7SVWXZ7ns59nvjxhr/2G3XRtvLlc/ImzuF0OrXRaBRy4QyHw4yTiW70ZI+2oUL1perCvOu1nZTw9fA62P8dky8tOy+CSu9VQplr6Q8cZp1jlrWDEjiqk7QukFY47ETUAk9GIxfD4TDIIhFE1WrVfvGLX1ixeH6qHc4puq3f74c8eWZmL168yBA5KquFQsHOzs7s7OwsOHQqkz46KyYXXItuRMeUy2Xb3NwMW/pisqGkiUY5e4KPdmHM6UIDgOAzs0sEoie7Yv34PqHPJnK30WiEBQNvDyl8O+qihXfkdc5cx8ZVW0j7G9uKOQyiU+XC7CJCDqAniUbRvlS9m3I+XSxeVSqVkBuONibFg7d3zS6ISLPL+nEZyRfzi8ziB6h4AtjDX49O0O2u6El9RqlUCjshiICv1WqZNBS6cER5EFEclFKv163dbocoZuYzjR5HR85ms/C3mQX5wx5DJ+W9633ArRBPN2F+b5ukuWvSxxsAMTw0hz1hOWL9WSicb4l49uxZMJz0O2W7dbuEAsWEUeMn11evXtnh4WHUCfaK5VNffbkq6aS/+XtnZ8f+43/8j9ZoNDLRQHpd3rYUvjO7iHby2wNiq82+rJhh7Fdv/XeeeFJDCvmbTCZ2cnIS9tjHJmd1SHUl1r9HoVAIk+vTp09D8lq2kB0dHVmv17NOp5NJyvqh5TNPRvLGt0etVrOnT59atVoNjm+v17PxeHzJ8dCx7h1uJVe8nGDcENmDE6fEk0aGcC3EE31NktZut2v1ej0YfpTb6/VCDjDIi/F4HMrFoFJSic+VGMOgwtBUAkBXL4m44Nm63cyTaDp+MMJY7eN/jKtGo2FPnz61fr8ftmXEHMRVdkEe2ahYJr9epyjpo9d4QkeJvcePH9v29naItPDkk9nFtis1YGu1WnBmVQepDCKTnpBifCrZqEY18kz/UZbqIo2m88435ULUqkOtUTu69RcZhchuNptWqVRsPB6H7S66TZOEzf6QBx9don2tf8dIGn+PtoMvV+Vc+17lVMtbRjwpaaQEg7a56m2tO/f6+cT/7R073ZqkuXUYk9r3ENBPnjyxzz77LFMnJSTp6+FwGBx0VvY3Njbs888/z8gFukyTZ0+nU9ve3rYXL14EvQcxNJ/Pg8M3n8/t5OQkRP1pn9A+6BltZ81jxf/M5dPpNGx57XQ6YXuvX0TkPuZZdCJlqbNJ2xCxUCwWL+lytjTSR2zliyVFf19+Rh4pwGeVSsWeP39urVYr08be9vHy58tCd6guIcLDRwHGoHaMkrbUhbZDZyrxpONfFz3ULucedA12PykGPkVoH5LPq9Fo2O7u7iWiXG0es8unVfo5eBlZtMr/1p+8smJ2gv6NHCHjavswP5Lns1KpWLvdDuRbtVrN2EGan05B5C76QreZkmwcnQTxiTxC8I3HYzs7Owt6hWfpu3xo29vjTiKeroIPQdKseqYXyGUCyt50v7roDYL5fB62ZCQ8TKDIWq2W1et1a7VaQTGpsecdKTO7NBGbxZOEqqzV63V7+vTppZUjNWK63a4NBoNLhsh9UzT3GZubm7azsxNIxBgpo6vpQHVDzMHUaI88h8CXq6dzeEfDG/neudIVFn3OfH5+6k6r1crko0BGfd3V6fBGpw+N9tEu1WrVms1m2AplZiECytfJt9ddI29MrPpcZUGjxcwsk4g7RgrybjHHFP3g29zMMs4FBgt/+62RmoMHw11PiSJaRGWl0WiE06A0CgYnk35VImowGIRIBIwwHNLRaJQhRXzEEg4j32tuId82i8UiE2Gg7UdCTn1X3r1er9ticZ68ViMJYv27iojKuz4PvpyYLOh4KpVKITpDtx34vG5mdkkfqBGfByWaVNdQHvooj2BRXeIdSe8E8r9uiYttdeG9gR6fjZxoechNv98PfUpkXr/fD3pNnVOtW4y48+2q//toB72efvJtxTUxJ0fffV1503J8f8UWAfwYydsKFCPg+E7bzBOTjDnmRpzv3d1dazQamZxUnlDXuc3nSOEen5eN7aLoiHq9HsgkPQhDCepGo2E7OzuXyB7Kh8BWmVfdSjuj5zQCB5ILnRODyqq2JbrRy4eSIjEZ5BrmVKIZYvL8PhB7JnPS9vZ2iB4CXj/EdOGy56hTT6Sdj/SOgT5FtnQO428f6aTRcdyjZemYUpKQ9+Xksk8VOnZpX6JxdAHULGtDqr2yTFbynqmIzZX+87xxo/o5do2335SEYsGORRR0hi40+q296CfVlWoPcx1RYugmIkHJJarlmFmIdPe56JQ0v0+4NvF0UwV4VcNvXdykPO9IeueTz0GxeL6nGQICI1gnMjMLKyA//fTTB0+4e512j92z7P735UjeNWJGa7lctufPn9ujR4/C50xKeUYt3+m+X73XOwZ8trm5GZJzepnium+//TazdSURTqvlz4+/J0+e2N/+7d+GFQtd6cCgJJpHI9e8s+HbHkeJvtfJS69RQwmSwOzyFgkmKCY7dI0a1P5YWb6vVqu2t7cXZJXrNaJLiQklsnAmkX81iguF82gXPZ2tUqnYZDKxbrdrGxsb9u7dOzs5OQlla2i6d8zy+uqu4Q0k/7lGIWiuL7OLLRKsSGtOHMpTg1Yjh3TrpToiOs7NLsicGHCIMc7p78ViEQwS8m4RObS9vR3ehUgT7iV6iXdncYVEvyTbxziaTqd2dHRk0+k0nP7Iyhyh48hDtVq1Z8+eWaVSCWQCP9pumh9FSVbanrbg70KhEFYeyQmj/XeTOWnVnKl2Qoxc9joCR3Zvby9DZGpEmuoW5E7v1/bRvjK7fHoZwA5RHaZbO7lXf3ujWb8DEE66lYptWHmOx2QyCYcdqK6JOSdsZ/URfcVi0XZ3dy9FPKGvGGNK4GiduEajHLzcKNmrkXgazcRYjel3r1vXIZ54DnMHEbi6Mu4XsXg35MKTFLyD1ot+U3JICSK2blSrVfv1r39t29vbmbwsRCAyjvVUT21T3U6LgwaxrFtji8ViSF+ws7Nje3t7IcrNtzlz62KxsFarZbVazc7Ozmx/fz8ToUX0FI6eOomMV9qZHFVKpJK4npyJGhGlhAgEkc6fOIE+F6QnPqiDkoq072g0yiRb93L1IcA7tlot+4u/+IsMKefH+zLyNfYO3lZintHxvQz0w2QyCYQlbUlUCqSBEoJ5BC19rBEpKltE7H1q8HOOmYVDAiBkzC73udqbjKWYXUP5Ogf6OU7L9bou9rlHjBBVmVUdRlkQ4Sywqk6jXoxZLYfyfWoFnTM00pjozcXi/DCbyWRiZ2dnNhwOg61JW7L4UigUgl1H3b/55puPi3i6KksZw104FcsMTIyEVXuk1yVnYORjeXxU+BEQVmQ1n8b7VlrXeeZV++ljIJ0AK9NKHDFpxRSL2YUDoox/Xrt7wkKVEfeZZbdCKPS4WrPzFRi2T3yKE6LZ1eWP0yf0aFOz/PBc71yqHGD0m2WdDV+Wyow6NHrvqnfTyUrrqPfiWHL9YrHIECR+8lMHReuvDodvI3Vo+axQKNjW1lYg0kqlko1Go5Dzw2/Jib3jh9CNsc9oZ3VkVR54X23rvHJjhlTMIdXVfTVMdFuGrpoBnYeIHFAjZxmBxvtACiqhQP9pfiI1lDR5phqXujJI/ah7XmQf32s76XjhmbpVhiiuYrFoZ2dna/XtbeIqBq7ZxWo80Wb+fi8T9LX/XPWLXhMrS8kclcOYLKqj799Rx7l3BtRp12gClUfKx/lGXpTk13Kxl3ieT+LvkzirE8CzY/2AfvMRP1zrCSSv530bxyK81LmNtZlep5GQeo/vg5i+oExvJ1BfL2N87iPj0BFETe7u7lq73bbd3V1rtVoZwogcW2pPK0msskTUDs9WBwyHjm1LmpBeiSx++BxQf6LQzS5OSgMqh779vJ7V9uQzH0Hp7bIY/ByuY88/R+vn6+FlM9b/7wO1Wi2Qc5BxuoVxXay6VvUcc2qtVsuQQOuUTz01bUJM1y6rj5//zS4ijJnrNNjgU0OhUAhbyzQ/YYzU0d+rsEyHml3Oc+bHt36WZx+rzsurl+pPDuTQgxu0bpSBb6+LBMwNPk+d3o98QkxrxCT6slqthvyd+m5qt8f+v2/4YFvt7kJxqnDHJoRC4XxVdGtrK6NQvGHiJ+uYolejW4VOV/BUuAhPns1mdnh4GIzjvHZYZajcBB9i0npI0PZpNBr21VdfhQkXqDIxi4d/qvEVm+y8QxUzbPOMF7C3txeirwqFgp2cnITj7a8ywT5krJJnb7j571ih1+SReSvfODrq+KhB7B0WDCfvlPhtFGaX80ep4xQLIfaTi5IQPMsTRUQL8C7kZ1JHEIdYDS7y/WibmJ1Psr1eL6zQqNFBqPCzZ8+s0+nYjz/+aN98803GCc5L2prXXzfBsvJi3/GZRnn5lWnACreeOBIrKzbn6DzCXDIYDMJJSZzy02w2Q7SR2cVpJ5qAG4fRn2BFe5NfqVqtRus7m81ClEC32w2k4mJxHoG5vb0dkjwD8hyYWTA8kUOtr5bPKj7yqXXQMcA8i6HF6p7Ot6wQ1mq1kGOM7cceq5yM2wL9qg6tGsRsS2D8cR2EnsqHOjZeF1AWfVIsFjNzlcoW/yvJ4d+de8lb4smJQuEiTwX6TnNLmV30MRFxSoZCQmLAI6+z2cy63W7QTxj5tKHq12KxGGRKt+BpxKYSVL6+1AfZ5x6zC31Nn3CtOr2x7ZBmFzaBzvn0l5Jknijz/cR91AEdSV+rjclzGT8snigB6KPcKNdH13EPuvzx48f2d3/3d9ZsNm13d9eKxaK9ffvWer2eHR4e2vHxse3t7dmLFy8CMa1tR1049ht9pmODU+OePHlim5ubtr+/b2dnZzYajWx/f/9SdOxsNgu53NCHkNuVSsW2trZsPB6H5ylZT/uqfa7kl9pfSiToooo6iXoP32mUBPXWdveEBX6Gbq32uoPytQ534VTm2Un8v7u7a0+fPg36VuXG2zDLyLGY7Me+Y9EXGa7X65m8kaugOoZ5w+vW2Dv7evvtl2bZKGPmyE8J9HGxWLRnz57Z06dPM4sInpyP9bm3J9WP9jahH8dqa67rI8f8LbXftRxfrkb7TqdTazabmYOlsA2Rh/n8PEfhYDDIRGf6iFRypeqcSIQ5By/wnthN33//fTjNztuPsW2599Hv++A5nu4KMYMeo0lDbZVcUiFTZaNKNO83z/SfAZ7NJAmb6Qenj56JvVPC3YH2RQnU6/WwGgf8qkseu+8VqV/l9wSD9n1exIt/hpdvZEsNV3V+7qMS+lCo1+vBMcYhio2/WJv51XI/YS4bp6v6QMuKGYExI8n3r/a7Pi9GZMbkT8uIES36fL+KzP+aB6FQOF8Z48hYjHAcv/sol3qSGwlJzS4nV161eBCbK/ifz9Sw0XBtHNVisRjylOiWIsrRlTJdjfPOLPCyETPI9Frd2gYRoeX5rYH6frFV5tlsFlYOVS/yXWxehEj18qJzvTqY2ka3hXXLi/U1Rir19ItjsciWPHtA9bsaz34l1pfn7ZlYXX2dNe9drC8xjLlW66sLdP5/7U8IIr8y7O0rfUfGhPZ/XntdxUHh3fPmAP/+ec6KXruuY6Rl0646j68qK9a3Sp55vaXXo++wdZBVZA2nC72Ek6URSHl2K+VpPrPFYnFpvCpB5t9nVRv6LaSQ8cjZMv2nz+N33rsg67HP8+oY0wcxOeE39oWfY+7a/vfvj98CUQ7RF9P3d1EX9ITK5Coo2asyvMomW/a9Eo6QhMy399F2uWugV/CT1D8yy49wikXQrrpHn6fzp783rx+0XCWrtC5+vPl7gRKNmuZCfQHVkxBBSjyZXfht6CdkS3/0fc0uFhXY7lcoFDILGYvFxW4q0iXcV7w34ul9kCbe8SqVSrazsxNOnGDi84NE7zfLJgKOGWqUr/doGdzvlRJCT/iyGo0IMqvMy5y9hNW4qrx5Y21ra8s+//zzIC9quJldlpFlilavjZFLfrXkKhOZl5F6vW5fffWVjUYjOzg4CPuB81ZpP4ZJ86p9zQT0N3/zN/arX/0q5JUgT4U6RMuMXu/4meWHwS+bGLnXR1tpOTj7ec9QctHfh9NAfZvN5iUHh9+6gkOOj8XiPMFvoVAIUWHo02q1atvb2+FaIhh0AiXXBY4hk2Wv17Mff/zRRqPR2gT+TbBM1mMy9OTJE3v27FlmJY9IH3UQMDh0nNM2Stro/MJWMZznfr8fDBT9zf3D4TAk9j46OsqsiBE5w29OFCSnhVk2l9hisQgnp9CX9EuhUAj5TJijlAQoFM5zzmxubgZDh/dBZljp1wS/PDcWJao6FRlH7mg35kRdsGHOZLxubGwEQ5hjilW3Xkee8sgHj9j8oJ+xgMEJg3ocsq5oavQQUWn6fN1iVCgUglwoQamEEXXQaKCY80a9NZqgUCiESJK8+YprzC5O4ELXEDmjhIBuy0WekC36j2fwHO/gebJtPp+HfC7Itb6Tzw2j+lZX6PU7HxWhxAjjBdnT8jXyQ8lDL+MxInY8HmeiTWnX4XCYieqCrFHwLHQ99YZIIgpNr/WRcc+ePbPnz5/b6empHR4e2unpqf3hD3/I5DPhuO7F4jy30nA4tK+//jroIbV3NOKn1Wpl+tHLcafTsV6vF+YT318agbm5uXlpEY+5h0U3jazTqFBORNT+81ux8nYx6DvpNt9CoRBOWaS9C4WLhReVHR1/qu/8/Edeqxjh6yOybgu+DrTJ8+fPbWdnJ5M42mMZMbvq89g1tLeeJlatVq3f74d8hTEUi8UQCUf6BO/U59loq+pEPdCryDu20cdgS68L3l/nB/+jiPmy3m+KkcA6Z8VS2+SRVHnwuh7dwv/L3kExGo2s3++HiGWdU4nsHAwG1ul0MmUpn6C2SqvVCqe36s4LjSBkbnj27Jk1m007PT21d+/e2WAwsKOjIxsOh3Z2dmaz2cyeP38eUl0sa/cPhY824snswijiJAM6L7Zaob/1/tjfsWv1GiWfYsQUKwjquDIxakJyDIm85yXEcZO2QqnVarUQSqkTfqzsPCWFwoix6eqQ+jqvM4nnXVsqlcKpYuyLz1uNXKVcPybo2MR52N7eDomOvTOh15rlR4L4NlxllAGvgzzJdVXjLY+soX44JGYXhIBu18gj2H00hd7L9YSde5n24dHtdts2NzczTrJPwOrb932s2uSNAfIW8A4YFEoyahnewPDbD2LP5J1xhiCJdRXLLJugdjqdWrVaDRFYuqpLn0IqAU/46Cl3fA65iXGuK7tKGvGdkpq8K+NH50BtG7/NKBblkyfD/h3UydVIHwy0u3LQ8qB19++B0axOPO8BPJkSW03X/4vFYpBJjZjT75WMoF58550BbWONTNJtQWbxZLA61nmeOvLqvHtyR9vPz7f6zlonf6+uDvutrn5cep0Xm3vziHAd17Ht2HlgTOQ5vUqmqdOv9+k13jb184efwxgLWn/Nt4UjSR4nPudAAPpTIx9JLj4YDDJR/F7fqdPItkr0FHVWstqfIKf6BNtMZYNVfr+AYnZxXDn6MJYPzEeNx/oyr209GZQXcahlLHsOwCfwefi8HrxN+PrRjrqtSNtBkWf/5j1nWf096Wdml0i8ZYhFjeiC2k1sCtoFwlLJw08NejBGHmHj7TlFnix5eLJGdX9sHOX97WVK0xB4uVhmr7EootFLWif93i96+MVjnWMJkNHAGH0u3AW5omezmZ2dnYXviPLUA2t0oeQ++XrvjXha14G+qaPhhY6G15BeL2AMHP3cKyp1ImL11P/zjF2uwaBQ45PVcVh0HIOTkxPr9/uZctYRoPfltN1H3OS9Hz9+bE+fPs0cR64hlLHfeSSkGnVKMgI1nrS/lpFY/h3V0FFUq1V78uRJMLrm83lYDdaTpvJyoTwkrOpv7wD+6le/skePHtmLFy9CH5HUlEmD1WFOyvJ9R7lqiIDYZJvXtzpx5vWllhWTA/08ZtT6aCwl03AotH6eUIBc4llKWnCtEiVE5jAhcwrI1taW/epXvwp1mc1m9jd/8zc2GAzst7/9rR0dHdnp6Wk4pfG29ddVyzs4OLB+vx8Mb5UBdYLNLiKK1GBHp2ubLhaLsDpODoDpdBpyAahjHtPhxeLFVrvBYBDKUQNGHVS/mocuUBJLn6ERN3myOxwOQx8hsziO3AsZyXvru6k86hYsoKS5EiHFYjGMzZgDRvTVz372M3v58qV988039vbt2yv1+TKs4zD5LQAYi+SWZEVToydoX5+7SyMveK6OXX7rtqdarXYpmkThSQhff6CklSdB9bn8rfqH6BccfX1WHik4nU6t3++HiMJqtZqJ1C0Wz/M6bW9vhzJms5m9ffvWhsNhJum1OhjICePSO0n+HbhXn+tJHSVX9TslovS7PFLIg7LZfqyRkvS7OtTaj2xbRd6UxPJ5aeijzc1NK5VK1uv1wtgxO5dDFmQ4BUy3TWt/ElmC4zQej+3k5MRms5k9fvw4fKd6QvWKzjWLxcK63W447dDPU8gPiwGMj6Ojo6BTVccUCoVA8mLPff/993Z2dhai8SC6CoVsjhY9CU/liLprfcrlsjWbzVAv2t8vpmikGnLobUBki0gIdSg7nU6QY5+A/6agPzn9lnZBd+WRK8t0Yozs9c/Ta2P+F/2oh1d4m8eX0+v1wmmMRMD5/E55dc2rn36mQQz0qSfnP0Z4uxOShPGh8rxqgdYjz4fiN32InotFjXq7l2u8DldbCF2ri3D6t7eBVNcPBoMwx6n9TpoETvnU+up1zD+j0chqtVom7YSOGT9/8BmHPxAFOhwObT6/OMF4PB7b1taW/eVf/qWdnp7a27dvV/bD+8KDj3jSRvTCoZN+bJWMa7zTr6sx6kho2b7zrqJwvCDpAILtZPLr9/u5yfTyCIqb4qYkYB5J4nHfiLFCoWCtVsuePXt2yUlTxaqOnTdEVE5iMqIOQ55C9gZ+7G81omNyXSwWwwkvGJ69Xi8cx0nb40DeB2X0PlAsFu3p06f28uVLa7fblwgXfmgjXV3240KjLfQ6T1IDLxMxPbVsTMR0zLLIKX9fbPKMQeVcnUnfTjhHSqqo8aGRM6zU4AhgvJmdy+Xr169tNBpZr9eLGpQfAowXDAK/ggogRDQ3oJJAeY7rYDAI20f0eG6Fkt/II/9z2pyfHwiBh3RWqPFFfaijN+Z8PwKcYzMLWy/89iuNvtItg17fca2PfNKIYN8OPmG6vlOxWLSdnR0rlUr25s2beMfmICZ3eWM2D37sq8FMQlQcSR1jyAxjha1DPJP35EfbkTFHxLRvYz+W+UyN4Nh7QnLGjjFXwoAfdQyWHSXvtxRTHmNNF/2oS6FwHpGjxNNkMrHDw0MrFC62YvqIVd832paeYFXk9bm2ubZT7HO9X52avDnf609PYCmhhm7Rz4rFi6O9lXjWa7Qt2AkAwUedIZwqlUomOs+Xt1gsMlupiQqFTIfwod01Mk91A2XzP7IUyyNUKpUCYYSu7Xa7oU4+ogkCpd1uW71et/39/dD/JPaF8GXLlPYVfRHLO6d963dSKOmk8686nb7f/dyJriCKj8MDbjOCIUYmtNvtDKG4Kp9TzNb1xFDsGv08j0TwZHHMCffP1W3qtJdGaitigQS+3DyyShfX/OLjxw7sBbULvS+kn/v5KjaP5ulttU2UTIpda3b54C9NhE/9dGz6SEVvj2g9tAyVM60TW6N1EY86+KhB9C4LNDpXx9pHxxPk+WJxvu251+tZs9kMOnU2m1mj0Qh5Vd+9e3dvZPTBE09+wCNwHP0Z2w/vESOBlHTiu7x7qMcq8inmkOYZshgR29vbYWLHODs9Pb1zAbqJ4+fvzavrfRgE9DOyMp+fR5kpUJqxqKW8MvV3zNnSz1Y5O3lAXmOKKjYRsuqHUTEYDIIxyVafjwl5CrzRaFir1Qrtof2giXSBP4nHG7meUPROfcwp8SSV/o4ZVssMNy3T660YvGGgK/UYa6yOUzarOvxoHjofBYTzgxOqJ8vwHc+D3H3x4oU1Gg0bjUbhxI4PBdq51WoFh4VcScBvf1Dw7u12O6xUE5mkzjrRh3nOqMoC85huRVEC0Ds/k8kkk8+QsmNkI/criRqDGnQQTl7OfDTcYrEIehUZVkfGjx/eS09/4TPeSw1cfT5labsqYvog5jBdZ+7zdTE7b9d2ux1yjUAU6vuoIatjSldI1fn15B1GM9FA6HfaWucs1SHeJorJs/aLGvKUgyOsZCtOHtF+GjWC3lAii+jb8Xgc8nptbm6amdnx8bENBgPb3t4OuTq5hy0FRJBRhte3eQ6RWZaIwgGgHWLb03kPL3Pahvques0yx9bMAgGixKpPRKtOknfAuZY2RK9CQjPH6zuenp4GouHRo0e2ubmZOQEQYHeaXZxayRibTCYhIp/nUme+84ezqAyhjygXOwRiXYl+TlYlUgFy3+x8Tqd96FvGBU7fdDq1drttX375ZYboYVxub29njkp/+/atvXv37pIzqnOc2QURP5/PQ5TNYrEICwJcq9F/3kbktxKKi8UiI9Pkt4F0vYmNDpDNer0eTvbd2NjInAK37Dl5c8U6BNE6dq62S6FQsEePHlm9XrezszM7OTm5kg8Ri3iK1RFdnkeG+UWAWq2WOU3xY7OjzeIkfrvdDnmJ1A40u0zQaxl58hRr70KhEFIeIPs8P3atkjtK3qqtovOafqbET6xulFEsFjNpGJREV1KL6/yzffugM2ezWdgaDKmkZcR0PlFVzJ8sFmhe62KxGE6yvi+4NvGUx8jlfbdOeesqIf8c/7xS6SKZoZ5gt04dFDEnUCfNdeutrD3/x56tTivXbG1theS97OlkX+ddYVlb5RlR90mo14UqE3KBLRYL63Q6wZBWeGcoZkDkIUY0LWu7ZXKVZ8R6MsNPgJpjAeU2Go3CVoWHimXOov+OVVjyYKlBqU6UOsd+FVWN1hix5K8xy4/G9IST1y96j3+GJ5tik6+uyACNmtHyWKVR0snnmdEVdUgAyqfd2GaDM0G9IU1oFxyX+Xxuz549s62tLfv+++/X6tf3gWazaXt7e5l8Sn5rjh9jSgK1Wq0QTTAcDq3X64XtIJThI8ViOkEde3VQe72ezWazYJjofn6SO/sVSV/nWPuqzOr39DHP8XWEjNDoLXUcfVt5wlY/18TSZlki3Uc56X2FQiGTAPgmyBuDsevU2NR7Wq1WcEpIPuzLBnk5IxRsdVKw1QfChvookaX97reG0KfeBtH30nwefjunPxIa+dBtnJSvxz2zTUG3jJZK5wfClMvlQNRubW3ZkydPgn6azWaBoEDfnJ2dZZ7n5Rx59HrSLzzo/zF9zrvo5xqBRzl5TnfenI5u1G1eutWO8cO4jjkhkB3o1dlsZru7u+FIesgK+rnb7Vq5XLanT5/a7u5u0Nv6XMqHeOJkUg5DGI/Hdnp6msl5gt6GHNITyXz78ywcWK07BCzzEYQqWwM1/1G9Xg/kmi52kPzYzMKWlFqtZsPh0DqdToY4297eto2NDdva2goO4PHx8aW+g3giIhB5ZD4k2pRto1yrUTiqS9Um4H2YF5VgVeJpXZ9mHVDnvb29ML8oSROzJ/0YWceGjensvGv9d+iVnZ2doOdOT08zddC6edLZk7WxZ3Bv3rVqX6sOQ94Gg4H1er2PjnjSttGxy5yji2fA90mefCjy7tGE25pPVKF9pvMQYzVGPPE+kM9m2chG/75qY0E8qQ5TWy5mv/BsrtXf2NO6bZlnxcY7z0DvoMv8VkT0H7rTcxextnwfuDbxlMcK3jWKxfNkd5rwFKNO2UgaHMWgk/dVkMfWx/5eVv46nauDQ4VClSf7OsfjsXW73Rsb11dFnjJ+aFDlCbvM5K5yA/L6PNYeMSWhjljsGsU6sqJO+VXIP288wY6zQonh+pCwDulHzqt2ux1yUejkpDpi2QSqz/N96Ld5aHnaX/6+mEysY1guu0ajmHy99blev8R0ZkyetQx+a/6RvDaLGYnz+dzOzs6s1+tZq9Wyzz//3DqdTiay8670jDegWcmrVqth8cJsOeGkDoOSLN1u99L2EraQ+a1pMTmDFJjNZiFajBX/xWJxqb1xrPWddHV2HSgJyw/RVrFyvUHF9Up4eFJbI3KUrFLCI494AdyrJICPvIOU0K2BV8FtyByyocYv486X74kGM8u0EQTAYrHIjFPaHLnzRJPXadq2Ppeb3s89GkmnRIvKn9eZPuJMn0F9GQvq5DJPsngI6UtZmuMFEmY6ndrR0VFGd3p9q/BOh17jt4LF9LHPi+Z1SCzCXtszBo1487pXiSb6grpp0uXFYhFIQKIQdMsqOhobZ3Nz06rVaoh0oSyITDMLRDmydXp6ap1OJzhFsf4nMgmSqlAoZCJ3VF/q1lCeo6QlkaOMZeq0WCzs+Pg4RFQRVUV5EJNsFVTdovLN+2MDQshygAORrsViMdjcyB5jx+w84opnQUb57elK7vLj88N4mVE5UIf2OvpsGdBRGl3Be8cIJ/07jzDIsz1ienWVzevJOSXs8ognrvc2jK+LXhsbp36sq85Qf23VzpqPAeXy+aE8LCrGfIVlfZknB34+LBQKQScReW52OVcl0MU59BHbffWHfmIONTvX52rfxN5Hx4PqPZ03VLf4cROLvvbkKGWwCKGLnWpzcaIedhNzqJ4AST10rKj+XTUf3TXu1Va7dQy9Uqlke3t7YRVnOp2GKCCMmVqtljn22zuWKgSq8GOf+7BLOktXN1V5Ub4XSsUyo9qvmqnRYHa+4tRoNKzf74cVQbDMyeT76xrTN7n3PkHfoVQq2ebmZgjjhMmGiPGKkUEd23LnjUW9zyyrmJiglvVRnsPtlYcCxeSj5vLagaOL2Qs8mUzs7du3lyaTh9r3Ombr9br91V/9lW1vb4ctXUweGKxmlpmAfB9rmfztnUQ10tXJVIdG7/VlKbRcfi8zivR/dWJUJvN0Gd+psasrJ/xWh1KvY+LjPZBxLzsxI3E2m4XE4js7O7a3t2d/+tOfAvHkHcnbho6pQqFgjx8/DnmC6EvIE/qEMQIZxDvTFrPZzA4PD0MkADpcV+xUVmKGCc+hXBxwku9C4HA/9aTf1PhiHuS6mBHu9QZGC44s860nNSgXowk5IQJhOBxm2kiJLJxETexbLF7kCPIyyjOJ/lAjSrey0T6bm5vW7/dzyfSrytS6RjX/s2LJe2s5ajNwvSYj1dVRQuohnkj4i7PInMXKqSLPIeJaT9iYXRi7GunEPbS7OuqqE2IRlSrvjAO2gDHuuB6Hnq2DtAt10fQJECtv3rzJ6EvtC69HY5F26qyovtN5GHvMkwVKalCWkjHqCOh1CiVHdax4m4I6Mp/4CADdWstnSlSTa2xjY8O+/PLLYE9q3jGiXsbjsR0dHQUCy8xsf3/fRqNRiJLyUcOlUsk2NjbCYRL1ej1EetJWup2NJPGQPZSBDDYaDdvb28sQ+pBKr1+/tlevXtkXX3xhX3zxhZXL54nHiWYCqmuQVZ7ZbDbtq6++smKxmNkKPZlMrF6vh2cXCoVMNJkScoVCwba2tqzdblu327XT01Obz+eXDpdgaz96VElfdZi9P6G6m3aJbSW+CSD2NIpM7UfvJOd97klIs/ydKcvsmTy7xtsozGWeEONzxtAy2ypGhsRsP60v87n2MeM3z3Z/qNC2rVar9tlnnwVbRMmdGPL6cdl1lNdsNq1er9vOzo7t7OzYeDwOczmJtNGr6D2NLiTiElnhOyUiibpFRywjWhmnughIOZ4Yjs0PWibypfoGW2g8Hluz2Qw5epU8KhQK1u/3QwJ9FqRUtxeLxRBFrHX37Z2IpxWgE2FAtRNYweE7yANv6K0q3wuY/h0bLGos6m8liW4D/tnK1rIir6e/XMUwvkk9HjqQHxwDVhJjERt+IuE3faGf502chLD70Gr/nDwn+zqTWcww0XdT5agn3jC5f0wTaKFQyES0oUd8f6sTpI56zEBaNtnqhOdlRH/rPWBdkmUZcUXddKJdZ/LxRJp3lvheoyDUOfKklhIyGpWBYcDhCUqkUO/3KXcYJnqakLaBOqYK78wAPx9QHsQzxgZ5V9QY0bL5zbYWfR715m8lUL1hgzPBCY0xxyWvvTGqVT+xyubJbt/vnmTCWF22GBPTv6pzNXLUOxAadYjz9z63ESvBqE6cOkrqrOnY4V4v+8iPOvlEtmiErspabFx7glVJY69/zLJJySmDz80ub0FWUkqfa5ZNDu/r5vvSz6NaV91KqnVttVo2n88zJ+P591+mY2O60DvGnoTy1/ryfV/7NlHoO6ltS/twjZYZc5LVEfLvb3Y+/nd3d0PSWV31p1zsFEgi1SOcUMrn1E/7TvOr6ne6bcSDd9D5WAlMyFf04Gw2s1arZY8fPw5bXhaLRUhQjyOKvtFIBCXrSD2AjtOFXm1T6s57kZaB00h1gUH7YFl/aJt5OVEZUL3BZ7p4cBOo/vF6YBmxlUei5hE5V4W2Y6ysdWwZCEhyVi0bFzG/KWaraV8pGbruXPqxIM/XWSUPMXi9TzQVc1yhUMjkAtSctGpXQJ7rYgj9gy4tlUqZfL56mrXvRy9TPA99pIsmyIPO96rTvL3j5wO1rSC3Ob0XO4rxqVvotW7eBlWeZHNz0z777DMbDodhQfRD4l4ST9rhCG2tVgtHvMJoml2c3kWYKz8+YmWdZ6pzgMCsq6h0EHqlnOegquDoqqQ+I6Yszc4jn16+fGmj0ch++OGHSydyLDN01nVsr4q7Kve2EHP+Wf2LRTjlJeL1UTHeSPbXe+czr42031URxe7J69/Y58sIJJQZq544aurA3XesI3eFQiEkzmw2m2H10a/Y+607TEpKZPsxzgSjTpI35Hwd+c5HLC57lzxdEPsuRiSuus9Pst5oLhSySVXzjC5tDxYMNMkiKzX9ft9ev35t4/E49M3Z2Zn1+/0MQXObK7ux92dssuUE54rVJ90WRK4TddjMLiIW/FZFMwtOCu8CicB2QnWiNeqD++fz7Ilf5BAhNwlGCVtOyOdiZiGyjx9ym52dnWVWDVkx03YBGHkQchqZFNN/zL+6TVET8PZ6vUurpOoMajvouNRwet+HtNl8fr7FEdKp3W7fGvG0TB/6sc2hIGw10mt02ybvo+2v70+ft1qtYKOocYtDrLqDPGo+v5vfchWzS7gGB1+j+OhvSEj0IiQbDjjOvdpURG0gc2ob6Rj0coHhjTzhMPg8SJ999pk9f/7cfvjhB3v9+vUl/Uwd9DPVU9o/eo86/Kr31NZCRnUbHLKoeaX03li7D4fDDOGgP7SdRrOpnKgT5Ffi1bFpt9v2m9/8xur1eriXiEMlfBjfW1tbNp1Og7Py7NmzcDAJC54QnfQ7kU6caEd9Wq2W7ezs2Gg0yuQpLRaLmUjHarUanC6zcwJhOBzad999Z5PJxLa2tqxardqXX35pv/zlL0NiXfLolUol29raCvMrn6E7NzY2MvoYfYFsoueIasIuKhQKtr29HRw5M7Ovv/7aTk5OMrpUtxrTlzoGkTU+14gHP97oP95RcyienZ1dkqN1QX00ilB9J+qqY0HHjbcpY7/V7lhG4saQR/J6mV5mBx8eHtrx8bG9ePEi6M88m9iTDDG7KW+hTQ+zWGajPTQs8znMlu+o8PfltYnqf2wnDjlAh8zn56kYsBknk8mlNDOMJ8hjZFlzllH+kydPQsAGO4c096Z/d50n0L/0t87blK/bcPmtulplTxfvzC50b7/ft8PDw+CP6QKT5tFEd6qNw1jWxfUvv/zS/uIv/sJevXpl//N//k/r9XqX+vp9+nv3knjyg13D1ZetjKoyXzb4dTUjBgRiGWLO2qpr173eK8C8d2HCJ7Gi5g5ZJkh3pRjvs8KNkQJKJKzT574873QtuzYGfV5sxSSmsFVprVpdWCVrftLV6EEMqY8JauiqIxtrR2/UgFh/x4yfWJ/H+keNfTWo8uofK0N1kTfSvCPn65v33p4890Trsogkb2wy+aqxyP0Y9BjTkBMsMLyvyRBSjXnGE27MGX7+8YsHXo/gfKujjkFA/hpNxq3j3sugj8LTVXwvd3lRLFovvSdmlPO39iN9oo6bvnOeMxDTYz5aKnadtn/MGYg9R/vlfRpTWhcfjh+LfkGetM/MLLMCy+f0D+MFaESERmj4+sQ+p2xtf20vdUCRTf5WXbNsRVdlhs+9Mc7/GqHuZVP7PxY15aNXVY963eX/jyEmN56A8nVdhVXX6TiMjd0YAbDscy8ntVotE/EbSwqseifm8KO/vMyiz4i69Ndwnfa9r6PXA94ZU7lDHpTUUYISWdB8S9xDGZDozDl+bPKjCc8h03A2eb7PIxez4fWdPXnudW5szN4FqQEZp/0VwzKb6DpY5eiuek/yk04mk7D9mHpyP7oK4hKSIM/Wz5t7AGUTJaM+l5IBHyPwl/TAmGWI6ZS8PlUdr+SnLnQQ5QRJrtGFZhdzFfML0MUJyF3VJavsfF9vLU8XxVTX+TlP3y8vNQ7QtqW+kEq0Y4zAismptin6udFoRPvgfeNeEk+gUCjYxsaGPX78OKNIvNLX6/2gUENEr80bPKsU/bpE07KBpnVQA9kr4zwDRw2gcrlsz549s+l0am/evLGzs7NcIVy3/h8beHdWi/Q3xocqOgb3svJihtl1cRXSyRswfO6v07KWEVxqABWLRXv27JlNJhN78+ZNOK72vsvMOm2/WCys3+9bv98PR3Nr+9EuGnYfW7GMGYXqXOp41r/V2DW7OPZaT6pR+fOOvdZNDXfVBciGJ1c1z9067YShrWQI76nHZauT4vuhUCiEfEOcXKV1IrfI5uamLRYXSaLPzs5sMBhYv9+377//PuO03xVoQyJnNVpDnZ9isRiS7mrScDPLJGVVEkajPzxRROLc4XBoR0dHmXBvb1ip86Xb/bQPaCMfFYPhQZ9QJpEyngDRZyqxpM/mXckRREJhDUPX7cUKnqUOnz5X301lTwlBlU0No6d9Z7OZ9ft963Q6l7Yzrqurfb3ynKWYbdFqtazVamW2mPG+nlBiTNDn6ClWfZmvVMfoNiwlcLTu6At0jL6DP/FODXGIX1ZbT05OwrZQs4vk8GrQa4SGRm4hL4wPck/wzpRLhJpGXEAiQJQUChdH0qOHeJbmzfF2FX978ju28KDbQlW35hn5qtP1GZ589lFcXgbJz6G6nLrR7tR5PB5n8snoPfSnJmGfz+fWarVse3s7RAAqiY7s4Fhqn9AOJLol2mCxWIRT6Ph+b28vY1vpyW+8B7m4eH+iN80uk1LIAe9KgmGSone7XTs7OwuEU71eD9fwXpTFglqv17Nut2u1Wi20N+2gW1Tn8/NcUppMvNVq2c9+9jMrlUpBjpF3HGMtT/Uq7TCfz0Mkx2g0ssFgEMahj6gxu8jnVCgUMsmGb3oADO/ZarXs0aNHISpEv6MuefZlzD/i82XlxOzaPHvak3X8//jxY3v8+LEdHh7a73//+0ukj5Z1cnJig8EgbM30J/fF5h1v987n89Dn7969y5yopzaZLh49dGifbGxs2JMnTzILKn7BIs9vium7mN/OODbLRoB2Op1wUAsR5/Qbh0P5aCCgZDNzXK/Xy0QsxZKF6yKOt8mZv5Rg0shU9IjaTbQD84Pa8mZZm43PY5Ga5EXUdjO7mAd95KL+eBtPZfR9y+u9JJ4wHjHaSTQa27uv8MKdRzqtg5sQCeAqRi7X6/OVaMgrp1gsZvI9oJzVyPqUoUacGrFEWMSc8XUifWJExFVwleiqq2CV0eDroHXX/c+0k06qDy0CSseO7y+/Cu/JnmURBP4ZHt4Q0efyTCVwvJ7S+uRFRPlJQ8tWY02NK91qom2ibaNlxUgBNcyVKItB21PrQb3USdX3xInAwdX8I/6dbwu0j26XoZ4q92yjiN2vzr1C31vbHp2Eow9RQ7/rc9iKwt+U6+sQ+zxGPGv75W1Lj+kSCCWVQyU/lFzz23W1HbzM8bevu3esPREQK9tHN/B97N3vCmqImmWPcOb5SiApIBkhD1S2vIPK+2mEFO+4LI9D3phVnUebscKvhBHbYBmf/I8Mo9+UVFBiBFnxkV1eRmI6KrZqzPbSWMS31xuxz2PtEyOeYvALBlrnmLzHoH3sCYBYZKN/Bz+Xa324F0LIL2jwfO+II4dm2eg3T1TzfKKpYk4mzhYkpebcQYZ0DtB2UDLN7MK5Qjaxe1nVp56xOniZ07ZS21mhhDvkqOZf8Vt8/Bwe03V5esHLB/XxC6PL5t2rQG2+ZTrxNp8J8sZEbH7wdSN6bzgchj73izUAUrpQuNgiic4yi+cU9FElbD0ej8fW6/UubVXyNtXHhmKxGNJx+HeMyYS3HfSzvDby9i1jmIVQTSHgI9Nj29Xz7AmN4FWSRokkrxv9e6EbmfdoI5UBylJdyXN4T5VBnVNVD6EbYwt/eq/W1ddFde1VfM+74hDuJfFUKJzvRd/a2spEAvhIJ9+oCjXOzOLKLfZ3TPFzTawDVhkUsc9jjov/zDucMej7F4tFe/TokbXbbTs9PQ0na9xnRfi+6tZut217e9vK5XImt4+GjWPILFuBj+E67+ANrFXlehnMM6r1er0mTw40mkXrVigU7MmTJ7a9vR0m28FgYMfHx3eihG6K2CTnPy+VSra9vW27u7shcgfHWFcePfREGZ0UmLDMsicikVOC/EDkwSDaQQ35Uun8hM52u20bGxu2sbER6u2dTU+CxAxBnUjpR13R0VXwQqFw6ZQPLddHfmmYsjqP3kHTttd6q66izQHOrBIHL1++DKcq/fDDD8HgW4cMvA54D5wZDBydsOfzecg/5aHOYWzlWJ+hPxg7jx49sul0Gt7ROzTcT8SBJ8M8sU40E/3oE3pzP8+JERVqLNGPulWB+mAQIW/e+KFNcBC073AE/bP5nDBzn6Scemnb+nfixFKSKI/H48xpV6uwroyprFP30Wh0aVuHd2wLhYucEfo9IfGawF+jXmJ1U7Inr97oHzVyqbdG7dDu8/k85L8ol8u2u7trZheGsG67UCOZ6A99L+STxNOFQiEky/d5oHTlW2WXMrh2Op1at9u16XRqb9++DSvZKh86FmMOQt7cqLJEtIpG5Ghd/FzsySctT/WmgvGnepj2UX2Nc6XbxHSMYd/0ej0bDAahLUejUZB9dabNLER/KImlcxrlmpmdnp4G2YbE8hHBRAIxdrEhPLnlyTb0yWAwCFGxyKI6ncPhMIwNTlYkEuD4+NgqlYrt7OxkyK5erxeio1h0RE739/etVCrZ48ePQ5qB2WwW8rRRvnf+aBdyRhE1RgQUW8DoP96bHC7a39p+uujlt/WovNwG1Bn1ZOKqZ3nbI494WUVoxXyxvPHh9d/Gxob99V//tfV6Pfv6668zOeR0Lqbdj46Ogi1ULBZD9DttjpyNx+MQ7WZ2oTsXi/OE8nnveB/t4+vA9xltxhwOdD6O+STrzKHIPLYEegF912w2rdFohBxuGnWEneDzJqrt6RelmIP4DtuCyHy1t7Qs/87II3qW6zW6iDpoFJS2o7d9dX7Q+Yr24X9+yK3IXMbf/B9bzNG+WSWvdyXP95J4MjtntNvt9iVmT38DvSY26fO5Xu+/9/Cdsk4HrENYrBs14ld9YvXz74GRrUaG1utjUYpXBcdqY0D4ydbMMpO9J26u6uT6aAX9/DpYd1KLyWvsPdQYipEGhcJ5CGuz2Qz7432bPDQUCoWQONrsIm8Jhq2PplRjWp0HTyow0Wi7YDyTuBADl1wAZhZClhuNRohW1HIp2+szb6B6vaYkgco5hoOWzUqxjgPgjQEmZORaSVrvcOXpG627rvp4XVcqlazdbtvz58+tWCza/v6+mVlIpn1X4F3UsVACD8eIOio8IRYbY3qtOhg4UJpLBIcHApN+Jc+BEjVaT4wRTmvCWYrlMVksLrYbqf7TchU6D7Ny540k3dZF+SqDtMdisQhGE9dq+3iD0kcGaH18e+szcSp0pfAudJjXvboiqu3niQi/QEb9dYusyqSfi/hfiUU1MrW9vWGqZWEYI9+0Pc5WqVSyRqNhi8UizAeq+3DyMcapCwQXdVAin2t1tdav1Kqc62o7v9Hdp6endnZ2ltkKEnMaaHOvp/LmeK2T7+fYZzHbQZ+zzInX62KROX7LBG2u9YQg0WggdMBoNAoHHeh48YeK0EY+Go327vf7IeJE5xituwLiCAfPy6eZhVPy9Folz1U/6VYaHFTemUgkZIUyer2eDYfDsMXb7GL7K0SX6k0zC4R1tVq1ZrMZiE5tc59/Vkld39869mP6SMeql5nr+CNXRR5xpM/UvvX2iZaTVz7l5H237NnaJuixarVqrVbLut2uvXr1KiyQUT/Vr8gHYOeD2QVhznauwWBgJycna/trHwvyZABZj9mKZjePiFMihzkHe1UjGnVeMstG3qsN5rkCrb/fXkc5ZtnTV7UsnUd4R8Y4skV9tX24V4l936aaaxi9r89RvaHzd8x3U32tz4z5ER/Sp7sV4umuKu/JlWWEk34G8kio2HO4Xv+Pvde6yjP2/XWUWMzZjTkzfF4qnZ/ooQltx+OxHR8f33hf+G3jfQk8BrGPBlk1QV6VcALrkE5XlYWbkk55BEbsHZU4I8pwNBoFRXbfyKd19Y/uo1bHCAMz5tiqQ685IGK6qdls2nw+D2HYGNLIH6vDZhdG29u3b+3w8NAajUY4YXF3dzfjYKghxfP03XkPnVwxhtWJ1QgM7+Tpe/nIP7PLTlNelIrWy0/WSuDwmU74MdKG1WFyYt0VZrOZHR0dWa/Xs2azGbaNeN3rCSe/BYK28++l7+1Xl7kfGdL35Nhz+olTnzTCBWieJQxwjSjS/uEZy3JS+Og6hSd26B9dQdQfymF8qGOmUSoqh7plziybx0cdVzWGVaa4H8dR7/OIkVlXgb+PdvdEgdm5k6NJnjc3N61YLFq32w2nELZarYwxru8E4RAjCrVNNCIH4pH/fZ/SB0Q40c4k8dXIOI1c05Vl3Q7R7/dD25fL5Uw+nWKxGAgGZMYsu41rNpvZ2dlZaCt9JpGBrFAjF0Tg0IZq0NM+686jsa0L/rO87Vyqt9U5WOWc0Z5ED6pTDEHn+57IJ42I4/n1et22t7fDyXRE/rx588aq1WrId8MiCXprPB5fOvGSMQ0hjlzrd4B2V7vLH2evp2L69ucdmUf9CYmcOoqcMj5o2/F4bIeHh0GOFotFiATDiaUe9Xo95JDlet5rOByGXGvM4/1+P1PHs7OzkH/G7ILM8g4i76ZzBPOCj8jQORg9otENt5nImkji2MKA2oF584OSTzGfxCPPn1p2TaxcxonOtV988UVmTGq0ZqVSCQQ1C4Hj8dj29/fDGKJcnT8/NajOin2udmFszo7B+x2qU/V+XdQ0szB/cq0mlNd+1/GkP37cYQdja2uduNYnqvfbumOyrjsnfFSztoFyGDpHM/b0O++H6PN10Zxn+XQUekopnyshru/0IXBnEU/rKKFliBmIMQLGT/B5Za37TP17lZLMe+ZVOnMVscUkFGOZY9cWChfRKkxavV4vJMNbty436bv7An0HwqD9Ns08p+qmWBbddFerKF6B63iJkZTLxhjAyCQ59Lokz/vGqnrlkSwofb/dSMO6tfw8eSkUCmEyw0DGiNdVDL8Cd3x8HLYOVKtV29vbC86az5ehK05+VYWJC7JE8zZg4OokZ7Y8hD62Yusnct0nH5soAWV5/a2kg/aFvhvGPobgXcgffXF2dpYh5fxWLrOL7VBAIyuor66Ic43qcE+U6HU4mzgvup2JcjjFVI2kQqGQSWLuI4XUOOO53rDyyDMweR6Gkw9Nx8HTyBP6ejabhShA2tobQ1o+URWa50GNTPS56lTKQ5YgLdBhy3BTu8Ub6J6M0C0E5DHb2Niwcrls3W7XxuNxIKCJbIsZ1j5CTb9DDnTRQLciaHsjU+gonDXkWA8A4L5qtXpp7NLuOHU4s5BXEEM6R2nOKD9uCoWCnZ2dWb/ft1arZRsbG6GOo9HITk5OQt4pJUfY1qVEhxJB3mby/abjXOcL+k6v18UL6q31V3niJ2+86fVE/LAlkUTfvAekM+NMiV/aguid7e1te/z4sXU6Hdvf37fhcGgHBwfWaDTs8ePHYVseSXvNLqKaqA+RIRA4tVottBMRZgolnpAxHVPcGyPD0SG8o9+WAqHGMetevzFvn56ehnkQHUB7aj9VKhXb3t7OjCsIIAhO5IrxwXvP5+dbrzXBudbHyxe/qafmE6Q+fm5GztAZjLHbWERGrw4Gg7Bowecq36rTboJldnbM1tLPY99D0EJQfPbZZ5l5m6TiJJY/OTmxXq93Kdpd66Dz+TI746bzxH3HMvJpmR22DvmUd22enaK2BnLqF3S1Xp7QVp2OXq3X65n7dEzmyV6ePOhcjEx6/0ptPOqovgd1i+kAwDyu2769v+L1hra1zrHLbP9Y39w27ox4uinpZJYfsRRzooFfkV523zJoB2hn5pUXq7PvXHWoNJQvBj+wVenHCLhlZTG5YhDmTVofqyJVh9y3mSdr+EzbIo9EWiey6bqIKYZ1He5YHbwi9kpRnYcYCoXzEyYxVO6KPLsrxAxBdVh1xcvf59sOwsUsHkq7u7tr9Xrdut2u7ezsWKfTsXfv3mXK1ogUs4vIGYhiPXlFt8iZXRiofKcOuK4O+5Vp7wAAJjHvQPK3GvhMXkx+fisRbcL/3gnjnb3upG4QC2/evLFvv/3Wjo6OQpnLSJKbQp0O/se4pR1jBgXXaCSO2cXx4vrearBpW/BuanTEttJxnebYUZlSI0bnCD0BC8T0QaxNzLKnKOGIat2U5MAR9UaOGpVatn6n0VFaB08IKHQ8+tVEvlOH4iZYpX91XBIxorKiERg67+jKPXJInhkliMwsQxB4eLtAiZFi8eJ0Md22oNsbkEUlvXHcVcfxQ4SRJ4qZK5BVMwsnfhGZo88rFArh9DzI1kKhYL1eL8guBBPtRb19XyvZsG5/e9JB4Ykj7Tvu5bd3gGLX+ft9PdRW8Sv6tK+OV/5HP3HKE+/f7/ft7du3mSiqvb29QN7oPME4JMIMx0adFuqeFxGqZBL3aCSNj1b0UJKQcolsolwWInS88D3vTk4q8mQ1Go2wjY46QYhCsnkbsVwuW7vdzugVvy2U74mgYWtejPyPLWYo8UE7K0lNhKvOjcj3Ml2wLrDnWq1WaP+YDaR6S/svb1Fc3yn297LrYvBOdYwU8IujnA6KPlosFqGf8uzXdQm2j9VXWgb6WseD2fWjZmL+q/dFdOEFcgYSVud3PgNqE7N4R9SjRsKqHlU9ovA2of7t/2cMo291wTs2tyhh7nM0qm1Fu2tOYnSpzju+TrSjzpvL5Pt9yfW1iSet4HUFb1W5/rM8wklXhGOdm1eGNw5izGbMcdJn6sqmlh8zPhR6fx7yhCC20umhRlm1WrUnT57YeDy2H3/88d5tubtL4ISjdMwuG3/LGO1lk+p1HJlYf9+EZFIsk7c8OVMG3pelyrVSqdjW1pYNh8OwAntf4Im02Pf+fzWilFzhvXCkcdY0OkNXcnWcM9k9ffrUqtWqDQYD6/V69uOPP9rh4WEoGzJAt5Zw73Q6tZOTk8wk6bcrcS1JiHVii225yzuxhnqzVYV3UqNZJ0cmeogIrvETeWxc6CSoddFtD2YWEr1///339n/+z/8J15hdjkK7Lfi6xVY9dcuc3gNBoLlJ2M5BsnhWWbnPR4jpdypPOrfgKPmTXRRqnOh3+n6+b2KGiofm+kEX4OzyTLYDcnLWYDAIkU1+SyBtwPtpTgccRt82fIbzpqudSt4i+z6CUR3aGNF2U4OLujHu+v2+jcfj4NzrMzBKuW84HGYcPqJ2FJB5nU7HptNpSD7u7RElAniOOtTIgEZP6OqpriwTeanjQceERrboHMr9k8nEjo6OQh4dInOm02nQS4ynXq8XCBKtLw4kZdN3Gs1JHSBNVPbz5nrtD9Vbq0gh1f9e38WcVnU+PIkfg5ITnvxX0sm/N225ubkZCJbFYmFnZ2f2+vVr29jYsHa7bfV63V6+fBlW/c0uCGvqTt4cIsqIOsU5ms/nISmz6imcQ3XA9BQ75hlPMKvseyIL3aPOVafTCTqHLXcQmmynIeK/0+nYeDwOekmjxYjcQocj77RtvV63Vqtlk8kkpBqgLtR/Z2fH2u227e/v22g0snK5bK1Wy+bziy13bM9jmyKgXPS7RkEw7vhNYmXd7niVgxLyQP8S1ej7g35VXUsd8+Z6s5vr05gfFyNtdTwSAcxn/X4/RDwhl8PhMLPtOO9Znyq83R8jl7zvv8zvyPPdlz1bSU0lSpD9QuHidEK11xmfRAiSQgNSlXdS0prP0U1+ccwTsTH+QN9d9bQuGOqPQrfLqZ5njkOf+IVkIjJVllVHan1oF377Nv8Q8n5t4um+DU4vEOt8v8wgyTNOYwNtmVPnWVIFwnkTJz5WT/98Ffr3xWjeB7DKtbGxcWkPLVh3hcPD37MuCRUjHGNyse5k6OUsr3/9FiEPT576CQPj8T6SluvKNJOLjoMYyRybXPwqLuOWCVL7gFVW2qrRaNjTp08zjgS5SchfxAoGJwiyzUVXd3TrHRMMdYhFgugkGIsmAUxk2h6qt3gX7zSpLMfazfdN7DN9DzUAbjNSZRVw3La3tzMr1lrvvHbGeVHiD2dB5UJlLhbJ4KGOMM4SiW31pDff7vS1QiMa8gxLoDoyjyD021/89Wr8UH8lRfVZEBVKAqtD4x1SnceUTNHv/HbqmEF2HaxjYFMfyDSNgtPIB9Ur9CdGohqf2g7q9Gkb8j0OtR4prWUwznHAfOQQMqLOr7cjIBQon99KvMX6mK1gPFO3Go1GoxC94eUOxBxP/T8W6cd3foypjvPzQGxe0H6N9b+2A4jpaW2P2PyuEQXqjHjCib7RMcy40dw0+j0LR+12O7S7EjpeTrS+qt8hhj2Z6t9D20MXMnx+MEhpohK0n327UgcWP1QH6cIA1ywWi8yWc8YU8yhzjT+xFfgDP7CBtM3Z8oxNwPxPfZXk9XOnjjGNjFBZ4zm0uTrkt4VVZGhsIUrn5NiCxnXh9X7Mfli1XVUjRdDBbLPzZYLYGE7Ix20QFnly48e+X1xiHCq0z5V40uTdPu8l0MVUv32Pspe9Q4wn0M94z5ivqTstvJ2itoSvh+prnocPwb2Ui55jG3we7/E+8d5OtVvmFOchZoTkkSzaKTpJr3pmHoGUN7DyDJO8+q9TVowUWOc5qpxjxIM3AG8yOVyn/z4kisWiPX782Pb29jJ5CPwE440ks8uRdOsQU95B8mXF6ufvXXaPN2T1/5hD7+8BMYNOSRM1gLQckvJ5x+m+IeZAYFQOBgPrdrthBcETN7wb96seYfVSJ0Idd2YXK9REMPD99va2/f3f/30gVohcGI1G9sMPP9jR0VGIEGH1lognDH3dPqJkhBrbumKPka0G/8bGxqV+KxQKmZVrJUW0/XS7A+SGRiIpIaATofaL10G6oqWrw5oDCONcDd/b1EPIRqPRsF/+8pe2ublp7969s06nE9oZw0EjiXCYNjc3Q4JeDfVHDmgHdap8Mm1tL/5W+RyPx3Z0dBS2HfL91tZWZnudEjxaFpEg+rnfCqf19FvpyKug0XM4pBAGSiqp4aZRD2wZyYs8zSNPVD95coGoDIxOL4NarkaqrCsb/vo83axtzThXkkGNSiUm2Vqrn+MM87/ZReSlHhqgJMTZ2ZkdHx9btVq1nZ0dM7NMwmkI1VqtZmdnZyHnI/VmJZk6ax4dXYEFGgGhzmij0QgyS/3m8/OE8mx7UfnzpIySCJ6Yjc1dfE8EmJc977T4vlWHQHWW5q9Cj87n8e2gfn7lPbRtaGufMF/vU7IRnYvsMoY1R4lGqtFeZ2dn4V0pp1qt2u7urn355ZdWr9dDpBNJ/nUuY3wzt+h4NzvXd3qkujpe/EY30mZEaXKqLPIxm83s4ODAFouFPXv2zKrVaohI8bYL89R8fp5XaTqdhq3oyAwRwCzomJ1HJDF/4JBygiiLPugGf7Itp0QDCHfG93R6fsodp59p3ifmbvTefD4POduIxMjbWkwbqh4hgpboQR+1c134xTMlA6iL6liz7OmzKsuqc7Xf8hYR+Cy2eKHzpTruywg37tfI18XiPN/X69evQ1vq3JqQhfcvbrPcmI+KTo1dr7I5nU6tVqsFX44trtyr8ys6T3O6abSmRnCbWTjFENvby53KpW+XPN/d+1CeoFLCSf9WWxD5REdh3+hCItvdPaHm50De//j4+BI59SHw3oindeEFc91BoA6V7/R177su1ikjrz4x43bZ9f4+z4LG6qROzbr1/RiAURIz9MxWR7nd14nJ920eaen/9/escy9QhecJl/sO6trpdMJKCMZg3vgBKPSYoaKOtk4UOmkpeaKGF8Y7SYQ1cSKTa6vVCkliccR1BZyyeGaMPPVynddnOll6EkvHEXXIKy8mT3nkKCs0GBesPHkD9a7ljP4hcS7tj6G6TBdr3dSJVQPO616VFd/mlKnRDkQ5ERnHdciNEnMAIgbnR/Ox8Ax13nWrh/Yz32G8qWPgnXxtD3Jp6AlP3snwJD3leFLTv5f+HStDZRP5U6JtWR+uGifL7vcEhMq0J11xKs3skn5Z9mx1rLjWn+zlowVi8quOXLFYDM4+5fuoMT9uqbd+rkY413iZVp2peWN4RmzuUgLIX6PtEJuv88pbdd06iN0Tm2vXKTumv2MOuV7vn6vPZmxyKubGxkaIKoqNKa/ntK9i0TDaj+glIoli44l6xcjKmM2v98eiG3QLqNojurWW3zq/aL15jpd1rxtj12h7eWJFHWDtGx2jsbbMk2vqrfPJqnnpKvD19e/hCWDeGV2dV491/I28hVqVCZ0v14HqMYjgZePwodix7xPXJZ+uq1/X1ZPIvy64mV2OatYFKg+/6MFCj1+oyKujH69+/l827+bZy3ntrfMaOtnP8XymZem78YM9pu/zoWT/3hFPZpe3kajh4eGN+qvAN3ze3/6eVc/Km3yXGQuxZyyrU8zojk1c+ltXUJcJXR4ZtgrXVVZ3gcViEbYtFQqFzCkGfK9yZnZ5dQYjJrZSyvXvGzED1H+mDjD3xIyAPEXpjSv+xyHXVb/7MGnnERs67gaDgf3zP/+ztdtt+8//+T9bs9mMngLmFbju/cZJQx5YOWM11YOJEaVvlt1uU6vV7NmzZ7a3txeOeGXVludrtEan0wl5DBaLRSAWWAmP5VrSSXoVMNbMsjJE1AKrJko46ITvt1TF5MnLFBEeSg5oXq3FYhESNd+FftEtKKxCN5tNKxYvEsbStqo7cYb6/X4mhJ8cVazAYzSr/lUSQp0JlSWivjhxiogz7tVVaNqb/DlENezs7NgXX3xh5XLZdnZ2gk6kfLMLA02jjOhf3YpVKpVCe+jcjGwMBoPMGNJtrZC8PkcBY9BD9TIyoU4w7UV+F66HPPE5giDt1tkmHNNn6xiUujqqGAwGIRKIiFGMWx9VQoSLRv3ESBfVT6yGzufzsLUAQrLRaFza+jkej61ardrW1paNRqMQeXlycmKFQsGePHkSykEX+D4iCrNQuIio9OQnfUy+IV1t9gRbzI7RMcGPRlj4tsa4Vh3jV6Nj/afypM/y/eidHJ0HeBeeh9zG9K46PYqYg882Xt2qpRFQ2obaJujM6XRqX375pf3yl78M0TpE5NCvREoq0aTzlTowzKOqY/b39+2bb76xzc1N+/nPf57R5zqXFArnxDURWWB3dzcThcJ7IDPNZtP29vZsPj/P1zSbzezRo0e2WCys2WyGqDzGOAdzbG5uWrF4nhuJKCpd/eeks3K5HPLF+C2ImrBct20xNxF1yomU6FRkiP89kY8MKCmtWxD1Ho00Roe22+0wdm+y5U7lnPZeLBYZu8bngOOeWMRWzPbKc/7z/B7Kj0XF6sKF2rfAL1TxDBbwzs7Ownb1+2C33nes8gO1bxQxOcgrx+txT7brXKAypRHcsbpomX77HLKOPYMNp1GPaqP6CGOdg3xbeH/d+5sx5C1+c4/mhOQdsPV1TlLijL97vV44pIPoap6p/Mr7xr0knswuGlKNhWWGnzZgjLjJGzx5JM9VkGfcXKc8X8+891rn/vdJjNwHRe6ZXwyocrmcWdGNKYnYBMkkqL/1WevUZx1cdUVnnWdCqPC3/sTuWUU66f8xJ+g+g7bodrtmdpFQUw2nVX3gx6AnvGMEsY8IMMtGcBQKhRBh02q1rNVqhS1xShJ4R1xJGLaXqDz7flu2Our1S4yY5Tt16GLvR73UoY6NK0+04Exh5OqJV7q9766Ac66raBqlFjMMlJhT0oF3Uvi6L5vL1Mj3OQfMsqteOC3IFCtafAfZjpOMw0QZfm6lXO8g8dzRaBQMM5UpzZHA++oWRU846mfatr4Nvb5V2fTtq4SBkg5+1e8u5ShWNnOQbk8yy9o3moOGOsdyrvlnaV/hlOp33mDPI3HQNch0HrQ/tXyVJ+1jzWGjY+Iq86j/Xh0T/a2Evr5v3jP0mmX2oieirio//r5lDogHbeudbZ2nlr0rDgpEod+axzNi+knnG8az2cUWRMqE9ME5UpnSenAv12muFp0PdO700UZcg5zrAgfvo1u0lfDR92E7L2MPsBWYseiJUo9C4SKq1J8w5/WR9r9Gfa0aC36cx/TmTaD14tAY7WtvW/j7roo8WyTm9+jfasuuA2/bszh3lfGXcI7r6C6zm/miec/Js3Pznp13vRJQamdpxKTaunzm7Wmd/5a9yzr8w6o20vnb2+wxHwG7DP2sB9O8T24ghvdGPF3lRQuFgnW73WCwsTLRaDQuTVYxxR4TtqsQBXnGiF6nBo9/v7wJxP99VSMk5vjxna+/Tpb8H3MwY7iOUN4HEsIbXycnJ9btdjOnAzx+/NjMLvIQsCpM26oBq0aJlqu4StSZ1tHXe5khoX3pjSCVRSVRyAWgBv/m5mY47SVm9MTGinduzCyz+ndbhNlNsExe1RHFCTo9PbVarWbPnz+37e3tsFrKioe2ATLABKNbkvgOI1xXJjHYNA+TWdYgxdhjUuh2u2ErII7+dHp+yh2TB4RZsXhxqk/exErf5TmUKp86aXGCjq50c10eIck7DAYDe/PmjU2nU9vd3Q3bB3WVSFftMXZpO04D4/QuJdp4r3X6fV3MZjPrdrtWrVZtb2/Pdnd3rdfr2enpqRWLRdvY2AiTN6u8OCY4Hqpvye2BvGlfEEWge/TNLNMe3tEj4fn+/r69efMmyBnleGeEcumP4XCYkT3knPbTlW6e3+/3M0SXkjaz2cweP35sX3zxRWi7xWJhu7u7oX9VLswukuJ6kpdoG+per9dtc3MzyKDKH+NNIz2QFU7c0jxIKhu6orlsHFDuMqyja/Q68rEQ4UW/6XN8NA2/dbwgQ4wJVjBxqJBRnUe846xRQdSv3W6HU/TIWTMcDm1ra8sajUamXVX3IDuxxUHVkUQ8ed0VI5PzCB59puoq9OtisQgr4NyrY8hHM/m+VjLX23Ne3/j29eWorvQkEe8SkyG2WqMnvJ2n9cJZgvSgn80uTndqt9tWKBTs8PDQ/vEf/zFcW6/X7fHjx5lTBamzkoqlUsnG47EdHh6G9i0Wi9bpdEJdarWabW1t2S9+8YuQE4w20qTbg8HARqNRiJiu1WrWarUyBAqLLDhHyHOv17P9/f1MOzOnoN/Q09h0qieINKT8wWAQdASRxd6OoU6j0cjOzs6sWq0G2fUn4TWbTWs0GmGcq6wgt5DOnOyoUYJEQepJpeg29Ibm62LOJNLzJlAZPz09tX/9138N/Ueb8nx0qn6vNlXM1jW72MatJJ+3V/z/3sczu8iXqNuKPWKfoVN07tY6JKwHbLJqtRryK5nl+8zL5km/iB3TqciL9hN2wWJxkTYDGaUstRepk8ozOgAdw1jyW791gZiFIF2U1OgiPw94xHwr3z4xTkCv9YSX+hm8x2w2C1HTqu+I+ux2uxmb+kPi3kY8sXqLocTkB2LMuXaa7zyFj27wysiTKDFSxTtt/vNVUGNlHXgh9J/pb5wRTz7dRNlehbi7zTJvAk7L0XbZ2tqyQqEQVu5Jqqo/q9rJR0Cscur950o8XAVqPPvyvTI3OyfX9Fhu7sNh1ed7mQKqxLk+5gjcZ/h2Icn4bDYLEUN5EU9+vPloDU/2aHuos2aWdUx0glNDm+i8+XwetggcHx9nnEqMKJKZxkiZmDPk4T/XFWEmMgxiXaFm4tU2wdGaTCZ2eHho4/E4OC9M2sieTpQYEkC3leXV8zahK/bqjEyn0+DM6gqSQg0bs4uE7l42NGoo1lc4aX6cFQrnEXHNZtNOTk4ufRebA3WVX40pno1hos4M1+H0QSYhtyTz1fLb7XaQk8XifNuLJk5W4i3W5sg7CwMaYaardrq4otvPNIoJY4q6KBlidpE8dB14R2iVHaDfxeC37cT6zRM3fhzzTko8QUqrU0jbajurXoOMpC3ZDmp2QYb5LXH6owQl5fK3zkMQhegL9GvMTonBOzFe3+o44QdikrFGPfWZ/nkx4msdXaMkgF6vi1aeyNL31jlDy2Re1uhsX0/eA7sY8N6MQQiowWBgJycn4XTfVqsVEm77eVEJBeqPXmIss4UPOalUKmG7HPXRKAGIkn6/b/V6PbNNneeo46byhrz3+/0M0cGz8BEgtNBrPBfCQRdelBj30Qw+UlW33rDdjmTj6EwIuWKxGJ0T/XOoG7aHJj5X2cZ28wugqhtvAi9/Gs1qdt6Hu7u7IQJbt0mrjKzjX/lneqKJz7x9pWSVyte6iJEPCdcD45jx6ttymS/ndbn3t2L3xvx33ZoK8apR3dyn+kPHosov1+o8p7YZ8qvzSWz+8iSVws95Xtf69s1rN+9nUB9dgNKtu/q5ntypKSs+NK5NPN0laaAOnK6csEqj2eox7P0WFl1l1Y7zDKUKWYxc8opR68g1eflT/L0xEsJjHYHEwOY7NSJU6ev7qbFwX/A+BoC2cb/ft9evX2eMYmXvqVOeIvFkocoWz8obF74vKAcjQ/9XufGOhxpQOB0Y93qtGic8T4+UBavYenX8GGvk/PDh5R8Kfmz6z2nzs7MzGw6H4XSwer0enG1/og3loXt05VEnLlYVdPJD2ZNXgxM2dAVH+0e3l5XL5UAODAaDcF3s/VT3ENkC0aUkAPJAufquKmPki9HvgDqZKoPqkLJ6u7W1ZYPBwI6Pj+3w8DBsJ9zc3LStrS1rtVr27NmzDGmjY2E2m9mrV6/sxx9/tOPjY/vxxx8zRv1tgjYcDof2j//4jyFvyWAwCI4B/cOpS7qF0BPBlKkECD9+nqCfkBVIMG137mk0GiE6T6PReJb+Jv9Kq9XK6CZPiCIrRFooCbdYLILDsbW1FeZiyvjzn/8c6lipVGxnZ8dqtVrG4PHzDn3Is09PTzMRgcPh0E5PT61UOs+zxbvofI6ziR0wn8+t1WoFJ1HHCqdW4TRSnzx9of3n+3JdMKaVsJ/P53ZycmLD4dA2Njas3W6H/F1mF6dgKiEECaF6XW0XlU1INU8G0dc6byBzqs9qtZrt7u5mrmPbkb4L/8dOuFIjn8gQ5H46nYaTRHu9XiZ/kN7r5z0ltHVeVtLHE3lKmmlZwJM4+ty8OcTPyd7W9KSGlufbJ0/u1Hajz4kGhNRlbHIIwmKRjaJUXU9kD/MPOmswGNjvf/97q9fr9vnnn2dObUM3T6fnp3xyCmqhcH4ya6lUCtGFHL4AuTObnedvKhaLYWcCMkxUORFX8/nc3rx5k9GRzWbTqtVqIIo0jxjkjpJOyCGRQeiFyWRitVrNdnZ2Apm6WCxCdCVzc6fTsU6nE2RG++/09DTstiCS6ujoyIrFYoiEhbA9ODiw0WgUCHQdp/Qffe9zz9FPvCP9uVgsQh8rmcf8rluqr4tV987n8/BOzIUawaWn7qrOUr/E+zLLxok+1/s2Zhfb/q7yLmqv0+8J18NkMgn2M/OpPyk3Bt/XsQVyHxHN3IFs6ZjXvEzoRHZFMcerDazP0V0NesotviD2t86ZuqjIPM3iMLnytI6FwkVEqifKtQ1i7UA78b9G6Ok8o9GhLAww56nvhy2En9hqtW5Fd9wGbiXiaZUhdxOgwHUCM7u83U1XiXRVg46PMagxg07hmUY18PUahTdsFFo3X1f/TpStilgNeTWAWOnRsGnP3qrivqox/TEAp+Xg4MBKpfOjaTHeYkRPDF6G1Oj1/ervUQdC+1MJARSGOuPa75SHI6YKWxWOrkxrORhaWj8tV+8BuvLEhBCLZFilA2Lj7zaxjHwyu1jtJ3weo0kjPYgAoA8Xi4uQ+kajEaJ9cPgojyNKMRSJRmBrjRptShBoFAPGs/albnnyjh5AH6qRi+Gu5JNGLXB8O+3Dd8Ph0EajUTgFieeqXFBnlXMiGkheC+Hxww8/WL/fD2MNgmJjY8OePn1q5XI5ODc+MkePd//xxx+vJAfaXqvAe0wmE/vd7353qW11LqlUKhlCkVVy1b9M8rSLkiaUx7sib8iThokDjBS2p7BtTPuE/sBQgVBvNBoZWVYwF7CKr4YWepHk35SrTtsPP/xg1Wo1k5iX9kGnacJf1UuQP5pMu1gsWq/XCyQFhqRGFFCHxWIRtqkgIxiGnoBnhTR28t9VsIycUHg9Sjt3u13rdru2ubkZHHWN9oNk87LlCXHV/6z8jkajjJHrdbjaN7SF6jlPLmKAK+nDvWaWsbVisgWZyftDRhQKhUBc6L2+fJ6p+jJvsdBHXsTmyphtpzpM6+L7VwnE2L0KrS99qrYFiMmQn8eZX+gbtnvRNzhdvV4v6CazCwed7STb29thOwrE08HBQYikbLfbQS9tb29ndIFunXv06JFVKpUwt3U6Hev3+5mFr263e2nu4X+uq9fr1uv17Pj4OCwql0ole/nyZSZhNT88X99R22c8Htvp6WmICJ3NZkF3lEqlMLcfHx8HksfMQkJw7U/IpHfv3lm327UXL17Y06dPbTweh6TojJ9Hjx5ZqVSy09PTsP1QI4Gx59TO14UG+pJIW+ZOCMONjY2MPlUiDz18WzZ8bAxj+5hdjDHkrlqthrkBfcMWQR1Hy0hW/a3PzJunlJCNYVlbIBd6f2xcJuSD8Q0Zi92iY1ThyRR+xwgYHd/MHegLXUxhvOjuAJ1rVH58xLWOG3SCLlKhb4D6Dbw/hBacBAtHbP2lPmxt4+Afxm6MVNLPlWTWtlJbfbFYhPpDwCnBqtfpnO93i33oAJRbIZ7uypk0u9j7DssOu8lvLyx5DaoEjjLzGDgqtDHDAax61zyjwiy+nSlm0Oj/ngzBscD4NrtsfHGdGnQ4N7rF4lNSutq2arjrKQZmFphwT9xQhllWaeSx134VQCNcdGJW5RibFNWJihnBPvlloVDInIqm13jjN0a6+jHAtcgdwCheF3epI9YtH2W+tbVljx8/tp2dnUv71f34Y3WB7Szq3E2n0+As4hAoGaGnAPpycYo1uSHXaK4a6qXEFRMcq6ToMK7RlRLtYyZaf0qVRowqGeL1kToBKqtan2KxaM+fP7fRaGTNZtOGw2HQ1+1227a3t4Njgk7yDm6hULCNjQ17/PhxIK4gMlbprKvKmY4xf+8XX3xhL1++tE6nY8fHxxmnVtvb7IJc9GXyP+Sakmw+UlffTaOq1PngB/K8WCwGncU99B/3qhGjv5FjPY1pPp8H0hHZ5npkol6v29bWVqhrqVTKRCZjRHKPRhupAwHxpP2GA4gMU3+ftwnjT0FZyDfRFdSfbZxXRd587a/Rd1AiRO9jKyPvyfjhf13d1TGS91yVQ3SQth+yp/MRba8kKfLCb++Y6Rjx5ak8Mz7oN9qArTyxiC2N+OWdeCZjRnW01xWMqVjke6wv/Of6vl4HrIpm1/oqfH/5Od1Dt0cogV0oFDJRhDpP6LtqPbFvfZQgEVNq+/A9+oP5imgDjW7WbdBED+CIlUol297eDrJFmf7dcACJbiI6ajKZhFNbZ7Pzk+seP36cmecYuxBikGMQIdRLHTcWNlqt1qXFPogn2pPynzx5Ys+ePQun5jUajZCTCgcOB5D2pv11YTjPN9GoRO1jdYQ1YbuXNbULbgPrzKk+asP/pu5aX+aCPBJKiSrvLOtz9VmxNtF65L2XjtFPzfe5Tczn5yelsesGMlltXP/bzz2xvtN5j/lE5wUdu+gQnSdPT08zi2TLFpFJHRAbp54/UJuOd0EPtNvt8Hyu0UVYnZf0wB1tF52f0QneD2S+4130f3yPWH457Qd0NLqWfKx5UYR3jVsjnq47kH0j+3LL5XII04YJbTQaVq/XwwoNgo8wEU7HquJ8frGFQRWcTozewFKsYgc9g6hGknfg/d95DH/epKKTnBpoCjXYuE7JqvvAeH4I6CDHwCJBLZ9joKmD5AkfjH0fEWF2YdSqw2Z2QTzpVgccDVWQMaWsdcB5I1yUHy2TyEB1Pnh/7xTHECPcVIFjuF2FeLpLrDLA9F1LpZLt7e3ZZ599Zu12O6zeEOXBZMSPRgr6SYLPiBbwxLLqGF8PjcDCAeAajCuVD+/Ma0gw7+VlUg05/i4UCplIGDMLq9gY+J60UjkGyCPPRD8XCoVASjCOMAgwQLgeWfIGIo5CoVCwXq9n7XY7RMPcxUSp76iT9S9+8Qv7r//1v9oPP/xgv//9763X69m7d+/Ce+uKH+/IapySVP7dNGqM9kP++Jxt5Tp3UQYO4e7ublh1x6FU4tDMgoGmxCnkEVuf1AErlUqBjEXuaBPkDx0zHo/t6Ogo1JGcJDyPd6KNVZ9iLKlRqauUSpoDJUM14bWOAV05bTabmZXIQqEQ8lctQ8w45vOY7ozpbnVEkS+c59PT02C/qJPvSRSIazXCKUfJSOQE+WCbojdYdS4iNw5tw3ylkU5qQ/j5j7rwHXVGVn2UynA4DAY/dggypHk20HtKiCB3+h76bsi5n69idhh1W+YIaZ/ytye7Ys/xJOMy29YDm5U+0LbzDoLar6pH0A28I21KZB2ODfNHv9+34XBox8fHNhwOw5htt9thURfylkg1cjwhDyqrbCF9+/atTSaTEAmgkU3IMTLPYScnJyfW6XTs9PQ0LDa02+2ga9juNp/Prd1uh7ExHA5tZ2cnRP51Op2Mo9dut0O0aK1WC3rq4OAg066LxSKQVl999ZU9efLEer1e2MaKzHLi7MnJSeaET41A1H5nrKquQpZob41+xPGEpIVYA3dBPK0CcsUz1Rbgf3W6dbyh1/V6b2Nom3i/RO1obR9kPnYP5eoztYyE62M2m4UdA8wh7XY7zLXehoKYjpHzfK7zJz4Y8qRkEzaVzsMnJydmdp6KAL2mi3O6YMaY8vKsdpFZVn/7xUTKRhfwHovFIuxQ4LmaZgCbXoNlYu/u5xPVH7oYqQQYPiD11TLwCbEP0R1+ceB949a22t0WYspUw8i1USGhIKLoYIxtTbRFiCtGBErIR3vkKbJl8Nd75tKv5K1D1Pl79X5vYPn78hSxTn6fogLWyU73uRK5gkIi3FxXcrnOzC4ptxihqPuLvQJWJ1yR1yd+ElXFCXAgYuGi3mFa1ffL2PeHDiaIs7OzzIlrhMn7VQYdh/5vP0b1fu+seD0TW7XPg8qROoX6nW7ni0XicS3PV6LMy5fqEO+0+ggVfT8vmzjElIm+ipUPqLOefvT48WOr1WqZJNd3KY+808HBgf3xj38MuS4gCYgsUaJP35H6qXGj0ChH3l9X97SNtJ0gcjB4IHp82LsSCjjtGOmUq9FH3jHgmcyjWn/N46SRlBqZ4g19HR8x513nM/+DnKOTlGDwzgoyrTmlGBs4navGWqy/1oEfDzEdWyxebJlUwknL0Gf7cRKDGvRqnKutofYHthSRJhoZZ3Zx2quuOvtT1mJbrVXHeP2mUYKNRiNEqzPPemjkh29X/ke2ls1lah/F2naVLKi+Uv3l6+bL9c/2ZeY9y+sP/66xuYUxrxHVANk3s4zzhj28s7NjjUbDms2mTSYTa7fbgQTBudRoRerpCUkIB9VXfAd5UiwWgy3Odh106nw+D/nk0K2FQiHkaOOQDXIzMnbYGq4OqkaGa99otB1Ef7vdzpAZmrOSxRhfJu+JTuFvHDmcQPSwlyU/B/t+o97q6yiB5eXlroEMMcfgvOJAx/wyvVfrq36PJ5/MLvtRnsTgd2wMcj3lxIgtTwwnXB3MYcv63exy3+NP+D72+W697cPffheKjhOe53/0+b7P1a4A/pmx94hxBpo3UudG7F9dVFF7zMuxtqfaOLoAozad1m2dvE3M4eTPo36xueOu8cFPtYspEP0MBa8r+qBer1u73batrS3b2toKHTwajezo6ChMHjHDINbQPvIpdp+ve941sfKXkUh5n/sJzxvyeo/WQ+uiExzE3KcKjDS2O2heDaI2/FYlDe9Uw0ijSyib31dxXq4y6Ckb5xLD0K82qNMWM2z8hJ1XB54XI69iBt59hNZtPp/bu3fvQg6mvb29jMLHQFajU99VJyc/+XkdQdvllaPbp2LQtlWHnsgCdKMaA37Fg/t0wvZ9jXxr+ZAORB/o1id/LeQFzyW6Bhnk3XlX5E3Dob3Bzbh8+vSp/dVf/ZW9e/fO3r59G6IC8hy76yDPuPjtb39rf/jDH+z58+f2l3/5l1YoFGxzczOzrY0ftkyq0ath37TVYrEI/aSkjRoOtLPWia0p6Clyi5mZPX/+3BqNRsh/sLGxEVYAMTLU6ZzP5yE3AH2ssqvh4dy7WFycXMfRvGZ2qf90NQ8yl3fUE6IoVyMOMLJiBiZ10TGkiyjYCrSz6jS2y+jn+r6r5MjrOH+9kmw+yk0JglKpZJubm/by5cuMTs1bDKI9lMxVI1HHOPpqOp3aYDAIOoHvqEOxWAxbXrmWbU5EYOo7jMdjGw6HYWsBBKa+G2NB503K0C1ZGp2u73R6epppa9+GSm4AVqiV/PR6IUZW+T7Jm99832tZSiivIgB8Xfy8GXtvyqT/cDgoD12jq/mc3qvvpKQ0/UpEZrVata+++sqePn0anre/vx+S4J+cnNjm5qZ9+eWXYUwxj/BsJZPQJZ4oLhaLtrm5aY1Gw46Ojmx/f9+q1ao9e/Ys45jVajWbTqfhtMxSqZRJQD4ajezg4CCUS747zTfGdkBkgDEJmTabzazdbocIjefPn1uxWAwEKFG18/k8RFfxbH/iW6PRyJBXP/74ox0dHQWilogslTe10ZADyC7khLGNXuV6xjZl3DV5orqu2WyG5O9s49Vtwv56/W2W76covG8Ui/5QuVbC0I9HZIQ60Ha3mRfrU0WpVLJHjx5ZuXxx+rL6QZ5MiZFJsTLN8v1YJa4oF/nQ9ALKEWg98ux09ZH439v3Wg76TedsHcOa98wv+nK/2sXeBvHXssDX6XSCzuaQHtKpkF8PXaWpV5T0okzm3Wq1GvIDsivsfeKDE0/AGwwoOYgANWrU8NRwYxVGVlKIdNIVXxUgHRRml0NBqc9N34eyQV5Hx0gC/XuZcbSqvrHyPhX4QQ1xo9ECfsJTwxKjCwWh1y971lWxrkOtypA6qfKKrTD4/vfGTl59+P2xyIzmu9CJTSccXeX0P94p9r/5O+bUaDuqE6xGlsqYGlue0NAVSN3OpmXE4J00b8jyjrFn55Wn78W1mjBdx4mf+L3sKnTr2F2Sm749aF9NcMnckdcmOo7U+FLnwX/vSQeVGZ2TKIdxrTml/PZrJaUhpn3dtO392I4RcdQHA14NQa4zu8hPpv2p+YPyVp7zdJHOodom/jv/25PisUWCdXXtdeHLRn50O5vqHb1P71XdoDLk21HbUOcr/Y5+JzKDaBJPjPs5zm854DkxfajXKYnvnUsfNajvpfOulql6SdsmRub4vojNYdfp/1XzYMxp4fNlelnfif7TuULL1b5RuY+Vjw0MycJiLeQ+7cocgl3ND3WB/MOW1u0bWj+dt2h3SDW+U12i76Xbyvz8i/wQWeQXUXU7qpcpbSfVoXweG4daLyX/eEae7ad2oepy/o5BdT31XeY/3LUtxjuzeIHTq1FOWqd1xlFs4T32ucqOzjOx+cI/V9tYddCnvNPjNsCYUpvT7CKPl1k+sejtTQ9dfOJZ/O8XTPOewXf0t46fmG3hbVbVDfq/1oln+AX92DvF5pk8+9AsnhNY517aXedh/y7+PVRv6vXq234oXJt4uq1Ka8fq37u7u/b8+fNLRvNicZEkrNPphMmq2WwGI4b9l+SwKBaLwdEERA2woqHGWp5xTN3WbQf/3XWu9Uo075qY8PsBnJTveVtUKhV7+fJlYMnN7FIeGq41uzBaNMfIKtJm2YScJ1MxZbdqQo89hzquYrG98orVLUYo8Pd9UGBmVyPrCoVCWPX1CW/VUUI3cI8fOzop+giEmAGrv7VfF4vzved6dKzuTcdZ0EgDv/JIpJ6X3Zihpn8rMYDzptF9eQY80AUAnAizi6TO7969s7OzM3v27Jnt7OxkJkGNiCgUCiEvGX2Jfma8+oToqxCT2Tz48bexsWH1et2eP39uT548CRFCrO550P84bZTpnXZ9HnLIapmPoNJIMmQB/UPf7+7umpmF/3EAOQod+fCJNHk2/azzYl4I+GKRTQauJ17RdovFIuRQog3r9Xo4or1cLod5W/N1YVBxVLJGz6hRyxxNu1Cejw7DyVajDv2eNybWkY88MAZ8fdXxVl3hiSe/dalQuIjeokyi0jRnhN8K7uvDbyKMeP7JyUmICO92u1YqlYL9RL3Jfac5mHS7lr6XJmz3kUjcT24goltarVaQEZK0ojdOT08z+b9UbywWF1F6OMdeNn3fqUPC/To+/aLDMhmg7dU59tvbKS+2MKVkhi9fIyQXi0U4hQ3dTluy1UmJJ78Sz4/mfqzX67a3t2f/4T/8h9C/5Iqk7VqtVtjexlhdLBaZPHLVatXOzs5sMBhYq9WyJ0+eZJJ1t1otM7uIdiPvUrl8fhrcYrGwd+/eZWSHaEq2WA+HQxsMBhlbvtvthntIRE6bEGWELtT2MbNQxmw2C+3KoRVHR0chMTn1r9froQ1qtVrmlFczCxGrtJ+2tT9tk/ZF9lQuS6WLgxmY67XeejQ7OkCjGm4TqoNKpZI9e/YspDHRPKR5C1ExYixPdy4jm/SHa1Wm84IE9JnFYjbVymAwuHQYRcJyqG1fqVRCnjTmikajEdo/Rgit6xfk+R5qRyOTZvHtcfztZXRZ3WIy5eeAGKmjv4vFi8hiM8sQ6bEyGNtEpGuwg0IjnClXCV/NPYdO1HlM7YPYAhVz5ofK83QvI57MLk6z0wlBr8Vo9lscdPLGGFcDF8Ao6oStK8CKqzrXy5RuXjmrSKpVhFHMmNEBclv7ONd18u8jMOgxbnCelikof7/+Vvh24f/Y57FrYshzkvKIq9i9vvw8OVlFPD3UPo8BGdAoSG+wx/rEf+YjylZd7wknH4HhiScl0nVFWeuvKyGxVcRlddD/KV//9wahv99/v0x29H6VNf7WFSv90eiMq+AmhCg5RCBwRqNR5thafb91SAnqo8SUf2/aMubEejnhh/lM71W50f99/3mCMtaHWneuxwmK6RDmUBLV+21hnvhRMknLi61s+vu8zMb646p6a93rl+nr2ByB0cyPtndsfAFvRPv+0NVXs8srzjEnEQIJko9op2azeen5EHZmF9tV8trAj/NY26DzPGmDftOccHlyGtPNec9dpy/z7s2z4WLPXzWPr1Mvr3f9gqvXAToGGC8a4ebfA1Kj2Wzazs5OyHmmWzTN7NI8AjGk27Fj9dWxHcsbBvEE+eMPYIBM9jaPrvhr9Ca6xhOi1CcWAYz+1cNYCoVCJorT9wdtl7eoo/WIya32d8yW8jKu13u9sMreuAm8HYyNDOl03Yjjq+rgVfojdn1sPCpZhb7zW3gTrga1O72dYrZc3+bJwTK/No/w8fcWCheL7GrH8Dy/HVTv9bKS54frtQpv//pyvB3O4qVGkC5rN+ZF1fm6G8Mv5OpisK9L7Dl3pU9W4YMTT74x+F/3jntHh4blpAxO5oF51Alwc3MzGFUoVE2YyKke5MxgtcfMooIGljnzeQMldu+q63VSWmaIxAaVhksPBoNbYTevO/lc1wm8TbRaLXv27FmYVNUoMVs+CNXR8Ygp1Zgjwf/LjNqrIG/SXVZezLnU/llWB69cl9XjfWJdmcTx+eqrr+zzzz+3zc3NMGkReYOxylbd2GTinTM1aNRA9MYi5ZpdOICEs29sbNjm5mbQS6yk6Oot0ESfGvlkls1TxztrRA6/VWdgtGP4NxoN29raCu3Be6FTdJz4Oqhj/ezZM3v06FF0rHl5QU+h41k5Oj4+tt/+9rd2cnISkhzruy3r+6vIBSgWi7azs2O7u7tWrVbDKrsSRsjLYrEIubV4Fu/PKpTOXSR0JtJusbiIXqIM6qKre+gdHLjYe+rYpN+Q5cXi4mh15JLnQkCwpYLnaLkabYUM8G5EnBDdQBsRMcd2Lo38IrKFiDZyC6mxhMPryRaMX9Wv3ggzu4gswtnsdrs2GAyizp+2o9dry2RFP9PxbnYxDhkv7XbbHj16ZJVKxfr9fmbMKhmjcqgruSy+qf6gnXx+MPqeSEnmffQGdYJg9QQT/abjXA1lHHwiqfSEPZU31RX1et1ms5nt7e2FCKf5fB5W0jWKi/fXtlTHwuyC1PBzt3fqVZ7X6WPvwPC3ypbqMq9DF4tFZjz78arXKeg3lSEfmcWYRT9q+doe+gNp//jxY/vyyy9tY2MjtLM/vdc7L5PJJETEkVOk2+3adDq1Vqtle3t7ViqVQp4wZEDnrfl8HiKTGHulUilERWni+UKhYJ1Ox0ajUTjVjveoVCr25MmTDNGjyXY5YYttYeQjY2xQj36/H07N83mKtB3QnRymwAET9XrdzC6SlWvurNiOgkKhEO5Rcgs55DMdfzoPQhjGiLDbBO9WrVZte3s75JLRqIyYHR+bj71+zYtE1O8pX/WovybPj/ALVhq1TcTd0dHRJdsoYX1Uq1Xb2tq6lDBfkdf/Zvl+vpbjy0PGkQuNtlVdqXY79+l3XseojaBlexIqr276foxXM7tUJz8X6TM7nU7Qq5rPTevGj26F55kxoknrzt86h+mYii1SxfrgrvDBiac8qMOUp2Q16omEhN44IDwVI5RIFyVkuLfb7V5iIa8a1XAVksULdYxYin3H/6uE5/9v79ye40iOc589A8wVNwLgLhmUtZI3HOfhhK03+9l/tv8E+RL2saSwFJJ3V+TuEiRugxnMFQP0eUD8Cl8nqnsagwEIkP1FIADMdNc1qyrzq6wsNVY0ps1TwTIk1n3AYqrG9F0RI1nyiJdV1K9oMs/LO498yntWZXbRmOOZpyRHd0Gtdh3slACJGKZqsJvdGAK6IMUWEt++Om+oAQDppQaJGokozYxRnlVPCSU3/A/95fsmZhTHFkW/M6zKuMKTb+pRowt7kiTh6ml9r2hnXkkB6jGZTOzk5MSGw+Gj7c7gGeCJNq2LGgyezKD8vKeKCYF+YwqU5uHlyI9TzSsG/zntjryTrx41VYKL//nN+5SBNZN31GOYOtN2uInr8TzS02NcKmv87ZU6JfnyNgK0DegLyJf7zFtF78aMLe0rjhxS5zRNA4HmyWkdS2rMqryg66i3B+/rnILseEWUZ+kTPz51TvQKMSAfzduPby1Pklwfqd3Y2Ahu/nocVL1utKw6h/ly5M3DsX5btB4XjS/KoLphLG/fZjEDJs8Q9/Oyh87x6mHjdWWdTyBE1tfX7eXLl5k1DTmMzXGkC3ED8USaEIYc49WxxTyndcYA1Js4IaFUPjkWBQlC+SC/r66uwlqAbGmdyRu51vGBvUCgXm1XPw51swZZTdM0Q/yqt5g3YjVtLQtrO/Bzr76r+oGXlVWDPuHoK8f5PQG07PwZ00PzyKnYvK7/az/5snmSgv7haFKF5YB8qPf9ssiT3zzCSm0gtc9j+jjrvX6ueoDPD3nxx9L8fKifmWX1Ml2b/Jgt0nOZ15TY9XmrbqTv+c0CTzjF7BJdk72++dhYCfGUZxTfB0WKNQ2L0sy1qnp8hobFu8nv8qsCzGe6c+EXkLIKP9/FlJhYJ+cRSz69GBGg6XrFBo+wfr8fPLv4/LGRp1A9ltCrga7xGTwWEUj6O6ZsFv1dJh+FTyf2fZnPYmmqrMTkzyvX+jOdTu3jx4+3bnr5lCgz/yRJEpSp4XBoJycntr+/b+12O7Pj4Y0fNdhYTNRIQxnVOSe2KLLAsGOEV+XLly9tZ2cnI6M8S9wj3mEOw2tTiawixde3FWNADV/q6Mvu6+yPYvg21t/+qFWsTF6B1HeZ01+/fm29Xs96vd6Du8trG0D8EW+EHSoMGI6BU07dDdR+o817vV5ob3a5qCveOJ5wUi8TbbMkSWxjYyPIlBKVV1dX1u/3w3eqUFFObn8iwLDOC/yv6dZqNRuNRiE+CuUmbdJDPlSZw6CkLrrDhzKLIYcXBoaeygplVGVLDT81FvF20PgqRfPEMvOplssbaMjQ7u6utVqtIDf0X5qmNhqNgkcD/US+SgjEys7nGLY6h/EuN1NquvQBXpS0Pe2ElxRQbybi3Hi9CGNcxzC3HlEO/Q5vNr1aOk1T29raytR/OBzadDq1fr8fYg0BJe59u5OeztO+3MyZ6hVuZhmDwa/jnlj36er3lC9GUsXkivmO9mA8QNj4PCm/jynCczre2+22bW5u2sbGRvhOf7SNzCzswjMOa7WabWxsWL1et06nkyGJaLt6vW47Ozt2eXlpx8fHt+JgKXFNuVWWGfcEscZL6OLiwvr9vtXr1zdC8p2S3PQjdbi8vLSTk5Mw/6G3IIfb29thXtfbAQGEiyeCLi4urNfrWZpex9/ycw+eV0rcM7a0T7Q9vBwjh8zx/rIG5uVV21zNZjN4+eKxFtNj83TSmIGdB5VV3o3pBLH8dA5VnY01SG0cNhs0Bl2F5ZEnbzECKO8Z/Z4xUERk+c+91xK/9cbHmGeTT8sTNfpb38lDLE3mNB+vU+Vb12ez6xtddXOGOmoe6umu9r2u94vKrWuE8hsxkuox7PJ7E09+wSvzfBkjMfbbCw7KksYq8IudFwBvUPv0i0gn/dsbaHkKhX8/9nmesJQd0LFBhCJDIFd1x//SoF4ZZjfnbGPEYBHxFPvMkzlllYEiUikPZRbzMmnomC1DeOo4uby8tF6vF0jfpyJTi+YVjKG1tevr4AeDge3u7gbvR5Rh7+2hRp/vZ/3RdlBPkDRNw3E0FFzmLowtdlXxImEnxN/oSV+gnKuRhYKqRJmSGEpKMU9qAOPY836O9J8tAu2qCoafM30fqdJAe+zu7t7aVXoM0G94i2LI0D8YIBw98bvoPtAyx8nYUQbM1VdXN4Gndc3yaxGEA0f3aA82XtjVr9VqwQBEJnme9ZKjnkoUKcGpGzaUU0k1DVKu8oEcqlGvG0CkoWXSMiOrMcNDlT6MP0/OqGGu834ZLKN8xcZFrVazzc3NYJBTBj0eVa/XQ2BlHaOxnVedu6kzcwHtwJjTPgCkT9+yLprdkIjIvL5DTBwlIzyxg+FOGsQQGg6HZpaNr0m9IUr5jjkSD5GjoyM7Pz+3yWRya42O6WFKzvh50L+jOpMSF36n2ueTp6R72df5zstF7DNPFOo8XeQh548capnNLMSpI0i0mQW9mfT92CEO1Gw2s36/H9Jh/azVatbr9WwwGGRIl263a9Pp1H788ccQBiNJklvBqRm3WmZkl6Ny5DOfz+38/Dwc9cFDzs+JOt/M53MbDodWr9dtc3MzEEKTycS63a51u93MUUPmI/qeudJvckBusKnrv9fNAu1j5iDtF/rQr4veYOZ/5knGi86Nq8D6+rptbm5mYl+VtW9AjBDgcw+fll/XPSEaWwPpbzaBuACE59HnKuJpeZRdC4tspDzSyc9lRTKTJ0M6DlRGPKmlZI9/P0bc+PXCl0Xfia0JOqcosaZl1Q0fPZ7tPRy9zaakk5JH3p6LbRB7PUrr8Fh6tdkKiKe7Kml3qdyiyUkXeryVdKfFG9i1WvYqRJQobjzwLsOxOuYt8DEFqKyi63d1Y79j7RFrC1WAWATLluNzBUoRipdZsWeSKjCqCMewSJ7994tk664Els8nNnl746OIcNIFwSsCKGvP8az8+vq6vXr1Ktz2hTcgN+E0m83M817R8pO/fq675bFdDlWeNOYE76rirzcWYQCiOKk3Au/zXczQAnmyxDuxs+m6s66/Nf/YLosafRpU1i+mMYXDK+YEN+10OqHf/Jy3CujczcIfC6bqXfYpI+QfpIw/DkV/8D+el1pn702CLHHdPccgdOwOBgMzuyGcVNFRbyuVXb0ZxRvoSn5o+yLfGo+HH2JVUeZutxs8cEhD1zdVAr0iiBGRpmlm99Dsxlj26cTIBH8LGzdY4lW2CHed2xjXGIa1Wi2QSWYWCLXYvJokSTDSIRZU+fTzNW0JQc18owa0braRB8ov3il4gkMikZ+2s29DyAHGALG7tMykrQGb/Vqr415JKyWqkUduUNrZ2bF+v29HR0eFcuDJJD+vFRkTvO+Nf//cIqNcy+Lzi5FOPn3mDyVNlbDR+mnbxub9/f19++Uvf2nNZtMODw+DLkRcwSRJMkd/aS9IcuSCjRH6dDQa2WQyycR/G41GYbMAz0r+1hhx9Xo9xJPDS4W1Tj0gIRKY+4mnpES1EoYq13oEWmVayYrRaGRmlhkbyJ/2vXob8Ix6w7LO0TY+mDHt6i83SpIkxFjTgOyx+Ufll/5fpQ7m012kQ8R0Z7+O65zs84rlH8tnUZkpN8STxgb0gfMr3A158uXnRK/bLYu79n2Me9Cy5dngumaofPp1RZ+NpeH1X92s1r91DdI12Z8mUKJZ2yNvffNraZGdn1cP/8xjYWni6SHYsdiC7hH7DMUPZSdvp8krVExW7KqRBoLjhXhR2fXv2IScl44XtiIlZRGxwP9pmoYFPLZIlTFMY9B6PXVQR3ZzUG5iCqGfaFCwdWfeG1F3kY/Yc7Ey5PVpWRSVwxsxMRlQxdrXdTKZhCM1z43MbDQa9ubNmxCXYjwe29nZmaVpGlz4dTFTo5gFTI1pXbT0eJ5vPzU00/Q2UaQGOMQTlyHwHPOSXotOvup9wPt+B5XnFeSN0qvkkzda9TdQ7wrgSSmMFYKjMq+qQhAjn1iUW62WXVxc2Obmpo1Go1Kk0zIKrH+WNvE7RhhDZpa5TZBrycfjsTUajRAPRUkBbR/ahXZaW1uzzc1NS9M0EDkQRwTDZR6ir2ezWTj2QaBcvAUwwlDIY7KrxBj9ot5z2u+sl5Ci0+nUhsNh2PmnPfAw2NjYCIYp33nPJDMLhqQfb/SjGmvqpZG3dvG57nAnSWLD4dB6vV6hsVa0VntDykM9wTgeiwccRrwexVSvmjRNA5GDd4au++qVwjvahzrXeJJFiU+z7CUCePJxXJp8CfTu2xTvAbxJ0C8gSNI0DfLHUSj6C6hBjzwq0aBzGcQ7R4DW19ftxx9/tNPT00zb+x1q1ibmVfVi0vaL9W2eLqDQuTFmvHhgTGj/FK3tzD3eI8j3hR9LeXrzq1ev7O///u/t6OjIfvjhh0DiNxoN29/ft0ajEQgj2mA8HgdSG8IIcqrf72eCknc6nRBEfDgchnQ44qdEqG7mtdttu7y8DJc3QIbpsV6ITeLt4fnW6XRsbW0txF5inJGu2U2MOWK4et1/Op2GwOlsSPpg6/QFZBTyT7uYWTgOqkdSmad1Xde1GRKXTS+fj45Z6lFEdK4CjBtPHlH+ovxi82NsPC16h89jdk9eeekvjmSqDXdfHfoxDfHnhDzbaVG/FdmOefNXGbnz6Xi7zOdbZt72z+r/eRum/NbNE283qleTelnqEd28dtL070I4aTt4LBrbD4UnFVxcG2kymViv1wuKjBpCPMeErIsI7rh5pAsLB94bLDZFHgOKZSalRYNNBc0TT77OecSVosziERuQ96nLU0dsAtHf/llVFNSwfyjCZZWDv2ihV8QMbq8woFRxbMJ7HjwFlJVJ9UhIkiRcNKDHRPxEnqfca97+WnsPv8j53Wo1Hv1RDyWDSMvvdpRpF80jVl4tWywN/5waP7pToz8ssLznn9H0yMO3d5qmGYV/EZadnyBNIKeJv4OhEJsHdE5FofC3vyVJEo6Z6M45ZaW83gNK28vsmqTp9XpBRpS4QmEhRgw/KiNKRuRtqlAn2gA5wRjkXW6WM7Ng6DGOIDvUAEMRU9KR9siTYS0T7eHHodaN3152YspaERYpYjH5UqJSiRP1QMOojpUf+NvnSIf20ne1nWNpad397qtZ9mgd6fk60RaQo0pSQ2CRHv2Ll4uHyh0kJp4w6sVldjOWADKeJIl1u90QgNrPI95wV5nT53Te8zJUZESVMVT8O35s5c1PyAvjgr5RfdTfXqg6nHrM8H2tdh3La2try6bTqW1tbVmtVrN+vx+8lSDN8W5KksTOz88z8ej0NjfqovOTeunoPKG/SQv5gBAnPiJpacwo4kkpgaN958kaNpSQFyUnVFaZL6mTygfPKxHKM2trayGunh7LY27mWCnto2ugltF71PoNgtj6SN21jR4CtJn31i1joPrv7zqP+vdi+rbqD/QRZKh6WK5Cn6bv8Ib3tuLnjpjNuEwa/m9dj2L5ebt4kT2j7zAfaH5l5JLxFfN60r8X6Sux+uatI0VjuMhWjen/sbbUudE/43XRx8a9iKdlyYtFSNPUer2e9ft9297etl/84hchP74n34uLCxsMBkFp29jYyLgR07As5kzanPmGfPKGTZ4C4f8vGhR5hFAsLTVCy+SfBz9YY4bcXdNclN+q0noo0O9qKKth5uuAwoqnhtlixXGZMsX+BmUW+rukq38XebN4g2M0Gtnp6anNZjM7Pz9f2aL+mKC8eI1g2G1tbQUvA6A7o54kiY1nCKxYf6lxoIS3Kpp6c52PqUMaSt6oEp4396jhq4uVJ7XMsrEm9DN/PMXPJ554islajAQhPx+bxLsdkze71hzJ8OVf1frTaDTs17/+tXW7XRsMBnZ0dBTagP6h/b3yUavVwpEJDCUudMC7BAJL30fZMctuiJCm2Y0cYiw2m81A9qjBh5fPdDq1ZrOZiZ9E+6rhpzvpOt45TsfaigHsvb/SNA1HIfH0ob0wHNXLQY0I6gp5FvOwy1u3Nf5KLC5PbIxq7DbNIw93XXvxmtA6Qs5BrujxS9pFbxS8vLwMnkTb29uZ44pmN/LgSZkiBVQ97SCLAO2BUeV1OZV5+kjroPMPwahVt8IzkPSQu+FwaLPZLOPZSf974om5hgD+SXJ9dEy90z1hoXOXn0u1LVWG9Bld5/Vz367+uzS9ObLs5ymIEJ0LYzIECYNXkMrU1dWVjcdjm81m1mq1wrFb8mUNU28dyPSvv/461Pfs7Mx+/PFHM7v21lEvcOKFnZyc2MHBQZCPdrtt3377rTUaDTs5OcnUBeNf24t66HpGWsT+Oj8/tyRJwlxDzCTartvt2s7Ojo3HYzs9PQ3p6RhSD2AzCyTE5eVl8JBlfWcOI7QGXqasRWoE4n0wHo9tOByGGylbrVa4GdDL1J///OdAeqlhSL+ura3ZcDi0+Xxu3W7XOp1O9DIF0qUtdKOMeUO9elYJnUuYa8voqXlp5ekofkzFxliebalGO/G/Dg4OMrJzn3ZRvQtZ3t/fNzOz09PTsBGrXsGfM2J9WNbm821pdjs4eN47mpe3Z83it7zr++g/fFfGFtf5Wp/TcREjvGL1Iz3v8cT76EDaHkp8eZ1by1Xk7eTXuxhRxpz3Ke24exFPD1lwJpeiPOh4JiEWCw1OqBM5ygmTN67mGqxrFeVeBquaxLQ9nmMsnlVClVJ2mpCZRYtUTGFlAvNG2EPhLuTTMgpCHsmZpmk4DgQ5q7dDPUdcXV0fFdQb4bwnUYw4iv3tyZE8eFJG8/CkhhJQ3nNKAwFrnxUpZpp/rA6aR5HXhKapC6Aq1373xC/IXjZ9W8cMfcYthke/339Qb0Nkntu4MP4oj8bn8OX1xqt6CajhyLt+Zy0G2lePOHkShXZXDzZ/rMh7pdBn1EnnRMoGGUF+Sgp6oh555f8iIsTXO88I1zTU48e3sTcAV7WGFpGZi+Y/yq7GuZbXg/pp2+ixShRUv17FxpbvX18PzcMfgdN0vfJMub0SDXzfaLr0EfoYBK16mlIvJV01TYz3q6srazabGe9Afrxyr++rh44vb2zuKQNvFJQxwhat5954UUNIx4P/3ssZ76RpamdnZ/bzzz9br9ezk5OTcFxNNxxi6elxsYuLCzs/Pw+xu7RM2re0h29fncvW1tYyhrvKqq4pPKNHUCCeioxBHU+6viq5AUG5qN/wuoKQUyKNsmp8p6I+999jh9COMdn3GzdFHqKrgF+/8/QL6uY/z3vWP19Gh8xLT+05jmOqp9Oy8OsK0LlPbx71ZMhD9stTAMS36qc6Z8T6umgd9euSz0ufi/Ur41z1aU2nSBaLsEg/0/Lk2U95n1EOPxZitocvtyefit7JS4e5huP0n9LraWni6aEKGxPWmHDzP4tUkiQ2GAzs4ODAms2m7ezsZM5Qs9s8nU6DhxONz81EMQNxGSjDGjO8tE55dYth0WRMGuy23/Umu7JKlMLnvSrlf5UgLoUqLXky5o17BQu/32mLKeLATxj6mX++iDDKM9AW/a2LQ56RFlNyDw8Pw/X19z0z/9CITea+7y4uLuznn3+2jY2NjNcIu4rUTf9O02yQQJ+29o0nfJIkyRh3iiS58ZJiN1aP4vhArHnBG+krJYJQaHnXGxQKFAg1atRwUGPAHw1Uzx71JtH6+2M3pB+bx3mHMo/HYxuNRvbTTz/Zv/3bv9lkMgmxZ7zx7ftlGUynU/vrX/8avGVjXiqaB54CxBCBaEC2CIx8cXFhHz9+tPl8bq1WK9yw5HfhSB9vJHbCz8/P7ezsLOMpMxgMMsYJRjyB2PlufX09E7QcQylNU2u1WuGoDeXCy4Z+xZMY+cI7WBVtNQR0ntB+9ga1BvFVOVN4pUg9cNL05vY1ldG8OSpv/MQQG+eL5j1P9sznczs5ObF6/TooNkd6/M11fh6BYO52u7a1tRWOk7EBoPl4wk9vUNQ4O6pEY1Sh+/CZ/+3lXucN5gKFeushX5AEzLOUZWdnJ3Pd9Gw2C96MeO3pWOJ40/r6evC4jQUNJj/kV728lLjII9z9/APUg0iJPe23mCepyhBGa56sA54lPfV0urq6CmNU5yYlKMwsjInz83ObTqf2r//6r/aXv/wlePpsb2/b//k//yd4TeGtp/JEzMPxeGwfP3602Wxmf/jDHyxJkhCLCS/Uzc3NEOMJAl49k5IkCR5r6+vrYSOLo8yQQLSdBjAnbl6v1wveW8S/UlnUeYbjeZDnzMXo+hrXDK8xD2RrZ2fHNjc3MwQQ8zMeqB8+fAg3R2t/89vMQqw75EA9+OhnxizHsvVCmzRNwzjhxsj7rnceXo9QvSA2f8Z0WNUPYihT3iI9TufL8/Nze/fu3UpIJ02/1WqFWw9ZoxizxDNTspEfjYv3OcC3+2g0srdv31qj0Qi2NWOLdjLL6nKx9JSw8uuf78fYRqjqDXhxml17SHp9QPWCvDrm2em6RnhdQOu7CDH7j3Rj38f0J/4ueibPZmVM411JWCLV1z4FHi3GUx5zuQgoM3rNdAwsQkwAelNHrXYTGBDlWYORx46M3JXBLhpsZXCfRcS3K/WsbnO4gVeegTf+9PMYgVSUrqZ3X6VgkeFTlnRaVC6fh3oEMoY+h90cPJ5iuxm64+gRm7diYz1PPjyRowsank7q7cR8pYuKGiI6P8UWcDVo8xQ3/lbDJU9uYu0Rq2MevCLh2zNvUdejDhzPWaWi7cuYpmmQD+9BVJRvTCnQdzGMYmPI110NKWRSSQpVgklff0MiqbGrgXM1XyWdOCrVbrczBBPGEYq294QBfp6MkUBafvU48G2jHk5F8Ips0XP3lZu76i6QRSh8i3SK2LjU/327x+qUp9AXpa1l8u8rsZHXfjH59XnpnJYkSZA7oIQHx8W8twpjEq8TyHqNdbOonEXI69884/ouaej3i8qgngQx48M/QxvFysq7o9EojDHIb75ToljLh8cdN9RBfpndxHLTti/yEND5kTkNIi9Jbkho9Hvd6OB7/34sbcrBbz2SmtcvqttoW7Ius4mgeUA4MD9y+UPM40L7UcvBZ/4dLw+qM6g8rGJOy2sPn09ZrJoIK5PfKgkn+oJ5Bs88bx94IoKyfG7wddSNgaKxHtM9Y/Lk9U8l+XhHdQHVq1SXiK2DekS8qLy6cXOXNaKMt2Reu4D72FRFZFqsXLQFnAf63KeU20cjnu6quJllmdZ2u22vXr2KKmFmFiaJJLneYWHRJDC5xlbRY3cMKFUSVejL1MEvDnkL3l3boIxg64BAmAaDgR0eHt5ZuO6zcDzmonMXJMn1Lt3+/v6t3V8zyygbMaNK01GDVCefRYrAMvIU+130rJaz6P/YO2ooEUeCXejnuqj6cl9eXtrx8XG4wQdygxvDdHc/trDocVyd+JWc4Hmdo+h7b8jhNafH6PxC6GVVy+Ld7imTGnpqwKnREtuhV0VO51/g28Q/E9vRiXm4xNrPz2GXl5f2888/27t37+zg4KDUIl1m/lk0jlhD8DD66quvbHNz08zsFomvMaqQH4w0jqUoaaTeLrpeqHJ0eXkZPFv0WSUe8YhZX1+37e3tjCH+6tUr29vbs62tLdve3s6sd9we5Xfa2u22tVotazQawTuKvIhpgfcEN9pBTKshyNzI95rP5eVlJkAxbaMKkSc+aB8Nou5l1BvhStB5sqPI207lJ0+OvNLsv/NeDpRVCUiIzZh+oO+en59n2gRSkbqo7Ph8vPFtdjOm/DykxgTktx6b8uulnz9Uv6AMeM3pcdCYFw8GnpJOOzs7GaOBeYN8ms2m7e3tWaPRsPPzcxuPx3Z4eJgJAq0yoeOP8U1dqRvvxch9+sX/KOmvchR7V7/XPvZoNBrB08IHMcbDxesc1BWPC32HDQ2Iona7bVtbW5Ykib19+zasQWtra/b69WvrdrsZz076c2NjI0Oikhe6NcQ1hIzKlPYvZBbE+N7ens1mMzs+PrbLy8vgganHfznuvLGxEfqG9vdygpxxnI/4YWdnZxlv062trVAnvOD5jnd2d3dDHvX6dfBwjnShP/R6vbCBTV/4scV3jNnJZGKXlzeXBzB3Ywiq/KlBTlk6nU5GvlcJHbP+9s3YvMm8oN5Qqq/G5tOYXqHfxYgJ/y4yuL6+bl999ZWNx2M7OTm59wYpMbyIv4X8cXqEulIuJcQp73PVlfMQm8vq9XrwLtK5LKb/KUmqaSnBlyRJ0Aewv5k/GNM6pyH/yCgnmXq9nk2n06ADsVGpenLMroqRNNTH66p57ZNHqOl3ZWy4vN/q4VlGxmJrzXg8vuXp9EUQT8uAwY/SHJtYEGomew0yh8KnN9zpMxq4tKyQ5X2+qBPLMKpm2R3IsuQToE64VVe4Rr1eD8qbKi95BFMMsYXUL45lSR7/eUw2VjEpFC3++psxgMegXnP+ueDq6irjwcE8YHZzO47GEskjCj05Y3bbFT2mGKphysKrhp7f/fQLdawceYucfu7zzTN+/PzjF9WYZ5/uVKlyoWWirNqW+rdfmFkYB4OBHR8f22AweBQ51D5VY5Wgyf44offS4UePAGFAxupJ+vqjyleM9ONv5FQD43MkaWtry3Z3d21vby94jakhi7xh7HBlfaPRCOQG9SBguL/dieNUOkfkKV8+lhBlZc7hGW9QMSZjXruxXVBv7CiRHCMayuCu66+W35dbyxybGxT0DaECzG7mGJR1SFKNL6Ykjv6vY5T82NHnf03D94WST7RtTH6VYNL508+jOncpIbG9vR3KlaZpMPYx8CE7Li4uAhmxvr6eUcypgyeCWPN5zhsfSubF+tTPaSprfi3NM2Y0PQ/6xLepEqxFsotOq2SVHsljvpjNZiFYN0TPixcvose31MDz8bggVNRT1xttsRhs2t/0k3p2+jYlnxixp+XhfeRXyavpdBrmNuSTdUblVY1pT2qpFzgbcxi9Xk48ya3jENJE5d9vyqgsab38rZirBGVTLxPkLm8DLAYvQ2Xn0CK9WkFf1OvXF1qsKsg3GyOsh4wPPeas/altdJej3M8V2o9l6pwnM5qGziE8p/a613N1TdcYdJCmELsQWZqfH1uxMsXm3rvoC14Oi+Qyryw+zzL5x+w8/32apkEPjK1zj42liaeHmPwW5cFCocwnCzPQBUMnbW1w/d7sZqHMO27jFQc+80KyiN3MIyb8QlsE/7zZjTcGHh3cKJNXhy8JaXp9I9R8PrdOp2MvX740s5sboTRQqSrrqqjzvf/OL5CxSUQVKm/U573nv1t2rHnl2k9oKGUY+vzPJPVcZCZvwvdjijr/5S9/sY8fP9rr169td3c3xMZhBxJlS5VdVXq9gcMOjQYejXlAsNB67wQ/l/j6QHqoMe+VWq27GpAxQ9IvekULrpeZmOeJKskKyomHKYaOV9IxpK+urm9RnE6ndnR0ZO/evcvcZpfX32VR9j3qjMcAZKy2i8bBMcsa5YC5BfLAG0Wj0ciGw2GYIxqNhn399dfBUyBNU/vrX/8arulmHZvNZraxsWHffvttZhd8b2/PNjc3M8dDmOd0F5t20BgsxHNh48LshsCACNE4S5Qb2VT51rVU5Xw4HAavmFqtFow4jIkYcUM6lEXbFs9F8tE4OrQ7sWFevHhh0+n0FpGZJxN+rJeBN06SJLF+v2+j0ci63W6IiaGxtPRZNVBpEz1i6mMu+Xc0cHTeHEib+j7mc53bPGkdq6sn4j05gOFA/47H45AfxBoefDyvefj0k+Q6/s3+/r7t7OyE3e3vv//eer1eKGvM8Nd28O0SIzXU2ImRwv43sq/pazv4vlOw9hL/CNLHexV4PVYJTk9Q4wF0cXER4jB1u137+uuv7fLy0j58+BDGtXpz6zhkPtve3g7zCBu69Gm/3w9yrWSKPqseREpmbG1thbrjtYXRjwGqfWF2HTOJi0IgzdM0DUT7ZDKx4+Pj0BYaW4p2oXzkU6vVwmYtxPrZ2ZkNBgPrdDq2tbVlzWbTtra2bDQahdhO6AwQU5RJy6tzGHmpwQwxGJNPLS+XXzB/rNIGm81mdnR0lNGDdA7wUN1FEbNlVmE8+7WXZ3X9uQ+azWbw5NFbjpvNptXr9SBbkHPqDfYYtvBTwWw2sw8fPlij0bC9vb3gwRizLxTIK+3H816384SWn09VTubzufX7fbu4uLDd3V17/fp10Nf0BuFFJJLXg31+dyWfYsRpns13F5LJk7O+nPpb127aWB1uyuT3kFipx1NZ8mSZd5RQ0t0X4CdCNfZZ6FQI8zyoilA0Kd5VQHXCKqMIF6VDu5yfn1uv13s2hMFDwbcrigrKAJOWGkh+kHpCyQ/o2OSiz/Pbk5v+mVgeeZNULL+Y3MWe98aB2U0Q+slkEgKJf2omPA/LyHSsvS4vL+3g4MCOjo7CDrrZjXu5juUYCcOP9j+Kappmg5HH3NBjsVN8ur7eSqBr2WJ11HT93/z2BKj/38utAhnxsuW9CZRw4re2m28H5jB2k8/Ozuzo6OjR5rLYWMH40xiAeOfowu7bWA0OlFQMWN9/esy7VqvZ9vZ28DRK09Tev39/y2OFZ7/++mvb2dkJ5e52u0FRph5qyFE2yqDHO0ajkZ2enoarzmu1mu3t7Vmz2Qx9x+6kxnrQucQTqnoMD+MS4gkyQj01FH5N9KRLmt6Q47oLilGHkUwQVI4REqC6CMvKnMoN/cUxHfW8Yp3RMaaErIYCAJAaeQQB7VGr1cKc5pVtJVnoL9LjOfWCUo+ZWPvoWNc5KtYmSkBdXV2FWEN46hV59fjP1tbWbGtry9I0tf39fbu4uLD3799n1nLeU3LOj3E+ixlAtC39pRuVfu3349/Ph7R5Xln4npuW6Ue8dGI6K/OrH1N+c8zHMW02m/bmzRubz+d2dnZmo9EokC9eftUrAdmFTCKGKEdI9cIOJYP5Qd6UKDUz63Q6oR4Q3LSVD44P6c1xXt0o0naHhDWzQGqi5+h8TF2YL/UYMRcEHB0d2cuXL21vby9c1sCaMB6PwxjRCyboX+Zwys8Y101xxgBzvs7N6u2hnj4P4WVD+dM0tZ2dndDvKuvqxVKGOPD6jB/HMT2lCMz1zJf1ej1cwHAfPYG64vWrHqPMaXi7LWPjPmd4HfXy8tLOzs7C0Whdh2L94D9TfQH4uQFdPNbGOhem6fXm3Ww2C0fsIJiZm/xGhk/X22QxOSqS4bznfJn934tsQU0vZpd6GyRWFv++50A+JVZ+1O6uA7Loee2A+Xxux8fHgfGv1+vhXC6CyMJkdnPFNSizQ+/zXfQZZcsbIMvWeZGgUxeODJ2dnWVcQu9Sls8RMWXb7Pqc6/v374M8md3Ee+h2u8H9m51ClBez68GLYqWBK8kvb/Lwfxd9t6xB5BX2MpMRkxC3csV2fJ8SVrHQq+Gepql9+PDBJpOJ7e/vhzgXHOHwC5w3egGKI+NWjSxPsqhXDIt4zIDx/+uuuxIgZvFbqdQAIR316lQPLa2PNxrVO8fsZteed0hTlTTNi+9UWeZ/NWSurq5sOBzaaDSyg4MD6/V6dnp6Gm2TxwLl5Jhut9u1q6urcHlFzBvBH6/C8FDCQUFcldlsZsPh0BqNhg0Gg7CzCjEDaaJtjSeBHjWgzGY3pBeGnR4XQJ6TJAkesupxoOQ8dcUITpIkeFURJ4XjOxrvROVQCairqyvr9/tmZhnXb4XOpzquqJcaZmbX45lA6RgQGOPr6+u2t7dn3377rb17987+/d//PXPba56iWTQXFimnfi1gnLCWsEPvvQlUfjCKFTzrFVCeZYfXy5jKhB670hg5amTqPOGPsWhdVE+BMCBuh459jPtOp2P1ej3EyGm1WrazsxPGlrYd65GSBDr3URfGo85navh7r4SYbuWVfB1jtIfKqM6tfp738qHpUzbdhVfonO6PX/uxoDIB4RQjvxjneOHQB+fn53Z5eRn06Ha7nSGYWSPSNM144tAexFFqtVo2Go1sPB6HY/rkh56ONxD1JqYiY5T1tla7ueEQ4k1JGB0TyAbkG/DGJvKoxJAndnQcMg6QG44kzmazsKELAUGMPfqKukLS+c0WyqflwhvNzDJEE8/q2oG8891db6wui4uLCzs5ObFGo2H7+/vhdsAYARWD10Pz9FIvr8DrGwrmkyS5uX2uXq/bDz/8kPECLwvNezqd2nA4tDS9uZETWR+NRpkNNz/GnrLefF/k2S6Mvdlsduv24rw2UZ3R/696clGeqgcQKoDxzakNPw/E1mTgZTK2TuS1Rxl5zoN/N0+n4DtP2CuppJ/7cuqa+ZRkdWniqUj5eggwITL5aPBEVSxU6aGcnmhSJcIrH0Wkj1dSip5dpLwWwZdfy0Z5UQxns5mdnJyE20uKSI7HQtHAfWxoP4zH4+DqjwJJLAQMFxZ5dv6BGjQ+XbPb7RzzAFmmb8rKkZcX/cz/rx4JGLlP1dOpDPy4jH2v37E4vX//3t6/f2/ffPNN8BLw5IkaOnqUwhsKjEl+6xyhRoTf9TS77UWnruQ67jGCVElVYszPXwqUqIuLi+D14QNEUkc1rjR/VS5U0fN5ekPNB+VXbwoU8MFgYL1ez969e2cfPnwI5ISm/1hzmc4PtMfa2lowcGk7nY8x1LTe9JF6PIE0TW1zc9O2trZsPB4H4m4wGNjl5WVQdpMksY2NjdB3Kk963ExJTZQyJZ748UTqdDq109PTTBwrvoMAaLfb4ca7q6vr4zrdbjesPcPh0D5+/BiC9UJuaLBgsxvPJzZKlIyMEQLIvBrfeIaotxaySKDjra2tsHNdr9fDkaz/+q//sv/6r//KGKteX1AZKCIqYvISg5I1eLOgw2xsbGSMOdo/Ji9AFXXaF4OceUfnd9JTMkW9NFgPOTKhO8kY/FpnYm5eXl4HhK7X6zaZTGw6nQZiQ8mCdrsdgjqrbHa7XXvx4kW4TRFDRokZ0tLjWpQFmcCTBfmizRkLKh+xNVvJB08UJUlya22kHRkLajCRpk9fn9HyeDlRskGPpWnfkwZl5JgZMu3llT5Xgq/f71uaXns/ESC82WxmyO7JZBL0ayWBiKOi5DPzEMffvvrqq/Buo9EI8wixR5FXyEfI/YuLi3A0Vdc5+ghCQI+K0JaMH+ZMCBvmIbydgHoQ+fZmU4FNkclkYqenpzaZTIIXLhuVGo/Njz3KxvyH/BJHCPlK0zRzmYCOXWwd3jezUM+HwMXFhR0fH1uz2bTNzc1bOsEivV51GsDY83aT/606DH3udQm8kl68eGH7+/vBW0bTuYu+TH7qDccGM+0xHA5DP8XG5FMx5h8LzJN4aKIn8V3eO/43YxldxZ9k0g1M5Mp7MOllFj4WdMzu8rY/8PJQBouei+kLXq/wPEVe+p6A8t97L/fY358F8fSYiBn1qkz7c+Mx5O2sLspLP1chKSIeigSySLjy/lcBYucGV18G/1MhnZ4aivpYd5n5TA00duhRxvLS0l1RVfbz8tfPF8lNmT6MTWSx9EhLr0v3E/XniJgRaZYdx35ixujJexdFTPtRDQ2zrFeDKu9m2flIFWxVbLxCpUptbDdQy1mkAOqxK62DN3S1Lirn+uPbzRtppKtkjtYfowlFX3cYtdyPjTS9vh2UeAZ41ioZqIaDmUUNXTMLhpdPH/lgrmH+UCVMDW5tzzRNgwGpZGa/3w/KXLPZtI2NjVvkipdzDCglW1Hyue2p2+3a6emp9Xq9UAeI64uLi0AwkC6kiBqJakSqLMdIU02HtZ2NFjWQSYfjOmY3O+N7e3shboemG5t7YyirgCq8ThDTXfAQgagBStCqR5JZ9oguaeN5oso0efg8zSxjCCtxrnMHearceWUfY1jnAV3vdD6BfOCd7e3tcPyJo02MdT3+rmmo4c14oT54PUAweFJH20y9Namvn5f1e21XXV+9LpknUzrfaZ5FeoRCSQgdP75MfEffes/cNE1DfDO9WY7yQUChS+LlQl9A0JhZIEzMLBPMl/7Dc8kbSrppgucXt8NBXvKZtq/31lMST/uHTYx2u50hV5V48/2N3KqHpJnZ8fFxCFvBnANxDDk8m80yZdO5m/lZiRPto5ie7j0ZdD2l3XS8LuPhcxdcXl4GD5LNzc3QNqtAGZ03Ty/TDTS8PJGL+xjW6jGrQHb0MgbAOqnjbZk147mBOXA4HAZPV5WPvDlOoXOTzuf+GbWpvK5tZrfe9fNw3tzsbaY8wim2+eMRIzyRDf+d6pAx+DLGfvu8PRGqa7Gul08JKyGeVj3gitJL0zTslrIgqDtwHvvtlYhYJ8YW9aIy5qVf9I6fdGOTsFfAWWhQrvv9flAkvEvhqrGob5/jZKuyoYYMu/woTuwC6vWeqhSpMghhxbvsBscmvrx+yluQi2RZ3/XveDmm/OPxOATl+xRG/UOhjKya3W63mKGhynTMYEDZjeXviSdVgFkgY0QmJDoLht9hJB2IZzVmPNHp5wQUc2RT5YN0ND9fZ2RHf2u7KYlL+5CWGkPUj/KjPK6tXV+BfXFxYWdnZ59MLlGqzMw+fvxovV7P9vb27Be/+EXG6OE3R330amztW3bM1dgBustO8F/aAxdyJeFUnubzuX38+NH6/X54Vg3Uy8tL29rastevX4cAznhJ6TrHbVcYfpShVquFgNj7+/u2sbFhHz9+tB9//DHcOMgc2Wg07Jtvvgm3DClhOZ1OQx34DnmAePAkAO2GUZgkNwHOMQB5BoLLzMIxxbOzM6vX67a/v297e3uhT1V+i+ZX/cx/XhZ+jaBuEP7tdtu2t7dDvWPegLqx5nfaWbP8kbxYeakz76gXg77j2whii7Zmjex2u8EwRRfT+FpgbW3NNjc3g1fT2tqa7e7uWqPRCGuQEgGkBSHHnMF8hQ6khFer1QreVgSW9Yq2J/8Zn54Uog3IS+dI+kaJMn/MQcl+nf88YRTbBKV9VYcF6ChA1xPKr95yWif+Hg6HdnBwYBsbG/b69etMm3S7XdvZ2bHRaBS8hDqdjk2nU+v1eqFseA+22207OTkJx8/QdTSv2WxmL1++DMQosozOgccdXuV5Y8x7XTHnqO6mXksQTD4+Ed6FfOdRr19fQpCmqf3+97+377777tbmim7yMj9BohLUXIOiKykeM6CRB75T+dOjmcgAuqXK8EMA+f/48aPV6/WMR7jXsXwZYjppbH6N5enJN97RdVPXAeL7IMeeuCiCr0er1crcEktZmY9UZ9FNZnSXLw1XV1d2enpqtdp1TEE9MltGD/c/Okfqc+Tl5zP/rMZYy7OjPXR+Z/5S/sDXoYxtoTq5r8Nd0oh97jeTda3QdtcyqF6vn5chBx8Sz3rEMNFzmwTnzs2Kj92UQZnnip7J+66M4OnfLEgorPz2bukPhUWk0nMjnczs1sRA+3JUhJ1TNZZYjHWHXhUToOn6nWKPmIKcV8ZYOmVIP52wqYv3HNBnnjOK2qJoop3NZsGAp09xfdc+8gaBX2xiZdHdSl0E+N63vyqeMS8H72WEgutlgfpqvf3ivajtVIb9rrumpUSbwi+2KNNqqCGHvV4vHJv5lLKoeSMHeqSNxV5jc/j3zLLyRh/544lqaKq3C++Y3RzjjM0nelyNdyjzxcWFra2t2WAwyNyqh+HnjSJNl345Pz8PO/vE4DK7VtJ3d3eD0tlsNm1nZ8darZZNJpPgtaDzpuaphpmXJe9KrkqTyiDP4qlAO11dXQXvF+Tt7OzMTk9P7cOHD7mydR+Zi41/HY9afsAGgMbzodyqWMbiXpAWfQ1JVaRzePJF6+zHuR+3Skghd77OWldkstlshh+CMmvcH38jFf2lZSVNnZ90DoWQIeYL6caME80rb62IGS36rn8/77m8dBcZ3/qjeemRx7I6pJYZXWYymYTbJSHEx+NxIDZ0PdL2ixEKPoaWEiykz9rEkUAIG5Utysec4Nc92oL0Y8+SJ8/7dVbzVuNL60TYAR9jjLnbE9bUVdPU9tKTGJDkvIfu5fvfXx6g84aXj4fWvakv5fcbYYveLUtCAO0r3/dqOHv9Z1kUjSfNVwlq3dDjp4xXzOeIorYvmu/8OClCHglTVKaYnPr5NK88/O/n9zJ2cExOwSLPoyLdvKyMxwhbvDTZrHsqWJp4uovw3Cdts7g3R5reXHfKZ9vb2/b69etbSgrfxwZDTMjoNK8AxIQ+b6GP1ckTC7Hf/M2CjCI/GAyCJ4AabosG4qKJ/yHwHMgob2AeHR3ZycmJvXr1yl69emXn5+d2enqaWXS51YJdDl9P9YDR94A3Rj2KiCj/XBn3XvJCEefmmPPz83Ct+EN6yz0mysicLgr62fHxsQ0GA/vlL39pv/71r4NBl6ZpCMAa29VCKfPeR/xgBGHwr62tWafTySjMkMm6q4z3jFnWU0lJEDUGYwq33803s0w5eZ5nY4q6Ek3+CIRPQ8cDCie7wyjvkGl6THowGNhwOLQ//OEPdnp6amdnZ6WMtIeAV0wY63iX4gmAtwceJxxdAj4ujtnNEQGNB4IBQswPPxZpLx27SojjcaJxlJC1wWBgo9EoEKrb29sZTwntE4h2+ub8/Nzm87n99NNP4fhMklwHFe92u/bmzRt78+ZNOLYDaWJmdnR0FEiq8XgcApdzpM/MMhsn+j/eAlo+HXdKTiHf7Xbbdnd3zewmWDnl7HQ6tra2Zr///e/tX/7lX4Jxndfv2vf+87Ky49dxxpceWWo0Gjabzezg4CCMH/Um6Xa7maDFOhbVK43PiXHEuqCB4KkTfc0Y1t9KNilJSH+Rl/d21HS1Hq1Wy7a2tqzT6YQrt/0NiZBQxAZC3tX41o01bd8kSQJ5BTm6t7dn7Xbb3r17Z5PJJIw3vLFoH9pD1wKv58WeUZJA51g1MjyZovMr8YJix25J08s8pBr9qRsY9LXO814WtfyMazxFrq6uL6Wp1Wq2tbWVqR/pe09LjhtBKHW73VBHPE8gK9I0tYODA7u6urKvvvrKXrx4EQwglTnmMjyw8Z4ilg91oa/xiL24uLA3b97Yzs5O2LzQIz+8R9vhhUVdmFv5mc1m9vbt2zBntVqtIKPcTAmprenrTXy6hiZJYu12O7Qr7zI/4+mFzOh4J13dtNI51vf3quF1Y3QO9JKY3eHnv7xNVIUfj2qcs54xp3iSjrbxOs0ydY1tIGsZyI+j5DpHqmfmc7B7VoEim9fPmyBPp1uWQM0jcvzGShGJVGQ3eXLXk+FaF68zx2x03WiL5Rd7Ny8fJXV9PfSZ+fz6Qrbj4+PMGv8U8Kw9ntTt2cyCcq7K0CIjPe+z2N/3gU9TFbm878yuvbrwUHlqrOXnBOQI4572jxnk/I7Jjp9cPPkUQ57ho+/6SUN3/ReRi8iTxgd76BgBTxWxnQ/IBY4F6Q5jGaUm9kzeIsLRANLXhckrYnokhGe9Mabv+kXWG1P6jn6mBoPfsfF5FbWr/0Fh9As2RhCEznA4tMFgEIwPTZMyfgrQNhxxxmBmPM3n88xRp5giUvSbv2NyQjqMb7yEYkqTGqBAyUnILfWig+DBmPEGPuSGzhXEccK1nuvF1WjA81iNcyW5YsqSb78YVK7US0iPtvCjXlr9ft96vZ4dHx+bWdaYWCXy5uAi5VaDuTMHYXRDKKq88R5gPlikuMcC4vJbDXv9LNZOsflF+5e+5xZEva5eb/vyAbsh5PxOdcwg1HLRhhBjefMF3xXJntYxD96QKcKiNTkvb2/E+Dk15jkZ6xefN/OAblgQWJ4xwpjStUjbJG/90LKoF5QSbXynY1WheVNeJTFY93y5PKHKGFL9X9c0XW/NbgLy4+HJsWBdd7U8avBpetrmqrfp3OyJwkV95vv4UwH7Q71rgdcxFGV0XxDTp3VdIR/dOIGcXAWQVTb6/FyksqllooxF7fC5A/1IN8DMimVjFVjkRXQXKJmTN9Z0nMbqpXNh2bLFSKe8NouNj1g91CZg7D412bwX8aQT+qKJcZmFWPPxacUwmUzsw4cPIaiqxn8wux2sF6jB578va3TGBNIv2HpsjhtluGEqT0hVUVhmIH/KBWsRnlLZaNfT01Mbj8fW6XTs66+/tiRJMkSELjT6nn6nO6F58BOTKjNeiSlKI4aY3OEhQcDIpzYRedxnvlgEP45QqPr9vv3ud7+zzc1N+/Wvfx0ClVIe9UhROfB95ZVnPRrgY6J4JR4FSHfViHGhQZV93AiOBkIwqJLrySQvz7rL6OOSaX39DqA3jKgP3/nr1TEU379/b//+7/8ePHLUy8YvvI+pdMfWmaurq7Bbvra2FmLVbG1thb+9sqUGttntceqNJQ1aGyOYMczb7XYgW/As4XY04uCYWTCeII7YpaZ/kT8MQSXPLi8vA8GknmlmZltbW7a7u2vr6+t2fn5urVYrePBpm6m84HUEscIOvpLgWidvuM7n2VuqILqUzIJswiPi3bt3Np/P7Y9//KNtb2/bzz//nAnCXabfPQlQhDxiRNNXby4+8/oGJOxoNLJOp2Pb29v28uXLDHGi3oTq9aLjXQ197Wv1lqJPYyQ2iHnHKYEIqcBcxrFLCEnGAVeVz2Yz+/jxo52fn4fy4vFE4PFarRaOfOHtjYFJrCj16Ds4OAgevJPJJHjyal/ofEe9tN88ycF3Os/rUSue8elqO9K/2lakH/OWpu0ZG8iMmYUxoGVR7zn1CMGrxsdyU6LJrwf/8z//Y999910maPzl5fXNdb/85S8Dkch4Xl9ft9FoFPqU/tvY2MjoPhsbG6HdBoNBuBmYttA22t/ft1qtZkdHR3Z2dmYbGxthfmq321av10MMqu3t7QzhzFHO4+Nj++GHH6zT6djf/u3fWq1WC5ct6OYN/aEe4NPp1D5+/Bg2oFhnCbruN7TpY9pdj+RNp9PMeFEvKcaLzq/aJ+pVn6ZZz0BN97H0tzRN7ejoyPr9vu3v74cj1osIBtqHdSf2rMoh7+SRT/zdarWs0WjYq1ev7Fe/+lWGlMorSxFo+36/b7PZzHZ3d8NaGvPa0rVN9bkvFWma2uHhYYiF+fLly8zalmcL+bWvrI4X093Nbt92p3/7PGKELrLq11BPQNL3um6qHkcaRbpDTOZ1k6WsnqLtwfvE6iSdmK33FGy/lXk8FRmKj1FRBIcYIbiJ626DnwRj5SpDoC16zreFKhUofp54UkH06X9KguYhCYCnAp3MUEZQtlAuFk0K3ghXkiIvryKsot2VdEJx+dQxdMpgmfLdtb38s0mSBNfU+Xxub968CcdcvKKOAajv5j3nFxXdWVFFVtPhh11GFkD16tB0qb/fiYu1SYxU8gux/yw2n3llz38fm9MwmM7Pz+3g4MBGo1HGw+wpQeuoQZ6vrq7CDXdq8HtD1RuwRfn4H7PbBAbpEjsHBUiP56hxyhykO/rIGvVQMkIVbdKDkKIddCMHj5xYP/MORCgKOkaVV9iob0xhU3nGENUjMvQPBvtkMrGTk5MQt+b09NRGo9GtdJeZX+/6vFeQY4qv/tbAy2YWSDbNnzGuMka/5in5PJvnHcU6of+rPJM2BJNe5qLHTfVmKPoJox+SajQahdvVML41fpqut3yHvCZJEkhUvp9MJjYej204HIbA81ruWHto36ucxQzI2LxX9H9sDCDrMUPGl0vXCP+591zTvmEs0NexNUWJKB0H3I5JjDHmjfl8bl999ZWZZccncnZ5eRmIp9iFFciL2c3GiF97zCyQlpDL3iNbSZwkSUJAb++ZzhFoTVuPiXGUGB18MpmEAOrT6TQc21RyChnOWyd9v9N2+p3OgfSRJzZIT/NSHSEWV+0xgB5ycXFhGxsbYR3UvtZnPVQOYwRAGX1Y34O8bDabYYNEn1u2fZhL9ARN3jj1xPOXjDRNQ2zObrd7S5cwu90vRfNfmTU21s+aX2z+LMNNKPlUJEsxnVqPofvyFNmMXheKrSFloJsWKsNPVUbvRTx5BSoPj0Fc6EKoygyeT+wOe6H0XgteSGNCFvutz6uirAsSt+4Q00LZyDxDMZbHY+Ih++5T1kvhlSH66vvvv4+6TL58+dK63W40DVV6Fy2Enl1fBl52zW6CiBMskyNMxNJ4Lig7v5R9Jg94GTHpn5+f23g8tm63a7/5zW9sf38/lMcvqpq/J45833jDQpVLMwsGliq+vB8jMrQsmr8em0Hh1vL4894xg8fn6xVHPXrgjSmMwuPjY5tOpyHezsnJiR0dHdnBwYENBoOg5MfaknJ9CuQp0M1m0/b29qxer4dbjF68eJG50ELjfeDtpWnQ7xro3+y2B6TOIXqzmJmFnW/In1arFY7Tra2thZ1pjHw9pqKeZVdXN/GQKIMax5ubm2ZmdnJyYpPJJNyit7OzY69fv7arq5s4MSoPeoMUMcz0+mtIMupPfhi7tJ1Z1qtECRZkZDwe24cPH4LnAsZovV4PN5zF5GyRIhpbi/MMP+0rn4+SBtpOsTKQBu3UarWCdxDPqgec957xhjHPExSesqg8UF41prSeMbJPY0hBxBJfh+/IRy9ESZIkeJEwBoh7R4D6JEmCPFMu5sXpdGpmFkgDZL7dbtvx8XG43hsZ8bvh3tNTCSFP6qje5udCJUO1H/38H+tbTdt/7zdFGefc8kc9IHQgaVRWNQ6UL5/3ZkV2eJ7+4pmzszP705/+ZNvb2/aP//iP4davJElsY2PDGo1GCFSOpxrzJGMYeUYGuAmLunrvXG7H4qjm1dWV9fv9sJaZWSCMKOeHDx+s1+uZmYVLDkajUTgW3Gg0wuUVZ2dndnZ2Fm6VHI/HdnJyEuZSiDfaDeK03W5nZEnXRSXqkiTJHP/SOUFtAtqbMaBHoD0BBQHW7XZz7Y6HBvLAODa7Duj/6tWrDKFHv3ryM09vUujc7nUKZHV/f99evHhhh4eH9t///d92dHR0r9uZdY31Fzt4Yk31sjRNrdfrhbXR23FfEphrzs7ObDab2cbGhr18+fKWDHjcVWePtW1sjV4kZzFSX/sv5vnE2PZrsZ/r1WNb88irR4xoymsXXYd0jZ3P58H7lLifgDXzqWFp4ukpDi5V6vAWMLMQIFgnfoTIe0GBRQRQERuqE60qLng4qau7J7meYrt+SWAiwLA0y/ZRrVYLgVP5btFOz6I+jbmLLoInCIDuFrMDjCv5U4c3yIqMQMV9SCfSR6HAcOn3+9bpdOzv/u7vMs8tWhi88RlTXmIGqvdsYlFRIyqWb4wYMrsxsvyRPj+H6W6LGlR+xwo59nXBcPAL6eXlpfV6Pev3+/bVV19ZvV63Xq9nP/74o52engaXYM0j1p5PAaqcMu5PT08tTVN78eLFrcCTKD+sNWqsaJvreqWeazpnqPeS9pH3+lBsbm7a1taWDYdDOzo6yhxDg4CG3DDLejNQz3q9Ho7OYPgNBoNg4O3t7VmSXN+IRbnTNA3HrWKB8NWjBw8FzV+PHLIm844elVMZnc1m1uv1gmGrRh5l8Iqdx6L5pQxi5I+2i5Y7Rgro37QbBjZxR8yywb/9OI2R3bRhHiEWM5j85+pZBxGlii/GvQYf1qC/rKdmFp5hruX4FselzG4C5KsHgidr+SE9Nh29/kVbxcggPtN2jK3Vvo1iBJ/+ju1eF5FOmhZlgUBijlUPH+89p2n6tcf/rXMIawPpsmMOxuNx2LxqNpu2vb0d+g2SEUKQflHigU0PxjCBu9fW1qzb7QYSU9ueywq0Pty+xxigDOD09NR+/PFH29raslevXtn6+nrwfGMOI9TA0dGRHR4e2u7urnW73WC0cbRQvTjVG7TRaGQ2bLTM9Jd6Vmlf6xqg9dK1N7a+6/eMO9ULHmt9pB5cGEH7QDAoeWkWDwGxqLy6/uh45B3moG63ay9evLDvv//e/vM//zPj4XEf2wkS3x8L1Pr4cTYajYIeoM9/iXYc45t5ns1akLc+6vt+bYzN2XnrZyzdPLtM12GvF/t08vT02JjWzYvYWsP7zCle9/NttagelGE+n9toNAqbb6uOBb0K/cjjWQcXj8EbVuoBpccRgBJS/uw9kzzf8Znu1LLzk7fzj/svu3QswmWEq8LTgjcaYwqgGj7+3UUoIqDyJkR+Q2rqTrYGB34OWKSc52EVE6M3upLkepcDZbndbt/ayfRl1t1n9XbUOQfFRmVId4C17ioParArYeHrwDzF7p2/SlVl1JcvpjjhOcrcSFoomqPRKNz4w+4LO194PJ2cnNja2lq41h7lVdvvMVAkV0UyxHvIA+1hZsGLdWNj4xYZrUFq+TxGQvIdQPFWgknlU8czHgHD4TDEeprNZsFgRCln8wXvCQgCjEez7C61HlvRuAFm15s6/X7fut1uuC2PuuDd0O/3Q9ucn59ngmNzq5be3ESbIWe6w8h7+o4eQYGwyhsTi/o9r//vMg/FjA/9TV+pPPh8vVfjZDKxw8NDa7fbwcCjHdBbdH736eTt/KpBC5BNTVs/B3jF8LfZzQUoGG54Pyn5o/HbiNsEKUDbMLfgEa7jgzJDkPDOhw8fQnwn3+Yqc7F21zWbfvBt6J/Pa1etq/arl6uy812tVgskjJJ8Xs8gfSVlVDdRI0vlJE3TcLOa5sF6pF6W8/ncfv/739v29rZ9++23trOzkyFniCeHxyHEEHJCGXV+8cfkOp1OIHe8F6h/n8+Z35CltbU1m06n1mw27c2bN2Zm9sMPP4Qbiol9x21zeEqSPuVRjzE/l3t9j76AaNM4Wb7+KofoCN1uN9PeKo/eM/FTrJkeWob5fG4fPnzIeOtubm6GG1p9jF3gx4+OW5Vbnk2SJKxfV1dX4VitHxN3gepjeLSh4zGOqRNzEfLDTa2ESdF2qXBti7x//z7cZqq67V1kV8da7G99pkxasWd1zi5TRrXN/HgsIwPIuG6I5a3TeaQaMjsej0NsMvX21vdXIZcPMd+shHjyCsyqkdfBi/Jit8TMgru5BwsAC70qXRqcFVdb0kVJajabwbWYAcYihpKFYoRCFatbhU8PP+nEWGtVgM1uX50eO+Nrlp2w8ryVisqVBxSSwWBgBwcHucbX54pV1M2TTmY3xNBkMrHhcJjZmdXjGYxz5gSOnnhvF7O4EeoNAoUnGb0Rrs+o7GL81Wq1sEvJgqdKrn/Pyz5lU4VQjwinaRpuDMObZjqd2vv378P/V1dX4XixekLE6vup4GVIjQTtA5RO4kyYWQiOjnKcJNceQ96rFXnRtsZg8esna0mSJBkvHsoBkD9itGBUccRON1MI+kygXowDTdMb5oPBIBhQqtDMZjM7OzsL76qBAQmBscdNkaQP8YQcqNcchBh1oS3JR728MLbx3uKzWB/G/l8lVFbyiCfqqs/4Mazkj5mFOFU7Ozv28uXLYHjRViiwPlizJ568953OOaTH++qxom2p5fIbGUpYQG5iUHvvFZTjjY0N29raCvOmEhXIm98ZVi8g/v/w4YOdnp7eanvta1XwY+Si9p0e51TEyCltH20nzX9ZeYPIUAJay6G6iHrEef2SPvDeOldXV4EQ1lg5jCviG0IE/e53v7NOp2OvX78Ox2xVF+KiCMau2Q1h3W63rdlsZtpKY8+RX6fTCTE2Y0Qe7yP7w+Ew6Occ72Wj5M2bNzafz+1f//Vf7aeffgoyxtHM2Wxmh4eHGdlQYhRS3s9HSkroD/2ltzeqbkCdr65ugosTR1RlDY82JVlj+XzqtZO+Ozg4uGUQa31if8fGj5+7dB6q1WrhGDlri65Jy5BOmh8B7Le2tjKbi7Q5uky/3w8xwfR43eesX98FzI94Pm1ubtqLFy+CR2rsebPFeqCuAXlzb97zse9if+eln2cDFqWja0BRffKIp0VlZA44Pz+3k5OTsCEac1h4qliaeFqGdVxFXnfNrwzLSof5wFx6Mwj5IjAsRExGOuHynBoruhB96kXjKZThKaKoTXSRUUMqRjDEgEKLkqVKvs/XK+uxcrGrqIHqP5cF8C5M/SrkmPx8vvP53N6/f59Rcrw7NkaXmQXvkTJGrio/Wo+YLOlCpsaqJ63UQFEZwqjwLuO+fCi5augxB56cnAQDg2MMGI3MfxojgXc1jTxPrU+NPBnyn19eXt+0hSFXr9cDkYN3ghIMOr49qZNHSOozXoa8J4PPD6PJx6vRMuBZQLwOvfYew4nbHCGRODpHHVqtVoiZqIaBmWV2o5vNZmYXzhMH6nnlCVD1buC3Grts6Oius2+/ov9j8CRVWfix7EkPr4zqd1pn9SpTcgrPJ4zmWq2W8WLUgNu849P39dSxqASoN/jMsl6PebKLwY0s6TyVJDdxbyAJPdmlshyTezXiLy4ubDgchhvsYt5JWjb/W9vGG8N+bvTkpbavT7Mo/zLGlf8hL4iQGKmleqbmTf9pv+maAQGifcbnGidK2308Htt3330XPBavrq5sb2/PXr16Zc1mM0Mop+nNBT96gyZzBV5H5+fnITgxuhQxg/TopHrdoj9BUjFHsPFhZvaHP/whQ65RXtajNL05vus94/RoKX1D++HNRJ9oH/AM+RWNF10PddxrWbUfaYM874hPCZ1H0EM5fmtmIe6bWT5RQP30BIr+Ru86Ojqy8Xhsh4eHGa/IMvO1zjXqLEDeEEzD4TDUC1vv8vL6Vkg9vn0fYvlLwMXFRfB29x5xZvcjkYr4h0XcRNFcvIw9wbiP6d5e7tFjkDXmRp1vfNrMNZyYYh4gfILOH/7dp4qVeDzdVVF7bBSVTSdNv1sEYnE0gLp456Ud+/3QbVakdOZ9X5aB/tKg/ZSmqZ2enoZd1rxn/XdcB93tdm1raysoYXnkA/AeVeqJw/XRw+HwVhmfO3R8PIY85pF7//M//2Nra2thF7bb7drGxkaGBECBQdEsc7zRG9WemNC666635qtzlhos6trMosZ3xKLwMuIVdxRibkJ89+6djUYjOzs7CzvZeC5sbm5ap9Ox3d3djLINKeoJ/cdATHYWyVHeuOFz4oRg+K+vr9s333xjW1tbmT6h7xuNxi3DWA0/f8SCdosRj1ofDDAltshXFSBf33q9bru7u3Z1dRWOwhEcHS+uRqNh+/v7liRJiH2ieZMmpBvlwOPgw4cP1u/3w1iBaNBde9JrNpvheAxEio+36I/HI3v9ft+Oj49DmrG1zJNBvk2KFNpFz/l39Ait9hd9GpMP75nEONFYSRjnw+HQWq2W/epXv7JWqxW8pzleyZFDNaRJ23vxoPgC9aRSAhmPKkgBZIGx7AnOTqeTiamjxiNHPPHiQu6Zn6irygdjwpPXBJSHVNA1Ms+LTKEbgN770xuUGlMLwjnPkzE2TtSo1vLlyZHXCej/+XweSGMlK/iBpFFSF2MdY4fvGWuQmORJ3SiHzkfE3Prtb3+biYP0z//8z/ZP//RPgcieTCYhDtzm5qY1Go2wHjLHsFaMRiN7//69zefzcHwPQoyjTEqI4/WCR7EaYmYWLkA4ODiw//3f/830uz+iCflA3ZQgajQatzaXzCyQZtQHnUDJQORX08dr1ROKrN/6nv9fA4/HiMlPhdiceHl5HdcxSa6DzxMont9FBLHqUPS5EkWQV+/evbM//vGPGU9P0qAP8tqGdNbX121nZ+fW2Mc7l2PqjJMiMvpzxrI2Ku9MJhN7+/Zt+Lxer4f1y2+uL8pf13GdT2PvFL2bV948faEoj5gOTX10HtfysjYSQ5j1kvlCy8T8gF5+dHQUNtp0vom111PHZxfjaVks22HLkkifSkAo612Z4Ao3yNtlKepTlLrpdGrj8Thz5bSmi1KpASSVYOAZ3X15Ti6Wd8FTmEhRTHu9nn348MG63a5NJhNrNpu2ubkZFCbK6w0RZMUvlMgDCpYaTosWSLPbZ9P1GWRHd+bUayDPSONInNnNMS712uSHYwscCzCz4MWgwatR0NUD4zGx7HxWhqCijUejUUahNcsGkNQfVZpiRLHKSZHh7Odvr4j4nXTyViOTuCh61AOyACMWcsMbxCrbGmvIzAK5TnnUIzTP41e9M3z91VvK7Ob4GV6I91m38z5fhdzEFF/+XmSA+bbmGXbdlViCHNb6aBv6dBjXsSC6QEkKX04vt0VGHs8oOcgxAQinmNGtx+xULiaTifX7/XCsS4+7aDv6v8sYE2XgjQhN20P7VA0ET2zp83k75koe+jnEe+uQhrYlfU563quN/JTkoW903jC72aClT4fDYThSi+HUbDYD0aTx3/jczMJaAqnGBQaQa8gfZYKAYK5hXdYjzZCmPk6U7z+dW1SGPbEQI0DxMNBNA9/f/n8/h5NebDPGy5OXN51LnyK0bpPJxNbW1mwwGISLOehDs3hsG18/yD1IKSWh89bQIjAeaHtIdrzn2CxTopL0VzWPPBfch3Tib7+GEPNRwwDoBga6kyJvLV2E2FjKey72XWx9i5FN+oz3SFcySk+ooEebWbALvXMLcyyBw9W76bnL4EputXvujXAXrHryWWZA5aXjFdw8lDGsVlGmzx13kQFIIq705Yp5NUJZUAeDQTBo8bY5Ozu7Neb8xP45jsOysvqQSNPU/vd//9f++te/2tbWlr148cK+/vpr+7//9/8Gl22zG0WeI0iqxNBPuB2zq8bzqlABfxRTvUaU5OI7VWbZDcRNF2Ot0WjY5uZm5jvaEC+YVqsVPFhQyk5OTmwwGGQC/6bpdQBkvP9oBx/b4lPI5V3nrjzFI/Z9mqahb9++fWu1Ws2+/vpr293dtUajEa6LBz5wvBqOyID2o1k24C+fqwHErhoKje7me881rcPGxobV63Xb2dkJMXbwguACDNInfhXH6rQ+eB9gEBLfZWdnx/b39+38/DwEvyQuGIqWkq0YcXhdQUho/CoUNVXYNHD6sv2bhyJ5vYssaz/Tn/5YmdkNqUa92ZRQrwrk4+PHj7a2tma7u7vh2nhi1zAXqSelQr1sIQRUriAVkiQJxKrGD1LyQn+zTunnEBekh5cTV9z72+1QvrVMxCKjTu/fv7f/9//+363AvmZxwt57mcRIHyUX/G+vT3kjKUYyaD4K0tMx7cuK9w4ywjhpt9uZ/iF4uxKvfm7A+817vCZJYq1W6xYpSd3UixEZQH5Jj7Xt8vLSfv75Z/u3f/s3297etjdv3mS84tR7xcxCTKPBYGBv3761wWBgP/74Y9is2NjYsL/7u7+z169fh7mtXq+HDR7KAFl1enpqw+HQptNpINN3dnZCDDoMvTRNM/GX6vV6yJNNAx0D/viK9ieXS+AtFjsG6eWONZ90NPh6mqbBi0vrqPqCBl1nTnjqG454dAwGA/v48aN1Op1w46Ae7VbyU9cx/icA/t/8zd/YxsZG4RheBMYFco3nU71et8FgENYwPxfcNZ8KN/Bz9MHBgX38+DF4xLFRpRdSKDGsZDvpeV3MrHh9L+Nt6sndRTKm5dRxztypRDl61Wg0srdv3wb9RfWCIujcniebzw0P4vEUE4YYe/i5YFkheO7CU6E8/ESGIabeUygT7OhjHOitTXkTbSVLDweIhtlsFoysVqtl/X7fWq1WIBBZGDRYcizeif74XZEYVEZ8/+vC7JWmvAVLSQp+zLJxw0ajUSgjt7igtHmDtWjx/1znfTUizCyzY0VgXn9szHssxPq7aFdOjyTp+zF369gPhhJ/axBc0tGjmH7XV+VI36Mdrq5u4prgTo5nEkRRTOb5X49bKRkBkcauH3kV9Y3+XqX8FaXlSYu8ndRFO69+h1eVbl0jcNvX+QVD2iwbOFzLp3PHorYpIks0LTXcY8q0kmsY1/qOHjvS+Yz4hcxJw+Ewc1Onv4mYMsXKm0cG5SFPj421S8wwuWt+/lnmfU3Tl6eorkqAaJ/E1iFNV4nLGPmmf08mEzs6OrIkSez169eBAPJeDEpmpmkaLtvRDTkzC0ed9FIMNuGoF7HnuFGVucWPAyVwtD5FRKSSR76tdO0kPe1X3xc+fS87lNEb1T6t2Fr7VPU96qBrE5srbGowP7F2xvQUs+s5g3hLEM2QdXetv29Pv0Gn61OFh4NuROCxquR0bO2LzYEPBT++/HiOzZdm2TnTLBvPkrryo6EulvFcfKpj/y54EOIpzyi+qxHylIwWVYZWhcdSiD9lWp8r7isHxM2JKbUYdWqgLmLgv1Q8hqyqYoii3e/37f3797axsWF/+7d/a/V63b7//ns7Pz8Pi9Df//3f229+8xszy3oLEPMkTdPMrh9GlCrNqmyx6PnYKrH5VpXner0ePOz0e/4mn0ajEW5v+etf/xrIUb0goUz8qpjRrN89xfnFGx9538eUDjOzk5MT6/f7tru7m9nRNbsJGOs942JHxfTYm5Ir7BRPJpNgkOkOG7LEZyjUagCwftVqtXA9tR4foZ4ao2p9fd02Nzet3W7b+fm5jUajjOxAnhPostfrWZqm9v79e/v48WPwtIPQpC6xNoao5Xpgf6xHSYpFfeg/Lytzsfl4EWgzNbjU6OYZ7wnh9Qm+U69GjZmmMoixrz8EuWcX38dJUWLPk5VqDDMXxXaBtV2URIIcTJJrD51utxvSxuPy6urK2u12IO7x2oFkHI/HZmbBI+f09DTEczo8PLR+v597e48SVt5g8X3i6+I9DvV7TUO/03Hny6PH4nw6eTKFh5M+q7GHmJ81ILZ6R+qaoX2psQfJH1n1V917OSMt74VGWdfW1uz09NT+4z/+w/7mb/7GdnZ2rNvt2u7urtVqN8Fv8XA7PDy08/NzGwwGdnZ2ZuPxOLQhccz++Mc/2o8//miDwSBzM6dvXzPLzFmAtuO4L/OT/16PypGO3gyoRwXx1FIZpR19kGCgXmdepohtR//g/eTlAbJOvVpV7p7iOmoWJ3i57bbb7dqrV6+s0+nYd999Z2dnZ9Zut63RaIRjWLoGQRC9e/fO6vX6rbiDd5mj9W9i83IxCp6lFR4OakOzmanzkPfw393dtU6nE9aKu2zUKfx7MeLSz9dFcuX1cPUoNbu5YIUTBKxvaXpznFzbIy+/2Hefi4xWMZ4qVHhkoMyhxHhUpNLdsIrJuIwihyKIET0cDm08HgdF++DgwM7OzoLS/4tf/CJzzEh3XFls9TM1/HQHEMXfE06Uu+h/TReXf5Rx9ZrRHVU90qRHWrxh4vMp08afEg+RP2niEdfpdILB6I1Zf4wuj8TSd3z/qdHhd+BIm/e1jPyw+4zhoztzmreWU+O+eIMeGfXxMc7OzqzX69l0Og3Eqd7EFtvEQfan06kNBoNcWdM0lsUiIiBWxqL+KlJY80iIvDypt84FXilWV30vTxrfRolsTTtPmdV3YkG7i9oIWfLEc5IkwZgnTT1Oiezg9YKcYYj2ej07OjoKHhNlCUZtu0XQesRkk/Tz/o/Jsh/Dsec0fyUpzbIxH7V+Og97oo18lWBRQlPT1/T8515OfDsq4TgYDGxra8sGg4ElSWJbW1uZMvEuBIvGAKTuyDPHufFu823HfOTXTV07lVRClvxcEusTT7R68o73tC3Ua1gNZ9+G+o6midcpJFWMqNQ8dLw/JxCfTvUedCjWkfPz8xBSwh/r5SZpxTLrufYN5arwePBrRZIkt/QCs2v56HQ6mdtSeX+RvvMQ5dW1P++H5/HO5TKe2Bp0V+L0c8OjEE+qJBfBP/OUJtenUJanvMtRoTxi5ECFG5Qx0FaNu+bFYsIV02aW8Qa5urqyP//5zyHWxNXVlW1sbNi3335rnU7HXrx4kblmGOOe91Hoza5viyKmhCrRqtjqURZVznX3dn19PRirV1dXIV7TwcFBUPrOz8+t0+nYN998Y4PBwP7yl79kPCQW9c1DEQWrQNn8i+bZRYrC+fm5vX371tbX10M8JRQTdrrVUyTvOJ6WA5KIo2wvXrwI3kAQSUpScNxKj815Igqlr9/v29nZmXU6HdvZ2bEkSTJHtcxujiOsr69n8p5Op/bTTz9lDObhcJghZSEPFKSXp/RrefNIAO2fvPm0LOGgz8Z0EE8wxJRI/5l6J5hlFWR/K5pCjUxvrPryKMFAm+nxSI41QPJoeX2AZH8kKdZ+6jWlRrq2AWQER3V9O/d6Pbu8vAxz2ng8trOzMxsOh/bTTz8FcipJknCMinhhOvd4g8Mb+bE+jBFiSqLG+tMb+dRf+0TLonlrObUN8+YXT35xZJeA8v6GSOL/6LuU18fcYn5g3vf9Qtkon97opeXl4gHmsLW1Ndvc3LTJZGL/8R//Eea9ZrNpv/rVr6zb7dqf/vQn+/jxYyCUiP3jYx/ShpAw6umkZDl1ZG1j7by4uLDhcBg8OpXQ0nxYQ5Fj1sXJZJIhdzhGT5sxn6pc0NZKzFMP9Vo0s0zfeQ9TjlFD0nPpA3WkDjHPuKcML+vj8dj+9Kc/2draWtiYuLi4CHG7/JrwUIb5c2i7LwExotXsevz0ej0bDodhbLXbbdvY2AhzjG4s6CaJIs9LKq//i7gK5lG9affq6vqCBWLOKanuvS2XbZtFnz1HPJrH0yoG+qcwSB8Li0ilPMW4wvOH33ksMqqeGr50eby4uLCjo6PMZ/TZ4eGhHR4ehs92dnZsb2/P0jS17e3tjFES2+HEA2Bzc83//1AAACMQSURBVDMTGJgrVlFaMWb9zq+/mUgXZ5RdjtGdnp5ar9ezfr9vb968sb29PTOz4IYeO67g8dRltQgxgmEZEAuLgLXsbNMn5KVGYSw/7Tc1bElPZcCTBWpAalr8rcbPdDq1fr+fCeqt5TS7IYhwedfg3qenp5mgxMRuQQHD48nsxpXeE6dFbe6VxLv0S4zEuw+K8o7tYCoRoIqqHqOOeV7QX97zSWVGSSf+V8IKYzVG3JE2ZYh5g6ix7skTs/wjabzHERaMbp4jyKoGsD88PLSzs7MQeDWWF0Z3zOsuRvz5uvj1VedKf/RQyxvb0Y59rt9p3h5F5fT/46FK2ZnjtT0ogy+XP+4HYeHjaOkzHM1UYsRDZYV8OKL97t07M7MQQP7FixfWbDbt559/tj//+c+ZMaBzl1n2MgWNlagEIJspvjx8n6ZpkLu8TRo9kqhjgHzn83kgfdbX163T6YTYLHr8mTGsJJwfz0CPBvqxBSgD/aPHkf040zXhuWE+n9uHDx/M7GYsaKynIqzC/nvOOspTwyrtcZ0LkHfGHXlsbGxkPA/zyCFNQ736F3lHxTYr/Heqa/EMOs7R0VFm8zkv7QpP7Kjdos75nDuvTN0fetIsUs4fgmD4nPvzrliF0fsp8BB9eNc0H5v88vnFjBL/vNm10fWXv/zF2u22HR0dWbfbtc3NTet2u7a9vW07OzthZ3symdgf//jHcHzLX92M0swPu+PcDAVB8e2339o333wTdsd7vZ59//33NhwOrdfr2Ww2s+Pj47ATPZ1O7fDwMNz6o4EQF+E5j+eYkrHsOMSAOD8/zxiBHDUgFgqGdB7UuOR/NaKJexDzvPCkhVe6SLPT6dhXX30V4kdpbCDy4oY1POROT0/t/fv3Ge+AdrttZhYCQQ+Hw7ATiKzqLn+MLMgjSbS890HRPHHf9TVGRJAnnhV8j4cF8IqxPquEYoxIVIWYNj47OwveEmbXnpjc4LSxsREIQZ5RGYX4id3WRXq0I/LCDrDGZ5nP5yE+mHpcEaup3W5bu90OxxGQLa0T0ON/kDH+yJ1vO21/j5j8+Xb0ZVBjRUmSPLIpz7jRsanQGGgQJtrW3oPJLBtLyh/Li3lq4VFCW/E+fc1RWe8JpySQ1pl+gDhQYnk2m9mf//xn++mnn+z9+/c2Ho/DzYtmFuYU6qx9rO2ksfK0fvxfq9VCOniBra2tBQ9h2pFbZLWt+BtCiNsD2Si4uLiwk5OTKDGp86rKDOniEapEkbYfY8t77DE3QOwTD40xlUduPWXEyOllyv+c6vwlYNX9UbT2o9uenp7a2tqanZ+fW71eD17lxKyMzele94k9o9A1DW8r9Bhiu4KYN2SZun3pWAnxtIzStkqFclncpQxPobyPgVUY8V9KW1V4/rirvKvxF9ulzns+Sa4DWf7www9Wr9ft+PjYOp2O/eIXv8gEUdSrlr/77jvr9/u30lTDg6DTm5ublqapHR8fZ4zJ3d1d+4d/+Idw1A7Pgl6vZz///HMgqlQphoyqcHfQ3xgOZlkvBPqMQO958TpiJJInjfRIXMyQNbs5WqKBc1V2IQAIDq3H9cgLgowjMMfHx/b9999ndv1brZbV6/VAIJTxZoohj/SLrSl5aRbltUjpXHbNyiMsIEgw3pEDJU88geK9G9TgXkSacBNUmqaZGwzx4NjY2AjKshrFGOp4IhHjjb7H8DW7ISwgJ1qtlq2trYXA98Ph0Pr9vjUaDdvf37dms2mdTsfq9br9+OOP1uv1rNls2vr6ejiWV9SGfKcEFrJIWbxHmG8nL4uMJ/WkUoI2Jn+MG/9MzLCOlT+PcEVOaG/11kEmtH6xo5NaH8gTX37kTYknoF6QeDZqnTUNn6fGjeOZ2Wxm3333XTAYqRsENWmoh4/2pXrsNRqNkI+2Id/7euNxpeXh9jzfTvzP0TrkzOzmhj02bfy4VG9Wne9oR44lKnHmySdtfzMLxBPHKxuNhrVarSDvz5F4Al6W9PMKFfKA3BBH08zCuPr666+t1Wrd0qPy9Cod93nvKOHEugUpf3h4aD/99FNm7Fbye3eshHhapuGfwsR5lzI8hfKaPWw5itJ+iLaqBmyF++K+MnTX8bQMye6N5aurq7ADe3BwEG7wef/+fSAsTk5OQrwHn44quBj5GLN6hMDM7O3bt/bb3/42KMqnp6f28ePHkP+ioypfMu7rBaNQQ4OYRxhJ3JqkR9Z8HBOza6MkdgxG5StvBw/lTANP12q1oMxBdpKn2e34Ofzu9Xq3dg/1xsOybVZEJsXaPm+sFj37GHKdV36z7DE1DNxFx9S8p4qiqD6+fTQQfZJcX0t/fHwcjkGSdr1eD0cayIPYKxqPTOWOXeZarRY8nTTAPH0yHo/DzV9JkoQ4OsiYeuD48iuxo6Sr/h0zxGNkk5cHJblihJN/1/eXerhoeSifGtkqn0os+rr6eTjv9lKIFC2DJwXpN4355ceJxiHTuiTJjReUEiK1Wi2QQL4tlOjUsvjjgHqLIeuWltvXF5LU7IY01/ZRstSPJ10fMTSVtPPypccafR/QDsRl1CPJpOHHB3M55JQ3dmNlViKMZ/SoO98/16DYeeRThQpFiI0TNlk46ubJdr/2+vHu1w719tbxjt6EN3HeZsZT4QieA57UUbuHxiLhKKvorhoxBYnPK2GuUOFp4b4kLC67SZLYyclJxkABXpHlM4UaFSjnzBksrv/93/9tv/vd7zJpVLs1t1FEaoBl24r3MJCOj4/t5OTE1tfXrdlsWqPRsJ2dHWu1WraxsRGuTU+SJHgLqMv3ZDLJrA1qWKoBjVJVr9fDkSf6HmPo7OwsEE9ceW+WNdr6/X4gKryBjKz568Bj9S/6Ls/Lpeh7/Tzv2bz+KyI5/HdlDCUlHfQdPX6kHjbahjFyyj8TK6Ma9L4tvCyYXQf27vV64Zm8I2tJkmQ8TvRYEfNSrVazzc1NW19ft36/H2SSNPA2OTs7y5SNMaAElTcAPDGnt+VRX21fTwwV9ZWXDfV00rnRE0Vab/XMgWjRPtF+1vf13Zj8eQ8nNYI0fY5iaxkoW7fbDWR2vV4PGwxad3/0BOKbclxcXIRg7mmaBuKaY45mN0Sz9hkECfnhLUB96Hc9hgZ5qSSVyjCbNDGCTy/M8Leg0WYcg6EevKMBvZUw0/GUpjeeYzyvGwM+P73ogbldQRv4H54nHTWK2RBQOVHvreeI51ruCp8enjg/PT29d5qM4UajETzRz8/Po5tous7EvqtQDl8U8XRfg/GhUMboKXquQoUKzwdqQK1qscrbffHXm1dYHn43fBmo0qLHMTAQMQLxMIB4YqeeYx+Xl5fW7/czRgrkFJ4nlBlDS29NxAAeDofh1jBv4GHcqCdTHkGTt2lTtKniP3tMPMSmTmwMaj5567m2lf6dNz+UJdM8Ceb/1zz0GT83xchq5IJ3vKdWUdvEZKNo08+TbLE2KZpLY7vlMfIuVgbff7FnfT9qurEyxsoJWae/Y/XwJJQScBp7CrLO94uSJnnyoN4B/sIB3z6+nkok+jhI+n8sNpKXMd+ePl/qGRtjeiRQP9d6ax1jbUzd9VY52tOnoePG95G2txJWKg/ei09l1NfPH72sUOFLRFn9edHGEd/7S3uKdOeKZLofPjnx9KkVUMV9y5CnzD6lOlaoUOHxcZcFcpnnyzwXI06qBfUGsXnaz+ll2muRogMwDLkGPEkSOzg4MDO7FTPJ7NpAev36tf3mN7+x8/Nz+/3vf2+j0ch2dnZCHJ1Wq2WHh4d2dHSUyd8HMY8Rk7FjXZ6c8EFyFxn7sTbL+6wojaJn8oidRX1T9G4MZYhH9VrRdL33UZLcxJLxeasnoz4fI6owWr03DcQQXhsxTzhvzJI3RrTGotK68/d4PLYkSYKniD9WpWX1Y8p7f2nZNMYRBEAs9pLm449SQBqoVxdp0C54G2r8KqD50R55hI2/ua/IY80bNGB9fT1cOKBeNvqcP3ar5fRtT4wg5IKy+OMkSm7g4Ug+BLamLZMkycimBvNVmYI0x5tJ0/Okmsqdl2eI8rw1i37zpBb19+2j8sFxRcppZsGrk3ZYX1+3drsdbtdSsofyMl7a7bY1m83gzaVxtNgQ0CN/auxq4HA8qnhWx6PGlfJzdYUKFYqxaI2fz+chPmJs7s5DZd/fHZ+ceKpQoUKFZfG5TvbeyI39f9f0YulUWIy8DYVVpKu/zSxzfKVWq4Vg82bXfTcej0PQW7yhiM+DIUjcJlWeyhIrvjxPBcv0waeozyIiq4iU8eWM/R8jgFZdbk9OlSFX80i/PNIx5i2j7xW9X2QQ6PuL2nNVKLujvugZbY8iYiHmCeTjDcUIS4U+s8jAggDJi08FPNnq1yv9Ue9LNfTy4kf58sTaI/aMHzP+PW0f8o/VQb3JiqDfq7eZEsk6xvxRzLxxoWXI+75ChQr3g/dkrPAweBDiaRll9zlDFTX+N/s86lahwlPHcxhni8q4yCvkIciPZT1RnisWKRNFHjNl5vQ8A7PIMI2lC3nEzrd+fnR0ZL/97W/t8vIyxNUZDoc2Go2s1+sFsuoua1CeYRdrj/ukm/e5puX/9n2Q92xRuWMG4zJyXkZ+8FbxR5NiRAjveG8jnvVeNnilmFnwWvHxkTQfvGJi9fD5qFeFP8qDUey95ohDBjEBvPGu7a9Gtg/yDDQAft4cBcmqRIWvI2XS9jXLxoUiLtEiWdXvY+XybUo5+VlUXtKYz+fhBjjaV4+TaQBd0tP+p44ExY2ROnqcxNeHtIhHhFcbXkzeG4336vV6CDzOpRiUne/pB70ljltVNZA5ZfLB1akDcZuazaatra1ljgIrsWV2492mxBFtxhgibUj+VqsVxg7xldrtdiZ+FWUjNpaZhXalr4nFhMegj1FVq9VCTJkiMpk0Na/PeZ2uUGGVWDWJ5MdoNRbvjpUTTxVTGEclnLdRtUmFp4aHIHiK8CnGQDXunj50912hVwqz1mIM3VcZeggF7UuB33wyixMufO4RI45iHh9l+tiTVjHyxH+uXhj+J1bGvGd8XnlkrG8fX67YZl6MUPQEiM8r5h2in+kOd5myxtLLq4Mnc8rC77rHZMeT0r4s6k3jn9P0fZ2UfFSSxsdSipVJiSIlvHwekEoQMnn9o2XSNtW8lQhTj6wiDzDgn9Hjn5RPg8THyqhBwD3hqp6qKuv6bqwMvsy+3HxfocJTQd5c/jniS6nnQ2LlxNOXpGyC2MJpVnk+LUI1gCs8NTzVsbpsuZ5qfT4FyrTFfebsIk+hZVBWmfMGyiKSo2w+D0XClqlXkVeIX1/z3l1U9rz389bvRUSJfueNfWLjaOwabnXzMXd82fHgUMObPNSo9YQFhr3Gm1H50Dw0rpM3hvPqqvlrvB/K7Ikjn44nHmJyrF5EPv6U5uMJgDzCTkk53vXPp2l6y7Mldnue7yvvnaZ/x0gkhbYh+VxcXGTSgBjBIwfvKN+P9L1CA2PjDeRjKGlcLC4k0BvxPBGlXnIqB81mM0o6qZebBuxO05vb47QueCv5uviYU9ywh5eWemap5xPyprLDTXv6nsqallXHjC+TkkieqGN8EzvKv+dv1vPjAM83+pF+r/TnCk8FlSxWuAtWSjw9Juv5UErxKvAlsb8VKnxqVARvBY9lZCJmqJZ59i7flS3DqmR5Ebmi//u8YwTFquAN/SJvk0+NIu8ZfUbbyxuPGqTb/w/ZU9RX3mvCfx8jRNToV+PfE1yeqPTPeGLN/+Y931Z57ej/9nX3sqE/kHex42GexMojn/LaRPPzgaDpJ/otVi/NP0Y4afoevkwQDL7ulHNtbS1DiMQ8Z7y8Xl1dZW6/A+rZw/c+QHqsHuplpGMYYofyexKV97Ud/ZFRygQpo23Esb9Yf3nZ17LkEbt6HE/byre9L7/+cDTPjx/+r9Vqmfp6WaWuvs0Ixq7PapD5ChUq3B2rsNEfQlf7UmyYpYmnRYrFQyOmKD8VPNVygS9JwCt8/qhkuYLHMjLh38lbz5Zd5/K8P8qmed86LarPQ5Jdi9LOI3fy2qrImyaGsn1b9F0RaeCPGSm8Z4iSBzyP4Zmmt29kUwOa573RamYZEoD/VU9SYz7v9j31ulBCIXbcyHtv8JwSH5p2zGiPpZOHWq2WiVtFWyl5BjHhYwZp/nif0c6+X9X7iLooybNIdrR/fHypvLhV5KGxjfAcIg4SmM/nIb4bsZIoU6PRCDKm5JPemKZeRyp3s9nMptOpra+v37o1j3d4XtvOkz60g5Z3Pp+HW+74DG8jyu2PhirhR1lqtVqoIzGU6vW6dbvdTJ7UTb2FyFcJYC231tGTxBBTeC/x3mw2y5BSkFRJkoT2pk70g5J/eXHBIJxoX9rbzKpb7SpUuCdWwVWs2u74kuyYR7vV7iHJjodI+ymRM6s0DPyO0GNgkbJWoUKFCp8Ssfmw7K5YmeeWnWuL3ouRKUXlWMUun+ZVVJZVo4iMKkOulfl+2fZR49jHeVEvC29Y6/E0PU7F9etK4OQF4laiwxM83itE89JjfxjEZvEA50peaDv5gM7e20PL4L1e1HD2bZanoyghpMSAGvC0nRIM+j51VCIg1ud6bM4fYbzLvOBJoDxoXyvJBzmjeV9eXtp0OrV6vR5INj22Wa/XbTqdhmNyZjfBv6lbzKMKIsfMrNlsZtoBIoSyUEb1vskjZTkaRhkuLy9DUHe8mVS+PdnJ/xA2kGKz2SwQWtQN+SVdTcPshnhSrzmV3SRJApmknoh4d3niU+uv44Ijh/ShyrgPrO9JTzML/eiJLd71gdcrVHhMPCX7uEI53KXPHrp/lyaeyipoXil6CDxE2k9xUD3Xwf7Q/V+hQoUKi7As6VLGA6fs+2WxKmJn0aZFmTbx686y3kLLEnsesbqU1TMW1WOZMilpoKQJ6Skx4gkiT8J48iXPwNT2VO8Ns9s36sXq6I+r+WNP3hjWcvq6aTm0DJ70URLGt5O+z48/TmeWJalIT/PRtvS38Onn5DGfz3MJKE+q6edFZdK65bWHhz9mBdGC94vKkJaD/yFE9BnvJae3BXriiTTW19eDRw2eVbwDfL3JB+8l9dyj/Joveaks+PZR8s3HotJ64P0EmaieadpGSixpjCfIVwXl1n6IkWBaTtpO5U9jdCkokx8L2s5KdlE+yLrYexUqPCYqe+754S599tD9ey+Pp1UotffBfRtnlZ5EDwlVRlft/fTU616hwiLEdgyLnqtkvoJHnkwUyYoamWVkqujZ+66VZd9X414/i5UvRqTcJX9P4sTqr3n7dln0rv9uEUFWRHzFylRUN/+9EiD8n6Zp8FyIETn+aBzQoz5qFMf6Qo/TqReT2Y1nj4eSGhAaGPPEz9F2gTDwN5t5Ykjr4j20Yrd/5cETF+r94wOm65FBykCgadohLz88fDSODvUrOoqoHj95RJmSC9qPebJ0eXlps9ksxAKq1+vWarUsSa6P3KlH3Hw+D8GoeZb0CZStXnP6nsodRAb1bzQaGUJoNpvZ+fm5Jcm1J5X2pRKpHAvl+B9t1263bW1tzRqNRkYm1fMJmVLvI/5XDye8vNI0DQTX+vq6NRqNcNOnP16pMuk9nPhcPcFoDw2wr+8iS+opqMHYO51O8Ai7vLy08XicqRvyTBkJjK7EZh7xNJ/PbTweZ9q/QoUKFVaBx+YC7n3Urqxi/lzwlMkYbyDcJ437plOhwlPDXbwdKlRYBcqucasilsrKcJlyfWnjoYigLlr3F6276h3hvYHUEPcxl5S0yCPNYmSZvstn+r6vZxnSzqeraSjJoO/EiMEi5BGbpF3k3eQJoLy20rJ5Dy0PTdc/k3cET8sZI6diBKPvn1g/QDAo4QLxQD7e20VJJfL1Mby0jbRfY3+TlpKMPoZW7B0lTTwB571zlBxUMo2jgnq8TYlO337av9oHfvz5vo3NAb7tYmSVvq8knn4eO6aq6Supqc8osVVUfiWsF3k1VqhQoUJZPLYueC/iqUxhV1khrwjcN+277mwui7saDY+Fp1aeCk8TT5mMNavkuEI5LCMnXva9ge4JB59PbE0pWmeKyIFYeRallWc8F+UdM34W5XeXtlVjMi+fovSf2jqNwWxmt4KBE1h5bW0tHGHysYc8iaRl8fBGOZ9pWhjFsYDQ3svKkye87+UbYiRN08wRIi2vEi2+XuqpFKu79/qgjrSdtokSAhrryafp6+ZjScUMfqD9GTP88Qiq1WrBMwmPGR87SIkHPa6lwGNGyTD1CKLd6Ruti6YPoUM5NAg4xymV8OE9yB/kk3ypG+XxR0Z5V4kzPRqm5cEzC+8uJWvIr9vtBg+fi4uL0EcaX4l8iRWFV5USVXo8ETnV8jI+aFf9Tbu0Wi1rNpthDKs8TyaTjPzpu3oEUdNVMg5Sz7cZ+fjyk54+W+k9FSo8Ppaxh+5rQz11G+yueLa0+efUCXfFl1z3Co+PSt4qVCjGIsKozPt5RFEeyjxbhtQpSn9RHsumvyx59FCkU5k8liGkNM289swjnhaRiotIqiJiL68uZUiwIoKJ/9Wrw6edN1ZixNJdCEn/WZ6ni6+jevQUIa8d9LtYO5eRAyW11LPH7IaA8h4+mrd+v4hA9v0H8OSJxRzz5V9Udg8vK0oIKfnn5YDP8+TJeyn5usW8v3yb5JVF42DF2gDCjXr7uEuxNlevxzLzzKL5okKFCo+LT2EPfW422KPdancfLLsTeVfcR4EuevdzE5oKFSpU+JzgDWLvhZE3z+t7iwyGsuuAz2sV61LM4C+7i5ZnTJVBGTJNy3HfvHwai9JaRN6UTYf31btCDVm8OtRQjQXx9vFzNH19VgNH661i3qAmXQ3QTBnU08T/4CnDM+qpxZXyGtBZvTJ41ux2YOgYWaW/8UQxs4x3EIZ97P1FBJXP2xM4sfGWR0xBAiVJYo1Gw9I0tel0GuoeIxuUGFFvIoV6lGmgd7Nr75r5fB7ib6nsQIAQ96jVaoU4Uer1RDtqPlovSJbLy0trNBrWarXCbXQqb54YUjJFPbW0LymrelXRl9z8Rr9QF+I38T8xpLQslBcPKvJTGeHdZrOZiVOl/TqdTi1JEut0Olar1Ww0GtlsNrPRaGRm1zJMOX2/NRoNq9frwbsrRvLhqUXMK2Jh+baKtaHKMONqOp0GL6oKFSo8fXxKDqCsnveYeLYeT4+N5zbJP3R5n1t7VKhQocJj4SEX+mV3vJ/SnL2K9injEXOXtFb1rCeTPFmSV+4ioimPTIt50OTlFyNU8tKPlbGI6PHvxzxUYnXzdVRSw3s+LSJ2Y2Uv4+nj3/VliZVf09M+WERklhmDtJ160igZmRd7yMwC0eTJT98mRfGLvIzmtWHej2+PGIGvafm+9sSWb5eYzCjJ6vPyxGZsnCkhq/l5D7C88bZoTGgdY0HofXvFyFp+65HHChUq3B1f8th5CnV/0h5PRUrafdJbBot2TJ8aFu0A3rfcT7XeFb4sxBS0ClmUGe9PcVdk1VhkrPrvtU3KtI1vw7sSFPo7ZviWSTuvjouIjtjneaRB0TOLCAl9Rtt80Vofa6tF9SgqxyrHQ2wOUu8cvdVKy8Jvvd6d394I9+VWkiBWpzwDm7LlzZt6k5x6YOTlqflpmp780HZRI9+nSRrqiaVl0Xf0PX9EzZNYMXJEy+Ph6+EJhzRNMwGxfb5aB20j4nx52SKeFV5GxI4yM2s2myEWkCdj8L7C04nfeLSp95h/lzYlZhCeO/V6PdwMuLOzE+qapqk1m83gUaX1xCsIjxwf6yrmHUW6ZhZiGlG++XwePJF4ntvnNEaSyidl0ODfzWYzyMtsNrNGoxE81TQdMwv9mUdQ+aN3KktJkli73bbZbBZu3+M5vLIoS71eD20FiaQ3DlJH6oTMUEbarEKFCsvhc9d1i/AU6v4gxNNTNmIew0h9yobwXdnOp9yXnzOqdr87lmmzuxqYy/ZJWfLHbLXzhjfsi55ZRV5fiswWEUQPhWXy8X0Sk7FVyh35lS1rEclV9HxZ3KUsHsvMDb4+MULRx5yJ3Wi1iED0ZM1dNpqKZNZ7fXiixhM6sbz0PU90+Pe9N4n+9kcOSS/mgVJmg1Jvn+PdWPwfRVEdIJAgTXwbxcrmy6D1gIiYz+cZwkiPj3nyjPTX1tYywapj5FasLuQRCzpfr9et1WqFMkGa6FE3T6wpMeiJV82LI5kEGafcAAKuXq+Ho53+uJ8/qkr9/VFPMwtkGGXwXmRmljnimEfc+nhSEH+QgzEPKf7X/Dj+COGkR3T1XfWSIo0KFSpUKIunqJM/CPG0qoquusG8cvAQeTxUmqvCMor7Q8Evsk+53R4SMVn8UtvisXGXdi7zbJ4cl3n3U81FT3W+XiX8vO+/K0tO+Oc80aD9v2iNia1HZRHLx6eZV2b//jL9VlTeRXXJ+97XI/ZsUdoxkiePzFlUxkVETux5JQSUGFJPDzUu9VYxLXss2LHWQY1w3tebzDRWUIy4UVLElz9WP71ljv95jvRjHlo+DyVhMLp9G2m7aD94g9+TXpQvRvKQB+WP9VWsvck3j7TTPohB84kRvf5ZyAh/xI5y4R2jBAakF2WFyLi4uMjEFFNCWG+30/KQHkSTmdl4PM60v96sRxuT/nA4vBU3TGWCsuvYIHaSxhCjLMS0ihFXvt9VNnX84alFfrPZLJSf9iEGk29XPKg8yQdxpmWjzldXV4Hs0r41u5a/yWSSeUdlVklGLSOg3hqjq0KFChWeG570UbuHQEw5uo9BeV88hwUkZhA8VD73Sf8hycSHwl0NuEUG0XOq+0PgMdogL48y5MFTkNFVlaGoHcqmHSvLY8035KVGRez7PIO8KM2i/7+UMRojwR4bnnhZpjx55BXw5IIaokoWqbeLNyrVgwMD1pNOCu+lwjvko4SmEiVKtvj0YmNQSQ8ljsxu3wYW06v8b30Xo5t6etJAySHNT8kC/Tx2vMu3De3gy+uJJ09eemIuj0zS3zHiKUb6aX6QD2Z2i4ihnATVXl9fD95ApI1McWxPPZS0rjH5WFtbs/X19Qx5xHE3nuOYlxIvHM0bj8e35lFN35NLtVotEE+TyeRWYH49fuf7Rsk0JXAoH31OcHHaAY8kvl9fXw9l4Du8x6jj5eVlSJeyNBqNjAxp0Hh/9FL7Jk3TkL4fs7SJtp/GrgJ4ixXhsXTBp6DPVKhQ4XlhaeKJ2y4qVCiD2LW03NbypaNavMvBzzlpmtpkMqliHlQoDS8rV1dXNh6PC438p44y88eqya/nMmcVlXMZgtMTRmbXMjUcDkM6Sp7wmfemiZE/3rsn5i3Dc+phRFp4cODlsegolE8zRtDxOcSOWdzjKdamWidfByUkfB1jxrb3OsG4jx1j8mn6MnnvLE+C5cmCliFWp7y6+We1LcF0OrXBYBCIJS0nUK8ayqz6k8oLJEqsPj5vyqokknpOxZ7VtuLoGnKnxJLvB5WhJEnCTXV6RC0m79rn2r6MR2TfewJyi57GvYqRQZQB4oh68Y62Pe0SI1tjUBml7hBavq/5X28ljBHWsZsRiS1VoUIZeNsLfbqyySqUxbI8UJKWnKmeuoJZoUKFChUqVKhQoUKFChUqVKhQ4fFQhlK6HR2yQoUKFSpUqFChQoUKFSpUqFChQoUVoCKeKlSoUKFChQoVKlSoUKFChQoVKjwIKuKpQoUKFSpUqFChQoUKFSpUqFChwoOgdHDxKmhdhQoVKlSoUKFChQoVKlSoUKFChbug8niqUKFChQoVKlSoUKFChQoVKlSo8CCoiKcKFSpUqFChQoUKFSpUqFChQoUKD4KKeKpQoUKFChUqVKhQoUKFChUqVKjwIKiIpwoVKlSoUKFChQoVKlSoUKFChQoPgop4qlChQoUKFSpUqFChQoUKFSpUqPAgqIinChUqVKhQoUKFChUqVKhQoUKFCg+CiniqUKFChQoVKlSoUKFChQoVKlSo8CCoiKcKFSpUqFChQoUKFSpUqFChQoUKD4KKeKpQoUKFChUqVKhQoUKFChUqVKjwIPj/YnAgO8/1isYAAAAASUVORK5CYII=",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "grid = torchvision.utils.make_grid(\n",
+ " torch.cat([images[:8], reconstruction[:8]]), nrow=8, padding=2, normalize=True, scale_each=False, pad_value=0\n",
+ ")\n",
+ "plt.figure(figsize=(15, 5))\n",
+ "plt.imshow(grid.detach().cpu().numpy()[0], cmap=\"gray\")\n",
+ "plt.axis(\"off\")"
+ ]
+ },
+ {
+ "attachments": {},
+ "cell_type": "markdown",
+ "id": "b00071e2",
+ "metadata": {},
+ "source": [
+ "## Evaluate Latent Space\n",
+ "\n",
+ "First, obtain the latent space from the entire training and validation datasets.\n",
+ "Then, we train a logistic regression classifier on the latent space."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 19,
+ "id": "775401d4",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# get latent space of training set\n",
+ "latents_train = []\n",
+ "classes_train = []\n",
+ "# 15 slices from each volume\n",
+ "nb_slices_per_volume = 15\n",
+ "for _ in range(nb_slices_per_volume):\n",
+ " for batch in train_loader:\n",
+ " images = batch[\"image\"].to(device)\n",
+ " latent = model.semantic_encoder(images)\n",
+ " latents_train.append(latent.detach().cpu().numpy())\n",
+ " classes_train.append(batch[\"slice_label\"].numpy())\n",
+ "\n",
+ "latents_train = np.concatenate(latents_train, axis=0)\n",
+ "classes_train = np.concatenate(classes_train, axis=0)\n",
+ "\n",
+ "# get latent space of validation set\n",
+ "latents_val = []\n",
+ "classes_val = []\n",
+ "for batch in val_loader:\n",
+ " images = batch[\"image\"].to(device)\n",
+ " latent = model.semantic_encoder(images)\n",
+ " latents_val.append(latent.detach().cpu().numpy())\n",
+ " classes_val.append(batch[\"slice_label\"].numpy())\n",
+ "latents_val = np.concatenate(latents_val, axis=0)\n",
+ "classes_val = np.concatenate(classes_val, axis=0)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 20,
+ "id": "f4d22437",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "((5760, 512), (5760,))"
+ ]
+ },
+ "execution_count": 20,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "print(latents_train.shape)\n",
+ "print(classes_train.shape)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 21,
+ "id": "fcfd10aa",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "(0.8217013888888889, 0.7395833333333334)"
+ ]
+ },
+ "execution_count": 21,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "clf = LogisticRegression(solver=\"newton-cg\", random_state=0).fit(latents_train, classes_train)\n",
+ "print(clf.score(latents_train, classes_train))\n",
+ "print(clf.score(latents_val, classes_val))"
+ ]
+ },
+ {
+ "attachments": {},
+ "cell_type": "markdown",
+ "id": "a8b174a0",
+ "metadata": {},
+ "source": [
+ "## Manipulate Latent Space\n",
+ "\n",
+ "The logistic regression classifier learns a direction `w` in the latent space that separates the healthy and abnormal slices. We can use this direction to manipulate the images by `latent = latent + s * w`, where `s` controls the strength of the manipulation. Negative `s` will move the image in the opposite direction."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 26,
+ "id": "809e8aed",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 100/100 [00:02<00:00, 42.02it/s]\n",
+ "100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 100/100 [00:02<00:00, 41.93it/s]\n"
+ ]
+ }
+ ],
+ "source": [
+ "s = -1.5\n",
+ "\n",
+ "w = torch.Tensor(clf.coef_).float().to(device)\n",
+ "scheduler.set_timesteps(num_inference_steps=100)\n",
+ "batch = next(iter(val_loader))\n",
+ "images = batch[\"image\"].to(device)\n",
+ "noise = torch.randn_like(images).to(device)\n",
+ "\n",
+ "latent = model.semantic_encoder(images)\n",
+ "w_ = torch.cat([w] * images.shape[0], 0)\n",
+ "latent_manip = latent + s * w[0]\n",
+ "\n",
+ "reconstruction = inferer.sample(\n",
+ " input_noise=noise,\n",
+ " diffusion_model=model.unet,\n",
+ " scheduler=scheduler,\n",
+ " save_intermediates=False,\n",
+ " conditioning=latent.unsqueeze(2),\n",
+ ")\n",
+ "manipulated_images = inferer.sample(\n",
+ " input_noise=noise,\n",
+ " diffusion_model=model.unet,\n",
+ " scheduler=scheduler,\n",
+ " save_intermediates=False,\n",
+ " conditioning=latent_manip.unsqueeze(2),\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "525702b5",
+ "metadata": {},
+ "source": [
+ "Although not perfectly, the manipulated slices do not present a tumour (unlike the middle - \"reconstructed\" - ones), because we tweaked the latents to move away from the abnormality cluster: "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 28,
+ "id": "7cf1fdc6",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABBAAAAGrCAYAAAB5UGThAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjkuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8hTgPZAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOx9d5ykVZn1qaruyl3VOU4OMIgoMCgoWf3AgBgWWMBFwYB5xbiu7gqIYc34uYt5FTFnPwMquLgqyKoEkTiByalzV67qrnq/P3rPrfPeqp4ZBpjuYe75/frX3VVvvOG5z3OecAOe53lwcHBwcHBwcHBwcHBwcHBw2AuC8/0ADg4ODg4ODg4ODg4ODg4OCx+OQHBwcHBwcHBwcHBwcHBwcNgnHIHg4ODg4ODg4ODg4ODg4OCwTzgCwcHBwcHBwcHBwcHBwcHBYZ9wBIKDg4ODg4ODg4ODg4ODg8M+4QgEBwcHBwcHBwcHBwcHBweHfcIRCA4ODg4ODg4ODg4ODg4ODvuEIxAcHBwcHBwcHBwcHBwcHBz2CUcgODg4ODg4ODg4ODg4ODg47BOOQHBwOAxw1VVXIRAIHNC5X/3qVxEIBLB58+bH9qEEmzdvRiAQwFe/+tX9Ov673/0uOjs7kcvlHrdn2htOOukkvOtd75qXezs89ng08+OxwLZt2xCNRnHrrbc+Ztd8JPN22bJluPTSSw/ommeccQbOOOOMR/x809PTWLx4Ma677rpHfO5CxYG2xSPBI5WVBwuP5N1zuRx6e3vxjW98w3x26aWXIplMPk5Pt/Dw7ne/GyeeeOJ8P4aDg4PDAcERCA4OCxj33Xcf/uEf/gFDQ0OIRCIYHBzEy172Mtx3333z/Wjzhmq1iiuvvBJvfvObfQrnhz70Ifz4xz8+KM/wT//0T/iP//gP7N69+4CvcemllyIQCJifSCSCI444Au973/tQKpUew6edfxQKBVx11VX47W9/e1g/w1x4//vfjxNPPBEnn3zyfD/KQUNrayve9ra34YMf/OCjGu9nnHEGAoEAVq9e3fT7m266ycyx73//+wd8nycCbrvtNlx11VWYnJyc1+f49Kc/jba2Nlx44YWP633mWhMWQjtcccUV+Otf/4r/9//+37w9w2OFP/3pT3jDG96AtWvXorW19RGTsZzD9s9zn/vcx+mJHRwcHi0cgeDgsEDxwx/+EMcffzx+85vf4LLLLsN1112HV73qVbjllltw/PHH40c/+tF+X+tf/uVfUCwWD+g5LrnkEhSLRSxduvSAzn+s8dOf/hQPPfQQLr/8ct/nB5NAeNGLXoRUKvWovaeRSAQ33HADbrjhBnzyk5/EsmXLcM011+BVr3rVY/SkCwOFQgFXX331vBMIcz3Do5kfjxYjIyO4/vrr8brXve4xve5Cm7fNcNlll2F0dBTf/OY3H9V1otEoNmzYgD/96U8N333jG99ANBp9VNffX/z617/Gr3/964NyrwPBbbfdhquvvnpeDefp6Wl8+tOfxqtf/WqEQqHH9V57IxDmux36+/vxohe9CB//+Mfn7RkeK/ziF7/Al770JQQCAaxYseKArrFo0SKzFvLHRfk5OCxctMz3Azg4ODRi48aNuOSSS7BixQr87ne/Q09Pj/nuLW95C0499VRccskluOeee/a6YOfzeSQSCbS0tKCl5cCmeygUetwVvUeCr3zlKzj55JMxNDQ0b88QDAZx3nnn4Wtf+xquvvrqAw5/b2lpwT/8wz+Y/9/whjfgmc98Jr71rW/hk5/8JPr6+h6rRz6kwHF7sPBo5sejxde//nW0tLTghS984WN63YU2b5uhvb0dZ511Fr761a/ila985QFfZ+XKlZiZmcG3vvUtPP3pTzefl0ol/OhHP8ILXvAC/OAHP3gsHnmvCIfDj/s9DnX87Gc/w8jICC644IL5fpR5xwUXXIDzzz8fDz/88AEb3gsBr3/96/FP//RPiMVieNOb3oR169Y94muk02nfWujg4LCw4SIQHBwWID72sY+hUCjgC1/4go88AIDu7m58/vOfRz6fx0c/+lHzOfO477//flx88cXo6OjAKaec4vtOUSwW8Y//+I/o7u5GW1sbzj33XOzYsQOBQABXXXWVOa5Z3vOyZctwzjnn4A9/+AOe/vSnIxqNYsWKFfja177mu8f4+Dje8Y534JhjjkEymUQqlcLznvc8/PWvfz2gdimVSvjlL3+J5zznOb7PA4EA8vk8rr/+ehP+qDndd911F573vOchlUohmUzi2c9+Nm6//XbfNfiev/vd7/Da174WXV1dSKVSePnLX46JiYmGZ/k//+f/YMuWLbj77rsP6F2aIRAI4JRTToHneXj44Yd9391444049dRTkUgk0NbWhhe84AVNU1kefPBBXHDBBejp6UEsFsORRx6J9773vb5jHkl73HrrrXjb296Gnp4eJBIJvOQlL8HIyIjv2L/85S84++yz0d3djVgshuXLlxuDcPPmzWYMk2zRMcbc540bN+L5z38+2tra8LKXvQzA3Ln5zfKtS6USrrrqKhxxxBGIRqMYGBjAS1/6UmzcuHGfz9BsfszMzOCaa67BypUrEYlEsGzZMrznPe9BuVz2Hbe/c2Eu/PjHP8aJJ57YkP99xhln4MlPfjLuuecenH766YjH41i1apUJw//v//5vnHjiiaaPb775Zt/5zeat53n4wAc+gEWLFiEej+PMM8+cMx3qvvvuw7Oe9SzEYjEsWrQIH/jAB1Cr1fbrncrlMq688kqsWrUKkUgEixcvxrve9a6GtgNm59Ef/vAHjI+P79e158JFF12E73znO75n/OlPf4pCodDUWN2yZQve8IY34Mgjj0QsFkNXVxfOP//8hpoRj2Qe2OPyt7/9LQKBAL7zne/gPe95D/r7+5FIJHDuuedi27ZtvnMfyVi3cc899+DSSy/FihUrEI1G0d/fj1e+8pUYGxszx1x11VV45zvfCQBYvny5mQP6vl//+texdu1axGIxdHZ24sILL2x4TgD4whe+gJUrVyIWi+HpT386fv/73+/1+RQ//vGPsWzZMqxcubLp9w8//DDOPvtsJBIJDA4O4v3vfz88z/Mdk8/n8fa3vx2LFy9GJBLBkUceiY9//OO+4+ZaE/bVDo903v/2t7/FCSecgFgshmOOOcZEOP3whz/EMcccg2g0irVr1+Kuu+5qeFeuYz/5yU/22W57k7Hzjb6+PsRisUd9nZmZmXmra+Tg4PDI4CIQHBwWIH76059i2bJlOPXUU5t+f9ppp2HZsmX4+c9/3vDd+eefj9WrV+NDH/pQg+KluPTSS/Hd734Xl1xyCU466ST893//N17wghfs9zNu2LAB5513Hl71qlfhFa94Bf7zP/8Tl156KdauXYujjz4awKwy+OMf/xjnn38+li9fjj179uDzn/88Tj/9dNx///0YHBzc7/sBwB133IFKpYLjjz/e9/kNN9yAV7/61Xj6059uUhuooN5333049dRTkUql8K53vQutra34/Oc/jzPOOMMYYYo3velNaG9vx1VXXYWHHnoIn/3sZ7FlyxZjDBBr164FANx666047rjjHtF77A1UZDs6Onzv94pXvAJnn302PvKRj6BQKOCzn/0sTjnlFNx1111YtmwZgFlD4tRTT0Vraysuv/xyLFu2DBs3bsRPf/pTfPCDHzyg9njzm9+Mjo4OXHnlldi8eTOuvfZavOlNb8J3vvMdAMDw8DDOOuss9PT04N3vfjfa29uxefNm/PCHPwQA9PT04LOf/Sxe//rX4yUveQle+tKXAgCe8pSnmHvMzMzg7LPPximnnIKPf/zjiMfjj6jNqtUqzjnnHPzmN7/BhRdeiLe85S3IZrO46aabcO+99+I5z3nOPp/Bxqtf/Wpcf/31OO+88/D2t78d//M//4MPf/jDeOCBBxrSh/ZnLjTD9PQ0/vznP+P1r3990+8nJiZwzjnn4MILL8T555+Pz372s7jwwgvxjW98A1dccQVe97rX4eKLL8bHPvYxnHfeedi2bRva2trmvN/73vc+fOADH8Dzn/98PP/5z8edd96Js846C5VKxXfc7t27ceaZZ2JmZgbvfve7kUgk8IUvfGG/jIRarYZzzz0Xf/jDH3D55ZfjqKOOwt/+9jd86lOfwrp16xpCyteuXQvP83DbbbfhnHPO2ef158LFF19salw861nPAgB885vfxLOf/Wz09vY2HP/nP/8Zt912Gy688EIsWrQImzdvxmc/+1mcccYZuP/++xvG4L7mwd7wwQ9+EIFAAP/0T/+E4eFhXHvttXjOc56Du++++zExvG666SY8/PDDuOyyy9Df34/77rsPX/jCF3Dffffh9ttvRyAQwEtf+lKsW7cO3/rWt/CpT30K3d3dAGCItQ9+8IP413/9V1xwwQV49atfjZGREXzmM5/Baaedhrvuugvt7e0AgC9/+ct47Wtfi2c+85m44oor8PDDD+Pcc89FZ2cnFi9evM9nve222xrkN1GtVvHc5z4XJ510Ej760Y/il7/8Ja688krMzMzg/e9/P4BZEuzcc8/FLbfcgle96lU49thj8atf/QrvfOc7sWPHDnzqU58CMPeakEgk9toOj3TeX3zxxXjta1+Lf/iHf8DHP/5xvPCFL8TnPvc5vOc978Eb3vAGAMCHP/xhXHDBBXjooYcQDNb9dul0GitXrsStt96Kt771rXO22b5k7N6Qy+X2q8ZIa2sr0un0Po97vLBu3TokEglUKhX09fXhNa95Dd73vvehtbV13p7JwcFhL/AcHBwWFCYnJz0A3ote9KK9Hnfuued6ALxMJuN5nuddeeWVHgDvoosuajiW3xF33HGHB8C74oorfMddeumlHgDvyiuvNJ995Stf8QB4mzZtMp8tXbrUA+D97ne/M58NDw97kUjEe/vb324+K5VKXrVa9d1j06ZNXiQS8d7//vf7PgPgfeUrX9nrO3/pS1/yAHh/+9vfGr5LJBLeK17xiobPX/ziF3vhcNjbuHGj+Wznzp1eW1ubd9pppzW859q1a71KpWI+/+hHP+oB8H7yk580XDscDnuvf/3r9/rMc+EVr3iFl0gkvJGREW9kZMTbsGGD9/GPf9wLBALek5/8ZK9Wq3me53nZbNZrb2/3XvOa1/jO3717t5dOp32fn3baaV5bW5u3ZcsW37G81oG0x3Oe8xzf+W9961u9UCjkTU5Oep7neT/60Y88AN6f//znOd91ZGSkYVxpOwDw3v3udzd8t3Tp0qZ9evrpp3unn366+f8///M/PQDeJz/5yYZj+ex7ewZ7ftx9990eAO/Vr36177h3vOMdHgDvv/7rv3zPuD9zoRk2bNjgAfA+85nPNH1HAN43v/lN89mDDz7oAfCCwaB3++23m89/9atfNcwfe94ODw974XDYe8ELXuDrz/e85z0eAF87X3HFFR4A73/+539875ROpxtkgd0XN9xwgxcMBr3f//73vvf53Oc+5wHwbr31Vt/nO3fu9AB4H/nIR/baVnPh9NNP944++mjP8zzvhBNO8F71qld5nud5ExMTXjgc9q6//nrvlltu8QB43/ve98x5hUKh4Vp//OMfPQDe1772NfPZ/s4DPou2Be87NDRk5LTned53v/tdD4D36U9/2ny2v2O9maxs9i7f+ta3Gsblxz72sYb+8zzP27x5sxcKhbwPfvCDvs//9re/eS0tLebzSqXi9fb2escee6xXLpfNcV/4whc8AL7nbIbp6WkvEAg0nReUA29+85vNZ7VazXvBC17ghcNhb2RkxPM8z/vxj3/sAfA+8IEP+M4/77zzvEAg4G3YsMF8NteaMFc7HMi8v+2228xnnIexWMwngz//+c97ALxbbrml4VnOOuss76ijjmr4XLE/MnYusF339bOvvttfvPGNb/TJ0v3BK1/5Su+qq67yfvCDH3hf+9rXjG5zwQUXPCbP5ODg8NjDpTA4OCwwZLNZANirJ1G/z2Qyvs/3pxjbL3/5SwAwHhLizW9+834/55Oe9CRfhERPTw+OPPJIX+h9JBIxHpdqtYqxsTEkk0kceeSRuPPOO/f7XgRDctU7vzdUq1X8+te/xotf/GJfjunAwAAuvvhi/OEPf2hov8svv9zn9Xj961+PlpYW/OIXv2i4fkdHB0ZHRx/xexD5fB49PT3o6enBqlWr8I53vAMnn3wyfvKTn5hoh5tuugmTk5O46KKLMDo6an5CoRBOPPFE3HLLLQBmi/H97ne/wytf+UosWbLEdx9e60DbQyMvTj31VFSrVWzZsgUAjGfyZz/7Gaanpw+4Lebywu8PfvCDH6C7u7vp+D2Q+hTs67e97W2+z9/+9rcDQEPkz/7MhWbY13hOJpO+SvVHHnkk2tvbcdRRR/kiRfj33u538803o1Kp4M1vfrOvTa644oqGY3/xi1/gpJNO8tUT6OnpMakle8P3vvc9HHXUUVizZo1vvDIqgOOV4Ls/mnlEXHzxxfjhD3+ISqWC73//+wiFQnjJS17S9Fj1/E9PT2NsbAyrVq1Ce3t7U9m0r3mwN7z85S/3yfPzzjsPAwMDTWXKgUDfpVQqYXR0FCeddBIA7Jec/eEPf4harYYLLrjA12f9/f1YvXq16bO//OUvGB4exute9zpfvYdLL710v7zX4+Pj8Dxvr/L7TW96k/k7EAjgTW96EyqViknR+cUvfoFQKIR//Md/9J339re/HZ7n4cYbb9znc8yFA5n3z3jGM8z/nIfPetazfDJ4b/Nzf9aQRyNj3/Wud+Gmm27a588nPvGJR3TdxxJf/vKXceWVV+KlL30pLrnkEvzkJz/Ba17zGnz3u99tSK1zcHBYGHApDA4OCwxUNEkkzIW5iIbly5fv8x5btmxBMBhsOHbVqlX7/Zy2kQrMKkNaL6BWq+HTn/40rrvuOmzatAnVatV819XVtd/3suHtJTVDMTIygkKhgCOPPLLhu6OOOgq1Wg3btm3zhZnb28Elk0kMDAw05EbzOQ60gCIwWz3+pz/9KQBg+/bt+OhHP4rh4WGfQbB+/XoAMAaYjVQqBaCunD75yU+e834H0h52P1P5Zz+ffvrp+Lu/+ztcffXV+NSnPoUzzjgDL37xi3HxxRcjEonsvQH+Fy0tLVi0aNF+HdsMGzduxJFHHvmYFULk/LDnQ39/P9rb2xuMxv2ZC3vDXON50aJFDeMrnU43hIrTeNvb/fjM9vju6elpMOi2bNnSdI/6ZuPGxvr16/HAAw801G4hhoeHff/z3R/NPCIuvPBCvOMd78CNN96Ib3zjGzjnnHPmJGKLxSI+/OEP4ytf+Qp27Njh64OpqamG4/c1D/YGu80DgQBWrVrVVKYcCMbHx3H11Vfj29/+dkP7NnsXG+vXr4fneXNuhUlCda4x1Nra+oiKAM413oPBYMN1jjjiCAD11K4tW7ZgcHCwoV+POuoo3zMeCB7tvOc8fCTzc3/WkEcjY5/0pCfhSU960l6P2R/kcjlffYJQKDTnHH8s8Pa3vx1f/OIXcfPNNxsyzMHBYeHAEQgODgsM6XQaAwMDuOeee/Z63D333IOhoSFjQBKPRU7t/mCuCu+qHH7oQx/Cv/7rv+KVr3wlrrnmGnR2diIYDOKKK67Y74JsCpIOExMTj8rgfKwwOTlpcmgPBKFQyFcQ8uyzz8aaNWvw2te+1uwPzna64YYb0N/f33CNx3v3gH31cyAQwPe//33cfvvt+OlPf4pf/epXeOUrX4lPfOITuP322xuKAzaDRqoo5lKsq9XqQdlhYH+N2v2ZC82g4/mRXPdA73cwUKvVcMwxx+CTn/xk0+9t44rv/mjmETEwMIAzzjgDn/jEJ3DrrbfudeeFN7/5zfjKV76CK664As94xjOQTqcRCARw4YUXNpVNj3ebP5qxfsEFF+C2227DO9/5Thx77LFIJpOo1Wp47nOfu19ytlarIRAI4MYbb2x6r/2Zw/uDzs5OBAKB/SbW5guPdt4/krEyMTGxz7H/aGTs1NTUfm1RGw6H0dnZOef3H//4x3H11Veb/5cuXfqYEWDNQDnxaIurOjg4PD5wBIKDwwLEOeecgy9+8Yv4wx/+YHZSUPz+97/H5s2b8drXvvaArr906VLUajVs2rTJ503asGHDAT9zM3z/+9/HmWeeiS9/+cu+zw/U8F6zZg0AYNOmTTjmmGN83zVT+np6ehCPx/HQQw81fPfggw8iGAw2GDTr16/HmWeeaf7P5XLYtWsXnv/85/uO27FjByqVivF8PRYYGBjAW9/6Vlx99dW4/fbbcdJJJ5likL29vQ27Tyjoubv33nvnPOZA2mN/cdJJJ+Gkk07CBz/4QXzzm9/Ey172Mnz729/Gq1/96gP2Lnd0dDTdq33Lli0+T+XKlSvxP//zP5ienp6z6NYjeQbOj/Xr1/v6d8+ePZicnMTSpUv3/yX2giVLliAWi2HTpk2PyfX2Bj7z+vXrfW03MjLSYNAtXbrURL4omo0bGytXrsRf//pXPPvZz96vNue7P1bz6OKLL8arX/1qtLe3N8xZxfe//3284hWv8IVul0qlpuPt0cJuS8/zsGHDBl8Rz/0d6zYmJibwm9/8BldffTXe9773zXlPYO45sHLlSnieh+XLlxuPfzPoGNKIqOnpaWzatAlPfepT5zwXmCU7V65cOed4r9VqePjhh33PwC0BWSh26dKluPnmm5HNZn1RCA8++KDvGYG533euzw/WvFfsT7sRe5Oxc+Etb3kLrr/++n1e+/TTTzc7SDTDy1/+cp8u8ng7KhhR93hGOTg4OBw4XA0EB4cFiHe+852IxWJ47Wtf69uKC5hl5F/3utchHo+b7ageKc4++2wAwHXXXef7/DOf+cyBPfAcCIVCDV6X733ve9ixY8cBXW/t2rUIh8P4y1/+0vBdIpFoUMBDoRDOOuss/OQnP/F5S/bs2YNvfvObOOWUUxoiOL7whS/48kw/+9nPYmZmBs973vN8x91xxx0AgGc+85kH9C5z4c1vfjPi8Tj+7d/+DcBsX6VSKXzoQx9qmv/KreR6enpw2mmn4T//8z+xdetW3zHsgwNpj31hYmKioY+PPfZYADBbn7Gi/SM1zlauXInbb7/dt0vAz372s4at5f7u7/4Oo6Oj+Pd///eGa/DZHskz0PC89tprfZ/Tq/5IdivZG1pbW3HCCSc0Hc+PNZ7znOegtbUVn/nMZ3z9Zb8jMPv+t99+O/70pz+Zz0ZGRvCNb3xjn/e54IILsGPHDnzxi19s+K5YLCKfz/s+u+OOOxAIBHy55I8G5513Hq688kpcd911vjx9G81k02c+8xlfmtVjha997Wu+lLTvf//72LVrl0+m7O9Yt0Fvt/0uzfo1kUgAaJwDL33pSxEKhXD11Vc3XMfzPLMGnXDCCejp6cHnPvc533N+9atf3e+5/YxnPGOv413nsOd5+Pd//3e0trbi2c9+NoDZsVmtVhvm+qc+9SkEAgFfmzZbE/g50NgOB2veE1NTU9i4ceM+15D9kbFz4bGqgbBixQo85znPMT8nn3zyvl+wCR588EHf+pTJZBrewfvf7WaBuq7i4OCwsOAiEBwcFiBWr16N66+/Hi972ctwzDHH4FWvehWWL1+OzZs348tf/jJGR0fxrW99a869tPeFtWvX4u/+7u9w7bXXYmxszGzjSG/PY5GPDMxGUrz//e/HZZddhmc+85n429/+hm984xuPKF9WEY1GcdZZZ+Hmm28223oRa9euxc0334xPfvKTGBwcxPLly3HiiSfiAx/4AG666SaccsopeMMb3oCWlhZ8/vOfR7lcxkc/+tGGe1QqFTz72c82225dd911OOWUU3Duuef6jrvpppuwZMmShi0c6Sk70PDOrq4uXHbZZbjuuuvwwAMP4KijjsJnP/tZXHLJJTj++ONx4YUXoqenB1u3bsXPf/5znHzyyUaZ/r//9//ilFNOwfHHH4/LL7/cjJmf//znuPvuuwHgEbfHvnD99dfjuuuuw0te8hKsXLkS2WwWX/ziF5FKpYxCHovF8KQnPQnf+c53cMQRR6CzsxNPfvKT91qvAZjdUu373/8+nvvc5+KCCy7Axo0b8fWvf71h3L/85S/H1772NbztbW/Dn/70J5x66qnI5/O4+eab8YY3vAEvetGLHtEzPPWpT8UrXvEKfOELX8Dk5CROP/10/OlPf8L111+PF7/4xb4IlUeLF73oRXjve9+LTCbziMmbR4Kenh684x3vwIc//GGcc845eP7zn4+77roLN954Y0M00Lve9S7ccMMNeO5zn4u3vOUtZhvHpUuX7jO16pJLLsF3v/tdvO51r8Mtt9yCk08+GdVqFQ8++CC++93v4le/+hVOOOEEc/xNN92Ek08+uaEmSiAQ2KdXtBnS6TSuuuqqfR53zjnn4IYbbkA6ncaTnvQk/PGPf8TNN9/8qGqzzIXOzk6ccsopuOyyy7Bnzx5ce+21WLVqFV7zmteYY/Z3rNtIpVI47bTT8NGPfhTT09MYGhrCr3/966Zefm49+973vhcXXnghWltb8cIXvhArV67EBz7wAfzzP/8zNm/ejBe/+MVoa2vDpk2b8KMf/QiXX3453vGOd6C1tRUf+MAH8NrXvhbPetaz8Pd///fYtGkTvvKVr+y3TH/Ri16EG264AevWrWuIdohGo/jlL3+JV7ziFTjxxBNx44034uc//zne8573GE/0C1/4Qpx55pl473vfi82bN+OpT30qfv3rX+MnP/kJrrjiCl97zbUmzNUOB3PeA7OFTT3Pw4te9KK9Hrc/MnYuPFY1EPaGLVu24IYbbgAAQw6RAFi6dCkuueQSc+xRRx3lm9d33nknLrroIlx00UVYtWoVisUifvSjH+HWW2/F5ZdfPueWnw4ODvOMg7DTg4ODwwHinnvu8S666CJvYGDAa21t9fr7+72LLrqo6TaG3IqO2101+06Rz+e9N77xjV5nZ6eXTCa9F7/4xd5DDz3kAfD+7d/+zRw31zaOL3jBCxruY285ViqVvLe//e3ewMCAF4vFvJNPPtn74x//uF9bk82FH/7wh14gEPC2bt3q+/zBBx/0TjvtNC8WizVsS3fnnXd6Z599tpdMJr14PO6deeaZvu239D3/+7//27v88su9jo4OL5lMei972cu8sbEx37HVatUbGBjw/uVf/qXh+bq7u72TTjppn+/BbRybYePGjV4oFPK9wy233OKdffbZXjqd9qLRqLdy5Urv0ksv9f7yl7/4zr333nu9l7zkJV57e7sXjUa9I4880vvXf/1X3zGPpD3srcO4NR23JLvzzju9iy66yFuyZIkXiUS83t5e75xzzml4rttuu81bu3atFw6Hfdsp7q0dPM/zPvGJT3hDQ0NeJBLxTj75ZO8vf/lLw/jxvNmt7N773vd6y5cvN3PlvPPO821XOdczNJsf09PT3tVXX22ut3jxYu+f//mfvVKp5Dtuf+fCXNizZ4/X0tLi3XDDDQ3nc3vC/bkfAO+Nb3yj+b/ZvK1Wq97VV19t5uMZZ5zh3XvvvU23ELznnnu8008/3YtGo97Q0JB3zTXXeF/+8pf3uY2j581u9/eRj3zEO/roo71IJOJ1dHR4a9eu9a6++mpvamrKHDc5OemFw2HvS1/6ku/8bDbrAfAuvPDCuZptn+2kaLaN48TEhHfZZZd53d3dXjKZ9M4++2zvwQcfbGiL/Z0HzdqCx3zrW9/y/vmf/9nr7e31YrGY94IXvKBhq1XP27+x3kxWbt++3cz5dDrtnX/++WZ7THvb0muuucYbGhrygsFgQ1/+4Ac/8E455RQvkUh4iUTCW7NmjffGN77Re+ihh3zXuO6667zly5d7kUjEO+GEE7zf/e53+z3ey+Wy193d7V1zzTW+zykHNm7c6J111llePB73+vr6vCuvvLJhK+BsNuu99a1v9QYHB73W1lZv9erV3sc+9jHfNpuet/c1Ya52eLTz3p6Hnlfvs4997GO+z//+7//eO+WUU/bZZvsrY+cLHOfNfuwxYX/28MMPe+eff763bNkyLxqNevF43Fu7dq33uc99rqE/HRwcFg4CnrcAqi45ODgsCNx999047rjj8PWvf32/tmybD1SrVTzpSU/CBRdcgGuuueYxu+5Xv/pVXHbZZfjzn//s85A2w49//GNcfPHF2LhxIwYGBszn999/P44++mj87Gc/e8zDXR2euHjVq16FdevW4fe///18P8pBxbXXXouPfvSj2Lhxoy+n+he/+AXOOecc/PWvf22odXIo4be//S3OPPNMfO9738N5550334+zYHDNNdfgK1/5CtavX39QiqEuROzevRvLly/Ht7/97X1GIDg4ODgsNLgaCA4OhymaVWa+9tprEQwGcdppp83DE+0fQqEQ3v/+9+M//uM/fNtKHUx85CMfwZve9CYfeQDM7nH/jGc8w5EHDo8IV155Jf785z/j1ltvne9HOWiYnp7GJz/5SfzLv/xLQ0G2W265BRdeeOEhTR44zI23vvWtyOVy+Pa3vz3fjzJvuPbaa3HMMcc48sDBweGQhItAcHA4THH11VfjjjvuwJlnnomWlhbceOONuPHGG3H55Zfj85///Hw/3kHHI4lAcHBwcNgXXASCg4ODg8MTEa6IooPDYYpnPvOZuOmmm3DNNdcgl8thyZIluOqqq/De9753vh/NwcHBwcHBwcHBwWEBwkUgODg4ODg4ODg4ODg4ODg47BOuBoKDg4ODg4ODg4ODg4ODg8M+4QgEBwcHBwcHBwcHBwcHBweHfcIRCA4ODg4ODg4ODg4ODg4ODvvEfhdRXL58+eP5HA4ODg4ODg4ODg4ODg4ODvOETZs27fMYF4Hg4ODg4ODg4ODg4ODg4OCwTzgCwcHBwcHBwcHBwcHBwcHBYZ9wBIKDg4ODg4ODg4ODg4ODg8M+4QgEBwcHBwcHBwcHBwcHBweHfcIRCA4ODg4ODg4ODg4ODg4ODvuEIxAcHBwcHBwcHBwcHBwcHBz2CUcgODg4ODg4ODg4ODg4ODg47BOOQHBwcHBwcHBwcHBwcHBwcNgnHIHg4ODg4ODg4ODg4ODg4OCwTzgCwcHBwcHBwcHBwcHBwcHBYZ9wBIKDg4ODg4ODg4ODg4ODg8M+4QgEBwcHBwcHBwcHBwcHBweHfcIRCA4ODg4ODg4ODg4ODg4ODvuEIxAcHBwcHBwcHBwcHBwcHBz2CUcgODg4ODg4ODg4ODg4ODg47BOOQHBwcHBwcHBwcHBwcHBwcNgnHIHg4ODg4ODg4ODg4ODg4OCwT7TM9wM4ODg4ODg4ODg4zBeCwVl/WiAQQCAQwMzMzDw/kYODg8PChSMQHBwcHBwcHBwcDhtEIhG0trYiFAohFAohlUohFouhu7sb4XAYd999N8bGxub7MR0cHBwWJByB4ODg4OBw2KGlxb/8eZ7n+z8QCJjP9btAIADP81Cr1R7/h3RwcJgTwWAQgUAA1Wq14fNm85NRBrVaDaFQCJFIBKFQCMFgEMlkEm1tbejr60MsFsNDDz2ElpaWBrlg38vBwcHhcIQjEBwcHBwcDisEg0GsWrUKXV1dyOfzmJ6eRj6fN4ZFKBRCa2srPM9DoVBApVJBsVhEKBRCLBZDsVjE+Pj4fL+Gg8Nhi1AohJ6eHoRCIUxMTJiUg0AggNbWVgDwpSGEQiFDCNRqNaRSKaRSKeRyOZRKJYyOjmJychKFQsFEIrS3tyOfz8PzPITDYUxPT2PHjh2oVCrz8s4ODg4OCwWOQHBwcHBwOORBo59/M4LABo2Kjo4O9Pb2IpvNolKpoLW1FdVqFS0tLQiFQohGo6hWq8Zw4OfxeBwtLS0oFAqo1Wqo1WrwPM95Jh0cDgIYRUAyr7W1FcVisYFA0AgEz/MQCAQQCoVQq9UQDAbR0tKClpYWBINBeJ6HUqkEAGhtbUWlUkEikUAkEjGEQzgcNtEKjHzg/QC4mgkODg6HFRyB4ODg4OBwyKOrqwtHH3002tra0NHRgUgkglgsZkKQZ2ZmUK1WMTw8jGw2i8WLFyOdTqNWq6FarSKXy2FmZsYUUaPBwWsUCgVzLUYgZLNZjI2NYXJy0uVLOzg8zmDKAY1/1i0YGBhAMBhEKBTCzMwMJicnUSqVMDk5ienpaZTLZdRqNeTzebS0tKC1tRWZTAaZTAZAnZTwPA/lchme5yGbzRqyAZglLEgotrS0IBqNIhwOI51OI5/PY/v27S6tycHB4bCBIxAcHBwcHA4Z0Ki3kUql0NXVhXQ6je7ubkSjUcTjcVPDgARCMBhENBpFW1sbYrGYqWkQDAZRrVYNSeB5njFSPM9DNBo1ZINGOkxPT5sUCN6rWq26iITHGZFIZM4oExp9gL9mhUamaD/bnxGlUskZhQsAqVQK0WgUsVjMRAwEAgETFcDfmn7EaCIAZl5r5MHMzAxqtZqJQmAkESMJKpWK73vObb1GOBxGPB43cgWAGy8HGdFoFC0tLSYajP2mCAaDRmY3kxkzMzMugmQBgtE+/FvlNPuY83JfNU8cHns4AsHBwcHB4ZBBMpnEGWecgVgs5lMiWlpaEI/HkUgkEIvFEAqFzHc8LhQKoa+vDz09PUbxUKOyWq1ienoatVrNRCPYRRQ9z0Nrayva2tqMAdHe3o6uri6USiVUKhWMjo5iamrqILfM4YNIJIIVK1YgGo0axbKlpQWBQMAonTT8QqEQyuUyisUiUqkU0uk0KpUKpqenDanEc6enp82YqFQquOuuu5DL5eb7dQ9rhEIhvOQlL8HatWuRTCYRCASwbt06jI+P48EHH0Qmk8Ho6KgxIHUsdHZ2AoAh/WKxGGZmZlCpVEyUUbFYRLlcNqlMJAI5fiqViiEtObZ4L5UTqVQK5XIZ+Xx+nlvs8EFLSwtOOOEEtLe3I5PJIJ/P47777jPpKEQ8Hsfy5ctN//GHhNO2bduwdevWeXoLh7kQDoeRTCYRj8cRj8fNOl2pVDAzM2PqF5VKJczMzDQUO45EIgAcEfx44bAhEOit4ACjd2hv7JWDg4ODw/wiGAyira3N5B+n02l0dnYaAkE9g62trcb7qF5ohiIzLQEApqenUa1WfSkL6vGYmZkxnkcbNFJqtRpisZiJQmB4dSKRQLVaNYqNw6NHIpEwRfBaW1uRTCYRiUR8hIH2oxIIWmk/kUigtbXVkAccGzQWNUc+mUw2fRZ6r10xvccHTBMIh8MIh8OIRqNGf6NhEI/HEYvFjDHBH8oBEoo0Ong9zlWOFWJ6ehoAjCHS2tpqZIHtteb8J/lopz05nfLxQzgc9s35aDSKaDSKcrmMarWK9vZ2QyCwtkUkEjFkIzC7pnCMMcqsvb294V4cCySVbfLI4fEB+4XEQSwWQzQaNfOacz0ejxvSjzIZ8O+yAsCkJSl4bKVSQaFQaIhwsOH6uxEBr1lLNcHy5csf72d53BAKhbBs2TLEYjGj0BWLRVSrVbP4UPg4ODg4OCwcRKNRPPvZz0Z3dzeSyaRPMdAChtFo1FRNHx0dRVtbGzo7O8333PMdqOc6K5FM45FpCZs3b0YwGMSiRYtMbjXXDAAm5WF6etp4QQkqmOvWrcOePXsOcos98dDS0oKnPe1p6OzsNEq9Knw0CDSHvVqt+nbT4BjQAnskFvibHi0aDAx9VwOyUqlgcnIS2WzW5b0/ThgaGkJ/fz+WLVuG3t5ebNq0CWNjYyiXywCANWvWoK2tzRzPuclaB7VaDa2trYZ0ikajKBQKyGazxtAn8ZjJZJDL5UxUSjPUajVMTU2ZegotLS1ob29HOBxGIpFALpfDli1bzFiYmZlp8II7PDZYtGgR0um0kedMXymXywiFQhgaGkI4HAYAZLNZPPDAAwiFQujq6jJ1MKLRKJLJpC8tRrcDJRk5MjKCQqGAXbt2oVAomKKaw8PDjhh+HNHe3o7FixejpaXFtLnneejp6UFXVxfi8bjv80Kh4Kt1QrNW5bvOe8r2crmMbdu24e677zYEoxJElP0klw+nPt+0adM+jzlkIxA44VtbWw2zqHlqWiE3FAqZHDoqD+Fw2LfgUOloVlG7WaVtDWt1CsTCQjweNwvI/sDm0HQc8H8KHwopBweHxw9UzgEYJT0ej6Otra1BzjPagMokd1TQ4wA0/K2RBjrfCXsnB/Vs839ei4Yqr8Nj4vG4z4vtIhL2jWbyW4vWab4z117tJxa70wJ47DvNcScCgYAvkkWPV8UTqK8V0WjUeMDoDXM7cTx60OPIHVDsflGdi/OMfUXyj3qdhqnTOGhtbW3oz2g0Cs/zEIlEGtZ9olqtYmZmxuzGEgwGkUgkDIlIGcLoh2QyiXA4jEwmg8nJyYPbiE9Q0ODv6OhAMpk0famRZqFQyEQYMQKMfcKoMG7JSTKRRAR38yiVSuZzjg32NSOg2tvbMTMzY6JNaFw60ujAwT5IJBJmi1UWPKVOzl1XGIlA2LVMiGbRaVwDKC/a2trQ3d1t7qXzWWUMt3Nm5CLvY9dZOJzswUOWQOCCMDQ0hMHBQSSTSRPOpmGpVCQ5cMgwa2EtXaToUeIWXVyMmNtaLpd94XI8xikOCweLFy/GsmXLjAKgXgVdbPi3fs8xwSgV9i+Z0N27d2P79u0H6U0cHA4/tLS04LjjjsPixYt9nmLmLVNxoFIRDAZRLpfNd8lk0kcO0FiwjU6GwmazWd86wGPS6bRRPrl+cHtH5j7TwxEOhxGJRMw6QQW1v78f7e3tRvFct26dqfzu0BzLly/H4sWLfd5/GgqlUskY9XZ/AfViaVzLde0H6mSRXlPlP9dxFlyz82oZ1UADkUbH5OQkyuWyq5fwKLF06VI85SlPwYYNG7B582ZMT09jdHQUAwMDWLRokVHc2T+VSsXnJaQOODExYQgjprl4nod4PG7WdHVCtbe3N6Q26Tir1Wro6enBzMwMcrmcIRCKxSI2b96MYrEIYHbcpFIprF69GieeeCJuu+02/OY3v5m39nwiYfXq1Vi5cqUvjN3zPBNBwF1yOP9zuZyJKEokEliyZAkAGBthZmbGpMgAs+sJ9bv+/n6kUikzpvr7+030med5WLx4sTF2Z2ZmsHv3bmQyGWzcuNHZAgcAkgf9/f047rjjTAoDjXp73S+Xyz6nr5KNAHwpRTxH1wotljw0NIShoSFfTRTOZ943GAxidHQU+Xweu3fvRi6XMzZiKpVCIBBoSKM4HHDIEAjMK+VA48Bqa2szngkuKro4UMFTNonKBRcdHWSaA8tBx0WpXC4bBoohjnYxnVqthlKp5EiFg4hEIoG2tjbTX4w20SJpGpXCPtfcSPU6aGEt9ivHRTKZRFdXly9KQb0izsN4cEG5wP7QrftIBs7MzJjoI2J0dBSVSsV4O+mpIuGoEUeaAwnUc+YcHnt0d3cbj0BbW5tvoae3j0o/ow+0aFqzXFX2LeD3DnDu6o9+T8VBCQj1cGg1eBZoo7eDXi16yrLZrFkXHPyg11n/Z38q7P6ZK3IMgCEJgDopoGu1HZnA+W7nvO9tl4fW1lbzrMFgEMVi0YTAArPRJs4juXdEo1GkUilUKhUUi0VEIhFTOK2zs9PUuVD9DvB7+3TtVnIQqM9RRg3qloyEXeWd40WjT7hzi85fRjZwJxeu+4xSJJmUTCZRqVRcvYxHCHqh2XahUMgQiEC93yhrNbWJ+rcaltqfaiMwhZkEdTqdNjYFz6FnempqylzXjnqiPUIHFD9z+kJzcK1kpEEkEkFHRwfi8XhD9JDq60oeqx3GawJ1pyD7jzKC+oQez/tQB+Cz2DYkn4t6I+czIw9VBqg9+ESOTjtkCIRkMomVK1cikUigo6MDQL1QBgU8O4+DwvY8aZSBRg8oa6WLgh2uSmFEI5GDkAN8amoKpVIJW7ZsMWzo4cRGzRcGBwdx7LHHmhDD1tZWRCIR39ZNWijL3sqLuVSc6DQolUDgItDb24uBgQGziJBQ4vjaunWrq75+EEG5wH7q6+vD0qVLTb+MjIxgfHwcS5cuRVdXlwlxvemmm7Bz506sWLEC6XTa5NT19/cbb3e1WjUVusfHx43cGB4e3q/8MIdHhmAwiGOPPRZHHHGE8fDS40OvUjabRTAYRFdXF4C6oUglnt9raLFGECh5aHsubFmtxBKPsUOVufZw/Nhe8Xg8jnK5jIcffhi7du16QioRjxZ9fX1YtWqVLxyZRe4A+JQ/oB5Voms/AF/bK3FMRY9ruNbDoJeLMrxZES3Nl+f/ra2tZgcOXocV+Nn327Ztc9Fq+0B3dzeOO+44jIyMYPPmzYhEIpiZmcGiRYuwePFiM5dJCNB5o30B1NMM+bujo8OMEcpvFl5kf1FfUENSdUWbxOKWsLFYzFcLZWhoCNPT08hms5iamsL27duxefNmswYtXboUe/bs8dVIcdg3VqxYgbVr12J4eBijo6MoFArYsGEDFi9ebKK61KHIuc95zv5legEjV1paWkyESaFQQD6fx9jYGMbGxrB06VIsX77c9DuNR16zVCqZGjvUK/ldOBzGsmXLzI4e8XgcHR0dTl9oAiUPjjvuOFMIk6lq6sgF6jYc+5zymPoZDX7aa7TRbPnBNYROB9bNodOQawtT5VRf6OzsRLVaRW9vL4BZxyUAjI+Po1QqYc+ePcZ+mJ6eNlFpmUzGXP+JhgVLIITDYfT09JiJnEwmkUqlEIlEDBOtSh8HC6GMlQ0dFHqcFlNSI5PH8LtIJGIEliqlLNjT19dnvE18Ph2kXATd1iIHBhZLYx91dHT4iqMB8HmM2Xf83o4aIOx8Z+1/eiBY0ZtgnyrLmcvljJLD7ycnJ11kwmOIeDyOvr4+tLW1oaury7Q/GWxgtm+j0Sja2tqM3KDyODQ0ZMYRc+t5jBokXJQ0jam1tRXpdNp85vDo0dXVhVQqhY6ODlNxXRdczi0q9aoI2EaEGgEcF3otJZd5Db2P/T/nspLNek16OTVCgXKCz0JZtWTJEoTDYWzfvv2wHTucd8DsHEskEkbG0pOobWb3h/7dLAqh2XEqn22SwI461GPmqqivuoMqqQyBzefzhlg63Ipv7Q+i0aiJMmJhw4GBAaTTaZ/hrsabHYmk0OM14oh9z2uyL2lcqpGhUQ08RseNneNMEpFjlgYJAGOYkLBipOzk5KRLc5kDNLij0Sji8TiGhoYQi8WQTCYxMzODSCRi0hGog1P2zszMIJvNmshREogkDFRns2WGOg45FjRSReUPo4pSqZSpdTE9PW227mSRXyWYo9Eoent7jbzI5XKH9Rhgv7AoMue4Ru4BjWkHKoPVq6/R3lyDGT2i11YncrOIQ5XlGp3eLBJOyUqOnWg0CgCm1kY0GsX09DTS6bRJiS6VSsjlciZK5VDHgiUQkskknva0p5lq20Djwg/Ui9vwNyc8BbkKDqCu7HFw2aGM+jk9VPZg0i2FdBCn02kAsx4VXpPf12qz1V/L5bLJpdm5c2eDouywb7S3t+O4444zoY1AXdjQk6CTk8ymRgrwHP1NJUOJBwCGXaawI4lEDyU9UsFgEKtWrTLeiHK5jEKhgEKhgLvvvvsJITAWCjo6OvCsZz3LLNKMOlHvc6FQMCkK9FADszJh7dq1qNVqmJiYQK1WM0V0qKhyLDB9qVarYXJyEqOjowiHw1i0aBHGxsawe/fueW6JJwaOOOIIrFmzBul02nghdb7Q00MvYKlU8hkGmtdOkpYKiaYh8ZxmBLHKEDt9hf9TYVDCQFPnKF9UEQoEZredSyQSOPnkk9HZ2Ykf/OAHh+3Y6ezsxFOe8hTUajUTasr+Yl+qQWaTvoB/1wygbvSxfxU2eaC5tOxPOyTeJhD0O4WOIxIju3btQjabRSgUQmdnpzMam6CrqwvPfOYzMT4+jvXr12PRokU47rjjTFuqx45rOlD3XKpBwXMYeqxEgUYo8bp2JKoaDJr6RIJPI5iUOGTRVq79PHflypWYmpoylfoLhYLZVeKee+5xY2EOdHZ2Yu3atejr68Py5cuN7qROATUKOfeYgrBz505UKhUkk0lTC4eFTilHlOTlmKLx19bWZo5TEgqoOyvHx8dRKBTwtKc9zYTeT0xM4I477kBLSws6OzvR2tqKzs5OU0utvb0dfX19hlRev379YTsGuF4mk0k86UlPQjgcRrlcNusAv+carvYdI0j4tzpj1cHL6/N6KtsZWcprMzVGiSPbwQDUHQY8D6jrDRxT3Gqa0TFqm+gYXbduHfL5/BNiDCwYAoEeXk6+trY2H2vcLJrAjiJQL4J6/pt5H+y/7c/4m4NDz7eZLB2gGgVBAcXjqGhSSdZ3IyNeKBSeEAPrsQRDyykMdAsfZSttzzGheUj8n6BgaOaF4jncNo4V4KnEqIeMIU80WMg+Tk5OIhKJYMmSJSbihIYJBZIrvrVvRKNRLF++3ISyd3R0mDQjzUfkPMrn88jn8yZsVQ06nb9MX2kmC3Rux2Ixk5bE4xOJBPr7+814yWazDbmOwWAQHR0daG1txfj4uMuD/V90d3djYGDA/N/f349YLNbg8bHlONA8ooifq+Gnslq9mPROaBoaSSg1EHVM6X00VJbKAe/RzGPueZ7ZNqxUKpmQxsMN9DozBVE9QyqTKV/VmLNltnqjbXlv9+FcHiT+rUqq/b3qATpW+KM5tpTt4XAY7e3tRrmlR4wOhMMJ6qWncUZjYWxsDNPT08brTI+/RhNou9rEjsoArvHcfUGjf3Te2kSUEgPNokF1HNjfc4wCjTUZIpGIMSb57mp8ONTR3t6O5cuXm4KETDtgm7Kv+WPnsXMLTupgTFMB6tu7KgnE+V6pVJDP55HJZBAIBEy9GpXvRKFQMPqbRijTmbR48WJjPPI5S6WSme+adnW4gR76vr4+4+SJRCK+KBKtdaCpx0Cjo09lP52DvA7JYU13A/zbPeuawr7W3VzsyEclFNTZwOMp19i3JCT4jDzf8zyk02kMDg6iVCqhWCwik8kgk8k0rHGHChYUgZBKpZBOp3HMMcf4tsRSpZ1Q0oCLha14qtfITltQ5YT3b0YyqKDiuZorx3NtNopslw4Ke2uYvr4+M5koyHbs2OGMSQuJRAJPfepTDftIKGnEkFcKAPYnPVVAPcJAvRmqnOi11GvJbeS6u7uNQLCVEm4vowpOrVbDrl27UCwWfWFM3NmjUqkgk8lgamrKVHR1aI5kMonTTz8dbW1tPsXCzmEvFovIZrOYnJzExMSELyw2FAoZbzKjUbRYjt3+NA7p+c7lcr6w9fb2dgwMDJh7b9q0qSmBsGTJEiQSCdxzzz2OQPhfrFixAqeeeioAvyfYDlvXqvi6cFPRY40EwL9Ya7Fcfk7FNJFIGIVejX+SupQPJJeKxaI5RuWCejdUoQD80XK12mylZs/zMDk5iUwmM+d+809kcG0H4IvmAPxFD1URZJSCkgRsOx0T/J/X5rn2eLLnOK9fLpdNXrSC46gZSaT7htM4nJ6eNtsQ6njL5/PYunXrYUcg0PvP7feq1arZhWTz5s2+/d655Z7WptBt01T20tvHtZrbcefzeYRCIeOxto0Bu0Ai9QUtuKdpELZuRzDaAfCHU/N54vE4Ojs7kcvlkE6nzbp0OM77faG/vx/nnnsuRkdHcf/99xtdGPBvw8d0BOpQbG8WRGZaAXPTGaXG+QjUdbtKpYJSqYSJiQls374dQ0ND6O3tNTLEjkRiFBGNTSU5k8kknvrUpzYQBHQosEAodUw7iumJDtaUe+pTn2q2v9T2ZeoX5TujAmx9XwlezktGAQOzsoZrhe7QYBOHSiBwy04lM+zoR8oi3oO/KSNU77fBZ6Qs6enpMeRypVLBhg0bzFg8FPX/eScQyNrFYjEMDAz48ps4YFQhINiBdlijhqHoAmB7pJWB0s5X5VALZuk99Vq8rypA+rzNvJvqNeE7kDnt6+tDa2srCoUCisWiISEOp+1BWlpaDKOby+XQ1tZmvM1UJtSDDzTmw2roqU0MaQirsoZqyAAwxbba2tqM0TEX1LhRkooKJpVQ9iWjGli9XY3hXC6HsbGxx7hVDw2EQiGsWLHCKAHsD9YX4QKu/W8b7ZxLAHzeCF1M6HGkh8gmH+0qvkC9LgsVVJUT09PTGBoaMlWYARilIZ1Om2KPzIMrlUoYHR097DzR3d3dWLx4MYaGhnzMvh2WSrlos/rqUbTBfmvmdabBR4Igl8th586dyGQyvn3dWVwtFAqZQmwMdaSBQ2VUr83n0vWHz93S0mKilzj/e3t7kUwmsWfPnifsGNDIMQCmDQA0KHZK+HI9tddZrSkE+D1R+r8WvdToJN5HlXwlIHUsqkdZn7WZomgTIQTJae7WMDQ0hK6uLuzevdvkTD9REQqFTBQpPfCsdcHdtGKxGCKRiFHCucuBbr1KUrFSqfiMefUkU06orFaimE4aAD6dUp0HQGMaK+9DmaLHMTVBSQl+p7oHDc1CoYDR0VH09/djyZIl2LhxI4aHhw9OZyxwcD2ORCIYHBxEJBJBuVw2shOYbceJiQkUi0UTKcCaRIxy4VjTNYIyiMQA00unp6dRLBYRDAYxODjok01A3VnIwui5XM6Qf7a9oAYt+151PcoEGrfhcBjd3d3GzhkdHUWxWMSiRYuQSCTMe42MjBzyDodQKGS2xPQ8z9evnGcaLQLU56HOR0LnP+cvPwfmjkjk/3PZcypTmsl5XQfsqKNmdgN/0y6kjkidNRicrY8zODiIWCyGfD6PUqlkxtuhspvbvBMIgUDADLClS5eaSQXAZyiwY1V55EKv3gUqg1owzR4gAJoyzvagVKVBB5vtpZgrNM0mPPRv3o+DmlWdk8kk+vv7sWfPHoyMjJiBdaiGuBwIIpEIjjzySESjUezcudNUuyYCgYDxPGpFZvYX+90WJBTmHF+coGRA1btJwzAcDvu29bHJItu7pYKPoYw0XhjSqjm6qVQK1WoVPT09Zhxt27btsCYQnvzkJ2NoaMj0B/NXSaaRSKAwzmazhjVOJBJIpVJIJpNIJpMmxE0NBXquq9WqUWYJfq/eC4L7QXMnGLLIxWIRhULBREfwWcbGxlAul9HV1YW2tjZ0dHSYzzOZzGFZWHNgYACnnnqqL2/YjhAD6jKSc4XGgS2beaz2qy2rlcyjzMjn89i4cSP27NljivP29PQgHA6bed/X12fmLaOHmBJDLxbBZ9DQaqAe9dTZ2YloNIrR0VGUy2VTuf2JPAai0SiOOOIIQ6KyP5p5lQiucyyGZnuXVFln/3OMaC4s1wiNNPQ8z4Q5A/7CxjxHU1/4PKo32GMUqHtJVXfgu+muQN3d3QgEAia96omMQCCArq4uY+gxL5n1aEicM5ScazxDxdm2rDXE9Vv7h8QeAEPo8rtCoWDa39YfCCUrlISyyUreQ2UVo91UL+M6z3txrIbDYeRyOWzbtg1nnXUWjjvuOPzwhz90BML/grI0Eolg2bJlKBQKyGQyRncCZtt+ZGQEu3btwqpVq9DV1YVcLme2daTdQAKYfcIChvRKl8tlTExMoFwuo1gsoqurC4sXLwbQWBwPmE2zmZiY8BETai+owUn5QduCeoASCKVSCdFoFAMDA0ilUojFYua5Vq9ejcHBQYyOjpodPQ51AiEQCGDx4sXo7u42zh6mIGtdKvsc/lb5r8QcyRgtlg6ggYwA/KlLej87wojrAe9n6/b2NXSN4LqvkUiAn6hklBTrcsTjcSxfvhyrVq3C+Pg4crkctmzZgrGxsUOmyOK8EQihUAjLly83VdQpLBhyyoVABwm9CSpUgMa9gAkNYbGrdmrIqQ5Ym6CwGW/94bFzeUZsA3Z6etqXH6MD0X4vhsClUinz7LVaDXv27PFtFXUoIxgMYuXKlWhvbzdtnMvlTHhgS0uL2XpPF3rNl6JgV68F2U3tI2UONQIEqPePhs0CMHlazKFXUkLDofR9eG9eyx7XSlopA6sMdiwWQ2dnp2EiD4ctoILBIFavXo3u7m50dnYaQ47KIABjdHIukKkPBAKGKCDxY3sFbcKH48ee8+o5UsaaIZSMkLKNVD6bMuGtra2majSjV7itYCwWw5o1a5DL5bB58+ZDYrF4NOju7sbq1avR399v5hF3tNB5xflEgpDhf6oEAI3hjFr1XD+3FT31bvf09PgKb6ZSKd/+8dlsFp7n+SLBADTIaho3fB8eo6ARRKOGObLNFKhDHeFwGENDQ0gkEkY221ECBNuERrxNGPEcVdI5d5UI0LGh3kdCFUoaonQ06NxlP7O/eD3KbSp2xWLRRzgEArOe9XQ6bf5nmo2SkjQsDgdwfHd1dfmIA7u+hdYu4NygQ4VeSxI9Wnmfbayynm3LNFHOdY1O0c9VjnOM6FZxgJ/U4v+EGhqMtOB44vO2tbWhr68PMzMzyOfzuP/++5FKpXDMMcccVts+x+NxHH300T5iAJgl5rdv3454PI729nYTtcM1gu3f3t5udmiYmZnx7YqlurQacxpJzP5jHyWTyQYHAscEC53XajXjGGC/a549ZUO5XPbJDxr+7e3tPjuE9gydRblcDrFYDN3d3eZ/YHb8rly5Evl8Htu2bTvkUp80soMR5oxAovxmGynJ38yZ0Ew/Y4o7d7hRWwvw24T2GqsktL3G2O+gsIvz2v1q113gfVRvoC7JH65DlFdM91IZtJDtvHkjEAKBAFauXIn+/n4fy0+hy/+pmGmYoZ2P0qyBbUWT7I/NGOp1mv2twkUFkYavNPvR57JDpFX5VMGkEymRSPi8dHxnFmZ5IuTSBYOzuxYsXbrUtMXIyAimp6dNaGNXV5ePGbT3dCfjrISQKgPNPARKHtiEEVAveMOwSp3QvI5ObFVGqATTkND9q9WIUfKAubQM8+S+6JlMBhMTE5iZmTksCIQjjjgCK1asMPsAs+8KhYLpD6DuOdS9fsPhMNra2gzLr95Lne+2EcLv51o8SD7Q2FCZoOONfagFfbidD/P0SGrRS9XT04PJyUls3779CW9UdHd348QTTzTKHaM3VLYB/voj1WoV8Xjc5EKrUmCHDypBw7VDZbzmJwOzfdfd3Y329nafokiltFabrbhNg1ELd/G6qoTYEQkqgwKBgElXYjQMveW2kvJEAPdDj0ajxksbj8fn9DapB5KfEc28R5SdHDdaB0ONQ0Y+aJ+p11kLeLEfisUipqenTUFnXk9Dk4vFotnzW2ts9PX1GTJc5QXHLj2NT/S5DsAY/qxMzwg+e84ooaKkH6M22B92DQqgXviUMpn9EwwGTcojDXkaYJqqSFlg6wwkLQmOIY5lQp9DDQOtxRGJRBCNRk1q6sTEBIaHhzE0NIShoSFMTEwcNgRCLBbD2rVrkU6nfWvzxMQE1q1bh1QqZXY4o17HSMFqtWqKbbIYKYkA9hUjde2IUiX/gDqB0Eyv43Nxh6XBwUEkk0nzHNRLeX3KBzo5dBy2tLSgo6PDZ2h6nmeibBhBQW90rVav4RGNRrFs2TKUSiXs3r37kCMQAoEABgcHMTAw4Is8CgaDxhbT9GOdyyoj7LXWNqipS9i1TnRXB8CvL9jPqWuHOrDtY3WsADB1FmxbzHZa6tql+iLXHxIIgUC9Xkw4HDZjTkmIhYZ5TWHgNneELvKq6CtzB/irYuvCYoc86m877YAdZw9KFQxquOpnzTpT76dGoq0MqUdGFzD7OLLZ+r3neSbdI5/PY3p6GsPDw4dkmFNXV5fZbocFrFSQqFdIDQI72sQmX+x+V6WD5zYjArQ/arWayVvlIsNn4nlclLhgqFKrgoYGCcNvmbKgyitDMVtaWszx/JvFogYGBrB+/Xrs2LHj4HXSQcLq1avR29uLnp4eY4hrPhkVOI6TYrFozqWCyrYE6sQff9i3ykhrH9kLUiAQ8OW5c5ww75XGoG2Q8jcXPBbhU5a6VqshFouhVquZ/l2+fLmRCblcDrt27VqwC8YjBSts9/X1+YxwzmebdGXfscgo01dsgxyYHRv06nIhz+VyZu5yHmnUDwlE/q9GvT5PMBhEZ2enj8yg0hoOh32GKAmMtrY2n6yhYqPeCT6/yqonCli7hnuhU/G3ZSvnh7YLCT3Kes/zzBxtFpYKwEcqK1QfsCMX1TOsawSfK5FI+NYIXYO5LrS2tiKbzZp7MzSXYyQajfq8rBybJD07OjqQSCQwNjZmtgp8ooFjIZVKGc8j54JGdyjRouu51h1Qp5FGFakjgAYW9QaOG5JISiaxMCMjDCmf1etnyyPV5Xj/UqlkjlPCKpfLIRwOGyLc8zyTYpFMJs2uS9u2bfOtZU9UhMNhrFy5Ep2dnQ0GH/+fnp7G+Pg4MpkM2tvb0d/f7ytuWqvVkM1mTeSPRpUQqp/Z63G1WjW7LTC6hf2tcp/RzolEAj09PSb6lDo2ownVocf8dqJarRo9QQsEaqQV631w7WDkaSgUMjUaSKiuWbMGlUoFk5OTKJVKGBsba5oyvVBAgobt3dbWZmpR6Ny39e9mqeOce3TkqZ7neZ7ZVpP9YKeqKuxxoyQB76Xrkq5Nup6pM1vJS44B25ZjxBvXHI5TLZxIsoztxy3jVYeg7FpIuuG8EwgM/bE7kP9z8dDO04gFe7Bp5+nftvLBgcxBxM7nvfk3O2tvE3YuRVBZVlVSOFmoqDYL0dXP+SzArOHd3t6ObDZrqsgeagRCMDgbLtzV1YVgMGgWdCUDNFTRjvbQCaQkjP5W2Mq6EjbKDqqhRyOSwp2GrQocfS5VdjkWARivC71ZVFDViNCFhcKXjG06nUY8HsfAwAAmJiaeUMYlMNsXixYtwqpVq0xxJPUq0FvLokflchmjo6MIhUJm3+Z0Ou0jYShH9IeLC+e7Eorap+pNAvzMNQ1Wjsu5Ihc4nrhgkHHn+OI4oqE7ODhoyKjR0VHs3r37cW/3gwEqzGvWrEE0GvXNL203Hc+c9+xvDWnWecW2pyHPvhkbG/OljGheooa26ndqTBKBwOy2XoFAwFyf1aHpHdDxQqWS/cw5rTVa9Nr8/UQiEVpaWkzqgpLldAJ4nmfmqB0doIo820/TjID6mq2KIvUDXkM/V1JZiR32mcp9rhskcDWFRq9NA5WpL/F43NRAIWlkE4wce1QSU6kUADyhPc+hUAh9fX0mpaNWqxnZqbCdRJStmpJo9xfgNzIA+GohaCQn5YZtFGjKDMkdrvWqi1BO6zjTea6yJBKJmO3ZABjixPM8QyqlUinUajXce++9GB4ePuQ8yweC1tZWLF26FB0dHWYtpt7PVEU6BrjTQU9Pjy/6WAlbGvVq+AN1J6HtRKKOVSgUTFFsOnqaGXszMzOIxWLGcaQySAt/0m7g+KGc4NrFa+r5XOcpDzzPMx56vg8LLbN+yuLFi+F5Hnbs2IGpqSmMj48fnI47QDB6iKQq25M1UQB/wUTbNmqmUzHlhPohzyPBxGgAJa3ta2gkmjohbUKfc5vzWx19HItcG2wnJ+BPddDxSWeFpnDyPqqfqgOkWCz6It8XWuT5vBIIZIDpSbANI/t/m2BQRZ7QwaDK6t6iAjhIeD7P09BG28hvpgjrNXktvgcHmF7PJi/0PXVA22QJAGPcrlixAsViEVu3bj0kiITly5ebKAqG6+hCoH9rG7MvqJhxwmnhLKBO9FBp0D7n9dTLAfiNPi5qXFx4T3oU2P4kPVS55TPqvSk0uH0NDSmNQKDiSeNEjV4q4JFIBMceeyyWLFmCu+66C9u3bz+o/fZ4YnJyEsPDw6b9duzYYYQmFTaGeZGIYd9TEdR+BRqrodskAbeC4haPGk7H4wD/9q6RSAS9vb1mznJsqQdL57yGVKoHTXOj1dMN1Ld6HR0dxaZNmx7PZn9c0d7ejuOOO84UtAyHw8ajYstrzmcq8S0tLUgkEsaYo1wgsQDU5yxD40n4sTBbLpfzpSMA9ar4JCSobJAcoBfD3plDc11VuWjmreQ9SCqQLObWjXymJxI08oBkP/vHzncG/BGENqhAaSSXHb2gkUW8v677uhMH+1IVS3vbLXt94XkavaCKXzAYRHd3t08J5U49kUgEsVjMeJB03DJ6RRXYJwI4V2hYpVIpMy9VJ1EFXuWrTRqo3mMTBRppoCltqrRrpJOGQxOM7tNwYnUCMCrBluu240r1AaalMfSeawrHnDoXgsEgent7EQ6HzfaAT0S0tLRg6dKlZqtOygeNPGI7LlmyxBib5XIZ69evN/aBpoUA/rXZnsdAnUjgWsG0IRJ7qqvxR9cGyhC7wCYA5PN5E1quz6H1VlpbW82Wkhx7lIu6VvDdSIjwuZcsWYJSqYSNGzeaNYOOEvt5FhI4f7q6upBOp9HZ2YlYLGZqn+j6DdTlhjpzAfjaidfVv9lulOssmM3IHqZHqlFPmavGuK5BKmPscUH9RIlM1UFtG1KvyevxvQhen22gsoXRFpVKBVNTUyYtl/KTkbALwZE4rwSCLsoq9NUjoAPJDj9p1mH2YkGlj+fbC4ptMCh4fXacGrWKfSkDtkHM+ymrNdc76rvpAKSHrbu7G6VSCbt27fJVfF2o6O7uxooVK4wAV2FBpdxWIAB/7pAq9AwPUs8irzWXgtqMANJxYYdL8/pq+PHePE9DlCgQAH9dCx3XNIrV+2KPDw2VopK+aNEibNmyBbt27VrQYWz7A7ZzpVJBJpMxxVS5lQ0w2w6s2qsEAqOXdM7b/a3z3v6OCgKNBh2H9vzj75aWFlM1OZ/P+8aLTVzqPTQlg+SRGprqsWXF8EAggK1btx6SfRwKhZBMJk0Ffn6m5A+AhgWaJBpQLz6qBgQ9SQSVMF4LmPVAZjIZZLNZM7d4rJLIdhSSze5T2QDQoGzYBLZGrfF7W4YwfJ2K4kJVAh8pqARxpxEAPgLBThXgbzXydc7oZ9pOzWS1Kuh6DyWDNWKE/WI7A9iXOi6UdNZ7EixuXC6XjWwi+UWyjKQYr8G+b6ZDHMpgP9Pz2NHRYVKPmqUqaTuyze3xAPgjQAnqOJSpnJvN9D4ez/7ks9okko431SPYd+oUINkP+A0bvrvneb4tI/n8JFcIRjftbWvoQx0k2np6ekz9As4JnYOtra3o6uoCMNsXO3fuxPbt25FKpYxepf2iOpqOGbY15T6NO44Fkk6ae64Els57e77zb5IHHCt8T404CgQCPqJ4ruvxebSWAx0llUoF999/P/L5vEnzZo2nZrbKQgDX+EQigfb2dnR2dhpSlREXulaq3NA5r0Y55ziPp85MEoFRqMFg0KQUMbpFSSpdq4HmEeXqELLtCY2I47U0goDPx+vob8KOtLSJcABmK2lGsjC6gjKS7bNQUp/mlUCwQ0K42DDPiQK62YSxFQ/9rX9rKBrvp8xPMwaTgkQHgL0A6v1txkyZLD1flaFareYLz+Iz8XwqtKpg2/cg89nS0oIjjjgCxWIRIyMjprbEQlRSlCRSaPEcu084adQroIq7CiSg3r66OPBaNtMI1BUBW5m0FT4tfmUrsLZBon2pYyUWi/mUUvWwKoNODwYNaVU0jj/+eCxevBh/+ctfsGfPnkfdJ/OFo48+GsuWLTNjO5vNolKpIJ1OG4WCCyrnhOd5virKtVoNu3fvNp4jwF+Mi/2m/wOzChxhG44aJUAPGsdONpv1yRFVOqiYaBi1kpwcH1QIqEQC9YWTz9je3o41a9aYYk6HClKpFI4//ni0t7f7PD0AjGeOxSXVuKBiR08FwflOpYBzhOeqR4Cfx2IxDA4ONsxLNRDZTwCQTqeNd4wKSigUMiHIdgFHwL8m2QQD0JhK1dPTY8JoWQSXBNihilAohGXLlploMiVdON7VS6zyV4lgGvmAn+jh3GL+OOcV+6NYLBpiT2U+65cwdYh9wXoFDKXXPuQ6oYZBKBTyyR41EJjCoIVAeR/KIkY5MRqFBfW2bdtmUhCfCGB4vm7PGIvFTBiuGnKUqSobdc3VtXquecXjaJDYpAShESSqt7G/7K3SuH6oZ5RQ3ZBjl9EQjFhg2DnvTVK0UqkY8pty7v7778f27duf0MWRaUirbGAhSiWRgXqqIqM0jzjiCLNWc+7YzhVNV9Q1QB1pqqdxC20tTq5jD6jLDEbHajFfO4oJgKmForv58L1o6FJ/pBxQ4sI2ID3Pw9TUlNERgsEgxsbGUCgUfBEvCw0ki7q7u816YJPHnH+acgbUo4p0DWfbcdeNWCzm25GJY4j9BMzK91wu1xCJPZf9qLKeJL8W5OV7qQ3JcRcI1OvlcG2grOLYnotY0M80uo7vQB0JAHp7ezEzM4PJyUkUi0Xs2LHDpOLwmecT80ogsEP0t+3R0YW+mSex2TX39TkZJqB55xI2QcEfW2ABjeEpNtuoRqSGq/B5AH+hR04Q/qgCS6HHdgqHw+js7EShUDBbj2lxyoUAJWxUKbA98joxbCPMJh60PZr1Fb+zlRB+rgyyfYyy3HPdz2bAbeW3Gbmhlb2VzdTnJoEA1HM19TmYArJu3TqMjY01JWQOBXR3d2PlypXYvXu32fPY8zx0dXWZPYKVSGTBPLYH8+ympqbMYkNo29vjCKjXplBlRscQv9P+5FxUWUDoWAD84Ws2qUmhrx4vvVcwGDQ5g4dSjizDMRcvXmy2x6KSpMaX1pdgm6vRpos2oQonFUi7vXWBj8ViRim1vU28N+CPYtD3IIHIeykZzfP4nX1/jVTiuKNHlqGINF4OxXlLBAIBtLe3o6Ojw+cM4He27LTnC+cCx4Qt23X+t7S0+Mg8zXtl/zD9ROc1iQeVtbqdsn6uzgW+B8NrbbJHj+H72AYJx7Z+HgwGUSwWn1D1D2iU0Qtve3rVkAcat0FU2QA0OoGayVmdb3otm0yw5YReh9fnb9ULeT372hwjOr54Hy0OyDGqxdHUGTQyMvKESkO0oREpGnFHg1xJfV1PuRVuPB43aWVKFGj/qkxX/Yvrq+rInJOaSmL/0MsLwEd8UqbbBIHq8IQ917n22Tu/KOmo7+95s2R5qVQyeqDWErCdlQsBbM9kMomOjg7T57YdBNQJQLttbJBsIXmk8kT1NH7Gwsb2eLDtNEKJRKAuBzSq2H52HXvUD3iO7eTVe/JvJbMVtu6nY4O6BDC7Fo2Pj5sILN57PjGvBALgDx+zJ3Ozz2zowgOgYVHR/DYADQNQjflmRroKBJvtVkHWLAy6mdEK1IkCLS5F0Eihx902Vmxvpy5gVFTtRXQhYNmyZcZbZSvYZIe1PW2lnUW3aGQyDE5zoDmBKXh5DbaVHULFa9vjisdRaDVbdAh7LFBJsPNsCbLIewtNJ1OvYVMKeriOP/54LFu2DHfccceCL6zTDFQyOBba2tpMHqkSPGqc2EZGNBrF4OAgAP/uGNofqugplHhpRvpwMSdJN9f5fH47Z5veSyqXfMaenp4GecbxS29srVYz1YsPBSQSCRx33HEm3QRojPpiWgJD8sLhsK9gGaEGAueiTSyoAtfM+KMyz9xXrbbO76ig8Hz1iNNzquNQxxU/V8WBz9Da2mqiDNTLUavVjFe2UCgcEjVr9gW2qf2e7EOtmq7kEVBXEjWVkX3NNaFYLCKfzxvlCoCv3ZgyoMqgGinsHx7X0tKCVCrl2yJLI080koHyxDYwVGcgwacFd6vVqtkaNBwOm75mOPKhmJa0N7Dg79DQkNm5SOUgd50pFAo+Mo26DtPBbH1L5QDnJj+nPLWjBThndSzY6zevxzHBH3rAC4WC2dGlVquZegX0nnPup1Ipc61qtWpCqPneXN8SiYR57gceeABbt27F5OTkQe6lg4eWlhaceOKJ6O/vx+LFixEOh818AGbrCKxfvx7hcBhLliwx7UR9rlwuY3x8HNFo1OiLjBjRtUB33ADqJLMdlcC12fb+63pP3ZJjiTKE859kCMcRAOPsUH1byUrV1W25pzodxzYLojN6p62tDcViEffccw8mJibwt7/9zTzXQgDbtKOjAx0dHSaNjWkLSsSrnOU6TjnK9mA6B8/nb8pWyledz+oEZMSYTVbZ9+Kx1AVUB6QcUTturlQ5nsdxqdu86rPxeNtOVVuzGVmheiN1Y9Z4yufzmJycxB133DGvesS8EwhqPNtkgk402xvMc20lXJlu+7p2R6lxrgarGh/2MzTzGKlQsa+t72iTAfa9mnmzmpEQdtvwPBWuCw3JZBL9/f0NwlMFeLVaNblk2lbN+o7nKoPYzNvEz5mD1ew6ej27j7St7Z9m7azn6vccS7bno9k7UfjtjQgKBALo7Ow0WwUdilCPJQBTqFIFL+DfyhHwkzUkU2xDTtGMgda21fmp7W3Pv7nmuD1vbTZZiQ8ulCS0FCr/uJhq8UGSDPPNOjdDKBRCT0+PyVtV2HJU5yi/B5rvWmP3nbajzlc1/Ox+sMknHUtUJGxygjLJVlKIZt4oBb/T59RrM7x5oXmT9heqFNdq9bDOZn1I2J4dHss1y65vwTnNlAUtZmefr8QbI5XsNZ3ygiHoOi61b1UOKBlijydeg/OVhg7gz58H6sYyI6hopDTTJw4l0DCIRCKIx+Mmh5ftrV439a5x3Ks3mrCjAJo5bXT+2oq9Hqef6edKelHGqhxhqkszucF7UldhJXi7GLYaknzPyclJ7Ny589E2+4JGMDhbJHJoaMgU/mN6oufNbn+ZzWYRjUYN4aM7XbDoIQCf59mOUrP1Mo1S0zWdc9i2FfRHZZXtlKPsUSPYTsHQNcW+hz6zfqZGrco6Og50x4eZmRlkMhnfM8637CCBwJoHTFsgYc/35btrBAHJWP2e85BpCYlEwtSX4Xpjk4yEzjWOmWY6nm3L2Sl3evzebA+7v3VdANCgA9lQO4HPZdt1+tx8f3Uu6f/zpRPOG4HASahhH7Y3EGhkcvR7Kn+20bc3A1rZSlVGeC0KE3onNKSFg7eZshgMBk3eL40gLjQcbJVKBTMzM0aY0svcbGsO+/30cxVEXLxYHTafz/v2J14oUKLAFnzqneJCwhQMRlTonqkUUjZRYLeZveDQw0TFzR4ntrAol8umFgEnK49TVhPwM5L8noymXlOVRlWmlEUslUrI5XLmHcikcvyo8qvViQ817NmzB+vWrTPh+lx0COYjqveenmx6fNTrqaGL/MzuI9tQ0DGl57A/ksmkT75oCooSBc2MWTtFieD+yDqPKXMA/44eK1asMNudhkIhPPjggwtyd4ZgMGiqIetirosht0Gkd5KKIueu9iHnieaWep6/ijLHgvarvQ60trZiz549GB4eRm9vr2lL+3oKEo2cW81ytu0xoH2uRoeGcQcCAUxNTSGTyWD79u1mZ4ZDDRyX3NddU3LUYAb89WX4W+WWKpCFQgGFQsHIOM4PVqWmPKAczmazCAZnt1IEYNIMeC9NnSEJwflGg5fHa5/Zij6vrcbl5OQkPK++PV8ymTSKtCqT9IAzl7dWq5n87gcffPAJkcrQ29uL3t5eE4Wp3lbP80ytCra/Krtse35P4lTnOPtLjSZ1MqlxSXlAqMfZlkkcq/RC8jnoqeZOGtyxgZEUWkQxn89jy5YtAODzcNP7Sv1uy5Yt2LZt2xN2xwUbJNQoOznX7r77bniehyOPPNIYiSqPPc8z211yPNm2gOppGsXL+a7XImwigXOZ48n27PPa+j+hMkhJSoU+t0ZYAX75ojoKdyzieOMYWrlyJXK5HIaHh83cKZfLPkJhPpBMJo3TgI4su74EUI8Y41jQ8PxwOIz29nZfpAIjxTRtxSZwgXp6L1CvGxaLxRAMBo1dxGfgemMT2hp1Rtiyn/flGNHdtShTQqGQ0RX1OjoOVc+h3OM7MsrCXnt0xyLVSQKB2fTBY489FmNjY1i3bt28RKbMewQC0czgVSJBYTOH9iJkLyD2gFAhop/x+LkmpU56HRRcUGKxmC830mbIKOA42O132Nvz7a3dbC+belYWSrhTM+iEoiAgYWO/uwpfTnz9HPC3GxcLhba3ftbsbwoMO1dZmULAT3rZ19B3tFluvSeVak1f0Xs2M0zYBtwyiKG+C9E7PRfK5TKy2axvX2VdkO1FXueMbbDbc97uL4WyzLyO3feqbHAe2eNH76Hznphr/jaTO7wvxzcA397HvEc6nUYikfB5aRYK5kr10f5QuWnLPT2O8tz2NDSbbzq37FBnYFZxyeVySKfTxqDjfNO1Q+W7TS7qIm4/t45T9XzrseyvYrFo5upCLXS7P2CILVMBgPruC2xbHcval7aCCdRlHL1w9u4lvIa99iqU0LE/B+rEEAATYmsbs7bc0HfTv3kelV0q0BoKr89KxZneOc/zbz14KIIGA4smqlzU+aNbr6oDxnbe2P2mc07Xdp3fzcZSM12vmUziPWzdkbKW6xKP1Vx+ACaKSNN0lMwA6s6AiYmJJ3TBRIJkX7OoIpJJwWDQV52/mR5sk8+6TtuebdsoVKJQ761jyZY9zf6eyxFp2xRKYKt9YI89Hms/k62v6tpI8qVWq/nkxULQ61nzSFMLdC7a8xxorDNFmUhCQeeR3T46PprpdLyevfbY8oGf2bB1Chuqm+p6YEd9N3tf1THt9ct+r7l0Vr6jzpFkMmnkz3xg3lYwLjJqOAD+0FBtSFXoddGg16pYLKJUKiGfz5u8xEBgdgs4Ltoaiqr3U4OBHc7Jyvtrx/IYbiW3e/duk+PFxUiFFSt8t7e3mwIxSigo9J3VcCHU2wn4twPUfK329nZMT08vGA+HssStra1mz3UuNlTKJiYmUK1WTehbJpMBUC9sprUsVNnjZ/xfhbftieaYs2ELgVwuZ9qUCi1z4WyygmNLxzKVE61loOOO4FioVCqYnJw044rkBQUVw7vIaJOdfOlLX4qpqSn84Ac/wPDw8GPUY48/uA0aDanp6WnfHsoc17oQAHVGm4xtM6iM0IWN891WLgjOLba5rXSqALeNTX5neyfsCCpdSGq1mm/XGVVWGWnBrSNLpRJWrVqFJUuW4J577sHmzZsPsOUfH3CsUxFQGaipAkAjSUoFhJXM+Tmr3PPYfD4PAKZ2AVn8aDSKfD6PkZERY9Ro5BG95ZVKxVyfSipldzqd9nk+KKto8HFMUJZxftK7reQE3yeXy6FUKmHTpk2YmpoysmR8fPyQI/wUnAOajsN1k2sQvUm6pgP1fFWChIoS7/T4hsNhlEols15wDASDQXR0dPh27eAYIYljh5/r/RlVZitr7A9+p1FNwWDQhLUzsoyGZiKR8NXpYd0GXQMYrUDD81DHihUr0N/fb3YrYT9wdwlu60mjsbOz07QpI+poTLJNbGVcDXzAH5nE+ann6JpMo4SyVI0RvZe9NZ+tG2iEDeVDuVzGjh07zNas6lDQsbdt2zZs2LDhCVHvZF8IhUI45phjMDg4iFQqZWrNVKv13WcGBwd9UcC6LnNMlMtlUwuA/asefLa3FkylPOY6qmusOmNUjivpr3qCTeTze+rjavjp8+s72cSn1sPhNajjcfxlMhmzY0dLS4spCq1kNHWmhZD+xD6IxWJmO0WmW2p6HvUa6vokHChDAfj6j/OUzkQeqz8avq+2mxIZ2p/6zIDfEWETFNrHCtXn1Ams1+M99hbRwONp8/D+jHjme+hY5m+2UzabRaFQMPZus+c9GJhXClyVSDvvjb9VeddO0ElI4oCKCAkEKjBqvNoLVDN2Wg10hSqO1WoVxWLRGEBUBtWAVENPUyTUGOb72wX+5noG+3ko6MiO69YzfL/5FjSAvyilzcrye6BuhHBM2JEEtsGohgq/twWKTehoH9nXAvzMMAU8DQ81QLWvlKxoRvzYz2v/DaBhHGh4FgBTjVaLhnmeZ7xfXV1dqFQqZqvBhQq+B3/zvanE2REFzcgZ+3NltQmbSOJn+pt/22NE76MLOP/nec3Ybb1us7/V+2WP3WbMs+Z80sOzEFNXbC9iM4/PXG3FeU/vs63A2V59/ZzzTesK0LhQZYPzhnOa96ACxxxdjkM1JvXZ1UNERYAVw21FZmJiAvl8HqOjo8hkMkbpoZf6UIOGqRK2t0iVaiVxgLrnTFMX2RZKvgP1dlZvj44juzgZsT/KlObe244BoDF6yB63Nlmt36uXWmHvwDPXXDhUwOKJc5G49vpoyz3+rcfsa820I0Q4j0nq29A5ahN/nOe6feBc7wI0Om9I9Nv3YZHYYDCIbDZ72KQtAH6d3W4TkssaXaD9qg4e1RXtsUO5MtearnPT1hd0/jXra+qe1NH1GXlv2yDVa+n4tNdDRbNoKW0L/eGayDVfo+zmQ7en7cK+5P9a40ChZLwWs9ToE8Vc66z+7E1X4vPYjjtb5uj19UeP0efhb+rdfP5maRtKROi9dXyofaNzxSZD1aahrkxybq615mBhXgkE26DXztNFRwcaDfd8Po+pqSmUSiUUi0VkMhmfF4MDulKpGGGgxiZDGOk5YG6sPWiB+h613NN3amoK+XzeeJdo9MXjcbS2tqKzs9NUJY5Go0gmkz7GSvPiSX5o9ATzLe3wL8AfHqgCk2x/R0cHKpUKxsfHkclkTLXf+SYRWGxFJz0nAoUjozMoJHieCmgthKhC21ZEgEZyiEqG5lGrEccFQ9uK1ZgBmLxZm4HU8aTVvXUMKRvL5+TnFAqq1CQSCWMs8p34rHw/LsrcF/ass87C2NgYfvazny3oKs+LFy/G0qVL0dbWhmg0iomJCUxNTRmPoy6+KkA5H+jh1hB0LlC6COj8oSyxF3Rlm2mUAH5Bz/6xr8lFlIKcQt2+hxq1NKY4bjjudZGkQUrCikZwPB5HqVQy8mGhQftM56EqDtPT0w37PgPA2NiYqfsRCMzuVME5BcAY96yxwP6g95+ymQpXpVJBe3s70uk0gHq4Xzwex8TEBEZGRsy6QI8Io9goY/L5vNkil4QXn9tWFEZHR80ezcz59jwPo6OjyOVyPmKQRsyhiKGhIXR3d5t8cDv9g/9r2g29VDQkcrkcxsfHfe0IoIFEyGazZk6qB0uNRSr7hMpcPVfnOA1P3SI1mUz6KnCTAOYYZsQAtwtTQqtWq5m6Q1QubcNF9Zz5VvoeKxSLRWSzWbS1tfn0NBoIGn2iSjLnF+UBt+FNJpM+WQs0ksdcH1j34uGHH0a1WsXAwICJNOXx1BX5P8cMCUQ9rlar77Zgp0+pN1ANA1vuszbG9u3bzbp1OEQeENVqFffccw/WrVuH5z3veUgmkybai+3EdlFji7oP1zjP80yRON0Ji+C5drraXJGldEYx+odbQ3JHLJVfGv1AstfzPLN7CscC57fqmpTr6oTgcRoFqYaoOoLsfHxGuuzevRvVahVDQ0MAZmu/zCcxxdoH6XTaRInYRKqSx3R4aGQp4NellHgnUWIXzySRzPGiOjaPYfQGj6OM4Rqsu+ho5IHKHHt86hqlcoT3SqfTCIfDSKfTxkExMzODXC5nHHqsecfrK5FCOaH6H8ePyiklP7nLE+fIfGHBRCDwf8BfJHEuRpO5ZyQQlA1WFIvFpg3MqIBqterLdbOZKFupZz5toVAwyibJClZPZUXSVCpliiepEqEKj3qZ1SOjhqcSK8paqYJjh7zQ4zbfiMfjZvsRO8KiGQNMIaoCyZ7APH8uI0o/bza2+H8zb5cewwVKJ21ra6svp3MuBtVmw/U7+zg9VgkTKkS6INnst7KczK9eiMYlAFNkr6enB11dXcabyZBXz/NMoT0uCsGgv+Ca3Y8Km/ib6zP7nL1hrvGn125GOtr3oOKkBrbOYXss2DII8BsiJCYpgxYSVCHTwqh2G1EJtCNu7HbguQB8yqIqpbwm5R8VD8pM9XxxLvMYJYo9zzPVoWmw2ClwJO3GxsYMITIyMoLx8XFDIPDZM5mMKQj7RACLBHPdtmWSjmkNCS8Wi2bNZgiuKmp2OKhtwOnYt/UGJZdVMeR3tmNCx5Mt/+3Pbag+ANTXbeoBapBoVJrKBX5HA+tQS2Uhua2EOUFSVOevrX/NJfeajSWgHmrO39qW3M1irn7X9ZH3VKJK72mTSkrYq/yyi3xSN8zlcqa2yeEK6ka5XM6E5LN9aADqnLQJd8pY24gDGg05+0e/I7hGsM+q1XrxZZ1zHIMkg9ThqH3ebJ1WndaOpLafWWWb6sCe5zVU1OfalEgkUKvVjJOQY87WOw8WOMc1fYjvonPaTiXQ+ayEnOoDSsjws7kMeZ3vqlvQ8C6VSpiamjK1tjSSjbDXH10beF07YoY6B7elBeAr+Kl6hKa06A5zQD16ku+g7zNXlEUz8oGRj/OBeSUQtOIu4C+UB9SNPDY6JzK32GEEAL1yBJULevF4LX4XCMxWw96boWV7+fX5eF48HkcymURfXx+SySS6urrMHq6ah0sGlcVCyKxRkHZ1daFQKGBqasp4junFaubVtBlQDXWhtzKZTPpYuvnC8uXLcfzxx8PzPJO7SuFC759Ofs0fV4FsKyk8RhUD27hUzy8NB1UQ1dPA6ymYt0YhoOQGoyk0V1b7SY2hZte2FadarWZyZG3lit9TEdM5we8KhQJuuukm7Nq1a8F6PY466iiccsopRqBSGUyn06jVati6dSsmJiZ886elZXbfdvUYaIoS+wDwGxBAY0TTXIsRr6WwDQk1DtjmWiiN/5OYtI1e9aTZz6+/7XMoAygrgdmxtWjRIsRiMWzatAljY2OPVRc9KthRHtyCKZVKmUW8WfpApVJBOp1GT0+PkXeAv5CibYDRszA5OYlgMGjGColT5lUXi0WEQiETyTMzM7vPezabRSqVQltbG7LZrK/uCOcPyY9MJoNEIoHBwUEAs+Nsw4YNuOmmm3xjgorfXMrsEwHqMSORr99x/WF/tLa2olgsYvPmzWbNjsVi6OjoQCwWM0VCW1tbkcvlUCwWjSzltex6BGpE8p61Ws14ZZgTahOJlOMk4NQDqe/CY4D6OkSvFsdwqVRCMDi7AwQJKSrWnldPK2ttbTX532qEhMNhHHXUUSiVSrjzzjsXTK2i/cHq1auxatUq7NixA5OTkyaKk95F6jkk4uhVJlHMegT0oKXTaZ9hpwo7PdCUp6OjoyiXy2ZOr1y5EgAwNTVlvI7UK3hNzk0duxxPjH5saWnB5OQkxsfHkU6nzVqsKZC8zuTkJKanp03hyLGxMUxOTmLLli1PiMiSRwN67h944AFs3rzZRPbYRremrHFt5xjifLPz/Dkv+bkdHUTofRiNW6lUTBSB5uerXhAIBExaJT3rvI5NflO3p3HMtVl36uA1OS6JZhFJ6lzjfUOhEOLxOE444QRzLtencDiM+++//7HoskcM2jKU2/aPEgSaqk0SibIxlUoZxxfbjNcnVP5qRArlB1A36jnfi8UiNm7ciImJCTz44IPGtmIUIp283O2Du4Hw+ow2J/HE52X/79y5E9lsFmNjY2bNUd2fkTSDg4PGPoxGo6aWFXcaYlSlPRYJtV04LzRdgohGo7jrrrse935vhnklEJTJtxWtudhGfqdGKH9sFt8WPjabaedPkqDgb/tcKvlcXBjC09PTg0QiYYQlQ2KbCU19Z0WxWDSEBxc4u2CgGrs2y2p7b6hMt7W1mbDR+QAXcy7W2o9si7mU7LmMQY0UUW8uv5/Lm8S20cm3N+aumRFPBVUXACqN9rPrPXSxmOu+djSOfYw+u3rmp6enEY1G0dfXBwDYsWPHgiQRdKHl//p3LBYDUK+QTgOiWd/y/2YeCmX17e9s2GNkb98383Q0iwrZ1/VsY9ieu3pNfSfNDaUnOJVKIRAIGG/PQoLdV7aiRBk+V4FUe67yHAC+vFBeR4kijUjgNdRbyjFG+aRhhCzqqUoRDdpqtYpcLofdu3cf0rsoPFLofATqfcc1jeud7YXi/KWyF4/HjbGghqHKPVsBbUa2AvUILC1iqbUS6PGxvdC2XND5Z5N6tieS407XFI1KUALMJjw0BBeoh8AyXWd8fPyQiERgFBnDgrUfOWdV32Ibq7Ngb+s+wf4mKQA0kjs654G6nGGal2348XrNHEsaharjSGXY9PQ0stmsifwqFAomfXYhFLabTwSDs1uZMzWRaxSNSqBuFHFLP9Wr2dbsd+0Hnst5pASCvS7bOjf/Zr8z9bNZX1He28+t4FrDsUibQN9Rn6uZbqjrvM4bylIAvjVM9RdGPx9skOhJJpOIxWKGYLPTM+wfJVl0vQf881nJOqC+TaOuJTbBaJM7TGVkbTwSCjreqCdFIhFMT08jHA6jUCiYZ+M6QpuFY5n3mJyc9BUw1PQDthOJh5mZGUOS21vMEtpGdtsRunbZMjYej6Ozs9PIooOJeSUQ2Mm62KjnDWjc312ZQu5uQEWmWQoDz1PDi+w1JwSvOz09jUwmYzwMfAYNQQmHwxgcHER3dzf6+vrQ3t6OeDzuC+dTZky9aPy+WCz6FB9VPjj4Q6GQMagA+Jh0VYpsMoLMJ6MQVq5cifHxcTz88MPzsrhp/2mOFxd4fqd5rWoYak4Zv9PQHyUYuPjzc05KXUT02uqN0La0w5rUW0olgnU42tvbzTjUcUYlk9fQAjgKfSYqmCo4+PyqYPP5GNrG7f7OP/98jIyM4Etf+tKC3DKKYZ6qUGoNgcWLFzconp7nGY8iybVm0RwkVOYyDghVTHQe2YaqnXur49AmpFQJ4jk8z46M0XupIaSGCBVmDf2l7OEYYQGzNWvWwPM83HnnnfO+A4e+H40tErv8AeCbKzoHOSaAurGvNRCAeljn6OgogsEguru7GxTOarWKiYkJJJNJtLe3m+iCsbExZDIZBINB9Pb2mgJwPT09Rv5PT09jZGTEVMNmpEMwGMT27duRzWaxefPmw85YSKfTxlsD1HdA4Ryyw1kB+OZ4rVZDMpnE4sWLfUQ9FTV6oTgmVKnSmgNAY02R8fFx8zlQJ1cTiYTZEcHeeYNrus5pjjeOTXoAAZg8VkYKcG3WcGN7DVGjVddunsP900866STk83n813/91yERidDT04PVq1cjFAqZ+aXhwexDDflmJBlzg1VfozzUyBbKOyr/jGih4cL1kruy2GTV1NSUiYZQg4TRq8Vi0aRW0qsZj8eNh5vRh9wFhDpHpVLBpk2bDGFQLBZNzYPDSR40QyAQwJo1a7B06dKG7zgfSqUSKpUKJiYm0Nraiu7u7oa1lvOdP6r3q07N/lYdW9d7rkda12JmZsbIA8ocyiDVzSjPtDYK5YFNFAQCAePZTqfTvshqtQWakVyMwtH0Zl4/k8n4UqUikQjy+Tw2bNiAqampfRJwjzWSySSWLFmCdDqN3t7epoa9ErDq7GhtbTVtw37jmq7ymHOUfa+ENUln1fMJevRZm44ki5JNtVrNGNhjY2M+/UvHju1s5v3t76iXci2jM4P24+TkJNrb21GtVpFMJtHd3e0bM9pe1DX0fXRcchxxjdLx0tHRgRNOOAE7duzAX//614MqhxZEDQSgPsE4oZVtIdQrpQKfnRAOh42HwM5vosLD8DoSB1o4icfS4NPcWYa38H+tds+QIhu6FZ0KPioRJCmUDJgrBI5CxWbf+Mx2xIOd9zVfYB/zOZR1BfzhSvb/2vfN2F2gMTqEwoXjR5lqe2KpN4RQEsBmArXvKPwYIk2PJgWc3UdzTWrbo0ZFZW/PYLcPhS8jTo488kh0dHRg06ZNC8qjxQVVvXsKFdrNFAFtE37O65JgIDRCRI+xFwq7AJstB3ThV9jeBb1mM0+79qkdgcDfmjNo97l6UOh9IKM/1zMebPDZ9T1UbtkFUYHG8E2VhTo3SN7Z767hjIxiIdlj52IDMB6FSCRivEyU01Rw6Lmg14LPqSTv4WYssMCtHbWnfWnPL5W/7e3tvjVSFUBd85uRcITqBPzczqm2iUbKa5UfaqjYyiLHHfuec5H9zs+1Ng3P0+e0jRlbFvB5AoGACYdeunSpSaehkbUQQ+K1TZuts3YqGeUy9TLNDQbmXuOULCcoU9hP9lgD6sXWOBaoo1H/oxyiHLDDo9nXmUzGl19MwoIeSJIgjjyAicYNBGYLg9M7zfGrBK/necZjPxc5wDZVHccm/4HGdF7Ar6cB9bWH8isQCJgt8zRqSCNkbV1Do1P0uZo5KfQ9+L8+lzoz7TVRx5Gm3vJ687nWcz6RCNWISL4PnbJa/FJT0eaKGgH8u7Wog0HT2GydS9cDpjBoYXu9BseDzlcSULyWPoeOy2YElT1GlUDldSjvNOrJ7kOVofyfv20ZqH/znemYm5eolIN+RwELVFE5tBccNrTmwbOzYrEYEomE8S7x/JGREbNLgob0svCPRi3wmmQDgXrFVgoc7jWtIa+Tk5MYHh7Gnj17AAC9vb1IJBKmyij3RE0kEoaNpPJbKpWQzWZNKBzQWJGff9sGtJIRmuoA+Fl8sqwkOeazajvbksWFVNgA8HlZucBz4WF7NFNKNZ9VFRAlGngsBYgWp9RrcZxQmNvFXVS4awQIPROlUgltbW3Go9FMGaJRo8JFFxqbDLAVc0LbQ73nfO5UKoWXvOQl2LVrF770pS8tKI8WQz6pBLJv2Od2pJEqEnw/JYmUINN6BAAMUQj4Fz7ei31s78zBftIFC/BvwcZrEqp0sF/Uk6L9Q4VHmWueq/ltlElKcrGacCaTQUtLi4lA4TPPN2iMU07qtmgcm5yj7DstqAfAlyuu5B69loy+oKwlaVwqlUwon+akK9hnbW1tRkZrSOTSpUvheR6OPPJIFItFkz+pu/scrmCNH1sBtLel5BjmXKEBtnTpUl+kgW0A6LlKeqtsVznMsaPGPMcVPU/Mqec4bBZVpGQmDQvPm90BQj2gLNjMNUwJBMoXJUeBetSQKtn6bpQD1B2e/exno1wuY+fOnRgdHcWf//znBTnuCoUCJiYmjKLOH5JLLCLKPqOsY5szakDDgtluavgBdc8r249/Ux4QvL7mt3P8sZhaKpVCKpUyUQdKdJJ8bGlpwdTUlMmb9rzZGlUtLS1mt6/t27ebQomHO3FALFmyBIODg6hUKti+fTv6+voMmQvUCYB8Po9QKISenh7fXOE8sm0B6giBQMBH3HJM8dqqF1AW5fN5tLS0mChh1ishEVgoFMzfSjYqMcQ1QuWa6qVc72xDt5njhnqKEoe6qwvlFtuDNVoymYzvnvToH2yUy2VMTEygpaUFpVLJVyeE8zQWi6G7uxttbW1mXtk6t02sqJ5NPYjX09RGHqu6lu1cyWazhvhTx67neT4dU/uB927m+OF6ZEc78Bz9bae9895ckzgeudaoA43jzrZn2M/259SNWJPl4YcfRi6XO+jyaN4jEAB/uJ+tpNuGoy7qaljwuEQiYQYLoxGUmaZSoUoHlYyZmRlfnl4gEDCKAwsAhkIhlEolkzvDwa3GnC5KXBR5b4b7Af7ceb4fn8dm52yop93+jG2kXv+DjVQqhZ6eHrS3t5u0img02sAe0yi0lSo1BhU2+2h7ruxw12ZeDTXW9Vwep+G1AIxyZOdqA/B5qtjmXGx0bKo3VKF9ps+gjKfNTvN7JVOU3Fio0AXaJnrYrioL+N6cD+pF0v5kaowNHT9qJPB/Gvs8Vtua/WqnnmhYrj6/TXaqQsP72V4Nkhg8Xo0xyhJ9LioPutXpvuTEwcL09DQ2bNiAzs5OrFixAqFQyOx0oOSZymqbJAIa65To957nGaWFRB3birn1HCu6OGezWYyMjKBarfqIYDufUhWCQCCA7u5uZDIZszBTmW1vbzes/+ECNQa5/qqMspU89hfbViNKmnlbdA1QBZHjR5VN/q2hnCTo9Xsa8Epk2X1NmakyW0k+puGQfKZRNDY2ZuZsIpFAV1dXA5nHNuFawh9VAsvlMh5++GEAwODgoJE587k1176wa9cu3HvvvYZA4JyyvWQaCUCZb48D26unijflhx2ySznItgTqOzXQeONY4Jzt7+9vWqQYqMtwrV9B/bFWqxmyYPfu3cjlcg2OCAeYlBE60+iMAWCcNJ7nmUgPoLGAIfvNjmJT/UdrV9hjh58DfuLJ1p/UU86/tfYZw8Q5Zpt5zfk5bQDOAdokOrZVJ+WapSkVeg+7Pdhm+h2Ldy5ZsgT5fP6gpS6S5GB6D3VirseJRMKQcGyvZpET9m+u1TZZrONHixoqcci2ZD0C/qYcZZqi7vSluobKe8BPRhG2jaBplwq+NwmnRCJhnIoca2wT+/q2HWs7peyoVF1DPM8zhXoPNuaVQFBFgA3bjEXmsbb3FWjcUoRKpm6RxMFHT1UwGDSFLRiZ0NPTYxZ0GvuTk5PYvXu37zxO4EgkgkQigUQiYYxH+3loEJH1nJqaMpMgEJgtfqGhUzwfqIf72QOKx8wV/q1Mv517fDDR39+PE088EZ43u4UXDR87NJhtxXZnNADbk5NS2V+CY4ULjZJLGp2gY0dBAscWKlzsNArCrszLscZtyVhNmIsnWWIKVAoAVTxs41dJFN5DFWkl0Oz5YudLLUTPFZ9V31eViVQq5ctX1IgDehTIUPN6VCZtzxUA3+Ks4XYqiOkRpcLDmgyZTMYsBHxW3oOfK8kE1HOvbQLQJnz4vmp0UeFhpXqmaNlkEhelyclJY8AuBGU2n8/j97//PXp7e7Fs2TJ43uyuKxyrVNio1Nmkn038aagpx3UgEDChsrFYDNPT0xgdHUVrays6Ozt9Ra9Upo6MjODee+/F0NAQ+vv7G0gEJXFVfi9duhQTExPYtm2bGVvhcBhDQ0OYmpo67AgErrvqgeEcZdtr6DgAX3SgyjHbW0PvEEOLda5yzVRDgB5jytRyuWzyW3U3AOoCVNZto4OFizmvk8mkkRWMmAgE6vm6HR0dmJqawkMPPWTeYdGiRejr6zPeTIKkse3d1OtXKhXceuutKJfLeN7znoe2tjZjZDUjnBcC7r33Xtx///3o7Ow0dZYSiYT5njJTI6jUUFOPK0ke6jQ0TJjDnEgkfNtsq5JN8pz35HpMpw91oe7ubqxZs8as7dSJeD5lBne+AmBqH3jerAe4XC7jb3/722E15x8Jtm7dip07d2LJkiVYsmSJaX/qX4y27erqaog6pVwolUrIZDK+SGEWoqPcYURTIBBoiDJUQ0z1B+qGGtmsxq+SWiSN7FQKOzpA62bwt22XAPWaPaVSyaw5NHS5xTx3/eB5HOOMfKOcA2COT6fTWLp0KXbs2IGxsbGDou9RvjEqm3puW1sbUqmUKa6okSCqs9vGsG0U6/9qIM/MzJjIS7YbdQbqB7Qf1PnCSEVGIClBROjfLS0tvh1DVL9Tg1/HHH/r2OMOP93d3YjFYmhvb28Yh2rD8W+dF1qzhzKxGdlKzFcR7XklEAD/7gS25xGoG2qqJFOBUKNRmWMWpKjVZreIa+aNpkAge8X/aXzZQkMVTubRkXXjZKIXTHPr1IjVSq0qaNTzYr+PQgeQbUzzHkC9oAiNkflgprjY0yhgP3OS2Qa+zTra3gydOGwfCnKbjaYgsplP9Yzo57a3TAUeJ7EaO/xtM+RUoJm2wbFIYsGOXrDZcbutuAhr2Ku+B59Vwzd5nhYBXShgHjWfV8P+1BhRTzBQN5C5OKmwBhqjB5T11++VwLGZbvvzSCQCAD6hzEWJz9oszLpWq5nw3nQ6beQAAFO1nKRXOp02iy2fo1QqYefOnWhra/OF8Gmqhi6oJK/mI//NBscwiQO2L8chF0577lPG6wJPRY5FbZlyQCWSSiIVN1X62J7crjGZTOIpT3kKUqmU2X5VCR2NGgHqaw7lS3t7uyE+S6USxsfHD7u93rm9MAkcyj2OS/6t3txm0LWe8pOgkc3xoYoixwaP04gD9r2Se7ZsVh1AfyifbVB+qycVqG/tqcjlcnj44YeRSqVMCg29mKqMDg8PI5vN+mRYIBDA4OCgiZSgfpFOp3HUUUcZGZPJZLB169YFQRYCs31Ag5tkK5+fHkCuY7lczlS2V2Ke/UTomqbyGahv50gZyn6zdSbqchwLnZ2dSKVS5ro2satRIVq7QeXSQor0WsjQ9qUuzVQTOlJ0rbcNRRrw1BvtH3Ue2P0UDAabGlCUN0pSaxSUOps47kh8qA7BYqqEnd/fTH/V8as6CrepZkSy5usricH78Dw+F8k6jU44mMhkMnj44YfR2dmJ7u5u077c4YJkskb4qQxVw1t/2+SLyhBtK10TbHDOagoqHUTUzZXUtaE2qOrjhG2f2CQCdQ8dGzxeSdK5nFr29XltEiMsLs3f1WoVe/bsmbd1Yd4jENg4HISqpKtRbIe404DQrblolLDjaLDQwKcyzrDBQqGA8fFxFItF7N692+et57EUWPQoc6En60jWjZXw7b2tddAwKoLCAICJjtBFkIo20LgFoBoq2j4Er8P9RicmJuZlcFH51kWZFWfVo6BkiQryZvlthCqLVCL4Y+cVcbxwXNHTpQqlLkSAv/YGBZKyqgzhUvacz5PL5XzsNw1IRia0tbX5jEZ7j2SgrkjncjlTL0PDNTn+7Jx6HscqtAtF2SRaW1sNIzw9PW2UQo3sCATqBU81rBCYzV3XsU9FQ8cK21IVBqBuEHCuqbEINNZdicViqFarKBQK5pmo3PM5OX45Pvkse/bswfj4OFatWmUYaZID9I61tLQYJl8V5kKhgIcffhh9fX3o6ekx8oxtxoV0YmIC4+PjmJqaMl63hYBqtWr2ZOdYB/zRJzSuOHcZ9QHU5SGVhZ07d6JareLpT3862trakMvljJLZ0jK70wyVLsCfn1goFLBjxw6sWLECT3va04y3mUXQOI50Uee5/K61tRU9PT0oFouYmppCuVzGrl27FmSEz+OJ4eFhDA8P46ijjkIqlTKyh8XkKO8o62ncU2HjdzbppkYa1z4qXcxlpbxTj1a1WsXk5KQvd5QV0jlXeR/bANQ+5xpdLBZ9kY/0CPJ7lRc2gTA5OYnJyUkcccQRWLFihdldivKNBsHOnTuxZcsW37nRaBTPe97zTFVzoL6PeG9vr3neTZs2mWr/CwX0BnIXjK6uLhNFBdSLiE1OThrPKdcpbUfbgcB31JowdNrs2bMH+XweAwMDPhKXSrUWoUylUhgaGjLyRdcD6gGUSRqtqXndQN0b6LBvqK5XqVQwOTkJz/OwbNky49SzI0mUPObaqPow/+b6q9GAnueZNZlruI4rGl1KXCmpQEcgxxmjZOh0U91D5z3fgykxtlPM1t+VSKc827lzJzKZDJLJpJE3wGwkzMzMjJFnGqEdCARMZf9isejTiw8WxsbGMDY2hkWLFhkisVAoIJVKIR6Pm6ghtb34/krcqN6uESIE9ThGglFGN1t7mzmdSPIAMM4HygybIAQa62ro5+pgtG0yQskHTWvR96FNqQ5We53ksTo/GCU3MTFh5tX09DQKhYKxOeYD80og2OH7hHqGbG+Vdj4VvGYsjhp8NKpUSRkfHzceeio7AHwCIRqNmkJlZLEYFsOiUolEwggPjUbgZ4Qak4FAwGewqEAD6kYNB7F6l/VYHeD8jGFG9JjNF0qlEoaHhxGLxUwodq1WM+ykMs/K8qlhT7Dt2J806GzYglpZRrZhs3xavRfQuOMDn9MOkbefXwUAv6chwty+TCbjG6MUcna4nRII+iz0vNFLrkwpz2P450LzmrANKURpBFLh1/BnKvk05tX7oNdTQUyGmcqpVsjWsGEaKRr1oPIFqJMRmh7BviQY6cN5yXYfGxtDoVDAzp07MTk5acYEZRDfm8aEzu1MJmO2k92yZYuRQUqQRaNRtLe3G1nDAqXzEWlko1gs4v7770d3dzeOPfbYhgWR7UqSizmCVN4590ZGRpDNZo1xMj4+jmq1vl0giTe7kB5lYKFQgOd56OnpMTmjthdayUUaoUDznWE4hxdCG88nOEcoazVlhPMuFAoZI9KWpRptws+VQOcc5Y8aC4VCAdPT02Yt0JQAlcUqU23ZrpE8lC2UQRpRQe86lXg+t667c7UPZRdQJ/3tMRUMBjE4OGiKjVUqFV/khK4lC5msqtVmI66YesIUkEAgYIwiRt8Bs+/NLTBVH+N8pjGSSCRM2wB1Q45EPPuI/cv1XcmMRCLRoOg30z3o1OH6wzlOMnPPnj2m4J7D3PA8D+vXr8f4+Dh6enoQiUQM6U95y/4gqaZ6Uyg0uy2oRupynmqqp034qrcZaMwPt73IqiPSu20b4urcUf2B40ffWXUyjVyiTmbrDXy+yclJ7NixwzgSKFt0O0Cu+ar/UMfPZDLzGglXKpUwMTEBAEanAWD0q+npaUSjUUO+qJGvY4J1RXRLVsC/dpD8VyOdx6hdyH6nPqkR5CSLdJcevZaOEXXY6Wc8vpndwDZgiqXagbY9U61WTSpLoVAwx9qOVa6DJOrZDozOo0PqsCUQNOwR8BdJAvyF9rTTNI/GXpwJZR+ZI8KaCPTsFgoFYxyEQiETnkmvcWdnp2FTSSD09fWho6PD7IvN57ejHfgMVFKj0ai5DwkETZmgMmQzncqQk520K9LSkGFO93zVPiCKxSL27Nlj2or9SsOxGWkA1ItR8hiGtKohR0HFNuOYoIC3x5J6KYD6PvQaBqUTXIUSv1MyQoUfQaHExY/CXz1mHAf6o2kxNA6VQMjlcuYYm/DQonH6M99CZS5QyWNRGVUElAjh3OBcZAEaNUIpTLmw8tqco+Vy2cwzGjxclEksaNgt21eLPfHaJAdsJUMjCkgcMNSbimgwWA+tpFzp6OgAMOvVZT+zxgMwO44ZJphMJk1tCJKX3G2A+dLxeBzDw8MLIj+3UCjgb3/7G5YsWYJjjz3Wx7JrH+ZyOezatQs9PT2mn2ZmZowBOjU1heHhYd++zZ7nobe317QFlQ/Kao6dYrGIsbExJBIJ9PT0mO8Af3oS5a4SG4C/+J0afwt1Xh1M6DoFNKYZaaivRo6RFFSyTxVsnSNcu3RtBGCiTwiub7YBwXlLb6XKeY1YAmC2HKM8IEnB/GPKZhoEdg6tQtcS25veTIlcvHgxuru7EQwGjRFjrw37Q1rMNxgJxZQselg18lIjTpjXTo8iU55aWlowOTmJ0dFRLF68GD09PeYeNB7a2toAzEZ9lMtlH4leLpcxNjaGaDSK1atXm8gvjjM1VNX7SNKKjiS2N+f79u3bF4RsXeio1WpYt24dWlpa8IxnPAO9vb1IpVI+o5v9Qf2VcoEGZmdnp4/Q12Ll7BebvLQNQL0Xfzcz4IHGWmNqxOk4sR2WfD6tmaZzXMlIva/ef3JyEtu3b8fq1asRDofNGCeZyXodGgWtjgruFjJf61GlUsH4+LhPj7KdbtT3uKbazt5qtYpsNotisYiJiQkjI2w5yHnJ/3kN1atVP2f7A7PjUqNUSNhSH1RPv/aXrl+ETXqpTkriKBqN+gonanvwWJIHIyMjGBsbM3oPf3NNIznLqE62I+0LTYGZD8wrgRCNRk0hQfXwajiQehiB+jaL/F+9FZx8tleRA1mPozBoa2vzeQWTySQikQiSySQ6OjowMDBgOlQHiKYycFBR4NgKDdBY60GNX+4Awf9VeDFnl+cwlJnKFVl+MlNTU1MmlK9QKBgF/GAjm81iy5YtCAZn9wDXdyZjW61WTZ44hSUAowxoG7Gd6S3QbfV4nG4hp4sE251Gugp5Ciw18tVrpONSjSBbWDXzYvN7XbxUkCpTTk8qBRt/qAQBMKGxGm2g7CTfld7dheYxUcZaiyOxf0iC2cw7UCcf2Cac0yyEqkx/My8nw9ZJ8mnUhxqT+kN54HkeYrFYA4nEvF5+3tXV1bBlqufNFpCqVqtm60EWRaLwLxaLyGaz2LZtG1pbW9Hd3W3Yct6DRjNTqciwkwC12fD5BscnF3adB2zPnp4e47HM5XKYnJw0c2tyctJsjxqLxdDX12dymdUDTvlHb6TObxLFHCNKCPA4m9igrOF3lFXZbBa7d+82BO3hitHRURQKBQwMDCCZTPrWKm0zKr2cq6rg2aA8161+1cPEfonH44hEIkb2M0VOi6tSp9A8XJUxjCxUeTE9PY2JiQkjR9Xop+zX7RjnmmsjIyO444470N3djf7+fuzatQsjIyNGFlH2EaqbMD1J20RJTRJoCxWe52HPnj2YnJw0inB/f79PXum6pQY9CdM9e/YgFothcHAQyWTSJ9e4vrHNdNttoJ761tXVhVgsZrZe5JznvVRvIEgEkzCynTYLud0XImq1GjZt2oTh4WGk02mfg4+GHHU2pixwzjK6SPubep2ue+rV5xzltRk9RP2hWboE1281vvQYWy/gGs5xpNvBq5NTCVNG2xSLReMMYk2ycrmMkZERtLS0YPPmzZicnDTXoHOToCFKJyqdINlsdl627lOoTKSXn6RsR0eHqQmnu9tRRyJJTKco+8kmEGxdWYkbvrs6jpQ05vrOYvmRSMQ4l9TLr/Od96Ls4ljU9PZAIGAcXExZTyaTvjRlfV6VIRrdok5HjdCgDOL9Ozs7jWOLdigd3sViETt27MDk5CR27tx5UMfDvBEIwWDQbP9Br5+ygCr09YcDgh5IMsc0oDlQ2MmaR61eYXZWIpEwg42EArdl6unpwdKlS01eDxdGrdqsLJgKJ6AurGxvCz+jQNL8bII1FOj9ILTqKACjxOm+pxSgzcJwDhby+Tzy+TzS6bQhC0iAlMtlI0gDgdmiMDSEgHoetUZYsN1UCeR3DINkW9lsnubKKUuqgo+Ggk4+Xaxs8L7KgtveDtuzyb7m+YTtkaOA4PGqaFLY1mo1k5M9NjZmiIdqtZ4bvNBAYovbEOpiwDGtealA3ZNfrVaNoZBMJgHMjhMWHFOlkIJW05t2796NsbExLF++HB0dHQ2Lk85NJa60EI7Ou0AgYJQdNVT0vTjHR0dHMT09jb6+PuMxY39SiRofH8fIyAiSySQWLVpkirLqYsaxANSjZKLRqEmPWWhQw009RkA9eoZ9RDae/ZDNZlGpVNDZ2Yl0Oo2Ojg4kk0mjyLHvSERREdWiRTTMSDARVCo1MkXnql4DgPEWjI6OLsh5dTAxPj6OyclJtLW1GcVQiRsqWwzDjUQiPvJfU/cUXP+y2axRQHldQkk8zjuuKeqFZNqBrvXBYNAQjjQc+Kwk3mn8ck3id2qEAv4izwrWQlizZg0GBgYwMjKCBx54YK/tSd3E8+q7lmioLAmEiYmJBW3I1mo1jI6Omv+p01CXUgKB/WdHJO3YsQMrV65Eb2+v0fFsQ44kM8+zCd10Oo14PI5UKmU8fWpkRKNRE1EK1NeXXC5ndAf2uR294rB/qNVq2L59O0KhkKnjQ/JfCyEz+i4SiSCVSpmdzajP8VokDZPJpNnJi+Q0UC90TIJ5cnLS50yMx+NG5gP1yDINubf1ZK4HPJ4pgnwuktdco+1aKTMzs1vCsyYI663t2bMHExMTmJqaMinNO3bswI4dOwyZTicgCYVm6bq1Ws2nM88XbLnIaMBYLGbWCOrd1Fup5/H5OUfVoWcTCWxbym2mcfAY6lW0JTWSiOQzHRcaacSxpjvoUFfhs3MdoZwmocV0Ku620NnZaQx8ktJKVGt0BtchkgC2/cBnpH6k62pLSwtSqRRisZjZajoajWLHjh3YtWvXQe3/eSMQ6GXSkCB2nO21VcMAqOegkGjQ/CFlBQkKG/UyMWeWHsGenh6TW8zUhba2NrM9mBojAHyGKJ+t2UKjxAKfW73lNPqZlsBjbdaV12K4Je9FD3U8Hjch3fSkBAIBU3RjvnKldu3ahUqlgsWLF2NoaMgYx/QI6jZNShS0tbU1ePN1AjKci8KfCwJ/NMzJJnY0RFGvzTZje+s1bc+2GovKTAONrCwA34LoeZ4vZFdZ5Uwm42NDOT60dgSfjWSZFpOiMjTfC0sz8H1YZHBwcNDML6CumKvSp2NC+x+AEbCM4CGzrCGIxIoVKzA0NGRYYi7OmrJAg1ajRLTIqS5M9DCoB5bPqx5wHkcPJgBf4VfO6Xg8jr6+PsTjcbPtj8osXo/nkDBU5n6hoZlMpBG5c+dOo2QGg0FMTEwgl8v5KrnPzMxg0aJF6O3tNV7jqakpBAKzhaRCoZBPGQDqufjxeBz5fB4TExM+o1AXa8pjLvK2Isl1o7e311x3Ic6r+QDnMseptovnzUbdBAIB442hMcz5wRQUTcljyo+mmimxox4jrqHsVw1X1bQ3Hqvr8FyEMO/JflbymNcnGd7d3W2KffL9kskk0uk02trakMlk0NbWhtWrV2NkZMSkNgWDQSxZsgTpdNqEd1N2kFjl81Du6Dqy0BEMBk2RTUbBcbs6GkgAGvqBxgW3z2ZtFB7LccB6JjyX5D8LbnJnmh07diAWiyGdThvigdfRdYRjNBqNmv5mnzIa9VBp+4WCYDCI/v5+xONxU8dC21TXZxJNGjGknmPKaNUVleChLkXjMBCo197g+Vpfyh53dlShvoPOu1QqZQxOOwJBz7F3iaBjh+0Qj8exZMkSk5pBfb1cLmN8fBzlchkrVqxAKBTCxo0bfalNlLG8B8f+fIEOIcphpiNNT0+bCCL2L50EJA5UltNeYdvqmIhEIiayBPDbgKz/xKKpdOjpHGfkMnUlpiVxdxAlNHldYFbe03GlY83zPBPtyPRi2rEaFcCC4TYRxXGhBcSBul1AOUh5xDHJtZY19ziP+O62vnuwMK+SMZ/PG6+xepUVzRZ7ChUOTLvqKlAXBuplsr3FPDcSiaC3t9fkFjMEjgXMdBAo28bBx7+bKfFKHOhza3gVDRXdg7ZZKgahRIhOXrZfOBw2VTqZkzpfBAK9MqlUCsuWLfMZU2ok2YOf/8+Vb9rS0tLgedSFSYWrehJVKeRkpXBgm2o4kYa6a9gTvW12CBzvZRuxZC85ZlTx1HA+KkCaW8/tQdvb201/kgQDYEglAE0LAi0kMOdtZmbG7AnNtuK4YD8pONaB+v7iQL0qOsmDlpYW304JlAn0FNhkHu9FY4XjRr0kVFJ0IafXX1OYeE9dhDRKhWNDQ3g53uiFicfjpo/VE2kTKQy7pfzhcfMZzqhQDx7gJ33Izm/atMm8PwkDpjSx3Ts7O9HX12c8g9wVg/2tRQ11bsZiMZPKQy8XiRqV4dqulANqsFL5YzEwh1nQ6Of6o+TA9PS0yRmnbNa6PpxnjBpkSK96FTlvlDRV8o7X5hyll1PlOeX1IwHXESV4dRxzjW5ra/MVe2XIbn9/v1GKo9Eo+vv7TSohx1N3dzd6enoaCkAzwojtqTrFoWLEUsltbW31bX3K9domEOjA4byjEcK5ymPVScDjgHrNjFKpZHaFmJmZwfj4OFKpFNrb2wHAN2Z4TYI5y8Vi0ch5GqK8n8P+IxAIIJ1OG30lGAyaIoPpdNrnWe/s7DR9q8a9kvqM+GVhOo0cojxgNKJGD/Faqu/z2ko6K5RopAwB6sa6EqDq7FRngq4llGk0Ku30KpLn+XzeROX29fUhGo1iy5YtPmJWDUrOhflc7znvCoWCaR+uCcBsW2qo/tTUlDHiqbcw5Za6NOcdHUNKotpOYMp81k/gzitcb2xdTAkEEsHq8AHq8p7vRzmsRJP2CYkRoJ7iTH1Ba8GwPfibz0+CkoQ1xzKfw7Zp2TYc63r8fOgn87oqMYWBncwOU4OtmaeISqh67IHGsEigLkRIVLDhNYQ2HA6jo6MD8Xgc3d3dJpRKF4+5vKBq3OtCox7LZp/RICKJoCE3XEybXc+GzahzMWbYbldXF4LBoFFg5gsUqqoAMO1ADR++i+3R4vlc4LVAFttKhZDC7jtOYIYn8d6q0OkY07AoTl4qRlwIOLZU2aQ3TMHwOo5vLgrMH1P2leFWFEi6lSgXZU19YI7wQlV4kskkhoaGzEIQiUQwNTWFtrY2RCIRE8KrCwTgZ2c1+qNWq/mIJ747yR2VFyTkKGN0LikByL6jIqA7OeiCpDuLcNxpHRY1XrgIUpFWmcZ7RaNRs5WbesL5vgB878WFm+N6yZIl6OjowNatW82CNp8YGxvDb37zG6MIdHV1YcWKFYhGo0ilUjjyyCNNqHIgEMDU1JQxOtnejC4gy16r1Yznhwsv570SCWyzSCSCzs5ODAwMYHBwEAB8803DodnflKEkKVRWO8yiVquZXTLWrFnjCwulckzChRFythKlijXnlF25nP1oh/ZzzeM4J2HIcUHvfTabNXJDCQDVGzj+KIM4P1mPgPVIKCO4DS3TBDW9SQuBccy0trZiYGAAHR0d2L59uyFPVelT4lnHPd9969atC772Br3OjN5krQGgTqZTPmuKEN9TCT5dv+xaSVoUl21VrVZ9ecS1Ws1sbcZCs6zFQQISgBkHJB20rlQkEjFFOxdyuy9EcN4nk0kzfzjftSCykmeA37usacz6txr9nF/Un20DU5+H19Q1Wwk6XcfVY62yA6jnv1M2qX0A+Akq2y6hgUj9jtegQbt8+XKEQiETgXj00UejUqmYFM2xsTGEQiETETcxMYHR0dF5q4NAwoDyuVwuIxwOo1KpmEhKjgMa9dRz+bzUW9UZq3afRqDomkBwDZmLLKaMYU24kZERX1SaPodtN+j/9n15bxLYQH1Ny2azZo3kLhRqzzFalvJOo1NV7yV5RruHhJZGddjO5YONeSUQbM+Edqoa6M06kpOxmWGoYMfYdRVY08DOr2Jeixav0wGsHj99Pttoo5FsM5r2MTxXjRolBOx7azvob4JeURqaZNYXApR5o/LebPA3eze+P3PDlKED4BPqNsnDRcFeYKjU8juypUA9hEkVUC2oRXJAIyjskDLtd/YxjRLNhQfq4XYqZJnjpR5QLsIamsVzVZGmsbyQwG2d+I4sHEZjnMKShiHbDWisg6EGhb1483jKCVtG2N4HW4FRaN0UHse+ZvuqZ5QElp7De/I7yiKdzwxv1OPYBhpFxe+p8BIkmA52DtxcKJVK2LRpE8LhsKlZsWjRIhOSSO8TMNv+Y2NjyGQyyOfzqFQqhozTMHGgXjVfvVia00zQuGM+dGdnp6lerR4vDYVXb5N6OW0y1wFm+2PPm03BUQWHskjHOmFHKzD9UNdnjm/Kba2JovoA55+SEDpHdO7pOqpyUaOf2O8qH2iAMrKLNR2YNqaeSRoDGn1GcqKtrQ3j4+PGsFXyW0E5yGcoFouHRO0NvidTM+zUP84hrnF2NBdQ37tdvY3sf44Vto06DXTNAGC2uAuFQigWi4YQoDzhGFJimkSBrs30jKqO5rB/oEOFaSA633XM6/qsOr+dGmBDiQfAv3bb3moerwU0GbmiMkd1BPUG27qCks0cE82MS5VZhK3nqyzgjkE8t7e3F57nmSLkJB6GhoZ8WyXOh+eZzw/Uo9EAmLlI3ZjRYeocU73G87ymNR70+qq/qZMVqEemUg5TPlBeqlwuFoumqLwdCdVsfWlGbrHfdXzZBAd1csoPdfxpLT72qS0j9TmaEVxsczovlRA72JhXAoGsoAoRGllc1NVDD/iNefU+a/4U4A8hV0ON31HhpkHDiAMOCOYu22kP2tHqKbHZLNvg0QljCz49TqHfAf5oA/s4CjzmBHGRpcI932DbqVFHRlnf0yZkisWiz1OlxROVjdPJbE96jg07pNw2QNUg1P6gIqwhtYlEwuctCQQCvp0kqNDQ0BseHobneaY6tApNFhPyvLrHhEo5jSnN52WbMQSYhTQpxNeuXYtsNou//vWvC27felX6OCYYas5UDQpDPrsdiaCsv23caaFDIhAI+DxXyuyyP5sx0YFAwCieatQrEaSRCUo6qvBnPQ8SPPZWgDS+eJ4usNpuLS0tplI9xyCP27BhA8bGxhbMdmOMqOjo6MCqVauQTCZNkSFdQPl3MDibV5rJZJDNZs2Cf/fddyMej+MZz3iGqehdrVaxdetWhMNhDA0NGaKUMlCjhHTucE1Rua1yR40cJRgKhcKCIWEXGhgJo+sz4N+urRnBrmsgSXyeTyLOJt1J8NLj1dHRgWq1ikwmY8ieQqGABx54AKlUCosXL24gDEgC2MYBU5nUw6gOBkYAUGGlF5Cf0/jVfF31tgMwWxNyu0PAb1BQLkSjURQKBaxbt25BFEo7EPDdGV3FeeR5ngl51gLW1MX0XKAeOk4vHLfZ5LrPPGMlbwEYo2F0dBTJZNLUUFGyn8fxWrYSPzIygmq1ir6+PqTTaezevXvB7Wy0UKGpZwpdK3UOUHdi+1JuAGiQyZzTOrfYr2p4Ucfi/KSx3cwu0PVfjTzen/NUt1oEGg1KgtdWw5/yxI6Y6+joMGubpsRy+1M+a09Pj88h2tfXN2+pyQBMlAG3LCRRR4Oeji6b8LUdQITt2NNjCXXINXMu8V7UnbndKwuOE6rPqT1H8LNmdSbsMaO2AgnJQqGAXbt2+SLCu7u7fdegXsm1iERWrVaPrKIdwagUtpOmV2QyGdx3331mq8eDiXklEGzDD6g3rP5uxtJrp1IgKNFAppO/dSByYNhbMtqKI4+12SAOLpsM4LPZxIIyjXpNfQ/7neZ6Vz0e8E9GLrIUwvZiOZ9QbznfXYWshqfaHkIV0soiNxPczdjYZp+p0LH7xyZy9Jk4Fqlw6PvNpejRkwTAjDsNYaPQISHCHxIJNtPI5+QY0LzdQCBgwgbtuhILBWxfLowUhqyeroQbj1MjX+ci/wf80QU6V3nPWq1e1ZbH2uNHof2t19R+4zVsYlHJMA1J47k8T9tDlRt73tueVyVMA4EAstksxsfHH1W/PFagIZVOp9HZ2YnBwUHDwAPwyXclk9RY4LsyP5Q7ttD447ZrKuO4GJMoAOoGmpI2tszlj7axyoRisWiUD+eJnIWSsnszcJutaYTKUtZxsRVBrhPsewCGSCUxxIKNjBopFApGGde1wpbjKkf1PbRmiW248HwWbiVIPuiuOTaZyCjHZnJZxyHHrq30LjRQd2Kkni1HVS+js0A9iLaRZtfJ4DU1UpDGHeWtrd+pYUESQSNkVLbwPjyea66tw7F4XyaTaTB6Hfyg7sK6EjbY3loHi+OAY6SZR1iNRf2ttoHq6kpCcZ7akQSqg9vyQWUAz21GNKsuA6BBp9D3oMxkvRd+zrbQyCO2Jd+PTjR9fnuHtoMNFgFk3SaSCGp820Y+UI/qtL3mShQRtm3QbD3RflSCiUUeuf259r/aTyoztP/sMWDra/bf+j+fIRAImCKy+rz2+3Ft4RhQUoGktUZdqzONBTh1G+CDhXlPYeC+nPaCrsJeBQM9SVQ6dLBq0UEuMPF4HC0tLWbSZrNZALPsmQoueg91kGiYoSr3VDZsNkxZITUytAI/oYuUHV0B+AWcQvOydBLyMxWagcBsHu9CIBA2btyIXbt2Yc2aNRgaGjKfq3IG1AW1rWTRMNCQUTVC9HtbCVWSRduTbWcTBzRWaZCrEU9Ph2002oJPizbF43EMDg7C8+r7o9Og4bOSraUCyv5TogHwh17RY8PthRgqPjo6Ou81L5qB70sCBajn9bNfVMG0lXfdZod9TaHLY7hYUB7Yiq0W3yJZoVEHHFdKwvF4fk+ossFr8VmA+njS8G49h8fZhIGObXtcKcnENqQxtRAQjUYxMDCA9vZ2rFq1yqSE8R0pI9XY1/djOgu9y7t370apVMKDDz6IHTt24GlPexpisRiWLVsGACZ/VD2WSu6GQiFs2LABO3bsMBXyGVZrrzf8m7Kd68Vdd92FbDaL9vZ2UyX+cEYwGMTixYuRTqeNIa2EsCpfTA8hbDJc1zuOec5dQostco5zvodCISxZsgQAzJjiGr9582bjJSOBpecFg0GTSqdpMdQzqtWqqTLO583n8w0EB5+fhK/qAww15nqhpDVlPo2JZDJpZM/B9iQ9UgSDQVx88cU48cQT8YMf/ADr1q0zxRNVH1FnixprMzMzZttMRgUxekjXWf5P+U8PJ4/PZDI+gpBjSPOoc7kcHnzwQfPsdl42dQDKqcnJSRPpNTMzuxNMLBbDk5/8ZAAwMuCPf/zjvCjtCxWhUAgnnngiFi1aZOpgqOHd0tLii/xlH9Fjy/7Wtc821jViR1MBleDTqFSVN7YjkXKKvxmJDMB3r2bOANVT9Fhbl+f9lcykXcIxbqdi816q7/DebC+uTRMTEwehZ5uDEViUY1p0XkFjmIRIM0eCygzbOag7z6nOr+D33AWCxchzuZxZO3SNV6KAbas2gu28UgeWji1bp9ExR1uyVCqZHSMikYghWXhPFoRWZwjrMPHajFCmncp3YG0H6v4HOwJ1/i3LOWAzSqpoagfZEQLKQOp3hO3ts1nHZka7nqMTXQ00FWT28+v/PE8njgod/raf2x7EHOwUPiqg1PjSKqDziVwuh1wuh6VLl5rPVDjbn6kwBfx9oG2hba4hPtqHKhhs9lDTZ5TpVI+GCjSSWvrsXFT0/rwPlWGGMtmkhu2N5z3U26WLlD47lXN6qahoaYG9hQY1MGwDGvCH9M71/uwTZf117Ov4mesZ9qZg2Oezj5XYUVZa/7cNJD6fji31mug76jEK/V+9elqMzD7nYCMUCplQxvb2drS3t5vQYbY1oX1kG2Mklalk0Bhk2Dq3NdVieUosa5+yXcrlMiYnJxv6z+4LPgPHAHdwmJyc9JFSzaIQtD9omB6Koef7C+7zba9xhEYXKOx+15QyBY1OhaZvAfWceSpbrBnDSLxcLmeMGMoYe72goT/X2kFDhucyV15z9Xme6h18DkL1DVVONWyZ92DEy0KU34qBgQEceeSR6Orq8hGFNhlL2ESt1nChzqLHAvV1UccM1zmgXqBWd81QY4uygQSDGh+aDqm6AY063iuRSCCZTJp0CXoUWUeL19A1XeX54QRGnBG2jsy1yy72rLu5qFdYHTV2nQLVl1TnVc89P7edSs3sBf1tr1G2Ea8pjDQeOb7tc+15QONRCWxtJ3tNYnvodaanpw3RNd9yQu2nZjqwTapoHyia2VV6PRv2e1Om0IlEp7E6dud6fn0PW3+w9dW5np+f8R3VGa3nckzbbaLvyra0bUXKTJIt1PXnC/O+jePU1FTDQFPlnqEoqiTzt71YURHQaAbb0xsMzoa9cYuZ9vZ2X+isDR3wGj6ng4eLmHZ2s0mtUQt8Xh0UvF+zAUyhqEoKjUWGbWpkBCewhucsBJCBbJb3DdQXdV1IgHoYGvtQt/xUskiVBI0Asb3cNCL5v2188h7sJz6n/ub19PtmbDEFgt5bvZyqyNppHmwLfQ9eT/O6A4GAGQf3338/stmsb1wtBHAe2kYcvUwcs7axqV4M/U7zqyk71Lici5gD4Lu3gmHStpeCHmt760TAXwxVvYwEx5FtaGnxPiUZ9Pl0btCYYXvxWqpYzRfa2trwwhe+EIlEwixofDZGQbGwHr09bGseV61WkUgkzPZN1epsYan29nZMTU0BAHbs2IF4PG6qsqfTaTNuyuUy8vk8wuGw8YREIhEsW7YMfX192LlzJ4aHh40CyDWAHgGVScViEbfffrsxQmu1minw2EwRGRoawurVq83C/8ADD2Dz5s0Hp/HnEbbizd+6lSrgr07OdUqNQDWqVXYrqcRjKG91HVQiNxqNIh6Po7e3F/l8Hrt27Wqarsh5RRkaDAZNRX7bQ0X5OzY2hlqtZjxJnZ2d5p2U7LTXd5V5KluA2bGWz+exfv163w4MC52A2r17N9avX49gMIjOzk5TR4ogWUIym6SgGn1sD9ZK4O5MjAipVCool8smuoFjggq9vR1bLBYz2/1RpnB3rUwmg127dpk+YVQKq/lrLQ4WqwuFZqvea857NBpFT08PzjjjDEMmsd5CsVjE1NQUstksRkdHD36nzCM4/219mv3FvlaDnPPGLh5dKBRMv/A7jRhVo52krhI61JmpI6sRpo476lxKUtj6ezNiVI1DXodzX/UUyhHqg4w4ojxgIURtQ9UX9d4q9yYmJvCnP/1pXndn0V3rPK9xS2y2gcrpYLBeYFd1YR6naKYP0SGqRKDqXdwyd8+ePb5UEYLtaTv9VD/j8ycSCV+BXsoa1vyxiREbfN62tjZ0dHRg8eLFAPypWEpaUgdRHZfzhHVkdu7ciUKhgOHhYbOulMtlTExMzAthOa8Egt3wzRgdPc4mEXSA6nF6XZv94aLBhYMD0maX5nomvZcKCdsAbfYcqhTxHJ0Ic7GVShooS6Wf2eyZPv9c7TpfsA06fXZ9F23ruUgZPV+vr/ewIxVsT2+zvtPv9bpKHjRrb41a0IgF21NhX5efcXFTYWqPGc191zbkrgYMv1yImIu11XndjFkG6t5MNRp4DttEFxNVUGzywL633efaXzZhpISFzsG5BPhchoPC9jDwfjbpwGfjeODOAvNtbIRCIeOJZD0O1v3Q6ADbo2hH29jMO4vAUgmkh4FErp3m0WwOc3s+GhYk2mKxmK9SfD6fN6x+Pp/H5OQkCoWC2YaJYZrqXefzc99zrint7e1IpVKHbBG8/YESBnOtUUBdwQPq80llrs4NlfnN5liztVH7Wok89WpS0WJfa2FWfVZ7HOr78VpqMGh0gr0ONYu+sO/neY2RLocKyuWyUaYZgaN1qPiOupsJf7PfVS4wdaGZHmR7EFWvYtuzz2g8hkIhEznEqCaS7YxK0egUkhe8lhJOugME9cj29nYAs/1MOawECp07C7mOxWMF5r+TiNOCedqfdvi53dd21MHeZAr7njo8iXWOLV5DUxlJZqiTydYLdM1ttv7ax9o2zFw6t3rom52j17IjrXg+j5+ZmcHU1NS8ri1s22YOL31/RgdxHdZi9ZShPK8ZtE3tPuL6y79ZA45bP+uz8lr8n2NEnRlAvZ/UuUAjnttw2mnPSpipjIjH4yZtUndvazY+VO/nWqF1JPiO1PMpW/i+84F5JRASiQTS6XRDiIkuLioA9qaA20LKNhKYm6h7k7JoDtA8dFqNCRVstofEVi70hwsTFVN7ktjEgirU+q523j3z9+gBoVJNJZiLoXpSFgLoJVRPPQ0O7XdGGNhedPatKopAI0tMJYH/69jiImMznLYiwnM0XNUmAHisRs00I4ea1aHguOSzcDs6e/HTueB5nmmzSCRi2m56ehrj4+NmD9qFCL4PlTnOD/5mWKPt5eX70wtUqVTQ2trqC0G1Fxb72oT+z7FgKwNUQD3PM6HoutWYHj8zM4NYLIZIJGKK/ekzE6occLEiyaN503zmmZnZnTnC4TDi8bi5JudMsVhEqVTC3XffjR07dsw7YUQ5V6vVTB2D7du3m/GdSCSMF1G3XuRvto9GZahMD4fDJo+Sc6JSqWDbtm2+LSEZeaCeJqK/vx89PT247777sGXLFkxMTJg9pIHZquskD5hLT2IuEolg+fLlxrPNVI1MJoPh4WHEYjFTbC0cDuMpT3kKli1bhjvvvBNbt26dlz55PEGDzzYYNGVFZTSjcKrVqi88346e0WgwynFVoBmBo7DJX5J5jFrp6elBoVAwUVmlUsl4m5XQ4tzS7+gt47NQXwFgjGXKcSqifA4SVHzGsbExFItFxONxM84rlQrWrVuHycnJQ64oHz3F1N84t4vFolmnPM9DNps1uhcAY6RzHeNv9VTSu8Y5RWWZspJ1IjQdQWWGGluU1+l0Gslk0kS+cq7y3oVCwRCL3P6VO7zYHmfek0YLiYhUKoWuri6TBrFp0yasW7fuIPfMwcfRRx+NJUuWoLe3F4FAwJDa7A87spL1b7jW6fa6gUB9hyHAT7wpScV1mvNMDVOgcXtnzmWgvluTTVjb+e32tqEcV3bdArVVeG/1MuuuT1z3bANaw9RrtZpZh2ZmZnec6Onp8dUAm2/oXCM5oLWYisUiKpUKRkZGUKlU0NnZaaK2WltbzbyijKeubzuG+KMkAPWKbDaLSqWC8fFxFItFQ8Ky3VW/UyKK8iqdTqO7uxtLly41855jkP1HI57PqtsK81p05rDfW1tbzQ5/3PqX0S0abcexx+e0I3XYz5SpqVTKkBqFQgFjY2Pm3eZD719QNRB0Ibc9GjZjBzRWZFXhocfxWhoSxUFpK/p6ng5Ym/2yGSdVWO16BBw0tifcVnwU9v88z353NSqAujHC51losPtWP2/mhW12PuD3SjczNvU6dlj5XCyvspJ2nyt5ZJMx+k4agXAgpI3NXtusrgpEjiktHLOQCQTboNf5urd+V+FtyweeS/AYlRn2HNPj55p39ty0vV+qZOgx9rWbjZW5xoctd1S5orzivYrFInK5HDKZjNnbeL5B+aZGoy7+Oqe0Te120HbjO6vM1jmgc4Hn6rhQwpHGCiuEU4mjYsncSZKwlKv0rtGT0NXVZf6nMUPlicYQFZGuri4T+qih+wz3PJQxl2eo2bhXj6GuZbZzgMdqP6o85n1tqExhuLMd+dKsAJqSA7yXGrW2DqGF2/TdVcG120jbSu+Rz+fNdqWHUuQBMTk5iZ07d/q2smzm/LD7i0ZYM+eGkoeqM3H+qMGhJJNeR2U99SHVAbWwpX0OiQ9GEmk4tr02q+EJwHcs9UzWT3iiRyLQAULiROefgnOd40THDcH5YZ+j3thAoB4Cr2uAPZZULugaxH6mIclnt8F765wH0PRYvfZc12kmH/U9VG/R/9UhspDSm9hvGo0ANOpkdiSJwtax1C6z+02vx/mvbWKPJUKjENmX4XAYqVQKqVTKpE7qThc2ecHnsglsJRR0rCaTSXMOiUZbz7XfT3VAlUn8nNFQJDbms4gmMM8EApU1Qr2taizZBILC7hB78FDxZPiq7lVKdkgHtSoGKjz4DBr6xAFLL6XNIPL5+D+JBSUabINVGUZ7UNKzogJGSQxlUPl8zXK65hORSMTsbxsIBEykBEMLWZwGqIdqKXRS2QQP4Fc2tWYAPZhA3UBjv2lIkfaHKgRKINgKTTNFVJUKfW7tU9uIUrZS35PPzbGseU+VSgXDw8MoFArGg7pQFhcb09PTZr4rKaAKgLYlFS6OF43OaBYeDDQSSJzHVBBsI1/PAerzSPPT+LxzkRyM/mnGoCvpwfHEMdksgoJjj97IQqGA0dFRs1USn2HLli3YvXu38bLONygHGeIXi8Vw1FFH+WQXF+5KpWIMJ3ov2NbMQWebxONxn8dR92xnBNbMzAwymYxZpKPRKFKplIluoKznvFi5ciWWL1+Oe++9FyMjIxgcHEQ0GjV5t6qUtLa2YsmSJaZoYCwWM9EO9Kql0+mGnQMoz0466SR4noepqSmUSiWMjIwgl8th/fr1vrXvUIMdisz5yDmraznbhvtyU6YxP1RJBV0fOSd03jQjl7Q+DpVEjkPKdyqQtiFHckgVP5XlvJ/tdWZdD/7o9sJEuVxGuVw2URoc69wZ6s4778Tw8PAhF3kAzM733/3ud7j99tsxNDSEtrY2ZDIZRCIRX1RPIBAwfcz5lUqlTESmylPNh6feksvljPdNj2M7s211HaUcCIVCpjq5GquUT+xHmzRqa2tDPB4317aNP9sAAGDIAu7QwCjXwcFBpNNpbNq0CVu2bHl8O2Uecf/992P9+vU4+eSTsWjRIt98UdKXei/7gvNTtzDkfNKIFCWA1GglGau6utZUsu0I1bN5jZaWFuRyORMhrP1sG6XqFOS9NILATlNuNm5JNvN7FvxjVDTHVCQSMbstALPyrVwuI5PJzLvhyOehfGSbslbNzMyMWauZ+8/0Ro0UYf/zb36v0Rx6L0J1cqYmsa4JIz04HsLhMHp6epBOp7F69WrfzkD8XavVjE6iYwnwp54wElYJ8VwuZ55dSWamcNryw9Yr1b7Vsa1jmPYOozaGhoYwNjY279GN80ogqJfcbkRbcOgAshntvYEdxPA6JRBsb5ZtlNrPqgygDoZmEQhqKCqT3oxxtaEsVDNPpQ5wW+miEKPBxIV4oUAXCS4omvdvt4sdTWFHLdgeAYJjRRlRZS2pbOoipcQBz1VmkP/b6SRKHNh9NRcjbbPRNvGggkMXQP5oqB3DcxcyeQDAKNBcdKlkNvMwNpuLJGzUg2UrdUoG6HfNlD6imVdA5y/P0b60lYNm3nS9ZrPn0vnLYzTMjcoSfzO1Q8nIhQT1jGjEBEGjThdjnUeeV9/m1G53zslSqYRgMGjSOhR2H6pXhOQr5QyNiHg8bkhfKpuJRML0AaMKNLRdt37j2qLeEo5PVYRDoZDxMtPQyOVyh6wBSTQjp1VGsk/sdYhjgGulRgWo7FbCrZkCpvfkb1s2U76rwmmvI3o/m9jcm/NCI1XsZ9O12V5DPM8zRNqhilKpZNIYGEqucpB/s99tGarKu36vkVaELbObeSl5nBohulZoPzPCQMcF5zbrY9m6oepx+lzUZRjRxFoINF4ANHgtn2iYK6WE4da2vqPEXLP5rOu2EjxqD1Bu6DjScWd7vHU82fqCHqvX1DGg59oGoe15V72R//M7226wdQOCY5kEO4mxTCazIHbZ0ne05abqqEoI2OcA8Mlnez7bTjm7LziHaVh7nmfGHB2DTFVoa2szRLJeh2uYbcvpvdlPdlq06mK2zFJiW/ve/l9lk70WUX5RH9YfjaafL8w7gaCTzxbM/FFlXgeXfmZPJg03aW1tRTKZRCwWQ09Pj1nsVMnVRUw7mYNGB4mSCVxYeAwnuQpGDlDdW14XHn0ffQZbsNpGigpghsTSiCwUCiiXy2af0IWCUqmEbDZr9gNmFVxVHID6hCELy7oJmo9oe7FVYQMaDVO732iUsA/ogWC0gu7DqwsWCRBGJNhRIYDfm24roiR49Blp4NCzpRWrGVrFkFcaNFzostksxsfH90pKLQTQI/P/2XvT3kiy7L775MLckzurWEt3dXX3dE/PotGMVlgLHm+wXxjwF/En8IfxO7+yJdgCLBk2YAGS4FWypNb0LBp391R1FauKazL3JHN5XhC/m/84jMiFZHUtHQcgSGZG3Lhxl7P8z3IZSw0TxVvoATZVNFQgsOb5XNeBD39Ug0SBF7PLyitzHQe66T1+rHUfxykX2q+4Sv7wGSJLiNQpl8tWq9VCugLemslkYrVazRqNxnWn5UZoMpkEjyvhdcqnSMUgyoYwfzWozKb1IYgOYkyr1aoNBgN79OiRZTKZcHpOr9cLc8W+wWjXM+Qnk0kkSmQymdjt27dtY2PDnjx5Es6kLxaLtrOzY9ns9FQG1gbeY7wszC17cTQaBVDCKwp89u6779pkMrHf+q3fstPTU/u3//bfvrHV2jGWzKJeGv5nT7CvM5lM5ESSXq8XIkc07Y950/oK4/E4KIbMOd/riTwK/nqggPO48T7Dz5V/6F6F73hlD96OXMLT5vUI5QPcA59/naICr0Pj8dhOT09tMBhYpVIJehX7B50kl7uoD8D8mU3HU4FFNeZzuWm+OPPIvMA78D575Zrv4ee6BvUsdtUhiDrw4AFzjoeaaBPWSb1eD/xqPL44m13z7nFafRMIoPXu3buRwnGHh4ch+kd1NY0KRLarMQ1PrdVqER1rMplGdWlhW9pU0FnBSr2fZyI3yuVyREc3s4geRhuj0SjwIHiHd3agG3IvMhB9Re0F5IraEbqmAbRbrZY1m0378ssvXwsAAXmpof7qACCaAj7sdSrGhXvQZ71TDvLzb2ZhbxFphG6koACEjhWX6uL1N/qjxD3UOvD3q72q9p7arXE6uge8NW1CQXT6pDZztVoNzo9XQa8UQADt1c2nSBCf6eAkGQe6WNRgILyF490AFHiWRhNou3F/K2k/8fQrM4xDmlShjkPbFnmuX4DaDwzT8/Nz6/V6oajI6wQggCTr2Cup0IbG4/ElRs73ceivb09RPY/4KanRp+i2zqV+Z2aR9aNzrNfTD97Ze6n0HdSgUgWcEDtCLr2C+rqDB2bTdQ8T7/V6IR9VwSOPXHOvepP4zCwerfV8Q5WUOPJzor91Tj1fUvCKviyydxUY9eOjufTeO8J7IKw9+PiqaDgc2rNnz6zb7dru7m7EA2B2uTKzWTQCwfPNJIFLjiLgkSp2Ct7Bj/lODVTdPyhw+p0WVjOzUPCpVqsFjwfeY50HBajMogCvfxef8vCmkQd+lK+i8Og16uk1mxaxorK1KtgK8prZpbXg+Z8CObpXvGcGXQNwySzqGdb3Ud6vBJ9RoNHLdh0j/a3rU2XIm04Y+F6P0nlQgEXnVfk2QILn417nM7NLepuOuwLAOvZexuqehe8qeOBluycFh0lhODs7s3q9bvl83gaDQXhmuVy23d1da7Vab3Tq0jzSKATP/+CVvgq/3wtqiJpZZJ+ZRU898zKe+728pB1t08sb73BSPUKBQJ13+q1t69rR6zXKSvug0YTeEB2NRtZoNEKIvMqxV02DwcAajUZ4v8lkEil6rs4alf/e7vF8ms+9DIE839R1ofMZZ1v5fTzrf89TkvRCBTvURvD9ibsvLgpeo/V8JBXjOx6Pg02gx09/3fTKNBi8yaurq5cMNNA9NgmbB6biN7TZ5ZBiFAry2dbX161cLofQKu/p1EnVZyhT8osDxZQjNRTlNosyKUVEWTDqpdF2lfl4RqiGM8Sio8J0v9+3o6Mja7Va9stf/vJSPverJPKTOQLKzCKoJaRHP+VyOVtbWwufq8Bh7FQI8Jl6lJQ8cOSRSWon+IgRlFwUpqTQITUO1fNkZsH7AoiC4UM/tGIryszJyUkolIfxyHvpGepvCpGb/otf/MKePXsWmGSpVLJ8Ph9OSrlz507kPPlSqRQiD7LZbAT9xigARFNDwsxCZI4qFx4U4jlxwB9zqnl6rDddO37vQ16p9WuQ/gNyqgDMZDLB48DnmgryOlCn07G/+Iu/sO3tbfvn//yfWy4XPZJNhaXZdE8B6MLv2d9JgvjevXs2Gk0r7AMsajQXila/37dutxuOOaJYElW7e72edbtd29zctHw+H5Qh1iFeTO65c+eOnZ+f28nJifV6PTs+PrZarRZOfjCLAkiqDNB/vJj5fP61TjeaR2p46VypkaaKJWOiNWGKxaKtr6+HI/A4flYVbwAd5XXlctkmk0ngiegGzJvyR1KBiHajn6yF09NT6/V6ES+h2VR51f0F76WwJjUdcE6wfhkP1rY3FIjSeVVK300Tp8+o9w+D3MwioJvZ5TQT0nu63W6oSWFml/il/vR6vYi8V3CGsSbyVIEKn/pgZgE4UGfWZDIJ0Q+qt/lnmVkwijc3N61er1sul7N2ux3y1CeTie3s7NiDBw/sb/7mb+zzzz9/6XPyqojje9GN2c/IN50D1gpRqMhX6pUx1z4qAMcDOr62hUxRwNF7nD0QwV7U2htqfyi4ibFGMT767YFEPiPljs/iQI9ms2nj8ThEwFCXrdPpWLvdtv/zf/6PDYdD+/jjj4PseB3A55OTE2s0Grazs2Pb29uhX7VaLURVwLfNpgCuAu5q5Osxhwq2+LlTncDrCBB73qcreB1N7Th11vj6C9ofz0N0/WkEidqmkOpByCxOmWG/KCDAtRsbG5bL5azZbNrZ2Vk4SebFixexp/t9XfTKViETp0c6xRnHZhYRSqr06/dKCAsmiNA69Sxxvyo36kXw3pV55AUc7+Hbj2Nk/ntVvvx7eQ8nm4cFCIBAJIJ64l4HOjo6si+//DIYif5dPBrHb1VOeGc11BFSakzrJp71mUcK9TM1KFVIxbXjyd/n21OPHc8FUFCh470wjIEeQ/Ym0NHRkf3kJz8JSmKxWLTt7e1IyDKGmy+0YzY17hkrDd1iz6CMIIjj9reCfB448LxH58cLDS8A9R6zqKKi/MR7JvUeP9cIQZ7V6XRC2oIqV68DAa51u13LZDJByYpTAHTv6P7jbwVnUShoE7BJPVt6RBf8QnmoesUwRH20BzncAFPwFD//hLzWarVwJB/kwcqk/1kT7733ntVqNXvy5MlrxafnEQBOrVZLzMNkHpVH+bO5VfEj0kMVQp/qRbtmU4VTgXZdQ947qM4BZKb2Q/c+f2sBRPqo+kW1Wg1F2AAXkGNm0+OXfd/fNppMJnZ8fGyj0cju3bt3KZKAeVL9RqPO2FfwNA/863Wep5hN1xVyw69JlSXaNiBTNpsNwLSXDd6jzeda+4D/s9ms1Wo1G41G4XQkjF30z7eVJpOJHRwcWCaTsc3NzYhBpnuPPYLBhdHlZZ3XqVVW+0gvs2g0kepvPhqFvnoQPy46gL/pL3qodyDF6foq//2zIRwhyjMUmKIYJ6m/mUwmpMO96kKKqnubTeeW2j/IVp03b2NxvwKsnm/H8QEIfqI8Re/xupmfV0jXqdp/cfab74/vU5xdoLoicsKvYT7X/mtU3WQyCYUecSqSOvWq6JXCWN1uN3IEmZ8cv8DIlTeLosH+HjZluVy2tbW14G0AKdZnKXNAiCVtdrN4AZbE6LRuAkLNo1+6gHSRadQADEj7q/2GsVHzAG8OSO3r5KH+f//v/9nnn39uv/M7v2Pvv//+JabhvaqMQ7vdjswF4+q9ySqofHSKKgTajiKeCi7xPcAEBisKqCLbnjl69FQFTyYz9XQp4gmghoeL+zKZTDCQMpmLmgeDwSAYOl6Zel2Juf/Wt75lDx8+tFu3boUK915xMLPIeclmU4WNCCLyr/X9B4OB9Xq9EEaqngQ/t0qMLetR+QzkDX8VXtzrvR1xQKUaIR4s0vYnk6nHk5/Dw8OIB+t1iSyChsOhHR0dhYrIXlCqV8gsGhKuyjtRA41GIxyvmM1m7e7du1Yul219fT1Eo1DZnedToNDsYqzVICHyQEEm5r5erwc+rX1U3s5eLBaLwdvoT1rxAKECm8wthvU/+Af/wI6Pj+0//If/EPr8utN4PLbHjx9bPp+3Tz75xNbX1wPf9qG7mt8OwJfErwD7Ab47nU5E5mvhXa4fj8fh6FpdWyonmTeUN2RDp9OxyWQS1ohGEWkoLsqwGryAWbVazTqdju3v71u1Wg1nnOdyuZDmQrQQMsPrGG8DjUYj+/LLL61YLNrq6mqIvjCb5o0j89S4V7ldqVRsMBiEuhJxhQd17JRvEpFQrVaD/qd8lD5y5Cr3o5ir11mLoppNj4BDnuDxI8KCtcN7bG9vWzabDTU+kOF6OsXbSOPx2H7+85/bF198EfgzDgKvJwEQA7AwLwCy6AFq4KMLYqDqmMPbzS4biQpcKSmfjvNiKw9n/TL38LVqtWpmU6cOp38QQQEpcKYRC4Dh+Xz+UjRDtVoN9SSazabt7e1ZoVCw9957zwqFgu3t7b3U+VyGMplMcAxxJCI2l0YVml22oZALRCSrPuCBHX2etqXRTGrb+bRytQVo0+sf2i9NnfG6to86MZvaE/RRbUrV9flBnikgpc5BXdOcwNFsNu3JkyfW7XYjNaBeBb1SAMGH/qpxHWeYQd5oVIMOIa8hJ3HGPW37xeORb2VkUFyb/n9dfPRRDQ41llSZVmRUF5aOjRLtIhwBDigw469/1cQ7Mfd+w4PWE7oOk61WqxGjEdICjGq0qyFqNvU8TiaTSFEXZWoqqJR03SShl8x5kjea98TL0u/3Lwk9RXD12R7t9kbJ6zbHSaSK/9bWVvDgKnhgFt3XavQrTzCzyDixBsymURx6RJc35GlD14DyIVU64wBDfW7cfvdKjP6vhqXnLfps9jV7W9OkXlcaDAb29OnTkBpAioeOrQKiZtOaBR4AxMMLGGwWTSXjfwXk+EyPyDw9PQ2FWyny5UPdzaJHeJpN1xGGDHUX4FEouroP1futfFwVVABRDWl/E0n3qK5vs8seJvi0pufEAQm0yRxSv0i9mF7e8j1eaI0u0f2vPMDv51lRAvSfZ+u65T1IjVQDFTATRZDoKMbnk08+scFgYD/96U/fGPBoHrHmMQ6VZ2uqGftG14IHeQBQPU/0ESN6nTcEfKoZRr9eC7FW4AH0l5QTfZbybn4DVGLcqpNgNBpFjqh+W4m9qSkhyq+90YiDiz3i93jcuvBpiHqNWRScjiMvl7lW9ei4CAN1DjC3mpOuzgpv9MZFOvix8EbzwcFBKDpZKBQCuPK6RZ2SzseeRF5ms9lLDiDdc5pS5veF19Pi9HmekSRHVD6Zxddh8oR+Eqd/QgoWKe+Bd/hnqNynPbU1NA2XHwXdkT+DwcDOzs6Cnfc62HevBYCgRiSkyqTP99FB0wWoRjcIpwIJLCAv1CA1Hrwh6g0ABQrokzckfASC2fQIIWViasR4Q0dzxvy76wJHOWk0GtZut+3FixevVeSBJzz6hIAiZCkwhAeBMdjY2Aho9Xg8juQ5q/fLLGpUIMxQ7tiwbEq+13XhAQT6YXbZGGTDezDMLGqQss6o4K4hl6wV0GjIG0r+ma9TQZ1laHV11e7evWulUil45uJQYjO7JMjNLsbFF2IijF0Z/tnZWVDszSyyP3WulbkTdq+RMcyf8gM+58QOzfePA5v0cwwc7YMKIN4b0It6IZy08jpTv9+3n/3sZ3b37l379re/HcZc34/50vBGPXUBg4wQTrMpz+33+0E5B83nuYrua3j7aDSy4+PjcAIPRgRtImd6vV7gpeplIo8aj/X5+Xmkmr+fe21D51iVy+Pj48C7fHTVm0JqhKkM898D/LIP4yJOzKKhvtlsNkR4eOMDowPlnZoI5F5TmX1rayukRVAfSOdclUX1BqkjwuxyqhDvBZ/I5S5OGMA7zfrq9XrWarWCMUVEwmRyUf/h937v96xUKtmzZ8/eGgDBzIIuwjh7pbhUKtloNAq1J7R+CTxBgXfvHDCzS7LCK+DwG8aedDaN1vRgMXoCqQc8p9PpWCaTCRF/KrPNpnwE8EgVftVHiah52ymTuYi2IBrEbCpn0aW63W6YC3RidZ74yEHdnz6vHVIAwQOYns9445T74R8Y6ypDVPZiQOr7IZd0vXKtt0F0rBgbIlR41qNHj6zX69na2lqIpmasXqdIFrzimq7D+CCL0c/Q9ZGjyFklP1/sUW+b6X6HGF8PDMEPvLff8xP2NTqZ6n60ia7S6/UCgA2vASTX9jQSmmcjY+BVRKn5As5EN1FnhhQGTr551fRKAQRdXEq68WAaniHwWzeqfs9mhpGTO+vD1/1z1YMEefTQPxOhoag6SqQuJG9YeNBEmYwaqZ5xscjH44sCLIPBwF68eBHyo18HZGoWjcdj29vbs8FgYO+//76tra0FAcIRKTDRdrsdMQgYQ1XQdRxV8ECqvGcyGTs8PLTJZBI8kipA2OQ6fjoXPqxIkXDa9yCPGk+E22ooLc/GQEKQ+oKNXEuxnWfPnoWUlTeJ/LpHGBDCpx4HD7BBOt4g3njo1UBVj7b/MYsWddPP1YCIe6YCeyg4fp8yp2oUKe/yQJMa2Ci5h4eH4XSDTqcTSfl6nandbtvf/d3f2cbGhj18+DDsCxQGvFO8O4a9V7o8UIRxZjYNSUZZAXBg7bB/crmcbW5uRs4k1z2oQKWZRYwYVUq73W4IT/WpcLxLu922TqcTCVtXhYf3o1ZNuVx+Y8+IH4/Htr+/b91u127fvh3SQRRE1zH0HrY4pVDHUh0Cfm8yDzqueIsB2ihIBf/XcFYFidXTo3wB3sI78V70QRVXLwe4ln0Mf9DxqdVq4WSPt4VGo5E9e/bMms2m7e7uBgCXuVfPndk05DeOV5tZMEogrlFQ2MyCcV8qlSLrBN2M+gaq6POjxh/rQr2CcU4i+q3GKnyD1FHup6BcuVy2999/39bX1+3x48d2dHT0sqfjldBoNLIf//jHdnh4aN///vfDEYyMnxrkjJPKYbNoOh9jzX6MC3HXe8yiIF+czq96OX2mPxi2ep32W0FxlRPaDy2mSn/47WUb/wNI0A/Ac0Aniu199dVX1ul0XjvHEbo76bU7OztWrVaDnNVUH/Q6P86MB5/F8VVktwcOzKZ8wYNHquPHARIQ+zhO/2O/Y7PG2abaV08qx7zuBziAvNJoE/iaT6F4HeiVSi7OyGVQFJ3VSVAlwjMYRfVgKCjg+Xw+olDECWpv+GnUApOroAILWDev5sypYaiKifZZPS36DnynFZqTmAQhzQcHB9Zut21vby+EEr0JxbgeP35sT58+Deiqntus0SOtVisYaBqKhCKnocg+4sSHGrLO9vf37ezszD788MOIQaLKLs9RQYMBQzi1XudBH98mgMDp6allMhnb2toys+kRWOTA4cHCAOr1eqEAqJkFxdPM7NNPP7WnT5/e5LR8bRTH4BGcWq03DkDQv0G28TByLZ8nodFqrHjSdcbz1HOgAAJKqec/HtRUYaVhfYqkK785Ozuzk5MT+/LLL+1v/uZvbnLovxZqNpv2l3/5l/bgwQN79913Ay/U6AHd1+xj9lK3241cx1z4vOput2vn5+fBaF9dXQ0KKWsin8/bzs6O1Wq1SLQQoCXto3zoaT8QnqlisRhyO7meNZDP50Nl6u3t7XCsm3ozeI9er2f9ft92dnYiBSDfJAIILhQKtrGxEWR5JjNNF9P0JL+vIA8gsBY0Z173KQYgEUfMKfejXLfb7VDfwCxaFwfSZ6EcwnvU88n7+Do4Gr5Ke3ynhUDNpp5RZEW9Xrf19fW3DkB4/PhxOG0pm80GYBAeqOej8zl73Sxa+AxQGF6LHNSIsGw2G1LhKMxM+hp7m1opWrCXPYeOSKoCvJ21AeChhmQcSLayshJqOGgqpv6sr69bNntRH+FtBRCGw6H99V//tVUqFbt7926kHgW8l70B8Gt2uXaB8v7z8/NIIXQ12jUUXnUDDyB4Z43X5wkPVwBBv9dnmU2jB3S9KKCt/VDwmLWjRijRS/CoyWQSjMjj42ObTC5qIpyfn9vnn3/+Wur47Xbb2u22HR4eRiKO2GuMiab2qFxQfpBk4HvHYRKpfun1PygOPNCoBt5BZTb8H96PzRjnGPL98UC4fk7q+dHRkXW7Xdva2rJSqRSKza+vrwceGWdnvCp6pZLLK/F4mVVIm0Wrq6qxDXlj3COG3pMbtzD1f++B1gWtfdYiYSgHusCpKK0nCCiD0L7SB56vTEsXJaEseH6Ojo5C0bDXPT/a02QysS+//NIODw9DyPK7775ra2trYQw3NjbM7PLZzQjrVqsVOTIGBUMFhN6Ty+WsXq8HpUDDpv3GjzMuz87OQrEXswsQDKWzWCxGUFZoPB4H4xbFlDlVAMMXT6R9IjGgvb09a7fboRL6m0ZffvmlnZ2d2ccff2z3798P3iMtnqQCUr0EZtGUJsYWY1FDzuPAHNpTNFcNVNpUb5jvB/cwL+xhFAnPW5KiTdToIcS12WzaL3/5y3Ac1quutHxdajQa9ld/9Ve2vr5ud+7cCeHE6kGImyfNJ1RwBsJQ42heUqFKpZJ1Oh17/vx5UFDX19dtfX3dKpVKRKnROQblVyVR65V4kFCBXoxWjizb3t4OxwYqGK3vt7a2FrwK5XLZfvu3f9tOTk7s7/7u7964MOfRaGRfffWVVatVu3PnTjiOVOWWB89VEVJ+6QF9vo9L81OZznVmFmQB36kHUkOEaYt2uU77osYCgIJZNFyaNaIRDmYXa5QichiNAMKkPdy+fdv+yT/5J/bhhx/aX/zFX7w1qQzD4dCePHlitVrN3nvvvUsOALMp36WgKXOI84ex9gALa0iBXUAg79FUGo1GIXVBnTsYfQpm0Aa6gZkFnQEDApCTAo70E1mgAIpPo8MoQG9720nnBR2M4omqe7Ev+V/1M/gKfFX3N5EfrAUPyuueVp7CeiM0HLAX3gKpA0kdiPyttQr43DsGzaKRjc1mM/Lcer0e9EnW2Hg8rSmAfhmnl75uNB5f1HDodrv28OFDq9frEfnrSYEGsynv1TQX5lYBJy1YGEfYXmqzeWeP3q9yRtOSeSe1K2iXtFcFNSeTSUiJhF+xVhWchCg8WSgUQlSO2QUo02g07Be/+IX1+307ODh45YUTlV459K1KvCKKZlPFm00X57mIQ5SYNAUPQAphPF64xKFRvp9emfUGiAogBAoCCuEFoMA9sxazKlcsylarZe1227744gs7PT19owXQeDy2R48ehf9LpZI9ePDAarWaNZtNy2Qyobq6KtVswMFgYO1228bjcQgrVoMcpQ6GhdFRrVbDdYRPxoUH6WfMvRp1mcxF5XazaaVmHwWhfaGfun7wsrO2S6VSMHxYQyieMKFHjx7Z8+fPb2YSXgE9fvzYHj9+bLVazW7dunUph4x94o0KSBUOBRAGg4FVq1WrVqth37Ov4C/aBvvTLB5E4Dol5i2Xy4UiacwfIfJxqLc3IAEU6MdoNLJms2lPnz61v/zLv3xtBMR16fT01P7mb/7G7t27Z7Vazer1ejjtQJVzSHmqphf5MdT8QcA79ke73bb9/f2gAKyurtr6+nokB5OIJTXu8V42m82g6GIosIbgxxoFlclkrNvt2osXL2xnZ8e2traCJ8uH4XM9yiJ9/7Vf+zXb39+3n/70p28kgLC3t2elUimcV42Shyz2ILwa/SrvPOk1gKoK3DDnZlOjnggx9SJBGv2jfNqfjKCGotllZ4eC/HguUXZpc3t72zY3N8M60PoM2ezFcX/b29v2e7/3e/bee+/Z3/zN37xVAMLTp0+tVquFCCTlsbqfkdFaT0aVbbPoOjKbrhX1ZuZyuUhIvOfBk8kkGHoadeL5tYaqE61gZuHIcYokkiLDsbpci+cYw0L7wtolQuNVH8P2sinOUZfLXZxeMBgM7PT0NPBG3evwWgxojD8cKnyuvAS9Ia4oc1yf0MWpMUSNG9YAqUcKQPBMQCfWENeur6+b2eWaN6qDoFe2Wq3gcT4/P7fd3d2Q0oTsUadTsVgMUQpvAh0eHlqj0bCdnZ0AluPE8xE8RIxC8AF0YXgBUUSsAcbZ6+rMMXq32VSfV8eFBzN59mg0Cqc1wT+YB+aT9jhFQ9cjcoBIG+ad6/ihLd69Xq8HO28wGNjR0ZF1Oh37yU9+8lrKhlcGIOB9Pjo6sg8++CDiNdBc2DiAwDMEVQoR5GYWPITD4TAYZhpORZteGfTP8j/eOPRhTrSniBULLk5p9u+l4AIbiIW0v78fUCkNtXpbCEbu3wvlgnBQvI07OzuxwgKGDaqJIFeUmA2tRRzN4iNeVNFcX18PTAYPKMakWbT6rII//m8EGOtFUUxlkgcHB/b8+fPwjm9KHvw8+ulPf2qHh4f2rW99y7a3t8NxjihZ3W43gEgofOwnFaiNRsNWVlZCbQizaFVkRYDVUwR4hKGgawAhh9Koxg/CzezCWCFFqtlshvw1DUvnfoSdRiKMxxfH0J2entrPfvYzOz09jTWk3nQ6PT21H//4x3b//v0wTx4g0DFiTMmhhGfHhYxD7KlarWYfffRR4CFra2vheWq4Kr82iyoR6lnE4DOzCOCHfDk+PraVlZWQjqC1ODTKgTWtaUuAg7lcLuSQvqk0HA7t0aNHVqlU7P3334/kmrN/kO3q5TWLPwXHG4nq4WHPKkijoKxZtJiaAnUK3PFMPldZwP8euEK5hA+cn59bt9sNR3sqIGU2TZOg6Oa3vvUtu337dsgN9+Dm20T9ft9++tOfWr1etw8//DAynoy9php6wDXub40U4TuNTtPQ4263G/YanwPmeL6ugILZNH2CZyPTdT2SvpPP561ardpkMglH2Gp6LoD2yclJKCBYrVYD+PA20tnZmf2P//E/bGtry37jN37DarVa2Js4dzTikvlRkE6jVjD2+Q57AV2ZGhRq4JlNQRvmV4uwjkajEFmC7uFltAeVzKa8yadbUX9M0+90vRN1oXUNaB+56K9ZW1uzs7Mz+/u///s3zmE4Hl8c+XtycmL1ej1iNHsbD71O97hGGGF0U5BWbTHV21TH00gl2lPSiBDWkqanFovFS0AQ645nnJycBD5OdI3qjsrD1B5E59RIGd776OgoHNdIpMrrSK8MQBiNLortNBoNe+eddwKAoIxgEUWaicYQVKFCWBMC33sZ1ThUhsF3HizQ30mggjcO9R10gXrQQIWZ9m84HIZiaoeHh7a/vx9OKngbiZAuRZaTPFaFQsFWV1cjxY88EKOKGf+zTjyzUuagbTG3CAXOKj8/Pw8hZ+Q0+6OL6Isastq2rhVFUTXUttFovLG1DmbRkydPbG9vLyj2Ozs7wXtIZAFMWY/+IsWJeex2u1apVIL30ywKDJJvqKixKoZqvKhQm0ym+bpcp1FSeEXY54Sx5/P5gCh7wYHyqiARnojXNbfxJoj8yGKxaB988MGldA8FEFDqUKpUwHpBy9yhJI7HY6tUKsGQU8+xT19jf3qZwA/GBwAW3i2uG40uqiO/ePHCbt++bTs7OxHPivIT/ucoJj5HMSAH8k2m4XBoL168sFqtZg8ePIhNE1lZWQnGlJlFvjeLgm1qPCjIo8olSjn3qNdaZa/3ZGvEge5NNRjU8wgBLpAvj3xm35OeoP3kd6FQsFKpZPfu3bMHDx6EiJe3mUhlWF9ftwcPHlwyqFgXPjpM/9b55FqfGhQXKYISr+Aj4D77Tvm6ntLkwWSNOPH6BfUNNjc3rd/v2+npaTB0FAQbj8cBcMxkMoG3va00HA7tpz/9qa2trdn3vve9UIPGzIIH359ipGCR/lZZ7oFZyPMFjVxG7hIFpN5h9WKrcaeOBXVI8Cx0SV2HWu+EtDizqD5CrSuzKeA1mVykR1CzRSPXOGXmyZMnkfTZN4HG44tCu81m077zne8EkE31LL+H1YmmQIyG//s0NNXb1VmIjsh4qtM1zvHIs3RuuReer3YDeh/rV2sjqVNa9QB1XhCRoLoCvKjT6djBwcFrDTK+0hQGNvNXX31lp6entrW1lVhQSA10DXPShaiKJgoFNQNOT09tOBxatVqNpDGwQAAaQBAVHSI0HgSM9r1io2EqZhY5csxfo8qsesKoxrm3t2cvXrwIYTTtdtv6/f5rcXTHy6Lz83P78Y9/bLVazb797W+HfGazqfIAQ1YhwJifn58H8MHMLilyoJanp6d2fn5u29vbIRTdbIqA8jyf/4ThpxEDWq+jUCgEZF09D5lMJqwr1ql6IWnv+PjYnjx5Eq5jTbzODOS6NB6P7csvv7SDgwP7lV/5FdvZ2Qnvr/nD4/E41BwxmzL/4XBox8fHkcglPZ9XQw6ZCwVqPNDD/PtoFH9ag/IdDUujkFKr1QoeF7zpWgtlNBqFqKLPP//8tayq/DLIA3SQjj9rX8P/tLAhewLlSlF8NTo9gKhzn81mw9GYCiohA+AlGKgrKyuhtkaj0Qje5lKpFOp4aHV5nqeKy3A4DJEQrMdGo2G9Xs8+++yzEJ3wphNHeVar1UgBTbOpN9CnD5ldLi6sEUdqILI3FQiCAHUUxPMAv8p+dVqoJywO0ADUZG3yu1AohNoP3D+ZTEJtjuPj41DQcWdnx7797W/bhx9+aAcHB/bFF1/Yf/yP/9EeP378VvP5s7Mz29vbs3K5HAoJamg6exX+qgaAOg/UwFNAWJVvs4t0AzzM6GDoAnGgoRqorEP6oPqBWTSihDWBHKIdTZEgivTs7MwODw/tq6++su9///t2+/Zte/HixVs972YXxef+23/7b7azs2P/9J/+U6tWqyEaB9moALDqXBoFgn5MCir7ElLZASn/8E4bjUiAAARpn/WE/Nf0yuFwaO122zKZTAAD9fhSMwt1mTAKiThTAIGaQETMIIsePXpk/X7fvvjiiwA8vKl0fn5uf/3Xf231et2+//3vR8Az5qDdbkcAOVJRMdzx6JtNZYN3vLJedHwVZFIbkXbUZqMtBTbV4I9z9KqOGmdPwHPQZ/RkoEqlYtVq1R4/fmwHBwehzVardane2utIrxRAQFAfHx/b+fl5COHB4PPokPcSqiBRIaLGF2geYaLkwKmwZwGfnZ1Zs9mMCAGQZLNoTjz9UxBAF6YqwTAolCZ9P4+QUhDx+fPn9sUXX1w6VuZtptHoIpe2Wq2GEFgUttHoIhesWq1G5hUFDm8uHgdVRlgXmq+mQkM9hsocNK1AQSUUCbOpkEPZYQ5JlVHFeTweR0KiEDSsk2azaY8fP/5GzLXS4eGhnZychEgkGDFHX5GDrsgu84LBgJdYlQWNTGK9qFdQeUkSaUicN0Qg+sIP+5Uj+hAc6ik9Pz+309NTOz09tadPn77RysEypPzOK/2qeHmlXnNRUdqZF815RRGL20NxngAKuGEosH+RB+PxRRQbxzKiJLI2c7lcKPoKQKU/vAPGDH3VthuNRiic+TbQcDi058+fW61Ws93d3ci52Aq4q9xUQM4sKtv1txoIcd4j5sHMIjm1zLePANNIFtUbVLlF3nDaB54jnlUqlcIagNQIxQFw69YtW19ft+3tbdve3rbPP//cHj9+bH/1V39lT548eTmT8ZoQkXQcT6fH8WnKoJ8PBQch3d9+v5lNQ8VVFqiX0vMcZL6mL2j76A2Q5qQDOHpDlD4qeIBDq9FoWKlUCgD5206E3zcaDfv93/99q9VqQQ/SfanRhWaXeQAymNoSqvubXS5+rnOpP+q085EsPkpQ102c44GjffGs67rR5+Hg0hM/tPZTsVi0drsdHEsAUm9LuupoNLInT55YtVq1jz/+OAD/6hTudDphv5lZ0PXZf8hNTT0zizoi2MO0QRScT330ALHaC5CPjogDD7RNeIpPwdPIGPQLTVHJZrP27Nkz+/LLLxN1l9eVXnkRxfF4bIeHh9ZsNoPX7qOPPrp0tJVudrPLk6sb3iwaipLNZgMqtL+/b8Vi0ba2tiIIU6/XC3nsKPjkuFE9VPN3lCFxvEer1QpMQtFyRc3G47E1m80QFUFRPsKaYF6dTidS/fubRJnMRWVTPLhsulwuFwqqEJ3QbDYvzTUMg+gNjkJhHra3t20yuShUkslkbHNz08wsIKBqNDKvGjXCeqJwDmj6aDQK1VRZmwoa0TYKUavVsp/97GeRvO9v2lxDo9HIfvKTn9gXX3xhZheV1B88eGD1ej2Mb6vVMjOLFMAcDAbWaDSsWq1ar9cLtTHgFzD1ZrNpJycndvfu3RASCHnjRoEnFDzNlVNCWFCDIZPJ2NOnT+309NR2d3cDiq45jGYWMUre1rSFOHr69Kn96Z/+aRjfjz76yD744AMzu3z6hUZrqWKn0QV4IsymnkFIZYHZ9Ex5gIJ8Pm9ra2tBbhDl1Wg0QsXjQqFgH330UaRmA38DYmhfUQa73W6QKaxD9WY0m80AGFI7420jIhFIaSASSD0+KIw69x5E4tp5KSg+TUGjw5DlXp76iBitXUFUk9mFF7VQKFi9Xg/Go/aRfmJUTiYTOz4+tqdPnwbg8Dd/8zftO9/5jv3kJz+xP/uzP7P//b//t7148cIODw9f9lS8choOh3Z4eGjHx8d2cHBglUol1IFQoAeeq4WN1Tnjowcw2vk+rrYG16Mn+vQpNSLUsMDZpOChtrm3txdAomw2a6VSKcKjNAea51erVdve3rbz83M7Ojp6KyKOFqXT01P7gz/4A7t79679y3/5LwOQNBwOg66mMlhP4jCbhvsrMKNrQ2uu0AZgM/NCvRKzqbwhJVWdeApKKH+hltrR0ZENh8OwVtVg5X2azabt7+9btVq1tbW1oCsSRYuOwrVbW1u2srJin376qR0fH7/23uer0GAwsP/5P/+nbWxs2I9+9KOwBtC1zaYFlHXOkP8KFqqe7gEBr0topBIEcOFBaWS2t/XgG5qaN5lMgo7oa6TQLwVDWde9Xi+kdZpd1FF4E2291wJAAJFhsXAWvCJ+IMQ+JNUsvhCiMgC8UlTtHw6HwTj1CxWFHuOQCVfFwCOaZ2dnIQ+Svz1SxbsOh8NQKPDg4MBarZbt7++HkNk3bQG9bGLjabE7lPhMJhMRwBQuggBlUA7Y2Hi5T09PIyg2f0NseM4qVvRSw+5UyGgYuzITlB/N4ev3++G4uZQsci52rVYL+0kVBrNpJWSNHOJHc+R8aBuAnFcyoDjvppnF8hxIhRrCpd/v28nJiVUqlSDQBoOBPX/+/K0PV51HKjTNLsC8+/fvR/YXpAaDeqvUwPNGgFm0Dop6l1SxPz8/t3q9HnJwuZZ1osVcOX9cAQnWH0T/WX94QTV1QYGQTqdj7Xbbms3ma1ld+SYIRVvBdE3j8A4Cr+j5KDK+8ykMkFcOVYk0u+yh9KQ8QeWO2RScYh4VJNbwW7zTeKYpsFkoFMJRpn/+539un332mf34xz+O8Ly3mUajUTCI2u221Wq14JjhaDqd47j9rYCh9wyqB1l1Px9poPxfeYrZZQCSz/V0HTML6QmkS5Lbz5pWPRGCt+TzeavVasEx8U2S/YPBwP7+7//eut1u8NwzXhr6r55e1bk0KoioPp1vX0tD7QL0B3gyxLx5GaOgkz5beTvRR3FRqQAR6Jhcp4AT/W80GtbtdkMKd7PZfGv5AtFp/X7f+v1+JIJQ60YpwMccMndE8plF09/MLst+LyOUFITWz5hf/x39VCALGaORp5oqy/v452Jjore+qbbfKwcQIBS70WgUzg3/wQ9+EDkb1B95x+QhDLTghhIKjNm08jqLV88UJedEPd4YI2bTyv8KMpDHyobQfBkYFp6oVqsV+tLtdm1/fz8wNi9wvsnU7/ftz//8zwOzXl1dtR/+8IeRCBBqI+zs7ATGAjNCWCuKaHb5KKi1tTUbDAb2i1/8wrLZbMhjJdRdBRLzCWKK54RQM63yjjf96OgoMJx79+6Zmdlnn30WlAYMmpQuU7/ftz/8wz8MQmV1ddV+93d/16rVavBkkj++tbVltVotss8h9hVRKJlMJiiwpMiAIuOFNpuCTHoEK0AiCoXmzCrwgEeBXF+zdK6T6O///u9tb2/PPv74Y3v33Xcjyr3ZRXrL+fl5iDR69913rVwuB+NDw6BR/uDj8G+ua7VawZOMUVepVELkWKfTsVarFVLq6vV6CKOEbyCntMq6ehk0V3NlZcW63W4ArrLZrLVaLet2u/a3f/u3dnJy8tpWV75Jarfb9tlnn4X/t7a27IMPPoiMHePnPUz6HXwcMEcjF7gnTrHESMHAU8cEbQAAaU0a5SfscwwWTaExm0Yo6Xz2ej07PT21er1uuVzO/vAP/9D++I//2H7xi1+8VeHJVyFqXxGVwH7a3NwMHnqvS+HMiQMGiDDVU5fMprofIIV6qXVN8QwzCznpGHjeE06fcFYQ1aAGIu1S0+rp06f25MkTW1tbs52dHXv8+LG1Wq0QVfdNosPDQ/s3/+bfBAMLg+rjjz+2f/SP/lHQvzHkGEvm8uTkxDKZ6fF5CvapIeeBS/RvbAAiS1hThUIhUihvMpkWNgQAAHze3NwMqUnwD2qXcTrY2tpaOK6To31Jk26327axsRFqpDx9+tSePn1quVwuHBP+NlO73bY///M/D2O7urpq3/72t61QKET2cLlcjhx3ykldzB2ALZHjyFr4gp6MBhEpqIAwxFpT0Ii9zbU+Qo71Bb/gaNLV1VVbWVmxer0eHManp6e2v78fIhAU4HoT6bUBEMymDIJiNAhjzTFRL5MHCuLC1vR6M4ucu8tCUgQJcAAmBHNQtEhDYamWCUigi5dcWo7haDQaoV+6gFKKEuGO+j/CXVE+QsLUe4Hg1/AjHw2CEojRodX+NVRdFVxPKKFaVZ37hsOhnZychHfgqKdMJmMnJydvdSHMm6LhcBjJC97a2grF0Qh3Q1igSPjQZp0TziGGyXuPNeuDdYZyCPLtz5g2s4gRo54Q+AaGJu+T7vXLRCj/7du3bXNz85Ih2Gq1rN/vW6fTicgBlEU1CtXzx3xo1AJ8RI0+VWIxWFgjWqwLQ1UjInx4Iu1o1BHXItuIVDs5OfnGRKMAskMUnNT5iwP+PTijESBx10E+kiUuSsHvVfV6arQaxLPVEYGs0GiJOMCan729PTs7O3vrT1JahFThNrtYE+VyORQm1L2jeyguSinuf+X9yuv1fh+pmuSNVOeUtu11ClJm9HlEQRJxtLGxYfV63R49evSNSF2Jo36/b59//vmlz9fW1kJUh48kwMGngIKmPMF3uY71outH9ULuU/6NXNG6FMgW5L4eN0kELO0zz7RHpFK5XLZisRj6NhgMrNlsWqlUCid4+ci8t52Gw6Ht7+9bLndRjBTj32w65lojws+D1pzStGAPDsZFAykY6KNRdf97ACEuRZK+TCbTNGWcmRo5RQou+g7p8m+64zgzmRXTJ/Tw4cOX3ZcIEepVKpVsY2MjHAOUJPg9Ku0VBb84FDHWkBWYjObKFYvFwAjIxx6Px6Fq9tOnT0MNBwAIhN1odHE+vEeZ3mTU6esm1gIblQ13584d+5Vf+ZWIB1Ln/quvvrLj42N7//33bWNjI3g1QKIJPcTY8N4NBAQAQzabDQKgWq1atVoNHsajoyNrtVp2cnISlAXml/xIs+npESktR/l83tbX121ra8t+8zd/M9S4YD1Uq1Xb3NwMjB4k2ywKKGpaxGQyCYXwJpOLY/v++q//2jKZjH3yySchUuns7CwczUVxTBUQKMP8kKpwdHQUyWPkpJeULlO1Wg3RJtls1j755BNbXV21v/u7v7Nut2vf+c53bGNjw959991g1OOhiPMmwn85ZhODFUXD7EJhLRQKAeB9/vy5dbtdazQaNhqNgpdje3s7Ug2e3FfWjubzIzNYN0TJoHjs7+9bq9WyTz/99Bvrgc7n81apVGx3d9cePnx4KbScfcXnPpeUeeh0OpFUJVIVtWixeicxDJT/Auxovj3XoBxyndnlwo1mFlEiUVo1ZJrfa2trViwW7bPPPvvGGo+ekKv8PHjwwN5//32r1WrhxCyNTvWk+chm0RBzM4usJ7ydGPt8740IjSgzm8691xk1naLb7drz58+D/qfGquqn3//+9+3Bgwf2x3/8x5GonJQuZMDGxoZ9//vft3/4D/9h2Ls47g4ODqzZbNrGxoZVKpXgRSY6gHFHvnswD71cIxAKhUIo6EgEoh6n673OnIT2+eefh2hlMwsh+Ds7OxFgIpfLhaM7OV745z//uX3++eeh/5wU900lZCjRpZlMxt555x374Q9/GAH99bQWDwqxX71D4ejoKAA2yBjsCY7+hn8r72dfK2+oVCohIn08Hod1As/BNnj27JmZWXBslctle/bsmX366afBgY2ceJ3pyy+/nHvNaxWBoITXAubARoN5e2+x2WXU2aPTfG42BSBYjHpEiMdU+F4FGTmOHNkGgkhuHEJDFZ2UrkbegwXVarXgldZ0BQ15VQ8j84FCRxh0pVIxs2l0g0+V0bxM1kChUAie6X6/b61WyxqNhp2cnFwqfgPYlNLViagUfhcKhSBYNOxYQ8i1Or96nQlFHI1GkYrO5KYTWaJeaVVKffSC1lBhbZlZOFElpfnU6XSCVzaXy4WUhWazGUAfBC9jjtBXj6DOt49I4ngoTTfRaCOAJ+rd0IavY+KjEHxxJ4BHwmGJPBgOL479+qbLg+Hw4sSZWq0WwBUUPw8EmVmiTPfXQxp9NM+RkBRh5iNL4tYMPAO5ot5qIplQZEmFWtBf840hb6yTRgQhexXg0UgUn/6ihoBZ1MOoOcn6o6CA2bQwI9d7Q1QdDGbTUx/UUcSer1QqVqvVYj3hKUUJGXD//n0bjUYhvQA9W+vf+Ppomcy0GKv+VvL1czxP0HXFHPqoZ+o34EVGf9A058lkEimw22w27fj4OESx0EZKF6TReVC1WrVmsxnZo5rO7lMH4qJJzCxxrr0c0IhlDyhCrCd1Nms76IAaWZXJZCJpK2/bvn9tIxAgDS3S8OE7d+7Y+++/H3KUvMDnf0KeVAEwi+a6qOdaFxvEwiB/td1uW7fbjXgxqcQ6HA7txYsXIRznTUCa3lSiJoVnEPz94YcfhmPEFCj48Y9/bP1+39577z0rlUrBYGg0GlYoFGx3d9cmk0nwGCuijWHAeb5HR0d2enoa8Tq8bUzidSJC3gBzqtWq7ezs2Obmpr3zzjvWbrft5OTEdnZ27Pbt21av161Wq5mZRXIYX7x4Yb1ez959991Q16TVatmf/dmf2Wg0svfffz+c4w6wMBgMrNPp2OHhoT1+/NjMooAkpIIm3ftXI1JOyIUtlUpWr9ft//v//j9bW1sL50grr9YaFfxPxWOO+sSLoCHLgD6NRiNEm2jBJryX9Xo9AkwSWmk2lTc8c29vz46OjoIR8tlnn0UKCmrF8W8qMV/379+3Bw8emFlUPmsxM40iSqp67VNM/DwhozEC9UefbTZVKAEetUI4IDJrhXBb5p7imCiigMoYPoBJKV0m3cO5XM4++ugju3fvnq2urobUF0D+OJnP/x4EMLNIbSvu13BorXmhehvrA8eQhlZraPLjx4+tXC7b5uamtVotOzo6st///d+3f/bP/pn9+3//7+1P/uRPrFgshjXyTfY6z6Lvfve79ju/8zt269Ytu337tn3++ef26NEju3v3rq2vr0cK7jJ/6pXWukXwb6JEOT7Tp68BBqIfPHv2zE5PT21zczNyagKn5jx58sSKxaL943/8j21lZcX29vas0+nY8+fPQ7F2SFNgNKIipWQqFApWLpdtZ2fH7t+/b7du3bJbt26F75kn0sTVNvTpDGbTIqbtdtsymUyIRtrY2AigH8Av68tHlppZcAhrAc1+v2/D4TCcqvf06dNLQISmaLwp9EZHIECK2ipVKhVrNpuXim7EFb/zqQtKXnkA5QZF0oKJrVYroKQUTISo5q3KS2o8vFzCo5dEpBewcfEUYhyQcuJTUtrtdjAaEUgIGdYDoW5En6T09dBoNLoknCl6Va1WA4BAYR4UC/Y3gocCdhyrRLFTeIWe7T0ajcIxUxgHp6enr+T9vynkhS0eG+rjYKzhidKcRw09N4t6ndVgwJOgaS+ABWbTAnx4GtQj7vm81ubIZi+KOgF+jMfjYGSkNCUUM7zOyGIK1fpoQSjJ56FgDvepBysuIlEJ76S25dtWpRCDA683fWa9oEOkBsPipMq62cXRf7VaLThqfJTRcDiMnSs1JuK8jhqpiM7nI1YUhFIvtS+ijWzgvkwmY/V6PUQf4EFXXSSlZOp2u/bixYtg/L948cKOjo5sc3Mz8G54LXUnzKJOQd2nHLnNd1zro0L0x+vyAIntdjsYijiZWAMamZDqhNcjeCbAPY5i0k6Q2zrP0Hg8DvJfT/vB2OdvH3nkCUABkIJ9j2PRAwjNZjM4Fr8ptt9rH4GQRFoZV0MQK5VKCEOl0jbKIZ4Ccuapb+AXYLvdtmfPnlmz2bTDw8OI4qgINRS3gL/p3qXXgTQ/Mpu9qIrK2phMJra/v29mZvfu3QspMnghqMquhgPkw5jTuX51pIJAj2P64IMP7MMPPwyeQrwR3W7XBoOBHR0dRWpbjMdjKxQKdv/+/bBuer2ePXr0KBJyqikLKX29RBjj+vq6/fZv/3bIk+ZUFICeYrEY6pswj51Ox9bW1sLpKfl8PqwJ5AjKX7PZDFFnEF5NDAjWACdu1Go1q9frQdlAAf3888/DSRLfFKViWfJV7j/55BN75513glcQBQ2FEe+xFkvjc9UFVMkkh9ZHigFAIc9pQyMfzKI1EMh/7XQ69uzZsyAvyHHmfZ49exb0h1RGXI0UKMzlcvbtb3/btra27Pbt2+EUJNaA2TQ6RY1J9iz/w8MxRnwYNEYHaau0eXp6GqJOut2uffXVV2ZmEV7DOvv1X/91+xf/4l/Yf/7P/9n+3b/7d2nY+hKkUSga2fv7v//79p3vfMdu3bpllUrFHj9+bJ1OJ6wFIpKYYxw9X3zxhRUKBbt7924igIBjELsAHY//t7a2bDKZ2B/8wR/Y3t5eWC/lctnMoqe0xOmMKV2NAItwCn/88cf28OHDUDOJ1EYvW7VWldm05lyj0QigYKlUsq2trUhEoPIBoosPDw+DA4DT+8zskg7I/2+LbvhWRCAkkUeqITyS5EezkGBI/EZR8Mf+EKKCZzll+m8uea8P8w1zp6Bhq9UK4dIadfJNr5T9JpAq5zrfrVbLDg8PL6HH/B9XuKhQKIQoFDMLRkJq+L0eNB6PQ12Jw8ND63a7VqlUrFwuh5oYHJuH11LvqVarkTB3lETkCOsIBRKlUI+GRUlUrxO1b/SkHohIhJSSycvydrsdTiwi/BiPDwalRhZohJHZdP7MojmwcfnukA93JYpA7wVEYu711CUiVXq9Xuhjko6S0uKkY5jNZq3RaFg2m7VKpRI5iUeB4Lj8ZU1X4HpfvV1lCXntAImTySRSPZ1oAvLlCbk2u1g/OKGeP3+eFsxckpL2zfHxse3t7YXaA3t7e0FeU5NKo0gAlKmZpJFlhLDzv56wpmnNEDoAYCb3pTriyyVNK2L/HxwcWKfTCZGj+j2OYl8jD5CA6IDRaBTAQ2Q6+x2e0Gg0wlGretIe6RKaDmdm30jQ6I2NQJhFcWkJs67zpMrlN3FRvK3k14VWV4Z8YZWU3kxCgMRFj5hZIiigntA0Den1JPUSZjIZu337tv3u7/6udbtde/z4sd2/f99+9Vd/NSgNe3t79uTJE/uVX/kV+9a3vhVRFgAYUFp1fVC4lcrtnU4nGC2dTseOj4+t0+lYo9Gwfr8fwGZdc6n3eXnSfFazaUjq3bt3rVqt2vb2djhhhRoWzBu1bgABNMpQjUSAAI1qoEbKcDiMVFjP5XK2urpqo9HI9vf3rd/v28nJSTBa4TWdTieS2pTO/c0T4MzDhw+tUqnY4eGhTSYT29nZsUKhYPV6PcwpgE+1WrXbt2+HSFSdF001AVTmfj4/ODiwbrdre3t7Nh6PbW1tzcwuwEG80PV63d55551QF4noVYosp3R90jpoWrjQLJq25A06H01kZnb//n37/ve/H/4HEMJYJFKx3W5H0iTSSLJXSzr/7PFMJhOii3d3d61SqYR0FwX9+/1+qFUB3yDtPQ7w9Y6Gbxovf6sjEGbRN22iU1qMktZFKhDePlLkehlKPYavP+Exglqtlu3t7Vm/37fj42Or1+shDYEQx1KpFOqcQBiLekLCeDwOnil9HgbqYDAIBkWr1QqKJ3nOKV2fkiILu91uCD8FQMIAJEVNi6kNBgNbWVmJFFn29RA0NcEDDOrR1NpIWuMAQxNlNeUfL5cYe/Zeu922fD5v29vb4YhtTTdiHZycnASvM6CPXkvEIWCiAgutVivwkaQ+kfqEEdpqtdI6OTdMNxnR02q17Pnz5wFUIPoAT3Ov1wtgcbqnXx9KmgsAAMD88/PzyAlM6AzULtMixupsSud6OXorIxBSSimllFL6ZpBW0p9MJnb//n37wQ9+EBTAzc1N29zcDLmU9XrdSqWSHR8fh7Och8Ohffnll9bv9+3u3btWKpWsUqkEIxUFZG9vz/7iL/4iGB9xp3Ck9HJII8h81f21tTX7wQ9+ECITer1eOHt9Y2Mj5KZzHwYDhgLh7KQ3cH641rsgdB5vNcdzQeka+PpIoww2NzftX/2rf2X1et1+/vOfh/Q1vNHdbtcODg6sUCiEWiXr6+sBJCL1CFACIIAUlXK5HAyMXC4XIhAAHDXFAq/1N9Fj+SaRygxIC2yapfv5TSMFhuOizlN5vRx9YyMQUkoppZRS+maQDxXvdDr29OnTUM+EQocoGNRMaDabod7FaDSy58+f23g8ttXVVTs7OwtGiNZK4DzvNGrp66dZSt9gMLDDw8OQjsapSUSGaF4s9TL0zG5fB0m9zhptwHogaiVVRF8N6bifnZ3Zz3/+cyuXy/bkyRPr9Xp2enoaalgw14QyDwaDcAw3wCDtUWiT+jhxR7WSkqBgFPenvOHNoDS96O2jdD6/fkojEFJKKaWUUnqryHuX5h3hZ2bhjPfvfve7ls1m7Sc/+cml/OXUs/j6UlJNI6VKpWLVajUYeuRVY1AAGHDWd0pvBvnTNFStLZfLtrGxEUlpGg6HkYKcZmZ37tyxer1uv/jFL+z4+DjU2tAIAwokkjIzHA7t4OAgBQ1SSimlt4rSCISUUkoppZS+cXRVI384HNrh4aFlMpm0YNYbRovMOREppKBQv4B5BkhY0K+S0mtCs/bp+fl5SCsAOCJ6hMiSTCZjJycnoZ4JxVWppeOPBzQz63a74buUUkoppW8apREIKaWUUkoppZRSSimllFJKKaX0DadFIhDmx/yllFJKKaWUUkoppZRSSimllFJK33hKAYSUUkoppZRSSimllFJKKaWUUkppLqUAQkoppZRSSimllFJKPQrPWAABAABJREFUKaWUUkoppTSXUgAhpZRSSimllFJKKaWUUkoppZRSmkspgJBSSimllFJKKaWUUkoppZRSSinNpRRASCmllFJKKaWUUkoppZRSSimllOZSCiCklFJKKaWUUkoppZRSSimllFJKcykFEFJKKaWUUkoppZRSSimllFJKKaW5lAIIKaWUUkoppZRSSimllFJKKaWU0lxKAYSUUkoppZRSSimllFJKKaWUUkppLqUAQkoppZRSSimllFJKKaWUUkoppTSXUgAhpZRSSimllFJKKaWUUkoppZRSmkspgJBSSimllFJKKaWUUkoppZRSSinNpRRASCmllFJKKaWUUkoppZRSSimllOZSCiCklFJKKaWUUkoppZRSSimllFJKcykFEFJKKaWUUkoppZRSSimllFJKKaW5lAIIKaWUUkoppZRSSimllFJKKaWU0lzKv+oOpPR2UDabtUwmY5PJxMbj8aXv/GeTycTMzHK5nJmZjUYjm0wmls3OxrRGo5FlMpnE67LZrGWzWcvlcjYcDkO7k8nEMplMuJe+mln4ezQahf+139p32tZ2J5NJeA/fL//eSRQ3RnHEe/jr6Yf2wV+r/3uirVnzmFJKrDEl9ovuJzOz4XBomUzm0t7w63Y8Hlsul5u5TpP4h+8D38FLeLbvp/Ka4XAY27Zer/uIPmq7/CjBJ8bjsa2srFgmkwn3s8+45/z8PPJM/+70mXv1e57B59p/z+eU4KXKF3X8U7o5SuLvi/L9m3hWSimllFJKKd0UXRtAWMRgilMcF/neC8J57ST1aZF7FqVlDcRZwnwRQb/oOyfdBy1jyM67Xo1N/cnn8zYajWwwGFz6fjQaBUVXFeKVlRXL5/PWaDRsOBxarVYLirfv0/n5uXU6Hctms1YqlSyXywUDQZXger1u1WrVDg8PrdVq2dnZmY3HYysWi5bL5WxlZSXyDJTsfr9vmUzGisViaG88Hlu/3w99qVQqVi6Xrd/vW6/Xs7OzMzs/P7darWalUiny3mZm/X7fxuOx5fP5yNjl8/kAWvix0/fSewBEyuWyrayshPE8Pz8P92YyGVtdXbVMJmO9Xi+MVSaTsW63a/l83vL5fDBgeP/hcGjD4dAKhYIVCgU7Ozuz4XB4CUD5OsivQf1/llG5TPuz7p33jFl7JK7tWXtx1rP4To1AvS6OP153rma1wXqAMDRXVlbC92ZmKysrNhwOrdlsWi6XC3u6UCiENczaGwwGNhgMbHV11QqFQthT1Wo17BnaZr+Mx+Owd9W4p83RaBTaqFarkT2Xy+Ws3+/bYDAIzzg9PbWzs7PQHtfncrnwzHw+b6VSKfAg+Bl7t1AoWKlUCp8Xi0UrFArWarXC+1WrVTs9PbXhcBj6UiwWbTQa2eHhYQAaaNPMwv47Ozuzs7Mz6/f7VqlUrFKphPduNpvW7XatUqmEMTYzKxQKYT6ZJwVNOp2OZTKZ0P9isWjD4dB6vd4lHqRrA36ma5dnKiCs9wFs8PkiBjUyIp/PWyaTibQZR3HAj/6vwG8cCJv0rmYWWeNJ4JYCU/l8PtzPWCKHkC26vnmmjuU88nxI54V1mMvlLoFrkIJ788b2baer6llvMi37zsvIl1k6/SLPXEQuXkX+XkdnuMr9iwKH8953lh20iD4zbwwX1YkWsceua3sse++ssVzm+cvQIrJjliNiFqmse1n75aZA5pcWgbBoB+cNZtLivynj4bqCY15fMHrirrmJZ96k4NO5mPVecd42/c4bx3Fz7L3lKOv6nRIKHMokir72QxWws7Mzy+fzVqlUgpGtip4aIXymY4lHlHa5Rz2BamjotbSh15+fn8d6KlX5oy017OPIMyd+8HLqmHplWsfaMyk1WJm3qwCCN00KHHgQ4SbIv+d1nvEyxiQOPHhZz5pF7BmMdb+e1YBnD2EoY9j4cfXGMgYepJE1+hxv+Kjxpt970INrs9lsJEKJPQ5v8UCCgji0rZ56/1y/lyaTiQ2Hw8gYAHSoUel5GgRPVYOaMctmswGIVWPdR1pwPWBMsVgMn8/i6Xqv582ej+tnel9c28vK8Xmy20dOeGPZR5jNeo4nvybnRWmpjNB+z+LpSZQUEeLv8esnbk7j5MGbRjel/L6u9Dq+n+oIixjo82ToPBBg3n1xfYmTLfPouuDCIrpQnLF+lX4uChLE2QeLABmznsF83rTuNYuuYj/G9e+q+2nW3HqddBFaNKrvpnnzy9CZoWsDCIugHUkvkLSxvFHlvQHz2pm1kfzfcW3NQmriGNYiiNeiCN+sNmZdn/TdMihnUjv+Wox5rxiiIFerVRsMBuF/vGzD4dByuVxYD6oEl8vliIcRowLDu16vh/bOz8+Dd12NdJR1vGtbW1u2tbVlz549s1arFcKE8cLjuecZpVLpEnqI5xFlfzQaWa/XC+9HNAPePcaq3+8HD9BkMrFut2uTycSq1WrEAOHZvHO5XA5Kvk+l0LkDIKH9bPYi8sJfi+GiId14wxhDjDiMEMZRvWgQxlTcnr4phHMe2LYooDhL2eG7pH00r+8Yi6yTeWi0f/4iz1nWuNLf11FAk8ZzOBza+fl58Gyz5guFQhiP4XBo3W43RMLk8/kQ0WMWNWomk4mVSiWrVCp2dnZm7XY7AiDkcjkbDAYRfsD7FQqFEDXEfmBt88zRaGStVis8i+/ZB41Gw87Pz61SqQQDnWsBHeFnZtM0g0qlEviB9rVUKkWAQyINstlsiHqA9+AhPj09NTMLxny/3w+RWYx5LpezSqUSmQf41nA4tHK5HPhKJpMJYCm8lMgr5q/ZbFqxWLR79+7ZeDy2brcbWZfLKDoY5cyPRiIwBn5tKfmoAJUNavArgKMAFhQHbtBHn97FTxwIAG9Wg1/fU8Ee+qvjxvXIFvqlkXJ+HHh/3xayUuUbAD3AGGuZqB7mXde6vo+fp2WV1evw9Xm86aZ411XaeBXPfNW0aH+vYvDS/jJjE9fuLMDQG7RJBvpVdOB5a3SZd9DvZvUlSYbPMt6T5mYZQ3rROUoa36TruHaenaf/x/VlkTm+qh63CM1bF0k24lXA4rhnJn0f90zGe9lnXHWcXmkEwnWM5GXb8tct03bSu9wksnPdtrSPSW3x+SLgwSyKM5pUMYNQaDC2UYZVUURB8gqh9/hwP+2q4avX8QOIgKIdx5Doixo0yqzjAAodRwwnlL18Ph88itynz+J3nLKu6xJFf2VlxVZWVoJSyA+Gm46l95ryPry/Pku9rqqsM770Ic576+cG8td9XcrUrLU7a89et3+LKt6zAEed8+v25yZ5kVl8n9TD7fe7N9T4TNsiTUBrA7AfWNNqdLFvPVA5Hk/TihToM7MIsMaPghK0D6hG/3Svq3Gp3+k+U6OQdjTNQr3/7Ccfju+NOG1b+ZjyHoxKHxapxqwa5P46orJI5VCZgdG7CM1br/O8/YuuV30Hz9t8X2jPvzOfeR6uz/B9i3t+0tqOeze9l3WocpMf7bOPKvP90+gy3Z86Zz4iz79bXHSI2RTweZVG8E0o1m8DvWlAxMuilzkO83Tlr/uZixjlV+2nBydmgSOLjPkyfUkCAm6i7UXbelnr6Cq25FVpGUAojhaxta8yTjcOICQt1llIot6r3/vP/Xfz0LRZA5JkRCc9axZKtwhQkoSWxrWz6HW+b0njPe8Zi7yD0vn5eVA2UJhzuVzwnqtXipxacnhrtZqVy2Uzi4bwFovFSJ+8gthut81sqqQXCoWQu4uCRj41njm8/l6ZB3jQcRsOh9Zut4OSzc9wOLR+vx8BK3ytAIz9UqkUageoYaPvpXnJZlEP13h84WkdDAbW7XatVqtZpVIJ70W7pVIpRAzkcjnrdDohkoF+M74AKdlsNuSDU6NCPcftdtva7batra1ZJnNRL2EwGITxhW4yN2sezXtG3P5MelYSX1i0/9fZN4sIGM/A1Yj1z0kyWmb1ZdF5mCXAMTwx7BXAMpt6xiFqB+Tzeev1esHzXa1Ww9pkP5bLZSsUCtbv9204HIY170E+ntdsNi2TyVi5XA6RO4PBwE5PT0N9FI1u4Adwjr4BXDD+mUzGCoWCmU0jrfiO9zs7Owv7XQG4Xq93CQCo1+tWLBbt8PDQBoOBlcvlECVAlBHvxDgCHAC6aJQD40kf1QCERwAgVCqVCDACv1hdXbXz83N78eKF5XI5q9frEYAnSVnhPfkNIKL8gedxna/9on+zhtR4Zf1hLOv7wf90nCBNH6FtxjZu7fMs3/8kMELrdrDW9f0gACvAcuZM638oKIbs9G1oXxQwV1L+oJ9xve4bnRclBZboWxIlGSGLyoIknrzIvbMMrmX5uZ/jReXSsjJPeek8GbaIPnrTtOy8zbrer41lgP1F5SP3LjpmcYD9ovq0b2tRG2RRPWGW8Zk03kn2QVJ/kozCuOuXNYIX0cnm2SBX/X8eCOLvuapxrGPjea23tZblZfP21Dx9z38Xt0YWmaPr0mt/CsMiG3eRxbGocu3vuWk0bNFrtV/zNtBV+nndd1NFDobLZ4ThqpKJEusN5mw2G7xqeg3t8Sz6rF5ylF6tuaD9Q2FGGVel1EdDoMxqtAP9Rkmk7wqe0BeURr7XVACuUfJV5wE4UFQxNFDqMfY1B93MIgqoKp6MLR5HiM8YL/q1srJi9Xo9YjRp0bVXQcsoIvP6eVVFbFEhOK+NJKNsluG/bHjxon1Z5JpZ4+n3BdEACtCxpkejUUjnYT1pEUEtuqoRRhoNpAaUGsP0hecpEMHnXM/+Vn7Ds3hngBH6qWH1PIv/FdDQz+OK9CWdRkGbk8kkjKEvGMj3jDepDrQJIKnEcwAVARvgT4y7Ksr6DK5XiotmiPNue6VL14KOpcoC/xxI16p65+Ou9dczDsoLVZ4qb9bx9uSjaDywoM9UYEXXnplFjHMPavj3iVMC/ZqbRSofVHZq1EzceOn1856hdB3eel35suyzr6s3LfuMRa59VTL2psCJJIDOf6fXJ81D3H1Jf98UxRlb1x2bRQ3zWfP/MtbGMjrT60rL7q+boFm62MsE++aBZa+abvwUBrP5SPOiG2MRtDDpGcv0d5k+xKFHy7alyvAi/b4KgjaLISchZ8tuBDyIqsSen59HQo+LxWIwhrVCNPUE6vW65fP5kP+shQBVAUM5xStJxXC8/8ViMShuXFsul61Wq1m32w2GOP1WI4T3JV2ASAQNr+Y6H3nBdT58GS+okoIPGAKMG8YTedJra2shEqFYLFqpVAqRHAAf3KMnK5hZeFc+x+NLrnOpVLJ+vx/Al5WVFatWq1Yul4OnlirySWkMfs3E0SzjeFG6yv1xComnWUL7Kv2Zt0fjvlM+MOt6b/zM4p+LINrXoUxmWs0fg4n9Tg0OntftdsNpDEQJkJrA3jw8PLTT09Ng9HOSAO+pxh7GNEBBJnNxYooa6Wtra8Hra2bB0z8ej8MzIHgQ95PyRKSFgn/sG40u0igGPLhEVGn6hNaC8UVSafPw8NCy2axtbW2FvhFFQRulUslqtZr1ej1rt9uBt2qaA++eyWSs0WjYeDy27e1ty+fzIVJJgV0PIOh7av0CBXEUeFSAgHbMLheDVRBh0fQDvveh9foMbcNHJHBSDSlcen1SdALvqEC3jpXfR3HAA3NAxIGOJW3HgSc+jcDLQWpy6Ge+/z5Fjj3kU2ho39eoSIqs0PHhPW6Cp8TxsiSDblEdbxFKAm+v+l5J9yyi687i/zf5zjdBVzVAF5njpOdcl5Jkb9z/fk0sO/5e/s6zFRaxh+bpMrPmZJ5+No+S5mme3jJrfJM+uymesizNsmFn9WlZ+29ZIOyqIIHn0Yus4WUAY6WXUkQxDmGcd99VnxW3Uf3AL/OsRRnb14EAJT3rKuO5yDstC+xwPCAeSfV4qUKqnkWUIvX+qxJD2ygyKysrkYgFLVqoniNV5DAUJpOJ9Xo9G4+n3lJVClXx1A1E33gWBg2GCIoeYIa2zf1nZ2fBwMH4MZsWYqO/qljq3iFNRE+diIt84LmqjHovk3qIVWn0yiyKLgYPczZrDVxnr90kxTHKWUrLdRXSmxB2sxSbZfb4PF7r219GIUjqm+4H9ZLrfmbfeI88gFy/3w8GLUYp9+uxohhjmhrgc+zhF6xjf1wg+wBAEO+01iuAb9E/741lH1NEUVO5eAddV2po8z336HiMx+OQilGv1yPRTHFpBcpX4BE8w2waxcBxmsyHnrowHo8j0Qy8f9JpGd6QVyNb3znJU6NGqxrPPjKBZ+nzfdqUP6mDcVQPvvI5jGrPJ/VdPFDN5x6k8MdreiAgLjLDj6Neq/d6vu4/9+TTE5KiN5grbcvPgx6vumj/4+hlGgFXaXcRgHbRZyTpR9fRvebR6wAaKMUZJYuQ1xdmGWV+7V5X5573zGWJ9192XS1jzF8VuFjkWXrPVdfurPsWAQ8Woa8LULgKkHUd/XFZO+uq1y36ucq/ZemVH+PItWaXUbtF7lmWbgpNmtVWUrtx76eLaRZTikPr4vqwKNKbhMDHMWu9RkPfq9VqUDbOzs6s2+1aoVCwSqUSriNKQMEDlHieT/ve60P18fF4bK1WK3jsstlsRPk1m+aoZrPZUJ+g3W5br9ezcrkcgAg1xLlHlVgMomw2G2oNEO2gZ8V3u13rdruh+rkWhSMfGmOJPtFfjBwdSzyWKysr1u/3L9VdUAPFz7XWT/BKL/nkvA+KNWtKlW7eUUPM59FVlAnf/7g2Z12/KMOfp3hcte+MWxIgcRNCbxEg8yoC1vd72T4RbaNrvFKpRIz3brcbomjMoqkJrFGuo2YJ659riRzAw69pRcojdD/zDNY478oa51nVajVELuhehLcwPoPBILSHEUpUD9ELGPnsH8aI/co+IjJLIxQUXCV9aGNjw87Pz63b7dr5+bn1+/3Ag+iXesPhMYAsZnbpdAwiRFZXVy2TyQR+UCwWw7O4HvAhLj1AjU/GyXuwvSKiay3O46/fcb9PUwBA8JFXep/33tNfAF59Fv3mf38f7Y3HYyuVSmZm4WQRrYND35AdCozreLB+5hWo9CCFJz8nOg96v76/ptJp1JyCe35ul/FGLWPgLWp0aXtfBy+ddZ/v01X57ptOOhbXAd4X1ZnnrZNZeu6yxtk80D5OP0/Su2fp50l6/DwdPum7pGfos/x7LmofxD13WZBjUd3Kv1MSgHRVeln7dRn71ttai+ieXhbS1rxnx4Eby4BXy9BLLaIYR4tM5jKD5Ntb1Ci4Cmjh770OgrfMNYug3kmAwKJGWtw4xhFKlCp2KGN6FrlXSlD0VRE3s1AJPC7EUhUeCjSi1AMA4DGkoCFKPEqShvd3u91IlXdvbKDsFwqFEPKv4IBWkdd0CfV4aqhuNpsNEQco8woaKKlXlTWM4YCSh5HFeKmnV+dMPXQYClrIK64opHrrULi9cXDTNEvYeoq7ZhnBkHTdVZhnEo+5CSEV1/asvi8KWnCdDwef1Q9PmqfPHoMPqMEaZ+iZTY8kzGazofYBQIOeMpLJZELdDvYde09Tf1TAsh/pmxqN9ImCoOrx1ur4Oj6050EPM4uAABDRBT71AdJ6IvBB2mJMzcwajUYECOB92fcUVVQAhb7AhwFseVfGSU99gG8pX4H/zTIgFXCMW0vMC2tT68/4duIUR9++hukrb9X54nptS0mBAu2bgtq0qWAF/FujE/wYesBEebs+15/MEdd3Pvd1fma9q+ovXpdRucv/ep/KQO1T3PwvavzPopdhbC5KVzEiFjUev84+val00+8at9+TZGGSDux15mXW+DL2w3WMN/99nH5w3b25LOByledctX83rVO9zP12lfUzi+L48HX13SS66v68MoCwKGo3615/T9J3el/SZCxi/F6X4vq2zMAvglLOeuYiRsIi45PU/qLv4ov1aWiwAggaZsy1KKjUTeAUA8019QBCLpezWq1m/X4/nJuuFcw1UqHX64W++Xzq8/PzSGV33p1+0v9yuWz9ft+Oj48jEQDkJWOcKICgxooHJyaTSTCI4pRAHUs15AuFQoh+4HmMrXrQqCOhx2WiqOZyuRApQr+pIq9tEylSr9etVCpZu922fr9/6XSMq9KstbUov0hSGq4KKszrr/bvutf5exYRyFfZz0mk4eZXpcFgEOqWqKcSYAADlD0ImMe600r2AFnUQmi1WqFmQiaTsVqtZisrK9bpdMKJDLy7elLgLewr+oBHnrWlaUmsdz5TsIE9TdsAb+wb+IimNvFuePoVjIQ4ktVsCnYoKEENhZOTEzOzEI0EcKrggKaLxIXAkyuvAKFPh+B9eLaCL4uQGscQa0JBAI0M4zM12BXAiTO8aVfXfFx0BL8VOPFrXteKRpX4Z6sc0qMuFYRR48NHT3jAQv9W2eDnjd/+xAelJDBA1wPjpVEPmq6gY6YylGcn0Txg82Ubw3F8b1GwNe7+RZwryotv0ghJkl+vI/m9m/TdIu3MM6bmGcyLggO+jZdFs3STZfoTNzaz9KVFnuOvuYohexVQxtNVx//r3hc3sb8X4UfL8Kyvg66j318ZQEhaUPOMgTiGoIbRrPuTNthNGDjzKEn4LDP5VxG4XoDNYyrzaBnkNIm0JgARAGrEcwqDn1P1PnLEIqAC+cd4IX2BQxQ3jiJUZWg4vDiCcTKZWLVaDc9ScMNs6uVDadKibNBkMgmGkh5hmMtFj6nkGDdVIol2UM+PKswAJ/osNQZU6fOpGUq+onev1wuGjyqtvC8hy3zH2DIHtIc3eTAYBIOHvs2iJMXiphhjXPtJfCLumdftx3UR/qT7FgUSZn1+1T5cBXTVYoFaxT/O2JpMLoq+kYKgRj3h+Vw3Ho9DbQH2ihr/3vgGzAMQKJfL9uDBA+t2u3ZwcBA5CYHUpbOzMyuVSpFIJdIQuN7XQKDOih6lyB6dTCaR2iL+VBn6ijHrIx14f8bL13TQvaz8IZvNWq/XixwZWS6XAxhoZqGA62AwiN0npILs7OzYcDi0VqsVgFBfhM+TN3Y979S+M/76nnrSDaSAgkZnKC1ieCgg7EEH7aOPXPHGNWOkn9NHLz99YUadZzXMk/aXvq9vU6+hPf0dNxYKTngwwIMO+tki4OKiRuKi1y5Ls3jwLJ0xqU9JMuQmdL15xLNftfGwCHk5sYhDalm9OAmY8H2YJbeuooMk8RC/rhZdO3G0yLVXBQXi+jbru1nzc905m/X510XL8Kike6663xe9fhZPiqNZwOkyz3wZdOMpDEkM2Ww5A9ozhqso2vP6dV1apo+zaBb4ooa+fneVRe7vX5S5+vf0Ie4AAKVSKZwc4BVp/kdhoYAaHm4MXIxalHcPIFB1XOsRYARwWgH91nx+NXQgPVZNvT8oU/QBJW9lZSWSs02kAoo31wBMqNcP5ZOQZDUM8P6bRYt0EZ2BAaXRC6p44p1VZd0bOjqXKysrIb8aUqUzk8kEY6vb7V6ZSekam6VwqIGU1N5VgLOr7slZvEL7exN0Xb6xDO9LChtflNg/GNTsK9Zdp9OJgHsYYWZTjzqRBwo0ACAA+mFgsmf5ARAEnMBALZVK9uDBAzs6OrJnz55FAMJCoRAinLLZ7KWoAaJ24FHsP57J/uF9WadaW8Tn2KtRBqlHnPfz3mhvxDIWCkT6PgEgaCFXarcoCKPtAY5ubGxYv9+3VqsV4efMZxx5kEBBT/1cwR8FDHQM4gzhuJD6JPBAr9F39Clis9a4B0QgfR/tk+5/AAJt3wMhcak8/tkKIHhA21McMML/3DdrX/tIg0X1iGV1rFdtHOt7zdMdFwERXga9CeBBHF3V6Fnk+0WdArP6lbQO/VqfZewuMv9+zy3S73ljMuu6ZYADrn+ZBuayYME8cGYRYOo6fX2daN78LgoovUzAdhG6VgpDHDLJ39ehpMGNG9R5C26eAXMTfZzFhOKun9XWos+8Ci06VrOuV0UTrwyGfrPZjCiV6jn0ghxFiDQDwpcxsH0BMEg9W75/GOwokdRGoM/ea6afqWKLcaKh19yHEUIbpEXgPT07O7N+vx+8gFrrgd/ZbDZSsI1xZJx89IameMStNT1WT0lrIWA4aHgryqQqyBhOHmCYR8uAg0nXLbKnbuKZs2gWmHdTz7gpWmaMF1U+ZglxzQfXtcY6oV6H1v0wm0bAUMuAEHv2J1EBGGVqdLHffUqA1ls4Ozuzzz//3M7OzsJRkQoc0k6z2QxHSrLWfZi3eo3pE/tOjVb6yD1EWWg9AfaR8jDv4VdAwewiegA+NhqNrN1uW6FQsFqtFqlfUq/Xw/0UaaTvpDEBbrK3dWyI2mJO4Q/Mpzeodc49H1I+o4AIEU2sK+7160fHEzCJaxVo8h50f5oOxP2sZZ8uoEAs4LEHLrSv2gff56RUA9VVeKaPLEDm+DHS5/s+aduQ1lfwgAbtepBKxzguciTpvWYR4/kqeCTP9mO1qIETF4WyjHH0suhVAzFJfUhyLkHzZPOyxnmcDJunty5qfOk9iwJx84zhuOcv+s6z2lzkfa5i8yS9600Ai/7aZewN/W6ReZlHSWBhUl9ntXGdfenX3nV5zbJr7aboWhEIs0CEpGuuyxAXaX/Z9hbpz00AJItM8nUWU1z/lmUii9znGQHeLi3Oh6LM/1oIDSKkn8gFVfoBHghV9v1UA1v7hcE9HA6DgYLHk2u9kQKpMq+KPko4yqgaMzwPpRrFv1gsRrxFKMekG2AAAVJo/7WPKMo82xduY/x1HfsaFfp+6jXjGZoPrHnsRD+8CkXqpgBJr3zMUwiS+rDoc5ahV6UYzhqDpNBv7uNkAa43s2C8UrGedUkx0n6/H9YYxrQ3tonCoQ+sXV3zquSzXomI2N/ft1wuZ6VSKVIUVI2hXq9nZ2dnVqvVQmFRNaz0HvayV1x0X+ra4D0UZCTSR9Mk4oxExpb7SNEglUnrMBCZUS6Xw/164oNGbcEHAQyJXmCOABi8Ub1I8dQko9wfaat8Zh7xLh4MjQMzeAf9nnuS9qxPD9Gx0rlTHqwRFXERBzzP81ltX/uv0WlaNBdZoO9FW7PGjr7pM/X9dc1q28jXeSdDLEs3wauv8+yryCqVg7qWF6WXbeQnGfBXNSxfRt+Sxn3eM+MA+yRj/iZpUV131n033Revr82ieQZu0vdJQNu8+xaluPm8Ls3jgTdNSfZq0vskraVFx3MRu3DRPQwPW2YurzNXN1YDYdHrrsIIFzWIl5nsq6B0szblIp/Hvbt+fp3Ntwjaukg/F0FA1SjmGvW2Z7MXIb69Xi9ikKh3g/8bjUZEsaNo4ubm5sz+EbavpKGzesyjHr02Ho+Dce+9P+RAa4qCz/WmP6rc1+v1EJVAsUT1AhL+DGDi5wKAQOsqnJ2dxaKURGWoIefPikchjTP+MSa0DfqG95JnU/PhOhTHHBdlhrMY6bzr/HeLPutVIblxNGvPLgqILMPndAzinr29vW0rKyvWaDRCqpKZhWgajVAwi9YaMbvYnxQGhaiH4g0ZwAjqkej619/FYtHK5bLdunUrrO1Op2MnJyc2GAxCbRQzs42NjZDmlM/nrd/v22g0srW1NVtZWbFerxf4D0Y8AKHWaQEE4VST8/PzAIQqCMl38BzqEigwB7jC9woCaqHGw8NDy+fzYVx4T06yyGazgSeura0F0AG+lc1mw/sBymrtA2pJsA6UNzJ3yr99eL4aYPxPWwoIKL/1CjNrZZbc0c/9s2alRfCerG1khQLF9EejGvhO29Bnxnmu1WD3oJEW79Q2lOLSKhhzrX+j76/AsgcSkGE6nkQJ6bOTAJI4etlG8zLPXEZX4h3ZH8Vi0YrFYnA25HI5e/bsmbVarUhkTdzzrqJDXoWSwNw4ihuj6/Zvnj46T+9eZK0sAkAkgQm+/UVk4yI6Q1z/FtETFgUnrmq0XReku+k249q9Sf6gsoS25/GCWetxHg+Jm79Zc3WVtb9Iu1w37x30+2XAz6uCaErXroHgB+g6aN51kNJ5iv8iBvZVn30TNMvQmnftMs/QhXvVcY7zUrLJUci0ToEi/F7RxMBWwxpFEiVf84W5hnB871Uaj8fhXjML/2s/MTRUgfPRAPyv3ka+VyMBUEAjLjCmSG8Yj8dWLpeDUaDvSVsaqq1Kpi/KZWYRDyFjDQChkRJ8z3rRkGvGjDnTeRkOh1YqlULO+jwv1Sxm7hXsWWt6GfTWv8Oi9Kr3+U3SrGgBaNF9nrSflcrlspXLZWu32yFiyMwixqTuU91r7FmMYP7HS+6fp6k/uv4UsGS/lEol29zcjKx5+AZRDdnsRdqQRh+QKlCtVq1UKlkmkwkGmhqWWsiUfvMc3W86huwb+IXyM2oQmEVrCfgxgOdoWpSmT/Ec3k+NS+WBPKvX64V+AUTyTlwHMBy3ZhRAUAN1Ue9Q3F5Vvq1txe3vOENb++EjJ/QdNIoAAIG2ud+H8vOdPlejvua9p/ZdU2X8u3gF0I9THDCiYDnfITv0GT4Ng3tZA1oHSN/3piMTbooWMRCSSPlDPp8P4GO5XLZSqRRk3snJSajnYhZfMPTrotdZTs0DFsxudsyuC1JclZZ5h5uyMxYxfJfVZV4WeODbWsQonkXL6CzLtDuvT4vaW9exT5cFrub1zX9/3bWwLN1oCoN+Ds1CBpdFCGd5Jq4KGNCeZ05J/89rZ9HnxT3D0zILah46dxVUOgk508gCNWC5niMC9bx4FB6f56rHN+Jxy2Qyocp4q9WyTCYTTnjA68nzMXLx9HmF9Pz8/NK57Rwz55VE3oEIhU6nE3l3nsOzdHw0HFuPjEMp1xQB5keVQCIX8BL699B7eX/mg7HUqAvGmnsJWV5ZWbFarRYMKg29pj08VlTcT6JFmFCc0RAHFCQhqrPujevPvHX9spSMm2w3bkzinqdK/yxeEdf2vOvi5q3X64Xn4jGfTCaX0o2ISMBgwyDp9XpBUSc6B8+3puko+QimjY0Nq1ar9sknn9h4PLavvvoq9K3X69nh4WEkhWFjY8NqtZrV6/VQA2F9fT0CBh4dHVkmk4nUPMhkMlav1204HNrBwUGYj7OzM2s0GlYsFq1er0eKpmrNEAq40l6/37dcLhdOiYE04kijA9Rjz14dDod2eHgYvKZmFuoaKIBIlIQHHrWobbFYtN3dXev3+/b8+fPw+dnZWUizijsNwRcX9OQ/Y169wc16UwNWxz6uTQVZdX36GhZxQIxZtDhkpVIJESOaMsL1fuz4m3HnWgAcPSVE5ZDvI9do+37vJUUmKHihe0vb1XEimkbTJhRgiAN2r8rHXpYBp/3yPE9JQS0Fw3U+uE6PNT09PY0UagWEqdVq4X74wmAwWAgMn6XXvWxA4GXOQdLz1EmxTH+W1dGXBSvmGX7LGFHz9JNF29J2vOG3bH+T+rSILuXthbjnLUtJds0yNqL/fpk5S9pvcesiSQeat4bmPVfbnrdm48Yg6b11ny2q6/n+zGr/qnStIoovk5JefNF7r/OsRduZtziSBMmsRbIoJS1Oz9AXNSCWIZSXOKUJQtnynrs4sMbMIh73TCYThDUeRH027XO9FkNU5Uw3snr59Jg3bUvbNrOIh5XvyDdWJTHO40Q7qtB4pVznEGNd60ToWMV5KX0Egc8Vx8vE3+Sqq/Ku/fF9neVZXGSPLSL0b4K+jme8jvSyxjepXQ3fVoPQG38a/aN7Qz3k8AOKD3ry3mUIwOHWrVvBoCbaqdvtWqPRCH0slUpWLpetXq/b+vp6MPDZK75IKnubd8IgVwB0PJ6mNJhNc+eJEmAvxhmQk8nEarVaAD117HyqhkYo8BzekwK1HsBl7D3op7yO91pZWQmgpYIVvF/cvHijLG5+4tYElCR3tI1FI4o8sKTvoR557Ys+r1KpWLlcDhEwemJFHJAFqSzwMkTfMSmKYJb8jQMt4tpIGvdZYxcnN5hP/7xF9INFlNUkuooSq237qDYFUtgTumfZI/756A0axZPNXqTued0GkG/ZiLdZ7/G60KJ9ukl586pl9tf9/Flrfpk9c5VnLnP9q1ibs547b9z0HT1fSLruJmleuzf57FltLTpvNz2/mcmCHPHhw4eR/+cJgUWFxCzkLAl9moW8vayFokbvIshfHN00+jOPkhCuRRQ5vcdfg1edoom1Ws3MLOTVE4KP52M8HgclTY3z8XgcjiDDY1Yul4P3n/kErEDxV888ecVUesdIz+fzId+YsF81kM0sgBRaQIvPIRRmzrPnf55JxIGmMODN1IJgmvetniA11jHytR0zuxS1QBt+3lCYiWIAQMAYYTyZF67BYODIu+FwGNIykiIQFlkrs+65iT1wnb34qmkRYb3oNWbLha5dp81sNhupeTAcDsNRn+xPvOKAYRhd5NoXi0UbDAbW7/etXC6H6CLWpJmFKJ9qtRoBK6g7cvfuXTOzcPIL67jT6YRIod3dXXvvvffC2vagGEY9kTiE+DebTev3+/bs2bNQ/FXBPOUhq6urtrOzY8+ePbMnT57Y5uamra+vh+/7/X7gQ7wPoKeOjdZKoRgkx0yaRYvvAQBonQX4rvJUxg0+B4+q1WoB6Dg/P7eTk5NLgKjWtJm1dmgH40qBFeZrHikQQhvwQy/T4/a4GsGcWFEqlWx1dTWALfBLTcPpdrvW6XQCsDSZTKzT6YTUs7j30CgOvxboEz9x0RBJ728WjaRQ8sAwclSPD2XevDGtchLve9yzFURatL8vi8cm6XCAgrlcLqQCIT/Z3+gJcX1k7AAWkemsM9KeuFaLXI7HY2u329dS1F+GfJrl/LrJ+Zkn75O+n/f5vHb0vq/b6NdnztMz/HXL2ipXAREWGbtF7bPr6hFXBQUX6WvcPXHra1G7xlMcuKptznqGjsOsvs3rY1Kfr7qHb2L/f/nll3OvuXYNBOgqHZ41seoN8J9ftX9K3kO0zP3aL11g88bgZQvcuLGaxcCvO5aaAmA2NYa9h4PnolRxDV51/ldFSJXJbDYbwjF9tIBX5DTcVb/znnbIG+LqJfWex7hnxXnr/bvEKZFxnjlV4Mfj8aXK7toH/x7aLn3yXhffT64nN917fed5zHz/l6HrMribVia+TnDv61aEboo0ikD3sKYlARSYTcPvzaZ7UD22GLl6WoEn8v7J3edElUajEdaQPrNYLIbPi8WiVavVsI6r1aqVy+XQlhqVACN6hCtef00zyOVyViwWwzNJJ6BeihoxZhdACFEBChz6kHbGxEctKcELASzjChiOx9P6MBoNobxXjWL2PkBEEtEnNaBpU9/D8zsP+CaRjoFfX0pJCjn/Y0yS365AiplZrVYLR2IOBoNL65JxZQ3F6Q1KScrnouCBb8u373lxXPQcz/aRJnHf+ffRdpb1rt+0kUqb2je/H9hr7D/mnGhH5jquRgUylbUBsKg8zaceqRPDg0ezxutljM2rpCRj+ptCSTJ7nix/Wesgrs1XAbIsQouum0XHKk4vveoYz+J/3sZLGvNZ/79suumxXZZeWgTCLJq3yGchOMtcA2UyGavVahGPOIpoUqXdm6RlJ3fe/3H3z3vWrDbmocH+cw1RhogSwCtGwTItJIgSzveqWHMNoYPUWVhdXTWz6FFxemSkgjc8m7PmyZeOKwTow4tRPIfDoZ2cnIRnqRKhIc9J4f94KwkBJpICRZYIC2/46Byi3FarVavVaiFSwNeaIA8dbwxKIv2mhoOmklBnAoOB96MSNR5Qfh8fH0dyu5NoEbR12XW2yLNmGRRXQcNfhXIUh1wvisZfFbSd96y4z1kTeNPxbLNn2aNE26jiz97ntAI8wRjeL168sOPj4wCYUdBsd3c3nDxwfn5ue3t7ZnZxIkS5XLb19XUbjUZ2enoa6ntw+kKtVrPNzc3wHuvr67a6umqFQsHy+XyIOMDz6D23nU4nRDYAXuTz+RD6n81mrdls2uHhoZ2dnQWvNWMzGAwi/A4eBT/Ay65jRUSCAhlJfC7Oa6xAI/NTq9Usk8mEKAeACHgwPJU0jE6nE4CduLXj14/vA2sFAnhSxU/57yxvPiAzCh7/53I5W1tbC+MB78vn86HOhB87+FyxWLR2ux3RAUgJOTw8tF6vF+QRa9kXBFZSY1bBCO237iUPnjN2HmDjOi3iqXPBWPoin6wv9qqOofaL52ifrssz4/jGPL7viX2QzWZtfX09pP3wk81OT3zx/QcE0xNIFPjkhCEF4xSAU4cBUYTs/263G4n48afOeJolm+LGYxYtw6dfFi0qd/X7OHkz67pF21+GkoC8l633Q8vYM0rL6jNxdsOs+/X6efrPIt/Pe4fr6n1mUx3ERwfNoyReFQdUz9tnN6XHLtLHRa5ZdO6gRfv3UiMQXjUKuQzj9N5pNQbxonjPySIbetEohptm8jfZ3lWYs48w0BMRvGKoUQrem6AKUFzbqvzFEfOHElAoFC4dxag5wX6joeQCBKhXT8krGChkGlYc13ffhv6G1DDQ9vU+H02hz2IM+PGKoiqFGCeqwHsPnL5vSm8nLcI74q5hnSjwZZa8XtQT7r0FAI76ma5zDFjlFxQhzGQy4eQEAELAiVqtFlJ2MNrpGyCeGg/wLzzxWl8ARYWfbrdr+Xw+FCGl3Xa7bYVCwarVqnU6nVAA1vODuKgBP4bsd+Vffl7i9jrvp2MfZ6irUa7fw2t1vOPWRJwyooayPstHPyjxvedncRTHoziGj/Q3rlPgwxvtADNEguj61DWhYI6+r76TN1zjdIE4mbgIxY19XCSbN/j9nCaBNC+TrqM868kqzAkpTsw1e0kj5nguz4a30KbZVLZ72cpv/dExVN0BQErXgUYscl2xWAxOgNeNXibgEMcfrkrzjKJ5+wqA1Cx6ZClzZha/p1Qv/Tp17K8TCIIWATYWoZuacyWVfQoaK4Cg8swsuiZ0/3q5x7WQ3hcX3bAsver7Pd3kvvR0oykMnhYdhEWM9UWemTRQ4/FF/hoKUi6Xs/X1dTOzcN4vubXqwfJEBXGo2+2G3M9FkOgkpjhvnK77/axrdMwWRaqUAZtZ8KT1er3g4e52u9ZsNoNC508h8EeTeU8JdRXUs453CUWAs+g5ueHhw4f2wQcf2KNHj2xvby8oD/1+387OzoIng/4TDlmv120ymZ74UK/Xg4dB85H1GDrWEgYBXgm8qtQhIJyZyAMEGDUbCLmmlgORF/Sz3W4HZZcoAdrAUNF0D7Novi5t8KzRaGSNRiNSRG0ymQRvnIa7xgEhy66vRa65itdL71OhEKdUxz2PsbrKcWWzUPW4a5fdv9fhm3HP12tvQjCxRqrVqplZWDtqSJJbjyLHsWmAD3jz9AdwIJO5OHWlWCyG0xXgz9/+9retUqlYrVaz8fjiVJZcLme3bt0K/EVPdNFig0TskOfO3gSA0LBmxoqoHKIuisViqHEwHo9DQcd+v2/dbtceP35snU4n3Md4a+RBnAEK4eFsNpsRAEXHHl7I//AmBcbhOWZT77nyDsaEuhGslfF4HJFxfs49af+8Mu55N2PKfdpfzT1XANTMrFqt2srKim1tbdnKykqIiCLSAO8/88Zz8Dargjgejy/VhODeXC5nGxsbVqlUwvrUe/x48M6048dWn6kguwInyosU6GUPAYwr0M7aox/ahu53le3ew8bnRLLwjJvgD0k8J0mWZDIXUXPr6+vhR9eOAlvIWe+E4H/WAOPrx0zv1bH2hojZ9PhT1igRHQoinJ+f2+npaXiXzc1Ne/jwoe3v70c8eNcd15uWnctQkryL+3xRL+iifYoz+KBZYFi1WrUf/ehHNh6P7fPPP7fJZBL4eLfbjdQ5UarValapVEIdnDhQNImuE9EwS2dJsh/idItlvM1X9Uz7Z88yUGfZdkl8AR381q1bQTasr6/bxsZG4AOaZmR2uWAuOkWj0bB+v28HBweRSDWfWjerNozKtzj5lDQ+syhuXBZZA/Pu8/cvovfNA+tm0Y0BCC+bVGDoIlGaNWlxaDH3sKBQcs0sMA/vvTabhtGwcfwpAPME53URJp77dSOWcf1QhUiVNfWUIbT1uEBVsPR/723y7+iRQkAHQhYxtAEFMPoV9NA2eB590NQEr2zMA4KUtH/8T5uqDOr19C/OM+f/j/Ok4KFRr6Iqhd5bpn2AGaviqXPyddGi6/omvQMvcx+96j2aRFfxsrAWVHCzRlDQvMD1Hl6iBiAEPfwXHhFXnFTDmFHq1UDieYAA+nx4E5EE3W7XKpVKyP9XfqV7DEMOEI/9S9uaYz+ZTGx9fT2SRkVKE7wJ49WPEfPBM9VoUi9+nMfM7HIkkn5Hm1oTgc+Ro6oczeJvi/ID5Tn6e956wwj0hQ8BbjXtTdcb68NsClwwfqxRHRcvR7jWF+yEV/siioyZ7iM96UbfR//2Yxens/i+Jt07awy1fRRuL0t0LmYZJUm0jFHr35P55L1Ia8JJwz6LW8sKVvp15sE2/Yx7/FiqTqA8xes2AHp6PcA/tLKyspSekNJ84shVL688gMEexRFIrRPq3sCr8/m8nZ2dBf6he57INsBez1d9QW7WI3yeaIfrgAlXpVmG/E21f1PtxIEG7C9SEavVaphXeINZNIJc97a2CdAIiMxa8NEKcc7QON1Y11cSH/af3wTo97rTlWsgeFqEWS6KeMUtLsLZWFytVstOTk7C9/Newwty9YrRJs8ZDAbWarWs3+8HLy/9ymaztrm5afV6PfSz3W4HD9V4PA456R7BXJbiwI4kxHHeWF5FQZjVr8lkEoqKVSqViEer3W5HTi1Q7zmbmKgEck3NokqS7y/IP161bDZr/X7fWq2WbWxsBC9gv9+3e/fu2a1bt6zX69nZ2ZkdHh5ap9MJnkcUAkIj6X8mc3F85PHxcTAWeJZGTBAFEcdQ1AAym0a4wPx6vV5YJ0Q3EI7LM7QtNaRQaPmtoImZBYWMqvgYR0Qg8L1Z9Mg6nqWoLHttMBjMrKR+HSUp7t6rrs9lvCTL9mlWv75OIG+ZZ83jtVfpN2sa7yxRNRhTgK/qudWaAcPh0N5991377ne/a8fHx7a/v28nJyfWaDQCf9ja2rJKpRIibx48eGDlcjkoaKoQwENY4+wnvBf9fj8Secae/fzzz+358+d2+/btAGZkMpkAKFQqlbCPzs/PrdVqhciAQqFg6+vrocq/WRSYo87CF198YXt7e3ZwcGCtVivwwl/+8pfW6/WCUaxGvZ66oIDK2dmZtdvtUPwNHgBf6Ha74UQYFDDdy0R3acqGemsVuNBTC+LqxiQpT14B84Yfyh581q9DorXy+bzdu3fPtra2ghKooevj8bQaPidaaFs8azy+iBrg2E+iuxjXXq9n/X7fKpVK5LhO+kbdGPg1ugE1aRqNRlgzg8HAms2mdbvdwO8VhCWX3tfN4VlJ/FX3cByobBaN8lDyKR/oJ9qW15vUmFrk9Iy4cZ/3HtDm5qZ997vfDbLy7OwsEsEIeU+j1l1RI87XEvLvqp9rpIiOwaLygX1EX6BMJmOtVsv29/cjAEhcu7PG6jryRN9zWdk3r804StJH/ff+vZL6aXZZV//e975nH330UahNwvesAfjH8+fPbTKZ2O3btwMPRP8DAC6Xy7a9vR14KnWmzC4f2TkcDq3X64WIsOFwGGry1Ov1EOHZ7/ft0aNH1ul07ODgYOG6aklRQfMAqEXmNe6aWfddVY+7Kf2nVCrZ7du3rVKphGhCX7BXeahGEWtdJu0XfIE5hYcTAQkwzLM8cE0No1arFXi8HrPu16kveE5knwf5Fx3DJHtvno19Uzri13oKwzya1dk4BkVouZmFhYOSSY4ZC0A9BYsACXisQcFXVlYixpXZ9Lgwr5SoBznOG+yf9SqQyFl0E5vdI/p8xubUfFLmLs4DpPlJqlhpP1XIo/SidFDzYHV1NRxNZjZNTSAMmqPd8F7BTDBCUBZ1bagn0BdPBChRz6QaEdpP7/3yY2ZmkbHQMVbFCG+LV8y5X39D9N0XE/NhWOrNoQ2MjEXW700xtHltLUpxincSg8Z4mKXsLdPf6wjURe5dtP153ojrjLMac0keVAVd1fNTr9cDz8Xgp7Ahxh6pDpPJxRGLxWIxgLLcp2HfGL66vr0HEwJIq9frwbPFPZpmYDb1YvDOgKLIDjW8vYGHbKnX6wHIIyVKjWyepUaO95rrdZ5PqGKkY6+h9H7O/Z7wPEXnL25u9Vo+88btIt5yDyaoPEZmxIHK+tw48FnfgWu8ka21LrwiyGfMeZwCTn8Bn3u9XgA6kvp3VfL3sn5m8eZFI0XinvEydBbaxxGkhS5VX/DrWPew9kvn1+zyGk56F8+3ZoEHurdpW9eZ11ngQ8h/wFV0hEV4+03QTQPdSXz+qsamtuX/Rk5o4edyuRzWBlFG6rGmzWq1aqPRKKQj0T89khobwsyCfqjHc8dFy2oKkabHaTQUdXHUHvF7ClBCQ+lVTsaNiY5b3HeLjnvSXLxqgh+USqUgj1Vuqa7BPCuwzfgDkmsUrueRKifR+7wujBOEa1ljg8HAisVieA7zqffTP2Q1skOLrsZR0jy8LJBR278uz7lxAGEZpNGTbrhKpWI/+tGPAqrrBcra2pqtrKzY6empNRoNa7Va1ul0YlF633Y+n7ft7e0QLuc9AzAEZSqj0UWl79PT04BM6fVqBGoIpfZlUcGs3otFrlW6KpK4DGnIv1faiUjgM/Wi9fv9YPRTP0KVRe6h/zByNmuxWLRbt24FJR4FHYLZwMA3NzeD9zKTydg777xj1WrVTk9PbTgc2traWsQQIYJB+1EqlWxjY8NqtZptbGzY8fGxHRwchPPdDw8P7fT0NHL8UyZzcXoEni9FR0mt6Pf7EQVVo1XUY0qonU//UKalygmGgQIhSjA01icRFc1mM0SO5HK54EnDU5pEV11/yzCuech8kqeO7/R/vSebvajyTV41nmzvDaCNRRm3V5QW3YvzrlO+sIiSuIyAWBS8AHTxQt170b0hub6+bu+//344IQTwd3t7O2JMoFxtbGyEPT4ej+3o6MhGo5F95zvfsVKpZGdnZ8E7kMtdVOQfj8fhVIUXL15EZIbZhUwpl8v28ccfm9k05Yd0g8ePH4d9rSlqRJtlsxcRUDs7O8GDpWOQzWbt4ODAnj9/HqKOHj58aPl83r744gs7OTkJSggyAoWJ8dL8d9peWVmxer1u/X7fTk9PQyQC/AaFlmgh+B0RIihdRHFpcTHmAkCWMYwzxOBtcYa6v97XPPCeYP7XqIhKpWJbW1uWy+UikVhEZfhTIQBXkTtEZ+j44kXE4KDPlUrFVldXA9/WNc7zAW4ymUxY09S2abVatra2Zmtra5bP50MUiJIquowPwI4nD7oxdjpe2kfmWfkbRpIa3RpdoessznumgPU8igOm5hGg/Ycffmi5XC7MC0Y3fQWg96cO8Y4KwOlvM4sA7r6vHoyKA5b0nsFgEImAUcOEMeOZ4/H0mNfd3d2wjnq9nrVaLev1etbtdi89I0mmXZU8/78pSjJgk+TLLONHSeeyXC7bxsZGiChFL4f/63wBzqjjY21tzcyiaXHZbDZEGPBs9iB6KlHGuo74mygn6nJwSguRa/Ce3d3d8E4aSaYpckdHR7a/v2/dbtd6vV7o0zww0I+b12H0fw8KJ+3TWXpE0vPjrp11/7w1jfz79re/HdEp4P0ahWcWX4MAvQ1CT2bM2cPIPhx7up+JTtvY2AiRJRqJyE+1Wg312s7Pz+3JkyfhZKbRaGTHx8c2Ho9DZPP6+rp1u117+vSp9ft9azQagUcnzeci45o01p5XJj3jJnnEjQMISS8wj5ggGG+1Wg0by28ShA4IEYqDIr5alCnuWdzvUWSPNvNMFC9FFlUYKQNSjzQK2Xh8UfBLBbgvILXIuN0U+nSddrxSo0q6fx+UAf7mXjVK/ZpRpVzDciuVSvDogVJrYTY1tGkDAxxFnX7r/BMeTb8Aj1DMiWgAEFHFHIPbHylWq9WsWCwG8IO0Ap6va4sxUAUbxVrrMcA81aDNZDKXkE0+ZwwQpuRn6lxlMtOj5BgP9bpdx3M2ixYxbmcpJ3izNQyN+WDcPRCnY806wQCAZ3B0n895Zpx84b+4Iy5fJnj3MtueRx6ognSN6j7SnGYUcjWSVldXQxFVPPSscfa2eqFon/kmIgCjgrXrPZcQn6FY6vc802wKhqJsaFV/Qla1HgJKJGOgBQ1RjGiXlCldZ0nrnLXLHve1dvy65pmMoxqYKC7KYxToUp7iUxcYHy8r6Ye/jrGK+9wD/ESVKJhPKgNjyXz6Gg4KaOg7oUPoMbUeSNR+MQ5xRql/D52z8fginYKCuAAgHmA5OTkJRZnhy3H98O+l3ng/tvrufky1rSTAQo2pmybPZ9fW1kIfMcji9A9V6vU9vBdRv1OKAwOUF/jx8+Po+59E9Nuno6is8GAZEVYAlMvoxq8zJcnxOHDEE0YWhSipXUX6pO5N3Y/KT/W3WXIkjepbOuceZFYjlefDTzB4iSjRZ3j+o23Ae6vVakh/GwwG1ul0Fjoiex4tAj7NAnRehU5BOhg1J4he1n6pUwJ5F+cMiiMvG5kLwEDV/5ErWmfBg4VmU97PZ0TG+FoZGnFJ0WWOnUd/8XbqorQM4BN3z03P9ZUBBM8Ull28/n5yHwllMbMQeeDv0/ATQh7JTTw9PbVOpxM83F6gKPCAEavIvGcIPCeXy9nm5qZtbm6GxcF7KWBgZhGD2cxCLYVf/vKXEUO3VqtZv9+3ZrMZedascYxDHeeNtSe/uZa9V5F33eBmFilcoqH/hCYzH4R8kVcU1xdAm1KpFM59397eDkoYjB0UEi8az2k2m3ZychIQZJBDPa89k7mIcBmPx0HZ397eDgbQeDz1aFFVfm1tzUqlUqjB0Ov17P3337dbt26FXDmYIor8V199FSnM6b0YcV5+1ikRLyrQGF+v/NAW6Cv5XghnMwsGG/NHrhZ7CWVnWebGmLJOdM3EXbMIiODHA2FfKpXswYMHQfnIZi/Cz1ZXV21ra8vOzs5CXjh7TYUD+98rexiyzDXeCz7nmL7T01M7Pj6+pAAsw6xnCf5lBfsssCXp+ll9jXs++eCE56qxb2bWbDbDnJbLZfvwww8jofd7e3sh4mV9fd0++OCDME/tdts6nU5A77kO0HV3d9fG43FQulZXVwOwB1BItBCeerOpUYEnC+Udo5z3yWaztrW1ZcPhMOQwU/3f7IKnw2cwxBk3eI8qoqReYASz3zY2Nmw0GtmjR48CsIhnxBPRXMgIlVEaNaA1UcwuPPaDwSAoLevr6+H9ledglDPfKLpxXmqfzscz/ZpJWku6Pr2BvrW1Zbu7u+F5jJ2eQMM76/14fKkjw7xWq9XAMz0I4N+B8aBOgaas6LswNoASpFH+8pe/DOD21taWvf/++1YulyMRjP/rf/0v+9nPfnaJ1zAG6DN8pvKTtafylH5r2o4CZhq+jfz1irTvgzpcFgGNFwWAS6WSffTRR8HwYh4xqiE16OKAP8gb7fwo+OjvMbPI+zEmCgbpmGgYM9+pnNX9r/0C9NKUWvqBd3Nvby/oh8vKv6vQTRmIs/qZpIvOuieTuYjS/OEPf2iNRsP+7u/+zur1ut27dy8CbsU5R8ziI6Li3pPPVD+Nc95o+3EOHvQ5s4v9SNSCGqS0xedKRD1vbm4GvvDzn//cnjx5EsYDmheN4N8tadyvYmwu8iw/XovKAaWVlRX78MMPrVKphJpiROXqyUkA9uj1Ctqzf+DFylu8c5h5Ys2oDs06q1Qqtra2FmQnUY7MJfo7/SNtmvfd3t4O70Ef0VP5HL5zcnJih4eHIeo5DgxbhuaBdXHzw33LrhelG4lAWPTBcYIcQqDAvJW851U3uCpAKiw9SqjCAaPMLN5wS+p70uR47wo5VQAThIaurq5GlD3Cw7UPvnCjkjfKZgnar5N0fnhvBSnUQ6IbHdRRQRvWwa1btwJCvbKyEvKkVfnlSB4N22TeVTlAOSyXyxEBxLMJ9We9qJGuipkqX/xdLBYDioonjVw7ns24KHjgC87xTh4kilv7en0cM+DHMzyMXe99YUyZBxTv6yofs/a7frboc3iXtbU1q1arVq/XbTwehzxkjAk9AxwPNUq6hsvGAYdcQ5QJSi6CAuWA2hnlcjmAUhRm854SPxazPtPvlmHsV1FGrwJSKIqPAa5hw4w1VdUx7BDKGlUDuIYQ7fV6IcUJXo4QJ12ANUCEmhZw1Cr8AAUYfhRAJWKJ55tNQWVVKuAtGEFcR/vcz1pRTye8SfdruVwO0VPs6V6vZy9evAi8kPHg+8nkItUJJVpDOumLFo9jPuE9yls8+GBmEZ6p6SJxRqQfM54JeW+5/1wNNcBZ+kwBY0hPMlBgxssJfe9MJhNAVsYOEJT3JdII8EU9R0l7DX7BM2jTh8R6+aOOgnv37lkul7OnT58GZ4EfP+U/CtbwmRr5cSBAHGmbcaBAXMTCIuCB73vS9+vr61apVC71HT7qPwP4YO/PUqbnKdwKRugzFbhKeg/l36q76I/XQ/2z/d/wE/jVVQ2FZekmwYObADzgr2tra1ar1UJKEMcnah0ReJXOA/0wm86x/95fp+TnJm4evOfZbOok1HoW4/E4InPixiapD5nMxVGF29vboS2Ksd/E+pg371edy0VsjrjPstmLiEN4G/IGHpzJZCL1iPS3Gulqa+k68fZGnH2o9ysvUF6qKccKwjInOi/weX2Wl4+qU3gnAVFy8Ab0II1wW4bm6ZtJdB0ecWUA4bqMSRk0C6BcLlu5XA4GtCKLirirEYgyD3GesM+hU09kPp8PpyygyOjCMru80HSx+bA/L6iV4WKEZLNZu3PnTvAIawEm7f+LFy/s6dOnl8ZrHqCQNB9x6GDSBr8KKbP14brMD0rgaDQKkSHqMfKoY6VSsV/7tV+LnHShaDNoXrfbtaOjo+ABIkSaucXrzJm+GPps0m63aysrK7a+vm7j8diOj48jygHvQfEz1p8qeKwn5hLDBmbBGkTp5N05VgaFEqMFI4qQbeZdvVQ6xipMuZ7xxvCoVCo2HA4j51Wzn4rFYoRxU+kY726cpzGOFmF4s75fFBAjZw5eUSgUwpiDJPtjtQCqUOoxCnTM/J6u1+thjOBPpML49cFJAo8ePQqVoJW0nbj3mjd2iwqTq/DkOCMkiReo8M9ms0H503oe7IFarRbq1ORyuVA/hvvNLJyS0Gq1rNFohAgEs6nHn3zRZ8+e2dnZWdjTpLuxVldXVyNGeLvdDlFPnU7HGo2GbW5uBnBCeTZRN2YWjOnRaGQvXrwI+a2aGsNaOjs7s9XVVdvc3LRWqxXxmI/HF9EOhONiTBHV8NFHH1m327X/9J/+U6gFQw0OAMbJ5CI6COOqWCwGgwyeQrQT3hkzC1Ez7XY7AhaYTfnZZDIJEUq9Xs9WV1dte3vbzKaV7r0CraCIl8Xavq5XjELuBTzY3d0NvIf3APjl9Bw/L+xV9i86BEoiOeZ8hkzghA4iDbrdbkid4V3h75omY3bBOzXyCSC22WyG8FS+o0I8bVSrVatUKvarv/qrViqV7I/+6I/sxz/+ceijRufoelR+rGASqWiaE6whtToX3tD1inUcr00yiD0toncUCgX78MMPrVQqhbpReHEBt4iQ0TBixl5lm0bGYKjpc1Wx955crlNPtgeLPb/WdWZmET3S7wva0HZ9P8wu9mKj0YgYHNc1xl8FecMzzoGRROx/6mCMx2N78eKFmZnt7u4GXmk25VP9fj/oIt6w1mghHW8P9HoHXxLgwDsosS5xvqA76mle7ENNZfOAq18bmUzGbt26ZRsbG8FW+eKLL+z09DSy52f1LYnm6fdqGOv3L8sByfu88847IbUXuWtmQb9eW1sLxjT9U/5gFt1v6mRjHlRH1znmWsbVR6IgGzSilH77cWH+KM7Onq5Wq4H/e56rkXLFYtE2NjZsPJ6mUz5+/Nj29/ft4OAg6ABxtIxT6eugl3YKwyIINV5lQqZVICp5hV1JGbp6FDGa1JDNZqNVNrnfM74kVJlFocCHXj+rn/QPIwRFQBUgswvl79atWxEl12x6VCQG6+npaUQo+oW1DENImqu4xarKlfcgKJMfDoeXcv30fQghB+3DsH748GE4Hg2FDC+fKtggenpEHM/wniG80hgXGJH8Zp0omszzERaqQPDOFFQhj1f/1/cslUrhxAfGFYOB8STsKW5tcQ3MRpVFM7uk6KjHkjlj7XuvDPdpao8+d1G6LiiV9CydS8DC/f39EO6o96oQ4R10LJWhq8fQ7PJ+xZvp874ViaatQqFg9XrddnZ2wh5Qr2Sj0QjIdlLO8csU4PNo0edq9A+Cczweh0gDBCQnLcADut2uZTIZW19fDyAePzom9Xo9RAgQrYBw3tzcNDML91EwizkCnIOXcLwTaxvvlnoetDo3x8mqQba6umqZTCbMnRrNk8lFdMDKykpQJMyiueXD4TAAKPRHn5nNZu2DDz6wTqcTlBeiGTCcvQKq4es+xQjPrd8PSijx4/E49AlFhvb0LHu9z4Ng3Mf3cV4dwHtSzzRKSAE8NXrhzQoSICt5R2/g0Qc/HiiqPoWDtgEtMBRUWdXxVAWUlEntD2sPHsr8Au4Ui0W7e/eu9ft9Ozk5Cfye99bx1ggMP29xa4K/tQ3vzPDXez1B9ZZFQAQl1RNyuZxtbGxEvMmsJzWy9PlxhnocMT8eBFE+78eEz5W/xl3r393z+DgjNA644Tvei3Y0+opTZeKqst8UmHzTpO+WRDoOXp9GdnNMr6ZIYlDlcrkQsak1EGhj0bWZZHzFXcN687qCvrfXIVi/Ohdc54GtOD4Kse6RBxsbG5F6Oz6FK8l4XMQhkQQWvEyDFPtOT0WDFyOb0FeVr+t487/WFlLZ4u2tpPdQMCkOMGTdeQco9+gziD7jO/gc61kjmfmcPtOuyjpsByJyzCwcH+rfadY8zQPwXgZduwZC3OJNutZ/tr29bfV63dbX1y2fz1u73Q4hnJAyDVVYdII9o8cLpoqQAhQojLQZt6GUYfG9KpBJIIP/2yPpMEcVnGrYbGxs2OrqakSQTiYTe/LkibXb7XBWKkrtrLH27xUnnJPQ5FnECRQ6PhiojCceKzXAVIDjfWo2myGMB+/y9va2vXjxwprNZjAgqYJ7dHRkhUIhnLCQzWZDpWM2qtbRGI/HQdmjUjaFnJgjjEWiAih4iBFAVXZVhIh6gLGhJOraRYHM5/PhXHOq0OuxdO12O0Qi+KOJstlsMI7IPVfBqh45GLHmkplZxIiCYetaJX9cFT5f3davmesKnEUFVyaTCYKnUqnY+fm5ffnll7axsWF3794NRib7SUPEzaZF7WiL3yirSZ4r+APtMpYoDwgzDGfm//bt28FAYo/+9Kc/Dd6nWe/uP/cKqRcQs0Cbq87PLB6AcYXyyzqiGBJFEfHKdrtdazab9vjxY7t165Z973vfC4qk7lEAgkwmY41GI6SCKLjwzjvvRJQRat5ks9mwR8/OzqzT6YS1jqcBkFoNPjML7XW73QgAQYj71taWjUYX54ubTWuEsI+oHaLRQaxBajUAGFBwCblyfn5u+XzefvSjH1mv17PPPvvMstlsqFOiUU68H+tSo4OQAewDXdd6TKEqwApOsHfwwDAutKVzrwC/Gr4KtHEPvMrswkB49913g0EFD0NG+LUK0MK70D+zi3VNrQ0+g39rbQ7ezcwifBr+poCHgjJ6aoHqCXjNFGgFrCJSRh0DRDtxNFmxWLSPPvrItra27NNPP7X9/f1gIDAX9AngXPvCM/28qDLK/KLUYpjovEBqNMXxlFmG2iywN5/P2/3794OjYzKZ1ougkCRrG97K96xxXSP0RSPB+MzLITXg4pR/vd7rjlyrz/dtQ97DzZjoXlDQS/cxPOTo6CixFsJ1QYSryoCkdhcBD/y1Suh7lUrFHj58GClWm81eRB7fu3fPOp2OHR8fB91Q9eI40j2j69/PMX2I6yv7XwEff41+5kFknqP7ic+SQD1tS/Xj3d3dYP8Mh8NQN0tz5OcRczRvDbxsQzObvagptL6+HiL/iHzTCFCceoBH3t4zi46lRjSbTceUudT0Qh1reHxcZAIFLUlJTZo31oLaXapzKijMfcwlDk91qo7H45A2SDQb13rg6CYBnkUAp0Xp2hEI8x4+i/kQ5mo2DTHzGxDSSfXMQFEqvkeYe+SYxaAMyr+PXo/xpcIcikOr4whhp+BH3DsoE/TvSfVW3mt7e9tqtVpQQjBI/XtASXN0VSNE+wsT1srik8nkUnVVlFcUv+FwGI5lLBaLIbz49PTUms1mqFugxhsGeLPZDMJahbYakvSDteWjW0D7WAt8ryGiZhY5lpJ1CKCEAcn7Y4yQfkH/OKPYAzkomGoswQjxfqFMjsfTMFmdGxRtHQszC8yKfH4YGv3QsdI6Cd1uN3weBzrdBDNLaiOXy9m9e/esWCzas2fPgtKVzWbDkX137961Wq0WUGPCjFGwGR+fnoBCrWPrz4JnjlUQe0Gk9TU0XI11A8qO8bi7u2v1ej1UbD8+Pg73+33EM/V/j0Br3646F1dpB2CNPpPTz7gC4tXrdRsMBvb06dOIMUT6h+5BBehA4TH2IV238BrCPgFpMD40LNIrAvxPTRSNAMtkMhEvstnUQKAIIUd3sW4INQe0QJHg/TA6CcuHD+i8A4LCF5kLUimoseHnDV6FEspnHCulHhEvC/hc+RiAT1yupo4F5NtUAIVxBuhlHLxXh7kA4GFe+fHzwP/wQuQoc65RQyqrWTc6XsyLRmwwJnqPyio1tuHLOlbMP7xgMBjYyclJSJWjIOjGxkZYbyovWaP0j2cpeKKkhnacB07bjONri8xrHMVdk8lkbGdnJ8hr5C5rjHWre1LHljnX9tSA9EaF7zdj4A07DyR4ICLJ4OW3PlvnmvdRw8KT6gs4E0i7I2opzgm0iD49i64jE5aheWslm5068nZ2diJOCrOL8QR0hn9jaB4dHZnZ5aKZalB5B1wS+e/UVtD7/T5hbn3kFf2KA6PUgNW1rg6fuD6ZWeS0r9FoZLdv3w7A9tnZme3v70fktratuoKX5/5//91NEXxrd3fX1tbWwtxqVCuGNqASY6J7VQFq3X8eZGMO/L3qNPKAJGPB53qMr36v/Ff1BtaD8qa4ei3cjz3B3wp2jMfjEM2ALKE4dLVatfPz8+BUVwfUy6Cr6pI3ksIwD7lUUiawtrZmGxsbdnJyEgbSM2NdGJCGc/OdRwAxSP01HnFWxuEFlobUxIV1epqFEoJ+xY1LHCKkHsdM5iIyQftOVfK9vT3rdDqXzqCeBQwkfb8s6eZkgzHOHK+pYYswDZTb8/Nzu3v3rm1vbwcl/eTkJOQss/k0JIgaBsfHxyGUOc4Y1vx9Pe9c+06uFfULEOaah4eBhJGCYZrNXkSSACyRW9vr9SKeBtYpUSUABSinGJZ44zAC8NaguJLLrcU/WRvUDMGgw7Dt9Xq2srISwr+9UcWYYaCDArfb7ZBrHqfgLLKWVNAlXRNHmUzGPvjgA1tdXbVWqxVOkDAzOzg4sHK5bN/5zndClITOOQY746YGJ4KZNcpaYP7ijBD6o8qr5mpDGF2sFf0Zj8d2//59Gw4valBwHrieyMFaSxrjWWN3kyDCPAIAQdHZ2dmJ5KhT32R7e9s6nY49evTIstlsiDCDH+iaYr3joSd/H+OKfsK7+ezs7CzUDGHv6Wk87FVV/DBS2EfkY1J0kPQoeBXjs7W1FdJUzs/Pw0kr5XLZzs7OrNVqhaJQeIgBBpEjKB+aU29mQcHWND7ekzFD9sDnqBDNZ6y1s7OzcEa58j/WMPLHH29IKlm73Q5Kftxa0T6o0q3APmuea3d3dwP/ZD7UeCXdBF6TyWTC/iA1hvdgf1P0FoCU+g/tdjviHIAUUGSc8Qyxl3WdKOgMSKRV11m3+Xw+jLWCR3jVKayqoIWZ2dbWltXr9XCKi1egNQ2K+WFNqAEFKWjDe5pFHRWqy7AWvEzkWfC5RYg1gOFA/Sn6oW2hRHtgiz3DfOraUj2PvaT7WtNNuIZ31zFQg41n6LizT2hDfwCZNbxcDQoFl/Q5tMteBoQslUrW6XQujVMcLSIDrkrLtD1LPsQZpIwHBY/fe+89KxQKES9zPp8PugkAKzUz9vf3rVarWb1ej0Ru0bZfFx5ggryhru9Bex7Y8rLYA9Fm00gEeGncNdyrsoT/dW/Sp3K5bGZTcAxn2Wh0UTvs+Pg4RIn5d/Eggqd5cz1Pj0j6ns/RZwuFgj18+NDefffdwFu1MOBkMgmOO1K9ksADrVOgAIDfa7p/NaJLeUXc/owDkHVMmWP2OSnN2Au65pQnaV+1TbWX0IOQ3zgRNjY2QhuTycSeP39u7XY7Eq22DCXp4NfRG5WuDSAs04nV1dVQSArjXgtwsQhUmMcxf0Xo4za7R46VNKxMF5W2qWg1vxWdiiPP4PRz379ZpMIzjmlzPxsP7zLeP23HLN57OW/OFp1TZeD8Ruj7cDA8LbrpGFMEy3g8jhy/ScGRTCYTEDg1lmHgIN0oh51OJ4QkqVGp6HEmkwnGCsxGj9/Udca7YchrwUd9R94ZpkQIs1dmMZTG44s8N5RIFLharWa1Ws2azWYkxQOUkvHUfGpFRmFmeDe1KA1KM4ThR7/xBqPozVuvjNcyfCCJqf3whz+027dvB0H68OHDoKirAtxqtQJo0Ol0bH9/P1S5RyHT6APeQ0EmjEbmUgUZa5i1QT9VUGFIqHLDmmB+IHgOhs2DBw9sMBiEPdvr9SybzYaj3zCqteilUpwXIu67q9Cs+1dXV4NxBRhTKBTsW9/6lpmZffbZZ9bv963RaNh4PLa7d+/a6upqONrObLrXGo2GHR4eBuFItBL7hTWlUUlmFiIU9CgleAcee/gP64D9w3XFYtHOz89DxIoCn7r3OR0AoOLk5CSkMGDssw7oE/yKcYDH4Xlkfa2urobnFAoFe++99+z4+NgODg5CvwEn+Js1rwZuJpMJqRRm0yMQMUJ5f/gOPGIymaZRKaCZNPfK73yOp/I9s4v1fvv27TB3ZlOPnR5HS18VvIP/o7AxT1qfRsE/9q6ZBTDZG8dEwTH2ANqMpfZtHrjPmGuqmRqf9JFwVuUL1Pig5sXm5mYwJtnzACPKdzAamCMPgKgBq8Cyzp0HhTQKRXWlOG8abSSR6k2sOfqlY6iylGepEaXy2Bvi3kjzxpfqE/q9B2d8P1TX4zrVDWkjDlTR9cN1+r60C5DIPWYWeJV3/Hh6GcDBVdr2Mscbr0oAh9VqNRTS5fhjTcNM6gO8Vz3XCviYXS5cnkR+LcXdm81mw9G37K+4PsYBTTo+ceRtAb+uZ90Lf4HHbm9vhyOkrwISJF2/KM2zf27fvh0iTfR0NH7DD0n1hddo7TTv1PCAj4IV3KNt6LVKRLRxDYCe6jOedygP0+hn9G4P2PCZj47yPFZ5mI6Dvjs8ZW1tLRxt3ev17PHjx0vxjEX0wevwmJdyCgPf+QW9urpqGxsbIdSNvNUkgwLSwfeGvy4ij+5puwgrDTOEMCq80OXZKpBn9VUFEPfyO0koe1RI3zXuHi8QNTyd9pKQyTiKW1yLLKg4xu0/U6MPL4P2HWWWfHGUKD33GmZ+enoaFDOOcUOxppgiobBUPN7e3r5U2Zd+mlkISVZFjO9ZE974x8sJo/AoNu/Nj4bg0YdMJhPqWDQajUuovOZioWyqAQETRQnGk6GeU7Mpgg2AoAxODV3aJxdNAZebUGCSEF7+Z81+//vft48//th+8YtfWLvdtgcPHpiZBS8zgh4AgWNROXFDx1q9P6w7ABgMPb1ec860nwg972HwxpgqsB7QYf8TlUK49osXL0KIP/UTxuOL3HpOLfDjpkIrSTDMAhg8P4ib36S2fQFXPMPvv/++ZbNZ+8lPfmL9ft9arZYVi0Xb3d213d1d+7Vf+zXr9Xp2eHgY5qTVatnJyUmYH5RLTSnRVCSANLMLnre2thY8euTvwwcIAaRtUos42QQAAZCBCCDWBBFMACYUvXv27FlIu9N0IXgYSkapVLK9vb0wf6w7XSsACMzJu+++a6VSyf72b//WzKa8k6gI5gkwTcFYwjB5NuAYax6FQ6N11MhVQztpTfG+ymt4N/qritSdO3dCfRfAHSXWvB7ZCVBDf9gbRPcoKMj9yJZcLhdAZYxY9WibResAMHcogxyxx/5nPpMMUE2D4DNVgjWyAL5AGiJK6/r6uq2urgYZ0Gq1IqfIMJ4K2JhZiHTh+YCs2i+zaY65Al3wdPWYMWf6rHmkPIL3U5mi/NTLXV0zkB4jqjyOHw9s+DQPSPeU9jUODPc6Jc/wKTA6j9zHWJtZcH7pHlAdGABBdQQiNFut1kLj/brRPMPk9u3bIX1pMrnwpI7HY9vc3Ax6SJLBp5FoZtGIkLj15GmW08P3G56nzpM43VaNV+3XrGfPAjZm9VfXGX2jAGW73Q5yxdtZUJzsj9MDPC3iCIrTQ+jr9va2PXz4MPBxD67yv4LBavxrWx4E1WhEtR/4mzZox4NNfOb5JD8qT3lPbBZ1AOmzAB7ibE1I5YcCkjwDIFgBRpXdnAa2ublp3W7Xnj17NhNAWFSfuylg8kZPYYhj3vyfyVzkf66vr1smk7mE9qswUu8Bn+nffnH5azx5BCiuTe+lnoW0qUKngkUnPuk+ZRYsKn2WR1j1b2Wi/hpoEVRRmcAiCJW/l5BRGJkq0T4kSA1x9cBp2LmOPwrdZDKJVLsm9J++AjJQIIujuvh+c3MzKJ0wD1VwYRpqHKqXxnvhuZeiNhDvprlUZlOmhRKLt4L6AoRPr66uBtBEFdpMJhOqWQO0Ea1AeLcqlgo+0Q/AF2o4MOf0h9QA3tdsusYwomadHEB7SetkUSZF2PTPfvYzOzg4sK2trVABfzKZhOO+1tbWIkit5kLncrmQ/60hwBiF/M8cK49B4R+Px0FI6DzquPAZwkMNIG13PJ6ehoGhA+pdr9dDyC4h3Ofn5/b06dMw9tVq1b773e/a0dFRUL4WHftZ3y2rIPix4J0LhYLt7u5aqVSyTz/91DKZTCRVQ8Gtvb29YLBmMpngjd/Y2LBWq2WtVisSpp/P521vb8+63a69//77kaKynCWtdRCIxiEdYTy+OJJVve+s5fF4bOvr62E/IhtQ0jKZTDAm6S8GM/dh5JZKpQhQqAbU/fv37b333rOTkxPr9Xp27969EFWEYQzwMRwOrdFoWKvVCgYm76jKgkbW6B6Fr7LuSd/AQPeh7xgt8HEiYPS0giQl3BujSisrK3bnzp1g4MYpUtynvHcwGFi/3w/jklQAmd8ACAoMa5oA+xR+Wq1WI0duEQVB27x7Pp+/VAiLMfERR6rkaxQHa5HxVR4FqEDqA3yftjc3N0Mh0DjnBOOmtUi0Tzo/WgvGX6P7XOdkFsWBkhTBVvmv6QmsNzX+PYgAsQ+8fqf8XXUfrwv5CAs1Dubpix4k1og11pka/zpu3vBVg9SvCS22qkaNp2Vk5zy6ybZ8u7PoyZMndnx8bB988IGVSqXAwxlHeJiOh5Lq1HwfN+ZJujbX+e/VRtF51xo9hNv7Z+va8wYt7c2yQ+Laifsd926sS+Wps2S19l/fdxYtuk78dVtbW0FnU36jJ5TRH3Qns2hNEe+gMbtsC+q8KwiqoLKCEb7N8fgi4jebnaYNoOcD8KtcUnBA+TiEA0KBAMbar23lhx4k9aQOFF0rxWLRPv74Y2u1WvbLX/4yONXi7Gjf7ssCEW4MQJjFUBhMjrPzxpYKfFXqPGqsE7MouhfXT0WDtH9KccxHBRbXxCHT+r2+n++DXmNmEQYb12+uiWtPPZ1KiwAEXjmYxZhUkdPQYc0D9akUGAXaPxR+DRdjo/J8mDpt0K7mSxYKhUhO8GQyCefEq0KQZICpIPOoJN/r+5ydnUU8W5wnToi0hrZyPe+PEqkMFeMeg4vIg8lkYrVazTY2NsJ+OTg4CKANBizeN117KtS0KJoyYwAc5kg99XyPp1wpaW0sqqjE3YdB+uTJEzs4OLDf+q3fsvX19TDXXKfFEvU9mWOtIs8+wTCIU0jMpkaZr6yr3jO/p1EKVRnSvYuAYDy1FkY2mw3ecdJuisWinZ6e2tHRkeXz+XDc4f379208HodTAK5Cs/bysqQeBDWof/7zn1s2m7Uf/ehHNh6PQ7QQ43h0dBTWJ3PNDyCfD1dtNpvWaDTso48+ChE/7InJZBIJ7UdxYE33+/2QY8zJJ6RQjMcXdQhWV1dDZAv7gj1Kagl7l73EOc8AeMqrlP+Ox2Pb3t62ra0te/LkiTUaDdva2rJarWatVisSxs8ebrfb1uv1Qt0DjFmih9RQZU2yF3whUI6A0hoCquSSl0+KEwCdRtQkAQgqo72Cls9fHNdImL7yVq98adim1nyBp6o3Wg1lVYwBPVH4VY4wZkSlwCcJVVb5C4/gHn0moJ/ONesI0rYUTGSMtdYCY0/NB4BreBV7QnmxGjt4SiF9X9Vr4vixzpdP80jSVWbR6uqq7ezsBBkOQKP9Up7oSXmTRhcqGKRjEKcb6fe0pTI8SV+kbTVA6KeP6FPDX5+p60RlPN/RFmtvXpi1vsfrSMi4pD7qmB4dHVmr1bJ3333XyuVyAOZ9VEpSOx708ffErVMvq5PAA/8/+4bTQDzwyW/WBO/h+xU3LnGGHH3ztoPvs46nAlKLUJLef931Fff81dVVu3v3bgDvVQ/V9+VzX2uMa+FrOhY6/sqjlB9yv+rwcQAd+jeyDp1B09l8pBNtqjHvv1P+xlpiDet46bj48fTrwtuH6Dj37t2zVqtlT548ia2JEGcDJtFNAAo3VkRxFt27d89u3boVKkvqhkti8CwIjwSZXQYc4kgXr6ckYcKC8N/pxHvGoYDHIkJ41gTr+/lFmdRvFJ9bt25Zv98PYcLaZhxC5WnRxYOgn0wm4bg2RWzVcFUPN96We/fu2c7OTmTjnp+fh3xc7gexp7iOKo0ADf1+354/fx68TLrx1NAhnArPIkS+dKVSCQqQWbQ6tG5kjAZCoWHoRCTggVFBq57JbDYbwqKPjo4igoGjJbVGR7vdtuPj4zAWzDmgBe+jSKd6fDDiVOgxRnhweQf6zfXKXK9SvGUZZrSxsWGbm5vB80i4OEWDGF/W1M7OTmRd03+u88dd6r5RnjOZTIJnkkgXxomx1ggD5RG0qcAL+0C9ZrRjZiG0HKN1fX3dxuOLHOdKpRKMXN7p8PDQzs/PbXV1NawTVdL1nZLG+6rAQVybGnmTzWbtiy++sFKpZN/73vcixuqdO3fC+sOI17WZyWSCF1XnTI84XV9fj1R011oDjDtgHmskm83a6elpMBoxuhXRX1lZCekhgAycWa/zNZlMQvg9RZ8w/NbW1mwwGAQwT/cTfX7y5Ik9fvw47GeOp0SZpk6LmUWii+r1unU6nVBYmHdQjzLgC8+Gx+jpErlcLqQlEUmhJw9NJtOjShljPQs7DgxX5UjXFikLpVIpHMHpZRV9xJBQkK5er9vW1lYonsh3zIVGFOneVSCAyBeid5TXMtfdbjdEvFDcDTBaFc9sNhtA4vX19ciRlCpf+A3o02g07OjoKJL7r/KWSCsiRDgOlD6QKqPgph9D7YPXi9B5kmS+6h3XARRp/+DgwNrttr3zzjsh5Bzep/oLYwvAqzzSLBr15vs6D7Txa1Vlrf7OZKa1TIi+UzBd5x9ZSH98uoonNZrgS8jVYrEYUr/Ui0kfkvSxmwJ+49bBsm369aWfKal8fPDgQahXk+TAidODkz7zayXOZkjqF5SklyvQCe9Jsh90/+veS7pO17M3Zv3z/XfwR414U0dFHHimpPwnCchYFFBIsiHU8OV/1X9UnnhCpnnQFh7sU8h0nLytxB4FuAb0U9lvNnUuKcGrPOAAse99KpnKAO7zNWqSnuH5l64TwJThcBhAfr6bTC6iJYhE+OKLLyLjonx31hzqe1yHbuQYx3m0vr5ud+/eDYNidjnETNvyxnPcZk1Scub11S94T4p+xSlQceiQ/+3bSnpO3IaA/EKj/TjEkpD4fD4fig1eV/DQp7h2UGzL5XLECKA/9AkhracLVCoVu3XrVkRpYLNpwRKMf5Q776EkZL3ZbIYjYxg32iLCAUUZRY31pApCNjuNcIh7b9ql+BHKOc/C8B4MBpc8qjpXhPeq8eH7Qn/G43E4EQGGqN9pKCsACP97IIH317nFMFFQj34q8OHH4SYJRXp1ddXW1tZCsZh2u23Pnz8PRg19qlQqoXKzVyjxHqingPWiDJvxY+2ORqOQ8sJa9mCBXxteiMQp/TrvgGqZzDQnvVKpBOOY6Cw8361WKxTU4yg/1q6S551XUQ4XvYf1xZo+OzuzarVqd+7csVqtZgcHBzaZTGxtbS3UHlDBSdoR78heYQxQsBGcGG5quDKmRC6whjudjmUyFyeSrK2t2draWiRtQucCDz055z4EnDGhf1oh3MyCIqekygGAQavVCsftAqCura2FOhLD4TCAjlowUPkI/dK1TXQQfFWNF63sDECoR0VBXq7GgYh6vSqcXnnLZDK2trZm5XI5AKNqHClv0VxVMwsRIpzCw/Uq6zwvIs0C4I4cdP4HzNKTEKgEDqBSr9fDGDJOClZoOL16jhXYoJ9EGjSbzZBG1e/3Q2qSKomkrZhNgRuMLACUJFIl0Y+R/u+Vffrq5/46lM1mw2kmd+7cCXOi7fs9q2vIr79Zxpg3mHgGY+Lv9Toc3zPPWttIo0V8P3zUiQeRkvRN9RQDLqmOwR72aReM0U0o9q+SMpmLnO3Nzc0wz/N081ljqnMdR8qP4q6bdb/XexRE4Htv4Ou9/tn+e79X/fvp53HgJA4GM4tEm81KK70qLaMLmE3BXXW60mddx2rjJNl1fn+rnea/43MdT56FPk7f9N3gv+jG/OZ5cXxRx9rPj7cH2eM+rRWaBSJ52ewjdfSZFCkuFov2y1/+MtLnm9bP59GNnsKQxPhAZRVZYuEwqUoIVlBfrZJtFo/YeYM/yQhMIs984t4lDolVxueFmqdZgEMcKhYHVsS1nclkQuXt9957z3q9nj19+jQisJUp8ZlHEr0RosaWEhsUZQflS8dwNBpFDAizqZfRC1QzC96YVqsVQpDNLHjmUaxhonjl8cSpMaKKAmstl8vZ1tZW+HsymeakAogoE8pkpt5nr0gPBoPg5cQwQHlkfROe3mw2g5GDoomXjPt6vV6IpKAQGPm7d+/etU6nY8fHx7a2tma7u7t2eHgYCeEm7JXKt+wzf5yZggYwOg39N7NLSnwcLbu3ZlE2exGuzjoClBqPL6r4Z7PTNA8tOBiHuJIf75U+9XjB2Dn+FMMVPsS9hNmpIuh5Eeuc5yjyroqxPtdsCuSwdtlnrLfz8/MAVGEAPnnyxB49enRj4z6Lktrc3t62UqkUPPObm5tWr9dDcUhqArB2qPOxtrYWTpXQnPLxeOrlq9frVq/X7ejoyAaDQfDQqSE/Ho/txYsXkXkARGDPVCqVEM1B7i0g2f7+vj179szef/99293dDfVFdM1ns9lwT6fTCWCg7l32GcVOMdYHg0F4Pu3Apzh2knVBAUn4Hjxpb28vpFbAR7gPUBIwAeBJa0Gwv3VdKQ9U4FdPcqB9/TxJnrPWMYQULPDKd9x60r1IW6oke7CD+cEBAbBEAWHGhdQQfrMeOd6y2WxauVy2zc3NkPNaq9VCSpFGlbGOj46OrFwu261bt4L8Yg4w+keji6KguVwu1AUpl8vhKFyVi6oYK+Ch+x++zD7T8VQ5Ba9Bjur3Xt57Xq4yXud1FnnjlmMbAWoULFS+rPNhNjXa0fviAAR4CO2xRmk7LlVC30sBZN6LyD2tb2JmQX7SF02NGQ6HIaKFNeEjwOiT5nbzXG9gqZHqv/Nzc9N0XXBiGZCaefE55Urq3PDP8Pq4gkEKLHKP/84/R3/7v/W5GLPqdOBZukaTwAptX/eAB/ri+qHvpYYz6Zxcr/xR70+a25fh9Mlms7a9vW13794NOoBfH3E2B+RBZF0L7DXS9xQk8DYJ/I+9qZFQPId7lf8qYBi3DvUevvdzTqoTJ0jpvLHH4/prNgUZ9Rlqx+oRsegeOueZzMUpcj/4wQ/s9PTUvvzyy8g7eNsuaR6vSzdaRNEsGqKvzBgmqwxUAQTdsHp/nPd0Hpq5DCUJUI/uzyMPICTd799x1iQmGXEeQIGxYXQinGZFInhhsoxgoV9JKChzqXnlZtMiQwhONhZ9Ua8A4ARVfHluHKrIPbSliqBuZkJIyVUEaPAKDaH/KlQ0XQaDBQMHQUFBPDMLYcYo5DAvwqVLpVIomAWYwfe0R1E4PKbFYtE2Njas2WzGCnO/XnzuJqTMizb8WlUl+mWQrjdADIwm5gwvYb1eNzOL5Enzm/HX1A8PZilazdh2Oh1rtVpWr9cj+c/apke3tY04wNCPv/ZDlQmEkb9WhZrm3Y1Go5Ca9DKUAWgeD6C2CIr1+vp6KKJmNvUuK3/S+gOdTifC99lXGE8AKhiJGp3E73a7HSm4poo/nnly2nkG+4eIpUwmE4xGNXghDAry1c0sRFRpiKsCmvA89qyCo8q/+AxQRPnZeBw91pX3U0OR6xSoUo+K8mW+T1K8VbHjWarwL0Lek+q9Sap0xyk12n/6prJB1xLyDD6htQP0vdlrgCqs1/Pzc6vX66HYl+ojgKrcS3uAluxJLfqbzU7PCNeoPD0+2IMhXheADyMT9f0xdpPkLP1inSfpCrr+FHzwbS1CrHv2kKYx6nMYW1W+kW38n7Q+eY5fRzpmcXyY771uBDGmWrBT+a3OM/1kzLS2kdfz6C/keVwSxRmxL9uDeJX2lwUedF/xf5wRP4+SQASVxzqH3rj3c+M/17WiMlwBXUhrdc17d9rT58ftT90j2pe496MdDc2P0yM8efl+U+trPB5buVy27e3tS+k5nt/NeybXqDzy/Fn5qDfI4d/ozNlsNpLelkSq70FJIIca+zoGyGFkg9lUThGVxdh4RyvPU2BD+TOyDr6lurHZxZrc3t62bDZrX331lZlNbROll8lXrgwgeAMmTjC988479s4774SBVMBADTqEsleQYOJsFoS1MnEvQDz6vSixETV/UdtWFNwbl96Ioz39P07Y+XfWNpIWvzIdnq/f4cF4+PChdTod29vbuyQAPDKotAhyRdVvPO4YzTq/hOXSLy1UhSGhjAEFBOVrc3MzbBxlHIVCwQaDQXgvvApayBGli03Hu6BwghzyriigmmvP2sNIyGSmldqVaaG4UxsBxVXrQmguF0W8ODqOnF9yiFHI1Ci4deuW3blzJwghwt0JkUXRWVtbMzOz09PTSP/xnmsIutn0bFwMPJ6LBzROYC6jSMwiFQD379+3e/fuhefu7+9HwthRzgFkNGybftOWChxVxtk3fP7uu+9GQpeVWefz+Yi3WI0r35YCdXynYXEYFblcLnK+Pf3m2fCebDYbagHQBvunUqkEoCVuPubt56Rr9LtZ80sxx9XV1VALoFar2cnJiWWz2VB3AKCHCB2iiTDqFeQjkufs7MyOj49tOBwGhUQNQ9I3OMUHRYF92Gq1gjGpNUz09JZ3333Xbt26ZWtrawGsKxaL1m63g1cym82Go8bwbKtBQV/y+bzV6/UQITIYDKzb7YboGCKnOIWB9Bzmudvthv3H/1qjBZ5KFITyE+aw0+mE6B3Wkjesdc7hbxwNyVjh3UDOxoVWK1ihEQ5bW1sRDy3ADB75jY2NiEKsShVRJoPBwJrNZgT4JtWAUwrgv4Bpk8nEtre3rVAoBF6FsUedgdPT08APSqWSbW1tBWCIPcsPfEILG66srNju7m5Ixet2u6E2AmtCxwpg6+TkxE5PT0NtF9aZygPGDzCTtuF71WrV3nnnHWu32/aLX/zCzCwSMcZYKgCuPFE9XXG8Ms44mUdcS3QPcsXzKlW6zaYnWRBRxZHEFETVeaCP3gmgY8fcaP8VBI4DHhgLZDZrX2WEBzJoG+BQjUD2wXg8TeH0Oo0fd02XefbsmZ2enoZ7b0quvixS2TDL6DK7HBUSp8smyao4QIl2POCkII2uBShJ9/b98XLPgwr6mW/HR1v5Z6uRqm35vsSBUXGGIHpmJpOJpFvGja3OwU06Hxhv+qLEmBFhqPaapoXRbw9+s79nPZdnMxeMbRzAB2mUIv/TFnVK6BP6u0YOw2/VgYCs16hKbBR1wCnwzVxo5JHKbN7JH2nLe3oQI5PJ2Orqqv3gBz+w4+PjSCSCrp84/nIT6+GlFlEslUq2sbER8jv1evXeEE6ogscj1WZRJYbBjtvYsxTpuO88s4pDuHXSvZDwbeszkhBC7T8CMqlvcfd7pE+vzeVyQTjH0XURKZiDb1ONKgVczC6EMKE+ZtMwRgAC9YqzCeO8W7y7InMagq45YurFVfCHZ6kQ8qCTZ8LK/GnT59xTEDIOUeX5vLdGTACmafVxBbL4XFMz1MvKGvVKlCcvrGBwysz0NAsEgV9nN0WAh9VqNRhjjCmKvIaoK39QvuAVDj5L4ksYu4BGzEOcwqB7XdtWgeLXjldglYeoh1ejqhAw7B0PIubzF0e/mUWLD+l1i+zr6+x9zTknnB+0P5vNBkOSsWRcAckIYfYKHSCAKgM6lowPzwZMYV44AcUselydgmYABhj2rHsPsKkhrsdvAvwwdnyuhg79ZU9rqg38QY0q5hV+RloG1/s+MQ48B2OMcfBhtvqb9eblKjxWx1wBVE86D6wDDa9UXpLJZCLHYymoN5lMQkoAhpXKUT5TcI45Zc8y5zpnENcBcLP+lDfDZzAodW/AWwG0/ZnfegQZa4H9rBFVerSsygTm1zsAdNxWV1eDLM9kMuFEB4AVTbPyugjt8E46tioPk2SFJ21X01Y8n4qTFX6dKRCADEoy0PwPz1AnjufbqiN64vN54AHvqW3656hxpPvPG75cA/+nmKOPqHvdaR7ArLTM2jKLByH0t3cO6Hgrz9c97HVsfvy6mLWOfJtqe0B+D8zaD4uMifZZ/0cXJSpX+Q19uw4tez/72Bu6STqGH5c4EEXH3I+V18XUbtA244AijXBTPYP9rydCcC86As9EJiA/fdRrHB9h7gDCPciq96rtCW/UvvCOnvL5i5O79HQn5uRl85YrAwhJxpZOer/ft0ajcUlYoTiQI+oHzxfrUk8Qz1HmrQo6NGvAPelCUkYVxxTiGIffLCow9HsvKHUj6MbzxoHeoxTXBkqJLkzP4HQM9X+dy1lE+/V6PSi/LFZV3AAByOXHm4PXaDQahZD+Vqtlg8HA1tbWLJfLhTbIr67X6zYYDOzg4MAKhYK988474R37/X44ylE9LigtvCsKDMJf1xXKuJlFqpXDXDAUUISp4K4KUC6XC0cNmlkokuZRY2W4nDygxiEeTZ7NcW61Wi0YQewjfSf1ZuTz+RCRoFXklQiVnkyiESLcr0qSru15a2ORNTSZTOy9996ze/fuWaFQCLnGeN8Y606nc6k/RAfAxMkj9yFiGl3A/DCPeLAUsNEwXNaGT/fwykuc0FKQjLB7vVeVV8ZUeRmeaECwYrFod+7csdu3b9vjx49tb28v1Dw5OjoKHn6eofN0k16HBw8e2Orqqr333ntWqVTs+fPn1ul0IgUPMX6Gw2HwKpPjrZFJ8DtqA7D+mEfmfXV11VZWVkLUAMaT8phcLmfb29vBIMxms5F9BsBQrVZDAVQEOgpZPj8tQIuHmvmhvwh0anKwZkhd4rSMVqsV+B6VyNvttp2cnAR+h2e+Xq9bu922Tz/9NBx/qUoGoAtRMfAF1iDvr3tVjWDmbjQaWbvdtkwmE4qyUrSz2+1G9oeP8GEtq0y9c+dOiKrQPY8yyxGfnG6iHiA1IlkrWuhWgVnWCesaZQk+yU8+nw81buirRi5oiClzajaNGoD3VyqVwK9zuYtilv1+31qtVpAZCoaxBmu1WujLrVu37Fvf+pa1Wi3rdDphLbLOWW+M5fb2tp2dnYVTGJhfoiZ+8IMfWK1Ws9u3b4e5+O///b/bH/3RH0V0J8Bllfke3PAKOL9pw9cDgpQHAhwpOOGVZgXScBJVq9WILqRFPj14SL8VcPHPUJmuwJsq56wz+HmSzqak+0uBK30ua0zHmKgh3Sfcx3o9PDwMp4LwrNedvAGt+9FTnLGjIPAs8kCNGlb+J05n1z7o8+Jsg0XsAl0rzDd8SR1A+q4KeCipfbMIqbxRoCSfz9v9+/dD+is8p9vtWqPRSGxP5/A6TgTtn4Kw6iBmDDzP8baT8iLeU78DyFYe48lHX+m+1HUIiA1I70Fn7JJSqRT0bdJbPW8h/VCdHmYW0TlUZ1WAQp2X2m9+o0cpoK5jpfITfUjfk6hkjXaAdM9e1fbzdOM1EJRQzL0nmMFVA0/v8eTRHaVZ4IHvSxxpe/ocv2A9U1JwwG9Ivyj4Ow48SOqv3q8LJA5U0LZ0LDHAtcCWXzjLolSK1vrwbTXQmGO85xiHPooD8lEBSoBKeo169+KUI99f/c63zzh475mCDTxXlXTeHaNRhZ56mrUtfaZXUsymtQcAH2hLQTW8sIyrGr60rW36MWGelNH6ftK3RQWeH+tFlAVSMdRIR0Efj8d2enoaUQIYH/+3AmX6vh699vuR9+NeBYO0vXlt+ffS32ZRIRfHW/hODQH/TMCiarUaOfLTKyovkzCU6vW6VSoVe/HiRQT8gJg/9Yzoemc/853Z1OutigOk61GVCjOLGIcKwPpCZ9qON0L8usWg0T2ka0vfQfeO5jpqqLl6+JlbACxAAdJ3FIjy/MobShqZo+sgDrDW/zXyQoFu9qHKbD9+9IcCknGAejabDUCJKlFqEDBepJ+R3qGANH3SGhOsFVXIAQp17Oin52/+XXTMdI4BtGjf83rPX/Ve6rag2JtZGNPJZBLx3ptZABQ0lUzfj1Nqtre3w7N3d3dta2srAOf+3ZPecxbvirvfk8ofL0e9kUBf1VNnNj3u2ANFOob6o7LJv5ff02rA6R5N0unU4QLNMli8Qan98Yo498NT+v2+9Xq9UHjzbSed00UAGyhOb44DEVhfcfOqcl3X0TxS3pkEICjP9DpH0jjMsk90jcf1Ufl8JpMJp8yYWZAfcfIujq4LWKmsNIvuhySdM278/X5lHj2v1n2LzFPS+73cj7MVvQ0Ej6BwNbyNWkaFQiECSPOOAM/IA7PLa0d5k9drFGBQmcx7qH6jTmXtN2Ov9le1WrVutxtJc32ZdOMpDHEbwCOH+rca5HiQESy6OOMM37iFmSRI4za63qtGttlUwfMbRp8NEwFJR5BrJWkELn3wzGcWU0t6L72PTUf/1JCt1+v27W9/O+SYdjqdcMyWR5Lj0MlZyJS+93A4DOkqeGswbjY2NuzevXuWyUxzo80uPO+cG45ypRuYKIDRaBRqHuTzedvc3IwoIHqWOUotJznQb/I1OcpLQQCYis49jEjfm+gCnpnNZoM3U3O7er1e5D7+7na7QfEmf3o8HocjxhqNRlA8CVNlHGgH72s2e+GZ/eijj2wwGNijR48CGj0ej4MyfnR0FAmBVe+lens9IDKLPJrs33URAUXaCV5RcurVY8pYTSaTYBzqsZWTySRyJCfrRol+KjPHS8T/eCXVgPE8RxUHLyx0feg4cG2cEaZGJvdms9PcOXLs9Zx4+Mv6+rpVq1U7PDwM+e8+39DPl/Z3Hto8y0vBXqTw59ramlUqFWu1Wtbtdq3dbgdDKJ/Phzz/g4MDq1artrOzY7VazVZXV+3Fixf2/Plzq1QqIQpkNBrZ6upqmCOeOZlMQkTCvXv3zMxsf38/eGE0PSqXywWPCPyAEy0mk0lIpygWi5dqlQBmtVotOzs7s263a/l8PuTakzah/IexGo1GIdKHiINmsxny3znq7tmzZ2EdDwYD+9nPfmbNZjPUdFFPBTxWFWL2DpFJWlBQ0yG87MhmsyGKAzmrgC+nZPA+pBVBHImrXhdNIWAsSqWSVSoVe/jwoWUyGTs5OQn7jrWsNWpWV1eDMsX8ffXVV5Fimcwt+xy5g7cG/sY4KUjNmuaZ8GlSDACOPRCG11oN/fPz8zBGRKUMh8OwLsbjcUjj4aSe7e3tkMKJrNra2gprzcxCJN+9e/ci0XS//OUvbTgc2l/+5V/arVu37Ic//KHVajXb2NiwDz74wP71v/7X9qd/+qf2X//rf720T+EpunZ0TJTXKc0CJOGZAL/aDn8roSAzt76wmffgJRnuOrceeKe/fs7NLpT8o6OjCEipNZVIkSGyDz7A9awB9iRH/iJn45wZZlF9GL7w4sWLALiyt72sjOPJ8/h10vXL3LNou4vKd/ZbUh0l365ZFAjyIAFriM/426ds8exFSPVwrw/yt9og3pERt+50b9EX3x9/jRrKHkTQtaigFPsJfQE+zDHKy6yrZcfNzIJeigPRAwP0D3nEO+ItV9tK+4tu6/umkQkaKYxuyP5T0MiT6nTK++C37Xbbbt26FU6D2tjYCHOKQb6xsWGlUinULmk0GnZ+fh5qJmmEPOtT9Um/xvV/5CuyWaOvxuNx0Ik0aosx4Blra2v2G7/xG/b06VP79NNPY+fO233XpZcagaCbSg1+nUyEt9+4ZpeNZW3XgwhxCi9txP3PgvNMkTY96ucVcM/sWLzaB4+yzUNAZ6GUSeSZjn8mC49q/tclZYrK1DyQo95SvOQa/uX/huGoAqHjAcgAc4pDf9nEXpnwv1VYxI0zn3vPsTIEzwDixkeFmwfBIO2Tvo8/QUERXwgFl+KN9FfnR9d5HHrrhbsHtxZdh74NJQw5CMHva5+osOGdPVDhFQbuo9/+nfzc+799+6ooeF6hey1Jafb99s9Tgsck8TcVSFyjyoOP3krigTdF8DrAD+0f/TaLKllciwGF0qOhzRy3p/tK158q6yo4eSbjxXMwIhXk1TWCd9lHLjF+eIhReFBYtPaIgnAKKsF/4GvtdjsABisrK5GCeQC7FHFEIdK59PtRlREde/UA6Trw/EIBBn4r/47jaYyzGlhx/ETHkjHSI5m1b3EGLGteFZy4/eXD2f36U17ggRS+1+d57xn36+fwfk1nQ5kFOOb5KHhxPF+Nevqjniw1lBhL3T8rKys2GAxsY2PDdnZ27O7du/bOO+/Y0dFRADeuS7MMPr6Pew9/jfJqxhPQRY02P0ZeDvCZ/608WZ+p1+n9ahQqX/Fr0UeA+fbjZIyvI8KcURyVCKOvi16mHIh7lpfJcXXPkvoUN676v9/vi5Kfv6RrPJgwS74rz1EQQ9cdvGGe7rSoXeD7q+NiNi1S+nURTgJ1ukBx85SkC3n9yiy6lnhXr5PFta97V9tQ3Yl9qvfxP3qV8l7tg+r7amcg1+N0MeZEAV21K7VNHAOqhyq44vmN2iL6/ryHl30vi24EQIhjIChTeHpU2cBLywJMMrI8Mgh5w51r+S5u889a1OqZUMUD4a0LazweR5QjMwtVmlVIeQST5/DsuB/t26zJT3oXv3knk2mUQNx7+42m4ziLEAyKDk8mk3DU3Pn5ue3s7Nh3vvOdSKXvXC4XjikjlI8cXo6DA7kmn598483NzUjKC8ocRbj0WCY8DYpsqnfdnycOaZETNVoAlDQ0mecwDmpUKSNYW1uzTCYTjATQeUJbzSyMAeuM47E0X1wNbiIR6PudO3dsMBjYV199FTzBk8kkGO2ETFKkD0VVT5dg7r2i5dcDayZpncR9fvfuXfv1X//18I7Hx8d2cnISKuI3m01rtVqRwny6h3lXHxUEqSeLSBQ1IjR0TMPRJpNJJCpF35fn+KMEIQ8kaLqHGsF6ve4xvZf35WxyfT+MbMaCtUv9mNPT0+BFX3Q+lJL2fdx9IPP0FcWlXq9bJpMJtTmIUCBPWo3mcrlsJycnVi6X7e7du1apVALAOBxenKZwcnISvMNE7BCl8Nlnn5mZ2fb2dsixhw80m0178eKF1et1u3v3boiWoOYBzyqVSoFnj8fjCG8aj8f2ySefWDabtcePH1u73Q6eHaJCdnd3bWVlxVZXV0NUD0Yj4A7z+Omnn9qTJ08C36IWyv7+vo1GI9vY2LBarWbHx8eWyUxrHjAeeGVyuVzk2FczC+Cs8gP90X0NXxmPx9ZoNAI/0DoFZlMvbRyhzMHj8aibTSvVm13ssdPTUyuVSra5uWnD4dAajYZlsxepDfDjwWBgx8fHgWfhhcnlcra+vh7x9mpdBgqgAsxQAwF9gpoOmh/vwS/2ldaxUGCg3W6HqBP2Xj6ft93dXRsMBvbs2bNL6wv5RGQdkTC1Wi0c75jNXkQ/MAfj8Th4yTWSMZfL2QcffBDmpVKp2Nra2qVc/t/+7d+2X/3VX7U/+IM/sP/yX/5LJPXCyy/mUH/gPRr6G6eke8BAFWvWBHxPPcMK4iFXkEcewPNKMvPlQYZMJhMpGJbJTKMAdHxyuZzt7OxEAEaiO/r9fjhJhigD5ACRbRoqns1O662gz7I3AXO1uF2j0bAvv/wyeDh1fJN4cpxcXQYImKXDeYDsJkiBOE/Hx8d2dnZmm5ubkaNPPek61N8aYeLXone2eLBQ0w30OWqMxek5Xgfw/dN2NGpQDTr4YqfTidynXnQdOz6LA8iSdC/6z/uhV8UBEnFzlLQ+FlkX4/HY6vW6fetb3wq6qB8r5aOqhxFVDMivdhf363ioLkbEGCmUUKvVCvJkMpmC/WqbIBuoNUYRZnR1CGcGvJjjXmkDHcZsWotnNBrZ+vp6kO/oMNi/RBszxj6CIs6OzWQyAYCL0wexBbAjiJbs9XrWbDbt+Pj40pwtMq9XoRs5xnGW8somxbhSJmGWbEzHbeoko1qRIRalR6886Ub14IEuaPV2a5v6zosiPWzSWRs9rq1Z7+2/88x0mT4us4i8sOcZipwpU+O9GUeYnyo2OqaMu35vZsFYUiVJDUhlXjAAZfi0o0qU/q/oXRKiqKFWjJkHI2ASiljyPknGLd97IRMnXPR3nFGt3/M8792LE6g61suABHGEwUUhOc/MvdJAn5MUBAUO+R9G7YU460yZs44FfEKN+aQ94kFN5Rf0UcdQ/4+bD8jvoTjF3iwKTiDwCOteXV0NhRpftodLDQYVfow/e5OoJ9Y6RrE3LtTg9EaLenZ03FQ51NBzPseAUj7Ac7VgIAqCpiLwTD3ZwBsx2WzWWq1WMJiRbRj7vAOF0lQByWazAUjE+6+eal3rGtWgvEk9D16xZg17b6hX7HQu4AnsS5Qeb7Qx5uqx8XJSgUl+SPsi+o13xvCGT7Nn1dng90QcIOd5gtnl6vfalvI/rlEdRWtp0Bf+1+cRScP1Xv4of/feKwVhVMdR2aDvyXwqcN9sNiMn1WgxLd6LsfDrxK8ZnqP/L0Jx8lM/8zoS76gyzt/j+6Ljpt8rv2ZsvFwzm0bmKADCmHtgSmWG/kDeGGSdsk401azValmv17PBYBDhyzdlvMfRPF38pp8VRzqPqrvHrcO4ufdtKMXJaOVBcfd5HhD3nepZ/r38WlaAA36n6wdjNom8bhnHx/27+T75MUiKbn1ZlATsQNo/1ZFVt4t7J/9eHvzgt9o4qjOrvut1Sw9Sjsfj2BpSypP9uNJvQG6c42qDaEQ1OoJGlaneST9Vx+B/rXHhdSMvy3iGgprUvlOQP25c4/TUZejaEQhJDItBIcebnFRQHi0kxKLSydAJ9CCCMnqv0CtooAvNC2aNEshkpsi1DyH0ijL3msUzIH2G9jOuP7TvQ0G9gej/jht/fbYCISjOPr/dz1vSd3GMSb2ymUw0rxyvC6gYiqSOt86F1lFg7rLZbKgR0Gw2w2ej0fQMdjxZnU4nrCm8s6Bx1ELAeMVrq54u5lMFgnqd8PpVKhVbX18PeU+8FwxnY2PDyuVyQAS1ngfG+2Ry4Z1lHPD+IXjMonmWtVotfK/MDKWSvaFeDpRavC0KHJC3qoADTIQ+YdwjCL0xsgxtbm7aBx98EAq70DZjAoOjiJryAdaHMn7fZwQ5Snw+n7dOp2PHx8eXBAdj4Ne4F1JarwRepHtBvU6QghneGFQleJai4JVk3V9qeCOYoGq1ar1ez/7v//2/tr+/H3mXuPfTz/zf8wjvCn1BOSfSBa/zhx9+aOPxOEQS4HlAYGt6DvUGKpVK2KdacBUPA0oC6Trkx/d6vcBfcrmcvfPOO3Z2dmbHx8dh/Emhefr0qR0eHgaDnugG1iD742c/+1nIbfeRZf1+346Ojmx1ddXu3btng8HA2u12UByYy88++8wePXpkn3zyiX3yySchEulP/uRPbH9/3+7fvx9OH9GoJvgbOaaAFAAD/nxoFKF8Pm+9Xi/wFWoFqPw5OTkJe6xQKNjm5qaZWdjnRJDEKbWkXOzu7trq6mrwziqAms1mQ1TErVu3rFwuh0iqQqFg3W7XDg4O7PDw0D7//HMrl8u2uroaUep4T+QwOgMRGAoY4nVmL+KVrlardnZ2Zs1m07LZbFhvpK3wGx7JSQvD4dB2d3ft/2fvzH8jS478HnWwbhbvvqZnpNFKWklrrAwsDPg3Awbsv932roFdS7vy7mjn6u7pbl51XySryj8Qn6zvi8736lWR7OmxGABBsuq9PCMjI74RGVmv1wMgRzt0TReLRTs5OQn7j/e2Uefu7m6IdPEKJjysY62g82JxG5kAX7Kfkn/g7OzMXr16Zd1u1zqdTrhhQ8kr6mrEqVxTQCTL+IFUrvI+n3ujStuheYkKhVW0jQdMVEdCXnh5zXjC47ErO29ubsJewP+sNQz7fr8f9AHAL/IzweP0Bz5Ad1gubyPCer2ezWazoG9wiw4gYZZhf9/k5bkacHelWB/8Z7pHoUexLpRfPPCk7fdgg9dteQ/dnTXKPKnTjz1b151GAqMjexBSgW7tpx5fQwapLnN+fm5myRxqacAJ5Wpbtb+qP2jfVTe6urqy4XCYOJ6s/ObnP4sX8vIK+yDRfN42gxgjviOyhz7hdIuBCloWMhtdeDKZhP6xjhXIXS6XCSNfDXKVARoZrU4HxkIBdrWniJZmHPT2JuaepLcKbuIsxNlApJnqiuiA+/v7ZmbB4YAOgLwDGFDHHEciG42GvXjxwjqdTnguNrcqa7elB82BgHBFmKigVgRLvUpstgok+AXlvSNm8TOxupB0cUIqxLQcrSeGdEFpAEJswXsESSdU//foe+zvWJ89ad8wsnySuW3JKxkeUCkWV6E8hAwhyJV0oSPk1ZBSw49NAS8n39VqtbBIEewYBwgslHE/BhoChlLt0WRFDDlOQJu1rXgePI/oWOmc6FlqM0tsgoRZ4iVVI5T3GRMFEDAwNFmlrgeAH43+iBkLCkptS/DAaDQKArvdbtv+/n7CiKT+LB7WNeZBQ8AW5pz5gmIotn5PeWlr1Y9B1jr0f+v69mMT29S9sqKyi3VF+SoDvTfAKxBKaQpCHuUBBdsrCt5jzP9s2iofeM6fg4bPuSKJ0Ej6xcaJLMFYRD6o7EVxUPCZcHc1SjEQiObwIKt6ExSYRgHAeFRFczAYhASK19fXNhwOQ7g6/aYsZCIZoD3IpXuOtsMr4sggf75TwSc+U9IIijykSpVfs6rsodSqI4BcECR7pa0xJYq6kNXeK6MGK/+jfOln6gxQ/uNdlY0oYvSB9aD7je+zN4L8nsD7zCFzz7gAPvv2aT8BsbUfhUIh7EWMdWxv9bJM54m/18mmNIqNg86jkjqC1FmSpR/pb29c0E7WhQIOurfpda88wxzo3qvvsx4BHZgLAFFAVH0WsAnnATIsprBnje99Gfofg9IAEZyDHgxfB6B4MErfhdLGR2WzymL9m/e97aD6EO30PKwgg4bGU+/19bV1u91gzKrsitkYsfb7/Vvlod9vlbRNPPcxwCpv9+jn/m/VWWI2Umx9axn6jH8eXTKWlwj9EJBd26Aefz2WpBFLejW11sP76N1myWP13FJFW9L0WHRg5Tc/DjwTA1joL3IOByD1qZProWTLnQGELHSVxD6//e1v7cWLF+GMs4Ywm1lA4hkEDe80sw8WkTec0wwgH0Kvvz144c8A6sT7CIGYUq7t8wJBw9S9AqiInDIKf8fACD8W+pwfC4xsFGodgzRSJo9teHhKYFAWEW3CG/btt9/aixcvQjQBZ4RV4cfzeHl5GTKa6oJqNpthocAbtAtPZbfbtdPTU2u329ZqtYKHligF9SSYWcKryYIvFArhDC2RDBjiZDznnC5h43j7qtVqyO2AtxXCsNdwpkLh1ksGoexWq1VrNpshymE6nVq/37d2ux3ObCGoCoVVZvPBYGD9ft+Ojo7MzEJ+BQVLMJS0f8yHet01NDlNCV1HzE+/37d/+Zd/CREGv/zlL0OkhirZ+p5X6syS6w9eoI7xeGzn5+dWq9XCvb2KiiuirN4kD/rpXeTaLt0QAX5U6dAy0t5VflCjj00M2eMBM9pJbgTdpAiP1fooM43usokUCrfZ7o+OjkJkAWPJDSPkI+h2u8GjjXf36urKJpNJ2IhHo5ENh0NrNpvWaDQSnpSrqyt79+6dTadT++1vf2u7u7shx0m73bb5fG5v37615XIZvAH0bzabhbP31I3Xu1wu297enp2cnNje3l4ikzRlzmaz4IkfDAZhU4aYq/l8bqenp4HvmJevvvrK/umf/imAFK9fv7YffvghzN/NzU3wpHBjjZmFWxo8SMFaRsnxIZesBz1GQn90negeA9+w1vAMA9DEciCwdoi8AiiCt73BRlJB9jIiCLg55OjoKPRRn0GxwqBXRwLjrJ5ds5Uype0m4oy1SV28R19YL+1220qlko3HY5tOp9ZoNILcN7OQz0NDS/EiMa5EwjHegFbMg7ZFDRkvH3Qc5vN5iKTgjnIdw8FgELzxqltoP3UPj4F5vi0KAqZRzLPKZ/QPvUePWtA2bYsCf17Owc8epPBgmUYksEbH47H1ej0rFoshckqjnCD6r8lFcTjA91dXV/ZP//RPQSbAY7xH/1kHXofiR8fVG7cPQfdRrtfx03T+YvH2elFue1Hdlu/XkerrMfArBiho/hf0XdYqn2l7YmvF78EY4hqZ4sPRl8tlOHf+hz/8wZbLpbVarRC9QnneHvB98kCoB2ZjeoWWSUJDT2nyZVvy4DYRXAq6+Dbqe3zvAVPVX9Ct1L7RKEAPCnEDkx9DnuH2Jo1So07ki9lKDqLTl0qlYHvgkGi1WsG2mU6n9u7dO5vNZnZ8fBz0+2q1ap9//nnipjHN46NjqQAC4AW30sGvRFxiPynP0q+rqyt7+/at1et1e/bsWdAb1JHo51EBJz7bRlY8aASCHldgUlThQIEGsQXZZZL9huM9CPz2wIInb7QrMXBpC8sb6rTDL3J9TutSJYrvYoiaRzx9HTG0PK3P2l+URRanJ884eRjJG38Kjqi3iE2YJGmqKGhYoP9cw299PzB6WUCABRr2SrnqQSAMShcudaNc8DleTrx+CB8NV2N+NHJAbxUAjIDvFZxgnHUMmVfqbDQawSuLYqRX1mAIaJiyzgtlMa58rpuK9xjRJh3DTcEDJdrOetakWQpueEAQHswCGehfsbi6c14VX11f+r96rNLq17/9szEZpP/r2tP+0G7/PXMXAxhVmYbv9LgGn3k5qe28L2/Ecrm04XBoFxcXZmYB0NO6MGSR5wAaqmyhdC+Xy3DHMlEqyGFF8bnmkXXMen/27JmZrULnb25uApgHqOHHo1arhWsiWYuA1Dpefmx1o/eep9FoFBIEFgqFYNxRluZYiPGUKrkYXzrmChiogQYvxK6U1GgtxkjLQClWpdrLA79XoACp7FMgzivngF4K4GHcKUimBhU6gRq9utehQPl9xwOMnue9oaAKuBoGvOsjLPy6VWNYM5HDO5QBoAIYQYSazoWXvTr+3ovt9ZzlchmSena73aAs67EX7zDxpDpJ1nP0W//WNvvy0uYgRjE56v9XA1HL90YqfdHoQ3/Mza8p/Zs1gbOCsGR410clFou3x3ZQ/nXOvMH1UCDBp0C1Wi3II9YV84VMh9IMatU3vK5slp0nzMsjZDVyGtmCDPDtienU9MODEdp21jj9xN5RoCHWVy9j1T5IM+68XkH9nU7HRqNR6txk2TebEGOqfVN7TvuWVYafK7MPnUdajup89EdlsZKXB+iZ3qZUUIPylVcV8NW9D/mKbYuuT8JddY7HQCv6p0cjaM9yuUru7W1DeFD1JN7DMVIsFhN5ndaBwDpm29KD5UAoFG69RUdHR7a3txcWlYZNariqD/UzSy5kj0D5hemROt3cvDHkhZNX4LVuM0ucYeT5WP1eEPmr+DwYoQq4N9pihr0qVYyVBy6UsQghBxnTxeOZMEZpjIUSP5lMEkIPRQxUsNVq2f7+vh0eHtr19e0d2hjqGAWK+u3s7CTOPvM5YYIKNNAflGOMSPpDPWa3GYExXkCH2Vg4agG/4p3AaCcRGMZJr9ezi4sLq1ariagCMwu5B5bLWyQaNJxn1Hvp5w+BymZ0dHRko9EoeJhGo5Ht7+/bwcFBmJvLy0vr9XpWKBTC+lIhi8KtRx10PdRqtXCWXMdNjahNAYQYMELd1MNce0WZutTDo2vTjxWh0E+fPg1IL0Akz9Nf6ta+8psxUsGta1HBB78B6UYUC6GOKUte8dby9Xv+5uo2jORSqRTOHxJNk6ag5t0cYp4B//2bN2+s0+nYL37xi5DXgjHRDbXb7QYjkjWHN1DX4MHBgV1eXtrFxUUI//3ss89sb2/Pjo6OrFKpWLvdTkSrocT89V//dahjPB7bDz/8ELzOo9EonB/XBI6Hh4f28uVLGw6HNpvNQqb8ZrMZ5lqPwgDg4XlAnvBdt9u1t2/f2h//+MeEfNZrneBTeJ0jAABk3MqALMTjzfvkPFDlhfwu3J6guU+0Xu8thZ84m6ze3XL59owpZzk9z+oNARw7UMBBIwkUOPDh+4wTRhxgLeOkyRSRpZxj5ZYM5hRCftAuPJAq6+Bh5ASyhKhI6vPHJNTjzbxpf3Z3d4MRAYiMvB8OhzYYDEIeA/ItaERgTMbqeMC79FOfmc9vb/F49uyZ/du//Zt9++23H+Qc4kcNOm8sqa7j9Q6tz7cvRtRB2dp+9TDyvQcbVPdRfoLf9Pggz2s5RAuwL56cnHxgwMZ0L+UReKHf74f8XYAHqpgXCreRhM+ePbPxeJxYb2lj5z+/L4D3ocnrop729/dtb28vAGqq97Bfe8NS5551p3q551FvVMUMzuVyGYxp3b9Zs7rPeoB5uVyG+Wa/Vd0j1gf2hcPDQ6tWq+GIpt/7VY/wZelzaca3rkv9ezQa2Z///OdEW2PkQa0YyLVOV0C24sjyNklsfmN1qTxTsInPNfJMjXk/ZpQdA35YW41GwxaLRbAfFADgWXQsBW+0HD26vFwug+51cnISboaoVCp2cHAQgHL2RGxHBZd1b/EE32gONbPVVZ26JzAGtVrNfvazn9lgMLA3b94E+ZaVVPu+AM0HO8IAmoKCpGcJ2dz47YECSDdWRa58PfpbQQQIBtTyvYDyi0DL0w1HBYE3GLS+dW2MTWDMUOK3Ml6sD2mEgqkhLbE5y7uZqYcj1ndF7AghRiFtt9thISkPKGo/Ho+DosAP4bsIANrrBboKbp0zjAKUXA3Z573FYhFCscvlcuI4zXg8Dp7NcrlsBwcHYZNRBdhsdRsDdanRocBBtVoNCRo5uoCShOAolW4TtmDka0goZ435bj6/PWdcLBbt6Ogo/M8Ye15C4WZ8GA9VgNTLvC3p/HC11cHBQbgOUMPVIFX+lVQZUKKNGuXEnDA2HjHXteiVZlWCvbKrIA1rIdYmylEggh+/ZlVB9kqN2So5nF5zqQCNPvuQxJgyZ4wnx2s4ZgAICNDIs1wjiILO3CBLAQtJFmdmIXeOGn3FYjGARGzuKG5ewS8Wb4867e3tmZmFIwOabV8BCpTfxWJhz549C5EUGNgkyhoMBnZ+fm79fj8B/Oj6UplFHTyroe+seb8fKr+yhyEXyC2jhOylDPYnH8lDmSqPtAy//2jfMGx1T1X57z2O7Pf6v8oeD3ojfwFc6RPlIP8UwNe1Ax8BJCqQrOCFdwIAEACyMnZeGaQ9HKVTRbVer4dEnMvlMvC7XhmmYERaSD+k+77u9Ywh7WAeGSMFcLwcpRwvB32dWfJkNBqFI4N6ZM/rLz6CQuuIfaZ8qW33YJX3JjPvKp9inmPlbX3ej43qZ4vFIkRIYXjo1XVKHoiJ/f0x5PR9k+pcaToiV2NqlLGur9he7vnSU8x49z9aNp/5daV6g74Xmwt0Ic9fZpaIZKF/tVotJEzVo2R+LXsdTO0IjnCzXiifo2WUq+fbkW/+9pUsuitYVa/X7fnz54njP6rXIJf8XKs+psAPf8eAFv7W55CDHnhRPovZdco7tI/1DACEzsKRAOQ7pGUxT0Qb4LzTHDfKsz6yAZCNcnW/N1utMwADbb9fU7pH0B+A+HW5jdbJ+Ty0NYDgEekYc5JlHkSFZxSZ0cFThChmHMcYxuxDFN1sJQAo1z/rjU+PDMY2F1UsvEEW2xQ9mKGCK4bo+s+0Lh86pRtijBlVcZ1MJvbmzZsPkoT5OtNQSk9+HNTjoIrzYnHrBev1elapVOz4+DjMPR5H5gl0jnDgo6OjcBZWFdBSqRTOS8cMTww8NdiJFiAJ0t7eXsIQxHDh/lSUO128tVrN5vO5tVotOzk5sbdv31q32w3eRoQ8guji4iKcpcS4Ymw4ojCfz+3y8jJkdOfZyWQSjCjOh5NpdrFYhDNYnBdHYHDrxa9//evQhslkYufn5wnBrqAS3mDmC2DEe1yzKKYgeWFYKBTs3bt3dnp6an/7t39re3t7CQXTA0HwmX6nZSKY2eTL5XIYU4xTPIOAUsx5DM1H2PozjvzA65Sh64ux09BWbbMqsWarDOK6EbLeGW94mDDaZrMZ8makKVBZc5Nno1i3/nV9E51TKpVCxuBOp2PlctmeP38ewvqur6+t3+8HhJ6Qf43KWS5XZ+/x0pIJnbwmZDqmTXj7WBfPnz+3q6urkD+EcSmVSiGHyGQysffv39vx8XFQ+JQXyH3APAAUnp2d2c7Ojj158sQuLi7s4uLCLi8v7dWrVzYajT5QcJhjjQDa3d21nZ2dIPeQX0Q9IRc1mkSVA6KbOMrUarXCPqKGF3yDTIWnle90H/Z7XBpfwcNEKKhnXvdCgFblv8VikVB0kWEAu6qgm62OPqIE0W71qivYQEQFilq1WrXJZBJy1qjco72ay2GxWASPGokxMUC5YYP1Tz9UOWs2m3ZwcGDNZtP29vYSt5XoneU6Z7RXZYfKDNV19M5v+AlZDc+w12iuB9WndP16nmBOtF6/9nWdnJ+fW6fTsS+++CLsE7F3yCngIxJUhmr52i9VuBVAQLZy04HyznK5DLLl8PDwgzL8umLc6D/zoGeQ0WGQd3qbg45pGnjgyX/3MQCFrD1gEyMiq1+TySSAsd6jHAMPfFnoeLrXqq5ulpRPWUAAn2tuBH1fy9O2qVzgf3iC/erw8DAY8uwt6H8qo9SG0NwwGJ0afcvtHfAz3vFOpxP010qlYkdHR6Geq6urtUcXNgEM0nhAeWd3d9d+85vf2Gw2C8elFDRHhqm8ZRzR2xVEYE3qfPO8B5h0PljDqlPpHqg8retYdb/ZbBZuZyKPUb1et2azab1ez3q93gdjwfxyNTw5eTTCl/7wrDoP+BtbQh0oCsLCb7Rf9+mY/Um/2Au5QtYfA9e5VhDsLjLowXIg0CgdTAYiJnBVuKvSbpY0LlT4KNP55/zA+AH3qKQycxrphqQTEGuLtskj9PqO/o710y9G/5wqN2ar0EbO904mkyDcsxDkTUnnyCseurH3ej17+/at7e3tWbvdDnOimVOXy2VIooiXVa8rAXDA6w7yi6FPW1AIqDuGAnPFG8JcDcOTk5Og3JZKpRAaT3iq9rXRaISjGerh5ppGlEkWPGdgz8/Pg6Kt56/ZQDShmQIhZhYSfHW73RASPp1Ow6aHB2AwGNhisbD3798Hz4CZBTCG/4meQCCaJa8v8us0Rnm9K8vlMlzbRlSSmUX525Pf5FUhVTBLNzD1BuAlUAXVb1I+CiMmsH07PKCnxhJn1JVHNRkYSgDv0l6VSYoqa7gbfQU0gufS5ua+lFQ9GqKyifWOzOn1egEQgNdR+iuVSkh8yJgVCqt8Hs+fP7e9vb1gcL9//94uLi7CvHK8oNfrhXZgcOjccq1rt9sNIZfISvVYY3CpUkJ/WDvv3r2z5XJpZ2dn1uv17IcffgjHN5RHYvwIoRTACyiJyrMeUEKmcTRBwyE1agEeUWIfYN5QMJg/5QtksfYnjVRGcWREI7YUGDJLN5gYJ62XOWTPgic4KqbGN2PI/DOWtFH/9p5R3tfzpGpQs2+qrsH7KIPsdYwtiUI7nU6C3/S8NfIUj7YHWzTCTNcZ/VF5oYYK0Q0kWfQ5NxSAV1IjTHWaGMWMNKJ5OKKatlcoSKG/tT6NovBKMjKZvxeLxQfzyXckw4Q3VDeJ9UP1RHXSzOe3uVkmk0kw3Dj6dHl5GUDAxWJ1XW3amOXdIx+KsvS++2oPc1wqrY4Q6R4R2z9j5N/hMzX+zD50linvqYzhez73PKrfwWPsBRxJ0OSoevVoDDClXpXTGn1Ef8xWPO/PzPP94eFhor2j0SiUcXV1FQzFbcjzQ5ohqWDtcDi0r7/+OkRa+TIU3ORds+TVlx5g0DLYA/08eVstpo95XtA1bWaJJPIQx5eJ5CDpM445P1b0gflibiFkMvsGkRqqyyugoVGHyHgFklT/R/fi6Df7D89j+zB2Kk9jdF+24L0ACGkN0Y2TTdEjRh6N9Oii/g3T+OeVMRRpji0SJa+Q8L6vQ1E2FXCxNntlkHZrHXzmPa3++RjF0CSzlQFEn/BSc8+6jmEa0JKXoTwIxLhw/hCFbT6fW7fbtclkErKM80PYD+E8r1+/tn6/b0+ePAkeObxdeNin02nw2H/55Zfh7Cptubm5vTkhluTFbJXwhgRrBwcHQdmrVCr29OlTu76+tvfv31uz2bQvv/zShsOhvXnzJvQTHuTcU7fbDUcHisViUCa4+53ESsvlMkQWLJfLACiYrZSV4XBo79+/t1qtZnt7ewnFXxOonJ6ehvO1Nzc39uTJk6AwzefzcP/rd999Z4vFIoAyjCueuUajEY6aoMwzJ4x/XgXDP6c8xd+tVsuePn0aopLgEQ+oeVJjRNeNKv8qYwBs1DtJtAseRhX+KKMYjQh03udZ3ZS8QaeKPl5mzs57b5m/vQSlRKMZkDfkDPBGHQYF1wZ6BfYu4EHa5sJmpca2mYXoGr3SCKWJJG+0g8gEBW5LpVI4YvXb3/7WfvGLXwT+e/XqlV1f397OwuZ5fX1tP/zwgy2XyxBNRJQJcgVPwtdff21HR0d2dHQUxpT54/gPYIDeS31zcxPW9vfffx+ubJpMJnZ6epowOlX2aiIxD3Bq6DVzTsg8YJ6On1+bei4SJXU+n4fkTRBzpB5qjRRRrxXzZGYJ/lTg0vOAvotyDYiF4cyew9pQwESVLwU1mB88cpDyCf2jjEKhEOpSbwx7AnxEqKlZMupIIykom/2mWCwmEqIhDzDWAcuQ7cPh0Dqdjh0fH9uLFy+Cp1oN0+VyGfZEzk1TNzzAWKoMZX9j3ClLx1ePCDGWqoyqXqOKNoYQPJwXNObmIZ/rSRV82u31Od2bUaavr68D2KukgDrl+0TIjA17C+3UPVuNE0AIr8foWfzLy0tbLpf261//2vb29gJfIm+Qh6enpwlDy9OPARo8RBt0X/A6I7KGtaHh9p5inzN2MZ1YdWvdB2mDyil4S+WB6qteB+c71jxl1mq1cLZ8f38/RKyRJZ9nfdSXEvLRzIL+ppGxvEf0E+3nO/JdYdCenZ2FMnAe6Fr3/fNzp/MVozQQgbEaDAb2z//8z/by5Uv77W9/m5gb3ldAhjH3icRVHlKG1u8BZZ7RPngAQQFVJfYbzSXEGHPlKvttq9UKN+fwHvUgJ3HWqVOH5zUyiehJdE7lFd3beAcAmn7oXocdRLnMx3w+D1f4ooMpv38MuhcAIU3h1GRWCBaYyWw16T4JmGcOPlOjUDfALOHtyQMDHh1KC6umDTCOLgKPsqahrYqeUT/9V+NEhahuuFpWrF98x2LVBaeJ6xCAZtkJftI+13BUlHb6xyasgrBUug3hJ8QZzxWLerm8PS/K53ommRAjFj/Xvh0eHgZkjoWt3tpCoZDwxjB2aozhCcdjyrl8DPHLy8uwMOk74VtsApVKJVxbNJ/PQ5iqV3Dw2h0fHyeOMfzVX/1VaF+z2bSXL18mbq5gnswsgexjWJit1hGGf7fbtcViEYxn7/HXPA3KU4vFIhiszF/WppJFMQAOXlksFsHgo3y/KaD8KzAAsRGx0eg7rB8iVzASMbL0M8ZG17Iq6YvF6qwz86jRJiDXrC14oN/vh8gA730wWyUJwqMA4IYXl3P9Ki8wvNlQ4PfpdGq9Xm/tebdNKc0boWeBfU4RAKnBYGA7Ozt2fHxsy+VtdNFoNArGFnPLPADWgNhzLIf1wrpdLpf2ww8/2PX1dSIRIGOqwAXXrT5//jycT+dGh8PDQ2s0GnZxcRGO6wBioAQz9sgUjhOxjhkLDRNUwxQeQk6gNPA8yrKGw8LDCnTQFrydfi2zR3ilVPmH/mlkBe1DjvO+KvFKarypokciU+aH9Yeiw9om9Jt5x0BX7xQKnRr9tFFDPVGaWTd6vEK9NXpWlz7iQWIekCGAKii8uneqLFOvjhrgzBXvcmynUqkEA4Dr1ojCYu41Qkn5znveVI56XSWW+E2jE1XnUOJ/lR955b2CE2m6lzfeqdPrMSqD1fjgWeoBHAPY9cR8MD8xQ0UNCXUOMZ44FDqdTpBnfK880263A79qn9YBMD9FUh0oS89WfdBslaNGdVwdc5V/Xm/WuTdL3twW41EP1KnMgpQPqQOnCUddifjSSJZutxvWl/KYl8WAjVqfmX2wtumbAi3wvAemaQMRvMhyQKxerxeOOup4KWXN2bo51X6Y3UYV//nPf7b9/f0AzCP70YtUbjHeXkfRvUvHRKPp+AyAStujjgzkuXrnFbSEd4jOVbvPLKnvQX7/4QgZzzPXzCtJpDXaVXkN+YXNYra6DlhvVGNOGDPdc9SpR9s5CqjjiuNYx9GvmfsAGR7sCEOxuLqjnYW5u7sbwhGLxWJAXNRLCxruNxmMYK/MM0kYpjxrlvS2q4GigspvbjCaerb5HoZRAaObui/bb3AxAAEljDpiNzd45c2XqX2G4f2tC16o+/OvWm4WYymCRog2HgPNIM5xAxb1bDazi4uLACLxLv0GGNDM4mYWFqUq2LVazQ4ODmw8HgehqQn0VCHVXAncDkHYGWeR+v1+iAhAgcaTrzywXC7D4udzFEESVJLRXQEEBYlIcNjv961ardqLFy9CmHS1WrWTk5Og5HILAzwJKs652oODA9vZ2bHXr1+HfAYANShZhUIhZKLVc3i0if4qjzcajSDUtiHPo7q5kuBsNBoFT4WuTUXiEZ6sRTyPjD38heEDMlypVIIBPx6PbTabhfupEdiEEavBCO8Xi6vsvXrcQdFxMwvzg3GJDOv1ejYajUI0w9HR0QcCXjckQC0yQINYc74fpYZjKtfX1+Ec/2QyiQIID4FA0z/mURHzYvE2ZG82m9np6anVajV7/vy5LRaLkIuj2+0GPhuPxyE5KTyA0ckcmZk9ffo0hEdPJhN7+/at3dzc2C9/+csA/nnlDB5ot9tmtrri9eDgIBylqtVq1u12AwhoZgFQ0FsZNGqKJIrMDedAMUwBrjiPrt46f/6TvUxDrVXW8C4G6XA4DHymxqPyJfzs9wyUVG9gM66q2AC+pAHVkCo4HDNQ5RiQTz35EHkx2LvpFwqxmSXWs/dIafJX9hL4in5Uq1Xb29sLnwNcsJ5UMQOMgBcUYFD5SFleOYbn9Iz8YDCwvb09azab1u/3w20MGALsJfQHOebni7lhLlX/MVspx0T+qd5iljSq6AtlKxihdeSZe/Zo5VdvuHjjSr16MSCD79RL66NUAPDQIz0xhjp3vk2MaczZoWWztv1d8vQbrzTnpdOMN0/bgvKfCmW1HVmLfNIjQTHDXXkB3V/5JqaXesNM9QvPu/CA8oI6CDkHf3h4aAcHB7a/vx9yDZnd7gmj0chevXoVcmTBCwpeatQZclkBPjV26RN87Z2XerTXzIKeSlk41KbTqY1Go6CjbHKcIS//6R7G/91u17rdrn355Zd2eHgY+qWRcroHKbjN/0pqCHtdX2UH5GWvgrB6rbOWgZz1uQ2QOdgrJFJnjlnzi8Ui2BqUDQ/Ae8fHxyEhI/XpfozOqsfj0Bdwpni7F3nOHqSOX8ok1yA8js6Vluz1PunBrnE0u/Uk9fv9cE8unYNR+MGbxMT5TU8ZVBegDqIi3WYfnvPUzxV5VtIFzsbCO7TbI6XU7T04HqTgtzKTomq854EIj+Ip+gmxsaoSihfo6dOniU1tuVyGa9Pu4l1mQd3c3CQWGe1DgW632/bkyZOE4c73hG/Rb0UQfUi2bkgo76pQocAAAnClFxEBZhaUdq9cHR0dmZmFBEyq/BIVwRxgxKsX4+bmJng41UvBOV5FznmedvJ9vV4PiRwbjUYIf2I8FTwjbAmepAw1RBaLRQIAYGzUkFdBTRsJSzWzEC5+V2K88eig9L948cKOjo4+QJfV0DJLRgXACzqmCF7e5dnd3d1w8wdAD5sLfMFn8J8aJ6w/Bcm8EkTZejaSuQSk2Nvbi4bljsdjM1sh3RiLzWYzeBaQLdVq1Q4ODsJmY2bB07+7uxu8I3nJj5d+niUT5vO5ffXVVyEpq5nZycmJVavV0EeiiCaTiVWrVXv27Jn1+32bTCbW6XTs/fv31mq17PDw0HZ3d63ZbNrp6an1er1wfOfNmzc2Go1CVAMG3xdffGHFYtGOj48Ta4r5IzIH+Y6xo1ewwguEkvPucDi0m5ub4E0HBCKz/s7OTjjSpPIYvoEXiajAM8A6UiWSOWd9MffqeTZbKdEoqJSvoasK4igA7Q1QZJiCdAqkqhHnSXmiVCqFKA4IUJ12UyeK8cXFRfgbmcrY4bkHRKJdjKF64jD2AduLxWJCXpmtbrjQPRVZrjoIeWgAEfUaTCI9aCN9I48HIBNRYZp4DaBavVfqeVLZQv91zBUMYrwVzFTgF4OZa4wvLy8Dbyj/sCdQppcVXh6kgQgxB4YmiTNbJa/TozGqj6kXzZelgIHyqRr3jBFAkepc2g/VHSEFVxgTBdFULgOmwwe0hbrZd1utVsJA+BiK+8ek2B4Ro+Vyaa9evbJOp2MnJyfhyBk/qnernCH6LKb/eucCPAw/6Hx64NSXQV+YZ5x3HE07Pz9PyIjF4jZKcDabhdt21DZRp6fKY22LGv5mqwhjDwJqf9TjzPfIacZLeRggi/3PAwkq8zeZ57TPKKvT6dhXX30V9jKNMFdwxQMiGmGg/fOgM7oPEWkKQCpgQdnKF57fKP/o6OiDsWbf0/bQd6LHkPGLxSLkxdDoGbVBkA2Xl5dh3gAnzFZ6BNfHa3+8E8CDMTxXr9dDm9Ve5WjL+fn5B3LoIYDLOwEIMaZUZtWzhGYrBYAFop5gZQYt2wsRj0pSZ8w7oN95z4xOCPXxmdatGz0TFeuzCpWY4GLyFJn0yZI8sKKbn27+lKvAgHoQeAZ0FeL52AanCCOUZmRQNxsooaQ6ZigQrVYrZKgGmcNjguKmxllanfoeqHatVrP9/f2weNVTjYJJ2LqZBUVNeaRUuj0brKHX2k7OcTN+3FrAQseYbzabibBulHcNeaZPHp0HOb2+vg5ChfOsGBV65gphxHdqnNBOxkp5j0zSoKuaDZZ2AQq1Wq3gTcsizzexeeO74XAYQnsxfMkToWgtdTYajTCvCE4/fvTVzMJ6UpBC+Y7x8mNltjoWofNFXWw++ryuzXq9noia2t3dtcViEXITkAtBlXPAC9Y+G/BicRumPhgMwlEZeLndbgeZSpQDIFm3282cpzTadFNZLBb2+vXr0HcUhnq9Hgxz5g0F//DwMIzx9fXtrQYABdwf3u/3rdPpWK1Ws2azGaKH2HTZxJ89e5Y4g47nWA159WKpYd3pdKzT6QTPtjesqYv/iYzTZEg3Nzd2dnZmhUIhcZwAeYHsgdfMVjd7KECAcamZm5kPb7zp/qdROShq9B8e1HPcPK8GkAcQiEhS3lbQmmcVLN/f37f9/f0ACgKUKJDCe8g19dxp9AP8r3Ni9mEEH0oTbVN5yH6nhPKqx9YURCGHDnJeHQQYjkQDMc6atZ+x8wBvq9WyVqsVzrWqPFZQUsEJ5g2+M0vek+71G0Bg+kmUJ1FXMR1E5zSmlG4qByAAcfQX71FU3uJ5ldu8A5iCAYBiTn0KtgD8IJeZX8/bCqTEDE4dD36zB6hBq+1nLofDoZVKpQ+OU2kUTWy8Phal7cl3LS+NlsvbRLOXl5cBEOCoCfNEGfA6uiORplqHykrkg86hAgEeDFJ9wRvjrHl1jvT7fTNbnTmnbPRNkvp6flC7gvar8att8jYN7fFrW20IJc1zw1guFovEcTEzSwAIeUCBbQzLQqEQ9mciSXESEuGniZS1L3ymawpZrU4zZK4a1Sr39T2v08X20XK5bLu7uwlQl70DA1z5iKN2yKt2u22VSsWePHkSEkFTrtqKRBlwfF+jock9dn19bZ1OJ0Rg8hw2FbypSdrhG/ZPBddV9yDReppNp3N9V1DhwY4wmK2E+O7urh0dHSVCPhS5MVt5Fc2SHY4Z4mkAggcH/GcefeYzDCdVEMxW10mpAedRUtqo9UJpoTpqwHpBpBu/3/y1v3zmy9TvzT7MIu/HLzaWsc8h5o3FokysBpLZyqBT44wFCbihHlUdB/rkk2khQIhc0M1Az4n7sUTAYJDe3NyEkGo2u729vSBMKAP+mM1mIYwYniiVSiEUGwUKjzZKCONBeWymJycnZrbKkE69KIV6JgqhqmGA8COCT8PzeFeVW+ZBwZZ+vx/Ggs/pL16kTYVLmtKi/HtycmJPnjwJURYov17gw2cxkAIjQBVqNlLGHGGu9ft1h4IPSKFniFVmKFpM+br2fJ8BhfA+M57Ku3qtm26ogKp42fFoq2HA9YbNZtMmk4mdnZ2FYzRZ8wDFlIhtCCBxZ2cnXHHlI5LevXsXwh5brZb9p//0n6zdbtv+/r5Np1N7+/atzedz293dDYlST09Prdvt2m9/+1s7OTkJily/37dCoWDHx8dmZuEKUrxDREKoYskYcvSJz73swavMvHsjjPUJ/+g5fta+gk96fEr5ysyCsas8xTpmTDGKFVTTcfek+w0ADh5/DRdm/WsuGwxqXftKtFO9iTc3t7lFFFjQ/ZwxNrNgkJtZOCbB3Khi5MeQtqlXkP1GZTRrl7owNGmDevVU98B4YRyQqwoYEvpKP6+ursLNIBptwlEMMwvJcovFYuArPSZCO+gf7VdZp8axRsYxvvA8c1cul+3i4iIxdwrgennu9RfVDbLkhtchADM1ckC9Y/CTfs+ce6VdQ+DJT6IAms+XxT5LJNHJyUkC9I8BJrSBvnswhed5Rm8dKRaL9vLlSxuNRvZv//ZvwYGCPPA6n9ZHWz4WmHCf9XgwJGu/WCxub4Dq9/v2/PnzYEzCfwrm8DkRLCqj1JBWUFPlupeD3jjX7PTMj79NiLXJXMbmELBeAVB15LEWAZsVwEDOaHSN6nW+DwpI8D/jStn87Ozs2NHRUbgWNxZZpHzg5ar/Oy/PLJdL29/fTxy5Ze/lFh3kMPOGPaAAixK5E+ARgAH2RAVpFJTROdcoIm9Tqi7sAQPd772t+Pz5c2u1Wra/vx8ivfhOo0lw5KETPHv2zCqViu3v7yduylosVlEjgMx+7JH9ulcUi8VQv+ryqpuwD2XN57a6XozuBCDEmNE3brlchnPbuuB4Vjc7mN+jyB6V9Ia1Nwp823x78JDw++bmJnj7mExVdlTZSIuU0DphPl0gMSUwhmxTrvfoe1LQRDdUHRNV6nShxcpTWoec62Jkw2csGSsWL4ucRYpxy6aiict8nSjSOh5sOpq4kTN2zI0PAdM2844a5Bo+64EbNiqOTWiCr0pldW+9IqOcoVUPCfMFDzWbzRD1wMajm46irvARAAyeXspSg1pBABQeD3hRPggrXltVmjUyIYtH8m44Kh/a7bY9e/bMzCwACMxdTLjFQD9fL55v3RDgQTx/vkyMCwWbYutIUXEtR9uq61iNETMLfKNeGOYF/vUyjOgdolQ0DJsNRA2LWGTUNpQ1n6q4qPEBrzabzbCGUBiWy6X1+/1wNObg4CBEEZCrgnOJRLwQ3gdiv7u7GxLsnZ+fB1mqBmeptLr1QedMf5DlRLzAIxAhtwoo6dpR/lRFBxmnyqF6nxlXldMKnvMO4wlPIF+RrWarvDlpc4eM4R1kq+5hGMk+Ek2jGfy+C3nAmLIUAI+NkWb5V2+i8pYq8zouyGcUNJRSNdiYcwxvlU+6p6vuQT80n4eCuapQAs5hmHKFoYLCGv6s+XQARzki441V6lEAQZVd314zC14u+glw56M29H3dV2M6gK7rTYxP+Ii1Ao+QYBb5pWMK6MFa8/OiUWZqeOm+VCwWwzoeDAZWLt+eQ1bwRSOCtF8KIKiRoeCxGiX8rlQqIfcQvKoGqo73OvLG3adKaTpu1l5NIuGDg4OwT8XKUWeT7ok6LvCVRq4o37BmdU6pg3kBMFUAQWUiehD7DLJev1cnEJ/DMyqz1MilHj3KobqJ6g0qb1QX8HYWzzGugLOqY2wyp9tQoXAbgXd8fBzGAQCBEH76zvqivxqppOtN+6tOStU5vA1JWyDGdjweB8cNddJG5IOON060mPzc29uzJ0+eJG7kUfAC0qg7nDxEwS6XyxC5jDOjXq9bt9uN6tlqh+h8N5vND2xD5TfkKt+vm+e7yp97j0BIEyxZRqsXJl6J1zKU6ZSR/ED4TdoDHD7MldAWRZCYDK80a7sRBDEk0bfHI4qxz2AUBKUuGh/CpcLUK6iq9Gr7Y+3UTVUVLzVIlRTkUC9CTCCen5/bZDKxn/3sZ/by5cugWHBtG+0i1I1rGxH2GMLkKcCIQgBom1E8VAD7RW1moeyDg4MAJJDMREOuGX88iZyFXi6X1ul0bDQaBS+wCkU8TSjPpVIpnPntdrsBBLi5uQnnvkGuMRhHo9EHIEW9Xg/5GFAwCcMFbCFDPRuKGr46lypo1HNIKDp8krZuPU9kCaLDw0P7/PPPw9EFkGn4xwMCqujG+I6+6GaJMqebgCqzalBq2aqwKICgQls3Mk+6iajSq99Tj3plFUXXKBo1MHXtqndTQVD4YB0oGGu3kp+/2LontwHjAn/+/Oc/t2azGa4J5BgMnjv6+8UXXyTO6rG29/f3gxL+zTffBMBH1ydyoV6v23x+e6aeDXU+X13POZvNApiEIqMeeJUZfIaHmHvf4Q0iWtj0+/1+SLiKAsV6BSzUdVOtVsMxlpOTE6vX6yFaCcUG/qJNHGNh7DXqRA1v1o4qzbE9iveKxWIIbcX7D+9ipBG5wdWSMVJwWsEOrwjyjMpp2qO8h8xUwIR+IkNZm8yXHlVQEEfBXvYQjsqQl4BIFtadygezlZLLd+12O8hT5PpyuTpyhvHMjSzD4TBE12BcwtsooACmeoRRx1TBK5VzOiesHY3e0jL8GtfjAl7hpg3UmUVaJrKWJLF6HE/ll8onrV/lrhpr/Oha0L1C9Q6Anb/6q78K9cznt9dHM3YqL33UmPIhnyOnP//8c2u1WkEuM9+s4YODg5Ac1sxC4uo0PdCD7j8F8MATc+D74vcTZAo85XnaE3uv32t1T0a2eh2P73hO92EFspnHtHLgLXQ6ZAYyV8FMolYBK/lcj+N6vQZ5izygfwqc8lt1en1O5afXZfR7HRuv06dRHn5cLG5vRnr58mU4uun3AsaG6FycCvSLo4K+/8gefvvjC9pXCLmrc602HO94+0dvb1N7T4125h25gr7Ns+h5uufr/klE37fffmvtdttevnwZHCbsDfV6PRxxYM/RueQHmep5QO1A8h+wz2fZo1AM1NuEHvQIQxrpBpbGGLpwECyx52LvZNWryhiTQfgRz8Q8ENpOFTwoLSqYtA5ff1obddMvFouJRaOInN/8lYE8A1A/bfJCN43yMJJXBPityhCAwGg0sqdPnwZjd2dnJ9yrDmqJ8MUQQClnkapnXoUOcxXLb8C46cZCGSCCy+Uy1KnzAGl4PwYCxlGv17N6vZ4whjHiNXoAAaAgC+AI3hkFghAu5CHgeZQqvWPdK5WgrYw1fBObP+pVoYRwzArH3JQajYY9ffo0ZEBnHDAWEPo6dzGQTXnOC1E1IuhDGgimf8f4mM/1+zSDyssyLwd0E/dGiq5deEFJz1yizOhzMeAvD23rfWD+4HXApqOjo6Bw6aav4GqlUgnJxrT9eAXMbr2q3W7X+v2+vXjxIiQlRUlQOY3HUfN4sCZZM3iN+FHlVRUMwgJJesl+4w1VkipqJJqGSfIuaxDZg3FMQkj6qgAxpAAB78a8tyoDdc9RntNnzFZXSNJveFfBhDwUU+79moViSq/WQxnMrTdkfVm6NwNGqfKqvMARLZQ0D/Yx3jp26gxQg6HRaAQwgPYpWMjfRNchc9QYUAM5S3FLmz8leIJjlvCTH3edGwArlYcxXSCP4kkb8ICS84GIMpV3ClQrxUBLxog+s6a8Qk0fWI+Am0R7EdKtkYvrdB8PyAEEAV72er1gIMzn88TRF97Pozvlfe6+370r6X66jpgv5Tfdy83iTkXVR3hG9TnaoePu9U+NCEG2+HXNvkud1IeRSFJs9gbepT8cYwVggOd13asuoHOmOqyCJsg/7ZfXI5S8vPVjm3cdb0q1Ws2ePHnyQd1eZpIfzEfKasRPDASnXB27NPvQ5xxTpxn6rdfRvG2gcsXbblovIDv8SVkaCbNYLAI4sVzeRiKSnJO8ZmpvqJ6g68uvDQVYGCvtD33HGfpQc+/p3m9hiAkXVaK8wgTphKQZ7jposc0k9qw3Hn3Y0WAwCAoH7ahUKgFd09DymNGi4VUe+YsJem+MaD+8MqMKKQvBo6c+AiE2niwwPChp2Tl9e2PtV1R/PB4nQqw1E716mll0p6enCUGsAno+n4eQzNj5JBSkXq8XvcJJDWUV2OrZZazwinGTw8nJSWJjZoHTDxS0fr8fyi4UCiGB43Q6tVarFY5kAJJQvwIheFDfvHkTxmE+n9v5+XlQUHWjKhaLIVM9wgjDknBuNrN2ux2OOSBIzFbnrfXYjo6XepNRtNk0QUbvQhiJi8Uiij5DGJasA89/equEBxIUZGGuvQeCNRsT0vodskHbn7ZG8HiiFPB8DIygX2pQ6BpGPqoXVttGPV4Z0g05ppQraR82BRLwtJEs6fDwMCRMIrpksViE8G48+2rsDAYDGwwGiVtLFPzkZoZf/vKX1m637d27d/bmzZvQBpSRZrNphULBOp1OkMPchsFaJSyVzZ269Pwg8qlSqdju7q5VKhXr9Xo2nU7t9evXViwW7cmTJ3Z1dRX2iidPniSOXig/wQ8KHJHbQZUnvKsa9o1MLRQK4SYPeJe59QoSx0DUm4FCww0keGjgUT3+ZbYCM9gHuV7TJyUENNLkpn6tKn+jzCNfdC3QRvqm3mMPvGmiXcYKo94seZ71+vo6JGolqosz6jGjGRmB0cFccl+4ghLFYjHI/EqlkkiQqPLCv6f8XSgUgoKJogdPsC/xHOM6nU4DWMY8csQJfnv9+rW9ffs27O1eGU0DLPRz1T3SjFQA2nL59oYC1r0H3LRsD95qVnNtG/xJn4gI1COj7COUiRPg1atXiTFCLiCbuJoPGaU84L2PXP+pOXVKpdv8CqzRq6urxP6rvLyO7gIA5H33oYAG+CqrnkKhYC9evLBWqxX0Z9avvqt6uu7FMUDN//AO/KIAoj+eplFFWp62l/kHqG80Glav10NybG/QqSG5WCwSiQu1bd5GUdlN/9WhoGPkwVZvy/gxUvAtTXf3ZW3jTNDoQnQu5LImk1XglroULIg5WOmL6utKGkGEbFQHFLox+4juG7RRdTYAK82FRBk+ASJHEvxVkcic09PTcASGY9YceVoul/bNN98EvYFyeJ59iGSi5C/S43eMB7KTecTG6XQ69vXXX4frqbPmV9fxXeTEvUcg+M0fUqEdQx7N4iH9/vtYfWllUa9/l4V5c3MTvE4IgGJxlfTHbHXXZ1ofIRRUb5TEKAYg6NlSj0KqINEFFBOqOoZ+HPDmKaq/Dem5JgSzCkUWJQKFjVhDY9WLx00JasRpXVouyoduDjzD/x71ZWNRj0ihUAjzjMDwyqQfVz2Dh7BmYVM2BrqeE6ZNKjRR9EiShpLv5w+FjeQ09B+DcrFYBB5VhFfr1A1HASgfLgWlgXzbkm6gKOKQ53U/5ryvRolvm0djPdKt68cDD1q+2epIg2+Xf47P1SuiUUJpMoJnY2PgPXAerPT90jbEwL91c6jPeKUjtqloeKBvK+/QPr5HqVfe9+Oraw3Dtd1uW7vdtsvLSxuPxwlgS0Oi9ay5huFr5AE/eiuQni+nbt5lrEmc2W63E2edMf75Xs+ms7aQZyhRyBV/ZEF5Qw1V6ojNB/zAGOj8I8eWy1VCOpQ91o7ylbZZf6ftXXp8zCvhXnZpu3VNeCOAdmv/9L3Yb31HAT4zC2fr9ZiB7h3Kh4CpjCFjA69rUjWAJvYt6lDDBLnrgb6YkcXnvO+jJNTo0LlbLm8B5mq1Grzjg8HALi8vEwo75MfHt4O2a51ZBF9pRBLv6hzGdDnfH+/pQ47qPqprVfcS1t5isQhJ7lDsAZuRRz7pWExf8nKX96lXj4roGgUIVQAEUvBIy/upUVa7vRwrl8vWarVCojhvOPo9NKav6nO6P8RkjuqGgHf6vBqjuhaZR3gKo5EjpXqzkI9k8XuZlq+gAXJC69Z6vd7l34+Nux8D/3dMBucxFtcBD/odfK2faWSb7vdpuhfPq/OF/sVsG7+OVNfF+eSju1SW8r3nAa8/8re2j+N02j/fb/QMjaYzWyWRHwwG4TgyegByjv7AazGdPbYOmAf2ORLa5qH7kEV3BhA8kqWTfXh4GG5fYDNQRcEb5lpmbDGocFElTP+OGY3KLHr1IAOvRhW/QY+UWZhEFFHKVqSMhRND2LzSBPPqxqWKqkYX+DK8EqYCjrFVwU3ZoOeeYsIjTeiooYsisVwug0cfJUcz4P/iF78Injw8N2qM4L0AyGm1WlYsFu3g4MDMLHht9vf3E55c6iVhEwr0zc2NtdvtxJV4XKfnFb5Xr14Fo4LPlM+43lHvnOZcNnPNFYUgm4S6ev7Fa4lHRFFFrqXkeAf3E1POzs5O8LyaWfAwwu9///d/n7jDWsOltS1qeGDg4Xlkw/T8to48/+j/hG8BkuiRD+89VwUsxo+6XjAaEbj+1gr4kHf5n3JVsWQeyAaNski79Mw6bVNe8ZsSpIAC/dONgzIwShaLRbhrXpUPszi4MR6PE9n0lfx83JWIKIBXzs/PbTabBUXx8vLSSqWSffbZZwleR/aQ1+Ply5c2HA6Dl1CNZ/gPT8bJyUmIcFKDg/li8+YWFPrpvaRmlliX6jE+PT21YnGVWImjGMXibd6AP/7xj2F8iaw6PDy03//+9wGUHQwG1u127d27d4kEez4yBRk0GAwSt3Mw1zyPwkJbuO5Mz2NOp9PgKac+BQZVMSkWi7a3txc+J/qOHBR8vrOzE3JPeELBwXDy18QyPmarvZ1wfjzHADj6A08r0EO79R2i1bihgrHQSAAzS4QT06fZbGa9Xi9EvWlEhq4Nn0RZ7173uoDuuypD4HW/dn04vo+QgP/0aADyEOMGQB7+vri4sH//93+3yWQS9mHapnPPjx5jUVlLP2K6gSeuWt3d3U2MtfIJY+TlkgfvdP9jDBkD8ptwZbEaXtpP+G8+n4fry9gDiGrUqBR0FjVCFNhg/mezWYhgYP5oP/Nwc3NjL1++TABVqnuenp7aDz/8kOi/0kMBCvdZbgychnx/nj59au122w4ODhIRqR4Q9KQ6V9pzXodhvhhvkmKjk8EjmgNB28Kz6F7tdtt+/vOf27Nnz6zdboekwKpvIpfV8ahgoT+ypMCJGoL6oyCHGolp+jhtUacb46yf+znz6zQvxXhJ9yI/pmqjaLsh1j9tx4mmupSuSW9jMlbsn/xg6BcKq2u3NUKOvcIDuxrBps7Am5ubcF00EQhmq/wzyCp0yMPDw7B/zee3V7yrvJvP5yGPGf0kyexoNAq6VLPZDDd0XV5eJo5N6k1RRILwG16MAZYxUDk2rpvSg+ZAUO8TlIaeKcW8Gfq/AghqsPKd99ApqKGh/DALCwtGYnNWI9zXoQqD748aDXlJBYtHLP3YefDAUxq6afYhIn4XUuRePd7MAf2BqcvlcuKctyo5MaWHYxEIbrPVmSGPZPNelgeZOeZZ2ooxoWPkx1PH1G9khUIhcd4aAahgkoJPZpYI96QsjcbQq6FY4CRw8RsUQqvb7dpoNLJ2ux3qjkU/6Jh5r5FHldcBCHk2JAX4mD/6yfqL1ZcmKxThVuDQz3uWfPFlqZGn5evnKLD81mNLvs3wM8/q98pnqhSrMRUbdw9UeuNn3brO+l43k7TnYgYfhv9yuQyh7yjnXtmbzWaJY2EkPPSgMpsz46sZ7hlDeNUrT6qosumyxr2Sh3LhIysUHFJvJkeFqtWqtVotOzk5CZs3xlmz2Ux4AAA1VFElKsArtTruyCQ9kqNgMHOm4IrytSoZjIePlIjNOWPGOGl58BvgpFfwKFfHX8dAy9HoJyhNgY4p2hjVumcov+i+raAf72r4qtc1dE1rvoXYnq5toByUW90f1+kE+j3KuXr0VPmnv7PZzMbjsQ0Gg0x9gL3X1+f/Xyfrtc+AGYDusf5AjEuWcejbqwCz8pkvR4Fn+N3zjfKOAj48Bz9oHcViMXHUgn6ogaq3SNzc3IQ9TT2RJJHjM09Z8vanRhhTyDjkiNmH5/V5ns9if/uyY3+bJedZATo/9yrXqYs1RbLV/f19Ozw8tFarFcBn3Z9whi4Wi0QyXG2/r1eJz2L6vh+rtDHwa8vzb4zS9LQ0AzOLVEdiL0h738+V7lPenvEghP4wnxByXPd03bOQo0SYqZyPjVHMRvW8glNPr9PVcvVYy/X1dTiixtgAGHCMWfd+ZA7AJJ9rsn/2ZnRPnXsfxZZ3Hu8qex4EQFBG4BybKiUacq7MRIdU8HhSRYYytCxlZphIF6v3OiD0OMt7cHAQwuZQZlUR0U1NzzminHim92CAXxjKQDwfQxBpqzcgGDs+j4UTMmZ4sPXe0SxmS1toJC4D3ce7RFuINsFYV2WSOWi1WlatVsO5YoAmRZF3dnbs4uLCzFZeGm/cLZe3ZxD5qVariUSG0+nUms1mYjPwBh9IuT8qQZJEzjDx+Xx+ezXa3t5eQuGmPJRblFkECgJksVjYcDgMxoga1zqnKGqUxXlQ+jYYDEIfdXwIkfJGF0imKjrwMUYRIVbaFk8xwZP2P0bSeDy2nZ2dEEFSLpfDWXMEL2gqWXx1jSrppsD3gCgQdejaYExjYBCeUpRCfx+0D42DR7VONSJUTvCenpmjDv5XAwED6OrqKkS+4PWn7STYLJVKIZEn7VTlKW1+1n0eI24oYBzb7XZYA+Vy2Q4ODqxYLFqv17NSqRS87Ts7OzYcDu39+/ch3BcPDklUNdP8crm0d+/ehbEpl8v29OlTK5fL1u12rVAo2NHRkS0Wi8RZZ6IBWH+M3XA4tNFoFMaY5E77+/tWrVbDlU+Afv1+30ajkV1cXFixWLS//uu//uDaTM7J4o3Y2dmx3d1d+/zzzxN7TK/Xs8lkEiKDXr58adVq1d6+fWvj8djOzs7s6uoq4YU2Wx3N4n/WJNFCRKkxzowTfIfxgqzy4EGhUAhAI+3lmdj+Q7h6o9EIc2ZmiTrgWZ5nz2HtsP+wV5KrhbHUTNTKD/AoddA+XXvsO9SDAqf7BTcFMK8KDEN7e3vhuBhzi2zW9cJ4wQO0hdt8AJPIF8Hzy+UyHCNkPTGPeLv13LiCR9zI0+12rdPp2OnpaSJfD2NEXgx4SENiGQ8PkvNdHqUSPkR59s/rnqNyyMtc1QkUENVn9JYJnWt+FPxjrCgHnmVPhj8BBljH8DXjCGBJDie/F3odTKNtWHs8U6/X7cWLF/bNN9/Yd999Fx3PtDGPgcPr5uehAIm8Rok3kM2Sx5f8s96Y5DkPEmkbFPhhzpFhCgirkYWeQ9uok+Nyv/71r+1v//ZvA3CgPMY6Mkte686a1ytgfTSLBwXon34eAxK8s8DLKvbg0WhkZ2dnQb7o8Y20ubsP/qAfGkGn6wEj1wPR9A0CgKedMXCIejSXGbkPNGG59hlQnx/0bO07+yu6okZ0MGbX19fhmV6vF3LIqa2ofIAsQh8ol8tBnmNDEj24XC5tMpnY2dmZPX361D7//HPb29uzWq0W9BhuchgOhwnAm6Nrmuy81WrZb37zG3v79q31+/1c83hXefGgEQi6MLLQd79QzNJD6j0ar+g+5AEGXZiAGertYEPkzJP36OhvXSDUT3keKGBiVZh4QapgQwxw8GOkY6X91b9ji9DMEl64u5BXMOmfKnf8r5uBtlEFJYq/zrmOo/bBgyaLxSqpkyb+QsCjUGi9kBpDKoBAVX27dUPRfBXMsxqUfKbCUucGoargAZ/DJwAA6kllXOFDLR9BpeewaFdMyGqfeE7nM229ZpHf5GMbjdbNWMb4md+UqX31YWS6jhTx9X1VRZXPlM/gQf2Mdvh1QzmxDVuVYD821Et7tP+qRNNPlF4N/6a+2WwWjPGHJvXQmVmQmQpw0WYzS4Cwer5bjYrYvJmtNmPe1fFU+a9jDUimMoOrHLnxBRmlGfVZL6xdDHQzCwY6HleUDiIp1OjlM9rllaX5fB6Azt3dXSuVSuG4g09sqwSP6PjA97RJ50gVa92L/NrUtYg8iRmESsgqxszzuBqDuleqIY4M88/6Ovw+yHwxx/qe503db3WvVq+Vgu1e5ujnym9+b9ex88/58vR/r/Poc7GIEvp3dXUVrkAmUWiWsQB5+Zb2fR7dQMc0pqP4Z2Mydx1YofOnfUt7nueYY5272FzE1gVyBqBe918tb50eq+MA3zcajcTxwzTD51OkvOCBWZyfsyhLz/Cgksp83Td83TG7wWwVvcrxUbNbnanVatn+/n5IkofxqxGC1KVzpfJHjVW/z2t71hlsafyg8sqXy3d+D43RXXR/D2j5+ckz5zo+jC9Aj69HdQUFEPzepmOma51ndV/zOh3j5qMU0BN4FichegP/a/2eV1U26x6IbarzCYgJiMz4wIt6jMuDTdRB9ALO2Dxy5a624L3dwqCeNn6DLqn3Rg3+NKTMLzi/CXmAwCy58ECXY+/HjGtVCGBUSBUDVSb0b38HLEKCSQdN4nM9q+2VEX1f+6a//d9euPKZ2QqlJTP5mzdvEsZrjGLzAM3n8+AFZGHiXSsUVkcXKAeF7erqKkQsNBoNG41G1ul0QuRHp9Oxm5sbOzk5sZ2dHev3+zafz4NCzlgx5+PxOAifvb09Ozw8TBjW8GOhUAiebs6vwXu0Gy/FZDKxnZ0dOz4+Tnjzut1uWJzwnd7vvVwuwzV2CC5uY+B5vLPMNwYN3stKpWKj0cjOz8/DlXfqRTezUCdjtr+/b4vFwnq9nl1dXYUrp/74xz+GSA4Mu0Kh8AG4offWg6Kj2HiPu1IeoaM8RGZ0D/SAorJu8MzruTWdLw9swE946rRukG+/uXlBTy4UNU7MLCEDeI+5U4WSMDmvDKp8YLw508xZNbL1qtKiCkm5XLZOpxOuAULOYJTf3NzYP/zDP9irV69CmD11xYwZPz+xz7PmllA56j85ObHj4+NQD2eWh8NhKKdUKgUkXjddPTNM7hSN/MKrRFZsxvbo6CjMz2KxSmjIufP3798Hr1K327XLy8sg04+OjkIeADOzi4sLWy6XAVTGK8BVcCcnJ2Gd1ev14J3mhp5Wq2UXFxf27bffhvnmCAe8Df9quPdyubQvvvgiyEryIQB28DwyiWgP5odom3a7ba1WK1yV65UL+F5vL4E38Xj79UHd6tkws8RNI9Vq1fr9vk2n0xDZpRnQNfoJPsZ4UtAMzw7z6b9DJpF8SiP+NCrF74+UQ6QVa5kx1TGk78hiPdqgAA3yiLHVUHn6yE0eHGfzY6vAGeuCdY9SrDkYVDklSqXb7dqrV69sMpkEfsXIQRb5/V2NDeSCX+fMtQdmYsT86vN8ztgq0K3HVXy/GBcvn73zJQ2I8VFizDO8GgPFdF0Mh8OwZvH+IQ98NnbKV72NeSPKjjnmc5Vbh4eHoQ2vX7+2TqcTIkUgldmqU0Pr9t67GgR5yO+1Shjjqgt5o20dqSxSWeJBVOYAO4P/0f39nO/s7NjPfvYz+y//5b+EuZzNZjaZTKzZbFqpVArHgtT5FFsP8BQyXh1Aqrso8OBtGDUIPbhFHbqOdE1QV6lUsqdPn4b3ucWH97MoLzCkNoWOGxE83o5D/iAHVB6z7yyXS+t2uyF/EPNgZonoMy87Y/pVoVBIyG0dO9VvKQcdVKOE+Z/9BL7SaGp1FuO4ub6+DnlVNK8ZshonV6VSsUajkQB6arWaHR0dWbFYDMdm0O1pK0mk2Rs0Gk3nAznVarXs8vIyFw/ch6x40AgElOSYp8F3LCZcPIPHFnGaUFKD2iOF+luZUo15bR9GgzKtWTKsWQ0TXVBeeCpKmtb2POBB2ruxz/2CuC/Em35o2CAMzaJGOdPM6WYrJQSjQQUFil1snLw3QedFFbTYvPC+gkuq8HihjwJKPZTnNyZPurBj84fCicKlXjHfXspScIZxVkQWQ0jbxvloVbJ1TFTZ0SgM/fyuQkbnQc9p6bhmrU0/hroh8RnjwljpGvWbv9anY8K4xtaGtl2BP+ZJ546ytE/K2ygT2ha/McIXAA3ab+Qpc0u4/ccgXdv0Tdd8LLoJcIZ1pwYd44qRofPkz5z78cVjr6HlKp8VTCYMmSsIVcFZLBYfXImk7dFkmmpMKt8pkKxG83L54fEonuX6OUKnNXpIx5h3MG5RhFSZ9vysfYdUgVVvCwoV/ckCnZbLZThKo3Pt5ygGpul8wjPKG7p+zSwAKuxZOv8+RFZ5hnml//oepDzLfKjM8Hu26gXe2FPdhnLpB3Ou46fk9y3mSI0X5ABjOh6PE+CUL0+VZsbKy5j7IC1L1y3y0Mt0/57KwXWGpeclJf+/3+v8HGi72Ic80MIc+2g5TwoowSNef1QgW/cejqogy9P0so8BCGxC69oDMOwjo9JoHQ+ozPIRIcpbHB3y+rzZao1Xq1V7+vRpuIoV2a+8oD+6j/vfChLpb57xe6W2Q8ti/0jTdfQzDywgL9gbiJxLW+dZwE8eYi7gadXbtT2+7V5foC1EBnLkWPPG8Dx1epBC5S3yJi1CQ/9W54/qun5+/R5Bm1V/0b14uVwGPYJ+sQ70SLE/Wsv+D4Dt9w2/L3lg0evPfpwemu4NQIgxJCg5GfUVeYtNmgpzPo+BDmkDpIYX5AfUe/t5xi9ORfnY1H17fN1+09TnvIEII2u9fvNJM2b0d9qGqv0APFDFLgvZ9ka43zRUKaZsEDXmeTKZWK/Xs6dPn9rz58/tyZMn1m63Qyj20dFRWEiLxSLkZri8vDQzC2flQSUZH7Ktg+YBQOABAE2u1+s2HA7DHdqVSiUsZM4uFYu3ZyLJ3IwnmIzWe3t7YTwJHUWAaKgQPI33sFwuB88s76jBzPmoxWIRzmYjNPBUMvbqaeSKFsCETqdjk8kkeHw504ziMxgMEkqubkT8XF9f29XVle3u7oaQbD1frW2BlG9jBqMnFe5sPsybGmWx6CRvXJtZ4qyz/q/8QMioVwgoy9/77jc89bBhxOhca7ZyD/gpCKBrHS8xHi2MyH6/b6VSKaDglUrFOp2Offfdd9ZoNBI5OM7Ozuz09DTcvkDf88xDnu+zDEiiYrgZBF6Bl8/Ozmy5XCYynd/c3Njr168TETwkIcJboiAje0Cr1Qo8g/fbzELUwsXFhZXLZfvss8/Cc81m0549exaUqVqtZi9evAheRdZRt9sNddOO2WwW7nHGM8waQOaY3crxfr8f+JNjJURBdbtd63a7tru7G2TIzc1NOD/JUQhyRzx79ix4LshxAVCAYsvPdDq10WiUiD5CPmpSVgxrBeSWy2VQUOr1eojY0DXFNbuspdhe/PbtWzs7O7O9vb0QwaSRS+yTmkeFvUFlG7qAgl/ckHB5eWmj0Sh4eJiHw8PD4HlhHtTY29/ft+VyGW77IJM1/Mx61FtmaCPt0uNfCmbr+dtSaXVDgnq4GTdCUVEiaYPm4FG5pNF28Daeuul0GrL4l0qlMC5ZugH90DnXo3E8ozqLPwqRRcyzlqHGkBrePM9vb0yo/uJBJPQUD7DE3tfIKy2PchTk4W9yX/Esd7KjxB8eHgY5p2tJ26N1+gRuRBViJOn6Z3/C+3p+fp7rBowfk9YZoMvl0t6+fWvdbtd+9atfWavVCt95vTRGykvqZNFbL4j8qlartre3l7hGlAgQH4WHjkE+ErNVNCde3bQEl75tHhBEn9V1roApz5mtdD+eQWaqPhaLZvT6idZDHZ1Ox7766qu1QFRsfWTt+TEipF5vPVO7ijaqfacAGnLx7du34fYAnqMdChypjIjpilm2lMp/7AbeIw8Nuj/7irZVo2E5Zk3kB/IVoAAeIOK52+2GPZLbjXw+ot3d3VCuyk72Bt8GHCf0odlshv4S6au5qtbNPRTTIfPQvV3jSCOUFCkzSy7CGKrMIFFWlsGuC4nnszbVdYMTM9r9Z7F+xD7X/qgQ0U0nhjiuq1PbFRsTTwhTjT7YhNLGzNev/dR3EC54UJgjXRigeQom8L96yhgHlGmtlw2fH7NVmCHCq1i8PTphtkrwBbHI4TkEhApq5o4NCU+LKjEYGwAdPBNTYGgnwgEUWVFUhAJIL8YiygjIrV4lpF5+FbIeXFMhSxuoX4GRGJ9tI2j8+lSFW8dQn1EPkX6v8x4DIlW+ACowD3p2mzljrLV+2pvmuctafwogeqWV7+EpjBSMJNpUKpUCEMYVmBpxAvDDWG5L22wcuv7Z1DQpnPdCqkEGT9NfgDwNZ9d1AI+ot9mXrc/wnCoAtFMRfBQK2oripQoJskkNJJX7lE+yNZUP9IOyMVK9QYdi3G63rVwuB4NDr/JlbXrFEX7WqAhIeU1lZ9o+ybPKrzGC99QoRJYAgHpFEHBCFXuUNRQvPWbBPCrwikylH2ar+7XhL8ZZPTbMh4/kUVIlVWWzV960v5Svxw88qIpB4BX0WLQZxki5XA7JUfkBaKStfo71f6+8r4sG8PwcK9cTxz+8MuzJ82QaKchNu6C8silm0Oq4q85glsydpcYG/DGfzwOAxdqkbTFnk/+Mz+EXlT/wBAaDgn0/ddI+xpx1Zh/yRRq/xYxmXb/8zTwqiGqWlGfsNWYr48wbVlqWb4Nvl9atYFaajWBmwbmhNkBMl89aNyrfcIANh0MbDoeZ0QeeNnE4wJ/0mWsHq9XqB1FgWWUAxnIcS+W8WVIOQxr9rf/rXBUKK1CYtcg4Uzb5j/R4BOOox5P4ziypG6ms5DN0bcBXnvfHgFV2s+YZS5Urup+oHFJQCdK9TvlpMpl8kAcqD22rQ24NIGR5vdKEIZtzLGTbLIkuqRKoC5zfXgBlGbv6238e+z/PBpbWFi+EPIjg31Mmz2pzDFiICV4FCebzeTAyOZPvCeHg5zPLsMDTjsBWTyFlmlnIdYBH7ssvvwwKMmgw/edc/P7+ftjUUf7m83nIqkpUgG66ZPdG+cJTB+rMPHz22WdWq9Ws2+0GhXY+n4d70EGwUd51fPkcZZ9oB/gTr6tGKiyXSW+zCkIUf7yduhkwd+Px2EajkfX7fSsWi9Zut61er9vZ2ZkNh8NgqHQ6HRuNRtbr9Wy5XIY7jBUgUE87Btx0Og1nuzEAd3d37ejoKHh9/VnoNErjF+pF6PPDWLKxFwqFMCe0t16vJ4xRzrursaFGBgIej4CZhXt1WYeDwSCAPGos6FpUg1GT6VGH/s9n6n1S5VDBBIArTZJDf3iPzxqNhv3ud78L4/Pu3buQe6RerwfUfp3gX+dd2ESR0GSOOm5v374NOVbMLOQSabfbIWfAcrkM3oZer2eFQsH29/eDdwlvBleR0hbO2BNlQxQD9yETYdRoNMKtBvV6PXij4fPBYBAUWyIQSJrV7/dtOByGDR3lAxlycnISAAV4GW8Sz3OWs1AohPwLw+EwbOiEKCIHer1e8HzgCSUZZr/fD1FRCoKhGCEfmQtkjPc+MUc+xwjHYBQoUGBWI8s8qUG0WCxCHhl4nuSQfK/gdaVSscPDw/A5INlwOLSLi4vA+wp2s7aIyigUCra7u2vVatWePHkSQFsiycrlcojuYA9pNpshrBSZRh/02AnjQD9Za3iZCDWHN5HRgGLqYWQdkOtGQQzGn7P3rVbLbm5u7Pz83IrFoh0fH4eIjWazac1mMxwHLRQKdn5+nlBkabcqk8gwgEb/vffQeZBhnRwYDodhnJV8m3QPjRlK2hZtWwwM5n8FqLyXmGdoh4KUfKfGnhq8EHve5eWlFYtF+4//8T+G44GqmLP3sJ9Qvua40sgP1VPh5WJxlSE+NoafKqXp+sjD6XSaiKqL6apZQJWfGwV0WT8Alqxh1ipeZuaAHGSMuc696h8K9CvfKQCEcYasUvkBT0AApPQVGUufkJHITvYWnlc+UGNZ29ntdu0Pf/jDRob8NqSG9GAwsNFoZIvFItwApVcb6vrVfnDdLIBxWrQEPKXga1ofmD/sCcpk3NmzNT+B2pTKm94W86AV+z7zhu5BRK3mz0IP0Hnlb9rBHsjtOldXV+FWHfqDLYMegR6NDqz94EYHdAs/nnntu03oThEIsUbEJpzEJISlepQPim0S/rmYsZ5mTGcZ4rFnYsBBHqAh67MsdDUGPqQBHv7ddV4CX8Z9ItwIOfXQ8Rthi+BgsQ4GA3vz5k0isRheI80uj0BFIBG9gALKAtJzriiQGrZJOwEhUCIQ+mZmR0dHic1elQJtDwqFRnOYJc9pq7HeaDRCP4lW8Kik95DqhsT3GNiawKxUWmWF53MNhVdF0yt3yl9suLrB6Ubm+ecupKCgbweGNgq/Kny6sSufqbIWUy7hQ3jr6uoqHE9BMWcjh6ifu3s94uvXs4YuM5cKiHovhiq1GoFjZolz9pSjHivlO5KRbhpNdB9EmzQqxPMNQI+GajNGzLPepc2PeiLK5XIwrhTQM1vJHNqAksZGbpZMomu2iujA+6FlAfIBQJitlDV4hasLmRvATAUQ4A81dmmPepPpJ+0j+Rd3xXMWVMFVla8apRHjNVVIlS917NQbr+uLedIIijTSIxaMhRriur4xZIvFYmJ98bnfR5BbyiPaNxTLyWSSiFwDlFVepI3aF/Xg6fhpNJTKWx1/fQde8ESbAdm9nsTYKy/rngPQQX2sg8FgkLj6UUmNHE+qIPt3vB6RR6lk7tvtdpDrvqx1+oYC9N7Tp+3Wvqq+x/dqyMb0nSw9yRtkrFn4jn4CiProRtUZFCRQ8Eq9pbo2aBeAKHtd2p6bB9h5SMprfOhxD9UBs/RzyPdf9UTGWYGELJ2CutVxEpOXsX1a2+b5UXUQ+F7XnvKmrgGeAWxSAFjzmais8TaQ51WAZm+Ie2CNMeG72Od5DUp9hjB9QOPYOGn/qaNQKCSubo4BCVm6pwI1yGp1CFG+9tHrwro/qHxUHtR3/Dz7zwERtGzVdzQSUsFxyiDnD7KffRge8fyEXNGxAljIoxvelxx5kFsYlPBScGYVQakKeBqpgPcLlO/TBAOUxogeOFAlRX+nvad1p1Fa/2KLeRPwIK09/nPd0FB2NYyU37E2Mp8xgUNUAHewk+MCRU29uEQBvHv3zt69e2cvX7604+Pj0CaScrVaLSsUCuEMYqvVsvl8Hm6N0IzIenZNDRTGoFqt2u7ubhibo6Mjq1arIfKgXq/b7u6uPX/+3Obzub1+/TpkxAcwYEwx2HwoEUABY83i55y4eu4Xi0WIDuB77m3nztfBYBBAAzY9MrKen5/b5eVlQNt/9rOfWaVSsW+++SbkmWBDGQ6H1uv1wvtmK0VceYwcDgguhK6iv7FEXWmU9pwCQvyv2WQZA/rG8zFlFOGogI5XzDDoFJEnDLVer4dwVJR8DEp46v3798FAUeWE9pqtUG8Fy+BdzZWi7+rGg5IF/xBZ4QEqjcAiSVS/3w+5BrbxOKQp9nnKgh/UuML4xktbKpXCTQlE9OCdVWV5MBhYt9sN/YU3AbYODg6sWq3axcWFzWaz8C4IPUa8XnukfEybyI/C/GLAgtgvl7cRO/v7+/bDDz8Eg7BUus2Vwn3PKKvj8dhOT0+DQsQYtFot29vbs8FgEM41A1wRfVAoFAJgwK0snU7HzMyOj49tPp+HyAU1iHRs8HRwblJBNnhCj0UVCoXgLQIwUeOUtYlsK5dvs0mPRqNEpI/fd8nBcXx8bJVKJUSEKChUKBQCEKzjTn90PqrVaiKs2MyCMqUhrgDGGHq0F77UnBEaKeIzWNMPzYHAXAJM8Ywqjpp0jUzc6gFjLTH35N7xIAnggyZ+Y6xOT08Dj+/u7tpf/dVf2Ww2s2+//TYhk3VOFFBTGepBVx8yq3MKb8QUbiXW0snJSfCeaZ1efntSsM0rxto2BVO9fFJHlK9LASRfphoH/DC/hIKrMVcul+3i4iLcfgSAxfcqv1SnAixEX+JzDALmibweb968SUSJrgNgtK8PDSpk6bD+mfF4HDyxAF9qXPk58aQGXAxAZa2gy/oEuGpf8I7efqN16zpSwF55hXLUKYXBx5qjjwqkqexR8F9BAyKa1CGioJMfb3SO+fz2Zpp//Md/TOydsfnIy0c8u4m+x+04z58/D3JTDWcF1hg79mzGCtmosl+P+KTxi44dY10ulxM3PplZwkGmvKCyJwaiqk3ho+5UNiFzGTsPqqMbkDCVcrTexeL26EG/3w8RsowT0QfqAOW75XIZcjjAY37f1vlfByJtI0fuJYmi9xD4zwnr7vf7tlgsgvGkAhzSCVAkM21D8xtDXiOc7/1mvO59/X7dgPsylGHy9EHfSSPdQL3Rw9EFRbc2EShpwIJ6183sA4NLFQkWNgIWg5H3Dg8Pw7U/ZrdXqxHGa3Ybgo5nmIUGaDGdTq3f79vV1VUIj2JzKZVKITEgAABCB9QST6l6Ohk7VWwUyPILn78Jm9fwdPqIglworMLwu91uuPvV8zn1qEKCUoxBRKQB4aQo4uVyOYTKe37y6whBg+HORpgWWrYtjUYje/36dWjL7u6u7e7uBqWdTdG3Vz2Rurmrcc488L8/gqB90/FBoec9PIX8eN7XOnWtem8GbdaNwsyC50QVE01EpjzAWDC/XHHEhpYXPIhRmozOQygwtPf09DQY7YVCIYAz9JGx1AR1lKP8qTJMI3Yg9WyjaLB2+c3zgG54eFQZAXxKA7AJtyXcEQVJj2bo9UyNRiOsGQxT+I8xUBCRNiyXywASEFarRqZf9yii8ISuT1VW9bpkxlQVH/WCMK5mq5BLIpl6vd5aLwZlEg0DSKJA2XK5TAAyKFseVFMngd+P1XngPXKME+AAc6HJIVnvmjTVe8voDwCB/s+c+DFjngmXVn0GcODmZnW9nM4DtyjQFg/mcz0tY0p9CoKw93hdJmaQaz999JB/Js0R4+fezMKRHZXjfqz8PhIzdnQuvR7kDT3a6Q08zx9pffCgCkf3mC+AnFKpFPZHfV7n0bdJwXc1BrVONVC17wCKAKZ+vLMcPT82xfYU+Fp1pNi8xPbRGOm+q3qK2SqyClnEevRgmQcH/NEZz3f8qO6HbcJtPjFvslkyqSftBcj24EHamoCUh25ubuzy8jJxxC3t3TSQ574IGUg7VLb6/pt9OK5qH9A3bXcMAPQ2Bp9rkmae1zWpehb86etgjHg3bVw9KIvuqBFJyv/8APr7qDbGEFmqBj3jo3oLY8UYKgHsb0J34YutAYS0SmOfc1785ubGBoOBPX36NBgQquQwyQyi39D8bzNLLMA0tDpGaYBBDN2P9Stm7Kf9ndX+2Aapz6Qxs2dAv0DwYJyfn4dEe/dBy+UyGPEo0HjyENwYy/yPUc3tBeQxuLm5sc8//zxky57NZtbr9Ww8HgcD++c//3mIEpjP59br9azVatmzZ8+s2+1ap9Ox4XCYOIuKJ/dXv/qV1Wq1AC4o6qmZ0KvVqi2Xy+CpI4SI0CNdpCiKKJcIhOl0GowCMi1jGJjdZojXUOmvvvrKms2mPX/+PCHM1DvGeLNxVatVq9Vq1u/3bTweh7Nor1+/DkqnT0ZHO/HsshESWVGtVq1eryc2N9bQuk09RjE08/z8PJzvLZVK9h/+w3+wFy9ehLaiyCnia7a6Dxivs6K+eHh0XuF7BREAXeiTnslXzwERL+o58hu0Kh0qn3RD5DmVJ8wHnjrdLOE/DG1VLiaTiXU6HXv//n0AXTRsc5P50DmJKaR5UGgFAhaLhX311VfhLHqr1bLf/OY3ViqV7OLiwsxW52EBDMnMj9GvdeHBoB16Q4MCDqw58ieQyGkwGFilUrGnT58GY6vX69nZ2ZkdHBzYwcFBAGNYn2bJUNTd3V0zs8SZdHjv+vo6gJvX19fhHD6epbSx1LPO1LdcLu3s7CzwRKFQCJ4GBRAXi0U4P8+tMtysososSoYmd1VDXc+FqlIPcDoej63RaNje3p51u1179+5dkAtKKg/oL2BKs9kM4KjZ6khQv9+3crlsh4eHZpaUSZTpQWaN8kI2a7SRvmNm4VYCDGwiRK6vr8P+A9/pMTgPACsf+mggiHeREUdHR0G2IH+ZJ/rCERhAIiJUmEeAK7yVg8HAdnZ27Pnz5yHLNvJAATnGk7YoaK9ADuOs/fL5CZhTVW5jpHKDyLgXL16EtWOW7XzxoJ0aC3q0SY08lfFeTnkFmr00Js98v/AIDwaDEHlQKBRClv9Op5M4WoIST1sUEOUZ5Q2NhvHjosDiYrGwFy9e2OHhYXAGeDm8jZKfR6bnLWcTfZ93PLiTBewwdpAa7/yveyc6DH+zDkqlUrghYH9//4MoE4x2dSpoPcyjN+xZX3qTEI4uPMbKr6oTACTiCNBjMrG14Enl3mw2s++++y6RZys2H1lOgth3aXWnETyhkbbozOSy8vsN40O7Va9VYFRBJWQo5OeEeSXXFXux6okKIvC/OhZoF3V5vY62eKLvOAHJj8Hepfv4bDaz4XAY+qtt5JlicZWrAR5ET6FseBm7AnsEPRodZRNiPtbJ/hjd6zWOWYKKDZ2wVrO48FGklnK1U7G/PTqpdaa1Je1zNdaz+qPPxVBVvs8SmusQxFjZvv8KJMBYgAd4OjZlqCxCoaf9urHrOVg2Ut1E5vPba+jm87l99tlntr+/b/1+Pxj0CAoSsBWLRev1egmjDXBiOBzafD633d3dD4ATwvP39vYS/EO7UORoNzkFEIgAJCxONp3r6+uQ7JG6EBQcTfBePhVMbDRXV1dBuKL8YkQS7ucNjmLx1uP75s2bIKAvLy9DkhUiKsxWwkbPgTMGGvJGWxFGbLa6OW8qVNK8JCqoSWpHErvYOvbtQqDCZ4SpQyj7RNpwhp45rNVq1mw2A4/i3VMji/k1s1worsob5bGYDIJ3dUPU9YsBpJutAjqARXrt3TpaJ5M9rXuW9a5GFmtJlSIUbb3Nw2x1qwYbL0av3k7A+Gh+Ag+Kwp8o+woyMIZaBxs4P8gUQD3k9GAwCHWUSiU7Pj5OGDbICIAoIh3UeAcAKpVWV/2hKBUKhcR1X2qgDofDxPV8ukfymR4DUbnKtVgKHqoyiwxiXlhj1E10Q7fbTYAYMfLtU0OUda7PYbBDqrybJfd35lrlE/sZdaFwqcHBb5Qv5KUmaWUOaANjyBpWRU5Dammb9xr5SAU18tWoYT/RcpXfAUPMVsnh4C3yYnz77bfB269jH2ubfq6f+QhO1V10TrMUZk/aDq+nxeri2Zj3TWWV8p8CPAom+LI9X6rOEDNmzSwcMUF+AOwA9DM2GtHn9yjqVOPWt0GNZ13zCviwN21qyGXRXYEDpU32kuXy9hjOZDKx4+PjBIAfM2aVB3V+tDwFELyhqWCT2QoMJOkc8k2P4KUBbLF6zZJRJcyjGvDwF/sUOiN7JMeVNOrAj4dfGypLSRI7Go0Sx0Q2nScPHqzjN/997B2vf/OZn3PGjrHXdTifzxP6qgcO/J6kOUkUNPWk8l31UK2H8rP67kEmfVd5U8dE+RWeKRRWVwKrfQiY6WWMOp0UGKau+fw2ke+bN2/C0dZ1lAbCbgoemN0TgKAITxbapeddzFYhdwyy75gOupaXtll5gRIbTP+ZKvBKMWZch2rrgo8xnNYB0+mGmLUJe8BCx00VCwQVyCghlJvQOuQapVs3SwwklBmMH1XaiCR4/fp18Hidn5+bmYWETJTfaDRsPp/bu3fvgvKO0bhY3B4B2NnZCXc1q+L5/PlzOz4+tsFgYOPxOLSJqAAUOjaE/f39YAgAcqkRi8EyHo8Tip2euWWTHA6HCWVHPW4okYT8lkq32dgrlUrw3vGDcathXd999529efMm9AeASA02MwvJ4Ig4UOEIj+CZQ8nlvBb8dHNzEzyTzKHyxzbKCet+NBrZ5eWl1Wq1AACZra69Yww0tNps5a3FA0DuDYTydDoN4X2cPceoajQawWuMcQevXV9f29nZmc1ms5AlX0OPPeptlh5Sp+Pj1yuRD4AAqjwtFqsjNLxP5neMO0LLszwIeT0K28yfHhOoVCp2eXkZ2onnoVgsBgOcm1HoP2Ac4B8eYTWoGAMMMYA5QAXAPX4rIITxD0+jlCwWt1FSHAn54YcfrNfr2ZdffhnyNZjd3mZCwrRGo2G///3vEx5wQCXyEOi946xJ2sjxKfoP8DkYDEK0j9nKg8w56zQADoO60Wgk6kJezWYz293dDaCN2WqPQfYwP2qUaR4WctroGVIlXQeqOKt80GMRy+UyGPEATny+WKy83awBjjZSD4oyMtBHqVAOsnt3d9cWi9uIimq1GnLAqLzCgNCbK+bzeeAzBbAgBR+oX6O8ICIPtE7NscI8tlqthLyFB8iTs7+/b/V6PUSb/elPf/pgT/DAHH1jTLXPzDlz4OUW7+q8Zjk9/N+MR5pM8XV5hVWNKfZTyoQX2esYR40c0v5oXYDN8LTup2a3t0TVarUQbYO+xL7E7UysYW90Quzx6izQcWSdMdfoFAogEPXk1906XexjUl5wYz6f2/fffx/26Gq1GmSQGr7s417vVcPK77cqa5VUn+Z/9BwzS6xB1jb1eB0pVp7qJuia+r3yCM4i5szvFcqzMcDE2w3sPd9//72NRqNEng76lmXox+ZtW36KgSxmHyZWV1nDM3rkWccepw0AAno4+h77u/KKPzLn83UpYEh/0WsVLKat3oZlv0X38PuVWfLWOXWcehnhjx14mYU+A1i+XCaPKuLE0GNVGgV9eXlp/+t//a+EUzTP/Ho5rIBNXrq3HAhpwkW/Y9DOz89tMpnYyclJ8KjoIsrqvBrPKtQ9mpcGIPhyvDDIes/3MwuxiXkBPNLKZ7EEM/qMvs9YqRBFsF5dXdnl5eUHtxLk6csmpEJT0TGv4KjAINSXhXZxcWHF4sr77xcXivDTp0/t+vrahsNh2IwZM8I9a7VaSFRSr9ft8PDQ9vb2grGOcEGo4DnkjDN5FvDykIARw7pcLidQXzxYGKM6jijBHIfAQPZKj17fyHywySG8JpOJjcdjOz8/t263G4wMPfrD2CuPACQwVzzrQ+d0U9ZNS/MoxAyJu2w+gD/L5er8KjwAXzH36nlkTBh/fY4NpdlsBmUQfqzX6+Ez5kYVbH5UWUHxROHjM8ZX26Cka5oQbiU1pOm/bmYk0eI4zMXFRfAu6xndGEiQZhDkpTzPwxOcGaY+bv8YDodWrVZDVAB8pYas2a2nGAUBxRqvDfzJ5o3SwNhwkw/9xLA4Pz9PhOuz3tVTjAwiyaqZhU27XC7bkydPEvOHskY4Om0ir0q32w3yWK+yKhQKAfyBvxQsUsMX75QHFljD8AagE8qF2cqbDwijV1ctl8vgReV4jhr6us/R/na7HcbI70WeP+gLPA6gq0AwbdR3lPc98KtgAX2vVCoBGFFPDt8XCoVEMttCoRASOqIs+jBW1qEPT9eIKx1L5LLKXNpNe5kLzkZfXV3Z0dGRvXjxIoQvUzbKL6DS+fl5AKNVl0Fp9uOuv5mbGFCsf7MHeWKN5tUFYsppt9sNUYQYw9qXmJ6kuovyou7vuo5RrFWBV71RvZFeT6Jc6oM0vwXHbJrNZgCstU1Qmn7oDQIFFGgfPKeRfsg/HD/K258K+fle1zbdg8h7pjewKRjvnRNKsb2OvYLyY+tB31VjXq9zZB7RE+A31r2PPvUAG/qTGnnKmzjMNOJO9S5IeVllE2Xc3NxYp9MJV3rT9k3mQ0nnMgY6xJ5fV36/37dXr17Z0dFRAG2V/5l3X77KB7+mibbTvirgol586lK+8iAMv9l/fKSElk/bkO2xeYO3zCxhX2hfeE5lGoRdwvrXerU+zxckPueo99u3b4NjSdu3CU9k2cnr6N6OMGQpoDAhA352dmadTidkRo8Nuv5OW3AqjPzkpwl6FTge4aQcX5YXUusQPf+cKtF+IakRqe/H0G41QDCEGFOU0YuLi8SGFyMdX1+3/p+GZPGeorsoMIrSIgA0gQweKUCkly9fWrvd/iBZld6RrQYL4cFk2u/3+1YoFOzg4MDa7bYdHx9bu922ZrMZPHNEQ6DgACD0+/2E90TPUbPhLBaLoMz3+/0ALOA99fxDJAFnp8n10el0EiAKAIKOr3o5K5WKjUYjOz8/t1evXtkPP/yQ4AOvgKvSRHuZB1V22dRYj4qKE15L/QA7eY7A5NmMoG63G3JcwDfq4SNyQjdnxpdNFUWcfqOQt9ttOzg4COHqAAh4m1TOMP4a0kyYGCCNKoU6T7wTk1sa1h2TXSp7qBdP8ng8tsvLSxsMBvbu3btQxjboMH1cNx95ifXT7/ft+vo6RIB0u92Qk8Ps9kaB5XKVIdhsxdsY7xhUjA8AAc9rVnyzlaFPSCzynUz45HrhmFCxeJvoqt1uhzLx2MPbZpbwcvziF78IxjbI/ng8tnfv3gVgEZlGnhZkka452gtIot4oojLgMyIWvv322wA4EmkAn5ChGf6kH2a3vASPs56pb29vL0RgaMitKl2UoflZWF+edC/kPeQDBjBjq3uDX3MeOFBFHKVJI7tUdwBoUAAOec7tM8hgjFqtn3IBDOAz+AtQWPP2IPNVqaQtCt5zuw/7xpMnT+zp06d2dnYW8hoogElE0tnZWRg/yjWzRC4dP+5+XvTzNANXlWz9DBmk8xKTN2l6T6fTsW63m8jzo/uSzrPvC2X479UA1P/pp4I5+pnKVn0OYE5lBwY76//o6ChEQSmwjFwCjNCx8Xqoji398s+r0cocE5ru9chNlfu83se7UB4Am886nY5dXV2FqBuV+WYfHllW0jlXMOdjNocAAQAASURBVIk6dA/Wfqsuz3PIRQB6ylPg1yx5Owf7P3zodTVtv/Ic3xNt4oFtTx70UucG4Ljm+criibxzv4m+to6IjqxUKiFqR4Fy9GRv9Ps1r+OH7GfscADomvbHFrwebPahnedtMeU/fiDWPmXrHLKuC4XbaGuV694xCIAAn7E3cVyKPZp6lOfY/+gTEZE4FP/whz+Ecc0CDdL47q50bwCCWXbiDhUwDL4alX7zS2NoHWjdiDxg4MvzIIBnHn2PBRwDEWJo7DaLzzO6b3dsIUDz+e0Vimp0awhMjPK2URkx7R2/APWKPoxkCGG8s7MTlGPGbDab2fHxsT1//jyc9dnf30+AE3j+G41GmAeAhUajEYwYsqOrV48waZBlwvEV6VdjnGSOb9++DX3UDafRaITEjYTI47Ggzf7sNvNlZkG51XWiG+JoNLJXr16F8RoOh9bv9wNIQnuVNxkPVWQQdD6sFGGkyLvZCm1XsAHeymu45kGqPT+dn5+HucLYYVMgXwDtVsGNIofxh2Kh1zzSHmQNCfz0TDbCXc/w63V/bF6Ms65Bxo+jK8vlMhiLej5P+64bHLxlZsFA/PrrrxPnJc3WR1J9TFIwSfmFcf7+++9DokeigswscQsKRD+JDCF7MLzI+MIDKCYkYEXJn0wmwTuMFx4lnfBkBZ0o28zs8PAw7D2sX0LJOQa2WCzs+Pg4fF8orK5ipC18jvFbrVZD0lpkFIR8gAAeXr58mZBhGMV6FMMsCXBjkDI3yluAF/DZYrEKgVcFGuMXIlIhBiCo7PF7l4YWA7AUi7dJoVjT8/k8JAJUkEBlmYaeqvEVA+tU5ilwqoqpKnAosQCptJt3GEflF1V4zZLHBbQdGCIaOUbOEg+isHYYE9b73t6emZn1ej3r9/v21VdfBcA5Nh9+XrRdUJqBy3s+qiuLsnQIwLzFYhHkMp58BYdicxwDSGK6ne6B8I3Xj9RwiemE3rmiwAl99MaiGqL6f6GwirLiPdqgZWp/6/V6AOnNzL7//vsw/9fX16lXp+alhwAPdGz07xivKS2XyxCd5iNI/Pym6cExPZ962QPQv3QNaDSXgpTIVN2P2XM4zlWtVkM0ipmFI43aX414oU5vGHu7wo+THwvaRzQaRibXj6vet468Dn8XY9HrdrEyAUKvrq7s+fPn4bioP96mof5EfDGWKqfUoZN2hFb3AI2iVdtEI6x8+arnKtAQc6LqPPEue7KC1PRLdSP0yW63G/itXq+HyDk9coltoiCjgqBv3761wWBg33zzTXBS6lykAQUPBSxuDSDcB0NqyKpXDpQ8CMDznoGzBFHMEI9R2ve+DWkUa4Nf9Kr0xOpWpoX8Bkd4M+TPReWl2Dt50CzahqK+WCxC7gDmFAQNlN2HoV5dXdn+/r49e/bMXr9+HQxJDR/1QABeo2azGdowmUzCTQso6CjdIHZ49ViQPpFRoXAbCjudThP3vF9fX9toNAo5Gy4uLuz9+/chAoFEa5xNpn5/HQtz6D1iqhhPJhN79+5d4A0UUb/RUB7Kj55ZVkPNrxGNWlEDUIWVeipVQOflpTS+ifEZ+QroO+cl4Sf67I1x+q2h3Ipws2mgZMJrapwqiqwAAoCChh0ylsrzgDwkAFIvh9kqkZsq91oO8g+Fu9vt2ps3bxIGZox/1q3xdd/nUSxUuVLy4eW8i4f43bt3NhwO7ejoyAqFgp2cnIT1oyGcADqz2SysI8ZOeRqDfrlchrBostIjC1C+GVPAG8AE9WIwd8wLN1son83ncxsOhyE5ablctmfPnoV1o0cvNH8H36n3CoOBSBs8B3pOFDnx5MkTGwwGdnp6mpCv8DjniNUYw1POmGpkA2CYGuF4/xSE0JBe1tG68+y6NnVfVAWeMeJ6Ot7j/LcCPSrPFLxXeeK9U9SjPAroqGuIsfCGD+33/dQoDeVz2hJTZvlcZQsAGV5D6tdyFaC+urqydrsdFHHCVLXvHuxg3OFbBQFUl/DvaNt1THgvr7zXfpitooSILtIrimNtiOlxSjE9yXuwPamRjz6gHjzKpG6dG5XXyhe+PnUsaV9UPqaBPjgd2F/evn0bkp/BY1mOOE8PZRik1bXJ5wCJOja6h3pHlFIa6IWsUyPdHw/Q0HPkmso9LYN2soYBtNFDmRPksIJg2m4PNnoe8f2B19gXzFZRCxcXF4mrRUnumyWT181HDAS4iw2nRPu73a71+33b398Pt+6gGywW8fwsPMM8KUDtI7LMVvwD2KLywwOHOvZq4PMZvEIZMaeI1s33yBh0eX90TPUT9LzZbBYintnv9/f3E4C2RvORP4m+oZu+efPGOp2OvXr16oOIjB9DVtw5AiEP86a99+7dO+v3+/aLX/wieBnNVuieX3SeIfje/+jzWQBCDCWkTEW0sjYs3o8h6WqA+UWwbpNWhFMVMBiJOjVh37o2xigNufJos3+HzRevEs/xGWguCxNji2MFLNp//Md/tO+//z4kZhuPxyHCwCtrHFloNpv29OnTMI6DwSAhbBhbTXICaLBYLMJNCgAVGBnKDyqM1LDg+MKLFy/syZMn1u127fT01BqNRiLqAGNWzy4zZiiYpdLt1YrT6dQuLi7ClZSENRFOi1ChjbVaLXFrhfKFej/8+U8NwVKFFP7CyK5UKsGbtOkms42Auri4sNFoZM+ePbNWqxWS8DFHCFLaomvTbCUnfOSLrjMUNxX2hcLqGATzNR6PEwaIB5oUlFCgRvmdKAa+ow2ATPAqCgIbr86PCvusNaoUUzzXvaOf6/sx+aRrTAFb3sNr/6//+q+2u7sbvNCLxSIcMWFekV16zEgNQ701gfHe2dkJnhiMK/JdtNvtIHsUJGMTr9VqiUR2jH+hsLqaCxmLEnl8fBw8xPTbbJULwgOpXMNJmxUohbgZRs/WTiYTOz09TdykAC/Q7uFwmAitV3nFHgBv4+XUow4owRjvrHf1BAHSxrzRfr69gc+8kduG+VTvHrKUdxRMA7TA4NN9GPL3bTMOHJ3heByJdjUUXctSY9KvE4ANTbQbWxuxs9vwX61Ws88++8yKxWI4eqJKMkDzxcVFiLy5vr62V69eJdqtoFfM2FJlV5X0GClAwP+sy7s6g/z/yHO9NjOm89AvledqWGl71UjQeVPdStejrkutS2Uqyr++r8eNvE6VpkvC1/RT++vBvUKhEG7IQu4pj3uZv+n4PzTF6lunJ1xdXdnXX39tzWbTvvzyyw90/TTdVWWO3+/1hyg01Q+0DF3H+pkarApOAtay13gwaT6f22g0suvr6+AAIe+P56EYkOSNXniAHAeTySQBIKzT72O6gtmHvOSN9nXPKK2bdzViX716Fa53JR+Nt610/VIGejb7MnWo3NM9g3brnqRy1iwZdetB72JxdYxMeQDeUEDB95Hn4F8FPFQvhy+JMq1UKlav10PeAj3WRh0asYQ++u7dOxsMBvb999+HiE6eWUc6T1n8sQ3d6xEGs/XeMh38fr9vk8nEvvjii6iBrQCBvhsbNA8eKHmkUMvQ34qO8VuZKqZUr5tARd4YFz8WSrrYaI+2Xw1FM0sIq7T6ffl3ZRxdsAAIhUIhYYgXi8Wg7LK4UIwnk0lQXL799lt7//69/eY3v7G9vb1EJnr1rKMAkyUZRZz2qBdZUTvGHyULpVyVurRx0E1guVwlL+Os1+eff26DwSAYf9ymoJ58VUxVodDr0obDob19+zYc18DgYQww5vkhmgOjF4GC4UJInwo8+DsGtqnxZGaJOlWwplEWsrkO9VwsFuF8H/kiMHz0FgkMT7NVGDhC1IN+MaUTxcDLCUAk1iihpH4j8gqtKvgARxiWGpLGuypPOAtHdA23hfjNScdwHd2nEZAFHGL86qbLGqXfJPbZ2dlJJLDUK9MwKnW8VU4yxyhxGL0g9SQw1Fs2yCeg/cI4Jp8HxHqmPRpKj6FKbpZXr14lvB2amFHHhRs9GB/khiY42t/fD0ApEQtmFq6QUzmpYzSbzUJ0jnpNGROATfirVCqFfAZqvKu8U/mgY7QuB4K+5wFuboBBAdMEj/THGwP628tc6mWcvcGhADZ8xRgp0KftjQH9atBoBIn22a9Jr5Ai80nmy9WchEVTHnIBwBhZcXFxEdrAvOo8axu9fqDjhCKeNn+01c+x3zO2IeQ5MlwjfjzRTq/A++djupuOO0Ad78b6pPKc/mkCM90nPd+lGa9K1KEh2War8/cA8xrFxE0zaeP4qdBd27JYLOz09NSazaZ98cUXiSMcsTlXsMyD1GpM8g4RaGnHcfyeqnqY/jZbOVnYy/w80zYM/NPT01CeRnHq3qDyi/pVvhAthv5H0lXNxL/OzkjTs+6iF+SpT2UqY3NxcWGXl5e2v7+fyOWjdpyuLQ8a6vrTvmeBSP57jbpT8nKdCD7WIXYC8tGDgVAMXFYeVuCa/RtHRLVaDY4TcnPFgNbFYhHkxPv3763X64Uk+ToP90HrdPw0ujOA4Bk3hmylKahmtxP95z//OXh1UTh1wph0yvJn6PziyvrfM50ubt1EPKUNsC6MtD7yXCz8MYay0neMbUIhESigdL6t65DgtLZlCZ7Y3AEMoJyS0Zy50bNOGAhkPy8Wi0HZpx/z+dy++uorazab9p//83+2vb29hKJZKt1mdm61WiFSwWyFFu/s7IRcCNSJh3+xWIQEPsPhMISMlkqlcAyCLOvcxQwijJExHA6D4YBQLBaL9u7dOysWi3Z8fBzGB4NGNyQVUKpoX11d2Z///OfgYTRbeakxlDTEHj4BLNBcB6VSKXGDg6K6eGe50lI9+rRP/2dDI0vsOlqnYKxDt/mO5KpnZ2dWr9ft97//vR0cHNjBwcEHGzN9U9CPDZ/IjkajETZiyG/mKDP+eiQUFSIU1Bg0S4bSma08wnymobOaE2E2mwXA4N/+7d/CMRU1MnXcvAdkHW2q7OX1QCjB35pXoFC4PfNMe+fzuf3www92dHRkn3/+uU2nU3v9+nUwgvldq9US77EGMUK8Yqkhf8hJ5CDrArmA0o4c1dwYhUIhkbTSzBJXJALsab80NJtoi9jYYMAqeAmpcjidTu1Pf/qTDQaDEFGBoen5TcPB9cYFMwugqQJ+xWIx3Cajmbv9HoeRz9ovFm/zFvhcNmbpxpMC+/AE7SMKBTAUgJXIClX0eI+QT++94zgXBgORFk+ePAk8Z7aKuALQ0RBnzRu0XC7D2tTnACu53lLbZ2ZhD/PyALnNvg4PKhC+XN5e48q+4pOH6ngqyE29uhaoS2U93/n1jJ4Rk+dqROVVSNcBwzc3N/bq1Sur1+v25ZdfWrlcDnscdaiXkDZ6Rd2TNyY0woCydV60Pn1PAQXGUMEwlcXoIsqLqrcxpmm6brlcDjetAKjt7e3Z/v6+nZ2dReXIp0QxHd/3c51TCjD4n//5n63VagWeUP7lOV+32Qok0rnxe6OCDryjZbJ+iEzzUVzX17e3fZXLt7ducaQB+YDOBVhQr9ft2bNnoQ0kPKQuACV0ANYZvEMUCnuTWTLKzwNanvx6zVq7mzok8pCWo+XT5u+++85OT0/tiy++CLmRzCyh6+gc6Z7EZx40VtmoubEUwGD/5PkYOMFnzCfP8VvBRd3DY+1WHUT1IcoHVCdnEtGUehucly+9Xs+m06m9e/fOxuNxAmiOUV69L+25dQBVGm0NIHjkJasDWd8vFgu7vLy0SqUSzkui0HjDP09daeCBTryi3Upe+KyrK/ZebLOKIej6vy9LFwPM0+/3Q/KrWD89ynoXyjImdMNE4dRzxn5jV6WSsvGwYYQsl8sQ9qiLX+tE0dPcB2YrrxNAQqVSsW63mwCfOLKAl1cNCRDHxWIRFBkSr/FDu9UTztwUCoUEIOI9LswjG0ehsLq/fTQa2bt378J33BbA8woeqHcdgcUPCg5rRjdlxs6PmfYJoanzxfxsK1jWUWwNomByNecvf/nLoKibfYhc0wcFFxgjjEjvdYa85wPQybeP+YRnNVTSey1iHhRdl4wpiTFfvXoVvODbUF755N/Rtm9CyidsjmarMEH4ln4OBoOQ14IQPjbOdrsdAEXkx2KxCOAC56kxylQmqmKlngA1CJg7DFLWvNmKD/hMcwBg8AFEcjUhRxG0TPVaUEez2UwciVDvCnwGGDEej0OGfmSpZgRXo1gjmJB5avTp+qdN9EPlmILurBXkLWOHsuuJ59MUR+UR2qTAqeaFQQ5fX19/kGla9wyti3UGsME5UVXEmEdktcpNeFdluz6nxwP9GHuAX48yMd5KGOs+wZaZhZtD9KgT5SrpHuq/j+33/n2vVOszXg7E+rgNqRwgTFfri5WdJpPSHES8E2trDNxiHLz8Z2xUXvi2sI48eGC2Wi/sp2o0aD2lUilcxYv8QFeJ1RmjPEZ82nvryt6G0upPA6FY02dnZzadTu3ly5cfGL9puq3KDOVl/9tH1agurbyivMP7uv7RBUjwrnUTzcS8NZvNAFzjCCoWiwF09nyv+ibHFTjC5GWF179iIM060G/d95sAhlqmrhvaynP8zdFMQJY0O4iydF/if5Xduu9jD1Cu6gheF9N6FaTQdnvZ4HlEeQnS9tMGxkDbPJ1OQxJ3ZCP7LPPv7cfLy8ugIwJA6Fykree8IFKez/PQnSIQ0gTIus9iC+H6+tq+++67IJAbjYZ98cUXibNjvKubnTJNjBnUkIyBB34B6Ebrjfk0QiBwxtc/mwUkqBJCWRqO789H39WguysSieJHWZqsS5V53Xi5Gg0hbZa8Lod23Nzc2P/8n//Tdnd37de//nW4ks/MwllSvYbJbLVB6/lDDG4WMgi/Rhbc3NyEZIkAFyjOGIudTifRF7yZ19fX1mg0rNFo2MXFhfX7/dA3PG5EVsCvo9HICoVCSC5zfn4ezjxjnFSrVTs4OLDpdBqM6Rifq/eVcdP5pE4NxSfywsxCgjM2RwxwReV9OFUWZRkUaZ/HylVFYTab2f/+3/87nBlrt9v2d3/3d7a7uxuQXOaGYw+FQiEAbnh46af3ZsILeIQ5RwlpZAFh0SpLlA/9GiZHxZs3b6zX6wUDEfKgUBqtE+z6/Trlc91zeTYRjF8MU71GE54zSxqaw+HQ/uEf/iEkitzf3w+5Q/QaxJOTE2u32wmPol7hx9re398PMoexwxBdLpeJjNz1et2ePHlil5eXNp/Pg/fv4uLChsOhHR4eWr1e/+B+cMBITchI/xkr1gsRcyiBGMIYB4PBIAARgJk3Nzf2T//0TyGEXY1c+EiTdikAiWFarVbDGVnGizEHgCfiyiti1AcPj0ajAIxqtJOSB9x0P6ad2g4+Y23o/oBHlu/29/ft6OgosWew76ss1RwzzLuGISu4BzhK3USpKfCj9TAvmmhWo4oYQ/hL62ZPhFfYwwGjiOa6vLy04XAYgANNuOrHWD/nf/rHuMT2cl2HOhaQlxnwgjeS11FeOTKbzexf//VfrVar2dOnTxPXlsHjAE2s6di+o7yPLIgZ9fSX41L6Lv3VIypmltjzzJLZ4tWYYG1SLkaI5hYxs+hYFgq3uVYajYZVq1X7+uuv7fz8PJyhTzMO08Y1r9KfxiObkgKiad9pnWkggtltJNEf//hH293dtV/96lcJYNFspdMpYMznmicnBiTEwCQ+1+gb5pX1xNxxFXqj0QhGH87NxeL2Wkp0C/RfMwtn6c1WV6rP53O7vLxM2CwKsCG/0VfYX0k8uc0cr/s+BpDlLceXYZbuyNTvX716Ze/fvzczC0mJ2R8VLOaHo6oxoJF1qLJLn/P8ofuOt598FIPaWIw/gDX1YN8BDJiZtdvtxN6l/FosFoM+SOR0oVD4IAcO+w3XP3c6nRCdhsMiFn1wH8DgXeTCvedA2IZoOEaT2a2R8/TpUzP7EBFaLBaJTTQGDMSMfv+Mp5hxnmdTTUO387zPAqIMNlIUHQRLGm266GOCfhNPJguXv2ML1G/WqshRD0YImzbj9O7dO+v1evbkyRMzs8Q1YCgGOnbwgj9Xh4KMAqcKOO+xCWiiNhXyGBResYPnNExKEVYdJ8pVRZu61cDXjYz2eDDLjzHt1P+VqN8nE2PTU4XZo79a70NQmgIMAfCYWTAcf/WrX4UQ8tgmpkCUXqeo86TlcxZVQxPNkuexveeW73Xs08ZoPB7bYDAIYJG2N2tc09bjJutU31n3fV4lk01O+SOtfBQ2lCjOeJK7w5+R3t3dtXa7HfhUQUH1RmBE+lDsmCEEeIQxQWJSlJCdnZ1wXE6jbjAqqV+NTq9cmFkAsJCl+qNAngJ1l5eXdnFxkTBmFayOjb/KWq8c6/9atzd6tC71hqnik8UrMb6NeW88sMBvzdmDoc3NGn7sNBJNv+cIjRp+jBm8Qx2qKAPieJCB/5Wn/BwzzsoTOh8eDNR5xas5HA4DmKh7go6vkjfEmCfVL7IozZBT8rIzjbYxNHj28vLSms2mnZycJPh1XX/N4lGbatz7tvi9ms98JJqvR3UJNWbSeN63O9YG/RtdhD1pMBgkbl/wbeb/+zAQfkyKzSnyT42wtKOSaWMQMwi9Dqb7uALRXq9invVoHqAfzxIZxr6geh08qcAU+xtGIPsmsgnZh/6JE0OdOGnj91Oi5fL2Kk/Gdmdnxw4ODj4Aob1c9sRnqo8pGAjxvyaa53dsHWs7cD5q2/0+r/zmj0nFAEuzla2j7dWoFX5ubm5sNBrZdDq1fr9vV1dXCSD0LhTba/SzbesoLPPsRGb25ZdfftCAWONiCmletEu/LxaL4Q5tIhFUOWTCsgxYFp8OjqLKSt7A5Z00pvD9Q7ikIeiQlrFY3HqmT09Pg9BSxQvjj/DWbciPvf6ftjmtQ6Q05FXf0R9C9ugHuQEwQvjf8wQh3U+ePAnnUCuVSrgybT6f29HRkf3N3/xN2JAR+uo1Wi6Xdnh4aK1WK3h9+E6T16nS4HmH+Tk/P7d2u21Pnz61yWQSzssTrlYoFOz58+fBk1apVOxf//Vfww0N8/ncTk5ObD6f2//9v/83tIUzd5VKJaCYpVIphLiWSqXEcQ8/p5wnjgkss5WAA8DBg6Xn7NjodKx3dnZCUre8guW+lR0vN8rlsh0eHgaeqdfrwaPVaDRsf3/fPvvsszBmfuz29/fDveTL5dJ6vV44h8yVaRiPi8UicdzFe7zUUOU7HdP/83/+j71+/TqMoSoQZtujxnmAhU3r0Oe9TPXEWALi8QzgnQJmlUolRNswnr1eL8gHxo6x+eyzz+z4+NgODw8DmLCzs2NnZ2eJW1tarZaZWci8j2JOGDvAkeZX4MgIyjtn0PEyYdRx3pXInMFgYMPh0L7++mtrNBr2+9//Psz7aDSyTqdj9Xrd9vf3Q79YQ+/fv7eLi4tg7BBd8S//8i92eXlpP/zwg11dXYU6UU586D48SXSAT6CETPR7n5kFftccL5pMlLI444syT/1qwOt+mrUXKSDswQM+h2grc/XkyRM7OjoKkRmtVssqlUoAelutVgIc0KMM8/ltMkUFQrVO1miacuqBGR+FwbwDQNF+Bfp1LJHxqpvwHlcw61EZ3o2BEHrEQsffOymWy5WH3u8ZackrvRIMWBfzdm0rv3RtVKvVIIsPDg4Shpju4fQnzUDw+pl+D18p+KjHKD0o4cv2ADplkaQUw1KPNPm6ifhDb+U6Vw1NJvpgk7H9MUCFtPWex7jNchIQaXxwcGC/+tWvgszwDiEPqqrc0/8h5RF1mJglnUsa/YlRz3o9Pj623d1de/HiRQC25/PVTVyDwSCsc+T7bDYL2fLfvHmT0EfRbWM3O6Djq6xIG+NtHQhZ85BV7joHQ562KTjE/ko+MX5TTqlUCvPicyXQFv3RG8mWy2UAieEN9lXvDMSY19wU7HnqkGP9K4DtZSf6Asl8cSicn5+HqOLxeGynp6fBZiGfmzqw5vO5fffdd3Z5eRnk4jqdbB3lAWnT5u+bb75ZW/4nEYEQo8ViESISJpNJNKRUyW8kih7HEPsYIuXR4JjxlAaIeI+QCgIPciiAQBI1fx6SMmP4zjphkEZ5GXDdxuBRPfUMma1CAClrPp8HZUnHLlYHgoA7Uzk6wE0PoMij0SiR1VgXIUaFP8uvioqei1ahohtOsVgMIWalUimcV+KIQbfbTQAhCDOUXOZUQSHADJR72obhSggTwAbtUD5QAafnfD2pMq9ePXI8UM/19XXw7DLmRG58CsScnZ+fh3nkPBl5I66vr213dzcYn6r8wYN6pESvCdTr/TD42FhYgx6E9JuRKr29Xs8uLi4yk9782BTzdq0jVa5B672s0HFCHmikAWsPXiRkfjgcBhm/XC5DHgE1AsxWsofneEYNJ10XGl3iAU94H2WFvUUBN7wBalTr9Z2QvmtmIeKiXq9bpVIJa+ny8tLOz88TZ2n1DDV91D3CK1Hwm8pZ5XU9zoFc8d4GD8Sr0pUGgK8DBNKe9YarN1AxtpB98ATgHf2hLEBTNQgZRx/t5T1d9Fm/1zGOkXop1TClDD9fyH34SpVdBRp1TnUfShvLPGOtn2WVqd4+r0+k6Ql5DMY0AkTUxLwkX6Ze9k2VuZ4X03gzxmOx73XePBDDb+WTmOKun/GOHxc92mlmIQppNBpZr9cLMuSnTHl4QfnJ88/NzU3wTqPfLZe3R8g03Fvfi/FmjD/W6fY+gllBI9a0hspr1JDqE+wbarCaWTgWq31Hd9R9EwBxE8D/xwaZssCG2Pf8zx4zGo0SwBpAHM8qEOfL0TWqNpXaWzr/yBTdP7yjkHlVm489RUEL3Qc80IstZ2ZBd+AIYaPRsPF4bN1uNwAIZhaiMVU31WjHrLG+b9q2njtHIGyDiK3bsFTIFIvFBOq/v79vL168CFfmQV5AKLPFmEy96H6hewXLgwqeUf0QUiYbJuHqACIodXpUwSOPUNb4xtClvJQlZNaVqyh7sVgMxjDfARhw1nU8HodNIab8YrR7gwBD7ubmxgaDgZVKJdvd3bVarRbOpDG+Gu3wd3/3d/a73/3OptOpXV1d2dHRkVWrVev3++F4gNnKK4OQwZjEY3d1dWWXl5f25z//OQi7er1urVYrlIE383e/+509ffrU/vznP9vl5aVdXl7abDYL5/URJmpUqhcDg1hDpeENHUs9j0USOjbb0WgUBLB+zpzgnW02m6EuwBD6lrXx5uWfPN9vQypzADr0987Ojv3d3/2d/ff//t8/2GBI5seZdNYmUQIkqiEShM1GDVFVLDQM/7vvvgv5WwC3YkrBXdYr76+bi7x1bONJgDhCQsglPKuRCIVCIXHciLWq3iOULyII8IybmZ2cnFiz2bT9/f2QZ8ADFV4JMEt6aykb+YAMArDV3BiFQiFEJOzu7tp8Prfvv/8+gFVECbFmqdODc4wHuVEODw+t0WjYH/7wBzs9PQ1XrvIesrPT6QTgBL5jXki21Wg0bHd3NwCmKB0+T9BkMrHFYhESzlL24eFhaKMqyMgkZAuyQ/fXGL8BgDCf+r83xnhP541xU+CSM/KALuybNzc39vOf/9xarVbCE6zlaxSHN/LS1BwFjMxWUV3eU0gIM9Ew/K8RCLpfKWh2enpqnU7nA4PBG7D+DK2OkVky103ankydABh6vlzL8sAHawfg9CHAY+afNtZqNdvf37eXL1+mzhvvMNeaoFRBJOWh5XKZAJ34Pq09/jgJz8aSeSv45cFL5m4+n4dbF/B0n52d2eXlZSL/zX1EpX0MWqejp+1JSlnvaz4mM7PPPvvMfvOb3yQMONXTFRBUIMgsCXKzflW/hu/QqVRP0PfJg7O3txf2CbNbHQvvMnpAqVRKOITev39vf//3f584t0699XrdBoOBjUaj0OZ1Jtg2e/i6d30ZeZ9fV1bMW+7rYK2wV2ALlMtla7Va9vz58zA/uoZjoCB7H3NMyD8AXa1WC7aYgpIKDrJ3q5NAj0mxVr2cwEn5zTff2Gg0Crkr4Fnktcok7TuAt/YNh0fWGJvljxhJ+zyPvvdJRiBkMVba83q3t96hjaEaCz3zA5a2SLddvLzrFwtKBu2+ubkJvzFSNNFSVv15wAMVHpsYbTGBnvdd7xWE2FwVpNGzYdpOs+QRCEUItW8YA2Qw5gYEMwuKG+fHKOfy8tK63W64HgfDAEOCOlAeVakiTA0PQr/fD4gpi5t3isVi4nxrrVazi4sLOz8/t8FgYPP53FqtVlBI9V1QS8ZHNzHGWNHQGLLOODCOipTSH75XYMwj9jo/uuHF5ljpY4MIWhaAjx+Ps7MzOz8/D7yjYAq8g+Lm83BQBsJeDTzGVm/QwFDodDrW6XRSvX0PTduMcQzdzyOP1eDTd2OAqx698gg+yhyKAs8D1JCw9ODgICjy6pnkHQwdL0v47cNIqVfnXI1efz69WCyGK2L11gaUTPWUA6oAyundzxyjYDxUhqgSq2NE/Rgm64B3D2yrgaIyQZUWFB1fVoyXY4qgp5h80v/TlFyUPkLNS6VS8OQDlsxmsxCi6oF8+pMF7qvBqZ/pnqXPeZ72hnVMPvvvlAfVME6TFWmALe3IQ3nkQU6/0b0S888c39zcWKVSCfoS8hrDLtZWlTWx37E5S+NllSmUrd/78v3+rM/wPetYjVe8rjgm/n+i++gPEWjQeDwOEQnsD+jMsTWWRjHgUPf9mGz0+xpn0vkcnXI8Hge5USgUgi6CAwFZFgM4qSuL8u7HH4tiBui2c++duXq0tlgsBodj7Dic1u8BWP+91qWk69rbHfqd6tfaZtVvALhHo1FwDqRR1nxuO5YxQCE2N7HyVcfZtv57j0DIg2xsSlomjGZmwSO9v79vBwcH4botVQBAc9IUJGUKZQ6PaurfipRjyMBMNzc3IVNrrHzKyPKKxNqbF/G9z/lIY0685YPBIBhZACf0lXPIeozA7NbD22g0rNvthmsQzT5UfmFqveEBox9vIKCMKvGK7j19+tTa7bb9zd/8jR0fH9t3330X8hbs7OzYZ599Frz48/ncOp2OnZ+f2//4H/8jcS4NRYd74vFY+ZBoVVr7/b4tl0t7+fKlVatVe//+feBF2u3RcMbKn/vUJCx4Cj0a6oGAQqEQvEmTySREOWBM44X3Gyr9iG2AaXwV4627eFbuwrOcp4b29vas1WrZf/2v/9X+5m/+JkShYBReXl7aZDKx9+/fB16bTqf26tUr29nZsS+++MKWy9Wdzf1+P5xhh/zZ9LS+xOgh5KduCJt6GLI2E8Bas9v1OhqNEp5/QpJZiyDvuk44FkBUAbynER3z+Tx4wP/bf/tvdnx8bK9fv7br62trtVohSgAZRJmsDfKVwOMYotTF2XqMfLyaep2i2crjC5jBmr65ubH9/X37/PPPrdvt2rt370L/3r9/H5J/6hpQj3DsWAGAVaPRCHkKAKw04mU2m4UoKJWti8UqRByPGUAN0VnkW6BtGHPcEIPcxaOqvKNH0HTv8ryix1b4X3kA+aR8BNEP6vJ7p3oCi8XbK9Sq1Wq4Juzi4sLMVmdS0QM0JJZjMgr4wBsqc4mm4T0AQ8ZysVhYo9GwZ8+eBcARsJufXq8XeMbrFgA8ecjLUgUgvB6hirXOlQJXMWLfWtemTZTNmJMj9gy3MpiZPX/+3F6+fJk4/jefz4NBwY1Uh4eHIaJRx0PBQB1zfUb3OgXJATL8taJpQIOX1RrRQ9QQt83oOv2UaJv5VEozXNL2nTxGMWuUqLRf/epX9rOf/czMkvMIf2uEAf8zH17HJgKTaCe1E9RQBCx++/ZtyIVDtAG6FUl4r66u7NWrV6EdyAna68fPr9lNxibteT8Psc+V7tNOiwExWX1K+465KJfLtre3Zy9evAi5uZhPiKPDHHtDj04D/rBNPOiEXYEOjixiP9Xk19TBXvz69esADKpNmDW2se/yrMF1a28dZdWRpqt/khEIaZTH4GBi9RkNe1TUmWtCdNNYR15p4jPPdHjKEGAeQODIQhplbURpY+AZ8y4G2l3Jh9gw5goCqEGt3m2dw+VymVBMvcLjjWj1xKlXR9/hjPJkMgmhroSPauiYJjaiT71ez3q9XlAq1RumfWCz8ccLUHRU+cUg4UcVGuUD3QSJrFHiXY+cxxRT/tZ2qHBTsIwxo02Ue1dl58dSlKbTaYhGQTGYTqf27t0729/fD4rAcDi0crkcAIVutxuMPP5H2TCzEOkyGAwSfHQX9PY+3o/RQ86brkltu0YHQPAyoJgHxnivVCqFCB14kPdIMqqJDlHwC4VVKDnHd1TeeG8ucgmA0T+rZ9ZV6eA7jgYga7hidzgchvUyHA5tMpmE8mMyStuC0urXK+Pp87TEFBL1aqk3RetUGeCNZdqkRlPMU69zzWeef9Vo12f1HQ8a+zny4KxX8r3cQsmjHDyGPKNgP1F/CqAQqcGzvp2eXykPYAd+1aMlRLBpdIqWwXjnWat+fH17YsQc+L3a98sDEboHPCTRJ91nALsBwjyIrXJC91FPyvOeZ3WPVJ1F14c/1uqvGYTvdN9kzwTEJHIGcJO6PyXapD13NWDWvavl+zwo6GWxMtCxtAyvDxHhiSxdLpchooF178FYjot2u92w55O/o1AohHxXmsMn6yjyXcfrp0BetmzK74wdDga9wcLbGIA5egWiHjtQZyL7KG0CMPDzwR6vdhxH01jf7BlEoerNGdrnu4ByeekhdMdN6U4RCHkRjSwDOWsA86BnyijKvE+ePLHd3V07OjpKnJ/14Sh+0etmpoafKlXff/99uNfUzBKCxyypyPF/nv7lZYhNEMZNv1/XBha4WfLOVeaALKoAO2ykbKY6lsVi0Q4PD61WqwWBPRwObblc2sHBgRWLRev3+2ZmIVyY2wnq9XoCyLm5ubFWq2WtVivkJcBjyrlZ2ouwxztGwhvlH8rmLmC8gpyXR6g1m02r1WpB6dEzqMvlMgAKeMX0/uAYEo2Cr+HRrVbLGo1G8ILr2TGz1Z3xmghRle5OpxPmi3OumhOBpIqau+Kut394ismE+xR+WR6PQqEQvN2Mu57Dhc90Dev5NW0vP4xNDMSJtcHsQ6XcG7ixPsW+954e34ZNykp7NlYmfEckC8q8KmY8h9G9WCxCvgGiBlgby+Uy5N7gyBHAr/I4sqJWq9nf/u3fWrvdtqOjo8C73W7X/vjHP4a75qmb/CiMP2uVzV5vZlksVglMCVv9/vvvgxexVCpZu90OaxMjEUKJgK98ZAV1EcVEOCuyR416wM3JZGLn5+fhf77nphTmirWK4oOn3p+152/OheqtC2bJpLgxEIG2ac4A3tN9tVhc3Zahnjh/lMrzHGMGX9E2+CEGvBeLt5EIOzs7dnR0ZLPZzE5PT61Sqdj+/n4If1aDnmihYrEY+I39gbwdAA2asBkDkX1IjU+MDvYvjBMFb+i/nu32Y0CfY+sZmaPKb2wfV70FvlOlWkFo2uEdHvcBIORVpvU5H+UEMT/sdb/4xS+s2WwGPmR90Fc9FuUNCgV4NNEhffYGwe7ubogcUp7B+cCeAMD87t07Gw6HISJG+/9jK/zb0F30zby2QEzPUI+0d6goIbfIl8NNOE+ePAl5NiaTif3www82GAzs/fv3Vq/XbW9vL0S0qlNqPp/b2dmZDYfDwAc+IbJfq/4s+10obW2nzUPac1lje1enR1pZWfrPOt5QSnM4KGmkkd9TsEF2d3cT8hD+ODo6CpHAlUrF6vW6XV5e2vv370M+A8okBxLOJ/Y6/b1NP/OsK09ZY5/2bJoOua6MB41A2JYB71uAKnIMFQqFwAA7OzsBRaJ+BRA0zEk/RxHy3oNicRX26D3rsbal0aewkcTakKddiuarJ9uXo8mC0p5XoyymcPl6NTRXy1TPgjeANJzWK6hs/GYWQlshwtR4D5TaA1YqwGi3ejm8d1Y9hP4dDwBkCQHKQ7nmfz1Tpl5PrygpsupBNeYkzZD41EkNfjML8kBDXplTeEKfhxQoMLMPNgtPsbXw0HQfSosSRo4fC+VpNUCUT70xqd45zfmi60UjD4gOoCwNv9fjYYQt7u7u2nA4DPM3GAxCO/11elxXqhFrZhYixshbAuCJB0JlDeUqYGK2yryMcaEeE13PXh7Ap7r+NcrJk8oF75VRuUI9Kis9YBlTwNatdS+Xda9UINl/79sSI+UrD+imPV8oFIKXX+/VNrOQN0e9mRiOapTQdl3rzLEaoGYrQ0KBRP4GsFE5orJAy9lm//fv+j3Pl8n/fl71c8/H9ynrN+mjArf8rfygt1qYWSLqx2x1bEqTM5utohE0ETfjocAK/KYh6marxJI+PNoseSf9bDazXq8XIpBwbPz/RPfRnyyj1hOyg3WbJTvQ+XkWkBVHzHQ6DfODA8nMPkjWh76Kd1n3fZWf/vfHpG2NxrT38wJ9+v5D6zg+Cm0TQhZqjiv2HwB9gESuWuV4Ks4DBZnZz33007bt8vRQcuJjzNPWEQhQFpJulm9wYsZnVhm+zphHzix+JMFTHnQ8hqR5ZSytrLxjsQl6lQeF2gbdyls+Y8wi1OSQLDgELka3z3qLgsZ5ZA8o+A1Ds6UrqdBn09Azzz5DuZkl8iaYrdBKvJO9Xi+cs0aB0KzKJF9UAEG9rXjyi8ViGJOYcof3DI+W9wyZrUJ6ddxRYoluYKzI6krEAeirKjqc20OR1vaoYomg9OGbtCOPpyFtjWbRJgh2Wtl56zJLRtHEKKs//pk02nYt5hnntLbFxm7TNvtndJ2araI0OKIAX+F5Q2lHDkyn03C2lXXEOkSe4k3GqMeAOzo6skKhYN1uN/BlvV63zz//PGTFNrOQyfno6ChEIXQ6Hbu8vAxt/+u//utwk0+5XLbXr1/bYDCw169f23Q6tVarZYvFwn744QdbLBbBA9lqtUJILfc706/hcGj9fj94v5BByDcNbS8UCtZsNhPe0F6vZ4VCwVqtVgJURNnRG1WI2iAprAe+kAckACW5E7KQz5kXcqTgUU0jBYU4k46hRCSPen4Zm0JhdSMHskgBY/1f5RtgMbKWfur/eCjVe+yPDTA2CkoQ1dVsNsP8aMQVnmmOrXAOdzgcWqFQCDkqNOcB7ffn8r3hqbdH0E79XsEhv+cBDnmgLRax4Mvz82i2kn8KYOmYfUzK0jtie5CnSqVih4eHiXPutVrNWq2WPX36NAHyAE4iZwAXiTDi3WJxdWsG+oIaH7Tl8vLS/vSnPwWZGPNMxvq07Z74Y1JsT1m3V697Lmt/zUt+rShw66MEYutNaR1AoLqfUpbRFgNPsj7T9sU+999nvb/tu+vKyKsLZlEaD6xrbx57ytsLaQCpl8Fmq2OUfv/Zhrbhidj7eXXiTdqUVsZHyYHwUKjkXdATFjVhhPfRtjzt8Yr7JgyXt7933Uw2EQRZZfC8CuNYNIca0bpA1VNAcrFCoRAUYi2fvlIGvzWaQduuXjANJ/VKW7F46xHzYABjrCFKmvOC93hef3vBRRu9wqY8qhEsGqqXpjjSP1WMdW74Ts9f41VRVJZ+sLHG5ifv+rlvxeZjKUrKv5soMJu0L8ajD0V5FYJ1FHtPZWGWJwbDB/5izaCQ84zPY+LLi4G0vMO8kVRNj1UhczAm9XhRuVwOxxJoC8cnSLhISKv3VOrZXM5fMuYackl/1Wj2URpmSQ+wzwyOIaLAAe8ALMBXeo7fbAW2AhgAFPo1rR4ejCv1zMd4IAbi6mcKKmn0hc6j5xU+8zJeZbRvjz7v+8FvnUPlJQBSIrU0eSdE+4lAYf3qMTx9jjq9/Nf16D3gvm1eofPjTBu8XNbxVRDDj4lvR+y7T8FANVvfrjRFmjPMzIVGEQH4tFota7fbYfw55lKv1xPJ2NBJ1CtN2fCCyqF1t2rd11h8KpS1R/p5WdeHPHvvOoPU7xdZdeZ9Ls/7Snn0JZUTd7VP8tJd9Y+0d7cpM2se17VzU7swbxSDgk3873WRhwIP+DvLNtuWssbzPuTK1gBCFiKyDcoaozRkK+u5H1vYahvvihJ5QCJvvUqb1J0XwOAMLedA9Uw9yp/mQyBbshoLnEnHYw/qzzkjMroTwqxhuWYWDIRY/xQxVNSZZ4kgQECgKKCIE76oSfXMkoni8DqpIb5YLBJlxVBvvH+0HQ/IdDoNY6WKJaSAAx43Tfyj/Wg0GqHdvFetVhPezULhNhGQKs6a+Iw6vGKdl/Iqpl4+3HWt6MYc22y8bErbHPKuu3XtSavX15FlsPv3YpFVaf/fp2yEpzXiRcEXDD49/80a5CzqdDoNdzLrneiQhu/rvMCzGp58dXVl79+/t8ViddNIrVYL16/62zF2d3et0WhYp9MJCRDJlWJ2CyToWmAM8aLjieQs/WQyCTcikCsFIwVjhOMVgHcYHRjq5N4gIgG5Nh6PgyeVugBASNbH/3hDkWtcW9toNBJyTcOzGWfkA3U2Gg1rNBofyFbWSSwsVOUyHntkGACIykMFlyh7sViFnJolb5WJ5YtR/tYoF96lLsZdZTHHGq6vr8P4K+CsyhxlakQdpCCFHluhDsrzpACPmSXAaVVifQSDRuFpf5SYG9rs5ZiOL2tQ/+fvNE9djO7DGwalybw0ndLLUKLvtP3e2/y73/3OPv/887B/sscdHh6G9abn4Qld/u6770JGft9OH3GwTu7et+H4YwHUZpsZdbF9ahPgPg+l7d2+nV7HikUVpAFVSlltztuWrGfT6skCZ/RZ3ZvTnt+UNikrL3+sG2t4JUtv2tZO8iCzt2Oz2pW3jnU6cJaOuCndpx2aRfd2C4My6V0Bgzxl5K0ntiizGNp/F0OJ0spOq+sufVDmWieo0oymPKTvrWuTbw/J6biKDM8Xiow/U68ecsrg/CpKFGGoZiuPkf4f8/z7/AgoqhoZweeqiFG2et+0XE2k5UNUY2Ol3iRfJ4RSi/JKeDgeLn1PnzNboaqafTjmFdTcCMViMZGAEUJJqlarVq1Wg9EVM1KhTUGprOc3WcN5yIMIPyZtIgs3eTYLDX/oPmOAmq2OKGCEkMyPhGa6ISvwoMANfKrGIvLCG1T0j8+Xy9sQ82KxGI7zeKOPzNkY74vFIqw11rE36GgPR5o0LJnnmYOrq6twI4c3Qq+urj7I2K5goxq8zCd/E7WlhjxrEuNXn1WvPf2i3142KCCq8prwbVU2dd6pL7bPqWFttjLslU9V7vK/zitjp3Ph26Dl+/GEVP77SBZkpVfYvDHu1xftVgBLeTFmUPpy6JOXrSqv/N5G2Sof1smKmFHk++E/u4uSua3OsS3lAVtjpCDDv//7vwceYA/sdDrh6mkAgcViEZIyc+1rnvPZ97HvbUIfAzzIU38eIDv2f+zdNPDLP7MOTE/73IN720aP5OH/PDr1JuXdR5uy2vAQz983pcmBbQAdP/dpfbuLzbkJZQGQ29p3voz7mL97vcbRgwi68LMExqbf5SH//joBlneys5BD//99bappIEIa0u0VjnVtSxujGKEYm6081a1WKyQeQ/GGD7jGSJVG7lUnXLhQKNhgMAhKZ6GwSoJZr9eDIaAeL7xqRAHoDQSqcKvBr5+psk2STW5K4IyjGveqEGLk+3lRw4L2aJSDjjFnaDEyODeNMcIcaVSAmSXySNAvvWECYpxVWRyPx1YsFkPbaC8RHwcHB9bpdEJUxCZeKNqrfdTPH3Kz8Yp11vpbt3bTyt6mTd4Qu8sYbALu6Tt53ttU1pKngPVC1NBgMLBisWgHBwe2WCwSnjrNlaLzpJnNy+WynZ+f22g0CmeYY3c746m/vr62i4uLkAuBW1wAwbSOarUasitzKwtzhLzC04jXWm9tYa0CoCwWixA5NBqNrNFohBwJZhZua2m329ZsNsMZe9acylAzS4Aw5ClYLBaJK0kx9mezmU0mkyBbuNoSw4ckYTxvZgkwl7Wt4drMgcpHJUAWorLMksetNIs/IIfZCkxVEBZeY//QNUuEld6YouNEHwqFQuIKXp7RKAcPEGs5yE812jWqxu8XOo4esMhj0Cpg5sfYJ7ul34xRllzz691HWvhz+FoexF4Bj9POTWgTA36TMu6i//mx4f/vvvvOXr16ldrHmCc6bwjzTwm03qRMM0vlQa0zBnZtWoenNKPwrnX6cmLvrgMj0nTnNNtnGzvjYxjq9wUexIDRmO1yn+1Js4M2pTR5kaevsefy6Fzrnkt7z/P6NnXfh6z46Lcw+DKyBIM3CPMKiG0MmU2fzbMY7mtRxuretOz73Fi88ktWdA0Hpy49FqDZbtUbo4Siqefy8Y6hyMWiAAhFxiBGiTRbCTBNCLhYJK+dw4DQxIvqefTeMv2hn36DjYXIKRChyh79UEOBs5kYH7ynCi2GDMYJ/dExVI+KeiVVkVVgCKU+S5GMrbGsdfHQIEKM0jbhu7Ql77tZG8RDjsM2SkdeecbaHY1GwcBjnSgQh2HHGoDvvdzgGQxyzWPAj+YhUeNN5YrmA+Fv6taoJAXPlGazWQAGeF8NYtasyi/K9mvaH9VCJuhRIn8MhDGJhcgrwGj2YW4Bs9U6V2NR5QPv8DwylnFlbAFKNeoCUo9rDGDQOU2LwFLPepaXXMfHG3FmKzDDk785xD+TdawA8muBcQaQoXzd63gua815z7/K/picZYz1dyy02rc9rS2qN7CHeD7i3Yeijy3/s+rOGqt1yv3HNOw2pR9jj92kDXcx7rJ48776HatnG71G30lbj9tQmj5zlzIp465juE52pMmkdWBM2vvrPr8L5bXF7lL+fRnyD2Fn5qV7jUAw29zTlWchbLIA1yGG61CjNEpj8rss6PucyLR+pSHFm5aj/+Ml5z50VZhVaVajmuvT8GDh/dJ7Vc1WScM0eZUq99yfrpmsiWYg9Jg28Y4P6dUzjlonAML+/n7C6MZQ0qud1IAoFm8jLfQsqwd6+I0R4hV0nsGgqtVq4Rx1t9sNV8wtl8uQL0LnYz6fhyvkOPuM4kvYJSAK7+qtGWrA6TxtSmmbxCa0rdHv61JAJ6uNWWXH2r6uLZtu6HnW5KagBe/kHfs8YwIPweetViuAe2Tz17VK3fAhkUjwHABZrVazwWAQvOrczb2zsxPO1CvgRkSSmYVbD1hPrFEMPtYo3mb1ulMm8qzdbluxWLR+v58w7tTjrh7tYnGVwI86NLdAzOCr1WpWKpWs0+nYfD63er2eyGUwGo0SwMB0OrVqtWrNZjMBBqB4FQqFxLEjs9URDJVfi8Uq+V69Xrflchnkwmw2Cx5oZKsn7xFXcNYTsjHmtfXjonzKPFMPdShIu1wuQ6SE51H2Bj3aRXl+b4gdj/FzBf9QN2Mb65fOmcpUbb+Wr7LJR4/Rbo2U0zp0LfAM46p87YEcAC49tuPH0eeL2IQ+NcM6r5z2z92HceedXw9Nm+h2n8r8rKOsvTxmePp39N208mM6xjpAwP+v5Wib/Dt525vW9lhZsT6lva/PbPJ5HkoD3bLmKTZGecq8S3vz2El5y9jWdtyGYryXxqt5KOYU3aasewcQlGJG1H0g3Fkd9XX6z++bHnqzyGMA5Xk/TfhkjVOWcqi/VSHT93zyRM5IoxijgKsy50N2KUu9UtoO7ZP3qvuzzT5KQMNqFazwni4+03PHjJEqaoQd6w+84ROCqbJPAspicZW5nYgOxgzlmHFQgEZzThQKhXDGWQ0GDDide+0n8+N5JI3X8m7KPJu1Sax7/iHWra/vIZ7dduPYVpasW7t3JYwL1h1n7wHzSHyqBibGVqlUst3d3cC38CvZzwEfMLA1RwjyQqN0/A0H8C7P+7p91I7yOm1mzDTvAKCDrjezpIdYZWG1Wg1XLGLY39zcJJKSXl9fB2+/lqlja2YBDFRjlHIAGjUqQg1HytOxUllGXQqMau4T76X3UQf+ex/1xP9+LXuj3ee78Oue9nqZy7tKPkpCyRv9MeUpFiHgy8kyrNPklPKMN9pj0RDwE/umzj38rX3x0Rx6dMG3TdvC56yru9KPZZim7SHr6L7bex8gxH3UfZdn7ovy7kPrjMTY53mN7m30hhgvpYEAm9gUMXBf2xprbxpPZ9WZZwwf0g5SyuKB+1grH/s9s811s7xjsI507u/D1vT72rblPSiAYLa5gZr1rqcs5C+tvDwCa1vaRGhuI/CzhFuesVQ0MOudLMGoxwhQElHGVRkpl8vBMwizKoDglVwSr43HY1ssFsEz57Ng673olKv5BtRLCWE4kD2dcSDUGo8qn6vHEQOECAOeUVBiPp9bo9EIeQ0Wi9vz3xoFoccrzCwaUVGpVKxarYaoAa60rNVqVqvVwv+Mt4ZWq8FGJAHeVrKq45VlblXZB6zQCAU9NpGHNt3Y1j2/bqPbBHzIq8jE5EmsHZsY6jFPh29z7POsMtIoC9jJ096sNmAks/bwbgNYcTUa/2ubKpVKuIUBIAvjvNls2nA4DHJAeZ06ABhoB2tebzNRzzdrQxO1Ip/IA6ByDLkFUIBc0vP4GhVFeYCDUKPRsFqtZv1+P5F0bW9vz3Z2dkK/dnd3rVBYXUMJn7H2+LvVaoVxIDJjsVgE+aHrXq+Y02MWjJU/SgLwyDGpXq8XAJ2YoaxKh+dnr5AwNv5oBp8jZ/Xom8pJfVaBgpjyzXxoHYxJjGKAgV8fjCF98ABJLHIBflEPPvUoMK1AQuyIhh9neJh2+6TAWqZGWvi50Gf5XCMn0vp1V/oYOtcmz/9YQMdPlfLqnHnmIu3dTXRdnk8zWPOQyvAsXWMbgCDtvbxG4Kb7/DY8ndW+H5PSwBX/nX7mn90GYPHlr9PZ0j7/mODEp0D3BiDch/G86bvboFibGhJ53t1UaV/HxNu0M8979wXeqCcvpmTxHYaCJomi/ul0mgi71xwH1E04s9nK04j3hpBfogK0bowc9dSrUVGtVoOiRR+0X2qUoFAT8qtnhQFKfF4GDCaUPW27hkFzrKJYXCUww8BgDFQp9KGutN0nygIYoS88Ezv/rcYGSr2GaP/YAm0dP2/6zn23Ie35LKU5DTDQ97I2Uihrfh5CaVc+w7AjpFzrUSDPbHX+HXCQZxeLhfX7fZtMJjYajcJa1avlSK4Yy37P0SXC8FlfpVIpgHnkB2FsNYrBt5OyWd8kHeVaVE3kamYfGLasXxLHap0+5wHGvkYg6LEPxgcDmzbrvKqRqnOsdQBwquxlfDUyQmVkmuGt/VTwMebt14gI5Y1YeUqx6BGlmFIXO1agUW06pv7/WLlm9sG79DHWV8YjBlzEFE8fMcCPHpPQshXgAmjxYATP+2gNeMPLnLR++dDW+6Afew9Ruo+2fEr9+TEo1v9tgJys8ngmZtB5QGwbiu3JWXtvWn159XRf7iYUAzfzvpcX5LkrT991PvKWsY5v0uyidbStPZTXpsoz9+vWld/nPwW6M4AQm6C0Sb4vJtsUaMirTN9H+7LKzcPwH4Nii2uT+jHyUUSLxWLCwEUpvrq6CmeUUdRRWDU0H+MZBTumDGuUA0aChv6jHGJ0kJhNzyTzPkYJ7/i6aDvZ1cmJwDPVajV4Fnd2dkIG9FjUA4aRggB6hpt2cTe7XrHGb5RIBRBUCSXjPGCERlZoKC6GnifaVywWg0GmCSdjlEcJX0fe0Pblr9v88tSXVse2m3JaOb6MrL759uVpb1q96+THNnOi5SrpzSRmK4OFowxqgGIca0g1UQIalj4YDMJzGFEYqYVCIUTo+Cgb+Bo5Ali5WHwYsaNgHMqn8hdGOnKM3C69Xs/MkvIOjz2yxRuZrB8dK/o1n89D3ghufFDZZLbKS8L7atgD2tB+Pieni0Y7AWYgiwFXzFayFEPUJx9Uw9+TD8FPAxqVD/xnyl861x7EYBx4Lo03eV/XMuWqgU9f1ejmOd923740UkPeAx46T7Ex8REH+hy/lb9i+RV89Iz2n3e0Hn9NMQQv6I0WH4vuogPdp970Y+hi90U/ZtvXAeFZ7YoBBOvK34RidkAeY9C3JwbAbTvW1JNWRtbnsbZkGbEPZdPkoZgus61tqN8j1/OABbRhE5snzxxvw6934ZnY+9us+TSAeNu23RlASJuYTRoUG4jY+3ddsGnlxp6LfZeHNmW6TfqUZaytE0r+OV/OJvPFc5pUUJUPs5X3UEPqY0oLRgDf6/lOFCWUdT5XLxV1qJKk52r9Gd/FYmHj8ThhkCOQSOJGPRxLMFsBB4vF7fEExhojQD1FtE2jM1Dk1NgwW4EtmhyN4x/0m+f4gQBSmDs1jlQRR6nFS+s9XrQ3z/xvigBvS/epCMV4fF356zaHTYDItHfWtSFtQ+T3XTekLIqVCz+pAWaWjEwwS145yP+sH014Ss4QM0vwNiAAR5j8kSTawroxW11l2Gq1giwql8tWr9cTzy+XywBq0t5+vx+ODJlZwsgCFCgWi7a3txc+p19e9vAbkNKf00fWqYzSd/XmFwz0arUarojU4yE+YaO/mQJj0wOHehPEfD4Pck8jINIIOadRWwCPCtT4NadRWMyxzqVXCLPWihrgnhf92MXa7I3tWB99XT76S8vzdfv/fY4gX49/x+tUmkuI8tLmKk0ueDADUmBcx81HfjwkfSoG+6fSjm3ox2p7GqifZtRt2s51+nrsf63T7/kxHXkTvSCt7li7Y89R16Z7f+x5LxPvYrtsq0us0wfT7JS0MtKI91SmezA6bQyy9pI0myyPHbWu/HU8kIfWzeumANF9A8P3doRhnXK8DaCQl7Z5Pq9QyqpvHdq3TqDdN+UFEdZRXqQW5ZHPNCIBJYSQ5JiXBYUGcECNXlX29BkFBswsePQ11wLP0Q5/XppkYbVaLaGA+rvjm81miI7Qs8KTycSq1WowiNRjT1lqVKnxEgMQNEqAca3Vaolxi40RtzGoMKVO+oHxpgaaT9QGUOPLiZHv3zraxAPhP/sx6K4ASJYsyuNZ2ESW5dng7gvQMYtfv5fF22pk4dnn+UqlEtZlsVgMyVNZLxwNou3qQeYzXefkD2m1WiF6iDXOc6z/arVqtVotAIvj8diur69DxAIRFdDNzY1VKpWQj2A8HoeoBAUxVPbSP3+biRrafix1jBVcqFQqtre3Z8Ph0CaTScIYVLkXO/fOWKr803P6tB+wIY+Cod57rUf5V8EE7WsWP+r4+dB8yuL7LGMXY93zpPfU5yEFIvwYpI1VDBzRPnkl2IML2l8FiPU7M/sAFFFAxQPC7E36vgI7sTm8b7pPWeTLfeg942PU8anTQ/DFNrpxmuzI+26sH/c1v3cZo/tce9ustYe00fJQXvslS0/dFgTJY7/67/wYbzp+ed+7KzgUq3vbdz09eBJFaNNN2yz/BMUUl7vUn0VZC2cTI2nTMnz9eRh8E8pC1GLPopjq9Wwaqsz1bI1GwyqVik2n08R1gmpkaFgpCh5hxXjcECz6HH1GySKagUSAnAGmrTzrcwGoAYQivbOzE84+dzqd8CyJzfSuegUmtGw1+s1Wnkk1ZlDe1Uu4WCwS4cdqLGDM0D/1SGIYDIdDM7v1ynp0nX4xxvxm7lTRV0AE0rO+abzBu1m85Ndyns1zk3WU9f4mdazbWLapI+u9rHV9l3IpK2s+st41WxlDo9EoAF167KDRaFixWLTxeJx4B76azWbhyAHHa1jPrCv4vtvtJt6ljR784npYeJrrTrV+SG8j0KgG6idagd+j0SjIBcrWNrG+KQv5Q6JWBTeRQ41Gw8rlsg2HQ1ssFtZoNMzMQpJI1k6tVgu5FBgvTZKoRiLgpTfaFVBV41CvcdV+0O5qtRqORcRIy0P2az4G5Sn2BW8Aq7xV3tcjLDqHAB/aR54DCGJM9NYNBU59tEfalYxKPjIEgzttvVKPAgN6dE35MRa54sES5L6CZ1Da/BChgEz3ESE6X5SpETHrQORt6aEM8I9h2P8lgwdpumWWLpq1PjahNLDAfxezEbLshTyfaX3r9k3t77o9O6u8vPrSXeg+nDX3AXZkzWMapcmnvP3IO4+blLXpu5vqlJu2a9Oy7jKPHw1AyKL7YMasMvIsvrugMpu8+9AbUZbAjT3nBW5aGUrq9dA8BChkKKJmFm4BwMD2nhsf7qweG5Rv2qZ1eMNcr73iMxRSf7QCD6M/c0tbyGtAXoLJZBJABb5Xz32xWAxJIdXgj3lsFQRhDCkTZd4seeWkGjwY8OVy2SaTSeL8OISXcnd314rF2/BiNcI0ckLDoL0HMgYg5OGP2FrMswbvQw5sS3fZoB/Ks6Zl3qdnYtt2wguAewpQwVeE/MNvauTAc6xLygRYw2O/WCwSOUbUc+sTzHEcodFo2HQ6tX6/b2b2gbFF3xlHb1TC+8ViMSRNBQjBsNP8JPRBAQVkH1EHamgzZuRnIUIC43c0GoV2ap4F5KAmg4zNC/1Sw1zBVk8qv3Z2dsL1kryTxm/0hzL9PHqjWNun8lD/hofoq8p5M0uMr7ZNAREfjQGo7I0ZBZ01kiINCNC/NZIgbQ15uY9cpT9pRr8fLyWfrDP2TOwzjdhIewZi/POCB/dhhHxKdJ8G2n3SQ+4tD0F59in/TB5QYpu60wylTcrmnU34Iw9I78u7DxtF5dsmjoJtaVvdJK+e5+W81rlNvXelTe2kj7lmN3XY+fe2pcIy547x5ZdfblTwpyKQ8072ps8p5UW11o3JQwMd91UX7/ojCyiJKFneE2a2MiL0+IPZKp+CR65R0heL2wRVzWYzRD3o57zvw0GV/DlWnkepU4+kByswGCi7VqsFgwkwQhU9vIXVatWKxWJIpogRxOf8lMtlm81mNhwOw9V24/E4hHZrn4hyQAnWTPTKa7VaLTGWWpd+7r2pGBXbCJc8yoH/PK2Mh+Lx2OebrP+8ZW7SznV1fwyFfZ0CRoRBt9sNnnGzVf4B9aabJT3gavyzZtXjTt2j0ShcaapGHvkJSEKoxp8CiLPZLBG5UywWE+fHNaSfdTAYDEIUTrlcDrkOzs7OzMzC/wCllUrFrq+vbTKZJIxeXaOtVivIqvl8buPx2G5ubsLVqvrsfD4PAILeoKJjB4g4m82s0WhYq9Uys9u1O5lMQl4JwJhisZgAX3U+9beCFeRnuA9SxdvsQ8BG557PFYDVdyGfENBHEgCAML4+esADEEo8q/l1KIsysvYWBUG0PD1G4a+C9AppHn0BPtOIEuY6Bt7E2ql1QOuiMT4Vfe7HoG33o7/kMctLeffThzC4s8patxdu89y69t9V79nGhslb17YG6iZlb9MeT3fR67LeX/ddnjo+NVrX/m+++WZtGVtHIGQZ0h8bGUqj+2iHXxh36WMeAyFNsDw0c25SB20lPBLj3WwVpq+eRg271+f0DKj37KiRq0qZ996rkqyhomYrL5u/Kk0TFmJ8eK8RhgFlKpCBga3eOn82mzZhrNBX2lKv161cLifOW/MMY6peOB/yS7tRHtX4x4BQZTgGHKjxRmi5NzI+lbX80JSX92NePehjKYz3Uc+6MmLfEZUDTwAgNhqNRESPT6qoEUvwPJ/rMSDNc0IiUd4DnGStKV8ul8vEzQJmFkLr+V7Lpm0KMBA67+WAGpwKwKlhqEcx9BnWqH5OO5rNZhgzHSvmRROzmq2AV3/EqFQqBeCQpKr000dhULY/gsE7gDCAKWlrXw1plW1pfONJx0PD7PkOUgPZLGnca0i/zq3uIchPlZnU4Y1lnSev6MfmKa2fuq/oZ9p3/5lvWx6ld7FIjxbwe4a2O61c5d+sSImfKj2kbP5LAwo+hf5+rPrX1aOA50NQ1lhvOw8/9txl0bo+bTLWsWe3sXPyUJ4y70tvy1vffdWZRVsDCJ8yE5ptPtBpz236+abP6LNpkx0DMO6b1tWrRIgyxgRnU8nyDxWLxWAoe+UXw5okhf4IgBolxWIxZFcn8gBwQHMHeMUH459nfLit3pdeKBTCLQsKFhCSTNTAZDKx4XAY2o3hDWEQoRiT4ZzEbZwt7na7IRM9Y10qlazValmhULDRaBS8qYAvGDrUrcZUqVQKEQd4MWmX5l3Qa+XIF4FXVPM56PrxCnUWb6R51bLeSSvjrrRNOSj/Cm4p6f9ZxlNav1njWZtT3jGOvZP1zLrv172Dl7zT6dhsNrN2ux3WMWCA2QqA07HUdhYKhbCu4FWMKN5l3cLDu7u7Yf2rgViv1+3q6souLi6sVqvZycnJB/kN4GHkC21WMBBZVSgUrNvtJj6nDYAUs9ksREPNZjObzWbhOlqOGmiEBuNDeyiDsaK9rOGbm5tEskQSuk4mkxDJNB6PE3Neq9USBrnWNR6Pbbm8zb9QKpVCG4fDYcKA5/lYpBbz5g1Lv94x6pGpCsoAjCpo7OWLB5V1n/G8pLymdRMREjOCaQ9lxyIPtGz2LU1AS788QKWgrgejqE/5ACBNbx/RNuiY6RhDemQv5ujwfVRAhXH2ORLS6FPX99bRXdq/7dj81Mcsje6zX3nH7mMbypvq7ps+k3f/3QQ8eEh+82WnOVbvUvY6g33d91njoft9nnfXtS+2F26qg21Defkhrb+xffQu7XyQHAgPjcr9VNqwKf1UNhxV2NRrw5h7pcUrSqp8qffen4vVZ9W49d9nCQYtAyPCfxf72/fXe/CpD8PcL0qUSQAPbnxAqaMv/uiG/q8KoE9yCKn3U2+mYLxRZtVDrKG9lItRRRmbAnDrSJXtWIjtp+DV8KTgwDova2zzuk/5kwUwfizykS66tmO8r39rlJHZyujiusU0Ysz15gA9jsBnGPX6nj+PnkasD+/tJ8eDWXI9ar9IZsra0WR7lB0jP4/qAfbgVcwwVRnko6BidcXGQI9uUa/3nqeRX8cKGK0bcx8B4MEVDyB4mR+LIOB7nXMvc2JzEZNH64AFbavvr88jw/dp8tS3ScGDrEiPtEiNmHxYx/8+GuKRHumR7kYPvVd/rHX6Y+sceeljGut59sdNyvO07ZjnfS/W/m3H78FyIDzSXw7BuDHlRhWfGJOqR1xJjWCeSysjq10xRc8rpGn/m8WVWz3akAeF1HBbBR5iz3vPtTdEPTjDZx59zOqXB3y8Yu7b/0iPpKQ3m/i1brbeSOKZmGEHX2pkg9mKN/16AwDT20xigGIsrNsTnwNQpBl3tEflXuz/TUiBQgBGBSU1CV9a2Vnr3ssgLct7Vh6SNlGOYvvJj0XbzOk6ygvSpq2fR3qkR3qkR3qkTSnPPpwnB8IjgPBIj/RIj/RIj/RIj/RIj/RIj/RIj/QXTnkAhJ9WjP8jPdIjPdIjPdIjPdIjPdIjPdIjPdIj/Sj0IDkQHukvj7KS5a0LlyHhVVZ4sZYdS6alZfHDmW0fCpv3XDLkQ5c1URnHItJyKdz3uScfLq2faz6ErHd9G7Wd646cPNIj5SW/VrPOaMd4ept1FCsT0mNI5HAws2iyvRj5o1q6nrLyenB8wB8d0vfytCFtjdMfv6bXhdx7ufZID0c/lbPEj/RIj/RIj/RIeehOAELa2bw8Z8tj769THvMqlOuS4aWV6T+P1bHJecR17U3LnBkrY925/Vj787Qxq71p86Z16A85Acgwrt+R/MwnI+OWhl6vZzc3N9ZsNhMGuq93NBqFGxE0cZgmIWu1WtZoNOzy8tKGw6FdXV3ZYrEId8tzdaIa/8vl0obDoZnd3mJAeWREp456vW71et0mk4lNp9OQ0bzZbCZuR2DsyBrvr1D0GcN17Lhhwo83gEitVrOdnZ0wntzsQOZzbnLgKrtarWaLxcKm02kYO+ZHDZibm5twVR/Xb8bOkz/SXybFkniarfKV6PWp8/ncxuNxuCmBdQefQdfX13Z9fW2NRsN2dnbCzSPVavWDWx00K35aEkKzVWJTbj6BkBfUwc0Fo9Eo0SaVbyojWBfj8Tgkk6RMbo2gfTs7O1Yul20ymdj19XWQD5PJJORQKRQKIWdDr9cLQANJY6Gbm5sgZ7i5gn7R/ul0arVaLVzJyLywp2giRuYKucYNLLTl6uoqIcN0/Dwgwvzo3Csv8J4HSrL2Vw/SZCUIVPJAsSbt3DZHhY4l7Y+969vLzUQAVSTQVVBNP9d2bwpoaRuYl+vr60RiS99O6tsmt9AjPVLe/B2P9GlQHlsk7Tv/vqc0uy2rvrx15LVb7qsN68qO1bGp02Odk1Tf3SZPzjobks82rSNa78ZvrCswxRN7n+X+mGVsW27euh9q/PLUl+dzs+Q93l6ZUkXVe7X1t1dQ9X9vpKCQoayrMsaPGhaaiA2l2uzDTOoKaOhVZrEFqAkGfTJG3lOPJ0YMz2KQx5RcNdJ9Fm9PakxpOYw7Y5+VUV0Vcn+9pmaj/xj890g/HfK8Z/bh7QsemFvHi7pmWI9pkTTeGFT+9LcW6DrUda/GGbctaNt9f2Pf6Xr3n6XJRG8kQgAqGh0RIwUqPLioxmjMYIyBK8hH5KqP1ohRWvQI7eP/tESsOdMtmVk8Ea+nGA/4v7NuGEjbb9JI++HrjvEOPJdWvr9JIe3ZtPdj8+HXZ6zOx2iTR7oLPYRe8KhrfHxizD/22KeB09uWtUk5sbrv8twmdd+lrKyytxmD+6I7RSB4L/VdG5bmAfcISZpnJPZuWtv8/z7yIA2dSetnDAFKa69/LqusNNrG8E9r46bz5q8ehDDCm82mXV1dhbvMUXrVYNf24FVXAMBfRdhut8N1g0QFoJh7g2W5XNpkMrH9/X07Ojqyt2/f2nA4DF48vX4ND36hUAieebOVNwcQAg8/dV9dXYX2VKtV29nZSUROzGaz4KE0MxuNRmZm4S526sB4oD7qivGw2coYubq6ClnwAQ6IPKDsarWaADIwQorFYrirXt/Ha2pmCQ9aHkTzp0B5vJg/hTp+LCKKCL7D+FTvLFE0yAG96tEsCV6ZmVUqFavVaoEfYzJFbxDQq0qXy2WILkL20DaiHfCymyWBh2JxFXlAtAOGF+uFMvH28zkRPcgN2oMHX0FDvWVmOBwGo502E/XEu9fX1+GGC+pELkC8yw8RCRjaPtKLyCieH4/HVi6X7fj42JbLZZgv/xMjNXJ95AGymXmm/UoeNKZdAB1ep2DeNIKA92IGeIzU8PdAi/e+e/DbRwVQP/uMkgJo7C20S3UZv9/GomqQy8pPlK9XGut6YvyIcNEoEQWotT+P0QePtCk9BL888uDDUhrYmPZd2rObgMzrAIqssrIiCvLYc3ehPLZizD7lu3WUN6oibx9jc6N7mN8n1pW3Cd1LDoS7Lv60AcgiVSY2aVuehbCu7HVlpBkRP4bhlQWsaJs2IRQnHQdVztRTiAGLwpOm+Hnvv/cmofxqu9Vb7p9dLpc2nU7NbBX67/usIZwxj5f3CvrQWIARNcK98k5d6tWPKeeLxSrUlTaXy2Xb2dkJSiG/Mdz40cgGSJVjvtf++DPijC+f6ZzF2vpTpI/R7p/q2OQh5XVd41BabgDkIcakX1cAW2ZJT2xatAPGeRof+zWnckM3Ve89Z814GUb7tRwFNbRs33bduHWNq4zQdilRlobNY1RqpIf2wUdxULYqO5VKxYrF2zB3rUtlbFqYv5YZ+9yPcxoQsW7vjvGXUiyywM9jWtt8+7M88mn8reXHFEwfvcI+4+vWevw7fgzTokTy9iVGaY6SR3qkR3qk/18pS97F7DuVz3lsx03bche5m/f9h5DtdwYQvIFq9mHId5oHM+v9WB2beObXDZY3KPOGfaSV6xWi+2ayWH2xevL2e917WW3ES6YKrnrJUELxlEynU7u6ugpngYk2wKu/WCyCUgt5LxcefAyHnZ0dKxaLwfNWLBbt6urKrq6ugvHLO6qI8SweQz7HG6jAAHkJrq6uEmDFzc2NVSoVazQaISqBSAXqp/0Y+9RDuzECAF8YQyIjJpOJNRoNq9frNpvNQsTDYnEbrUH7i8Wijcfj4Kmkb2oQjMdjKxaLVq/XbbFYhBwVtIUyRqNRGCuiLHjmp0hZQN6nqCiva9eP3W7Wt0b8mK3WF/ypRiZykdwBOzs7Vq1WQ/QAhhI5TVi7nPuHP30Y/ng8NjMLeU2q1apdX1/bcDgM0UDUpWUSIaHrDQBDoxhiXmj6w1pjbbDXAViqbCS3Q7/ft+vra6tWq1YqlUK0BWPoAVPAO4z82WwW2kkUA20i6oJcKBiw5HIB0KBfrVbLbm5urNPpBBmK1zwtAkGjBTTyy+drUbDEzBLt1N/87T3+6ilXuQlv6DMeJIjljfFGtweQNCJB51j7DG/ruBA5prkqaLcHyojsUtBLASkPRClopf97/UL5TEEG7Y9fNz6/Au9qxNkjPdIjPVIWZTlI057Z1q7LstXW2ZZ3seti7dMyN7FL0+pUYP8+QQQfcfBQcv3ebmHwg+g9onkHaFtjJeZZz8PkD0F5GOuhjYGPYWyol02VFMKKNZzVe840bDWmvKR5jVDc+P76+joo1apYEgZcLBYTdVG/hhfzjgIE9I1Fru/Gwk3V029mHyimnhcwWDD2GUfaifKPAaFh4NoW2qd9UcPNLJkUEoCBZ2h7uVwOxg51rMvH8KlTFtj3KdImoOePRWpos14AAWM8gxHsve/FYtGq1WoiqSJrQY0jyoB31ZjS+lg3JAHle/hc14O+F4tqUFnCd2aWKFMNNk1cqEafyhp9348nxrs+o3KEsdDjIAp2eNJoBJ0nBXpihiRjHyszBirEvPMxr3nsaAHzFYucgtbto2lRD/57leEK3kKxvTIG7Ph+xb73SSJj+0Ws7f4z/7xvc9ZeqXxOG2mLByc8+Wi7R3qkR3okCFm6qX0Rk+ExQ3rTtmz6XVpdaaDEOhtuU8rrZL4vemg78F4AhNhAxDb/Tb3lac/kHZAYU3glLqbcqDIYAybW1RWrM1beJgy0CSPEUK3Y2K+bmyx0DsW4WCwGhV2jCvi7Wq0GT7ka9IAMrVbLyuWyjUajRHi+nyOUIDKEY3xMp9OQh8B7Rev1ujUajRABAaGse+8YxwWIXNDcADznIy9Q0PXcNN6/rH5w7lqjBcxuPY3lctna7XbII8E5cTK6Y/xopIdGOtBXPm80GmGsGLvZbGaz2SxEczSbTatWqyGCgvZ9Sl6pH9sDr5TVlqx1cx/P/9jEmXoMwMlkYovFIiQsLRQK4caAxWIRbmNgjXIDQq1Ws36/b/1+P0T9UIauLwXIWC+AYj5XSqvVShjBumY16oh3+F5zMBDVBFE3MkejoxQApRxATsAWjlUo8AHRn36/b4VCwdrttplZiL4gN8J8Pg9y4OrqyqbTaYiwUICUsTK7zbuyXC6t3W5bsXgboYX8Ue8/hPz0wA5E+/WYCHJfy9AxUyM2BhqkGdb+uEAM0IkZw/odY6fzocCpglI6nzomPkrAt9ePEc/qmlbAxoPRfny1Dv0f3tL2eVBc/9fxUDCfdcO8+fazjnxUxCP95dJD7k8/tb3vL41iNlQaiJDHOE+jPPaIPpfX+59mP24KDOQ5vpBFdwUL0gDuPHXkqXtbwPjeciDkNbT1HU+bGtTbUgw08GVvimBllXWX99PKyssseZ/bBNxgbBQYUEVtZ2cnER7qvXJmlvhOPfeq4KrBQGiuP16AAqQeNc1UPpvNwnu+fI1Y8B4p+qHXz/EOyhpghpbN+4QD6xgpUKBJubRODZHVMVRFOibMlF99KC+GA+Vr5nlIxwUl8lMy2M0+LSVjG/R72/I+FVIPvFky0kW93nyvnnz1irIWOP6j5QAaaCJRDHE1nHQ96LpUBSNmgHHcyEcn0F6M6BjvY4RWKpUEWOjb4I1grYu1pWMCiAeAonLCJyXUMVRZytir8acGM/3jfYBfxofvPcABqQxWXvB7adbeivxJi0pIIwVg1q0TLdsb7So7aavuAT6KwuxD4EAT4LJHaZkxAz4rsiCNdHw9YOXriinU2iYPkvCu/q85cB7pkTw95P70U9j7/lJJ5UpM/q5zpOSZ27vYSHmevStIlResuE/KqnOTduQdy032Y6V7O8KQ1WGduDQmzCpT/1dlNa38bduZ9nwWA24DnuStN1betsycNubbGjvFYtEajUbCk4G3vNlsBoWTs8yq7KgwUgWXsvFgFovFcO6abOV4ByuVSvCWm1nCW8mtCKPRyCaTidVqtQBqYPjjGdLwZ9oCAIEXnnPUGOJmZuPxOOQp0L5g7OCVRSlXT6J6fjSKg6SJ0+nUZrNZAEronx8rxlSvZVMDAoNFozb0eVUs9VmMrJ/6EYZN6Mf0hPxUFCjllcViESJY9Kw9OQZKpZI1m00z+9CQY60RGcQaUG8pBo3P7q/GshqAHqT0gJyZBQChVquF9ciaNLMP8rDouXdkFpEI5CRhLevaRAaoN1fBC9aWyoFGoxEij4iGIJpLo6BioKJGdmkuFIBP2tFoNMI4FAqFcOMLkUmaW8GTGt/eC657YEwR0bB/v5f5/VNlsc7DfD4PIItPCuvLVIDJH2/jeY0M0bFUcBYQ2cxCfguVxwrGAjzp0bV1ek9aNEZeuevH1e+j9B/e1fUCAEWficrza8bTpwYqP9LD0yN48EieVG6rTPDyfFtbaFMQIa2uPJ/l5cFYPdsCGJv2LeudWPvz2MH3YafeG4CQRlmTk2fgYwMYY9KHFnIx4MK3KY28xymrnrR39f+79vWuC9xnEtezw7HQR1VU+H5nZ8cKhUIIG/bXtXmFjqvTSCamHj8MbwwPTXClSjEeT/XA+6MAKJyEZvO3GuIKOnhPJG1X494saZyoRwlSr6OG0mLoMFf0HYMExV/JK7UkmuOIBte2aZg3CSg1JDsWnvv/Kz0qMuuJtafRBPAtx30KhVXeDn/OXo0XNY4bjUaiHCJ3zFZHpZQX1XhU2aIGnDeC9BYU2uIN4VjZvKtGrUYHad8UCOF9yvf5Vnwb+ZujXLzDGvXAib+GT6/80+gNNVK1fQpeMKf+dpcYKYjkDX3KUlBB5WKMfD3ee8+8UqfynlKWouWjDGh7zNjXsUd+854HDHR/guBh3Z80+kH7oxEPyg8+j4JSbDw1CiY2lgqu+fc8CLPOE/UoJx/pkf6yKK/TdxP75j6corHys6IZ0sqnf3mdSOu+X1fOXUAV/35WW9JAnfukrQGEtEHSTt7nAGYxxrr6sihtYfj+3WUS1i2QdePkPRW+bWkMtQlQEAsrTWuXerjVqFfvmir9lK0efjzu3M6AYowSi7KFQtZsNm02m1m/3zezlRfN7NYgaTabNhqNgqdosViEpIDUPRgMAgig3nfKom3NZtOm06l1Op3Ene1XV1cJgIF26llqHc9isRjyQfhx8KRgDGNcqVQSkQsYXjxHOeSRILu8jjsGGvNDdINmqAdYubm5sUajYY1Gw0aj0b3cwvCX5rHK43nM++42ZWxbRx4iGWKj0UgY6pRXrVYTclKPwvC/enBns5lVq1Wr1+s2mUwC/xYKBavX61YsFoMnXo85aSg8pJ5jwAz1yCtgpgZuzKjSslg3RC6x3mPl0V/Wna4bva1guVwGzzbygbWNfON5xpQfnlejWMthnGkDY63zYbYCPJBTCgClHWFQ8vXH5gW5pUCKjjtRGLFytWw18jG2Y88rMMB7+owa8n6OtH3I9mKxGI7AQQq6aHsUVCaywQMWWvc6oCSN/LM87wEL5jTt1gXfdubiL0lWP9IjPVI23ZfhmWYn5nlm24gBfT5vlAB/pwEKm+pzsfeznk+zR/0+F3Ms63N5QY670tYAQh5EapPv87637QaXt/4YAOI36zT0bRNPS9a7/tk0r4AqMXc1MtQbokpVrExNXMb/en6XawK9kqVXdqmhr4o1oaV6TtlspQTX6/UPPD8cGVgul+GKQ7xAgBvabpQm/tfxpv0aMsszREHQZj0WoZ5GHTdVmAl/VuVbgRVV+jTRJKRlqlLMNY/eK8YYAppQF8YLxyy0PAwkAB6vgG5Kf2kKaZ6NMu+725SxbR15SPN4qBGG4alHfLQujDHAsOl0GmSHGvMapaNedLNkXg/1wANG7u/vh6sitQ3+ukOOQygIh+HFevFyQaMf1PjTzxVAjBng3lj2uVvSbkXwCgFAoY51pVJJrFXG0Yf6azmAshxhwNiPGfX0yctdb8h677yX+Tqm2t88QHeMbz1AomXHwvpjpJFkvj6dUw826TjGIk74X2/RSKvfR91l7f9pAA91xyIZ+N73Tz9/BA8eKY3yemYf6adLP4ajJw9fpUUPbKIrbeuwzgNy6Gcxx25e8GBbeqjIgrz0YLcwpH2vBpUqjzHy3/mJ8ROXZvTn7UPeBeTRqTQ0KPZerC710mW9s65NeShPpEEWiIBHziwZykuG8Ovra5tMJsEYNvvwfKiZBSMCZRcDFyBAFX8FErhRAJCCdnBzAN52s9WRBZRYTTxmtlJAVQnU4wgcs6CPRExcXV1ZpVKxer0eznGrkaSeScK5IQ3NxkjSYxeq/C0WixAF4L2dzAVjqSG5qrwvFouQg4Lx3NnZsevr6wDiKG9QJ0CMGnt56C8t4uDHoDxj/BBKn4Z16/l+gDQMUbMP+ZRnZ7NZ4tpHDcHXMHz18qssIe+Cfl+pVOzo6MhGo5H1+/2EhxvAgFsMOMbDutPoJ/Veq6zS8+H0h3dpm4KAapTpe2qEx4x7/z9E2Zo7QeUfMod3ObJEH2PeiXK5bLu7uwk54PNMxIg++Yi4GChaLBYTgKk++//Y+5PmRrPszhM+AEiCmAiCBOkk3en0KcIzPSIUmSoNJimlllWWrEqL2nTXpldlbW296s/TX6GW3YvutrZuK1WVVFZSllVKOUVmRkRmhE90OmfMEwkC74Lv7/L/HD4AwcEjPCL9mNFIAs9wh3PP8D/nnuv7Gvf3uIwtHee4/o3KUvDv0P7ofX47GZ8z/rrVQUFyzTzw2yBGjSV98Xzmx5l2xI2htnGcfIgDXTyAHMeDbyO90zXv6B2NpknXx0UBw7jv4vyecb7KpEHYm6Y4pz6Oxvmhk9J1gkfQZUCVi54TF3yMe8d1+n0jWxguw0z8PwqRn9QwHtXpi5CquPaoAo37blQ7Rzn+kywQnj3p5HHtZSY97vmjMg0mpXHADYUOMaqJDprZOSMKgyeTyYTCgQAKROrNLBj4nnAEtE+aZuwdBn2/Rqo0OqTGvUaP1NhKJpORtP5+v2+9Xi+kXB8fHweAQY9WxGnCmdfjtLzTBeCiqdE+IuvHwuy84a9GMP9reivP0ugV80Y/LisE3xl0b54mGeM3MQ+sF7NotFWPDTU7c0RxRBRgYz0rr2lWAPeNAi0hHOZk8jTSXqlUgvyg/96Z73Q61ul0ImtAAVV10LQffOfBBa1ar0CHAh9++4Vfo7rtAAASx5/sgKmpqZD9RJ0S6kbQNt3ShQyh0CP9Qk6wrpG5Ou6aGRJHClD69+kY+nkcBaooaR0cDx6MyqTwf5udzxbw7/I6kGfDh76t2gdt0yhH24Nnmlng2xUHCPt2jrJptJ167bjx0Ow0/vf3fFNAhHe65quhd+P8dtJFzuZVAqLX+e6iICjXXDbAGvf8ScGRSX2sUf5anOMd195xnyuwPamvFffuSZ5zlTG6Dt3oKQzjGHoUyOCRKaVR4AM0SRZDXDv8s8Y55qMAh5ugyyI/Fy2qi671n180bqOe4fe1knavxflwDvifyL0SRi1nm5udGeJa+NC3BSHkgR/+14rnMzMz56LocSmeZmeGGMXdtNYDxrD2D3Dh+Pg4nA7Bnm0cGa7DaG+326F/+hw/5j5aqc6NN9w1ess76U+cYci1CiBolkYymQyRYgVB3tG3jy4jz3yhU7OzLBvAQK4zO9vyAHiGQ80WJfhW64zA5wBm6sh4flVertfroWaAFkpVgqc5lQWHX/vH8+OcX43w+lRzZJICCFNTU5FtQqy/uPXEWlUAgd8AC3pihQIqXMdapd3+JAjuQRbpSRJKozKOFGzxgQAPkNBX5lAd2HGOd9z2A3WQ40AE/50vbhnXfv+9blvxMlN/+7Uyri/0X9unJ0LAb4yR6ptJSUFn3hHXJq/zNMPPA+jfBPDgHb2jd3SzNGmw1F93GXl1kc8X99llZFJcGy8TdPXtHHfPpLbTVX3Gq/ieXse9aRDhxmog8Jk6d6PQqVEITRxi4z/X54xC6MfRJMhNXL/0mkkmJQ5QGfX/Re0dh4L5d12Wxj17lMBgMasxy7xrVJDUenWGuR/DpdFoWLPZPJf6urCwEN7nMxdwyP33GunRSKSPcuI8kHJNGzHetTo8Bi3P4B16zFwulwtbMXCiKE6IsQ6YwrsBBszOHLNE4vRoNY2CeUomkyHLgvE+Pj4O6dQ6HnHHsikAocfkYcBqajVj+I6+vXQZ5VIsFm1qasparVbgbbMz0E8dzzg9MBwOz/Ek68g7gZq55JF3fqtDz/Xw8czMTIjg8+x0Oh2pkcJ7fQYPoARAhgdN9NhUBURU5ngHnXeSgaHp7YyhvoN+8Fmj0QhrEnlFAVqVA2ZmuVzuHJhhdpbNpVuaaC9jpp95R1oBEN6psktJQU6u9TJe38E1vgCiPi8OWNBrRxmavFsBKn2vt01op4JE47IP4uwBbZM+XwttemBKx1p/cw3v0fbFActx4+Dbp1lC2g4Fot/RO3pHby+pDPu61uxVnHN/ryfvd3hd4q+b5FmXpUnumyQj4LrtGPfuUYEIf92oNtxEm66dgRDn9Hu0apKJvojiJmvUIOrncWDGpO+7CH0a9ZkHQOL6cRl6ExHg66BicdF/DBEi2aT2q3GiPxA1D3DAfSEwnHwvLLWCuEaH1FjnWjXWMajV4KJ9msKq12EE8r3ZWbHBROJ0OwKGLwABThbtZ4sD7dI2a3TSO/xaHRs+0JoJjDXACEa9Gpa8L64iOmOlQA/1JHxq+Tt6MzQKqIu77uuci0wmY7Ozs9btdkN9ETML23Hiig2qvDA7c/b1OEKfLeCdXu8scY3Kxbh9++os817NqPFbk9Sp8jorLvId5wTrNXo6C+sMUMFHm9XJ1v9xdrvdbsjW4jvAToq90hYFPPXkBQAE3umPKARA1ag05KPTXidNGiGKiy55x3wcyB/3Hj+f3nn3toOCGX7cuY974raFjWtjXN888DGqb3qff47P4lCdoOBLXHHKuPfqNiK9VoGhd/SO3tHbR3Gy5E3aBm/C/5j0vZP26Sr+3ST3x/mB44Lnl3n3dcf1pp5zHboWgBCnoC5COSZhikmeO8n9/hlXpUkZ2bc3boIv049xzHvRM0eNwaTOyrg26SkLZmcROZ5JNM6nheIwaNTfH99IhI1q6tRVyGazwZDmfpwCov1qVPFsjGyNVlE0zBvrtF/b4MeQaL8amWQsADLgkNM2DFW+9+OZTJ5lLihg4jMt1PlRVJYsAiKIvFOPHGOLyfT0tGWz2QB8+L3bvJu2eqDoHd08TTq+X/c86NoDrDI7X/sAQMEsWuW+1+tF6pKwbrSeiScFtRTYS6fTkfWhUX+IzAF1ptvtdpBNyCOATg+IKvCInOr3+9ZsNoMzr5kD/ihFrbFCHQgFG80sOO16MoTZ2TYJiDFqNBqR2jLUiqGvgDPq6KvMAJDk5Irj42OrVqthDAF+RznrGv2Pi6DHRb69Q6zPiasJ4Z1l/0xfCDDO2VX57IFknqH/+wy5uPcDsvBOdbSZD91SoJkEccCJjpfnPf0N6fYD1aHaVm2z6gbNnIvLcLiuXfCO3tE7+mrIr9GbWLPjnuH9h1H+0GX9tctkEFzHX5k0m+AiP0o/G/fcy/Z9XJv8tXHjMUlbbiqY7enaRRSvQ1cFCG7ivZM45kpfNcrjoyZfB41iMIwnjKY4JxMHFANHo10alYF0T3MikQip/5qab3Y+9ZLv1GDTdtI+DGyfpq/P0iiYvkuFpqZc+x811nmO1hvAUadtaqSTDq1OiEYUaYcalWqE6l5yBQK4TqOxmu0A8OHTYEc5EBfRpGDb1x1N/zbSqMiE2c0oC10PCoR5ZytuL7eChzhUROLjop7qSCrP6vsVQOCZcfJB1y9HlCr5YqOacaSOPGtftwAoyOBPO/Hrbzg8O2ZWZQ0ZRYyNl2usVbYs8F6dW5xFBXXjSLMTNJvBzxPv0PtU1vHZOH3pwYOLIvCT8qjygb7jInkVp29GPX+UE6/ZDnEgis650iSZCBf1w29ZuAyNAkri6DKy4p0cvzq9G7t3dB26Lv+8Sf67rN9ymQytm6C4932dvta493/d7RpH197C4B3vywzCRU78uLQSJZ+COOo6fe9F74pr20WT6JGpi66PG7u4919mkY9CrXz7/QKalEGTyaTlcrkQUUwkEuF/jOBerxcpEIjhrg4CzgQGtR4JaWbWbDYj2QS8i2rkcZEqddI5Lx2HQY1rLSbGO/14Kz9xFKQ+R4sMAkyo0Q8AgkOlldvVSKd/FH4k5Vh5SI1dzWjwc+fnHvCF1G32RqtzQ2G26enpcLzjycnJyAJrF9GbiqZ/U4ytr7OdbwplhnBg2aZDX1utVoT3WFd+SwAZL75NpF4DCpid8bkepYocUacXXuZHr0un05GsnFQqFTJ9FKjTExM0WkwWlNnpmiZziQwerTlwfHxsrVbLstmsZbPZcA9yTzMYtK3aD5VFZCaQuQBgi/Ov9Rd0LTNmKpMAWZiz2dlZS6VSobgscpr+qlyFFBjyc8d4KvniqxcZh+qI++0EOkYK6Pgx1Hu0bbxjMDjbsqXjptkJ2mbd4qBgNO307/AUN45x46CgxLjxYWwU4NGMB9Up/NZr44AH/tc1dhn6Jsjkt5Xejd07ug5dl3+uAhSqnh8VrIi7V983Klh7kb83qU82ab98sG9SW/ei518UjJ7kGdzvx2zUdRe9O87nvQm6sVMYxpGPpk/iWE/SyTeByox796QgwlXf+ybpKu0a5QwRVfdRQo0IYaypUa5Rd4SROiLquGPgs51gVLTSp536SIuPiupYxEVj1CDTqJsKGG/wep7mGRim+nwoblx5ly50rdeAw6BG36iMhDiDUM+K13t8ZXe95rp8+VU41JO+45sCQrytxNhpBF+dYhwaLQ6qay9OqcHbfm7gXe5XZ1mdJe7RiLCuYZ7LqSzeedQ2+Mg2z1QHD0BO3+0dO/88rtX1yBgxZnHp5HFOvK/v4udHZY5P0efZuuWE68mCiHuv9kmdd3+tykpIndxJyQMF/jt9nyfeNU7feR7gPtUL9M3rlDgjLO57/fw6pLykIJfKeO2D8rB+rs9T0jbeRHvf0Tt6R+/opmiU3ojTfeOecR2/7LKB4OvQZZ91EUg/rv1xgevL0hsHEC4zedqhSToOjUKOvJHlncBR7eOzm3Q2xkUetK1xkxrX1osYbRxqF/f+Uff5cSAqZnYWyedoQnWWZ2ZmLJvNWr/ft6Ojo2C0UXyNzAON0mmUD+dDI4hEKXXfMu3k9IKTkxPrdDrW7/dtbm7O8vn8OQNdCzWqs0HNAk6PmJ2dNbMzwxiDm3bkcrnIWBKVHAzOTnrodDqRY+yIgGpGgY43WyyOjo4sm83a7OzsOeeE+WCvOdkCnBGfTqdDO3WMcMbYJ02GAvUTZmZmgtNBEctqtRrm5Co0ag1ddn3dxFr8KsCDbzNAAZhFlopmCZhFI6hE0XF0fPSCtYUD32w2g5zgHgW84F2tFQDvajYUfMszkAnqWNMuvvPHyxK9Rz4oKME7WUfUREgkElYsFiNtpJ2DwSC0S512szOnk0wL+tvtdiPOvs9CiiuWx5gyzq1WK3yOnFB5zPgWCoUwn0dHR0H+KV0U7RkFZur/o773xQ95rgeB9W/v2Pt3jFqHPgtExxA56+Wt/q/8rG0F7FJATEEXD1YoYEFf48BmfTcUlykxap1pRo4HF+IA93f0jr5tdBOO0u8yqS/gPx/ls4y73pP3OTy47wPQo66Na8Ood/k2etnn5bv31UY9T/s5ygeLG4dxflrcdaPGZFz/J33HZeiNbqwY18CbRLuvOxDekLgqeOCNkm8yjeuHjzRhfI6r3AzAgFGlR5TxLjUYzeycwaOfaVYD12gmAAadnnft++ANPf1Of4/KatBooF5Pe9To1e/UAPQRUL8uMAJHtYW+6Q/jy3OVLzFWtS3aB/qlY/mO3pHZGa9qJoB+rgTP+awaJV9jQHnYP0tJ14iuPY3UqkPl14/PmvLv8M/xvyliqNu0FPDAYdNaKd7p846ovsPsrN6Cko5T3PYinw0VN+7cq/JaZYCXhf7eUXMTl9k0qg36/SgH1n8/6n6lUW3Q/zU7bBSpzI7TTdo3vS5Ozk9i58Tdc1Ff+CwuIDDqWv+ed/SOfpdonD0Tp8O8TfmOztNXMTZv0/hP6t9dBDJ8VXRRgPm6lBhOCDvfv39/5HfjJvgipEWvuQ6jxD1jVBR/knddpk2TokmTfn7Z9kyCOl2EaI175zjCOB4MBpE990ROiHTp8Y4amaMqebvdtpOTkxAdjBsrov5kGRwdHVmn07Hp6WlLp9OWy+Usk8lYu922brcbHJR2u23Hx8eWy+VsamoqbI8A1ABkwLAmY0CrxPv+YHRjyBOVzWQylkqlrNfrRQx0CpbxHM0W4Fn0h3u0ejxjQ/vVgdD6EUR++fzk5CREM9lXTe0GIpaMrxrECih8HaQg3lUjCFcFAt9RPPmjVYmaa70PTbVuNptBHui6UQffO3X8z5r0jhxtwHHXIorqjPpaImanWy9mZmbCuiCq3+127eTkJMgi7iE7iLoNR0dHNjMzY6VSKbwHRx+5QYYVzxi1hYnvtQ6L2ZmD3263LZVKhXoKfj2os6jywUc/uEbbQNTCn2Qxbp15uaD9SCRGH/un4IqPpnvAVwFQpThnmrbouPisjnHkQXDVT3q/r/GgvMtz/G91PBgbssEmARV0K1Dc2Hmwm4yWuLn3oIIH5bnWn6Tyjt7R20g3rdNH2dNXdQC/bTbHJH7SuLHy4zHJeF+Wxt0/qd+junWcP3fdtsa1a9IxiqO4sb9ojEf1z3/+9OnTsX0w+4pqIPwu000Ik5sWmDf1vFHRJ74bVRF9VPTIX8dz4trrI4xm5/f5avqotsenp8b1x7dH06DVUI0jHQ8f6eQ57KcGGFGDVJ0rnzHgSQ1DP77eoMRo1nfrc9SIx/gdV638KnST/PdtU9ZvO+HceedL+c1TXNRT71MgbByfTbIGdO3EnRKhwMC4GgRxz/fZEd4RZGzYuhSXNTSKRkWb9XM9mtHfqyCLzoEHQrzjqf3y2RD0KW4svgp5EPcO35+LIoqTygY/l8yjymDkIeAsgMJFmQJx62VUv1ROI/d9uybtj3++PzWC9/nP3snUd/Q209fBm7/La+ImnPubfF4c3eTzxs3z28wDV233dcfuRgCEcUwxaYR7kkU6DjWKe8+kn42juDbFRWHG3Xsd1G2SLIVJUSg+Y6xHjedF78PwIEJP5CubzYZq5ES4NXKv78hkMpZIJMK+W04B8MYUjjFGf6/XMzMLkXkcerIY6vV6OGueSD0G4dHRUbgfg5kIqr5Xz9smgkQ7vRMSB3oMh8MQ3W+1WpF91kRvPRgRN+48O51OhznT4l8YufzPO3mHbkXgR88F173fWrV9OByGmgjsm56Urqps/X3jENNJ6bKRA73nuu9+W+m6xpAWM/SnLPjignNzc8Hp4nr4Sp14jTrDo2Q1wPtc6+uv0B8yeoisZ7PZcGoEQBg83263rdfrReqwmEXrrPD/cHh2OgGy7ODgwGZnZ21hYcEGg0F4RyJxWk+gUCjYzs6OHR4ehnFDRpJpRb/S6fS5sU2lUlYoFMJaPT4+tm63GzKtFOSDGF/WPf01iwIsOKfIPeaPZ+AoxznCcaROL9dpBJ//qVGhzrq2mTZp5D4OFIH0Ox9l59ma/cC74C8dK96n8zQ/P2/J5GkNGPRBOp2227dvW7fbtRcvXoS50v56+a0ZC9pWHQcvXzX7AXmsoJj2U4vq6pjHFdD0WzL0e3iY8XiXifCOvml0UYQVuijarGvUg+MX6c5vm71gNt4vuIqdFHftRf7QRXM6KcW1N85/9LZo3HcXteEiH2vUM+Lum7R9cXbsJBkOV6WvLQPhJqOQb4LeJOr4NgqZcUCJ/w7BqkaQGkv6m8UQZ1Sajd7ryrU+ldkbtr4GAe/RlFG+06wF3umN51FtwkHyUf24tg0Gg3PF3EYZmHH3awaCFkLUbAQ1SscJOAUG9N0+DVjbyPdv4hjH6yqaqz7rHd0c+TXlyYN//B6VzaLr0DtYPmIap0i9LIpzlHxauh6/6h1r5Xmf4ZNOpy2fz4ejEAFBdVx8hX9doz5bwMsY/7c/mk9lgPZbv48DArz81f5ddo37eY/LRlG94Nsb97y472jvJMbl1NSUpdPpCFg7LuqPk61tNbOwbQy5qGAXYDJzkE6nbX5+3nq9ntXr9VidECejJs0kGNVnzWoY9TyvJy56r5/Pr4MYc4IDcfP/Vch8tjJdFjx/R18PTRrQi/t+lJ0/Shb9rtNlHNGbCABdxr+77PV6n9IoQOGyz77M9eMCaG8zvTEAYdwAxEX5vJK4yGCIm+TLtMGTN4C0fZelixaMOqHjkKU49GiUYcpzRrV5nJC9LLqnUX91ugeDQWTf7nA4DIY6UTQikO12O2QeaLRMn6WRQ/3R6CdRd61PwCkN2WzWMpmM1et1Oz4+tkKhYNPT09bpdGwwGEQAAcYBx1n7inFaKpWs1+tZr9eLRLI40UAd7sXFxXC6gRohuVwuEpEjOtbtds85K+yrxqhVJ0uBD3VY9BoKvXknTGtAzM7OWiaTsWazGTJHUqmUNZtNGwwGwVG6LL1JAO5N0ChU+evsx5t493WehzzCmdIxU6eGyL3Z2ekBZAH5GgOaEWMWdZjJsDGzsD6KxWJog64jPXnEr0WeyXooFApmdgZOIosbjca54yDNLNQeSafTVi6X7fd+7/es0+nYzs5OqGFAn6rVqm1vb0dOX9CTVZBpyDCfLaAghMpUTplpNpshw8rXWNHTMcj80LnRbCx9B+2PO00DGpUNMMr599d5oEP76nWv51F4Ku5e5m5qasoePnxonU7Hvvzyy3P30ibAbH8qBvOSzWZtZmYmZIPMzc3ZYDCwSqVivV7Pnj17FmTo8vKy/fCHP7RXr17Z3//9359zOJWP4oDquHHUsYsDmfge3aBAm9oVjKE/3SMOdEAP6Vh91USf8/m8lUolq9VqVq/XbTgcRvSPrpU3IZdTqZQtLS1ZoVCwly9fhjoub+p93wR6W3X5TTlYF8mkN9X3bwpfjfIVVJZN4k9cJSCkvt6o7y9Do673OiwOUPWfxfmx+n8cxflso/6PA04vAjYmaUPcfVelKwMIFzHF24CevMk2+EjVJO/Xyb1IKMdFozxNyixXufaiRWAWL2TVufdRNDUg2frg2xaXdouBFxdB8Smk+g5vPPIuH73x0SI1yvSd6pRg2OO0YIR541sjKko+8kgfdXwUzCBV1Wd8KKmwJVrG57RPn+3Hmnvp13UiUTcl2K9Lkyqvq8qKN2lcvW2GhQeq4pxes/MnnEAe5PJp1spzWnARvlZ+9DUOeJam/I+L0Prn0R7awv+sX117OOr0T9eN9lP77k9VoL8+au3/5r1c6x3NOCNOt5iocxnnoOoYjtNpGrFXirvej/eoyLfyiyddV+PkUCqVsrm5OSsUCra4uBic+EajYXt7e+eu97otDhDxp1OkUinLZDJhex7PGAwGVq1WrdPp2MzMjGUymQBS4ZAPh0M7PDw8d984UkCDNnkQ2OsqJZ1H3eKg33u6SibKTVEyeXq8cT6ft2w2GwH4er1eBChRQMzsbCzYtncTVCwWbWFhwfb29gLoZxa/Zt82Gf2OztYEOoJ6JXHEdjfWLDLfZ8uxnvf3963b7Vq32/2dyU7xOmbSAOmkNImNdtnn5fP5SLCDrYIA0QQeKYQ+GAwCLwBeInsgH1i4TrBpUntzkuddBQy4Kd/42hkIcZM/znEe9wz9f9w9F3V+XErfqGt9GuwoUmUel7UwSfvirouL5sWhS+P+1+f4Z3mKWwiTMCsGtdnZHmE1BIkAch0OdjqdDicODAYDy+fzlkqlQnYAnzP3PFP36WrUU/dAkwWA4Mfg73a74dkzMzOhSjqf0WatGUCETqMyWmUdw04/Ozo6skKhYOl0OuzdxoAnqqfjw9+q5NQhgjgBotfrhfoLakjRX61loDyMo4OBWygUIv1h/vS8eDWAxx3L+bbRRXLoIpk0Cl2+6H38fROG5Nsa6YHgbc0MMLMABFIrgDWC0laHVp1eoup6rCC8TbYCCjybzdpweFrDYGpqyvL5fMjwGQxOayBks1lbXV21/f39SAVhdaAVUMQhx2jMZDJhvQyHw3Bqi55W0Gq17NmzZ5GjHHU8kD1an4S0euRBMpkMa4sTUuLWP2PEeyGfNcD48oxWqxXkUjKZDAayAju01esdnu/1IP3iek0x1/bG8S+ySoFadcY80IT8Yczi9BefZTIZ++ijj2x+ft42NjZsamrK/uiP/sh++9vf2v/9f//fYWxULnoHXPVUp9MJ/MWpHRikvV7PXrx4EdZAvV63//gf/6PNzMzYwsKC3bp1y+7fv2/z8/O2uLhorVbLWq2W/ef//J/t5z//eQBuPcALSKF6w+sfbSffAzAw7nGgAv1SOad6xxcWHge6vSlKJBK2srJiv/d7vxc5BWk4HNr29rZVKpUgDzKZTGRbY7fbtV6vZ69evYroweu05d69e3bv3j2rVqtmdja+8LzWRHnbZfZN0FfRv5sE+uFvatQcHh6eA2rh71u3btnDhw+tWCxasVi0fD4fgEB02NTUVMhE+j//z//TNjc37YsvvjgHJl2Wvkl8cxUQ4SbfPeqZXpYy948ePbJsNhuyatfW1mw4HFqtVrPZ2VlbW1uz2dlZy+fz1u12rdls2tramt2/f9/+4R/+wf7rf/2vtrW1Zfv7+2Pb4f2rSfzhcf/7+/w4jxr3OD3q77kK0HARvbWnMFylozCPppbrd2bR44qmp6dtZWUlKG9PnU4npNorEoWQaTab1u12w+c3heBP+pxxY6RR+Ou8YxJS8EUj4GbR6KCPoGmkW6MLOM5m0TRjvlMjlBRibYuPvPNOjGDNJEgmk7aysmInJydWrVYjjr2mstIXb2jzuZIa6dyLIewzCDQ1V8cibmz03dpf/z9j1uv1QqZEIpEIvMoY+cwEnuWdrLedLguA4Zglk8ngFGs0IQ5Ewqh90+PxNo+58qGuI3+8nGbvKGqvTiNKX8EDUvrNounsOEGaMUMBRJx4tuKUSqUAANAWgAN11FUWabuREQo28BlbGdTZwrjsdrvWbrdHyl0fQfXZCpCvO6KFYDUi7rM+vAOuRlUcMW/MSdx2K3+9zwjwIJpmjOjnZvHHA3p5qu9hvgCIVI5ls9kwl7lczvL5fACIadvs7KxtbGxYvV633d3dc+/QeVeZ62VxNpsNzsTs7KyVy2XrdrvWaDTM7BQ8Y888+ohivYlEwjKZjK2vr9twOLStrS2rVqsRXvDjqGvMj3/cqUa0ddSc6fVx3426/qsi+jAzMxPWUavVCnzAlj/GRAsKwyejTii5KvV6Pet0OjY/P29mp3bg8fGxNZvNADjqOwF21FB/R5enUeM2DvxPJpM2NzcX1qGCz3Nzc3ZycmLFYvEcgAAtLCyEwAnyBfmg18FrZB/8Ls7xVRzQ64zTOFtIgdBUKmXz8/NhHmdmZuzOnTuWTqet1WqF79HX09PTlslkwlZACNA6l8vZ2tpa0CetVivi53ldclEfrkrX5bHL3H/Vd10ZQJgk3WTSwfPXX5ZR1QDM5XKWyWSsVqtFJh3KZDKWTCat2Wza3Nyc/eVf/qVls9mIgYNh9fr1a/vyyy+tUqnYwcFBeMfa2pqtr6/bp59+atvb2+cMq8v0d9RYXWVCx91zUaaCb8+kc6B9poiVfs4C55lkBWCsIQhw2PhMT2TwxgGOB6nKAA44GqQepdPpUPOg3+9bLpez6enpYHQMBqdpS3/0R39k/X7f/u7v/s56vV6IgBH90xRKVTIaGfKOFG3W0yMUJcxkMmZmkVoIWididnY24kxolFOdFH0n1xOtJWpJZLVer4cxpC+8C4VJRAfkPS7S+Cbpqg70RffwPTU4bt++bdls1ra3tyNGK+OCgikUCnZ0dGSVSsWOjo6CTFHk+XfFmNAMHbMzgEor7KvMUDBOC9HBtwBoRB3JXFIDXaN+rNfp6WkrlUoh86FYLNrjx4/D2tS1lkqlQt0Sf+pCnONoZgGArtfrQRbMzMyEtEiMyePjY1taWrK7d+/a4eGh7e7uhjXnq/wjA31BU6KZ9JmtFwoCMrYYyT4LAGCDNUwNGmq9mEUjzNyHHDw6Ogop5GbRrC9IAVCV0woaKLDgdRwAvAINHhDmGejiubk5S6fTYT4Zz4cPHwZZTm0aMwvO+fT0tGWzWfsX/+Jf2Keffmq7u7uReaWuDKA2z9XsNT4vl8sBRDg5ObGFhQU7PDy0n/zkJzY7O2urq6sBYOx0Ora9vW2tVsuazaYVi0Wbm5uzP/uzP7Mf/vCH9u/+3b+zH//4x4EX9NQSzR7QTD0+Y1xoI6Q1O3TcGVM/3pqZoKTZP18VqR6bnZ215eVlq1arkSyExcVFW1xcDLzK2JFCfnx8HORKnD01qWzWtuzt7VkqlbKNjQ179OiRPX361BqNhvV6vdAGBXoINLDeflf0wU1S3JiNi6bqNQ8ePLCFhQVbXl4ORW69jaQyn9/YoziZ1JjpdrtBHrD2W62W9Xo9297etr29vcBzvi3f1LmfdL2MiohPMlfjnomOVKB6lA+i4AH+3h//8R/b6upq0AtqX6tugReYP2Tq3NycHR8f24sXLyyXy9kf/MEf2Pz8vG1ubtpvfvObcwACAZRRYzBOjvqsBaVx8zAqUyGOvgrwwOyaNRDiFvM4GsUQF6V4eFLAYH5+3kqlUjAscXzq9bp1u91zThfH+2F4mVkw4LgORHl+ft7W1tYiaU3T09O2trZmpVLJNjY2ArqpY4GTvLe3F8lcmCS95To0ahFPkqkwaXs0WqugC4aNGjvsH1SjHcIwx5gl3Vb3KtGeqakpy2azNhgMrNlsmtn5IwwxnjHyKKCYTqeD8evvmZ6ettnZ2YBOPnny5JxB0mg0QpoxbdFj6VA4OOJHR0exdRDMotElNbY1wq1RMTVkMVzishA028Eb6zyL/mr0TaODut+bdrwJZfgmlOxgMLC5uTlbWloK/2uhOY2sIR9yuVzIQOj1epbJZMI4Ew03syBDSqVShK+JNmuqtR5NeJX+vu3GB7yrPDkYnN/SAI/6iJw6zvxNpg2Aoa4NHOlUKmV37961TCYT1vX6+rolk8kAdjHXOPCLi4t2fHwcKXiq0SXaQPt07BVsgkfMzpwsnH0y1JrNph0dHQVALpfLheNbRzly2j8dO5955SNh6uh53lJn0ux8NFuzFVQm0T4FfT0vqvOpRp6vl+Lv82Pt5ZcHD4bDoS0vL1upVIoU2FUewsGG7/R4XfqjGS3FYjGsW67R9mrEUWU8oLR/dz6ft42NDUulUpbL5azX61m73Y5sMdDsFeySxcVFW1tbC/wySs7GZY6gR3VM/TjrczTLRfWAnyd4yGdjfFW0sLBg9+7ds6WlpaBrB4PoEccKUMHTAO4KrmFHXJdYH+hcnJFisRhqYQBqUpRVj4hWgEdB/nd0ffJO2tTUlGUymeBIUrRW17gW3mQNAD51Oh2r1+uWzWYjtirriSg0subevXtWLBZtc3PTOp2O1Wq1SBbpNxlEuGq7byr4OYkvsrq6aktLS0FGpdPpAO4z5yqzdS7NzvSV+oXHx8fWaDSCDY9MmZubs5WVFRsOh7a0tGTVajVkGqqdN6r/o3ypUeDBJKCA8tkk90xC1+HZa21h4MUXOZ3awHENvWjg1TDiuvX1dfv444+tVCrZ3NxciD6jpHkWYAH7EjlXG8NCIxAw4vLysi0vL1uj0bDDw0Obm5uzubm5oGBgLq+M9/b2rFar2Y9+9KPYPZyTgAbjFuU4BCuO/BxdNM4XkVfSGOhEx1KpVNiHq4WgfJRldnbW6vV6iIJhFOKUaeoiqclEB+bn54Pji6OAgbG+vm7f+c53LJfL2ezsbFAq9Xrd+v2+zc/Pxzo9Dx8+tOPjYzs4OAjKZWtry3Z3d0OWA6nSGLdbW1t2dHRk+Xze8vl8KL5Cn+mvpjuSLcD//X7fOp1OUIjwEfwIj+qpCgrKqOEKqs5YYsCQgqsAA20i8osTNzMz87UVCbqqIFtaWrI//dM/DQqjUCgEw07rR8AL+/v71m63LZvNBv4BEOp0Ora5uRmAwGKxaPfv3w8AYqVSsZcvX9rs7Kxls9lwgkWz2YxVLDehYN80TaJEMOrhDQXm1EgzO3PMiKoTFVaHWjN31BlUAId9iv/yX/5LW1lZCZkH+Xze+v1+KGpVq9Ws0+nY7u6uDYdDe/jwoe3v79urV6/CmtF1Z2ah3awbBUYSiUQALdnGhnGBEVKr1SIR41QqFfbOs6ZZq77GAf0DpGAOMplMJNOJaxnr4+PjsE69o4dhzBrQ7Q4qixSk0NoxenqDB8N4Dp8xvxhjyHnG15/ooAUYaTtgnQIIZmbvvfeeffDBB9Zut+3k5CScBJNMnmasvHjxIgA2yWQyRBDViKQGRCqVsvX1dTs8PLSdnZ2gUxhXb2wi/4g8kj2GfZDJZCyTyVi5XA52BoYlwBLZccwvcntjY8PMzD755BM7ODiI9Jm5oe3Mj2Z5qJzXOfegGDxHe5TfdH364Aqf05abolGyZTAY2Pr6uv2bf/NvbHd3N5yeMRwOg2Og/VcgENmcyWRsdnbWXr9+HQGALytj1cEA9GEtzc3NWS6XC/xPltOrV69senra1tfXrV6vW61WO2fnfhsL7d2kk3yRIxRn63KPZoYVi0XLZrORbNe4tcXvo6MjazabdnBwYDs7O1YulyPyUAM2Ki//9E//1I6Ojuzv//7vbW9vLxRHvUyfvs10nT6PC6zy3Xe+8x370z/907DGmeNOpxOyjwF00Bdalw1djc7CL3j58qWVy2W7fft2kKflctkWFxft0aNHdnJyYp988ont7u7as2fPwhY2s9G18MYF2K/qg427bxJf/LJB/4voxooojqNJmWqSZ2GIFotFK5fLtrq6GhBijE9NAdV0MwyEVCplxWIxYti12+3IPqpkMmmdTscajYZNTU3Z6upqcCDi+qeGCamg6XQ6KLrrOPyeJkGwPFKrpFHEqzKQtgHDlTRj5oCx1GwCjHazszoUGsXCgEJ5oyQePHgQHBecwnw+b7du3Qp7FpnP27dvW6FQCO8hPdrvL+50OmZmwWjne802YVwxTBA6ABOzs7NWKpWCwU0kIpfLnSuM5VFRBBnCDN70EUOzsyrAOMPaDz2WUQtyEX1lvz/vRkmqo4LB6SMpPjr7ddAohZxMJm1hYcGePHliKysrtr6+Hok8Ar7oOONYEAEslUqRiDkZJcViMTjHuVwuZDeQfQAgeXR0FMAwjaAzV1/32E1Kk7QTkI61ioFvdiYD1JkkfVCdV3V0iCIOh8MAwLH2cKwB7jAOWYvICNY2qf7FYjFkI+CEoBfoo+oIn4mj61K3KGWz2XA06/T0tB0dHQVH+/DwMESZ2SML73je9VFkdcw1SnZychJ4eJSxwDhqxBRDCX6O0xW6nQGggfnyKfL+HkjHTQn+vyhQwHX9ft9WV1ftzp071ul0rNvt2snJiT1//jzoBpVjZmfFXmkH2UOVSiUAOpACKjq32hbaoxHHwWAQspVIUY/LBMnn8yHYgAwFgABk6na7AVzPZrNBdwDEe12q2RSatRI3n1yjfVQ9o/Oszx4nU2+a4ngBUHZlZcUqlYrVajVrt9tBf6Fv/dGvCkwig4bDoZVKJZudnQ32VrVavXLkn4wS2oKsX1paCn1hnSnP5HK5sAbhsW9jtf43qdOU9/ldKBRCajrzwc/U1JTNz89HwCa/Rvy6xw7lhyK5nU4n6B4NrkC6BW9jY8MWFhaCA/rq1atz2z2/SdkI18k+GOf4X/UdyGScevTkyspKeA86DzAU+67f7587pldJgVoChQp0oxOwD8g4ws64fft2BNx/9erVlfw87Sd9mnSMLutTx13vfcSr8MAbK6Ko6SQX0UVoDIOcSJyed724uGj379+3jz76KHJNu90O78b4UoNNU1AXFxcje+cbjYZlMpkQnUYw7Ozs2O3bt21jYyNUw/eRZQxUGG5hYSEYEXEK5CopLHFjM0kmwmURKX/PRYagpoxiOA8Gg3Csle5dxGnAYNZ9ySxaDEjNQMhkMvbhhx8Gh2R/f9+++OILKxaL9gd/8AehiirZAWxdoH4BexfVcKYmAIABUQUMUECpcrls7733nrXb7WCU9Pt9y2azlsvlbHV11ZrNpv3617+2169fhxoCFHXx+4218Jwa61q0D+J6kFMioWYWcSwYdyrTIzjZy1cqlYIg9BkzKGSMpaOjI2s0GsHQHXcE0lXoskJqHBBmZnbnzh37H/6H/yGc8kEdiU6nE7I6lEg/I1V2fX3d8vl8iDCROaNbZXAi2u227e/vW6vVCs5jp9OxxcXFYExg/DLvOuZvwjj/Kqndbof940R8de0qgIA8VkDBLBoJ0mwctottbGxYqVQK8oLMJKLL6uSztpnvVCoVUqHJJiG1GSMAA//k5CQYoBgjAD4K4OG4FgoFW11dNbNT4LHX6wUe2NvbC8X82u122AtNTRgFELVII+PBelVnHocPGaJGBgAY//PDeABm+e07cVkEfM6awHiOi6YwNvzwOc/nt4Iv43Q687K+vm5/9Vd/Zfv7+1apVOzLL7+0Tz75xFZWVqxQKIR2avbJcHhW4yWfz1un07Fnz55ZMpm0YrEY+MuDXr7t+sP6T6VS1ul0Qkr07OxseBf9xLnN5/MRQKDdblsmk7G5uTk7Ojqyvb29iLGLrCFbyQNHOk/YPArSebCB67VmiK9DRHt1fnzGiPKS2ZuPnC8sLNhf/MVfWL/ft62tLavX69ZoNAIYq9mgus1Ht4uxPqampmx5eTnYDM1m02q1WuR9kxjI9J3AEbVEyCIpl8sR4Gt+ft7q9bo9e/bMBoOBFYtFOz4+jsi94XAYW4vrq6K31Yn18kPlhAf5FhcXw/722dnZsJUEPtGtWZ50bakMnZqaCsf2ZTKZwDfYfWZn8l9BIWzb73znOyEAsbOzE+oifFspzhEdZ8/o/F3WqYYGg4Hdvn3b/vk//+dBbzIHyEgPICDvtYYXcpJ2aYCn1WpFAAQNtGkWF/qm1WrZ7//+7wf/sdvt2n/8j//RKpVKeNc43r6IWK/jAN6rrGe9z/t317FLbwRAiGOqyzDNuA7Mzc3ZBx98EJQjKa0Y7LrPVKPYWrwPIYBzmEwmbXFxMTAj/2s6aSJxmsK6vLxs+Xw+gi5pHxXc0Kg5Ti9RlV6vZ3t7e9bpdOzg4CBiDMDUfhx0wuMm/7JZDReN9Ti0ypMaOPxPPzD+tX84w2pgaqYIY4cBBEq8vr4ecQpyuZzNzMxYuVy2YrEYCt3Mzs6Gn0ajYfv7+8EApC2KMuIAQUQzaT/gkqLWGBI8k6yAVCplDx8+DEWgcNwxyPr9vr18+TKAI4nEWRoxjiyfwwcKJOB86H2DwSAAXQhRxp35I+WaTAvWCO8yswjwoxkOOidfF43jx3w+b/fu3bPl5WXb3t62bDYbqi6TZQDKTDQpmTw70o71v7i4GCnAicHKWeTwOPNfKBQCqAUAQ6S7XC6HfZHsjwfQ6PV6dnh4eCN7dL8uwmhTBwWnGPDP7IxfifDoOjOz4PxrxLxQKFi5XLZCoRAAPbOzLJh6vR4yDBhv5CzbmKamTo/fox7G2tqa3blzx169emWvX7+2er1uzWYzyB/aSl98VhARb4yH3/72t5bL5WxhYSGS4UY7U6lU0EuvX7+2SqUSkfOszUQiEaKaZmc1OwAaeCdrVwFHvlPHTx0UZJSm8iJrfZ0JPmcedduEJ73PA5Bm548BVNCI/7k3l8tZuVy2+fl5W1paslu3bpmZWbPZtO3tbavX63Z0dGSHh4fWbrdtaWkpGPnwjZmFdFR4iLoYRPvJRALooZii8qHqMPSOB3K0toQ67QrSoAsAb7QmCvxEtXjdLqJ60lOc3FPQ2QN3zIk6YLqOlPx8cd2bcDY9CMzaBUQB6Lt37164jvXEmsG2Awj04LdGoFOplN25c8e63a5Vq1UbDC5XG0FlgJlF7DrVSel02orFot29ezc4I41GI1JHB16aNJh20/RVvvOyzg2FM5E7/OjaJfv31q1bgW98bRR4GJ5mTeqx27rOzSxkkc7Pz1smk7GdnR3b2dmxpaWlcMqLt/MAxY+Pj21+ft6SyaTlcjkrlUr28OFDa7fbIeOIgtWXsam/CTRpfy5rN2LPsU2Y9a2n5Cnw7bcfaiYzPMF3yHCdS53fZDIZsu+UpzRYPD09bQ8ePAh2RT6fD0GI7373u9Zut0NBzs8//zwC+l+HLgIUboKu88w3cgrDuGvinORxA10qlewHP/iBJZPJyD5xs6jSwxDCAVUjyuyMoTE+MTIwPhRQQJCxD1LP2ua9AAZ6vb47k8nYxx9/HARZs9m0X/7yl3Z4eBibXqdRn3GZBaPGaxxA4OdhUhTxIlIjy+x8jQqNeuCgazTF7Cw1n7HUzIPZ2Vm7e/euzc3NBYGcyWRsaWnJVldXQwQYJJl5rVartru7GxY6Tre+0+wUnDKzMG+k7gMeYKDyGQW0iDRobQEKMdZqNev1elapVMIezX6/HyIiRDmJTuqRVfARwIUaMGoMw4u+EKUqYDMLpysQEUEYIUy177pnWAXppMLlJgTcZZ6Rz+ftww8/tOnpadva2gqRSrNoyi5RQfpVKpWsUChE0h6Hw2EwNAEQcrlcaAsKiNToYrFo6+vrNjs7a7lcLqTCMV6vXr0KhkS/37dqtWrNZtMajUbEkJ20vxcZZlcZ+6sg2TjrFAhUwIVxUkWPMbCwsBDmgXcSRWdeCoWCLS0tWaFQCOnfyIHBYGAHBwdhy9NwOAxblPL5fIhKzszM2Pz8fFin7Xbb6vW6ffLJJ6EPpMOrA8WaVEOWdW126tj2ej3b39+3crkcjF6zs2w39MTCwoLNz89brVaz169fh/fqdgYiJKxVDCB1OnzKPPwcd7SsZlRgZLOGdT8+Y43TSr/he41Ae2Js1IHj/ZA+Cxmm26XoL8bio0eP7Pd///etVqtZpVKxer1ur1+/DuNNRhgAAn0BMCmXy2GLAw4o72CPczabDZFitRfoj26nY7y0/RrBVJBJ+6dOImNC9htrIZFIBHDLAwh+Hep7zM4f1algkzpbcfaOBxQ040Lbq9sIR4FIVyV9HtuBABCOj4+t1WrZ8vKy3b17N8y7t+fQgYyFHuOqQAK1C5LJZJC3ZI5eRPCFbzNySqOgAIyzs7Oh9la1WrV0Oh3q6LBWNEpu9vZmBYyiy2RvTPI9/Dc7OxtqCzGuZA1h1wEysNXQzMK4eiBVHUe2k7JW/dwBNBKQqlQqtr+/b4VCIXIPbeOd1Drp9/vh/mQyaY8fP7ZGo2Gbm5tWq9UCkKRZD7Tx20Y34eTmcjn78MMPg22mti4ZyQrKUjgZOUFgmPerLYg+wHdEzyGLzCxknqneRYazrfLBgwehrVNTU9Zut212dtaePHkS5PDe3p49ffo0st1lElL/za+lUWsrbrx90DnOL2SuboIXb+wUBu2MLpqLnFUfXc9ms/bxxx8HBVMoFKzRaAQFjRFkdlZ1XhWiDhoTSJs0GoRxqkaE3u+jbKpcYTK2LnAONIod44R2pFKnxZcePnxoq6urkUgl2yS8sah0GYffAwxx914HNEDwnpycWKPRiGQcKBhgdmaYMB4seLMzJaDIsz5jenraCoWCPXnyJER9B4NBQAoR5DgbjUYjLL5kMmnLy8sh8qTbBjQSp2NNP2gzxjIErzUajZDejsIjAgoYxZnWGHZmZh988IHV63X70Y9+FOERhKSeWAHgYmbBMGJe4T8ElkbEdF3QT42kqqAnhY/+6/GEqkA14jeOrusE8wyQZz8PmUzGvve97wV0OpvNWrlcjgA8rVYrZIhAhUIhso+W+8k2gS9qtVpIMWa8zeJTedU4UUCHNrMdgmyUxcVFy+fz9vr164CqDwYDe/bs2URpj5OM22XpKvcwXihheJWtYzjBGOsYWvV6PWRtLC4uhj2NKOFOp2MrKysBcEin0/bs2TNrt9v23nvv2dzcXJDBGBca5UMGAw6fnJzYwcFByALJZDJ2794963Q6tr+/H7ZeAPDAG96ZZP2zRuArjnQDoNPsIbZmffe737XHjx/br3/9a9ve3ra1tTXLZrO2tbUVtgoQqR4OhwG8NLOwZhWMMTu/hpgH2q1bFJA93IOcwJhivvhfZY/22ZPqS89DPCPuO9rPdpClpSVLJpOhSO329rbVarVwLCNja3YK9ALo0m7WnoIUmlnF+9hKCOAU53h4gIO5p3BmPp8Pc49+UbBc5cjx8XGYW4qsIh/YHsYZ5V988YU1m81zRp43ArF9eAcgu2Z7qBw0OwMd1AbxY6PzfNOODWPPs5HZMzMzViwWQyYReqbVatkvf/nLkEkG0Q+u8/1hbIkIAuojp5DDz58/n6iPw+HQDg4OrNvtBl2BvPBbgrzhzhbY27dvW61Ws729PTOzr3ULw03QJOPm7U4ojqdZ46VSKdSsUeBGC1Uz7wqaxoGr+rnKIW3fKJk2HA5tfn7e7t+/b8fHx/b06VO7fft2OB6WawBwp6amgu1P0Xac0ZWVFZubm7NMJmP1et22t7cj7/2mgUfjyPt6UNyce8pmsxF7Dr2g2aAa3GL+8duwtwFR8Quw7b1fyHrFFoHn0CVsXQe8NIsCtxpUw3bEZ9Giw5lMxj766KNQzLHRaNjLly/D9XGZSKMAgDhS/mH8PYDj5+Gi/6/Dj2+sBsJViKj/xx9/bLOzs7azs2ODwSBEEOOO7lNnn89UyOt3GAkaMYgDEDQCwPvUOOF/UDFFK83ODBJV8OyZ7/f7trKyYo1GI6TW7uzsxI6HB1dGURxDTopixQEO/lp9vkZfWGz036caqTOqjM5YxxnHzAV7XR88eGD5fD5sYQAVbLfbAQFmbxICI5PJ2MLCQpgnwAqMdY/AKfqtDqwam/BEp9OxVqsVov+kXLP/GOSU+YdnOAbmv/7X/xoMXgQZ42EWzeqA51UZatsZQ3W2zSwiaKempiKp2KwH2u95GtLshnF0kUK8ClhFmxgbtq5873vfC86E9pM5Jt0bwzWRSFgulwsFLTVqiuJBUQGGESHUOdc2wRe9Xi84zJoRkkwmA0LN3jqKvHE+9cbGhvX7fdvc3Azj+00xLFRpYdDj0OhJNyhXUpQxEFZWVuz73/++ZbNZy+fztre3Z4eHh5HtQdPT03Z4eGiHh4f2ne98J8zJcHhaqGw4HIYsiLhq951Ox6rVaqiPkE6n7fbt27a5uRkAnkwmEwAe5tkrVOZGnZhkMmntdjtEPdALANTww4MHD+zOnTvWaDSsWq3a6uqqzc3N2d7eXgSANDsvCwGjkXdc6w0i5AfPUZBVU4D9GgZ8zeVyEQDBZ5TFkU/H9rrBO7AQPEPWzsLCgpmZ7e3t2dbWlr148SLM49rami0tLUWAUr6D75gPnScFpHknDitbjrheI/Sq8xRAIKuFLXLe7oB4HvPId1rEk3E+OTmxW7du2fz8vG1vbwdeYPy8Y+rbhQFLO+ADfYb2S0nbPWrryVUozmHAUSQbA0ecbD2cBbPTed3d3bXnz58HoM2T1g5R0J/2E0hgSyCOKMVX4a+LaDAYhIwxMhhV1nl7UglniHnkJDA/Tt9WmiSIgD3IFtRCoRDklMqUk5OzIrIA0WZRPlX5CS8MBoNIarqCs+rE+aycQqFgt2/fti+++MJevXplc3NzVigUzt1D5gsyU2Ut8ub4+DgEDNS2v84a+7ppFEA06vM4Uvk2Oztr3/ve90Ixe2wwxhobGTnsM8D5nPWO7V0qlULgS/05fEGCHQpckMloZiHrzSz+FDWzKFBFIARemJ2dtffffz/Yo9vb27a5uXmjcx8n29W2VR9n0ueZXQ1IuJEtDN5h9jTOIeX7bDZrf/7nfx4ESyKRsHK5bM1m016+fGmFQiHskSNFTZ290CGJgHCMlho2kN6jisgrY402ABhou1WxKHLlIxT6TJxjom7cq0bCwcGBVSqV2PG8Ck3CUJMw0MnJSUDUi8ViMGp9JoGPBLPgiTpoyqc66blcLoBIi4uLkXRGRfympqasXq/bixcvLJ/Phy0EasjRBtDB169fBwGSSp0WXKMoDxEsBZfUQWWOMSjVuGUbwvT0dIhqKsLJ72KxaD/84Q/t8PDQfvGLXwR+wvlSXkMIIhhBZgFZNDtAoyOKvKoiVh7nOs3O8Cc5oLyvyzOXFUqqJLRQXLfbtZ/85Ce2sLBg77///rm00F6vZ7VaLRimKhtUQCLsmePXr1/b0dFRqIVgFo1wkDWj48MzkslkJBqocmlmZsYWFxdDMU0zsx/+8IfBiTg6OrI/+ZM/sWq1ar/61a9uvFjlmyCNkptZJJJtFs184f9MJmPr6+sB1FtcXDQzC0UuAX3YhoQTUC6XQ3qp7ifkN4Ya1Y/Z3lapVMIWMo1Qmp0W41pfX7dms2mVSiVy1K/yCTKb/noni20rOh4KKB8fH9svf/lL+8UvfmG7u7sBDD88PLRE4rSquNZc0egYvIXTicEFUIhB7Z0swBrkA//r1jEy5DRbQkFbrvMGE32Pc1j9+tasKMYyn8/bkydPQjQf0JXit+VyOYDqjUYjFG/l2Zp2ihE/HA4D+EP7arVaqIsBeGhmVqlUwqk97Lv3Dqkai3yOM0LdDwVwVMZmMhnLZrO2s7Nju7u7gaeU9+BZUrQHg9MCrnNzc/b06dNQH0dplJGoQIbOE+3xBib9URqVVebnfRLyQQ547cmTJyHFu9Pp2NOnT+3k5CTIw4ODg1BsOZ/P2/3798Pcw8OqE3WdqGNgdlY9nVoZ6Db0/Pe//33b39+3Z8+ejewH7cduKBaLtrCwEJwMBZ50fH10UY/hXFpasuXl5fAdcuB3jZLJZIjO5nI5KxQKYcuVkgfszaJbo7z8gZCNGkzRNcxz9Nlq45Hxyna7arUaMp8BPZhPwETk5vT0dNBrPPfo6MiWl5dtZWXFXr58aZ9++mlkLL4JwQJP6kNM4pzqtTMzM/b48WObnZ0NNauwq9BvOO9sF8bm1SLoGnjTDDsA4u3tbTs5OQnAlMoRtjiP659f12YWbDyfgcQ16FHs9GKxGGr4NJvN4CN6e+SisR43zvTbX6dy/jIgwlXpjRzj6JHoSZ6hTiORO/a31mq1wFQwGvd5cIB3+orhXtkqwRw+kqtospmFlCWY0kdcPGNo5FhRT/pSLBbNLHrcGQul2+1GAIRxzDDOoFNhdVMMhaFJZBUnXwU86J7uW+I8eB1fxob70+m0FQoFe/z4caTWgKaQMoYHBwe2ublpt2/ftuXl5fAs9lcTlWTh1mq1kKpOyhnOsjqkKhzUEQcAKRQKYV+lOvk4lLq3m2ezjeWDDz6wnZ0d+8UvfhHZxqG8wvVEULXaMIIKFFwNKQQZn2HwAHop+MWYMDfcg+OtjvLXQbomAUieP39u7Xbb7t69G3GGQKo5hkkdBDVA6bdGiyuVinW7XVtfX7dsNhsi22ZnqWtecei2HB/dZS6mpqZCKi7bUNbW1uzk5MSePn1qvV4vRKQ/++yzbwSAEFdrA2dBlaMCVul02paXly2Xy1mxWLS5ubkQQWD9mJ3VSyCrIJ/PR8719nOIw4BMpkbK1NRUeA/rHMrn81YqlcIeZcAH5seTymSzs7nFAVKHhutYc5ubm7a/vx8q9Nfr9eA8TU1NWbVajWxx8lExzeIyi27XI8tJ94Qr0ADPq3Gmxpw+U8dS9+X7daPOPM9RYwU9oyAsxF5n6hEo9Xo9K5VKdufOHdve3ra9vb1zkV6fPYRBRv85yg/9gtznJB6y09LpdDghg+dq9oCCJ8ytRpg8qMxn09Onx4zu7+9bvV63mZmZyJGYukVGM85KpZKl0+mwrSXOeVJSHaXAB+3g74uCO+NsoeuQD+SQBj4zM2PVatWePn1qg8Eg6GRkLXvd8/l8mFPPr+his2i2HM9ifLH1AHDMLBwDaGb24sWLsQY8/EWggOw1xk35wssFDwbq9hk+JyPpm+hAjqI4wEqJNYUcYEuqWZSP+V/vMTtz7FhHzK+ClLxXbXj0k77H28CsZTKyqFOyv78fCu4C2AImsuaRMWSiwoPMdalUsuXlZRsMBvbpp59G2vJto1G+hQYU19fXw1pQGwwgQU+60LoYzJsGZtUHGwwGoWB4vV4P2cnYsPqbdatBQbMof3hS4NDs/DHIqk+wP46OjoLtrgACz1OKWz9XlQ/+PvXFRwHScfdNSje2hYEBHuWweiXGtbOzs/ZXf/VXtrKyYtlsNhKVBRV89OiRzczMhGryPvUa4aILlGtGLVplRP+5GlBqKKnyHwzOUhJ5V61Ws36/H5SmV94Y2VRlr1arwZCl2A8pnqMMWh27uM/iFvE4htTrPUONAhtYQGQiqDFFPweDQUjP9Man2VmBP5TB7//+71uhULCDg4MgcCmYiHORSqXCGeCgiRTD5Pg9HArdh51MnqZTPn78OCj/RCJh3W43RLd17BBkIKBemVHgJ5/Ph6JPr1+/tmq1GqJMpM1yvAuCJJPJ2K1bt+zf/Jt/Y/v7+/bTn/40FH0EWMKJIopGlgORLhwVTbNlP7kCCuzF1/lVJJfUMU2z1P3Nagy9afI8OjU1Zd/97netWCza2tpayLgge0evHw6HwdlUZ1CNDq4l6vuzn/3M9vf3zcwiNSIYL67rdrsREEP34yEffAqmghdmFlEcw+Fplg11U5g/BXLeVqI6tQeutG4HTtLc3Jzdv3/fSqWS3b9/PxgJrGPmhrnCeKP4JAYAchZ+3N/fD6CdGuyg/zyHWgqAfd1u1w4ODuzXv/61ra2t2d27d+3zzz+3w8PDCFCooLAaDnze7Xbt+fPnZnZ2lB+FtxKJ072Ui4uLNjU1FcBwwBKMCrOzGjA++0G3TSDvdJuStouxVpAW3qTNXpeZnRXh8+nYPk07Tgepk+rlQ5xRj3wn4ugjTsPhMGw50WJ13Ku6XLOA4Bmzs0K8uqVBQRIKeJKhcOvWraAj4EG/7obD0wyUX/7yl1Yul+2DDz4IToQavDjB9Xrd0um0vf/++yHCCg965x5eqVQqVqvVbDgchq0O48jPK2OeTJ7V0vDAgMrIuM9Vx18HVCDSPzMzY4eHh6FNjUbDvvjiC0skEvb973/f+v3TorIUx1OAXWUpxHrwNQ8IujAW2B9aOZ37uL5QKNjHH39su7u79urVq5F9IXPs+PjYKpVKOAFAedfMAi+og0OggPWkAazBYGDZbHbk8d7fBvL25MbGRtiuhg2kcoe/dS79s5B9PhtFAT/lAy+D4AHkFbaVgq0QmW/IDfT948ePw0ltKlfRZ/pe3k32qfb7bdbvk9AooGhcYJI1o1u4sNXMLGxJ3tvbC4WQAdpw+nU9Ie8Hg7PtKqxNPcmFdilfqf5QQEq3knpAmXlTXjMz29/ft5OTk+CjwBu0JZPJ2Nramv3gBz+wRqMROQWIop2Tjrf39+A/72uPm4frABOj6FpFFM2uV9Ef5P7x48e2trYWzmhX4zydTtvi4mKYZBjK7DyqqJ8jdLzijEM4+T/uGv0MJtY9lxopIutBi4F444SFxJEfGMcACzgWXydpe+OMCsZ91P5JlLkqSBauN3ww/O7cuRPqFrRarbAvGmdLUV+NOmBsaPpwt9u1brcbtlgwb8ViMaTNDYdD29raCkoCYxyBoagl7YSf+v1+OD8Y4sgoirxRCGhvby84oWpAfPe737WdnR179uzZua0MajirgwCSC4CAYFPhqIIOg9oT96mjrXOtQumrIC836NPKyootLy/bw4cPLZVKWb1ej0Sw1HCLq7SskQ2zMz7t90/PHn/16lU4fcUsWmgMg4MosablAySMAho1au7BJ+aVudR90jdtUN60wtBCZpr+Th9RyLlcLhSlmp+ft9XV1ZAl4DNDuId1zZxqtJYoRb9/epoJYGsicZb9wPWZTCakP6pRiUFYrVbt0aNHtra2Zjs7O2EbA/ONHvGRMTUmqtVqiFIq35lZ2HfN3wcHB5F97nFbjVQuwiMKyKsRBemWBn2uRkQURNexUCBC+0YbNONmFGk7R+lS2gfQm0qlAujJb8YU3U/7kJeqy1VX8mx4h2v5Xv9WwBWdAj/4NarODYAVfeFeHFVAiMHgNG19enralpaWgnEMT+t46ri2221rtVphnpU8QKpEWycJGHgZ6AMqcfN3WYKv8vm8ZTKZUAMFx/3169ehCC6nmQCk+jbAs+gobaca95qR4wMfCqQoMJdOp21paSkEojwhdzKZjBUKhcAj8JhZdJ3pmqXN8ImS2krIfHT6t5WSydOU8YWFBSsWi2FvOrzpedSDqWrT+DWqMpl58GBCXHvi1oQGlBKJRLDrcrlcCHIlEolwfB/Alcpfbau+CxuMHzOLOKrfBjBhEp8P/geMYWui6iFOzaFGiv5P4EJ1oWa6AeyfnJyErajUTDOLAq6Q+oY6n16PqZ2pvgA6S8F2bA615QuFgm1sbIQjvHnG0dHRRADCRRTnh09y/WXuGUdvZAtDHPlIxfT0tP31X/91SGsBnVLhr3tLPKnR7x2hUYpX/49zkokk9PunxwNi/BBBAk1GuGAoeqSTAh1q3PFsrpuenrZbt24FJcg7OEsYlDRufOMmftJ5UATLP0ed+1FjaHaWiYFjzL4iFgcgi68sbmbnHI+PPvoo7Cvr9/u2uroajIupqdNz3XV8yUR5+fKlHR0dWalUCvOhqf1E/b1TMhwOQ0qrmQXncDgchpQ15k8dGQQJ1ycSZ0d1kXK9vLwchCHbGjB+ETRknNTrdavX6wHVBqFm3IhUEqHW8+4xkhhDAJC5uTkbDoehICARYU33RrHxbFB05lqN7esYlVch5btkMmkLCwuRYmpETrVqvIImCrypc0rfdD7/6I/+yNrttrXb7RAt63Q6gUfYmw8veCNFs2C0DUQuB4NBcJqoAA9geHBwEFJ3j46O7L333rPDw0P7/PPPLz1O4+imDZRms3lOjjNWHKOn6cg4CLu7uxFAjrYxRqz9Wq0WACIFFDA+BoOBLSwsRAw35o7jGbW+ijoZ09PT9od/+Idhq8r09LR99NFHdufOHfvkk0/s8PAwXE8EcZQ87Ha7kawLMn/gUY5ynJmZsVqtZu12OxxDpkfLjYoKqxNCajt1VZS63W7gU3W0kQv85j1EuLUODFlP8DX6Nk434CQxDnwOoQtYA4uLi/bXf/3XIUNDnXMzC45au922ra0ty2QyYX9xnLzCGdfIj9Z/4flkKxHxSSaTVi6X7cmTJ6HOgm7/oO0QTsns7Kx9+OGHtrS0ZGYWtlaqYamF8zqdjvX7p0d57ezsWLlcDhFN9uYPBqc1PpA9rVYrRKN9tEn5WNunxixjxX3Ks1w7KjhyXeCA95DaXS6XbW5uLhTIZA7X1tYCsKeOM3aDZozQNu5lnpCl/LD9U0Exggzcp98PBgOr1Wq2vb0d7DDfD8aDYwTL5XKQFQpqad9wPnT9mZ2d2ILsYgunnv7zTaZx9ubU1JT9/u//vi0uLgadi42j8wGpPPcAgl7jAwMKEnn9HxcEVADKgwjoJ2yGDz/80N5///3QFrbe8T912pjber0edD3vQjcUCgX7/ve/b5ubm/b06VMz++qCM2+KLvI3vFwhYNftdu39998P9Y6Q08hDso2piaTv84EHDegxb5o1qHpbwb3h8OyEJTMLgQfkM7JYA3eqT9ED8/PzEdAT/uAdGkikmDe2PfU1GBsF1q4zH5d5RhyYd1l6o6cwjOoIe8M2Njbs/v37AcVX0kWugmKU8zwKcY+juO+TyWRQPCh4HD8MVIxaDEx1UMzOFL5GYHgXqfUYWRrV5HtAFFItcTDijDn9LA5Vioto6PfXcUAwMLWvLAZSUPU7HQuNIExNTdnCwoKtrq4GQwGFPTc3FwABVTgY7SzAbDYbjAuED0Yl8+NTzFD+aqghzFAy9I/79f16Pe2GL6gKq5EyHQcMG47/ocgURjd8pyntRLN8hFGNfuZFlayOPf3WefGpyj6Cp0LzIroJRJ10NLNT5yKTyZyrdcDYxQEGnt/UWPFR3XK5bMPh0Pb394PSYf71GT510uxsncOfmpqIowR/KXoNuAQSz7sWFhbOOQk3NaY3SfC6AgF8Pj09bfPz82HOMplMAFABGDQ1XcmnmMZFnPiOta5V9dURZK7UGOCZy8vLViwWw5axcrls6XTanj59GslEgHdUpvEs3sc8K+gGmNLr9QKA4nlFU3iVhz0w4+VQ3LipzKKdPFd5Vp+lcgnHSA0zHUPv8KscGSUTtL+5XM4ePnwY0tq9UU96L440+169Llc7gOiNbiPS63XNszUNB3dxcdH6/X7ICPEyQeUm72IeqbbOutUTl8hGwSjluMZsNht4HzlmZsGIRBYoCBA33jpefk68TPf3jiI1eHnOVWl2dvacoWx2tk2Hwsge2FKwI87h07n3EWrv0PMM/yyuR/agn9kqOEpPAmqQ4cQ79DdrXmU/v5VHFGjwmRXfBvK8k0icRuxXVlZsf38/MnejaFTW3qjP/HdxvsYoOyiOlK9SqVQAfLFJWP++vQBEnMwFoIhjSy2ucrn8VhfPnNTWmMQ59XOH3lOgn/U4GAyCLcz16lehW72OYr789gLNEBrVNg346FpV2zdO96jdfHJyVs9I7RS9Fptd295ut61arUZqwXGvju0ouRz3uZ+TqwARV7U1bwRA8E7rqMbAHP/iX/wLe/Dgga2urkaEgzea+NxvRfAMEgce+AiJTnKcoY7gUCRKSQ1+RUj1WRi1GKI4gEQYuE8r89NHlNHCwoLl83m7c+eOHR0d2c9//nN78eLFuQUxKWI1igH1uzgGHEWKBFIQhX6yoBESWv02zhianp625eVlu3Pnjn3++efWbrftzp07Njs7G7IBcEjm5uas3W7bixcvQj0D2sF57xjUvEcBBN6JUQAybmbBqCeyzf5reIJtBETliSYrWDAcDi2TyURS9QCdyKSgrRpRX19fDzzR6XSsUqnY06dP7Wc/+1loM4pIHWqNZMBDWlyUd5qdRR791hiyHIg6aoE0xm6UcetpUuGjssELzD//8z+3u3fvRhyYw8PDcNSP5y/6yXF0moamgIAaB6xNitvhvMNDZHMwdj6lmYwQDAUzi2QsoTjS6bTV63Xr9Xq2tbVlw+FpnYapqSkrl8uh/RpZ9tud/HhddqxvmihUxFw0Go1Isbj19fVwQoGZhZogHL0JsAjvsu6azWbk++FwGKJ1jBljhPOIcwjP5vP54MxzvwJiRDGz2WxoNw7ixx9/bJVKxX7605+G6LSuFa3CbHa2jlj/zOH09LRtbm7a3t6effDBB3bv3r1Q8+Tly5fhmCqzs+irniigshR5qlsxMFb5n+/hQ+9waSo14IaZhTHVd/NMBUqU4gAeNfoVGM5ms/bP/tk/s+Xl5fBMBXEZA9YLqZ4YcWbndazq2fn5+dBOtqwlk8mwvQB9o/pnZmbGSqVSALqeP39+Duxlbulbv9+3v/3bvw18mclk7NGjR1YoFGx1dTUig9CFtVrN7t27Z9/97netXq9bs9m0VqsVDMdWq2UHBwfWarVCIU3GQmW66kx4XLPJcFD4XEFM7CXVcZ53vT5W4HOUQxZHyWTS3n//fVtZWQlzSAYWbc/lciEzADkxPT0d0T86x4ypBiM8aOlBZX0fgI7ZKd8Xi0V7+PBh0PGVSiXUQXj9+nUIBODgw1OAIu1227rdbgATNFuEsaPNtIv1S4Zis9m0w8NDq9Vq1mw2zzkAbxNQPAmNsysnIR8Y9LKB8dPv4gBIlYXaNg8ecF8cqIAchcd0bWFTYDewbek3v/lNyCSjntns7KxtbGyEtUQ6vkbFv2nk11ec4xrHCzq33//+921xcTEEFchSMzudQzKWGDuyvcmMY/0ju5QnfEYzMswDrWanPEcWpdrOw+Ew6FEFOgh0I0sVLFD5jD0OyERtHTJPsQ3y+XzwI7EhNSMrLkAwybyoHxhns49bm5ddt55uNAPBdySOEonTSNDdu3cjWxPUaY9bbHECwYMKcX/rZ6MQTIiJhTkVKVYjyU8Q1yBs4sANs2hxNRV6uiAQZOyvLxaLNjs7G1HKN0UXKa5RAiJO2HsDFKNfgRclCgJmMplIqrKmJqkDgCIG0SXKYRY9hztuXryCUqWjAAOf+2sVmGLuaQv/AwqRLUCUGb7zWRC8m/3apHgmEgnb2dkJ109NTZ1LcY2bB/jV923cvKsg1f6zjj1w96aI1OWVlRW7c+dOMJJfvXoVSTVjrBkHeMs7Gjpn3ljw0ayZmZlIqqxGh3HwuV7HKS5dUqOkjCPGKFEveASjHx7gKDO2uLyNBD/6Inf0mzVNZJXtIVzDmOg6YN1r1pI6xB5E9iCz2dmWOF3/cQYE12lhu1QqZeVyOWQ9aZaBXyc6DmZnckej0hxNWK1WQ80O+EhPa/HGcRxhtCg/+WiIyiy/vcDrPMYeGYux5MdqlBOpYxAHoHNNMpm0tbW1YBjq8/w40h5NE9dnxeltjRap8++Bas97yeTZdi0ii6NsDvrHSUj9ft8ymUworgcIQ9CBrMRE4rR4bblctsFgYO12O0TYONarWq0GgOzk5CQC9FxEjFfc9gsfPBn3jFE8dxl5jywoFAoBODeLZiOaWaQWBOODvjKL2o0qY71tNspe0f6r84LDp7UySJ3udDphDllXjClAA31QEJLv4+RCHOAFYEpWqy+eeF0D/uugi+xGHZdRNoTnv3E86e/ReVb5x3fj7o3729uzZucdZuQkv8k0wy5FZwMSYzdwkpwGEfW53xS6DMilmcPT06dHXC4vL8eCPaxLsokZW76LswF84NTPX5yOQd5o1pECtUdHR6Edvm3ILd0SqEE8bBd4AwCEdiqwS2COwAo8xDU3UQvLz5Ufr5ukKwMIcZEC/VzJO2VqvCC4mRCNdMQJAz84/jqPUvrr1MDQ30Qr1diJE2remRwOz44N/PLLL63T6diTJ09CBJNopjo1cWmI/MCEvPfevXtWKpXs17/+te3u7l5a8FzEOCrQLgJ//BioUE2n0zY3NxfQdhY/z+Jaxu6jjz6yR48e2fT0tG1vb9v09On5qQAopVLJzE6VdavVsp/85CcB4U2n02HhsQeYdNhsNhsiPxh4VMplccJvGn3SdGSMB++QcyJCp9OxROK04A7RC4QL+7gZJ4QBR5ESpSmVSsHA7HQ6tr+/Hwyc+fl5K5fL4Uihly9f2u7ubki/xbkfJTAxSCuVSmi3j9zj1HC/GuQ6zzdNXrClUin7i7/4i3BmuIKKgCtEvpvNZlg7bDVibnHM40BG/dFzgBWw8vvLFclWUDCbzVoikYhkuuCYIDNYx3NzczY3NxfWgCLYR0dH9uLFixAZz+fz9q//9b+2ly9f2t/+7d+eAynfBhoMBiEaD59NTU2FtQigxjrBuHr16lU4lYQiopVKxQ4PD8N+R8aNoqmMJfPGmuMYwFqtFtb/1NRU2BOt4w9YwNyyvkm57nQ6wXAgwlitVu0nP/mJ1Wq1YMiQBaAZOt7xxPBhfj/77DP78ssvwzqdnZ2127dv28HBwbliSmZnJ79gjCif8x4FcLTWi4ICHmRTkIVMHRxXxgodRm0EMwvRV4h+aNq2AgI8Bxn28ccfWy6Xs62trci1elIOsplnUFCUo7iwBzT6xFgjm32dHG2rgk16Egbj5oFvlR0ayabfJycn9sknn9jU1JR9+umn4ftbt27ZkydPbDgcRrIQp6ZOj3L9+c9/bl988UWINul+b03X9RlImk6rOll5Qe0a5R0F4pl/1oeuq3HRw3GUTJ4WuZ2fnw9gvjpbGrFjHsiQU7BPZTP91zZ4oJH/PSDvwadEImEHBwf205/+NMy5gi9sg2w0GufAiVarFeogHB8f2/z8vKVSqYjMob04SaojNOuD6vI7Ozu2u7sb1vU31ZGchNCPR0dHkYK2cWBgXDANUnDZZ08qwKk8Ehdk8fYscx0HHOl6NDs7jYmCecjFjz76KMI3bMPihB4yig4PD+358+f2q1/9KvgYPjr8NvNAnJ8XB/wpra+v29LSks3Nzdns7Kytrq5aOp0OtrFuC1JggKxjsgGYF60nwtpl7evpB2bnt5EriMz7zCzoPLKBBoPT+kq3bt0KWWrwAqfmURMF8Ghzc9OOj4/t7t27gc8JbgISME7YJMPhad2c999/3x4+fBhqP/Cuf/qnf7LNzc1IwCVuPuLmSW2mrwqYfKM1EM697P+flsJgegWiAkAFchyN+v6i+/y1SvpufntFpu/w71JH1CwakfSKkL/ps0+hU9SKI7DU2LkMXWZMLiI1TnW84owOH7VVw4V90vSbxRb3nMHgdBuIRm+9oaxGtF88Xolo1MosfkuM8mIymQzGEKAA7/HIp49i853fL+kj2BiWU1NTls1mbWFhIewnpQqtti9OoOvY6bu0P97Q9uPgwbub4Bsi7LwTAUzflpaWbHFx8VwEdZQQ1P2valiOAg+1f8oLOia6zvlcnTB1NvR/bauCpCDTyju8F/BBeQWgpFqthsKtHon+ug0N+G5c5of+D39hwFOp3ixacFUdfI3M8xlzoUYF5MFjzfoZxQfMC4YI6fz1et2SyaQtLy/b9PR0AO3UUPLP9O2k7WyJARDVGhA6nvzWNe0jF/psL/f8s8bpB6IiWkncyz2eMQmNAhuTyWQAA/Q71ZnqsCtIq46ggpqauq8UZyypI6dOp37PnGumWBx53lYAAnmdSqVsb28vyHQ9CajdbgdAOw4M8GMXR2ofKcUBH77t/ruLwIFx6wZijrLZrBWLxUjG4Lh3eX7W+h1qK/j7/bO9nhtlp/E9gBVtwAkBZGQOdeup2VmdImQZ46kyxkfCaevx8XEAKJrNZgArv62kMhKHmyr6ulVX58rrTLP4+fM2Vtw1tEH/jyMPkKkN7nnM8x99JB0dvsEp1LplOIWcPkRmwiTg3DedGAfsV7+F2I8rckwBnDjAKQ4g0u88eZvOzCI8qtui1B9VWy1OvqqN57P1VFZoH1XXkZGFrd/pdML9BMRGbcN42+jGjnFUw2WUAXLr1i0rlUp2cnJie3t7kYgjDDQcnp3n7J3xOPIM5j+Lu06vj1Ny9MULN57jHVIiKX/wB38QnosSiQMMFDRg7wwOAwZKq9WyTqcT9r0nk8lIkb5RYxz3uR87j4COum8U4QAhGNgnVK1Wg2FASj4GIE4UqZtbW1uWSJwW28nn8yGNmKhlrVYLz56enrYHDx4EgY3zSISHfWgQxiHt02JVw+EwpJMxrsyvPw5MHW4yIXSPk6ZV614sTcculUqWSp0eQchYoFTMTvkpnU6H/bnpdNoePnxo9+7ds3q9HiK1+Xw+vIN9eIrCqmHO/JCuyxE3RMU0pZOxhE94BmtvUqd1lOOSTJ6eBf1Hf/RHlsvlLJ/P2z/+4z/az3/+c/vv/rv/zj7++GNrtVq2s7MT9sqaRdORyZwge0DXJMYha4mTEeiDOrpcj6Li2dpfjRCBIqvRyPtpozp+fO/366pDze+pqSlbWVkJ9/f7p6cQnJyc2J07d6zZbFqlUomAkpeNWt10dIMx82sDvmU7EkfTUTiNbRlbW1vB6ZiZmQmnrzBfw+FplJI6BACNAA0nJye2ublpZhYME3QINURqtZpls1krlUph2wDtxanVqFi/3w9R8L29PTMz+7f/9t9at9u1f/fv/p3t7u5apVIJmReAmMlkMuxh1LXH/CpYRARDDSicFPbtazok3+PoaMaeyjqOR+z1esGQ8QYavxOJRDjhgGga9T7I8GGOPdChz2AtqJEHr0H9ft+2t7dtbm4uZGkBzrCekDsKLqnRODs7GzmaV2UR8pWTLFhDbEfSLSUKeKXT6VAss1wuh2N2OfVI9TTvZp54x9zcnA0Gg+AUnpycHuv54sWLcB26QefQLLr9QIFa5LUCSgBbZhYZb0/IHs1c1FRflZO0QX+QWwpWxtlFSmw5W11dtdXVVTOzkMnjDWh9JuuQApLtdjtE7DCq6Se/NQuD9tPeOOeT/pycnFg+n7c//dM/DbzQaDRsb2/Ptra27NmzZ7a6umrlcjnoxGfPntn+/n6wDwBzqcDPFjTqsABAAA4SEEHW/f3f/33gobcNDL4Oqf0Z14+TkxP7xS9+Yfl83v74j/84ZIeZxdcvUJ5RmaLfm513xkb5Bv5z5Q8PYvlgErJbgV+9N5/PR3gVWQSfPH782J4/f27/3//3/4Xn6/bTOJ38NmQhjHt/XNYE98T1hawefBeKwnPEoq4f7Fez81lEGhjDPyLLGF4h00VtV+5R/mGN67yZma2srER0IUA1eodtJ5lMJtgx9J9tavgotJn6SxokSaVSQV+zhSuRSFihULDhcBieTdZqtVqNyOG48fefj/IL4+aIMTIbD8xcRDeWgTBJA/L5fGAiXbxXTbdQYcP/l6U40MFHnMYpVEVIyRLAoPPv8AipOmsqaBRg0MV2FbpsVOmyz9ZFp4ZRHGOrIGcrgHe8MRYhdSTU+NK6BVyvWxMwAtVZ5LfOmbZJBY4KTXUAR+09RSDxGfOlkTXGSJ1UNdaZc4xhnB1Sv0nr1T7wN7/jooKK9CofK0944Ut7rkMgrKSl53I5KxaL4RzgQqFgxWIxOBEeYFODkHb5OUKJqBPvj8qKE7jcO4pv4wxgHXcfMdPvFeU2i+6nV7mC40w6Osb08vKyzczMBOAHA9SvjYvopo0SdfwgVZDdbjcYXswVjnvcHGhWjwdldXzj5AH8wTzzeVz2gtmZnFAZwee8Vw0TMwt90TboMz04BXlAQXlN+6frLC7KgczwDl/c9bQNkEPHWcdd7+V5zCH8qQ6ov5/7vLFvZsFI0n3lWolanVmiLrOzsxH958da+8X7vbOh86BymzYwlswpQIPZ6TYv5saDdKq3vD5TeUG02ctZvscp8fJ2UsNtFHjg2+TtlFEGZRx5XTKOKA6HgxBX0DfOKWKOda3qj9fJvm1KXvZ64MyDfcjaVqsVqZ6u99EOtlSpfKK9CrDheFSrVUulTgsrExA6PDy0RqPxtTuGXxd5x1nJg+u6XlQXeF7Q7/n/MhQnT7xNrnJL24Ec0+1HnudOTk5CtgG2rW/j28gPNwVgMK/UfDCLBlO8vvN6xI8n5O0/f53qNF2rceTXu2Y86P3+uTpGnieYe9UHZtGtWupDaL/i/Ezsf8bqMuDOm/T34ujaAMI4xMM7jffv37cnT54EJNfszOkzs3OGS5wB6QczTshMQvoO70RiMKjRr4aBGg/6Pi34pu2DNNUPp1iBFBA5FFg6nba9vT2r1WpWr9dD9sFl+ueR4lFGb9w9owgFStTDH0lCtJ8IkTfaiZhQcIzIju5fKhaLIbrDZ0Sb2WdLpoai/2RudLvdsJcRoxb0WLeD0G/egdOrfWm32yFyWqvV7PDwMKDTjEGpVAoVm4+Ojqxer9vR0VHYow2fsI9/MBiEvVYYIuoMUairUCjYrVu3zMzsxYsXtr+/H9rJMz24xNpCiCMkqcvhnTV4mjZpEci4aNI43oGSyaQtLi7a48ePbWZmxnZ2dgKvgEYPh0Or1+thHGgD/KNbUrxRwY/O5/T0dKh2jVMbZ6Bqe72TpxEHdUxZ70SEtWaC8qdGQJkfxlAjhGYWtnXwu1wuW7/ft/fff982NzftJz/5SRiTSqUSjpz8uowQlZn6Q+2Szz77zJaWlkLUr1arBQBMozp6XF+n07Fms2nZbDYUICWDKJlMWrvdjhhiegoJ0X2i86lUKmyFaTQaod2AcbxLC6slEolQ7PHevXvW6XTs//1//1/b29sLsoM5g3fI5PFp9WqQ0L58Ph+AwEQiYdvb29br9WxpacmmpqZC/wAOyW7C+FDDWo8DVJ7zKdiasaBGiVZ/p2gk85pIJELGUhx/aRaMOlEKKkxPT9vKykrYK4qDSdFKZGmtVrNnz57ZwsJCBGwDMNOxZuxTqVQkS8DsLFuCzCSiSJwEgm6hOBZzPjs7G05G2N7ejmwfpFK4P3kDGavbXsyiRxp70IgfD1j59eT1EP/zbmS9GqLaNq5VUI1n+S0c/O0L+alOv4jW19ft/fffD6A+88dvD2ChX4jMmZ2CEGx/UIBfgWAFcOKcP/7WsfKAGPNIVpPWGep2u/b06dOwfgC1lpaWLJvN2srKSsg+0LbAX/1+3yqViv3sZz8LNRPos25DfRvoppzEcc/SMVpcXAz7yOPsCJ0n1cnIXF+ryINjZuMzjnkH13nQgB/vjML/yGvaqdk1ura13a9evbL/4//4PyL1W+KAzbeJJnE0RwHJo+6lRkgmkwmFdIfDobVarci61pOudH3HOfPYBMPhMJJ9i07wPohme6q9i32mNVHU59O2qPxWuai6H1tDr4FfONEPn0UzLbAPyIzo9XqRo6TRjbu7u+eKantg+KI59D4gv31w5Cr0ldRAKBaLwRkitVyVgtnFaUgerY/r9CSOziQEE2OMKTqpAIIqMG3bRROqQgsDaFSUIZPJhHNmSfW8Ko1r12WEm9+b4yNH6nzp82F8bQdGsS9KxzUYTxgVmrpIhAFBwvjxORkIus9REUAPdClaqsqGOaeNLHoPQqjRoM59HJ+jiNQoV+OQis3w2OzsbKjoCzCixiCGW5yxSB81cqK/PQjn23pVItLY6/Ws1WqFCC81HogEjnq/b4vnL+YIh84suvWB/7WPOsZ8rjTKSIlrz6j2jZJVcUoSHlDkOZU6PYd6bW3N2u22NRqNCN9+XeQdG/qg20JQuOpk6bW6rnQ8cKDhZf5XR0idK9aij17xmQJstFHn3BuwCgDxPdFE7YM3cPR5Oh46XvqZtjmRONuqoIY0z9axgjTzys+Lj25wXRzv0Oa4d8RR3PvixkS34en2EeYQhw65rbxEn2mbRpB5rzfc1eH0YGPcnlueQ82RQqFgnU4nbEfxzr5fy+okjRonP49KcfLkorG/SA7r99749obmdWW6mQXw3I+vvpe2eLBR36/j6MFhrzO9DPXkAQbmTYF51jfBBIqGIm8AYdiOwbzAFxRRBDxoNpshuEPU9W10Es2+msj3KKfGz1nc2lGbLs5OVTlzEXDg+UhtdM+fcfYATh/bYLAL44IZXMuRoOoETkpfJ8+8iXdrQEznEnvcy0+V+3Hk5Ya/x8sOs7O59WCHgo9x13rfxvsrCt76rUm+Pfq5PltlHj4JNeE4jUv9pbiMQA8i+P8noXFjPildG0CIa7j//8MPP7QPPvjA5ufnI4aSIo9m5yNbTLQ3xr0AGeU0+bbEtTXu3V5YKfPGLbg4MCGuTTphMI4eLQSSyR53IlgUbNrb2wsR+UkAC6+g4/qtyOikDAh6B6KGkU3/9cx2NeZ1TzoLY3Fx0Uqlku3v79vR0ZHdunUrsk8WlBJnU88sz+fztrS0ZJVKxba3t21+ft7y+XxAj8lSIKqEwdNsNiNVuKmaSpqjHkOXSCRCOnmz2bR0Om3FYjFShCmZTAYjgv2QjDtRDd2/T+0GBFcymQz7SguFgu3v71ur1bL9/X1rNBoh1X9mZsZWVlbst7/9re3v74f5Yi9uPp8PiP9wOIw4cCC4OEga9dRopd9Kclkho8Z+tVq1n/3sZ6Gf6XTanjx5Ynfu3LGFhYVgtPsok44LfKVtUQCy0WjYq1evLJvN2uLioqVSqSCA4bnBYBABkPy6VgdV13Bc3zS1jLaOkxHaXv1enSD4TIto3r1719bW1uzLL78MY+iR6K86qsGaRVZhUDWbTTM7rXEzPz9vtVotnKF8cnISouxk48zMzFiv17Nut2vZbDaciMDe436/H+TB3bt3wzo2O8tAoEYKx+eZnTkCbI/BYQXdJwqgkXGc636/b8+fP7dms2n37t2zYrFon3/+eahLobqGfvM5z0kmk+FUFU2V19MZmGMzi1R0L5VKER7BQNFoC32EFAjRqK+CEszbKEKmwsPaPk8KRvh2MPY7OzvW6/Vsb28v9A0Z0+v1wskw9+7dC2Ogxh86kfFTYLZQKFgikQgghEZUkLGMCRkWXKf1MIbDU0CW0wNWVlaCDPjFL34RUtITiUSQg7RPozbco+tDyRuqHlzW8eNzbxDTdgV8uF+39Onc6PM0isZ8a1sU8KN/vl9KcQ6YBllwqMyimYreOFfgivdqv3VdKvjnx0z7wue8q9/vW7vdPmdTzs7O2p07d4LMqVQqVq/Xg85vt9s2NTUVsoTIfPybv/kbq1arkfHVaPbvCo3SjUrI9zinSf9XXmLNm0XrfvgIqgfJILWtuQ97zkeX/XpRQDuROD3Bo9Pp2KNHj0KdHQURaFO327W9vT37v/6v/8tqtVpkrdLmyzp2bzOpLBnlNyAzAdo8OK7bnnlOnOxBrzB33t9Te9XbqMwtutdvCeCdcf4m8+czo+AratZxqoT3awkIq82KHQTv4Pehb2dmZmxhYcEqlYrNzMzYF198YdVq1ZLJ04y5SY72HsVrfr2OCrpcRYa98QyE4XAYzk9Gwcdd46P6o1AnSI2qUeSRIB+JGaWU/HOV0VHK/hp1gFgA3nFQAaUFm2irmYXIDAaZOsvD4TBU82XCx4EHcX3U/qiz55ln3LN9iuIox88sevIGKTs4yvPz8yHCpGgc6bjKA+12OygDjTixQElT5Vlq2KMgcPa1gJrZmRHL2GM0aJVmM4vcx/t5JymTvE/bw95g2q9j5UErxp00SYq2DAanxVry+Xw4orJSqQTBorzrHW7mwxu7oxx3/fsy4IEneJjnIbQR5v7cXf8ub2zo3/QvmUyG9Hd9ryoiXQNq6CrFredRfdJr/PqOGz+PkKti0n6qYQJYkcvlbGFhwQ4ODmLH5qsmH10nqoec18KCmkI/HA5DjQSzs/opGOfqwKI0UayaTcDfhULBzCxyKosqfa0XoetK5Svpj8gT1v7c3FxwXDRDZhSvqlPmM168I6bjoeMIn/h03bioHteoAexT++NAZjWM6LP2R8GBOL3Bu0fxHusdZx2ZyFhgUJJ1pvVgdM50y49mMGjBSg/YqTzQMfXXqcOdSCRCRiSOOnOPzFUe9n1VI9QTc6lAmzopcRRnK4wjz0P8Pcq5HvUMrwPGUSJxCsDv7u6GOgj6nQIKcfLcB4Mm1THeNlP7xgMPyH6yopTHVB+SZcD2R6LOFOU9ODgI/EoWqGb+vaPRRMaxd+7UrozTkR4sgC893+hvJewMszM5yTpUmyjuPp45GAxCEWNORtL28Ruw7PDw0JrNZgSIhSbR0191IOCmKQ5IiPPdWJ+MoQIFPtjpnVsvZ5UvVIZ4fkGXYIfGZQcqH3qZFMcr6Mnp6emgD9U2GOUf+h/9HL+ErVUvXryIABtvkq7z/DdSAwGiYfl83m7duhUMNlXkcQvcp2qYnUUJ/SIep3THOUEqSDRjwDMW1xIFGQwG547k8oxPpIMq5PpO7Y/uw8EJxWkws1BhtNfr2fr6eojqciSUtnUUGnhRdgGLJu5ZoxiLPa0ITF0EpONARHqIxOVyOSuVSraxsWF37twJhiT7nxkz0Fyi4VoLAVACBz+RSAQnUtsBEri/v2+dTic4G2R8kFJVr9fDfVoDAcCDon+ZTMaq1art7e2Fs+Q1s0ELRFElHhBDjWnACb+HldoJyWTSbt++HY5AIitlfX3dyuWyLS0tWbPZtL/5m7+xw8PDMCYaHeMdRObor84VNRziCj6OikJOSp53NAWdSrpcp0a9kt9S4p/PqQt3794Nxj79VAWEUaHIM5/z2ztd6pypXPIOol9XatCqsvRySwEc7wCoEbWwsGDf/e53rVar2a9//etzytQbXJelyxgvjCtrDoObtiwsLFg+n7darRaAslTqtMp/r9cLmQkADblcLmzR4HSW1dVVm5ubs9XV1bBWNVqBg3nr1q2wlo6OjkKl52w2GyLdvAveYC2zNQF+4ZhUTpGgZgpOBd/HpWxzDfM4GJydOAPfxW2f0Ki5WfRkAf43O8u4UEMJWcoJFgAwAHLwKinV1DZgvvkfGcH7eFfccXOa/h1Harghx7iHLAdkjtkZGMu9tJcsFI5DU31LDQcNRHAvAAMAkLaJdpF+zvn06Frm+ujoyNbX161YLAYegS8ZO30n/O2BUl2jurXnojGMG3Oeqb+1DcgLX+9C+Q9gTu2duHmjjxfJg5cvX9r+/r59+OGHYZ3q+tAostoWXlbp9kIPpPmIMG33QQIFFtHf/f7pCQpmZ+uH8VGwjzFJpU6Pyk6lUlatVkN9pk8++SQy7hoFfUdR0vWQSqVsZWXFlpeXQ/0b7+h58GDcfuxRYAL/+0CdZrzonHtS25X7kRGvXr2y58+f26effmpmZ6c16fv1OVrc1+zyAP/XASJc5Z2+f95XwwdivvUdWgMA/yGRSIRTCczObDHWLGsdG8yDQB6U1YAhum44HIZMJK5BByqwof1Q3lAe4pn6OUFQPVGJvqidplksmglLWxOJhK2trVmpVLIvv/wy1GFScFzH2c9l3PyMojhg7ip0I1sYoFGNfvXqlf3sZz+zu3fv2vz8fBgU7veMpsaBFz7j0CGdMBx+H+X0aXT+fj+gyrzqFPCdR8YwcNQxUoeaa9QZ0RoCmrqqhVh0H79/52UoTvh5GidYWACqTOOcKAgDG2OZPT7D4Wk2BdF/Fl2r1QoOrP5GEDAfCjqZnSkkbyhhKKTT6UhxPu4xOzPeARRUCCjQQ2otR8RpoS34AxAD4xdDmWdzLe2pVquhvoECDRjRIJK9Xi/wUa/XC0ex6ZhTSI7rFBiAtzUaps6Dzhuf++jNJBQn3KD9/X37xS9+Yaurq3br1q1z2wYgNYC1Xfo77m/GjnYwjygiv3aUn5SPaINvmzr73Kv/ewOd9/nfPMsDCypfUCyNRsNevHhh/X7f1tbWrF6vW6fTudScjKPLKBAvb+k7/fryyy9tfn4+bEPS7QWqtDUtWZ3jVCoVjHctuMjncaAJUWkAO+SuRq9ZEzjoXo6TmQTYMD09bcVi0f7wD//QdnZ27MWLFzYYnEYq2d+p46c87w1ZPkMuqX6KczZ1DY4Cs5GlcXUTNOtm1DqKcyQZ11H84Pl31DU45rybsQUYAWDQdE7vfOg2KnUW1GbQ8Ubesf2B44PjsrM8qVFJ2wGMjo+P7fXr10H+e9niDUAvD3xkSuXHZYx3D6J6O0VllDoxXBvX71HArLfF4ojtSDs7O9bv921paSkEPdQYx5Hz7/Jp4Ppes2hGibf54HHAS++c6Hxo/9WO1AwX77jAt9qOd6DB5UmdJNaJjqWf/zg7w/O4Avme55U/kBvIWLVvvLzUz9XOzmazls1mrdlsBlBh1JqL+39cX94W8r7bJG0c5bjGEXOFngKEUX9nlHzSZ+j3qtP1Xq/rRvVV1zdzjnPP/9iMXm94XvZ2ndcLXt7Bi/gE3pfVNcER30+fPg21WiYZ81H9flN0LQDBN84zJB398Y9/bD/96U/t3/7bf2t37961Wq0WOU/TbLSToAtTJ1//9ot3MBiEVH9SXZlcdTzVgIszALmPexQt1/75ezhv++DgIKDsvEOjz4paUsW3Xq9btVq1ubm5UMCFvWH6/jiBHEfjIpTjQIJx9+miUYOBvsRF1qempqxYLFqpVLLFxUU7Pj62g4OD8B4i9bu7u2H/IX3W1NVkMmndbteq1Wpw1iHNTFBFMjs7a5lMJpznzp4lxo/aAJxfzzu5BiUyHJ5mFty6dcu2trZse3s7ZDUAdBDRoto6n7MfkIqshULBGo1GSAVdX1+PXNtuty2TyVipVAqFCEmZOjw8DHuNlRjnhYWFSFYE2z+U1zECAXWYMzIS4Dvm8DIUh4Imk0n77LPP7LPPPrO/+qu/CgCCOkoKBEBxckANCNYOe9s1bfXk5MSazaY1Go3AG/65cU6/ot6KJqMA1EjVo3wwmFnf8CfPxJlSZ5j58O3r9/shEvJ3f/d3trS0ZB999JF9/vnn9vz580ibL0PXiXQwBuowTU9PB+fhP/yH/2DLy8v2P//P/7MVCoVQyLTRaNjMzIyVSqVwOgoOImOFwUnEN51Oh0J36XQ6nF5CGxhrgLWlpaWQZkyUWaP47MFHtnJ2s8ovjdQXCgX7n/6n/8levnxp/9v/9r9Zt9sN7d/f3w/XeWOW9qEzGCfqsJAVgFFA/RXVCwqcq66Bt+B1BS/U6eJv7qN/ZBZoMVUP5Cigo7J1nH5hPugPYCjykGg+fUT25PN5KxaLEdlOJgRZK560j/SPCNZwOAwZCO12O2Rz6Ykpcbx8cnISTv0gEr2wsGDHx8f26aefRuSPgjzaDrULsDOQ51yroFXcmHo5641iBYQhv5Z1Tumn189mZxlWGpFXm2oUAQb1ej377LPPLJlM2p/8yZ9EskJYRwSKGFvSfTUSqTYUAKDWxdC2wmcnJ6enM1G4cDgchkzGRqNhmUzG7t+/H7IR4oDfVCoV5ATv1kwIaBLwYJyt9LtCcWDQKIBdHTZdz3q/2vaq61mvPohgdrY+CN6gA+bn5yOgmw8YsDbJeJuamrJyuRwKWROs8XJe3x3nC03i6H2TeEbB7kn6hyxCNhAURY9rDaJxdgn6iL8VGPJBAB9YVJ9P70EOYL/jW83MzFir1bJWqzVSB8Jn6tcNh8MQUFT9yjsVoMrlcoGX4UXaAn8/efLEHjx4ELbH+DaMmyMdt1HjeRUgO46uDCBc5qUY159++qkdHx/b7du3Q6EzOsAEq4BgYnifOvxqAHgBxDt9hMvs/P4URajjmEWNKRgMwRgHNgyHw+CAYixiSCiq5Y0Q0rqz2azNzc0Fw5l3895SqRSKgmGYjQMHLssgkwg979BxH8JFI9hm0aOhOF6NQmUsLhxuCuEhKI6OjoLBiYOQSqUsk8mETA9VIJrdou0yO4vcA16x/5X55CjBbrdrs7OzwYikEKIa5RwFhRMEHR4e2mAwCPOohcx6vZ7t7OwEA4YjJ6empmx/fz+8mzEkIuZT/Pf3921vby9c6w0xjHQUqWYaoFjhS8ZFwQWErHeOLkPKd97A8tEebzBA3kDQZ8dFM9QxxyDEkcWIJXVdDRw1dFB6GJYq/LUtjJ0a3tTOYD8kPIpiYZxZF4ATpL5pESGitOzBRQErwu3X9iRr/SYMFg+6Iq/7/dPK5P/0T/9k8/Pztra2Zul0OpI9RA0UdWqGw7PaLmtra1YsFsN8NRqNcPyT2Vkx1UqlElHQ2gact0ajYTs7O5bNZoPShhhnjA6zaG2Xk5OTUGGdVHYKpXr5FhcJ8Z/zTp6v/OOjLN5pBMxTgFZBsrgtRwqYQ3HAnOd/+jBq3tUI98+CxxuNhj179iyAk/ArACqGFEabOsY4dug39DfjrbyngBx8yPaOTqcTgCoNAkC6xtHZfH58fGyHh4dhvXnnKG5O1dbw48J9Ov8awNBn872fCw+gxtEoZxc+jyOe63lgFOm70Unobtbi7du3wzbHwWBg9Xo9AKJcQwaNjolm7IwaY76nECqyBcrlcpG6RWr/qd7QZ0HU6qLOEvL3MmPyu06AvgR/VP4wx9jRyH3dbjrJ9h7m0csg1jBySkE9vU75ifWNHaf1T+AvbHlAa+4d1bZJ6LqO203TRW3xcmiSfr58+dJ6vZ598MEHwadhfpEDKtPRadhx+qMyXO1S9QO9U652EltmNWvA7Kwg/PHxcaiJgo73tint9cEfszO9gf5JpVKhiC98QxBS5ZEGugBGsXfIWn6b6caKKHrkwyNUw+HQ/st/+S/23/7bf7P/8X/8H+3JkydhcGAqFjCOEQoGJ8ksul9Z3+fRQSYKRsDYGMX4PtWQd/CD0iNdUg1FNV7NztLpcJYxlmB0GBEh6hWcXzBa0OvWrVuWTqdta2srONU+3VXJC4ZxTod/xihgQo0ldTinpqZCzYY4fjg5ObHd3V3b39+3hw8fhvOWB4OBffLJJ3ZwcGC5XC6k9xM9B0BoNpu2ublppVLJPvroo7DgGTMFGPSHcecMcuop3L592zKZjGWzWUun07aysmLHx8e2tbVlhULBHj16ZPV63Z49e3bOwMYx3d3dDSBAMpm0ra0tazab9ud//ue2tLQUzp8eDE4L8+zt7YX5xNim1kKr1QoOD+CDGtrwwObmpm1uboasBgQzfIAgI1KKwwaI1Wq1QqquKk3qKFA0ShXmJDQpOurTG70h7ZW0Knq9Fv7DUNFsAbJ2cGDoD84FBqzyLg4Qc0M2B9/Dx5pirdtzGMdms2nVatUWFhbC3m2ArUQiEfZoEyE1s9Ae3o0D1O/3w0kkGDEoWu/cvGnySluBOeTf4eGh/T//z/9j5XLZ/uRP/sSWl5ftyZMnlkgkrNFoRIx7nomzXqvV7NGjR3b79u1gSLBeOIWEuh1sK2DrQqVSCZF5eOLVq1f2q1/9yu7cuRPWOo6N2RmwyVjqkbC9Xs+2trZsa2vLWq1WqM4OKRCkYIiCTh7E5p36Ln/KAuOLXD4+Pg78x/rnPs+PEDpPAcRkMhkyRfSYMaIvGlVSIEv763lBnWDGkOjN/v6+JRKJAIyvrq6GytXT09OWz+dDVgYynHFkyxb62usZ+F4j3ax/xr7Valm9Xg9gPkS/FVBAzmI8drvdcP62Zr/pWNAO3TLC/MAbcUAA8zMYDCJHBSo/abRT0+zjnF7/bJ1X7acHXHketkdclsYoUvl7cnJiX375ZWgX2/Hm5+fD+3d3dyO6JJk8LQpN5gh8THaNtsU7EvBbsViMBC0A+XkvulGBd69P9LvB4PSUD+o1wTfKOx4If0fniSAY9Zv0aMvBYBAyR/P5fMimnJmZsfn5+cjJK2bxIKXZ6GJ9cbrQ848+xwfZ4Gd0D6f5qL+BbeVpEttnlJ39baTBYGC//OUv7YsvvrD79+/b8vJyGFcyLXUdmlnQI7pFkO/JesJ29E68PzoTWaFbUhKJs8KN2Ml6Sgv2Iu9SexMQAvsBH5GAnZkF36fValkul7PV1VXr9/sBQD06OgpyilOgACvINMCnAxjXsRg1zvTnsvNzE3z4Rk5hiDM2NKLyySef2N7eXgR50okiBVKVNAaE7hMnikAxNYwyjDgVXBop5LeiV0wk6d6KdsHUZAWQXgvxTNJhmHwMM8YA41HBCpxejQTB6BiQCiSwlxhj8CpMcF30U50h+q3PZoEzbz5SyYJn0Q+Hw7CtoFAohMrOLGp1bJPJpM3NzVmpVAoCgPeooTAcDsMpBcwhzrzWGWi327azsxOKIg4Gg5AG/ezZM+t0OuHopkTi7AgXNS7y+XxoC8axRjvMzpw/hArK8sMPPwxCMp1OBwAlk8lEotDHx8cR9JTIrplF+EqNXcYRdN/szLlGgCoBlDEOjOukvHLRdYzFl19+acnkaaHIxcXF8L06ZIrcqtGvzhbKXo+cRE60222rVqvBGSkWi5bJZAIQdXh4aGYWDBf6j5MIz+mebF2DqVTKGo2G1Wo1m5ubs0KhEOGzer1uX3zxRQBvWNOJRCIUQaV459zcXCggijxgO9Ph4WEky+iyoM5NE3ymkV+zM75i3tgjTds7nU44wk8NNuVL0vkVNAU8gdd3d3ft+Pg4jLc6RzjD7INfWlqyhw8fhuNdMWwxbkH44TsttMS+VzU4NJtI9RaOiPIlfULmsX2A/3knDq860rzDLFpwSrfFIF+YEx99gUd8O9EpvAOehHfjAHqz8QZH3He0EX4FvGRekf29Xs/m5uZsbm4ujDnyjLnU4AHvAzBWZx4DbX9/31KpVDj2cXp6OrKvVU+AACyhoBfGJkUgFcyZhHwWAffqs/xee73ePwcaBR6Mut+DFxpFU4pzii/qq/9e9Zw6YRoVJDswlUoF/ag2mfZN+VjfMYqvkTmJRCLUh9HsFQVR9DN9jtmZHl1cXAzFYBU0fAccnCeV34nEaRG4paWlYEMoEAdAr1tEsen4X/nR87rPSvFBQw/Ewpe6FuEBlbOJRCIA+IDMKysr1uv17NWrV1atVu3Xv/51qKkyzuYeBRryv9oz32ZSe+W3v/2tVSqV8BlBHWQvNhXgnc/UBphuNpsR/w67TMFyAgj4KIDUusVpMBiEgJtulyKoi46iDcjrfD5v09PT1ul0zuk8AHpqpE1NTQXggEAQvmq32w3ZLXxWr9dD1h1rxYMplyUPWsXx3XV58Y0f4wipAvjHf/xHM7MQOYUZiFZ85zvfCU4p9+DYYByS3t7tdq3T6QREmsnWNGyMRI0OqTNGxKndbtvBwUHYImB2lupIWjtHEGaz2dAnhE+pVAoVOjGaIDXcVPFRnZy2syhQejAY4xAHIHjnmc89c8QJvssiURhbGkXzBcpYnEdHRyGVjXnA6SAtmDYuLCzY/Px8cOi4DgUDLS4uWjabtcXFRavValapVELfGHcUxf7+vu3v7wcnRvkN5LDT6djnn39u6XTaFhcXLZlMBseuWq2GiDBzzZ56qFgsWqFQsL29vRDZJ/1alWCn07F+v2/r6+sBcczlcvbw4UNrtVr27NmzgHjTxr29vQBMdLvdAC6wBnA8KfRFvzCOQF1J89RoOcLJR75YZ6yvm6ZEImGff/65/eY3v7Ef/vCHViwWw3fwP3yG4akRAw9QaT+IPBOBPDg4sP39fatWq/b48WNbWVkJe6NZ50tLS2E8BoPTLSSpVCocO8s71TmG3/b29mx7e9uWl5dtaWkptLtSqVilUrHXr1/bcDi01dXVcFQYNBgMQgYCUXTO+61WqwG4gu8URBwl9N+0YeJBGuYGHmedt9tta7VatrW1ZYeHh4E/m81mSHHFWSyVSmHNA3Qxr8PhMKwHjIJXr17ZYDCwjY0NGw6Hdnh4GIAvssTS6XSoH4OzgoGiJyoQuUbGVCoV6/V6IZuENjLfXhZ5IARdQsQfp1n7A6HztA6DRllxNgEWOp1OGCMFTXwEV6N3XKNyAX1mZpGMC2Sz6ixPqisUvFAnjHHR6xR00u05BwcH9vz5c3vvvffsyZMnQSeYnRVHpK6Jvk8zFwEaABCazaZtbW1ZqVSyx48fB6BBo4ozMzNhKxPP8yc+mEWP/Bq1tnQeaDef02fmR20QromLtupWGv9dXHv8nOs9ahv4AAXzBu9o+0cBFaNI7TvleeTWycnpOejoL60dw/u033GOlgZh0PH8xkYaBYjAQzxD16gGsPr9vpXLZZuamrLnz59bvV7/nXD4rkvM38bGht27dy84SltbW1atViOny0xNnR5Bnc/n7dGjR2Z2likTN3+sL7UDmEvVP8whpPqK9ef5invwPW7dumXlcjnwzBdffGG7u7v27NmzkFXFsz3FgXijQIS3iSZpU9z3cX6DzhP3/epXvwrrniAhTr2ZhVNxyuVyZA51rGu1WjjKWuUd6xefZGlpyaanp8NpKpzilEqdHg2/tbVlZtGMcwUi9J20A5nJs7ATFLTK5/P2/e9/P9T1IatST3yiHtTBwUHwJbEx6vV6CBIgo1RXjxrvSUj7MWqNXZVu/BjHSRxSFj1CHKfw7t27ls1mQxE4TQ9E2CuaxCAT0VVl4BHruDbob4w1PXYPA4904vn5eZubmztXAVvTsTHCABT0exxtVWIYLfSPBaQLMZlM2ubmptVqtbBXuNFoRPbjxgm0cfOk/ytKFXdNXHQEIIE0NdqAYYLRz5xopGg4HNru7q4lk0m7d+9eSNcfDM5OLVDDXQ2TVqsVjlJkztTxBHQxszBXLErmVsdVjWbavrq6GuYIVJr+oWjUkB0Oh6FqKgYOKe4AQGo46rgDbhQKhbAXCpCKY8ZwaCjwk0gkQsQMntMoF2PMXk7ayP+6vUOFMUYe80kfrksK6rD2UQq6FYd1wPxoZIj28DnAgWZnkNXB/GQyGdvY2LD79+9bqVQKtQbm5+dteXnZ+v1+yBDAoAU41KyEmZmZUOxNI2DHx8fWaDSsVCrZ8vJy6C+ZDhzDc+fOnbAHn76dnJweH2pmAXACQJidnQ3gB3ObTqetUChYrVY7p6QZ4zdNylc4ZShx2sQaNrOwjWN9fT2ANmznuHXrlq2trdny8rKVy+UQ7QMc3d3dDRk9eqrN2tqaJRIJm5+fjzjm8DlRTsYEwzGVSkXS2ln7KOlEIhGymUgt/OSTT2x3d9fMomCBbvnR9zBXOKoaKVGwReWjpsP6TCqIz+A/nw6uwJbuMeXZ+g4PAgCO+SzAi0AqNerpl46RGmLdbtdevXplJydnJyNw7C4pz8hMIkhkDqhBCV/xXq5DhrLG1FYAMAXAVSNK17jKxEQiYY8ePbJOp2M//vGPI4AxPO6NXOURnTN1dJCxo5wk/7k61/w/zqbR6+KAAHWeFMykvVxzWfBAqd/v29OnT21vby/IRCJwmrlEUEZP7GBc4/iPfsN3yB94hLmE/9Xw1nHx2Qj0mf+Hw2Go6aDFh7nuHcUTY/v555/bzs5OkMtEhfUErEwmY3fv3rWpqSmr1WqWy+UCaOOBViW1DZQfzM5OJlEd69eN/njQjQyZ3d1dq1argQd/9rOf2atXr6xWq4XrR9Eoh9rf97aBCDfZFg9c4njncjkrFosBKEDnMF9TU1ORmgEAUhSxpPigDxCjRwhGEiBgKxPyBf9idXU10laCy5pRjow4PDy0er0esoCLxaLNzc3ZyspKsDFUVy0sLAQAGp03PT1t5XI5bEsFYKhWq3Z4eBjA1HK5bMlk0nZ3d63RaFiv14v4dzpPPogRR5f16a5KVwYQxoEEcUI3TuGy4Ofn561cLtuHH34Y9sSDKus9KHoABFWUGt1WJAmiIBLkAQRNYfGRLAzP5eXliKPgjYRarRYxLtnrDLMRoVPgA4NbAQQl+nJ4eGgvX74M6WAavR81BxfN01WJNmK4EbVVYa5GsrYBo58igOvr68ExZn4Hg7NsDUAX+lyr1cI+o4WFBdvY2AigEinJ8FU+n7eFhYXwbiKc8BfXzs/PW79/enb01NRUOCGg2WxaLpezlZWVMM/sXYL/KHpSKpXC/imNXuLk6h56RdLhy1wuF9LuVSghEAGgEKC8BwBBBTfP9nvJ2CMMEqxbFTDIEJYAF9cxJpWUV+lPrVaznZ0d293dDdFpAJ5EImHFYjFEdc3O0tiZO9YC/QLVzefzVigUAlCwsLAQxl6zDczODGlS5VnDjAcnOJDhpMRJGcViMWQgmJmVy2UbDof29OlTazQaAUBQmdPv963RaATlybYUQDmUh0bLcrlc7JGw4+imFQYAAs/UaDnvQM41Gg3L5/O2tLQUHHWAhHK5bCsrK7a2tma3bt2yZ8+eWbfbtXQ6bdls1o6OjqzVaoU0dLJMVlZWAg/rViKfIuvHJ5VKWb1et3q9HmQ8bcepJf2ZtfLpp5/awcFBMHzNzgq1enkHfylvaQRao8Cqn3yWjwcQ9D76w3uQrcgiBW21XSofVGfyGfuORznDei2/eZduUdD7NXrf6/Xs9evXQaZRq4KidQC0umVB+6EAgoIf6Aoyq6jpopl8/ChYS191KySylR9qNvz85z+PAFR+206cfvVguTotOq5qe6ieVMfWR8V0Dj1gEOeY6DMVaPLghYLJ16HBYGDPnz8PQGAqlbJOp2MnJycBHEK+EpUGBMCY90C7tp8+q62nEUStK6EUB8IwXgqwmZnt7OxYpVI5d3zaOzpPPjjwxRdfhO+SyaQ9ePDAZmdnAwhHpt2dO3fs6OjIvvzyy5AdZmbnAhbMuQYU48Ax2mIWPYY6DmzXZ7PGsKW0JpWZ2a9+9St79uxZxG6Lk6Fx5P2QuGvfFjDhsu0Ydb3KQ2RsNpu1QqFg5XLZcrmc3b59O9j1EPYPdh33UriYrHPdgkiNKgI22EncizzAH4OPzM5sSGpdaXBXC6PzXLKLi8WibWxsWD6fHzm32Ejb29tWLBbt7t274X35fN5u3boVToSan5+32dnZEODCRqEOQxzPqH8d991l6Lr890a3MIwDD8zM1tfXbX5+3h4/fmxzc3PBgTGLpipy32AwCI4mPxCGG4vWL16EHA6bGjjHx8dBYVSr1fD5wsJCQEY5nsqnukA4gfRZU+ZIr9PCVyguhBgOnzcOARsQvL7q/02QRo4uAhxYhIlEIkRvNSWTa8zOKogj/NXQv337tt25c8emp6cjNSAQ1FrUyuyMlzA82WdHdI9oBmg36fhxqcEYUhyzmclkLJVKWblcDs4F84DjA2hBfQKEEvvd2WrA2CB4GBM9+WBmZsaWl5dD9EyNIKLR8AK8NBgMrFKpWKfTCVFqCB5SJ4cx9MJUDc1msxkcDI1w6j60N6ncAJGKxaKVy+UgTHEiQI9VjjB31AqAbzVzSZ2HweA0/VsjgIwZ0VF1gJS/1RGER1X+pFIpW1xcDFtE/M/CwkJwgHE6iXyytcc7EWan22KOjo7s8ePHIdvm6OjIXr9+HTnSx4My/rO4/69LKvvUmYO3tT3D4WlNiZ/97GdhnczPz9uHH35o6+vrdvv2bUsmk3Z4eGiJxGktiH6/b7VaLUSC7t69a/Pz82G7QbvdDmCKmYXUSI0kIDtUzmIUch9yGZmXSCQCwMheepW1mkXF/awRnGlfddxnZqnh6SuGcx3jBmACj3gnxzv02iZIo346Xzhr3lj36ex+3vW3tlfJ86HqWaJI5XLZHj16FHiJrWWMsep2gBGepTaBykgom83ae++9F+SI6nyftqrZaPQLuUFdGz0CNM6B9X332w90XXs5zbPUqPVGddzYKun1ccCT6vS47/XvUdH/iyju+n7/tNApspMxZS4BZZWvGD+1A/wPc4ldBDixv79v6XTafu/3fi8URuZ79KE6gSrvzaKFsAH+VTbo+L8NDt/bSh6YOjg4CDKZGjQcdT01NWX37t0LR+fp+tG1xv/89uvE2/u6TnTe9be+AxC23+/by5cvbXt7OzyD+le8R3/7v7Wdcd+xvbXb7Z6za79umrQd4/wDDaiamd2/fz/4UDMzMyFrenl5OdjtkMpz/B9kNnKD4J3qd7XtVT+z5jX7F9kCwQu8V2U191CnLJ/PR7LPyfblWt5pdqrbC4VCCIgvLy+HYyHZQnf37l0rFoshGyuTyYTtnWx3JQPY6/6L5mCS+bypwPK1AQQ17rXR48ADJnxpaclu3bplt2/ftmw2G9A/FLtOEvd5RMYrGA8gxC16jfwSIWk2m5EIMHt1mFQ+i0vH55k4EgoO0A99p6Lg9AHDTSOqON4wN+eh3ySx4C8DIqhSVUMMgxqBrCm5CpQMBoOQ2jwYDMKRdzqftEGNXMYAJBBiTy2ZI4nEaVEVNUaUmJNarRbSIFOpVNhKoYIGQ7vdblulUgmFT3AAqTpOhItsCoot6t55jGEcGaLQ8BZGNoi48hYgV7VajTyXZ+uc6B5hRV8VNYfPEGAINn2mV4A3TRSOKRaLViwWbXl5OexT1y1CkDqDjAFzOz8/bysrK2FuMQiGw2HkPHkfiSJrBcVgFo0g8psopxohyeTpaRxUFValZmYBpW6325FiPfAY2QSqCGlbv9+3O3fu2NTU2SkOur3k6yY1FFSB45yaWUhB/OKLL6zfP603srGxYR999JGVSqVQx4ToFEY/25Sq1WpwOgHVOOKIda7rQLcb6ZiqUcJ2IOURQCOAxG63Gzm2S3WY8o86g4AXAEysf13D3Mez1LHnc3jM64BJSKOByBDa6LcoaGaPtkX5N279ewNM7/X3qA4H1MtkMra4uGjvvfct1JAcAACOHklEQVRe2Cet86e6Q3UB86+AAqCSElt94EXkmxqIGKasP8BClc+AGkSwNMtD51FtDp6l8kHHbFx6Nm0YZfipfPfOsH4fp+802j7OwVGbaVKeG0WDwSCcAkTwQ8c/mUxaJpMJRn5cH7yNpLIdw5ptgq9evbJsNmvf+973wtyhJxRYU8dU+0u71A5T4MfPBX18R6MjothYMzMzduvWrQAeUNgOUIGoM+sO0nH3OtLsbK3pHPI579dnjVo3yJajoyPb3d21p0+fhu/JaFJ573Ufz4nzT7T9FMnWwNg3mfyce2AF347szoODg2Bzqn026tkKMGPHomPRr2ZRnarOPHofv8HbydpWzX5Se2Z6eto2Njbszp07EX2ja1/5g2fPzs7axsaGzczMhFplGhheXl6227dvhxpdtB2QBHuRrTOjxvyiuZnEn7sOXQtAGCdAfaM9o0xNTdn9+/dtY2MjON44DYreKymqHvf9qHepcOFdnAuKUgL1uXPnTjA0c7lc2EvjhZkKNEWvlYkQKt5wULBDnWUikzC0GlErKyth32+lUjl3bMlVSZX0pIzmIxaMiV+gGHCNRiOSmnxycnr0ExFGHEgAEvaWa2bBysqKmZ0ajTjvKjDMLCCDPvrF2OMskP7P0TI4ZuyJZ5sK2Qe1Ws2Gw2FwCE9OTmx7e9tqtVpoOyAEqZlUamWc5ubmbDAYhIKZZJPU6/UwNmZnR8E0m82AWLMPq1AoWD6ft2q1avV6PRjuunWDcdC5UQWrUXVIBRtbd940DYdD++ijj+zhw4fhTG9S9Gmvd2SUPzXtzMxCSrsahThOahx6xa/HRuk61WegiLhPHR5VOlwXB8ThhAA06Xf6OUZxMnmarp/P521xcTEolp/+9Kf261//+sbW/2WIzBsv93BIiarzuRpJKysr9t3vfjcUS2XLEWsBg+K3v/1tOBaVbSGk84HKD4entSqSyWSYP9LTuQagDwNC+cnsLMKQSqUsm83a9PR0OEbpyy+/tMPDw5DFZHamJzA09N3IfZWlZhbq5/T7/RC90HYqwIphSgFZnqPglwcB1OFSx4j2Kg8DqtIuvZ52MLbUhIgjn/Xi++wpmTzdWnD79m3L5XJh/pmDZDIZCiGTnso4MH86h6S6mp0Z92psAkhTpJFtEolEIpxsQ3uR98gO1d2M0/e+9z1bW1uzf/zHfwyZTMpPcXYBcwXP6Fjw2zvp6oholsUog1f/9pkK+i7IZ3Nqm3k/zxpl1F+WBoPT7ZkrKyvBgD45OQkAscpjBdHhV5WltBGeQ98CwP+rf/WvwvHHw+EwZAWi19kShmzVsWBsut2utVqtUMzsj//4j61YLNqPfvQjq1QqEXBo3Fj/LgMLOhY4RMlk0lqtlpmZ3bt3L3JKFfPP3MfZ7uMccw/q8jvuenhJ1wA8wp7zhYUFy2azVi6XQ+R7OBzaj3/8Y6tUKvbw4cNz2zvRBbwbAFiBrqOjo+D8/uY3vwnZn28LTQqKTeorDIdD+/TTT+3Vq1f26NGjiO2/ubkZMnkBldV+8HpMI/vIBnxFsoxUH3Kt3hsH/qtfqGAh17JtFVvF+3fILwUpzE63ttLGTqdjm5ubls/nwzHxgOaaedDpdMJ2CtaCtk/H/zKAwCTXXgcQ/cpOYdDGYQyXy2W7detW2HetHVHU3D9HnQSz85U/zeL3GzGpZhYxDEEH1TGg4B6MqNFzNRZhII8qatRHDULfNg82gLLp/hcAD46R9I7zuLG+iK4qxOIEt48WJJNn+x01OmdmVqlUrNVqhSOTcAjNLOxNIrNgMBhEolOaBQKP8LmPPCpvsNBBPjmLWI/sov08BxADnmCu6/W6bW9vh4gabdICc+rQUE0cJxeHSSPKvI8x47QP2o6jrenPSgg/jaTH8Qr/E93Ua1D4calTN0Ws7dXVVfvggw+CwabRvnGROEjPEzY7c4Q0PRUhHAfiMQajIk36PuUNf686Uh5EUBnF/z66hWGtR45OT58eB6o1Hebm5mxra8s+++yzayuWuH5eJAtQbjqWrE0FUnScGH+2LqjDB+8hY5PJpO3v79vh4aE9ePDACoWCmUWPVKSd3W43zDWyF3mhRRe5R1Pp1Rk1swAgUKT29evXAUBQ+aHGE+9WJ5Fx8ZEqgAiia0S74owx3YakoKzu4VQdGLc3GPIOqEZ6+V4B+7i9555UtuuYjCKcCAzycrkcxkFBTYwnxkqdNWSxGo86l7rFgTZ1u13b29sLp+SgfwCReTZjG2dnTE9P261btwJoodkScXJV59PbJArY+HsVtFT5otfrdUo6v6OcL/8OXeveFrkp8MDszFabm5sLWxkUNFP9Qrt8mjGkY86co09nZ2ft8ePHls/nbX9/3zqdTgDukBsakInjWdYp+ncwGNjdu3dtZWXFfvrTn4Y26noxizfQr2OQfxNpVCSaeVKdns/nI/vHFUBSAGEcz48iz+uT3I+tyQ8g5927dyPbEzc3N204HNq9e/esVCqF2lS0naMJ4aNutxuCSTiN9Ov169cT9+mbRjpv+/v7VqlUbHFxMSLLyUoxswAkKNDNGlM/y+sy/kbPazFWvqcdHlznc357Wcy7yGbUTHCVz2rjo+fMLADwyWTSOp2ObW9v2+rqquVyubAFWe0CsiPImo7bbvG20pUBhDghGtdhL0RTqZT98Ic/tAcPHoQIsCoPRXd8BFkRY4SNRlrHOTzeqdCoI4gh78WgIBoKaTtxWH0/PYPxnY6D7vPSMdSUc963u7sbjiKkMEez2YzdgzmpE+Hnjv/j7o9D24m8sf+w1WqFNEX6xXU+ashYrK2t2eLiot2+fTsUnet0OhEjWecf9PLw8DCkNNF2zzu62DEK1OnBUW00GpZIJGxlZSU8K5FIhPNb4QVSig4PDyNgxdLSUjCM2NenRdbISNDj4Ii2bm1tBUdjMDg9L9kfY0aabalUsnw+b5988ok9ffo0FJZpNpsRgQewAEDinY+44ndmFkArCompkXnTQILylxpzzDHXqDHL3/RrFCCiES34DL7RZymy64v5qPGn98QdO0b7eYfvp4+EqNLDuBoOhxHeYL6Y+37/7Cgi5gMF5Ok6Busk9xJF8spN9433+32rVCo2MzNjGxsbtrCwYI8ePbJSqWRLS0vhGE2AMDXu+/2+LS4uWqFQsAcPHtj8/Hw4NtVHK+F1auYgfygMqvspkbea3aEAgp7ecXR0ZPv7+7a9vR2O0czlcmG+Vf5TdFHHgr6os052G9svzM7ALwXzhsNhKCBFoeA4gFENKvaS9vv9iJNsdnbetm7ZUP0Cf2q9EzKgkAmedO2pvvBgCP8jg9bW1sL8AFAyp4AricTZPljAZ2SkbsNi3jDwtD9slcnn8/bgwYMg91QnaPYaBqDWzTk5ObF/+qd/CsfrNptNq9Vqkf6OitRP8pnKBdqsY+eNYMYQmaJOOM+gf16+xtlm4xxgdeKuSzybI0gzmYwNBgPb2dkJZ6qTeUa7mBd4Wp1R5o6xTyaTduvWLUskEvbb3/42coITxXDjAgpx7Uwmk0H2kHHYaDTCGshkMra+vm5mZk+fPj1XoNiP6+8SxfEd+u29996zubk5m5ubs5mZmVCnCPL6mHs9EO3XjN7vdW8cIKe2htftOJ/sXffFP5PJpH3wwQf28OFDy+fzETsJHVOv1yNOMu1ARk9PT1u9XrdKpRL02dtGcW0aJTfi/mdeWdt6ikkqlbJSqWSJRCJ8Pz8/HwkExvkuChB7m1CJsceHon0q/9SuVV5Q0gClFu0la1SBDHgVuUZNNXxHtlsvLi5aIpGwFy9eWKfTsXq9HmrqNRqNkDHX6/VsYWHBSqWSffbZZ5HsQz/uk/ja0GV9wsvQjR/jGBex8d+vr6/bd77znUiKqU6Od8A9afTAC5U4QaOTrYqXd6CA1UnBuPXOlhd4/jMvqFRY6bX+M4wkjZAlk8lw8kCr1QqF/JSxtB0KBoxb+ONI7x91nzoQGGB8zhhqdBajVh3A2dlZm5ubs3w+b9lsNhhwOraMCwg2iK4ilBpFYuzVWMCgwIimnWYWUqgRZFqYSQ0P3ofjxrMx0NUYxhHSbApFKTFQKaqCw0PRNi8gMaATiUQ49hDivbqXV+fRC0n6wzjrVgflb92bHQdUXZf0vbpeGUNdbxDtpl26pvV7NRq03x65pq86zsp73thkPcQZJ8gOz7vadv9u33bGBeDAI9H6Lg9IflWkTpiCdvzN+qduzMLCgq2srNjjx4/DcYwe0PH90ur8xWLRdnZ2QraBWRRYM7OQ0YNjMTU1FbKA/DjFOV8eSCNqQN2JOIfZA9neeNZxYi4V0NM15tugTr7yL7/5TMFwbZsa4vTHFxvk3Qqax7V9FI0C8EYR4BKGOu9UXQOQpzLA60/VnTqGCsjzHTVdqF+DU+ptAAA8LZg5GAzs9evXVqlU7Pnz5+cKKCpY7cdBx82Po/ZLaRKHPc5ojHOQFBgZZRv4Z0zy2WXItxPQDj3f6XQslUpFjlz1fYQX4WHlew0cUEehUqmEOiaA+BqEGEW6prQOUSqVCsfH8R1FH7PZbATY8/p11P+/K4RtkU6nbXFx0RYXF21+fj6yTWFUMMAsCiLEAQBeB+tnoyhOhvIM1jMgNHYdthzgkpmd0138RkZoRqf3G7Dl35Y6RkqX5dFx16P/NWsQGU/9L0BjbEwdK+8beXkSxzdqR44DGlSWXOQ7qk0DQO/9R/qLzMEe0YAkwYJGo2GdTsdarVaQK2RNttttOzo6slKpFHgwrg5YHF1FvsSB/1ehGymi6A2ouM+Vut3uuWPbVGioEaEpmn7CvaA2i099imOQuGceHx9bs9m0TCYTHDtVXAiIuJQ4FXKjFLffq6joHD9UaKWQV71et0ajEQSPT0OdhMYxyjhGGvW5Cn8iVcPhMBhqyWQyOAoaHdPqqTgUOEicBV6v1y2ZPK0ZkEgkwn5ZhEypVAqLDwOBlEXagjE4NzcXqt62223L5XLhe7MzA/r58+cRpFMLLiWTSavVaueOGGu322HvVSqVskqlYsPhMOy5pFq8Ahwg1YlEIhSBVAOHAkPNZtMqlYptbW3Zb37zG6vX69ZqtUJkF8HstzLU63Uzs7DHlH6QUqXpzzr3HD/J6Q4aeZzEuL0MDQYD++CDD+zjjz+2QqEQybhQJ123MSjwo4CHgm3aL59izzxiFKiSZ849YKQRTxSId/x07fNMb7CqgQLxDK3Sj4IlAp7JZCLHT2oq5E0YpOMAwlGkBUoB27RfBwcHtrCwYP/9f//f29TU6Qkl8/PzQT7An+Vy2TqdTqTCNSAb+0uZl1wuFwwNNTIUtDQ7m3OVi8gDIvMQfET/9/f3rd/vhyOU6CvpqwAJahQA/pmd8YHKO0j1TDKZDGPI51zLuxS0Njs7ElNP8aCPOGOqe4jCMKb84PjQpsFgEArPEgEG+C0UCrG84Q23OKNeKZFIWC6XC7VNkL26vY8+zszMhCw76l0QQQZsXVhYiOyT1X3HugYZI95jdhoFPzg4CHVk0LOMRbVaDTwJgKR7b+OA+Tjy/Kmfefsgzm7S6xX0VPJGLPPrt6Co/aJgEuAS1+g7bhIwxlms1Wo2OztrhUIhROS08KzKVtYR88v3HthSeW1mQefTPwXuIQ/wAhxRU4j6B61Wy46Pj+0Xv/hFqI3Cfdls1v7sz/7MpqZOj+mG146OjkI0sdFo2OHhob1+/TrYcd92Ur5OpVL2h3/4h7a0tBSR/1p/wgPoHrDnc37H/T1K9sQ9B75SG14dV+T97Oxs5LjsuAALz9D3esdUZTIFkLe3t+3zzz8PmXzfBIrTA6NkIOPRbDYjRTHZgkkmJTUwvL7ytXf4XkEI5Z84sJY17WUh16NTuJ4AHX6otz/V/zSLnq5HIBdbsVgshrYOBoNg6yMHj4+PLZ1OhwwMbIJUKmXVatX29/dDUPWDDz6wu3fvhq3eo8Ze5fcoey7OF/c+qj7rMnQjNRB8Ay9qCIuXlDOz+H2BLNbLDo5GKbxwGYVYemHG33qd35KgDO7bZHa+oIxvB332ERH28wIkYFhdt3KrjmPcmF7WqdDI3cnJSRAA6sjx41MPFXggbUidCaKvVHCt1WrBqPBOHPuHGFPNduB5KCgfScbpHw6HwSFQo1/7wzFvur8ZwqnSeheaPg0vgVDqcXK8Q9Ooadfh4aFVKpWQVukXvo61plXSThV4ngdZOzrufmvOTQAIajBTkfnevXvBiNd0QF1/cc/x6L4KaNobt+a9PND/vdLy7zGLj8rFPXMUxaHifmuFOoY4LbT96OgobF3hvZeRuTdBCqDomGKkk/K5uroa1jprBoQe4NAXDVJlTjQah1YBHd7NmtbsDN8ufx99gJAFFFHlVBB1RFV2cP9wOIzUfIiLcnpdpm1UI4hnq7PHMzGYtK/qAOEgxUVFzKI84R1M1V86Hgraa79GGcvj3kntF47bVV2nvIuxjvOHHMKIQ6/wWzOReCf8Akij/YYXe71e2I6GY4fjSf0LjpZlbJhnT37uFUAaZXt4ipMtPtrO2MfNL9/F3RtHcXaS/n0Tsl7fo/JMa3hQOEz1qL5b5ZvKQO846vXeSfQAQ9wYoq/ZVgV4xFqr1Woh/Vyzw1ZWVkKWFHq21+uFY5YpuNhoNALvwRvfZlLdSfaZ6jqz+MCe8jn/x/Fi3L1xPOG3COt3yit6xB/2F/OpspY20S6/PvUafQc2GUVi2Y6ncvUqQP7XSRcBqDpHAAisdQ/ma8aX3qtB5Tg+iBszBXbQjV4H865xz/Y8pnym9qn6fehqBcZPTk7CtgfV98g/iOvwG7CROREOkPwi+rp46EaLKPpOxDnS6jwqEqSoD8ojLppndiYgvJGvlX09k02CspA+q5UwtQ/qWKlxp+hVHHlFCHEPRsdwOAzHAoKkcaTZpMonDqHy4+8Nx8sQaO1gMAgReAQDfcIJ1XnyRvP8/Lzdvn3barWaHR4ehkJLnL7AHOA4++MrtU+gxuw7IoV5ODzNiqD4JBkP3hkgDVKVfa/XC5GThYWF8DlAAXu4MCzgWwwV+EejtmYWxk6PqENQcE+v17ODgwPrdrvhmkQiEfZJ0X7d8kB/+ByBnUqlgtNJBID91RqlYS8qxYQmTZ+ahOC1x48f2+/93u/ZxsaGLS4u2qtXr6zZbIYIJQbY0tJSqBVhFo0y8xs5wpjjoMJrrFcdn1HggNkZiuzPjmdc4/bhaTaD2ZnC0W03w+HZ6TIYLOyZOzw8tEQiYYuLi8ER1shWu90O8/jpp5/a3/7t31qz2YwAPtedk8uQHovmxzCZTIZqyltbW5bP521paSkUKOx0Ora/vx8ikWTwIG/9fB4cHES2c2Csg8bn83kbDAZhPIhW6lYo0miPjo7CWfSsh36/H8CN3d1dq1QqtrOzE4w8nEvmS+cTfsnlcgHYxWhBDtEn3YcN/9A2dWr0hAQ1VDAgcI6J4pOinUwmg3yD79AnXOPXMvpRazuojNb2Qur8K2jHu/Re2pTP5+3Ro0c2NzcX1qw690dHR9bpdCybzVo2mw1pnPC8Gmq6jiDNFANoUL2sxazQSa9evbJKpRIyeuAXotzsTYWvyuWyZTIZK5fLQc6zJYM+Az7t7OzYs2fPInJA24scU8CD9vO9B3romwd6GX+eBf/B48ofXKuZV2/K4Ewmk0EvUvMI4IBMEz2KmfZ40Jr+0h8PCvC3bh80ixYyNYvWquF7LWJ6cnJizWYznP6kY0Y2FNHTu3fv2tzcnC0sLASwX21PUpkXFxdtfX3dHj9+bIeHh7a3t2fPnj2zzc3NNzLmbwupfEBGEST0Dr/qELWLPdDudcwo0EHtyziw17eR9qnuYTvt7OxsxN5WAFf9AQUQ9TuyYpvNpu3t7Vm73bZarRaya7Xd/t63jbzf5P0J/7+Z2Z07d6xcLoe1y7ZCMj6o84O+rlarQcfHzZWCAyr3FHjQa2mXAgk+01RBTuUX1r4CXzzXg2DU7UHHU4+JLTAU2tTj0TX7sd/v29OnT+23v/2tffe737UnT56E05o43npmZsby+XwIzijF8Yzn0UnoOrz3lZ3CoOQFh3es4xwXjwb66+KcgrjIzCgHWxWZCidlRM9s3jH2yKkXEoqO8W4WhqKiGh1So31UH26arhrZ9Ea2H3sWrho1RIAoxKgpRmo88uOBCEXtMFB4N0ahAhmQzqMi1ggbFqsayzjc7M1Ug5DnKFhE+7yAYl7Nzk7rQMB1Op3gvCo4oycUMNZqOHkj3vfPp0Zzj86xN3BvCkCAUqlUJD0doAZE1gNbo/jcjy1rSg1r7Z//W2WF/9zfrw6WXkf7/JjyOc/Re71s6Xa7Ye6JwGLMMB4o3r29Pdve3j4n475K8o4l8pD+AuR1u11Lp9ORbT8q7zUzSedc5StyT1F9b0yqU+vXldkZmKm1U5AxChDpNjF1JFQe8EN7cIBIWSaaqQ6s/mibVD76dUzffAE570CqzPF8xW99v64ldUqVJjFk49aBEu/HEdeTZHQteEdQHT3G2mdA+G0fyle65UnnXYFEjNdqtXpumwTjwfYvZCFOBU4xsh8AgWcmk6f1ijjZR3UE/dKsuOuSnyfvOOlc6N+j5vgm2qXrhB+dT2Sd6jRv+41qj+ox/h91n3+mfoaM0C2WWjPFzEKUlC2FCwsL4UhvHMw4/a8AKODlYDAIWwN9OvS3kcgwM4vqizidPO7/UTb+ReR5X/W8ygG1uzTLZJTti40Rx1dxhAwi+wDnMpvNBnBv3P3fZNJ1rs5y3FwPBmfb846OjsJ8qL3gfUXu1d/+b/4fNV/ej9O/VdaMs4OR/+gPBcXibEv9zT0UQ0+lUuEoe8aPjJg4P5b3XwQivGm60SKKFyFTfG52OpD+qEIMJVXqSn4SlLHUaaMtccZ2nLGvbVAB7xGpUc9Dkaiha2YB5aZtRDBwCnq9XjgOkH6Uy2VbXl62w8NDa7fbEfBg1JheRKPuu+hZcUx4cnISqpNzP8JRF5OZhX34CpzMz89bLpcL0b4HDx7Y4uKivXz50o6OjuzBgweWTqft8PAwVKDnvbxzODzN1GDPI4Yq444iIMJGQTStIg//mVk4wpPiJouLixEnl2NncHSHw2HYMw3PFYvFUMCp3+/bwcFBpPbA2tqaTU9PhxoJ1WrVcrmcra2thWdvb2/bJ598ErIOlG/MLEToieAwzghn+IvoKWuKLAicK3icPg6HZ6dcKIB100DVb3/7W9vc3LQ/+ZM/sUTi7IQRskP0yDWzKLChaxxSJ8oDV/QFUMcTnzFO6vgxpjpG6uzi5ANceQXJWkYBIOeIYlarVWs0GvbixQvLZrP28OHDyHYedZJ/9rOf2d/8zd+EbJ+vkwDPGCvd0jM9PW3379+3bDYbMnXgM1Ly1tbWIkYB6cPdbjcAgBohQl5QH2A4HIYtTWan44yRDt9rZk+j0QjZXP1+3+bn5y2fz4csr/39fWs2m7a7u2vtdjtk/XCsqEanbt26ZX/5l39pxWLRlpaWbGZmxmZnZ21nZ8e++OILq9VqVqlUAi8/e/bMXr9+HWQFhLGkPO51g+oUIvK5XO4ciMn2gH6/H9Lu1dBSMEYJvQbYGpcppluxdP6Zb41w03bem06n7Xvf+16QvwoiaYYB78f5Zp4AGXkeWQLIfBz227dvn8tUQM/wXk5lAJDRCLRuCdTsr36/HwpZvffee1YoFIJThM5QPTc9PW2rq6u2uLhoDx8+DFks8AJHdz179swqlUoYa9265fWmko9ajgKPVf7rfbSXz+IMTJ2/q4CUyeTpSRuZTMYqlYq12+2w15cMmWw2GyL3yjPaf5XX8LuX+WbRbDTmnntYc2rg93q9IJe4fm9vz/b398NnrPXV1VUrFot2//59m5+ft42NDctmsyGyCPhI25F1rEFsHj2+j1Mo0P/fNmKs79y5YwsLC1YsFiMZnZB3sNQf0IAPmQvMy7ig1jgn3PsMzHGhUAinfw0Gg5BlRi0olct+Pejfuq74DjD96Ogo2K/Hx8ch02pra8v29vaCH+DH8aty/iahuPFXivt8c3MznLRCIU2Ox2T9D4fDkFlNwcWdnR3LZDK2tLR0Lljr7T8AIP5X/8AsGhxT8Ac9oHW+FKDHDvNzEAfS8zfvLZVKoV29Xs92dnYCL2jgVINLnEyCHQNw8ODBAzs6OrL/9J/+U+Q0i0lpkmtvgs++lgyEarVqOzs7QZFclhSV4v+4SR+HHinpNR7Q4G8PSIxCmPQ5Hu1So8xHlYi4UZETI0QFzHUcCGXASYXUqOu0D2ZnaT4sDpB4HylSIasomxrT7Hvm/X4MNcoEMS9qRMZFKFBmmgqrzp8acThIupdp1PioUuS59M9HHDD0MJKJVhElJb2L96FQSeXmfZptwBgo2IXhrfvJ4oh+q1Dzht1NEc5Zo9GwdrsdibIOh8PgNPhoqbbJC2+da6/kld88v/jr9T3eYFBDVg1Y2socel7V93EPv3nPcDiMRCTMzhyqWq1me3t7tre3dyWj/qbJyyz9n2hjnAxWIEH3ieu+P5+2rXPHZ2ZnMlCzdJA1ceg/1xAFBaSA34lIsvb8Fg3eNz09beVy2ebn5wPASOG/UqkUAAUMCPbUm51tdWGOT05OQju8sx83xwqSqXziXboFTn/UmPJ9inuPl+ujyI+tXyuJRCIUJNNtBDov2hblEXUcvE5XGce6Uz3D+/lf150W2FMd4p9JW7LZbCisBlCGQ+Flqe7tRZ/5orupVCoUb7zIifT2jepuPyZxck0/1/lRWT9qTq9DjBfAKfYd+6A9r3t5qfI9jp9HtZM5VJkap0NYh4D86izyHAV02IYDeKC1WTQwZGZBjvC3l1ffZoobaz6/yNm/6H+zaJQ4Ts/H2TdxDr/KIXVAtY6J2hlx4IC3HVROKX+jcziKGQBtbm4uBAbjtia/TeABdFnnFRAWe1WPAtdxU/BP17dfj3zOb68r4+Z+lCxR8rJ0Elt53P/4OQCVFFI3O8vMgffgF06j84V6NZh3E7L5TdEbARAYCL8AzU4H/d//+39v//AP/2B//dd/bbdv344YF7oYfXaAfsdEeCbQNuj9PAPyBqJnOI90q5GhikaVYFxREFAtItaJRCIoo3w+b7lczgqFgu3u7trz58/txYsX9sUXX4SK4Gpke9TWo7LeSPPXKI2LTvjr/PiyEPgOYaFIGydtpNPpUDDQ7BREaTab9gd/8Af28OHD8P5SqWSdTsdevHhhiUTCVldXQ/SGsSRiOTU1FVJNSfnp9XohVSyXy1k2mw0nV2DQMF8cKdZoNEJxuuHw7Mg17pmfnw9zjUDA8MhkMmEPJMY9KbPUTUilUlav14OAPDk5CY7G0tKS9fv9SESq1WqFKE0yeXac3OzsrC0vLwdHEsNZo7wY7Yz9YHBWvRzDinFUZ5gUznw+b5lMJlI/AiV400ZQo9Gw7e3tUFARoAZHlHYiQP2pELofnOuYB4x1nEV1uszOhDzrSpFldUC12jvV7nm2jxx4BYXzQDuJXL18+dJOTk6sVCpZNpu1jY0NOz4+tl/+8peWyWTszp07gac/++wz+9//9/897NOEvk4Dgz19FB1lzoiC//KXv7S5uTn74z/+4+Cw9/t9293dDVElnDAKhGqBMq5PJpPhLG6ihxjv8DwFzjhei3lLpVKR/beLi4vhHfA4UVEighRPpGDtzMxMZJ0x1/Pz85ZOp8NJDRhHCwsLtrGxYfPz8yGqubCwYB9++KH9/Oc/t83NTdvf3w/jBp8zDhrJ1+0rytPJZDLUDKBeidnZSR7KIz71kt9q1A4GpzVs1KAjIu/BciiZPDvWFflA273hTToqugE5okCGWbSOATKVavi6RqempiJnyJ+cnJ5ow3U46MPhMBy/RzYMeoNjtBhTBZIZY97HaQ1mFgxg1vfU1OmRfsyZytLhcBgKyLVarUj06N69e7a6umq//vWvQxafAh4KGvN/HJDinek4Q5pnA34gB1lTOse04TqGKjw9Oztr6+vrlkyeZbgQ4Scrw2831Pbq88zOsmN8RowPPGmGCfOr9iIZCMjyZrMZCiZCjPurV69sd3fXHj58aIlEwiqVijWbzTDncQCCB67QP9QxQna9zc7ApORtQv375cuXtrOzY6urq1YoFCJHTTM/ZtHtkkrIRW9rQ2qze7vEPysOyI/7DPut2Wyes3dUz3nwlTmlVhm6kGfOzMyEjMpUKmWlUskWFhZseXnZ+v2+/fjHP7bf/OY3E4z4zdCkgcPLkPokGtTC/uz1era0tBTsUDLC0BHYAdiCyWQycjRz3Pyr3OLHBxx067PZ2VGymvVFhhBZERo8UF0V9zzGU3+TQXd4eGjNZtO2t7eD3cG8I/cAMTc2NqxcLofPAFQ+++wz293dtVqtFt4XB+RMaptfBAJdlTe+kgwE33hSCknx4Gi+OEXooxtKFwlj/14dIAUO+D0OfcKg0wilR4fUGNPPNPqk36NYETYcp1ev189tX5iULnP9TQkTnSN1VnU8WLwIEfYYUhwEZ4/tBH4vFGOon6vx5wWLFi+jTT5ll8WqGQ/MlxrhahhjHKixqWOOwUqqsoJhCCacX9ri+YX+Eq3X6uEINu0f7cT5ok0+OhinGHHoGA94UcfzpqnVatne3l4osqftittCpO1n3anB79vq16QXnGpYco1f/z7CoM/z4+Lv8fyo1ysPkLZWr9dD9hG8zbwPh8NYIORtIeVFtgkBii0tLZlZNHJDRo/KBAwslQ/woEab4XOdc1X4fGd2HvDV9gIwkDLrI5EQ6yGfz5/bOgEhC4i8zs7OBmBR26tt4hlxqb3wtDrmtMUbL8gpjZ7r8zzfTwIGjlrz4+7zehUjEEBCQWbaCT/TD773a8XLXzUCtT88R0kBfI02quz08pEimGRQkIGArvbZDegQPT5QDVraDHBjZud0Bn2MI+UBlXdxbdfnaPu8Ph5FNyXr0dH0FwdMgXTdjx5HowI/49quoJYnv2VinDyFjw4PDwPQqHqa9an90edpW8zOgDuytL7NxDo5PDwMQSXld28DK6kzeFleHOUzTEIeHPAgQdx74mwI/fGBDI4jzmQygV98gclvIo1rO+sEoADAmmCAz8zz+lprIPEuL1ch1RX8r+0bZa+NsuX877g+q35XPQYYSyCQ6zXrWu0cgPbj42M7ODgws1PZ4zPQr0MX6f2ryqUrAwg6kf7zOKfdT3i/37e//du/tWw2az/4wQ9scXExpLyxsPxCVocu7t1xxDXc4/d/x6WY81uNjDgDBRoFPNB2kGecY5Aq0tVTqdOjPTY2NgIiF9cm3hHHDKMYRI2PuM/9dx5JjCMKktEfFrhPEaUmQKPRCCdcYLgDEpDug7EGWsm44zgTcSyVSmYWPa+a8UNRcyYzwgplv7S0ZOl0OpxmQHbAwsKCJRKJ4NgQrdBoIO3MZDJWKpXCFhOMWDIHdnd3rV6vB+ePbIdbt25F0pY1qumVEVkBOzs7oTaEClPaxzrBkKlWq5ZMJkNKlPK6Otzq8FEV/+TkJGRvlEqlEHXT9LPLkDfklMdevHhhm5ub9oMf/CDUBSCyj3HJ3AGMwAtmFskO8I6Y8oYCUfod80m7fGQV0qiR7tfGMOIath/BiygFFAZyYGFhwcxOq/cOBoMQAd/d3Y0UUuRIsVu3boUjXLvdbqg1Mmq8zd5shoJmWOk41Wq1sD6Ojo7sRz/6ka2srNj8/LzNzc3Z4uJimMdGoxHqg1DfgCyldDptrVYrUu8hl8uFUxxUKeOks6ee7QREM4hGw+fM+/HxsW1tbYW6M/1+P+zZNIs6Xt1u1wqFgn388ce2vLwccYR1W9HMzEzIZJqamrJyuWwvXrywarVqlUolRJtxIpA1zFtctE0dFOQaACpGC8aKrzCthKNtZkEW6lGgECAIf6uzrNeok+TfyRqdmjo9PafX64VMiVqtFtJ4mQd0PVFhXat6UgzyD72DfAOgYo1ohl8ikQiAK+uu1WrZYHB6cgc6mzXK7/X19bB3N5PJ2Pr6us3OzgaZjoGHsUgwhHPPkbtEJVutVggO6JwCTvmoHYCHn0MFJ7nWXxN3jy9GanY+dTfu/quQ8iM8y7ofDAZB/xGBJFqr72bOGRv6Os5R8UCwWbTuRzKZDJXMyQK6yGkbDof2ox/9yPL5vP0v/8v/YouLi0Hv4vRo7QPdmqVABU4CUchqtRrk+DcVTLio3UTXZ2dn7Qc/+IGVSqVIFN/s7CQl3b4KiM6WEdaLgqFxwKwP0iifx/E6z1HSrW0etFRZyf8KaE9PT1uxWIz4KBoURFdRAwFw1WdAeXvppvnjOs8bda+PwiuxTvb29kKGBkVJyRT0taOw+3q9XshgpmaC2nnYWPAUMhzdhs5jC51uP6K91MLg3SoTvN9odgaM4ufoj2ZADYenWxPu3r1rx8fHoUgi/J7NZq3ZbNrBwYEtLS1ZuVy2zc1NOzw8tF/96le2s7NjCwsLkRpyF83HOH887r5JMxcuojeagTCusRjnicRp6jZp/QiGuNoIOjiXXQxxqL1vjwol/Vzfp8oq7jN9lyLUowAGj37q824KmbwpZoEUMDA7L4zj0EGUgQpeFiPGF0KTxW1mYZvB0dFRMNgR7DxTowOqQCCUg9kZYJRIJEKhQo1o8VyNyiPoOM9a0+3VMaeNRNVxeEhPUkeUdmJg6b4xxojicxgd8AiOCETtAOZDa0+MIiLgPMfzotnN8Z8nhC3ghFabVUPAR848COjJA2xqPPj+MWZ8pnzl0WxPfozUqdNnqlDn2QpEAkQAYKVSKWu320Hh+krx4+irMEbVYDOLP+VGDS3S7XEqtOI120AYG7JneK46Y2bRudf5Zx59to8WQ9I29Xq9kM7OfnT0kDcKMDwWFhZsbm4uyHLd3+lrP6DwkVlTU1MBSPXRFvpDn+mnRpm9Ecx1angpvyr/eT7mXeOAAcY+LvJBu0cZ5NoHwNn5+flztS/U6NL55HMF9fgehwMjTYFFnV8cZT6D59hCqIWbldjWQiFXjhvUZ/E8dYJarVZEH/E3bVRDF/BxVIQz7jP9XPnjMqSAhX/PTQAHPKvdbgeHSvVTnH0DyKJOpD4r7mdc1BpSPo4DgwEoka3jSIFb3VKjILTPPojjLbKYyuVysCNuKrL4thK2yN7envX7/XNZxmbneZkMINLAyQTiWm/DK29AKofU1vOkz1F7Q+39OH5TGYre0XdrW+iPyih4kG1aSnGB17edvK0fR9i3bCtEFvmaV2SsITvGZaLo9ja1HVUHeuDHLD4zwduanp/UH1M5T/u8jYk8g9/ZNonOI9tRfZ5qtWpbW1u2v79vlUolyMVRcuKrCBhNQjd6CoPSqI55AXBycmL7+/sBkTazMNhcwyCzN0YN9MsiMSo0uG6cgqINcaQRIlWStAulo3trcBrUcUulUiGS4Q3kixCki/73yO1FCJX+HzeWMPbJyelpDDjiGEdqJCNciLi22+0wlhhsRCRRMKRx37592/r9vv3qV7+y4+Pj4Eyn0+lIwTMWI/vozSw4xqTTcTwKe5PIdlhYWAiLV/lPjXDaTVYA/Zueno6kNdOehYUFW11dDdEKnnF4eGjD4dCKxWLoO2NWr9dtb28vRIoY86WlJVteXrbPPvssRNfMLHLO9vHxcahJQZVyzhumfT7qzhgVi8UQ3VPDDydXj7a6LF1033A4DCnvpH9zn+c71gr90CrY8CP90+PBmCvWGOPtDVqzs7RiIt1+zSuwwHO4DucYw1R5R9sNX8EX8GGhUAjzVq1W7bPPPotk6lw2A+RNRC/MohXPdRxQlP1+36anp21hYcEymYwdHh7aYDAIR/llMhnL5/MhUsCpKNybTJ7Wi0in06F4WaPRsJOTk5BhxJrmCEwtwopjT40ADAuc+VarZdVq1Q4ODmx/f9+eP38eTm3IZrPWbrcj8pfI4YMHD0KkgsiI7382mw1Rznq9brVazVqtVjgdBkDo4ODA+v1+OAaQPY7IHj0phjFXYAzHGufZO6RqmMDrWh1e+YlrAEGYg9nZ2QCsePJgG2tVo36cOFAqlezJkyc2PT0dxkwNMOrKqNM/GAwCUMwpGrQ3k8kEuU5kXTMnWF9kKmHgT01NWb1et9/85jeRNquNkc/nrVgs2sbGRsiYUcMW2a/ZkUdHR7a7uxt0k+rYk5OTED3DYUSOqeHox5Y5Zy4V7NQ269/IFOT2KBCJ9cG9cYayboO7iHz2xOvXr8NaINtFnTOMfHitXq+HAovaJg/60Sdts3cEfH88sEdW4ubmZlg/4/rF8/v9vr1+/Tpi52imJXZpXLvgv2QyaaurqyG7kkysq2T2fVOIOfvpT39quVzO/uIv/iLoZR0jPXWGmgGbm5v2+eef2507d+zevXtmFg3Oce8oXvcAAhQHnGnGgQKZ2OK6/Unfi/NPtpMHK7ALNMMC3fD69etwApUC599U8jabytfhcGjNZjPIUJUvfqsTNVKYE9YbpDKz1+vZ8fFxkB9aB8uDAGZnQSvkArrD8w7t1kxY7B5kBr8VTKZ9KjuHw9Osc07xAXAmU5gaa61Wyz799FP78Y9/HGx4shY8yATRx1H+2yhghzH0Ph33XJZuLAPBN3icEasGEcg1aAtC16PlMIc+P04gxCHBGCbavjjhzaQoiqWfefQUY9MbBLyP1DZ9Pr9hZo4RwynGoLxpoTIKBIEmQRK5DuGq20AUudWFyVwyt3y+ubkZHMc7d+6E4252d3dDWreZhXR6DElSoXK5nLVarVAvgndoKno+nw+VwHE8ETT9fj848VyvYJKml3oDXhccc0oBNtIy+Q7hg2DMZrPW7/ft5cuXNjMzY7dv37bBYBAiWcpjcQ6bN4zUUdXvPXLKtWbRQoJmZ1Fc5lajmzdFcfyFM4YS9qRGHKToMv1mHeo2AsZIDXDu9YasmQX+gwe0DTp+cUasXqvKw8sdHDlFzTUCp8pwkqyDUfSmUGld12ZnMpD3EbElcodBoAYahhVjo/Oie+CJ4vuxxlgna0W3uZidbnnAeSHDgHubzabVajVrNpvWbreDXND+mZ0HrEh5h89It0+n0wFYNLOInNNnoh/UuMWQ4tpR+gj5CQ97MEqNZsZVx1HlmgJb3IPTiT4yswCYjiPPY3Hrstvt2vPnzy2fz9v8/HwAPzzf6JqkjzwPeaZ8oGOJQ6eyn/YDBpqZHRwcjF0Xfh6RH1rHQeUzsgZQgzHH2WBrja4VDFdvo8TJPq8LzEY7RMgY1Uf+Gd4+0nWsz4v7fBR5mY6u0uryejSrtkvXk65/n42iOkzbPol+Gg7PtpepA3MZ3eYdTAU0PF8it3TtKJ8iM5BZvwtE9Pn169fWarWsXC5HMkJH2dV6tKa/TjOZzKJga9wa92CTvitunal8oT0aiMPpjbtX+ZU5p729Xs9qtVrY2nZ0dBRrc78p/f2mKC7o6Onk5LTwMWsjnU5bqVSywWAQTjnT2gDqN+h4+JR+bHrksG5RUH3LZxpY5ceDft5ujrOj0VPoKLUNfRvMokAo4wGoDFBAdpzqwFE0iQy7jE93VboygOAj3Xx2UQTb3zMcDm1/f996vZ7du3cvRKC8Molz5tVBY7I06si7WMyqaNmD6lOMVLmpQ8b/GFw8o9/vRwxnDA+cXTMLtR000pJInEZ8nz9/bv/+3//7yHiMmnQdx7jxj/s/bvxHXTsJww2Hw3AyAvtZ+R/hqvvJdN+vvvMf/uEf7L/9t/9m/+v/+r/a9773vbAPdmdnx6rVqj179syy2az92Z/9mfX7pxXeifgUi0W7ffu27e3t2ebmpnU6HTs8PAwOQ7vdtk6nYx999JFtbGxYrVaLRK6JXur+J1Vag8EgVEtVIARnz6OYyWTSms1myBLgCLBkMhkQRI56KxaLtru7a//5P/9nK5VKtrKyYsfHx1apVGx6ejpELBlnIpc6lmrsTk1NBadKI1zqsCGQceZwuFqtVjh6i75j4L4JJaY8m0icFgrc3d21ROJ0Lzv73VXJmFmoZK5VeXGE1NDvdrshGsnnGp1ELlBHgjEwM5ubm4s4OFoAx4NM6oSpUaOV5tXYxdg4PDwMxTWRbxqxI909zrF9k6DApM/WaIpZ9FjKRCJhhUIhAMKMBxEcHHqtHQChhPk8kUiEOiWMC+9lPXG6AimvrVbLpqambGlpKfDD7u6ubW5uhujy69evbX9/33Z3d61SqdhgMIhEd3kPPMM2h1evXoVCetDs7GzY26tFGb3uISLhwSX2YnO9d9g9eEBFdwpReZAW2aTP4vm6L5PPmU8MWyIl7M30VfJHkRpcnprNpv3d3/2drays2L/6V/8qUtdAU1DpI2muuoeekxRU1tJfavBohOvo6Mh6vZ41Gg3b2toKWU4KSoxqq4KOZBz4/a7IX+yHW7duBVkLb/t6JfAwpwTp6TnwiQeO1TBlnHmHbg/wgFKcQQw/8ZmCTH4eJ8k8UPKyo9/v27Nnz2xmZsbu379v2WzWFhcXIxkmtJf+kLmkess76XzmMyhGZVTQNrLCOB57Et3Guvr/tXdmzW1dyR1vgCCJlbslepMlZ5yxM1OVhyRTSaqm5iVfIR80ecrbTPIwL6mUM/bELo2tXZQoihQJEhs3IA+s38H/ts4FLkBQoqTbVSoKwL1nP326/70chHvWm7+mkc+MOXwOxVDfpUxi4rnJ5X0lPTO73a79z//8jy0vL9tvf/vb19a72dADEI9dlCnNTg+R80RDH82GAAJ7Dwu2BxBiiiLPsbfUyMI5AY9V3sNZnQYG6po4PDy0ra0t29rasu3t7ZmO91XSNMZM1SUYHzx57t27Z9Vq1X71q1/Z3NyctVqt4O1nZmH/4G3MmTc3NxdCPxqNhlUqleDJg9cxiQeZJ03SrXxPjUsqz+g5owq/EnNMWPHa2lrQAZDN0YPgT+ohQZ+RWUqlkrXb7bCWvHFlUvlv3LNeL6euSXm/2Qw9ELRRMaU29j0HBEJDs9m0YvHCtUNRSkWcPUKuQr8/EPmr7yvKE0PbPTPSOP+Y8KGghlqJzIYCt97/CaNqt9u2tbVlz549SwguacBAVoq9fxkFxL+ngrAexgAiavFV9yzmWtsHMNBut+3zzz8P+QXm5uZsbW3N5ufnbXt7O+HpgSszCbFWVlZC/QAIq6urVihcJNtScInEPIRSsDnxClCwSF17NaHP4uJicEfiuWJxmLhQXfFVyGBNHBwc2OHhYXCpvH//vvV6vTAeuH2fnV1cPYbwG0NjWdMqyCDoKKDA+Jgl3WM10YzZ8NBUATp22M+CBoOBHR0d2dzcnC0tLVm9Xk8oPqpcqRVI++PzSaCE7OzsWK1Ws3q9Ht5TRQ7FBbDHzAJIw80IWr8fwzQrn9nre015DcnZANwU9Gy1Wnb//n17+vTprId6ZqR7l36q4sL+BplnPwLsMLbq/glo4NF6QkHMLHhlsHcR7JhzFfY5wAEgEN5arZbt7+/bzs6O7e3thSty6Q/1otyXy2X7+uuvbWlpyZaXl4PiSF85+BUoNbMgAOOOWygUQsgaHmYeaIhZwtIsY7EEw+xfn/XZK2He60HdSfGsUNfONPL7cBx/OD9P3ryh54AqsnNzc8EbSRU2PTsUnGNNaFI+wtoGg0EQSDVURknHf21tzVZXV8M8q+Ia67uGeulcwnvn5+cTN30UCoUQ1sLvsTPZGxA8LzR7PZ7Xzxdj7L9j33hgQesYBbJMQv1+P1yjjLKHC796l3LuKWlyNNoCf2ZMvMu4uhkrH2LP1mq11CS0Xna9efNmWDvkwtB1pwojbeFc0TNa+wCfwDNrnIfPu05e3geoxPOyVLq48hOPBM0t0O8Pw5h0Per5Ezs3PC9SHuPXdwxc0/f0edqPDEi5ypd0L+r6PD09tVevXoUkeS9fvkxc7XrdaVZt1HE0sxDGA1+s1Wp28+bNoHibDWVVFHH4AnnG9Ipas2GyerMhb1Eei6ylbYI/6D7lt5icwz/qUUWf972HKWcFz9N/zi09w2JjZjZ7j3RfZpoRYBxdSRLFNBDBEwPP4O3s7NjJyYmtr6+HK0+80M4kxRBnjyzqRPM9B7jG2tBmf7hhlSYRnm+LWhsLhUIok/h3FhVZWLWOV69e2e9///vEgaML6CoZjC83DVxI+14zmiqT1jHl8NbwDhVeEHb/4z/+wxYWFuxf//Vf7ZNPPglW2Y8//tjOzs7s7t27dn5+HrK0Ly8vW79/kdmVEACz4QF1fHxs6+vrtrKyYs1m0zqdTmgDc9hutxPu7tyEQAy0uiZh/cMVEguCZtKdm5sLliisYcw/AiWoeafTsb29vaBY/fd//7dVKhVbWVmxVqsVssEXi8XggcA44oIJQ2X8NWbbzIKgtLq6mhDQYFZYwUH3T09PQ+4AFepQpBSImAWxZkgYc/PmTVtfX3/tqjT2AN4BKAy0EQ8FZeyPHz+2+/fv2+3bt4M1+vz8PBErbzZMcIOgiJdKpVIJSiSorBdQ+KfAnxdmVOBkPjc2Nqzf79vW1lYixu709NS2t7ft3/7t3xLeB/7QuQylgYiTlM2artfrViqVAhDnXf6Zp3a7bUdHR9ZqtaxYLFqj0bBer2etVsvMLrw+NLmiCl+MA2WTcBOQmTvZsVxSN9ZfzXaO5Xdra8sePXpke3t71mq1rF6vJ1ysVeEol8v2u9/9LuwhL7yqFVoVerIuc7NEo9EIAEa327Xd3d3gcq/CjHq4QV7oKhaLIexK20s8aLVaTXjpMJYKhsdAdhTvV69eBb6XdvZ4wdpbsrU/ZkOvDqxMuk9UKDQbhgP4vaNnB/sfPq23X9y8eTPcYlQsFoPlu9lsJoB9PVsp89NPP7Vbt26FGzUUfKGfOk8oPfDSQqEQvKDUekYepMFgYC9evAgWM85QHU/OCh0jvlfhVoVe1gWkIKmSN8ak8Zg0pWpSOjs7C2GIZhd7fW1tLZz7ZkOgQBOqImvRNgXpOIMVBIf4njNc8xIgNwDc+jHRz8Vi0X7xi1/Y559/HuYAT0vGx8+btoe95sefOSVJrh9/aBa8/rqQ32fdbte+//57M7tYXxsbG/aP//iPZmZBEeTsQO5Q3scca0gYZfMMfJHv4Re6jxRQ0H2h4Cp1aUz9YDAIYK3yV30fjwMA036/b0+ePLE//vGPwbNCx+d9pZi8obzm5OTEdnd3bTAY2N7enq2vr4f9joEOj8VqtRq+V3kOgyMKOPKIymgK8Hr9jXNFvaaZP+Ye2V+NhQoqcL6avX4WUp43KgIetFqt4IlA6LqOE+/4sfPPZBl7T9pOPdsmpUtrBlnBgnHvETt3fn5uT548sVqtZjdu3EgciBzedJjJ9oeiF+49o1HhRQUWFhSLggR/y8vL4VoNmA/9VHRZUWWECDYFi63X69mLFy/s5cuXQUjxCHhsjLwyMi3F3k1bcGnfqxVGQRHtpwqiCHtYvBStR1l4+vSp9Xo929vbs0KhYJ999lm4CoUEaAgb1I1gXi6XA8DA9VsqBKsXCfNCYq1er2dLS0t2fn5ue3t7wftBxx23VA43rHR4Q6glirqJd8dDAleshw8f2tHRURhbcjhwxdTh4WHCms64+Zhh/qpgCSnD0gNTy/GWJ7XGsi/o31WQju/W1laIKy+VSvbVV19Zo9EIB77GzLOHaJ9Z0i13ZWXF7ty5E4Am3of5ax+VT+jvvOPHWonx0oOJ/arlmFnCTVsVE4RckivFBM9Z0SzKVUVJ+8//GTOAHUILHj16ZLVazfb3961arYYbDRTsBZBT5F7npNvt2vn5eQAvEPZQ2ra2tkJODYA6bR+KPd9rRnAUMvVYKZfL9uzZM9vf3w/Cw8rKSnD1Jy8L7dQrWovFYsh/s7u7a4eHh8H1EjdHBb8RbilLBRH6j9eGAresI3W1NhsCPYTW8XzsLITYT/CCmFVOSc9cD7Ao0bcXL15YtVoNyXIBQnhXw62UrxHiA5Crwhv7dGVlxfr9fvDu4HrU7e3tEE7jQwa034VCIVydfPv27cCHzCwoArSPcphrVVZY+/x/aWkp3KLTbrdDAlHWMnOFR5q3oKoBRCntDE+b27TvzJICKXxwVqRrptfr2ePHj61er9tHH32UCD1AoeDWFvIEEBONnKc8w/+DFHCATk5O7OHDhyFsSdunz33yySe2vr4erpMle7ryJd4bJRdBgHucuRgYYmf2+0oxsM5sCBjo/lKQk5wpR0dHYey8gublIdaChgmrnKPzp7KPAgp+/1GuUsx4qc/SL5TEnZ2dqa/DflM0ysBwFWsVgx17qdfr2dOnT21pack+++wzM7PXdD/Wis4luhoyiQLSfi7V8KNeux74039qJPWhVerhqFeLa8iiypxzc3NBznn58qX99NNP4bMHN9P0vbS58PM0bs7SzoNJaSamRWUKMfSE3/x3dJpNt7+/H6zDy8vLAWViknkeS4ZaRvV3lHlFED0yhNCFEoyipm5uBwcHdu/ePfv000/DfdbKDH1sK4IB7QNAgEERi3f//v2QlV/JWwl0jPwzWeYkNuax30eVHWMsvKuxyfSTjVgsDrNjM7Z4c2jWfP7eu3fPdnZ2ggBYKpVsaWnJVldXrdPp2E8//WSFQsG63W4Q2Nvttr148cJWV1dDlndyaChKrdlfVVDmuhQUO4TcL774worFYhDq1IoGs+JOX+ZLs3QjNPf7/YCsMuffffednZychHvqEVwZJ7wByuVyGDcsLzEB0yurhUIhWNHNLCD2CiAA8Oj4qzJiNgy7mfXBp2uMg/jBgwf24MEDKxQuvHi+/PJLW1paCsIX+wuhg5sb6JcCDRsbG8GbAcaOQqCHC8oIc0q/aR/zqGCh2dDKxI0ZvIdCwxjquoHXqAcEB9DZ2Zm9fPkyhK5cZ0Lphs+RMFQBBPY9PPXw8NB+/PFHq1ar1mg07M6dO7a5uRn2nXrmaM4DH95AjPrNmzcT1/32ej07ODiwn376yVqtVrDu9ft9q9frtrq6Grx9AOtYZ2rJLhaLtrq6GtrOnjW7UH6q1arduXPHlpaWwj3VWL5RGlkjc3MXNwgQorSzsxOAjZjVGCCkWCwGbzXlX1iu+KxeUmaWULYQjvr9vtVqtbAG1VKia5W2AKwqWOuJ9yAFziD9P/un1+vZkydPbGVlJfB2eBRtpk94tCjAr+FNCGwKnCwtLVmv17N79+6Fz51Oxx49ehQFOFSeoI7t7W3b29uzjY2NkHy3UCgEIRFe5F3P9czj1gV49urqqi0vL9ujR4/s5OTElpeXQ/JfACOUSh1PpZgS489kNYykCYbec0TlC2QYtbbOWtnp9Xr2008/2draWlAO1ZBArgoAhEajkVjvKrxrX7yM6cHzQuEi186PP/4Y7ZOuiy+//NK++uore/HihTWbzXB2aL4ssyF4rAYkb5xiDXQ6neB91O12rdlsJuZU/39d+f8oOTILeZBK553bx5CfOIvX19fNzALoAz9X2cYDBqwPzl+V1eHPlOXBA20rz/KbB3sVOFSZAiIcbG9vz+7fvx/C5WaltF0VXRWIEFs/AKdQu922e/fu2c2bN21jYyPhiaDGRwWPzYZJFZGl1AChoIEHlDhPVc7zwKAP91KQC0MW55GZJbwYzIZeR6zFUqkUQuyePXtmf/rTn14DGdLGbhTR5lHzFJvXWQBDb+QaxyyKLIIGi0CtjFx9V61W7fj42HZ3d21paSkwGRWysFb4ODoWHEqt1q9KAgIkAvLq6qoNBhcJQDj8lCFRt6JVLHD6jYD8888/2+Hhob148SI1Hi/r+I573o//ZZm/kqK1hUIhcWgruqfJhEqlktVqtfB/GDCKYKfTsdPTU7tz504YY2Jyua6FuguFQrhGkQMEAR23e57nLzF3eC70+/0gJHLo43mwvb0d5pa5LhQuksS9ePEieMjUajX76KOPwl3nCOAgoYzB6emp/fTTT7a3txcOStBXFTzMhi6yMCnN76FtUvQdxVStYnqwMi9qJVWLJQcpjFcPyFkLkmnIKnN7dnZm3333nT1+/DjM48cffxySKwJ+MLZqkaUMtVioRYB5ATDin3cJ5lDQuVflnzWPVVQVJW7iQLlB4e73++Fauh9++CEkBur3++Fe6JiAcZ2ESlVaVVlmzfj1DF9gH7PHm81m2Nebm5t248YNazabtre3Z0tLS4GHA+IVi8WgUGDFZc739/dDrPXZ2VkirAUrd7vdtp2dnRALD2meHf4SugMwValU7IsvvrBqtRr2OYDV0tJS4GeMAYICYIaGB5kN4/Z1HGkrQrDZ0LuLcQV0Vasre9gryJxf8DkVrAErdG2rUqyAXYxUwI4pQv78YQ8QWkCoxcbGhi0vL9vGxkYoW8FQ7SuCXkxBVqWgUqkET0Ysl9oW/u8FWahQuEjeeXR0FOZY+TDzomOnQCFzcXx8HK7qKpUukieS3BGvI3i8ygyqCOka8fPheYKCQf43PTP8O/r7m7KOdjode/jwYVi7mmRRQ5qU39L2mLKnBK9nzfd6PXv58qUdHh6OVd4Yb5VXtG6tT/kcnxW480oHFsZ2u22bm5t2+/Zte/jwoe3u7prZ1SbJnQXNqm0q65sNPdS8rK68zBvpNMwB/gZQqoq8ykEqK6lso89CXi5VGZA2KQDtDQsARQcHB+GfJsy9znTV7WOd+zOCz3gg/+Uvf7GNjQ27fft2AtjU+cV4oMYZ5AW9GpTyAebh25zjzWbTSqVSCK3Surx8ql6k/X4/XN2Lp58Hkmj7/Py87ezshCvpe72ePX/+fKTuPInep+Ppx9SPvX/nsnQpAGFcI/T3cYACAhtoJEmI6vW6ff7559ZoNKzRaNjx8bFtb2/bYDAIAIKZBSbtExZ6Zd+7zsUQbA7TcrlsKysr4SAiSz7EIsMi5w9hRbsODg7sxx9/DMrCqPGLHXYqKMUWQ9rCiVEMsYqVkcZQ9D0U836/n4g/VKUVrwOUebUCIZS/ePHCBoOB/cM//EOIXSfh0GAwCIqBCtgATFznSMxUvV4PicyoE0BI47UR2lkba2trIcQEMAnlc2VlxT7++GP7+eef7c9//rPV63Wr1Wr2zTffBM8HBFg8EcwsxGT//PPPCSszIIvZ6+5vepB6V/mY5RAmSj896MDzHIjqmaMCkyrWum9G0WWsEzFh9+zszL7//vsQ07y0tGS1Wi14jSDowS8UQFArBMybMWVcq9VqQohQ92YFELgCjrL4nfHCw0hRckJqzIauzFgxj4+P7cGDB7a/v29/+tOfgufDKMHiugkcXtnyFjhdu4wPQqLZ8Madv/zlL0Hg+s1vfmObm5vWbDZDbgisTbgPz81d3JhC8iQIvtpsNgNIw2HOmi4ULnKekIyVOQYU8tfMnZ2dBW8HkvsCINBPPKlIkogVWnOndLvdEKaGgGI2TLKnCih7GNDULAkEmFnYmxrbjWKt54KCOTybBkqYDeNAdW/hMu7JK7dpCr32D35L+MaLFy+sUqnY/v6+ffHFFyGxnlr9FAxU4CMNYKB/1Wo13LOtYJECHNo2+k+ZAAitVitYqKiTOmIWbsaM9XZ8fGyvXr0K5w+JBAEQFADVfAsxQNXs9SRwfk7UC8ID0mnzBDHefhxmQbGzodfr2YMHD8JneHy5XA57TNeNtpu+Ks+JWQjh9ySm9QpjGlEu+5EyVWbU9aaE8qh7k3nBgNRqtezOnTt2584dOzg4CADCVfD56wpKaJs4GxhfgCPWIzKJ3toDD4dXnp+fB+XQAwisA92r2gblZ+wd+DhyK7xCQ5eKxYvwVfXY0Ru+4EH883qG0nWZp0nbkEXJ9fqf8lN9RseQ3EXn5+f213/91+FdPSsLhULg0awZPHa5QlZDmDW8gH4CIBweHgY+jX4Qa6fZ0MOSq6EJp9R2mQ2NgJwJ8/Pztre3Z//1X/8VeL3qojFQhfZ6vj1Kz9O1FNO3PYAzC5oaQJhWsRj1nh4ICwsLduPGDSuVSmFRkZQIq64e8hpDZ/Z6LJzWqwKUWlp5nolDaH358mVw62QSBoML10O9wovfUUq2trZCezX+NesExjab/t8DAFnHOW0hpX1Os2rAoEFYVZlDgVBhfmFhIVgh2URHR0fBtaff79t3331ny8vL9s0331itVgtCBc8cHh5asVgMye+84qiWGwQ02kYduPwSV+z7qa5IikricrWysmJfffWVffnll/b48WP7z//8T1tcXAzW6H7/Ih6Xumm3uuHiwsohpQfd3NzwnmEALT3k9Go7ysPNS4ED+qXKso6RCjuUoWOtCmEazerw8/uTwwDBbH5+3mq1WrCYqhKh7+hBUywWwxptNBoBTFLBH5dIrI0PHz608/NzW15eDskNWRONRsM2NzcDuMVaZ21zbdTTp09tf3/fjo6OguszLnsoDCiEsTG4DgJFjNgH6o6J4qNgl/IWb001s+CB1O/37fHjxyGxKPzx5cuXtr29nfDy+PTTTxM3ORD6U6lU7OzszJaXl8M924RF0D54DJ9V4VClhHXDtZq//vWvE1dLYaUol8uvWRzgcbu7u/bq1avQH+WRCqjq+OlfFZbZi7h4q2KlSjZjzNmn1yArOMb8eJdfxkF5kSdVvBWk8GeGtks/q+BDaAu5Idi7GpoAaKBWI65D5rzlms2nT5+GsZ2fn7dbt27Z3t5eAGzpJxRTJtTyWK/XE8lrOe/0nz939TxcXFy0Tz75xE5PT+3JkyfhxiBy3UCacFfnB9L1qQAPbdd20Zc0fq1Kk5+PWQqUsTpHUavVCqEn8/Pz9tFHH9nm5mbos3rKqcKnVyqqt43GGKd5dSmpLESIgRpp2Avq/aDtoQ2FQiFxvvC3WLzwNGk0Gra0tGS7u7u2vb0dwIOroqs8Q2al9J6cnARLbKFwkffgs88+C3NOiANnAMmjVYn3YKlZXHlS+cB79ABGdLvdEJoKn2UuNSzx/Pzcnj17FryqBoNBeAeD1pMnT0JSv1F0Xc/6cTQpz0h7Xs8QBRLUeHh+PkyCjUygIaGUMT8/b8vLy8HDt1AohBuU/Dhj5Ltx40b4TnPsYIBU/g/hPen1BYxGXLf89OnTAB4+e/bsNUPVNGM5bu/Ffh+lJ16WZpJEUWmc4hp7J1bW3NxcuGd7e3vb5ubmEi6ZCBwwGxB+siCTAM4f+FoHi1OBCxYbAkmj0Qju5mZJRN/f68yCpi3/93//F6xZWrffMP57L5ilWRCyLobYeMfa4McorXxvdcQdm8zUKBV4DSAIM7bdbjccAriwAbrcu3fPKpVK2Nhc6ck96AiTmkBPBVDclxTIYc40wy8CCm3VeeCw8IICTKnRaNjt27ft7/7u7+znn3+2b7/9NvQTBeDg4CAIuqwrHWti6H34h1okKZOwCN4FMUUJQ5llfDS5o65x6veWFBWWFEBgfGZlkcpKtKvVatlgMAjjSE6RmGsiY6hu3QAIZhay4iswwvc6Bs+fP7fBYGC1Wi1cCYkV6saNG3bjxo2EQqiKDQLk3t6e3bt3z54+fRo8EqiDtZu2168zsScUwNHDlfXi+6RWUeaFf9vb27a1tRU+c7cySi7gDHPCPt7a2rKFhQX74osvEndI4zGE8g7Aq+2GVGFTfrCwsGArKyv2N3/zN7a4uGgvX74MVikUbW/tAkDodDq2s7MTboBhX7OfWCve+4S1pN5EfFavPK/QUgbtMxvyL+L3FTDgPW0DgJaGlsXIW7fThGMFETygAE8ioSVnR7FYDJ46eJko74EvefCl2+3a48ePbTAYhNt38GDTc0XL8/xM54AkvITZ8A5z7q1N9EctnsRwP3v2zHZ2dsJ8EufPuJDgkXJjcoDKLrF95J9nfcTO/Jjnhd+rbxrEVI9M6r9582bYNx7c0zFgv3L+s55PTk5sb28vXNk9rl/MJ/PDdzzrY+G97MR+UmukAm7n5+fhWuG7d+9e66t6x5GuuWnWiL5HJn7GHwWRMxzejaXXG3Q4u/v9ZCK7GF9iXSh/1d/IaVOtVoN86NsNDxoMLm4OODg4CHlyPvroI6vX6/bZZ5+FBK6sYd59V8GCLKQ6yjj9YdQ4wEfJxWM2NEL4PanzzZog1PXg4CCcCZwZ8BPmhbBqAHrmSXORqTypZ62XjzUXEgDD1taWHR0dhfBJD/DGZL8s62ScvDgJD7+s/DmzHAhpDRn13Sjwodfr2d27d4OCVK/XgzJZLpft+PjYvvvuu4RggZKpbk5MvipwZq8LQTHrmgIJJMPjSjKYXqlUChn6UejI/oxClzY+/kBKG7NxKKaOZZpFKAuN2/j8psmESHJFO3W8eQbAB6uBKr9sSLMhUyiVSnb//n17+vSp/fjjj7a2tmb//M//bNVq1T799NNgCWQtVCoVq9fr4XDBWwVmgCcJyauIncIFGSEW9BJEEWZEaMT8/Lxtbm6G/v7www/W6XRC0i7ACxVa/diy7vBW8K7yuMap4u+9CzgwNdcB48dn/a7RaASgR2PKYFa6NqnL53KYNXlGOUrgXV5etnq9Hqw2KswTQsPzrIFqtWq1Ws1evXoVrvKs1WohaZN6KPX7F9eCcv3e+fl5yLD/y1/+Mng/7O/v2x//+McEUKVKLkDi9vZ2iMuP9Ukz6l9mv74t0jhweK1+x0HJWmS/a6Iss6GCrNY9UH8Pjj158iQRLnJ0dBSARfhAu922Z8+evSa4cahz4FM3ij18Sa1MZmbPnz+3RqMRXGTNLPTn5OQkxMqToPHVq1chYSNzrAKPWqkhnzcHYYd24xWkngmaX4O+eMAZXkIdqnTzV9cvAEuxWEwkcFVSC3yM1MrnAVN9hjJ2d3ft22+/DYoD2ff39vZC3hu1AnHFLUDu2tqaNRoN+6d/+ic7Pj62vb09KxaLQXnc2NiwVqtl+/v7iX7TJoBd+t7v9+3Zs2chASLyBPOnyhPWT2+A0NwJi4uLtra2FjxisKR2u90A7uh4+nGNKTE6196bUZ9X0EH/6brxcs51oBcvXiSEedYAf/Hq44wmz4nZUDYhFw1eSKNIQYpGo2Hr6+vhjGDOAa6VFID399YrMDc3N2fLy8t2cHBgjx49sqOjo1kO1xsnr8hN836MBoOBHRwc2Pfffx/W+erqqq2urob99PTpU2s2m3br1i1bWVkJ8+Y9DmIAq+41wiQ4k+AdOzs7iVuCVE/Z3d1NGA1WVlZCUlQszp1Ox7799ttg+KA9o/r9vpAHD/T/0yior169sm+//dZu3Lhht27dMjMLN5VhtOF61RiQSNJ7zrBKpZIA/DifVCagzcgUmgx/bm4u5HLiamo8krmaV+V1QMzT09PAT2JAbWycPGAc0x2z6mqxdafvXtZ4NbV2MA65yIJsjAIf1H2YCYeZNxoNOzo6ssePHwcBYH19PRzWWCt1ocSELOr2FnUI5oOSjPukopgoqRxW5+cX2fyViVyWeYx6P7awJlkUaeBETPjjewUHAAtgyGqZoXwOfdqGG5gqG5QN6vfy5cuADG9ubtpvfvObYB0yG7og8TwCaLlctt3d3SA0wmwAnVQZh0HgVkouB9pEHg68Wubn521paSmsv+fPn9vJyYktLi4Ga1LapvT9BAn1VhLAGWWI3pNCLb2sT00ipMIuSglAiNlQ4GHtatvUkuaZ65sm1p5eu2lmASyCJ2iMMO8BLADoKCBkNnQVLxaLiWzZ8IJut2uVSsU2NzetUqnYyspKyGWBcMqaVyACq7d6Ofj1QBuuA3gwqTDoFXCz4fWNXhFh/2EpYswQ2r0lD4WO3AmM5/n5RWI8FD0sFAsLC7a/v2/z8/NWqVTs6OgoJK+DNwBsqBLthUt4PvwJgIlwqeXlZSsUCiGhY6lUCiFzuFo+f/7cHj16FOIoVflGGFXAjvNDvWnUwurH2+9vHbOYQg//SpsXHQsPRuiYxcqFdO14gMILS7EwglarZUdHRyH+dGVlJVx72O12rV6vh9Awxh+BrFQq2fLycgCVSX4I+EeyRr3C14MIjB0KR7/fD9fo3rhxI+HV4hV9vfXCzxd9nZubs1qtFjyWGFtAsFFjyzzrmOrvyuv8+14G8MCZgse+vDQw401Rs9lMKNnVajXIfCQpNrNE/LHKeGoIUg+7cYRsWa/XEwI2gLuCnGbDsEGVK/25DD+rVCr2/PnzIM/GlId3iWbR5ti5wxmsihSeqHgrPH/+POx7dTlXfqhAm8qY3mgAgKx5CwCsFUAYDAbWbDZDnq2FhQXb3NwMvB539VarZY8fPw7y7vtMMR5zWdIxa7Va1mq1bH5+3m7fvp2QBfr9fggzhL+z15Eb1DuFtqrMwmd/hjLvet6yljCCctbAAwhn8d5L3sjiwSQ9k2Jjqs9OC8aMkjEn1RVjNFPz4ih00n/nBYxRnRkMLlwe7969G5QlcgrwudPpJOKpsFzU63WrVqt269atcA0Mz2g7ONBjYAOxzVirdnZ27PDwMORm0HvRsSqn9TVt3EY9N2qjpo3ruDLHLZ40BoiVhTIUPNEDlMO3UCgEIUqtb2pViwk7zE+pVLKjoyP793//94TlDWGhVCrZ6uqqbW5uhpsR9HeueyQxi1ppDg4OzGxo0dI1wVUrjCN3Qnc6HWu321ar1eyTTz6xu3fv2s7OTgAnYBZYPHU+VJkiB4JeeUdiNg41s2S4iAonMFKz1xVSnkG5RRngOipAMNqirr7qLjbK2nhZGnfg0Jdut2u///3vbW5uznq9njUaDfv7v//74OLI+sHlbXt72x4+fGhra2u2vr4e9j/rATACIZ77mn/44Qfb29uz7e3tMHeMEWv18PDQ9vb2XgMaY5QGHuh3b1N4VCEqK6kypoesPwh5hjEgeRxu9rj6qfUWpd/MEjwCYY45QZkktwxWZ6z7yoMqlYqtr69bv39x0wVgIx5jrAXNEXJ+Pky2yj/APrzbSqWSvXr1yh48eBD6gOIDsMH6AQDUkAwzS4CqjJf2XRVM+qTx2OrxokowZx/jruFLKiQpUIDFl89e2df5VNAnZsHxVnPaD/9TfkJd6p2C0sU6WVxctMPDwxBHXi6XQ31bW1s2Pz9vL168sG63a/fu3UucHer1Vq/XbXl5OYw3+TTq9XoQRAeDgW1sbASQGsuRnmfk5NGEz+pua2YByIL29/et1WoF5cSDBx4g8BYoBSdVOdK963mKnj3KgxQ80ud9uN7bJO0XexWvwc3NzeBdxjkNQDMYXCRb5iYmfh8ll6rhiH8opoy1Ana8w1o+PT0N4CZ18ixrJOaR6Pv5odGovvPby5cvg9ckPP/8/NyOjo4Cj1UeqlZlsyHIDU9eW1uzarVqq6ur1m637enTpyFnxunpqdVqNdvb27Ner2cbGxu2tLQUrnT99a9/bWZmu7u71u127dGjRyFZqtnQqJHmefq+0Si5xixbmHrad1rO8+fPrdvtBo8P5grjAH/NLngbSbLVWBHjnYCCGJXg4Vz13Ov1Qh4r3sEwxDlPnXiTwR80ZM4sPedBFpApzRiZ9l1WsHRWNBMAIYZkX7YcJRSE/f396Dv9fj9kZDUbCkjFYtHW1tasVqvZ6upqQJm9EKQokT/EVSDDunh0dGS7u7u2u7sbYpz9wXxdadQYZ31fLXYwcLXqeIESDwX9HUVAwZwYQsjBcffu3YR1XwVVElahLAIU1Wq1kMndK/ODwSCgiLidqmJEghzqQjjpdDrWbDZDyMzZ2VmIb/KCmaLhKrSbJZV+hBsYok+24pW0NIuin0MUKn+dG+VoqAPlUB+C1dsQKLUfZ2dn9ujRo9AuhDK1CBMr2W63bW9vzx49ehRirD/55JPE1ayUD+ADmvzixQvb2dkJV+/5PAvTtH2WjPo6EOtOE0yNWh/eGqjWdAVcKZO1mGbVNUsmGVTFAQVV+QNCveY0wasIC7EKH2p5AjSA58MnADFarVYAL/BiIqzFLCkk0LYYWMozygdj604VQ28x8XNBHShEMauyPq/8fBT5c3Pcc9o+rVcpDRRVBQ4vsKWlpcBzCWMpFArBE4SM57F9x7W/1MktOsvLy1Yul8PcNhqNBPCj4IfZUElRAKHb7drR0VEAwQ4PD213dzfMN+CSB2cZDx0jPS9iVr5J+HEWC1PMY+Q6EfNAHhOzYZgTa+P09DR4fDIv4/J5mMVBFwXpRnn68B1nCGc3z7E2MDq9C7Lh26I0vtPpdBLGHTUW4lWp7yqoCRG6WalUQugrMhEJvVEMCVnieTwY5+bm7KOPPgrz22w27dGjR9ZsNsPtbCiu74oe4CkNYOO3LO+Pe2ca3ZA8ORjD8P5stVpB3tertNXrTsFzD9R70B3QgdCEZrNpz58/DwajWPu9vJyVvCwPpZWR9jz0NkGqwiDjar9z507icxraNMlATvueki4A7QoLBasTWXB/+9vf2traWoijZuMAQGhSJ1zmsWR8//339uc//zmg4jAes2xo0jQ0izGKlRdjGFk3vQrw+q4K7yTEUqUBy+/5+flrNwkoY0dZ1zaqJRK3QOYYS5UeNPPz8/a73/3Ovvnmm+AlgqfI9va2HR4e2s8//xwSOjLn3oqPy1K1WrXl5eVwwCBcvHr1yg4PD4OrLe0gozxCH4cRngUIOHrDgLrU46aLFdYDBvQbcEZ/Z1yxvmm4BEKuuleRcZY+lEqlkCH8bQmWMf5C29fX14PFWVHks7Mz29zctFu3boUYuZ2dHdvf37df/OIXtrm5GQ6YJ0+ehKsDW61WCEfRWzu07mnbPm0Z15FQXlmn3nqpiqjmRlGBzZO6HAIqUibKoQI/eM3gTaM5V9gHPKcJ8biJYW5uLpH0FqGk3x+GVRDzSG4N8pz86le/Cs+TKJPnsWQBLLbb7YQrK8AH/YU36v3TOob6WRMcKvDoAQDq4i/jSTZw+IUHMZkjf7WsBwK88hsjL5T5d6mL7xX4XFpasmq1Gqz1tJe5/vrrr63RaATlbGtrKyj9x8fH9vz581TviYWFhXDVLuABILNajklyidIH/9ZM28xfu91OJMpi3nz8vfJvv29QNvWzvqfv+BC5GMDL7/7MUJdcxkTr0HezeFi9LSJ0gTXs1zKKJbce+bNxFP3t3/6tff7551YulxPXu2K9XF5eNrMLjxIS5RWLRVtaWgo8qNvt2sHBgR0dHdne3l7C003XxPtyJlwlxZTSYrGYkB0xEpLXoFQq2a1bt4J8T5JV5Lhi8cLr85NPPrGvv/7aXr58aU+ePEl4KxUKBdvc3LTl5WX7+OOPrVarBZ5ETqWnT5+GhLl4rfX7/cTNH2keL9dx7kd56JjFQxbSZMMsekXsudjzPIN8wHd4BN+4cSN4I5VKJfvlL39p9Xo98APO5u3t7QBEM2+Li4u2vLxsnU7H9vf3wzlMjoOYPBhr+7j+pY1hGmV5btzYZa1rVJl63W4aXU2GtCui2KCkIX58B9PGDQ5lUAVGhCd1ReQQ5i9X8SEoTNLGUd9fFaVZMcwmAyJijMWPN4wdpj43NxesgyCBOtYqyMSUrbTNijDgNy/hLBp7WiqVQkwb1kF1ez44OAhXyCFoK+NHMWXey+WyNZvNIAwgzKvArLkIUBbUcqWWRfU8UOQUa61ae2OCPPOquTj8uFGnKmW4PyPYsPYB2kgImMWCEyOvJExLaUjr8fFxiCWNPbeyshKSrS4sLNjx8bHt7u7a6upqQvDc2tqyg4MDe/jwYbiO1QNi+nfaPl1HYeEypHs3tleVvDcGlgC1BqjVRsdKQ5W0Pg0183VRPv/HOwhlUOdXrRLsNw2R6vf7tre3ZycnJ/bq1StbW1uz27dvm5nZ4eFhcG/UfaIKIPtKLZl8z7ipt0OaZZ7/08c0ZZLnsIqaWQAn/Dmg8dxe4VTvPd+e2Fnr2+09I/jOJ/iLWdMBLElCSegHIAptY0zhwT6Pi7fqM8eAsuTQABAgtEZ5OX3waxBA6/j4OIQqHB0dBe9Ib8xQ/gsv99awtPHwFPt91P5L+03nl7oVGHobXmdZiRh55kUz5isoMo3Vv9vthjw7g8Hw5iT2GvyDeGcSuS4tLSVA0v39fWs2m6/Jim8LjH8XKU2hHQwGAYhmDWD9JwwUWVQ9KXu9XrAmFwqFhPWacs2SXpkqbx4dHVmn0wn5WQCEkNdYN9D7du6bTQYiTEJ+rmNjh0ESAhQHQEZuRZ5X4JewA/SEw8NDe/LkSUi8jOdquVy2Wq322s0wZnFPMU8eMIjRpGOWpczY89PUNQ1d2gMhhrJ4SrPITYOQZEV7ID0M5+bmgnLhD0mvnMKcNEEbbtHT0rQTOs3GjVk8+Dxpm2IAAgwbRNf/hmBMjPnCwkJQXAEUNEkUyj9tQdjCAkBCMwQGTcSo3iBkYMXaRL3qZsyzeDVoQjNVzkuli+sM2+12ULy9BY53iM/FmomFEU+JmDKO2xSxtaogMSa4Y2L5VAUKSyljBmCjVlkYH54GuNtRF8IQ40XZsIXrZIlK4zG6xol1Zo5Akf/qr/7KPvroo+B5gFcKLvCX7ed1tSxcBWGxJcbeW811/0DsUxRW3lPwEctvTJjwFlQtV5/z86CKJmUAGPjYZs2bY3YR79rv90MG+LW1tYR1U2/ZUBCgWCwGLwes6PAcf74Q048LNuFyqhRhcdfrW+Fd8Ezl4VhN8Hqi7EajEcaeM421D69Rzz2E6zSCdzKm+jk2L/THA6kxxVVBJXjsyspKwvrowxb1/yrWeEs841UsFu3OnTt248aNkJRrY2MjhKoBNFBeq9Wy//3f/w08HiCB+YmBD4w3603XrF/PmoyUvzGvgDRQX9eC97LRsU7j74DmKMPXlRT0yGLdHMWXdSxZA7dv37aVlZVwBRz77fDwMACKAI6lUsmq1aqdn5+HcLjnz59Hc118SGfEZSkG3Md0DpREfU9v5gA80MSl8MKbN28GqzQ5UVZXV63RaAQLt4bK9Ho9++GHH6zZbIb9BR/29L7Nc1a9xfP3LO/G5Lm03zwhk7MWarVa8EY0s/B/AAcN6+V3dBn0Pe/FNk5FHtfGNF15VDmjZN20d0eNm/KeLPWbXSMPhDeBhHiKCZvn5+e2t7dnZpOFHMQGfhZ9ygqkTINYzfpZJW851PIQSlEKNIGYWbIvKrykbR4FcNjgKqiptV4te4PBIFyjQi4Ef+82YESa9U+TH6kAp0q7Wv69wKvPctCoyyUCNyEG3mpHmdTDuHvXZT8WvKdu0FmsUd4Cz2/X6TBMawvt5Kodb2Ftt9tWLpdtb28vCIDTAAfXbTzeJOmaUMXPI/NeefTrlv2n4IEvj3+qSKvio8/q3lHlS8ECno1Zqb2V2fcZpZWYWUAn5U2eB/CuKoA6HvAF1pOW4UFKs+QeVhAmtq89f45Z47WtCkbo2MbGAkqzmHuPEf9/LcODB4xDDITo9y/cg8mCDk+l/V6Z1Pd1zypvKBQKIcaWcel2uwEABhgALCCJqr+eNW0OVGHnuVEgmF/DsfKyUFb+FLOoeeE/jd4mH9Q9Pss2cP1jp9OxSqUSvFSQA0iuhjJCcmjkilarFdZoTrOnmMyNEUZJE1DzjJ4fKIzcjKLX3XJekFtDgUxi5FutVuZ1977JC29alxtlmDYbeq3xOyHoyuNH8TQNE/Nn9DhgKKveluWdScodVZd+fhPrbuYeCEpp6Mk4pGXUAMYGZRqrelq5sywrrX3+mVluyHF1Zx0//d63tVKphIMTBgyDZRNyN7u6mJpZiD8lvEBJPRDYABqLWiwOr2erVqtBwPPxa94aU6/XbX5+3prNZuI5Mmprv+mXVwpwiUco1IRYXig2G3oDbGxshJwCPH9+fnHVGF4EWDIYQw9qoGBhKdQkf5AKmByW6q6rNxBo/gWeMxtaUbFgzVpAu2rS/pslBXaSpTWbzYQrHH0cd1DlZIlEh4PBIChbZhdjX61WzcwSaL4/vNmzes0ingcaVsMaJr4RizDlYnVSBY+/CwsLgT+wTzQLM/WyR9lf8C/to+4PysLlvVqthnvE8YrCwwmAgPXHGGARhkfBr/DO0Fs/VLlXd314K/1VAVfdeNULZzAYhPwsqtgSkmU25CFe8WXu4ckKNvj94mPS0/LlePCJctmLHiDSsvQ95ocxpHydP31HgWz1MlRARwEuxhfeq66zug49EKnAkAJFWndW8NLzJu2HB4h8XXoW+jFUUk+1D5mKxaJ9/vnntrS0FM5LeBDebLu7u4kbFjjb1ZMnpzdHafJzDIRl7/3617+2f/mXfwm50f7whz/YH/7wh8R7Kkvyf2RDs7hukEXnuY40qp1ZfjN7HdSfVq8ZpYv5urMaYdPKnkU702haAGHUc1na4nWacWsw7fdr44Fglg2t8ZM56eJ4m/SmkbksdFXt8ZiTt6Cp8Kn/90INFnlFCbUMtWZqtnQVKlWAKhaLwWVZDwtI3ZNiljKtn7JVwERQ9ZY9rBQqqPmx0THwQh/9UcugP/x0f9AmLYu69T0dw7Q58zcxxJSed4382JpZwu04I2aa0xjySmZMYdP17124PeCjc0PZft8oyMV+SOM9vq36l/p1jat1Si1W/ppaz4P0fa0vpnD7/aleRP436vT8g7bHxtvX45XNGMWU6jQvBF/2OEtHzJID3/EghIKgCt769jCmaW2M8fC05wBQvIeLV8THKdaTWHx0vLO8M+6ZWP80LE/Jj4cHImLr9EMjwi7VuonsQLgk/wiDe9fA9g+NPA9SHg74CAAbkx9igGdWel/XxdvUdy5Td8zgNwtKU8TfphfKVc/RzDwQ/PfQKJRuXOfSLOGTeDtMSuOAAFV2r2JysqJa454fhxp6154YcBMjBOqYpQ4FHpdf7ion4QwHsgqp6+vrVi6Xw4FNFtuVlRUzs3BNJvkTOp1OyJCO8IflpFqtWqVSCbdkIAT6u2KJswYQ6Ha7UeXk5OQk3PiAtYlEjAgM1Wo13D2tdVIHFkXyROD+HEvyRJmMHRaOWq1m1Wo1JO/RdppZIp5Lf8PC2Gw2w++MB54JPjcFHgocptcRFJuEGce8EpTe98M9bf9P02/WFmvZ5xLxwADrmVs+arXaa7HBZFfudDp2fHycWMNqAaK9rGGAR13jus8UlFNLsyqoHkzUPqBcwnOKxWK4KcUnRNV20naf00H5gYYteV5KH+GdzWYz8FTq0mStZsM8LMyHuvj7/hUKFzcSKDDif08DEOBtsfXjczIwD8x1DGSOlY1niI/Nj1nVPSiEkqceMJTtwZ9Y37xiPwp80PcgbR/t0jMyzSPBl+XPZoi1HBOAvQWK71nDOq/6O6Q3cNCGD5U0w7/+hRQsiIGJ74rV+X2hrHoEz8JnCGGdm5sLoUyjZPu0ffmh0DjreZpelkV/09+1vmn0m1HPZ6FRumQWfXYanXhcG2LlpL03Tj/OqkNeqQfCdd5Es0CnJgUIrgpQuKrDSIUo3+5xCoYqCgjiXrDp94c5BFRQ183mreP+O28pUcXYC6J8r8KRCsIxS5Ym1dHf1etBFRpNYOit/doWVSxYF15o1bHiUNJy0yywvj5vjeVZgAidp9iY+bJV0I3Nw9umafdB7IaF68zDrpKm7bd6tOja4zdffkwhj1mCVCD3fEQTx2n58BzW+DjPA91jkF8HMWsTCrG6uWvZ/NOQJtpEG/VZ+KWGOHggl/7FchPoP79ndey0r96ar+33XhOjiDK914YfDyXlIcVicawlX9+LWcrT2qn8P9Zu39a0Nqed4Wk8I+3cj50n2vZZ8J7Y3otRzINDv4+dKx8yzSIE4UM9W94mZTWGqcdBWhmxfZ3R1vpe0pswJHkeOw48mISyGq2zljULHfOqaJZ9HUdTeyBAWdElfca/O47S0JNx6NakTDz2bhY0ZxS6M4rS6vDfI6BmaU9aO2Io2bhnxpVPjD25ELAOaqiA3iSgbvdY5Gq1WojNpS7AB7Okd0OakoAFjrhqvB08AIAwi4WLMeUZ7vjmerZ6vR4sjsfHx9ZqtRK5EHwbsOr1+8NEYMQ8pwmeeFL0er0E+JG2FguFQsKDgpAN+nF+fm4HBwdmdpFvQoX2weAil0OlUgmx6FqHsgIUotiNJZPQODBqljTKqufpTbTpfQMq2E+sE9YViuX8/LwNBoNwpZVmx8bjBeu63qSiwEKlUgn7TXOnkF+BvAso4FjT8UQyG1rpzYbAhSrjZNiGr+Btwz5aXFy0wWAQvJ/wQCIvQa/XC55J8Diui8Wjghhp4qj1hhez4U0WfMe1UdycwLjiBaQ3WuA1hBu1lst77PVisZhI+siYMTbMi68jRgpmwAPxoKAuD2ISHsDa8AK6P4/gbwqy+DwKaZ/5ThVk325IAQc9X/ktjY/g3aDrKyYP6LmlbaEM/44HMRg/D4LzV+crZgUfRQrq6Fh+6MCBp6yWuveNz7/v5OdVQbQs8sO7Ms+zWJej9sA4y/yo77PQVey3NHl01DynyeLjPBXSyo3VM+sx0jaN6+9b8UDQymOCwPtMOinTggeTPH9VyKefq6zKnr/POs2SjZCiWdZh1mrNU7dbhF0tX93KvBdCzMKvghtCspbnrWEqwHmXXwRShFrN2aCghI4hdcS8B3wcuLrV+r3kBTodA0jLoX7Gg7YznvPz8wm3Xn1O6+N5X9c09LYP2zeJxsbqft94oSqrni8BHHrFRwEGf3B5hc+v57S9xX7R/cNvWkeWvclvo8qhLOqk7VqeXmOpn2OeDb4fHiBV5Vj5DeXrDTFe2aTt3gPJA5T+Ngb4pPbD0yh+4AVxbZMquDonHvjQECzl4Vko5t0yzjMl9p62yc+VPjtKac/CNz044NekL0O9WXRt6rjHAJFRbfN9zUGE6ehtn3M5TU+j+Au8+V2d31m1O0s5s5a1xinpo+ZlFMhw2fnM0r9JxuCqZcSrXL9TAwijJmgUcuPfT3t+3Dt8jll2+e2ySJV/1y/erJTVKjrqmXGW1CyW1iwI4bi2FYvFcHc5VjMsicRRquUIaxlWFyxW5EnA8lev18NtBXw2G+YM8C7I1Kn94zeEUBXyVfhTSyrWs0KhENqI4I2ngsYKU4YmalSLEQCDZk+n/kJhGD9O26mj1+sF74aYcEvfEbIZO/UiQCDlXmrG2uzCqlqr1RJ9WFxcDMCIBy2YQ36/TpS2r0ft81kdbqMOtXG88DoJIdPwRtZyDHjzIJxZ0l17fn7e6vW6nZ6ehoSW7E+1fvJ/vZ5VFUp/5al6OgGSQSjaZsM77jV3gIKCKNkKuOlNCLTTf15YWLBKpfKaVX9xcdEWFhZCzhRCIDwwgMcSuRH8zSnceHN8fBzGgFtnNDcA3h3FYjF4PSwuLibapPkZdD4Z75OTE1tcXLRyufwab4VXUgfzTTJEQAfmlnLxEInNpwdRKYN2auiY946KgTvqes5clkolm5+fD2stZun3inNMmffAAeUrWKTgmiaJVFKwif7hPaMAkIILCi558NyTAsPaHgWOaIcfM+17DiRk543Xia/nNJ5U5vXy8SidIgtdp3N+Fu3IortMWs8kshjj6fVF5WejdJy0OiapO+09v4ay6mIx42uW96dpY9pzs1qjM7+FIYtgmnWA0gZ6krqzDtS0isX7aGUcRzGhBFd6hCO1ZMWER7OkUIbyrgo6hIDLu/qcV1ZUMFVPA/WI8AKahjJ4K6gK3JDP5K/WH8ivCS+UIXBCWGdVqNfyAQ50/GOKnNbnrVSxKyIV+CBxm87VdaTLML/LMs5RIMFV1nsVNG2b9Mo7tWSjkGvYi7c2+32j/IJ9Puo2BgW4+v0LzyD2qFdKNS8Bv52dnb2Wy8AnJeV53O4VBOR3+kP4EeXAp/hNlUVtPwq9V4zhP7RRQ60oS8Mt+E6vbqTNmmhSeYTf3woGKMCiRDnKL1RRVaBW/3rhzivraXV5PuVJzyCvTKd5DWh/VbmO1e+JOfc31tAfX5b23/fbg7X6ewyEowz9f6y/fmxifdF9FPPOuY58KqecYnSZNXtVcvuHtn+uur9p5Y8CEca9fx31tTSddVqgY9zzvp5p6dIAglfy/cE0CcXAgiwW8SxW9GmRMx3sNKaTlRlpWWnI0zgrahrCNm7R+br9M5O0AeEVkKBWq4W8A+QSQBg6OzuzbrebUAT8LQCFQsGOjo6CUFsoFEJeBaxhKAq0G8EaaxReBdp+yvIKvwrU/f6FF4C2G+VEhXAVUokZTlv7aqnjd39fOBZLxqBcLtvJyYl1Op3EnHlwAM8DLYu+K2H903fJJq/9HAwu8jZUq1VbWlqyw8NDa7fbiXmeJV0FQn+dUP93haYdr2KxGOL3sXB3u107OzsL66vRaNhgMLzdhPpQtP2+QVkvlUp2cHBgvV4vkSHbK5x8z+0LCwsLtr6+HurwOQ/wgsIboFwuh32NhZr+qEdCuVwO1n3lQaVSKSjNXOOG5R7C06JSqVitVgu5ChTIAGAwS3p30JZ+/yKHgPYdnqU5H/A44IwiTwRjxbvMw8nJSeDD6lEAD/Hgps4TACPPQeolAM81S8brezCJ80N5K+OveXS0/TxDv3XsPGCgbVPgiTFkrPU93yb1GFCeCRgWGyv65/+v4WP6l7FhbXivOQ94xGQHvvfguX/H7yWdHzMLXmvXATz2fD3n8zldJU1ibHzf1mHWPqkOktXynZXS9CL9Lfadtj+LwTmmR43Sn8aV6ds8jk+Pa19au8a1gWez8sxZrONL38LgO5QGHlxGwc7SjmkoNoBpdWdZPFdJWRG2y25i/3ysXoRaBJCTk5NwLaG3BmlYgFrcvHLg3Vi91U29GjwooJsW4Vyt8wh7CMu8o20pFovhGkZVxnnOC15euac9aZsXQVQ9LBAW1bLHe4ACXKmo8c4quKPoY1n1Qq62DeEc66f2hTYxHu/SAfkutfVdJ5TXmBcLihpgmbewxrxrVLmEr7DPVSGK7XX2gvIrBQe9xVm9HXRvkqhQlUvvxo6i5etRhZXnlLcoDQaD4NUQSwBolrwtBCVXvaBinlSMfexMVld2r7hSlg9R8uELftzTlEvl5WmeBfzuv/N1afu0L7Q/9p7nWzGvFV9/jGKWeX+exIS1SciPu2+r/s1q/BhlBIgJ4Dzr9+N1oVgfcsppVjTtevoQ12EWQ+5V1pFVf1S+PEmbZgUKpZUzrm1ZFP1xoMgk34/7LSvNLImifjYbjwD5Z2KozzgkKIbyT6ssTzqYaRM6DkWL1Zn2eVz9SuMADu8ZEvMUSQMftK7BYJj7ALdZH6KgCgUC7MLCgi0uLgYLFjkQcHtWa1qhUAj5FBBw+B4BXO+t1phhLFcxSxaWR+pE0McboNvtRmOHfXw11ksUETML1wIpk2As1MUVITZm3WftMFaVSsXK5bIdHBxYq9UK/VhcXAzjggs1ruPETQOynJ2dhbhkfcZsGDaB9ZJ8CoQyZM3MPQnznXSfvY9o/yxoUr6V9flR482+xrNAs/cDLJgNATkFzdijatHFZX5hYcE6nU4ioz/rlD3lgTbdu2rd9lcoskcBJ7VtZhb6YWZh33Q6ndcAScqmLx6E4FkfgsH3PAcfYz+zl2kjXhqM9/Hxceij8lTtg+clCiLqLRco9twywXjDSxVQ8GeDWuQVPI3lR9H6Y+EEMS8B7bMCq2bDtUs/9QYNHX/1wtD5BWjSs8GHDNBG2qD1at2sAb9HNIGoXxve+q9rmN99aIT2wQNCjB1j5D0oGEMPerGPKJN39Rld4znldJ0plwtmR6OU11HPTqJvTaqjZfESGNWWNEXeP6PAegxsH7fOfL+yegmMMvZmLVOfzUppuuM0+2kmORDSlP0sA8nnSevT90Yp81nLmqQt45CkNMqKoo2rexq0LyYQapmTkE925bP4U54KIyioeAcg1Pms7erdoIq3CvTeumhmibAJ3kdIoh1q9ad9Oh7qTaD9Q0DDwsqzWPMR1HA7Vk8MhEn1rNC62At4PwBmEPrBdXCa9BGLKf3x3hkoRHxPGAiJ2Py80wZNyDgJU7nKgzwXEuJ02UNjmufYT6wNTcYHQKfPQaxRVfA0oR/hBWaWiOWnPewP3XuaD6RYLAYlWPcfz/f7w+SmtCemdHtPAvpCMkWv+MYAcMAPQEo8AxTwY+x8QkhVGimT5IoKQDIHmlvBzFKVPubJe0EpH2ceeS5G6vXAOHrrCO30PFqBhJj3CvMVG1N/3qsCPck5pr/7PvrPHsTw7Y3RKMMBY6BKe0zJpy0qI6lnmAI8/kzXskcJif788e3NKac3Tbmh4HoSvCtNqZ5WH5lVu3xboFm0KWt5acDFOEDDj12MF48b31kY5C6z764kiWJsQvnN/3+UEh5DYUahSiowxuoc1+5paNwET8IYs6B9HiHL0j4tO03IiT0bI3WnRfD03gII7Ny+wLxg1dabDRCC1Po3GFzc1Y6SbGYJoQmhHoHJ5ymIWabMLIRa0E6UdY1PVkEPhYd29Hq9BChhNryNoVqtJtyTu91uwuIPAICipN/jvbCwsGDVajXcrtDr9azfv8jQvri4GDwJNFyE/qnCBQhDbDRlAjz4/YVgenp6GhQbHyZxnWhaYWMWwvKbFHSum1Dls/jDi1hv3Jzi77nv9/uJtU3OEfZgpVIJ+QkWFxdtfn4+rFespnoTigJt6t1glhwz9ojGngNSEsajlljeU8WUus7Pz4PnFd8rv6BttL/T6YQ+9ft9q9VqViqVwliRR6LdbicADwU1NY+KB2H0alz66ttOmYwVpCAGdZ6enlq73Q5826+7mOLvx0G/1/YpYMN3mgxS58lb4rVMP7/+vNI6aDMUA21HKdGqaOu8eLDcl68gGeV4AZwyPeCj9bEeYx4vPmGlguYahqNjFhsTXT/jwKOccroqmrUCmoNik9MoWWMcWBD7PgYq+/JibUirP3bGxL7PspbGrYtxZWTRk8aVn3aGxdp2WSDjKmkmAEIaAGA23WSNQmpGLXQV+q4T8xg1sVnRpUkWa0yJHtWuNAEtrU5/G4C6JZsN3UZRuL3rL3H9Z2dntrCwEARjs6EbKkKlJh9U91m9OlLrpt0Ktvgs6tSJ8I/yoUIiilGpVLJKpZJQtgEKVKhX92qzIUDgPSx0LHgfIR/lJmaV0zGiL2q5ZB7oH6ReF4QsKHlBWbO+X7d9BE3bpln05U2Ox3Ube+/+zNpRQMH/ZW31+/1EiA+8gNAFwDK9iYB97m9JUJdt3PAJj1ClWL2fVLn03gnekgsvwWNHr3OE1+he13fU80BDDbzXE+V5d3qff8XfIOOVXLMkL9D9rYqmAgCMhZ6r+mxsTCDfHw8sQL6c2BnjPQ58n9IEUy1H/+pvMU8R5cOet8UAE+2v/17rYV5i52UMuE/zHPCeBt5ThPHUsvz465mh+9Cf1X4vKRCVgwg5vUm6bufch0jjlPpRgMAkNAsl97KA0yT6qdJlgYMsZXsaV1cMjJimnmlpJrcwTEP+wI11TBesBxFi5V22TWav5wbI0s5JFtaodo4TQrLQJItpXPlpZaDkq+eBBwr4nfvQvYsqArZmAteytS5vPdLcBsRheyV9YWEhZCr3Sjx1+j6qoHZycmLtdtsqlYo1Go2gmHBbA1ZM4pN94jHKJ55aPRdot1qQuKu81+slLEoeNDFLWhvNhpmzAUUAXfBUoO/eEqnCPe/iJeKfnZZmAUJcVyAjRtO0ddw7Wcsc9dwsDn+1iKoSz3rzoBYKN+3yyRcJq9FYbrxkvELtkw3SDpRwAATaUy6XQ/gPz+l+0varEq+AAR4HKMyabJH28w4eDexFDW1SMBNPK4AG9RjQPrJv/XW2yse0/exhteJrHWqpUTBF2xdzi/fkFfA08EDHgPdiQIcq6AqWMHZ6tqads4BCkD9HvXeaPu/L0vb69RIjfd7X69+jXwqSxMpS8EUBghjo4teXPoeXh7YRME7r5vu0Wy/eFXqXzomcro7yNTB7GiU/ZFFyJ/nd83nPyyHPP2N62qQ6Waw8byxIq2NcnaOemxTI8GfANDKnL2uafTPzEIYspAedLpKskx57bpwSPA50gCZZlNOiZ5OiTWnAQuz3yyoKMYDDl8VnFAcvmJoNlWJ12/eWDr0uEfIuuGxef+sCvwNOeEFOr6MiPwIWUFyoNTZ4MBgEwIHyK5VKSHKmrr3tdjuh8PicCbRNrUVe2FZroI4BdXHVJf3C3VfHSq9gU5DCW7BogyaxU4uXjrV+ngXN4jB/lwSCado67p2sZY56bhZj6NcU6967jpsNlRL+j2KOIu7BLs0V0O/3EwlaNfzGew7QL4C8SqUS2losDvOSaPt5lja32+0QNqT7Av4B+FCr1RJjof9XLwkAOG0rhMeUAo5eSeQv9ZdKpcSVkgpgqOKvQAJjBT/Rc8eHoMArFWRII8rU54vFYgAreUb7pv3yn3UsR52N+r1/JqbsMg4KxupvaUD7qLKUxp3HSmm5KdKEYS9naOJGHWN/dS/vekDFt1d/03CWYrGY8LJ51+hdOidyyuldoizAwaT7L4seNAkQkFbHqHfH6Uv+/Zh+5J9Lq/OyfYnVexmaBb+cyS0MZqMV9Fl1WMuchjzyPss6p+mjLzdLGd7aMO65WH1eEM+KoEEq2PK8ur4jZGIBQWjW99XCpEK2CsReUdB/KlyphZEyeIaQg1KpFJQUFIVyuZwQ3gEY+v1+yB2AJR5l5/j42Hq9XrgpAQBBvSzM7LWxSBtbf50jAn+5XE4ABrTLu7ZqKIa3WPEcfffhHig+ADleeL7uAllucXo7pEpZmtXaW0rZh7q/AAnMLvYe+9JsCKSZDcEtLOlmw/3AdwsLCzY/P5/Is2BmAcRU3sFNK5R/fHycyLmgOUXMLNzoUqlUAtDIPku7hYArWBVgNHs9P4QfU88P8Ryq1+shp4KS8pnYeTIYDF5TNPlex3ASpVE9IJgPD5RoXdSjayLtWSzhSt4qrgAz7/nzRV3zFWDNcnYqxfiitkXb7vulyjzlKH9O2z/eY4B15Pvn69TzJ7YW/Jnv95S2Oaeccsopi5I/6t2r4CXK27PoczHZe1TbRp0PMVk+9nxMrxpFabLsVejQsyxrZh4I01q/siyyWblrxFD+UTQOdVPBRJ+/DFoWI19e1oWZ9p5ZUvhKez6tDhU4B4OBdbvdhPXt9PTU5ufnw1WE8/Pz1uv1QrJCLRMFVoXDfn8YHqG3Mvh8A7QXJZq6Ed5x4dV+zM3NJRIwKkihFjW1+h0eHiZAExImaigFbdY8A17hV6UI4MDfvsB7evWiuqOSN4L+MT5mQ0uVJmpTQpkgpwPzgUVY20tb9brM60Y5ePDmSRVo713DelMlF3DMbKg8s0/NhooY+4rcKIT+eO8irZdwomKxGOrmiskY6f7Gu4c1pKABexEQAiWw2+2aWdLVXpVw3aO8B7DKGNBeTZCqYwZvwnNCwQ310lAvI/ifgg7q/eGVYH/7gu+DV1g9we8UjE07K1Vx9cpyDLD0IKjZ68kwvVcB86UCpbrle9BF2zeOh3hAWIFe33bfXh17wDPvuaL1+Paz7jSfxqi2K3jAuNNelU30Xb8G0gDBnHLK6cMlz2+yggOjdKhRCrw+E+OtWevzBoe0OidV9tM+jwLR09oZ+923R0Hf2HPjzrJYv2cBJLyVEIY0GucCEns2Rn5yYt+nlTOLSZglqBB7zyNvs1gIfsxHjYNagDQPAfeLoxSbXVgAcf1VLwH9662NanHUOGoFLVQYU2ugCtEox969Vt01tT+Uw1Vs5FHodDrBgko/1fo/NzdnvV4vkdld26iWIc3poACBz/KNstDvD6+7pH+MFzc90G6e73a7ViwWrV6vW7FYfC3fgnpOMEYxAd1b9nJ6M/QmPCsmOTA9ofyrmz77xizpsq0WTl3DPps9YTsoeyjY/qYEzTKv3kW1Ws2Oj4+t1WolnlfyQKV6A+geRCHVMCjtN+8rCMFfFH14oYYXDAaDcBsD4AR18pl2osRruezvmOKoSm1MMdff+F2TwfpQrLR1obyLOdUxitUf84pCIda6lN/56ylVKda1y7PeSyEWTqbghI5ZrK8xrwD1JBg1PirkAtqO2m+x8VJSMCdtjmNlpvUv9m5sXeWUjd4Ev75O9KH1N6cLmmTeJ3k2piN5EGHUs9OQfz+rN8MsaBSYMMl7+p0HhseNv5cJpqXCIOOo3blzZ6KCJ2Uyo6zfow7fLL+l/Z6lHN+PUahZ2jOT9GNUWZMo+eMoDayJ1Z1Wj7++URVn764JoUSgGJglhXcV1MyGlnoU3EqlEpKvIbhrPgMvzCrFYkbVQuqzzOuVXF7p4WpF6vKuyoAWKCPdbjehEOG+rR4PJycn1mq1gudGr9cL3h1K+m6hMEzIhsKDcI51U+dDwRrGmDHQvnKLRC4o5ARx9eDR0VHCuwdADS8APGBG8U5dj/q9AnGqBMJruN7VA5AAgrRL3bzVA8BsqFyipHY6neCFMzc3FwDPg4MDMzOrVqtmZoln4EGe30GVSiWEIfX7/ZAsUnmG8lf2uVc2fT9OT0+tXC4H7ygzC14byksAVGP80Fu+UcBVUb3svvfCXwys1blXHpRmafdgrAdlNURLLfr+NopY2Wqx12cpyycjjPVXlXAFL3QstI5phGHK0FAE1v6os0/f17rHfT8p5cplTjm9fzStDpalrHFG3En44zi+FmvrOH0ta7veBN+bZqzTnh3X/gcPHowt/1IeCOMGflzjJxnwtGfTvBVmYZXXssahOVkpy7Ox+qZFrbK2aZL5QLHG+o3l0WwYs6tu/efn58FS6C1B6gaswpVP9OWRNbWcqbCnSq9aK/U7vfNaBWgf4oJnBdZAtQgipKsQq3Xp98XihcvyYDAISdAqlUqwutIv7cvCwkIAIWiXuiqrsqFWXZR/vjcb5jrwwIEmfkMJ8ZbFWe6j94k+REGZ0CCvFKIUs2bgC2avx68r8MX3mp+E/aU5CqiL9YjlWsv3XjSad8WHG+hzCjAAgJol+asHJzX5Kn+9VVvDBHRva84G3aP+zGSPw88IN9LxxAPEK7f+HKadCpQyHp6nwENi4C+kimoWIcrbKBQ80Lq1rVoefAoQybfP55FRL4RYyIRX9nUOPanHQ6x9sb6qku8tW95Tw/N37benLLxY68wS9qBtUSNAWuLHUZSfFTnl9OGRApl8TqOr5hEeFM5CMdD6Ktql9V0XuqznxaUAhEkOuVGCxriFF1sQ+uw4D4G0uqZpUxpgMa69k1Ba32KfL2M5GFXPKMLNeH5+PmGp5950bVulUkncm44Con81BIDxVatfsXjhjt/v94OrL2CBghfqucAzCPMqaKtybzZUNjQjvJklQBCE/l6vZ+12O/QdxVuFVs16DnCAxwKKUrPZDFZbFTZrtZoVCgXr9Xoh/lmvijw7Owt1qxBOPLiZhb+aYVvHEoWm2+2GXBXqNq1r3AvaHwpl5UkfErH3Wq2WnZ6ehr3trc3Ee6NIeauvegvo/kV5we17YWEhrMdqtRp4jAKQi4uLdnp6aoeHh7awsGBLS0sJMM17EakSbmYJnoRC3mq1XrPumg29IOAX5CkAFNTrXPE4oF9+vahFXq3J9LnT6SQAznK5bCcnJ4FPel4LaBgToJQHQefn5yHUySveaYB8zELvz0yUdg+MQD4xZkyR915oWn/Mm0IBUeZU25pGehbos7o+AKnh8bpetb2aq0YBBNoDeWBKzyV+82EeMc85X55fYxo6oyAIz3n+psD+tALlh8gTc8ppGnpXDBCjPJam0R9iz40zPGfRuWLlT6NjKvk60wD5tOen7cMoSmu/H7MYSM73aefoNHQtciDManAv2wZoVm2ZhEFc1RhcBaPyFmz/vVoYUfLVSqa/AyCYvX5NnD6rGc29VUjr9oRQyziMEiq9xYo2YTXUPAUq5Ood82rZLBQKIdQCKy3v4Znhb0TADdzHZ2uSQ0++bg8Y4PnhwQF+J8u8Wk555k3FheV0/Yk9zD5UrxazpEXeX+FollRWYsqjpxjwQG4EvkNpJ7EjhOXaK4NKGh6g7dTwIwU1dP/pLQu6/5Q3aHJST6MEHfWEUK8H6tLx03eUryrFeB58zSuZozwPslJMCVXQh89e4fUeI/pP+ZaOgb7LuCnf9GWbWWq9WrcXEmNeFNoW9QCJgWa+Xp71QqnOu/eKG2VA8eCR9m0UD4/1/11QbHLKKacPh8bpR1fBs2atk2Vt47Q6W9b3Lnu+J8oaZNQQJs2BkNOHQyxc767Mb17g879hhVFSJdhsaF2axLXSC8TesuXLjAl6vk8oBigQWVBIdZmm7DQgRJUelAR9xis9WAFHoa2xz1q2F8x9+3PKSUmt+1kUpaxeYXzPflFFWi29SppgtFgsJq6K9BTjT7F2jgrf0TLSUP9piH3tLfjeHV/DQ2JtNxu97/msfNArsVdJk4zRuPl6k3QVbcnqPThu/+SUU0455ZRTVspy9mTJgZADCDnllFNOOeWUU0455ZRTTjnl9IFTFgAhz3qTU0455ZRTTjnllFNOOeWUU045jaUcQMgpp5xyyimnnHLKKaeccsopp5zGUuYQhpxyyimnnHLKKaeccsopp5xyyunDpdwDIaeccsopp5xyyimnnHLKKaecchpLOYCQU0455ZRTTjnllFNOOeWUU045jaUcQMgpp5xyyimnnHLKKaeccsopp5zGUg4g5JRTTjnllFNOOeWUU0455ZRTTmMpBxByyimnnHLKKaeccsopp5xyyimnsZQDCDnllFNOOeWUU0455ZRTTjnllNNYygGEnHLKKaeccsopp5xyyimnnHLKaSzlAEJOOeWUU0455ZRTTjnllFNOOeU0lnIAIaeccsopp5xyyimnnHLKKaecchpL/w8geIpm6kdWOwAAAABJRU5ErkJggg==",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "nb = 8\n",
+ "grid = torchvision.utils.make_grid(\n",
+ " torch.cat([images[:nb], reconstruction[:nb], manipulated_images[:nb]]),\n",
+ " nrow=8,\n",
+ " normalize=False,\n",
+ " scale_each=False,\n",
+ " pad_value=0,\n",
+ ")\n",
+ "plt.figure(figsize=(15, 5))\n",
+ "plt.imshow(grid.detach().cpu().numpy()[0], cmap=\"gray\")\n",
+ "plt.axis(\"off\")\n",
+ "plt.title(f\"Original (top), Reconstruction (middle), Manipulated (bottom) s = {s}\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "9cf8fbf9",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "if directory is None:\n",
+ " shutil.rmtree(root_dir)"
+ ]
+ }
+ ],
+ "metadata": {
+ "jupytext": {
+ "formats": "py:percent,ipynb"
+ },
+ "kernelspec": {
+ "display_name": "Python 3 (ipykernel)",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.10.14"
+ },
+ "vscode": {
+ "interpreter": {
+ "hash": "4f1513a79f82193cb81c96943579af15c6a44d6347609348bde584197ab7b1ab"
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}