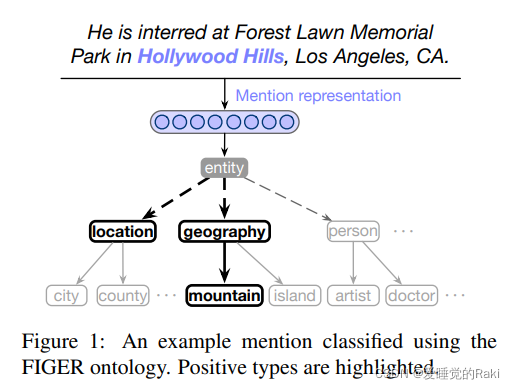
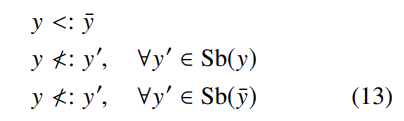一个树状层级的粗粒度到细粒度的模型,拥抱了本体论结构(?这是什么)
- 研究任务 hierarchical entity classification
- 已有方法和相关工作:FET的进展主要集中在以下方面
- 更好的mention表示
- 融入层次结构
-
面临挑战 研究人员提出了替代的FET方法,其类型不在类型层次中形成。
-
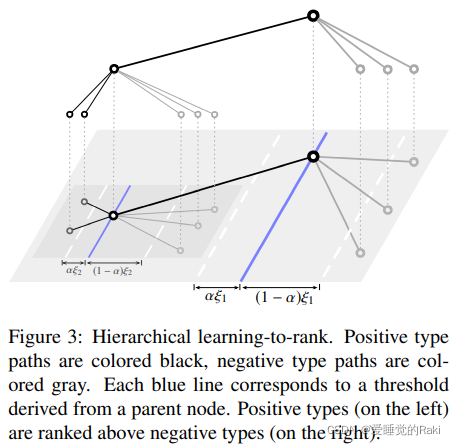
创新思路 提出了一种新的方法,将明确的本体结构考虑在内,通过多层次的学习排名方法,以给定的实体提法为条件对候选类型进行排名,直观地说,较粗的类型更容易,而较细的类型则更难分类:我们通过在排名模型的每一级允许不同的边际来捕捉这一直觉
-
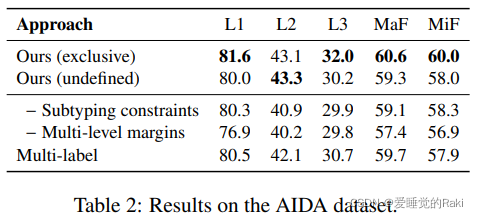
实验结论 achieves state-of-the-art results according to multiple measures across vari�ous commonly used datasets.
首先,使用mention中的词的表征,得出一个mention表征。我们在线性转换后,在mention的顶部应用一个maxpool层
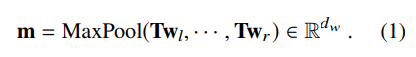
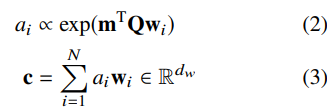
用一个两层的fc,并与y的 type embedding 来学习一个 mention 与类型 y 之间的 embedding
本文提出了一个novel的 hierarchical learning-to-rank loss
- 允许进行自然的多标签分类
- 考虑层次化的本体
首先从多类hinge loss开始,将正样本排在负样本上面
这是用ranking SVM,模型学会去将正样本的y的排名高于一个
然而,这种方法认为所有的候选类型都是 flat,而不是 hierarchical ,所有的类型都被给予同样的处理,没有任何关于它们在类型层次中的相对位置的先验。
我们通过以下方式对这一直觉进行编码:
(1)学习只在类型树的同一层次上对类型进行排序
(2)对不同层次的排序模型设置不同的间隔参数

给定父节点的情况下,模型应该学习到接上一个正确的子节点的置信度要高于其他的负样本
总结就是:"一个正子样本应该比它的父类型排名高,而它的父类型应该比它的负子样本排名高"



- 正样本的的分数应该比所有的父节点高
- 父节点的分数应该比所有负兄弟样本节点高
- 正>负
本体中的每个类型y∈Y都被赋予一个类型嵌入y∈R dt。我们注意到类型上的二元子类型关系 " <: "⊆Y×Y的类型。Trouillon等人(2016)提出了关系嵌入方法ComplEx,它能很好地处理反对称和传递性关系,如子类型。它之前已经被运用于FET中--在Murty等人(2018)中,ComplEx被添加到损失中以调节类型嵌入。ComplEx在复数空间中操作--我们使用实数空间和复数空间之间的自然同构,将类型嵌入映射到复数空间中(嵌入向量的前一半为实数部分,后一半为虚数部分)
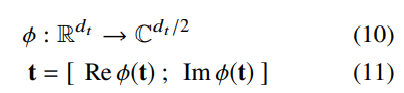

将这些关系约束转化为原始SVM下的二元分类问题("是或不是一个子类型"),我们得到一个hinge loss
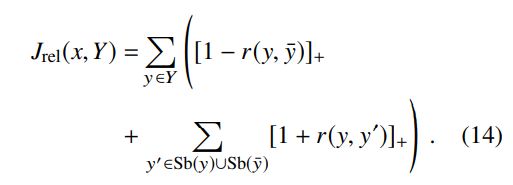
训练对的结构:我们使用兄弟姐妹和父母的兄弟姐妹作为负样本(这些类型比较接近于的类型),因此在训练中使用了更有竞争力的负样本。
我们的最终损失是分层排名损失和子类型关系约束损失的组合,并使用L2正则化
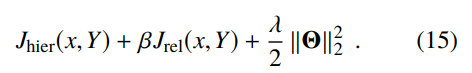
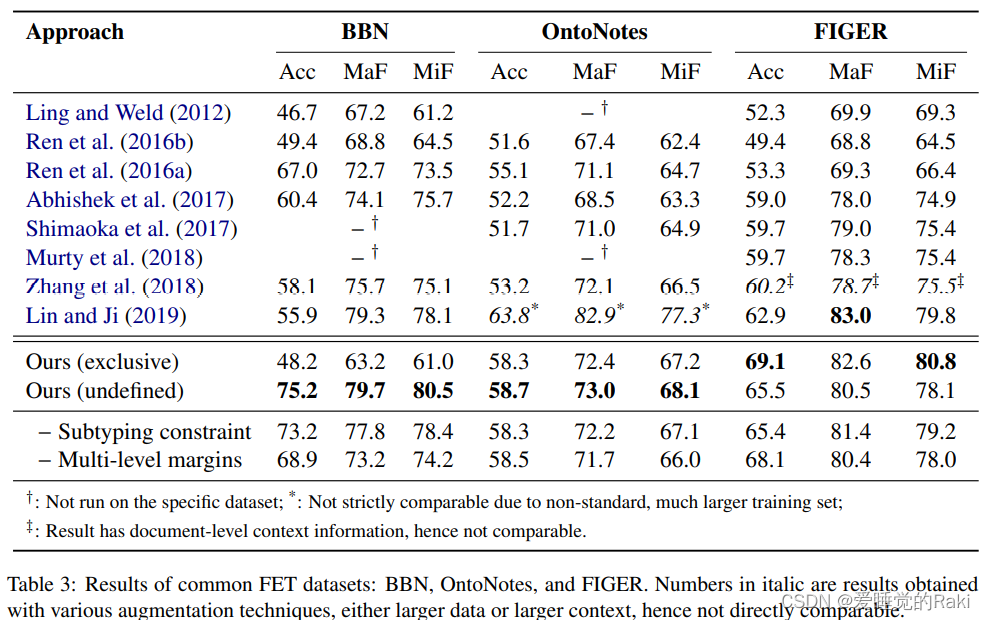
我们提出了(i)一种新的多层次学习到损失函数,在类型树上操作。和(ii)一个伴随的从粗到细的解码器 以充分接受本体论结构的类型的本体结构,进行分层实体打字。我们的方法在各种数据集上取得了sota,并在严格的准确性上取得了实质性的改进(4-8%)
此外,我们主张仔细研究部分类型路径:它们的解释依赖于数据的注释方式,并反过来影响类型的性能
第一感觉就是,这篇paper真的很抽象很难读懂,一字一句读了很久,感觉自己还是理解的不到位,属于是我目前读过的paper里面最复杂的,method部分满满的三页
方法我觉得并不novel,用树形结构从粗粒度到细粒度,但是能实现出来并让它work确实很厉害,这就是约翰霍普金斯大学的含金量吗orz