README.md

flash1dkmeans

An optimized k-means implementation for the one-dimensional case.

Exploits the fact that one-dimensional data can be sorted.

For the lower level functions prefixed with numba_, Numba acceleration is used, so callers can utilize these functions within their own Numba-accelerated functions.

Note that this library is not an implementation of optimal 1D k-means, which is known to be possible through dynamic programming approaches and entails $O(n)$ runtime. Instead, this is a $O(\log{n})$ optimization of the commonly used (greedy) k-means++ initialization and Lloyd's algorithm - thus it should run faster at the cost of possible non-optimal clusterings.

Important Notice

This library utilizes Numba, a JIT compiler, for acceleration. As there is a compile time overhead, the first invocation may be slower than usual.

Numba caches the compiled functions, so execution times should stabilize after the first invocation.

Features

Two clusters

Finds a Lloyd's algorithm solution (i.e. convergence) for the two-cluster case, in $O(\log{n})$ time. The algorithm utilizes binary search and is deterministic. The convergence is guaranteed, but the global minimum is not guaranteed. Desirable when a very fast and deterministic two-cluster k-means is needed.

K clusters

Uses the greedy k-means++ initialization algorithm to find the initial centroids. Then uses the Lloyd's algorithm to find the final centroids, except with optimizations for the one-dimensional case. The algorithm is non-deterministic, but you can provide a random seed for reproducibility.

Time Complexity

For number of elements $n$, number of clusteres $k$, number of Lloyd's algorithm iterations $i$, and assuming one-dimensional data (which is the only case covered by this implementation):

• Two clusters: $O(\log{n})$
  ($+ O(n)$ for prefix sum calculation if not provided, $+ O(n \cdot \log {n})$ for sorting if not sorted)
• $k$ clusters: $O(k ^ 2 \cdot \log {k} \cdot \log {n}) + O(i \cdot \log {n} \cdot k)$
  (The first term is for greedy k-means++ initialization, and the latter for Lloyd's algorithm)
  ($+ O(n)$ for prefix sum calculation if not provided, $+ O(n \cdot \log {n})$ for sorting if not sorted)

This is a significant improvement over common k-means implementations. For example, general implementations for $d$-dimensional data using a combination of greedy k-means++ initialization and Lloyd's algorithm for convergence, when given one-dimensional data, spends $O(k ^ 2 \cdot \log {k} \cdot n)$ time in initialization and $O(i \cdot n \cdot k)$ time in iterations.

Note that you must use the underlying numba_ functions directly in order to directly supply prefix sums and skip sorting.

How fast is it?

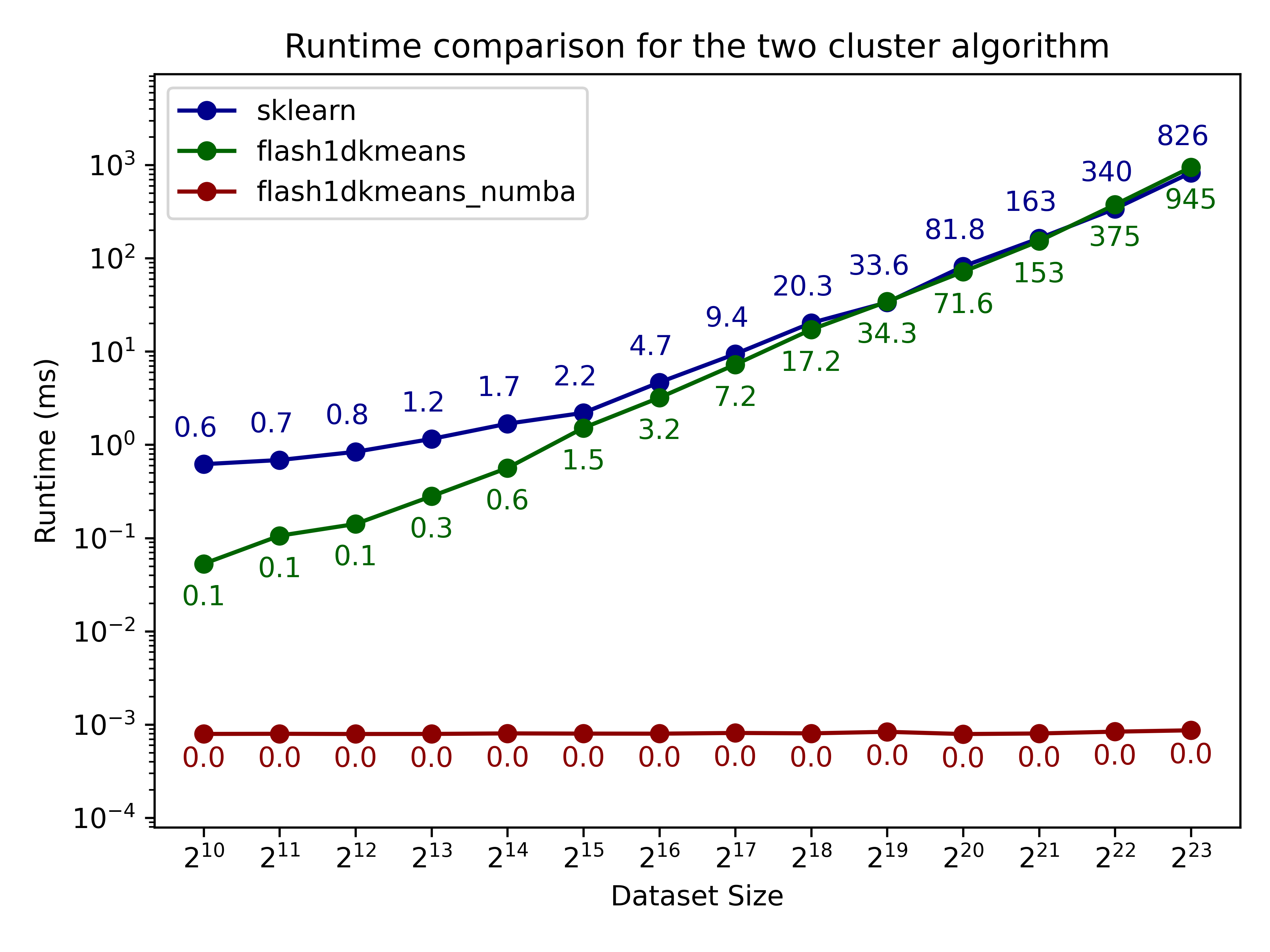
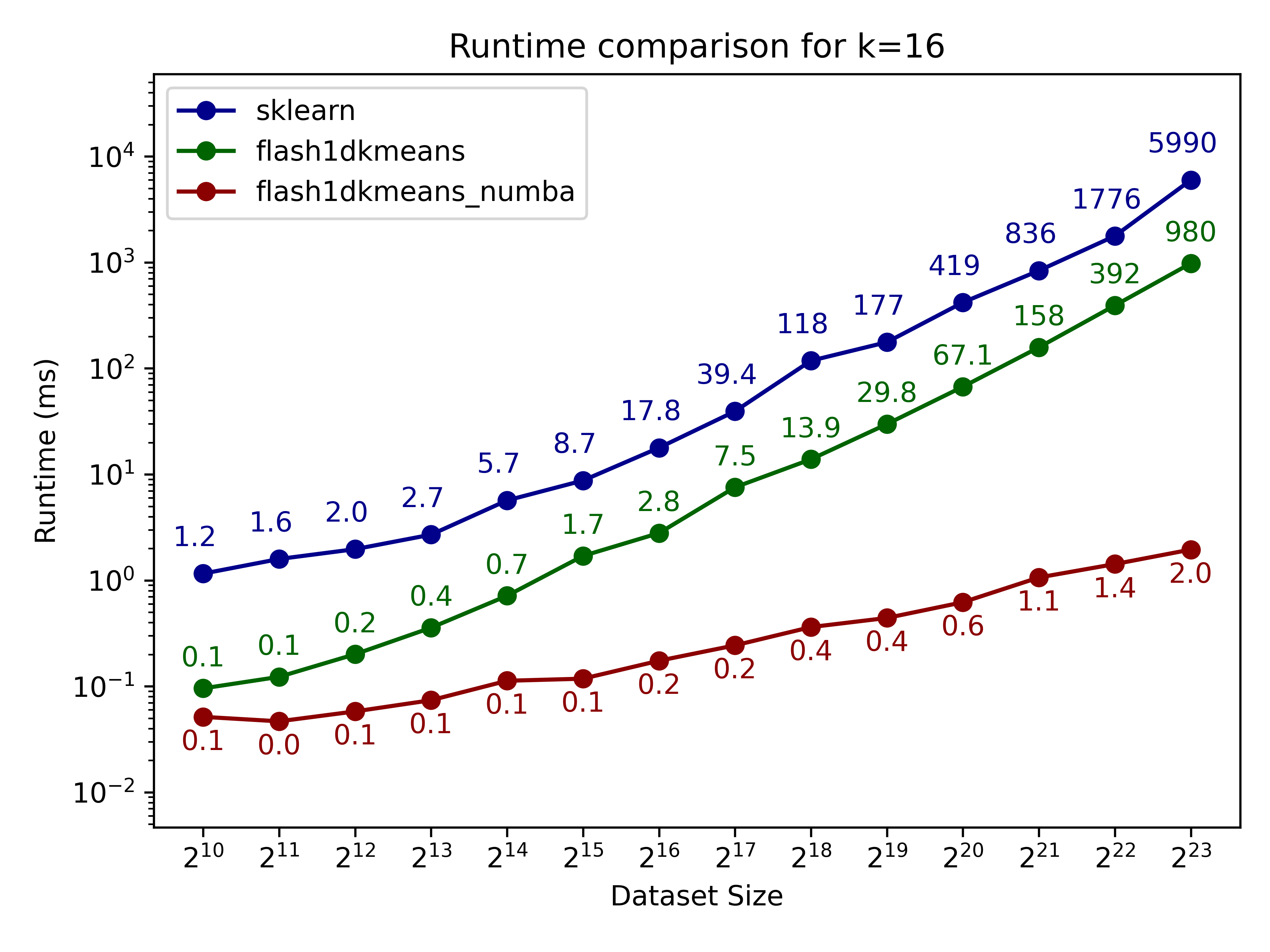
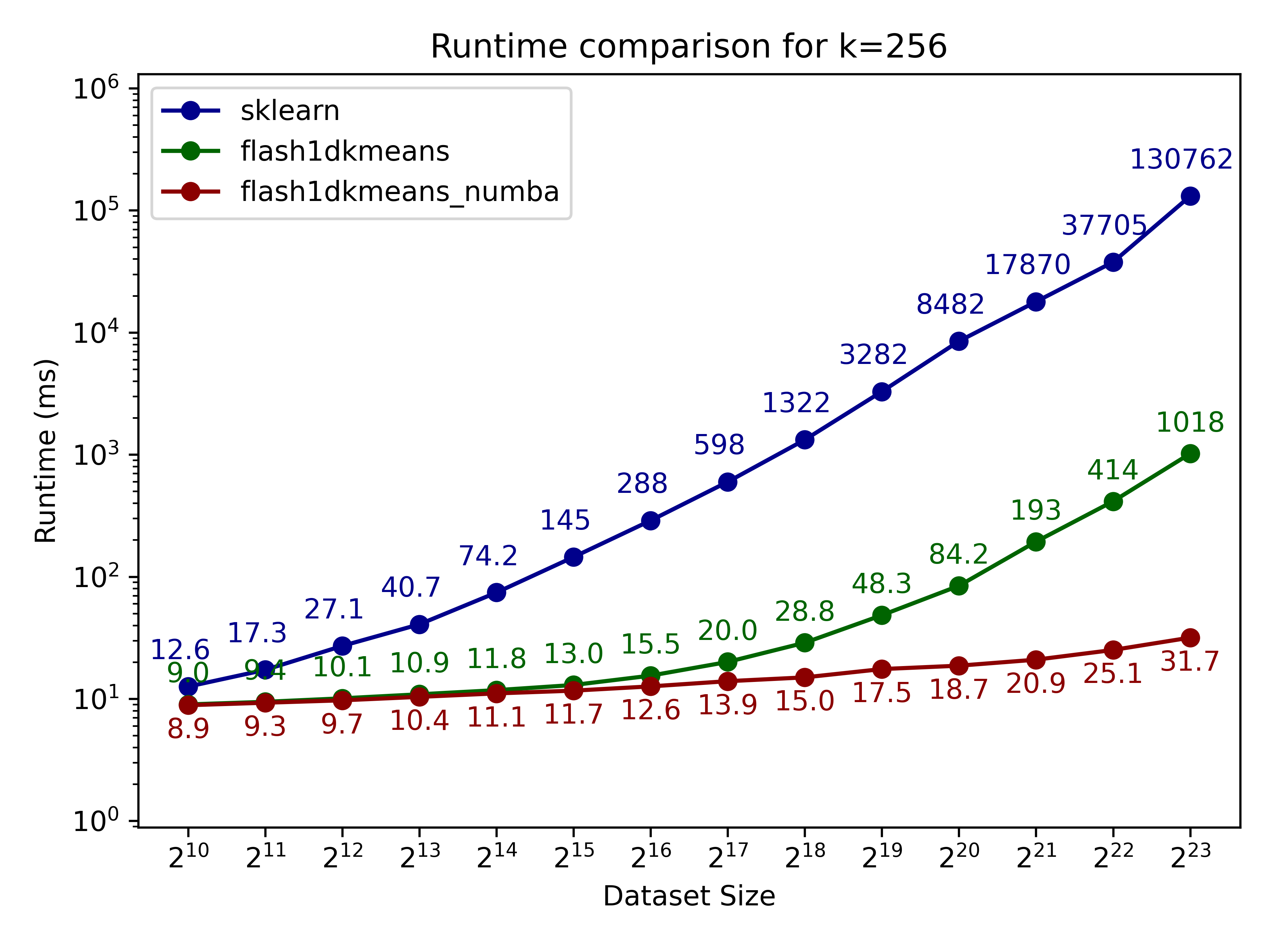
Here we compare flash1dkmeans against one of the most commonly used k-means implementations, sklearn.cluster.KMeans.

In the figures below, we show the k-means clustering runtime on randomly generated data of various sizes.

• flash1dkmeans measures the wrapper function kmeans_1d, which includes the sorting and prefix sum calculation overheads.
• flash1dkemeans_numba measures the underlying Numba-accelerated functions, excluding the sorting and prefix sum calculation overheads. (A case where this performance is useful is when you only have to sort once, while calling k-means multiple times on different segments of the same data - or if you already have the sorted prefix sum calculations ready. Both happened to be the case for Any-Precision-LLM.)

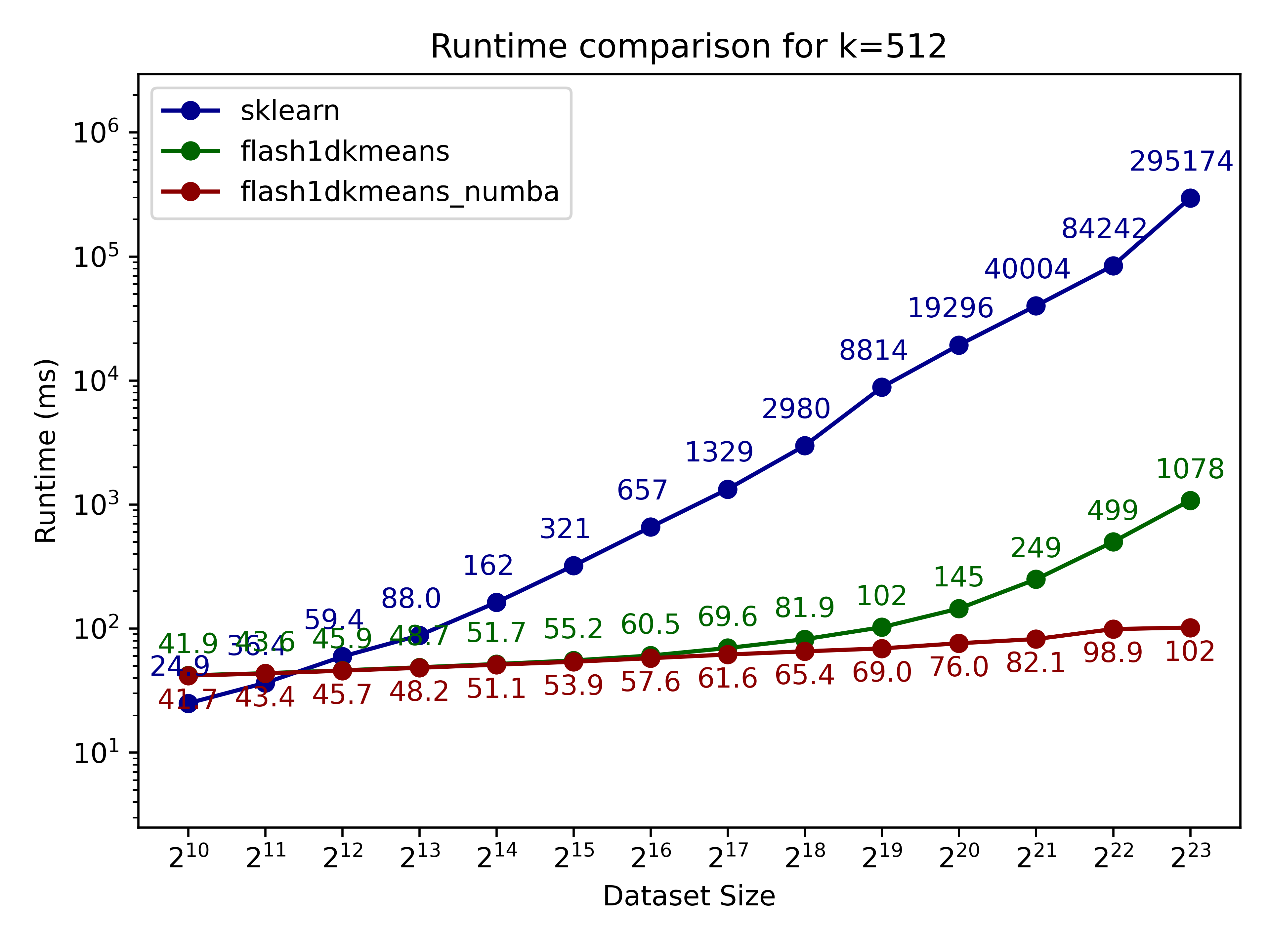You can confirm that flash1dkmeans is several orders of magnitude faster, even when measured with the wrapper function, including the sorting and prefix sum calculation overheads.

These speeds are achieved while running an optimized but mathematically equivalent algorithm to sklearn’s implementation for the k-cluster algorithm, ensuring identical results apart from numerical errors and effects from randomness.

Additionally, you can see that for the two-cluster algorithm, the algorithm indeed is $O(\log{n})$ - the Numba function's runtime barely grows. This algorithm does not use Lloyd's algorithm, but converges to a Lloyd's algorithm local minima in $O(\log{n})$ time.

The figures below compare the squared error of the clusterings on real and generated datasets obtained using scikit-learn. Results demonstrate that flash1dkmeans indeed produces clustering results near identical to those of scikit-learn's k-means implementation.

Installation

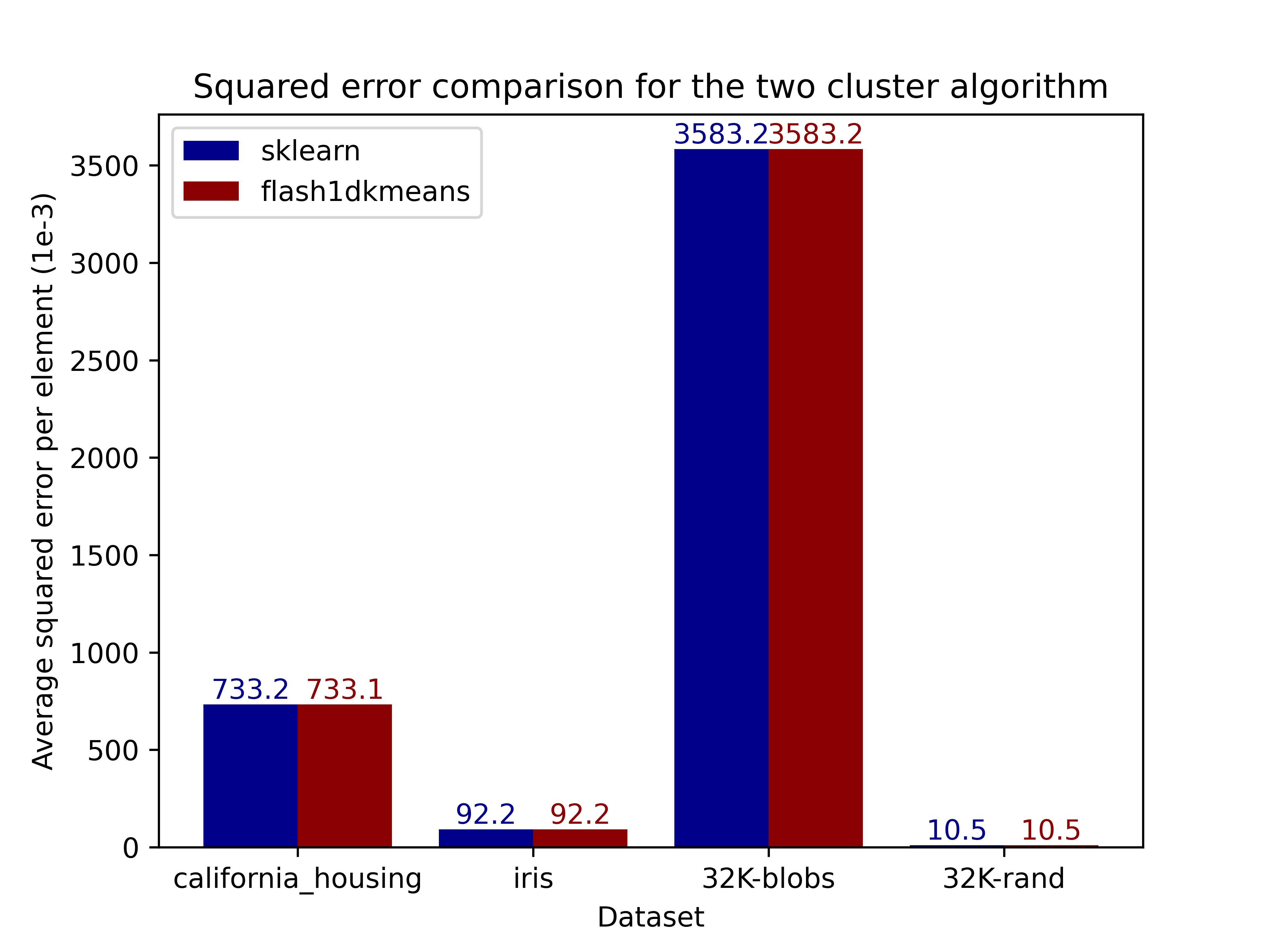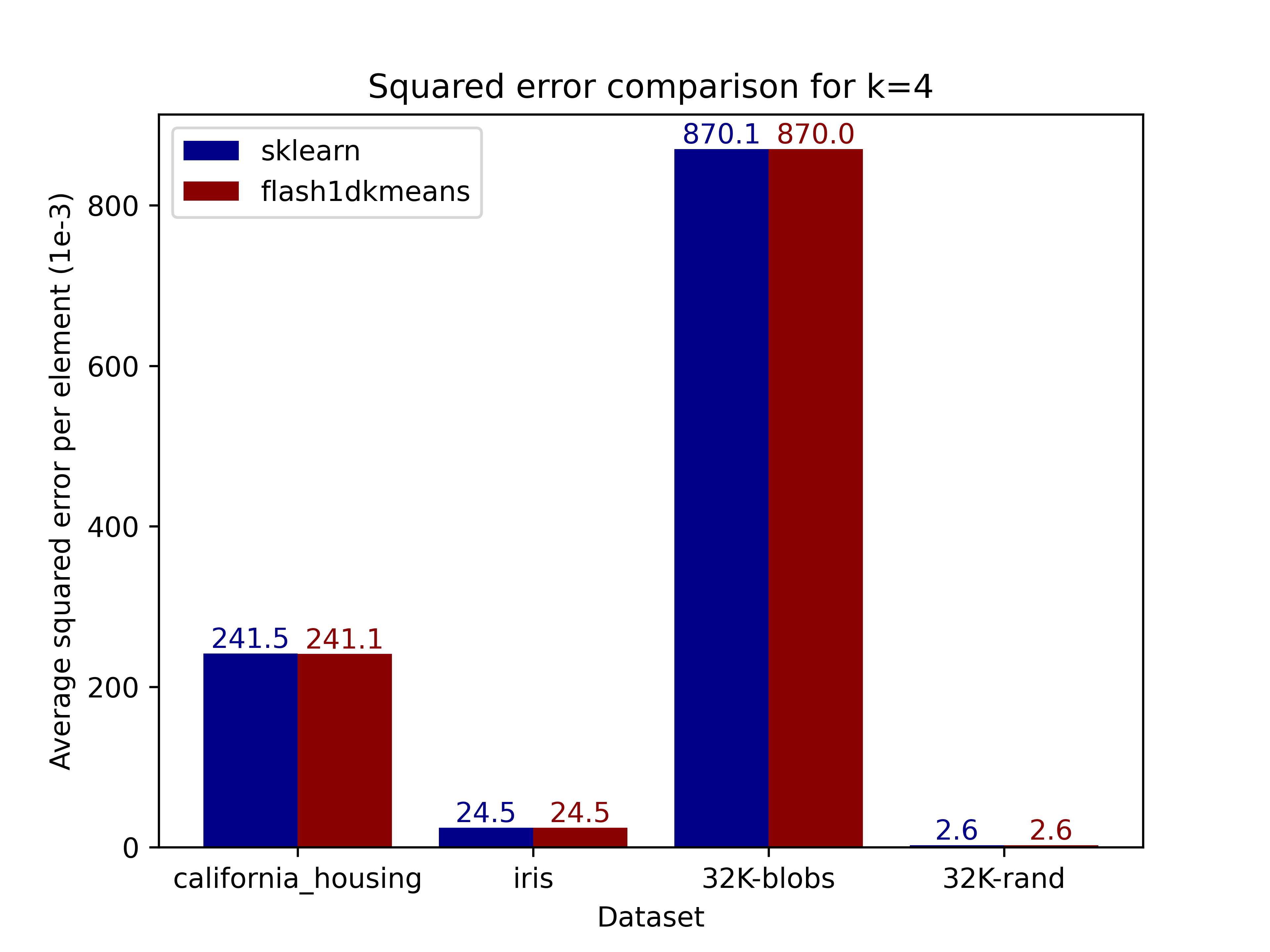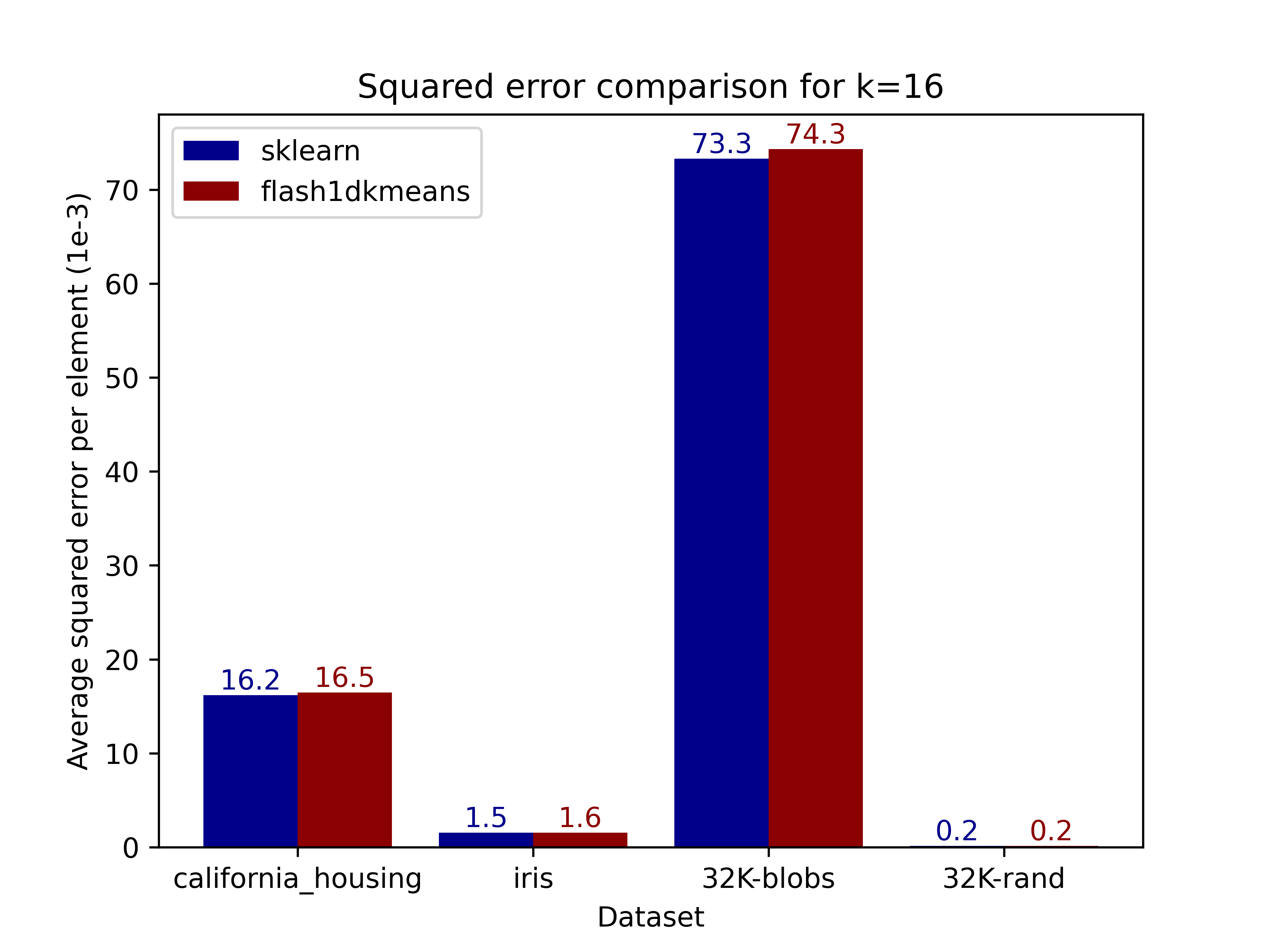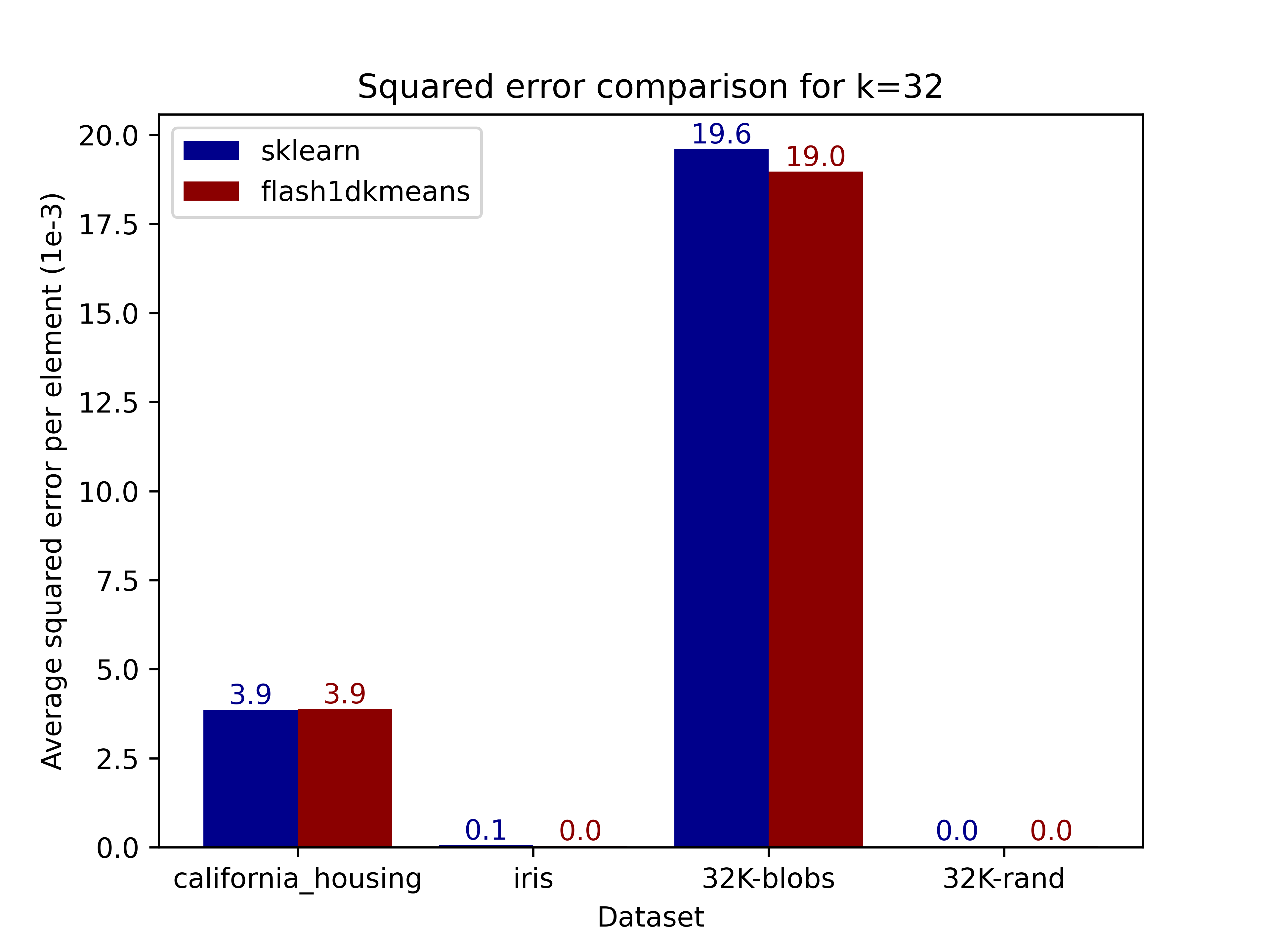pip install flash1dkmeans

Usage

Basic usage

from flash1dkmeans import kmeans_1d, kmeans_1d_two_clusters

data = [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0]
k = 2

# The optimized k-means++ initialization and Lloyd's algorithm
centroids, labels = kmeans_1d(data, k)

# The faster two-cluster deterministic algorithm
centroids, labels = kmeans_1d_two_clusters(data)

More Options

from flash1dkmeans import kmeans_1d
import numpy as np

data = np.array([1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0])
weights = np.random.random_sample(data.shape)
k = 3

# The optimized k-means++ initialization and Lloyd's algorithm
centroids, labels = kmeans_1d(
    data, k,
    sample_weights=weights,  # sample weights
    max_iter=100,  # maximum number of iterations
    random_state=42,  # random seed
)

# The faster two-cluster deterministic algorithm
centroids, labels = kmeans_1d_two_clusters(
    data,
    sample_weights=weights,  # sample weights
)

Advanced Usage

Optional arguments is_sorted can be set to True if the data is already sorted. Optional argument return_cluster_borders can be set to True to return the cluster borders (i.e. the indices where the clusters change) instead of the labels. Refer to the docstrings for more information.

Even More Options

The underlying Numba-accelerated function numba_kmeans_1d_k_clusters can be used directly for more control.

This is useful when the algorithm is run multiple times on different segments of the data, or to use within another Numba-accelerated function.

The list of available functions are as follows:

• numba_kmeans_1d_two_clusters
• numba_kmeans_1d_two_clusters_unweighted
• numba_kmeans_1d_k_cluster
• numba_kmeans_1d_k_cluster_unweighted

All of these functions assume the data is sorted beforehand.

from flash1dkmeans import numba_kmeans_1d_k_cluster
import numpy as np

n, k = 1024, 4

# Generate random data
data = np.random.random_sample(n)
data = np.sort(data)

# Generate random weights
weights = np.random.random_sample(data.shape)

# Calculate prefix sums
weights_prefix_sum = np.cumsum(weights)
weighted_X_prefix_sum = np.cumsum(data * weights)
weighted_X_squared_prefix_sum = np.cumsum(data ** 2 * weights)

middle_idx = n // 2

# Providing prefix sums reduces redundant calculations
# This is useful when the algorithm is run multiple times on different segments of the data
for start_idx, stop_idx in [(0, middle_idx), (middle_idx, n)]:
  centroids, cluster_borders = numba_kmeans_1d_k_cluster(  # Note that data MUST be sorted beforehand
    data, k,  # Note how the sample weights are not provided when the prefix sums are provided
    max_iter=100,  # maximum number of iterations
    weights_prefix_sum=weights_prefix_sum,  # prefix sum of the sample weights, leave empty for unweighted data
    weighted_X_prefix_sum=weighted_X_prefix_sum,  # prefix sum of the weighted data
    weighted_X_squared_prefix_sum=weighted_X_squared_prefix_sum,  # prefix sum of the squared weighted data
    start_idx=start_idx,  # start index of the data
    stop_idx=stop_idx,  # stop index of the data
    random_state=42,  # random seed
  )

Refer to the docstrings for more information.

Notes

This repository has been created to be used in Any-Precision-LLM project, where multiple 1D k-means instances are run in parallel for LLM quantization.

However, the algorithm is general and can be used for any 1D k-means problem.

I am currently working on my undergrad thesis, where I delve into the detailed explanations and proofs of the algorithms. The thesis will be linked here shortly.

Feel free to leave issues or contact me at [email protected] for inquiries.