The requested file was not found.
Please click here to go to the home page, or have a look at the website modules below.
The requested file was not found.
Please click here to go to the home page, or have a look at the website modules below.
Homework 1 is in the form of a jupyter notebook. You must complete it and submit it on moodle (for students enrolled on this course).
This homework will run fine on regular CPU (no need for GPU). If you want to run it locally (on your laptop), you can follow the procedure described in Module 0. Note that if you cloned the GitHub repository, the homework will be in the folder /notebooks/HW1
Homework 1 is in the form of a jupyter notebook. You must complete it and submit it on moodle (for students enrolled on this course).
This homework will run fine on regular CPU (no need for GPU). If you want to run it locally (on your laptop), you can follow the procedure described in Module 0. Note that if you cloned the GitHub repository, the homework will be in the folder /notebooks/HW1

Homework 2 is in the form of a jupyter notebook. You must complete it and submit it on moodle (for students enrolled on this course).
This homework will run fine on regular CPU (no need for GPU). If you want to run it locally (on your laptop), you can follow the procedure described in Module 0. Note that if you cloned the GitHub repository, the homework will be in the folder /notebooks/HW2

Homework 2 is in the form of a jupyter notebook. You must complete it and submit it on moodle (for students enrolled on this course).
This homework will run fine on regular CPU (no need for GPU). If you want to run it locally (on your laptop), you can follow the procedure described in Module 0. Note that if you cloned the GitHub repository, the homework will be in the folder /notebooks/HW2

Homework 3 is in the form of a jupyter notebook. You must complete it and submit it on moodle (for students enrolled on this course).

Homework 3 is in the form of a jupyter notebook. You must complete it and submit it on moodle (for students enrolled on this course).
This site collects resources to learn Deep Learning in the form of Modules available through the sidebar on the left. As a student, you can walk through the modules at your own pace and interact with others thanks to the associated Discord server. You don’t need any special hardware or software.
The main goal of the course is to allow students to understand papers, blog posts and codes available online and to adapt them to their projects as soon as possible. In particular, we avoid the use of any high-level neural networks API and focus on the PyTorch library in Python.
The course is divided into sessions (containing possibly several modules), each session requiring a significant amount of coding. At the end of this course, students were able to read very recent papers and reproduce (or even ameliorate) their experiments.
All the code used in this course is available on the GitHub repository dataflowr/notebooks. You will find the solutions to the practicals on this repo! You can fork the repo if you want to run the code locally: GitHub Docs about fork then follow the steps in Module 0. Most of the code will not require a GPU.
⚠ When a GPU is required , you can launch the code on colab by following the corresponding link given in the module (see for example Module 1).
Pre-requisites:
Mathematics: basics of linear algebra, probability, differential calculus and optimization
Programming: Python. Test your proficiency: quiz
Start right away and train a deep neural network on a GPU with Module 1 - Introduction & General Overview
Be sure to build your own classifier with more dogs and cats in the practicals. Things to remember
you do not need to understand everything to run a deep learning model! But the main goal of this course will be to come back to each step done today and understand them...
to use the dataloader from Pytorch, you need to follow the API (i.e. for classification store your dataset in folders)
using a pretrained model and modifying it to adapt it to a similar task is easy.
if you do not understand why we take this loss, that's fine, we'll cover that in Module 3.
even with a GPU, avoid unnecessary computations!
Module 2b - Automatic differentiation + Practicals
MLP from scratch start of HW1
Pytorch tensors = Numpy on GPU + gradients!
in deep learning, broadcasting is used everywhere. The rules are the same as for Numpy.
Automatic differentiation is not only the chain rule! Backpropagation algorithm (or dual numbers) is a clever algorithm to implement automatic differentiation...
Module 5 - Stacking layers and overfitting a MLP on CIFAR10
how to regularize with dropout and uncertainty estimation with MC Dropout: Module 15 - Dropout
Loss vs Accuracy. Know your loss for a classification task!
know your optimizer (Module 4)
know how to build a neural net with torch.nn.module (Module 5)
know how to use convolution and pooling layers (kernel, stride, padding)
know how to use dropout
Module 8b - Collaborative filtering and build your own recommender system: 08_collaborative_filtering_empty.ipynb (on a larger dataset 08_collaborative_filtering_1M.ipynb)
Module 8c - Word2vec and build your own word embedding 08_Word2vec_pytorch_empty.ipynb
Module 16 - Batchnorm and check your understanding with 16_simple_batchnorm_eval.ipynb and more 16_batchnorm_simple.ipynb
start of Homework 2: Class Activation Map and adversarial examples
know how to use dataloader
to deal with categorical variables in deep learning, use embeddings
in the case of word embedding, starting in an unsupervised setting, we built a supervised task (i.e. predicting central / context words in a window) and learned the representation thanks to negative sampling
know your batchnorm
architectures with skip connections allows deeper models
Module 9a: Autoencoders and code your noisy autoencoder 09_AE_NoisyAE.ipynb
Module 10: Generative Adversarial Networks and code your GAN, Conditional GAN and InfoGAN 10_GAN_double_moon.ipynb
start of Homework 3: VAE for MNIST clustering and generation
Module 11b - Recurrent Neural Networks practice and predict engine failure with 11_predicitions_RNN_empty.ipynb
Correcting the PyTorch tutorial on attention in seq2seq: 12_seq2seq_attention.ipynb
Build your own microGPT: GPT_hist.ipynb
Build your own Real NVP: Normalizing_flows_empty.ipynb
Train your own DDPM on MNIST: ddpm_nano_empty.ipynb
Finetuning on CIFAR10: ddpm_micro_sol.ipynb
and check the
Marc Lelarge, Andrei Bursuc with Jill-Jênn Vie
Super fast track to learn the basics of deep learning from scratch:
Have a look at the slides of Module 1: Introduction & General Overview
Run the notebook (or in colab) of Module 2a: Pytorch Tensors
Run the notebook (or in colab) of Module 2b: Automatic Differentiation
Check the Minimal working examples of Module 3: Loss functions for classification. If you do not understand, have a look at the slides.
Have a look at the slides of Module 4: Optimization for Deep Learning
Try playback speed 1.5 for the video from Module 5: Stacking layers.
Run the notebook (or in colab) of Module 6: Convolutional Neural Network
Try playback speed 2 for the video from Module 7: Dataloading
Have a look at the slides of Module 8a: Embedding layers
Well done! Now you have time to enjoy deep learning!
Join the GitHub repo dataflowr and make a pull request. What are pull requests?
Thanks to Daniel Huynh, Eric Daoud, Simon Coste
Materials from this site is used for courses at ENS and X.


This site collects resources to learn Deep Learning in the form of Modules available through the sidebar on the left. As a student, you can walk through the modules at your own pace and interact with others thanks to the associated Discord server. You don’t need any special hardware or software.
The main goal of the course is to allow students to understand papers, blog posts and codes available online and to adapt them to their projects as soon as possible. In particular, we avoid the use of any high-level neural networks API and focus on the PyTorch library in Python.
The course is divided into sessions (containing possibly several modules), each session requiring a significant amount of coding. At the end of this course, students were able to read very recent papers and reproduce (or even ameliorate) their experiments.
All the code used in this course is available on the GitHub repository dataflowr/notebooks. You will find the solutions to the practicals on this repo! You can fork the repo if you want to run the code locally: GitHub Docs about fork then follow the steps in Module 0. Most of the code will not require a GPU.
⚠ When a GPU is required , you can launch the code on colab by following the corresponding link given in the module (see for example Module 1).
Pre-requisites:
Mathematics: basics of linear algebra, probability, differential calculus and optimization
Programming: Python. Test your proficiency: quiz
Start right away and train a deep neural network on a GPU with Module 1 - Introduction & General Overview
Be sure to build your own classifier with more dogs and cats in the practicals. Things to remember
you do not need to understand everything to run a deep learning model! But the main goal of this course will be to come back to each step done today and understand them...
to use the dataloader from Pytorch, you need to follow the API (i.e. for classification store your dataset in folders)
using a pretrained model and modifying it to adapt it to a similar task is easy.
if you do not understand why we take this loss, that's fine, we'll cover that in Module 3.
even with a GPU, avoid unnecessary computations!
Module 2b - Automatic differentiation + Practicals
MLP from scratch start of HW1
Pytorch tensors = Numpy on GPU + gradients!
in deep learning, broadcasting is used everywhere. The rules are the same as for Numpy.
Automatic differentiation is not only the chain rule! Backpropagation algorithm (or dual numbers) is a clever algorithm to implement automatic differentiation...
Module 5 - Stacking layers and overfitting a MLP on CIFAR10
how to regularize with dropout and uncertainty estimation with MC Dropout: Module 15 - Dropout
Loss vs Accuracy. Know your loss for a classification task!
know your optimizer (Module 4)
know how to build a neural net with torch.nn.module (Module 5)
know how to use convolution and pooling layers (kernel, stride, padding)
know how to use dropout
Module 8b - Collaborative filtering and build your own recommender system: 08_collaborative_filtering_empty.ipynb (on a larger dataset 08_collaborative_filtering_1M.ipynb)
Module 8c - Word2vec and build your own word embedding 08_Word2vec_pytorch_empty.ipynb
Module 16 - Batchnorm and check your understanding with 16_simple_batchnorm_eval.ipynb and more 16_batchnorm_simple.ipynb
start of Homework 2: Class Activation Map and adversarial examples
know how to use dataloader
to deal with categorical variables in deep learning, use embeddings
in the case of word embedding, starting in an unsupervised setting, we built a supervised task (i.e. predicting central / context words in a window) and learned the representation thanks to negative sampling
know your batchnorm
architectures with skip connections allows deeper models
Module 9a: Autoencoders and code your noisy autoencoder 09_AE_NoisyAE.ipynb
Module 10: Generative Adversarial Networks and code your GAN, Conditional GAN and InfoGAN 10_GAN_double_moon.ipynb
start of Homework 3: VAE for MNIST clustering and generation
Module 11b - Recurrent Neural Networks practice and predict engine failure with 11_predicitions_RNN_empty.ipynb
Correcting the PyTorch tutorial on attention in seq2seq: 12_seq2seq_attention.ipynb
Build your own microGPT: GPT_hist.ipynb
Build your own Real NVP: Normalizing_flows_empty.ipynb
Train your own DDPM on MNIST: ddpm_nano_empty.ipynb
Finetuning on CIFAR10: ddpm_micro_sol.ipynb
and check the
Marc Lelarge, Andrei Bursuc with Jill-Jênn Vie
Super fast track to learn the basics of deep learning from scratch:
Have a look at the slides of Module 1: Introduction & General Overview
Run the notebook (or in colab) of Module 2a: Pytorch Tensors
Run the notebook (or in colab) of Module 2b: Automatic Differentiation
Check the Minimal working examples of Module 3: Loss functions for classification. If you do not understand, have a look at the slides.
Have a look at the slides of Module 4: Optimization for Deep Learning
Try playback speed 1.5 for the video from Module 5: Stacking layers.
Run the notebook (or in colab) of Module 6: Convolutional Neural Network
Try playback speed 2 for the video from Module 7: Dataloading
Have a look at the slides of Module 8a: Embedding layers
Well done! Now you have time to enjoy deep learning!
Join the GitHub repo dataflowr and make a pull request. What are pull requests?
Thanks to Daniel Huynh, Eric Daoud, Simon Coste
Materials from this site is used for courses at ENS and X.


Table of Contents
0:00 Intro
0:31 Goal of this lecture
2:08 What is deep learning?
7:06 Why deep learning now?
9:33 Deep learning pipeline
12:17 General overview
16:02 Organization of the course
18:24 A first example in Colab (setting)
19:35 Dogs vs cats (data wrangling)
25:50 Data processing (dataset and dataloader)
40:51 VGG model
45:55 Modifying the last layer
49:50 Choosing your loss and optimizer for training
57:40 Precomputing features
1:03:39 Qualitative analysis
⚠ Dogs and Cats with VGG: static notebook, code (GitHub) or running in colab GPU is required for this notebook ⚠
⚠ More dogs and cats with VGG and resnet in colab GPU is required for this notebook ⚠
Table of Contents
0:00 Intro
0:31 Goal of this lecture
2:08 What is deep learning?
7:06 Why deep learning now?
9:33 Deep learning pipeline
12:17 General overview
16:02 Organization of the course
18:24 A first example in Colab (setting)
19:35 Dogs vs cats (data wrangling)
25:50 Data processing (dataset and dataloader)
40:51 VGG model
45:55 Modifying the last layer
49:50 Choosing your loss and optimizer for training
57:40 Precomputing features
1:03:39 Qualitative analysis
⚠ Dogs and Cats with VGG: static notebook, code (GitHub) or running in colab GPU is required for this notebook ⚠
⚠ More dogs and cats with VGG and resnet in colab GPU is required for this notebook ⚠
Table of Contents
Table of Contents
Table of Contents
Understanding LSTM Networks by Christopher Olah
Table of Contents
Understanding LSTM Networks by Christopher Olah
Table of Contents
RNNs can generate bounded hierarchical languages with optimal memory (2020) John Hewitt, Michael Hahn, Surya Ganguli, Percy Liang, Christopher D. Manning arXiv:2010.07515
Self-Attention Networks Can Process Bounded Hierarchical Languages (2021) Shunyu Yao, Binghui Peng, Christos Papadimitriou, Karthik Narasimhan arXiv:2105.11115
Table of Contents
RNNs can generate bounded hierarchical languages with optimal memory (2020) John Hewitt, Michael Hahn, Surya Ganguli, Percy Liang, Christopher D. Manning arXiv:2010.07515
Self-Attention Networks Can Process Bounded Hierarchical Languages (2021) Shunyu Yao, Binghui Peng, Christos Papadimitriou, Karthik Narasimhan arXiv:2105.11115
Table of Contents
Table of Contents
Table of Contents
The first attention mechanism was proposed in Neural Machine Translation by Jointly Learning to Align and Translate by Dzmitry Bahdanau, Kyunghyun Cho, Yoshua Bengio (presented at ICLR 2015).
The task considered is English-to-French translation and the attention mechanism is proposed to extend a seq2seq architecture by adding a context vector in the RNN decoder so that, the hidden states for the decoder are computed recursively as where is the previously predicted token and predictions are made in a probabilist manner as where and are the current hidden state and context of the decoder.
Now the main novelty is the introduction of the context which is a weighted average of all the hidden states of the encoder: where is the length of the input sequence, are the corresponding hidden states of the decoder and . Hence the context allows passing direct information from the 'relevant' part of the input to the decoder. The coefficients are computed from the current hidden state of the decoder and all the hidden states from the encoder as explained below (taken from the original paper):

In Attention for seq2seq, you can play with a simple model and code the attention mechanism proposed in the paper. For the alignment network (used to define the coefficient ), we take a MLP with activations.
You will learn about seq2seq, teacher-forcing for RNNs and build the attention mechanism. To simplify things, we do not deal with batches (see Batches with sequences in Pytorch for more on that). The solution for this practical is provided in Attention for seq2seq- solution
Note that each is a real number so that we can display the matrix of 's where ranges over the input tokens and over the output tokens, see below (taken from the paper):

We now describe the attention mechanism proposed in Attention Is All You Need by Vaswani et al. First, we recall basic notions from retrieval systems: query/key/value illustrated by an example: search for videos on Youtube. In this example, the query is the text in the search bar, the key is the metadata associated with the videos which are the values. Hence a score can be computed from the query and all the keys. Finally, the matched video with the highest score is returned.
We see that we can formalize this process as follows: if is the current query and and are all the keys and values in the database, we return
where .
Note that this formalism allows us to recover the way contexts were computed above (where the score function was called the alignment network). Now, we will change the score function and consider dot-product attention: . Note that for this definition to make sense, both the query and the key need to live in the same space and is the dimension of this space.
Given inputs in denoted by a matrix and a database containing samples in denoted by a matrix , we define:
Now self-attention is simply obtained with (so that ) and . In summary, self-attention layer can take as input any tensor of the form (for any ) has parameters:
and produce (with same and as for the input). is the dimension of the input and is a hyper-parameter of the self-attention layer:
with the convention that (resp. ) is the -th column of (resp. the -th column of ). Note that the notation might be a bit confusing. Recall that is always taking as input a vector and returning a (normalized) vector. In practice, most of the time, we are dealing with batches so that the function is taking as input a matrix (or tensor) and we need to normalize according to the right axis! Named tensor notation see below deals with this notational issue. I also find the interpretation given below helpful:
Mental model for self-attention: self-attention interpreted as taking expectation
where the mappings and represent query, key and value.
Multi-head attention combines several such operations in parallel, and is the concatenation of the results along the feature dimension to which is applied one more linear transformation.

To finish the description of a transformer block, we need to define two last layers: Layer Norm and Feed Forward Network.
The Layer Norm used in the transformer block is particularly simple as it acts on vectors and standardizes it as follows: for , we define
and then the Layer Norm has two parameters and
where we used the natural broadcasting rule for subtracting the mean and dividing by std and is component-wise multiplication.
A Feed Forward Network is an MLP acting on vectors: for , we define
where , , , .
Each of these layers is applied on each of the inputs given to the transformer block as depicted below:

Note that this block is equivariant: if we permute the inputs, then the outputs will be permuted with the same permutation. As a result, the order of the input is irrelevant to the transformer block. In particular, this order cannot be used. The important notion of positional encoding allows us to take order into account. It is a deterministic unique encoding for each time step that is added to the input tokens.
In Transformers using Named Tensor Notation, we derive the formal equations for the Transformer block using named tensor notation.
Now is the time to have fun building a simple transformer block and to think like transformers (open in colab).


Table of Contents
The first attention mechanism was proposed in Neural Machine Translation by Jointly Learning to Align and Translate by Dzmitry Bahdanau, Kyunghyun Cho, Yoshua Bengio (presented at ICLR 2015).
The task considered is English-to-French translation and the attention mechanism is proposed to extend a seq2seq architecture by adding a context vector in the RNN decoder so that, the hidden states for the decoder are computed recursively as where is the previously predicted token and predictions are made in a probabilist manner as where and are the current hidden state and context of the decoder.
Now the main novelty is the introduction of the context which is a weighted average of all the hidden states of the encoder: where is the length of the input sequence, are the corresponding hidden states of the decoder and . Hence the context allows passing direct information from the 'relevant' part of the input to the decoder. The coefficients are computed from the current hidden state of the decoder and all the hidden states from the encoder as explained below (taken from the original paper):

In Attention for seq2seq, you can play with a simple model and code the attention mechanism proposed in the paper. For the alignment network (used to define the coefficient ), we take a MLP with activations.
You will learn about seq2seq, teacher-forcing for RNNs and build the attention mechanism. To simplify things, we do not deal with batches (see Batches with sequences in Pytorch for more on that). The solution for this practical is provided in Attention for seq2seq- solution
Note that each is a real number so that we can display the matrix of 's where ranges over the input tokens and over the output tokens, see below (taken from the paper):

We now describe the attention mechanism proposed in Attention Is All You Need by Vaswani et al. First, we recall basic notions from retrieval systems: query/key/value illustrated by an example: search for videos on Youtube. In this example, the query is the text in the search bar, the key is the metadata associated with the videos which are the values. Hence a score can be computed from the query and all the keys. Finally, the matched video with the highest score is returned.
We see that we can formalize this process as follows: if is the current query and and are all the keys and values in the database, we return
where .
Note that this formalism allows us to recover the way contexts were computed above (where the score function was called the alignment network). Now, we will change the score function and consider dot-product attention: . Note that for this definition to make sense, both the query and the key need to live in the same space and is the dimension of this space.
Given inputs in denoted by a matrix and a database containing samples in denoted by a matrix , we define:
Now self-attention is simply obtained with (so that ) and . In summary, self-attention layer can take as input any tensor of the form (for any ) has parameters:
and produce (with same and as for the input). is the dimension of the input and is a hyper-parameter of the self-attention layer:
with the convention that (resp. ) is the -th column of (resp. the -th column of ). Note that the notation might be a bit confusing. Recall that is always taking as input a vector and returning a (normalized) vector. In practice, most of the time, we are dealing with batches so that the function is taking as input a matrix (or tensor) and we need to normalize according to the right axis! Named tensor notation see below deals with this notational issue. I also find the interpretation given below helpful:
Mental model for self-attention: self-attention interpreted as taking expectation
where the mappings and represent query, key and value.
Multi-head attention combines several such operations in parallel, and is the concatenation of the results along the feature dimension to which is applied one more linear transformation.

To finish the description of a transformer block, we need to define two last layers: Layer Norm and Feed Forward Network.
The Layer Norm used in the transformer block is particularly simple as it acts on vectors and standardizes it as follows: for , we define
and then the Layer Norm has two parameters and
where we used the natural broadcasting rule for subtracting the mean and dividing by std and is component-wise multiplication.
A Feed Forward Network is an MLP acting on vectors: for , we define
where , , , .
Each of these layers is applied on each of the inputs given to the transformer block as depicted below:

Note that this block is equivariant: if we permute the inputs, then the outputs will be permuted with the same permutation. As a result, the order of the input is irrelevant to the transformer block. In particular, this order cannot be used. The important notion of positional encoding allows us to take order into account. It is a deterministic unique encoding for each time step that is added to the input tokens.
Have a look at Brendan Bycroft’s beautifully crafted interactive explanation of the transformers architecture:
In Transformers using Named Tensor Notation, we derive the formal equations for the Transformer block using named tensor notation.
Now is the time to have fun building a simple transformer block and to think like transformers (open in colab).


Table of Contents
notebook (you need to install Julia) or use:
Table of Contents
notebook (you need to install Julia) or use:
Table of Contents
Table of Contents
Table of Contents
Table of Contents
Table of Contents
Table of Contents
Table of Contents
Table of Contents
Table of Contents
Table of Contents
Table of Contents
Table of Contents
(J. Ho, A. Jain, P. Abbeel 2020)

Given a schedule , the forward diffusion process is defined by: and .
With and , we see that, with :

The training of this notebook on colab takes approximately 20 minutes.
ddpm_nano_empty.ipynb is the notebook where you code the DDPM algorithm (a simple UNet is provided for the network ), its training and the sampling. You should get results like this:

Here is the corresponding solution: ddpm_nano_sol.ipynb
The training of this notebook on colab takes approximately 20 minutes (so do not expect high-quality pictures!). Still, after finetuning on specific classes, we see that the model learns features of the class.

With a bit more training (100 epochs), you can get results like this:



Note that the Denoising Diffusion Probabilistic Model is the same for MNIST and CIFAR10, we only change the UNet learning to reverse the noise. For CIFAR10, we adapt the UNet provided in Module 9b. Indeed, you can still use the code provided here for DDPM with other architectures like more complex ones with self-attention like this Unet coded by lucidrains which is the one used in the original paper.
In the paper, the authors used Exponential Moving Average (EMA) on model parameters with a decay factor of . This is not implemented here to keep the code as simple as possible.
(J. Ho, A. Jain, P. Abbeel 2020)

Given a schedule , the forward diffusion process is defined by: and .
With and , we see that, with :

The training of this notebook on colab takes approximately 20 minutes.
ddpm_nano_empty.ipynb is the notebook where you code the DDPM algorithm (a simple UNet is provided for the network ), its training and the sampling. You should get results like this:

Here is the corresponding solution: ddpm_nano_sol.ipynb
The training of this notebook on colab takes approximately 20 minutes (so do not expect high-quality pictures!). Still, after finetuning on specific classes, we see that the model learns features of the class.

With a bit more training (100 epochs), you can get results like this:



Note that the Denoising Diffusion Probabilistic Model is the same for MNIST and CIFAR10, we only change the UNet learning to reverse the noise. For CIFAR10, we adapt the UNet provided in Module 9b. Indeed, you can still use the code provided here for DDPM with other architectures like more complex ones with self-attention like this Unet coded by lucidrains which is the one used in the original paper.
In the paper, the authors used Exponential Moving Average (EMA) on model parameters with a decay factor of . This is not implemented here to keep the code as simple as possible.

in Zeroshot_with_CLIP.ipynb we build a zero-shop classifier using the pretrained CLIP network and improve its performance with descriptors generated with GPT.
CLIP Learning Transferable Visual Models From Natural Language Supervision (ICML 2021) Alec Radford et al.
Visual Classification via Description from Large Language Models (ICLR 2023) Menon, Sachit and Vondrick, Carl

in Zeroshot_with_CLIP.ipynb we build a zero-shop classifier using the pretrained CLIP network and improve its performance with descriptors generated with GPT.
CLIP Learning Transferable Visual Models From Natural Language Supervision (ICML 2021) Alec Radford et al.
Visual Classification via Description from Large Language Models (ICLR 2023) Menon, Sachit and Vondrick, Carl
Table of Contents
0:00 Recap
1:43 Introduction to tensors
4:32 Sizes
5:25 Bridge to numpy
11:10 Broadcasting
14:35 Inplace modification
16:30 Shared memory
18:40 Cuda
22:34 CIFAR dataset
To check your understanding of the material, you can do the quizzes
Table of Contents
0:00 Recap
1:43 Introduction to tensors
4:32 Sizes
5:25 Bridge to numpy
11:10 Broadcasting
14:35 Inplace modification
16:30 Shared memory
18:40 Cuda
22:34 CIFAR dataset
To check your understanding of the material, you can do the quizzes
Table of Contents
0:00 Recap
0:40 A simple example (more in the practicals)
3:44 Pytorch tensor: requires_grad field
6:44 Pytorch backward function
9:05 The chain rule on our example
16:00 Linear regression
18:00 Gradient descent with numpy...
27:30 ... with pytorch tensors
31:30 Using autograd
34:35 Using a neural network (linear layer)
39:50 Using a pytorch optimizer
44:00 algorithm: how automatic differentiation works
Automatic differentiation: a simple example static notebook, code (GitHub) in colab
notebook used in the video for the linear regression. If you want to open it in colab
backprop slide (used for the practical below)
To check your understanding of automatic differentiation, you can do the quizzes
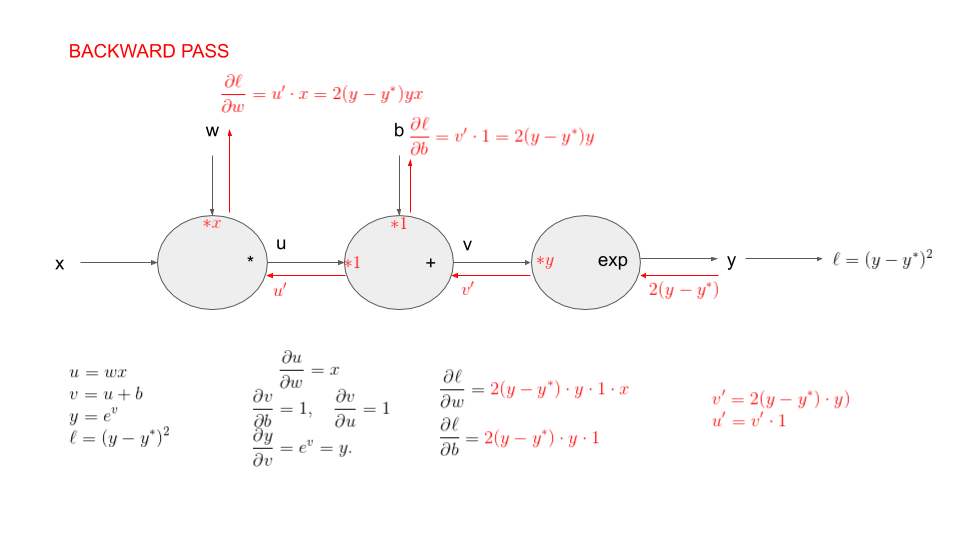
practicals in colab Coding backprop.
Adapt your code to solve the following challenge:
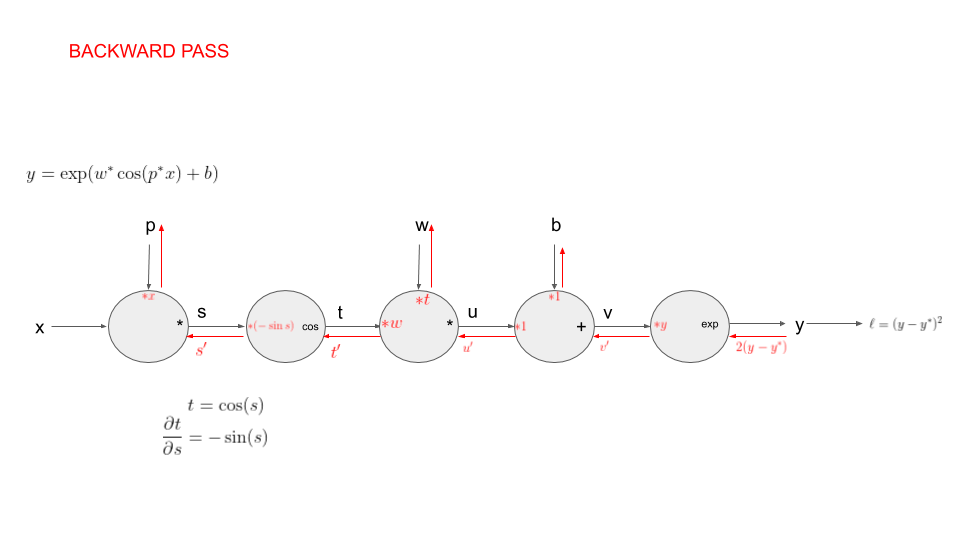
Some small modifications:
First modification: we now generate points where , i.e is obtained by applying a deterministic function to with parameters and . Our goal is still to recover the parameters and from the observations .
Second modification: we now generate points where , i.e is obtained by applying a deterministic function to with parameters , and . Our goal is still to recover the parameters from the observations .
Table of Contents
0:00 Recap
0:40 A simple example (more in the practicals)
3:44 Pytorch tensor: requires_grad field
6:44 Pytorch backward function
9:05 The chain rule on our example
16:00 Linear regression
18:00 Gradient descent with numpy...
27:30 ... with pytorch tensors
31:30 Using autograd
34:35 Using a neural network (linear layer)
39:50 Using a pytorch optimizer
44:00 algorithm: how automatic differentiation works
Automatic differentiation: a simple example static notebook, code (GitHub) in colab
notebook used in the video for the linear regression. If you want to open it in colab
backprop slide (used for the practical below)
To check your understanding of automatic differentiation, you can do the quizzes

practicals in colab Coding backprop.
Adapt your code to solve the following challenge:

Some small modifications:
First modification: we now generate points where , i.e is obtained by applying a deterministic function to with parameters and . Our goal is still to recover the parameters and from the observations .
Second modification: we now generate points where , i.e is obtained by applying a deterministic function to with parameters , and . Our goal is still to recover the parameters from the observations .
You can have a look at Module 2b to learn more about this approach as well as MLP from scratch.
Here we will implement in numpy a different approach mimicking the functional approach of JAX see The Autodiff Cookbook.
Each function will take 2 arguments: one being the input x and the other being the parameters w. For each function, we build 2 vjp functions taking as argument a gradient , and corresponding to and so that these functions return and respectively. To summarize, for , , and, ,
Then backpropagation is simply done by first computing the gradient of the loss and then composing the vjp functions in the right order.
intro to JAX: autodiff the functional way autodiff_functional_empty.ipynb and its solution autodiff_functional_sol.ipynb
Linear regression in JAX linear_regression_jax.ipynb
You can have a look at Module 2b to learn more about this approach as well as MLP from scratch.
Here we will implement in numpy a different approach mimicking the functional approach of JAX see The Autodiff Cookbook.
Each function will take 2 arguments: one being the input x and the other being the parameters w. For each function, we build 2 vjp functions taking as argument a gradient , and corresponding to and so that these functions return and respectively. To summarize, for , , and, ,
Then backpropagation is simply done by first computing the gradient of the loss and then composing the vjp functions in the right order.
intro to JAX: autodiff the functional way autodiff_functional_empty.ipynb and its solution autodiff_functional_sol.ipynb
Linear regression in JAX linear_regression_jax.ipynb
To check you know your loss, you can do the quizzes
To check you know your loss, you can do the quizzes
Table of Contents
0:00 Recap
0:31 Plan
1:14 Optimization in deep learning
3:44 Gradient descent variants
7:58 Setting for the jupyter notebook
9:49 Vanilla gradient descent
12:14 Momentum
15:38 Nesterov accelerated gradient descent
18:00 Adagrad
20:06 RMSProp
22:11 Adam
24:39 AMSGrad
27:09 Pytorch optimizers
An overview of gradient descent optimization algorithms by Sebastian Ruder
Gradient-based optimization A short introduction to optimization in Deep Learning, by Christian S. Perone
Table of Contents
0:00 Recap
0:31 Plan
1:14 Optimization in deep learning
3:44 Gradient descent variants
7:58 Setting for the jupyter notebook
9:49 Vanilla gradient descent
12:14 Momentum
15:38 Nesterov accelerated gradient descent
18:00 Adagrad
20:06 RMSProp
22:11 Adam
24:39 AMSGrad
27:09 Pytorch optimizers
An overview of gradient descent optimization algorithms by Sebastian Ruder
Gradient-based optimization A short introduction to optimization in Deep Learning, by Christian S. Perone
Table of Contents
0:00 Recap
1:35 Plan of the lesson: define a NN model
2:24 MLP with pytorch Sequential
6:41 Using Torch.nn.module
10:08 Writing a pytorch module
Table of Contents
0:00 Recap
1:35 Plan of the lesson: define a NN model
2:24 MLP with pytorch Sequential
6:41 Using Torch.nn.module
10:08 Writing a pytorch module
Table of Contents
0:00 Recap
0:52 MNIST dataset
2:56 A simple binary classifier
6:21 Precision and recall
8:44 Filters and convolutions
19:40 Max pooling
Table of Contents
0:00 Recap
0:52 MNIST dataset
2:56 A simple binary classifier
6:21 Precision and recall
8:44 Filters and convolutions
19:40 Max pooling
Table of Contents
0:00 Recap
1:09 Plan of the lesson
2:08 Dataloading
4:40 Example 1: torchvision.datasets.Imagefolder
9:45 Example 2: dataset from numpy arrays
14:47 Example 3: custom dataloader
Table of Contents
0:00 Recap
1:09 Plan of the lesson
2:08 Dataloading
4:40 Example 1: torchvision.datasets.Imagefolder
9:45 Example 2: dataset from numpy arrays
14:47 Example 3: custom dataloader
Table of Contents
Table of Contents
Table of Contents
Table of Contents
Table of Contents
-word2vec Explained: deriving Mikolov et al.'s negative-sampling word-embedding method by Yoav Goldberg and Omer Levy
Table of Contents
-word2vec Explained: deriving Mikolov et al.'s negative-sampling word-embedding method by Yoav Goldberg and Omer Levy
Table of Contents
Table of Contents



Table of Contents
The image below is taken from this very good blog post on normalizing flows: blogpost

Here we only describe flow-based generative models, you can have look at VAE and GAN.
A flow-based generative model is constructed by a sequence of invertible transformations. The main advantage of flows is that the model explicitly learns the data distribution \(p(\mathbf{x})\) and therefore the loss function is simply the negative log-likelihood.
Given a sample \(\mathbf{x}\) and a prior \(p(\mathbf{z})\), we compute \(f(\mathbf{x}) = \mathbf{z}\) with an invertible function \(f\) that will be learned. Given \(f\) and the prior \(p(\mathbf{z})\), we can compute the evidence \(p(\mathbf{x})\) thanks to the change of variable formula:
where \(\dfrac{\partial f(\mathbf{x})}{\partial \mathbf{x}}\) is the Jacobian matrix of \(f\). Recall that given a function mapping a \(n\)-dimensional input vector \(\mathbf{x}\) to a \(m\)-dimensional output vector, \(f: \mathbb{R}^n \mapsto \mathbb{R}^m\), the matrix of all first-order partial derivatives of this function is called the Jacobian matrix, \(J_f\) where one entry on the i-th row and j-th column is \((J_f(\mathbf{x}))_{ij} = \frac{\partial f_i(\mathbf{x})}{\partial x_j}\):
Below, we will parametrize \(f\) with a neural network and learn \(f\) by maximizing \(\ln p(\mathbf{x})\). More precisely, given a dataset \((\mathbf{x}_1,\dots,\mathbf{x}_n)\) and a model provided by a prior \(p(\mathbf{z})\) and a neural network \(f\), we optimize the weights of \(f\) by minimizing:
We need to ensure that \(f\) is always invertible and that the determinant is simple to compute.
Real NVP (introduced by Laurent Dinh, Jascha Sohl-Dickstein, Samy Bengio in 2016) uses function \(f\) obtained by stacking affine coupling layers which for an input \(\mathbf{x}\in \mathbb{R}^D\) produce the output \(\mathbf{y}\in\mathbb{R}^D\) defined by (with \( d < D \) ):
\[\begin{aligned} \mathbf{y}_{1:d} &= \mathbf{x}_{1:d}\\ \mathbf{y}_{d+1:D} &= \mathbf{x}_{d+1:D} \odot \exp\left(s(\mathbf{x}_{1:d})\right) +t(\mathbf{x}_{1:d}) , \end{aligned}\]where \(s\) (scale) and \(t\) (translation) are neural networks mapping \(\mathbb{R}^d\) to \(\mathbb{R}^{D-d}\) and \(\odot\) is the element-wise product.
For any functions \(s\) and \(t\), the affine coupling layer is invertible:
The Jacobian of an affine coupling layer is a lower triangular matrix:
Hence the determinant is simply the product of terms on the diagonal:
Note that, we do not need to compute the Jacobian of \(s\) or \(t\) and to compute \(f^{-1}\), we do not need to compute the inverse of \(s\) or \(t\) (which might not exist!). In other words, we can take arbitrary complex functions for \(s\) and \(t\).
In one affine coupling layer, some dimensions (channels) remain unchanged. To make sure all the inputs have a chance to be altered, the model reverses the ordering in each layer so that different components are left unchanged. Following such an alternating pattern, the set of units which remain identical in one transformation layer are always modified in the next.
This can be implemented with binary masks. First, we can extend the scale and neural networks to mappings form \(\mathbb{R}^D\) to \(\mathbb{R}^D\). Then taking a mask \(\mathbf{b} = (1,\dots,1,0,\dots,0)\) with \(d\) ones, so that we have for the affine layer:
Note that we have
and to invert the affine layer:
Now we alternates the binary mask \(\mathbf{b}\) from one coupling layer to the other.
Note, that the formula given in the paper is slightly different:
\[\mathbf{y} = \mathbf{b} \odot \mathbf{x} + (1 - \mathbf{b}) \odot \Big(\mathbf{x} \odot \exp\big(s(\mathbf{b} \odot \mathbf{x})\big) + t(\mathbf{b} \odot \mathbf{x})\Big),\]but the 2 formulas give the same result!

Table of Contents
The image below is taken from this very good blog post on normalizing flows: blogpost

Here we only describe flow-based generative models, you can have look at VAE and GAN.
A flow-based generative model is constructed by a sequence of invertible transformations. The main advantage of flows is that the model explicitly learns the data distribution \(p(\mathbf{x})\) and therefore the loss function is simply the negative log-likelihood.
Given a sample \(\mathbf{x}\) and a prior \(p(\mathbf{z})\), we compute \(f(\mathbf{x}) = \mathbf{z}\) with an invertible function \(f\) that will be learned. Given \(f\) and the prior \(p(\mathbf{z})\), we can compute the evidence \(p(\mathbf{x})\) thanks to the change of variable formula:
where \(\dfrac{\partial f(\mathbf{x})}{\partial \mathbf{x}}\) is the Jacobian matrix of \(f\). Recall that given a function mapping a \(n\)-dimensional input vector \(\mathbf{x}\) to a \(m\)-dimensional output vector, \(f: \mathbb{R}^n \mapsto \mathbb{R}^m\), the matrix of all first-order partial derivatives of this function is called the Jacobian matrix, \(J_f\) where one entry on the i-th row and j-th column is \((J_f(\mathbf{x}))_{ij} = \frac{\partial f_i(\mathbf{x})}{\partial x_j}\):
Below, we will parametrize \(f\) with a neural network and learn \(f\) by maximizing \(\ln p(\mathbf{x})\). More precisely, given a dataset \((\mathbf{x}_1,\dots,\mathbf{x}_n)\) and a model provided by a prior \(p(\mathbf{z})\) and a neural network \(f\), we optimize the weights of \(f\) by minimizing:
We need to ensure that \(f\) is always invertible and that the determinant is simple to compute.
Real NVP (introduced by Laurent Dinh, Jascha Sohl-Dickstein, Samy Bengio in 2016) uses function \(f\) obtained by stacking affine coupling layers which for an input \(\mathbf{x}\in \mathbb{R}^D\) produce the output \(\mathbf{y}\in\mathbb{R}^D\) defined by (with \( d < D \) ):
\[\begin{aligned} \mathbf{y}_{1:d} &= \mathbf{x}_{1:d}\\ \mathbf{y}_{d+1:D} &= \mathbf{x}_{d+1:D} \odot \exp\left(s(\mathbf{x}_{1:d})\right) +t(\mathbf{x}_{1:d}) , \end{aligned}\]where \(s\) (scale) and \(t\) (translation) are neural networks mapping \(\mathbb{R}^d\) to \(\mathbb{R}^{D-d}\) and \(\odot\) is the element-wise product.
For any functions \(s\) and \(t\), the affine coupling layer is invertible:
The Jacobian of an affine coupling layer is a lower triangular matrix:
Hence the determinant is simply the product of terms on the diagonal:
Note that, we do not need to compute the Jacobian of \(s\) or \(t\) and to compute \(f^{-1}\), we do not need to compute the inverse of \(s\) or \(t\) (which might not exist!). In other words, we can take arbitrary complex functions for \(s\) and \(t\).
In one affine coupling layer, some dimensions (channels) remain unchanged. To make sure all the inputs have a chance to be altered, the model reverses the ordering in each layer so that different components are left unchanged. Following such an alternating pattern, the set of units which remain identical in one transformation layer are always modified in the next.
This can be implemented with binary masks. First, we can extend the scale and neural networks to mappings form \(\mathbb{R}^D\) to \(\mathbb{R}^D\). Then taking a mask \(\mathbf{b} = (1,\dots,1,0,\dots,0)\) with \(d\) ones, so that we have for the affine layer:
Note that we have
and to invert the affine layer:
Now we alternates the binary mask \(\mathbf{b}\) from one coupling layer to the other.
Note, that the formula given in the paper is slightly different:
\[\mathbf{y} = \mathbf{b} \odot \mathbf{x} + (1 - \mathbf{b}) \odot \Big(\mathbf{x} \odot \exp\big(s(\mathbf{b} \odot \mathbf{x})\big) + t(\mathbf{b} \odot \mathbf{x})\Big),\]but the 2 formulas give the same result!

We see that we get a pretty good approximation of our target polynomial. Below is the a gif showing the convergence of our network towards the target:

By stacking convolutions with kernel of size 3, we obtained a network with a receptive field of size 9.
Follow on twitter!

We see that we get a pretty good approximation of our target polynomial. Below is the a gif showing the convergence of our network towards the target:

By stacking convolutions with kernel of size 3, we obtained a network with a receptive field of size 9.
Follow on twitter!
author: Marc Lelarge, course: dataflowr
date: April 23, 2021
As shown in the module on GNN, invariant and equivariant functions are crucial for GNN. For example, the message passing GNN (MGNN) layer is defined by:
where means that nodes and are neighbors and the function should not depend on the order of the elements in the multiset . This layer is applied in parallel to all nodes (with the same function ) producing a mapping from to with where is the number of nodes in the graph (and only real hidden states are considered for simplicity). It is easy to see that is an equivariant function, i.e. permuting its input will permute its output.
Another example of invariant and equivariant functions is given by the attention layer defined for a tensor of row queries, the keys and the values, by
The queries are obtained from a tensor by and the keys and values are obtained from a tensor by and . We see that when the queries are fixed, the attention layer is invariant in the pair (keys, values):
hence is invariant in . Similarly, when the pair (keys, values) is fixed, the attention layer is equivariant in the queries:
hence is equivariant in . If , we get the self-attention layer so that is equivariant in .
In this post, we will characterize invariant and equivariant functions following the ideas given in the paper Deep Sets.
We start with some definitions.
For a vector and a permutation , we define
Definitions:
A function is invariant if for all and all , we have .
A function is equivariant if for all and all , we have .
We can now state our main result:
Theorem
invariant case: let be a continuous function. is invariant if and only if there are continuous functions and such that
equivariant case: let be a continuous function. is equivariant if and only if there are continuous functions and such that
We give some remarks before providing the proof below. For the sake of simplicity, we consider here a fixed number of points on the unit interval . For results with a varying number of points, see On the Limitations of Representing Functions on Sets and for points in higher dimension with , see On Universal Equivariant Set Networks and Expressive Power of Invariant and Equivariant Graph Neural Networks.
Our proof will make the mapping explicit and it will not depend on the function . The mapping can be seen as an embedding of the points in in a space of high-dimension. Indeed this embedding space has to be of dimension at least the number of points in order to ensure universality. This is an important remark as in learning scenario, the size of the embedding is typically fixed and hence will limit the expressiveness of the algorithm.
Coming back to the GNN layer (1), our result on the invariant case tells us that we can always rewrite it as:
and the dimension of the embedding needs to be of the same order as the maximum degree in the graph. Note that (8) is not of the form of (7) as the sum inside the function is taken only on neighbors. Indeed, we know that message passing GNN are not universal (see Expressive Power of Invariant and Equivariant Graph Neural Networks).
As a last remark, note that the original PointNet architecture is of the form which is not universal equivariant. Indeed, it is impossible to approximate the equivariant function as shown below (we denote ):
and these quantities cannot be small together. Hence PointNet is not universal equivariant but as shown in On Universal Equivariant Set Networks, modifying PointNet by adding the term inside the function as in (7) makes it universal equivariant. We refer to Are Transformers universal approximators of sequence-to-sequence functions? for similar results about transformers based on self-attention.
We first show that the equivariant case is not more difficult than the invariant case. Assume that we proved the invariant case. Consider a permutation such that so that gives for the first component:
For any , the mapping is invariant. Hence by (6), we have
Now consider a permutation such that and for , then we have
hence and (7) follows.
Hence, we only need to prove (6) and follow the proof given in Deep Sets. We start with a crucial result stating that a set of real points is characterized by the first moments of its empirical measure. Let see what it means for : we can recover the values of and from the quantities and . To see that this is correct, note that
so that . As a result, we have
and clearly and can be recovered as the roots of this polynomial whose coefficients are functions of and . The result below extends this argument for a general :
Proposition
Let , where , be defined by
is injective and has a continuous inverse mapping.
The proof follows from Newton's identities. For , we denote by the power sums and by the elementary symmetric polynomials (note that all polynomials are function of the ):
From Newton's identities, we have for ,
so that, we can express the elementary symmetric polynomials from the power sums:
Note that and since
if then so that and , showing that is injective.
Hence we proved that where is the image of , is a bijection. We need now to prove that is continuous and we'll prove it directly. Let , we need to show that . Now if , since is compact, this means that there exists a convergent subsequence of with . But by continuity of , we have , so that we get a contradiction and hence proved the continuity of , finishing the proof of the proposition.
We are now ready to prove (6). Let be defined by and . Note that and , where is the vector with components sorted in non-decreasing order. Hence as soon as f is invariant, we have so that (6) is valid. We only need to extend the function from the domain to in a continuous way. This can be done by considering the projection on the compact and define .
Follow on twitter!
author: Marc Lelarge, course: dataflowr
date: April 23, 2021
As shown in the module on GNN, invariant and equivariant functions are crucial for GNN. For example, the message passing GNN (MGNN) layer is defined by:
where means that nodes and are neighbors and the function should not depend on the order of the elements in the multiset . This layer is applied in parallel to all nodes (with the same function ) producing a mapping from to with where is the number of nodes in the graph (and only real hidden states are considered for simplicity). It is easy to see that is an equivariant function, i.e. permuting its input will permute its output.
Another example of invariant and equivariant functions is given by the attention layer defined for a tensor of row queries, the keys and the values, by
The queries are obtained from a tensor by and the keys and values are obtained from a tensor by and . We see that when the queries are fixed, the attention layer is invariant in the pair (keys, values):
hence is invariant in . Similarly, when the pair (keys, values) is fixed, the attention layer is equivariant in the queries:
hence is equivariant in . If , we get the self-attention layer so that is equivariant in .
In this post, we will characterize invariant and equivariant functions following the ideas given in the paper Deep Sets.
We start with some definitions.
For a vector and a permutation , we define
Definitions:
A function is invariant if for all and all , we have .
A function is equivariant if for all and all , we have .
We can now state our main result:
Theorem
invariant case: let be a continuous function. is invariant if and only if there are continuous functions and such that
equivariant case: let be a continuous function. is equivariant if and only if there are continuous functions and such that
We give some remarks before providing the proof below. For the sake of simplicity, we consider here a fixed number of points on the unit interval . For results with a varying number of points, see On the Limitations of Representing Functions on Sets and for points in higher dimension with , see On Universal Equivariant Set Networks and Expressive Power of Invariant and Equivariant Graph Neural Networks.
Our proof will make the mapping explicit and it will not depend on the function . The mapping can be seen as an embedding of the points in in a space of high-dimension. Indeed this embedding space has to be of dimension at least the number of points in order to ensure universality. This is an important remark as in learning scenario, the size of the embedding is typically fixed and hence will limit the expressiveness of the algorithm.
Coming back to the GNN layer (1), our result on the invariant case tells us that we can always rewrite it as:
and the dimension of the embedding needs to be of the same order as the maximum degree in the graph. Note that (8) is not of the form of (7) as the sum inside the function is taken only on neighbors. Indeed, we know that message passing GNN are not universal (see Expressive Power of Invariant and Equivariant Graph Neural Networks).
As a last remark, note that the original PointNet architecture is of the form which is not universal equivariant. Indeed, it is impossible to approximate the equivariant function as shown below (we denote ):
and these quantities cannot be small together. Hence PointNet is not universal equivariant but as shown in On Universal Equivariant Set Networks, modifying PointNet by adding the term inside the function as in (7) makes it universal equivariant. We refer to Are Transformers universal approximators of sequence-to-sequence functions? for similar results about transformers based on self-attention.
We first show that the equivariant case is not more difficult than the invariant case. Assume that we proved the invariant case. Consider a permutation such that so that gives for the first component:
For any , the mapping is invariant. Hence by (6), we have
Now consider a permutation such that and for , then we have
hence and (7) follows.
Hence, we only need to prove (6) and follow the proof given in Deep Sets. We start with a crucial result stating that a set of real points is characterized by the first moments of its empirical measure. Let see what it means for : we can recover the values of and from the quantities and . To see that this is correct, note that
so that . As a result, we have
and clearly and can be recovered as the roots of this polynomial whose coefficients are functions of and . The result below extends this argument for a general :
Proposition
Let , where , be defined by
is injective and has a continuous inverse mapping.
The proof follows from Newton's identities. For , we denote by the power sums and by the elementary symmetric polynomials (note that all polynomials are function of the ):
From Newton's identities, we have for ,
so that, we can express the elementary symmetric polynomials from the power sums:
Note that and since
if then so that and , showing that is injective.
Hence we proved that where is the image of , is a bijection. We need now to prove that is continuous and we'll prove it directly. Let , we need to show that . Now if , since is compact, this means that there exists a convergent subsequence of with . But by continuity of , we have , so that we get a contradiction and hence proved the continuity of , finishing the proof of the proposition.
We are now ready to prove (6). Let be defined by and . Note that and , where is the vector with components sorted in non-decreasing order. Hence as soon as f is invariant, we have so that (6) is valid. We only need to extend the function from the domain to in a continuous way. This can be done by considering the projection on the compact and define .
Follow on twitter!
Table of Contents
Slides for a short overview
Course: Node embedding
Course: Signal processing on graphs
Related post: Inductive bias in GCN: a spectral perspective
Course:Graph embedding
Related post: Invariant and equivariant layers with applications to GNN, PointNet and Transformers
Table of Contents
Slides for a short overview
Course: Node embedding
Course: Signal processing on graphs
Related post: Inductive bias in GCN: a spectral perspective
Course:Graph embedding
Related post: Invariant and equivariant layers with applications to GNN, PointNet and Transformers
Table of Contents
Table of Contents
Table of Contents
Inductive bias in GCN: a spectral perspective (run the code or open it in Colab)
Table of Contents
Inductive bias in GCN: a spectral perspective (run the code or open it in Colab)
Table of Contents
Table of Contents
by Daniel Huynh
Table of Contents
by Daniel Huynh
Table of Contents