| comments | difficulty | edit_url | rating | source | tags | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
true |
Hard |
2137 |
Weekly Contest 295 Q4 |
|
You are given a 0-indexed 2D integer array grid of size m x n. Each cell has one of two values:
0represents an empty cell,1represents an obstacle that may be removed.
You can move up, down, left, or right from and to an empty cell.
Return the minimum number of obstacles to remove so you can move from the upper left corner (0, 0) to the lower right corner (m - 1, n - 1).
Example 1:
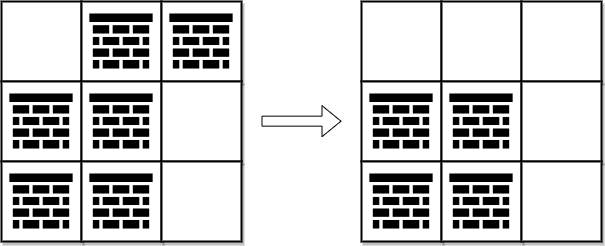
Input: grid = [[0,1,1],[1,1,0],[1,1,0]] Output: 2 Explanation: We can remove the obstacles at (0, 1) and (0, 2) to create a path from (0, 0) to (2, 2). It can be shown that we need to remove at least 2 obstacles, so we return 2. Note that there may be other ways to remove 2 obstacles to create a path.
Example 2:
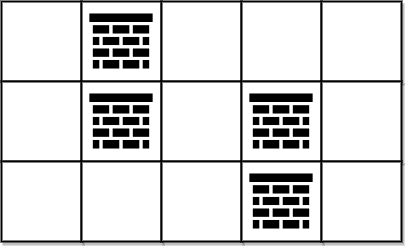
Input: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]] Output: 0 Explanation: We can move from (0, 0) to (2, 4) without removing any obstacles, so we return 0.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 1052 <= m * n <= 105grid[i][j]is either0or1.grid[0][0] == grid[m - 1][n - 1] == 0
class Solution:
def minimumObstacles(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
q = deque([(0, 0, 0)])
vis = set()
dirs = (-1, 0, 1, 0, -1)
while 1:
i, j, k = q.popleft()
if i == m - 1 and j == n - 1:
return k
if (i, j) in vis:
continue
vis.add((i, j))
for a, b in pairwise(dirs):
x, y = i + a, j + b
if 0 <= x < m and 0 <= y < n:
if grid[x][y] == 0:
q.appendleft((x, y, k))
else:
q.append((x, y, k + 1))class Solution {
public int minimumObstacles(int[][] grid) {
int m = grid.length, n = grid[0].length;
Deque<int[]> q = new ArrayDeque<>();
q.offer(new int[] {0, 0, 0});
int[] dirs = {-1, 0, 1, 0, -1};
boolean[][] vis = new boolean[m][n];
while (true) {
var p = q.poll();
int i = p[0], j = p[1], k = p[2];
if (i == m - 1 && j == n - 1) {
return k;
}
if (vis[i][j]) {
continue;
}
vis[i][j] = true;
for (int h = 0; h < 4; ++h) {
int x = i + dirs[h], y = j + dirs[h + 1];
if (x >= 0 && x < m && y >= 0 && y < n) {
if (grid[x][y] == 0) {
q.offerFirst(new int[] {x, y, k});
} else {
q.offerLast(new int[] {x, y, k + 1});
}
}
}
}
}
}class Solution {
public:
int minimumObstacles(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
deque<tuple<int, int, int>> q{{0, 0, 0}};
bool vis[m][n];
memset(vis, 0, sizeof vis);
int dirs[5] = {-1, 0, 1, 0, -1};
while (1) {
auto [i, j, k] = q.front();
q.pop_front();
if (i == m - 1 && j == n - 1) {
return k;
}
if (vis[i][j]) {
continue;
}
vis[i][j] = true;
for (int h = 0; h < 4; ++h) {
int x = i + dirs[h], y = j + dirs[h + 1];
if (x >= 0 && x < m && y >= 0 && y < n) {
if (grid[x][y] == 0) {
q.push_front({x, y, k});
} else {
q.push_back({x, y, k + 1});
}
}
}
}
}
};func minimumObstacles(grid [][]int) int {
m, n := len(grid), len(grid[0])
q := doublylinkedlist.New()
type tuple struct{ i, j, k int }
q.Add(tuple{0, 0, 0})
vis := make([][]bool, m)
for i := range vis {
vis[i] = make([]bool, n)
}
dirs := [5]int{-1, 0, 1, 0, -1}
for {
v, _ := q.Get(0)
p := v.(tuple)
q.Remove(0)
i, j, k := p.i, p.j, p.k
if i == m-1 && j == n-1 {
return k
}
if vis[i][j] {
continue
}
vis[i][j] = true
for h := 0; h < 4; h++ {
x, y := i+dirs[h], j+dirs[h+1]
if x >= 0 && x < m && y >= 0 && y < n {
if grid[x][y] == 0 {
q.Insert(0, tuple{x, y, k})
} else {
q.Add(tuple{x, y, k + 1})
}
}
}
}
}function minimumObstacles(grid: number[][]): number {
const m = grid.length,
n = grid[0].length;
const dirs = [
[0, 1],
[0, -1],
[1, 0],
[-1, 0],
];
let ans = Array.from({ length: m }, v => new Array(n).fill(Infinity));
ans[0][0] = 0;
let deque = [[0, 0]];
while (deque.length) {
let [x, y] = deque.shift();
for (let [dx, dy] of dirs) {
let [i, j] = [x + dx, y + dy];
if (i < 0 || i > m - 1 || j < 0 || j > n - 1) continue;
const cost = grid[i][j];
if (ans[x][y] + cost >= ans[i][j]) continue;
ans[i][j] = ans[x][y] + cost;
deque.push([i, j]);
}
}
return ans[m - 1][n - 1];
}