-
Notifications
You must be signed in to change notification settings - Fork 67
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Transform between cartesian and frenet coordinate system #7
Comments
|
Hi @hcv1027 interesting problem. I think there could be an issue with the angle of your reference path (too high relative to your x-axis). Depending on the coordinate frames you are using, representing the reference path as a spline might be problematic because one x value could map to multiple y values. So far I've only used the code in this repo to test reference paths that lie in the first quadrant of a global coordinate frame, which leads to one x value mapping to only one y value (bijection). If you work in a (moving) local reference frame this shouldn't be a problem though. You might also try to use a polyline (x,y points) to represent your reference path. This is something I'd like to have implemented in this repo in the near future. However, this would require to rewrite the transformation functions and you would still have to work in a local (moving) reference frame. High curvature could also be a problem but from the image you provide, the curvature seems not that large - although I don't know the value :-) I am not entirely sure if the bijection thing leads to your problem but you could try using a reference path with similar curvature only this time let your robot travel in the the first quadrant similar to this: |
|
Hi @fjp , thanks for your reply. For the one x could map to multiple y problem, I already fixed it by using two spline function: But even the problem is coming from curvature, I still don't know how to fix it. |
|
You're right, I forgot that this formula from wikipedia is used in the spline class to calculate the curvature. It isn't that exact to calculate the curvature this way. Another approach is to use for example a clothoid where it is possible to get the exact curvature at a specific s coordinate (running length). Maybe you could try to fit clothoids to your reference path (which is not that easy) and use them as your reference path. However, this would again require to modify the transformation methods. And even then it seems you get into trouble with too high curvatures... Let me cite the main reference (Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame) of this approach:
I am not entirely sure because I don't know the values you get for ∆θ, κr or d, but I guess one of these constraints are not met in your case. Unfortunately there are no further details in the paper on how to deal with this. If there's no hard requirement on your side to use the Frenet space, I'd also try to stay in the Cartesian frame. However, I know that planning can be much simpler in the Frenet frame. |
|
This hasn't been active for a while, but have you looked at the Centripetal Catmull-Rom spline? Here it is applied separately to the x and y coordinate of points in blue to give the reconstructed green path: Note that the first and the last point (which are omitted from the interpolation) happen to the the same at (-3,10). I was experimenting with this here. |
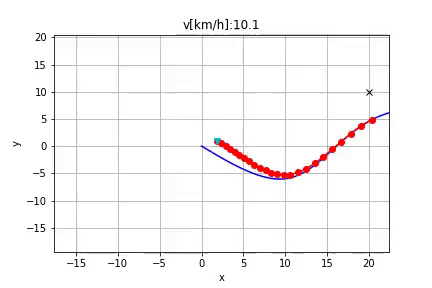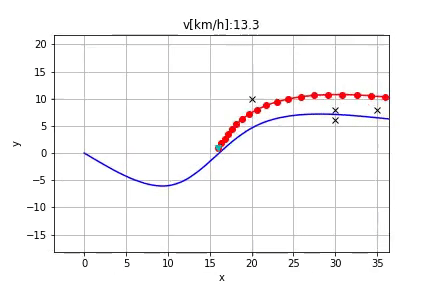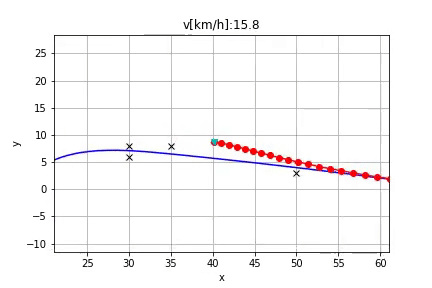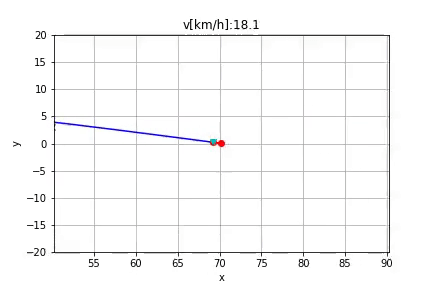



Hi @fjp , I'm working on my own version of this algorithm to generate a local path to avoid obstacles.

Currently I have a problem which I have no idea about how to fix. Here is the image to show my problem, the pink path is the original reference path, the left blue path is the generated path to avoid the obstacle lies on the original path, and the red circle marks my problem. When I try to convert my path from Frenet coordinate (s, d) to Cartesian coordinate (x, y), sometimes the path will suddenly turn back like the red circle part shows.
I use the spline function to map between s-to-x and s-to-y according to the original reference path. And I calculate the new path point which has d distance away from the original reference path and is perpendicular to the tangent direction of the relative point on the original path. I think the problem is coming from the curvature of the original path, but I have no idea about how to fix it. Can you give me some suggestion?
The text was updated successfully, but these errors were encountered: