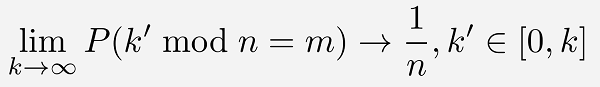Extending the ChainBet protocol to go beyond a simple coin flip can begin with dice. Games like craps offer many different kinds of bets. Here we will focus on a simple one-time dice roll. For example, a standard 6-sided die could be rolled and Bob could choose a number at random, say "5". Alice could then offer Bob bet odds at a 6:1 payout. Bob can wager 1 BCH and if a 5 is rolled, he will collect 6 BCH from Alice. If he loses, Alice will collect his 1 BCH.
We can extend the base protocol by introducing a new bet type designating a dice roll. It can configured to allow:
- different types ('cardinalities') of dice: 6-sided, 12-sided, 20-sided, etc
- different betting odds
- different roles (giving or taking odds)
The changes are fairly modest:
- Alice needs to advertise the bet differently, specifying the parameters of the bet.
- The participants need to fund the bet according to the parameters chosen.
- The main betting script should contain changes to handle the bet odds.
This phase is modified from the base protocol. Here we use a different bet type (0x02) instead of the coin flip (0x01). The presense of a different bet type will effect the "various_phase_dependent_data" that follows. In other words, the phase dependent data is not only dependent on the phase, but also on the bet type.
Alice could choose to either give odds (pay a bet multiple to Bob if he successfully guesses the outcome of a multi-sided dice roll), or take odds (the roles would reverse: Alice would win the multiple if Bob loses -- if his guess is unluckily rolled).
Alice can also choose the number of sides of the virtual die.
Since giving or taking odds is a binary decision, it would be a waste of space to consume an entire byte. Thus, we shall combine the "role" field (giving or taking odds) with the "number of sides of the die" in the same byte, with the most significant bit signaling the role, and the least significant 7 bits designating the number of sides.
A value of 0 for the "role" indicates Alice is giving odds to Bob (Bob wagers 1 BCH to win 6 BCH) and a value 1 indicates Alice is taking odds. 7 bits for the number of sides allows up to a 128-sided die.
Bob can also guess the actual outcome (more detail on this in the "Funding Transaction" section below).
The next 2 fields in the payload designate payout and payIn amounts. Rather than having a single amount, we need two fields since this is an assymetrical bet. Note that the amounts do NOT need to correspond to fair probabilities. If we always wanted a fair bet, only a single amount field would be needed.
However, by providing the flexibility to give slightly less-than-fair bets, it incentivizes liquidity to enter the system. This is analogous to how a market maker profits from a spread in a speculative marketplace. Therefore, it is essential for implementations to check and handle fairness parameters in a way that makes sense for their users.
OP_RETURN OUTPUT:
| Bytes | Name | Hex Value | Description |
|---|---|---|---|
| 1 | Phase | 0x01 | Phase 1 is "Bet Offer Announcement" |
| 1 | Bet Type | 0x02 | Denotes what kind of bet will be contructed. 0x02 for Dice Roll. |
| 1 | Role & Sides | <odds and sides> | Most significant bit designates who is giving odds; the least significant 7 bits designates the number of sides to the die |
| 1 | Guess | <guess > | Bob's guess at the outcome of the roll |
| 8 | Payout Amount | <payout amount> | Payout amount in Satohis for the bet host (Alice). |
| 8 | PayIn Amount | <payIn amount> | PayIn amount in Satohis for the bet participant (Bob). |
| 20 | Target Address | <target> | Optional. Restricts offer to a specific bet participant. |
In the base protocol (coin flip), the bet outcome is deteremined from the sum of 2 random secrets. Here is no different. But instead of merely picking odd or even, the result is based on the remainder of a modulo operation, where the divisor is the number of sides of the die.
It should be fairly clear why this works: Iterating the modulo operation over a divisor and a set of adjacent dividends produces a simple repeating sequence of integer values, and since the secrets being used are far larger than the set of possible values in the sequence, there is an essentially equal probability of choosing any particular number in the set. (This is actually the same algorithm as the coin flip, with the divisor always being 2).
Mathematically:
The construction of the Bitcoin script can simply plug in the value (number of sides) desired.
Although the "result of a dice roll" is already an abstraction derived from large secret numbers, it is fun for players to guess their lucky numbers. It is therefore valuable to include a way for Bob to choose the number he wants. This is done with the "guess" field in the payload, and needs to be implemented in the script, with an IF-ELSE path. If the guess matches the remainder (plus one), the participant taking odds wins the bet, otherwise he/she loses.
Jonald Fyookball