读论文推荐系统之ctr预估-AFM模型解析

[guevara]

（读论文）推荐系统之ctr预估-AFM模型解析



https://ift.tt/fVqDrxA



Jesse_jia

本人才疏学浅，不足之处欢迎大家指出和交流。

因个人原因最近都没更新，今天补上一篇FM家族的论文（AFM），接下来会将阿里的几个模型进行汇总下分享，希望大家一起学习呀。

话不多说，今天要分享的是一个Attentional Factorization Machine模型，是17年FM家族的成员。它和NFM是同一个作者，其在FM上的改进，最大的特点就是使用一个attention network来学习不同组合特征(二阶交叉)的重要性。下面我们一起来看下。

原文：《Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Network》

1、Introduction

首先介绍对于监督学习问题，类别特征作为输入，一般采用One-hot编码，所以需要引入特征交互来做出更精确的预测；但是如果直接以product的方式来显示交互，对于稀疏输入数据集，只能观察到一些交叉特征；所以提出FM，利用隐变量来做内积实现交互，但是FM也存在问题，也就是所有交互特征的权重是一样的，但是在实际中，对于预测性较低的特征，其对应权重也较低，所以AFM就是基于这个思想来做交叉特征的权重。

2、FM

FM全称Factorization Machine（详情可见之前的文章FM），通过隐向量内积来对每一对特征组合进行建模。

提出FM仍存在有下面两个问题：

在一次预测中，并不是所有的特征都有用的，但是FM对于所有的组合特征都使用相同的权重。AFM就是从这个角度进行优化的，针对不同的特征组合使用不同的权重。这也使得模型的可解释性更强，方便后续针对重要的特征组合进行深入研究。

虽然多层神经网络已经被证明可以有效的学习高阶特征组合。但是DNN的缺点也很明显（参数多，可解释性较弱，这里AFM未采用，智者见智吧）

3、AFM

3.1 Model

AFM的模型结构如下：

可以看到Sparse Input和Embedding Layer和FM中的是相同的，Embedding Layer把输入特征中非零部分特征embed成一个dense vector。剩下的三层为重点，如下：

Pair-wise Interaction Layer:

这一层主要是对组合特征进行建模，原来的m个嵌入向量，通过element-wise product（哈达玛积）操作得到了m(m-1)/2个组合向量，这些向量的维度和嵌入向量的维度相同均为k。形式化如下：

也就是说Pair-wise Interaction Layer的输入是所有嵌入向量，输出也是一组向量。输出是任意两个嵌入向量的element-wise product。任意两个嵌入向量都组合得到一个Interacted vector，所以m个嵌入向量得到m(m-1)/2个向量。

如果不考虑Attention机制，在Pair-wise Interaction Layer之后直接得到最终输出，可以形式化如下：

其中p和b分别是权重矩阵和偏置。当p全为1的时候，我们发现这就是FM。这个只是说明AFM的表达能力是在FM之上的，实际的情况中后面还使用了Attention机制。NFM中的Bilinear Interaction Layer也是把任意两个嵌入向量做element-wise product，然后进行sum pooling（求和池化，同NFM）操作。

Attention-based Pooling Layer:

Attention机制的核心思想在于：当把不同的部分拼接在一起的时候，让不同的部分的贡献程度不一样。AFM通过在Interacted vector后增加一个weighted sum来实现Attention机制。形式化如下：

这里aij是交互特征的Attention score，表示不同的组合特征对于最终的预测的贡献程度。可以看到：

1. Attention-based Pooling Layer的输入是Pair-wise Interaction Layer的输出。它包含m(m-1)/2个向量，每个向量的维度是k。（k是嵌入向量的维度，m是Embedding Layer中嵌入向量的个数）

2. Attention-based Pooling Layer的输出是一个k维向量。它对Interacted vector使用Attention score进行了weighted sum pooling（加权求和池化）操作。

但Attention score的学习是一个问题。一个常规的想法就是随着最小化loss来学习，但是存在一个问题是：对于训练集中从来没有一起出现过的特征组合的Attention score无法学习。

为了解决泛化问题，引入多层感知机（MLP），这里称为Attention network，其形式化定义如下：

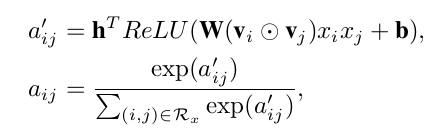
可以看到，本文中的Attention network实际上就是一个one layer MLP，激活函数使用ReLU，网络大小用attention factor表示，就是神经元的个数。它的输入是两个嵌入向量element-wise product之后的结果(interacted vector，用来在嵌入空间中对组合特征进行编码)；它的输出是组合特征对应的Attention score（aij）。最后，使用softmax对得到的Attention score进行规范化。

总结一下，AFM模型总形式化如下：

前面一部分是线性部分；后面一部分对每两个嵌入向量进行element-wise product得到Interacted vector；然后使用Attention机制得到每个组合特征的Attention score，并用这个score来进行weighted sum pooling；最后将这个k维的向量通过权重矩阵直接得到预测结果。

3.2 Learning

AFM可以用于不同的任务：回归、分类、排序等，一般对于回归问题是平方损失，二分类是Logloss，本文使用平方损失函数，且使用SGD算法来最优化模型参数；

防止过拟合： 防止过拟合常用的方法是Dropout或者L2 L1正则化。AFM的做法是：

1. 在Pair-wise Interaction Layer的输出使用Dropout

2. 在Attention Network中使用L2正则化

Attention Network是一个one layer MLP。不使用Dropout是因为，作者发现如果同时在interaction layer和Attention Network中使用Dropout会使得训练不稳定，并且降低性能。

所以，AFM的loss函数更新为：

4、Experiments

数据集：MovieLens和Frappe；

数据集划分：70% 训练, 20%验证， 10% 测试；

使用RMSE作为性能衡量，且和LibFM、HOFM、Wide&Deep和DeepCross进行性能对（Embedding大小256维）；这里用FM Embedding向量预训练AFM会导致更好的性能表现（相比于随机初始化）；

5、总结：

AFM是在FM的基础上改进的。相比于其他的DNN模型，比如Wide&Deep，DeepCross都是通过MLP来隐式学习组合特征。且这些Deep Methods都缺乏解释性，因为并不知道各个组合特征的情况。相比之下，FM通过两个隐向量内积来学习组合特征，解释性就比较好。

通过直接扩展FM，AFM引入Attention机制来学习不同组合特征的权重，即保证了模型的可解释性又提高了模型性能(但个人觉得这里的缺点是使用了物理意义并不明显的哈达玛积)。

但是，DNN的另一个作用是提取高阶组合特征，而AFM由于最后的加权累加，二次项并没有进行更深的网络去学习高阶交叉特征，这应该是缺点之一。

实现AFM的一个Demo，感兴趣的童鞋可以看下我的[github]。

via Jesse's Blog

December 5, 2024 at 06:31PM