Skip to content

Latest commit

 

History

History
729 lines (496 loc) · 21.9 KB

dp.md

File metadata and controls

729 lines (496 loc) · 21.9 KB
Raw

动态规划

背景

先从一道题目开始~

如题  triangle

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

例如，给定三角形：

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

自顶向下的最小路径和为  11（即，2 + 3 + 5 + 1 = 11）。

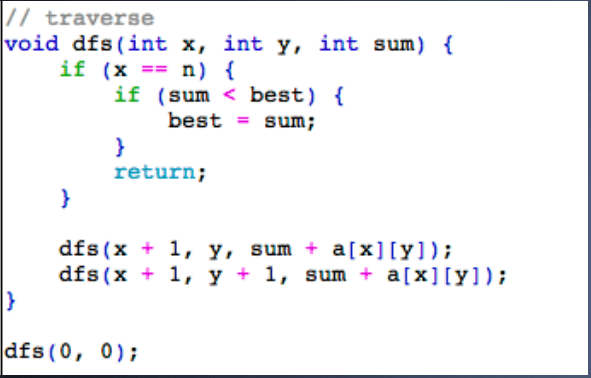
使用 DFS（遍历 或者 分治法）

遍历

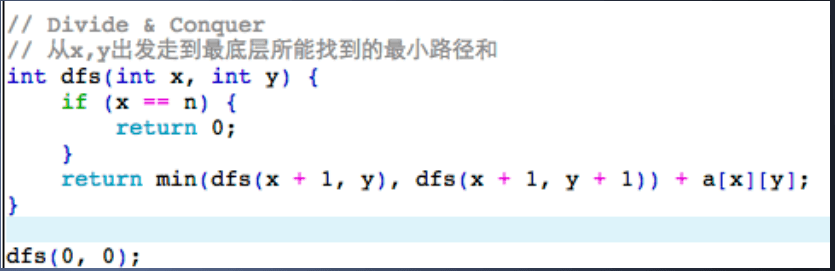
image.png

分治法

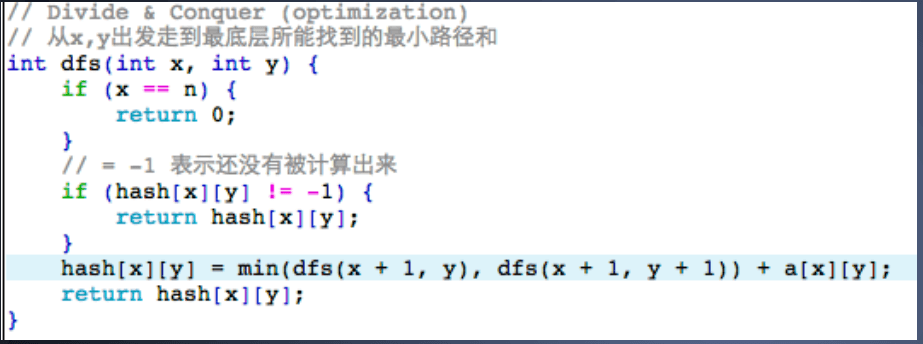
image.png

优化 DFS，缓存已经被计算的值（称为：记忆化搜索 本质上：动态规划）

image.png

动态规划就是把大问题变成小问题，并解决了小问题重复计算的方法称为动态规划

动态规划和 DFS 区别

  • 二叉树 子问题是没有交集，所以大部分二叉树都用递归或者分治法，即 DFS，就可以解决
  • 像 triangle 这种是有重复走的情况，子问题是有交集，所以可以用动态规划来解决

动态规划，自底向上

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        if len(triangle) == 0:
            return 0
        
        dp = triangle[-1].copy()
        
        for i in range(-2, -len(triangle) - 1, -1):
            for j in range(len(triangle[i])):
                dp[j] = triangle[i][j] + min(dp[j], dp[j + 1])
        
        return dp[0]

动态规划，自顶向下

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        if len(triangle) == 0:
            return 0
        
        dp = triangle[0]
        for row in triangle[1:]:
            dp_new = [row[0] + dp[0]]
            for i in range(len(dp) - 1):
                dp_new.append(row[i+1] + min(dp[i], dp[i+1]))
            dp_new.append(row[-1] + dp[-1])
            dp = dp_new
        
        return min(dp)

递归和动规关系

递归是一种程序的实现方式：函数的自我调用

Function(x) {
	...
	Funciton(x-1);
	...
}

动态规划：是一种解决问题的思想，大规模问题的结果，是由小规模问题的结果运算得来的。动态规划可用递归来实现(Memorization Search)

使用场景

满足两个条件

  • 满足以下条件之一
    • 求最大/最小值（Maximum/Minimum ）
    • 求是否可行（Yes/No ）
    • 求可行个数（Count(*) ）
  • 满足不能排序或者交换（Can not sort / swap ）

如题：longest-consecutive-sequence  位置可以交换，所以不用动态规划

四点要素

  1. 状态 State
    • 灵感，创造力，存储小规模问题的结果
  2. 方程 Function
    • 状态之间的联系，怎么通过小的状态，来算大的状态
  3. 初始化 Intialization
    • 最极限的小状态是什么, 起点
  4. 答案 Answer
    • 最大的那个状态是什么，终点

常见四种类型

  1. Matrix DP (10%)
  2. Sequence (40%)
  3. Two Sequences DP (40%)
  4. Backpack (10%)

注意点

  • 贪心算法大多题目靠背答案，所以如果能用动态规划就尽量用动规，不用贪心算法

1、矩阵类型（10%）

minimum-path-sum

给定一个包含非负整数的  m x n  网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

思路：动态规划

  1. state: f(x, y) 从起点走到 (x, y) 的最短路径

  2. function: f(x, y) = min(f(x - 1, y), f(x, y - 1]) + A(x, y)

  3. intialize: f(0, 0) = A(0, 0)、f(i, 0) = sum(0,0 -> i,0)、 f(0, i) = sum(0,0 -> 0,i)

  4. answer: f(n - 1, m - 1)

  5. 2D DP -> 1D DP

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        
        dp = [0] * n
        dp[0] = grid[0][0]
        for i in range(1, n):
            dp[i] = dp[i-1] + grid[0][i]
        
        for i in range(1, m):
            dp[0] += grid[i][0]
            for j in range(1, n):
                dp[j] = grid[i][j] + min(dp[j-1], dp[j])
        return dp[-1]

unique-paths

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。 问总共有多少条不同的路径？

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        
        if m < n:
            m, n = n, m
        
        dp = [1] * n
        
        for i in range(1, m):
            for j in range(1, n):
                dp[j] += dp[j - 1]
        
        return dp[-1]

unique-paths-ii

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。 问总共有多少条不同的路径？ 现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

class Solution:
    def uniquePathsWithObstacles(self, G: List[List[int]]) -> int:
        
        m, n = len(G), len(G[0])
        
        dp = [1] if G[0][0] == 0 else [0]
        for i in range(1, n):
            new = dp[i-1] if G[0][i] == 0 else 0
            dp.append(new)
        
        for i in range(1, m):
            dp[0] = 0 if G[i][0] == 1 else dp[0]
            for j in range(1, n):
                dp[j] = dp[j-1] + dp[j] if G[i][j] == 0 else 0
        
        return dp[-1]

2、序列类型（40%）

climbing-stairs

假设你正在爬楼梯。需要  n  阶你才能到达楼顶。

class Solution:
    def climbStairs(self, n: int) -> int:
        if n < 2: return n
        
        step1, step2 = 2, 1
        
        for _ in range(n - 2):
            step1, step2 = step1 + step2, step1
        
        return step1

jump-game

给定一个非负整数数组，你最初位于数组的第一个位置。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个位置。

解法：直接DP无法得到O(n)的解，考虑间接DP

  • tail to head
class Solution:
    def canJump(self, nums: List[int]) -> bool:
        
        left = len(nums) - 1 # most left index that can reach the last index
        
        for i in range(len(nums) - 2, -1, -1):
            
            left = i if i + nums[i] >= left else left # DP
        
        return left == 0
  • head to tail
class Solution:
    def canJump(self, nums: List[int]) -> bool:
        
        max_pos = nums[0] # furthest index can reach
        
        for i in range(1, len(nums)):
            if max_pos < i:
                return False
            max_pos = max(max_pos, i + nums[i]) # DP
        
        return True

jump-game-ii

给定一个非负整数数组，你最初位于数组的第一个位置。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 你的目标是使用最少的跳跃次数到达数组的最后一个位置。

class Solution:
    def jump(self, nums: List[int]) -> int:
        
        cur_max = 0
        step_max = 0
        step = 0
        
        for i in range(len(nums)):

            if cur_max < i: # can't reach i, don't have to consider in this problem
                return float('inf')
            
            if step_max < i: # can't reach i in current number of steps
                step += 1
                step_max = cur_max
            
            cur_max = max(cur_max, i + nums[i]) # DP
        
        return min_step

palindrome-partitioning-ii

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。 返回符合要求的最少分割次数。

  • Why is hard

仅目标DP, 判断回文时间复杂度高 -> 目标DP + 回文二维DP, 回文DP空间复杂度高 -> 一点trick, 回文DP空间复杂度降为线性

class Solution:
    
    def minCut(self, s: str) -> int:
        
        dp_min = [0] * len(s)
        dp_pal = [True] * len(s)
        
        def isPal(i, j):
            dp_pal[i] = (s[i] == s[j] and dp_pal[i+1])
            return dp_pal[i]
        
        for j in range(1, len(s)):
            
            min_cut = dp_min[j - 1] + 1
            
            if isPal(0, j):
                min_cut = 0
            
            for i in range(1, j):
                if isPal(i, j):
                    min_cut = min(min_cut, dp_min[i - 1] + 1)
            
            dp_min[j] = min_cut
        
        return dp_min[-1]

longest-increasing-subsequence

给定一个无序的整数数组，找到其中最长上升子序列的长度。

  • DP(i) 等于以第i个数结尾的最长上升子序列的长度，容易想但不是最优
class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        
        if len(nums) == 0: return 0
        
        dp_max = [1] * len(nums)
        
        for j in range(1, len(nums)):
            for i in range(j):
                if nums[j] > nums[i]:
                    dp_max[j] = max(dp_max[j], dp_max[i] + 1)
        
        return max(dp_max)
  • 最优算法使用 greedy + binary search，比较tricky
class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        
        if len(nums) == 0: return 0
        
        seq = [nums[0]]
        
        for i in range(1, len(nums)):
            ins = bisect.bisect_left(seq, nums[i])
            if ins == len(seq):
                seq.append(nums[i])
            else:
                seq[ins] = nums[i]
        
        return len(seq)

word-break

给定一个非空字符串  s  和一个包含非空单词列表的字典  wordDict，判定  s  是否可以被空格拆分为一个或多个在字典中出现的单词。

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        
        dp = [False] * (len(s) + 1)
        dp[-1] = True
        
        for j in range(len(s)):
            for i in range(j+1):
                if dp[i - 1] and s[i:j+1] in wordDict:
                    dp[j] = True
                    break
        
        return dp[len(s) - 1]

小结

常见处理方式是给 0 位置占位，这样处理问题时一视同仁，初始化则在原来基础上 length+1，返回结果 f[n]

  • 状态可以为前 i 个
  • 初始化 length+1
  • 取值 index=i-1
  • 返回值：f[n]或者 f[m][n]

Two Sequences DP（40%）

longest-common-subsequence

给定两个字符串  text1 和  text2，返回这两个字符串的最长公共子序列。 一个字符串的   子序列   是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

  • 二维DP若只与当前行和上一行有关，可将空间复杂度降到线性
class Solution:
    def longestCommonSubsequence(self, t1: str, t2: str) -> int:
        
        if t1 == '' or t2 == '':
            return 0
        
        if len(t1) < len(t2):
            t1, t2 = t2, t1

        dp = [int(t2[0] == t1[0])] * len(t2) # previous row
        dp_new = [0] * len(t2) # current row
        
        for j in range(1, len(t2)):
            dp[j] = 1 if t2[j] == t1[0] else dp[j - 1]
        
        for i in range(1, len(t1)):
            dp_new[0] = 1 if dp[0] == 1 or t2[0] == t1[i] else 0
            for j in range(1, len(t2)):
                if t2[j] != t1[i]:
                    dp_new[j] = max(dp[j], dp_new[j - 1])
                else:
                    dp_new[j] = dp[j - 1] + 1
            dp, dp_new = dp_new, dp
        
        return dp[-1]

edit-distance

给你两个单词  word1 和  word2，请你计算出将  word1  转换成  word2 所使用的最少操作数   你可以对一个单词进行如下三种操作： 插入一个字符 删除一个字符 替换一个字符

思路：和上题很类似，相等则不需要操作，否则取删除、插入、替换最小操作次数的值+1

class Solution:
    def minDistance(self, w1: str, w2: str) -> int:
        
        if w1 == '': return len(w2)
        if w2 == '': return len(w1)
        
        m, n = len(w1), len(w2)
        if m < n:
            w1, w2, m, n = w2, w1, n, m
        
        dp = [int(w1[0] != w2[0])] * n
        dp_new = [0] * n
        
        for j in range(1, n):
            dp[j] = dp[j - 1] + int(w2[j] != w1[0] or dp[j - 1] != j)
        
        for i in range(1, m):
            dp_new[0] = dp[0] + int(w2[0] != w1[i] or dp[0] != i)
            
            for j in range(1, n):
                dp_new[j] = min(dp[j - 1] + int(w2[j] != w1[i]), dp[j] + 1, dp_new[j - 1] + 1)
                
            dp, dp_new = dp_new, dp
        
        
        return dp[-1]

说明

另外一种做法：MAXLEN(a,b)-LCS(a,b)

零钱和背包（10%）

coin-change

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回  -1。

思路：和其他 DP 不太一样，i 表示钱或者容量

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        
        dp = [0] * (amount + 1)
         
        for i in range(1, len(dp)):
            dp[i] = float('inf')
            
            for coin in coins:
                if i >= coin and dp[i - coin] + 1 < dp[i]:
                    dp[i] = dp[i - coin] + 1
            
        return -1 if dp[amount] == float('inf') else dp[amount]

backpack

在 n 个物品中挑选若干物品装入背包，最多能装多满？假设背包的大小为 m，每个物品的大小为 A[i]

class Solution:
    def backPack(self, m, A):
        
        n = len(A)
        
        dp = [0] * (m + 1)
        dp_new = [0] * (m + 1)
        
        for i in range(n):
            for j in range(1, m + 1):
                use_Ai = 0 if j - A[i] < 0 else dp[j - A[i]] + A[i]
                dp_new[j] = max(dp[j], use_Ai)
            
            dp, dp_new = dp_new, dp
        
        return dp[-1]

backpack-ii

有 n 个物品和一个大小为 m 的背包. 给定数组 A 表示每个物品的大小和数组 V 表示每个物品的价值. 问最多能装入背包的总价值是多大?

思路：dp(i, j) 为前 i 个物品，装入 j 背包的最大价值

class Solution:
    def backPackII(self, m, A, V):
        
        n = len(A)
        
        dp = [0] * (m + 1)
        dp_new = [0] * (m + 1)
        
        for i in range(n):
            for j in range(1, m + 1):
                use_Ai = 0 if j - A[i] < 0 else dp[j - A[i]] + V[i] # previous problem is a special case of this problem that V(i) = A(i)
                dp_new[j] = max(dp[j], use_Ai)
            
            dp, dp_new = dp_new, dp
        
        return dp[-1]

补充

maximum-product-subarray

最大乘积子串

处理负数情况稍微有点复杂，注意需要同时 DP 正数乘积和负数乘积

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        
        max_product = float('-inf')

        dp_pos, dp_neg = 0, 0
        
        for num in nums:
            if num > 0:
                dp_pos, dp_neg = max(num, num * dp_pos), dp_neg * num
            else:
                dp_pos, dp_neg = dp_neg * num, min(num, dp_pos * num)
            
            if dp_pos != 0:
                max_product = max(max_product, dp_pos)
            elif dp_neg != 0:
                max_product = max(max_product, dp_neg)
            else:
                max_product = max(max_product, 0)
            
        return max_product

decode-ways

1 到 26 分别对应 a 到 z，给定输入数字串，问总共有多少种译码方法

常规 DP 题，注意处理edge case即可

class Solution:
    def numDecodings(self, s: str) -> int:
        
        def valid_2(i):
            if i < 1:
                return 0
            num = int(s[i-1:i+1])
            return int(num > 9 and num < 27)
        
        dp_1, dp_2 = 1, 0
        for i in range(len(s)):
            dp_1, dp_2 = dp_1 * int(s[i] != '0') + dp_2 * valid_2(i), dp_1
        
        return dp_1

best-time-to-buy-and-sell-stock-with-cooldown

给定股票每天的价格，每天可以买入卖出，买入后必须卖出才可以进行下一次购买，卖出后一天不可以购买，问可以获得的最大利润

经典的维特比译码类问题，找到状态空间和状态转移关系即可

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        
        buy, buy_then_nothing, sell, sell_then_nothing = float('-inf'), float('-inf'), float('-inf'), 0
        
        for p in prices:
            buy, buy_then_nothing, sell, sell_then_nothing = sell_then_nothing - p, max(buy, buy_then_nothing), max(buy, buy_then_nothing) + p, max(sell, sell_then_nothing)
        
        return max(buy, buy_then_nothing, sell, sell_then_nothing)

word-break-ii

给定字符串和可选的单词列表，求字符串所有的分割方式

思路：此题 DP 解法容易想但并不是好做法，因为和 word-break 不同，此题需要返回所有可行分割而不是找到一组就可以。这里使用 个人推荐 backtrack with memoization。

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:
        
        n = len(s)
        result = []
        mem = collections.defaultdict(list)
        wordDict = set(wordDict)
        
        def backtrack(first=0, route=[]):
            if first == n:
                result.append(' '.join(route))
                return True
            
            if first not in mem:
                for next_first in range(first + 1, n + 1):
                    if s[first:next_first] in wordDict:
                        route.append(s[first:next_first])
                        if backtrack(next_first, route):
                            mem[first].append(next_first)
                        route.pop()
                if len(mem[first]) > 0:
                    return True
            elif len(mem[first]) > 0:
                for next_first in mem[first]:
                    route.append(s[first:next_first])
                    backtrack(next_first)
                    route.pop()
                return True
            
            return False
        
        backtrack()
        return result

burst-balloons

n 个气球排成一行，每个气球上有一个分数，每次戳爆一个气球得分为该气球分数和相邻两气球分数的乘积，求最大得分

此题主要难点是构造 DP 的状态，过程为逆着气球戳爆的顺序

class Solution:
    def maxCoins(self, nums: List[int]) -> int:
        
        n = len(nums)
        nums.append(1)
        dp = [[0] * (n + 1) for _ in range(n + 1)]
        
        for dist in range(2, n + 2):
            for left in range(-1, n - dist + 1):
                right = left + dist
                max_coin = float('-inf')
                left_right = nums[left] * nums[right]
                for j in range(left + 1, right):
                    max_coin = max(max_coin, left_right * nums[j] + dp[left][j] + dp[j][right])
                dp[left][right] = max_coin
        nums.pop()
        return dp[-1][n]

练习

Matrix DP (10%)

Sequence (40%)

Two Sequences DP (40%)

Backpack & Coin Change (10%)