Skip to content

Latest commit

 

History

History
168 lines (109 loc) · 5.41 KB

README.md

File metadata and controls

168 lines (109 loc) · 5.41 KB
Raw

Metaheuristics

Metaheuristics logo

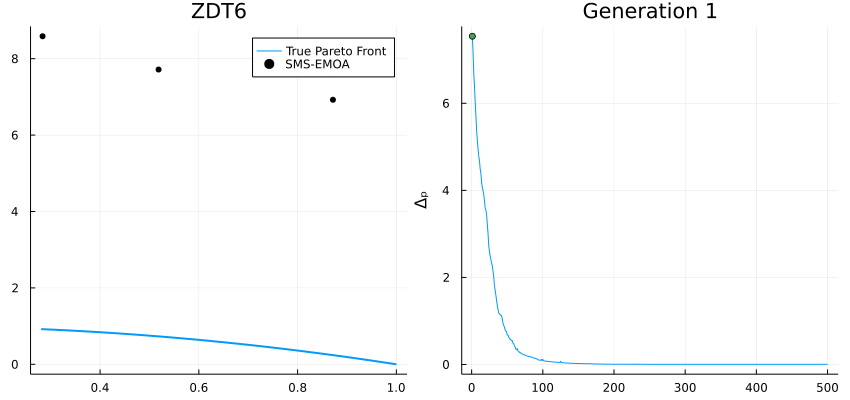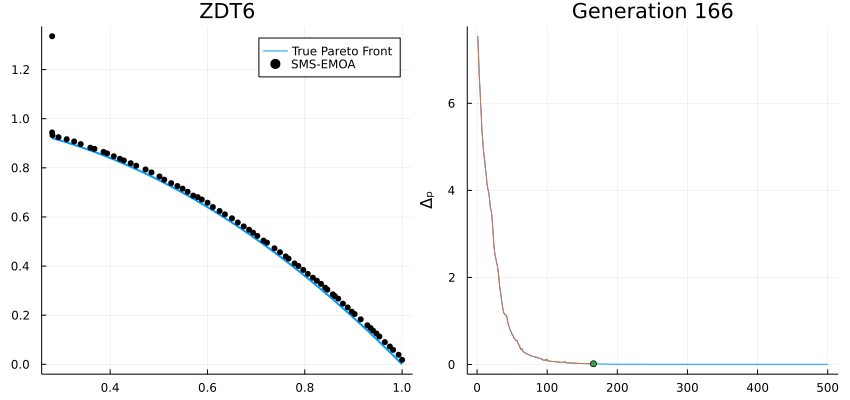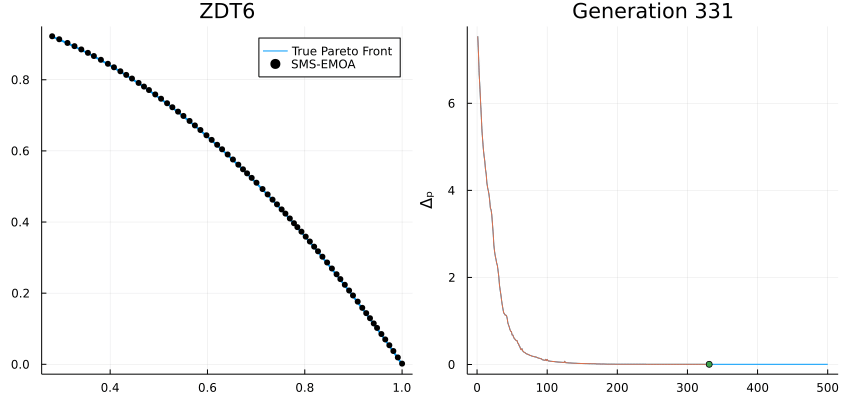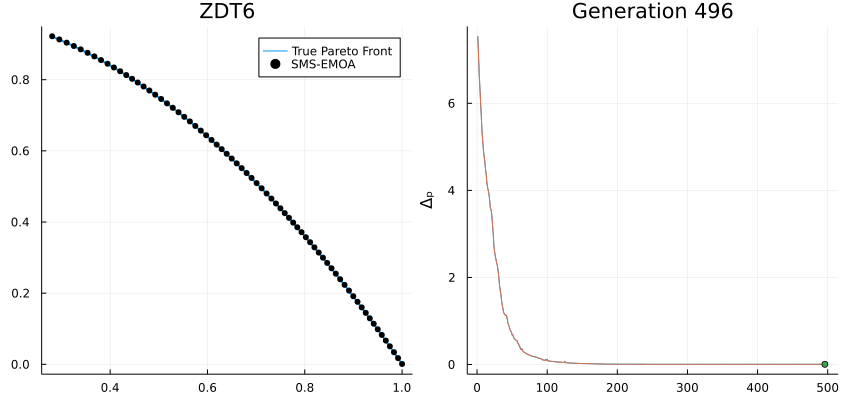
High-performance metaheuristics for global optimization.

Build Status codecov Aqua QA Doc Doc DOI

Installation

Open the Julia REPL and press ] to open the Pkg prompt. To add this package, use the add command:

pkg> add Metaheuristics

Or, equivalently, via the Pkg API:

julia> import Pkg; Pkg.add("Metaheuristics")

Algorithms

Some representative metaheuristics are developed here, including those for single- and multi-objective optimization. Moreover, some constraint handling techniques have been considered in most of the implemented algorithms.

Single-Objective Optimization

  • ECA: Evolutionary Centers Algorithm
  • DE: Differential Evolution
  • PSO: Particle Swarm Optimization
  • ABC: Artificial Bee Colony
  • GSA: Gravitational Search Algorithm
  • SA: Simulated Annealing
  • WOA: Whale Optimization Algorithm
  • MCCGA: Machine-coded Compact Genetic Algorithm
  • GA: Genetic Algorithm
  • BRKGA: Biased Random Key Genetic Algorithm

Multi-Objective Optimization

SMS-EMOA in Metaheuristics.jl

  • MOEA/D-DE: Multi-objective Evolutionary Algorithm based on Decomposition
  • NSGA-II: A fast and elitist multi-objective genetic algorithm: NSGA-II
  • NSGA-III: Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach
  • SMS-EMOA: An EMO algorithm using the hypervolume measure as the selection criterion
  • SPEA2: Improved Strength Pareto Evolutionary Algorithm
  • CCMO: Coevolutionary Framework for Constrained Multiobjective Optimization

Performance Indicators

  • GD: Generational Distance
  • IGD, IGD+: Inverted Generational Distance (Plus)
  • C-metric: Covering Indicator
  • HV: Hypervolume
  • Δₚ (Delta p): Averaged Hausdorff distance
  • Spacing Indicator
  • and more...

Multi-Criteria Decision-Making

Multi-Criteria Decision Making methods are available, including:

Quick Start

Assume you want to solve the following minimization problem.

Rastrigin Surface

Minimize:

$$f(x) = 10D + \sum_{i=1}^D x_i^2 - 10\cos(2\pi x_i)$$

where $x\in [-5, 5]^D$, that is, each coordinate in $x$ is between -5 and 5. Use $D=10$.

Solution

Firstly, import the Metaheuristics package:

using Metaheuristics

Code the objective function:

f(x) = 10length(x) + sum( x.^2 - 10cos.(2π*x)  )

Instantiate the bounds:

D = 10
bounds = boxconstraints(lb = -5ones(D), ub = 5ones(D))

Also, bounds can be a $2\times 10$ Matrix where the first row corresponds to the lower bounds whilst the second row corresponds to the upper bounds.

Approximate the optimum using the function optimize.

result = optimize(f, bounds)

Optimize returns a State datatype which contains some information about the approximation. For instance, you may use mainly two functions to obtain such an approximation.

@show minimum(result)
@show minimizer(result)

Documentation

See the documentation for more details, examples and options.

How to cite?

Please cite the package using the bibtex entry

@article{metaheuristics2022, 
  doi = {10.21105/joss.04723}, 
  url = {https://doi.org/10.21105/joss.04723}, 
  year = {2022}, 
  publisher = {The Open Journal}, 
  volume = {7}, 
  number = {78}, 
  pages = {4723}, 
  author = {Jesús-Adolfo Mejía-de-Dios and Efrén Mezura-Montes}, 
  title = {Metaheuristics: A Julia Package for Single- and Multi-Objective Optimization}, 
 journal = {Journal of Open Source Software} }

or the citation string

Mejía-de-Dios et al., (2022). Metaheuristics: A Julia Package for Single- and Multi-Objective Optimization. Journal of Open Source Software, 7(78), 4723, https://doi.org/10.21105/joss.04723

in your scientific paper if you use Metaheristics.jl.

Contributing

Please feel free to send me your PR, issue or any comment about this package for Julia.