Alice 和 Bob 共有一个无向图,其中包含 n 个节点和 3 种类型的边:
- 类型 1:只能由 Alice 遍历。
- 类型 2:只能由 Bob 遍历。
- 类型 3:Alice 和 Bob 都可以遍历。
给你一个数组 edges ,其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下,找出可以删除的最大边数。如果从任何节点开始,Alice 和 Bob 都可以到达所有其他节点,则认为图是可以完全遍历的。
返回可以删除的最大边数,如果 Alice 和 Bob 无法完全遍历图,则返回 -1 。
示例 1:
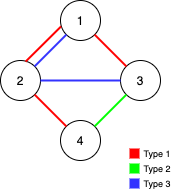
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]] 输出:2 解释:如果删除 [1,1,2] 和 [1,1,3] 这两条边,Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。
示例 2:
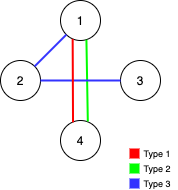
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]] 输出:0 解释:注意,删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。
示例 3:
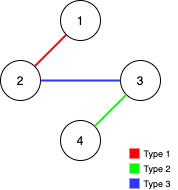
输入:n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]] 输出:-1 解释:在当前图中,Alice 无法从其他节点到达节点 4 。类似地,Bob 也不能达到节点 1 。因此,图无法完全遍历。
提示:
1 <= n <= 10^51 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)edges[i].length == 31 <= edges[i][0] <= 31 <= edges[i][1] < edges[i][2] <= n- 所有元组
(typei, ui, vi)互不相同
方法一:贪心 + 并查集
题目要求我们删除最多数目的边,使得 Alice 和 Bob 都可以遍历整个图。也即是说,我们需要保留尽可能少的边,并且要求这些边能够使得 Alice 和 Bob 都可以遍历整个图。
我们可以用两个并查集
接下来,我们优先遍历公共边,即
然后,我们再遍历 Alice 独有的边,即
最后,如果 Alice 和 Bob 都可以遍历整个图,那么答案就是我们删除的边数;否则答案就是
时间复杂度
class UnionFind:
def __init__(self, n):
self.p = list(range(n))
self.size = [1] * n
self.cnt = n
def find(self, x):
if self.p[x] != x:
self.p[x] = self.find(self.p[x])
return self.p[x]
def union(self, a, b):
pa, pb = self.find(a - 1), self.find(b - 1)
if pa == pb:
return False
if self.size[pa] > self.size[pb]:
self.p[pb] = pa
self.size[pa] += self.size[pb]
else:
self.p[pa] = pb
self.size[pb] += self.size[pa]
self.cnt -= 1
return True
class Solution:
def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:
ufa = UnionFind(n)
ufb = UnionFind(n)
ans = 0
for t, u, v in edges:
if t == 3:
if ufa.union(u, v):
ufb.union(u, v)
else:
ans += 1
for t, u, v in edges:
if t == 1:
ans += not ufa.union(u, v)
if t == 2:
ans += not ufb.union(u, v)
return ans if ufa.cnt == 1 and ufb.cnt == 1 else -1class UnionFind {
private int[] p;
private int[] size;
public int cnt;
public UnionFind(int n) {
p = new int[n];
size = new int[n];
for (int i = 0; i < n; ++i) {
p[i] = i;
size[i] = 1;
}
cnt = n;
}
public int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
public boolean union(int a, int b) {
int pa = find(a - 1), pb = find(b - 1);
if (pa == pb) {
return false;
}
if (size[pa] > size[pb]) {
p[pb] = pa;
size[pa] += size[pb];
} else {
p[pa] = pb;
size[pb] += size[pa];
}
--cnt;
return true;
}
}
class Solution {
public int maxNumEdgesToRemove(int n, int[][] edges) {
UnionFind ufa = new UnionFind(n);
UnionFind ufb = new UnionFind(n);
int ans = 0;
for (var e : edges) {
int t = e[0], u = e[1], v = e[2];
if (t == 3) {
if (ufa.union(u, v)) {
ufb.union(u, v);
} else {
++ans;
}
}
}
for (var e : edges) {
int t = e[0], u = e[1], v = e[2];
if (t == 1 && !ufa.union(u, v)) {
++ans;
}
if (t == 2 && !ufb.union(u, v)) {
++ans;
}
}
return ufa.cnt == 1 && ufb.cnt == 1 ? ans : -1;
}
}class UnionFind {
public:
int cnt;
UnionFind(int n) {
p = vector<int>(n);
size = vector<int>(n, 1);
iota(p.begin(), p.end(), 0);
cnt = n;
}
bool unite(int a, int b) {
int pa = find(a - 1), pb = find(b - 1);
if (pa == pb) {
return false;
}
if (size[pa] > size[pb]) {
p[pb] = pa;
size[pa] += size[pb];
} else {
p[pa] = pb;
size[pb] += size[pa];
}
--cnt;
return true;
}
int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
private:
vector<int> p, size;
};
class Solution {
public:
int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {
UnionFind ufa(n);
UnionFind ufb(n);
int ans = 0;
for (auto& e : edges) {
int t = e[0], u = e[1], v = e[2];
if (t == 3) {
if (ufa.unite(u, v)) {
ufb.unite(u, v);
} else {
++ans;
}
}
}
for (auto& e : edges) {
int t = e[0], u = e[1], v = e[2];
ans += t == 1 && !ufa.unite(u, v);
ans += t == 2 && !ufb.unite(u, v);
}
return ufa.cnt == 1 && ufb.cnt == 1 ? ans : -1;
}
};type unionFind struct {
p, size []int
cnt int
}
func newUnionFind(n int) *unionFind {
p := make([]int, n)
size := make([]int, n)
for i := range p {
p[i] = i
size[i] = 1
}
return &unionFind{p, size, n}
}
func (uf *unionFind) find(x int) int {
if uf.p[x] != x {
uf.p[x] = uf.find(uf.p[x])
}
return uf.p[x]
}
func (uf *unionFind) union(a, b int) bool {
pa, pb := uf.find(a-1), uf.find(b-1)
if pa == pb {
return false
}
if uf.size[pa] > uf.size[pb] {
uf.p[pb] = pa
uf.size[pa] += uf.size[pb]
} else {
uf.p[pa] = pb
uf.size[pb] += uf.size[pa]
}
uf.cnt--
return true
}
func maxNumEdgesToRemove(n int, edges [][]int) (ans int) {
ufa := newUnionFind(n)
ufb := newUnionFind(n)
for _, e := range edges {
t, u, v := e[0], e[1], e[2]
if t == 3 {
if ufa.union(u, v) {
ufb.union(u, v)
} else {
ans++
}
}
}
for _, e := range edges {
t, u, v := e[0], e[1], e[2]
if t == 1 && !ufa.union(u, v) {
ans++
}
if t == 2 && !ufb.union(u, v) {
ans++
}
}
if ufa.cnt == 1 && ufb.cnt == 1 {
return
}
return -1
}