​「隐语小课」联邦学习之“隐私保护图神经网络”GNN

[halosecret00]

  

前言：

本文对隐语团队发表在Peer-to-Peer Networking & Applications期刊中的一篇“ASFGNN: Automated separated-federated graph neural network.”进行解读，介绍了联邦GNN的一种实践方式。公众号后台回复GNN，获取原论文。

一、背景知识

图神经网络模型（GNN）利用图数据聚合节点特征和邻居信息，丰富了自身的特征信息，在计算机视觉、推荐系统、金融欺诈等领域有广泛的应用。对于神经网络模型来说，参与训练的数据量越多，模型的性能往往越好，GNN也不例外。然而在实际应用时，特别是在金融场景中，多方联合GNN建模存在很多需要解决的问题。首先，拥有数据的机构之间由于数据安全的原因或者数据隐私法规的限制，往往无法互通数据，造成数据孤岛问题，大大减少了参与训练的数据总量。其次，由于数据采集的地域、目标人群、时间窗口的不同，数据集之间的图/特征/标签分布也往往不同，即非独立同分布数据（Non-IID），因此在进行联合建模时需要采用不同的网络结构和超参数来表征参与方数据集之间的差异性，从而大大增加了超参的搜索空间。此外，由于在联合建模中，需要进行大量的数据通信，受限于通信环境，模型单次训练的时间较长，超参数搜索空间的增大，进一步增加了训练了整体时间。

  

综上所述，在保证数据隐私的前提下，针对多方非独立同分布数据（Non-IID），实现图神经网络模型的联合训练及自动超参调优是目前急需解决的问题（如下图所示）。

二、先验知识

2.1图神经网络

GNN通过聚合节点信息和邻居信息的方式获取/交换周围节点的信息，得到节点（node）的embedding，作为节点新的特征，然后基于新的特征进行分类或回归训练。因此GNN模型训练可以分为embedding生成和损失函数计算两个步骤，其中embedding有多种生成算子，例如structure2vec、GCN、GraphSAGE等。我们采用GraphSAGE作为本文的embedding生成算子，首先对节点的embedding进行初始化，即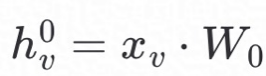：，然后对邻居进行k度传播，得到节点最终的embedding，如公式（1）所示：

其中AGG是聚合函数，有三种类型：mean、max和LSTM；k为邻居传播的深度，u是图数据集的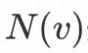节点，是节点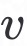的邻接节点函数。

2.2联邦学习

联邦学习是一种保护数据隐私的多方联合建模的训练方法，由Google在2016年首次提出。联邦学习借鉴了参数服务器的思路，参与训练的成员分为服务器端和客户端，客户端拥有数据集，服务器负责进行模型聚合。

  

具体训练过程如下：客户端利用自身数据集进行训练，更新本地模型；客户端将加密后的模型上传至服务器端，服务器端进行模型融合，得到全局模型；客户端从服务器获得全局模型，更新本地模型，完成一次训练过程。联邦学习通过共享模型而非数据的方式，防止隐私数据的泄漏。然而联邦学习基于独立同分布数据集假设，因此对于非独立同分布数据集，训练效果较差。

2.3JS散度

JS散度可用于度量两个数据集分布之间的相似性，是KL散度的变体，具有对称性、平滑性等特点，取值区间为[0,1]，可用于表征两个Non-IID数据集之间分布的差异性，如公式（2）所示：

2.4秘密分享

本文基于t-n秘密分享算法，将需要保密的信息分成n份密文，只有得到大于等于t份密文时，才可以恢复出原始明文信息。假设客户端i(i∈P,P={1,2,...,I})中有一个l位的数a，是需要进行分享的秘密。特别的，令t=n，我们设计了一个n-n加法秘密分享算法，即若想恢复原始秘密，则需要得到所有的密文。

  

设密文生成算法为Shr(.) 秘密恢复算法为Rec(.)

**Shr(.)为：**客户端i生成个I−1随机数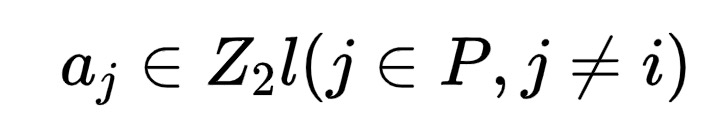，并把aj发送给客户端j,同时得到：

于是我们得到明文a在所有客户端上的密文，用⟨a⟩表示。**Rec(.)**为：

2.5贝叶斯优化

贝叶斯优化算法是一种解决黑箱问题的有效算法。我们将模型的超参调试过程作为一个黑箱问题，即黑箱的输入为超参数的不同组合，黑箱的输出为模型的性能，贝叶斯优化算法可以表示为：

其中x表示超参数，X为超参数的搜索空间，f为模型性能关于超参数x的函数。对于GNN模型来说，超参数可以是学习率、正则化系数、网络结构、传播深度等，模型的性能评价指标可以是准确率、AUC、mae等。贝叶斯优化算法的关键在于分布函数，以及选择合适的获得函数（acquisitionfunction），利用已有的试验数据得到下一个需要测试的x点。本文中我们选择高斯分布（GP）作为分布函数和expectedimprovement（EI）作为获得函数。

  

三、算法模型

3.1简介

我们提出了AutomatedSeparated-Federated Graph Neural Network(ASFGNN)算法框架，该算法框架主要包括三个部分，如Figure2所示：

•   （1）SeparatedGNN learning（SGNN）：客户端采用不同的超参数分别计算得到各自节点的embedding。
      
•   （2）FedaratedGNN learning（FGNN）：客户端将（1）中得到的embedding作为新的节点特征，利用联邦学习算法，进行隐私保护的联合训练；利用JS散度优化联邦学习中的Non-IID数据集问题。
      
•   （3）贝叶斯超参优化：针对Non-IID的超参爆炸问题，利用贝叶斯优化算法进行超参调优，从而减少超参调试的训练时间。
      

综上SGNN和FGNN完成了在某个超参组合下的模型训练，总体称为SFGNN模型；贝叶斯优化部分完成了对SFGNN模型的自动调参。

3.2SGNN

客户端利用GraphSAGE算子生成embedding，如Algorithm1中所示，其中输入数据为客户端i的图数据集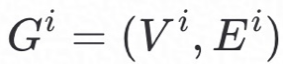，邻接函数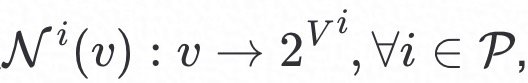非线性函数σ，传播深度K，最终得到客户端在第t次训练时的，作为FGNN的输入。

3.3FGNN

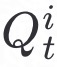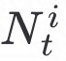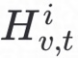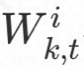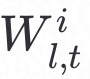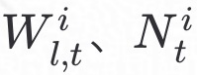我们将SGNN中生成的embedding作为客户端节点的新特征，然后基于联邦学习进行隐私保护联合训练。以分类任务为例，具体过程如下：在第t次训练过程中客户端i首先得到该次训练过程中的训练样本的label分布的概率密度函数和每个分类的样本数量，然后利用SGNN中生成的新特征前向传播计算得到损失函数和性能指标Mti;客户端利用后向传播算法更新SGNN模型权重和FGNN的模型权重；客户端将和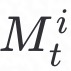利用秘密共享算法**Shr(.)进行加密上传至服务器端；服务器端利用Rec(.)**得到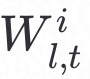均值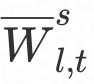、概率密度函数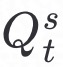和性能均值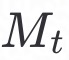，传给所有的客户端;客户端利用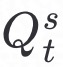和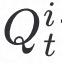计算得到JS散度，利用算法2中第24行中的公式更新本地FGNN模型得到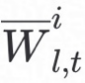，完成一次训练。

3.4超参优化

我们利用贝叶斯优化算法对模型进行自动调参，将整个模型作为一个黑箱问题，输入为超参，输出为性能均值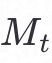，具体优化算法如下图所示。

  

4.实验

4.1实验设置

假设参与训练的客户端有两方分别为A和B。数据集选取Cora,Pubmed,andCiteseer三个常用的GNN分类数据集，根据label将数据集拆分成两部分N1和N2，两部分之间的数据不重叠，三个数据集对应的拆分结果如Table3所示。为了分析数据分布对模型的影响，设Non-IID参数为α，客户端A从N1抽取α⋅N1个样本，从N2抽取(1−α)⋅N1个样本，同理客户端B从N1抽取(1−α)⋅N2个样本，从N2抽取α⋅N2个样本。另外我们采用客户端准确率的均值作为模型的性能指标。

4.2性能比较

4.2.1联邦学习与SFGNN模型

针对4.1中构造的Non-IID数据集，针对α=1.0的情况，我们比较了联邦学习模型和SFGNN在三个数据集上的准确率，如Table4所示，本文模型在三个数据集上的准确率均高于联邦学习模型，平均准确率提升5.7%.

注：联邦学习模型指embedding的生成模型和损失函数的计算模型均采用联邦学习进行权重平均。

  

4.2.2数据分布对性能的影响

针对不同的数据分布参数α，比较SFGNN、联邦学习（FL）、分割学习（SP）在Cora数据集上的性能。如下图所示，当数据集分布均匀性较差时（α>0.75），SFGNN模型性能优于FL和SP；联邦学习更适用于均匀分布数据集的训练；当数据集分布差异性非常大时（α>0.89），联邦学习的性能差于分割学习。

注：分割学习模型指客户端A和B独立计算，互相之间不进行任何数据交互，完成训练后对性能指标进行平均作为最终的性能结果。

4.2.3JS散度对性能的影响

在Cora数据集上分别比较采用JS散度和不采用JS散度对模型性能的影响，如Table8所示，JS散度提升了模型性能，并提升效果随着分布不均匀性程度的增加而增加。

  

4.3效率比较

我们利用SMAC3框架中的贝叶斯优化算法对SFGNN进行超参优化，对比GridSearch方法，得到相应的训练时间，如Table9所示。我们可以发现，利用贝叶斯优化算法大幅度减少了模型的训练时间；数据集越大，加速效果越明显。

  

四、参考文献

**[1]**WillHamilton, Zhitao Ying, and Jure Leskovec. 2017. Inductiverepresentation learning on large graphs. In NeurIPS. 1024–1034.

**[2]**JakubKonecný, H. Brendan McMahan, Daniel Ramage, and PeterRichtárik.2016. Federated Optimization: Distributed Machine Learningfor On-Device Intelligence. ArXiv abs/1610.02527 (2016).

**[3]**J.LIN and S. K. M. WONG. 1990. A NEW DIRECTED DIVERGENCE MEASURE ANDITS CHARACTERIZATION. International Journal of General Systems 17, 1(1990), 73–81.

**[4]**AdiShamir. 1979. How to share a secret. Commun. ACM 22, 11 (1979),612–613.

**[5]**EricBrochu, Vlad M. Cora, and Nando de Freitas. 2010. A Tutorial onBayesian Optimization of Expensive Cost Functions, with Applicationto Active User Modeling and Hierarchical Reinforcement Learning.arXiv:cs.LG/1012.2599

  

 隐语官网：

 https://www.secretflow.org.cn

 隐语社区：

https://github.com/secretflow

https://gitee.com/secretflow

 联系我们：

公众号：隐语的小剧场

B站：隐语secretflow

邮箱：[email protected]