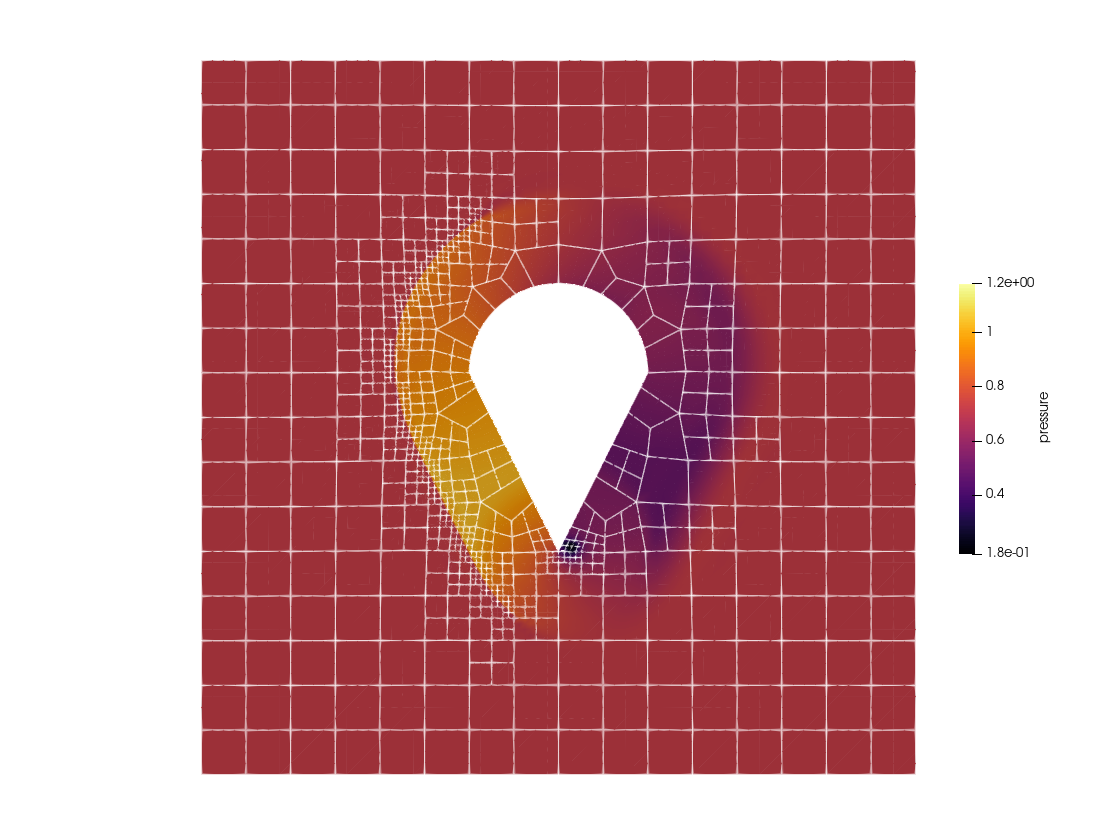
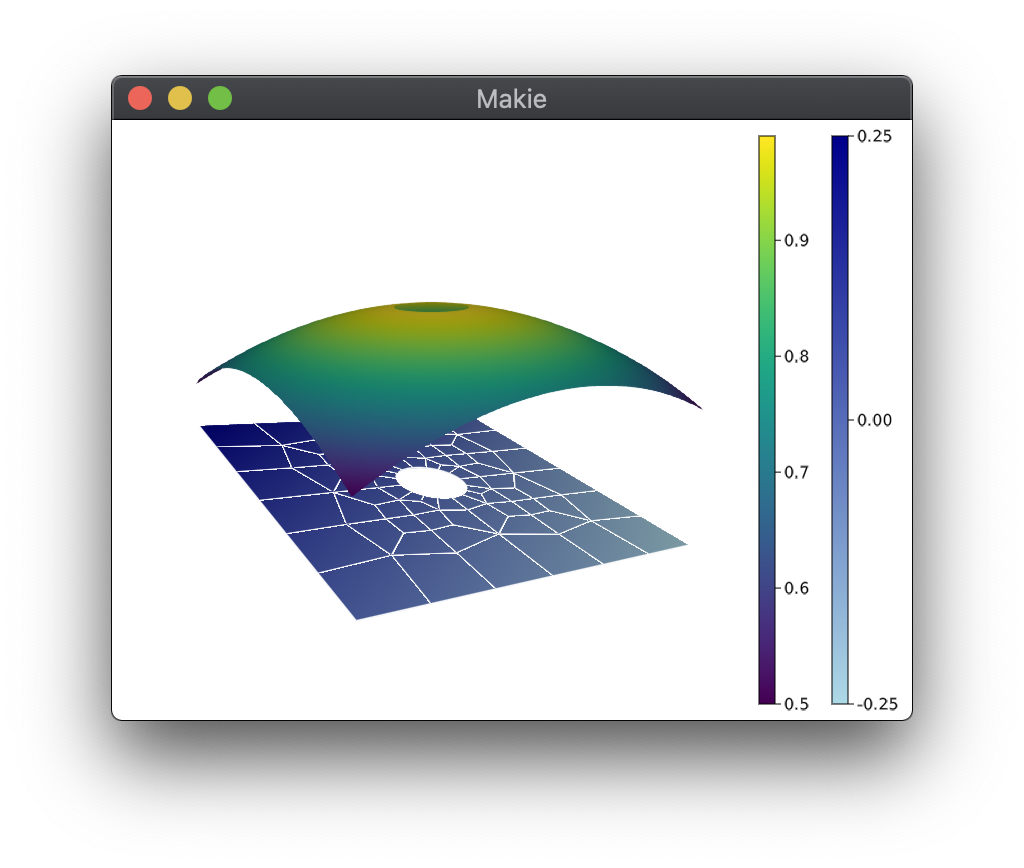
The P4estMesh is an unstructured, curvilinear, nonconforming mesh type for quadrilateral (2D) and hexahedral (3D) cells. It supports quadtree/octree-based adaptive mesh refinement (AMR) via the C library p4est. See AMRCallback for further information.
Due to its curvilinear nature, (numerical) fluxes need to implement methods dispatching on the normal::AbstractVector. Rotationally invariant equations such as the compressible Euler equations can use FluxRotated to wrap numerical fluxes implemented only for Cartesian meshes. This simplifies the re-use of existing functionality for the TreeMesh but is usually less efficient, cf. PR #550.
One available option to construct a P4estMesh is to read in an Abaqus (.inp) mesh file. We briefly describe the structure of this file, the conventions it uses, and how the mesh file is parsed to create an initial unstructured, curvilinear, and conforming mesh.
For this discussion we use the following two-dimensional unstructured curved mesh with three elements:

We note that the corner and element connectivity information parsed from the Abaqus file creates a straight sided (linear) mesh. From this linear mesh there are two strategies available to make the mesh curvilinear:
- Apply a
mapping function to describe a transformation of the linear mesh to another physical domain. The mapping is approximated using interpolation polynomial of a user specified polynomial degree. The default value of this polynomial degree is 1 that corresponds to an uncurved geometry. - High-order boundary information is available in the
.inp mesh file because it was created with the HOHQMesh mesh generator, which is available via the Julia package HOHQMesh.jl. This information is used to create appropriate transfinite mappings during the mesh construction.
We divide our discussion into two parts. The first part discusses the standard corner and element information contained in the .inp mesh file. The second part specifically deals with the mesh file parsing of an Abaqus file created by HOHQMesh.jl.
An Abaqus .inp mesh file typically begins with a *Heading. Though optional, the *Heading is helpful to give users some information about the mesh described by the mesh file. In particular, a .inp mesh file created with HOHQMesh will contain the header
*Heading
+ File created by HOHQMesh
This heading is used to indicate to the mesh constructor which of the above mapping strategies to apply in order to create a curvilinear mesh. If the Abaqus file header is not present then the P4estMesh is created with the first strategy above.
Next, prefaced with *NODE, comes a list of the physical (x,y,z) coordinates of all the corners. The first integer in the list of the corners provides its id number. Thus, for the two-dimensional example mesh this block of corner information is
*NODE
+1, 1.0, -1.0, 0.0
+2, 3.0, 0.0, 0.0
+3, 1.0, 1.0, 0.0
+4, 2.0, 0.0, 0.0
+5, 0.0, 0.0, 0.0
+6, 3.0, 1.0, 0.0
+7, 3.0, -1.0, 0.0
The element connectivity is given after the list of corners. The header for this information block is
*ELEMENT, type=CPS4, ELSET=Surface1
The Abaqus element type CPS4 corresponds to a quadrilateral element. Each quadrilateral element in the unstructured mesh is dictated by four corner points with indexing taken from the numbering given by the corner list above. The elements connect a set of four corner points (starting from the bottom left) in an anti-clockwise fashion; making the element right-handed. This element handedness is indicated using the circular arrow in the figure above. Just as with the corner list, the first integer in the element connectivity list indicates the element id number. Thus, the element connectivity list for the three element example mesh is
*ELEMENT, type=CPS4, ELSET=Surface1
+1, 5, 1, 4, 3
+2, 4, 2, 6, 3
+3, 7, 2, 4, 1
The construction of the element neighbor ids and identifying physical boundary surfaces is done using functionality directly from the p4est library. For example, the neighbor connectivity is created in the mesh constructor using the wrapper read_inp_p4est function.
If present, any additional information in the mesh file that was created by HOHQMesh is prefaced with ** to make it an Abaqus comment. This ensures that the read in of the file by a standard Abaqus file parser, as done in the read_inp_p4est function, is done correctly.
The high-order, curved boundary information and labels of the physical boundary created by HOHQMesh is found below the comment line
** ***** HOHQMesh boundary information ***** **
Next comes the polynomial degree that the mesh will use to represent any curved sides
** mesh polynomial degree = 8
The mesh file then, again, provides the element connectivity as well as information for curved surfaces either interior to the domain or along the physical boundaries. A set of check digits are included directly below the four corner indexes to indicate whether the local surface index (-y, +x, +y, or -x) within the element is straight sided, 0, or is curved, 1. If the local surface is straight sided no additional information is necessary during the mesh file read in. But for any curved surfaces the mesh file provides (x,y,z) coordinate values in order to construct an interpolant of this surface with the mesh polynomial order at the Chebyshev-Gauss-Lobatto nodes. This list of (x,y,z) data will be given in the direction of the local coordinate system. Given below is the element curvature information for the example mesh:
** 5 1 4 3
+** 0 0 1 1
+** 1.000000000000000 1.000000000000000 0.0
+** 1.024948365654583 0.934461926834452 0.0
+** 1.116583018200151 0.777350964621867 0.0
+** 1.295753434047077 0.606254343587194 0.0
+** 1.537500000000000 0.462500000000000 0.0
+** 1.768263070247418 0.329729152118310 0.0
+** 1.920916981799849 0.185149035378133 0.0
+** 1.986035130050921 0.054554577460044 0.0
+** 2.000000000000000 0.0 0.0
+** 0.0 0.0 0.0
+** 0.035513826946206 0.105291711848750 0.0
+** 0.148591270347399 0.317731556850611 0.0
+** 0.340010713990041 0.452219430075470 0.0
+** 0.575000000000000 0.462500000000000 0.0
+** 0.788022294598950 0.483764065630034 0.0
+** 0.926408729652601 0.644768443149389 0.0
+** 0.986453164464803 0.883724792445746 0.0
+** 1.000000000000000 1.000000000000000 0.0
+** 4 2 6 3
+** 0 0 0 1
+** 2.000000000000000 0.0 0.0
+** 1.986035130050921 0.054554577460044 0.0
+** 1.920916981799849 0.185149035378133 0.0
+** 1.768263070247418 0.329729152118310 0.0
+** 1.537500000000000 0.462500000000000 0.0
+** 1.295753434047077 0.606254343587194 0.0
+** 1.116583018200151 0.777350964621867 0.0
+** 1.024948365654583 0.934461926834452 0.0
+** 1.000000000000000 1.000000000000000 0.0
+** 7 2 4 1
+** 0 0 0 0
The last piece of information provided by HOHQMesh are labels for the different surfaces of an element. These labels are useful to set boundary conditions along physical surfaces. The labels can be short descriptive words up to 32 characters in length. The label --- indicates an internal surface where no boundary condition is required.
It is important to note that these labels are given in the following order according to the local surface index -x +x -y +y as required by the p4est library.
** Bezier --- Slant ---
+** --- Right --- Top
+** Bottom --- Right ---
For completeness, we provide the entire Abaqus mesh file for the example mesh in the figure above:
*Heading
+ File created by HOHQMesh
+*NODE
+1, 1.0, -1.0, 0.0
+2, 3.0, 0.0, 0.0
+3, 1.0, 1.0, 0.0
+4, 2.0, 0.0, 0.0
+5, 0.0, 0.0, 0.0
+6, 3.0, 1.0, 0.0
+7, 3.0, -1.0, 0.0
+*ELEMENT, type=CPS4, ELSET=Surface1
+1, 5, 1, 4, 3
+2, 4, 2, 6, 3
+3, 7, 2, 4, 1
+** ***** HOHQMesh boundary information ***** **
+** mesh polynomial degree = 8
+** 5 1 4 3
+** 0 0 1 1
+** 1.000000000000000 1.000000000000000 0.0
+** 1.024948365654583 0.934461926834452 0.0
+** 1.116583018200151 0.777350964621867 0.0
+** 1.295753434047077 0.606254343587194 0.0
+** 1.537500000000000 0.462500000000000 0.0
+** 1.768263070247418 0.329729152118310 0.0
+** 1.920916981799849 0.185149035378133 0.0
+** 1.986035130050921 0.054554577460044 0.0
+** 2.000000000000000 0.0 0.0
+** 0.0 0.0 0.0
+** 0.035513826946206 0.105291711848750 0.0
+** 0.148591270347399 0.317731556850611 0.0
+** 0.340010713990041 0.452219430075470 0.0
+** 0.575000000000000 0.462500000000000 0.0
+** 0.788022294598950 0.483764065630034 0.0
+** 0.926408729652601 0.644768443149389 0.0
+** 0.986453164464803 0.883724792445746 0.0
+** 1.000000000000000 1.000000000000000 0.0
+** 4 2 6 3
+** 0 0 0 1
+** 2.000000000000000 0.0 0.0
+** 1.986035130050921 0.054554577460044 0.0
+** 1.920916981799849 0.185149035378133 0.0
+** 1.768263070247418 0.329729152118310 0.0
+** 1.537500000000000 0.462500000000000 0.0
+** 1.295753434047077 0.606254343587194 0.0
+** 1.116583018200151 0.777350964621867 0.0
+** 1.024948365654583 0.934461926834452 0.0
+** 1.000000000000000 1.000000000000000 0.0
+** 7 2 4 1
+** 0 0 0 0
+** Bezier --- Slant ---
+** --- Right --- Top
+** Bottom --- Right ---
As an alternative to an Abaqus mesh generated by HOHQMesh, .inp files with boundary information encoded as nodesets *NSET,NSET= can be used to construct a p4est mesh. This is especially useful for usage of existing meshes (consisting of bilinear elements) which could stem from the popular gmsh meshing software.
In addition to the list of nodes and elements given above, there are nodesets of the form
*NSET,NSET=PhysicalLine1
+1, 4, 52, 53, 54, 55, 56, 57, 58,
present which are used to associate the edges defined through their corner nodes with a label. In this case it is called PhysicalLine1. By looping over every element and its associated edges, consisting of two nodes, we query the read in NSETs if the current node pair is present.
To prevent that every nodeset following *NSET,NSET= is treated as a boundary, the user must supply a boundary_symbols keyword to the P4estMesh constructor:
boundary_symbols = [:PhysicalLine1]
+
+mesh = P4estMesh{2}(mesh_file, polydeg = polydeg, boundary_symbols = boundary_symbols)
By doing so, only nodesets with a label present in boundary_symbols are treated as physical boundaries. Other nodesets that could be used for diagnostics are not treated as external boundaries. Note that there is a leading colon : compared to the label in the .inp mesh file. This is required to turn the label into a Symbol. Important: In Julia, a symbol cannot contain a hyphen/dash -, i.e., :BC-1 is not a valid symbol. Keep this in mind when importing boundaries, you might have to convert hyphens/dashes - to underscores _ in the .inp mesh file, i.e., BC_1 instead of BC-1.
A 2D example for this mesh, which is read-in for an unstructured mesh file created with gmsh, is presented in examples/p4est_2d_dgsem/elixir_euler_NACA6412airfoil_mach2.jl.
The 3D Abaqus file format with high-order boundary information from HOHQMesh is very similar to the 2D version discussed above. There are only three changes:
- The element connectivity would be given in terms of the eight corners that define a hexahedron. The corners are numbered as shown in the figure below. The header of the element list changes to be
*ELEMENT, type=C3D8, ELSET=Volume1
where C3D8 corresponds to a Abaqus hexahedral element. - There are six check digits included directly below the eight corner indexes to indicate whether the local face within the element is straight sided,
0, or is curved, 1. For curved faces (x,y,z) coordinate values are available in order to construct an face interpolant with the mesh polynomial order at the Chebyshev-Gauss-Lobatto nodes. - The boundary labels are given in the following order according to the local surface index
-x +x -y +y -z +z as required by the p4est library.
For completeness, we also give a short description and derivation of the three-dimensional transfinite mapping formulas used to compute the physical coordinates $\mathbf{x}=(x,y,z)$ of a (possibly curved) hexahedral element give the reference coordinates $\boldsymbol{\xi} = (\xi, \eta, \zeta)$ which lie in $[-1,1]^3$. That is, we will create an expression $\mathbf{x}= \mathbf{X}(\boldsymbol{\xi})$.
Below we provide a sketch of a single hexahedral element with curved faces. This is done to introduce the numbering conventions for corners, edges, and faces of the element.

When the hexahedron is a straight sided (linear) element we compute the transfinite mapping directly from the element corner points according to
\[\begin{aligned}
+\mathbf{X}_{linear}(\boldsymbol{\xi}) &= \frac{1}{8}[\quad\, \mathbf{x}_1(1-\xi)(1-\eta)(1-\zeta)
+ + \mathbf{x}_2(1+\xi)(1-\eta)(1-\zeta)\\[-0.15cm]
+ & \qquad\; + \mathbf{x}_3(1+\xi)(1+\eta)(1-\zeta)
+ + \mathbf{x}_4(1-\xi)(1+\eta)(1-\zeta) \\
+ & \qquad\; + \mathbf{x}_5(1-\xi)(1-\eta)(1+\zeta)
+ + \mathbf{x}_6(1+\xi)(1-\eta)(1+\zeta) \\
+ & \qquad\; + \mathbf{x}_7(1+\xi)(1+\eta)(1+\zeta)
+ + \mathbf{x}_8(1-\xi)(1+\eta)(1+\zeta)\quad].
+\end{aligned}\]
Next, we create a transfinite mapping function, $\mathbf{X}(\boldsymbol{\xi})$, for a hexahedron that has one or more curved faces. For this we assume that have a set of six interpolating polynomials $\{\Gamma_i\}_{i=1}^6$ that approximate the faces. The interpolating polynomial for any curved faces is provided by the information in a HOHQMesh Abaqus mesh file or is constructed on the fly via a bi-linear interpolation routine for any linear faces. Explicitly, these six face interpolation polynomials depend on the computational coordinates $\boldsymbol{\xi}$ as follows
\[ \begin{aligned}
+ \Gamma_1(\xi, \zeta), \quad && \quad \Gamma_3(\xi, \eta), \quad && \quad \Gamma_4(\eta, \zeta),\\[0.1cm]
+ \Gamma_2(\xi, \zeta), \quad && \quad \Gamma_5(\xi, \eta), \quad && \quad \Gamma_6(\eta, \zeta).
+ \end{aligned}\]
To determine the form of the mapping we first create linear interpolations between two opposing faces, e.g., $\Gamma_3$ and $\Gamma_5$ and sum them together to have
\[\begin{aligned}
+ \boldsymbol\Sigma(\boldsymbol{\xi}) &= \frac{1}{2}[\quad\,(1-\xi)\Gamma_6(\eta,\zeta) + (1+\xi)\Gamma_4(\eta,\zeta) \\[-0.15cm]
+ &\qquad\;+ (1-\eta)\Gamma_1(\xi,\zeta) + (1+\eta)\Gamma_2(\xi,\zeta) \\%[-0.15cm]
+ &\qquad\; +(1-\zeta)\Gamma_3(\xi,\eta) + (1+\zeta)\Gamma_5(\xi,\eta)\quad].
+\end{aligned}\]
Unfortunately, the linear interpolations $\boldsymbol\Sigma(\boldsymbol{\xi})$ no longer match at the faces, e.g., evaluating at $\eta = -1$ we have
\[\boldsymbol\Sigma(\xi,-1,\zeta) = \Gamma_1(\xi,\zeta) + \frac{1}{2}[\;(1-\xi)\Gamma_6(-1,\zeta) + (1+\xi)\Gamma_4(-1,\zeta)
+ +(1-\zeta)\Gamma_3(\xi,-1) + (1+\zeta)\Gamma_5(\xi,-1)\;],\]
which is the desired face $\Gamma_1(\xi,\zeta)$ plus four edge error terms. Analogous edge error terms occur at the other faces evaluating $\boldsymbol\Sigma(\boldsymbol{\xi})$ at $\eta=1$, $\xi=\pm 1$, and $\zeta=\pm 1$. In order to match the faces, we subtract a linear interpolant in the $\xi$, $\eta$, and $\zeta$ directions of the edge error terms, e.g., the terms in braces in the above equation. So, continuing the example above, the correction term to be subtracted for face $\Gamma_1$ to match would be
\[\left(\frac{1-\eta}{2}\right) \bigg[ \frac{1}{2} [ \; (1-\xi)\Gamma_6(-1,\zeta) + (1+\xi)\Gamma_4(-1,\zeta)+(1-\zeta)\Gamma_3(\xi,-1)
+ + (1+\zeta)\Gamma_5(\xi,-1)\;] \bigg].\]
For clarity, and to allow an easier comparison to the implementation, we introduce auxiliary notation for the 12 edge values present in the complete correction term. That is, for given values of $\xi$, $\eta$, and $\zeta$ we have
\[ \begin{aligned}
+ \texttt{edge}_{1} &= \Gamma_1(\xi, -1), \quad && \quad \texttt{edge}_{5} = \Gamma_2(\xi, -1), \quad & \quad \texttt{edge}_{9} &= \Gamma_6(\eta, -1),\\[0.1cm]
+ \texttt{edge}_{2} &= \Gamma_1(1, \zeta), \quad && \quad\texttt{edge}_{6} = \Gamma_2(1, \zeta), \quad & \quad \texttt{edge}_{10} &= \Gamma_4(\eta, -1),\\[0.1cm]
+ \texttt{edge}_{3} &= \Gamma_1(\xi, 1), \quad && \quad \texttt{edge}_{7} = \Gamma_2(\xi, 1), \quad & \quad \texttt{edge}_{11} &= \Gamma_4(\eta, 1),\\[0.1cm]
+ \texttt{edge}_{4} &= \Gamma_1(-1, \zeta), \quad && \quad \texttt{edge}_{8} = \Gamma_2(-1, \zeta), \quad & \quad \texttt{edge}_{12} &= \Gamma_6(\eta, 1).
+ \end{aligned}\]
With this notation for the edge terms (and after some algebraic manipulation) we write the complete edge correction term, $\mathcal{C}_{\texttt{edge}}(\boldsymbol{\xi})$, as
\[\begin{aligned}
+\mathcal{C}_{\texttt{edge}}(\boldsymbol{\xi}) &= \frac{1}{4}[\quad\, (1-\eta)(1-\zeta)\texttt{edge}_{1}\\[-0.15cm]
+ & \qquad\; + (1+\xi)(1-\eta)\texttt{edge}_{2} \\
+ & \qquad\; + (1-\eta)(1+\zeta)\texttt{edge}_{3} \\
+ & \qquad\; + (1-\xi)(1-\eta)\texttt{edge}_{4} \\
+ & \qquad\; + (1+\eta)(1-\zeta)\texttt{edge}_{5} \\
+ & \qquad\; + (1+\xi)(1+\eta)\texttt{edge}_{6} \\
+ & \qquad\; + (1+\eta)(1+\zeta)\texttt{edge}_{7} \\
+ & \qquad\; + (1-\xi)(1+\eta)\texttt{edge}_{8} \\
+ & \qquad\; + (1-\xi)(1-\zeta)\texttt{edge}_{9} \\
+ & \qquad\; + (1+\xi)(1-\zeta)\texttt{edge}_{10} \\
+ & \qquad\; + (1+\xi)(1+\zeta)\texttt{edge}_{11} \\
+ & \qquad\; + (1-\xi)(1+\zeta)\texttt{edge}_{12}\quad].
+\end{aligned}\]
However, subtracting the edge correction terms $\mathcal{C}_{\texttt{edge}}(\boldsymbol{\xi})$ from $\boldsymbol\Sigma(\boldsymbol{\xi})$ removes the interior element contributions twice. Thus, to complete the construction of the transfinite mapping $\mathbf{X}(\boldsymbol{\xi})$ we add the transfinite map of the straight sided hexahedral element to find
\[\mathbf{X}(\boldsymbol{\xi}) = \boldsymbol\Sigma(\boldsymbol{\xi})
+ - \mathcal{C}_{\texttt{edge}}(\boldsymbol{\xi})
+ + \mathbf{X}_{linear}(\boldsymbol{\xi}).\]
Also for a mesh in standard Abaqus format there are no qualitative changes when going from 2D to 3D. The most notable difference is that boundaries are formed in 3D by faces defined by four nodes while in 2D boundaries are edges consisting of two elements. A simple mesh file, which is used also in examples/p4est_3d_dgsem/elixir_euler_free_stream_boundaries.jl, is given below:
*Heading
+<SOMETHING DIFFERENT FROM "File created by HOHQMesh">
+*NODE
+1, -2, 0, 0
+2, -1, 0, 0
+3, -1, 1, 0
+4, -2, 1, 0
+5, -2, 0, 1
+6, -1, 0, 1
+7, -1, 1, 1
+8, -2, 1, 1
+9, -1.75, 1, 0
+10, -1.5, 1, 0
+11, -1.25, 1, 0
+12, -1, 0.75000000000035, 0
+13, -1, 0.50000000000206, 0
+14, -1, 0.25000000000104, 0
+15, -1.25, 0, 0
+16, -1.5, 0, 0
+17, -1.75, 0, 0
+18, -2, 0.24999999999941, 0
+19, -2, 0.49999999999869, 0
+20, -2, 0.74999999999934, 0
+21, -1.75, 0, 1
+22, -1.5, 0, 1
+23, -1.25, 0, 1
+24, -1, 0.24999999999941, 1
+25, -1, 0.49999999999869, 1
+26, -1, 0.74999999999934, 1
+27, -1.25, 1, 1
+28, -1.5, 1, 1
+29, -1.75, 1, 1
+30, -2, 0.75000000000035, 1
+31, -2, 0.50000000000206, 1
+32, -2, 0.25000000000104, 1
+33, -2, 0, 0.24999999999941
+34, -2, 0, 0.49999999999869
+35, -2, 0, 0.74999999999934
+36, -2, 1, 0.24999999999941
+37, -2, 1, 0.49999999999869
+38, -2, 1, 0.74999999999934
+39, -1, 0, 0.24999999999941
+40, -1, 0, 0.49999999999869
+41, -1, 0, 0.74999999999934
+42, -1, 1, 0.24999999999941
+43, -1, 1, 0.49999999999869
+44, -1, 1, 0.74999999999934
+45, -1.25, 0.25000000000063, 0
+46, -1.25, 0.50000000000122, 0
+47, -1.25, 0.7500000000001, 0
+48, -1.5, 0.25000000000023, 0
+49, -1.5, 0.50000000000038, 0
+50, -1.5, 0.74999999999984, 0
+51, -1.75, 0.24999999999982, 0
+52, -1.75, 0.49999999999953, 0
+53, -1.75, 0.74999999999959, 0
+54, -1.75, 0.25000000000063, 1
+55, -1.75, 0.50000000000122, 1
+56, -1.75, 0.7500000000001, 1
+57, -1.5, 0.25000000000023, 1
+58, -1.5, 0.50000000000038, 1
+59, -1.5, 0.74999999999984, 1
+60, -1.25, 0.24999999999982, 1
+61, -1.25, 0.49999999999953, 1
+62, -1.25, 0.74999999999959, 1
+63, -2, 0.24999999999982, 0.24999999999941
+64, -2, 0.49999999999953, 0.24999999999941
+65, -2, 0.74999999999959, 0.24999999999941
+66, -2, 0.25000000000023, 0.49999999999869
+67, -2, 0.50000000000038, 0.49999999999869
+68, -2, 0.74999999999984, 0.49999999999869
+69, -2, 0.25000000000063, 0.74999999999934
+70, -2, 0.50000000000122, 0.74999999999934
+71, -2, 0.7500000000001, 0.74999999999934
+72, -1.25, 1, 0.74999999999934
+73, -1.25, 1, 0.49999999999869
+74, -1.25, 1, 0.24999999999941
+75, -1.5, 1, 0.74999999999934
+76, -1.5, 1, 0.49999999999869
+77, -1.5, 1, 0.24999999999941
+78, -1.75, 1, 0.74999999999934
+79, -1.75, 1, 0.49999999999869
+80, -1.75, 1, 0.24999999999941
+81, -1, 0.25000000000063, 0.24999999999941
+82, -1, 0.50000000000122, 0.24999999999941
+83, -1, 0.7500000000001, 0.24999999999941
+84, -1, 0.25000000000023, 0.49999999999869
+85, -1, 0.50000000000038, 0.49999999999869
+86, -1, 0.74999999999984, 0.49999999999869
+87, -1, 0.24999999999982, 0.74999999999934
+88, -1, 0.49999999999953, 0.74999999999934
+89, -1, 0.74999999999959, 0.74999999999934
+90, -1.75, 0, 0.74999999999934
+91, -1.75, 0, 0.49999999999869
+92, -1.75, 0, 0.24999999999941
+93, -1.5, 0, 0.74999999999934
+94, -1.5, 0, 0.49999999999869
+95, -1.5, 0, 0.24999999999941
+96, -1.25, 0, 0.74999999999934
+97, -1.25, 0, 0.49999999999869
+98, -1.25, 0, 0.24999999999941
+99, -1.75, 0.25000000000043, 0.74999999999934
+100, -1.75, 0.25000000000023, 0.49999999999869
+101, -1.75, 0.25000000000002, 0.24999999999941
+102, -1.75, 0.5000000000008, 0.74999999999934
+103, -1.75, 0.50000000000038, 0.49999999999869
+104, -1.75, 0.49999999999995, 0.24999999999941
+105, -1.75, 0.74999999999997, 0.74999999999934
+106, -1.75, 0.74999999999984, 0.49999999999869
+107, -1.75, 0.74999999999972, 0.24999999999941
+108, -1.5, 0.25000000000023, 0.74999999999934
+109, -1.5, 0.25000000000023, 0.49999999999869
+110, -1.5, 0.25000000000023, 0.24999999999941
+111, -1.5, 0.50000000000038, 0.74999999999934
+112, -1.5, 0.50000000000038, 0.49999999999869
+113, -1.5, 0.50000000000038, 0.24999999999941
+114, -1.5, 0.74999999999984, 0.74999999999934
+115, -1.5, 0.74999999999984, 0.49999999999869
+116, -1.5, 0.74999999999984, 0.24999999999941
+117, -1.25, 0.25000000000002, 0.74999999999934
+118, -1.25, 0.25000000000023, 0.49999999999869
+119, -1.25, 0.25000000000043, 0.24999999999941
+120, -1.25, 0.49999999999995, 0.74999999999934
+121, -1.25, 0.50000000000038, 0.49999999999869
+122, -1.25, 0.5000000000008, 0.24999999999941
+123, -1.25, 0.74999999999972, 0.74999999999934
+124, -1.25, 0.74999999999984, 0.49999999999869
+125, -1.25, 0.74999999999997, 0.24999999999941
+******* E L E M E N T S *************
+*ELEMENT, type=C3D8, ELSET=Volume1
+153, 54, 21, 5, 32, 99, 90, 35, 69
+154, 99, 90, 35, 69, 100, 91, 34, 66
+155, 100, 91, 34, 66, 101, 92, 33, 63
+156, 101, 92, 33, 63, 51, 17, 1, 18
+157, 55, 54, 32, 31, 102, 99, 69, 70
+158, 102, 99, 69, 70, 103, 100, 66, 67
+159, 103, 100, 66, 67, 104, 101, 63, 64
+160, 104, 101, 63, 64, 52, 51, 18, 19
+161, 56, 55, 31, 30, 105, 102, 70, 71
+162, 105, 102, 70, 71, 106, 103, 67, 68
+163, 106, 103, 67, 68, 107, 104, 64, 65
+164, 107, 104, 64, 65, 53, 52, 19, 20
+165, 29, 56, 30, 8, 78, 105, 71, 38
+166, 78, 105, 71, 38, 79, 106, 68, 37
+167, 79, 106, 68, 37, 80, 107, 65, 36
+168, 80, 107, 65, 36, 9, 53, 20, 4
+169, 57, 22, 21, 54, 108, 93, 90, 99
+170, 108, 93, 90, 99, 109, 94, 91, 100
+171, 109, 94, 91, 100, 110, 95, 92, 101
+172, 110, 95, 92, 101, 48, 16, 17, 51
+173, 58, 57, 54, 55, 111, 108, 99, 102
+174, 111, 108, 99, 102, 112, 109, 100, 103
+175, 112, 109, 100, 103, 113, 110, 101, 104
+176, 113, 110, 101, 104, 49, 48, 51, 52
+177, 59, 58, 55, 56, 114, 111, 102, 105
+178, 114, 111, 102, 105, 115, 112, 103, 106
+179, 115, 112, 103, 106, 116, 113, 104, 107
+180, 116, 113, 104, 107, 50, 49, 52, 53
+181, 28, 59, 56, 29, 75, 114, 105, 78
+182, 75, 114, 105, 78, 76, 115, 106, 79
+183, 76, 115, 106, 79, 77, 116, 107, 80
+184, 77, 116, 107, 80, 10, 50, 53, 9
+185, 60, 23, 22, 57, 117, 96, 93, 108
+186, 117, 96, 93, 108, 118, 97, 94, 109
+187, 118, 97, 94, 109, 119, 98, 95, 110
+188, 119, 98, 95, 110, 45, 15, 16, 48
+189, 61, 60, 57, 58, 120, 117, 108, 111
+190, 120, 117, 108, 111, 121, 118, 109, 112
+191, 121, 118, 109, 112, 122, 119, 110, 113
+192, 122, 119, 110, 113, 46, 45, 48, 49
+193, 62, 61, 58, 59, 123, 120, 111, 114
+194, 123, 120, 111, 114, 124, 121, 112, 115
+195, 124, 121, 112, 115, 125, 122, 113, 116
+196, 125, 122, 113, 116, 47, 46, 49, 50
+197, 27, 62, 59, 28, 72, 123, 114, 75
+198, 72, 123, 114, 75, 73, 124, 115, 76
+199, 73, 124, 115, 76, 74, 125, 116, 77
+200, 74, 125, 116, 77, 11, 47, 50, 10
+201, 24, 6, 23, 60, 87, 41, 96, 117
+202, 87, 41, 96, 117, 84, 40, 97, 118
+203, 84, 40, 97, 118, 81, 39, 98, 119
+204, 81, 39, 98, 119, 14, 2, 15, 45
+205, 25, 24, 60, 61, 88, 87, 117, 120
+206, 88, 87, 117, 120, 85, 84, 118, 121
+207, 85, 84, 118, 121, 82, 81, 119, 122
+208, 82, 81, 119, 122, 13, 14, 45, 46
+209, 26, 25, 61, 62, 89, 88, 120, 123
+210, 89, 88, 120, 123, 86, 85, 121, 124
+211, 86, 85, 121, 124, 83, 82, 122, 125
+212, 83, 82, 122, 125, 12, 13, 46, 47
+213, 7, 26, 62, 27, 44, 89, 123, 72
+214, 44, 89, 123, 72, 43, 86, 124, 73
+215, 43, 86, 124, 73, 42, 83, 125, 74
+216, 42, 83, 125, 74, 3, 12, 47, 11
+*NSET,NSET=PhysicalSurface1
+1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
+11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
+21, 22, 23, 24, 25, 26, 27, 28, 29, 30,
+31, 32, 33, 34, 35, 36, 37, 38, 45, 46,
+47, 48, 49, 50, 51, 52, 53, 54, 55, 56,
+57, 58, 59, 60, 61, 62, 63, 64, 65, 66,
+67, 68, 69, 70, 71,
+*NSET,NSET=PhysicalSurface2
+1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
+11, 12, 13, 14, 15, 16, 17, 21, 22, 23,
+24, 25, 26, 27, 28, 29, 33, 34, 35, 36,
+37, 38, 39, 40, 41, 42, 43, 44, 72, 73,
+74, 75, 76, 77, 78, 79, 80, 81, 82, 83,
+84, 85, 86, 87, 88, 89, 90, 91, 92, 93,
+94, 95, 96, 97, 98,