diff --git a/Makefile b/Makefile
new file mode 100644
index 0000000..4b77896
--- /dev/null
+++ b/Makefile
@@ -0,0 +1,24 @@
+JL = julia --project
+
+default: init test
+
+init:
+ $(JL) -e 'using Pkg; Pkg.precompile(); Pkg.activate("docs"); Pkg.develop(path="."), Pkg.precompile()'
+
+update:
+ $(JL) -e 'using Pkg; Pkg.update(); Pkg.precompile(); Pkg.activate("docs"); Pkg.update(); Pkg.precompile()'
+
+test:
+ $(JL) -e 'using Pkg; Pkg.test()'
+
+coverage:
+ $(JL) -e 'using Pkg; Pkg.test(; coverage=true)'
+
+serve:
+ $(JL) -e 'using Pkg; Pkg.activate("docs"); using LiveServer; servedocs(;skip_dirs=["docs/src/assets", "docs/src/generated"])'
+
+clean:
+ rm -rf docs/build
+ find . -name "*.cov" -type f -print0 | xargs -0 /bin/rm -f
+
+.PHONY: init test coverage serve clean update
\ No newline at end of file
diff --git a/README.md b/README.md
index aff2941..e2df687 100644
--- a/README.md
+++ b/README.md
@@ -20,7 +20,7 @@ Einstein summation can be implemented in no more than 20 lines of Julia code, th
*Note: why the test coverage is not 100%* - GPU-code coverage is not evaluated although we test the GPU code properly on gitlab. Ignoring the GPU-code, the actual coverage is at about _97%_.
-*Warning: since v0.4, OMEinsum does not optimize the contraction order anymore. One has to use nested einsum to specify the contraction order manually, e.g. `ein"(ijk,jkl),klm->im"(x, y, z)`.*
+*Warning: since v0.4, OMEinsum does not optimize the contraction order anymore. One has to use nested einsum to specify the contraction order manually, e.g. `ein"(ijk,jkl),klm->im"(x, y, z)`.* Please check out the [documentation](https://under-Peter.github.io/OMEinsum.jl/dev/contractionorder/) for more details.
## Install
@@ -89,32 +89,7 @@ which is closer to the standard way of writing einsum-operations in physics
julia> @ein c[i,j] := a[i,k] * b[k,j];
```
-#### A table for reference
-| code | meaning |
-| ---------------- | --------------- |
-| `ein"ij,jk->ik"` | matrix matrix multiplication |
-| `ein"ijl,jkl->ikl"` | batched - matrix matrix multiplication |
-| `ein"ij,j->i"` | matrix vector multiplication |
-| `ein"ij,ik,il->jkl"` | star contraction |
-| `ein"ii->"` | trace |
-| `ein"ij->i"` | sum |
-| `ein"ii->i"` | take the diagonal part of a matrix |
-| `ein"ijkl->ilkj"` | permute the dimensions of a tensor |
-| `ein"i->ii"` | construct a diagonal matrix |
-| `ein"->ii"` | broadcast a scalar to the diagonal part of a matrix |
-| `ein"ij,ij->ij"` | element wise product |
-| `ein"ij,kl->ijkl"` | outer product |
-
-
-Many of these are handled by special kernels
-([listed in the docs](https://under-peter.github.io/OMEinsum.jl/stable/implementation/)),
-but there is also a fallback which handles other cases
-(more like what [Einsum.jl](https://github.com/ahwillia/Einsum.jl) does, plus a GPU version).
-
-It is sometimes helpful to specify the order of operations, by inserting brackets,
-either because you know this will be more efficient,
-or to help the computer see what kernels can be used.
-For example:
+It is sometimes helpful to specify the order of operations, by inserting brackets, either because you know this will be more efficient, or to help the computer see what kernels can be used. For example:
```julia
julia> @ein Z[o,s] := x[i,s] * (W[o,i,j] * y[j,s]); # macro style
@@ -140,107 +115,13 @@ julia> Zl = ein"is, oij, js -> os"(x, W, y);
└ @ OMEinsum ~/.julia/dev/OMEinsum/src/loop_einsum.jl:26
```
-To see more examples using the GPU and autodiff, check out our asciinema-demo here:
-[](https://asciinema.org/a/wE4CtIzWUC3R0GkVV28rVBRFb)
-
-## Application
-
-For an application in tensor network algorithms, check out the [TensorNetworkAD](https://github.com/under-Peter/TensorNetworkAD.jl)
-package, where `OMEinsum` is used to evaluate tensor-contractions, permutations and summations.
-
-#### Toy Application: solving a 3-coloring problem on the Petersen graph
-Let us focus on graphs
-with vertices with three edges each. A question one might ask is:
-How many different ways are there to colour the edges of the graph with
-three different colours such that no vertex has a duplicate colour on its edges?
-
-The counting problem can be transformed into a contraction of rank-3 tensors
-representing the edges. Consider the tensor `s` defined as
-```julia
-julia> s = map(x->Int(length(unique(x.I)) == 3), CartesianIndices((3,3,3)))
-```
-
-Then we can simply contract `s` tensors to get the number of 3 colourings satisfying the above condition!
-E.g. for two vertices, we get 6 distinct colourings:
-```julia
-julia> ein"ijk,ijk->"(s,s)[]
-6
-```
-
-Using that method, it's easy to find that e.g. the peterson graph allows no 3 colouring, since
-```julia
-julia> code = ein"afl,bhn,cjf,dlh,enj,ago,big,cki,dmk,eom->"
-afl, bhn, cjf, dlh, enj, ago, big, cki, dmk, eom
-
-julia> code(fill(s, 10)...)[]
-0
-```
-
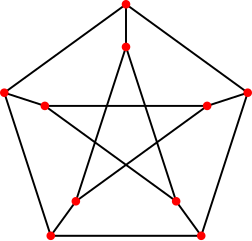
-The peterson graph consists of 10 vertices and 15 edges and looks like a pentagram
-embedded in a pentagon as depicted here:
-
-
-
-`OMEinsum` does not optimie the contraction order by default, so the above contraction can be time consuming. To speed up the contraction, we can use `optimize_code` to optimize the contraction order:
-```julia
-julia> optcode = optimize_code(code, uniformsize(code, 3), TreeSA())
-SlicedEinsum{Char, DynamicNestedEinsum{Char}}(Char[], ago, goa ->
-├─ ago
-└─ gcojl, cjal -> goa
- ├─ bgck, bojlk -> gcojl
- │ ├─ big, cki -> bgck
- │ │ ├─ big
- │ │ └─ cki
- │ └─ bhomj, lhmk -> bojlk
- │ ├─ bhn, omnj -> bhomj
- │ │ ├─ bhn
- │ │ └─ eom, enj -> omnj
- │ │ ⋮
- │ │
- │ └─ dlh, dmk -> lhmk
- │ ├─ dlh
- │ └─ dmk
- └─ cjf, afl -> cjal
- ├─ cjf
- └─ afl
-)
-
-julia> contraction_complexity(optcode, uniformsize(optcode, 3))
-Time complexity: 2^12.737881076857779
-Space complexity: 2^7.92481250360578
-Read-write complexity: 2^11.247334178028728
-
-julia> optcode(fill(s, 10)...)[]
-0
-```
-We can see the time complexity of the optimized code is much smaller than the original one. To know more about the contraction order optimization, please check the julia package [`OMEinsumContractionOrders.jl`](https://github.com/TensorBFS/OMEinsumContractionOrders.jl).
-
-Confronted with the above result, we can ask whether the peterson graph allows a relaxed variation of 3 colouring, having one vertex that might accept duplicate colours. The answer to that can be found using the gradient w.r.t a vertex:
-```julia
-julia> using Zygote: gradient
-
-julia> gradient(x->optcode(x,s,s,s,s,s,s,s,s,s)[], s)[1] |> sum
-0
-```
-This tells us that even if we allow duplicates on one vertex, there are no 3-colourings for the peterson graph.
-
## Comparison with other packages
Similar packages include:
- [TensorOperations.jl](https://github.com/Jutho/TensorOperations.jl) and [TensorKit.jl](https://github.com/Jutho/TensorKit.jl)
- [ITensors.jl](https://github.com/ITensor/ITensors.jl)
-Comparing with the above packages, `OMEinsum` is optimized over large scale tensor network (or einsum, sum-product network) contraction. Its main advantages are:
-- `OMEinsum` has better support to very high dimensional tensor networks and their contraction order.
-- `OMEinsum` allows an index to appear multiple times.
-- `OMEinsum` has well tested generic element type support.
-
-However, `OMEinsum` also has some disadvantages:
-- `OMEinsum` does not support good quantum numbers.
-- `OMEinsum` has less optimization on small scale problems.
+Comparing with the above packages, `OMEinsum` is optimized over large scale tensor network (or einsum, sum-product network) contraction.
## Contribute
-Suggestions and Comments in the _Issues_ are welcome.
-
-## License
-MIT License
+Suggestions and Comments in the [_Issues_](https://github.com/under-Peter/OMEinsum.jl/issues) are welcome.
\ No newline at end of file
diff --git a/docs/Project.toml b/docs/Project.toml
index 8f7ee43..3964eda 100644
--- a/docs/Project.toml
+++ b/docs/Project.toml
@@ -1,5 +1,6 @@
[deps]
Documenter = "e30172f5-a6a5-5a46-863b-614d45cd2de4"
+LiveServer = "16fef848-5104-11e9-1b77-fb7a48bbb589"
OMEinsum = "ebe7aa44-baf0-506c-a96f-8464559b3922"
OMEinsumContractionOrders = "6f22d1fd-8eed-4bb7-9776-e7d684900715"
Zygote = "e88e6eb3-aa80-5325-afca-941959d7151f"
diff --git a/docs/make.jl b/docs/make.jl
index ba56981..7769e8c 100644
--- a/docs/make.jl
+++ b/docs/make.jl
@@ -5,11 +5,13 @@ makedocs(;
format=Documenter.HTML(),
pages=[
"Home" => "index.md",
- "Parsing" => "parsing.md",
- "Implementations" => "implementation.md",
+ "Background: Tensor Networks" => "background.md",
+ "Basic usage" => "basic.md",
"Contraction order optimization" => "contractionorder.md",
- "Extending OMEinsum" => "extending.md",
- "DocStrings" => "docstrings.md"
+ "Automatic differentiation" => "autodiff.md",
+ "CUDA" => "cuda.md",
+ "Applications" => "applications.md",
+ "Manual" => "docstrings.md"
],
repo="https://github.com/under-Peter/OMEinsum.jl/blob/{commit}{path}#L{line}",
sitename="OMEinsum.jl",
diff --git a/docs/src/applications.md b/docs/src/applications.md
new file mode 100644
index 0000000..c8a0f59
--- /dev/null
+++ b/docs/src/applications.md
@@ -0,0 +1,55 @@
+# Application
+
+## List of packages using OMEinsum
+- [GenericTensorNetworks](https://github.com/QuEraComputing/GenericTensorNetworks.jl), solving combinational optimization problems by generic tensor networks.
+- [TensorInference](https://github.com/TensorBFS/TensorInference.jl), probabilistic inference using contraction of tensor networks
+- [YaoToEinsum](https://github.com/QuantumBFS/Yao.jl), the tensor network simulation backend for quantum circuits.
+- [TensorNetworkAD2](https://github.com/YidaiZhang/TensorNetworkAD2.jl), using differential programming tensor networks to solve quantum many-body problems.
+- [TensorQEC](https://github.com/nzy1997/TensorQEC.jl), tensor networks for quantum error correction.
+
+## Example: Solving a 3-coloring problem on the Petersen graph
+Let us focus on graphs
+with vertices with three edges each. A question one might ask is:
+How many different ways are there to colour the edges of the graph with
+three different colours such that no vertex has a duplicate colour on its edges?
+
+The counting problem can be transformed into a contraction of rank-3 tensors
+representing the edges. Consider the tensor `s` defined as
+```@repl coloring
+using OMEinsum
+s = map(x->Int(length(unique(x.I)) == 3), CartesianIndices((3,3,3)))
+```
+
+Then we can simply contract `s` tensors to get the number of 3 colourings satisfying the above condition!
+E.g. for two vertices, we get 6 distinct colourings:
+```@repl coloring
+ein"ijk,ijk->"(s,s)[]
+```
+
+Using that method, it's easy to find that e.g. the peterson graph allows no 3 colouring, since
+```@repl coloring
+code = ein"afl,bhn,cjf,dlh,enj,ago,big,cki,dmk,eom->"
+afl, bhn, cjf, dlh, enj, ago, big, cki, dmk, eom
+code(fill(s, 10)...)[]
+```
+
+The peterson graph consists of 10 vertices and 15 edges and looks like a pentagram
+embedded in a pentagon as depicted here:
+
+
+
+`OMEinsum` does not optimie the contraction order by default, so the above contraction can be time consuming. To speed up the contraction, we can use `optimize_code` to optimize the contraction order:
+```@repl coloring
+optcode = optimize_code(code, uniformsize(code, 3), TreeSA())
+contraction_complexity(optcode, uniformsize(optcode, 3))
+optcode(fill(s, 10)...)[]
+```
+We can see the time complexity of the optimized code is much smaller than the original one. To know more about the contraction order optimization, please check the Julia package [`OMEinsumContractionOrders.jl`](https://github.com/TensorBFS/OMEinsumContractionOrders.jl).
+
+Confronted with the above result, we can ask whether the peterson graph allows a relaxed variation of 3 colouring, having one vertex that might accept duplicate colours. The answer to that can be found using the gradient w.r.t a vertex:
+```@repl coloring
+using Zygote: gradient
+gradient(x->optcode(x,s,s,s,s,s,s,s,s,s)[], s)[1] |> sum
+```
+This tells us that even if we allow duplicates on one vertex, there are no 3-colourings for the peterson graph.
+
diff --git a/docs/src/assets/matmul.png b/docs/src/assets/matmul.png
new file mode 100644
index 0000000..f16d4ec
Binary files /dev/null and b/docs/src/assets/matmul.png differ
diff --git a/docs/src/assets/perm.svg b/docs/src/assets/perm.svg
new file mode 100644
index 0000000..d572238
--- /dev/null
+++ b/docs/src/assets/perm.svg
@@ -0,0 +1,36 @@
+
+
diff --git a/docs/src/assets/starcontract.png b/docs/src/assets/starcontract.png
new file mode 100644
index 0000000..43e5a8c
Binary files /dev/null and b/docs/src/assets/starcontract.png differ
diff --git a/docs/src/assets/tensors.svg b/docs/src/assets/tensors.svg
new file mode 100644
index 0000000..a31dee4
--- /dev/null
+++ b/docs/src/assets/tensors.svg
@@ -0,0 +1,112 @@
+
+
diff --git a/docs/src/autodiff.md b/docs/src/autodiff.md
new file mode 100644
index 0000000..53b3473
--- /dev/null
+++ b/docs/src/autodiff.md
@@ -0,0 +1,22 @@
+# Automatic differentiation
+
+There are two ways to compute the gradient of an einsum expression. The first one is to use the `OMEinsum` package, which is a custom implementation of the reverse-mode automatic differentiation. The second one is to use the [`Zygote`](https://github.com/FluxML/Zygote.jl) package, which is a source-to-source automatic differentiation tool.
+
+## Built-in automatic differentiation
+The `OMEinsum` package provides a built-in function [`cost_and_gradient`](@ref) to compute the cost and the gradient of an einsum expression.
+
+```@repl autodiff
+using OMEinsum # the 1st way
+A, B, C = randn(2, 3), randn(3, 4), randn(4, 2);
+y, g = cost_and_gradient(ein"(ij, jk), ki->", (A, B, C))
+```
+This built-in automatic differentiation is designed for tensor contractions and is more efficient than the general-purpose automatic differentiation tools.
+
+## Using Zygote
+The backward rule for the basic einsum operation is ported to the [`ChainRulesCore`](https://github.com/JuliaDiff/ChainRulesCore.jl), which is used by the `Zygote` package.
+Zygote is a source-to-source automatic differentiation tool that can be used to compute the gradient of an einsum expression.
+It is more general and can be used for any Julia code.
+```@repl autodiff
+using Zygote # the 2nd way
+Zygote.gradient((A, B, C)->ein"(ij, jk), ki->"(A, B, C)[], A, B, C)
+```
\ No newline at end of file
diff --git a/docs/src/background.md b/docs/src/background.md
new file mode 100644
index 0000000..597558e
--- /dev/null
+++ b/docs/src/background.md
@@ -0,0 +1,65 @@
+# Background Knowledge
+
+## Tensors and Tensor Networks
+Tensor networks serve as a fundamental tool for modeling and analyzing correlated systems. This section reviews the fundamental concepts of tensor
+networks.
+
+A tensor is a mathematical object that generalizes scalars, vectors, and matrices. It can have multiple dimensions and is used to represent data in various mathematical and physical contexts. It is formally defined as follows:
+
+*Definition* (Tensor): A tensor $T$ associated to a set of discrete variables $V$ is defined as a function that maps each possible instantiation of the variables in its scope $\mathcal{D}_V = \prod_{v\in V} \mathcal{D}_{v}$ to an element in the set $\mathcal{E}$, given by
+```math
+T_{V}: \prod_{v \in V} \mathcal{D}_{v} \rightarrow \mathcal{E}.
+```
+Within the context of probabilistic modeling, the elements in $\mathcal{E}$ are non-negative real numbers, while in other scenarios, they can be of generic types. The diagrammatic representation of a tensor is given by a node with the variables $V$ as labels on its edges, as shown below:
+
+```@raw html
+
+```
+
+*Definition* (Tensor Network): A tensor network is a mathematical framework for defining multilinear maps, which can be represented by a triple $\mathcal{N} = (\Lambda, \mathcal{T}, V_0)$, where:
+* $\Lambda$ is the set of variables present in the network $\mathcal{N}$.
+* $\mathcal{T} = \{ T_{V_k} \}_{k=1}^{K}$ is the set of input tensors, where each tensor $T_{V_k}$ is associated with the labels $V_k$.
+* $V_0$ specifies the labels of the output tensor.
+
+Specifically, each tensor $T_{V_k} \in \mathcal{T}$ is labeled by a set of variables $V_k \subseteq \Lambda$, where the cardinality $|V_k|$ equals the rank of $T_{V_k}$. The multilinear map, or the **contraction**, applied to this triple is defined as
+```math
+T_{V_0} = \texttt{contract}(\Lambda, \mathcal{T}, V_0) \overset{\mathrm{def}}{=} \sum_{m \in \mathcal{D}_{\Lambda\setminus V_0}} \prod_{T_V \in \mathcal{T}} T_{V|M=m},
+```
+where $M = \Lambda \setminus V_0$. $T_{V|M=m}$ denotes a slicing of the tensor $T_{V}$ with the variables $M$ fixed to the values $m$. The summation runs over all possible configurations of the variables in $M$.
+
+For instance, matrix multiplication can be described as the contraction of a tensor network given by
+```math
+(AB)_{\{i, k\}} = \texttt{contract}\left(\{i,j,k\}, \{A_{\{i, j\}}, B_{\{j, k\}}\}, \{i, k\}\right),
+```
+where matrices $A$ and $B$ are input tensors containing the variable sets $\{i, j\}, \{j, k\}$, respectively, which are subsets of $\Lambda = \{i, j, k\}$. The output tensor is comprised of variables $\{i, k\}$ and the summation runs over variables $\Lambda \setminus \{i, k\} = \{j\}$. The contraction corresponds to
+```math
+(A B)_{\{i, k\}} = \sum_j A_{\{i,j\}}B_{\{j, k\}}.
+```
+
+Diagrammatically, a tensor network can be represented as an *open hypergraph*, where each tensor is mapped to a vertex and each variable is mapped to a hyperedge. Two vertices are connected by the same hyperedge if and only if they share a common variable. The diagrammatic representation of the matrix multiplication is given as follows:
+
+```@raw html
+
+```
+
+Here, we use different colors to denote different hyperedges. Hyperedges for $i$ and $k$ are left open to denote variables of the output tensor. A slightly more complex example of this is the star contraction:
+```math
+\texttt{contract}(\{i,j,k,l\}, \{A_{\{i, l\}}, B_{\{j, l\}}, C_{\{k, l\}}\}, \{i,j,k\}) \\
+= \sum_{l}A_{\{i,l\}} B_{\{j,l\}} C_{\{k,l\}}.
+```
+Note that the variable $l$ is shared by all three tensors, making regular edges, which by definition connect two nodes, insufficient for its representation. This motivates the need for hyperedges, which can connect a single variable to any number of nodes. The hypergraph representation is given as:
+
+```@raw html
+
+```
+
+## Einsum notation
+The einsum notation is a compact way to specify tensor contractions with a string. In this notation, an index (subscripts) is represented by a char, and the tensors are represented by the indices. The input tensors and the output tensor are separated by an arrow `->` and input tensors are separated by comma `,`. For example, the matrix multiplication $\left(\{i,j,k\}, \{A_{\{i, j\}}, B_{\{j, k\}}\}, \{i, k\}\right)$ can be concisely written as `"ij,jk->ik"`. A general contraction can be defined with pseudocode as follows:
+```
+Let A, B, C, ... be input tensors, O be the output tensor
+for indices in domain_of_unique_indices(einsum_notation)
+ O[indices in O] += A[indices in A] * B[indices in B] * ...
+end
+```
+
+Please [Einsum examples](@ref) for some examples.
\ No newline at end of file
diff --git a/docs/src/basic.md b/docs/src/basic.md
new file mode 100644
index 0000000..91bd7af
--- /dev/null
+++ b/docs/src/basic.md
@@ -0,0 +1,65 @@
+# Basic Usage
+
+In the following example, we demonstrate the einsum notation for basic tensor operations.
+
+## Einsum notation
+To specify the operation, the user can either use the [`@ein_str`](@ref)-string literal or the [`EinCode`](@ref) object.
+For example, both the following code snippets define the matrix multiplication operation:
+```@repl tensor
+using OMEinsum
+code1 = ein"ij,jk -> ik" # the string literal
+ixs = [[1, 2], [2, 3]] # the input indices
+iy = [1, 3] # the output indices
+EinCode(ixs, iy) # the EinCode object (equivalent to the string literal)
+```
+
+The [`@ein_str`](@ref) macro can be used to define the einsum notation directly in the function call.
+```@repl tensor
+A, B = randn(2, 3), randn(3, 4);
+ein"ij,jk -> ik"(A, B) # matrix multiplication
+@ein C[i,k] := A[i,j] * B[j,k] # equivalent to the above line
+```
+Here, we show that the [`@ein`](@ref) macro combines the einsum notation defintion and the operation in a single line, which is more convenient for simple operations.
+Separating the einsum notation and the operation (the first approach) can be useful for reusing the einsum notation for multiple input tensors.
+
+For more than two input tensors, *the [`@ein_str`](@ref) macro does not optimize the contraction order*. In such cases, the user can use the [`@optein_str`](@ref) string literal to optimize the contraction order.
+```@repl tensor
+optein"ij,jk,kl,lm->im"(randn(100, 100), randn(100, 100), randn(100, 100), randn(100, 100))
+```
+
+Sometimes, manually optimizing the contraction order can be beneficial. Please check [Contraction order optimization](@ref) for more details.
+
+## Einsum examples
+We first define the tensors and then demonstrate the einsum notation for various tensor operations.
+```@repl tensor
+using OMEinsum
+s = fill(1) # scalar
+w, v = [1, 2], [4, 5]; # vectors
+A, B = [1 2; 3 4], [5 6; 7 8]; # matrices
+T1, T2 = reshape(1:8, 2, 2, 2), reshape(9:16, 2, 2, 2); # 3D tensor
+```
+### Unary examples
+```@repl tensor
+ein"i->"(w) # sum of the elements of a vector.
+ein"ij->i"(A) # sum of the rows of a matrix.
+ein"ii->"(A) # sum of the diagonal elements of a matrix, i.e., the trace.
+ein"ij->"(A) # sum of the elements of a matrix.
+ein"i->ii"(w) # create a diagonal matrix.
+ein"i->ij"(w; size_info=Dict('j'=>2)) # repeat a vector to form a matrix.
+ein"ijk->ikj"(T1) # permute the dimensions of a tensor.
+```
+
+### Binary examples
+```@repl tensor
+ein"ij, jk -> ik"(A, B) # matrix multiplication.
+ein"ijb,jkb->ikb"(T1, T2) # batch matrix multiplication.
+ein"ij,ij->ij"(A, B) # element-wise multiplication.
+ein"ij,ij->"(A, B) # sum of the element-wise multiplication.
+ein"ij,->ij"(A, s) # element-wise multiplication by a scalar.
+```
+
+### Nary examples
+```@repl tensor
+optein"ai,aj,ak->ijk"(A, A, B) # star contraction.
+optein"ia,ajb,bkc,cld,dm->ijklm"(A, T1, T2, T1, A) # tensor train contraction.
+```
\ No newline at end of file
diff --git a/docs/src/contractionorder.md b/docs/src/contractionorder.md
index 428fcdb..b035257 100644
--- a/docs/src/contractionorder.md
+++ b/docs/src/contractionorder.md
@@ -1,33 +1,49 @@
# Contraction order optimization
-OMEinsum does not implicitly optimize the contraction order.
-Functionalities related to contraction order optimization are mostly defined in [OMEinsumContractionOrders](https://github.com/TensorBFS/OMEinsumContractionOrders.jl)
+The [`@ein_str`](@ref) string literal does not optimize the contraction order for more than two input tensors.
-Here, we provide an example, advanced uses can be found in [OMEinsumContractionOrders](https://github.com/TensorBFS/OMEinsumContractionOrders.jl) and the [performance tips](https://queracomputing.github.io/GenericTensorNetworks.jl/dev/performancetips/) of [GenericTensorNetworks](https://github.com/QuEraComputing/GenericTensorNetworks.jl).
-Let us first consider the following contraction order
-
-```@example 3
+```@repl order
using OMEinsum
code = ein"ij,jk,kl,li->"
```
The time and space complexity can be obtained by calling the [`contraction_complexity`](@ref) function.
-```@example 3
-size_dict = uniformsize(code, 10)
+```@repl order
+size_dict = uniformsize(code, 10) # size of the labels are set to 10
-contraction_complexity(code, size_dict)
+contraction_complexity(code, size_dict) # time and space complexity
```
The return values are `log2` values of the number of iterations, number of elements of the largest tensor and the number of elementwise read-write operations.
-```@example 3
+## Optimizing the contraction order
+To optimize the contraction order, we can use the [`optimize_code`](@ref) function.
+
+```@repl order
optcode = optimize_code(code, size_dict, TreeSA())
```
-The output value is a binary contraction tree with type [`NestedEinsum`](@ref) type.
-The time and readwrite complexities are significantly reduced comparing to the direct contraction.
+The output value is a binary contraction tree with type [`SlicedEinsum`](@ref) or [`NestedEinsum`](@ref).
+The `TreeSA` is a local search algorithm that optimizes the contraction order. More algorithms can be found in the
+[OMEinsumContractionOrders](https://github.com/TensorBFS/OMEinsumContractionOrders.jl) and the [performance tips](https://queracomputing.github.io/GenericTensorNetworks.jl/dev/performancetips/) of [GenericTensorNetworks](https://github.com/QuEraComputing/GenericTensorNetworks.jl).
-```@example 3
+After optimizing the contraction order, the time and readwrite complexities are significantly reduced.
+
+```@repl order
contraction_complexity(optcode, size_dict)
+```
+
+## Using `optein` string literal
+For convenience, the optimized contraction can be directly contructed by using the [`@optein_str`](@ref) string literal.
+```@repl order
+optein"ij,jk,kl,li->" # optimized contraction, without knowing the size of the tensors
+```
+The drawback of using `@optein_str` is that the contraction order is optimized without knowing the size of the tensors.
+Only the tensor ranks are used to optimize the contraction order.
+
+## Manual optimization
+One can also manually specify the contraction order by using the [`@ein_str`](@ref) string literal.
+```@repl order
+ein"((ij,jk),kl),li->ik" # manually optimized contraction
```
\ No newline at end of file
diff --git a/docs/src/cuda.md b/docs/src/cuda.md
new file mode 100644
index 0000000..ca264d8
--- /dev/null
+++ b/docs/src/cuda.md
@@ -0,0 +1,52 @@
+# CUDA Acceleration
+
+By uploading your data to the GPU, you can accelerate the computation of your model.
+
+```julia repl
+julia> using CUDA, OMEinsum
+
+julia> code = ein"ij,jk,kl,li->" # the einsum notation
+ij, jk, kl, li ->
+
+julia> A, B, C, D = rand(1000, 1000), rand(1000, 300), rand(300, 800), rand(800, 1000);
+
+julia> size_dict = OMEinsum.get_size_dict(getixsv(code), (A, B, C, D)) # get the size of the labels
+Dict{Char, Int64} with 4 entries:
+ 'j' => 1000
+ 'i' => 1000
+ 'k' => 300
+ 'l' => 800
+
+julia> optcode = optimize_code(code, size_dict, TreeSA()) # optimize the contraction order
+SlicedEinsum{Char, DynamicNestedEinsum{Char}}(Char[], kl, kl ->
+├─ ki, li -> kl
+│ ├─ jk, ij -> ki
+│ │ ├─ jk
+│ │ └─ ij
+│ └─ li
+└─ kl
+)
+```
+
+The contraction order is optimized. Now, let's benchmark the contraction on the CPU.
+
+```julia repl
+julia> using BenchmarkTools
+
+julia> @btime optcode($A, $B, $C, $D) # the contraction on CPU
+ 6.053 ms (308 allocations: 20.16 MiB)
+0-dimensional Array{Float64, 0}:
+1.4984046443610943e10
+```
+
+The contraction on the CPU takes about 6 ms. Now, let's upload the data to the GPU and perform the contraction on the GPU.
+```julia repl
+julia> @btime CUDA.@sync optcode($cuA, $cuB, $cuC, $cuD) # the contraction on GPU
+ 243.888 μs (763 allocations: 28.56 KiB)
+0-dimensional CuArray{Float64, 0, CUDA.DeviceMemory}:
+1.4984046443610939e10
+```
+
+To learn more about using GPU and autodiff, please check out the following asciinema video.
+[](https://asciinema.org/a/wE4CtIzWUC3R0GkVV28rVBRFb)
+
diff --git a/docs/src/extending.md b/docs/src/extending.md
deleted file mode 100644
index 24a859d..0000000
--- a/docs/src/extending.md
+++ /dev/null
@@ -1,48 +0,0 @@
-# Extending OMEinsum
-
-Adding a new subtype of `EinRule` is bothersome - the list of rules
-that's considered needs to be fix and thus one has to change the code before
-`using` OMEinsum. A limitation due to liberal use of `generated` functions.
-If a useful rule is found, we might add it to the package itself though so feel free to reach out.
-
-Extending `einsum` for certain array-types on the other hands is easy,
-since we use the usual dispatch mechanism.
-Consider e.g. adding a special operator for index-reductions of a `Diagonal`-operator.
-
-First, we need to add a method for the `asarray`-function that ensures that we return 0-dimensional arrays for operations.
-
-```@example 1
-using OMEinsum, LinearAlgebra
-
-OMEinsum.asarray(a::Number, ::Diagonal) = fill(a,())
-```
-
-Now reducing over indices already works but it uses the `sum` function
-which does not specialize on `Diagonal`:
-```@example 1
-ein"ij -> "(Diagonal([1,2,3]))
-```
-
-we can do better by overloading the unary rule `einsum(::Sum, ixs, iy, ::Tuple{<:Diagonal}, <:Any)`:
-```@example 1
-function OMEinsum.einsum(::OMEinsum.Sum, ixs, iy, xs::Tuple{<:Diagonal}, size_dict::Dict)
- length(iy) == 1 && return diag(xs[1])
- return sum(diag(xs[1]))
-end
-```
-
-where we use that the indices `iy` and `ixs` have already been checked in `match_rule`.
-We now get our more efficient implementation when we call any of the below:
-```@example 1
-ein"ij -> i"(Diagonal([1,2,3]))
-```
-
-```@example 1
-ein"ij -> j"(Diagonal([1,2,3]))
-```
-
-```@example 1
-ein"ij -> "(Diagonal([1,2,3]))
-```
-
-(To make sure the custom implementation is called, you can add a `print`-statement to the method for `Diagonal`)
diff --git a/docs/src/implementation.md b/docs/src/implementation.md
deleted file mode 100644
index b6015cd..0000000
--- a/docs/src/implementation.md
+++ /dev/null
@@ -1,107 +0,0 @@
-# Implementations
-
-## Identity
-To test whether a specification `ixs,iy` is the identity, it is checked whether
-`ixs` is made up of _one_ tuple of index-labels that is equal to `iy` _and_
-that all index-labels in `iy` are unique - the latter to distinguish identity
-from e.g. projection to the diagonal like `ein"ii -> ii"`.
-
-The identity operation simply returns the first (and only) tensor argument to `einsum`.
-
-## Permutations
-
-A specification `ixs,iy` is an index-permutation if `ixs` is a tuple containing
-one tuple of index-labels that are all unique and are a permutation of the labels
-in `iy`.
-
-Index-permutation is implemented with `permutedims` and a permutation that's calculated
-at runtime.
-
-## Tr
-
-A specification `ixs, iy` is a trace if `iy` is empty and `ixs` contains one
-2-tuple containing the same index-label twice.
-
-A trace dispatches to the `LinearAlgebra.tr` although the result is wrapped in
-a 0-dimensional array for type stability since all `einsum` return `AbstractArray`s.
-
-## Sum
-
-A specification `ixs,iy` is a sum or a reduction over indices if all indices in `iy`
-are unique and contained in the only tuple in `ixs` that additionally contains
-unique labels (that are reduced over).
-
-Index-reductions are implemented using `Base.sum` and `Base.dropdims` - the latter
-to remove the singleton-dimensions left over after summing over a dimension.
-
-## Repeat
-The inverse rule of `Sum`, e.g. `ij->lijk`.
-
-## Diag
-A unary operation that remove multi-edges from a tensor, e.g. `ijkj->ikj`.
-
-## Duplicate
-The inverse rule of `Diag`, e.g. `ikj->ijkj`.
-
-## SimpleBinaryRule
-The contraction between two tensors with the following restriction
-* a tensor can not be simplified by unary rules, e.g. `iij,jk,ik` is not valid, the first index can be simplified to `ij` using the unary rule `iij->ij`.
-* no multi-edge
-
-A complete list of rules are
-* ein",->"
-* ein",k->k"
-* ein"i,->i"
-* ein"j,j->"
-* ein"i,k->ik" and ein"i,k->ki",
-* ein"j,jk->k" and ein"j,kj->k"
-* ein"ji,j->i" and ein"ij,j->i"
-* ein"ji,jk->ik" and its index permutations (within a tensor)
-* ein"l,l->l"
-* ein"l,kl->kl"
-* ein"il,->il"
-* ein"jl,jl->"
-* ein"il,kl->ikl" and ein"il,kl->kil",
-* ein"jl,jkl->kl" and ein"jl,kjl->kl"
-* ein"jil,jl->il" and ein"ijl,jl->il"
-* ein"jil,jkl->ikl" and its index permutations (within a tensor, except the batch dimension)
-
-Here, the batch dimension always appears as the last dimension.
-
-## Fallback
-
-The fallback is called for any specification that does not satisfy the criteria
-outlined above.
-
-The dispatch calls `loop_einsum` which is defined in `loop_einsum.jl`.
-
-`loop_einsum` is based on the `EinArray`-struct.
-An `EinArray` is a subtype of `AbstractArray` that represents an intermediate
-step in a general einsum-expression _before_ reductions remove indices.
-Consider a specification `ixs,iy` - the `EinArray` for that specification is
-the array with an index for each (distinct) label in `ixs` and `iy`.
-As an example, in `ein"ij,ik,il -> jkl"(a,b,c)`, the distinct labels are `(i,j,k,l)`
-and the corresponding `EinArray` `einarr` would be a rank-4 tensor with an index each for
-each distinct label.
-
-If an entry of `einarr` is requested, e.g. `einarr[i₁,j₁,k₁,l₁]`, it's values is lazily
-constructed as `einarr[i₁,j₁,k₁,l₁] = a[i₁,j₁]*a[i₁,k₁]*a[i₁,l₁]` upon access - the lazy evaluation avoids constructing the whole array.
-
-To get to the final result, we reduce over the dimensions that are missing in
-the output. By first allocating an array of the correct size, we can fill it
-up with the entries of the `EinArray` which are calculated on the fly,
-avoiding the allocation of the intermediate result.
-
-Thus effectively we split an operation like `ein"ij,ik,il -> jkl"(a,b,c)` into
-two piece: `einarr = ein"ij,ik,il -> ijkl"(a,b,c)` and `ein"ijkl -> jkl"(einarr)`
-but treat the first operation as a lazy one - this way we can use `mapreduce(identity, +)`
-over the dimensions we want to remove which is implemented efficiently for both
-regular `Array`s and `CuArray`s.
-
-## Debugging
-
-Calling `allow_loops(false)` will cause an error to be printed when if the
-fallback `loop_einsum` is used. This is an `@error` which does not interrupt execution.
-
-Alternatively, a log of all methods used can be saved using `@debug` logging macro.
-This is switched off by default, but can be printed by setting `ENV["JULIA_DEBUG"] = "all"`.
diff --git a/docs/src/index.md b/docs/src/index.md
index 431f451..e20cbe8 100644
--- a/docs/src/index.md
+++ b/docs/src/index.md
@@ -1,38 +1,16 @@
# OMEinsum.jl
-This package mainly exports one function, `einsum`, with three interfaces.
-`einsum` implements functionality similar to the `einsum` function in `numpy`,
-although some details are different.
+This package provides
+- The einsum notation, which is similar to the einsum function in `numpy`, although some details are different.
+- Highly optimized algorithms to optimize the contraction of tensors.
-`einsum` operations are specified by a tuple of tensors `xs = (x1, x2, x3...)`
-, a tuple of index-labels for the tensors in `xs`, `ixs = (ix1, ix2, ix3...)`,
-and output index-labels `iy` specified as `einsum(EinCode(ixs,iy), xs)`.
-Alternatively, operations can be specified using the `@ein`-macro or
-the `@ein_str`- string literal (see examples or help).
+The source code is available at [OMEinsum.jl](https://github.com/under-Peter/OMEinsum.jl).
-Let `l` be the set of all unique labels in the `ixs` without the ones in `iy`.
-`einsum` then calculates an output tensor `y` with indices labelled `iy` according
-to the following specification:
-```math
-\forall iy : y[iy] = \sum_l x_1[ix_1] * x_2[ix_2] * x_3[ix_3] \ldots
-```
+## Quick start
-where the sum over `l` implies the sum over all possible values of the labels in `l`.
+You can find a set up guide in the [README](https://github.com/under-Peter/OMEinsum.jl). To get started, open a Julia REPL and type the following code.
-As an example, consider the _matrix multiplication_ of two random 2×2 tensors, where we have:
-```julia
-xs = (rand(2,2), rand(2,2))
-ixs = (('i','j'),('j','k'))
-iy = ('i','k')
-```
-Now `l = ('j',)` since all unique indices are `('i','j','k')`
-but both `'i'` and `'k'` are in `iy`.
-The output `y` is then defined by
-```math
-\forall i,k : y[i,k] = \sum_j x_1[i,j] * x_2[j,k]
-```
-which is just the regular definition of matrix multiplication. Alternatively it could've been specified with a custom string-literal as `ein"ij,jk -> ik"(rand(2,2),rand(2,2))`, see [Input (flat)](@ref).
-
-The structure of an `einsum` evaluation with the string-literal is depicted
-in the flowchart below:
-
+```@repl intro
+using OMEinsum
+optein"ij,jk,kl,lm->im"(randn(100, 100), randn(100, 100), randn(100, 100), randn(100, 100))
+```
\ No newline at end of file
diff --git a/docs/src/ome-flowchart.png b/docs/src/ome-flowchart.png
deleted file mode 100644
index 0bceac0..0000000
Binary files a/docs/src/ome-flowchart.png and /dev/null differ
diff --git a/docs/src/parsing.md b/docs/src/parsing.md
deleted file mode 100644
index 7105e33..0000000
--- a/docs/src/parsing.md
+++ /dev/null
@@ -1,102 +0,0 @@
-# Input (flat)
-
-An einsum specification should be given via the `ein_str` string-literal
-or with the `@ein`-macro as e.g.
-```@example 2
-using OMEinsum
-a, b = randn(2, 2), randn(2, 2)
-
-c = ein"ij,jk -> ik"(a,b)
-@ein c[i,k] := a[i,j] * b[j,k]
-```
-where both specifications encode the same operation - a matrix multiplication.
-The `ein_str`-literal is parsed directly into an `EinCode` struct that holds
-the indices of the input `ixs = (('i','j'),('j','k'))` and output `iy = ('i','k')`
-as type parameters, making them accessible at compile time.
-
-The string-literal form gets turned into
-```@example 2
-c = EinCode((('i','j'),('j','k')),('i','k'))(a,b)
-```
-Calling an `EinCode`-object gets lowered to
-```@example 2
-c = einsum(EinCode((('i','j'),('j','k')),('i','k')), (a,b), Dict('i'=>2, 'j'=>2, 'k'=>2))
-```
-The third argument `size_dict` is a dictionary to specify the dimensions of degree of freedoms, which could also allow to provide dimensions for index-labels that only appear in the output.
-
-In the next step, a singleton-subtype of the abstract type `EinRule` is chosen which is later used for dispatch.
-Subtypes of `EinRule` specify the kind of operation and are created in such a way that they allow useful dispatch.
-They are defined in `EinRule.jl`.
-
-The possible types are:
-- `Identity` - operation is the identity on _one_ tensor, e.g. `ein"ijk -> ijk"`
-- `Permutedims` - operation is a permutation of the indices of _one_ tensor, e.g. `ein"ijk -> jki"`
-- `Tr` - operation is a trace of _one_ matrix, e.g. `ein"ii ->"`
-- `Sum` - operation is a reduction over one or more indices of _one_ tensor, e.g. `ein"ijkl -> il"`
-- `SimpleBinaryRule` - operation is a pairwise contraction that can not be reduce by unary operations, e.g. `ein"ijl,jkl-> ikl"`
-- `DefaultRule` - default if none of the above match, e.g. `ein"ij,ik,il -> jkl"`
-
-Since `ixs` and `iy` are saved as type-parameters, the operation-matching can happen at compile time.
-The operation is chosen using `match_rule(ixs,iy)` by testing all subtypes of `EinRule` in the sequence above (top to bottom) and picking the first match.
-
-This enables us to chose fast BLAS functions for a matrix multiplication which is also a legal tensor-contraction.
-
-We proceed by calling `einsum(<:EinRule, <:EinCode, xs, size_dict)` which
-dispatches on the `EinRule` and the type of `xs` - the latter enables us to dispatch to e.g. cuda-specific routines for certain operations (as done in the `cueinsum.jl` file).
-
-In the case of the matrix-multiplication above, `einsum` calls `*` which can dispatch
-to efficient routines for most `Array`-types including `CuArray`.
-
-# Input (Nested)
-
-Whether with the `ein_str` string-literal or the `@ein` macro, nested expressions are mapped to a nested struct.
-Consider the example
-```@example 2
-c = ein"(ij,jk),kl -> il"(a,b,c)
-@ein c[i,l] := (a[i,j] * b[j,k]) * c[k,l]
-```
-which is a simply a product of three matrices evaluated as
-two matrix products in sequence.
-
-This is equivalent to
-```@example 2
-c = ein"ik,kl -> il"(ein"ij,jk -> ik"(a,b),c)
-@ein ab[i,k] := a[i,j] * b[j,k]
-@ein c[i,l] := ab[i,k] * c[k,l]
-```
-and is expressed as a nested structure `NestedEinsum`
-which contains the `EinCode`s for the intermediate calculations
-as well as some logic to assign the correct input and output tensors
-to the correct `EinCode`.
-
-`NestedEinsum` has the following definition:
-```@example 2
-struct NestedEinsum
- args
- eins
-end
-```
-`args` holds the arguments to that `EinCode` which can either be a integer to label a tensor or a `NestedEinsum` itself.
-The labeling works such that the `i`th input is represented by the number `i`.
-
-Upon application to tensors, a `NestedEinsum` evaluates its arguments.
-If the argument is an integer `i`, the `i`th provided tensor is chosen,
-otherwise the `NestedEinsum` is evaluated.
-
-To make it more concrete, consider the `NestedEinsum` for the expression above, where for easier reading the type signatures were removed and the `EinCode`-structs were replaced by `ein`-string literals.
-```@example 2
-ein"(ij,jk),kl -> il"
-```
-Evaluating this expression with three arguments leads to the inner `NestedEinsum` to be evaluated first with the first and second argument and the specification `ein"ij,jk -> ik"`. Then the result of that is given
-as the first argument to `ein"ik,kl -> il"` with the third argument as the second input.
-
-To improve understanding, you might replace the integers with `getindex` operations in your head
-```julia
-ein"(ij,jk),kl -> il"(xs...)
-⇒ NestedEinsum{...}((NestedEinsum{...}((xs[1], xs[2]), ein"ij,jk -> ik"), xs[3]), ein"ik,kl -> il")
-```
-and finally turn it into
-```julia
-ein"(ij,jk),kl -> il"(xs...)
-⇒ ein"ik,kl -> il"(ein"ij,jk -> ik"(xs[1], xs[2]), xs[3])
-```
\ No newline at end of file
diff --git a/examples/random_tn.jl b/examples/random_tn.jl
deleted file mode 100644
index 48b5b3f..0000000
--- a/examples/random_tn.jl
+++ /dev/null
@@ -1,58 +0,0 @@
-using OMEinsum
-using StatsBase, Random
-
-function test()
- for i=1:50
- ranka = rand(1:8)
- rankb = rand(1:8)
- ta = [1:ranka...]
- rankab = rand(1:min(ranka, rankb))
- tb = sample(ta, rankab; replace=false)
- tout = setdiff(ta, tb)
- for k=1:rankb-rankab
- push!(tb, ranka+k)
- push!(tout, ranka+k)
- end
- shuffle!(tb)
- shuffle!(tout)
- A = randn(fill(2, ranka)...)
- B = randn(fill(2, rankb)...)
- OMEinsum.batched_contract(Val((ta...,)), A, Val((tb...,)), B, Val((tout...,)))
- end
-end
-
-@time test()
-
-function batched_contract2(iAs, A::AbstractArray, iBs, B::AbstractArray, iOuts)
- pA, iAps, iAbs, iAss, pB, iBps, iBbs, iBss, pOut = OMEinsum.analyse_batched_dim(iAs, iBs, iOuts)
- sAb, sAs, sAp, sBs, sBb, sBp, sAB = OMEinsum.analyse_batched_size(iAs, iAps, iAbs, iAss, size(A), iBs, iBps, iBbs, iBss, size(B))
-
- A, B = OMEinsum.align_eltypes(A, B)
- Apr = reshape(OMEinsum.tensorpermute(A, pA), sAb, sAs, sAp)
- Bpr = reshape(OMEinsum.tensorpermute(B, pB), sBs, sBb, sBp)
- AB = OMEinsum._batched_gemm('N','N', Apr, Bpr)
- AB = OMEinsum.tensorpermute(reshape(AB, sAB...), (pOut...,))
-end
-
-function test2()
- for i=1:10
- ranka = rand(1:8)
- rankb = rand(1:8)
- ta = [1:ranka...]
- rankab = rand(1:min(ranka, rankb))
- tb = sample(ta, rankab; replace=false)
- tout = setdiff(ta, tb)
- for k=1:rankb-rankab
- push!(tb, ranka+k)
- push!(tout, ranka+k)
- end
- shuffle!(tb)
- shuffle!(tout)
- A = randn(fill(2, ranka)...)
- B = randn(fill(2, rankb)...)
- batched_contract2(ta, A, tb, B, tout)
- end
-end
-
-
-@time test2()
\ No newline at end of file
diff --git a/src/OMEinsum.jl b/src/OMEinsum.jl
index ff90099..e617382 100644
--- a/src/OMEinsum.jl
+++ b/src/OMEinsum.jl
@@ -13,6 +13,7 @@ export getiyv, getixsv, uniquelabels, labeltype
export flop
export loop_einsum, loop_einsum!, allow_loops
export asarray, asscalar
+export cost_and_gradient
# re-export the functions in OMEinsumContractionOrders
export CodeOptimizer, CodeSimplifier,
diff --git a/src/slicing.jl b/src/slicing.jl
index 18beb57..7c7570f 100644
--- a/src/slicing.jl
+++ b/src/slicing.jl
@@ -1,3 +1,12 @@
+"""
+ SlicedEinsum{LT, Ein} <: AbstractEinsum
+
+A tensor network with slicing. `LT` is the label type and `Ein` is the tensor network.
+
+### Fields
+- `slicing::Vector{LT}`: A vector of labels to slice.
+- `eins::Ein`: The tensor network.
+"""
struct SlicedEinsum{LT, Ein} <: AbstractEinsum
slicing::Vector{LT}
eins::Ein