- 时间: 2020-10-18
- 题目链接:https://leetcode-cn.com/problems/n-queens-ii/
- tag:n皇后
- 题目描述:
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
来自力扣官方 同0051题 方法一使用三个集合记录分别记录每一列以及两个方向的每条斜线上是否有皇后,每个集合最多包含 N 个元素,因此集合的空间复杂度是 O(N)。如果利用位运算记录皇后的信息,就可以将记录皇后信息的空间复杂度从 O(N) 降到 O(1)。
具体做法是,使用三个整数 columns、diagonals1和 diagonals2分别记录每一列以及两个方向的每条斜线上是否有皇后,每个整数有 N个二进制位。棋盘的每一列对应每个整数的二进制表示中的一个数位,其中棋盘的最左列对应每个整数的最低二进制位,最右列对应每个整数的最高二进制位。
那么如何根据每次放置的皇后更新三个整数的值呢?在说具体的计算方法之前,首先说一个例子。
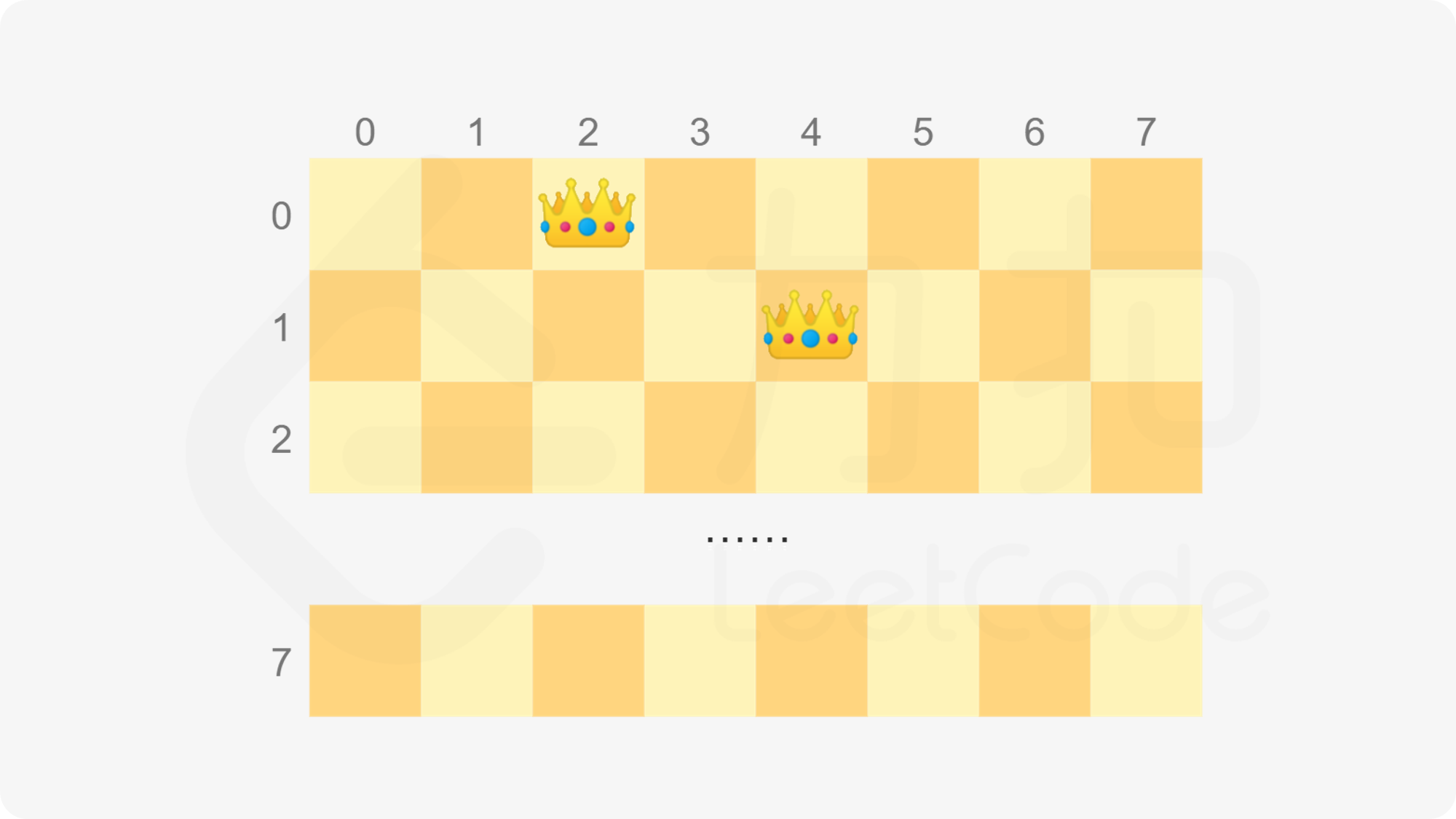
棋盘的边长和皇后的数量 N=8。如果棋盘的前两行分别在第 2 列和第 4 列放置了皇后(下标从 0 开始),则棋盘的前两行如下图所示。
class Solution:
def totalNQueens(self, n: int):
res=0
def solve(row: int, columns: int, diagonals1: int, diagonals2: int):
if row == n:
nonlocal res
res+=1
else:
availablePositions = ((1 << n) - 1) & (~(columns | diagonals1 | diagonals2))
while availablePositions:
position = availablePositions & (-availablePositions)
availablePositions = availablePositions & (availablePositions - 1)
#记录当前选择点所处的位置,column和columns无关,小心看错。后者是用二进制表示已经占据位点的情况
solve(row + 1, columns | position, (diagonals1 | position) << 1, (diagonals2 | position) >> 1)
solve(0, 0, 0, 0)
return res