Skip to content

Latest commit

 

History

History
367 lines (317 loc) · 9.65 KB

README.md

File metadata and controls

367 lines (317 loc) · 9.65 KB
Raw

面试题 07. 重建二叉树

题目描述

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

 

示例 1:

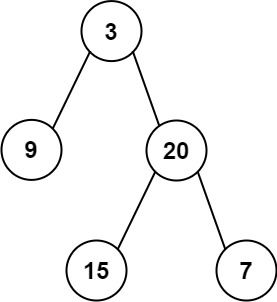
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

 

限制：

0 <= 节点个数 <= 5000

 

注意：本题与主站 105 题重复：https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

解法

方法一：哈希表 + 递归

由于我们每一次都需要在中序序列中找到根节点的位置，因此我们可以使用哈希表 $d$ 来存储中序序列的值和索引，这样可以将查找的时间复杂度降低到 $O(1)$。

接下来，我们设计一个递归函数 $dfs(i, j, n)$，表示在前序序列中，从第 $i$ 个节点开始的 $n$ 个节点，对应的中序序列中，从第 $j$ 个节点开始的 $n$ 个节点，构造出的二叉树。

函数 $dfs(i, j, n)$ 的执行过程如下：

如果 $n = 0$，说明已经没有节点了，返回 $null$；

否则，我们取前序序列的第 $i$ 个节点作为根节点，创建一个树节点，即 root = new TreeNode(preorder[i])，然后我们在中序序列中找到根节点的位置，记为 $k$，则根节点左边的 $k - j$ 个节点为左子树，右边的 $n - k + j - 1$ 个节点为右子树。递归地调用函数 $dfs(i + 1, j, k - j)$ 构造左子树，调用函数 $dfs(i + k - j + 1, k + 1, n - k + j - 1)$ 构造右子树。最后返回根节点 root。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点个数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None


class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        def dfs(i, j, n):
            if n < 1:
                return None
            root = TreeNode(preorder[i])
            k = d[preorder[i]]
            l = k - j
            root.left = dfs(i + 1, j, l)
            root.right = dfs(i + 1 + l, k + 1, n - l - 1)
            return root

        d = {v: i for i, v in enumerate(inorder)}
        return dfs(0, 0, len(preorder))

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private Map<Integer, Integer> d = new HashMap<>();
    private int[] preorder;
    private int[] inorder;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = inorder.length;
        for (int i = 0; i < n; ++i) {
            d.put(inorder[i], i);
        }
        this.preorder = preorder;
        this.inorder = inorder;
        return dfs(0, 0, n);
    }

    private TreeNode dfs(int i, int j, int n) {
        if (n < 1) {
            return null;
        }
        int k = d.get(preorder[i]);
        int l = k - j;
        TreeNode root = new TreeNode(preorder[i]);
        root.left = dfs(i + 1, j, l);
        root.right = dfs(i + 1 + l, k + 1, n - l - 1);
        return root;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        unordered_map<int, int> d;
        int n = inorder.size();
        for (int i = 0; i < n; ++i) {
            d[inorder[i]] = i;
        }
        function<TreeNode*(int, int, int)> dfs = [&](int i, int j, int n) -> TreeNode* {
            if (n < 1) {
                return nullptr;
            }
            int k = d[preorder[i]];
            int l = k - j;
            TreeNode* root = new TreeNode(preorder[i]);
            root->left = dfs(i + 1, j, l);
            root->right = dfs(i + 1 + l, k + 1, n - l - 1);
            return root;
        };
        return dfs(0, 0, n);
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(preorder []int, inorder []int) *TreeNode {
	d := map[int]int{}
	for i, v := range inorder {
		d[v] = i
	}
	var dfs func(i, j, n int) *TreeNode
	dfs = func(i, j, n int) *TreeNode {
		if n < 1 {
			return nil
		}
		k := d[preorder[i]]
		l := k - j
		root := &TreeNode{Val: preorder[i]}
		root.Left = dfs(i+1, j, l)
		root.Right = dfs(i+1+l, k+1, n-l-1)
		return root
	}
	return dfs(0, 0, len(inorder))
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function (preorder, inorder) {
    const d = new Map();
    const n = inorder.length;
    for (let i = 0; i < n; ++i) {
        d.set(inorder[i], i);
    }
    const dfs = (i, j, n) => {
        if (n < 1) {
            return null;
        }
        const k = d.get(preorder[i]);
        const l = k - j;
        const root = new TreeNode(preorder[i]);
        root.left = dfs(i + 1, j, l);
        root.right = dfs(i + 1 + l, k + 1, n - l - 1);
        return root;
    };
    return dfs(0, 0, n);
};

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function buildTree(preorder: number[], inorder: number[]): TreeNode | null {
    const d = new Map<number, number>();
    const n = inorder.length;
    for (let i = 0; i < n; ++i) {
        d.set(inorder[i], i);
    }
    const dfs = (i: number, j: number, n: number): TreeNode | null => {
        if (n < 1) {
            return null;
        }
        const k = d.get(preorder[i]) ?? 0;
        const l = k - j;
        const root = new TreeNode(preorder[i]);
        root.left = dfs(i + 1, j, l);
        root.right = dfs(i + 1 + l, k + 1, n - l - 1);
        return root;
    };
    return dfs(0, 0, n);
}
/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function buildTree(preorder: number[], inorder: number[]): TreeNode | null {
    if (inorder.length === 0) {
        return null;
    }
    const val = preorder[0];
    const i = inorder.indexOf(val);
    return new TreeNode(
        val,
        buildTree(preorder.slice(1, i + 1), inorder.slice(0, i)),
        buildTree(preorder.slice(i + 1), inorder.slice(i + 1)),
    );
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    fn help(preorder: &[i32], inorder: &[i32]) -> Option<Rc<RefCell<TreeNode>>> {
        if inorder.is_empty() {
            return None;
        }
        let val = preorder[0];
        let i = inorder.iter().position(|num| *num == val).unwrap();
        Some(Rc::new(RefCell::new(TreeNode {
            val,
            left: Self::help(&preorder[1..i + 1], &inorder[..i]),
            right: Self::help(&preorder[i + 1..], &inorder[i + 1..]),
        })))
    }

    pub fn build_tree(preorder: Vec<i32>, inorder: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
        Self::help(&preorder, &inorder)
    }
}

C#

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public TreeNode BuildTree(int[] preorder, int[] inorder) {
        if (preorder.Length == 0) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[0]);
        int idx = Array.IndexOf(inorder, root.val);
        root.left = BuildTree(preorder[1..(index+1)], inorder[0..idx]);
        root.right = BuildTree(preorder[(index+1)..], inorder[(idx+1)..]);
        return root;
    }
}

...