原始 Markdown文档、Visio流程图、XMind思维导图见:https://github.com/LiZhengXiao99/Navigation-Learning
[TOC]
以非差非组合双频 PPP 模型为例,假如某一时刻观测到
观测噪声的方差矩阵 $\mathbf{R}{k}$ 可根据卫星高度角或信噪比随机模型确定,即:
$$
\mathbf{R}{k}=\left[\begin{array}{ccccccccc}\left(\sigma_{p_{1}}^{1}\right)^{2} & 0 & 0 & 0 & & & & & \ 0 & \left(\sigma_{l_{1}}^{1}\right)^{2} & 0 & 0 & & & & & \ 0 & 0 & \left(\sigma_{p_{2}}^{1}\right)^{2} & 0 & & & & & \ 0 & 0 & 0 & \left(\sigma_{l_{2}}^{1}\right)^{2} & & & & & \ & & & & \ddots & & & & \ & & & & & \left(\sigma_{p_{1}}^{m}\right)^{2} & 0 & 0 & 0 \ & & & & & 0 & \left(\sigma_{l_{1}}^{m}\right)^{2} & 0 & 0 \ & & & & & 0 & 0 & \left(\sigma_{p_{2}}^{m}\right)^{2} & 0 \ & & & & & 0 & 0 & 0 & \left(\sigma_{l_{2}}^{m}\right)^{2}\end{array}\right]
$$
式中,$\sigma_{p_{1}}$ 和
对于 PPP 定位,其状态转移矩阵 $\boldsymbol{\Phi}{k, k-1}$ 为单位阵,因此状态方程可描述为:
$$
\hat{\mathbf{X}}{k, k-1}=\mathbf{X}_{k-1}
$$
其中,相位模糊度参数当作常数处理,其初值由伪距和载波观测值扣除电离层延迟得到,初始方差设为
状态向量
N 开头的宏定义是参数数量:
#define NF(opt) ((opt)->ionoopt==IONOOPT_IF12?1:(opt)->nf) /* number of frquencies */
#define NP(opt) ((opt)->dynamics?9:3) /* number of position solution */
#define NC(opt) (NSYS) /* number of clock solution */
#define ND(opt) ((opt)->nf>=3||(opt)->ionoopt==IONOOPT_UC12?1:0) /* number of receiver DCB */
//#define ND(opt) ((opt)->nf>=3?1:0) /* number of receiver DCB */
#define NICB(opt) ((opt)->gloicb==GLOICB_OFF?0:((opt)->gloicb==GLOICB_LNF?1:((opt)->gloicb==GLOICB_QUAD?2:((opt)->gloicb==GLOICB_1SAT?NSATGLO:13))))
/* number of GLONASS ICB */
#define NT(opt) ((opt)->tropopt<TROPOPT_EST?0:((opt)->tropopt==TROPOPT_EST?1:3)) /* number of tropospheric parameters */
#define NI(opt) ((opt)->ionoopt==IONOOPT_UC1||(opt)->ionoopt==IONOOPT_UC12?MAXSAT:0) /* number of ionospheric parameters */
#define NR(opt) (NP(opt)+NC(opt)+ND(opt)+NICB(opt)+NT(opt)+NI(opt))
#define NB(opt) (NF(opt)*MAXSAT) /* number of phase ambiguity parameters */
#define NX(opt) (NR(opt)+NB(opt)) /* number of estimated parameters */-
NF:频率数量:电离层与双频的线性组合时为 1,否则为设置的频率数
-
NP:位置参数数量:正常为 3( XYZ坐标),dynamics 动力学模式还有估计速度加速度为 9。
-
NC:系统数量、钟差参数数量:设为卫星系统数量,GPS 对应的是接收机钟差,其它系统对应的是与 GPS 之间的系统间偏差 ISB(包括系统间时间偏差和硬件延迟等)。
-
ND:接收机 DCB 参数数量:如果频率数量 nf>=3,或者双频非差非组合,设为 1,否则为 0。
-
NICB:GLONASS 伪距频间偏差 ICB 数量:不估计是为 0,线性模型为 1,二次多项式模型为 2,每颗卫星估计一个 GLONASS 卫星数 NSATGLO,否则是 13(13 是啥意思,没看懂)。
-
NT:对流层参数数量:不估计对流层时为 0,
TROPOPT_EST时为 1,TROPOPT_ESTG时为 3。 -
NI:电离层参数数量:非差非组合模式为最大卫星数 MAXSAT,否则为 0 不估计电离层。
-
NR:除模糊度之外的参数数量:上面的几个相加。
-
NB:模糊度参数数量:频率数 NF 乘以卫星数 MAXSAT。
-
NX:总参数数量:除模糊度之外的参数数量 NR + 总参数数量 NX。
I 开头的宏定义是参数下标:
#define IC(s,opt) (NP(opt)+(s)) /* state index of clocks (s=0:gps,1:glo,2:bds,3:gal) */
#define ID(opt) (NP(opt)+NC(opt)) /* state index of receiver DCB */
#define IICB(s,opt) (NP(opt)+NC(opt)+ND(opt)+(s)-1) /* state inde#define ID(opt) (NP(opt)+NC(opt))x of GLONASS ICB */
#define IT(opt) (NP(opt)+NC(opt)+ND(opt)+NICB(opt)) /* state index of tropospheric parameters */
#define II(s,opt) (NP(opt)+NC(opt)+ND(opt)+NICB(opt)+NT(opt)+(s)-1) /* state index of ionospheric parameters */
#define IB(s,f,opt) (NR(opt)+MAXSAT*(f)+(s)-1) /* state index of phase ambiguity parameters */为啥直接从 IC 开始,没有 IP?因为位置参数在最前面,就是前 3 或者前 9,直接取就行。
-
IC:钟差、ISB 参数下标
-
ID:DCB 参数下标
-
IICB:GLONASS 伪距频间偏差 ICB 下标
-
IT:对流层参数下标
-
II:电离层参数下标
-
IB:模糊度参数下标
-
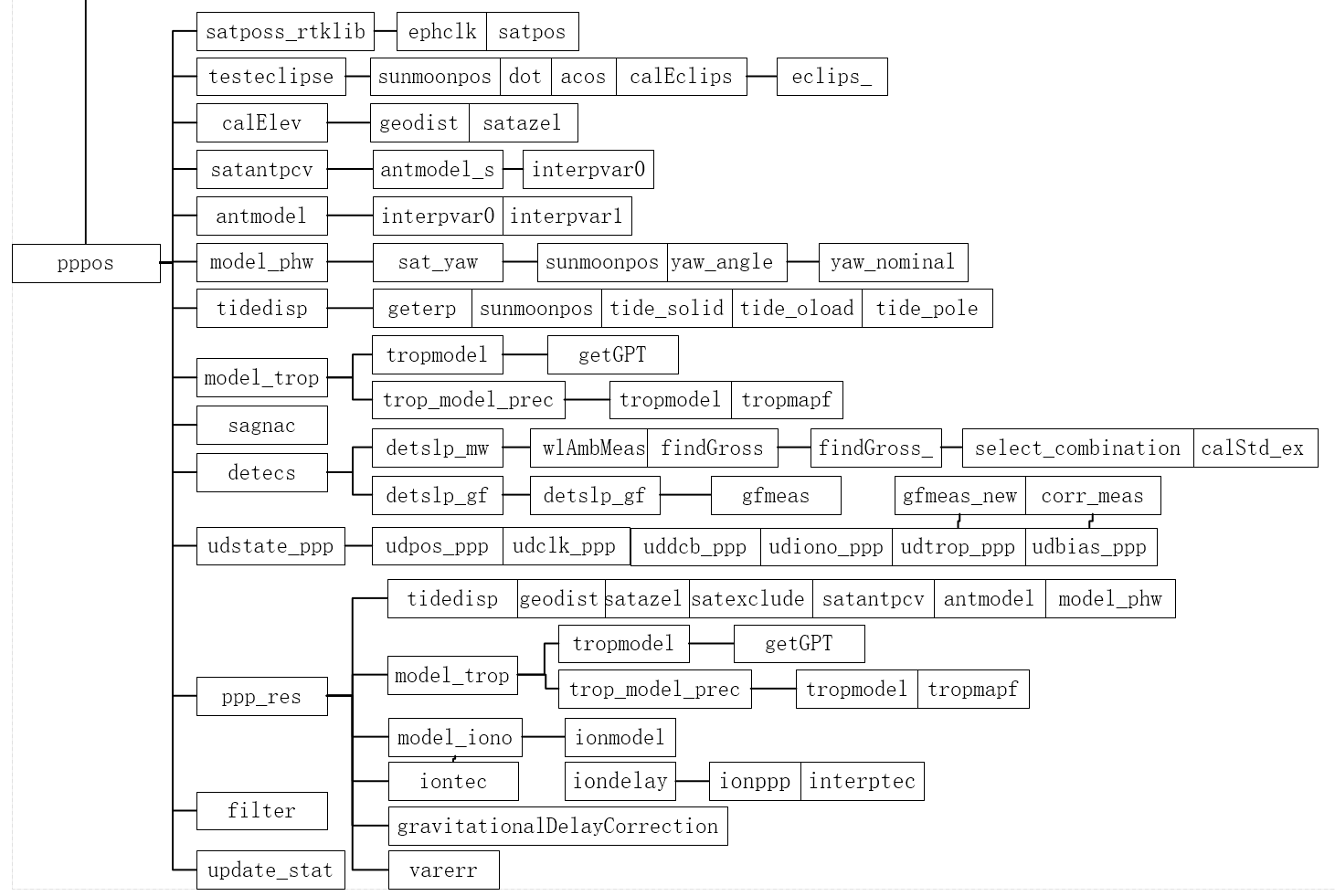
调用 satposs_rtklib() 精密星历计算卫星位置、钟差。
-
调用 testeclipse() 排除日食卫星卫星。
-
调用 calElev() 其通过调用 geodist()、satazel() 计算近似几何距离、方位角高度角。
-
计算 RCVEX 的数据,存到 PPP_Info 里,对解算好像不起做用。
-
调用 detecs() 周跳检测。
-
调用 udstate_ppp() 时间更新,注意时间更新在迭代计算之前。
-
for 循环迭代进行,最多迭代 8 次,超出迭代次数输出错误信息。
- 调用 ppp_res() 计算残差 V、设计矩阵 H。
- 调用 filter() EKF 估计。
- 调用 ppp_res() 计算后验残差,符合限制则输出为精密单点定位状态
-
如果 PPP 解算成功,调用 update_stat() 保存结果。
-
free() 释放开辟的矩阵。
- 调用 sunmoonpos() 计算太阳 ECEF 坐标 rsun,调用 normv3() 单位向量 esun
- 遍历观测值,
- 先把 azel 全赋值 0。
- 如果有静态 PPP 参考坐标,赋值 rr[i],否则用状态向量 rtk->x 或者结果 rtk->sol.rr 赋值 rr[i]。
- 遍历当前历元每颗卫星:
- 调用 geodist() 计算改正了 sagnac 效应的近似距离、单位视线向量 e。
- 调用 satazel() 计算方位角高度角到 azel。
extern void calElev(rtk_t *rtk, const obsd_t *obs, int n, double *rs)
{
int i,sat;
double rr[3]={0},pos[3],r,e[3];
// 先把 azel 全赋值 0
for (i=0;i<MAXSAT;i++)
rtk->ssat[i].azel[1]=0.0;
// 如果有静态 PPP 参考坐标,赋值 rr[i]
if ( 0.0!=PPP_Glo.crdTrue[0] ) {
for (i=0;i<3;i++)
rr[i]=PPP_Glo.crdTrue[i];
}
// 否则用状态向量 rtk->x 或者结果 rtk->sol.rr 赋值 rr[i]
else {
for (i=0;i<3;i++)
rr[i]=rtk->x[i];
if (rr[0]==0.0) {
for (i=0;i<3;i++)
rr[i]=rtk->sol.rr[i];
}
}
if (norm(rr,3)<=100.0) return ;
ecef2pos(rr,pos);
// 遍历当前历元每颗卫星
// 调用 geodist() 计算改正了 sagnac 效应的近似距离、单位视线向量 e
// 调用 satazel() 计算方位角高度角到 azel
for (i=0;i<n&&i<MAXOBS;i++) {
sat=obs[i].sat;
if (!PPP_Glo.sFlag[sat-1].sys) continue;
/* geometric distance/azimuth/elevation angle */
if ((r=geodist(rs+i*6,rr,e))<0) continue;
satazel(pos,e,rtk->ssat[sat-1].azel);
}
}周跳的探测与修复就是运用一定的方法探测出在何时发生了整周跳变,并求出丢失的整周数,然后将中断后的整周计数恢复为正确的计数,使这部分观测值正常使用。
- 在 GNSS 测量中,接收机开机时,观测载波相位的小数部分,并初始化整周计数。连续跟踪的情况下,小数部分的相位从
$2\pi$ 变成0时计数器加1。 - 因此,在某一给定的历元下,观测的累积相位
$\Delta_\phi$ 等于相位整周计数N加上小数部分。整周数 N 被认为是一个未知数。在接收载波信号过程中不发生失锁的倩况下,整周数 N 就一直保持某一固定值。 - 当累积相位出现整周数的跳变时,整周计数就要重新进行初始化。由于卫星信号受到阻挡等原因而导致卫星信号失锁,当某个历元载波信号重新被接收到后,计数器整周计数丢失,整周数发生错误,但小数部分仍然是正确的,这就是周跳现象。
- 引起整周计数中断原因主要有:
- 信号遮挡,特别是基于载波相位的动态定位。
- 低信噪比,如恶劣的电离层条件、多路径效应、接收机的高速运动或者卫星高度角过低。
- 接收机软件问题、卫星振荡器故障。
- 观测数据中大于10 周的周跳,在数据预处理时不难发现,可W消除。而对于小于10周的周跳,特别是 1-5 周的周跳,以及半周跳和 1/4 周跳不易发现,而对含有周跳的观测值,周跳的影响视为观测的偶然误差,因而严重影响测量的精度。
- 即使只有一颗卫星存在一个周跳,也会对测点产生几厘米的误差。一个点位坐标是由4颗上卫星所确定的,故周跳对点位坐标的影响取决于卫星数、几何结构、周跳影响各分量的大小和周跳次数。
- 凡精度要求达到厘米级或分米级的 GNSS 测量,都必须将观测数据中的周跳全部清除。
- 载波相位观测量的时间序列,表现出来的是一条随时间变化的光滑曲线,因为整周模糊度不随时间变化,一旦出现周跳,这种光滑性就被破坏,而且自该历元起,后继历元相位观测值序列均发生等量阶跃。
- 判读周跳实质上就是探测观测序列是否发生阶跃突变,在探测之前最好能尽量消除观测序列中的各项误差项,使得观测序列能准确反映出周跳的变化。
- 由载波相位的观测方程可知,在方程中随时间变化的项主要有接收机至卫星间的几何距离、接收机和卫星的钟差以及及大气层延迟等三项。对GNSS观测值进行适当的組合,将上面三项中的大部分误差消除,即可构成周跳检测量。
- 范围为 0-7,对应二进制数 000-111;有三个位,其中 bit0、bit1 仅用于相位
- 0 或空格:正常或未知
- Bit0:先前与当前观测值之间失锁,可能发生了周跳(只针对相位观测值)
- Bit1:接收机进行半周模糊度解算,或程序不能处理半周数据而跳过该观测值的记录(只对当前历元有效)
- Bit2:bit 2 置 1 表示为反欺骗(AS)下的观测值(可能会受到噪声增加的影响)
- 理论上只要板卡足够好,它自身的LLI标志就能把载波数据的周跳、半周跳告知你,就不需要其他探测方法了。LLI 的是从信道方面探测周跳的,效果应该比我们从数据方法探测周跳更灵敏。
- 有的板卡或许 LLI 探测太灵敏了,把没有问题的数据也当作周跳进行标志,可能会导致观测数据不足,故有时会把 LLI 周跳探测方法关闭(GAMP 中就是如此)。
GAMP 中联合使用 Geometry-free (GF) 和 MW 组合观测值进行周跳探测,其充分利用了双频观测值线性组合的特点。GF 和 MW 组合观测值分别为:
$$
\begin{array}{c}
L_{\mathrm{GF}}(i)=\lambda_{1} \Phi_{1}(i)-\lambda_{2} \Phi_{2}(i)=\left(\gamma_{2}-1\right) I_{1}(i)+\left(\lambda_{1} N_{1}-\lambda_{2} N_{2}\right) \
\left{\begin{array}{l}
\lambda_{\delta} \Phi_{\delta}(i)=\left(f_{1} \lambda_{1} \Phi_{1}(i)-f_{2} \lambda_{2} \Phi_{2}(i)\right) /\left(f_{1}-f_{2}\right)=\rho(i)+f_{1} f_{2} /\left(f_{1}^{2}-f_{2}^{2}\right) \cdot I_{1}(i)+\lambda_{\delta} N_{\delta} \
P_{\delta}(i)=\left(f_{1} P_{1}(i)+f_{2} P_{2}(i)\right) /\left(f_{1}+f_{2}\right)=\rho(i)+f_{1} f_{2} /\left(f_{1}^{2}-f_{2}^{2}\right) \cdot I_{1}(i) \
N_{\delta}=N_{1}-N_{2}=\Phi_{\delta}(i)-P_{\delta}(i) / \lambda_{\delta} \
\lambda_{\delta}=c /\left(f_{1}-f_{2}\right)
\end{array}\right.
\end{array}
$$
式中,$i$ 表示观测历元号;$\lambda_{\delta}$ 和
extern int calCsThres(prcopt_t *opt, const double sample)
{
int b=0;
if (sample>0.0) {
if (PPP_Glo.prcOpt_Ex.bUsed_gfCs==1&&fabs(PPP_Glo.prcOpt_Ex.csThresGF)<0.01) {
if (sample<=1.0) PPP_Glo.prcOpt_Ex.csThresGF=0.05;
else if (sample<=20.0) PPP_Glo.prcOpt_Ex.csThresGF=(0.10)/(20.0-0.0)*sample+0.05;
else if (sample<=60.0) PPP_Glo.prcOpt_Ex.csThresGF=0.15;
else if (sample<=100.0) PPP_Glo.prcOpt_Ex.csThresGF=0.25;
else PPP_Glo.prcOpt_Ex.csThresGF=0.35;
b=1;
}
if (PPP_Glo.prcOpt_Ex.bUsed_mwCs==1&&fabs(PPP_Glo.prcOpt_Ex.csThresMW)<0.01) {
if (sample<=1.0) PPP_Glo.prcOpt_Ex.csThresMW=2.5;
else if (sample<=20.0) PPP_Glo.prcOpt_Ex.csThresMW=(2.5)/(20.0-0.0)*sample+2.5;
else if (sample<=60.0) PPP_Glo.prcOpt_Ex.csThresMW=5.0;
else PPP_Glo.prcOpt_Ex.csThresMW=7.5;
b=1;
}
return b;
}
else {
//sample<=0.0
PPP_Glo.prcOpt_Ex.csThresGF=0.15;
PPP_Glo.prcOpt_Ex.csThresMW=5.0;
b=0;
}
return b;
}- 先后调用 detslp_mw()、detslp_gf() 进行周跳检测
-
存下当前历元时间字符串 str,用于 Trace 输出。
-
遍历当前历元卫星,初始化 azel;如果是反向滤波,resc_pri、resp_pri 设为 0;如果是正向滤波,resc_pos、resp_pos 设为 0。
-
rr 设为传入的接收机 ECEF 坐标 x,如果 rr 过小,说明取值有误,return。
-
调用 tidedisp() 算出潮汐改正量 dr,加到接收机 ECEF 坐标 rr 上。
-
用潮汐改正后的测站 ECEF 准备计算测站纬经高 pos。
-
接下来是两层 for 循环:外层遍历卫星,索引为 n;内层遍历伪距载波观测值,索引为 j。 *
-
如果是 GLONASS,
时间更新函数对理解 PPP 模型至关重要,PPP 的核心是参数估计,
而且初始协方差也在此函数中设置。
- udpos_ppp():位置参数时间更新,
- udclk_ppp():钟差、ISB 参数时间更新,
- udtrop_ppp():对流层参数时间更新,
- udiono_ppp():电离层参数时间更新,
- uddcb_ppp():DCB 参数时间更新,
- udbias_ppp():模糊度参数时间更新,
下面将对这些函数做具体介绍。
GAMP 只支持三种定位模式:SPP、static PPP、kinematic PPP;PPP 只有静态和动态两种,只估计位置,不估计速度、加速度。
- 如果是 PPP 固定解模式:直接用已知点的固定坐标初始化,给一个极小的协方差 1E-8。
- 如果是首历元:赋值单点定位的解,设协方差 VAR_POS ((60.0)*(60.0))。
- 如果是 静态 PPP 模式:状态量不变,P 矩阵也不加过程噪声。
- 如果是 动态 PPP 模式:状态量不变,设固定协方差 VAR_POS ((60.0)*(60.0))。
static void udpos_ppp(rtk_t *rtk)
{
int i;
// GAMP 只支持三种定位模式:SPP、static PPP、kinematic PPP
// 如果是 PPP 固定解模式,直接用已知点的固定坐标初始化,给一个极小的协方差 1E-8
/* fixed mode */
if (rtk->opt.mode==PMODE_PPP_FIXED) {
for (i=0;i<3;i++) initx(rtk,rtk->opt.ru[i],1E-8,i);
return;
}
// 如果是首历元,赋值单点定位的解,设协方差 VAR_POS ((60.0)*(60.0))
/* initialize position for first epoch */
if (norm(rtk->x,3)<=0.0) {
for (i=0;i<3;i++) initx(rtk,rtk->sol.rr[i],VAR_POS,i);
}
// 如果是 PMODE_PPP_STATIC 模式,状态量不变,P 矩阵也不加过程噪声
/* static ppp mode */
if (rtk->opt.mode==PMODE_PPP_STATIC) {
/*for (i=0;i<3;i++) {
rtk->P[i*(1+rtk->nx)]+=SQR(rtk->opt.prn[5])*fabs(rtk->tt);
}*/
return;
}
// 动态 PPP 模式,状态量不变,设协方差 VAR_POS ((60.0)*(60.0))
/* kinmatic mode without dynamics */
for (i=0;i<3;i++) {
initx(rtk,rtk->sol.rr[i],VAR_POS,i);
}
}相关的配置选项有很多,
- 获取对流层参数下标 i、历元间时间间隔 tt
- 如果对流层状态量为 0,相当于要给协方差赋初值:
- 用 0.15、0.3*0.3 初始化天顶方向对流层延迟。
- 如果是 ROPOPT_ESTG 对流层梯度估计模式:用 1E-6、VAR_GRA 初始化东向、北向的对流层梯度系数。
- 对流层状态量不为 0,就是加过程噪声:
- 增加过程噪声
SQR(rtk->opt.prn[2])*fabs(tt),就是设置的对流层过程噪声标准差取平方得到方差,再乘以历元间时间间隔 tt。 - 如果是 ROPOPT_ESTG 对流层梯度估计模式:给东向、北向的对流层梯度系数加过程噪声
SQR(rtk->opt.prn[2]*0.1)*tt,就是设置的对流层过程噪声标准差的十分之一取平方得到方差,再乘以历元间时间间隔 tt。
- 增加过程噪声
static void udtrop_ppp(rtk_t *rtk)
{
// 获取对流层参数下标 i、历元间时间间隔 tt
double var,tt=fabs(rtk->tt);
int i=IT(&rtk->opt),j;
// 如果对流层状态量为 0,相当于要给协方差赋初值
if (rtk->x[i]==0.0) {
var=SQR(0.3);
// 用 0.15、0.3*0.3 初始化天顶方向对流层延迟
initx(rtk,0.15,var,i);
// TROPOPT_ESTG 模式,用 1E-6、VAR_GRA 初始化东向、北向的对流层梯度系数
if (rtk->opt.tropopt>=TROPOPT_ESTG) {
for (j=i+1;j<i+3;j++) initx(rtk,1E-6,VAR_GRA,j);
}
}
// 对流层状态量不为 0,就是加过程噪声
else {
// 增加过程噪声 SQR(rtk->opt.prn[2])*fabs(tt)
// 设置的对流层过程噪声标准差取平方得到方差,再乘以历元间时间间隔 tt
rtk->P[i+i*rtk->nx]+=SQR(rtk->opt.prn[2])*tt;
// TROPOPT_ESTG 模式,给东向、北向的对流层梯度系数加过程噪声 SQR(rtk->opt.prn[2]*0.1)*tt
if (rtk->opt.tropopt>=TROPOPT_ESTG) {
for (j=i+1;j<i+3;j++) {
// 设置的对流层过程噪声标准差的十分之一取平方得到方差,再乘以历元间时间间隔 tt
rtk->P[j+j*rtk->nx]+=SQR(rtk->opt.prn[2]*0.1)*tt;
}
}
}
}与电离层参数相关的选项有 ionoopt、ionopnoise、ionoconstraint。当 ionoopt 选 3 单频估计和 4 双频估计时才会进入这个函数。
-
ionoopt:电离层处理选项:0 不处理、1 广播星历克罗布歇模型、2 消电离层、3 单频估计、4 双频估计、5 电离层格网模型。
-
ionopnoise:估计电离层随机模型:0 静态、1 随机游走、2 新随机游走、3 白噪声。
- 静态:
- 随机游走:
- 新随机游走:
- 白噪声:
-
ionoconstraint:增加电离层的虚拟观测参数及其对观测方程的相应约束:0 关闭、1 打开。
执行流程:
- 遍历每颗卫星,获取电离层参数下标 j,载波中断计数都大于 gap_resion(默认120),重置电离层参数为 0。
static void uddcb_ppp(rtk_t *rtk)
{
int i=ID(&rtk->opt); // 取 DCB 参数下标 i
// 如果 DCB 参数为 0,用 1E-6、VAR_DCB 初始化
if (rtk->x[i]==0.0) {
initx(rtk,1E-6,VAR_DCB,i);
}
}- 判断当前历元是否在日界线上。
- 遍历每个频率:
- 三种情况会重置模糊度,重置为 0,0
- 载波中断计数大于阈值
- 模糊度固定模式为 instantaneous
- 当前历元处于日界线上
- 遍历当前历元卫星,得到各卫星载波伪距偏差与模糊度的差值总和 offset
- 调用 corr_meas() 获取天线改正、DCB 改正后的伪距载波观测值 P、L,消电离层组合后的伪距载波观测值 Pc、Lc
- 如果是消电离层组合用 Lc - Pc 得到载波伪距偏差 bias[i]
- 如果是非差非组合模式
- 如果有周跳、载波伪距偏差为 0、模糊度参数为 0,跳过当前观测值
- 三种情况会重置模糊度,重置为 0,0
抗差 Kalman 滤波通过构造等价权对含有小周跳或粗差的观测值进行控制,降低异常观测值对于参数估计的影响。本文使用 IGGIII 等价权函数: $$ \bar{p}{i}=\left{\begin{array}{cc} p{i}, & \left|\tilde{v}{i}\right| \leq k{0} \ p_{i} \frac{k_{0}}{\left|\tilde{v}{i}\right|}\left(\frac{k{1}-\left|\tilde{v}{i}\right|}{k{1}-k_{0}}\right)^{2}, & k_{0}<\left|\tilde{v}{i}\right| \leq k{1} \ 0, & \left|\tilde{v}{i}\right|>k{1} \end{array}\right. $$
式中,$p_{i}$ 为观测量
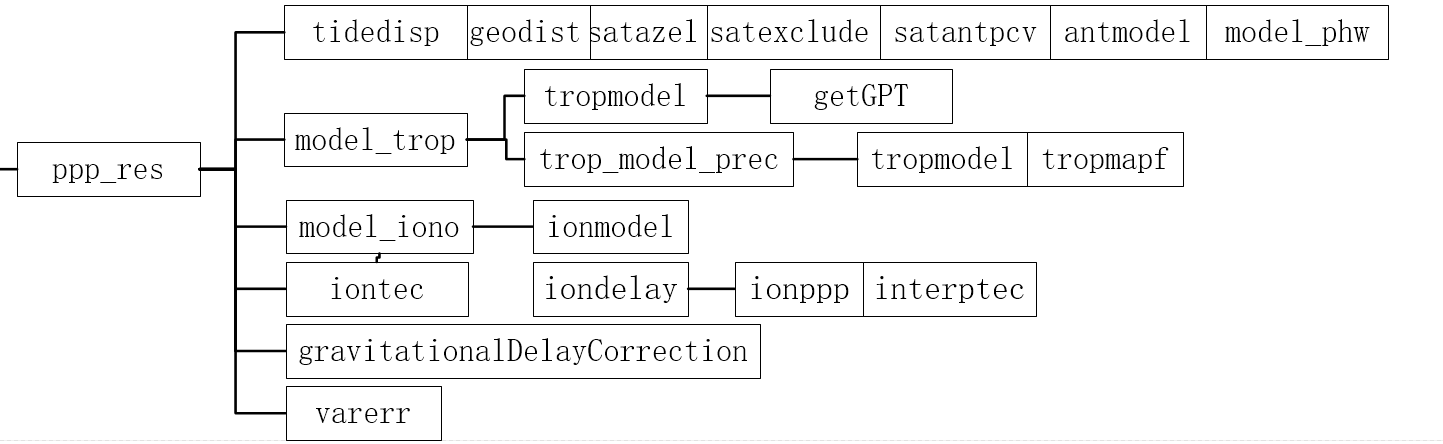
PPP 的核心是参数估计,看一下三个方面:
-
看各个参数的初始值、协方差,在 udstate_ppp() 函数。
-
看各个参数的过程噪声咋加的,什么样的情况会重置参数估计值和对应的协方差,在 udstate_ppp() 函数。
-
看各个参数对应的设计矩阵,在 ppp_res() 函数。