ref https://zhuanlan.zhihu.com/p/388620573
[toc]
VAE可以理解为通过网络学习出每个属性正太分布的mean和std编码,然后通过mean和std和N ( 0,1 )正态分布恢复每个属性的正态分布,最后随机采样得到每个属性的离散值。VAE相对于AutoEncoder的好处是,当采样输入不同时,VAE对于任意采样都能重构出鲁棒的图片。VAE的生成过程是可控的,对输入噪声不敏感,我们可以预先知道每个属性都是服从正态分布的。
VQVAE通过Encoder学习出中间编码,然后通过最邻近搜索将中间编码映射为codebook中K个向量之一,然后通过Decoder对latent code进行重建。另外由于最邻近搜索使用argmax来找codebook中的索引位置,导致不可导问题,VQVAE通过stop gradient操作来避免最邻近搜索的不可导问题,也就是通过stop gradient操作,将decoder输入的梯度复制到encoder的输出上。
什么是 Vector Quantization
计算机智能处理离散的数字信号,所以在将模拟信号转换为数字信号时,可以用区间内的某一个值去代替一个区间,比如:[0, 1]上的值全变为0,[1,2]上的值全变为1。这样VQ就将一个向量空间中的点用其中一个有限子集来进行编码的过程。
【这样其实实现的是一种压缩的效果】
找到最接近的VQ table 上的 z
几个问题?
如何保证生成的多样性呢?
是为了学到一个离散的隐空间
Neural Discrete Representation Learning
Aaron van den Oord, Oriol Vinyals, Koray Kavukcuoglu
[NeurIPS 2017] (``)
VQ (Vector Quantisation) 指的是
为了解决过去VAE的“后验崩塌” (posterior collapse) 问题,
z空间是由一个codebook(例如m个
CNN输出
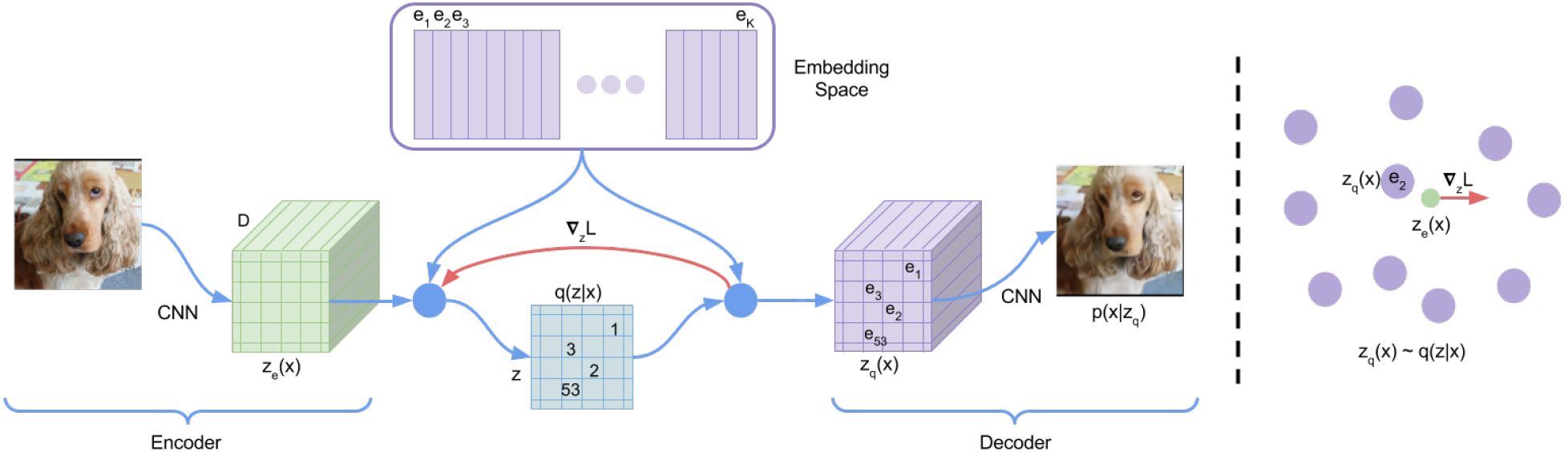
$m \times n$ 个 D 维向量 (用z表示),codebook 是$K$ 个 D 维向量 (用e表示)。然后通过算法找到这$m \times n$ 个最接近的 e,图中用数字标注出来了对应关系。总共有$K^{(m\times n)}$ 种组合方式,也就是可以重建出$K^{(m\times n)}$ 个不同的图像局部结果。
$$ z_{q}(x)=e_{k}, \quad \text { where } \quad k=\operatorname{argmin}{j}\left|z{e}(x)-e_{j}\right|_{2} $$
损失函数 $$ L=\log p\left(x \mid z_{q}(x)\right)+\left|\operatorname{sg}\left[z_{e}(x)\right]-e\right|{2}^{2}+\beta\left|z{e}(x)-\operatorname{sg}[e]\right|_{2}^{2} $$
第一项是autoencoder的重建loss;第二项是codebook loss,sg 表示 stop gradient,也就是不计算这一项的梯度,这个loss只更新codebook,也就是希望e趋向于encoder出来的z;commitment loss,跟第二个loss恰恰相反,这就体现了一种交替更新的思想。
第二项loss是不连续的: $$ \sum_j^{n_i} |z_{i,j} - e_i| \ e_i = \frac{1}{n_i} \sum_j^{n_i} z_{i,j} \ $$ 当使用minibatches训练时,由于数据量不足,这么更新是不准确的,因此使用指数滑动平均来更新 e_i
但在训练第一个step时,由于数据不足,n_i可能为0,怎么会产生nan,因此要引入拉普拉斯平滑
$$
n_i = \frac{n_i + \epsilon}{N + K\epsilon} \cdot N
$$
在训练过程中,隐向量满足均匀分布。训练完成后,可以重新学习一个分布来生成有意义的结果。也就是说codebook是杂乱的,你怎么选择一个序列出来生成呢。训练一个自回归模型,一个接一个的来生成z,这样最后的
他的好处是:
Generating Diverse High-Fidelity Images with VQ-VAE-2
Ali Razavi, Aaron van den Oord, Oriol Vinyals
[arXiv 2019] (``)
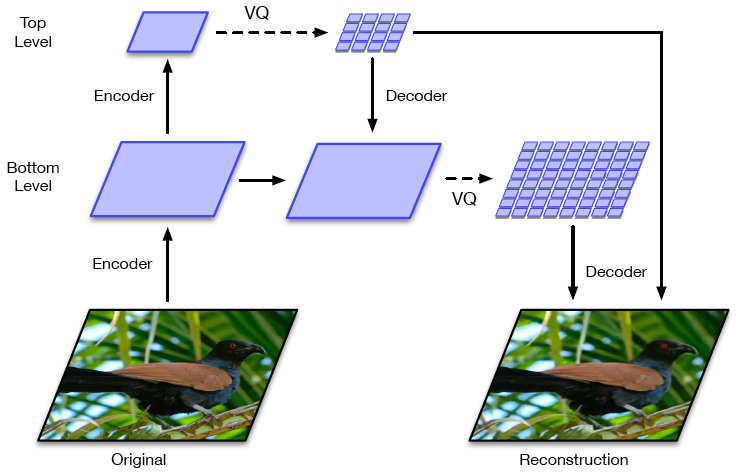
Hierarchical-VQ-VAE,把隐空间分成两个,一个上层隐空间,一个下层隐空间。上层隐空间表示全局信息,下层隐空间表示局部信息。