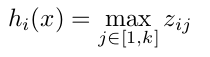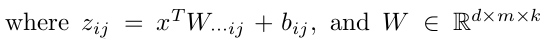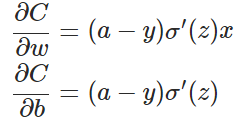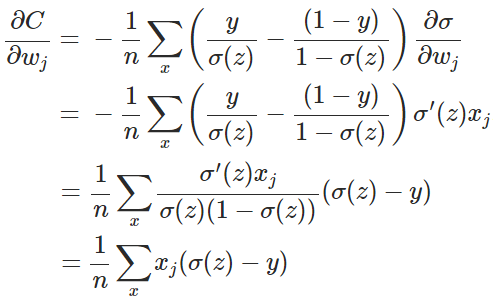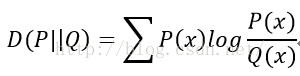- 均值和方差都是在wx+b计算得到的z上求得的
- 不能在batch小的情况下使用
- BN使用的一般位置是在wx+b之后,激活函数之前
- 测试阶段记录之前数据集中全部batch的均值方差,使用均值和方差的期望作为测试时的均值和方差,其中var是无偏估计
- 当
$(\mu,\delta)$与$ (\gamma,\beta)$对应相等的时候,那么BN就相当于没有做 当$(\mu,\delta)$与$ (\gamma,\beta)$不等的时候,就是BN起作用的时候了
- 优点
- 加速收敛
- 缓解梯度消失梯度爆炸
- 可以使用更大的学习率
- 避免overfit,可以降低正则项权重和丢弃dropout
https://blog.csdn.net/lanran2/article/details/79057994 https://blog.csdn.net/shwan_ma/article/details/78203020
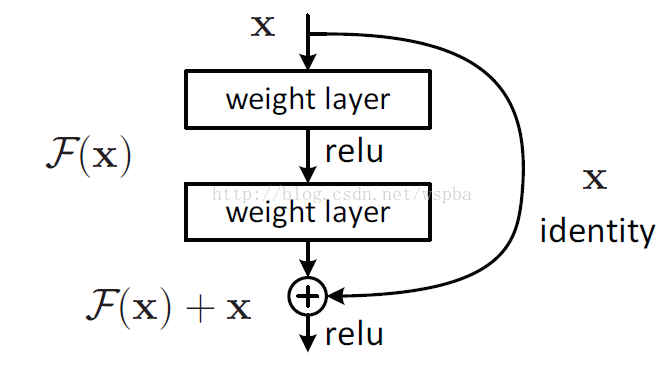
- 解决的问题:不是梯度消失,而是网络退化(degradation)
网咯加深,效果应该不差于浅层网络,实际并不是 说明网络拟合恒等映射也很困难。 如下图,可以看出拟合输入输出之间残差,拟合难度就会降低。
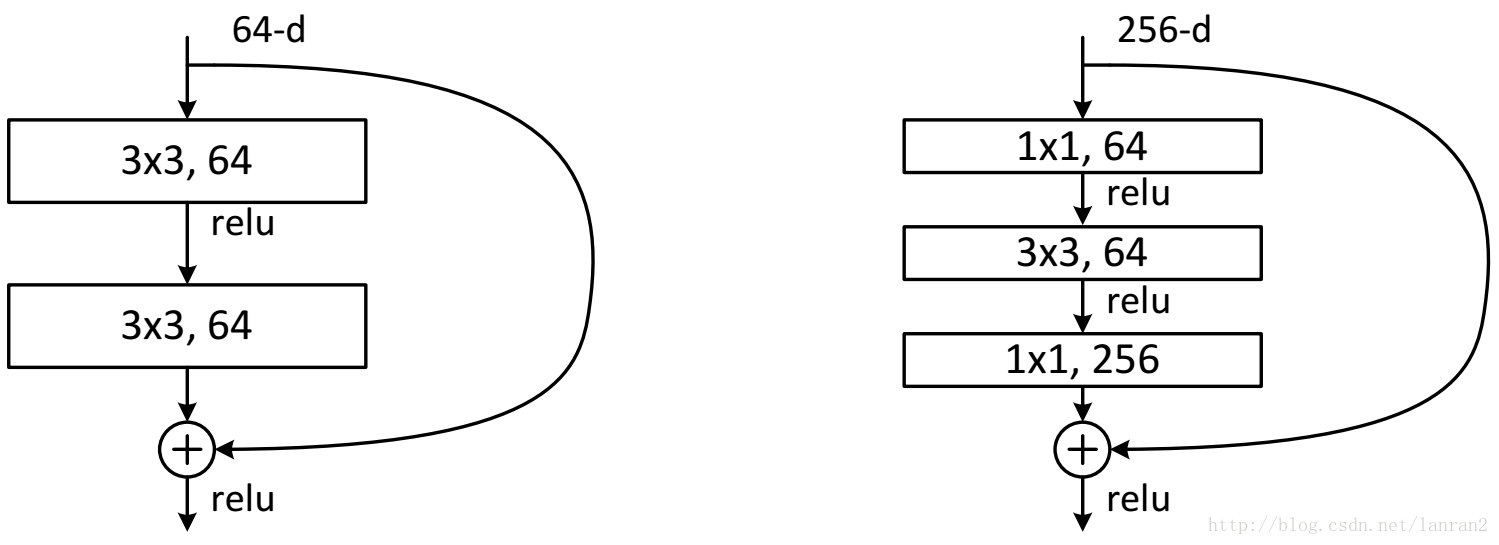
- 两种结构:左边是basic结构,resnet18和34采用,后面resnte50,101,152使用右边的bottlecnk结构,减少参数和运算量。
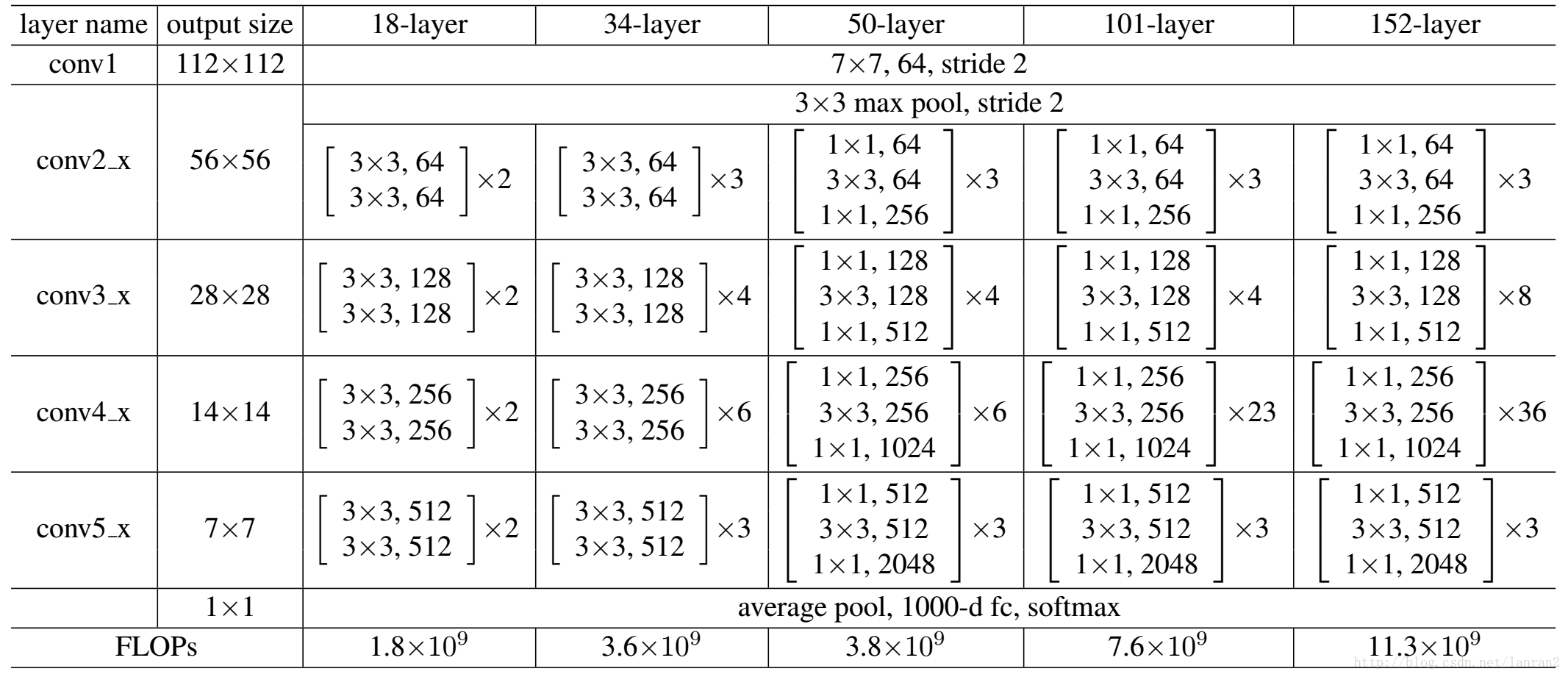
- 网络结构
- 注意:
- resnet第一层使用7*7大卷积核卷积,后面则使用3*3卷积核
- 无全连接层,直接7*7平均池化
- block层间无pooling结构,每个block的首层使用stride=2实现降采样,四个block依次减半。变化为224->112(conv1)->56(max pool)->28(block2)->14(block3)->7(block4)->1(avg_pool)
- 图像通道变化3->64->64->128->256->512
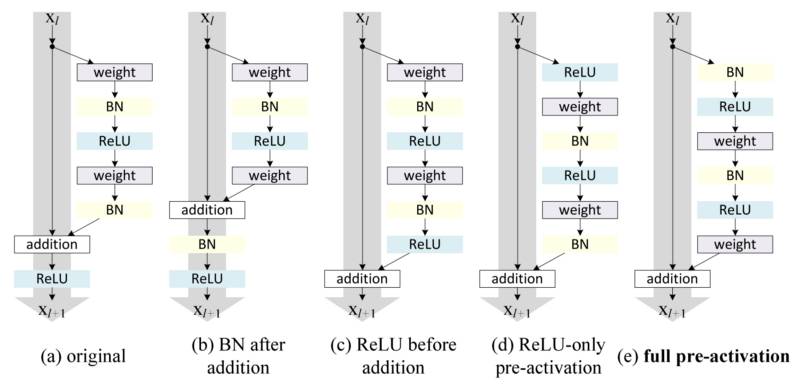
- 变体:
- preact-resnet:在激活之后加残差,使得block真正拟合的是残差。
- resnetXt: 加入googlenet的思路,网络变宽了
- denseNet: 之前的若干层也连接起来,不加和,而是使用concat
- Early stop:在模型训练过程中,提前终止
- Data expending:用更多的数据集,或者对原始数据做数据扩张,进行图像随机变换
- 正则:L1 L2正则,pytorch中叫weight decay,一般去e-4数量级
- Droup Out:以一定的概率使某些神经元停止工作,可以从ensemble的角度来看,一般取0.5
- BatchNorm
- sigmoid
$f(x)=1/1+exp(-x)$,求导$f'(x) = f(x)(1-f(x))$- 取值0-1之间,有梯度饱和区
- 不是0均值的
- 目的:降输出压缩到0-1之间== ==
- tanh
$f(x)=exp(x)-exp(-x)/exp(x)+exp(-x)$- -1-1之间,梯度饱和区
- 是0均值的
- relu
$f(x)=max(0, x)$- 无饱和区 不易产生梯度消失
- 训练小于0后会dead
- Leaky ReLU
$f(x)=max(x, alpha * x)$- alpha取值在0.01左右
- 防止dead发生
- prelu
$f(x)=max(x, alpha * x)$- alpha是一个参数加入训练
- Maxout==:==
https://blog.csdn.net/garfielder007/article/details/50581021
参数增加了k倍,因为是在k组参数中选出最大的一组
https://www.jianshu.com/p/244c7340984e
col2img
多个卷积核只需要把卷积核按行排列,矩阵乘法就可以得到所有的feature map
-
交叉熵
用于分类问题
$z_i = \sum_j{w_{ij} x_{ij} + b}$$a_i = \frac{e^{z_i}}{\sum_k{e^{z_k}}}$$C = -\sum_i{y_i \ln {a_i}}$与softmax的关系
当cross entropy的输入P是softmax的输出时,cross entropy等于softmax loss https://blog.csdn.net/u014380165/article/details/77284921
优点:
加大对预测错误的惩罚,相对于直接normalize
缓解梯度消失现象
加快收敛,错误越大,loss下降越快
-
平方误差
-
KL散度
不对称性 非负性
- center loss
- constrc loss
- L-softmax
- angloe loss
- AM loss
input是H*W*C, 卷积输出是H*W*D, 卷积核尺寸大小K*K,卷积参数为
降低卷积参数量的操作
1*1卷积
depth-wise卷积
- squeeze net
- mobile net
- mobile net v2
- shuffle net
- RNN
- 简单解释
https://zhuanlan.zhihu.com/p/28871960
前馈神经网络(包括全连接层、卷积层等)可以表示为 $ F=f_3(f_2(f_1(\mathbf{x}W_1)W_2)W_3) $,那么网络输出对 $W_1 $求偏导 $\frac{\partial{F}}{\partial{W_1}}=\mathbf{x}*f'_1*W_2*f'_2*W_3*f'_3 $,这里 $W_1,W_2,W_3$是相互独立的,一般不会有数值问题,主要问题在于激活函数的导数 f'在饱和区接近于零,导致梯度消失。
循环神经网络的状态循环部分可以表示为 $\mathbf{h}_3=f_3(f_2(f_1(\mathbf{h}_0W)W)W)$,这里的问题不仅在于激活函数的导数,还有 W 在不同时刻是共享的,网络输出对 W 的偏导包含 W 的连乘项,稍有不慎( W值偏小或偏大)就会出现梯度消失或爆炸。
- 复杂解释加数学推导
https://zhuanlan.zhihu.com/p/33594517
https://www.cnblogs.com/rongyux/p/6715235.html
https://www.cnblogs.com/pinard/p/6509630.html
https://zhuanlan.zhihu.com/p/26892413
BPTT主要更新的参数有三个,跟别是U,W,V
其中V是输出权重,比较好求,类似于标准BP
难点在于U和W的更新
- 方向1,沿时间方向反向传播,与w有关
- 方向2,沿输入传播,与U有关,类似于普通bp
- 各个时间步的梯度求和,更新权重
目标是求这两个东西
其中第二项是好求的,就看第一项怎么求。
具体展开求解参考第一个链接的内容
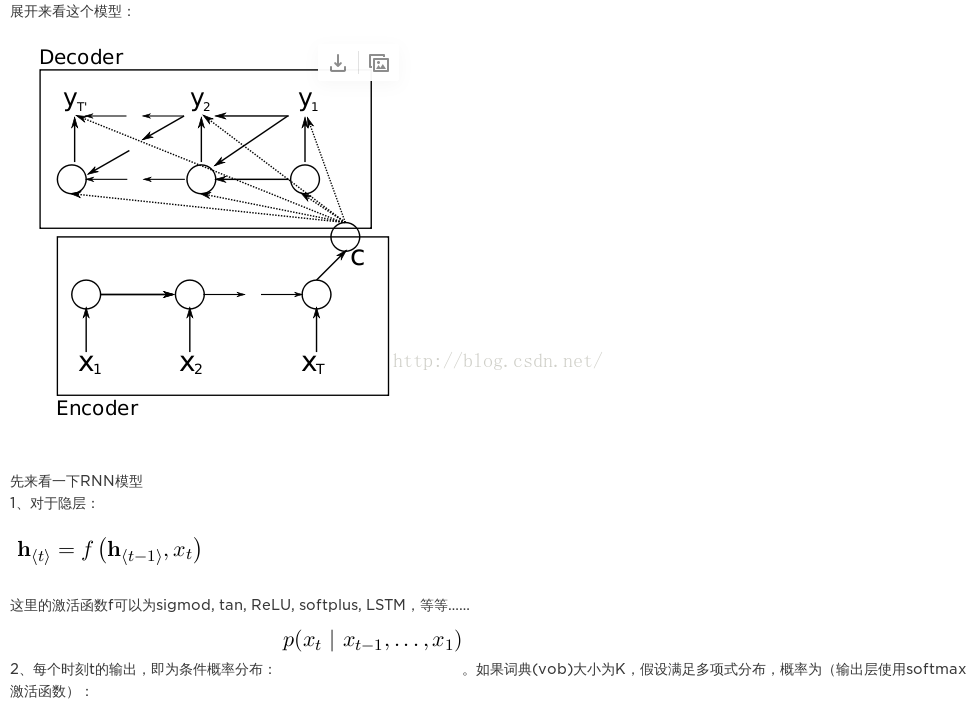
- seq2seq
- 四种解码模型,包括attention机制
http://jacoxu.com/encoder_decoder/
- attention机制
我的博客解析了pytorch的 toy 代码
https://zhuanlan.zhihu.com/p/35955689
- sgd
- bgd
- mini batch sgd
- adam
- RMSrop
- adadelta
- 旋转
- 水平垂直翻转
- jittering
- 随机crop
- 中心crop
- 缩放
- 加噪声
- RCNN
- fast RCNN
- faster RCNN
- SPP net
- YOLO
- SSD
- vgg
- google net
- inception v1-v4
- resnet
- ZF net
- SE net