隐藏博客
+ + + ++
2022级推免基本告一段落,刚开始夏令营的时候其实还没有什么疫情,但是各大高校仍然基本选择了线上夏令营,因此造成了夏令营非常非常卷。我本人将比我们学校好的985基本全部报了一遍,总共报了20多个,最后入营的非常少。不幸中的万幸我以为根本不可能考虑我的中科院计算所在我没入营没联系老师的情况下仍然打电话叫我过去考试,最终拿到了offer。计算所offer确认的时间比较早,是9月10日,而经过夏令营入营惨痛的经历,我决定就不参加预推免了。
+ +南京大学今年养了一个大鱼塘,就拿我们专业来说,65人的小专业前三名都通过了南大的初审。当时接到了南大的邮件激动坏了,然而南大先搞了一波笔试。。。
+我实在是太菜了,有一半的题里面的名词都没听说过。。。所以就挂了,也没有然后了。
+面试后就结束了,几周后公布了优营名单,一共三四百入营的,优营给了不到二百个,承诺优营一定录取。
+北航最后拿到了候补,一共500个入营的,过了机试有400左右,优营给了110多个,候补给了100个。不过整个夏令营的阶段都没有北航的同学参与,而看去年的录取名单基本都是北航的。。不知道是什么原因
+入营有五百左右,给了三百的优营,要自己联系老师,8月底联系不到的认为放弃优营资格。
+入营只有200左右,大多数给了优营,但是是唯一一个没有后续的学校,没人说过优营有什么用接下来干什么。。。
+吐槽吐槽!!!!中山真的是太烦人了,就算过了也真心不想去。
+入营资格要一个一个电话确认,还没开始夏令营就开了三场会,一个面试环境检查会,一个笔试环境检查会,一个面试分组抽签会。更为奇葩的双机位要求:两个机位互相能看见,次机位看清电脑屏幕,主机位能看到脑袋+肩膀且能看到双手???你来教教我咋能主机位看到双手???我双手举起来编程吗???更为奇葩的机试监考,要共享屏幕到腾讯会议中。好家伙总共五百多人参加机试你找了五百多个研究生坐五百多个电脑前面开五百多个腾讯会议盯着我们???面试环境检查会都已经查看完了承诺书,正式面试还要再看一遍???程序无比繁琐,而且充斥着学校对学生的满满的不信任感!
五百多人给了300优营和100候补,还承诺优营一定录取,还说不搞预推免了。祝愿中山被鸽穿!
+中科院计算所本来是没有入营的(意料之中),看QQ群里面的报名号有六千多人报名,入营名单发了400多。但是实验室秘书有一天早上打电话过来希望我能去北京参加机试面试,难得的机会就过去了。在报名后和入营名单公布之前会在QQ群里面让选意向导师,实际上就是意向实验室,才会有实验室秘书联系你,所以要多关注群消息。
+面试结束当天晚上就打来了电话并发送了拟录取的邮件。一个月后在官网公布了拟录取的名单,入营的优营与没入营的优营(比如我)各占一半,总共给了200优营,承诺一定录取。其中查了一下,网数实验室面试38进12。
+理论上的防疫政策:低风险地区提前三天向酒店等报备,第一天和第三天两次核酸。
+实际:基本只看“青岛一码通”的绿码和7天内核酸阴性报告(有的地方可能要48小时核酸阴性报告)
+具体措施:
+| 日期 | +计划 | +备注 | +
|---|---|---|
| Day0 | +晚上到达青岛,做核酸、住酒店 | +可以去旁边的丽达生活超市买一些水和吃的 | +
| Day1上午 | +信号山公园、栈桥 | ++ |
| Day1中午 | +王姐烧烤午餐 | ++ |
| Day1下午 | +小青岛公园、鲁迅公园、小鱼山公园、青岛第一海水浴场、八大关风景区 | ++ |
| Day1晚上 | +台东步行街小吃晚餐、回酒店 | +可以去大商场买一点点吃的和水果等 | +
| Day2上午 | +小麦岛公园 | ++ |
| Day2中午 | +船歌鱼水饺午餐 | ++ |
| Day2下午 | +燕儿岛公园、奥帆中心、情人坝、五四广场、海天云上艺术中心 | +看天气,太热了就先去海天云上艺术中心 | +
| Day2晚上 | +探海岛海鲜自助(探鲜岛海鲜自助餐厅)晚餐、栈桥附近的夜景、回酒店 | ++ |
| Day3上午 | +去崂山风景区 | ++ |
| Day3中午 | +吃一些提前买的面包等,景区内应该也有一些吃的 | ++ |
| Day3下午 | +崂山风景区、回市区 | ++ |
| Day3晚上 | +前海沿晚餐、回酒店 | ++ |
| Day4 | +返程 | ++ |
备注:
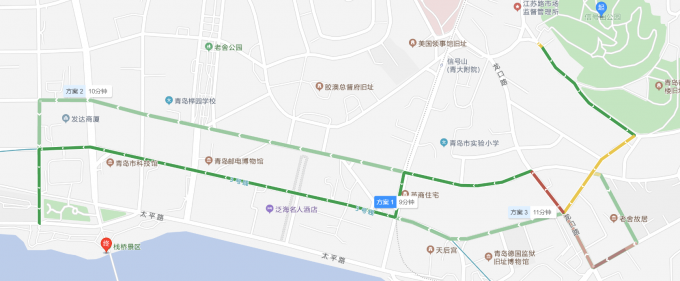
+交通方式:酒店——信号山公园,公交前往,37分钟,步行680米
+ + +预约:已经预约好 7月24日 6:00-20:30,包括收费5元的旋转观景楼
+时间:1个小时左右
+简介:信号山公园位于青岛市中心,因曾在山顶建有为船只引航的信号台而得名。信号山海拔98米,山顶三幢红顶蘑菇楼尤为显眼,其中较高的一幢是旋转观景楼,在这里你可以360度俯看青岛“红瓦绿树,碧海蓝天”的景色。进入景区大门,南坡上有踏浪观景台,就在连心桥下面一点,是拍摄南边德国古堡式建筑迎宾馆的好位置。连心桥上一把把红色爱心造型的锁挂在绿色栏杆上,情侣们可以在此买一把同心锁把彼此的山盟海誓锁在信号山上,据说手拉手走过连心桥可以得到祝福,单身的话自个儿的左手拉右手一样很好!再往前,可以看看五龙潭喷泉等景点,周围四条小龙围着中间一条大龙,与信号山又叫五龙山对应,因为山周边有龙江路、龙华路、龙口路、龙山路、伏龙路五条带“龙”字的路而得此别名。最后到达山顶的旋转观景楼,登上楼上观景台观景,一幢幢掩映在绿树中红瓦黄墙的德式建筑令人惊叹。往西南看,近处有绿色钟楼屋顶的基督教堂在一片红屋顶中非常出挑。
+
 +
+交通方式:步行,共3公里左右
+ +预约:小鱼山公园开放时间08:00-17:00,网上找不到预约入口
+时间:2-3小时
+简介:小青岛故称为“琴岛”,是青岛湾内的一座小岛,青岛这个城市的名称就来源于它。小青岛与陆地之间有长长的海堤相接,岛上矗立着德国人建于1898年的灯塔,是青岛的标志之一。小青岛面积很小,岛上绿树成荫,岛的四周礁石环绕,海水清澈、蔚蓝,岛上常能见到来垂钓的游客。坐在礁石上吹吹海风,赤脚踩踩海水,看看四周青岛湾边林立的高楼和红顶的小洋房,仿佛置身于海上花园。每当夕阳西下时景色尤其美,阳光把整个海湾都镀成了金色。小青岛的南侧有一尊姿态优美的琴女雕像,雕像周围是花坛,种植着五颜六色的鲜花。岛的较高处有当年德国人建造的灯塔,整个岛的海拔也不高,才17米,走到灯塔脚下不需要爬多少路。灯塔通体洁白,由大理石构筑,是海上过往船只进出胶州湾的重要航标。每当夜幕降临,灯塔与岛上的灯光倒映在海面上,像一匹飘动的彩绸,形成青岛的一大胜景“琴屿飘灯”,在这里拍摄夜景很不错。鲁迅公园是青岛市内一处对外开放的临海公园,海边有大片的红褐色礁石,景色很特别,常有不少新人在此拍摄婚纱照。沿着海边步道慢慢走、听听海浪拍壁之声,或是走上岩石高处的亭子远眺大海,很是惬意。公园的东部紧邻青岛海底世界,再往东走是第一海水浴场,沿途风光很美。小鱼山公园是青岛佳风景眺望点之一,一是因为它位于市中心,是青岛离海近的一座山,地理位置;二是因为它的海拔仅60米,爬山不累,登到山顶能看到“红瓦绿树,碧海蓝天”具青岛代表性的景色。
+交通方式:步行,毗邻青岛第一海水浴场
+景区图:
+ +预约:无需预约,内部场馆单独售票,营业时间:9:00-17:00;换票时间:9:00-15:00
+时间:2小时
+简介:八大关是青岛市区南部相交错的十几条马路的总称,它们大多取名于我国知名关隘的名称。这里环境清幽,春季有碧桃盛开、夏季有紫薇盛放,秋季可见银杏红枫夹道,还坐落着许多各国风格的别墅,是摄影胜地。在这里,你可以进入欧洲古堡风格的“花石楼”参观、登上楼顶遥望大海,或者外观开国元帅住过的日式洋楼“元帅楼”、流传着唯美爱情故事的丹麦建筑“公主楼”等经典别墅,让你仿佛身处欧洲的某个角落。
+交通方式:地铁,24分钟,步行248m
+ +预约:无需预约
+时间:晚上
+简介:“朝观壁画夜赏灯,购物休闲在台东”,台东步行街是青岛有名的街区,街内有国内外知名的沃尔玛、万达广场、百信鞋业、利群集团、苏宁电器、三联家电、亚泰电器、新华书店、医保城等各类业态的企业245家。步行街两侧的21座楼6万余平方米的墙面为统一彩绘,精心绘制了色彩斑斓、造型生动的大型壁画,形成了独特的彩色画廊,这是大型的手工彩绘一条街。台东三路经过精心的景观设置,夜景迷人。这里还有男士、女士特色广场,营造出优美的购物和休闲环境,使市民在购物消费的同时,还享受着文化特色的盛宴。
+美食推荐(有人排队多的肯定好吃):
+
 +
+交通方式:地铁+公交(打车)(或公交),58分钟,步行1.2公里
+ +预约:无需预约
+时间:1-2小时
+简介:小麦岛公园位于崂山区麦岛路西50米,小麦岛属环形岛屿,有大片平坦宽广的绿化草地,远处就是湛蓝的海水,可在这里眺望到遥远的海岸线,一派海滨美景,非常适宜拍照。
+就在小麦岛公园的公交站旁边,逛后吃午餐。
+重点菜:鲅鱼、墨鱼、三鲜、虾仁水饺,海菜凉粉
+
 +
+交通方式:公交34分钟,步行883米
+ +预约:无需预约
+时间:1-3小时
+简介:燕儿岛山公园位于山东省青岛市南部,处在浮山湾东端,是一个突出海中的岬角。园内环境优美,集生态、景观、文化、健身、休闲等为一体,是市民休闲锻炼、观光游玩的好地方。公园里的海滨栈道是一大亮点,木栈道与阶梯相连,一边是大海,一边是峭壁,峭壁底下鲜花盛开,在这里拍照仿佛置身于美丽的垦丁,有着独特的韵味。登上阶梯高处的平台放眼望去,可以将整个大海纳入眼帘,景色十分迷人。
+交通方式:步行,直线距离2公里左右
+ +预约:无需预约,奥帆中心其他景点待确定
+时间:2-3小时
+简介:青岛奥帆中心景区位于青岛市浮山湾畔,与青岛市标志性景点——五四广场近海相望,总占地面积约45公顷,是2008年北京第29届奥运会奥帆赛和第13届残奥会帆船比赛举办场地,奥帆中心景区依山面海,景色宜人,是全国唯一“国家滨海旅游休闲示范区”。青岛被誉为“帆船之都”,作为最能体现青岛城市特色和展示城市形象的景区,奥帆中心景区内不仅有飞帆渺渺的优雅,有青岛十大旧景代表燕岛秋潮,有青岛新时代景观鸥翔彩虹,更有众多惊险刺激的娱乐体验,是游客来青必看的景点。
+交通方式:公交或地铁,20分钟
+ +预约:已经预约好 7月25日 9:00-20:00,80F+81F联票
+时间:没查到。。。
+简介:海天中心城市观光厅是山东省超高层垂直建筑之上的高空观光平台。在这里,向西可揽胜八大关老城区红瓦绿树,向东承接新城区璀璨繁华,360°俯瞰壮美海景、山景、城景,全方位感受身处"天空之城"的独特体验。其内部设置的透明观景区、沉浸式体验区、多媒体展示区与空中水吧等多个功能空间,将内部游览体验与外部自然景观融为一体。站在369米之上的城市观光厅,可以看尽因海而生、向海而兴的魅力青岛在时间长河中的风貌变迁与发展动线。随着观光者的漫步,不同姿态的青岛都将尽收眼底。
+回青岛站附近吃晚餐,美团可以订座,顺便可以游览栈桥附近的夜景。
+
 +
+交通方式:地铁接公交
+预约:已经预约好 7月26日 6:00-12:00太清,12:01-17:30 华严和仰口
+时间:一天
+路线:大河东检票——第三站下车游览太清宫、太清索道——索道往返——走到垭口乘坐公交618路前往华严(或仰口)——景区游览车到仰口(或华严)——原路返回大河东(或者直接从仰口出去)
+这个位置暂定,美团可以排队
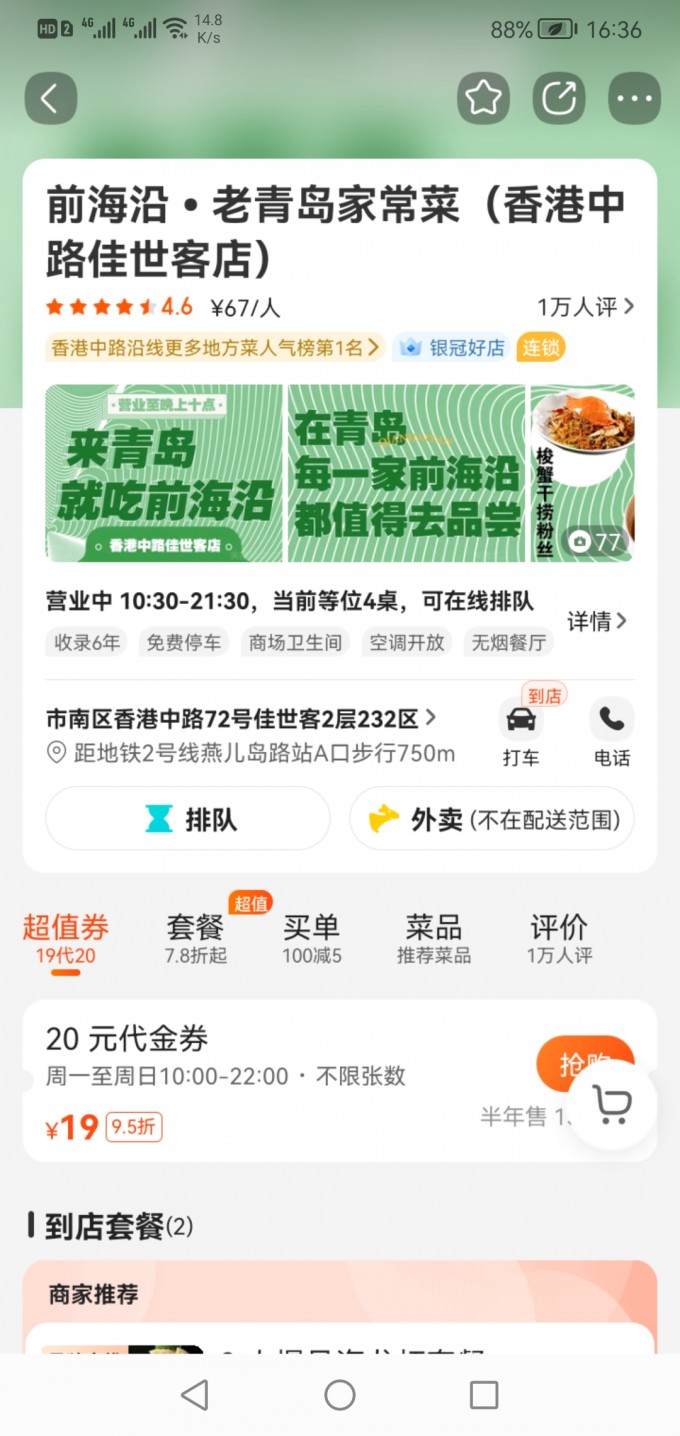
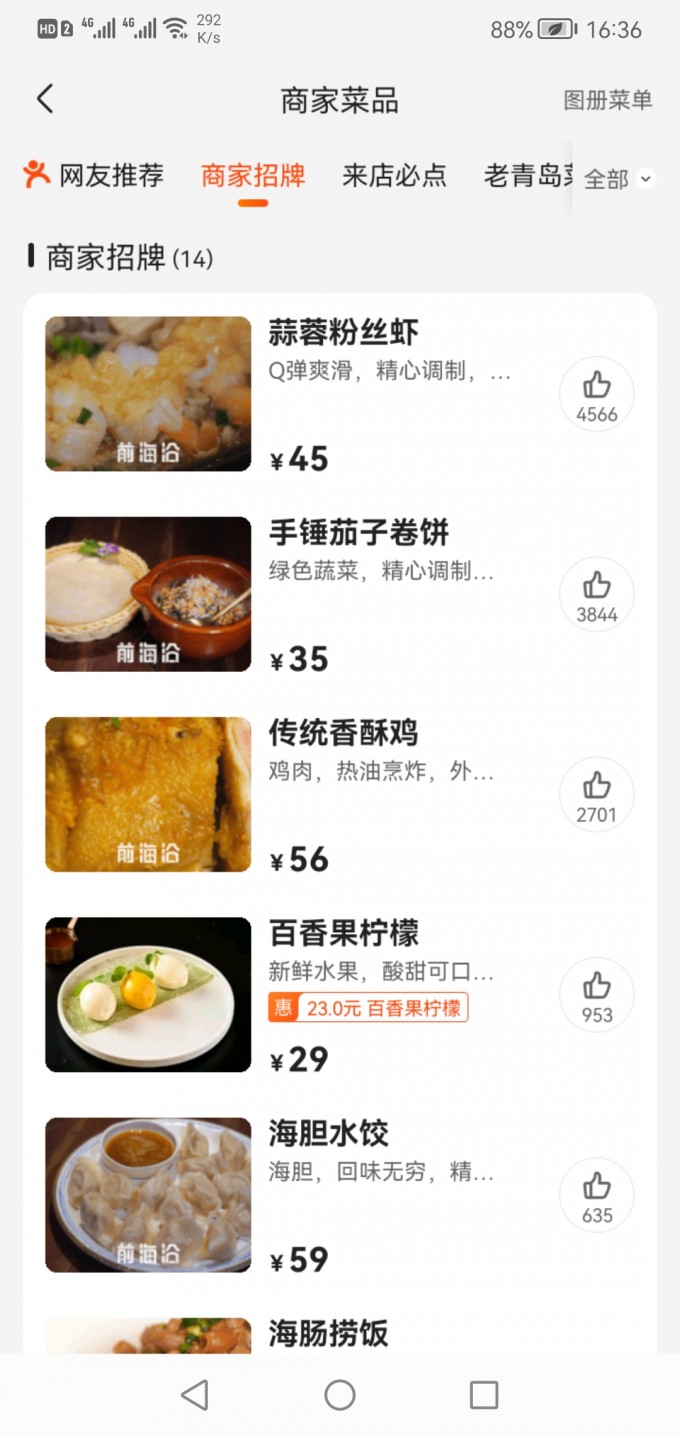
+ +重点菜:蒜蓉粉丝虾、手锤茄子卷饼
+
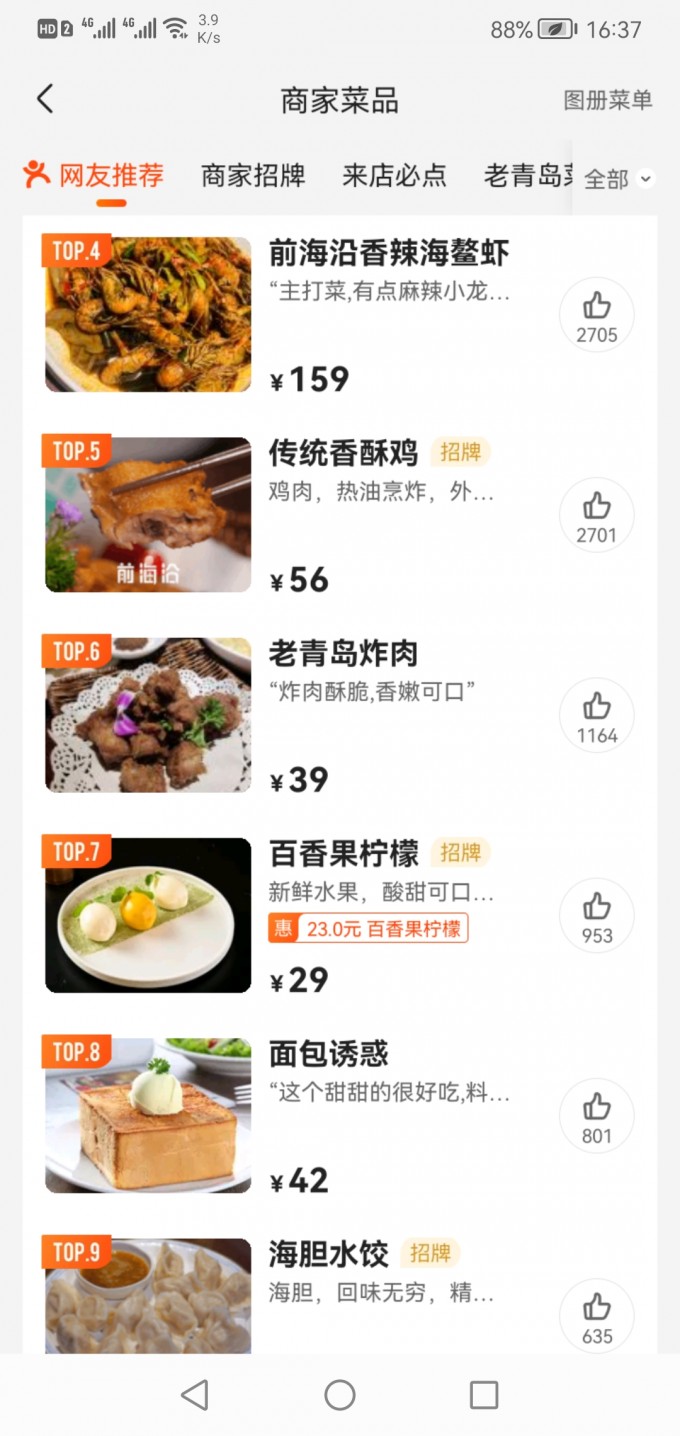 +
+数学在机器学习领域的应用一:线性代数
+ +总是觉得自己数学有一点差,可能是因为上大学学习的时候题目做的比较少,我的脑子又不太灵光,因此一直不能很好的理解数学相关的一些公式、定理等,平时编程的时候尽量找简单的方法绕开复杂的数学公式。假期有时间了,试一下帝国理工的线性代数课程,注重记录,注重理解。这也是第一次看没有中文字幕的全英文课。加油!
+In this course on Linear Algebra we look at what linear algebra is and how it relates to vectors and matrices. Then we look through what vectors and matrices are and how to work with them, including the knotty problem of eigenvalues and eigenvectors, and how to use these to solve problems. Finally we look at how to use these to do fun things with datasets - like how to rotate images of faces and how to extract eigenvectors to look at how the Pagerank algorithm works.
+Since we’re aiming at data-driven applications, we’ll be implementing some of these ideas in code, not just on pencil and paper. Towards the end of the course, you’ll write code blocks and encounter Jupyter notebooks in Python, but don’t worry, these will be quite short, focussed on the concepts, and will guide you through if you’ve not coded before.
+At the end of this course you will have an intuitive understanding of vectors and matrices that will help you bridge the gap into linear algebra problems, and how to apply these concepts to machine learning.
+Linear algebra is a mathematical system for manipulating vectors in the spaces described by vectors.
+Linear algebra is linear, because it just takes input values, and multiplies them by constants, everything is linear.
+Linear algebra is algebra, that is it’s a notation describing mathematical objects and a system of manipulating those notations.
+How vectors are transformed by matrices is the heart of linear algebra.
+ ,可以转换为
,可以转换为 ,然后进行求解。
,然后进行求解。在计算机科学中,向量被认为是描述一个物体的属性的集合。
+向量有两种操作:向量与向量之间的加法,以及向量与标量之间的乘法。
+向量与向量之间的加法满足结合律(associativity)。
+向量与标量之间的乘法,要将标量与向量中的每一个属性相乘
+如果不以坐标系的角度去观察向量,那么一个向量由两个属性构成:向量的方向和向量的模长
+向量的模长指的是向量各组成成分的平方和开根号
+向量的点乘指的是向量对应位置的数值相乘之和,满足交换律(commutative)
+同时满足向量的加法分配律(distributive over addition),即
向量与标量相乘满足结合律和交换律,即
向量模长与点乘之间的关系:向量自身的点乘与模长的平方相等,即
向量的余弦定理:
向量投影(projection):
+




向量投影是一个标量,但是,如果需要投影向量的方向,直接与被投影的单位向量相乘即可。
+两个不共线的向量可以确定一个坐标系(coordinate system)。要描述一个向量,首先要定义一个坐标系,决定坐标系的是基向量。
+基向量是
 维的向量彼此之间不线性相关,也就是线性独立的
维的向量彼此之间不线性相关,也就是线性独立的 维向量。
维向量。 维的。
维的。虽然并不要求基向量正交,但是如果它们正交,会为解决数学问题带来很大的方便。
+如果二维的基向量互相垂直,转换坐标系只需将向量投影到转换后的基向量,计算数值即可。
+设原始坐标系


首先验证

然后将待转换的向量










从而得出

找到一个合适的坐标系,帮助我们解决数学问题,是非常重要的。
+矩阵与向量相乘,相当于将向量转换到不同的坐标系。
+矩阵的乘法满足结合律,但是不满足交换律.
+如

如

通过矩阵的转换实际上可以看作不同转换向量之间的和。
+如果我们对

单位矩阵(identity matrix)不对向量做任何变换
+设单位矩阵


根据逆矩阵的定义,
因此

通过初等行变换求解逆矩阵:
对于二维矩阵


二维行列式(determinant):
行列式为0的矩阵,维度不满足当前矩阵的维度,因此在矩阵操作前要首先检查行列式。
+矩阵的转置:


设

则


如
因此

设原始坐标系



如果将


反之,将原始坐标系中的向量转换到

如果基向量是正交的,可以使用投影来实现坐标系的转换:
+设原始坐标系



则将




正交的基向量会给我们解决问题带来很多的方便,需要一种方法将基向量转换为正交的基向量。
+设原始的

对特征向量的直观感受:在进行变换的时候方向仍然保持不变的向量。
+


求特征值,即
对角矩阵(diagonal matrix)会使矩阵的乘法变得更加容易,
因此可以通过特征值与特征向量的转换,将矩阵转化为对角矩阵,然后求矩阵的幂。
+设特征向量

矩阵
# GRADED FUNCTION
+import numpy as np
+
+# Our function will go through the matrix replacing each row in order turning it into echelon form.
+# If at any point it fails because it can't put a 1 in the leading diagonal,
+# we will return the value True, otherwise, we will return False.
+# There is no need to edit this function.
+def isSingular(A) :
+ B = np.array(A, dtype=np.float_) # Make B as a copy of A, since we're going to alter it's values.
+ try:
+ fixRowZero(B)
+ fixRowOne(B)
+ fixRowTwo(B)
+ fixRowThree(B)
+ except MatrixIsSingular:
+ return True
+ return False
+
+# This next line defines our error flag. For when things go wrong if the matrix is singular.
+# There is no need to edit this line.
+class MatrixIsSingular(Exception): pass
+
+# For Row Zero, all we require is the first element is equal to 1.
+# We'll divide the row by the value of A[0, 0].
+# This will get us in trouble though if A[0, 0] equals 0, so first we'll test for that,
+# and if this is true, we'll add one of the lower rows to the first one before the division.
+# We'll repeat the test going down each lower row until we can do the division.
+# There is no need to edit this function.
+def fixRowZero(A) :
+ if A[0,0] == 0 :
+ A[0] = A[0] + A[1]
+ if A[0,0] == 0 :
+ A[0] = A[0] + A[2]
+ if A[0,0] == 0 :
+ A[0] = A[0] + A[3]
+ if A[0,0] == 0 :
+ raise MatrixIsSingular()
+ A[0] = A[0] / A[0,0]
+ return A
+
+# First we'll set the sub-diagonal elements to zero, i.e. A[1,0].
+# Next we want the diagonal element to be equal to one.
+# We'll divide the row by the value of A[1, 1].
+# Again, we need to test if this is zero.
+# If so, we'll add a lower row and repeat setting the sub-diagonal elements to zero.
+# There is no need to edit this function.
+def fixRowOne(A) :
+ A[1] = A[1] - A[1,0] * A[0]
+ if A[1,1] == 0 :
+ A[1] = A[1] + A[2]
+ A[1] = A[1] - A[1,0] * A[0]
+ if A[1,1] == 0 :
+ A[1] = A[1] + A[3]
+ A[1] = A[1] - A[1,0] * A[0]
+ if A[1,1] == 0 :
+ raise MatrixIsSingular()
+ A[1] = A[1] / A[1,1]
+ return A
+
+# This is the first function that you should complete.
+# Follow the instructions inside the function at each comment.
+def fixRowTwo(A) :
+ # Insert code below to set the sub-diagonal elements of row two to zero (there are two of them).
+ A[2] = A[2] - A[2,0] * A[0]
+ A[2] = A[2] - A[2,1] * A[1]
+ # Next we'll test that the diagonal element is not zero.
+ if A[2,2] == 0 :
+ # Insert code below that adds a lower row to row 2.
+ A[2] = A[2] + A[3]
+ # Now repeat your code which sets the sub-diagonal elements to zero.
+ A[2] = A[2] - A[2,0] * A[0]
+ A[2] = A[2] - A[2,1] * A[1]
+ if A[2,2] == 0 :
+ raise MatrixIsSingular()
+ # Finally set the diagonal element to one by dividing the whole row by that element.
+ A[2] = A[2] / A[2,2]
+ return A
+
+# You should also complete this function
+# Follow the instructions inside the function at each comment.
+def fixRowThree(A) :
+ # Insert code below to set the sub-diagonal elements of row three to zero.
+ A[3] = A[3] - A[3,0] * A[0]
+ A[3] = A[3] - A[3,1] * A[1]
+ A[3] = A[3] - A[3,2] * A[2]
+ # Complete the if statement to test if the diagonal element is zero.
+ if A[3,3] == 0:
+ raise MatrixIsSingular()
+ # Transform the row to set the diagonal element to one.
+ A[3] = A[3] / A[3,3]
+ return AA = np.array([
+ [2, 0, 0, 0],
+ [0, 3, 0, 0],
+ [0, 0, 4, 4],
+ [0, 0, 5, 5]
+ ], dtype=np.float_)
+isSingular(A)
+A = np.array([
+ [0, 7, -5, 3],
+ [2, 8, 0, 4],
+ [3, 12, 0, 5],
+ [1, 3, 1, 3]
+ ], dtype=np.float_)
+isSingular(A)
+fixRowZero(A)
+fixRowOne(A)
+fixRowTwo(A)
+fixRowThree(A)# GRADED FUNCTION
+import numpy as np
+import numpy.linalg as la
+
+verySmallNumber = 1e-14 # That's 1×10⁻¹⁴ = 0.00000000000001
+
+# Our first function will perform the Gram-Schmidt procedure for 4 basis vectors.
+# We'll take this list of vectors as the columns of a matrix, A.
+# We'll then go through the vectors one at a time and set them to be orthogonal
+# to all the vectors that came before it. Before normalising.
+# Follow the instructions inside the function at each comment.
+# You will be told where to add code to complete the function.
+def gsBasis4(A) :
+ B = np.array(A, dtype=np.float_) # Make B as a copy of A, since we're going to alter it's values.
+ # The zeroth column is easy, since it has no other vectors to make it normal to.
+ # All that needs to be done is to normalise it. I.e. divide by its modulus, or norm.
+ B[:, 0] = B[:, 0] / la.norm(B[:, 0])
+ # For the first column, we need to subtract any overlap with our new zeroth vector.
+ B[:, 1] = B[:, 1] - B[:, 1] @ B[:, 0] * B[:, 0]
+ # If there's anything left after that subtraction, then B[:, 1] is linearly independant of B[:, 0]
+ # If this is the case, we can normalise it. Otherwise we'll set that vector to zero.
+ if la.norm(B[:, 1]) > verySmallNumber :
+ B[:, 1] = B[:, 1] / la.norm(B[:, 1])
+ else :
+ B[:, 1] = np.zeros_like(B[:, 1])
+ # Now we need to repeat the process for column 2.
+ # Insert two lines of code, the first to subtract the overlap with the zeroth vector,
+ # and the second to subtract the overlap with the first.
+ B[:, 2] = B[:, 2] - B[:, 2] @ B[:, 0] * B[:, 0]
+ B[:, 2] = B[:, 2] - B[:, 2] @ B[:, 1] * B[:, 1]
+ # Again we'll need to normalise our new vector.
+ # Copy and adapt the normalisation fragment from above to column 2.
+ if la.norm(B[:, 2]) > verySmallNumber :
+ B[:, 2] = B[:, 2] / la.norm(B[:, 2])
+ else :
+ B[:, 2] = np.zeros_like(B[:, 2])
+ # Finally, column three:
+ # Insert code to subtract the overlap with the first three vectors.
+ B[:, 3] = B[:, 3] - B[:, 3] @ B[:, 0] * B[:, 0]
+ B[:, 3] = B[:, 3] - B[:, 3] @ B[:, 1] * B[:, 1]
+ B[:, 3] = B[:, 3] - B[:, 3] @ B[:, 2] * B[:, 2]
+ # Now normalise if possible
+ if la.norm(B[:, 3]) > verySmallNumber :
+ B[:, 3] = B[:, 3] / la.norm(B[:, 3])
+ else :
+ B[:, 3] = np.zeros_like(B[:, 3])
+ # Finally, we return the result:
+ return B
+
+# The second part of this exercise will generalise the procedure.
+# Previously, we could only have four vectors, and there was a lot of repeating in the code.
+# We'll use a for-loop here to iterate the process for each vector.
+def gsBasis(A) :
+ B = np.array(A, dtype=np.float_) # Make B as a copy of A, since we're going to alter it's values.
+ # Loop over all vectors, starting with zero, label them with i
+ for i in range(B.shape[1]) :
+ # Inside that loop, loop over all previous vectors, j, to subtract.
+ for j in range(i) :
+ # Complete the code to subtract the overlap with previous vectors.
+ # you'll need the current vector B[:, i] and a previous vector B[:, j]
+ B[:, i] = B[:, i] - B[:, i] @ B[:, j] * B[:, j]
+ # Next insert code to do the normalisation test for B[:, i]
+ if la.norm(B[:, i]) > verySmallNumber :
+ B[:, i] = B[:, i] / la.norm(B[:, i])
+ else :
+ B[:, i] = np.zeros_like(B[:, i])
+ # Finally, we return the result:
+ return B
+
+# This function uses the Gram-schmidt process to calculate the dimension
+# spanned by a list of vectors.
+# Since each vector is normalised to one, or is zero,
+# the sum of all the norms will be the dimension.
+def dimensions(A) :
+ return np.sum(la.norm(gsBasis(A), axis=0))V = np.array([[1,0,2,6],
+ [0,1,8,2],
+ [2,8,3,1],
+ [1,-6,2,3]], dtype=np.float_)
+gsBasis4(V)
+# Once you've done Gram-Schmidt once,
+# doing it again should give you the same result. Test this:
+U = gsBasis4(V)
+gsBasis4(U)
+# Try the general function too.
+gsBasis(V)
+# See what happens for non-square matrices
+A = np.array([[3,2,3],
+ [2,5,-1],
+ [2,4,8],
+ [12,2,1]], dtype=np.float_)
+gsBasis(A)
+dimensions(A)
+B = np.array([[6,2,1,7,5],
+ [2,8,5,-4,1],
+ [1,-6,3,2,8]], dtype=np.float_)
+gsBasis(B)
+dimensions(B)
+# Now let's see what happens when we have one vector that is a linear combination of the others.
+C = np.array([[1,0,2],
+ [0,1,-3],
+ [1,0,2]], dtype=np.float_)
+gsBasis(C)
+dimensions(C)# PACKAGE
+# Run this cell first once to load the dependancies.
+import numpy as np
+from numpy.linalg import norm, inv
+from numpy import transpose
+from readonly.bearNecessities import *
+# GRADED FUNCTION
+# You should edit this cell.
+
+# In this function, you will return the transformation matrix T,
+# having built it out of an orthonormal basis set E that you create from Bear's Basis
+# and a transformation matrix in the mirror's coordinates TE.
+def build_reflection_matrix(bearBasis) : # The parameter bearBasis is a 2×2 matrix that is passed to the function.
+ # Use the gsBasis function on bearBasis to get the mirror's orthonormal basis.
+ E = gsBasis(bearBasis)
+ # Write a matrix in component form that performs the mirror's reflection in the mirror's basis.
+ # Recall, the mirror operates by negating the last component of a vector.
+ # Replace a,b,c,d with appropriate values
+ TE = np.array([[1, 0],
+ [0, -1]])
+ # Combine the matrices E and TE to produce your transformation matrix.
+ T = E @ TE @ inv(E)
+ # Finally, we return the result. There is no need to change this line.
+ return T
+# First load Pyplot, a graph plotting library.
+%matplotlib inline
+import matplotlib.pyplot as plt
+
+# This is the matrix of Bear's basis vectors.
+# (When you've done the exercise once, see what happns when you change Bear's basis.)
+bearBasis = np.array(
+ [[1, -1],
+ [1.5, 2]])
+# This line uses your code to build a transformation matrix for us to use.
+T = build_reflection_matrix(bearBasis)
+
+# Bear is drawn as a set of polygons, the vertices of which are placed as a matrix list of column vectors.
+# We have three of these non-square matrix lists: bear_white_fur, bear_black_fur, and bear_face.
+# We'll make new lists of vertices by applying the T matrix you've calculated.
+reflected_bear_white_fur = T @ bear_white_fur
+reflected_bear_black_fur = T @ bear_black_fur
+reflected_bear_face = T @ bear_face
+
+# This next line runs a code to set up the graphics environment.
+ax = draw_mirror(bearBasis)
+
+# We'll first plot Bear, his white fur, his black fur, and his face.
+ax.fill(bear_white_fur[0], bear_white_fur[1], color=bear_white, zorder=1)
+ax.fill(bear_black_fur[0], bear_black_fur[1], color=bear_black, zorder=2)
+ax.plot(bear_face[0], bear_face[1], color=bear_white, zorder=3)
+
+# Next we'll plot Bear's reflection.
+ax.fill(reflected_bear_white_fur[0], reflected_bear_white_fur[1], color=bear_white, zorder=1)
+ax.fill(reflected_bear_black_fur[0], reflected_bear_black_fur[1], color=bear_black, zorder=2)
+ax.plot(reflected_bear_face[0], reflected_bear_face[1], color=bear_white, zorder=3);
+# PACKAGE
+# Here are the imports again, just in case you need them.
+# There is no need to edit or submit this cell.
+import numpy as np
+import numpy.linalg as la
+from readonly.PageRankFunctions import *
+np.set_printoptions(suppress=True)
+# GRADED FUNCTION
+# Complete this function to provide the PageRank for an arbitrarily sized internet.
+# I.e. the principal eigenvector of the damped system, using the power iteration method.
+# (Normalisation doesn't matter here)
+# The functions inputs are the linkMatrix, and d the damping parameter - as defined in this worksheet.
+# (The damping parameter, d, will be set by the function - no need to set this yourself.)
+def pageRank(linkMatrix, d) :
+ n = linkMatrix.shape[0]
+ M = d * linkMatrix + (1-d)/n * np.ones([n, n])
+ r = 100 * np.ones(n) / n
+ lastR = r
+ r = M @ r
+ i = 0
+ while la.norm(lastR - r) > 0.01 :
+ lastR = r
+ r = M @ r
+ i += 1
+ return r# Use the following function to generate internets of different sizes.
+generate_internet(5)
+# Test your PageRank method against the built in "eig" method.
+# You should see yours is a lot faster for large internets
+L = generate_internet(10)
+pageRank(L, 1)
+# Do note, this is calculating the eigenvalues of the link matrix, L,
+# without any damping. It may give different results that your pageRank function.
+# If you wish, you could modify this cell to include damping.
+# (There is no credit for this though)
+eVals, eVecs = la.eig(L) # Gets the eigenvalues and vectors
+order = np.absolute(eVals).argsort()[::-1] # Orders them by their eigenvalues
+eVals = eVals[order]
+eVecs = eVecs[:,order]
+
+r = eVecs[:, 0]
+100 * np.real(r / np.sum(r))
+# You may wish to view the PageRank graphically.
+# This code will draw a bar chart, for each (numbered) website on the generated internet,
+# The height of each bar will be the score in the PageRank.
+# Run this code to see the PageRank for each internet you generate.
+# Hopefully you should see what you might expect
+# - there are a few clusters of important websites, but most on the internet are rubbish!
+%pylab notebook
+r = pageRank(generate_internet(100), 0.9)
+plt.bar(arange(r.shape[0]), r);Formula Sheet: Sheet summarising all the formulae covered in this course.
+ + +旅行物品清单
+ +机器学习-监督学习:回归和分类
+ +吴恩达的机器学习课程终于更新了!!!想当初应该是大二的时候,看了吴恩达的课程,对机器学习有了初步的了解。当时听的不是很明白,英语看不太懂,一些给了充分提示的代码也写不太好,也就是入了一个门而已。这次有一些时间,正好捡一捡机器学习的基础知识,推一推那些一直在调包的数学公式。注重记录!
+In the first course of the Machine Learning Specialization, you will:
+• Build machine learning models in Python using popular machine learning libraries NumPy and scikit-learn.
+• Build and train supervised machine learning models for prediction and binary classification tasks, including linear regression and logistic regression
The Machine Learning Specialization is a foundational online program created in collaboration between DeepLearning.AI and Stanford Online. In this beginner-friendly program, you will learn the fundamentals of machine learning and how to use these techniques to build real-world AI applications.
+This Specialization is taught by Andrew Ng, an AI visionary who has led critical research at Stanford University and groundbreaking work at Google Brain, Baidu, and Landing.AI to advance the AI field.
+This 3-course Specialization is an updated and expanded version of Andrew’s pioneering Machine Learning course, rated 4.9 out of 5 and taken by over 4.8 million learners since it launched in 2012.
+It provides a broad introduction to modern machine learning, including supervised learning (multiple linear regression, logistic regression, neural networks, and decision trees), unsupervised learning (clustering, dimensionality reduction, recommender systems), and some of the best practices used in Silicon Valley for artificial intelligence and machine learning innovation (evaluating and tuning models, taking a data-centric approach to improving performance, and more.)
+By the end of this Specialization, you will have mastered key concepts and gained the practical know-how to quickly and powerfully apply machine learning to challenging real-world problems. If you’re looking to break into AI or build a career in machine learning, the new Machine Learning Specialization is the best place to start.
+监督学习是学习从输入

监督学习的基本类型有两种:回归和分类
+回归任务是在大量的数值空间中,对某一个具体数值进行预测
+分类任务是在给定的数值空间中(如0和1),对某一个具体数据进行预测
+






线性回归的机器学习模型可以表示为:
度量预测值与实际目标值之间的差异
+线性回归中使用的平方损失函数:
目标就是要找出最合适的


使用梯度下降算法:
+


梯度下降在更新的时候需要同时更新



具体计算:
+学习率的选择:
+如果学习率过小,梯度下降算法运行会比较慢
+如果学习率过大,梯度下降算法可能运行过头,最终导致算法不能收敛
+如果使用固定的学习率,梯度下降算法运行到局部最小值后不会再变化。因为到达局部最小值的附近后,梯度下降的每一步会变得更小,更新的值也会逐渐变小。
+通过损失值随着迭代次数的变化可以看出一些错误:
+将学习率调整足够小,损失值在每一次迭代的过程中都会减小
+







令

可以通过Numpy的向量化进行计算
+当具有不同的值范围的不同特征时,可能会导致梯度下降算法运行较慢
+需要对不同的特征重新缩放到相同或相似的范围
+均值归一化:

Z-score归一化:
sigmoid函数:
逻辑回归:
不同的决策边界:
+逻辑回归损失函数:
+简化写法:
欠拟合:函数对于训练集的拟合效果不好——高偏差(high bias)
+过拟合:函数对于训练集的拟合效果好,对于测试集的效果不好——高方差(high variance)
+避免过拟合的方法:
+通过将损失函数加上特别大的常数与某一参数的乘积,使得这个参数在优化的过程中变得非常小
+例如回归问题:
+由于不知道哪些特征是比较重要的,哪些特征不重要,因此加上参数平方求和的正则项,让优化算法自行选择。
+对于线性回归来说:
+进一步推导:
+因此正则项的加入实际上相当于将参数略微减小
+记于2022年7月28日,已于2022年9月24日正式分手,公开于2023年11月19日
+ +青岛的五天旅行结束了,251天后的初次见面,美好的时光总是短暂。
+回家后心里一直不太舒服,一直在胡思乱想,想着想着有时还偷偷抹抹眼泪。父母也是真的了解我,虽然并没有表现出什么,一直在不断追问我怎么了。当然就算有明确的原因也不会说,对爸妈只能是报喜不报忧,何况我现在也不知道我为什么这样。
+可能是不舍得吧,分开了251天,再次见面的时间只有短短的五天,下一次见面还不知道什么时候。
+可能是由于毕业季的几乎分手吧,可能现在自己的信心没有那么足了。
+可能是对自己未来的迷茫吧,本科取得了不错的成绩,研究生一切从头开始,不知该从何做起。
+这一段时间,对我影响最大的就是那一次的几乎分手。女孩子真的需要陪伴,异地太久了,感情是真的会变淡的。而且之前并没有很明确的聊过未来的规划。可能随口的一句“杭州南京”,就成为了一道跨不过去的坎。
+我出生在东北的一个小城,从小的梦想就是要走出去,给我自己,甚至给我的下一代创造一个更好的生活环境。高二那年清华暑校遇到全国的优秀学生,发现不同地区顶尖学生之间的差异居然也有如此之大,更加坚定了我走出去的决心。我也很庆幸在高考失利的情况下能选到一个好专业,在房价居高不下的大环境下,至少目前来看毕业后的薪资还是非常有竞争力的。
+我很开心可以遇到我的女朋友,我们在一无所有的情况下愿意去尝试。我也从此有了另外的一个前进动力,从高考失利和大一的挫折中走了出来,拿下了年级排名和无数的竞赛奖项、荣誉称号,成功保研。保研的时候也没有选择华师大,想着自己应该获得更好的学历,以后赚更多的钱,才能和她一起有更好的生活。我按照我的道路一步一步在走。
+然而由于我早去北京的提前异地,我们之间的沟通就少了许多。地理上的距离造成了心的距离,找到了一个很好的教师编职位后,她便产生了分手的想法。整个过程我甚至都是毫不知情的状态。虽然靠着一条时间轴挽回,但是我需要对自己做一个深刻的反思。我自认为我的爱没有变,但是异地半年多,确实很难将爱表达出来,同时也忽略了她的感受,我们之间的交流变得更少,最终导致了单方面无吵架的分手。
+能有一个爱人时刻陪伴在身边,确实是一件非常美好的事情。才分开两天,五天的回忆一波一波涌上心头,真的很难受。想起她忘记带伞的时候,只能躲在小店内等待雨停,却无法等到一个送伞的我。异地恋真的难熬。然而这还不到一年的时间。最少需要三年才能奔现,要是找一份更高薪的工作,甚至需要五年的时间,我才能在合肥站稳脚跟,真正地和她在一起。“所以你就选定我了是嘛”“是的”“为什么呢”“。。。”是啊,为什么呢,我回答不上来。后来我也认真考虑了很久,我是一个纯理性思维的人,这一次我选择听从我的心。我相信我三年前的选择,不管是现在,三年后,三十年后,我还会作出同样的选择。
+我是一个很坚定的人,我作出了选择,就会坚定的走下去。这几年我会尽全力维护这一段感情,改正掉我之前的错误,尽量多见面,尽量提升自己以后拿到更好的薪资,尽量多关心,多询问她的感受。三年前我还是一个懵懂无知的学生,我不知道三年后,甚至五年后我会成为什么样的人,但是我的爱是永远不变的。
+如果她熬不住了,我会坦然接受。因为我知道,我才是那个最对不起她的人。长三角省会城市工作稳定,我又何德何能拴住她数年的时间,忍受着屏幕那边可有可无的关心,忍受着几个月甚至半年才有的一次短短几天的见面。
+我真的希望最终我们可以幸福地走到一起。
+为你,千千万万遍。
+ + +数学在机器学习领域的应用二:多元微积分
+ +This course offers a brief introduction to the multivariate calculus required to build many common machine learning techniques. We start at the very beginning with a refresher on the “rise over run” formulation of a slope, before converting this to the formal definition of the gradient of a function. We then start to build up a set of tools for making calculus easier and faster. Next, we learn how to calculate vectors that point up hill on multidimensional surfaces and even put this into action using an interactive game. We take a look at how we can use calculus to build approximations to functions, as well as helping us to quantify how accurate we should expect those approximations to be. We also spend some time talking about where calculus comes up in the training of neural networks, before finally showing you how it is applied in linear regression models. This course is intended to offer an intuitive understanding of calculus, as well as the language necessary to look concepts up yourselves when you get stuck. Hopefully, without going into too much detail, you’ll still come away with the confidence to dive into some more focused machine learning courses in future.
+函数是从输入到输出的映射,选择函数来建模世界的过程是伟大天才的科学目的,微积分只是对这些函数如何相对于它们的输入变量如何变化的研究。
+对于线性函数而言,斜率(梯度、gradient)=‘rise over run’,也就是任意取两点,

对于梯度一直在变化的函数来说,设函数为


即,
导数的求和法则:
幂函数求导法则:令
不连续(discontinuity)的函数,例如



例如

三角函数:
导数乘积法则:令
求导的链式法则:若

偏导数求导法则:
偏导数仍然遵循导数的求导法则
+设函数
这样给予一组
设函数
对雅可比行列式再求一次偏导数,构成的二阶偏导数矩阵为海森矩阵
+设函数

雅可比行列式求得的值为0的情况下,首先求海森矩阵的行列式,如果行列式为正数,说明目前的点是一个极值点;然后看海森矩阵的第一个数字,如果第一个数字是正数,说明目前在极小值点,否则在极大值点;如果海森矩阵的行列式为负,说明目前的点是一个鞍点。
+最简单的神经网络:




输入可能不仅仅是一个,设输入的神经元有
输出可能也不仅仅是一个,设输出的神经元有
可以简化表示为:
如果神经网络不止一层,则可以表示为:
神经网络(分类任务)的损失函数为
泰勒展开式是对一个复杂函数的简化估计函数
+
泰勒形式:
+


+

迭代求解方程的近似根:
+这种方法会存在一些问题,如果选取的点比较靠近函数的拐点,会得不到正确的结果,或者得到的结果并不是与选取的点最接近的。
+如何使用梯度找到多元函数的最大值或者最小值
+函数的梯度:
如果希望找到最大值,将梯度与它的单位向量相乘,则
梯度下降:
计算函数在某些约束下的最大值或者最小值
+

即:
设函数
计算平方误差:
求解使得误差最小:
则可以解得:
+Formula Sheet: Sheet summarising all the formulae covered in this course.
+ + +机器学习-高级学习算法
+ +In the second course of the Machine Learning Specialization, you will:
+• Build and train a neural network with TensorFlow to perform multi-class classification
+• Apply best practices for machine learning development so that your models generalize to data and tasks in the real world
+• Build and use decision trees and tree ensemble methods, including random forests and boosted trees
The Machine Learning Specialization is a foundational online program created in collaboration between DeepLearning.AI and Stanford Online. In this beginner-friendly program, you will learn the fundamentals of machine learning and how to use these techniques to build real-world AI applications.
+This Specialization is taught by Andrew Ng, an AI visionary who has led critical research at Stanford University and groundbreaking work at Google Brain, Baidu, and Landing.AI to advance the AI field.
+This 3-course Specialization is an updated and expanded version of Andrew’s pioneering Machine Learning course, rated 4.9 out of 5 and taken by over 4.8 million learners since it launched in 2012.
+It provides a broad introduction to modern machine learning, including supervised learning (multiple linear regression, logistic regression, neural networks, and decision trees), unsupervised learning (clustering, dimensionality reduction, recommender systems), and some of the best practices used in Silicon Valley for artificial intelligence and machine learning innovation (evaluating and tuning models, taking a data-centric approach to improving performance, and more.)
+By the end of this Specialization, you will have mastered key theoretical concepts and gained the practical know-how to quickly and powerfully apply machine learning to challenging real-world problems. If you’re looking to break into AI or build a career in machine learning, the new Machine Learning Specialization is the best place to start.
+生物神经元:通过树突接收到来自不同地方的输入,然后通过轴突将神经冲动传递出去。
+但是目前对于人脑的运作方式了解的还不是很透彻。
+model = Sequential(
+ [
+ tf.keras.Input(shape=(400,)), #specify input size
+ tf.keras.layers.Dense(25, activation='sigmoid'),
+ tf.keras.layers.Dense(15, activation='sigmoid'),
+ tf.keras.layers.Dense(1, activation='sigmoid')
+ ], name = "my_model"
+)model.compile(
+ loss=tf.keras.losses.BinaryCrossentropy(),
+ optimizer=tf.keras.optimizers.Adam(0.001),
+)
+
+model.fit(
+ X,y,
+ epochs=20
+)prediction = model.predict(X[0].reshape(1,400)) # a zero
+print(f" predicting a zero: {prediction}")
+prediction = model.predict(X[500].reshape(1,400)) # a one
+print(f" predicting a one: {prediction}")def my_dense_v(A_in, W, b, g):
+ """
+ Computes dense layer
+ Args:
+ A_in (ndarray (m,n)) : Data, m examples, n features each
+ W (ndarray (n,j)) : Weight matrix, n features per unit, j units
+ b (ndarray (1,j)) : bias vector, j units
+ g activation function (e.g. sigmoid, relu..)
+ Returns
+ A_out (ndarray (m,j)) : m examples, j units
+ """
+ z = np.matmul(A_in,W)+b
+ A_out = g(z)
+ return(A_out)def my_sequential_v(X, W1, b1, W2, b2, W3, b3):
+ A1 = my_dense_v(X, W1, b1, sigmoid)
+ A2 = my_dense_v(A1, W2, b2, sigmoid)
+ A3 = my_dense_v(A2, W3, b3, sigmoid)
+ return(A3)Prediction = my_sequential_v(X, W1_tmp, b1_tmp, W2_tmp, b2_tmp, W3_tmp, b3_tmp )
+Prediction.shape人工智能(AI)可以分为两种,ANI和AGI:
+ANI指在某一特定领域应用的人工智能,目前已经取得了很好的效果;
+AGI指通用人工智能,人工智能可以做任何人类可以做到的事情。
+鉴于对人脑的了解还不够,如果通过模拟人脑的方式达到通用人工智能比较困难。
+不过目前有一些进展,让通用人工智能看到了一点点希望。
+如果不使用激活函数,那么不管多么复杂的神经网络都会退化成线性回归方法可以实现的效果。
+Sigmoid激活函数:
ReLU激活函数:
如何选择输出层的激活函数:
+隐藏层中大多数使用ReLU激活函数而非Sigmoid激活函数
+多类别分类是指输出不止两种情况的分类问题,如对手写数字进行分类,输出的类别会有10个
+可以使用Softmax回归算法:
+损失函数:
多标签分类:可以看成很多多类别分类问题,也可以使用一个神经网络预测所有的类别
+Adam优化方法:自动调节学习率
+如果梯度下降的方向一直是同一方向则增大学习率,让算法运行更快
+如果梯度下降的方向一直在波动,则减小学习率。
+如果发现训练好的模型在预测上存在很大的问题,可以从以下几个方面入手查找原因:
+ 、
、 、
、 等等——高偏差
等等——高偏差 ——高方差、高偏差
——高方差、高偏差训练时对训练集进行划分,可以划分为训练集和测试集,如果希望使用交叉验证的方式,可以划分为训练集、验证集和测试集。通过测试集的表型评估模型的效果。模型的选择上,可以从多项式的次数从低到高依次进行选择,找出测试集误差最小的模型。
+更大规模的神经网络的偏差往往更小
+如果恰当选择正则化参数,更大规模的神经网络的表现比小规模的神经网络表现更好
+欠拟合:函数对于训练集的拟合效果不好——高偏差(high bias)
+过拟合:函数对于训练集的拟合效果好,对于测试集的效果不好——高方差(high variance)
+避免过拟合的方法:
+正则项参数
 导致模型的训练集拟合效果不好——高偏差(high bias)
导致模型的训练集拟合效果不好——高偏差(high bias) 导致模型对于训练集的拟合效果好,对于测试集的效果不好——高方差(high variance)
导致模型对于训练集的拟合效果好,对于测试集的效果不好——高方差(high variance)学习曲线:
+评价分类(尤其针对分布不平衡的数据)
+熵(Entropy)
信息增益
如果一个决策结点有三个可选项,可以通过独热编码的方式将其转换为多个二分类形式。
+如果变量是连续的数值,可以计算从那里开始划分的信息增益最高,从而转化为判断大小于的二分类形式。
+决策树解决回归问题,则将熵替换为节点上数据的方差进行计算。
+随机森林:
+XGBoost:采样训练数据的时候更倾向于采样前面的树中被分类错误的数据
+决策树更适用于结构化的数据,快速,但是不适用于其他类似于图片文本等的数据
+神经网络适用于所有类型的数据,运行可能稍慢一些,可以迁移学习,更适合将不同的神经网络结合到一起。
+机器学习-无监督学习,推荐系统与强化学习
+ +In the third course of the Machine Learning Specialization, you will:
+• Use unsupervised learning techniques for unsupervised learning: including clustering and anomaly detection.
+• Build recommender systems with a collaborative filtering approach and a content-based deep learning method.
+• Build a deep reinforcement learning model.
The Machine Learning Specialization is a foundational online program created in collaboration between DeepLearning.AI and Stanford Online. In this beginner-friendly program, you will learn the fundamentals of machine learning and how to use these techniques to build real-world AI applications.
+This Specialization is taught by Andrew Ng, an AI visionary who has led critical research at Stanford University and groundbreaking work at Google Brain, Baidu, and Landing.AI to advance the AI field.
+This 3-course Specialization is an updated and expanded version of Andrew’s pioneering Machine Learning course, rated 4.9 out of 5 and taken by over 4.8 million learners since it launched in 2012.
+It provides a broad introduction to modern machine learning, including supervised learning (multiple linear regression, logistic regression, neural networks, and decision trees), unsupervised learning (clustering, dimensionality reduction, recommender systems), and some of the best practices used in Silicon Valley for artificial intelligence and machine learning innovation (evaluating and tuning models, taking a data-centric approach to improving performance, and more.)
+By the end of this Specialization, you will have mastered key concepts and gained the practical know-how to quickly and powerfully apply machine learning to challenging real-world problems. If you’re looking to break into AI or build a career in machine learning, the new Machine Learning Specialization is the best place to start.
+无监督学习是在没有标签的数据中自动寻找某些规律
+聚类任务是典型的无监督学习任务,通过某些特征将相似的人或事物自动归为一类
+无监督学习任务还有异常检测(找出一些不寻常的数据)和维度降低(使用更少的数字对数据进行压缩)
+聚类是一种典型的无监督学习算法,不定义标签,让算法自己去寻找数据中有趣的特征
+聚类可以在下面几个方面得到应用:
+K-means聚类步骤:
+ 个中心点
个中心点 (
( 预先定义)
预先定义)如何决定聚类的数量?Elbow method
+多种聚类数量都尝试一下,找到“肘点”,也就是增加聚类数量后代价函数也不能明显减小的点
+如何随机初始化最初的类别中心点?
+已经拥有一些数据,增加一条数据,判断其是否符合已有的数据的特征,如果不符合则为异常数据
+正态分布:
异常检测:

实际应用中,可以找一些有标记的异常点,指导算法选取合适的阈值
在某种类别(异常)的数据量很少的情况下,且异常的种类较多,特征无法很好区分出来的时候,使用异常检测算法比较好。
+场景:很多用户对电影进行打分,分数从0-5,如何向用户推荐合适的电影?
+设用户的数量为

如果用户










预测用户

代价函数:
对所有用户来说,

前面是有特征,通过类似于线性回归的方式可以进行预测,但是如果没有特征应该怎么做呢?
+已知
代价函数:
将两个代价函数结合到一起:
如果评分是二值化的,则类似于线性回归与逻辑回归的区别:
+如果一个人没有对任何电影进行评分,则选取其他所有人的评分平均值作为他的评分。
+协同过滤算法的局限性:
+协同过滤算法是基于用户的评分,根据比较相似的评分情况来进行推荐
+基于内容的过滤算法是基于用户和物品的特征来寻找比较合适的匹配对
+设用户


比较两个特征之间相似度的方法是点乘,但是两者的维度不同,因此要对输入的特征增加几层神经网络,使其输出相同,再进行点乘。
+通过神经网络后,



代价函数为::
检索和排序策略:
+强化学习不告诉应该怎么做,而是只告诉做什么,如果做的好有奖励,做的不好有惩罚,从而让算法自动向着奖赏最多的方向优化,最终学习出最好的结果。
+目前的状态、动作、奖励、下一个状态,下一个状态的动作
每一个时间步后,会有一个权重


一般来说,权重按照幂的方式变化,如第一步是



措施

强化学习的目标就是找到合适的措施
马尔可夫决策过程:未来只取决于现在所处的位置,与之前是怎么到达现在这个位置的无关。
+状态-动作方程:


因此,可以得出两个结论:
+ 开始的最佳的返回奖励是
开始的最佳的返回奖励是
 开始的最好的动作是能达到
开始的最好的动作是能达到 的动作
的动作
贝尔曼方程:
在更为复杂的环境下,状态之间的转移可能并不是确定的,有一定的几率到达其他的状态
+因此得到的返回奖励实际上是期望的返回奖励,即
状态空间可能是连续的,对于月球车来说,有方向(前后左右和旋转)和速度两种变量,因此
训练神经网络:输入是




训练步骤:
+

 作为输入,
作为输入, 作为输出训练
作为输出训练 使得
使得
 ,重复上述步骤
,重复上述步骤



mini-batch:在
soft update:
Numpy是个好东西,但是ndarray的轴感觉弄不太明白。可能二维三维数组还好,要是再增加几维就无法在脑海中想象这个东西,对于一些有关轴的操作就稀里糊涂,只能一个个尝试。现在准备把它彻底弄明白!
+ +首先从二维入手,然后扩展到三维以及更高的维度(从特殊到一般),然后找出普遍的规律,再进行验证(从一般到特殊)
+官方文档应该是最权威的,首先看官方文档是怎么说明的,然后查找一些资料,看看其他人是怎么理解的,最后总结出自己的一套规律
+import numpy as np感受一个ndarray,最简单的方法就是打印ndarray的shape。
+官方文档里面是这样写的:
+the dimensions of the array. This is a tuple of integers indicating the size of the array in each dimension. For a matrix with n rows and m columns, shape will be (n,m). The length of the shape tuple is therefore the number of axes, ndim.
只列举了矩阵的例子,尝试一下:
+a1 = np.arange(15).reshape(3, 5)
+print(a1,'\n',a1.shape,'\n',a1.ndim)输出结果:
+[[ 0 1 2 3 4]
+ [ 5 6 7 8 9]
+ [10 11 12 13 14]]
+ (3, 5)
+ 2简单推断:最开始有2个方括号,因此矩阵是2维的,且第1个方括号内部有3个“2级方括号”,每一个“2级方括号”内部都有5个元素,因此这个shape可能是从外向里数的。
+尝试1维ndarray:
+a2 = np.arange(15)
+print(a2,'\n',a2.shape,'\n',a2.ndim)输出结果:
+[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14]
+ (15,)
+ 1尝试3维ndarray:
+a3 = np.arange(24).reshape(3,2,4)
+print(a3,'\n',a3.shape,'\n',a3.ndim)输出结果:
+[[[ 0 1 2 3]
+ [ 4 5 6 7]]
+
+ [[ 8 9 10 11]
+ [12 13 14 15]]
+
+ [[16 17 18 19]
+ [20 21 22 23]]]
+ (3, 2, 4)
+ 3尝试4维ndarray:
+a4 = np.arange(24).reshape(3,2,1,4)
+print(a4,'\n',a4.shape,'\n',a4.ndim)输出结果:
+[[[[ 0 1 2 3]]
+
+ [[ 4 5 6 7]]]
+
+
+ [[[ 8 9 10 11]]
+
+ [[12 13 14 15]]]
+
+
+ [[[16 17 18 19]]
+
+ [[20 21 22 23]]]]
+ (3, 2, 1, 4)
+ 4因此可以得出结论:对于给定的ndarray,判断ndim就是计数最前面有多少个相连的方括号,判断shape就是从外向内看,每一层分别有多少个“元素”。
+也可以看出,数组超过4维后,肉眼就有些难以区分了。
+索引就是取数组中的某些元素,官方文档有下面的举例:
+>>> a = np.arange(30).reshape(2, 3, 5)
+>>> a
+array([[[ 0, 1, 2, 3, 4],
+ [ 5, 6, 7, 8, 9],
+ [10, 11, 12, 13, 14]],
+
+ [[15, 16, 17, 18, 19],
+ [20, 21, 22, 23, 24],
+ [25, 26, 27, 28, 29]]])
+>>> a[0, 2, :]
+array([10, 11, 12, 13, 14])
+>>> a[0, :, 3]
+array([ 3, 8, 13])索引操作是与shape相对应的。如上述例子,a[0]即为取数组的第1个维度(2)的第1个元素,这样原来3维的数组就降到了2维;a[0, :]就是在a[0]的基础上取数组的第2个维度(3)的全部元素,数组的维度不变,还是2维;a[0, :, 3]就是在a[0, :]的基础上取数组的第3个维度(5)的第4个元素,即可得出上面的结果。
+索引操作后的维度与索引的数量以及是否有“:”相关。如果索引的数量与ndim相同,则最后取出来的是一个数。如果数量不同或者有“:”(数量不同可以看成在后面补“:”),则最终取得的数组的维度与“:”对应的原数组的维度相同。
+以numpy.sum为例:
+官方文档:
+Axis or axes along which a sum is performed. The default, axis=None, will sum all of the elements of the input array. If axis is negative it counts from the last to the first axis.
+If axis is a tuple of ints, a sum is performed on all of the axes specified in the tuple instead of a single axis or all the axes as before.
+以三维数组为例:
+print('origin')
+print(a3,a3.shape)
+print('axis=0')
+print(a3.sum(axis=0),a3.sum(axis=0).shape)
+print('axis=1')
+print(a3.sum(axis=1),a3.sum(axis=1).shape)
+print('axis=2')
+print(a3.sum(axis=2),a3.sum(axis=2).shape)
+print('axis=(0,1)')
+print(a3.sum(axis=(0,1)),a3.sum(axis=(0,1)).shape)
+print('axis=(1,2)')
+print(a3.sum(axis=(1,2)),a3.sum(axis=(1,2)).shape)
+print('axis=(0,2)')
+print(a3.sum(axis=(0,2)),a3.sum(axis=(0,2)).shape)
+print('axis=(0,1,2)')
+print(a3.sum(axis=(0,1,2)),a3.sum(axis=(0,1,2)).shape)origin
+[[[ 0 1 2 3]
+ [ 4 5 6 7]]
+
+ [[ 8 9 10 11]
+ [12 13 14 15]]
+
+ [[16 17 18 19]
+ [20 21 22 23]]] (3, 2, 4)
+axis=0
+[[24 27 30 33]
+ [36 39 42 45]] (2, 4)
+axis=1
+[[ 4 6 8 10]
+ [20 22 24 26]
+ [36 38 40 42]] (3, 4)
+axis=2
+[[ 6 22]
+ [38 54]
+ [70 86]] (3, 2)
+axis=(0,1)
+[60 66 72 78] (4,)
+axis=(1,2)
+[ 28 92 156] (3,)
+axis=(0,2)
+[114 162] (2,)
+axis=(0,1,2)
+276 ()axis为多少,就是在这个维度上进行操作,最终的结果就是这个维度消失
+不要从行列什么的去思考怎么变化,直接从shape的角度入手。设置axis为多少,这个维度就没有了!比如原来是(3,2,4)的维度,要是axis=0,第一个维度就没有了,加和得到的矩阵就是(2,4)。
+如果希望保留维度,可以增加keepdims=True的选项,这样被操作的维度就会变为1而不是直接消失。
+print('axis=(0,1)')
+print(a3.sum(axis=(0,1),keepdims=True),a3.sum(axis=(0,1),keepdims=True).shape)axis=(0,1)
+[[[60 66 72 78]]] (1, 1, 4)这样想应该会比较好理解,尤其是对于更高维的数组来说,行列的概念基本失效,从shape的角度思考会好。
+另外一个比较常用的操作是np.concatenate,可以将数组进行合并,在数据处理或者神经网络中很常用。
+在np.concatenate上检验一下对于axis的理解:
+ta = np.arange(24).reshape(3,2,4)
+tb = np.arange(24,36).reshape(3,1,4)
+print(ta,ta.shape)
+print(tb,tb.shape)[[[ 0 1 2 3]
+ [ 4 5 6 7]]
+
+ [[ 8 9 10 11]
+ [12 13 14 15]]
+
+ [[16 17 18 19]
+ [20 21 22 23]]] (3, 2, 4)
+[[[24 25 26 27]]
+
+ [[28 29 30 31]]
+
+ [[32 33 34 35]]] (3, 1, 4)两者合并,第2个维度不相同,应该是可以合并的,合并后的shape应该为(3,3,4)
+print(np.concatenate((ta,tb),axis=1),np.concatenate((ta,tb),axis=1).shape)[[[ 0 1 2 3]
+ [ 4 5 6 7]
+ [24 25 26 27]]
+
+ [[ 8 9 10 11]
+ [12 13 14 15]
+ [28 29 30 31]]
+
+ [[16 17 18 19]
+ [20 21 22 23]
+ [32 33 34 35]]] (3, 3, 4)np.concatenate除了在待合并的axis上之外,必须具有相同的shape
+之前的结论也得到了验证。
+我们处在三维空间中,二维和三维是比较直观的,可以在脑海中想象出来。因此我们会觉得axis的设计有些反直觉。以后应该从shape的角度去看待axis的设计思想,首先理解上比较直观,其次在更高维度的数组上也能合理的进行操作。不要去思考数组实际中应该是个什么样子,直接观察axis就足够了。
+上大学之前,父母特意嘱咐借钱的问题,我当时觉得现在和以前不一样了,以前父母上学的时候可能零花钱限额比较严格,生活也不太好。现在大家基本都是独生子女,而且正规的借钱手段也不少,比如“花呗”等等。因此我不觉得有人会向我借钱,我自己也决定把不借给别人钱作为一条原则。大学四年风平浪静,然而今天下午就突然碰到了这个问题。
+大学有三个室友,分别用QLD代替吧。Q保研了本校,L在深圳工作,D在二战考研。首先要说明的是,在我2年对他们的了解下,人品都没有问题。今天下午Q突然打微信电话给我,要借6000元钱。(可惜是微信电话没有留下录音证据)首先他说的是个人原因,明天就会还我,不好找父母要。再三追问下,他说是“类似于赌博的平台,自己是内部参加的,就是自己操作失误了,现在急需这些钱,明天肯定能赚回来”云云。他还说就算赚不回来明天也会找父母要还我。当然我非常相信他的人品,但是我感觉这个就是一个非常经典的骗局,我不想看到他越陷越深,就劝了他一阵,主要说的就是希望他能冷静下来好好想想。我劝不回来他,中间有一句话骗了他一下说我现在没有钱,也要找父母要。最终也没有借给他。后面打过电话后我也劝了几句话,但是他没有回复我。
+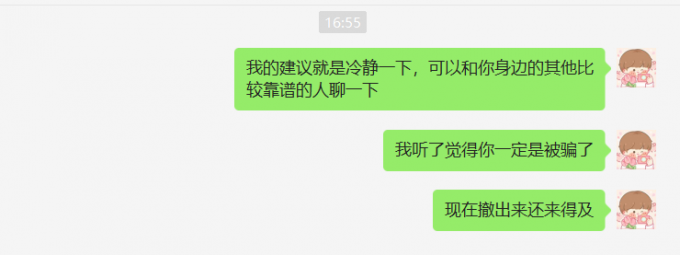 +
+我也想到了他会找我的另外的室友,我也知道这件事情知道的人越少越好,所以我找了和他关系更好一点的L。结果L一直都没有回复我,差不多半个多小时后,我们才交流了一下。L告诉我Q除了找我之外也找了L和D,他们俩一人借了3000元钱,算是Q借钱成功了。
+我不知道D怎么想的,但是可能他家比较有钱,可能人家也不在乎这个。L和我交流了一下,大意就是他也知道十有八九是一个骗局,但是还是借给他了。
+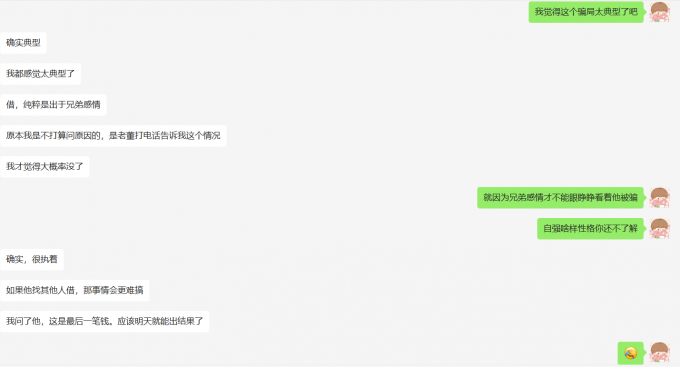 +
+我本来还是挺理直气壮的,我认为我做的没什么问题,而且很遗憾没有把他们俩及时劝住。但是L一句话让我没话说了。
+“如果他找其他人借,那事情会更难搞”
+不是黑Q,主要是大学几年我们都看在眼里,确实没有什么很好的朋友。可能平时聊天最多的就是我们三个了。真的如果我们三个都不借给他,那他会怎么办呢?难道我们几个真的能劝住吗?而且已经毕业了我们又不在身边,谁知道他会做什么?高利贷?我不敢往下想了。都毕业了不可能找学校的任何人帮助他,又不知道他家庭的电话,打110也只能打到我自己家。所以是不是在充分了解这个人的情况下,劝说无效后借钱给他才是最好的帮助他的办法?
+所以我一直到晚上一直都不太舒服,感觉自己一直坚守的底线被我自己动摇了。以后再遇到这样的事情怎么办?
+还这么办!坚守底线!听对象的话!
+当然我有十足的把握是了解Q的,才会这么纠结。一般的同学或者同事什么的肯定坚守底线的。
+明天就出结果了,当然我还是认为99%是被骗了,现在又比较担心骗子还有后招,他会不会继续借钱。
+后续:
+ +
+果然是被骗了,傻孩子,咋办啊。。。。
+后续更新:一直都没有理我,估计是认为我不够意思了。哎,心情复杂,没有什么办法,朋友没了就没了吧。
+ + +C++ Primer 阅读笔记 - 第一部分 C++基础
+ +大一学过C语言,当时学的不是很好,但是后面接触到算法竞赛的时候就慢慢补上来了,而且增加了一些C++特性以及STL标准模板库,也靠着半吊子C++拿了一些小奖,但是确实没有系统的学过C++。总之听说C++比较难,这次准备半系统性的学习一下。之前会的东西就做做题简单过一下,不会的重点看,尤其是指针和面向对象方面。希望以后能更加得心应手地使用C++,也为后面求职打打基础。
+std::cout << "/*";
+std::cout << "*/";
+std::cout << /* "*/" *.;
+std::cout << /* "*/" /* "/*" */;前两行没问题,注释只有一边,编译运行顺利通过
+第三行注释全,但是字符串不全,缺少右边的",编译运行不能通过
+第四行两边分别有两组注释,且中间的字符串是全的,因此编译运行顺利通过
+int sum = 0,value = 0;
+while(std::cin >> value){
+ sum += value;
+}
+std::cout << sum << std::endl;读取数量不定的整数,将其加和。
+std::cin属于一种 istream对象,将其作为条件时是检测流的状态,遇到文件结束符或者无效输入时会变为无效,从而退出循环。
在Ubuntu中输入 Ctrl+D来输入一个文件结束符。
定义好的头文件:
+#ifndef SALESITEM_H
+// we're here only if SALESITEM_H has not yet been defined
+#define SALESITEM_H
+
+// Definition of Sales_item class and related functions goes here
+#include <iostream>
+#include <string>
+
+class Sales_item {
+// these declarations are explained section 7.2.1, p. 270
+// and in chapter 14, pages 557, 558, 561
+friend std::istream& operator>>(std::istream&, Sales_item&);
+friend std::ostream& operator<<(std::ostream&, const Sales_item&);
+friend bool operator<(const Sales_item&, const Sales_item&);
+friend bool
+operator==(const Sales_item&, const Sales_item&);
+public:
+ // constructors are explained in section 7.1.4, pages 262 - 265
+ // default constructor needed to initialize members of built-in type
+ Sales_item() = default;
+ Sales_item(const std::string &book): bookNo(book) { }
+ Sales_item(std::istream &is) { is >> *this; }
+public:
+ // operations on Sales_item objects
+ // member binary operator: left-hand operand bound to implicit this pointer
+ Sales_item& operator+=(const Sales_item&);
+
+ // operations on Sales_item objects
+ std::string isbn() const { return bookNo; }
+ double avg_price() const;
+// private members as before
+private:
+ std::string bookNo; // implicitly initialized to the empty string
+ unsigned units_sold = 0; // explicitly initialized
+ double revenue = 0.0;
+};
+
+// used in chapter 10
+inline
+bool compareIsbn(const Sales_item &lhs, const Sales_item &rhs)
+{ return lhs.isbn() == rhs.isbn(); }
+
+// nonmember binary operator: must declare a parameter for each operand
+Sales_item operator+(const Sales_item&, const Sales_item&);
+
+inline bool
+operator==(const Sales_item &lhs, const Sales_item &rhs)
+{
+ // must be made a friend of Sales_item
+ return lhs.units_sold == rhs.units_sold &&
+ lhs.revenue == rhs.revenue &&
+ lhs.isbn() == rhs.isbn();
+}
+
+inline bool
+operator!=(const Sales_item &lhs, const Sales_item &rhs)
+{
+ return !(lhs == rhs); // != defined in terms of operator==
+}
+
+// assumes that both objects refer to the same ISBN
+Sales_item& Sales_item::operator+=(const Sales_item& rhs)
+{
+ units_sold += rhs.units_sold;
+ revenue += rhs.revenue;
+ return *this;
+}
+
+// assumes that both objects refer to the same ISBN
+Sales_item
+operator+(const Sales_item& lhs, const Sales_item& rhs)
+{
+ Sales_item ret(lhs); // copy (|lhs|) into a local object that we'll return
+ ret += rhs; // add in the contents of (|rhs|)
+ return ret; // return (|ret|) by value
+}
+
+std::istream&
+operator>>(std::istream& in, Sales_item& s)
+{
+ double price;
+ in >> s.bookNo >> s.units_sold >> price;
+ // check that the inputs succeeded
+ if (in)
+ s.revenue = s.units_sold * price;
+ else
+ s = Sales_item(); // input failed: reset object to default state
+ return in;
+}
+
+std::ostream&
+operator<<(std::ostream& out, const Sales_item& s)
+{
+ out << s.isbn() << " " << s.units_sold << " "
+ << s.revenue << " " << s.avg_price();
+ return out;
+}
+
+double Sales_item::avg_price() const
+{
+ if (units_sold)
+ return revenue/units_sold;
+ else
+ return 0;
+}
+#endif
+暂时不用怎么管,先试着使用:
+Sales_item book; // 创建一个对象
+std::cin >> book;
+std::cout << book << std::endl;
+return 0;0-201-70353-x 4 24.99
+> 0-201-70353-x 4 99.96 24.99Sales_item book1,book2; // 创建一个对象
+std::cin >> book1 >> book2;
+std::cout << book1+book2 << std::endl;
+return 0;0-201-70353-x 3 20.00
+0-201-70353-x 2 25.00
+> 0-201-70353-x 5 110 22Sales_item book1,book2; // 创建一个对象
+std::cin >> book1 >> book2;
+if(book1.isbn() == book2.isbn()){
+ std::cout << book1+book2 << std::endl;
+}
+else{
+ std::cerr << "Error!" << std::endl;
+}
+return 0;0-201-70353-x 3 20.00
+0-201-70343-x 2 25.00
+> Error!#include <bits/stdc++.h>
+#include "Sales_item.h"
+int main(void){
+ Sales_item total;
+ if(std::cin >> total){ // 读取第一条数据,确保有数据可以处理
+ Sales_item trans;
+ while(std::cin >> trans){
+ if(total.isbn() == trans.isbn()){
+ total += trans;
+ }
+ else{
+ std::cout << total << std::endl;
+ total = trans;
+ }
+ }
+ std::cout << total << std::endl; // 打印最后一本书
+ }
+ else{
+ std::cerr << "No data!" << std::endl;
+ }
+ return 0;
+}0-201-70353-X 4 24.99
+0-201-82470-1 4 45.39
+0-201-88954-4 2 15.00
+0-201-88954-4 5 12.00
+0-201-88954-4 7 12.00
+0-201-88954-4 2 12.00
+0-399-82477-1 2 45.39
+0-399-82477-1 3 45.39
+0-201-78345-X 3 20.00
+0-201-78345-X 2 25.00
+>
+0-201-70353-X 4 99.96 24.99
+0-201-82470-1 4 181.56 45.39
+0-201-88954-4 16 198 12.375
+0-399-82477-1 5 226.95 45.39
+0-201-78345-X 5 110 22这个程序的局限性在于,必须是连号的输入,不连号的输入就失效了。
+当然这个时候学到的还不多,后面会将这个程序继续完善。
+整型可以分为带符号类型和无符号类型(在前面添加 unsigned)
选择类型的原则:
+创建变量时赋予其一个初始值(赋值指的是将对象的当前值用一个新值来替代,含义不同)
+初始化的4种方式:
+int a = 0;int a = {0};int a{0}; // 列表初始化int a(0);变量声明:“一个文件如果想使用别处定义的名字,必须包含对那个名字的声明”
+与定义的区别在于不赋初值
+extern int i;
如:
+int a = 0;
+int main(void){
+ std::cout << a << std::endl;
+ int a = 1;
+ std::cout << a << std::endl;
+ std::cout << ::a << std::endl; // 显式指定访问全局变量
+ return 0;
+}0
+1
+0相当于为对象起一个另外的名字,通过 &符号来定义
int ival = 1024;
+int &refVal = ival;引用必须初始化,因为引用需要和它的初始化对象一起绑定在一起,不能重新绑定到其他对象。
+定义引用之后,对其进行的所有操作都是在它的绑定对象上进行的
+refVal = 12;
+std::cout << refVal << std::endl;12引用本身不是一个对象,不能定义引用的引用
+如下面的方式,实际上是绑定到了该引用对应的绑定对象上:
+int &refVal2 = refVal;
+std::cout << refVal2 << std::endl;12引用的类型要与绑定的对象严格匹配
+引用不能绑定到字面值上
+指针也实现了对其他对象的间接访问,但是指针本身也是一个对象,通过 *符号来定义
&int ival = 42;
+int *p = &ival;指针的类型也要与它所指向的对象严格匹配
+*来访问这个对象int ival = 42;
+int *p = &ival;
+std::cout << *p << std::endl;42符号的多重含义:
+int i = 42;
+int &r = i; // &随类型名出现,是声明的一部分,r是一个引用
+int *p; // *随类型名出现,是声明的一部分,p是一个指针
+p = &i; // &出现在表达式中,是一个取地址符
+*p = i; // *出现在表达式中,是一个解引用符
+int &r2 = *p; // r2是一个引用,*是一个解引用符
+std::cout << i << std::endl << r << std::endl << *p << std::endl << r2 << std::endl;42
+42
+42
+42空指针:int *p1 = nullptr
建议:初始化所有的指针
+指针与引用不同,是可以赋值的。赋值的时候永远改变的是等号左侧的对象。
+void*指针,可以用于存放任意类型对象的地址
double obj = 3.14;
+double *pd = &obj;
+void *pv = &obj;
+pv = pd;
+std::cout << *pv << std::endl;error: ‘void*’ is not a pointer-to-object typevoid*指针只能与其他指针作比较,作为函数的输入和输出,或者赋值给另外一个 void*指针。
甚至连访问对象都不可以
+指向指针的指针
+int ival = 1024;
+int *pi = &ival;
+int **ppi = π
+std::cout << ival << std::endl;
+std::cout << *pi << std::endl;
+std::cout << **ppi << std::endl;1024
+1024
+1024指向指针的引用
+int i = 42;
+int *p;
+int *&r = p;
+r = &i; // p = &i;
+std::cout << i << std::endl;
+std::cout << *r << std::endl;
+std::cout << *p << std::endl;42
+42
+42阅读定义要从右往左,离变量名最近的符号对变量类型有最直接的影响
+最近的是 &,因此 r是一个引用
然后是 *,说明 r引用的是一个指针
const对象一旦创建,值不可以再改变,因此在创建的时候必须初始化
const int a = 45;
只能在 const类型的对象上执行不改变其内容的操作
可以添加extern关键字,使const变量在文件间共享
+extern const int bufSize = fcn(); // file.cpp定义并初始化了这个常量,可以被其他文件访问
+extern const int bufSize; // file.h 和上面的变量是同一个,只是一个声明,说明定义会在其他地方出现const的引用是对常量的引用,不能改变引用的值,引用的时候也要添加 const限定符
const int ci = 1024;
+const int &r1 = ci;初始化常量引用时可以使用任意的表达式,只要表达式的结果能转化成引用的类型即可
+int i = 42;
+const int &r1 = i;
+const int &r2 = 42;
+const int &r3 = r1 * 2;
+std::cout << r1 << std::endl;
+std::cout << r2 << std::endl;
+std::cout << r3 << std::endl;
+i = 56;
+std::cout << r1 << std::endl;
+std::cout << r2 << std::endl;
+std::cout << r3 << std::endl;42
+42
+84
+56
+42
+84因此,对 const的引用可以并非一个 const的对象,不能通过这种引用改变被引用的对象的值,但是可以通过其他方式改变这个对象的值
指向常量的指针也不能用于改变其所指对象的值,且指向常量的指针所指的对象也不一定是一个常量
+const double pi = 3.14;
+const double *cptr = &pi
+std::cout << *cptr << std::endl;
+double dval = 3.14;
+cptr = &dval;
+std::cout << *cptr << std::endl;3.14
+3.14const指针:将指针本身定义为常量,也就是指针所指的地址不变
int errNumb = 0;
+int *const curErr = &errNumb; // curErr将一直指向errNumb,不能改变
+const double pi = 3.14159;
+const double *const pip = &pi // 一个指向常量对象的常量指针
+*curErr = 56;
+std::cout << errNumb << std::endl;56指针所指的地址不变,但是如果指向的不是常量,还是可以改变指向的值的
+顶层 const可以表示任意的对象是一个常量,底层 const与复合类型有关,指的是下一层对象是常量。
常量表达式:值不会改变且在编译过程就能得到计算结果的表达式
+将变量声明为 constexpr来由编译器验证是否为一个常量表达式:constexpr int limit = mf + 1;
在 constexpr中如果声明了一个指针,那么一定是常量指针,即顶层 const
类型别名的两种定义方式:
+typedef double wages;
+using wages = double;如果别名是一个复合类型,不能仅仅将其替换进行理解。
+auto类型:将类型交给编译器自己去分析,一般会忽略掉顶层 const,如果需要保留要加 const auto进行推断
decltype类型指示符:通过表达式的类型推断出要定义的变量的类型
const int a = 0,b = 0;
+decltype(a+b) x = 0;
+std::cout << x << std::endl;0如果希望得到引用类型,可以添加两层括号,即 decltype((a+b))
struct Sales_data{
+ std::string bookNo;
+ unsigned units_sold = 0;
+ double revenue = 0.0;
+};读取单价和数量,输出总价格
+Sales_item book; // 创建一个对象
+std::cin >> book;
+std::cout << book << std::endl;
+return 0;0-201-70353-x 4 24.99
+> 0-201-70353-x 4 99.96 24.99头文件:包含只能被定义一起的实体
+通过头文件保护符来确保不允许重复包含:
+#ifndef SALES_DATA_H
+#define SALES_DATA_H
+#include <string>
+struct Sales_data{
+ std::string bookNo;
+ unsigned units_sold = 0;
+ double revenue = 0.0;
+};
+#endifusing声明:使用命名空间中的成员
using std::cin;头文件不应包含 using声明
string s1;
+string s2(s1); // string s2 = s1;
+string s3("value"); // string s3 = "value";
+string s4(10,'c');
+cout << s1 << endl;
+cout << s2 << endl;
+cout << s3 << endl;
+cout << s4 << endl;
+
+value
+cccccccccc初始化分为直接初始化和拷贝初始化,有 =的为拷贝初始化,一般只用于单个初始值的情况下
输入输出与对整数等的操作相同
+使用getline读入一整行(可以带空格)
+string line;
+while(getline(cin,line)){
+ cout << line << endl;
+}
+return 0;> fds fdsfdsf dsf
+fds fdsfdsf dsf
+> dsfdsfdsfds fdsfds
+dsfdsfdsfds fdsfdsstring.size()返回的是无符号整形数,不要去负数值混用
字面值不为字符串,不能将字面值相加,只能将字符串相加,如 "df"+"fdsfs"是不合法的
基于范围的 for语句:遍历给定序列中的每一个元素
string str("some string");
+for (auto c : str){
+ cout << c;
+}
+cout << endl;some string如果要改变字符,需要使用引用类型:
+string str("some string");
+for (auto &c : str){
+ c = toupper(c);
+}
+cout << str << endl;SOME STRINGvector属于一个类模板,模板不是类或者函数,但是可以看作编译器生成类或函数编写的一份说明,编译器根据模板创建类或函数的过程称为实例化。
vector<int> ivec;
+vector<int> ivec2(ivec);
+vector<int> ivec3 = ivec;
+vector<string> articles{"a","an","the"};
+vector<string> svec(10,"hi");
+for(auto i : svec){
+ cout << i << " ";
+}
+cout << endl;hi hi hi hi hi hi hi hi hi hi值初始化:只初始化 vector的大小,不赋值具体数值 vector<int> i(10)
vector在设计上事先指定容量是不好的做法,比较适合运行时再添加具体的值
循环内部如果包含向 vector添加元素的语句,不能使用范围 for循环
不能用下标形式添加元素,也就是下标操作只能对确知已经存在的元素进行
+vector<int> vi = {1,2,4,5,7,8,9,5,6,4};
+for(auto it1 = vi.begin();it1 != vi.end();it1++){
+ *it1 *= 2;
+}
+for(auto it2 = vi.cbegin();it2 != vi.cend();it2++){
+ cout << *it2 << " ";
+}
+cout << endl;2 4 8 10 14 16 18 10 12 8int a2[] = {0,1,2};
+int a3[5] = {1,2,4}; // 多余的初始化成默认值
+char a4[8] = "Daniel"; // 至少是7,要有一个空字符
+for (auto i: a3){
+ cout << i << " ";
+}
+cout << endl;
+for (auto i: a4){
+ cout << i << " ";
+}
+cout << endl;1 2 4 0 0
+D a n i e l数组不允许拷贝和赋值
+复杂的数组声明:
+int *ptrs[10]; // 含有10个整型指针的数组
+int arr[10];
+int (*Parray)[10] = &arr; // Parray指向一个含有10个整数的数组
+int (&arrRef)[10] = arr; // arrRef引用一个含有10个整数的数组
+int *(&arry)[10] = ptrs; // arry是数组的引用,该数组含有10个指针使用数组的时候编译器一般将其转化为指针
+string nums[] = {"one","two","three"};
+string *p = &nums[0]; // p指向nums的第1个元素
+string *p2 = nums // 等价于上面的语句使用 auto推断时会返回一个指针,但是只用 decltype推断的时候会返回数组
利用指针对数组可以起到迭代器的效果
+int ia[] = {1,2,3,4,5,6,7,8,9};
+int *beg = begin(ia); // 指向ia的第一个元素
+int *last = end(ia); // 指向ia的最后一个元素的下一个位置
+for(auto it = beg;it != last;it++){
+ cout << *it << " ";
+}
+cout << endl;string转化为C风格字符串
string s("Hello World!");
+const char *str = s.c_str();
+cout << *str << endl;使用数组初始化vector
+int int_arr[] = {0,1,2,3,4,5};
+vector<int> ivec(begin(int_arr),end(int_arr));
+for(auto it : ivec){
+ cout << it << " ";
+}
+cout << endl;0 1 2 3 4 5int ia[3][4] = {{1,2,3,4},{5,6,7,8},{9,10,11,12}};
+int (*p)[4] = ia; // p指向含有4个整数的数组
+p = &ia[2]; // p 指向ia的尾元素
+for(auto p = ia;p != ia+3;++p){
+ for(auto q = *p;q != *p+4;q++){
+ cout << *q << " ";
+ }
+}
+cout << endl;
+for(auto p = begin(ia);p != end(ia);++p){
+ for(auto q = begin(*p);q != end(*p);q++){
+ cout << *q << " ";
+ }
+}
+cout << endl;通俗的讲,左值就是能够出现在赋值符号左面的东西,而右值就是那些可以出现在赋值符号右面的东西.
+左值:指表达式结束后依然存在的持久对象,可以取地址,具名变量或对象
+右值:表达式结束后就不再存在的临时对象,不可以取地址,没有名字。
+当一个对象被用作右值的时候,使用的是对象的值(内容);当一个对象被用作左值的时候,用的是对象的身份(在内存中的位置)
+m%n的符号与 m相同
强制类型转换:
+int i = 52;
+int j = 9;
+double slope = static_cast<double>(j) / i;
+cout << slope << endl;0.173077switch语句:
int a;
+while(cin >> a){
+ switch(a){
+ case 0: cout << '1' << endl;break;
+ case 1: cout << '2' << endl;break;
+ case 2: cout << '3' << endl;break;
+ case 3: cout << '4' << endl;break;
+ case 4: cout << '5' << endl;break;
+ case 5: cout << '6' << endl;break;
+ case 6: cout << '7' << endl;break;
+ case 7: cout << '8' << endl;break;
+ case 8: cout << '9' << endl;break;
+ case 9: cout << '0' << endl;break;
+ default: cout << 'N' << endl;break;
+ }
+}> 0
+1
+> 9
+0
+> 45
+Ntry语句块和异常处理:
throw语句抛出异常:
int a = 1;
+throw runtime_error("fdsdfds");terminate called after throwing an instance of 'std::runtime_error'
+ what(): fdsdfds
+Abortedcatch语句捕捉异常:
double m, n;
+cin >> m >> n;
+try {
+ if (n == 0)
+ throw - 1; //抛出整型异常
+ else if (m == 0)
+ throw - 1.0; //拋出 double 型异常
+ else
+ cout << m / n << endl;
+}
+catch (double d) {
+ cout << "catch (double)" << d << endl;
+}
+catch (...) {
+ cout << "catch (...)" << endl;
+}> 0 6
+catch (double)-1
+> 6 0
+catch (...)局部静态对象:程序第一次经过时被初始化,直到程序终止时才被销毁。
+int count_calls(){
+ static int ctr = -1;
+ return ++ctr;
+}
+
+int main(void){
+ for(int i = 0;i != 10; ++i){
+ cout << count_calls() << " ";
+ }
+ cout << endl;
+ return 0;
+}0 1 2 3 4 5 6 7 8 9函数声明(函数原型):在使用函数之前对函数的名字进行声明
+函数声明可以忽略形参的名字,也可以加上形参的名字。
+函数声明最好写在头文件中
+分离式编译:编译和链接多个源文件
+指针形参:
+void reset(int *ip){
+ *ip = 0;
+}
+
+int main(void){
+ int i = 42;
+ reset(&i);
+ cout << i << endl;
+ return 0;
+}0传引用参数:
+void reset(int &i){
+ i = 0;
+}
+
+int main(void){
+ int i = 42;
+ reset(i);
+ cout << i << endl;
+ return 0;
+}0尽量使用引用形式从而避免拷贝
+还可以通过引用形式返回一些额外信息。因为函数只能返回一个返回值,但是如果某个值是引用的形式传到函数中的,也会保留下修改后的值。
+不修改的变量尽量使用常量引用
+数组形参:
+void Print(const int i[]){
+ cout << i[0] << endl;
+}
+
+void Print(const int *i){
+ cout << i[0] << endl;
+}
+
+void Print(const int i[10]){
+ cout << i[0] << endl;
+}
+
+int main(void){
+ int i = 5;
+ int j[2] = {6,7};
+ Print(&i);
+ Print(j);
+}5
+6数组不能直接进行传递,直接作为指针的形式传递,因此丢掉了数组大小的信息
+可以使用指针的形式进行提示,也可以传入一个表示数组大小的参数。
+void print(const int *beg,const int *end){
+ while(beg != end){
+ cout << *beg++ << " ";
+ }
+}
+
+void print(const int i[] ,size_t size){
+ for(size_t a=0;a<size;a++){
+ cout << i[a] << " ";
+ }
+}
+
+int main(void){
+ int i[10] = {6,7,5,4,7,8,9,6,5,4};
+ print(begin(i),end(i));
+ cout << endl;
+ return 0;
+}6 7 5 4 7 8 9 6 5 4数组引用形参:(缺点是只能作用于大小固定的数组)
+void print(int (&arr)[10]){
+ for(auto elem : arr){
+ cout << elem << " ";
+ }
+}含有可变形参的函数:
+void error_msg(initializer_list<string> il){
+ for(auto beg = il.begin();beg != il.end();++beg){
+ cout << *beg << " ";
+ }
+ cout << endl;
+}
+
+int main(void){
+ error_msg({"a","b"});
+ error_msg({"a","b","c"});
+}a b
+a b c函数返回时不要返回局部对象的引用或指针
+调用一个返回引用的函数会得到左值
+char &get_val(string &str,string::size_type ix){
+ return str[ix];
+}
+
+int main(void){
+ string s("a value");
+ cout << s << endl;
+ get_val(s,0) = 'A';
+ cout << s << endl;
+ return 0;
+}a value
+A value返回值也可以是一个花括号包围起来的列表
+定义相同名称的函数,但是形参列表不同,可能是数量上的不同,也可能是类型上的不同。使得函数调用的时候根据不同的形参列表自动判断指定哪一个函数。
+顶层 const不影响传入的参数
在不同的作用域中无法重载函数,会覆盖掉
+默认实参:在函数的声明中给一个默认值,调用时可以覆盖掉,也可以不写以使用默认值。
+内联函数:将函数在调用点展开,但是编译器不一定支持
+constexpr函数:能用于常量表达式的函数,函数的返回值和所有形参的类型都要是字面值类型,函数体中有且只有一条 return语句。
assert表达式:用于调试的时候对程序进行检查 assert(s == "dfdsf");如果不满足条件程序会中断退出。
完全不明白。。。没有示例程序看不懂
+成员函数是类定义的一部分,通过特定的对象来调用。非成员函数就是普通的函数。
+成员函数的声明必须在类的内部,定义可以在类的内部或者外部。非成员函数的声明和定义都在类的外部。
+构造函数:控制对象的初始化过程
+访问控制与封装:
+定义在public说明符后的成员在整个程序内可被访问,public成员定义类的接口。
+定义在private说明符之后的成员可以被类的成员函数访问,但是不能被使用该类的代码访问,private部分封装了类的实现细节。
+使用class和struct定义类的区别在于默认的访问权限不同,struct默认访问权限都是public的
+友元:令其他类或成员成为访问它的非公有成员。但是友元只算一个权限控制,在类外一样要进行声明。
+上述代码:
+#include <bits/stdc++.h>
+using std::string;
+using std::vector;
+using std::cin;
+using std::cout;
+using std::endl;
+using std::begin;
+using std::end;
+using std::runtime_error;
+using std::initializer_list;
+using std::istream;
+using std::ostream;
+
+class Sales_data{
+friend Sales_data add(const Sales_data&,const Sales_data&);
+friend std::ostream &print(std::ostream&,const Sales_data&);
+friend std::istream &read(std::istream&,Sales_data&);
+public:
+ // 构造函数
+ Sales_data() = default; // 默认构造函数
+ // 构造函数初始值列表
+ Sales_data(const std::string &s):bookNo(s){ }
+ Sales_data(const std::string &s,unsigned n,double p):bookNo(s),units_sold(n),revenue(p*n){ }
+ Sales_data(std::istream &);
+ // 常量成员函数
+ std::string isbn() const {
+ return bookNo;
+ }
+ Sales_data &combine(const Sales_data&);
+private:
+ double avg_price() const;
+ std::string bookNo;
+ unsigned units_sold = 0;
+ double revenue = 0.0;
+};
+Sales_data add(const Sales_data&,const Sales_data&);
+std::ostream &print(std::ostream&,const Sales_data&);
+std::istream &read(std::istream&,Sales_data&);
+
+
+// 在类的外部定义成员函数
+double Sales_data::avg_price() const {
+ if(units_sold){
+ return revenue / units_sold;
+ }
+ else{
+ return 0;
+ }
+}
+
+// 定义一个返回this对象的函数
+Sales_data& Sales_data::combine(const Sales_data &rhs){
+ units_sold += rhs.units_sold;
+ revenue += rhs.revenue;
+ return *this;
+}
+
+// 类相关的非成员函数
+istream &read(istream &is, Sales_data &item){
+ double price = 0;
+ is >> item.bookNo >> item.units_sold >> price;
+ item.revenue = price * item.units_sold;
+ return is;
+}
+
+ostream &print(ostream &os,const Sales_data &item){
+ os << item.isbn() << " " << item.units_sold << " " << item.revenue << " " << item.avg_price();
+ return os;
+}
+
+Sales_data add(const Sales_data &lhs,const Sales_data &rhs){
+ Sales_data sum = lhs;
+ sum.combine(rhs);
+ return sum;
+}
+
+// 在类的外部定义构造函数
+Sales_data::Sales_data(std::istream &is){
+ read(is,*this);
+}
+
+int main(void){
+ return 0;
+}
+
+inline写在类内或者类外,一般写在类外const里面也可以变化class Screen{
+ public:
+ typedef std::string::size_type pos; // 定义类型的成员
+ Screen() = default;
+ Screen(pos ht,pos wd,char c): height(ht), width(wd),contents(ht*wd,c){ }
+ char get() const {
+ return contents[cursor]; // 隐式内联函数
+ };
+ inline char get(pos ht,pos wd) const; // 显式内联函数
+ Screen &move(pos r, pos c); // 后面设置为内联函数
+ size_t some_member() const;
+ Screen &set(char);
+ Screen &set(pos,pos,char);
+ Screen &display(std::ostream &os){
+ do_display(os);
+ return *this;
+ }
+ const Screen &display(std::ostream &os) const {
+ do_display(os);
+ return *this;
+ }
+ private:
+ pos cursor = 0;
+ pos height = 0,width = 0;
+ std::string contents;
+ mutable size_t access_ctr = 0;
+ void do_display(std::ostream &os) const {
+ os << contents;
+ }
+};
+
+inline Screen &Screen::move(pos r,pos c){
+ pos row = r * width;
+ cursor = row + c;
+ return *this;
+}
+
+char Screen::get(pos r,pos c) const {
+ pos row = r * width;
+ return contents[row + c];
+}
+
+size_t Screen::some_member() const{
+ ++access_ctr;
+ return access_ctr;
+}
+
+inline Screen &Screen::set(char c){
+ contents[cursor] = c;
+ return *this;
+}
+
+inline Screen &Screen::set(pos r,pos col,char ch){
+ contents[r*width+col] = ch;
+ return *this;
+}
+
+// 类数据成员的初始值
+class Window_mgr{
+ private:
+ std::vector<Screen> screens{Screen(24,80,' ')};
+};
+
+int main(void){
+ Screen myscreen;
+ char ch = myscreen.get();
+ cout << myscreen.some_member() << endl;
+ ch = myscreen.get(0,0);
+ cout << myscreen.some_member() << endl;
+ myscreen.move(4,0);
+ myscreen.set('#');
+ cout << myscreen.get() << endl;
+ Screen myScreen(5,3,'!');
+ const Screen blank(5,3,'?');
+ myScreen.set(2,1,'#').display(cout);
+ cout << endl;
+ blank.display(cout);
+ cout << endl;
+ return 0;
+}1
+2
+#
+!!!!!!!#!!!!!!!
+???????????????类之间的友元关系:不存在传递性
+class Screen{
+ friend class Window_mgr;
+
+// 类数据成员的初始值
+class Window_mgr{
+ public:
+ using ScreenIndex = std::vector<Screen>::size_type;
+ void clear(ScreenIndex);
+ private:
+ std::vector<Screen> screens{Screen(24,80,' ')};
+};
+
+void Window_mgr::clear(ScreenIndex i){
+ Screen &s = screens[i];
+ s.contents = string(s.height * s.width, ' ');
+}class Screen{
+ friend class Window_mgr;
+ public:
+ typedef std::string::size_type pos; // 定义类型的成员
+ Screen() = default;
+ Screen(pos ht,pos wd,char c): height(ht), width(wd),contents(ht*wd,c){ }
+ char get() const {
+ return contents[cursor]; // 隐式内联函数
+ };
+ inline char get(pos ht,pos wd) const; // 显式内联函数
+ Screen &move(pos r, pos c); // 后面设置为内联函数
+ size_t some_member() const;
+ Screen &set(char);
+ Screen &set(pos,pos,char);
+ Screen &display(std::ostream &os){
+ do_display(os);
+ return *this;
+ }
+ const Screen &display(std::ostream &os) const {
+ do_display(os);
+ return *this;
+ }
+ private:
+ pos cursor = 0;
+ pos height = 0,width = 0;
+ std::string contents;
+ mutable size_t access_ctr = 0;
+ void do_display(std::ostream &os) const {
+ os << contents;
+ }
+};
+
+inline Screen &Screen::move(pos r,pos c){
+ pos row = r * width;
+ cursor = row + c;
+ return *this;
+}
+
+char Screen::get(pos r,pos c) const {
+ pos row = r * width;
+ return contents[row + c];
+}
+
+size_t Screen::some_member() const{
+ ++access_ctr;
+ return access_ctr;
+}
+
+inline Screen &Screen::set(char c){
+ contents[cursor] = c;
+ return *this;
+}
+
+inline Screen &Screen::set(pos r,pos col,char ch){
+ contents[r*width+col] = ch;
+ return *this;
+}
+
+// 类数据成员的初始值
+class Window_mgr{
+ public:
+ using ScreenIndex = std::vector<Screen>::size_type;
+ void clear(ScreenIndex);
+ ScreenIndex addScreen(const Screen&);
+ private:
+ std::vector<Screen> screens{Screen(24,80,' ')};
+};
+
+void Window_mgr::clear(ScreenIndex i){
+ Screen &s = screens[i];
+ s.contents = string(s.height * s.width, ' ');
+}
+
+Window_mgr::ScreenIndex Window_mgr::addScreen(const Screen &s){
+ screens.push_back(s);
+ return screens.size() - 1;
+}
+
+int main(void){
+ Screen myscreen;
+ char ch = myscreen.get();
+ cout << myscreen.some_member() << endl;
+ ch = myscreen.get(0,0);
+ cout << myscreen.some_member() << endl;
+ myscreen.move(4,0);
+ myscreen.set('#');
+ cout << myscreen.get() << endl;
+ Screen myScreen(5,3,'!');
+ const Screen blank(5,3,'?');
+ myScreen.set(2,1,'#').display(cout);
+ cout << endl;
+ blank.display(cout);
+ cout << endl;
+ return 0;
+}构造函数初始值列表:定义变量的时候习惯对其立即进行初始化,有时初始化的值是必不可少的,且要注意成员初始化的顺序。
+委托构造函数:使用它所属类的其他构造函数执行它自己的初始化过程
+默认构造函数
+类类型转换
+聚合类:就是比较简单的结构体
+字面值常量类
+类的静态成员存在于任何对象之外,对象中不包含任何与静态数据成员有关的数据
+ + +C++ Primer - 第二部分 C++标准库
+ +iostream定义了用于读写流的基本类型
fstream定义了读写命名文件的类型
sstream定义了读写内存 string对象的类型
用法都是完全相同的,得益于继承机制
+流的状态:
+auto old_state = cin.rdstate(); // 获取流的当前状态
+cin.clear(); // 将所有条件状态复位,将流的状态置为有效
+cin.setstate(old_state); // 根据给定的标志位对流进行复位输出缓冲:每个输出流都管理一个缓冲区,保存程序读写的数据。
+控制输出缓冲:
+cout << "hi!" << endl; // 多输出一个换行符,然后刷新缓冲区
+cout << "hi!" << flush; // 输出后直接刷新缓冲区
+cout << "hi!" << ends; // 多输出一个空字符,然后刷新缓冲区
+cout << unitbuf; // 所有输出操作后都立即刷新缓冲区
+cout << nounitbuf; // 回到正常的缓冲方式关联输入和输出流:如果某一个输入流和输出流关联,则从输入流读取的操作会对这个输出流进行刷新。
+标准库将 cout和 cin关联在一起
cin.tie(&cerr); // 将cin和cerr关联在一起ifstream in("infile");
+ofstream output("outfile");
+string s;
+while(getline(in,s)){
+ output << s << endl;
+}
+return 0;显式打开或者关闭文件流:
+ofstream output; // 空文件流对象
+output.open("outfile"); // 调用open进行关联
+output.close(); // 关闭文件流文件模式:
+ofstream output("outfile");这种方式其实隐含了以输出模式打开文件并进行截断,显式控制如下:
+ofstream output("outfile",ofstream::out | ofstream::trunc);为了保留之前的文件内容,需要显式指定 app模式
ofstream output("outfile",ofstream::out | ofstream::app);ifstream in("infile");
+ofstream output("outfile",ofstream::out | ofstream::app);
+string s;
+while(getline(in,s)){
+ string a,b,c;
+ istringstream s1(s);
+ ostringstream s2;
+ s1 >> a;
+ s2 << a;
+ s1 >> b;
+ s2 << b;
+ s1 >> c;
+ s2 << c;
+ cout << s2.str() << endl;
+}
+return 0;一个容器就是一些特定类型对象的集合,顺序容器为程序员提供了控制元素存储和访问顺序的能力。
+vector是可变大小数组,支持快速随机访问。但是在尾部之外的位置插入或者删除元素可能很慢。
deque是双端队列,支持快速随机访问,在头尾部插入或者删除元素的速度很快。
list是双向链表,只支持双向顺序访问,在 list中任意位置进行插入/删除的速度都很快
forward_list是单向链表,只支持单向顺序访问,在链表中任意位置进行插入/删除的速度都很快
array是固定大小的数组,支持快速随机访问,不能添加或者删除元素
string是与 vector相似的容器,专门用于保存字符,随机访问快,在尾部插入/删除的速度很快
顺序容器几乎可以保存任意类型的元素
+各种迭代器:
+auto it1 = a.begin(); // list<string>::iterator
+auto it2 = a.rbegin(); // list<string>::reverse_iterator
+auto it3 = a.cbegin(); // list<string>::const_iterator
+auto it4 = a.crbegin(); // list<string>::const_reverse_iterator元素的拷贝初始化:
+list<string> a = {"Milton","SHakespeare","Austen"};
+list<string> a2(a);array具有固定的大小,并且可以进行拷贝
+array<int,10> ia1 = {0,1,2,3,4,5,6,7,8,9};
+array<int,10> ia2 = ia1;使用 assign对不同但相容的类型进行赋值
list<string> names;
+vector<const char*> oldstyle;
+names.assign(oldstyle.cbegin(),oldstyle.cend());添加元素三种方法:push_front(),insert(),push_back()
新标准对应了三种直接构造元素的方法:emplace_front()、emplace()、emplace_back()
更安全的访问元素的方法:svec.at(0)
改变容器大小并使用某个元素填充更大的部分:ilist.resize(15,-1)
管理容量的成员函数:
+c.capacity(); // 不重新分配内存空间的话最多能保存多少元素
+c.reserve(n); // 分配至少能容纳n个元素的内存空间
+c.shrink_to_fit() // 请求将capacity()减小为size()一样的大小数值转换:
+int i = 42;
+string s = to_string(i);
+double d = stod(s);
+cout << s << " " << d << endl;42 42对于容器的其他操作,并没有通过定义成员函数的方式实现,而是定义一套泛型算法,实现了一些算法的公共接口。
+在容器中对值进行查找使用 find,返回查找元素的指针的位置
auto result = find(vec.cbegin(),vec.cend(),val)返回元素在容器中出现的次数:
+vector<int> a;
+int temp;
+for(int i=0;i<10;i++){
+ cin >> temp;
+ a.push_back(temp);
+}
+cin >> temp;
+auto result = count(a.cbegin(),a.cend(),temp);
+cout << result << endl;泛型算法本身不会执行容器的操作,只会运行于迭代器之上,执行迭代器的操作。
+因此泛型算法永远不会改变底层容器的大小。
+元素求和:
+vector<int> a{1,2,3,4,5,6,7,8};
+int sum = accumulate(a.cbegin(),a.cend(),0);
+cout << sum << endl;36可以推广到字符串中用来连接字符串:
+vector<int> a{1,2,3,4,5,6,7,8};
+vector<string> b{"df","fsfds","rte"};
+string sum = accumulate(b.cbegin(),b.cend(),string(""));
+cout << sum << endl;dffsfdsrte确定两个序列中保存的值是否相同(假定第二个序列至少与第一个序列一样长)
+vector<int> a{1,2,3,4,5,6,7,8};
+vector<string> b{"df","fsfds","rte"};
+vector<string> c{"df","fsfds","rte","fdsf"};
+auto sum = equal(b.cbegin(),b.cend(),c.cbegin());
+cout << sum << endl;1使用 fill和 fill_n填充元素:
vector<int> a{1,2,3,4,5,6,7,8};
+fill(a.begin(),a.end(),0);
+for(auto i : a){
+ cout << i << " ";
+}
+cout << endl;
+fill_n(a.begin(),a.size(),1);
+for(auto i : a){
+ cout << i << " ";
+}
+cout << endl;0 0 0 0 0 0 0 0
+1 1 1 1 1 1 1 1算法是不会检查写操作的,泛型算法也不能更改容器的大小。因此需要自行检查容器是否越界等问题。
+安全的方式:插入迭代器
+vector<int> a{1,2,3,4,5,6,7,8};
+vector<string> b{"df","fsfds","rte"};
+vector<string> c{"df","fsfds","rte","fdsf"};
+fill_n(back_inserter(a),10,1);
+for(auto i : a){
+ cout << i << " ";
+}
+cout << endl;1 2 3 4 5 6 7 8 1 1 1 1 1 1 1 1 1 1将 a1的内容拷贝到 a2:copy(begin(a1),end(a1),a2)
对元素进行排序去重:
+vector<string> d{"the","quick","red","fox","jumps","over","the","slow","red","turtle"};
+sort(d.begin(),d.end()); // 排序
+auto end_unique = unique(d.begin(),d.end()); // 将重复的移到末尾,并同时返回最后一个不重复的元素的后一位置
+d.erase(end_unique,d.end()); // 使用容器操作删除重复的元素(因为泛型算法无法改变容器大小)
+for(auto i : d){
+ cout << i << " ";
+}
+cout << endl;fox jumps over quick red slow the turtlelambda表达式:
一个 lambda表达式表示一个可调用的代码单元,可以理解为一个未命名的内联函数。
auto f = []{return 42;};
+cout << f() << endl;42int a = 0, b = 1;
+auto f6 = [&a, &b]{ return a + b; };
+cout << f6() << endl;1lambda表达式还有其他的一些用法。
+插入迭代器:
+back_inserter:创建一个使用 push_back的迭代器
front_inserter:创建一个使用 push_front的迭代器
inserter:创建一个使用 insert的迭代器
list<int> lst = {1,2,3,4};
+list<int> lst2 = {5,6};
+list<int> lst3 = {9,10,11};
+list<int> lst4 = {12};
+copy(lst.cbegin(),lst.cend(),front_inserter(lst2));
+for(auto i : lst2){
+ cout << i << " ";
+}
+cout << endl;
+copy(lst.cbegin(),lst.cend(),inserter(lst3,lst3.begin()));
+for(auto i : lst3){
+ cout << i << " ";
+}
+cout << endl;
+copy(lst.cbegin(),lst.cend(),back_inserter(lst4));
+for(auto i : lst4){
+ cout << i << " ";
+}
+cout << endl;4 3 2 1 5 6
+1 2 3 4 9 10 11
+12 1 2 3 4流迭代器:
+istream_iterator<int> in(cin),eof;
+cout << accumulate(in,eof,0) << endl;> 2 1 4 5 6 7 8 9
+42ostream_iterator<int> out(cout," ");
+for(int i=0;i<10;i++){
+ out = i;
+}
+cout << endl;0 1 2 3 4 5 6 7 8 9反向迭代器:
+vector<int> vi{1,2,3,4,5,6,7,8,9,10};
+for(auto i = vi.crbegin();i != vi.crend();i++){
+ cout << *i << " ";
+}
+cout << endl;10 9 8 7 6 5 4 3 2 1要注意反向迭代器真的是反的。。。比如下面的例子:
+string line = "first,middle,end";
+auto rcomma = find(line.crbegin(),line.crend(),',');
+cout << string(line.crbegin(),rcomma) << endl;
+cout << string(rcomma.base(),line.cend()) << endl;dne
+end关联容器中的元素是按关键字来保存和访问的,而顺序容器中的元素是按它们在容器中的位置来顺序保存和访问的。
+map是关键字-值对的结合
map<string,size_t> word_count;
+string word;
+while(cin >> word){
+ ++word_count[word];
+}
+for(const auto &w : word_count){
+ cout << w.first << " " << w.second << endl;
+}> a b c d e d b c
+a 1
+b 2
+c 2
+d 2
+e 1关联容器的元素都是根据关键字存储的,因此不支持位置相关的操作。
+multimap和 multiset允许相同关键字:
vector<int> vi{1,2,3,4,5,5,4,3,2,1};
+set<int> iset(vi.cbegin(),vi.cend());
+multiset<int> miset(vi.cbegin(),vi.cend());
+cout << iset.size() << " " << miset.size() << endl;关联容器的迭代器:
+vector<int> vi{1,2,3,4,5,5,4,3,2,1};
+set<int> iset(vi.cbegin(),vi.cend());
+for(auto set_it = iset.cbegin();set_it != iset.cend();set_it++){
+ cout << *set_it << " ";
+}
+cout << endl;1 2 3 4 5插入元素:
+iset.insert(8);查找元素的下标操作:
+c[k]; // 如果没有会添加,并对值进行初始化
+c.at(k); // 如果没有会抛出异常访问元素:find和 count
在 multimap中查找元素:
multimap<string,int> mi{make_pair("as",1),make_pair("as",2),make_pair("ab",2),make_pair("ac",2),make_pair("ac",5)};
+for(auto pos = mi.equal_range("as");pos.first != pos.second;++pos.first){
+ cout << pos.first->second << " ";
+}
+cout << endl;根据转换规则对文件内容进行转换:
+转换规则:
+brb be right back
+k okay?
+y why
+r are
+u you
+pic picture
+thk thanks!
+l8r later文件内容:
+where r u
+y dont u send me a pic
+k thk l8r转换代码:
+// 实际的转换工作,生成转换文本
+const string & transform(const string &s, const map<string,string> &m){
+ auto map_it = m.find(s);
+ if (map_it != m.cend()){
+ return map_it->second;
+ }
+ else{
+ return s;
+ }
+}
+
+
+// 读入给定文件,建立转换映射
+map<string,string> buildMap(ifstream &map_file){
+ map<string,string> trans_map;
+ string key,value;
+ // 读取第一个单词存入key,剩余内容存入value
+ while(map_file >> key && getline(map_file,value)){
+ if(value.size() > 1){
+ trans_map[key] = value.substr(1);
+ }
+ else{
+ throw runtime_error("No rule for " + key);
+ }
+ }
+ return trans_map;
+}
+
+int main(void){
+ ifstream map_file("rules");
+ ifstream input("text");
+ auto trans_map = buildMap(map_file); // 保存转换规则
+ string text; // 保存输入中的每一行
+ while(getline(input,text)){
+ istringstream stream(text); // 读取每个单词
+ string word;
+ bool firstword = true; // 控制是否打印空格
+ while(stream >> word){
+ if(firstword){
+ firstword = false;
+ }
+ else{
+ cout << " ";
+ }
+ cout << transform(word,trans_map);
+ }
+ cout << endl;
+ }
+ return 0;
+}输出:
+where are you
+why dont you send me a picture
+okay? thanks! later无序容器:不适用比较运算符来组织元素,而是使用哈希函数组织元素。
+一般情况下的性能要比有序容器更好,但是不能按照顺序输出。
+前面都是静态对象,由程序自动分配内存并销毁。而动态对象需要被显式进行释放。
+动态内存需要显式进行分配和释放,因此很容易忘记释放导致一些问题。因此定义了两种智能指针来管理这些动态对象,自动进行释放。
+shared_ptr<string> p1; // 指向string的shared_ptr
+shared_ptr<list<int>> p2; // 指向int的list的shared_ptr默认初始化的智能指针中保存着一个空指针。
+最安全的分配和使用动态内存的方式是调用 make_shared的标准库函数。
shared_ptr<int> p3 = make_shared<int>(42);
+shared_ptr<string> p4 = make_shared<string>(10,'9');
+shared_ptr<int> p5 = make_shared<int>();shared_ptr会自动记录有多少个其他 shared_ptr指向相同的对象,如果没有了,会自动销毁所管理的对象并自动释放相关联的内存。
离开作用域也会被销毁。如果返回这个指针,也不会被销毁(就是挺智能的)
+直接管理内存:使用 new和 delete
int *pi = new int;
+string *ps = new string(10,'9');
+const string *pcs = new const string;
+delete pi;
+delete ps;
+delete pcs;delete不会抛出任何异常,尽管可能已经释放过了,甚至有可能都不是指针也会释放,会造成一些问题。
delete还可能会造成空悬指针,因此这个 delete只提供了有限的保护。
不要混用智能指针和普通指针,不要使用 get初始化另一个智能指针或者赋值。
unique_ptr“拥有”它所指向的对象,某个时刻只能由一个 unique_ptr指向一个给定对象。销毁指针就一起销毁了。
weak_ptr指向一个 shared_ptr管理的对象,不会改变 shared_ptr的计数,计数为 0后会自动释放。
使用 new分配一个 int数组:
int *p = new int[42];实际上并没有得到一个数组类型的对象,而是得到一个数据元素类型的指针。
+动态分配并初始化数组:
+int *pia3 = new int[10]{0,1,2,3,4,5,6,7,8,9};动态分配的数组的大小可以为0,会返回一个类似于尾后迭代器的指针。
+释放动态数组:delete [] p
智能指针管理动态数组:
+unique_ptr<int[]> up(new int[10]);
+for(size_t i = 0;i != 10;++i){
+ up[i] = i;
+}
+up.release();allocator将内存分配和对象构造分离开来,提供一种类型感知的内存分配方法。
int n = 5;
+allocator<string> alloc;
+auto const p = alloc.allocate(n);这个 allocator为5个 string分配了内存
在内存中构造对象:
+auto q = p;
+alloc.construct(q++,"hi");
+cout << *p << endl;hi在一个给定文件中查询单词,最终返回单词在文件中出现的次数及其所在行的列表。
+ + +开学第一周,或者算是第二周,开学但是没有任何课程,也没有什么活动,开了一次班会,然后一个学院的开学典礼。新认识的人呢,也就一个室友+之前室友的同学,也就寥寥几人,同一个套间住着的人几乎都不认识。这几天就一直有些不太舒服,写些文字简单发泄一下。
+总的来说,这里确实是一群学霸。首先可以拿我室友来说,早上7点起床,晚上11点左右睡觉,几乎每时每刻都在看论文做实验,甚至在看比赛的过程中间也会去看论文。他的目标就是要发文章,发一篇顶会文章,因此现在在努力完成这个目标。之后的方向他还没有想好,可能出国或者找音频算法相关的工作。其次是图书馆的同学们,才开学没有几天,图书馆就已经爆满了。大家都是思维缜密且有计划的人,昨天一窝蜂去抢机房,抢各种台式电脑去选课,选过课后去找相关的书籍,这在之前都是我的标准操作,在这里却被其他人不断模仿甚至比我做的更好。我有一种压力感,同时也有一种恐惧。
+我的内心真的很脆弱。感觉其他人都还很适应的,我表面上也是这样,但是内心里已经稍稍有点崩溃了。我不禁回想我本科阶段,如果我高考真的考的好了,去了一些顶级985的学校,那么我是会坚持住学下去拼下去,还是会基本上崩溃掉,完全没有任何的竞争实力了呢?或许去了中南大学,并不是考的不好,而是帮我减轻了同龄人的压力。现在研究生的阶段,我是真真正正感受到了同龄人的压力。这么多优秀的人当中,我又能排到一个什么水平?如果真的在各个方面都比不上别人,我会不会崩溃呢?这些都是我现在所担心的。
+其实换个角度来想,我没有必要去和任何人去比较。大家的人生道路都是不一样的,也无所谓好与不好,只是适不适合,以及过的是否开心罢了。对于我现在来说,虽然我知道不要去和其他人比较,总有人比你更强,比你过的更好。但是我还是时不时会看看想想别人现在在做什么,看看别人取得的成就,想想自己有没有可能赶得上甚至超过。这样就造成了现在每一天都非常不开心,学习也没有什么动力,学到后面甚至有一点混时间的感觉。这种想法困扰了我很长的一段时间,目前仍然在困扰着我。
+我现在能做的,就是找准自己的目标,制定好计划,坚定不移地实施下去。至于我脆弱的内心,慢慢调解吧。没有人能帮助我,最后能靠得住的只有我自己。
+ + +学习计划
+ +1. C++初步了解与练习(2022年8月-2022年9月)#6f42c1
+2. 面试算法题重做,加深理解,记录笔记(2022年9月-2022年10月)#777
+3. 确定研究方向和实习面试岗位方向(2022年10月-2022年11月)#5cb85c
+4. 实习面试(2022年12月-2023年1月)#d9534f
+5. 上课+复习+考试(尽量考好一点)(2022年9月-2023年1月)#f0ad4e
+6. 根据本科毕设尝试发论文(2022年9月-2022年10月)#428bca
+7. 竞赛初步尝试(2022年9月-2023年1月)#3c4858
+8. 其他计划(2022年9月-2023年1月)#ffc0cb
+1. C++练习(在算法题中练习+额外知识补充)
+2. Leetcode 101练习,加深理解,记录笔记
+3. 上课(充分利用课堂时间弄懂,拒绝耽误课后太长时间)
+4. 根据本科毕设尝试发论文(与师兄和导师了解目前情况)
+5. 竞赛初步尝试(学习、练习为重点)
+周总结(第2教学周):
+周总结(第3教学周):
+周总结(第4教学周):
+周总结(第5教学周):
+周总结(第6教学周):
+1. 面试算法题重做(重点代码随想录),加深理解,记录笔记
+2. 确定研究方向和实习面试岗位方向,首先确定到底是算法还是开发
+3. 上课+预习+各种大作业+复习,拒绝耽误课后大量时间
+4. 竞赛初步尝试(练习为重点)
+周总结(第7教学周):
+周总结(第8教学周):
+周总结(第9教学周):
+周总结(第10教学周):
+1. 面试算法题重做,加深理解,记录笔记,重点代码随想录一定要完成
+2. 确定研究方向和实习面试岗位方向,多问问人,问问同龄人和学长学姐,克服社恐
+3. 上课+复习+考试,应该只有信息检索(尽量考好一点)
+4. 小样本分类竞赛,再多跑一跑,争取进前十
+5. Go后端学习,不仅仅是Go这一门语言,对整个后端的知识要有体系,以面试为目的进行准备
+周总结(第11教学周):
+周总结(第12教学周):
+周总结(第13教学周):
+周总结(第14教学周):
+周总结(第15教学周):
+1. 完成代码随想录,回顾前面做过的题目,做一些没有在讲解中的题目检验学习成果
+2. 上课+复习+考试,不要耽误太长时间,但是要稳步推进复习
+3. 后端知识学习,学习八股文的资料,对整个后端的知识要有体系,以面试为目的进行准备
+4. 实习面试,克服恐惧,迎难而上
+周总结(第16教学周):
+周总结(第17教学周):
+周总结(第18教学周):
+周总结(第19教学周):
+周总结(第20教学周):
+回顾刚上研一定下的计划,看看完成情况:
+1. C++初步了解与练习(2022年8月-2022年9月)
+完成情况★★★
+C++了解还是不太够,不过算法题使用C++过了一遍
+2. 面试算法题重做,加深理解,记录笔记(2022年9月-2022年10月)
+完成情况★★★★
+算法题重做了大概两遍,第一遍是C++,第二遍是Go,现在有一些找到方法了
+3. 确定研究方向和实习面试岗位方向(2022年10月-2022年11月)
+完成情况★★★★★
+确定了目前的目标是Go后端开发相关
+4. 实习面试(2022年12月-2023年1月)
+完成情况★★★★
+实习面试推荐稍慢,不过最终还是成功找到理想的岗位
+5. 上课+复习+考试(尽量考好一点)(2022年9月-2023年1月)
+完成情况★★★★★
+考试还不错,在周围人中间也算考的最好的了
+6. 根据本科毕设尝试发论文(2022年9月-2022年10月)
+完成情况★
+不能找老师,暂时不要在论文上耽误时间,研二再看
+7. 竞赛初步尝试(2022年9月-2023年1月)
+完成情况★★★★★
+在室友大佬的加持下还拿了一个比较好的奖项,又丰富了算法的简历
+ + +Leetcode 刷题笔记-Leetcode 101 第2章 贪心算法
+ +贪心算法或贪心思想采用贪心的策略,保证每次操作都是局部最优的,从而使最后得到的结果是全局最优的。
+有一群孩子和一堆饼干,每个孩子有一个饥饿度,每个饼干都有一个大小。每个孩子只能吃一个饼干,且只有饼干的大小不小于孩子的饥饿度时,这个孩子才能吃饱。求解最多有多少孩子可以吃饱。
+class Solution {
+public:
+ int findContentChildren(vector<int>& g, vector<int>& s) {
+ sort(g.begin(),g.end());
+ sort(s.begin(),s.end());
+ int childrenCount = 0;
+ for(size_t i = 0;i<s.size() && childrenCount < g.size();i++){
+ if(s[i] >= g[childrenCount]){
+ ++childrenCount;
+ }
+ }
+ return childrenCount;
+ }
+};分析:用最小大小的饼干 (s)去满足最小饥饿度的孩子 (g),一直满足到饥饿度最大的孩子,相当于双指针的移动。
贪心策略是给剩余孩子里最小饥饿度的孩子分配最小的能饱腹的饼干。
+错误:忘记检查g是否越界,可能发生所有饼干都能满足所有孩子,然而饼干还剩着的情况。下标运算一定要确认是否越界。
+一群孩子站成一排,每一个孩子有自己的评分。现在需要给这些孩子发糖果,规则是如果一个孩子的评分比自己身旁的一个孩子要高,那么这个孩子就必须得到比身旁孩子更多的糖果;所有孩子至少要有一个糖果。求解最少需要多少个糖果。
+class Solution {
+public:
+ int candy(vector<int>& ratings) {
+ vector<int> candyNum(ratings.size(),1);
+ for(size_t i = 0;i<ratings.size()-1;++i){
+ if(ratings[i+1] > ratings[i] && candyNum[i+1] <= candyNum[i]){
+ candyNum[i+1] = candyNum[i] + 1;
+ }
+ }
+ for(size_t i = ratings.size()-1;i>0;--i){
+ if(ratings[i-1] > ratings[i] && candyNum[i-1] <= candyNum[i]){
+ candyNum[i-1] = candyNum[i] + 1;
+ }
+ }
+ return accumulate(candyNum.cbegin(),candyNum.cend(),0);
+ }
+};分析:首先至少有一个糖果分配好,然后从左向右扫一遍,如果右边的孩子评分高,则右边孩子的糖果=左边孩子的糖果+1,再从右往左扫一遍,如果左边的孩子评分高,则左边孩子的糖果=右边孩子的糖果+1。最后求和即可。
+贪心策略:在每次遍历中,只考虑并更新相邻一侧的大小关系
+错误:没有更新为相邻孩子+1,而是仅仅加了1,考虑不够完整。
+给定一个区间的集合 intervals ,返回 需要移除区间的最小数量,使剩余区间互不重叠。
class Solution {
+public:
+ static bool cmp(vector<int> &a,vector<int> &b){
+ return a[1] < b[1];
+ }
+ int eraseOverlapIntervals(vector<vector<int>>& intervals) {
+ sort(intervals.begin(),intervals.end(),cmp);
+ int intervalsCount = 1;
+ int searchBack = intervals[0][1];
+ size_t n = intervals.size();
+ for(size_t i=0;i<n;++i){
+ if (intervals[i][0] >= searchBack){
+ intervalsCount += 1;
+ searchBack = intervals[i][1];
+ }
+ }
+ return n - intervalsCount;
+ }
+};分析:假设第一个区间是 k,k的左边没有任何区间,因此使用其他任何一个区间,只要右端点小于 k的右端点就可以了。而且右端点向左移动,比 k更优。因此首个区间就是所有可以选择的区间中右端点最小的那个区间 。后面只要去寻找其中与首个区间不重合并且右端点最小的区间即可。
贪心策略:优先保留结尾小且不相交的区间
+错误1:没想明白右端点的问题
+错误2:函数要加 static(但是不太明白)
错误3:使用引用传参,防止拷贝浪费时间
+建议:一些比如数组大小的数字提前计算出来,避免反复计算。
+有一个很长的花坛,一部分地块种植了花,另一部分却没有。花不能种植在相邻的地块上。 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 表示没种植花,1 表示种植了花。另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?能则返回 true ,不能则返回 false。
class Solution {
+public:
+ bool canPlaceFlowers(vector<int>& flowerbed, int n) {
+ int flowerCount = 0;
+ size_t m = flowerbed.size();
+ if(m == 1){
+ if(flowerbed[0] == 0){
+ return true;
+ }
+ else if (flowerbed[0] == 1 && n == 1){
+ return false;
+ }
+ }
+ if(flowerbed[0] == 0 && flowerbed[1] == 0){
+ flowerbed[0] = 1;
+ flowerCount += 1;
+ }
+ if(flowerbed[m-1] == 0 && flowerbed[m-2] == 0){
+ flowerbed[m-1] = 1;
+ flowerCount += 1;
+ }
+ for(size_t i=1;i<m-1;i++){
+ if(flowerbed[i] == 0 && flowerbed[i-1] == 0 && flowerbed[i+1] == 0){
+ flowerbed[i] = 1;
+ flowerCount += 1;
+ }
+ }
+ return flowerCount >= n;
+ }
+};分析:遍历即可,尤其注意开头部分和结尾部分。
+错误:最后没有考虑等于条件也为 true
建议:判断太多,有更为简洁的解法,大致思路是计算相邻的 1之间能种多少个 0。
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,不知道具体位置,但是知道一个位置的范围。一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,射进了气球的位置范围后,该气球就会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。给你一个数组 points , 返回引爆所有气球所必须射出的最小弓箭数 。
class Solution {
+public:
+ static bool cmp(vector<int> &a,vector<int> &b){
+ return a[1] < b[1];
+ }
+ int findMinArrowShots(vector<vector<int>>& points) {
+ sort(points.begin(),points.end(),cmp);
+ int n = points.size();
+ int arrowCount = 1;
+ int endPoint = points[0][1];
+ for(size_t i=0;i<n;i++){
+ if(points[i][0] > endPoint){
+ ++arrowCount;
+ endPoint = points[i][1];
+ }
+ }
+ return arrowCount;
+ }
+};分析:拿第一个气球来说,要是想射爆,最佳的方法就是射最右侧的位置,这样能射到的其他的气球数量也会增加,以此类推,构成贪心算法。
+一遍AC
+字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
class Solution {
+public:
+ vector<int> partitionLabels(string s) {
+ vector<int> last(26,-1);
+ for(int i = s.size() - 1;i >= 0;i--){
+ if(last[s[i] - 'a'] == -1){
+ last[s[i] - 'a'] = i;
+ }
+ }
+ vector<int> result;
+ int start = 0;
+ int end = 0;
+ for(int i=0;i<s.size();i++){
+ end = max(end,last[s[i] - 'a']);
+ if(i == end){
+ result.push_back(end - start + 1);
+ start = i + 1;
+ }
+ }
+ return result;
+ }
+};分析:首先得到字符出现的最后的下标位置,然后重新遍历字符串,得到每个字符最后出现的位置。一旦前面的所有字符都出现完了,就算一个区间。
+上述做法使用贪心的思想寻找每个片段可能的最小结束下标,因此可以保证每个片段的长度一定是符合要求的最短长度,如果取更短的片段,则一定会出现同一个字母出现在多个片段中的情况。由于每次取的片段都是符合要求的最短的片段,因此得到的片段数也是最多的。
+错误:思路有问题,没有做对
+给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。在每一天,你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买,然后在同一天出售。返回你能获得的最大利润 。
class Solution {
+public:
+ int maxProfit(vector<int>& prices) {
+ int stockSum = 0;
+ for(size_t i=0;i<prices.size()-1;i++){
+ if(prices[i+1] > prices[i]){
+ stockSum = stockSum+prices[i+1]-prices[i];
+ }
+ }
+ return stockSum;
+ }
+};分析:什么都不限制,涨了就卖就完事了,比较简单。贪心策略就是只要价格上涨就直接出售。
+一遍AC
+假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面正好有 ki个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
class Solution {
+public:
+ static bool cmp(vector<int> &a,vector<int> &b){
+ if(a[0] != b[0]){
+ return a[0] < b[0];
+ }
+ return a[1] > b[1];
+ }
+ vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
+ vector<vector<int>> result(people.size());
+ sort(people.begin(),people.end(),cmp);
+ for(size_t i=0;i<people.size();++i){
+ int pos = people[i][1];
+ for(size_t j=0;j<result.size();j++){
+ if(result[j].empty()){
+ pos--;
+ }
+ if(pos == -1){
+ result[j] = people[i];
+ break;
+ }
+ }
+ }
+ return result;
+ }
+};分析:将人员从低往高先排列,然后一个个进行插入。插入的人只会对后面的人有影响,因为后面的人的身高都会大于等于他。而对已经插入的人没有影响。因此插入的时候给后面的人要留出空位置,以便后面的人插入进去。如果身高相同,就去比较 ki。 ki更小一点的,说明这个人在靠前一点,也就是最小的 ki前面是不会有相同身高的人的,由于相同身高也会算在内,因此要先插入大 ki。
错误:思路有问题,没有做对
+给你一个长度为 n 的整数数组 nums ,请你判断在最多改变 1 个元素的情况下,该数组能否变成一个非递减数列。
class Solution {
+public:
+ bool checkPossibility(vector<int>& nums) {
+ int count = 0;
+ for (int i = 1; i < nums.size(); i++) {
+ if (nums[i] < nums[i - 1]) {
+ if(i == 1 || nums[i] >= nums[i - 2]){
+ nums[i - 1] = nums[i];
+ }
+ else{
+ nums[i] = nums[i - 1];
+ }
+ ++count;
+ }
+ }
+ return count <= 1;
+ }
+};分析:要多种情况一起考虑。。。。
+错误:思路有问题,没有做对。另外不要去改 i+1啊。。判断什么修改什么好吧,要不就乱套了。
贪心算法确实是比较好理解的,但是怎么贪心?什么时候贪心?这些问题都要去详细认真的思考,真正出题的时候不会如此直白,要多练多想。
+ + +Leetcode 刷题笔记-Leetcode 101 第3章 双指针
+ +双指针主要用于遍历数组,两个指针指向不同的元素,从而协同完成任务。也可以延伸到多个数组的多个指针。
+若两个指针指向同一数组,遍历方向相同且不会相交,则也称为滑动窗口(两个指针包围的区域即为当前的窗口),经常用于区间搜索。
+若两个指针指向同一数组,但是遍历方向相反,则可以用来进行搜索,待搜索的数组往往是排好序的。
+在一个增序的整数数组里找到两个数,使它们的和为给定值。已知有且只有一对解。
+class Solution {
+public:
+ vector<int> twoSum(vector<int>& numbers, int target) {
+ vector<int> result;
+ int left = 0;
+ int right = numbers.size() - 1;
+ while(left < right){
+ if(numbers[left] + numbers[right] < target){
+ ++left;
+ }
+ else if(numbers[left] + numbers[right] > target){
+ --right;
+ }
+ else{
+ result.push_back(left+1);
+ result.push_back(right+1);
+ break;
+ }
+ }
+ return result;
+ }
+};分析:左右两个指针分别进行移动,加和小了就把左边的指针往右移动一下,加和大了就把右边的指针往左移动一下。这道题比较特殊,限定了一定有答案而且答案只会有一个,因此不需要添加任何其他的额外条件。
+错误:没看清下标的表示方式,直接输出数组下标了。
+给定两个有序数组,把两个数组合并为一个。
+class Solution {
+public:
+ void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
+ if(n == 0){
+ return;
+ }
+ if(m == 0){
+ nums1 = nums2;
+ return;
+ }
+ int mi = m - 1;
+ int ni = n - 1;
+ int numIndex = m+n-1;
+ while(numIndex >= 0){
+ if(mi >= 0 && ni >= 0){
+ if(nums1[mi] > nums2[ni]){
+ swap(nums1[mi],nums1[numIndex]);
+ --mi;
+ }
+ else{
+ swap(nums2[ni],nums1[numIndex]);
+ --ni;
+ }
+
+ }
+ else if(mi == -1){
+ while(ni != -1){
+ nums1[numIndex] = nums2[ni];
+ --ni;
+ --numIndex;
+ }
+ break;
+ }
+ --numIndex;
+ }
+
+ }
+};分析:从后边开始安排数字,填充0的空位
+错误:挺简单的一道题,首先是刚开始没有想到非常好的解法,看了答案后双指针又有一些问题。。真的是生疏了。
+给定一个链表,如果有环路,找出环路的开始点。
+class Solution {
+public:
+ ListNode *detectCycle(ListNode *head) {
+ ListNode* slow = head;
+ ListNode* fast = head;
+ do{
+ if(fast == nullptr || fast->next == nullptr){
+ return nullptr;
+ }
+ slow = slow->next;
+ fast = fast->next->next;
+ }while(slow != fast);
+ fast = head;
+ while(slow != fast){
+ slow = slow->next;
+ fast = fast->next;
+ }
+ return fast;
+ }
+};分析:有一个通用的解法——快慢指针(Floyd判圈法)。给定两个指针,分别命名为slow和fast,起始位置在链表的开头。每次fast前进两步,slow前进一步。如果fast可以走到尽头,那么说明没有环路;如果fast可以无限走下去,那么说明一定有环路,且一定存在一个时刻slow 和fast 相遇。当slow和fast第一次相遇时,我们将fast重新移动到链表开头,并让slow和fast每次都前进一步。当slow和fast第二次相遇时,相遇的节点即为环路的开始点。
+错误:算法忘记了,没有思路。
+给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 ""
class Solution {
+public:
+ string minWindow(string s, string t) {
+ size_t s_size = s.size();
+ size_t t_size = t.size();
+ map<char,int> mp1;
+ for(size_t i=0;i<t_size;i++){
+ if(mp1.count(t[i])){
+ mp1[t[i]] += 1;
+ }
+ else{
+ mp1[t[i]] = 1;
+ }
+ }
+ int left = 0,cnt = 0,min_l = 0,min_size = s_size+1;
+ for(int r=0;r<s_size;++r){
+ if(mp1.count(s[r])){
+ --mp1[s[r]];
+ if(mp1[s[r]] >= 0){
+ ++cnt;
+ }
+ while(cnt == t_size){
+ if(r - left + 1 < min_size){
+ min_size = r - left + 1;
+ min_l = left;
+ }
+ if(mp1.count(s[left]) && ++mp1[s[left]] > 0){
+ --cnt;
+ }
+ ++left;
+ }
+ }
+ }
+ return min_size > s_size ? "" : s.substr(min_l,min_size);
+ }
+};分析:滑动窗口典型题目
+首先对子字符串进行计数,记录是否出现,以及出现的次数。然后采取滑动窗口的策略,两个指针都从左开始滑动,以右指针为基准构成外侧的大循环。右指针滑动的过程中,对之前的计数进行更改,滑动到了一个字符就减小1。等到0的时候,说明右指针滑动过了的字符串一定包含子字符串的全部字符,然后将左指针向右滑动来减小这个字符串的长度。左指针碰到了某个子字符串内部的字符,就会将计数+1,从而不满足这个字符串包含整个子字符串的要求,因此重新开始移动右字符串,以尝试再次包含整个子字符串。
+错误:算法忘记了,没有思路。
+给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a^2 + b^2 = c 。
class Solution {
+public:
+ bool judgeSquareSum(int c) {
+ long long left = 0;
+ long long right = sqrt(c);
+ while(left <= right){
+ if(left * left + right * right < c){
+ ++left;
+ }
+ else if(left * left + right * right > c){
+ --right;
+ }
+ else{
+ return true;
+ }
+ }
+ return false;
+ }
+};分析:仍然是双指针的问题,多了一点点细节问题。
+错误:left = right,right的范围考虑的不太好。
给你一个字符串 s,最多可以从中删除一个字符。请你判断 s是否能成为回文字符串:如果能,返回 true ;否则,返回 false 。
class Solution {
+public:
+ bool judge(string &s,int left,int right){
+ while(left <= right){
+ if(s[left] == s[right]){
+ ++left;
+ --right;
+ }
+ else{
+ return false;
+ }
+ }
+ return true;
+ }
+ bool validPalindrome(string s) {
+ size_t s_size = s.size();
+ int left = 0;
+ int right = s_size - 1;
+ while(left <= right){
+ if(s[left] == s[right]){
+ ++left;
+ --right;
+ }
+ else{
+ return judge(s,left+1,right) || judge(s,left,right-1);
+ }
+ }
+ return true;
+ }
+};分析:双指针移动就好
+错误:没有考虑到删除一个字符后有两种情况,应该共同考虑而不是仅仅使用某一种情况进行判断。
+给你一个字符串 s 和一个字符串数组 dictionary ,找出并返回 dictionary 中最长的字符串,该字符串可以通过删除 s 中的某些字符得到。如果答案不止一个,返回长度最长且字母序最小的字符串。如果答案不存在,则返回空字符串。
class Solution {
+public:
+ static bool cmp(string &a,string &b){
+ if(a.size() != b.size()){
+ return a.size() > b.size();
+ }
+ return a < b;
+ }
+ string findLongestWord(string s, vector<string>& dictionary) {
+ sort(dictionary.begin(),dictionary.end(),cmp);
+ size_t s_size = s.size();
+ for(auto t : dictionary){
+ size_t t_size = t.size();
+ int si = 0,ti = 0;
+ while(si != s_size){
+ if(s[si] == t[ti]){
+ ++ti;
+ }
+ ++si;
+ if(ti == t_size){
+ return t;
+ }
+ }
+ }
+ return "";
+ }
+};分析:先排序,然后双指针进行移动匹配,如果子字符串的指针移动到字符串的末尾了,说明已经匹配成功了,可以直接输出这个字符串。如果原始的字符串的指针移动到末尾了,说明没有匹配成功,因此转为匹配下一个字符串。
+错误:题目要求的排序条件没有看好,返回了长度比较短的字符串。
+给定一个字符串 s,找出至多包含 k个不同字符的最长子串 T
分析:还是滑动窗口的策略,以右边指针为基准,滑动一下就记录一下最长的长度,滑动到不满足条件了,就将左边的指针收回来,收到满足条件了就继续放右边的指针去滑动。
+class Solution {
+public:
+ int lengthOfLongestSubstringKDistinct(string s, int k) {
+ size_t s_size - s.size();
+ map<char,int> mp;
+ int maxlen = 0;
+ int l = 0;
+ for(int r=0;r<s_size;r++){
+ if(mp.size() <= k){
+ ++mp[s[r]];
+ }
+ while(mp.size() > k){
+ if(--mp[s[l]] == 0){
+ mp.erase(s[l]);
+ }
+ l++;
+ }
+ maxlen = max(maxlen,r-l+1);
+ }
+ return maxlen;
+ }
+};错误:会员题,无法提交。
+双指针的题目还可以,感觉重要的是判断条件。滑动窗口的题目比较困难,可能也是做的题目比较少。后面还需要加强练习。
+ + +Leetcode 刷题笔记-Leetcode 101 第4章 二分查找
+ +二分查找也常被称为二分法或者折半查找,每次查找时通过将待查找区间分成两部分并只取一部分继续查找,将查找的复杂度大大减少。
+二分查找也可以看作双指针的一种特殊情况,但我们一般会将二者区分。双指针类型的题,指针通常是一步一步移动的,而在二分查找里,指针每次移动半个区间长度。
+因为我们初始化 right = nums.length - 1,所以决定了我们的「搜索区间」是 [left, right],所以决定了 while (left <= right),同时也决定了 left = mid+1 和 right = mid-1,因为我们只需找到一个 target 的索引即可,所以当 nums[mid] == target 时可以立即返回。
因为我们初始化 right = nums.length,所以决定了我们的「搜索区间」是 [left, right),所以决定了 while (left < right),同时也决定了 left = mid + 1 和 right = mid,因为我们需找到 target 的最左侧索引,所以当 nums[mid] == target 时不要立即返回,而要收紧右侧边界以锁定左侧边界。
因为我们初始化 right = nums.length,所以决定了我们的「搜索区间」是 [left, right),所以决定了 while (left < right),同时也决定了 left = mid + 1 和 right = mid,因为我们需找到 target 的最右侧索引,所以当 nums[mid] == target 时不要立即返回,而要收紧左侧边界以锁定右侧边界,又因为收紧左侧边界时必须 left = mid + 1,所以最后无论返回 left 还是 right,必须减一。
给定一个非负整数,求它的开方,向下取整。
+class Solution {
+public:
+ int mySqrt(int x) {
+ long long left = 0;
+ long long right = sqrt(x) + 1;
+ while(left <= right){
+ long long mid = (right - left) / 2 + left;
+ if(mid * mid < x){
+ left = mid + 1;
+ }
+ else if(mid * mid > x){
+ right = mid - 1;
+ }
+ else{
+ return mid;
+ }
+ }
+ return left - 1;
+ }
+};思路很简单,主要是细节问题,已经整理了笔记。
+给定一个增序的整数数组和一个值,查找该值第一次和最后一次出现的位置。
+class Solution {
+public:
+ vector<int> searchRange(vector<int>& nums, int target) {
+ vector<int> result;
+ int n = nums.size();
+ if (n == 0){
+ return vector<int>{-1, -1};
+ }
+ int left = 0;
+ int right = n;
+ while(left < right){
+ int mid = (right - left) / 2 + left;
+ if(nums[mid] >= target){
+ right = mid;
+ }
+ else if(nums[mid] < target){
+ left = mid + 1;
+ }
+ }
+ if(right >= n || nums[right] != target){
+ return vector<int>{-1, -1};
+ }
+ else{
+ result.push_back(right);
+ }
+ left = 0;
+ right = n;
+ while(left < right){
+ int mid = (right - left) / 2 + left;
+ if(nums[mid] > target){
+ right = mid;
+ }
+ else if(nums[mid] <= target){
+ left = mid + 1;
+ }
+ }
+ result.push_back(left - 1);
+ return result;
+ }
+};分析:也是最基础的二分查找,实现了 upper_bound和 lower_bound两个函数。
错误:判断的时候忘记判断是否越界。
+一个原本增序的数组被首尾相连后按某个位置断开(如[1,2,2,3,4,5] - [2,3,4,5,1,2],在第一位和第二位断开),我们称其为旋转数组。给定一个值,判断这个值是否存在于这个旋转数组中。
+class Solution {
+public:
+ bool search(vector<int>& nums, int target) {
+ int n = nums.size();
+ int left = 0;
+ int right = n;
+ while(left < right){
+ int mid = (right - left) / 2 + left;
+ if(nums[mid] == target){
+ return true;
+ }
+ else if(nums[mid] < nums[right-1]){
+ // 说明右端是排好序的
+ if(target >= nums[mid] && target <= nums[right-1]){
+ left = mid + 1;
+ }
+ else{
+ right = mid;
+ }
+ }
+ else if(nums[mid] > nums[right-1]){
+ // 说明左端是排好序的
+ if(target <= nums[mid] && target >= nums[left]){
+ right = mid;
+ }
+ else{
+ left = mid + 1;
+ }
+ }
+ else{
+ --right;
+ }
+ }
+ return false;
+ }
+};分析:旋转数组是一类经典题目,需要抓住旋转后二分会有一个区间是单调的性质进行判断,从而对所查找的数字进行区间的锁定。
+错误:条件考虑不全面,没有对旋转数组充分理解。
+寻找旋转排序数组中的最小值
+class Solution {
+public:
+ int findMin(vector<int>& nums) {
+ int n = nums.size();
+ int left = 0;
+ int right = n;
+ int minnum = 10000;
+ while(left < right){
+ int mid = (right - left) / 2 + left;
+ if(nums[mid] > nums[left]){
+ // 左边一定有序
+ minnum = min(minnum,nums[left]);
+ left = mid + 1;
+ }
+ else if(nums[mid] < nums[left]){
+ // 右边一定有序
+ minnum = min(minnum,nums[mid]);
+ right = mid;
+ }
+ else{
+ minnum = min(minnum,nums[mid]);
+ ++left;
+ }
+ }
+ return minnum;
+ }
+};分析:比查找还要稍稍简单一点,只需要想好最小值可能出现的位置即可。
+错误:相等的时候没有判断,会导致漏掉元素。
+给你一个仅由整数组成的有序数组,其中每个元素都会出现两次,唯有一个数只会出现一次。请你找出并返回只出现一次的那个数。
+class Solution {
+public:
+ int singleNonDuplicate(vector<int>& nums) {
+ int n = nums.size();
+ int left = 0;
+ int right = n;
+ if(nums.size()==1){
+ return nums[0];
+ }
+ while(left < right){
+ int mid = (right - left) / 2 + left;
+ if(mid % 2 == 0){
+ if(nums[mid] == nums[mid+1]){
+ left = mid + 2;
+ }
+ else{
+ right = mid;
+ }
+ }
+ else{
+ if(nums[mid] == nums[mid-1]){
+ left = mid + 1;
+ }
+ else{
+ right = mid;
+ }
+ }
+ }
+ return nums[left];
+ }
+};分析:如果mid是偶数,则比较nums[mid]和nums[mid+1]是否相等;如果mid是奇数,则比较nums[mid−1]和nums[mid]是否相等。
+错误:感觉需要判断很多条件?其实不用,只需要考虑长度为1的数组,然后根据下标寻找规律就可以。
+给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数 。
分析:二分的解法太难了。。后续补充吧
+错误:没有思路。。。
+二分查找是非常好的降低时间复杂度的方法之一,整体的思想不是很难,但是细节的部分需要多多注意。当然也有难题,还要多练习。
+ + +Leetcode 刷题笔记-Leetcode 101 第5章 排序算法
+ +排序自然都有C++的STL搞定了,但是在实际中仍然需要这些排序算法,一方面夯实基础,另一方面有一些题目是从这些排序算法中引申出来的,掌握这些排序算法对于做题也会有很大的帮助。
+int main(void){
+ vector<int> nums = {1,3,5,7,2,6,4,8,9,2,8,7,6,0,3,5,9,4,1,0};
+ vector<int> temp(nums.size());
+ sort(nums.begin(), nums.end());
+ quick_sort(nums, 0, nums.size());
+ print(nums);
+ merge_sort(nums, 0, nums.size(), temp);
+ print(nums);
+ insertion_sort(nums, nums.size());
+ print(nums);
+ bubble_sort(nums, nums.size());
+ print(nums);
+ selection_sort(nums, nums.size());
+ print(nums);
+ return 0;
+}void quick_sort(vector<int> &nums,int left,int right){
+ int l = left;
+ int r = right;
+ if(left+1 >= right){
+ return;
+ }
+ int k = nums[left];
+ while(left+1 < right){
+ while(left+1 < right && nums[right-1] >= k){
+ --right;
+ }
+ nums[left] = nums[right-1];
+ while(left+1 < right && nums[left] < k){
+ ++left;
+ }
+ nums[right-1] = nums[left];
+ }
+ nums[left] = k;
+ quick_sort(nums,l,left);
+ quick_sort(nums,left+1,r);
+}错误:while内部的 left < right的条件没有加,导致内部会出问题,而且也是要+1的
void merge_sort(vector<int> &nums,int left,int right,vector<int> &temp){
+ if(left + 1 >= right){
+ return;
+ }
+ int mid = (right - left) / 2 + left;
+ merge_sort(nums,left,mid,temp);
+ merge_sort(nums,mid,right,temp);
+ int p = left;
+ int q = mid;
+ int i = left;
+ while(p < mid && q < right){
+ if(nums[p] <= nums[q]){
+ temp[i++] = nums[p++];
+ }
+ else{
+ temp[i++] = nums[q++];
+ }
+ }
+ while(p < mid){
+ temp[i++] = nums[p++];
+ }
+ while(q < right){
+ temp[i++] = nums[q++];
+ }
+ for(int j=left;j<right;++j){
+ nums[j] = temp[j];
+ }
+}错误:应该是 left + 1 >= right,只剩下一个数字后就应该返回了。
void insertion_sort(vector<int> &nums,int n){
+ for(int i=1;i<n;i++){
+ int a = i;
+ while(a - 1 >= 0 && nums[a] < nums[a-1]){
+ swap(nums[a],nums[a-1]);
+ --a;
+ }
+ }
+ return;
+}void bubble_sort(vector<int> &nums,int n){
+ for(int i=0;i<n-1;i++){
+ for(int j=0;j<n-i-1;j++){
+ if(nums[j] > nums[j+1]){
+ swap(nums[j],nums[j+1]);
+ }
+ }
+ }
+ return;
+}void selection_sort(vector<int> &nums,int n){
+ for(int i=0;i<n;i++){
+ int minnum = nums[i];
+ int minindex = i;
+ for(int j=i+1;j<n;j++){
+ if(nums[j] < minnum){
+ minnum = nums[j];
+ minindex = j;
+ }
+ }
+ swap(nums[i],nums[minindex]);
+ }
+ return;
+}在一个未排序的数组中,找到第 k大的数字
class Solution {
+public:
+ static void quick_selection(vector<int> &nums,int left,int right,int k){
+ int l = left;
+ int r = right;
+ int k2 = nums[left];
+ if(left + 1 > right){
+ return;
+ }
+ while(left+1 < right){
+ while(left+1 < right && nums[right-1] < k2){
+ --right;
+ }
+ nums[left] = nums[right-1];
+ while(left+1 < right && nums[left] >= k2){
+ ++left;
+ }
+ nums[right-1] = nums[left];
+ }
+ nums[left] = k2;
+ if(k <= left){
+ quick_selection(nums,l,left,k);
+ }
+ else{
+ quick_selection(nums,left+1,r,k);
+ }
+ return;
+ }
+ int findKthLargest(vector<int>& nums, int k) {
+ quick_selection(nums,0,nums.size(),k-1);
+ return nums[k-1];
+ }
+};分析:与快速排序相同的思路,但是不需要对没有用的一侧进行快速排序,只需要对k在的区间一侧进行快速排序即可。
错误:开始快速排序有问题,然后k的值想不清楚造成错误。
class Solution {
+public:
+ static bool cmp(pair<int,int> &a,pair<int,int> &b){
+ return a.first > b.first;
+ }
+ vector<int> topKFrequent(vector<int>& nums, int k) {
+ map<int,int> mp1,mp2;
+ for(auto i : nums){
+ ++mp1[i];
+ }
+ vector<pair<int,int>> pr;
+ vector<int> result;
+ for(auto i = mp1.cbegin();i != mp1.cend();++i){
+ pr.push_back(make_pair(i->second,i->first));
+ }
+ sort(pr.begin(),pr.end(),cmp);
+ for(auto i = pr.cbegin();i != pr.cend();++i){
+ if(k != 0){
+ result.push_back(i->second);
+ }
+ else{
+ break;
+ }
+ k--;
+ }
+ return result;
+ }
+};分析:也是比较简单的一道题,通过这道题可以复习一下各种 STL数据结构,总也不用生疏了。
错误:STL有一些生疏,调了一段时间才调好。
给定一个字符串 s ,根据字符出现的频率对其进行降序排序。一个字符出现的频率是它出现在字符串中的次数。返回已排序的字符串。
class Solution {
+public:
+ static bool cmp(pair<char,int> &a,pair<char,int> &b){
+ return a.second > b.second;
+ }
+ string frequencySort(string s) {
+ string result = "";
+ map<char,int> mp;
+ for(auto i : s){
+ mp[i] += 1;
+ }
+ vector<pair<char,int>> pr;
+ for(auto i = mp.cbegin();i != mp.cend();i++){
+ pr.push_back(make_pair(i->first,i->second));
+ }
+ sort(pr.begin(),pr.end(),cmp);
+ for(auto i = pr.cbegin();i != pr.cend();i++){
+ for(int j=0;j<i->second;j++){
+ result += i->first;
+ }
+ }
+ return result;
+ }
+};分析:桶排序的变形题,没有什么新意,还是数据结构
+一遍AC
+void sortColors(vector<int>& nums) {
+ int n = nums.size();
+ int p0 = 0;
+ int p1 = 0;
+ for(int i=0;i<n;++i){
+ if(nums[i] == 1){
+ swap(nums[i],nums[p1]);
+ ++p1;
+ }
+ else if(nums[i] == 0){
+ swap(nums[i],nums[p0]);
+ if(p0 < p1){
+ swap(nums[i],nums[p1]);
+ }
+ ++p0;
+ ++p1;
+ }
+ }
+}分析:荷兰国旗问题,双指针一次遍历就可以得到三个数字的排序。
+错误:想复杂了。
+排序算法基本都可以写,就是变形的题目还是有些不太熟练。还是要多多练习。
+ + +《现代信息检索》课程笔记:第0讲 课程简介
+ +信息检索应用例子的共同特征:
+给定需求或者是对象,从信息库中找出与之最匹配的信息或对象。
+数据形式是无固定结构的自由文本(谷歌搜索)或者结构化数据(京东商品)
+信息检索与其他的学科关系密切,包括自然语言处理、数据挖掘和机器学习。
+信息检索技术广泛应用于搜索、推荐、挖掘、舆情分析、情报处理和内容安全。
+从信息规模上分类,信息检索可以分为:
+《现代信息检索》课程笔记:第1讲 布尔检索
+ +现在提到信息检索,通常会首先想到Web搜索,但是除此之外还有很多其它的搜索应用,如电子邮件搜索、笔记本电脑(桌面)搜索、知识库搜索、法律文献搜索等。
+本课程主要关注文本检索,因为文本检索是最早的检索应用,也仍然是目前最主要的应用,且文本检索理论可以用于其他领域。
+信息检索与数据库的区别主要在于数据的区别,信息检索关注的是非结构化的数据,而数据库关注的是结构化的数据。
+数据库常常支持范围或者精确匹配查询。
+非结构化数据通常指自由文本,允许关键词加上操作符号的查询和更复杂的概念性查询,经典的检索模型一般都针对自由文本进行处理。
+文档集(Collection): 由固定数目的文档组成
+目标:返回与用户需求相关的文档并辅助用户来完成某项任务
+相关性(Relevance):主观的概念,反映对象的匹配程度不同,应用相关性不同。
+检索效果的评价:准确率和召回率(准确率是自己的,召回率才是真正的)
+布尔检索:针对布尔查询的检索,布尔查询是指利用 AND,OR或者 NOT操作符将词项连接起来的查询。
需求:莎士比亚的哪部剧本包含Brutus及Caesar但是不包含Calpurnia
+将需求表示为布尔表达式: Brutus AND Caesar AND NOT Calpurnia
+从头到尾扫描所有剧本,对每部剧本判断它是否包含Brutus AND Caesar ,同时又不包含Calpurnia
+暴力方法的优点:①实现简单②很容易支持文档动态变化
+暴力方法的不足:
+关联矩阵:
+| + | Antony and Cleopatra | +Julius Caesar | +The Tempest | +Hamlet | +Othello | +Macbeth | +
|---|---|---|---|---|---|---|
| Antony | +1 | +1 | +0 | +0 | +0 | +1 | +
| Brutus | +1 | +1 | +0 | +1 | +0 | +0 | +
| Caesar | +1 | +1 | +0 | +1 | +1 | +1 | +
| Calpurnia | +0 | +1 | +0 | +0 | +0 | +0 | +
| Cleopatra | +1 | +0 | +0 | +0 | +0 | +0 | +
| mercy | +1 | +0 | +1 | +1 | +1 | +1 | +
| worser | +1 | +0 | +1 | +1 | +1 | +0 | +
行表示单词,列表示文本,若文本中包含这个单词,则记录为1,反之记录为0
+使用关联矩阵进行查询的时候,即将关联矩阵有关单词的行向量取出来后进行按位与或非操作即可。
+但是这种词项-文档的关联矩阵将非常大,由于是 one-hot存储,矩阵高度稀疏,需要更好的表示方式,因此有了倒排索引。
对每个词项 t,记录所有包含 t的文档列表,每篇文档用一个唯一的 docID来表示,通常是正整数。
词典 ➡ 倒排记录(Posting)
+Brutus ➡ 1 2 4 11 31 45 173
+Calpurnia ➡ 1 2 4 5 6 16 57 132
+Caesar ➡2 31 54 101
+倒排索引的存储通常采用变长表方式
+文本预处理:
+构建词条序列:<词条,docID> 类型的二元组
按词项排序:每个词项按 docID排序
某个词项在单篇文档中的多次出现会被合并
+拆分成词典和倒排记录表两部分
+每个词项出现的文档数目(doc.frequency, DF)会被加入
+最终构成倒排索引:
+ +对于布尔查询来说,对倒排记录表进行操作即可。
+每个倒排记录表都有一个定位指针,两个指针同时从前往后扫描, 每次比较当前指针对应倒排记录,然后移动某个或两个指针。合并时间为两个表长之和的线性时间。时间复杂度为 O(m+n)
这也是倒排记录表按照 docID排序的关键原因!
查询处理中存在处理的顺序问题:n个词项的 AND我们希望查询的次数越少越好,因此要按照表从小到大(即 df从小到大)的顺序进行处理,每次从最小的开始合并(这样可以尽量提前结束合并)
按照直接加和的方式对 Or的 df进行估计。
每个布尔表达式都能转换成(合取范式)
+获得每个词项的 df
通过将词项的 df相加,估计每个 OR表达式对应的倒排记录表的大小
按照上述估计从小到大依次处理每个 OR表达式
构建简单,是构建信息检索系统的一种最简单方式
+Leetcode 刷题笔记-Leetcode 101 第6章 搜索
+ +深度优先搜索和广度优先搜索是两种最常见的优先搜索方法,它们被广泛地运用在图和树等结构中进行搜索。
+岛屿是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直的四个方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。岛屿的面积是岛上值为 1 的单元格的数目。计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
class Solution {
+public:
+ static int DFS(vector<vector<int>> & grid,int x,int y,int m,int n){
+ if(x < 0 || x >= m || y < 0 || y >= n || grid[x][y] == 0){
+ return 0;
+ }
+ grid[x][y] = 0;
+ return 1 + DFS(grid,x+1,y,m,n) + DFS(grid,x-1,y,m,n) + DFS(grid,x,y+1,m,n) + DFS(grid,x,y-1,m,n);
+ }
+ int maxAreaOfIsland(vector<vector<int>>& grid) {
+ int m = grid.size();
+ int n = grid[0].size();
+ int maxarea = 0;
+ for(int i=0;i<m;++i){
+ for(int j=0;j<n;++j){
+ if(grid[i][j] == 1){
+ maxarea = max(maxarea,DFS(grid,i,j,m,n));
+ }
+ }
+ }
+ return maxarea;
+ }
+};分析:标准的DFS,重点要判断是否越界以及返回值的处理。
+错误:基本思路是正确的,返回值的处理有问题,以及想的有些复杂。
+有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。返回矩阵中 省份 的数量。
class Solution {
+public:
+ static void DFS(vector<vector<int>>& isConnected, vector<bool>& visit,int x,int n){
+ if(x < 0 || x >= n || visit[x] == true){
+ return;
+ }
+ visit[x] = true;
+ for(int i=0;i<n;i++){
+ if(isConnected[x][i] == 1){
+ DFS(isConnected,visit,i,n);
+ }
+ }
+ return;
+ }
+ int findCircleNum(vector<vector<int>>& isConnected) {
+ int n = isConnected.size();
+ int sumCount = 0;
+ vector<bool> visit(n);
+ fill(visit.begin(),visit.end(),false);
+ for(int i=0;i<n;i++){
+ if(visit[i] == false){
+ DFS(isConnected,visit,i,n);
+ ++sumCount;
+ }
+ }
+ return sumCount;
+ }
+};分析:还是比较基本的DFS,只不过是一个一维的DFS,比较简单
+错误:开始的思路有一些偏差,后面纠正过来没什么问题了。
+有一个 m × n 的矩形岛屿,与太平洋和大西洋相邻。 太平洋”处于大陆的左边界和上边界,而“大西洋”处于大陆的右边界和下边界。这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights , heights[r][c] 表示坐标 (r, c) 上单元格高于海平面的高度 。岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。返回网格坐标 result 的 2D 列表 ,其中 result[i] = [r<sub>i</sub>, c<sub>i</sub>] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。
class Solution {
+public:
+ static void DFS(vector<vector<int>>& heights,vector<vector<bool>>& Ocean,int x,int y,int m,int n){
+ Ocean[x][y] = true;
+ if(x+1 < m && Ocean[x+1][y] == false && heights[x+1][y] >= heights[x][y]){
+ DFS(heights,Ocean,x+1,y,m,n);
+ }
+ if(x-1 >= 0 && Ocean[x-1][y] == false && heights[x-1][y] >= heights[x][y]){
+ DFS(heights,Ocean,x-1,y,m,n);
+ }
+ if(y+1 < n && Ocean[x][y+1] == false && heights[x][y+1] >= heights[x][y]){
+ DFS(heights,Ocean,x,y+1,m,n);
+ }
+ if(y-1 >= 0 && Ocean[x][y-1] == false && heights[x][y-1] >= heights[x][y]){
+ DFS(heights,Ocean,x,y-1,m,n);
+ }
+ return;
+ }
+ vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
+ int m = heights.size();
+ int n = heights[0].size();
+ vector<vector<bool>> pOcean(m,vector<bool>(n,false));
+ vector<vector<bool>> aOcean(m,vector<bool>(n,false));
+ for(int i=0;i<m;++i){
+ if(pOcean[i][0] == false){
+ DFS(heights,pOcean,i,0,m,n);
+ }
+ if(aOcean[i][n-1] == false){
+ DFS(heights,aOcean,i,n-1,m,n);
+ }
+ }
+ for(int i=0;i<n;++i){
+ if(pOcean[0][i] == false){
+ DFS(heights,pOcean,0,i,m,n);
+ }
+ if(aOcean[m-1][i] == false){
+ DFS(heights,aOcean,m-1,i,m,n);
+ }
+ }
+ vector<vector<int>> result;
+ for(int i=0;i<m;++i){
+ for(int j=0;j<n;++j){
+ if(pOcean[i][j] == true && aOcean[i][j] == true){
+ result.push_back(vector<int>{i,j});
+ }
+ }
+ }
+ return result;
+ }
+};分析:仍然是比较普通的DFS,不过只要对周围的一圈进行DFS就足够了,不需要全部遍历。
+错误:细节问题,写的时候一定好好检查 m和 n有没有用反。
给定一个不含重复数字的数组 nums ,返回其所有可能的全排列。
class Solution {
+public:
+ static void backtracking(vector<int>& nums,int level,vector<vector<int>>&result){
+ if(level == nums.size()-1){
+ result.push_back(nums);
+ return;
+ }
+ for(int i=level;i<nums.size();i++){
+ swap(nums[i],nums[level]);
+ backtracking(nums,level+1,result);
+ swap(nums[i],nums[level]);
+ }
+ }
+ vector<vector<int>> permute(vector<int>& nums) {
+ vector<vector<int>> result;
+ backtracking(nums,0,result);
+ return result;
+ }
+};分析:对于每一个当前位置 i,我们可以将其于之后的任意位置交换,然后继续处理位置 i+1,直到处理到最后一位。为了防止我们每此遍历时都要新建一个子数组储存位置 i之前已经交换好的数字,我们可以利用回溯法,只对原数组进行修改,在递归完成后再修改回来。
错误:学习一下回溯法的基本框架。
+给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
class Solution {
+public:
+ static void backtracking(vector<vector<int>> &result,vector<int> &temp,int n,int level,int k){
+ if(temp.size() == k){
+ result.push_back(temp);
+ return;
+ }
+ for(int i=level+1;i<=n;++i){
+ temp.push_back(i);
+ backtracking(result,temp,n,i,k);
+ temp.pop_back();
+ }
+ }
+ vector<vector<int>> combine(int n, int k) {
+ vector<vector<int>> result;
+ vector<int> temp;
+ backtracking(result,temp,n,0,k);
+ return result;
+ }
+};分析:类似于排列问题,也可以进行回溯。排列回溯的是交换的位置,而组合回溯的是是否把当前的数字加入结果中。
+错误:需要有一个记录状态的数值,要不然就变成全排列了。
+给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
class Solution {
+public:
+ static void backtracking(vector<vector<char>>& board, string &word,int x,int y,int m,int n,vector<vector<bool>> &visited,bool &find,int level){
+ if(x < 0 || x >= m || y < 0 || y >= n){
+ return;
+ }
+ if(visited[x][y] == true || word[level] != board[x][y] || find == true){
+ return;
+ }
+ if(level == word.size() - 1){
+ find = true;
+ return;
+ }
+ visited[x][y] = true;
+ backtracking(board,word,x+1,y,m,n,visited,find,level+1);
+ backtracking(board,word,x-1,y,m,n,visited,find,level+1);
+ backtracking(board,word,x,y+1,m,n,visited,find,level+1);
+ backtracking(board,word,x,y-1,m,n,visited,find,level+1);
+ visited[x][y] = false;
+ return;
+ }
+ bool exist(vector<vector<char>>& board, string word) {
+ int m = board.size();
+ int n = board[0].size();
+ vector<vector<bool>> visited(m, vector<bool>(n, false));
+ bool find = false;
+ for(int i=0;i<m;++i){
+ for(int j=0;j<n;++j){
+ backtracking(board,word,i,j,m,n,visited,find,0);
+ }
+ }
+ return find;
+ }
+};分析:典型回溯题,判断条件需要多一些
+错误1:回溯法不要有返回值,都使用引用传参
+错误2:判断条件:①是否越界②访问过③不匹配④已经确定对的了
+n皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数 n ,返回所有不同的n皇后问题的解决方案。
class Solution {
+public:
+ void backtracking(vector<vector<string>> & result,vector<string> tempresult,vector<bool> &column,vector<bool> &ldiag,vector<bool> &rdiag,int n,int level){
+ if(level == n){
+ result.push_back(tempresult);
+ return;
+ }
+ for(int i=0;i<n;++i){
+ if (column[i] || ldiag[n-level+i-1] || rdiag[level+i]) {
+ continue;
+ }
+ tempresult[level][i] = 'Q';
+ column[i] = ldiag[n-level+i-1] = rdiag[level+i] = true;
+ backtracking(result,tempresult,column,ldiag,rdiag,n,level+1);
+ column[i] = ldiag[n-level+i-1] = rdiag[level+i] = false;
+ tempresult[level][i] = '.';
+ }
+ return;
+ }
+ vector<vector<string>> solveNQueens(int n) {
+ vector<vector<string>> result;
+ string tempstring = "";
+ for(int i=0;i<n;i++){
+ tempstring += ".";
+ }
+ vector<string> tempresult(n,tempstring);
+ vector<bool> column(n,false);
+ vector<bool> ldiag(2*n-1,false);
+ vector<bool> rdiag(2*n-1,false);
+ backtracking(result,tempresult,column,ldiag,rdiag,n,0);
+ return result;
+ }
+};分析:最典型的回溯法之一。类似于在矩阵中寻找字符串,本题也是通过修改状态矩阵来进行回溯。不同的是,我们需要对每一行、列、左斜、右斜建立访问数组,来记录它们是否存在皇后。本题需要判断满足条件的结果中每一行或列有且仅有一个皇后。这是因为我们一共只有 n行和 n列。所以如果我们通过对每一行遍历来插入皇后,我们就不需要对行建立访问数组了。
错误:再理解吧。
+在给定的二维二进制数组 A 中,存在两座岛。(岛是由四面相连的 1 形成的一个最大组。)现在,我们可以将 0 变为 1,以使两座岛连接起来,变成一座岛。返回必须翻转的 0 的最小数目。(可以保证答案至少是 1 。)
class Solution {
+public:
+ static void DFS(vector<vector<int>>& grid,queue<pair<int,int>> &points,int x,int y,int n){
+ if(x < 0 || x >= n || y < 0 || y >= n || grid[x][y] == 2){
+ return;
+ }
+ if(grid[x][y] == 0){
+ points.push({x,y});
+ return;
+ }
+ grid[x][y] = 2;
+ DFS(grid,points,x+1,y,n);
+ DFS(grid,points,x-1,y,n);
+ DFS(grid,points,x,y+1,n);
+ DFS(grid,points,x,y-1,n);
+ return;
+ }
+ int shortestBridge(vector<vector<int>>& grid) {
+ int n = grid.size();
+ queue<pair<int,int>> points;
+ bool find = false;
+ for(int i=0;i<n;++i){
+ if(find == true){
+ break;
+ }
+ for(int j=0;j<n;++j){
+ if(grid[i][j] == 1){
+ find = true;
+ DFS(grid,points,i,j,n);
+ break;
+ }
+ }
+ }
+ int level = 0;
+ vector<vector<int>> d = {{0,1},{0,-1},{1,0},{-1,0}};
+ while(!points.empty()){
+ ++level;
+ int n_points = points.size();
+ while(n_points--){
+ auto [r,c] = points.front();
+ grid[r][c] = 2;
+ points.pop();
+ for(int k=0;k<4;k++){
+ int x = r + d[k][0];
+ int y = c + d[k][1];
+ if(x >= 0 && y >= 0 && x < n && y < n){
+ if(grid[x][y] == 1){
+ return level;
+ }
+ else if(grid[x][y] == 0){
+ grid[x][y] = 2;
+ points.push({x,y});
+ }
+ }
+ }
+ }
+ }
+ return 0;
+ }
+};分析:先通过任意搜索方法找到其中一个岛屿,然后利用广度优先搜索,查找其与另一个岛屿的最短距离
+错误:BFS好久没有练习了,也是生疏了。
+给定一个起始字符串和一个终止字符串,以及一个单词表,求是否可以将起始字符串每次改一个字符,直到改成终止字符串,且所有中间的修改过程表示的字符串都可以在单词表里找到。若存在,输出需要修改次数最少的所有更改方式。
+class Solution {
+public:
+ vector<vector<string>> findLadders(string beginWord, string endWord, vector<string> &wordList) {
+ vector<vector<string>> res;
+ // 因为需要快速判断扩展出的单词是否在 wordList 里,因此需要将 wordList 存入哈希表,这里命名为「字典」
+ unordered_set<string> dict = {wordList.begin(), wordList.end()};
+ // 修改以后看一下,如果根本就不在 dict 里面,跳过
+ if (dict.find(endWord) == dict.end()) {
+ return res;
+ }
+ // 特殊用例处理
+ dict.erase(beginWord);
+
+ // 第 1 步:广度优先搜索建图
+ // 记录扩展出的单词是在第几次扩展的时候得到的,key:单词,value:在广度优先搜索的第几层
+ unordered_map<string, int> steps = {{beginWord, 0}};
+ // 记录了单词是从哪些单词扩展而来,key:单词,value:单词列表,这些单词可以变换到 key ,它们是一对多关系
+ unordered_map<string, set<string>> from = {{beginWord, {}}};
+ int step = 0;
+ bool found = false;
+ queue<string> q = queue<string>{{beginWord}};
+ int wordLen = beginWord.length();
+ while (!q.empty()) {
+ step++;
+ int size = q.size();
+ for (int i = 0; i < size; i++) {
+ const string currWord = move(q.front());
+ string nextWord = currWord;
+ q.pop();
+ // 将每一位替换成 26 个小写英文字母
+ for (int j = 0; j < wordLen; ++j) {
+ const char origin = nextWord[j];
+ for (char c = 'a'; c <= 'z'; ++c) {
+ nextWord[j] = c;
+ if (steps[nextWord] == step) {
+ from[nextWord].insert(currWord);
+ }
+ if (dict.find(nextWord) == dict.end()) {
+ continue;
+ }
+ // 如果从一个单词扩展出来的单词以前遍历过,距离一定更远,为了避免搜索到已经遍历到,且距离更远的单词,需要将它从 dict 中删除
+ dict.erase(nextWord);
+ // 这一层扩展出的单词进入队列
+ q.push(nextWord);
+ // 记录 nextWord 从 currWord 而来
+ from[nextWord].insert(currWord);
+ // 记录 nextWord 的 step
+ steps[nextWord] = step;
+ if (nextWord == endWord) {
+ found = true;
+ }
+ }
+ nextWord[j] = origin;
+ }
+ }
+ if (found) {
+ break;
+ }
+ }
+ // 第 2 步:回溯找到所有解,从 endWord 恢复到 beginWord ,所以每次尝试操作 path 列表的头部
+ if (found) {
+ vector<string> Path = {endWord};
+ backtrack(res, endWord, from, Path);
+ }
+ return res;
+ }
+
+ void backtrack(vector<vector<string>> &res, const string &Node, unordered_map<string, set<string>> &from,
+ vector<string> &path) {
+ if (from[Node].empty()) {
+ res.push_back({path.rbegin(), path.rend()});
+ return;
+ }
+ for (const string &Parent: from[Node]) {
+ path.push_back(Parent);
+ backtrack(res, Parent, from, path);
+ path.pop_back();
+ }
+ }
+};分析:比较复杂的BFS+回溯法
+错误:太复杂暂时还理解不了,慢慢来吧。。。
+给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
class Solution {
+public:
+ static void DFS(vector<vector<char>>& board,int x,int y,int m,int n){
+ if(x < 0 || y < 0 || x >= m || y >= n){
+ return;
+ }
+ if(board[x][y] == 'X' || board[x][y] == 'A'){
+ return;
+ }
+ board[x][y] = 'A';
+ DFS(board,x+1,y,m,n);
+ DFS(board,x-1,y,m,n);
+ DFS(board,x,y-1,m,n);
+ DFS(board,x,y+1,m,n);
+ return;
+ }
+ void solve(vector<vector<char>>& board) {
+ int m = board.size();
+ int n = board[0].size();
+ for(int i=0;i<m;++i){
+ DFS(board,i,0,m,n);
+ DFS(board,i,n-1,m,n);
+ }
+ for(int i=0;i<n;++i){
+ DFS(board,0,i,m,n);
+ DFS(board,m-1,i,m,n);
+ }
+ for(int i=0;i<m;++i){
+ for(int j=0;j<n;++j){
+ if(board[i][j] == 'A'){
+ board[i][j] = 'O';
+ }
+ else{
+ board[i][j] = 'X';
+ }
+ }
+ }
+ return;
+ }
+};分析:也是比较普通的DFS,注意记录是否访问过即可。
+一遍AC
+给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
class Solution {
+public:
+ static void DFS(TreeNode* &root,vector<string> &paths,string temp){
+ if(root != nullptr){
+ temp += to_string(root->val);
+ if(root->left == nullptr && root->right == nullptr){
+ paths.push_back(temp);
+ return;
+ }
+ else{
+ temp += "->";
+ DFS(root->left,paths,temp);
+ DFS(root->right,paths,temp);
+ }
+ }
+ }
+ vector<string> binaryTreePaths(TreeNode* root) {
+ vector<string> paths;
+ DFS(root,paths,"");
+ return paths;
+ }
+};分析:使用深度优先搜索。在深度优先搜索遍历二叉树时,我们需要考虑当前的节点以及它的孩子节点。如果当前节点不是叶子节点,则在当前的路径末尾添加该节点,并继续递归遍历该节点的每一个孩子节点。如果当前节点是叶子节点,则在当前路径末尾添加该节点后我们就得到了一条从根节点到叶子节点的路径,将该路径加入到答案即可。如此,当遍历完整棵二叉树以后我们就得到了所有从根节点到叶子节点的路径。
+错误:陷入回溯法的坑了。
+给定一个可包含重复数字的序列 nums ,按任意顺序返回所有不重复的全排列。
class Solution {
+public:
+ static void backtracking(vector<int>& nums,vector<vector<int>> &result,int level){
+ if(level == nums.size() - 1){
+ result.push_back(nums);
+ return;
+ }
+ set<int> st;
+ for(int i=level;i<nums.size();++i){
+ if(st.find(nums[i]) == st.end()){
+ st.insert(nums[i]);
+ swap(nums[level],nums[i]);
+ backtracking(nums,result,level+1);
+ swap(nums[level],nums[i]);
+ }
+ }
+ return;
+ }
+ vector<vector<int>> permuteUnique(vector<int>& nums) {
+ vector<vector<int>> result;
+ backtracking(nums,result,0);
+ return result;
+ }
+};分析:与全排列基本相同,添加一个set用于记录曾经交换过的数字,如果这个数字曾经交换过就不换了
错误:看了网上的思路。
+给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次 。
class Solution {
+public:
+ static void backtracking(vector<int>& candidates,vector<vector<int>> &result,vector<int> &path,vector<bool> &used,int level,int sum,int target){
+ if(sum > target){
+ return;
+ }
+ else if(sum == target){
+ result.push_back(path);
+ return;
+ }
+ else{
+ for(int i=level;i<candidates.size() && sum + candidates[i] <= target;++i){
+ if(i > 0 && candidates[i] == candidates[i-1] && used[i - 1] == false){
+ continue;
+ }
+ sum += candidates[i];
+ path.push_back(candidates[i]);
+ used[i] = true;
+ backtracking(candidates,result,path,used,i+1,sum,target);
+ used[i] = false;
+ sum -= candidates[i];
+ path.pop_back();
+ }
+ }
+ }
+ vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
+ vector<vector<int>> result;
+ vector<int> path;
+ vector<bool> used(candidates.size(),false);
+ sort(candidates.begin(),candidates.end());
+ backtracking(candidates,result,path,used,0,0,target);
+ return result;
+ }
+};分析:还是组合数,但是数字内部有重复的,因此需要对同一树层上的“使用过”进行去重。
+错误:没什么思路。
+编写一个程序,通过填充空格来解决数独问题。
+class Solution {
+public:
+ static bool isValid(int i,int j,char k,vector<vector<char>>& board){
+ set<char> st;
+ for(int x=0;x<9;x++){
+ st.insert(board[i][x]);
+ st.insert(board[x][j]);
+ }
+ int p = i / 3;
+ int q = j / 3;
+ for(int x = p*3;x < p*3+3;++x){
+ for(int y = q * 3;y < q*3+3;++y){
+ st.insert(board[x][y]);
+ }
+ }
+ if(st.find(k) == st.end()){
+ return true;
+ }
+ return false;
+ }
+ static bool backtracking(vector<vector<char>>& board){
+ for(int i=0;i<9;++i){
+ for(int j=0;j<9;++j){
+ if(board[i][j] != '.'){
+ continue;
+ }
+ for(char k = '1';k <= '9';++k){
+ if(isValid(i,j,k,board)){
+ board[i][j] = k;
+ if(backtracking(board) == true){
+ return true;
+ }
+ board[i][j] = '.';
+ }
+ }
+ return false;
+ }
+ }
+ return true;
+ }
+ void solveSudoku(vector<vector<char>>& board) {
+ bool judge = backtracking(board);
+ return;
+ }
+};分析:二维的回溯问题,说白了就是去尝试填充每一个数字,合理就填上,不合理就删掉之前填充的重新进行尝试。
+错误:看题解。
+给你一棵包含 n 个节点的树,标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表(每一个边都是一对标签),其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。可选择树中任何一个节点作为根。当选择节点 x 作为根节点时,设结果树的高度为 h 。在所有可能的树中,具有最小高度的树(即,min(h))被称为 最小高度树 。请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。
class Solution {
+public:
+ vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
+ int m = edges.size();
+ vector<int> result;
+ if(m == 0){
+ result.push_back(0);
+ return result;
+ }
+ vector<int> degree(n,0);
+ vector<vector<int>> tree(n);
+ for(int i=0;i<m;++i){
+ ++degree[edges[i][0]];
+ ++degree[edges[i][1]];
+ tree[edges[i][0]].push_back(edges[i][1]);
+ tree[edges[i][1]].push_back(edges[i][0]);
+ }
+ queue<int> q;
+ for(int i=0;i<n;++i){
+ if(degree[i] == 1){
+ q.push(i);
+ }
+ }
+ while(!q.empty()){
+ int size = q.size();
+ result.clear();
+ for(int i=0;i<size;++i){
+ int top = q.front();
+ result.push_back(top);
+ q.pop();
+ --degree[top];
+ for(int j=0;j<tree[top].size();++j){
+ --degree[tree[top][j]];
+ if(degree[tree[top][j]] == 1){
+ q.push(tree[top][j]);
+ }
+ }
+ }
+ }
+ return result;
+ }
+};分析:拓扑排序的思想,从多端同时BFS到中心点,直到到达最后一层,输出这一层的结点即为最小的高度。
+错误:看了思路后自己实现,注意判断边界条件。
+深度优先、广度优先和回溯法,理解的还是并不是非常深入,今后还要多加练习。
+ + +《模式识别与机器学习》课程笔记:第1章 概论
+ +模式识别的目的:利用计算机对物理对象进行分类,在错误概率最小的条件下,使识别的结果尽量与客观物体相符合。
+模式识别的数学化:Y= F(X),X的定义域取自特征集,Y的值域为类别的标号集,F是模式识别的判别方法。
机器学习:研究如何构造理论、算法和计算机系统,让机器通过从数据中学习后可以进行分类和识别事物、推理决策、预测未来等工作。
+在特征空间和解释空间之间找到一种映射关系,这种映射也称之为假说。
+c个类别的集合表示为Ω,称为解释空间。机器学习的目标:针对某类任务 T,用 P衡量性能,根据经验 E来学习和自我完善,提高性能。
假说的两种获得方法:
+数据聚类
+统计分类
+结构模式识别
+神经网络
+监督学习
+无监督学习
+半监督学习
+强化学习
+集成学习
+深度学习
+元学习
+多任务学习
+多标记学习
+对抗学习
+模式识别系统与机器学习系统构成对比
+

在传送带上用光学传感器件对鱼按品种分类
+《高级人工智能》课程笔记:第1讲 人工智能概述
+ +首先讲授人工智能基础知识,进而分三个专题(联结主义、符号主义、行为主义)介绍人工智能的新进展。
+智能:个体适应环境并能在不同环境中实现其目标的能力。
+蕴含众多方面的能力
+人工智能:
+机械智能 ➡ 理性思考 ➡ 数理逻辑 ➡ 计算思维
+萌芽期
+孕育期(文艺复兴以来)
+形成期(1956年-1961年)
+发展期(60年代)
+寒冬期(60年代末到70年代初)
+艰难前行(70年代)
+走向工业(80年代)
+今天
+Can Machine Think?
+图灵测试:一个人(C)在完全不接触对方(A和B)的情况下,和对方进行一系列的问答,如果在相当长时间内,他无法根据这些问题判断对方是人(B)还是计算机(A),那么,就认为该计算机具有同人相当的智能(即计算机是能思维的)。
+质疑:
+图灵预言:到2000年,机器可以做到5分钟内以30%的可能性让普通人分辨不出其是机器还是人。
+图灵测试案例
+达特茅斯会议:1956年在达特茅斯学院发起
+发起人
+会议成就
+并且出现了人工智能三大学派:
+衍生出:逻辑、专家系统、知识库
+衍生出:人工神经网络、认知科学、类脑计算
+衍生出:控制论、多智能体、强化学习等
+三大层次
+四大问题
+弱人工智能
+强人工智能
+人工智能恐慌
+人工智能实现了会怎样?
+人工智能伦理
+“准人”水平的人工智能:手写识别、物体识别、语音识别、自然语言处理、词义消歧、机器翻译
+“过人”水平的人工智能:游戏、双陆棋、国际象棋、桥牌、填词、拼字、七巧板、自动驾驶、智力竞赛问答、OCR字符识别
+“许多尖端的人工智能由于应用广泛,已经不再被称为人工智能。因为,人们一旦觉得某些东西非常有用并广泛使用,就不再称之为人工智能了。”
+人工智能是国家战略:2017年,国务院印发了《新一代人工智能发展规划》,人工智能成为国家战略,大数据在人工智能中将扮演越来越重要的角色。
+人工智能经过60余年的发展取得了长足进步,近年来呈现出爆发之势,但总体上还处于初级阶段,通用智能之路任重道远。
+ + +Leetcode 刷题笔记-Leetcode 101 第7章 动态规划
+ +动态规划和其它遍历算法(如深/广度优先搜索)都是将原问题拆成多个子问题然后求解,他们之间最本质的区别是,动态规划保存子问题的解,避免重复计算。解决动态规划问题的关键是找到状态转移方程,这样我们可以通过计算和储存子问题的解来求解最终问题。同时也可以对动态规划进行空间压缩,起到节省空间消耗的效果。
+假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
class Solution {
+public:
+ int climbStairs(int n) {
+ vector<int> num(n+1);
+ if(n <= 2){
+ return n;
+ }
+ else{
+ num[1] = 1;
+ num[2] = 2;
+ for(int i=3;i<=n;++i){
+ num[i] = num[i-1] + num[i-2];
+ }
+ }
+ return num[n];
+ }
+};分析:num[i]表示在第 i阶的方法数,则到达第 i阶的方法是到达第 i-1阶的方法和到达第 i-2阶的方法数之和。因此 num[i] = num[i-1] + num[i-2]。判断边界条件即可。
一遍AC
+你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统, 如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。给定一个代表每个房屋存放金额的非负整数数组,计算你不触动警报装置的情况下,一夜之内能够偷窃到的最高金额。
+class Solution {
+public:
+ int rob(vector<int>& nums) {
+ int n = nums.size();
+ vector<int> dp(n+1);
+ if(n == 1){
+ return nums[0];
+ }
+ else if(n == 2){
+ return max(nums[0],nums[1]);
+ }
+ dp[1] = nums[0];
+ dp[2] = max(nums[0],nums[1]);
+ for(int i=3;i<=n;++i){
+ dp[i] = max(dp[i-1],dp[i-2] + nums[i-1]);
+ }
+ return dp[n];
+ }
+};分析:定义一个数组 dp,dp[i]表示抢劫到第i个房子时,可以抢劫的最大数量。我们考虑 dp[i],此时可以抢劫的最大数量有两种可能,一种是我们选择不抢劫这个房子,此时累计的金额即为 dp[i-1];另一种是我们选择抢劫这个房子,那么此前累计的最大金额只能是 dp[i-2]。因此本题的状态转移方程为 dp[i] = max(dp[i-1],nums[i-1] + dp[i-2])。然后判断边界条件即可。
一遍AC
+给定一个数组,求这个数组中连续且等差的子数组一共有多少个
+class Solution {
+public:
+ int numberOfArithmeticSlices(vector<int>& nums) {
+ int n = nums.size();
+ if(n == 1 || n == 2){
+ return 0;
+ }
+ vector<int>dp(n+1);
+ dp[0] = 0;
+ dp[1] = 0;
+ dp[2] = 0;
+ for(int i=2;i < n;++i){
+ if(nums[i] - nums[i-1] == nums[i-1] - nums[i-2]){
+ dp[i+1] = dp[i] + 1;
+ }
+ }
+ return accumulate(dp.begin(),dp.end(),0);
+ }
+};分析:这道题略微特殊,因为要求是等差数列,可以很自然的想到子数组必定满足 num[i] - num[i-1] = num[i-1] - num[i-2]。然而由于我们对于 dp数组的定义通常为以 i结尾的,满足某些条件的子数组数量,而等差子数组可以在任意一个位置终结,因此此题在最后需要对 dp数组求和。
错误:最开始写的时候越界了
+给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
class Solution {
+public:
+ int minPathSum(vector<vector<int>>& grid) {
+ int m = grid.size();
+ int n = grid[0].size();
+ vector<vector<int>> dp(m,vector<int>(n,0));
+ dp[0][0] = grid[0][0];
+ for(int i=1;i<m;++i){
+ dp[i][0] = dp[i-1][0] + grid[i][0];
+ }
+ for(int j=1;j<n;++j){
+ dp[0][j] = dp[0][j-1] + grid[0][j];
+ }
+ for(int i=1;i<m;++i){
+ for(int j=1;j<n;++j){
+ dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j];
+ }
+ }
+ return dp[m-1][n-1];
+ }
+};分析:定义一个同样是二维的 dp数组,其中 dp[i][j]表示从左上角开始到 (i, j)位置的最优路径的数字和。因为每次只能向下或者向右移动,我们可以很容易得到状态转移方程 dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j],其中 grid表示原数组。
错误:注意区间,开多大的 dp数组以及怎么进行状态转移,不要把自己转蒙。
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。两个相邻元素间的距离为 1 。
class Solution {
+public:
+ vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
+ int m = mat.size();
+ int n = mat[0].size();
+ vector<vector<int>> dp(m,vector<int>(n,0));
+ if(mat[0][0] == 0){
+ dp[0][0] = 0;
+ }
+ else{
+ dp[0][0] = 10002;
+ }
+
+ for(int i=1;i<m;++i){
+ if(mat[i][0] == 0){
+ dp[i][0] = 0;
+ }
+ else{
+ dp[i][0] = dp[i-1][0] + 1;
+ }
+ }
+ for(int j=1;j<n;++j){
+ if(mat[0][j] == 0){
+ dp[0][j] = 0;
+ }
+ else{
+ dp[0][j] = dp[0][j-1] + 1;
+ }
+ }
+ for(int i=1;i<m;++i){
+ for(int j=1;j<n;++j){
+ if(mat[i][j] == 0){
+ dp[i][j] = 0;
+ }
+ else{
+ dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + 1;
+ }
+ }
+ }
+ for(int i=m-2;i>=0;--i){
+ if(mat[i][n-1] == 0){
+ dp[i][n-1] = 0;
+ }
+ else{
+ dp[i][n-1] = min(dp[i][n-1],dp[i+1][n-1] + 1);
+ }
+ }
+ for(int j=n-2;j>=0;--j){
+ if(mat[m-1][j] == 0){
+ dp[m-1][j] = 0;
+ }
+ else{
+ dp[m-1][j] = min(dp[m-1][j],dp[m-1][j+1] + 1);
+ }
+ }
+ for(int i=m-2;i>=0;--i){
+ for(int j=n-2;j>=0;--j){
+ if(mat[i][j] != 0){
+ dp[i][j] = min(dp[i][j],min(dp[i+1][j],dp[i][j+1])+1);
+ }
+ }
+ }
+ return dp;
+ }
+};分析:从左上到右下进行一次动态搜索,再从右下到左上进行一次动态搜索。两次动态搜索即可完成四个方向上的查找。
+错误:看了一下题解的思路,还是有点不敢想。另外要细心,注意越界!!!
+在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
class Solution {
+public:
+ int maximalSquare(vector<vector<char>>& matrix) {
+ int m = matrix.size();
+ int n = matrix[0].size();
+ vector<vector<int>> dp(m+1,vector<int>(n+1,0));
+ int maxside = 0;
+ for(int i=1;i<=m;++i){
+ for(int j=1;j<=n;++j){
+ if(matrix[i-1][j-1] == '1'){
+ dp[i][j] = min(dp[i-1][j-1],min(dp[i][j-1],dp[i-1][j])) + 1;
+ }
+ maxside = max(maxside,dp[i][j]);
+ }
+ }
+ return maxside * maxside;
+ }
+};分析:dp[i][j]表示以 (i, j)为右下角的全由 1构成的最大正方形边长。
错误:状态转移方程没有想太好。
+对于分割类型题,动态规划的状态转移方程通常并不依赖相邻的位置,而是依赖于满足分割条件的位置。
+给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
class Solution {
+public:
+ int numSquares(int n) {
+ vector<int> dp(n+1,100000000);
+ dp[0] = 0;
+ for(int i=1;i<=n;++i){
+ for(int j=1;j*j<=i;++j){
+ dp[i] = min(dp[i],dp[i-j*j]+1);
+ }
+ }
+ return dp[n];
+ }
+};分析:dp[i]表示数字 i最少可以由几个完全平方数相加构成。
错误:没有思路
+输入是一个由数字组成的字符串,输出是满足条件的解码方式总数。
+class Solution {
+public:
+ int numDecodings(string s) {
+ int n = s.size();
+ if(s[0] == '0'){
+ return 0;
+ }
+ if(n == 1){
+ return 1;
+ }
+ vector<int>dp(n+1,1);
+ int prev = s[0] - '0';
+ for(int i=2;i<=n;++i){
+ int cur = s[i-1] - '0';
+ if((prev == 0 || prev > 2) && cur == 0){
+ return 0;
+ }
+ if((prev == 1) || (prev == 2 && cur < 7)){
+ if(cur){
+ dp[i] = dp[i-1] + dp[i-2];
+ }
+ else{
+ dp[i] = dp[i-2];
+ }
+ }
+ else{
+ dp[i] = dp[i-1];
+ }
+ prev = cur;
+ }
+ return dp[n];
+ }
+};分析:dp[i]表示以当前第i个位置上的数字为结尾的表示方法总数。dp[i]取决于两个数字,当前的数字和前一个数字。如果当前数字是 0,而前一个数字不是 1或者 2,说明这两个数字不可能构成字符,因此直接返回 0。如果前一个数字是 1,当前的数字是什么都行,或者前一个数字是 2,而当前的数字是 0-6的某一个数,说明这两个能构成一种组合。同时如果当前的数字不是 0,那么这个数字自己也能构成一种。如果前一个数字是其他,说明不能和当前的数字产生关系了,就只能是当前的数字自己了。
错误:不明白
+给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s
class Solution {
+public:
+ bool wordBreak(string s, vector<string>& wordDict) {
+ int n = s.size();
+ vector<bool> dp(n+1,false);
+ dp[0] = true;
+ for(int i=1;i<=n;++i){
+ for(const string & word : wordDict){
+ int len = word.size();
+ if(i >= len && s.substr(i-len,len) == word){
+ dp[i] = dp[i] || dp[i-len];
+ }
+ }
+ }
+ return dp[n];
+ }
+};分析:类似于完全平方数分割问题,这道题的分割条件由集合内的字符串决定,因此在考虑每个分割位置时,需要遍历字符串集合,以确定当前位置是否可以成功分割。注意对于位置0,需要初始化值为真。
+对于子序列问题,第一种动态规划方法是,定义一个 dp数组,其中 dp[i]表示以 i结尾的子序列的性质。在处理好每个位置后,统计一遍各个位置的结果即可得到题目要求的结果。第二种动态规划方法是,定义一个 dp数组,其中 dp[i]表示到位置 i为止的子序列的性质,并不必须以 i结尾。这样 dp数组的最后一位结果即为题目所求,不需要再对每个位置进行统计。
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
class Solution {
+public:
+ int lengthOfLIS(vector<int>& nums) {
+ int n = nums.size();
+ vector<int> dp(n+1,1);
+ dp[0] = 0;
+ for(int i=1;i<=n;++i){
+ for(int j=0;j<i;j++){
+ if(nums[i-1] > nums[j]){
+ dp[i] = max(dp[i],dp[j+1]+1);
+ }
+ }
+ }
+ return *max_element(dp.begin(),dp.end());
+ }
+};分析: dp[i]表示以 i结尾的子序列的性质。简单动态规划即可。
错误:下标指代不清,初始化应该全部为1
+给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列,返回 0 。
class Solution {
+public:
+ int longestCommonSubsequence(string text1, string text2) {
+ int m = text1.size();
+ int n = text2.size();
+ vector<vector<int>> dp(m+1,vector<int>(n+1,0));
+ for(int i=1;i<=m;++i){
+ for(int j=1;j<=n;++j){
+ if(text1[i-1] == text2[j-1]){
+ dp[i][j] = dp[i-1][j-1] + 1;
+ }
+ else{
+ dp[i][j] = max(dp[i][j-1],dp[i-1][j]);
+ }
+ }
+ }
+ return dp[m][n];
+ }
+};分析:建立一个二维数组 dp,其中 dp[i][j]表示到第一个字符串位置 i为止、到第二个字符串位置 j为止、最长的公共子序列长度。
错误:没想到是二维的动态规划。
+给定一个正整数数组,求是否可以把这个数组分成和相等的两部分。
+class Solution {
+public:
+ bool canPartition(vector<int>& nums) {
+ int n = nums.size();
+ int sum = accumulate(nums.begin(),nums.end(),0);
+ if(sum % 2 == 1){
+ return false;
+ }
+ sum /= 2;
+ vector<vector<int>> dp(n+1,vector<int>(sum+1,false));
+ dp[0][0] = true;
+ for(int i=1;i<=n;++i){
+ for(int j=0;j<=sum;++j){
+ if(j < nums[i-1]){
+ dp[i][j] = dp[i-1][j];
+ }
+ else{
+ dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i-1]];
+ }
+ }
+ }
+ return dp[n][sum];
+ }
+};分析:背包问题,价值是一半,背包容量没有限制。比较重要的是 dp[0][0] =true,后续的判断都是从这个 true继承过来的。
错误:思路不够完善
+给你一个二进制字符串数组 strs 和两个整数 m 和 n ,请你找出并返回 strs 的最大子集的长度,该子集中最多有 m 个 0 和 n 个 1
class Solution {
+public:
+ static vector<int> getzerosandones(string &str){
+ vector<int> result(2);
+ int n = str.size();
+ for(int i=0;i<n;++i){
+ if(str[i] == '0'){
+ ++result[0];
+ }
+ else{
+ ++result[1];
+ }
+ }
+ return result;
+ }
+ int findMaxForm(vector<string>& strs, int m, int n) {
+ int l = strs.size();
+ vector<vector<vector<int>>> dp(l+1,vector<vector<int>>(m+1,vector<int>(n+1,0)));
+ for(int i=1;i<=l;++i){
+ vector<int> && zerosones = getzerosandones(strs[i-1]);
+ int zero = zerosones[0];
+ int one = zerosones[1];
+ for(int j=0;j<=m;++j){
+ for(int k=0;k<=n;++k){
+ dp[i][j][k] = dp[i-1][j][k];
+ if(j >= zero && k >= one){
+ dp[i][j][k] = max(dp[i][j][k],dp[i-1][j-zero][k-one]+1);
+ }
+ }
+ }
+ }
+ return dp[l][m][n];
+ }
+};分析:三维的背包问题,要同时考虑两个背包的容量。
+错误:还是不理解
+给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1 ,可以认为每种硬币的数量是无限的。
class Solution {
+public:
+ int coinChange(vector<int>& coins, int amount) {
+ int n = coins.size();
+ vector<vector<int>> dp(n+1,vector<int>(amount+1,amount+1));
+ dp[0][0] = 0;
+ for(int i=0;i<=amount;++i){
+ for(int j=1;j<=n;++j){
+ if(coins[j-1] <= i){
+ dp[j][i] = min(dp[j-1][i],dp[j][i-coins[j-1]]+1);
+ }
+ else{
+ dp[j][i] = dp[j-1][i];
+ }
+ }
+ }
+ return dp[n][amount] == amount+1 ? -1 : dp[n][amount];
+ }
+};分析:完全背包问题。
+错误:就是不理解
+给定两个字符串,已知你可以删除、替换和插入任意字符串的任意字符,求最少编辑几步可以将两个字符串变成相同。
+class Solution {
+public:
+ int minDistance(string word1, string word2) {
+ int m = word1.size();
+ int n = word2.size();
+ vector<vector<int>> dp(m+1,vector<int>(n+1,0));
+ for(int i=0;i<=m;++i){
+ dp[i][0] = i;
+ }
+ for(int j=0;j<=n;++j){
+ dp[0][j] = j;
+ }
+ for(int i=1;i<=m;++i){
+ for(int j=1;j<=n;++j){
+ if(word1[i-1] == word2[j-1]){
+ dp[i][j] = dp[i-1][j-1];
+ }
+ else{
+ dp[i][j] = min(dp[i-1][j-1],min(dp[i][j-1],dp[i-1][j])) + 1;
+ }
+ }
+ }
+ return dp[m][n];
+ }
+};分析:使用一个二维数组 dp[i][j],表示将第一个字符串到位置 i为止,和第二个字符串到位置 j为止,最多需要几步编辑。当第 i位和第 j位对应的字符相同时,dp[i][j]等于 dp[i-1][j-1];当二者对应的字符不同时,修改的消耗是 dp[i-1][j-1]+1,插入 i位置/删除 j位置的消耗是 dp[i][j-1] + 1,插入 j位置/删除 i位置的消耗是 dp[i-1][j] + 1。
错误:初始化没有做好。
+给定一个字母A,已知你可以每次选择复制全部字符,或者粘贴之前复制的字符,求最少需要几次操作可以把字符串延展到指定长度。
+class Solution {
+public:
+ int minSteps(int n) {
+ vector<int> dp(n+1,0);
+ for(int i=2;i<=n;++i){
+ dp[i] = i;
+ for(int j=2;j * j <= i;++j){
+ if(i % j == 0){
+ dp[i] = dp[j] + dp[i/j];
+ break;
+ }
+ }
+ }
+ return dp[n];
+ }
+};分析:我们使用一个一维数组dp,其中位置i表示延展到长度i的最少操作次数。对于每个位置j,如果j可以被i整除,那么长度i就可以由长度j操作得到,其操作次数等价于把一个长度为1的A延展到长度为i/j。因此我们可以得到递推公式dp[i] = dp[j] + dp[i/j]
+错误:还是不会想。
+给定一个字符串和一个正则表达式,求该字符串是否可以被匹配。
+class Solution {
+public:
+ bool isMatch(string s, string p) {
+ int m = s.size();
+ int n = p.size();
+ vector<vector<bool>> dp(m+1,vector<bool>(n+1,false));
+ dp[0][0] = true;
+ for(int i=1;i<=n;++i){
+ if(p[i-1] == '*'){
+ dp[0][i] = dp[0][i-2];
+ }
+ }
+ for(int i=1;i<=m;++i){
+ for(int j=1;j<=n;++j){
+ if(p[j-1] == '.'){
+ dp[i][j] = dp[i-1][j-1];
+ }
+ else if (p[j-1] != '*') {
+ dp[i][j] = dp[i-1][j-1] && p[j-1] == s[i-1];
+ }
+ else if (p[j-2] != s[i-1] && p[j-2] != '.') {
+ dp[i][j] = dp[i][j-2];
+ }
+ else {
+ dp[i][j] = dp[i][j-1] || dp[i-1][j] || dp[i][j-2];
+ }
+ }
+ }
+ return dp[m][n];
+ }
+};分析:使用一个二维数组 dp,其中 dp[i][j]表示以 i截止的字符串是否可以被以 j截止的正则表达式匹配。
错误:没有思路
+给定一段时间内每天某只股票的固定价格,已知你只可以买卖各一次,求最大的收益。
+class Solution {
+public:
+ int maxProfit(vector<int>& prices) {
+ int sell = 0, buy = INT_MIN;
+ for (int i = 0; i < prices.size(); ++i) {
+ buy = max(buy, -prices[i]);
+ sell = max(sell, buy + prices[i]);
+ }
+ return sell;
+ }
+};分析:遍历一次就行,记录一下最小的价格,然后遍历到每个价格的时候看看是不是比这个价格更大就行了。
+错误:简单的问题也不会想了。。。
+给定一段时间内每天某只股票的固定价格,已知你只可以买卖各 k次,且每次只能拥有一支股票,求最大的收益。
给定一段时间内每天某只股票的固定价格,已知每次卖出之后必须冷却一天,且每次只能拥有一支股票,求最大的收益。
+class Solution {
+public:
+ int maxProfit(vector<int>& prices) {
+ int n = prices.size();
+ if(n == 0){
+ return 0;
+ }
+ vector<int> buy(n),sell(n),s1(n),s2(n);
+ s1[0] = buy[0] = -prices[0];
+ sell[0] = s2[0] = 0;
+ for(int i=1;i<n;++i){
+ buy[i] = s2[i-1] - prices[i];
+ s1[i] = max(buy[i-1],s1[i-1]);
+ sell[i] = max(buy[i-1],s1[i-1]) + prices[i];
+ s2[i] = max(s2[i-1],sell[i-1]);
+ }
+ return max(sell[n-1],s2[n-1]);
+ }
+};分析:状态机求解
+错误:完全不懂
+你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
+class Solution {
+public:
+ int rob(vector<int>& nums) {
+ int n = nums.size();
+ if(n == 1){
+ return nums[0];
+ }
+ else if(n == 2){
+ return max(nums[0],nums[1]);
+ }
+ vector<int> dp(n+1);
+ int answer_a;
+ dp[0] = dp[1] = dp[2] = nums[0];
+ for(int i=3;i<n;++i){
+ dp[i] = max(dp[i-1],dp[i-2] + nums[i-1]);
+ }
+ answer_a = dp[n-1];
+ dp[0] = dp[1] = 0;
+ dp[2] = nums[1];
+ for(int i=3;i<=n;++i){
+ dp[i] = max(dp[i-1],dp[i-2] + nums[i-1]);
+ }
+ return max(answer_a,dp[n]);
+ }
+};分析:分两种情况进行讨论,选第一个和不选第一个。
+错误:看了一下思路,最后调通了
+给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
class Solution {
+public:
+ int maxSubArray(vector<int>& nums) {
+ int n = nums.size();
+ vector<int> dp(n+1);
+ dp[0] = -20000;
+ for(int i=1;i<=n;++i){
+ dp[i] = max(nums[i-1],dp[i-1] + nums[i-1]);
+ }
+ return *max_element(dp.begin(),dp.end());
+ }
+};分析:dp数组记录以当前位置为结尾的子数组的最大和,因此后面再加一位有两种可能,一是和这个一起,二是自己一组。最后取最大的部分即可。
+错误:开始没想太懂,后来自己调通了。
+给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
class Solution {
+public:
+ int integerBreak(int n) {
+ vector<int> dp(n+1);
+ for(int i=2;i<=n;++i){
+ for(int j=1;j<i;++j){
+ dp[i] = max(dp[i],max(j*(i-j),j*dp[i-j]));
+ }
+ }
+ return dp[n];
+ }
+};分析:对于正整数n,当n≥2时,可以拆分成至少两个正整数的和。令x是拆分出的第一个正整数,则剩下的部分是n-x,n−x可以不继续拆分,或者继续拆分成至少两个正整数的和。每个正整数对应的最大乘积取决于比它小的正整数对应的最大乘积。
+错误:分割问题还是没有什么思路
+给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的 最小步数 。每步可以删除任意一个字符串中的一个字符。
class Solution {
+public:
+ int minDistance(string word1, string word2) {
+ int m = word1.size();
+ int n = word2.size();
+ vector<vector<int>> dp(m+1,vector<int>(n+1,0));
+ for(int i=0;i<=m;++i){
+ dp[i][0] = i;
+ }
+ for(int i=0;i<=n;++i){
+ dp[0][i] = i;
+ }
+ for(int i=1;i<=m;++i){
+ for(int j=1;j<=n;++j){
+ if(word1[i-1] == word2[j-1]){
+ dp[i][j] = dp[i-1][j-1];
+ }
+ else{
+ dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + 1;
+ }
+ }
+ }
+ return dp[m][n];
+ }
+};分析:不相等的时候看两边的字符串,相等的时候看前一位
+错误:字符相等的时候有些没想明白,后来调通了
+给出 n 个数对。 在每一个数对中,第一个数字总是比第二个数字小。现在,我们定义一种跟随关系,当且仅当 b < c 时,数对 (c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。给定一个数对集合,找出能够形成的最长数对链的长度。你不需要用到所有的数对,你可以以任何顺序选择其中的一些数对来构造。
class Solution {
+public:
+ static bool cmp(vector<int> &a,vector<int> &b){
+ return a[0] < b[0];
+ }
+ int findLongestChain(vector<vector<int>>& pairs) {
+ int n = pairs.size();
+ sort(pairs.begin(),pairs.end(),cmp);
+ vector<int> dp(n+1,1);
+ for(int i=1;i<=n;++i){
+ for(int j=0;j<i-1;++j){
+ if(pairs[i-1][0] > pairs[j][1]){
+ dp[i] = max(dp[i],dp[j+1]+1);
+ }
+ }
+ }
+ return dp[n];
+ }
+};分析:排序后进行动态规划即可
+错误:排序有问题。
+如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。给你一个整数数组 nums ,返回 nums 中作为摆动序列的最长子序列的长度 。
class Solution {
+public:
+ int wiggleMaxLength(vector<int>& nums) {
+ int n = nums.size();
+ if(n == 1 || (n == 2 && nums[0] != nums[1])){
+ return n;
+ }
+ if(n == 2 && nums[0] == nums[1]){
+ return 1;
+ }
+ vector<int> up(n),down(n);
+ up[0] = down[0] = 1;
+ for(int i=1;i<n;++i){
+ if(nums[i] > nums[i-1]){
+ up[i] = max(up[i-1],down[i-1] + 1);
+ down[i] = down[i-1];
+ }
+ else if(nums[i] < nums[i-1]){
+ up[i] = up[i-1];
+ down[i] = max(down[i-1],up[i-1] + 1);
+ }
+ else{
+ up[i] = up[i-1];
+ down[i] = down[i-1];
+ }
+ }
+ return max(up[n-1],down[n-1]);
+ }
+};分析:每当我们选择一个元素作为摆动序列的一部分时,这个元素要么是上升的,要么是下降的,这取决于前一个元素的大小。那么列出状态表达式为:up[i]表示以前 i个元素中的某一个为结尾的最长的「上升摆动序列」的长度。down[i]表示以前i个元素中的某一个为结尾的最长的「下降摆动序列」的长度。
错误:没有思路
+class Solution {
+public:
+ int findTargetSumWays(vector<int>& nums, int target) {
+ int sum = 0;
+ for (int& num : nums) {
+ sum += num;
+ }
+ int diff = sum - target;
+ if (diff < 0 || diff % 2 != 0) {
+ return 0;
+ }
+ int n = nums.size(), neg = diff / 2;
+ vector<vector<int>> dp(n + 1, vector<int>(neg + 1));
+ dp[0][0] = 1;
+ for (int i = 1; i <= n; i++) {
+ int num = nums[i - 1];
+ for (int j = 0; j <= neg; j++) {
+ dp[i][j] = dp[i - 1][j];
+ if (j >= num) {
+ dp[i][j] += dp[i - 1][j - num];
+ }
+ }
+ }
+ return dp[n][neg];
+ }
+};分析:转化为0-1背包问题
+错误:背包问题一直都不怎么理解,就先这样,后续再补充。
+给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。返回获得利润的最大值。
class Solution {
+public:
+ int maxProfit(vector<int>& prices, int fee) {
+ int n = prices.size();
+ vector<vector<int>> dp(n, vector<int>(2));
+ dp[0][0] = 0, dp[0][1] = -prices[0];
+ for (int i = 1; i < n; ++i) {
+ dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
+ dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
+ }
+ return dp[n - 1][0];
+ }
+};分析:股票问题的变形,比较类似于状态机,不是很能想得到
+错误:股票问题后面也要再做一做
+动态规划比较有难度,一是状态转移方程的写法,二是在实现状态转移中的各种细节。以后对于动态规划还要勤加练习,多练习思考方法。
+ + +《机器学习》课程笔记:第1章 绪论
+ +什么是人工智能?
+“人工智能就是让机器来完成那些如果由人来做则需要智能的事情的科学”;
+“人工智能就是研究如何使计算机去做只有人才能做的智能工作”
+“人工智能是研究使计算机来模拟人的某些思维过程和智能行为 (如学习、推理、思考、规划等)的学科 ”
+图灵测试思考的问题:
+我们研究的是弱人工智能
+对人工智能的期望
+人工智能创新发展引领新一轮产业变革之势,推动人类社会进入智能化时代,人工智能成为世界各国竞相战略布局的新高地,我国人工智能综合实力不断提升。
+机器学习是一门人工智能的科学
+“机器学习是一门人工智能的科学,该领域的主要研究对象是人工智能,特别是如何在经验学习中改善具体算法的性能 。 Langley(1996)“
+“机器学习是对能通过经验自动改进的计算机算法的研究 。 Tom Mitchell (1997)“
+“机器学习是用数据或以往的经验,以此优化计算机程序的性能标准”。 Alpaydin (2004)
+机器学习发展时期
+推理期➡知识期➡学科形成➡蓬勃发展期
+应用领域
+机器学习研究意义
+机器学习的一般过程
+ +x到输出 y的映射,训练数据会有标签 y,分为回归问题和分类问题。x到输出 y的映射,不会提供标签,但是会给一个反馈表示目前的选择有多好。机器学习流程:
+《机器学习》课程笔记:第2章 贝叶斯学习
+ +某地全年365天,晴朗265天,非晴朗100天。判断明天天气如何?
+令




令





今天有晚霞,判断明天天气如何? 即计算
今天没有晚霞,判断明天天气如何? 即计算
利用贝叶斯决策原理:
+

因此可以求得
贝叶斯公式:
+因此
贝叶斯决策:
+基于观察特征、类别的贝叶斯公式:
+也就是:
因此
如果存在



更改为比值的形式:
可以定义类别相似性函数
分母都是相同的,因此可以将
概率有很多都是


对于两变量决策问题来说,可以计算决策边界
 中
中 特征向量的各维属性独立;
特征向量的各维属性独立; 中
中 的各维属性存在依赖;
的各维属性存在依赖; 服从正态分布;
服从正态分布;采用了“属性条件独立性假设”
+关键问题:由训练样本学习类别条件概率和类别先验概率







类别先验概率
类别概率密度 
对于






若

拉普拉斯平滑:避免因训练集样本不充分而导致概率估计值为零。
+平滑后:




若

多维正态分布的概率密度:
在每个维度上都是正态分布:
贝叶斯学习将公式化简为对数的形式:
不同的高斯参数情况:
+

《现代信息检索》课程笔记:第2讲 索引构建
+ +语料通常很大,而服务器内存通常相对较小,因此需要在内存有限的情况下的索引构建策略。
+词项:一个语料中不同的词的数量
+词条:一个语料中所有词的数量(包括重复的)
+在构建索引时,每次解析一篇文档,因此对于每个词项而言,其倒排记录表不到最后一篇文档都是不完整的。
+如果每个 (termID, docID)对占用 8个字节, 那么处理大规模语料需要大量的空间。
一般内存的容量比较小,没有办法将前面产生的倒排记录表全部放在内存中,需要在磁盘上存储中间结果。
+内存的典型配置是几G ~ 几十G的内存或上百G或1-2T
+磁盘空间通常有几T(小型服务器)或10T以上(磁盘阵列)
+硬盘空间更大,但是在内存中访问数据会比从硬盘访问数据快很多(大概10倍以上的差距)
+硬盘寻道时间是闲置时间:磁头在定位时不发生数据传输(假设使用的是机械硬盘)
+因此一个大(连续)块的传输会比多个小块(非连续)的传输速度快
+硬盘 I/O是基于块的:读写时是整块进行的。块大小:8KB到256KB不等
+不能在硬盘上对倒排索引表进行排序,因为寻道的时间很慢,导致排序的时间也很慢。
+一种减少寻道操作的排序:Blocked sort-based Indexing
+将所有记录划分为每个大小约为10M的块,收集每一块的倒排记录,排序,将倒排索引写入硬盘,最后将不同的分块合并为一个大的倒排索引。
+关键决策:块的大小-块越大,最后的合并操作就越少
+合并的过程中需要在磁盘中同时保存数据的两份拷贝(合并前与正在合并),因此磁盘空间要足够大。
+ +词项字符串的占用空间比较大,因此维护一个全局词典来将字符串映射到唯一的全局ID
+合并的过程中,将每一个小块的一点点数据放入内存中进行排序,排序好了就放在写缓冲区中,写缓冲区满了就写回硬盘,直到排序完成。
+可以将两两合并的方式优化为多项合并(multi-way merge):
+termid的优先级队列(priority queue),每次迭代从队列中选取一个最小的未处理 termidtermid的倒排记录,并写入磁盘。BSBI算法的问题:
+term映射成 termID。实际上倒排记录表可以直接采用 (term,docID)方式而不是(termID,docID)方式,但是此时中间文件(即待合并的倒排记录表)将会变得很大(字符串比整型数空间消耗更大)内存式单遍扫描索引构建算法:Single-pass in-memory indexing
+关键思想:
+term-termID的映射)在扫描文档的同时,直接在内存中维护一个不断更新的倒排索引
+因此对每个块生成一个完整的倒排索引,这些独立的索引最后合并成一个大索引
+最终合并词典的过程中,需要进行词项字符串的比较,因为此时没有全局词典提供词项-整数ID的映射。
+ +BSBI算法:在分块索引阶段,BSBI算法维护一个全局Term (String) – Termid (int) 的映射表,局部索引为Termid及其倒排记录表,仍然按词典顺序排序。
+SPIMI算法:分块索引阶段与BSBI算法不同在于建立局部词典和索引,无需全局词典。在合并阶段,将局部索引两两合并,最后产生全局词典建立Term – Termid的映射。
+实际中文档会增加、删除和修改,因此词典和倒排记录表必须要动态更新。
+最简单的方法:主索引(Main index)+辅助索引(Auxiliary index)
+删除的处理:
+问题:
+辅助索引方式: 每次合并都需要处理每个倒排记录,索引构建时间为

对数合并(Logarithmic merge):
+对数合并算法能够缓解(随时间增长)索引合并的开销 → 用户并不感觉到响应时间上有明显延迟。
+ 置于内存
置于内存 置于磁盘
置于磁盘 ,则将它作为 $I_0 $写到磁盘中(如果 $I_0 $不存在)
,则将它作为 $I_0 $写到磁盘中(如果 $I_0 $不存在) 合并(如果
合并(如果 已经存在),并将合并结果作为
已经存在),并将合并结果作为 写到磁盘中(如果
写到磁盘中(如果 不存在),或者和
不存在),或者和 合并(如果
合并(如果 已经存在),依此类推
已经存在),依此类推因此每次两两合并中两个索引的大小相同
+索引数目的上界为



Leetcode 刷题笔记-Leetcode 101 第10章 位运算
+ +按位异或:x ^ 0s = x, x ^ 1s = ~x, x ^ x = 0
按位与:x & 0s = 0, x & 1s = x, x & x = x
按位或:x | 0s = x, x | 1s = 1s, x | x = x
n & (n - 1)可以去除 n的位级表示中最低的那一位,例如对于二进制表示 11110100,减去 1得到 11110011,这两个数按位与得到 11110000。
n & (-n)可以得到n的位级表示中最低的那一位,例如对于二进制表示 11110100,取负得到 00001100,这两个数按位与得到 00000100。
给定两个十进制数字,求它们二进制表示的汉明距离(Hamming distance,即不同位的个数)。
+class Solution {
+public:
+ int hammingDistance(int x, int y) {
+ int diff = x ^ y;
+ int ans = 0;
+ while(diff){
+ ans += diff & 1;
+ diff >>= 1;
+ }
+ return ans;
+ }
+};分析:将x和y按位异或,则不同的位置为1,相同的位置为0。然后将得到的结果与1进行与操作,为0说明是0,为1说明是1,就计数了1。然后将这个结果逐步右移就可以看出下一位了。
错误:第一道题不太熟悉。
+颠倒给定的 32 位无符号整数的二进制位
+class Solution {
+public:
+ uint32_t reverseBits(uint32_t n) {
+ uint32_t ans = 0;
+ for(int i=0;i<32;++i){
+ ans <<= 1;
+ ans += n & 1;
+ n >>= 1;
+ }
+ return ans;
+ }
+};分析:摆出一个0,然后左移,逐步加上n右移的数字。
错误:不太明白左右移这种东西
+给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
+class Solution {
+public:
+ int singleNumber(vector<int>& nums) {
+ int ret = 0;
+ for (auto e: nums) ret ^= e;
+ return ret;
+ }
+};分析:一个数字和 0进行按位异或会得到本身,一个数字和本身进行按位异或会得到0。因此在数组内部进行循环,两次的元素出现了一定会变为0,最后剩下的一个就是这个数字本身。
错误:不熟练
+给定一个整数,判断它是否是4 的次方。
+class Solution {
+public:
+ bool isPowerOfFour(int n) {
+ return n > 0 && !(n & (n - 1)) && (n & 1431655765);
+ }
+};分析:首先我们考虑一个数字是不是2 的(整数)次方:如果一个数字n 是2 的整数次方,那么它的二进制一定是0…010…0 这样的形式;考虑到n - 1 的二进制是0…001…1,这两个数求按位与的结果一定是0。因此如果n & (n - 1) 为0,那么这个数是2 的次方。如果这个数也是4 的次方,那二进制表示中1 的位置必须为奇数位。我们可以把n 和二进制的10101…101(即十进制下的1431655765)做按位与,如果结果不为0,那么说明这个数是4的次方。
+错误:不理解
+给你一个字符串数组 words ,找出并返回 length(words[i]) * length(words[j]) 的最大值,并且这两个单词不含有公共字母。如果不存在这样的两个单词,返回 0 。
class Solution {
+public:
+ int maxProduct(vector<string>& words) {
+ unordered_map<int, int> hash;
+ int ans = 0;
+ for (const string & word : words) {
+ int mask = 0, size = word.size();
+ for (const char & c : word) {
+ mask |= 1 << (c - 'a');
+ }
+ hash[mask] = max(hash[mask], size);
+ for (const auto& [h_mask, h_len]: hash) {
+ if (!(mask & h_mask)) {
+ ans = max(ans, size * h_len);
+ }
+ }
+ }
+ return ans;
+ }
+};分析:怎样快速判断两个字母串是否含有重复数字呢?可以为每个字母串建立一个长度为26的二进制数字,每个位置表示是否存在该字母。如果两个字母串含有重复数字,那它们的二进制表示的按位与不为0。
错误:看了思路后自己实现的。
+给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
class Solution {
+public:
+ vector<int> countBits(int n) {
+ vector<int> ans(n+1,0);
+ for (int i = 1; i <= num; ++i){
+ dp[i] = i & 1? dp[i-1] + 1: dp[i>>1];
+ }
+ return ans;
+ }
+};分析:本题可以利用动态规划和位运算进行快速的求解。定义一个数组dp,其中dp[i] 表示数字i的二进制含有1 的个数。对于第i 个数字,如果它二进制的最后一位为1,那么它含有1 的个数
+则为dp[i-1] + 1;如果它二进制的最后一位为0,那么它含有1 的个数和其算术右移结果相同,即dp[i>>1]。
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
class Solution {
+public:
+ int missingNumber(vector<int>& nums) {
+ int n = nums.size();
+ int total = n * (n + 1) / 2;
+ int arrSum = 0;
+ for (int i = 0; i < n; i++) {
+ arrSum += nums[i];
+ }
+ return total - arrSum;
+ }
+};分析:高斯求和后相减即可
+给定一个正整数,检查它的二进制表示是否总是 0、1 交替出现:换句话说,就是二进制表示中相邻两位的数字永不相同。
+class Solution {
+public:
+ bool hasAlternatingBits(int n) {
+ int pre = 0;
+ int sign = 0;
+ while(n){
+ int ans = n & 1;
+ if(sign == 1){
+ if(pre == ans){
+ return false;
+ }
+ }
+ pre = ans;
+ sign = 1;
+ n >>= 1;
+ }
+ return true;
+ }
+};分析:存储并判断即可
+错误:有一点小问题,很快调通
+给你一个整数 num ,输出它的补数。
class Solution {
+public:
+ int findComplement(int num) {
+ uint t = 1u << 31;
+ while (! (t & num)) {
+ num |= t;
+ t >>= 1;
+ }
+ return ~num;
+ }
+};分析:前边补1,然后就可以直接取反了
+错误:没有思路
+给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
class Solution {
+public:
+ vector<int> singleNumber(vector<int>& nums) {
+ map<int,int> mp;
+ for(int i=0;i<nums.size();++i){
+ ++mp[nums[i]];
+ }
+ vector<int> result;
+ for(const auto &[a,b] : mp){
+ if(b == 1){
+ result.push_back(a);
+ }
+ }
+ return result;
+ }
+};分析:哈希表算了。。。
+一遍AC
+这东西和计组挺相关的,面试中应该不会怎么考察这种数学题,但不失为一种运算加速的好办法。
+ + +Leetcode 刷题笔记-Leetcode 101 第8章 分治法
+ +顾名思义,分治问题由“分”(divide)和“治”(conquer)两部分组成,通过把原问题分为子问题,再将子问题进行处理合并,从而实现对原问题的求解。我们在排序章节展示的归并排序就是典型的分治问题,其中“分”即为把大数组平均分成两个小数组,通过递归实现,最终我们会得到多个长度为1的子数组;“治”即为把已经排好序的两个小数组合成为一个排好序的大数组,从长度为1 的子数组开始,最终合成一个大数组。
+给定一个只包含加、减和乘法的数学表达式,求通过加括号可以得到多少种不同的结果
+class Solution {
+public:
+ vector<int> diffWaysToCompute(string expression) {
+ vector<int> ways;
+ for(int i=0;i<expression.size();++i){
+ char c = expression[i];
+ if(c == '+' || c == '-' || c == '*'){
+ vector<int> left = diffWaysToCompute(expression.substr(0,i));
+ vector<int> right = diffWaysToCompute(expression.substr(i+1));
+ for(const int &l : left){
+ for(const int &r : right){
+ if(c == '+'){
+ ways.push_back(l+r);
+ }
+ else if(c == '-'){
+ ways.push_back(l-r);
+ }
+ else{
+ ways.push_back(l*r);
+ }
+ }
+ }
+ }
+ }
+ if (ways.empty()){
+ ways.push_back(stoi(expression));
+ }
+ return ways;
+ }
+};分析:利用分治思想,我们可以把加括号转化为,对于每个运算符号,先执行处理两侧的数学表达式,再处理此运算符号。注意边界情况,即字符串内无运算符号,只有数字。
+错误:想不通的
+class Solution {
+public:
+ vector<int> beautifulArray(int n) {
+ vector<int> ans;
+ if(n==1){
+ ans.push_back(1);
+ return ans;
+ }
+ int odd_num=(n+1)/2;
+ int even_num=n/2;
+ vector<int> left_arry=beautifulArray(odd_num);
+ vector<int> right_arry=beautifulArray(even_num);
+ //将左侧数组映射为奇数
+ for(auto &val:left_arry){
+ ans.push_back(val*2-1);
+ }
+ //将右侧数组映射为偶数
+ for(auto &val:right_arry){
+ ans.push_back(val*2);
+ }
+ return ans;
+ }
+};分析:不懂
+错误:不懂
+class Solution {
+public:
+ int maxCoins(vector<int>& nums) {
+ int n = nums.size();
+ vector<vector<int>> rec(n + 2, vector<int>(n + 2));
+ vector<int> val(n + 2);
+ val[0] = val[n + 1] = 1;
+ for (int i = 1; i <= n; i++) {
+ val[i] = nums[i - 1];
+ }
+ for (int i = n - 1; i >= 0; i--) {
+ for (int j = i + 2; j <= n + 1; j++) {
+ for (int k = i + 1; k < j; k++) {
+ int sum = val[i] * val[k] * val[j];
+ sum += rec[i][k] + rec[k][j];
+ rec[i][j] = max(rec[i][j], sum);
+ }
+ }
+ }
+ return rec[0][n + 1];
+ }
+};分析:不懂
+错误:不懂
+不懂不懂不懂啊啊啊啊啊
+ + +Leetcode 刷题笔记-Leetcode 101 第9章 数学问题
+ +利用辗转相除法求得两个数的最大公因数,将两个数相乘再除以最大公因数即可得到最小公倍数
+int gcd(int a, int b) {
+ return b == 0 ? a : gcd(b, a% b);
+}
+int lcm(int a, int b) {
+ return a * b / gcd(a, b);
+}进一步也可以通过扩展欧几里得算法在求得 a和 b最大公因数的同时,也得到它们的系数 x和 y,从而使 ax + by = gcd(a, b)
int xGCD(int a, int b, int &x, int &y) {
+ if (!b) {
+ x = 1, y = 0;
+ return a;
+ }
+ int x1, y1, gcd = xGCD(b, a % b, x1, y1);
+ x = y1, y = x1 - (a / b) * y1;
+ return gcd;
+}给定整数 n ,返回所有小于非负整数 n 的质数的数量 。
class Solution {
+public:
+ int countPrimes(int n) {
+ if(n <= 2){
+ return 0;
+ }
+ vector<bool> nums(n,true);
+ for(int i=2;i<n;++i){
+ if(nums[i] == true){
+ for(int j=2*i;j<n;j += i){
+ nums[j] = false;
+ }
+ }
+ }
+ return accumulate(nums.begin(),nums.end(),0) - 2;
+ }
+};分析:使用埃拉托斯特尼筛法即可。
+错误:有点忘记算法了。
+给定一个整数 num,将其转化为7进制,并以字符串形式输出。
class Solution {
+public:
+ string convertToBase7(int num) {
+ int sign = 0;
+ if(num < 0){
+ num = -num;
+ sign = 1;
+ }
+ if(num == 0){
+ return "0";
+ }
+ string result = "";
+ while(num/7){
+ char c = num%7 + '0';
+ result = c + result;
+ num /= 7;
+ }
+ if(num != 0){
+ char b = '0' + num;
+ result = b + result;
+ }
+ if(sign == 1){
+ return '-' + result;
+ }
+ return result;
+ }
+};分析:直接进制转换就行,注意进制转换的时候用十进制进行过渡比较方便。
+错误:磕磕绊绊调通了。
+给定一个整数 n ,返回 n! 结果中尾随零的数量。
class Solution {
+public:
+ int trailingZeroes(int n) {
+ return n == 0? 0: n / 5 + trailingZeroes(n / 5);
+ }
+};分析:每个尾部的0由2*5 = 10而来,因此我们可以把阶乘的每一个元素拆成质数相乘,统计有多少个2和5。明显的,质因子2的数量远多于质因子5的数量,因此我们可以只统计阶乘结果里有多少个质因子5。
+错误:没想到这么好的思路
+给定两个字符串形式的非负整数 num1 和 num2 ,计算它们的和并同样以字符串形式返回。
class Solution {
+public:
+ string addStrings(string num1, string num2) {
+ int n1 = num1.size();
+ int n2 = num2.size();
+ --n1;
+ --n2;
+ string result = "";
+ int cnt = 0;
+ while(n1 >= 0 && n2 >= 0){
+ int temp = num1[n1] - '0' + num2[n2] - '0' + cnt;
+ if(temp >= 10){
+ cnt = 1;
+ }
+ else{
+ cnt = 0;
+ }
+ char c = temp%10 + '0';
+ result = c + result;
+ --n1;
+ --n2;
+ }
+ while(n1 >= 0){
+ int temp = num1[n1] - '0' + cnt;
+ if(temp >= 10){
+ cnt = 1;
+ }
+ else{
+ cnt = 0;
+ }
+ char c = temp%10 + '0';
+ result = c + result;
+ --n1;
+ }
+ while(n2 >= 0){
+ int temp = num2[n2] - '0' + cnt;
+ if(temp >= 10){
+ cnt = 1;
+ }
+ else{
+ cnt = 0;
+ }
+ char c = temp%10 + '0';
+ result = c + result;
+ --n2;
+ }
+ if(cnt == 1){
+ return '1' + result;
+ }
+ return result;
+ }
+};分析:大数相加,没什么新的东西
+一遍AC
+给定一个整数,写一个函数来判断它是否是 3 的幂次方。如果是,返回 true ;否则,返回 false
class Solution {
+public:
+ bool isPowerOfThree(int n) {
+ if(n == 1){
+ return true;
+ }
+ for(long long i=3;i<INT_MAX;i*=3){
+ if(i == n){
+ return true;
+ }
+ }
+ return false;
+ }
+};分析:比较简单,有更好的解法,需要数学能力
+错误:n=1没有考虑
给定一个数组,要求实现两个指令函数。第一个函数“shuffle”可以随机打乱这个数组,第二个函数“reset”可以恢复原来的顺序。
+class Solution {
+public:
+ Solution(vector<int>& nums) {
+ this->nums = nums;
+ this->original.resize(nums.size());
+ copy(nums.begin(), nums.end(), original.begin());
+ }
+
+ vector<int> reset() {
+ copy(original.begin(), original.end(), nums.begin());
+ return nums;
+ }
+
+ vector<int> shuffle() {
+ if (nums.empty()) return {};
+ vector<int> shuffled(nums);
+ int n = nums.size();
+ for (int i = n - 1; i >= 0; --i) {
+ swap(shuffled[i], shuffled[rand() % (i + 1)]);
+ }
+ // 正向洗牌:
+ // for (int i = 0; i < n; ++i) {
+ // int pos = rand() % (n - i);
+ // swap(shuffled[i], shuffled[i+pos]);
+ // }
+ return shuffled;
+ }
+private:
+ vector<int> nums;
+ vector<int> original;
+};分析:经典的Fisher-Yates洗牌算法,原理是通过随机交换位置来实现随机打乱,有正向和反向两种写法
+错误:类什么的还是不太会写
+给定一个数组,数组每个位置的值表示该位置的权重,要求按照权重的概率去随机采样。
+class Solution {
+ vector<int> W;
+public:
+ Solution(vector<int>& w) {
+ partial_sum(w.begin(), w.end(), back_inserter(W));
+ }
+
+ int pickIndex() {
+ int pos = rand() % W.back();
+ return upper_bound(W.begin(), W.end(), pos) - W.begin();
+ }
+};分析:我们可以先使用 partial_sum求前缀和(即到每个位置为止之前所有数字的和),这个结果对于正整数数组是单调递增的。每当需要采样时,我们可以先随机产生一个数字,然后使用二分法查找其在前缀和中的位置,以模拟加权采样的过程。
错误:没思路
+给你一个单链表,随机选择链表的一个节点,并返回相应的节点值。每个节点被选中的概率一样 。
+class Solution {
+ vector<int> arr;
+public:
+ Solution(ListNode* head) {
+ while (head) {
+ arr.emplace_back(head->val);
+ head = head->next;
+ }
+ }
+
+ int getRandom() {
+ return arr[rand() % arr.size()];
+ }
+};分析:用一个数组记录链表中的所有结点值,然后随机输出即可。
+错误:思路简单就是不会写
+给你一个整数 columnNumber ,返回它在 Excel 表中相对应的列名称。
class Solution {
+public:
+ string convertToTitle(int columnNumber) {
+ string ans;
+ while (columnNumber > 0) {
+ int a0 = (columnNumber - 1) % 26 + 1;
+ ans += a0 - 1 + 'A';
+ columnNumber = (columnNumber - a0) / 26;
+ }
+ reverse(ans.begin(), ans.end());
+ return ans;
+ }
+};分析:进制转换的变形题
+错误:减法操作没想好
+给你两个二进制字符串,返回它们的和(用二进制表示)。
+class Solution {
+public:
+ string addBinary(string a, string b) {
+ int a_size = a.size();
+ int b_size = b.size();
+ --a_size;
+ --b_size;
+ int cnt = 0;
+ int sign;
+ string result = "";
+ while(a_size >= 0 && b_size >= 0){
+ sign = a[a_size] - '0' + b[b_size] - '0' + cnt;
+ if(sign == 0){
+ result = "0" + result;
+ cnt = 0;
+ }
+ else if(sign == 1){
+ result = "1" + result;
+ cnt = 0;
+ }
+ else if(sign == 2){
+ result = "0" + result;
+ cnt = 1;
+ }
+ else if(sign == 3){
+ result = "1" + result;
+ cnt = 1;
+ }
+ --a_size;
+ --b_size;
+ }
+ while(a_size >= 0){
+ sign = a[a_size] - '0' + cnt;
+ if(sign == 0){
+ result = "0" + result;
+ cnt = 0;
+ }
+ else if(sign == 1){
+ result = "1" + result;
+ cnt = 0;
+ }
+ else if(sign == 2){
+ result = "0" + result;
+ cnt = 1;
+ }
+ else if(sign == 3){
+ result = "1" + result;
+ cnt = 1;
+ }
+ --a_size;
+ }
+ while(b_size >= 0){
+ sign = b[b_size] - '0' + cnt;
+ if(sign == 0){
+ result = "0" + result;
+ cnt = 0;
+ }
+ else if(sign == 1){
+ result = "1" + result;
+ cnt = 0;
+ }
+ else if(sign == 2){
+ result = "0" + result;
+ cnt = 1;
+ }
+ else if(sign == 3){
+ result = "1" + result;
+ cnt = 1;
+ }
+ --b_size;
+ }
+ if(cnt == 1){
+ result = "1" + result;
+ }
+ return result;
+ }
+};分析:还是大数加法
+错误:忘记了,应该没什么错误
+给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
class Solution {
+public:
+ vector<int> productExceptSelf(vector<int>& nums) {
+ int n = nums.size();
+ vector<int> left(n);
+ vector<int> right(n);
+ int start = 1;
+ left[0] = start;
+ for(int i=1;i<n;++i){
+ left[i] = start * nums[i-1];
+ start = left[i];
+ }
+ int end = 1;
+ right[n-1] = end;
+ for(int i=n-2;i>=0;--i){
+ right[i] = end * nums[i+1];
+ end = right[i];
+ }
+ vector<int> result(n);
+ for(int i=0;i<n;++i){
+ result[i] = left[i] * right[i];
+ }
+ return result;
+ }
+};分析:前缀积+后缀积
+错误:看了一下思路,后面自己想通了实现了
+给你一个长度为 n 的整数数组 nums ,返回使所有数组元素相等需要的最少移动数。在一步操作中,你可以使数组中的一个元素加 1 或者减 1 。
class Solution {
+public:
+ int minMoves2(vector<int>& nums) {
+ int n = nums.size();
+ sort(nums.begin(),nums.end());
+ int num = nums[n/2];
+ int sum2 = 0;
+ for(int i=0;i<n;++i){
+ if(nums[i] > num){
+ sum2 += nums[i] - num;
+ }
+ else{
+ sum2 += num - nums[i];
+ }
+ }
+ return sum2;
+ }
+};分析:如果仅仅考虑最大的数字和最小的数字,那么这个数字一定在这两个数字中间,去除掉后这个数字也一定在次大的和次小的数字之间。因此是中位数
+错误:思路不对,开始想成平均数了
+给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
class Solution {
+public:
+ int majorityElement(vector<int>& nums) {
+ int candidate = -1;
+ int count = 0;
+ for (int num : nums) {
+ if (num == candidate)
+ ++count;
+ else if (--count < 0) {
+ candidate = num;
+ count = 1;
+ }
+ }
+ return candidate;
+ }
+};分析:Boyer-Moore 算法:维护一个候选众数 candidate 和它出现的次数 count。初始时 candidate 可以为任意值,count 为 0;我们遍历数组 nums 中的所有元素,对于每个元素 x,在判断 x 之前,如果 count 的值为 0,我们先将 x 的值赋予 candidate,随后我们判断 x:如果 x 与 candidate 相等,那么计数器 count 的值增加 1;如果 x 与 candidate 不等,那么计数器 count 的值减少 1。在遍历完成后,candidate 即为整个数组的众数。
+错误:算法想的不太好,没有想到最优的解法。
+给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数,试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数。
class Solution {
+public:
+ int rand10() {
+ int row, col, idx;
+ do {
+ row = rand7();
+ col = rand7();
+ idx = col + (row - 1) * 7;
+ } while (idx > 40);
+ return 1 + (idx - 1) % 10;
+ }
+};分析:调用两次rand7(),找到一些等概率的数字,然后拒绝掉另外的数字。
+错误:想当然认为是直接乘法了。
+编写一个算法来判断一个数 n 是不是快乐数。
class Solution {
+public:
+ bool isHappy(int n) {
+ int sum = 6;
+ while(sum--){
+ string s = to_string(n);
+ int t = 0;
+ for(int i=0;i<s.size();++i){
+ t += (s[i] - '0') * (s[i] - '0');
+ }
+ if(t == 1){
+ return true;
+ }
+ n = t;
+ }
+ return false;
+ }
+};分析:看看会不会跳出循环
+一遍AC,但是解法不够好,后面要用更好的方法进行尝试。
+数学问题需要有数学基础,一般面试中应该用的比较少,有些问题还是挺有意思的。
+ + +《现代信息检索》课程笔记:第3讲 索引压缩
+ +举例:将长编码串用短编码串来代替:111111111111111111➡18个1
+为什么要压缩?
+为什么在IR中需要压缩?
+IR中压缩的两个基本要求:无损压缩和随机访问
+压缩的一个基本问题:对齐,即建立不同压缩单元之间的分界标识
+有损压缩:丢弃一些信息-很多常用的预处理步骤可以看成是有损压缩
+无损压缩:所有信息都保留-索引压缩中通常都使用无损压缩
+词典压缩中词典的大小即词汇表的大小是关键
+词汇表大小会随着文档集的大小增长而增长,没有办法估计数量。
+存在一个经验规律可以进行估计:
+Heaps定律:





Heaps定律在对数空间下是线性的。
+在容许拼写错误或者对拼写错误自动纠错的情况下,Heaps定律的效果如何?
+倒排记录表压缩中词项的分布情况是关键
+我们还需要知道在文档集中有多少高频词项和低频词项
+Zipf定律:第




实际统计中可以发现拟合度并不是很高,但是可以发现高频词项很少,低频罕见词项很多。
+一般而言,相对于倒排记录表,词典所占空间较小。但是我们想将词典放入内存,另外满足一些特定领域特定应用的需要,如手机、机
+载计算机上的应用或要求快速启动等需求。因此,压缩词典也很重要。
定长数组方式下的词典存储:每个词项需要20(字符串)+4(词频)+4(指向倒排索引表的指针)=28个字节。
+不足之处:
+将整部词典看成单一字符串:4(词频)+4(指向倒排索引表的指针)+3(指向字符串的指针,按照实际大小决定,例如8*400000个位置需要$log_2(8 * 400000)< 24 $位来表示)+8(每个字符串平均需要8个字节)=19个字节
+按块存储,假设块大小k=4,此时每4个词项只需要保留1个词项指针,但是同时需要增加4个字节(比较短,1个字节就可以)来表示每个词项的长度,因此每4个词项需要3+4=7B,比之前的节省了12-7=5B
+但是不采用块存储方式下的词项查找是典型的二叉查找,而采用块存储方式下的词项查找需要进行顺序查找,块如果太大会影响效率。
+每个块当中,会有公共前缀,可以采用前端编码方式继续压缩。
+哪些前缀应该用于前端编码?需要在哪些方面有所权衡?
+倒排记录表空间远大于词典,压缩关键是对每条倒排记录进行压缩
+关键思想:存储 docID间隔而不是 docID本身
设计一个变长编码(variable length encoding):可变长编码对于小间隔采用短编码而对于长间隔采用长编码
+可变字节(VB)码:设定一个专用位 (高位) c作为延续位(continuation bit),如果间隔表示少于7比特,那么c置1,将间隔编入一个
+字节的后7位中;否则将高7位放入当前字节中,并将c置0,剩下的位数采用同样的方法进行处理,最后一个字节的c置1(表
+示结束)
一元码:将n表示成n个1和最后一个0
+基于位的编码:
+
偏移部分是


 编码是前缀无关的,也就是说一个合法的
编码是前缀无关的,也就是说一个合法的 编码不会是任何一个其他的合法
编码不会是任何一个其他的合法 编码的前缀,也保证了解码的唯一性。
编码的前缀,也保证了解码的唯一性。 编码在最优编码的2或3倍之内
编码在最优编码的2或3倍之内 编码适用于任何分布,是通用性编码
编码适用于任何分布,是通用性编码 编码是无参数编码,不需要通过拟合得到参数
编码是无参数编码,不需要通过拟合得到参数组变长整数编码:
+
 字节(在4–16之间)存放4个整数
字节(在4–16之间)存放4个整数Simple9编码:每块4字节,前4位标识块内结构,剩余28位存储若干个数字,每个数字占用相同的位数。
+ + +《模式识别与机器学习》课程笔记:第2章 统计判别
+ +统计学(statistics)是用以收集数据,分析数据和由数据得出结论的一组概念、原则和方法。
+给定观测值


最小化误差概率条件下,若



两类模式集的分类:
+目的:要确定





根据概率判别规则,若



由贝叶斯定理,后验概率






与概率判别规则结合,则若



不等式转换一下:
+若

若

其中,

此判别称为贝叶斯判别。
+贝叶斯判别的推广:
+可以通过引入一个更一般的损失函数来替代误差概率
+特征
当考虑到对于某一类的错误判决要比对另一类的判决更为关键时,就需要把最小错误概率的贝叶斯判别做一些修正,提出条件平均风险
对




若

若

意义:
+ 类的模式
类的模式 来说,它来自
来说,它来自 类的概率应为
类的概率应为
 是属于
是属于 类,但它实际上来自
类,但它实际上来自 类,也就是说分类器失败,这时
类,也就是说分类器失败,这时 为失分,对应的条件风险为后验概率进行
为失分,对应的条件风险为后验概率进行 的加权运算。
的加权运算。 的自然属性可能来自
的自然属性可能来自 类中的任一类,因此可将观察样本指定为
类中的任一类,因此可将观察样本指定为 类的条件平均风险用
类的条件平均风险用 的公式运算。
的公式运算。分类器对每一个模式




按贝叶斯公式,最小平均条件风险可写成:
+可以舍去公共项,则可以简化为:
+也是贝叶斯分类器,只是它的判别方法不是按错误概率最小作为标准,而是按平均条件风险作为标准。
+举例若
当分类器将

当分类器将

若


此时:
即:
通常
当
左边为似然比:
因此两类模式的贝叶斯判别条件为:
+ ,则
,则 ;
; ,则
,则 ;
; ,则可以做任意判别。
,则可以做任意判别。通常,当判别正确时,不失分,可选常数
判别错误时,可选常数
此时:
对于
贝叶斯最小错误判别是计算得到某个类别的概率,而最小风险判别是计算得到某个类别后存在风险的概率。两者正好相反。
+出发点:当已知或者有理由设想类概率密度函数

其中,每一类模式的分布密度都完全被其均值向量

当协方差矩阵的全部非对角线上的元素都为零时,多变量正态类密度函数可简化为

已知类别
可以取自然对数的形式以方便计算:
代入正态类密度函数,可以得到:
+去掉与
即为正态分布模式的贝叶斯判别函数。
+因此判别函数是一个超二次曲面,对于正态分布模式的贝叶斯分类器,两个模式类别之间用一个二次判别界面分开,就可以求得最优的分类效果。
+ 时:
时:两类模式的正态分布:





判别界面



当
 时:
时:
因

由此可导出类别

判别界面为
当
决策边界的特征:
+贝叶斯分类规则是基于统计概念的。如果只有少数模式样本,一般较难获得最优的结果。
+defBayesian(data,label,P):
+ if data.shape[0] != label.shape[0]: # 如果数据和标签的数量不相同
+ print('Error!')
+ sys.exit()
+ M = data[0].shape[0] # 获取数据的维度
+ data_list = [[],[]] # 将不同类别的数据分开存储
+ data_list[0] = np.array([data[i] for i inrange(len(label)) if label[i] ==0])
+ data_list[1] = np.array([data[i] for i inrange(len(label)) if label[i] ==1])
+ # 计算均值向量
+ m0 = np.sum(data_list[0],axis=0) / data_list[0].shape[0]
+ m1 = np.sum(data_list[1],axis=0) / data_list[1].shape[0]
+ # 计算协方差矩阵
+ C0 = np.sum(np.array([np.dot((data_list[0][i] - m0).reshape(-1,1), \
+ (data_list[0][i] - m0).reshape(1,-1)) for i inrange(data_list[0].shape[0])]),axis=0) / data_list[0].shape[0]
+ C1 = np.sum(np.array([np.dot((data_list[1][i] - m1).reshape(-1,1),\
+ (data_list[1][i] - m1).reshape(1,-1)) for i inrange(data_list[1].shape[0])]),axis=0) / data_list[1].shape[0]
+ return np.dot(m0-m1,np.linalg.inv(C0)),np.log(P[0]) - np.log(P[1]) +0.5* (np.dot(np.dot(m1.reshape(1,-1),\
+ np.linalg.inv(C0)),m1.reshape(-1,1)) - np.dot(np.dot(m0.reshape(1,-1),np.linalg.inv(C0)),m0.reshape(-1,1)))在贝叶斯分类器中,构造分类器需要知道类概率密度函数
对均值向量和协方差矩阵的估计即为贝叶斯分类器中的一种参数估计问题。
+参数估计的两种方式:
+设模式的类概率密度函数为

若以样本的平均值作为均值向量的近似值,则均值估计量


协方差矩阵
其中的每个元素
其中,





协方差矩阵写成向量形式为:
协方差矩阵的估计量(当
假设已经计算了

其中

协方差矩阵估计量的迭代运算与上述相似:
将概率密度函数的参数估计量看成是随机变量



Leetcode 刷题笔记-Leetcode 101 第11章 数据结构
+ +给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
class Solution {
+public:
+ vector<int> findDisappearedNumbers(vector<int>& nums) {
+ int n = nums.size();
+ vector<bool> vt(n+1,false);
+ for(int i=0;i<n;++i){
+ vt[nums[i]] = true;
+ }
+ vector<int> result;
+ for(int i=1;i<=n;++i){
+ if(vt[i] == false){
+ result.push_back(i);
+ }
+ }
+ return result;
+ }
+};分析:扫一遍确认一下,再扫一遍找出结果。
+一遍AC
+给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像原地顺时针旋转 90 度。
class Solution {
+public:
+ void rotate(vector<vector<int>>& matrix) {
+ int temp = 0, n = matrix.size()-1;
+ for (int i = 0; i <= n / 2; ++i) {
+ for (int j = i; j < n - i; ++j) {
+ temp = matrix[j][n-i];
+ matrix[j][n-i] = matrix[i][j];
+ matrix[i][j] = matrix[n-j][i];
+ matrix[n-j][i] = matrix[n-i][n-j];
+ matrix[n-i][n-j] = temp;
+ }
+ }
+ }
+};分析:转转转
+错误:没想到原地旋转的思路。
+编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:每行的元素从左到右升序排列,每列的元素从上到下升序排列。
class Solution {
+public:
+ bool searchMatrix(vector<vector<int>>& matrix, int target) {
+ int m = matrix.size();
+ int n = matrix[0].size();
+ int x = 0;
+ int y = n-1;
+ while(x >= 0 && x < m && y >= 0 && y < n){
+ if(matrix[x][y] == target){
+ return true;
+ }
+ else if(target < matrix[x][y]){
+ y -= 1;
+ }
+ else{
+ x += 1;
+ }
+ }
+ return false;
+ }
+};分析:从右上角开始查找,若当前值大于待搜索值,我们向左移动一位;若当前值小于待搜索值,我们向下移动一位。如果最终移动到左下角时仍不等于待搜索值,则说明待搜索值不存在于矩阵中。
+错误:找到思路后一遍AC
+给定一个长度为 n 的整数数组 arr ,它表示在 [0, n - 1] 范围内的整数的排列。我们将 arr 分割成若干 块 (即分区),并对每个块单独排序。将它们连接起来后,使得连接的结果和按升序排序后的原数组相同。返回数组能分成的最多块数量。
class Solution {
+public:
+ int maxChunksToSorted(vector<int>& arr) {
+ int n = arr.size();
+ int result = 0;
+ int maxnum = 0;
+ for(int i=0;i<n;++i){
+ maxnum = max(maxnum,arr[i]);
+ if(maxnum == i){
+ ++result;
+ }
+ }
+ return result;
+ }
+};分析:从左往右遍历,同时记录当前的最大值,每当当前最大值等于数组位置时,我们可以多一次分割。
+错误:看了思路后实现的
+请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty)
class MyQueue {
+ stack<int> st1;
+ stack<int> st2;
+public:
+ MyQueue() {
+
+ }
+
+ void push(int x) {
+ st1.push(x);
+ }
+
+ int pop() {
+ while(!st1.empty()){
+ st2.push(st1.top());
+ st1.pop();
+ }
+ int a = st2.top();
+ st2.pop();
+ while(!st2.empty()){
+ st1.push(st2.top());
+ st2.pop();
+ }
+ return a;
+ }
+
+ int peek() {
+ while(!st1.empty()){
+ st2.push(st1.top());
+ st1.pop();
+ }
+ int a = st2.top();
+ while(!st2.empty()){
+ st1.push(st2.top());
+ st2.pop();
+ }
+ return a;
+ }
+
+ bool empty() {
+ return st1.empty();
+ }
+};分析:比较简单,也没有算法
+错误:全局变量没定义好,返回值漏掉了,调通了。
+设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
class MinStack {
+ stack<int> s1;
+ stack<int> mins;
+public:
+ MinStack() {
+
+ }
+
+ void push(int val) {
+ if(mins.empty() || val <= mins.top()){
+ mins.push(val);
+ }
+ s1.push(val);
+ }
+
+ void pop() {
+ int a = s1.top();
+ s1.pop();
+ if(mins.top() == a){
+ mins.pop();
+ }
+ }
+
+ int top() {
+ return s1.top();
+ }
+
+ int getMin() {
+ return mins.top();
+ }
+};分析:可以额外建立一个新栈,栈顶表示原栈里所有值的最小值。每当在原栈里插入一个数字时,若该数字小于等于新栈栈顶,则表示这个数字在原栈里是最小值,我们将其同时插入新栈内。每当从原栈里取出一个数字时,若该数字等于新栈栈顶,则表示这个数是原栈里的最小值之一,我们同时取出新栈栈顶的值。
+错误:没有思路
+给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
class Solution {
+public:
+ bool isValid(string s) {
+ stack<char> st;
+ int n = s.size();
+ for(int i=0;i<n;++i){
+ if(s[i] == '(' || s[i] == '{' || s[i] == '['){
+ st.push(s[i]);
+ }
+ else{
+ if(st.empty()){
+ return false;
+ }
+ else if(st.top() == '[' && s[i] == ']'){
+ st.pop();
+ }
+ else if(st.top() == '(' && s[i] == ')'){
+ st.pop();
+ }
+ else if(st.top() == '{' && s[i] == '}'){
+ st.pop();
+ }
+ else{
+ return false;
+ }
+ }
+ }
+ if(st.empty()){
+ return true;
+ }
+ return false;
+ }
+};分析:用栈进行匹配即可
+错误:没有考虑只有一个左括号的情况,改正后调通了
+给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
class Solution {
+public:
+ vector<int> dailyTemperatures(vector<int>& temperatures) {
+ int n = temperatures.size();
+ vector<int> answer(n);
+ stack<int> s;
+ for(int i=0;i<n;++i){
+ while (!s.empty()) {
+ int pre_index = s.top();
+ if (temperatures[i] <= temperatures[pre_index]) {
+ break;
+ }
+ s.pop();
+ answer[pre_index] = i - pre_index;
+ }
+ s.push(i);
+ }
+ return answer;
+ }
+};分析:我们可以维持一个单调递减的栈,表示每天的温度;为了方便计算天数差,我们这里存放位置(即日期)而非温度本身。我们从左向右遍历温度数组,对于每个日期p,如果p的温度比栈顶存储位置q的温度高,则我们取出q,并记录q需要等待的天数为p-q;我们重复这一过程,直到p的温度小于等于栈顶存储位置的温度(或空栈)时,我们将p插入栈顶,然后考虑下一天。在这个过程中,栈内数组永远保持单调递减,避免了使用排序进行比较。最后若栈内剩余一些日期,则说明它们之后都没有出现更暖和的日期。
+错误:感觉并不是非常理解。
+给你一个链表数组,每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中,返回合并后的链表。
+class Solution {
+public:
+ struct Comp{
+ bool operator()(ListNode* l1,ListNode* l2){
+ return l1->val > l2->val;
+ }
+ };
+ ListNode* mergeKLists(vector<ListNode*>& lists) {
+ if(lists.empty()){
+ return nullptr;
+ }
+ priority_queue<ListNode*,vector<ListNode*>,Comp> q;
+ for(ListNode* list:lists){
+ if(list){
+ q.push(list);
+ }
+ }
+ ListNode* dummy = new ListNode(0), *cur = dummy;
+ while (!q.empty()) {
+ cur->next = q.top();
+ q.pop();
+ cur = cur->next;
+ if (cur->next) {
+ q.push(cur->next);
+ }
+ }
+ return dummy->next;
+ }
+};分析:即把所有的链表存储在一个优先队列中,每次提取所有链表头部节点值最小的那个节点,直到所有链表都被提取完为止。
+错误:优先队列不是很熟悉
+给定建筑物的起止位置和高度,返回建筑物轮廓(天际线)的拐点。
+Hard难度,想不太明白,暂时不做了
+分析:使用优先队列储存每个建筑物的高度和右端(这里使用pair,其默认比较函数是先比较第一个值,如果相等则再比较第二个值),从而获取目前会拔高天际线、且妨碍到前一个建筑物(的右端端点)的下一个建筑物。
+错误:没有思路
+给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。
class Solution {
+public:
+ vector<int> maxSlidingWindow(vector<int>& nums, int k) {
+ vector<int> result;
+ deque<int> dq;
+ int n = nums.size();
+ for(int i=0;i<n;++i){
+ if(!dq.empty() && nums[i] > nums[dq.back()]){
+ while(!dq.empty() && nums[dq.back()] < nums[i]){
+ dq.pop_back();
+ }
+ }
+ dq.push_back(i);
+ if(i >= k-1){
+ result.push_back(nums[dq.front()]);
+ if(nums[i-k+1] == nums[dq.front()]){
+ dq.pop_front();
+ }
+ }
+ }
+ return result;
+ }
+};分析:利用双端队列进行操作:每当向右移动时,把窗口左端的值从队列左端剔除,把队列右边小于窗口右端的值全部剔除。这样双端队列的最左端永远是当前窗口内的最大值。
+错误:理解了思路后调通了。
+给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出和为目标值 target的那两个整数,并返回它们的数组下标。
class Solution {
+public:
+ vector<int> twoSum(vector<int>& nums, int target) {
+ vector<int> result;
+ unordered_map<int, int> hash;
+ int n = nums.size();
+ for(int i=0;i<n;++i){
+ if(hash.count(target - nums[i])){
+ result.push_back(hash[target - nums[i]]);
+ result.push_back(i);
+ break;
+ }
+ hash[nums[i]] = i;
+ }
+ return result;
+ }
+};分析:利用哈希表存储遍历过的值以及它们的位置,每次遍历到位置i 的时候,查找哈希表里是否存在target - nums[i],若存在,则说明这两个值的和为target。
+一遍AC
+给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
class Solution {
+public:
+ int longestConsecutive(vector<int>& nums) {
+ unordered_set<int> hash;
+ for(const int & num:nums){
+ hash.insert(num);
+ }
+ int ans = 0;
+ while(!hash.empty()){
+ int cnt = *(hash.begin());
+ hash.erase(cnt);
+ int pre = cnt - 1;
+ int next = cnt + 1;
+ while(!hash.empty() && hash.count(pre)){
+ hash.erase(pre);
+ --pre;
+ }
+ while(!hash.empty() && hash.count(next)){
+ hash.erase(next);
+ ++next;
+ }
+ ans = max(ans,next-pre-1);
+ }
+ return ans;
+ }
+};分析:把所有数字放到一个哈希表,然后不断地从哈希表中任意取一个值,并删除掉其之前之后的所有连续数字,然后更新目前的最长连续序列长度。重复这一过程,我们就可以找到所有的连续数字序列。
+错误:看了思路后实现了
+给你一个数组 points ,其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
class Solution {
+public:
+ int maxPoints(vector<vector<int>>& points) {
+ unordered_map<double, int> hash; // <斜率, 点个数>
+ int max_count = 0, same = 1, same_y = 1;
+ for (int i = 0; i < points.size(); ++i) {
+ same = 1, same_y = 1;
+ for (int j = i + 1; j < points.size(); ++j) {
+ if (points[i][1] == points[j][1]) {
+ ++same_y;
+ if (points[i][0] == points[j][0]) {
+ ++same;
+ }
+ }
+ else {
+ double dx = points[i][0] - points[j][0], dy = points[i][1] -
+ points[j][1];
+ ++hash[dx/dy];
+ }
+ }
+ max_count = max(max_count, same_y);
+ for (auto item : hash) {
+ max_count = max(max_count, same + item.second);
+ }
+ hash.clear();
+ }
+ return max_count;
+ }
+};分析:对于每个点,我们对其它点建立哈希表,统计同一斜率的点一共有多少个。这里利用的原理是,一条线可以由一个点和斜率而唯一确定。另外也要考虑斜率不存在和重复坐标的情况。
+错误:好麻烦先算了
+给你一份航线列表 tickets ,其中 tickets[i] = [from<sub>i</sub>, to<sub>i</sub>] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。
class Solution {
+public:
+ vector<string> findItinerary(vector<vector<string>>& tickets) {
+ vector<string> ans;
+ if (tickets.empty()) {
+ return ans;
+ }
+ unordered_map<string, multiset<string>> hash;
+ for (const auto & ticket: tickets) {
+ hash[ticket[0]].insert(ticket[1]);
+ }
+ stack<string> s;
+ s.push("JFK");
+ while (!s.empty()) {
+ string next = s.top();
+ if (hash[next].empty()) {
+ ans.push_back(next);
+ s.pop();
+ }
+ else {
+ s.push(*hash[next].begin());
+ hash[next].erase(hash[next].begin());
+ }
+ }
+ reverse(ans.begin(), ans.end());
+ return ans;
+ }
+};分析:本题可以先用哈希表记录起止机场,其中键是起始机场,值是一个多重集合,表示对应的终止机场。因为一个人可能坐过重复的线路,所以我们需要使用多重集合储存重复值。储存完成之后,我们可以利用栈来恢复从终点到起点飞行的顺序,再将结果逆序得到从起点到终点的顺序。
+错误:多重集合的第一道题,也是唯一一道题,不是很明白
+设计一个数据结构,使得其能够快速查询给定数组中,任意两个位置间所有数字的和。
+class NumArray {
+ vector<int> frontsum;
+public:
+ NumArray(vector<int>& nums) {
+ for(int i=0;i<nums.size();++i){
+ if(i == 0){
+ frontsum.push_back(nums[i]);
+ }
+ else{
+ frontsum.push_back(nums[i] + frontsum[i-1]);
+ }
+ }
+ }
+
+ int sumRange(int left, int right) {
+ if(left == 0){
+ return frontsum[right];
+ }
+ return frontsum[right] - frontsum[left-1];
+ }
+};分析:前缀和即可
+一遍AC
+设计一个数据结构,使得其能够快速查询给定矩阵中,任意两个位置包围的长方形中所有数字的和。
+class NumMatrix {
+ vector<vector<int>> frontmatrix;
+public:
+ NumMatrix(vector<vector<int>>& matrix) {
+ int m = matrix.size();
+ int n = matrix[0].size();
+ for(int i=0;i<m;++i){
+ vector<int> temp;
+ for(int j=0;j<n;++j){
+ if(i == 0 && j == 0){
+ temp.push_back(matrix[i][j]);
+ }
+ else if(i == 0){
+ temp.push_back(matrix[i][j] + temp[j-1]);
+ }
+ else if(j == 0){
+ temp.push_back(matrix[i][j] + frontmatrix[i-1][j]);
+ }
+ else{
+ temp.push_back(matrix[i][j] + frontmatrix[i-1][j] + temp[j-1] - frontmatrix[i-1][j-1]);
+ }
+ }
+ frontmatrix.push_back(temp);
+ }
+ }
+
+ int sumRegion(int row1, int col1, int row2, int col2) {
+ if(row1 == 0 && col1 == 0){
+ return frontmatrix[row2][col2];
+ }
+ else if(row1 == 0){
+ return frontmatrix[row2][col2]-frontmatrix[row2][col1-1];
+ }
+ else if(col1 == 0){
+ return frontmatrix[row2][col2]-frontmatrix[row1-1][col2];
+ }
+ return frontmatrix[row2][col2]-frontmatrix[row2][col1-1]-frontmatrix[row1-1][col2]+frontmatrix[row1-1][col1-1];
+ }
+};分析:二维上的前缀和(积分图)即可
+一遍AC
+给你一个整数数组 nums 和一个整数 k ,请你统计并返回该数组中和为 k 的连续子数组的个数。
class Solution {
+public:
+ int subarraySum(vector<int>& nums, int k) {
+ int count = 0, psum = 0;
+ unordered_map<int, int> hashmap;
+ hashmap[0] = 1; // 初始化很重要
+ for (int i: nums) {
+ psum += i;
+ count += hashmap[psum-k];
+ ++hashmap[psum];
+ }
+ return count;
+ }
+};分析:本题同样是利用前缀和,不同的是这里我们使用一个哈希表 hashmap,其键是前缀和,而值是该前缀和出现的次数。在我们遍历到位置i 时,假设当前的前缀和是 psum ,那么 hashmap[psum-k]即为以当前位置结尾、满足条件的区间个数。
错误:直接使用前缀和会超时,然而这个短代码挺难理解的样子。
+在 MATLAB 中,有一个非常有用的函数 reshape ,它可以将一个 m x n 矩阵重塑为另一个大小不同(r x c)的新矩阵,但保留其原始数据。给你一个由二维数组 mat 表示的 m x n 矩阵,以及两个正整数 r 和 c ,分别表示想要的重构的矩阵的行数和列数。重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序填充。如果具有给定参数的 reshape 操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
class Solution {
+public:
+ vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {
+ int m = mat.size();
+ int n = mat[0].size();
+ if(m*n != r*c){
+ return mat;
+ }
+ int rowindex = 0;
+ int colindex = 0;
+ vector<vector<int>> result(r,vector<int>(c));
+ for(int i=0;i<r;++i){
+ for(int j=0;j<c;++j){
+ result[i][j] = mat[rowindex][colindex];
+ ++colindex;
+ if(colindex == n){
+ ++rowindex;
+ colindex = 0;
+ }
+ }
+ }
+ return result;
+ }
+};分析:很简单的小题,没有任何难度。
+一遍AC
+用两个队列实现一个栈
+class MyStack {
+ queue<int> q1;
+ queue<int> q2;
+public:
+ MyStack() {
+
+ }
+
+ void push(int x) {
+ q1.push(x);
+ return;
+ }
+
+ int pop() {
+ while(q1.size() != 1){
+ q2.push(q1.front());
+ q1.pop();
+ }
+ int a = q1.front();
+ q1.pop();
+ while(!q2.empty()){
+ q1.push(q2.front());
+ q2.pop();
+ }
+ return a;
+ }
+
+ int top() {
+ while(q1.size() != 1){
+ q2.push(q1.front());
+ q1.pop();
+ }
+ int a = q1.front();
+ q2.push(q1.front());
+ q1.pop();
+ while(!q2.empty()){
+ q1.push(q2.front());
+ q2.pop();
+ }
+ return a;
+ }
+
+ bool empty() {
+ return q1.empty();
+ }
+};分析:也是很简单的题,倒腾倒腾数字就行了
+一遍AC
+给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的下一个更大元素 。
class Solution {
+public:
+ vector<int> nextGreaterElements(vector<int>& nums) {
+ int n = nums.size();
+ stack<int> st;
+ vector<int> result(n,-1);
+ for(int i=0;i<2*n-1;++i){
+ while(!st.empty() && nums[i%n] > nums[st.top()]){
+ result[st.top()] = nums[i%n];
+ st.pop();
+ }
+ st.push(i%n);
+ }
+ return result;
+ }
+};分析:使用单调栈解决本题。单调栈中保存的是下标,从栈底到栈顶的下标在数组 nums中对应的值是单调不升的。每次我们移动到数组中的一个新的位置 i,我们就将当前单调栈中所有对应值小于 nums[i]的下标弹出单调栈,这些值的下一个更大元素即为 nums[i]。随后我们将位置 i入栈。
错误:没有想到单调栈,看了一下思路后自己实现的。
+给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
class Solution {
+public:
+ bool containsDuplicate(vector<int>& nums) {
+ unordered_map<int,int> mp;
+ int n = nums.size();
+ for(int i=0;i<n;++i){
+ if(mp.find(nums[i]) == mp.end()){
+ mp[nums[i]] = 1;
+ }
+ else{
+ return true;
+ }
+ }
+ return false;
+ }
+};分析:非常简单的哈希表,没什么难度
+错误:下标和数字插入看的不太对
+给定一个非空且只包含非负数的整数数组 nums,数组的度的定义是指数组里任一元素出现频数的最大值。你的任务是在 nums 中找到与 nums 拥有相同大小的度的最短连续子数组,返回其长度。
class Solution {
+public:
+ int findShortestSubArray(vector<int>& nums) {
+ unordered_map<int,vector<int>> mp;
+ int n = nums.size();
+ for(int i=0;i<n;++i){
+ if(mp.find(nums[i]) == mp.end()){
+ mp[nums[i]].push_back(i);
+ mp[nums[i]].push_back(i);
+ mp[nums[i]].push_back(1);
+ }
+ else{
+ if(i < mp[nums[i]][0]){
+ mp[nums[i]][0] = i;
+ }
+ if(i > mp[nums[i]][1]){
+ mp[nums[i]][1] = i;
+ }
+ ++mp[nums[i]][2];
+ }
+ }
+ int maxnum = 0;
+ int result = n+1;
+ for(auto it = mp.cbegin();it != mp.cend();++it){
+ if(it->second[2] > maxnum){
+ maxnum = it->second[2];
+ result = it->second[1]-it->second[0]+1;
+ }
+ else if (it->second[2] == maxnum){
+ result = min(result,it->second[1]-it->second[0]+1);
+ }
+ }
+ return result;
+ }
+};分析:比较简单的数据结构应用题
+错误:语法问题,还有下标数字问题,后面自己调通
+和谐数组是指一个数组里元素的最大值和最小值之间的差别 正好是 1 。现在,给你一个整数数组 nums ,请你在所有可能的子序列中找到最长的和谐子序列的长度。数组的子序列是一个由数组派生出来的序列,它可以通过删除一些元素或不删除元素、且不改变其余元素的顺序而得到。
class Solution {
+public:
+ int findLHS(vector<int>& nums) {
+ int n = nums.size();
+ int ans = 0;
+ unordered_map<int,int> mp;
+ for(int i=0;i<n;++i){
+ if(mp.find(nums[i]) == mp.end()){
+ mp[nums[i]] = 1;
+ }
+ else{
+ ++mp[nums[i]];
+ }
+ }
+ for(auto it = mp.cbegin();it != mp.cend();++it){
+ if(mp.find(it->first-1) != mp.end()){
+ ans = max(ans,it->second + mp[it->first-1]);
+ }
+ if(mp.find(it->first+1) != mp.end()){
+ ans = max(ans,it->second + mp[it->first+1]);
+ }
+ }
+ return ans;
+ }
+};分析:看起来挺像动态规划,实际上并不是,统计一下就好了
+错误:还是map迭代器不太熟练,后面调通。
+给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
class Solution {
+public:
+ int findDuplicate(vector<int>& nums) {
+ int n = nums.size();
+ int len = nums.length;
+ for (int num : nums) {
+ int idx = Math.abs(num);
+ if (nums[idx] < 0) {
+ return idx;
+ }
+ nums[idx] = -nums[idx];
+ }
+ return len;
+ }
+};分析:考虑到数组元素值的范围是 [1,n],但数组长度为 n+1,那么很显然在遍历数组的时候,我们将数组的值变为其对应的负数,那么再次遇到负数就得到了答案。
错误:上面不是最优解,没有想到最优解
+超级丑数 是一个正整数,并满足其所有质因数都出现在质数数组 primes 中。给你一个整数 n 和一个整数数组 primes ,返回第 n 个 超级丑数 。题目数据保证第 n 个 超级丑数 在 32-bit 带符号整数范围内。
class Solution {
+public:
+ int nthSuperUglyNumber(int n, vector<int>& primes) {
+ vector<long> dp(n + 1);
+ int m = primes.size();
+ vector<int> pointers(m, 0);
+ vector<long> nums(m, 1);
+ for (int i = 1; i <= n; i++) {
+ long minNum = INT_MAX;
+ for (int j = 0; j < m; j++) {
+ minNum = min(minNum, nums[j]);
+ }
+ dp[i] = minNum;
+ for (int j = 0; j < m; j++) {
+ if (nums[j] == minNum) {
+ pointers[j]++;
+ nums[j] = dp[pointers[j]] * primes[j];
+ }
+ }
+ }
+ return dp[n];
+ }
+};分析:动态规划,没有思路
+错误:没有思路
+给定两个大小相等的数组 nums1 和 nums2,nums1 相对于 nums 的优势可以用满足 nums1[i] > nums2[i] 的索引 i 的数目来描述。返回 nums1 的任意排列,使其相对于 nums2 的优势最大化。
class Solution {
+public:
+ vector<int> advantageCount(vector<int>& nums1, vector<int>& nums2) {
+ sort(nums1.begin(),nums1.end());
+ vector<pair<int,int>> vt;
+ for(int i=0;i<nums2.size();i++){
+ vt.push_back(make_pair(nums2[i],i));
+ }
+ sort(vt.begin(),vt.end());
+ vector<int> ans(nums2.size());
+ int l1=0,r1=nums1.size()-1,l2=0,r2=nums2.size()-1;
+ while(r2>=0){
+ if(nums1[r1]>vt[r2].first){
+ ans[vt[r2].second]=nums1[r1];
+ r1--;
+ }
+ else{
+ ans[vt[r2].second]=nums1[l1];
+ l1++;
+ }
+ r2--;
+ }
+
+ return ans;
+ }
+};分析:田忌赛马,能打就打,打不过让最菜的送人头。
+错误:没思路
+线段树先算了
+数据结构是最最基础的算法,没有合适的数据结构就不可能有高效的算法。普通的数据结构掌握的还不错,但是有一些比较高级的数据结构练的比较少,掌握的不太好。今后要注重这些比较高级的数据结构,并尽量去在实际中应用。
+ + +《高级人工智能》课程笔记:第2讲 搜索
+ +搜索问题是对原问题的建模
+搜索问题的构成:状态空间➡后继函数(状态转化为另一个状态,采取的动作,付出的代价)➡初始状态和目标测试
+解是一个行动序列,将初始状态转换成目标状态
+例1:罗马尼亚旅行:
+ +解:从Arad到Bucharest的最短路径
+例2:吃豆子游戏
+ +状态空间包含了环境中的每一个细节:Agent,Ghost,大的豆子和小的豆子
+搜索状态只保留行动需要的细节:
+对于走到终点来说:
+对于吃掉所有豆子来说:
+状态数量计算:
+

例3:三个传教士和三个野人
+状态空间:{(M, C, B)},表示河左岸的传教士数量、野人数量和船目前的方位
+后继函数:{P01, P10, P02, P20, P11, Q01, Q10, Q02, Q20, Q11},P表示现在是从左岸到右岸,后面两个数字表示船上的传教士数量和野人数量
+初始状态:(3, 3, 1)
+目标状态:(0, 0, 0)
+状态空间图:搜索问题的数学表示,在状态空间图中,每个状态只出现一次
+搜索树:
+状态空间图的每一个结点表示每一个状态
+搜索树的每一个结点不表示状态,而是从初始状态到这个状态的一个路径(因此要尽量少构建搜索树的结点)
+基于搜索树的搜索:
+搜索算法特性:
+所有搜索算法都是相同的,除了对边缘的处理策略
+ ,最大深度为
,最大深度为 ,时间复杂度为
,时间复杂度为 ,空间复杂度为
,空间复杂度为 (因为只保留了路径上的结点)
(因为只保留了路径上的结点) 无穷大,无法在可以接受的时间内找到解
无穷大,无法在可以接受的时间内找到解 ,最大深度为
,最大深度为 ,解的深度为
,解的深度为 ,时间复杂度为
,时间复杂度为 ,空间复杂度为
,空间复杂度为
 一定是有限的
一定是有限的结合DFS的空间优势与BFS的时间优势
+深度优先按照层数进行约束,不要搜索到
通常绝大多数的节点都在底层,所以上层的节点生成多次影响不是很大
+代价一致搜索(Uniform Cost Search):将之前的走过的路径的代价进行一个累加,然后寻找其代价最低的路径。
+可以看成代价敏感搜索的一种实现。
+ ,每条结点间连线的代价大概为
,每条结点间连线的代价大概为 ,时间复杂度为
,时间复杂度为 ,空间复杂度为
,空间复杂度为
启发策略:估计一个状态到目标距离的函数,问题给予算法的额外信息,为特定搜索问题而设计。
+策略:扩展你认为最接近目标状态的节点
+启发式:对每个状态估计到最近目标的距离(曼哈顿距离或者欧氏距离),只使用启发函数
通常情况下最佳优先使你直接(或很快)到达目标,最坏情况类似DFS
+结合代价一致搜索和贪婪搜索
+重点搜索评价函数:


A* 搜索将两个代价进行组合
+A* 搜索结束条件是目标出列的时候,而不是目标入列的时候,因为目标入列的时候可能路径并不是最优的。
+A*搜索不一定是最优的,启发函数要好好选择
+启发函数


前提:启发函数
对于解决难的搜索问题,大部分工作就是想出可采纳的启发函数。通常可采纳启发函数是松弛问题的解的耗散
+A*图搜索与树搜索的区别在于图搜索不允许访问相同结点
+图搜索中,如果启发函数是一致的,A* 搜索是最优的。
+一致的:启发函数不仅仅要是可采纳的,同时在每一个局部的位置也要合理。
+也就是:如果沿路径的节点估计耗散

通常,天然的可采纳启发函数是倾向于一致的,特别是从松弛问题中获得的启发函数
+树搜索在边缘集合中保留未探索的替代路径(确保完备性)
+局部搜索: 改进单一选项直到不能再改善为止
+爬山法搜索
+模拟退火搜索:避免局部极大(允许向山下移动)
+遗传算法——自然选择
+《现代信息检索》课程笔记:第4讲 通配查询与拼写矫正
+ +词典是指存储词项词汇表的数据结构:作用:存储词项以及定位词项
+词项词汇表指的是具体数据,而词典指的是数据结构
+采用定长数组的词典结构对每个词项需要存储文档频率和指向倒排记录表的指针
+词项定位(查词典):在词典中查找给定关键字
+用于词项定位的数据结构:主要是哈希表和树
+有些IR系统用哈希表,有些系统用树结构
+采用哈希表或树的准则:
+哈希函数:输入词项,输出正整数(通常是地址)
+树
+树可以支持前缀查找(相当于对词典再建一层索引)
+最简单的树结构:二叉树,搜索速度略低于哈希表方式,时间复杂度为

且
B-树:每个内部节点的子节点数目在

通配查询:包含通配符的查询
+mon*: 找出所有包含以mon开头的词项的文档
+如果采用B-树词典结构,那么实现起来非常容易,只需要返回区间mon ≤ t < moo上的词项t
+*mon: 找出所有包含以mon结尾的词项的文档
+将所有的词项倒转过来,然后基于它们建一棵附加的树,返回区间nom ≤ t < non上的词项t
+词项中间的*号处理:mnchen
+轮排索引:(主要思想:让星号出现在词汇的末尾)
+轮排索引的查找过程:
+相对于通常的B-树,轮排索引(轮排树)的空间要大4倍以上 (经验值)
+k-gram索引:枚举一个词项中所有连读的k个字符构成k-gram
+k-gram存在两个倒排索引:
+k-gram索引 vs. 轮排索引
+涉及的任务:拼写错误检测和拼写错误矫正(并不是先后的关系)
+错误种类:非词汇错误(纠正的时候不需要考虑上下文)和真实词汇错误(纠正的时候需要考虑上下文)
+两个主要用途
+非词汇拼写错误检测:词典中不存在的词均视为错误
+非词汇拼写错误矫正:
+词独立法:
+采用拼写噪声通道模型:通过贝叶斯定理求解:
+正确拼写为


产生候选词的方法:
+语言模型
+若有包含


通道模型概率-计算错误概率
然后可以计算噪声通道模型
+计算的过程中可以添加加一概率平滑:上述混淆矩阵的例子很难避免某种操作样本数为0,要避免这种概率为0的情况
+真实词汇错误的纠正通常需要考虑上下文
+上下文敏感法:
+真实词汇拼写矫正的噪声通道:二元语言模型,将一元模型与二元模型插值
+通道模型的改进:
+《模式识别与机器学习》课程笔记:第3章 判别函数
+ +模式识别系统的主要作用:判别各个模式(也称样本)所属的类别
+模式分类若可用任一个线性函数来划分,则这些模式就称为线性可分的,否则就是非线性可分的。
+一旦线性函数的系数
对一个两类问题的判别,就是将模式


这两类可以通过一个直线方程
若



用判别函数进行模式分类依赖的两个因素:
+一个
权向量(参数向量):

增广模式向量:
多类情况1:用线性判别函数将属于





多类情况2:采用每对划分,即 
判别函数为

因此要分开

多类情况1和多类情况2的比较
+ 类模式的分类,多类情况1需要
类模式的分类,多类情况1需要 个判别函数,而多类情况2需
个判别函数,而多类情况2需 个判别函数,当
个判别函数,当 较大时,后者需要更多的判别式
较大时,后者需要更多的判别式 种类别的模式分开,而不是将一种类别的模式仅与另一种类别的模式分开。
种类别的模式分开,而不是将一种类别的模式仅与另一种类别的模式分开。 种模式的分布更为聚集,因此多类情况2对模式是线性可分的可能性比多类情况1更大一些。
种模式的分布更为聚集,因此多类情况2对模式是线性可分的可能性比多类情况1更大一些。多类情况3:没有不确定区域的 



线性判别函数简单,容易实现,而非线性判别函数复杂,不容易实现。
+若能将非线性判别函数转换为线性判别函数,则有利于模式分类的实现。
+设有一个训练用的模式集













一个非线性判别函数可如下表示:


若定义成广义形式:
此时有:
非线性判别函数已被变换成广义线性,因此只讨论线性判别函数不会失去一般性意义。
+当

式中各项的组成应包含



+
若


也就是说,可以使用一个二次判别函数进行分类的地方,也可以使用一个分段线性判别函数来逼近这个二次曲线。
+可以采用最小距离分类的方法,只有在类别密集地分布在其均值附近时才有效。
+对于各类交错分布的情况,若再用每类一个均值代表点产生最小距离分类器,就会产生很明显的错误率。在这种情况下,可以运用聚类方法将一些类分解成若干个子类,再用最小距离分类。
+模式空间:
+对一个线性方程


把

若

模式空间即为增广向量决定的平面或非增广向量决定的直线。
+权空间:
+若将方程


问题描述:
+ 维空间的样本投影到一条直线上,形成一维空间,即把维数压缩到一维。
维空间的样本投影到一条直线上,形成一维空间,即把维数压缩到一维。 维空间里形成若干紧凑的互相分得开的集群,当把它们投影到一条直线上时,也可能会是几类样本混在一起而变得无法识别。
维空间里形成若干紧凑的互相分得开的集群,当把它们投影到一条直线上时,也可能会是几类样本混在一起而变得无法识别。Fisher判别方法所要解决的基本问题:如何根据实际情况找到一条最好的、最易于分类的投影线。
+从
假设有一集合















实际上,




Fisher准则函数中的基本参量:
+在

各类样本的均值向量
样本类内离散度矩阵:
总样本类内离散度矩阵:
样本类间离散度矩阵:
在一维
各类样本的均值:
样本类内离散度:
总样本类内离散度:
我们希望投影后,在一维
Fisher准则函数:

然后使用Lagrange乘数法求解,最终解得
事实上,Fisher的降维就相当于找一个线性判别函数。投影后的

多类情形:
+类间散度矩阵与两类情形略有不同:原来度量的是两个均值点的散列情况,现在度量的是每类均值点相对于样本中心的散列情况
+推导可得:
一旦判别函数的形式确定下来,不管它是线性的还是非线性的,剩下的问题就是如何确定它的系数。在模式识别中,系数确定的一个主要方法就是通过对已知样本的训练和学习来得到。感知器算法就是通过训练样本模式的迭代和学习,产生线性(或广义线性)可分的模式判别函数。
+基本思想:采用感知器算法能通过对训练模式样本集的“学习”得到判别函数的系数。不需要对各类别中模式的统计性质做任何假设,因此称为确定性的方法。
+感知器作为人工神经网络中最基本的单元,由多个输入和一个输出组成。
+已知两个训练模式集分别属于


若
第
若




若




若以上情况不符合,则表明该模式样本在第
 加上一个正比于
加上一个正比于 的分量。
的分量。感知器算法的收敛性:只要模式类别是线性可分的,就可以在有限的迭代步数里求出权向量。
+采用多类情况3,将感知器算法推广到多类模式。
+多类情况3:对



设有







若其中第

其中

这里的分类算法都是通过模式样本来确定判别函数的系数,但一个分类器的判断性能最终要受并未用于训练的那些未知样本来检验。要使一个分类器设计完善,必须采用有代表性的训练数据,它能够合理反映模式数据的整体。
+要获得一个判别性能好的线性分类器,直观上训练样本越多越好,但实际上能收集到的样本数目会受到客观条件的限制,且过多的训练样本在训练阶段会使计算机需要较长的运算时间。一般来说,合适的样本数目可如下估计:若


感知器算法的解与初值的选择和迭代过程中误分类点的选择顺序有关。
+设函数


从



梯度是一个向量,它的最重要性质就是指出了函数

定义一个对错误分类敏感的准则函数



C值的选择是很重要的。若C值太小,则收敛太慢;若C值太大,则搜索可能过头,引起发散。
+设取准则函数为:
则


则由梯度法中

其中


若模式是线性可分的,选择合适的准则函数
感知器算法只是当被分模式可用一个特定的判别界面分开时才收敛,在不可分情况下,只要计算程序不终止,它就始终不收敛。即使在模式可分的情况下,也很难事先算出达到收敛时所需要的迭代次数。这样,在模式分类过程中,有时候会出现一次又一次迭代却不见收敛的情况,白白浪费时间。为此需要知道:发生迟迟不见收敛的情况时,到底是由于收敛速度过慢造成的呢,还是由于所给的训练样本集不是线性可分造成的呢?
+最小平方误差(LMSE)算法,除了对可分模式是收敛的以外,对于类别不可分的情况也能指出来。
+求两类问题的解相当于求一组线性不等式的解,因此,若给出分别属于


设两类模式的训练样本总数为
H-K算法:
+模式类别可分性的判别:
+当不等式组


 ,即
,即 ,有解。
,有解。 ,此时隐含
,此时隐含 的条件,有解。若继续进行迭代,可使
的条件,有解。若继续进行迭代,可使 。
。 的全部分量停止变为正值(但不是全部为零),表明该模式类别线性不可分。因此,若
的全部分量停止变为正值(但不是全部为零),表明该模式类别线性不可分。因此,若 没有一个分量为正值,则
没有一个分量为正值,则 不会再变化,所以不能求得解。
不会再变化,所以不能求得解。固定增量算法与LMSE算法的比较:
+ 求逆(维数高时求逆比较困难),但对两类情况,提供了线性可分的测试特征。
求逆(维数高时求逆比较困难),但对两类情况,提供了线性可分的测试特征。用势函数的概念来确定判别函数和划分类别界面
+基本思想:
+ 和
和 的模式样本,这些样本可看成是分布在
的模式样本,这些样本可看成是分布在 维模式空间中的点
维模式空间中的点 。
。 的点比拟为某种能源点,在点上,电位达到峰值。
的点比拟为某种能源点,在点上,电位达到峰值。 附近空间
附近空间 点上的电位分布,看成是一个势函数
点上的电位分布,看成是一个势函数 。
。 的样本集群,其附近空间会形成一个“高地”,这些样本点所处的位置就是“山头”。
的样本集群,其附近空间会形成一个“高地”,这些样本点所处的位置就是“山头”。 的模式样本,在其附近空间就形成“凹地”。
的模式样本,在其附近空间就形成“凹地”。模式分类的判别函数可由分布在模式空间中的许多样本向量







从势函数可以看出,积累位势起着判别函数的作用:
+ 属于
属于 时,
时, ;
; 属于
属于 时,
时, ,则积累位势不做任何修改就可用作判别函数。
,则积累位势不做任何修改就可用作判别函数。由于一个模式样本的错误分类可造成积累位势在训练时的变化,因此势函数算法提供了确定

判别函数表达式:取
选择势函数的条件:一般来说,若两个



 ,并且当且仅当
,并且当且仅当 时达到最大值;
时达到最大值; 与
与 的距离趋于无穷时,
的距离趋于无穷时, 趋于零;
趋于零; 是光滑函数,且是
是光滑函数,且是 与
与 之间距离的单调下降函数。
之间距离的单调下降函数。第一类势函数:可用对称的有限多项式展开:
+

将这类势函数代入判别函数:
因此,积累位势可写成

第二类势函数:选择双变量


例如:
+

用第二类势函数,当训练样本维数和数目都较高时,需要计算和存储的指数项较多。
+因为势函数由许多新项组成,因此有很强的分类能力。
+决策树,或称多级分类器,是模式识别中进行分类的一种有效方法,对于多类或多峰分布问题,这种方法尤为方便。利用树分类器可以把一个复杂的多类别分类问题,转化为若干个简单的分类问题来解决。它不是企图用一种算法、一个决策规则去把多个类别一次分开,而是采用分级的形式,使分类问题逐步得到解决。
+一般来讲,一个决策树由一个根节点



如果用

决策树的一种简单形式是二叉树,它是指除叶结点外,树的每个节点仅分为两个分支,即每个非终止节点


二叉树结构分类器可以把一个复杂的多类别分类问题转化为多级多个两类问题来解决,在每个非终止节点
二叉树结构分类器概念简单、直观、便于解释,而且在各个节点上可以选择不同的特征和采用不同的决策规则,因此设计方法灵活多样,便于利用先验知识来获得一个较好的分类器。
+在设计一个决策树时,主要应解决以下几个问题:
+把一个多类别分类问题转化为两类问题的形式是多种多样的,因此,对应的二叉树的结构也是各不相同的。通常的目的是要找一个最优的决策树。一个性能良好的决策树结构应该具有小的错误率和低的决策代价。但是由于很难把错误率的解析表达式和树的结构联系起来,而且在每个节点上所采用的决策规则也仅仅是在该节点上所采用的特征观测值的函数,因此,即使每个节点上的性能都达到最优,也不能说整个决策树的性能达到最优。在实际问题中,人们往往提出其它一些优化准则,例如极小化整个树的节点数目,或从根节点到叶结点的最大路经长度,或从根节点到叶结点的平均路经长度等,然后采用动态规划的方法,力争设计出能满足某种准则的“最优”决策树。
+ + +《现代信息检索》课程笔记:第5讲 文档评分、词项权重计算及向量空间模型
+ +布尔检索的优点:
+布尔检索的不足:
+在布尔检索中,需要大量技巧来生成一个可以获得合适规模结果的查询
+排序式检索会对查询和文档的匹配程度进行排序,即给出一个查询和文档匹配评分
+自由文本查询:与布尔查询不同,在排序式检索应用中,用户查询通常都是一个或几个关键字
+排序式检索可以解决返回结果过少或过多的问题,可以把相关的结果排在前面
+希望文档集中相关度高的文档排名高于相关度低的文档:对每个查询-文档对赋一个[0, 1]之间的分值,度量了文档和查询的匹配程度
+Jaccard系数:计算两个集合重合度的常用方法,也就是计算查询文档之间的词项重合度——交集/并集
+Jaccard系数的不足:
+查询-文档匹配评分计算:
+从单词项查询(查询只包含一个词项)开始,若该词项不出现在文档当中,该文档得分应该为0,该词项在文档中出现越多,则得分越高。
+即为词项频率 (term frequency,TF)评分
+词袋(Bag of words)模型:不考虑词在文档中出现的顺序
+利用tf来计算文档评分的方法:采用原始的tf值(raw tf)
+但是原始tf不太合适:某个词项在A文档中出现十次,即tf = 10,在B文档中tf = 1,那么A比B更相关,但是相关度不会相差10倍。
+替代原始tf的方法:对数词频
+罕见词项比常见词所蕴含的信息更多
+考虑查询中某个词项,它在整个文档集中非常罕见,但是某篇包含该词项的文档很可能相关,因此需要提高权重
+常见词项的信息量不如罕见词,一篇包含该词项的文档当然比不包含该词项的文档的相关度要高,但是,这些词对于相关度而言并不是非常强的指示词。
+文档频率(Document frequency, df):出现词项的文档数目
+idf 权重
+



于是可以定义词项t的idf权重(逆文档频率):



对于单词项查询,idf对文档排序没有任何影响,idf 会影响至少包含2个词项的查询的文档排序结果
+词项的tf-idf权重是tf权重和idf权重的乘积:
tf-idf权重:
+二值-tfidf矩阵
+文档表示成向量:每篇文档表示成一个基于tfidf权重的实值向量 ∈ R|V|。有一个|V|维实值空间,空间的每一维都对应词项,文档都是该空间下的一个点或者向量。
+查询看成向量:
+向量空间下相似度:利用余弦相似度
+文档长度归一化:一个向量可以通过除以它的长度进行归一化处理(防止长度影响)
+问题:
+余弦归一化倾向于短文档,即对短文档产生的归一化因子太大,而平均而言对长文档产生的归一化因子太小,因此余弦归一化对长文档的惩罚过重,实际上长文档中虽然词频较高,但也会包含较多的信息。
+可以先找到一个支点(pivot,平衡点),然后通过这个支点对余弦归一化操作进行线性调整。因此短文档的相似度降低,而长文档的相似度增大,可以去除原来余弦归一化偏向短文档的问题
+回转归一化:基本思想是旋转归一化曲线,使得两条曲线尽量重合
+向量空间模型小结:
+Leetcode 刷题笔记-Leetcode 101 第12章 字符串
+ +给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。注意: 若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t互为字母异位词。
class Solution {
+public:
+ bool isAnagram(string s, string t) {
+ sort(s.begin(),s.end());
+ sort(t.begin(),t.end());
+ if(s == t){
+ return true;
+ }
+ return false;
+ }
+};分析:哈希表或者直接排序
+一遍AC
+给定两个字符串 s 和 t ,判断它们是否是同构的。如果 s 中的字符可以按某种映射关系替换得到 t ,那么这两个字符串是同构的。每个出现的字符都应当映射到另一个字符,同时不改变字符的顺序。不同字符不能映射到同一个字符上,相同字符只能映射到同一个字符上,字符可以映射到自己本身。
class Solution {
+public:
+ bool isIsomorphic(string s, string t) {
+ unordered_map<char,char> mp1;
+ unordered_map<char,char> mp2;
+ for(int i=0;i<s.size();++i){
+ if(mp1.find(s[i]) == mp1.cend()){
+ mp1[s[i]] = t[i];
+ }
+ if(mp2.find(t[i]) == mp2.cend()){
+ mp2[t[i]] = s[i];
+ }
+ if(mp1[s[i]] != t[i] || mp2[t[i]] != s[i]){
+ return false;
+ }
+ }
+ return true;
+ }
+};分析:通过字典比较即可
+错误:开始想用统计的方法去做,后面用字符字典的方式也有一些小错误,应该是比较两遍的。
+给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。回文字符串 是正着读和倒过来读一样的字符串。子字符串 是字符串中的由连续字符组成的一个序列。具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
class Solution {
+public:
+ int countSubstrings(string s) {
+ int countsum = 0;
+ int n = s.size();
+ for(int i=0;i<n;++i){
+ countsum += 1;
+ int leftindex = i-1;
+ int rightindex = i+1;
+ while(leftindex >= 0 && rightindex < n && s[leftindex] == s[rightindex]){
+ ++countsum;
+ --leftindex;
+ ++rightindex;
+ }
+ }
+ for(int i=0;i<n-1;++i){
+ if(s[i] == s[i+1]){
+ ++countsum;
+ int leftindex = i-1;
+ int rightindex = i+2;
+ while(leftindex >= 0 && rightindex < n && s[leftindex] == s[rightindex]){
+ ++countsum;
+ --leftindex;
+ ++rightindex;
+ }
+ }
+ }
+ return countsum;
+ }
+};分析:遍历扩展即可,注意分两种情况讨论一下
+一遍AC
+给定一个字符串 s,统计并返回具有相同数量 0 和 1 的非空(连续)子字符串的数量,并且这些子字符串中的所有 0 和所有 1 都是成组连续的。重复出现(不同位置)的子串也要统计它们出现的次数。
class Solution {
+public:
+ int countBinarySubstrings(string s) {
+ int n = s.size();
+ int countsum = 0;
+ for(int i=0;i<n-1;++i){
+ if(s[i] != s[i+1]){
+ ++countsum;
+ int leftindex = i-1;
+ int rightindex = i+2;
+ while(leftindex >= 0 && rightindex < n && s[leftindex] == s[leftindex+1] && s[rightindex] == s[rightindex-1]){
+ ++countsum;
+ --leftindex;
+ ++rightindex;
+ }
+ }
+ }
+ return countsum;
+ }
+};分析:和上一道题目相同,甚至只考虑一种情况就可以了,比上一道题目还要简单一点。
+一遍AC
+给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。整数除法仅保留整数部分。
class Solution {
+public:
+ int calculate(string s) {
+ vector<int> stk;
+ char preSign = '+';
+ int num = 0;
+ int n = s.length();
+ for (int i = 0; i < n; ++i) {
+ if (isdigit(s[i])) {
+ num = num * 10 + int(s[i] - '0');
+ }
+ if (!isdigit(s[i]) && s[i] != ' ' || i == n - 1) {
+ switch (preSign) {
+ case '+':
+ stk.push_back(num);
+ break;
+ case '-':
+ stk.push_back(-num);
+ break;
+ case '*':
+ stk.back() *= num;
+ break;
+ default:
+ stk.back() /= num;
+ }
+ preSign = s[i];
+ num = 0;
+ }
+ }
+ return accumulate(stk.begin(), stk.end(), 0);
+ }
+};分析:栈和字符串的应用
+错误:最后的运算顺序有问题,没有能自己实现。
+给你两个字符串 haystack和 needle,请你在 haystack字符串中找出 needle字符串的第一个匹配项的下标(下标从 0开始)。如果 needle不是 haystack的一部分,则返回 -1。
class Solution {
+public:
+ int strStr(string haystack, string needle) {
+ int m = haystack.size();
+ int n = needle.size();
+ for(int i=0;i<m-n+1;++i){
+ if(haystack.substr(i,n) == needle){
+ return i;
+ }
+ }
+ return -1;
+ }
+};分析:可以使用KMP算法,但是不会,简单一点就直接字符串匹配即可。
+一遍AC
+给定一个包含大写字母和小写字母的字符串 s ,返回通过这些字母构造成的最长的回文串。在构造过程中,请注意区分大小写 。比如 "Aa" 不能当做一个回文字符串。
class Solution {
+public:
+ int longestPalindrome(string s) {
+ unordered_map<char,int> mp;
+ int n = s.size();
+ for(int i=0;i<s.size();++i){
+ if(mp.find(s[i]) == mp.cend()){
+ mp[s[i]] = 1;
+ }
+ else{
+ ++mp[s[i]];
+ }
+ }
+ int ans = 0;
+ int sign = 0;
+ for(auto it : mp){
+ if(it.second % 2 == 0){
+ ans += it.second;
+ }
+ else{
+ if(sign == 0){
+ ans += it.second;
+ sign = 1;
+ }
+ else{
+ ans = ans + it.second / 2 * 2;
+ }
+ }
+ }
+ return ans;
+ }
+};分析:统计数数即可
+一遍AC
+给定一个字符串 s ,请你找出其中不含有重复字符的最长子串的长度。
class Solution {
+public:
+ int lengthOfLongestSubstring(string s) {
+ map<char,int> mp;
+ int n = s.size();
+ int right = 0;
+ int maxlen = 0;
+ int left = 0;
+ while(left < n){
+ while(right < n && (mp.find(s[right]) == mp.cend() || mp[s[right]] == 0)){
+ ++mp[s[right]];
+ ++right;
+ }
+ maxlen = max(maxlen,right-left);
+ --mp[s[left]];
+ ++left;
+ }
+ return maxlen;
+ }
+};分析:滑动窗口经典算法
+错误:与或非的括号忘记添加了
+付费题目
+给你一个字符串 s,找到 s 中最长的回文子串。
class Solution {
+public:
+ string longestPalindrome(string s) {
+ int countsum = 1;
+ string result = s.substr(0,1);
+ int n = s.size();
+ for(int i=0;i<n;++i){
+ int temp = 1;
+ int leftindex = i-1;
+ int rightindex = i+1;
+ while(leftindex >= 0 && rightindex < n && s[leftindex] == s[rightindex]){
+ temp += 2;
+ --leftindex;
+ ++rightindex;
+ }
+ if(temp > countsum){
+ countsum = temp;
+ result = s.substr(leftindex+1,rightindex-1-(leftindex+1)+1);
+ }
+ }
+ for(int i=0;i<n-1;++i){
+ if(s[i] == s[i+1]){
+ int temp = 2;
+ int leftindex = i-1;
+ int rightindex = i+2;
+ while(leftindex >= 0 && rightindex < n && s[leftindex] == s[rightindex]){
+ temp += 2;
+ --leftindex;
+ ++rightindex;
+ }
+ if(temp > countsum){
+ countsum = temp;
+ result = s.substr(leftindex+1,rightindex-1-(leftindex+1)+1);
+ }
+ }
+ }
+ return result;
+ }
+};分析:还是这种题,都第三道了
+错误:开始有些索引没考虑好错了一些,后来调通了。
+字符串还可以,主要是熟悉一下字符串的处理过程,其余的知识点其他的数据结构中都有。
+ + +《高级人工智能》课程笔记:第3讲 人工神经网络
+ +联结主义学派:又称仿生学派或生理学派
+核心:智能的本质是联接机制。
+原理:神经网络及神经网络间的连接机制和学习算法
+生物神经元
+神经元特性
+工作状态
+结构的可塑性:神经元之间的柔性连接:突触的信息传递特性是可变的——学习记忆的基础
+从生物学结构到数学模型
+人工神经元
+ +


组合函数:
+权重和:

径向距离:
激活函数
+ +生物系统中的学习:
+ANN的学习规则:能量最小
+对人工神经网络,需要确定合适的能量定义;可以使用数学上的优化技术来发现如何改变神经元间的联接权重。
+两个主要问题:结构和学习方法
+ANN结构
+ANN的学习方法:通过神经网络所在环境的模拟过程,调整网络中的自由参数。
+学习策略:Error Correction:最小化实际输出与期望输出之间的误差,属于监督学习。
+感知机实质上是一种神经元模型
+阈值激活函数:
判别规则:
+输入空间中
+ ,另一边对应
,另一边对应
单层感知机学习:用现在的权重进行分类,如果分类正确,权重不改变;如果分类错误,用分类错误的样本调整权重
感知机收敛定理:若训练数据集是线性可分的,则感知机模型收敛。
+感知机存在的问题:如果存在噪声,或样本不是线性可分的,不会收敛。(例如不能处理异或操作),且泛化性比较差。
+多层感知机:三层可以学习全部连续的函数,四层就可以学习全部的函数。层间神经元全连接,层内神经元不连接。
+学习方法:反向传播
+

全局误差度量:(最小平方误差)
权值更新规则采用梯度下降的方法:
误差反向传播:
+ +实际应用中要对数据进行归一化,并且选择合适的学习率
+优点:
+缺点:
+多层感知机解决了一般性学习问题,并且与生物系统相联系。
+层数增加使用BP算法会存在梯度消失的问题:在后面的几层,误差反向传播后可能变得非常小,权重不太好更新。
+采用sigmoid函数,多个相乘使得传递过来的残差会越来越小。
+时代背景:数据爆炸、计算性能提升
+传统机器学习解决问题的思路:
+使用深度学习去自动学习特征!
+人脑视觉机理
+为什么使用深度学习?
+深层 vs 浅层神经网络
+BP算法的问题:
+Deep learning训练:
+自下向上的非监督学习(greedy layer-wise training)
+自顶向下的监督学习
+对输入的结构建模:建立产生输入的生成式模型,调整参数使得生成式模型的概率最大。
+学习过程:无标签数据,用非监督学习学习特征
+利用人工神经网络本身的层次结构特点
+自动编码器就是一种尽可能复现输入信号的神经网络。
+为了实现这种复现,自动编码器就必须捕捉可以代表输入数据的最重要的因素
+网络结构
+自动编码器可以只训练单组参数,不需要关心另一半的参数。
+Deep结构——逐层训练
+监督学习
+两隐层自编码网络MNIST手写数字识别:
+训练一个包含两个隐含层的栈式自编码网络,用来进行MNIST手写数字分类
+ 训练第一个自编码器,学习得到原始输入的一阶特征表示
训练第一个自编码器,学习得到原始输入的一阶特征表示

栈式自编码器神经网络
+Hopfield Network
+结构:
+Hopfield网络按动力学方式运行,其工作过程为状态的演化过程,即从初始状态按能量减小的方向进行演化,直到达到稳定状态。稳定状态即为网络的输出。
+二值随机神经元(Bernoulli variables):以一定的概率产生1
+波尔兹曼机(Boltzmann Machine):
+BM基本原理:
缺点:网络结构复杂、训练代价大、局部极小
+受限波尔兹曼机(Restricted Boltzmann Machines):
+Deep Belief Networks:
+Deep Boltzmann Machines:
+Leetcode 刷题笔记-Leetcode 101 第13章 链表
+ +(单)链表是由节点和指针构成的数据结构,每个节点存有一个值,和一个指向下一个节点的指针,因此很多链表问题可以用递归来处理。不同于数组,链表并不能直接获取任意节点的值,必须要通过指针找到该节点后才能获取其值。同理,在未遍历到链表结尾时,我们也无法知道链表的长度,除非依赖其他数据结构储存长度。
+给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
class Solution {
+public:
+ ListNode* reverseList(ListNode* head) {
+ ListNode* p = nullptr;
+ ListNode* q = head;
+ while(q){
+ ListNode* r = q->next;
+ q->next = p;
+ p = q;
+ q = r;
+ }
+ return p;
+ }
+};分析:两种方式,迭代法和递归法反转链表。
+错误:算法忘记了,稍稍看了一眼后明白了
+将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
+class Solution {
+public:
+ ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
+ ListNode* result = new ListNode(-1);
+ ListNode* head = result;
+ while(list1 != nullptr && list2 != nullptr){
+ if(list1->val > list2->val){
+ head->next = list2;
+ list2 = list2->next;
+ }
+ else{
+ head->next = list1;
+ list1 = list1->next;
+ }
+ head = head->next;
+ }
+ if(list1 != nullptr){
+ head->next = list1;
+ }
+ else{
+ head->next = list2;
+ }
+ return result->next;
+ }
+};分析:按照顺序一点一点合并即可,前面设置一个头结点,后面把它扔掉返回。
+错误:链表操作忘记了
+给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
+class Solution {
+public:
+ ListNode* swapPairs(ListNode* head) {
+ ListNode* pre = new ListNode(-1);
+ pre->next = head;
+ head = pre;
+ while(pre->next != nullptr && pre->next->next != nullptr){
+ ListNode* p = pre->next;
+ ListNode* q = p->next;
+ pre->next = q;
+ p->next = q->next;
+ q->next = p;
+ pre = p;
+ }
+ return head->next;
+ }
+};分析:链表操作
+错误:已经不熟练了,不知道什么时候加结点什么的。
+给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
class Solution {
+public:
+ ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
+ if(headA == nullptr || headB == nullptr){
+ return nullptr;
+ }
+ ListNode* pa = headA;
+ ListNode* pb = headB;
+ while(pa != pb){
+ if(pa == nullptr){
+ pa = headB;
+ pb = pb->next;
+ }
+ else if(pb == nullptr){
+ pb = headA;
+ pa = pa->next;
+ }
+ else{
+ pa = pa->next;
+ pb = pb->next;
+ }
+ }
+ return pa;
+ }
+};分析:当链表headA和headB都不为空时,创建两个指针pA和pB,初始时分别指向两个链表的头节点headA和headB,然后将两个指针依次遍历两个链表的每个节点。具体做法如下:每步操作需要同时更新指针pA和pB。如果指针pA不为空,则将指针pA移到下一个节点;如果指针 pB不为空,则将指针pB移到下一个节点。如果指针pA为空,则将指针pA移到链表headB的头节点;如果指针pB为空,则将指针pB移到链表headA的头节点。当指针pA和pB指向同一个节点或者都为空时,返回它们指向的节点或者null。
+错误:不会做
+给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
class Solution {
+public:
+ bool isPalindrome(ListNode* head) {
+ vector<int> vt;
+ while(head != nullptr){
+ vt.push_back(head->val);
+ head = head->next;
+ }
+ int n = vt.size();
+ for(int i=0;i<n/2;++i){
+ if(vt[i] != vt[n-i-1]){
+ return false;
+ }
+ }
+ return true;
+ }
+};分析:复制到数组中判断
+一遍AC
+给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。
class Solution {
+public:
+ ListNode* deleteDuplicates(ListNode* head) {
+ ListNode* p = head;
+ if(p == nullptr){
+ return nullptr;
+ }
+ while(p->next != nullptr){
+ ListNode* q = p->next;
+ if(p->val == q->val){
+ p->next = q->next;
+ q = p->next;
+ }
+ else{
+ q = q->next;
+ p = p->next;
+ }
+ }
+ return head;
+ }
+};分析:遍历判断即可
+错误:没有考虑链表中没有结点的情况。
+给定单链表的头节点 head ,将所有索引为奇数的节点和索引为偶数的节点分别组合在一起,然后返回重新排序的列表。
class Solution {
+public:
+ ListNode* oddEvenList(ListNode* head) {
+ if(head == nullptr){
+ return head;
+ }
+ ListNode* odd = head;
+ ListNode* even = head->next;
+ ListNode* evenhead = even;
+ while(even != nullptr && even->next != nullptr){
+ odd->next = even->next;
+ even->next = even->next->next;
+ odd = odd->next;
+ even = even->next;
+ }
+ odd->next = evenhead;
+ return head;
+ }
+};分析:单独存储奇偶结点即可。
+错误:还是不熟练
+给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
class Solution {
+public:
+ ListNode* removeNthFromEnd(ListNode* head, int n) {
+ ListNode* p = head;
+ int sum = 0;
+ while(p != nullptr){
+ ++sum;
+ p = p->next;
+ }
+ p = head;
+ int num = sum - n;
+ if(num == 0){
+ return head->next;
+ }
+ ListNode* pre = new ListNode(-1);
+ pre->next = p;
+ for(int i=0;i<num;++i){
+ pre = p;
+ p = p->next;
+ }
+ pre->next = p->next;
+ return head;
+ }
+};分析:先数一遍一共有多少个结点,然后再遍历一遍删掉即可。
+一遍AC
+给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
class Solution {
+public:
+ ListNode* sortList(ListNode* head) {
+ if(head == nullptr){
+ return head;
+ }
+ vector<int> result;
+ ListNode* p = head;
+ while(head != nullptr){
+ result.push_back(head->val);
+ head = head->next;
+ }
+ sort(result.begin(),result.end());
+ head = p;
+ int index = 0;
+ while(head != nullptr){
+ head->val = result[index++];
+ head = head->next;
+ }
+ return p;
+ }
+};分析:可以用一些比较高大上的链表排序方法,也可以耍赖,直接读入数组中排序即可。
+一遍AC
+链表不难,就是太容易忘记了,后面要经常复习。
+ + +《现代信息检索》课程笔记:第6讲 概率检索模型
+ +向量空间模型的优缺点
+优点:
+缺点:
+检索系统中,给定查询,计算每个文档的相关度
+检索系统对用户查询的理解是非确定的(uncertain),对返回结果的猜测也是非确定的
+而概率理论为非确定推理提供了坚实的理论基础,可以计算文档和查询相关的可能性
+概率检索模型是通过概率的方法将查询和文档联系起来
+定义3个随机变量R、Q、D:相关度R={0,1},查询Q可以是q1,q2,…中的一个查询,文档D可以是d1,d2,…中的一篇文档,则可以通过计算条件概率P(R=1|Q=q,D=d)来度量文档和查询的相关度。
+概率排序原理(PRP):
+回归分析:回归分析是处理变量之间相关关系的一种工具,回归的结果可以用于预测或者分类
+一元线性回归:根据观测点,拟合出一条直线,使得某种损失 (如离差平方和)最小
+Logistic回归是一种非线性回归,可以转化成线性回归来实现。
+基本思想:为了求Q和D相关的概率P(R=1|Q,D),通过定义多个特征函数fi(Q,D),认为P(R=1|Q,D)是这些函数的组合。
+求解和使用过程:通过训练集合拟和得到相应系数 ,对于新的文档,代入公式计算得到概率P
+优缺点:
+二值独立概率模型
+BIM模型通过贝叶斯公式对所求条件概率P(R=1|Q,D)展开进行计算,是一种生成式(generative)模型
+对每个Q定义排序(Ranking)函数RSV(Q,D)
+其中,P(D|R=1)、P(D|R=0)分别表示在相关和不相关情况下生成文档D的概率。Ranking函数显然是随着P(R=1|D)的增长而增长。
+两种常用的文档生成的总体分布:多元贝努利分布和多项式分布
+BIM中P(D|R=1)或P(D|R=0)的计算:类比M次独立试验
+BIM模型公式的推导:pi qi参数的计算,RSJ权重
+BIM计算过程:目标是求排序函数P(D|R=1)/P(D|R=0)
+优点:
+缺点:
+二重泊松分布
+泊松分布是一个经典的随机分布:分布公式参数:均值 λ,分布形式随参数取值变化
+关于文本中词频分布的一个经典结论:在高质量精英文档集(Elite Set)中:均值较高,接近正态分布;在整个语料中:均值低,接近指数分布
+优点:
+缺点:
+BM25被视为现实应用中最好的IR模型之一。即便现在基于BERT预训练语言模型的方法可以获得更好的效果,仍然需要使用BM25进行无监督过滤来保证检索精度。
+ + +《机器学习》课程笔记:第3章 线性分类
+ +

向量空间:所有分量为实数的


超平面表达式:
线性判别函数表达式:
线性函数刻画了样本到超平面的距离
+相似性测度:
+





常用的统计量:
+
 ,
,



分类问题
+ ,其中
,其中 ,要求寻找
,要求寻找 上的决策函数
上的决策函数
 类,其中
类,其中 类做测试,
类做测试, 类做训练;进行
类做训练;进行 次实验取平均。
次实验取平均。 次随机取一个样本, 共
次随机取一个样本, 共 个样本,放入
个样本,放入 中;由
中;由 训练,
训练, 测试。
测试。 ,
,
 检验
检验线性分类问题
+

线性决策的多分类问题:
+
需要训练好
根据最大相似性决定类别。
+基本知识:
+
 ,其中
,其中


 +
+
感知机结构
+ +感知机学习准则:目标:最小化错分样本的误差代价。
+代价函数(错分样本的误差函数):

感知机优化:Batch Perception和Online Perception
+误差修正基本规则:
+ 。
。 ,修正
,修正 ;当错分样本的正确标签为
;当错分样本的正确标签为 ,修正
,修正
基本思想:求线性变换

目标函数:

样本投影后的类别间距离:


样本投影后的类别内距离:投影后的各类样本方差
计算:
基本思想:假设likelihood ratio的对数为线性判别函数
+两类问题:
+
学习目标:
+标签 





《机器学习》课程笔记:第4章 非线性分类
+ +非线性问题:对于线性不可分数据,采用非线性决策的方法
+线性扩展的思想:线性扩展模型
非线性的思想:最近邻、决策树、神经网络、集成学习
+决策问题一定是一个二判决问题
+样本根据问题一定可以分成两部分,两部分之间没有交集,两部分的并集包括所有的情况
+决策树的目标:在树结构上,根据节点的判断,搜索类别。
+树结构的优点:可以不必测试所有特征和区域。
+设属性
 产生的候选问题数为
产生的候选问题数为 (切分太快,容易过拟合)
(切分太快,容易过拟合) 产生的候选问题数为
产生的候选问题数为
属性
方法:每个特征上的样本特征值作为候选问题,属性
无论特征值是连续还是离散,确定每个属性所产生的候选问题,候选的问题总数为
非纯度(Impurity Measure)需要满足两条性质:
+非纯度的熵度量(C4.5):
非纯度的基尼度量(CART):
划分目标:选择最大减少类别非纯度的问题作为划分节点。
+基于非纯度变化量的三个指标:
+信息增益(熵度量):




增益率(信息增益与数据集


增益率改善信息增益:



基尼指数(基尼度量):
节点类别设置:叶子节点纯度达到预设阈值后,停止划分,并对叶子节点进行类别设置。(按概率最大的类别设定)
+决策树生成过程
+从顶向下(不断增加一个节点)
+ (非纯度减少量)最大的划分为节点,加入决策树。
(非纯度减少量)最大的划分为节点,加入决策树。ID3 决策树:属性特征作为结点问题,划分选择实际是特征选择过程,最大化信息增益作为划分选择依据
+C4.5 决策树:属性特征作为结点问题,划分选择实际是特征选择过程,最大化信息增益率作为划分选择依据
+CART 决策树:属性特征离散值作为结点问题,本质是二叉树,最小化基尼指数作为划分选择依据
+连续值二叉决策树
+ID3、C4.5决策树剪枝
+泛化性能评估法
+原理:将样本分类为离之最近的样本类别
+
决策规则:
最近邻分类隐含的决策边界是非线性的
+原理:将样本分给




判别函数:
决策规则:
误差讨论
+近邻法的缺点:
+原理:将样本分成不相交的子集,基于子集的搜索
+规则1-找最近子集:如果



规则2-找最近样本:如果


k 近邻快速搜索推广:子集搜索过程与最近邻一致,样本搜索时,

原理:通过剪掉边界样本(错误分类样本),缩减样本规模
+剪辑规则:两分剪辑近邻法
+ ,
,
 做分类参考,对
做分类参考,对 进行剪辑(错分样本被剪掉)
进行剪辑(错分样本被剪掉) 作为最终的训练集训练近邻分类器
作为最终的训练集训练近邻分类器原理:去掉中心附近样本,保留错误样本,在剪辑基础上进行压缩
+基本思想:分类中通常被正确分类的样本,较少支持决策,将常分误的样本保留。
+压缩规则:
+ ,
, ,
, 中仅
中仅 个样本;
个样本; 中
中 个
个 作为训练,分类
作为训练,分类 中第
中第 个样本;如果错误,将该样本放入
个样本;如果错误,将该样本放入 中
中 无错分样本,或
无错分样本,或 为空
为空 中样本放弃,
中样本放弃, 是最终压缩样本集
是最终压缩样本集原理:对于与各类别相似度较低的样本,不做判断
+优点:在样本压缩时,给可是可非的样本机会。
+ , 拒绝分类
, 拒绝分类原理:不同的分类器对样本有不同的鉴别力;综合优势,使错误率最小。
+问题描述:已知一组训练分类器,分类器的类别后验为


目标是对
概率分布相似性的计算:
+
 和
和

Geometric Average Rule
+

Arithmetic Average Rule
+

Majority Voting Rule
+Bagging:通过随机采样,训练分类器,保证分类器的差异。从训练集中不断随机抽取样本构造分类器,分类时通过投票进行类别判断。
+随机森林:多决策树的Bagging;决策树随机属性选择;从训练集中不断随机构造决策树分类器,分类时通过投票进行类别判断。
+随机森林较一般Bagging效果好
+Boosting原理:一系列弱分类器,在不同子集上学习,得到增强分类器。
+AdaBoost加权分类器
+AdaBoost 目标函数
+两个核心思想
+KKT:任何目标函数有解的充要条件
+一个原始问题总有它的对偶问题
+对于特殊的凸优化来说,原始问题

如果原始问题和它的对偶问题都满足KKT条件,对于条件好的凸优化,可以构造

目标:找到最大间隔分类超平面(类别集合到分类超平面的最小距离最大化)
+函数间隔:给定的训练数据集
 关于样本
关于样本 的函数间隔定义为
的函数间隔定义为
 关于训练数据集
关于训练数据集 的函数间隔定义为
的函数间隔定义为 ,即所有样本点
,即所有样本点 的函数间隔的最小值。
的函数间隔的最小值。 和
和 ,函数间隔会相应变化。
,函数间隔会相应变化。几何间隔:给定的训练数据集
 关于样本
关于样本 的几何间隔定义为
的几何间隔定义为
 关于训练数据集
关于训练数据集 的几何间隔定义为
的几何间隔定义为 ,即所有样本点
,即所有样本点 的几何间隔的最小值。
的几何间隔的最小值。 和
和 ,几何间隔不会相应变化。
,几何间隔不会相应变化。最大几何间隔等价的问题:
函数间隔
支撑向量(SV):支撑最小距离最大化的样本
+支撑超平面:通过支持向量,平行于分类面的超平面
+间隔:支撑向量到分类面的距离
+支持向量机学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。
+根据KKT条件成立求解
+避免直接求非线性映射,由核函数替代内积运算
+硬间隔SVM
+软间隔SVM
+ + +Leetcode 刷题笔记-Leetcode 101 第14章 树
+ +给定一个二叉树,找出其最大深度。
+class Solution {
+public:
+ static int DFS(TreeNode* &root,int sum){
+ if(root == nullptr){
+ return sum;
+ }
+ return max(DFS(root->left,sum+1),DFS(root->right,sum+1));
+ }
+ int maxDepth(TreeNode* root) {
+ return DFS(root,0);
+ }
+};分析:递归计算最大高度即可
+错误:开始递归写的有问题,变成引用传参了,后面改对后调通。
+给定一个二叉树,判断它是否是高度平衡的二叉树。
+class Solution {
+public:
+ static int DFS(TreeNode* &root){
+ if(root == nullptr){
+ return 0;
+ }
+ int left = DFS(root->left);
+ int right = DFS(root->right);
+ if(left == -1 || right == -1 || abs(left - right) > 1){
+ return -1;
+ }
+ return max(left,right)+1;
+ }
+ bool isBalanced(TreeNode* root) {
+ return DFS(root) != -1;
+ }
+};分析:解法类似于求树的最大深度,但有两个不同的地方:一是我们需要先处理子树的深度再进行比较,二是如果我们在处理子树时发现其已经不平衡了,则可以返回一个-1,使得所有其长辈节点可以避免多余的判断
+错误:思路不对,看了解析
+给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
+class Solution {
+public:
+ static int DFS(TreeNode* &root,int &maxsum){
+ if(root == nullptr){
+ return 0;
+ }
+ int left = DFS(root->left,maxsum);
+ int right = DFS(root->right,maxsum);
+ maxsum = max(maxsum,left+right+1);
+ return max(left,right)+1;
+ }
+ int diameterOfBinaryTree(TreeNode* root) {
+ int maxsum = 0;
+ int a = DFS(root,maxsum);
+ return maxsum-1;
+ }
+};分析:还是递归,要留两个变量进行记录
+错误:没看解析调通,但是自己想的挺艰难的。
+给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
class Solution {
+public:
+ static long long DFS(TreeNode* &root, long long sum){
+ if(root == nullptr){
+ return 0;
+ }
+ long long count;
+ if(root->val == sum){
+ count = 1;
+ }
+ else{
+ count = 0;
+ }
+ return count + DFS(root->left,sum-root->val) + DFS(root->right,sum-root->val);
+ }
+ int pathSum(TreeNode* root, int targetSum) {
+ if(root == nullptr){
+ return 0;
+ }
+ return DFS(root,targetSum)+pathSum(root->left,targetSum)+pathSum(root->right,targetSum);
+ }
+};分析:递归每个节点时,需要分情况考虑:(1)如果选取该节点加入路径,则之后必须继续加入连续节点,或停止加入节点(2)如果不选取该节点加入路径,则对其左右节点进行重新进行考虑。因此一个方便的方法是我们创建一个辅函数,专门用来计算连续加入节点的路径。
+错误:两层的递归有点做不了
+给你一个二叉树的根节点 root , 检查它是否轴对称。
class Solution {
+public:
+ static bool DFS(TreeNode* &left,TreeNode* &right){
+ if(left == nullptr && right != nullptr){
+ return false;
+ }
+ if(left != nullptr && right == nullptr){
+ return false;
+ }
+ if(left == nullptr && right == nullptr){
+ return true;
+ }
+ if(left->val != right->val){
+ return false;
+ }
+ return DFS(left->left,right->right) && DFS(left->right,right->left);
+ }
+ bool isSymmetric(TreeNode* root) {
+ if(root == nullptr){
+ return true;
+ }
+ return DFS(root->left,root->right);
+ }
+};分析:判断一个树是否对称等价于判断左右子树是否对称。笔者一般习惯将判断两个子树是否相等或对称类型的题的解法叫做“四步法”:(1)如果两个子树都为空指针,则它们相等或对称(2)如果两个子树只有一个为空指针,则它们不相等或不对称(3)如果两个子树根节点的值不相等,则它们不相等或不对称(4)根据相等或对称要求,进行递归处理。
+错误:不明白
+给出二叉树的根节点 root,树上每个节点都有一个不同的值。如果节点值在 to_delete 中出现,我们就把该节点从树上删去,最后得到一个森林(一些不相交的树构成的集合)。返回森林中的每棵树。你可以按任意顺序组织答案。
class Solution {
+public:
+ void DFS(TreeNode* &root, vector<int>& to_delete,vector<TreeNode*>& result){
+ if(root == nullptr){
+ return;
+ }
+ DFS(root->left,to_delete,result);
+ DFS(root->right,to_delete,result);
+ auto it = find(to_delete.begin(),to_delete.end(),root->val);
+ if(it != to_delete.end()){
+ if(root->left != nullptr){
+ result.push_back(root->left);
+ }
+ if(root->right != nullptr){
+ result.push_back(root->right);
+ }
+ root->left = nullptr;
+ root->right = nullptr;
+ root = nullptr;
+ }
+ return;
+ }
+ vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) {
+ vector<TreeNode*> result;
+ DFS(root,to_delete,result);
+ if(root != nullptr){
+ result.push_back(root);
+ }
+ return result;
+ }
+};分析:遍历,然后置为空指针就好
+错误:开始的判断条件不太够,后来自己调通。
+给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10<sup>-5</sup> 以内的答案可以被接受。
class Solution {
+public:
+ vector<double> averageOfLevels(TreeNode* root) {
+ vector<double> result;
+ queue<TreeNode*> q;
+ q.push(root);
+ while(!q.empty()){
+ int num = 0;
+ double sum = 0.0;
+ int nowsize = q.size();
+ while(nowsize--){
+ TreeNode* t = q.front();
+ q.pop();
+ num += 1;
+ sum += t->val;
+ if(t->left != nullptr){
+ q.push(t->left);
+ }
+ if(t->right != nullptr){
+ q.push(t->right);
+ }
+ }
+ result.push_back(sum/num);
+ }
+ return result;
+ }
+};分析:层序遍历即可
+一遍AC
+给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的 先序遍历 , inorder 是同一棵树的 中序遍历 ,请构造二叉树并返回其根节点。
class Solution {
+private:
+ unordered_map<int, int> index;
+public:
+ TreeNode* myBuildTree(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
+ if (preorder_left > preorder_right) {
+ return nullptr;
+ }
+
+ // 前序遍历中的第一个节点就是根节点
+ int preorder_root = preorder_left;
+ // 在中序遍历中定位根节点
+ int inorder_root = index[preorder[preorder_root]];
+
+ // 先把根节点建立出来
+ TreeNode* root = new TreeNode(preorder[preorder_root]);
+ // 得到左子树中的节点数目
+ int size_left_subtree = inorder_root - inorder_left;
+ // 递归地构造左子树,并连接到根节点
+ // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
+ root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
+ // 递归地构造右子树,并连接到根节点
+ // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
+ root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
+ return root;
+ }
+ TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
+ int n = preorder.size();
+ // 构造哈希映射,帮助我们快速定位根节点
+ for (int i = 0; i < n; ++i) {
+ index[inorder[i]] = i;
+ }
+ return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
+ }
+};分析:很老的题,好好判断,数据结构设计对即可
+错误:太久远了忘记怎么判断了
+给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
class Solution {
+public:
+ static void dfs(TreeNode* &root,vector<int> &result){
+ if(root == nullptr){
+ return;
+ }
+ result.push_back(root->val);
+ dfs(root->left,result);
+ dfs(root->right,result);
+ }
+ vector<int> preorderTraversal(TreeNode* root) {
+ vector<int> result;
+ dfs(root,result);
+ return result;
+ }
+};分析:递归遍历即可
+一遍AC
+给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。 请在不改变其结构的情况下,恢复这棵树。
class Solution {
+public:
+ void inorder(TreeNode* root, TreeNode*& mistake1, TreeNode*& mistake2, TreeNode*& prev) {
+ if (!root) {
+ return;
+ }
+ if (root->left) {
+ inorder(root->left, mistake1, mistake2, prev);
+ }
+ if (prev && root->val < prev->val) {
+ if (!mistake1) {
+ mistake1 = prev;
+ mistake2 = root;
+ }
+ else {
+ mistake2 = root;
+ }
+ cout << mistake1->val;
+ cout << mistake2->val;
+ }
+ prev = root;
+ if (root->right) {
+ inorder(root->right, mistake1, mistake2, prev);
+ }
+ }
+ void recoverTree(TreeNode* root) {
+ TreeNode *mistake1 = nullptr, *mistake2 = nullptr, *prev = nullptr;
+ inorder(root, mistake1, mistake2, prev);
+ if (mistake1 && mistake2) {
+ int temp = mistake1->val;
+ mistake1->val = mistake2->val;
+ mistake2->val = temp;
+ }
+ }
+};分析:我们可以使用中序遍历这个二叉查找树,同时设置一个prev 指针,记录当前节点中序遍历时的前节点。如果当前节点大于prev 节点的值,说明需要调整次序。有一个技巧是如果遍历整个序列过程中只出现了一次次序错误,说明就是这两个相邻节点需要被交换;如果出现了两次次序错误,那就需要交换这两个节点。
+错误:没有思路
+给你二叉搜索树的根节点 root ,同时给定最小边界 low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在 [low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
class Solution {
+public:
+ TreeNode* trimBST(TreeNode* root, int low, int high) {
+ if(root == nullptr){
+ return root;
+ }
+ if(root->val > high){
+ return trimBST(root->left,low,high);
+ }
+ if(root->val < low){
+ return trimBST(root->right,low,high);
+ }
+ root->left = trimBST(root->left, low, high);
+ root->right = trimBST(root->right, low, high);
+ return root;
+ }
+};分析:利用二叉查找树的大小关系递归进行树的处理。
+错误:看了解析
+尝试建立一个字典树,支持快速插入单词、查找单词、查找单词前缀的功能。
+class Trie {
+private:
+ vector<Trie*> children;
+ bool isEnd;
+
+ Trie* searchPrefix(string prefix) {
+ Trie* node = this;
+ for (char ch : prefix) {
+ ch -= 'a';
+ if (node->children[ch] == nullptr) {
+ return nullptr;
+ }
+ node = node->children[ch];
+ }
+ return node;
+ }
+public:
+ Trie() : children(26), isEnd(false) {}
+ void insert(string word) {
+ Trie* node = this;
+ for (char ch : word) {
+ ch -= 'a';
+ if (node->children[ch] == nullptr) {
+ node->children[ch] = new Trie();
+ }
+ node = node->children[ch];
+ }
+ node->isEnd = true;
+ }
+
+ bool search(string word) {
+ Trie* node = this->searchPrefix(word);
+ return node != nullptr && node->isEnd;
+ }
+
+ bool startsWith(string prefix) {
+ return this->searchPrefix(prefix) != nullptr;
+ }
+};分析:字典树的典型实现方法
+错误:没做过,尝试理解
+给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
class Solution {
+public:
+ TreeNode* invertTree(TreeNode* root) {
+ if(root == nullptr){
+ return nullptr;
+ }
+ TreeNode* left = invertTree(root->left);
+ TreeNode* right = invertTree(root->right);
+ root->left = right;
+ root->right = left;
+ return root;
+ }
+};分析:递归反转即可
+错误:翻转值是不对的,需要反转结点
+给你两棵二叉树: root1 和 root2 。想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。返回合并后的二叉树。
class Solution {
+public:
+ TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
+ if (t1 == nullptr) {
+ return t2;
+ }
+ if (t2 == nullptr) {
+ return t1;
+ }
+ auto merged = new TreeNode(t1->val + t2->val);
+ merged->left = mergeTrees(t1->left, t2->left);
+ merged->right = mergeTrees(t1->right, t2->right);
+ return merged;
+ }
+};分析:递归处理即可
+错误:自己尝试的方法有问题,不太明白错在哪
+给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
class Solution {
+public:
+ static bool check(TreeNode* root, TreeNode* subRoot){
+ if(root == nullptr && subRoot == nullptr){
+ return true;
+ }
+ if(root == nullptr && subRoot != nullptr){
+ return false;
+ }
+ if(root != nullptr && subRoot == nullptr){
+ return false;
+ }
+ if(root->val != subRoot->val){
+ return false;
+ }
+ return check(root->left,subRoot->left) && check(root->right,subRoot->right);
+ }
+ static bool DFS(TreeNode* root, TreeNode* subRoot){
+ if(root == nullptr){
+ return false;
+ }
+ return check(root,subRoot) || DFS(root->left,subRoot) || DFS(root->right,subRoot);
+ }
+ bool isSubtree(TreeNode* root, TreeNode* subRoot) {
+ bool judge = DFS(root,subRoot);
+ return judge;
+ }
+};分析:递归判断即可
+错误:自己写了前半部分,看了一眼后写了后半部分
+给定二叉树的根节点 root ,返回所有左叶子之和。
class Solution {
+public:
+ bool isLeafNode(TreeNode* node) {
+ return !node->left && !node->right;
+ }
+
+ int dfs(TreeNode* node) {
+ int ans = 0;
+ if (node->left) {
+ ans += isLeafNode(node->left) ? node->left->val : dfs(node->left);
+ }
+ if (node->right && !isLeafNode(node->right)) {
+ ans += dfs(node->right);
+ }
+ return ans;
+ }
+ int sumOfLeftLeaves(TreeNode* root) {
+ return dfs(root);
+ }
+};分析:递归判断结点
+错误:没有思路
+给定一个二叉树的 根节点 root,请找出该二叉树的最底层最左边节点的值。
class Solution {
+public:
+ int findBottomLeftValue(TreeNode* root) {
+ queue<TreeNode*> q;
+ q.push(root);
+ int result = root->val;
+ while(!q.empty()){
+ int tempsize = q.size();
+ int sign = 0;
+ while(tempsize--){
+ TreeNode* t = q.front();
+ q.pop();
+ if(sign == 0){
+ result = t->val;
+ sign = 1;
+ }
+ if(t->left != nullptr){
+ q.push(t->left);
+ }
+ if(t->right != nullptr){
+ q.push(t->right);
+ }
+ }
+ }
+ return result;
+ }
+};分析:广度优先遍历即可
+一遍AC
+给出二叉搜索树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
class Solution {
+public:
+ void DFS(TreeNode* root,int &sum){
+ if(root == nullptr){
+ return;
+ }
+ DFS(root->right,sum);
+ root->val = root->val + sum;
+ sum = root->val;
+ DFS(root->left,sum);
+ return;
+ }
+ TreeNode* convertBST(TreeNode* root) {
+ int sum = 0;
+ DFS(root,sum);
+ return root;
+ }
+};分析:反向的中序遍历
+错误:开始顺序弄反,后面修正了
+给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
+class Solution {
+public:
+ vector<TreeNode*> getPath(TreeNode* root, TreeNode* target) {
+ vector<TreeNode*> path;
+ TreeNode* node = root;
+ while (node != target) {
+ path.push_back(node);
+ if (target->val < node->val) {
+ node = node->left;
+ }
+ else {
+ node = node->right;
+ }
+ }
+ path.push_back(node);
+ return path;
+ }
+ TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
+ vector<TreeNode*> path_p = getPath(root, p);
+ vector<TreeNode*> path_q = getPath(root, q);
+ TreeNode* ancestor;
+ for (int i = 0; i < path_p.size() && i < path_q.size(); ++i) {
+ if (path_p[i] == path_q[i]) {
+ ancestor = path_p[i];
+ }
+ else {
+ break;
+ }
+ }
+ return ancestor;
+ }
+};分析:从根节点开始遍历;如果当前节点就是p,那么成功地找到了节点;如果当前节点的值大于p的值,说明p应该在当前节点的左子树,因此将当前节点移动到它的左子节点;如果当前节点的值小于p的值,说明p应该在当前节点的右子树,因此将当前节点移动到它的右子节点。对于节点q同理。在寻找节点的过程中,我们可以顺便记录经过的节点,这样就得到了从根节点到被寻找节点的路径。
+错误:没有思路
+给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
class Solution {
+public:
+ void DFS(TreeNode* &root,vector<int>& result){
+ if(root == nullptr){
+ return;
+ }
+ DFS(root->left,result);
+ result.push_back(root->val);
+ DFS(root->right,result);
+ }
+ int getMinimumDifference(TreeNode* root) {
+ vector<int> result;
+ DFS(root,result);
+ int minval = 100000;
+ for(int i=0;i<result.size()-1;++i){
+ if(result[i+1]-result[i] < minval){
+ minval = result[i+1]-result[i];
+ }
+ }
+ return minval;
+ }
+};分析:中序遍历存在数组内部,然后遍历判断即可
+一遍AC
+给定两个整数数组,preorder 和 postorder ,其中 preorder 是一个具有 无重复 值的二叉树的前序遍历,postorder 是同一棵树的后序遍历,重构并返回二叉树。
class Solution {
+ int preIdx = 0, postIdx = 0;
+public:
+ TreeNode* constructFromPrePost(vector<int>& preorder, vector<int>& postorder) {
+ TreeNode *node = new TreeNode(preorder[preIdx++]);
+ if(node->val != postorder[postIdx]){
+ node->left = constructFromPrePost(preorder, postorder);
+ }
+
+ if(node->val != postorder[postIdx]){
+ node->right = constructFromPrePost(preorder, postorder);
+ }
+ postIdx++;
+ return node;
+ }
+};分析:利用前序遍历来构建Tree,然后通过后续遍历来检验当前树是否构建完毕 。
+错误:思路不对
+给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
class Solution {
+public:
+ TreeNode* DFS(vector<int>& inorder, int inleft,int inright,vector<int>& postorder,int postleft,int postright){
+ if(inleft > inright){
+ return nullptr;
+ }
+ TreeNode* root = new TreeNode(postorder[postright]);
+ int k;
+ for(k=inleft;k<=inright;++k){
+ if(inorder[k] == postorder[postright]){
+ break;
+ }
+ }
+ int rightsize = inright - k;
+ root->left = DFS(inorder,inleft,k-1,postorder,postleft,postright-rightsize-1);
+ root->right = DFS(inorder,k+1,inright,postorder,postright-rightsize,postright-1);
+ return root;
+ }
+ TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
+ int n = inorder.size();
+ TreeNode* root = DFS(inorder,0,n-1,postorder,0,n-1);
+ return root;
+ }
+};分析:与前面的题目相同
+一遍AC
+给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
class Solution {
+public:
+ static void dfs(TreeNode* &root,vector<int> &result){
+ if(root == nullptr){
+ return;
+ }
+ dfs(root->left,result);
+ result.push_back(root->val);
+ dfs(root->right,result);
+ }
+ vector<int> inorderTraversal(TreeNode* root) {
+ vector<int> result;
+ dfs(root,result);
+ return result;
+ }
+};分析:普通递归
+一遍AC
+给你一棵二叉树的根节点 root ,返回其节点值的后序遍历。
class Solution {
+public:
+ static void dfs(TreeNode* &root,vector<int> &result){
+ if(root == nullptr){
+ return;
+ }
+ dfs(root->left,result);
+ dfs(root->right,result);
+ result.push_back(root->val);
+ }
+ vector<int> postorderTraversal(TreeNode* root) {
+ vector<int> result;
+ dfs(root,result);
+ return result;
+ }
+};分析:普通递归
+一遍AC
+给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
+class Solution {
+public:
+ TreeNode* ans;
+ bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) {
+ if (root == nullptr) return false;
+ bool lson = dfs(root->left, p, q);
+ bool rson = dfs(root->right, p, q);
+ if ((lson && rson) || ((root->val == p->val || root->val == q->val) && (lson || rson))) {
+ ans = root;
+ }
+ return lson || rson || (root->val == p->val || root->val == q->val);
+ }
+ TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
+ dfs(root, p, q);
+ return ans;
+ }
+};分析:不太明白
+错误:不太明白
+给定一个单链表的头节点 head ,其中的元素 按升序排序 ,将其转换为高度平衡的二叉搜索树。
class Solution {
+public:
+ ListNode* getMedian(ListNode* left, ListNode* right) {
+ ListNode* fast = left;
+ ListNode* slow = left;
+ while (fast != right && fast->next != right) {
+ fast = fast->next;
+ fast = fast->next;
+ slow = slow->next;
+ }
+ return slow;
+ }
+
+ TreeNode* buildTree(ListNode* left, ListNode* right) {
+ if (left == right) {
+ return nullptr;
+ }
+ ListNode* mid = getMedian(left, right);
+ TreeNode* root = new TreeNode(mid->val);
+ root->left = buildTree(left, mid);
+ root->right = buildTree(mid->next, right);
+ return root;
+ }
+ TreeNode* sortedListToBST(ListNode* head) {
+ return buildTree(head, nullptr);
+ }
+};分析:每一次找中位数,然后递归构造两边就可以了
+错误:以为要调整平衡,没有思路
+给你一棵二叉搜索树的 root ,请你 按中序遍历 将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
class Solution {
+public:
+ void inorder(TreeNode *node, vector<int> &res) {
+ if (node == nullptr) {
+ return;
+ }
+ inorder(node->left, res);
+ res.push_back(node->val);
+ inorder(node->right, res);
+ }
+ TreeNode* increasingBST(TreeNode* root) {
+ vector<int> res;
+ inorder(root, res);
+
+ TreeNode *dummyNode = new TreeNode(-1);
+ TreeNode *currNode = dummyNode;
+ for (int value : res) {
+ currNode->right = new TreeNode(value);
+ currNode = currNode->right;
+ }
+ return dummyNode->right;
+ }
+};分析:遍历建树就可以,注意不要在函数中建树,原因没明白
+错误:在函数中建树不行
+给定一个二叉搜索树 root 和一个目标结果 k,如果二叉搜索树中存在两个元素且它们的和等于给定的目标结果,则返回 true。
class Solution {
+public:
+ void DFS(TreeNode* root,vector<int> &result){
+ if(root == nullptr){
+ return;
+ }
+ DFS(root->left,result);
+ result.push_back(root->val);
+ DFS(root->right,result);
+ return;
+ }
+ bool findTarget(TreeNode* root, int k) {
+ vector<int> result;
+ DFS(root,result);
+ int left = 0;
+ int right = result.size()-1;
+ while(left < right){
+ if(result[left] + result[right] == k){
+ return true;
+ }
+ else if(result[left] + result[right] < k){
+ ++left;
+ }
+ else{
+ --right;
+ }
+ }
+ return false;
+ }
+};分析:读出来二分就可以了
+一遍AC
+给定一个二叉搜索树的根节点root和一个值key,删除二叉搜索树中的key对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
+class Solution {
+public:
+ TreeNode* deleteNode(TreeNode* root, int key) {
+ if (root == nullptr) {
+ return nullptr;
+ }
+ if (root->val > key) {
+ root->left = deleteNode(root->left, key);
+ return root;
+ }
+ if (root->val < key) {
+ root->right = deleteNode(root->right, key);
+ return root;
+ }
+ if (root->val == key) {
+ if (!root->left && !root->right) {
+ return nullptr;
+ }
+ if (!root->right) {
+ return root->left;
+ }
+ if (!root->left) {
+ return root->right;
+ }
+ TreeNode *successor = root->right;
+ while (successor->left) {
+ successor = successor->left;
+ }
+ root->right = deleteNode(root->right, successor->val);
+ successor->right = root->right;
+ successor->left = root->left;
+ return successor;
+ }
+ return root;
+ }
+};分析:解析
+错误:不明白应该怎么调整
+看起来树的题目并没有特别复杂的。主要的难度在于递归的思路,想明白后就简单了。另外就是各种边界条件的判断,也要多想多练。
+ + +Leetcode 刷题笔记-Leetcode 101 第15章 图
+ +二分图算法也称为染色法,是一种广度优先搜索。如果可以用两种颜色对图中的节点进行着色,并且保证相邻的节点颜色不同,那么图为二分。
+判断一个图是不是二分图
+class Solution {
+private:
+ static constexpr int UNCOLORED = 0;
+ static constexpr int RED = 1;
+ static constexpr int GREEN = 2;
+ vector<int> color;
+public:
+ bool isBipartite(vector<vector<int>>& graph) {
+ int n = graph.size();
+ vector<int> color(n, UNCOLORED);
+ for (int i = 0; i < n; ++i) {
+ if (color[i] == UNCOLORED) {
+ queue<int> q;
+ q.push(i);
+ color[i] = RED;
+ while (!q.empty()) {
+ int node = q.front();
+ int cNei = (color[node] == RED ? GREEN : RED);
+ q.pop();
+ for (int neighbor: graph[node]) {
+ if (color[neighbor] == UNCOLORED) {
+ q.push(neighbor);
+ color[neighbor] = cNei;
+ }
+ else if (color[neighbor] != cNei) {
+ return false;
+ }
+ }
+ }
+ }
+ }
+ return true;
+ }
+};分析:广度优先遍历,需要判断
+错误:想简单了
+拓扑排序(topological sort)是一种常见的,对有向无环图排序的算法。给定有向无环图中的N个节点,我们把它们排序成一个线性序列;若原图中节点i指向节点j,则排序结果中i一定在j之前。拓扑排序的结果不是唯一的,只要满足以上条件即可。
+给定N个课程和这些课程的前置必修课,求可以一次性上完所有课的顺序。
+class Solution {
+public:
+ vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
+ vector<int> result;
+ vector<int> indegree(numCourses,0);
+ vector<vector<int>> graph(numCourses,vector<int>(numCourses,0));
+ int m = prerequisites.size();
+ for(int i=0;i<m;++i){
+ graph[prerequisites[i][1]][prerequisites[i][0]] = 1;
+ ++indegree[prerequisites[i][0]];
+ }
+ while(1){
+ if(result.size() == numCourses){
+ return result;
+ }
+ int sign = 0;
+ for(int i=0;i<numCourses;++i){
+ if(indegree[i] == 0){
+ indegree[i] = -1;
+ result.push_back(i);
+ sign = 1;
+ for(int j=0;j<numCourses;++j){
+ if(graph[i][j] == 1){
+ graph[i][j] = 0;
+ --indegree[j];
+ }
+ }
+ }
+ }
+ if(sign == 0){
+ break;
+ }
+ }
+ result.clear();
+ return result;
+ }
+};分析:经典拓扑排序
+错误:有一点小错误,基本一遍AC
+付费题目
+付费题目
+经典的节点最短距离问题
+class Solution {
+public:
+ int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {
+ // 先构建图
+ vector<vector<pair<int, int>>> graph(n);
+ for (vector<int>& edge : edges)
+ {
+ int s = edge[0];
+ int e = edge[1];
+ int cnt = edge[2];
+ graph[s].emplace_back(e, cnt);
+ graph[e].emplace_back(s, cnt);
+ }
+
+ // 保持一个从起点到当前点的距离
+ unordered_map<int, int> distances;
+ distances[0] = 0;
+ for (int i = 1; i < n; ++i)
+ {
+ distances[i] = maxMoves + 1;
+ }
+
+ // 点到点的“额外扩展距离”,最大是cnt
+ // 二维变一维 int<<32 + int
+ unordered_map<long, int> extras;
+
+ // 结果记录
+ int res = 0;
+
+ // 从起点到改点的距离的小顶堆
+ priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int, int>>> q;
+ q.push({0, 0});
+
+ while (!q.empty())
+ {
+ int dist = q.top().first;
+ int curr = q.top().second;
+ q.pop();
+
+ // 忽略更大的距离
+ if (dist > distances[curr])
+ {
+ continue;
+ }
+
+ distances[curr] = dist;
+ ++res;
+
+ for (auto& pair : graph[curr])
+ {
+ int next = pair.first;
+ int cnt = pair.second;
+ // 这里取最小的距离, 取(cnt和 maxMoves-dist)的最小值
+ extras[((long)curr << 32) + next] = min(cnt, maxMoves - dist);
+
+ // 计算基于当前点到下一个结点的距离,额外走一步,如果找到更小,则插入队列里
+ int dist2 = dist + cnt + 1;
+ if (dist2 < distances[next])
+ {
+ q.emplace(dist2, next);
+ distances[next] = dist2;
+ }
+ }
+ }
+
+ // 最后加上“额外扩展距离”
+ for (vector<int>& edge : edges)
+ {
+ int s = edge[0];
+ int e = edge[1];
+ res += min(edge[2], extras[((long)s<< 32) +e] + extras[((long)e<<32) +s]);
+ }
+
+ return res;
+ }
+};各种高级用法,还比较简单,但是应该不是很常见
+ + +《现代信息检索》课程笔记:第7讲 基于语言建模的IR模型
+ +统计语言模型(Statistical Language Modeling,SLM)
+SLM广泛使用于语音识别和统计机器翻译领域,利用概率统计理论研究语言。
+规则方法:词、句、篇章的生成比如满足某些规则,不满足该规则就不应存在。
+统计方法:任何语言片断都有存在的可能,只是可能性大小不同
+对于n-gram,n越大,则模型越复杂,估计的参数(即估计的概率)也越多。当然,当数据量足够大的情况下,模型阶数越高越对片段概率的计算也越准确。
+理论上说,在数据充足的情况下,利用更多的历史高阶的模型更准确,但是总计算量也越大
+数据规模总是有限的,即用于训练模型参数的语料存在稀疏性 (Data Sparseness ,即某参数在训练语料中没有出现问题。
+数据稀疏性导致零概率问题,但是训练集上不出现的事件并不代表在新的语料上不出现。
+SLM的一个重要工作就是进行平滑重新分配概率,即使没出现的事件也会赋予一个概率。
+总体分布&抽样
+文档的模型风格实际上是某种总体分布
+(待评分)文档和查询都是该总体分布下的一个抽样样本实例
+根据文档,估计文档的模型,即求出该总体分布(一般假设某种总体分布,然后求出其参数),然后计算该总体分布下抽样出查询的概率
+查询似然模型(Query Likelihood Model)
+文本生成的多项式模型
+数据平滑的一般形式
+其它SLMIR 模型
+基于翻译模型的IR模型:
+基本的QLM模型不能解决词语失配(word mismatch)问题,即查询中的用词和文档中的用词不一致
+翻译概率P(qi|wj)在计算时可以将词项之间的关系融入。
+KL距离(相对熵)模型
+统计语言建模IR模型优缺点
+优点:
+缺点:数据稀疏性,需要参数估计
+SLMIR vs. VSM :
+共性:
+不同:
+基于统计建模的IR模型 : 假设
+Leetcode 刷题笔记-Leetcode 101 第16章 复杂数据结构
+ +并查集(union-find, 或disjoint set)可以动态地连通两个点,并且可以非常快速地判断两个点是否连通。假设存在n个节点,我们先将所有节点的父亲标为自己;每次要连接节点i和j时,我们可以将i的父亲标为j;每次要查询两个节点是否相连时,我们可以查找i和j的祖先是否最终为同一个人。
+在无向图找出一条边,移除它之后该图能够成为一棵树(即无向无环图)。如果有多个解,返回在原数组中位置最靠后的那条边。
+class Solution {
+public:
+ int Find(vector<int>& parent, int index) {
+ if (parent[index] != index) {
+ parent[index] = Find(parent, parent[index]);
+ }
+ return parent[index];
+ }
+
+ void Union(vector<int>& parent, int index1, int index2) {
+ parent[Find(parent, index1)] = Find(parent, index2);
+ }
+
+ vector<int> findRedundantConnection(vector<vector<int>>& edges) {
+ int n = edges.size();
+ vector<int> parent(n + 1);
+ for (int i = 1; i <= n; ++i) {
+ parent[i] = i;
+ }
+ for (auto& edge: edges) {
+ int node1 = edge[0], node2 = edge[1];
+ if (Find(parent, node1) != Find(parent, node2)) {
+ Union(parent, node1, node2);
+ } else {
+ return edge;
+ }
+ }
+ return vector<int>{};
+ }
+};分析:在一棵树中,边的数量比节点的数量少1。如果一棵树有n个节点,则这棵树有n−1条边。这道题中的图在树的基础上多了一条附加的边,因此边的数量也是n。树是一个连通且无环的无向图,在树中多了一条附加的边之后就会出现环,因此附加的边即为导致环出现的边。可以通过并查集寻找附加的边。初始时,每个节点都属于不同的连通分量。遍历每一条边,判断这条边连接的两个顶点是否属于相同的连通分量。如果两个顶点属于不同的连通分量,则说明在遍历到当前的边之前,这两个顶点之间不连通,因此当前的边不会导致环出现,合并这两个顶点的连通分量。如果两个顶点属于相同的连通分量,则说明在遍历到当前的边之前,这两个顶点之间已经连通,因此当前的边导致环出现,为附加的边,将当前的边作为答案返回。
+错误:不知道怎么使用并查集
+请你设计并实现一个满足 LRU (最近最少使用) 缓存约束的数据结构。
+class LRUCache {
+public:
+ //定义双链表
+ struct Node{
+ int key,value;
+ Node* left ,*right;
+ Node(int _key,int _value): key(_key),value(_value),left(NULL),right(NULL){}
+ }*L,*R;//双链表的最左和最右节点,不存贮值。
+ int n;
+ unordered_map<int,Node*>hash;
+
+ void remove(Node* p)
+ {
+ p->right->left = p->left;
+ p->left->right = p->right;
+ }
+ void insert(Node *p)
+ {
+ p->right = L->right;
+ p->left = L;
+ L->right->left = p;
+ L->right = p;
+ }
+ LRUCache(int capacity) {
+ n = capacity;
+ L = new Node(-1,-1),R = new Node(-1,-1);
+ L->right = R;
+ R->left = L;
+ }
+
+ int get(int key) {
+ if(hash.count(key) == 0) return -1; //不存在关键字 key
+ auto p = hash[key];
+ remove(p);
+ insert(p);//将当前节点放在双链表的第一位
+ return p->value;
+ }
+
+ void put(int key, int value) {
+ if(hash.count(key)) //如果key存在,则修改对应的value
+ {
+ auto p = hash[key];
+ p->value = value;
+ remove(p);
+ insert(p);
+ }
+ else
+ {
+ if(hash.size() == n) //如果缓存已满,则删除双链表最右侧的节点
+ {
+ auto p = R->left;
+ remove(p);
+ hash.erase(p->key); //更新哈希表
+ delete p; //释放内存
+ }
+ //否则,插入(key, value)
+ auto p = new Node(key,value);
+ hash[key] = p;
+ insert(p);
+ }
+ }
+};分析:采用一个链表 list<pair<int, int>>来储存信息的 key和 value,链表的链接顺序即为最近使用的新旧顺序,最新的信息在链表头节点。同时我们需要一个嵌套着链表的迭代器的 unordered_map<int, list<pair<int, int>>::iterator>进行快速搜索,存迭代器的原因是方便调用链表的 splice函数来直接更新查找成功(cash hit)时的信息,即把迭代器对应的节点移动为链表的头节点。
错误:不明白
+付费题目
+设计一个插入、删除和随机取值均为
class RandomizedSet {
+private:
+ vector<int> nums;
+ unordered_map<int, int> indices;
+public:
+ RandomizedSet() {
+ srand((unsigned)time(NULL));
+ }
+
+ bool insert(int val) {
+ if (indices.count(val)) {
+ return false;
+ }
+ int index = nums.size();
+ nums.emplace_back(val);
+ indices[val] = index;
+ return true;
+ }
+
+ bool remove(int val) {
+ if (!indices.count(val)) {
+ return false;
+ }
+ int index = indices[val];
+ int last = nums.back();
+ nums[index] = last;
+ indices[last] = index;
+ nums.pop_back();
+ indices.erase(val);
+ return true;
+ }
+
+ int getRandom() {
+ return nums[rand()%nums.size()];
+ }
+};分析:变长数组 + 哈希表可以实现
+错误:随机数不太会,剩下的自己实现了
+设计一个increaseKey,decreaseKey,getMaxKey,getMinKey 均为
class AllOne {
+ list<pair<unordered_set<string>, int>> lst;
+ unordered_map<string, list<pair<unordered_set<string>, int>>::iterator> nodes;
+
+public:
+ AllOne() {}
+
+ void inc(string key) {
+ if (nodes.count(key)) {
+ auto cur = nodes[key], nxt = next(cur);
+ if (nxt == lst.end() || nxt->second > cur->second + 1) {
+ unordered_set<string> s({key});
+ nodes[key] = lst.emplace(nxt, s, cur->second + 1);
+ } else {
+ nxt->first.emplace(key);
+ nodes[key] = nxt;
+ }
+ cur->first.erase(key);
+ if (cur->first.empty()) {
+ lst.erase(cur);
+ }
+ } else { // key 不在链表中
+ if (lst.empty() || lst.begin()->second > 1) {
+ unordered_set<string> s({key});
+ lst.emplace_front(s, 1);
+ } else {
+ lst.begin()->first.emplace(key);
+ }
+ nodes[key] = lst.begin();
+ }
+ }
+
+ void dec(string key) {
+ auto cur = nodes[key];
+ if (cur->second == 1) { // key 仅出现一次,将其移出 nodes
+ nodes.erase(key);
+ } else {
+ auto pre = prev(cur);
+ if (cur == lst.begin() || pre->second < cur->second - 1) {
+ unordered_set<string> s({key});
+ nodes[key] = lst.emplace(cur, s, cur->second - 1);
+ } else {
+ pre->first.emplace(key);
+ nodes[key] = pre;
+ }
+ }
+ cur->first.erase(key);
+ if (cur->first.empty()) {
+ lst.erase(cur);
+ }
+ }
+
+ string getMaxKey() {
+ return lst.empty() ? "" : *lst.rbegin()->first.begin();
+ }
+
+ string getMinKey() {
+ return lst.empty() ? "" : *lst.begin()->first.begin();
+ }
+};分析:双向链表+哈希表
+错误:好难
+付费题目
+基本上都是要自己写数据结构的题目,应该也不是很常见了。
+ + +《模式识别与机器学习》课程笔记:第4章 特征选择和提取
+ +特征选择和提取是模式识别中的一个关键问题,前面讨论分类器设计的时候,一直假定已给出了特征向量维数确定的样本集,其中各样本的每一维都是该样本的一个特征;这些特征的选择是很重要的,它强烈地影响到分类器的设计及其性能;假若对不同的类别,这些特征的差别很大,则比较容易设计出具有较好性能的分类器。
+例如,描述人可以用好多特征,如肤色,体重,身高等,但是如果要判断软件工程师,显然编程这个特征比较有判别性;如果要判断是不是篮球员,则体重、身高有很强的判别性。
+特征选择和提取是构造模式识别系统时的一个重要课题。在很多实际问题中,往往不容易找到那些最重要的特征,或受客观条件的限制,不能对它们进行有效的测量;因此在测量时,由于人们心理上的作用,只要条件许可总希望把特征取得多一些;另外,由于客观上的需要,为了突出某些有用信息,抑制无用信息,有意加上一些比值、指数或对数等组合计算特征;如果将数目很多的测量值不做分析,全部直接用作分类特征,不但耗时,而且会影响到分类的效果,产生“特征维数灾难”问题。
+为了设计出效果好的分类器,通常需要对原始的测量值集合进行分析,经过选择或变换处理,组成有效的识别特征;在保证一定分类精度的前提下,减少特征维数,即进行“降维”处理,使分类器实现快速、准确和高效的分类。为达到上述目的,关键是所提供的识别特征应具有很好的可分性,使分类器容易判别。为此,需对特征进行选择:
+特征选择和提取这一任务应在设计分类器之前进行;
+ +所谓特征选择,就是从



所谓特征提取,就是使


其目的都是为了在尽可能保留识别信息的前提下,降低特征空间的维数,以达到有效的分类效果。
+距离和散布矩阵:
+ ,其中,
,其中,  和
和  为
为  维向量, 其第
维向量, 其第  个分量分别是
个分量分别是  和
和 
 到点集
到点集 之间的距离为
之间的距离为
类内距离:


类内散布矩阵:考虑一类内模式点集

对属于同一类的模式样本,类内散布矩阵表示各样本点围绕其均值周围的散布情况。
+在考虑有两个以上的类别,如集合
为简化起见,常用两类样本各自质心间的距离作为类间距离,并假设两类样本出现的概率相等,则
其中







两类模式的类间散布矩阵:
对三个以上的类别,类间散布矩阵常写成


多类情况的类内散布矩阵可写成各类的类内散布矩阵的先验概率的加权和,即


有时,用多类模式总体分布的散布矩阵来反映其可分性,即:


设有

从


对于独立特征的选择准则:类别可分性准则应具有这样的特点,即不同类别模式特征的均值向量之间的距离应最大,而属于同一类的模式特征,其方差之和应最小。假设各原始特征测量值是统计独立的,此时,只需对训练样本的

对于 
















上述基于距离测度的可分性准则,其适用范围与模式特征的分布有关。假若类概率密度函数不是或不近似正态分布,均值和方差就不足以用来估计类别的可分性,此时该准则函数不完全适用。
+一般特征的散布矩阵准则:
+

直观上,类间离散度越大且类内离散度越小,则可分性越好。因此,可推导出散布矩阵准则采用如下形式:
+

其中,



前面讨论的特征选择是在一定准则下,从




K-L变换就是一种适用于任意概率密度函数的正交变换。
+离散的有限K-L展开式的形式:
+设一连续的随机实函数








将上式写成离散的正交函数形式,使连续随机函数




写成向量形式:
将展开式写成离散形式:







+它将

对各个模式类别,正交函数都是相同的,但其展开系数向量
K-L展开式的根本性质是将随机向量



正交向量集
设随机向量





因为
K-L展开式系数的计算步骤:
+ 的自相关矩阵:
的自相关矩阵:
 的特征值
的特征值 和对应的特征向量
和对应的特征向量 ,
, ,得矩阵:
,得矩阵:

K-L展开式用于特征选择相当于一种线性变换。若从









从K-L展开式的性质和按最小均方差的准则来选择特征,应使





将K-L展开式系数







K-L变换是在均方误差最小的意义下获得数据压缩(降维)的最佳变换,且不受模式分布的限制。对于一种类别的模式特征提取,它不存在特征分类问题,只是实现用低维的

通过K-L变换能获得互不相关的新特征。若采用较大特征值对应的特征向量组成变换矩阵,则能对应地保留原模式中方差最大的特征成分,所以K-L变换起到了减小相关性、突出差异性的效果。在此情况下,K-L变换也称为主成分变换(PCA变换)。
+需要指出的是,采用K-L变换作为模式分类的特征提取时,要特别注意保留不同类别的模式分类鉴别信息,仅单纯考虑尽可能代表原来模式的主成分,有时并不一定有利于分类的鉴别。
+ + +机器学习算法竞赛实战-基础篇
+ +一直想学,前面看过觉得太难,这回一定要坚持看完!
+分析数据进而抽象出建模目标和方案。自行利用主办方提供的数据构造训练集与测试集。
+EDA(探索性数据分析),Exploratory Data Analysis。在大致了解问题建模方式后,需结合对赛题背景业务的理解去看数据长什么样子、数据是否和描述相符、包含哪些信息等。首先需要对数据有清晰认知,主要是宽表中各个字段的取值含义、范围和数据结构等。然后更深层次地结合标签分析特征的分布状态、训练集与测试集的同分布情况、特征之间的业务关联以及隐含信息表征等。
+Feature Engineering。特征决定机器学习预测效果上限,算法不断逼近这个上限。最费时的模块。
+选模型、调参数
+找找队友,看看Code
+从直观上梳理问题,分析问题可解的方法、赛题背景等
+业务理解:从个人生活的直观角度对业务进行分析
+数据理解:在问题建模阶段,只需对数据做基本的分析。可以将数据理解分为数据基础层和数据描述层两个部分。主办方提供的原始数据质量良莠不齐,往往需要对原始数据进行清洗、加工和计算等处理。
+分类指标:
+错误率:分类错误的样本数占样本总数的比例
+精度:分类正确的样本数占样本总数的比例
+精度=1-错误率
+查准率P反映真实情况与预测结果都为正例的样例在预测结果为正例的样例中的占比
+查全率R反映真实情况与预测结果都为正例的样例在真实情况为正例的样例中的占比
+(查准率与查全率是一对矛盾的度量,一般来讲,查准率高时,查全率偏低;查全率高时,查准率偏低)
+
# 构建一个计算准确率、召回率和F1-score的评价代码
+y_train = np.array([1,0,1,0,1,0,1,0,1,1])
+y_pred = np.array([1,1,1,1,0,0,0,0,1,0])
+precision = precision_score(y_train,y_pred) #准确率
+recall = recall_score(y_train,y_pred) #召回率
+f1 = f1_score(y_train,y_pred) #f1度量
+print(precision,recall,f1)0.6 0.5 0.5454545454545454先根据学习器的预测结果对样例进行排序,按此顺序逐个把样例作为正例进行预测,每次计算出“真正例率”(True Positive Rate,简称TPR)和“假正例率”(False Positive Rate,简称FPR),分别以他们为纵、横轴作图,就得到了ROC曲线。
+

ROC曲线对正负样本的数量和分布不敏感。
+AUC定义为ROC下方的面积,在互联网的搜索、推荐和广告的排序业务中都极为常见。AUC作为一个数值,其值越大就代表分类器的效果越好。
+值得一提的还有AUC的排序特性。相对于准确率、召回率等指标,AUC指标本身和模型预测的概率绝对值无关,它只关注样本间的排序效果,因此特别适合用作排序相关问题建模的评价指标。AUC是一个概率值,我们随机挑选一个正样本与一个负样本,由当前分类算法根据计算出的分数将这个正样本排在负样本前面的概率就是AUC值。
+为什么AUC与模型预测的分数值无关是个很好的特性?假设采用的是准确率等指标,而模型预测的分数是个概率值,那么必须选择一个阈值来决定把哪些样本预测为1,哪些预测为0。阈值的选择不同,准确率的值就会不同。而AUC可以直接使用模型预测分数本身,参考的是相对顺序。在竞赛中,省去了参赛者试探阈值的麻烦。
+对数损失可用于评价分类器的概率输出。对数损失通过惩罚错误的分类来实现对分类器的准确度的量化。最小化对数损失基本等价于最大化分类器的准确度。为了计算对数损失,分类器必须提供概率结果,即把输入样本喂入模型后,预测得到每个类别的概率值(0~1),而不只是预测最可能的类别。
+AUC与对数损失的区别
+对数损失主要评价模型预测的概率是否足够准确,更关注和观察数据的吻合程度;AUC评价的则是模型把正样本排列到前面的能力。两者侧重不同,故应用不同。对于广告CTR问题,如果考虑广告排序效果,则可以选择AUC,这样不会受极端值影响。此外,对数损失反映了评价偏差,更偏向于将样本数量多的那类划分准确。由于使用AUC或对数损失可以避免把预测概率转换成类别的麻烦,在各种数据竞赛的分类问题中,AUC和对数损失基本是最常见的模型评价指标。
+回归指标:
+ ,又称L1范数损失
,又称L1范数损失MAE不是二阶连续可微的,其二阶导数总为0。
+ ,又称L2范数损失
,又称L2范数损失MSE的量纲与数据标签不一致,为了保证量纲的一致性,通常需要对均方误差进行开方(均方根误差RMSE)
+平均绝对误差MAE与均方误差MSE的区别
+均方误差对误差(真实值-预测值)取了平方,若误差>1,则均方误差会进一步增大误差。如果数据中存在异常点,那误差值就会很大,而误差的平方则会远大于误差的绝对值。因此,相对于使用平均绝对误差计算损失,使用均方误差的模型会赋予异常点更大的权重。简而言之,均方误差对异常值更加敏感。
+为什么在XGBoost里通常选择Huber损失替换MAE?
+由于MAE不是连续可导的(0处不可导),所以需要使用可导目标函数来逼近平均绝对误差。而对于均方误差MSE,梯度又会随着损失的减小而减小,使预测结果更加精确。在这种情况下,Huber损失就非常有用,它会由于梯度的减小而落在最小值附近。比起均方误差MSE,Huber损失对异常点更加健壮。因此,Huber损失结合了MAE和MSE的优点。但是Huber损失可能需要我们不断调整超参数delta。
+
MAPE与MAE一样,不存在二阶导数。但不用于MAE,平均绝对百分比误差MAPE除了考虑预测值与真实值的误差,还考虑了误差与真实值之间的比例。因此真实值越大,误差会越小。
+主办方提供的数据往往令人脑壳疼,主要是以下四个原因:
+问题1:在数据量非常大的情况下,为了降低成本,如何提高模型的训练速度?
+问题2:针对正负样本分布不均衡的问题,如何通过数据采样解决这类问题?
+思考:在什么场景下需要处理样本的不均衡问题?
+由于需要数据集对模型的效果进行线下验证,所以需要考虑如何对数据进行划分,构建合适的线下验证集。针对不同类型的问题,需要不同的线下验证方式。
+书中将这些问题大致分为强时序性与弱时序性两类,然后以此确定线下验证方式。
+定义:先将总数据集D划分为k个大小相似的互斥子集,每个子集都尽可能保持数据分布的一致性(即从D中分层采样得到)。然后每次用K-1个子集的并集作为训练集,余下的自己作为测试集。这样可以获得K组训练/测试集,从而可进行k次训练和测试,最终返回这k个测试结果的均值。
+注意:
+以下为交叉验证代码,其中参数NFOLDS用来控制折数**(未实际验证)**
+from sklearn.model_selection import KFold
+NFOLDS = 5 #五折交叉验证
+folds = KFold (n_split = NFOLDS,shuffle=True,random_state=2021)#random_state只要是一个固定的值就可以了,不一定是2021
+for trn_idx,val_idx in folds.split(X_train,y_train):
+ train_df,train_label = X_train.iloc[trn_idx, :],y_train[trn_idx]
+ valid_df,valid_label = X_train.iloc[val_idx, :],y_train[val_idx]参数random_state默认设置为None,这意为着每次进行KFold(…, shuffle=True)时,打散都是不同的。
+为了保证结果的可重复性(在相同的平台上),应该给random_state设定一个固定的值。
+如何确保自己准备好竞赛使用的算法模型?如何为数据集选择最合适的算法?如何定义可用于算法模型的特征变量?数据探索可以帮助回答以上三点。
+一般而言,数据探索可以分为三个部分:
+赛前数据探索,主要包含分析思路、分析方法和明确目的。
+在实际竞赛中,最好使用多种探索思路和方法来探索每个变量并比较结果。在完全理解数据集后,就可以进入数据预处理阶段和特征提取阶段了,以便根据所期望的业务结果转换数据集。此步骤的目标是确信数据集已准备好应用于机器学习算法。
+数据探索的分析主要采用以下方法:
+可以检查每个变量的分布,定义一些丢失值,最终找到替换它们的可能方法。
+在竞赛中跳过数据探索阶段可能会导致数据倾斜、出现异常值和过多的缺失值,产生以下糟糕结果:
+数据探索阶段必须要明确:
+数据探索最基本的步骤之一是获取对数据的基本描述,通过获取对数据的基本描述从而获得对数据的基本感觉。以下方法有助于我们认识数据:
+DataFrame.describe():查看数据的基本分布,具体是对每列数据进行统计,统计值包含频次、均值、方差、最小值、分位数、最大值等。DataFrame.head(n):可以直接加载数据集的前n行,n默认为5DataFrame.shape:得到数据集的行列情况DataFrame.info():可以快速获得对数据集的简单描述,比如每个变量的类型、数据集的大小和缺失值情况。下面通过一段代码展示nunique和缺失值的情况:
+stats = []
+for col in train.columns:
+ stats.append((col, train[col].nunique(), train[col].isnull().sum() * 100 / train.shape[0], train[col].value_counts(normalize=True, dropna=False).values[0] * 100, train[col].dtype))
+stats_df = pd.DataFrame(stats, columns=['Feature', 'Unique_values', 'Percentage of missing values', 'Percentage of values in the biggest category', 'type'])
+stats_df.sort_values('Percentage of missing values', ascending=False)[:10]上图展示了经过上述代码生成的数据基本信息,我们从中找到特殊变量进行细致分析,这里选择nunique值低和缺失值多的变量进行观察。一般而言,nunique为1是不具备任何意义的,表示所有值都一样,不存在区分性,需要进行删除。可以发现有些变量的缺失值很多,比如缺失比例达到95%以上,我们可以考虑将其删除。
+用柱状图的形式可以更加直观地展示变量的缺失值分布情况,以下为变量缺失值可视化图的具体生成代码:
+missing = train.isnull().sum()
+missing = missing[missing > 0]
+missing.sort_values(inplace=True)
+missing.plot.bar()单变量可以分为标签、连续型和类别型
+标签是最重要的变量,首先应当观察标签的分布情况。对于房屋价格预测,其标签SalePrice为连续型变量。
+通过可视化的方式观察SalePrice的分布情况
+sns.distplot(train['SalePrice'], color='b', bins=100, hist_kws={'alpha': 0.4})可见,SalePrice呈偏离正态分布,属于向右倾斜类型,存在峰值状态,一些异常值在500000以上。我们最终会想办法去掉这些异常值,得出能够让算法模型很好学习的、符合正态分布的变量。
+ +下面对SalePrice进行对数转换,并生成可视化图
+sns.distplot(np.log(train['SalePrice']), color='b', bins=100, hist_kws={'alpha': 0.4})可以看出 ,对数转换后的标签的分布为正态分布形式,比较适合算法模型学习。
+类似于标签的查看方式,这里主要使用直方图这种可视化方式观察值的分布、每个值出现的频率等。以下为连续型变量的分布可视化的生成代码:
+df_num = train.select_dtypes(include = ['float64', 'int64'])
+df_num.hist(figsize=(16, 20), bins=50, xlabelsize=8, ylabelsize=8)实际中要对全部的变量进行查看,分析每一个变量的分布情况。
+接着进行更加科学的分析,首先是相关性分析。相关性分析只能比较数值间特征,所以对于字母或字符串特征,需要先进行编码,并将其转换为数值,然后再看有什么关联。在实际竞赛中,相关性分析可以很好地过滤掉与标签没有直接关系的特征。
+正相关和负相关
+在搭建或训练模型时,如果同时使用这两个特征,可能其中一个会是多余的。我们应尽量消除冗余特征,因为它会使训练时间变长,同时影响其他优势
+以下代码为生成有关SalePrice的相似性矩阵图
+corrmat = train.corr()
+f, ax = plt.subplots(figsize=(20, 9))
+sns.heatmap(corrmat, vmax=0.8, square=True)从生成的相似性矩阵中,可以找出与房价相关性最强的变量,其中OverallQual(总评价)、GarageCars(车库)、TotalBsmtSF(地下室面积)、GrLivArea(生活面积)等特征与SalePrice呈正相关
+从相似性矩阵中,我们还能发现变量之间的关系,如何利用相似性矩阵进行分析就成为了关键
+数据探索的目的是为了帮助我们了解数据并且构建有效特征。
+比如,我们找到了与标签有着强相关的特征,那么就可以围绕着这个强相关特征进行一系列的扩展,具体可以进行交叉组合,比如强相关加弱相关、强相关加强相关等组合,挖掘更高维度的潜在信息。
+首先,观察类别型变量的基本分布情况,即观察每个属性的频次。根据频次,我们不仅可以发现热点属性和极少出现的属性,还可以进一步分析出现这些情况的原因,比如淘宝网的女性用户多于男性,主要是因为平台在服饰和美妆业务方面拥有强大的影响力。这是从业务角度考虑,自然也有可能是数据采样的原因。
+对部分类别变量的分布进行可视化展示
+df_not_num = train.select_dtypes(include = ['O'])
+fig, axes = plt.subplots(round(len(df_not_num.columns) / 3), 3, figsize=(12, 30))
+for i, ax in enumerate(fig.axes):
+ if i < len(df_not_num.columns):
+ ax.set_xticklabels(ax.xaxis.get_majorticklabels(), rotation=45)
+ sns.countplot(x=df_not_num.columns[i], alpha=0.7, data=df_not_num, ax=ax)
+fig.tight_layout()单变量分析太过于单一,不足以挖掘变量之间的内在联系,获取更加细粒度的信息,所以有必要进行多变量分析。分析特征变量与特征变量之间的关系有助于构建更好的特征,同时降低构建冗余特征的概率值。
+此处选用本赛题中需要特别关注的特征变量进行分析
+从相似性矩阵中,我们已知房屋评价与SalePrice呈正相关。进一步扩展分析,通过可视化来考虑房屋评价和房屋位置是否存在某种联系。
+plt.style.use('seaborn-white')
+type_cluster = train.groupby(['Neighborhood','OverallQual']).size()
+type_cluster.unstack().plot(kind='bar',stacked=True, colormap= 'PuBu', figsize=(13,11), grid=False)
+plt.xlabel('OverallQual', fontsize=16)
+plt.show()上图为不同房屋位置的评价分布条状图,我们可发现颜色越深代表评价越高。NoRidge、NridgHt和StoneBr都有不错的评价
+再进一步看看不同位置房屋的SalePrice
+var = 'Neighborhood'
+data = pd.concat([train['SalePrice'], train[var]], axis=1)
+f, ax = plt.subplots(figsize=(26, 12))
+fig = sns.boxplot(x=var, y="SalePrice", data=data)高评价位置对应高SalePrice,说明房屋位置评价与房屋售价有比较强的相关性。除了通过这样的分析证明原始特征与SalePrice强相关外,还可以通过分析来构建新的特征。
+既然房屋位置和房屋评价的组合能够出现更高售价的房屋,那么我们可以构造这两个类别特征的交叉组合特征来进行更细致的描述,也可以构造这个组合特征下的房屋均价等。
+学习曲线是机器学习中被广泛使用的效果评估工具,能够反映训练集和验证集在训练迭代中的分数变化情况,帮助我们快速了解模型的学习效果。我们可以通过学习曲线来观察模型是否过拟合,通过判断拟合程度来确定如何改进模型
+学习曲线广泛应用于机器学习中的模型评估,模型会随着训练迭代逐步学习(优化其内部参数),例如神经网络模型。这时用于评估学习的指标可能会最大化(分类准确率)或者最小化(回归误差),这也意味着得分越高(低)表示学习到的信息越多(少)。
+以下是学习曲线图中观察到的一些常见形状
+欠拟合是指模型无法学习到训练集中数据所展现的信息,这里可以通过训练损失的学习曲线来确定是否发生欠拟合。在通常情况下,欠拟合学习曲线可能是一条平坦的线或者有着相对较高的损失,也就表明该模型根本无法学习训练集
+过拟合是指模型对训练集学习得很好,包括统计噪声或训练集中的随机波动。过拟合的问题在于,模型对于训练数据的专业化程度越高,对新数据的泛化能力就越差,这会导致泛化误差增加。泛化误差的增加可以通过模型在验证集上的表现来衡量。如果模型的容量超出了问题所需的容量,而灵活性又过多,则会经常发生这种情况。如果模型训练时间过长,也会发生过拟合。
+通过模型训练可以得到特征重要性。对于树模型(如LightGBM和XGBoost),通过计算特征的信息增益或分裂次数得到特征的重要性得分。对于模型LR和SVM,则是使用特征系数作为特征重要性得分,例如LR(逻辑回归),每个特征各对应一个特征系数w,w越大,那么改特征对模型预测结果的影响就会越大,就可以认为该特征越重要。我们假定特征性得分和特征系数w都是在衡量特征在模型中的重要性,都可以起到特征选择的作用。
+误差分析是通过模型预测结果来发现问题的关键。
+一般而言,回归问题中看预测结果的分布,分类问题中看混淆矩阵等。
+在真实问题中,误差分析会更加细致。比如,在进行一个用户违约预估的二分类任务中,验证集结果中有200个错误分类样本,进一步分析发现有70%的错误分类样本是由于大量特征缺失而导致的误判,这时就需要调整,既可以通过挖掘更多能够描述这些误判样本的特征信息帮助增强模型的预测能力,还可以在模型训练中赋予这些误判样本更高的权重。
+尽量得到标准、干净、连续的数据,供数据统计、数据挖掘等使用,视情况尝试对缺失值进行处理,比如是否要填充,填充什么。此外,有些竞赛提供的数据集以及对应的存储方式可能使得需要占用超过参赛者本身硬件条件的内存,故有必要进行一定的内存优化,这也有助于在有限的内存空间对更大的数据集进行操作。
+除了XGBoost和LightGBM等算法在训练时可以直接处理缺失值以外,其他很多例如LR、DNN、CNN、RNN等都并不能对缺失值进行直接处理。故而在数据准备阶段,要比构建算法阶段花更多时间,因为像填补缺失值这样的操作需要细致处理。
+首先,需找到缺失值表现形式。除了None、NA和NaN外,还有例如-1或-999来填充的缺失值。还有一种看上去像缺失值,但实际上有实际意义的业务,此时需特殊对待。例如没有填“婚姻状态”的用户可能是对自己隐私比较敏感,应为其单独设为一个分类;没有“驾龄”可能是没有车,为其填充0比较合适。
+数据缺失可以分为类别特征的缺失和数值特征的缺失两种。
+填充方法总结如下:
+实际数据中可能会发现某个或某些字段(特征)根据某个变量(如时间序列问题中的时间)排序后,经观察存在一些数值远高于或低于其一定范围内的其他数值。还有些不合理的存在,这些都可以视作异常值,他们可能会给算法性能带来负面影响。
+首先,找到异常值,总结了两种方法:
+离散型异常值(离散属性定义范围以外的所有值均为异常值)、知识型异常值(如大学生脱发情况:从无)等,都可以当做类别缺失值来处理。
+数据集太大而自己的硬件条件有限就有可能会因为内存不够导致代码出现memory error,介绍Python的内存回收机制和数值类型优化这两种有助于优化内存的常见方法。
+我们可以用np.iinfo类来确认每一个int型子类型的最大值和最小值
+import numpy as np
+np.iinfo(np.int8).min
+np.iinfo(np.int8).max无量纲化指的是将不同规格的数据转换到同一规格。常见无量纲化方法有标准化和区间缩放法。标准化的前提是特征值服从正态分布,标准化后,特征值服从标准正态分布。区间缩放法利用了边界信息,将特征的取值区间缩放到某个特定的范围,例如[0,1]
+单特征转换是构建一些模型(如线性回归、KNN、神经网络)的关键,对于决策树相关模型并无影响。还有些纯粹的工程原因,即在进行回归预测时,对目标取对数处理,不仅可以缩小数据范围,而且压缩变量尺度使数据更平稳。
+然而,数据要求不仅是通过参数化方法施加的。如果特征没有被规范化,例如当一个特征的分布位于0附近且范围不超过(-1,1),而另一个特征的分布范围在数十万数量级时,会导致分布于0附近的特征变得完全无用。
+扩展:cbox-cox变换,一种自动寻找最佳正态分布变换函数的方法。
+log变换可以将倾斜数据变得接近正态分布。
+离散化后的特征对异常数据有很强的健壮性,更便于探索数据的相关性。常用的离散化分为无监督和有监督两种。
+无监督的离散化分桶操作可以将连续变量离散化,同时使数据平滑,即降低噪声的影响。一般分为等频和等距两种分桶方式。
+有监督的离散化对目标有很好的区分能力,常用的是使用树模型返回叶子节点来进行离散化。如在GBDT+LR经典模型中,就是先使用GBDT来将连续值转化为离散值。具体方法:用训练集中的所有连续值和标签输出来训练LightGBM,共训练两棵决策树,第一棵有4个叶子节点,第二棵树有3个叶子节点。如果某一个样本落在第一棵树的第三个叶子节点上,落在第二棵树的第一个叶子节点上,那么它的编码就是0010100,一共7个离散特征,其中会有两个取值为1的位置,分别对应每棵树中样本落点的位置。最终我们会获得num_trees*num_leaves维特征。
+在实际数据中,特征并不总是数值,还有可能是类别。对于离散型的类别特征进行编码,一般分为两种情况:自然数编码(特征有意义)和独热(one-hot)编码(特征无意义)。
+自然数编码:一列有意义的类别特征(即有顺序关系)可以使用自然数进行编码,利用自然数的大小关系可以保留其顺序关系。以下是两种自然数编码的常用方式:
+①调用sklearn中函数:
+from sklearn import preprocessing
+from f in columns:
+ le = preprocessing.LableEncoder()
+ le.fit(data[f})②自定义实现(速度快)
+for f in columns:
+ data[f] = data[f].fillna(-999)
+ data[f] = data[f].map(dict(zip(data[f].unique(),range(0,data[f].nunique()))))独热编码:当类别特征没有意义(即无顺序关系)时,需要使用独热编码。例如,红>蓝>绿不代表任何东西,进行独热编码后,每个特征的取值对应一维特征,最后得到一个样本数×类别数大小的0~1矩阵。可直接调用sklearn中API进行生成(或者是使用哑变量的方式)
+不规则特征可能包含样本的很多信息,比如身份证号,各段表示不同的信息。一般不会提供这种比较敏感的信息。
+机器学习模型很难识别复杂的模式,特别是很难学习到不同特征组合交叉的信息,所以我们可以基于对数据集的直觉分析和业务理解创建一些特征来帮助模型有效学习。下面我们将介绍结构化数据的特征提取方式。
+(结构化数据由明确定义的数据类型组成,非结构化数据由音频、视频和图片等不容易搜索的数据组成。)
+类别特征又可以称为离散特征,除了每个类别属性的特定含义外,还可以构造连续型的统计特征,以挖掘更多有价值的信息,比如构造目标编码、count、nunique和ratio等特征。另外,也可以通过类别特征间的交叉组合构造更加细粒度的特征。
+目标编码可以理解为用目标变量(标签)的统计量对类别特征进行编码,即根据目标变量进行有监督的特征构造。如果是分类问题,可以统计目标均值、中位数和最值。目标编码的方式可以很好地替代类别特征,或者作为新特征。
+使用目标变量时,非常重要的一点是不能泄露任何验证集的信息。所有基于目标编码的特征都应该在训练集上计算,测试集则由完整的训练集来构造。更严格一点,我们在统计训练集的特征时,需要采用K折交叉统计法构造目标编码特征,从而最大限度地防止信息泄露。如用五折交叉统计构造特征时,我们将样本划分为五份,对于其中每一份数据,我们都将用另外四份来计算每个类别取值对应目标变量的频次、比例或者均值,简单来说就是未知的数据(一份)在已知的数据(四份)里面取特征。
+目标编码方法对于基数较低的类别特征通常很有效,但对于基数较高的类别特征,可能会有过拟合的风险。因为会存在一些类别出现频次非常低,统计出来的结果不具有代表性。一般会加入平滑性来降低过拟合风险。在处置妥当的情况下,无论是线性模型,还是非线性模型,目标编程都是最佳的编码方式和特征构造方式。
+count:计数特征,用于统计类别特征的出现频次
+nunique和ratio常常会涉及多个类别特征的联合构造。例如在广告点击率预测问题中,对于用户ID和广告ID,使用nunique可以反映用户对广告的兴趣宽度,也就是统计用户ID看过几种广告ID;使用ratio可以反映用户对某类广告的偏好程度,即统计用户ID点击某类广告ID的频次占用户点击所有广告ID频次的比例。
+交叉组合能够描述更细粒度的内容。对类别特征进行交叉组合在竞赛中是一项非常重要的工作,这样可以进行很好的非线性特征拟合。如用户年龄和用户性别可以组合成“年龄_性别”这样的新特征。一般我们可以对两个类别或三个类别特征进行组合,也称作二阶组合或三阶组合。简单来讲,就是对两个类别特征进行笛卡尔积的操作,产生新的类别特征。
+并非所有组合都是需要考虑的,我们会从两个方面进行分析。
+这里所说的数值特征,我们认为是连续的。数值特征的大小是有意义的,通常不需要处理就可以直接“喂”给模型进行训练。除了之前对数值特征进行各种变换外,还存在一些其他常见的数值特征构造方式。
+在实际数据中,通常给出的时间特征是时间戳属性,所以首先需要将其分离成多个维度,比如年月日小时分钟秒钟。如果你的数据源来自于不同的地理数据源,还需要利用时区将数据标准化。除了分离出来的基本时间特征外,还可以构造时间差特征,即计算出各个样本的时间与未来某一个时间的数值差距,这样这个差距是UTC的时间差,从而将时间特征转换为连续值,比如用户首次行为日期与用户注册日期的时间差、用户当前行为与用户上次行为的时间差等。
+在竞赛中,可能会遇到某一列特征中每行都包含多个属性的情况,这就是多值特征。例如广告大赛中的兴趣类目,其中包含5个兴趣特征组,每个兴趣特征组都包含若干个兴趣ID。对于多值特征,通常可以进行稀疏化或者向量化的处理,这种操作一般出现在自然语言处理中,比如文本分词后使用TF-IDF(词频-逆文档频率)、LDA(隐含狄利克雷分布)、NMF(非负矩阵分解)等方式进行处理,这里则可以将多值特征看作文本分词后的结果,然后做相同的处理。
+对多值特征最基本的处理办法是完全展开,即把这列特征所包含的n个属性展开成n维稀疏矩阵。使用sklearn中的CountVectorizer函数,可以方便地将多值特征展开,只考虑每个属性在这个特征的出现频次。
+还有一种情况,比如在广告算法大赛中,需要根据用户的历史点击行为预测用户的属性标签。这时候用户的点击序列尤为重要,当我们构造好用户对应的历史点击序列后,除了使用上述的TF-IDF等方法外,还可以提取点击序列中商品或广告的嵌入表示,比如用Word2Vec、DeepWalk等方法获取embedding向量表示。因为要提取用户单个特征,所以可以对序列中的嵌入向量进行聚合统计,这种方法本质上是假设用户点击过的商品或广告等同重要,是一种比较粗糙的处理方式。我们可以引入时间衰减因素,或者使用序列模型,如RNN、LSTN、GRU,套用NLP的方法进行求解。
+当我们添加新特征时,需要验证它是否确实能够提高模型预测的准确度,以确定不是加入了无用的特征,因为这样只会增加算法运算的复杂度,这时候就要通过特征选择算法自动选择出特征集中的最优子集,帮助模型提供更好的性能。特征选择算法用于从数据中识别并删除不需要、不相关以及冗余特征。这些特征可能会降低模型的准确度和性能,特征选择的方法主要有先验的特征关联性分析以及后验的特征重要性分析。、
+特征关联性分析是使用统计量来为特征之间的相关性进行评分。特征按照分数进行排序,要么保留,要么从数据集中删除。关联性分析方法通常是针对单变量的,并独立考虑特征或者因变量。常见的特征关联性分析方法有皮尔逊相关系数、卡方检验、互信息法和信息增益等。这些方法速度快、使用方便,但是忽略了特征之间的关系,以及特征和模型之间的关系。
+不仅可以衡量变量之间的线性相关性,解决共线变量问题,还可以衡量特征与标签的相关性。共线变量是指变量之间存在高度相关关系,这会降低模型的学习可用性,可解释性以及测试集的泛化性能。但这三个特性都是我们想增加的,所以删除共线变量是一个有价值的步骤。我们将为删除共线变量建立一个基本的阈值(根据想要保留的特征数量决定)。
+下面代码用于解决特征与标签不具有相关性的问题,根据皮尔逊相关系数的计算提取top300的相似特征:
+def feature_select_pearson(train,features):
+ featureSelect = features[:]
+ #进行皮尔逊相关性计算
+ corr=[]
+ for feat in featureSelect:
+ corr.append(abs(train[[feat,'target']].fillna(0).corr().values[0][1]))
+ se = pd.Series(corr,index=featureSelect).sort_values(ascending=False)
+ feature_select = se[:300}.index.tolist()
+ #返回特征选择后的训练集
+ return train[feature_select]用于检验特征变量与因变量的相关性。对于分类问题,一般假设与标签独立的特征为无关特征,而卡方检验恰好可以进行独立性检验,所以使用与特征选择。如果检验结果是某个特征与标签独立,则可以去除该特征。
+互信息是对一个联合分布中两个变量之间相互影响关系的度量,也可以用于评价两个变量之间的相关性。互信息法之所以能够用于特征选择,可以从两个角度进行解释:基于KL散度和基于信息增益。互信息越大说明两个变量相关性越高。
+但是想把互信息直接用于特征选择其实不太方便,由于:
+在实际竞赛中,经常用到的一种特征选择方法是基于树模型评估特征的重要性分数。特征的重要性分数越高,说明特征在模型中被用来构建决策树的次数越多。这里我们以XGBoost为例来介绍树模型评估特征重要性的三种计算方法(weight、gain和cover)。(LightGBM也可以返回特征重要性)
+params ={
+ 'max_depth':10,
+ 'subsample':1,
+ 'verbose_eval':True,
+ 'seed':12,
+ 'objective':'binary:logistic'
+}
+xgtrain = xgb.DMatrix(x,label=y)
+bst = xgb.train(params,xgtrain,numm_boost_round=10)
+importance = bst.get_score(fmap='',importance_type='weight')importance =bst.get_score(fmap='',importance_type='gain')importance = bst.get_score(fmap='',importance_type='cover')技巧:虽然特征重要性可以帮助我们快速分析特征在模型训练过程中的重要性,但不能将其当做绝对的参考依据。一般而言,只要特征不会导致过拟合,我们就可以选择重要性高的特征进行分析和扩展,对于重要性低的特征,可以考虑将之从特征集中移除,然后观察线下效果,再做进一步判断。
+可以将一组特征的选择视作一个搜索问题,在这个问题中,通过准备、评估不同的组合并对这些组合进行比较,从而找出最优的特征子集,搜索过程可以是系统性的,比如最佳优先搜索;也可以是随机的,比如随机爬山算法,或者启发式方法,比如通过向前和向后搜索来添加和删除特征(类似前剪枝和后剪枝算法)。这种方法比较耗时。
+from sklearn.feature_selection import RFE
+from sklearn.linear_model import LogisticRegression
+#递归消除特征法,返回特征选择后的数据
+#参数estimator为基模型
+#参数n_feature_to_select 为选择的特征个数
+RFE(estimator=LogisticRegression(),n_features_to_select=2).fit_transform(data,target)技巧:在使用封装方法进行特征选择时,用全量数据训练并不是最明智的选择。应先对大数据进行采样,再对小数据使用封装方法
+以上三种特征选择方法按需使用或组合使用,建议优先考虑特征重要性,其次是特征关联性。
+此外还有null importance。其思想:将构建好的特征和正确的标签喂给树模型得到一个特征重要性分数,再将特征和打乱后的标签喂给树模型得到一个特征重要性分数,然后对比两个分数,如果前者没有超过后者,那么这个特征就是一个无用的特征。
+参考资料 :《机器学习算法竞赛实战》整理 | 五、模型训练
+Lasso回归是对普通的线性回归采用L1正则化进行优化,通过惩罚或限制估计值的绝对值之和,可以使某些系数为零,从而达到特征稀疏化和特征选择的效果。当我们需要一些自动的特征、变量选择,或者处理高度相关的预测因素时,很方便。
+from sklearn.linear_model import Lasso
+lasso_model = Lasso(alpha = 0.1, normalize = True)只保留不相关的特征,其他为0,可能会导致信息损失
+Ridge回归是对普通的线性回归采用L2正则化进行优化,对特征的权重系数设置了惩罚项。
+from sklearn.linear_model import Ridge
+ridge_model = Ridge(alpha = 0.05, normalize = True)不会减少特征数量,不利于特征缩减。
+两者合并:Elastic Net Regression
+本节将介绍竞赛中常见的树模型,这些模型简单易用,能够带来高收益。
+可将树模型分为随机森林(Random Forest, RF)和梯度提升树(GBDT), 这两者最大的差异是前者并行、后者串行。在梯度提升树部分我们将介绍如今竞赛中大火的三种树模型: XGBoost、 LightGBM 和CatBoost。能够灵活运用这三种模型是竞赛中的必备技能。接下来将详细介绍各种树模型的数学形式、优缺点、使用细节和应用场景。
+随机森林就是通过集成学习的思想将多个决策树集成在一起,各个决策树之间没有任何关联。随机森林算法对多个决策树的结果进行投票得到最终结果,也是最简单的bagging思想 。
+随机森林的优点:
+很多缺点都是相对而言的:
+from sklearn.ensemble import RandomForestClassifier
+rf = RandomForestClassifier(max_ features=' auto', oob_ score=True, random state=1, n_ jobs=-1)梯度提升树(GBDT)是基于Boosting改进而得的,在Boosting算法中,一系列基学习器都需要串行生成,每次学习一棵树,学习目标是上棵树的残差。和AdaBoost 一样,梯度提升树也是基于梯度下降函数。梯度提升树算法已被证明是Boosting算法集合中最成熟的算法之一,它的特点是估计方差增加,对数据中的噪声更敏感(这两个问题都可以通过使用子采样来减弱),以及由于非并行操作而导致计算成本显著,因此要比随机森林慢很多。
+梯度提升树是XGBoost、LightGBM和CatBoost的基础。
+import xgboost as xgb
+params = {'eta': 0.01, ' max depth': 11, 'objective': 'reg:linear', 'eval_ metric': 'rmse' }
+dtrain = xgb.DMatrix(data=X_train, label=y_train)
+dtest = xgb.DMatrix(data=X_valid, label=y_valid)
+watchlist = [(train.data, 'train'), (valid_data, 'valid_ data')]model=xgb. train(params, train_data,num_boost_round=20000,evals=watchlist,early_stopping_rounds=200,verbose_eval=500)y_pred = model. predict(xgb .DMatrix(X_test), ntree_limit=model.best_ntree_limit)LightGBM是微软的一个团队在Github上开发的一个开源项目,高性能的LightGBM算法具有分布式和可以快速处理大量数据的特点。LightGBM虽然基于决策树和XGBoost而生,但它还遵循其他不同的策略。
+XGBoost使用决策树对一个变量进行拆分,并在该变量上探索不同的切割点(按级别划分的树生长策略),而LightGBM则专注于按叶子节点进行拆分,以便获得更好的拟合(这是按叶划分的树生长策略)。这使得LightGBM能够快速获得很好的数据拟合,并生成能够替代XGBoost的解决方案。从算法上讲,XGBoost将决策树所进行的分割结构作为一个图来计算,使用广度优先搜索(BFS),而LightGBM使用的是深度优先搜索(DFS)。
+主要特点
+import lightgbm as lgb
+params = {'num_leaves': 54, 'objective': 'regression', 'max_depth': 18,'learning_rate': 0.01, 'boosting': 'gbdt', 'metric': 'rmse', 'lambda_11': 0.1}
+model = lgb.LGBMRegressor(**params, n_estimators = 20000, nthread = 4, n_jobs = -1)
+model.fit(x_train, y_train, eval_set=[(X_train, y_train), (X_valid, y_valid)], eval_metric='rmse', verbose=1000, early_stopping_rounds=200)
+y_pred= model.predict(X_test, num_iteration=model.best_iteration_)CatBoost是由俄罗斯搜索引擎Yandex在2017年7月开源的一个GBM算法,它最强大的点是能够采用将独热编码和平均编码混合的策略来处理类别特征。
+CatBoost用来对类别特征进行编码的方法并不是新方法,是均值编码,该方法已经成为一种特征工程方法,被广泛应用于各种数据科学竞赛中,如Kaggle。
+均值编码,也称为似然编码、影响编码或目标编码,可将标签转换为基于它们的数字,并与目标变量相关联。如果是回归问题,则基于级别典型的平均目标值转换标签;如果是分类问题,则仅给定标签的目标分类概率(目标概率取决于每个类别值)。均值编码可能看起来只是一个简单而聪明的特征工程技巧,但实际上它也有副作用,主要是过拟合,因为会把目标信息带入预测中。
+主要特点
+from catboost import CatBoostRegressor
+params = {'learning_rate': 0.02, 'depth': 13,'bootstrap_type': 'Bernoulli', 'od_type': 'Iter', 'od_wait': 50, 'random_seed': 11}
+model = CatBoostRegressor(iterations=20000, eval_metric='RMSE', **params)
+model.fit(X_train, y_train, eval_set=(X_valid, y_valid), cat_features=[], use_best_model=True, verbose=False)
+y_pred = model.predict(X_test)每类树模型都其与众不同的地方,接下来将从决策树的生长策略、梯度偏差、类别特征处理和参数对比四个方面深入理解这些树模型,帮助参赛者更好地将它们应用到竞赛中。
+XGBoost,LightGBM 和 CatBoost是三个非常核心的树模型,本节将对它们进行分析,因为三者之间有着千丝万缕的关系,只有厘清其中的关系,才能更好地运用这三个模型。
 ,然后使用第1条到第i-1条数据来建一个修正树M,累加到原来的模型
,然后使用第1条到第i-1条数据来建一个修正树M,累加到原来的模型 上。
上。随着拥有数据量的增加,神经网络战胜传统机器学习模型的可能性也会加大。
+#接第5章实战案例代码,构造训练集和测试集
+x_train = data[:ntrain][all_cols]
+x_test = data[ntrain:][all_cols]
+#对售价进行log处理
+y_train = np.log1p(data[data.SalePrice.notnull()]['SalePrice'].values)XGBoost:使用比较常规的五折交叉验证
+import xgboost as xgb
+from sklearn.model_selection import KFold
+kf = KFold(n_splits=5,shuffle=True,random_state=2020)
+for i,(train_index,valid_index)in enumerate(kf.split(x_train,y_train)):
+ trn_x,trn_y,val_x,val_y = x_train.iloc[train_index],y_train[train_index],x_train.iloc[valid_index],y_train[valid_index]
+ params ={'eta':0.01,'max_depth':11,'objective':'reg:linear','eval_metric':'mae'}
+ dtrain = xgb.DMatrix(data=trn_x,label=trn_y)
+ dtest = xgb.DMatrix(data=val_x,label=val_y)
+ watchlist =[(dtrain,'train'),(dtest,'valid_data')]
+ model=xgb.train(params,dtrain,num_boost_round=20000,evals=watchlist,early_stopping_rounds=200,verbose_eval=500)多层感知机:要确保数据中没有缺失值,并且要对数据进行归一化处理。
+from sklearn. model_selection import train_test_split
+from sklearn.preprocessing import StandardScaler
+x_train = x_train. fillna(0)
+x_train = StandardScaler(). fit_transform(x_train)
+trn_x, val_x, trny, val_y = train_test_split(x_train, y_train, random_state=2020)
+def create_mlp(shape):
+ x_input = Input((shape, ))
+ X = Dropout(0.2)(BatchNormalization()(
+ Dense(256, activation=' relu')(X_input)))
+ X = Dropout(0.2)(BatchNormalization()(Dense(128, activation=' relu')(X)))
+ X = Dropout(0.2)(BatchNormalization()(Dense(64, activation=' relu')(X)))
+ X = Dense(1)(X)
+ model = Model(inputs=X_input, outputs=X)
+ model. compile(optimizer=' adam', loss=' mse', metrics=[' mae'])
+ return modelmlp_model = create_mlp(trn_x. shape[1])
+mlp_model.fit(x=trn_x, y=trn_y, validation_data=(val_x, val_y), epochs=30, batch_size=16)本章将向大家介绍在算法竞赛中提分的关键步骤,这也是最后阶段的惯用方法,即模型融合(或者集成学习),通过结合不同子模型的长处进行模型融合,当然这是在理想状态下。
+本章主要分为构建多样性、训练过程融合和训练结果融合三部分。
+模型融合常常是竞赛取得胜利的关键,相比之下具有差异性的模型融合往往能给结果带来很大提升。了解的模型融合方法越多,最后取胜的概率就会越高。
+本章从这三个部分介绍不同模型融合方法的应用场景,同时给出使用技巧和应用代码。
+介绍三种模型融合中构建多样性的方式,分别是特征多样性、样本多样性和模型多样性。其中多样性是指子模型之间存在着差异,可以通过降低子模型融合的同质性来构建多样性,好的多样性有助于模型融合效果的提升。
+构建多个有差异的特征集并分别建立模型,可使特征存在于不同的超空间(hyperspace),从而建立的多个模型有不同的泛化误差,最终模型融合时可以起到互补的效果。在竞赛中,队友之间的特征集往往是不一样的,在分数差异不大的情况下,直接进行模型融合基本会获得不错的收益。
+另外,像随机森林中的max_features,XGBoost中的colsample_bytree 和LightGBM中的feature_fraction都是用来对训练集中的特征进行采样的,其实本质上就是构建特征的多样性。
+样本多样性也是竞赛中常见的一种模型融合方式,这里的多样性主要来自不同的样本集。
+具体做法是将数据集切分成多份,然后分别建立模型。我们知道很多树模型在训练的时候会进行采样(sampling),主要目的是防止过拟合,从而提升预测的准确性。
+有时候将数据集切分成多份并不是随机进行的,而是根据具体的赛题数据进行切分,需要考虑如何切分可以构建最大限度的数据差异性,并用切分后的数据分别训练模型。
+例如,在天池“全球城市计算AI挑战赛”中,竞赛训练集包含从2019年1月1日到1月25日共25天的地铁刷卡数据记录,要求预测1月26日每个地铁站点每十分钟的平均出入客流量(2019年1月26日是周六)。显然,工作日和周末的客流量分布具有很大差异,这时会面临一个问题,若只保留周末的数据进行训练,则会浪费掉很多数据;若一周的数据全部保留,则会对工作日的数据产生一定影响。这时候就可以尝试构建两组有差异性的样本分别训练模型,即整体数据保留为一组,周末数据为一组。当然,模型融合后的分数会有很大提升。
+不同模型对数据的表达能力是不同的,比如FM能够学习到特征之间的交叉信息,并且记忆性较强;树模型可以很好地处理连续特征和离散特征(如LightGBM 和CatBoost),并且对异常值也具有很好的健壮性。把这两类在数据假设、表征能力方面有差异的模型融合起来肯定会达到一定的效果。
+对于竞赛而言,传统的树模型(XGBoost,LightGBM、CatBoost)和神经网络都需要尝试一遍,然后将尝试过的模型作为具有差异性的模型融合在一起。
+还有很多其他构建多样性的方法,比如训练目标多样性、参数多样性和损失函数选择的多样性等,这些都能产生非常好的效果。
+模型融合的方式有两种,第一种是训练过程融合,比如我们了解到的随机森林和XGBoost,基于这两种模型在训练中构造多个决策树进行融合,这里的多个决策树可以看作多个弱学习器。其中随机森林通过Bagging的方式进行融合,XGBoost通过Boosting的方式进行融合。
+Bagging的思想很简单,即从训练集中有放回地取出数据(Bootstrapping),这些数据构成样本集,这也保证了训练集的规模不变,然后用样本集训练弱分类器。重复上述过程多次,取平均值或者采用投票机制得到模型融合的最终结果。
+当在不同的样本集上训练模型时,Bagging通过减小误差之间的差来减少分类器的方差,因此Bagging可以降低过拟合的风险。Bagging算法的效率在于训练数据的不同,各模型之间存在着很大的差异,并且在加权融合的过程中可以使训练数据的错误相互抵消。
+Boosting的思想其实并不难理解,首先训练一个弱分类器,并把这个弱分类器分错类的样本记录下来,同时给予这个弱分类器一定的权重;然后建立一个新的弱分类器,新的弱分类器基于前面记录的错误样本进行训练,同样,我们也给予这个分类器一个权重。重复上面的过程,直到弱分类器的性能达到某一指标,例如当再建立的新弱分类器并不会使准确率显著提升时,就停止选代。最后,把这些弱分类器各自乘上相应的权重并全部加起来,就得到了最后的强分类器。其实,基于Boosting的算法是比较多的,有Adaboost、LightGBM、XGBoost和CatBoost等。
+模型融合的第二种方式是训练结果融合,主要分为加权法、Stacking和Blending,这些方法都可以有效地提高模型的整体预测能力,在竞赛中也是参赛者必须要掌握的方法。
+加权法对于一系列任务(比如分类和回归)和评价指标(如AUC,MSE 或 Logloss)都是很有效的,比如我们有10个算法模型并都预测到了结果,直接对这10个结果取平均值或者给予每个算法不同的权重,即得到了融合结果。加权法通常还能减少过拟合,因为每个模型的结果可能存在一定的噪声,加权法能够平滑噪声,提高模型的泛化性。
+分类问题:对于分类问题,需要注意不同分类器的输出结果范围一致,因为输出的预测结果可以是0/1值,也可以是介于0和1之间的概率。另外,投票法(Voting)也是一种特殊的加权法。
+回归问题:对于回归问题,使用加权法会非常简单。这里主要介绍算术平均和几何平均。
+算术平均:基于算术平均数的集成方法在算法中是用得最多的,因为它不仅简单,而且基本每次使用该算法都有较大概率能获得很好的效果。
+几何平均:根据很多参赛选手的分享,基于几何平均数的加权法在算法中使用得还不是很多,但在实际情况中,有时候基于几何平均数的模型融合效果要稍好于基于算术平均数的效果。
+一般推荐问题中的主要任务是对推荐结果进行排序,常见的评价指标有mAP(mean Average Precision),NDCG(Normalized Discounted Cumulative Gain),MRR(Mean Reciprocal Rank)和AUC,这里主要介绍MRR和AUC。
+MRR:给定推荐结果q,如果q在推荐序列中的位置是r,那么MRR(q)就是1/r。可以看出,如果向用户推荐的产品在推荐序列中命中,那么命中的位置越靠前,得分也就越高。显然,排序结果在前在后的重要性是不一样的,因此我们不仅要进行加权融合,还需要让结果偏向小值。这时候就要对结果进行转换,然后再用加权法进行融合,一般而言使用的转换方式是log变换。
+其基本思路如下:首先,输人三个预测结果文件,每个预测结果文件都包含M条记录,每条记录各对应N个预测结果,最终输出三个预测结果文件的整合结果。统计三个预测结果文件中记录的所有推荐商品(共N个商品)出现的位置,例如商品A,在第一份文件中的推荐位置是1,在第二个文件的推荐位置是3,在第三个文件中未出现,此时我们计算商品A的得分为log1+log3+log(N+1),此处我们用N+1来表示未出现,即在N个推荐商品中是找不到商品A的,所以只能是N+1。对每条记录中的商品按计算得分由小到大排序,取前N个作为这条记录的最终推荐结果。
AUC:作为排序指标,一般使用排序均值的融合思路,使用相对顺序来代替原先的概率值。很多以AUC为指标的比赛均取得了非常不错的成绩。使用过程如下:对每个分类器中分类的概率进行排序,然后用每个样本排序之后得到的排名值(rank)作为新的结果。对每个分类器的排名值求算术平均值作为最终结果。
+使用加权法进行融合虽然简单,但需要人工来确定权重,因此可以考虑更加智能的方式,通过新的模型来学习每个分类器的权重。这里我们假设有两层分类器,如果在第一层中某个特定的基分类器错误地学习了特征空间的某个区域,则这种错误的学习行为可能会被第二层分类器检测到,这与其他分类器的学习行为一样,可以纠正不恰当的训练。上述过程便是Stacking融合的基本思想。
+这里需要注意两点:第一,构建的新模型一般是简单模型,比如逻辑回归这样的线性模型;第二,使用多个模型进行Stacking融合会有比较好的结果。
+Stacking融合使用基模型的预测结果作为第二层模型的输入。然而,我们不能简单地使用完整的训练集数据来训练基模型,这会产生基分类器在预测时就已经“看到”测试集的风险,因此在提供预测结果时出现过度拟合问题。所以我们应该使用Out-of-Fold的方式进行预测,也就是通过K折交叉验证的方式来预测结果。这里我们将Stacking融合分为训练阶段和测试阶段两部分,将并以流程图的形式展示每部分的具体操作。如图6.2所示为训练阶段。
+特征加权的线性堆叠,可参考相应论文“Feature-Weighted Linear Stacking two layer stacking",其实就是对传统的Stacking融合方法在深度上进行扩展。通过传统的Stacking融合方法得到概率值,再将此值与基础特征集进行拼接,重新组成新的特征集,进行新一轮训练。
+不同于Stacking融合使用K折交叉验证方式得到预测结果,Blending融合是建立一个Holdout集,将不相交的数据集用于不同层的训练,这样可以在很大程度上降低过拟合的风险。
+假设构造两层Blending,训练集等分为两部分(train_one和train_two),测试集为test。第一层用train_one训练多个模型,将train_two和test的预测结果合并到原始特征集合中,作为第二层的特征集。第二层用train_two的特征集和标签训练新的模型,然后对test预测得到最终的融合结果。
+以stacking为例。选择ExtraTreesRegressor、RandomForestRegressor、Ridge、Lasso作为基学习器,Ridge为最终分类器。
+依然采用5折交叉验证
+kf = KFold(n_splits=5, shuffle=True, random_state=2020)然后构建一个sklearn中模型的功能类,初始化参数然后训练和预测。这段代码可复用性很高,建议完善、储存。
+class SklearnWrapper(object):
+ def __init__(self, clf, seed=0, params=None):
+ params['random_state'] = seed
+ self.clf = clf(**params)
+
+ def train(self, x_train, y_train):
+ self.clf.fit(x_train, y_train)
+
+ def predict(self, x):
+ return self.clf.predict(x)封装交叉验证函数。可复用性也很高。
+def get_oof(clf):
+ oof_train = np.zeros((x_train.shape[0],))
+ oof_test = np.zeros((x_test.shape[0],))
+ oof_test_skf = np.empty((5, x_test.shape[0]))
+
+ for i, (train_index, valid_index) in enumerate(kf.split(x_train, y_train)):
+ trn_x, trn_y, val_x, val_y = x_train.iloc[train_index], y_train[train_index],\
+ x_train.iloc[valid_index], y_train[valid_index]
+ clf.train(trn_x, trn_y)
+
+ oof_train[valid_index] = clf.predict(val_x)
+ oof_test_skf[i, :] = clf.predict(x_test)
+
+ oof_test[:] = oof_test_skf.mean(axis=0)
+ return oof_train.reshape(-1, 1), oof_test.reshape(-1, 1)预测四个模型的验证集结果和测试集结果。并辅助最后一步的stacking融合操作:
+et_params = {
+ 'n_estimators': 100,
+ 'max_features': 0.5,
+ 'max_depth': 12,
+ 'min_samples_leaf': 2,
+}
+rf_params = {
+ 'n_estimators': 100,
+ 'max_features': 0.2,
+ 'max_depth': 12,
+ 'min_samples_leaf': 2,
+}
+rd_params={'alpha': 10}
+ls_params={ 'alpha': 0.005}
+et = SklearnWrapper(clf=ExtraTreesRegressor, seed=2020, params=et_params)
+rf = SklearnWrapper(clf=RandomForestRegressor, seed=2020, params=rf_params)
+rd = SklearnWrapper(clf=Ridge, seed=2020, params=rd_params)
+ls = SklearnWrapper(clf=Lasso, seed=2020, params=ls_params)
+
+et_oof_train, et_oof_test = get_oof(et)
+rf_oof_train, rf_oof_test = get_oof(rf)
+rd_oof_train, rd_oof_test = get_oof(rd)
+ls_oof_train, ls_oof_test = get_oof(ls)最后就是stacking部分,使用ridge模型。
+def stack_model(oof_1, oof_2, oof_3, oof_4, predictions_1, predictions_2, predictions_3, predictions_4, y):
+ train_stack = np.hstack([oof_1, oof_2, oof_3, oof_4])
+ test_stack = np.hstack([predictions_1, predictions_2, predictions_3, predictions_4])
+
+ oof = np.zeros((train_stack.shape[0],))
+ predictions = np.zeros((test_stack.shape[0],))
+ scores = []
+
+ for fold_, (trn_idx, val_idx) in enumerate(kf.split(train_stack, y)):
+ trn_data, trn_y = train_stack[trn_idx], y[trn_idx]
+ val_data, val_y = train_stack[val_idx], y[val_idx]
+
+ clf = Ridge(random_state=2020)
+ clf.fit(trn_data, trn_y)
+
+ oof[val_idx] = clf.predict(val_data)
+ predictions += clf.predict(test_stack) / 5
+
+ score_single = sqrt(mean_squared_error(val_y, oof[val_idx]))
+ scores.append(score_single)
+ print(f'{fold_+1}/{5}', score_single)
+ print('mean: ',np.mean(scores))
+
+ return oof, predictions
+
+oof_stack , predictions_stack = stack_model(et_oof_train, rf_oof_train, rd_oof_train, ls_oof_train, et_oof_test, rf_oof_test, rd_oof_test,ls_oof_test, y_train)实际运行后发现,基分类器的分类效果差别很大,且最终融合后的模型效果确实要比基分类器的模型效果好很多。
+ + + +机器学习算法竞赛实战-用户画像
+ +用户:产品的使用者
+数据收集方为了推广产品同时持续维护和改善用户体验需要对由用户操作而产生的数据进行挖掘,以期从中发现群体乃至个体的行为偏好,形成数据层面上的所谓画像。
+用于商业分析和数据挖掘的用户画像。基于给定的数据对用户属性及行为进行描述,然后提取用户的个性化指标,再以此分析可能存在的群体共性,并落地应用到各种业务场景中。
+核心就是给用户打标签,用来分析社会属性、社会习惯、生活习惯、消费行为。
+通过分析一个用户的特征来展示标签分类方式:
+ +标签获取方式也可以看作特征获取方式
+事实类:直接来自原始数据,比如性别、年龄、会员等级。也可以进行简单统计,比如用户行为次数、消费总额。
+规则类:由运营人员和数据人员经过共同协商设定。例如,地域属性、家庭类型、年龄层等。所用技术知识:数理统计类,如基础统计、数值分层、概率分布、均值分析、方差分析等。
+模型类:经过机器学习和深度学习等模型处理后,二次加工生成的洞察性标签。比如预测用户状态、预测用户信用分、划分兴趣人群和对评论文本进行分类。特点:综合程度高、复杂,依托数学建模,多种算法组合。
+LSA:非概率主题模型,与词向量有关,主要用于文档的话题分析。其核心思想是通过矩阵分解的方式发现文档和词之间基于话题的语义关系。
+具体:将文档集表示为词-文档矩阵,对矩阵进行SVD(奇异值分解),从而得到话题向量以及文档在话题向量的表示。
+举例:2020腾讯广告大赛,首先构造用户点击的广告素材id序列(creative_id),然后进行TF-IDF计算,最后经过SVD得到结果。
+(代码与书中不同,未验证)
+from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
+# 稀疏特征降维 TruncatedSVD
+from sklearn.decomposition import TruncatedSVD
+from sklearn.pipeline import Pipeline
+# 提取用户点击序列
+docs = data_df.groupby(['user_id'])['creative_id'].agg(lambda x:"".join(x)).reset_index()['creative_id']
+# tf-idf
+tfd = TfidfVectorizer()
+svd = TruncatedSVD(n_components=100, n_iter=50, random_state=2020)PLSA:PLSA(概率潜在语义分析)模型是为了克服LSA模型潜在存在的一些缺点而提出的。通过一个生成模型来为LSA赋予概率意义上的解释。该模型假设每一篇文档都包含一系列可能的潜在话题,文档中的每一个词都不是凭空产生的,而是在潜在话题的指引下通过一定的概率生成的。
+LDA:LDA(潜在狄利克雷分布)是一种概率主题模型,与词向量无关,可以将文档集中的每篇文档的主题以概率分布的形式给出。通过分析一批文档集,抽取出他们的主题分布,就可以根据主题进行聚类或分类。同时,它是一种典型的词袋模型,即一篇文档由一组相互独立的词构成,词和词之间没有先后顺序。
+word2Vec:可调用gensim包,参数:窗口大小、模型类型选择、生成词向量长度
+对于Skip-Gram和CBOW:
+DeepWalk
+对于Word2Vec的衍生Item2Vec以及更多图嵌入方法,比如LINE、Node2Vec和SDNE
+特点:
+参考资料:《机器学习算法竞赛实战》整理 | 八、实战案例:Elo Merchant Category Recommendation
+Imagine being hungry in an unfamiliar part of town and getting restaurant recommendations served up, based on your personal preferences, at just the right moment. The recommendation comes with an attached discount from your credit card provider for a local place around the corner!
+Right now, Elo, one of the largest payment brands in Brazil, has built partnerships with merchants in order to offer promotions or discounts to cardholders. But do these promotions work for either the consumer or the merchant? Do customers enjoy their experience? Do merchants see repeat business? Personalization is key.
+Elo has built machine learning models to understand the most important aspects and preferences in their customers’ lifecycle, from food to shopping. But so far none of them is specifically tailored for an individual or profile. This is where you come in.
+In this competition, Kagglers will develop algorithms to identify and serve the most relevant opportunities to individuals, by uncovering signal in customer loyalty. Your input will improve customers’ lives and help Elo reduce unwanted campaigns, to create the right experience for customers.
+train.csv 训练数据集,包括 first_active_month,card_id,feature_1,feature_2,feature_3,target字段test.csv 测试数据集,包括 first_active_month,card_id,feature_1,feature_2,feature_3字段first_active_month表示的是信用卡产生第一笔交易的时间,feature是信用卡类型的脱敏特征。最后一列 target是要预测的数值
historical_transactions.csv 信用卡在给定商家的历史交易记录,文件比较大,基本都是一些脱敏的特征
merchants.csv所有商家的附加信息
new_merchant_transactions.csv two months’ worth of data for each card_id containing ALL purchases that card_id made at merchant_ids that were not visited in the historical data .(每张信用卡在新商家的购物数据)
评价指标使用RMSE
《现代信息检索》课程笔记:第8讲 检索评价
+ +评价什么?
+使用相同的文档集合,相同的查询主题集合,相同的评价指标,对不同的检索系统进行比较。
+评价指标:某个或某几个可衡量、可比较的值
+评价过程:设计上保证公平、合理
+IR中评价的难点:相关性(Relevance)是一个主观概念,文档相关性依赖于查询(数据标记工作量庞大)
+召回率(Recall):返回的相关结果数占实际相关结果总数的比率
+正确率(Precision):返回的结果中真正相关结果的比率
+虽然Precision和Recall都很重要,但是不同的应用、不用的用户可能会对两者的要求不一样。
+问题①:召回率难以计算:
+对于大规模语料集合,列举每个查询的所有相关文档是不可能的事情,因此,这种情况几乎不可能准确地计算召回率可以采用Pooling方法,或者不考虑召回
+缓冲池(Pooling)方法:对多个检索系统的Top k个结果组成的集合(并集)进行人工标注,标注出的相关文档集合作为整个相关文档集合。这种做法被验证是可行的(可以比较不同系统的相对效果),在TREC会议中被广泛采用。
+问题②:两个指标需要融成一个指标,或者只采用单一指标
+F值(F-measure):召回率R和正确率P的调和平均值
+Fβ:表示召回率的重要程度是正确率的β(>=0)倍,β>1更重视召回率, β<1更重视正确率
+E(Effectiveness)值:召回率R和正确率P的加权平均值,b>1表示更重视P
+精确率是所有判定中正确的比率,一般不使用这一评价指标
+问题③:两个指标都是基于(无序)集合进行计算,并没有考虑(排)序的作用
+R-Precision:检索结果中,在所有相关文档总数位置上的准确率,如某个查询的相关文档总数为80,则计算检索结果中在前80篇文档的正确率。
+正确率-召回率 曲线:检索结果以排序方式排列,用户不可能马上看到全部文档,因此,在用户观察的过程中,正确率和召回率在不断变化。
+在上面的曲线对应的系统结果更好,也就是线下的面积(AUC)
+P-R 曲线的插值问题:利用存在的召回率点对不存在的召回率点进行插值
+优点:
+缺点:单个查询的P-R曲线虽然直观,但是难以明确表示两个查询的检索结果的优劣
+基于P-R曲线的单一指标:P-R曲线上P=R的那个点(Break Point)
+平均正确率(Average Precision, AP):对不同召回率点上的正确率进行平均
+不考虑召回率的指标:
+Precision@N:在第N个位置上的正确率,对于搜索引擎,大量统计数据表明,大部分搜索引擎用户只关注前一、两页的结果,
+平均的求法:
+MAP(Mean AP):对所有查询的AP求宏平均
+整个IR系统的P-R曲线:
+在每个召回率点上,对所有的查询在此点上的正确率进行算术平均,得到系统在该点上的正确率的平均值。
+两个检索系统可以通过P-R曲线进行比较。位置在上面的曲线代表的系统性能占优。
+MRR(Mean Reciprocal Rank): 对于某些IR系统(如问答系统或主页发现系统),只关心第一个标准答案返回的位置(Rank),越前越好,这个位置的倒数称为RR,对问题集合求平均,则得到MRR
+Bpref:在相关性判断不完全的情况下,计算在进行了相关性判断的文档集合中,在判断到相关文档前,需要判断的不相关文档的篇数。
+相关性判断完全的情况下,利用Bpref和MAP进行评价的结果很一致,但是相关性判断不完全的情况下,Bpref更鲁棒
+GMAP:几何平均值
+NDCG:对于返回结果,相关度级别越高的结果越多越好,相关度级别越高的结果越靠前越好。
+优点:
+缺点:
+现有评价体系远没有达到完美程度
+TREC
+总目标:支持在信息检索领域的基础研究,提供对大规模文本检索方法的评估办法
+《高级人工智能》课程笔记:第4讲 图像数据的深度学习模型
+ +计算机视觉需要应用大量的图像数据
+卷积神经网络是一种特殊的深层神经网络模型
+20世纪60年代,Hubel和Wiesel研究猫脑皮层
+局部连接
+局部感知野:图像的空间联系也是局部的像素联系较为紧密,而距离较远的像素相关性则较弱,减少了需要训练的权值数目
+参数共享:图像的一部分的统计特性与其他部分是一样的。在输入的不同位置检测同一种特征具有平移不变性
+一维、二维、三维卷积
+其中三维卷积:假设输入数据的大小为a1×a2×a3,过滤器大小为f,即过滤器维度为f×f×f。三维卷积最终的输出为(a1−f+1)×(a2−f+1)×(a3−f+1)。
+多卷积核:
+边缘检测示例:卷积运算是输入图像与过滤器(也叫核)进行的运算,得到输出图像。卷积核与图像对应的位置相乘求和得到一个新值。
+假定要识别图像中的特定曲线,也就是说,对这种曲线有很高的输出,对其他形状则输出很低,这也就像是神经元的激活。
+Padding:边缘不填充
+卷积步长:卷积中的步幅是另一个构建卷积神经网络的基本操作
+输入与输出的尺寸关系:
单层卷积网络:每一个卷积核的输出对应一个实数b(偏差),然后在进行激活函数的非线性转换得到输出
+Pooling池化:
+通过卷积获得了特征之后,下一步利用这些特征去做分类。
+池化层中没有需要学习的参数,所以通常不把池化层当做独立的一层来看。
+池化层是一般不会设置padding,即一般padding为0。
+fitter为2,stride为2是最常见的参数设置,尺寸图像缩小为原来的一半。
+卷积时用的尺寸计算公式同样适用于池化层。
+CNN基本结构:卷积层和子采样层
+卷积神经网络是一个多层的神经网络
+CNN训练过程
+监督训练:Bp算法
+向前传播
+ ,将
,将 输入网络
输入网络
反向传播
+ 与相应的理想输出
与相应的理想输出 的差
的差卷积网络的核心思想:将局部感受野、权值共享以及时间或空间亚采样这三种结构思想结合起来获得了某种程度的位移、尺度、形变不变性。
+层间联系和空域信息的紧密关系,使其适于图像处理和理解:图像和网络的拓扑结构能很好的吻合
+避免了显式的特征抽取,而隐式地从训练数据中进行学习:特征提取和模式分类同时进行,并同时在训练中产生;权重共享可以减少网络的训练参数,使神经网络结构变得更简单,适应性更强。
+CNN的改进:
+Rectified linear function:加速收敛和稀疏化
+dropout:将隐层节点以一定概率清0
+局部对比归一
+非线性变换、池化
+残差网络(Residual Networks(ResNets))
+《机器学习》课程笔记:第5章 回归分析
+ +回归问题:
+根据给定的训练集


要求寻找
性能评价:
+均方误差:
泛化误差可分解为偏差、方差和噪声之和
+线性回归原理:使用线性函数来预测数据的分布
+目标函数:最小误差平方和
+求解:
正态分布假设的似然函数
+误差服从正态分布:
似然函数:
高斯误差的最大似然估计
优化学习:梯度下降方法
+正态分布的先验似然函数:
最大后验估计目标函数:
高斯分布的最大后验估计 = 正则化最小二乘估计
+正则化最小二乘估计解:
正则项解决过拟合问题
+线性基函数回归
+线性回归:
扩展的非线性回归:
基函数形式:多项式函数、高斯分布函数、sigmoid类型的函数、tanh类型的函数
+多项式回归:
正则项对Bias和Variance的影响
+参数估计
+最小二乘估计是无偏估计
+正则化最小二乘估计是有偏估计
+使得参数估计更加稳定
+相当于增加正则项
+相当于加入白噪声
+ + +《现代信息检索》课程笔记:第9讲 完整搜索系统中的评分计算
+ +不排序的问题严重性
+排序的重要性:
+倒排索引中的词项频率存储
+两种常见的评分累加算法:
+以词项为单位(term-at-a-time, TAAT),首先获得词项t的posting list,然后累加得分
+以文档为单位的计算,首先获得包含查询词的所有文档,将这些文档按照静态评分排序,然后依次累加得分
+精确top K检索及其加速办法:
+目标:从文档集的所有文档中找出K个离查询最近的文档
+步骤:对每个文档评分(余弦相似度),按照评分高低排序,选出前K个结果
+加速方法:
+快速计算余弦:不考虑查询词项的权重
+堆法N中选K:不对所有文档进行排序,只需要挑出最高的K个结果
+提前终止计算:得到了top K结果,不需要再进行后续计算
+精确topK检索的问题:仍然无法避免大量文档参与计算
+非精确topK检索:非精确topK的结果如果和精确topK的结果相似度相差不大,应该也能让用户满意
+找一个文档集合A,K<|A|<<N,利用A中的top K结果代替整个文档集的top K结果
+方法一:索引去除
+从查询词的角度:只考虑那些包含高idf查询词项的文档
+从文档的角度:只考虑那些包含多个查询词项的文档
+仅考虑高idf词项、仅考虑包含多个词项的文档
+方法二:胜者表
+对每个词项t,预先计算出其倒排记录表中权重最高的r篇文档,如果采用tfidf机制,即tf最高的r篇
+方法三:静态质量得分排序方式
+为每篇文档赋予一个与查询无关的[0,1]之间的值,记为g(d),例如Pagerank
+最终文档排名基于g(d)和相关度的线性组合
+目标是找net-score最高的top K文档
+方法四:影响度(Impact)排序
+提前结束法:
+遍历倒排记录表时,可以在如下情况之一发生时停止:
+将词项按照idf排序:
+方法五: 簇剪枝
+随机选 
非docID的倒排记录表排序方法
+与查询无关的一种反映结果好坏程度的指标
+以文档为单位(Document-at-a-time)的处理、以词项为单位(Term-at-a-time)的处理方式
+WAND(Weak AND) 评分算法
+多层次索引基本思路:
+机器学习算法竞赛实战-时间序列
+ +时间序列是按时间顺序索引(或列出或图示)的一系列数据点。组成时间序列的数据由相对确定的时间戳组成。
+对时间序列的分析基于以下假设:数据文件中标签的数据值表示以等间隔时间进行的连续测量值。假设数据存在相关性,然后通过建模找到对应的相关性,并利用它预测未来的数据走向。
+可以从变量角度将这些问题归纳为单变量时间序列和多变量时间序列
+可以从预测目标角度将这些问题归纳为单步预测和多步预测
+单变量时间序列仅具有单个时间相关变量,所以仅受时间因素的影响。这类问题重点在于分析数据的变化特点,受相关性、趋势性、周期性和循环性等因素的影响。
+多变量时间序列具有多个时间相关变量,除了受时间因素的影响,还受其他变量的影响。需要考虑更多的因素,挑战也更大。
+单步预测问题比较基础,仅在训练集的时间基础上添加一个时间单位便可以作为测试集
+多步预测问题比较复杂,是在训练集的时间基础上添加多个时间单位作为测试集
+交叉验证的时候为了保留时间相关性,需要采用滚动交叉验证的方式:
+加权平均:离当前时间点越近的数据的重要性越高
+指数平滑:将每个时间单位的权重按照指数级进行衰减(指数平滑像是拥有无限记忆且权值呈指数级递减的移动平均法)
+趋势性:在很长一段时间内呈现的数据持续上升或持续下降的变动
+周期性:在一段时间序列内重复出现的波动,是各种因素综合影响的结果。
+相关性:在某一段序列往往存在正相关或负相关,前后时间点会有很大的关联
+随机性:除了上述三种模式外的随机扰动
+历史平移:直接将历史记录作为特征
+窗口统计:从多个序列单位中提取特征
+序列熵特征:描述序列的确定性和不确定性
+还有时间特征与统计特征
+传统的时序模型:ARIMA(差分自回归滑动平均模型)
+树模型:对时间序列进行平稳性调整
+深度学习模型
+《机器学习》课程笔记:第6章 聚类分析
+ +聚类是无监督机器学习问题
+影响聚类结果的因素:
+样本-样本:(向量相似性)
+样本-集合:
+到集合最远点距离:
到集合最近点距离:
到集合平均点距离:
集合为平面:
集合为圆:
集合-集合:(类间距离)
+集合间最远点距离:
集合间最近点距离:
集合间所有点平均距离:
集合表征点间距离(如平均值):
集合内样本间距离(类内距离):
聚类性能的外部指标指通过已知类簇划分,对聚类结果进行评价;判别同类别样本对标签一致与否,避免相同类簇划分,不同标签名称导致的不一致。
+Jaccard系数、FM系数和Rand系数
+聚类性能的内部指标:没有已知的类簇划分进行参考,通过聚类具有的类内相似和类间相异的特点进行评价。
+DB指数:
Dunn指数:
基本思想:逐一比较单个样本与类簇的相似性,有相似类则归类,无相似类则建立新类。
+优点:一种简单的,快速算法
+相似性的关键度量:类别相似性:样本—类簇(样本—集合)。
+缺点:所有样本过滤一遍后才知道类别总数,而先出现的样本不能找到(后出现的)合适类别
+改进算法:采用两个阶段,类别确定、分类。
+两阶段序贯方法:
+缺点:以上两种方法依赖于阈值
+改进方法:弱化阈值作用,采用两个阈值,形成灰色带。
+双阈值序贯方法
+三种算法缺点:
+增强算法
+增强处理1:对类别集合进行合并操作
+增强处理2:对样本类别重置
+基本思想:
+聚类嵌套定义:






层次聚类策略:类簇之间(依据相似性)不断合并、或不断的分化, 直到满足聚类停止条件。
+自底向上/归并算法:
+第
缺点:没有归并的类簇间相似性,被重复计算
+基于矩阵的归并算法
+利用矩阵记录类簇间的相似性
+优点:不必重新计算“没有合并的类簇间”的相似性
+分化算法:过程与归并相反
+第
缺点:没有划分的类簇间相似性,被重复计算
+如何确定聚类个数?
+Kmeans:将样本分给最近的类心,然后重新调整类心;通过多次迭代,逐步进行类别划分。
+最优准则:最小化误差平方和



一般方法:最近类心原则,批量划分后修正类心
+改进方法:单个划分最优原则,单个划分后修正类心
+ + +公开于2023年11月19日
+ +四年相识、三年相恋、抵不过些许距离。
+并没有表现得太过于悲伤,甚至都没有留下眼泪。可能是因为从日常的点点滴滴中已经知道这个结果了,最后的两三个月完全就是在硬撑着,我一厢情愿地在努力,但是她的心里早就已经有了答案。
+相识的第一天,2018年9月24日,中秋节。两个人走进教室,拿出简历,面试。面试后一起下楼,简单的说了第一句打招呼的话语,分开。那是第一次见面,内心里有一种悸动,真的似乎有点喜欢。此时的我,刚刚经历了高考的失利,急于在这个看起来与我的能力并不匹配的学校中证明我自己。去竞选班干部,去参加各种学生组织,去认识更多的人,同时也不再压抑内心的感情,积极去找寻自己的爱情。当初对爱情只是懵懂,被拒绝了一次,拒绝了别人一次,有点怕了。有时候我也毫不掩饰我对她的喜欢,去车站接,送奶茶,约出来走走等等。就这样默默暗恋了一年。
+第二年的中秋节,2019年9月13日,我终于鼓起勇气,约出来转到了湖大再转回来,说出了压在心底一年的话。这样就收获了我的初恋。当时的我,并不优秀,对未来一片迷茫,不知道四年大学毕业后要去到哪里。“我们在一无所有的情况下选择去尝试”,我同时也坚定了要共度一生的想法,想要给她今后一个更好的生活,于是我努力学习,从一个将将摸到保研边的中等生,逐渐变成了一个强者,拿下了很好的成绩排名,拿到了学校里面的绝大部分奖项,拿到了国家奖学金,成功保研。因为有了动力,一切都变得理所应当,再苦再累真的值得。
+我们之间的感情没有那么多的激情燃烧,更多的是平淡。我尽量在她需要我的时候出现在她的身边,平时四周转一转,一起去图书馆学习,感冒了送她去医院,脚伤了每天接送,中午晚上点好饭送到身边。我很享受这种平淡的生活,因为我已经认准了她,什么东西都不能减少我对她的爱。我也认为她是和我一样性格的人,有自己的个性,有上进心进取心,不安于现状希望改变。就这样过了两年的美好时光,我们走入了大四的毕业季。
+大四开始的我,松弛了下来,暂时与紧张的学习生活说了再见,开始无底线的放松。而她却要每天准备考研,还有两节课要上。而且由于搬校区的缘故,我见到她并不是很容易了。在这期间有了一些她不怎么讲话的迹象,甚至在我离开长沙和她吃的最后一顿饭上也是心不在焉。我把它归结为考研焦虑,并没有太过在意。也还是因为我对这段感情太有信心了吧,我相信时间距离都不是问题,我们只要努力把自己变得更好,总有一天会克服种种困难生活在一起衣食无忧。这也导致了大四下学期去实习的时候有点忽略了对她的关心,感觉是因为都忙,说的话也变少了。这种下了分手的种子。
+6月正式本科毕业,2022年6月21日,突然的完全不理我,突然的提出分手,我直接崩溃掉。原来她并没有任何的信心,只是我自己自作多情罢了。原来这半年我基本不知道任何有关她的生活,我不知道她实习的工作怎么样,不知道她去面试了教师岗位,不知道她成功考上教师编制。我终于发现了这个问题,但是事实上已经晚了。虽然这一次分手我用回忆挽回,但是并没有打消她的念头,也并没有增加很多她对我的爱。而且由于距离,也阻隔了表达爱的方式。就好像“inception”一样,动了念头就很难再忘记掉了。
+然后是短短四天的青岛旅行,差不多一年以来的首次见面。尤其是最后一天的晚上,最后一次吃饭基本上全程都在看手机。虽然是在修朋友圈的照片,但是我当然也是有一点点不高兴的。从上次几乎分手后我就十分在乎她的感受,但是我从来都没有勇气当面问出这些话语。这样过了两个月,我不断询问她的感受,不断讲给她我现在的想法。然而一切都是没有作用的。不爱了真的就不爱了。2022年9月24日,正式分手。我拼了命的想要挽回,我真的放不下,也不可能放得下三年的感情,换回来的仅仅是“不甜”、“不爱了”如此冰冷的字眼。我也并没有像我想象中的那么悲伤绝望,甚至一滴眼泪都没有落下。也许是因为早已经知道了这个结果吧。但是还是一夜没有睡着觉,真的无法接受这个冰冷的事实。
+人,真的是会变的,会根据环境而变化。上大学的时候我们周围什么都没有,只有彼此。而步入社会,找到了稳定的工作,接触了各种各样的有趣的人,就会重新审视自己之前的生活,自己之前爱过的人。“我想换人了”“我倾向于比较条件,你的条件不如我”“及时止损”如此冰冷的话语,真的很难相信是从她的聊天框里面弹出来的。或许她发现自己面前存在着无数种可能性,为什么还要等着可能一年仅能见几次面,至少还要等上三年的远方的人呢?总之她不再怀念我们共度的三年时光了,毅然放手投入了新生活的怀抱,只能留下我在这里独自悲伤。
+所以什么是爱情?我这几天不断在问自己这个问题。我一直认为爱情是一份承诺,是能克服重重困难一起走下去的勇气。现在我觉得这个想法确实太过于理想化了。可能我自己是这种想法,但是我不能要求别人有完全相同的想法。女孩子可能需要的并不是这种承诺,也不愿意有勇气,更愿意的是就在此时此刻,能有一个人在身边照顾她,关心她,两个人在一起的样子才是爱情。爱情也不可能没有物质需求,如果没有面包,只有爱情 ,那么这段爱情能撑到什么时候呢?如果能有一个人在身边照顾她,不愁吃穿,稳定工作,未来立刻触手可及,有人会不希望过上这种生活吗?可能以前觉得,两个人向着一个目标而努力,最终实现了理想,爱情自然修成了正果。但是如果不努力就能得到爱情,还努力做什么呢?为什么还要体验那种拼搏痛苦的生活,为什么不能躺在现实中直接享受呢?我这个人,对待每一件事情都很认真,对待每一个人也很认真,过于认真就过于理想化,理想化的目标,我能坚持但是并不能保证别人也坚持。世界是很残酷的,人也是很残酷的,坚持初心的人真的很少。
+我的第一段恋爱之旅就这样结束了。我不恨她,她没有什么错误,也从来没有对我做出过任何的承诺,也没有做任何对不起我的事情。只能说,我们的爱情观确实不一致。好的恋爱让我们都成长了很多,学会更好地爱自己、爱他人。如果我还能有下一段爱情,我会更加谨慎地做出选择,没有结果,或者是短期内看不到结果的爱情,我宁愿不要,也不会去轻易去做出承诺,即使我知道我的承诺我一定坚持。
+我不能这样悲伤下去,我要抬头向前看。虽然可能以后都不会有合适的人,合适的爱情,但,还是要过好每一天,珍惜自己现在的生活。最近纠结于这段感情,对父母疏远了一些,但其实他们才是这个世界上真的真的无条件爱我的人,我又有什么理由不爱他们呢?
+放下过去,原谅自己,弥补过错,重新开始。
+ + +《现代信息检索》课程笔记:第10讲 相关反馈及查询扩展
+ +考虑查询q: [aircraft] . . .
+某篇文档 d 包含“plane”, 但是不包含 “aircraft”
+显然对于查询q,一个简单的IR系统不会返回文档d,即使d是和q最相关的文档
+提高召回率的方法:
+局部(local)方法:对用户查询进行局部的即时的分析
+全局(Global)方法: 进行一次性的全局分析(比如分析整个文档集)来产生同/近义词词典
+关于相关反馈和查询扩展:
+相关反馈的本质是将检索返回的文档的相关性判定(不同的判定来源:人工或非人工)作为返回信息,希望提升检索效果(召回率和正确率)。
+相关反馈常常用于查询扩展,所以提到相关反馈往往默认为有查询扩展
+而查询扩展的最初含义是对查询进行扩充,近年来越来越向查询重构偏移,即现在的查询扩展是指对原有查询进行修改。
+相关反馈的基本思想
+显式相关反馈:用户显式参加交互过程
+隐式相关反馈:系统跟踪用户的行为来推测返回文档的相关性,从而进行反馈。
+伪相关反馈或盲相关反馈:没有用户参与,系统直接假设返回文档的前k篇是相关的,然后进行反馈。
+相关反馈中的核心概念:矩心
+矩心是一系列点的中心
+Rocchio算法是向量空间模型中相关反馈的实现方式
+相关反馈中的假设:
+假设 A1: 对于某初始查询,用户知道在文档集中使用哪些词项来表达
+假设A2: 相关文档中出现的词项类似 (因此,可以基于相关反馈,从一篇相关文档跳到另一篇相关文档)
+相关反馈的评价:
+基于存留文档集(residual collection):用户没有判断的文档集
+一轮相关反馈往往非常有用,相对一轮相关反馈,两轮相关反馈效果的提高有限。
+用户相关反馈存在的问题:
+隐式相关反馈
+通过观察用户对当前检索结果采取的行为来给出对检索结果的相关性判定。
+判定不一定很准确,但是省却了用户的显式参与过程。
+用户行为种类:鼠标键盘动作和用户眼球动作
+隐式相关反馈小结:
+优点:
+缺点:
+伪相关反馈
+伪相关反馈对于真实相关反馈的人工部分进行自动化
+伪相关反馈算法:对于用户查询返回有序的检索结果,假定前 k 篇文档是相关的进行相关反馈 (如 Rocchio)
+优点:
+缺点:
+相关反馈小结:
+查询扩展是另一种提高召回率的方法
+使用 “全局查询扩展” 来指那些 “查询重构(query reformulation)的全局方法”
+在全局查询扩展中,查询基于一些全局的资源(同义词或近义词)进行修改,这些资源是与查询无关的
+查询扩展的方法
+交互式查询扩展 (Interactive QE):用户通常很懒,用户提交的扩展词项并不一定有用
+基于词项相似度的查询扩展:
+基于候选词和原始查询词项共现 (co-occurrences)的查询扩展
+查询扩展的优点:
+使用外部资源进行查询扩展(External QE)
+选择性查询扩展(Selective QE)
+搜索引擎中的查询扩展主要依赖的资源:查询日志
+ + +《高级人工智能》课程笔记:第5讲 序列数据的深度学习模型
+ +序列数据建模:
+为什么不使用标准的神经网络?
+RNN的特点:
+一般来说,RNN每一时间的输入和输出是不一样的
+序列学习:对于序列数据是将序列项依次传入,每个序列项再对应不同的输出
+时序展开:在RNN中每一个时间步骤用到的参数都是一样的
+RNN可看作权值共享的多层、前向网络,训练权值约束的前向网络
+Back Propagation Through Time:前向传播和反向传播
+示例:
+语言模型
+新序列采样
+字符级别的语言模型
+序列生成
+训练长序列 (100 time steps) RNN中,梯度很容易膨胀或消散
+即使好的初始化,也难以检测当前目标输出对很多步之前的输入的依赖关系
+GRU
+LSTM:
+解决了RNN长期(like hundreds of time steps)记忆的问题
+LSTM是一个存储单元,使用logistic和linear单元执行乘法运算
+记忆单元:存储RNN的长期信息
+LSTM vs GRU
+GRU是更加简单的模型,更容易创建一个更大的网络,而且它只有两个门,在计算性上也运行得更快,可以扩大模型的规模。
+LSTM更加强大和灵活,有三个门而不是两个。
+双向循环神经网络(Bidirectional RNN)
+深层循环神经网络(Deep RNNs)
+机器翻译
+图片说明
+使用集束搜索(Beam search algorithm)而不使用贪心搜索
+改进集束搜索(Refinements to Beam Search),序列长度归一化
+注意力模型
+ + +机器学习算法竞赛实战-计算广告
+ +计算广告是指借助大数据的分析建模,使得广告能够覆盖广泛区域和实现消费者的多跨度精准曝光,让同一份广告尽可能接触到更多有效的流量和更多对广告感兴趣的人,从而用同样低的成本,让广告的效果尽可能更好,使产品和服务获得更多商业上的成功。
+如何协调广告主、平台和消费者三方之间的利益
+在线投放引擎:
+分布式计算平台:
+流式计算平台:
+合约广告:包括CPT广告和定向广告。CPT广告指的是按照时间成本计算,广告主以固定的价格买断一段时间内的广告位来展示自己的广告;定向广告指的是广告主选择自己要投放的兴趣标签,然后算法为其匹配相应的受众人群并进行广告投放。
+竞价广告:采用“价高者得”的方案来决策每次展示哪个广告,使得媒体主可以实时对不同广告进行比价,从而最大化收益。
+程序化交易广告:广告主可以实时地在每一次广告展示中选择自己的目标受众,并且参与竞价。
+根据用户或商品属性以及页面上下文属性从广告索引中检索符合投放条件的候选广告。
+布尔表达式召回:根据广告主设置的定向标签组合成布尔表达式。
+向量检索召回:通过传统的Word2Vec方式获取广告的向量表示,然后通过相似度计算对受众人群进行召回;或者通过深度学习模型获取广告的向量表示。
+基于TDM(深度树匹配模型)的召回:基于深度学习的大规模推荐系统算法框架。
+目前的找回策略大多是多路召回与权重检索相结合。
+为用户侧特征和广告侧特征构建不同的塔,在经过多层全连接后,计算相似度并进行广告检索。
+广泛应用于搜索、推荐等领域的召回和排序问题中。
+对广告召回模块送来的广告候选集计算值,并按照所得值的大小倒排序。
+点击率预估:向用户投放一个广告,然后预测用户点击广告的概率
+特征处理:特征交叉组合、连续值特征的处理、点击率平滑、向量化表示
+常见模型:
+在广告竞拍机制中,广告的实际曝光量取决于广告的流量覆盖大小和在竞争广告中的相对竞争力水平,其中前者取决于广告的人群定向(匹配对应特征的用户数量)、广告素材尺寸(匹配的广告位)以及投放时段、预算等设置项;影响后者的因素主要有出价、广告质量、以及对用户体验的控制策略等。
+机器学习算法竞赛实战-自然语言处理
+ +《现代信息检索》课程笔记:第11讲 文本分类
+ +常设查询(Standing Queries)
+从检索到文本分类:假设某用户有一个经常关注的信息需求,用户会经常输入这个查询来寻找关于这个主题的新内容,关注于浏览新内容,此时排序问题变成了一个分类问题(相关 vs. 不相关)
+需要构建分类函数
+专家分类一般都是准确的
+当数据规模不大、标注者人数较少时,分类一致
+当数据规模变大,人工分类困难且代价昂贵
+新闻机构,情报机构等使用的一个技术,广泛部署于政府和企业
+供应商提供“ IDE”来编写此类规则,商业系统具有复杂的查询语言
+如果领域专家花时间精心完善规则,则准确性会很高,但是建立和维护这些规则非常昂贵
+监督学习分类器可以使用各种特征
+仅使用词项特征,使用文本中的所有词项
+最简单的特征选择方法:
+更聪明的特征选择方法:卡方(chi-square)等
+朴素贝叶斯分类的目标是寻找具有最大后验概率的类别
+对数计算:通过取对数将原来的乘积计算变成求和计算
+参数估计:极大似然估计
+避免零概率:加一平滑
+朴素贝叶斯对于训练集的大小和测试文档的大小而言是线性的,在某种意义上是最优的。
+分类结果的评价:评估必须在独立于训练数据的测试数据上完成
+评价指标:正确率(Precision),召回率(Recall),F1,分类准确率r/n ,其中 n 是所有测试文档的数量,r是正确分类的测试文档数量
+训练集包含一系列文档,每篇都标记着它的类别
+在向量空间分类中,该集合对应着空间中一系列标记的点或向量。
+利用Rocchio方法进行向量空间分类
+基本思想:计算每个类的中心向量(所有文档向量的算术平均),将每篇测试文档分到离它最近的那个中心向量
+Rocchio简单地将每个类别表示成其中心向量,分类基于文档向量到原型的相似度或聚类来进行,并不保证分类结果与训练集一致,即得到分类器后,不能保证训练集中的文档能否正确分类。
+很多情况下,Rocchio的效果不如朴素贝叶斯:Rocchio算法不能正确处理非凸、多模式类别问题
+将每篇测试文档分给训练集中离它最近的那篇文档所属的类别。
+线性分类器计算特征值的一个线性加权和
+很多常用的文本分类器都是线性分类器:朴素贝叶斯、Rocchio、logistic回归、线性SVM等等
+不同的方法选择超平面的策略不同,造成了在测试文档分类性能的巨大差异
+不能通过更强大的非线性分类器来获得更好的分类性能
+不存在某个学习方法对于任何分类问题都最优
+kNN高方差低偏差,而朴素贝叶斯分类器低方差高偏差
+单标签问题:类别之间互斥,每篇文档属于且仅属于某一个类
+多标签分类问题:一篇文档可以属于0、1或更多个类,针对某个类的决策并不影响其他类别上的决策
+对于给定的分类问题,要考虑很多因素从而选择合适的分类器算法。
+ + +《机器学习》课程笔记:第7章 降维与特征选择
+ +机器学习算法的有效性和计算复杂度是敏感于数据的特征表达和维度。
+特征降维的意义:
+数据压缩:简化数据表示,加快数据通信传输、节省存储资源、…
+学习算法效率:
+特征选择:从D个特征中选择d个,来表达模式
+特征提取:采用特征变换的方法,生成d个新的特征
+特征选择问题:从D维特征中选择d维(d<D)特征子集
+特征选择的处理过程:
+ +特征子集生成问题:D维特征中,选择d维(d<D)特征子集,子集个数为
基于距离的可分性判据:
+通常依赖于类内类间的距离度量,前提是数据具有类别标签。可分性评估是在选择的特征子集维度上计算数据统计量。
+距离的可分性判据的特点:
+基于概率分布的可分性判据:从类别概率密度的角度,讨论两个类别的交叠程度
+常见的概率距离准则:
+熵可分性判据:
+Filter 方法:
+不依赖于学习算法(如分类器)的结果,直接由数据构建评估函数,对选择的特征子集进行评估。
+通常方法:根据特征评价准则进行评估,选择最优的特征子集。
+评价准则:距离准则、概率可分、熵可分准则。
+优点:计算复杂度低,效率高。
+缺点:选择的特征之间存在冗余信息。
+Wrapper 方法:
+原理:通过学习算法(如分类器),对选择的特征子集进行评估。
+优点:选择的特征可以支持学习算法。
+缺点:算法的计算复杂度高。
+Embedded 方法:
+原理:特征选择过程在学习算法中完成,目标是完成学习过程。
+特点:不是专门的特征选择过程
+缺点:计算复杂度高。
+优点:
+不同的应用问题会有不同的特征提取研究问题
+特征提取目标:学习变换矩阵
+给定 
两种降维表示途径:
+

目标函数:均方误差最小原则(求最优重构子空间)
+
最小误差等价于最大投影
+求解目标函数:
特征值的意义:样本在w方向的投影平均值(或和)最大
+PCA算法流程:
+
 特征值,并降排序
特征值,并降排序 对应非零特征向量
对应非零特征向量

PCA能保证类别区分的有效性,LDA特征的优点:类内最小、类间最大。
+特征方向的提取:
 的特征值,对应特征向量
的特征值,对应特征向量 的问题:
的问题:
 的特征值降序
的特征值降序 ,前
,前 个特征值对应特征向量
个特征值对应特征向量
 \boldsymbol{\Lambda}=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \ldots, \boldsymbol{\alpha}_d\right)
\boldsymbol{\Lambda}=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \ldots, \boldsymbol{\alpha}_d\right) W=\Phi \boldsymbol{\Lambda}$
W=\Phi \boldsymbol{\Lambda}$
 的低维表示:
的低维表示:

LLE方法是一种流形学习,保持样本间的局部线性关系,整体实现非线性映射。
+基本思想:通过矩阵分解,进行数据降维;分解后的矩阵为非负矩阵
+不同的目标函数情况:
+《现代信息检索》课程笔记:第12讲 支持向量机和排序学习
+ +线性可分情况下,不仅要区分开,而且要使得区分间隔最大
+最优超平面)是使得两类的分类间隔(Margin)最大的超平面,即每类中离超平面最近的样本到超平面的距离最大。距离这个最优超平面最近的样本被称为支持向量。
+求解最优超平面就相当于,在上述约束条件下,求2/||W||的最大值 ,即以下损失函数最小值
+二次优化问题可以采用Lagrange方法求解
+非线性可分情况下的处理
+广义最优分类面方法:在线性不可分的情况下,就是某些训练样本不能满足约束条件,因此可以在条件中增加一个松弛项ζ(发音Zeta,也称
+引入Soft Margin,软边界),变换约束条件。
变换到高维空间的支持向量机
+为什么要使间隔最大化?
+SVM用于支持多类问题:结构化SVM
+权重学习主要方法:
+给定训练样例集合,每个样例表示为三元组<q, d, R(d,q)>
+从上述样例中学习权重,使得学到的评分接近训练集中的相关性判定结果。
+评分函数是两个因子的线性组合:
+我们的一个因子取决于查询词项在文档中的词袋统计量,另一个因子取决于邻近度权重
+基于机器学习的检索结果排序
+将IR排序问题看成序回归
+对于同一查询,文档之间可以按照相对得分排序即可,并不一定要求每篇文档有一个全局的绝对得分。因此,只需要一个排序,而不要得到相关度的绝对得分,问题空间可以减小。
+排序SVM的构建
+排序学习算法现在一般分为以下三类
+虽然近年来基于深度学习和大规模预训练语言模型的方法已成功应用于IR,排序学习仍然是一种整合不同文本特征的有效方法。
+ + +在下一段感情之前,必须要将这一段感情的问题想清楚,不能上头!
+ +首先,我要好好剖析一下自己的性格。我的性格在我看来是存在很大的缺陷的,但是其实我自己并不是很了解自己。这次要好好想想。
+人,都是会变的。虽然我不愿意承认我自己在变化,但是事实是所有人都在改变,包括我自己在内,区别在于大家在潜移默化中接受了自己的变化,而我总愿意回头去看,不承认自己已经改变了的事实。我的前女友也在变。可能大一大二的时候,她只是需要一个人陪在她的身边,帮助她度过这些单调无聊的生活,但是大三开始,免不得要为自己以后的前程考虑。似乎用这种眼光来看,我们两个并不合适。但是我仍然纠结于自己之前的感情,认为我们还是和之前相同的,但是实际上已经不一样了。
+我以为平平淡淡就是美,就是真爱,但是我还年轻啊,为什么不更有激情一点,聊天更有意思一点?恋爱脑最近还有点想大学同学。拜托?人家和你根本就不是同一路人,城市都不在同一个,怎么谈?人家会答应一个异地的矮子吗?
+和gxgg聊了关于他女朋友的事情,我觉得他现在的状态也不是很好的状态,说不定保了研就基本告别了。我不知道为什么我们在感情生活中如此悲惨。是不是就是因为我们太在意了?是不是,没那么在意会好很多?
+表白是水到渠成,不是破釜沉舟不要相信自己的朴实,别人不信没有用的,多看看别人的经验
+不咬手指,前期用指甲刀修,尽量不撕嘴皮,把眼皮养好,这样太难受了
+不要胡思乱想,好好学习!好好学习后端!
+20221009
+没写完,在下面继续写吧
+一焦虑就咬手指,控制不住,毕竟都差不多二十年的毛病了。今天下午又开始emo,感觉计算机现在就不应该学,到处都是会计算机的,互联网大厂又基本上没有国家的支持,以后是不是会非常非常难啊。。。我一直在踏踏实实的学习,希望能学以致用,以后过的轻松一点,换一个城市生活。但是现在我感觉自己没有什么大的变化,环境却翻天覆地的变了。早出生几年,房子也不贵,学个计算机现在就已经财务自由了,基本都能做到OG级别了。可是我还有三年啊。。。这三年会变成什么样子啊。。。真的不敢想象。是不是还会经历战争?小时候还知道“和平和发展”是世界的主题。然而现在一切都变了。疫情、动乱、封锁。真的不知道我自己的努力方向在哪里,真的好想好想预测一下三年后究竟是个什么样子。。。
+太焦虑了,太焦虑了。不学习感觉过的不踏实,学习又焦虑效率不太高。
+可能什么时候真正把咬手指戒掉了,什么时候我才是一个正常的状态吧。。。
+ + +Go基础学习(微软教程)
+ +Go 语言表现力强,且简单明了。 它在设计时考虑了惯用语言,这使程序员能够高效地编写高效且可靠的代码。 以 Go 语言编写的程序可以在 Unix 系统上运行,例如 Linux 和 macOS,还有 Windows。 Go 语言之所以值得注意,部分原因在于它独特的并发机制,使得编写可同时利用多个内核的程序非常容易。 它主要是一种强化静态类型的语言,这意味着变量类型在编译时是已知的。 不过,它确实具有一些动态类型化功能。
+下面是 Go 编程语言的基本原理优势:
+如果不想在本地安装 Go,可以使用 Go Playground。 Go Playground 是一款 Web 服务,可在浏览器中运行 Go 应用程序。
+本地安装包下载地址
+wget https://go.dev/dl/go1.19.1.linux-amd64.tar.gz // 版本号可能改变提取本地安装包
+sudo tar -C /usr/local -xzf go1.19.1.linux-amd64.tar.gz编辑配置文件,添加到环境变量:
+vim ~/.bashrc
+export PATH=$PATH:/usr/local/go/bin
+source ~/.bashrc确认是否已经安装好:
+go versiongo version go1.19.1 linux/amd64Go 在组织项目文件方面与其他编程语言不同。 首先,Go 是在工作区的概念下工作的。 工作区就是应用程序源代码所在的位置。 所有 Go 项目共享同一个工作区。 不过,从版本 1.11 开始,Go 已开始更改此方法。 你尚且不必担心,因为我们将在下一个模块中介绍工作区。 现在,Go 工作区位于 $HOME/go,但如果需要,可以为所有项目设置其他位置。
+若要将工作区设置为其他位置,可以使用 $GOPATH 环境变量。 在处理更复杂的项目时,此环境变量有助于避免将来出现问题。
+export GOPATH=/mnt/d/Programming_Design/Go每个 Go 工作区都包含三个基本文件夹:
+例如,工作站文件夹结构树可能与下面的示例类似:
+bin/
+ hello
+ coolapp
+pkg/
+ github.com/gorilla/
+ mux.a
+src/
+ github.com/golang/example/
+ .git/
+ hello/
+ hello.go在安装插件之前要先更改go的源
+The "gopls" command is not available. Run "go install -v golang.org/x/tools/gopls@latest" to install.然后点击上边的窗口的install All,即可完成插件的安装
+文件夹组织形式:
+ +package main
+
+import "fmt"
+
+func main() {
+ fmt.Println("Hello World!")
+}
+运行:
+go run main.goHello World!只生成二进制文件但是不运行:
+go build main.go我们在 package main 语句中告诉 Go,我们将要创建的应用是一个可执行程序(可以运行的文件)。 我们的“Hello World!”应用是 main 包的一部分。
包是一组常用的源代码文件。 每个可执行应用都具有此第一行,即使项目或文件具有不同的名称。
+import 语句使你的程序可以访问其他包中的其他代码。 在本例中,fmt 为标准库包。
你需要此 import 语句,因为你将在此程序的稍后部分使用此包中的函数将消息打印到屏幕上。 可以在程序中包含你想要或需要的任意数量的 import 语句。 但是,Go 在这方面是惯用的。 如果导入包,但不使用包中的相应函数,应用将不会进行编译。 Visual Studio Code 的一大功能是,当你保存文件时,它会自动删除程序中未使用的导入。
VSCode 是自动帮助我们删除的,但是和Python什么的不一样,如果多了冗余的包程序是无法运行的。
+# command-line-arguments
+./main.go:4:8: imported and not used: "math"func 语句是用于声明函数的保留字。 第一个函数名为“main”,因为它是程序的起始点。 整个 package main 中只能有一个 main() 函数(在第一行中定义的那个)。 在 main() 函数中,你调用了 fmt 包中的 Println 函数。 你发送了你希望在屏幕上看到的文本消息。
var firstName string // 声明单一变量
+var secondName, lastName string // 如果多个变量的类型相同,可以用逗号分隔一起声明多个变量
+var age int
+
+// 也可以在一个括号内批量声明变量
+var (
+ thirdName, fourthName string
+ secondage int
+)(VSCode会自动进行格式化,完全不用担心格式的问题)
+可以在声明的时候直接对变量进行初始化,会自动对变量的类型进行推断,不用显式指定类型
+var (
+ firstName string = "John"
+ lastName string = "Doe"
+ age int = 32
+)等价于下面的写法:
+var (
+ firstName, lastName, age = "John", "Doe", 32
+)package main
+
+import "fmt"
+
+func main() {
+ firstName, lastName := "John", "Doe"
+ age := 32
+ fmt.Println(firstName, lastName, age)
+}John Doe 32请注意,在定义变量名称后,需要在此处加入一个冒号等于号 (:=) 和相应的值。 使用冒号等于号时, 要声明的变量必须是新变量 。 如果使用冒号等于号并已经声明该变量,将不会对程序进行编译。
用于声明常量的关键字是 const
const HTTPStatusOK = 200
+
+const (
+ StatusOK = 0
+ StatusConnectionReset = 1
+ StatusOtherError = 2
+)常量和变量之间既有相似之处,也有一些重要差异。 例如,你可以在不使用常量的情况下声明常量。 你不会收到错误消息。 不能使用冒号等于号来声明常量。 如果采用这种方式,Go 会发出警告。
+在 Go 中,当你(在函数内部)声明一个变量但不使用它时,Go 会抛出错误,而不是像某些其他编程语言一样抛出警告。
+一般来说,定义整数类型的关键字是 int。 但 Go 还提供了 int8、int16、int32 和 int64 类型,其大小分别为 8、16、32 或 64 位的整数。 使用 32 位操作系统时,如果只是使用 int,则大小通常为 32 位。 在 64 位系统上,int 大小通常为 64 位。 但是,此行为可能因计算机而不同。 可以使用 uint。 但是,只有在出于某种原因需要将值表示为无符号数字的情况下,才使用此类型。 此外,Go 还提供 uint8、uint16、uint32 和 uint64 类型。
var integer8 int8 = 127
+var integer16 int16 = 32767
+var integer32 int32 = 2147483647
+var integer64 int64 = 9223372036854775807不能进行隐式转换,如果两个变量的类型不同,需要进行强制转换,否则编译不能通过。
+Go 提供两种浮点数大小的数据类型:float32 和 float64。 如果需要存储较大的数字,则可以使用这些类型,这些类型无法适应前面提到的任何一个整数类型。 这两种类型的区别是它们可以容纳的最大位数。
var float32 float32 = 2147483647
+var float64 float64 = 9223372036854775807
+fmt.Println(float32, float64)可以使用 math 包中提供的 math.MaxFloat32 和 math.MaxFloat64 常量来查找这两种类型的限制。
package main
+
+import (
+ "fmt"
+ "math"
+)
+
+func main() {
+ fmt.Println(math.MaxFloat32, math.MaxFloat64)
+}3.4028234663852886e+38 1.7976931348623157e+308布尔类型仅可能有两个值:true 和 false。 你可以使用关键字 bool 声明布尔类型。 Go 不同于其他编程语言,在 Go 中,你不能将布尔类型隐式转换为 0 或 1。
var featureFlag bool = true最后,让我们看一下编程语言中最常见的数据类型:string。 在 Go 中,关键字 string 用于表示字符串数据类型。 若要初始化字符串变量,你需要在双引号(")中定义值。 单引号(')用于单个字符(以及 runes,正如我们在上一节所述)。
var firstName string = "John"
+lastName := "Doe"
+fmt.Println(firstName, lastName)John Doe到目前为止,几乎每次声明变量时,都使用值对其进行了初始化。 但与在其他编程语言中不同的是,在 Go 中,如果你不对变量初始化,所有数据类型都有默认值。 此功能非常方便,因为在使用之前,你无需检查变量是否已初始化。
+下面列出了我们目前浏览过类型的几个默认值:
+int 类型的 0(及其所有子类型,如 int64)float32 和 float64 类型的 +0.000000e+000bool 类型的 falsestring 类型的空值Go 中隐式强制转换不起作用。 接下来,需要显式强制转换。 Go 提供了将一种数据类型转换为另一种数据类型的一些本机方法。
+一种方法是对每个类型使用内置函数,如下所示:
+var integer16 int16 = 127
+var integer32 int32 = 32767
+fmt.Println(int32(integer16) + integer32)Go 的另一种转换方法是使用 strconv 包。 将 string 与 int
package main
+
+import (
+ "fmt"
+ "strconv"
+)
+
+func main() {
+ i, _ := strconv.Atoi("-42")
+ s := strconv.Itoa(-42)
+ fmt.Println(i, s)
+}-42 -42有一个下划线 (_) 用作变量的名称。 在 Go 中(或Python中),这意味着我们不会使用该变量的值,而是要将其忽略。
在 Go 中,函数允许你将一组可以从应用程序的其他部分调用的语句组合在一起。 你可以使用函数来组织代码并使其更易于阅读,而不是创建包含许多语句的程序。 更具可读性的代码也更易于维护。
+与之交互的函数是 main() 函数。 Go 中的所有可执行程序都具有此函数,因为它是程序的起点。 你的程序中只能有一个 main() 函数。
package main
+
+import (
+ "fmt"
+ "os"
+ "strconv"
+)
+
+func main() {
+ number1, _ := strconv.Atoi(os.Args[1])
+ number2, _ := strconv.Atoi(os.Args[2])
+ fmt.Println("Sum:", number1+number2)
+}os.Args 变量包含传递给程序的每个命令行参数。 由于这些值的类型为 string,因此需要将它们转换为 int 以进行求和。
+> go run main.go 3 5
+Sum: 8使用 func 关键字来定义函数,然后为其指定名称。 在命名后,指定函数的参数列表。 你可以指定零个或多个参数。 你还可以定义函数的返回类型,该函数也可以是零个或多个。 (我们将在下一节中讨论如何返回多个值)。在定义所有这些值之后,你可以编写函数的正文内容。
package main
+
+import (
+ "fmt"
+ "os"
+ "strconv"
+)
+
+func main() {
+ sum := sum(os.Args[1], os.Args[2])
+ fmt.Println("Sum:", sum)
+}
+
+func sum(number1 string, number2 string) int {
+ int1, _ := strconv.Atoi(number1)
+ int2, _ := strconv.Atoi(number2)
+ return int1 + int2
+}此代码创建一个名为 sum 的函数,该函数采用两个 string 参数,并将它们强制转换为 int,然后返回求和所得的结果。 定义返回类型时,函数需要返回该类型的值。
在 Go 中,你还可以为函数的返回值设置名称,将其当作一个变量。
+func sum(number1 string, number2 string) (result int) {
+ int1, _ := strconv.Atoi(number1)
+ int2, _ := strconv.Atoi(number2)
+ result = int1 + int2
+ return
+}package main
+
+import (
+ "fmt"
+ "os"
+ "strconv"
+)
+
+func main() {
+ sum, mul := calc(os.Args[1], os.Args[2])
+ fmt.Println("Sum:", sum)
+ fmt.Println("Mul:", mul)
+}
+
+func calc(number1 string, number2 string) (sum int, mul int) {
+ int1, _ := strconv.Atoi(number1)
+ int2, _ := strconv.Atoi(number2)
+ sum = int1 + int2
+ mul = int1 * int2
+ return
+}> go run main.go 3 5
+Sum: 8
+Mul: 15将值传递给函数时,该函数中的每个更改都不会影响调用方。 Go 是“按值传递”编程语言。 每次向函数传递值时,Go 都会使用该值并创建本地副本(内存中的新变量)。 在函数中对该变量所做的更改都不会影响你向函数发送的更改。
+指针是包含另一个变量的内存地址的变量。 当你发送指向某个函数的指针时,不会传递值,而是传递地址内存。 因此,对该变量所做的每个更改都会影响调用方。
+在 Go 中,有两个运算符可用于处理指针:
+& 运算符使用其后对象的地址。* 运算符取消引用指针。 也就是说,你可以前往指针中包含的地址访问其中的对象。package main
+
+import "fmt"
+
+func main() {
+ firstName := "John"
+ updateName(&firstName)
+ fmt.Println(firstName)
+}
+
+func updateName(name *string) {
+ *name = "David"
+}
+首先要做的就是修改函数的签名,以指明你要接收指针。 为此,请将参数类型从 string 更改为 *string。 (后者仍是字符串,但现在它是指向字符串 的 指针。)然后,将新值分配给该变量时,需要在该变量的左侧添加星号 (*) 以暂停该变量的值。 调用 updateName 函数时,系统不会发送值,而是发送变量的内存地址。 这就是前面的代码在变量左侧带有 & 符号的原因。
Go 包与其他编程语言中的库或模块类似。 你可以打包代码,并在其他位置重复使用它。 包的源代码可以分布在多个 .go 文件中。 到目前为止,我们已编写 main 包,并对其他本地包进行了一些引用。
你可能注意到,在 Go 中,甚至最直接的程序都是包的一部分。 通常情况下,默认包是 main 包,即目前为止一直使用的包。 如果程序是 main 包的一部分,Go 会生成二进制文件。 运行该文件时,它将调用 main() 函数。
换句话说,当你使用 main 包时,程序将生成独立的可执行文件。 但当程序非是 main 包的一部分时,Go 不会生成二进制文件。 它生成包存档文件(扩展名为“.a”的文件)。
在 Go 中,包名称需遵循约定。 包使用其导入路径的最后一部分作为名称。 例如,Go 标准库包含名为 math/cmplx 的包,该包提供用于处理复数的有用代码。 此包的导入路径为 math/cmplx,导入包的方式如下所示:
import "math/cmplx"在名为 calculator 的目录中 创建名为 sum.go 的文件。 树目录应如下列目录所示:
用包的名称初始化 sum.go 文件:
package calculator你现在可以开始编写包的函数和变量。 不同于其他编程语言,Go 不会提供 public 或 private 关键字,以指示是否可以从包的内外部调用变量或函数。 但 Go 须遵循以下两个简单规则:
接下来,让我们将以下代码添加到我们要创建的计算器包:
+package calculator
+
+var logMessage = "[LOG]"
+
+// Version of the calculator
+var Version = "1.0"
+
+func internalSum(number int) int {
+ return number - 1
+}
+
+// Sum two integer numbers
+func Sum(number1, number2 int) int {
+ return number1 + number2
+}让我们看一下该代码中的一些事项:
+logMessage 变量。Version 变量。 建议你添加注释来描述此变量的用途。 (此描述适用于包的任何用户。)internalSum 函数。Sum 函数。 建议你添加注释来描述此函数的用途。若要确认一切正常,可在 calculator 目录中运行 go build 命令。 如果执行此操作,请注意系统不会生成可执行的二进制文件。
你已将计算器功能放入包中。 现在可以将包放到模块中。 Go 模块通常包含可提供相关功能的包。 包的模块还指定了 Go 运行你组合在一起的代码所需的上下文。 此上下文信息包括编写代码时所用的 Go 版本。
+此外,模块还有助于其他开发人员引用代码的特定版本,并更轻松地处理依赖项。 另一个优点是,我们的程序源代码无需严格存在于 $GOPATH/src 目录中。 如果释放该限制,则可以更方便地在其他项目中同时使用不同包版本。
(下面与教程不同,自己探索出了一个可用不报错的方法)
+VSCode GOPATH设置:"go.gopath": "/mnt/d/Programming_Design/Go"
首先设置 go env -w GO111MODULE=on
如果 helloworld要引用 calculator,则文件夹的组织形式如下:
在 $GOPATH/src/calculator创建 go.mod文件,其中文件第一行与文件夹同名
module calculator
+
+go 1.19在 $GOPATH/src/helloworld创建 go.mod文件,其中文件第一行与文件夹同名,下面要写好版本号和包的路径
module helloworld
+
+go 1.19
+
+require "calculator" v1.0.0
+replace "calculator" => "../calculator"然后可以导入这个包并运行主文件
+package main
+
+import (
+ "calculator"
+ "fmt"
+)
+
+func main() {
+ total := calculator.Sum(3, 5)
+ fmt.Println(total)
+ fmt.Println("Version: ", calculator.Version)
+}
+8
+Version: 1.0有时,程序需要引用其他开发人员编写的包。
+测试后不是很明白,基本上是在主文件和 .mod文件中写入包的名称和版本即可。然后根据控制台的输出将包安装好即可使用
main.go:
package main
+
+import (
+ "calculator"
+ "fmt"
+
+ "rsc.io/quote"
+)
+
+func main() {
+ total := calculator.Sum(3, 5)
+ fmt.Println(total)
+ fmt.Println("Version: ", calculator.Version)
+ fmt.Println(quote.Hello())
+}go.mod:
module helloworld
+
+go 1.19
+
+require (
+ calculator v1.0.0
+ rsc.io/quote v1.5.2
+)
+
+require (
+ golang.org/x/text v0.0.0-20170915032832-14c0d48ead0c // indirect
+ rsc.io/sampler v1.3.0 // indirect
+)
+
+replace calculator => ../calculator输出:
+8
+Version: 1.0
+Ahoy, world!与其他编程语言不同的是,在 Go 中,你不需要在条件中使用括号。 else 子句可选。 但是,大括号仍然是必需的。 此外,为了减少行,Go 不支持三元 if 语句,因此每次都需要编写完整的 if 语句。
package main
+
+import "fmt"
+
+func givemeanumber() int {
+ return -1
+}
+
+func main() {
+ if num := givemeanumber(); num < 0 {
+ fmt.Println(num, "is negative")
+ } else if num < 10 {
+ fmt.Println(num, "has only one digit")
+ } else {
+ fmt.Println(num, "has multiple digits")
+ }
+}其中,有一个在 Go 中常见的约定进行高效编程的方式 if num := givemeanumber(); num < 0,同时接收函数的返回值,但是不重复进行接收,然后使用到if语句中进行判断。当然这个 num变量在 if的外部是无法使用的。
像其他编程语言一样,Go 支持 switch 语句。 可以使用 switch 语句来避免链接多个 if 语句。 使用 switch 语句,就不需维护和读取包含多个 if 语句的代码。 这些语句还可以让复杂的条件更易于构造。 请参阅以下部分的 switch 语句。
普通的switch语句:
+package main
+
+import (
+ "fmt"
+ "math/rand"
+ "time"
+)
+
+func main() {
+ sec := time.Now().Unix()
+ rand.Seed(sec)
+ i := rand.Int31n(10)
+
+ switch i {
+ case 0:
+ fmt.Print("zero...")
+ case 1:
+ fmt.Print("one...")
+ case 2:
+ fmt.Print("two...")
+ default:
+ fmt.Print("no match...")
+ }
+
+ fmt.Println("ok")
+}有时,多个表达式仅与一个 case 语句匹配。 在 Go 中,如果希望 case 语句包含多个表达式,请使用逗号 (,) 来分隔表达式。 此方法可避免代码重复。
package main
+
+import "fmt"
+
+func location(city string) (string, string) {
+ var region string
+ var continent string
+ switch city {
+ case "Delhi", "Hyderabad", "Mumbai", "Chennai", "Kochi":
+ region, continent = "India", "Asia"
+ case "Lafayette", "Louisville", "Boulder":
+ region, continent = "Colorado", "USA"
+ case "Irvine", "Los Angeles", "San Diego":
+ region, continent = "California", "USA"
+ default:
+ region, continent = "Unknown", "Unknown"
+ }
+ return region, continent
+}
+func main() {
+ region, continent := location("Irvine")
+ fmt.Printf("John works in %s, %s\n", region, continent)
+}
+John works in California, USA在 case 语句的表达式中包含的值对应于 switch 语句验证的变量的数据类型。
switch 还可以调用函数。 在该函数中,可以针对可能的返回值编写 case 语句。
第一种是在switch上调用函数,对返回值进行判断
+package main
+
+import (
+ "fmt"
+ "time"
+)
+
+func main() {
+ switch time.Now().Weekday().String() {
+ case "Monday", "Tuesday", "Wednesday", "Thursday", "Friday":
+ fmt.Println("It's time to learn some Go.")
+ default:
+ fmt.Println("It's weekend, time to rest!")
+ }
+
+ fmt.Println(time.Now().Weekday().String())
+}
+It's time to learn some Go.
+Wednesday第二种是在case上调用函数
+package main
+
+import (
+ "fmt"
+ "regexp"
+)
+
+func main() {
+ var email = regexp.MustCompile(`^[^@]+@[^@.]+\.[^@.]+`)
+ var phone = regexp.MustCompile(`^[(]?[0-9][0-9][0-9][). \-]*[0-9][0-9][0-9][.\-]?[0-9][0-9][0-9][0-9]`)
+
+ contact := "foo@bar.com"
+
+ switch {
+ case email.MatchString(contact):
+ fmt.Println(contact, "is an email")
+ case phone.MatchString(contact):
+ fmt.Println(contact, "is a phone number")
+ default:
+ fmt.Println(contact, "is not recognized")
+ }
+}
+foo@bar.com is an email上面的 switch 语句中省略了条件,就像在 if 语句中那样。 此模式类似于比较 true 值,就像强制 switch 语句一直运行一样。
一个条件 switch 块比一长串的 if 和 else if 语句更易于维护。
在某些编程语言中,你会在每个 case 语句末尾写一个 break 关键字。 但在 Go 中,当逻辑进入某个 case 时,它会退出 switch 块,除非你显式停止它。 若要使逻辑进入到下一个紧邻的 case,请使用 fallthrough 关键字。
package main
+
+import (
+ "fmt"
+)
+
+func main() {
+ switch num := 15; {
+ case num < 50:
+ fmt.Printf("%d is less than 50\n", num)
+ fallthrough
+ case num > 100:
+ fmt.Printf("%d is greater than 100\n", num)
+ fallthrough
+ case num < 200:
+ fmt.Printf("%d is less than 200\n", num)
+ }
+}
+15 is less than 50
+15 is greater than 100
+15 is less than 200请注意,由于 num 为 15(小于 50),因此它与第一个 case 匹配。 但是,num 不大于 100。 由于第一个 case 语句包含 fallthrough 关键字,因此逻辑会立即转到下一个 case 语句,而不会对该 case 进行验证。 因此,在使用 fallthrough 关键字时必须谨慎。 该代码产生的行为可能不是你想要的。
另一个常用控制流是循环。 Go 只使用一个循环构造,即 for 循环。 但是,你可以通过多种方式表示循环。
package main
+
+import (
+ "fmt"
+)
+
+func main() {
+ sum := 0
+ for i := 1; i <= 100; i++ {
+ sum += i
+ }
+ fmt.Println("sum of 1..100 is", sum)
+}
+sum of 1..100 is 5050package main
+
+import (
+ "fmt"
+ "math/rand"
+ "time"
+)
+
+func main() {
+ var num int64
+ rand.Seed(time.Now().Unix())
+ for num != 5 {
+ num = rand.Int63n(15)
+ fmt.Println(num)
+ }
+}只要 num 变量保存的值与 5 不同,程序就会输出一个随机数。
可以在 Go 中编写的另一种循环模式是无限循环。 在这种情况下,你不编写条件表达式,也不编写预处理语句或后处理语句, 而是采取退出循环的方式进行编写。 否则,逻辑永远都不会退出。 若要使逻辑退出循环,请使用 break 关键字。
package main
+
+import (
+ "fmt"
+ "math/rand"
+ "time"
+)
+
+func main() {
+ var num int32
+ sec := time.Now().Unix()
+ rand.Seed(sec)
+
+ for {
+ fmt.Print("Writing inside the loop...")
+ if num = rand.Int31n(10); num == 5 {
+ fmt.Println("finish!")
+ break
+ }
+ fmt.Println(num)
+ }
+}
+在 Go 中,可以使用 continue 关键字跳过循环的当前迭代。 例如,可以使用此关键字在循环继续之前运行验证。 也可以在编写无限循环并需要等待资源变得可用时使用它。
package main
+
+import "fmt"
+
+func main() {
+ sum := 0
+ for num := 1; num <= 100; num++ {
+ if num%5 == 0 {
+ continue
+ }
+ sum += num
+ }
+ fmt.Println("The sum of 1 to 100, but excluding numbers divisible by 5, is", sum)
+}
+The sum of 1 to 100, but excluding numbers divisible by 5, is 4000在 Go 中,defer 语句会推迟函数(包括任何参数)的运行,直到包含 defer 语句的函数完成。 通常情况下,当你想要避免忘记任务(例如关闭文件或运行清理进程)时,可以推迟某个函数的运行。
可以根据需要推迟任意多个函数。 defer 语句按逆序运行,先运行最后一个,最后运行第一个。
package main
+
+import "fmt"
+
+func main() {
+ for i := 1; i <= 4; i++ {
+ defer fmt.Println("deferred", -i)
+ fmt.Println("regular", i)
+ }
+}
+regular 1
+regular 2
+regular 3
+regular 4
+deferred -4
+deferred -3
+deferred -2
+deferred -1在此示例中,请注意,每次推迟 fmt.Println("deferred", -i) 时,都会存储 i 的值,并会将其运行任务添加到队列中。 在 main() 函数输出完 regular 值后,所有推迟的调用都会运行。 这就是你看到输出采用逆序(后进先出)的原因。
defer 函数的一个典型用例是在使用完文件后将其关闭。
package main
+
+import (
+ "fmt"
+ "io"
+ "os"
+)
+
+func main() {
+ newfile, error := os.Create("learnGo.txt")
+ if error != nil {
+ fmt.Println("Error: Could not create file.")
+ return
+ }
+ defer newfile.Close()
+
+ if _, error = io.WriteString(newfile, "Learning Go!"); error != nil {
+ fmt.Println("Error: Could not write to file.")
+ return
+ }
+
+ newfile.Sync()
+}
+创建或打开某个文件后,可以推迟 .Close() 函数的执行,以免在你完成后忘记关闭该文件。
运行时错误会使 Go 程序崩溃,例如尝试通过使用超出范围的索引或取消引用 nil 指针来访问数组。 你也可以强制程序崩溃。
+内置 panic() 函数可以停止 Go 程序中的正常控制流。 当你使用 panic 调用时,任何延迟的函数调用都将正常运行。 进程会在堆栈中继续,直到所有函数都返回。 然后,程序会崩溃并记录日志消息。 此消息包含错误信息和堆栈跟踪,有助于诊断问题的根本原因。
调用 panic() 函数时,可以添加任何值作为参数。 通常,你会发送一条错误消息,说明为什么会进入紧急状态。
例如,下面的代码将 panic 和 defer 函数组合在一起。 尝试运行此代码以了解控制流的中断。 请注意,清理过程仍会运行。
package main
+
+import "fmt"
+
+func highlow(high int, low int) {
+ if high < low {
+ fmt.Println("Panic!")
+ panic("highlow() low greater than high")
+ }
+ defer fmt.Println("Deferred: highlow(", high, ",", low, ")")
+ fmt.Println("Call: highlow(", high, ",", low, ")")
+
+ highlow(high, low+1)
+}
+
+func main() {
+ highlow(2, 0)
+ fmt.Println("Program finished successfully!")
+}
+Call: highlow( 2 , 0 )
+Call: highlow( 2 , 1 )
+Call: highlow( 2 , 2 )
+Panic!
+Deferred: highlow( 2 , 2 )
+Deferred: highlow( 2 , 1 )
+Deferred: highlow( 2 , 0 )
+panic: highlow() low greater than high
+
+goroutine 1 [running]:
+main.highlow(0x4b8018?, 0xc000012018?)
+ /mnt/d/Programming_Design/Go/src/helloworld/main.go:8 +0x285
+main.highlow(0x2, 0x2)
+ /mnt/d/Programming_Design/Go/src/helloworld/main.go:13 +0x211
+main.highlow(0x2, 0x1)
+ /mnt/d/Programming_Design/Go/src/helloworld/main.go:13 +0x211
+main.highlow(0x2, 0x0)
+ /mnt/d/Programming_Design/Go/src/helloworld/main.go:13 +0x211
+main.main()
+ /mnt/d/Programming_Design/Go/src/helloworld/main.go:17 +0x25
+exit status 2下面是运行代码时会发生的情况:
+highlow() 函数中的高值和低值。low 的值大于 high 的值,则程序会崩溃。 会显示“Panic!”消息。 此时,控制流中断,所有推迟的函数都开始输出“Deferred...”消息。Program finished successfully!”消息。有时,你可能想要避免程序崩溃,改为在内部报告错误。 或者,你可能想要先清理混乱情况,然后再让程序崩溃。 例如,你可能想要关闭与某个资源的连接,以免出现更多问题。
+Go 提供内置 recover() 函数,让你可以在程序崩溃之后重新获得控制权。 你只会在你同时调用 defer 的函数中调用 recover。 如果调用 recover() 函数,则在正常运行的情况下,它会返回 nil,没有任何其他作用。
尝试修改前面的代码中的 main 函数,以添加对 recover() 的调用,如下所示:
package main
+
+import "fmt"
+
+func highlow(high int, low int) {
+ if high < low {
+ fmt.Println("Panic!")
+ panic("highlow() low greater than high")
+ }
+ defer fmt.Println("Deferred: highlow(", high, ",", low, ")")
+ fmt.Println("Call: highlow(", high, ",", low, ")")
+
+ highlow(high, low+1)
+}
+
+func main() {
+ defer func() {
+ handler := recover()
+ if handler != nil {
+ fmt.Println("main(): recover", handler)
+ }
+ }()
+
+ highlow(2, 0)
+ fmt.Println("Program finished successfully!")
+}
+Call: highlow( 2 , 0 )
+Call: highlow( 2 , 1 )
+Call: highlow( 2 , 2 )
+Panic!
+Deferred: highlow( 2 , 2 )
+Deferred: highlow( 2 , 1 )
+Deferred: highlow( 2 , 0 )
+main(): recover highlow() low greater than high在 main() 函数中,你会将一个可以调用 recover() 函数的匿名函数推迟。 当程序处于紧急状态时,对 recover() 的调用无法返回 nil。 你可以在此处执行一些操作来清理混乱,但在本例中,你只是简单地输出一些内容。
panic 和 recover 函数的组合是 Go 处理异常的惯用方式。 其他编程语言使用 try/catch 块。 Go 首选此处所述的方法。
首先,编写一个用于输出数字(1 到 100)的程序,其中有以下变化:
+Fizz。Buzz。FizzBuzz。尝试使用 switch 语句。
package main
+
+import (
+ "fmt"
+ "strconv"
+)
+
+func fizzbuzz(num int) string {
+ switch {
+ case num%15 == 0:
+ return "FizzBuzz"
+ case num%3 == 0:
+ return "Fizz"
+ case num%5 == 0:
+ return "Buzz"
+ }
+ return strconv.Itoa(num)
+}
+
+func main() {
+ for num := 1; num <= 100; num++ {
+ fmt.Println(fizzbuzz(num))
+ }
+}编写一个程序来查找小于 20 的所有质数。 质数是大于 1 的任意数字,只能被它自己和 1 整除。 “整除”表示经过除法运算后没有余数。 与大多数编程语言一样,Go 还提供了一种方法来检查除法运算是否产生余数。 我们可以使用模数 %(百分号)运算符。
在本练习中,你将更新一个名为 findprimes 的函数,以检查数值是否为质数。 该函数有一个整数参数,并返回一个布尔值。 函数通过检查是否有余数来测试输入数字是否为质数。 如果数字为质数,则该函数返回 true。
package main
+
+import "fmt"
+
+func findprimes(number int) bool {
+ for i := 2; i < number; i++ {
+ if number%i == 0 {
+ return false
+ }
+ }
+
+ if number > 1 {
+ return true
+ } else {
+ return false
+ }
+}
+
+func main() {
+ fmt.Println("Prime numbers less than 20:")
+
+ for number := 1; number < 20; number++ {
+ if findprimes(number) {
+ fmt.Printf("%v ", number)
+ }
+ }
+ fmt.Println()
+}Prime numbers less than 20:
+2 3 5 7 11 13 17 19编写一个要求用户输入一个数字的程序。 在开始时使用以下代码片段:
+此程序要求用户输入一个数字,然后将其输出。 修改示例代码,使之符合以下要求:
+0 is neither negative nor positive”。 继续要求用户输入数字。You entered: X”(其中的 X 为输入的数字)。 继续要求用户输入数字。package main
+
+import "fmt"
+
+func main() {
+ val := 0
+ for {
+ fmt.Print("Enter number: ")
+ fmt.Scanf("%d", &val)
+ if val < 0 {
+ panic("Negative!")
+ } else if val == 0 {
+ fmt.Println("0 is neither negative nor positive")
+ } else {
+ fmt.Printf("You entered: %d\n", val)
+ }
+ }
+}Go 中的数组是一种特定类型且长度固定的数据结构。 它们可具有零个或多个元素,你必须在声明或初始化它们时定义大小。 此外,它们一旦创建,就无法调整大小。 鉴于这些原因,数组在 Go 程序中并不常用,但它们是切片和映射的基础。
+要在 Go 中声明数组,必须定义其元素的数据类型以及该数组可容纳的元素数目。 然后,可采用下标表示法访问数组中的每个元素,其中第一个元素是 0,最后一个元素是数组长度减去 1(长度 - 1)。
+package main
+
+import "fmt"
+
+func main() {
+ var a [3]int
+ a[1] = 10
+ fmt.Println(a[0])
+ fmt.Println(a[1])
+ fmt.Println(a[len(a)-1])
+}0
+10
+0已声明的数组访问其元素时不会遇到错误。 默认情况下,Go 会用默认数据类型初始化每个元素。 这样的话,int 的默认值为零。 不过,你可为特定位置分配值。 这就是为什么你会看到 a[1] = 10。 你可采用上述表示法来访问该元素。 另请注意,为了打印出第一个元素,我们使用了 a[0]。 为了打印出最后一个元素,我们使用了 a[len(a)-1]。 len 函数是 Go 中的内置函数,用于获取数组、切片或映射中的元素数。
声明数组时,还可使用非默认值来初始化数组。
+package main
+
+import "fmt"
+
+func main() {
+ cities := [5]string{"New York", "Paris", "Berlin", "Madrid"}
+ fmt.Println("Cities:", cities)
+}Cities: [New York Paris Berlin Madrid ]如果你不知道你将需要多少个位置,但知道你将具有多少数据,那么还有一种声明和初始化数组的方法是使用省略号 (...)
package main
+
+import "fmt"
+
+func main() {
+ cities := [...]string{"New York", "Paris", "Berlin", "Madrid"}
+ fmt.Println("Cities:", cities)
+}另一种有趣的数组初始化方法是使用省略号并仅为最新的位置指定值。
+package main
+
+import "fmt"
+
+func main() {
+ numbers := [...]int{99: -1}
+ fmt.Println("First Position:", numbers[0])
+ fmt.Println("Last Position:", numbers[99])
+ fmt.Println("Length:", len(numbers))
+}
+First Position: 0
+Last Position: -1
+Length: 100注意数组的长度是 100,因为你为第 99 个位置指定了一个值。
+如果需要处理复杂数据结构,请记住 Go 支持多维数组。
+package main
+
+import "fmt"
+
+func main() {
+ var twoD [3][5]int
+ for i := 0; i < 3; i++ {
+ for j := 0; j < 5; j++ {
+ twoD[i][j] = (i + 1) * (j + 1)
+ }
+ fmt.Println("Row", i, twoD[i])
+ }
+ fmt.Println("\nAll at once:", twoD)
+}
+Row 0 [1 2 3 4 5]
+Row 1 [2 4 6 8 10]
+Row 2 [3 6 9 12 15]
+
+All at once: [[1 2 3 4 5] [2 4 6 8 10] [3 6 9 12 15]]与数组一样,切片也是 Go 中的一种数据类型,它表示一系列类型相同的元素。 不过,与数组更重要的区别是切片的大小是动态的,不是固定的。
+切片是数组或另一个切片之上的数据结构。 我们将源数组或切片称为基础数组。 通过切片,可访问整个基础数组,也可仅访问部分元素。
+切片只有 3 个组件:
+array[0]。要声明切片,可采用与声明数组相同的方式操作。
+package main
+
+import "fmt"
+
+func main() {
+ months := []string{"January", "February", "March", "April", "May", "June", "July", "August", "September", "October", "November", "December"}
+ fmt.Println(months)
+ fmt.Println("Length:", len(months))
+ fmt.Println("Capacity:", cap(months))
+}[January February March April May June July August September October November December]
+Length: 12
+Capacity: 12Go 支持切片运算符 s[i:p],其中:
s 表示数组。i 表示指向要添加到新切片的基础数组(或另一个切片)的第一个元素的指针。 变量 i 对应于数组 array[i] 中索引位置 i 处的元素。 请记住,此元素不一定是基础数组的第一个元素 array[0]。p 表示创建新切片时要使用的基础数组中的元素数目。 变量 p 对应于可用于新切片的基础数组中的最后一个元素。 可在位置 array[i+1] 找到基础数组中位置 p 处的元素。 请注意,此元素不一定是基础数组的最后一个元素 array[len(array)-1]。package main
+
+import "fmt"
+
+func main() {
+ months := []string{"January", "February", "March", "April", "May", "June", "July", "August", "September", "October", "November", "December"}
+ quarter1 := months[0:3]
+ quarter2 := months[3:6]
+ quarter3 := months[6:9]
+ quarter4 := months[9:12]
+ fmt.Println(quarter1, len(quarter1), cap(quarter1))
+ fmt.Println(quarter2, len(quarter2), cap(quarter2))
+ fmt.Println(quarter3, len(quarter3), cap(quarter3))
+ fmt.Println(quarter4, len(quarter4), cap(quarter4))
+}[January February March] 3 12
+[April May June] 3 9
+[July August September] 3 6
+[October November December] 3 3注意,切片的长度不变,但容量不同。 我们来了解 quarter2 切片。 声明此切片时,你指出希望切片从位置编号 3 开始,最后一个元素位于位置编号 6。 切片长度为 3 个元素,但容量为 9,原因是基础数组有更多元素或位置可供使用,但对切片而言不可见。
切片容量仅指出切片可扩展的程度。 因此可从 quarter2 创建扩展切片
package main
+
+import "fmt"
+
+func main() {
+ months := []string{"January", "February", "March", "April", "May", "June", "July", "August", "September", "October", "November", "December"}
+ quarter2 := months[3:6]
+ quarter2Extended := quarter2[:4]
+ fmt.Println(quarter2, len(quarter2), cap(quarter2))
+ fmt.Println(quarter2Extended, len(quarter2Extended), cap(quarter2Extended))
+}[April May June] 3 9
+[April May June July] 4 9切片与数组之间有何不同? 第一个区别是切片的大小不是固定的,而是动态的。 创建切片后,可向其添加更多元素,这样切片就会扩展。
+Go 提供了内置函数 append(slice, element),便于你向切片添加元素。 将要修改的切片和要追加的元素作为值发送给该函数。 然后,append 函数会返回一个新的切片,将其存储在变量中。 对于要更改的切片,变量可能相同。
package main
+
+import "fmt"
+
+func main() {
+ var numbers []int
+ for i := 0; i < 10; i++ {
+ numbers = append(numbers, i)
+ fmt.Printf("%d\tcap=%d\t%v\n", i, cap(numbers), numbers)
+ }
+}0 cap=1 [0]
+1 cap=2 [0 1]
+2 cap=4 [0 1 2]
+3 cap=4 [0 1 2 3]
+4 cap=8 [0 1 2 3 4]
+5 cap=8 [0 1 2 3 4 5]
+6 cap=8 [0 1 2 3 4 5 6]
+7 cap=8 [0 1 2 3 4 5 6 7]
+8 cap=16 [0 1 2 3 4 5 6 7 8]
+9 cap=16 [0 1 2 3 4 5 6 7 8 9]当切片容量不足以容纳更多元素时,Go 的容量将翻倍。 它将新建一个具有新容量的基础数组。 无需执行任何操作即可使容量增加。 Go 会自动扩充容量。
+Go 没有内置函数用于从切片中删除元素。 可使用上述切片运算符 s[i:p] 来新建一个仅包含所需元素的切片。
package main
+
+import "fmt"
+
+func main() {
+ letters := []string{"A", "B", "C", "D", "E"}
+ remove := 2
+
+ if remove < len(letters) {
+
+ fmt.Println("Before", letters, "Remove ", letters[remove])
+
+ letters = append(letters[:remove], letters[remove+1:]...)
+
+ fmt.Println("After", letters)
+ }
+
+}Before [A B C D E] Remove C
+After [A B D E]Go 具有内置函数 copy(dst, src []Type) 用于创建切片的副本。
更改切片中的元素时,基础数组将随之更改。
+package main
+
+import "fmt"
+
+func main() {
+ letters := []string{"A", "B", "C", "D", "E"}
+ fmt.Println("Before", letters)
+
+ slice1 := letters[0:2]
+ slice2 := letters[1:4]
+
+ slice1[1] = "Z"
+
+ fmt.Println("After", letters)
+ fmt.Println("Slice2", slice2)
+}
+Before [A B C D E]
+After [A Z C D E]
+Slice2 [Z C D]创建副本则不会产生影响
+package main
+
+import "fmt"
+
+func main() {
+ letters := []string{"A", "B", "C", "D", "E"}
+ fmt.Println("Before", letters)
+
+ slice1 := letters[0:2]
+
+ slice2 := make([]string, 3)
+ copy(slice2, letters[1:4])
+
+ slice1[1] = "Z"
+
+ fmt.Println("After", letters)
+ fmt.Println("Slice2", slice2)
+}Before [A B C D E]
+After [A Z C D E]
+Slice2 [B C D]Go 中的映射是一个哈希表,是键值对的集合。 映射中所有的键都必须具有相同的类型,它们的值也是如此。 不过,可对键和值使用不同的类型。 例如,键可以是数字,值可以是字符串。 若要访问映射中的特定项,可引用该项的键。
+若要声明映射,需要使用 map 关键字。 然后,定义键和值类型,如下所示:map[T]T。
package main
+
+import "fmt"
+
+func main() {
+ studentsAge := map[string]int{
+ "john": 32,
+ "bob": 31,
+ }
+ fmt.Println(studentsAge)
+}
+map[bob:31 john:32]如果不想使用项来初始化映射,可使用内置函数 make() 在上一部分创建切片。
要添加项,无需像对切片一样使用内置函数。 映射更加简单。 你只需定义键和值即可。 如果没有键值对,则该项会添加到映射中。
+package main
+
+import "fmt"
+
+func main() {
+ studentsAge := make(map[string]int)
+ studentsAge["john"] = 32
+ studentsAge["bob"] = 31
+ fmt.Println(studentsAge)
+}若要访问映射中的项,可使用常用的下标表示法 m[key]
在映射中使用下标表示法时,即使映射中没有键,你也总会获得默认值的响应。
+package main
+
+import "fmt"
+
+func main() {
+ studentsAge := make(map[string]int)
+ studentsAge["john"] = 32
+ studentsAge["bob"] = 31
+ fmt.Println("Bob's age is", studentsAge["bob"])
+ fmt.Println("Christy's age is", studentsAge["christy"])
+}Bob's age is 31
+Christy's age is 0在很多情况下,访问映射中没有的项时 Go 不会返回错误,这是正常的。 但有时需要知道某个项是否存在。 在 Go 中,映射的下标表示法可生成两个值。 第一个是项的值。 第二个是指示键是否存在的布尔型标志。
+package main
+
+import "fmt"
+
+func main() {
+ studentsAge := make(map[string]int)
+ studentsAge["john"] = 32
+ studentsAge["bob"] = 31
+
+ age, exist := studentsAge["christy"]
+ if exist {
+ fmt.Println("Christy's age is", age)
+ } else {
+ fmt.Println("Christy's age couldn't be found")
+ }
+}
+Christy's age couldn't be found若要从映射中删除项,请使用内置函数 delete()。
package main
+
+import "fmt"
+
+func main() {
+ studentsAge := make(map[string]int)
+ studentsAge["john"] = 32
+ studentsAge["bob"] = 31
+ delete(studentsAge, "bob")
+ delete(studentsAge, "christy")
+ fmt.Println(studentsAge)
+}
+map[john:32]如果你尝试删除不存在的项,Go 不会执行 panic
+最后,让我们看看如何在映射中进行循环来以编程方式访问其所有的项。 为此,可使用基于范围的循环
+package main
+
+import (
+ "fmt"
+)
+
+func main() {
+ studentsAge := make(map[string]int)
+ studentsAge["john"] = 32
+ studentsAge["bob"] = 31
+ for name, age := range studentsAge {
+ fmt.Printf("%s\t%d\n", name, age)
+ }
+}
+john 32
+bob 31range 会首先生成项的键,然后再生成该项的值。 可使用 _ 变量忽略其中任何一个
有时,你需要在一个结构中表示字段的集合。在 Go 中,可使用结构将可能构成记录的不同字段组合在一起。Go 中的结构也是一种数据结构,它可包含零个或多个任意类型的字段,并将它们表示为单个实体。
+若要声明结构,需要使用 struct 关键字,还要使用希望新的数据类型具有的字段及其类型的列表。
若要访问结构的各个字段,可使用点表示法 (.) 做到这一点
可使用 & 运算符生成指向结构的指针以修改结构中的项
package main
+
+import "fmt"
+
+type Employee struct {
+ ID int
+ FirstName string
+ LastName string
+ Address string
+}
+
+func main() {
+ employee := Employee{LastName: "Doe", FirstName: "John"}
+ fmt.Println(employee)
+ employeeCopy := &employee
+ employeeCopy.FirstName = "David"
+ fmt.Println(employee)
+}{0 John Doe }
+{0 David Doe }通过 Go 中的结构,可将某结构嵌入到另一结构中。
+package main
+
+import "fmt"
+
+type Person struct {
+ ID int
+ FirstName string
+ LastName string
+ Address string
+}
+
+type Employee struct {
+ Person
+ ManagerID int
+}
+
+type Contractor struct {
+ Person
+ CompanyID int
+}
+
+func main() {
+ employee := Employee{
+ Person: Person{
+ FirstName: "John",
+ },
+ }
+ employee.LastName = "Doe"
+ employee.ManagerID = 2
+ fmt.Println(employee)
+}
+{{0 John Doe } 2}最后,可使用结构来对 JSON 中的数据进行编码和解码。 Go 对 JSON 格式提供很好的支持,该格式已包含在标准库包中。
+你还可执行一些操作,例如重命名结构中字段的名称。 例如,假设你不希望 JSON 输出显示 FirstName 而只显示 name,或者忽略空字段, 可使用如下例所示的字段标记:
然后,若要将结构编码为 JSON,请使用 json.Marshal 函数。 若要将 JSON 字符串解码为数据结构,请使用 json.Unmarshal 函数。 下例将所有内容组合在一起,将员工数组编码为 JSON,并将输出解码为新的变量:
package main
+
+import (
+ "encoding/json"
+ "fmt"
+)
+
+type Person struct {
+ ID int
+ FirstName string `json:"name"`
+ LastName string
+ Address string `json:"address,omitempty"`
+}
+
+type Employee struct {
+ Person
+ ManagerID int
+}
+
+type Contractor struct {
+ Person
+ CompanyID int
+}
+
+func main() {
+ employees := []Employee{
+ {
+ Person: Person{
+ LastName: "Doe", FirstName: "John",
+ },
+ },
+ {
+ Person: Person{
+ LastName: "Campbell", FirstName: "David",
+ },
+ },
+ }
+
+ data, _ := json.Marshal(employees)
+ fmt.Printf("%s\n", data)
+
+ var decoded []Employee
+ json.Unmarshal(data, &decoded)
+ fmt.Printf("%v\n", decoded)
+}[{"ID":0,"name":"John","LastName":"Doe","ManagerID":0},{"ID":0,"name":"David","LastName":"Campbell","ManagerID":0}]
+[{{0 John Doe } 0} {{0 David Campbell } 0}]在这第一个挑战中,你将编写一个程序来计算某个数字的斐波纳契数列。 这是在学习新语言时要编码的一个典型的编程练习。 你将编写一个函数,它返回一个包含按斐波纳契数列排列的所有数字的切片,而这些数字是通过根据用户输入的大于 2 的数字计算得到的。 让我们假设小于 2 的数字会导致错误,并返回一个 nil 切片。
请记住,斐波那契数列是一个数字列表,其中每个数字是前两个斐波那契数字之和。 例如,数字 6 的序列是 1,1,2,3,5,8,数字 7 的序列是 1,1,2,3,5,8,13,数字 8 的序列是 1,1,2,3,5,8,13,21,以此类推。
package main
+
+import "fmt"
+
+func fibonacci(n int) []int {
+ if n < 2 {
+ return make([]int, 0)
+ }
+
+ nums := make([]int, n)
+ nums[0], nums[1] = 1, 1
+
+ for i := 2; i < n; i++ {
+ nums[i] = nums[i-1] + nums[i-2]
+ }
+
+ return nums
+}
+
+func main() {
+ var num int
+
+ fmt.Print("What's the Fibonacci sequence you want? ")
+ fmt.Scanln(&num)
+ fmt.Println("The Fibonacci sequence is:", fibonacci(num))
+}
+编写一个程序来转换罗马数字(例如将 MCLX 转换成 1,160)。 使用映射加载要用于将字符串字符转换为数字的基本罗马数字。 例如,M 将是映射中的键,其值将为 1000。 使用以下字符串字符映射表列表:
M => 1000D => 500C => 100L => 50X => 10V => 5I => 1如果用户输入的字母与上述列表中的不同,则打印一个错误。
+请记住在有些情况下,较小的数字会排在较大的数字前面,因此不能仅仅将数字相加。 例如,数字 MCM 应打印为 1,900。
package main
+
+import (
+ "fmt"
+)
+
+func romanToArabic(numeral string) int {
+ romanMap := map[rune]int{
+ 'M': 1000,
+ 'D': 500,
+ 'C': 100,
+ 'L': 50,
+ 'X': 10,
+ 'V': 5,
+ 'I': 1,
+ }
+
+ arabicVals := make([]int, len(numeral)+1)
+
+ for index, digit := range numeral {
+ if val, present := romanMap[digit]; present {
+ arabicVals[index] = val
+ } else {
+ fmt.Printf("Error: The roman numeral %s has a bad digit: %c\n", numeral, digit)
+ return 0
+ }
+ }
+
+ total := 0
+
+ for index := 0; index < len(numeral); index++ {
+ if arabicVals[index] < arabicVals[index+1] {
+ arabicVals[index] = -arabicVals[index]
+ }
+ total += arabicVals[index]
+ }
+
+ return total
+}
+func main() {
+ fmt.Println("MCLX is", romanToArabic("MCLX"))
+ fmt.Println("MCMXCIX is ", romanToArabic("MCMXCIX"))
+ fmt.Println("MCMZ is", romanToArabic("MCMZ"))
+}
+编写程序时,需要考虑程序失败的各种方式,并且需要管理失败。 无需让用户看到冗长而混乱的堆栈跟踪错误。 让他们看到有关错误的有意义的信息更好。 正如你所看到的,Go 具有 panic 和 recover 之类的内置函数来管理程序中的异常或意外行为。 但错误是已知的失败,你的程序应该可以处理它们。
Go 的错误处理方法只是一种只需要 if 和 return 语句的控制流机制。 例如,在调用函数以从 employee 对象获取信息时,可能需要了解该员工是否存在。 Go 处理此类预期错误的一贯方法如下所示:
employee, err := getInformation(1000)
+if err != nil {
+ // Something is wrong. Do something.
+}注意 getInformation 函数返回了 employee 结构,还返回了错误作为第二个值。 该错误可能为 nil。 如果错误为 nil,则表示成功。 如果错误不是 nil,则表示失败。 非 nil 错误附带一条错误消息,你可以打印该错误消息,也可以记录该消息(更可取)。
当函数返回错误时,该错误通常是最后一个返回值。 正如上一部分所介绍的那样,调用方负责检查是否存在错误并处理错误。
+你可能还需要在传播错误之前添加更多信息。 为此,可以使用 fmt.Errorf() 函数,该函数与我们之前看到的函数类似,但它返回一个错误。 例如,你可以向错误添加更多上下文,但仍返回原始错误,如下所示:
func getInformation(id int) (*Employee, error) {
+ employee, err := apiCallEmployee(1000)
+ if err != nil {
+ return nil, fmt.Errorf("got an error when getting the employee information: %v", err)
+ }
+ return employee, nil
+}另一种策略是在错误为暂时性错误时运行重试逻辑。 例如,可以使用重试策略调用函数三次并等待两秒钟
+func getInformation(id int) (*Employee, error) {
+ for tries := 0; tries < 3; tries++ {
+ employee, err := apiCallEmployee(1000)
+ if err == nil {
+ return employee, nil
+ }
+
+ fmt.Println("Server is not responding, retrying ...")
+ time.Sleep(time.Second * 2)
+ }
+
+ return nil, fmt.Errorf("server has failed to respond to get the employee information")
+}有时错误消息数会增加,你需要维持秩序。 或者,你可能需要为要重用的常见错误消息创建一个库。 在 Go 中,你可以使用 errors.New() 函数创建错误并在若干部分中重复使用这些错误,如下所示:
var ErrNotFound = errors.New("Employee not found!")
+
+func getInformation(id int) (*Employee, error) {
+ if id != 1001 {
+ return nil, ErrNotFound
+ }
+
+ employee := Employee{LastName: "Doe", FirstName: "John"}
+ return &employee, nil
+}最后,如果你具有错误变量,则在处理调用方函数中的错误时可以更具体。 errors.Is() 函数允许你比较获得的错误的类型
employee, err := getInformation(1000)
+if errors.Is(err, ErrNotFound) {
+ fmt.Printf("NOT FOUND: %v\n", err)
+} else {
+ fmt.Print(employee)
+}在 Go 中处理错误时,请记住下面一些推荐做法:
+日志在程序中发挥着重要作用,因为它们是在出现问题时你可以检查的信息源。 通常,发生错误时,最终用户只会看到一条消息,指示程序出现问题。 从开发人员的角度来看,我们需要简单错误消息以外的更多信息。 这主要是因为我们想要再现该问题以编写适当的修补程序。
+log 包对于初学者,Go 提供了一个用于处理日志的简单标准包。 可以像使用 fmt 包一样使用此包。 该标准包不提供日志级别,且不允许为每个包配置单独的记录器。 如果需要编写更复杂的日志记录配置,可以使用记录框架执行此操作。
package main
+
+import (
+ "log"
+)
+
+func main() {
+ log.Print("Hey, I'm a log!")
+}
+2022/10/05 15:37:16 Hey, I'm a log!默认情况下,log.Print() 函数将日期和时间添加为日志消息的前缀。 你可以通过使用 fmt.Print() 获得相同的行为,但使用 log 包还能执行其他操作,例如将日志发送到文件。 稍后我们将详细介绍 log 包功能。
你可以使用 log.Fatal() 函数记录错误并结束程序,就像使用 os.Exit(1) 一样。
package main
+
+import (
+ "fmt"
+ "log"
+)
+
+func main() {
+ log.Fatal("Hey, I'm an error log!")
+ fmt.Print("Can you see me?")
+}
+2022/10/05 15:38:56 Hey, I'm an error log!
+exit status 1使用 log.Panic() 函数时会出现类似行为,但是还会获取错误堆栈跟踪。
另一重要函数是 log.SetPrefix()。 可使用它向程序的日志消息添加前缀。
package main
+
+import (
+ "log"
+)
+
+func main() {
+ log.SetPrefix("main(): ")
+ log.Print("Hey, I'm a log!")
+ log.Fatal("Hey, I'm an error log!")
+}
+main(): 2022/10/05 15:40:36 Hey, I'm a log!
+main(): 2022/10/05 15:40:36 Hey, I'm an error log!
+exit status 1除了将日志打印到控制台之外,你可能还希望将日志发送到文件,以便稍后或实时处理这些日志。
+package main
+
+import (
+ "log"
+ "os"
+)
+
+func main() {
+ file, err := os.OpenFile("info.log", os.O_CREATE|os.O_APPEND|os.O_WRONLY, 0644)
+ if err != nil {
+ log.Fatal(err)
+ }
+
+ defer file.Close()
+
+ log.SetOutput(file)
+ log.Print("Hey, I'm a log!")
+}最后,可能有 log 包中的函数不足以处理问题的情况。 你可能会发现,使用记录框架而不编写自己的库很有用。 Go 的几个记录框架有 Logrus、zerolog、zap 和 Apex。
面向对象编程 (OOP) 是一种广受欢迎的编程模式,大部分编程语言都支持(至少部分支持)。 Go 是其中一种语言,但它并不完全支持所有 OOP 原则。
+Go 中的方法是一种特殊类型的函数,但存在一个简单的区别:你必须在函数名称之前加入一个额外的参数。 此附加参数称为 接收方 。
+如你希望分组函数并将其绑定到自定义类型,则方法非常有用。 Go 中的这一方法类似于在其他编程语言中创建类,因为它允许你实现面向对象编程 (OOP) 模型中的某些功能,例如嵌入、重载和封装。
+到目前为止,你仅将结构用作可在 Go 中创建的另一种自定义类型。 在此模块中你将了解到,通过添加方法你可以将行为添加到你所创建的结构中。
+在声明方法之前,必须先创建结构。 假设你想要创建一个几何包,并决定创建一个名为 triangle 的三角形结构作为此程序包的一个组成部分。 然后,你需要使用一种方法来计算此三角形的周长。 你可以在 Go 中将其表示为:
type triangle struct {
+ size int
+}
+
+func (t triangle) perimeter() int {
+ return t.size * 3
+}结构看起来像普通结构,但 perimeter() 函数在函数名称之前有一个类型 triangle 的额外参数。 也就是说,在使用结构时,你可以按如下方式调用函数:
func main() {
+ t := triangle{3}
+ fmt.Println("Perimeter:", t.perimeter())
+}如果尝试按平常的方式调用 perimeter() 函数,则此函数将无法正常工作,因为此函数的签名表明它需要接收方。 正因如此,调用此方法的唯一方式是先声明一个结构,获取此方法的访问权限。 这也意味着,只要此方法属于不同的结构,你甚至可以为其指定相同的名称。 例如,你可以使用 perimeter() 函数声明一个 square 结构,具体如下所示:
package main
+
+import "fmt"
+
+type triangle struct {
+ size int
+}
+
+type square struct {
+ size int
+}
+
+func (t triangle) perimeter() int {
+ return t.size * 3
+}
+
+func (s square) perimeter() int {
+ return s.size * 4
+}
+
+func main() {
+ t := triangle{3}
+ s := square{4}
+ fmt.Println("Perimeter (triangle):", t.perimeter())
+ fmt.Println("Perimeter (square):", s.perimeter())
+}
+Perimeter (triangle): 9
+Perimeter (square): 16通过对 perimeter() 函数的两次调用,编译器将根据接收方类型来确定要调用的函数。 这有助于在各程序包之间保持函数的一致性和名称的简短,并避免将包名称作为前缀。
有时,方法需要更新变量,或者,如果参数太大,则可能需要避免复制它。 在遇到此类情况时,你需要使用指针传递变量的地址。 在之前的模块中,当我们在讨论指针时提到,每次在 Go 中调用函数时,Go 都会复制每个参数值以便使用。
+如果你需要更新方法中的接收方变量,也会执行相同的行为。 例如,假设你要创建一个新方法以使三角形的大小增加一倍。 你需要在接收方变量中使用指针,具体如下所示:
+func (t *triangle) doubleSize() {
+ t.size *= 2
+}如果方法仅可访问接收方的信息,则不需要在接收方变量中使用指针。 但是,依据 Go 的约定,如果结构的任何方法具有指针接收方,则此结构的所有方法都必须具有指针接收方,即使某个方法不需要也是如此。
+方法的一个关键方面在于,需要为任何类型定义方法,而不只是针对自定义类型(如结构)进行定义。 但是,你不能通过属于其他包的类型来定义结构。 因此,不能在基本类型(如 string)上创建方法。
尽管如此,你仍然可以利用一点技巧,基于基本类型创建自定义类型,然后将其用作基本类型。 例如,假设你要创建一个方法,以将字符串从小写字母转换为大写字母。 你可以按如下所示写入方法:
+package main
+
+import (
+ "fmt"
+ "strings"
+)
+
+type upperstring string
+
+func (s upperstring) Upper() string {
+ return strings.ToUpper(string(s))
+}
+
+func main() {
+ s := upperstring("Learning Go!")
+ fmt.Println(s)
+ fmt.Println(s.Upper())
+}
+在之前的模块中,您已了解到可以在一个结构中使用属性,并将同一属性嵌入另一个结构中。 也就是说,可以重用来自一个结构的属性,以避免出现重复并保持代码库的一致性。 类似的观点也适用于方法。 即使接收方不同,也可以调用已嵌入结构的方法。
+例如,假设你想要创建一个带有逻辑的新三角形结构,以加入颜色。 此外,你还希望继续使用之前声明的三角形结构。 然后,你可以初始化 coloredTriangle 结构,并从 triangle 结构调用 perimeter() 方法(甚至访问其字段)
package main
+
+import "fmt"
+
+type triangle struct {
+ size int
+}
+
+type coloredTriangle struct {
+ triangle
+ color string
+}
+
+func (t triangle) perimeter() int {
+ return t.size * 3
+}
+
+func main() {
+ t := coloredTriangle{triangle{3}, "blue"}
+ fmt.Println("Size:", t.size)
+ fmt.Println("Perimeter", t.perimeter())
+}
+Size: 3
+Perimeter 9让我们回到之前讨论过的 triangle 示例。 如果要在 coloredTriangle 结构中更改 perimeter() 方法的实现,会发生什么情况? 不能存在两个同名的函数。 但是,因为方法需要额外参数(接收方),所以,你可以使用一个同名的方法,只要此方法专门用于要使用的接收方即可。 这就是重载方法的方式。
如果你仍需要从 triangle 结构调用 perimeter() 方法,则可通过对其进行显示访问来执行此操作
package main
+
+import "fmt"
+
+type triangle struct {
+ size int
+}
+
+type coloredTriangle struct {
+ triangle
+ color string
+}
+
+func (t coloredTriangle) perimeter() int {
+ return t.size * 3 * 2
+}
+
+func (t triangle) perimeter() int {
+ return t.size * 3
+}
+
+func main() {
+ t := coloredTriangle{triangle{3}, "blue"}
+ fmt.Println("Size:", t.size)
+ fmt.Println("Perimeter (colored)", t.perimeter())
+ fmt.Println("Perimeter (normal)", t.triangle.perimeter())
+}
+“封装”表示对象的发送方(客户端)无法访问某个方法。 通常,在其他编程语言中,你会将 private 或 public 关键字放在方法名称之前。 在 Go 中,只需使用大写标识符,即可公开方法,使用非大写的标识符将方法设为私有方法。
Go 中的封装仅在程序包之间有效。 换句话说,你只能隐藏来自其他程序包的实现详细信息,而不能隐藏程序包本身。
+package geometry
+
+type Triangle struct {
+ size int
+}
+
+func (t *Triangle) doubleSize() {
+ t.size *= 2
+}
+
+func (t *Triangle) SetSize(size int) {
+ t.size = size
+}
+
+func (t *Triangle) Perimeter() int {
+ t.doubleSize()
+ return t.size * 3
+}package main
+
+import (
+ "fmt"
+ "geometry"
+)
+
+func main() {
+ t := geometry.Triangle{}
+ t.SetSize(3)
+ fmt.Println("Perimeter", t.Perimeter())
+}
+Go 中的接口是一种用于表示其他类型的行为的数据类型。 接口类似于对象应满足的蓝图或协定。 在你使用接口时,你的基本代码将变得更加灵活、适应性更强,因为你编写的代码未绑定到特定的实现。 因此,你可以快速扩展程序的功能。
+与其他编程语言中的接口不同,Go 中的接口是满足隐式实现的。 Go 并不提供用于实现接口的关键字,因此,如果你之前使用的是其他编程语言中的接口,但不熟悉 Go,那么此概念可能会造成混淆。
+Go 中的接口是一种抽象类型,只包括具体类型必须拥有或实现的方法。 正因如此,我们说接口类似于蓝图。
+假设你希望在几何包中创建一个接口来指示形状必须实现的方法。 你可以按如下所示定义接口:
+type Shape interface {
+ Perimeter() float64
+ Area() float64
+}Shape 接口表示你想要考虑 Shape 的任何类型都需要同时具有 Perimeter() 和 Area() 方法。 例如,在创建 Square 结构时,它必须实现两种方法,而不是仅实现一种。 另外,请注意接口不包含这些方法的实现细节(例如,用于计算某个形状的周长和面积)。 接口仅表示一种协定。 三角形、圆圈和正方形等形状有不同的计算面积和周长方式。
正如上文所讨论的内容,你没有用于实现接口的关键字。 当 Go 中的接口具有接口所需的所有方法时,则满足按类型的隐式实现。
+让我们创建一个 Square 结构,此结构具有 Shape 接口中的两个方法
type Square struct {
+ size float64
+}
+
+func (s Square) Area() float64 {
+ return s.size * s.size
+}
+
+func (s Square) Perimeter() float64 {
+ return s.size * 4
+}请注意 Square 结构的方法签名与 Shape 接口的签名的匹配方式。
func main() {
+ var s Shape = Square{3}
+ fmt.Printf("%T\n", s)
+ fmt.Println("Area: ", s.Area())
+ fmt.Println("Perimeter:", s.Perimeter())
+}main.Square
+Area: 9
+Perimeter: 12此时,无论你是否使用接口,都没有任何区别。 接下来,让我们创建另一种类型,如 Circle,然后进行相同的操作:
package main
+
+import (
+ "fmt"
+ "math"
+)
+
+type Shape interface {
+ Perimeter() float64
+ Area() float64
+}
+
+type Square struct {
+ size float64
+}
+
+func (s Square) Area() float64 {
+ return s.size * s.size
+}
+
+func (s Square) Perimeter() float64 {
+ return s.size * 4
+}
+
+type Circle struct {
+ radius float64
+}
+
+func (c Circle) Area() float64 {
+ return math.Pi * c.radius * c.radius
+}
+
+func (c Circle) Perimeter() float64 {
+ return 2 * math.Pi * c.radius
+}
+
+func printInformation(s Shape) {
+ fmt.Printf("%T\n", s)
+ fmt.Println("Area: ", s.Area())
+ fmt.Println("Perimeter:", s.Perimeter())
+ fmt.Println()
+}
+
+func main() {
+ var s Shape = Square{3}
+ printInformation(s)
+
+ c := Circle{6}
+ printInformation(c)
+}
+main.Square
+Area: 9
+Perimeter: 12
+
+main.Circle
+Area: 113.09733552923255
+Perimeter: 37.69911184307752使用接口的优点在于,对于 Shape的每个新类型或实现,printInformation 函数都不需要更改。 正如之前所述,当你使用接口时,代码会变得更灵活、更容易扩展。
假设你具有以下代码,并且希望通过编写负责处理某些数据的 Writer 方法的自定义实现来扩展其功能。
通过使用以下代码,你可以创建一个程序,此程序使用 GitHub API 从 Microsoft 获取三个存储库:
+package main
+
+import (
+ "fmt"
+ "io"
+ "net/http"
+ "os"
+)
+
+func main() {
+ resp, err := http.Get("https://api.github.com/users/microsoft/repos?page=15&per_page=5")
+ if err != nil {
+ fmt.Println("Error:", err)
+ os.Exit(1)
+ }
+
+ io.Copy(os.Stdout, resp.Body)
+}改写后:
+package main
+
+import (
+ "encoding/json"
+ "fmt"
+ "io"
+ "net/http"
+ "os"
+)
+
+type GitHubResponse []struct {
+ FullName string `json:"full_name"`
+}
+
+type customWriter struct{}
+
+func (w customWriter) Write(p []byte) (n int, err error) {
+ var resp GitHubResponse
+ json.Unmarshal(p, &resp)
+ for _, r := range resp {
+ fmt.Println(r.FullName)
+ }
+ return len(p), nil
+}
+
+func main() {
+ resp, err := http.Get("https://api.github.com/users/microsoft/repos?page=15&per_page=5")
+ if err != nil {
+ fmt.Println("Error:", err)
+ os.Exit(1)
+ }
+
+ writer := customWriter{}
+ io.Copy(writer, resp.Body)
+}
+最后,我们一起来探讨接口的另一种用例,如果你要创建服务器 API,你可能会发现此用例非常实用。 编写 Web 服务器的常用方式是使用 net/http 程序包中的 http.Handler 接口
package main
+
+import (
+ "fmt"
+ "log"
+ "net/http"
+)
+
+// 创建 float32 类型的自定义类型,然后编写 String() 方法的自定义实现
+type dollars float32
+
+func (d dollars) String() string {
+ return fmt.Sprintf("$%.2f", d)
+}
+
+// 写入 http.Handler 可使用的 ServeHTTP 方法的实现。
+
+type database map[string]dollars
+
+// 通过使用 database 类型作为接收方来写入 ServeHTTP 方法。
+func (db database) ServeHTTP(w http.ResponseWriter, req *http.Request) {
+ for item, price := range db {
+ fmt.Fprintf(w, "%s: %s\n", item, price)
+ }
+}
+
+// 在 main() 函数中,我们将 database 类型实例化,并使用一些值对其进行初始化。 我们使用 http.ListenAndServe 函数启动了 HTTP 服务器,在其中定义了服务器地址,包括要使用的端口和实现 ServerHTTP 方法自定义版本的 db 对象。
+func main() {
+ db := database{"Go T-Shirt": 25, "Go Jacket": 55}
+ log.Fatal(http.ListenAndServe("localhost:8000", db))
+}编写一个程序,此程序使用自定义程序包来管理在线商店的帐户。 你的挑战包括以下四个要素:
+Account 的自定义类型,此类型包含帐户所有者的名字和姓氏。 此类型还必须加入 ChangeName 的功能。Employee 的自定义类型,此类型包含用于将贷方数额存储为类型 float64 并嵌入 Account 对象的变量。 类型还必须包含 AddCredits、RemoveCredits 和 CheckCredits 的功能。 你需要展示你可以通过 Employee 对象更改帐户名称。Account 对象,以便按包含名字和姓氏的格式打印 Employee 名称。package main
+
+import (
+ "errors"
+ "fmt"
+)
+
+type Account struct {
+ firstname string
+ lastname string
+}
+
+func (a *Account) ChangeName(afterfirstname string) {
+ a.firstname = afterfirstname
+}
+
+type Employee struct {
+ Account
+ credit float64
+}
+
+func (e Employee) String() string {
+ return fmt.Sprintf("Firstname:%s,Lastname:%s,Credit:%.2f\n", e.firstname, e.lastname, e.credit)
+}
+
+func CreateEmployee(firstname, lastname string, credit float64) (*Employee, error) {
+ return &Employee{Account{firstname, lastname}, credit}, nil
+}
+
+func (e *Employee) AddCredits(amount float64) (float64, error) {
+ if amount > 0.0 {
+ e.credit += amount
+ return e.credit, nil
+ }
+ return 0.0, errors.New("invalid amount")
+}
+
+func (e *Employee) RemoveCredits(amount float64) (float64, error) {
+ if e.credit-amount < 0 {
+ return 0.0, errors.New("too much")
+ }
+ if amount < 0 {
+ return 0.0, errors.New("invalid amount")
+ }
+ e.credit -= amount
+ return e.credit, nil
+}
+
+func (e Employee) CheckCredits() float64 {
+ return e.credit
+}
+
+func main() {
+ bruce, _ := CreateEmployee("Bruce", "Lee", 500)
+ fmt.Println(bruce.CheckCredits())
+ credits, err := bruce.AddCredits(250)
+ if err != nil {
+ fmt.Println("Error:", err)
+ } else {
+ fmt.Println("New Credits Balance = ", credits)
+ }
+
+ _, err = bruce.RemoveCredits(2500)
+ if err != nil {
+ fmt.Println("Can't withdraw or overdrawn!", err)
+ }
+
+ bruce.ChangeName("Mark")
+
+ fmt.Println(bruce)
+}
+并发是独立活动的组合,就像 Web 服务器虽然同时处理多个用户请求,但它是自主运行的。 并发在当今的许多程序中都存在。 Web 服务器就是一个例子,但你也能看到,在批量处理大量数据时也需要使用并发。
+Go 有两种编写并发程序的样式。 一种是在其他语言中通过线程实现的传统样式。
+通常,编写并发程序时最大的问题是在进程之间共享数据。 Go 采用不同于其他编程语言的通信方式,因为 Go 是通过 channel 来回传递数据的。 这意味着只有一个活动 (goroutine) 有权访问数据,设计上不存在争用条件。 学完本模块中的 goroutine 和 channel 之后,你将更好地理解 Go 的并发方法。
+可以使用下面的标语来概括 Go 的方法:“不是通过共享内存通信,而是通过通信共享内存。”
+goroutine 是轻量线程中的并发活动,而不是在操作系统中进行的传统活动。 假设你有一个写入输出的程序和另一个计算两个数字相加的函数。 一个并发程序可以有数个 goroutine 同时调用这两个函数。
+我们可以说,程序执行的第一个 goroutine 是 main() 函数。 如果要创建其他 goroutine,则必须在调用该函数之前使用 go 关键字
func main(){
+ login()
+ go launch()
+}许多程序喜欢使用匿名函数来创建 goroutine
+func main(){
+ login()
+ go func() {
+ launch()
+ }()
+}由于我们只想将重点放在并发部分,因此我们使用现有程序来检查 API 终结点是否响应。
+串行程序:
+package main
+
+import (
+ "fmt"
+ "net/http"
+ "time"
+)
+
+func main() {
+ start := time.Now()
+
+ apis := []string{
+ "https://management.azure.com",
+ "https://dev.azure.com",
+ "https://api.github.com",
+ "https://outlook.office.com/",
+ "https://api.somewhereintheinternet.com/",
+ "https://graph.microsoft.com",
+ }
+
+ for _, api := range apis {
+ _, err := http.Get(api)
+ if err != nil {
+ fmt.Printf("ERROR: %s is down!\n", api)
+ continue
+ }
+
+ fmt.Printf("SUCCESS: %s is up and running!\n", api)
+ }
+
+ elapsed := time.Since(start)
+ fmt.Printf("Done! It took %v seconds!\n", elapsed.Seconds())
+}
+SUCCESS: https://management.azure.com is up and running!
+SUCCESS: https://dev.azure.com is up and running!
+SUCCESS: https://api.github.com is up and running!
+SUCCESS: https://outlook.office.com/ is up and running!
+ERROR: https://api.somewhereintheinternet.com/ is down!
+SUCCESS: https://graph.microsoft.com is up and running!
+Done! It took 5.163787068 seconds!同时检查所有站点?我们需要并发运行的代码部分是向站点进行 HTTP 调用的部分。 换句话说,我们需要为程序要检查的每个 API 创建一个 goroutine。为了创建 goroutine,我们需要在调用函数前使用 go 关键字。
首先创建一个新函数:
+func checkAPI(api string) {
+ _, err := http.Get(api)
+ if err != nil {
+ fmt.Printf("ERROR: %s is down!\n", api)
+ return
+ }
+
+ fmt.Printf("SUCCESS: %s is up and running!\n", api)
+}修改 main() 函数中的代码,为每个 API 创建一个 goroutine
for _, api := range apis {
+ go checkAPI(api)
+}Done! It took 3.42e-05 seconds!即使看起来 checkAPI 函数没有运行,它实际上是在运行。 它只是没有时间完成。
添加 time.Sleep(3 * time.Second)
ERROR: https://api.somewhereintheinternet.com/ is down!
+SUCCESS: https://api.github.com is up and running!
+SUCCESS: https://management.azure.com is up and running!
+SUCCESS: https://dev.azure.com is up and running!
+SUCCESS: https://outlook.office.com/ is up and running!
+SUCCESS: https://graph.microsoft.com is up and running!
+Done! It took 3.001536063 seconds!Go 中的 channel 是 goroutine 之间的通信机制。 这就是为什么我们之前说过 Go 实现并发的方式是:“不是通过共享内存通信,而是通过通信共享内存。”需要将值从一个 goroutine 发送到另一个时,可以使用通道。
+由于 channel 是发送和接收数据的通信机制,因此它也有类型之分。 这意味着你只能发送 channel 支持的数据类型。 除使用关键字 chan 作为 channel 的数据类型外,还需指定将通过 channel 传递的数据类型,如 int 类型。
每次声明一个 channel 或希望在函数中指定一个 channel 作为参数时,都需要使用 chan <type>,如 chan int。 要创建 channel,需使用内置的 make() 函数,如下所示:
ch := make(chan int)一个 channel 可以执行两项操作:发送数据和接收数据。 若要指定 channel 具有的操作类型,需要使用 channel 运算符 <-。 此外,在 channel 中发送数据和接收数据属于阻止操作。
如果希望 channel 仅发送数据,则必须在 channel 之后使用 <- 运算符。 如果希望 channel 接收数据,则必须在 channel 之前使用 <- 运算符
ch <- x // sends (or write) x through channel ch
+x = <-ch // x receives (or reads) data sent to the channel ch
+<-ch // receives data, but the result is discarded可在 channel 中执行的另一项操作是关闭 channel
+close(ch)关闭 channel 时,你希望数据将不再在该 channel 中发送。 如果试图将数据发送到已关闭的 channel,则程序将发生严重错误。 如果试图通过已关闭的 channel 接收数据,则可以读取发送的所有数据。 随后的每次“读取”都将返回一个零值。
+使用 channel 来删除睡眠功能并稍做清理:
+package main
+
+import (
+ "fmt"
+ "net/http"
+ "time"
+)
+
+// 通过 channel 发送该消息,而不是在 checkAPI 函数中打印结果
+func checkAPI(api string, ch chan string) {
+ _, err := http.Get(api)
+ if err != nil {
+ ch <- fmt.Sprintf("ERROR: %s is down!\n", api)
+ return
+ }
+ ch <- fmt.Sprintf("SUCCESS: %s is up and running!\n", api)
+}
+
+func main() {
+ // 创建channel
+ ch := make(chan string)
+
+ start := time.Now()
+
+ apis := []string{
+ "https://management.azure.com",
+ "https://dev.azure.com",
+ "https://api.github.com",
+ "https://outlook.office.com/",
+ "https://api.somewhereintheinternet.com/",
+ "https://graph.microsoft.com",
+ }
+
+ for _, api := range apis {
+ go checkAPI(api, ch)
+ }
+ fmt.Print(<-ch)
+
+ elapsed := time.Since(start)
+ fmt.Printf("Done! It took %v seconds!\n", elapsed.Seconds())
+}
+ERROR: https://api.somewhereintheinternet.com/ is down!
+Done! It took 0.088759104 seconds!但是事实上并没有实现功能
+使用 make() 函数创建 channel 时,会创建一个无缓冲 channel,这是默认行为。 无缓冲 channel 会阻止发送操作,直到有人准备好接收数据。 这就是为什么我们之前说发送和接收都属于阻止操作。 这也是上面的程序在收到第一条消息后立即停止的原因。
我们可以说 fmt.Print(<-ch) 会阻止程序,因为它从 channel 读取,并等待一些数据到达。 一旦有任何数据到达,它就会继续下一行,然后程序完成。
其他 goroutine 发生了什么? 它们仍在运行,但都没有在侦听。 而且,由于程序提前完成,一些 goroutine 无法发送数据。
+读取数据和接收数据都属于阻止操作
+要解决此问题,只需更改循环的代码,然后只接收确定要发送的数据
+package main
+
+import (
+ "fmt"
+ "net/http"
+ "time"
+)
+
+// 通过 channel 发送该消息,而不是在 checkAPI 函数中打印结果
+func checkAPI(api string, ch chan string) {
+ _, err := http.Get(api)
+ if err != nil {
+ ch <- fmt.Sprintf("ERROR: %s is down!\n", api)
+ return
+ }
+ ch <- fmt.Sprintf("SUCCESS: %s is up and running!\n", api)
+}
+
+func main() {
+ // 创建channel
+ ch := make(chan string)
+
+ start := time.Now()
+
+ apis := []string{
+ "https://management.azure.com",
+ "https://dev.azure.com",
+ "https://api.github.com",
+ "https://outlook.office.com/",
+ "https://api.somewhereintheinternet.com/",
+ "https://graph.microsoft.com",
+ }
+
+ for _, api := range apis {
+ go checkAPI(api, ch)
+ }
+ for i := 0; i < len(apis); i++ {
+ fmt.Print(<-ch)
+ }
+
+ elapsed := time.Since(start)
+ fmt.Printf("Done! It took %v seconds!\n", elapsed.Seconds())
+}
+ERROR: https://api.somewhereintheinternet.com/ is down!
+SUCCESS: https://api.github.com is up and running!
+SUCCESS: https://management.azure.com is up and running!
+SUCCESS: https://graph.microsoft.com is up and running!
+SUCCESS: https://dev.azure.com is up and running!
+SUCCESS: https://outlook.office.com/ is up and running!
+Done! It took 1.029620196 seconds!无缓冲 channel 在同步发送和接收操作。 即使使用并发,通信也是同步的。
+默认情况下 channel 是无缓冲行为。 这意味着只有存在接收操作时,它们才接受发送操作。 否则,程序将永久被阻止等待。
+有时需要在 goroutine 之间进行此类同步。 但是,有时你可能只需要实现并发,而不需要限制 goroutine 之间的通信方式。
+有缓冲 channel 在不阻止程序的情况下发送和接收数据,因为有缓冲 channel 的行为类似于队列。 创建 channel 时,可以限制此队列的大小
+package main
+
+import (
+ "fmt"
+)
+
+func send(ch chan string, message string) {
+ ch <- message
+}
+
+func main() {
+ size := 4
+ ch := make(chan string, size)
+ send(ch, "one")
+ send(ch, "two")
+ send(ch, "three")
+ send(ch, "four")
+ fmt.Println("All data sent to the channel ...")
+
+ for i := 0; i < size; i++ {
+ fmt.Println(<-ch)
+ }
+
+ fmt.Println("Done!")
+}
+All data sent to the channel ...
+one
+two
+three
+four
+Done!channel 与 goroutine 有着紧密的联系。 如果没有另一个 goroutine 从 channel 接收数据,则整个程序可能会永久处于被阻止状态。
+func main() {
+ size := 2
+ ch := make(chan string, size)
+ send(ch, "one")
+ send(ch, "two")
+ go send(ch, "three")
+ go send(ch, "four")
+ fmt.Println("All data sent to the channel ...")
+
+ for i := 0; i < 4; i++ {
+ fmt.Println(<-ch)
+ }
+
+ fmt.Println("Done!")
+}现在,你可能想知道何时使用这两种类型。 这完全取决于你希望 goroutine 之间的通信如何进行。 无缓冲 channel 同步通信。 它们保证每次发送数据时,程序都会被阻止,直到有人从 channel 中读取数据。
+相反,有缓冲 channel 将发送和接收操作解耦。 它们不会阻止程序,但你必须小心使用,因为可能最终会导致死锁(如前文所述)。 使用无缓冲 channel 时,可以控制可并发运行的 goroutine 的数量。 例如,你可能要对 API 进行调用,并且想要控制每秒执行的调用次数。 否则,你可能会被阻止。
+Go 中 channel 的一个有趣特性是,在使用 channel 作为函数的参数时,可以指定 channel 是要发送数据还是接收数据。 随着程序的增长,可能会使用大量的函数,这时候,最好记录每个 channel 的意图,以便正确使用它们。 或者,你要编写一个库,并希望将 channel 公开为只读,以保持数据一致性。
+要定义 channel 的方向,可以使用与读取或接收数据时类似的方式进行定义。 但是你在函数参数中声明 channel 时执行此操作。 将 channel 类型定义为函数中的参数的语法如下所示:
+chan<- int // it's a channel to only send data
+<-chan int // it's a channel to only receive data通过仅接收的 channel 发送数据时,在编译程序时会出现错误。
+让我们使用以下程序作为两个函数的示例,一个函数用于读取数据,另一个函数用于发送数据:
+package main
+
+import "fmt"
+
+func send(ch chan<- string, message string) {
+ fmt.Printf("Sending: %#v\n", message)
+ ch <- message
+}
+
+func read(ch <-chan string) {
+ fmt.Printf("Receiving: %#v\n", <-ch)
+}
+
+func main() {
+ ch := make(chan string, 1)
+ send(ch, "Hello World!")
+ read(ch)
+}运行程序时,将看到以下输出:
+Sending: "Hello World!"
+Receiving: "Hello World!"程序阐明每个函数中每个 channel 的意图。 如果试图使用一个 channel 在一个仅用于接收数据的 channel 中发送数据,将会出现编译错误。 例如,尝试执行如下所示的操作:
+func read(ch <-chan string) {
+ fmt.Printf("Receiving: %#v\n", <-ch)
+ ch <- "Bye!"
+}运行程序时,将看到以下错误:
+# command-line-arguments
+./main.go:12:5: invalid operation: ch <- "Bye!" (send to receive-only type <-chan string)编译错误总比误用 channel 好。
+最后,让我们讨论一个关于如何在使用 select 关键字的同时与多个 channel 交互的简短主题。 有时,在使用多个 channel 时,需要等待事件发生。 例如,当程序正在处理的数据中出现异常时,可以包含一些逻辑来取消操作。
select 语句的工作方式类似于 switch 语句,但它适用于 channel。 它会阻止程序的执行,直到它收到要处理的事件。 如果它收到多个事件,则会随机选择一个。
select 语句的一个重要方面是,它在处理事件后完成执行。 如果要等待更多事件发生,则可能需要使用循环。
package main
+
+import (
+ "fmt"
+ "time"
+)
+
+func process(ch chan string) {
+ time.Sleep(3 * time.Second)
+ ch <- "Done processing!"
+}
+
+func replicate(ch chan string) {
+ time.Sleep(1 * time.Second)
+ ch <- "Done replicating!"
+}
+
+func main() {
+ ch1 := make(chan string)
+ ch2 := make(chan string)
+ go process(ch1)
+ go replicate(ch2)
+
+ for i := 0; i < 2; i++ {
+ select {
+ case process := <-ch1:
+ fmt.Println(process)
+ case replicate := <-ch2:
+ fmt.Println(replicate)
+ }
+ }
+}
+Done replicating!
+Done processing!请注意,replicate 函数先完成。 这就是你在终端中先看到其输出的原因。 main 函数存在一个循环,因为 select 语句在收到事件后立即结束,但我们仍在等待 process 函数完成。
实现并发的改进版本。 完成此操作需要几秒钟的时间(不超过 15 秒),应使用有缓冲 channel。
+package main
+
+import (
+ "fmt"
+ "math/rand"
+ "time"
+)
+
+func fib(number float64, ch chan string) {
+ x, y := 1.0, 1.0
+ for i := 0; i < int(number); i++ {
+ x, y = y, x+y
+ }
+
+ r := rand.Intn(3)
+ time.Sleep(time.Duration(r) * time.Second)
+
+ ch <- fmt.Sprintf("Fib(%v): %v\n", number, x)
+}
+
+func main() {
+ ch := make(chan string, 15)
+
+ start := time.Now()
+
+ for i := 1; i < 15; i++ {
+ go fib(float64(i), ch)
+ }
+
+ for i := 1; i < 15; i++ {
+ fmt.Printf(<-ch)
+ }
+
+ elapsed := time.Since(start)
+ fmt.Printf("Done! It took %v seconds!\n", elapsed.Seconds())
+}
+编写一个新版本以计算斐波纳契数,直到用户使用 fmt.Scanf() 函数在终端中输入 quit。 如果用户按 Enter,则应计算新的斐波纳契数。
+使用两个无缓冲 channel:一个用于计算斐波纳契数,另一个用于等待用户的“退出”消息。 你需要使用 select 语句。
+package main
+
+import (
+ "fmt"
+ "time"
+)
+
+var quit = make(chan bool)
+
+func fib(c chan int) {
+ x, y := 1, 1
+
+ for {
+ select {
+ case c <- x:
+ x, y = y, x+y
+ case <-quit:
+ fmt.Println("Done calculating Fibonacci!")
+ return
+ }
+ }
+}
+
+func main() {
+ start := time.Now()
+
+ command := ""
+ data := make(chan int)
+
+ go fib(data)
+
+ for {
+ num := <-data
+ fmt.Println(num)
+ fmt.Scanf("%s", &command)
+ if command == "quit" {
+ quit <- true
+ break
+ }
+ }
+
+ time.Sleep(1 * time.Second)
+
+ elapsed := time.Since(start)
+ fmt.Printf("Done! It took %v seconds!\n", elapsed.Seconds())
+}
+《机器学习》课程笔记:第8章 信息论模型
+ +信息量(信息增益量)定义:
信息量性质:概率越小的状态,信息量越大
+信息熵定义:信息量在全部数值域上的概率平均值
+
 (微分熵不是严格意义的信息熵)
(微分熵不是严格意义的信息熵)微分熵性质:平移不变、尺度变化,且可以是负值
+当根据不完整的信息作为依据进行推断时,应该由满足分布限制条件的具有最大熵的概率分布推得。
+最大微分熵问题:
已知均值和方差,高斯分布的微分熵最大
+条件信息量:
条件熵:
+ ,
, 的条件熵:
的条件熵:
 ,
, 的条件熵:
的条件熵:
联合熵:
+


互信息:信息熵与条件熵的差:
互信息性质:非负性、对称性、不变性
+相对熵是衡量两个分布的平均信息差异
+相对熵和互信息之间的关系:
最大熵模型:最大化 

最大互信息模型: 最大化 
最小互信息模型:最小化 

《现代信息检索》课程笔记:第13讲 决策树与面向文档的机器学习
+ +面向文本分类的决策树
+决策树的学习
+学习一个序列的特征测试,典型的做法是由上到下的贪心搜索,每一步选择具有最高信息收益的未使用特征
+叶节点标记:yes/no 类别标记,或连续值
+如果有

我们可以通过在每个节点上递归选择最佳拆分特征,以贪心的方式创建树
+属性选择基本思想:(理想情况下)一个好的特征能够把所有样本划分成“全部正样本”和“全部负样本”两个子集
+利用信息论:
+信息熵(Entropy):考虑每个节点的类分解
+信息增益
+对每个节点,我们选择使信息增益最大的特征f
+数值特征 (例如tf-idf):通常使用二元的切分 (f < t), t怎样确定?
+穷尽式(搜索):评估观察值之间的每个分割点的信息增益。
+分箱(Discretize into bins)
+(树的构建)什么时候停止?
+宏平均:计算每个类别的性能指标,然后取平均值
+微平均:收集所有类别的决策(分类)结果,计算列联表,评价
+判别式 (discriminative) 分类方法: Logistic Regression (逻辑回归) 与 Support vector machines (支持向量机)
+Ensemble 方法
+随机森林 (Random Forests)
+从原始数据集重复采样(bootstrap采样),在采样数据上构建K个树,p=特征数量
+原则:我们希望在不同的学习器(learner)之间进行投票,因此我们不希望这些模型过于相似。这两个标准确保了各个树的多样性
+优点:
+缺点:
+Boosted Decision Trees (BDT, 增强决策树)
+随机森林(RF) vs 增强树(BDT)
+ + +Go语言圣经-入门
+ +os 包以跨平台的方式,提供了一些与操作系统交互的函数和变量。程序的命令行参数可从 os 包的 Args 变量获取;os 包外部使用 os.Args 访问该变量。
os.Args 的第一个元素:os.Args[0],是命令本身的名字;其它的元素则是程序启动时传给它的参数。
package main
+
+import (
+ "fmt"
+ "os"
+)
+
+func main() {
+ var s, sep string
+ for i := 1; i < len(os.Args); i++ {
+ s += sep + os.Args[i]
+ sep = " "
+ }
+ fmt.Println(s)
+}> go run main.go 4 2 5 4 1
+4 2 5 4 1for 循环的另一种形式,在某种数据类型的区间(range)上遍历
func main() {
+ var s, sep string
+ for _, j := range os.Args[1:] {
+ s += sep + j
+ sep = " "
+ }
+ fmt.Println(s)
+}使用 strings 包的 Join 函数:
func main() {
+ fmt.Println(strings.Join(os.Args[1:], " "))
+}// Dup1 prints the text of each line that appears more than
+// once in the standard input, preceded by its count.
+package main
+
+import (
+ "bufio"
+ "fmt"
+ "os"
+)
+
+func main() {
+ counts := make(map[string]int)
+ input := bufio.NewScanner(os.Stdin)
+ for input.Scan() {
+ counts[input.Text()]++
+ }
+ // NOTE: ignoring potential errors from input.Err()
+ for line, n := range counts {
+ if n > 1 {
+ fmt.Printf("%d\t%s\n", n, line)
+ }
+ }
+}
+> abc
+> abc
+> def
+> efd
+> efd
+2 abc
+2 efdPrintf的多种转换形式:
+%d 十进制整数
+%x, %o, %b 十六进制,八进制,二进制整数。
+%f, %g, %e 浮点数: 3.141593 3.141592653589793 3.141593e+00
+%t 布尔:true或false
+%c 字符(rune) (Unicode码点)
+%s 字符串
+%q 带双引号的字符串"abc"或带单引号的字符'c'
+%v 变量的自然形式(natural format)
+%T 变量的类型
+%% 字面上的百分号标志(无操作数)以 ln 结尾的格式化函数,则遵循 Println 的方式,以跟 %v 差不多的方式格式化参数,并在最后添加一个换行符。
第二个版本,可以接收文件并判断重复行
+// Dup2 prints the count and text of lines that appear more than once
+// in the input. It reads from stdin or from a list of named files.
+package main
+
+import (
+ "bufio"
+ "fmt"
+ "os"
+)
+
+func main() {
+ counts := make(map[string]int)
+ files := os.Args[1:]
+ if len(files) == 0 {
+ countLines(os.Stdin, counts)
+ } else {
+ for _, arg := range files {
+ f, err := os.Open(arg)
+ if err != nil {
+ fmt.Fprintf(os.Stderr, "dup2: %v\n", err)
+ continue
+ }
+ countLines(f, counts)
+ f.Close()
+ }
+ }
+ for line, n := range counts {
+ if n > 1 {
+ fmt.Printf("%d\t%s\n", n, line)
+ }
+ }
+}
+
+func countLines(f *os.File, counts map[string]int) {
+ input := bufio.NewScanner(f)
+ for input.Scan() {
+ counts[input.Text()]++
+ }
+ // NOTE: ignoring potential errors from input.Err()
+}
+map 是一个由 make 函数创建的数据结构的引用。map 作为参数传递给某函数时,该函数接收这个引用的一份拷贝(copy,或译为副本),被调用函数对 map 底层数据结构的任何修改,调用者函数都可以通过持有的 map 引用看到。
package main
+
+import (
+ "fmt"
+ "os"
+ "strings"
+)
+
+func main() {
+ counts := make(map[string]int)
+ for _, filename := range os.Args[1:] {
+ data, err := os.ReadFile(filename)
+ if err != nil {
+ fmt.Fprintf(os.Stderr, "dup3: %v\n", err)
+ continue
+ }
+ for _, line := range strings.Split(string(data), "\n") {
+ counts[line]++
+ }
+ }
+ for line, n := range counts {
+ if n > 1 {
+ fmt.Printf("%d\t%s\n", n, line)
+ }
+ }
+}
+引入了 ReadFile 函数(来自于 os包),其读取指定文件的全部内容,strings.Split 函数把字符串分割成子串的切片。
// Lissajous generates GIF animations of random Lissajous figures.
+package main
+
+import (
+ "image"
+ "image/color"
+ "image/gif"
+ "io"
+ "math"
+ "math/rand"
+ "os"
+ "time"
+)
+
+var palette = []color.Color{color.White, color.Black}
+
+const (
+ whiteIndex = 0 // first color in palette
+ blackIndex = 1 // next color in palette
+)
+
+func main() {
+ // The sequence of images is deterministic unless we seed
+ // the pseudo-random number generator using the current time.
+ // Thanks to Randall McPherson for pointing out the omission.
+ rand.Seed(time.Now().UTC().UnixNano())
+ lissajous(os.Stdout)
+}
+
+func lissajous(out io.Writer) {
+ const (
+ cycles = 5 // number of complete x oscillator revolutions
+ res = 0.001 // angular resolution
+ size = 100 // image canvas covers [-size..+size]
+ nframes = 64 // number of animation frames
+ delay = 8 // delay between frames in 10ms units
+ )
+
+ freq := rand.Float64() * 3.0 // relative frequency of y oscillator
+ anim := gif.GIF{LoopCount: nframes}
+ phase := 0.0 // phase difference
+ for i := 0; i < nframes; i++ {
+ rect := image.Rect(0, 0, 2*size+1, 2*size+1)
+ img := image.NewPaletted(rect, palette)
+ for t := 0.0; t < cycles*2*math.Pi; t += res {
+ x := math.Sin(t)
+ y := math.Sin(t*freq + phase)
+ img.SetColorIndex(size+int(x*size+0.5), size+int(y*size+0.5),
+ blackIndex)
+ }
+ phase += 0.1
+ anim.Delay = append(anim.Delay, delay)
+ anim.Image = append(anim.Image, img)
+ }
+ gif.EncodeAll(out, &anim) // NOTE: ignoring encoding errors
+}
+// Fetch prints the content found at a URL.
+package main
+
+import (
+ "fmt"
+ "io"
+ "net/http"
+ "os"
+)
+
+func main() {
+ for _, url := range os.Args[1:] {
+ resp, err := http.Get(url)
+ if err != nil {
+ fmt.Fprintf(os.Stderr, "fetch: %v\n", err)
+ os.Exit(1)
+ }
+ b, err := io.ReadAll(resp.Body)
+ resp.Body.Close()
+ if err != nil {
+ fmt.Fprintf(os.Stderr, "fetch: reading %s: %v\n", url, err)
+ os.Exit(1)
+ }
+ fmt.Printf("%s", b)
+ }
+}
+改进:
+避免申请缓冲区、url参数没有 http:// 前缀、打印出HTTP协议的状态码
// Fetch prints the content found at a URL.
+package main
+
+import (
+ "fmt"
+ "io"
+ "net/http"
+ "os"
+ "strings"
+)
+
+func main() {
+ for _, url := range os.Args[1:] {
+ if !strings.HasPrefix(url, "http://") {
+ url = "http://" + url
+ }
+ resp, err := http.Get(url)
+ if err != nil {
+ fmt.Fprintf(os.Stderr, "fetch: %v\n", err)
+ os.Exit(1)
+ }
+ _, err = io.Copy(os.Stdout, resp.Body)
+ if err != nil {
+ fmt.Fprintf(os.Stderr, "fetch: reading %s: %v\n", url, err)
+ os.Exit(1)
+ }
+ fmt.Println(resp.Status)
+ resp.Body.Close()
+ }
+}
+// Fetchall fetches URLs in parallel and reports their times and sizes.
+package main
+
+import (
+ "fmt"
+ "io"
+ "net/http"
+ "os"
+ "time"
+)
+
+func main() {
+ start := time.Now()
+ ch := make(chan string)
+ for _, url := range os.Args[1:] {
+ go fetch(url, ch) // start a goroutine
+ }
+ for range os.Args[1:] {
+ fmt.Println(<-ch) // receive from channel ch
+ }
+ fmt.Printf("%.2fs elapsed\n", time.Since(start).Seconds())
+}
+
+func fetch(url string, ch chan<- string) {
+ start := time.Now()
+ resp, err := http.Get(url)
+ if err != nil {
+ ch <- fmt.Sprint(err) // send to channel ch
+ return
+ }
+ nbytes, err := io.Copy(io.Discard, resp.Body)
+ resp.Body.Close() // don't leak resources
+ if err != nil {
+ ch <- fmt.Sprintf("while reading %s: %v", url, err)
+ return
+ }
+ secs := time.Since(start).Seconds()
+ ch <- fmt.Sprintf("%.2fs %7d %s", secs, nbytes, url)
+}
+goroutine是一种函数的并发执行方式,而channel是用来在goroutine之间进行参数传递。main函数本身也运行在一个goroutine中,而go function则表示创建一个新的goroutine,并在这个新的goroutine中执行这个函数。
+// Server1 is a minimal "echo" server.
+package main
+
+import (
+ "fmt"
+ "log"
+ "net/http"
+)
+
+func main() {
+ http.HandleFunc("/", handler) // each request calls handler
+ log.Fatal(http.ListenAndServe("localhost:8000", nil))
+}
+
+// handler echoes the Path component of the request URL r.
+func handler(w http.ResponseWriter, r *http.Request) {
+ fmt.Fprintf(w, "URL.Path = %q\n", r.URL.Path)
+}为访问的url添加某种状态。比如,下面这个版本输出了同样的内容,但是会对请求的次数进行计算
+// Server2 is a minimal "echo" and counter server.
+package main
+
+import (
+ "fmt"
+ "log"
+ "net/http"
+ "sync"
+)
+
+var mu sync.Mutex
+var count int
+
+func main() {
+ http.HandleFunc("/", handler)
+ http.HandleFunc("/count", counter)
+ log.Fatal(http.ListenAndServe("localhost:8000", nil))
+}
+
+// handler echoes the Path component of the requested URL.
+func handler(w http.ResponseWriter, r *http.Request) {
+ mu.Lock()
+ count++
+ mu.Unlock()
+ fmt.Fprintf(w, "URL.Path = %q\n", r.URL.Path)
+}
+
+// counter echoes the number of calls so far.
+func counter(w http.ResponseWriter, r *http.Request) {
+ mu.Lock()
+ fmt.Fprintf(w, "Count %d\n", count)
+ mu.Unlock()
+}
+handler函数会把请求的http头和请求的form数据都打印出来,这样可以使检查和调试这个服务更为方便
+// handler echoes the HTTP request.
+func handler(w http.ResponseWriter, r *http.Request) {
+ fmt.Fprintf(w, "%s %s %s\n", r.Method, r.URL, r.Proto)
+ for k, v := range r.Header {
+ fmt.Fprintf(w, "Header[%q] = %q\n", k, v)
+ }
+ fmt.Fprintf(w, "Host = %q\n", r.Host)
+ fmt.Fprintf(w, "RemoteAddr = %q\n", r.RemoteAddr)
+ if err := r.ParseForm(); err != nil {
+ log.Print(err)
+ }
+ for k, v := range r.Form {
+ fmt.Fprintf(w, "Form[%q] = %q\n", k, v)
+ }
+}Go语言圣经-程序结构-基础数据类型
+ +var形式的声明语句往往是用于需要显式指定变量类型的地方,或者因为变量稍后会被重新赋值而初始值无关紧要的地方。
+简短变量声明语句中必须至少要声明一个新的变量
+如果用“var x int”声明语句声明一个x变量,那么&x表达式(取x变量的内存地址)将产生一个指向该整数变量的指针,指针对应的数据类型是 *int,指针被称之为“指向int类型的指针”。
指针是实现标准库中flag包的关键技术,它使用命令行参数来设置对应变量的值,而这些对应命令行标志参数的变量可能会零散分布在整个程序中。
+// Echo4 prints its command-line arguments.
+package main
+
+import (
+ "flag"
+ "fmt"
+ "strings"
+)
+
+var n = flag.Bool("n", false, "omit trailing newline")
+var sep = flag.String("s", " ", "separator")
+
+func main() {
+ flag.Parse()
+ fmt.Print(strings.Join(flag.Args(), *sep))
+ if !*n {
+ fmt.Println()
+ }
+}程序中的 sep和 n变量分别是指向对应命令行标志参数变量的指针,因此必须用 *sep和 *n形式的指针语法间接引用它们。
另一个创建变量的方法是调用内建的new函数。表达式new(T)将创建一个T类型的匿名变量,初始化为T类型的零值,然后返回变量地址,返回的指针类型为 *T。
p := new(int) // p, *int 类型, 指向匿名的 int 变量
+fmt.Println(*p) // "0"
+*p = 2 // 设置 int 匿名变量的值为 2
+fmt.Println(*p) // "2"下面的两个newInt函数有着相同的行为:
+func newInt() *int {
+ return new(int)
+}
+
+func newInt() *int {
+ var dummy int
+ return &dummy
+}变量的生命周期指的是在程序运行期间变量有效存在的时间段。对于在包一级声明的变量来说,它们的生命周期和整个程序的运行周期是一致的。而相比之下,局部变量的生命周期则是动态的:每次从创建一个新变量的声明语句开始,直到该变量不再被引用为止,然后变量的存储空间可能被回收。函数的参数变量和返回值变量都是局部变量。它们在函数每次被调用的时候创建。
+一个类型声明语句创建了一个新的类型名称,和现有类型具有相同的底层结构。新命名的类型提供了一个方法,用来分隔不同概念的类型,这样即使它们底层类型相同也是不兼容的。
+type 类型名字 底层类型在Go语言中,一个简单的规则是:如果一个名字是大写字母开头的,那么该名字是导出的
+Unicode字符rune类型是和int32等价的类型,通常用于表示一个Unicode码点。这两个名称可以互换使用。
+标准库中有四个包对字符串处理尤为重要:bytes、strings、strconv和unicode包。strings包提供了许多如字符串的查询、替换、比较、截断、拆分和合并等功能。
+bytes包也提供了很多类似功能的函数,但是针对和字符串有着相同结构的[]byte类型。因为字符串是只读的,因此逐步构建字符串会导致很多分配和复制。在这种情况下,使用bytes.Buffer类型将会更有效,稍后我们将展示。
+strconv包提供了布尔型、整型数、浮点数和对应字符串的相互转换,还提供了双引号转义相关的转换。
+unicode包提供了IsDigit、IsLetter、IsUpper和IsLower等类似功能,它们用于给字符分类。每个函数有一个单一的rune类型的参数,然后返回一个布尔值。而像ToUpper和ToLower之类的转换函数将用于rune字符的大小写转换。所有的这些函数都是遵循Unicode标准定义的字母、数字等分类规范。strings包也有类似的函数,它们是ToUpper和ToLower,将原始字符串的每个字符都做相应的转换,然后返回新的字符串。
+将一个整数转为字符串,一种方法是用fmt.Sprintf返回一个格式化的字符串;另一个方法是用strconv.Itoa(“整数到ASCII”)
+如果要将一个字符串解析为整数,可以使用strconv包的Atoi或ParseInt函数,还有用于解析无符号整数的ParseUint函数
+常量声明可以使用iota常量生成器初始化,它用于生成一组以相似规则初始化的常量,但是不用每行都写一遍初始化表达式。在一个const声明语句中,在第一个声明的常量所在的行,iota将会被置为0,然后在每一个有常量声明的行加一。
+type Weekday int
+
+const (
+ Sunday Weekday = iota
+ Monday
+ Tuesday
+ Wednesday
+ Thursday
+ Friday
+ Saturday
+)Go语言圣经-复合数据类型
+ +数组是一个由固定长度的特定类型元素组成的序列,一个数组可以由零个或多个元素组成。因为数组的长度是固定的,因此在Go语言中很少直接使用数组。
+一个nil值的slice的长度和容量都是0,但是也有非nil值的slice的长度和容量也是0
+如果你需要测试一个slice是否是空的,使用len(s) == 0来判断,而不应该用s == nil来判断。
+一个slice可以用来模拟一个stack
+最初给定的空slice对应一个空的stack,然后可以使用append函数将新的值压入stack:
+stack = append(stack, v) // push vstack的顶部位置对应slice的最后一个元素:
+top := stack[len(stack)-1] // top of stack通过收缩stack可以弹出栈顶的元素
+stack = stack[:len(stack)-1] // pop要删除slice中间的某个元素并保存原有的元素顺序,可以通过内置的copy函数将后面的子slice向前依次移动一位完成:
+func remove(slice []int, i int) []int {
+ copy(slice[i:], slice[i+1:])
+ return slice[:len(slice)-1]
+}
+
+func main() {
+ s := []int{5, 6, 7, 8, 9}
+ fmt.Println(remove(s, 2)) // "[5 6 8 9]"
+}如果删除元素后不用保持原来顺序的话,我们可以简单的用最后一个元素覆盖被删除的元素:
+func remove(slice []int, i int) []int {
+ slice[i] = slice[len(slice)-1]
+ return slice[:len(slice)-1]
+}
+
+func main() {
+ s := []int{5, 6, 7, 8, 9}
+ fmt.Println(remove(s, 2)) // "[5 6 9 8]
+}type Movie struct {
+ Title string
+ Year int `json:"released"`
+ Color bool `json:"color,omitempty"`
+ Actors []string
+}
+
+var movies = []Movie{
+ {Title: "Casablanca", Year: 1942, Color: false,
+ Actors: []string{"Humphrey Bogart", "Ingrid Bergman"}},
+ {Title: "Cool Hand Luke", Year: 1967, Color: true,
+ Actors: []string{"Paul Newman"}},
+ {Title: "Bullitt", Year: 1968, Color: true,
+ Actors: []string{"Steve McQueen", "Jacqueline Bisset"}},
+ // ...
+}
+这样的数据结构特别适合JSON格式,并且在两者之间相互转换也很容易。将一个Go语言中类似movies的结构体slice转为JSON的过程叫编组(marshaling)。编组通过调用json.Marshal函数完成:
+data, err := json.Marshal(movies)
+if err != nil {
+ log.Fatalf("JSON marshaling failed: %s", err)
+}
+fmt.Printf("%s\n", data)另一个json.MarshalIndent函数将产生整齐缩进的输出。该函数有两个额外的字符串参数用于表示每一行输出的前缀和每一个层级的缩进:
+data, err := json.MarshalIndent(movies, "", " ")
+if err != nil {
+ log.Fatalf("JSON marshaling failed: %s", err)
+}
+fmt.Printf("%s\n", data)编码的逆操作是解码,对应将JSON数据解码为Go语言的数据结构,Go语言中一般叫unmarshaling,通过json.Unmarshal函数完成。
+var titles []struct{ Title string }
+if err := json.Unmarshal(data, &titles); err != nil {
+ log.Fatalf("JSON unmarshaling failed: %s", err)
+}
+fmt.Println(titles) // "[{Casablanca} {Cool Hand Luke} {Bullitt}]"《现代信息检索》课程笔记:第14讲 面向信息检索的分布式词项表示
+ +怎样更鲁棒的匹配用户搜索意图?
+查询扩展/Query expansion:
+文档扩展/Document expansion:
+使用锚文本/anchor text可以通过提供人工创作的同义词(即锚文本)来解决此问题,但不适用于新的或不太受欢迎的网页(注:链接稀疏,锚文本少)或无超链接的语料
+基于查询日志的查询扩展
+不考虑上下文语境的查询扩展可能会导致问题
+从查询日志学习考虑上下文语境的查询重写:识别同一用户基于同一信息需求的多次查询请求
+自动同义词库生成
+表示词项之间的关系
+使用词项的标准符号编码,每个词项都是一个维度
+不同的词项没有内在的相似性
+基于分布式相似度的表示:用相邻词项的意义来表示一个词项
+解决方案:低维向量
+基本思想: 将“大部分的”重要信息存储在一个维度固定的低维向量中 - 即“密集向量”
+传统方法:潜在语义索引/分析
+使用奇异值分解(Singular Value Decomposition,SVD)–或只是随机映射(random projection)以找到低维基向量或正交向量
+词项的意义由向量表示:为每个词类构建一个密集向量,该向量应当能够准确的预测其上下文词项
+学习神经词嵌入:基本思路
+思路:直接基于预测能力学习低维词向量
+Word2Vec包含一组算法预测每个词的上下文(或者反过来)
+神经网络的优化:(求导的)链式法则
+Word2vec里的线性关系
+Word2vec的向量表示非常善于对相似性和相似性的维度编码!
+仅通过在嵌入空间中进行向量减法就可以很好地解决类比测试相似度的问题
+Dual Embedding Space Model (DESM)
+一种简单的利用词嵌入的检索模型
+文档由其词项嵌入的中心向量表示
+查询-文档相似度:查询词向量与文档向量的平均相似度
+DESM 是一个弱排序模型,但是具有发现微妙相似性/关联性的能力
+ + +《机器学习》课程笔记:第9章 概率图模型
+ +图结构:有向无环图
+结点:一个或一组随机变量
+边:随机变量之间的单向、直接影响
+联合概率分布分解形式:


条件独立性 D-分离准则(D-separation criterion):判断贝叶斯网络结点之间的条件独立性。
+贝叶斯网络的全局马尔科夫性:给定结点集合A,B,C,若A到B中结点的所有无向路径都是被C阻塞的(blocked),则称A和B被C D-分离(D-separated),即A和B关于C条件独立。
+若一条无向路径包含结点x满足以下条件之一,则称其是阻塞的:
+

贝叶斯网络的局部马尔科夫性:
+图结构:无向图
+结点:一个或一组随机变量。
+边:随机变量之间的相互依赖(非“因果关系”)。
+团:对于图中的结点子集,若其中任意两个节点之间都有连边,则称该结点子集为一个团(clique)。
+极大团:若在团中加入其他任意一个结点都不再形成团,则称该团为极大团(maximal clique)。
+分解形式:
其中, 





条件独立性:
+马尔可夫随机场的全局马尔科夫性:给定结点集合A,B,C,若从A中的结点到B中结点必须经过C中的结点,则称A和B被C分离,即A和B关于C条件独立。
+局部马尔科夫性:给定某变量的马尔可夫毯(邻接变量),则该变量条件独立于其他变量。
成对马尔科夫性:给定其他所有变量,两个非相邻变量条件独立。
基本定义
+推断:已知联合概率分布 





学习:从观测数据

推断:已知联合概率分布 

枚举 : 假设 


推断的核心问题 : 如何高效地计算边际分布
推断方法
+精确推断:计算

变量消去(variable elimination)
+思路:利用图模型的紧凑概率分布形式来削减计算量。
+优点:简单直观,代数上的消去对应图中结点的消去。
+缺点:针对不同证据变量会造成大量冗余计算。
+信念传播(belief propagation)
+思路:将变量消去过程中产生的中间结果视为可复用的消息,避免重复计算。
+消息传递仅在邻接变量之间发生,与边的方向性无关。
+树结构:有向树=无向树
+树结构上的消息传递:
+消息计算公式:
+边际分布:
+二次扫描算法:
+近似推断:在较低的时间复杂度下获得原问题的近似解。通过采样一组服从特定分布的样本,来近似原始分布,适用范围更广,操作性更强。
+前向采样(forward sampling)
+思路:依据贝叶斯网络的(条件)概率直接采样。采样后,进行需要的概率统计。
+缺点:对于小概率事件采样困难,可能经过很多次采样也无法获得足够多的样本
+仅适用于贝叶斯网络,不适用于马尔可夫随机场。
+吉布斯采样(Gibbs sampling)
+思路:直接依照条件概率
马尔可夫毯的性质:
+优点:
+ 采样,解决小概率事件采样难的问题
采样,解决小概率事件采样难的问题隐马尔可夫模型是关于时序的概率模型,是最简单的动态贝叶斯网络模型。
+状态变量



观测变量仅依赖于当前时刻的状态变量,当前状态仅依赖于前一时刻的状态。状态集合 
联合概率:
状态转移矩阵





观测概率矩阵




初始状态概率向量 


生成过程:
+给定
 ,并根据初始状态概率
,并根据初始状态概率 生成初始状态
生成初始状态
 和观测概率矩阵B生成
和观测概率矩阵B生成
 和状态转移矩阵A 生成
和状态转移矩阵A 生成
 ,则设置
,则设置 ,并转到第(2)步;否则,停止。
,并转到第(2)步;否则,停止。三个基本问题
+ 和观测序列
和观测序列 ,计算在模型
,计算在模型 下观测
下观测 到的概率
到的概率 。(评估模型与观测序列之间的匹配程度)
。(评估模型与观测序列之间的匹配程度) 和观测序列
和观测序列 ,求使得
,求使得 最大的状态观测序列
最大的状态观测序列 。(根据观测序列推测状态序列)
。(根据观测序列推测状态序列) ,调整模型
,调整模型 参数,使得该序列出现的概率
参数,使得该序列出现的概率 最大。(训练模型使其更好地描述观测序列)
最大。(训练模型使其更好地描述观测序列)条件随机场(Conditional Random Field) 是给定随机变量




线性链条件随机场(linear-chain CRF)是随机变量





《高级人工智能》课程笔记:第7讲 图卷积神经网络
+ +卷积神经网络在欧式数据(图像、文本、声音和视频等)上获得了巨大的成功,广泛应用于图像分类、目标检测、机器翻译等
+卷积神经网络可以学习局部小结构,使用局部的卷积核,然后形成多维的模式
+卷积如何迁移到非欧空间上去?
+卷积是在函数

连续形式:
离散形式:
在图上定义卷积的方法:
+谱方法:在谱空间中定义卷积:
+空间方法:在向量空间中定义卷积
+定义一个图
图上的每个结点


图的拉普拉斯算子:
归一化的拉普拉斯算子:
图



对于一个信号
两个信号的卷积的傅里叶变换是两个信号的傅里叶变换的逐点相乘
图卷积神经网络:
+ +缺点:
+
ChebyNet:参数化-将参数的数量从n降为K
+ +优点:
+ 下降到
下降到
Graph wavelet neural network:图小波神经网络
+将傅里叶基换为小波基:稀疏、局部化、计算代价低
+方法类比卷积:
+GraphSAGE:从每个结点开始随机游走,采样
图卷积网络(GCN):通过归一化的拉普拉斯矩阵从不固定数量的邻居结点中聚合信息,通过特征变换共享参数
+GAT:Graph Attention Network:通过注意力机制学习聚合矩阵
+MoNet:空间方法的一般意义框架:所有的空间方法都是定义多个核函数,来测量目标结点和其他结点之间的相似度
+谱方法是空间方法的特例
+图粗化:将结点进行聚类,每一类作为一个超级结点
+结点选择:学习一个评价标准去挑选比较重要的结点
+图神经网络在结点分类、链接预测、图分类上取得了巨大的成功,但是图神经网络的设计大多基于直觉、启发式方法或者实验试错,缺少对于图神经网络的理论理解。
+ + +《模式识别与机器学习》课程笔记:第5章 统计机器学习
+ +桑克(R.Shank)“一台计算机若不会学习,就不能说它具有智能。”
+机器学习更强调面向算法,而统计学更偏重于面向模型。换而言之,机器学习强调算法的结果要好,所以机器学习很关注损失函数。而统计学要先扔出来一大堆模型假设,然后站在模型上面通过严格的数学推导做出结果。
+统计机器学习:是基于数据构建概率统计模型并运用模型对数据进行预测分析的一门学科。
+机器学习的学习过程:
+机器学习的特点:
+机器学习方法分类:
+自监督学习是自主监督学习。它提取并使用自然可用的相关上下文和嵌入式元数据作为监督信号。
+输入训练样本,目标是损失函数期望风险最小化
+期望风险最小化:
+经验风险最小化:(导致过拟合)
+结构风险最小化:
+怎么样在测试数据上预测得好?
+两方面:
+正则项:在原来的经验损失函数中添加一个惩罚项,不鼓励复杂的模型
+偏差-方差分解:expected loss=bias2+variance+noise
+偏差:度量了模型的期望预测和真实结果的偏离程度
+方差:刻画了数据扰动所造成的影响
+噪声:与f相互独立,刻画了问题的难易程度
+由正则化参数
大的

对模型复杂度问题的深刻理解:
+《现代信息检索》课程笔记:第15讲 基于深度神经网络的IR模型
+ +最简单的神经网络-神经元
+激活函数:主要作用是引入非线性,增强网络的表示能力。
+最简单的多层神经网络-多层感知机
+Softmax归一化是在使用神经网络进行分类时常用的方法,对于分类问题,通常需要给出可能属于每一个类别的概率,即需要输出介于 0 和 1 之间,且加和为 1
+参数的学习
+正则化
+卷积神经网络
+循环神经网络
+Neural IR 模型分类
+Representation based:学习文本的分布式表示 在高维空间匹配
+Matching function:文本之间先进行交互匹配,再对匹配信号进行融合
+Combination of both: 既考虑 Representation 又考虑 Matching function
+DSSM:Deep Structured Semantic Models
+word hashing: Bag of letter trigrams representation
+模型:DNN学习查询,文本的语义表示, cosine相似度作为匹配评分
+MatchPyramid:
+考虑各种层次的匹配信号,包括单词层次、短语层次以及句子层次等等;
+在图像领域,基于 CNN 特征提取的图像金字塔被证明是有效的
+DRMM:相比普通的文本匹配任务,检索任务更需要关注相关性匹配
+通过显式地对精确匹配信号,查询词重要度以及多样匹配要求进行建模,得到的模型更加适合于检索任务。
+DRMM是第一个在 TREC 数据集能够取得比传统检索模型更好效果的基于 DNN 模型
+DRMM的设计思路在一定程度上借鉴了传统的 TF-IDF
+K-NRM:使用kernel pooling 技术提取多层次的软匹配 (soft match)特征
+PACRR:通过将具有不同大小(k= lg 卷积核的卷积层作用于查询与文档间的单词-单词相似度矩阵,来对 k gram 匹配信息进行建模。
+DUET:Representation与Matching function 的方法是互补的
+SNRM:监督学习得到文本稀疏表示,解决效率问题
+NPRF:将反馈文档视为原始查询的扩充表示,通过增强与查询相关的信息匹配信号获得更好的交互矩阵
+总结与展望
+基于BERT的检索模型
+稠密向量检索模型
+直接改变了原有第一阶段的检索模式,通过BERT等预训练语言模型,将查询和文档都映射到语义空间中,编码成单个稠密向量表示,用ANN 算法来进行检索。在一定程度上缓解了词汇不匹配问题,并将检索阶段的匹配效果推到了一个新的台阶
+模型框架:一般采用双塔结构对查询和文档单独地编码得到二者独立的表达,从而使文档可以进行离线索引。
+RepBERT:平均词项表示作为文档的单个向量
+ANCE:利用k-1的模型来检索得到top-n文档并随机采样负样本,每隔一段时间都需要对训练数据中的负样本进行更新,因此该方法的训练代价较大。
+RocketQA:与ANCE相比,做了额外的denoised操作;
+TCT-ColBERT:通过蒸馏技术,将ColBERT的强建模能力蒸馏到类似于RepBERT这样的双塔架构上去
+Condenser:为了将更完整的序列信息压缩到CLS 位置上
+DAR:通过插值、扰动的方式在文档表示层面进行数据增强
+JPQ:除了直接采用乘积量化(Product Quantization, PQ )方法来压缩向量外,将乘积量化后的文档d†表示用于模型训练,通过排序排序训练目标来优化 PQ 的聚类中心表示
+ + +对自己未来方向的调研
+ +2022.10.16 要失业了,商汤都要裁员了,NLP还是可以的
+目前先学算法,然后找算法实习,也是学一些开发
+实验室的学长:有个拿了农行offer,带我的学长快手转正了
+都有暑期实习:2个字节算法,1个字节产品,2个快手算法,还有个好像去电信了
+我可能就没什么发论文的想法,打打算法比赛,学学开发,找个大厂实习,然后毕业银行、国企,或者如果机会好,再考虑
+我学长他们没论文,也能找到算法岗
+如果不是上海广州,我觉得,得学开发吧,毕竟其他城市可能算法岗更少
+算法岗不动摇
+我觉得,现在能做的就两点 1. 多卷一点 2. 降低预期
+准备下一个实习去开发
+开发的话,就那些技术,我觉得方向上不会错太多,不像算法,跳坑里就出不来了
+我最近在做一个自己想的项目,学了学web前端,之后再学学后端,把项目做出来,然后争取寒假前找个实习
+前端是 vue,后端现在想的是 node + mogoDB + SQL,但后端还没咋研究,不好说
+我本来想的是,去微软苏州,或者先去微软北京再rebase苏州,我实在不想加班
+而且微软苏州人多,也买得起房,但现在进微软也好难的,不知道2年后咋样
+我选这个导师,也是考虑到他和微软有合作,但进来才知道他合作的都是MSRA,每年全国就要几个人,都是博士打架。。。
+八股内容很多,感觉很难搞,写程序的时候,经常觉得底层懂得太少,包的源码也看不懂
+挺想再学学计网,偏实践的,还想做csapp
+今年秋招的算法岗比开发岗还惨,搞算法投开发岗直接简历挂
+赛道还是挺重要的,要是搞算法没发好一点的论文应该就直接寄了,还是趁早转赛道
+可以去搞大数据嘛
+去年秋招和今年秋招比是一个天上一个地下,今年阿里腾讯秋招hc大概只有几百个,而且大部分都要留给实习生,基本等于不招人。其他大厂的hc也基本缩减50%以上
+大厂hc少导致一些中厂的简历也是暴涨,我知道的网易的java岗有10w份简历。还有小红书也是几万几万的简历
+今年字节卡简历很严重,实习成了进大厂的捷径
+web3这条赛道挺好
+看到知乎上好多ict的学长去lab实习的,感觉学长也可以考虑下这个,不过好像准备硕士直接工作的话,去做一下面向业务的岗好像帮助要大点
+《机器学习》课程笔记:第10章 神经网络与深度学习
+ +ANN到DL的技术发展
+DL在AI的成功应用
+语音识别
+2009年, Hinton把深层神经网络介绍给做语音识别的学者们。2010年,语音识别就产生了巨大突破。本质上是把传统的混合高斯模型(GMM)替换成了
+深度神经网络(DNN)模型,但相对识别错误率一下降低20%多,这个改进幅度超过了过去很多年的总和。这里的关键是把原来模型中通过 GMM 建模的手工特征换成了通过 DNN 进行更加复杂的特征学习。
在此之后,在深度学习框架下,人们还在不断利用更好的模型和更多的训练数据进一步改进结果。现在语音识别已经真正变得比较成熟,并且被广泛商用,目前所有的商用语音识别算法没有一个不是基于深度学习的。
+计算视觉:通过组合低层特征形成更加抽象的高层特征
+DL在图像识别
+Yann LeCun早在1989年就开始了卷积神经网络的研究,取得了在一些小规模(手写字)的图像识别的成果,但在像素丰富的图片上迟迟没有突破,直到2012年Hinton和他学生在ImageNet上的突破,使识别精度提高了一大步;截至2015年最好的模型ResNet
+2012年 Google Brain 用 16000 个 CPU 核的计算平台训练 10 亿神经元的深度网络,无外界干涉下自动识别了“Cat”
+2014年香港中文大学教授汤晓鸥研究组DeepID的深度学习模型,在 LFW 数据库上获得了99.15%的识别率,人用肉眼在LFW上的识别率为97.52%,深度学习在学术研究层面上已经超过了人用肉眼的识别 。
+自然语言处理
+词向量表示学习
+词向量是指通过对大量文本的无监督学习,根据前后文自动学习到每个词的紧凑向量表达,包括NNML 、 Word2Vector 、预训练模型等。
+预训练模型:ELMo、 GPT和BERT 等,全线提升自然语言领域的多项任务的Baseline
+递归神经网络 RNN:文本的各个词之间是有顺序的,RNN能更好的挖掘和利用这个性质,在自然语言各个领域都在尝试进行中。 已经有BPTT 、 LSTM等。
+神经网络模型学习框架
+ +损失函数:
+平方损失:
交叉熵损失:
单个神经元模型:
+ +单个神经元模型:
+多层感知机
+卷积网络
+核函数网络:单隐层神经网络、非线性体现在径向基核函数
+自组织映射
+RBM
+ 层为隐层,
层为隐层, 层为可见层
层为可见层递归网络
+深度前馈网络
+常见的结构:
+递归神经网络
+常见的结构:
+生成对抗网络(GAN)
+两个网络博弈:G(Generator)和D(Discriminator)
+深度强化学习
+强化学习:学习目标:策略概率
值函数网络:Deep Q-Learning
+策略网络:Deep Policy Network
+含有数据输入层、1个以上隐藏层、 1个输出层;各层神经元全连接,同一层神经元之间无连接。
+ +多层感知机的运算:
+ +激活函数(包括硬门限阈值函数),是导致网络运算非线性的直接原因。
+学习问题:
+学习目标:调整神经元连接权重值,使得平均误差能量最小。
+两种方法:批量学习和在线学习。
+目标:最小化损失函数
+批量学习(Batch Learning)
+在线学习(Online Learning):sample by sample 调整权值
+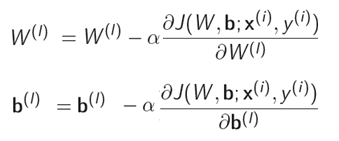
+优点:容易执行、存储量小、有效解决大规模和困难模式的分类。
缺点:学习过程随机、不稳定。
+两个方向的信号流、两个方向的函数运算
+函数信号:计算输出函数信号
+误差信号:计算梯度向量
+数据前馈运算
+ +梯度反馈运算
+ +BP 算法小结
+激活函数
+异或问题
+改善性能的试探法
+函数逼近
+卷积层:卷积层具有局部连接和权重共享特点。
+一维、二维卷积
+卷积层的输出尺度
+卷积层的参数个数
+子采样层:每个通道,通过下采样,缩减尺度。
+典型实例:LeNet-5
+四种基本递归结构
+通用逼近定理:如果网络具有充分多的隐藏神经元,任意的非线性动态系统可以由递归神经网络以期望的精度来逼近,对于状态空间的紧致性没有限制。
+计算能力
+Recurrent 网络
+RNN分回合训练
+RNN连续训练
+RNN长期依赖
+RNN扩展的递归结构
+深层结构:神经网络 + 深层结构 + 优化 + 计算资源 + 人工智能应用
+梯度消失:解决梯度消失
+视觉识别
+自然语言处理
+生成对抗模型原理
+生成器(Generator):尽可能去学习真实样本的分布,迷惑鉴别器。
+鉴别器(Discriminator):尽可能的正确判断输入数据是来自真实数据还是来自生成器。
+损失函数:
训练过程:生成器与鉴别器交替训练,互相提升各自的生成能力和鉴别能力,最终寻找二者之间的一个纳什均衡。
+马尔科夫决策过程:
+智能体环境交互-智能体的目标是最大化将来的期望累积奖励
+背景
+知识图谱的概念最早出现于Google公司的知识图谱项目,体现在使用Google搜索引擎时,出现于搜索结果右侧的相关知识展示。
+截止到2016 年底,Google知识图谱中的知识数量已经达到了600亿条,关于1500个类别的5.7亿个实体,以及它们之间的3.5万种关系。
+实体、关系和事实:
+狭义知识图谱
+狭义知识图谱:具有图结构的三元组知识库。
+节点:实体。 边:事实(由头实体指向尾实体)。 边的类型:关系。
+链接预测、三元组分类:知识图谱上的链接预测
+分布式知识表示方法分类:
+KMP算法详解
+ +一直都没弄明白,也没下决心去弄明白。昨天感觉基本上差不多了,整理一下,再加深一下印象。
+给你两个字符串 haystack和 needle,请你在 haystack字符串中找出 needle字符串的第一个匹配项的下标(下标从 0开始)。如果 needle不是 haystack的一部分,则返回 -1 。
AC代码:
+func strStr(haystack string, needle string) int {
+ needlelen := len(needle)
+ haystacklen := len(haystack)
+ next := make([]int,needlelen)
+ next[0] = 0
+ j := 0
+ for i:=1;i<needlelen;i++{
+ for j > 0 && needle[i] != needle[j]{
+ j = next[j-1]
+ }
+ if needle[i] == needle[j]{
+ j++
+ }
+ next[i] = j
+ }
+ j = 0
+ for i:=0;i<haystacklen;i++{
+ for j > 0 && needle[j] != haystack[i]{
+ j = next[j-1]
+ }
+ if needle[j] == haystack[i]{
+ j++
+ }
+ if j == needlelen{
+ return i-j+1;
+ }
+ }
+ return -1
+}判断一个字符串(模式串)是不是另外一个字符串(文本串)的子串,怎么做?
+最容易想到的:暴力匹配。
+比如有下面的两个字符串:
+abacac和 ac
开始肯定是第一个 a开始和 ac进行匹配,匹配失败了,然后从 b再开始匹配。最坏情况,每一个都要判断到匹配字符串的最后一个字符,两层循环,时间复杂度很容易想到就是
但是事实上,如果从人工匹配的角度来看,我们都知道 b不可能匹配成功,让你用肉眼匹配,傻子才会去看 b。但是计算机程序为了全部判断还是要去尝试一下。
那么怎么把这种无效的匹配让开呢?直观上可能想到,我判断第一个能不能匹配上不就行了,应该能降低时间复杂度?
+那么再举一个例子:aaaaaaaaaa和 ab,时间复杂度一样是
所以不仅仅要看第一个,看第一个也无法完全抹去无效的匹配。这时候需要一种高效的匹配算法,核心思想就是在匹配的过程中要记录,匹配失败后从第一个可能成功的地方开始即可,不要做无效工作。
+因此就有了超难理解的KMP算法以及各种比KMP还要复杂的算法。这里就先好好的讲一下KMP,希望以后可以真正理解,抬手就来。
+前缀表:记录下标 i之前(包括 i)的字符串中,有多大长度的相同前缀后缀。
前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串 。
+后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串 。
+啥意思?举例子就好了
+| 模式串下标 | +0 | +1 | +2 | +3 | +4 | +5 | +6 | +7 | +8 | +9 | +10 | +11 | +12 | +
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 字符串 | +a | +b | +c | +d | +a | +b | +c | +a | +b | +c | +d | +a | +b | +
| 前缀表 | +0 | +0 | +0 | +0 | +1 | +2 | +3 | +1 | +2 | +3 | +4 | +5 | +6 | +
怎么算的?
+下标为 0,字符串为 a,前缀为空(因为不包含最后一个字符,因此字符就没了),后缀为空(因为不包含第一个字符,因此字符就没了),因此相同前缀后缀长度为0(因为都是空串)
下标为 1,字符串为 ab,前缀为 a,后缀为 b,因此相同前缀后缀长度为 0
下标为 2,字符串为 abc,前缀为 ab,后缀为 bc,因此相同前缀后缀长度为 0
下标为 3,字符串为 abcd,前缀为 abc,后缀为 bcd,因此相同前缀后缀长度为 0
下标为 4,字符串为 abcda,前缀为 abcd,后缀为 bcda,因此相同前缀后缀长度为 1,也就是 a
下标为 5,字符串为 abcdab,前缀为 abcda,后缀为 bcdab,因此相同前缀后缀长度为 2,也就是 ab
下标为 6,字符串为 abcdabc,前缀为 abcdab,后缀为 bcdabc,因此相同前缀后缀长度为 3,也就是 abc
下标为 7,字符串为 abcdabca,前缀为 abcdabc,后缀为 bcdabca,因此相同前缀后缀长度为 1,也就是 a
…
+下标为 12,字符串为 abcdabcabcdab,前缀为 abcdabcabcda,后缀为 bcdabcabcdab,因此相同前缀后缀长度为 6,也就是 abcdab
人工计算还是挺好算的,用眼睛看看简单算算就行了。网上有些资料是从 -1开始,然后右移一位,我认为不好理解,不如保留前缀表的本意
所以算来算去,前缀表有什么用处呢?
+前缀表可以帮助我们在匹配不成功的时候找到前面最佳的重新开始的位置,从而保证我们只遍历文本串一次就能判断模式串与文本串是否匹配。(废话)
+先举例:后面的 i指文本串的下标,j指模式串的下标。(文本串下标保证递增,绝对不回退)
| 文本串下标 | +0 | +1 | +2 | +3 | +4 | +5 | +
|---|---|---|---|---|---|---|
| 字符串 | +a | +c | +b | +a | +b | +a | +
| 模式串下标 | +0 | +1 | +2 | +3 | +4 | +
|---|---|---|---|---|---|
| 字符串 | +a | +c | +b | +a | +c | +
| 前缀表 | +0 | +0 | +0 | +1 | +2 | +
开始匹配,i和 j匹配的很顺利,转眼就到了 i=j=4,然后发现糟了,匹配不上了,现在 j要回退,找到重新开始匹配的位置。
j退到哪里呢?因为 j是没有匹配上的,而 j-1如果有意义(j≠0),一定是能匹配上的!(为什么?因为只有匹配上了 j才会移动,j移动过的位置一定是之前匹配好了的)
那么 j-1是匹配上的又说明了什么呢?说明对于 0~j-1的字符串,如果有相同的前缀后缀,一定也是能和i-1匹配的上的,因此就不需要回退超过前缀的位置!
还是上面的例子,模式串的 j-1前缀表的值是 1,说明 j-1位置的 a在模式串的前面也出现过,就是模式串 0位置的 a。由于 j-1是和 i-1匹配上了的,因此 j=0和 i-1也是匹配上了的,不需要再去看模式串 0的位置,只需要看0的后一个位置 1和 i是否能匹配上就好了!
流程步骤:
+i和 j匹配不上了,隐含条件是 i-1和 j-1是可以匹配的j-1后缀的相同长度的前缀长度,也就是 next[j-1]的值j到 next[j-1]的位置,隐含了这一步将相同长度的前缀绕过然后 j=next[j-1]后就去判断 j和 i是不是相同就好了,很不幸的是,还是不相同,i指向的是 b,j指向的是 c。
那么没办法,留着这个前缀也无法匹配了,只好再次回退,这一退就退到 j=0了,但是还是不相等。
j=0就没有办法再次回退了,只好 i++,舍弃这一个部分的文本串,开始新的文本串。
到这里应该明白了前缀表的作用了,字面上很难理解,跟着流程走一遍就明白它的思想了,确实精妙
+所以在已知 next数组的前提下,这个字符串匹配的代码就很简单了。虽然简单,但是结构一点都不可以修改,循环和顺序都是精心设计的。
j = 0
+for i:=0;i<haystacklen;i++{
+ for j > 0 && needle[j] != haystack[i]{ // 匹配不上就一直回退,j=0说明真的匹配不上了,跳出来i++
+ j = next[j-1]
+ }
+ // j=0也会跳到这里尝试一下
+ if needle[j] == haystack[i]{ // 匹配上的就能j++去看模式串的下一个字符了,然后进入下一个循环i++,判断文本串的下一个字符能不能和模式串的这个字符匹配上
+ j++
+ }
+}还有一个问题,next数组怎么求?
next数组首先要明确一点,next数组是针对模式串而言的,与文本串半毛钱关系没有
| 模式串下标 | +0 | +1 | +2 | +3 | +4 | +5 | +6 | +
|---|---|---|---|---|---|---|---|
| 字符串 | +a | +b | +a | +a | +b | +a | +e | +
| 前缀表 | +0 | +0 | +1 | +1 | +2 | +3 | +0 | +
其实思想和匹配是相同的,不同的地方在于上面的是用模式串和文本串进行匹配,这里是用自己和自己进行匹配,匹配的过程中看看能匹配上多少,就能得出 next数组的数值了
next[0]=0,初始化毫无争议,因为空串一定是0
指针 i同样一直向前,指针 j会进行回退,因为 next[0]确定了,因此直接初始化i=1
最开始,j指向的是 0的位置,就在这里等着到底哪个 i能和我这个可爱的 j匹配上
到了 i=2,匹配上了!这时候 j不满足了,是不是 i+1也能和 j+1匹配上呢?所以就 j++,尝试匹配下一个
要是匹配不上了怎么办呢?比如 j=3,i=6匹配不上了,也隐含了条件,就是 j=2是能和 i-1匹配上的(要是匹配不上j也不可能不等于0)
那么j=2时候的相同长度的前后缀在哪里呢?因为如果相同也不需要去看了,所以更新j=next[j-1]就可以了,和上面的字符串的匹配思想是完全相同的。
如果还是匹配不上,那么j只好乖乖变为0,等待着下一个能匹配上的将j+1了
代码如下:
+next[0] = 0 // 初始化
+j := 0 // j指向首位
+for i:=1;i<needlelen;i++{ // 遍历模式串,不回退
+ for j > 0 && needle[i] != needle[j]{
+ j = next[j-1] // 匹配不上了,绕过已知的相同长度的前后缀,直到变为j=0的初始状态
+ }
+ // 如果j=0还是有一次判断的机会的
+ if needle[i] == needle[j]{ // 匹配上了将j解放出来,+1再试试
+ j++
+ }
+ next[i] = j // 赋值next数组
+}设 n为文本串长度,m为模式串长度
在匹配的过程中,根据前缀表不断调整匹配的位置,如果没有一个字符能匹配的上,时间复杂度就是文本串的指针从头移到尾,也就是
如果能匹配上一些字符,回退的次数也不可能超过 n次。因此时间复杂度是
生成 next数组,不会比匹配的时间复杂度高(因为如果模式串比文本串还要长,根本就不需要匹配了)
所以从平方级别的时间复杂度直接降到了线性的时间复杂度。
+看过很多遍,应该也曾经懂过,就是从来没有整理过,因此可能也没有真正懂过。
+希望这次能真真正正懂了,后面忘记了再来看看这篇文章,希望能快一些想起来。
+ + +《高级人工智能》课程笔记:第8讲 逻辑
+ +什么是“数理逻辑”?
+一个算法,以任何作为输入,输出的都是正确答案
+输入:
+输出答案:该查询在此知识库上的正确答案
+如果有上面的算法,那么所有难题都能得到解决
+如果有这样的一种“终极算法”,首先要将自然语言表达的知识库和查询表示成形式语言表达的知识库和查询,然后通过自动的知识推理,得到形式语言表达的答案
+解决如下问题:
+研究形式化定义的sentences之间的关系
+ +左侧是语义的蕴含关系(逻辑推导),
右侧是语法的演绎关系(形式推演),
如果左侧的是右侧的子集,说明正确的结论都在算法推导的里面,那么说明这个算法是完备的,但是有一些结论可能算法计算出来是错误的
+如果右侧的是左侧的子集,说明算法推出来的结论都是正确的,因此算法是可靠的,但是有可能有一些正确的结论算法算不出来
+如果兼具完备性和可靠性,那么证明这个算法是正确的。
+如果

true,那么称

model,句子
KB指的是一些句子的集合



KB蕴含
因此



命题是一种声明,要么是真的,要么是假的,不存在第三种可能
+命题逻辑通常不考虑时间
+原子命题指的是最小的命题,用大写字母表达
+文字是原子命题,或者是原子命题的否
+一个句子是一个原子句或者复杂句
+一个原子句表示为:
复杂句有五种表示形式,与复杂句之间的真值表:
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+
|---|---|---|---|---|---|---|
| false | +false | +true | +false | +false | +true | +true | +
| false | +true | +true | +false | +true | +true | +false | +
| true | +false | +false | +false | +true | +false | +false | +
| true | +true | +false | +true | +true | +true | +true | +
连接词和集合之间的联系:
+两个句子是逻辑等价的-两个句子的model相同:

定理:
+KB: 满足命题逻辑语法的sentence的集合
+假设:这组sentence中,一共有n个原子命题
+真值指派(truth assignment):对每个原子名字赋值
+一共有
在此基础上,在命题逻辑中,我们可以明确的定义
 当且仅当
当且仅当 是永真的
是永真的 当且仅当
当且仅当 是不可满足的
是不可满足的

推出:
共有两套规则(11条规则和归结原理)
+11条形式推演规则:(不需要背诵)
+形式可推演性:A在命题逻辑中由


句子

可靠性:任意时刻当


完备性:任意时刻当


合取范式:子句(文字和析取符号)的合取形式,子句内部是没有合取的(CNF)转换为合取范式是多项式时间复杂度的
+归结原理:互补文字可以互相消去(但是每一次只能消去一对)
+归结原理是既可靠又完备的
+证明:若



使用上述证明来证明知识库可以推出某个子句
+在研究可靠性与完备性问题时,应当把语法层面的知识理解为Groundtruth
+因此可靠性可以大概表述为:语义上推演得到的知识在语法上正确。因此要证明归结原理的可靠性,即证明
+ +使用真值表进行证明即可
+完备性可以大概表述为:如果语法上能够推理得到的,那么语义上正确。
+即证明:如果
RC(S):对S内部的全部子句进行归结后的集合。
+完备性证明
+




则只需要证明:如果
等价于证明逆否命题:如果RC(S)不包含空子句,则
证明:针对S中的原子命题
首先,因为RC(S)中不包含空集,即RC(S)中不包含永假的子句。
+从


如果RC(S)中包含一个子句,此子句包含


我们用反证法证明:这个真值指派使得RC(S)中的子句都为真。
+假设,在此过程的第i步,我们这样来指派

显然,如果RC(S)中只包含以上两个子句之一,子句C是不会在此真值指派中为False的。因此, RC(S)此时应该同时包含了以上两个子句。
+以上两个子句显然是满足归结条件的,也就是说,它归结后的子句也应该在RC(S)中;同时,该子句已经被指派为False了;这与我们之前的假设矛盾。
+因此这个真值指派使得RC(S)中的子句都为真,进而S是可满足的。
+可以转换为搜索问题,如何使用A*搜索实现呢?
+以限制知识库里面的句子形式为代价,获得时间复杂度上的提升
+上述提到的归结原理具有完备性,这是很好的性质,对于许多现实世界的应用,如果添加一些限制,可以实现更高效的推理。为了换取更好的inference的时间效率,缩小命题逻辑的表达范围,得到适用于Horn Form的Modus Ponens规则,是另外一种形式的归结原理。
+KB为Definite clause的合取形式:
+ +Definite clause: 每一个句子有且只有一个文字是正文字的析取形式
+只有两种形式:①原子命题②命题的合取
Horn clause: 每一个句子最多一个文字是正文字的析取形式
+PPT例子:KB是全部句子的情况下是否能推出Q
+前向推理:从条件出发去推结论
+前向推理是数据驱动的,可能推出一些结论与我们要推出的结论是无关的
+后向推理:从结论返回推出条件
+后向推理是目的驱动的,找为了推出这个结论所需要的条件,因此通常情况下后向推理比前向推理好,但是也存在某种情况前向推理比后向推理好
+(全连接神经网络)
+证明是可靠的,即证明
通过真值表进行证明即可
+证明是完备的:
+若




证明:RC(KB)是KB中原始的句子和通过Modus Ponens推出的句子的全部集合
+ :对于任意的symbol a,a指派为True当且仅当
:对于任意的symbol a,a指派为True当且仅当
(如果一个正文字在
 下,
下, 为真。
为真。反证:若此时

若该子句为






若该子句为



 ,根据蕴含的定义:在
,根据蕴含的定义:在 中,
中, 为真;则根据1中的定义,
为真;则根据1中的定义, ,也就是说:
,也就是说:
命题逻辑的缺点:能表达的东西比较有限。
+命题逻辑假设世界上都是事实(fact),一阶谓词逻辑认为世界上还包括对象、关系和函数等等。
+基本元素:
+ ,
, 为真当且仅当
为真当且仅当 和
和 指向现实世界中的同一个对象
指向现实世界中的同一个对象 和存在量词
和存在量词
简单句:

嵌套函数会造成很大的问题。命题逻辑的算法一定会停止(decidable可判定的),但是由于嵌套函数的存在,谓词逻辑只是半可判定的。
+复杂句:使用连接词对简单句进行连接构成复杂句
+在谓词逻辑中,要将每一个符号指派到现实世界中,将常量转化为对象、将谓词转化为关系、将函数符号转化为真正的函数
+量词与变量是对应的,有变量一定要有量词来量化
+全称量词:变量所有实例的合取形式
+错误的形式:
存在量词:变量所有实例的析取形式
+错误的形式:
量词的属性关系
+两种量词之间可以相互转换
+全称实例化:实例化全称量词蕴含的每一个实例
+注意在实例化的过程中,第n次循环只能嵌套n次函数
+因此算法可能不会停止,为semi-decidable的
+存在实例化:赋予一个新的常量符号
+去掉存在量词和存在量词修饰的变量,使得句子里面的每一个变量都是全称量词修饰的变量,且为合取范式
+合一算子:替换后等价的替换方式(只能将常量赋值给变量)
+归结原理:
尤其注意要赋值
归结原理既完备又可靠,证明比较复杂不讲
+可能有很多的归结策略,选择哪种方式进行归结呢?
+没有一种归结策略适用于全部情况
+广度优先策略:扩展所有可能的情况然后归结
+优点:
+缺点:
+广度优先对大问题的归结容易产生组合爆炸,但对小问题却仍是一种比较好的归结策略。
+常用的归结策略可分为两大类:
+删除法主要想法是:把子句集中无用的子句删除掉,这就会缩小搜索范围,减少比较次数,从而提高归结效率。
+删除纯文字:
+ 在子句集中不存在可与其互补的文字
在子句集中不存在可与其互补的文字 ,则称该文字为纯文字。
,则称该文字为纯文字。重言式删除法:
+限制策略要慎重,防止可以得到空子句但是限制后就得不到空子句了
+支持集策略:每一次参加归结的两个亲本子句中,至少应该有一个是由目标公式的否定所得到的子句或它们的后裔。(就是别自己本身进行归结,带上
支持集策略是完备的,即当子句集为不可满足时,则由支持集策略一定能够归结出一个空子句。
+单文字子句策略:每次参加归结的两个亲本子句中至少有一个子句是单文字子句
+采用单文字子句策略,归结式包含的文字数将少于其非单文字亲本子句中的文字数,这将有利于向空子句的方向发展,因此会有较高的归结效率。
+单文字子句策略是不完备的,即当子句集为不可满足时,用这种策略不一定能归结出空子句。原因: 没有可用的单文字字句
+祖先过滤策略:满足以下两个条件中的任意一个就可进行归结:
+祖先过滤策略是完备的
+GMP的可靠性证明:将量词去掉变量替换为
同样有前向推理和后向推理,同样是半可判定的
+但是,如果仅包含一阶谓词的definite子句且没有函数,那么是decidable的(也叫Datalog)
+清晰的概念:对象是否属于这个概念是明确的。
+模糊性的概念:对象从属的界限是模糊的,随判断人的思维而定
+取得精确数据不可能或很困难,也没有必要获取精确数据
+要使计算机能够模仿人脑,对复杂系统进行识别和判断,出路何在?
+1965年扎德(Zadeh)教授开创了对“模糊数学”的研究。他认为数学是可以模糊的,主张从精度方面“后退”一步。他提出用隶属函数使模糊概念数学化。
+设













模糊集














模糊性:事件发生的程度,而不是一个事件是否发生
+随机性:描述事件发生的不确定性,即一个事件发生与否
+离散且为有限论域的表示方法
+设论域
为了能够表示出论域中的元素与其隶属度之间的对应关系,扎德引入了一种模糊集的表示方式:先为论域中的每个元素都标上其隶属度,然后再用“+”号把它们连接起来,即




连续论域的表示方法:如果论域是连续的,则其模糊集可用一个实函数来表示。
+设





设





设





设



两个模糊集之间的运算实际上就是逐点对隶属函数作相应的运算
+经典集合的关系:
+笛卡尔积:设



从




对于








模糊集合的关系:在二元关系上定义隶属度函数
+设

为

在



设











模糊逻辑:定义模糊谓词、模糊量词、模糊修饰语等
+模糊谓词:设



模糊量词:模糊逻辑中使用的模糊量词,如极少、很少、几个、少数、多数、大多数、几乎所有等。
+模糊修饰语:
+设



模糊修饰语的四种主要运算:
+



演化计算(Evolutionary Computation, EC):
+典型代表:
+演化计算:一种模拟自然界生物进化过程与机制进行问题求解的自组织、自适应的随机搜索技术。
+演化规则:“物竞天择、适者生存”
+演化操作:繁殖(Reproduction)、变异(Mutation)、竞争(Competition)、选择(Selection)
+遗传算法的基本思想是从初始种群出发,采用优胜劣汰、适者生存的自然法则选择个体,并通过杂交、变异来产生新一代种群,如此逐代进化,直到满足目标为止
+基本概念:
+遗传算法主要由染色体编码、初始种群设定、适应度函数设定、遗传操作设计等几大部分所组成,
+算法基本步骤:
+二进制编码是将原问题的结构变换为染色体的位串结构。假设某一参数的取值范围是



优点:易于理解和实现,可表示的模式数最多
+缺点:海明悬崖。当算法从7改进到8时,就必须改变所有的位
+要求两个连续整数的编码之间只能有一个码位不同,其余码位都是完全相同的。有效地解决了海明悬崖问题。
+基本原理:
+个体染色体编码串中的基因值取自一个无数值含义,而只有代码含义的符号集。
+适应度函数是一个用于对个体的适应性进行度量的函数。个体的适应度值越大,它被遗传到下一代种群中的概率越大
+常用的适应度函数
+ 定义为遗传算法的适应度函数。
+
定义为遗传算法的适应度函数。
+ 时,
时, 即为
即为 的原始适应度函数。
的原始适应度函数。
选择(selection)操作:根据选择概率按某种策略从当前种群中挑选出一定数目的个体,使它们能够有更多的机会被遗传到下一代中
+ ,其中,
,其中, 是个体
是个体 的相对适应度,即个体
的相对适应度,即个体 被选中的概率,
被选中的概率, 是个体
是个体 的原始适应度。
的原始适应度。交叉(crossover)操作:按照某种方式对选择的父代个体的染色体的部分基因进行交配重组,从而形成新的个体。
+二进制交叉:二进制编码情况下所采用的交叉操作
+实值交叉:在实数编码情况下所采用的交叉操作,主要包括离散交叉和算术交叉
+ 的概率进行交换,从而生成子代中的两个新的个体。
的概率进行交换,从而生成子代中的两个新的个体。变异(Mutation)操作:对选中个体的染色体中的某些基因进行变动,以形成新的个体。遗传算法中的变异操作增加了算法的局部随机搜索能力,从而可以维持种群的多样性。
+精英主义 (Elitism)
+仅仅从产生的子代中选择基因去构造新的种群可能会丢失掉上一代种群中的很多信息。也就是说当利用交叉和变异产生新的一代时,我们有很大的可能把在某个中间步骤中得到的最优解丢失。
+使用精英主义(Elitism)方法,在每一次产生新的一代时,我们首先把当前最优解原封不动的复制到新的一代中,其他步骤不变。这样任何时刻产生的一个最优解都可以存活到遗传算法结束。
+《现代信息检索》课程笔记:第16讲 Web搜索
+ +搜索是Web上使用最多的应用之一
+没有搜索引擎,Web甚至无法运转
+兴趣聚合:具有相同兴趣的人,即使所处地理位置分散,也可以通过Web找到对方。
+搜索引擎是实现兴趣聚合的关键事物
+在Web上,搜索不仅仅是一个好的特点
+Web是一个充满噪声数据且组织失调的集合体→大量的重复需要检测
+用户可以(某种意义上)无控制和无限制地发布内容→大量作弊内容需要检测
+传统广告:品牌广告、直接营销、
+传统广告的不足:
+互联网广告的优点:
+互联网广告的主要形式:图片广告、文本广告、搜索广告、网页广告、
+第一代搜索广告:Goto
+第二代搜索广告:Google
+如何对广告排序?
+Web查询“长尾”现象:基于AOL查询频次的统计、基于查询频次的流量统计
+长尾效应的解释
+近似重复的检测:采用编辑距离指标计算页面之间的相似度
+将每篇文档表示成一个shingle 集合
+每个shingle 是一个基于词语的 n-gram
+使用shingle 来计算文档之间的语法相似度
+两个文档的相似度定义为它们的shingle 集合的Jaccard距离
+每篇文档的shingle的个数非常大
+为提高效率,接下来我们使用文档的梗概来表示文档,它由文档的shingle集合中精巧挑选出的子集构成
+高效的近似重复检测:局部敏感哈希或排序
+ + +《现代信息检索》课程笔记:第17讲 信息采集
+ +基本的采集过程
+上述简单采集器的问题:
+采集器必须做到
+任意一个采集器应该做到:
+待采集URL池:
+基本的采集架构
+URL规范化
+内容重复判别
+分布式采集
+分布式采集器
+待采集URL池 : 主要考虑两点
+采集器陷阱
+《现代信息检索》课程笔记:第18讲 链接分析
+ +链接无处不在
+为什么我们对链接分析感兴趣?
+链接分析对目前为止的完全基于文本的IR任务进行了补充
+Web可以看成一个有向图
+对锚文本构建索引
+PageRank背后的假设
+Google炸弹:指由于人为恶意构造锚文本而导致的结果很差的搜索。用户群体有意创建链接误导搜索引擎
+锚文本索引:将从指向文档D的链接的锚文本(也可能包含锚文本附近的文本)包含在D的索引中
+有时会产生低于期望的效果,例如:垃圾邮件过滤应用全然失败
+可以根据锚页面网站的权威性对锚文本进行加权
+链接服务器:低成本地获取所有链接信息
+Boldi and Vigna:基本目标-维护内存中的节点邻接表
+邻接表压缩中利用到的属性:
+间隔编码
+给出整数x,y,z 的已排序列表,用 x y-x z-y 来对 x,y,z 进行表示
+使用编码来压缩整数
+BV算法的主要优势
+引用分析:科技文献中的引用分析
+另一个应用:引用频率可以用度量一篇文档的影响度
+更好的度量方法:对不同网页来的引用频率进行加权
+原始PageRank的一个不足:图中存在一个循环通路,每次迭代,该循环通路中的每个节点的 PageRank不断增加,但是它们并不指出去,即不将PageRank分配给其他节点!
+改进的PageRank公式:随机冲浪或随机游走(Random Walk)模型
+每个网页计算两个值:
+Hub:作为目录型或导航型网页的权重
+Authority:作为权威型网页的权重
+一个网页被越重要的导航型网页指向越多,那么它的Authority越大;
+一个网页指向的高重要度权威型网页越多,那么它的Hub越大。
+HITS算法也是收敛的,也可以通过迭代的方式计算。
+HITS算法的实际计算过程
+PageRank vs. HITS
+网页的PageRank 与查询主题无关,可以事先算好,因此适合于大型搜索引擎的应用。
+HITS算法的计算与查询主题相关,检索之后再进行计算,因此,不适合于大型搜索引擎。
+ + +Go项目-家庭收支记账软件
+ +func main() {
+ // 声明一个变量保存用户的输入
+ key := ""
+
+ // 声明一个变量,控制是否退出for循环
+ loop := true
+
+ // 显示主菜单
+ for loop {
+ fmt.Println("---------------------家庭收支记账软件---------------------")
+ fmt.Println(" 1 收支明细")
+ fmt.Println(" 2 登记收入")
+ fmt.Println(" 3 登记输出")
+ fmt.Println(" 4 退出软件")
+ fmt.Print("请选择(1-4):")
+ // 接收用户的输入
+ fmt.Scanln(&key)
+ // 对用户的输入进行判断
+ switch key {
+ case "1":
+ fmt.Println("---------------------当前收支明细记录---------------------")
+ case "2":
+ case "3":
+ fmt.Println("登记支出------")
+ case "4":
+ loop = false
+ default:
+ fmt.Println("请输入正确的选项------")
+ }
+ }
+ fmt.Println("-------------------退出家庭收支记账软件-------------------")
+}没啥有意思的,基础编程,效果如下:
+ +case "1":
+ fmt.Println("---------------------当前收支明细记录---------------------")
+ fmt.Println(details)
+case "2":
+ fmt.Println("-------------------------登记收入-------------------------")
+ fmt.Print("本次收入金额:")
+ fmt.Scanln(&money)
+ fmt.Print("本次收入说明:")
+ fmt.Scanln(¬e)
+ balance += money
+ details += fmt.Sprintf("收 入\t%v\t%v\t%v\n", balance, money, note)
+ fmt.Println("收入登记成功!")其中明细是用字符串拼接实现的,实际中应该是要操作数据库的
+case "3":
+ fmt.Println("-------------------------登记支出-------------------------")
+ fmt.Print("本次支出金额:")
+ fmt.Scanln(&money)
+ if money > balance {
+ fmt.Println("余额的金额不足!")
+ break
+ } else if money <= 0 {
+ fmt.Println("支出金额应为正数!")
+ }
+ fmt.Print("本次支出说明:")
+ fmt.Scanln(¬e)
+ balance -= money
+ details += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", balance+money, money, balance, note)
+ fmt.Println("支出登记成功!")注意支出的金额要小于账户余额,也要注意收入和支出的时候用户输入的数字需要为正数。
+case "4":
+ var choice byte
+ for {
+ fmt.Print("确定退出?(y/n):")
+ fmt.Scanf("%c\n", &choice)
+ if choice == 'y' {
+ loop = false
+ break
+ } else if choice == 'n' {
+ break
+ } else {
+ fmt.Println("输入有误!!请重新输入")
+ }
+ }注意scanf字符的时候与C语言是差不多的,需要考虑回车符号
+// 判断当前是否有输入或者输出的记录
+flag := false也没啥好说的,加个标志位,有记录的时候将这个标志位改掉就可以了
+将上面的面向过程的代码修改成面向对象的代码
+主要思想:将记账软件的功能封装到结构体中,然后调用这个结构体的方法完成功能。
+// 定义结构体
+type FamilyAccount struct {
+ // 声明一个变量保存用户的输入
+ key string
+ // 声明一个变量,控制是否退出for循环
+ loop bool
+ // 定义账户的初始值
+ balance float64
+ // 定义每次收支的金额和说明
+ money float64
+ note string
+ // 收支的详情使用字符串来记录
+ // 当有记录时对这个字符串进行拼接
+ details string
+ // 判断当前是否有输入或者输出的记录
+ flag bool
+}注意定义结构体的时候不能进行初始化
+// 编写一个工厂模式的构造方法,返回结构体的指针
+func NewFamilyAcount() *FamilyAccount {
+ return &FamilyAccount{
+ key: "",
+ loop: true,
+ balance: 10000.0,
+ money: 0.0,
+ note: "",
+ details: "收 支\t收支前账户余额\t收支金额\t收支后账户余额\t说 明\n",
+ flag: false,
+ }
+}注意如果结构体是私有的是一定要有的,公开的也可以有,以后就要记得一定要有这样的一个方法
+简单改造一下面向过程的代码即可完成面向对象的效果
+将显示明细写成一个方法
+func (fa *FamilyAccount) showDetails() {
+ if !fa.flag {
+ fmt.Println("当前没有任何收支记录!")
+ } else {
+ fmt.Println("---------------------当前收支明细记录---------------------")
+ fmt.Println(fa.details)
+ }
+}将登记收入写成一个方法
+func (fa *FamilyAccount) income() {
+ fmt.Println("-------------------------登记收入-------------------------")
+ fmt.Print("本次收入金额:")
+ fmt.Scanln(&fa.money)
+ // 收入金额不能是负数
+ if fa.money <= 0 {
+ fmt.Println("收入金额应为正数!")
+ return
+ }
+ fmt.Print("本次收入说明:")
+ fmt.Scanln(&fa.note)
+ fa.balance += fa.money
+ fa.details += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", fa.balance-fa.money, fa.money, fa.balance, fa.note)
+ fmt.Println("收入登记成功!")
+ fa.flag = true
+}将登记支出写成一个方法
+func (fa *FamilyAccount) pay() {
+ fmt.Println("-------------------------登记支出-------------------------")
+ fmt.Print("本次支出金额:")
+ fmt.Scanln(&fa.money)
+ if fa.money > fa.balance {
+ fmt.Println("余额的金额不足!")
+ return
+ } else if fa.money <= 0 {
+ fmt.Println("支出金额应为正数!")
+ }
+ fmt.Print("本次支出说明:")
+ fmt.Scanln(&fa.note)
+ fa.balance -= fa.money
+ fa.details += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", fa.balance+fa.money, fa.money, fa.balance, fa.note)
+ fmt.Println("支出登记成功!")
+ fa.flag = true
+}将退出系统写成一个方法
+func (fa *FamilyAccount) exit() {
+ var choice byte
+ for {
+ fmt.Print("确定退出?(y/n):")
+ fmt.Scanf("%c\n", &choice)
+ if choice == 'y' {
+ fa.loop = false
+ break
+ } else if choice == 'n' {
+ break
+ } else {
+ fmt.Println("输入有误!!请重新输入")
+ }
+ }
+}显示主菜单
+func (fa *FamilyAccount) MainMenu() {
+ // 显示主菜单
+ for fa.loop {
+ fmt.Println("\n---------------------家庭收支记账软件---------------------")
+ fmt.Println(" 1 收支明细")
+ fmt.Println(" 2 登记收入")
+ fmt.Println(" 3 登记输出")
+ fmt.Println(" 4 退出软件")
+ fmt.Print("请选择(1-4):")
+ // 接收用户的输入
+ fmt.Scanln(&fa.key)
+ // 对用户的输入进行判断
+ switch fa.key {
+ case "1":
+ fa.showDetails()
+ case "2":
+ fa.income()
+ case "3":
+ fa.pay()
+ case "4":
+ fa.exit()
+ default:
+ fmt.Println("请输入正确的选项------")
+ }
+ }
+}func main() {
+ utils.NewFamilyAcount().MainMenu()
+}添加一个用户登录的功能,即只有将用户名和密码输入正确后才能打开软件,否则无法看到主界面
+实现:在显示菜单之前增加一个无限循环要求用户输入用户名和密码,只有输入正确才能退出循环
+for {
+ var username, password string
+ fmt.Print("请输入用户名:")
+ fmt.Scanln(&username)
+ fmt.Print("请输入密码:")
+ fmt.Scanln(&password)
+ if fa.login(username, password) {
+ break
+ } else {
+ fmt.Println("用户名或密码错误!")
+ }
+}用户登录的方法
+func (fa *FamilyAccount) login(username string, password string) bool {
+ if (username == fa.username) && (password == fa.password) {
+ return true
+ }
+ return false
+}package main
+
+import "fmt"
+
+func main() {
+ // 声明一个变量保存用户的输入
+ key := ""
+
+ // 声明一个变量,控制是否退出for循环
+ loop := true
+
+ // 定义账户的初始值
+ balance := 10000.0
+
+ // 定义每次收支的金额和说明
+ var money float64
+ var note string
+
+ // 收支的详情使用字符串来记录
+ // 当有记录时对这个字符串进行拼接
+ details := "收 支\t收支前账户余额\t收支金额\t收支后账户余额\t说 明\n"
+ // 判断当前是否有输入或者输出的记录
+ flag := false
+
+ // 显示主菜单
+ for loop {
+ fmt.Println("\n---------------------家庭收支记账软件---------------------")
+ fmt.Println(" 1 收支明细")
+ fmt.Println(" 2 登记收入")
+ fmt.Println(" 3 登记输出")
+ fmt.Println(" 4 退出软件")
+ fmt.Print("请选择(1-4):")
+ // 接收用户的输入
+ fmt.Scanln(&key)
+ // 对用户的输入进行判断
+ switch key {
+ case "1":
+ if !flag {
+ fmt.Println("当前没有任何收支记录!")
+ } else {
+ fmt.Println("---------------------当前收支明细记录---------------------")
+ fmt.Println(details)
+ }
+ case "2":
+ fmt.Println("-------------------------登记收入-------------------------")
+ fmt.Print("本次收入金额:")
+ fmt.Scanln(&money)
+ // 收入金额不能是负数
+ if money <= 0 {
+ fmt.Println("收入金额应为正数!")
+ break
+ }
+ fmt.Print("本次收入说明:")
+ fmt.Scanln(¬e)
+ balance += money
+ details += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", balance-money, money, balance, note)
+ fmt.Println("收入登记成功!")
+ flag = true
+ case "3":
+ fmt.Println("-------------------------登记支出-------------------------")
+ fmt.Print("本次支出金额:")
+ fmt.Scanln(&money)
+ if money > balance {
+ fmt.Println("余额的金额不足!")
+ break
+ } else if money <= 0 {
+ fmt.Println("支出金额应为正数!")
+ }
+ fmt.Print("本次支出说明:")
+ fmt.Scanln(¬e)
+ balance -= money
+ details += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", balance+money, money, balance, note)
+ fmt.Println("支出登记成功!")
+ flag = true
+ case "4":
+ var choice byte
+ for {
+ fmt.Print("确定退出?(y/n):")
+ fmt.Scanf("%c\n", &choice)
+ if choice == 'y' {
+ loop = false
+ break
+ } else if choice == 'n' {
+ break
+ } else {
+ fmt.Println("输入有误!!请重新输入")
+ }
+ }
+ default:
+ fmt.Println("请输入正确的选项------")
+ }
+ }
+ fmt.Println("-------------------退出家庭收支记账软件-------------------")
+}
+.
+├── Family-Ledger
+│ ├── main
+│ │ └── main.go
+│ └── utils
+│ └── familyAccount.go
main.go
+package main
+
+import (
+ "Go-Projects/Family-Ledger/utils"
+)
+
+func main() {
+ utils.NewFamilyAcount().MainMenu()
+}
+familyAccount.go
+package utils
+
+import "fmt"
+
+// 定义结构体
+type FamilyAccount struct {
+ // 用户名和密码
+ username string
+ password string
+ // 声明一个变量保存用户的输入
+ key string
+ // 声明一个变量,控制是否退出for循环
+ loop bool
+ // 定义账户的初始值
+ balance float64
+ // 定义每次收支的金额和说明
+ money float64
+ note string
+ // 收支的详情使用字符串来记录
+ // 当有记录时对这个字符串进行拼接
+ details string
+ // 判断当前是否有输入或者输出的记录
+ flag bool
+}
+
+// 编写一个工厂模式的构造方法,返回结构体的指针
+func NewFamilyAcount() *FamilyAccount {
+ return &FamilyAccount{
+ username: "admin",
+ password: "password",
+ key: "",
+ loop: true,
+ balance: 10000.0,
+ money: 0.0,
+ note: "",
+ details: "收 支\t收支前账户余额\t收支金额\t收支后账户余额\t说 明\n",
+ flag: false,
+ }
+}
+
+// 给结构体绑定相应的方法
+
+// 将显示明细写成一个方法
+func (fa *FamilyAccount) showDetails() {
+ if !fa.flag {
+ fmt.Println("当前没有任何收支记录!")
+ } else {
+ fmt.Println("---------------------当前收支明细记录---------------------")
+ fmt.Println(fa.details)
+ }
+}
+
+// 将登记收入写成一个方法
+func (fa *FamilyAccount) income() {
+ fmt.Println("-------------------------登记收入-------------------------")
+ fmt.Print("本次收入金额:")
+ fmt.Scanln(&fa.money)
+ // 收入金额不能是负数
+ if fa.money <= 0 {
+ fmt.Println("收入金额应为正数!")
+ return
+ }
+ fmt.Print("本次收入说明:")
+ fmt.Scanln(&fa.note)
+ fa.balance += fa.money
+ fa.details += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", fa.balance-fa.money, fa.money, fa.balance, fa.note)
+ fmt.Println("收入登记成功!")
+ fa.flag = true
+}
+
+// 将登记支出写成一个方法
+func (fa *FamilyAccount) pay() {
+ fmt.Println("-------------------------登记支出-------------------------")
+ fmt.Print("本次支出金额:")
+ fmt.Scanln(&fa.money)
+ if fa.money > fa.balance {
+ fmt.Println("余额的金额不足!")
+ return
+ } else if fa.money <= 0 {
+ fmt.Println("支出金额应为正数!")
+ }
+ fmt.Print("本次支出说明:")
+ fmt.Scanln(&fa.note)
+ fa.balance -= fa.money
+ fa.details += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", fa.balance+fa.money, fa.money, fa.balance, fa.note)
+ fmt.Println("支出登记成功!")
+ fa.flag = true
+}
+
+// 将退出系统写成一个方法
+func (fa *FamilyAccount) exit() {
+ var choice byte
+ for {
+ fmt.Print("确定退出?(y/n):")
+ fmt.Scanf("%c\n", &choice)
+ if choice == 'y' {
+ fa.loop = false
+ break
+ } else if choice == 'n' {
+ break
+ } else {
+ fmt.Println("输入有误!!请重新输入")
+ }
+ }
+}
+
+// 用户登录的功能
+func (fa *FamilyAccount) login(username string, password string) bool {
+ if (username == fa.username) && (password == fa.password) {
+ return true
+ }
+ return false
+}
+
+// 显示主菜单
+func (fa *FamilyAccount) MainMenu() {
+ for {
+ var username, password string
+ fmt.Print("请输入用户名:")
+ fmt.Scanln(&username)
+ fmt.Print("请输入密码:")
+ fmt.Scanln(&password)
+ if fa.login(username, password) {
+ break
+ } else {
+ fmt.Println("用户名或密码错误!")
+ }
+ }
+ // 显示主菜单
+ for fa.loop {
+ fmt.Println("\n---------------------家庭收支记账软件---------------------")
+ fmt.Println(" 1 收支明细")
+ fmt.Println(" 2 登记收入")
+ fmt.Println(" 3 登记输出")
+ fmt.Println(" 4 退出软件")
+ fmt.Print("请选择(1-4):")
+ // 接收用户的输入
+ fmt.Scanln(&fa.key)
+ // 对用户的输入进行判断
+ switch fa.key {
+ case "1":
+ fa.showDetails()
+ case "2":
+ fa.income()
+ case "3":
+ fa.pay()
+ case "4":
+ fa.exit()
+ default:
+ fmt.Println("请输入正确的选项------")
+ }
+ }
+}
+Go项目-客户信息管理系统
+ +主要是用于表示一个客户的信息,包含结构体以及在其他地方如果调用它的工厂模式的方法
+package model
+
+import "fmt"
+
+// 定义Customer结构体,表示一个客户信息
+type Customer struct {
+ Id int
+ Name string
+ Gender string
+ Age int
+ Phone string
+ Email string
+}
+
+// 工厂模式返回Customer的结构体,在CustomerService里面使用
+// 感觉就是新建一个Customer的实例
+func NewCustomer(id int, name string, gender string, age int, phone string, email string) *Customer {
+ return &Customer{
+ Id: id,
+ Name: name,
+ Gender: gender,
+ Age: age,
+ Phone: phone,
+ Email: email,
+ }
+}
+
+func (cu *Customer) GetInfo() string {
+ return fmt.Sprintf("%v\t%v\t%v\t%v\t%v\t%v", cu.Id, cu.Name, cu.Gender, cu.Age, cu.Phone, cu.Email)
+}以及如果我们要返回一个客户的信息,操作也是在Customer的实例上进行的,因此后面的方法也要写在这个结构体的下面
+完成对Customer结构体的操作的代码在CustomerService里面,定义另外一个结构体,里面包含一个切片,存储全部实例化的Customer
+// 完成对Customer的操作,包括增删改查
+type CustomerService struct {
+ // 存储当前的客户
+ Customers []model.Customer
+ // 声明一个字段,表示当前切片含有多少个客户
+ CustomerNum int
+}主菜单:
+func (cv *CustomerView) MainMenu() {
+ for {
+ var username, password string
+ fmt.Print("请输入用户名:")
+ fmt.Scanln(&username)
+ fmt.Print("请输入密码:")
+ fmt.Scanln(&password)
+ if cv.login(username, password) {
+ break
+ } else {
+ fmt.Println("用户名或密码错误!")
+ }
+ }
+ // 显示主菜单
+ for cv.loop {
+ fmt.Println("\n---------------------客户信息管理软件---------------------")
+ fmt.Println(" 1 添加客户")
+ fmt.Println(" 2 修改客户")
+ fmt.Println(" 3 删除客户")
+ fmt.Println(" 4 客户列表")
+ fmt.Println(" 5 退 出")
+ fmt.Print("请选择(1-5):")
+ // 接收用户的输入
+ fmt.Scanln(&cv.key)
+ // 对用户的输入进行判断
+ switch cv.key {
+ case "1":
+ cv.addCustomer()
+ case "2":
+ cv.changeCustomer()
+ case "3":
+ cv.deleteCustomer()
+ case "4":
+ cv.showCustomer()
+ case "5":
+ cv.exit()
+ default:
+ fmt.Println("请输入正确的选项------")
+ }
+ }
+}主菜单里面有的变量是需要定义在结构体中的
+type CustomerView struct {
+ key string // 接收用户输入
+ loop bool // 表示是否循环的显示主菜单
+ username string // 用户的用户名
+ password string // 用户的密码
+ customerService *service.CustomerService // 获取用户服务
+}同时也编写一个工厂模式的方法,方便main.go文件进行调用
+func NewCustomerView() *CustomerView {
+ return &CustomerView{
+ key: "",
+ loop: true,
+ username: "admin",
+ password: "password",
+ customerService: service.NewCustomerService(),
+ }
+}main.go:
+package main
+
+import (
+ "Go-Projects/Customer-Management-System/view"
+)
+
+func main() {
+ view.NewCustomerView().MainMenu()
+}
+要注意,全部的功能实现细节都应该是在customerService里面进行编写的,customerView.go 文件只负责调用,并对返回的结果进行判断等。
+首先要对CustomerService进行初始化,也是相当于工厂模式了
+// 初始化CustomerService
+func NewCustomerService() *CustomerService {
+ customerService := &CustomerService{} // 初始化
+ customerService.CustomerNum = 0
+ return customerService
+}func (cv *CustomerView) showCustomer() {
+ if cv.customerService.CustomerNum == 0 {
+ fmt.Println("没有客户!")
+ return
+ }
+ fmt.Println("\n-------------------------客户列表-------------------------")
+ fmt.Println("编号\t姓名\t性别\t年龄\t电话\t电子邮件")
+ for _, eachCustomer := range cv.customerService.ShowCustomerSlice() {
+ fmt.Println(eachCustomer.GetInfo())
+ }
+}func (cs *CustomerService) ShowCustomerSlice() []model.Customer {
+ return cs.Customers
+}对切片增加一个客户的实例,然后将记录的数量+1
+func (cv *CustomerView) addCustomer() {
+ id := cv.customerService.CustomerNum + 1
+ var name, gender, phone, email string
+ var age int
+ fmt.Print("请输入姓名:")
+ fmt.Scanln(&name)
+ fmt.Print("请输入性别:")
+ fmt.Scanln(&gender)
+ fmt.Print("请输入年龄:")
+ fmt.Scanln(&age)
+ fmt.Print("请输入电话:")
+ fmt.Scanln(&phone)
+ fmt.Print("请输入电子邮件:")
+ fmt.Scanln(&email)
+
+ if cv.customerService.AddCustomer(*model.NewCustomer(id, name, gender, age, phone, email)) {
+ fmt.Println("-------------------------添加成功-------------------------")
+ } else {
+ fmt.Println("-------------------------添加失败-------------------------")
+ }
+}func (cs *CustomerService) AddCustomer(customer model.Customer) bool {
+ cs.Customers = append(cs.Customers, customer)
+ cs.CustomerNum += 1
+ return true
+}根据客户的ID寻找客户在切片中的位置,然后将它删除即可。
+func (cv *CustomerView) changeCustomer() {
+ var id int
+ fmt.Print("请输入修改的ID号:")
+ fmt.Scanln(&id)
+ if cv.customerService.ChangeCustomer(id) {
+ fmt.Println("-------------------------修改成功-------------------------")
+ } else {
+ fmt.Println("-------------------------添加失败-------------------------")
+ }
+}func (cs *CustomerService) DeleteCustomer(id int) bool {
+ for index, cus := range cs.Customers {
+ if cus.Id == id {
+ cs.Customers = append(cs.Customers[:index], cs.Customers[index+1:]...)
+ cs.CustomerNum -= 1
+ return true
+ }
+ }
+ return false
+}根据客户的ID寻找客户在切片中的位置,然后修改需要修改的字段即可。
+func (cv *CustomerView) changeCustomer() {
+ var id int
+ fmt.Print("请输入修改的ID号:")
+ fmt.Scanln(&id)
+ if cv.customerService.ChangeCustomer(id) {
+ fmt.Println("-------------------------修改成功-------------------------")
+ } else {
+ fmt.Println("-------------------------添加失败-------------------------")
+ }
+}func (cs *CustomerService) ChangeCustomer(id int) bool {
+
+ reader := bufio.NewReader(os.Stdin) // 标准输入输出
+
+ for index, cus := range cs.Customers {
+ if cus.Id == id {
+
+ fmt.Printf("请输入修改的姓名(%v):", cus.Name)
+ name, _ := reader.ReadString('\n')
+ name = strings.TrimSpace(name)
+ if len(name) != 0 {
+ cs.Customers[index].Name = name
+ }
+
+ fmt.Printf("请输入修改的性别(%v):", cus.Gender)
+ gender, _ := reader.ReadString('\n')
+ gender = strings.TrimSpace(gender)
+ if len(gender) != 0 {
+ cs.Customers[index].Gender = gender
+ }
+
+ fmt.Printf("请输入修改的年龄(%v):", cus.Age)
+ age, _ := reader.ReadString('\n')
+ age = strings.TrimSpace(age)
+ if len(age) != 0 {
+ t, _ := strconv.ParseInt(age, 10, 64)
+ cs.Customers[index].Age = int(t)
+ }
+
+ fmt.Printf("请输入修改的电话(%v):", cus.Phone)
+ phone, _ := reader.ReadString('\n')
+ phone = strings.TrimSpace(phone)
+ if len(phone) != 0 {
+ cs.Customers[index].Phone = phone
+ }
+
+ fmt.Printf("请输入修改的电子邮件(%v):", cus.Email)
+ email, _ := reader.ReadString('\n')
+ email = strings.TrimSpace(email)
+ if len(email) != 0 {
+ cs.Customers[index].Email = email
+ }
+
+ return true
+ }
+ }
+ return false
+}修改的时候回车表示对这个字段不修改,因此要调一个reader的包来完成这个工作,自己无法作出这种判断。
+.
+├── Customer-Management-System
+│ ├── main
+│ │ └── main.go
+│ ├── model
+│ │ └── customer.go
+│ ├── service
+│ │ └── customerService.go
+│ └── view
+│ └── customerView.go
main.go
+package main
+
+import (
+ "Go-Projects/Customer-Management-System/view"
+)
+
+func main() {
+ view.NewCustomerView().MainMenu()
+}
+customer.go
+package model
+
+import "fmt"
+
+// 定义Customer结构体,表示一个客户信息
+type Customer struct {
+ Id int
+ Name string
+ Gender string
+ Age int
+ Phone string
+ Email string
+}
+
+// 工厂模式返回Customer的结构体,在CustomerService里面使用
+// 感觉就是新建一个Customer的实例
+func NewCustomer(id int, name string, gender string, age int, phone string, email string) *Customer {
+ return &Customer{
+ Id: id,
+ Name: name,
+ Gender: gender,
+ Age: age,
+ Phone: phone,
+ Email: email,
+ }
+}
+
+func (cu *Customer) GetInfo() string {
+ return fmt.Sprintf("%v\t%v\t%v\t%v\t%v\t%v", cu.Id, cu.Name, cu.Gender, cu.Age, cu.Phone, cu.Email)
+}
+customerService.go
+package service
+
+import (
+ "Go-Projects/Customer-Management-System/model"
+ "bufio"
+ "fmt"
+ "os"
+ "strconv"
+ "strings"
+)
+
+// 完成对Customer的操作,包括增删改查
+type CustomerService struct {
+ // 存储当前的客户
+ Customers []model.Customer
+ // 声明一个字段,表示当前切片含有多少个客户
+ CustomerNum int
+}
+
+// 初始化CustomerService
+func NewCustomerService() *CustomerService {
+ customerService := &CustomerService{} // 初始化
+ customerService.CustomerNum = 0
+ return customerService
+}
+
+func (cs *CustomerService) ShowCustomerSlice() []model.Customer {
+ return cs.Customers
+}
+
+func (cs *CustomerService) AddCustomer(customer model.Customer) bool {
+ cs.Customers = append(cs.Customers, customer)
+ cs.CustomerNum += 1
+ return true
+}
+
+func (cs *CustomerService) DeleteCustomer(id int) bool {
+ for index, cus := range cs.Customers {
+ if cus.Id == id {
+ cs.Customers = append(cs.Customers[:index], cs.Customers[index+1:]...)
+ cs.CustomerNum -= 1
+ return true
+ }
+ }
+ return false
+}
+
+func (cs *CustomerService) ChangeCustomer(id int) bool {
+
+ reader := bufio.NewReader(os.Stdin) // 标准输入输出
+
+ for index, cus := range cs.Customers {
+ if cus.Id == id {
+
+ fmt.Printf("请输入修改的姓名(%v):", cus.Name)
+ name, _ := reader.ReadString('\n')
+ name = strings.TrimSpace(name)
+ if len(name) != 0 {
+ cs.Customers[index].Name = name
+ }
+
+ fmt.Printf("请输入修改的性别(%v):", cus.Gender)
+ gender, _ := reader.ReadString('\n')
+ gender = strings.TrimSpace(gender)
+ if len(gender) != 0 {
+ cs.Customers[index].Gender = gender
+ }
+
+ fmt.Printf("请输入修改的年龄(%v):", cus.Age)
+ age, _ := reader.ReadString('\n')
+ age = strings.TrimSpace(age)
+ if len(age) != 0 {
+ t, _ := strconv.ParseInt(age, 10, 64)
+ cs.Customers[index].Age = int(t)
+ }
+
+ fmt.Printf("请输入修改的电话(%v):", cus.Phone)
+ phone, _ := reader.ReadString('\n')
+ phone = strings.TrimSpace(phone)
+ if len(phone) != 0 {
+ cs.Customers[index].Phone = phone
+ }
+
+ fmt.Printf("请输入修改的电子邮件(%v):", cus.Email)
+ email, _ := reader.ReadString('\n')
+ email = strings.TrimSpace(email)
+ if len(email) != 0 {
+ cs.Customers[index].Email = email
+ }
+
+ return true
+ }
+ }
+ return false
+}
+customerView.go
+package view
+
+import (
+ "Go-Projects/Customer-Management-System/model"
+ "Go-Projects/Customer-Management-System/service"
+ "fmt"
+)
+
+type CustomerView struct {
+ key string // 接收用户输入
+ loop bool // 表示是否循环的显示主菜单
+ username string // 用户的用户名
+ password string // 用户的密码
+ customerService *service.CustomerService // 获取用户服务
+}
+
+func NewCustomerView() *CustomerView {
+ return &CustomerView{
+ key: "",
+ loop: true,
+ username: "admin",
+ password: "password",
+ customerService: service.NewCustomerService(),
+ }
+}
+
+func (cv *CustomerView) login(username, password string) bool {
+ if username == cv.username && password == cv.password {
+ return true
+ }
+ return false
+}
+
+func (cv *CustomerView) addCustomer() {
+ id := cv.customerService.CustomerNum + 1
+ var name, gender, phone, email string
+ var age int
+ fmt.Print("请输入姓名:")
+ fmt.Scanln(&name)
+ fmt.Print("请输入性别:")
+ fmt.Scanln(&gender)
+ fmt.Print("请输入年龄:")
+ fmt.Scanln(&age)
+ fmt.Print("请输入电话:")
+ fmt.Scanln(&phone)
+ fmt.Print("请输入电子邮件:")
+ fmt.Scanln(&email)
+
+ if cv.customerService.AddCustomer(*model.NewCustomer(id, name, gender, age, phone, email)) {
+ fmt.Println("-------------------------添加成功-------------------------")
+ } else {
+ fmt.Println("-------------------------添加失败-------------------------")
+ }
+}
+
+func (cv *CustomerView) changeCustomer() {
+ var id int
+ fmt.Print("请输入修改的ID号:")
+ fmt.Scanln(&id)
+ if cv.customerService.ChangeCustomer(id) {
+ fmt.Println("-------------------------修改成功-------------------------")
+ } else {
+ fmt.Println("-------------------------添加失败-------------------------")
+ }
+}
+
+func (cv *CustomerView) deleteCustomer() {
+ var id int
+ fmt.Print("请输入删除的ID号:")
+ fmt.Scanln(&id)
+ if cv.customerService.DeleteCustomer(id) {
+ fmt.Println("-------------------------删除成功-------------------------")
+ } else {
+ fmt.Println("-------------------------删除失败-------------------------")
+ }
+}
+
+func (cv *CustomerView) showCustomer() {
+ if cv.customerService.CustomerNum == 0 {
+ fmt.Println("没有客户!")
+ return
+ }
+ fmt.Println("\n-------------------------客户列表-------------------------")
+ fmt.Println("编号\t姓名\t性别\t年龄\t电话\t电子邮件")
+ for _, eachCustomer := range cv.customerService.ShowCustomerSlice() {
+ fmt.Println(eachCustomer.GetInfo())
+ }
+}
+
+func (cv *CustomerView) exit() {
+ var choice byte
+ for {
+ fmt.Print("确定退出?(y/n):")
+ fmt.Scanf("%c\n", &choice)
+ if choice == 'y' {
+ cv.loop = false
+ break
+ } else if choice == 'n' {
+ break
+ } else {
+ fmt.Println("输入有误!!请重新输入")
+ }
+ }
+}
+
+func (cv *CustomerView) MainMenu() {
+ for {
+ var username, password string
+ fmt.Print("请输入用户名:")
+ fmt.Scanln(&username)
+ fmt.Print("请输入密码:")
+ fmt.Scanln(&password)
+ if cv.login(username, password) {
+ break
+ } else {
+ fmt.Println("用户名或密码错误!")
+ }
+ }
+ // 显示主菜单
+ for cv.loop {
+ fmt.Println("\n---------------------客户信息管理软件---------------------")
+ fmt.Println(" 1 添加客户")
+ fmt.Println(" 2 修改客户")
+ fmt.Println(" 3 删除客户")
+ fmt.Println(" 4 客户列表")
+ fmt.Println(" 5 退 出")
+ fmt.Print("请选择(1-5):")
+ // 接收用户的输入
+ fmt.Scanln(&cv.key)
+ // 对用户的输入进行判断
+ switch cv.key {
+ case "1":
+ cv.addCustomer()
+ case "2":
+ cv.changeCustomer()
+ case "3":
+ cv.deleteCustomer()
+ case "4":
+ cv.showCustomer()
+ case "5":
+ cv.exit()
+ default:
+ fmt.Println("请输入正确的选项------")
+ }
+ }
+}
+《现代信息检索》期末复习
+ +考试主要涉及概念上的问题,可能没有特别复杂的计算的内容
+倒排索引基本结构:
+对每个词项t,记录所有包含t的文档列表。每篇文档用一个唯一的docID来表示,通常是正整数,如1,2,3…
+为什么要用倒排索引:
+当用户发起查询时(假设查询为一个关键词),搜索引擎会扫描索引库中的所有文档,找出所有包含关键词的文档,这样依次从文档中去查找是否含有关键词的方法叫做正向索引 。
+为了增加效率, 搜索引擎会把正向索引变为倒排索引即把“文档→单词”的形式变为“单词→文档”的形式 。
+倒排索引是实现“单词-文档矩阵”的一种具体存储形式,通过倒排索引,可以根据单词快速获取包含这个单词的文档列表。
+布尔查询的处理优化:
+问题:什么是倒排索引?为什么说倒排索引能加快检索的速度?假设“信息”、“检索”在倒排索引中是两个独立的term,试说明检索短语“信息检索”的基本流程。
+答案:倒排索引指的是从词项到文档的一种索引结构。由于它直接可以从查询词定位到文档,所以能够大大加快检索的速度。检索短语“信息检索”的基本流程:从词典中分别查找到“信息”和“检索”这两个词,分别返回它们的倒排记录表,然后求这两个表的交集,在求交集时要考虑它们在文档中的位置相对关系。
+词条 :一段文本中有效词的子序列,其中每个子序列称为一个词条。
+词条类 :相同词条构成的集合。
+词项 :一个词项指的是在信息检索系统词典中所包含的某个可能经过归一化处理的词条类。(词项集合和词条集合可以完全不同,比如可以采用某一个分类体系中的类别标签作为词项。当然,在实际的信息检索系统中,词项往往和词条密切相关)
+注意:①文档-词项关联矩阵只包含01②要按字典序进行排序
+ +在构建索引时,每次解析一篇文档,因此对于每个词项而言,其倒排记录表不到最后一篇文档都是不完整的。
+如果每个 (termID, docID)对占用 8个字节, 那么处理大规模语料需要大量的空间。
一般内存的容量比较小,没有办法将前面产生的倒排记录表全部放在内存中,需要在磁盘上存储中间结果。
+一种减少寻道操作的排序:Blocked sort-based Indexing
+将所有记录划分为每个大小约为10M的块,收集每一块的倒排记录,排序,将倒排索引写入硬盘,最后将不同的分块合并为一个大的倒排索引。
+内存式单遍扫描索引构建算法:Single-pass in-memory indexing
+关键思想:
+term-termID的映射)在扫描文档的同时,直接在内存中维护一个不断更新的倒排索引
+因此对每个块生成一个完整的倒排索引,这些独立的索引最后合并成一个大索引
+最终合并词典的过程中,需要进行词项字符串的比较,因为此时没有全局词典提供词项-整数ID的映射。
+BSBI算法:在分块索引阶段,BSBI算法维护一个全局Term (String) – Termid (int) 的映射表,局部索引为Termid及其倒排记录表,仍然按词典顺序排序。
+SPIMI算法:分块索引阶段与BSBI算法不同在于建立局部词典和索引,无需全局词典。在合并阶段,将局部索引两两合并,最后产生全局词典建立Term – Termid的映射。
+使用文本预处理步骤可以大大减小系统所需要存储的倒排记录表的数目,从而提高索引构建和检索的速度
+有损压缩:丢弃一些信息-很多常用的预处理步骤可以看成是有损压缩
+无损压缩:所有信息都保留-索引压缩中通常都使用无损压缩
+定长数组方式下的词典存储:每个词项需要20(字符串)+4(词频)+4(指向倒排索引表的指针)=28个字节。
+将整部词典看成单一字符串:4(词频)+4(指向倒排索引表的指针)+3(指向字符串的指针,按照实际大小决定,例如8*400000个位置需要$log_2(8 * 400000)< 24 $位来表示)+8(每个字符串平均需要8个字节)=19个字节
+按块存储,假设块大小k=4,此时每4个词项只需要保留1个词项指针,但是同时需要增加4个字节(比较短,1个字节就可以)来表示每个词项的长度,因此每4个词项需要3+4=7B,比之前的节省了12-7=5B
+前端编码:每个块当中 (k = 4)会有公共前缀,可以采用前端编码方式继续压缩
+如果使用词干还原,由于将同一词汇的不同形式还原到词根,因此前端编码的压缩效果有限
+倒排记录表的压缩:两种经典编码VB和γ编码(注意对gap进行编码,第一个id,后面都是gap)
+可变字节(VB)码:设定一个专用位 (高位) c作为延续位(continuation bit),如果间隔表示少于7比特,那么c置1,将间隔编入一个
+字节的后7位中;否则将高7位放入当前字节中,并将c置0,剩下的位数采用同样的方法进行处理,最后一个字节的c置1(表
+示结束)

通道模型:
+若有包含


通道模型概率-计算错误概率
轮排索引:(主要思想:让星号出现在词汇的末尾)
+轮排索引的查找过程:
+相对于通常的B-树,轮排索引(轮排树)的空间要大4倍以上 (经验值)
+k-gram索引:枚举一个词项中所有连读的k个字符构成k-gram(在首尾添加k-1个首尾符号)
+k-gram索引 vs. 轮排索引
+tf-idf词频及log词频
+TF是词项t的词项频率,是与文档相关的一个量,可以认为是文档内代表度的一个量,也可以认为是一种局部信息。
+IDF是反映词项t的信息量的一个指标,是一种全局性指标,反应的是词项在全局的区别性,可视为一种词项全局信息量的指标。
+向量空间模型基本思想:把查询和文本表示成向量(早期表示成TF-IDF权重)
+向量空间模型的不同实现方案(不用背表,但是有很多情况,要看好题)(比如有时候idf不用算):
+ +注意:看好题目,不说对数、归一化什么的就不要做
+ +主要是BM25模型的基本概念,IDF是怎么计算的,以及它的基本假设,伯努利分布
+BIM的基本假设,BM25的二重泊松分布,考虑了哪些因素,如长度归一等等。
+ +以往的向量空间模型是将query和文档使用向量表示然后计算其内容相似性来进行相关性估计的,而概率检索模型是一种直接对用户需求进行相关性的建模方法,一个query进来,将所有的文档分为两类-相关文档、不相关文档,这样就转为了一个相关性的分类问题。
+对于某个文档



使用贝叶斯公式转换一下,则在搜索排序过程中不需要真正的分类,只需要保证相关性由高到底排序即可,所以只需要
+这样就最终转为计算
为了能够使得上述两个计算因子可行,二元独立模型做出了两个假设
+类似于布尔模型中的文档表示方法,一篇文档在由特征(或者单词)进行表示的时候,以特征(或者单词)出现和不出现两种情况来表示,不考虑词频等其他因素。
+指文档里出现的单词之间没有任何关联,任意一个单词在文档的分布概率不依赖于其他单词是否出现。因为词汇之间没有关联,所以可以将文档概率转换为单词概率的乘积。
+上述提到的文档D表示为


同理在不相关文档中出现的概率为
可以推导出:
设文档统计量如下:
+| + | 相关文档 | +不相关文档 | +文档数量 | +
|---|---|---|---|
 |
+ |
+ |
+ |
+
 |
+ |
+ |
+ |
+
| 文档数量 | + |
+ |
+ |
+
则可以得出(加1平滑):
因此最终的公式为:
+其代表的含义是:对于同时出现在用户查询Q和文档D中的单词,累加每个单词的估值,其和就是文档D和查询的相关性度量。
+在不确定哪些文档是相关的,哪些文档是不相关的的时候,可以给公式的估算因子直接赋予固定值,则该公式将会退化为IDF因子。
+优点:BIM模型建立在数学基础上,理论性较强
+缺点:
+BM25模型计算公式其实融合了4个考虑因素:IDF因子,文档长度因子,文档词频和查询词频。并对3个自由调节因子
IDF因子:设BIM模型中的相关文档数量为0,则退化为
查询权重:
TF权重(基于二重泊松分布):
最终形式为三项相乘
+例题:
+ + +优点:
+缺点:
+问题:BM25和向量空间模型(VSM)为何需要长度归一?语言模型为何需要平滑处理?两个问题之间有何联系?
+答案:由于长文挡中词项反复出现的可能性大,包含更多的不同词项,所以词项频率和词汇量可能更大。这显然是不公平的。长度归一化,可以使长文档和短文档的向量中的权重都处于同一数量级。平滑处理是为了解决数据稀疏引起的0概率问题。两者都是常见的数据预处理方法,提高了数据质量,为了保证模型的鲁棒性。
+流行的是基于多项式分布,对于生成模型的计算有零概率的问题,需要进行平滑,基本概念要知道
+ +指标计算,如正确率召回率等等,F1,未插值的AP
+题目:什么是非插值的MAP?为什么说它在引入序的作用的同时考虑了召回率?
+答案:单个查询的非插值MAP指的是所有相关文档(不论是否在结果出现,若不出现就假定出现在无穷远处)在结果出现位置上的正确率的算术平均值。系统的非插值MAP是所有查询上的非插值AP的算术平均值。从非插值AP的定义看,一方面,如果出现在结果中的相关文档越多,求和结果也越大,那么非插值AP值也越大。另一方面,如果相关文档在结果中出现位置越靠前,那么非插值AP值也越大。因此,可以认为非插值MAP同时考底了召回率和序的作用。
+Bpref:在相关性判断不完全的情况下,计算在进行了相关性判断的文档集合中,在判断到相关文档前,需要判断的不相关文档的篇数。相关性判断完全的情况下,利用Bpref和MAP进行评价的结果很一致,但是相关性判断不完全的情况下,Bpref更鲁棒。
+NDCG:每个文档不仅仅只有相关和不相关两种情况,而是有相关度级别,比如0,1,2,3。我们可以假设,对于返回结果:相关度级别越高的结果越多越好,相关度级别越高的结果越靠前越好
+优点:
+缺点:
+考试基本不涉及
+相关反馈的本质是将检索返回的文档的相关性判定(不同的判定来源:人工或非人工)作为返回信息,希望提升检索效果(召回率和正确率)
+反馈信息的来源:显式(用户点击)、隐式(用户行为等)、伪相关反馈(返回的前几个结果算相关)
+Rocchio算法
+查询扩展的最初含义是对查询进行扩充,近年来越来越向查询重构偏移,即现在的查询扩展是指对原有查询进行修改。
+通过在查询中加入同义或者相关的词项来提高检索结果。
+相关词项的来源: 人工编辑的同义词词典、自动构造的同义词词典、查询日志等等。
+查询扩展和相关反馈对检索效果的提升是非常有用的经验性的方法
+问题:什么是伪相关反馈?为什么说有时候伪相关反馈会降低某个查询的检索效果?
+答案:伪相关反馈指的是系统对上次返回的检索结采进行“伪”判定(比如假设前几个结果是相关的),然后根据这个结果进行反馈。伪相关反馈依赖于上次检索的结果,那么在上次检索结果不可靠情况下,假设成立的可能性很小,此时就进行伪相关反馈反而可能降低后一次检索的效果。
+注意:负权重要记为0,同时也要进行排序
+ +问题:文本分类当中,什么是宏平均?什么是微平均?为什么说微平均计算时易受大类影响?
+答案:宏平均指的是在每个类别上分类效果的平均值,也即将每个类别看成一个单位。而微平均是将所有类别看成一个类别后求到的效果值,即将每篇文档看成一个单位。由于微平均将文档看成单位,而大类文档数目较多,因此它在计算时易受大类影响。
+使用log将乘积计算变为求和计算
+最大似然估计(零概率的情况下怎么进行加一平滑)
+计算每个类的中心向量(所有文档向量的算术平均)
+将每篇测试文档分到离它最近的那个中心向量
+Rocchio分类器是要训练的
+kNN分类决策取决于k个邻居类中的多数类
+类别之间的分类面是分段线性的
+kNN分类器几乎不需要训练
+但是像kNN这种非线性学习方法在某些情况下也会产生一个线性分类器
+SVM分线性SVM和非线性SVM,SVM本身是一个线性决策,但是核函数可以是线性或非线性的
+算法本身是转化成一个线性公式,但是最终得到的是一个非线性的决策面,只不过把样本投射到高维空间里面
+问题:总结SVM中处理线性不可分数据的方法,给出其基本原理。
+问题:什么是核函数?它的作用是什么?为什么核函数的引入常常称为核技巧?
+答案:核函数是满足若干性质的相似度计算函数。它的主要作用是计算两个对象的相似度,具体地说,它可以基于原始空间上的点来定义映射后空间上的内积函数。核函数避免知道空间映射的具体函数形式,能够直接基于核函数进行映射后的对象相似度计算,所以它的引入常常称为核技巧。
+对于像Rocchio和NB一样的线性方法来说,对于非线性问题它们的偏差就比较大
+像kNN一样的非线性方法的偏差较小,方差较大
+如果拥有的训练数据非常少,而又要训练出一个基于监督学习的分类器,应该采用具有高偏差的分类器,在这种情况下NB能取得较好的结果,诸如kNN的低偏差模型大概是不可取的。
+现有检索排序算法存在哪些问题,怎么改进?
+很多传统的IR权重计算机制中都包含了基本指标的非线性缩放过程(比如词项频率或idf 的对数权重计算)。目前为止,机器学习非常擅长特征线性组合(或者其他类似的受限模型)中的权重优化,但是并不擅长基本指标的非线性缩放。这个领域仍然需要人工的特征工程方法。
+给定训练样例集合,每个样例表示为三元组,相关或者不相关
+从上述样例中学习权重,使得学到的评分接近训练集中的相关性判定结果。
+设置评分函数是两个因子的线性组合:查询和文档的向量空间相似度评分和查询词项在文档中存在的最小窗口宽度
+相关记为1,不相关记为0,我们的目标是寻找一个评分函数,该函数能够组合特征因子的值,并尽量接近0或1,希望该函数的结果尽量与训练集上的结果保持一致
+为什么将IR排序问题看成一个序回归问题?
+方法:
+ , 我们都有针对该查询的一系列文档集合,这些文档已经由人工按照其与查询的相关度排序
, 我们都有针对该查询的一系列文档集合,这些文档已经由人工按照其与查询的相关度排序 ,这里的特征可以采用前面的特征
,这里的特征可以采用前面的特征 和
和 ,可以计算特征向量之间的差异向量
,可以计算特征向量之间的差异向量 中的一个更相关
中的一个更相关 比
比 更相关,记为
更相关,记为 (在检索结果中,
(在检索结果中, 应该出现在
应该出现在 前面), 那么分配给
前面), 那么分配给 向量的类别为
向量的类别为 ,否则为
,否则为

词项表示:通过分析文档集来自动生成同义词库-基于共现的同义词库
+词嵌入:得到每个词的低维密集向量表示
+Neural IR 模型分类
+Representation based(基于表示学习的模型):学习文本的分布式表示,在高维空间匹配
+Matching function(基于交互匹配的模型):文本之间先进行交互匹配,再对匹配信号进行融合
+Combination of both: 既考虑 Representation 又考虑 Matching function
+BERT在检索应用中的特点:
+问题:简述BERT的基本结构?如何预训练一个BERT(涉及什么任务)?
+BERT的基本结构:
+BERT的训练任务有两类:
+Google次高竞标价格拍卖机制:
+ +bid:每个广告商为每次点击给出的最大投标价格
+CTR:一旦被显示后被点击的比率
+ad rank=bid × CTR:这种做法可以在广告商愿意支付的价钱和广告的相关度高低之间进行平衡。
+排名第1的C,需要支付的价格是它的下一位的
排名第2的B,需要支付的价格是它的下一位的
这样做避免了“保底”行为的产生,可以使收益更大化。
+采集器必须做到
+锚文本是人为创建的超链接,可以理解为质量认证的信号。
+邻接表:一个节点的邻居集合,可以视为一个结点(URL)所有指向它的页面的集合
+假设每个URL由一个整数表示,对于40亿页的网站,每个结点需要32位甚至64位,存储开销非常大
+BV算法可以降低到平均3位
+压缩中使用到的属性:
+BV算法主要思想:由于模板的缘故,一个节点的邻接列表类似于字典顺序中的7个先前的URL之一,根据这7个中的之一表示邻接表,否则重新编码。
+BV算法的主要优势
+起源 : 引用分析
+特点:
+PageRank背后的假设:
+PageRank的计算:迭代法计算
+如果存在循环通路,需要虚拟一个结点,或者以一定的概率选取一个其他结点到达
+每个网页计算两个值:
+计算方法:
+





实际计算过程:
+PageRank算法是Google提出的一个链接分析的算法,它可以根据节点之间的链接关系计算出每个节点的重要性,反映的是“越多越重要的节点指向该节点则该节点越重要”这个事实。
+HITS是IBM提出的另一种链接分析算法,它根据节点之间的链接关系对每个节点计算出两个值:权威度(authority值)和导航度(hub值).
+相同点:两者都是基于链接分析的排序算法,并且在算法中两者都利用了特征向量作为理论基础和收敛性依据。
+不同点:网页的PageRank是一种静态评分,与查询主题无关,可以事先算好,因此适合于大型搜索引擎;HITS算法的计算与查询主题相关,检索之后再进行计算,因此不适合于大型搜索引擎。
+ + +Go项目-海量用户通讯系统
+ +用户注册、用户登录、显示在线用户列表、群聊(广播)、点对点聊天、离线留言
+package main
+
+import "fmt"
+
+// 定义两个变量,一个表示用户ID,一个表示用户密码
+var userId int
+var userPwd string
+
+func main() {
+
+ // 接收用户的选择
+ var key int
+ // 判断是否还能继续显示菜单
+ var loop = true
+ // 循环展示菜单
+ for loop {
+ fmt.Println("---------------欢迎登录多人聊天系统---------------")
+ fmt.Println("--------------- 1 登录聊天室")
+ fmt.Println("--------------- 2 注册用户")
+ fmt.Println("--------------- 3 退出系统")
+ fmt.Println("请选择(1-3):")
+ fmt.Scanln(&key)
+ switch key {
+ case 1:
+ fmt.Println("登录聊天室")
+ loop = false
+ case 2:
+ fmt.Println("注册用户")
+ case 3:
+ fmt.Println("退出系统")
+ loop = false
+ default:
+ fmt.Println("输入有误,请重新输入")
+ }
+ }
+ if key == 1 {
+ fmt.Println("请输入用户ID")
+ fmt.Scanln(&userId)
+ fmt.Println("请输入用户密码")
+ fmt.Scanln(&userPwd)
+ // 先把登录的函数写在另外一个文件
+ err := login(userId, userPwd)
+ if err != nil {
+ fmt.Println("登录失败")
+ } else {
+ fmt.Println("登录成功")
+ }
+ } else if key == 2 {
+ fmt.Println("进行用户注册的逻辑")
+ }
+}登录逻辑的判断首先写在另外的文件中,后续再进行修改
+package main
+
+import "fmt"
+
+func login(userId int, userPwd string) (err error) {
+ fmt.Printf("userId=%d, userPed=%s\n", userId, userPwd)
+ return nil
+}注意这种在同一个包下引用函数的方式需要在src文件夹之外进行编译,然后手动运行
+重点是如何发送包以及如何对包进行校验,同时要保证多线程
+ +要对发送的消息进行序列化等操作,首先定义好处理这些数据的结构体
+package message
+
+// 确定消息类型
+const (
+ LoginMesType = "LoginMes"
+ LoginResMesType = "LoginResMes"
+)
+
+type Message struct {
+ Type string `json:"type"` // 消息类型
+ Data string `json:"data"` // 消息内容
+}
+
+// 定义两个消息,后面需要再增加
+type LoginMes struct {
+ UserId int `json:"userId"` // 用户Id
+ UserPwd string `json:"userPwd"` // 用户密码
+ UserName string `json:"userName"` // 用户名
+}
+
+type LoginResMes struct {
+ Code int `json:"code"` // 返回的状态码 500 表示用户未注册,200 表示成功
+ Error string `json:"error"` // 返回错误信息
+}客户端发送消息(消息的长度)
+package main
+
+import (
+ "Go-Projects/Mass-Communication-System/common/message"
+ "encoding/binary"
+ "encoding/json"
+ "fmt"
+ "net"
+)
+
+func login(userId int, userPwd string) (err error) {
+ // fmt.Printf("userId=%d, userPed=%s\n", userId, userPwd)
+ // return nil
+ // 连接到服务器端
+ conn, err := net.Dial("tcp", "localhost:8889")
+ if err != nil {
+ fmt.Println("net.Dial err=", err)
+ return
+ }
+ defer conn.Close()
+ // 准备通过conn发送消息给服务
+ var mes message.Message
+ mes.Type = message.LoginMesType
+ // 创建一个LoginMes结构体
+ var loginMes message.LoginMes
+ loginMes.UserId = userId
+ loginMes.UserPwd = userPwd
+ // 将loginMes序列化
+ data, err := json.Marshal(loginMes)
+ if err != nil {
+ fmt.Println("json Marshal err=", err)
+ return
+ }
+ mes.Data = string(data)
+ // 将mes进行序列化
+ data, err = json.Marshal(mes)
+ if err != nil {
+ fmt.Println("json Marshal err=", err)
+ return
+ }
+ // data为发送的消息
+ // 先把data的长度发送给服务器
+ var pkgLen = uint32(len(data))
+ var buf [4]byte
+ binary.BigEndian.PutUint32(buf[0:4], pkgLen)
+ // 发送长度
+ n, err := conn.Write(buf[:4])
+ if n != 4 || err != nil {
+ fmt.Println("conn.Write err=", err)
+ return
+ }
+ fmt.Println("客户端发送的消息长度为", len(data))
+ fmt.Println("客户端发送的消息内容为", string(data))
+ return
+}
+服务器端接收消息
+package main
+
+import (
+ "fmt"
+ "net"
+)
+
+func process(conn net.Conn) {
+ // 延时关闭连接
+ defer conn.Close()
+ // 读取客户端发送的信息
+ for {
+ buf := make([]byte, 1024*4)
+ fmt.Println("等待读取客户端发送的数据.....")
+ n, err := conn.Read(buf[:4])
+ if n != 4 || err != nil {
+ fmt.Println("conn.Read err=", err)
+ return
+ }
+ fmt.Println("读到的长度为", buf[:4])
+ }
+
+}
+
+func main() {
+ fmt.Println("服务器在8889端口监听.....")
+ listen, err := net.Listen("tcp", "localhost:8889")
+ defer listen.Close()
+ if err != nil {
+ fmt.Println("net.Listen err=", err)
+ return
+ }
+ // 一旦监听成功,等待客户端连接服务器
+ for {
+ fmt.Println("等待客户端连接服务器.....")
+ conn, err := listen.Accept()
+ if err != nil {
+ fmt.Println("listen.Accept err=", err)
+ }
+ // 一旦连接成功,则启动一个协程和客户端保持通讯
+ go process(conn)
+ }
+}
+将服务器端的消息接收封装成一个函数
+func readPkg(conn net.Conn) (mes message.Message, err error) {
+ buf := make([]byte, 1024*4)
+ fmt.Println("等待读取客户端发送的数据.....")
+ _, err = conn.Read(buf[:4])
+ if err != nil {
+ fmt.Println("conn.Read err=", err)
+ return
+ }
+ // fmt.Println("读到的长度为", buf[:4])
+ // 转换为一个uint32类型
+ var pkgLen = binary.BigEndian.Uint32(buf[0:4])
+ // 发送长度
+ n, err := conn.Read(buf[:pkgLen])
+ if n != int(pkgLen) || err != nil {
+ fmt.Println("conn.Read err=", err)
+ return
+ }
+ // 把pkgLen反序列化成message
+ err = json.Unmarshal(buf[:pkgLen], &mes)
+ if err != nil {
+ fmt.Println("json.Unmarshal err=", err)
+ return
+ }
+ return
+}客户端发送消息
+// 发送消息本身
+_, err = conn.Write(data)
+if err != nil {
+ fmt.Println("conn.Write err=", err)
+ return
+}服务器端封装一个发送消息的函数
+func writePkg(conn net.Conn, data []byte) (err error) {
+ // 先发送一个长度
+ var pkgLen = uint32(len(data))
+ var buf [4]byte
+ binary.BigEndian.PutUint32(buf[0:4], pkgLen)
+ // 发送长度
+ _, err = conn.Write(buf[:4])
+ if err != nil {
+ fmt.Println("conn.Write err=", err)
+ return
+ }
+
+ //发送data本身
+ n, err := conn.Write(data)
+ if n != int(pkgLen) || err != nil {
+ fmt.Println("conn.Write err=", err)
+ return
+ }
+ return
+}将这种请求通用化,为后面的其他消息做准备
+// 编写serverProcessLogin函数,专门处理登录的请求
+func serverProcessLogin(conn net.Conn, mes *message.Message) (err error) {
+ // 从mes中取出data,并反序列化
+ var loginMes message.LoginMes
+ err = json.Unmarshal([]byte(mes.Data), &loginMes)
+ if err != nil {
+ fmt.Println("json.Unmarshal error, err=", err)
+ return
+ }
+ // 先声明一个resMes
+ var resMes message.Message
+ resMes.Type = message.LoginResMesType
+ // 声明一个LoginResMes
+ var loginResMes message.LoginResMes
+ // 如果用户的id为100,密码为123456,认为合法,否则不合法
+ if loginMes.UserId == 100 && loginMes.UserPwd == "123456" {
+ //合法
+ loginResMes.Code = 200
+ } else {
+ //不合法
+ loginResMes.Code = 500
+ loginResMes.Error = "该用户不存在,请注册再使用..."
+ }
+ // 将loginResMes序列化
+ data, err := json.Marshal(loginResMes)
+ if err != nil {
+ fmt.Println("json.Marshal error, err=", err)
+ return
+ }
+ // 将data赋值给resMes
+ resMes.Data = string(data)
+ // 对resMes进行序列化,准备发送
+ data, err = json.Marshal(resMes)
+ if err != nil {
+ fmt.Println("json.Marshal error, err=", err)
+ return
+ }
+ // 发送data,封装到writePkg函数
+ err = writePkg(conn, data)
+ return
+}
+
+// 根据客户端发送消息种类不同,决定调用哪个函数来实现
+func serverProcessMes(conn net.Conn, mes *message.Message) (err error) {
+ switch mes.Type {
+ case message.LoginMesType:
+ // 处理登录的逻辑
+ err = serverProcessLogin(conn, mes)
+ case message.RegisterMesType:
+ // 处理注册的逻辑
+ default:
+ fmt.Println("消息类型不存在,无法处理")
+ }
+ return
+}客户端对消息进行处理
+// 处理服务器端返回的消息
+mes, err = readPkg(conn)
+if err != nil {
+ fmt.Println("readPkg(conn) error, err=", err)
+ return
+}
+// 将mes的data部分反序列化
+var loginResMes message.LoginResMes
+err = json.Unmarshal([]byte(mes.Data), &loginResMes)
+if loginResMes.Code == 200 {
+ fmt.Println("登录成功")
+} else if loginResMes.Code == 500 {
+ fmt.Println(loginResMes.Error)
+}改进主要是将前面编写的函数封装进方法之中,减少不同函数之间参数的传递,通过结构体直接调用即可
+客户端的改进增加了一个与服务器端保持联系的函数
+// 和服务器端保持通讯
+func serverProcessMes(conn net.Conn) {
+ tf := &utils.Transfer{
+ Conn: conn,
+ }
+ for {
+ fmt.Println("客户端正在等待读取服务器发送的消息")
+ mes, err := tf.ReadPkg()
+ if err != nil {
+ fmt.Println("tf.ReadPkg err=", err)
+ return
+ }
+ // 如果读取到消息,下一步进行处理
+ fmt.Println(mes)
+ }
+}MVC开发模式,增加models,从而从数据库中进行读取和接收,验证用户的有效性
+models层
+package model
+
+import (
+ "Go-Projects/Mass-Communication-System/common/message"
+ "encoding/json"
+ "fmt"
+
+ "github.com/gomodule/redigo/redis"
+)
+
+// 使用工厂模式创建一个UserDao的实例
+func NewUserDao(pool *redis.Pool) (userDao *UserDao) {
+ userDao = &UserDao{
+ pool: pool,
+ }
+ return
+}
+
+// 在服务器启动后初始化一个userDao实例
+var (
+ MyUserDao *UserDao
+)
+
+// 定义一个userDao的结构体
+type UserDao struct {
+ pool *redis.Pool
+}
+
+// 根据用户id返回user实例
+func (ud *UserDao) getUserById(conn redis.Conn, id int) (user *User, err error) {
+ res, err := redis.String(conn.Do("HGET", "users", id))
+ if err != nil {
+ if err == redis.ErrNil {
+ err = ERROR_USER_NOTEXISTS
+ }
+ return
+ }
+
+ user = &User{}
+
+ // 把res反序列化成User实例
+ err = json.Unmarshal([]byte(res), user)
+ if err != nil {
+ fmt.Println("json.Unmarshal err=", err)
+ return
+ }
+ return
+}
+
+// 完成登录的校验
+func (ud *UserDao) Login(userId int, userPwd string) (user *User, err error) {
+ conn := ud.pool.Get()
+ defer conn.Close()
+ user, err = ud.getUserById(conn, userId)
+ if err != nil {
+ return
+ }
+ if user.UserPwd != userPwd {
+ err = ERROR_USER_PWD
+ return
+ }
+ return
+}
+
+// 注册
+func (ud *UserDao) Register(user *message.User) (err error) {
+ conn := ud.pool.Get()
+ defer conn.Close()
+ _, err = ud.getUserById(conn, user.UserId)
+ if err == nil {
+ err = ERROR_USER_EXISTS
+ return
+ }
+ // 说明该用户还没有注册过,则可以完成注册
+ data, err := json.Marshal(user)
+ if err != nil {
+ return
+ }
+ _, err = conn.Do("HSET", "users", user.UserId, string(data))
+ if err != nil {
+ fmt.Println("保存注册用户错误,err=", err)
+ return
+ }
+ return
+}
+处理注册的请求
+// 编写ServerProcessRegister函数,专门处理注册的请求
+func (u *UserProcess) ServerProcessRegister(mes *message.Message) (err error) {
+ // 从mes中取出data,并反序列化
+ var registerMes message.RegisterMes
+ err = json.Unmarshal([]byte(mes.Data), ®isterMes)
+ if err != nil {
+ fmt.Println("json.Unmarshal error, err=", err)
+ return
+ }
+ // 先声明一个resMes
+ var resMes message.Message
+ resMes.Type = message.RegisterResMesType
+ // 声明一个RegisterResMes
+ var registerResMes message.RegisterResMes
+
+ err = model.MyUserDao.Register(®isterMes.User)
+
+ if err != nil {
+ if err == model.ERROR_USER_EXISTS {
+ registerResMes.Code = 505
+ registerResMes.Error = err.Error()
+ } else {
+ registerResMes.Code = 506
+ registerResMes.Error = "注册发生未知错误"
+ }
+
+ } else {
+ registerResMes.Code = 200
+ }
+
+ // 将loginResMes序列化
+ data, err := json.Marshal(registerResMes)
+ if err != nil {
+ fmt.Println("json.Marshal error, err=", err)
+ return
+ }
+ // 将data赋值给resMes
+ resMes.Data = string(data)
+ // 对resMes进行序列化,准备发送
+ data, err = json.Marshal(resMes)
+ if err != nil {
+ fmt.Println("json.Marshal error, err=", err)
+ return
+ }
+ // 发送data,封装到writePkg函数
+ tf := &utils.Transfer{
+ Conn: u.Conn,
+ }
+ err = tf.WritePkg(data)
+ return
+}完成对当前在线用户的增删改查
+package process2
+
+import "fmt"
+
+// 在服务器端实例只有一个,在很多的地方都会使用到
+
+var (
+ userMgr *UserMgr
+)
+
+type UserMgr struct {
+ onlineUsers map[int]*UserProcess
+}
+
+// 完成对userMgr初始化工作
+func init() {
+ userMgr = &UserMgr{
+ onlineUsers: make(map[int]*UserProcess, 1024),
+ }
+}
+
+// 完成对onlineUsers的增删改查
+
+func (um *UserMgr) AddOnlineUser(up *UserProcess) {
+ um.onlineUsers[up.UserId] = up
+}
+
+func (um *UserMgr) DelOnlineUser(userId int) {
+ delete(um.onlineUsers, userId)
+}
+
+func (um *UserMgr) GetAllOnlineUser() map[int]*UserProcess {
+ return um.onlineUsers
+}
+
+func (um *UserMgr) GetOnlineUserById(userId int) (up *UserProcess, err error) {
+ up, ok := um.onlineUsers[userId]
+ if !ok {
+ err = fmt.Errorf("用户%d不存在", userId)
+ return
+ }
+ return
+}
+显示当前在线用户列表
+// 因为用户登录成功,要将用户放入全局变量中以返回列表
+u.UserId = loginMes.UserId
+userMgr.AddOnlineUser(u)
+// 将当前在线用户的id放入到loginResMes.UsersIds
+for id := range userMgr.onlineUsers {
+ loginResMes.UsersIds = append(loginResMes.UsersIds, id)
+}
+fmt.Println(user, "登录成功")// 显示当前在线用户列表
+fmt.Println("当前在线用户列表如下:")
+for _, v := range loginResMes.UsersIds {
+ fmt.Println("用户id,\t", v)
+}服务器端对用户列表进行处理
+// 通知所有用户在线
+func (u *UserProcess) NotifyOthersOnlineUser(userId int) {
+ for id, up := range userMgr.onlineUsers {
+ if id == userId {
+ continue
+ }
+ up.NotifyMeOnline(userId)
+ }
+
+}
+
+func (u *UserProcess) NotifyMeOnline(userId int) {
+ var mes message.Message
+ mes.Type = message.NotifyUserStatusMesType
+ var notifyUserStatusMes message.NotifyUserStatusMes
+ notifyUserStatusMes.UserId = userId
+ notifyUserStatusMes.Status = message.UserOnline
+
+ data, err := json.Marshal(notifyUserStatusMes)
+ if err != nil {
+ fmt.Println("json.Marshal err=", err)
+ return
+ }
+ mes.Data = string(data)
+
+ data, err = json.Marshal(mes)
+ if err != nil {
+ fmt.Println("json.Marshal err=", err)
+ return
+ }
+ tf := &utils.Transfer{
+ Conn: u.Conn,
+ }
+ err = tf.WritePkg(data)
+ if err != nil {
+ fmt.Println("NotifyMeOnline err=", err)
+ }
+}客户端对用户列表进行处理
+package process
+
+import (
+ "Go-Projects/Mass-Communication-System/common/message"
+ "fmt"
+)
+
+// 客户端要维护的map
+var onlineUsers map[int]*message.User = make(map[int]*message.User, 10)
+
+// 在客户端显示当前在线的用户
+
+func outputOnlineUser() {
+ fmt.Println("当前在线用户列表")
+ for id, user := range onlineUsers {
+ fmt.Println(id, user)
+ }
+}
+
+// 处理返回的NotifyUserStatusMes
+func updateUserStatus(notifyUserStatusMes *message.NotifyUserStatusMes) {
+
+ user, ok := onlineUsers[notifyUserStatusMes.UserId]
+ if !ok {
+ user = &message.User{
+ UserId: notifyUserStatusMes.UserId,
+ }
+ }
+ user.UserStatus = notifyUserStatusMes.Status
+ onlineUsers[notifyUserStatusMes.UserId] = user
+ outputOnlineUser()
+}
+客户端显示用户列表
+// 显示当前在线用户列表
+fmt.Println("当前在线用户列表如下:")
+for _, v := range loginResMes.UsersIds {
+ fmt.Println("用户id,\t", v)
+ user := &message.User{
+ UserId: v,
+ UserStatus: message.UserOnline,
+ }
+ onlineUsers[v] = user
+}直接调用前面写好的就行,代码很少了
+package process
+
+import (
+ "Go-Projects/Mass-Communication-System/client/utils"
+ "Go-Projects/Mass-Communication-System/common/message"
+ "encoding/json"
+ "fmt"
+)
+
+type SmsProecss struct {
+}
+
+func (sp *SmsProecss) SendGroupSms(content string) (err error) {
+ var mes message.Message
+ mes.Type = message.SmsMesType
+
+ var smsMes message.SmsMes
+ smsMes.Content = content
+ smsMes.UserId = CurUser.UserId
+ smsMes.UserStatus = CurUser.UserStatus
+
+ data, err := json.Marshal(smsMes)
+ if err != nil {
+ fmt.Println("json.Marshal err=", err)
+ return
+ }
+ mes.Data = string(data)
+ data, err = json.Marshal(mes)
+ if err != nil {
+ fmt.Println("json.Marshal err=", err)
+ return
+ }
+ tf := &utils.Transfer{
+ Conn: CurUser.Conn,
+ }
+ err = tf.WritePkg(data)
+ if err != nil {
+ fmt.Println("tf.WritePkg err=", err)
+ return
+ }
+ return
+}
+也是和上面的差不多
+package process2
+
+import (
+ "Go-Projects/Mass-Communication-System/common/message"
+ "Go-Projects/Mass-Communication-System/server/utils"
+ "encoding/json"
+ "fmt"
+ "net"
+)
+
+type SmsProecss struct {
+}
+
+func (sp *SmsProecss) SendGroupSms(mes *message.Message) (err error) {
+
+ var smsMes message.SmsMes
+ err = json.Unmarshal([]byte(mes.Data), &smsMes)
+ if err != nil {
+ fmt.Println("json.Unmarshal err=", err)
+ return
+ }
+
+ data, err := json.Marshal(mes)
+ if err != nil {
+ fmt.Println("json.Marshal err=", err)
+ return
+ }
+
+ for id, up := range userMgr.onlineUsers {
+ if id == smsMes.UserId {
+ continue
+ }
+ sp.SendMesToEachOnlineUser(data, up.Conn)
+ }
+ return
+}
+
+func (sp *SmsProecss) SendMesToEachOnlineUser(data []byte, conn net.Conn) (err error) {
+
+ tf := &utils.Transfer{
+ Conn: conn,
+ }
+ err = tf.WritePkg(data)
+ if err != nil {
+ fmt.Println("tf.WritePkg err=", err)
+ return
+ }
+ return
+}
+Go项目-Gee Web框架
+ +net/http库以及 http.Handler接口路由(router)独立出来,方便之后增强。上下文(Context),封装 Request 和 Response ,提供对 JSON、HTML 等返回类型的支持。Logger中间件,能够记录请求到响应所花费的时间,Go语言内置了 net/http库,封装了HTTP网络编程的基础的接口,使用这个库:
package main
+
+import (
+ "fmt"
+ "net/http"
+)
+
+func main() {
+ // 设置两个路由
+ http.HandleFunc("/", indexHandler)
+ http.HandleFunc("/hello", helloHandler)
+ // 启动Web服务,在9999端口进行监听,处理所有的HTTP请求的实例
+ http.ListenAndServe("localhost:9999", nil)
+ // 最后的nil即为实现框架的入口
+}
+
+// 根路由
+func indexHandler(w http.ResponseWriter, req *http.Request) {
+ fmt.Fprintf(w, "URL.Path=%q\n", req.URL.Path)
+}
+
+// hello路由
+func helloHandler(w http.ResponseWriter, req *http.Request) {
+ for k, v := range req.Header {
+ fmt.Fprintf(w, "Header[%q] = %q\n", k, v)
+ }
+}使用curl进行测试:
+> curl http://localhost:9999/
+URL.Path="/"
+> curl http://localhost:9999/hello
+Header["User-Agent"] = ["curl/7.68.0"]
+Header["Accept"] = ["*/*"]其中代码的nil就是一个接口,需要实现方法 ServeHTTP ,也就是说,只要传入任何实现了 ServerHTTP 接口的实例,所有的HTTP请求,就都交给了该实例处理了。
+拦截一下请求进行尝试
+package main
+
+import (
+ "fmt"
+ "net/http"
+)
+
+// 定义一个空结构体,因为后面实现的是一个方法,比如在一个结构体的基础上进行实现
+type Engine struct{}
+
+// 实现ServeHTTP方法
+func (engine *Engine) ServeHTTP(w http.ResponseWriter, req *http.Request) {
+ switch req.URL.Path {
+ case "/":
+ fmt.Fprintf(w, "URL.Path=%q\n", req.URL.Path)
+ case "/hello":
+ for k, v := range req.Header {
+ fmt.Fprintf(w, "Header[%q] = %q\n", k, v)
+ }
+ default:
+ fmt.Fprintf(w, "404 NOT FOUND: %s\n", req.URL)
+ }
+}
+
+func main() {
+ engine := &Engine{}
+ // 多设置一个路由
+ http.HandleFunc("/hi", indexHandler)
+ // 启动Web服务,在9999端口进行监听,处理所有的HTTP请求的实例
+ http.ListenAndServe("localhost:9999", engine)
+ // 最后的nil即为实现框架的入口
+}
+
+// 根路由
+func indexHandler(w http.ResponseWriter, req *http.Request) {
+ fmt.Fprintf(w, "URL.Path=%q\n", req.URL.Path)
+}
+测试:
+> curl http://localhost:9999/hello
+Header["User-Agent"] = ["curl/7.68.0"]
+Header["Accept"] = ["*/*"]
+> curl http://localhost:9999/
+URL.Path="/"
+> curl http://localhost:9999/hi
+404 NOT FOUND: /hi因此就将所有的HTTP请求转向了自己的处理逻辑,代码的运行结果与之前的是一致的。
+我们拦截了所有的HTTP请求,拥有了统一的控制入口。在这里我们可以自由定义路由映射的规则,也可以统一添加一些处理逻辑,例如日志、异常处理等。
+因此就可以从这里入手完成这个Web框架,最终的代码结构是这样的
+.
+├── gee
+│ └── gee.go
+└── main.gomain.go:
+使用 New()创建 gee 的实例,使用 GET()方法添加路由,最后使用 Run()启动Web服务。
package main
+
+import (
+ "Go-Projects/Gee/gee"
+ "fmt"
+ "net/http"
+)
+
+func main() {
+ r := gee.New()
+ r.Get("/", func(w http.ResponseWriter, req *http.Request) {
+ fmt.Fprintf(w, "URL.Path=%q\n", req.URL.Path)
+ })
+ r.Get("/hello", func(w http.ResponseWriter, req *http.Request) {
+ for k, v := range req.Header {
+ fmt.Fprintf(w, "Header[%q] = %q\n", k, v)
+ }
+ })
+ r.Run("localhost:9999")
+}gee.go
+package gee
+
+import (
+ "fmt"
+ "net/http"
+)
+
+// 定义一个普遍使用的函数类型,避免后面再次定义
+type HandlerFunc func(http.ResponseWriter, *http.Request)
+
+// 定义路由表
+type Engine struct {
+ router map[string]HandlerFunc
+}
+
+// 工厂模式的构造方法,返回一个实例
+func New() *Engine {
+ return &Engine{
+ router: make(map[string]HandlerFunc),
+ }
+}
+
+// 将路由添加到路由表中
+func (engine *Engine) addRoute(method, pattern string, handler HandlerFunc) {
+ key := method + "-" + pattern
+ engine.router[key] = handler
+}
+
+// 实现GET方法
+func (engine *Engine) GET(pattern string, handler HandlerFunc) {
+ engine.addRoute("GET", pattern, handler)
+}
+
+// 实现POST方法
+func (engine *Engine) POST(pattern string, handler HandlerFunc) {
+ engine.addRoute("POST", pattern, handler)
+}
+
+// 实现Run方法
+func (engine *Engine) Run(addr string) (err error) {
+ return http.ListenAndServe(addr, engine)
+}
+
+// 完成统一的控制入口方法ServeHTTP
+func (engine *Engine) ServeHTTP(w http.ResponseWriter, req *http.Request) {
+ key := req.Method + "-" + req.URL.Path
+ if handler, ok := engine.router[key]; ok {
+ handler(w, req)
+ } else {
+ fmt.Fprintf(w, "404 NOT FOUND: %s\n", req.URL)
+ }
+}
+测试后的效果和之前完全相同。
+整个 Gee框架的原型已经出来了。实现了路由映射表,提供了用户注册静态路由的方法,包装了启动服务的函数。
最终调用的效果:
+package main
+
+import (
+ "Go-Projects/Gee/gee"
+ "net/http"
+)
+
+func main() {
+ r := gee.New()
+ r.GET("/", func(c *gee.Context) {
+ c.HTML(http.StatusOK, "<h1>Hello Gee</h1>")
+ })
+ r.GET("/hello", func(c *gee.Context) {
+ c.String(http.StatusOK, "hello %s, you're at %s\n", c.Query("name"), c.Path)
+ })
+ r.POST("/login", func(c *gee.Context) {
+ c.JSON(http.StatusOK, gee.H{
+ "username": c.PostForm("username"),
+ "password": c.PostForm("password"),
+ })
+ })
+ r.Run("localhost:9999")
+}
+Handler的参数变成成了 gee.Context,提供了查询Query/PostForm参数的功能。gee.Context封装了 HTML/String/JSON函数,能够快速构造HTTP响应。*http.Request,构造响应 http.ResponseWriter。但是这两个对象提供的接口粒度太细,比如我们要构造一个完整的响应,需要考虑消息头(Header)和消息体(Body),而 Header 包含了状态码(StatusCode),消息类型(ContentType)等几乎每次请求都需要设置的信息。因此,如果不进行有效的封装,那么框架的用户将需要写大量重复,繁杂的代码,而且容易出错。针对常用场景,能够高效地构造出 HTTP 响应是一个好的框架必须考虑的点。*http.Request和 http.ResponseWriter的方法,简化相关接口的调用,只是设计 Context 的原因之一。对于框架来说,还需要支撑额外的功能。例如,将来解析动态路由 /hello/:name,参数 :name的值放在哪呢?再比如,框架需要支持中间件,那中间件产生的信息放在哪呢?Context 随着每一个请求的出现而产生,请求的结束而销毁,和当前请求强相关的信息都应由 Context 承载。因此,设计 Context 结构,扩展性和复杂性留在了内部,而对外简化了接口。路由的处理函数,以及将要实现的中间件,参数都统一使用 Context 实例, Context 就像一次会话的百宝箱,可以找到任何东西。context.go
+package gee
+
+import (
+ "encoding/json"
+ "fmt"
+ "net/http"
+)
+
+// 给map[string]interface{}起了一个别名gee.H,构建JSON数据时,显得更简洁。
+type H map[string]interface{}
+
+type Context struct {
+ // 原始的两个参数
+ Writer http.ResponseWriter
+ Req *http.Request
+ // 请求信息
+ Path string
+ Method string
+ // 响应信息
+ StatusCode int
+}
+
+// 创建一个Context实例
+func newContext(w http.ResponseWriter, req *http.Request) *Context {
+ return &Context{
+ Writer: w,
+ Req: req,
+ Path: req.URL.Path,
+ Method: req.Method,
+ }
+}
+
+// 根据key返回用户输入的value,属于POST方法的工具
+func (c *Context) PostForm(key string) string {
+ return c.Req.FormValue(key)
+}
+
+// 根据key返回用户输入的value,属于GET方法的工具
+func (c *Context) Query(key string) string {
+ return c.Req.URL.Query().Get(key)
+}
+
+// 写入状态码并更改Context的状态码
+func (c *Context) Status(code int) {
+ c.StatusCode = code
+ c.Writer.WriteHeader(code)
+}
+
+// 帮助下面的方法快速构造响应
+func (c *Context) SetHeader(key, value string) {
+ c.Writer.Header().Set(key, value)
+}
+
+// 构造字符串类型的响应
+func (c *Context) String(code int, format string, values ...interface{}) {
+ c.SetHeader("Content-Type", "text/plain")
+ c.Status(code)
+ c.Writer.Write([]byte(fmt.Sprintf(format, values...)))
+}
+
+// 构造JSON类型的响应
+func (c *Context) JSON(code int, obj interface{}) {
+ c.SetHeader("Content-Type", "application/json")
+ c.Status(code)
+ encoder := json.NewEncoder(c.Writer) // 流数据构造json
+ if err := encoder.Encode(obj); err != nil {
+ http.Error(c.Writer, err.Error(), 500)
+ }
+}
+
+// 构造data类型的响应
+func (c *Context) Data(code int, data []byte) {
+ c.Status(code)
+ c.Writer.Write(data)
+}
+
+// 构造HTML类型的响应
+func (c *Context) HTML(code int, html string) {
+ c.SetHeader("Content-Type", "text/html")
+ c.Status(code)
+ c.Writer.Write([]byte(html))
+}
+将和路由相关的方法和结构提取出来,放到了一个新的文件中 router.go,方便我下一次对 router 的功能进行增强,
package gee
+
+import (
+ "log"
+ "net/http"
+)
+
+type router struct {
+ handlers map[string]HandlerFunc
+}
+
+func newRouter() *router {
+ return &router{
+ handlers: make(map[string]HandlerFunc),
+ }
+}
+
+// 将路由添加到路由表中
+func (r *router) addRoute(method, pattern string, handler HandlerFunc) {
+ log.Printf("Route %4s - %s", method, pattern)
+ key := method + "-" + pattern
+ r.handlers[key] = handler
+}
+
+// 路由处理
+func (r *router) handle(c *Context) {
+ key := c.Method + "-" + c.Path
+ if handler, ok := r.handlers[key]; ok {
+ handler(c)
+ } else {
+ c.String(http.StatusNotFound, "404 NOT FOUND: %s\n", c.Path)
+ }
+}
+调整主框架入口gee.go
+package gee
+
+import (
+ "net/http"
+)
+
+// 定义一个普遍使用的函数类型,避免后面再次定义
+type HandlerFunc func(*Context)
+
+// 定义路由表
+type Engine struct {
+ router *router
+}
+
+// 工厂模式的构造方法,返回一个实例
+func New() *Engine {
+ return &Engine{
+ router: newRouter(),
+ }
+}
+
+// 实现GET方法
+func (engine *Engine) GET(pattern string, handler HandlerFunc) {
+ engine.router.addRoute("GET", pattern, handler)
+}
+
+// 实现POST方法
+func (engine *Engine) POST(pattern string, handler HandlerFunc) {
+ engine.router.addRoute("POST", pattern, handler)
+}
+
+// 实现Run方法
+func (engine *Engine) Run(addr string) (err error) {
+ return http.ListenAndServe(addr, engine)
+}
+
+// 完成统一的控制入口方法ServeHTTP
+func (engine *Engine) ServeHTTP(w http.ResponseWriter, req *http.Request) {
+ c := newContext(w, req)
+ engine.router.handle(c)
+}
+测试代码
+启动程序后:
+2022/11/21 21:05:40 Route GET - /
+2022/11/21 21:05:40 Route GET - /hello
+2022/11/21 21:05:40 Route POST - /login> curl -i http://localhost:9999/
+HTTP/1.1 200 OK
+Content-Type: text/html
+Date: Mon, 21 Nov 2022 13:05:47 GMT
+Content-Length: 19
+
+<h1>Hello Gee</h1>
+> curl "http://localhost:9999/hello?name=geektutu"
+hello geektutu, you're at /hello
+> curl "http://localhost:9999/login" -X POST -d 'username=geektutu&password=1234'
+{"password":"1234","username":"geektutu"}
+> curl "http://localhost:9999/xxx"
+404 NOT FOUND: /xxx之前,我们用了一个非常简单的 map结构存储了路由表,使用 map存储键值对,索引非常高效,但是有一个弊端,键值对的存储的方式,只能用来索引静态路由。那如果我们想支持类似于 /hello/:name这样的动态路由怎么办呢?
实现动态路由最常用的数据结构,被称为前缀树(Trie树),每一个节点的所有的子节点都拥有相同的前缀。这种结构非常适用于路由匹配。
+首先设计树节点上应该存储哪些信息
+type node struct {
+ pattern string // 待匹配路由,例如 /p/:lang
+ part string // 路由中的一部分,例如 :lang
+ children []*node // 子节点,例如 [doc, tutorial, intro]
+ isWild bool // 是否精确匹配,part 含有 : 或 * 时为true
+}
+将匹配的逻辑,包装为一个辅助函数:
+// 查找第一个匹配的节点,用于插入
+func (n *node) matchChild(part string) *node {
+ for _, child := range n.children {
+ if child.part == part || n.isWild {
+ return child
+ }
+ }
+ return nil
+}
+
+// 查找全部匹配的节点,用于查找
+func (n *node) matchChildren(part string) []*node {
+ nodes := make([]*node, 0)
+ for _, child := range n.children {
+ if child.part == part || n.isWild {
+ nodes = append(nodes, child)
+ }
+ }
+ return nodes
+}实现节点的递归插入和查找
+// 插入节点
+func (n *node) insert(pattern string, parts []string, height int) {
+ // 到达高度了就停止
+ if len(parts) == height {
+ n.pattern = pattern
+ return
+ }
+ part := parts[height] // 获取当前的规则
+ child := n.matchChild(part) // 尝试用当前的规则进行匹配
+ // 如果没有匹配成功,就新建一个节点,并加入到当前节点的孩子们中去
+ if child == nil {
+ child = &node{
+ part: part,
+ isWild: part[0] == ':' || part[0] == '*',
+ }
+ n.children = append(n.children, child)
+ }
+ // 递归进行插入
+ child.insert(pattern, parts, height+1)
+}
+
+// 查询节点
+func (n *node) search(parts []string, height int) *node {
+ if len(parts) == height || strings.HasPrefix(n.part, "*") {
+ if n.pattern == "" {
+ return nil
+ }
+ return n
+ }
+ part := parts[height] // 获取当前的规则
+ children := n.matchChildren(part) // 尝试用当前的规则进行匹配
+ // 遍历所有当前匹配的节点进行递归匹配
+ for _, child := range children {
+ result := child.search(parts, height+1)
+ if result != nil {
+ return result
+ }
+ }
+ return nil
+}使用 roots 来存储每种请求方式的Trie 树根节点。使用 handlers 存储每种请求方式的 HandlerFunc 。getRoute 函数中解析了 :和 *两种匹配符的参数,返回一个 map 。
// 将字符串解析成一个切片
+func parsePattern(pattern string) []string {
+ vs := strings.Split(pattern, "/")
+ parts := make([]string, 0)
+ for _, item := range vs {
+ if item != "" {
+ parts = append(parts, item)
+ if item[0] == '*' {
+ break
+ }
+ }
+ }
+ return parts
+}
+
+// 将路由添加到路由表中
+func (r *router) addRoute(method, pattern string, handler HandlerFunc) {
+ parts := parsePattern(pattern)
+ key := method + "-" + pattern
+ // 先看看是不是Get或者Post方法
+ _, ok := r.roots[method]
+ if !ok {
+ r.roots[method] = &node{}
+ }
+ r.roots[method].insert(pattern, parts, 0)
+ r.handlers[key] = handler
+}
+
+// 从路由表中查找路由
+func (r *router) getRoute(method, path string) (*node, map[string]string) {
+ searchParts := parsePattern(path)
+ params := make(map[string]string)
+ root, ok := r.roots[method]
+ if !ok {
+ return nil, nil
+ }
+ n := root.search(searchParts, 0)
+ if n != nil {
+ parts := parsePattern(n.pattern)
+ for index, part := range parts {
+ if part[0] == ':' {
+ params[part[1:]] = searchParts[index]
+ }
+ if part[0] == '*' && len(part) > 1 {
+ params[part[1:]] = strings.Join(searchParts[index:], "/")
+ break
+ }
+ }
+ return n, params
+ }
+ return nil, nil
+}对 Context 对象增加一个属性和方法,来提供对路由参数的访问。我们将解析后的参数存储到 Params中
更改路由处理的方法
+// 路由处理
+func (r *router) handle(c *Context) {
+ n, params := r.getRoute(c.Method, c.Path)
+ if n != nil {
+ c.Params = params
+ key := c.Method + "-" + n.pattern
+ r.handlers[key](c)
+ } else {
+ c.String(http.StatusNotFound, "404 NOT FOUND: %s\n", c.Path)
+ }
+}测试:
+> curl "http://localhost:9999/hello/geektutu"
+hello geektutu, you're at /hello/geektutu
+> curl "http://localhost:9999/assets/css/geektutu.css"
+{"filepath":"css/geektutu.css"}真实的业务场景中,往往某一组路由需要相似的处理。例如:
+/post开头的路由匿名可访问。/admin开头的路由需要鉴权。/api开头的路由是 RESTful 接口,可以对接第三方平台,需要三方平台鉴权。一个 Group 对象需要具备哪些属性呢?
+首先是前缀(prefix),比如 /,或者 /api;
要支持分组嵌套,那么需要知道当前分组的父亲(parent)是谁;
+中间件是应用在分组上的,那还需要存储应用在该分组上的中间件(middlewares)。
+还需要有访问 Router的能力
// 分组路由
+type RouterGroup struct {
+ prefix string
+ middlewares []HandlerFunc
+ parent *RouterGroup
+ engine *Engine
+}将 Engine作为最顶层的分组,也就是说 Engine拥有 RouterGroup所有的能力。
// 扩展Engine
+type Engine struct {
+ *RouterGroup
+ router *router
+ groups []*RouterGroup
+}更改下面的其他Engine方法即可
+// 工厂模式的构造方法,返回一个实例
+func New() *Engine {
+ engine := &Engine{
+ router: newRouter(),
+ }
+ engine.RouterGroup = &RouterGroup{
+ engine: engine,
+ }
+ engine.groups = []*RouterGroup{engine.RouterGroup}
+ return engine
+}增加一个Group的方法,创建一个新的RouterGroup
+// 创建一个新的RouterGroup
+func (group *RouterGroup) Group(prefix string) *RouterGroup {
+ engine := group.engine
+ newGroup := &RouterGroup{
+ prefix: group.prefix + prefix,
+ parent: group,
+ engine: engine,
+ }
+ engine.groups = append(engine.groups, newGroup)
+ return newGroup
+}后面的Get方法和Post方法就都换成RouterGroup的方法就可以了
+测试:
+> curl "http://localhost:9999/v1/hello?name=geektutu"
+hello geektutu, you're at /v1/hello
+> curl "http://localhost:9999/v2/hello/geektutu"
+hello geektutu, you're at /v2/hello/geektutu
+> curl "http://localhost:9999/index"
+<h1>Index Page</h1>中间件(middlewares),简单说,就是非业务的技术类组件。Web 框架本身不可能去理解所有的业务,因而不可能实现所有的功能。因此,框架需要有一个插口,允许用户自己定义功能,嵌入到框架中,仿佛这个功能是框架原生支持的一样。因此,对中间件而言,需要考虑2个比较关键的点:
+Gee 的中间件的定义与路由映射的 Handler 一致,处理的输入是 Context对象。插入点是框架接收到请求初始化 Context对象后,允许用户使用自己定义的中间件做一些额外的处理,例如记录日志等,以及对 Context进行二次加工。另外通过调用 (*Context).Next()函数,中间件可等待用户自己定义的 Handler处理结束后,再做一些额外的操作,例如计算本次处理所用时间等。即 Gee 的中间件支持用户在请求被处理的前后,做一些额外的操作。举个例子,我们希望最终能够支持如下定义的中间件,c.Next()表示等待执行其他的中间件或用户的 Handler:
package gee
+
+import (
+ "log"
+ "time"
+)
+
+func Logger() HandlerFunc {
+ return func(c *Context) {
+ t := time.Now() // 开始计时
+ c.Next() // 等待用户自己的Handler处理结束
+ log.Printf("[%d] %s in %v", c.StatusCode, c.Req.RequestURI, time.Since(t)) // 打印时间
+ }
+}
+中间件是应用在 RouterGroup上的,应用在最顶层的 Group,相当于作用于全局,所有的请求都会被中间件处理。
给 Context添加了2个参数,定义了 Next方法:
func (c *Context) Next() {
+ c.index++
+ s := len(c.handlers)
+ for ; c.index < s; c.index++ {
+ c.handlers[c.index](c)
+ }
+}index是记录当前执行到第几个中间件,当在中间件中调用 Next方法时,控制权交给了下一个中间件,直到调用到最后一个中间件,然后再从后往前,调用每个中间件在 Next方法之后定义的部分。
定义 Use函数,将中间件应用到某个 Group 。
func (group *RouterGroup) Use(middlewares ...HandlerFunc) {
+ group.middlewares = append(group.middlewares, middlewares...)
+}ServeHTTP 函数也有变化,当我们接收到一个具体请求时,要判断该请求适用于哪些中间件,在这里我们简单通过 URL 的前缀来判断。得到中间件列表后,赋值给 c.handlers。
// 完成统一的控制入口方法ServeHTTP
+func (engine *Engine) ServeHTTP(w http.ResponseWriter, req *http.Request) {
+ var middlewares []HandlerFunc
+ for _, group := range engine.groups {
+ if strings.HasPrefix(req.URL.Path, group.prefix) {
+ middlewares = append(middlewares, group.middlewares...)
+ }
+ }
+ c := newContext(w, req)
+ c.handlers = middlewares
+ engine.router.handle(c)
+}handle 函数中,将从路由匹配得到的 Handler 添加到 c.handlers列表中,执行 c.Next()。
// 路由处理
+func (r *router) handle(c *Context) {
+ n, params := r.getRoute(c.Method, c.Path)
+ if n != nil {
+ key := c.Method + "-" + n.pattern
+ c.Params = params
+ c.handlers = append(c.handlers, r.handlers[key])
+ } else {
+ c.handlers = append(c.handlers, func(c *Context) {
+ c.String(http.StatusNotFound, "404 NOT FOUND: %s\n", c.Path)
+ })
+ }
+ c.Next()
+}测试:
+> go run Go-Projects/Gee
+2022/11/22 15:45:00 Route GET - /
+2022/11/22 15:45:00 Route GET - /v2/hello/:name
+>
+2022/11/22 15:45:11 [200] / in 3µs
+>
+2022/11/22 15:45:25 [500] /v2/hello/geektutu in 39.4µs for group v2
+2022/11/22 15:45:25 [500] /v2/hello/geektutu in 77.6µs> curl http://localhost:9999/
+<h1>Hello Gee</h1>
+> curl http://localhost:9999/v2/hello/geektutu
+{"message":"Internal Server Error"}Web 框架如何支持服务端渲染的场景
+解析请求的地址,映射到服务器上文件的真实地址:
+// 解析请求的地址,映射到服务器上文件的真实地址
+func (group *RouterGroup) createStaticHandler(relativePath string, fs http.FileSystem) HandlerFunc {
+ absolutePath := path.Join(group.prefix, relativePath)
+ fileServer := http.StripPrefix(absolutePath, http.FileServer(fs))
+ return func(c *Context) {
+ file := c.Param("filepath")
+ // Check if file exists and/or if we have permission to access it
+ if _, err := fs.Open(file); err != nil {
+ c.Status(http.StatusNotFound)
+ return
+ }
+
+ fileServer.ServeHTTP(c.Writer, c.Req)
+ }
+}
+
+func (group *RouterGroup) Static(relativePath string, root string) {
+ handler := group.createStaticHandler(relativePath, http.Dir(root))
+ urlPattern := path.Join(relativePath, "/*filepath")
+ // Register GET handlers
+ group.GET(urlPattern, handler)
+}HTML 模板渲染
+// 扩展Engine
+type Engine struct {
+ *RouterGroup
+ router *router
+ groups []*RouterGroup
+ htmlTemplates *template.Template // 模板渲染
+ funcMap template.FuncMap // 模板渲染
+}
+
+func (engine *Engine) SetFuncMap(funcMap template.FuncMap) {
+ engine.funcMap = funcMap
+}
+
+func (engine *Engine) LoadHTMLGlob(pattern string) {
+ engine.htmlTemplates = template.Must(template.New("").Funcs(engine.funcMap).ParseGlob(pattern))
+}对原来的 (*Context).HTML()方法做了些小修改,使之支持根据模板文件名选择模板进行渲染。
// 构造HTML类型的响应
+func (c *Context) HTML(code int, name string, data interface{}) {
+ c.SetHeader("Content-Type", "text/html")
+ c.Status(code)
+ if err := c.engine.htmlTemplates.ExecuteTemplate(c.Writer, name, data); err != nil {
+ c.Fail(500, err.Error())
+ }
+}进行测试:
+package main
+
+import (
+ "Go-Projects/Gee/gee"
+ "fmt"
+ "html/template"
+ "net/http"
+ "time"
+)
+
+type student struct {
+ Name string
+ Age int8
+}
+
+func FormatAsDate(t time.Time) string {
+ year, month, day := t.Date()
+ return fmt.Sprintf("%d-%02d-%02d", year, month, day)
+}
+
+func main() {
+ r := gee.New()
+ r.Use(gee.Logger())
+ r.SetFuncMap(template.FuncMap{
+ "FormatAsDate": FormatAsDate,
+ })
+ r.LoadHTMLGlob("Gee/templates/*")
+ r.Static("/assets", "./static")
+
+ stu1 := &student{Name: "Geektutu", Age: 20}
+ stu2 := &student{Name: "Jack", Age: 22}
+ r.GET("/", func(c *gee.Context) {
+ c.HTML(http.StatusOK, "css.tmpl", nil)
+ })
+ r.GET("/students", func(c *gee.Context) {
+ c.HTML(http.StatusOK, "arr.tmpl", gee.H{
+ "title": "gee",
+ "stuArr": [2]*student{stu1, stu2},
+ })
+ })
+
+ r.GET("/date", func(c *gee.Context) {
+ c.HTML(http.StatusOK, "custom_func.tmpl", gee.H{
+ "title": "gee",
+ "now": time.Date(2019, 8, 17, 0, 0, 0, 0, time.UTC),
+ })
+ })
+
+ r.Run("localhost:9999")
+}
+错误处理也可以作为一个中间件,增强 gee 框架的能力
+package gee
+
+import (
+ "fmt"
+ "log"
+ "net/http"
+ "runtime"
+ "strings"
+)
+
+// print stack trace for debug
+func trace(message string) string {
+ var pcs [32]uintptr
+ n := runtime.Callers(3, pcs[:]) // skip first 3 caller
+
+ var str strings.Builder
+ str.WriteString(message + "\nTraceback:")
+ for _, pc := range pcs[:n] {
+ fn := runtime.FuncForPC(pc)
+ file, line := fn.FileLine(pc)
+ str.WriteString(fmt.Sprintf("\n\t%s:%d", file, line))
+ }
+ return str.String()
+}
+
+func Recovery() HandlerFunc {
+ return func(c *Context) {
+ defer func() {
+ if err := recover(); err != nil {
+ message := fmt.Sprintf("%s", err)
+ log.Printf("%s\n\n", trace(message))
+ c.Fail(http.StatusInternalServerError, "Internal Server Error")
+ }
+ }()
+
+ c.Next()
+ }
+}
+《高级人工智能》课程笔记:第13讲 群体智能
+ +集群智能:众多无智能的个体,通过相互之间的简单合作所表现出来的智能行为
+博弈:具备一定智能的理性个体,按照某种机制行动,在群体层面体现出的智能
+众包:设计合适的机制,激励个体参与,从而实现单个个体不具备的社会智能
+分布式 、 自组织的(自然/人造)系统表现出的一种群体智能
+集群智能系统一般由一群简单的智能体构成,智能体按照简单的规则彼此进行局部交互,智能体也可以环境交互
+灵感通常来自生物系统(蚁群、鸟群、兽群、粒子群)
+特点:
+一种解空间搜索方法,适用于在图上寻找最优路径
+算法形式化:
+TSP问题蚁群算法流程
+蚁群大小:一般情况下,蚁群中的蚂蚁个数不超过TSP图中节点的个数
+终止条件:
+思想:局部随机搜索+自增强
+缺点:
+是一种随机优化方法,通过粒子群在解空间中进行搜索,寻找最优解(适应度最大的解)
+ 在第
在第 轮的位置:
轮的位置:
 在第
在第 轮的速度:
轮的速度:
 :粒子
:粒子 的历史最好位置
的历史最好位置 :全局历史最好位置
:全局历史最好位置
 和
和
 和
和



粒子速度更新公式:
+ 权重参数:一般取值为2
权重参数:一般取值为2 随机参数:0和1之间的随机数
随机参数:0和1之间的随机数算法终止条件:
+速度更新参数:又称加速度参数,用来控制粒子当前最优位置

 :每个微粒执行局部搜索;
:每个微粒执行局部搜索; :微粒群转化为一个随机爬山法
:微粒群转化为一个随机爬山法 :微粒逐渐移向
:微粒逐渐移向 和
和 的加权均值
的加权均值 :算法比较适合于单峰优化问题
:算法比较适合于单峰优化问题 :算法比较适合于多峰优化问题
:算法比较适合于多峰优化问题惯性权重:速度冲量导致微粒按照先前速度方向继续移动。提出一个惯性权重
优点:
+缺点:和其它演化计算算法类似,不保证收敛到全局最优解
+import numpy as np
+
+def cal(x):
+ return x*x*x-5*x*x-2*x+3
+
+x_min = -2
+x_max = 5
+
+p_num = 1000
+
+g_best_max = 1
+g_best_max_i = 0
+
+g_best_min = 1
+g_best_min_i = 0
+
+x_MAX = (x_max - x_min) * np.random.random_sample((p_num,)) + x_min
+v_MAX = (x_max - x_min) * np.random.random_sample((p_num,)) + x_min
+
+x_MIN = (x_max - x_min) * np.random.random_sample((p_num,)) + x_min
+v_MIN = (x_max - x_min) * np.random.random_sample((p_num,)) + x_min
+
+p_best_max = np.ones_like(x_MAX)
+p_best_min = np.ones_like(x_MAX)
+
+for i in range(1,10000):
+
+ f_max = cal(x_MAX)
+ f_min = cal(x_MIN)
+
+ t_max = cal(p_best_max)
+ t_min = cal(p_best_min)
+
+ p_best_max = np.where(t_max > f_max, p_best_max, x_MAX)
+ p_best_min = np.where(t_min < f_min, p_best_min, x_MIN)
+
+
+ if np.max(f_max) > g_best_max:
+ g_best_max = np.max(f_max)
+ g_best_max_i = x_MAX[np.argmax(f_max)]
+
+ if np.min(f_min) < g_best_min:
+ g_best_min = np.min(f_min)
+ g_best_min_i = x_MIN[np.argmin(f_min)]
+
+ v_MAX = v_MAX + (p_best_max - x_MAX) + (g_best_max - x_MAX)
+ x_MAX = x_MAX + v_MAX
+
+ x_MAX = np.where(x_MAX > x_max,x_max,x_MAX)
+ x_MAX = np.where(x_MAX < x_min,x_min,x_MAX)
+
+ v_MIN = v_MIN + (p_best_min - x_MIN) + (g_best_min - x_MIN)
+ x_MIN = x_MIN + v_MIN
+
+ x_MIN = np.where(x_MIN > x_max,x_max,x_MIN)
+ x_MIN = np.where(x_MIN < x_min,x_min,x_MIN)
+
+print(g_best_max_i)
+print(g_best_min_i)《高级人工智能》课程笔记:第14讲 强化学习
+ +目标:学习从环境状态到行为的映射(即策略),智能体选择能够获得环境最大奖赏的行为,使得外部环境对学习系统在某种意义下的评价为最佳。
+区别于监督学习:监督学习是从标注中学习;强化学习是从交互中学习
+评价性反馈
+指导性反馈
+试错搜索和延迟奖励,用于判断某一问题是否适用于强化学习求解。
+利用和探索之间的矛盾
+主体:智能体和环境-状态、行为和奖励
+要素:
+一台赌博机有多个摇臂 ,每个摇臂摇出的奖励(reward)大小不确定 ,玩家希望摇固定次数的臂所获得的期望累积奖励最大
+行为:摇哪个臂
+奖励:每次摇臂获得的奖金
+



第

假如摇臂
当


但是一般情况下,





利用:
+ 最大的行为
最大的行为
 只是对
只是对 的估计,估计的不确定性导致按照贪心策略选择的行为不一定是
的估计,估计的不确定性导致按照贪心策略选择的行为不一定是 最大的行为
最大的行为探索:
+每步选择在“利用”和“探索”中二选一
+如何平衡“利用”和“探索” 是关键
+贪心策略形式化地表示为:


 按照贪心策略进行行为选择(Exploitation)
按照贪心策略进行行为选择(Exploitation) 在所有行为中随机选择一个(Exploration)
在所有行为中随机选择一个(Exploration) 的取值取决于
的取值取决于 的方差,方差越大
的方差,方差越大 取值应越大
取值应越大根据历史观测样本的均值对
约定:
+
 收敛到
收敛到
行为估值时,一个行为被选择了


行为的初始估值
+乐观初值法:Optimistic Initial Values
+
 或
或
贝尔曼方程定义了状态估值函数的依赖关系
+ 个)的估值根据贝尔曼方程形成了一个具有
个)的估值根据贝尔曼方程形成了一个具有 个方程和
个方程和 个变量的线性方程组
个变量的线性方程组求解贝尔曼最优性方程寻找最优策略的局限性
+
算法面试题准备
+ +void mergesort(vector<int> & nums, int start, int end){
+ if(start >= end){
+ return;
+ }
+ int mid = (end - start) / 2 + start;
+ mergesort(nums, start, mid);
+ mergesort(nums, mid+1, end);
+ vector<int> temp;
+ int l1start = start;
+ int l1end = mid;
+ int l2start = mid + 1;
+ int l2end = end;
+ while(l1start <= l1end || l2start <= l2end){
+ if(l1start > l1end){
+ temp.push_back(nums[l2start]);
+ l2start += 1;
+ } else if(l2start > l2end){
+ temp.push_back(nums[l1start]);
+ l1start += 1;
+ } else{
+ if(nums[l1start] < nums[l2start]){
+ temp.push_back(nums[l1start]);
+ l1start += 1;
+ } else{
+ temp.push_back(nums[l2start]);
+ l2start += 1;
+ }
+ }
+ }
+ for(int i=0;i<temp.size();i++){
+ nums[start+i] = temp[i];
+ }
+}
+
+void quicksort(vector<int> &nums, int start, int end){
+ if(start >= end){
+ return;
+ }
+ int x = nums[start];
+ int left = start;
+ int right = end;
+ while(left < right){
+ while(left < right && nums[right] >= x){
+ right--;
+ }
+ nums[left] = nums[right];
+ while(left < right && nums[left] < x){
+ left++;
+ }
+ nums[right] = nums[left];
+ }
+ nums[left] = x;
+ quicksort(nums, start, left-1);
+ quicksort(nums, left+1, end);
+}double binarysearch(double x, double threshold){
+ double left = 0;
+ double right = x+1;
+ while(right - left >= threshold){
+ double mid = (left + right) / 2.0;
+ if(mid * mid < x){
+ left = mid;
+ } else{
+ right = mid;
+ }
+ }
+ return left;
+}
+
+double gdtosqrt(double x, double threshold){
+ // y^2 = x -> x - y^2 = 0
+ // min (x - y^2)^2
+ // x^2 - 2 * x * y^2 + y^4
+ // 对y求导
+ // -4*x * y + 4 * y ^ 3
+
+ double now = x;
+ double pre = x + threshold*2;
+ double lr = 0.00001;
+ while(abs(now-pre) >= threshold){
+ pre = now;
+ now = now - lr * (-4 * x * now + 4 * now * now * now);
+ }
+ return now;
+}
+
+double gdtocube(double x, double threshold){
+ // y^3 = x -> x - y^3 = 0
+ // min (x - y^3)^2
+ // x^2 - 2 * x * y^3 + y^6
+ // 对y求导
+ // -6*x * y^2 + 6 * y ^ 5
+
+ double now = x;
+ double pre = x + threshold*2;
+ double lr = 0.00001;
+ while(abs(now-pre) >= threshold){
+ pre = now;
+ now = now - lr * (-6 * x * now * now + 6 * now * now * now * now * now);
+ }
+
+ return now;
+}
+
+int main(){
+ double a = 1;
+ double threshold = 0.00000000001;
+ double res = binarysearch(a, threshold);
+ cout << res << endl;
+ double res2 = gdtosqrt(a, threshold);
+ cout << res2 << endl;
+ double res3 = gdtocube(a, threshold);
+ cout << res3 << endl;
+ return 0;跑不通调整学习率,大数学习率要小,小数学习率要大
+class MultiHeadAttention(nn.Module):
+ def __init__(self, hidden_size, num_heads):
+ super(MultiHeadAttention, self).__init__()
+ self.num_heads = num_heads
+ self.head_dim = hidden_size // num_heads
+
+ self.q_linear = nn.Linear(hidden_size, hidden_size)
+ self.k_linear = nn.Linear(hidden_size, hidden_size)
+ self.v_linear = nn.Linear(hidden_size, hidden_size)
+
+ self.o_linear = nn.Linear(hidden_size, hidden_size)
+
+ def forward(self, hidden_state, attention_mask=None):
+ batch_size = hidden_state.size()[0]
+
+ query = self.q_linear(hidden_state)
+ key = self.k_linear(hidden_state)
+ value = self.v_linear = nn.Linear(hidden_state)
+
+ query = self.split_head(query)
+ key = self.split_head(key)
+ value = self.split_head(value)
+
+ attention_scores = torch.matmul(query, key.transpose(-1,-2)) / torch.sqrt(torch.tensor(self.head_dim))
+
+ if attention_mask != None:
+ attention_scores += attention_mask * -1e9
+
+ attention_probs = torch.softmax(attention_scores, dim=-1)
+
+ output = torch.matmul(attention_probs, value)
+
+ output = output.transpose(-1,-2).contiguous().view(batch_size, -1, self.head_dim * self.num_heads)
+
+ output = self.o_linear(output)
+
+ return output
+
+ def split_head(self, x):
+ batch_size = x.size()[0]
+ return x.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1,2)import numpy as np
+import torch
+import torch.nn as nn
+
+nn.Softmax()
+
+def softmax(logits):
+ max_logits = np.max(logits)
+ exp_logits = np.exp(logits - max_logits)
+ return exp_logits / np.sum(exp_logits)
+
+print(softmax([1,2,3,4,5,6]))
+
+class Our_CrossEntropy(torch.nn.Module):
+
+ def __init__(self):
+ super(Our_CrossEntropy,self).__init__()
+
+ def forward(self, x ,y):
+ P_i = torch.nn.functional.softmax(x, dim=1)
+ y = torch.nn.functional.one_hot(y)
+ loss = y*torch.log(P_i + 0.0000001)
+ loss = -torch.mean(torch.sum(loss, dim=1),dim = 0)
+ return loss
+Go面试题准备
+ +make 关键字的主要作用是创建 slice、map 和 Channel 等内置的数据结构
+new 的主要作用是为类型申请一片内存空间,并返回指向这片内存的指针
+最常见的垃圾回收算法有标记清除(Mark-Sweep) 和引用计数(Reference Count),Go 语言采用的是标记清除算法。并在此基础上使用了三色标记法和写屏障技术,提高了效率。
+标记清除的执行过程可以分成标记和清除两个阶段:
+标记清除算法的一大问题是在标记期间,需要暂停程序(Stop the world,STW),标记结束之后,用户程序才可以继续执行。为了能够异步执行,减少 STW 的时间,Go 语言采用了三色标记法。
+三色标记算法将程序中的对象分成白色、黑色和灰色三类。
+标记开始时,所有对象加入白色集合(这一步需 STW)。首先将根对象标记为灰色,加入灰色集合,垃圾搜集器取出一个灰色对象,将其标记为黑色,并将其指向的对象标记为灰色,加入灰色集合。重复这个过程,直到灰色集合为空为止
+标记阶段结束。那么白色对象即可需要清理的对象,而黑色对象均为根可达的对象,不能被清理。
+三色标记法因为多了一个白色的状态来存放不确定对象,所以后续的标记阶段可以并发地执行。当然并发执行的代价是可能会造成一些遗漏,因为那些早先被标记为黑色的对象可能目前已经是不可达的了。所以三色标记法是一个 false negative(假阴性)的算法。
+三色标记法并发执行仍存在一个问题,此时用户从已经被标记成黑色的对象新建了引用指向了白色对象,白色不可达对象将被收集
+为了解决这个问题,Go 使用了内存屏障技术,当对象新增或更新时,会将其着色为灰色。这样即使与用户程序并发执行,对象的引用发生改变时,垃圾收集器也能正确处理。
+一次完整的 GC 分为四个阶段:
+进程:进程是系统进行资源分配的基本单位,有独立的内存空间。
+线程:线程是CPU调度的基本单位,线程依附于进程存在,每个线程会共享父进程的资源。
+协程: 协程是一种用户态的轻量级线程, 协程的调度完全由用户控制,协程间切换只需要保存任务的上下文,没有内核的开销。
+Goroutine的并发编程模型基于GMP模型:
+G: 表示goroutine,每个goroutine都有自己的栈空间,定时器,初始化的栈空间在2k左右,空间会随着需求增长。
+M: 内核线程,每个m对象对应一个内核线程,p对象需要挂载到m上才能运行,每个m都有一个g0协程负责进行调度
+P: 代表调度器,表示执行 Go 代码所需的资源,负责调度goroutine,维护一个本地goroutine队列,M从P上获得goroutine并执行。
+线程想运行任务就得获取 P,从 P 的本地队列获取 G,P 队列为空时,M 也会尝试从全局队列拿一批 G 放到 P 的本地队列,或从其他 P 的本地队列偷一半放到自己 P 的本地队列。M 运行 G,G 执行之后,M 会从 P 获取下一个 G,不断重复下去。
+复用线程:避免频繁的创建、销毁线程,而是对线程的复用。
+1)work stealing 机制
+当本线程无可运行的 G 时,尝试从其他线程绑定的 P 偷取 G,或者从全局队列中获取G。
+2)hand off 机制
+为了保证多个P之间任务的平衡,所有M共享P全局队列,为保证数据竞争问题,需要加锁处理
+Go的代码库中为开发人员提供了一下两种锁:
+第一个互斥锁指的是在Go编程中,同一资源的锁定对各个协程是相互排斥的,当其中一个协程获取到该锁时,其它协程只能等待,直到这个获取锁的协程释放锁之后,其它的协程才能获取。
+第二个读写锁依赖于互斥锁的实现,这个指的是当多个协程对某一个资源都是只读操作,那么多个协程可以获取该资源的读锁,并且互相不影响,但当有协程要修改该资源时就必须获取写锁,如果获取写锁时,已经有其它协程获取了读写或者写锁,那么此次获取失败,也就是说读写互斥,读读共享,写写互斥。
+乐观锁和悲观锁是两种思想,用于解决并发场景下的数据竞争问题。
+乐观锁:乐观锁在操作数据时非常乐观,认为别人不会同时修改数据。因此乐观锁不会上锁,只是在执行更新的时候判断一下在此期间别人是否修改了数据:如果别人修改了数据则放弃操作,否则执行操作。
+悲观锁:悲观锁在操作数据时比较悲观,认为别人会同时修改数据。因此操作数据时直接把数据锁住,直到操作完成后才会释放锁;上锁期间其他人不能修改数据。
+乐观锁的实现方式主要有两种:CAS机制和版本号机制
+如果内存位置V的值等于预期的A值,则将该位置更新为新值B,否则不进行任何操作。
+许多CAS的操作是自旋的:如果操作不成功,会一直重试,直到操作成功为止。
+atomic 包可以在不形成临界区和创建互斥量的情况下完成并发安全的值替换操作,这个包应用的便是乐观锁的原理。
+版本号机制的基本思路是在数据中增加一个字段version,表示该数据的版本号,每当数据被修改,版本号加1。
+Golang中的sync包,提供了各种锁,如果使用了这个包,基本上就以悲观锁的工作模式了。
+乐观锁没有加锁和解除锁的步骤,直觉上会快一些;但是乐观锁这么做的前提是总认为不会发生并发,如果并发发生的概率很大,重试的次数会增加,这种情况下乐观锁的性能就差很多了。
+悲观锁有加锁和解除锁的步骤,直觉上会慢一些;但是当有很多进程或者线程对同一个数值进行修改时,能避免大量的重试过程,这种情况下悲观锁的性能相对就很高了。
+例如,CAS只能保证单个变量操作的原子性,当涉及到多个变量时,CAS是无能为力的,而synchronized则可以通过对整个代码块加锁来处理。
+再比如版本号机制,如果query的时候是针对表1,而update的时候是针对表2,也很难通过简单的版本号来实现乐观锁。
+当竞争不激烈 (出现并发冲突的概率小)时,乐观锁更有优势,因为悲观锁会锁住代码块或数据,其他线程无法同时访问,影响并发,而且加锁和释放锁都需要消耗额外的资源。
+当竞争激烈(出现并发冲突的概率大)时,悲观锁更有优势,因为乐观锁在执行更新时频繁失败,需要不断重试,浪费CPU资源。
+channel 是一个通道,用于端到端的数据传输,这有点像我们平常使用的消息队列,只不过 channel 的发送方和接受方是 goroutine 对象,属于内存级别的通信。
+无缓冲的 channel,一旦有 goroutine 往 channel 发送数据,那么当前的 goroutine 会被阻塞住,直到有其他的 goroutine 消费了 channel 里的数据,才能继续运行。
+有缓冲的 channel,第二个参数表示 channel 可缓冲数据的容量。只要当前 channel 里的元素总数不大于这个可缓冲容量,则当前的 goroutine 就不会被阻塞住。
+channel 创建后返回了 hchan 结构体,包括:
+qcount uint // channel 里的元素计数
+ dataqsiz uint // 可以缓冲的数量,如 ch := make(chan int, 10)。 此处的 10 即 dataqsiz
+ elemsize uint16 // 要发送或接收的数据类型大小
+ buf unsafe.Pointer // 当 channel 设置了缓冲数量时,该 buf 指向一个存储缓冲数据的区域,该区域是一个循环队列的数据结构
+ closed uint32 // 关闭状态
+ sendx uint // 当 channel 设置了缓冲数量时,数据区域即循环队列此时已发送数据的索引位置
+ recvx uint // 当 channel 设置了缓冲数量时,数据区域即循环队列此时已接收数据的索引位置
+ recvq waitq // 想读取数据但又被阻塞住的 goroutine 队列
+ sendq waitq // 想发送数据但又被阻塞住的 goroutine 队列
+
+ lock mutex
+ ...G1往channel写数据,G1 暂时被挂在 sendq 队列里,然后 G1 调用了 gopark 休眠了起来
+G2从channel读数据,发现 sendq 等待队列里有 goroutine 存在,于是直接从 G1 copy 数据过来,并且会对 G1 设置 goready 函数,这样下次调度发生时, G1 就可以继续运行,并且会从等待队列里移除掉。
+G1 暂时被挂在了 recvq 队列,然后休眠起来。
+G2 在写数据时,发现 recvq 队列有 goroutine 存在,于是直接将数据发送给 G1。同时设置 G1 goready 函数,等待下次调度运行。
+面对一个并发问题的时候,应当选择合适的并发方式:channel还是mutex。 选择的依据是他们的能力/特性:channel的能力是让数据流动起来,擅长的是数据流动的场景:
+mutex的能力是数据不动,某段时间只给一个协程访问数据的权限擅长数据位置固定的场景:
+map就是一种状态内存逃逸:在一段程序中,每一个函数都会有自己的内存区域存放自己的局部变量、返回地址等,这些内存会由编译器在栈中进行分配,每一个函数都会分配一个栈桢,在函数运行结束后进行销毁,但是有些变量我们想在函数运行结束后仍然使用它,那么就需要把这个变量在堆上分配,这种从"栈"上逃逸到"堆"上的现象就成为内存逃逸。
+在 Go语言中堆内存的分配与释放完全不需要我们去管了,Go语言引入了 GC机制,GC机制会对位于堆上的对象进行自动管理,当某个对象不可达时(即没有其对象引用它时),他将会被回收并被重用。
为了减少 GC造成的压力,Go语言引入了逃逸分析,也就是想法设法尽量减少在堆上的内存分配,可以在栈中分配的变量尽量留在栈中。
逃逸分析就是指程序在编译阶段根据代码中的数据流,对代码中哪些变量需要在栈中分配,哪些变量需要在堆上分配进行静态分析的方法。堆和栈相比,堆适合不可预知大小的内存分配。但是为此付出的代价是分配速度较慢,而且会形成内存碎片。栈内存分配则会非常快。栈分配内存只需要两个CPU指令:“PUSH”和“RELEASE”,分配和释放;而堆分配内存首先需要去找到一块大小合适的内存块,之后要通过垃圾回收才能释放。所以逃逸分析更做到更好内存分配,提高程序的运行速度。
+逃逸分析原理:
+对逃逸做一个总结:
+GC压力,提高程序的运行速度GC处理,堆上内存使用完毕会交给 GC处理GC压力,提高性能MySQL面试题准备
+ +MySQL 常见索引有 B+Tree 索引、HASH 索引、Full-Text 索引
+B+Tree 索引类型是 MySQL 存储引擎采用最多的索引类型。
+O(logdN),其中 d 表示节点允许的最大子节点个数为 d 个。而二叉树的每个父节点的儿子节点个数只能是 2 个,意味着其搜索复杂度为 O(logN)InnoDB 引擎通过什么技术来保证事务的这四个特性的呢?
+binlog是二进制文件,记录了对数据库执行更改的所有操作,不包括 select、show,因为这两个操作没有对数据本身做修改。但是若操作了数据,但是数据没有发生变化,也会记录到 binlog。常用来数据恢复,数据备份。
MVCC是通过在每行记录后面保存两个隐藏的列来实现的。这两个列,一个保存了行的创建时间,一个保存行的过期时间(或删除时间)。当然存储的并不是实际的时间值,而是系统版本号(system version number)。每开始一个新的事务,系统版本号都会自动递增。事务开始时刻的系统版本号会作为事务的版本号,用来和查询到的每行记录的版本号进行比较。
+脏读:如果一个事务「读到」了另一个「未提交事务修改过的数据」,就意味着发生了「脏读」现象。
+不可重复读:在一个事务内多次读取同一个数据,如果出现前后两次读到的数据不一样的情况,就意味着发生了「不可重复读」现象。
+幻读:在一个事务内多次查询某个符合查询条件的「记录数量」,如果出现前后两次查询到的记录数量不一样的情况,就意味着发生了「幻读」现象。
+Mysql 在可重复读的隔离级别下基本不会有幻读的情况,但是在特殊的情况下也可能会有。
+第一范式:列不可再分:每一列属性都是不可再分的属性值,确保每一列的原子性
+第二范式:数据库表中的每个实例或行必须可以被惟一地区分,属性完全依赖于主键
+第三范式:数据不能存在传递关系,即每个属性都跟主键有直接关系而不是间接关系。
+优点:
+缺点:
+解耦:一个系统或者一个模块,调用了多个系统或者模块,互相之间的调用很复杂,维护起来很麻烦。但是其实这个调用是不需要直接同步调用接口的,如果用 MQ 给它异步化解耦,也是可以的
+异步:将数据放到消息队列中,直接对用户返回响应,后续再等待慢慢写入
+削峰:从消息队列到数据库的流速固定,不受外界突然的高请求数量的干扰
+缺点:
+系统可用性降低:系统引入的外部依赖越多,越容易挂掉。
+系统复杂度提高
+一致性问题:不知道后续对数据库的操作是否完成
+解决方法:
+计算机网络面试题准备
+ +浏览器根据请求的 URL 交给 DNS 域名解析,找到真实 IP ,向服务器发起请求;
+服务器交给后台处理完成后返回数据,浏览器接收⽂件( HTML、JS、CSS 、图像等);
+浏览器对加载到的资源( HTML、JS、CSS 等)进行语法解析,建立相应的内部数据结构 (如 HTML 的 DOM);
+载⼊解析到的资源⽂件,渲染页面,完成。
+OSI七层模型从上到下依次为:
+TCP/IP:应用层、传输层、网络层、数据链路层
+TCP 是面向连接的、可靠的、基于字节流的传输层通信协议。
+TCP和UDP的区别如下:
+TCP对应的典型的应用层协议:
+UDP对应的典型的应用层协议:
+
客户端在发送完给服务端的回执报文后没有立刻进入CLOSED状态,而是进入TIME-WAIT状态,然后等待2*MSL(最长报文段寿命)的时间后才进入CLOSED状态,原因有以下两点:
+ARQ协议,即自动重传请求(Automatic Repeat-reQuest),意思是如果发送方在发送后一段时间之内没有收到确认回执,它通常会重新发送。ARQ协议包括停止等待ARQ协议和连续ARQ协议。
+(1)停止等待ARQ协议
+停止等待ARQ协议是指,在停止等待中如果接收端没有收到发送端发来的分组,接收端就不会给发送端发送确认回执,此时发送端会重新发送之前的报文分组。发送端会维护一个超时计时器,超时时间会设置的比数据在传输往返过程的时间要长一些。
+(2)连续ARQ协议
+连续ARQ协议是指,发送端维护一个“窗口”,“窗口”内可以有多个分组,窗口的大小就是窗口中分组的个数,凡是位于“窗口”内的分组可以连续发送出去而不必等待接收端返回的确认回执,对按序到达的最后一个分组,接收端会向发送端发送确认回执,如果有分组没有正确到达,会返回最后一个正确达到的分组序号,该序号后面的分组会重新发送给接收端。
+在连续ARQ协议中,发送端会维护一块发送端的数据缓存,“窗口”里的分组都会在这个缓存中,当需要重新发送“窗口”中的分组报文时,便会从缓存里读取分组并发送。
+连续 ARQ 协议可提高信道利用率。
+流量控制是为了控制发送端发送数据的速率,保证接收端能将本应接收的所有报文分组接收成功,否则会触发自动重传机制造成网络流量的浪费。
+流量控制的具体操作是:接收端会通知发送端自己能接收的数据大小,于是发送端会发送不超过这个数据量的数据,这个大小被称为“窗口”的大小,在TCP首部中专门有一个字段表示“窗口”的大小,该值越大代表网络的吞吐量越高。
+计算机网络都处在一个共享的环境,在通信开始时如果立即把大量数据注入到网络,可能会引起网络阻塞,甚至带来网络瘫痪。TCP为了防止该问题的出现,采用了拥塞控制的策略
+常见的拥塞控制策略有慢启动、拥塞避免、快重传与快恢复
+cwnd 「超过」慢启动门限 ssthresh 就会进入拥塞避免算法:每当收到一个 ACK 时,cwnd 增加 1/cwnd,变成了线性增长cwnd = cwnd/2 ,也就是设置为原来的一半; ssthresh = cwndcwnd = ssthresh + 3 ( 3 的意思是确认有 3 个数据包被收到了);如果客户端连续不断的向服务端发送数据包时,服务端接收的数据会出现两个数据包粘在一起的情况。
+基于上面两点,在使用 TCP 传输数据时,才有粘包或者拆包现象发生的可能。一个数据包中包含了发送端发送的两个数据包的信息,这种现象即为粘包。
+采用 TCP 协议传输数据的客户端与服务器经常是保持一个长连接的状态(一次连接发一次数据不存在粘包),双方在连接不断开的情况下,可以一直传输数据。但当发送的数据包过于的小时,那么 TCP 协议默认的会启用 Nagle 算法,将这些较小的数据包进行合并发送(缓冲区数据发送是一个堆压的过程);这个合并过程就是在发送缓冲区中进行的,也就是说数据发送出来它已经是粘包的状态了。
+一句话:要发送的数据小于 TCP 发送缓冲区的大小,TCP 将多次写入缓冲区的数据一次发送出去,将会发生粘包。
+接收方采用 TCP 协议接收数据时的过程是这样的:数据到接收方,从网络模型的下方传递至传输层,传输层的 TCP 协议处理是将其放置接收缓冲区,然后由应用层来主动获取(C 语言用 recv、read 等函数);这时会出现一个问题,就是我们在程序中调用的读取数据函数不能及时的把缓冲区中的数据拿出来,而下一个数据又到来并有一部分放入的缓冲区末尾,等我们读取数据时就是一个粘包(放数据的速度 > 应用层拿数据速度)。
+一句话:接收数据端的应用层没有及时读取接收缓冲区中的数据,将发生粘包。
+浏览器输入地址,然后浏览器这个进程去调操作系统某个库里的gethostbyname函数(例如,Linux GNU glibc标准库的gethostbyname函数),然后呢这个函数通过网卡给DNS服务器发UDP请求,接收结果,然后将结果给返回给浏览器。
+为什么域名解析用UDP协议?
+UDP的DNS协议只要一个请求、一个应答就好了。UDP协议传输内容不能超过512字节。不过客户端向DNS服务器查询域名,一般返回的内容都不超过512字节,用UDP传输即可。
+为什么区域传送用TCP协议?
+因为TCP协议可靠性好啊!你要从主DNS上复制内容啊,你用不可靠的UDP? TCP协议传输的内容大
+com域,因此根域DNS服务器会返回它所管理的 com域中的DNS 服务器的IP地址,意思是“虽然我不知道你要查的那个域名的地址,但你可以去 com域问问看”com域的DNS服务器发送查询消息。com 域中也没有 www.tmall.com这个域名的信息,和刚才一样,com域服务器会返回它下面的 tmall.com域的DNS服务器的IP地址。http协议是一种无状态协议,协议自身不对请求和响应之间的通信状态进行保存,即对发送过来的请求和响应都不做持久化处理,把http协议设计的如此简单是为了更快地处理大量事务。
+为了解决http协议不能保存通信状态的问题,引入了Cookie状态管理。Cookie技术通过在请求和响应报文中写入Cookie信息来控制客户端的状态。Cookie会根据从服务端发送的响应报文的一个叫Set-Cookie的首部字段,通知客户端保存Cookie。当下次客户端再往该服务端发送请求时,客户端会自动在请求报文中加入Cookie值发送出去,服务端发现客户端发来的Cookie后,会检查是哪一个客户端发来的连接请求,对比服务器上的记录,最后得到之前的状态信息。
+面试项目准备
+ +您好,我是张兆,就读于中国科学院计算技术研究所,是预计25年夏季毕业的硕士研究生。我本科来自于中南大学计算机学院,是通过推荐免试的方式进入到中科院计算所就读研究生的。我在本科期间获得了国家奖学金和省级优秀毕业生的荣誉称号,同时拿过一些程序设计竞赛、数学建模和英语竞赛的奖项。
+我的主要经历大概这样,有哪些经历您比较感兴趣我可以更加详细的介绍一下。
+目标:基于Qwen进行医疗行业垂直领域大模型建设,包括医疗领域数据增量预训练、监督微调、强化学习等大模型全链路方法,同时增加检索增强、密态隐私安全等相关特色能力;
+方法:收集爬取4.5B医学领域开源数据和中英文通用领域开源数据,并使用 PPL 、MinHash等方法对数据进行清洗、过滤等,随后在Qwen2系列LLM上进行继续预训练尝试;在SFT阶段针对医疗任务的指令特点,设计了一种基于多轮对话的指令扩充方法,增强模型指令能力;在SFT的基础上,设计奖励模型数据获取流程,对PPO、DPO及变体等进行了简单尝试;
+目前成果:设计了完备的多维度模型评测流程,与其他著名开源医疗模型相比胜和率平均达到 64.8% ,选择题准确率超出 35% ,同时在三项中文医疗领域著名算法竞赛上取得 第一名 。
+隐语团队要打造大模型密算平台,其一要吸引外部客户在密算平台上训练模型,所以需要向外展示隐语团队有较强的打造垂域模型的能力。其二医疗作为目前是受众最多的垂域领域之一,结合密算平台推出隐语自研的安全医疗大模型,可以和医疗机构合作达到落地的目的。
+垂域能力打造:在安全框架下针对特定医疗领域达到或超过蚂蚁医疗大模型的能力。
+Why:垂域模型需要有自主的技术,选择医疗领域考虑是受众最多的垂域领域之一。
+Todo:
+继续预训练:共2.7B token,其中通用语料约1.4B token,医疗领域约1.3B token
++英文数据:
+pmc_llama_instructions row 513999 tokens:151723250
+pubmed abstracts 5.4B token row:112165 tokens:29505846
+共1.8B token
+ +SFT:SFT 训练数据(100w条左右)
+混入30%的通用数据(medical_and_daily)
+困惑度(perplexity ppl)基本内容
+ ,其中,W=w1w2w3…wN表示一个句子。
,其中,W=w1w2w3…wN表示一个句子。基本解释:困惑度越小,说明文本语义等内容越流畅。挑选困惑度较小的数据进行训练
+用文档中所有词最小的K个哈希值做特征集合来表征这篇文档,然后基于特征集合的Jaccard距离计算文档之间的相似度。适合海量文档,是一种大规模文本去重算法。代表是GPT-3和Gopher.
+针对医疗任务的指令特点,设计了一种基于多轮对话的指令扩充方法
+原始指令:
+请你基于患者当前及历史的问题给出回复,说话方式要像医生,在必要时如果无法明确诊断患者的疾病,可以询问患者更多的信息。但请切记,不要重复之前轮次的询问。\n
+共分为三个部分:
+基本说明:上述的原始指令+约70条英文指令,共n条
+补充说明+限制:共m条(当前使用m=2)
+多轮对话的优势:
+目标:在有限的资源条件下尽量全面评测自研医疗大模型的能力
+模型:与下面开源医疗大模型进行对比(模型开源能跑通且较新)
+数据:评测数据分为单轮对话、多轮对话和选择题三种类别
+评测流程:
+动机:为了保证隐私安全,需要部署本地小型LLM,且我们希望其拥有大型LLM的能力,因此需要对大型LLM进行 知识蒸馏 ,将大型LLM的语言理解能力迁移到小型LLM上;
+受教育学中响应式教学的启发,创新性地考虑 学生模型的反馈 ,提出ARTE框架,让 大型LLM(教师模型)根据小型LLM(学生模型)的偏好来生成为知识蒸馏量身定制的训练数据 ;
+ARTE框架通过 知识提取 、偏好收集和偏好对齐的三个步骤,经过Llama-3-70B对Gemma-2B的知识蒸馏实验,在BIG-Bench-Hard评测标准上面相比于其他方法提升超过 3% ;
+小型LLM在其他的数据集的微调效果展示了 学生模型的良好泛化性能 ;经过对齐后的大型LLM在其他任务方面与其他相似尺寸的小型LLM层面展示了 教师模型的良好泛化性能 。
+大型语言模型在自然语言处理的很多任务中都表现的比较出色。其中很大一部分原因是因为参数量比较大,模型的能力比较强,但是在处理隐私敏感数据时,为了保证隐私数据不被泄露,我们可能会需要在自己的设备上本地部署 LLM,而不能使用其他服务器或者是提供的api这种。 但是我们自己有的一般是小型设备,不太能直接部署大规模的 LLM。因此我们需要一种方法将大规模的模型的能力迁移到小规模的模型上,也就是一个知识蒸馏的过程。
+目前已经有很多工作来探究这种知识蒸馏的过程,有些是采用COT的方式让大模型生成一个回答问题的过程从而让小模型进行模仿。让大模型生成小模型的训练数据并不困难,难点是保证数据的多样性和高质量。有些研究通过一些相似性度量方式(如ROUGE-L等)找出冗余的数据从而保证数据的多样性,phi模型是希望找到一些比较类似于教科书的数据,还有人认为生成数据的时候对于不同的任务应该采取不同的策略。这些工作都是聚焦于训练数据本身,而并没有考虑如果有了学生模型的反馈,对大模型的数据进行更有针对性的提取,会对这个教师模型生成数据的过程产生促进作用。这个就类似于教学法中的响应式教学,老师就是大规模的大模型,学生就是小规模的大模型,一个老师应该根据学生的反馈来调整自己的教学内容。
+我们提出了ARTE的框架,让教师模型根据学生模型的偏好来生成为知识蒸馏量身定制的训练数据。主要有三个步骤
+使用对齐的教师模型重新生成问题和答案,这个训练数据就是为学生模型量身定制的,使用它们来微调学生模型,在下游任务上取得的效果更好。
+我们的知识蒸馏方法在BBH数据集上面要比不采用我们这个方法提升3个点以上,我们同时也测试了这个方法的泛化性能。
+我们的贡献主要有三个方面:
+我们的主实验是在BBH上面进行的,这个数据集总共有27个子任务
+使用自己编写的种子问题作为prompt对教师模型进行推理,令教师模型草拟生成一些问题和答案
+首先是第一个知识提取的步骤,我们使用三个种子问题来构建一个问题生成提示作为Prompt对教师模型进行推理,引导教师模型集思广益,生成多个问题,在temperature=1的情况下多次进行推理,最终在每一个任务上得到大概250个问题。
+然后,对于每个问题我们让教师模型生成一个经过思考后的答案,我们使用不同的Prompt推理让其进行生成,例如直接一句简单的Prompt然后回答、详细解释后回答,先说一下一些基本原理然后回答,step by step等,因为我们认为对于不同的问题和不同的模型,最好的推理Prompt可能是不同的。例如给定一个相同的数学问题,更强大的语言模型可能更喜欢纯粹基于数学符号的基本原理,因为它有这个能力,而小模型可能更喜欢将数学符号和自然语言组合在一起的一个推理过程。我们人为的设计了4个Prompt来生成答案。
+最后,我们将每个问题和相应的回答两两结合起来,这样我们获取了task * 250 * 4=1000个问题回答对作为最初的数据集,也就是从教师模型中提取知识的过程。
+在验证集上进行1-shot的上下文学习推理来收集上面生成的问题和答案的偏好,也就是哪些问题和答案比较好,哪些问题和答案不太好,就可以从提取出最具辨别力的top k的问题和答案对。
+第二个步骤是偏好收集。在这一步中,我们的目标是收集学生模型在问题和答案两个层面的偏好。也就是说我们的目标是确定哪个问题或回答更有可能被学生模型接受。有研究指出,语言模型在上下文学习期间也会进行上下文示例的梯度下降。因此我们认为小模型对于这些问题和回答的偏好可以通过上下文学习的方式来获得,这样就不需要对模型进行微调,可以比较快速获取结果。我们具体的做法是从big-bench里面抽取了一个验证集,然后通过上下文学习的方式验证上面的问题和答案的有效性。也就是把上面的问题和答案对分别作为1-shot,加入到上面的有答案的验证集的前面,然后将temperature置为1推理100次,统计这100次中回答正确的次数。由于上面我们生成数据的时候对于每一个问题有不同的回答方式,这里我们对每一种回答方式都进行统计,最终对于每一个回答都可以获得一个分数,就是答案层面的一个偏好。然后一个问题的所有四个回答的分数的平均值就作为这个问题的分数,就是问题层面的一个偏好。
+(IRT theory 待补充)不用全部的BBH数据,用十条数据测一下就行了
+通过直接偏好优化 (DPO)让教师模型的偏好与学生模型保持一致
+在收集了问题和回答的偏好分数后,我们的目标是使教师模型与学生模型的偏好保持一致,也就是我们调整教师模型之后,教师模型能够有为目标任务生成量身定制的训练数据的能力。我们不仅要生成量身定制的回答,还要生成量身定制的问题。我们的实现方式是采用直接偏好优化的方式(DPO)。这种方式比较简单且稳定。
+最后,我们将问题和回答的DPO数据混合在一起进行教师模型的DPO,以使教师模型与学生模型的偏好保持一致。
+经过上面的三个步骤后,我们就获得了经过对齐的教师模型。那么我们使用对齐的教师模型来重新生成问题和答案,这个训练数据就是为学生模型量身定制的,使用它们来sft微调学生模型,然后在下游任务上进行测试。
+实验就是在没有相关benchmark数据的情况下,用什么数据来微调小模型才能让这个小模型在benchmark上面表现得更好
+首先我们整个过程都是在BBH上面进行的,我们将BBH的23个子任务分成了四大部分的任务,分别是逻辑推理、常识推理、世界知识和数学能力。我们使用多种数据对小模型进行微调,每个数据都是250*27=6750条左右,从而证明我们方法的有效性。我们的大模型是Llama-70b-instruct,小模型是gemma-2b,DPO学习率1e-7,SFT学习率2e-5。
+其他的指令微调数据集包括:
+除了用上面的流程生成的数据之外,我们也使用了一些其他的数据,分别在0-shot和3-shot两种实验设置下进行了实验。
+我们的效果比其他的都好,同时我们发现问题的质量比回答的质量起着更重要的作用。
+然后我们探究了我们的框架的泛化性能
+尽管使用的大多数数据都是由教师模型自动生成的,但仍然需要一些手动工作来构造提示并收集偏好分数。
+主要有两个方面:
+通过分析小模型的偏好的答案,我们有下面的一些启示:
+答案越详细并不一定意味着小语言模型的性能越好。我们发现,答案的长度与偏好分数之间没有显着的线性相关性,即小语言模型在1-shot上下文学习中的准确性。具有完整而简洁的推理步骤的基本原理更有利于小语言模型的学习。原因可能有两方面:
+尽管同一任务中的不同问题更喜欢不同的推理策略,但在监督微调中,小语言模型更喜欢为一个任务使用一致的推理策略。
+我们还有一个问题可以进行探索,就是在偏好对齐后用大模型生成回答数据的时候,用哪个Prompt是更好的。(因为我们上面设计了四种Prompt对一个问题来生成答案)
+训练语料库的多样性对于语言模型的预训练阶段至关重要,为了研究训练数据集中推理策略多样性的影响,我们在 Big-Bench-Hard 上使用四个不同的训练数据集对 Gemma-2B 进行了微调。
+结果是使用Most Preferred数据集微调的 Gemma-2B 的性能与Randomly Selected数据集相似,而Task Consistent和Aligned Teacher数据集的性能都优于其他两个数据集。这说明在微调阶段,特别是当我们尝试增强小语言模型的一两个特定能力时,一致的推理策略更有益。这背后的原因是,当推理策略对于一项任务来说过于多样化时,小语言模型可能会感到困惑,而一致的推理策略为小语言模型提供了明确的指导,以模仿特定的能力增强。
+使用停留时间的用户历史行为特征从输入侧与模型侧两个角度优化Unium特征向量,解决用户误点击及停留时间过长等问题,同时增强模型的鲁棒性。线上AUC+0.51%;
+利用GPT和Ada2 Embedding升级原始多级主题模型,不依赖于人工标注,并保证对其他市场和其他主题的 泛化能力 。线下精确率在英语市场提升1.9%,在非英语市场提升7.4%;
+分析线上用于推荐的特征,将线上用于对Top 30 Bing首页新闻进行CTR预估的简单DNN模型升级为以DeepFM为基础的推荐模型,完善模型训练流程并上线,线上AUC+0.37%;
+针对线上问题,如Linkoff点击率过高、新闻文章质量、不同市场之间效果差异较大等,在GPT能力加持下训练深度学习模型进行解决,满足需求同时确保线上指标不变或有增益。
+如何利用用户停留时间实现更为高效的推荐?
+为什么要使用用户停留时间的特征?因为只看用户是否点击是不够的。
+用户停留时间可以帮助过滤掉不相关的新闻,并有助于在用户建模中准确衡量特定点击行为的相关性。
+但是有下面的问题:
+对停留时间进行分析:
+之前的版本:新闻表示+用户表示 + 多头注意力 双塔结构
+DweW(停留时间权重)
+之前的工作将停留时间作为一个过滤条件,过滤掉停留时间比较短的用户点击行为。但是这种方法没有考虑在现实场景下面的收集用户点击时间延迟的问题,以及用户的个性化问题(如某些用户就是停留时间比较短)。首先将用户的停留时间进行离散化,按照0和5为阈值,筛选出停留时间大于0的用户点击行为和停留时间大于5的点击行为。然后使用用户表示方法送入相同的多头注意力层和Attention pool层获取语义信息。
+考虑到每一个用户都有独一无二的阅读习惯,我们引入了一个阅读偏好网络。将用户的停留时间编码进矩阵,过Attention层,获取大于0和大于5的两个部分的权重,使用门控网络将这些向量合并,形成一个更细微的用户兴趣表示。
+DweA(停留时间Attention)
+之前的工作过于依赖停留时间,且没有考虑语义和停留时间的交互过程。DweA将用户的停留时间编码进矩阵,拼接到原始的嵌入维度中(Q和K),使模型能够权衡被点击新闻的语义内容和停留时间。
+随机抽取4条在同一会话中出现但未被该用户点击的新闻作为负样本。此外,我们扰乱新闻的顺序,以避免可能的位置偏见。
+数据集:
+至关重要的是,我们的方法对用户停留时间信息表现出鲁棒性,即使在停留时间数据完全缺失的极端情况下,也能保持推荐高质量内容的能力。
+主题模型可以推荐给用户他们感兴趣的东西,主要有两点问题
+通过多个角度利用GPT的能力:作为先知(标注数据)和编码器(获取ada2 embedding)
+之前是一个分级的model,第一级13个,第二级400,第三级10w
+现在一共4000topic左右
+在Ada2 Embedding上面搭建的LightGBM
+ +模型结构:title embedding和body embedding各1536维直接取平均,query(也就是主题)直接送给ada2 embedding,也是1536维,两个向量逐个元素相乘成为1536维,query与title body 和刚才平均的进行点乘作为剩下的三维,1539维输入到LightGBM里面进行打分
+评价:主要关注精确率,不关心召回(召回也很难算)
+一周的数据,70w行,来自11个市场的7个语言,4k多主题
+从已有的topic model上面拿数据,然后用GPT标,0.77是对的,0.23是错的,很多主题没有出现过,因此采样了一些,保证主题覆盖率的同时增加负样本的数量。同时也采样了一些正样本,让GPT给10个主题这样的方式
+最后50对50的数据,8:2分训练集和验证集
+测试集构造:为了包括全部的文档类别,用GPT Embedding进行聚类然后随机采样
+7天的数据,还包括了2个非英语市场,一个市场聚100类然后取10个,是用GPT-4标注的
+精确率在英语市场上提升1.9%,在非英语市场上提升7.4%
+| feature | +example value | +possible values | +description | +
|---|---|---|---|
| AbstractLength | +102 | ++ | + |
| AbstractWordCount | +18 | ++ | + |
| BrandAuthority | +800 | ++ | + |
| ImageScore | +1419822 | ++ | + |
| Score | +1473 | ++ | + |
| timeSlot | +18 | ++ | + |
| TitleLength | +140 | ++ | + |
| TitleWordCount | +23 | ++ | + |
| TrendingScore | +0 | ++ | + |
| IsLocalContent | +0 | ++ | + |
| delayMinutes | +1939 | ++ | current datetime minus “DateCreated” in IntAttributes | +
| isWeekend | +7 | +1-7 | +day of week | +
| Clicks5 | +0 | ++ | total clicks in the past 5 minutes | +
| Clicks10 | +0 | ++ | total clicks in the past 10 minutes | +
| Clicks30 | +0 | ++ | total clicks in the past 30 minutes | +
| CTR5 | +10 | ++ | ctr in the past 5 minutes | +
| CTR10 | +10 | ++ | ctr in the past 10 minutes | +
| CTR30 | +10 | ++ | ctr in the past30 minutes | +
| Udi[0-67] | ++ | + | element wide product between user’s unium_v4 and item’s unium_v4 vector | +
| Cosine[0-10] | ++ | + | cosine similarity of unium_v4 vectors between user’s pass 10 clicks and the item | +
| dotProd[0-10] | ++ | + | dot product of unium_v4 vectors between user’s pass 10 clicks and the item | +
| neastCosine | +1339050 | ++ | largest cosine-similarity | +
| neastCosinePos | +6 | ++ | index of the largest consine similarity in user’s click history | +
| neastDotprod | +921662 | ++ | largest dot product | +
| neastDotprodPos | +2 | ++ | index of largest dot product in user’s click history | +
| vertType | +1 | ++ | + |
| Locale[0-54] | ++ | 0,1 | +one-hot encoding of locale | +
| Product[1-5] | ++ | 0,1 | +one hot encoding of locale | +
| vertType[0-18] | ++ | 0,1 | +one-hot encoding of vertical type | +
| ContentType[0-3] | ++ | 0,1 | +one-hot encoding of ContentType | +
训练参数:hidden_units 512 256 64,batch_size 4096 Adamw lr 5e-2
+这是一个名为 FM_Layer的因子分解机(Factorization Machine)层的实现。因子分解机是一种用于处理稀疏数据的机器学习算法,它可以捕获特征之间的交互关系。
在 __init__方法中,初始化了一个线性层和一个嵌入层。线性层用于处理输入特征的线性关系,嵌入层用于将输入特征映射到一个低维空间,以便处理特征之间的交互关系。
在 forward方法中,首先计算了线性项,然后计算了交互项。交互项的计算使用了因子分解机的一个重要特性,即通过嵌入向量的内积来模拟特征之间的交互。具体来说,交互项的计算公式为:(sum(v*x))^2 - sum((v*x)^2),其中 v是嵌入向量,x是输入特征。这个公式可以有效地计算所有特征对的交互,而且计算复杂度是线性的,这是因子分解机的一个重要优点。
最后,将线性项和交互项相加,得到最终的输出。
+class FM_Layer(nn.Module):
+ def __init__(self, n_features, k):
+ super(FM_Layer, self).__init__()
+ self.linear = nn.Linear(n_features, 1)
+ self.embedding = nn.Embedding(n_features, k)
+
+ def forward(self, x):
+ linear_term = self.linear(x)
+ interaction_term = torch.sum(self.embedding(x), dim=1) ** 2 - torch.sum(self.embedding(x) ** 2, dim=1)
+ return linear_term + interaction_termFM模型的二次项等价化简过程如下:
+
FM部分结构图如下:
+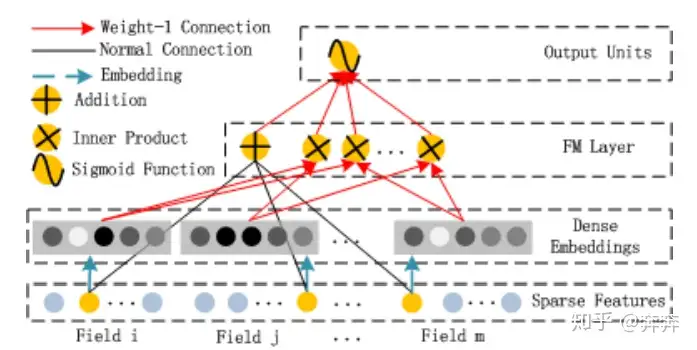
下图为DNN部分的结构图:
+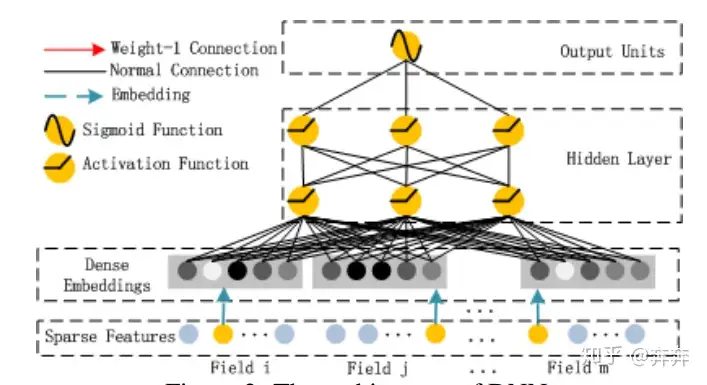
上面分别介绍了FM和DNN,下面把他们融合起来。典型网络融合有两种方式,一种是并行结构,一种是串行结构,DeepFM采用的是并行的方式。
+在 forward方法中,模型首先通过输入层处理输入数据,然后将稀疏特征进行嵌入,接着将嵌入的稀疏特征和密集特征拼接在一起。如果启用了批量归一化,那么会对输入进行归一化。最后,模型将处理过的输入通过全连接层和逻辑回归层,然后将两者的输出相加,得到最终的预测结果。
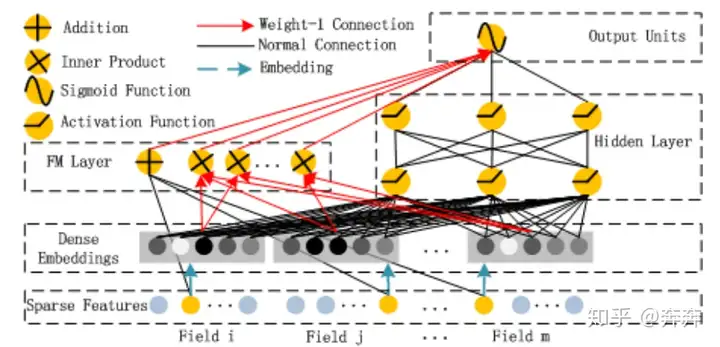
与 Wide&Deep 的异同:
+相同点:都是线性模型与深度模型的结合,低阶与高阶特征交互的融合。
+不同点:DeepFM 两个部分共享输入,而 Wide&Deep 的 wide 侧是稀疏输入,deep 侧是稠密输入;DeepFM 无需加入人工特征,可端到端的学习,线上部署更方便,Wide&Deep 则需要在输入上加入人工特征提升模型表达能力。
+DeepFM 优缺点:
+优点:
+缺点:
+1 将类别特征对应的稠密向量拼接作为输入,然后对元素进行两两交叉。这样导致模型无法意识到域的概念,FM 与 Deep 两部分都不会考虑到域,属于同一个域的元素应该对应同样的计算。
+sparse_features = ['IsLocalContent', 'isWeekend', 'vertType', 'timeSlot', 'HeadLineWholePageOrder', 'WholePageOrder', 'hostAuthority0', 'hostAuthority1', 'hostAuthority2', 'hostAuthority3', 'hostAuthority4', 'hostAuthority5', 'hostAuthority6', 'hostAuthority7', 'hostAuthority8', 'hostAuthority9', 'hostAuthority10', 'minAuthority', 'avgAuthority', 'Product_OHIndex_0', 'Product_OHIndex_1', 'Product_OHIndex_2', 'Product_OHIndex_3', 'ContentType_OHIndex_0', 'ContentType_OHIndex_1', 'ContentType_OHIndex_2', 'ContentType_OHIndex_3', 'vertType_0', 'vertType_1', 'vertType_2', 'vertType_3', 'vertType_4', 'vertType_5', 'vertType_6', 'vertType_7', 'vertType_8', 'vertType_9', 'vertType_10', 'vertType_11', 'vertType_12', 'vertType_13', 'vertType_14', 'vertType_15', 'vertType_16', 'vertType_17', 'vertType_18', 'blingMatchCount', 'userBlingCtrCount', 'userBlingNegCount', 'IsMale', 'IsFemale', 'NoGender', 'IndexedAgeIntValue', 'IsSemiFresh']class DeepFM(nn.Module):
+ def __init__(self,
+ feature_config,
+ hidden_units=[512,64],
+ output_dim=1,
+ emb_size=10,
+ embedding_cols=230,
+ bucket_cols=54,
+ dropout=0.0,
+ activation='relu',
+ use_senet=False,
+ sparse_batchnorm=True,
+ mlp_normalization='batch',
+ non_blocking=False,
+ device='cuda'):
+
+ super(DeepFM, self).__init__()
+ self.device = device
+ self.non_blocking = non_blocking
+ self.sparse_batchnorm = sparse_batchnorm
+ self.bucket_feat = ['IsLocalContent', 'isWeekend', 'vertType', 'timeSlot', 'HeadLineWholePageOrder', 'WholePageOrder', 'hostAuthority0', 'hostAuthority1', 'hostAuthority2', 'hostAuthority3', 'hostAuthority4', 'hostAuthority5', 'hostAuthority6', 'hostAuthority7', 'hostAuthority8', 'hostAuthority9', 'hostAuthority10', 'minAuthority', 'avgAuthority', 'Product_OHIndex_0', 'Product_OHIndex_1', 'Product_OHIndex_2', 'Product_OHIndex_3', 'ContentType_OHIndex_0', 'ContentType_OHIndex_1', 'ContentType_OHIndex_2', 'ContentType_OHIndex_3', 'vertType_0', 'vertType_1', 'vertType_2', 'vertType_3', 'vertType_4', 'vertType_5', 'vertType_6', 'vertType_7', 'vertType_8', 'vertType_9', 'vertType_10', 'vertType_11', 'vertType_12', 'vertType_13', 'vertType_14', 'vertType_15', 'vertType_16', 'vertType_17', 'vertType_18', 'blingMatchCount', 'userBlingCtrCount', 'userBlingNegCount', 'IsMale', 'IsFemale', 'NoGender', 'IndexedAgeIntValue', 'IsSemiFresh']
+ self.bucket_size = [2, 8, 19, 24, 16, 16, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 10, 10, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 11, 129, 129, 2, 2, 2, 11, 2]
+
+ self.embedding_dim = emb_size
+ self.use_senet = use_senet
+
+
+ input_size = embedding_cols + bucket_cols * self.embedding_dim
+
+ if sparse_batchnorm:
+ self.sparse_norm = nn.BatchNorm1d(embedding_cols + bucket_cols * self.embedding_dim)
+ self.sparse_norm_wide = nn.BatchNorm1d((embedding_cols + bucket_cols) * 1 )
+
+ # Deep
+ self.dnn = MLP_Layer(input_dim=input_size,
+ hidden_units=hidden_units,
+ output_dim=1,
+ dropout=dropout,
+ activation=activation,
+ bn_name=mlp_normalization)
+
+ self.fc = nn.Linear(hidden_units[-1] + 1, 1, bias=True)
+
+
+ self.emb_layer = nn.ModuleList([nn.Embedding(self.bucket_size[i], self.embedding_dim) for i, _ in enumerate(self.bucket_feat)])
+
+ self.input_layer = CustomInputLayer(feature_config,device)
+
+ # self.alpha = nn.Parameter(torch.FloatTensor([0.05]))
+
+ # Wide
+ self.lr_layer = LogisticRegression_Layer(input_size, use_bias=False)
+ self.fm_layer = FM_Layer(embedding_cols + bucket_cols, 5)
+
+ self.initialize()
+
+
+ def initialize(self):
+ def init_weights(m):
+ if isinstance(m, (nn.Linear, nn.Embedding)):
+ nn.init.xavier_uniform_(m.weight)
+ if isinstance(m, (nn.Linear)) and m.bias is not None:
+ m.bias.data.fill_(0.01)
+ self.apply(init_weights)
+
+ def forward(self, X):
+ sparse_feature, dense_feature = self.input_layer(X)
+
+ # wide_input = torch.cat([sparse_feature, dense_feature], -1)
+
+ sparse_embedding = [layer(sparse_feature[:,i]) for i, layer in enumerate(self.emb_layer)]
+
+ input = torch.cat(sparse_embedding + [dense_feature], -1)
+
+ if self.sparse_batchnorm:
+ input = self.sparse_norm(input)
+
+ lr_logit = self.lr_layer(input)
+ #print(lr_logit)
+ # input = torch.cat((input, dense_feature_log), -1)
+
+ return self.dnn(input) + lr_logit立场检测任务:从某人的言论中判断他对某个目标的立场(支持、反对、中立),相比于普通的情感分析的难点在于 目标(较短)不同的相同言论(较长)的立场标签可能完全相反 ;
+充分利用大模型的语言理解能力,对言论与目标的关系进行 显式深度分析 ;使用生成式小模型(BART)微调立场标签的 生成 ,并创新性应用原型聚类对比学习的训练策略增强语义理解;
+提出的立场检测方法在Zero-Shot与Cross-Target两种类型的立场检测任务上分别超越前SOTA **2.5%**及 10-15% 。消融实验证明了上述每一个模块的有效性。论文地址。
+立场检测任务是指从某人的言论(也就是文本text)中判断他对某个目标(也就是target)的立场。这个言论是发表在一些公开场合的文字,如Twitter,Facebook或者辩论会上面。需要判断的立场一般分三种,分别是支持、反对和中立,表示这个人发表的言论text对于target的一个立场态度,(支持target,反对target,或者仅仅是对target的客观评价,并没有情感倾向),也有的数据集可能会包括“不相关”的第四个立场,也就是这个言论与这个target完全没有关系。这个任务类似于文本分类任务中的情感分析的任务,不同的是target很重要,比如美国总统大选的时候,target一般就指Trump和Biden,如果一个人发表了一大段支持特朗普的言论,则对于拜登的立场就会是完全相反的。target的变化在数据集中可能仅仅是一个单词的变化,结果会导致立场标签完全不同,也就是立场检测相比于普通的情感分析的难点所在。
+根据target在测试集中是否可见,立场检测可分为三类: 一、训练集与测试集有相同的target;二、target在测试集中不存在,但是测试集中有相似的target(也就是cross-target的分类);三、target在测试集中不存在,也没有相似的target存在(也就是立场检测中的zero-shot)。我这篇论文主要是做zero-shot的任务,因为后两个任务要比第一个任务更为困难一些。
+之前的工作普遍希望使用各种方法扩充target的信息,如在wiki上面查找target的相关知识并拼接一起输入到模型等,或者是在模型结构上对target语义进行更为详尽的提取。但是很少有工作对target与text之间进行显式的分析。我们有了大模型,这个问题正好可以使用大模型来解决,可以利用类似于ChatGPT等大模型的语言理解能力,去显式提取text与target之间的关系,也就是增加额外的“LLM驱动的知识”。这个知识与之前相比更加具体,语义更加丰富。
+我们具体的做法是将text与target一起送给GPT-3.5,让它分析关键词、修辞手法、隐藏情感,最后说一下对这个立场的看法,但是并不允许直接给出表明立场的词汇。提取关键词的目的是让模型更为关注这些关键词语,修辞手法和隐藏情感的目的是找到一些表达立场的证据,如果这个是一个讽刺的言论,那么立场应该是完全相反的。最后只让它分析立场而并不是直接给出立场,因为我们前期实验发现让大模型直接给出立场的效果并不好,在VAST数据集上面只有69左右,因此不让其给出立场词汇是会防止其误导模型,有助于最后的立场检测效果。
+我们后面做了一些消融实验证明了这里面的每一个部分对于我们整个模型的效果都是起促进作用的。如果不加这些LLM驱动的知识的话效果大概是不到75的样子,像之前的工作添加wiki的知识的效果大概是76多,我们添加关键词的效果可以到达75多,修辞手法和隐藏情感大概76多,加上分析立场的文字后大概是77多,如果一起加上的效果最终是79.6
+因为立场标签也是有语义的,为了弥补这个知识与立场标签之间的语义的gap,我们使用了双向自回归语言模型-BART作为我们的主干网络,因此我们把这个分类问题转换成了一个立场标签的生成问题,输入是文本和LLM驱动的知识,输出是利用了丰富的语义进行解码的立场标签的文字。
+我们后面做了消融实验证明了BART的有效性,我们分别实验了将上面的LLM驱动的知识直接使用LLM进行分析,以及使用BERT或者BART作为主干网络,最终效果最好的是BART
+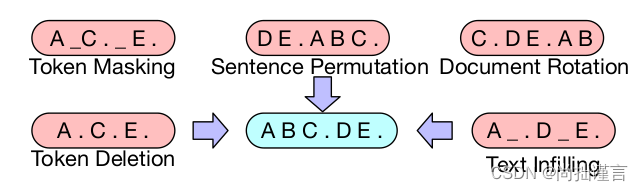
之前的工作一般使用对比学习的方式,也就是将立场标签相同的文本在向量空间中拉近,将立场标签不同的文本在向量空间中推远,这样最终立场标签的表示应该会形成类别数量的簇。
+但是虽然标签相同的文本,在语义上可能是不太相同的,将其强行归为一个类别并不是很合理。因此为了更好的align立场的表示与标签的语义,我们在上述框架的基础上进一步采用原型聚类对比学习的方式,与普通对比学习的区别在于我们并不强制相同类别的标签一定将彼此拉近,而是采用多个原型来对分类特征空间进行建模,然后优化对比损失,使得立场标签被相应标签的最近的原型吸引,并被其他立场的原型排斥。这样最终的立场标签的表示会更为鲁棒,会形成原型类别的簇,立场的表示与标签的语义就会更为统一。
+具体的做法是在最初对每个类别都初始化一个原型,对比学习的时候将样本归到最相近的原型中,这也会有一个问题,也就是之前的归类更多的原型后面的相似度越来越高导致所有样本都聚类到这个原型上面,可能导致我们最终只有一个原型起作用。因此我们训练5个epoch后使用Kmeans对最近的1000个类别向量重新设定类别中心来缓解这个问题。实验表明原型的数量为3的时候效果最好,总体上大概有1-2个点的提升。
+class MCContrastiveLoss(torch.nn.Module):
+ def __init__(self, training_steps, seed, bert_config):
+ super(MCContrastiveLoss, self).__init__()
+ self.prototype_contrastive_class = bert_config["prototype_contrastive_class"]
+ self.prototype_contrastive_num = bert_config["prototype_contrastive_num"]
+ self.encoder_label_pos = bert_config["encoder_label_pos"]
+ self.decoder_label_pos = bert_config["decoder_label_pos"]
+ self.label_id_list = bert_config["label_id_list"]
+ self.prototype_contrastive_project_dimension = bert_config[
+ "prototype_contrastive_project_dimension"
+ ]
+ self.prototype_contrastive_temperature = bert_config[
+ "prototype_contrastive_temperature"
+ ]
+ self.prototype_contrastive_ema = bert_config["prototype_contrastive_ema"]
+ self.loss_combination_ratio = bert_config["loss_combination_ratio"]
+ self.kmeans_step = bert_config["kmeans_epoch"] * training_steps
+
+ self.kmeans = KMeans(
+ n_clusters=self.prototype_contrastive_num, random_state=seed, n_init="auto"
+ )
+ self.kmeans_deque = [
+ deque(maxlen=bert_config["kmeans_deque"])
+ for i in range(self.prototype_contrastive_class)
+ ]
+
+ self.project = nn.Linear(768, self.prototype_contrastive_project_dimension)
+ self.anchor = torch.randn(
+ (
+ self.prototype_contrastive_class,
+ self.prototype_contrastive_num,
+ self.prototype_contrastive_project_dimension,
+ ),
+ dtype=torch.float32,
+ )
+ self.anchor = F.normalize(self.anchor, p=2, dim=-1)
+
+ def forward(self, outputs, labels):
+ # judge when to apply kmeans
+ self.kmeans_step -= 1
+
+ # to gpu
+ self.project = self.project.to(labels.device)
+ self.anchor = self.anchor.to(labels.device)
+
+ # predict label now
+ predict_label = (
+ outputs.logits[:, self.decoder_label_pos, self.label_id_list]
+ .squeeze(1)
+ .detach()
+ )
+ # transform predict label to one-hot
+ predict_label_index = F.one_hot(
+ torch.max(predict_label, dim=1)[1],
+ num_classes=self.prototype_contrastive_class,
+ ) # (64, 3)
+
+ # transform actual label to one hot
+ contrastive_mask = F.one_hot(
+ labels, num_classes=self.prototype_contrastive_class
+ ) # (64, 3)
+
+ # project encoder_last_hidden_state into smaller dimension
+ contrastive_vector = F.normalize(
+ self.project(
+ outputs.encoder_last_hidden_state[:, self.encoder_label_pos, :].squeeze(
+ 1
+ )
+ ),
+ p=2,
+ dim=-1,
+ ) # (64, 128)
+
+ for i in range(self.prototype_contrastive_class):
+ # only extract same label both label and predict
+ temp_mask = contrastive_mask[:, i] * predict_label_index[:, i]
+ if torch.count_nonzero(temp_mask) != 0:
+ # contrastive_vector for class i
+ contrastive_vector_class = contrastive_vector[temp_mask.bool()].detach()
+
+ self.kmeans_deque[i].extend(contrastive_vector_class)
+
+ if self.kmeans_step == 0:
+ now_deque_tensor = torch.stack(list(self.kmeans_deque[i]))
+ self.kmeans.fit(now_deque_tensor.cpu().numpy().astype("float32"))
+ cls_centers = torch.tensor(self.kmeans.cluster_centers_)
+ cls_centers = F.normalize(cls_centers, p=2, dim=-1)
+ self.anchor[i] = cls_centers
+
+ # choose the most similar one
+ max_index = torch.max(
+ torch.einsum("bd,nd->bn", contrastive_vector_class, self.anchor[i]),
+ dim=1,
+ )[1]
+ # print(max_index)
+
+ for j in range(self.prototype_contrastive_num):
+ proto_index = (max_index == j).nonzero()
+ if proto_index.size(0) == 0:
+ continue
+ cur_mean_vector = torch.mean(
+ contrastive_vector_class[proto_index], dim=0
+ )
+
+ self.anchor[i][j] = self.anchor[i][
+ j
+ ].data * self.prototype_contrastive_ema + cur_mean_vector * (
+ 1 - self.prototype_contrastive_ema
+ )
+
+ self.anchor[i][j] = F.normalize(self.anchor[i][j].data, p=2, dim=-1)
+
+ feat_sim_mat = torch.max(
+ torch.matmul(self.anchor, contrastive_vector.T).permute(2, 0, 1), dim=-1
+ )[0]
+ feat_sim_mat = torch.div(feat_sim_mat, self.prototype_contrastive_temperature)
+
+ logits_max, _ = torch.max(feat_sim_mat, dim=1, keepdim=True)
+ feat_sim_mat = feat_sim_mat - logits_max.detach()
+
+ # compute log_prob
+ exp_logits = torch.exp(feat_sim_mat)
+ log_prob = feat_sim_mat - torch.log(1e-7 + exp_logits.sum(1, keepdim=True))
+ # print(log_prob)
+ # print(log_prob.shape)
+ contrastive_loss = -(
+ (contrastive_mask * log_prob).sum(1) / (contrastive_mask.sum(1) + 1e-7)
+ ).mean()
+ # print(contrastive_loss)
+
+ return outputs.loss + contrastive_loss * self.loss_combination_ratio我们在P-Stance和VAST两个数据集上面取得了SOTA的效果,实验表明在zero-shot(VAST数据集)与cross-target(P-Stance数据集)两种类型的立场检测任务上分别超越前SOTA 2.5% 及10-15%。
+比赛目标:在给定上下文对话和最多5篇 参考文档 (小红书文本笔记)的基础上,根据用户的最终问题生成正确的回答,评价指标主要为ROUGE-L,要求模型总参数量不超过14B;
+方案简介:以SOLAR 10.7B大模型为基座进行LoRA 微调 ,结合Prompt设计、多轮对话训练方式、混合训练、不相关参考文档的联合过滤、生成式任务的模型集成等策略;
+比赛结果:在三个评价指标上分别领先亚军网易互娱与季军华为2012实验室 1.6% , 0.9% 和 2.3% 获得冠军,受邀投稿并在WSDM 2024会议进行汇报。Github仓库Star 140+ 。
+WSDM Cup 2024是一个解决多文档对话式问答的比赛。
+对话式问答是根据对话中识别的用户意图生成正确且有意义的答案,(在现代搜索引擎和对话系统中发挥着至关重要的作用)。 目前的挑战是训练模型的数据中可能不包含时效性高的信息,因为在语言模型在训练阶段是无法获得当下或者是训练时间之后的知识。 尽管可以通过检索增强的方式为模型提供多个相关文档作为上下文信息,但模型仍然面临着无法从长文本中获取有效信息,被大量无关信息输入误导的风险。本次比赛就是鼓励对这种对话式多文档问答类问题进行进一步的探索。
+本次比赛提供的数据集是json的格式,其中训练集包括12557 条数据,验证集包括1794条数据,测试集包括3588条数据。所有数据中都包含uuid,历史的问答对,最多5篇小红书的参考文档和用户的问题。数据就类似于一个人在询问如何将iPhone中的照片导入到电脑中,然后回答说可以通过这样的方式,需要一个USB线,然后用户说如果我没有这根线该怎么办。然后会给几篇小红书上面的参考文档,我们的目标就是生成最终的答案,尽量与标准答案越相似越好。其中训练集包括主办方给出的回答的标准答案,验证集和测试集需要我们自己生成答案提交到竞赛平台上面进行评测。评价标准有三个,包括字符级别的rouge l,文字级别的rouge l和keywords recall(关键词的召回率),这个关键词也是数据集中的预先标注的,不过在训练、验证和测试三个数据集中都不会公开给我们,仅用于评测。参赛模型的参数量要求不允许超过14B
+最近,ChatGPT 等大语言模型在多项自然语言处理任务上表现出了 SOTA 性能,我们希望通过利用大模型的理解和推理能力来探索这一问题。 我们做了很多的尝试,最work的方案是首先根据任务微调 LLM,然后设计了一种混合训练策略,以充分利用无标注的验证集数据和测试集数据。并使用一个文本嵌入模型来过滤潜在的不相关文档,最后设计和比较了几种模型集成的方法,拿到了这个比赛的冠军。
+首先使用LLM进行微调的时候,由于我们的输入有很多信息,包括历史对话、参考文档和问题等。我们仔细设计了三者的输入顺序,最终确定了历史对话、问题、参考文档的格式。首先历史对话与问题是相关的,我们发现在问题中会存在一些代词,可能要去历史对话中找答案,且问题有可能很简短,实际上的信息都保存在历史的对话中。因此历史对话与问题是要连在一起输入的。其次有研究表明,在RAG中与问题越接近的文档,模型的关注度会越高,而我们参考的小红书的文档顺序是直接从搜索引擎中得来的,因此最相关的文档排序靠前,也就与问题更为接近。经过实验我们的这种组织方式效果是最好的。我们并没有仔细设计prompt,因为我们前期做了一些简单的尝试发现Prompt对于最终结果的影响并不是很大。
+然后我们对大模型进行微调。虽然我们发现历史的答案与最终的答案并不是很相似,最终的答案的长度要大于历史的答案,但是我们经过实验后还是采用多轮对话的方式进行训练。我们猜测多轮对话的模式可以使大模型更加关注上下文信息,帮助解决我们上面提到的最终问题中可能存在的指代消解。
+为什么Work?答案在于因果语言模型的attention mask。以GPT为代表的Causal Language Model(因果语言模型),这种模型的attention mask是一个对角掩码矩阵,每个token在编码的时候,只能看到它之前的token,看不到它之后的token。
+最后我们对目前比较流行的多个开源且参数量小于14B的大模型进行了尝试,发现SOLAR的模型表现最好。它是两个Llama结构(使用了mistral的权重)拼接在一起后使用高质量的训练数据进行再次预训练后得到的大模型,因此最后我们使用SOLAR大模型进行微调。
+SOLAR模型:
+Depthwise scaling的过程如下:
+然后,从原始模型中移除最后m层,并从其复制体中移除最初的m层,这样就形成了两个各有(n-m)层的独特模型。
+在SOLAR 10.7B-Instruct中,由于基础模型n为32层,并且考虑到硬件限制以及扩展模型效率(模型参数量介于70亿至130亿之间),SOLAR 10.7B-Instruct设置s为48层。因此,需要移除的中间层数目m计算得出为8层(即m=8)。
+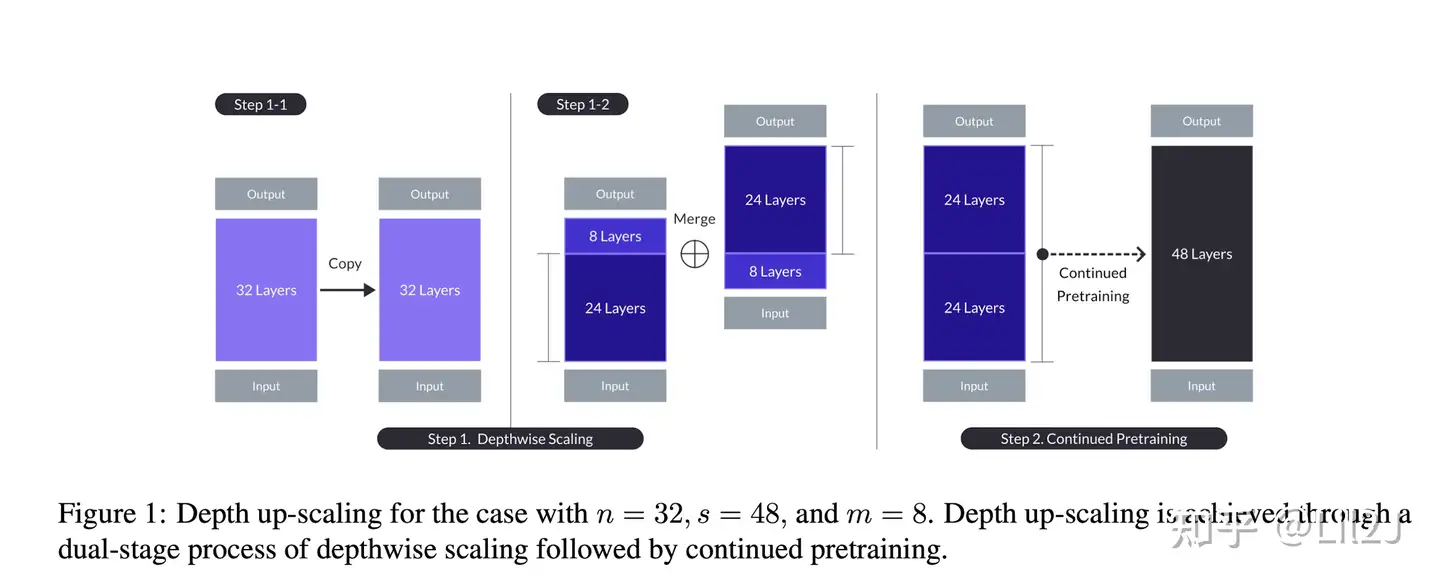
在大模型的训练或微调中,高质量的数据要比数量更为重要。但是由于小红书的数据比较特殊,我们无法找到很相似的数据进行数据增强。不过我们在评测测试集的效果的时候,验证集是可以使用的。因此我们使用我们第一阶段的最好的模型对验证集进行推理,推理得到的结果加入到训练数据中再次进行训练,也就是训练数据从12000条增长到了14000条。一方面可以被视为对域内无标签数据的知识蒸馏过程,另一方面,因为我们只为最终答案生成伪标签,历史问题的答案仍然是官方标注的,这有利于多轮对话的训练模式。实验结果表明这样训练会将各个指标提升半个点到一个点。不过我们不会进一步加入测试数据集的伪标签,因为它可能会过度校正模型,实验结果表明这样反而会降低最终的模型性能。
+其次我们发现有一些不相关的文档,一种不相关的文档是这个文档可能是视频或者图片的形式,因此提取出来的文字就只有对问题的重复,因此对于回答这个问题来说并没有任何的帮助。另一种不相关的文档是真正的不相关的文档,描述的内容与问题或者是历史的对话都是完全不相关的。因此在不存在真实答案的情况下量化相关性就显得至关重要,相似度太高的和相似度太低的文档是都要进行剔除的。
+我们从语义和词汇的角度使用了多种方式进行联合判断,如计算单词或字符级的 ROUGE-L ,也可以被视为词汇相关性标准。或者使用文本嵌入模型计算文档与相应问题(或与对话历史问答一起)之间的余弦相似度,或者我们对每个评价指标都设置了一个较高的和一个较低的阈值,如果计算的分数不在这个阈值的区间范围内我们就将其进行剔除。最终,我们在第二阶段过滤掉了 193 个噪声文档,分数有一点点的提升。一方面是这个参考文档本身就比较短,我们将全部的数据拼接在一起也不会超过3072个token,另一方面我们也发现大模型是有一定的过滤不相关文档的能力的。
+此外,之前的工作表明,将重要的信息放在大模型的开头或结尾处有利于其更好地利用有效信息,因此,我们也尝试了对输入数据的参考文档进行顺序调整。 然而,我们发现原数据中参考文档的索引(即其出现顺序)和官方标注的答案中其出现的相对顺序之间存在很强的相关性,相关实验也表明,对参考文档重新排序可能会导致严重的性能下降,因此我们实际上并没有对文档的顺序进行调整。
+模型集成已被证明在判别类任务中是有效的,但是,很少有工作在生成任务上对其进行探索。在这项工作中,我们希望找到一种方法可以近似评估不同模型生成答案的质量,然后从中选择选择最好的一个作为最终结果。我们想象这样一个现实场景,假设有 N 位候选者都提出了自己的方案,那么最终的方案应该是获得赞成最多的方案。因此,我们最终选择的答案应该是与最多候选模型达成一致的代表。具体地,假设给定一个测试样本,我们有M个候选答案进行集成,对于每个候选r_i,我们计算r_i和r_j之间的相关性分数,将它们加在一起作为r_i的质量分数q_i。这个质量分数我们也尝试了一些,例如上文提到的余弦相似度,rouge l等。虽然使用我们上面的方案就已经超出第二名很多了,我们通过这种方式进行集成也可以显著提升最终模型的效果,且集成的数量越多,效果提升就越明显。最终我们训练出了8个比较好的单模型一起集成。
+赛题目标:以ChatGLM2-6B大模型为中心制作一个问答系统,根据上市公司的原始PDF年报,回答用户的 金融相关问题 。问题包括基本查询、统计分析、联合对比、开放性问题等;
+将原始金融年报的文字与表格提取到数据库中,利用通用模型的上下文多轮对话能力提取问题的关键部分。针对不同的问题类型,首先微调LoRA权重进行问题分类,对于查询统计对比类问题,使用 NL2SQL (微调的LoRA权重)+正则匹配+查表的联合方法解决;对于开放性问题使用 多路检索召回 +Prompt设计解决,最终实现了完整的金融年报问答系统,得分85.89。
+任务是以ChatGLM2-6B模型为中心制作一个问答系统,根据上市公司的原始PDF年报,回答用户的金融相关的问题。上市公司每一年都会发布一个公开的金融年报,格式基本相同,且大部分是表格形式的数据,一个年报的总页数大概在400页左右。主办方提供了1万多篇年报文档和五千的待回答的问题,所有问题都没有答案,只能在天池的线上系统进行评测。评测指标:首先要包括最重要的答案数字,占0.25分,但是如果数字答案不对直接为0分,其次查找答案中的关键词,满分为0.25分,没有关键词会按照缺失比例扣分,最后的0.5分是根据语句的相似度匹配进行计算给出的分数。
+问题类型有三种,实际上是五种问题:
+方案介绍 – PDF2TXT工具优化
+年报数据主要包括公司的基础信息,例如公司名称、注册地址等,财务的数据,主要都是表格,利润表负债表等等,以及综合信息部分,包括财务指标业务概要等
+有人开源了处理pdf文件的代码,基于pdfplumber将pdf年报提取成为txt文件,表格也作为一行一行的文字存储在txt文件中。
+有一些表格txt提取的不太好,我们使用html文件进行了二次提取,有几个年报是图片形式的,我们使用paddleocr进行提取。最终将提取到的表格存储在csv文件中,文字以txt的形式保存
+同时将提供的计算公式引入,将计算的字段名称直接作为已知条件插入到数据库中
+对问题进行结构化解析,提取公司名称、年份和问题的关键词(研发费用等词语),模拟多轮对话的方式,使用In Context Learning的关键词抽取方案,无需微调,保留大模型的通用能力,拓展性和灵活性更好。
+然后将问题与关键词一起输入到大模型中,训练一个Lora对问题进行分类(训练大模型做选择题),我们人工对给定的问题进行标注,将其分为基本统计题目,计算题目,SQL题目,根据文档的开放性问题和纯开放性问题。由于问题的特征都比较明显,因此这个Lora是非常好训练的,准确率可以达到99%之上。
+基本统计题目和计算题目直接通过关键词与csv文件中的标题字段名等进行匹配,定位到正确的关键词,通过向量相似度和编辑距离进行匹配(金融特有词汇使用向量语义匹配的效果不是很好)
+答案通过规则的方式进行生成(也就是只需要找到正确的数字)
+训练一个LoRA解决复杂的SQL问题(哪家在上海注册的上市公司,2020年营业收入最高?金额是?)
+提供的数据量不够,大模型对微调数据质量要求非常高,重要性在数据量之上。使用GPT-4+人工修改的方式进行数据集的扩充。
+生成SQL后实际进行运行,运行不通重新进行生成(通过分词和 sqlparse 校对 SQL ,并编写算法)
+基于向量语义匹配的广度优先搜索
+首先语义匹配数据库字段,再语义匹配文档树中章节标题节点,最后深度向量语义检索文档树子叶,或全文向量语义检索,保证系统的泛化和可靠
+如果未能精准匹配到章节标题,扩大检索范围,检索faiss向量数据库,召回top-n条文本块。
+将文档解析成文档树,根据提取出来的关键词,通过BM25与向量检索两者融合选出相关的top5文档块,输入到大模型的上下文中作为prompt让大模型直接进行回答
+简单设计了一个prompt让大模型回答纯开放性问题
+使用大规模公开的代码数据集提升通用模型的代码能力,同时 利用GPT-4扩充 “代码修复”任务相关数据,并参考测试集的Prompt****组织方式 ,对Qwen1.8B模型进行参数高效微调;
+采用多任务学习的微调方式,添加额外语义相关任务进行 联合训练 ,显著提升代码能力,同时探索最佳训练推理参数。初赛Pass@1为0.2594(第一名),复赛Pass@1为0.3001。
+任务:使用Qwen系列的大模型生成可以实际运行的实际代码,探索Qwen大模型的代码生成的能力
+初赛任务:只允许使用Qwen 1.8B模型,在MFTCoder训练框架上进行数据收集与微调,评测指标是pass@1,使用humanevalpack和mbpp的benchmark进行评测。
+评测指标:humanevalpack是人工编写的164个问题的代码解决方案,每一个问题都用六种编程语言实现。这些代码会被组织成三种任务,包括代码编写、代码解释和代码修复,这个比赛在评测的时候只评测代码编写和代码修复的任务。mbpp是python代码生成任务,数据量要稍大一些。评测指标使用pass@1,就是让模型生成一个解决方案,然后将代码放到可以实际运行的环境中进行编译执行。如果这个代码可以通过所有的测试样例,证明这个解决方案正确;反之如果不能通过任何一个测试样例则认为这个解决方案是错误的。它不单单关注代码的语法是否正确,更重视代码能否正确执行功能,这种评估方式更符合实际编程工作中的要求。
+数据集:数据集是可以自行收集的,比赛中给出了建议使用的CodeExercise-Python-27k和Evol-Instruction-66k,但是不允许使用humanevalpack或者mbpp这些测试数据进行训练。
复赛任务:使用Qwen-72B进行微调,不需要自行操作,使用阿里平台提供的api进行在线训练,我们只能上传数据和模型的参数,具体的训练方式是不可见的,训练结束之后我们可以通过api自行进行代码生成效果的测试。提供的验证集A榜是Leetcode上面的50道问题,验证集B榜是更大规模的Leetcode的数据。数据限定问题都只是中文的语言描述,最终只会要求生成Python的代码。
+初赛的亮点:数据组织与生成、多任务学习、参数尝试
+数据组织:按照humanevalpack和mbpp的prompt的组织方法,将不同数据集的组织形式更改成与他们尽量相似的形式,使得训练过程与测试过程尽量相似。
+MFTCoder是一个多任务的学习框架,可以接受不同组织形式的输入同时进行训练,得到多个loss的汇总结果。借助PHI-1的思想,我们除了让其通过写代码的方式进行训练之外,也让其学习对代码进行解释。因为在代码数据中会存在一些注释,正常在我们写代码的时候注释会给我们很大的帮助。因此除了写代码的任务之外,我们还加入了对代码进行解释的任务,实验效果表明确实会增强写代码的效果。
+为了解决数据量不平衡的问题
+复赛:
+复赛的时候是通过api的方式提交进行训练,我们并没有在训练技巧上面的发挥空间,只能在训练数据和训练参数上面简单尝试。在72B模型上,我们测试zero-shot能力已经达到了0.5,由于模型已经具备较强的推理能力,想要在特定任务上获得更好的模型效果,需要加入特定任务的高质量的数据集。因此我们使用了公开的Leetcode中文数据集(由于事先告知全部为中文Python评测数据),同时也加入了代码解释的任务。由于已知测试集都是中文数据,因此并没有加入英文的数据进行训练。同时我们制作了本地的单样例的评测脚本,使用Leetcode上面公开的测试样例进行测试,与线上结果相差10个点左右(50道题中本地测试要比线上测试多正确5道题目)。最终版本模型加入了测试集A榜的数据进行训练,最终模型在B榜的效果也不错,在10支决赛队伍中排名第5。
训练参数:直接zero-shot的方式性能有0.5,尝试过增大lora_rank,增大epoch,效果下降。
+使用Baichuan2-7B大模型进行LoRA微调,配合数据增强、风格适应、NEFTune、探索最佳推理参数、集成学习等策略,完成对多文档搜索摘要进行组织的任务,性能达到0.5032。
+任务:针对用户查询检索返回的不超过5个的文档,利用生成模型进行组织,生成一个正确、语义通顺、满足用户需求的答案。
+评价指标:BLEU-4与ROUGE-L,BLEU-4侧重于衡量答案的准确性和精确匹配程度,类似于精确度Precision,ROUGE-L更侧重于衡量答案的信息完整性和涵盖程度,更类似于召回率Recall。
+数据集:百度提供的数据集,训练集、验证集、测试集分别包含8000条、1000条和1000条查询及从网页搜索结果中抽取的摘要,除了测试集外都包含了人工撰写的答案。
+限制条件:模型可以在单卡A100使用最多40G显存完成推理,允许使用外部数据集但不允许使用api,如chatgpt等直接进行回答。
我们选择了合适的大模型基座,基于LoRA进行微调,对于训练、推理参数进行了调优,并尝试了噪声微调、知识蒸馏、等方式进一步提升模型性能。
+模型选择:我们进行了一些实验进行基座模型的选择,包括不同模型尺寸的Baichuan2,Qwen,ChatGLM-3,Lingowhale等尝试进行相同配置下的训练与推理,最后发现Baichuan2-7B和Qwen-14B的效果比较好。此外我们利用Baichuan2-7B模型比较了Base和Chat权重对于模型性能的影响,发现Base权重要好于Chat权重,可能是由于我们的任务形式相对较为单一,可能并不需要Chat模型多轮对话、理解问题意图的能力。
+性能调优:我们主要在Baichuan2-7B上对训练和推理时的一些重要参数进行选择,训练时需要考虑的主要是LoRA的秩的大小,它决定了可训练参数的量,但是我们实际发现一些比较常用的秩,比如8和16的微调效果都差不多。在推理参数上,我们发现温度系数对于模型效果的影响十分显著,较大的温度系数使得预测输出分布更为均匀,更多的词有机会被输出,继而生成答案也更加丰富多样,但同时也有偏离主题的风险,而较小的温度系数使得预测输出分布更加尖锐,模型输出的准确性和真实性更高一些,实验发现0.7左右的温度系数可以取得较好的表现。此外,topp和topk等采样参数也会在一定程度上影响推理表现,但是我们发现没有温度系数影响的更为明显,因此我们维持了默认参数。
+训练的时候打乱检索摘要能提升两个点 不打乱的话loss降的很快
+推理的时候我们还采取了风格适应的策略,在prompt里面给几个例子让它照着生成,并且在推理结束之后让模型自行反思推理的质量。
+之后,我们尝试纳入更多的训练数据来提升模型的表现,主要想法是搜集一些问答数据集,然后利用一个在原训练集训练好的大语言模型产生回答作为伪标签,得到的问题-摘要-伪标签对作为新数据与原训练集合并,然后指导一个模型从零开始训练。在这里,我们称产生伪标签的模型为教师模型,而从零开始训练的模型为学生模型,当教师模型与学生模型相同时,相当于一个同样容量的模型在自举地生成数据,即Bootstrap,当教师模型比学生模型能力更强、容量更大时,相当于通过蒸馏,即Distillation的方式在两个模型之间传递知识。
+对于上述训练流程,最重要的是如何选择与所提供数据集分布较为一致的数据集,经过调研,我们选择了百度整理的WebQA中文问答数据集作为额外的训练集,选择它的一个重要原因是相较于其它数据集,WebQA对于每个问题都有多个从百度知道等渠道返回的检索摘要,虽然数据集当中也有标注的问题答案,但是考虑到其可能与本次竞赛人工撰写答案存在分布不一致的情况,因此我们舍弃了这些答案,而使用前述的伪标签生成的方式重新生成答案。此外,我们也对数据集进行了简单的自动化清洗,比如限制问题对应的检索摘要数目大于等于3条小于等于5条,并去掉了其中总字数过短的样本。之后,我们利用合并后的数据集对于不同设置下的模型进行重新训练,使用自举,也就是保持师生一致的情况下,模型性能的提升较小,而采用性能较好、参数量更大的教师模型向性能稍差、参数量更小的学生模型蒸馏知识时,则可以较为显著地提升学生模型的性能,但是其性能相较于规模更大的教师模型还有一定差距。因此,我猜想如果我们获得了性能更好、但是由于参数量过大而无法在40G A100 GPU 上完成推理的模型,是否也可以通过这样蒸馏的方式获得一个效果稍差一点、但是参数尺寸符合参赛要求的模型呢。
+之后,我们使用了一系列技巧尝试进一步提升模型的性能,首先尝试的是NEFTune,其想法来源于Noisy Embeddings Improve Instruction Finetuning这篇文章。主要方法较为简单,就是在训练过程中对于输入指令的问题部分还及多条检索摘要部分的嵌入表示随机添加均匀采样的噪声,希望以此提升模型的鲁棒性,缓解过拟合,同时,也有研究表明其可以使得生成结果包含额外的细节,增强答案的丰富性。实验发现,NEFTune可以较大地提升7B模型的表现,但是对于13B模型性能提升则相对较少,除此之外可以看出,这种方法对于ROUGE-L,也就是召回,提升更为明显,说明模型生成的答案更多地包含了之前所没有的细节。
+最后我们采取了一系列的集成策略,首先是由于我们将temperature设置的很高,所以我们获取结果的时候推理多次,然后取这个结果中与原始的材料重合度最高的作为我们的最终答案。
+赛题目标:对小样本训练数据的中文专利文本进行分类,数据包括标题、发明人和专利摘要,共36个数值类别(类别标签 无语义信息 ),训练集: 测试集≈1: 20,评价指标为F1-Score;
+提出基于类别动态阈值伪标签与尾部类别数据增强的小样本文本分类方法,采用恰当的Prompt组织策略,使用ERNIE-3.0中文预训练模型微调文本分类任务,利用无标签的大量测试集数据标注 伪标签 、采用多语言回译等文本数据增强方法并加入对抗训练策略提升模型的鲁棒性,在A榜测试集分数为0.6516,在B榜测试集分数为0.5955。解决方案在Github开源。
+数据是专利文本数据,包括专利名称、专利发明单位(一般是企业)和专利的摘要,最后有一个专利的类别标签。专利的类别标签共有36个,是数字形式的,也就是说从标签本身是无法获取标签的语义信息的。训练集数据总共900条左右(带标签),测试集(不带标签)A、B榜数据分别都是两万条左右。在比赛的前两个月是可以获得训练集和A榜测试集的,其中A榜测试集的预测标签每一天可以在网站上提交三次,网站会返回这个测试集的得分。评价标准是宏平均的F1-Score,即求出每一个类别的F1-Score后取平均(也就是除以36)。最后一天开放B榜的数据,只能提交一次且无法看到自己的成绩,比赛结束后统一公布B榜成绩,按照B榜成绩决定团队的名次。
+预训练模型+伪标签+尾部类别数据增强+对抗训练+模型集成
+尝试了一些huggingface上面的预训练模型,包括bert-chinese、mengzi、macbert、roberta-wwm等等,最终我们发现使用百度的ernie作为主干效果最好。
+因为我们的训练数据比较少,因此在训练集上训练第一个模型后,我们对测试集进行了标签的预测,根据预测的softmax分数打了测试集的伪标签。
+在长尾识别任务下,尾部类别虽然召回率Recall较低,但却有着较高的精确度Precision,而头部类别则相反。这启发我们根据标签分布情况及模型预测情况为每一个类别设置不同的阈值:头部类别较多,模型学习情况较好,应为其设置较高的阈值,保证其精确度;尾部类别较少,模型学习情况较差,应为其设置较低的阈值,从而获得较高的召回率。
+对于每一类别,我们先得到预测标签为该类的所有记录,之后将这些记录按照对于该类预测概率由大到小进行排序,进一步地,我们求其




这种方式的伪标签产生流程可以迭代进行,即训练得到一个较好的模型A,利用其产生的伪标签再训练一个模型B,再利用模型B对无标签测试数据打伪标签,并由此再训练一个新的模型C。在这个过程中我们会将标准定的越来越严格。最终的训练数据大概在1万5左右。
+提升大概是从0.55-0.62左右
+为了缓解类别不平衡的问题,我们对尾部类别(类别12、22、32、35)应用两类数据增强方法。
+ 个非停用词,随机选择它们的同义词进行替换)
个非停用词,随机选择它们的同义词进行替换) 次)
次) 次)
次) 判定此单词是否被删除)。
判定此单词是否被删除)。提升大概是0.62-0.63左右
+其他的数据增强方法:
+对抗训练是一种引入噪声的训练方式,可以对参数进行正则化,提升模型鲁棒性和泛化能力。
+对抗训练的假设是:给输入加上扰动之后,输出分布和原Y的分布一致
+往增大损失的方向增加扰动
+在计算对抗扰动时虽然计算了梯度,但不对参数进行更新, 因为当前得到的对抗扰动是对旧参数最优的 。
+用一句话形容对抗训练的思路,就是 在输入上进行梯度上升(增大loss),在参数上进行梯度下降(减小loss) ,实际的做法是在embedding table上进行梯度上升 。
+接下来介绍不同的方法,后续方法优化的主要方向有两点:得到更优的扰动 & 提升训练速度
+FGM
+对于每个x:(输入的梯度是g)
+PGD小步走多走几步
+训练模型的时候采用了5折交叉验证的方式,因此实际上每一次训练后我们可以得到6个推理结果,分别是五个小模型的结果和最终投票的结果。但是我们在实际提交的时候发现,并不总是最终投票的结果的得分最高,有可能是其中的某一折或某几折的效果更好。因此通过前期多种模型的线上提交返回的F1分数,我们最终选择了效果较好的9个模型作为参赛系统的最终结果。9个模型的具体参数细节各不相同,训练数据也采用了不同阶段得到的伪标签。同时为了满足模型的总大小不超过2G的要求,我们将单精度模型转换为半精度,实验表明这种转换对于最终的推理结果影响不大。最后我们通过投票法将9个模型集成在一起得到最终的推理结果。
+最终A榜成绩是0.65159296/0.65780034,评测后的B榜成绩是0.59547145/0.61387745
+项目目标:进行场馆级别多相机跟踪与动作捕捉研究:通过相机架设、目标感知、多视角多目标匹配、三维关键点重建、动作分析等模块,最终实现篮球场景下的动作分析和技术统计;
+辅助完善多相机匹配模块,在多相机感知的基础上利用多种特征、考虑时间连续性与相机的空间连续性,优化层级式匈牙利匹配算法,最终离线性能达到 **99.5%**以上 ;
+独立设计实现相机架设优化算法模块,满足全链路中 不同模块的需求 ,与原始的相机架设相比性能提升 50%以上 ;并设计小工具辅助相机架设算法在实际场景中进行验证,效果良好。
+项目的整体目标是完成球类运动(主要是篮球)的动作分析和技术统计,动作分析包括球员动作的标准程度等,技术统计包括球员得分、球员跑动距离、球速统计等等。背景是选择一个篮球场馆,然后架设多台相机,通过相机实时拍摄到的视频流进行实时的效果输出。
+项目整体分为五大模块:
+除此之外,在感知的层面还需要对篮球单独跑一个模型进行检测,同时项目后期我们加入了人脸的检测,在感知到的人体的框中切割出人脸的部分并进行人脸识别,后面准备也添加进去作为一种特征。我们在算法研究的时候是采集了小部分的数据,包括三个场馆的不同数量的球员的打球的视频,请外部团队进行标注后供我们进行算法研究。后期我们在实际的篮球场馆中进行验证,主要是根据实际情况对一些超参数进行调整。最终的效果达到了验收的标准。
+上一层感知模块的输出包括人体的检测框,深度学习模型提取出来的人体的唯一特征向量,和检测出来的人体的21个关键点(平面关键点)。关键点的信息没有使用,主要是使用了检测框和提取出来的特征向量。同时也通过相机的内外参计算检测框的底边中点在真实世界中的位置,作为另外一个特征。
+运用信息及评价标准:(归一化到0-1)
+算法流程:第一张图片有几个检测框就认为有几个tracklet,然后外层循环遍历全部帧,内层循环遍历全部相机,将一帧、一个相机中的检测框与这些tracklet进行匈牙利匹配。匹配的过程中会包含一个阈值,因此会有匹配不上的,或者前期有可能检测框的数量多于tracklet的数量。产生了这些情况就新建一个tracklet。最终选择匹配到的数量最多的球员数量的tracklet作为该球员的tracklet。
+我们将我们使用到的特征进行了分类:
+同时探究了空间连续性对相机匹配顺序带来的影响,因为一个相机对于它的相邻的相机的重合部分更高,用两个重合度更高的相机进行匹配的准确率也会更高。
+核心代码:
+这段代码的主要目的是预测视频中物体的轨迹。具体来说,它首先加载视频数据和特征点,然后对每一帧进行处理。在处理每一帧时,它会提取出人脸、特征点、轨迹等信息,并根据输入的匹配函数进行匹配。匹配结果会被存储在 new数组中,最后将预测结果用于评估。
以下是代码的主要步骤:
+np.load()函数加载 homopath、trackpath、norm_feature_path和 id_feature_path中的文件,分别得到特征点矩阵 track_np1、norm_feature_np1、id_feature_np1和 id_feature_path。T1、最大跟踪数 max_track_num、布尔值 humannum等。frame,然后根据 framenum和 camnum计算出当前帧的最大跟踪数 max_track_num。featurelist,然后提取特征点 featurelist和轨迹信息 tracklist。homomat,然后根据输入的匹配函数 match_function进行匹配。匹配结果会被存储在 new数组中。count、count2等。new保存到文件中,以便后续评估。在原始的相机架设方案中,相机的架设一般都是纯人为架设的,通俗来说,就是简单观察一下球场,让相机尽量的平均分布一下,相机的位置和朝向等全凭借着在场人员的经验进行实施。整个的过程没有任何数学上的依据,比较简单粗暴。
+我们将相机架设的问题看成一个最优化问题,最优化问题主要需要明确下面的四个问题:设计变量、目标函数、约束函数和优化方法
+设计变量即是相机的架设可变的量,也就是相机的架设相关参数。
+对于单个相机来说,分为外参和内参的变化。
+ ,以及相机的架设角度
,以及相机的架设角度
目标函数是变量到评价标准之间的映射模型,使用其来评估相机架设的好坏,可以从感知,匹配以及重建,或者功能的好坏等方面来进行评估。
+首先对于感知来说,对于人体的大小和人脸的大小有要求,也就是适合感知的区域要尽可能大。因此需要满足人体和人脸大小的有效区域尽可能大,同时要考虑是否能够覆盖全场。其次对于匹配来说,对于人体大小和人体拍摄视角有一定的要求,这些会影响特征提取,框的重叠程度,homo点的误差等。同时对于相机之间的空间连续性有一定的要求,相机拍到的非目标区域要尽可能少,目标区域要尽可能大,使得相机的拍摄范围内基本都是我们关注的球员,减少其他场外人员的干扰。最后考虑重建的方面,同一个区域是否有多个相机可以看到,如果没有几个相机拍摄到同一个位置就很难进行重建。并且相机和相机,相机和目标之间的角度关系是否合适。最终希望适合重建的区域要尽可能多,适合重建的相机也要尽可能多。
+约束函数也就是相机架设的物理限制,比如说相机架设的高度,架设的数目等等。
+ 与
与 中一定有一个的搜索空间比较小;相机只能架设在已有的墙上,已有的屋顶上,会对
中一定有一个的搜索空间比较小;相机只能架设在已有的墙上,已有的屋顶上,会对 产生一些约束。除此之外还会有客户对于架设提出的约束要求,以及在实际架设相机时,架设的困难和容易的程度。
产生一些约束。除此之外还会有客户对于架设提出的约束要求,以及在实际架设相机时,架设的困难和容易的程度。定义了优化问题之后,可以使用一些优化方法来进行优化。我们采用的是遗传算法进行优化。
+一种展示中长期信号时变特征的新的视觉抽象方法,负责数据处理、时间片划分算法的损失函数并设计算法效果评价标准,发表二作专利、一作软著并协助撰写部分论文。论文地址。
+项目目标:设计一种新的视觉抽象方法,可以在有限屏幕空间内显示中长期无线电信号的时变特征。
+承担工作:设计了系统核心部分的时间片划分算法及其对应的损失函数,创新了无线电信号的度量方法。
+项目背景:如何在有限屏幕空间内显示中长期无线电信号的时变特征,无线电信号只有0和1两个数值
+视觉抽象设计:采用五种基本图形编码无线电信号,菱形表示短联,正方形表示长联,空白表示中断,长方形+三角形表示先出联后消失,X形表示中间中断两边出联。异常使用红线表示,横竖两种红线表示不同的异常种类
+时间分割算法:平均分算法+微调 优化目标
+优化目标:
+参与推荐广告、激励视频广告、用户特征等后端服务研发;使用Hertz、Kitex等新框架升级旧系统架构,引入泛型等新特性降低服务资源消耗3-4%;协助周末假期等高峰期的故障排除。
+由于服务端直接与数据库交互导致响应客户端时间过慢,因此在完成点赞模块基本功能的基础上,增加缓存减少数据获取的时间从而减少响应时间,使用具有高性能特点的Redis作为缓存数据库。考虑到实际情况下,用户在客户端刷视频时,使用率最频繁的是点赞、取消赞功能,因此在变更点赞状态时,直接更新缓存中的数据进行返回响应,提高用户刷视频的流畅度。同时查询点赞数量、获取点赞列表、判断是否点赞、点赞总数、被点赞总数都可根据缓存中的已有数据进行性能优化
+在大量用户同时使用客户端的情况下,会出现请求数量过大导致数据库压力过大、处理能力下降甚至是宕机的问题。因此,设计在服务端与数据库操作间加入消息队列。计划使用具有较高可靠性和稳定性的rabbitMQ作为消息队列。当需要对数据库进行操作时,将数据库操作放入消息队列,服务端取出消息队列中的信息,在对数据库操作后再取出下一个信息进行处理,从而避免数据库在一段时间接收大量响应出现异常,同时为了避免数据库操作失败,设置了update失败重试机制。
+最初的设计是客户端在发起请求后,需要在Mysql的likes表中添加或者更新相应点赞关系的信息,响应时间较久,影响客户体验。
+优化方案:考虑将这些信息存进缓存中,当点赞或者取消赞的时候,只需要添加或者删除对应的信息即可,响应时间更快,再采用往rabbitmq中传递需要修改数据库的关键信息,通过协程的方式修改数据库。
+设计两种Redis存储信息内容:
+当进行点赞或者取消赞的操作时,同时维护这两种数据结构。这边考虑到脏读的情况,所以每个key首次加载的过程中,加入永不读取或者更新的值“-1”。
+使用缓存进行性能优化提升后,需要解决一个新的问题,即数据的脏读问题。在多个用户进行删除、读取评论操作时,若某一个操作恰好将缓存中的数据清空,而此时数据库还未来得及对数据做出同样的操作(脏数据),此时,读取数据的用户在读取不到缓存中信息的情况下,很可能将数据库中的脏数据重新写入缓存,此时就会出现大量用户读取到脏数据且无法恢复正确值的情况。
+针对上述情况,计划对缓存中的键值设置一个固定的、不会被删除的id值。经过项目组成员讨论一致决定,使用-1作为首次添加新key时对应的预设value值。
+ + +Redis面试题准备
+ +关系型数据库
+优点:
+缺点:
+非关系型数据库
+优点:
+缺点:
+String 是最基本的 key-value 结构,key 是唯一标识,value 是具体的值,value其实不仅是字符串, 也可以是数字(整数或浮点数),value 最多可以容纳的数据长度是 512M。
SDS 使用 len 属性的值而不是空字符来判断字符串是否结束,并且 SDS 的所有 API 都会以处理二进制的方式来处理 SDS 存放在 buf[] 数组里的数据。所以 SDS 不光能存放文本数据,而且能保存图片、音频、视频、压缩文件这样的二进制数据。len 属性记录了字符串长度,所以复杂度为 O(1)。应用场景:
+List 列表是简单的字符串列表, 按照插入顺序排序 ,可以从头部或尾部向 List 列表添加元素。
+列表的最大长度为 2^32 - 1,也即每个列表支持超过 40 亿个元素。
List 类型的底层数据结构是由双向链表或压缩列表实现的,在 Redis 3.2 版本之后,List 数据类型底层数据结构就只由 quicklist 实现
+压缩列表:由一个连续内存组成的顺序型数据结构,一个压缩列表可以包含任意多个节点,每个节点上可以保存一个字节数组或整数值。
+quicklist 实际上是 zipList 和 linkedList 的混合体,它将 linkedList 按段切分,每一段使用 zipList 来紧凑存储,多个 zipList 之间使用双向指针串接起来。
+应用场景:消息队列
+Hash 是一个键值对(key - value)集合
+Hash 类型的底层数据结构是由压缩列表或哈希表实现的,在 Redis 7.0 中,压缩列表数据结构已经废弃了,交由 listpack 数据结构来实现
+listpack 也叫 紧凑列表 ,它的特点就是用一块连续的内存空间来紧凑地保存数据,同时为了节省内存空间,listpack 列表项使用了多种编码方式,来表示不同长度的数据,这些数据包括整数和字符串。
+它最大的改进就是每个listpack节点中,不再保存前一个节点的长度了,所以也就不存在出现连锁更新的情况了。
+应用场景:
+Set 类型是一个无序并唯一的键值集合,它的存储顺序不会按照插入的先后顺序进行存储。
+一个集合最多可以存储 2^32-1 个元素。概念和数学中个的集合基本类似,可以交集,并集,差集等等,所以 Set 类型除了支持集合内的增删改查,同时还支持多个集合取交集、并集、差集。
Set 类型和 List 类型的区别如下:
+Set 类型的底层数据结构是由哈希表或整数集合实现的
+应用场景:
+Set 类型比较适合用来数据去重和保障数据的唯一性,还可以用来统计多个集合的交集、错集和并集等,当我们存储的数据是无序并且需要去重的情况下,比较适合使用集合类型进行存储。
+Zset 类型(有序集合类型)相比于 Set 类型多了一个排序属性 score(分值),对于有序集合 ZSet 来说,每个存储元素相当于有两个值组成的,一个是有序集合的元素值,一个是排序值。
+有序集合保留了集合不能有重复成员的特性(分值可以重复),但不同的是,有序集合中的元素可以排序。
+Zset 类型的底层数据结构是由压缩列表或跳表实现的,在 Redis 7.0 中,压缩列表数据结构已经废弃了,交由 listpack 数据结构来实现
+应用场景:
+Bitmap,即位图,是一串连续的二进制数组(0和1),可以通过偏移量(offset)定位元素。BitMap通过最小的单位bit来进行 0|1的设置,表示某个元素的值或者状态,时间复杂度为O(1)。
由于 bit 是计算机中最小的单位,使用它进行储存将非常节省空间,特别适合一些数据量大且使用 二值统计的场景 。
+Bitmap 本身是用 String 类型作为底层数据结构实现的一种统计二值状态的数据类型。
+String 类型是会保存为二进制的字节数组,所以,Redis 就把字节数组的每个 bit 位利用起来,用来表示一个元素的二值状态,你可以把 Bitmap 看作是一个 bit 数组。
+应用场景:
+统计一个集合中不重复的元素个数,但是并不准确,不过非常节省空间
+应用场景:百万级网页 UV 计数
+Redis GEO 是 Redis 3.2 版本新增的数据类型,主要用于存储地理位置信息,并对存储的信息进行操作。
+GEO 类型使用 GeoHash 编码方法实现了经纬度到 Sorted Set 中元素权重分数的转换,这其中的两个关键机制就是「对二维地图做区间划分」和「对区间进行编码」。一组经纬度落在某个区间后,就用区间的编码值来表示,并把编码值作为 Sorted Set 元素的权重分数。
+应用场景:叫车等需要地理位置的场景
+Redis Stream 是 Redis 5.0 版本新增加的数据类型,Redis 专门为消息队列设计的数据类型。
+应用场景:消息队列
+Redis 单线程指的是「接收客户端请求->解析请求 ->进行数据读写等操作->发送数据给客户端」这个过程是由一个线程(主线程)来完成的 ,这也是我们常说 Redis 是单线程的原因。
+但是, Redis 程序并不是单线程的 ,Redis 在启动的时候,是会 启动后台线程 (BIO)的:
+虽然 Redis 的主要工作(网络 I/O 和执行命令)一直是单线程模型,但是 在 Redis 6.0 版本之后,也采用了多个 I/O 线程来处理网络请求 , 这是因为随着网络硬件的性能提升,Redis 的性能瓶颈有时会出现在网络 I/O 的处理上 。
+Redis 6.0 版本之后,Redis 在启动的时候,默认情况下会 额外创建 6 个线程 ( 这里的线程数不包括主线程 ):
+SDS比C语言的字符串多了一个SDSHDR表头。里面存放free(空闲空间)、len(已用空间)、buf(缓冲区)
+优点:
+根据键值对的键计算哈希值和索引值,然后根据索引值,将包含键值对的哈希节点放到哈希数组的指定索引上
+如何解决冲突:redis采用链地址法解决键冲突。每个哈希节点有一个next指针,多个哈希节点通过next指针构成一个单向链表。总是将最新的节点添加到表头
+扩容:redis的扩容通过rehash(重新散列)实现,为字典ht[1]分配空间,ht[1]的大小为第一个大于等于ht[0].used * 2 的 2n
+redis使用MULTI、EXEC、DISCARD、WATCH四个事务命令
+使用MULTI开启事务,客户端可以向服务器发送任意多个命令,这些命令不会立马执行,而是被放到一个队列中,当调用EXEC命令时,所有队列中的命令才会被执行。如果在执行事务的过程发生异常,而没有执行EXEC,那么事务中的所有命令都不会被执行。至于在执行EXEC命令之后发生了错误,及时事务中某个命令发生了错误,其他事务也会正常执行,没有回滚操作
+通过调用DISCARD,客户端可以清空事务队列,并放弃执行事务
+WATCH命令可以为redis提供CAS行为
+redis 是单线程为什么还那么快?
+主从模式:主从复制是 Redis 高可用服务的最基础的保证,实现方案就是将从前的一台 Redis 服务器,同步数据到多台从 Redis 服务器上,即一主多从的模式,且主从服务器之间采用的是「读写分离」的方式。
+哨兵模式:在使用 Redis 主从服务的时候,会有一个问题,就是当 Redis 的主从服务器出现故障宕机时,需要手动进行恢复。为了解决这个问题,Redis 增加了哨兵模式,因为哨兵模式做到了可以监控主从服务器,并且提供主从节点故障转移的功能。
+cluster集群模式:当 Redis 缓存数据量大到一台服务器无法缓存时,就需要使用 Redis 切片集群 方案,它将数据分布在不同的服务器上,以此来降低系统对单主节点的依赖,从而提高 Redis 服务的读写性能。
+ + +2022年12月2日
+ +最近心情不太好,自己也不怎么在状态,想写点什么东西又感觉写不出来,就随便写写吧。
+首先是一句关心,真的当场吓到我了。现在想想,前女友上一次的关心已经都想不起来是什么时候了。最近一年一直都是我在说我到了之类的话,一丁点的关心都没有。所以我真的早就应该意识到,早就没有了当初的感觉,真的不应该弄得如此狼狈,好聚好散,哪有那么多的舍不得,只不过是自己骗自己罢了。
+但是也就是这么一句关心吧,有点开始想入非非了。我应该清醒一下,以我的条件根本不可能的嘛,人家大美女,数学竞赛一等奖,家里有钱有势,我又有什么?就只能尽量当个朋友吧,毕竟现在能和我说话的女生也不多了。可能有个饭局,就尽量表现得好一点,留下点好印象,不要减分就可以了。
+人家就是客气客气罢了,早有意思也不能拖到现在了,还是自己想太多了。
+然后呢,按照自己的计划,现在应该开始找实习了,身边的人确实也都已经开始找了。但是自己又不会太多的东西,很不敢开始下一步,这几天一直迷茫,用一些其他的游戏视频等让自己暂时开心,开心后又是不断的悲伤。上课现在也是听不太明白,考试也没有什么着落,每天过的都不怎么开心。
+无人可以倾诉,只能自己慢慢调整。
+ + +Go项目-分布式缓存GeeCache
+ +FIFO:先淘汰缓存中最早添加的记录
+LFU:淘汰缓存中访问频率最低的记录,需要维护一个访问频率的表
+LRU:最近最少使用,认为如果数据最近被访问过,那么将来被访问的概率也会更高。维护一个队列,如果一条记录被访问,则移动到队列尾端,这样保证队首一定是最近最少访问的数据
+package lru
+
+import "container/list"
+
+// LRU cache 结构体
+type Cache struct {
+ maxBytes int64 // 允许使用的最大内存
+ nbytes int64 // 当前已使用的内存
+ ll *list.List // cache链表
+ cache map[string]*list.Element // 查找键值对的字典
+ OnEvicted func(key string, value Value) // 某条记录被移除时的回调函数
+}
+
+// 双向链表节点的数据类型
+// 主要目的是为了删除节点后能从字典中删除该键值对
+type entry struct {
+ key string
+ value Value
+}
+
+// 值的类型可以是任意的,定义一个空接口,实现Len()方法返回值的占用空间大小
+
+// Len the number of cache entries
+func (c *Cache) Len() int {
+ return c.ll.Len()
+}
+
+type Value interface {
+ Len() int // 包含一个方法返回值占用的内存大小
+}
+
+// 工厂模式,返回实例化的cache
+func New(maxBytes int64, onEvicted func(string, Value)) *Cache {
+ return &Cache{
+ maxBytes: maxBytes,
+ ll: list.New(),
+ cache: make(map[string]*list.Element),
+ OnEvicted: onEvicted,
+ }
+}
+
+// 查找功能,在字典中进行查找,然后移动到队尾(Front)
+func (c *Cache) Get(key string) (value Value, ok bool) {
+ if ele, ok := c.cache[key]; ok {
+ c.ll.MoveToFront(ele)
+ kv := ele.Value.(*entry)
+ return kv.value, true
+ }
+ return
+}
+
+// LRU删除策略:从队首(Back)拿到节点,然后将其删除
+func (c *Cache) RemoveOldest() {
+ ele := c.ll.Back()
+ if ele != nil {
+ c.ll.Remove(ele)
+ kv := ele.Value.(*entry)
+ delete(c.cache, kv.key)
+ c.nbytes -= int64(len(kv.key)) + int64(kv.value.Len()) // 更新当前已经使用的内存
+ if c.OnEvicted != nil {
+ c.OnEvicted(kv.key, kv.value)
+ }
+ }
+}
+
+// 新增节点/修改节点
+func (c *Cache) Add(key string, value Value) {
+ // 如果在链表中找到则将其更新,同时更新占用的空间大小等,并移动到队列尾端
+ if ele, ok := c.cache[key]; ok {
+ c.ll.MoveToFront(ele)
+ kv := ele.Value.(*entry)
+ c.nbytes += int64(value.Len()) - int64(kv.value.Len())
+ kv.value = value
+ } else { // 如果找不到则直接插入
+ ele := c.ll.PushFront(&entry{key, value})
+ c.cache[key] = ele
+ c.nbytes += int64(len(key)) + int64(value.Len())
+ }
+ // 如果占用空间超过了链表的最大空间,则删除掉队首的节点
+ for c.maxBytes != 0 && c.maxBytes < c.nbytes {
+ c.RemoveOldest()
+ }
+}
+多个协程(goroutine)同时读写同一个变量,在并发度较高的情况下,会发生冲突。确保一次只有一个协程(goroutine)可以访问该变量以避免冲突,这称之为 互斥,互斥锁可以解决这个问题。
当一个协程调用了 Lock() 方法时,其他协程被阻塞了,直到 Unlock()调用将锁释放。因此被包裹部分的代码就能够避免冲突,实现互斥。
抽象了一个只读数据结构 ByteView 用来表示缓存值:
package geecache
+
+// 只读数据结构用来表示缓存值
+type ByteView struct {
+ b []byte
+}
+
+// 返回缓存值的长度
+func (v ByteView) Len() int {
+ return len(v.b)
+}
+
+// 返回拷贝从而防止这个值被外部操作修改
+func (v ByteView) ByteSlice() []byte {
+ return cloneBytes(v.b)
+}
+
+// 将数据作为一个字符串进行返回
+func (v ByteView) String() string {
+ return string(v.b)
+}
+
+func cloneBytes(b []byte) []byte {
+ c := make([]byte, len(b))
+ copy(c, b)
+ return c
+}
+为 lru.Cache 添加并发特性(加锁):
+package geecache
+
+import (
+ "Go-Projects/GeeCache/lru"
+ "sync"
+)
+
+type cache struct {
+ mu sync.Mutex
+ lru *lru.Cache
+ cacheBytes int64
+}
+
+func (c *cache) add(key string, value ByteView) {
+ c.mu.Lock()
+ defer c.mu.Unlock()
+ // 延迟初始化
+ if c.lru == nil {
+ c.lru = lru.New(c.cacheBytes, nil)
+ }
+ c.lru.Add(key, value)
+}
+
+func (c *cache) get(key string) (value ByteView, ok bool) {
+ c.mu.Lock()
+ defer c.mu.Unlock()
+ if c.lru == nil {
+ return
+ }
+
+ if v, ok := c.lru.Get(key); ok {
+ return v.(ByteView), ok
+ }
+
+ return
+}
+Group 是 GeeCache 最核心的数据结构,负责与用户的交互,并且控制缓存值存储和获取的流程。
+在缓存不存在时,调用这个函数,得到源数据:
+type Getter interface {
+ Get(key string) ([]byte, error)
+}
+
+// 定义函数类型 GetterFunc,并实现 Getter 接口的 Get 方法
+type GetterFunc func(key string) ([]byte, error)
+
+func (f GetterFunc) Get(key string) ([]byte, error) {
+ return f(key)
+}核心Group:
+// 缓存的命名空间
+type Group struct {
+ name string // 每个Group拥有一个唯一的名称
+ getter Getter // 缓存未命中时的回溯
+ mainCache cache // 并发缓存
+}
+
+var (
+ mu sync.RWMutex
+ groups = make(map[string]*Group)
+)
+
+// 创建Group实例,并且将group的名称存在全局变量中
+func NewGroup(name string, cacheBytes int64, getter Getter) *Group {
+ if getter == nil {
+ panic("nil Getter")
+ }
+ mu.Lock()
+ defer mu.Unlock()
+ g := &Group{
+ name: name,
+ getter: getter,
+ mainCache: cache{cacheBytes: cacheBytes},
+ }
+ groups[name] = g
+ return g
+}
+
+// 获取指定的group
+func GetGroup(name string) *Group {
+ mu.RLock()
+ g := groups[name]
+ mu.RUnlock()
+ return g
+}Group的Get方法,完成对缓存的查找以及未命中后的回调操作
+// 找到缓存值
+func (g *Group) Get(key string) (ByteView, error) {
+ // 如果没有键则报错
+ if key == "" {
+ return ByteView{}, fmt.Errorf("key is required")
+ }
+ // 从 mainCache 中查找缓存,如果存在则返回缓存值
+ if v, ok := g.mainCache.get(key); ok {
+ log.Println("[GeeCache] hit")
+ return v, nil
+ }
+
+ return g.load(key)
+}
+
+// 缓存不存在,则调用 load 方法
+func (g *Group) load(key string) (value ByteView, err error) {
+ return g.getLocally(key)
+}
+
+// getLocally 调用用户回调函数 g.getter.Get() 获取源数据,并且将源数据添加到缓存 mainCache 中
+func (g *Group) getLocally(key string) (ByteView, error) {
+ bytes, err := g.getter.Get(key)
+ if err != nil {
+ return ByteView{}, err
+
+ }
+ value := ByteView{b: cloneBytes(bytes)}
+ g.populateCache(key, value)
+ return value, nil
+}
+
+func (g *Group) populateCache(key string, value ByteView) {
+ g.mainCache.add(key, value)
+}
+分布式缓存需要实现节点间通信,建立基于 HTTP 的通信机制是比较常见和简单的做法。如果一个节点启动了 HTTP 服务,那么这个节点就可以被其他节点访问。
+承载节点间 HTTP 通信的核心数据结构:
+package geecache
+
+const defaultBasePath = "/_geecache/"
+
+type HTTPPool struct {
+ self string // 记录自己的地址,包括主机名/IP 和端口
+ basePath string // 节点间通讯地址的前缀
+}
+
+// 返回HTTP实例
+func NewHTTPPool(self string) *HTTPPool {
+ return &HTTPPool{
+ self: self,
+ basePath: defaultBasePath,
+ }
+}实现最为核心的 ServeHTTP 方法:
// 使用服务器登录
+func (p *HTTPPool) Log(format string, v ...interface{}) {
+ log.Printf("[Server %s] %s", p.self, fmt.Sprintf(format, v...))
+}
+
+// 处理HTTP请求
+func (p *HTTPPool) ServeHTTP(w http.ResponseWriter, r *http.Request) {
+ // 判断访问路径的前缀是否是 basePath,不是返回错误
+ if !strings.HasPrefix(r.URL.Path, p.basePath) {
+ panic("HTTPPool serving unexpected path: " + r.URL.Path)
+ }
+ p.Log("%s %s", r.Method, r.URL.Path)
+ // /<basepath>/<groupname>/<key> required
+ parts := strings.SplitN(r.URL.Path[len(p.basePath):], "/", 2)
+ if len(parts) != 2 {
+ http.Error(w, "bad request", http.StatusBadRequest)
+ return
+ }
+
+ groupName := parts[0]
+ key := parts[1]
+ // 通过 groupname 得到 group 实例,再使用 group.Get(key) 获取缓存数据
+ group := GetGroup(groupName)
+ if group == nil {
+ http.Error(w, "no such group: "+groupName, http.StatusNotFound)
+ return
+ }
+
+ view, err := group.Get(key)
+ if err != nil {
+ http.Error(w, err.Error(), http.StatusInternalServerError)
+ return
+ }
+
+ w.Header().Set("Content-Type", "application/octet-stream")
+ // 将缓存值作为 httpResponse 的 body 返回
+ w.Write(view.ByteSlice())
+}一致性哈希算法将 key 映射到 2^32 的空间中,将这个数字首尾相连,形成一个环
+package consistenthash
+
+import (
+ "hash/crc32"
+ "sort"
+ "strconv"
+)
+
+// 定义了函数类型 Hash,采取依赖注入的方式,允许用于替换成自定义的 Hash 函数
+type Hash func(data []byte) uint32
+
+// 一致性哈希算法的主数据结构
+type Map struct {
+ hash Hash
+ replicas int // 虚拟节点倍数
+ keys []int // 哈希环
+ hashMap map[int]string // 虚拟节点与真实节点的映射表
+}
+
+// 允许自定义虚拟节点倍数和 Hash 函数
+func New(replicas int, fn Hash) *Map {
+ m := &Map{
+ replicas: replicas,
+ hash: fn,
+ hashMap: make(map[int]string),
+ }
+ if m.hash == nil {
+ m.hash = crc32.ChecksumIEEE
+ }
+ return m
+}
+
+// 实现添加真实节点/机器的 Add() 方法
+func (m *Map) Add(keys ...string) {
+ for _, key := range keys {
+ for i := 0; i < m.replicas; i++ {
+ hash := int(m.hash([]byte(strconv.Itoa(i) + key)))
+ m.keys = append(m.keys, hash)
+ m.hashMap[hash] = key
+ }
+ }
+ sort.Ints(m.keys)
+}
+
+// 实现选择节点的 Get() 方法
+func (m *Map) Get(key string) string {
+ if len(m.keys) == 0 {
+ return ""
+ }
+
+ hash := int(m.hash([]byte(key))) // 计算 key 的哈希值
+ // 顺时针找到第一个匹配的虚拟节点的下标 idx
+ idx := sort.Search(len(m.keys), func(i int) bool {
+ return m.keys[i] >= hash
+ })
+
+ return m.hashMap[m.keys[idx%len(m.keys)]]
+}
+抽象 PeerPicker
+package geecache
+
+// PeerPicker 的 PickPeer() 方法用于根据传入的 key 选择相应节点 PeerGetter
+type PeerPicker interface {
+ PickPeer(key string) (peer PeerGetter, ok bool)
+}
+
+// 接口 PeerGetter 的 Get() 方法用于从对应 group 查找缓存值
+type PeerGetter interface {
+ Get(group string, key string) ([]byte, error)
+}
+节点选择与 HTTP 客户端
+const (
+ defaultBasePath = "/_geecache/"
+ defaultReplicas = 50
+)
+
+type HTTPPool struct {
+ self string // 记录自己的地址,包括主机名/IP 和端口
+ basePath string // 节点间通讯地址的前缀
+ mu sync.Mutex // 锁
+ peers *consistenthash.Map // 新增成员变量 peers,类型是一致性哈希算法的 Map,用来根据具体的 key 选择节点
+ httpGetters map[string]*httpGetter // 映射远程节点与对应的 httpGetter
+}
+
+// 实现 PeerGetter 接口
+type httpGetter struct {
+ baseURL string
+}// 使用 http.Get() 方式获取返回值,并转换为 []bytes 类型
+func (h *httpGetter) Get(group string, key string) ([]byte, error) {
+ u := fmt.Sprintf(
+ "%v%v/%v",
+ h.baseURL,
+ url.QueryEscape(group),
+ url.QueryEscape(key),
+ )
+ res, err := http.Get(u)
+ if err != nil {
+ return nil, err
+ }
+ defer res.Body.Close()
+
+ if res.StatusCode != http.StatusOK {
+ return nil, fmt.Errorf("server returned: %v", res.Status)
+ }
+
+ bytes, err := ioutil.ReadAll(res.Body)
+ if err != nil {
+ return nil, fmt.Errorf("reading response body: %v", err)
+ }
+
+ return bytes, nil
+}实现 PeerPicker 接口
+// Set() 方法实例化了一致性哈希算法,并且添加了传入的节点,为每一个节点创建了一个 HTTP 客户端 httpGetter
+func (p *HTTPPool) Set(peers ...string) {
+ p.mu.Lock()
+ defer p.mu.Unlock()
+ p.peers = consistenthash.New(defaultReplicas, nil)
+ p.peers.Add(peers...)
+ p.httpGetters = make(map[string]*httpGetter, len(peers))
+ for _, peer := range peers {
+ p.httpGetters[peer] = &httpGetter{baseURL: peer + p.basePath}
+ }
+}
+
+// PickerPeer() 包装了一致性哈希算法的 Get() 方法,根据具体的 key,选择节点,返回节点对应的 HTTP 客户端
+func (p *HTTPPool) PickPeer(key string) (PeerGetter, bool) {
+ p.mu.Lock()
+ defer p.mu.Unlock()
+ if peer := p.peers.Get(key); peer != "" && peer != p.self {
+ p.Log("Pick peer %s", peer)
+ return p.httpGetters[peer], true
+ }
+ return nil, false
+}修改主方法
+// 将 实现了 PeerPicker 接口的 HTTPPool 注入到 Group 中
+func (g *Group) RegisterPeers(peers PeerPicker) {
+ if g.peers != nil {
+ panic("RegisterPeerPicker called more than once")
+ }
+ g.peers = peers
+}
+
+// 使用实现了 PeerGetter 接口的 httpGetter 从访问远程节点,获取缓存值
+func (g *Group) getFromPeer(peer PeerGetter, key string) (ByteView, error) {
+ bytes, err := peer.Get(g.name, key)
+ if err != nil {
+ return ByteView{}, err
+ }
+ return ByteView{b: bytes}, nil
+}
+
+// 缓存不存在,则调用 load 方法
+// 若非本机节点,则调用 getFromPeer() 从远程获取。若是本机节点或失败,则回退到 getLocally()
+func (g *Group) load(key string) (value ByteView, err error) {
+
+ if g.peers != nil {
+ if peer, ok := g.peers.PickPeer(key); ok {
+ if value, err = g.getFromPeer(peer, key); err == nil {
+ return value, nil
+ }
+ log.Println("[GeeCache] Failed to get from peer", err)
+ }
+ }
+
+ return g.getLocally(key)
+}并发了 N 个请求,假设对数据库的访问没有做任何限制的,很可能向数据库也发起 N 次请求,容易导致缓存击穿和穿透。针对相同的 key,如何做到只向远端节点发起一次请求呢?
+实现了一个名为 singleflight 的 package 来解决这个问题
+package singleflight
+
+import "sync"
+
+// call 代表正在进行中,或已经结束的请求。使用 sync.WaitGroup 锁避免重入
+type call struct {
+ wg sync.WaitGroup
+ val interface{}
+ err error
+}
+
+// Group 是 singleflight 的主数据结构,管理不同 key 的请求(call)
+type Group struct {
+ mu sync.Mutex // protects m
+ m map[string]*call
+}
+实现 Do 方法
// 针对相同的 key,无论 Do 被调用多少次,函数 fn 都只会被调用一次,等待 fn 调用结束了,返回返回值或错误。
+func (g *Group) Do(key string, fn func() (interface{}, error)) (interface{}, error) {
+ g.mu.Lock()
+ if g.m == nil {
+ g.m = make(map[string]*call)
+ }
+ if c, ok := g.m[key]; ok {
+ g.mu.Unlock()
+ c.wg.Wait() // 如果请求正在进行中,则等待
+ return c.val, c.err // 请求结束,返回结果
+ }
+ c := new(call)
+ c.wg.Add(1) // 发起请求前加锁
+ g.m[key] = c // 添加到 g.m,表明 key 已经有对应的请求在处理
+ g.mu.Unlock()
+
+ c.val, c.err = fn() // 调用 fn,发起请求
+ c.wg.Done() // 请求结束
+
+ g.mu.Lock()
+ delete(g.m, key) // 更新 g.m
+ g.mu.Unlock()
+
+ return c.val, c.err // 返回结果
+}《高级人工智能》期末复习
+ +人工智能的三大主义:行为主义、联结主义、符号主义
+ +图灵测试是做什么的?给几个论断,哪些是哪些不是?
+图灵测试:一个人(C)在完全不接触对方(A和B)的情况下,和对方进行一系列的问答,如果在相当长时间内,他无法根据这些问题判断对方是人(B)还是计算机(A),那么,就认为该计算机具有同人相当的智能(即计算机是能思维的)。
+ +g(x)为从根节点到x节点的代价总和
+h(x)为从x节点到目标节点的估计代价总和
+代价一致搜索 f(x) = g(x)
+贪婪搜索 f(x) = h(x)
+A*搜索 f(x) = g(x) + h(x)
+ 是可采纳的,那么
是可采纳的,那么 ,其中
,其中 是到最近目标的真实耗散。
是到最近目标的真实耗散。 是可采纳的,那么A* 树搜索是最优的
是可采纳的,那么A* 树搜索是最优的
蚁群优化算法和粒子群优化算法是群体智能优化算法的两个代表,请从蚁群优化算法和粒子群优化算法中任选一个阐述其基本原理、算法过程及适用范围。
+基本原理:
+粒子群优化算法中的每个粒子模拟一只鸟,代表待求解问题搜索解空间中的一个潜在解,“飞行信息”包括粒子当前的位置和速度两个状态量。每个粒子都可以获得其邻域内其它个体的信息,对所经过的位置进行评价,并根据这些信息和位置速度更新规则,改变自身的两个状态量,随着这一过程的不断进行,粒子群最终能够找到问题的近似最优解。
+算法过程:
+ 和
和
 和
和



适用范围:适用于求解连续解空间的优化问题
+基本原理:
+蚁群算法是一种用来寻找优化路径的概率型算法。用蚂蚁的行走路径表示待优化问题的可行解,整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多,随着时间的推进,较短的路径上累积的信息素浓度逐渐增高,选择该路径的蚂蚁个数也愈来愈多。最终,整个蚂蚁会在正反馈的作用下集中到最佳的路径上,此时对应的便是待优化问题的最优解。
+算法过程:
+ 只蚂蚁随机放置在
只蚂蚁随机放置在 个城市,位于城市
个城市,位于城市 的第
的第 只蚂蚁选择下一个城市
只蚂蚁选择下一个城市 的概率为:
的概率为:其中




其中: 




适用范围:适用于求解离散解空间的优化问题,适用于在图上寻找最优路径
+A*树搜索的最优性条件
+ 是可采纳的,那么
是可采纳的,那么 ,其中
,其中 是到最近目标的真实耗散。
是到最近目标的真实耗散。 是可采纳的,那么A* 树搜索是最优的
是可采纳的,那么A* 树搜索是最优的A*图搜索的最优性条件
+
传教士和野人问题通常描述如下:三个传教士和三个野人在河的一边,还有一条能载一个人或者两个人的船,找到一个方法让所有的人都渡到河的另一岸,要求在任何地方野人数都不能多于传教士的人数(可以只有野人没有传教士)。
+(1) 精确地形式化该问题,只描述确保该问题有解所必须的特性,画出该问题的完全状态图
+ +(2) 用一个合适的算法实现和最优地求解该问题,检查重复状态是个好主意吗?
+采用先深搜索、先广搜索以及图搜索都可以,注意检查重复状态,重复状态的检测避免程序陷入死循环。
+(3) 这个问题的状态空间如此简单,你认为为什么人们求解他却很困难?
+虽然状态空间比较简单,但是要检测重复状态是一个困难:另外,在当前状态选取下一个合法状态,要能够不漏举所有合法状态也存在困难,当在某个状态无下一个合法状态时,需要回溯,这些都使得人为求解它变得困难
+已知知识库里包含如下的句子:
+请用归结原理证明该知识库蕴含如下的句子:$\neg A \land \neg B $
+Forward chain 证明7<3+9
+ +kb中所有句子都为definite子句,请构造一种真值指派使得kb中所有子句为真
+将所有的原子命题指派为True即可。
+归结原理及证明:
+ +设计一个可靠但不完备的规则
+ ,为全部自然数的集合
,为全部自然数的集合描述语义蕴含、
 是命题逻辑里面的连接词,用于知识表示(实际上是可以替代的,但是引入这个符号进行知识表示比较方便)
是命题逻辑里面的连接词,用于知识表示(实际上是可以替代的,但是引入这个符号进行知识表示比较方便)设计A*启发式函数来使归结次数最少
+构想一个A启发式函数,使得A归结结果为最优,并证明
+h(n)为集合中的最短子句的长度
+胜者为王,败者为寇
+不到长城非好汉,到了长城就是好汉;两个句子是否语义等价,并证明
+成绩好的人都很刻苦,刻苦的人,一定成绩好;两个句子是否语义等价,并证明
+理发师只给不给自己理发的人理发
+ +将如下的一阶谓词逻辑的句子转化为合取范式:(不需要包含存在量词)
+构造一个一阶谓词逻辑的知识库


(刻画模糊量词、模糊修饰词等)
+很少有成绩好的学生特别贪玩
+很少有成绩好的学生特别喜欢玩游戏
+普通编程的步骤:了解问题-收集条件-寻找解决方法-编程解决-将问题数据化-用程序运行数据-debug
+逻辑编程的步骤:了解问题-收集条件-不寻找解决方法-将条件写进KB-将问题转换为fact-问query-寻找错误的事实
+C :- A,B 如果AB,则implyC(definite 子句)
+[E | L]:将list拆解成第一个是E,后面的剩下
+trace 和 notrace是debug的过程
+DFS+backward chaining
+不教程序怎么算,只列出事实
+Prolog缺点:
+谱方法:在谱空间中定义卷积:
+空间方法:在向量空间中定义卷积
+谱方法是空间方法的特例
+聚合,更新是什么?
+图神经网络的框架:聚合邻居节点的信息从而更新中心节点的表示
+GraphSAGE:从每个结点开始随机游走,采样
图卷积网络(GCN):通过归一化的拉普拉斯矩阵从不固定数量的邻居结点中聚合信息,通过特征变换共享参数
+证明感知机不能表示异或逻辑
+异或的逻辑为:
+ |
+ |
+ |
+
|---|---|---|
| 0 | +0 | +0 | +
| 1 | +0 | +1 | +
| 0 | +1 | +1 | +
| 1 | +1 | +0 | +
两个变量的感知机模型为
代入上面的异或逻辑:
+ ,则
,则
 ,则
,则
 ,则
,则
 ,根据上面三个式子是明显不可满足的
,根据上面三个式子是明显不可满足的因此感知机不能表示异或逻辑
+设计用于异或问题的二层感知机
+ +(以下简答题目答案来源于shmily)
+描述BP算法
+BP算法由正向传播与反向传播两个过程组成。正向传播时,输入由输入层经过隐藏层到输出层;反向传播时,输出结果与真实结果通过损失函数计算误差,误差信号再沿相反方向传播至输入层,获得各层各单元的误差信号(梯度),并将其作为修正权值的依据。通过梯度下降算法更新权值,使得网络的整体误差迭代减小。
+试论述在深度神经网络中BP算法遇到的困难,并说明为什么会出现“梯度消失”问题
+当网络变深时,BP算法会遇到梯度消失或者梯度爆炸的现象,此时浅层的神经元几乎接受不到来自输出层的误差信号或者误差太大,无法更新其参数或参数剧烈波动。
+根据链式求导法则,浅层参数的梯度来源于深层参数梯度的乘积。由于中间梯度矩阵的范数可能远小于1,再加上许多激活函数的导数小于1,随着传播层数的增多,误差信号反向传播的过程中以指数形式衰减,当传播到浅层时便出现了梯度消失现象。
+简述对抗式生成网络(GAN)的基本原理及其学习算法
+GAN的思想来源于博弈论当中的均衡理论,其由生成器G与判别器D构成。生成器G希望生成更接近于真实分布的数据,判别器则希望尽可能分辨所给数据是由生成器生成的还是从真实分布中采样的。
+GAN的学习算法交替地更新判别器D与生成器G:
+首先训练判别器D,
+ ;
; ,送入生成器G生成数据
,送入生成器G生成数据 ;
; ;
;接着训练生成器G,
+ ,送入生成器G生成数据
,送入生成器G生成数据 ;
; ;
;重复进行以上各步骤直至收敛。
+描述ResNet(ResNet的原理和结构图)
+ResNet由如下多个Residual Block堆叠构成
+ +残差网络容易优化恒等式函数,学习优化残差映射比原始映射更加容易,随着网络加深,网络至少不会变得更差,有效地缓解了梯度消失等现象;此外,残差连接隐式地扩展了模型的特征空间,可以看作一种模型集成。
+利用RNN构建一个翻译器
+采用编码器-解码器结构,二者都是RNN网络,示意图如下:
+ +其中,编码器RNN接受输入(原文token) 


解码器的RNN同样编码隐藏状态




预测时,通过自回归与束搜索的方式得到翻译序列。
+多臂赌博机:
+一台赌博机有多个摇臂,每个摇臂摇出的奖励大小不确定,玩家希望摇固定次数的臂所获得的期望累积奖励最大
+优化目标:期望累计奖励最大化
+探索和利用的关系:
+策略:
+ 贪心策略
+
贪心策略
+ 按照贪心策略进行行为选择(利用)
按照贪心策略进行行为选择(利用) 在所有行为中随机选择一个(探索)
在所有行为中随机选择一个(探索)马尔可夫状态过程的要素:
+奖励假设:最终目标是通过最大化累积的Reward实现的
+策略学习方法:
+博弈的要素
+剪刀石头布:所有玩家的收益之和为0-零和博弈
+最佳应对:针对局中人2的策略t,若局中人1用策略s产生的收益大于或等于其任何其他策略,则称策略s是局中人1对局中人2的策略t的最佳应对
+纳什均衡:如果一个局势下,每个局中人的策略都是相对其他局中人当前策略的最佳应对,则称该局势是一个纳什均衡
+帕累托最优:对于一组策略选择(局势)若不存在其他策略选择使所有参与者得到至少和目前一样高的回报,且至少一个参与者会得到严格较高的回报,则这组策略选择为帕累托最优。(“不可能再改善某些人的境况,而不使任何其他人受损。”)
+社会最优:使参与者的回报之和最大的策略选择,社会最优的结果一定也是帕累托最优的结果
+ +应用案例:
+讨价的对象是双方对商品估价之差
+ +maxmin策略:最大化自己最坏情况时的效用
+minmax策略:最小化对手的最大效用
+零和博弈情况下:
+匹配市场:
+市场结清价格:给定买方报价的情况下,如果卖方的某种价格使得对应的买方偏好图中存在完全匹配,则称卖方的这组价格为市场结清价格。市场结清价格总是存在,且使得买卖双方总效用最优。
+ +议价权:
+不稳定边:对于结局中未参与配对的边,如果边的两个端点获得的收益之和小于1,则称这条边为不稳定边,不稳定边的存在意味着其两个端点可以通过改变报价而改变结局
+稳定结局:如果一个结局中不存在不稳定边,则称该结局为稳定结局
+纳什议价解:
+




均衡结局:给定一个结局,如果结局中的任意一个参与配对的边都满足纳什议价解的条件,则称该结局是均衡结局
+均衡结局一定是稳定结局
+ +画一个图,什么什么路径,上课那种,阻断、D分离
+ +后门准则:Z满足关于(X,Y)的后门准则
+《机器学习》期末复习
+ +监督学习:贝叶斯分类器、支持向量机、Logistic回归、决策树、线性回归、最大熵、CRF
+无监督学习:主成分分析、K-Means、高斯混合聚类、层次聚类
+线性分类方法:感知机、线性鉴别分析、最小距离分类器
+非线性分类方法:决策树、最近邻、集成学习、核SVM
+线性分类器最佳准则:感知准则函数、支持向量机、Fisher准则
+生成式模型:朴素贝叶斯、隐马尔可夫模型、高斯混合模型
+判别式模型:支持向量机、线性分类器、神经网络、线性判别分析
+Logistic回归使用最大似然估计
+回归问题和分类问题的区别:前者预测函数值为连续值,后者为离散值
+最小二乘回归方法的等效回归方法:线性均值和正态误差的最大似然回归
+正则化的回归分析,可以避免过拟合
+假如使用一个较复杂的回归模型来拟合样本数据,使用岭回归,调试正则化参数λ,来降低模型复杂度。若λ较大时,偏差增大,方差减小
+在线性回归中使用正则项,你发现解的不少coefficient都是0,这个正则项可能是L0-norm或L1-norm
+LR模型的损失函数是交叉熵
+在Logistic Regression 中,如果同时加入L1和L2范数,可以做特征选择,并在一定程度上防止过拟合
+逻辑斯蒂回归没有利用回归的思想
+二项式分布的共轭分布是Beta分布
+多项式分布的共轭分布是Dirichlet分布
+朴素贝叶斯分类器的特点是假设样本各维属性独立
+最大似然估计没有考虑先验分布
+对于正态密度的贝叶斯分类器,各类协方差矩阵相同时,决策函数为线性决策函数
+下面关于贝叶斯分类器描述错误:是基于后验概率,推导出先验概率
+朴素贝叶斯模型属于生成式模型
+贝叶斯分类器参数估计的准则:最大高斯后验、最大beta后验、极大似然
+错误:以贝叶斯估计的角度来看朴素贝叶斯时,其没有估计联合概率
+以下模型中属于贝叶斯网络的有( BD )
+A.马尔可夫随机场
+B.隐马尔可夫模型
+C.条件随机场
+D.朴素贝叶斯分类器
+支持向量机属于判别式模型
+SVM的原理:最大间隔分类
+SVM的算法性能取决于:核函数的选择、核函数的参数、软间隔参数C
+支持向量机的对偶问题是凸二次优化
+支撑向量:最大间隔支撑面上的向量
+避免直接的复杂非线性变换,采用线性手段实现非线性学习的方法是:核函数方法
+软间隔SVM的阈值趋于无穷:只要最佳分类超平面存在,它就能将所有数据全部正确分类
+核函数并不是把特征映射到的空间维度越高越好
+如果SVM模型欠拟合, 以下方法哪些可以改进模型:增大惩罚参数C的值,增大核系数(gamma参数)
+密度聚类方法充分考虑了样本间的密度可达关系
+混合高斯聚类使用了EM算法
+k-means算法初始值不同,最终结果可能不同
+k-means不适合处理非凸型数据
+以下可用于聚类性能测量的评估方法:Jaccard系数、FM指数、Rand指数、DB指数
+主成分分析方法是一种降维方法
+PCA在做降维处理时,优先选取中心化样本的协方差矩阵的最大特征值对应特征向量
+可以用于特征降维的:SVD、PCA和LDA
+不可以用于特征降维的:蒙特卡洛方法
+特征降维带来的好处:节省数据通信开销、节省数据存储资源、加快模型计算速度
+关于决策树节点划分指标描述正确的是信息增益越大越好
+决策树不受数据归一化影响,SVM、神经网络、Logistic回归都会受影响
+增加决策树的深度可能导致随机森林模型过拟合数据
+我们想在大数据集上训练决策树, 为了使用较少时间, 我们可以减少树的深度,减少树的数量
+Bootstrap数据:有放回地从总共N个样本中抽样n个样本
+集成学习中基分类器多样,差异大,学习效率通常越好,每个基分类器的正确率的最低要求50%以上
+Bagging方法的特点:构造训练集时采用Bootstraping的方式
+Boosting方法的特点:预测结果时,分类器的比重不同
+随机森林方法属于Bagging方法
+Adaboost算法:
+Adaboost方法中,需要迭代调整的两个重要参数是:样本权重和分类器权重
+以下关于深度网络训练的说法正确的:
+在训练神经网络时,如果出现训练error过高,增加训练数据不能大幅度降低训练error
+Tanh可以导致梯度消失
+ReLU在神经网络中引入了非线性
+关于CNN,Pooling层用于减少图片的空间分辨率
+卷积神经网络可以有多个卷积核,可以不同大小
+GRU和LSTM的说法正确的是:GRU的参数比LSTM的参数少
+与普通反向传播不同的是,BPTT会在每个时间步长内叠加所有对应权重的梯度
+在RNN中,梯度裁剪可以较好地处理梯度爆炸问题
+循环神经网络有反馈连接并常被用来处理序列数据
+数据增强会增加模型的欠拟合风险
+过拟合现象中训练样本的测试误差最小,测试样本的正确识别率却很低
+过拟合:训练误差小,测试误差大
+容易引起过拟合:SVM算法中使用高斯核代替线性核
+不容易引起过拟合:增加训练集量、减少神经网络隐藏层节点数、删除稀疏的特征
+神经网络处理过拟合:Dropout、Batch Normalization、regularization
+在HMM中,如果已知观察序列和产生观察序列的状态序列,那么可用极大似然估计直接进行参数估计
+解决隐马模型中预测问题的算法是维特比算法
+K-NN最近邻方法在什么情况下效果好:样本较少但典型性较好
+以下可行的最近邻分类的加速方案:分层搜索和训练样本缩减
+线性鉴别分析:找到一个投影方向,使得类内距离最小,类间距离最大
+KL散度是根据类概率密度构造的可分性判据
+最大似然估计没有考虑先验分布
+多层感知机方法中,可用作神经元的非线性激活函数:logistic 函数
+在有限支撑集上,均匀分布的熵最大
+已知均值和方差,高斯分布的熵最大
+受限玻尔兹曼机属于概率图模型
+余弦距离会侧重考虑向量的方向
+除了EM算法,梯度下降也可求混合高斯模型的参数
+下列哪个不属于常用的文本分类的特征选择算法(D)
+A. 卡方检验值
+B. 互信息
+C. 信息增益
+D. 主成分分析
+解决样本类别不平衡的手段:欠采样、过采样、使用focal loss
+对于k折交叉验证, 以下对k的说法正确的是:
+A.k越大, 不一定越好, 选择大的k会加大评估时间
+B.选择更大的k, 就会有更小的bias ,因为训练集更加接近总数据集
+C.在选择k时, 要最小化数据集之间的方差
+下列选项中,关于KNN算法说法不正确的是(D)
+A.能找出与待测样本相近的K个样本
+B.可以使用欧氏距离度量相似度
+C.实现过程相对简单,但是可解释性不强
+D.效率很高
+73.关于特征预处理,下列说法中错误的是(B )
+A.包含标准化和归一化
+B.标准化在任何场景下受异常值的影响都很小
+C.归一化利用了样本中的最大值和最小值
+D.标准化实际上是将数据在样本的标准差上做了等比例的缩放操作
+交叉验证不能够提升模型的准确率
+76.EM算法(Expectation Maximization Algorithm)是机器学习领域的一个经典算法,下面关于EM算法的说法中不正确的有:(A)
+A.EM算法属于一种分类算法
+B.EM算法可用于隐马尔科夫模型的参数估计
+C.EM算法可以分为E-step和M-step两步
+D.EM算法可用于从不完整的数据中计算最大似然估计
+将一个k分类问题分解成一对一问题时总共需要k(k-1)/2个分类器
+在有限支撑集上,下面分布中熵最大的是均匀分布
+在机器学习中,当模型的参数量大于样本量时参数估计使用梯度下降法
+A. GRU通过output gate控制memory;
+B. LSTM对memory不做控制,直接传递给下一个unit
+C. GRU不对上一时刻的信息做任何控制;
+D. GRU的参数比LSTM的参数少;
+以下哪些算法, 可以用神经网络去构造( BD )
+A.KNN
+B.Logistic回归
+C.决策树
+D.最小二乘估计
+给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近,异类样例的投影点尽可能远离;
+在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来判断新样本的类别。
+答案:SVM是一个分类算法,它的目标为确定一个分类超平面,从而将不同类别的数据分隔开达到分类的目标。
+当训练数据线性可分时,通过硬间隔最大化,学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机;
+当训练数据近似线性可分时,通过软间隔最大化,也学习一个线性的分类器,即线性支持向量机,又称为软间隔支持向量机;
+当训练数据线性不可分时,通过使用核技巧及软间隔最大化,学习非线性支持向量机。
+给定训练集,SVM最优决策边界由支持向量决定。
+当增加噪声时,那么该噪声有极高的可能是含噪声训练集的一个支持向量,这意味着决策边界需要变。
+不引入非线性激活函数的情况下,不管神经网络有多少层其输出都是输入的线性组合,与没有隐藏层的效果相当
+在实际问题中,我们使用的样本通常是多维数据,每一维对应一个特征,这些特征的量纲和数量级都是不一样的
+这时需要对数据进行标准化处理,试所有的特征具有同样的尺度
+如果单用线性函数作为激活函数,无论多少层的神经网络会退化成一个线性回归,不能处理非线性分类任务。
+如果学习率太低,每次下降的很慢,使得迭代次数非常多。
+如果学习率太高,在后面迭代时会出现震荡现象,在最小值附近来回波动。
+前面层上的梯度是来自于后面层上梯度的乘积。当存在过多的层次时,且激活函数的梯度小于1时,就会使前面层的梯度变得很小,更新速度过慢,导致梯度消失。
+一种解决方案是使用Relu激活函数替换sigmoid,relu函数的梯度不会随着x的增大而变小,sigmoid在x取值较大时梯度趋近于0。
+对3个32×32的特征图进行卷积层操作,卷积核10个5×5,Stride是1,pad为2,输出特征图的尺度是多少?卷积层的参数是多少?写出公式和结果。
+输出尺度:(N+2P-F)/stride+1
+卷积层的参数:(F×F×n+1)×N
+答案:输出尺度( 32+2×2-5)/1+1 = 32
+卷积层的参数 (5×5×3+1)×10=760
+随机森林是Bagging算法的一个扩展变体,以决策树为基学习器构建Bagging集成,
+Bagging在选择划分属性时需要考察结点的所有属性,而随机森林只需随机地考察一个属性子集
+所以随机森林比决策树Bagging训练速度更快,泛化能力越强。
+L1范数为向量各个元素绝对值之和可以使权值稀疏,方便特征提取。
+L2 范数为向量各个元素平方和的1/2次方可以防止过拟合,提升模型的泛化能力。
+基于L1范数的特征选择:不能直接设置最终选择特征的个数k;通过设置正则化系数λ来隐式控制k;
+λ值越大,模型越关注稀疏性,得到的非零系数个数越少;
+反之,非零稀疏个数越多;
+可以设置一个选择特征个数的上限,通过设置不同λ值,得到满足要求的特征。
+从有条件极值问题的角度来看,L1范数相当于将模型界空间限制在了L1-ball上,目标函数的等高线有很大的概率与坐标轴和边相交,这样的解具有稀疏性。
+根据给定的训练集



泛化误差 = 偏差+方差+噪声
+偏差:度量了学习算法的期望预测与真实结果的偏离程度,刻画了学习算法本身的拟合能力
+方差:度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响
+噪声:表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即刻画了学习问题本身的难度
+过拟合是指模型对于训练数据拟合呈过当的情况,反映到评估指标上,就是模型在训练集上的表现很好,但在测试集和新数据上的表现较差。
+欠拟合是模型在训练和预测时表现都不好的情况。
+降低过拟合:
+降低欠拟合:
+K均值算法缺点:例如受初值和离群点的影响每次的结果不稳定、结果通常不是全局最优而是局部最优解、无法很好地解决数据簇分布差别比较大的情况、不太适用于离散分类等。
+K均值聚类的优点:主要体现在对于大数据集,K均值聚类算法相对是高效的,计算复杂度是 O(NKt) 接近于线性,其中N是数据对象的数目,K是聚类的簇数,t 是迭代的轮数。
+调优方法:数据归一化,离群点预处理,采用核函数,合理选择K值。
+优点:
+缺点:
+在较大学习率设置下Relu可能会出现大量神经元死亡问题。后面神经元方向传播梯度为正,且学习率较大,Relu的梯度为1,梯度下降此时会导致该神经元的参数为负值,可能之后不会再被激活,造成神经元死亡。
+生成模型估计的是联合概率分布,然后求出条件概率分布P(Y|X)作为预测的模型,即生成模型:P(Y|X)= P(X,Y)/ P(X)。
+生成方法关心的是给定输入x产生输出y的生成关系。
+判别模型估计的是条件概率分布,有数据直接学得决策函数P(X)或者条件概率分布P(Y|X)作为预测的模型。
+判别式方法关心的是给定输入X,应该预测什么样的输出Y
+不同之处:
+相同之处:
+



根据最大熵模型, 推导出x概率密度函数是一个常函数,所以最大熵分布为均匀分布。
+根据最大熵模型推导出x概率密度函数是一个高斯分布 。
+写出概率图模型联合分布的因子分解式
+无向图看团,有向图看条件概率
+贝叶斯网络计算概率
+前向算法
+后向算法
+维特比解码
+Kmeans:
+层次聚类自底向上:初始每一个点为一类,逐步合并更新中心即可,注意更新的时候要使用原始的点重新进行计算
+贝叶斯最小错误分类
+贝叶斯最小风险
+抛一枚硬币问题,观察数据情况是:一枚硬币包括正反两面,共抛了30次,其中12次是正面,18次是反面。采用Maximum Likelihood方法,估计正面出
+现的概率和反面出现的概率。
在机器学习中常常采用基于数据驱动的方法进行图像分类。所谓基于数据驱动的方法,就是给计算机很多数据,然后实现学习算法,让计算机学习到每个类的外形的方法。基于这种方法的完整流程如下
+[
《模式识别与机器学习》期末复习
+ +模式识别:利用计算机对物理对象进行分类,在错误概率最小的条件下,使识别的结果尽量与客观物体相符合
+在特征空间和解释空间之间找到一种映射关系:
机器学习:利用大量的训练数据,获得产生数据的模式或预测
+什么是线性判别函数?
+统计模式识别中用以对模式进行分类的一种最简单的判别函数称为线性判别函数。线性判别函数的一般形式是



为什么需要非线性判别函数?
+对于复杂的实际应用,线性分类器往往无法满足要求,不同类别的样本之间并不总是线性可分的,比如著名的异或问题,这就需要寻找能够实现非线性分类的判别函数分类器。
+多类情况:
+权重分量数量计算:



多类情况增广向量不需要变为负数,要求这个类别的比其他的类别都要大,否则这个类别+样本,其他的类别-样本
+H-K算法可以发现类别不可分的情况
+期望风险:机器学习算法的目标就是降低式所示的期望泛化误差(这个数据量被称为风险),选择期望风险最小的模型。
+经验风险:用训练集的分布代替真实情况下的数据分布,最小化训练集上的期望损失
+结构风险:在经验风险最小化的基础上再引入参数的正则化来限制模型能力,使其不要过度地最小化经验风险
+简述偏差方差分解及其推导过程,并说明偏差、方差和噪声三部分的内在含义
+ +过拟合:当学习器把训练样本学的“太好”了的时候,很可能已经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质,在训练集上效果好。但是在测试集上效果差,这样就会导致模型的泛化性能下降。
+欠拟合:模型尚未学习到数据的真实结构。在训练集和验证集上的性能都很差。
+如何判断一个模型处在过拟合状态还是欠拟合状态?
+给出3种减轻模型过拟合的方法:
+过拟合:
+欠拟合:
+假设某研究者在 ImageNet 数据上使用线性支持向量机 Linear SVM 来做文本分类的任务,请说明在如下情况下分别如何操作才能得到更好的结果, 并说明原因。
+如果使用SVM做二分类问题得到如下结果,分别应该采取什么措施以取得更好的结果?并说明原因。
+如果使用逻辑回归算法做二分类问题得到如下结果,分别应该采取什么措施以取得更好的结果?并说明理由。
+2018-2019
+ +2021-2022
+ + +径向基函数(RBF)gamma和C的影响:
+最小化VC维h等价于最大化间隔,使分类器的复杂度小!
+简述SVM算法的原理
+ +K均值:CE
+密度:AF
+高斯混合:BD
+Kmeans:Kmeans的判别界面应该是簇的中垂线
+K-Means与GMM
+K-Means
+GMM
+层次聚类:最小距离层次聚类可以做同心圆相关聚类
+DBSCAN
+PCA的优化目标:
+平滑假设:如果高密度区域中两个点

聚类假设:如果两个点在同一个簇,那么它们很有可能属于同一个类别
+流形假设:输入空间由所有数据点所在的多个低维流形构成,位于同一流形上的数据点具有相同的标签,流形上距离近的点的标签相似
+自我训练算法:假设输出的高度置信的预测是正确的
+协同训练:假设特征可分裂




生成式模型:假设所有数据(带标签&不带标签)都由一个潜在的模型生成(GMM,HMM,朴素贝叶斯)
+半监督支持向量机:假设来自不同类别的无标记数据之间会被较大的间隔隔开
+基于干扰的半监督:基于连续性假设:考虑对输入



基于图的半监督学习:假设在所有数据点(标注数据和无标注数据)定义一个相似性图,相似的数据点之间存在边,边的权重表示两个数据点之间的相似程度,相似图中“紧密”连接的点趋向于有相同的标签
+贝叶斯球:
+ + +降低模型的方差,偏差不变
+原理:通过对训练样本进行bootstrap采样(有放回的随机采样),然后训练多个模型,最后对多个模型作平均,得到最后的融合模型。
+Bagging适合对偏差低、方差高的模型进行融合,如决策树、神经网络等
+降低模型的偏差,方差不变
+原理:每次迭代顺序的把一些模型加进去,最后一些子模型的加权平均是我们最后的集成模型
+Adaboost:在弱学习器失败的样本上,学习第二个弱学习器
+开始初始化的时候每个样本的权重相同
+分对的样本,其权重除以
分错的样本,其权重乘以
最后对模型进行加权融合
+Adaboost 原理:先从初始训练集训练出一个学习器,再根据基学习器的表现来对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续得到更多的关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直到基学习器达到事先指定的值T,最终将这T个基学习器进行加权结合。
+Adaboost 损失函数:使用指数损失函数
Adaboost算法流程:
+ +为什么AdaBoost经常可以在训练误差为0后继续训练还可能带来测试误差的持续下降?
+在训练误差下降到接近0的时候,更多的训练,会增加分类器的分类margin,这个过程也能够防止测试误差的上升,随着Margin的变大,测试误差会逐渐收敛。
+AdaBoost优缺点:
+优点:实现快速简单、灵活、通用性高
+缺点:AdaBoost性能取决于数据和弱学习器,如果弱分类器过于复杂,可能会产生过拟合情况,如果弱分类器太弱有可能造成欠拟合,还容易收到均匀噪声的影响。
+Sigmoid函数:
+在早期的神经网络中较为普遍,逐渐被更简单的ReLU函数取代
+容易导致梯度消失问题:
+Tanh函数:形状和sigmoid函数的形状很像,但tanh函数在坐标系的原点上对称:使用tanh激活函数收敛会更快,减轻消失梯度的现象
+ReLU函数:
+ 时,导数为
时,导数为 ,解决了梯度消失问题,收敛速度更快
,解决了梯度消失问题,收敛速度更快 时,导数为
时,导数为 ,无法更新权重
,无法更新权重梯度爆炸:梯度值超出范围:无穷大值
+对学习率敏感
+梯度消失:梯度值趋近0
+无论如何选择学习率,训练都没有进展
+只有顶层训练有效,底层训练基本无效,使网络更深可能并没有更好
+模型的深度增加,梯度会逐渐消失:
+其他技巧:
+MIT-6.824(Spring 2022)LEC 1 Introduction
+ +(WordCount)
+map(String key, String value):
+// key: document name
+// value: document contents
+ for each word w in value:
+ EmitIntermediate(w, "1");
+reduce(String key, Iterator values):
+// key: a word
+// values: a list of counts
+ int result = 0;
+ for each v in values:
+ result += ParseInt(v);
+ Emit(AsString(result));map函数输出每个单词和计数的数量,reduce汇总其中某个特定单词的数量并输出。
+<target, source>键值对,reduce函数对目标URL汇总source并输出如上图所示,map的过程是在多机器上调用的,其中分配的过程是自动化的,共分配了

其中有一个master节点,这个节点负责将任务进行分配,有些机器进行map操作,有些机器进行reduce操作等。
+被分配到map任务的节点读取输入,将处理好的内容写入缓存,周期性的存入硬盘。存入时直接分为
当一个节点被master通知要进行reduce时,通过RPC的方式从硬盘中读取数据到缓存中,进行处理并排序,保证相同的key出现在相同的位置
+最终输出的时
对于每一个map任务或者reduce任务,都要保存任务的状态(已经完成或者未完成)以及工作节点的信息
+对于每一个完成后的map任务,还要保存完成后的中间数据的位置和大小等信息
+机器太多了肯定有的机器会失效
+Worker失效:Master会定期ping每一个Worker,如果没有得到响应,将这个节点标记为失效
+Master失效:Master的数据要经常备份,且由于只有一个Master,不太可能失效(因为被保护好了?),因此如果Master失效了会终止整个任务
+故障时处理的机制:用户提供的Map和Reduce操作是输入确定性函数时,分布式的计算要保证任何情况下的输出都要一致没有错误.
+使用map和reduce的原子提交特点来实现。map和reduce操作都写入临时文件中,完成操作后通知Master节点。如果Master节点被通知了另外一次,则直接忽略掉。reduce操作结束后将临时文件重命名为最终输出的文件,重命名操作也是原子性,最终只会有一个符合条件的文件名。
+尽量存储在本地的硬盘中,通过GFS把每个文件按64MB一个块,并在不同的机器上存储三份冗余的数据。
+理想情况下

在我们的具体实现中对







MapReduce的合适执行比例:


在运算过程中,如果有一台机器花了很长的时间才完成最后几个Map或Reduce任务,会导致MapReduce操作总的执行时间超过预期。
+当一个MapReduce操作接近完成的时候,master会调度备用任务进程来一起执行最后的任务,谁完成了整个任务都算完成。
+在具体的实现上,对上面描述的简单mapreduce过程可以进行优化
+MapReduce的成功取决于采用MapReduce库能够在不到半个小时时间内写出一个简单的程序,这个简单的程序能够在上千台机器的组成的集群上做大规模并发处理,极大的加快了开发和原形设计的周期。另外,采用MapReduce库,可以让完全没有分布式和/或并行系统开发经验的程序员很容易的利用大量的资源,开发出分布式和/或并行处理的应用。
+MapReduce的成功有几个方面:
+从MapReduce开发过程中也学到了不少东西。
+判断系统是否正常工作非常困难,例如两台机器间的网络挂掉,两边都认为对方挂掉了,因此对外提供了两份服务。
+课程不关注应用程序,只关注基础设施,也就是支撑这些应用程序正确工作的部分。
+关注的三个方面:存储、计算和通信
+抽象:分布式系统的抽象与单机系统的抽象基本相同
+容错机制
+一致性:分布式系统与单机的行为相同
+性能:不同类型的一致性和容错机制与性能相关
+实现细节:如何实现并发、远程过程调用等等
+在Google早期的数据中心,有一个搜索引擎,需要构建万维网的倒排索引,允许用户上网查询。
+在这个过程中处理TB级别的数据需要耗费几个小时。
+为每一个应用都编写一个这种系统很困难,因此提出了MapReduce,使得构建不同应用的分布式程序比较轻松
+不过这些应用必须要能分成map和reduce两个部分,然后放到MapReduce框架下运行,不需要再关注其他细节(如容错机制等等)
+主要的网络通信在于传输map产生的中间文件给reduce使用
+如果一个机器在一定的时间内没有对Coordinator作出响应,就认为这个机器已经挂掉了,因此Coordinator会重新安排其他机器重启它的任务。
+map和reduce任务可能会运行两次,例如Coordinator认为这个机器挂掉了,把它的任务分配给别人了,但是实际上这个机器并没有挂掉。最终使用重命名操作的原子性确保只存储一个结果。
+Coordinator会挂掉吗?挂掉了整个任务就都要重新跑了,一般不会挂掉。
+一些机器可能会运行很慢从而拖累整个任务的进程。当整个任务快要结束的时候,会复制任务到其他的空闲节点上一起做,谁先做完取谁的。
+ + +MIT-6.824(Spring 2022)LEC 2 RPC and Threads
+ +How do Go channels work? How does Go make sure they are synchronized between the many possible goroutines?
+https://golang.org/src/runtime/chan.go
+At a high level, a chan is a struct holding a buffer and a lock. Sending on a channel involves acquiring the lock, waiting (perhaps releasing the CPU) until some thread is receiving, and handing off the message. Receiving involves acquiring the lock and waiting for a sender. You could implement your own channels with Go sync.Mutex and sync.Cond.
+在一个进程中并行运行多个线程
+线程原语:开启线程、退出线程(隐式)、停止线程(挂在一边不懂)、恢复线程
+支持并发
+数量可以不考虑,按照需求创建线程即可
+channels和condition variables
+分配条件变量并且和锁关联,不满足条件进入睡眠状态,并释放关联的锁。
+在goroutine运行的最后唤醒睡眠状态的线程,重新进行判断
+package main
+
+import "sync"
+import "time"
+import "math/rand"
+
+func main() {
+ rand.Seed(time.Now().UnixNano())
+
+ count := 0
+ finished := 0
+ var mu sync.Mutex
+ cond := sync.NewCond(&mu)
+
+ for i := 0; i < 10; i++ {
+ go func() {
+ vote := requestVote()
+ mu.Lock()
+ defer mu.Unlock()
+ if vote {
+ count++
+ }
+ finished++
+ cond.Broadcast()
+ }()
+ }
+
+ mu.Lock()
+ for count < 5 && finished != 10 {
+ cond.Wait()
+ }
+ if count >= 5 {
+ println("received 5+ votes!")
+ } else {
+ println("lost")
+ }
+ mu.Unlock()
+}
+
+func requestVote() bool {
+ time.Sleep(time.Duration(rand.Intn(100)) * time.Millisecond)
+ return rand.Int() % 2 == 0
+}
+package main
+
+import "time"
+import "math/rand"
+
+func main() {
+ rand.Seed(time.Now().UnixNano())
+
+ count := 0
+ ch := make(chan bool)
+ for i := 0; i < 10; i++ {
+ go func() {
+ ch <- requestVote()
+ }()
+ }
+ for i := 0; i < 10; i++ {
+ v := <-ch
+ if v {
+ count += 1
+ }
+ }
+ if count >= 5 {
+ println("received 5+ votes!")
+ } else {
+ println("lost")
+ }
+}
+
+func requestVote() bool {
+ time.Sleep(time.Duration(rand.Intn(100)) * time.Millisecond)
+ return rand.Int()%2 == 0
+}
+package main
+
+import (
+ "fmt"
+ "sync"
+)
+
+//
+// Several solutions to the crawler exercise from the Go tutorial
+// https://tour.golang.org/concurrency/10
+//
+
+//
+// Serial crawler
+//
+
+func Serial(url string, fetcher Fetcher, fetched map[string]bool) {
+ if fetched[url] {
+ return
+ }
+ fetched[url] = true
+ urls, err := fetcher.Fetch(url)
+ if err != nil {
+ return
+ }
+ for _, u := range urls {
+ Serial(u, fetcher, fetched)
+ }
+ return
+}
+
+//
+// Concurrent crawler with shared state and Mutex
+//
+
+type fetchState struct {
+ mu sync.Mutex
+ fetched map[string]bool
+}
+
+func ConcurrentMutex(url string, fetcher Fetcher, f *fetchState) {
+ f.mu.Lock()
+ already := f.fetched[url]
+ f.fetched[url] = true
+ f.mu.Unlock()
+
+ if already {
+ return
+ }
+
+ urls, err := fetcher.Fetch(url)
+ if err != nil {
+ return
+ }
+ var done sync.WaitGroup
+ for _, u := range urls {
+ done.Add(1)
+ go func(u string) {
+ defer done.Done()
+ ConcurrentMutex(u, fetcher, f)
+ }(u)
+ }
+ done.Wait()
+ return
+}
+
+func makeState() *fetchState {
+ f := &fetchState{}
+ f.fetched = make(map[string]bool)
+ return f
+}
+
+//
+// Concurrent crawler with channels
+//
+
+func worker(url string, ch chan []string, fetcher Fetcher) {
+ urls, err := fetcher.Fetch(url)
+ if err != nil {
+ ch <- []string{}
+ } else {
+ ch <- urls
+ }
+}
+
+func coordinator(ch chan []string, fetcher Fetcher) {
+ n := 1
+ fetched := make(map[string]bool)
+ for urls := range ch {
+ for _, u := range urls {
+ if fetched[u] == false {
+ fetched[u] = true
+ n += 1
+ go worker(u, ch, fetcher)
+ }
+ }
+ n -= 1
+ if n == 0 {
+ break
+ }
+ }
+}
+
+func ConcurrentChannel(url string, fetcher Fetcher) {
+ ch := make(chan []string)
+ go func() {
+ ch <- []string{url}
+ }()
+ coordinator(ch, fetcher)
+}
+
+//
+// main
+//
+
+func main() {
+ fmt.Printf("=== Serial===\n")
+ Serial("http://golang.org/", fetcher, make(map[string]bool))
+
+ fmt.Printf("=== ConcurrentMutex ===\n")
+ ConcurrentMutex("http://golang.org/", fetcher, makeState())
+
+ fmt.Printf("=== ConcurrentChannel ===\n")
+ ConcurrentChannel("http://golang.org/", fetcher)
+}
+
+//
+// Fetcher
+//
+
+type Fetcher interface {
+ // Fetch returns a slice of URLs found on the page.
+ Fetch(url string) (urls []string, err error)
+}
+
+// fakeFetcher is Fetcher that returns canned results.
+type fakeFetcher map[string]*fakeResult
+
+type fakeResult struct {
+ body string
+ urls []string
+}
+
+func (f fakeFetcher) Fetch(url string) ([]string, error) {
+ if res, ok := f[url]; ok {
+ fmt.Printf("found: %s\n", url)
+ return res.urls, nil
+ }
+ fmt.Printf("missing: %s\n", url)
+ return nil, fmt.Errorf("not found: %s", url)
+}
+
+// fetcher is a populated fakeFetcher.
+var fetcher = fakeFetcher{
+ "http://golang.org/": &fakeResult{
+ "The Go Programming Language",
+ []string{
+ "http://golang.org/pkg/",
+ "http://golang.org/cmd/",
+ },
+ },
+ "http://golang.org/pkg/": &fakeResult{
+ "Packages",
+ []string{
+ "http://golang.org/",
+ "http://golang.org/cmd/",
+ "http://golang.org/pkg/fmt/",
+ "http://golang.org/pkg/os/",
+ },
+ },
+ "http://golang.org/pkg/fmt/": &fakeResult{
+ "Package fmt",
+ []string{
+ "http://golang.org/",
+ "http://golang.org/pkg/",
+ },
+ },
+ "http://golang.org/pkg/os/": &fakeResult{
+ "Package os",
+ []string{
+ "http://golang.org/",
+ "http://golang.org/pkg/",
+ },
+ },
+}RPC:在客户端上调用在服务器端实现的函数-传递参数并返回结果
+实际过程:
+package main
+
+import (
+ "fmt"
+ "log"
+ "net"
+ "net/rpc"
+ "sync"
+)
+
+//
+// Common RPC request/reply definitions
+//
+
+type PutArgs struct {
+ Key string
+ Value string
+}
+
+type PutReply struct {
+}
+
+type GetArgs struct {
+ Key string
+}
+
+type GetReply struct {
+ Value string
+}
+
+//
+// Client
+//
+
+func connect() *rpc.Client {
+ client, err := rpc.Dial("tcp", ":1234")
+ if err != nil {
+ log.Fatal("dialing:", err)
+ }
+ return client
+}
+
+func get(key string) string {
+ client := connect()
+ args := GetArgs{"subject"}
+ reply := GetReply{}
+ err := client.Call("KV.Get", &args, &reply)
+ if err != nil {
+ log.Fatal("error:", err)
+ }
+ client.Close()
+ return reply.Value
+}
+
+func put(key string, val string) {
+ client := connect()
+ args := PutArgs{"subject", "6.824"}
+ reply := PutReply{}
+ err := client.Call("KV.Put", &args, &reply)
+ if err != nil {
+ log.Fatal("error:", err)
+ }
+ client.Close()
+}
+
+//
+// Server
+//
+
+type KV struct {
+ mu sync.Mutex
+ data map[string]string
+}
+
+func server() {
+ kv := new(KV)
+ kv.data = map[string]string{}
+ rpcs := rpc.NewServer()
+ rpcs.Register(kv)
+ l, e := net.Listen("tcp", ":1234")
+ if e != nil {
+ log.Fatal("listen error:", e)
+ }
+ go func() {
+ for {
+ conn, err := l.Accept()
+ if err == nil {
+ go rpcs.ServeConn(conn)
+ } else {
+ break
+ }
+ }
+ l.Close()
+ }()
+}
+
+func (kv *KV) Get(args *GetArgs, reply *GetReply) error {
+ kv.mu.Lock()
+ defer kv.mu.Unlock()
+
+ reply.Value = kv.data[args.Key]
+
+ return nil
+}
+
+func (kv *KV) Put(args *PutArgs, reply *PutReply) error {
+ kv.mu.Lock()
+ defer kv.mu.Unlock()
+
+ kv.data[args.Key] = args.Value
+
+ return nil
+}
+
+//
+// main
+//
+
+func main() {
+ server()
+
+ put("subject", "6.824")
+ fmt.Printf("Put(subject, 6.824) done\n")
+ fmt.Printf("get(subject) -> %s\n", get("subject"))
+}MIT-6.824(Spring 2022)Lab 1 MapReduce
+ + +构建一个MapReduce系统
+在 src/main/mrsequential.go 中提供了串行的mapreduce程序,在单进程里面直接顺序执行Map操作和Reduce操作
同时提供了一些MapReduce的应用程序:
+mrapps/wc.go:WordCount程序
mrapps/indexer.go:text-indexer
按照如下的方式运行串行的mapreduce程序:
+cd src/main
+go build -race -buildmode=plugin ../mrapps/wc.go
+rm mr-out*
+go run -race mrsequential.go wc.so pg*.txt
+more mr-out-0输出的文件中是对文件的WordCount结果
+Go是静态编译型语言,在编译时就将所有引用的包(库)全部加载打包到最终的可执行程序(或库文件)中,因此并不能在运行时动态加载其他共享库。Go Plugin提供了这样一种方式,能够让你在运行时动态加载外部功能。
+type Plugin即Golang加载的插件,与之有关的两个方法:
+因此这一行命令将 wc.go文件编译成了一个插件 wc.so(默认文件名),从而可以插入到MapReduce主程序中运行。
// The map function is called once for each file of input. The first
+// argument is the name of the input file, and the second is the
+// file's complete contents. You should ignore the input file name,
+// and look only at the contents argument. The return value is a slice
+// of key/value pairs.
+func Map(filename string, contents string) []mr.KeyValue {
+ // function to detect word separators.
+ ff := func(r rune) bool { return !unicode.IsLetter(r) }
+
+ // split contents into an array of words.
+ words := strings.FieldsFunc(contents, ff)
+
+ kva := []mr.KeyValue{}
+ for _, w := range words {
+ kv := mr.KeyValue{w, "1"}
+ kva = append(kva, kv)
+ }
+ return kva
+}对每一个传进来的字符串,通过 strings.FieldsFunc函数找到字符串的分割点,分割成单独的单词,构造成KeyValue结构体并合并成切片返回
// The reduce function is called once for each key generated by the
+// map tasks, with a list of all the values created for that key by
+// any map task.
+func Reduce(key string, values []string) string {
+ // return the number of occurrences of this word.
+ return strconv.Itoa(len(values))
+}直接以字符串的形式返回values的长度
+// load the application Map and Reduce functions
+// from a plugin file, e.g. ../mrapps/wc.so
+func loadPlugin(filename string) (func(string, string) []mr.KeyValue, func(string, []string) string) {
+ p, err := plugin.Open(filename)
+ if err != nil {
+ log.Fatalf("cannot load plugin %v", filename)
+ }
+ xmapf, err := p.Lookup("Map")
+ if err != nil {
+ log.Fatalf("cannot find Map in %v", filename)
+ }
+ mapf := xmapf.(func(string, string) []mr.KeyValue)
+ xreducef, err := p.Lookup("Reduce")
+ if err != nil {
+ log.Fatalf("cannot find Reduce in %v", filename)
+ }
+ reducef := xreducef.(func(string, []string) string)
+
+ return mapf, reducef
+}从编译好的*.so文件中查找Map函数和Reduce函数,通过函数的返回值类型进行类型推断,最终返回两个函数通过主函数里面的变量进行接收
+mapf, reducef := loadPlugin(os.Args[1]) //
+// read each input file,
+// pass it to Map,
+// accumulate the intermediate Map output.
+//
+intermediate := []mr.KeyValue{}
+for _, filename := range os.Args[2:] {
+ file, err := os.Open(filename)
+ if err != nil {
+ log.Fatalf("cannot open %v", filename)
+ }
+ content, err := ioutil.ReadAll(file)
+ if err != nil {
+ log.Fatalf("cannot read %v", filename)
+ }
+ file.Close()
+ kva := mapf(filename, string(content))
+ intermediate = append(intermediate, kva...)
+}pg-*.txt会匹配到所有满足条件的文件,将文件逐个打开,读取文件内容,通过Map函数处理成中间数据格式,存入中间变量intermediate
+对中间变量的切片按照键的字典序进行排序
+sort.Sort(ByKey(intermediate))
+// for sorting by key.
+func (a ByKey) Len() int { return len(a) }
+func (a ByKey) Swap(i, j int) { a[i], a[j] = a[j], a[i] }
+func (a ByKey) Less(i, j int) bool { return a[i].Key < a[j].Key }这里是通过实现Sort的接口实现了自定义排序
+//
+// call Reduce on each distinct key in intermediate[],
+// and print the result to mr-out-0.
+//
+i := 0
+for i < len(intermediate) {
+ j := i + 1
+ for j < len(intermediate) && intermediate[j].Key == intermediate[i].Key {
+ j++
+ }
+ values := []string{}
+ for k := i; k < j; k++ {
+ values = append(values, intermediate[k].Value)
+ }
+ output := reducef(intermediate[i].Key, values)
+
+ // this is the correct format for each line of Reduce output.
+ fmt.Fprintf(ofile, "%v %v\n", intermediate[i].Key, output)
+
+ i = j
+}由于已经排好顺序了,从左到右遍历一遍就可以统计每一个键出现的数量,然后输出到文件即可。
+实现一个分布式MapReduce,由coordinator和worker两个程序组成。
+coordinator进程只有一个,worker进程有一个或多个并行执行。
+worker进程将通过RPC与coordinator进程进行通信。每个worker进程将向coordinator进程请求任务,从一个或多个文件中读取任务的输入,执行任务,并将任务的输出写入一个或更多个文件。
+coordinator进程应该注意到一个worker进程是否没有在合理的时间内完成其任务(10秒),并将相同的任务交给另一个worker进程。
+coordinator和worker的“main”函数在 main/mrcordinator.go和 main/mrworker.go中
实现应该在 mr/coordinator.go、mr/worker.go和 mr/rpc.go中。
测试运行:
+go build -race -buildmode=plugin ../mrapps/wc.go
+rm mr-out*
+go run -race mrcoordinator.go pg-*.txt
+
+go run -race mrworker.go wc.so
+go run -race mrworker.go wc.so测试脚本:
+bash test-mr.sh待补充的代码提供了一个RPC的示例
+启动Worker后,会调用CallExample()函数
+// example function to show how to make an RPC call to the coordinator.
+//
+// the RPC argument and reply types are defined in rpc.go.
+func CallExample() {
+
+ // declare an argument structure.
+ args := ExampleArgs{}
+
+ // fill in the argument(s).
+ args.X = 99
+
+ // declare a reply structure.
+ reply := ExampleReply{}
+
+ // send the RPC request, wait for the reply.
+ // the "Coordinator.Example" tells the
+ // receiving server that we'd like to call
+ // the Example() method of struct Coordinator.
+ ok := call("Coordinator.Example", &args, &reply)
+ if ok {
+ // reply.Y should be 100.
+ fmt.Printf("reply.Y %v\n", reply.Y)
+ } else {
+ fmt.Printf("call failed!\n")
+ }
+}函数构建了RPC的结构体,然后调用call函数并接收响应
+在这里体现了RPC的核心思想:在这里看起来就是调用的本地函数call,但是实际上call内部是与coordinator进行通信,然后在远程得到返回值后返回给reply结构体,因此为“远程过程调用”
+call函数:
+// send an RPC request to the coordinator, wait for the response.
+// usually returns true.
+// returns false if something goes wrong.
+func call(rpcname string, args interface{}, reply interface{}) bool {
+ // c, err := rpc.DialHTTP("tcp", "127.0.0.1"+":1234")
+ sockname := coordinatorSock()
+ c, err := rpc.DialHTTP("unix", sockname)
+ if err != nil {
+ log.Fatal("dialing:", err)
+ }
+ defer c.Close()
+
+ err = c.Call(rpcname, args, reply)
+ if err == nil {
+ return true
+ }
+
+ fmt.Println(err)
+ return false
+}注意coordinatorSock()方法,会获取一个临时文件,通信是通过这个临时文件进行的。
+在coordinator.go内部,RPC指定的方法"Coordinator.Example":
+// an example RPC handler.
+//
+// the RPC argument and reply types are defined in rpc.go.
+func (c *Coordinator) Example(args *ExampleArgs, reply *ExampleReply) error {
+ reply.Y = args.X + 1
+ return nil
+}因此返回的结构体中reply.Y的值就为100
+在启动Worker前要先启动Coordinator,启动后首先创建一个Coordinator结构:
+// create a Coordinator.
+// main/mrcoordinator.go calls this function.
+// nReduce is the number of reduce tasks to use.
+func MakeCoordinator(files []string, nReduce int) *Coordinator {
+ c := Coordinator{}
+
+ // Your code here.
+
+ c.server()
+ return &c
+}其中调用server方法,监听Worker的RPC:
+// start a thread that listens for RPCs from worker.go
+func (c *Coordinator) server() {
+ rpc.Register(c)
+ rpc.HandleHTTP()
+ //l, e := net.Listen("tcp", ":1234")
+ sockname := coordinatorSock()
+ os.Remove(sockname)
+ l, e := net.Listen("unix", sockname)
+ if e != nil {
+ log.Fatal("listen error:", e)
+ }
+ go http.Serve(l, nil)
+}Coordinator会不断检测Done方法的返回值,一旦为true,Coordinator就会退出:
+// main/mrcoordinator.go calls Done() periodically to find out
+// if the entire job has finished.
+func (c *Coordinator) Done() bool {
+ ret := false
+
+ // Your code here.
+
+ return ret
+}首先考虑简单一些,不考虑并行、容错处理等,先把整个的流程跑通。
+首先跑通Map流程
+Coordinator的数据结构:
+type Coordinator struct {
+ // Your definitions here.
+ MapTask []MapTaskInformation // Map任务列表
+ ReduceTask []ReduceTaskInformation // Reduce任务列表
+}内部有两个切片,分别对应Map的任务列表和Reduce的任务列表。
+两个任务列表是在Coordinator启动的时候就设置好:
+// create a Coordinator.
+// main/mrcoordinator.go calls this function.
+// nReduce is the number of reduce tasks to use.
+func MakeCoordinator(files []string, nReduce int) *Coordinator {
+
+ mapTaskSlice := []MapTaskInformation{}
+
+ for id, fileName := range files {
+ mapTaskSlice = append(mapTaskSlice, MapTaskInformation{
+ Id: id + 1,
+ State: 0,
+ NReduce: nReduce,
+ OriginFileName: fileName,
+ IntermediateFileName: "mr-" + strconv.Itoa(id+1) + "-",
+ })
+ }
+
+ reduceTaskSlice := []ReduceTaskInformation{}
+
+ for i := 0; i < nReduce; i++ {
+ reduceTaskSlice = append(reduceTaskSlice, ReduceTaskInformation{
+ Id: i + 1,
+ State: 0,
+ OriginFileName: "mr-0-" + strconv.Itoa(i+1),
+ OutputFileName: "mr-" + strconv.Itoa(i+1),
+ })
+ }
+
+ c := Coordinator{
+ MapTask: mapTaskSlice,
+ ReduceTask: reduceTaskSlice,
+ }
+
+ // Your code here.
+
+ c.server()
+ return &c
+}其中为Map和Reduce暂时设计的数据结构:
+type MapTaskInformation struct {
+ Id int // 任务唯一编码
+ State int // 0表示未开始,1表示正在进行,2表示已经完成
+ NReduce int // 分成Reduce任务的数量
+ OriginFileName string // 原始文件名称
+ IntermediateFileName string // Map任务完成后的文件名称(中间文件)
+}
+type ReduceTaskInformation struct {
+ Id int // 任务唯一编码
+ State int // 0表示未开始,1表示正在进行,2表示已经完成
+ OriginFileName string // Reduce的初始文件名称(中间文件)
+ OutputFileName string // Reduce任务完成后的最终文件名称
+}Worker启动时,通过RPC向Coordinator要一个任务
+// main/mrworker.go calls this function.
+func Worker(mapf func(string, string) []KeyValue,
+ reducef func(string, []string) string) {
+
+ args := TaskInformation{}
+ reply := TaskInformation{}
+
+ ok := call("Coordinator.AsssignTask", &args, &reply)Coordinator会遍历自己内部的所有任务列表,找到第一个还没有完成的任务分配给这个Worker:
+// 分配任务
+func (c *Coordinator) AsssignTask(args *TaskInformation, reply *TaskInformation) error {
+ isMapfinished := true
+ //遍历所有的Map任务信息,将未开始的分配给这个节点
+ for i, mapTask := range c.MapTask {
+ if mapTask.State == 0 {
+ isMapfinished = false
+ reply.Id = mapTask.Id
+ reply.TaskType = "map"
+ reply.InputFileName = mapTask.OriginFileName
+ reply.OutputFileName = mapTask.IntermediateFileName
+ reply.NReduce = mapTask.NReduce
+ c.MapTask[i].State = 1
+ return nil
+ } else if mapTask.State == 1 {
+ isMapfinished = false
+ }
+ }
+ // 如果所有的Map任务都完成了,就遍历Reduce任务
+ if isMapfinished {
+ for _, reduceTask := range c.ReduceTask {
+ if reduceTask.State == 0 {
+ return nil
+ }
+ }
+ }
+ return nil
+}Worker接收到任务后使用插件中的Map函数进行处理,并将成功完成任务的消息通过RPC的方式返回给Coordinator
+if ok {
+ fmt.Println("Call Success!")
+ if reply.TaskType == "map" {
+ fmt.Printf("Map Task!\n")
+ intermediate := []KeyValue{}
+ file, err := os.Open(reply.InputFileName)
+ if err != nil {
+ log.Fatalf("cannot open %v", reply.InputFileName)
+ }
+ content, err := io.ReadAll(file)
+ if err != nil {
+ log.Fatalf("cannot read %v", reply.InputFileName)
+ }
+ file.Close()
+ kva := mapf(reply.InputFileName, string(content))
+ intermediate = append(intermediate, kva...)
+
+ // 排序
+ sort.Sort(ByKey(intermediate))
+
+ fmt.Println(intermediate)
+ args = reply
+ call("Coordinator.TaskFinish", &args, &reply)Coordinator接收消息,将自己内部的任务状态修改,后续就不会再将这个任务分配给Worker了。
+// 接收任务已经完成的信息
+func (c *Coordinator) TaskFinish(args *TaskInformation, reply *TaskInformation) error {
+ if args.TaskType == "map" {
+ c.MapTask[args.Id-1].State = 2
+ } else if args.TaskType == "reduce" {
+ c.ReduceTask[args.Id-1].State = 2
+ }
+ return nil
+}问题:
+首先在Worker的主函数增加一层循环,从而使Worker不断请求任务,由Coordinator按需分配
+首先要构造中间文件,也就是map结束后的文件需要存起来,然后才能用reduce去处理
+// 循环创建NReduce个文件准备保存
+encoderList := make([]*json.Encoder, 0)
+for i := 0; i < reply.NReduce; i++ {
+ fileName := reply.OutputFileName + strconv.FormatInt(int64(i+1), 10)
+ tempFile, err := os.Create(fileName)
+ if err != nil {
+ log.Fatalf("cannot create %v", fileName)
+ }
+ defer tempFile.Close()
+ encoderList = append(encoderList, json.NewEncoder(tempFile))
+}
+for i, v := range intermediate {
+ encoderList[ihash(v.Key)%reply.NReduce].Encode(&intermediate[i])
+}map在保存的时候要直接分成NReduce的文件,文件的内容是由哈希函数对键进行映射后得到的,保证键大致平均分到NReduce个节点上
+保存文件的时候使用的是json的格式,保存的过程有些慢,需要对整个map的结果全部遍历一遍,后续可以考虑并行处理?
+Reduce内容:
+} else if reply.TaskType == "reduce" {
+
+ ofile, _ := os.Create(reply.OutputFileName)
+
+ fmt.Printf("Reduce Task!\n")
+ kva := make([]KeyValue, 0)
+ for p := 1; p <= 8; p++ {
+ filename := strings.Replace(reply.InputFileName, "*", strconv.FormatInt(int64(p), 10), 1)
+ fmt.Println(filename)
+ file, err := os.Open(filename)
+ if err != nil {
+ log.Fatalf("cannot open %v", filename)
+ }
+ dec := json.NewDecoder(file)
+ for {
+ var kv KeyValue
+ if err := dec.Decode(&kv); err != nil {
+ break
+ }
+ kva = append(kva, kv)
+ }
+ }
+ // 排序
+ sort.Sort(ByKey(kva))
+ //
+ // call Reduce on each distinct key in intermediate[],
+ // and print the result to mr-out-0.
+ //
+ i := 0
+ for i < len(kva) {
+ j := i + 1
+ for j < len(kva) && kva[j].Key == kva[i].Key {
+ j++
+ }
+ values := []string{}
+ for k := i; k < j; k++ {
+ values = append(values, kva[k].Value)
+ }
+ output := reducef(kva[i].Key, values)
+
+ // this is the correct format for each line of Reduce output.
+ fmt.Fprintf(ofile, "%v %v\n", kva[i].Key, output)
+
+ i = j
+ }循环读取map保存下来的内容,这里写死了,后面需要调整。
+读取内容后汇总并排序,排序后直接使用串行的Reduce代码即可
+对于Coordinator,将Reduce的内容添加进去即可:
+// 如果所有的Map任务都完成了,就遍历Reduce任务
+if isMapfinished {
+ for i, reduceTask := range c.ReduceTask {
+ if reduceTask.State == 0 {
+ reply.Id = reduceTask.Id
+ reply.TaskType = "reduce"
+ reply.InputFileName = reduceTask.OriginFileName
+ reply.OutputFileName = reduceTask.OutputFileName
+ mu.Lock()
+ c.ReduceTask[i].State = 1
+ mu.Unlock()
+ return nil
+ }
+ }
+
+}Reduce结束后需要告知主Coordinator在无限循环的Done(),返回True让其退出:
+// main/mrcoordinator.go calls Done() periodically to find out
+// if the entire job has finished.
+func (c *Coordinator) Done() bool {
+ ret := true
+ mu.Lock()
+ // Your code here.
+ for _, v := range c.ReduceTask {
+ if v.State != 2 {
+ ret = false
+ break
+ }
+ }
+ mu.Unlock()
+ return ret
+}中间添加了锁,但是添加的有些问题,后面需要调整。
+到这里的代码除了异常处理外已经都能测试通过了,只不过是有data race问题
+问题:
+首先将Coordinator对于任务的数据结构更改,内部维护三个双向链表,分别表示未开始的任务,正在进行的任务和已经结束的任务,链表外面使用map的数据结构,从而支持快速查找。在生成任务的时候自动赋值一个全局唯一的id。
+数据结构中要包括全部的信息,主要变化部分是对输入和输出的信息,将Map的输入、输出和Reduce的输出都在初始化的时候直接写在结构体中,避免后续进行多次判断和修改。
+结构体:
+// Coordinator存储的主要信息,包括Map和Reduce两部分任务的信息以及工作节点的信息
+type Coordinator struct {
+ UniqueIdSlice []*list.Element // 通过任务Id找到任务信息的切片,相当于一个Map
+ MapTaskNum int // map任务总数量
+ ReduceTaskNum int // reduce任务总数量
+ WorkerNum int // 目前正在工作的节点数量
+ MapTask // Map任务信息链表
+ ReduceTask // Reduce任务信息链表
+ WorkerInformation // Worker的信息
+}
+
+// Map任务信息链表,包括三个链表,分别表示未开始、正在进行和已经完成的任务
+type MapTask struct {
+ MapListReady *list.List // 未开始的Map任务
+ MapListRunning *list.List // 正在进行的Map任务
+ MapListComplete *list.List // 已经完成的Map任务
+}
+
+// Reduce任务信息链表,包括三个链表,分别表示未开始、正在进行和已经完成的任务
+type ReduceTask struct {
+ ReduceListReady *list.List // 未开始的Reduce任务
+ ReduceListRunning *list.List // 正在进行的Reduce任务
+ ReduceListComplete *list.List // 已经完成的Reduce任务
+}
+
+// Map任务具体信息
+type MapTaskInformation struct {
+ Id int // 任务唯一编码
+ OriginFileName string // 原始文件名称
+ IntermediateFileName []string // Map任务完成后中间文件列表
+}
+
+// Reduce任务具体信息
+type ReduceTaskInformation struct {
+ Id int // 任务唯一编码
+ IntermediateFileName []string // Reduce的初始中间文件列表(从Map处获得)
+ OutputFileName string // Reduce任务完成后的最终文件名称
+}Worker中分为几个步骤:
+主程序如下:
+// main/mrworker.go 调用的函数
+func Worker(mapf func(string, string) []KeyValue, reducef func(string, []string) string) {
+
+ // 1. 告知Coordinator自己已经上线
+ args := WorkerArgs{TaskType: "None"}
+ reply := WorkerReply{TaskType: "None"}
+ call("Coordinator.WorkerOnline", &args, &reply)
+
+ // 无限循环向Coordinator请求任务
+ for {
+ // 2. 向Coordinator请求任务
+ args = WorkerArgs{TaskType: "None"}
+ reply = WorkerReply{TaskType: "None"}
+ ok := call("Coordinator.AsssignTask", &args, &reply)
+
+ if ok {
+
+ fmt.Println("Call Success!")
+
+ if reply.TaskType == "map" {
+
+ fmt.Printf("Map Task!\n")
+
+ // 读取文件,调用map函数进行处理
+ intermediate := []KeyValue{}
+ file, err := os.Open(reply.MapInput)
+ if err != nil {
+ log.Fatalf("cannot open %v", reply.MapInput)
+ }
+ content, err := io.ReadAll(file)
+ if err != nil {
+ log.Fatalf("cannot read %v", reply.MapInput)
+ }
+ file.Close()
+ kva := mapf(reply.MapInput, string(content))
+ intermediate = append(intermediate, kva...)
+
+ // 循环创建NReduce个文件准备保存
+ encoderList := make([]*json.Encoder, 0)
+ for _, fileName := range reply.MapOutput {
+ tempFile, err := os.Create(fileName)
+ if err != nil {
+ log.Fatalf("cannot create %v", fileName)
+ }
+ defer tempFile.Close()
+ encoderList = append(encoderList, json.NewEncoder(tempFile))
+ }
+ // 将map后的结果存入文件中(最费时间)
+ for i, v := range intermediate {
+ encoderList[ihash(v.Key)%len(reply.MapOutput)].Encode(&intermediate[i])
+ }
+
+ // 3. 向Coordinator返回自己的Map任务已经完成
+ args.TaskType = "map"
+ args.Taskid = reply.Id
+ call("Coordinator.TaskFinish", &args, &reply)
+
+ } else if reply.TaskType == "reduce" {
+
+ fmt.Printf("Reduce Task!\n")
+
+ // 创建输出文件
+ ofile, _ := os.Create(reply.ReduceOutput)
+
+ // 遍历输入文件,汇总Map产生的所有结果
+ kva := make([]KeyValue, 0)
+ for _, filename := range reply.ReduceInput {
+ // fmt.Println(filename)
+ file, err := os.Open(filename)
+ if err != nil {
+ log.Fatalf("cannot open %v", filename)
+ }
+ dec := json.NewDecoder(file)
+ for {
+ var kv KeyValue
+ if err := dec.Decode(&kv); err != nil {
+ break
+ }
+ kva = append(kva, kv)
+ }
+ }
+
+ // 排序
+ sort.Sort(ByKey(kva))
+
+ // 在已经排好序的键值对上进行统计,并写入到文件中
+ i := 0
+ for i < len(kva) {
+ j := i + 1
+ for j < len(kva) && kva[j].Key == kva[i].Key {
+ j++
+ }
+ values := []string{}
+ for k := i; k < j; k++ {
+ values = append(values, kva[k].Value)
+ }
+ output := reducef(kva[i].Key, values)
+
+ fmt.Fprintf(ofile, "%v %v\n", kva[i].Key, output)
+
+ i = j
+ }
+
+ // 4. 向Coordinator返回自己的Reduce任务已经完成
+ args.Taskid = reply.Id
+ args.TaskType = "reduce"
+ call("Coordinator.TaskFinish", &args, &reply)
+
+ } else if reply.TaskType == "finish" {
+
+ // 5. 向Coordinator返回自己退出的消息
+ call("Coordinator.WorkerFinish", &args, &reply)
+ fmt.Printf("Bye!\n")
+ return
+ }
+ } else {
+ fmt.Printf("Call failed!\n")
+ }
+
+ // 间隔1秒请求一次
+ time.Sleep(time.Second)
+ }
+}其中将RPC的发送和接收的结构体更改的更为合理:
+// Worker向Coordinator传递的信息
+type WorkerArgs struct {
+ Id int // Worker的唯一ID
+ Taskid int // 任务全局唯一ID
+ TaskType string // 任务类型
+}
+
+// Coordinator向Worker传递的信息
+type WorkerReply struct {
+ Id int // 任务id
+ TaskType string // 任务类型
+ MapInput string // Map任务的输入
+ MapOutput []string // Map任务的输出
+ ReduceInput []string // Reduce任务的输入
+ ReduceOutput string // Reduce任务的输出
+}// Worker告知Coordinator自己上线了
+func (c *Coordinator) WorkerOnline(args *WorkerArgs, reply *WorkerReply) error {
+ mu.Lock()
+ if c.WorkerNum == -1 {
+ c.WorkerNum = 0
+ }
+ c.WorkerNum += 1
+ mu.Unlock()
+ return nil
+}这里暂时比较简单,后续需要进行处理,以进行异常处理
+// Worker向Coordinator请求任务
+func (c *Coordinator) AsssignTask(args *WorkerArgs, reply *WorkerReply) error {
+
+ mu.Lock()
+
+ // 首先查看map任务是否已经全部完成,如果全部完成了就去完成Reduce任务,如果也全部完成了就发送Worker可以退出的消息
+ // 判断方式:通过完成链表的节点数量与初始化时侯计算的数量是否相同
+
+ if c.MapListComplete.Len() != c.MapTaskNum {
+
+ // 分配map任务
+
+ if c.MapListReady.Len() == 0 {
+
+ // 没有没开始的Map任务
+ reply.TaskType = "waiting"
+
+ } else {
+
+ // 将一个未完成的任务从未开始的链表中取出,插入到正在进行的链表里面
+ e := c.MapListReady.Front()
+ c.MapListReady.Remove(e)
+ c.MapListRunning.PushBack(e)
+
+ // 构建返回消息,告知Worker这个任务的信息
+ reply.TaskType = "map"
+ value := e.Value.(MapTaskInformation)
+ reply.Id = value.Id
+ reply.MapInput = value.OriginFileName
+ reply.MapOutput = value.IntermediateFileName
+ }
+ } else if c.ReduceListComplete.Len() != c.ReduceTaskNum {
+
+ // 分配reduce任务
+
+ if c.ReduceListReady.Len() == 0 {
+ // 没有没开始的Reduce任务
+ reply.TaskType = "waiting"
+
+ } else {
+
+ // 将一个未完成的任务从未开始的链表中取出,插入到正在进行的链表里面
+ e := c.ReduceListReady.Front()
+ c.ReduceListReady.Remove(e)
+ c.ReduceListRunning.PushBack(e)
+
+ // 构建返回消息,告知Worker这个任务的信息
+ reply.TaskType = "reduce"
+ value := e.Value.(ReduceTaskInformation)
+ reply.Id = value.Id
+ reply.ReduceInput = value.IntermediateFileName
+ reply.ReduceOutput = value.OutputFileName
+
+ }
+ } else {
+
+ //告知Worker已经没有任务了,可以退出了
+ reply.TaskType = "finish"
+ }
+
+ mu.Unlock()
+
+ return nil
+}收到请求后操作全局链表,构建消息并返回即可
+// Worker告知Coordinator刚才分配的任务已经完成
+func (c *Coordinator) TaskFinish(args *WorkerArgs, reply *WorkerReply) error {
+
+ mu.Lock()
+
+ // 将节点从正在进行的链表中取出,插入到已经完成的链表中
+ if args.TaskType == "map" {
+
+ // 操作节点
+ e := c.UniqueIdSlice[args.Taskid]
+ c.MapListRunning.Remove(e)
+ c.MapListComplete.PushBack(e)
+
+ // 如果是Map任务,需要将产生的nReduce个中间文件分配给Reduce节点
+ for _, file := range e.Value.(MapTaskInformation).IntermediateFileName {
+
+ // 计算是哪个Reduce节点
+ reduceTaskNum, err := strconv.Atoi(strings.Split(file, "-")[2])
+ if err != nil {
+ log.Fatalf("cannot parseInt %v", file)
+ }
+
+ // 将产生的nReduce个中间文件分配给Reduce节点(需要重新构建节点)
+ value := c.UniqueIdSlice[reduceTaskNum].Value
+ tempSlice := append(value.(ReduceTaskInformation).IntermediateFileName, file)
+ c.UniqueIdSlice[reduceTaskNum].Value = ReduceTaskInformation{
+ Id: value.(ReduceTaskInformation).Id,
+ IntermediateFileName: tempSlice,
+ OutputFileName: value.(ReduceTaskInformation).OutputFileName,
+ }
+ }
+ } else if args.TaskType == "reduce" {
+
+ // 操作节点
+ e := c.ReduceListRunning.Remove(c.UniqueIdSlice[args.Taskid])
+ c.ReduceListComplete.PushBack(e)
+ }
+ mu.Unlock()
+ return nil
+}对于Map任务需要传递Map输出,Reduce输入的文件信息,将结构体填充完整
+// Worker告知Coordinator自己退出了
+func (c *Coordinator) WorkerFinish(args *WorkerArgs, reply *WorkerReply) error {
+
+ mu.Lock()
+
+ // 退出时将Coordinator内部存储的Worker数量-1
+ c.WorkerNum -= 1
+
+ mu.Unlock()
+
+ return nil
+}将全局的WorkerNum减去1,后续需要进行处理。
+经测试,除异常检测完已经都能顺利pass,多次运行的结果也完全相同
+有一个小问题是它的脚本给的超时时间不够,调大一些后才能顺利运行,后续可以进行更改。
+原文与异常处理相关的部分:
+The coordinator should notice if a worker hasn’t completed its task in a reasonable amount of time (for this lab, use ten seconds), and give the same task to a different worker.
+The best you can do is have the coordinator wait for some amount of time, and then give up and re-issue the task to a different worker. For this lab, have the coordinator wait for ten seconds; after that the coordinator should assume the worker has died (of course, it might not have).
+To test crash recovery, you can use the mrapps/crash.go application plugin. It randomly exits in the Map and Reduce functions.
+可以先查看crash.go,看看是如何模拟线程崩溃的:
+func maybeCrash() {
+ max := big.NewInt(1000)
+ rr, _ := crand.Int(crand.Reader, max)
+ if rr.Int64() < 330 {
+ // crash!
+ os.Exit(1)
+ } else if rr.Int64() < 660 {
+ // delay for a while.
+ maxms := big.NewInt(10 * 1000)
+ ms, _ := crand.Int(crand.Reader, maxms)
+ time.Sleep(time.Duration(ms.Int64()) * time.Millisecond)
+ }
+}阅读代码,可以发现这个设置是有1/3的概率直接崩溃掉,有2/3的概率线程睡眠不到10s,模拟的环境还是比较简单的。
+实现:
+Worker部分:
+Worker上线后,由Coordinator为其分配一个ID,随后在Worker的每一个rpc请求中都带有这个ID
+WorkerID := reply.WorkerIDWorker上线后每5秒发送心跳信号给Coordinator,表明自己在线
+// 心跳信号
+go func() {
+ for {
+ args := WorkerArgs{TaskType: "None"}
+ args.Id = WorkerID
+ reply := WorkerReply{TaskType: "None"}
+ time.Sleep(time.Second * 5)
+ call("Coordinator.WorkerAlive", &args, &reply)
+ }
+}()Coordinator部分:
+维护一个切片结构体,索引表示Worker的ID,结构体内部包括任务ID和上一次心跳信号的时间
+type HeartBeat struct {
+ WorkID int
+ Time int64
+}
+var WorkerList []HeartBeat接收到Worker上线的RPC后,记录当前的时间戳,记录任务ID为-1,即表示这个索引ID已经分配给Worker了
+// 分配任务ID并记录时间
+WorkerList = append(WorkerList, HeartBeat{
+ WorkID: -1,
+ Time: time.Now().Unix(),
+})
+reply.WorkerID = len(WorkerList)接收心跳信号后更新切片结构体
+// Coordinator接收心跳信号
+func (c *Coordinator) WorkerAlive(args *WorkerArgs, reply *WorkerReply) error {
+ mu.Lock()
+ WorkerList[args.Id-1].Time = time.Now().Unix()
+ fmt.Printf("接收到%d心跳信号\n", args.Id-1)
+ mu.Unlock()
+ return nil
+}分配任务后在切片结构体内更新任务ID信息
+WorkerList[args.Id-1].WorkID = value.Id开启协程每10秒检查切片结构体的时间戳,如果时间戳与当前时间间隔大于10秒,将任务的状态更改为未完成,重新分配。
+// Worker信息存储
+WorkerList = make([]HeartBeat, 0)
+// 每间隔10秒进行验证
+go func() {
+ for {
+ time.Sleep(10 * time.Second)
+ mu.Lock()
+ for i := 0; i < len(WorkerList); i++ {
+ if WorkerList[i].WorkID != -1 && time.Now().Unix()-WorkerList[i].Time > 10 {
+ fmt.Printf("%d心跳信号过期\n", i)
+ e2 := *(c.UniqueIdSlice[WorkerList[i].WorkID])
+
+ // 这里不太懂为什么要这样写
+ if WorkerList[i].WorkID < c.MapTaskNum {
+ c.MapListRunning.Remove(&e2)
+ c.MapListReady.PushBack(e2.Value)
+ } else {
+ c.ReduceListRunning.Remove(&e2)
+ c.ReduceListReady.PushBack(e2.Value)
+ }
+
+ c.WorkerNum -= 1
+ WorkerList[i].WorkID = -1
+ }
+ }
+ mu.Unlock()
+ }
+}()至此,可以单独通过全部的test,但是仍然存在一些问题
+总之基本功能已经没有什么问题了,以后有时间再进行重构。
+ + +互联网公司整理
+ +岗位投递 | 腾讯校招:https://join.qq.com/post.html
+字节跳动校园招聘:https://jobs.bytedance.com/campus/position
+阿里巴巴集团校园招聘:https://talent.alibaba.com/campus/home?lang=zh
+百度校园招聘:https://talent.baidu.com/jobs/list
+京东校招:https://campus.jd.com/#/jobs
+网易校园招聘:https://campus.163.com/app/index
+快手校招 - 首页:https://campus.kuaishou.cn/recruit/campus/e/#/campus/index
+校园招聘 | 美团招聘:https://zhaopin.meituan.com/web/campus
+滴滴招聘:https://talent.didiglobal.com/
+新浪集团 | 校园招聘:https://career.sina.com.cn/campus-recruitment/#/
+搜狐 - 校园招聘:https://app.mokahr.com/campus_apply/sohu/5682#/
+360校园招聘:https://360campus.zhiye.com/
+可以发现北京一堆在线教育的公司,可能教育要紧盯了政策变化,所以都要在北京吧
+华为(上海)
+MIT-6.824(Spring 2022)LEC 3 GFS
+ +参考资料(感谢Alex!这篇论文翻译得非常有质量!)
+ + +Google GFS文件系统是一个面向大规模数据密集型应用的、可伸缩的分布式文件系统。GFS运行在廉价的普遍硬件设备上,但是依然了提供容错机制,为大量客户提供了高性能的服务。
+GFS的设计目标与许多传统的分布式文件系统有很多相同之处,不过还是以我们对自己的应用的负载情况和技术环境的分析为基础进行设计,和早期的分布式文件系统有明显的不同。
+GFS完全满足了我们对存储的需求。GFS作为存储平台已经被广泛的部署在Google内部,存储我们的服务产生和处理的数据,同时还用于那些需要大规模数据集的研究和开发工作。目前为止,最大的一个集群利用数千台机器的数千个硬盘,提供了数百TB的存储空间,同时为数百个客户机服务。
+在本论文中,我们展示能够支持分布式应用的文件系统接口扩展,讨论我们设计的许多方面,最后列出了小规模性能测试以及真实生产系统中性能的相关数据。
+GFS与传统的分布式文件系统有着很多相同的设计目标,比如,性能、可伸缩性、可靠性以及可用性。但是,我们的设计还基于我们对我们自己的应用的负载情况和技术环境的观察的影响,和早期文件系统的假设都有明显的不同。
+所以我们重新审视了传统文件系统在设计上的折衷选择,衍生出了完全不同的设计思路。
+首先,组件失效被认为是常态事件,而不是意外事件。GFS组件的数量和质量导致在任何给定时间内都有可能发生某些组件无法工作,且某些组件无法从它们目前的失效状态中恢复。因此,持续的监控、错误侦测、容错以及自动恢复的机制必须集成在GFS中。
+其次,我们的文件非常巨大,GB的文件非常普遍。当我们经常需要处理快速增长的、并且由数亿个对象构成的、数以TB的数据集时,采用管理数亿个KB大小的小文件的方式是非常不明智的。因此,设计的假设条件和参数,比如I/O操作和Block的尺寸等都需要重新考虑。
+第三,绝大部分文件的修改是采用在文件尾部追加数据,而不是覆盖原有数据的方式。一旦写完之后,对文件的操作就只有读,而且通常是按顺序读。对于这种针对海量文件的访问模式,客户端对数据块缓存是没有意义的,数据的追加操作是性能优化和原子性保证的主要考量因素。
+第四,应用程序和文件系统API的协同设计提高了整个系统的灵活性。比如,我们放松了对GFS一致性模型的要求,这样就减轻了文件系统对应用程序的苛刻要求,大大简化了GFS的设计。我们引入了原子性的记录追加操作,从而保证多个客户端能够同时进行追加操作,不需要额外的同步操作来保证数据的一致性。
+GFS提供了一套类似传统文件系统的API接口函数,虽然并不是严格按照POSIX等标准API的形式实现的。文件以分层目录的形式组织,用路径名来标识。支持常用的操作如创建新文件、删除文件、打开文件、关闭文件、读和写文件。
+另外,GFS提供了快照和记录追加操作。快照以很低的成本创建一个文件或者目录树的拷贝。记录追加操作允许多个客户端同时对一个文件进行数据追加操作,同时保证每个客户端的追加操作都是原子性的。多个客户端可以在不需要额外的同步锁定的情况下,同时对一个文件追加数据。这些类型的文件对于构建大型分布应用是非常重要的。
+一个GFS集群包含一个单独的Master节点 (alex注:这里的一个单独的Master节点的含义是GFS系统中只存在一个逻辑上的Master组件。后面还会提到Master节点复制,因此,为了理解方便,我们把Master节点视为一个逻辑上的概念,一个逻辑的Master节点包括两台物理主机,即两台Master服务器)、 和多台Chunk服务器,并且同时被多个客户端访问。Chunk服务器和客户端也可以放在同一台机器上。
+GFS存储的文件都被分割成固定大小的Chunk。在Chunk创建的时候,Master服务器会给每个Chunk分配一个唯一不变的64位的Chunk标识。Chunk服务器把Chunk以linux文件的形式保存在本地硬盘上,并且根据指定的Chunk标识和字节范围来读写块数据。出于可靠性的考虑,每个块都会复制到多个块服务器上,默认是3份。
+Master节点管理所有的文件系统元数据。这些元数据包括名字空间、访问控制信息、文件和Chunk的映射信息、以及当前Chunk的位置信息。Master节点还管理着系统范围内的活动,比如,Chunk租用管理、孤儿Chunk的回收、以及Chunk在Chunk服务器之间的迁移。Master节点使用心跳信息周期地和每个Chunk服务器通讯,发送指令到各个Chunk服务器并接收Chunk服务器的状态信息。
+GFS客户端代码以库的形式链接到客户程序里。客户端代码实现了GFS文件系统的API接口函数、应用程序与Master节点和Chunk服务器通讯、以及对数据进行读写操作。客户端和Master节点的通信只获取元数据,所有的数据操作都是由客户端直接和Chunk服务器进行交互的。
+无论是客户端还是Chunk服务器都不需要缓存文件数据。客户端缓存数据几乎没有什么用处,因为大部分程序要么以流的方式读取一个巨大文件,要么工作集太大根本无法被缓存。无需考虑缓存相关的问题也简化了客户端和整个系统的设计和实现。(不过,客户端会缓存元数据。)Chunk服务器不需要缓存文件数据的原因是,Chunk以本地文件的方式保存,Linux操作系统的文件系统缓存会把经常访问的数据缓存在内存中。
+单一的Master节点可以通过全局的信息精确定位Chunk的位置以及进行复制决策。不过我们必须减少对Master节点的读写,避免Master节点成为系统的瓶颈。客户端并不通过Master节点读写文件数据。而是向Master节点询问它应该联系的Chunk服务器。客户端将这些元数据信息缓存一段时间,后续的操作将直接和Chunk服务器进行数据读写操作。
+一次简单读取的流程:首先,客户端把文件名和程序指定的字节偏移,根据固定的Chunk大小,转换成文件的Chunk索引。然后,它把文件名和Chunk索引发送给Master节点。Master节点将相应的Chunk标识和副本的位置信息发还给客户端。客户端用文件名和Chunk索引作为key缓存这些信息。之后客户端发送请求到其中的一个(一般是最近的)副本处。请求信息包含了Chunk的标识和字节范围。在对这个Chunk的后续读取操作中,客户端不必再和Master节点通讯了,除非缓存的元数据信息过期或者文件被重新打开。实际上,客户端通常会在一次请求中查询多个Chunk信息,Master节点的回应也可能包含了紧跟着这些被请求的Chunk后面的Chunk的信息。在实际应用中,这些额外的信息避免了客户端和Master节点未来可能会发生的几次通讯。
+Chunk的大小是关键的设计参数之一。我们选择了64MB,远远大于一般文件系统的Block size。每个Chunk的副本都以普通Linux文件的形式保存在Chunk服务器上,只有在需要的时候才扩大。惰性空间分配策略避免了因内部碎片造成的空间浪费,内部碎片或许是对选择这么大的Chunk尺寸最具争议的一点。
+选择较大的Chunk尺寸有几个重要的优点。首先,它减少了客户端和Master节点通讯的需求,一次和Master节点的通信就可以获取Chunk的位置信息,之后就可以对同一个Chunk进行多次的读写操作。即使是小规模的随机读取,客户端可以轻松的缓存一个数TB的工作数据集所有的Chunk位置信息。其次,采用较大的Chunk尺寸,客户端能够对一个块进行多次操作,这样就可以通过与Chunk服务器保持较长时间的TCP连接来减少网络负载。第三,选用较大的Chunk尺寸减少了Master节点需要保存的元数据的数量。
+另一方面,即使配合惰性空间分配,采用较大的Chunk尺寸也有其缺陷。小文件包含较少的Chunk,甚至只有一个Chunk。当有许多的客户端对同一个小文件进行多次的访问时,存储这些Chunk的Chunk服务器就会变成热点。在实际应用中,热点不是主要问题。
+然而,当我们第一次把GFS用于批处理队列系统的时候,热点的问题还是产生了:一个可执行文件在GFS上保存为single-chunk文件,之后这个可执行文件在数百台机器上同时启动。存放这个可执行文件的几个Chunk服务器被数百个客户端的并发请求访问导致系统局部过载。我们通过将这个文件复制更多份,并错开批处理队列系统程序的启动时间的方法解决了这个问题。一个可能的长效解决方案是,在这种的情况下,允许客户端从其它客户端读取数据。
+Master服务器(alex注:注意逻辑的Master节点和物理的Master服务器的区别。后续我们谈的是每个Master服务器的行为,如存储、内存等等,因此我们将全部使用物理名称)存储3种主要类型的元数据,包括:文件和Chunk的命名空间、文件和Chunk的对应关系、每个Chunk副本的存放地点。所有的元数据都保存在Master服务器的内存中。前两种类型的元数据(命名空间、文件和Chunk的对应关系)同时也会以记录变更日志的方式记录在操作系统的系统日志文件中,日志文件存储在本地磁盘上,同时日志会被复制到其它的远程Master服务器上。采用保存变更日志的方式,我们能够简单可靠的更新Master服务器的状态,并且不用担心Master服务器崩溃导致数据不一致的风险。Master服务器不会持久保存Chunk位置信息。Master服务器在启动时,或者有新的Chunk服务器加入时,向各个Chunk服务器轮询它们所存储的Chunk的信息。
+因为元数据保存在内存中,所以Master服务器可以在后台简单而高效的周期性扫描自己保存的全部状态信息。这种周期性的状态扫描也用于实现Chunk垃圾收集、在Chunk服务器失效的时重新复制数据、通过Chunk的迁移实现跨Chunk服务器的负载均衡以及磁盘使用状况统计等功能。
+将元数据全部保存在内存中的方法的问题:Chunk的数量以及整个系统的承载能力都受限于Master服务器所拥有的内存大小。但是在实际应用中,这并不是一个严重的问题。Master服务器只需要不到64个字节的元数据就能够管理一个64MB的Chunk。每个文件的在命名空间中的数据大小通常在64字节以下,因为保存的文件名是用前缀压缩算法压缩过的。
+即便是需要支持更大的文件系统,为Master服务器增加额外内存的费用是很少的,增强了系统的简洁性、可靠性、高性能和灵活性。
+Master服务器并不保存持久化保存哪个Chunk服务器存有指定Chunk的副本的信息。Master服务器只是在启动的时候轮询Chunk服务器以获取这些信息。Master服务器能够保证它持有的信息始终是最新的,因为它控制了所有的Chunk位置的分配,而且通过周期性的心跳信息监控Chunk服务器的状态。
+最初设计时,我们试图把Chunk的位置信息持久的保存在Master服务器上,但是后来我们发现在启动的时候轮询Chunk服务器,之后定期轮询更新的方式更简单。这种设计简化了在有Chunk服务器加入集群、离开集群、更名、失效、以及重启的时候,Master服务器和Chunk服务器数据同步的问题。
+可以从另外一个角度去理解这个设计决策:只有Chunk服务器才能最终确定一个Chunk是否在它的硬盘上。我们从没有考虑过在Master服务器上维护一个这些信息的全局视图,因为Chunk服务器的错误可能会导致Chunk自动消失(比如,硬盘损坏了或者无法访问了),亦或者操作人员可能会重命名一个Chunk服务器。
+操作日志包含了关键的元数据变更历史记录。这对GFS非常重要。这不仅仅是因为操作日志是元数据唯一的持久化存储记录,它也作为判断同步操作顺序的逻辑时间基线 (alex注:也就是通过逻辑日志的序号作为操作发生的逻辑时间,类似于事务系统中的LSN) 。文件和Chunk,连同它们的版本,都由它们创建的逻辑时间唯一的、永久的标识。
+操作日志非常重要,我们必须确保日志文件的完整,确保只有在元数据的变化被持久化后,日志才对客户端是可见的。否则,即使Chunk本身没有出现任何问题,我们仍有可能丢失整个文件系统,或者丢失客户端最近的操作。所以,我们会把日志复制到多台远程机器,并且只有把相应的日志记录写入到本地以及远程机器的硬盘后,才会响应客户端的操作请求。Master服务器会收集多个日志记录后批量处理,以减少写入磁盘和复制对系统整体性能的影响。
+Master服务器在恢复时,通过重演操作日志把文件系统恢复到最近的状态。为了缩短Master启动的时间,我们必须使日志足够小 (alex注:即重演系统操作的日志量尽量的少)。 Master服务器在日志增长到一定量时对系统状态做一次Checkpoint (alex注:Checkpoint是一种行为,一种对数据库状态作一次快照的行为), 将所有的状态数据写入一个Checkpoint文件 (alex注:并删除之前的日志文件)。 在灾难恢复的时候,Master服务器就通过从磁盘上读取这个Checkpoint文件,以及重演Checkpoint之后的有限个日志文件就能够恢复系统。Checkpoint文件以压缩B-树形势的数据结构存储,可以直接映射到内存,在用于命名空间查询时无需额外的解析。这大大提高了恢复速度,增强了可用性。
+由于创建一个Checkpoint文件需要一定的时间,所以Master服务器的内部状态被组织为一种格式,这种格式要确保在Checkpoint过程中不会阻塞正在进行的修改操作。Master服务器使用独立的线程切换到新的日志文件和创建新的Checkpoint文件。新的Checkpoint文件包括切换前所有的修改。对于一个包含数百万个文件的集群,创建一个Checkpoint文件需要1分钟左右的时间。创建完成后,Checkpoint文件会被写入在本地和远程的硬盘里。
+Master服务器恢复只需要最新的Checkpoint文件和后续的日志文件。旧的Checkpoint文件和日志文件可以被删除,但是为了应对灾难性的故障 (alex注:catastrophes,数据备份相关文档中经常会遇到这个词,表示一种超出预期范围的灾难性事件), 我们通常会多保存一些历史文件。Checkpoint失败不会对正确性产生任何影响,因为恢复功能的代码可以检测并跳过没有完成的Checkpoint文件。
+GFS支持一个宽松的一致性模型,这个模型能够很好的支撑我们的高度分布的应用,同时还保持了相对简单且容易实现的优点。本节我们讨论GFS的一致性的保障机制,以及对应用程序的意义。我们也着重描述了GFS如何管理这些一致性保障机制。
+文件命名空间的修改(例如,文件创建)是原子性的。它们仅由Master节点的控制:命名空间锁提供了原子性和正确性的保障;Master节点的操作日志定义了这些操作在全局的顺序。
+数据修改后文件region (alex注:region这个词用中文非常难以表达,我认为应该是修改操作所涉及的文件中的某个范围) 的状态取决于操作的类型、成功与否、以及是否同步修改。如果所有客户端,无论从哪个副本读取,读到的数据都一样,那么我们认为文件region是“一致的”;如果对文件的数据修改之后,region是一致的,并且客户端能够看到写入操作全部的内容,那么这个region是“已定义的”。当一个数据修改操作成功执行,并且没有受到同时执行的其它写入操作的干扰,那么影响的region就是已定义的(隐含了一致性):所有的客户端都可以看到写入的内容。并行修改操作成功完成之后,region处于一致的、未定义的状态:所有的客户端看到同样的数据,但是无法读到任何一次写入操作写入的数据。通常情况下,文件region内包含了来自多个修改操作的、混杂的数据片段。失败的修改操作导致一个region处于不一致状态(同时也是未定义的):不同的客户在不同的时间会看到不同的数据。
+数据修改操作分为写入或者记录追加两种。写入操作把数据写在应用程序指定的文件偏移位置上。即使有多个修改操作并行执行时,记录追加操作至少可以把数据原子性的追加到文件中一次,但是偏移位置是由GFS选择的 (alex注:这句话有点费解,其含义是所有的追加写入都会成功,但是有可能被执行了多次,而且每次追加的文件偏移量由GFS自己计算) 。(相比而言,通常说的追加操作写的偏移位置是文件的尾部。)GFS返回给客户端一个偏移量,表示了包含了写入记录的、已定义的region的起点。另外,GFS可能会在文件中间插入填充数据或者重复记录。这些数据占据的文件region被认定是不一致的,这些数据通常比用户数据小的多。
+经过了一系列的成功的修改操作之后,GFS确保被修改的文件region是已定义的,并且包含最后一次修改操作写入的数据。GFS通过以下措施确保上述行为:(a) 对Chunk的所有副本的修改操作顺序一致(3.1章),(b)使用Chunk的版本号来检测副本是否因为它所在的Chunk服务器宕机(4.5章)而错过了修改操作而导致其失效。失效的副本不会再进行任何修改操作,Master服务器也不再返回这个Chunk副本的位置信息给客户端。它们会被垃圾收集系统尽快回收。
+由于Chunk位置信息会被客户端缓存,所以在信息刷新前,客户端有可能从一个失效的副本读取了数据。在缓存的超时时间和文件下一次被打开的时间之间存在一个时间窗,文件再次被打开后会清除缓存中与该文件有关的所有Chunk位置信息。而且,由于我们的文件大多数都是只进行追加操作的,所以,一个失效的副本通常返回一个提前结束的Chunk而不是过期的数据。当一个Reader (alex注:本文中将用到两个专有名词,Reader和Writer,分别表示执行GFS读取和写入操作的程序) 重新尝试并联络Master服务器时,它就会立刻得到最新的Chunk位置信息。
+即使在修改操作成功执行很长时间之后,组件的失效也可能损坏或者删除数据。GFS通过Master服务器和所有Chunk服务器的定期“握手”来找到失效的Chunk服务器,并且使用Checksum来校验数据是否损坏(5.2章)。一旦发现问题,数据要尽快利用有效的副本进行恢复(4.3章)。只有当一个Chunk的所有副本在GFS检测到错误并采取应对措施之前全部丢失,这个Chunk才会不可逆转的丢失。在一般情况下GFS的反应时间 (alex注:指Master节点检测到错误并采取应对措施) 是几分钟。即使在这种情况下,Chunk也只是不可用了,而不是损坏了:应用程序会收到明确的错误信息而不是损坏的数据。
+使用GFS的应用程序可以利用一些简单技术实现这个宽松的一致性模型,这些技术也用来实现一些其它的目标功能,包括:尽量采用追加写入而不是覆盖,Checkpoint,自验证的写入操作,自标识的记录。
+在实际应用中,我们所有的应用程序对文件的写入操作都是尽量采用数据追加方式,而不是覆盖方式。一种典型的应用,应用程序从头到尾写入数据,生成了一个文件。写入所有数据之后,应用程序自动将文件改名为一个永久保存的文件名,或者周期性的作Checkpoint,记录成功写入了多少数据。Checkpoint文件可以包含程序级别的校验和。Readers仅校验并处理上个Checkpoint之后产生的文件region,这些文件region的状态一定是已定义的。这个方法满足了我们一致性和并发处理的要求。追加写入比随机位置写入更加有效率,对应用程序的失败处理更具有弹性。Checkpoint可以让Writer以渐进的方式重新开始,并且可以防止Reader处理已经被成功写入,但是从应用程序的角度来看还并未完成的数据。
+我们再来分析另一种典型的应用。许多应用程序并行的追加数据到同一个文件,比如进行结果的合并或者是一个生产者-消费者队列。记录追加方式的“至少一次追加”的特性保证了Writer的输出。Readers使用下面的方法来处理偶然性的填充数据和重复内容。Writers在每条写入的记录中都包含了额外的信息,例如Checksum,用来验证它的有效性。Reader可以利用Checksum识别和抛弃额外的填充数据和记录片段。如果应用不能容忍偶尔的重复内容(比如,如果这些重复数据触发了非幂等操作),可以用记录的唯一标识符来过滤它们,这些唯一标识符通常用于命名程序中处理的实体对象,例如web文档。这些记录I/O功能 (alex注:These functionalities for record I/O) (除了剔除重复数据)都包含在我们的程序共享的库中,并且适用于Google内部的其它的文件接口实现。所以,相同序列的记录,加上一些偶尔出现的重复数据,都被分发到Reader了。
+我们在设计这个系统时,一个重要的原则是最小化所有操作和Master节点的交互。带着这样的设计理念,我们现在描述一下客户机、Master服务器和Chunk服务器如何进行交互,以实现数据修改操作、原子的记录追加操作以及快照功能。
+(alex注:lease是数据库中的一个术语)
+变更是一个会改变Chunk内容或者元数据的操作,比如写入操作或者记录追加操作。变更操作会在Chunk的所有副本上执行。我们使用租约(lease)机制来保持多个副本间变更顺序的一致性。Master节点为Chunk的一个副本建立一个租约,我们把这个副本叫做主Chunk。主Chunk对Chunk的所有更改操作进行序列化。所有的副本都遵从这个序列进行修改操作。因此,修改操作全局的顺序首先由Master节点选择的租约的顺序决定,然后由租约中主Chunk分配的序列号决定。
+设计租约机制的目的是为了最小化Master节点的管理负担。租约的初始超时设置为60秒。不过,只要Chunk被修改了,主Chunk就可以申请更长的租期,通常会得到Master节点的确认并收到租约延长的时间。这些租约延长请求和批准的信息通常都是附加在Master节点和Chunk服务器之间的心跳消息中来传递。有时Master节点会试图提前取消租约(例如,Master节点想取消在一个已经被改名的文件上的修改操作)。即使Master节点和主Chunk失去联系,它仍然可以安全地在旧的租约到期后和另外一个Chunk副本签订新的租约。
+在图中,依据步骤编号,展现写入操作的控制流程。
+ +如果应用程序一次写入的数据量很大,或者数据跨越了多个Chunk,GFS客户机代码会把它们分成多个写操作。这些操作都遵循前面描述的控制流程,但是可能会被其它客户机上同时进行的操作打断或者覆盖。因此,共享的文件region的尾部可能包含来自不同客户机的数据片段,尽管如此,由于这些分解后的写入操作在所有的副本上都以相同的顺序执行完成,Chunk的所有副本都是一致的。这使文件region处于2.7节描述的一致的、但是未定义的状态。
+为了提高网络效率,我们采取了把数据流和控制流分开的措施。在控制流从客户机到主Chunk、然后再到所有二级副本的同时,数据以管道的方式,顺序的沿着一个精心选择的Chunk服务器链推送。我们的目标是充分利用每台机器的带宽,避免网络瓶颈和高延时的连接,最小化推送所有数据的延时。
+为了充分利用每台机器的带宽,数据沿着一个Chunk服务器链顺序的推送,而不是以其它拓扑形式分散推送(例如,树型拓扑结构)。线性推送模式下,每台机器所有的出口带宽都用于以最快的速度传输数据,而不是在多个接受者之间分配带宽。
+为了尽可能的避免出现网络瓶颈和高延迟的链接(eg,inter-switch最有可能出现类似问题),每台机器都尽量的在网络拓扑中选择一台还没有接收到数据的、离自己最近的机器作为目标推送数据。假设客户机把数据从Chunk服务器S1推送到S4。它把数据推送到最近的Chunk服务器S1。S1把数据推送到S2,因为S2和S4中最接近的机器是S2。同样的,S2把数据传递给S3和S4之间更近的机器,依次类推推送下去。我们的网络拓扑非常简单,通过IP地址就可以计算出节点的“距离”。
+最后,我们利用基于TCP连接的、管道式数据推送方式来最小化延迟。Chunk服务器接收到数据后,马上开始向前推送。管道方式的数据推送对我们帮助很大,因为我们采用全双工的交换网络。接收到数据后立刻向前推送不会降低接收的速度。在没有网络拥塞的情况下,传送B字节的数据到R个副本的理想时间是 B/T+RL ,T是网络的吞吐量,L是在两台机器数据传输的延迟。通常情况下,我们的网络连接速度是100Mbps(T),L将远小于1ms。因此,1MB的数据在理想情况下80ms左右就能分发出去。
+GFS提供了一种原子的数据追加操作–记录追加。传统方式的写入操作,客户程序会指定数据写入的偏移量。对同一个region的并行写入操作不是串行的:region尾部可能会包含多个不同客户机写入的数据片段。使用记录追加,客户机只需要指定要写入的数据。GFS保证至少有一次原子的写入操作成功执行(即写入一个顺序的byte流),写入的数据追加到GFS指定的偏移位置上,之后GFS返回这个偏移量给客户机。这类似于在Unix操作系统编程环境中,对以O_APPEND模式打开的文件,多个并发写操作在没有竞态条件时的行为。
+记录追加在我们的分布应用中非常频繁的使用,在这些分布式应用中,通常有很多的客户机并行地对同一个文件追加写入数据。如果我们采用传统方式的文件写入操作,客户机需要额外的复杂、昂贵的同步机制,例如使用一个分布式的锁管理器。在我们的工作中,这样的文件通常用于多个生产者/单一消费者的队列系统,或者是合并了来自多个客户机的数据的结果文件。
+记录追加是一种修改操作,它也遵循3.1节描述的控制流程,除了在主Chunk有些额外的控制逻辑。客户机把数据推送给文件最后一个Chunk的所有副本,之后发送请求给主Chunk。主Chunk会检查这次记录追加操作是否会使Chunk超过最大尺寸(64MB)。如果超过了最大尺寸,主Chunk首先将当前Chunk填充到最大尺寸,之后通知所有二级副本做同样的操作,然后回复客户机要求其对下一个Chunk重新进行记录追加操作。(记录追加的数据大小严格控制在Chunk最大尺寸的1/4,这样即使在最坏情况下,数据碎片的数量仍然在可控的范围。)通常情况下追加的记录不超过Chunk的最大尺寸,主Chunk把数据追加到自己的副本内,然后通知二级副本把数据写在跟主Chunk一样的位置上,最后回复客户机操作成功。
+如果记录追加操作在任何一个副本上失败了,客户端就需要重新进行操作。重新进行记录追加的结果是,同一个Chunk的不同副本可能包含不同的数据–重复包含一个记录全部或者部分的数据。GFS并不保证Chunk的所有副本在字节级别是完全一致的。它只保证数据作为一个整体原子的被至少写入一次。这个特性可以通过简单观察推导出来:如果操作成功执行,数据一定已经写入到Chunk的所有副本的相同偏移位置上。这之后,所有的副本至少都到了记录尾部的长度,任何后续的记录都会追加到更大的偏移地址,或者是不同的Chunk上,即使其它的Chunk副本被Master节点选为了主Chunk。就我们的一致性保障模型而言,记录追加操作成功写入数据的region是已定义的(因此也是一致的),反之则是不一致的(因此也就是未定义的)。正如我们在2.7.2节讨论的,我们的程序可以处理不一致的区域。
+(alex注:这一节非常难以理解,总的来说依次讲述了什么是快照、快照使用的COW技术、快照如何不干扰当前操作)
+快照操作几乎可以瞬间完成对一个文件或者目录树(“源”)做一个拷贝,并且几乎不会对正在进行的其它操作造成任何干扰。我们的用户可以使用快照迅速的创建一个巨大的数据集的分支拷贝(而且经常是递归的拷贝拷贝),或者是在做实验性的数据操作之前,使用快照操作备份当前状态,这样之后就可以轻松的提交或者回滚到备份时的状态。
+就像AFS (alex注:AFS,即Andrew File System,一种分布式文件系统), 我们用标准的copy-on-write技术实现快照。当Master节点收到一个快照请求,它首先取消作快照的文件的所有Chunk的租约。这个措施保证了后续对这些Chunk的写操作都必须与Master交互交互以找到租约持有者。这就给Master节点一个率先创建Chunk的新拷贝的机会。
+租约取消或者过期之后,Master节点把这个操作以日志的方式记录到硬盘上。然后,Master节点通过复制源文件或者目录的元数据的方式,把这条日志记录的变化反映到保存在内存的状态中。新创建的快照文件和源文件指向完全相同的Chunk地址。
+在快照操作之后,当客户机第一次想写入数据到Chunk C,它首先会发送一个请求到Master节点查询当前的租约持有者。Master节点注意到Chunke C的引用计数超过了1 (alex注:不太明白为什么会大于1.难道是Snapshot没有释放引用计数?) 。Master节点不会马上回复客户机的请求,而是选择一个新的Chunk句柄C 。之后,Master节点要求每个拥有Chunk C当前副本的Chunk服务器创建一个叫做C的新Chunk。通过在源Chunk所在Chunk服务器上创建新的Chunk,我们确保数据在本地而不是通过网络复制(我们的硬盘比我们的100Mb以太网大约快3倍)。从这点来讲,请求的处理方式和任何其它Chunk没什么不同:Master节点确保新Chunk C`的一个副本拥有租约,之后回复客户机,客户机得到回复后就可以正常的写这个Chunk,而不必理会它是从一个已存在的Chunk克隆出来的。
+Master节点执行所有的名称空间操作。此外,它还管理着整个系统里所有Chunk的副本:它决定Chunk的存储位置,创建新Chunk和它的副本,协调各种各样的系统活动以保证Chunk被完全复制,在所有的Chunk服务器之间的进行负载均衡,回收不再使用的存储空间。
+Master节点的很多操作会花费很长的时间:比如,快照操作必须取消Chunk服务器上快照所涉及的所有的Chunk的租约。我们不希望在这些操作的运行时,延缓了其它的Master节点的操作。因此,我们允许多个操作同时进行,使用名称空间的region上的锁来保证执行的正确顺序。
+不同于许多传统文件系统,GFS没有针对每个目录实现能够列出目录下所有文件的数据结构。GFS也不支持文件或者目录的链接(即Unix术语中的硬链接或者符号链接)。在逻辑上,GFS的名称空间就是一个全路径和元数据映射关系的查找表。利用前缀压缩,这个表可以高效的存储在内存中。在存储名称空间的树型结构上,每个节点(绝对路径的文件名或绝对路径的目录名)都有一个关联的读写锁。
+每个Master节点的操作在开始之前都要获得一系列的锁。通常情况下,如果一个操作涉及/d1/d2/…/dn/leaf,那么操作首先要获得目录/d1,/d1/d2,…,/d1/d2/…/dn的读锁,以及/d1/d2/…/dn/leaf的读写锁。注意,根据操作的不同,leaf可以是一个文件,也可以是一个目录。
+我们演示一下在/home/user被快照到/save/user的时候,锁机制如何防止创建文件/home/user/foo。快照操作获取/home和/save的读取锁,以及/home/user和/save/user的写入锁。文件创建操作获得/home和/home/user的读取锁,以及/home/user/foo的写入锁。这两个操作要顺序执行,因为它们试图获取的/home/user的锁是相互冲突。文件创建操作不需要获取父目录的写入锁,因为这里没有”目录”,或者类似inode等用来禁止修改的数据结构。文件名的读取锁足以防止父目录被删除。
+采用这种锁方案的优点是支持对同一目录的并行操作。比如,可以在同一个目录下同时创建多个文件:每一个操作都获取一个目录名的上的读取锁和文件名上的写入锁。目录名的读取锁足以的防止目录被删除、改名以及被快照。文件名的写入锁序列化文件创建操作,确保不会多次创建同名的文件。
+因为名称空间可能有很多节点,读写锁采用惰性分配策略,在不再使用的时候立刻被删除。同样,锁的获取也要依据一个全局一致的顺序来避免死锁:首先按名称空间的层次排序,在同一个层次内按字典顺序排序。
+GFS集群是高度分布的多层布局结构,而不是平面结构。典型的拓扑结构是有数百个Chunk服务器安装在许多机架上。Chunk服务器被来自同一或者不同机架上的数百个客户机轮流访问。不同机架上的两台机器间的通讯可能跨越一个或多个网络交换机。另外,机架的出入带宽可能比机架内所有机器加和在一起的带宽要小。多层分布架构对数据的灵活性、可靠性以及可用性方面提出特有的挑战。
+Chunk副本位置选择的策略服务两大目标:最大化数据可靠性和可用性,最大化网络带宽利用率。为了实现这两个目的,仅仅是在多台机器上分别存储这些副本是不够的,这只能预防硬盘损坏或者机器失效带来的影响,以及最大化每台机器的网络带宽利用率。我们必须在多个机架间分布储存Chunk的副本。这保证Chunk的一些副本在整个机架被破坏或掉线(比如,共享资源,如电源或者网络交换机造成的问题)的情况下依然存在且保持可用状态。这还意味着在网络流量方面,尤其是针对Chunk的读操作,能够有效利用多个机架的整合带宽。另一方面,写操作必须和多个机架上的设备进行网络通信,但是这个代价是我们愿意付出的。
+Chunk的副本有三个用途:Chunk创建,重新复制和重新负载均衡。
+当Master节点创建一个Chunk时,它会选择在哪里放置初始的空的副本。Master节点会考虑几个因素。(1)我们希望在低于平均硬盘使用率的Chunk服务器上存储新的副本。这样的做法最终能够平衡Chunk服务器之间的硬盘使用率。(2)我们希望限制在每个Chunk服务器上”最近”的Chunk创建操作的次数。虽然创建操作本身是廉价的,但是创建操作也意味着随之会有大量的写入数据的操作,因为Chunk在Writer真正写入数据的时候才被创建,而在我们的”追加一次,读取多次”的工作模式下,Chunk一旦写入成功之后就会变为只读的了。(3)如上所述,我们希望把Chunk的副本分布在多个机架之间。
+当Chunk的有效副本数量少于用户指定的复制因数的时候,Master节点会重新复制它。这可能是由几个原因引起的:一个Chunk服务器不可用了,Chunk服务器报告它所存储的一个副本损坏了,Chunk服务器的一个磁盘因为错误不可用了,或者Chunk副本的复制因数提高了。每个需要被重新复制的Chunk都会根据几个因素进行排序。一个因素是Chunk现有副本数量和复制因数相差多少。例如,丢失两个副本的Chunk比丢失一个副本的Chunk有更高的优先级。另外,我们优先重新复制活跃(live)文件的Chunk而不是最近刚被删除的文件的Chunk(查看4.4节)。最后,为了最小化失效的Chunk对正在运行的应用程序的影响,我们提高会阻塞客户机程序处理流程的Chunk的优先级。
+Master节点选择优先级最高的Chunk,然后命令某个Chunk服务器直接从可用的副本”克隆”一个副本出来。选择新副本的位置的策略和创建时类似:平衡硬盘使用率、限制同一台Chunk服务器上的正在进行的克隆操作的数量、在机架间分布副本。为了防止克隆产生的网络流量大大超过客户机的流量,Master节点对整个集群和每个Chunk服务器上的同时进行的克隆操作的数量都进行了限制。另外,Chunk服务器通过调节它对源Chunk服务器读请求的频率来限制它用于克隆操作的带宽。
+最后,Master服务器周期性地对副本进行重新负载均衡:它检查当前的副本分布情况,然后移动副本以便更好的利用硬盘空间、更有效的进行负载均衡。而且在这个过程中,Master服务器逐渐的填满一个新的Chunk服务器,而不是在短时间内用新的Chunk填满它,以至于过载。新副本的存储位置选择策略和上面讨论的相同。另外,Master节点必须选择哪个副本要被移走。通常情况,Master节点移走那些剩余空间低于平均值的Chunk服务器上的副本,从而平衡系统整体的硬盘使用率。
+GFS在文件删除后不会立刻回收可用的物理空间。GFS空间回收采用惰性的策略,只在文件和Chunk级的常规垃圾收集时进行。我们发现这个方法使系统更简单、更可靠。
+当一个文件被应用程序删除时,Master节点像对待其它修改操作一样,立刻把删除操作以日志的方式记录下来。但是,Master节点并不马上回收资源,而是把文件名改为一个包含删除时间戳的、隐藏的名字。当Master节点对文件系统命名空间做常规扫描的时候,它会删除所有三天前的隐藏文件(这个时间间隔是可以设置的)。直到文件被真正删除,它们仍旧可以用新的特殊的名字读取,也可以通过把隐藏文件改名为正常显示的文件名的方式“反删除”。当隐藏文件被从名称空间中删除,Master服务器内存中保存的这个文件的相关元数据才会被删除。这也有效的切断了文件和它包含的所有Chunk的连接 (alex注:原文是This effectively severs its links to all its chunks) 。
+在对Chunk名字空间做类似的常规扫描时,Master节点找到孤儿Chunk(不被任何文件包含的Chunk)并删除它们的元数据。Chunk服务器在和Master节点交互的心跳信息中,报告它拥有的Chunk子集的信息,Master节点回复Chunk服务器哪些Chunk在Master节点保存的元数据中已经不存在了。Chunk服务器可以任意删除这些Chunk的副本。
+虽然分布式垃圾回收在编程语言领域是一个需要复杂的方案才能解决的难题,但是在GFS系统中是非常简单的。我们可以轻易的得到Chunk的所有引用:它们都只存储在Master服务器上的文件到块的映射表中。我们也可以很轻易的得到所有Chunk的副本:它们都以Linux文件的形式存储在Chunk服务器的指定目录下。所有Master节点不能识别的副本都是”垃圾”。
+垃圾回收在空间回收方面相比直接删除有几个优势。首先,对于组件失效是常态的大规模分布式系统,垃圾回收方式简单可靠。Chunk可能在某些Chunk服务器创建成功,某些Chunk服务器上创建失败,失败的副本处于无法被Master节点识别的状态。副本删除消息可能丢失,Master节点必须重新发送失败的删除消息,包括自身的和Chunk服务器的 (alex注:自身的指删除metadata的消息) 。垃圾回收提供了一致的、可靠的清除无用副本的方法。第二,垃圾回收把存储空间的回收操作合并到Master节点规律性的后台活动中,比如,例行扫描和与Chunk服务器握手等。因此,操作被批量的执行,开销会被分散。另外,垃圾回收在Master节点相对空闲的时候完成。这样Master节点就可以给那些需要快速反应的客户机请求提供更快捷的响应。第三,延缓存储空间回收为意外的、不可逆转的删除操作提供了安全保障。
+根据我们的使用经验,延迟回收空间的主要问题是,延迟回收会阻碍用户调优存储空间的使用,特别是当存储空间比较紧缺的时候。当应用程序重复创建和删除临时文件时,释放的存储空间不能马上重用。我们通过显式的再次删除一个已经被删除的文件的方式加速空间回收的速度。我们允许用户为命名空间的不同部分设定不同的复制和回收策略。例如,用户可以指定某些目录树下面的文件不做复制,删除的文件被即时的、不可恢复的从文件系统移除。
+当Chunk服务器失效时,Chunk的副本有可能因错失了一些修改操作而过期失效。Master节点保存了每个Chunk的版本号,用来区分当前的副本和过期副本。
+无论何时,只要Master节点和Chunk签订一个新的租约,它就增加Chunk的版本号,然后通知最新的副本。Master节点和这些副本都把新的版本号记录在它们持久化存储的状态信息中。这个动作发生在任何客户机得到通知以前,因此也是对这个Chunk开始写之前。如果某个副本所在的Chunk服务器正好处于失效状态,那么副本的版本号就不会被增加。Master节点在这个Chunk服务器重新启动,并且向Master节点报告它拥有的Chunk的集合以及相应的版本号的时候,就会检测出它包含过期的Chunk。如果Master节点看到一个比它记录的版本号更高的版本号,Master节点会认为它和Chunk服务器签订租约的操作失败了,因此会选择更高的版本号作为当前的版本号。
+Master节点在例行的垃圾回收过程中移除所有的过期失效副本。在此之前,Master节点在回复客户机的Chunk信息请求的时候,简单的认为那些过期的块根本就不存在。另外一重保障措施是,Master节点在通知客户机哪个Chunk服务器持有租约、或者指示Chunk服务器从哪个Chunk服务器进行克隆时,消息中都附带了Chunk的版本号。客户机或者Chunk服务器在执行操作时都会验证版本号以确保总是访问当前版本的数据。
+我们在设计GFS时遇到的最大挑战之一是如何处理频繁发生的组件失效。组件的数量和质量让这些问题出现的频率远远超过一般系统意外发生的频率:我们不能完全依赖机器的稳定性,也不能完全相信硬盘的可靠性。组件的失效可能造成系统不可用,更糟糕的是,还可能产生不完整的数据。我们讨论我们如何面对这些挑战,以及当组件失效不可避免的发生时,用GFS自带工具诊断系统故障。
+在GFS集群的数百个服务器之中,在任何给定的时间必定会有些服务器是不可用的。我们使用两条简单但是有效的策略保证整个系统的高可用性:快速恢复和复制。
+不管Master服务器和Chunk服务器是如何关闭的,它们都被设计为可以在数秒钟内恢复它们的状态并重新启动。事实上,我们并不区分正常关闭和异常关闭;通常,我们通过直接kill掉进程来关闭服务器。客户机和其它的服务器会感觉到系统有点颠簸 (alex注:a minor hiccup) ,正在发出的请求会超时,需要重新连接到重启后的服务器,然后重试这个请求。
+正如之前讨论的,每个Chunk都被复制到不同机架上的不同的Chunk服务器上。用户可以为文件命名空间的不同部分设定不同的复制级别。缺省是3。当有Chunk服务器离线了,或者通过Chksum校验(参考5.2节)发现了已经损坏的数据,Master节点通过克隆已有的副本保证每个Chunk都被完整复制 (alex注:即每个Chunk都有复制因子制定的个数个副本,缺省是3)。 虽然Chunk复制策略对我们非常有效,但是我们也在寻找其它形式的跨服务器的冗余解决方案,比如使用奇偶校验、或者Erasure codes (alex注:Erasure codes用来解决链接层中不相关的错误,以及网络拥塞和buffer限制造成的丢包错误) 来解决我们日益增长的只读存储需求。我们的系统主要的工作负载是追加方式的写入和读取操作,很少有随机的写入操作,因此,我们认为在我们这个高度解耦合的系统架构下实现这些复杂的冗余方案很有挑战性,但并非不可实现。
+为了保证Master服务器的可靠性,Master服务器的状态也要复制。Master服务器所有的操作日志和checkpoint文件都被复制到多台机器上。对Master服务器状态的修改操作能够提交成功的前提是,操作日志写入到Master服务器的备节点和本机的磁盘。简单说来,一个Master服务进程负责所有的修改操作,包括后台的服务,比如垃圾回收等改变系统内部状态活动。当它失效的时候,几乎可以立刻重新启动。如果Master进程所在的机器或者磁盘失效了,处于GFS系统外部的监控进程会在其它的存有完整操作日志的机器上启动一个新的Master进程。客户端使用规范的名字访问Master(比如gfs-test)节点,这个名字类似DNS别名,因此也就可以在Master进程转到别的机器上执行时,通过更改别名的实际指向访问新的Master节点。
+此外,GFS中还有些“影子”Master服务器,这些“影子”服务器在“主”Master服务器宕机的时候提供文件系统的只读访问。它们是影子,而不是镜像,所以它们的数据可能比“主”Master服务器更新要慢,通常是不到1秒。对于那些不经常改变的文件、或者那些允许获取的数据有少量过期的应用程序,“影子”Master服务器能够提高读取的效率。事实上,因为文件内容是从Chunk服务器上读取的,因此,应用程序不会发现过期的文件内容。在这个短暂的时间窗内,过期的可能是文件的元数据,比如目录的内容或者访问控制信息。
+“影子”Master服务器为了保持自身状态是最新的,它会读取一份当前正在进行的操作的日志副本,并且依照和主Master服务器完全相同的顺序来更改内部的数据结构。和主Master服务器一样,“影子”Master服务器在启动的时候也会从Chunk服务器轮询数据(之后定期拉数据),数据中包括了Chunk副本的位置信息;“影子”Master服务器也会定期和Chunk服务器“握手”来确定它们的状态。在主Master服务器因创建和删除副本导致副本位置信息更新时,“影子”Master服务器才和主Master服务器通信来更新自身状态。
+每个Chunk服务器都使用Checksum来检查保存的数据是否损坏。考虑到一个GFS集群通常都有好几百台机器、几千块硬盘,磁盘损坏导致数据在读写过程中损坏或者丢失是非常常见的(第7节讲了一个原因)。我们可以通过别的Chunk副本来解决数据损坏问题,但是跨越Chunk服务器比较副本来检查数据是否损坏很不实际。另外,GFS允许有歧义的副本存在:GFS修改操作的语义,特别是早先讨论过的原子纪录追加的操作,并不保证副本完全相同 (alex注:副本不是byte-wise完全一致的) 。因此,每个Chunk服务器必须独立维护Checksum来校验自己的副本的完整性。
+我们把每个Chunk都分成64KB大小的块。每个块都对应一个32位的Checksum。和其它元数据一样,Checksum与其它的用户数据是分开的,并且保存在内存和硬盘上,同时也记录操作日志。
+对于读操作来说,在把数据返回给客户端或者其它的Chunk服务器之前,Chunk服务器会校验读取操作涉及的范围内的块的Checksum。因此Chunk服务器不会把错误数据传递到其它的机器上。如果发生某个块的Checksum不正确,Chunk服务器返回给请求者一个错误信息,并且通知Master服务器这个错误。作为回应,请求者应当从其它副本读取数据,Master服务器也会从其它副本克隆数据进行恢复。当一个新的副本就绪后,Master服务器通知副本错误的Chunk服务器删掉错误的副本。
+Checksum对读操作的性能影响很小,可以基于几个原因来分析一下。因为大部分的读操作都至少要读取几个块,而我们只需要读取一小部分额外的相关数据进行校验。GFS客户端代码通过每次把读取操作都对齐在Checksum block的边界上,进一步减少了这些额外的读取操作的负面影响。另外,在Chunk服务器上,Chunksum的查找和比较不需要I/O操作,Checksum的计算可以和I/O操作同时进行。
+Checksum的计算针对在Chunk尾部的追加写入操作作了高度优化(与之对应的是覆盖现有数据的写入操作),因为这类操作在我们的工作中占了很大比例。我们只增量更新最后一个不完整的块的Checksum,并且用所有的追加来的新Checksum块来计算新的Checksum。即使是最后一个不完整的Checksum块已经损坏了,而且我们不能够马上检查出来,由于新的Checksum和已有数据不吻合,在下次对这个块进行读取操作的时候,会检查出数据已经损坏了。
+相比之下,如果写操作覆盖已经存在的一个范围内的Chunk,我们必须读取和校验被覆盖的第一个和最后一个块,然后再执行写操作;操作完成之后再重新计算和写入新的Checksum。如果我们不校验第一个和最后一个被写的块,那么新的Checksum可能会隐藏没有被覆盖区域内的数据错误。
+在Chunk服务器空闲的时候,它会扫描和校验每个不活动的Chunk的内容。这使得我们能够发现很少被读取的Chunk是否完整。一旦发现有Chunk的数据损坏,Master可以创建一个新的、正确的副本,然后把损坏的副本删除掉。这个机制也避免了非活动的、已损坏的Chunk欺骗Master节点,使Master节点认为它们已经有了足够多的副本了。
+详尽的、深入细节的诊断日志,在问题隔离、调试、以及性能分析等方面给我们带来无法估量的帮助,同时也只需要很小的开销。没有日志的帮助,我们很难理解短暂的、不重复的机器之间的消息交互。GFS的服务器会产生大量的日志,记录了大量关键的事件(比如,Chunk服务器启动和关闭)以及所有的RPC的请求和回复。这些诊断日志可以随意删除,对系统的正确运行不造成任何影响。然而,我们在存储空间允许的情况下会尽量的保存这些日志。
+RPC日志包含了网络上发生的所有请求和响应的详细记录,但是不包括读写的文件数据。通过匹配请求与回应,以及收集不同机器上的RPC日志记录,我们可以重演所有的消息交互来诊断问题。日志还用来跟踪负载测试和性能分析。
+日志对性能的影响很小(远小于它带来的好处),因为这些日志的写入方式是顺序的、异步的。最近发生的事件日志保存在内存中,可用于持续不断的在线监控。
+在建造和部署GFS的过程中,我们经历了各种各样的问题,有些是操作上的,有些是技术上的。
+起初,GFS被设想为我们的生产系统的后端文件系统。随着时间推移,在GFS的使用中逐步的增加了对研究和开发任务的支持。我们开始增加一些小的功能,比如权限和配额,到了现在,GFS已经初步支持了这些功能。虽然我们生产系统是严格受控的,但是用户层却不总是这样的。需要更多的基础架构来防止用户间的相互干扰。
+我们最大的问题是磁盘以及和Linux相关的问题。很多磁盘都声称它们支持某个范围内的Linux IDE硬盘驱动程序,但是实际应用中反映出来的情况却不是这样,它们只支持最新的驱动。因为协议版本很接近,所以大部分磁盘都可以用,但是偶尔也会有由于协议不匹配,导致驱动和内核对于驱动器的状态判断失误。这会导致数据因为内核中的问题意外的被破坏了。这个问题促使我们使用Checksum来校验数据,同时我们也修改内核来处理这些因为协议不匹配带来的问题。
+较早的时候,我们在使用Linux 2.2内核时遇到了些问题,主要是fsync()的效率问题。它的效率与文件的大小而不是文件修改部分的大小有关。这在我们的操作日志文件过大时给出了难题,尤其是在我们尚未实现Checkpoint的时候。我们费了很大的力气用同步写来解决这个问题,但是最后还是移植到了Linux2.4内核上。
+另一个和Linux相关的问题是单个读写锁的问题,也就是说,在某一个地址空间的任意一个线程都必须在从磁盘page in(读锁)的时候先hold住,或者在mmap()调用(写锁)的时候改写地址空间。我们发现即使我们的系统负载很轻的情况下也会有偶尔的超时,我们花费了很多的精力去查找资源的瓶颈或者硬件的问题。最后我们终于发现这个单个锁在磁盘线程交换以前映射的数据到磁盘的时候,锁住了当前的网络线程,阻止它把新数据映射到内存。由于我们的性能主要受限于网络接口,而不是内存copy的带宽,因此,我们用pread()替代mmap(),用了一个额外的copy动作来解决这个问题。
+尽管偶尔还是有其它的问题,Linux的开放源代码还是使我们能够快速探究和理解系统的行为。在适当的时候,我们会改进内核并且和公开源码组织共享这些改动。
+Google文件系统展示了一个使用普通硬件支持大规模数据处理的系统的特质。虽然一些设计要点都是针对我们的特殊的需要定制的,但是还是有很多特性适用于类似规模的和成本的数据处理任务。
+首先,我们根据我们当前的和可预期的将来的应用规模和技术环境来评估传统的文件系统的特性。我们的评估结果将我们引导到一个使用完全不同于传统的设计思路上。根据我们的设计思路,我们认为组件失效是常态而不是异常,针对采用追加方式(有可能是并发追加)写入、然后再读取(通常序列化读取)的大文件进行优化,以及扩展标准文件系统接口、放松接口限制来改进整个系统。
+我们系统通过持续监控,复制关键数据,快速和自动恢复提供灾难冗余。Chunk复制使得我们可以对Chunk服务器的失效进行容错。高频率的组件失效要求系统具备在线修复机制,能够周期性的、透明的修复损坏的数据,也能够第一时间重新建立丢失的副本。此外,我们使用Checksum在磁盘或者IDE子系统级别检测数据损坏,在这样磁盘数量惊人的大系统中,损坏率是相当高的。
+我们的设计保证了在有大量的并发读写操作时能够提供很高的合计吞吐量。我们通过分离控制流和数据流来实现这个目标,控制流在Master服务器处理,而数据流在Chunk服务器和客户端处理。当一般的操作涉及到Master服务器时,由于GFS选择的Chunk尺寸较大 (alex注:从而减小了元数据的大小), 以及通过Chunk Lease将控制权限移交给主副本,这些措施将Master服务器的负担降到最低。这使得一个简单、中心的Master不会成为成为瓶颈。我们相信我们对网络协议栈的优化可以提升当前对于每客户端的写入吞吐量限制。
+GFS成功的实现了我们对存储的需求,在Google内部,无论是作为研究和开发的存储平台,还是作为生产系统的数据处理平台,都得到了广泛的应用。它是我们持续创新和处理整个WEB范围内的难题的一个重要工具。
+存储系统是容错系统的基础构件
+如果可以建立一个持久的存储系统,应用程序不需要特殊对自己的状态进行保存,因为存储系统已经存好了,从而简化了应用程序的设计。
+因此存储系统本身必须有很高的容错性能,设计这个并不容易。
+因此形成了一个环,主要矛盾是一致性和性能之间的矛盾
+理想情况下的一致性:分布式系统与单机系统在表现上完全相同
+然而在实际情况下很难实现
+两个线程



此时




解决故障一般是通过使用复制数据到其他机器上的方式。
+一个很烂的服务器之间复制数据的方案:客户端写入数据的时候,同时向两个服务器写入数据,不需要服务器之间同步。
+此时两个线程



相当于一个分布式系统的案例研究,包括了高性能、复制和容错、一致性等等主题
+GFS是第一个在上千台计算机上构建的分布式系统,后续的HDFS等都受到了GFS的启发。
+两个非标准做法:
+关键属性
+如果中间过程有错误,客户端一般会重试,希望下一次可以正常运行(也就是最少一次)
+这可能会造成在一个磁盘中有两份数据的拷贝。会有id和checksum协助控制不会将相同的数据读取两次。
+一个服务器暂时挂掉了,导致版本号没有更新,同时一个客户端的版本号也是一个老版本号,结果正好匹配到了这个刚刚挂掉的服务器,最终导致读取的数据和期望的不同。
+通过租约机制确保只会存在一个primary服务器,不会产生“脑裂”现象
+获得强一致性?更新所有的除primary外的其他服务器或者全部都不更新,GFS没有实现这个。
+ + +MIT-6.824(Spring 2022)LEC 4 Primary-Backup Replication
+ +通过提供故障容错性的虚拟机,我们实现了一个商业化的企业级系统,建立在复制一个主虚拟机的执行过程到另一个服务器上的备份虚拟机的基础上。系统很容易使用,同时保证了应用的性能仅有少于10%的降低。另外,为了让主VM和二级VM的执行活动保持一致,对于几个实际的应用而言,需要的数据带宽少于20Mbit/s,这也允许实现更长距离的故障容错的可能性。一种容易使用,在故障后自动恢复备份的商业化系统,在复制VM执行之前需要额外的组件。我们已经设计并且实现了这些额外的组件,并且解决了在支持VM运行企业级应用的时候,遇到的许多实际问题。
+一个实现故障容忍服务器的常见方法是主备机制,主服务器失败的同时另外一个备份服务器立即进行接管,此时对于外部客户端而言,故障就相当于被隐藏了起来,并且不会造成数据丢失。因此在任何时间,备份服务器的状态必须和主服务器几乎保持一致,在备份服务器上复制状态的一种方法是将主服务器的所有状态,包括CPU、memory、IO设备,连续地送给备份服务器。然而,这种发送状态的方法,尤其是涉及到内存中的变更,其需要的带宽非常大。
+另一种可以用更少带宽复制服务器的方法类似于状态机。这种思路是将服务器建模为确定性的状态机,他们从相同的初始状态开始,并且确保以相同的顺序接收相同的输入请求,这样就能保持同步。因为大多数服务器或服务有一些不确定性的操作,因此必须使用额外的协调机制来确保主备同步。然而,需要保持主备一致性的额外信息数目,远远少于正在变更的主服务器上状态(主要是内存更新)的数目。
+实现协调机制来确保物理服务器的确定性操作是困难的,尤其随着处理器频率增长。反之,一个运行在管理程序(hypervisor)上的VM,是一个实现状态机方法的很好的平台。 一个VM可以被当作一个定义好的状态机,它的操作是机器被虚拟化的操作(包括它所有的设备) 。和物理服务器一样,VM有相同的非确定性操作(例如读取时钟或发送中断),因此为了保持同步,额外的信息必须被发送给备份服务器。管理程序(hypervisor)有VM的全权控制权利,包括处理所有输入,因此它能够获得所有与主VM上的非确定性操作有关的必要信息,并且能正确地重放这些操作。
+因此,这个状态机方法可以通过商业化软件上的VM来实现,它不需要硬件更改,允许在最新的微处理器上立刻实现故障容错。另外,状态机方法需要的低带宽允许了主备服务器能更好地进行物理分隔。例如,被复制的VM可以运行在横跨一个学校的物理机器上,相比于运行在同一建筑内的VM而言,可以提供更多的可靠性。
+我们在VMware vSphere 4.0平台上使用主备机制实现了故障容忍的VMs,VMware vSphere实现了一个完整的x86虚拟机,所以我们自动地能够为任何x86操作系统和应用提供故障容忍。这种允许我们记录一个主服务器执行,并确保备份服务器一致执行的基础技术是确定性重放。VMware vSphere Fault Tolerance(FT)是基于确定性重放(Deterministic Replay) 的,但是为了建立一个完整的故障容忍系统,还增加了必要的额外协议和功能。除了提供硬件故障容忍,我们的系统在一次失败后,通过在局部集群中任何可接受的服务器上开始一个新的备份虚拟机,进行自动地存储备份。目前确定性重放和VMare FT的产品版本只支持单处理器的VMs。多处理器VM的操作记录和重放还在开发中,因为每个共享内存的操作都是一个非确定性的操作,因此还有重要的性能问题待解决。
+Bressoud和Schneider描述了一个针对HP PA-RISC平台的故障容忍VMs的原型实现。我们的方法是相似的,但是出于性能原因,以及在调查了许多可替代设计后,我们已经做了一些基础性的改变。另外,为了建立一个完整的系统,而这个系统是有效的并且能够被正在运行企业级应用的客户使用,我们已经设计并实现了系统中许多额外的组件,可以处理许多实际问题。与大多数其他实际系统讨论的类似, 我们只尝试应付fail-stop的故障 ,这是一种服务器故障,可以在故障服务器造成一次不正确的外部可见行为之前被检测。( Hades注:fail-stop故障指的是,如果某些东西出现故障,只是单纯的停止运行,而不是运算出错误结果。比如电源线、服务器风扇导致CPU过热停止运行、网络等故障 )
+
图1展示了我们系统在故障容忍VMs的基本步骤。对于一个给定的VM,我们希望提供故障容忍(主VM),我们在一个完全不同的物理机器上运行一个备份VM,保持和主VM同步并且执行一致,虽然存在短时间的滞后。我们说这两个VMs是虚拟的步调一致。VMs的虚拟磁盘是在一个共享存储中的(例如一个Fibre Channel或者iSCSI磁盘阵列),因此可以接受主备服务器的输入和输出。(我们将在4.1节中讨论带有分隔的非共享虚拟磁盘的主备VM的设计)只有主VM会说明它在网络中的存在,因此所有网络输入都会来到主VM上。相似地,所有其他输入(例如键盘和鼠标)也只会来到主VM上。
+所有主VM接收到的输入都会通过名为logging channel的网络连接,被发送到备份VM上。对于几个工作负载而言,主要的输入途径是网络和磁盘。为了保证备份VM和主VM使用相同的方式执行非确定性操作,下面2.1节讨论的额外的信息也需要发送。最终备份VM总是执行和主VM一致的操作。然而,备份VM的输出会被管理程序扔掉,因此只有主VM产生实际输出,并被返回给客户端。和2.2节中描述的一样,为了确保主VM失败后没有数据丢失,主备VM遵循一个具体的协议,包括备份VM明确的确认信息。
+为了检测主或备份虚拟机是否失败,我们的系统既使用相关服务器间的心跳机制,同时也监测 logging channel 上的流量。另外,我们我们必须确保只有主或备份VM执行操作,即使存在脑裂(split brain)的场景(在这种场景中主备服务器互相之间会失去通信)。
+正如我们已经提到的,复制服务器(或者VM)的操作可以被建模为确定性状态机的复制。如果两个确定性的状态机以相同的初始状态开始,并且以相同的顺序提供确切的输入,它们将经历相同的状态序列并且产生相同的输出。一个虚拟机有很宽泛的输入,包括到来的网络包,磁盘读,以及来自键盘和鼠标的输入。非确定性事件(例如虚拟中断)和非确定性操作(例如处理器的时钟周期计数器)也会影响虚拟机的状态。这显示了对于正在运行任何操作系统和工作负载的任何虚拟机而言,复制执行有 三个挑战 :
+另外,许多在x86处理器上的复杂操作还未被定义,因此会引起非确定性以及副作用。捕获这些未定义的操作并且重放它们产生相同的状态是一个额外的挑战。
+针对在VMare vSphere平台上的x86虚拟机,VMware确定性地重放恰好提供了这个功能。确定性重放记录了 VM 的输入以及与 VM执行相关的所有可能的不确定性的日志条目流,这些条目会被写入日志文件。在读取日志文件中的条目后,VM 操作会被精确地重放。 对于非确定性操作,为了允许操作以相同的状态变化和输出再现,需要记录足够的信息。 对于非确定性事件,例如定时器或 IO 完成中断,事件发生的确切指令也会被记录下来。 在重播期间,事件被传递在指令流中的同一位置。 VMware 确定性重放采用各种技术,实现了高效的事件记录和事件传递机制,包括使用AMD和英特尔联合开发的硬件性能计数器。
+Bressoud 和 Schneider提到将VM执行切分成不同的epoch,其中非确定性事件,例如中断仅在一个epoch结束时传递。 epoch的概念似乎被用作批处理机制,因为在它发生的确切指令处单独传递每个中断的成本太高。然而,我们的事件传递机制足够高效,以至于 VMware确定性重放不需要使用epochs。 每次中断在发生时被记录,并且在重放时有效地传递到适当的指令处。
+对于 VMware FT而言,我们使用确定性重放来生成必要的日志条目来记录主VM的执行情况,但是不是将日志条目写入磁盘,而是通过日志通道将它们发送到备份VM。备份 VM 实时重放日志条目,因此与主 VM 的执行保持一致。 然而,我们必须在日志通道中使用严格的 FT 协议以增强日志条目,从而确保我们实现故障容忍。 我们的基本要求如下:
+输出要求 :如果备份VM在主VM发生故障后接管,那么备份VM将继续以一种与主虚拟机发送到外部世界的所有输出完全一致的方式执行。
+请注意,在发生故障转移后(即备份 VM 需要在主VM故障后接管),备份VM开始执行的方式可能与主 VM 相当不同,因为在执行期间发生了许多非确定性事件。但是,只要备份VM满足输出要求,在故障转移到备份 VM期间 没有外部可见状态或数据的丢失 ,客户端将注意到他们的服务没有中断或不一致。
+可以通过延迟任何外部输出(通常是网络数据包)直到备份VM 已收到重放的所有信息来确保输出要求,这些信息允许它至少执行到该输出操作的点。一个必要条件是备份 VM 必须接收到输出操作之前生成的所有日志条目。这些日志条目将允许它执行到最后一个日志条目的点。但是,假设失败是在主VM执行输出操作后立即发生。备份 VM 必须知道它必须继续重播到输出操作点,并且到那时只能“上线”(停止重播并作为主VM接管,如2.3 节所述)。如果备份将在输出操作之前的最后一个日志条目点上线,一些非确定性事件(例如计时器传递给 VM 的中断)可能会在执行输出操作之前改变其执行路径。
+给定上述的限制,强制满足输入要求的最容易的方式是在每个输出操作时创建一个特殊的日志条目。然后,输出要求一定被下面特殊的规则限制:
+输出规则 :主VM可能不发送一个输出到外部世界,直到备份VM已收到并确认与产生输出的操作相关的日志条目。
+如果备份 VM 已收到所有日志条目,包括生成输出操作的日志条目,然后备份 VM 将能够准确地重现主 VM在输出点的状态,所以如果主VM死了, 备份将正确地达到一个与输出一致的状态 。相反,如果备份VM在没有收到所有必要的日志条目的情况下接管,那么它的状态可能会 迅速分歧 ,以至于与主服务器的输出不一致。输出规则在某些方面类似于 [11] 中描述的方法,其中“外部同步” IO 实际上可以被缓存,只要它在下一次外部通信之前确实被写入磁盘了。
+请注意,输出规则没有说明关于停止主VM执行的任何事。我们只需要延迟输出发送,但 VM 本身可以继续执行。由于操作系统通过异步中断来指示完成,因此可以执行非阻塞的网络和磁盘输出,VM可以轻松地继续执行并且不一定会立即受到输出延迟的影响。相比之下,以前的工作 [3, 9] 通常必须在执行输出之前完全停止主VM,直到备份 VM 已确认来自主 VM 的所有必要信息。
+
作为一个例子,我们在图2中展示了 FT 协议的需求。该图显示了一个主VM和备份VM上的事件时间线。从主线到备份线的箭头表示日志条目的传输,从备份线路到主线路的箭头表示确认。有关异步事件、输入和输出操作的信息必须作为日志条目发送到备份VM并确认。如图所示,到外部世界的输出被延迟,直到主VM收到来自备份 VM 的确认,它已经收到与输出操作相关的日志条目。鉴于遵循输出规则,备份VM将能够以这样一种状态接管,即与主VM最后的输出一致。
+我们不能保证一旦出现故障转移情况,所有输出都准确地产生一次。当主VM打算发送输出时, 没有使用两阶段提交事务 ,备份VM无法确定主VM是在发送它的最后一个输出之前还是之后立即崩溃。 幸运的是,网络基础设施(包括常用的TCP)旨在处理丢失的数据包和相同(重复)的数据包 。 请注意传入到主VM的数据包也可能在其故障的期间丢失,因此不会被传递给备份VM。 但是,传入的数据包可能会由于与服务器故障无关的任何原因被丢弃,因此网络基础设施、操作系统和应用程序都被写入,以确保他们可以弥补丢失的数据包。
+如上所述,如果另一个 VM 出现故障,主备VMs必须快速响应。如果备份VM出现故障,主VM将上线,即离开记录模式(因此停止发送条目到日志通道)并开始正常执行。如果主VM失败,备份VM应该同样上线(go live),但过程更为复杂。由于其执行的滞后,备份 VM 可能会有许多它已收到并确认,但尚未消耗的日志条目,因为备份 VM 尚未达到执行的适当点。 备份VM必须继续重放日志条目,直到它消耗了最后一个日志条目 。此时,备份 VM 将停止重放模式并开始作为正常VM执行。本质上备份VM被提升为主VM(现在缺少备份VM)。由于它不再是备份 VM,当操作系统执行输出操作时,新的主VM现在将向外部世界生产输出。在过渡到正常模式期间,可能会有一些特定设备的操作需要允许正确地发送输出。特别是, 出于联网目的,VMware FT 自动在网络上通告新的主VM的MAC 地址,以便物理网络交换机知道新的主 VM 所在的服务器 。此外,新提升的主VM可能需要重做一些磁盘 IO(如第 3.4 节所述)。
+有许多可能的方法来尝试检测主备VMs的故障。VMware FT在运行容错VMs的服务器之间使用 UDP心跳 ,来检测服务器何时崩溃。此外,VMware FT 监控日志流量,包括从主到备的发送以及从备到主的确认。因为定时器中断,日志流量应该是有规律的,并且永远不会停止。因此,在日志条目或确认流中的中断可能表明VM故障。如果心跳或记录流量已停止超过特定超时时间(大约几秒钟),就可能发生故障了。
+但是,任何此类故障检测方法都容易受到脑裂(split brain)问题的影响 。如果备份服务器停止接收来自主服务器的心跳,这可能表明主服务器出现故障,或者可能只是意味着所有仍在运行的服务器之间的网络连接丢失。如果备份VM随后上线,而主VM也仍然在运行,对于与VM通信的客户端而言可能会有数据损坏以及其他问题。因此,我们必须确保当检测到故障时,主VM和备份VM只有一个在线。为了避免脑裂问题,我们利用共享存储,来存储VM的虚拟磁盘。 当任一主或备份VM想要上线时,它会在共享存储中执行一个原子性的测试设置操作 。 如果操作成功,VM 被允许上线。 如果操作失败,那么另一个 VM 一定已经上线,所以当前虚拟机实际上停止了自己(“自杀”)。 如果尝试执行此原子操作时,VM 无法访问共享存储,然后它只是等待,直到可以访问。 注意如果由于存储网络上的某些故障而无法访问共享存储时,那么虚拟机可能无法做有用的工作,因为虚拟磁盘在同样的共享存储中,因此,为了解决脑裂问题而使用共享存储不会引入任何额外的不可接受性。( Hades注:使用共享存储这种解决方案本身使得主备又得以通信了,只不过是通过信号量,而非socket。 )
+这个设计的一个最终方面是一旦故障发生并且一个VM已经上线,VMware FT自动地通过在另一个主机上开始一个新的备份VM,来恢复备份。虽然这个过程不能覆盖过去大部分的工作,但是对于故障容忍的VM有用,它是基础,需要仔细设计。
+第二节描述了我们基础的设计以及FT协议。然而,为了创建一个有用的、健壮的以及自动化的系统,有许多其他组件必须设计实现。
+一个必须被设计的最大的额外组件是这种机制,即 启动一个拥有和主VM状态一样的备份VM 。当故障发生后重启一个备份VM时,这个机制也将变得很有用。因此,这个机制一定可用于一个处于任意状态的正在运行中的主VM。此外,我们希望该机制不会显著地中断主VM的执行,因为这会影响 VM 的任何当前客户端。
+对于 VMware FT而言,我们调整了VMware vSphere上现有的 VMotion 功能。 VMware VMotion [10] 允许以最少中断的方式,将正在运行的 VM 从一台服务器迁移到另一台服务器,VM的暂停时间通常不到一秒钟。我们创建了一个VMotion的修改形式,可在远程服务器上创建准确的 VM 运行副本,但不会破坏本地服务器的虚拟机。也就是说,我们修改后的 FT VMotion 将VM克隆到远程主机上而不是迁移它。 FT VMotion还设置了一个日志记录通道,并导致源VM作为主VM进入日志记录模式,而目的VM 作为备份进入重放模式。像平常的VMotion一样,FT VMotion 通常会中断主VM的执行不到一秒。因此,启用 FT在正在运行的 VM 上是一个简单的、无中断的操作。
+启动备份 VM 的另一个方面是选择一个运行它的服务器。容错 VM 在服务器集群中运行,可以访问共享存储,因此所有 VM通常可以运行在集群上的任何服务器中。这种灵活性允许VMware vSphere恢复FT冗余,即使一个或多个服务器失效。 VMware vSphere 实现了一种集群服务,用于维护管理以及资源信息 。 当发生故障并且主VM 现在需要一个新的备份 VM 来重新建立冗余时,主 VM 通知集群服务它需要一个新的备份。 集群服务基于资源利用率以及其他约束,决定运行备份VM最好的服务器,并调用 FT VMotion 以创建新的备份 VM。 结果是 VMware FT通常可以在几分钟内重新建立VM冗余,在一个故障容忍VM的执行上,所有这些都没有任何明显的中断。
+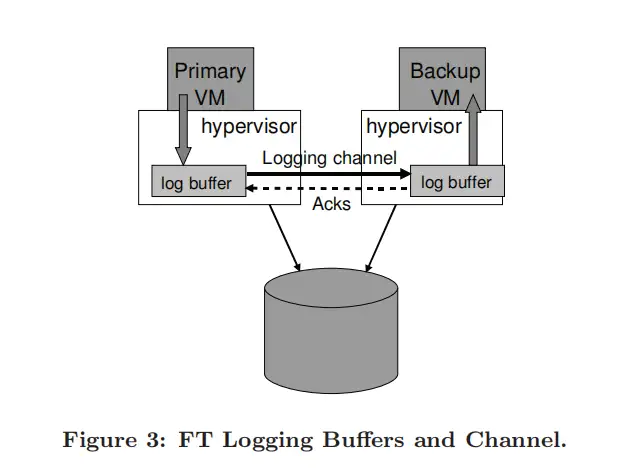
在管理日志通道上的流量时,有许多有趣的实现细节。在我们的实现中,管理程序为主备 VM 的日志记录条目维持了一个大的 缓冲区 。当主 VM 执行时,它生成日志条目到缓冲区中,类似地,备份VM从它的日志缓冲区中消耗日志条目。主日志缓冲区的内容会被尽快刷新到日志记录通道,这些日志条目一到日志通道,就会被读取到备份的日志缓冲区。备份每次从网络上读取一些日志条目到它的日志缓冲区时,都会发送确认返回给主VM。这些确认允许 VMware FT 确定一个被输入规则延迟的输出何时可以被发送。图3说明了这个过程。
+如果备份 VM 在需要读取下一个日志条目时,遇到空的日志缓冲区,它将停止执行直到有新的日志条目可用。由于备份 VM 是不与外部通信的,此暂停不会影响任何VM 的客户端。同样地,当主VM需要写入一个日志条目时,如果主VM遇到一个完整的日志缓冲区,它必须停止执行,直到可以刷新日志条目。这种执行的停止是一种自然的流控制机制,当主VM生产日志条目太快了,它会减慢主VM。但是,此暂停可能会影响VM的客户端,因为主 VM 将完全停止并且无响应,直到它可以记录其条目并继续执行。因此,我们的实现必须设计为尽量减少主日志缓冲区填满的可能性。
+主日志缓冲区可能填满的原因之一是备份 VM 执行速度太慢,因此消耗日志条目太慢。 一般来说,备份VM必须能够以与正在记录执行的主VM大致相同的速度重放执行 。幸运的是,在 VMware 确定性重放中,记录和重放的开销大致相同。然而,如果由于其他VMs,托管备份 VM 的服务器负载很重(因此过度使用资源),备份VM 可能无法获得足够的 CPU 和内存资源,来与主 VM 一样快地执行,尽管备份管理程序的VM调度器已经尽了最大努力。
+如果日志缓冲区填满,除了避免意外暂停,还有另一个原因是我们不希望滞后变得太大。如果主VM出现故障,备份VM必须通过重放它在上线和开始与外部世界交流之前已经确认的所有日志条目来“赶上”。完成重放的时间基本上是失败点的执行延迟时间,所以 备份上线的时间大约等于故障检测时间加上当前执行时差 。因此,我们不希望执行滞后时间太大(超过一秒),因为这将显著地增加故障转移时间。
+因此,我们有一个额外的机制减慢主VM,以防止备份 VM 获取太滞后了。在我们的发送和确认日志条目的协议中,我们发送附加信息来确定主备VM之间的实时执行滞后。通常执行滞后小于 100 毫秒。 如果备份 VM 有一个显著的执行滞后(例如,超过 1 秒),VMware FT 通过通知调度程序给它稍微少一点的CPU(最初只是百分之几)来减慢主 VM 。我们使用一个缓慢的反馈循环,这将尝试逐步确定适当的 CPU 限制,将允许主备 VM同步执行。如果备份 VM 继续滞后,我们继续逐步降低主VM的 CPU 限制。反之,如果备份VM赶上,我们逐渐增加主VM的 CPU 限制,直到备份虚拟机恢复轻微的滞后。
+请注意,主VM的这种减速很少见,通常只在系统处于低压力时发生。第 5 节的所有性能编号包括任何此类放缓的成本。
+另一个实际问题是处理各种控制操作,它们可以应用于主 VM 。例如,如果主VM明确关闭电源,备份 VM 也应该停止,而不是尝试上线。 再举一个例子,任何主VM上的资源管理更改(例如增加 CPU 份额)应该 也适用于备份。 对于此类操作,为了影响备份进行合适的操作,特殊的控制条目通过日志通道从主发送到备份。
+一般来说,VM 上的大部分操作都应该仅在主 VM 上初始化。 VMware FT 然后发送任何必要的控制条目以造成备份VM上适当的更改。 唯一可以独立在主VM和备份VM上完成的操作是 VMotion。 那即,主VM和备份VM可以独立被 VMotioned到其他主机。 请注意,VMware FT 确保两个 VM 都不会移动到另一个 VM 所在的服务器,因为这种场景将不再提供故障容忍。
+主VM的VMotion增加了比普通VM更多的复杂性,因为备份VM一定会与源主VM失去连接以及在适当的时间重连。备份VM的VMotion有一个相似的问题,但是只增加了一个额外的复杂性。对于一个正常的VMotion而言,我们需要当VMotion上最后的切换发生时,所有的磁盘IO停止(或完成)。对于一个主VM而言,这种停顿是容易应付的,通过等待直到物理IO完成并将这些完成信息发送给VM。然而,对于一个备份VM而言,没有容易的方式来使得所有IO在任何需要的时刻完成,因为备用VM必须重放主VM的执行过程,并在相同的执行点完成IO。主VM可能正运行在一个工作负载上,在正常执行过程中总是有磁盘IO。VMware FT有一个独一无二的方法来解决这个问题。当一个备份VM是在VMotion最后的切换点时,它需要通过日志通道来告知主VM临时停止所有IO。备份VM的IO将自然地被停止在一个单独的执行点,因为它需要重放主VM的停止操作的过程。
+有许多与磁盘IO相关的微小的实现问题。首先,假设磁盘操作是非阻塞的,因此访问相同磁盘位置的并行、同时执行的磁盘操作将引起非确定性。此外,我们的磁盘 IO 实现使用DMA 直接from/to虚拟机的内存,所以同时访问相同内存页的磁盘操作也可能导致不确定性。我们的解决方案是 经常检测任何此类 IO 竞争 (很少见),以及强制此类竞争磁盘操作在主备VM上按顺序执行。
+第二,通过 VM 中的应用程序(或操作系统)时,磁盘操作与内存访问也会存在竞争,因为磁盘操作通过 DMA 直接访问 VM 的内存。例如,如果一个VM 中的应用程序/操作系统正在读取内存块,同时对该块进行磁盘读取。( Hades注:这里的意思应该是,该块内存作为DMA操作的目的地址。 )这个情况也不太可能发生,但如果它发生,我们必须检测它并处理它。一种解决方案是临时设置页保护,在作为磁盘操作目标的页面上。如果VM 碰巧访问一个页,同时该页面也是磁盘操作的目标,页保护将导致一个陷阱( Hades注:trap,陷入系统调用 ),VM将暂停直到磁盘操作完成。 因为改变页上的MMU 保护是一项昂贵的操作,所以我们选择使用 弹跳缓冲区(Bounce Buffer) 代替 。bounce buffer是临时缓冲区,与正在被磁盘操作访问的内存大小相同。磁盘读取操作被修改为读取指定数据到bounce buffer,并在在IO完成时将数据复制到内存中。相似地,对于磁盘写操作,首先将要发送的数据复制到bounce buffer,磁盘写入修改为向bounce buffer写入数据。bounce buffer的使用会减慢磁盘操作,但我们还没有看到它会导致任何明显的性能损失。( Hades注:bounce buffer存在的意义是在内存访问这个操作之前加了一个拦截器,其最本质的意义是为了supervisor监控DMA操作,使得数据从bounce buffer拷贝到到内存和系统中断这两个步骤,能够同时在backup VM上被复制, 否则网卡直接将网络数据包DMA到Primary虚机中这个操作是无法通过log channel进行复制的 。 )
+第三,有一些与故障发生并且备份VM接管时,主VM未完成的磁盘 IO 相关的问题。对于新上线的主VM,没有办法确定磁盘IO是有问题的还是成功完成了。另外,由于磁盘IO没有从外部发布到备用VM上,而是通过主备传递,因此对于继续运行的新上任的主VM来说,将没有明确的IO完成信息,最终将导致VM上的操作系统开始中止或者重调度程序。我们能够发送一个错误完成,表示每个IO失败,因为即使IO成功完成了,它可以接受返回一个错误。然而,操作系统可能不能对这些来自本地磁盘的错误有很好的响应。反之,我们在备份VM上线的过程中,重新发送这些悬挂着的IO。因为我们已经限制了所有的竞争和所有的直接指定内存和磁盘的IO,这些磁盘操作可以被重新发送,即使它们已经成功完成了(即他们是幂等的)。
+VMware vSphere针对VM网络提供了很多性能优化。一些优化是基于管理程序(supervisor) 异步更新虚拟机的网络设备状态 。例如,当VM正在执行时,接收缓冲区可以由管理程序直接更新。不幸的是这些对 VM 状态的 异步更新会增加不确定性 。除非我们可以保证所有更新都发生在主备指令流上的同一点,否则备份VM的执行可能与主VM的执行不同。
+对于FT而言,网络仿真代码的最大变化是禁用异步网络优化。异步更新带有传入数据包的VM环形缓冲区的代码已被修改,以强制管理程序捕获到操作系统,它可以在其中记录更新然后将它们应用到 VM。同样,异步地将数据包从传输队列中拉出也被修改了,取而代之的是通过管理程序traps来完成传输(如下所述)。
+网络设备异步更新的消除结合第 2.2 节中描述的发送数据包的延迟带来了一些网络性能的挑战。我们采取了两种方法在运行 FT 时提高 VM 的网络性能。第一,我们实施了集群优化以减少 VM 的陷阱和中断。当 VM 以足够的比特率流式传输数据时,管理程序可以对每组数据包做一个传输trap,在最好的情况下零trap,因为它可以传输所接收新数据包的一部分数据包。同样地,通过仅对于一组数据包发布中断,管理程序可以将接收包的中断数量减少。
+我们对网络的第二个性能优化涉及 减少传输数据包的延迟 。如前所述,管理程序必须延迟所有发送的包直到它得到备份VM对于某些日志条目的确认。减少发送延迟的关键在于减少发送/接收备份VM信息的所需时间。我们的主要优化包括 保证收发信息在无需任何线程上下文切换的情形下就可以被执行 。VMware vSphere管理程序允许函数被注册到TCP栈中,只要TCP数据被接收到了,函数就会被一个延期执行的上下文调用(和Linux中的tasklet类似)。这允许我们快速处理备份VM上任何即将到来的日志消息,以及主VM接收的任何确认消息,而不需要任何线程上下文的切换。另外,当主VM有一个包要寄出去时,我们强制一次相关输出日志条目的日志刷出(正如2.2节中所描述的),通过调度一个延迟执行的上下文来执行这次刷出。
+在我们VMware FT的实现中,我们已经探索了许多有趣的替代设计。在这节中,我们探索一些替代设计。
+在我们默认的设计中,主备VM共享相同的虚拟磁盘。因此,如果一次故障转移发生,共享磁盘的内容自然是正确、可接受的。必要地,对于主备VM来说,共享磁盘被认为是外部的,因此任何共享磁盘的写入被认为是一次与外部世界的沟通。因此,只有主VM做这种实际的磁盘写入,并且为了遵循输出规则,这种写入必须被延迟。
+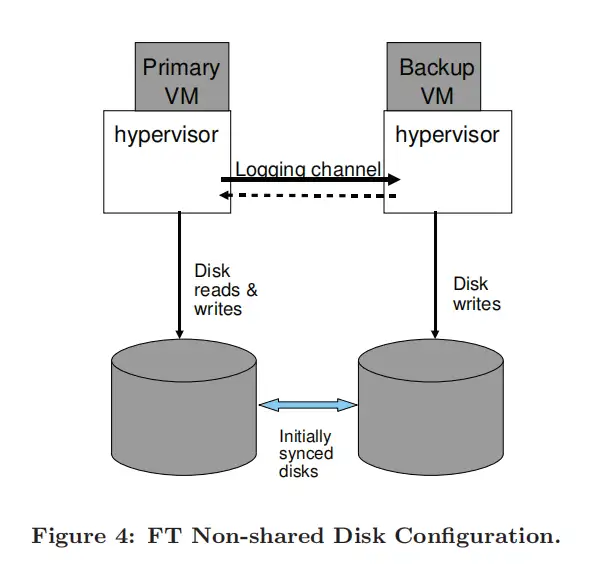
对于主备VM而言,一种可替代的选择是分隔的虚拟磁盘。在这种设计中,备份VM要执行所有虚拟磁盘的写入操作。而且这样做的话自然要保持它的虚拟磁盘内容与主VM虚拟磁盘内容一致。图4阐述了这种配置。在非共享磁盘的情况下,虚拟磁盘必须被认为是每个VM的内部状态。因此,依据输出规则, 主VM的磁盘写入不必延迟 。在共享存储不能被主备VM接受的情况下,非共享的设计是相当有用的。这种情况可能是由于共享存储不可接受或者太昂贵,或者由于运行主备VM的服务器相隔太远(“长距离FT”)。非共享设计的一个缺点是在首次启动故障容错时,虚拟磁盘的两个复制必须以相同的方式进行显示同步。另外,发生故障后磁盘 可能会不同步 ,因此当在一次失败后备份VM重启的时候,他们必须再显式地同步。FT VMotion必须不止同步主备VM的运行状态,还要同步他们的磁盘状态。
+在这种非共享磁盘的配置中,他们也能应付脑裂场景。在这种场景中,系统能够 使用一些其他的外部决策者 ,例如所有服务器可以沟通的一个第三方服务。如果服务器是超过两个节点的集群的一部分,这个系统能够基于集群关系使用一种majority算法。在这个例子中,一个VM能够被允许上线,如果它正在一个服务器上运行,这个服务器是包含大多数原始节点的正在通信的子集群的一部分。
+在我们默认的设计中,备份的VM从不会从它自己的虚拟磁盘上读取(无论共享还是非共享)。 因为磁盘读取被认为是一个输入 ,它是自然地通过日志通道将磁盘读取的结果发送到备份VM上。
+一种替代的设计是 让备份VM执行磁盘读取 ,因此消除了磁盘读取的日志。对于大多数时候都做磁盘读取的工作负载而言,这种方法可以很好地降低日志通道上的流量。然而,这种方法有很多小问题。它可能会减慢备份VM的执行速度,因为备份VM必须执行所有的磁盘读取,当到达VM执行中主VM已经完成的位置时,如果备份上的磁盘读取还没完成就必须等待。
+同样地, 为了处理失败的磁盘读取操作,必须做一些额外的工作 。如果一个主VM的磁盘读取成功了,但是相应的备份VM磁盘读取失败了,备份VM的磁盘读取必须重试直到成功。因为备份VM必须获得和主VM一样的数据到内存中。相反地,如果一个主VM的磁盘读取失败了,目标内存的内容必须通过日志通道发送给备份服务器,因此内存的内容将被破坏,不能被备份VM成功的磁盘读取复制。
+最后,如果这种磁盘读取被用于共享磁盘配置的话,还有一个小问题。如果主VM做了一次对具体磁盘位置的读取,然后紧跟相同磁盘位置的写入,然后这个磁盘写必须被延迟到备份VM已经执行了第一次磁盘读取。这种依赖可以被检测和正确处理,但是需要增加实现上额外的复杂性。
+在5.1节中,对于实际的应用而言,我们给出一些性能结果以表示在备份VM上执行磁盘读取会造成一些轻微的吞吐量减少(1-4%),因此在日志通道的带宽被限制的情况下,在备份VM上执行磁盘读取可能是有用的。
+在这节中,我们做了一次VMware FT性能的基础评估,针对许多应用负载以及网络基准。为了得到这些结果,我们在一样的服务器上运行主备VM,每个都带9个Intel Xeon 2.8Ghz CPUs and 8Gbytes of RAM。服务器间通过10 Gbit/s的交换机连接,但是在所有的例子中都能看到被使用的网络带宽远远少于1Gbit/s。从一个通过标准的4Gbit/s的光纤通道网络连接的EMC Clariion中,服务器可以连接他们的共享虚拟磁盘。客户端通过1 Gbit/s的网络来驱动一些连接服务器的工作负载。
+我们评估性能结果的应用如下所示。SPECJbb2005是工业标准的Java应用基准,非常耗费CPU和内存,但是IO非常少。Kernel Compile是一种运行Linux核编译的工作负载。由于许多编译过程的创建和毁灭,这个工作负载做很多磁盘读取和写入,是非常耗费CPU和MMU的。Oracle Swingbench是被Swingbench OLTP工作负载(在线事务处理)驱动的一个Oracle 11g的数据库。这个工作负载做连续的磁盘和网络IO,有80个同时在线的数据库会话。MS-SQL DVD Store是一种工作负载,运行了一个Microsoft SQL Server 2005的数据库,有60个同时在线的客户端。
+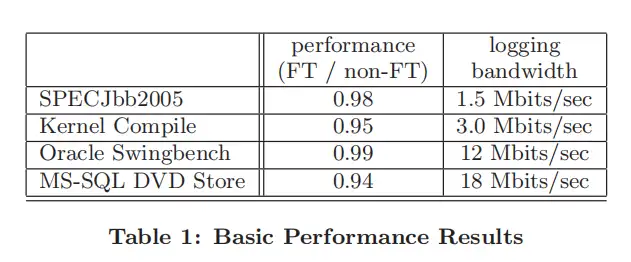
表 1 列出了基本的性能结果。对于每个应用程序,第二列给出了应用程序的性能比例,运行服务器工作负载的虚拟机上启用和未启用FT的情况。性能比小于 1 表示带FT的工作负载更慢。显然,这些有代表性的工作负载上启用FT 的开销小于10%。 SPECJbb2005 完全受计算限制,没有空闲时间,但其表现性能良好,因为它具有最小的除定时器中断以外的不确定性事件。另一个工作负载做磁盘 IO 有一些空闲时间,所以一些FT 开销可能被 FT虚拟机的空闲时间更少的真实情况隐藏。然而,一般的结论是VMware FT 能够支持故障容忍VM,并且具备相当低的性能开销。
+在表的第三列中,我们给出了当应用程序正在运行时,在日志通道上发送数据的平均带宽。对于这些应用程序,日志带宽相当合理,1 Gbit/s的网络就能满足 。事实上,低带宽要求表明多个 FT 工作负载可以共享相同的 1 Gbit/s网络,同时没有任何负面的性能影响。
+对于运行常见操作系统的 VM,例如Linux 和 Windows,我们发现当操作系统空闲时,通常的日志记录带宽为 0.5-1.5 Mbits/sec。"空闲"带宽主要是记录定时器中断发送的结果。对于具有活动中工作负载的 VM而言,日志带宽由网络和必须发送到备份的磁盘输入主导—网络收到的数据包和从磁盘读取的磁盘块。因此,对于非常高的网络接收或者磁盘读取带宽的应用而言,日志带宽高于表1中的测量值。对于这类应用而言,日志通道的带宽可能是瓶颈,特别是日志通道还有其他使用时。
+对于许多实际应用程序而言, 日志记录所需的带宽相对较低,这使得基于重放的故障容忍对于使用非共享磁盘的长距离配置非常有吸引力 。对于远距离配置而言,其主备VM可能相隔1-100公里,光纤可以轻松地支持延迟小于 10 毫秒的100-1000 Mbit/s带宽。对于表 1 中的应用而言,主备之间的额外往返延迟,可能会导致网络和磁盘输出最多延迟 20 毫秒。远距离配置仅适用于这类应用程序:他的客户端可以容忍每个请求的额外延迟。
+对于两个最占用磁盘空间的应用程序,我们测量了在备份 VM上执行磁盘读取(如第 4.2 节所述)与通过日志记录通道发送磁盘读取数据相比,对于性能的影响。对于 Oracle Swingbench来说,在备份VM上执行磁盘读取时的吞吐量降低约 4%;对于 MS-SQL DVD 存储,吞吐量约降低 1%。同时,Oracle Swingbench的日志带宽从 12 Mbits/sec 降低到 3 Mbits/sec,MS-SQL DVD 存储从 18 Mbits/sec 降低到 8 Mbits/sec。显然,对于具有更大磁盘读取带宽的应用程序,带宽可能会节省很多。如第 4.2 节所述,预计在备份 VM 上执行磁盘读取时,性能可能会更差。但是,对于日志通道的带宽是有限的(例如,远程配置)情况下,在备份 VM 上执行磁盘读取可能有用。
+出于多种原因。网络基准测试对我们的系统来说非常具有挑战性。第一,高速网络会有一个非常高的中断率,这需要以非常高的速度记录和重放异步事件。 第二,以高速率接收数据包的基准将导致高速率的日志流量,因为所有这些数据包必须通过日志通道发送到备份。第三,发送数据包的基准测试将受制于输出规则,延迟网络数据包的发送直到已收到来自备份VM的确认。 此延迟会增加对客户端测量的延迟。这种延迟还可能会降低到客户端的网络带宽,因为网络协议(如 TCP)由于往返延迟增加,可能不得不降低网络传输速率。
+
表 2 给出了我们通过标准的netperf 基准测试,多次测量的结果。在所有这些测量中,客户端 VM 和主 VM 通过 1 Gbit/s 网络连接。前两行给出了主备主机间通过1 Gbit/s 的日志通道连接时,发送和接收的性能。第三行和第四行给出当主备服务器通过10 Gbit/s的日志通道连接时,发送和接收的性能,不仅带宽更高,延迟也低于 1 Gbit/s。作为一个粗略的测量,在1 Gbit/s 网络连接的管理程序之间, ping 时间约为 150 微秒,而对于 10 Gbit/s 连接,ping时间大约需要 90 微秒。
+未启用 FT 时,主 VM 对于接收和发送,可以实现接近 (940 Mbit/s) 1 Gbit/s 的线路传输速率。当为接收工作负载启用 FT 时,日志记录带宽非常大,因为所有传入的网络数据包必须在日志通道上发送。因此,日志记录通道可能成为瓶颈,正如1 Gbit/s 日志网络的结果。对于 10 Gbit/s 的日志网络,影响则小了很多。当为上传工作负载启用 FT 时,上传数据包的数据不会记录,但仍必须记录网络中断。日志带宽要低得多,因此可实现的网络上传带宽高于网络接收带宽。 总的来说,我们看到 FT 在非常高的上传和接收速率情况下,可以显著地限制网络带宽,但仍然可以实现很高的速率 。
+我们在VMware vSphere 中设计并实施了一个高效完整的系统(FT) ,用于为服务器上运行的虚拟机提供容错。我们的设计基于复制主VM中的执行,再通过另一台主机上的备份VM执行VMware确定性重放。如果运行主 VM的服务器出现故障,备份 VM 能立即接管且不会中断或丢失数据。
+总体而言,在商业硬件上运行VMware FT时,故障容错VM的性能非常出色,并且对于某些典型应用程序,其开销低于 10%。大多数 VMware FT 的性能成本来自于使用 VMware 确定性重放来保持主备VM同步。因此,VMware FT 的低开销源自 VMware 确定性重放的效率。此外,保持主备同步所需的日志带宽非常小,通常小于 20 Mbit/s。因为日志带宽在大多数情况下很小,主备相隔很长的距离(1-100公里)似乎也是可行的实施配置。因此,VMware FT 可用于这种场景:可以防止整个站点发生故障的灾难。值得注意的是,日志流通常是可压缩的,因此简单的压缩技术可以显著地减少日志带宽,虽然有少量额外的 CPU 开销。
+我们对 VMware FT 的结果表明, 一个高效的故障容错VM的实现可以建立在确定性重放的基础上 。 这样的系统可以透明地为运行任何操作系统和应用的虚拟机提供容错能力,仅会带来极小的开销 。然而,对客户有用的故障容错VM系统而言,它必须还具有强大、易于使用和高度自动化的特点。一个可用的系统除了复制虚拟机执行之外,还需要许多其他组件。特别是VMware FT 故障后自动地恢复冗余,通过在本地集群中找到合适的服务器并在其上创建一个新的备份VM。通过解决所有必要的问题,我们已经展示了一个在客户的数据中心可用于实际应用的系统。
+通过确定性重放实现容错的权衡之一是当前确定性重放仅针对单处理器VM 。然而,单处理器虚拟机足够应付各种各样的工作负载,特别是因为物理处理器不断变得更加强大。此外,许多工作负载可以通过使用许多单处理器的虚拟机来扩展,而不是通过使用一个更大的多处理器虚拟机来扩展。多处理器 VM 的高性能重放是一种活跃的研究领域,并且可以潜在地被微处理器中的一些额外硬件支持。一个有趣的方向可能是扩展事务内存模型以促进多处理器重放。
+将来,我们也有兴趣扩展我们的系统处理部分硬件故障。通过部分硬件故障,我们的意思是服务器上功能或冗余的部分丢失,不会导致损坏或丢失数据。一个例子是到 VM所有网络连接的丢失,或在物理服务器中备用电源丢失。如果在运行主 VM 的服务器上发生部分硬件故障,在许多情况下(但不是all) 故障转移到备份 VM 将是有利的。这样的故障转移对于关键VM而言,可以立即恢复完整服务,并确保虚拟机从可能不可靠的服务器上快速地移走。
+我们希望复制方案可以处理的故障:
+如果发生了故障,主机器真的挂掉了吗?
+在分布式系统中,没有办法区分网络分区和机器故障的区别,因此很有可能主机器并没有挂掉,有一些客户端还能访问主机器,但是从机器和主机器之间的网络有问题,无法互相访问到,所以从机器认为主机器已经挂掉了。因此不能有两个主机器同时存在的情况,也就是脑裂问题。
+如何保持主从同步?
+如果主机器挂了,从机器要从主机器挂掉的地方直接开始,这就意味着从机器的状态与主机器的状态相同,都是最新的。从客户端的角度感知不到这种变化。
+非常困难:
+两种方法都是目前流行的方法,状态转移的缺点是如果一个操作生成了很多状态,这个传输的数据量非常大,因此如果只发送操作过去就很轻松。
+应用级别:文件追加写入,需要在应用程序上进行修改
+机器级别:寄存器指令级别的复制,只有x86指令,不涉及应用程序方面的更改,可以使用虚拟机实现,从而不用再硬件级别上实现。
+利用虚拟化技术,使得复制操作对应用程序是透明的,应用程序认为仅有一台服务器,并且也同时提供了很强的一致性。
+虚拟机监控器(hypervisor):在实际硬件上运行,虚拟出多个虚拟的硬件
+任何我们看到的外部事件实际上都经过了hypervisor,例如一个外部中断,hypervisor会先观察到并决定什么时候传递给虚拟机
+多个hypervisor之间通过logging channel进行通信,从而进行操作的精确复制
+ +storage server可以对谁当主机器进行仲裁
+如果主机器和从机器不能相互通信,但是都能看到storage server,两台机器都会进行test-and-set操作,比较早的那一个就会成为主机器。
+目标:多台虚拟机对外表现为单一的机器
+问题:差异来源导致两台机器表现不一样
+非确定性指令:
+确定性指令不需要通过logging channel进行通信
+中断发生后,会传递给从机器中断发生的前一个指令号,但是从机器并不会马上去执行,而是缓存下来,等到下一条中断指令传递过来之后,再执行前一条指令。这样会落后一条指令
+在机器启动之前会遍历全部的指令,确保浏览到全部的非确定性指令,不会直接执行,而会交给hypervisor进行控制。hypervisor执行的时候会额外记录下这些指令操作后的对应结果。传递的时候会同时对结果进行传递,这样从机器不需要真正去执行,直接修改结果就可以。
+指令级别的复制会付出性能的代价
+论文的实验表明带宽会降低大概30%左右,由于主机器接收来自客户端的输入,然后传递给从机器,这个过程中主机器必须等待,才能将响应传递给客户端。
+因此状态机复制的方法并不常用的原因之一是性能会下降。
+ + +操作系统面试题准备
+ +并发是指宏观上在一段时间内能同时运行多个程序,而并行则指同一时刻能运行多个指令。
+并行需要硬件支持,如多流水线、多核处理器或者分布式计算系统。
+操作系统通过引入进程和线程,使得程序能够并发运行。
+共享是指系统中的资源可以被多个并发进程共同使用。
+有两种共享方式:互斥共享和同时共享。
+互斥共享的资源称为临界资源,例如打印机等,在同一时刻只允许一个进程访问,需要用同步机制来实现互斥访问。
+虚拟技术把一个物理实体转换为多个逻辑实体。
+主要有两种虚拟技术:时(时间)分复用技术和空(空间)分复用技术。
+多个进程能在同一个处理器上并发执行使用了时分复用技术,让每个进程轮流占用处理器,每次只执行一小个时间片并快速切换。
+虚拟内存使用了空分复用技术,它将物理内存抽象为地址空间,每个进程都有各自的地址空间。地址空间的页被映射到物理内存,地址空间的页并不需要全部在物理内存中,当使用到一个没有在物理内存的页时,执行页面置换算法,将该页置换到内存中。
+异步指进程不是一次性执行完毕,而是走走停停,以不可知的速度向前推进。
+宏内核是将操作系统功能作为一个紧密结合的整体放到内核。
+由于各模块共享信息,因此有很高的性能。
+由于操作系统不断复杂,因此将一部分操作系统功能移出内核,从而降低内核的复杂性。移出的部分根据分层的原则划分成若干服务,相互独立。
+在微内核结构下,操作系统被划分成小的、定义良好的模块,只有微内核这一个模块运行在内核态,其余模块运行在用户态。
+因为需要频繁地在用户态和核心态之间进行切换,所以会有一定的性能损失。
+外中断:由 CPU 执行指令以外的事件引起,如 I/O 完成中断,表示设备输入/输出处理已经完成,处理器能够发送下一个输入/输出请求。此外还有时钟中断、控制台中断等。
+异常:由 CPU 执行指令的内部事件引起,如非法操作码、地址越界、算术溢出等。
+陷入:在用户程序中使用系统调用。
+当进程执行用户自己的代码时,则该进程处于用户态。用户态运行的进程可以直接读取用户程序的数据,但是,这时cpu访问资源受限。
+内核态(kernel mode):当进程执行系统内核代码时,则该进程处于内核态。系统态运行的进程或程序几乎可以访问计算机的任何资源,不受限制,这时cpu可以访问计算机的所有资源
+用户态进程通过系统调用申请使用系统态级别的资源,并由操作系统程序代为完成。
+在运行的用户态程序中,凡是与系统态级别的资源有关的操作(如文件管理、进程控制、内存管理等),都必须通过系统调用方式向操作系统提出服务请求,并由操作系统代为完成*。
+当外围设备接收到用户请求后,会向CPU发出相应的中断信号,这时CPU会暂停执行下一条即将要执行的指令,转而去执行与中断信号对应的处理程序,如果先前执行的指令是用户态程序,那么这个转换的过程自然也就发生了由用户态到内核态的切换。比如需要进行硬盘读写操作时,系统会切换到硬盘读写的中断处理程序
+当CPU在执行用户态程序时,发生了某些事先不可知的异常,这时会触发由当前运行进程切换到处理此异常的内核相关程序中,也就转到了内核态,比如缺页异常。
+研一上学期闭卷三科目考试重点
+ +25道选择题,5道大题(简答题与计算题结合在一起)
+非监督学习:不考死记硬背的概念,看一下作业题的例子,比如给一些具体样本分布的图,如果使用KMeans聚类会怎么样,Kmeans的判别界面应该是一个中垂线,两个簇的中垂线,如果不是大小均匀的球体可能KMeans就不适合,如果是有疏有密的,一个椭球形的,是不是考虑基于混合高斯的模型,或者簇是一个不规则的形状,比如是字母S或者C型,甚至有的簇是一个同心圆的,最适合的聚类算法应该是什么样的,可以考虑一下基于密度的聚类是不是可以,基于密度的聚类有没有不适合的情况,包括基于层次聚类会遇到什么问题,结合一些实际的例子请大家分析一下。
+降维:PCA每年都考,可能和前面讲K-L变换的知识结合起来,比如PCA为什么要先做零均值的平移,特征值的选择,为什么先做倒序的排序,选排在前面的特征值最大的几个特征值对应的特征向量来构成对应的变换核,基本原理希望掌握。后面的非线性降维,核PCA的主要思想是什么,先升维再降维,基于流形的非线性降维方法,说出一些经典方法的名字就行,不可能考太细。(前面讲了一些降维,这里不可能考大题,可以看看Fisher线性判别怎么做降维,选择最佳投影方向等等)
+半监督学习:半监督学习是基于一些假设的,最基本的假设有哪些,不同的半监督算法各自基于什么假设?比如半监督的SVM应该是基于低密度分割的假设,半监督SVM里面有一些比较关键的参数,C1,C2等等,分别表达什么意思,C2很小表达对未标注样本错分的容忍度比较大,很大表示不容忍错分,每一个未标注样本也要分对,但是所有的样本都必须要严格分对这种也可能有问题,过拟合等等,过拟合怎么办呢?可以把模型参数调简单点,怎么让模型参数调简单?不同的模型方法不一样,比如半监督SVM就可以把C2调小一点,或者把C1调小也行,如果是神经网络可以让结构简单一点,层数和节点变少参数就变少,欠拟合怎么办,如何让模型变复杂,除了从模型参数上调,增加数据样本是不是一定有用?
+概率图模型每年都会有大题,要么是考贝叶斯球判断条件独立性,或者大题问维特比解码,一般只考前向的推导。
+集成学习只考经典的bagging和boosting两种,其他的不考,考的时候从基本原理出发,比如bagging的基本原理是降低方差,但是不能改变偏差,boosting主要是降低偏差,考的时候可能会给实际的例子去判断哪种更适用,比如模型的单个基学习器都是偏差比较高的情况,要把多个集成起来增加学习能力,到底是用boosting还是bagging,如果选择boosting,不同的基学习器的权重是完全一样的吗,谁的权重大,或者是boosting作迭代训练的时候,训练样本每一次的权重在迭代的时候是不是都要改变,为什么要让分错的样本权重更大,分对的样本下一次权重就调小,要知道这些基本的调节权重的原则。
+人工神经网络只考基本原理和卷积神经网络,可能让你设计一个人工神经网络的结构,和前面几章的内容有结合,比如线性分类器,非线性分类器,两类分类的,多类分类的,都怎么来设计,能画出大概的结构,写出能用什么(激励?)函数就可以。卷积神经网络主要是考察基本原理,比如为什么卷积神经网络能够进一步降低(深度,参数量?)但是又不会降低性能。可能是基于局部连接和参数重用,池化等等技术,这几个技术的基本的动机是什么,是因为有一些很有判别力的局部模式,他是之前局部出现,并且能够在不同的位置出现,还有有的时候下采样也不会影响这种局部模式的识别。可能会问一些深度神经网络训练的时候遇到一些问题怎么解决,比如说层数很深的时候,会遇到梯度消失、梯度爆炸的问题,遇到问题怎么办呢,激活函数从sigmoid换成relu为什么这样能解决这个问题,比如说使用batch normalization也可以缓解梯度消失的问题,甚至还能带来一些正则化的效果,或者是残差网络的技术,将前层的信息引入进来,可能还带有一些集成学习的思想,把这些基本的原理说清楚。人工神经网络的训练可能也会遇到过拟合,模型的参数可能就过于复杂,除了简化模型的结构之外,还有什么其他的技术,比如是不是可以考虑添加正则化项,正则化也分为L1和L2,L1正则能让系数=0也能做特征选择,L2可以让参数趋向于变小,对整体的影响就变小了,相当于参数变简单了,也能防止过拟合,包括做数据增强,增加训练样本集尽可能让他多样化,也是可以增加模型的泛化能力,还有做梯度下降的时候收敛速度变慢怎么办,陷入局部极值点怎么办,一般是这种实际一些的问题
+不考:
+势函数、决策树、贝叶斯参数估计、后向算法、马尔科夫随机场、SMO、拉普拉斯平滑
+没有证明题,但是会有一点公式推导
+EM算法不作为重点考察,最多知道概念是拿来干什么的就行,是对含有隐含变量的模型做优化,不会考很细节的
+零碎考点:
+判别器有讲过贝叶斯风险,是每年都会考的,感知器算法、朴素贝叶斯、Fisher判别分析,都有可能考到的,K-L变换作特征提取或者后面的PCA,还有像LR,SVM,还有线性回归,另外就是机器学习一般的概念,过拟合、欠拟合应该怎么办,怎么判断模型处于哪种状态,正则的概念,可能放到多种模型中,都要能理解。
+降维需要掌握的知识点:PCA是怎么做的,Fisher判别分析要会
+Fisher判别分析是要考的但是不考计算,除了两类也要看一下多类的
+深度学习有一道大题,偏简答性质的
+HMM有计算题,判断独立性是选择题
+概率图掌握贝叶斯球就可以,概率的分布表示还是要的
+多类LR不需要特别掌握,知道有这回事就行,比如用softmax函数做最后一层就可以
+多类分类问题在SVM或者LR可以转化为两两的分类问题,算术题,转成多少个需要知道
+支持向量考的挺多的,给一个图,哪些点是支持向量,或者自己画图
+偏差方差分解具体的证明不考,但是要知道泛化误差是三部分,会判断模型什么时候偏差比较大,什么时候方差比较大,应该怎么办
+高斯判别分析今年没有大题,Fisher判别分析多看看
+SVM软间隔硬间隔都会有
+一般对线性回归、LR、SVM公式推导方面严一点,比如损失函数是怎么推导来的,极大似然估计是怎么回事,MAP估计是怎么样,这些基本概念需要掌握,SVM的模型推导可能少一些。SVM更多理解margin、支持向量、不同的C的影响等等、核函数,RBF核模型复杂度的参数是核函数的宽度,多项式核模型复杂度还有多项式的项数。
+类内类间散度矩阵应该怎么算是要求掌握的,与Fisher是什么关系,但是不会考察具体的数值计算
+多类感知器不考,感知器是有的
+PCA没有计算,需要知道PCA的计算过程,另外目的和达到的效果也需要知道。首先要减均值,然后再算协方差矩阵作矩阵分解,或者是作SVD分解都可以,测试的过程也一样,目的是去掉各个维度之间的相关性
+bagging知道功效和怎么做就行,是多个模型做平均,目的是偏差不变,降低模型的方差,boosting是降低模型的偏差,方差不变
+聚类:比如像K均值,GMM,DBSCAN这三类聚类方法需要掌握他的特点,我们什么时候用哪种方法来做,选择题
+降维:今年考的不是很多,稍微看一看就行
+半监督学习:不会考的特别细,但是半监督学习是基于一些假设的,最基本的假设有哪些,不同的半监督算法各自基于什么假设?
+概率图模型一方面考对于有向图模型,判断给定观测到某些节点的情况下,这个变量和那个变量是否独立,可以通过贝叶斯球的方式做,需要记忆贝叶斯球的规则,根据一个图模型把联合分布写出来,HMM要求掌握前向算法求观测概率和利用维特比算法求给定一个观测后最可能的隐含状态的序列
+集成学习主要是bagging和boosting,要知道bagging的原理是通过对训练样本进行bootstrap采样,然后训练多个模型,最后对多个模型作平均,得到最后的融合模型。它的好处是可以降低模型的方差,偏差不变。boosting对于Adaboost的过程,比如一开始初始化的时候每个样本的权重相同,经过一轮迭代之后哪些样本的权重会增加,哪些样本的权重会减小,最后模型是怎么融合的,没有计算题,知道Adabooost的过程就可以。对于boosting一般的原理也要知道,每次迭代顺序的把一些模型加进去,最后一些子模型的加权平均是我们最后的集成模型,boosting的好处是降低模型的偏差,方差不变。
+深度学习:知道神经元的结构(线性组合+激活函数),一个神经元可以起到一个什么样的作用,神经网络是把神经元组合起来,卷积神经网络为什么要局部连接,为什么要权重共享,这样做的基于对数据的假设是什么,局部连接我们认为是一个模式在一个比较小的范围内,而不是要看全局,权值共享是说不同位置可能都有这样的模式,这样做可以使得模型的参数变少,另外多层感知器很多层并不能带来性能提升,现在的模型采用哪些技术使得训练深度模型成为可能?比如说激活函数,sigmoid容易梯度消失,使用relu使得梯度消失的问题会减弱,这样网络层数可以更深,另外batch normalization会使得我们的训练会和好多因素(学习率、初始化)的要求没有那么高,这样也是一种技术,另外采用预训练网络作初始化也是一种方式,或者核初始化等等,也可以让模型的层数更深。另外Resnet,或者叫skip-connect,通过跳接的方式使得梯度消失的问题能减弱,使得模型可以很深很深甚至上千层。神经网络设计的时候也讲了一些其他的技术。不要求全部掌握,至少知道几点。为什么要用mini-batch的梯度下降,随机的梯度下降,有什么样的好处或者特点等等。
+第一章:模式识别和机器学习我们并不是很区分它们,可以看成一个问题的两个方面
+第二章:统计判别,主要是讲了错误率最小,错误率最小对应到分类问题等价于后验概率最大,后验概率怎么算需要大家一定掌握,后面也把风险带进来
+第三章:判别函数,作判别的时候一种方式可以使用生成式分类器,高斯分布的贝叶斯分类器采用的实际上是生成式分类器,指的是我们的联合分布可以由先验和似然相乘得到,有了联合分布可以从联合分布进行采样从而得到新的数据,也就是我们知道数据的产生过程,因此叫做生成式分类器。朴素贝叶斯,高斯判别分析,概率图模型,HMM都属于生成式分类器。好处是因为我们对数据的产生过程有比较强的假设,如果我们的数据符合这个假设,通常用很少量的数据就能得到很好的模型,或者说收敛的比较快,缺点是如果数据不符合这个假设,模型的性能就很不好。另外是判别式分类器,就是直接对后验概率进行建模,或者是定义一个判别函数,根据判别函数的值判断是哪一个类别。像逻辑斯蒂回归,决策树,SVM,深度学习都是判别式的。
+线性判别函数如何将多类分类任务转化成两类分类任务或者是直接用多类分类任务去做。线性判别函数处理的都是线性可分的问题,如果不是线性可分的需要用广义的线性判别函数,或者是分段线性判别函数实现。模式空间和权空间只是一些基本概念。重点掌握Fisher线性判别,协方差矩阵、类内类间,向量等都是怎么定义的,Fisher线性判别的准则是什么,都需要掌握,两类的情况,多类的情况,大家都去想想,感知器算法需要重点掌握,它是线性判别函数,只能在线性可分的时候可以使用,感知器多类也需要大家掌握。
+第四章:特征选择是很重要的内容,但是不作为重点考察。特征提取重点掌握K-L变换,比较简单,实际也比较有用,PCA实际上和K-L变换就是一回事。需要知道K-L变换的目的和过程,做了K-L变换之后能达到一个什么样的效果。
+第五章:期望风险:在没有见过的数据上的误差,也就是期望风险。结构风险:正则项,L1正则和L2正则,泛化误差的分解,证明过程不要求,结论要知道,用VC维计算泛化误差的上界,基本概念比较多
+第六章:线性回归的损失函数,目标函数包括两部分,L1损失或者L2损失,负log似然损失,需要掌握似然是怎么定义的,由负log似然损失怎么推到了L2损失,L2损失的问题是对噪声比较敏感,因为是平方的关系,预测差距比较大的时候损失也比较大,可以采用L1损失,但是是不连续的,因此一般采用Huber损失,实际上是L1损失和L2损失的分段的情况。正则可以是L1正则或者L2正则,目的是为了限制模型的复杂度,L2会使得w的绝对值会缩小,也叫权重缩减,但是一般不为0。L1会为0,可以起到特征选择的作用。然后讲了逻辑斯蒂回归,是一个分类问题,直接计算后验概率,多类分类需要softmax函数,损失也是负log似然,只是称为交叉熵损失,推导的时候都是从负log似然推导过来的。然后生成式分类器,高斯判别分析和朴素贝叶斯,两种分类器的先验是相同的,两类是伯努利分布,多类是多项式分布,两者不同的地方是类条件的定义不一样,高斯是在给定类别的条件下是高斯分布,朴素贝叶斯是独立的,
+第七章:SVM,考察的重点,需要掌握线性的SVM,核化的SVM,回归了解一下就行,首先要知道间隔的概念,硬间隔和软间隔的目标函数分别是什么,可以写成损失+正则的情况,合页损失+正则,什么样的样本是支持向量,了解原问题和对偶问题,核化也是很重要的,后面的PCA,包括逻辑斯蒂回归都可以核化,但是模型比较复杂,大家用的比较少,线性核,多项式核的复杂度体现在基数,RBF核的复杂度是核函数的宽度,软间隔的复杂度还有松弛因子C,概念需要掌握
+第八章:聚类:重点掌握K均值,GMM,DBSCAN,知道聚类的过程,对什么样的数据比较适合,K均值每一个类的都是高斯,方差相同等等,GMM更宽泛,不球形,DBSCAN不要求每一类的具体形式,找密度最大的作为中心,还可以处理带有噪声的情况。
+第九章降维:PCA就是K-L变换,目标是重构误差最小,MDS不作重点考察,非线性降维知道一些常用的非线性降维方法的做法就可以了
+第十章半监督学习:重点掌握三种基本假设,半监督学习算法了解就行,想一下每一种算法的背后是基于哪些假设在做
+第十一章概率图模型,考试时候主要是考察有向的图模型,无向图模型了解一下就行,给定一个概率图模型,能不能写出概率分布来,根据有向图模型,判断给定观测到某些节点的情况下,这个变量和那个变量是否独立,可以通过贝叶斯球的方式做,需要记忆贝叶斯球的规则,缺失的边实际上也蕴含了独立的关系,HMM要求掌握前向算法求观测概率和利用维特比算法求给定一个观测后最可能的隐含状态的序列。HMM的模型参数学习,全监督的用极大似然估计,隐含状态不知道用EM算法。
+第十二章集成学习主要是bagging和boosting,要知道bagging的原理是通过对训练样本进行bootstrap采样,然后训练多个模型,最后对多个模型作平均或者投票,得到最后的融合模型。可以并行训练,它的好处是可以降低模型的方差,偏差不变。基学习器的选择可以选方差比较大的模型。比如随机森林里面选取的决策树就是选层数比较深或者叶子节点比较多的。或者多个神经网络进行。boosting是多个基学习器采用顺序的方式进行训练,不能并行训练,每一个新加入的学习器希望能纠正前面的学习器的一些错误,实现的时候每个基学习器都是一样的,融合的方式是加权平均,权重和每个基学习器是相关的。boosting的好处是降低模型的偏差,方差不变。因此基学习器可以比较简单,决策树就树比较浅。重点考察Adaboost的过程,需要掌握。
+第十三章深度学习:知道神经元的结构(多个输入线性组合+激活函数得到输出),与人类神经元比较像,线性回归实际上也可以用一个神经元来表示,相当于激活函数是一个线性的激活函数(恒等映射函数)。逻辑斯蒂回归就相当于一个神经元+sigmoid函数,SVM也可以写成这样的形式。多层叠加就可以实现非常复杂的非线性函数的拟合。80年代层数不深,当时的训练方法有一些问题,sigmoid或者tanh会产生梯度消失的问题,relu可以解决梯度消失,计算简单。梯度消失是梯度传几层就没了,一个原因是激活函数,另外的原因是乘很多次,也会没了。神经网络之间的连接方式:全连接,每一个神经元都和其他的神经元相连。为了简化,图像可以采用卷积神经网络,通常只是局部连接,为什么要局部连接,因为图像里面一些局部的输入就可以判断模式的存在。为什么要权重共享,权值共享是说不同位置可能都有这样的模式,这样做可以使得模型的参数变少,计算量并不会减少。数据不满足这种特点不能使用卷积做。另外多层感知器很多层并不能带来性能提升,现在的模型采用哪些技术使得训练深度模型成为可能?Resnet,或者叫skip-connect,通过跳接的方式使得梯度消失的问题能减弱,使得模型可以很深很深甚至上千层。另外batch normalization相当于做一个标准化,使得输入的范围的差异不至于这么大。相当于在神经网络里面增加了一个层,学习这个层的参数。会使得模型训练更快更稳定,性能更好。dropout使得某些输出是0,不往下传,相当于集成学习的高效的实现方式,主要使用在全连接层里面。另外讲了一些神经网络的训练技巧,基本算法是梯度下降,梯度爆炸就是乘多了很大很大,梯度的计算首先是利用网络结构进行反向传播,批处理梯度下降是所有的样本一起,算一次很慢,一般不采用,随机梯度下降是每一个只选取一个样本,比较快,但是受单个样本的影响比较大。梯度的方向可能是锯齿的形状。通常使用小批量梯度下降,两者取中间。走一步的步长叫做学习率,下降的方法不一定是梯度,因为鞍点可能不动,平滑的区域也不怎么动,因此考虑动量法,进行自适应调整。参数初始化也比较重要。另外关于抗过拟合的问题,每一层的节点很多,模型就非常复杂,需要抗过拟合。及早停止,监控验证集上的误差,正则,数据增广,收集更多的训练样本,但是收集样本需要费用,可以采用一些图像处理的方法。还有dropout。
+非线性降维基本掌握流程就行
+大题没有画模型结构图
+RNN不作为重点考察内容
+极大似然:给一个应用场景,写似然的式子,概率分布都写的,无非是取一个log然后对所有的样本求和
+SVM二维计算量不大,侧重于概念,考了很多选择题
+考试不涉及求矩阵的逆、特征值的具体计算
+没有问概念的简答题
+选择题重点:过拟合欠拟合、偏差方差、概率图、深度学习等等
+MAP的概念需要知道,大题里面没有
+LDA需要知道
+K-L变换需要掌握过程,能达到什么目的,但是没有数值计算
+逻辑斯蒂回归需要知道正则,损失函数的推导,实际上是负log似然,关于似然的计算,这个过程需要大家知道。
+极大似然或贝叶斯求参数今年没有
+线性回归逻辑斯蒂回归损失函数的推导需要掌握,+正则
+Adaboost知道过程就行
+核函数表示两个样本的相似度,常用的核函数,比如多项式核,RBF核,还有核函数控制模型复杂度的超参数,就差不多了
+DBSCAN具体过程不考,需要知道对哪些数据合适
+EM算法不考察
+泛化误差不会考具体的公式,知道泛化误差的上界由两部分构成,一部分是和训练误差有关系,另外一部分是模型复杂度(VC维)有关系,是一个正关系还是反关系就行了
+贝叶斯估计、高斯分布参数求解不作为大题考试内容,MLE的计算过程希望大家了解,考试可能不考
+20道选择题
+3道简答题
+3道综合应用题
+确定性的知识:
+命题逻辑:语法和语义,蕴含和形式推演
+三种形式推演的系统:
+一阶谓词逻辑:与命题逻辑对应复习,不考证明
+Logic Programming:一种新的编程的思路
+不确定性的知识:
+模糊集合之间的运算,交并补、模糊关系、模糊关系的合成,用模糊逻辑表示自然语言
+模糊逻辑比一阶谓词逻辑多了模糊谓词、模糊量词和模糊修饰词
+深度学习部分:
+受限玻尔兹曼机原理理解就可以了
+卷积神经网络、循环神经网络用的比较多,对于具体模型来说,要了解模型的原理,为什么采用这种结构就可以
+更倾向于概念
+不会考公式,梯度下降应该熟练掌握的
+综合应用题分三个小问题,每一个是一个方面,各自独立
+A*树搜索和图搜索的最优性证明最好是了解一下
+简答题是搜索方面的,搜索这些算法相应的原理了解一下就可以了
+简答题不是要求证明的,没有证明题
+简答题是单个题目
+没有考公式推导
+野人传教士问题,实际上是考你搜索问题的形式化描述,形式化描述了解的话应该是没问题的
+对于GAN,基本概念和原理掌握,考试掌握基本原理就可以了
+对于启发式搜索,主要是设计一个合适的启发式函数(可采纳性和一致性),针对实际问题用松弛问题的解来作为启发式函数就可以
+综合应用题是神经网络相关
+综合应用题有要求画神经网络结构的,说明具体采用的算法
+选择题都是一些基本概念
+单选30题,每题1分
+多选15题,每题1分
+简答3题,每题5分
+计算3题,每题10分
+设计1题,每题10分
+ + +2022年终总结
+ +到了一年的末尾,伴着客厅的电视声音和窗外若有若无的鞭炮声,还是要写一点总结。
+我本想用“高开低走”来对这一年做一个精炼的总结,虽然说目前确实是“低”的状态,可是年初似乎也并没有什么“高”的事情,故这个词语还是不怎么恰当。
+回想去年的这个时候,应该是在科一招和两位同学一起跑赛车吧,当时虽然屋子里面很冷,心是火热的,幻想着这样的生活可以一直持续下去。今天屋子里面还是很冷,不同的是心也很冷,目前过的不怎么样,也看不到什么未来。
+再回想几年前,已经想不起来什么印象深刻的事情了,可能大多数都是在准备考试吧hh。
+现在我自己的状态,或许和2018年初是相同的,又或许是2019年,又或许不同,只是我自己的内心深处偏要找一个相同的历史时刻才能让我自己获得某种慰藉。
+我不知道应该写些什么关于今年的事情,写一写可能又写到了感情生活上,而这是我现在最不愿触及的部分之一。
+突然想起了五年前看到过的一篇文章,翻出来,最后就用它做一个总结吧:
+小时候,过年是头等大事。我们家的人不多,但是和父母一起,准备小零食,准备年夜饭,包饺子,看春晚。年少时的我总觉得,日子一天天过去,没有开端也没有终结。
+那时我总以为,过完了今天,明天还是一样的会来,过完了今年,还有明天这个时候的“今年”。可曾经那个心心念念的过年,曾经的那个“今年”,都像天上的云彩和海上的浪花一样,早已不知所踪。
+人不能两次踏进同一条河流,也不能,重新过一遍2022。
+季节流转,日升月落,星移斗转,世事如白衣苍狗。这一年有多少遗憾和侥幸,有多少悲恼和欣欢,多少披星染雾的启程和多少戴月荷锄的归途。新的一年终将随着初生的太阳喷薄而出,我们如同站在两个世界的边缘,愧疚地送别过去,紧张地等候未来。
+我不愿意用一句“新年新气象”,就将过去一年的得失通通扫净,尽管它们终将消失在记忆的犄角旮旯。
+新的一年,不是一切归零的重新开局,也不是一成不变的延续。
+回头再看看2022,我们有伤感的时候,有无奈的时候,有纠结的时候,也有骄傲的时候。总结过去,才能展望未来。
+2023,不是新的开始,而是新的征程。
+ + +MIT-6.824(Spring 2022)LEC 5 Fault Tolerance-Raft-1
+ +一致性算法,或者说 共识算法 ,让⼀组机器像⼀个整体⼀样工作,即使其中⼀些机器出现故障也能够继续工作。
+Raft 是⼀种为了管理复制日志的⼀致性算法。
+它将⼀致性算法分解成了几个关键模块:领导人选举、日志复制和安全性。同时它通过更强的⼀致性来 减少状态机的数量 。
+总之,对比传统的一致性算法 Paxos,Raft 更清晰易懂,易于实现。
+一致性算法允许多台机器作为一个集群协同工作,并且在其中的某几台机器出故障时集群仍然能正常工作。正因为如此,一致性算法在建立可靠的大规模软件系统方面发挥了重要作用。在过去十年中,Paxos 主导了关于一致性算法的讨论:大多数一致性的实现都是基于 Paxos 或受其影响,Paxos 已经成为教授学生关于一致性知识的主要工具。然而尽管很多人一直在努力尝试使 Paxos 更易懂,Paxos 还是太难理解了。此外,Paxos 的架构需要复杂的改变来支持实际系统。
+我们开始着手寻找一个新的一致性算法,希望可以为系统开发和教学提供更好的基础。 我们的方法是不寻常的,因为我们的主要目标是可理解性。在该算法的设计中,重要的不仅是如何让算法起作用,还要清晰地知道该算法为什么会起作用。这项工作的结果是一个称为 Raft 的一致性算法。在设计 Raft 时,我们使用了特定的技术来提高它的可理解性,包括:
+一项针对 2 所大学共 43 名学生的用户研究表明,Raft 比 Paxos 更容易理解:在学习两种算法后,其中 33 名学生能够更好地回答 Raft 的相关问题。
+Raft 在许多方面类似于现有的公式算法,但它有几个新特性:
+我们认为 Raft 跟 Paxos 以及其他一致性算法相比是更优的,这不仅体现在教学方面,还体现在工程实现方面。
+一致性算法基于复制状态机
+一致性算法一般都是在 复制状态机 的背景下实现的。在这种方法下,一组服务器在的状态机计算相同状态的相同副本,即使某些服务器崩溃,它们也可以继续运行。
+复制状态机是用来解决分布式系统中的各种容错问题。比如说,具有单个 leader 的大规模的系统,如 GFS,HDFS 和 RAMCloud ,他们通常都使用单独的复制状态机来管理 leader election 和保存 leader 崩溃后重新选举所需的配置信息。像 Chubby 和 ZooKeeper 都是复制状态机。
+复制状态机通常都是使用日志复制(log replication)来实现。
+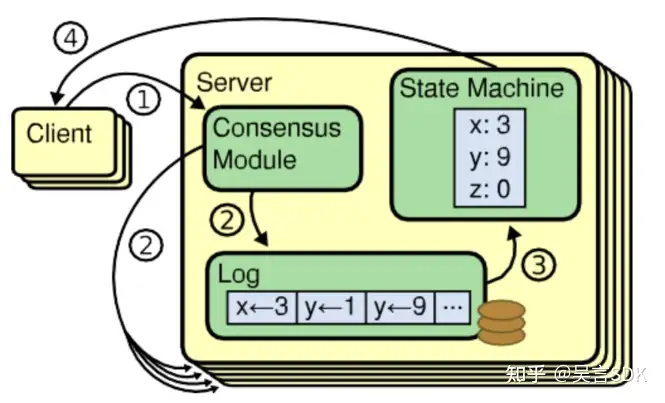
如图:每个服务器都保存着一份拥有一系列命令的日志,然后服务器上的状态机会按顺序执行日志中的命令。每一份日志中命令相同并且顺序也相同,因此每个状态机可以处理相同的命令序列。所以状态机是可确定的,每个状态机都执行相同的状态和相同的输出序列。
+一致性算法的主要工作就是保证复制日志(replicated log)的一致性 。每台服务器上的一致性模块接收来自客户端的命令,并将这些命令添加到其日志当中。一致性模块与其他服务器上的一致性模块进行通信,以确保每台服务器上最终以相同的顺序包含相同的命令,即使部分服务器崩溃了,这个条件也可以满足。一旦命令被正确复制,每台服务器上的状态机就会按日志顺序处理它们,并将输出返回给客户端。这样就形成了高可用的复制状态机。
+适用于实际系统的 一致性算法通常都包含以下几点特征 :
+在过去的十年间,Leslie Lamport 的 Paxos 协议 几乎成为一致性的同义词。它是课堂上被教授最多的一致性协议,大多数一致性的实现也是以它为起点。Paxos 首先定义了能在单个决策问题(例如单个复制日志条目)上达成一致性的协议。我们将这个子集称为 single-decree Paxos 。然后 Paxos 组合该协议的多个实例去实现一系列决策,比如日志(multi-Paxos)。Paxos 保证了安全性和活性,它也支持改变集群中的成员,它的安全性也已经被论证了,并且大多数情况下都是高效的。
+美中不足的是,Paxos 有两个严重的缺点:
+众所周知,Paxos 非常晦涩难懂,除非下了很大的功夫,很少有人能够成功理解它。因此,尽管目前已经有几个尝试希望将 Paxos 解释得通俗易懂一些,而且这些解释都集中在 single-decree Paxos,但是它们还是很难懂。在对 NSDI 2012 参会者的非正式调查中,我们发现很少人会喜欢 Paxos,即使是经验丰富的研究人员。我们自己也一直在跟 Paxos 作斗争,我们也无法完全理解整个 Paxos 协议,直到阅读了几个更简单的描述和自己设计了替代 Paxos 的协议,我们才对 Paxos 有了比较深刻的理解。但这个过程,花了将近一年。我们推测 Paxos 这么晦涩难懂,主要是因为作者选择了 Single-decree Paxos 来作为基础。Single-decree Paxso 非常搞人:它分为两个阶段,但是并没有对这两个阶段进行简单直观的说明,而且这两个阶段也不能分开了单独理解,所以使用者将就很难理解为什么该算法能起作用。Multi-Paxos 的合成规则又增加了许多复杂性。我们相信,对多个决定(日志,并非单个日志条目)达成一致性的总体问题可以用其他更直接和更明显的方式进行分解。
+其中一个原因是没有广泛认同的针对 Multi-Paxos 的算法。Lamport 的描述主要是针对 signle-decree Paxos 的,他描述了针对 multi-Paxos 的可能方法,但缺少了很多细节。目前已经有人在尝试具体化和优化 Paxos,但是这些尝试都互不相同并且它们跟 Lamport 描述的也不尽相同。虽然像 Chubby 这样的系统已经实现了类 Paxos 算法,但是他们并没有透露出很多的实现细节。
+此外,Paxos 的架构对于构建实际系统来说其实是一个糟糕的设计,这是 single-decree Paxos 分解的另一个结果。举个例子,这对于独立选择地日志条目的集合,然后再将它们合并到顺序日志当中没有任何好处,这只会增加复杂性。围绕日志来设计系统是更加简单和高效的方法,其中新条目按受约束的顺序依次附加。另外一个问题是 Paxos 在其核心使用了 对称对等方法 (尽管它最终表明了这会被用作一种性能优化的弱领导模式)。这在只有一个决策的情况下是有意义的,但是尽管如此,还是很少有实际系统采用了这种方法。如果有一系列的决策需要制定,更简单和更快速的方法应该是首先选择一个 leader,然后由 leader 去协调这些决策。
+因此,按照 Paxos 来实现的实际系统往往跟 Paxos 相差很大。几乎所有的实现都是从 Paxos 开始,然后在实现的过程中发现了一系列的难题,在解决难题的过程中,开发出了跟 Paxos 完全不一样的架构。这样既费时又容易出错,而且 Paxos 本身的晦涩难懂又使得问题变得更加严重。Paxos 公式可能是证明其正确性的一个很好的公式,但真正的实现与 Paxos 又相差很大,这证明了它其实没有什么价值。来自 Chubby 作者的评论非常典型:在 Paxos 算法描述和现实实现系统之间有着巨大的鸿沟,如果一直按照 Paxos 算法走下去,最终的系统往往会建立在一个还未被证明的协议之上。
+综合上述问题,我们觉得 Paxos 在教学端和系统构建端都没有提供一个良好的基础。考虑到共识性在大规模软件系统中的重要性,我们决定去尝试一下看看能不能设计一个替代 Paxos 并且具有更好特性的共识算法。
+Raft 算法就是尝试克服以上缺点,替代 Paxos 的一致性算法。
+设计 Raft 的初衷:
+在设计 Raft 算法的过程中,很多情况下我们需要在多个备选方案下做出抉择。在这种情况下,我们往往会基于可理解性来进行抉择:
+我们意识到这一的分析具有高度的主观性。所以我们采取了两种通用的措施来解决这个问题。
+Raft 是一种用来管理第2节中提到的复制日志(replicated log)的算法
+Raft算法的关键特性:
+ +Raft算法的简略版:
+ +Raft 选举一个 Leader ,给予管理所有复制日志的权限,由此实现一致性。
+Leader 从客户接受指令,写入日志,复制到其他 Backup Server 上,在保证安全性时通知其他 Server 根据日志执行指令更新状态机。
+Leader 大大简化了对复制日志的管理。leader 可以自行决定新日志写入位置,数据都从 Leader 流向其他 Server。当 Leader 宕机,从其他 Server 中选举一个新 Leader。
+Raft 将一致性问题分解为 三个子问题 :
+所有服务器上持久存在的:
+(在响应RPCs之前已在稳定存储上进行更新)
+| 状态变量 | +说明 | +
|---|---|
| currentTerm | +服务器最后⼀次知道的最新的任期号(初始化为 0,持续递增) | +
| votedFor | +在当前任期获得选票的候选人的id(如果没有则为 null) | +
| log[] | +日志条目集;每⼀个条目包含⼀个用户状态机执行的指令,和收到时的任期号 | +
所有服务器上经常变的:
+| 状态变量 | +说明 | +
|---|---|
| commitIndex | +已知的最大的已经被提交的日志条目的索引值 | +
| lastApplied | +最后被应用到状态机的日志条目索引值(初始化为 0,持续递增) | +
在leader里面经常改变的:
+(选举后重新初始化)
+| 状态变量 | +说明 | +
|---|---|
| nextIndex[] | +对于每⼀个服务器,需要发送给他的下⼀个日志条目的索引值(初始化为领导人最后索引值加1) | +
| matchIndex[] | +对于每⼀个服务器,已经复制给他的日志的最高索引值 | +
由 Leader 负责调用来复制日志(5.3);也会用作心跳机制(5.2)
+传入参数:
+| 状态变量 | +说明 | +
|---|---|
| term | +Leader的任期号 | +
| leaderId | +Leader的 id,以便于跟随者重定向请求 | +
| prevLogIndex | +新的日志条目紧随之前的索引值 | +
| prevLogTerm | +prevLogIndex 条目的任期号 | +
| entries[] | +准备存储的日志条目(表示心跳时为空;⼀次性发送多个是为了提高效率) | +
| leaderCommit | +Leader已经提交的日志的索引值 | +
返回值:
+| 状态变量 | +说明 | +
|---|---|
| term | +当前的任期号,用于Leader去更新自己 | +
| success | +跟随者包含了匹配上 prevLogIndex 和 prevLogTerm 的日志时为真 | +
接收者实现:
+false (5.1 节)prevLogIndex 位置处的日志条目的任期号和 prevLogTerm 不匹配,则返回 false (5.3 节)leaderCommit > commitIndex ,令 commitIndex = min(leaderCommit, 新日志条目索引)由候选人调用用来征集选票(5.2 节)
+传入参数 :
+| 状态变量 | +说明 | +
|---|---|
| term | +候选人的任期号 | +
| candidateId | +请求选票的候选人的 Id | +
| lastLogIndex | +候选人的最后日志条目的索引值 | +
| lastLogTerm | +候选人最后日志条目的任期号 | +
返回值 :
+| 状态变量 | +说明 | +
|---|---|
| term | +当前任期号,以便于候选人去更新自己的任期号 | +
| voteGranted | +候选人赢得了此张选票时为 true | +
接收者实现:
+false (5.2 节)votedFor 为 null 或者为 candidateId,并且候选人的日志至少和接受者一样新,那么就给它投票(5.2 节,5.4 节)所有服务器 :
+lastApplied 加一,并把 log[lastApplied] 应用到状态机中(5.3 节)currentTerm 等于 T,并切换状态为 Follower(5.1 节)Followers(跟随者)(5.2 节):
+Candidates(候选人)(5.2 节):
+currentTerm)Leader(领导人):
+nextIndex 开始的所有日志条目:
+nextIndex 和 matchIndexnextIndex 并重试| 特性 | +解释 | +
|---|---|
| 选举安全 | +对于一个给定的任期号,最多只会有一个 Leader 被选举出来(5.2 节) | +
| Leader 只追加 | +Leader 绝对不会删除或者覆盖自己的日志,只会增加(5.3 节) | +
| 日志匹配特性 | +如果两个日志在相同的索引位置的日志条目的任期号相同,那么我们就认为这个日志从头到这个索引位置之间全部完全相同(5.3 节) | +
| 领导人完全特性 | +如果某个日志条目在某个任期号中已经被提交,那么这个条目必然出现在更大任期号的所有领导人中(5.4 节) | +
| 状态机安全特性 | +如果一个 Leader 已经在给定的索引值位置的日志条目应用到状态机中,那么其他任何的服务器在这个索引位置不会提交一个不同的日志(5.4.3 节) | +
一个 Raft 集群通常包含 5 个节点,能容忍 2 个节点宕机。
+Raft 集群的服务器都处于三个状态之一:
+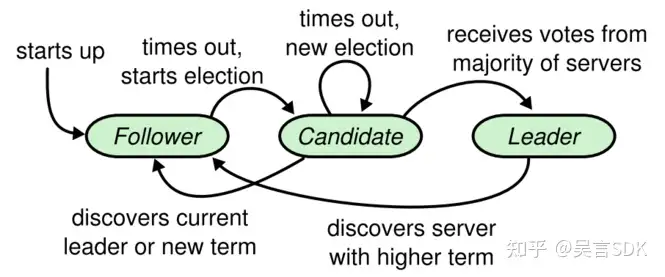
服务器状态。Follower 只响应来自其他服务器的请求。如果 Follower 接收不到消息,那么他就会变成 Candidate 并发起一次选举。获得集群中大多数选票的 Candidate 将成为 Leader。在一个任期内,Leader 保持身份直到自己宕机。
+Raft 把时间分割成任意长度的 任期(term) ,用 连续递增整数编号 ,任期开始即选举。Raft 保证一个任期只有一个 Leader。在某些情况下,一次选举无法选出 leader,这个时候这个任期会以没有 leader 而结束。同时一个新的任期(包含一次新的选举)会很快重新开始。
+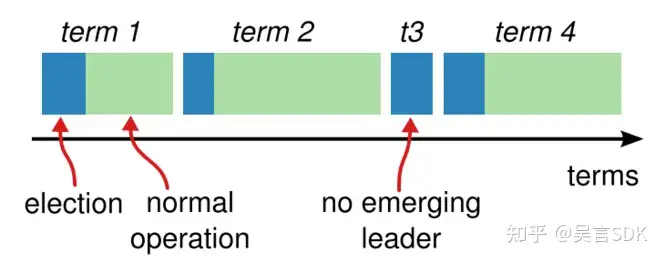
时间被划分成一个个的任期(term),每个任期开始都是一次选举。在选举成功后,领导人会管理整个集群直到任期结束。有时候选举会失败,那么这个任期就会没有领导人而结束。任期之间的切换可以在不同的时间不同的服务器上观察到。
+任期编号在 Raft 算法中充当逻辑时钟,每个节点都储存当前任期号, 节点之间通信会交换任期号 ,当一个节点:
+节点之间通信使用远程过程调用(RPCs) ,包含两种(第7节还增加了第三种传送快照的):
+当节点没有及时的收到 RPC 的响应时,会进行重试,而且节点之间都是以并行的方式发送 RPC 请求,以此来获得更好的性能。
+term(任期号)并转为 Candidate,并行向其他节点发送 RV RPC 等待给自己投票。
+commitIndex。leaderCommit,并放进所有 AE PRCs,其他节点由此得知 Leader 已提交位置,并按日志顺序应用到自己的状态机。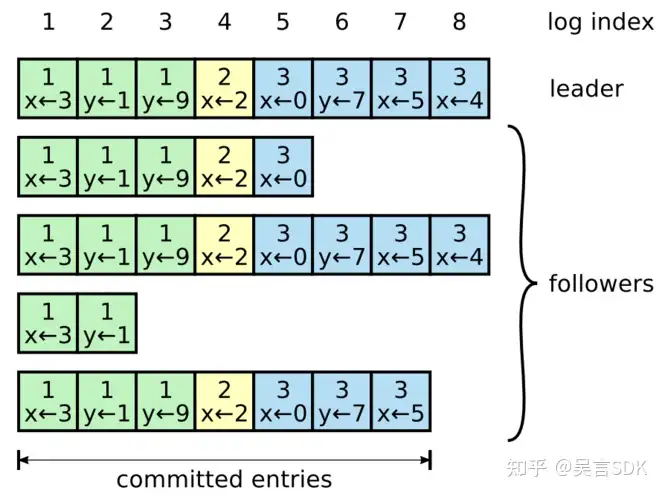
日志由序号标记的条目组成。每个条目都包含创建时的任期号和一个状态机需要执行的指令。一个条目当可以安全的被应用到状态机中去的时候,就认为是可以提交了。
+这样 Raft 能维持 日志的一致性 (日志匹配特性):
+正常情况下一致性检查不会失败,能一直保持一致。 但是 Leader 在未完全复制日志时宕机会使日志不一致 。例如 Follower 可能没有新 Leader 有的条目,也可能有新 Leader 没有的条目,或者都有,如下图。
+
当一个领导人成功当选时,跟随者可能是任何情况(a-f)。每一个盒子表示是一个日志条目;里面的数字表示任期号。跟随者可能会缺少一些日志条目(a-b),可能会有一些未被提交的日志条目(c-d),或者两种情况都存在(e-f)。
+例如,场景 f 可能会这样发生:f 对应的服务器在任期2的时候是 Leader,它追加了一些日志条目到自己的日志中,一条日志还没提交就宕机了,但是它很快就恢复重启了,然后再在任期3重新被选举为 Leader,又追加了一些日志条目到自己的日志中,在这些任期2和任期3的日志还没有被提交之前,该服务器又宕机了,并且在接下来的几个任期里一直处于宕机状态。
+Raft 中处理这种不一致方法是, Leader 强制 Follower 复制自己的日志,即覆盖 Follower 中所有冲突日志 (安全性在5.4)。
+Leader 找到最后和 Follower 一致的地方,删除 Follower 之后的冲突日志,发送自己的日志附加给 Follower。这些操作 在 AE RPCs 一致性检查时完成 :
+nextIndex,在刚上任时初始化为最新日志索引+1。nextIndex 重试直到成功 ,Follower 删除冲突日志并追加 Leader 日志。日志即保持一致。所以 Leader 无需特殊操作就能恢复一致性 ,Leader 也从不会覆盖删除自己的日志(图3 Leader 只追加特性)。
+日志复制机制展示了一致性特征:
+目前为止所讨论的机制并不能充分地保证每一个状态机会按相同的顺序执行相同的指令。比如说,一个 follower 可能会进入不可用状态,在此期间,leader 可能提交了若干的日志条目, 然后这个 follower 可能被选举为新的 leader 并且用新的日志条目去覆盖这些日志条目 。这样就会造成不同的状态机执行不同的指令的情况。
+故需 增加选举限制 ,保证图 3 中的领导人完整性,即 Leader 一定包含所有已提交日志条目 。
+某些一致性算法中需要额外复杂机制把缺少的日志传给 Leader。但是 Raft 保证 Leader 本来就有所有日志,所有日志都是单向从 Leader 传出去。
+Raft 在等待投票时,RV PRC 包含 Candidate 的日志信息, 投票人会拒绝日志没有自己新的 Candidate 的投票请求。
+投票人 比较最后一条日志的索引值和任期号 :
+(本小节是一种错误情况)
+前面介绍,一旦当前任期内的某个日志条目以及存储到过半的服务器节点上,Leader 就知道此日志在自己任期已提交。
+但 Leader 可能在提交之前崩溃 ,新 Leader 不知道保存在多数节点的的条目是否提交。例如下图,存在多数节点的老日志仍可能被覆盖。
+
所以 Raft 对日志提交条件增加一个额外限制: Leader 在当前任期至少有一条日志被提交 (即超过半数节点复制),如图 8 中的(e)所示。而©中并没有提交4任期的日志。
+所以新上任的 Leader 在接受客户写入命令前先提交一个 no-op(空命令),携带自己任期号的日志复制到多数节点,这样能保证选举限制成立。
+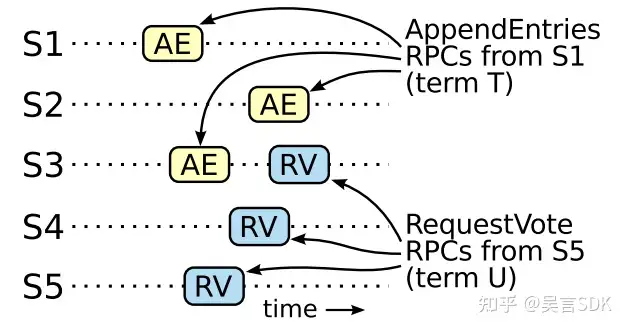
假设:
+假设任期 T 的 leaderT 在任期内提交了一个日志条目,但是该日志条目没有存在未来某些任期的 leader 中,假设 U 是大于 T 的没有存储该日志条目的最小任期号,处在任期 U 的 leader 称为 leaderU。
+反证法论证:
+通过 leader 的完整性特性,我们就可以证明状态机安全特性了,即如果某个节点已经将某个给定的索引处的日志条目应用到自己的状态机里了,那么其他的节点就不会在相同的索引处应用一个不同的日志条目。在一个节点应用一个日志条目到自己的状态机中时,它的日志和 leader 的日志从开始到该日志条目都是相同的,并且该日志条目必须被提交。现在考虑一个最小的任期号,在该任期中任意节点应用了一个给定的最小索引上面的日志条目,那么 Log 的完整性特性就会保证该任期之后的所有 leader 将存储相同的日志条目,因此在后面的任期中应用该索引上的日志条目的节点会应用相同的值。所以,状态机安全特性是可以得到保证的。
+因为 Raft 要求服务器节点按照日志索引顺序应用日志条目,再加上状态机安全特性,这样就意味着我们可以保证所有的服务器都会按照相同的顺序应用相同的日志条目到自己的状态机中了。
+前面都是讨论 Leader 崩溃,Follower和 Candidate 崩溃后的处理方式简单的多,Raft 只需要不断重试发送 RPCs 即可,崩溃重启后再执行 RPC。
+Raft 的 RPCs 都是幂等的,重试不会产生问题。如果 Follower 发现 AE RPC 中的日志已经有了,它直接忽略这个请求。
+Raft 的要求之一就是 安全性不能依赖时间 :整个系统不能因为某些事件运行的比预期快一点或者慢一点就产生了错误的结果。
+但可用性不可避免要依赖时间,最关键在于 Leader 选举,需要满足如下时间要求:
+broadcastTime<<electionTimeout<<MTB
+到目前为止,我们都假设集群的配置(参与共识算法的服务器节点集合)是固定不变的。但是在实际情况中,我们有时候是需要去改变集群配置的,比如说在服务器崩溃的时候去更换服务器或者是更改副本的数量。尽管可以通过下线整个集群,更新所有配置,然后重启整个集群的方式来实现这个需求,但是这会导致集群在更改过程中是不可用的。另外,如果这个过程中存在一些操作需要人工干预,那么就会有操作失误的风险。为了避免这些问题,我们决定将配置变更自动化并将其纳入到 Raft 的共识算法中来。
+为了让配置修改机制安全,在转换的过程中同一个任期里 不能够存在两个 Leader 同时当选 。问题在于, 一次性自动的转换所有服务器是不可能的 ,任何切换方法都是不安全的,所以在转换期间 整个集群可能分裂成两个独立的多数 。
+
直接从一种配置转到新的配置是十分不安全的,因为各个机器可能在不同时候进行转换。在中间位置 Server1 可以通过自身和 Server2 的选票成为 leader(满足旧配置下收到大多数选票的原则);Server3 可以通过自身和 Server4、Server5 的选票成为 leader(满足新配置线,即集群有 5 个节点的情况下的收到大多数选票的原则);此时整个集群可能在同一任期中出现了两个 leader,这和 Raft 协议是违背的。
+为了保证安全性,配置更改必须使用 两阶段方法 。有些系统在第一阶段停掉旧的配置,集群就不能处理客户端请求;然后在第二阶段在启用新的配置。
+在 Raft 中,集群先切换到一个过渡性配置,我们称之为 Joint Consensus ( 联合共识 );一旦联合共识被提交,那么系统就切换到新的配置上。
+Joint Consensus 是老配置和新配置的结合:
+Joint Consensus 允许独立的服务器在不影响安全性的前提下,在不同的时间进行配置转换,还可以让集群在配置转换的过程中依然响应客户端的请求。
+集群配置在复制日志中以特殊的日志条目来存储和通信。下图展示了配置转换的过程:
+在整个过程中 没有哪个时候让 C-old 和 C-new 同时产生影响 ,保证了安全性。
+
日志不能无限增长, Snapshotting ( 快照 )是最简单的压缩方法。在快照系统中,整个系统的状态都以快照的形式写入到稳定的持久化存储中,那个时间点之前的日志全部丢弃。
+增量压缩 ,例如日志清理或者日志结构合并树也可行,这些方法每次只对一小部分数据进行操作,分散了负载压力。首先,选择一个已经积累的大量已经被删除或者被覆盖对象的区域,然后重写那个区域还活跃的对象,之后释放那个区域。
+增量压缩需要增加复杂的机制来实现,而快照总是简单操作整个数据集合,简化了这个问题。日志清除方法需要修改 Raft,但是 状态机可以使用和快照相同的接口实现 LSM tree(日志结构合并树) 。
+
上图展示了 Raft 中快照的基本思路:
+lastIncludedIndex:被快照取代的最后的条目在日志中的索引值(状态机最后应用的日志)lastIncludedTerm:该条目的任期号保留这些数据是为了支持快照后第一个 AE RPC 时的一致性检查,因为这个条目需要前一日志条目的索引值和任期号。
+Leader 必须偶尔 通过 RPC 发送快照给一些落后的 Follower 。一般发生于当 Leader 已经删除下一条需要发送给某 Follower 的日志条目的时候。例如一个运行非常缓慢的 Follower 或者新加入集群的服务器(第 6 节),这时让这个 Follower 更新到最新的状态的方式就是通过网络把快照发送给他们。
+当 Follower 接收到 IS RPC 时,自己决定对于已经存在的日志该如何处理。
+由 Leader 调用,将快照的分块发送给 Follower。Leader 总是按顺序发送分块。
+| 参数 | +解释 | +
|---|---|
| term | +领导人的任期号 | +
| leaderId | +领导人的 Id,以便于跟随者重定向请求 | +
| lastIncludedIndex | +快照中包含的最后日志条目的索引值 | +
| lastIncludedTerm | +快照中包含的最后日志条目的任期号 | +
| offset | +分块在快照中的字节偏移量 | +
| data[] | +原始数据 | +
| done | +如果这是最后一个分块则为 true | +
| 返回结果 | +解释 | +
|---|---|
| term | +当前任期号(currentTerm),便于领导人更新自己 | +
接收者实现 :
+这种快照的方式背离了 Raft 的强 Leader 原则,因为 Follower 可以在 Leader 不知情情况下创建快照,但是这是值得的。Leader 的存在,是为了解决在达成一致性的时候的冲突,创建快照的时候一致性已经达成,不存在冲突了,所以没有 Leader 也是可以的。数据依然是从 Leader 传给 Follower,只是Follower 可以重新组织他们的数据。
+而只有 Leader 创建快照,发送给所有的 Follower 的方案有三个问题:
+还有两个问题影响快照性能:
+这一节将介绍客户端是如何和 Raft 进行交互的,包括:
+这些问题对于所有基于一致性的系统都存在,并且 Raft 的解决方案和其他的也差不多。
+可选项: Leader 可以通过心跳机制实现租约机制 ,但是这种方法依赖时间来保证安全性(假设时间误差是有界的)。
+算法的设计通常以正确性、效率和简洁性为主要目标。虽然这些都是有价值的目标,但我们相信可理解性同样重要。在开发人员将算法转化为实际实现之前,其他任何目标都不能实现,而实际实现将不可避免地偏离和扩展发布的形式。除非开发人员对算法有深刻的理解,并能对算法有直观的认识,否则他们很难在实现中保留算法理想的特性。
+在本文中,我们讨论了分布式共识的问题,在这个问题上,一个被广泛接受但难以理解的算法:Paxos,多年来一直让学生和开发人员非常挣扎。我们开发了一种新的算法:Raft,我们已经证明它比 Paxos 更容易理解。我们也相信 Raft 会为系统建设提供更好的基础。将可理解性作为主要设计目标改变了我们处理 Raft 设计的方式。随着设计的进展,我们发现自己反复使用了一些技术,比如分解问题和简化状态空间。这些技术不仅提高了 Raft 的可理解性,而且使我们更容易证实它的正确性。
+前面的系统都有单点故障:例如Coordinator、Master等等。因为要避免脑裂问题,因此并不设计成分布式的。
+这种在一般情况下是没有问题的,出错的概率很小,即使出错了也可以在很短的时间内恢复回来。
+Raft协议就是处理这种类型的问题,不允许单点故障产生,即使产生了也会更快恢复。
+客户端访问两台服务器,一台得到了响应,另一台没有得到响应,如果另一台服务器挂掉了最好,但是如果仅仅是网络不通,会造成网络分区的问题,也就是脑裂,导致服务器不一致。因此前面的方案中都使用单点服务器的方式。
+处理原则:少数服从多数
+客户端的操作需要在大多数服务器都成功,否则一直等待恢复,这样可以实现强一致性
+大多数:全部服务器,无论是开机的还是停机的,需要获得一半以上的服务器同意
+两种前协议:Paxos和View-stamped replication
+步骤:
+如果失败,需要选举新的Leader,重试操作
+K/V服务器是保留操作表的,为什么还需要日志呢?
+最终需要保证日志在所有的服务器上都是相同的
+日志条目包括序号、操作和Leader的任期(隐含表示了这个日志条目是哪个Leader追加的)
+Follower如果接收不到Leader发送的周期性的心跳信号,就认为Leader挂掉了,开始选举Leader
+具体实施:Follower自己有计时器,如果在一段的时间之内既没有接收到新的日志条目,也没有接收到Leader的心跳信号,则认为选举超时,开始进行选举。
+此时新的Leader的任期号要大于原来的Leader的任期号,如果此时客户端与旧的Leader进行交互,Leader给新的Leader发送了增加日志的请求,会被拒绝,发送给旧的Leader自己的任期号。旧的Leader发现任期号比自己大,不会再成为Leader。从而避免了脑裂的问题。
+挑战:两个Follower几乎同时发起选举,选不出Leader(分裂选举)
+因此设置选举超时时间,但是是随机的,如果选不出Leader,经过一段时间后就不会同时开始选举Leader,就可以最终选出Leader了。
+常用软件常用命令
+ +head -c 32 /dev/random | base64sudo visudotar -cvf temp.tar temp.txt temp/
+tar -xvf temp.tar -C temp/
+tar cvzf - pic | split -b 10m -d - pic
+cat pic* > pic.tar.gz
+tar xvzf pic.tar.gz| 描述 | +命令 | +
|---|---|
| 查看都有什么环境 | +conda info --envs | +
| 查看当前环境有什么包 | +conda list | +
| 创建环境 | +conda create -n env_name python=version package_names | +
| 安装包 | +conda install name=version | +
| 离线安装包 | +conda install --use-local name | +
| 导出当前环境 | +conda env export > name.yaml | +
| 导出base环境需要更换名称 | +conda create -n new_name --clone base | +
| 复制后导入 | +conda env create -f name.yaml | +
| 删除环境下的某个包 | +conda env remove -n your_env_name package_name | +
| 删除环境 | +conda env remove --name your_env_name | +
| 打包环境 | +conda pack -n my_env -o out_name.tar.gz | +
| 利用打包的环境复现 | +tar -xzf my_env.tar.gz -C my_env && source my_env/bin/activate | +
sudo apt update
+sudo apt install vim
+sudo cp /etc/apt/sources.list /etc/apt/sources.list.bak
+sudo vim /etc/apt/sources.list
+sudo apt update
+sudo apt upgrade
+sudo apt install python3-pip
+
+
+sudo mkdir ~/.pip
+cd ~/.pip
+sudo vim pip.conf
+# [global]
+# index-url=https://mirrors.aliyun.com/pypi/simple/
+# https://pypi.org/simple
+
+
+vim ~/.bashrc
+export PATH=~/mypath/bin:$PATH
+source ~/.bashrc添加%zhangzhao ALL=(ALL:ALL) NOPASSWD: ALL 到最后一行 , 后 ctrl+o, 回车 , ctrl+x 退出
+How can I install vscode-server in linux offline
+安装说明:https://www.v2fly.org/guide/install.html
+脚本下载地址:https://github.com/v2fly/fhs-install-v2ray
+执行脚本前首先临时更改hosts,避免github连接不上的情况
+参考仓库:https://github.com/521xueweihan/GitHub520
+执行脚本下载安装V2ray
+bash install-release.sh安装后的文件位置:
+installed: /usr/local/bin/v2ray
+installed: /usr/local/share/v2ray/geoip.dat
+installed: /usr/local/share/v2ray/geosite.dat
+installed: /usr/local/etc/v2ray/config.json
+installed: /var/log/v2ray/
+installed: /var/log/v2ray/access.log
+installed: /var/log/v2ray/error.log
+installed: /etc/systemd/system/v2ray.service
+installed: /etc/systemd/system/v2ray@.service按照上面的配置文件路径写入配置文件(可以直接从Windows客户端中copy过来)
+V2ray命令:
+# 启动V2ray
+systemctl start v2ray
+# 检查V2ray状态
+systemctl status v2ray
+# 设置V2ray开机自启动
+systemctl enable v2ray测试:
+curl -x socks5://127.0.0.1:10808 https://www.google.com -v下载地址:https://github.com/Dreamacro/clash/releases/tag/v1.12.0
+解压并赋予权限:
+gzip -d clash-linux-amd64-v1.11.4.gz
+chmod a+x clash-linux有的代理服务商会直接给出配置文件config.yaml,如果没有,可以将订阅链接直接粘贴在浏览器网址栏,然后搜索,会直接下载下来文件或者展示出配置文件,如果搜索到的是一大堆字符则需要在订阅链接的后面添加 &flag=clash ,然后会下载下来一个文件,将其更名为config.yaml即可
+然后替换~/.config/clash下自动生成的config.yaml,删除Country.mmdb文件,然后再次执行 ./clash-linux
+即可以使用
+释放9090端口后可以通过Web端查看:http://clash.razord.top
+(WSL2 git push时候可能会遇到错误,解决方法:将下述代码粘贴到~/.ssh/config文件中)
+Host github.com
+Hostname ssh.github.com
+Port 443安装proxychains从而避免全局代理
+apt install proxychains4配置文件:(/etc/proxychains.conf)
+# proxychains.conf VER 4.x
+#
+# HTTP, SOCKS4a, SOCKS5 tunneling proxifier with DNS.
+
+
+# The option below identifies how the ProxyList is treated.
+# only one option should be uncommented at time,
+# otherwise the last appearing option will be accepted
+#
+# dynamic_chain
+#
+# Dynamic - Each connection will be done via chained proxies
+# all proxies chained in the order as they appear in the list
+# at least one proxy must be online to play in chain
+# (dead proxies are skipped)
+# otherwise EINTR is returned to the app
+#
+strict_chain
+#
+# Strict - Each connection will be done via chained proxies
+# all proxies chained in the order as they appear in the list
+# all proxies must be online to play in chain
+# otherwise EINTR is returned to the app
+#
+#round_robin_chain
+#
+# Round Robin - Each connection will be done via chained proxies
+# of chain_len length
+# all proxies chained in the order as they appear in the list
+# at least one proxy must be online to play in chain
+# (dead proxies are skipped).
+# the start of the current proxy chain is the proxy after the last
+# proxy in the previously invoked proxy chain.
+# if the end of the proxy chain is reached while looking for proxies
+# start at the beginning again.
+# otherwise EINTR is returned to the app
+# These semantics are not guaranteed in a multithreaded environment.
+#
+#random_chain
+#
+# Random - Each connection will be done via random proxy
+# (or proxy chain, see chain_len) from the list.
+# this option is good to test your IDS :)
+
+# Make sense only if random_chain or round_robin_chain
+#chain_len = 2
+
+# Quiet mode (no output from library)
+# quiet_mode
+
+# Proxy DNS requests - no leak for DNS data
+proxy_dns
+
+# set the class A subnet number to use for the internal remote DNS mapping
+# we use the reserved 224.x.x.x range by default,
+# if the proxified app does a DNS request, we will return an IP from that range.
+# on further accesses to this ip we will send the saved DNS name to the proxy.
+# in case some control-freak app checks the returned ip, and denies to
+# connect, you can use another subnet, e.g. 10.x.x.x or 127.x.x.x.
+# of course you should make sure that the proxified app does not need
+# *real* access to this subnet.
+# i.e. dont use the same subnet then in the localnet section
+#remote_dns_subnet 127
+#remote_dns_subnet 10
+remote_dns_subnet 224
+
+# Some timeouts in milliseconds
+tcp_read_time_out 15000
+tcp_connect_time_out 8000
+
+### Examples for localnet exclusion
+## localnet ranges will *not* use a proxy to connect.
+## Exclude connections to 192.168.1.0/24 with port 80
+# localnet 192.168.1.0:80/255.255.255.0
+
+## Exclude connections to 192.168.100.0/24
+# localnet 192.168.100.0/255.255.255.0
+
+## Exclude connections to ANYwhere with port 80
+# localnet 0.0.0.0:80/0.0.0.0
+
+## RFC5735 Loopback address range
+## if you enable this, you have to make sure remote_dns_subnet is not 127
+## you'll need to enable it if you want to use an application that
+## connects to localhost.
+# localnet 127.0.0.0/255.0.0.0
+
+## RFC1918 Private Address Ranges
+# localnet 10.0.0.0/255.0.0.0
+# localnet 172.16.0.0/255.240.0.0
+# localnet 192.168.0.0/255.255.0.0
+
+# ProxyList format
+# type ip port [user pass]
+# (values separated by 'tab' or 'blank')
+#
+# only numeric ipv4 addresses are valid
+#
+#
+# Examples:
+#
+# socks5 192.168.67.78 1080 lamer secret
+# http 192.168.89.3 8080 justu hidden
+# socks4 192.168.1.49 1080
+# http 192.168.39.93 8080
+#
+#
+# proxy types: http, socks4, socks5
+# ( auth types supported: "basic"-http "user/pass"-socks )
+#
+[ProxyList]
+# add proxy here ...
+# meanwile
+# defaults set to "tor"
+socks5 127.0.0.1 10808
+http 127.0.0.1 10809需要走代理的命令在命令开头添加proxychains即可
+全局代理:(似乎对软件内部,例如go没有作用)
+export http_proxy=http://127.0.0.1:10809
+export https_proxy=https://127.0.0.1:10809网站说明:https://golang.google.cn/doc/install
+wget https://golang.google.cn/dl/go1.19.5.linux-amd64.tar.gz删除旧版本并解压安装包:
+rm -rf /usr/local/go && tar -C /usr/local -xzf go1.19.5.linux-amd64.tar.gz编辑配置文件,增加环境变量:
+vim ~/.bashrc
+export PATH=$PATH:/usr/local/go/bin
+source ~/.bashrc验证安装:
+go version查看配置:
+go env修改配置:
+go env -w GO111MODULE=on
+go env -w GOPROXY=https://goproxy.io,direct拉取私有仓库的包
+go env -w GOPRIVATE=gitlab.appshahe.com除配置私有仓库的地址外,还需要将走http或者https的协议转到git协议上
+具体命令:
+git config --global url."git@gitlab.appshahe.com:".insteadOf "https://gitlab.appshahe.com/"
+git config --global url."git@gitlab.appshahe.com:".insteadOf "http://gitlab.appshahe.com/"具体的更改会体现在 ~/.gitconfig里面
docker安装直接可以远程访问,不需要任何配置操作
+apt install mysql-server运行mysql服务并查看是否正在运行
+service mysql start
+service mysql status刚开始安装不能使用用户名和密码访问,需要更换为原来的密码验证方式
+mysql
+ALTER USER 'root'@'localhost' IDENTIFIED WITH mysql_native_password BY 'root';
+FLUSH PRIVILEGES;创建数据库:
+CREATE DATABASE simpledy取消bind-address=127.0.0.1
+vim /etc/mysql/mysql.conf.d/mysqld.cnf密码生成为随机字符串:
+head -c 8 /dev/random | base64创建用户:
+CREATE USER 'dymysql'@'%' IDENTIFIED BY 'gxnw21XxRhY';更改密码验证方式:
+ALTER USER 'dymysql'@'%' IDENTIFIED WITH mysql_native_password BY 'gxnw21XxRhY';授予用户某个数据库的全部权限:
+GRANT ALL PRIVILEGES ON `simpledy`.* TO `dymysql`@`%` WITH GRANT OPTION;撤销某个用户对某个数据库的全部权限:
+REVOKE ALL PRIVILEGES, GRANT OPTION FROM 'dymysql';刷新缓存:
+FLUSH PRIVILEGES;展示某个用户的权限:
+SHOW GRANTS FOR 'dymysql'@'%';查看已有用户以及是否可以远程登录:
+select host,user,plugin from mysql.user;docker安装配置成功
+apt install redis-server运行并查看是否正在运行
+service redis-server start
+service redis-server status打开redis配置文件 /etc/redis/redis.conf
找到requirepass,修改即可
+默认情况下,Redis 不允许远程连接。只能从127.0.0.1(localhost)连接 Redis 服务器
+打开redis配置文件 /etc/redis/redis.conf
注释掉 bind 127.0.0.1 ::1
关闭保护模式 protected-mode no
重启Redis服务:service redis-server restart
(注意WSL的ip要到WSL里面去看)
+官网安装脚本:https://www.rabbitmq.com/install-debian.html#apt-cloudsmith
+注意修改apt-get为apt,将软件源设置为对应版本(如Ubuntu22.04为jammy)
+查看安装状态:
+service rabbitmq-server status打开管理界面:
+rabbitmq-plugins enable rabbitmq_management通过http://localhost:15672/#/进行查看
+默认的guest用户,密码为guest,具有超级管理员权限,无法远程登录
+创建用户并设置密码:
+add_user root QxdkQeiIUNY管理用户角色:
+rabbitmqctl set_user_tags root administrator查看当前的用户及角色:
+rabbitmqctl list_users不需要开启远程连接,自动支持
+然后进入到管理页面中,对virtual hosts进行设置(相当于数据库中的db)
+然后即可使用程序等跑通
+apt install ffmpegapt install nginx配置文件:/etc/nginx/nginx.conf
+增加mp4支持:
+apt install nginx-extrasapt install vsftpd下载protobuf官方的protoc工具(tar.gz版本)
+编译安装:
+# 安装需要的工具包
+apt install autoconf automake libtool curl make g++ unzip
+# 解压安装包
+tar xvf protobuf-21.12.tar.gz && cd protobuf-21.12
+# 编译安装
+./autogen.sh
+./configure
+make && make install
+ldconfig
+# 验证安装
+protoc --version安装go语言插件:
+go get -u google.golang.org/protobuf/cmd/protoc-gen-go
+go get -u google.golang.org/grpc/cmd/protoc-gen-go-grpc将执行文件添加到环境变量中:
+export PATH=$PATH:/root/go/bin执行:
+protoc --go_out=. video.proto下载地址:https://developer.hashicorp.com/consul/downloads
+解压后直接执行即可
+核心思想:
+root@hecs-296470:/etc/apt/keyrings# cd /etc/apt/keyrings
+root@hecs-296470:/etc/apt/keyrings# ls
+docker.gpgroot@hecs-296470:/etc/apt/sources.list.d# ls
+docker.list
+root@hecs-296470:/etc/apt/sources.list.d# cat docker.list
+deb [arch=amd64 signed-by=/etc/apt/keyrings/docker.gpg] https://download.docker.com/linux/ubuntu jammy stable
+root@hecs-296470:/etc/apt/sources.list.d#apt install docker-ce docker-ce-cli containerd.io docker-buildx-plugin docker-compose-plugin换源:
+vim /etc/docker/daemon.json写入源:
+{
+ "registry-mirrors": [
+ "https://hub-mirror.c.163.com",
+ "https://ustc-edu-cn.mirror.aliyuncs.com",
+ "https://ghcr.io",
+ "https://mirror.baidubce.com"
+ ]
+}重启docker:
+systemctl daemon-reload
+systemctl restart docker准备重装编程环境,以Docker为基础,既能开发,又能方便部署,同时不损害原有的其他环境
+但是Docker Desktop坑点太多,且占用资源巨大,因此不安装Windows环境下面的Docker,而是在WSL内部安装Docker,VSCode通过SSH方式跨过WSL访问容器。
+与上面的Docker安装基本相同,不过注意每一次重启WSL的时候要手动重启Docker,否则无法使用Docker
+service docker start由于WSL的ip会总变化,这里准备配桥接模式,我的理解是WSL与主机的地位相同,在内网中都有自己的ip,这样无论是互相访问还是访问外网都没有什么问题。
+参考资料:
+ + + +| 描述 | +命令 | +
|---|---|
| 查询容器 | +sudo docker ps -a | +
| 删除容器 | +sudo docker rm 容器ID | +
| 查询镜像 | +sudo docker images | +
| 删除镜像 | +sudo docker rmi 镜像ID(要先删除掉容器才能删除掉镜像) | +
| 拉取镜像 | +sudo docker pull python:3.8.13(去dockerhub上找合适的版本) | +
| 根据镜像启动容器并挂载数据 | +docker run -v 绝对路径:/mnt --gpus all --shm-size=6g -it python:3.8.13 /bin/bash | +
| 启动已经停止的容器 | +sudo docker start ID | +
| 进入某个容器的终端 | +sudo docker exec -it ID /bin/bash | +
| 将容器转为镜像并上传到dockerhub-登录 | +docker login | +
| 将容器转为镜像并上传到dockerhub-提交 | +sudo docker commit 容器ID zhangzhao219/仓库名(也是将容器写回到镜像中的操作) | +
| 将容器转为镜像并上传到dockerhub-打标签 | +sudo docker tag zhangzhao219/仓库名 zhangzhao219/TAG | +
| 将容器转为镜像并上传到dockerhub-上传 | +sudo docker push zhangzhao219/仓库名:TAG | +
| 导出容器到文件 | +sudo docker export -o *.tar 容器ID | +
| 从文件导入容器(会直接变为镜像) | +sudo docker import IR.tar 名称 | +
Go 语言基础 - 基础语法
+ +本节课程主要分为四个方面:
+课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
+可以选择安装 VS Code , 或者 Goland ,对于 VS Code,需要安装 Go 插件
+go run example/01-hello/main.go 如果正确输出 hello world,则说明环境配置正确空余时间阅读 Go语言圣经(中文版)
+课程链接:
+package main
+
+import (
+ "fmt"
+)
+
+func main() {
+ fmt.Println("hello world")
+}
+注意常量没有类型,会根据使用的上下文自动推断类型
+package main
+
+import (
+ "fmt"
+ "math"
+)
+
+func main() {
+
+ var a = "initial"
+
+ var b, c int = 1, 2
+
+ var d = true
+
+ var e float64
+
+ f := float32(e)
+
+ g := a + "foo"
+ fmt.Println(a, b, c, d, e, f) // initial 1 2 true 0 0
+ fmt.Println(g) // initialapple
+
+ const s string = "constant"
+ const h = 500000000
+ const i = 3e20 / h
+ fmt.Println(s, h, i, math.Sin(h), math.Sin(i))
+}
+package main
+
+import "fmt"
+
+func main() {
+
+ i := 1
+ for {
+ fmt.Println("loop")
+ break
+ }
+ for j := 7; j < 9; j++ {
+ fmt.Println(j)
+ }
+
+ for n := 0; n < 5; n++ {
+ if n%2 == 0 {
+ continue
+ }
+ fmt.Println(n)
+ }
+ for i <= 3 {
+ fmt.Println(i)
+ i = i + 1
+ }
+}
+package main
+
+import "fmt"
+
+func main() {
+
+ if 7%2 == 0 {
+ fmt.Println("7 is even")
+ } else {
+ fmt.Println("7 is odd")
+ }
+
+ if 8%4 == 0 {
+ fmt.Println("8 is divisible by 4")
+ }
+
+ if num := 9; num < 0 {
+ fmt.Println(num, "is negative")
+ } else if num < 10 {
+ fmt.Println(num, "has 1 digit")
+ } else {
+ fmt.Println(num, "has multiple digits")
+ }
+}
+默认不需要添加break
+可以使用任意的变量类型
+package main
+
+import (
+ "fmt"
+ "time"
+)
+
+func main() {
+
+ a := 2
+ switch a {
+ case 1:
+ fmt.Println("one")
+ case 2:
+ fmt.Println("two")
+ case 3:
+ fmt.Println("three")
+ case 4, 5:
+ fmt.Println("four or five")
+ default:
+ fmt.Println("other")
+ }
+
+ t := time.Now()
+ switch {
+ case t.Hour() < 12:
+ fmt.Println("It's before noon")
+ default:
+ fmt.Println("It's after noon")
+ }
+}
+真实场景下很少用,一般使用切片
+package main
+
+import "fmt"
+
+func main() {
+
+ var a [5]int
+ a[4] = 100
+ fmt.Println("get:", a[2])
+ fmt.Println("len:", len(a))
+
+ b := [5]int{1, 2, 3, 4, 5}
+ fmt.Println(b)
+
+ var twoD [2][3]int
+ for i := 0; i < 2; i++ {
+ for j := 0; j < 3; j++ {
+ twoD[i][j] = i + j
+ }
+ }
+ fmt.Println("2d: ", twoD)
+}
+package main
+
+import "fmt"
+
+func main() {
+
+ s := make([]string, 3)
+ s[0] = "a"
+ s[1] = "b"
+ s[2] = "c"
+ fmt.Println("get:", s[2]) // c
+ fmt.Println("len:", len(s)) // 3
+
+ s = append(s, "d")
+ s = append(s, "e", "f")
+ fmt.Println(s) // [a b c d e f]
+
+ c := make([]string, len(s))
+ copy(c, s)
+ fmt.Println(c) // [a b c d e f]
+
+ fmt.Println(s[2:5]) // [c d e]
+ fmt.Println(s[:5]) // [a b c d e]
+ fmt.Println(s[2:]) // [c d e f]
+
+ good := []string{"g", "o", "o", "d"}
+ fmt.Println(good) // [g o o d]
+}
+实际中使用最频繁,完全无序
+package main
+
+import "fmt"
+
+func main() {
+ m := make(map[string]int)
+ m["one"] = 1
+ m["two"] = 2
+ fmt.Println(m) // map[one:1 two:2]
+ fmt.Println(len(m)) // 2
+ fmt.Println(m["one"]) // 1
+ fmt.Println(m["unknow"]) // 0
+
+ r, ok := m["unknow"]
+ fmt.Println(r, ok) // 0 false
+
+ delete(m, "one")
+
+ m2 := map[string]int{"one": 1, "two": 2}
+ var m3 = map[string]int{"one": 1, "two": 2}
+ fmt.Println(m2, m3)
+}
+package main
+
+import "fmt"
+
+func main() {
+ nums := []int{2, 3, 4}
+ sum := 0
+ for i, num := range nums {
+ sum += num
+ if num == 2 {
+ fmt.Println("index:", i, "num:", num) // index: 0 num: 2
+ }
+ }
+ fmt.Println(sum) // 9
+
+ m := map[string]string{"a": "A", "b": "B"}
+ for k, v := range m {
+ fmt.Println(k, v) // b 8; a A
+ }
+ for k := range m {
+ fmt.Println("key", k) // key a; key b
+ }
+}
+一般返回两个值,第一个值是真正需要的,第二个值是错误信息
+package main
+
+import "fmt"
+
+func add(a int, b int) int {
+ return a + b
+}
+
+func add2(a, b int) int {
+ return a + b
+}
+
+func exists(m map[string]string, k string) (v string, ok bool) {
+ v, ok = m[k]
+ return v, ok
+}
+
+func main() {
+ res := add(1, 2)
+ fmt.Println(res) // 3
+
+ v, ok := exists(map[string]string{"a": "A"}, "a")
+ fmt.Println(v, ok) // A True
+}
+对传入的参数进行修改
+功能比较有限,不如C++丰富
+package main
+
+import "fmt"
+
+func add2(n int) {
+ n += 2
+}
+
+func add2ptr(n *int) {
+ *n += 2
+}
+
+func main() {
+ n := 5
+ add2(n)
+ fmt.Println(n) // 5
+ add2ptr(&n)
+ fmt.Println(n) // 7
+}
+传入指针避免传递的开销过大,同时也可以对结构体进行修改
+package main
+
+import "fmt"
+
+type user struct {
+ name string
+ password string
+}
+
+func main() {
+ a := user{name: "wang", password: "1024"}
+ b := user{"wang", "1024"}
+ c := user{name: "wang"}
+ c.password = "1024"
+ var d user
+ d.name = "wang"
+ d.password = "1024"
+
+ fmt.Println(a, b, c, d) // {wang 1024} {wang 1024} {wang 1024} {wang 1024}
+ fmt.Println(checkPassword(a, "haha")) // false
+ fmt.Println(checkPassword2(&a, "haha")) // false
+}
+
+func checkPassword(u user, password string) bool {
+ return u.password == password
+}
+
+func checkPassword2(u *user, password string) bool {
+ return u.password == password
+}
+相当于一个类成员函数
+带指针就能对结构体进行修改
+package main
+
+import "fmt"
+
+type user struct {
+ name string
+ password string
+}
+
+func (u user) checkPassword(password string) bool {
+ return u.password == password
+}
+
+func (u *user) resetPassword(password string) {
+ u.password = password
+}
+
+func main() {
+ a := user{name: "wang", password: "1024"}
+ a.resetPassword("2048")
+ fmt.Println(a.checkPassword("2048")) // true
+}
+package main
+
+import (
+ "errors"
+ "fmt"
+)
+
+type user struct {
+ name string
+ password string
+}
+
+func findUser(users []user, name string) (v *user, err error) {
+ for _, u := range users {
+ if u.name == name {
+ return &u, nil
+ }
+ }
+ return nil, errors.New("not found")
+}
+
+func main() {
+ u, err := findUser([]user{{"wang", "1024"}}, "wang")
+ if err != nil {
+ fmt.Println(err)
+ return
+ }
+ fmt.Println(u.name) // wang
+
+ if u, err := findUser([]user{{"wang", "1024"}}, "li"); err != nil {
+ fmt.Println(err) // not found
+ return
+ } else {
+ fmt.Println(u.name)
+ }
+}
+package main
+
+import (
+ "fmt"
+ "strings"
+)
+
+func main() {
+ a := "hello"
+ fmt.Println(strings.Contains(a, "ll")) // true
+ fmt.Println(strings.Count(a, "l")) // 2
+ fmt.Println(strings.HasPrefix(a, "he")) // true
+ fmt.Println(strings.HasSuffix(a, "llo")) // true
+ fmt.Println(strings.Index(a, "ll")) // 2
+ fmt.Println(strings.Join([]string{"he", "llo"}, "-")) // he-llo
+ fmt.Println(strings.Repeat(a, 2)) // hellohello
+ fmt.Println(strings.Replace(a, "e", "E", -1)) // hEllo
+ fmt.Println(strings.Split("a-b-c", "-")) // [a b c]
+ fmt.Println(strings.ToLower(a)) // hello
+ fmt.Println(strings.ToUpper(a)) // HELLO
+ fmt.Println(len(a)) // 5
+ b := "你好"
+ fmt.Println(len(b)) // 6
+}
++和#号可以打印更为详细的信息
+package main
+
+import "fmt"
+
+type point struct {
+ x, y int
+}
+
+func main() {
+ s := "hello"
+ n := 123
+ p := point{1, 2}
+ fmt.Println(s, n) // hello 123
+ fmt.Println(p) // {1 2}
+
+ fmt.Printf("s=%v\n", s) // s=hello
+ fmt.Printf("n=%v\n", n) // n=123
+ fmt.Printf("p=%v\n", p) // p={1 2}
+ fmt.Printf("p=%+v\n", p) // p={x:1 y:2}
+ fmt.Printf("p=%#v\n", p) // p=main.point{x:1, y:2}
+
+ f := 3.141592653
+ fmt.Println(f) // 3.141592653
+ fmt.Printf("%.2f\n", f) // 3.14
+}
+注意结构体要保证大写,小写传参的问题使用反射解决
+package main
+
+import (
+ "encoding/json"
+ "fmt"
+)
+
+type userInfo struct {
+ Name string
+ Age int `json:"age"`
+ Hobby []string
+}
+
+func main() {
+ a := userInfo{Name: "wang", Age: 18, Hobby: []string{"Golang", "TypeScript"}}
+ buf, err := json.Marshal(a)
+ if err != nil {
+ panic(err)
+ }
+ fmt.Println(buf) // [123 34 78 97...]
+ fmt.Println(string(buf)) // {"Name":"wang","age":18,"Hobby":["Golang","TypeScript"]}
+
+ buf, err = json.MarshalIndent(a, "", "\t")
+ if err != nil {
+ panic(err)
+ }
+ fmt.Println(string(buf))
+
+ var b userInfo
+ err = json.Unmarshal(buf, &b)
+ if err != nil {
+ panic(err)
+ }
+ fmt.Printf("%#v\n", b) // main.userInfo{Name:"wang", Age:18, Hobby:[]string{"Golang", "TypeScript"}}
+}
+package main
+
+import (
+ "fmt"
+ "time"
+)
+
+func main() {
+ now := time.Now()
+ fmt.Println(now) // 2022-03-27 18:04:59.433297 +0800 CST m=+0.000087933
+ t := time.Date(2022, 3, 27, 1, 25, 36, 0, time.UTC)
+ t2 := time.Date(2022, 3, 27, 2, 30, 36, 0, time.UTC)
+ fmt.Println(t) // 2022-03-27 01:25:36 +0000 UTC
+ fmt.Println(t.Year(), t.Month(), t.Day(), t.Hour(), t.Minute()) // 2022 March 27 1 25
+ fmt.Println(t.Format("2006-01-02 15:04:05")) // 2022-03-27 01:25:36
+ diff := t2.Sub(t)
+ fmt.Println(diff) // 1h5m0s
+ fmt.Println(diff.Minutes(), diff.Seconds()) // 65 3900
+ t3, err := time.Parse("2006-01-02 15:04:05", "2022-03-27 01:25:36")
+ if err != nil {
+ panic(err)
+ }
+ fmt.Println(t3 == t) // true
+ fmt.Println(now.Unix()) // 1648738080
+}
+package main
+
+import (
+ "fmt"
+ "strconv"
+)
+
+func main() {
+ f, _ := strconv.ParseFloat("1.234", 64)
+ fmt.Println(f) // 1.234
+
+ n, _ := strconv.ParseInt("111", 10, 64)
+ fmt.Println(n) // 111
+
+ n, _ = strconv.ParseInt("0x1000", 0, 64)
+ fmt.Println(n) // 4096
+
+ n2, _ := strconv.Atoi("123")
+ fmt.Println(n2) // 123
+
+ n2, err := strconv.Atoi("AAA")
+ fmt.Println(n2, err) // 0 strconv.Atoi: parsing "AAA": invalid syntax
+}
+package main
+
+import (
+ "fmt"
+ "os"
+ "os/exec"
+)
+
+func main() {
+ // go run example/20-env/main.go a b c d
+ fmt.Println(os.Args) // [/var/folders/8p/n34xxfnx38dg8bv_x8l62t_m0000gn/T/go-build3406981276/b001/exe/main a b c d]
+ fmt.Println(os.Getenv("PATH")) // /usr/local/go/bin...
+ fmt.Println(os.Setenv("AA", "BB"))
+
+ buf, err := exec.Command("grep", "127.0.0.1", "/etc/hosts").CombinedOutput()
+ if err != nil {
+ panic(err)
+ }
+ fmt.Println(string(buf)) // 127.0.0.1 localhost
+}
+rand.Seed(time.Now().UnixNano())
+secretNumber := rand.Intn(maxNum)reader := bufio.NewReader(os.Stdin)
+input, err := reader.ReadString('\n')
+input = strings.Trim(input, "\r\n")最终代码:
+package main
+
+import (
+ "bufio"
+ "fmt"
+ "math/rand"
+ "os"
+ "strconv"
+ "strings"
+ "time"
+)
+
+func main() {
+ maxNum := 100
+ rand.Seed(time.Now().UnixNano())
+ secretNumber := rand.Intn(maxNum)
+ // fmt.Println("The secret number is ", secretNumber)
+
+ fmt.Println("Please input your guess")
+ reader := bufio.NewReader(os.Stdin)
+ for {
+ input, err := reader.ReadString('\n')
+ if err != nil {
+ fmt.Println("An error occured while reading input. Please try again", err)
+ continue
+ }
+ input = strings.Trim(input, "\r\n")
+
+ guess, err := strconv.Atoi(input)
+ if err != nil {
+ fmt.Println("Invalid input. Please enter an integer value")
+ continue
+ }
+ fmt.Println("You guess is", guess)
+ if guess > secretNumber {
+ fmt.Println("Your guess is bigger than the secret number. Please try again")
+ } else if guess < secretNumber {
+ fmt.Println("Your guess is smaller than the secret number. Please try again")
+ } else {
+ fmt.Println("Correct, you Legend!")
+ break
+ }
+ }
+}
+抓包:找到翻译网站,提交一个翻译后去控制台抓包,然后copy as cURL,可以将这个请求转到本地进行运行
+为了方便,可以将这个请求copy到一些在线将请求转换为Go代码的网站,最终得到可以直接运行的代码,运行代码获得与网页返回相同的结果。
+将请求的部分单独提取出来,通过用户的输入进行序列化
+解析返回的响应,进行反序列化提取真正需要的部分
+返回的响应也使用在线工具转换为go代码,减少工作量
+最后通过命令行读入即可
+最终代码:
+package main
+
+import (
+ "bytes"
+ "encoding/json"
+ "fmt"
+ "io"
+ "log"
+ "net/http"
+ "os"
+)
+
+type DictRequest struct {
+ TransType string `json:"trans_type"`
+ Source string `json:"source"`
+ UserID string `json:"user_id"`
+}
+
+type DictResponse struct {
+ Rc int `json:"rc"`
+ Wiki struct {
+ KnownInLaguages int `json:"known_in_laguages"`
+ Description struct {
+ Source string `json:"source"`
+ Target interface{} `json:"target"`
+ } `json:"description"`
+ ID string `json:"id"`
+ Item struct {
+ Source string `json:"source"`
+ Target string `json:"target"`
+ } `json:"item"`
+ ImageURL string `json:"image_url"`
+ IsSubject string `json:"is_subject"`
+ Sitelink string `json:"sitelink"`
+ } `json:"wiki"`
+ Dictionary struct {
+ Prons struct {
+ EnUs string `json:"en-us"`
+ En string `json:"en"`
+ } `json:"prons"`
+ Explanations []string `json:"explanations"`
+ Synonym []string `json:"synonym"`
+ Antonym []string `json:"antonym"`
+ WqxExample [][]string `json:"wqx_example"`
+ Entry string `json:"entry"`
+ Type string `json:"type"`
+ Related []interface{} `json:"related"`
+ Source string `json:"source"`
+ } `json:"dictionary"`
+}
+
+func query(word string) {
+ client := &http.Client{}
+ request := DictRequest{TransType: "en2zh", Source: word}
+ buf, err := json.Marshal(request)
+ if err != nil {
+ log.Fatal(err)
+ }
+ var data = bytes.NewReader(buf)
+ req, err := http.NewRequest("POST", "https://api.interpreter.caiyunai.com/v1/dict", data)
+ if err != nil {
+ log.Fatal(err)
+ }
+ req.Header.Set("Authority", "api.interpreter.caiyunai.com")
+ req.Header.Set("Accept", "application/json, text/plain, */*")
+ req.Header.Set("Accept-Language", "zh-CN,zh;q=0.9,en-US;q=0.8,en;q=0.7")
+ req.Header.Set("App-Name", "xy")
+ req.Header.Set("Content-Type", "application/json;charset=UTF-8")
+ req.Header.Set("Origin", "https://fanyi.caiyunapp.com")
+ req.Header.Set("Os-Type", "web")
+ req.Header.Set("Referer", "https://fanyi.caiyunapp.com/")
+ req.Header.Set("Sec-Ch-Ua", "\"Not?A_Brand\";v=\"8\", \"Chromium\";v=\"108\", \"Microsoft Edge\";v=\"108\"")
+ req.Header.Set("Sec-Ch-Ua-Mobile", "?0")
+ req.Header.Set("Sec-Ch-Ua-Platform", "\"Windows\"")
+ req.Header.Set("Sec-Fetch-Dest", "empty")
+ req.Header.Set("Sec-Fetch-Mode", "cors")
+ req.Header.Set("Sec-Fetch-Site", "cross-site")
+ req.Header.Set("User-Agent", "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/108.0.0.0 Safari/537.36 Edg/108.0.1462.76")
+ req.Header.Set("X-Authorization", "token:qgemv4jr1y38jyq6vhvi")
+ resp, err := client.Do(req)
+ if err != nil {
+ log.Fatal(err)
+ }
+ defer resp.Body.Close()
+ bodyText, err := io.ReadAll(resp.Body)
+ if err != nil {
+ log.Fatal(err)
+ }
+ if resp.StatusCode != 200 {
+ log.Fatal("bad StatusCode:", resp.StatusCode, "body", string(bodyText))
+ }
+ var dictResponse DictResponse
+ err = json.Unmarshal(bodyText, &dictResponse)
+ if err != nil {
+ log.Fatal(err)
+ }
+ fmt.Println(word, "UK:", dictResponse.Dictionary.Prons.En, "US:", dictResponse.Dictionary.Prons.EnUs)
+ for _, item := range dictResponse.Dictionary.Explanations {
+ fmt.Println(item)
+ }
+}
+
+func main() {
+ if len(os.Args) != 2 {
+ fmt.Fprintf(os.Stderr, `usage: simpleDict WORD
+example: simpleDict hello
+ `)
+ os.Exit(1)
+ }
+ word := os.Args[1]
+ query(word)
+}
+正常浏览器访问一个网站,先和对方的网站建立TCP连接,然后正常发起HTTP请求,服务器返回响应
+如果设置了代理服务器,浏览器要先和代理服务器建立TCP连接,然后代理服务器再去和真正的网站建立TCP连接,可以分为4个阶段:
+实现流程:
+nc 127.0.0.1 1080)进行测试curl --socks5 127.0.0.1:1080 -v http://www.qq.com进行测试,但是仅为协商,因此不会成功,但是服务器端会有正确的输出。最终代码:
+package main
+
+import (
+ "bufio"
+ "context"
+ "encoding/binary"
+ "errors"
+ "fmt"
+ "io"
+ "log"
+ "net"
+)
+
+const socks5Ver = 0x05
+const cmdBind = 0x01
+const atypIPV4 = 0x01
+const atypeHOST = 0x03
+const atypeIPV6 = 0x04
+
+func main() {
+ server, err := net.Listen("tcp", "127.0.0.1:1080")
+ if err != nil {
+ panic(err)
+ }
+ for {
+ client, err := server.Accept()
+ if err != nil {
+ log.Printf("Accept failed %v", err)
+ continue
+ }
+ go process(client)
+ }
+}
+
+func process(conn net.Conn) {
+ defer conn.Close()
+ reader := bufio.NewReader(conn)
+ err := auth(reader, conn)
+ if err != nil {
+ log.Printf("client %v auth failed:%v", conn.RemoteAddr(), err)
+ return
+ }
+ err = connect(reader, conn)
+ if err != nil {
+ log.Printf("client %v auth failed:%v", conn.RemoteAddr(), err)
+ return
+ }
+}
+
+func auth(reader *bufio.Reader, conn net.Conn) (err error) {
+ // +----+----------+----------+
+ // |VER | NMETHODS | METHODS |
+ // +----+----------+----------+
+ // | 1 | 1 | 1 to 255 |
+ // +----+----------+----------+
+ // VER: 协议版本,socks5为0x05
+ // NMETHODS: 支持认证的方法数量
+ // METHODS: 对应NMETHODS,NMETHODS的值为多少,METHODS就有多少个字节。RFC预定义了一些值的含义,内容如下:
+ // X’00’ NO AUTHENTICATION REQUIRED
+ // X’02’ USERNAME/PASSWORD
+
+ ver, err := reader.ReadByte()
+ if err != nil {
+ return fmt.Errorf("read ver failed:%w", err)
+ }
+ if ver != socks5Ver {
+ return fmt.Errorf("not supported ver:%v", ver)
+ }
+ methodSize, err := reader.ReadByte()
+ if err != nil {
+ return fmt.Errorf("read methodSize failed:%w", err)
+ }
+ method := make([]byte, methodSize)
+ _, err = io.ReadFull(reader, method)
+ if err != nil {
+ return fmt.Errorf("read method failed:%w", err)
+ }
+
+ // +----+--------+
+ // |VER | METHOD |
+ // +----+--------+
+ // | 1 | 1 |
+ // +----+--------+
+ _, err = conn.Write([]byte{socks5Ver, 0x00})
+ if err != nil {
+ return fmt.Errorf("write failed:%w", err)
+ }
+ return nil
+}
+
+func connect(reader *bufio.Reader, conn net.Conn) (err error) {
+ // +----+-----+-------+------+----------+----------+
+ // |VER | CMD | RSV | ATYP | DST.ADDR | DST.PORT |
+ // +----+-----+-------+------+----------+----------+
+ // | 1 | 1 | X'00' | 1 | Variable | 2 |
+ // +----+-----+-------+------+----------+----------+
+ // VER 版本号,socks5的值为0x05
+ // CMD 0x01表示CONNECT请求
+ // RSV 保留字段,值为0x00
+ // ATYP 目标地址类型,DST.ADDR的数据对应这个字段的类型。
+ // 0x01表示IPv4地址,DST.ADDR为4个字节
+ // 0x03表示域名,DST.ADDR是一个可变长度的域名
+ // DST.ADDR 一个可变长度的值
+ // DST.PORT 目标端口,固定2个字节
+
+ buf := make([]byte, 4)
+ _, err = io.ReadFull(reader, buf)
+ if err != nil {
+ return fmt.Errorf("read header failed:%w", err)
+ }
+ ver, cmd, atyp := buf[0], buf[1], buf[3]
+ if ver != socks5Ver {
+ return fmt.Errorf("not supported ver:%v", ver)
+ }
+ if cmd != cmdBind {
+ return fmt.Errorf("not supported cmd:%v", ver)
+ }
+ addr := ""
+ switch atyp {
+ case atypIPV4:
+ _, err = io.ReadFull(reader, buf)
+ if err != nil {
+ return fmt.Errorf("read atyp failed:%w", err)
+ }
+ addr = fmt.Sprintf("%d.%d.%d.%d", buf[0], buf[1], buf[2], buf[3])
+ case atypeHOST:
+ hostSize, err := reader.ReadByte()
+ if err != nil {
+ return fmt.Errorf("read hostSize failed:%w", err)
+ }
+ host := make([]byte, hostSize)
+ _, err = io.ReadFull(reader, host)
+ if err != nil {
+ return fmt.Errorf("read host failed:%w", err)
+ }
+ addr = string(host)
+ case atypeIPV6:
+ return errors.New("IPv6: no supported yet")
+ default:
+ return errors.New("invalid atyp")
+ }
+ _, err = io.ReadFull(reader, buf[:2])
+ if err != nil {
+ return fmt.Errorf("read port failed:%w", err)
+ }
+ port := binary.BigEndian.Uint16(buf[:2])
+
+ dest, err := net.Dial("tcp", fmt.Sprintf("%v:%v", addr, port))
+ if err != nil {
+ return fmt.Errorf("dial dst failed:%w", err)
+ }
+ defer dest.Close()
+ log.Println("dial", addr, port)
+
+ // +----+-----+-------+------+----------+----------+
+ // |VER | REP | RSV | ATYP | BND.ADDR | BND.PORT |
+ // +----+-----+-------+------+----------+----------+
+ // | 1 | 1 | X'00' | 1 | Variable | 2 |
+ // +----+-----+-------+------+----------+----------+
+ // VER socks版本,这里为0x05
+ // REP Relay field,内容取值如下 X’00’ succeeded
+ // RSV 保留字段
+ // ATYPE 地址类型
+ // BND.ADDR 服务绑定的地址
+ // BND.PORT 服务绑定的端口DST.PORT
+ _, err = conn.Write([]byte{0x05, 0x00, 0x00, 0x01, 0, 0, 0, 0, 0, 0})
+ if err != nil {
+ return fmt.Errorf("write failed: %w", err)
+ }
+ ctx, cancel := context.WithCancel(context.Background())
+ defer cancel()
+
+ go func() {
+ _, _ = io.Copy(dest, reader)
+ cancel()
+ }()
+ go func() {
+ _, _ = io.Copy(conn, dest)
+ cancel()
+ }()
+
+ <-ctx.Done()
+ return nil
+}
+Go 语言进阶 - 工程进阶
+ +本节课程主要分为四个方面:
+属于编程进阶内容,考虑到工程项目的可用性和可靠性,工程实践中经常会用到。
+了解Go依赖管理演进的历程,通过课程学习以及课后实践能能够熟练使用go module 管理依赖。
+需求模型来源
+青训营话题页forum.juejin.cn/youthcamp/p…
+需求
+组件及技术点
+课程链接:
+Go可以充分发挥多核的优势,高效运行
+线程:内核态,比较重量级
+协程:用户态,线程可以跑多个协程,比较轻量
+快速打印:
+func hello(i int) {
+ println("hello goroutine : " + fmt.Sprint(i))
+}
+
+func HelloGoRoutine() {
+ for i := 0; i < 5; i++ {
+ go func(j int) {
+ hello(j)
+ }(i)
+ }
+ time.Sleep(time.Second)
+}最后是使用time.sleep进行阻塞,防止在协程未运行结束前主线程先运行结束了。
+协程通过通信来共享内存
+func CalSquare() {
+ src := make(chan int)
+ dest := make(chan int, 3)
+ go func() {
+ defer close(src)
+ for i := 0; i < 10; i++ {
+ src <- i
+ }
+ }()
+ go func() {
+ defer close(dest)
+ for i := range src {
+ dest <- i * i
+ }
+ }()
+ for i := range dest {
+ //复杂操作
+ println(i)
+ }
+}
+var (
+ x int64
+ lock sync.Mutex
+)
+
+func addWithLock() {
+ for i := 0; i < 2000; i++ {
+ lock.Lock()
+ x += 1
+ lock.Unlock()
+ }
+}
+func addWithoutLock() {
+ for i := 0; i < 2000; i++ {
+ x += 1
+ }
+}
+
+func Add() {
+ x = 0
+ for i := 0; i < 5; i++ {
+ go addWithoutLock()
+ }
+ time.Sleep(time.Second)
+ println("WithoutLock:", x)
+ x = 0
+ for i := 0; i < 5; i++ {
+ go addWithLock()
+ }
+ time.Sleep(time.Second)
+ println("WithLock:", x)
+}func ManyGoWait() {
+ var wg sync.WaitGroup
+ wg.Add(5)
+ for i := 0; i < 5; i++ {
+ go func(j int) {
+ defer wg.Done()
+ hello(j)
+ }(i)
+ }
+ wg.Wait()
+}GOPATH:环境变量,项目代码直接依赖src下的代码,go get下载最新的包到src目录下
+Go Vendor:增加vendor文件,存放依赖包的副本,优先从vendor文件里面查找,但是仍然无法控制依赖的版本
+Go Module:go.mod:依赖管理基本单元、原生库、单元依赖
+func HelloTom() string {
+ return "Tom"
+}
+
+func TestHelloTom(t *testing.T) {
+ output := HelloTom()
+ expectOutput := "Tom"
+ assert.Equal(t, expectOutput, output)
+}添加–cover参数可以评价测试代码的覆盖率
+一些函数对本地的数据库、文件等有强依赖,在测试的同时找到这些依赖要求过高
+可以使用Mock进行测试,在函数执行的时候替换成另外一个函数(打桩),从而规避掉对本地其他的强依赖
+func ReadFirstLine() string {
+ open, err := os.Open("log")
+ defer open.Close()
+ if err != nil {
+ return ""
+ }
+ scanner := bufio.NewScanner(open)
+ for scanner.Scan() {
+ return scanner.Text()
+ }
+ return ""
+}
+
+func ProcessFirstLine() string {
+ line := ReadFirstLine()
+ destLine := strings.ReplaceAll(line, "11", "00")
+ return destLine
+}
+
+func TestProcessFirstLine(t *testing.T) {
+ firstLine := ProcessFirstLine()
+ assert.Equal(t, "line00", firstLine)
+}
+
+func TestProcessFirstLineWithMock(t *testing.T) {
+ monkey.Patch(ReadFirstLine, func() string {
+ return "line110"
+ })
+ defer monkey.Unpatch(ReadFirstLine)
+ line := ProcessFirstLine()
+ assert.Equal(t, "line000", line)
+}对函数的运行时间进行测试:go test -bench=.
+var ServerIndex [10]int
+
+func InitServerIndex() {
+ for i := 0; i < 10; i++ {
+ ServerIndex[i] = i+100
+ }
+}
+
+func Select() int {
+ return ServerIndex[rand.Intn(10)]
+}
+
+func FastSelect() int {
+ return ServerIndex[fastrand.Intn(10)]
+}
+
+func BenchmarkSelect(b *testing.B) {
+ InitServerIndex()
+ b.ResetTimer()
+ for i := 0; i < b.N; i++ {
+ Select()
+ }
+}
+func BenchmarkSelectParallel(b *testing.B) {
+ InitServerIndex()
+ b.ResetTimer()
+ b.RunParallel(func(pb *testing.PB) {
+ for pb.Next() {
+ Select()
+ }
+ })
+}
+func BenchmarkFastSelectParallel(b *testing.B) {
+ InitServerIndex()
+ b.ResetTimer()
+ b.RunParallel(func(pb *testing.PB) {
+ for pb.Next() {
+ FastSelect()
+ }
+ })
+}需求
+分层结构
+组件及技术点
+具体逻辑见代码
+Go 框架三件套详解(Web/RPC/ORM)
+ +搭建课程所需要的开发环境以及安装需要用到的软件。
+提前体验一下课程涉及的 HTTP/RPC/ORM 框架
+通过阅读 www.cloudwego.io/zh/docs/her… 尝试运行 Hertz 的示例代码(Hertz 框架地址: github.com/cloudwego/h…)
+go install github.com/cloudwego/hertz/cmd/hz@latesthz new -module github.com/cloudwego/hertz-examplesgo mod tidygo build -o hertz_demo && ./hertz_demo通过阅读 www.cloudwego.io/zh/docs/kit… 尝试运行 Kitex 的示例代码(KItex 框架地址: github.com/cloudwego/k…)
+go install github.com/cloudwego/kitex/tool/cmd/kitex@latestgo install github.com/cloudwego/thriftgo@latestgit clone https://github.com/cloudwego/kitex-examples.githello 目录 cd kitex-examples/hellogo run .go run ./client通过阅读 gorm.cn/docs/#Insta… 尝试运行 Gorm 的示例代码(Gorm 框架地址: github.com/go-gorm/gor…)
+go get -u gorm.io/gorm
+go get -u gorm.io/driver/sqlite直播链接:https://live.juejin.cn/4354/9899243
+Gorm是一个已经迭代了10年+的功能强大的ORM框架,在字节内部被广泛使用并且拥有非常丰富的开源扩展。
+Kitex是字节内部的Golang微服务RPC框架,具有高性能、强可扩展的主要特点,支持多协议并且拥有丰富的开源扩展。
+Hertz是字节内部的HTTP框架,参考了其他开源框架的优势,结合字节跳动内部的需求,具有高易用性、高性能、高扩展性特点。
+Gorm拥有丰富的扩展生态,可以使用代码生成工具、分片库方案、手动索引、乐观锁、读写分离、OpenTelemetry 扩展等等
+Go 高质量编程与性能调优
+ +总结
+注释应该解释代码作用
+注释应该解释代码如何做的
+注释应该解释代码实现的原因
+注释应该解释代码什么情况会出错
+公共符号始终要注释
+总结
+variable
+function
+package
+总结
+避免嵌套,保持正常流程清晰
+如果两个分支中都包含 return 语句,则可以去除冗余的 else
+尽量保持正常代码路径为最小缩进,优先处理错误情况/特殊情况,并尽早返回或继续循环来减少嵌套,增加可读性
+总结
+简单错误处理
+错误的 Wrap 和 Unwrap
+错误判定
+panic
+recover
+总结
+在满足正确性、可靠性、健壮性、可读性等质量因素的前提下,设法提高程序的效率
+性能对比测试代码,可参考 github.com/RaymondCode…
+性能调优的核心是性能瓶颈的分析,对于 Go 应用程序,最方便的就是 pprof 工具
+
Go 语言内存管理详解
+ +本节课程主要分为四个方面:
+课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
+Auto memory management: 自动内存管理
+Grabage collction: 垃圾回收
+Mutator: 业务线程
+Collector: GC 线程
+Concurrent GC: 并发 GC
+Parallel GC: 并行 GC
+Tracing garbage collection: 追踪垃圾回收
+Reference counting: 引用计数
+Generational GC: 分代 GC
+mmap() 系统调用什么是性能优化?
+为什么要做性能优化?
+性能优化
+软件质量
+测试驱动
+通过清晰的文档告诉用户这一项优化 做了什么 , 没做什么 ,能达到怎样的效果
+隔离,优化代码用选项和原先的路径隔离,保证优化未启用时的行为同以前一致
+可观测、可灰度、可回滚
+自动内存管理:由程序语言的运行时系统管理动态内存
+避免手动内存管理,专注于实现业务逻辑
+保证内存使用的正确性和 安全性 : double-free problem, use-after-free problem
+三个任务
+概念
+Mutator: 业务线程,分配新对象,修改对象指向关系
+Collector: GC 线程,找到存活对象,回收死亡对象的内存空间
Serial GC: 只有一个 collector
+Parallel GC: 并行 GC,支持多个 collectors 同时回收的 GC 算法
+Concurrent GC: 并发 GC,支持 mutator(s) 和 collector(s) 同时执行的 GC 算法
+Collectors 必须感知对象指向关系的改变!
+


每个对象都有一个与之关联的引用数目
+对象存活的条件:当且仅当引用数大于 0
+优点
+缺点
+说明
+TCMalloc: TC is short for thread caching
+目标:为对象在 heap 上分配内存
+提前将内存分块
+对象分配:根据对象的大小,选择最合适的块返回
+内存缓存
+mspan, mcache 和 mcentral 构成了内存管理的多级缓存机制。
+可以看到,用于分配对象的函数 mallocgc() 占用 CPU 较高
横轴是对象大小,纵轴是数目,可以看到绝大多数对象都小于 80 B。因此 优化小对象分配是关键 。
+if g.ab.end - g.ab.top < size {
+ // Allocate a new allocation buffer
+}
+addr := g.ab.top
+g.ab.top += size
+return addrtop 指针并返回,快速完成一次对象分配mallocgc() 进行对象分配的方式相比,balanced GC 缩短了对象分配的路径,减少了对象分配执行的指令数目,降低 CPU 使用从 Go runtime 内存管理模块的角度看,一个 allocation buffer 其实是一个大对象。本质上 balanced GC 是 将多次小对象的分配合并成一次大对象的分配 。因此,当 GAB 中哪怕只有一个小对象存活时,Go runtime 也会认为整个大对象(即 GAB)存活。为此,balanced GC 会根据 GC 策略, 将 GAB 中存活的对象移动到另外的 GAB 中 ,从而压缩并清理 GAB 的内存空间,原先的 GAB 空间由于不再有存活对象,可以全部释放,如下图所示。
+上图上方是两个 GAB,其中虚线表示 GAB 中对象的分界线。黑色表示 GAB 中存活的对象,白色表示死掉的对象。由于 GAB 中有存活对象,整个 GAB 无法被回收。
+Balanced GC 会将 GAB 中存活的对象移动到下面的 GAB 中,这样原先的两个 GABs 就可以被释放,压缩并清理 GAB 的内存空间。
+Balanced GC 只负责 noscan 对象的分配和移动,对象的标记和回收依然依赖 Go GC 本身,并和 Go GC 保持兼容。
+上图的程序转换成控制流图 (control-flow graph)
+定义:将被调用函数的函数体的副本替换到调用位置上,同时重写代码以反映参数的绑定
+优点
+缺点
+函数内联在大多数情况下是正向优化,即多内联,会提升性能
+采取一定的策略决定是否内联
+Go 内联的限制
+字节跳动的优化方案
+开销
+定义:分析代码中指针的动态作用域,即指针在何处可以被访问
+大致思路
+优化:未逃逸出当前函数的指针指向的对象可以在栈上分配
+简易抖音项目-用户模块
+ +用户模块包括用户注册、用户登录和用户信息三个部分。
+新用户注册时提供用户名,密码,昵称即可,用户名需要保证唯一。创建成功后返回用户 id 和权限token.
+接口定义:
+service UserRegister {
+ rpc UserRegister (douyin_user_register_request) returns (douyin_user_register_response) {}
+}
+
+message douyin_user_register_request{
+ string username = 1; // 注册用户名,最长32个字符
+ string password = 2; // 密码,最长32个字符
+}
+
+message douyin_user_register_response{
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ int64 user_id = 3; // 用户id
+ string token = 4; // 用户鉴权token
+}通过用户名和密码进行登录,登录成功后返回用户 id 和权限 token
+接口定义:
+service UserLogin {
+ rpc UserLogin (douyin_user_login_request) returns (douyin_user_login_response) {}
+}
+
+message douyin_user_login_request{
+ string username = 1; // 登录用户名
+ string password = 2; // 登录密码
+}
+
+message douyin_user_login_response{
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ int64 user_id = 3; // 用户id
+ string token = 4; // 用户鉴权token
+}获取登录用户的 id、昵称,如果实现社交部分的功能,还会返回关注数和粉丝数。
+接口定义:
+service UserInfo {
+ rpc UserInfo (douyin_user_request) returns (douyin_user_response) {}
+}
+
+message douyin_user_request{
+ int64 user_id = 1; // 用户id
+ string token = 2; // 用户鉴权token
+}
+
+message douyin_user_response{
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ User user = 3; // 用户信息
+}返回的状态码(虽然客户端并没有逻辑进行处理):
+简易抖音项目-视频模块
+ +视频模块包括包括视频Feed流获取、视频投稿和获取用户投稿列表三个模块
+不限制登录状态,返回按投稿时间倒序的视频列表,视频数由服务端控制,单次最多30个。
+接口定义:
+service Feed {
+ rpc Feed (douyin_feed_request) returns (douyin_feed_response) {}
+}
+
+message douyin_feed_request{
+ int64 latest_time = 1; // 可选参数,限制返回视频的最新投稿时间戳,精确到秒,不填表示当前时间
+ string token = 2; // 可选参数,登录用户设置
+}
+
+message douyin_feed_response{
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ repeated Video video_list = 3; // 视频列表
+ int64 next_time = 4; // 本次返回的视频中,发布最早的时间,作为下次请求时的latest_time
+}登录用户的视频发布列表,直接列出用户所有投稿过的视频。
+接口定义:
+service PublishList {
+ rpc PublishList (douyin_publish_list_request) returns (douyin_publish_list_response) {}
+}
+
+message douyin_publish_list_request{
+ int64 user_id = 1; // 用户id
+ string token = 2; // 用户鉴权token
+}
+
+message douyin_publish_list_response{
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ repeated Video video_list = 3; // 用户发布的视频列表
+}登录用户选择视频上传。
+接口定义:
+service PublishAction {
+ rpc PublishAction (douyin_publish_action_request) returns (douyin_publish_action_response) {}
+}
+
+message douyin_publish_action_request{
+ string token = 1; // 用户鉴权token
+ bytes data = 2; // 视频数据
+ string title = 3; // 视频标题
+}
+
+message douyin_publish_action_response{
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+}返回的状态码(虽然客户端并没有逻辑进行处理):
+MIT-6.824(Spring 2022)LEC 7 Fault Tolerance-Raft-2
+ +日志擦除可能会带来一些问题,论文中的Figure 8 说明了这个问题,因此需要有日志提交条件的额外限制: Leader 在当前任期至少有一条日志被提交
+前面的协议中一直是减1操作,因此如果Follower落后过多,通信开销会很大
+追赶更快的优化算法:并不按照索引后退,而是按照term后退,然后再扫描相同的位置
+此时Follower并不只是拒绝,而是返回前一个term以及这个term开始的索引
+重启机器会发生什么?
+需要持久化什么信息?我们应该尽量不保存信息,因为需要存入磁盘,开销很大,只需要保留必要的信息
+状态机通过apply channel获得一个快照,然后使用它来进行恢复
+步骤:
+客户端也需要保存Raft的Leader和Follower的信息,可以切换它的通信对象
+客户端如果没有接收到服务器的响应会进行重试,而服务器可鞥已经执行过这些操作了,因此需要对这些重复的操作进行检测。
+一种实现方法:客户端的每一个操作都带有一个id,通过id对重复的操作进行过滤
+模糊定义:多台机器的行为如同单独的一台机器一样
+精确定义:
+线性一致性:
+查看历史操作,即使是并行的程序是否可以在一台机器上执行相同的结果,从而判断是否满足线性一致性。
+ + +MIT-6.824(Spring 2022)Lab 2 Raft
+ + +这是构建容错k/v存储系统的一系列实验室中的第一个。这个实验室将实现复制状态机协议Raft。
+复制服务通过在多个副本服务器上存储其状态(即数据)的完整副本来实现容错。复制允许服务继续运行,即使某些服务器出现故障(崩溃或网络问题)。挑战在于,故障可能会导致复制副本保存不同的数据副本。
+Raft将客户端请求组织成一个序列,称为日志,并确保所有副本服务器都看到相同的日志。每个副本按日志顺序执行客户端请求,并将它们应用于服务状态的本地副本。由于所有活动副本都看到相同的日志内容,因此它们都以相同的顺序执行相同的请求,从而继续具有相同的服务状态。如果服务器出现故障,但稍后恢复,Raft会负责更新其日志。只要有大多数服务器处于活动状态,并且可以相互通信,Raft就会继续运行。如果没有这样的大多数,Raft将会暂时停机,但一旦大多数服务器能够再次通信,Raft就会恢复原来的状态。
+在这个实验中,将会把Raft实现为一个Go对象类型,并实现相关的方法,这意味着要在更大的服务中将Raft用作模块。一组Raft实例通过RPC相互通信,以维护复制的日志。Raft接口将支持无限序列的编号命令,也称为日志条目。条目用索引编号进行编号。具有给定索引的日志条目最终会被提交。此时,Raft应该将日志条目发送到更大的服务以供其执行。
+您应该遵循扩展的Raft论文中的设计,尤其是图2。您将实现本文中的大部分内容,包括保存持久状态,并在节点发生故障后重新启动后读取该状态。不实现第6节提到的集群成员资格更改。
+最具挑战性的部分可能不是实现解决方案,而是调试解决方案。为了帮助解决这一挑战,您可能需要花时间思考如何使实现更易于调试。
+我们还提供了一个Raft交互的图表,可以帮助阐明Raft代码如何与上面的层进行交互。
+ +(几年前编写,特别是2D部分已经发生了变化)
+Raft 是一种共识算法,旨在轻松理解。它与Paxos的容错和性能相当。不同的是,它被分解成相对独立的子问题,它干净地解决了所有主要部分的实际系统需求。我们希望Raft可供更广泛的受众使用,并且这些更广泛的受众将是能够开发各种更高质量的基于共识的系统。
+ +与所有分布式共识协议一样,细节很难理解。在没有故障的稳定状态下,Raft 的行为易于理解,并且可以直观地解释。例如,从可视化中很容易看出, 假设没有失败,最终将选出Leader,并且最终,发送给Leader的所有操作都将由Follower按照顺序正确执行。但是,当消息延迟,网络分区或者服务故障,细节变得至关重要。特别是,我们可能一遍又一遍地重复许多错误,仅仅是由于阅读论文时的误解或疏忽。这个问题并非Raft所独有。
+Raft 的最终指南在 Raft 论文的图 2 中。这个图片指定在Raft服务器之间交换的每个RPC的行为, 给出服务器必须维护的各种不变量,并指定何时应执行某些操作。我们将在本文的其余部分大量讨论图 2。它需要一字不差地遵循。
+图 2 定义了每个服务器在各种状态下应该对每个传入的 RPC应该做什么,以及何时发生某些其他事情(例如就像在日志中应用条目是安全的一样)。图 2 非常精确,每一条语句在规范术语中,它应该被视为必须,而不是应该。例如,您可以合理地重置一台服务器的选举计时器,只要您收到或RPC,都表明其他服务器要么认为它是Leader,或者是努力成为Leader。直觉上,这意味着我们不应该干扰。但是,如果您仔细阅读图 2,它会说:如果选举超时过去而没有收到当前Leader的RPC或投票给其他的服务器,则转换为Candidate。
+事实证明,区别很重要,因为前一种实现在某些情况下,可能导致活性显著降低。
+考虑一个例子。Raft论文在许多地方提到了心跳RPC。具体来说,领导者将偶尔(每个检测信号间隔至少一次)向所有服务器发送 RPC,以防止它们启动新的选举。如果领导者没有要发送到特定对等方的新条目, RPC 不包含任何条目,被视为心跳。
+我们的许多学生认为心跳在某种程度上是“特别的”,当服务器收到心跳时,它应该以不同的方式对待它。特别是,许多人会只在收到心跳时重置他们的选举计时器,然后返回成功,而不执行图2中指定的任何检查。这是极其危险的。通过接受 RPC, Follower隐式地告诉Leader他们的日志与Leader匹配并包括参数中包含的内容。收到回复后,领导可能错误地确定某个条目已被复制到大多数服务器,并开始提交它。
+许多人遇到的另一个问题是在收到心跳时,他们会截断Follower的记录,然后添加参数中包含的日志条目。这也是不正确的。图 2说明,如果现有条目与新条目冲突(相同的索引但 不同的任期),删除现有条目及其后面的所有条目。
+这里的如果至关重要。如果Follower拥有Leader的所有条目,Follower不得截断其日志。必须保留Leader发送的条目之后的任何元素。这是因为我们可能从Leader收到过期的RPC,截断日志将意味着“收回”我们可能已经告诉Leader的我们的日志。
+在调试时,Raft通常有四个主要的错误来源: 活锁、不正确或不完整的 RPC 处理程序、未能遵循规则和术语混淆。死锁也是一个常见问题,但它们通常可以通过记录所有锁和解锁来调试,并且弄清楚你正在占有哪些锁且没有释放。
+当系统活锁时,系统中的每个节点都在执行一些东西,但总的来说,你的节点没有取得进展。一个活锁场景特别频繁出现:没有领导人被选举出来,或者一个领导者被选举出来后另一个节点马上开始选举,迫使最近当选的领导人立即退位。
+出现这种情况的原因有很多:
+确保在图 2说明的时候准确重置选举计时器。具体来说,有三种情况:
+最后一种情况在不可靠的网络中尤其重要,其中Follower可能有不同的日志,在这些情况下, 只有少量的服务器使得大多数服务器都愿意投票支持。如果每当有人要求您投票给他们时都重置选举计时器,会使日志过时的服务器同样有可能向前迈进
+事实上,因为很少的服务器有足够的最新的日志,这些服务器不太可能在足够和平的情况下进行选举。如果您遵循图 2,具有最新日志的服务器不会被过时的服务器选举打断,因此更有可能完成选举并成为Leader。
+按照图 2 的说明操作了解何时应开始选举。 特别要注意的是,如果您是Candidate,但选举计时器触发,应该开始另一次选举。这对于避免由于 RPC 延迟或丢弃而导致系统停止非常重要。
+在处理传入的 RPC 之前 ,请确保遵循“服务器规则”中的第二条规则。第二条规则规定:如果 RPC 请求或响应包含术语set ,则转换为Follower
+例如,如果您已经在当前任期内投票,并且传入的RPC有一个更高的任期号,你应该首先下台并采用他们的任期(从而重置),然后处理RPC,处理的过程中就会进行投票
+尽管图 2 准确地说明了每个 RPC 处理程序应该执行的操作, 一些细节仍然很容易被忽略。
+如果步骤显示“回复错误”,这意味着您应该立即回复,不要执行任何后续步骤。
+如果你得到一个指向日志末尾的RPC,应该像确实有该条目,但该任期不匹配处理这个。
+如果领导者没有发送任何条目,RPC处理程序的检查 2 应执行。
+#5 是必要的, 并且需要使用最后一个新条目的索引进行计算。 这是因为日志中可能存在与领导者日志不同的条目。因为 #3 规定您只有在有冲突的条目情况下才会截断日志,这些条目不会被删除,如果超出领导发送给您的条目,您可能会应用不正确的条目。
+实施“最新日志”检查非常重要。只是检查长度!
+虽然 Raft 论文非常明确地说明了如何实现每个 RPC 处理程序,它还留下了许多规则的实现和未指定的不变量。这些列在“服务器规则”中 图 2 右侧的块。虽然其中一些是不言自明的,也有一些需要非常小心地设计,以免违反规则:
+如果在执行过程中的任何时候应用特定的日志条目。请务必确保仅由一个实体完成此应用程序。具体来说,您需要有一个专门的 “应用器”,或者锁定这些应用,以便其他一些例程不会同时检测到需要应用条目。
+确保定期更新,或更新后进行检查。例如,如果您在发送给同行的同时进行检查,您可能需要等到下一个条目追加到日志中后再应用您刚刚发送并得到确认的条目。
+如果领导者发出 RPC,并且被拒绝,但不是因为日志不一致(这只有在我们的任期中才会发生),那么您应该立即下台并且不更新。
+领导者不允许更新到上一任期(或就此而言,未来任期)的某个地方。因此特别需要检查。这是因为如果这不是他们目前的任期,Raft 领导者无法确定条目是否实际提交(并且将来永远不会更改)。
+一个常见的问题来源是nextIndex和matchIndex之间的区别。特别是,你可能会观察到matchIndex = nextIndex - 1,而干脆不实现matchIndex。这是不安全的。虽然nextIndex和matchIndex通常在同一时间被更新为类似的值(具体来说,nextIndex = matchIndex + 1),但两者的作用完全不同。它通常是相当乐观的(我们分享一切),并且只在消极的反应中向后移动。例如,当一个领导者刚刚当选时,nextIndex被设置为日志末尾的索引指数。在某种程度上,nextIndex是用于性能的–你只需要将这些东西发送给这个对等体。
+matchIndex是用于安全的。MatchIndex不能被设置为一个太高的值,因为这可能会导致commitIndex被向前移动得太远。这就是为什么matchIndex被初始化为-1(也就是说,我们不同意任何前缀),并且只在跟随者肯定地确认AppendEntries RPC时才更新。
+任期混淆是指服务器被来自旧任期的RPC所迷惑。一般来说,在收到RPC时,这不是一个问题,因为图2中的规则确切地说明了当你看到一个旧任期时你应该做什么。然而,图2一般没有讨论当你收到旧的RPC回复时你应该做什么。根据经验,我们发现到目前为止,最简单的做法是首先记录回复中的任期(它可能比你当前的任期高),然后将当前任期与你在原始RPC中发送的任期进行比较。如果两者不同,就放弃回复并返回。只有当这两个任期相同时,你才应该继续处理回复。
+一个相关但不完全相同的问题是,预设你的状态在你发送RPC和你收到回复之间没有变化。这方面的一个很好的例子是,当你收到RPC的响应时,设置matchIndex = nextIndex - 1,或者matchIndex = len(log)。这并不安全,因为这两个值都可能在你发送RPC后被更新。相反,正确的做法是将 matchIndex 更新为你最初在 RPC 中发送的参数中 prevLogIndex + len( entries[]) 。
+一个Raft实例必须处理外部事件的到来(Start()调用、AppendEntries和RequestVote RPC以及RPC回复),它必须执行定期任务(选举和心跳)。有许多方法可以构造Raft代码来管理这些活动,下面是一些想法。
+rf.mu.Lock()
+ rf.currentTerm += 1
+ rf.state = Candidate
+ for <each peer> {
+ go func() {
+ rf.mu.Lock()
+ args.Term = rf.currentTerm
+ rf.mu.Unlock()
+ Call("Raft.RequestVote", &args, ...)
+ // handle the reply...
+ } ()
+ }
+ rf.mu.Unlock()这个代码在单独的goroutine中发送每个RPC。这是不正确的,因为如果周围的代码是决定成为Candidate,args.Term可能与rf.currentTerm不同。当周围的代码创建goroutine和当goroutine读取rf.currentTerm时可能过去了很多的时间,这台服务器也可能不再是Candidate。一种方法是当外部代码持有锁的时候创建rf.currentTerm的副本从而让goroutine去使用。同样的,在调用之后的回复处理代码重新获取锁后必须重新检查所有相关的假设,例如,它应该检查自从决定成为Candidate后rf.currentTerm没有再次改变。
+一种方法是从没有锁的代码开始,然后仔细考虑需要在哪里添加锁以变得正确。另一个更务实的方法从观察开始,如果没有并发性(没有同时执行goroutine)则根本不需要锁。但是当RPC系统创建goroutine以执行RPC处理程序时,以及
+因为您需要在单独的goroutine中发送RPC以避免等待,并发性就有了。可以通过识别所有goroutine开始的位置(RPC处理程序、在Make()中创建的后台goroutine,&c),并且在每个goroutine开始的时候获得锁,只有当goroutine
+完全完成并返回的时候才释放锁,从而消除并发性。这个锁定协议确保任何重要的事情都不会并行执行;锁确保每个goroutine在其他goroutine执行之前完成,没有并行执行,很难违反规则1、2、3或5。如果每个goroutine的代码正确,在使用锁抑制并发时仍然是正确的。
然而,规则4可能是一个问题。所以下一步是找到代码等待的位置,然后根据需求添加锁释放和重新获取(或goroutine的创建),记得小心重新建立和重新获取后的情况。
+框架代码:src/raft/raft.go
+测试代码:src/raft/test_test.go,运行go test即可
+通过在src/raft/raft.go中增加代码实现Raft,必须遵循下面的接口:
+// create a new Raft server instance:
+rf := Make(peers, me, persister, applyCh)
+
+// start agreement on a new log entry:
+rf.Start(command interface{}) (index, term, isleader)
+
+// ask a Raft for its current term, and whether it thinks it is leader
+rf.GetState() (term, isLeader)
+
+// each time a new entry is committed to the log, each Raft peer
+// should send an ApplyMsg to the service (or tester).
+type ApplyMsg服务调用 Make(peers, me, ...)创建一个 Raft peer。peers 参数是所有 Raft peers(包括这一个)的网络标识符数组,用于 RPC。me参数是网络标识符数组中,属于这个peer的网络标识符的下标。Start(command) 要求 Raft 启动处理,将命令追加到日志副本中。Start()应立即返回,无需等待日志追加完成。该服务希望你将每个新的日志条目,封装为 ApplyMsg,发送给Make函数中的 applyCh参数(这是一个channel)。
raft.go包含发送 RPC sendRequestVote()和处理传入 RPC RequestVote()的样例代码。您的 Raft peers 应该使用 labrpc Go 包(源代码在 src/labrpc)交换 RPC。测试代码可以告诉 labrpc 延迟 RPC请求,重新排列它们,并丢弃它们以模拟各种网络故障。Raft 实例必须仅与 RPC 交互;例如,不允许它们使用共享的 Go 变量或文件进行通信。
后续的实验也在此实验上进行构建。
+参考翻译:https://zhuanlan.zhihu.com/p/248686289
+实现Raft算法中的Leader选举和心跳机制(AppendEntries RPC 且没有日志条目)。确保只有一个Leader被选中,且若无错误该Leader会一直唯一存在,当该Leader下线或发生其他错误导致发出的数据无法被成功接收,则会产生新的Leader来替代。
go test -run 2A 来验证代码的正确性raft.go中添加Figure 2的Leader选举的状态,同时也需要定义一个结构体保留日志条目的信息RequestVoteArgs和 RequestVoteReply结构。修改 Make()以创建一个后台 go 协程,该协程将在一段时间未从其他 peers 那里听到请求投票 RPC 时,发送 RequestVote RPC 来定期启动 Leader 选举。这样,如果已经有一个 Leader,或者自己成为 Leader,其他 peers 就会知道谁是Leader。实现 RequestVote() RPC 函数,以便服务器投票给别人。AppendEntries RPC 结构(尽管您可能还不需要所有参数),并让 Leader 定期发送它们。AppendEntries RPC 函数需要重置选举超时时间,以便其他服务器已当选时,不会以 Leader 的身份继续运行。time.Timer或 time.Ticker,这两个并不好用,容易出错。GetState()。rf.Kill()时,您可以先调用 rf.killed()再检查是否 Kill()。您可能希望在所有循环中执行此功能,以避免已经死亡的 Raft 实例打印令人困惑的信息。go test -run 2A > out,将日志收集到文件中。然后,通过研究 out 文件,可以确定实现中不正确的地方。您可能会喜欢用 util.go中的 Dprintf函数来调试,其可以在不同情况下打开和关闭日志。labgob包会警告您这一点,不要忽略警告。go test -race测试你的代码,并修复它报告的任何问题。输出应该如下面所示:
+$ go test -run 2A
+Test (2A): initial election ...
+ ... Passed -- 3.5 3 58 16840 0
+Test (2A): election after network failure ...
+ ... Passed -- 5.4 3 118 25269 0
+Test (2A): multiple elections ...
+ ... Passed -- 7.3 7 624 138014 0
+PASS
+ok 6.824/raft 16.265s
+$每一个“通过”的测试用例会输出五个数字;他们分别是
+首先需要对代码中不完整的结构体进行填充,论文中的Figure 2有的字段一定保留,其他的字段看情况保留
+首先定义服务器的状态,用字符串常量表示:
+// 定义Peer的状态
+type State string
+
+const (
+ Follower State = "follower"
+ Candidate State = "candidate"
+ Leader State = "leader"
+)然后定义Raft结构体:
+type Raft struct {
+ mu sync.Mutex // Lock to protect shared access to this peer's state
+ peers []*labrpc.ClientEnd // RPC end points of all peers
+ persister *Persister // Object to hold this peer's persisted state
+ me int // this peer's index into peers[]
+ dead int32 // set by Kill()
+
+ // Your data here (2A, 2B, 2C).
+ // Look at the paper's Figure 2 for a description of what
+ // state a Raft server must maintain.
+
+ // 在所有peer上面的持久性的状态
+ // 在对RPC进行响应之后要在稳定存储上更新
+ currentTerm int // this peer 看到的最新的任期号
+ votedFor int // 在当前任期获得选票的Candidate的id(如果没有则为-1)
+
+ log []LogEntry // 日志信息
+
+ // 在所有peer上面的变化的状态
+ commitIndex int // 已知的已经被提交的日志条目的最大索引值
+ lastApplied int // 最后被应用到状态机的日志条目索引值(初始化为 0,持续递增)
+
+ // 在Leader上面的变化的状态
+ // 每一次选举后都要重新进行初始化
+ nextIndex []int // 对于每⼀个服务器,需要发送给他的下⼀个日志条目的索引值(初始化为Leader最后索引值加1)
+ matchIndex []int // 对于每⼀个服务器,已经复制给他的日志的最高索引值
+
+ // 与时间相关的变量
+ electTimeout int64 // 选举超时时间
+ randomTimeout int64 // 随机时间
+ heartBeatTimeout int64 // 心跳周期
+
+ // 当前状态
+ state State // 当前Peer所处的状态(Leader、Candidate或Follower)
+ majorityVote int // 成为Leader需要获得的最少票数
+ lastReceive int64
+}其中多定义了6个变量,3个变量与时间相关,分别表示选举超时时间、随机的时间上限和Leader发送心跳的周期时间
+// 与时间相关的变量
+electTimeout int64 // 选举超时时间
+randomTimeout int64 // 随机时间
+heartBeatTimeout int64 // 心跳周期最后3个变量,第1个表示服务器当前所处的状态,第2个表示成为Leader需要获得的最少票数,这个值提前计算出来,最后一个值表示最后一次接收到Leader的心跳信号的时间
+// 当前状态
+state State // 当前Peer所处的状态(Leader、Candidate或Follower)
+majorityVote int // 成为Leader需要获得的最少票数
+lastReceive int64 // 最后一次接收到Leader的心跳信号的时间服务器不同状态之间的转换比较频繁,因此可以将这些服务器状态转换的代码提取出来编写成工具函数,方便后续直接调用
+// 转为Leader
+func (rf *Raft) toLeader() {
+ DPrintf("[%d]: convert from [%s] to [%s], term [%d]", rf.me, rf.state, Leader, rf.currentTerm)
+ rf.state = Leader
+ // rf.lastReceive = time.Now().Unix()
+}
+
+// 转为Follower
+func (rf *Raft) toFollower(newTerm int) {
+ DPrintf("[%d]: convert from [%s] to [%s]", rf.me, rf.state, Follower)
+ rf.state = Follower
+ rf.currentTerm = newTerm
+ rf.votedFor = -1
+ rf.lastReceive = time.Now().Unix()
+}
+
+// 转为Candidate
+func (rf *Raft) toCandidate() {
+ DPrintf("[%d]: convert from [%s] to [%s]", rf.me, rf.state, Candidate)
+ rf.state = Candidate
+ rf.currentTerm += 1
+ rf.votedFor = rf.me
+ // rf.lastReceive = time.Now().Unix()
+}然后补充一个预定义的获取服务器状态的方法
+// return currentTerm and whether this server
+// believes it is the leader.
+func (rf *Raft) GetState() (int, bool) {
+
+ var term int
+ var isleader bool
+ // Your code here (2A).
+ rf.mu.Lock()
+ defer rf.mu.Unlock()
+ isleader = false
+ term = rf.currentTerm
+ if rf.state == Leader {
+ isleader = true
+ }
+ return term, isleader
+}结构体定义完全按照论文即可,目前不需要其他字段
+// example RequestVote RPC arguments structure.
+// field names must start with capital letters!
+type RequestVoteArgs struct {
+ // Your data here (2A, 2B).
+ Term int // Candidate的任期号
+ CandidateId int // Candidate的 Id
+ LastLogIndex int // Candidate最后一条日志条目的索引
+ LastLogTerm int // Candidate最后一条日志条目的任期
+}
+
+// example RequestVote RPC reply structure.
+// field names must start with capital letters!
+type RequestVoteReply struct {
+ // Your data here (2A).
+ Term int // 当前的任期,接收到了之后Candidate可以更新自己
+ VoteGranted bool // 是否给这个Candidate投票
+}核心RPC:
+// example RequestVote RPC handler.
+func (rf *Raft) RequestVote(args *RequestVoteArgs, reply *RequestVoteReply) {
+ // Your code here (2A, 2B).
+ // RPC 请求不一定在什么时候应用,因此必须加锁
+ rf.mu.Lock()
+ defer rf.mu.Unlock()
+ DPrintf("[%d]: received vote request from [%d]", rf.me, args.CandidateId)
+
+ reply.VoteGranted = false
+
+ // 如果参数的任期号还没有我的大,不投票,直接默认值返回即可
+ if args.Term < rf.currentTerm {
+ // 响应中包含当前自己的任期号
+ reply.Term = rf.currentTerm
+ return
+ }
+ // 如果参数的任期号比我的大,则我在这个任期内就只能是它的Follower,则更改我的任期号,而且在这个任期内我要投票给它
+ if args.Term > rf.currentTerm {
+ rf.toFollower(args.Term)
+ }
+ reply.Term = rf.currentTerm // 注意这里任期号已经变化了,因此要重新赋值
+ DPrintf("[%d]: status: term [%d], state [%s], vote for [%d]", rf.me, rf.currentTerm, rf.state, rf.votedFor)
+ // 如果参数的任期号和我的相同,则任期号不变,需要通过日志确定是否投票给它
+ // 这里论文要求的 rf.VotedFor == args.CandidateId 不是很明白
+ if rf.votedFor == -1 || rf.votedFor == args.CandidateId {
+ // Todo:判断日志是否至少更新才可以投票
+ rf.votedFor = args.CandidateId
+ rf.lastReceive = time.Now().Unix() // 更新时间,上面操作相当于与可能的Leader通信过了
+ reply.VoteGranted = true
+ DPrintf("[%d]: voted to [%d]", rf.me, args.CandidateId)
+ }
+}核心就是计算返回的reply中的两个值,第一个是是否投票,第二个是当前服务器的任期号。其中任期号一定要小心,可能服务器自己的状态改变后任期号会随之改变,因此一定要及时更新。
+if args.Term < rf.currentTerm {
+ // 响应中包含当前自己的任期号
+ reply.Term = rf.currentTerm
+ return
+}if args.Term > rf.currentTerm {
+ rf.toFollower(args.Term)
+}(这个结构不返回,投票的逻辑在下一个结构)
+rf.votedFor == -1 承接上面的投票逻辑,把情况2的票投了
rf.VotedFor == args.CandidateId 在后面要加上对于日志的判断,这里仅仅是简单投票给它
if rf.votedFor == -1 || rf.votedFor == args.CandidateId {
+ // Todo:判断日志是否至少更新才可以投票
+ rf.votedFor = args.CandidateId
+ rf.lastReceive = time.Now().Unix() // 更新时间,上面操作相当于与可能的Leader通信过了
+ reply.VoteGranted = true
+ DPrintf("[%d]: voted to [%d]", rf.me, args.CandidateId)
+}在调用的时候,Candidate请求每一台服务器投票给它,如果得到的响应说我的任期号比你还大,也就是上面的情况2,也自动放弃Candidate的地位成为Follower。否则这个Candidate就会得到自己的票。
+// 向每一个Peer请求投票
+func (rf *Raft) requestVoteToPeer(index int, args *RequestVoteArgs, votesSum *int, votesGet *int, cond *sync.Cond) {
+
+ reply := RequestVoteReply{}
+ ok := rf.sendRequestVote(index, args, &reply)
+ rf.mu.Lock()
+ defer rf.mu.Unlock()
+ defer cond.Broadcast()
+ *votesSum += 1
+ if !ok {
+ return
+ }
+ if reply.Term > rf.currentTerm {
+ rf.toFollower(reply.Term)
+ // } else if reply.VoteGranted && reply.Term == rf.currentTerm {
+ } else if reply.VoteGranted {
+ *votesGet += 1
+ }
+}结构体定义完全按照论文即可,目前不需要其他字段
+type AppendEntriesArgs struct {
+ // Your data here (2A, 2B).
+ Term int // Leader的任期号
+ LeaderId int // Follower可以通过这个LeaderId重定向客户端
+ PrevLogIndex int // 新的日志条目紧随之前的索引值
+ PrevLogTerm int // PrevLogIndex日志条目的任期
+ Entries []LogEntry // 存储的日志条目,如果是心跳包则为空
+ LeaderCommit int // Leader的提交索引
+}
+
+type AppendEntriesReply struct {
+ // Your data here (2A).
+ Term int // 当前的任期,接收到了之后Leader可以更新自己
+ Success bool // Follower包含了匹配上 prevLogIndex 和 prevLogTerm 的日志时为真
+}这个RPC既作为日志更新的来源,在没有日志携带的时候也作为心跳包用于维持Leader的地位
+func (rf *Raft) AppendEntries(args *AppendEntriesArgs, reply *AppendEntriesReply) {
+ // Your code here (2A, 2B).
+ // RPC 请求不一定在什么时候应用,因此必须加锁
+ rf.mu.Lock()
+ defer rf.mu.Unlock()
+ // 更新至少为当前的任期
+ reply.Term = rf.currentTerm
+ reply.Success = false
+ // 如果Leader的任期还没有我的大,则直接拒绝请求
+ if args.Term < rf.currentTerm {
+ return
+ }
+ // 如果Leader的任期比我的大,则我转为这个任期的Follower
+ if args.Term >= rf.currentTerm || rf.state == Candidate {
+ rf.toFollower(args.Term)
+ }
+ // 如果Leader的任期和我的相同,则操作日志
+ // Todo:日志操作
+ rf.lastReceive = time.Now().Unix()
+ reply.Term = rf.currentTerm
+ reply.Success = true
+}核心也是计算返回的reply中的两个值,第一个是是否更新成功,第二个是当前服务器的任期号。其中任期号一定要小心,可能服务器自己的状态改变后任期号会随之改变,因此一定要及时更新。
+if args.Term < rf.currentTerm {
+ return
+}// 如果Leader的任期比我的大,则我转为这个任期的Follower
+if args.Term >= rf.currentTerm || rf.state == Candidate {
+ rf.toFollower(args.Term)
+}(同时要对我自己的日志进行更新,目前还没有实现)
+rf.lastReceive = time.Now().Unix()
+reply.Term = rf.currentTerm
+reply.Success = true主要是要对服务器的收到Leader的请求的时间进行更新,从而避免Follower转为Candidate,在Leader存在的情况下发起选举
+在调用的时候,Leader向其他的每一台服务器发送这个RPC,如果得到的响应说我的任期号比你还大,也就是上面的情况2,也自动放弃Leader的地位成为Follower。
+// 向指定的Peer增加日志条目或者发送心跳包
+func (rf *Raft) appendEntriesToPeer(index int, args *AppendEntriesArgs) {
+ reply := AppendEntriesReply{}
+ if ok := rf.sendAppendEntries(index, args, &reply); ok {
+ rf.mu.Lock()
+ defer rf.mu.Unlock()
+ // Todo:log相关
+ // 如果响应的任期比Leader更大了,说明Leader需要退位成Follower了
+ if reply.Term > rf.currentTerm {
+ rf.toFollower(reply.Term)
+ }
+ }
+}
+每一台服务器初始化的时候都是一个Follower,任期号为0
+除此之外还要设置选举超时时间,心跳发送时间等
+以及根据服务器的数量计算好需要多少张选票才能达成共识
+然后直接开始选举
+rf.toFollower(0)
+
+rf.electTimeout = 200 // 初始化选举超时时间
+rf.heartBeatTimeout = 100 // 初始化心跳间隔时间
+rf.randomTimeout = 100 // 设置随机时间的最大范围
+
+// 初始化成为Leader需要得到的票数
+if len(rf.peers)%2 == 0 {
+ rf.majorityVote = len(rf.peers)/2 + 1
+} else {
+ rf.majorityVote = (len(rf.peers) + 1) / 2
+}
+
+// start ticker goroutine to start elections
+go rf.leaderElection()所有的协程都不设置退出条件,因此内部要么是无限循环,要么是有状态变量等进行控制
+选举Leader是一个无限循环,在每一次循环的时候记录当前的时间后进行睡眠(固定时间+随机时间),然后在循环内部进行判断,如果上一次循环到这里的实时时间比上一次接收到心跳包的时间还大,说明在睡眠时间内一直没有接收到心跳包,则认为超时,此时就要放弃自己的Follower身份,转为Candidate开始竞选。
+// The ticker go routine starts a new election if this peer hasn't received
+// heartsbeats recently.
+func (rf *Raft) leaderElection() {
+
+ lastElectTime := time.Now().Unix()
+
+ for !rf.killed() {
+
+ // Your code here to check if a leader election should
+ // be started and to randomize sleeping time using
+ // time.Sleep().
+
+ time.Sleep(time.Duration(rf.electTimeout+rand.Int63n(rf.randomTimeout)) * time.Millisecond)
+
+ rf.mu.Lock()
+ // lastStartTime := startTime
+
+ // 如果上一次循环到这里的实时时间比上一次接收到心跳包的时间还大,说明在睡眠时间内一直没有接收到心跳包,则认为超时
+ if lastElectTime > rf.lastReceive {
+ //DPrintf("[%d]: current state is [%s].", rf.me, rf.state)
+ if rf.state != Leader {
+ DPrintf("[%d]: is not leader, start election.", rf.me)
+ rf.tryLeader()
+ }
+ }
+ lastElectTime = time.Now().Unix() // 更新“上一次”的时间
+ rf.mu.Unlock()
+ }
+}然后在 rf.tryLeader()中,首先将服务器的状态转为Candidate,然后构建请求,向其他的peer发送请求投票的RPC,收到响应后对收到的投票进行统计。如果得到了大多数的选票,则这个Candidate可以转为Leader,同时向其他的服务器发送心跳包说明自己已经成为了Leader,其他的peer需要放弃竞选。
func (rf *Raft) tryLeader() {
+ rf.toCandidate()
+
+ votesSum := 1 // 总共的票的数量
+ votesGet := 1 // 收到的票数,自己首先给自己投票
+ cond := sync.NewCond(&rf.mu) // 条件变量,控制投票结果的返回
+ args := RequestVoteArgs{
+ Term: rf.currentTerm,
+ CandidateId: rf.me,
+ }
+ for i := 0; i < len(rf.peers); i++ {
+ if i != rf.me {
+ go rf.requestVoteToPeer(i, &args, &votesSum, &votesGet, cond)
+ }
+ }
+ // 等待票数统计完毕并判断是否能成为Leader
+ go func() {
+ rf.mu.Lock()
+ defer rf.mu.Unlock()
+
+ for votesGet < rf.majorityVote && votesSum < len(rf.peers) && rf.state == Candidate {
+ cond.Wait()
+ }
+ if votesGet >= rf.majorityVote && rf.state == Candidate {
+ rf.toLeader()
+ // 发送心跳包
+ go rf.logReplication()
+ }
+ }()
+}内部的协程同步使用状态变量控制(虽然不明白为什么使用WaitGroup不可以实现功能)
+心跳包发送(或与日志更新一起)是只有Leader才可以发起的动作。
+注意定时发起请求即可
+// Leader定时发送更新log的请求,同时也作为心跳包
+func (rf *Raft) logReplication() {
+ for !rf.killed() {
+ rf.mu.Lock()
+ if rf.state == Leader {
+ args := AppendEntriesArgs{
+ Term: rf.currentTerm,
+ LeaderId: rf.me,
+ }
+ for i := 0; i < len(rf.peers); i++ {
+ if i != rf.me {
+ go rf.appendEntriesToPeer(i, &args)
+ }
+ }
+ }
+ rf.mu.Unlock()
+ time.Sleep(time.Duration(rf.heartBeatTimeout) * time.Millisecond)
+ }
+}目前最快的结果:
+Test (2A): initial election ...
+ ... Passed -- 3.0 3 72 18660 0
+Test (2A): election after network failure ...
+ ... Passed -- 4.9 3 166 31952 0
+Test (2A): multiple elections ...
+ ... Passed -- 5.3 7 522 111880 0
+PASS
+ok 6.824/raft 13.335s运行10次后均成功
+完善 Leader 和 Follower 的代码,使他们可以追加新的日志条目,并通过 go test -run 2B。
TestBasicAgree2B()。首先实现 Start(),然后按照 Figure 2,实现 RPC 函数 AppendEntries来收发新的日志条目。通过 applyCh发送每一个新提交的日志条目。time.Sleep(10 * time.Millisecond)。如果运行太慢,可能会没法通过接下来的测试。您可以使用 time命令检查您的解决方案使用了多少实时时间和CPU时间。这是典型的输出:
$ time go test -run 2B
+Test (2B): basic agreement ...
+ ... Passed -- 0.9 3 16 4572 3
+Test (2B): RPC byte count ...
+ ... Passed -- 1.7 3 48 114536 11
+Test (2B): agreement after follower reconnects ...
+ ... Passed -- 3.6 3 78 22131 7
+Test (2B): no agreement if too many followers disconnect ...
+ ... Passed -- 3.8 5 172 40935 3
+Test (2B): concurrent Start()s ...
+ ... Passed -- 1.1 3 24 7379 6
+Test (2B): rejoin of partitioned leader ...
+ ... Passed -- 5.1 3 152 37021 4
+Test (2B): leader backs up quickly over incorrect follower logs ...
+ ... Passed -- 17.2 5 2080 1587388 102
+Test (2B): RPC counts aren't too high ...
+ ... Passed -- 2.2 3 60 20119 12
+PASS
+ok 6.824/raft 35.557s
+
+real 0m35.899s
+user 0m2.556s
+sys 0m1.458s
+$“ok 6.824/raft 35.557s” 意味着 Go 运行 2B 的测试所用的实时时间为 35.557 秒。“user 0m2.556s” 表示代码运行了 2.556 秒的 CPU 时间,或实际运行(而不是等待或睡眠)所花费的时间。如果测试 2B 使用超过 1 分钟的实时时间,或超过 5 秒的 CPU 时间,则以后的实验可能会遇到麻烦。检查睡眠时间、等待 RPC 超时所花费的时间、没有睡眠或等待地检查条件或channel信息的循环、或发送大量 RPC 的地方。
+无论是转为Leader、Follower或者转为Candidate,实际上都可以看成是有一个隐含存在的Leader告诉他们这样做的,因此都要同步更新自己的选举超时时间,防止在有Leader的时候就已经超时,导致Leader的存在时间过短。
+// 转为Leader
+func (rf *Raft) toLeader() {
+ DPrintf("[%d]: convert from [%s] to [%s], term [%d]", rf.me, rf.state, Leader, rf.currentTerm)
+ rf.state = Leader
+ rf.lastReceive = time.Now().Unix()
+ // 选举为Leader后重新对所有的peer进行初始化
+ for i := 0; i < len(rf.peers); i++ {
+ rf.nextIndex[i] = len(rf.log)
+ rf.matchIndex[i] = -1
+ }
+}
+
+// 转为Follower
+func (rf *Raft) toFollower(newTerm int) {
+ DPrintf("[%d]: convert from [%s] to [%s]", rf.me, rf.state, Follower)
+ rf.state = Follower
+ rf.currentTerm = newTerm
+ rf.votedFor = -1
+ rf.lastReceive = time.Now().Unix()
+}
+
+// 转为Candidate
+func (rf *Raft) toCandidate() {
+ DPrintf("[%d]: convert from [%s] to [%s]", rf.me, rf.state, Candidate)
+ rf.state = Candidate
+ rf.currentTerm += 1
+ rf.votedFor = rf.me
+ rf.lastReceive = time.Now().Unix()
+}首先要注意由于论文中的索引是从1开始计算的,而计算机上切片的索引是从0开始算的,因此论文说明的初始化为0的地方都要初始化为-1
+nextIndex[]:leader要发送给follower的下一条log entry(各follower不同),follower与leader一致的时候只发最新一条log,有不一致的时候,nextIndex要减,一次发多条log。把不一致的部分都修正过来。
+matchIndex[]:已知follower上,从0开始有多少条连续的log entry与leader一致。即: 有多少条log entry已经被成功replicate到follower上了。如果过半数,就可以增加commitIndex, apply到状态机, 答复客户端操作成功了
+commitIndex: 已知被提交的最高日志项对应的index。当日志项被提交(committed)了,意味着该日志项已经成功复制到了集群中的多数派server上,属于“集体记忆”了。如果当前的leader宕机再次发生选举,只有拥有完整已提交日志的server才能够获得多数派选票,才能被选举为leader。根据Leader完整性(Leader Completeness),如果一个日志项在某个term被提交了,则该Entry会存在于所有更高term的leader日志中。
+lastApplied: 应用(apply)给状态机的最高日志项的index,也就是上层应用“消费”到Raft日志项的最新index。Leader使用nextIndex和matchIndex两个数组来维护集群中其它server的日志状态。
+其他结构体字段:
+Start函数是raft顶层的服务最开始调用的类似初始化的函数
+如果server不是leader则返回false。如果是leader的话,那么将command组装成LogEntry后追加到自己的日志中。此处要同时更新leader自己的matchIndex(由于自己就是Leader,自己肯定与自己一致)和nextIndex(如果自己是Follower,这条日志肯定就不能改了)
+func (rf *Raft) Start(command interface{}) (int, int, bool) {
+ index := -1
+ term := -1
+ isLeader := false
+
+ // Your code here (2B).
+ if !rf.killed() {
+ rf.mu.Lock()
+ defer rf.mu.Unlock()
+ if rf.state == Leader {
+ isLeader = true
+ // 只有是Leader才可以接收日志信息
+ // 添加日志信息
+ rf.log = append(rf.log, LogEntry{
+ Term: rf.currentTerm,
+ Command: command,
+ })
+ index = len(rf.log) - 1
+ term = rf.currentTerm
+ rf.matchIndex[rf.me] = index // 已经复制给他的日志的最高索引值
+ rf.nextIndex[rf.me] = index + 1 // 需要发送给他的下⼀个日志条目的索引值
+ }
+ // 论文与代码起始位置索引不同
+ index += 1
+ }
+
+ return index, term, isLeader
+}请求投票RPC:新增了最后一个日志项的信息
+新增日志RPC:(只有Leader才可能发出)
+AppendEntryReply结构体新增了XTerm、XIndex和XLen几个变量用于nextIndex的快速回退。
+论文中的nextIndex在AppendEntry RPC返回不匹配后,默认只是回退一个日志项(nextIndex[i]=PrevLogIndex)。如果follower能够返回更多信息,那么leader可以根据这些信息使对应server的nextIndex快速回退,减少AppendEntry RPC通信不匹配的次数,从而加快同步日志的步伐。这几个变量的具体含义:
+make()函数中除做一些初始化的工作之外,新增了将已经被提交的日志项返回给上层应用的goroutine
+// 初始化日志相关
+rf.log = make([]LogEntry, 0)
+rf.commitIndex = -1
+rf.lastApplied = -1
+rf.nextIndex = make([]int, len(peers))
+rf.matchIndex = make([]int, len(peers))
+
+rf.applyCh = applyCh
+rf.moreApply = false
+rf.applyCond = sync.NewCond(&rf.mu)
+
+go rf.appMsgApplier()这个新增的goroutine无限循环判断rf.moreApply字段,一旦发现为真,则触发返回的操作,返回新的提交过的日志给上层应用
+func (rf *Raft) sendApplyMsg() {
+ rf.moreApply = true
+ rf.applyCond.Broadcast()
+}
+
+func (rf *Raft) appMsgApplier() {
+ for {
+ rf.mu.Lock()
+ // 等待这个字段为真才可以继续
+ for !rf.moreApply {
+ rf.applyCond.Wait()
+ }
+ rf.moreApply = false
+
+ commitIndex := rf.commitIndex
+ lastApplied := rf.lastApplied
+ entries := rf.log
+ rf.mu.Unlock()
+ // 发送已经提交但是还没有返回的日志字段
+ for i := lastApplied + 1; i <= commitIndex; i++ {
+ msg := ApplyMsg{
+ CommandValid: true,
+ Command: entries[i].Command,
+ CommandIndex: i + 1,
+ }
+ DPrintf("[%d]: apply index %d - 1", rf.me, msg.CommandIndex)
+ rf.applyCh <- msg
+ // 及时加锁更新,否则可能会变化
+ rf.mu.Lock()
+ rf.lastApplied = i
+ rf.mu.Unlock()
+ }
+
+ }
+}返回给上层应用的情况两种:
+在前面选举Leader时,并没有对日志做限制,在这里需要补充日志层面的选举限制
+首先要在请求投票的结构体中附带自己最后一条日志的信息
+// Candidate最后一条日志的信息
+lastLogIndex := len(rf.log) - 1
+lastLogTerm := -1
+// 如果日志为空需要添加判断
+if lastLogIndex != -1 {
+ lastLogTerm = rf.log[lastLogIndex].Term
+}
+args := RequestVoteArgs{
+ Term: rf.currentTerm,
+ CandidateId: rf.me,
+ LastLogIndex: lastLogIndex,
+ LastLogTerm: lastLogTerm,
+}然后严格按照论文说明对请求投票的双方进行判断即可:
+总体原则:candidate的log是否至少和接受者的log一样新
+len(rf.log) ==0args.LastLogTerm > rf.log[len(rf.log)-1].Termargs.LastLogTerm == rf.log[len(rf.log)-1].Term,但是它的日志长度比我长或一样(它先请求我投票,那么我就投票给他吧)args.LastLogIndex >=len(rf.log)-1// 是否没投票或者投给的是这个candidate
+if rf.votedFor == -1 || rf.votedFor == args.CandidateId {
+ // candidate的log是否至少和接受者的log一样新
+ // 1. 我的log长度为0,那我肯定投票给他了
+ // 2. candidate的最后的log的任期比我的最后的log的任期大
+ // 3. candidate的最后的log的任期和我的最后的log的任期相同,但是它的日志长度比我长
+ if len(rf.log) == 0 || (args.LastLogTerm > rf.log[len(rf.log)-1].Term) ||
+ (args.LastLogTerm == rf.log[len(rf.log)-1].Term && args.LastLogIndex >= len(rf.log)-1) {
+ rf.votedFor = args.CandidateId
+ rf.lastReceive = time.Now().Unix() // 更新时间,上面操作相当于与可能的Leader通信过了
+ reply.VoteGranted = true
+ DPrintf("[%d]: voted to [%d]", rf.me, args.CandidateId)
+ }
+}// 找到日志的同步位置
+prevLogIndex := rf.nextIndex[index] - 1
+prevLogTerm := -1
+if prevLogIndex != -1 {
+ prevLogTerm = rf.log[prevLogIndex].Term
+}
+// 找到要发送的日志
+var entries []LogEntry
+if len(rf.log)-1 >= rf.nextIndex[index] {
+ entries = rf.log[rf.nextIndex[index]:]
+}
+// 补充结构体
+args := AppendEntriesArgs{
+ Term: rf.currentTerm,
+ LeaderId: rf.me,
+ LeaderCommit: rf.commitIndex,
+ PrevLogIndex: prevLogIndex,
+ PrevLogTerm: prevLogTerm,
+ Entries: entries,
+}论文的日志匹配性质:
+因此只需要判断PrevLogIndex和PrevLogTerm与follower的日志匹配的程度即可,这里只是Leader猜测一下,真正的判断在接收到RPC后完成
+在处理AppendEntry RPC的代码中,新增了日志匹配的逻辑。
+如果日志在prevLogIndex处不包含term为prevLogTerm的日志项,那么返回false,(需要回退才能找到对应的位置)。
+回退的逻辑:
+// Reply false if log doesn’t contain an entry at prevLogIndex
+// whose term matches prevLogTerm (§5.3)
+if args.PrevLogIndex >= len(rf.log) || (args.PrevLogIndex >= 0 && rf.log[args.PrevLogIndex].Term != args.PrevLogTerm) {
+ reply.Term = rf.currentTerm
+ // 回退
+ reply.XLen = len(rf.log)
+ if args.PrevLogIndex >= 0 && args.PrevLogIndex < len(rf.log) {
+ reply.XTerm = rf.log[args.PrevLogIndex].Term
+ for i := args.PrevLogIndex; i >= 0; i-- {
+ if rf.log[i].Term == reply.XTerm {
+ reply.XIndex = i
+ } else {
+ break
+ }
+ }
+ }
+ return
+}此外还要注意prevLogIndex可能为-1,意味着日志全都没有匹配上,或者leader此刻还没有日志,此时接收者就要完全服从。
+接下来是PreLogIndex与PrevLogTerm匹配到的情况,还要额外检查新同步过来的日志和已存在的日志是否存在冲突。如果一个已经存在的日志项和新的日志项冲突(相同index但是不同term),那么要删除这个冲突的日志项及其往后的日志。
+// If an existing entry conflicts with a new one (same index
+// but different terms), delete the existing entry and all that
+// follow it (§5.3)
+misMatchIndex := -1
+for i := range args.Entries {
+ if args.PrevLogIndex+1+i >= len(rf.log) || rf.log[args.PrevLogIndex+1+i].Term != args.Entries[i].Term {
+ misMatchIndex = i
+ break
+ }
+}将新的日志项追加到日志中
+// Append any new entries not already in the log
+if misMatchIndex != -1 {
+ rf.log = append(rf.log[:args.PrevLogIndex+1+misMatchIndex], args.Entries[misMatchIndex:]...)
+}最后根据论文,如果 leaderCommit > commitIndex,说明follower的commitIndex也需要更新。为了防止越界,commitIndex取 min(leaderCommit, index of last new entry)。同时要向上层应用发回响应。
// If leaderCommit > commitIndex, set commitIndex = min(leaderCommit, index of last new entry)
+if args.LeaderCommit > rf.commitIndex {
+ newEntryIndex := len(rf.log) - 1
+ if args.LeaderCommit >= newEntryIndex {
+ rf.commitIndex = newEntryIndex
+ } else {
+ rf.commitIndex = args.LeaderCommit
+ }
+ DPrintf("[%d]: commit index [%d]", rf.me, rf.commitIndex)
+ rf.sendApplyMsg()
+}由于RPC在网络中可能乱序或者延迟,我们要确保当前RPC发送时的term、当前接收时的currentTerm以及RPC的reply.term三者一致,丢弃过去term的RPC,避免对当前currentTerm产生错误的影响。
+reply.Term == rf.currentTerm && rf.currentTerm == args.Term当reply.Success为true,说明follower包含了匹配prevLogIndex和prevLogTerm的日志项,更新nextIndex[serverTo]和matchIndex[serverTo]。这里只能用prevLogIndex和entries来更新,而不能用nextIndex及len(log),因为后两者可能已经被别的RPC更新了,进而导致数据不一致。
+由于matchIndex发生了变化,我们要检查是否更新commitIndex。根据论文,如果存在一个N,这个N大于commitIndex,多数派的matchIndex[i]都大于等于N,并且log[N].term等于currentTerm,那么更新commitIndex为N。这里必须注意,日志提交是有限制的,Raft从不提交过去term的日志项,即使已经复制达到了多数派。如果要更新commitIndex为N,那么N所对应的日志项的term必须是当前currentTerm。
+在检查是否更新commitIndex的实现上,我们将matchIndex复制到了matches数组中,通过sort升序排序以方便遍历。然后对matches数组进行遍历,找到大多数都提交的索引位置,随后调用sendApplyMsg(),通知有更多的日志项已经被提交,上层应用可以应用。
+if reply.Success {
+
+ // 更新服务器的状态
+ rf.nextIndex[index] = prevLogIndex + len(entries) + 1
+ rf.matchIndex[index] = prevLogIndex + len(entries)
+
+ // If there exists an N such that N > commitIndex, a majority of matchIndex[i] ≥ N, and log[N].term == currentTerm:
+ // set commitIndex = N
+ matches := make([]int, len(rf.peers))
+ copy(matches, rf.matchIndex)
+ sort.Ints(matches)
+
+ for i := rf.majorityVote - 1; i >= 0 && matches[i] > rf.commitIndex; i-- {
+ if rf.log[matches[i]].Term == rf.currentTerm {
+ rf.commitIndex = matches[i]
+ DPrintf("[%d]: commit index [%d]", rf.me, rf.commitIndex)
+ rf.sendApplyMsg()
+ break
+ }
+ }
+}当reply.Success为false,说明follower的日志不包含在prevLogIndex处并匹配prevLogTerm的日志项,要将nextIndex缩减。此处更新不宜采用自减的方式更新,因为RPC可能会重发,正确的方式是 rf.nextIndex[serverTo] = prevLogIndex。
在AppendEntryReply中增加了几个变量,以使nextIndex能够快速回退(back up)。如果接下来要尝试匹配的prevLogIndex比follower当前所拥有的的日志长度(XLen)还要大,那么显然直接从XLen尝试匹配即可。如果接下来要尝试匹配的prevLogIndex在XLen以内,因为我们已经知道了follower的日志从XIndex到当前prevLogIndex的日志项的term都是XTerm,那么我们可以直接在leader侧遍历匹配一遍,而无需多次往返RPC通信。
+} else {
+ // In Test (2C): Figure 8 (unreliable), the AppendEntry RPCs are reordered
+ // So rf.nextIndex[index]-- would be wrong
+ rf.nextIndex[index] = prevLogIndex
+ // 如果接下来要尝试匹配的prevLogIndex比follower当前所拥有的的日志长度(XLen)还要大,那么显然直接从XLen尝试匹配即可。
+ if rf.nextIndex[index]-1 >= reply.XLen {
+ rf.nextIndex[index] = reply.XLen
+ } else {
+ // 如果接下来要尝试匹配的prevLogIndex在XLen以内,因为我们已经知道了follower的日志从XIndex到当前prevLogIndex的日志项的term都是XTerm,那么我们可以直接在leader侧遍历匹配一遍,而无需多次往返RPC通信
+ for i := rf.nextIndex[index] - 1; i >= reply.XIndex; i-- {
+ if rf.log[i].Term != reply.XTerm {
+ rf.nextIndex[index] -= 1
+ } else {
+ break
+ }
+ }
+ }
+}Test (2B): basic agreement ...
+ ... Passed -- 1.3 3 16 4546 3
+Test (2B): RPC byte count ...
+ ... Passed -- 2.7 3 48 114510 11
+Test (2B): agreement after follower reconnects ...
+ ... Passed -- 7.1 3 116 31767 8
+Test (2B): no agreement if too many followers disconnect ...
+ ... Passed -- 4.1 5 160 37664 3
+Test (2B): concurrent Start()s ...
+ ... Passed -- 1.2 3 12 3466 6
+Test (2B): rejoin of partitioned leader ...
+ ... Passed -- 5.6 3 166 40233 4
+Test (2B): leader backs up quickly over incorrect follower logs ...
+ ... Passed -- 34.1 5 2352 2038228 102
+Test (2B): RPC counts aren't too high ...
+ ... Passed -- 2.5 3 42 12630 12
+PASS
+ok 6.824/raft 58.652s
+
+real 0m59.353s
+user 0m1.744s
+sys 0m1.630s如果基于 Raft 的服务器重新启动,它应该在中断的地方恢复服务。这要求 Raft 在重启后,依旧能确保数据持久化。本文的Figure 2 提到的那些状态应该被持久化。
+真正的实现会在每次 persistent state 被修改时写磁盘,并在重新启动后从磁盘读取状态。您不需要使用磁盘,而应该通过 Persister 对象保存和恢复 persistent state (请参阅 persister.go)。调用 Raft.Make()时会提供一个 Persister, 其可能会包含 Raft 最近的 persistent state(也可能没有) 。Raft 应从 Persister 初始化其状态(对应方法 ReadRaftState()),并在每次 president state 更改后使用 Persister 保存(对应方法 SaveRaftState())。
完善 raft.go中的 persist()和 readPerisit()函数,实现保存和读取 persistent state。你可能需要使用 labgob encoder 来编码(或者说序列化)persistent state,让 Persister来存储二进制流。欢迎查看 persist()和 readPerisit()的注释了解更多。labgob很像 go 的 gob,只是会在序列化非导出字段时报错。实现完“ 在每次 persistent state 改变时调用 presist()”后,应通过其余测试。
您可能想优化为一次性保存多条日志。查看论文第7页的顶部到第 8 页顶部(用灰色线标记的地方)。论文没有描述清楚细节,你需要自己多考虑一下。 6.824 Raft 的讲座或许也能提供一些帮助。
+您的代码应通过所有 2C 测试:
+$ go test -run 2C
+Test (2C): basic persistence ...
+ ... Passed -- 5.0 3 86 22849 6
+Test (2C): more persistence ...
+ ... Passed -- 17.6 5 952 218854 16
+Test (2C): partitioned leader and one follower crash, leader restarts ...
+ ... Passed -- 2.0 3 34 8937 4
+Test (2C): Figure 8 ...
+ ... Passed -- 31.2 5 580 130675 32
+Test (2C): unreliable agreement ...
+ ... Passed -- 1.7 5 1044 366392 246
+Test (2C): Figure 8 (unreliable) ...
+ ... Passed -- 33.6 5 10700 33695245 308
+Test (2C): churn ...
+ ... Passed -- 16.1 5 8864 44771259 1544
+Test (2C): unreliable churn ...
+ ... Passed -- 16.5 5 4220 6414632 906
+PASS
+ok 6.824/raft 123.564s
+$最好能多次运行:for i in {0..10}; do go test; done
就目前情况而言,重新启动的服务器会重放完整的Raft日志,以恢复其状态。然而,对于长期运行的服务来说,永远记住完整的Raft日志是不现实的。相反,您将修改Raft以与持久存储其状态的“快照”的服务协作,此时Raft将丢弃快照之前的日志条目。其结果是持久数据量更少,重启速度更快。然而,现在有可能一个追随者远远落后,以至于领导者放弃了需要追赶的日志条目;然后领导者必须发送快照以及快照时开始的日志。
+您的Raft必须提供以下函数 Snapshot(index int, snapshot []byte),服务可以使用其状态的序列化快照调用该函数。
在Lab 2D中,测试代码定期调用 Snapshot()。在Lab 3中,您将编写一个k/v服务器调用 Snapshot();快照将包含k/v对的完整表。服务层对每个对等方(而不仅仅是Leader)调用 Snapshot()。
index参数指示快照中包括的最高日志条目。raft应该在这个参数之前丢弃其日志条目。您需要修改Raft代码以只存储日志尾部。
+您需要实现论文中讨论的 InstallSnapshot RPC,该RPC允许raft的Leader告诉落后的Raft服务器用快照替换其状态。您可能需要考虑 InstallSnapshot应该如何与图2中的状态和规则交互。
当Follower的Raft代码接收到 InstallSnapshot RPC时,它可以使用 applyCh将快照发送到 ApplyMsg中的服务。ApplyMsg结构定义已经包含了您需要的字段(并且是测试代码期望的)。请注意,这些快照只会增加服务的状态,而不会导致服务向后移动。
如果服务器崩溃,它必须从持久数据重新启动。您的Raft应该保持Raft状态和相应的快照。使用 persister.SaveStateAndSnapshot(),它对于Raft状态和相应的快照有单独的参数。如果没有快照,则传递nil作为快照参数。
当服务器重新启动时,应用程序层读取持久化快照并恢复其保存状态。
+以前,建议您实现一个名为 CondInstallSnapshot的函数,以避免在 applyCh上发送的快照和日志条目需要协调。这个残留的API接口仍然存在,但不希望实现它:相反,我们建议您只需将其返回true。
任务:实现 Snapshot()和 InstallSnapshot RPC,以及对Raft的更改以支持这些(例如,使用修剪日志的操作)。
提示:
+Snapshot(index)放弃索引之前的日志,并将X设置为索引。如果一切顺利,您现在应该通过第一个2D测试。InstallSnapshot RPC。InstallSnapshot RPC中发送整个快照。不要实现图13的用于分割快照的偏移机制。AppendEntries RPC中的新条目之前正确发送条目的术语和索引;这可能需要保存和引用最新快照的 lastIncludedTerm/lastIncludedIndex(请考虑是否应持久化)。输出示例:
+$ go test -run 2D
+Test (2D): snapshots basic ...
+ ... Passed -- 11.6 3 176 61716 192
+Test (2D): install snapshots (disconnect) ...
+ ... Passed -- 64.2 3 878 320610 336
+Test (2D): install snapshots (disconnect+unreliable) ...
+ ... Passed -- 81.1 3 1059 375850 341
+Test (2D): install snapshots (crash) ...
+ ... Passed -- 53.5 3 601 256638 339
+Test (2D): install snapshots (unreliable+crash) ...
+ ... Passed -- 63.5 3 687 288294 336
+Test (2D): crash and restart all servers ...
+ ... Passed -- 19.5 3 268 81352 58
+PASS
+ok 6.824/raft 293.456s【实践课】规则引擎设计与实现
+ +规则引擎是一种嵌入在应用服务中的组件,可以将灵活多变的业务决策从服务代码中分离出来。通过使用预定义的语义模块来编写业务逻辑规则。在执行时接受数据输入、解释业务规则,并做出决策。规则引擎能大大提高系统的灵活性和扩展性。
+在字节跳动,规则引擎已经在风控识别、活动运营、配置下发等场景得到了广泛的应用。开发人员可以将业务逻辑与服务代码解耦,实现灵活、高效的业务策略发布。目前公司内部基于规则引擎的动态决策系统已经承接了千万级别QPS的决策请求。
+规则引擎的实现需要在满足大容量、高请求、低延迟的基础上尽可能做到简单易上手。本次课程将会带领大家实现一个简单版的规则引擎。
+重点
+难点
+主要涉及到编译原理的部分
+课前必看!!!
+本部分是需要大家在上课之前了解的内容,主要是一些基本的概念和原理。
+在这门课程之前你可能根本没有听说过规则引擎这个东西,当然也可能是浅浅的大概知道这是个什么东西,或者是个规则引擎方面的资深专家(还没毕业,五年工作经验那种🐶,如果是这样请赶紧找我内推)。都没有关系,这门课包教包会!!!(学不会的下课后可以找我们运营人员联系我一对一教学)
+当然,这门课程还是有一定的门槛的,这也就是我为什么要说这么多一定要让你仔细看看这部分的原因。经过实验,课程的内容如果只依赖于课上老师的讲解,只能做到:能听懂,能跟上,来不及思考。要想能够理解掌握这部分内容,能跟别人battle下,再向自己的知识山峰上加那么一块小石头,得好好预习。
+开始之前先百度或者Google一下 “规则引擎”简单浏览下哈,📪📪📪另外掘金app上面也有许多不错的文章。可以先浏览看看。
+数据结构得学过吧,考多少分?😁
+这块的预习目标呢,包括以下几个部分
+是的,就这一个要求,其实学完青训营的前几节课就可以达到了
+编译原理被誉为"程序员的三大浪漫"之一,足以可见这块知识的深度与广度,我们这次课程也是简单的介绍一下与规则引擎相关的概念。
+那么可能会有疑问了,不是讲规则引擎么?为啥还得学编译原理?
+规则引擎的本质呢就是我们自己定义一套语法,然后去解析用这套语法写的表达式,然后根据解析的内容执行表达式。这个过程其实就是编译和执行的过程。
+因此呢需要自行了解以下的内容
+课程之前,大家需要根据项目工程,来完成环境的搭建和Demo的运行
+项目地址:
+ +相信大家已经完成了Go环境的搭建,项目工程依赖了hertz框架,如果在之前的课程中完成了项目环境搭建可以直接复用。
+项目环境:
+项目clone到本地后,可以执行测试脚本来测试环境的可用性。如果有错误欢迎百度和Google解决
+git clone https://github.com/qimengxingyuan/young_engine.git
+chmod a+x ./setup.sh
+./setup.sh脚本执行成功,则环境可以支持项目的执行
+项目说明:
+本项目是一个简单的规则引擎的实现,详细目录可以参考README.md
+项目实现时间有限,没有做比较完备的测试,如果在demo执行的过程中出现某些bug或者执行异常可以直接在github提交issue或者修复后提起PR
+ +编译的过程就是 把某种语言的源程序, 在不改变语义的条件下 ,转换成另一种语言程序(目标语言程序)
+解释型语言和编译型语言
+关于 Java 和 Python .
+JVM 和 Python解释器 | 为什么一个叫虚拟机一个叫解释器
+把源代码字符串转换为词法单元(Token)的这个过程。
+确定的有限自动机 DFA | Deterministic Finite Automaton
+确定的有限自动机就是一个状态机,它的状态数量是有限的。该状态机在任何一个状态,基于输入的字符,都能做一个确定的状态转换。
+词法分析是识别一个个的单词,而语法分析就是在词法分析的基础上识别出程序的语法结构。这个结构是一个树状结构。这棵树叫做抽象语法树(Abstract Syntax Tree,AST)。树的每个节点(子树)是一个语法单元,这个单元的构成规则就叫“语法”。每个节点还可以有下级节点。
+Token -> AST
+上下文无关语法 Context-Free Grammar
+语言句子无需考虑上下文,就可以判断正确性
++++... +a = 0; +... +这是一个赋值语句,无论此语句的前后是什么代码,此语句所代表的操作是确定的。即给变量a赋值等于0 +
编程语言为什么不用人类的语言(自然语言),而是用上下文无关的文法呢? 因为
+上下文无关语法G:终结符集合T + 非终结符集合N + 产生式集合P + 起始符号S
+G由T、N、S和P组成,由语法G推导出来的所有句子的集合称为G语言!
+终结符: 组成串的基本符号。可以理解为词法分析器产生的token集合。比如 + Id ( ) 等
非终结符: 表示token的的集合的语法变量。比如 stmt varDecl 等等
start:blockStmts ; //起始
+block : '{' blockStmts '}' ; //语句块
+blockStmts : stmt* ; //语句块中的语句
+stmt = varDecl | expStmt | returnStmt | block; //语句
+varDecl : type Id varInitializer? ';' ; //变量声明
+type : Int | Long ; //类型
+varInitializer : '=' exp ; //变量初始化
+expStmt : exp ';' ; //表达式语句
+returnStmt : Return exp ';' ; //return语句
+exp : add ; //表达式
+add : add '+' mul | mul; //加法表达式
+mul : mul '*' pri | pri; //乘法表达式
+pri : IntLiteral | Id | '(' exp ')' ; //基础表达式 产生式:表示形式,S : AB ,就是说S的含义可以用语法AB进行表达
+S : AB
+A : aA | ε
+B : b | bB展开(expand):将P(A->u )应用到符号串vAw中,得到新串vu **w
+折叠(reduce):将P(A->uu )应用到符号串vuu w中,得到新串vAw
+推导(derivate):符号串u 应用一系列产生式,变成符号串v ,则u =>v:S => ab | b | bb
+巴科斯范式
+BNF是描述上下文无关理论的一种具体方法,通过BNF可以实现上下文无关文法的具体化、公式化、科学化,是实现代码解析的必要条件。
+<expr> ::= <expr> + <term>
+ | <expr> - <term>
+ | <term>
+
+<term> ::= <term> * <factor>
+ | <term> / <factor>
+ | <factor>
+
+<factor> ::= ( <expr> )
+ | Num++BNF本质上就是树形分解,分解成一棵抽象语法树
+
递归下降算法 Recursive Descent Parsing
+基本思路就是按照语法规则去匹配 Token 串。比如说,变量声明语句的规则如下:
+varDecl : types Id varInitializer? ';' ; //变量声明
+varInitializer : '=' exp ; //变量初始化
+exp : add ; //表达式
+add : add '+' mul | mul; //加法表达式
+mul : mul '*' pri | pri; //乘法表达式
+pri : IntLiteral | Id | '(' exp ')' ; //基础表达式如果写成产生式格式,是下面这样:
+varDecl -> types Id varInitializer ';'
+varInitializer -> '=' exp
+varInitializer -> ε
+exp -> add
+add -> add + mul
+add -> mul
+mul -> mul * pri
+mul -> pri
+pri -> IntLiteral
+pri -> Id
+pri -> ( exp )而基于这个规则做解析的算法如下:
+匹配一个数据类型(types)
+匹配一个标识符(Id),作为变量名称
+匹配初始化部分(varInitializer),而这会导致下降一层,使用一个新的语法规则:
+ 匹配一个等号
+ 匹配一个表达式(在这个步骤会导致多层下降:exp->add->mul->pri->IntLiteral)
+ 创建一个varInitializer对应的AST节点并返回
+如果没有成功地匹配初始化部分,则回溯,匹配ε,也就是没有初始化部分。
+匹配一个分号
+创建一个varDecl对应的AST节点并返回++int a = 2
+
课上我们重点讲了规则引擎的设计和实现,结合前面课程的内容课后实现一个在线版本的规则引擎
+使用Hertz框架开发一个HTTP服务,服务使用mysql,支持表达式的增删查改和编译执行。
+并实现以下接口
+请求参数为待执行的表达式和表达式中参数的值,并输出编译结果
+实时编译并执行结果,不需要写入DB中
+POST api/engine/run{
+ "exp": "uid == 12345 && did > 0",
+ "params": {
+ "uid": 123456,
+ "did": 0
+ }
+}{
+ "code": 0,
+ "message": "success",
+ "data": { // 执行结果
+ "result": true
+ }
+}新增一条表达式到DB中,并返回表达式在DB中的ID
+需要检测表达式 是否已经存在 ,如果已经存在,直接返回表达式的ID
+需要检测表达式是否合法(编译是否通过) ,如果编译失败,返回错误码 20001和编译错误
POST api/engine/exp/new{
+ "exp": "uid == 12345 && did > 0",
+}{
+ "code": 0,
+ "message": "success",
+ "data": { // 表达式ID
+ "id": 1
+ }
+}
+
+// 编译失败时
+{
+ "code": -1,
+ "message": "compile error: xxxxx", // 编译失败的信息
+ "data": { // 表达式ID
+ "id": 0
+ }
+}查询数据库中所有的表达式
+GET api/engine/exp/list{
+ "code": 0,
+ "message": "success",
+ "data": [
+ {
+ "id": 1,
+ "exp": "uid > 0"
+ }
+ ]
+}根据ID删除表达式,表达式不存在时返回错误码 20002 , 和错误信息
删除成功返回被删除的表达式信息
+DELETE api/engine/exp/:id// 删除成功时
+{
+ "code": 0,
+ "message": "success",
+ "data": { // 表达式ID
+ "id": 1,
+ "exp": "uid > 0"
+ }
+}
+
+// 删除失败时
+{
+ "code": -1,
+ "message": "exp id 1 not exist", //查询失败的信息
+ "data": {}
+}根据表达式的ID,查询出表达式内容,并编译执行。表达式不存在时返回错误码 20002 , 和错误信息
POST api/engine/exp/run{
+ "exp_id": 1,
+ "parmas": {
+ "uid": 123456,
+ "did": 0
+ }
+}{
+ "code": 0,
+ "message": "success",
+ "data": { // 执行结果
+ "result": true
+ }
+}
+
+// 表达式不存在时
+{
+ "code": -1,
+ "message": "exp id 1 not exist", //查询失败的信息
+ "data": {}
+}架构初探 - 谁动了我的蛋糕
+ +为了帮助同学们更好地理解本课程,我为大家准备了本学员手册。它包含以下几大模块内容:
+本课程的包含以下四个方面:
+常见软件架构:
+一些小问题:
+Q:如何给架构下定义?
+A:架构,又称软件架构:
+Q:架构的重要性?
+A:那盖房子来做举例子。
+我们都知道,地基对于一栋楼房的主要性,架构对于一个软件的重要性也是类似的:
+All in one,所有的东西都在一个进程里,部署在一个机器上。
+优点:
+缺点:
+在单机架构的基础上,将进程部署到多个机器上。
+优点:
+缺点:
+在单机架构基础上,将进程按照某种依据切分开。比如,A 软件和 B 软件的后端原先采用单机架构部署,那就是一个进程部署在多个机器上;如果用垂直应用架构,可以将 A 和 B 的后端拆分为 A、B 两个进程,然后再按照单体模式的思路,部署在多个机器上。
+优点:
+缺点:
+SOA 架构中,服务为一等公民,将进程按照不同的功能单元进行抽象,拆分为『服务』。有了服务之后,SOA 还为服务之间的通信定义了标准,保证各个服务之间通讯体验的一致性。
+优点:
+缺点:
+在 SOA 架构中,ESB 起到了至关重要的作用。但从架构拓扑来看,它更像是一个集中式的模块。有一个 SOA 分布式演进的分支,最终的形态便是微服务。
+优点:
+缺点:
+云计算基础:
+云计算架构:
+云原生,实际是云原生(计算)的简称,它是云计算发展到现在的一种形态。
+云原生技术为组织(公司)在公有云、自由云、混合云等新型的动态环境中,构建和运行可弹性拓展的应用提供了可能。 它的代表技术:
+基于虚拟化技术,提供的可以快速扩缩容的能力。可以分为弹性计算资源和弹性存储资源两个方面。
+弹性计算资源:
+弹性存储资源:
+在云原生的大背景下,不论是计算资源还是存储资源,他们都像是服务一样供用户使用。
+微服务架构下,服务之间的通讯标准是基于协议而不是 ESB 的。
+如何在 HTTP 和 RPC 之间选择?
+什么是服务网格?
+没有什么是加一层代理解决不了的问题,服务网格相比较于 RPC/HTTP 框架:
+基础设施层面:
+Q:我们总说,云是弹性的,也就是说,在用户的角度,云提供的资源是无限的。然而,云背后的物理资源是有限的。在企业级后端架构里,云如何解决近乎无限的弹性资源和有限的物理资源之间的矛盾?
+Q:闲事的资源就这么空着呢?如何提高资源利用率,提高物理资源的价值转换率?
+用户层面:
+Q:上了云原生微服务后,服务之间的通信开销较大,应该如何做成本优化?
+Q:微服务看起来没有那么美好,抖动导致的运维成本较高,如何解决?
+Q:异构的物理环境应该对用户是透明的,如何屏蔽这些细节?
+考虑到在线业务的 潮汐性 ,物理资源的用量不是一成不变的。离在线资源并池,可以:
+微服务之间的通信成本较高,是否可以:
+亲合性部署,通过将微服务调用形态与资源调度系统结合,将一些调用关系紧密、通信量大的服务部署在同一个机器上,并且使用 IPC 代替 RPC 的方式,降低网络通信带来的开销
+Q:微服务之间的通信流量为什么需要治理?
+Q:都有哪些常用的治理手段?
+Q:微服务中心件和服务网格在其中扮演着怎样的角色?
+Q:基础设施层往往是个复杂的异构环境,比如,有些机器的 CPU 是英特尔的,而有些是 AMD 的。就算是同一个品牌,也可能是不同代际。如何将这些差异屏蔽掉,使用户尽可能不感知呢?
+Q:什么情况下,我们觉得,服务需要扩容了?异构环境会对这个评判标准产生怎样的影响?
+如何设计一个根据主机层面的资源信息,实时进行流量调度的系统,打平不同宿主机异构环境的算力差异。
+关键点:
+设计需求:
+注意: 不需要考虑与做蛋糕相关服务的交互
+分布式理论 - 现代架构基石
+ +本节课程主要分为6个方面:
+课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
+微服务框架 - 不变的基建
+ +本课程内容主要分为以下4个方面:
+微服务架构介绍
+微服务架构原理及特征
+核心服务治理功能
+字节跳动服务治理实践
+为了帮助大家更好地预习及理解本节课程,该学员手册列出了课前、课中、及课后这三个阶段所涉及到的专业内容大纲,其中课前部分供同学们提前预习参考,课中部分给出了课程大纲,帮助同学们整理思路,课后部分列出一些扩展性的问题让同学们进一步延伸思考。
+系统架构的演进历史
+微服务架构的三大要素
+微服务架构中的基本概念及组件
+服务间通信
+服务注册及服务发现
+服务发布
+流量治理
+负载均衡
+稳定性治理
+单体架构
+垂直应用架构
+分布式架构
+SOA架构
+微服务架构
+服务治理(本课程内容)
+可观测性
+安全
+服务
+实例
+实例与进程的关系
+常见的实例承载形式
+基本问题
+简单方案
+服务注册发现
+微服务流量特征
+何为服务发布
+服务发布难点
+蓝绿部署
+灰度发布(金丝雀发布)
+流量控制
+控制维度
+限流
+熔断
+过载保护
+降级
+请求重试的意义
+请求重试的难点
+重试策略
+重试效果验证
+Consul与Kong联合配置理解
+ +Consul 是 HashiCorp 公司推出的开源工具,用于实现分布式系统的服务发现与配置。与其他分布式服务注册与发现的方案,Consul的方案更“一站式”,内置了服务注册与发现框 架、分布一致性协议实现、健康检查、Key/Value存储、多数据中心方案,不再需要依赖其他工具(比如ZooKeeper等)。使用起来也较 为简单。Consul使用Go语言编写,因此具有天然可移植性(支持Linux、windows和Mac OS X);安装包仅包含一个可执行文件,方便部署,与Docker等轻量级容器可无缝配合 。
+consul主要由server和client两种组件组成。
+server负责核心数据的存储和处理请求,server可以部署多个实例(通常推荐3-5个),server只有一个leader实例,就是主节点,主节点是通过选举产生的,主节点负责数据的写入处理,同时将数据同步至其他server节点
+client负责跟server通信,处理转发服务注册、服务发现请求到server节点,client还负责服务的健康检查,client节点可以部署多个实例,甚至每个微服务节点都部署一个client实例。
+以开发模式启动consul,同时具备server和client的功能,不需要单独部署server和client
+consul健康检查机制制运行在consul client中,会定期的根据服务健康检查配置,去检测服务是否正常,如果服务异常,就将服务的实例标记为不用, 如果恢复了,就标记为可用。
+Kong是一款基于OpenResty(Nginx + Lua模块)编写的高可用、易扩展的,由Mashape公司开源的API Gateway项目。Kong是基于NGINX和Apache Cassandra或PostgreSQL构建的,能提供易于使用的RESTful API来操作和配置API管理系统,所以它可以水平扩展多个Kong服务器,通过前置的负载均衡配置把请求均匀地分发到各个Server,来应对大批量的网络请求。
+Konga是可以管理Kong的图形界面,带来的一个最大的便利就是可以很好地通过UI观察到现在kong的所有的配置,并且可以对于管理kong节点情况进行查看、监控和预警。
+微服务架构是由多个服务端和多个api端组成,客户端发起请求,需要单独的api进行接收和路由转发,然后通过与不同的服务端建立连接从而获得服务。
+这个过程中需要在程序中记忆大量的端口,且一旦有节点失效,整个服务都将不可用。
+Kong
+Consul
+api端
+服务注册:
+registerClient := consul.NewRegistryClient(global.GlobalConfig.Consul.Address, global.GlobalConfig.Consul.Port)
+err = registerClient.Register(global.GlobalConfig.MainServer.Address, global.GlobalConfig.MainServer.Port, "video-api", []string{"api", "video"})健康检查(注意是HTTP类型的):
+check := &api.AgentServiceCheck{
+ HTTP: "http://" + address + ":" + port + "/health",
+ Timeout: "5s",
+ Interval: "5s",
+ DeregisterCriticalServiceAfter: "10s",
+}连接服务端:
+conn, err = grpc.Dial(
+ "consul://"+global.GlobalConfig.Consul.Address+":"+global.GlobalConfig.Consul.Port+"/"+name+"?wait=14s",
+ grpc.WithTransportCredentials(
+ insecure.NewCredentials(),
+ ),
+ grpc.WithDefaultCallOptions(
+ grpc.MaxCallRecvMsgSize(1024*1024*size),
+ grpc.MaxCallSendMsgSize(1024*1024*size),
+ ),
+ grpc.WithDefaultServiceConfig(`{"loadBalancingPolicy": "round_robin"}`),
+)服务端
+注意监听的时候要监听内网地址
+lis, err := net.Listen("tcp", global.GlobalConfig.Address.In+":"+port)服务注册:
+register_client := consul.NewRegistryClient(global.GlobalConfig.Consul.Address, global.GlobalConfig.Consul.Port)
+register_client.Register(global.GlobalConfig.Address.Out, port, name, []string{"srv", "video"})健康检查(注意是GRPC类型的):
+grpc_health_v1.RegisterHealthServer(s, health.NewServer())check := &api.AgentServiceCheck{
+ GRPC: address + ":" + port,
+ Timeout: "5s",
+ Interval: "5s",
+ DeregisterCriticalServiceAfter: "10s",
+}连接api端:
+s := grpc.NewServer()【实践课】手把手教你做系统设计
+ +手把手教你做系统设计之秒杀系统
+本节课程主要分为四个方面:
+课前部分主要罗列课程中涉及到的中间件和相关背景知识。对于使用到的中间件,同学们需要体验了解概念,安装并正确使用。课中部分会详细讲解系统设计的方法论和秒杀系统实践,帮助同学们入门系统设计。课后部分会做一些总结,梳理核心思想和重点。
+高性能系统的通用设计思想
+黑灰产监控与防御
+ +企业的信息安全体系是非常庞大的,任何一个环节都可能会出现安全风险。其中,黑灰产是安全人员最为关注的一个风险来源,也是历年来导致企业和用户损失最大的因素。
+如果某个平台或者业务被黑灰产盯上,可能是因为这个业务存在安全隐患被黑灰产利用,也可能只是被黑灰产当做牟利的垫脚石。对黑灰产的监控和防御,就是要了解他们的意图、手段和行为模式,避免被黑灰产攻击或者利用。
+本次可能会给大家简单介绍国内黑灰产的情况,挑选了几种比较经典的黑产作弊手段进行详细分析,希望能帮助大家对黑灰产这个群体有一定的了解,提升各位的安全意识,在日后的工作和生活中,多一些安全角度的思考。
+本次课程偏科普性质,但内容不是大家在网络上可以随便看到的,课前可以阅读一些国内黑灰产的调研报告
+推荐 Freebuf 黑镜调查系列 ,其中部分内容是讲师参与调查编写,不一定权威,但内容和数据都比较真实
+《风控要略 互联网业务反欺诈之路》讲师参与编写
+《互联网平台智能风控实战》
+《白帽子讲web安全》
+《Web安全深度剖析》
+《Web安全机器学习入门》
+上述几本都是入门级的书,挑一本即可
+《 SQL注入攻击与防御》数据库安全进阶
+《 linux服务器安全攻防》 主机安全进阶
+《互联网企业安全高级指南》
+《大型互联网企业安全架构》
+ + +分布式定时任务
+ +本节课程主要分为五个方面:
+课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
+每年春节抖音都会有很多有意思的玩法,如果同学们是字节的后端同学,怎么设计今年春节集卡瓜分20亿的技术方案?
+业务流程
+技术体量
+方案引出
+方案一:腾讯字节方案
+方案二:Quartz方案——时间轮
+资源来源
+消息队列原理与实战
+ +本节课程主要分为五个方面:
+课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
+kafka使用场景,业务日志、用户行为数据、Metrics数据
+基本概念,Producer、Cluster、Consumer、Topic、Partition
+数据迁移、Offset、Partition选主
+一条消息从生产到消费是如何处理的,Producer端逻辑、Broker端逻辑、Consumer端逻辑
+Kafka在使用中遇到问题
+BMQ架构
+BMQ各模块是如何工作的,Broker、Proxy、HDFS、MetaStorage
+BMQ多机房容灾
+RocketMQ使用场景
+RocketMQ和Kafka对比
+RocketMQ架构介绍,Producer、Broker、Nameserver、Consumer
+一条消息从生产到消费是如何处理的,Producer端逻辑、Broker端逻辑、Consumer端逻辑
+一些最佳实践的场景,包括数据展示
+RPC 原理与实现
+ +本节课程主要分为四个方面:
+课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;
+课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;
+课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
+RPC的概念模型:User、User-Stub、RPC-Runtime、Server-Stub、Server
+IDL(Interface Definition Language) 文件
+生成代码
+编解码(序列化/反序列化)
+通信协议
+网络通信
+编解码层
+传输协议层
+网络通信层
+稳定性
+易用性
+扩展性
+观测性
+高性能
+相比本地函数调用,RPC调用需要解决的问题
+一次 RPC 的完整过程
+RPC 带来的问题将由 RPC 框架来解决
+数据格式
+选型考察点
+生成代码和编解码层相互依赖,框架的编解码应当具备扩展任意编解码协议的能力
+- LENGTH 字段 32bits,包括数据包剩余部分的字节大小,不包含 LENGTH 自身长度
+- HEADER MAGIC 字段16bits,值为:0x1000,用于标识 协议版本信息,协议解析的时候可以快速校验
+- FLAGS 字段 16bits,为预留字段,暂未使用,默认值为 0x0000
+- SEQUENCE NUMBER 字段 32bits,表示数据包的 seqId,可用于多路复用,最好确保单个连接内递增
+- HEADER SIZE 字段 16bits,等于头部长度字节数/4,头部长度计算从第14个字节开始计算,一直到 PAYLOAD 前(备注:header 的最大长度为 64K)
+- PROTOCOL ID 字段 uint8 编码,取值有: - ProtocolIDBinary = 0 - ProtocolIDCompact = 2
+- NUM TRANSFORMS 字段 uint8 编码,表示 TRANSFORM 个数
+- TRANSFORM ID 字段 uint8 编码,表示压缩方式 zlib or snappy
+- INFO ID 字段 uint8 编码,具体取值参考下文,用于传递一些定制的 meta 信息
+- PAYLOAD 消息内容
+第一种方式浪费线程(会占用内存和上下文切换开销),第二种方式浪费 CPU 做大量无效工作。而基于 IO 多路复用系统调用实现的 Poll 的意义在于将可读/可写状态通知和实际文件操作分开,并支持多个文件描述符通过一个系统调用监听以提升性能。
+网络库的核心功能就是去同时监听大量的文件描述符的状态变化(通过操作系统调用),并对于不同状态变更,高效,安全地进行对应的文件操作。
+从某种程度上讲超时、限流和熔断也是一种服务降级的手段 。
+请求成功率
+长尾请求
+开箱即用
+周边工具
+框架文档 Kitex
+自研网络库 Netpoll,背景:
+a. 原生库无法感知连接状态
b. 原生库存在 goroutine 暴涨的风险
+扩展性:支持多协议,也支持灵活的自定义协议扩展
+性能优化,参考 字节跳动 Go RPC 框架 KiteX 性能优化实践
+a. 网络优化
b. 编解码优化
+合并部署
+a. 微服务过微,引入的额外的传输和序列化开销越来越大
b. 将强依赖的服务统计部署,有效减少资源消耗
+带你认识存储的本质 - 状态
+ +存储系统和数据库系统往往是后端服务的最后一环,提供数据存储、查询能力。本课程会先用模拟案例导入,向学员介绍存储系统、数据库系统的特点,然后解析多个主流产品,最后分享存储和数据库结合新技术演进的方向。本节课程主要包含以下内容:
+跟存储 & 数据库系统相关的材料很多,涵盖开源项目、博客、论文等。下面提供部分资料作为参考
+static.googleusercontent.com/media/resea…
+作为各种开源分布式文件系统的鼻祖,GFS论文里面提到的架构非常经典,值得一学。
+本书介绍了很多Linux内核子系统的实现,其中第13章着重讲了单机的文件IO。学习完Linux中的文件IO栈,对单机存储系统会有更深的认识。
+通过一个模拟案例,描述了数据是怎么产生,在后端系统里怎么流通,最后怎么写入到存储/数据库系统。
+MySQL - 深入理解RDBMS
+ +RDBMS(关系型数据库)是目前使用最为广泛的数据库之一,同时也是整个信息化时代的基石。本节课程通过生活中常见的场景向大家介绍RDBMS的作用、发展历程及其核心技术,最后以字节为例,展示了RDBMS的企业级实践。本节课程主要包含以下内容:
+RDBMS有相关的数据和材料都非常多,这里主要给大家提供几篇经典论文,从经典的论文中,能够更有效的帮助大家理解RDBMS。
+暂时无法在飞书文档外展示此内容
+这篇论文是RDBMS的奠基之作,由RDBMS之父E.F.Codd博士于1970年发表。在这篇论文中,E.F.Codd首次提出了用于管理数据的关系模型,并将数据独立于硬件来存储,用户使用一个非过程语言来访问数据。
+暂时无法在飞书文档外展示此内容
+这本书被称为数据库领域的“红宝书”,由著名的图灵奖获得者,数据库领域专家,Michael Stonebraker撰写。其中介绍了数据库的基本概念,传统的RDBMS以及新的数据库架构等等,是一本非常棒的数据库领域入门文章。
+通过抖音红包雨的案例,介绍 RDBMS 中 ACID 的概念:
+数据库发展最初过程中,诞生过3种数据模型,最终关系型模型成为了应用最为广泛的数据库模型。
+| + | 网状模型 | +层次模型 | +关系模型 | +
|---|---|---|---|
| 优势 | +能直接描述现实世界 存取效率较高 | +结构简单 查询效率高 可以提供较好的完整性支持 | +实体及实体间的的联系都通过二维表结构表示 可以方便的表示M:N关系 数据访问路径对用户透明 | +
| 劣势 | +结构复杂 用户不易使用 访问程序设计复杂 | +无法表示M:N的关系 插入、删除限制多 遍历子节点必须经过父节点 访问程序设计复杂 | +关联查询效率不够高 关系必须规范化 | +
在SQL执行过程中,需要经历SQL引擎、存储引擎、以及事务引擎等模块。而其中SQL引擎又分为Parser、Optimizer、Executor几个部分:
+SQL引擎包括了:
+存储引擎负责了数据的底层存储、管理和访问工作。各大RDBMS存储引擎的设计都有不少的差异,这里选择MySQL的InnoDB存储引擎来向大家做一个介绍:
+事务引擎实现了数据库的ACID能力,这里还是以MySQL的InnoDB为例来介绍数据库内部是通过哪些技术来实现ACID:
+字节中是国内数据规模最大的互联网公司之一,公司内部有成千上万套RDBMS系统。这一章节还是以红包雨为案例,展示了字节是如何解决大流量、流量突增、高可靠等问题的。
+Redis - 大厂程序员是怎么用的
+ +本节课程主要分为三个方面:
+CIickHouse - 你没有见过的列存储
+ +本节课程分为四个部分
+课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
+数据库是结构化信息或数据的有序集合,一般以电子形式存储在计算机系统中。通常由数据库管理系统 (DBMS) 来控制。在现实中,数据、DBMS 及关联应用一起被称为数据库系统,通常简称为数据库。
+查询包含一系列含有最终结果的字段, 紧跟 SELECT关键词。星号(“*”)也可以用来指定查询应当返回查询表所有字段,可选的关键词和子句包括:
FROM子句指定了选择的数据表。FROM子句也可以包含 JOIN 二层子句来为数据表的连接设置规则。WHERE子句后接一个比较谓词以限制返回的行。WHERE子句仅保留返回结果里使得比较谓词的值为True的行。GROUP BY子句用于将若干含有相同值的行合并。 GROUP BY通常与SQL聚合函数连用,或者用于清除数据重复的行。GROUP BY子句要用在 WHERE子句之后。HAVING子句后接一个谓词来过滤从 GROUP BY子句中获得的结果,由于其作用于 GROUP BY子句之上,所以聚合函数也可以放到其谓词中。ORDER BY子句指明将哪个字段用作排序关键字,以及排序顺序(升序/降序),如果无此子句,那么返回结果的顺序不能保证有序。CREATE TABLE default.test_insert_local
+(
+ `p_date` Date,
+ `id` Int32
+)
+ENGINE = MergeTree
+PARTITION BY p_date
+ORDER BY id
+SETTINGS index_granularity = 8192
+复制代码b. 读写数据库数据
+insert into default.test_insert_local values ('2022-01-01', 1);
+
+select count() from default.test_insert_local;
+复制代码a. 数据压缩
+【LZ4】
+输入:abcde_bcdefgh_abcdefghxxxxxxx
+
+输出:abcde_(5,4)fgh_(14,5)fghxxxxxxx
+复制代码(5,4) 代表向前5个byte,匹配到的内容长度有4,即"bcde"是一个重复
+重复项越多或者越长,压缩率就会越高
+【Run-length encoding】
+输入:WWWWWWWWWWWWBWWWWWWWWWWWWBBBWWWWWWWWWWWWWWWWWWWWWWWWBWWWWWWWWWWWWWW
+
+输出:12W1B12W3B24W1B14W
+复制代码++压缩重复的数据
+
【Delta encoding】
+输入:105, 135, 112, 135, 143, 147
+
+输出:105(base),30, -23, 23, 8, 4
+复制代码将数据存储为连续数据之间的差异,而不是直接存储数据本身
+b. 数据处理
+【查询优化】1.可以选择特定的列做计算而不是读所有列 2.对聚合计算友好
+【延迟物化】
+【向量化】
+for (size_t i = 0; i < 100; ++i)
+ c[i] = a[i] + b[i];
+复制代码非向量化执行
+c[0] = a[0] + b[0];
+c[1] = a[1] + b[1];
+... ...
+复制代码如果这时候CPU也可以并行的计算我们写的代码,那么理论上我们的处理速度就会是之前代码的100倍,幸运的是SIMD指令就是完成这样的工作的,用SIMD指令完成这样代码设计和执行就叫做向量化
+a.文件组织
+b.文件内容
+++对于表
+
CREATE TABLE test.test_insert_local
+(
+ `p_date` Date,
+ `id` Int32
+)
+ENGINE = MergeTree
+PARTITION BY p_date
+ORDER BY id
+SETTINGS index_granularity = 8192
+复制代码++它的文件组织
+
├── 20220101_1_1_0
+│ ├── checksums.txt
+│ ├── columns.txt
+│ ├── count.txt
+│ ├── data.bin
+│ ├── data.mrk3
+│ ├── default_compression_codec.txt
+│ ├── minmax_p_date.idx
+│ ├── partition.dat
+│ ├── primary.idx
+│ └── versions.txt
+├── 20220102_2_2_0
+│ ├── checksums.txt
+│ ├── columns.txt
+│ ├── count.txt
+│ ├── data.bin
+│ ├── data.mrk3
+│ ├── default_compression_codec.txt
+│ ├── minmax_p_date.idx
+│ ├── partition.dat
+│ ├── primary.idx
+│ └── versions.txt
+├── detached
+└── format_version.txt
+复制代码c. part和partition
+d. part和column
+e. column和index
+CREATE TABLE hits_UserID_URL
+(
+ `UserID` UInt32,
+ `URL` String,
+ `EventTime` DateTime
+)
+ENGINE = MergeTree
+PRIMARY KEY (UserID, URL)
+ORDER BY (UserID, URL, EventTime)
+SETTINGS index_granularity = 8192, index_granularity_bytes = 0;
+复制代码SELECT
+ URL,
+ count(URL) AS Count
+FROM hits_UserID_URL
+WHERE UserID = 749927693
+GROUP BY URL
+ORDER BY Count DESC
+LIMIT 10
+复制代码CREATE TABLE test_multi_columns
+(
+ `p_date` Date,
+ `id` Int32,
+ `map_a` Map(String, Int32)
+)
+ENGINE = MergeTree
+PARTITION BY p_date
+ORDER BY map_a
+复制代码map中的每个key都是一列
+map中的每一列都可以单独的查询
+使用方式同普通列,可以做任何计算
+大宽表查询
+可以建非常多的列查询的时候引擎可以快速选择需要的列,查询的时候引擎可以快速选择需要的列
+++数据可以通过spark生成clickhouse格式的文件
+导入到hdfs上由hive2ch导入工具完成数据导入
+数据直接导入到各个物理节点
+
保证查询可以及时访问已有数据
+可以按需加载需要的列
+
select countDistinct(uid)
+from user_detial
+where tag_id = 'a' and uid in
+(
+ select uid from user_detail
+ wherer tag_id = 'b'
+)
+复制代码面试大数据题目准备
+ +正常来说,我们一般会想到用哈希表来统计词频,也就是 HashMap<Integer, Integer>,其中,key 表示数字,value 表示这个数字的出现次数。但在 Java 中 Integer 类型的占用空间是 4 Byte,我们暂时不考虑其他的占用空间,这样一个数的 key + value 的占用空间就是 8 Byte。假设最差情况,40 亿个数字,出现最多次数的数只出现了两次,也就是说我们需要保存 40 亿 - 1 个数,40 亿大约是 2 ^32。所以我们可以计算一下大概要花费的空间:2^32 * 8 Byte = 2^35 Byte = 32 GB。所以说这种方式肯定不符合题目的条件的。
我们可以使用哈希函数对 40 亿个数字进行分类这种方式 。具体步骤如下:
+(1)在磁盘上申请 100 个文件(具体申请多少个文件视情况而定)
+(2)对 40 亿个数依次进行遍历,对遍历到的数字用哈希函数计算出一个哈希值,然后再模除文件的个数,也就是 % 100 ,这样就能均匀的分配到 100 个文件中(相等的数他们的哈希值肯定是一样的,所以一样的数肯定能保存到一个文件中)
(3)依次对 100 个文件进行统计,统计每个文件中出现最多的数字,如何统计呢?我们可以使用哈希表进行统计,key 还是数字,value 还是出现次数。正常情况下,文件中的数大概是 40 亿 / 100 个,也就是只占用 32 GB / 100 = 0.32 GB,内存足够。
(4)再用一个哈希表保存每个文件出现最多的数字和出现次数(也就是只保存 100 个数)。然后再依次遍历哈希表,找出现次数最大值即可。
+注意:假设出现最差情况,一个数出现了 40 亿 - 1 次,这意味着一个文件中保持了将近 40 亿个数,也就是 32 GB 左右,但是也没事。我们统计的时候是分批读入数字,并且哈希表肯定不会溢出,因为你保存的本来就是 数字 + 出现次数 ,假设 2 出现了 40 亿次,我们在哈希表中就记录 2 : 40 亿 不就行了吗,也就是只记录一个数就行了。
32位无符号整数的范围是 0~4294967295,现在有一个正好包含40亿个无符号整数的文件, 所以在整个范围中必然存在没出现过的数。 可以使用最多1GB 的内存,怎么找到所有未出现过的数 ?
+进阶:内存限制为 10MB, 但是只用找到一个没出现过的数即可
+正常来说,我们想到的是范围多大就开多大的数组,只要出现过就在数组对应的下标标记,最后我们遍历数组,没有标记过的位置就是范围内没出现过的数。一个 int 类型在 Java 中是 4 个字节,计算空间占用:42 亿 * 4 Byte,大概为 16 GB,不符合题意。
我们可以使用位图的方式来做,也就是 bitMap。具体步骤如下:
(1)我们用 1 bit 来表示数字是否出现过,也就是说我们可以开 int[ 42 亿 / 8] 这么大的数组(一个 Byte = 8 bit),这里的 42 亿是范围,其实意思就是说我们的思路没有变化,只是换了一种数据的存储方式。空间占用:42 亿 Byte / 8,大概是 500 多 MB,满足条件。
(2)然后遍历这 40 亿个数,依次在对应的 bit 位上标为 1。
+(3)最后统计我们开的数组,bit 位上为 0 的就是没出现过的。
+我们可以使用范围划分的方式 。具体步骤如下:
+(1)10 MB 大概可以申请 int[2621440] 这么多数组空间,计算方式:10 MB / 4Byte = 2621440
(2)划分份数:42 亿 / 2621440 大概等于 1638,假设这个数组名为 arr,arr[0] 就代表 0 ~ 1637 这个范围出现的数字的个数,同理 arr[1] 就代表 1638~ (1638+ 1638- 1) 这个范围出现的数字的个数。也就是类似于词频统计。
+(3)依次遍历这 40 亿个数,arr[每个数 / 1638]++,也就是说 0 就是 arr[0]++,1638就是 arr[1]++,其实思路就是把范围划分成 1638份,每份统计对应的数字个数,如果对应的数字个数小于 1638,说明在这个范围内肯定有数字没出现过
(4)重复此过程,将范围逐渐缩小即可求出答案。
+注意:这里是因为能使用的空间比较大,所以只需一次划分即可。
+只能使用有限几个变量,如何做 ?
+二分法,一直二分下去。
+第一种办法:使用哈希函数进行分类。
+(1)申请 N 个磁盘文件
+(2)遍历所有的 URL,为每个 URL 计算哈希值,然后再模除 N,就能均匀地分类到对应的文件中,重复的 URL 一定会在同一个文件中。
+(3)依次统计每一个文件中重复的 URL,然后再汇总各个文件的信息即可。
+第二种办法:使用布隆过滤器。会有失误率,不过概率很低。
+(1)首先申请一个足够大的 bitMap,便建立边检查是否重复
+(2)遍历所有的 URL,遍历到一个 URL,就通过某种哈希函数计算它的哈希值,然后再模除 bitMap 的位数。
+(3)如果发现对应的槽位已经为 1 (初始都是为 0,一个 bit 位就两种状态,0 和 1),就说明这个 URL 是重复的。
+(4)如果发现对应的槽位为 0,说明不重复,将槽位置为 1。
+可以发现,如果重复的 URL 一定能找出来,但是可能不重复的 URL 也被找出来了(这也就是失误率,因为哈希冲突),如果可以允许有一定的失误率就可以使用这种办法。
+使用分类 + 大根堆方式 。
+(1)通过哈希函数将海量数据分类到一个个小文件中
+(2)依次对每个小文件建立大根堆,规则就是 URL 出现次数最多的就在大根堆的顶部
+(3)取每个小文件出现次数最多的 URL,也就是刚刚建立的大根堆顶部元素,再建立一个大根堆
+(4)这样建立出来的大根堆就是 Top 100 了
+32位无符号整数的范围是0~4294967295,现在有40亿个无符号整数,可以使用最多1GB的内存,找出所有出现了两次的数。
+第一种方式:哈希函数。
+(1)通过哈希函数对 40 亿个数进行分流,分到一个个小文件中。
+(2)依次用哈希表统计每个小文件中只出现了两次的数。
+(3)然后再汇总各个文件中只出现了两次的数即可。
+第二种方式:bitMap
+(1)正常来说我们都是用 1 bit 来表示对应的数字是否出现过,对应这个题目,我们可以变化一下。
+(2)用 2 bit 来表示对应的数字,00 代表这个数没有出现过,01 代表这个数出现过一次,10 代表这个数出现过两次,11 代表这个数出现了两次以上。
(3)容量大概使用:40 亿大概就是 2 ^32^ ,所以就是 2^32^ * 2 bit / 8 ,大概就是 1 GB 左右。
+小根堆方式。
+ + +23岁的自己,生日快乐!
+ +也许今天你很迷茫,不知道应该做一些什么事情
+也许今天你很失落,努力了两周的结果是从头再来
+也许今天你很懊恼,后悔自己之前的选择不够合适
+也许今天你很伤心,并不会有人记得你的生日
+但是今天是你的生日呀
+在这个并不算很特殊的日子里,也值得你对自己说一声
+张兆,生日快乐!
+ + +后端实习面试经历
+ +第一次自己找实习,借助各公司官网和第三方APP,在形式不好的情况下最终上岸MetaApp,公司虽然不大,但是岗位很符合预期。
+这样我就有了一次算法的实习经历,研二前加上一次开发的实习经历,之后的选择应该会更多了吧
+开始的时候还是低估了互联网寒冬,想当初在商汤算法岗实习的时候,一半以上的人都是实习生,篮球的组也基本都是一两个研究员在指导很多实习生。
+因此当时感觉不会很难,而且有过算法实习和一般的基础知识+好学历应该会比较简单(好天真…)
+第一阶段主要聚焦在大中厂,在boss和实习僧上沟通了滴滴、VMWare、小红书、小米、bilibili,再加上一个量化的岗位,只有小红书得到了一面的机会。
+总体面试考的题目都比较基础,但是算法题是没见过的“搜索二叉树转双向链表”,没有意识到题目的含义是更改指针的指向。
+总之一面之后就没有消息了。
+这里开始有一点点担心了,但是随后的期末考试也没有时间去想,我自己还是不能完全放下期末考试。
+期末考试结束后,参加字节跳动青训营,做了一个抖音的项目,简单完善了一下简历,继续投递
+这回就不光盯着头部大厂了,只要是评价还可以的公司就直接投,一个公司也不仅仅投递一个岗位
+日程大概如下(主要是有回应的):
+| 时间 | ++ | + | + |
|---|---|---|---|
| 2023.02.06 | +滴滴投递1 | +Momenta投递 | +图森未来投递 | +
| 2023.02.07 | +滴滴简历挂 | +Momenta转岗 | +百度投递1 | +
| 2023.02.08 | +好未来投递 | +Momenta简历挂 | +百度一面通知 | +
| 2023.02.09 | +SmartX一面通知 | +MetaApp笔试 | +百度一面 | +
| 2023.02.10 | +滴滴投递2 | +MetaApp一面通知 | ++ |
| 2023.02.13 | +蔚来投递 | +MetaApp一面 | ++ |
| 2023.02.14 | +SmartX一面 | +MetaApp二面通知 | +百度一面挂 | +
| 2023.02.15 | +SmartX感谢信 | +MetaApp二面 | ++ |
| 2023.02.16 | ++ | + | + |
| 2023.02.17 | ++ | 第四范式一面通知 | +图森未来感谢信 | +
| 2023.02.20 | ++ | MetaApp Offer | ++ |
总的来说面试机会还是太少,有多方面的原因:
+感觉一切事情都是有关联的,而且都是一个接着一个,很少有空闲时间,也没有很多事情冲突的时间
+12月看到了字节跳动青训营的通知,期末考试结束当天正好是青训营的笔试
+12月底从北大学长那里搞了一台免费的华为云一年的服务器,然后青训营正好使用上
+青训营需要下载飞书,然后入职后的工作软件也正是飞书
+开学前两个星期面试,正好在开学后面试完成,不用到处找空教室面试(也找不到)
+有一种感觉,所有的事情都是有人安排好的,虽然这些事情之间并没有太多的关联,但是在我自己的视角看来就是一个接着另外一个安排好的
+我也不知道这对我来说是好是坏,是幸运还是不幸
+package main
+
+import "fmt"
+import "container/list"
+
+type node struct{
+ key int
+ value int
+}
+
+type Cache struct{
+ cache map[int]*list.Element
+ nodelist *list.List
+}
+
+func NewCache() *Cache{
+ return &Cache{
+ cache : make(map[int]*list.Element,0),
+ nodelist : list.New(),
+ }
+}
+
+func (c *Cache) put(k,v int){
+ n,ok := c.cache[k]
+ if !ok{
+ c.cache[k] = c.nodelist.PushFront(&node{k,v})
+ } else{
+ n.Value.(*node).value = v
+ c.nodelist.MoveToFront(n)
+ }
+}
+
+func (c *Cache) get(k int){
+ n,ok := c.cache[k]
+ if !ok{
+ fmt.Println("-1")
+ } else{
+ c.nodelist.MoveToFront(n)
+ fmt.Println(n.Value.(*node).value)
+ }
+}
+
+func main() {
+ c := NewCache()
+ c.put(1,2)
+ c.put(2,3)
+ c.put(1,4)
+ var key int
+ for i:=0;i<3;i++{
+ fmt.Scanf("%d",&key)
+ c.get(key)
+ }
+}package main
+
+import "fmt"
+
+func putNum(n int, putNumChan chan int) {
+ for i := 1; i <= 2000; i++ {
+ putNumChan <- i
+ }
+ close(putNumChan)
+}
+
+func dealNum(x int) int {
+ res := 0
+ for i := 1; i <= x; i++ {
+ res += i
+ }
+ return res
+}
+
+func add(putNumChan chan int, resChan chan map[int]int, exitChan chan bool) {
+ for {
+ x, ok := <-putNumChan
+ if !ok {
+ exitChan <- true
+ return
+ }
+ a := dealNum(x)
+ m := make(map[int]int, 0)
+ m[x] = a
+ resChan <- m
+ }
+}
+
+func output(resChan chan map[int]int, exitChan chan bool) {
+ for i := 0; i < 8; i++ {
+ <-exitChan
+ }
+ close(exitChan)
+ close(resChan)
+}
+
+func main() {
+ n := 2000
+ putNumChan := make(chan int)
+ go putNum(n, putNumChan)
+ resChan := make(chan map[int]int)
+ exitChan := make(chan bool)
+ for i := 0; i < 8; i++ {
+ go add(putNumChan, resChan, exitChan)
+ }
+ go output(resChan, exitChan)
+ for v := range resChan {
+ fmt.Println(v)
+ }
+}
+https://leetcode.cn/problems/remove-nth-node-from-end-of-list/
+func removeNthFromEnd(head *ListNode, n int) *ListNode {
+ var dummy = &ListNode{}
+ dummy.Next = head
+
+ count := 0
+ for head != nil {
+ count += 1
+ head = head.Next
+ }
+ head = dummy.Next
+ pre := dummy
+ count -= n
+ for count != 0 {
+ pre = head
+ count -= 1
+ head = head.Next
+ }
+ pre.Next = head.Next
+ return dummy.Next
+}https://leetcode.cn/problems/reverse-linked-list/
+func reverseList(head *ListNode) *ListNode {
+ if head == nil {
+ return head
+ }
+ dummy := &ListNode{}
+ dummy.Next = head
+ post := head.Next
+ head.Next = nil
+ for post != nil {
+ dummy.Next = post
+ post = post.Next
+ dummy.Next.Next = head
+ head = dummy.Next
+ }
+ return dummy.Next
+}package main
+
+import "fmt"
+import "container/list"
+
+type TreeNode struct{
+ Val int
+ Left *TreeNode
+ Right *TreeNode
+}
+
+func convert(head *TreeNode, listhead *list.List){
+ if head == nil{
+ return
+ }
+ convert(head.Left,listhead)
+ listhead.PushBack(head.Val)
+ fmt.Println(head.Val)
+ convert(head.Right,listhead)
+}
+
+func main() {
+ testlist := list.New()
+ head := &TreeNode{
+ Val:2,
+ Left:nil,
+ Right:nil,
+ }
+ head.Left = &TreeNode{
+ Val:1,
+ Left:nil,
+ Right:nil,
+ }
+ head.Right = &TreeNode{
+ Val:3,
+ Left:nil,
+ Right:nil,
+ }
+ convert(head,testlist)
+}/**
+ 编程:输入一多行数据,每一行代表两个数有关系,将有关系的数在同一行输出。
+ 输入:
+ 1 2
+ 3 4
+ 1 3
+ 5 6
+ 5 7
+ 输出(不要求有序):
+ 1 2 3 4
+ 5 6 7
+*/
+
+package main
+
+import "fmt"
+
+type UFS struct {
+ father []int
+}
+
+func NewUFS(size int) *UFS {
+ return &UFS{
+ father: make([]int, size),
+ }
+}
+
+func (u *UFS) Init() {
+ for i := 0; i < len(u.father); i++ {
+ u.father[i] = i
+ }
+}
+
+func (u *UFS) FindFather(x int) int {
+ a := x
+ for x != u.father[x] {
+ x = u.father[x]
+ }
+ for a != u.father[a] {
+ z := a
+ a = u.father[a]
+ u.father[z] = x
+ }
+ return x
+}
+
+func (u *UFS) Union(a, b int) {
+ faA := u.FindFather(a)
+ faB := u.FindFather(b)
+ if faA != faB {
+ u.father[faA] = faB
+ }
+}
+
+func (u *UFS) Print() {
+ fathermap := make(map[int][]int, 0)
+ for i := 0; i < len(u.father); i++ {
+ father := u.FindFather(i)
+ _, ok := fathermap[father]
+ if ok {
+ fathermap[father] = append(fathermap[father], i)
+ } else {
+ fathermap[father] = make([]int, 1)
+ fathermap[father][0] = i
+ }
+ }
+ for k, v := range fathermap {
+ fmt.Println(k, v)
+ }
+}
+
+func main() {
+ u := NewUFS(10)
+ u.Init()
+ u.Union(0, 1)
+ u.Union(2, 3)
+ u.Union(3, 5)
+ u.Union(7, 5)
+ u.Union(4, 6)
+ u.Print()
+}
+package main
+
+import "fmt"
+
+// 没有重复元素的数组,打印全排列组合
+
+var arr []int
+var vis []bool
+
+func Printarr(temp []int) {
+ for i := 0; i < len(temp); i++ {
+ fmt.Printf("%d ", temp[i])
+ }
+ fmt.Println()
+}
+
+func backtracking(arr []int, temp []int, start int) {
+ if start == len(arr) {
+ Printarr(temp)
+ }
+ for i := 0; i < len(arr); i++ {
+ if !vis[i] {
+ vis[i] = true
+ temp = append(temp, arr[i])
+ backtracking(arr, temp, start+1)
+ temp = temp[:len(temp)-1]
+ vis[i] = false
+ }
+ }
+}
+
+func main() {
+ arr = []int{1, 2, 3}
+ temp := make([]int, 0)
+ vis = make([]bool, len(arr))
+ backtracking(arr, temp, 0)
+}package main
+
+// 1. 只能编辑 foo 函数
+// 2. foo 必须要调用 slow 函数
+// 3. foo 函数在 ctx 超时后必须立刻返回
+// 4. 如果 slow 结束的比 ctx 快,也立刻返回
+
+import (
+ "context"
+ "fmt"
+ "math/rand"
+ "time"
+)
+
+func main() {
+ rand.Seed(time.Now().UnixNano())
+ ctx := context.Background()
+ ctx, cancel := context.WithTimeout(ctx, time.Second)
+ defer cancel()
+
+ foo(ctx)
+}
+
+func foo(ctx context.Context) {
+ go func() {
+ slow()
+ }()
+ <-ctx.Done()
+}
+
+func slow() {
+ n := rand.Intn(3)
+ fmt.Printf("sleep %ds\n", n)
+ time.Sleep(time.Duration(n) * time.Second)
+}
+学习计划
+ +1. 后端实习(2023年02月-2023年07月)#6f42c1
+2. 后端知识学习,记录技术总结笔记(2023年02月-2023年07月)#777
+3. 算法题目重做(2023年05月-2022年07月)#5cb85c
+4. 抖音项目完善(2023年02月-2023年03月)#d9534f
+5. 抖音前端找demo修改实现(2023年03月-2023年04月)#f0ad4e
+6. 找合适的后端项目并开发(2023年05月-2023年07月)#428bca
+7. 开源初步尝试(2023年02月-2023年07月)#3c4858
+8. 其他计划(2023年02月-2023年07月)#ffc0cb
+1. 后端实习,尽快熟悉上手
+2. 后端知识学习,主要是部门的技术,不仅要会用,更要多看底层原理,多记录笔记
+3. 抖音项目完善,先把两位队友的代码看懂,找一找优化方向
+4. 开源初步尝试,了解开源组织贡献方法等(如GSOC等)
+1. 后端实习,尽快熟悉上手
+2. 后端知识学习,主要是部门的技术,不仅要会用,更要多看底层原理,多记录笔记
+3. 抖音项目完善,先把两位队友的代码看懂,找一找优化方向,整理青训营的资料,找一个比较完备的前端准备开始优化项目
+4. 开源初步尝试,了解开源组织贡献方法等(如GSOC等)
+周总结:
+周总结:
+周总结:
+周总结:
+基本就是做作业,完成实习任务,上手还是有点慢,没学习什么其他的知识,感觉时间不够而且晚上回家什么都不想干。时间还是要挤的,还是要多学一些其他的东西。
+1. 后端实习,可以用chatgpt等工具辅助阅读代码,效率要提上来
+2. 后端知识学习,在实际项目中体验新技术的使用,同时关注学习底层原理
+3. 抖音项目完善,先把两位队友的代码看懂,找一找优化方向,用Hertz框架进行重写,整理青训营的资料,找一个比较完备的前端准备开始优化
+4. 开源初步尝试,多关注关注群消息和一些时间节点等
+5. 完成学校大作业等杂事
+周总结:
+周总结:
+周总结:
+周总结:
+周总结:
+周总结:
+周总结:
+周总结:
+周总结:
+周总结:
+周总结:
+周总结:
+周总结:
+整理交接材料,结束实习回学校
+基本就是实习,没受到重视,除了实习之外也没有干什么其他的事情
+ + +Hertz和Thrift简单示例
+ +Hertz 是字节跳动服务框架团队研发的超大规模的企业级微服务 HTTP 框架,具有高易用性、易扩展、低时延等特点。
+官方文档:https://www.cloudwego.io/zh/docs/hertz/
+基本使用:
+定义路由:
+func main() {
+ h := server.Default(server.WithHostPorts("127.0.0.1:50000"))
+ h.GET("/ping", router.Deal)
+ h.Spin()
+}路由的Handler:
+其中与其他框架最大的不同点是将Context分成了两个部分:
+两个上下文主要有两点区别:
+Copy()方法获取一个协程安全的副本,而 context.Context 本身就是协程安全的。func Deal(c context.Context, ctx *app.RequestContext) {
+ ctx.JSON(consts.StatusOK, utils.H{"message": res})
+}Thrift是一个 轻量级 、跨语言的远程服务调用框架,最初由 Facebook开发,后面进入 Apache开源项目。它通过自身的 IDL 中间语言 , 并借助代码生成引擎生成各种主流语言的 RPC 服务端 /客户端模板代码。
官方安装:https://thrift.apache.org/docs/BuildingFromSource.html
+网上资料:
+注意安装的thrift的版本与go的插件版本一定要相同!
+安装go插件:
+go get github.com/apache/thrift/lib/go/thrift首先安装依赖:
+apt install libboost-dev libboost-test-dev libboost-program-options-dev libboost-filesystem-dev libboost-thread-dev libevent-dev automake libtool flex bison pkg-config g++ libssl-dev安装Thrift:
+git clone https://github.com/apache/thrift
+cd thrift
+./bootstrap.sh
+./configure --without-qt4 --wihout-qt5
+make
+make install编译使用:
+thrift -r --gen go compute.thriftnamespace go compute
+
+service MulRange {
+ string BigRange(1:i64 max)
+}func Deal(c context.Context, ctx *app.RequestContext) {
+
+ transportFactory := thrift.NewTTransportFactory()
+
+ protocolFactory := thrift.NewTBinaryProtocolFactoryConf(nil)
+ addr := "127.0.0.1:9999"
+
+ cfg := &thrift.TConfiguration{}
+
+ // 建立和服务器的连接socket,通过socket建立Transport
+ var transport thrift.TTransport
+ transport = thrift.NewTSocketConf(addr, cfg)
+ transport, _ = transportFactory.GetTransport(transport)
+ defer transport.Close()
+
+ // 打开Transport,与服务器进行连接
+ transport.Open()
+
+ iprot := protocolFactory.GetProtocol(transport)
+ oprot := protocolFactory.GetProtocol(transport)
+
+ client := compute.NewMulRangeClient(thrift.NewTStandardClient(iprot, oprot))
+
+ num, _ := client.BigRange(context.Background(), 10)
+ fmt.Println(num)
+
+ ctx.JSON(consts.StatusOK, utils.H{"message": num})
+}// 尽量一个struct对应一个service
+type mulrangeThrift struct {
+}
+
+func (m *mulrangeThrift) BigRange(_ context.Context, max int64) (string, error) {
+
+ result := max + 1253
+ return strconv.FormatInt(result, 10), nil
+}
+
+func main() {
+ // 创建服务器
+ serverTransport, _ := thrift.NewTServerSocket(net.JoinHostPort("127.0.0.1", "9999"))
+
+ // 创建二进制协议
+ transportFactory := thrift.NewTTransportFactory()
+ protocolFactory := thrift.NewTBinaryProtocolFactoryConf(nil)
+
+ mulrangeProcessor := compute.NewMulRangeProcessor(new(mulrangeThrift))
+
+ // 启动服务器
+ server := thrift.NewTSimpleServer4(mulrangeProcessor, serverTransport, transportFactory, protocolFactory)
+ server.Serve()
+
+ // 退出时停止服务器
+ defer server.Stop()
+}参考资料:https://juejin.cn/post/6844903622380093447
+Thrift是一个 轻量级 、跨语言的远程服务调用框架,最初由 Facebook开发,后面进入 Apache开源项目。它通过自身的 IDL 中间语言 , 并借助代码生成引擎生成各种主流语言的 RPC 服务端 /客户端模板代码。
通过编写 RPC接口 Thrift IDL文件,利用编译生成器自动生成 服务端骨架 (Skeletons)和 客户端桩 (Stubs)。从而省去开发者自定义和 维护接口编解码 、 消息传输 、服务器多线程模型等基础工作。
Handler)即实现类即可。IDL定义好的客户端桩和 服务对象 ,然后就像调用本地对象的方法一样调用远端服务。通过维护 Thrift格式的IDL( 接口描述语言 )文件(注意写好注释),即可作为给 Client使用的接口文档使用,也自动生成接口代码,始终保持代码和文档的一致性。且 Thrift协议可灵活支持接口的 可扩展性 。
因为其来自 Google Protobuf开发团队,所以其 IDL文件风格类似 Google Protobuf,且更加 易读易懂 ;特别是 RPC服务接口的风格就像写一个面向对象的 Class一样简单。
初学者只需参照:thrift.apache.org/,一个多小时就可以理解 Thrift IDL文件的语法使用。
Thrift支持 C++、 Java、Python、PHP、Ruby、Erlang、Perl、Haskell、C#、Cocoa、JavaScript、Node.js、Smalltalk等多种语言,即可生成上述语言的服务器端和 客户端程序 。
对于我们经常使用的 Java、PHP、Python、C++支持良好,虽然对 iOS环境的 Objective-C(Cocoa)支持稍逊,但也完全满足我们的使用要求。
Thrift在很多开源项目中已经被验证是稳定和高效的,例如 Cassandra、Hadoop、HBase等;国外在 Facebook中有广泛使用,国内包括百度、美团小米、和饿了么等公司。
Thrift可以让用户选择客户端与服务端之间传输通信协议的类别,在传输协议上总体划分为 文本 (text)和 二进制 (binary)传输协议。为 节约带宽 , 提高传输效率 ,一般情况下使用二进制类型的传输协议为多数,有时还会使用基于文本类型的协议,这需要根据项目/产品中的实际需求。常用协议有以下几种:
JSON文本的数据编码协议进行数据传输JSON只写的协议,适用于通过脚本语言解析Thrift和Protobuf的最大不同,在于Thrift提供了完整的RPC支持,包含了Server/Client,而Protobuf只包括了stub的生成器和格式定义。
+User.thrift
+namespace go Sample
+
+struct User {
+ 1:required i32 id;
+ 2:required string name;
+ 3:required string avatar;
+ 4:required string address;
+ 5:required string mobile;
+}
+
+struct UserList {
+ 1:required list<User> userList;
+ 2:required i32 page;
+ 3:required i32 limit;
+}Service.thrift
+include "User.thrift"
+
+namespace go Sample
+
+typedef map<string, string> Data
+
+struct Response {
+ 1:required i32 errCode; //错误码
+ 2:required string errMsg; //错误信息
+ 3:required Data data;
+}
+
+//定义服务
+service Greeter {
+ Response SayHello(
+ 1:required User.User user
+ )
+
+ Response GetUser(
+ 1:required i32 uid
+ )
+}thrift支持引入另一个thrift文件:
+include "User.thrift"注意:
+include 引入文件的使用,字段必须带文件名前缀:
+1:required User.User user不能直接写 User user,这样会提示找不到 User定义。
编译时只编译引用了其他文件的thrift文件即可:
+thrift -r --gen go Service.thriftnamespace go Sample
+namespace php Sample需要支持多个语言,则需要定义多行。
+命名空间或者包名是多层级,使用 .号隔开。例如golang对于 Sample.Model会生成目录 Sample/Model,包名是 Model。
struct User {
+ 1:required i32 id = 0;
+ 2:optional string name;
+}字段选项 支持 required、optional两种。
一旦一个参数设置为 required,未来就一定不能删除或者改为 optional,否则就会出现版本不兼容问题,老客户端访问新服务会出现参数错误。不确定的情况可以都使用 optional 。
bool:布尔值(true或false)
+byte:8位有符号整数
+i16:16位有符号整数
+i32:32位有符号整数
+i64:64位有符号整数
+double:64位浮点数
+string:使用UTF-8编码编码的文本字符串list<t1>:一系列t1类型的元素组成的有序列表,元素可以重复
+set<t1>:一些t1类型的元素组成的无序集合,元素唯一不重复
+map<t1,t2>:key/value对,key唯一typedef map<string, string> Dataenum TweetType {
+ TWEET,
+ RETWEET = 2,
+ DM = 0xa,
+ REPLY
+}默认从0开始赋值,枚举值可以赋予某个常量,允许常量是十六进制整数。末尾没有逗号。
+不支持枚举类嵌套,枚举常量必须是32位正整数。
+对于go,会生成 TweetType_开头的常量。
Thrift允许用户定义常量,复杂的类型和结构体可以使用JSON形式表示:
+const i32 INT_CONST = 1234
+const map<string,string> MAP_CONST = {"hello": "world", "goodnight": "moon"}exception BizException {
+ 1:required i32 code
+ 2:required string msg
+}结构体可以包含其他结构体,但不支持继承结构体。
+struct Response {
+ 1:required i32 errCode; //错误码
+ 2:required string errMsg; //错误信息
+ 3:required Data data;
+}Thrift编译器会根据选择的目标语言为server产生服务接口代码,为client产生桩(stub)代码。
+在go里是 interface。service里定义的方法必须由服务端实现。
service Greeter {
+ Response SayHello(
+ 1:required User.User user
+ )
+}参数是user,返回值是Response类型
+服务端主要完成4个部分的工作:
+服务端最终要创建这样的一个server
+func NewTSimpleServerFactory6(processorFactory TProcessorFactory, serverTransport TServerTransport, inputTransportFactory TTransportFactory, outputTransportFactory TTransportFactory, inputProtocolFactory TProtocolFactory, outputProtocolFactory TProtocolFactory) *TSimpleServer {
+ return &TSimpleServer{
+ processorFactory: processorFactory,
+ serverTransport: serverTransport,
+ inputTransportFactory: inputTransportFactory,
+ outputTransportFactory: outputTransportFactory,
+ inputProtocolFactory: inputProtocolFactory,
+ outputProtocolFactory: outputProtocolFactory,
+ }
+}说明:
+server := thrift.NewTSimpleServer4(processor, transport, transportFactory, protocolFactory)
+err = server.Serve()// 定义服务
+type Greeter struct {
+}
+handler := &Greeter{}
+processor := Sample.NewGreeterProcessor(handler)var transport thrift.TServerTransport
+transport, err = thrift.NewTServerSocket(*addr)不同类型可选
+//buffered
+var transportFactory thrift.TTransportFactory
+if *buffered {
+ transportFactory = thrift.NewTBufferedTransportFactory(8192)
+} else {
+ transportFactory = thrift.NewTTransportFactory()
+}
+
+//framed
+if *framed {
+ transportFactory = thrift.NewTFramedTransportFactory(transportFactory)
+}不同类型可选
+var protocolFactory thrift.TProtocolFactory
+switch *protocol {
+case "compact":
+ protocolFactory = thrift.NewTCompactProtocolFactory()
+case "simplejson":
+ protocolFactory = thrift.NewTSimpleJSONProtocolFactory()
+case "json":
+ protocolFactory = thrift.NewTJSONProtocolFactory()
+case "binary", "":
+ protocolFactory = thrift.NewTBinaryProtocolFactoryDefault()客户端定义好client后直接调用方法即可,如下所示:
+client := GetClient()
+rep, err := client.GetUser(ctx, 100)
+rep, err := client.SayHello(ctx, &Sample.User{
+ Name: "thrift",
+ Address: "address",
+ })iprot := protocolFactory.GetProtocol(transport)
+oprot := protocolFactory.GetProtocol(transport)
+client := Sample.NewGreeterClient(thrift.NewTStandardClient(iprot, oprot))涉及到protocolFactory与transport
+protocolFactory := thrift.NewTBinaryProtocolFactoryDefault()
+iprot := protocolFactory.GetProtocol(transport)
+oprot := protocolFactory.GetProtocol(transport)注意要与服务端定义的protocolFactory要一致
+创建socket连接:
+var transport thrift.TTransport
+var err error
+transport, err = thrift.NewTSocket(addr)注意要提前进行类型定义,否则后面类型不匹配
+定义transportFactory:
+transportFactory := thrift.NewTTransportFactory()
+transport, err = transportFactory.GetTransport(transport)
+transport.Open()注意transportFactory的类型要与服务端相同
+可以添加key同时使用SSL进行Socket连接从而确保安全性
+ + +Prometheus简单示例
+ +Prometheus 是一款基于时序数据库的开源监控告警系统。Prometheus的基本原理是通过HTTP协议周期性抓取被监控组件的状态,任意组件只要提供对应的HTTP接口就可以接入监控。不需要任何SDK或者其他的集成过程。
+wget https://github.com/prometheus/prometheus/releases/download/v2.37.6/prometheus-2.37.6.linux-amd64.tar.gz
+tar xvfz prometheus-2.37.6.linux-amd64.tar.gz
+cd prometheus-2.37.6.linux-amd64/
+./prometheus --config.file=prometheus.yml此时打开http://localhost:9090/即可以看到监控界面
+package main
+
+import (
+ "net/http"
+
+ "github.com/prometheus/client_golang/prometheus/promhttp"
+)
+
+func main() {
+ //提供 /metrics HTTP 端点
+ http.Handle("/metrics", promhttp.Handler())
+ //端口号
+ http.ListenAndServe(":2112", nil)
+}运行后访问http://localhost:2112/metrics可以看到采集的指标数据
+注册自定义应用程序指定指标:
+package main
+
+import (
+ "net/http"
+ "time"
+
+ "github.com/prometheus/client_golang/prometheus"
+ "github.com/prometheus/client_golang/prometheus/promauto"
+ "github.com/prometheus/client_golang/prometheus/promhttp"
+)
+
+func recordMetrics() {
+ //每2秒,计数器增加1。
+ go func() {
+ for {
+ opsProcessed.Inc()
+ time.Sleep(2 * time.Second)
+ }
+ }()
+}
+
+// 公开了 myapp_processed_ops_total 计数器
+var (
+ opsProcessed = promauto.NewCounter(prometheus.CounterOpts{
+ Name: "myapp_processed_ops_total",
+ Help: "The total number of processed events",
+ })
+)
+
+func main() {
+ recordMetrics()
+
+ http.Handle("/metrics", promhttp.Handler())
+ http.ListenAndServe(":2112", nil)
+}运行后访问http://localhost:2112/metrics可以看到自定义的指标,每2秒,计数器增加1
+可以修改配置文件:prometheus.yml
+# my global config
+global:
+ scrape_interval: 15s # Set the scrape interval to every 15 seconds. Default is every 1 minute.
+ evaluation_interval: 15s # Evaluate rules every 15 seconds. The default is every 1 minute.
+ # scrape_timeout is set to the global default (10s).
+
+# Alertmanager configuration
+alerting:
+ alertmanagers:
+ - static_configs:
+ - targets:
+ # - alertmanager:9093
+
+# Load rules once and periodically evaluate them according to the global 'evaluation_interval'.
+rule_files:
+ # - "first_rules.yml"
+ # - "second_rules.yml"
+
+# A scrape configuration containing exactly one endpoint to scrape:
+# Here it's Prometheus itself.
+scrape_configs:
+ # The job name is added as a label `job=<job_name>` to any timeseries scraped from this config.
+ - job_name: "prometheus"
+
+ # metrics_path defaults to '/metrics'
+ # scheme defaults to 'http'.
+
+ static_configs:
+ - targets: ["localhost:2112"]将最后的targets修改成客户端启动的端口即可
+ + +Kafka简单示例
+ +首先需要安装Java
+sudo apt install openjdk-11-jdk下载安装kafka
+wget https://dlcdn.apache.org/kafka/3.4.0/kafka_2.13-3.4.0.tgz
+tar -xzf kafka_2.13-3.4.0.tgz
+cd kafka_2.13-3.4.0启动zookeeper和kafka:
+bin/zookeeper-server-start.sh config/zookeeper.properties
+bin/kafka-server-start.sh config/server.properties使用给定代理地址和配置创建一个同步生产者
+// 使用给定代理地址和配置创建一个同步生产者
+SyncProducer, err := sarama.NewSyncProducer(
+ []string{conn},
+ config,
+)config可以自由配置:
+config := sarama.NewConfig()
+// 等待服务器所有副本都保存成功后的响应
+config.Producer.RequiredAcks = sarama.WaitForAll
+// 随机的分区类型:返回一个分区器,该分区器每次选择一个随机分区
+config.Producer.Partitioner = sarama.NewRandomPartitioner
+// 是否等待成功和失败后的响应
+config.Producer.Return.Successes = true构建发送的消息:
+// 构建发送的消息
+msg := &sarama.ProducerMessage{
+ Topic: topic,
+ Key: sarama.StringEncoder(time.Now().String()),
+ Value: sarama.StringEncoder(content),
+}生产者发送消息:
+// SendMessage:该方法是生产者生产给定的消息
+// 生产成功的时候返回该消息的分区和所在的偏移量
+// 生产失败的时候返回error
+partition, offset, err := SyncProducer.SendMessage(msg)创建一个消费者的实例
+config := sarama.NewConfig()
+consumer, err := sarama.NewConsumer(c.Node, config)查询这个 topic 有多少分区
+partitions, err := consumer.Partitions(c.Topic)每个分区开一个 goroutine 来消费
+wg.Add(len(partitions))
+// 然后每个分区开一个 goroutine 来消费
+for _, partitionId := range partitions {
+ //不开异步会导致一个消费完才会消费另外一个
+ go c.consumeByPartition(consumer, c.Topic, partitionId, &wg)
+}消费
+partitionConsumer, err := consumer.ConsumePartition(topic, partitionId, sarama.OffsetNewest)
+// 然后可以通过partitionConsumer.Messages()打印得到的消息func main() {
+ Conn := "127.0.0.1:9092"
+ topic := "test_log"
+
+ var wg sync.WaitGroup
+ wg.Add(2)
+
+ // 消费者
+ go func() {
+ defer wg.Done()
+ // 初始化consumer
+ var kafkaConsumer = consumer.KafkaConsumer{
+ Node: []string{Conn},
+ Topic: topic,
+ }
+ // 消费
+ go kafkaConsumer.Consume()
+ }()
+
+ // 生产者
+ go func() {
+ defer wg.Done()
+
+ index := 0
+ for {
+ // 生产者发送消息
+ _, err := producer.Send(Conn, topic, fmt.Sprintf("lox_%d", index))
+ if err != nil {
+ log.Print("测试失败:" + err.Error())
+ return
+ }
+ index++
+ time.Sleep(1 * time.Second)
+ }
+ }()
+ wg.Wait()
+}字节跳动青训营-抖音项目
+ +“NoBugVideo”基于Gin Web框架,采用微服务架构,使用Kong集成Consul做服务发现,实现了“抖音”的基本功能,包括视频流的推送、视频投稿、用户的注册与登录,以及社交(用户之间的关注与聊天)与互动(用户对视频点赞及评论)等功能。
+项目服务地址:http://124.221.120.88:8000
+Github地址:https://github.com/xu-jq/simple-DY
+我们团队实现了包括基础功能在内的两大方向:互动方向与 社交方向 ,根据项目考核的4个标准,自评如下:
+| 评价项 | +实现情况 | +
|---|---|
| 功能实现 | +微服务与其他资源能够正常运行,完全实现文档中定义的全部接口,边界情况处理良好 | +
| 代码质量 | +项目结构清晰,包划分合理,代码符合编码规范 | +
| 服务性能 | +数据表设置了合理的索引,代码中尽量使用并行处理提高性能 | +
| 安全可靠 | +通过GORM框架防止SQL注入,通过JWT进行用户的认证,防止越权 | +
| 团队成员 | +主要贡献 | +
|---|---|
| @汪辉 | +开发社交模块,搭建Kong集成Consul做服务发现 | +
| @许珺琪 | +开发用户互动相关模块包括点赞评论等相关接口、搭建redis服务 | +
| @张兆 | +开发用户模块与视频模块相关接口、搭建MySQL、RabbitMQ等服务 | +
抖音上线于2016年9月26日,一开始是定位于专注于新生代的音乐创意短视频App,视频时常限制在15s内。年轻人比较爱赶新潮,乐于尝试新鲜事物,通过清晰明确定位在“潮流”“炫酷”“技术流”的方式,抖音吸引了第一批忠实粉丝。当产品功能逐渐完善后,抖音在运营方面开始发力,用户迎来大幅增长。抖音的主力用户群体年龄段上升,已经从早期的18岁到24岁,上升到了25岁到30岁用户。随着用户的快速增长,在内容层面也向着更加主流化、多元化的方向转变。
+架构方面比较常见的有三种:
+所有的模块打包到一起部署运行,在开发小型项目上有独特优势:易于调试、部署,运维方便。缺点是容错性低,不可靠。只能通过运行更多的服务器水平扩展, 而不同的应用服务对资源的需求不同,且不可持续发展。
+面向服务架构是一种设计方法,设计上通常是自上而下的,服务间松散耦合。ESB集成不同协议的服务,做消息的转化、解释、路由从而联通各个服务,解决企业通信问题,服务松耦合、可扩展。缺点是SOA更多的面向企业服务,服务拆分粒度很大,更多的是为了复用。
+微服务是去中心化的SOA的扩展,强调服务彻底的组件化,一个组件就是一个产品,服务切分力度更小,设计上更多的是自下而上的。服务间通过轻量级的协议进行通信,并根据服务本身需要独立化部署。从产品视角出发,更多聚焦可扩展性,兼顾可维护性。
+综合上述几种服务的对比,我们最终选择了微服务架构,并使用下面的技术栈:
+用户模块包括用户注册、用户登录和用户信息三个部分。
+POST-/douyin/user/register/新用户注册时提供用户名,密码,昵称即可,用户名需要保证唯一。创建成功后返回用户 id 和权限token。
+接口定义:
+message douyin_user_register_request{
+ string username = 1; // 注册用户名,最长32个字符
+ string password = 2; // 密码,最长32个字符
+}
+
+message douyin_user_register_response{
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ int64 user_id = 3; // 用户id
+ string token = 4; // 用户鉴权token
+}POST-/douyin/user/login/通过用户名和密码进行登录,登录成功后返回用户 id 和权限 token
+接口定义:
+message douyin_user_login_request{
+ string username = 1; // 登录用户名
+ string password = 2; // 登录密码
+}
+
+message douyin_user_login_response{
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ int64 user_id = 3; // 用户id
+ string token = 4; // 用户鉴权token
+}GET-/douyin/user/获取登录用户的 id、昵称,如果实现社交部分的功能,还会返回关注数和粉丝数。
+接口定义:
+message douyin_user_request{
+ int64 user_id = 1; // 用户id
+ string token = 2; // 用户鉴权token
+}
+
+message douyin_user_response{
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ User user = 3; // 用户信息
+}视频模块包括包括视频Feed流获取、视频投稿和获取用户投稿列表三个模块
+GET-/douyin/feed/不限制登录状态,返回按投稿时间倒序的视频列表,视频数由服务端控制,单次最多30个。
+接口定义:
+message douyin_feed_request{
+ int64 latest_time = 1; // 可选参数,限制返回视频的最新投稿时间戳,精确到秒,不填表示当前时间
+ string token = 2; // 可选参数,登录用户设置
+}
+
+message douyin_feed_response{
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ repeated Video video_list = 3; // 视频列表
+ int64 next_time = 4; // 本次返回的视频中,发布最早的时间,作为下次请求时的latest_time
+}GET-/douyin/publish/list/登录用户的视频发布列表,直接列出用户所有投稿过的视频。
+接口定义:
+message douyin_publish_list_request{
+ int64 user_id = 1; // 用户id
+ string token = 2; // 用户鉴权token
+}
+
+message douyin_publish_list_response{
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ repeated Video video_list = 3; // 用户发布的视频列表
+}POST-/douyin/publish/action/登录用户选择视频上传。
+接口定义:
+message douyin_publish_action_request{
+ string token = 1; // 用户鉴权token
+ bytes data = 2; // 视频数据
+ string title = 3; // 视频标题
+}
+
+message douyin_publish_action_response{
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+}POST-/douyin/favorite/action/登录用户对视频进行点赞与取消点赞操作。
+接口定义:
+message douyin_favorite_action_request {
+ string token = 1; // 用户鉴权token
+ int64 video_id = 2; // 视频id
+ int32 action_type = 3; // 1-点赞,2-取消点赞
+}
+
+message douyin_favorite_action_response {
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+}GET-/douyin/favorite/list/登录用户的所有点赞视频。
+接口定义:
+message douyin_favorite_list_request {
+ int64 user_id = 1; // 用户id
+ string token = 2; // 用户鉴权token
+}
+
+message douyin_favorite_list_response {
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ repeated Video video_list = 3; // 用户点赞视频列表
+}POST-/douyin/comment/action/登录用户对视频进行评论。
+接口定义:
+message douyin_comment_action_request {
+ string token = 1; // 用户鉴权token
+ int64 video_id = 2; // 视频id
+ int32 action_type = 3; // 1-发布评论,2-删除评论
+ string comment_text = 4; // 用户填写的评论内容,在action_type=1的时候使用
+ int64 comment_id = 5; // 要删除的评论id,在action_type=2的时候使用
+}
+
+message douyin_comment_action_response {
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ Comment comment = 3; // 评论成功返回评论内容,不需要重新拉取整个列表
+}GET-/douyin/comment/list/查看视频的所有评论,按发布时间倒序。
+接口定义:
+message douyin_comment_list_request {
+ string token = 1; // 用户鉴权token
+ int64 video_id = 2; // 视频id
+}
+
+message douyin_comment_list_response {
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ repeated Comment comment_list = 3; // 评论列表
+}POST-/douyin/relation/action/登录用户对其他用户进行关注或取消关注。实现用户之间的关注关系维护,登录用户能够关注或取关其他用户,同时自己能够看到自己关注过的所有用户列表,以及所有关注自己的用户列表。
+接口定义:
+message douyin_favorite_list_request {
+ int64 user_id = 1; // 用户id
+ string token = 2; // 用户鉴权token
+}
+
+message douyin_favorite_list_response {
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ repeated Video video_list = 3; // 用户点赞视频列表
+}GET-/douyin/relatioin/follow/list/登录用户关注的所有用户列表。
+message douyin_favorite_list_request {
+ int64 user_id = 1; // 用户id
+ string token = 2; // 用户鉴权token
+}
+
+message douyin_favorite_list_response {
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ repeated Video video_list = 3; // 用户点赞视频列表
+}GET-/douyin/relation/follower/list/所有关注登录用户的粉丝列表。
+message douyin_favorite_list_request {
+ int64 user_id = 1; // 用户id
+ string token = 2; // 用户鉴权token
+}
+
+message douyin_favorite_list_response {
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ repeated Video video_list = 3; // 用户点赞视频列表
+}GET-/douyin/relation/friend/list/互相关注的用户列表。
+message douyin_favorite_list_request {
+ int64 user_id = 1; // 用户id
+ string token = 2; // 用户鉴权token
+}
+
+message douyin_favorite_list_response {
+ int32 status_code = 1; // 状态码,0-成功,其他值-失败
+ string status_msg = 2; // 返回状态描述
+ repeated Video video_list = 3; // 用户点赞视频列表
+}客户端通过定时轮询服务端接口查询消息记录
+GET-/douyin/message/chat/当前登录用户和其他指定用户的聊天消息记录
+message douyin_message_chat_request{
+ required string token=1;//用户鉴权token
+ required int64 to_user_id=2;//对方用户id
+ required int64 pre_msg_time=3;//上次最新消息的时间
+}
+
+message douyin_message_chat_response {
+ required int:32 status_code=1;//状态码,g-成功,其他值-失败
+ optional string status._msg=2;//返回状态描述
+ repeated Message message_list=3;//消息列表
+}
+message Message{
+ required int64 id=1;//消息id
+ required int64 to_user_id=2;//该消息接收者的d
+ required int64 from_user_id=3;//该消息发送者的id
+ required string content=4;//消息内容
+ optional int64 create_time=5;//消息创建时间
+}POST-/douyin/message/action/登录用户对消息的相关操作,目前只支持消息发送
+message douyin_relation_action_request{
+ required string token=1;//用户鉴权token
+ required int64 to_user_id=2;//对方用户id
+ required int32 action_type=3;//1-发送消息
+ required string content=4;//消息内容
+}
+message douyin_relation_action_response{
+ required int32 status._code=1;//状态码,g-成功,其他值-失败
+ optional string status_msg=2;//返回状态描述
+}运行流程:
+用户注册的逻辑比较简单,请求的参数中只包含用户的用户名与密码,不支持手机注册以及各种验证码操作。因此用户的唯一识别信息为用户名。如果数据库中存在相同的用户名,则认为这个用户已经存在,拒绝注册;否则则允许用户注册,并在数据库中分配给这个用户唯一的id。最后调用JWT生成Token返回响应,作为在Token生效期间的用户的唯一标识符。
+用户注册流程:
+用户登录请求的参数中只包含用户的用户名与密码,不支持手机登录以及各种验证码操作。因此用户的唯一识别信息为用户名。如果数据库中不存在相同的用户名,则认为这个用户不存在,拒绝登录;否则则允许用户登录,并返回数据库中这个用户的唯一id。同时调用JWT生成Token返回响应,作为在Token生效期间的用户的唯一标识符。
+用户登录流程:
+用户信息请求的参数包括要请求的用户的id和当前登录的用户的Token。返回的用户信息应该包括用户的名称,用户的关注人数和粉丝人数,以及用户与当前登录用户的关注关系。因此除了调用DY-api.UserInfo获取用户的基本信息之外,还需要调用DY-srv.GetFollowList与DY-srv.GetFollowerList获取用户的关注人和用户的粉丝列表。两个Count数值可以通过查看切片的大小获得,关注关系需要遍历切片进行搜索。
+在对不同的服务进行调用的时候采取并行调用的方式,服务全部返回后在api层进行拼接,从而提高效率。
+用户信息流程:
+获取视频流的请求参数包括视频的最新时间和当前用户的Token信息。如果当前用户在登录的状态下请求视频流,则通过最新时间在数据库中查询前30个视频的信息,包括视频本身的id和作者的id。获得最多30个视频的信息后,创建多个协程(视频数量个数),根据每个id获得视频的其他信息,如作者的详细信息,视频的点赞数量,作者的关注人数等等。在调用不同服务的时候也采用并行调用的方式。最后对返回的全部响应进行组织返回。
+如果用户没有登录,则Token信息为空,那么返回的响应中缺少一些交互信息,如当前用户是否已经对当前视频点赞等等。
+获取视频流流程:
+DY-api.Feed处理请求,准备请求服务
+首先请求DY-srv.Feed服务,根据时间戳查询数据库,查询出不超过时间戳的前30个视频,查询后返回视频列表
+随后并行请求视频列表中的每一个视频(即最大并发数为30)
+对每一个视频,根据前一个服务响应的作者的id并行请求DY-srv.UserInfo、DY-srv.GetFollowList和DY-srv.GetFollowerList,等待全部成功返回后记录Author响应相关的5个字段
+对每一个视频,根据视频id并行请求DY-srv.douyinCommentList和DY-srv.douyinLikeVideo,对于每个视频
+等待全部的视频返回响应后,构建响应结构体并返回给客户端
+获取用户视频发布列表的请求参数包括用户的id和当前用户的Token信息。两者不一定是相同的用户,因为用户在观看视频的同时点击用户头像即可以看到这个视频作者的信息和作者的视频发布列表。
+如果当前用户是查看自己的视频发布列表,则通过用户的id在数据库中查询发布的视频的信息。获得最多视频的信息后,创建多个协程(视频数量个数),根据每个id获得视频的其他信息,如视频的点赞数量,作者的关注人数等等。在调用不同服务的时候也采用并行调用的方式。最后对返回的全部响应进行组织返回。
+如果Token信息为空,则当前场景是用户查看其他用户的发布视频列表。那么返回的响应中缺少一些交互信息,如当前用户是否已经对当前作者的视频点赞等等。
+获取视频发布列表流程:
+DY-api.PublishList处理请求,准备请求服务
+首先请求DY-srv.PublishList服务,根据id查询数据库,如果id在数据库中不存在,则直接返回错误,然后根据用户id查询发布的视频列表并返回
+随后并行请求DY-srv.UserInfo、DY-srv.GetFollowList和DY-srv.GetFollowerList,等待全部成功返回后记录User响应相关的5个字段
+对每一个视频,根据视频id并行请求DY-srv.douyinCommentList和DY-srv.douyinLikeVideo,对于每个视频
+等待全部的视频返回响应后,构建响应结构体并返回给客户端
+视频投稿的请求参数中包括用户的Token,上传的视频流数据以及视频的标题。其中视频流是用户从本地上传得到的,视频的标题是用户自行输入得到的。上传视频必须是在登录的状态下,因此必须包含用户的Token信息。获得参数后,根据Token信息解析出当前用户的id,然后根据用户id判断是否存在这个用户的文件夹。如果不存在文件夹则新建用户文件夹。创建文件夹后将视频流写入这个文件夹下的视频文件,同时调用ffmpeg对视频的封面进行截取从而获得视频的首图。确认视频文件与图片文件都保存在本地后,构建返回的响应,并将上传文件的消息推送到消息队列中,此时消息队列将视频文件和图片文件异步上传到对象存储当中,上传结束后将视频信息写入数据库,在下次请求视频流的过程中就可以请求到这个视频了。
+其中使用RabbitMQ进行异步处理,在服务器带宽有限的情况下,上传视频对用户来说基本无感,增加了用户的体验。且上传到对象存储后视频和图片的展示和下载速度也会更快,方便用户查看视频。
+视频投稿流程:
+点赞操作分为对未点赞的视频点赞以及对已点赞的视频取消点赞。点赞操作接口的请求参数包括,用户token;视频id;操作类型(1–点赞,2–取消点赞)。通过解析用户token可获得用户id。构建一个redis集合,将用户已经点赞的视频将其按照k-v形式存入redis。
+2.1.1 对视频点赞
+当请求参数操作类型的值为1时,即为点赞操作,点赞操作是要对用户未点赞的视频进行点赞,首先在redis集合中查询该用户是否对此视频点赞过,若点赞过则返回视频已点赞,若未点赞,则将该条点赞记录先插入redis再插入数据库中,最后返回成功的响应码。
+2.1.2 对视频取消点赞
+当请求参数操作类型的值为2时,即为取消点赞操作,取消点赞操作是要对用户点赞的视频进行取消,首先在redis集合中查询该用户是否对此视频点赞过,若未点赞过则返回视频暂未点赞,若点赞了,则将该条点赞记录先从redis中删除再从数据库中删除,最后返回成功的响应码。
+喜欢列表接口的请求参数为用户id和用户token,先根据token验证用户身份与登录状态,若成功,则根据用户id查询用户的喜欢列表,将喜欢列表封装进响应结构体中,返回参数中还需要视频相关信息,通过调用视频服务接口,获取视频相关信息,并封装到响应结构体中,最终将响应结构体返回。
+评论操作分为发表评论和删除评论,评论操作接口的请求参数包括用户token,视频id,操作类型(1–发表评论,2–删除评论),评论内容(发表评论时),评论id(删除评论时)。首先根据token验证用户身份与登录状态,若成功,则解析token获取用户id。
+2.1.1 发表评论
+当操作类型等于1时,表示是发表评论,将对应评论内容,用户id,视频id,添加进数据库,并且将评论列表封装进响应结构体,同时调用社交服务,获取对应的用户信息,将用户信息也封装进响应结构体,最后将其返回。
+2.1.2 删除评论
+当操作类型等于2时,表示是删除评论,将评论id对应的数据从数据库中删除,并返回删除成功的信息。
+评论列表接口的请求参数为视频id和用户token,先根据token验证用户身份与登录状态,若成功,则根据视频id查询视频的评论列表,将评论列表封装进响应结构体中,返回参数中还需要用户相关信息,通过调用社交服务接口,获取用户相关信息,并封装到响应结构体中,最终将响应结构体返回。
+社交模块的整体设计如下图:
+其中 social-api程序是使用Gin框架搭建的Web服务。主要接受url请求,通过路由绑定handler处理函数,添加授权中间件。social-api部署了多个,并将自己注册在Consule服务上,支持负载均衡,并通过服务发现调用gRPC服务。
social-srv是业务处理代码,主要和MySQL数据库打交道。social-srv可以部署在多个不同服务器上,并将自己注册到Consul上来实现负载均衡,提供被其他服务发现。
详细设计:
+关注接口的请求参数为用户ID和被关注的用户ID,先根据token验证用户身份与登录状态,若成功,则向数据库插入数据,同时互相关注的用户会成为朋友,在朋友界面显示朋友列表,并展现最近的一条消息。用户也可以在信息详情页面来查看关注的用户和粉丝。
+通过用户ID和朋友ID可以新增一条消息。使用定时调用接口的方式来获取消息。
+字段如下:
+| 名称 | +类型 | +说明 | +
|---|---|---|
id |
+bigint | +视频唯一id,自增主键 | +
author_id |
+bigint | +视频作者id | +
file_name |
+varchar | +文件名称 | +
publish_time |
+bigint | +发布时间 | +
title |
+varchar | +视频标题 | +
索引设置:
+| 名称 | +类型 | +说明 | +
|---|---|---|
id |
+bigint | +用户id,自增主键 | +
name |
+varchar | +用户名 | +
password |
+varchar | +用户密码 | +
索引设置:
+| 名称 | +类型 | +说明 | +
|---|---|---|
id |
+bigint | +评论唯一id,自增主键 | +
user_id |
+bigint | +评论发布者的id | +
video_id |
+bigint | +评论发布位置的视频id | +
comment_text |
+varchar | +评论内容 | +
create_time |
+datetime | +评论创建时间 | +
索引设置:
+| 名称 | +类型 | +说明 | +
|---|---|---|
id |
+bigint | +关注关系id,自增主键 | +
user_id |
+bigint | +用户id | +
follower_id |
+bigint | +关注的用户id | +
索引设置:
+| 名称 | +类型 | +说明 | +
|---|---|---|
id |
+bigint | +喜欢关系id,自增主键 | +
user_id |
+bigint | +点赞用户的id | +
video_id |
+bigint | +被点赞的视频id | +
索引设置:
+| 名称 | +类型 | +说明 | +
|---|---|---|
id |
+bigint | +消息唯一id,自增主键 | +
user_id |
+bigint | +发送消息的用户id | +
to_user_id |
+bigint | +接收消息的用户id | +
sent_time |
+datetime | +消息发送时间 | +
content |
+varchar | +消息内容 | +
索引设置:
+后端项目总体分为两个大部分:
+simple-DY/DY-api/):使用Gin框架来获取用户请求,连接GRPC远程调用服务,最后返回数据。simple-DY/DY-srvs/):GRPC编写的微服务。项目的总体结构如下所示:
+├── simple-DY
+│ ├── db.sql // 数据库初始化文件
+│ ├── DY-api // web项目
+│ │ ├── interact-web // 互动模块
+│ │ ├── social-web // 社交模块
+│ │ └── video-web // 视频模块
+│ ├── DY-srvs // service项目
+│ │ ├── interact-srv // 互动模块
+│ │ ├── social-srv // 社交模块
+│ │ └── video-srv // 视频模块
+│ ├── go.mod
+│ ├── go.sum
+│ └── README.md代码结构:
+video-web
+├── api
+│ ├── base.go
+│ ├── feed.go
+│ ├── info.go
+│ ├── otherapi.go
+│ ├── publishaction.go
+│ ├── publishlist.go
+│ ├── userinfo.go
+│ ├── userlogin.go
+│ └── userregister.go
+├── config
+│ └── config.go
+├── config-debug.yaml
+├── config-pro.yaml
+├── global
+│ └── global.go
+├── initialize
+│ ├── config.go
+│ ├── logger.go
+│ ├── router.go
+│ ├── srv_conn.go
+│ └── validator.go
+├── logs
+│ └── video-web.log
+├── main.go
+├── middlewares
+│ ├── cors.go
+│ └── jwt.go
+├── models
+│ ├── base.go
+│ ├── jwt.go
+│ ├── other.go
+│ ├── request.go
+│ └── response.go
+├── proto
+│ ├── simpledy_grpc.pb.go
+│ ├── simpledy.pb.go
+│ └── simpledy.proto
+├── README.md
+└── utils
+ └── consul
+ └── register.go详细说明:
+api:编写路由的Handler处理函数config:读取yaml文件时的接收结构体*.yaml:配置文件
+config-debug.yaml:线下开发使用的配置文件config-pro.yaml: 线上配置文件global:存放全局变量,例如config信息,连接信息等initialize:初始化程序代码
+config.go:读取配置文件logger.go:日志配置router.go:gin路由srv_conn.go:连接微服务validator.go:翻译器logs:日志文件main.go:主程序入口middlewares:gin的自定义中间件
+cors.go:跨域中间件jwt.go:JWT中间件models:用户请求参数的结构体proto:编写和生成proto文件README.md:说明文件utils:工具类
+consul:调用consul api进行服务注册发现等操作代码结构:
+.
+├── config
+│ └── config.go
+├── config-debug.yaml
+├── config-pro.yaml
+├── global
+│ └── global.go
+├── handler
+│ ├── base.go
+│ ├── feed.go
+│ ├── publishaction.go
+│ ├── publishlist.go
+│ ├── userinfo.go
+│ ├── userlogin.go
+│ ├── userregister.go
+│ └── videoinfo.go
+├── initialize
+│ ├── config.go
+│ ├── db.go
+│ ├── handler.go
+│ └── logger.go
+├── logs
+│ └── video-srv.log
+├── main.go
+├── models
+│ ├── base.go
+│ └── db.go
+├── proto
+│ ├── simpledy_grpc.pb.go
+│ ├── simpledy.pb.go
+│ └── simpledy.proto
+├── README.md
+└── utils
+ ├── backup
+ │ └── backup.go
+ ├── consul
+ │ └── register.go
+ ├── dao
+ │ ├── followdao.go
+ │ ├── userdao.go
+ │ └── videodao.go
+ ├── ffmpeg
+ │ └── extractFirstFrame.go
+ ├── freeport
+ │ └── port.go
+ ├── jwt
+ │ └── token.go
+ ├── md5salt
+ │ └── md5.go
+ ├── oss
+ │ └── upload.go
+ └── rabbitmq
+ ├── base.go
+ ├── consumer.go
+ └── producer.go详细说明:
+config:读取yaml文件时的接收结构体*.yaml:配置文件
+config-debug.yaml:线下开发使用的配置文件config-pro.yaml: 线上配置文件global:存放全局变量,例如config信息,连接信息等handler:主要的逻辑代码,proto的service的实现类initialize:初始化程序代码
+config.go:读取配置文件db.go:数据库全局连接handler.go:监听客户端连接logger.go:日志配置logs:日志文件main.go:主程序入口models:用户请求参数的结构体proto:编写和生成proto文件README.md:说明文件utils:工具类
+backup:备份用户上传的视频和图片文件consul:调用consul api进行服务注册发现等操作dao:数据库相关操作ffmpeg:视频首页截图freeport:获取空闲网络端口jwt:鉴权Token的生成与解析md5salt:密码加密存储oss:七牛云对象存储相关操作rabbitmq:消息队列相关操作interact-web
+├── api
+│ ├── base.go
+│ ├── comment.go
+│ └── like.go
+├── config
+│ └── config.go
+├── global
+│ └── global.go
+├── initialize
+│ ├── config.go
+│ ├── logger.go
+│ ├── router.go
+│ ├── srv_conn.go
+│ └── validator.go
+├── main.go
+├── middlewares
+│ ├── cors.go
+│ └── jwt.go
+├── models
+│ └── request.go
+├── proto
+│ ├── simpledy_grpc.pb.go
+│ ├── simpledy.pb.go
+│ └── simpledy.proto
+├── router
+│ ├── comment.go
+│ └── like.go
+└── utils
+ └── register
+ └── consul
+ └── register.gointeract-srv
+├── build.sh
+├── config
+│ └── config.go
+├── global
+│ └── global.go
+├── handler
+│ └── interact.go
+├── initalize
+│ ├── config.go
+│ ├── db.go
+│ ├── logger.go
+│ ├── rdb.go
+│ └── srvs_conn.go
+├── main.go
+├── model
+│ ├── base.go
+│ ├── comment.go
+│ ├── like.go
+│ └── video.go
+├── proto
+│ ├── simpledy_grpc.pb.go
+│ ├── simpledy.pb.go
+│ └── simpledy.proto
+└── utils
+ ├── addr.go
+ ├── jwt
+ │ └── token.go
+ ├── key
+ │ └── key.go
+ └── register
+ └── consul
+ └── register.gosocial-web
+├── api
+│ ├── base.go
+│ ├── message.go
+│ └── relation.go
+├── config
+│ └── config.go
+├── config-debug.yaml
+├── config-pro.yaml
+├── forms
+│ ├── message.go
+│ └── relation.go
+├── global
+│ └── global.go
+├── initialize
+│ ├── config.go
+│ ├── logger.go
+│ ├── router.go
+│ ├── srv_conn.go
+│ └── validator.go
+├── main.go
+├── middlewares
+│ ├── cors.go
+│ └── jwt.go
+├── models
+│ └── request.go
+├── proto
+│ ├── simpledy_grpc.pb.go
+│ ├── simpledy.pb.go
+│ └── simpledy.proto
+├── router
+│ ├── message.go
+│ └── relation.go
+└── utils
+ ├── addr.go
+ └── register
+ └── consul
+ └── register.gosocial-srv
+├── build.sh
+├── config
+│ └── config.go
+├── config-debug.yaml
+├── config-pro.yaml
+├── global
+│ └── global.go
+├── handler
+│ └── social.go
+├── initialize
+│ ├── config.go
+│ ├── db.go
+│ └── logger.go
+├── main.go
+├── model
+│ └── base.go
+└── proto
+ ├── simpledy_grpc.pb.go
+ ├── simpledy.pb.go
+ └── simpledy.proto通过Apifox的自动化测试,构建不同实际使用中可能遇到的情况,对接口进行充分测试。
+/douyin/user/register/需要对如下的用例进行测试:
+测试结果:
+/douyin/user/login/需要对如下的用例进行测试:
+测试结果:
+/douyin/user/需要对如下的用例进行测试:
+测试结果:
+/douyin/feed/需要对如下的用例进行测试:
+测试结果:
+/douyin/publish/list/需要对如下的用例进行测试:
+测试结果:
+/douyin/publish/action/需要对如下的用例进行测试:
+测试结果:
+在参加青训营期间,官方提供了全面的课程,涵盖了创作技巧、内容制作、问题分析等多个方面。这些课程不仅提供了实用的知识和技能,还可以让我们更好地理解抖音平台和用户需求。抖音青训营项目还提供了多种资源支持,包括专业导师、团队合作等。这些资源可以帮助我们更好地实践和落地自己的创意。
+回顾整个项目的过程,我们团队做了如下总结:
+https://www.jianshu.com/p/4e4ff6be6af9
+https://www.apifox.cn/apidoc/shared-09d88f32-0b6c-4157-9d07-a36d32d7a75c/api-50707523
+https://juejin.cn/post/7174037539345399839
+https://blog.csdn.net/cc18868876837/article/details/90672971
+ + + +2023年3月19日,周日
+ +回了一次家,但是实际上回家并不是我先提出的(虽然打过了回家的招呼),主要是张曦元提出的(虽然她说了后直接撤回了,我再问才告诉我)。
+虽然我的感情生活并不是很顺利,但是似乎从来不缺少聊的比较好的女同学。大一的时候是这样,研一的时候也是这样。这次实在是太热情了,我也是完全想不到,一个之前几乎没有说过话的女生,也仅仅在班里不到一年的时间,而且还是一个绝对的大美女,对我还如此感兴趣。甚至在没有怎么访问我的空间的情况下知道我的一些小事,还有我的程序设计竞赛的奖项,这个我自己从网络上都搜索不到。
+感觉她对我来说是一个黑盒子,但是她已经得知我的很多事情了,但是我们都避开了个人感情方面,甚至她对我们共同同学的谈论兴致也不是很高。最让我惊奇的一点是上车后几乎没有看过手机,这个我觉得实在是太出乎意料了,这个评价一个人是否对你有兴趣是很关键的一个点(前女友就是这样引起我的注意的)。本来也是想问问杨青默的,可是似乎并没有给我这个机会。
+很热情,说了很多东西,但是感觉有点缺少感觉,似乎只是很好的朋友关系,但是为什么突然就变成很好的朋友了呢?为什么初次见面的时候她完全了解我,但是我却连她本科去了哪里都不知道。反复想请我吃饭,但是我一直在拒绝,也是我不太敢吧。我还是没有从上一段感情中走出来,这种过分的热情让我暂时无法承受。
+我甚至问了问chatgpt,它的回答和我想得差不多,就慢慢来慢慢培养,平时若有若无关心一下,主要看她的反应。虽然是个大美女,但是看起来她的社交圈也不是非常广泛的样子,可以慢慢来,毕竟之后能创造见面的机会还有很多,我也可以稍微主动一些,请她到望京附近转转之类的。
+虽然矮,但是并不能成为自卑的理由,还是要多学知识,多看书,争取能配得上人家。慢慢加油吧,你已经不是情窦初开的小孩子了。
+ + +2023年3月26日,周日
+ +最重要的,感情,一周没有任何交流,尝试着发了一条朋友圈,晚上点左右发的,结果第二天上午才点赞,不知道什么原因,下周要不要再主动一点还有点犹豫。
+亲情要多交流,要始终铭记这些人是世界上唯一无条件对你好的人。
+最近事情有点多,每天下班后还是要学些知识,上班没什么事情的时候也要多看书,学技术,不要发呆
+尽量控制住自己的坏毛病。
+ + +2023年5月2日,周二
+ +干什么事情都没有动力,学习也不知道学什么,玩也不知道去哪,打球也略显尴尬,聊天也不知道找谁,刷剧也没有看下去的动力。
+不管了,好久没有刷剧了,先刷一刷比较火的悬疑剧吧
+ + +深度学习面试题准备
+ +优点:
+缺点:
+适用场景:
+优点:
+缺点:
+适用场景:
+优点:
+缺点:
+适用场景:
+优点:
+缺点:
+适用场景:
+优点:
+缺点:
+适用场景:
+优点:
+缺点:
+适用场景:
+自回归语言模型,是通过上文一步一步预测下文,不能看见未来信息的模型。像坚持只用单向Transformer的GPT就是典型的自回归语言模型
+自编码语言模型是类似于bert 这种,使用了mask LM,可以使用上下文语境信息进行预测。这也是为什么bert是双向的原因。
+自回归语言模型没能自然的同时获取单词的上下文信息(ELMo把两个方向的LSTM做concat是一个很好的尝试,但是效果并不是太好);
+自编码语言模型能很自然的把上下文信息融合到模型中(Bert中的每个Transformer都能看到整句话的所有单词,等价于双向语言模型),但在Fine-tune阶段,模型是看不到[mask]标记的,所以这就会带来一定的误差。
+XLNet的思路采用的是自回归语言模型,根据上文来预测下一个单词,但是在上文中添加了下文信息,这样就既解决了[mask]带来的两阶段不一致问题和无法同时引入上下文信息的问题。实际上是通过排列组合的方式将一部分下文单词放到上文单词的位置,但实际形式还是一个从左到右预测的自回归语言模型
+使用小批量梯度下降的优点是:
+SGD方法中的高方差振荡使得网络很难稳定收敛 ,所以有研究者提出了一种称为 动量(Momentum)的技术 ,通过优化相关方向的训练和弱化无关方向的振荡,来加速SGD训练。在动量学习算法中,每一步走多远不仅依赖于本次的梯度的大小还取决于过去的速度。速度v是累积各轮训练参的梯度。
+RMSprop将学习率分解成一个平方梯度的指数衰减的平均。 Adam中动量直接并入了梯度一阶矩(指数加权)的估计。其次,相比于缺少修正因子导致二阶矩估计可能在训练初期具有很高偏置的RMSProp,Adam还包括偏置修正,修正从原点初始化的 一阶矩(动量项) 和(非中心的) 二阶矩估计 。
+本质上是带有动量项的RMSprop,它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳
+import torch
+
+def adam_update(parameters, gradients, m, v, t, lr=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8):
+ for param, grad in zip(parameters, gradients):
+ m[param] = beta1 * m[param] + (1 - beta1) * grad
+ v[param] = beta2 * v[param] + (1 - beta2) * (grad ** 2)
+ m_corrected = m[param] / (1 - beta1 ** t)
+ v_corrected = v[param] / (1 - beta2 ** t)
+ param_update = lr * m_corrected / (np.sqrt(v_corrected) + epsilon)
+ param -= param_updateSGD缺点是其更新方向完全依赖于当前batch计算出的梯度,因而十分不稳定。
+Adam的优点主要在于:
+但是Adam也有其自身问题:可能会对前期出现的特征过拟合,后期才出现的特征很难纠正前期的拟合效果。二者似乎都没法很好避免局部最优问题。不收敛、无法达到全局最优。
+Nesterov梯度加速法 ,通过使网络更新与误差函数的斜率相适应,并依次加速SGD,也可根据每个参数的重要性来调整和更新对应参数,以执行更大或更小的更新幅度。
+AdaDelta方法是AdaGrad的延伸方法,它倾向于解决其学习率衰减的问题。Adadelta不是累积所有之前的平方梯度,而是将累积之前梯度的窗口限制到某个固定大小w。
+Adagrad方法是通过参数来调整合适的学习率η,对稀疏参数进行大幅更新和对频繁参数进行小幅更新。因此,Adagrad方法非常适合处理稀疏数据。
+一般定义:模型在训练集上的表现很好,但在测试集和新数据上的表现很差。
+出现的原因:
+解决的方法:
+将这些输入值进行标准化,降低scale的差异至同一个范围内。这样做的好处在于一方面提高梯度的收敛程度, 加快模型的训练速度 ;另一方面使得每一层可以尽量面对同一特征分布的输入值,减少了变化带来的不确定性,也降低了对后层网路的影响,各层网路变得相对独立, 缓解了训练中的梯度消失问题 。
+训练时,均值、方差分别是该批次内数据相应维度的均值与方差;推理时,均值、方差是基于所有批次的期望计算所得。其中在推理时所用的均值和方差是通过移动平均计算得到的,可以减少存储每个batch均值方差的内存。
+LN层与BN相比,只考虑单个sample内的统计变量,因此也不用使用BN实现中的running mean, running var.,LN也完全不用考虑输入batch_size的问题。
+为什么transformer中不使用BN归一化
+解释一:CV和NLP数据特性的不同,对于NLP数据,前向和反向传播中,batch统计量及其梯度都不太稳定,一个Batch中每个句子对应位置的分量不一定有意义。
+解释二:要能在某个维度做独立同分布假设,才能合理归一化。对于CV来说,batch之间的图像是独立的,可以使用BN,而对于自然语言的token,相互是具有较强的关联性,不是相互独立的。
+BN是对每个特征在batch_size上求的均值和方差,如果BN应用到NLP任务中,对应的是对每一个单词作处理,也就是说,现在的每一个单词是对应到了MLP中的每一个特征,也就是默认了在同一个位置的单词对应的是同一种特征,比如:“我/爱/中国/共产党”和“今天/天气/真/不错”
+如果使用BN,代表着认为 "我"和“今天”是对应的同一个维度特征,这样才可以去做BN。但是每个单词表达的特征是不一样的,所以按照位置对单词特征进行缩放,是违背直觉的。
+layer-norm 做的是针对每一个样本,做特征的缩放。也就是,它认为“我/爱/中国/共产党”这四个词在同一个特征之下,所以基于此而做归一化。
+梯度消失的原因:主要是是网络层较深,其次是采用了不合适的损失函数,会使得靠近输入层的参数更新缓慢。导致在训练时,只等价于后面几层的浅层网络的学习。
+梯度爆炸的原因:一般出现在深层网络和权值初始化值太大的情况下。在深层神经网络或循环神经网络中,误差的梯度可在更新中累积相乘。如果网络层之间的梯度值大于 1.0,那么重复相乘会导致梯度呈指数级增长,梯度变的非常大,然后导致网络权重的大幅更新,并因此使网络变得不稳定。
+梯度爆炸会使得在训练过程中,权重的值变得非常大,以至于溢出,导致模型损失变成 NaN等等。
+解决方法:梯度剪切,对梯度设定阈值;权重正则化;batch normalization;残差网络的捷径(shortcut);
+防止梯度爆炸:
+防止梯度消失:
+以上问题可以拓展到具体的模型上,比如问BERT是如何防止梯度消失的,就可以从残差网络等方面回答
+优点:
+缺点:
+Dropout可以作为训练深度神经网络的一种trick供选择。在每个训练批次中,在前向传播的时候,让某个神经元的激活值以一定的概率p停止工作,这样可以使模型泛化性更强,因为它不会太依赖某些局部的特征
+L1正则化是指在损失函数中加入权值向量w的绝对值之和,即各个元素的绝对值之和,使权重稀疏,可以进行特征选择
+L2正则化指在损失函数中加入权值向量w的平方和,使权重平滑
+L1范数MAE 与 L2范数 MSE作为损失函数的对比:
+MAE相比MSE,鲁棒性更强。MSE对误差取了平方,如果数据存在异常值,误差会被放大。所以,MAE对于异常值比MSE更稳定。
+然而MAE存在一个严重的问题(特别是对于神经网络):更新的梯度始终相同,也就是说,即使对于很小的损失值,梯度也很大。这样不利于模型的学习。为了解决这个缺陷,我们可以使用变化的学习率,在损失接近最小值时降低学习率。
+而MSE在这种情况下的表现就很好,即便使用固定的学习率也可以有效收敛。MSE损失的梯度随损失增大而增大,而损失趋于0时则会减小。这使得在训练结束时,使用MSE模型的结果会更精确。
+Word2Vec是轻量级的神经网络,其模型仅仅包括输入层、隐藏层和输出层,模型框架根据输入输出的不同,主要包括CBOW和Skip-gram模型。 CBOW的方式是在知道词的上下文的情况下预测当前词,而Skip-gram是在知道了词的情况下,对词的上下文进行预测。
+Word2Vec提出两种加快训练速度的方式,一种是Hierarchical softmax,另一种是Negative Sampling
+在进行最优化的求解过程中:从隐藏层到输出的Softmax层的计算量很大,因为要计算所有词的Softmax概率,再去找概率最大的值。
+Hierarchical softmax相当于将线性的Softmax转换为哈夫曼树,从而将时间复杂度降低到log级别
+无需计算词表中所有单词的softmax并选择最大的作为输出,只需遍历树的深度个节点,即可找到softmax值最大的词作为输出
+Negative Sampling
+Word2vec 的优缺点
+优点:
+缺点:
+下溢出与上溢出
+解决方式:将全部的分量减去最大值
+加权交叉熵思想是用一个系数描述样本在loss中的重要性。对于小数目样本,加强它对loss的贡献,对于大数目的样本减少它对loss的贡献。带权重的交叉熵在正样本的判别上加了一个

focal loss的设计很巧妙,就是在cross entropy的基础上加上权重,让模型注重学习难以学习的样本,训练数据不均衡中占比较少的样本,相对放大对难分类样本的梯度,相对降低对易分类样本的梯度,并在一定程度上解决类别不均衡问题。
+focal loss相比交叉熵多了一个

相比交叉熵损失,focal loss对于分类不准确的样本,损失没有改变,对于分类准确的样本,损失会变小。 整体而言,相当于增加了分类不准确样本在损失函数中的权重。
+对抗训练是一种引入噪声的训练方式,可以对参数进行正则化,提升模型鲁棒性和泛化能力。
+对抗训练的假设是:给输入加上扰动之后,输出分布和原Y的分布一致
+往增大损失的方向增加扰动
+在计算对抗扰动时虽然计算了梯度,但不对参数进行更新, 因为当前得到的对抗扰动是对旧参数最优的 。
+用一句话形容对抗训练的思路,就是 在输入上进行梯度上升(增大loss),在参数上进行梯度下降(减小loss) 。由于输入会进行embedding lookup,所以 实际的做法是在embedding table上进行梯度上升 。
+接下来介绍不同的方法,后续方法优化的主要方向有两点:得到更优的扰动 & 提升训练速度
+FGM
+对于每个x:(输入的梯度是g)
+PGD小步走多走几步
+N-Gram是一种基于统计语言模型的算法。它的基本思想是将文本里面的内容按照字节进行大小为N的滑动窗口操作,形成了长度是N的字节片段序列。
+每一个字节片段称为gram,对所有gram的出现频度进行统计,并且按照事先设定好的阈值进行过滤,形成关键gram列表,也就是这个文本的向量特征空间,列表中的每一种gram就是一个特征向量维度。
+该模型基于这样一种假设,第N个词的出现只与前面N-1个词相关,而与其它任何词都不相关,整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。常用的是二元的Bi-Gram和三元的Tri-Gram。
+模型通过训练语句对指数级语义相关的句子进行建模。
+(1)每个单词的分布式表示
+(2)单词序列的概率函数。
+(3)泛化(Generalization)是指从未出现的单词序列,可以通过类似的词的组成的已经出现的句子来获得较高的概率。
+语言模型与其他学习问题的最基本的问题就是维度爆炸
+两者的含义基本相同,但是NNLM使用了神经网络模型
+编码器+解码器的结构:
+编码器处理输入序列中的每一项,将捕获的信息编译成一个向量(输入序列的编码)
+解码器接收编码器处理后的上下文,逐项生成输出序列
+应用:阅读理解,文本摘要,闲聊系统,看图说话
+添加Attention机制后:
+编码器向解码器传递更多的数据,编码器不仅仅传递编码阶段的最后一个隐藏状态,而是将所有的隐藏状态传递给解码器
+注意解码器在产生输出之前的额外的步骤,为了聚焦于与该解码时间步骤相关的输入部分,解码的每一时刻都通过编码器隐藏状态与编码器当前隐藏状态的相关性,对不同的编码器隐藏状态进行打分,打分后的编码器隐藏状态加权相加,并与当前的隐藏状态相结合,再进行最后的输出运算
+文本生成的评价标准:
+BLEU:比较候选译文与参考译文的n-gram重合程度
+BLEU专注于召回率(关注有多少个参考译句中的n-gram出现在了输出之中),而非精度(候选译文的n-gram有没有在参考译文中出现过)
+ROUGE-N:将BLEU的精确率优化为召回率
+ROUGE-L:将BLEU的n-gram优化为公共子序列(公共子序列不一定连续)
+ROUGE-W:在ROUGE-L的基础上对连续性添加一个权重
+ROUGE-S:对n-gram进行统计,但是允许跳词
+METEOR:考虑了基于整个语料库上的准确率和召回率,包括同义词匹配与同型词匹配
+Seq2Seq模型输入的方式:
+①将前一时刻的输出作为下一时刻的输入
+缺点:如果预测错了,后面都是错的,错误会一直累积
+②以正确的作为输入
+缺点:测试时候不知道输入,因此存在训练测试偏差
+③Curriculum Learning
+使用概率p决定是①还是②
+开始训练时候②概率较大,随着训练时间减小
+Beam Search:
+贪心的方法:一个步骤一个步骤去看,可能不太准确
+Beam search对每一个单词的预测概率进行搜索,生成多个候选输出序列
+一词多义的现象——应用同一词向量不合适
+基于双向两层的LSTM,训练动态词表征
+双向的循环神经网络能更好地学习词语间的上下文关系
+两层的循环神经网络能学习到更深层次的语义表征。
+低层能够提取语法等方面的初级信息
+高层擅长于捕捉语义等高级特征
+对原始输入进行字符级别的卷积,能更好的抓取字词的内部信息
+核心:基于语言模型的思路,利用上下文信息去建模某一单词
+为什么Work?
+答案在于因果语言模型的attention mask。以GPT为代表的Causal Language Model(因果语言模型),这种模型的attention mask是一个对角掩码矩阵,每个token在编码的时候,只能看到它之前的token,看不到它之后的token。
+ + +Transformer面试题准备
+ +引入Attention机制的原因
+假设我们要对一段原文计算Attention,这里原文指的是我们要做attention的文本,那么所用信息包括内部信息和外部信息,内部信息指的是原文本身的信息,而外部信息指的是除原文以外的额外信息。
+General Attention,这种方式利用到了外部信息,常用于需要构建两段文本关系的任务,query一般包含了额外信息,根据外部query对原文进行对齐。比如在阅读理解任务中,需要构建问题和文章的关联,假设现在baseline是,对问题计算出一个问题向量q,把这个q和所有的文章词向量拼接起来,输入到LSTM中进行建模。那么在这个模型中,文章所有词向量共享同一个问题向量,现在我们想让文章每一步的词向量都有一个不同的问题向量,也就是,在每一步使用文章在该步下的词向量对问题来算attention,这里问题属于原文,文章词向量就属于外部信息。
+Local Attention,这种方式只使用内部信息,key和value以及query只和输入原文有关,在self attention中,key=value=query。既然没有外部信息,那么在原文中的每个词可以跟该句子中的所有词进行Attention计算,相当于寻找原文内部的关系。还是举阅读理解任务的例子,上面的baseline中提到,对问题计算出一个向量q,那么这里也可以用上attention,只用问题自身的信息去做attention,而不引入文章信息。
+结构方面根据是否划分层次关系,分为单层attention,多层attention和多头attention:
+https://www.nowcoder.com/discuss/387725948110602240?sourceSSR=search
+Scale 的作用:矩阵点乘可能会导致 数值指数级增加 ,从而 使得 softmax 的梯度非常小 ,所以使用d_k进行缩放来避免这个问题
+Softmax 的作用:Softmax 将其归一化至 (0,1)区间便于后续与V相乘,同时也起到以对梯度进行缩放的作用(防负数以及过大的结果导致梯度问题)
+ +
GQA-N 是指具有 N 组的 Grouped Query Attention。GQA-1具有单个组,因此具有单个Key 和 Value,等效于MQA。而GQA-H具有与头数相等的组,等效于MHA。
+在基于 Multi-head 多头结构变为 Grouped-query 分组结构的时候,也是采用跟上图一样的方法,对每一组的 key-value 对进行 mean pool 的操作进行参数融合。 融合后的模型能力更综合,精度比 Multi-query 好,同时速度比 Multi-head 快 。
+ +
最后我们再来整体看一下 Transformer:
+其他优化细节:
+
Residual Dropout :对于残差连接的 当前层输出和上一层输出相加后再正则化这一组操作,对其来自上一层的输出(不包括当前层的输出)和残差连接后的结果均进行 Dropout。
 ;
; ;然后是[N, N] * [N, d]也为
;然后是[N, N] * [N, d]也为

建立矩阵进行变换,空间复杂度来源于建立的矩阵
+ 。
。 ,然后要过Layer Normalization,就是
,然后要过Layer Normalization,就是
 (权重矩阵和偏置项)。然后要过Layer Normalization,再加
(权重矩阵和偏置项)。然后要过Layer Normalization,再加
 (两个权重矩阵和偏置项)。然后要过Layer Normalization,再加
(两个权重矩阵和偏置项)。然后要过Layer Normalization,再加

Transformer模型可以学习输入到文本的长距离依赖关系和全局特性,但是在预测时候会受到训练时所设定的最大长度的限制(直接截长补短)
+缺点:语义残破,文本非常长
+Transformer-XL:通过引入循环的机制(RNN)与相对位置编码,解决了Transformer长度限制的问题
+Vanilla Transformer:基于Transformer的语言模型
+将原来的句子进行切片,上下文有限且计算速度非常慢
+Transformer-XL:
+①循环机制:分成子句,在训练和预测时候,依次将每个子句传入Transformer模型,并将每个子句在Transformer中各层的输出传递给下一个子句,可以捕获的最大依赖项增加了N倍
+②相对位置编码:由于是分段计算的,因此如果对每个段直接使用Transformer中的位置编码,会出现问题,相同相对位置将具有相同的位置编码
+与Transformer的Encoder基本相同,其中输入层略有不同,被改造成[CLS]+句子A(+[SEP]+句子B+[SEP])
+因为transformer无法获得字的位置信息,BERT和transformer一样也加入了 绝对位置 position encoding,但是和transformer不同的是,BERT使用的不是transformer对应的函数型(functional)的encoding方式,而是直接采用类似word embedding的方式(Parametric),直接获得position embedding。
+因为我们对输入进行了改造,使得模型可能有多个句子Segment的输入,所以我们也需要加入segment的embedding,例如 [CLS], A_1, A_2, A_3,[SEP], B_1, B_2, B_3, [SEP] 对应的segment的输入是 [0,0,0,0,1,1,1,1], 然后再根据segment id进行embedding_lookup得到segment embedding。
因此输入层为三个embedding相加(position embedding + segment embedding + token embedding)
+一个transformer的encoder单元由一个multi-head-Attention + Layer Normalization + feedforword + Layer Normalization 叠加产生,BERT的每一层由一个这样的encoder单元构成。在比较大的BERT模型中,有24层encoder,每层有16个Attention,词向量的维度是1024。在比较小的BERT模型中,有12层encoder,每层有12个Attention,每个head的神经元个数是64,12个head总的神经元的个数即为768,因此词向量维度是768。在所有情况下,将feed-forward/filter 的大小设置为 4H(H为词向量的维度),即H = 768时为3072,H = 1024时为4096。
+Mask Language Model(MLM)
+BERT第一次采用了mask language model(MLM)任务,这就类似于完形填空(Cloze task)。
+具体的做法: 我们会随机mask输入的几个词,然后预测这个词。但是这样子做的坏处是因为fine-tuning阶段中并没有[MASK] token,所以导致了pre-training 和 fine-tuning的不匹配的情况。所以为了减轻这个问题,文章中采用的做法是:
+对于要MASK 15%的tokens,
+Next sentence order
+为了适配下游任务,使得模型懂得句子之间的关系,BERT加了一个新的训练任务,预测两个句子是不是下一句的关系。
+具体来说:50%的概率,句子A和句子B是来自同一个文档的上下句,50%的概率,句子A和句子B不是同一个文档的上下句,具体的做法就是,采用从其他的文档(document)中,加入新的连续句子(segments)作为句子B。
+预处理:subword
+一般的词表示方法不能解决OOV
+subword的粒度在词与字符之间,能较好的平衡OOV问题
+Byte Pair Encoding:准备足够大的训练语料并确定期望的subword词表大小,将单词拆分为字符序列并在末尾添加后缀并统计单词频率,统计每一个字节对的出现频率,选择最高频率的合并成新的subword
+https://zhuanlan.zhihu.com/p/452369195
+Attention结构有什么优点
+position embedding的作用是什么
+对子中token次序信息进行编码
+Residual Connection的作用是什么
+减缓梯度衰减,加快收敛
+加入LayerNorm层有什么好处
+当使用梯度下降法做优化时,随着网络深度的增加,数据的分布会不断发生变化,加入Layer Normalization可以提高数据特征分布的稳定性,从而加速模型的收敛速度
+加入Next Sentence Prediction任务的目的是什么
+获得句子级的语义表征,对问答、推理、句⼦关系类的NLP任务帮助非常大。
+Mask-LM的样本中,选中的词在10%的概率不做Mask保持真实的词的原因是什么
+给模型一定的bias,相当于是额外的奖励,将模型对于词的表征能够拉向词的真实表征
+Mask-LM的样本中,选中的词在10%的概率下不做mask,而是被随机替换成为一个其他词的目的是什么
+因为模型不知道哪些词是被mask的,哪些词是mask了之后又被替换成了一个其他的词,这会迫使模型尽量在每一个词上都学习到一个全局语境下的表征,因而也能够让BERT获得更好的语境相关的词向量,提升模型的鲁棒性。
+为什么即便数量很小,基于BERT做微调也能取得很好的泛化效果
+这个问题最直观的解释是BERT提供了好的起点,模型的训练是站在巨人的肩膀上。但更恰当的解释是用BERT初始化模型,相当于提供了一种正则化,即便数据量很少也不容易过拟合。有了BERT做初始化,用少量的高质量数据可以训练出比大量劣质数据更好的模型。
+Bert的CLS
+与文本中已有的其它字/词相比,这个无明显语义信息的符号会更“公平”地融合文本中各个字/词的语义信息,因此用来做分类任务
+几种减少内存的方法,提升速度
+主要通过参数共享减少参数量
+核心思想:通过更好地训练BERT可以达到超过其他新的预训练语言模型的效果
+核心改动
+XLNet专注于预训练阶段。在预训练阶段,它提出了一个新的目标,称为重排列语言建模
+Bert的痛点:独立性假设:Bert假设不同[mask]相互独立,忽略了[mask]之间的相关性;Pre-train阶段和Fine-tune阶段数据分布不一致
+排列组合获取上下文信息
+双流注意力
+XLNet:自回归(AR)语言模型 + 自动编码器(AE)语言模型
+自回归(AR)语言模型:希望通过已知的前半句预测后面的词或字
+自动编码器语言模型:Mask
+XLNet:结合两种语言模型,用上下文预测,随机打乱顺序
+双流自注意力机制:一个流包含了位置信息和内容信息,另外一个流仅包含位置信息
+Bert聚焦在针对字或者英文Word粒度的完形填空学习上面,没有充分利用训练数据当中的词法结构,语法结构以及语义信息去学习建模
+ERNIE直接对先验语义知识单元进行建模,增强了模型语义表示能力
+LLM面试题准备
+ +动机:虽然无标注的文本很多,但是在下游任务上,有标注的文本很少。
+GPT提出了一种方法:采用语言模型的方式在无标注文本下进行预训练,之后再在各个下游任务上进行微调。
+模型主要是三个方向的贡献:
+预训练:输入含有大量token的语料库,GPT使用一个语言模型来极大化这个似然函数。具体的说,语言模型就是给定第 





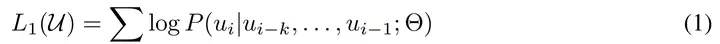
语言模型的损失函数其实是一个乘法规则,因为有log所以变成加法
+作者选择transformer的decoder作为骨干模型。
+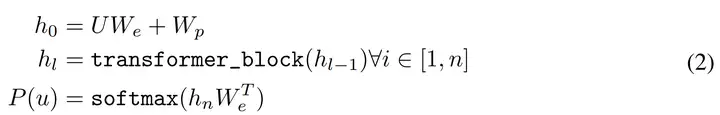
当输入是
而训练的过程其实非常的简单,就是将句子n个词的词向量(第一个为 <SOS>)加上Positional Encoding后输入到前面提到的Transfromer中,n个输出分别预测该位置的下一个词(<SOS>预测句子中的第一个词,最后一个词的预测结果不用于语言模型的训练)。
微调:当预训练后,作者将预训练好的参数直接迁移到下游任务中来。下游任务数据集中的每一个数据含有一系列的token:

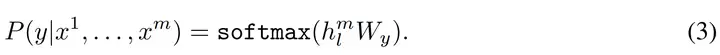
将预测值和真实值进行比对,得到有监督部分的损失函数,如下所示:
+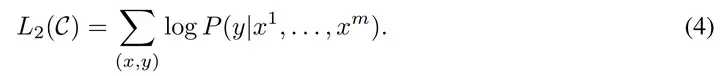
将预训练时的损失函数和有监督的损失函数加在一起,可以取得更好的效果
+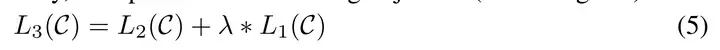
下游任务的损失=有监督的损失+预训练的损失
+如何把NLP里面很不一样的子任务表示成一个我们想要的形式(表示成一个序列+对应的标签)
+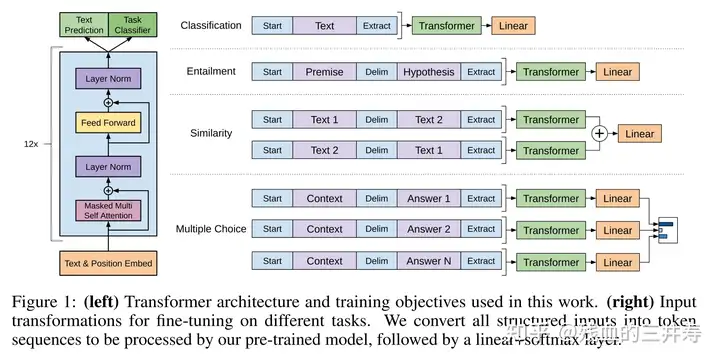
GPT2不仅仅使用一个更大的数据集,使用更大的模型去学习,还提出了一个新的更难的任务,zero-shot零样本学习,即将预训练好的模型,直接接诸多的下游任务,不再进行微调操作,在多个任务下都可以取得很好的效果。
+这两个模型的区别可以概括为:
+
关于 post-norm 和 pre-norm,两者的主要区别在于,post-norm 将 transformer 中每一个 block 的层归一化放在了残差层之后,而 pre-norm 将层归一化放在了每个 block 的输入位置,GPT-2 进行上述模型调整的主要原因在于,随着模型层数不断增加,梯度消失和梯度爆炸的风险越来越大,这些调整能够 减少预训练过程中各层之间的方差变化,使梯度更加稳定 。如下图所示:
+Pre Norm结构无形地增加了模型的宽度而降低了模型的深度,而我们知道深度通常比宽度更重要,所以是无形之中的降低深度导致最终效果变差了。Pre Norm结构会过度倾向于恒等分支(bottom layers),从而使得Pre Norm倾向于退化(degradation)为一个“浅而宽”的模型,最终不如同一深度的Post Norm
+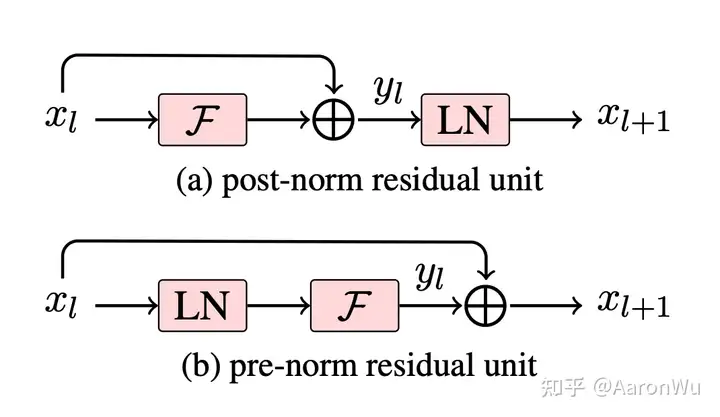
GPT3的参数量进一步的增大,并且使用few-shot learning的方法,取得了很好的效果。
+GPT3特别大,在计算子任务的时候无法计算梯度,性能非常好。
+最近一些年来,大家都使用预训练好的语言模型,之后再进行微调,这其实是有问题的:
+GPT-3提出了一种in-context learning的方法,就是给出任务的描述和一些参考案例的情况下,模型能根据当前任务描述、参数案例明白到当前的语境,即使在下游任务和预训练的数据分布不一致情况下,模型也能表现很好。注意的是,GPT并没有利用实例进行Fine-tune,而是让案例作为一种输入的指导,帮助模型更好的完成任务。
+在模型结构上,GPT-3 延续使用 GPT 模型结构,但是引入了 Sparse Transformer 中的 sparse attention 模块(稀疏注意力)。
+sparse attention 与传统 self-attention(称为 dense attention) 的区别在于:
+dense attention:每个 token 之间两两计算 attention,复杂度 O(n²)
+sparse attention:每个 token 只与其他 token 的一个子集计算 attention,复杂度 O(n*logn),具体来说,sparse attention 除了相对距离不超过 k 以及相对距离为 k,2k,3k,… 的 token,其他所有 token 的注意力都设为 0
+使用 sparse attention 的好处主要有以下两点:
+GPT3是一个1750亿参数的模型,评估用的是三种方法:
+
整体来看,GPT-3 相比于 GPT-2 有如下几点区别:
+GPT-3 虽然在各大 NLP 任务以及文本生成的能力上令人惊艳,但是他仍然还是会生成一些带有偏见的,不真实的,有害的造成负面社会影响的信息,而且很多时候,他并不按人类喜欢的表达方式去说话。在这个背景下,OpenAI 提出了一个概念“Alignment”,意思是模型输出与人类真实意图对齐,符合人类偏好。因此,为了让模型输出与用户意图更加 “align”,就有了 InstructGPT 这个工作。
+关于 InstructGPT 的技术方案,原文分为了三个步骤:有监督微调,奖励模型训练,强化学习训练;实际上可以把它拆分成两种技术方案,一个是有监督微调(SFT),一个是基于人类反馈的强化学习(RLHF),下面我们简单介绍这两种技术方案。
+
本质上来说,SFT 可以理解为人工标注了一批数据,然后去微调 GPT-3。
+这里标注的数据与 GPT-3 之前用来做下游任务使用的 few-shot 格式,有非常本质的区别。
+GPT-3 中的 few-shot 对于同一个下游任务,通常采用固定的任务描述方式,而且需要人去探索哪一种任务表述方式更好。显然这种模式与真实场景下用户的使用方式存在较大的 gap,用户在向 GPT-3 提问时才不会采用某种固定的任务表述,而是随心所欲地以自己的说话习惯去表达某个需求。
+InstructGPT 在 SFT 中标注的数据,正是为了消除这种模型预测与用户表达习惯之间的 gap。在标注过程中,他们从 GPT-3 的用户真实请求中采样大量下游任务的描述,然后让标注人员对任务描述进行续写,从而得到该问题的高质量回答。这里用户真实请求又被称为某个任务的指令,即 InstructGPT 的核心思想“基于人类反馈的指令微调”。
+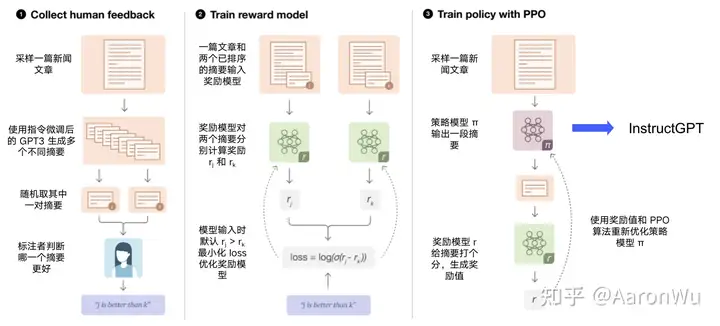
基于 SFT 得到的模型被用于后续的 RLHF 做进一步的模型优化。
+如上图所示,以摘要生成任务为例,详细展示了如何基于人类反馈进行强化学习,最终训练完成得到 InstructGPT 模型。主要分为三步:
+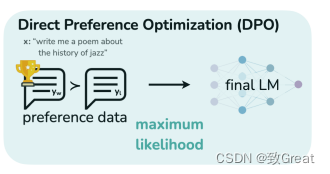
直接偏好优化 (DPO) 是一种微调大型语言模型 (LLM)以符合人类偏好的新颖方法。与涉及来自人类反馈的复杂强化学习 (RLHF) 的传统方法不同, DPO简化了流程。它的工作原理是创建人类偏好对的数据集,每个偏好对都包含一个提示和两种可能的完成方式——一种是首选,一种是不受欢迎。然后对LLM进行微调,以最大限度地提高生成首选完成的可能性,并最大限度地减少生成不受欢迎的完成的可能性。
+与 RLHF 相比,DPO 具有多项优势:
+总的来说,InstructGPT 相对于之前的 GPT 系列,有以下几点值得注意:
+单纯的扩大LLM模型的参数量无法让模型在算术推理/常识推理/符号推理等推理任务上取得理想的效果。 如何提升LLM在这些推理任务上性能呢?首次提出思维链(Chain-of-Throught,CoT)的概念,思维链就是一系列中间的推理步骤。
+在问LLM问题前,手工在prompt里面加入一些 包含思维过程(Chain of thought)的问答示例 ,就可以让LLM在推理任务上大幅提升。CoT的方法,就是在 In-Context-Learning 的范式中,增加了对推理的示范,从而希望LLM在给出答案的时候,也像模像样地进行推理。
+思维链提示作为一种促进语言模型推理的方法,有几个吸引人的特性。
+大模型,尤其是足够大的模型,可能不需要你写一堆CoT来作为prompt了,它自己可能就会推理了,秘诀就是加上一句咒语:“Let’s think step by step.”
+具体则是需要LLM两次生成:
+能不能利用 Zero-shot CoT 来让 LLM 产生很多带有推理的QA pair,然后把这些QA pair加入到prompt中,构成ICL的上文,再让LLM进行推理。
+有 一大堆的待测试的问题 (没有标注,不知道正确答案和推理过程),我们要怎么利用 LLM 和这么一个无标注问题集合,在不进行手工编写CoT的情况下,提升LLM回答这些模型的质量。
+作者的基本思路是这样的:
+关键就在于这个采样过程,作者分别先测试了两种简单的采样过程:
+实验发现,居然随机采样还要更好一些。经过探究,作者发现GPT-3自动产生推理过程是有一定比例出错的,而 出错的问题也容易聚集 ,因此基于相似度搜索的时候,容易导致采样出一批错误的示范,而随机采样的方法,则可能避免聚集性地出错。基于这样的考虑,作者设计了基于多样性的采样方法,先试用SentenceBERT对所有问题进行聚类,然后从每个cluster中进行采样
+Auto的方法居然可以比Manual更好。其实有一种解释,Manual方法其实给多个任务都使用的是同一套模板,比方6个数学任务里面5个都使用的同一套示例(为了省力,同时Manual-CoT的论文也不是为了刷榜,而是为了揭示这么一个现象,所以CoT没有进行仔细调优),而Auto-CoT则是每个任务都会有自己的一套示例产生,毕竟问题集合不一样,聚类的结果也会不一样。
+给定一个目标性能水平,首选的模型不是训练速度最快的,而是推理速度最快的,尽管训练一个大的模型以达到一定的性能水平可能更便宜,但训练时间较长的小模型最终会在推理中更便宜。
+ +tokenizer使用的是BPE算法
+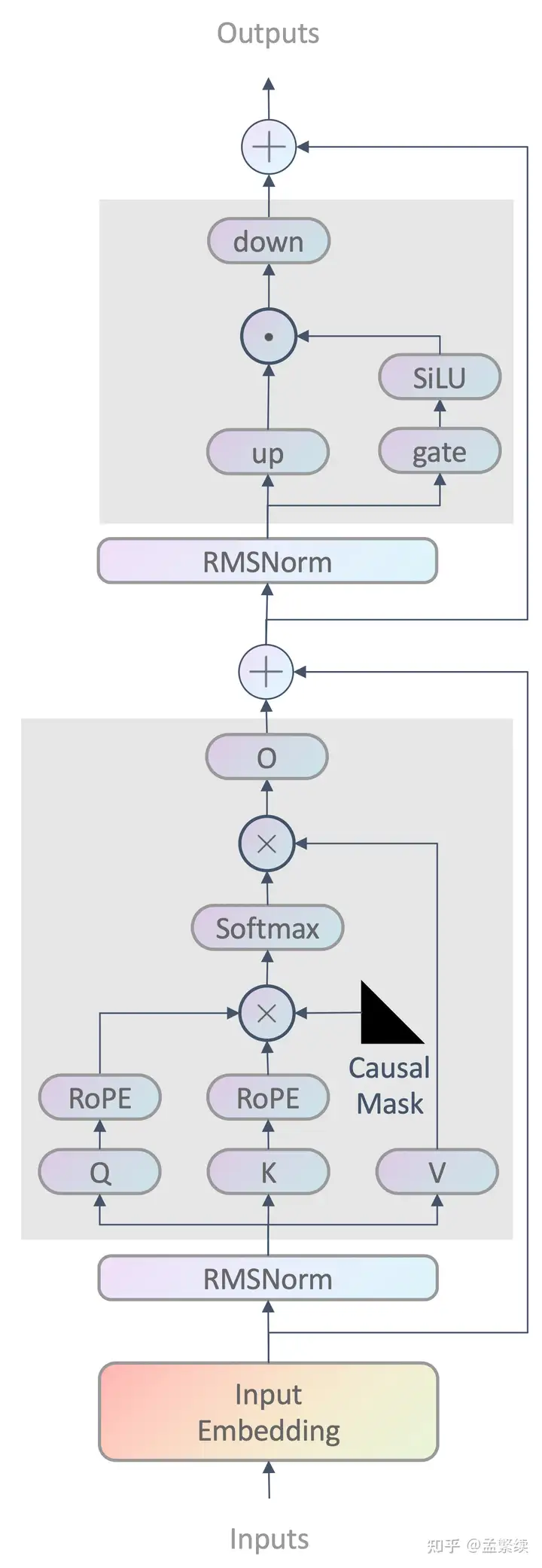

结构修改
+一般认为,Post-Norm在残差之后做归一化,对参数正则化的效果更强,进而模型的收敛性也会更好;而Pre-Norm有一部分参数直接加在了后面,没有对这部分参数进行正则化,可以在反向时防止梯度爆炸或者梯度消失,大模型的训练难度大,因而使用Pre-Norm较多
+加速技巧
+与Llama 1相比,主要的架构差异包括增加的上下文长度和分组查询注意力(GQA)
+Llama 2-Chat的训练过程:该过程始于使用公开可用的在线资源对Llama 2进行 预训练 。随后,我们通过有监督的微调创建Llama 2-Chat的初始版本。随后,我们使用强化学习与人类反馈( RLHF )方法,具体包括拒绝抽样和近端策略优化(PPO),对模型进行迭代优化。在RLHF阶段,迭代奖励建模数据的积累与模型改进密切相关,以确保奖励模型保持在分布内。
+Sliding Window Attention ,attention 中的操作数量与序列长度呈二次关系,通过Sliding Window Attention,可减少计算,但是会牺牲一点的效果。
+做法如下,第2层中的位置4的隐藏状态,关注来自前一层中位置在4- W和4之间的所有隐藏状态,下图中w=3
+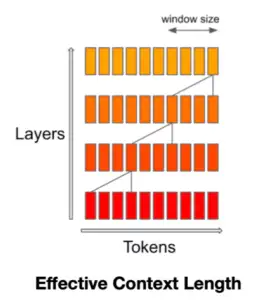
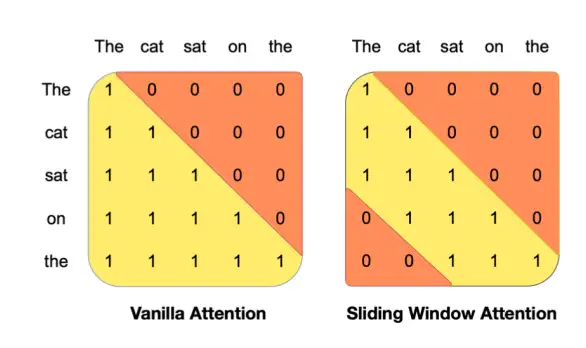
Rolling Buffer Cache, 显存消耗与序列长度呈二次关系。当长度比较长时,显存的消耗是比较多的
+Rolling Buffer Cache使用的是LRU算法,选择最久未使用的数据予以淘汰,相当于缓存最新数据。
+
缓存预处理
+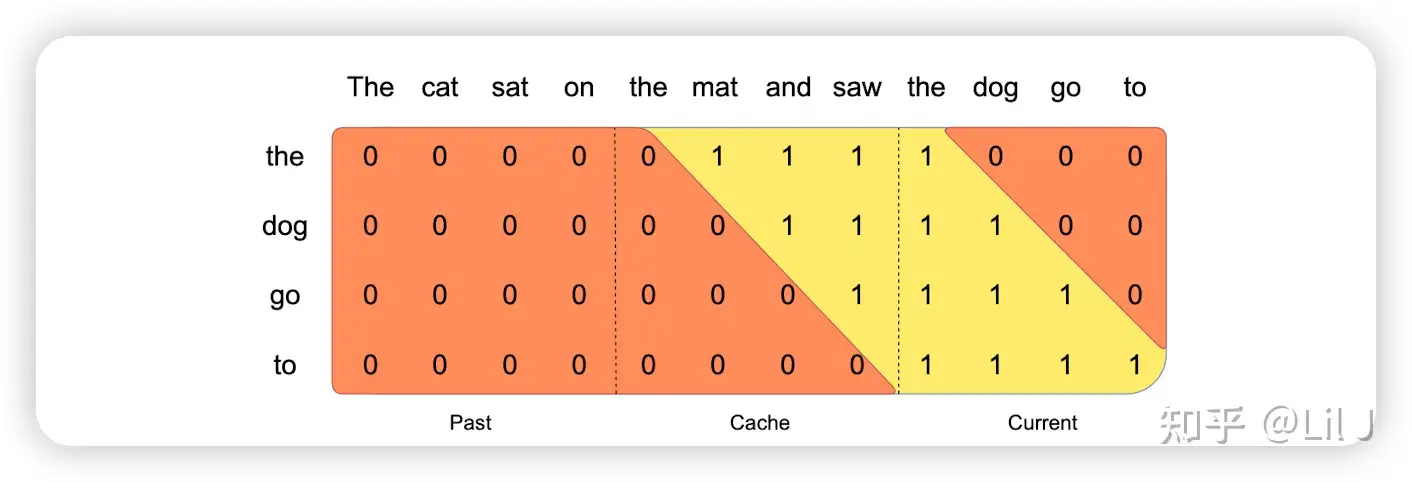
在生成序列时,由于每个标记的生成都依赖于前一个标记,因此需要逐个预测。但是,在开始生成之前,提示信息是已知的,我们可以预先将提示信息填充到(k, v)缓存中。
+具体而言,首先将已知的提示信息按照选定的块大小进行分段,并将每一小段的数据预处理后填充到滚动缓冲区缓存中。在生成新标记的过程中,模型会根据当前时刻的输入以及缓存中的历史信息来计算注意力权重,并更新隐藏状态。这样,在生成长序列时,通过预先填充和分块技术,可以有效地利用已知信息并保持内存使用量的可控性,同时确保模型能充分考虑整个上下文信息进行预测。
+Pretraining Data
+去重:标准化后进行完全匹配重复数据删除,以及使用 MinHash 和 LSH 算法进行模糊重复数据删除
+过滤质量低的数据:过滤低质量的数据,采用了规则型和基于机器学习的方法的组合。多个模型对内容进行评分,包括语言模型,文本质量评分模型以及用于识别潜在的攻击性或不适当内容的模型。 人工从各种来源中对文本进行抽样并审阅,以确保其质量 。
+高质量指令:由于多任务指令可以增强他们的零样本和少样本性能,预训练过程中加入了高质量的指令数据。
+Tokenizer
+使用基于bytepair encoding (BPE) 的tiktoken算法,其相当于BPE tokenizer分词更快。首先使用cl100k作为base token,针对连续数字分会拆为单独的数字,最终 词典大小为152K 。
+编码压缩率越小,则传递的信息就更多,每种语言100万个文档语料库来测试和比较不同模型的编码压缩率,
+可看到qwen编码压缩率是比较低的
+Architecture
+Embedding和output 投影层:解开输入嵌入和输出投影的权重,这一决定是为了以内存成本为代价获得更好的性能
+位置嵌入:RoPE,选择使用FP32精度的逆频率矩阵,而不是BF16或FP16,以优先考虑模型性能并获得更高的准确性。
+激活函数:SwiGLU
+normal方法:RMSNorm,前馈网络(FFN)的维度从隐藏大小的4倍减少到隐藏大小的83倍
+content长度:
+长度外推,在QKV注意力层中添加bias以增强模型的外推能力。下图可看到加上了bias,长度大于1024效果下降不是很多。
+NTK-aware interpolation,动态 NTK-aware 插值,则每个块比例不同:高频部分外推,低频部分内插。
+LogN-Scaling,q和v乘以一个系数,context length和training length的长度关系,来保持注意力的稳定。保证注意力的熵在上下文长度增加时也保持稳定,同时能提升外推表现。
+window attention,将注意力限制在有限的上下文窗口内,防止模型关注距离太远的标记。基于这一发现,我们为每个层分配不同的窗口大小,对较低层使用较短的窗口,对较高层使用较长的窗口。
+Pre-training
+来源收集数据,包括常规互联网网页、书籍、研究论文、代码库等,以构建一个广泛的世界知识体系。
+去重,构建了一个大规模的重复数据删除和聚类系统,支持LSH类似特征和稠密嵌入特征。最终只保留原始数据的31.68%的数据进行训练。
+Tokenizer
+字节对编码(BPE), 不对输入文本应用任何规范化,也不添加虚拟前缀 。将数字拆分为单独的数字,处理额外空格的代码数据,向分词器添加仅空格标记,最大标记长度设置为32,以处理长中文词组。
+Architecture
+位置嵌入:RoPE
+激活函数:SwiGLU
+注意力层:xFormers减少内存。
+normal方法:RMSNorm,并且 规范化输出嵌入lm_head 。
+norm_head loss
+最大z损失 ,在训练过程中,发现LLM的logits可能变得非常大。添加了一个最大z损失来规范化logits。其中z是最大logit值,这有助于稳定训练,并使推理更加稳健地适应超参数。
+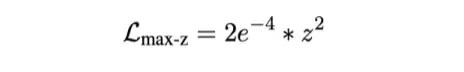
LLMs复读机问题(LLMs Parroting Problem)是指大型语言模型在生成文本时过度依赖输入文本的复制,而缺乏创造性和独特性。当面对一个问题或指令时,模型可能会简单地复制输入文本的一部分或全部内容,并将其作为生成的输出,而不是提供有意义或新颖的回应。
+为了缓解LLMs复读机问题,可以尝试以下方法:
+BPE,即字节对编码。其核心思想在于将 最常出现的子词对合并,直到词汇表达到预定的大小时停止 。
+BPE是一种基于数据压缩算法的分词方法。它通过不断地合并出现频率最高的字符或者字符组合,来构建一个词表。具体来说,BPE的运算过程如下:
+wordpiece算法可以看作是BPE的变种。不同的是,WordPiece基于概率生成新的subword而不是下一最高频字节对。WordPiece算法也是每次从词表中选出两个子词合并成新的子词。BPE选择频数最高的相邻子词合并,而 WordPiece选择使得语言模型概率最大的相邻子词加入词表 。即它每次合并的两个字符串A和B,应该具有最大的
与BPE或者WordPiece不同,Unigram的算法思想是 从一个巨大的词汇表出发 ,再 逐渐删除trim down其中的词汇 ,直到size满足预定义。
+初始的词汇表可以 采用所有预分词器分出来的词,再加上所有高频的子串 。
+每次从词汇表中删除词汇的原则是使预定义的损失最小
+SentencePiece,顾名思义,它是 把一个句子看作一个整体,再拆成片段 ,而没有保留天然的词语的概念。一般地,它 把空格space也当作一种特殊字符来处理,再用BPE或者Unigram算法来构造词汇表 。
+也就是词汇表外的词。在NLP中,通常会预先构建一个词汇表,包含所有模型能够识别的词。然而,总会有一些词没有出现在预先构建的词汇表中,这些词就是 OOV。传统的处理方式往往是将这些 OOV 映射到一个特殊的符号,如 UnKnow,但这种方式无法充分利用 OOV 中的信息。例如,对于词汇表中没有的词 “unhappiness”,如果直接映射为UnKnow ,则模型就无法理解它的含义。
+WordPiece/Byte Pair Encoding (BPE) 等基于子词的分词方法提供了一种解决 OOV 问题的方式。现在更多的语言大模型选择基于BPE的方式,只不过BERT时代更多还是WordPiece。BPE 通过将词分解为更小的单元(子词或字符),可以有效地处理词汇表外的词。对于上面的 “unhappiness” 例子,即使 “unhappiness” 本身不在词汇表中,但是它可以被分解为 “un”、“happiness” 等子词,而这些子词可能在词汇表中。这样,模型就可以通过这些子词来理解 “unhappiness” 的含义。另一方面就是,BPE本身的语义粒度也很合适,一个token不会太大,也不会小到损失连接信息(如一个字母)。
+理论上来说,LLMs(大型语言模型)可以处理任意长度的输入句子,但实际上存在一些限制和挑战 。下面是一些相关的考虑因素:
+要让大模型处理更长的文本,可以考虑以下几个方法:
+大模型在训练时和预测时的输入长度不一致,导致模型的泛化能力下降的问题 。在目前的大模型中,一般指的是超出预训练设置的上下文长度时,依旧保持良好推理效果的能力。
+我们将整数n以一个三维向量[a,b,c]来输入,a,b,c分别是n的百位、十位、个位。这样,我们既缩小了数字的跨度,又没有缩小相邻数字的差距,代价了增加了输入的维度——刚好,神经网络擅长处理高维数据。
+如果想要进一步缩小数字的跨度,我们还可以进一步缩小进制的基数,如使用8进制、6进制甚至2进制,代价是进一步增加输入的维度。
+简单来说,假如原来位置编码用三维向量表示,那外插就是直接增加一维。
+可以提前预留多几维,训练阶段设为0,推理阶段直接改为其他数字,这就是外推(Extrapolation)。
+然而,训练阶段预留的维度一直是0,如果推理阶段改为其他数字,效果不见得会好,因为模型对没被训练过的情况不一定具有适应能力。也就是说, 由于某些维度的训练数据不充分,所以直接进行外推通常会导致模型的性能严重下降 。
+就是将2000以内压缩到1000以内,比如通过除以2,1749就变成了874.5,然后转为三维向量[8,7,4.5]输入到原来的模型中。从绝对数值来看,新的[7,4,9]实际上对应的是1498,是原本对应的2倍,映射方式不一致;从相对数值来看,原本相邻数字的差距为1,现在是0.5,最后一个维度更加“拥挤”。所以,做了内插修改后,通常都需要微调训练,以便模型重新适应拥挤的映射关系。
+不过,内插方案也不尽完美,当处理范围进一步增大时,相邻差异则更小,并且这个相邻差异变小集中在个位数,剩下的百位、十位,还是保留了相邻差异为1。换句话说, 内插方法使得不同维度的分布情况不一样,每个维度变得不对等起来,模型进一步学习难度也更大 。
+有没有不用新增维度,又能保持相邻差距的方案呢? 进制转换 !三个数字的10进制编码可以表示0~999,如果是16进制呢?它最大可以表示163−1=4095>1999。所以,只需要转到16进制,如1749变为[6,13,5],那么三维向量就可以覆盖目标范围,代价是每个维度的数字从0~9变为0~15。
+这个进制转换的思想,实际上就对应着 NTK-aware scaled RoPE!
+长度外推需要关注的两个点:
+llama2、qwen和baichuan2的论文 都提到使用RoPE位置嵌入、SwiGLU激活函数、RMSNorm方法。并且都在尽可能实现更长长度的预测
+数据上,qwen和baichuan2 去重上做了许多工作 。并且qwen在数据质量上做了两方面工作首先 过滤低质量语料 ,其次加入高质量指令提高预训练效果。
+模型结构上:都在更长预测上下文长度进行提升,只是每个模型使用方式不一样。llama2使用 GQA ,Mistral 使用 Sliding Window Attention 和 Rolling Buffer Cache。 qwen在 QKV注意力层中添加bias以增强模型的外推能力、NTK-aware interpolation、LogN-Scaling和window attention 。
+另外,baichuan2使用规范化输出嵌入lm_head和最大z损失提升模型稳定性。qwen在 核心的矩阵计算中使用FP32换取更好效果 。
+联合采样:先top-k,k大一点,然后top-p,最后用temperature进行归一化
+
GLM 将 NLU 任务制定为包含任务描述的完形填空问题,这些问题可以通过自回归生成来回答。
+在前面的部分中,GLM掩蔽短跨度,并适用于NLU任务。然而,我们有兴趣预训练一个单一模型,可以处理NLU和文本生成。我们研究了一个多任务预训练设置,其中第二个目标是与空白填充目标联合优化的长文本生成任务。我们考虑以下两个目标:
+自回归空白填充任务的挑战之一是如何对位置信息进行编码。Transformers依靠位置编码来注入令牌的绝对位置和相对位置。GLM提出了2D位置编码来应对这一挑战。具体来说,每个令牌都使用两个位置id进行编码。第一个位置id表示mask文本Xcorrupt中的位置。对于掩码跨度,它是相应[MASK]标记的位置。第二个位置id表示跨度内的位置。对于A部分中的标记,它们的第二个位置id为0。对于B部分中的标记,它们的范围从1到span的长度。通过可学习embedding将两个位置id投影到两个向量中,这两个向量都被添加到输入token embedding中。GLM的编码方法确保模型在重建它们时,不知道掩蔽跨度的长度。
+对于分类任务:将NLU分类任务重新表述为空白填充的生成任务
+对于生成任务:给定的上下文构成输入的A部分,并在末尾附加一个掩码标记。该模型自回归地生成B部分的文本
+与BERT比较:BERT无法捕获掩码令牌的相互依赖性。BERT的另一个缺点是它不能正确地填充多个令牌的空白。为了推断长度为l的答案的概率,BERT需要执行l个连续预测。如果长度l未知,可能需要枚举所有可能的长度,因为BERT需要根据长度更改[MASK]令牌的数量。
+与XLNet比较:GLM和XLNet都是用自回归目标预训练的,但它们之间有两个不同之处。首先,XLNet使用mask前的原始位置编码。在推理过程中,需要知道或枚举答案的长度,这与BERT的问题相同。其次,为了避免Transformer内部的信息泄漏,XLNet使用two-stream自注意机制,而不是right-shift。这使得预训练的时间成本翻倍。
+与T5比较:T5提出了一个类似的空白填充目标来预训练编码器-解码器Transformer。T5对编码器和解码器使用独立的位置编码,并依赖于多个 sentinel tokens来区分掩码跨度。在下游任务中,只使用一个 sentinel tokens,导致模型容量的浪费和预训练和微调之间的不一致。此外,T5总是按照从左到右的固定顺序预测跨度。因此,在参数和数据更少的情况下,GLM在NLU和seq2seq任务上的性能明显优于T5。
+与UniLM比较:UniLM通过改变双向、单向和交叉注意之间的注意掩码,将不同的预训练目标组合在自动编码框架下。然而,UniLM总是用[MASK]令牌替换掩码跨度,这限制了它建模掩码跨度与其上下文之间依赖关系的能力。GLM输入前一个令牌并自回归生成下一个令牌。对下游生成任务的UniLM进行微调也依赖于掩码语言建模,效率较低。UniLMv2 (Bao等人,2020)对生成任务采用部分自回归建模,同时对NLU任务采用自编码目标。相反,GLM将NLU和生成任务与自回归预训练相结合。
+ChatGLM 参考了 ChatGPT 的设计思路,在千亿基座模型 GLM-130B 中注入了代码预训练,通过有监督微调(Supervised Fine-Tuning)等技术实现人类意图对齐。ChatGLM 当前版本模型的能力提升主要来源于独特的千亿基座模型 GLM-130B。
+具体来说,ChatGLM-6B 有如下特点:
+因此,ChatGLM-6B 具备了一定条件下较好的对话与问答能力。当然,ChatGLM-6B 也有相当多已知的局限和不足:
+Freeze方法
+Freeze方法,即参数冻结,对原始模型部分参数进行冻结操作,仅训练部分参数。
+大模型的Prompt构造方式严重影响下游任务的效果。比如:GPT-3采用人工构造的模版来做上下文学习(in context learning),但人工设计的模版的变化特别敏感,加一个词或者少一个词,或者变动位置都会造成比较大的变化。
+Prefix Tuning,在输入token之前构造一段任务相关的virtual tokens作为Prefix,然后训练的时候只更新Prefix部分的参数,而PLM中的其他部分参数固定。
+针对不同的模型结构,需要构造不同的Prefix。
+z = [PREFIX; x; y],合适的上文能够在固定 LM 的情况下去引导生成下文(比如:GPT3的上下文学习)。z = [PREFIX; x; PREFIX0; y]。Encoder端增加前缀是为了引导输入部分的编码,Decoder 端增加前缀是为了引导后续token的生成。为了防止直接更新Prefix的参数导致训练不稳定和性能下降的情况,在Prefix层前面加了MLP结构,训练完成后,只保留Prefix的参数。除此之外,通过消融实验证实,只调整embedding层的表现力不够,将导致性能显著下降,因此,在每层都加了prompt的参数。
+Prompt Tuning方法可以看作是Prefix Tuning的简化版本,它给每个任务定义了自己的Prompt,然后拼接到数据上作为输入,但 只在输入层加入prompt tokens ,并且不需要加入 MLP 进行调整来解决难训练的问题。
+与输出相关的tokens组成的上下文信息即可理解为是一个prompt。Prompt通常是一种短文本字符串,用于指导语言模型生成响应。Prompt提供上下文和任务相关信息,以帮助模型更好地理解要求,并生成正确的输出。例如,在问答任务中,prompt可能包含问题或话题的描述,以帮助模型生成正确的答案。Prompt通常是人类设计的,以帮助模型更好地理解特定任务或领域。
+简单总结就是说Prompt就是利用语言模型的生成能力帮我们完成任务。而Prompt-tuning的目的就是设计更加精巧的prompt,然后让模型输出我们想要的内容。
+以句子的情感分类为例,基于prompt方式让模型做情感分类任务的做法通常是在句子前面加入前缀“该句子的情感是”即可。本质上BERT这样的模型是一种生成模型,是无法完成特定任务的。它只是一个提取文本特征的通用模型。当你在句子前加入“该句子的情感是”这样的前缀,你实际上是将情感分类任务转换为一个“填空”任务。这是因为,在训练过程中,BERT可以学习到这个前缀与句子情感之间的关联。例如,它可以学习到“该句子的情感是积极的”和“该句子的情感是消极的”之间的差异。
+主要针对NLU任务
+P-tuning v1 微调方法是将 Prompt 加入到微调过程中, 只对 Prompt 部分的参数进行训练,而语言模型的参数固定不变 。
+P-Tuning方法将Prompt转换为可以学习的Embedding层,并用MLP+LSTM的方式来对Prompt Embedding进行一层处理。相比Prefix Tuning,P-Tuning加入的可微的virtual token,但仅限于输入层,没有在每一层都加;另外,virtual token的位置也不一定是前缀,插入的位置是可选的。这里的出发点实际是把传统人工设计模版中的真实token替换成可微的virtual token。
+之前的Prompt Tuning和P-Tuning等方法存在两个主要的问题:
+第一,缺乏模型参数规模和任务通用性。
+第二,缺少深度提示优化,在Prompt Tuning和P-tuning中,连续提示只被插入transformer第一层的输入embedding序列中,在接下来的transformer层中,插入连续提示的位置的embedding是由之前的transformer层计算出来的,这可能导致两个可能的优化挑战。
+P-tuning v2 微调方法是 P-tuning v1 微调方法的改进版,同时借鉴了 prefix-tuning 微调的方法。如下图所示:
+与 P-tuning v1 微调方法相比,P-tuning v2 微调方法采用了 prefix-tuning 的做法,在输入前面的每一层都加入可微调的参数。在 prefix 部分,每一层的 transformer 的 embedding 输入都需要被微调,而 P-tuning v1 只在第一层进行微调。同时,对于 prefix 部分,每一层 transformer 的输入不是从上一层输出,而是随机初始化的 embedding 作为输入。
+P-Tuning v2方法在每一层都加入了Prompts tokens作为输入,而不是仅仅加在输入层,这带来两个方面的好处:
+和prefix tuning的区别在于P-Tuning V2每一层的prompt是独立的,并不是由上一层计算得来
+具体做法基本同Prefix Tuning,可以看作是将文本生成的Prefix Tuning技术适配到NLU任务中,然后做了一些改进:
+LoRA(Low-Rank Adaptation of Large Language Models),直译为 大语言模型的低阶自适应 。LoRA 的基本原理 是冻结预训练好的模型权重参数,在冻结原模型参数的情况下,通过往模型中加入额外的网络层,并只训练这些新增的网络层参数 。由于这些新增参数数量较少,这样不仅 finetune 的成本显著下降,还能获得和全模型参数参与微调类似的效果。
+Lora方法的核心是在大型语言模型上对指定参数增加额外的低秩矩阵,也就是在原始PLM旁边增加一个旁路,做一个降维再升维的操作。并在模型训练过程中,固定PLM的参数,只训练降维矩阵A与升维矩阵B。
+原始论文加到Q和V上效果最好。
+先降维再升维,两个低秩矩阵A和B,一个高斯初始化,一个零初始化,目的是最开始的时候不会给模型带来噪声
+

当我们第一次做实验时,我们会尽量把

那么接下来,我们肯定就要往小的



 越小时,低秩矩阵表示的信息精炼,但不全面。我们通过调大
越小时,低秩矩阵表示的信息精炼,但不全面。我们通过调大 ,来放大forward过程中新知识对模型的影响。
,来放大forward过程中新知识对模型的影响。 越小时,低秩矩阵表示的信息精炼,噪声/冗余信息少,此时梯度下降的方向也更加确信,所以我们可以通过调大
越小时,低秩矩阵表示的信息精炼,噪声/冗余信息少,此时梯度下降的方向也更加确信,所以我们可以通过调大 ,适当增加梯度下降的步伐,也就相当于调整learning rate了
,适当增加梯度下降的步伐,也就相当于调整learning rate了在使用LoRA微调时,对模型的不同模块使用相同的秩,显然是不合理的
+LoRA微调过程中一直保持秩不变也是不合理的
+AdaLoRA的总体改进目标:找到一种办法,让模型在微调过程中,去学习每个模块参数对训练结果(以loss衡量)的重要性。然后,根据重要性,动态地调整不同模块的秩。
+LoRA是学习两个矩阵A和B,用来近似SVD分解的结果,而AdaLoRA是让模型去学习三个权重矩阵
 。其中,
。其中, 矩阵比较特殊,其大部分元素为0,只有对角线上的
矩阵比较特殊,其大部分元素为0,只有对角线上的 个元素有值。所以实操中我们可将其视为长度为
个元素有值。所以实操中我们可将其视为长度为 的向量,初始化时,我们将
的向量,初始化时,我们将 初始化为0,
初始化为0, 初始化为高斯随机矩阵 。这样做的目的和LoRA一样,都是为了避免引入噪声。
初始化为高斯随机矩阵 。这样做的目的和LoRA一样,都是为了避免引入噪声。 值置0 。这样,在下一次做forward时,这个三元组里对应的
值置0 。这样,在下一次做forward时,这个三元组里对应的 向量和
向量和 向量相当于被mask掉了,对Loss没有贡献。也就起到了变秩的效果。
向量相当于被mask掉了,对Loss没有贡献。也就起到了变秩的效果。 和
和 的参数。
的参数。 ,开启新一轮forward和backward,重复上面步骤,随时动态更新参数的秩。
,开启新一轮forward和backward,重复上面步骤,随时动态更新参数的秩。LoRA中是让模型学习BA,去近似SVD分解的结果,但是在训练过程中,没有引入任何SVD分解相关的性质做约束,所以模型就可能学歪了(因此LoRA作者在文章中写了很多实验,证明学出来的BA在一定程度上能近似SVD分解,能取得较好的效果)。而AdaLoRA则是直接将这一束缚考虑到了Loss中。
+Adapter Tuning 设计了Adapter结构 ,并将其嵌入Transformer的结构里面, 针对每一个Transformer层,增加了两个Adapter结构(分别是多头注意力的投影之后和第二个feed-forward层之后) , 在训练时,固定住原来预训练模型的参数不变,只对新增的 Adapter 结构和 Layer Norm 层进行微调,从而保证了训练的高效性 。
+每当出现新的下游任务,通过添加Adapter模块来产生一个易于扩展的下游模型,从而避免全量微调与灾难性遗忘的问题。
+
ChatGPT 模型上基本上和之前 GPT-3 都没有太大变化,主要变化的是训练策略变了,用上了强化学习
+监督调优模型
+收集演示数据,用监督学习去训练生成规则(把一些问题写出答案,把问题和答案都丢给GPT去训练,这个是有监督的训练,已经有答案了,让AI一葫芦画瓢,这种方法可以引导AI往人类所期望的方向去做答)
+但是,我们不可能人工穷举出所有可能的问题和答案,这个显然是不现实的,所以OpenAI只是提供了可能几万个这种有答案的数据,主要是为了让它在这个基础上进行泛化,然后提供一个方向上的引导,就是告诉模型,你就往这个方向上去答。
+训练回报模型
+让简化版的GPT监督训练之后变得更强,通过人工标注所有输出的优劣势
+先让ChatGPT输出很多个答案,然后基于它所生成的答案给他排序,我们只需要人工标注哪个答案是最好的,所以OpenAI做了大量的这种标注,
+使用 PPO 模型微调 SFT 模型
+通过PPO强化学习算法,实现模型的自我优化,强化学习就是让AI在不断的试错过程中自我调整优化策略,然后最大化预期的长期奖励,简单来说,就是让AI自己去不断尝试,前两步学习的模型在强化学习这一步都能派上用场。
+首先用监督版学习的ChatGPT来初始化PPO模型,让Reward模型去指导它,去给回答一个评分,然后AI就基于这个评分去调整自己的参数,试图在下一个回答中得到更高的分数,不断的重复这个过程,这个幼儿版的ChatGPT就成熟起来了,能够自我更新了。
+T5(Text-to-Text Transfer Transformer)和Bart(Bidirectional and Auto-Regressive Transformer)是两个常见的预训练模型,它们之间的区别如下:
+T5是一种基于Transformer的通用文本生成模型。T5的训练目标是将不同的自然语言处理(NLP)任务统一为文本到文本的转换任务。它采用了编码器-解码器结构,通过输入一个自然语言文本,输出另一个相关的自然语言文本,可以应用于机器翻译、摘要生成、问题回答等多个NLP任务。
+给定一系列的tokens , 我们迭代式的从中选择出tokens的子集 , 直到我们达到masking budget(例如,15%)。在每一次迭代中,我们首先从一个几何分布中采样出一个span length 。然后从中均匀地采样出一个starting point,作为该masked span的第一个token。
+与BERT保持一致的是,本文作者在SpanBERT中也同样会将15%的tokens给mask了,其中80%的用[MASK]来进行代替,10%的用random tokens,另外10%的就使用它本身的tokens。但是,对于同一个masked span来说,它们所做的替换操作是一样的(即,要么全用[MASK]来代替,要么全用sampled tokens来进行代替)。
+Bart是建立在T5模型基础上的一个变种,它专注于生成式任务。Bart模型使用了自回归解码器,通过训练一个自编码器来重构原始文本,同时采用了标准的语言模型预训练目标,从而使得生成的文本更加流畅和连贯。Bart的主要应用领域包括文本生成、摘要生成、对话系统等。
+在任务类型上,T5更加通用,适用于多种NLP任务的文本转换,而Bart则更加专注于生成式任务,并且在生成文本的质量和连贯性上有所优化。
+关于Bart的DAE(Denoising AutoEncoder)任务,它是Bart模型的一种预训练目标。DAE任务要求模型从输入的有噪声的文本中恢复原始的无噪声文本。通过在训练过程中向输入文本中添加噪声,并要求模型重建无噪声的文本,Bart可以学习到更好的文本表示和重构能力,从而提高生成文本的质量和准确性。
+BART的预训练任务是 将带噪声的输入还原 。如下图所示,输入为ABCDE,在AB中插入一个span长度为0的mask,再将CD替换为mask,最终得到加噪输入的A_B_E。模型的目标是将其还原为ABCDE。
+BART最终使用Text Infilling + Sentence permutation,其中Text Infilling起到了最主要的作用,其实就是Span级别的mask,只不过这里允许span长度为0,span的长度服从泊松分布,lambda = 3,总共mask30%的字符。Sentence permutation提升不大,之所以使用是作者假设模型规模提升后这个任务会有用。
+模型使用的是标准的Transformer结构中的Decoder
+PaLM做了以下修改:
+算法实习面试经历
+渠道:师兄组内内推+官网投递
+https://jobs.bytedance.com/campus/position/7225875094580119864/detail
+第一次正式面算法岗,经历、问题等回答的都不算太好
+Transformer的mask回答的不好,如何使用、mask的形状等等。
+算法题1:一个已经排好序的数组,给定一个目标值,求是否存在连续的子数组使得数组内部元素的和与目标值相等。滑动窗口实现,直接过
+算法题2:两个硬币有8种序列,两个人提前一人选择一种序列,然后抛这个硬币N次(N>3),从头开始匹配,先匹配到谁选择的序列就算谁赢,在已知两个人选择的序列的情况下求两个人赢的概率。
+模拟的方式做了一半超时,正规的解法应该是用马尔可夫的方法,没弄明白。
+def get_all_possible_list(possibilities, temparr, n):
+ if len(temparr) == n:
+ possibilities.append(temparr.copy())
+ return
+ for coin in [0, 1]:
+ temparr.append(coin)
+ get_all_possible_list(possibilities, temparr, n)
+ temparr.pop()
+
+
+def judge(arr1, arr2):
+ if len(arr1) != len(arr2):
+ return False
+ for i in range(0, len(arr1)):
+ if arr1[i] != arr2[i]:
+ return False
+ return True
+
+
+n = 5 # 第三方扔硬币的次数
+a = [0, 0, 1] # 第一个人选择的结果
+b = [0, 1, 0] # 第二个人选择的结果
+possibilities = []
+temparr = []
+get_all_possible_list(possibilities, temparr, n)
+# print(possibilities)
+all = len(possibilities)
+k = len(a)
+a_win = 0
+b_win = 0
+for arr in possibilities:
+ for index in range(0, n - k + 1):
+ if judge(arr[index : index + k], a):
+ a_win += 1
+ break
+ if judge(arr[index : index + k], b):
+ b_win += 1
+ break
+print(a_win / all) # 0.34375
+print(b_win / all) # 0.21875项目回答的还可以,出了一些数学题等
+有一个均匀分布的随机数发生器,如何产生正态分布的数字
+算法题:平面上有若干点,求最多可以连成多少条线
+应该通过斜率和截距唯一表示这个直线,同时要考虑斜率为无穷大的情况,也就是除数为0。
+提示下才写出来,也没有考虑除数为0的条件。
+排序挂,对方24届苏州大学NLP,五段经历,其中包括三篇论文
+渠道:微信公众号内推 https://mp.weixin.qq.com/s/y8zwSY0OYKZ5HfqqUoiLsw
+https://jobs.bytedance.com/campus/position/7259286117455235388/detail
+看了之前的面评,基础知识没有什么好问的,让手推Transformer的Attention的细节,也问了一些mask相关的内容
+算法题:https://leetcode.cn/problems/two-sum/
+秒杀
+简历上面的全部项目都讲了一遍,大概一个小时
+算法题:手写IOU,思路错误基本没有写
+概率题:圆上任取三点,能构成钝角三角形的概率
+讲解印象最深的一篇论文-InstructGPT
+讲解GPT的发展过程1-2-3-InstructGPT-4
+没有算法题及概率题
+渠道:boss直聘(对方主动联系)
+https://www.zhipin.com/job_detail/679790c8cb4e151e1X1y3dS4FFtX.html
+电话面试
+项目问题
+基础知识
+对大模型的了解程度
+算法题:排列数和组合数,快速排序和组合排序与树的关系
+约当天电话面试,拒绝后一面面试官联系我挽留
+渠道:boss直聘
+https://www.zhipin.com/job_detail/faa8bd495d022e241Xx80967F1dU.html
+没有问项目
+对大模型怎么看
+抽取网页的标题和正文怎么抽
+算法题:https://leetcode.cn/problems/longest-substring-without-repeating-characters/
+基本秒杀,但是还可以优化一个if,没有再继续做
+讲解Transformer的结构
+没有算法题
+最多只能拖两天
+微信拒绝:
+您好!我是下周一准备入职的张兆。
+很抱歉,之前可能刚刚回所低估了实验室的任务我今天接到导师的通知,从下周(甚至这周末)开始要有一个新项目需要我来主做,可能无法离开计算所保证实习时间去实习了。
+我不得不临时再拒绝您提供的百度的实习offer,给您造成的不便请您谅解,顺祝您工作顺利,也希望我们将来还有机会继续合作共事。
+回复:
+这样啊,那很遗憾
+理解,这边就先结束流程了哈
+渠道:boss直聘
+https://www.zhipin.com/job_detail/473e81a25baa5aaa1HR609u_FVtQ.html
+不开摄像头
+文本分类的机器学习算法有哪些,各自的优缺点和适用数据
+机器学习过拟合欠拟合的解决方法
+正则化为什么会有用
+算法题:
+对比赛不关心,只关心实习
+Bert和Transformer的结构
+矩阵转换 transpose和view的用法
+梯度下降法求平方根,调通一半吧
+ +最多考虑到2023-08-17中午
+被智能生成算法平台组-应用研究实习生捞
+GPT、RLHF、PPO的细节
+GPT4的置信度的图片
+Transformer的Self Attention的机制
+Decoder的mask的原理,mask和后面置0有什么区别
+做题:求三次方根
+深圳的部门,去不了直接挂
+约2023-08-22 10:00
+不打电话,直接微信通知,应该是AI平台部
+拒绝
+微软实习一段一段说,不太问细节,主要可能没说太清楚,她可能没理解好
+百度搜索比赛任务细节,不算搜索的,没讲完
+基础知识:交叉熵损失函数,transformer结构,beam search,temperature,topk,topp,前序中序后序遍历二叉树的原理,rope编码简单原理
+算法题:归并排序,白板写不需要运行
+微软实习第一个特征算法
+NAACL论文,主要是大模型方面
+没有算法题
+NAACL论文问了很多,质疑创新点
+微软实习质疑底层特征不能更改
+不开摄像头,共享屏幕讲论文
+微信底层开发平台人员面试
+5道编程题,100%,100%,60%,13.33%,0%
+NAACL论文,数据集,结合多轮对话场景如何判断立场转变
+微软实习没有问太多
+反转链表,力扣模式
+实验室干了啥,有啥帮助
+手撕二叉树的层序遍历
+为什么从微软离职,微软实习
+大模型没问比赛,问了做这些比赛有什么收获,有什么成长
+倾向于广告还是倾向于大模型
+发邮件及公众号询问
+入职时间暂定6月3日,一周下正式的offer
+48小时之内选择接受还是拒绝
+分析题11题、数学统计题11题、图形题11题、性格测试51题
+9道单选,6道不定项选择题,三道编程只做出来一个
+微软实习,扩展SSB问题
+WSDM Cup的比赛
+CodeQwen比赛
+softmax公式,数值过小怎么办
+梯度和导数的区别
+力扣原题:322 零钱兑换,初始条件有点问题
+说非常满意,会有二面的
+先拒了一个时间,然后约了第二个时间
+最近公共父节点及变形(如果结点不一定存在应该怎么办),询问时间复杂度
+有一个小bug,但是做的也很快
+问WSDM比赛,没问完,出了一个对用户评论进行总结的场景题目
+被发现看自我介绍了
+实习公司的氛围,更喜欢哪个
+自己的优缺点
+有什么兴趣爱好
+对部门的了解
+反问转正率
+直接更新到“等待面试结果”,应该是正向的
+一直没有消息,应该是简历挂了
+单选、不定项选择题
+WSDM比赛
+NAACL论文
+CodeQwen比赛
+ChatGLM比赛
+全部组合 本地写算法题
+说直接终面,二面免了
+WSDM比赛
+NAACL论文简要介绍
+对大模型的理解
+以后做什么方向
+自我介绍
+怎么安排时间,动力在哪
+与岗位最匹配的点
+压力最大的时候
+中间各种催
+没招了,就是不打电话
+算法实习生-风控
+职位描述
+ByteIntern:面向2025届毕业生(2024年9月-2025年8月期间毕业),为符合岗位要求的同学提供转正机会。
+团队介绍:风控研发作为业务的风控技术中台主要帮助解决各个产品(包括抖音、头条等)的各种黑灰产作弊问题,包括内容、交易、流量、账号等方面的风险,结合各场景业务(抖音短视频、电商、直播、生活服务、用户增长等)特性,进行模型和算法创新,打造业界领先的风控算法体系。
1、负责字节各产品(包括抖音、头条等)各种作弊风险的发现与治理,包括内容、交易、流量、账号等方面的风险;
+2、通过指标监控归因,及时感知风险及业务的变化,主动识别潜在攻击,持续优化调整风控方案,并推动风控治理建设及业务模式调整;
+3、通过CV、NLP、表征学习、图模型、深度学习、迁移学习、多任务学习等技术,提升问题发现的效率,从而快速阻断风险,优化平台的各项生态指标;
+4、挖掘和分析海量内容和用户行为进行用户长短期画像建设,提升模型的精准性和召回面;
+5、结合各场景业务(抖音短视频、电商、直播、生活服务、用户增长等)特性,进行模型和算法创新,打造业界领先的风控算法体系。
+职位要求
+1、2025届本科及以上学历在读,计算机、机器学习和模式识别等相关专业优先;
+2、热爱计算机科学和互联网技术,对人工智能类产品有浓厚兴趣;
+3、具备强悍的编码能力,熟悉 Linux 开发环境,熟悉 C++ 和 Python 语言优先;
+4、有扎实的数据结构和算法功底,熟悉机器学习、自然语言处理、数据挖掘、分布式计算、计算机视觉、计算机图形中一项或多项;
+5、优秀的分析问题和解决问题的能力,对解决具有挑战性问题充满激情。
+6、每周可实习4天以上,实习时间3个月以上。
都不太建议去,先面面看
+WSDM比赛
+GPT为什么有效
+大模型长度外推
+大模型的词表扩充
+大模型的微调方式
+Transformer的结构
+对于小样本数据如何作处理
+代码:最长公共子序列
+WSDM比赛,对着PPT详细介绍
+为什么大模型的参数量都是六七B这样,主要原因是模型的层数
+NAACL论文的贡献
+算法题
+IP 地址排序
+给定一组 IP 地址字符串组成的数组, 将其从小到大排序
+如 [“10.3.72.160”, “10.3.71.106”, “10.3.71.102”, “10.3.69.108”] 排序后得到 [‘10.3.69.108’, ‘10.3.71.102’, ‘10.3.71.106’, ‘10.3.72.160’]
样例1:
+[输入]
+[“10.3.72.160”, “10.3.71.106”, “10.3.71.102”, “10.3.69.108”]
+[输出]
+[‘10.3.69.108’, ‘10.3.71.102’, ‘10.3.71.106’, ‘10.3.72.160’]
#include <bits/stdc++.h>
+using namespace std;
+
+vector<int> splitstring(string s){
+ vector<int> result;
+ int temp = 0;
+ for(int i=0;i<s.size();i++){
+ if(s[i] == '.'){
+ result.push_back(temp);
+ temp = 0;
+ } else{
+ temp = temp * 10 + (s[i] - '0');
+ }
+ }
+ result.push_back(temp);
+ return result;
+}
+
+bool cmp(string a, string b){
+ vector<int> a_vt = splitstring(a);
+ // for(int i=0;i<a_vt.size();i++){
+ // cout << a_vt[i] << " ";
+ // }
+ // cout << endl;
+ vector<int> b_vt = splitstring(b);
+ // for(int i=0;i<b_vt.size();i++){
+ // cout << a_vt[i] << " ";
+ // }
+ // cout << endl;
+ for(int i=0;i<4;i++){
+ if(a_vt[i] < b_vt[i]){
+ return true;
+ } else if (a_vt[i] > b_vt[i]){
+ return false;
+ }
+ }
+ return true;
+}
+
+int main() {
+ vector<string> vs;
+ // string s;
+ // while(cin >> s){
+ // vs.push_back(s);
+ // }
+ vs.push_back("10.3.72.160");
+ vs.push_back("10.3.71.106");
+ vs.push_back("10.3.71.102");
+ vs.push_back("10.3.69.108");
+ sort(vs.begin(), vs.end(), cmp);
+ for(int i=0;i<vs.size();i++){
+ cout << vs[i] << endl;
+ }
+ return 0;
+}
+数组中重复的数据
+给定一个整数数组 a,其中1 ≤ a[i] ≤ n (n为数组长度), 其中有些元素出现两次而其他元素出现一次。找到所有出现两次的元素。
+你可以不用到任何额外空间并在O(n)时间复杂度内解决这个问题吗?
+样例1:
+[输入]
+[4,3,2,7,8,2,3,1]
+[输出]
+[2,3]
#include <iostream>
+using namespace std;
+int main() {
+ //int a;
+ //cin >> a;
+ vector<int> vt;
+ vt = [4,3,2,7,8,2,3,1]
+ for(int i=0;i<vt.size();i++){
+ if(vt[vt[i] - 1] < 0){
+ print(vt[i]);
+ } else{
+ vt[vt[i] - 1] = - vt[vt[i] - 1]
+ }
+ }
+}CodeQwen比赛
+算法题:
+给定两个字符串s1和s2,需要删除一些字符使得两个字符串相等。每删除一个字符,需要花费对应字符的ascii值代价。求使得两个字符相等,需要删除的字符花费最小和。
+例如: s1=‘sea’, s2=‘eat’
+在s1中删除s(115),在s2中删除t(116),两个字符串都等于 ea,代价和为 115 + 116 = 231
#include <bits/stdc++.h>
+using namespace std;
+int main() {
+ string s1 = "sea";
+ string s2 = "eat";
+ int m = s1.size();
+ int n = s2.size();
+ vector<vector<int> > dp(m+1,){vector<int>(n+1,0));
+ int tempsum = 0;
+ for(int i=0;i<=m;i++
+ dp[i][0] = tempsum;
+ if(i == m){
+ break;
+ }
+ tempsum += s1[i];
+ }
+ tempsum = 0;
+ for(int j=0;j<=n;j++){
+ dp[0][j] = tempsum;
+ if(j == n){
+ break;
+ }
+ tempsum += s2[j];
+ }
+ for(int i=1;i<=m;i++){
+ for(int j=1;j<=n;j++){
+ if(s1[i-1] == s2[j-1]){
+ dp[i][j] = dp[i-1][j-1];
+ } else{
+ dp[i][j] = min(dp[i-1][j] + s1[i-1], dp[i][j-1] + s2[j-1]);
+ }
+ }
+ }
+ for(int i=0;i<=m;i++){
+ for(int j=0;j<=n;j++){
+ cout << dp[i][j] << " ";
+ }
+ cout << endl;
+ }
+ cout << dp[m][n] << endl;
+ return 0;
+
+}CodeQwen代码大模型
+ChatGLM金融大模型
+NAACL论文
+对实习有什么预期
+实习期间需要弄一个论文,以论文和项目的进展判断最终转正的薪资
+WSDM Cup
+NAACL 论文
+反馈后面面试不太好,研究深度不够
+WSDM Cup 有没有更改过模型,模型的集成策略
+微软实习,各种业务问题,线上效果,优化策略
+小样本分类竞赛的难点
+机器学习树模型
+算法题:判断链表是否有环,计算环的长度
+自选项目做介绍
+先主动讲了WSDM Cup
+然后让我讲小样本分类比赛
+怎么通过计算机估算Π
+两个业务,一个是视频生成文本然后提取特征,一个是纯搜广推,主要是混排策略
+说会有HR面的
+在实习中对团队最有帮助的事情
+未来规划,为什么不读博
+不一定转正,和秋招是一起的,试用期可能会缩短
+实习工资9000,周末双休,五道口附近
+被推荐人是中科院计算所的硕士研究生,发表了NAACL 2024的一作文章,同时有NeurIPS 2024的一作文章在投;曾在商汤和微软实习,现在在蚂蚁集团作为蚂蚁星的候选人进行暑期实习;参加过五项算法竞赛,包括顶会竞赛WSDM Cup的冠军。
+(简答题)请简述你在文本大模型技术的研究或项目经历。
+研究经历:
+实习经历:
+项目经历(竞赛经历):
+(简答题)请罗列你玩过的游戏,并简述你对AIGC技术在游戏场景应用的思考。
+我平时一般不玩游戏,不过过年的时候可能会玩一点和平精英,其他游戏就有点不太了解了。
+下面是我对AIGC技术如果可能应用在和平精英中的一些思考:
+(简答题)最近看了什么paper?为什么要看这些paper?看完后有什么体会?
+(简答题)最近跟进了哪些开源项目?为什么跟进这些项目?有进一步的优化建议吗?
+(简答题)最近做了哪些算法应用实践?如果可以自由选择,想做什么样的应用实践?
+ + +Pytorch分布式训练学习整理
+ +源码解析:PyTorch 源码解读之 DP & DDP:模型并行和分布式训练解析
+简单小模型示例:pytorch中分布式训练DDP教程(新手快速入门!)
+ +系列文章:【分布式训练】单机多卡的正确打开方式(一):理论基础
+【分布式训练】基于PyTorch进行多GPU分布式模型训练(补充)
+较新较详细的教程:torch分布式训练
+ +把模型隔成不同的层,每一层都放到一块GPU上
+(1)GPU利用度不够。
+
如图,阴影部分所表示的时间段里,总有GPU在空转。GPU的数量越多时,空置的比例接近1
+(2)中间结果占据大量内存
+在做backward计算梯度的过程中,我们需要用到每一层的中间结果z。假设我们的模型有L层,每一层的宽度为d,则对于每块GPU,不考虑其参数本身的存储,额外的空间复杂度为
流水线并行的核心思想是: 在模型并行的基础上,进一步引入数据并行的办法,即把原先的数据再划分成若干个batch,送入GPU进行训练 。未划分前的数据,叫 mini-batch 。在mini-batch上再划分的数据,叫 micro-batch 。
+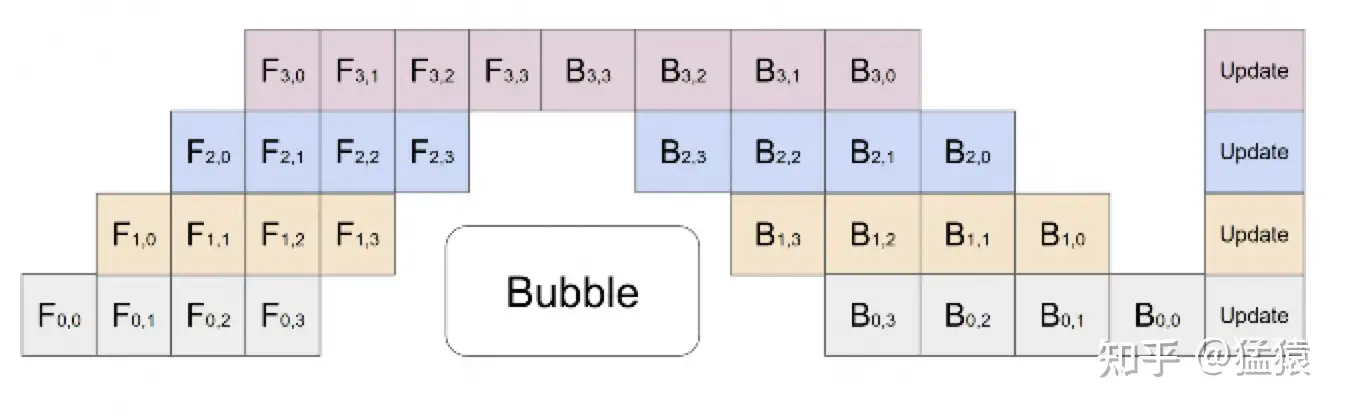
其中,第一个下标表示GPU编号,第二个下标表示micro-batch编号。假设我们将mini-batch划分为M个,则流水线并行下,bubble的时间复杂度为:

将batch切好,并逐一送入GPU的过程,就像一个流水生产线一样(类似于CPU里的流水线),因此也被称为Pipeline Parallelism。
+Gpipe采用用时间换空间的方法,几乎不存中间结果,等到backward的时候,再重新算一遍forward
+每块GPU上只保存来自上一块的最后一层输入z,其余的中间结果我们算完就废。等到backward的时候再由保存下来的z重新进行forward来算出。
+空间复杂度为
在实际应用中,流水线并行并不特别流行,主要原因是模型能否均匀切割,影响了整体计算效率,这就需要算法工程师做手调。
+数据并行的核心思想是: 在各个GPU上都拷贝一份完整模型,各自吃一份数据,算一份梯度,最后对梯度进行累加来更新整体模型 。理念不复杂,但到了大模型场景, 巨大的存储和GPU间的通讯量, 就是系统设计要考虑的重点了。在本文中,我们将递进介绍三种主流数据并行的实现方式:
+一个经典数据并行的过程如下:
+DP 基于单机多卡,所有设备都负责计算和训练网络,除此之外, device[0] (并非 GPU 真实标号而是输入参数 device_ids 首位) 还要负责整合梯度,更新参数。从图中我们可以看出,有三个主要过程:
+所有卡都并行运算(图中红色),将梯度收集到 device[0](图中浅蓝色)和 device[0] 分享模型参数给其他 GPU(图中绿色)三个主要过程。
+更详细的流程如下图所示:
+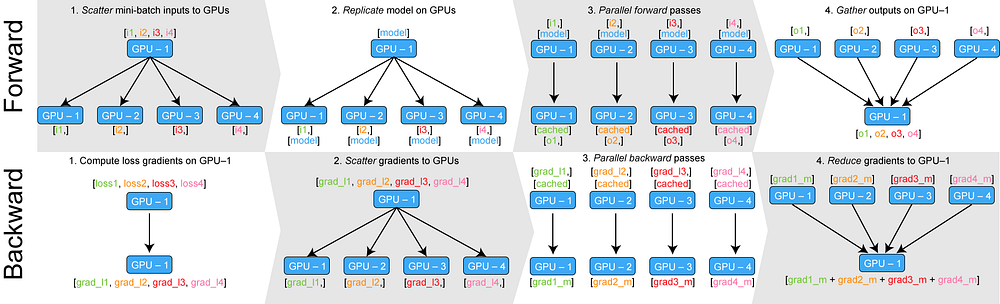
梯度异步更新:Worker并不会实际等到把聚合梯度拿回来,更新完参数W后再做计算。而是直接拿旧的W,吃新的数据,继续第11轮的计算。这样就保证在通讯的时间里,Worker也在马不停蹄做计算,提升计算通讯比。
+但是模型收敛的速度不会变快,只是多用了一些数据
+受通讯负载不均的影响, DP一般用于单机多卡场景 。
+DDP作为一种更通用的解决方案出现了,既能多机,也能单机。DDP首先要解决的就是通讯问题:将Server上的通讯压力均衡转到各个Worker上。实现这一点后,可以进一步去Server,留Worker。
+随着大模型的出现,简单的数据并行已经无法满足需求,毕竟一个模型的大小就有可能超过显卡的显存,更不可能将其复制多份。因此需要让每一张卡仅负责模型的一部分计算,承载模型的一小部分。
+使用DDP进行分布式训练有以下几个优势:
+Scatter Reduce过程:首先将参数分为


All Gather:得到每一份参数的累积之后,再做一次传递,同步到所有的GPU上。
+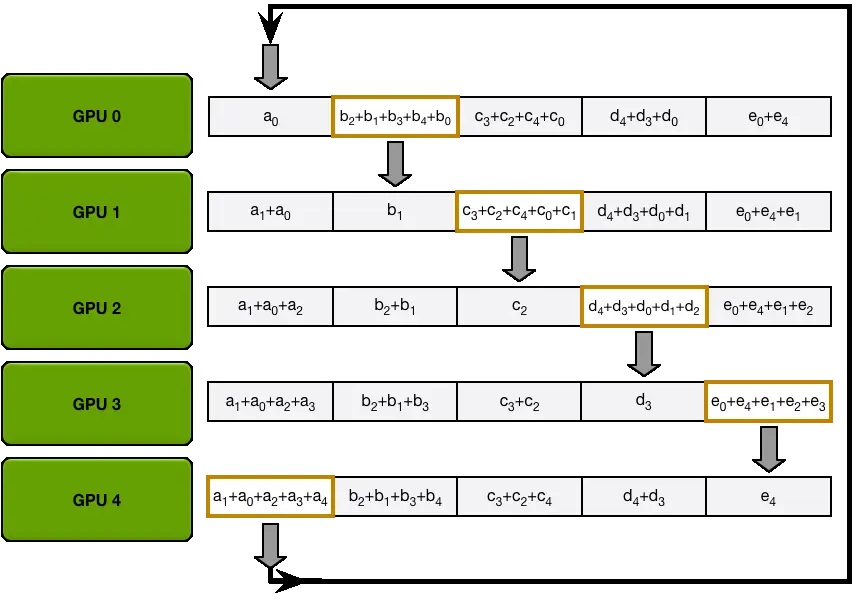
假设有





DP和DDP的总通讯量相同,但因负载不均的原因,DP需要耗费更多的时间搬运数据,但是DP不一定就比DDP差
+DDP采用多进程控制多GPU,共同训练模型,一份代码会被pytorch自动分配到n个进程并在n个GPU上运行。 DDP运用Ring-Reduce通信算法在每个GPU间对梯度进行通讯,交换彼此的梯度,从而获得所有GPU的梯度。对比DP,不需要在进行模型本体的通信,因此可以加速训练。
+需要注意以下几点:
+如下图所示,共有3个节点(机器),每个节点上有4个GPU,每台机器上起4个进程,每个进程占一块GPU,那么图中一共有12个rank,nproc_per_node=4,nnodes=3,每个节点都有一个对应的node_rank
+
rank与GPU之间没有必然的对应关系,一个rank可以包含多个GPU;一个GPU也可以为多个rank服务(多进程共享GPU),在torch的分布式训练中习惯默认一个rank对应着一个GPU,因此local_rank可以当作GPU号
+torchrun相当于原来的torch.distributed.launch,有一些额外增加的功能:
+torchrun命令与 python -m torch.distributed.run命令完全等同,为命令行命令
有一个参数 --use_env在目前版本的torchrun中是不存在的,因此需要做一点处理
--use_env参数旧版本代码:
+$ python -m torch.distributed.launch --use-env train_script.py
+import argparse
+parser = argparse.ArgumentParser()
+parser.add_argument("--local-rank", type=int)
+args = parser.parse_args()
+
+local_rank = args.local_rank新版本代码:
+$ torchrun train_script.py
+import os
+local_rank = int(os.environ["LOCAL_RANK"])| 参数名称 | +含义 | +示例 | +
|---|---|---|
| –nnodes | +节点数量,一个节点对应一个主机 | +1或MIN_SIZE:MAX_SIZE(弹性训练) | +
| –nproc-per-node | +一个节点中的进程数量,一般一个进程使用一个显卡,故也通常表述为一个节点中显卡的数量 | +[auto, cpu, gpu, int] | +
| –rdzv-backend | +rendezvous 后端 | +c10d etcd | +
| –rdzv-endpoint | +rendezvous 后端地址 | +<host>:<port> |
+
| –rdzv-id | +用户可以指定当前rendezvous的id,所有的node都要使用这同一个id | ++ |
| –rdzv-conf | +希望传入rendezvous的其他参数 | +<key1>=<value1> |
+
| –standalone | +单节点多卡的默认配置,不需要再传入上述的rendezvous参数,默认为C10d TCP 29400(–master-addr等也会失效) | +选项 | +
| –max-restarts | +worker group重启的最大次数 | ++ |
| –monitor-interval | +检测worker状态的时间间隔(以秒为单位) | ++ |
| –start-method | +创建子进程的方式 | +{spawn,fork,forkserver} | +
| –role | +User-defined role for the workers. | ++ |
| -m | +与python -m相同,将模块当作脚本运行 | +选项 | +
| –no-python | +不使用python命令而是直接执行(如果这个文件并不是一个py文件会使用这个) | ++ |
| –run-path | +使用runpy.run_path执行文件 | ++ |
| –log-dir | +日志文件存放目录 | ++ |
| –redirects | +将控制台输出的日志信息重定向到日志目录中的文件 | +[-r 3] 将所有worker的标准输出和标准错误进行重定向,[-r 0:1,1:2] 将rank 0的标准输出重定向,将rank 1的标准错误重定向 | +
| –tee | +除将日志输出到控制台外也输出到日志文件 | +日志文件流 | +
| –node-rank | +多节点分布式训练的时候该节点的Rank | ++ |
| –master-addr | +master 节点的 IP 地址,也就是 rank=0 对应的主机地址 | ++ |
| –master-port | +master 节点的端口号,用于通信 | ++ |
| –local-addr | +本地节点的IP地址 | ++ |
torchrun主要是对多节点作了分布式的优化,从而可以满足容错性和弹性伸缩。如果是单节点就不需要很复杂。
+| 名称 | +含义 | +示例 | ++ |
|---|---|---|---|
| LOCAL_RANK | +GPU在单节点中的序号 | +0 | +1 | +
| RANK | +GPU在全部节点的序号 | +0 | +1 | +
| GROUP_RANK | +worker组的rank | +0 | +0 | +
| ROLE_RANK | +相同ROLE的worker的rank | +0 | +1 | +
| LOCAL_WORLD_SIZE | +与–nproc-per-node相同 | +2 | +2 | +
| WORLD_SIZE | +job中worker的总数 | +2 | +2 | +
| ROLE_WORLD_SIZE | +相同角色的worker的数量 | +1 | +2 | +
| MASTER_ADDR | +rank为0的worker的地址 | +127.0.0.1 | +127.0.0.1 | +
| MASTER_PORT | +rank为0的worker的端口 | +29500 | +29500 | +
| TORCHELASTIC_RESTART_COUNT | +最近重启的worker组的数量 | +0 | +0 | +
| TORCHELASTIC_MAX_RESTARTS | +配置的最大重启次数 | +0 | +0 | +
| TORCHELASTIC_RUN_ID | +与–rdzv-id相同 | +none | +none | +
| PYTHON_EXEC | +执行这个脚本的python的位置 | +没有 | +没有 | +
import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from torch.utils.data import Dataset, DataLoader
+from torch.utils.data.distributed import DistributedSampler
+from torch.nn.parallel import DistributedDataParallel
+from torch.distributed import init_process_group, destroy_process_group
+import os
+import time
+
+class ToyModel(nn.Module):
+ def __init__(self):
+ super(ToyModel, self).__init__()
+ self.net1 = nn.Linear(10, 10)
+ self.relu = nn.ReLU()
+ self.net2 = nn.Linear(10, 5)
+
+ def forward(self, x):
+ return self.net2(self.relu(self.net1(x)))
+
+class MyTrainDataset(Dataset):
+ def __init__(self, size):
+ self.size = size
+ self.data = [(torch.rand(10), 0) for _ in range(size)]
+
+ def __len__(self):
+ return self.size
+
+ def __getitem__(self, index):
+ return self.data[index]
+
+class Trainer:
+ def __init__(
+ self,
+ model: torch.nn.Module,
+ train_data: DataLoader,
+ optimizer: torch.optim.Optimizer,
+ save_every: int,
+ snapshot_path: str,
+ ) -> None:
+ self.gpu_id = int(os.environ["LOCAL_RANK"])
+ self.model = model.to(self.gpu_id)
+ self.train_data = train_data
+ self.optimizer = optimizer
+ self.save_every = save_every
+ self.epochs_run = 0
+ self.snapshot_path = snapshot_path
+ if os.path.exists(snapshot_path):
+ print("Loading snapshot")
+ self._load_snapshot(snapshot_path)
+
+ self.model = DistributedDataParallel(self.model, device_ids=[self.gpu_id])
+
+ def _load_snapshot(self, snapshot_path):
+ loc = f"cuda:{self.gpu_id}"
+ snapshot = torch.load(snapshot_path, map_location=loc)
+ self.model.load_state_dict(snapshot["MODEL_STATE"])
+ self.epochs_run = snapshot["EPOCHS_RUN"]
+ print(f"Resuming training from snapshot at Epoch {self.epochs_run}")
+
+ def _run_batch(self, source, targets):
+ self.optimizer.zero_grad()
+ output = self.model(source)
+ # print(output,targets)
+ loss = F.cross_entropy(output, targets)
+ print(f"[GPU{self.gpu_id}] Loss {loss.item()}")
+ loss.backward()
+ self.optimizer.step()
+
+ def _run_epoch(self, epoch):
+ b_sz = len(next(iter(self.train_data))[0])
+ print(f"[GPU{self.gpu_id}] Epoch {epoch} | Batchsize: {b_sz} | Steps: {len(self.train_data)}")
+ self.train_data.sampler.set_epoch(epoch)
+ for source, targets in self.train_data:
+ source = source.to(self.gpu_id)
+ targets = targets.to(self.gpu_id)
+ self._run_batch(source, targets)
+
+ def _save_snapshot(self, epoch):
+ snapshot = {
+ "MODEL_STATE": self.model.module.state_dict(),
+ "EPOCHS_RUN": epoch,
+ }
+ torch.save(snapshot, self.snapshot_path)
+ print(f"Epoch {epoch} | Training snapshot saved at {self.snapshot_path}")
+
+ def train(self, max_epochs: int):
+ for epoch in range(self.epochs_run, max_epochs):
+ self._run_epoch(epoch)
+ if self.gpu_id == 0 and epoch % self.save_every == 0:
+ self._save_snapshot(epoch)
+ time.sleep(1)
+
+def ddp_setup():
+ init_process_group(backend="nccl")
+ print("Parameters")
+ print(f"LOCAL_RANK:{os.environ['LOCAL_RANK']}")
+ print(f"RANK:{os.environ['RANK']}")
+ print(f"GROUP_RANK:{os.environ['GROUP_RANK']}")
+ print(f"ROLE_RANK:{os.environ['ROLE_RANK']}")
+ print(f"LOCAL_WORLD_SIZE:{os.environ['LOCAL_WORLD_SIZE']}")
+ print(f"WORLD_SIZE:{os.environ['WORLD_SIZE']}")
+ print(f"ROLE_WORLD_SIZE:{os.environ['ROLE_WORLD_SIZE']}")
+ print(f"MASTER_ADDR:{os.environ['MASTER_ADDR']}")
+ print(f"MASTER_PORT:{os.environ['MASTER_PORT']}")
+ print("")
+ torch.cuda.set_device(int(os.environ["LOCAL_RANK"]))
+
+def load_train_objs():
+ train_set = MyTrainDataset(2048) # load your dataset
+ model = ToyModel()
+ optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)
+ return train_set, model, optimizer
+
+def prepare_dataloader(dataset: Dataset, batch_size: int):
+ return DataLoader(
+ dataset,
+ batch_size=batch_size,
+ pin_memory=True,
+ shuffle=False,
+ sampler=DistributedSampler(dataset)
+ )
+
+def main(save_every: int, total_epochs: int, batch_size: int, snapshot_path: str = "snapshot.pt"):
+ ddp_setup()
+ dataset, model, optimizer = load_train_objs()
+ train_data = prepare_dataloader(dataset, batch_size)
+ trainer = Trainer(model, train_data, optimizer, save_every, snapshot_path)
+ trainer.train(total_epochs)
+ destroy_process_group()
+
+if __name__ == "__main__":
+ import argparse
+ parser = argparse.ArgumentParser(description='simple distributed training job')
+ parser.add_argument('--total_epochs', default=10, type=int, help='Total epochs to train the model')
+ parser.add_argument('--save_every', default=2, type=int, help='How often to save a snapshot')
+ parser.add_argument('--batch_size', default=512, type=int, help='Input batch size on each device (default: 32)')
+ args = parser.parse_args()
+
+ main(args.save_every, args.total_epochs, args.batch_size)与单卡有几点不同:
+init_process_group(backend="nccl"),后端一般选择ncclsampler=DistributedSampler(dataset)self.model = DistributedDataParallel(self.model, device_ids=[self.gpu_id])训练脚本:
+torchrun \
+ --nnodes=1 \
+ --nproc_per_node=2 \
+ --master-addr=127.0.0.1 \
+ --master-port=29500 \
+ main.pyexport NCCL_DEBUG=info
+export NCCL_SOCKET_IFNAME=bond0
+export NCCL_IB_DISABLE=1
+
+torchrun \
+ --nnodes=2 \
+ --nproc_per_node=2 \
+ --master-addr=10.208.58.27 \
+ --master-port=29602 \
+ --node-rank=0 \
+ main.pyexport NCCL_DEBUG=info
+export NCCL_SOCKET_IFNAME=bond0
+export NCCL_IB_DISABLE=1
+
+torchrun \
+ --nnodes=2 \
+ --nproc_per_node=1 \
+ --master-addr=10.208.58.27 \
+ --master-port=29602 \
+ --node-rank=1 \
+ main.py注意事项:
+测试环境:
+master:10.208.58.27 2*V100
+Parameters
+LOCAL_RANK:0
+RANK:0
+GROUP_RANK:0
+ROLE_RANK:0
+LOCAL_WORLD_SIZE:2
+WORLD_SIZE:3
+ROLE_WORLD_SIZE:3
+MASTER_ADDR:10.208.58.27
+MASTER_PORT:29602
+
+Parameters
+LOCAL_RANK:1
+RANK:1
+GROUP_RANK:0
+ROLE_RANK:1
+LOCAL_WORLD_SIZE:2
+WORLD_SIZE:3
+ROLE_WORLD_SIZE:3
+MASTER_ADDR:10.208.58.27
+MASTER_PORT:29602worker:1*A100
+Parameters
+LOCAL_RANK:0
+RANK:2
+GROUP_RANK:1
+ROLE_RANK:2
+LOCAL_WORLD_SIZE:1
+WORLD_SIZE:3
+ROLE_WORLD_SIZE:3
+MASTER_ADDR:10.208.58.27
+MASTER_PORT:29602数据并行中,每个GPU上都复制了一份完整模型,当模型变大时,很容易打爆GPU的显存
+存储主要分为两大块:Model States和Residual States
+Model States指和模型本身息息相关的,必须存储的内容,具体包括:
+Residual States指并非模型必须的,但在训练过程中会额外产生的内容,具体包括:
+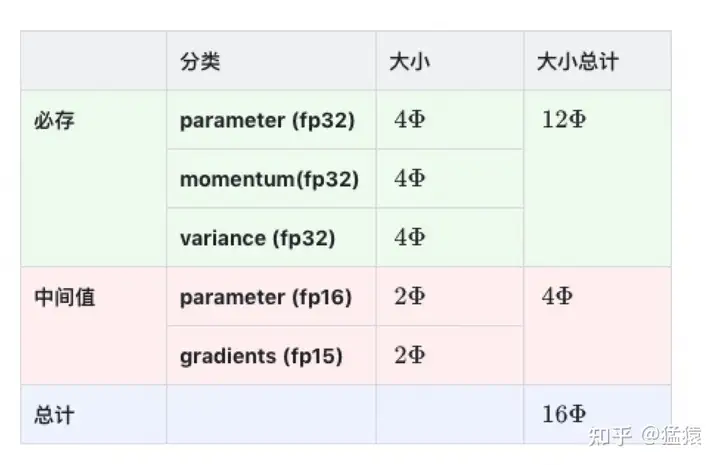
其中很大的momentum和variance是Adam保存的,首先就优化他们
+将optimizer state分成若干份,每块GPU上各自维护一份。这样就减少了相当一部分的显存开销。
+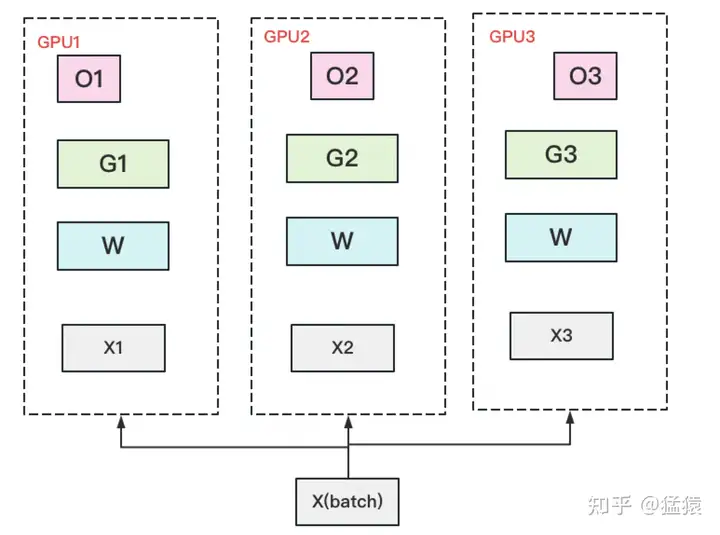
得到G是与DP一样的通信,然后还要聚合W
+显存和通讯量的情况如下:
+
把梯度也拆开,每个GPU格子维护一块梯度。
+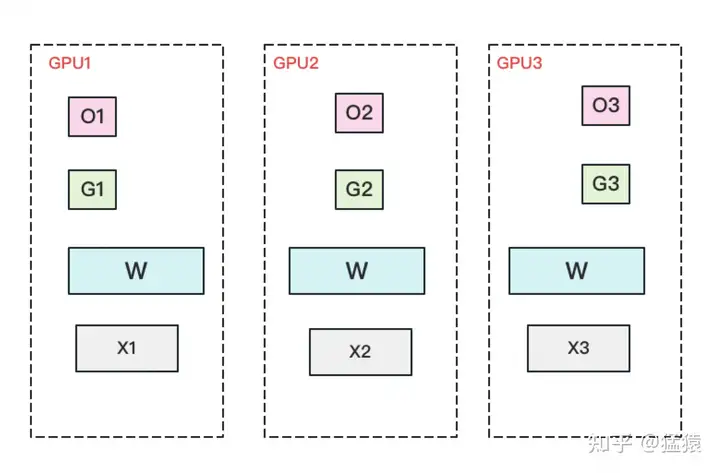
此时,数据并行的整体流程如下:
+对梯度做一次 Reduce-Scatter ,保证每个GPU上所维持的那块梯度是聚合梯度。例如对GPU1,它负责维护G1,因此其他的GPU只需要把G1对应位置的梯度发给GPU1做加总就可。
+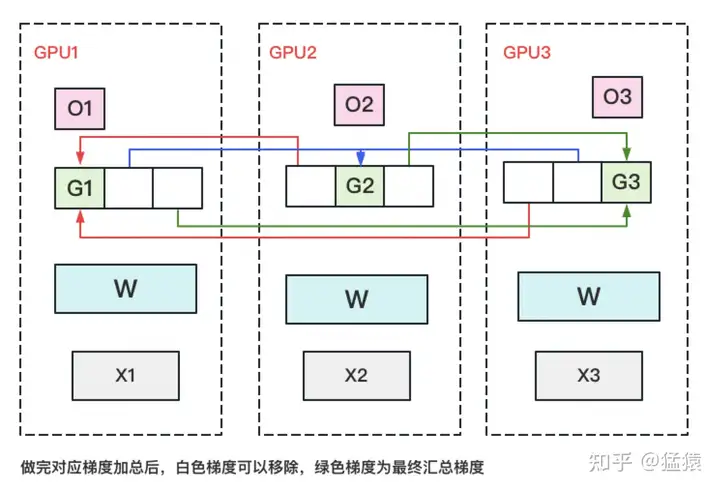
每块GPU用自己对应的O和G去更新相应的W。更新完毕后, 每块GPU维持了一块更新完毕的W 。同理,对W做一次 All-Gather ,将别的GPU算好的W同步到自己这来。单卡通讯量 Φ 。
+
每块GPU只维持对应的optimizer states,gradients和parameters
+
到这一步, 我们用1.5倍的通讯开销,换回近120倍的显存 。只要梯度计算和异步更新做的好,通讯时间大部分可以被计算时间隐藏,因此这样的额外通讯开销,也是划算的。
+ZeRO是模型并行的形式,数据并行的实质 。
+模型并行,是指在forward和backward的过程中,我只需要用自己维护的那块W来计算就行。即 同样的输入X,每块GPU上各算模型的一部分,最后通过某些方式聚合结果 。
+对ZeRO来说,它做forward和backward的时候,是需要把各GPU上维护的W聚合起来的,即本质上还是用完整的W进行计算。 它是不同的输入X,完整的参数W,最终再做聚合 。
+核心思想是: 显存不够,内存来凑
+把要存储的大头卸载(offload)到CPU上,而把计算部分放到GPU上
+ZeRO-Offload的做法是:
+具体切分如下图:
+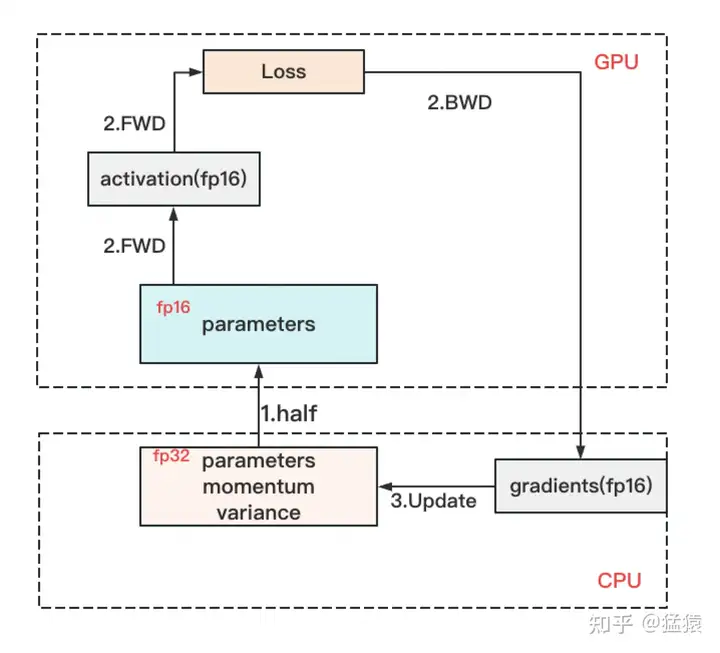
ZeRO-infinity也是同理,它们在解决的事情都是:找个除GPU之外的地方,存数据。感兴趣的朋友可以深入研究,这里就不展开了。
+把模型的参数纵向切开,放到不同的GPU上进行独立计算,然后再做聚合。
+假设现在W太大,导致单卡装不下。我们需要把W切开放到不同的卡上,则我们面临三个主要问题:
+forward
+我们用N来表示GPU的数量。有几块GPU,就把W按行维度切成几份。下图展示了N=2时的切割方式:
+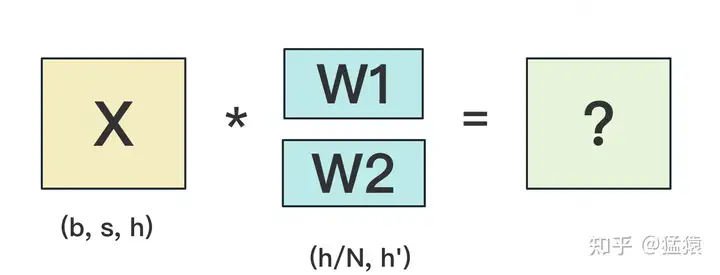
W按照行维度切开后,X的维度和它不对齐了,这可怎么做矩阵乘法呢?很简单,再把X“按列切开”就行了,如下图所示:
+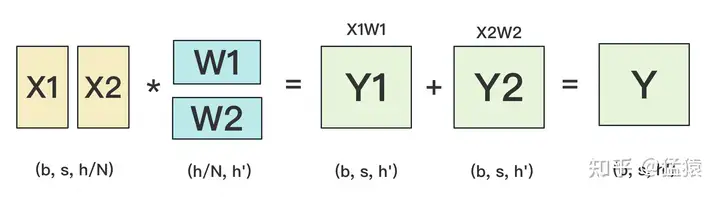
backward
+做完forward,取得预测值Y,进而可计算出损失L,接下来就能做backward了。我们重画一下forward的过程,并在其中加入backward的部分,整体流程图如下:
+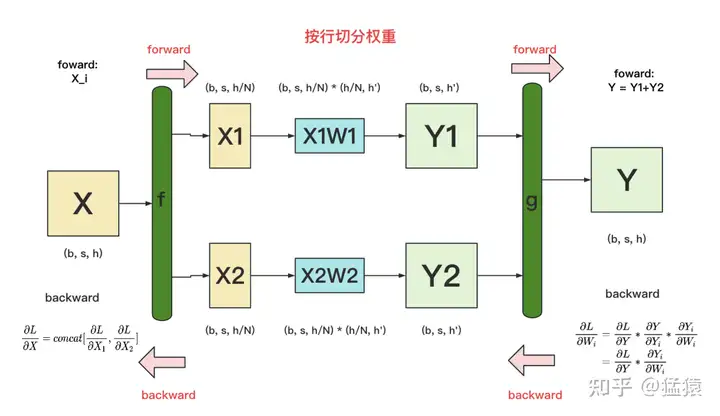
forward
+按列切分权重后,forward计算图如下:
+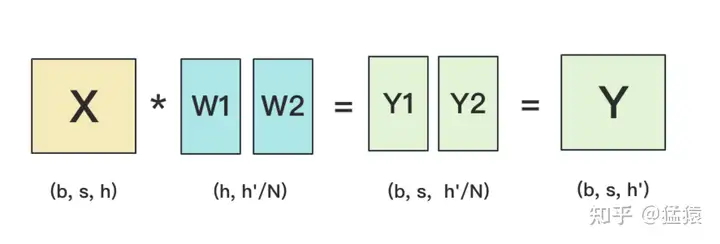
backward
+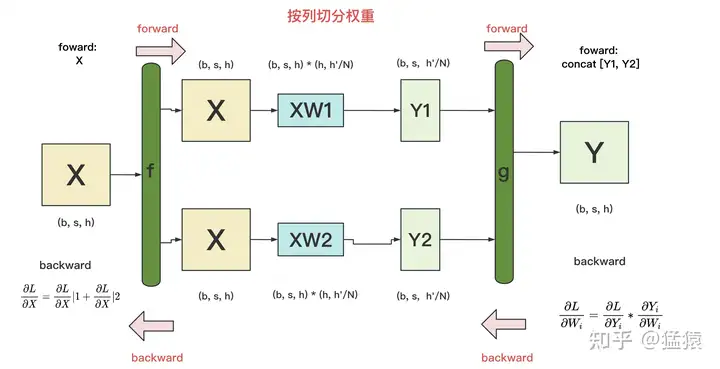
具体模型拆分方式:https://zhuanlan.zhihu.com/p/622212228
+在实际应用中,对Transformer类的模型,采用最经典方法是张量模型并行 + 数据并行,并在数据并行中引入ZeRO做显存优化。具体的架构如下:
+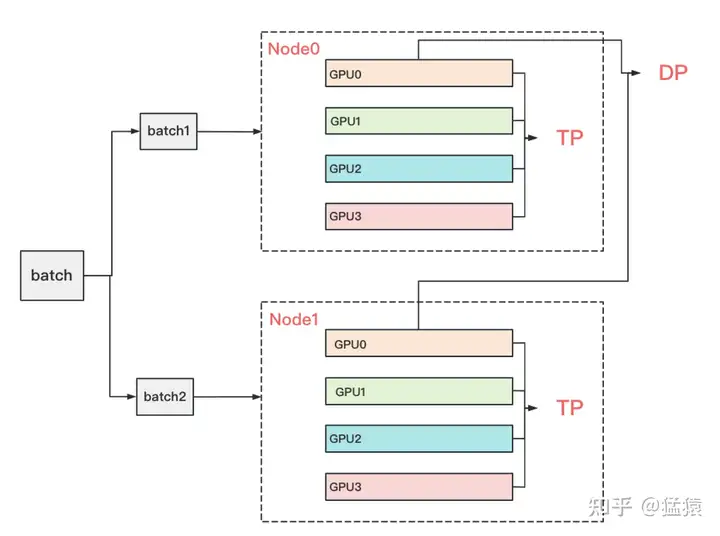
其中,node表示一台机器, 一般我们在同一台机器的GPU间做张量模型并行。在不同的机器上做数据并行 。图中颜色相同的部分,为一个数据并行组。凭直觉,我们可以知道这么设计大概率和两种并行方式的通讯量有关。具体来说, 它与TP和DP模式下每一层的通讯量有关,也与TP和DP的backward计算方式有关。
+ + +ICT周报月报
+ +月报:
+附上了 立场检测调研.docx 第一章内容
+月报:
+周报:
+与邱鹏师兄沟通立场检测项目,还没有得到师兄的反馈
+继续调研立场检测任务的新进展
+立场检测简单实验
+总结:
+月报:
+周报:
+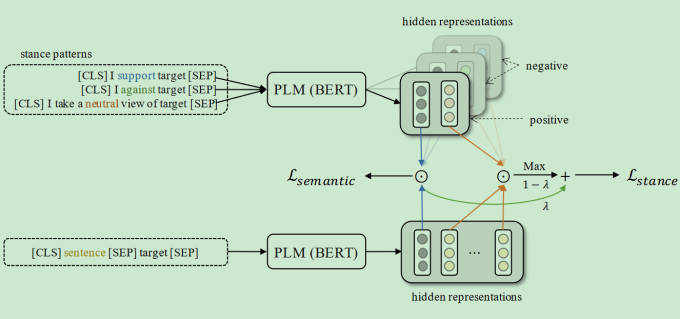
2023年10月6日,周五
+ +从7月中旬到9月底,我经历了到目前为止最忙碌的一段时间。现在十一假期已经过去,回头想想,感觉实现的成果还是很有限,白天有些困倦,自己也越发迷茫起来。
+硕士还是博士?硕士的工作准备足够吗?博士的论文可能吗?这个是摆在我面前的最急迫的选择了。可能一年前甚至半年前,我都会坚定选择硕士,但是按照目前看来,周围的绝大多数人都是向着博士的方向去准备的,就当比你强的人和比你弱的人都选择了博士的道路,无论之前有多么坚定硕士,也会发生一些动摇。可能我有一些家庭的因素,有一些自己的因素,希望我自己可以远离家乡,在另外的大城市定居。但是就当其他人没有任何这种想法的时候,你也会怀疑你自己的想法是否合理?其实历史都是相似的,想想你自己的高考之前,是不是也是这种想法?那么现在你又回到了这个地方,所以你的想法是否正确呢?你会不会走上高考之后沉沦的老路呢?这些问题都要一点一点想明白,不能放任自流,否则你自己的心态会崩溃的。现在你的状态就不怎么样,最多一个月的时间一定要把自己调整过来,后面要进入下一个阶段的考验了。
+至于个人问题,虽然还是很向往的,但是暂时也没什么办法考虑。果然大学才是最好的时机,越往后认识的人就越少了。只可惜自己大学时候没有遇到相同等级的人,过于感情用事了。现在毕竟硬件条件有限,只能慢慢随缘,相信有缘的人一定会来到,没有缘分强求也没有什么用。
+就这么多吧,自己的问题自己要慢慢克服,当下要先把每一天过好,争取每一天都有收获。
+ + +立场检测相关内容总结整理
+ +论文:Stance and Sentiment in Tweets
+数据集可视化:http://www.saifmohammad.com/WebPages/StanceDataset.htm
+Zero-shot数据集
+New data released in this submission. Short column descriptions
+相关链接:https://github.com/BinLiang-NLP/TPDG
+51284条英文Tweet
+关于公司的兼并收购的信息,第一个金融领域的数据集
+四个标签:
+21574条英文Tweet
+对三个target(Donald Trump(7953),Joe Biden(7296),Bernie Sanders(6325))的立场
+按照8:1:1进行划分
+时间:2017年4月
+等级:EACL 2017
+时间:2020年5月1日
+等级:ACL 2020
+ +思想:
+时间:2020年10月7日
+等级:EMNLP 2020(CCF B)
+思想:提出了VAST数据集
+同时提出了一个方法解决Zero-shot问题
+ +数据集:VAST
+时间:2021年4月
+等级:WWW 2021(CCF A)
+时间:2021年6月
+等级:NAACL 2021(CCF B)
+时间:2021年6月
+等级:NAACL 2021(CCF B)
+思想:使用对抗学习增强zero-shot的立场检测的效果
+ +数据集:Sem-16
+时间:2021年8月
+等级:ACL 2021(CCF A)
+思想:
+数据集:自行构建的COVID-19数据集
+时间:2021年8月
+等级:ACL 2021 Findings (CCF A)
+思想:topic在文本中是可以通过图推断出来的
+ +数据集:
+时间:2021年09月16日
+等级:EMNLP 2021 Findings
+ +思想:
+数据集:SemEval 2016
+时间:2021年08月
+等级:ACL 2021 Findings
+思想:
+数据集:SemEval-2016、Multi-Target stance datasets
+时间:2022年4月
+等级:WWW 2022(CCF A)
+ +思想:
+时间:2022年5月
+等级:ACL 2022 Workshop(WASSA)
+思想:从Wikipedia上预先查询到target的相关知识,融合到模型中进行立场检测
+数据集:P-Stance、COVID-19-Stance、VAST
+时间:2022年6月27日
+等级:SIGIR 2022(CCF A)
+ +思想:
+数据集:SemEval-2016、UKP
+时间:2022年5月
+等级:ACL 2022(CCF A)
+思想:
+ +图相关
+数据集:VAST、SEM-16、WT-WT
+时间:2022年7月
+等级:NAACL 2022 Findings(CCF B)
+思想:虚假新闻的立场检测,一篇综述性质的文章
+数据集:没有做实验,只是汇总之前人的数据、方法与结果
+时间:2022年7月
+等级:SIGIR 2022(CCF A)
+ +思想:
+数据集:VAST、SEM-16、WT-WT
+时间:2022年10月
+等级:COLING 2022
+思想:
+ +图相关
+时间:2022年12月
+等级:EMNLP 2022(CCF B)
+思想:在看见过的target的基础之上生成没有看见过的target的数据
+ +数据集:VAST、Sem-16
+时间:2022年12月30日
+等级:Arxiv
+思想:
+数据集:P-Stance
+时间:2023年2月20日
+等级:WWW 2023(CCF A)
+思想:
+ +数据集:
+时间:2023年3月31日
+等级:IEEE Transactions on Computational Social Systems(CCF C)
+思想:
+ +数据集:P-Stance,额外找到了作者的关系信息
+时间:2023年4月6日
+等级:Arxiv
+思想:通过思维链的方式,给一个例子帮助ChatGPT进行分析,在多个数据集上达到了SOTA(假)效果
+ +数据集:SEM-16、VAST、P-Stance
+时间:2023年4月
+等级:WWW 2023 Companion
+思想:
+时间:2023年4月22日
+等级:无
+思想:
+时间:2023年5月7日
+等级:ICWSM Data Challenge
+思想:
+数据集:COVID数据集
+(Contextual information integration for stance detection via cross-attention)
+时间:2023年5月25日
+等级:SEM2023(Co-located with ACL 2023)
+ +思想:
+时间:2023年5月31日
+等级:ACL 2023
+思想:
+ +数据集:SEM-16、P-Stance、VAST、Tweet-COVID
+时间:2023年6月
+等级:2023 ACM Transactions on Asian and Low-Resource Language Information Processing(SCI 4区 CCF C)
+ +思想:
+数据集:SEM16、VAST、P-stance、自己的数据集(ISD)
+时间:2023年6月
+等级:ACL 2023 Oral(CCF A)
+思想:
+ +数据集:16个benchmark数据集
+时间:2023年6月15日
+等级:Arxiv
+思想:
+数据集:x-stance
+时间:2023年7月
+等级:ACL 2023(CCF A)
+思想:第一个中文的Zero-shot数据集
+数据集:C-STANCE
+时间:2023年7月
+等级:ACL 2023(CCF A)
+思想:
+ +数据集:SemEval-2016、AM、COVID-19、P-Stance、自己构建的zero-shot数据集
+时间:2023年7月
+等级:ACL 2023 Findings(CCF A)
+思想:与知识蒸馏等相关
+数据集:AM、COVID-19、P-Stance
+时间:2023年7月
+等级:ACL 2023 Findings(CCF A)
+思想:将单语言的立场检测迁移到多语言上
+ +也是图相关的工作
+数据集:X-Stance-all
+时间:2023年7月
+等级:ACL 2023 Workshop(WASSA)
+思想:使用对比学习增强立场检测系统的鲁棒性
+数据集:DebateForum (DF), SemEval2016 (SE) ,ARC, Perspectrum, FNC-1, KSD-Biden, KSD-Trump
+时间:2023年7月
+等级:ACL 2023(CCF A)
+思想:
+数据集:VAST
+时间:2023年8月31日
+等级:Arxiv
+ +思想:
+数据集:VAST
+时间:2023年9月24日
+等级:ICWSM 2024 (CCF B)
+思想:
+数据集:covid-lies、election2016、phemerumors、semeval2016、wtwt
+时间:2023年9月26日
+等级:无
+思想:
+ +时间:2023年10月
+等级:投稿 EMNLP 2023 没中
+思想:
+ +数据集:SEM-16、VAST、WT-WT
+时间:2023年10月
+等级:Arxiv
+思想:多个LLM的Agent一起分析文本的各个方面,最后一正一反对立场进行推断,完全的Zero-shot
+ +数据集:Sem-16、WT-WT、VAST
+时间:2023年12月
+等级:EMNLP 2023(CCF B)
+思想:
+ +数据集:VAST
+时间:2023年12月
+等级:EMNLP 2023(CCF B)
+思想:多模态的信息不匹配会造成误解
+ +分别训练图片的立场检测分类器、文本的立场检测分类器,外加一些实体的知识进行识别
+数据集:NewsCLIPpings
+时间:2023年12月
+等级:EMNLP 2023(CCF B)
+思想:在文本审核中加入立场检测从而进行自动判断其是否应该被删除
+ +数据集:提出了多语言的Wiki的审核数据集
+时间:2023年12月
+等级:EMNLP 2023(CCF B)
+思想:
+数据集:
+时间:2023年12月
+等级:EMNLP 2023(CCF B)
+思想:
+ + +数据集:X-Stance、Semeval-2016、R-ita、Czech
+时间:2023年12月
+等级:EMNLP 2023(CCF B)
+思想:文字和图片的多模态立场检测,主要的贡献是数据集
+数据集:MMVAX-STANCE
+时间:2023年12月
+等级:EMNLP 2023(CCF B)
+思想:与价值观相关,不算立场检测任务
+数据集:非立场检测
+时间:2023年12月
+等级:EMNLP 2023(CCF B)
+思想:补充两种知识增强立场检测的效果
+ +数据集:Sem-16、P-Stance、VAST
+时间:2023年12月
+等级:EMNLP 2023 Findings
+思想:提出了与VAST对标的EZ-Stance数据集
+数据集:EZ-Stance
+时间:2023年12月
+等级:EMNLP 2023 Findings
+思想:思维链等zero-shot来增强直接使用大模型进行立场检测的效果
+ +数据集:
+时间:2023年12月
+等级:EMNLP 2023 Findings
+思想:用大模型对立场进行预测,然后输入到Roberta中进行再次预测
+ +数据集:Tweet-Stance、P-Stance
+时间:2023年12月
+等级:EMNLP 2023 Findings
+思想:关注一些情绪倾向
+ +数据集:SemEval、P-Stance、Climate、COVID
+时间:2023年12月
+等级:EMNLP 2023 Findings
+思想:使用大模型对人工编写的新闻的倾向进行判断,不算立场检测
+数据集:与立场检测无关
+ + +2023年10月28日,周六
+ +鼓起勇气约了一次,然而也没说什么更进一步的,就是普通同学的感觉。临走时还偏要与我AA,硬撑着没有要
+然后借比赛的幌子微信上主动找过两次,第一次还比较正常,第二次她说了好多,从比赛转到报告,又转到一点点生活(生活)。当然可能是我有想法所以我想的比较多,人家可能就是正常的一问。
+然而一条谁看了都会点赞的朋友圈,对于一个从来都会给我所有的朋友圈点赞的女生,这一次居然没有点。很伤心。这是故意的?还是为了引起我的注意?我一个如此单纯的小男生,经不住如此的试探。
+突然发现似乎每一次找她都是秒回,当然不排除都是正在看手机,但是我却从来都不敢快回复她。
+下回吃饭(要是还有下次)多试探一下吧,还是别太主动了,毕竟没有什么女性朋友,不想再失去了。
+ + +2023年11月16日,周四
+ +来北京整整两年了
+两年前的此时,我正在长沙黄花机场附近的酒店标数据(哈哈哈哈)记得那个任务很突然,也不太好做。当时应该是没有做完吧,记得后面过来之后还做了一小会时间。当然这些都不重要。
+当时是一个什么样的心情呢?对未来的憧憬?对大学三年多早已熟悉的长沙和学校的留恋?对周围优秀的同学和当时的女友的不舍?现在似乎早都忘记了。唯一记得的是,当时总体的心情还是比较愉悦的。如果给自己的心情评个分?1-10分,估计会给自己7分吧。
+然后就来到了既熟悉后陌生的北京。坐着地铁转了大半圈,遇见了老师与师兄师姐,有幸与三个健谈的室友一起度过每天的时光,与之前的同学相遇交流成长,独自一人或者与三五好友一起吃吃玩玩,同时入门了人工智能与自然语言处理。这一段时间应该算是最开心的时光了吧。没有忧愁也没有烦恼,每天有规律的做着不是很繁忙的事情,有很好的一群人陪在你身边,远方有牵挂着你的女友与家人。一切事情在有条不紊的进行当中。
+这样一直到了22年6月,开心的拿了一大堆的证书与奖品毕业的同时,几条QQ消息直接将我拉到谷底。原来我认为的“有感情基础,平稳期”就只是浮云罢了,原来人家根本就没把你当成可以走完一辈子的人。原来之前两年多三年的感情与行动全部付诸东流。我发疯了一样要挽回,虽然挽回了,但是也没有什么真正的作用。这一段感情最终还是在22年9月无疾而终了。
+从这时开始,我便没有真正的快乐过。我不断的怀疑自己,认为自己是一个很无趣的人,自己无法与别人相处,自己的情商很低,自己的先天条件不足,身高太矮等等。一直到现在,我也没有停止过任何这种想法。总是觉得自己可能就这辈子就这样了。之后也不会遇到太多的女同学,遇到了也不会喜欢我,我又不会去主动喜欢人家。我只能将自己埋在学习中,像本科一样进行各种尝试。
+写不下去了,不知道自己在说些啥,不知道自己今后的感情生活怎么办,什么都不知道。慢慢来吧,前方的道路从来都是黑暗的。
+ + +2023年11月19日,周日
+ +今天看了一些自己博客的文章,发现对外公开的居然全都是刷题或者学习的内容,对于外人来说是不是太枯燥了一些hh。
+于是挑了几篇过了很长时间的,或者已经没有隐藏的必要的文章,放出来也可以让其他人对我有更多的了解。
+当然没放出来的文章还有很多,没办法很多的内容利益相关,或者写的时候直呼其名,要是公开感觉对其他人不太好,后续我会慢慢调整一下。
+这些文章基本都在Life的标签下。
+文笔不好,请见谅。
+ + +2023年11月21日,周二
+ +又感冒了(or 发烧?)没什么区别吧,反正现在感冒必发烧。
+我还记得上初中的时候,有一次去辽工大打篮球,碰见了有一段时间没有见面的小学同学。他当时问了我一句话:“你还像小时候那样总生病吗?“当时我很奇怪,因为在我的印象里面小学时候生病不算很多。这个小学同学我至今也没有再见过了,也没有联系方式,但是这一次见面我始终都会记得,可能就因为他问了我这一句话吧。
+初中我已经不太记得了,但是高中确实一直在生病。几乎每一个月我都要感冒或者发烧一次。尤其是刚刚保送的一个月中,我还记得应该是周四的物理晚自习(当时物理老师给我的印象很恐怖),正好我也在生病,我就把卷子都扔给了我同桌,美美的回去休息了一个晚上,第二天就基本好的差不多了。从那之后我渐渐意识到,生病也并不是纯客观原因,其实自己的情绪、压力等主观因素才是生病的必要条件。
+上了大学之后我的感冒的次数就少很多了,但是每次有一些让我非常伤心难过的事情的时候,总会发一次烧。发烧逐渐成为了我宣泄的一个出口。心情难过了,无处抱怨,用较高的体温促使自己休息一下,帮助自己放松心情缓解压力。
+前一段刚刚发烧了一次,在床上躺了一天的同时出去吃了一些想吃的,完全没有看电脑。然而短暂的放松过后,自己的任务也并没有随之减轻,还是要一点一点继续推进。虽然发烧可以帮助我休息,但是实际上并没有对我的目标等起到任何的作用,短暂的麻痹过后还是要继续前行。可能我就是这样的人吧,目标很现实,丝毫不敢放松,完成一个目标后开心的同时又向着下一个目标推进,因此我现在过的并不快乐。
+如果有一天,我能真正放下一切好好休息一下,才算与自己达成了和解,内心可能才能真正快乐一些?
+写的稍微有点丧,心情不太好。
+ + +2023年12月02日,周六
+ +行了,今天基本摊牌了,估计大概率是不会再理我了,概率应该会到99.9%,就算理我估计也没有什么好结果。
+最近的一段时间感觉自己一直被这件事情主导了自己的情绪,感觉上很不好,也不能再这么下去了。总共两个月吧,今天基本就算彻底放下了。
+其实也还好,毕竟怎么看自己都是配不上人家的,对你热情一些已经很够意思了。
+还是要找一个足够喜欢你的吧,真的不要再碰你喜欢的了,真的就没有什么好结果。
+以后再说吧,我这种人真的很不适合谈恋爱,只适合好好过日子,就慢慢等待吧。
+后面认真学习,好好吃饭,在这样下去自己的胃都受不了了。
+慢慢与自己和解吧。
+ + +2023年终总结
+ +说是年终总结,然而今天才是12月18日,目前还有两项长期任务和两项短期任务压在肩上。当然年终总结嘛,我不会去絮絮叨叨那些小事,写的像那些杂谈一样。
+如果这个时候回看2022的年终总结,是可以看哭的。可能对于其他人来讲我一直都是一个较为冷漠的态度,没有什么情绪上的波动,但是实际上我的内心的活动是非常丰富的,总是有时候想着想着就有些想不开,甚至躺在床上自己偷偷哭一场。
+我很想把这个心理状态归结为ISFJ的普遍特征,最近刷小红书比较多,感觉对ISFJ的每一个特征都能对的上。然而我知道这只不过是自欺欺人罢了。ISFJ又怎样?ISFJ就要一直自己内耗下去吗?ISFJ就不配拥有快乐与幸福吗?
+又回到了我最近一直在思考的问题,什么是快乐?我一直在对自己说,对别人说,我自己不快乐,然而我真的不快乐吗?
+~我是一个可爱的分界线~
+2023的年终总结,然而现在已经是2024年的1月7日了。这期间一直发烧不舒服,反复来反复去,包括现在感觉我又有一点不舒服。这个年终总结注定难产,一方面是没有心情去写,另一方面是也还没想好写点什么,自己对于自己还是认识不清。
+想写一点就写一点,不写就抓紧把自己的任务完成吧,怎么说1月底有些东西要准备收尾了。
+ + +代码随想录-基本数据结构专题
+ +需要两点注意的是
+实际中一定要判断好自己的下标操作有没有越界!
+给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
+模板题,烂熟于心了
+第一种写法:定义 target 是在一个在左闭右闭的区间里, 也就是[left, right] (这个很重要非常重要) 。
+区间的定义决定了二分法的代码应该如何写,因为定义target在[left, right]区间,所以有如下两点:
+第二种写法:定义 target 是在一个在左闭右开的区间里,也就是[left, right) ,那么二分法的边界处理方式则截然不同。
+func search(nums []int, target int) int {
+ lennums := len(nums)
+ l := 0
+ r := lennums
+ for l < r{
+ mid := l + (r-l)/2
+ if nums[mid] == target{
+ return mid
+ } else if nums[mid] < target{
+ l = mid + 1
+ } else{
+ r = mid
+ }
+ }
+ return -1
+}class Solution {
+public:
+ int search(vector<int>& nums, int target) {
+ int left = 0;
+ int right = nums.size() - 1;
+ while(left <= right){
+ int mid = left + (right - left) / 2;
+ if (nums[mid] == target){
+ return mid;
+ } else if (nums[mid] < target){
+ left = mid + 1;
+ } else{
+ right = mid - 1;
+ }
+ }
+ return -1;
+ }
+};给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
+请必须使用时间复杂度为 O(log n) 的算法。
+func searchInsert(nums []int, target int) int {
+ lennums := len(nums)
+ l := 0
+ r := lennums
+ for l < r{
+ mid := l + (r-l)/2
+ if nums[mid] == target{
+ return mid
+ } else if nums[mid] < target{
+ l = mid + 1
+ } else{
+ r = mid
+ }
+ }
+ return l
+}class Solution {
+public:
+ int searchInsert(vector<int>& nums, int target) {
+ int left = 0;
+ int right = nums.size();
+ while(left < right){
+ int mid = left + (right - left) / 2;
+ if (nums[mid] == target){
+ return mid;
+ } else if (nums[mid] < target){
+ left = mid + 1;
+ } else{
+ right = mid;
+ }
+ }
+ return right;
+ }
+};给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
+如果数组中不存在目标值 target,返回 [-1, -1]。
+你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
+注意判断下标!!!思路没有任何问题,判断下标即可!!!!
+func searchRange(nums []int, target int) []int {
+ result := make([]int,2)
+ result[0] = lowerbound(nums,target)
+ result[1] = upperbound(nums,target)
+ return result
+}
+
+func lowerbound(nums []int, target int) int {
+ lennums := len(nums)
+ l := 0
+ r := lennums
+ for l < r{
+ mid := l + (r-l)/2
+ if nums[mid] == target{
+ r = mid
+ } else if nums[mid] < target{
+ l = mid + 1
+ } else{
+ r = mid
+ }
+ }
+ if l < lennums && nums[l] == target{
+ return l
+ }
+ return -1
+}
+
+func upperbound(nums []int, target int) int {
+ lennums := len(nums)
+ l := 0
+ r := lennums
+ for l < r{
+ mid := l + (r-l)/2
+ if nums[mid] == target{
+ l = mid + 1
+ } else if nums[mid] < target{
+ l = mid + 1
+ } else{
+ r = mid
+ }
+ }
+ if r-1 >= 0 && nums[r-1] == target{
+ return r-1
+ }
+ return -1
+}class Solution {
+public:
+ int searchbegin(vector<int>& nums, int target){
+ int left = 0;
+ int right = nums.size();
+ while(left < right){
+ int mid = left + (right - left) / 2;
+ if (nums[mid] >= target){
+ right = mid;
+ } else{
+ left = mid + 1;
+ }
+ }
+ if ((left < nums.size()) && (nums[left] == target)){
+ return left;
+ }
+ return -1;
+ }
+ int searchend(vector<int>& nums, int target){
+ int left = 0;
+ int right = nums.size();
+ while(left < right){
+ int mid = left + (right - left) / 2;
+ if (nums[mid] <= target){
+ left = mid + 1;
+ } else{
+ right = mid;
+ }
+ }
+ if ((right-1 >= 0) && (nums[right-1] == target)){
+ return right-1;
+ }
+ return -1;
+ }
+ vector<int> searchRange(vector<int>& nums, int target) {
+ vector<int> result = {-1,-1};
+ result[0] = searchbegin(nums, target);
+ result[1] = searchend(nums, target);
+ return result;
+ }
+};给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分,小数部分将被 舍去 。
+func mySqrt(x int) int {
+ if x == 1{
+ return 1
+ }
+ l := 1
+ r := x
+ for l < r{
+ mid := l + (r-l)/2
+ if mid*mid == x{
+ return mid
+ } else if mid*mid < x{
+ l = mid + 1
+ } else{
+ r = mid
+ }
+ }
+ return l-1
+}class Solution {
+public:
+ int mySqrt(int x) {
+ if (x == 0 || x == 1){
+ return x;
+ }
+ int left = 0;
+ int right = x;
+ while(left < right){
+ int mid = left + (right - left) / 2;
+ if((long long)mid * mid == x){
+ return mid;
+ } else if ((long long)mid * mid < x){
+ left = mid + 1;
+ } else{
+ right = mid;
+ }
+ }
+ return left - 1;
+ }
+};给定一个 正整数 num ,编写一个函数,如果 num 是一个完全平方数,则返回 true ,否则返回 false 。
func isPerfectSquare(num int) bool {
+ if num == 1{
+ return true
+ }
+ l := 1
+ r := num
+ for l < r{
+ mid := l + (r-l)/2
+ if mid*mid == num{
+ return true
+ } else if mid*mid < num{
+ l = mid + 1
+ } else{
+ r = mid
+ }
+ }
+ return false
+}class Solution {
+public:
+ bool isPerfectSquare(int num) {
+ if (num == 1){
+ return true;
+ }
+ int left = 0;
+ int right = num;
+ while(left < right){
+ int mid = left + (right - left) / 2;
+ if ((long long)mid * mid == num){
+ return true;
+ } else if ((long long)mid * mid < num){
+ left = mid + 1;
+ } else{
+ right = mid;
+ }
+ }
+ return false;
+ }
+};给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
+不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
+元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
+双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
+定义快慢指针
+func removeElement(nums []int, val int) int {
+ l := 0
+ numslen := len(nums)
+ for r := 0;r < numslen;r++{
+ if nums[r] != val{
+ nums[l] = nums[r]
+ l++
+ }
+ }
+ return l
+}class Solution {
+public:
+ int removeElement(vector<int>& nums, int val) {
+ int left = 0;
+ for(int right = 0;right < nums.size(); right += 1){
+ if (nums[right] != val){
+ nums[left] = nums[right];
+ left += 1;
+ }
+ }
+ return left;
+ }
+};给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。
+由于在某些语言中不能改变数组的长度,所以必须将结果放在数组nums的第一部分。更规范地说,如果在删除重复项之后有 k 个元素,那么 nums 的前 k 个元素应该保存最终结果。
+将最终结果插入 nums 的前 k 个位置后返回 k 。
+不要使用额外的空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
+还是双指针,思路不太好,想了一小会
+func removeDuplicates(nums []int) int {
+ l := 0
+ lennums := len(nums)
+ for r:=1;r<lennums;r++{
+ k := nums[l]
+ if nums[r] != k{
+ l++
+ nums[l] = nums[r]
+ }
+ }
+ return l+1
+}class Solution {
+public:
+ int removeDuplicates(vector<int>& nums) {
+ int left = 0;
+ for(int right = 1;right < nums.size();right++){
+ if (nums[right] != nums[left]){
+ nums[++left] = nums[right];
+ }
+ }
+ return left + 1;
+ }
+};给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
+func moveZeroes(nums []int) {
+ l := 0
+ numslen := len(nums)
+ for r := 0;r < numslen;r++{
+ if nums[r] != 0{
+ nums[l] = nums[r]
+ l++
+ }
+ }
+ for l != numslen{
+ nums[l] = 0
+ l++
+ }
+}class Solution {
+public:
+ void moveZeroes(vector<int>& nums) {
+ int left = 0;
+ for(int right = 0;right < nums.size();right++){
+ if(nums[right] != 0){
+ nums[left] = nums[right];
+ left += 1;
+ }
+ }
+ for(;left < nums.size();left += 1){
+ nums[left] = 0;
+ }
+ }
+};给定 s 和 t 两个字符串,当它们分别被输入到空白的文本编辑器后,如果两者相等,返回 true 。# 代表退格字符。
+注意:如果对空文本输入退格字符,文本继续为空。
+func backspaceCompare(s string, t string) bool {
+ s1 := []rune(s)
+ l := 0
+ slen := len(s1)
+ for r:=0;r<slen;r++{
+ if s1[r] == '#'{
+ if l > 0{
+ l--
+ }
+ } else{
+ s1[l] = s1[r]
+ l++
+ }
+ }
+ s1 = s1[:l]
+ s2 := []rune(t)
+ l = 0
+ tlen := len(s2)
+ for r:=0;r<tlen;r++{
+ if s2[r] == '#'{
+ if l > 0{
+ l--
+ }
+ } else{
+ s2[l] = s2[r]
+ l++
+ }
+ }
+ s2 = s2[:l]
+ return string(s1) == string(s2)
+}class Solution {
+public:
+ bool backspaceCompare(string s, string t) {
+ int slen = s.length() - 1;
+ int tlen = t.length() - 1;
+ int sskip = 0;
+ int tskip = 0;
+ while(slen >= 0 || tlen >= 0){
+ while(slen >= 0){
+ if (s[slen] == '#'){
+ sskip += 1;
+ slen -= 1;
+ } else if (sskip > 0){
+ sskip -= 1;
+ slen -= 1;
+ } else{
+ break;
+ }
+ }
+ while(tlen >= 0){
+ if (t[tlen] == '#'){
+ tskip += 1;
+ tlen -= 1;
+ } else if (tskip > 0){
+ tskip -= 1;
+ tlen -= 1;
+ } else{
+ break;
+ }
+ }
+ if (slen >= 0 && tlen >= 0){
+ if (s[slen] != t[tlen]){
+ return false;
+ }
+ } else if (slen >= 0 || tlen >= 0){
+ return false;
+ }
+ slen -= 1;
+ tlen -= 1;
+
+ }
+ return true;
+ }
+};给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
实现的是从中间往两边进行遍历,也可以修改成从两边往中间遍历的代码
+func sortedSquares(nums []int) []int {
+ lennums := len(nums)
+ minindex := 0
+ minnum := nums[0]*nums[0]
+ for i:=0;i<lennums;i++{
+ nums[i] = nums[i] * nums[i]
+ if nums[i] < minnum{
+ minnum = nums[i]
+ minindex = i
+ }
+ }
+ result := make([]int,lennums)
+ result[0] = nums[minindex]
+ l := minindex-1
+ r := minindex+1
+ i := 1
+ for l >= 0 && r < lennums{
+ if nums[l] < nums[r]{
+ result[i] = nums[l]
+ l--
+ } else{
+ result[i] = nums[r]
+ r++
+ }
+ i++
+ }
+ for l >= 0{
+ result[i] = nums[l]
+ l--
+ i++
+ }
+ for r < lennums{
+ result[i] = nums[r]
+ r++
+ i++
+ }
+ return result
+}class Solution {
+public:
+ vector<int> sortedSquares(vector<int>& nums) {
+ vector<int> result;
+ stack<int> temp;
+ int left = 0;
+ int right = nums.size() - 1;
+ while(left < right){
+ int a = nums[left] * nums[left];
+ int b = nums[right] * nums[right];
+ if (a < b){
+ temp.push(b);
+ right--;
+ } else{
+ temp.push(a);
+ left++;
+ }
+ }
+ result.push_back(nums[left] * nums[left]);
+ while(!temp.empty()){
+ result.push_back(temp.top());
+ temp.pop();
+ }
+ return result;
+ }
+};给定一个含有 n 个正整数的数组和一个正整数 target 。
+找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
+滑动窗口典型题目
+func minSubArrayLen(target int, nums []int) int {
+ lennums := len(nums)
+ l := 0
+ r := 0
+ minlength := lennums+2
+ nowsum := 0
+ allsum := 0
+ for r < lennums{
+ for r < lennums && nowsum < target{
+ nowsum += nums[r]
+ allsum += nums[r]
+ r++
+ }
+ minlength = min(minlength,r-l)
+ for nowsum >= target{
+ nowsum -= nums[l]
+ l++
+ }
+ minlength = min(minlength,r-l+1)
+ }
+
+ if allsum < target{
+ return 0
+ }
+ return minlength
+}
+
+func min(a int,b int) int{
+ if a < b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int minSubArrayLen(int target, vector<int>& nums) {
+ int result = nums.size() + 1;
+ int left = 0;
+ int right = 0;
+ int tempsum = 0;
+ while(right < nums.size()){
+ while(right < nums.size() && tempsum < target){
+ tempsum += nums[right];
+ right += 1;
+ }
+ while(tempsum >= target){
+ tempsum -= nums[left];
+ left += 1;
+ }
+ result = min(right - left + 1, result);
+ }
+ if (result == nums.size() + 1){
+ return 0;
+ }
+ return result;
+ }
+};你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示,其中 fruits[i] 是第 i 棵树上的水果 种类 。
+你想要尽可能多地收集水果。然而,农场的主人设定了一些严格的规矩,你必须按照要求采摘水果:
+你只有 两个 篮子,并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
+你可以选择任意一棵树开始采摘,你必须从 每棵 树(包括开始采摘的树)上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次,你将会向右移动到下一棵树,并继续采摘。
+一旦你走到某棵树前,但水果不符合篮子的水果类型,那么就必须停止采摘。
+给你一个整数数组 fruits ,返回你可以收集的水果的 最大 数目。
func totalFruit(fruits []int) int {
+ fruitmap := make(map[int]int)
+ lennums := len(fruits)
+ l := 0
+ r := 0
+ maxlength := 0
+ for r < lennums{
+ for r < lennums{
+ _, ok := fruitmap[fruits[r]]
+ if !ok && len(fruitmap) >= 2{
+ break
+ }
+ fruitmap[fruits[r]] += 1
+ r++
+ }
+ maxlength = max(maxlength,r-l)
+ if r < lennums{
+ for len(fruitmap) == 2{
+ if fruitmap[fruits[l]] == 1{
+ delete(fruitmap,fruits[l])
+ } else{
+ fruitmap[fruits[l]]--
+ }
+ l++
+ }
+ }
+
+ }
+ return maxlength
+}
+
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int totalFruit(vector<int>& fruits) {
+ int res = 0;
+ int left = 0;
+ map<int,int> mp;
+ for(int right=0;right < fruits.size();right += 1){
+ mp[fruits[right]]++;
+ while (mp.size() > 2){
+ mp[fruits[left]]--;
+ if (mp[fruits[left]] == 0){
+ mp.erase(mp.find(fruits[left]));
+ }
+ left++;
+ }
+ res = max(res,right-left+1);
+ }
+ return res;
+ }
+};给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
class Solution {
+public:
+ string minWindow(string s, string t) {
+ map<char,int> mp;
+ int zero_count = 0;
+ for (int i=0;i<t.size();i++){
+ mp[t[i]] += 1;
+ if (mp[t[i]] == 1){
+ zero_count += 1;
+ }
+ }
+ int min_begin = 0;
+ int min_end = s.size();
+ int left = 0;
+ bool istrue = false;
+ for(int right=0;right < s.size();right += 1){
+
+ mp[s[right]]--;
+ if (mp[s[right]] == 0){
+ zero_count -= 1;
+ }
+ while(zero_count == 0){
+ istrue = true;
+ if (right - left < min_end - min_begin){
+ min_end = right;
+ min_begin = left;
+ }
+ if(mp[s[left]] == 0){
+ zero_count = 1;
+ }
+ mp[s[left]] += 1;
+ left += 1;
+ }
+
+ }
+ if (istrue){
+ return s.substr(min_begin,min_end-min_begin+1);
+ }
+ return "";
+ }
+};给你一个正整数 n ,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
func generateMatrix(n int) [][]int {
+ result := make([][]int,n)
+ for i,_ := range result{
+ result[i] = make([]int,n)
+ }
+ boolmatrix := make([][]bool,n)
+ for i,_ := range boolmatrix{
+ boolmatrix[i] = make([]bool,n)
+ }
+ result[0][0] = 1
+ boolmatrix[0][0] = true
+ resultindex := 1
+ i := 0
+ j := 0
+ for resultindex < n*n{
+ for resultindex < n*n && j+1 < n && boolmatrix[i][j+1] == false{
+ j++
+ result[i][j] = resultindex+1
+ boolmatrix[i][j] = true
+ resultindex++
+ }
+ for resultindex < n*n && i+1 < n && boolmatrix[i+1][j] == false{
+ i++
+ result[i][j] = resultindex+1
+ boolmatrix[i][j] = true
+ resultindex++
+ }
+ for resultindex < n*n && j-1 >= 0 && boolmatrix[i][j-1] == false{
+ j--
+ result[i][j] = resultindex+1
+ boolmatrix[i][j] = true
+ resultindex++
+ }
+ for resultindex < n*n && i-1 >= 0 && boolmatrix[i-1][j] == false{
+ i--
+ result[i][j] = resultindex+1
+ boolmatrix[i][j] = true
+ resultindex++
+ }
+ }
+ return result
+}class Solution {
+public:
+ vector<vector<int>> generateMatrix(int n) {
+ vector<vector<int> > res(n, vector<int>(n));
+ int num = 1;
+ int x = 0;
+ int y = -1;
+ while(num <= n * n){
+ while(num <= n*n && y+1 < n && res[x][y+1] == 0){
+ y += 1;
+ res[x][y] = num;
+ num += 1;
+
+ }
+ while(num <= n*n && x+1 < n && res[x+1][y] == 0){
+ x += 1;
+ res[x][y] = num;
+ num += 1;
+ }
+ while(num <= n*n && y-1 >= 0 && res[x][y-1] == 0){
+ y -= 1;
+ res[x][y] = num;
+ num += 1;
+ }
+ while(num <= n*n && x-1 >= 0 && res[x-1][y] == 0){
+ x -= 1;
+ res[x][y] = num;
+ num += 1;
+ }
+ }
+ return res;
+ }
+};给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
func spiralOrder(matrix [][]int) []int {
+ m := len(matrix)
+ n := len(matrix[0])
+ result := make([]int,m*n)
+ boolmatrix := make([][]bool,m)
+ for i,_ := range boolmatrix{
+ boolmatrix[i] = make([]bool,n)
+ }
+ result[0] = matrix[0][0]
+ boolmatrix[0][0] = true
+ resultindex := 1
+ i := 0
+ j := 0
+ for resultindex < m*n{
+ for resultindex < m*n && j+1 < n && boolmatrix[i][j+1] == false{
+ j++
+ result[resultindex] = matrix[i][j]
+ boolmatrix[i][j] = true
+ resultindex++
+ }
+ for resultindex < m*n && i+1 < m && boolmatrix[i+1][j] == false{
+ i++
+ result[resultindex] = matrix[i][j]
+ boolmatrix[i][j] = true
+ resultindex++
+ }
+ for resultindex < m*n && j-1 >= 0 && boolmatrix[i][j-1] == false{
+ j--
+ result[resultindex] = matrix[i][j]
+ boolmatrix[i][j] = true
+ resultindex++
+ }
+ for resultindex < m*n && i-1 >= 0 && boolmatrix[i-1][j] == false{
+ i--
+ result[resultindex] = matrix[i][j]
+ boolmatrix[i][j] = true
+ resultindex++
+ }
+ }
+ return result
+}class Solution {
+public:
+ vector<int> spiralOrder(vector<vector<int>>& matrix) {
+ int m = matrix.size();
+ int n = matrix[0].size();
+ vector<int> res(m*n);
+ vector<vector<bool> > judge(m, vector<bool>(n));
+ int x = 0;
+ int y = -1;
+ int index = 0;
+ while(index < m * n){
+ while(index < m * n && y+1 < n && judge[x][y+1] == false){
+ y += 1;
+ judge[x][y] = true;
+ res[index] = matrix[x][y];
+ index += 1;
+ }
+ while(index < m * n && x+1 < m && judge[x+1][y] == false){
+ x += 1;
+ judge[x][y] = true;
+ res[index] = matrix[x][y];
+ index += 1;
+ }
+ while(index < m * n && y-1 >= 0 && judge[x][y-1] == false){
+ y -= 1;
+ judge[x][y] = true;
+ res[index] = matrix[x][y];
+ index += 1;
+ }
+ while(index < m * n && x-1 >= 0 && judge[x-1][y] == false){
+ x -= 1;
+ judge[x][y] = true;
+ res[index] = matrix[x][y];
+ index += 1;
+ }
+ }
+ return res;
+ }
+};链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,一个是数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(空指针的意思)。
+链接的入口节点称为链表的头结点也就是head。
+双链表:每一个节点有两个指针域,一个指向下一个节点,一个指向上一个节点。既可以向前查询也可以向后查询。
+循环链表:链表首尾相连,可以用来解决约瑟夫环问题
+数组是在内存中是连续分布的,但是链表在内存中可不是连续分布的。
+链表是通过指针域的指针链接在内存中各个节点。
+所以链表中的节点在内存中不是连续分布的 ,而是散乱分布在内存中的某地址上,分配机制取决于操作系统的内存管理。
+链表的定义:
+// 单链表
+struct ListNode {
+ int val; // 节点上存储的元素
+ ListNode *next; // 指向下一个节点的指针
+ ListNode(int x) : val(x), next(NULL) {} // 节点的构造函数
+};删除D节点,如图所示:
+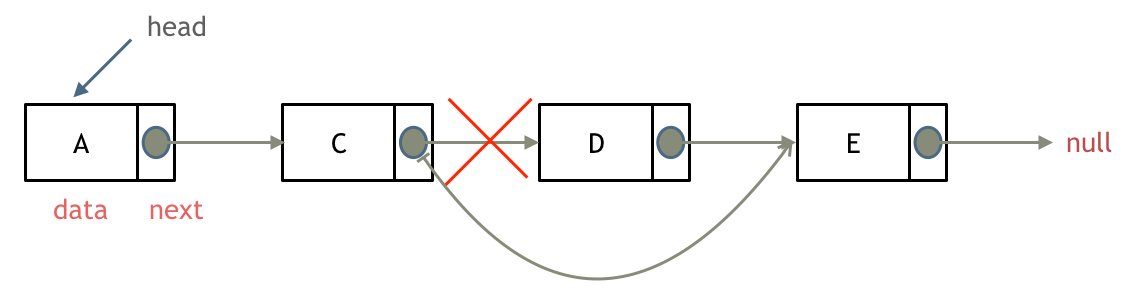
只要将C节点的next指针 指向E节点就可以了。
+那有同学说了,D节点不是依然存留在内存里么?只不过是没有在这个链表里而已。
+是这样的,所以在C++里最好是再手动释放这个D节点,释放这块内存。
+其他语言例如Java、Python,就有自己的内存回收机制,就不用自己手动释放了。
+如图所示:
+
可以看出链表的增添和删除都是O(1)操作,也不会影响到其他节点。
+但是要注意,要是删除第五个节点,需要从头节点查找到第四个节点通过next指针进行删除操作,查找的时间复杂度是O(n)。
+给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
/**
+ * Definition for singly-linked list.
+ * type ListNode struct {
+ * Val int
+ * Next *ListNode
+ * }
+ */
+func removeElements(head *ListNode, val int) *ListNode {
+ dummy := &ListNode{Val: 0, Next: head}
+ p := dummy
+ q := head
+ for q != nil{
+ if q.Val == val{
+ p.Next = q.Next
+ q = p.Next
+ } else{
+ p = q
+ q = q.Next
+ }
+ }
+ return dummy.Next
+}class Solution {
+public:
+ ListNode* removeElements(ListNode* head, int val) {
+ ListNode* dummy = new ListNode(-1);
+ dummy->next = head;
+ ListNode* p = dummy;
+ while(p->next != NULL){
+ if(p->next->val == val){
+ p->next = p->next->next;
+ } else{
+ p = p->next;
+ }
+ }
+ return dummy->next;
+ }
+};设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性:val 和 next。val 是当前节点的值,next 是指向下一个节点的指针/引用。如果要使用双向链表,则还需要一个属性 prev 以指示链表中的上一个节点。假设链表中的所有节点都是 0-index 的。
+在链表类中实现这些功能:
+get(index):获取链表中第 index 个节点的值。如果索引无效,则返回-1。
+addAtHead(val):在链表的第一个元素之前添加一个值为 val 的节点。插入后,新节点将成为链表的第一个节点。
+addAtTail(val):将值为 val 的节点追加到链表的最后一个元素。
+addAtIndex(index,val):在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度,则该节点将附加到链表的末尾。如果 index 大于链表长度,则不会插入节点。如果index小于0,则在头部插入节点。
+deleteAtIndex(index):如果索引 index 有效,则删除链表中的第 index 个节点。
type MyLinkedList struct {
+ dummy *Node
+}
+
+type Node struct {
+ Val int
+ Next *Node
+}
+
+func Constructor() MyLinkedList {
+ rear := &Node{
+ Val : -1,
+ Next : nil,
+ }
+ rear.Next = nil
+ return MyLinkedList{rear}
+}
+
+func (this *MyLinkedList) Get(index int) int {
+ head := this.dummy.Next
+ for index != 0 && head != nil{
+ index--
+ head = head.Next
+ }
+ if head == nil{
+ return -1
+ }
+ return head.Val
+}
+
+
+func (this *MyLinkedList) AddAtHead(val int) {
+ newnode := &Node{
+ Val : val,
+ Next : this.dummy.Next,
+ }
+ this.dummy.Next = newnode
+}
+
+
+func (this *MyLinkedList) AddAtTail(val int) {
+ head := this.dummy
+ for head.Next != nil{
+ head = head.Next
+ }
+ head.Next = &Node{
+ Val : val,
+ Next : nil,
+ }
+}
+
+
+func (this *MyLinkedList) AddAtIndex(index int, val int) {
+ newnode := &Node{
+ Val : val,
+ Next : nil,
+ }
+ if index <= 0{
+ newnode.Next = this.dummy.Next
+ this.dummy.Next = newnode
+ } else{
+ head := this.dummy.Next
+ for head != nil{
+ if index == 1{
+ newnode.Next = head.Next
+ head.Next = newnode
+ }
+ head = head.Next
+ index--
+ }
+ }
+}
+
+
+func (this *MyLinkedList) DeleteAtIndex(index int) {
+ if index >= 0{
+ dummy := this.dummy
+ head := this.dummy.Next
+ for head != nil{
+ if index == 0{
+ dummy.Next = head.Next
+ return
+ }
+ dummy = head
+ head = head.Next
+ index--
+ }
+ }
+}
+
+
+/**
+ * Your MyLinkedList object will be instantiated and called as such:
+ * obj := Constructor();
+ * param_1 := obj.Get(index);
+ * obj.AddAtHead(val);
+ * obj.AddAtTail(val);
+ * obj.AddAtIndex(index,val);
+ * obj.DeleteAtIndex(index);
+ */class MyLinkedList {
+public:
+ MyLinkedList() {
+ this->size = 0;
+ this->head = new ListNode(0);
+ }
+
+ int get(int index) {
+ if(index >= this->size || index <= -1){
+ return -1;
+ }
+ ListNode* p = this->head;
+ while(index != 0){
+ index -= 1;
+ p = p->next;
+ }
+ return p->val;
+ }
+
+ void addAtHead(int val) {
+ addAtIndex(0, val);
+ }
+
+ void addAtTail(int val) {
+ addAtIndex(this->size, val);
+ }
+
+ void addAtIndex(int index, int val) {
+ if(index > this->size || index <= -1){
+ return;
+ }
+ ListNode* dummy = new ListNode(-1);
+ ListNode* p = dummy;
+ dummy->next = this->head;
+ while(index != 0){
+ index -= 1;
+ p = p->next;
+ }
+ ListNode* newnode = new ListNode(val);
+ newnode->next = p->next;
+ p->next = newnode;
+ this->head = dummy->next;
+ this->size += 1;
+ }
+
+ void deleteAtIndex(int index) {
+ if(index >= this->size || index <= -1){
+ return;
+ }
+ ListNode* dummy = new ListNode(-1);
+ ListNode* p = dummy;
+ dummy->next = this->head;
+ while(index != 0){
+ index -= 1;
+ p = p->next;
+ }
+ p->next = p->next->next;
+ this->head = dummy->next;
+ this->size -= 1;
+ }
+private:
+ int size;
+ ListNode *head;
+};给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
/**
+ * Definition for singly-linked list.
+ * type ListNode struct {
+ * Val int
+ * Next *ListNode
+ * }
+ */
+func reverseList(head *ListNode) *ListNode {
+ var pre *ListNode
+ for head != nil{
+ temp := head.Next
+ head.Next = pre
+ pre = head
+ head = temp
+ }
+ return pre
+}class Solution {
+public:
+ ListNode* reverseList(ListNode* head) {
+ ListNode* pre = NULL;
+ ListNode* p = head;
+ while(p != NULL){
+ ListNode* q = p->next;
+ p->next = pre;
+ pre = p;
+ p = q;
+ }
+ return pre;
+ }
+};给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
+/**
+ * Definition for singly-linked list.
+ * type ListNode struct {
+ * Val int
+ * Next *ListNode
+ * }
+ */
+func swapPairs(head *ListNode) *ListNode {
+ dummy := &ListNode{
+ Val : 0,
+ Next : head,
+ }
+ var pre *ListNode
+ pre = dummy
+ for head != nil && head.Next != nil{
+ temp := head.Next.Next
+ pre.Next = head.Next
+ head.Next = temp
+ pre.Next.Next = head
+ pre = head
+ head = temp
+ }
+ head = dummy.Next
+ return head
+}class Solution {
+public:
+ ListNode* swapPairs(ListNode* head) {
+ ListNode* dummy = new ListNode(-1);
+ dummy->next = head;
+ ListNode* p = dummy;
+ while(p != NULL){
+ if (p->next != NULL && p->next->next != NULL){
+ ListNode* a = p->next;
+ ListNode* b = a->next;
+ ListNode* c = b->next;
+ p->next = b;
+ b->next = a;
+ a->next = c;
+ p = a;
+ } else{
+ break;
+ }
+ }
+ return dummy->next;
+ }
+};给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
还可以使用快慢指针做这个题
+/**
+ * Definition for singly-linked list.
+ * type ListNode struct {
+ * Val int
+ * Next *ListNode
+ * }
+ */
+func removeNthFromEnd(head *ListNode, n int) *ListNode {
+ dummy := &ListNode{
+ Val:0,
+ Next: head,
+ }
+ count := 1
+ for head != nil{
+ head = head.Next
+ count++
+ }
+ var pre *ListNode
+ pre = dummy
+ head = dummy.Next
+ for count-n != 1{
+ count--
+ pre = head
+ head = head.Next
+ }
+ pre.Next = head.Next
+ return dummy.Next
+}class Solution {
+public:
+ ListNode* removeNthFromEnd(ListNode* head, int n) {
+ ListNode* dummy = new ListNode(-1);
+ dummy->next = head;
+ ListNode* slow = dummy;
+ ListNode* fast = dummy;
+ while(n--){
+ fast = fast->next;
+ }
+ while(fast->next != NULL){
+ slow = slow->next;
+ fast = fast->next;
+ }
+ slow->next = slow->next->next;
+ return dummy->next;
+ }
+};给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
+题目数据 保证 整个链式结构中不存在环。
+注意,函数返回结果后,链表必须 保持其原始结构 。
+/**
+ * Definition for singly-linked list.
+ * type ListNode struct {
+ * Val int
+ * Next *ListNode
+ * }
+ */
+func getIntersectionNode(headA, headB *ListNode) *ListNode {
+ var p,q *ListNode
+ p = headA
+ q = headB
+ count := 60000
+ if p == nil || q == nil{
+ return nil
+ }
+ for p != q && count > 0{
+ p = p.Next
+ q = q.Next
+ if p == nil{
+ p = headB
+ }
+ if q == nil{
+ q = headA
+ }
+ count--
+ }
+ if count == 0{
+ return nil
+ }
+ return p
+}class Solution {
+public:
+ ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
+ ListNode* p = headA;
+ ListNode* q = headB;
+ int flag = 4;
+ while(flag > 0){
+ if(p == q){
+ return p;
+ }
+ if (p->next != NULL){
+ p = p->next;
+ } else{
+ p = headB;
+ flag -= 1;
+ }
+ if(q->next != NULL){
+ q = q->next;
+ } else{
+ q = headA;
+ flag -= 1;
+ }
+ }
+ return NULL;
+ }
+};给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
+如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
+不允许修改 链表。
+/**
+ * Definition for singly-linked list.
+ * type ListNode struct {
+ * Val int
+ * Next *ListNode
+ * }
+ */
+func detectCycle(head *ListNode) *ListNode {
+ slow, fast := head, head
+ for fast != nil && fast.Next != nil {
+ slow = slow.Next
+ fast = fast.Next.Next
+ if slow == fast {
+ for slow != head {
+ slow = slow.Next
+ head = head.Next
+ }
+ return head
+ }
+ }
+ return nil
+}class Solution {
+public:
+ ListNode *detectCycle(ListNode *head) {
+ if (head == NULL || head->next == NULL){
+ return NULL;
+ }
+ ListNode* slow = head;
+ ListNode* fast = head;
+ do{
+ if (slow == NULL || fast == NULL || fast->next == NULL){
+ return NULL;
+ }
+ slow = slow->next;
+ fast = fast->next->next;
+ }while(slow != fast);
+ slow = head;
+ while(slow != fast){
+ slow = slow->next;
+ fast = fast->next;
+ }
+ return slow;
+ }
+};
其实直白来讲其实数组就是一张哈希表。哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素
+一般哈希表都是用来快速判断一个元素是否出现集合里。
+给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
+注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
+func isAnagram(s string, t string) bool {
+ alphabet := make([]int, 26)
+ sBytes := []byte(s)
+ tBytes := []byte(t)
+ lens := len(sBytes)
+ lent := len(tBytes)
+ if lens != lent{
+ return false
+ }
+ for i:=0;i<lens;i++{
+ alphabet[s[i]-'a']++
+ alphabet[t[i]-'a']--
+ }
+ for i:=0;i<26;i++{
+ if alphabet[i] != 0{
+ return false
+ }
+ }
+ return true
+}class Solution {
+public:
+ bool isAnagram(string s, string t) {
+ unordered_map<char, int> mp;
+ for(int i=0;i<s.length();i++){
+ mp[s[i]] += 1;
+ }
+ for(int i=0;i<t.length();i++){
+ mp[t[i]] -= 1;
+ }
+ for(auto it = mp.begin();it != mp.end();it++){
+ if(it->second != 0){
+ return false;
+ }
+ }
+ return true;
+ }
+};给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
+字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母通常恰好只用一次。
+func groupAnagrams(strs []string) [][]string {
+ mp := map[string][]string{}
+ for _, str := range strs {
+ s := []byte(str)
+ sort.Slice(s, func(i, j int) bool { return s[i] < s[j] })
+ sortedStr := string(s)
+ mp[sortedStr] = append(mp[sortedStr], str)
+ }
+ ans := make([][]string, 0, len(mp))
+ for _, v := range mp {
+ ans = append(ans, v)
+ }
+ return ans
+}class Solution {
+public:
+
+ vector<vector<string>> groupAnagrams(vector<string>& strs) {
+ vector<vector<string> > result;
+ unordered_map<string, vector<string> > mp;
+ int arraylen = strs.size();
+ for(int i=0;i<arraylen;i++){
+ string t = strs[i];
+ sort(t.begin(),t.end());
+ mp[t].push_back(strs[i]);
+ }
+ for(auto it = mp.begin(); it != mp.end(); it++){
+ result.push_back(it->second);
+ }
+ return result;
+ }
+};给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
+异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
+func findAnagrams(s string, p string) []int {
+ alphabet := make([]int,26)
+ result := []int{}
+ lens := len(s)
+ lenp := len(p)
+ if lenp > lens{
+ return result
+ }
+ for i:=0;i<lenp;i++{
+ alphabet[p[i]-'a']++
+ alphabet[s[i]-'a']--
+ }
+ sign := 0
+ for i:=lenp;i<lens;i++{
+ sign = 0
+ for j:=0;j<26;j++{
+ if alphabet[j] != 0{
+ sign = 1
+ break
+ }
+ }
+ if sign == 0{
+ result = append(result,i-lenp)
+ }
+ alphabet[s[i]-'a']--
+ alphabet[s[i-lenp]-'a']++
+ }
+ sign = 0
+ for j:=0;j<26;j++{
+ if alphabet[j] != 0{
+ sign = 1
+ break
+ }
+ }
+ if sign == 0{
+ result = append(result,lens-lenp)
+ }
+ return result
+}class Solution {
+public:
+ bool judgemp(unordered_map<char, int> mp){
+ for(auto it = mp.begin();it != mp.end();it++){
+ if(it->second != 0){
+ return false;
+ }
+ }
+ return true;
+ }
+ vector<int> findAnagrams(string s, string p) {
+ vector<int> result;
+ unordered_map<char, int> mp;
+ for(int i=0;i<p.length();i++){
+ mp[p[i]] += 1;
+ }
+ int left = 0;
+ for(int right=0;right < s.length();right++){
+ mp[s[right]] -= 1;
+ if(right - left != p.length()-1){
+ continue;
+ }
+ if(judgemp(mp)){
+ result.push_back(left);
+ }
+ mp[s[left]] += 1;
+ left += 1;
+ }
+ return result;
+ }
+};给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。
func intersection(nums1 []int, nums2 []int) []int {
+ result := []int{}
+ nums := make([]int,1001)
+ for _,i := range nums1{
+ nums[i] = 1
+ }
+ for _,i := range nums2{
+ if nums[i] == 1{
+ nums[i] = 2
+ result = append(result,i)
+ }
+ }
+ return result
+}class Solution {
+public:
+ vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
+ vector<int> result;
+ unordered_map<int, bool> mp1;
+ unordered_map<int, bool> mp2;
+ for(int i=0;i<nums1.size();i++){
+ mp1[nums1[i]] = true;
+ }
+ for(int i=0;i<nums2.size();i++){
+ mp2[nums2[i]] = true;
+ }
+ for(auto it = mp1.begin();it != mp1.end(); it++){
+ if(mp2.find(it->first) != mp2.end()){
+ result.push_back(it->first);
+ }
+ }
+ return result;
+ }
+};给你两个整数数组 nums1 和 nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结果的顺序。
+func intersect(nums1 []int, nums2 []int) []int {
+ result := []int{}
+ nums11 := make([]int,1001)
+ nums22 := make([]int,1001)
+ for _,i := range nums1{
+ nums11[i]++
+ }
+ for _,i := range nums2{
+ nums22[i]++
+ }
+ for i,j := range nums11{
+ a := min(j,nums22[i])
+ for k:= 0;k<a;k++{
+ result = append(result,i)
+ }
+ }
+ return result
+}
+
+func min ( a int, b int) int {
+ if a < b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
+ vector<int> result;
+ unordered_map<int, int> mp1;
+ unordered_map<int, int> mp2;
+ for(int i=0;i<nums1.size();i++){
+ mp1[nums1[i]] += 1;
+ }
+ for(int i=0;i<nums2.size();i++){
+ mp2[nums2[i]] += 1;
+ }
+ for(auto it = mp1.begin();it != mp1.end(); it++){
+ if(mp2.find(it->first) != mp2.end()){
+ for(int i=0;i<min(mp2[it->first],it->second);i++){
+ result.push_back(it->first);
+ }
+ }
+ }
+ return result;
+ }
+};编写一个算法来判断一个数 n 是不是快乐数。
+「快乐数」 定义为:
+对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
+然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
+如果这个过程 结果为 1,那么这个数就是快乐数。
+如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
func isHappy(n int) bool {
+ for i:=0;i<6;i++{
+ result := 0
+ for n != 0{
+ result = result + (n%10) * (n%10)
+ n /= 10
+ }
+ if result == 1{
+ return true
+ }
+ n = result
+ }
+ return false
+}class Solution {
+public:
+ bool isHappy(int n) {
+ unordered_map<int,bool> mp;
+ while(1){
+ if(mp.find(n) != mp.end()){
+ return false;
+ }
+ if(n == 1){
+ return true;
+ }
+ mp[n] = true;
+ int res = 0;
+ while(n != 0){
+ res += (n%10) * (n%10);
+ n = n/10;
+ }
+ n = res;
+ }
+ return true;
+ }
+};给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
+你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
+你可以按任意顺序返回答案。
+func twoSum(nums []int, target int) []int {
+ result := make([]int,2)
+ mapnum := make(map[int]int)
+ for i,n := range nums{
+ if j, ok := mapnum[target-n]; ok {
+ result[0] = j
+ result[1] = i
+ return result
+ } else{
+ mapnum[n] = i
+ }
+ }
+ return result
+}class Solution {
+public:
+ vector<int> twoSum(vector<int>& nums, int target) {
+ vector<int> result(2);
+ unordered_map<int, int> mp;
+ for(int i=0;i<nums.size();i++){
+ if(mp.find(target-nums[i]) != mp.end()){
+ result[0] = i;
+ result[1] = mp[target-nums[i]];
+ } else{
+ mp[nums[i]] = i;
+ }
+ }
+ return result;
+ }
+};给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:
+0 <= i, j, k, l < n,nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
+func fourSumCount(nums1 []int, nums2 []int, nums3 []int, nums4 []int) int {
+ result := 0
+ numsmap := make(map[int]int)
+ for _,i := range nums1{
+ for _,j := range nums2{
+ numsmap[i+j]++
+ }
+ }
+ for _,i := range nums3{
+ for _,j := range nums4{
+ k,ok := numsmap[0-(i+j)]
+ if ok{
+ result += k
+ }
+ }
+ }
+ return result
+}class Solution {
+public:
+ int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
+ unordered_map <int, int> mp;
+ for(int i=0;i<nums1.size();i++){
+ for(int j=0;j<nums2.size();j++){
+ mp[nums1[i] + nums2[j]] += 1;
+ }
+ }
+ int count_result = 0;
+ for(int i=0;i<nums3.size();i++){
+ for(int j=0;j<nums4.size();j++){
+ if(mp.find(0-nums3[i]-nums4[j]) != mp.end()){
+ count_result += mp[0-nums3[i]-nums4[j]];
+ }
+ }
+ }
+ return count_result;
+ }
+};给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。
+如果可以,返回 true ;否则返回 false 。
+magazine 中的每个字符只能在 ransomNote 中使用一次。
+func canConstruct(ransomNote string, magazine string) bool {
+ alphabet := make([]int,26)
+ for i:=0;i<len(magazine);i++{
+ alphabet[magazine[i]-'a']++
+ }
+ for i:=0;i<len(ransomNote);i++{
+ alphabet[ransomNote[i]-'a']--
+ if alphabet[ransomNote[i]-'a'] < 0{
+ return false
+ }
+ }
+ return true
+}class Solution {
+public:
+ bool canConstruct(string ransomNote, string magazine) {
+ unordered_map<char,int> mp;
+ for(int i=0;i<ransomNote.size();i++){
+ mp[ransomNote[i]] += 1;
+ }
+ for(int i=0;i<magazine.size();i++){
+ mp[magazine[i]] -= 1;
+ }
+ for(auto it = mp.begin(); it != mp.end();it++){
+ if(it->second > 0){
+ return false;
+ }
+ }
+ return true;
+ }
+};编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
+不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
+func reverseString(s []byte) {
+ for i, j := 0, len(s)-1; i < j; {
+ s[i], s[j] = s[j], s[i]
+ i++
+ j--
+ }
+}class Solution {
+public:
+ void reverseString(vector<char>& s) {
+ int slen = s.size();
+ for(int left=0;left < slen/2;left++){
+ char t = s[left];
+ s[left] = s[slen-left-1];
+ s[slen-left-1] = t;
+ }
+
+ }
+};给定一个字符串 s 和一个整数 k,从字符串开头算起,每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。
+如果剩余字符少于 k 个,则将剩余字符全部反转。
+如果剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样。
+func reverseStr(s string, k int) string {
+ sbytes := []byte(s)
+ lens := len(s)
+ sign := 0
+ left := 1
+ right := len(s)
+ for i:=1;i<=lens;i++{
+ if i % k == 0{
+ if sign == 0{
+ sign = 1
+ right = i
+ } else{
+ sign = 0
+ x := left
+ y := right
+ for x < y{
+ sbytes[x-1],sbytes[y-1] = sbytes[y-1],sbytes[x-1]
+ x++
+ y--
+ }
+ left = i+1
+ }
+ }
+ }
+ if sign == 0{
+ right = len(s)
+ }
+ x := left
+ y := right
+ for x < y{
+ sbytes[x-1],sbytes[y-1] = sbytes[y-1],sbytes[x-1]
+ x++
+ y--
+ }
+ return string(sbytes)
+}class Solution {
+public:
+ string reversesmallstr(string s){
+ reverse(s.begin(), s.end());
+ return s;
+ }
+ string reverseStr(string s, int k) {
+ string result_str = "";
+ while(s.size() >= 2 * k){
+ result_str += reversesmallstr(s.substr(0,k));
+ s.erase(0,k);
+ result_str += s.substr(0,k);
+ s.erase(0,k);
+ }
+ if (s.size() >= k){
+ result_str += reversesmallstr(s.substr(0,k));
+ s.erase(0,k);
+ result_str += s;
+ } else{
+ result_str += reversesmallstr(s);
+ }
+ return result_str;
+ }
+};请实现一个函数,把字符串 s 中的每个空格替换成"%20"。
func replaceSpace(s string) string {
+ var newS []byte
+ for i := range s {
+ if s[i] == ' ' {
+ newS = append(newS, '%', '2', '0')
+ } else {
+ newS = append(newS, s[i])
+ }
+ }
+ return string(newS)
+}给你一个字符串 s ,请你反转字符串中 单词 的顺序。
+单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
+返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
+注意:输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
+func reverseWords(s string) string {
+ var result string
+ var store []string
+ sbytes := []byte(s)
+ sign := 1
+ point := 0
+ for i:=0;i<len(s);i++{
+ if sbytes[i] == ' '{
+ if sign == 0{
+ store = append(store,s[point:i])
+ sign = 1
+ }
+ } else{
+ if sign == 1{
+ point = i
+ sign = 0
+ }
+ }
+ }
+ if sign == 0{
+ store = append(store,s[point:len(s)])
+ }
+ for i:=len(store)-1;i>=0;i--{
+ result += store[i]
+ if i != 0{
+ result += " "
+ }
+ }
+ return result
+}class Solution {
+public:
+ string reverse_word(string s){
+ reverse(s.begin(), s.end());
+ return s;
+ }
+ string reverseWords(string s) {
+ string result_str = "";
+ int left = 0;
+ while(left < s.size()){
+ while(left < s.size() && s[left] == ' '){
+ left += 1;
+ }
+ int right = left;
+ while(right < s.size() && s[right] != ' '){
+ right += 1;
+ }
+ if(left == right){
+ break;
+ }
+ result_str = result_str + reverse_word(s.substr(left,right-left)) + " ";
+ left = right;
+ }
+ string result_str2 = result_str.substr(0,result_str.size()-1);
+
+ return reverse_word(result_str2);
+ }
+};给定两个字符串, s 和 goal。如果在若干次旋转操作之后,s 能变成 goal ,那么返回 true 。
+s 的 旋转操作 就是将 s 最左边的字符移动到最右边。
+例如, 若 s = ‘abcde’,在旋转一次之后结果就是’bcdea’ 。
+class Solution {
+public:
+ bool rotateString(string s, string goal) {
+ if (s.size() != goal.size()){
+ return false;
+ }
+ for(int left = 0;left < s.size();left++){
+ string comp = s.substr(1,s.size()-1) + s.substr(0,1);
+ s = comp;
+ if(s == goal){
+ return true;
+ }
+ }
+ return false;
+ }
+};字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如,输入字符串"abcdefg"和数字2,该函数将返回左旋转两位得到的结果"cdefgab"。
+func reverseLeftWords(s string, n int) string {
+ return s[n:]+s[:n]
+}给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
+func strStr(haystack string, needle string) int {
+ needlelen := len(needle)
+ haystacklen := len(haystack)
+ next := make([]int,needlelen)
+ next[0] = 0
+ j := 0
+ for i:=1;i<needlelen;i++{
+ for j > 0 && needle[i] != needle[j]{
+ j = next[j-1]
+ }
+ if needle[i] == needle[j]{
+ j++
+ }
+ next[i] = j
+ }
+ j = 0
+ for i:=0;i<haystacklen;i++{
+ for j > 0 && needle[j] != haystack[i]{
+ j = next[j-1]
+ }
+ if needle[j] == haystack[i]{
+ j++
+ }
+ if j == needlelen{
+ return i-j+1;
+ }
+ }
+ return -1
+}给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。
func repeatedSubstringPattern(s string) bool {
+ lens := len(s)
+ next := make([]int,lens)
+ next[0] = 0
+ j := 0
+ for i:=1;i<lens;i++{
+ for j > 0 && s[i] != s[j]{
+ j = next[j-1]
+ }
+ if s[i] == s[j]{
+ j++
+ }
+ next[i] = j
+ }
+ if next[lens-1] != 0 && lens % (lens-next[lens-1]) == 0{
+ return true
+ }
+ return false
+}class Solution {
+public:
+ bool repeatedSubstringPattern(string s) {
+ int slen = s.size();
+ if (slen == 1){
+ return false;
+ }
+ for(int i=1;i<slen / 2+1;i++){
+ if(slen % i != 0){
+ continue;
+ }
+ string t = s.substr(0,i);
+ bool flag = true;
+ for(int index=i;index < slen-i+1;index += i){
+ if(s.substr(index,i) != t){
+ flag = false;
+ break;
+ }
+ }
+ if(flag){
+ return true;
+ }
+ }
+ return false;
+ }
+};代码随想录-动态规划专题
+ +动态规划中每一个状态一定是由上一个状态推导出来的, 这一点就区分于贪心 ,贪心没有状态推导,而是从局部直接选最优的
+解决动态规划问题的五步曲:
+做动规的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,确定最后推出的是想要的结果 。
+然后再写代码,如果代码没通过就打印dp数组,看看是不是和自己预先推导的哪里不一样。
+如果打印出来和自己预先模拟推导是一样的,那么就是自己的递归公式、初始化或者遍历顺序有问题了。
+如果和自己预先模拟推导的不一样,那么就是代码实现细节有问题。
+斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
+F(n) = F(n - 1) + F(n - 2),其中 n > 1给定 n ,请计算 F(n) 。
dp[i]=dp[i-1]+dp[i-2]dp[0]=0, dp[1]=1因为每一个数字的求出只依赖于之前的两个数字,因此不需要存储整个数组,只需要存储前两个数字即可。
+func fib(n int) int {
+ a := 0
+ b := 1
+ if n == 0 {
+ return a
+ } else if n == 1 {
+ return b
+ }
+ var c int
+ for i := 2; i <= n; i++ {
+ c = a + b
+ if i == n {
+ break
+ }
+ a, b = b, c
+ }
+ return c
+}class Solution {
+public:
+ int fib(int n) {
+ if(n == 0 || n == 1){
+ return n;
+ }
+ vector<int> dp(n+1);
+ dp[0] = 0;
+ dp[1] = 1;
+ for(int i=2;i<=n;i++){
+ dp[i] = dp[i-1] + dp[i-2];
+ }
+ return dp[n];
+ }
+};假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
dp[i]=dp[i-1]+dp[i-2]dp[1]=1, dp[2]=2(注意 dp[0]是没有意义的,不要强行赋值进去)func climbStairs(n int) int {
+ dp := make([]int, n+1)
+ dp[0] = 1
+ dp[1] = 1
+ for i:=2;i<=n;i++{
+ dp[i]=dp[i-1]+dp[i-2]
+ }
+ return dp[n]
+}class Solution {
+public:
+ int climbStairs(int n) {
+ vector<int> dp(n+1);
+ dp[0] = 1;
+ dp[1] = 1;
+ for(int i=2;i<=n;i++){
+ dp[i] = dp[i-1] + dp[i-2];
+ }
+ return dp[n];
+ }
+};给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
+你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
+请你计算并返回达到楼梯顶部的最低花费。
+dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]),这里认为第一步是不要花钱的,最后一步需要花钱。dp[0]=0, dp[1]=0(因为第一步都不要钱)func minCostClimbingStairs(cost []int) int {
+ n := len(cost)
+ dp := make([]int,n+1)
+ dp[0],dp[1] = 0,0
+ for i:= 2;i<=n;i++{
+ dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
+ }
+ return dp[n]
+}
+
+func min(a, b int) int {
+ if a < b {
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int minCostClimbingStairs(vector<int>& cost) {
+ int n = cost.size();
+ vector<int> dp(n+2);
+ dp[1] = 0;
+ dp[2] = 0;
+ for(int i=3;i<=n+1;i++){
+ dp[i] = min(dp[i-1] + cost[i-2], dp[i-2] + cost[i-3]);
+ }
+ return dp[n+1];
+ }
+};一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
+问总共有多少条不同的路径?
+dp[i][j]=dp[i-1][j]+dp[i][j-1]func uniquePaths(m int, n int) int {
+ dp := make([][]int, m+1)
+ for i := 0; i < m+1; i++ {
+ dp[i] = make([]int, n+1)
+ }
+ for i:=1;i<m+1;i++{
+ for j:=1;j<n+1;j++{
+ if i == 1 || j == 1{
+ dp[i][j] = 1
+ } else{
+ dp[i][j] = dp[i-1][j] + dp[i][j-1]
+ }
+ }
+ }
+ return dp[m][n]
+}class Solution {
+public:
+ int uniquePaths(int m, int n) {
+ vector<vector<int> > dp(m, vector<int>(n));
+ for(int i=0;i<m;i++){
+ dp[i][0] = 1;
+ }
+ for(int j=0;j<n;j++){
+ dp[0][j] = 1;
+ }
+ for(int i=1;i<m;i++){
+ for(int j=1;j<n;j++){
+ dp[i][j] = dp[i-1][j] + dp[i][j-1];
+ }
+ }
+ return dp[m-1][n-1];
+ }
+};事实上使用一个一维数组就可以实现了,可以对代码的空间复杂度进行优化:
+func uniquePaths(m int, n int) int {
+ dp := make([]int, n+1)
+ for i := 0; i < n+1; i++ {
+ dp[i] = 1
+ }
+ for i:=2;i<m+1;i++{
+ for j:=2;j<n+1;j++{
+ dp[j] += dp[j-1]
+ }
+ }
+ return dp[n]
+}一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
+机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
+现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
+网格中的障碍物和空位置分别用 1 和 0 来表示。
+dp[i][j]=dp[i-1][j]+dp[i][j-1],但是,若该格子是障碍物,到达这个格子的路径数量为0,因此直接置 dp[i][j]=0class Solution {
+public:
+ int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
+ int m = obstacleGrid.size();
+ int n = obstacleGrid[0].size();
+ vector<vector<int> > dp(m+1, vector<int>(n+1));
+ if(obstacleGrid[0][0] == 1){
+ return 0;
+ }
+ for(int i=0;i<m;i++){
+ dp[i][0] = 0;
+ }
+ for(int j=0;j<n;j++){
+ dp[0][j] = 0;
+ }
+ for(int i=1;i<=m;i++){
+ for(int j=1;j<=n;j++){
+ if(i == 1 && j == 1){
+ dp[i][j] = 1;
+ continue;
+ }
+ if(obstacleGrid[i-1][j-1] == 1){
+ dp[i][j] = 0;
+ } else{
+ dp[i][j] = dp[i-1][j] + dp[i][j-1];
+ }
+ }
+ }
+ return dp[m][n];
+ }
+};直接给出状态压缩后的写法:
+func uniquePathsWithObstacles(obstacleGrid [][]int) int {
+ m := len(obstacleGrid)
+ n := len(obstacleGrid[0])
+ dp := make([]int, n)
+ var sign int = 0
+ for j:=0;j<n;j++{
+ if obstacleGrid[0][j] == 1{
+ sign = 1
+ dp[j] = 0
+ } else if sign == 1{
+ dp[j] = 0
+ } else{
+ dp[j] = 1
+ }
+ }
+ for i:=1;i<m;i++{
+ for j:=0;j<n;j++{
+ if obstacleGrid[i][j] == 1{
+ dp[j] = 0
+ } else{
+ if j != 0{
+ dp[j] += dp[j-1]
+ }
+ }
+ }
+ }
+ return dp[n-1]
+}给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
+dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j))dp[0]和 dp[1]都没有意义,dp[2]=1func integerBreak(n int) int {
+ dp := make([]int,n+1)
+ dp[2] = 1
+ for i:=3;i<=n;i++{
+ for j:=1;j<i-1;j++{
+ dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j))
+ }
+ }
+ return dp[n]
+}
+func max(a,b int) int {
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int integerBreak(int n) {
+ vector<int> dp(n+1);
+ dp[1] = 1;
+ for(int i=2;i<=n;i++){
+ for(int j=i-1;j>=1;j--){
+ dp[i] = max(dp[i],max(j * dp[i-j], j*(i-j)));
+ }
+ }
+ return dp[n];
+ }
+};给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
dp[i] = dp[i] + dp[j-1] * dp[i-j],j是遍历时候的标记。dp[0]=1,dp[1]=1,感觉 dp[0]也是很难解释。。。func numTrees(n int) int {
+ dp := make([]int,n+1)
+ dp[0] = 1
+ dp[1] = 1
+ for i:=2;i<=n;i++{
+ for j:=1;j<=i;j++{
+ dp[i] = dp[i] + dp[j-1] * dp[i-j]
+ }
+ }
+ return dp[n]
+}class Solution {
+public:
+ int numTrees(int n) {
+ vector<int> dp(n+1);
+ dp[0] = 1;
+ dp[1] = 1;
+ for(int i=2;i<=n;i++){
+ for(int j=i;j>=1;j--){
+ dp[i] = dp[i] + dp[j-1] * dp[i-j];
+ }
+ }
+ return dp[n];
+ }
+};有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。 每件物品只能用一次 ,求解将哪些物品装入背包里物品价值总和最大。
+再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
+那么可以有两个方向推出来dp[i][j],
+所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
+关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱 。
+首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
+ +状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
+dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
+那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
+当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量足够放编号0物品。
+要理解递归的本质和递推的方向 。
+dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
+dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向)
+先遍历物品再遍历背包这个顺序更好理解,但是怎么遍历都可以
+对于背包问题其实状态都是可以压缩的。
+在使用二维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
+其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
+与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了 ,只用dp[j](一维数组,也可以理解是一个滚动数组)。
+这就是滚动数组的由来,需要满足的条件是上一层可以重复利用,直接拷贝到当前层。
+在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值最大可以为dp[j]。
+dp[j]为 容量为j的背包所背的最大价值,那么如何推导dp[j]呢?
+dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
+dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
+此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,
+所以递归公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
+可以看出相对于二维dp数组的写法,就是把dp[i][j]中i的维度去掉了。
+关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱 。
+dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
+那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
+看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
+dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
+这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了 。
+那么我假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了。
+和二维dp的写法中,遍历背包的顺序是不一样的!
+二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。
+倒序遍历是为了保证物品i只被放入一次! 但如果一旦正序遍历了,那么物品0就会被重复加入多次!
+从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
+为什么二维dp数组历的时候不用倒序呢? 因为对于二维dp,dp[i][j]都是通过上一层即dp[i - 1][j]计算而来,本层的dp[i][j]并不会被覆盖!
+再来看看两个嵌套for循环的顺序,代码中是先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?
+不可以!因为一维dp的写法,背包容量一定要倒序遍历,如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品。
+给你一个 只包含正整数 的 非空数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
dp[j] = dp[j] || dp[j-nums[i]]dp[0]=truefunc canPartition(nums []int) bool {
+ var sum int = 0
+ for i:=0;i<len(nums);i++{
+ sum += nums[i]
+ }
+ if sum % 2 == 1{
+ return false
+ }
+ sum /= 2
+ dp := make([]bool,sum+1)
+ dp[0] = true
+ for i:=0;i<len(nums);i++{
+ for j:=sum;j>=nums[i];j--{
+ dp[j] = dp[j] || dp[j-nums[i]]
+ }
+ if dp[sum] == true{
+ return true
+ }
+ }
+ return dp[sum]
+}class Solution {
+public:
+ bool canPartition(vector<int>& nums) {
+ int numsum = 0;
+ for(int i=0;i<nums.size();i++){
+ numsum += nums[i];
+ }
+ if(numsum % 2 != 0){
+ return false;
+ }
+ int target = numsum / 2;
+ vector<vector<int> > dp(nums.size(), vector<int>(target+1,0));
+ for(int i=0;i<=target;i++){
+ if(i >= nums[0]){
+ dp[0][i] = nums[0];
+ }
+ }
+ for(int i=1;i<nums.size();i++){
+ for(int j=0;j<=target;j++){
+ if(j < nums[i]){
+ dp[i][j] = dp[i-1][j];
+ }
+ else{
+ dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]] + nums[i]);
+ }
+ }
+ }
+ return dp[nums.size()-1][target] == target;
+ }
+};有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
+每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
+如果 x == y,那么两块石头都会被完全粉碎;
+如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
+最后,最多只会剩下一块石头。返回此石头最小的可能重量 。如果没有石头剩下,就返回 0。
+分析:将石头分成重量大致相同的两堆,也就是看在不超过sum/2的情况下背包内最多能装多少石头,然后计算差值即可
+dp[j] = dp[j] || dp[j-nums[i]]dp[0]=truefunc lastStoneWeightII(stones []int) int {
+ var sum1,sum int = 0,0
+ for i:=0;i<len(stones);i++{
+ sum1 += stones[i]
+ }
+ if sum1 % 2 == 1{
+ sum = (sum1 -1) / 2
+ } else{
+ sum = sum1 / 2
+ }
+ dp := make([]bool,sum+1)
+ dp[0] = true
+ for i:=0;i<len(stones);i++{
+ for j:=sum;j>=stones[i];j--{
+ dp[j] = dp[j] || dp[j-stones[i]]
+ }
+ }
+ var result int = 0
+ for j:=sum;j>=0;j--{
+ if dp[j] == true{
+ result = j
+ break
+ }
+ }
+ return sum1 - result * 2
+}class Solution {
+public:
+ int lastStoneWeightII(vector<int>& stones) {
+ int numsum = 0;
+ for(int i=0;i<stones.size();i++){
+ numsum += stones[i];
+ }
+ int target = numsum;
+ numsum /= 2;
+ vector<vector<int> > dp(stones.size(),vector<int>(numsum+1, 0));
+ for(int i=0;i<=numsum;i++){
+ if(i >= stones[0]){
+ dp[0][i] = stones[0];
+ }
+ }
+ for(int i=1;i<stones.size();i++){
+ for(int j=0;j<=numsum;j++){
+ if(j < stones[i]){
+ dp[i][j] = dp[i-1][j];
+ } else{
+ dp[i][j] = max(dp[i-1][j], dp[i-1][j-stones[i]] + stones[i]);
+ }
+ }
+ }
+ return abs(target-2*dp[stones.size()-1][numsum]);
+ }
+};给你一个整数数组 nums 和一个整数 target 。
+向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
+例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
+返回可以通过上述方法构造的、运算结果等于 target 的不同表达式的数目。
+分析:假设加法的总和为x,那么减法对应的总和就是sum - x。所以我们要求的是 x - (sum - x) = S,x = (S + sum) / 2,此时问题就转化为,装满容量为x背包,有几种方法。
+dp[j] = dp[j]+dp[j-nums[i]]dp[0]=1,装0件物品对应的方法数量为1,就是什么都不装func findTargetSumWays(nums []int, target int) int {
+ var sum int = 0
+ for i:=0;i<len(nums);i++{
+ sum += nums[i]
+ }
+ x := target + sum
+ if x % 2 == 1 || x < 0{
+ return 0
+ }
+ x /= 2
+ dp := make([]int,x+1)
+ dp[0] = 1
+ for i:=0;i<len(nums);i++{
+ for j:=x;j>=nums[i];j--{
+ dp[j] += dp[j-nums[i]]
+ }
+ }
+ return dp[x]
+}class Solution {
+public:
+ int findTargetSumWays(vector<int>& nums, int target) {
+ int sum = 0;
+ for (int i = 0; i < nums.size(); i++) sum += nums[i];
+ if (abs(target) > sum) return 0; // 此时没有方案
+ if ((target + sum) % 2 == 1) return 0; // 此时没有方案
+ int bagSize = (target + sum) / 2;
+ vector<int> dp(bagSize + 1, 0);
+ dp[0] = 1;
+ for (int i = 0; i < nums.size(); i++) {
+ for (int j = bagSize; j >= nums[i]; j--) {
+ dp[j] += dp[j - nums[i]];
+ }
+ }
+ return dp[bagSize];
+ }
+};给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
+请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
+如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
+分析:相当于一个三维的0-1背包问题,可以通过压缩的方式压缩成二维背包,且需要对数据进行预处理
+dp[j][k] = max(dp[j][k],dp[j-strs[i]][k-strs[i]]+1)dp[0][0]=0func findMaxForm(strs []string, m int, n int) int {
+ dp := make([][]int, m+1)
+ for i := 0; i < m+1; i++ {
+ dp[i] = make([]int, n+1)
+ }
+ for _,str := range strs{
+ zero := strings.Count(str, "0")
+ one := len(str) - zero
+ for j:=m;j>=zero;j--{
+ for k:=n;k>=one;k--{
+ dp[j][k] = max(dp[j][k],dp[j-zero][k-one]+1)
+ }
+ }
+ }
+ return dp[m][n]
+}
+func max (a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int findMaxForm(vector<string>& strs, int m, int n) {
+ vector<vector<int> > dp(m+1, vector<int>(n+1,0));
+ for(int i=0;i<strs.size();i++){
+ string s = strs[i];
+ int zeronum = 0;
+ int onenum = 0;
+ for(int j=0;j<s.size();j++){
+ if(s[j] == '0'){
+ zeronum += 1;
+ } else{
+ onenum += 1;
+ }
+ }
+ for(int x=m;x >= zeronum;x--){
+ for(int y=n;y>=onenum;y--){
+ dp[x][y] = max(dp[x][y],dp[x-zeronum][y-onenum]+1);
+ }
+ }
+ }
+ return dp[m][n];
+ }
+};有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。 每件物品都有无限个(也就是可以放入背包多次) ,求解将哪些物品装入背包里物品价值总和最大。
+完全背包和01背包问题唯一不同的地方就是,每种物品有无限件 。
+01背包和完全背包唯一不同就是体现在遍历顺序上
+我们知道01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
+而完全背包的物品是可以添加多次的,所以要从小到大去遍历
+在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序同样无所谓!
+因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。
+给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
+请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
+假设每一种面额的硬币有无限个。
+题目数据保证结果符合 32 位带符号整数。
+dp[j]=dp[j]+dp[j-coins[i]]dp[0]=1,凑成金额0的组合数量为1,不影响后面的递推,解释起来就是凑成金额0的组合数量只有一种,就是什么都不凑class Solution {
+public:
+ int change(int amount, vector<int>& coins) {
+ int n = coins.size();
+ vector<int> dp(amount+1,0);
+ dp[0] = 1;
+ for(int i=0;i<n;i++){
+ for(int j=coins[i];j<=amount;j++){
+ dp[j] += dp[j-coins[i]];
+ }
+ }
+ return dp[amount];
+ }
+};给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
+题目数据保证答案符合 32 位整数范围。
+dp[j]=dp[j]+dp[j-nums[i]]dp[0]=1,凑成整数0的组合数量为1,不影响后面的递推func combinationSum4(nums []int, target int) int {
+ coinlen := len(nums)
+ dp := make([]int,target+1)
+ dp[0] = 1
+ for j:=0;j<=target;j++{
+ for i:=0;i<coinlen;i++{
+ if j-nums[i] >= 0{
+ dp[j] += dp[j-nums[i]]
+ }
+ }
+ }
+ return dp[target]
+}class Solution {
+public:
+ int combinationSum4(vector<int>& nums, int target) {
+ int n = nums.size();
+ vector<int> dp(target+1,0);
+ dp[0] = 1;
+ for(int i=0;i<=target;i++){
+ for(int j=0;j<n;j++){
+ if(i - nums[j] >= 0 && dp[i] < INT_MAX - dp[i - nums[j]] ){
+ dp[i] = dp[i] + dp[i - nums[j]];
+ }
+ }
+ }
+ return dp[target];
+ }
+};假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
改为:一步一个台阶,两个台阶,三个台阶,…,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢?
+实际上就是一个完全背包问题
+给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
+计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
+你可以认为每种硬币的数量是无限的。
+dp[j]=min(dp[j],dp[j-nums[i]]+1)dp[0]=0,凑成整数0的最少硬币个数为0,不影响后面的递推。同时要将整个dp数组初始化一个比较大的数值,从而不影响min的判断func coinChange(coins []int, amount int) int {
+ coinlen := len(coins)
+ dp := make([]int,amount+1)
+ for i:=1;i<=amount;i++{
+ dp[i] = amount+1
+ }
+ for i:=0;i<coinlen;i++{
+ for j:=coins[i];j<=amount;j++{
+ dp[j] = min(dp[j],dp[j-coins[i]]+1)
+ }
+ }
+ if dp[amount] == amount+1{
+ return -1
+ }
+ return dp[amount]
+}
+func min(a int,b int) int{
+ if a > b{
+ return b
+ }
+ return a
+}class Solution {
+public:
+ int coinChange(vector<int>& coins, int amount) {
+ int n = coins.size();
+ vector<int> dp(amount+1,INT_MAX);
+ dp[0] = 0;
+ for(int i=0;i<n;i++){
+ for(int j=coins[i];j<=amount;j++){
+ if (dp[j - coins[i]] != INT_MAX) {
+ dp[j] = min(dp[j], dp[j-coins[i]]+1);
+ }
+ }
+ }
+ return dp[amount] == INT_MAX ? -1 : dp[amount];
+ }
+};给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
+完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
+dp[j]=min(dp[j],dp[j-i*i]+1)dp[0]=0,凑成整数0的完全平方数的最少数量为0,不影响后面的递推。同时要将整个dp数组初始化一个比较大的数值,从而不影响min的判断func numSquares(n int) int {
+ dp := make([]int,n+1)
+ for i:=1;i<=n;i++{
+ dp[i] = n+1
+ }
+ dp[0] = 0
+ for j:=0;j<=n;j++{
+ for i:=1;i*i<=j;i++{
+ dp[j] = min(dp[j],dp[j-i*i]+1)
+ }
+ }
+ return dp[n]
+}
+
+func min(a int,b int) int{
+ if a > b{
+ return b
+ }
+ return a
+}class Solution {
+public:
+ int numSquares(int n) {
+ vector<int> nums;
+ for(int i=1;i<=n;i++){
+ if(i * i <= n){
+ nums.push_back(i*i);
+ } else{
+ break;
+ }
+ }
+ int m = nums.size();
+ vector<int> dp(n+1, INT_MAX);
+ dp[0] = 0;
+ for(int i=0;i<m;i++){
+ for(int j=nums[i];j<=n;j++){
+ if(dp[j-nums[i]] == INT_MAX){
+ continue;
+ }
+ dp[j] = min(dp[j],dp[j-nums[i]]+1);
+ }
+ }
+ return dp[n];
+ }
+};给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
dp[i] = dp[i] || dp[i-len(wordDict[j])]dp[0]=true,以0为结尾是一个空串,是可以拼接出来的,后续要用到这个真值进行递推。func wordBreak(s string, wordDict []string) bool {
+ lenword := len(wordDict)
+ lens := len(s)
+ dp := make([]bool,lens+1)
+ dp[0] = true
+ for i:=0;i<=lens;i++{
+ for j:=0;j<lenword;j++{
+ if i-len(wordDict[j]) >= 0{
+ if wordDict[j] == s[i-len(wordDict[j]):i]{
+ dp[i] = dp[i] || dp[i-len(wordDict[j])]
+ }
+ }
+ }
+ }
+ return dp[lens]
+}class Solution {
+public:
+ bool wordBreak(string s, vector<string>& wordDict) {
+ unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
+ vector<bool> dp(s.size() + 1, false);
+ dp[0] = true;
+ for (int i = 1; i <= s.size(); i++) { // 遍历背包
+ for (int j = 0; j < i; j++) { // 遍历物品
+ string word = s.substr(j, i - j); //substr(起始位置,截取的个数)
+ if (wordSet.find(word) != wordSet.end() && dp[j]) {
+ dp[i] = true;
+ }
+ }
+ }
+ return dp[s.size()];
+ }
+};有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。
+每件物品最多有Mi件可用,把Mi件摊开,其实就是一个01背包问题了。
+问能否能装满背包(或者最多装多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ,对应题目如下:
+ +问装满背包有几种方法:dp[j] += dp[j - nums[i]] ,对应题目如下:
+问背包装满最大价值:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ,对应题目如下:
+ +问装满背包所有物品的最小个数:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ,对应题目如下:
+ +在动态规划:关于01背包问题,你该了解这些! (opens new window)中我们讲解二维dp数组01背包先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
+和动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中,我们讲解一维dp数组01背包只能先遍历物品再遍历背包容量,且第二层for循环是从大到小遍历。
+一维dp数组的背包在遍历顺序上和二维dp数组实现的01背包其实是有很大差异的,大家需要注意!
+说完01背包,再看看完全背包。
+在动态规划:关于完全背包,你该了解这些! (opens new window)中,讲解了纯完全背包的一维dp数组实现,先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
+但是仅仅是纯完全背包的遍历顺序是这样的,题目稍有变化,两个for循环的先后顺序就不一样了。
+如果求组合数就是外层for循环遍历物品,内层for遍历背包 。
+如果求排列数就是外层for遍历背包,内层for循环遍历物品 。
+相关题目如下:
+如果求最小数,那么两层for循环的先后顺序就无所谓了,相关题目如下:
+ +对于背包问题,其实递推公式算是容易的,难是难在遍历顺序上,如果把遍历顺序搞透,才算是真正理解了 。
+你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
+给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
+dp[i]=max(dp[i-2] + nums[i-1], dp[i-1])dp[0]=0,偷第0个房间得到的金额为0;dp[1] = nums[0],偷第1个房间得到的金额只能是第一个房间的金额func rob(nums []int) int {
+ numslen := len(nums)
+ dp := make([]int,numslen+1)
+ dp[0] = 0
+ dp[1] = nums[0]
+ for i:=2;i<=numslen;i++{
+ dp[i]=max(dp[i-2] + nums[i-1], dp[i-1])
+ }
+ return dp[numslen]
+}
+
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int rob(vector<int>& nums) {
+ int n = nums.size();
+ if(n == 1){
+ return nums[0];
+ }
+ vector<int> dp(n,0);
+ dp[0] = nums[0];
+ dp[1] = max(nums[0], nums[1]);
+ for(int i=2;i<n;i++){
+ dp[i] = max(dp[i-1],dp[i-2]+nums[i]);
+ }
+ return dp[n-1];
+ }
+};你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
+给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
+分两种情况讨论就好,第一种情况是偷第一间房间,那么最后一间房间就不能偷了,第二种情况是不偷第一件房间,那么就可以偷最后一间房间。分类讨论即可。
+dp[i]=max(dp[i-2] + nums[i-1], dp[i-1])dp[0]=0,偷第0个房间得到的金额为0;dp[1] = nums[0],偷第1个房间得到的金额只能是第一个房间的金额func rob(nums []int) int {
+ numslen := len(nums)
+ if numslen == 1{
+ return nums[0]
+ }
+ dp := make([]int,numslen)
+ dp[0] = 0
+ dp[1] = nums[0]
+ for i:=2;i<numslen;i++{
+ dp[i]=max(dp[i-2] + nums[i-1], dp[i-1])
+ }
+ a := dp[numslen-1]
+
+ dp2 := make([]int,numslen)
+ dp2[0] = 0
+ dp2[1] = nums[1]
+ for i:=2;i<numslen;i++{
+ dp2[i]=max(dp2[i-2] + nums[i], dp2[i-1])
+ }
+ b := dp2[numslen-1]
+
+ return max(a,b)
+}
+
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int rob(vector<int>& nums) {
+ int n = nums.size();
+ if(n == 1){
+ return nums[0];
+ }
+ if(n == 2){
+ return max(nums[0], nums[1]);
+ }
+ if(n == 3){
+ return max(nums[0],max(nums[1], nums[2]));
+ }
+ vector<int> dp(n);
+ dp[0] = nums[0];
+ dp[1] = max(nums[0],nums[1]);
+ for(int i=2;i<n-1;i++){
+ dp[i] = max(dp[i-1], dp[i-2] + nums[i]);
+ }
+ vector<int> dp2(n);
+ dp2[1] = nums[1];
+ dp2[2] = max(nums[1],nums[2]);
+ for(int i=3;i<n;i++){
+ dp2[i] = max(dp2[i-1], dp2[i-2] + nums[i]);
+ }
+ return max(dp[n-2], dp2[n-1]);
+ }
+};小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
+除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
+给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
+这里我们要求一个节点 偷与不偷的两个状态所得到的金钱,那么返回值就是一个长度为2的数组。
+在遍历的过程中,如果遇到空节点的话,很明显,无论偷还是不偷都是0,所以就返回,这也相当于dp数组的初始化
+首先明确的是使用后序遍历。 因为通过递归函数的返回值来做下一步计算。
+通过递归左节点,得到左节点偷与不偷的金钱。
+通过递归右节点,得到右节点偷与不偷的金钱。
+如果是偷当前节点,那么左右孩子就不能偷,val1 = cur->val + left[0] + right[0];
+如果不偷当前节点,那么左右孩子就可以偷,至于到底偷不偷一定是选一个最大的,所以:val2 = max(left[0], left[1]) + max(right[0], right[1]);
+最后当前节点的状态就是{val2, val1}; 即:{不偷当前节点得到的最大金钱,偷当前节点得到的最大金钱}
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func rob(root *TreeNode) int {
+ res := DFS(root)
+ return max(res[0],res[1])
+}
+
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}
+
+func DFS(root *TreeNode) []int{
+ if root == nil{
+ return []int{0,0}
+ }
+ // 后序遍历
+ left := DFS(root.Left)
+ right := DFS(root.Right)
+
+ // 考虑去偷当前的屋子
+ robCur := root.Val + left[0] + right[0]
+ // 考虑不去偷当前的屋子
+ notRobCur := max(left[0], left[1]) + max(right[0], right[1])
+
+ // 注意顺序:0:不偷,1:去偷
+ return []int{notRobCur, robCur}
+}class Solution {
+public:
+ int rob(TreeNode* root) {
+ vector<int> result = robTree(root);
+ return max(result[0], result[1]);
+ }
+ vector<int> robTree(TreeNode* root){
+ if(root == NULL){
+ return vector<int>{0,0};
+ }
+ vector<int> left = robTree(root->left);
+ vector<int> right = robTree(root->right);
+ int val1 = root->val + left[0] + right[0];
+ int val2 = max(left[0], left[1]) + max(right[0], right[1]);
+ return vector<int>{val2, val1};
+ }
+};给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
+你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
+返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
+贪心:取最左最小值,取最右最大值,那么得到的差值就是最大利润。
+func maxProfit(prices []int) int {
+ pricelen := len(prices)
+ result := 0
+ minnum := prices[0]
+ for i:= 0;i<pricelen;i++{
+ minnum = min(minnum,prices[i])
+ result = max(result,prices[i] - minnum)
+ }
+ return result
+}
+
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}
+
+func min(a int,b int) int{
+ if a < b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int maxProfit(vector<int>& prices) {
+ vector<vector<int> > dp(prices.size(), vector<int>(2,0));
+ dp[0][0] = -prices[0];
+ dp[0][1] = 0;
+ for(int i=1;i<prices.size();i++){
+ dp[i][0] = max(dp[i-1][0], -prices[i]);
+ dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
+ }
+ return max(dp[prices.size()-1][0], dp[prices.size()-1][1]);
+ }
+};给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
+在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
+返回 你能获得的 最大 利润 。
+dp[0][1]=0,第0天持有股票 dp[0][0]=-prices[0],func maxProfit(prices []int) int {
+ lenprices := len(prices)
+ dp := make([][]int,lenprices+1)
+ for i,_ := range dp{
+ dp[i] = make([]int,2)
+ }
+ dp[0][1] = 0
+ dp[0][0] = -prices[0]
+ for i:=1;i<lenprices;i++{
+ dp[i][0]=max(dp[i-1][1]-prices[i],dp[i-1][0])
+ dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i])
+ }
+ return max(dp[lenprices-1][0],dp[lenprices-1][1])
+}
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int maxProfit(vector<int>& prices) {
+ int n = prices.size();
+ vector<vector<int> > dp(n,vector<int>(2,0));
+ dp[0][0] = -prices[0];
+ dp[0][1] = 0;
+ for(int i=1;i<n;i++){
+ dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]);
+ dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
+ }
+ return dp[n-1][1];
+ }
+};给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
+设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
+注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
+func maxProfit(prices []int) int {
+ lenprices := len(prices)
+ dp := make([][]int,lenprices+1)
+ for i,_ := range dp{
+ dp[i] = make([]int,5)
+ }
+ dp[0][0] = 0
+ dp[0][1] = -prices[0]
+ dp[0][2] = 0
+ dp[0][3] = -prices[0]
+ dp[0][4] = 0
+ for i:=1;i<lenprices;i++{
+ dp[i][0]=dp[i-1][0]
+ dp[i][1]=max(dp[i-1][0]-prices[i],dp[i-1][1])
+ dp[i][2]=max(dp[i-1][1]+prices[i],dp[i-1][2])
+ dp[i][3]=max(dp[i-1][2]-prices[i],dp[i-1][3])
+ dp[i][4]=max(dp[i-1][3]+prices[i],dp[i-1][4])
+ }
+ return dp[lenprices-1][4]
+}
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}
+class Solution {
+public:
+ int maxProfit(vector<int>& prices) {
+ int n = prices.size();
+ vector<vector<int> > dp(n,vector<int>(4,0));
+ // 第一次持有
+ // 第一次不持有
+ // 第二次持有
+ // 第二次不持有
+ dp[0][0] = -prices[0];
+ dp[0][2] = -prices[0];
+ for(int i=1;i<n;i++){
+ dp[i][0] = max(dp[i-1][0], - prices[i]);
+ dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
+ dp[i][2] = max(dp[i-1][2], dp[i-1][1] - prices[i]);
+ dp[i][3] = max(dp[i-1][3], dp[i-1][2] + prices[i]);
+ }
+ return max(dp[n-1][1], dp[n-1][3]);
+ }
+};给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
+设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
+func maxProfit(k int, prices []int) int {
+ lenprices := len(prices)
+ dp := make([][]int,lenprices+1)
+ for i,_ := range dp{
+ dp[i] = make([]int,k*2+1)
+ }
+ for i:=0;i<k*2+1;i++{
+ if i % 2 == 1{
+ dp[0][i] = -prices[0]
+ }
+ }
+ for i:=1;i<lenprices;i++{
+ dp[i][0]=dp[i-1][0]
+ for j:=1;j<=2*k;j++{
+ if j % 2 == 1{
+ dp[i][j] = max(dp[i-1][j-1]-prices[i],dp[i-1][j])
+ } else{
+ dp[i][j] = max(dp[i-1][j-1]+prices[i],dp[i-1][j])
+ }
+ }
+ }
+ return dp[lenprices-1][2*k]
+}
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int maxProfit(int k, vector<int>& prices) {
+ int n = prices.size();
+ vector<vector<int> > dp(n,vector<int>(k*2,0));
+ for(int i=0;i<k*2;i+=2){
+ dp[0][i] = -prices[0];
+ }
+ for(int i=1;i<n;i++){
+ dp[i][0] = max(dp[i-1][0], - prices[i]);
+ for(int j=1;j<2*k;j++){
+ if(j % 2 == 0){
+ dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] - prices[i]);
+ } else{
+ dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] + prices[i]);
+ }
+ }
+ }
+ int maxprofit = 0;
+ for(int i=0;i<2*k;i++){
+ maxprofit = max(maxprofit, dp[n-1][i]);
+ }
+ return maxprofit;
+ }
+};给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。
+设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
+卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
+注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
+func maxProfit(prices []int) int {
+ lenprices := len(prices)
+ dp := make([][]int,lenprices+1)
+ for i,_ := range dp{
+ dp[i] = make([]int,4)
+ }
+ dp[0][0] = -prices[0]
+ dp[0][1] = 0
+ dp[0][2] = 0
+ dp[0][3] = 0
+ for i:=1;i<lenprices;i++{
+ dp[i][0]=max(dp[i-1][0],max(dp[i-1][1],dp[i-1][3])-prices[i])
+ dp[i][1]=max(dp[i-1][1],dp[i-1][3])
+ dp[i][2]=dp[i-1][0]+prices[i]
+ dp[i][3]=dp[i-1][2]
+ }
+ return max(dp[lenprices-1][1],max(dp[lenprices-1][2],dp[lenprices-1][3]))
+}
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int maxProfit(vector<int>& prices) {
+ int n = prices.size();
+ vector<vector<int> > dp(n,vector<int>(4,0));
+ // 持有
+ // 不持有不是今天卖的
+ // 不持有是今天卖的
+ // 冷冻期
+ dp[0][0] = -prices[0];
+ for(int i=1;i<n;i++){
+ dp[i][0] = max(dp[i-1][0], max(dp[i-1][1], dp[i-1][3]) - prices[i]);
+ dp[i][1] = max(dp[i-1][1], dp[i-1][3]);
+ dp[i][2] = dp[i-1][0] + prices[i];
+ dp[i][3] = dp[i-1][2];
+ }
+ return max(dp[n-1][1], max(dp[n-1][2],dp[n-1][3]));
+ }
+};给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。
+你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
+返回获得利润的最大值。
+注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
+分析:卖出的时候扣除手续费即可。如果买入的时候扣除手续费,会导致买入的代价过大。卖出是获利的,卖出时候扣除手续费就可以了
+dp[0][1]=0,第0天持有股票 dp[0][0]=-prices[0],func maxProfit(prices []int, fee int) int {
+ lenprices := len(prices)
+ dp := make([][]int,lenprices+1)
+ for i,_ := range dp{
+ dp[i] = make([]int,2)
+ }
+ dp[0][1] = 0
+ dp[0][0] = -prices[0]
+ for i:=1;i<lenprices;i++{
+ dp[i][0]=max(dp[i-1][1]-prices[i],dp[i-1][0])
+ dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]-fee)
+ }
+ return max(dp[lenprices-1][0],dp[lenprices-1][1])
+}
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int maxProfit(vector<int>& prices, int fee) {
+ int n = prices.size();
+ vector<vector<int> > dp(n,vector<int>(2,0));
+ dp[0][0] = -prices[0]-fee;
+ dp[0][1] = 0;
+ for(int i=1;i<n;i++){
+ dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]-fee);
+ dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
+ }
+ return dp[n-1][1];
+ }
+};给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
+子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
+func lengthOfLIS(nums []int) int {
+ lennums := len(nums)
+ dp := make([]int,lennums)
+ for i,_ := range dp{
+ dp[i] = 1
+ }
+ var result int = 0
+ for i:=0;i<lennums;i++{
+ for j:=0;j<i;j++{
+ if nums[i] > nums[j]{
+ dp[i] = max(dp[i],dp[j]+1)
+ }
+ }
+ result = max(result,dp[i])
+ }
+ return result
+}
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int lengthOfLIS(vector<int>& nums) {
+ int n = nums.size();
+ vector<int> dp(n,1);
+ int result = 1;
+ for(int i=1;i<n;i++){
+ for(int j=0;j<i;j++){
+ if(nums[i] > nums[j]){
+ dp[i] = max(dp[i],dp[j]+1);
+ }
+ }
+ result = max(result, dp[i]);
+ }
+ return result;
+ }
+};给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
+连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。
+func findLengthOfLCIS(nums []int) int {
+ lennums := len(nums)
+ dp := make([]int,lennums)
+ for i,_ := range dp{
+ dp[i] = 1
+ }
+ var result int = 1
+ for i:=1;i<lennums;i++{
+ if nums[i] > nums[i-1]{
+ dp[i] = dp[i-1]+1
+ }
+ result = max(result,dp[i])
+ }
+ return result
+}
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int findLengthOfLCIS(vector<int>& nums) {
+ int n = nums.size();
+ vector<int> dp(n,1);
+ int result = 1;
+ for(int i=1;i<n;i++){
+ if(nums[i] > nums[i-1]){
+ dp[i] = dp[i-1] + 1;
+ }
+ result = max(result,dp[i]);
+ }
+ return result;
+ }
+};给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度。
注意题目中说的子数组,其实就是连续子序列。
+func findLength(nums1 []int, nums2 []int) int {
+ nums1len := len(nums1)
+ nums2len := len(nums2)
+ dp := make([][]int,nums1len+1)
+ for i,_ := range dp{
+ dp[i] = make([]int,nums2len+1)
+ }
+ var result int = 0
+ for i:=1;i<=nums1len;i++{
+ for j:=1;j<=nums2len;j++{
+ if nums1[i-1] == nums2[j-1]{
+ dp[i][j] = dp[i-1][j-1] + 1
+ }
+ result = max(result,dp[i][j])
+ }
+ }
+ return result
+}
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int findLength(vector<int>& nums1, vector<int>& nums2) {
+ int m = nums1.size();
+ int n = nums2.size();
+ int result = 0;
+ vector<vector<int> > dp(m+1, vector<int>(n+1,0));
+ for(int i=1;i<=m;i++){
+ for(int j=1;j<=n;j++){
+ if(nums1[i-1] == nums2[j-1]){
+ dp[i][j] = dp[i-1][j-1] + 1;
+ }
+ result = max(result, dp[i][j]);
+ }
+ }
+ return result;
+ }
+};给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
+一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
+例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
+两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
+func longestCommonSubsequence(text1 string, text2 string) int {
+ text1len := len(text1)
+ text2len := len(text2)
+ dp := make([][]int,text1len+1)
+ for i,_ := range dp{
+ dp[i] = make([]int,text2len+1)
+ }
+ for i:=1;i<=text1len;i++{
+ for j:=1;j<=text2len;j++{
+ if text1[i-1] == text2[j-1]{
+ dp[i][j] = dp[i-1][j-1] + 1
+ } else{
+ dp[i][j] = max(dp[i][j-1],dp[i-1][j])
+ }
+ }
+ }
+ return dp[text1len][text2len]
+}
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int longestCommonSubsequence(string text1, string text2) {
+ int m = text1.size();
+ int n = text2.size();
+ vector<vector<int> > dp(m+1,vector<int>(n+1,0));
+ for(int i=1; i<=m;i++){
+ for(int j=1;j<=n;j++){
+ if(text1[i-1] == text2[j-1]){
+ dp[i][j] = dp[i-1][j-1] + 1;
+ } else{
+ dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
+ }
+ }
+ }
+ return dp[m][n];
+ }
+};在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
+现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足:nums1[i] == nums2[j]
+且绘制的直线不与任何其他连线(非水平线)相交。
+请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
+以这种方法绘制线条,并返回可以绘制的最大连线数。
+分析:直线不能相交,这就是说明在字符串A中 找到一个与字符串B相同的子序列,且这个子序列不能改变相对顺序,只要相对顺序不改变,链接相同数字的直线就不会相交。
+本题说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度!
+func maxUncrossedLines(nums1 []int, nums2 []int) int {
+ nums1len := len(nums1)
+ nums2len := len(nums2)
+ dp := make([][]int,nums1len+1)
+ for i,_ := range dp{
+ dp[i] = make([]int,nums2len+1)
+ }
+ for i:=1;i<=nums1len;i++{
+ for j:=1;j<=nums2len;j++{
+ if nums1[i-1] == nums2[j-1]{
+ dp[i][j] = dp[i-1][j-1] + 1
+ } else{
+ dp[i][j] = max(dp[i][j-1],dp[i-1][j])
+ }
+ }
+ }
+ return dp[nums1len][nums2len]
+}
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
+ int m = nums1.size();
+ int n = nums2.size();
+ vector<vector<int> > dp(m+1,vector<int>(n+1,0));
+ for(int i=1; i<=m;i++){
+ for(int j=1;j<=n;j++){
+ if(nums1[i-1] == nums2[j-1]){
+ dp[i][j] = dp[i-1][j-1] + 1;
+ } else{
+ dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
+ }
+ }
+ }
+ return dp[m][n];
+ }
+};给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组是数组中的一个连续部分。
+func maxSubArray(nums []int) int {
+ lennums := len(nums)
+ dp := make([]int,lennums+1)
+ dp[0] = 0
+ var result int = nums[0]
+ for i:=1;i<=lennums;i++{
+ dp[i] = max(nums[i-1],dp[i-1]+nums[i-1])
+ result = max(result,dp[i])
+ }
+ return result
+}
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int maxSubArray(vector<int>& nums) {
+ int n = nums.size();
+ vector<int> dp(n,0);
+ dp[0] = nums[0];
+ int result = dp[0];
+ for(int i=1;i<n;i++){
+ dp[i] = max(nums[i], dp[i-1] + nums[i]);
+ result = max(result,dp[i]);
+ }
+ return result;
+ }
+};给定一个长度为 n 的环形整数数组 nums ,返回 * nums 的非空 子数组 的最大可能和 * 。
环形数组 意味着数组的末端将会与开头相连呈环状。形式上, nums[i] 的下一个元素是 nums[(i + 1) % n] , nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。
子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上,对于子数组 nums[i], nums[i + 1], ..., nums[j] ,不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。
class Solution {
+public:
+ int maxSubarraySumCircular(vector<int>& nums) {
+ vector<int> dp(nums.size(),0);
+ vector<int> leftMax(nums.size(),0);
+ dp[0] = nums[0];
+ int maxlength = dp[0];
+ int leftSum = dp[0];
+ leftMax[0] = dp[0];
+ for(int i=1;i<nums.size();i++){
+ dp[i] = max(dp[i-1] + nums[i], nums[i]);
+ maxlength = max(maxlength, dp[i]);
+ leftSum += nums[i];
+ leftMax[i] = max(leftMax[i-1], leftSum);
+ }
+ int rightSum = 0;
+ for(int j=nums.size()-1;j>0;j--){
+ rightSum += nums[j];
+ maxlength = max(maxlength, rightSum + leftMax[j-1]);
+ }
+ return maxlength;
+ }
+};给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
+字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
+func isSubsequence(s string, t string) bool {
+ slen := len(s)
+ tlen := len(t)
+ dp := make([][]int,slen+1)
+ for i,_ := range dp{
+ dp[i] = make([]int,tlen+1)
+ }
+ for i:=1;i<=slen;i++{
+ for j:=1;j<=tlen;j++{
+ if s[i-1] == t[j-1]{
+ dp[i][j] = dp[i-1][j-1] + 1
+ } else{
+ dp[i][j] = max(dp[i][j-1],dp[i-1][j])
+ }
+ }
+ }
+ return dp[slen][tlen] == slen
+}
+func max(a int,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ bool isSubsequence(string s, string t) {
+ int m = s.size();
+ int n = t.size();
+ vector<vector<int> > dp(m+1, vector<int>(n+1,0));
+ for(int i=1;i<=m;i++){
+ for(int j=1;j<=n;j++){
+ if(s[i-1] == t[j-1]){
+ dp[i][j] = dp[i-1][j-1] + 1;
+ } else{
+ dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
+ }
+ }
+ }
+ if (dp[m][n] == m){
+ return true;
+ }
+ return false;
+ }
+};给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。
+字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,“ACE” 是 “ABCDE” 的一个子序列,而 “AEC” 不是)
+题目数据保证答案符合 32 位带符号整数范围。
+func numDistinct(s string, t string) int {
+ slen := len(s)
+ tlen := len(t)
+ dp := make([][]int,slen+1)
+ for i,_ := range dp{
+ dp[i] = make([]int,tlen+1)
+ }
+ for i:=0;i<=slen;i++{
+ dp[i][0] = 1
+ }
+ for j:=1;j<=tlen;j++{
+ dp[0][j] = 0
+ }
+ for i:=1;i<=slen;i++{
+ for j:=1;j<=tlen;j++{
+ if s[i-1] == t[j-1]{
+ dp[i][j] = dp[i-1][j-1]+dp[i-1][j]
+ } else{
+ dp[i][j] = dp[i-1][j]
+ }
+ }
+ }
+ return dp[slen][tlen]
+}class Solution {
+public:
+ int numDistinct(string s, string t) {
+ vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1));
+ for (int i = 0; i < s.size(); i++) dp[i][0] = 1;
+ for (int j = 1; j < t.size(); j++) dp[0][j] = 0;
+ for (int i = 1; i <= s.size(); i++) {
+ for (int j = 1; j <= t.size(); j++) {
+ if (s[i - 1] == t[j - 1]) {
+ dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
+ } else {
+ dp[i][j] = dp[i - 1][j];
+ }
+ }
+ }
+ return dp[s.size()][t.size()];
+ }
+};给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的 最小步数 。
每步可以删除任意一个字符串中的一个字符。
+func minDistance(word1 string, word2 string) int {
+ word1len := len(word1)
+ word2len := len(word2)
+ dp := make([][]int,word1len+1)
+ for i,_ := range dp{
+ dp[i] = make([]int,word2len+1)
+ }
+ for i:=0;i<=word1len;i++{
+ dp[i][0] = i
+ }
+ for j:=1;j<=word2len;j++{
+ dp[0][j] = j
+ }
+ for i:=1;i<=word1len;i++{
+ for j:=1;j<=word2len;j++{
+ if word1[i-1] == word2[j-1]{
+ dp[i][j] = dp[i-1][j-1]
+ } else{
+ dp[i][j] = min(dp[i-1][j],dp[i][j-1])+1
+ }
+ }
+ }
+ return dp[word1len][word2len]
+}
+
+func min(a int,b int) int{
+ if a < b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int minDistance(string word1, string word2) {
+ int m = word1.size();
+ int n = word2.size();
+ vector<vector<int> > dp(m+1, vector<int>(n+1,1));
+ for(int i=0;i<=m;i++){
+ for(int j=0;j<=n;j++){
+ if(i == 0){
+ dp[i][j] = j;
+ }
+ if(j == 0){
+ dp[i][j] = i;
+ }
+ }
+ }
+ for(int i=1;i<=m;i++){
+ for(int j=1;j<=n;j++){
+ if(word1[i-1] == word2[j-1]){
+ dp[i][j] = dp[i-1][j-1];
+ } else{
+ dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + 1;
+ }
+ }
+ }
+ return dp[m][n];
+ }
+};给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
+你可以对一个单词进行如下三种操作:插入一个字符、删除一个字符、替换一个字符
+func minDistance(word1 string, word2 string) int {
+ word1len := len(word1)
+ word2len := len(word2)
+ dp := make([][]int,word1len+1)
+ for i,_ := range dp{
+ dp[i] = make([]int,word2len+1)
+ }
+ for i:=0;i<=word1len;i++{
+ dp[i][0] = i
+ }
+ for j:=1;j<=word2len;j++{
+ dp[0][j] = j
+ }
+ for i:=1;i<=word1len;i++{
+ for j:=1;j<=word2len;j++{
+ if word1[i-1] == word2[j-1]{
+ dp[i][j] = dp[i-1][j-1]
+ } else{
+ dp[i][j] = min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]))+1
+ }
+ }
+ }
+ return dp[word1len][word2len]
+}
+
+func min(a int,b int) int{
+ if a < b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int minDistance(string word1, string word2) {
+ int m = word1.size();
+ int n = word2.size();
+ vector<vector<int> > dp(m+1, vector<int>(n+1,1));
+ for(int i=0;i<=m;i++){
+ for(int j=0;j<=n;j++){
+ if(i == 0){
+ dp[i][j] = j;
+ }
+ if(j == 0){
+ dp[i][j] = i;
+ }
+ }
+ }
+ for(int i=1;i<=m;i++){
+ for(int j=1;j<=n;j++){
+ if(word1[i-1] == word2[j-1]){
+ dp[i][j] = dp[i-1][j-1];
+ } else{
+ dp[i][j] = min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]}) + 1;
+ }
+ }
+ }
+ return dp[m][n];
+ }
+};给你一个字符串 s ,请你统计并返回这个字符串中回文子串的数目。
+回文字符串 是正着读和倒过来读一样的字符串。
+子字符串 是字符串中的由连续字符组成的一个序列。
+具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
+func countSubstrings(s string) int {
+ slen := len(s)
+ dp := make([][]bool,slen)
+ for i,_ := range dp{
+ dp[i] = make([]bool,slen)
+ }
+ var result int = 0
+ for i:=slen-1;i>=0;i--{
+ for j:=i;j<slen;j++{
+ if s[i] == s[j]{
+ if j - i <= 1{
+ dp[i][j] = true
+ result++
+ } else if dp[i+1][j-1]{
+ dp[i][j] = true
+ result++
+ }
+ }
+ }
+ }
+ return result
+}class Solution {
+public:
+ int countSubstrings(string s) {
+ int n = s.size();
+ int result = 0;
+ vector<vector<bool> > dp(n, vector<bool>(n,false));
+ for(int i=n-1;i>=0;i--){
+ for(int j=i;j<n;j++){
+ if(s[i] == s[j]){
+ if(j-i <= 1){
+ result += 1;
+ dp[i][j] = true;
+ } else if(dp[i+1][j-1]){
+ result += 1;
+ dp[i][j] = true;
+ }
+ }
+ }
+ }
+ return result;
+ }
+};给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
+子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
+func longestPalindromeSubseq(s string) int {
+ slen := len(s)
+ dp := make([][]int,slen)
+ for i,_ := range dp{
+ dp[i] = make([]int,slen)
+ }
+ for i:=slen-1;i>=0;i--{
+ for j:=i;j<slen;j++{
+ if j == i{
+ dp[i][j] = 1
+ continue
+ }
+ if s[i] == s[j]{
+ dp[i][j]=dp[i+1][j-1]+2
+ } else{
+ dp[i][j]=max(dp[i+1][j],dp[i][j-1])
+ }
+ }
+ }
+ return dp[0][slen-1]
+}
+func max(a int,b int)int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int longestPalindromeSubseq(string s) {
+ int n = s.size();
+ vector<vector<int> > dp(n, vector<int>(n,false));
+ for (int i = 0; i < n; i++){
+ dp[i][i] = 1;
+ }
+ for(int i=n-1;i>=0;i--){
+ for(int j=i+1;j<n;j++){
+ if (s[i] == s[j]) {
+ dp[i][j] = dp[i + 1][j - 1] + 2;
+ } else {
+ dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
+ }
+ }
+ }
+ return dp[0][n-1];
+ }
+};代码随想录-图论专题
+ +dfs是可一个方向去搜,不到黄河不回头,直到遇到绝境了,搜不下去了,再换方向(换方向的过程就涉及到了回溯)。
+bfs是先把本节点所连接的所有节点遍历一遍,走到下一个节点的时候,再把连接节点的所有节点遍历一遍,搜索方向更像是广度,四面八方的搜索过程。
+回溯算法,其实就是dfs的过程,这里给出dfs的代码框架:
+void dfs(参数) {
+ if (终止条件) {
+ 存放结果;
+ return;
+ }
+
+ for (选择:本节点所连接的其他节点) {
+ 处理节点;
+ dfs(图,选择的节点); // 递归
+ 回溯,撤销处理结果
+ }
+}可以发现dfs的代码框架和回溯算法的代码框架是差不多的。
+深搜三部曲如下:
+void dfs(参数)通常我们递归的时候,我们递归搜索需要了解哪些参数,其实也可以在写递归函数的时候,发现需要什么参数,再去补充就可以。
+一般情况,深搜需要 二维数组数组结构保存所有路径,需要一维数组保存单一路径,这种保存结果的数组,我们可以定义一个全局变量,避免让我们的函数参数过多。
+例如这样:
+vector<vector<int>> result; // 保存符合条件的所有路径
+vector<int> path; // 起点到终点的路径
+void dfs (图,目前搜索的节点) 终止条件很重要,写dfs的时候,之所以容易死循环,栈溢出等等这些问题,都是因为终止条件没有想清楚。
+if (终止条件) {
+ 存放结果;
+ return;
+}终止添加不仅是结束本层递归,同时也是我们收获结果的时候。
+另外,其实很多dfs写法,没有写终止条件,其实终止条件写在了, 下面dfs递归的逻辑里了,也就是不符合条件,直接不会向下递归。
+一般这里就是一个for循环的操作,去遍历 目前搜索节点 所能到的所有节点。
+for (选择:本节点所连接的其他节点) {
+ 处理节点;
+ dfs(图,选择的节点); // 递归
+ 回溯,撤销处理结果
+}广搜的搜索方式就适合于解决两个点之间的最短路径问题。
+因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路。
+当然,也有一些问题是广搜 和 深搜都可以解决的,例如岛屿问题,这类问题的特征就是不涉及具体的遍历方式,只要能把相邻且相同属性的节点标记上就行。
+我们仅仅需要一个容器,能保存我们要遍历过的元素就可以,那么用队列,还是用栈,甚至用数组,都是可以的。
+用队列的话,就是保证每一圈都是一个方向去转,例如统一顺时针或者逆时针。
+因为队列是先进先出,加入元素和弹出元素的顺序是没有改变的。
+如果用栈的话,就是第一圈顺时针遍历,第二圈逆时针遍历,第三圈有顺时针遍历。
+因为栈是先进后出,加入元素和弹出元素的顺序改变了。
+下面给出广搜代码模板,该模板针对的就是,上面的四方格的地图: (详细注释)
+int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
+// grid 是地图,也就是一个二维数组
+// visited标记访问过的节点,不要重复访问
+// x,y 表示开始搜索节点的下标
+void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
+ queue<pair<int, int>> que; // 定义队列
+ que.push({x, y}); // 起始节点加入队列
+ visited[x][y] = true; // 只要加入队列,立刻标记为访问过的节点
+ while(!que.empty()) { // 开始遍历队列里的元素
+ pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
+ int curx = cur.first;
+ int cury = cur.second; // 当前节点坐标
+ for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
+ int nextx = curx + dir[i][0];
+ int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
+ if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 坐标越界了,直接跳过
+ if (!visited[nextx][nexty]) { // 如果节点没被访问过
+ que.push({nextx, nexty}); // 队列添加该节点为下一轮要遍历的节点
+ visited[nextx][nexty] = true; // 只要加入队列立刻标记,避免重复访问
+ }
+ }
+ }
+}当我们需要判断两个元素是否在同一个集合里的时候,我们就要想到用并查集。
+并查集主要有两个功能:
+int n = 1005; // n根据题目中节点数量而定,一般比节点数量大一点就好
+vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
+
+// 并查集初始化
+void init() {
+ for (int i = 0; i < n; ++i) {
+ father[i] = i;
+ }
+}
+// 并查集里寻根的过程
+int find(int u) {
+ return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
+}
+
+// 判断 u 和 v是否找到同一个根
+bool isSame(int u, int v) {
+ u = find(u);
+ v = find(v);
+ return u == v;
+}
+
+// 将v->u 这条边加入并查集
+void join(int u, int v) {
+ u = find(u); // 寻找u的根
+ v = find(v); // 寻找v的根
+ if (u == v) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
+ father[v] = u;
+}通过模板,我们可以知道,并查集主要有三个功能。
+给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特定顺序)
+graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节点 i 到节点 graph[i][j]存在一条有向边)。
+class Solution {
+private:
+ vector<vector<int> > result;
+ vector<int> path;
+public:
+ void DFS(vector<vector<int>>& graph, int node){
+ if(node == graph.size()-1){
+ result.push_back(path);
+ return;
+ }
+ for(int i=0;i<graph[node].size();i++){
+ path.push_back(graph[node][i]);
+ DFS(graph, graph[node][i]);
+ path.pop_back();
+ }
+ }
+ vector<vector<int> > allPathsSourceTarget(vector<vector<int>>& graph) {
+ path.push_back(0);
+ DFS(graph,0);
+ return result;
+ }
+};给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
+岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
+此外,你可以假设该网格的四条边均被水包围。
+class Solution {
+private:
+ vector<vector<bool> > isvisit;
+ int sumcount = 0;
+public:
+ void DFS(vector<vector<char>>& grid, int i, int j, int m, int n){
+ if(i < 0 || j < 0 || i >= m || j >= n || grid[i][j] == '0' || isvisit[i][j] == true){
+ return;
+ }
+ isvisit[i][j] = true;
+ DFS(grid,i-1,j,m,n);
+ DFS(grid,i,j-1,m,n);
+ DFS(grid,i+1,j,m,n);
+ DFS(grid,i,j+1,m,n);
+ }
+ void BFS(vector<vector<char>>& grid, int i, int j, int m, int n){
+ queue<pair<int, int> > q;
+ q.push({i,j});
+ isvisit[i][j] = true;
+ while(!q.empty()){
+ pair<int, int> cur = q.front();
+ q.pop();
+ int x = cur.first;
+ int y = cur.second;
+ if(x-1 >= 0 && grid[x-1][y] == '1' && isvisit[x-1][y] == false){
+ q.push({x-1,y});
+ isvisit[x-1][y] = true;
+ }
+ if(x+1 < m && grid[x+1][y] == '1' && isvisit[x+1][y] == false){
+ q.push({x+1,y});
+ isvisit[x+1][y] = true;
+ }
+ if(y-1 >= 0 && grid[x][y-1] == '1' && isvisit[x][y-1] == false){
+ q.push({x,y-1});
+ isvisit[x][y-1] = true;
+ }
+ if(y+1 < n && grid[x][y+1] == '1' && isvisit[x][y+1] == false){
+ q.push({x,y+1});
+ isvisit[x][y+1] = true;
+ }
+ }
+ return;
+ }
+ int numIslands(vector<vector<char>>& grid) {
+ int m = grid.size();
+ int n = grid[0].size();
+ for(int i=0;i<m;i++){
+ isvisit.push_back(vector<bool>(n));
+ }
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(isvisit[i][j] == true || grid[i][j] == '0'){
+ continue;
+ }
+ BFS(grid, i,j,m,n);
+ sumcount += 1;
+ }
+ }
+ return sumcount;
+ }
+};给你一个大小为 m x n 的二进制矩阵 grid 。
+岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
+岛屿的面积是岛上值为 1 的单元格的数目。
+计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
+class Solution {
+private:
+ vector<vector<bool> > isvisit;
+ int result = 0;
+public:
+ void BFS(vector<vector<int>>& grid, int i, int j, int m, int n, int nowsum){
+ queue<pair<int,int> > q;
+ q.push({i,j});
+ isvisit[i][j] = true;
+ while(!q.empty()){
+ pair<int,int> cur = q.front();
+ nowsum += 1;
+ q.pop();
+ int x = cur.first;
+ int y = cur.second;
+ if(x-1 >= 0 && grid[x-1][y] == 1 && isvisit[x-1][y] == false){
+ isvisit[x-1][y] = true;
+ q.push({x-1,y});
+ }
+ if(x+1 < m && grid[x+1][y] == 1 && isvisit[x+1][y] == false){
+ isvisit[x+1][y] = true;
+ q.push({x+1,y});
+ }
+ if(y-1 >= 0 && grid[x][y-1] == 1 && isvisit[x][y-1] == false){
+ isvisit[x][y-1] = true;
+ q.push({x,y-1});
+ }
+ if(y+1 < n && grid[x][y+1] == 1 && isvisit[x][y+1] == false){
+ isvisit[x][y+1] = true;
+ q.push({x,y+1});
+ }
+ }
+ result = max(result,nowsum);
+ }
+ int maxAreaOfIsland(vector<vector<int>>& grid) {
+ int m = grid.size();
+ int n = grid[0].size();
+ for(int i=0;i<m;i++){
+ isvisit.push_back(vector<bool>(n));
+ }
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(grid[i][j] == 1 && isvisit[i][j] == false){
+ BFS(grid,i,j,m,n,0);
+ }
+ }
+ }
+ return result;
+ }
+};给你一个大小为 m x n 的二进制矩阵 grid ,其中 0 表示一个海洋单元格、1 表示一个陆地单元格。
+一次 移动 是指从一个陆地单元格走到另一个相邻(上、下、左、右)的陆地单元格或跨过 grid 的边界。
+返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。
+class Solution {
+private:
+ vector<vector<bool> > isvisit;
+ int result = 0;
+public:
+ void BFS(vector<vector<int>>& grid, int i, int j, int m, int n, int nowsum, int mode){
+ queue<pair<int,int> > q;
+ q.push({i,j});
+ isvisit[i][j] = true;
+ while(!q.empty()){
+ pair<int,int> cur = q.front();
+ nowsum += 1;
+ q.pop();
+ int x = cur.first;
+ int y = cur.second;
+ if(x-1 >= 0 && grid[x-1][y] == 1 && isvisit[x-1][y] == false){
+ isvisit[x-1][y] = true;
+ q.push({x-1,y});
+ }
+ if(x+1 < m && grid[x+1][y] == 1 && isvisit[x+1][y] == false){
+ isvisit[x+1][y] = true;
+ q.push({x+1,y});
+ }
+ if(y-1 >= 0 && grid[x][y-1] == 1 && isvisit[x][y-1] == false){
+ isvisit[x][y-1] = true;
+ q.push({x,y-1});
+ }
+ if(y+1 < n && grid[x][y+1] == 1 && isvisit[x][y+1] == false){
+ isvisit[x][y+1] = true;
+ q.push({x,y+1});
+ }
+ }
+ if(mode == 0){
+ return;
+ }
+
+ result += nowsum;
+ }
+ int numEnclaves(vector<vector<int>>& grid) {
+ int m = grid.size();
+ int n = grid[0].size();
+ for(int i=0;i<m;i++){
+ isvisit.push_back(vector<bool>(n));
+ }
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(i != 0 && j != 0 && i != m-1 && j != n-1){
+ continue;
+ }
+ if(grid[i][j] == 1){
+ BFS(grid,i,j,m,n,0,0);
+ }
+ }
+ }
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(i == 0 || j == 0 || i == m-1 || j == n-1){
+ continue;
+ }
+ if(grid[i][j] == 1 && isvisit[i][j] == false){
+ BFS(grid,i,j,m,n,0,1);
+ }
+ }
+ }
+ return result;
+ }
+};二维矩阵 grid 由 0 (土地)和 1 (水)组成。岛是由最大的4个方向连通的 0 组成的群,封闭岛是一个 完全 由1包围(左、上、右、下)的岛。
+请返回 封闭岛屿 的数目。
+class Solution {
+private:
+ vector<vector<bool> > isvisit;
+public:
+ void BFS(vector<vector<int>>& grid, int i, int j, int m, int n){
+ queue<pair<int,int> > q;
+ q.push({i,j});
+ isvisit[i][j] = true;
+ while(!q.empty()){
+ pair<int,int> cur = q.front();
+ q.pop();
+ int x = cur.first;
+ int y = cur.second;
+ if(x-1 >= 0 && grid[x-1][y] == 0 && isvisit[x-1][y] == false){
+ isvisit[x-1][y] = true;
+ q.push({x-1,y});
+ }
+ if(x+1 < m && grid[x+1][y] == 0 && isvisit[x+1][y] == false){
+ isvisit[x+1][y] = true;
+ q.push({x+1,y});
+ }
+ if(y-1 >= 0 && grid[x][y-1] == 0 && isvisit[x][y-1] == false){
+ isvisit[x][y-1] = true;
+ q.push({x,y-1});
+ }
+ if(y+1 < n && grid[x][y+1] == 0 && isvisit[x][y+1] == false){
+ isvisit[x][y+1] = true;
+ q.push({x,y+1});
+ }
+ }
+ }
+ int closedIsland(vector<vector<int>>& grid) {
+ int m = grid.size();
+ int n = grid[0].size();
+ for(int i=0;i<m;i++){
+ isvisit.push_back(vector<bool>(n));
+ }
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(i != 0 && j != 0 && i != m-1 && j != n-1){
+ continue;
+ }
+ if(grid[i][j] == 0){
+ BFS(grid,i,j,m,n);
+ }
+ }
+ }
+ int result = 0;
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(grid[i][j] == 0 && isvisit[i][j] == false){
+ BFS(grid,i,j,m,n);
+ result += 1;
+ }
+ }
+ }
+ return result;
+ }
+};给你一个 m x n 的矩阵 board ,由若干字符 ‘X’ 和 ‘O’ ,找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。
+class Solution {
+private:
+ vector<vector<bool> > isvisit;
+public:
+ void BFS(vector<vector<char>>& board, int i, int j, int m, int n){
+ queue<pair<int,int> > q;
+ q.push({i,j});
+ isvisit[i][j] = true;
+ while(!q.empty()){
+ pair<int,int> cur = q.front();
+ q.pop();
+ int x = cur.first;
+ int y = cur.second;
+ if(x-1 >= 0 && board[x-1][y] == 'O' && isvisit[x-1][y] == false){
+ isvisit[x-1][y] = true;
+ q.push({x-1,y});
+ }
+ if(x+1 < m && board[x+1][y] == 'O' && isvisit[x+1][y] == false){
+ isvisit[x+1][y] = true;
+ q.push({x+1,y});
+ }
+ if(y-1 >= 0 && board[x][y-1] == 'O' && isvisit[x][y-1] == false){
+ isvisit[x][y-1] = true;
+ q.push({x,y-1});
+ }
+ if(y+1 < n && board[x][y+1] == 'O' && isvisit[x][y+1] == false){
+ isvisit[x][y+1] = true;
+ q.push({x,y+1});
+ }
+ }
+ }
+ void solve(vector<vector<char>>& board) {
+ int m = board.size();
+ int n = board[0].size();
+ for(int i=0;i<m;i++){
+ isvisit.push_back(vector<bool>(n));
+ }
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(i != 0 && i != m-1 && j != 0 && j != n-1){
+ continue;
+ }
+ if(board[i][j] == 'O' && isvisit[i][j] == false){
+ BFS(board,i,j,m,n);
+ }
+ }
+ }
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(board[i][j] == 'O' && isvisit[i][j] == false){
+ board[i][j] = 'X';
+ }
+ }
+ }
+ return;
+ }
+};有一个 m × n 的矩形岛屿,与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界,而 “大西洋” 处于大陆的右边界和下边界。
+这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights , heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。
+岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。
+返回网格坐标 result 的 2D 列表 ,其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。
+class Solution {
+private:
+ vector<vector<bool> > visit_p;
+ vector<vector<bool> > visit_a;
+public:
+ void BFS(vector<vector<int> >& heights, vector<vector<bool> >& visit, int i, int j, int m, int n){
+ visit[i][j] = true;
+ queue<pair<int, int> > q;
+ q.push({i,j});
+ while(!q.empty()){
+ pair<int, int> cur = q.front();
+ q.pop();
+ int x = cur.first;
+ int y = cur.second;
+ if(x-1 >= 0 && visit[x-1][y] == false && heights[x-1][y] >= heights[x][y]){
+ visit[x-1][y] = true;
+ q.push({x-1,y});
+ }
+ if(x+1 < m && visit[x+1][y] == false && heights[x+1][y] >= heights[x][y]){
+ visit[x+1][y] = true;
+ q.push({x+1,y});
+ }
+ if(y-1 >= 0 && visit[x][y-1] == false && heights[x][y-1] >= heights[x][y]){
+ visit[x][y-1] = true;
+ q.push({x,y-1});
+ }
+ if(y+1 < n && visit[x][y+1] == false && heights[x][y+1] >= heights[x][y]){
+ visit[x][y+1] = true;
+ q.push({x,y+1});
+ }
+ }
+ }
+ vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
+ int m = heights.size();
+ int n = heights[0].size();
+ for(int i=0;i<m;i++){
+ visit_p.push_back(vector<bool>(n));
+ visit_a.push_back(vector<bool>(n));
+ }
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(i == 0 || j == 0){
+ BFS(heights, visit_p, i,j,m,n);
+ }
+ if(i == m-1 || j == n-1){
+ BFS(heights, visit_a, i,j,m,n);
+ }
+ }
+ }
+ vector<vector<int> > result;
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(visit_p[i][j] == true && visit_a[i][j] == true){
+ result.push_back(vector<int>{i,j});
+ }
+ }
+ }
+ return result;
+ }
+};给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。
+返回执行此操作后,grid 中最大的岛屿面积是多少?
+岛屿 由一组上、下、左、右四个方向相连的 1 形成。
+class Solution {
+private:
+ int numindex = 2;
+ unordered_map<int, int> mp;
+public:
+ void BFS(vector<vector<int>>& grid, int i, int j, int n, int numindex){
+ queue<pair<int, int> > q;
+ q.push({i,j});
+ int nowcount = 1;
+ grid[i][j] = numindex;
+ while(!q.empty()){
+ pair<int, int> cur = q.front();
+ q.pop();
+ int x = cur.first;
+ int y = cur.second;
+ if(x-1 >= 0 && grid[x-1][y] == 1){
+ q.push({x-1,y});
+ nowcount += 1;
+ grid[x-1][y] = numindex;
+ }
+ if(y-1 >= 0 && grid[x][y-1] == 1){
+ q.push({x,y-1});
+ nowcount += 1;
+ grid[x][y-1] = numindex;
+ }
+ if(x+1 < n && grid[x+1][y] == 1){
+ q.push({x+1,y});
+ nowcount += 1;
+ grid[x+1][y] = numindex;
+ }
+ if(y+1 < n && grid[x][y+1] == 1){
+ q.push({x,y+1});
+ nowcount += 1;
+ grid[x][y+1] = numindex;
+ }
+ }
+ mp[numindex] = nowcount;
+ }
+ int largestIsland(vector<vector<int>>& grid) {
+ int n = grid.size();
+ for(int i=0;i<n;i++){
+ for(int j=0;j<n;j++){
+ if(grid[i][j] == 1){
+ BFS(grid,i,j,n,numindex);
+ numindex += 1;
+ }
+ }
+ }
+ mp[0] = 0;
+ int maxarea = 0;
+ for(int i=0;i<n;i++){
+ for(int j=0;j<n;j++){
+ int area = 0;
+ if(grid[i][j] == 0){
+ area += 1;
+ }
+ unordered_map<int,bool> mp2;
+ mp2[grid[i][j]] = true;
+ area += mp[grid[i][j]];
+ if(i-1 >= 0 && mp2.find(grid[i-1][j]) == mp2.end()){
+ mp2[grid[i-1][j]] = true;
+ area += mp[grid[i-1][j]];
+ }
+ if(j-1 >= 0 && mp2.find(grid[i][j-1]) == mp2.end()){
+ mp2[grid[i][j-1]] = true;
+ area += mp[grid[i][j-1]];
+ }
+ if(i+1 < n && mp2.find(grid[i+1][j]) == mp2.end()){
+ mp2[grid[i+1][j]] = true;
+ area += mp[grid[i+1][j]];
+ }
+ if(j+1 < n && mp2.find(grid[i][j+1]) == mp2.end()){
+ mp2[grid[i][j+1]] = true;
+ area += mp[grid[i][j+1]];
+ }
+ maxarea = max(maxarea, area);
+ }
+ }
+ return maxarea;
+ }
+};字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
+序列中第一个单词是 beginWord 。
+序列中最后一个单词是 endWord 。
+每次转换只能改变一个字母。
+转换过程中的中间单词必须是字典 wordList 中的单词。
+给你两个单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。
+class Solution {
+private:
+ int mincount = 0;
+public:
+ bool judgetwowords(string word1, string word2){
+ int sumcount = 0;
+ for(int i=0;i<word1.size();i++){
+ if(word1[i] != word2[i]){
+ sumcount += 1;
+ }
+ if(sumcount >= 2){
+ return false;
+ }
+ }
+ if(sumcount == 1){
+ return true;
+ }
+ return false;
+ }
+ int BFS(vector<vector<int> >& grid, int start, int end){
+ unordered_map<int, bool> visitMap;
+ visitMap[start] = true;
+ queue<int> q;
+ q.push(start);
+ int nowcount = 0;
+ while(!q.empty()){
+ int t = q.size();
+ nowcount += 1;
+ // cout << nowcount << " " << t << endl;
+ for(int j=0;j<t;j++){
+ int cur = q.front();
+ q.pop();
+ if(cur == end){
+ return nowcount;
+ }
+ for(int i=0;i<grid[cur].size();i++){
+ if(visitMap.find(grid[cur][i]) == visitMap.end()){
+ visitMap[grid[cur][i]] = true;
+ q.push(grid[cur][i]);
+ }
+ }
+ }
+ }
+ return 0;
+ }
+ int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
+ int sign = -1;
+ for(int i=0;i<wordList.size();i++){
+ if(wordList[i] == endWord){
+ sign = i+1;
+ }
+ }
+ if(sign == -1){
+ return 0;
+ }
+ vector<vector<int> > grid;
+ vector<int> tempgrid;
+ for(int i=0;i<wordList.size();i++){
+ if(judgetwowords(wordList[i], beginWord)){
+ // cout << i << "fgdgf" << endl;
+ tempgrid.push_back(i+1);
+ }
+ }
+ grid.push_back(tempgrid);
+ for(int i=0;i<wordList.size();i++){
+ vector<int> tempgrid2;
+ // tempgrid2.push_back(i+2);
+ for(int j=0;j<wordList.size();j++){
+ if(i+1 == j+1){
+ continue;
+ }
+ if(judgetwowords(wordList[i], wordList[j])){
+ tempgrid2.push_back(j+1);
+ }
+ }
+ grid.push_back(tempgrid2);
+ }
+ // for(int i=0;i<grid.size();i++){
+ // for(int j=0;j<grid[i].size();j++){
+ // cout << grid[i][j] << " ";
+ // }
+ // cout << endl;
+ // }
+ int mincount = BFS(grid, 0, sign);
+ return mincount;
+ }
+};有 N 个房间,开始时你位于 0 号房间。每个房间有不同的号码:0,1,2,…,N-1,并且房间里可能有一些钥匙能使你进入下一个房间。
+在形式上,对于每个房间 i 都有一个钥匙列表 rooms[i],每个钥匙 rooms[i][j] 由 [0,1,…,N-1] 中的一个整数表示,其中 N = rooms.length。 钥匙 rooms[i][j] = v 可以打开编号为 v 的房间。
+最初,除 0 号房间外的其余所有房间都被锁住。
+你可以自由地在房间之间来回走动。
+如果能进入每个房间返回 true,否则返回 false。
+class Solution {
+public:
+ bool canVisitAllRooms(vector<vector<int>>& rooms) {
+ int lenrooms = rooms.size();
+ vector<bool> isvisit(lenrooms);
+ queue<int> q;
+ q.push(0);
+ isvisit[0] = true;
+ while(!q.empty()){
+ int t = q.front();
+ q.pop();
+ for(int i=0;i<rooms[t].size();i++){
+ if (isvisit[rooms[t][i]] == false){
+ isvisit[rooms[t][i]] = true;
+ q.push(rooms[t][i]);
+ }
+ }
+ }
+ for(int i=0;i<lenrooms;i++){
+ if(isvisit[i] == false){
+ return false;
+ }
+ }
+ return true;
+ }
+};给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
+网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
+岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
+class Solution {
+public:
+ int islandPerimeter(vector<vector<int>>& grid) {
+ int result = 0;
+ int m = grid.size();
+ int n = grid[0].size();
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(grid[i][j] == 1){
+ result += 4;
+ if(i-1 >= 0 && grid[i-1][j] == 1){
+ result -= 1;
+ }
+ if(j-1 >= 0 && grid[i][j-1] == 1){
+ result -= 1;
+ }
+ if(i+1 < m && grid[i+1][j] == 1){
+ result -= 1;
+ }
+ if(j+1 < n && grid[i][j+1] == 1){
+ result -= 1;
+ }
+ }
+ }
+ }
+ return result;
+ }
+};有一个具有 n个顶点的 双向 图,其中每个顶点标记从 0 到 n - 1(包含 0 和 n - 1)。图中的边用一个二维整数数组 edges 表示,其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接,并且没有顶点存在与自身相连的边。
+请你确定是否存在从顶点 start 开始,到顶点 end 结束的 有效路径 。
+给你数组 edges 和整数 n、start和end,如果从 start 到 end 存在 有效路径 ,则返回 true,否则返回 false 。
+class Solution {
+private:
+ vector<int> father;
+public:
+ int findfather(int a){
+ if(a == father[a]){
+ return a;
+ }
+ return father[a] = findfather(father[a]);
+ }
+ void join(int a, int b){
+ a = findfather(a);
+ b = findfather(b);
+ if(a == b){
+ return;
+ }
+ father[a] = b;
+ }
+ bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
+ for(int i=0;i<n;i++){
+ father.push_back(i);
+ }
+ for(int i=0;i<edges.size();i++){
+ join(edges[i][0], edges[i][1]);
+ }
+ if(findfather(source) == findfather(destination)){
+ return true;
+ }
+ return false;
+ }
+};树可以看成是一个连通且 无环 的 无向 图。
+给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
+请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的边。
+class Solution {
+private:
+ vector<int> father;
+public:
+ int findfather(int a){
+ return a == father[a] ? a : father[a] = findfather(father[a]);
+ }
+ void join(int a, int b){
+ a = findfather(a);
+ b = findfather(b);
+ if(a == b){
+ return;
+ }
+ father[a] = b;
+ }
+ bool issamefather(int a, int b){
+ a = findfather(a);
+ b = findfather(b);
+ if(a == b){
+ return true;
+ }
+ return false;
+ }
+ vector<int> findRedundantConnection(vector<vector<int>>& edges) {
+ int n = edges.size();
+ for(int i=0;i<n+1;i++){
+ father.push_back(i);
+ }
+ for(int i=0;i<n;i++){
+ int x = edges[i][0];
+ int y = edges[i][1];
+ if(issamefather(x,y)){
+ return edges[i];
+ }
+ join(x,y);
+ }
+ return edges[0];
+ }
+};在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。
+输入一个有向图,该图由一个有着 n 个节点(节点值不重复,从 1 到 n)的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间,这条附加的边不属于树中已存在的边。
+结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi],用以表示 有向 图中连接顶点 ui 和顶点 vi 的边,其中 ui 是 vi 的一个父节点。
+返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案。
+这个不会
+代码随想录-二叉树
+ +type TreeNode struct {
+ Val int
+ Left *TreeNode
+ Right *TreeNode
+}确定递归函数的参数和返回值 :因为要打印出前序遍历节点的数值,所以参数里需要传入vector在放节点的数值,除了这一点就不需要在处理什么数据了也不需要有返回值,所以递归函数返回类型就是void
+确定终止条件 :在递归的过程中,如何算是递归结束了呢,当然是当前遍历的节点是空了,那么本层递归就要结束了,所以如果当前遍历的这个节点是空,就直接return
+确定单层递归的逻辑 :前序遍历是中左右的顺序,所以在单层递归的逻辑,是要先取中节点的数值
+func preorderTraversal(root *TreeNode) (res []int) {
+ var traversal func(node *TreeNode)
+ traversal = func(node *TreeNode) {
+ if node == nil {
+ return
+ }
+ res = append(res,node.Val)
+ traversal(node.Left)
+ traversal(node.Right)
+ }
+ traversal(root)
+ return res
+}将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。
+如何标记呢,就是要处理的节点放入栈之后,紧接着放入一个空指针作为标记。
+前序遍历统一迭代法:
+ /**
+ type Element struct {
+ // 元素保管的值
+ Value interface{}
+ // 内含隐藏或非导出字段
+}
+
+func (l *List) Back() *Element
+前序遍历:中左右
+压栈顺序:右左中
+ **/
+func preorderTraversal(root *TreeNode) []int {
+ if root == nil {
+ return nil
+ }
+ var stack = list.New()//栈
+ res:=[]int{}//结果集
+ stack.PushBack(root)
+ var node *TreeNode
+ for stack.Len()>0{
+ e := stack.Back()
+ stack.Remove(e)//弹出元素
+ if e.Value==nil{// 如果为空,则表明是需要处理中间节点
+ e=stack.Back()//弹出元素(即中间节点)
+ stack.Remove(e)//删除中间节点
+ node=e.Value.(*TreeNode)
+ res=append(res,node.Val)//将中间节点加入到结果集中
+ continue//继续弹出栈中下一个节点
+ }
+ node = e.Value.(*TreeNode)
+ //压栈顺序:右左中
+ if node.Right!=nil{
+ stack.PushBack(node.Right)
+ }
+ if node.Left!=nil{
+ stack.PushBack(node.Left)
+ }
+ stack.PushBack(node)//中间节点压栈后再压入nil作为中间节点的标志符
+ stack.PushBack(nil)
+ }
+ return res
+
+}中序遍历统一迭代法:
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+ //中序遍历:左中右
+ //压栈顺序:右中左
+func inorderTraversal(root *TreeNode) []int {
+ if root==nil{
+ return nil
+ }
+ stack:=list.New()//栈
+ res:=[]int{}//结果集
+ stack.PushBack(root)
+ var node *TreeNode
+ for stack.Len()>0{
+ e := stack.Back()
+ stack.Remove(e)
+ if e.Value==nil{// 如果为空,则表明是需要处理中间节点
+ e=stack.Back()//弹出元素(即中间节点)
+ stack.Remove(e)//删除中间节点
+ node=e.Value.(*TreeNode)
+ res=append(res,node.Val)//将中间节点加入到结果集中
+ continue//继续弹出栈中下一个节点
+ }
+ node = e.Value.(*TreeNode)
+ //压栈顺序:右中左
+ if node.Right!=nil{
+ stack.PushBack(node.Right)
+ }
+ stack.PushBack(node)//中间节点压栈后再压入nil作为中间节点的标志符
+ stack.PushBack(nil)
+ if node.Left!=nil{
+ stack.PushBack(node.Left)
+ }
+ }
+ return res
+}后序遍历统一迭代法:
+//后续遍历:左右中
+//压栈顺序:中右左
+func postorderTraversal(root *TreeNode) []int {
+ if root == nil {
+ return nil
+ }
+ var stack = list.New()//栈
+ res:=[]int{}//结果集
+ stack.PushBack(root)
+ var node *TreeNode
+ for stack.Len()>0{
+ e := stack.Back()
+ stack.Remove(e)
+ if e.Value==nil{// 如果为空,则表明是需要处理中间节点
+ e=stack.Back()//弹出元素(即中间节点)
+ stack.Remove(e)//删除中间节点
+ node=e.Value.(*TreeNode)
+ res=append(res,node.Val)//将中间节点加入到结果集中
+ continue//继续弹出栈中下一个节点
+ }
+ node = e.Value.(*TreeNode)
+ //压栈顺序:中右左
+ stack.PushBack(node)//中间节点压栈后再压入nil作为中间节点的标志符
+ stack.PushBack(nil)
+ if node.Right!=nil{
+ stack.PushBack(node.Right)
+ }
+ if node.Left!=nil{
+ stack.PushBack(node.Left)
+ }
+ }
+ return res
+}/**
+102. 二叉树的层序遍历
+ */
+func levelOrder(root *TreeNode) [][]int {
+ res:=[][]int{}
+ if root==nil{//防止为空
+ return res
+ }
+ queue:=list.New()
+ queue.PushBack(root)
+ var tmpArr []int
+ for queue.Len()>0 {
+ length:=queue.Len()//保存当前层的长度,然后处理当前层(十分重要,防止添加下层元素影响判断层中元素的个数)
+ for i:=0;i<length;i++{
+ node:=queue.Remove(queue.Front()).(*TreeNode)//出队列
+ if node.Left!=nil{
+ queue.PushBack(node.Left)
+ }
+ if node.Right!=nil{
+ queue.PushBack(node.Right)
+ }
+ tmpArr=append(tmpArr,node.Val)//将值加入本层切片中
+ }
+ res=append(res,tmpArr)//放入结果集
+ tmpArr=[]int{}//清空层的数据
+ }
+ return res
+}给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func levelOrder(root *TreeNode) [][]int {
+ result := make([][]int,0)
+ if root == nil{
+ return result
+ }
+ queue := list.New()
+ queue.PushBack(root)
+ for queue.Len() > 0{
+ length := queue.Len()
+ temp := make([]int,0)
+ for i:=0;i<length;i++{
+ node := queue.Remove(queue.Front()).(*TreeNode)
+ if node.Left != nil{
+ queue.PushBack(node.Left)
+ }
+ if node.Right != nil{
+ queue.PushBack(node.Right)
+ }
+ temp = append(temp,node.Val)
+ }
+ result = append(result,temp)
+ }
+ return result
+}class Solution {
+public:
+ vector<vector<int>> levelOrder(TreeNode* root) {
+ vector<vector<int> > result;
+ if(root == NULL){
+ return result;
+ }
+ queue<TreeNode*> q;
+ q.push(root);
+ while(!q.empty()){
+ int s = q.size();
+ vector<int> temp;
+ for(int i=0;i<s;i++){
+ TreeNode* t = q.front();
+ q.pop();
+ temp.push_back(t->val);
+ if(t->left != NULL){
+ q.push(t->left);
+ }
+ if(t->right != NULL){
+ q.push(t->right);
+ }
+ }
+ result.push_back(temp);
+ }
+ return result;
+ }
+};给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func levelOrderBottom(root *TreeNode) [][]int {
+ result := make([][]int,0)
+ if root == nil{
+ return result
+ }
+ queue := list.New()
+ queue.PushBack(root)
+ for queue.Len() > 0{
+ templen := queue.Len()
+ tempArr := make([]int,0)
+ for i:=0;i<templen;i++{
+ node := queue.Remove(queue.Front()).(*TreeNode)
+ if node.Left != nil{
+ queue.PushBack(node.Left)
+ }
+ if node.Right != nil{
+ queue.PushBack(node.Right)
+ }
+ tempArr = append(tempArr,node.Val)
+ }
+ result = append([][]int{tempArr},result...)
+ }
+ return result
+}class Solution {
+public:
+ vector<vector<int>> levelOrderBottom(TreeNode* root) {
+ vector<vector<int> > result;
+ if(root == NULL){
+ return result;
+ }
+ queue<TreeNode*> q;
+ q.push(root);
+ while(!q.empty()){
+ int s = q.size();
+ vector<int> temp;
+ for(int i=0;i<s;i++){
+ TreeNode* t = q.front();
+ q.pop();
+ temp.push_back(t->val);
+ if(t->left != NULL){
+ q.push(t->left);
+ }
+ if(t->right != NULL){
+ q.push(t->right);
+ }
+ }
+ result.push_back(temp);
+ }
+ vector<vector<int> > acresult;
+ for(int i=result.size()-1;i>=0;i--){
+ acresult.push_back(result[i]);
+ }
+ return acresult;
+ }
+};给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func rightSideView(root *TreeNode) []int {
+ result := make([]int,0)
+ if root == nil{
+ return result
+ }
+ queue := list.New()
+ queue.PushBack(root)
+ for queue.Len() > 0{
+ tempLen := queue.Len()
+ for i:=0;i<tempLen;i++{
+ node := queue.Remove(queue.Front()).(*TreeNode)
+ if node.Left != nil{
+ queue.PushBack(node.Left)
+ }
+ if node.Right != nil{
+ queue.PushBack(node.Right)
+ }
+ if i == tempLen-1{
+ result = append(result,node.Val)
+ }
+ }
+ }
+ return result
+}class Solution {
+public:
+ vector<int> rightSideView(TreeNode* root) {
+ vector<int> result;
+ if(root == NULL){
+ return result;
+ }
+ queue<TreeNode*> q;
+ q.push(root);
+ while(!q.empty()){
+ int s = q.size();
+ for(int i=0;i<s;i++){
+ TreeNode* t = q.front();
+ q.pop();
+ if(i == s-1){
+ result.push_back(t->val);
+ }
+
+ if(t->left != NULL){
+ q.push(t->left);
+ }
+ if(t->right != NULL){
+ q.push(t->right);
+ }
+ }
+ }
+ return result;
+ }
+};给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func averageOfLevels(root *TreeNode) []float64 {
+ result := make([]float64,0)
+ if root == nil{
+ return result
+ }
+ queue := list.New()
+ queue.PushBack(root)
+ for queue.Len() > 0{
+ tempLen := queue.Len()
+ sum := 0
+ for i:=0;i<tempLen;i++{
+ node := queue.Remove(queue.Front()).(*TreeNode)
+ if node.Left != nil{
+ queue.PushBack(node.Left)
+ }
+ if node.Right != nil{
+ queue.PushBack(node.Right)
+ }
+ sum += node.Val
+ }
+ result = append(result,float64(sum)/float64(tempLen))
+ }
+ return result
+}class Solution {
+public:
+ vector<double> averageOfLevels(TreeNode* root) {
+ vector<double> result;
+ if(root == NULL){
+ return result;
+ }
+ queue<TreeNode*> q;
+ q.push(root);
+ while(!q.empty()){
+ int s = q.size();
+ double nowsum = 0.0;
+ for(int i=0;i<s;i++){
+ TreeNode* t = q.front();
+ q.pop();
+ nowsum += (double)t->val;
+ if(t->left != NULL){
+ q.push(t->left);
+ }
+ if(t->right != NULL){
+ q.push(t->right);
+ }
+ }
+ nowsum /= (double)s;
+ result.push_back(nowsum);
+ }
+ return result;
+ }
+};给定一个 N 叉树,返回其节点值的 层序遍历 。(即从左到右,逐层遍历)。
+树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
+/**
+ * Definition for a Node.
+ * type Node struct {
+ * Val int
+ * Children []*Node
+ * }
+ */
+
+func levelOrder(root *Node) [][]int {
+ result := make([][]int,0)
+ if root == nil{
+ return result
+ }
+ queue := list.New()
+ queue.PushBack(root)
+ for queue.Len() > 0{
+ length := queue.Len()
+ temp := make([]int,0)
+ for i:=0;i<length;i++{
+ node := queue.Remove(queue.Front()).(*Node)
+ for j:=0;j<len(node.Children);j++{
+ if node.Children[j] != nil{
+ queue.PushBack(node.Children[j])
+ }
+ }
+ temp = append(temp,node.Val)
+ }
+ result = append(result,temp)
+ }
+ return result
+}class Solution {
+public:
+ vector<vector<int>> levelOrder(Node* root) {
+ vector<vector<int> > result;
+ if(root == NULL){
+ return result;
+ }
+ queue<Node*> q;
+ q.push(root);
+ while(!q.empty()){
+ int s = q.size();
+ vector<int> temp;
+ for(int i=0;i<s;i++){
+ Node* t = q.front();
+ q.pop();
+ temp.push_back(t->val);
+ for(int i=0;i<t->children.size();i++){
+ if(t->children[i] != NULL){
+ q.push(t->children[i]);
+ }
+ }
+ }
+ result.push_back(temp);
+ }
+ return result;
+ }
+};给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func largestValues(root *TreeNode) []int {
+ result := make([]int,0)
+ if root == nil{
+ return result
+ }
+ queue := list.New()
+ queue.PushBack(root)
+ for queue.Len() > 0{
+ maxVal := -1024*1024*1024*2
+ tempLen := queue.Len()
+ for i:=0;i<tempLen;i++{
+ node := queue.Remove(queue.Front()).(*TreeNode)
+ maxVal = max(maxVal,node.Val)
+ if node.Left != nil{
+ queue.PushBack(node.Left)
+ }
+ if node.Right != nil{
+ queue.PushBack(node.Right)
+ }
+ }
+ result = append(result,maxVal)
+ }
+ return result
+}
+
+func max(a,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ vector<int> largestValues(TreeNode* root) {
+ vector<int> result;
+ if(root == NULL){
+ return result;
+ }
+ queue<TreeNode*> q;
+ q.push(root);
+ while(!q.empty()){
+ int s = q.size();
+ int maxnode = q.front()->val;
+ for(int i=0;i<s;i++){
+ TreeNode* t = q.front();
+ q.pop();
+ maxnode = max(maxnode,t->val);
+ if(t->left != NULL){
+ q.push(t->left);
+ }
+ if(t->right != NULL){
+ q.push(t->right);
+ }
+ }
+ result.push_back(maxnode);
+ }
+ return result;
+ }
+};给定一个完美二叉树,其所有叶子节点都在同一层,每个父节点都有两个子节点。
+填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
/**
+ * Definition for a Node.
+ * type Node struct {
+ * Val int
+ * Left *Node
+ * Right *Node
+ * Next *Node
+ * }
+ */
+
+func connect(root *Node) *Node {
+ queue := []*Node{root}
+ if root == nil{
+ return root
+ }
+ for len(queue) > 0{
+ tempLen := len(queue)
+ for i:=0;i<tempLen;i++{
+ node := queue[0]
+ queue = queue[1:]
+ if i != tempLen-1{
+ node.Next = queue[0]
+ }
+ if node.Left != nil{
+ queue = append(queue,node.Left)
+ }
+ if node.Right != nil{
+ queue = append(queue,node.Right)
+ }
+ }
+ }
+ return root
+}class Solution {
+public:
+ Node* connect(Node* root) {
+ if(root == NULL){
+ return root;
+ }
+ queue<Node*> q;
+ q.push(root);
+ while(!q.empty()){
+ int s = q.size();
+ Node* pre = NULL;
+ for(int i=0;i<s;i++){
+ Node* t = q.front();
+ if(pre != NULL){
+ pre->next = q.front();
+ }
+ pre = t;
+ q.pop();
+ if(t->left != NULL){
+ q.push(t->left);
+ }
+ if(t->right != NULL){
+ q.push(t->right);
+ }
+ }
+ }
+ return root;
+ }
+};给定一个二叉树,填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
/**
+ * Definition for a Node.
+ * type Node struct {
+ * Val int
+ * Left *Node
+ * Right *Node
+ * Next *Node
+ * }
+ */
+
+func connect(root *Node) *Node {
+ queue := []*Node{root}
+ if root == nil{
+ return root
+ }
+ for len(queue) > 0{
+ tempLen := len(queue)
+ for i:=0;i<tempLen;i++{
+ node := queue[0]
+ queue = queue[1:]
+ if i != tempLen-1{
+ node.Next = queue[0]
+ }
+ if node.Left != nil{
+ queue = append(queue,node.Left)
+ }
+ if node.Right != nil{
+ queue = append(queue,node.Right)
+ }
+ }
+ }
+ return root
+}class Solution {
+public:
+ Node* connect(Node* root) {
+ if(root == NULL){
+ return root;
+ }
+ queue<Node*> q;
+ q.push(root);
+ while(!q.empty()){
+ int s = q.size();
+ Node* pre = NULL;
+ for(int i=0;i<s;i++){
+ Node* t = q.front();
+ if(pre != NULL){
+ pre->next = q.front();
+ }
+ pre = t;
+ q.pop();
+ if(t->left != NULL){
+ q.push(t->left);
+ }
+ if(t->right != NULL){
+ q.push(t->right);
+ }
+ }
+ }
+ return root;
+ }
+};给定一个二叉树,找出其最大深度。
+二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
+说明: 叶子节点是指没有子节点的节点。
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func maxDepth(root *TreeNode) int {
+ if root == nil{
+ return 0
+ }
+ queue := list.New()
+ queue.PushBack(root)
+ sum := 0
+ for queue.Len() > 0{
+ sum += 1
+ tempLen := queue.Len()
+ for i:=0;i<tempLen;i++{
+ node := queue.Remove(queue.Front()).(*TreeNode)
+ if node.Left != nil{
+ queue.PushBack(node.Left)
+ }
+ if node.Right != nil{
+ queue.PushBack(node.Right)
+ }
+ }
+ }
+ return sum
+}class Solution {
+public:
+ int maxDepth(TreeNode* root) {
+ int result = 0;
+ if(root == NULL){
+ return result;
+ }
+ queue<TreeNode*> q;
+ q.push(root);
+ while(!q.empty()){
+ int s = q.size();
+ for(int i=0;i<s;i++){
+ TreeNode* t = q.front();
+ q.pop();
+ if(t->left != NULL){
+ q.push(t->left);
+ }
+ if(t->right != NULL){
+ q.push(t->right);
+ }
+ }
+ result += 1;
+ }
+ return result;
+ }
+};给定一个二叉树,找出其最小深度。
+最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
+说明: 叶子节点是指没有子节点的节点。
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func minDepth(root *TreeNode) int {
+ if root == nil{
+ return 0
+ }
+ queue := list.New()
+ queue.PushBack(root)
+ level := 0
+ for queue.Len() > 0{
+ level += 1
+ tempLen := queue.Len()
+ for i:=0;i<tempLen;i++{
+ node := queue.Remove(queue.Front()).(*TreeNode)
+ if node.Left != nil{
+ queue.PushBack(node.Left)
+ }
+ if node.Right != nil{
+ queue.PushBack(node.Right)
+ }
+ if node.Left == nil && node.Right == nil{
+ return level
+ }
+ }
+ }
+ return level
+}class Solution {
+public:
+ int minDepth(TreeNode* root) {
+ int result = 0;
+ if(root == NULL){
+ return result;
+ }
+ queue<TreeNode*> q;
+ q.push(root);
+ while(!q.empty()){
+ int s = q.size();
+ for(int i=0;i<s;i++){
+ TreeNode* t = q.front();
+ q.pop();
+ if(t->left == NULL && t->right == NULL){
+ return result + 1;
+ }
+ if(t->left != NULL){
+ q.push(t->left);
+ }
+ if(t->right != NULL){
+ q.push(t->right);
+ }
+ }
+ result += 1;
+ }
+ return result;
+ }
+};给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func invertTree(root *TreeNode) *TreeNode {
+ if root == nil{
+ return root
+ }
+ DFS(root)
+ return root
+}
+
+func DFS(root *TreeNode){
+ if root == nil{
+ return
+ }
+ node := root.Left
+ root.Left = root.Right
+ root.Right = node
+ DFS(root.Left)
+ DFS(root.Right)
+}class Solution {
+public:
+ TreeNode* invertTree(TreeNode* root) {
+ if(root == NULL){
+ return root;
+ }
+ swap(root->left, root->right);
+ invertTree(root->left);
+ invertTree(root->right);
+ return root;
+ }
+};给你一个二叉树的根节点 root , 检查它是否轴对称。
/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func isSymmetric(root *TreeNode) bool {
+ return isSymmetricJudge(root.Left,root.Right)
+}
+
+func isSymmetricJudge(root1 *TreeNode,root2 *TreeNode) bool{
+ if root1 == nil && root2 == nil{
+ return true
+ } else if root1 == nil{
+ return false
+ } else if root2 == nil{
+ return false
+ } else{
+ if root1.Val == root2.Val{
+ return isSymmetricJudge(root1.Left,root2.Right) && isSymmetricJudge(root1.Right,root2.Left)
+ } else{
+ return false
+ }
+ }
+ return false
+}class Solution {
+public:
+ bool DFS(TreeNode* left, TreeNode* right){
+ if(left == NULL && right == NULL){
+ return true;
+ }
+ if(left == NULL){
+ return false;
+ }
+ if(right == NULL){
+ return false;
+ }
+ if(left->val != right->val){
+ return false;
+ }
+ return DFS(left->left, right->right) && DFS(right->left, left->right);
+ }
+ bool isSymmetric(TreeNode* root) {
+ if(root == NULL){
+ return true;
+ }
+ return DFS(root->left, root->right);
+ }
+};给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
+递归判断即可,注意留下一个true的值方便后续使用
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func isSameTree(p *TreeNode, q *TreeNode) bool {
+ if p == nil && q == nil{
+ return true
+ } else if p == nil{
+ return false
+ } else if q == nil{
+ return false
+ } else{
+ if p.Val == q.Val{
+ return isSameTree(p.Left,q.Left) && isSameTree(p.Right,q.Right)
+ }
+ return false
+ }
+ return false
+}class Solution {
+public:
+ bool isSameTree(TreeNode* p, TreeNode* q) {
+ if(p == NULL && q == NULL){
+ return true;
+ }
+ if(p == NULL){
+ return false;
+ }
+ if(q == NULL){
+ return false;
+ }
+ if(p->val != q->val){
+ return false;
+ }
+ return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
+ }
+};给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func isSubtree(root *TreeNode, subRoot *TreeNode) bool {
+ if root == nil && subRoot == nil{
+ return true
+ } else if root == nil || subRoot == nil{
+ return false
+ }
+ return isSameTree(root,subRoot) || isSubtree(root.Left,subRoot) || isSubtree(root.Right,subRoot)
+}
+
+func isSameTree(p *TreeNode, q *TreeNode) bool {
+ if p == nil && q == nil{
+ return true
+ } else if p == nil{
+ return false
+ } else if q == nil{
+ return false
+ } else{
+ if p.Val == q.Val{
+ return isSameTree(p.Left,q.Left) && isSameTree(p.Right,q.Right)
+ }
+ return false
+ }
+ return false
+}class Solution {
+public:
+ bool isSameTree(TreeNode* p, TreeNode* q) {
+ if(p == NULL && q == NULL){
+ return true;
+ }
+ if(p == NULL){
+ return false;
+ }
+ if(q == NULL){
+ return false;
+ }
+ if(p->val != q->val){
+ return false;
+ }
+ return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
+ }
+
+ bool isSubtree(TreeNode* root, TreeNode* subRoot) {
+ if(root == NULL && subRoot == NULL){
+ return true;
+ }
+ if(root == NULL || subRoot == NULL){
+ return false;
+ }
+ return isSameTree(root,subRoot) || isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
+ }
+};给你一棵完全二叉树的根节点 root ,求出该树的节点个数。
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
+对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
+对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func countNodes(root *TreeNode) int {
+ if root == nil {
+ return 0
+ }
+ leftH, rightH := 0, 0
+ leftNode := root.Left
+ rightNode := root.Right
+ for leftNode != nil {
+ leftNode = leftNode.Left
+ leftH++
+ }
+ for rightNode != nil {
+ rightNode = rightNode.Right
+ rightH++
+ }
+ if leftH == rightH {
+ return (2 << leftH) - 1
+ }
+ return countNodes(root.Left) + countNodes(root.Right) + 1
+}class Solution {
+public:
+ int countNodes(TreeNode* root) {
+ if(root == NULL){
+ return 0;
+ }
+ int leftCount = 0;
+ int rightCount = 0;
+ TreeNode* leftt = root->left;
+ TreeNode* rightt = root->right;
+ while(leftt != NULL){
+ leftCount += 1;
+ leftt = leftt->left;
+ }
+ while(rightt != NULL){
+ rightCount += 1;
+ rightt = rightt->right;
+ }
+ if(leftCount == rightCount){
+ return (2 << leftCount) - 1;
+ }
+ return countNodes(root->left) + countNodes(root->right) + 1;
+ }
+};给定一个二叉树,判断它是否是高度平衡的二叉树。
+写一个函数计算递归的深度,如果差值大于1,则直接返回-1标志位作为不满足条件,否则返回最大的深度确保后面计算的是最大的。
+如果是空结点,说明左右子树都是没有的,直接返回即可。
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func isBalanced(root *TreeNode) bool {
+ a := DFS(root)
+ if a == -1{
+ return false
+ }
+ return true
+}
+
+func DFS(root *TreeNode) int {
+ if root == nil{
+ return 0
+ }
+ leftheight := DFS(root.Left)
+ if leftheight == -1{
+ return -1
+ }
+ rightheight := DFS(root.Right)
+ if rightheight == -1{
+ return -1
+ }
+ if leftheight - rightheight == -1 || leftheight - rightheight == 0 || leftheight - rightheight == 1{
+ return 1+max(leftheight,rightheight)
+ }
+ return -1
+}
+
+func max(a,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int getHeight(TreeNode* root){
+ if(root == NULL){
+ return 0;
+ }
+ int left = getHeight(root->left);
+ if(left == -1){
+ return -1;
+ }
+ int right = getHeight(root->right);
+ if(right == -1){
+ return -1;
+ }
+ if(abs(right - left) <= 1){
+ return 1 + max(left, right);
+ }
+ return -1;
+ }
+ bool isBalanced(TreeNode* root) {
+ int a = getHeight(root);
+ if(a == -1){
+ return false;
+ }
+ return true;
+ }
+};给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
+与前面不同的是判断的时候要判断左右孩子的结点,不能只判断自己本身。
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func binaryTreePaths(root *TreeNode) []string {
+ result := make([]string,0)
+ tempstring := ""
+ DFS(root,tempstring,&result)
+ return result
+}
+
+func DFS(root *TreeNode, tempstring string, result *[]string ){
+ if root.Left == nil && root.Right == nil{
+ tempstring += fmt.Sprintf("%d", root.Val)
+ *result = append(*result,tempstring)
+ return
+ }
+ tempstring += fmt.Sprintf("%d->", root.Val)
+ if root.Left != nil{
+ DFS(root.Left,tempstring,result)
+ }
+ if root.Right != nil{
+ DFS(root.Right,tempstring,result)
+ }
+}class Solution {
+private:
+ vector<string> result;
+public:
+ void DFS(TreeNode* root, vector<int> temp){
+ temp.push_back(root->val);
+ if(root->left == NULL && root->right == NULL){
+ string s = "";
+ for(int i=0;i<temp.size();i++){
+ if(i != temp.size()-1){
+ s = s + to_string(temp[i]) + "->";
+ }
+ else{
+ s = s + to_string(temp[i]);
+ }
+ }
+ result.push_back(s);
+ return;
+ }
+ if(root->left != NULL){
+ DFS(root->left, temp);
+ }
+ if(root->right != NULL){
+ DFS(root->right, temp);
+ }
+ temp.pop_back();
+ }
+ vector<string> binaryTreePaths(TreeNode* root) {
+ if(root == NULL){
+ return result;
+ }
+ vector<int> temp;
+ DFS(root, temp);
+ return result;
+ }
+};给定二叉树的根节点 root ,返回所有左叶子之和。
判断条件进行递归操作即可
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func sumOfLeftLeaves(root *TreeNode) int {
+ sum := 0
+ if root.Left == nil && root.Right == nil{
+ return sum
+ }
+ DFS(root,&sum)
+ return sum
+}
+
+func DFS(root *TreeNode, sum *int){
+ if root.Left == nil && root.Right == nil{
+ *sum += root.Val
+ return
+ }
+ if root.Right != nil && (root.Right.Left != nil || root.Right.Right != nil){
+ DFS(root.Right,sum)
+ }
+ if root.Left != nil{
+ DFS(root.Left,sum)
+ }
+}class Solution {
+public:
+ int sumOfLeftLeaves(TreeNode* root) {
+ if(root == NULL){
+ return 0;
+ }
+ int sumleaves = 0;
+ if(root->left != NULL && root->left->left == NULL && root->left->right == NULL){
+ sumleaves = root->left->val;
+ }
+ return sumleaves + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
+ }
+};给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
+层序遍历即可(不能用一般的深度优先遍历!)
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func findBottomLeftValue(root *TreeNode) int {
+ queue := list.New()
+ queue.PushBack(root)
+ result := 0
+ for queue.Len() != 0 {
+ len1 := queue.Len()
+ for i:=0;i<len1;i++{
+ node := queue.Remove(queue.Front()).(*TreeNode)
+ if i == 0{
+ result = node.Val
+ }
+ if node.Left != nil{
+ queue.PushBack(node.Left)
+ }
+ if node.Right != nil{
+ queue.PushBack(node.Right)
+ }
+ }
+ }
+ return result
+}class Solution {
+public:
+ int findBottomLeftValue(TreeNode* root) {
+ if(root == NULL){
+ return 0;
+ }
+ int temp = root->val;
+ queue<TreeNode*> q;
+ q.push(root);
+ while(!q.empty()){
+ TreeNode* t = q.front();
+ q.pop();
+ temp = t->val;
+ if(t->right != NULL){
+ q.push(t->right);
+ }
+ if(t->left != NULL){
+ q.push(t->left);
+ }
+ }
+ return temp;
+ }
+};给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
+与找路径相同,递归寻找即可
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func hasPathSum(root *TreeNode, targetSum int) bool {
+ if root == nil{
+ return false
+ }
+ return DFS(root,0, targetSum)
+}
+
+func DFS(root *TreeNode,sum int,targetSum int) bool {
+ if root.Left == nil && root.Right == nil{
+ sum += root.Val
+ if sum == targetSum{
+ return true
+ }
+ return false
+ }
+ sum += root.Val
+ var a,b bool
+ if root.Left != nil{
+ a = DFS(root.Left,sum, targetSum)
+ }
+ if root.Right != nil{
+ b = DFS(root.Right,sum, targetSum)
+ }
+ return a || b
+}class Solution {
+private:
+ bool judge = false;
+public:
+ void DFS(TreeNode* root, int nowSum, int targetSum){
+ nowSum += root->val;
+ if(root->left == NULL && root->right == NULL){
+ if(nowSum == targetSum){
+ judge = true;
+ }
+ return;
+ }
+ if(root->left != NULL){
+ DFS(root->left, nowSum, targetSum);
+ }
+ if(root->right != NULL){
+ DFS(root->right, nowSum, targetSum);
+ }
+ nowSum -= root->val;
+ }
+ bool hasPathSum(TreeNode* root, int targetSum) {
+ if(root == NULL){
+ return false;
+ }
+ DFS(root,0, targetSum);
+ return judge;
+ }
+};给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
+新建一个数组记录每个结点的父亲即可
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+
+var result [][]int
+var pre map[*TreeNode]*TreeNode
+var target int
+
+func pathSum(root *TreeNode, targetSum int) [][]int {
+ result = make([][]int,0)
+ if root == nil{
+ return result
+ }
+ pre = make(map[*TreeNode]*TreeNode,0)
+ target = targetSum
+ DFS(root,0)
+ return result
+}
+
+func DFS(root *TreeNode, temp int){
+ temp += root.Val
+ if root.Left == nil && root.Right == nil{
+ if temp == target{
+ t := root
+ temp2 := make([]int,1)
+ temp2[0] = root.Val
+ for {
+ n,ok := pre[t]
+ if ok{
+ temp2 = append([]int{n.Val},temp2...)
+ t = n
+ } else{
+ break
+ }
+ }
+ result = append(result,temp2)
+ }
+ } else if root.Left == nil{
+ pre[root.Right] = root
+ DFS(root.Right,temp)
+ } else if root.Right == nil{
+ pre[root.Left] = root
+ DFS(root.Left,temp)
+ } else{
+ pre[root.Right] = root
+ pre[root.Left] = root
+ DFS(root.Left,temp)
+ DFS(root.Right,temp)
+ }
+}class Solution {
+private:
+ vector<vector<int> > result;
+public:
+ void DFS(TreeNode* root, int nowSum, int targetSum, vector<int> path){
+ nowSum += root->val;
+ path.push_back(root->val);
+ if(root->left == NULL && root->right == NULL && nowSum == targetSum){
+ result.push_back(path);
+ return;
+ }
+ if(root->left != NULL){
+ DFS(root->left,nowSum,targetSum, path);
+ }
+ if(root->right != NULL){
+ DFS(root->right,nowSum,targetSum, path);
+ }
+ nowSum -= root->val;
+ path.pop_back();
+ }
+ vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
+ if(root == NULL){
+ return result;
+ }
+ vector<int> path;
+ DFS(root,0,targetSum, path);
+ return result;
+ }
+};给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func buildTree(inorder []int, postorder []int) *TreeNode {
+ if len(inorder) < 1{
+ return nil
+ }
+ nodeValue := postorder[len(postorder)-1]
+ interval := findIndex(inorder,nodeValue)
+ root := &TreeNode{
+ Val:nodeValue,
+ Left:buildTree(inorder[:interval],postorder[:interval]),
+ Right:buildTree(inorder[interval+1:],postorder[interval:len(postorder)-1]),
+ }
+ return root
+}
+
+func findIndex(inorder []int,nodeValue int) int {
+ index := 0
+ for i:=0;i<len(inorder);i++{
+ if inorder[i] == nodeValue{
+ index = i
+ break
+ }
+ }
+ return index
+}class Solution {
+public:
+ TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
+ int postordersize = postorder.size();
+ int rootval = postorder[postordersize-1];
+ TreeNode* root = new TreeNode(rootval);
+ vector<int> newinorderleft;
+ vector<int> newinorderright;
+ vector<int> newpostorderleft;
+ vector<int> newpostorderright;
+ int inordersign = -1;
+ for(int i=0;i<inorder.size();i++){
+ if(inorder[i] == rootval){
+ inordersign = i;
+ newpostorderright.push_back(postorder[i]);
+ continue;
+ }
+ if(inordersign == -1){
+ newinorderleft.push_back(inorder[i]);
+ newpostorderleft.push_back(postorder[i]);
+ } else{
+ newinorderright.push_back(inorder[i]);
+ if(i != inorder.size() -1){
+ newpostorderright.push_back(postorder[i]);
+ }
+ }
+ }
+ if(newinorderleft.size() != 0){
+ root->left = buildTree(newinorderleft,newpostorderleft);
+ }
+ if(newinorderright.size() != 0){
+ root->right = buildTree(newinorderright,newpostorderright);
+ }
+ return root;
+ }
+};给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的 先序遍历 , inorder 是同一棵树的 中序遍历 ,请构造二叉树并返回其根节点。
/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func buildTree(preorder []int, inorder []int) *TreeNode {
+ if len(inorder) < 1{
+ return nil
+ }
+ nodeValue := preorder[0]
+ interval := findIndex(inorder,nodeValue)
+ root := &TreeNode{
+ Val:nodeValue,
+ Left:buildTree(preorder[1:interval+1],inorder[:interval]),
+ Right:buildTree(preorder[interval+1:],inorder[interval+1:]),
+ }
+ return root
+}
+
+func findIndex(inorder []int,nodeValue int) int {
+ index := 0
+ for i:=0;i<len(inorder);i++{
+ if inorder[i] == nodeValue{
+ index = i
+ break
+ }
+ }
+ return index
+}class Solution {
+public:
+ TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
+ int rootval = preorder[0];
+ TreeNode* root = new TreeNode(rootval);
+ vector<int> newinorderleft;
+ vector<int> newinorderright;
+ vector<int> newpreorderleft;
+ vector<int> newpreorderright;
+ int inordersign = -1;
+ for(int i=0;i<inorder.size();i++){
+ if(inorder[i] == rootval){
+ inordersign = i;
+ newpreorderleft.push_back(preorder[i]);
+ continue;
+ }
+ if(inordersign == -1){
+ newinorderleft.push_back(inorder[i]);
+ if(i != 0){
+ newpreorderleft.push_back(preorder[i]);
+ }
+ } else{
+ newinorderright.push_back(inorder[i]);
+ newpreorderright.push_back(preorder[i]);
+ }
+ }
+ if(newinorderleft.size() != 0){
+ root->left = buildTree(newpreorderleft,newinorderleft);
+ }
+ if(newinorderright.size() != 0){
+ root->right = buildTree(newpreorderright,newinorderright);
+ }
+ return root;
+ }
+};给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
nums 中的最大值。返回 nums 构建的最大二叉树。
/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func constructMaximumBinaryTree(nums []int) *TreeNode {
+ if len(nums) < 1{
+ return nil
+ }
+ maxIndex := findMaxindex(nums)
+ root := &TreeNode{
+ Val:nums[maxIndex],
+ Left:constructMaximumBinaryTree(nums[:maxIndex]),
+ Right:constructMaximumBinaryTree(nums[maxIndex+1:]),
+ }
+ return root
+}
+
+func findMaxindex(nums []int) int{
+ maxValue := nums[0]
+ maxIndex := 0
+ for i:=1;i<len(nums);i++{
+ if nums[i] > maxValue{
+ maxValue = nums[i]
+ maxIndex = i
+ }
+ }
+ return maxIndex
+}class Solution {
+public:
+ TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
+ if(nums.size() == 0){
+ return NULL;
+ }
+ int maxindex = 0;
+ int maxnode = nums[0];
+ for(int i=0;i<nums.size();i++){
+ if(nums[i] > maxnode){
+ maxindex = i;
+ maxnode = nums[i];
+ }
+ }
+ TreeNode* root = new TreeNode(maxnode);
+ vector<int> leftnums;
+ vector<int> rightnums;
+ for(int i=0;i<maxindex;i++){
+ leftnums.push_back(nums[i]);
+ }
+ for(int i=maxindex+1;i<nums.size();i++){
+ rightnums.push_back(nums[i]);
+ }
+ root->left = constructMaximumBinaryTree(leftnums);
+ root->right = constructMaximumBinaryTree(rightnums);
+ return root;
+ }
+};给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
+返回合并后的二叉树。
+注意: 合并过程必须从两个树的根节点开始。
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
+ if root1 == nil {
+ return root2
+ }
+ if root2 == nil {
+ return root1
+ }
+ root1.Val += root2.Val
+ root1.Left = mergeTrees(root1.Left, root2.Left)
+ root1.Right = mergeTrees(root1.Right, root2.Right)
+ return root1
+}class Solution {
+public:
+ TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
+ if(root1 == NULL){
+ return root2;
+ } else if(root2 == NULL){
+ return root1;
+ }
+ root1->val += root2->val;
+ root1->left = mergeTrees(root1->left, root2->left);
+ root1->right = mergeTrees(root1->right, root2->right);
+ return root1;
+ }
+};给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func searchBST(root *TreeNode, val int) *TreeNode {
+ if root == nil || root.Val == val{
+ return root
+ }
+ if val < root.Val{
+ return searchBST(root.Left,val)
+ } else if val > root.Val{
+ return searchBST(root.Right,val)
+ }
+ return root
+}class Solution {
+public:
+ TreeNode* searchBST(TreeNode* root, int val) {
+ if(root == NULL || root->val == val){
+ return root;
+ }
+ if(root->val > val){
+ return searchBST(root->left,val);
+ } else{
+ return searchBST(root->right,val);
+ }
+ return root;
+ }
+};给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
+不能单纯的比较左节点小于中间节点,右节点大于中间节点就完事了 。
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func isValidBST(root *TreeNode) bool {
+ result := make([]int,0)
+ DFS(root,&result)
+ for i:=0;i<len(result)-1;i++{
+ if result[i+1] <= result[i]{
+ return false
+ }
+ }
+ return true
+}
+
+func DFS(root *TreeNode, result *[]int){
+ if root == nil{
+ return
+ }
+ DFS(root.Left,result)
+ *result = append(*result,root.Val)
+ DFS(root.Right,result)
+}class Solution {
+private:
+ vector<int> result;
+public:
+ void inorder(TreeNode* root){
+ if(root == NULL){
+ return;
+ }
+ inorder(root->left);
+ result.push_back(root->val);
+ inorder(root->right);
+ }
+ bool isValidBST(TreeNode* root) {
+ inorder(root);
+ for(int i=0;i<result.size()-1;i++){
+ if(result[i] >= result[i+1]){
+ return false;
+ }
+ }
+ return true;
+ }
+};给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func getMinimumDifference(root *TreeNode) int {
+ result := make([]int,0)
+ DFS(root,&result)
+ minValue := 100000
+ for i:=0;i<len(result)-1;i++{
+ if result[i+1] - result[i] < minValue{
+ minValue = result[i+1] - result[i]
+ }
+ }
+ return minValue
+}
+
+func DFS(root *TreeNode, result *[]int){
+ if root == nil{
+ return
+ }
+ DFS(root.Left,result)
+ *result = append(*result,root.Val)
+ DFS(root.Right,result)
+}class Solution {
+private:
+ vector<int> result;
+public:
+ void inorder(TreeNode* root){
+ if(root == NULL){
+ return;
+ }
+ inorder(root->left);
+ result.push_back(root->val);
+ inorder(root->right);
+ }
+ int getMinimumDifference(TreeNode* root) {
+ inorder(root);
+ int minresult = INT_MAX;
+ for(int i=0;i<result.size()-1;i++){
+ minresult = min(result[i+1] - result[i], minresult);
+ }
+ return minresult;
+ }
+};给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
+假定 BST 满足如下定义:
+双指针法通过一次遍历快速找出众数
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func findMode(root *TreeNode) []int {
+ result := make([]int,0)
+ result2 := make([]int,0)
+ DFS(root,&result)
+ times := -1
+ p := 0
+ for q:=0;q<=len(result);q++{
+ if q == len(result) || result[q] != result[p]{
+ if times < q-p{
+ times = q-p
+ result2 = make([]int,0)
+ result2 = append(result2,result[p])
+ } else if times == q-p{
+ result2 = append(result2,result[p])
+ }
+ p = q
+ }
+ }
+ return result2
+}
+
+func DFS(root *TreeNode, result *[]int){
+ if root == nil{
+ return
+ }
+ DFS(root.Left,result)
+ *result = append(*result,root.Val)
+ DFS(root.Right,result)
+}class Solution {
+private:
+ unordered_map<int,int> mp;
+public:
+ void inorder(TreeNode* root){
+ if(root == NULL){
+ return;
+ }
+ inorder(root->left);
+ mp[root->val] += 1;
+ inorder(root->right);
+ }
+ vector<int> findMode(TreeNode* root) {
+ inorder(root);
+ int result = 0;
+ vector<int> res;
+ for(auto it = mp.begin();it != mp.end();it++){
+ if(it->second > result){
+ res.clear();
+ res.push_back(it->first);
+ result = it->second;
+ } else if (it->second == result){
+ res.push_back(it->first);
+ }
+ }
+ return res;
+ }
+};给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
+百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大( 一个节点也可以是它自己的祖先 )。”
+通过递归的方式将节点一层一层传递回去
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
+ if root == p || root == q || root == nil{
+ return root
+ }
+ left := lowestCommonAncestor(root.Left,p,q)
+ right := lowestCommonAncestor(root.Right,p,q)
+ if left != nil && right != nil{
+ return root
+ } else if left == nil && right != nil{
+ return right
+ } else if left != nil && right == nil{
+ return left
+ }
+ return nil
+}class Solution {
+public:
+ TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
+ if (root == q || root == p || root == NULL) return root;
+ TreeNode* left = lowestCommonAncestor(root->left, p, q);
+ TreeNode* right = lowestCommonAncestor(root->right, p, q);
+ if (left != NULL && right != NULL){
+ return root;
+ } else if (left == NULL){
+ return right;
+ }
+ return left;
+ }
+};给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
+百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大( 一个节点也可以是它自己的祖先 )。”
+利用二叉搜索树的性质,总体思想与上题相同
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+
+func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
+ if root.Val < p.Val && root.Val < q.Val{
+ return lowestCommonAncestor(root.Right,p,q)
+ } else if root.Val > p.Val && root.Val > q.Val{
+ return lowestCommonAncestor(root.Left,p,q)
+ }
+ return root
+}class Solution {
+public:
+ TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
+ if (root->val > p->val && root->val > q->val) {
+ return lowestCommonAncestor(root->left, p, q);
+ } else if (root->val < p->val && root->val < q->val) {
+ return lowestCommonAncestor(root->right, p, q);
+ } else return root;
+
+ }
+};给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意 ,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func insertIntoBST(root *TreeNode, val int) *TreeNode {
+ if root == nil {
+ return &TreeNode{Val:val}
+ }
+ node := root
+ var pnode *TreeNode
+ for node != nil{
+ if node.Val < val{
+ pnode = node
+ node = node.Right
+ } else if node.Val > val{
+ pnode = node
+ node = node.Left
+ }
+ }
+ if val > pnode.Val {
+ pnode.Right = &TreeNode{Val: val}
+ } else {
+ pnode.Left = &TreeNode{Val: val}
+ }
+ return root
+}class Solution {
+public:
+ TreeNode* insertIntoBST(TreeNode* root, int val) {
+ if(root == NULL){
+ TreeNode* node = new TreeNode(val);
+ return node;
+ }
+ if(root->val > val){
+ root->left = insertIntoBST(root->left, val);
+ } else{
+ root->right = insertIntoBST(root->right, val);
+ }
+ return root;
+ }
+};给定一个二叉搜索树的根节点 root 和一个值 key ,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
+有以下五种情况:
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func deleteOneNode(target *TreeNode) *TreeNode {
+ if target == nil {
+ return target
+ }
+ if target.Right == nil {
+ return target.Left
+ }
+ cur := target.Right
+ for cur.Left != nil {
+ cur = cur.Left
+ }
+ cur.Left = target.Left
+ return target.Right
+}
+func deleteNode(root *TreeNode, key int) *TreeNode {
+ // 特殊情况处理
+ if root == nil {
+ return root
+ }
+ cur := root
+ var pre *TreeNode
+ for cur != nil {
+ if cur.Val == key {
+ break
+ }
+ pre = cur
+ if cur.Val > key {
+ cur = cur.Left
+ } else {
+ cur = cur.Right
+ }
+ }
+ if pre == nil {
+ return deleteOneNode(cur)
+ }
+ // pre 要知道是删除左孩子还有右孩子
+ if pre.Left != nil && pre.Left.Val == key {
+ pre.Left = deleteOneNode(cur)
+ }
+ if pre.Right != nil && pre.Right.Val == key {
+ pre.Right = deleteOneNode(cur)
+ }
+ return root
+}class Solution {
+public:
+ TreeNode* deleteNode(TreeNode* root, int key) {
+ if (root == nullptr) return root; // 第一种情况:没找到删除的节点,遍历到空节点直接返回了
+ if (root->val == key) {
+ // 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
+ if (root->left == nullptr && root->right == nullptr) {
+ ///! 内存释放
+ delete root;
+ return nullptr;
+ }
+ // 第三种情况:其左孩子为空,右孩子不为空,删除节点,右孩子补位 ,返回右孩子为根节点
+ else if (root->left == nullptr) {
+ auto retNode = root->right;
+ ///! 内存释放
+ delete root;
+ return retNode;
+ }
+ // 第四种情况:其右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
+ else if (root->right == nullptr) {
+ auto retNode = root->left;
+ ///! 内存释放
+ delete root;
+ return retNode;
+ }
+ // 第五种情况:左右孩子节点都不为空,则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
+ // 并返回删除节点右孩子为新的根节点。
+ else {
+ TreeNode* cur = root->right; // 找右子树最左面的节点
+ while(cur->left != nullptr) {
+ cur = cur->left;
+ }
+ cur->left = root->left; // 把要删除的节点(root)左子树放在cur的左孩子的位置
+ TreeNode* tmp = root; // 把root节点保存一下,下面来删除
+ root = root->right; // 返回旧root的右孩子作为新root
+ delete tmp; // 释放节点内存(这里不写也可以,但C++最好手动释放一下吧)
+ return root;
+ }
+ }
+ if (root->val > key) root->left = deleteNode(root->left, key);
+ if (root->val < key) root->right = deleteNode(root->right, key);
+ return root;
+ }
+};给你二叉搜索树的根节点 root ,同时给定最小边界 low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在 [low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func trimBST(root *TreeNode, low int, high int) *TreeNode {
+ if root==nil{
+ return nil
+ }
+ if root.Val<low{//如果该节点值小于最小值,则该节点更换为该节点的右节点值,继续遍历
+ right:=trimBST(root.Right,low,high)
+ return right
+ }
+ if root.Val>high{//如果该节点的值大于最大值,则该节点更换为该节点的左节点值,继续遍历
+ left:=trimBST(root.Left,low,high)
+ return left
+ }
+ root.Left=trimBST(root.Left,low,high)
+ root.Right=trimBST(root.Right,low,high)
+ return root
+}class Solution {
+public:
+ TreeNode* trimBST(TreeNode* root, int low, int high) {
+ if (root == nullptr ) return nullptr;
+ if (root->val < low) {
+ TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
+ return right;
+ }
+ if (root->val > high) {
+ TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点
+ return left;
+ }
+ root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
+ root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
+ return root;
+ }
+};给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 的二叉树。
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func sortedArrayToBST(nums []int) *TreeNode {
+ if len(nums) == 0{
+ return nil
+ }
+ mid := len(nums) / 2
+ root := &TreeNode{
+ Val:nums[mid],
+ Left:sortedArrayToBST(nums[:mid]),
+ Right:sortedArrayToBST(nums[mid+1:]),
+ }
+ return root
+}class Solution {
+public:
+ TreeNode* sortedArrayToBST(vector<int>& nums) {
+ if(nums.size() == 0){
+ return NULL;
+ }
+ int mid = nums.size() / 2;
+ TreeNode* root = new TreeNode(nums[mid]);
+ vector<int> leftnums;
+ vector<int> rightnums;
+ for(int i=0;i<mid;i++){
+ leftnums.push_back(nums[i]);
+ }
+ for(int i=mid+1;i<nums.size();i++){
+ rightnums.push_back(nums[i]);
+ }
+ root->left = sortedArrayToBST(leftnums);
+ root->right = sortedArrayToBST(rightnums);
+ return root;
+ }
+};给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ * Val int
+ * Left *TreeNode
+ * Right *TreeNode
+ * }
+ */
+func convertBST(root *TreeNode) *TreeNode {
+ sum := 0
+ DFS(root,&sum)
+ return root
+}
+
+func DFS(root *TreeNode, sum *int){
+ if root == nil{
+ return
+ }
+ DFS(root.Right,sum)
+ root.Val += *sum
+ *sum = root.Val
+ DFS(root.Left,sum)
+}class Solution {
+private:
+ int nowsum = 0;
+public:
+ TreeNode* convertBST(TreeNode* root) {
+ if(root == NULL){
+ return NULL;
+ }
+ convertBST(root->right);
+ root->val += nowsum;
+ nowsum = root->val;
+ convertBST(root->left);
+ return root;
+ }
+};代码随想录-回溯算法
+ +回溯法,一般可以解决如下几种问题:
+回溯法解决的问题都可以抽象为树形结构 ,是的,我指的是所有回溯法的问题都可以抽象为树形结构!
+因为回溯法解决的都是在集合中递归查找子集, 集合的大小就构成了树的宽度,递归的深度,都构成的树的深度 。
+递归就要有终止条件,所以必然是一棵高度有限的树(N叉树)。
+回溯算法模板:
+void backtracking(参数) {
+ if (终止条件) {
+ 存放结果;
+ return;
+ }
+
+ for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
+ 处理节点;
+ backtracking(路径,选择列表); // 递归
+ 回溯,撤销处理结果
+ }
+}
+给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
+func combine(n int, k int) [][]int {
+ result := make([][]int,0)
+ temp := make([]int,0)
+ backtracking(n,k,1,temp,&result)
+ return result
+}
+
+func backtracking(n,k,s int,temp []int, result *[][]int){
+ if len(temp) == k{
+ b := make([]int, len(temp))
+ copy(b, temp)
+ *result = append(*result,b)
+ return
+ }
+ for i:=s;i<=n-k+len(temp)+1;i++{
+ temp = append(temp,i)
+ backtracking(n,k,i+1,temp,result)
+ temp = temp[:len(temp)-1]
+ }
+}class Solution {
+private:
+ vector<vector<int> > result;
+ vector<int> temp;
+public:
+ void backtracking(int start, int end, int k){
+ if(temp.size() == k){
+ result.push_back(temp);
+ return;
+ }
+ for(int i=start;i<=end;i++){
+ temp.push_back(i);
+ backtracking(i+1,end,k);
+ temp.pop_back();
+ }
+ }
+ vector<vector<int>> combine(int n, int k) {
+
+ backtracking(1,n,k);
+ return result;
+ }
+};找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
+func combinationSum3(k int, n int) [][]int {
+ result := make([][]int,0)
+ temp := make([]int,0)
+ backtracking(n,k,1,temp,&result)
+ return result
+}
+
+func backtracking(n,k,s int, temp []int,result *[][]int){
+ if len(temp) == k{
+ if sum(temp) == n{
+ t2 := make([]int,len(temp))
+ copy(t2,temp)
+ *result = append(*result,t2)
+ }
+ return
+ }
+ for i:=s;i<=9-k+len(temp)+1;i++{
+ temp = append(temp,i)
+ backtracking(n,k,i+1,temp,result)
+ temp = temp[:len(temp)-1]
+ }
+}
+
+func sum(temp []int) int{
+ res := 0
+ for i:=0;i<len(temp);i++{
+ res += temp[i]
+ }
+ return res
+}class Solution {
+private:
+ vector<vector<int> > result;
+ vector<int> temp;
+public:
+ void backtracking(int start, int end, int k, int n){
+ if(temp.size() == k){
+ int tempsum = 0;
+ for(int i=0;i<k;i++){
+ tempsum += temp[i];
+ }
+ if(tempsum == n){
+ result.push_back(temp);
+ return;
+ }
+ } else if(temp.size() > k){
+ return;
+ }
+ for(int i=start;i<=end;i++){
+ temp.push_back(i);
+ backtracking(i+1,9,k,n);
+ temp.pop_back();
+ }
+ }
+ vector<vector<int>> combinationSum3(int k, int n) {
+ backtracking(1,9,k,n);
+ return result;
+ }
+};给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
+func letterCombinations(digits string) []string {
+ alphamap := make(map[byte][]string,0)
+ alphamap['2'] = []string{"a","b","c"}
+ alphamap['3'] = []string{"d","e","f"}
+ alphamap['4'] = []string{"g","h","i"}
+ alphamap['5'] = []string{"j","k","l"}
+ alphamap['6'] = []string{"m","n","o"}
+ alphamap['7'] = []string{"p","q","r","s"}
+ alphamap['8'] = []string{"t","u","v"}
+ alphamap['9'] = []string{"w","x","y","z"}
+ result := make([]string,0)
+ n := len(digits)
+ temp := ""
+ backtracking(n,0,digits,alphamap,temp,&result)
+ if len(result) == 1 && result[0] == ""{
+ return make([]string,0)
+ }
+ return result
+}
+
+func backtracking(n,s int,digits string,alphamap map[byte][]string,temp string ,result *[]string){
+ if len(temp) == n{
+ *result = append(*result,temp)
+ return
+ }
+ index := digits[s]
+ letter := alphamap[index]
+ for i:=0;i<len(letter);i++{
+ temp += letter[i]
+ backtracking(n,s+1,digits,alphamap,temp,result)
+ temp = temp[:len(temp)-1]
+ }
+}class Solution {
+private:
+ map<int, vector<string> > mp;
+ vector<string> result;
+ vector<string> temp;
+public:
+ void backtracking(string digits, int start, int end){
+ if(temp.size() == end){
+ string t;
+ for(int i=0;i<end;i++){
+ t += temp[i];
+ }
+ result.push_back(t);
+ return;
+ }
+ for(int i=start;i<end;i++){
+ int index = digits[i] - '0';
+ vector<string> worddict = mp[index];
+ for(int j=0;j<worddict.size();j++){
+ temp.push_back(worddict[j]);
+ backtracking(digits,i+1,digits.size());
+ temp.pop_back();
+ }
+ }
+ }
+ vector<string> letterCombinations(string digits) {
+ if(digits.size() == 0){
+ return result;
+ }
+ mp[2] = vector<string>{"a","b","c"};
+ mp[3] = vector<string>{"d","e","f"};
+ mp[4] = vector<string>{"g","h","i"};
+ mp[5] = vector<string>{"j","k","l"};
+ mp[6] = vector<string>{"m","n","o"};
+ mp[7] = vector<string>{"p","q","r","s"};
+ mp[8] = vector<string>{"t","u","v"};
+ mp[9] = vector<string>{"w","x","y","z"};
+ backtracking(digits,0,digits.size());
+ return result;
+ }
+};给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
func combinationSum(candidates []int, target int) [][]int {
+ result := make([][]int,0)
+ temp := make([]int,0)
+ backtracking(0,candidates,target,temp,&result)
+ return result
+}
+
+func backtracking(s int,candidates []int, target int, temp []int,result *[][]int){
+ if sum(temp) == target{
+ t2 := make([]int,len(temp))
+ copy(t2,temp)
+ *result = append(*result,t2)
+ return
+ } else if sum(temp) > target{
+ return
+ }
+ for i:=s;i<len(candidates);i++{
+ temp = append(temp,candidates[i])
+ backtracking(i,candidates,target,temp,result)
+ temp = temp[:len(temp)-1]
+ }
+}
+
+func sum(temp []int) int{
+ res := 0
+ for i:=0;i<len(temp);i++{
+ res += temp[i]
+ }
+ return res
+}class Solution {
+private:
+ vector<vector<int> > result;
+ vector<int> temp;
+public:
+ void backtracking(vector<int>& candidates, int target, int start, int end){
+ int countsum = 0;
+ for(int i=0;i<temp.size();i++){
+ countsum += temp[i];
+ }
+ if(countsum == target){
+ result.push_back(temp);
+ return;
+ } else if(countsum > target){
+ return;
+ }
+ for(int i=start;i<=end;i++){
+ temp.push_back(candidates[i]);
+ backtracking(candidates,target,i,candidates.size()-1);
+ temp.pop_back();
+ }
+ }
+ vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
+ backtracking(candidates, target,0,candidates.size()-1);
+ return result;
+ }
+};给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意: 解集不能包含重复的组合。
+注意要去重!
+func combinationSum2(candidates []int, target int) [][]int {
+ sort.Slice(candidates,func(i,j int) bool{
+ return candidates[i] < candidates[j]
+ })
+ result := make([][]int,0)
+ temp := make([]int,0)
+ backtracking(0,0,candidates,target,temp,&result)
+ return result
+}
+
+func backtracking(s,sum int,candidates []int, target int, temp []int,result *[][]int){
+ if sum == target{
+ t2 := make([]int,len(temp))
+ copy(t2,temp)
+ *result = append(*result,t2)
+ return
+ } else if sum > target{
+ return
+ }
+ for i:=s;i<len(candidates);i++{
+ if i>s&&candidates[i]==candidates[i-1]{
+ continue
+ }
+ temp = append(temp,candidates[i])
+ sum += candidates[i]
+ backtracking(i+1,sum,candidates,target,temp,result)
+ temp = temp[:len(temp)-1]
+ sum -= candidates[i]
+ }
+}class Solution {
+private:
+ vector<vector<int> > result;
+ vector<int> temp;
+public:
+ void backtracking(vector<int>& candidates, int target, int start, int end){
+ int countsum = 0;
+ for(int i=0;i<temp.size();i++){
+ countsum += temp[i];
+ }
+ if(countsum == target){
+ result.push_back(temp);
+ return;
+ } else if(countsum > target){
+ return;
+ }
+ for(int i=start;i<=end;i++){
+ if (i > start && candidates[i] == candidates[i - 1]) {
+ continue;
+ }
+ temp.push_back(candidates[i]);
+ backtracking(candidates,target,i+1,candidates.size()-1);
+ temp.pop_back();
+ }
+ }
+ vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
+ sort(candidates.begin(), candidates.end());
+ backtracking(candidates, target,0,candidates.size()-1);
+ return result;
+ }
+};给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
+func partition(s string) [][]string {
+ result := make([][]string,0)
+ temp := make([]string,0)
+ backtracking(s,0,temp,&result)
+ return result
+}
+
+func backtracking(s string, start int, temp []string,result *[][]string){
+ if start == len(s){
+ t2 := make([]string,len(temp))
+ copy(t2,temp)
+ *result = append(*result,t2)
+ return
+ }
+ for i:=start;i<len(s);i++{
+ if judge(s,start,i){
+ temp = append(temp,s[start:i+1])
+ } else{
+ continue
+ }
+ backtracking(s,i+1,temp,result)
+ temp = temp[:len(temp)-1]
+ }
+}
+
+func judge(s string,start,end int)bool {
+ for start < end{
+ if s[start] != s[end]{
+ return false
+ }
+ start += 1
+ end -= 1
+ }
+ return true
+}class Solution {
+public:
+ vector<vector<string> > result;
+ vector<string> path;
+ bool judgepa(string s, int startIndex, int endIndex){
+ while(startIndex < endIndex){
+ if(s[startIndex] != s[endIndex]){
+ return false;
+ }
+ startIndex += 1;
+ endIndex -= 1;
+ }
+ return true;
+ }
+ void backtracking(string s, int startIndex){
+ if(startIndex >= s.size()){
+ result.push_back(path);
+ return;
+ }
+ for(int i = startIndex;i<s.size();i++){
+ if(judgepa(s,startIndex,i)){
+ string str = s.substr(startIndex, i-startIndex+1);
+ path.push_back(str);
+ } else{
+ continue;
+ }
+ backtracking(s,i+1);
+ path.pop_back();
+ }
+
+ }
+ vector<vector<string>> partition(string s) {
+ backtracking(s,0);
+ return result;
+ }
+};有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的 有效 IP 地址 ,这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。
func restoreIpAddresses(s string) []string {
+ result := make([]string,0)
+ temp := make([]string,0)
+ backtracking(s,0,temp,&result)
+ return result
+}
+
+func backtracking(s string, start int, temp []string,result *[]string){
+ if start == len(s) && len(temp) == 4{
+ t2 := temp[0] + "." + temp[1] + "." + temp[2] + "." + temp[3]
+ *result = append(*result,t2)
+ return
+ }
+ for i:=start;i<len(s);i++{
+ temp = append(temp,s[start:i+1])
+ if i-start+1<=3&&len(temp)<=4&&judge(s,start,i){
+ backtracking(s,i+1,temp,result)
+ } else{
+ continue
+ }
+ temp = temp[:len(temp)-1]
+ }
+}
+
+func judge(s string,start,end int)bool {
+ checkInt,_:=strconv.Atoi(s[start:end+1])
+ if end-start+1>1&&s[start]=='0'{//对于前导 0的IP(特别注意s[startIndex]=='0'的判断,不应该写成s[startIndex]==0,因为s截取出来不是数字)
+ return false
+ }
+ if checkInt>255{
+ return false
+ }
+ return true
+}class Solution {
+public:
+ vector<string> result;
+ vector<string> temp;
+ bool judgenum(string r){
+ if(r.size() <= 0 || r.size() > 3){
+ return false;
+ }
+ int num = stoi(r);
+ if(num > 255){
+ return false;
+ }
+ if(num != 0 && r[0] == '0'){
+ return false;
+ }
+ if(num == 0 && r.size() != 1){
+ return false;
+ }
+ return true;
+ }
+ void backtracking(string s, int startIndex){
+ if(startIndex >= s.size() && temp.size() == 4){
+ string r = "";
+ for(int i=0;i<3;i++){
+ r += temp[i];
+ r += ".";
+ }
+ r += temp[3];
+ result.push_back(r);
+ return;
+ } else if(temp.size() > 4 || startIndex >= s.size()){
+ return;
+ }
+ for(int i=startIndex;i<s.size();i++){
+ string r = s.substr(startIndex,i-startIndex+1);
+ if(judgenum(r)){
+ temp.push_back(r);
+ } else{
+ continue;
+ }
+ backtracking(s,i+1);
+ temp.pop_back();
+ }
+ }
+ vector<string> restoreIpAddresses(string s) {
+ backtracking(s,0);
+ return result;
+ }
+};给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
+func subsets(nums []int) [][]int {
+ result := make([][]int,0)
+ temp := make([]int,0)
+ for n:=0;n<=len(nums);n++{
+ backtracking(0,n,temp,&result,nums)
+ }
+ return result
+}
+
+func backtracking(s,n int,temp []int,result *[][]int,nums []int){
+ if len(temp) == n{
+ t2 := make([]int,n)
+ copy(t2,temp)
+ *result = append(*result,t2)
+ return
+ }
+ for i:=s;i<len(nums);i++{
+ temp = append(temp,nums[i])
+ backtracking(i+1,n,temp,result,nums)
+ temp = temp[:len(temp)-1]
+ }
+}class Solution {
+public:
+ vector<vector<int> > result;
+ vector<int> temp;
+ void backtracking(vector<int> nums, int startIndex, int maxIndex){
+ if(temp.size() == maxIndex){
+ result.push_back(temp);
+ return;
+ }
+ for(int i=startIndex;i<nums.size();i++){
+ temp.push_back(nums[i]);
+ backtracking(nums, i+1, maxIndex);
+ temp.pop_back();
+ }
+ }
+ vector<vector<int>> subsets(vector<int>& nums) {
+ for(int i=0;i<=nums.size();i++){
+ backtracking(nums,0,i);
+ }
+ return result;
+ }
+};给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
+func subsetsWithDup(nums []int) [][]int {
+ sort.Slice(nums,func(i,j int) bool{
+ return nums[i] < nums[j]
+ })
+ result := make([][]int,0)
+ temp := make([]int,0)
+ for n:=0;n<=len(nums);n++{
+ backtracking(0,n,temp,&result,nums)
+ }
+ return result
+}
+
+func backtracking(s,n int,temp []int,result *[][]int,nums []int){
+ if len(temp) == n{
+ t2 := make([]int,n)
+ copy(t2,temp)
+ *result = append(*result,t2)
+ return
+ }
+ for i:=s;i<len(nums);i++{
+ if i > s && nums[i] == nums[i-1]{
+ continue
+ }
+ temp = append(temp,nums[i])
+ backtracking(i+1,n,temp,result,nums)
+ temp = temp[:len(temp)-1]
+ }
+}class Solution {
+public:
+ vector<vector<int> > result;
+ vector<int> temp;
+ void backtracking(vector<int> nums, int startIndex){
+ result.push_back(temp);
+ for(int i=startIndex;i<nums.size();i++){
+ if(i > startIndex && nums[i] == nums[i-1]){
+ continue;
+ }
+ temp.push_back(nums[i]);
+ backtracking(nums, i+1);
+ temp.pop_back();
+ }
+ }
+ vector<vector<int>> subsetsWithDup(vector<int>& nums) {
+ sort(nums.begin(), nums.end());
+ backtracking(nums,0);
+ return result;
+ }
+};给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
+func findSubsequences(nums []int) [][]int {
+ result := make([][]int,0)
+ temp := make([]int,0)
+ backtracking(0,temp,&result,nums)
+ return result
+}
+
+func backtracking(s int ,temp []int,result *[][]int,nums []int){
+ if len(temp) > 1{
+ t2 := make([]int,len(temp))
+ copy(t2,temp)
+ *result = append(*result,t2)
+ }
+ history:=[201]int{}
+ for i:=s;i<len(nums);i++{
+ if len(temp)>0 && nums[i]<temp[len(temp)-1]||history[nums[i] + 100]==1{
+ continue
+ }
+ history[nums[i] + 100]=1
+ temp = append(temp,nums[i])
+ backtracking(i+1,temp,result,nums)
+ temp = temp[:len(temp)-1]
+ }
+}class Solution {
+public:
+ vector<vector<int> > result;
+ vector<int> temp;
+ bool judge(vector<int> t){
+ for(int i=0;i<t.size()-1;i++){
+ if(t[i+1] <= t[i]){
+ return false;
+ }
+ }
+ return true;
+ }
+ void backtracking(vector<int>& nums, int startIndex) {
+ if (temp.size() > 1) {
+ result.push_back(temp);
+ }
+ unordered_set<int> uset;
+ for (int i = startIndex; i < nums.size(); i++) {
+ if ((!temp.empty() && nums[i] < temp.back())
+ || uset.find(nums[i]) != uset.end()) {
+ continue;
+ }
+ uset.insert(nums[i]);
+ temp.push_back(nums[i]);
+ backtracking(nums, i + 1);
+ temp.pop_back();
+ }
+ }
+ vector<vector<int>> findSubsequences(vector<int>& nums) {
+ backtracking(nums,0);
+ return result;
+ }
+};给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
func permute(nums []int) [][]int {
+ result := make([][]int,0)
+ temp := make([]int,0)
+ used := make([]bool,len(nums))
+ backtracking(0,nums,temp,&result,used)
+ return result
+}
+
+func backtracking(s int, nums,temp []int, result *[][]int,used []bool){
+ if len(temp) == len(nums){
+ b := make([]int, len(temp))
+ copy(b, temp)
+ *result = append(*result,b)
+ return
+ }
+ for i:=0;i<len(nums);i++{
+ if used[i] == true{
+ continue
+ }
+ temp = append(temp,nums[i])
+ used[i] = true
+ backtracking(i+1,nums,temp,result,used)
+ temp = temp[:len(temp)-1]
+ used[i] = false
+ }
+}class Solution {
+public:
+ vector<vector<int> > result;
+ vector<int> temp;
+ void backtracking(vector<int>& nums, int startIndex, vector<bool> used){
+ if(temp.size() == nums.size()){
+ result.push_back(temp);
+ return;
+ }
+ for(int i=0;i<nums.size();i++){
+ if(used[i] == true){
+ continue;
+ }
+ used[i] = true;
+ temp.push_back(nums[i]);
+ backtracking(nums,i+1, used);
+ temp.pop_back();
+ used[i] = false;
+ }
+ }
+ vector<vector<int>> permute(vector<int>& nums) {
+ vector<bool> used(nums.size(), false);
+ backtracking(nums,0, used);
+ return result;
+ }
+};给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
used[i - 1] == true,说明同一树枝nums[i - 1]使用过
+used[i - 1] == false,说明同一树层nums[i - 1]使用过
+如果同一树层nums[i - 1]使用过则直接跳过
+func permuteUnique(nums []int) [][]int {
+ sort.Slice(nums,func(i,j int) bool {
+ return nums[i] < nums[j]
+ })
+ result := make([][]int,0)
+ temp := make([]int,0)
+ used := make([]bool,len(nums))
+ backtracking(0,nums,temp,&result,used)
+ return result
+}
+
+func backtracking(s int, nums,temp []int, result *[][]int,used []bool){
+ if len(temp) == len(nums){
+ b := make([]int, len(temp))
+ copy(b, temp)
+ *result = append(*result,b)
+ return
+ }
+ for i:=0;i<len(nums);i++{
+ if i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false || used[i] == true{
+ continue
+ }
+ temp = append(temp,nums[i])
+ used[i] = true
+ backtracking(i+1,nums,temp,result,used)
+ temp = temp[:len(temp)-1]
+ used[i] = false
+ }
+}class Solution {
+public:
+ vector<vector<int> > result;
+ vector<int> temp;
+ void backtracking(vector<int>& nums, vector<bool> used){
+ if(temp.size() == nums.size()){
+ result.push_back(temp);
+ return;
+ }
+ for(int i=0;i<nums.size();i++){
+ if((i > 0 && nums[i] == nums[i-1] && used[i-1] == false) || used[i] == true){
+ continue;
+ }
+ used[i] = true;
+ temp.push_back(nums[i]);
+ backtracking(nums, used);
+ temp.pop_back();
+ used[i] = false;
+ }
+ }
+ vector<vector<int>> permuteUnique(vector<int>& nums) {
+ vector<bool> used(nums.size(), false);
+ sort(nums.begin(), nums.end());
+ backtracking(nums, used);
+ return result;
+ }
+};给你一份航线列表 tickets ,其中 tickets[i] = [from<sub>i</sub>, to<sub>i</sub>] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。
所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。
["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小,排序更靠前。假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。
+type pair struct {
+ target string
+ visited bool
+}
+type pairs []*pair
+
+func (p pairs) Len() int {
+ return len(p)
+}
+func (p pairs) Swap(i, j int) {
+ p[i], p[j] = p[j], p[i]
+}
+func (p pairs) Less(i, j int) bool {
+ return p[i].target < p[j].target
+}
+
+func findItinerary(tickets [][]string) []string {
+ result := []string{}
+ // map[出发机场] pair{目的地,是否被访问过}
+ targets := make(map[string]pairs)
+ for _, ticket := range tickets {
+ if targets[ticket[0]] == nil {
+ targets[ticket[0]] = make(pairs, 0)
+ }
+ targets[ticket[0]] = append(targets[ticket[0]], &pair{target: ticket[1], visited: false})
+ }
+ for k, _ := range targets {
+ sort.Sort(targets[k])
+ }
+ result = append(result, "JFK")
+ var backtracking func() bool
+ backtracking = func() bool {
+ if len(tickets)+1 == len(result) {
+ return true
+ }
+ // 取出起飞航班对应的目的地
+ for _, pair := range targets[result[len(result)-1]] {
+ if pair.visited == false {
+ result = append(result, pair.target)
+ pair.visited = true
+ if backtracking() {
+ return true
+ }
+ result = result[:len(result)-1]
+ pair.visited = false
+ }
+ }
+ return false
+ }
+
+ backtracking()
+
+ return result
+}class Solution {
+public:
+ unordered_map<string, map<string, int>> targets;
+ bool backtracking(int ticketNum, vector<string>& result) {
+ if (result.size() == ticketNum + 1) {
+ return true;
+ }
+ for (pair<const string, int>& target : targets[result[result.size() - 1]]) {
+ if (target.second > 0 ) { // 记录到达机场是否飞过了
+ result.push_back(target.first);
+ target.second--;
+ if (backtracking(ticketNum, result)) return true;
+ result.pop_back();
+ target.second++;
+ }
+ }
+ return false;
+ }
+ vector<string> findItinerary(vector<vector<string>>& tickets) {
+ targets.clear();
+ vector<string> result;
+ for (const vector<string>& vec : tickets) {
+ targets[vec[0]][vec[1]]++; // 记录映射关系
+ }
+ result.push_back("JFK"); // 起始机场
+ backtracking(tickets.size(), result);
+ return result;
+ }
+};按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
+n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
func solveNQueens(n int) [][]string {
+ result := make([][]string,0)
+ temp := make([][]string,n)
+ for i:=0;i<n;i++{
+ temp[i] = make([]string,n)
+ }
+ for i:=0;i<n;i++{
+ for j:=0;j<n;j++{
+ temp[i][j] = "."
+ }
+ }
+ backtracking(0,temp,&result)
+ return result
+}
+
+func backtracking(s int,temp [][]string,result *[][]string){
+ if s == len(temp){
+ t2 := make([]string,0)
+ for i:=0;i<len(temp);i++{
+ s2 := ""
+ for j:=0;j<len(temp);j++{
+ s2 += temp[i][j]
+ }
+ t2 = append(t2,s2)
+ }
+ *result = append(*result,t2)
+ return
+ }
+ for i:=0;i<len(temp);i++{
+ if judge(temp,s,i) == false{
+ continue
+ }
+ temp[s][i] = "Q"
+ backtracking(s+1,temp,result)
+ temp[s][i] = "."
+ }
+}
+
+func judge(temp [][]string,p,q int) bool {
+ n := len(temp)
+ for i:=0;i<n;i++{
+ if temp[i][q] == "Q"{
+ return false
+ }
+ }
+ i := p
+ j := q
+ for i >= 0 && i < n && j >= 0 && j < n{
+ if temp[i][j] == "Q"{
+ return false
+ }
+ i--
+ j--
+ }
+ i = p
+ j = q
+ for i >= 0 && i < n && j >= 0 && j < n{
+ if temp[i][j] == "Q"{
+ return false
+ }
+ i--
+ j++
+ }
+ return true
+}class Solution {
+public:
+ vector<vector<string> > result;
+ vector<int> temp;
+ bool judge(int now, int end){
+ int now_size = temp.size();
+ for(int i=0;i<now_size;i++){
+ if(now == temp[i]){
+ return false;
+ }
+ }
+ int x = now_size - 1;
+ int y = now - 1;
+ while(x >= 0 && y >= 0){
+ if(temp[x] == y){
+ return false;
+ }
+ x -= 1;
+ y -= 1;
+ }
+ x = now_size - 1;
+ y = now + 1;
+ while(x >= 0 && y < end){
+ if(temp[x] == y){
+ return false;
+ }
+ x -= 1;
+ y += 1;
+ }
+ return true;
+ }
+ void backtracking(int start, int end){
+ if(start == end){
+ vector<string> s;
+ for(int i=0;i<end;i++){
+ int a = temp[i];
+ string temp_s = "";
+ for(int j=0;j<end;j++){
+ if(j == a){
+ temp_s += "Q";
+ } else{
+ temp_s += ".";
+ }
+ }
+ s.push_back(temp_s);
+ }
+ result.push_back(s);
+ return;
+ }
+ for(int i=0;i<end;i++){
+ if(judge(i,end)){
+ temp.push_back(i);
+ backtracking(start+1, end);
+ temp.pop_back();
+ }
+ }
+ }
+ vector<vector<string> > solveNQueens(int n) {
+ backtracking(0,n);
+ return result;
+ }
+};编写一个程序,通过填充空格来解决数独问题。
+数独的解法需 遵循如下规则 :
+1-9 在每一行只能出现一次。1-9 在每一列只能出现一次。1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)数独部分空格内已填入了数字,空白格用 '.' 表示。
func solveSudoku(board [][]byte) {
+ // numstring := []byte{"0","1","2","3","4","5","6","7","8","9"}
+ numbyte := []byte{'1','2','3','4','5','6','7','8','9'}
+ backtracking(numbyte,&board)
+}
+
+func backtracking(numbyte []byte, board *[][]byte) bool {
+ for i:=0;i<9;i++{
+ for j:=0;j<9;j++{
+ if (*board)[i][j] != '.'{
+ continue
+ }
+ for k:=0;k<9;k++{
+ if judge(*board,i,j,numbyte[k]) == false{
+ continue
+ }
+ (*board)[i][j] = numbyte[k]
+ if backtracking(numbyte,board) == true{
+ return true
+ }
+ (*board)[i][j] = '.'
+ }
+ return false
+ }
+ }
+ return true
+}
+
+func judge(board [][]byte, p,q int,c byte) bool {
+ for i:=0;i<9;i++{
+ if board[p][i] == c || board[i][q] == c{
+ return false
+ }
+ }
+ p = p / 3
+ q = q / 3
+ for i:=p*3;i<(p+1)*3;i++{
+ for j := q*3;j<(q+1)*3;j++{
+ if board[i][j] == c{
+ return false
+ }
+ }
+ }
+ return true
+}class Solution {
+public:
+ bool backtracking(vector<vector<char>>& board) {
+ for (int i = 0; i < board.size(); i++) {
+ for (int j = 0; j < board[0].size(); j++) {
+ if (board[i][j] == '.') {
+ for (char k = '1'; k <= '9'; k++) {
+ if (isValid(i, j, k, board)) {
+ board[i][j] = k;
+ if (backtracking(board)) return true;
+ board[i][j] = '.';
+ }
+ }
+ return false;
+ }
+ }
+ }
+ return true;
+ }
+ bool isValid(int row, int col, char val, vector<vector<char>>& board) {
+ for (int i = 0; i < 9; i++) {
+ if (board[row][i] == val) {
+ return false;
+ }
+ }
+ for (int j = 0; j < 9; j++) {
+ if (board[j][col] == val) {
+ return false;
+ }
+ }
+ int startRow = (row / 3) * 3;
+ int startCol = (col / 3) * 3;
+ for (int i = startRow; i < startRow + 3; i++) {
+ for (int j = startCol; j < startCol + 3; j++) {
+ if (board[i][j] == val ) {
+ return false;
+ }
+ }
+ }
+ return true;
+ }
+ void solveSudoku(vector<vector<char>>& board) {
+ backtracking(board);
+ }
+};代码随想录-栈与队列
+ +请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
+实现 MyQueue 类:
+void push(int x) 将元素 x 推到队列的末尾
+int pop() 从队列的开头移除并返回元素
+int peek() 返回队列开头的元素
+boolean empty() 如果队列为空,返回 true ;否则,返回 false
+说明:你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
+type MyQueue struct {
+ stack []int
+ back []int
+}
+
+
+func Constructor() MyQueue {
+ return MyQueue{
+ stack: make([]int, 0),
+ back: make([]int, 0),
+ }
+}
+
+
+func (this *MyQueue) Push(x int) {
+ for len(this.back) != 0{
+ val := this.back[len(this.back)-1]
+ this.stack = append(this.stack,val)
+ this.back = this.back[:len(this.back)-1]
+ }
+ this.stack = append(this.stack,x)
+}
+
+
+func (this *MyQueue) Pop() int {
+ for len(this.stack) != 0{
+ val := this.stack[len(this.stack)-1]
+ this.back = append(this.back,val)
+ this.stack = this.stack[:len(this.stack)-1]
+ }
+ val := this.back[len(this.back)-1]
+ this.back = this.back[:len(this.back)-1]
+ return val
+}
+
+
+func (this *MyQueue) Peek() int {
+ for len(this.stack) != 0{
+ val := this.stack[len(this.stack)-1]
+ this.back = append(this.back,val)
+ this.stack = this.stack[:len(this.stack)-1]
+ }
+ return this.back[len(this.back)-1]
+}
+
+
+func (this *MyQueue) Empty() bool {
+ return len(this.stack) == 0 && len(this.back) == 0
+}
+
+
+/**
+ * Your MyQueue object will be instantiated and called as such:
+ * obj := Constructor();
+ * obj.Push(x);
+ * param_2 := obj.Pop();
+ * param_3 := obj.Peek();
+ * param_4 := obj.Empty();
+ */class MyQueue {
+public:
+ stack<int> st1;
+ stack<int> st2;
+ MyQueue() {
+
+ }
+
+ void push(int x) {
+ while(!st2.empty()){
+ int a = st2.top();
+ st2.pop();
+ st1.push(a);
+ }
+ st1.push(x);
+ }
+
+ int pop() {
+ while(!st1.empty()){
+ int a = st1.top();
+ st1.pop();
+ st2.push(a);
+ }
+ int res = st2.top();
+ st2.pop();
+ return res;
+ }
+
+ int peek() {
+ while(!st1.empty()){
+ int a = st1.top();
+ st1.pop();
+ st2.push(a);
+ }
+ int res = st2.top();
+ return res;
+ }
+
+ bool empty() {
+ return st1.size() == 0 && st2.size() == 0;
+ }
+};请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
+实现 MyStack 类:
+void push(int x) 将元素 x 压入栈顶。
+int pop() 移除并返回栈顶元素。
+int top() 返回栈顶元素。
+boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。
+注意:你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
+type MyStack struct {
+ queue1 []int
+ queue2 []int
+}
+
+
+func Constructor() MyStack {
+ return MyStack{
+ queue1 : make([]int,0),
+ queue2 : make([]int,0),
+ }
+}
+
+
+func (this *MyStack) Push(x int) {
+ this.queue1 = append(this.queue1,x)
+}
+
+
+func (this *MyStack) Pop() int {
+ for len(this.queue1) != 1{
+ this.queue2 = append(this.queue2,this.queue1[0])
+ this.queue1 = this.queue1[1:]
+ }
+ val := this.queue1[0]
+ this.queue1 = []int{}
+ this.queue1,this.queue2 = this.queue2,this.queue1
+ return val
+}
+
+
+func (this *MyStack) Top() int {
+ for len(this.queue1) != 1{
+ this.queue2 = append(this.queue2,this.queue1[0])
+ this.queue1 = this.queue1[1:]
+ }
+ this.queue2 = append(this.queue2,this.queue1[0])
+ val := this.queue1[0]
+ this.queue1 = []int{}
+ this.queue1,this.queue2 = this.queue2,this.queue1
+ return val
+}
+
+
+func (this *MyStack) Empty() bool {
+ return len(this.queue1) == 0
+}
+
+
+/**
+ * Your MyStack object will be instantiated and called as such:
+ * obj := Constructor();
+ * obj.Push(x);
+ * param_2 := obj.Pop();
+ * param_3 := obj.Top();
+ * param_4 := obj.Empty();
+ */class MyStack {
+public:
+ queue<int> q1;
+ queue<int> q2;
+ MyStack() {
+
+ }
+
+ void push(int x) {
+ q1.push(x);
+ }
+
+ int pop() {
+ while(q1.size() != 1){
+ q2.push(q1.front());
+ q1.pop();
+ }
+ int a = q1.front();
+ q1.pop();
+ while(!q2.empty()){
+ q1.push(q2.front());
+ q2.pop();
+ }
+ return a;
+ }
+
+ int top() {
+ while(q1.size() != 1){
+ q2.push(q1.front());
+ q1.pop();
+ }
+ int a = q1.front();
+ q2.push(a);
+ q1.pop();
+ while(!q2.empty()){
+ q1.push(q2.front());
+ q2.pop();
+ }
+ return a;
+ }
+
+ bool empty() {
+ return q1.empty();
+ }
+};给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
+有效字符串需满足:
+func isValid(s string) bool {
+ result := make([]byte,0)
+ for i:=0;i<len(s);i++{
+ if s[i] == '(' || s[i] == '{' || s[i] == '['{
+ result = append(result,s[i])
+ } else{
+ if len(result) == 0{
+ return false
+ }
+ if s[i] == ')' && result[len(result)-1] == '('{
+ result = result[:len(result)-1]
+ } else if s[i] == '}' && result[len(result)-1] == '{'{
+ result = result[:len(result)-1]
+ } else if s[i] == ']' && result[len(result)-1] == '['{
+ result = result[:len(result)-1]
+ } else{
+ return false
+ }
+ }
+ }
+ return len(result) == 0
+}class Solution {
+public:
+ bool isValid(string s) {
+ stack<char> st;
+ for(int i=0;i<s.size();i++){
+ char a = s[i];
+ if(a == '[' || a == '(' || a == '{'){
+ st.push(a);
+ } else{
+ if(st.empty()){
+ return false;
+ }
+ if(a == ']' && st.top() == '['){
+ st.pop();
+ } else if (a == '}' && st.top() == '{'){
+ st.pop();
+ } else if (a == ')' && st.top() == '('){
+ st.pop();
+ } else{
+ return false;
+ }
+ }
+ }
+ return st.empty();
+ }
+};给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
+在 S 上反复执行重复项删除操作,直到无法继续删除。
+在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
+func removeDuplicates(s string) string {
+ result := make([]byte,0)
+ for i := 0;i<len(s);i++{
+ if len(result) == 0 || s[i] != result[len(result)-1]{
+ result = append(result,s[i])
+ } else{
+ result = result[:len(result)-1]
+ }
+ }
+ return string(result)
+}class Solution {
+public:
+ string removeDuplicates(string s) {
+ stack<char> st;
+ for(int i=0;i<s.size();i++){
+ char a = s[i];
+ if(st.empty()){
+ st.push(a);
+ continue;
+ }
+ if(st.top() == a){
+ st.pop();
+ } else{
+ st.push(a);
+ }
+ }
+ vector<char> c;
+ while(!st.empty()){
+ c.push_back(st.top());
+ st.pop();
+ }
+ string s2 = "";
+ for(int i=c.size()-1;i>=0;i--){
+ s2 += c[i];
+ }
+ return s2;
+ }
+};根据 逆波兰表示法,求表达式的值。
+有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
+注意 两个整数之间的除法只保留整数部分。
+可以保证给定的逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
+func evalRPN(tokens []string) int {
+ l := len(tokens)
+ numstack := make([]int,0)
+ for i:=0;i<l;i++{
+ if len(tokens[i]) == 1{
+ if tokens[i] == "+"{
+ b := numstack[len(numstack)-1]
+ a := numstack[len(numstack)-2]
+ numstack[len(numstack)-2] = a+b
+ numstack = numstack[:len(numstack)-1]
+ } else if tokens[i] == "-"{
+ b := numstack[len(numstack)-1]
+ a := numstack[len(numstack)-2]
+ numstack[len(numstack)-2] = a-b
+ numstack = numstack[:len(numstack)-1]
+
+ } else if tokens[i] == "*"{
+ b := numstack[len(numstack)-1]
+ a := numstack[len(numstack)-2]
+ numstack[len(numstack)-2] = a*b
+ numstack = numstack[:len(numstack)-1]
+
+ } else if tokens[i] == "/"{
+ b := numstack[len(numstack)-1]
+ a := numstack[len(numstack)-2]
+ numstack[len(numstack)-2] = a/b
+ numstack = numstack[:len(numstack)-1]
+ } else{
+ numstack = append(numstack,change(tokens[i]))
+ }
+ } else{
+ numstack = append(numstack,change(tokens[i]))
+ }
+ }
+ return numstack[0]
+}
+
+func change(s string) int{
+ sum := 0
+ sign := 1
+ lens := len(s)
+ for i:=lens-1;i>=0;i--{
+ if s[i] == '-'{
+ sum = -sum
+ } else{
+ c := int(s[i] - '0')
+ sum += sign * c
+ sign *= 10
+ }
+ }
+ return sum
+}class Solution {
+public:
+ int evalRPN(vector<string>& tokens) {
+ stack<int> st;
+ for(int i=0;i<tokens.size();i++){
+ string s = tokens[i];
+ if(s == "+" || s == "-" || s == "*" || s == "/"){
+ int a = st.top();
+ st.pop();
+ int b = st.top();
+ st.pop();
+ if(s == "+"){
+ st.push(a+b);
+ } else if (s == "-"){
+ st.push(b - a);
+ } else if(s == "*"){
+ st.push(a * b);
+ } else{
+ st.push(b/a);
+ }
+ } else{
+ st.push(atoi(s.c_str()));
+ }
+ }
+ return st.top();
+ }
+};给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
func topKFrequent(nums []int, k int) []int {
+ ans:=[]int{}
+ map_num:=map[int]int{}
+ for _,item:=range nums {
+ map_num[item]++
+ }
+ for key,_:=range map_num{
+ ans=append(ans,key)
+ }
+ //核心思想:排序
+ //可以不用包函数,自己实现快排
+ sort.Slice(ans,func (a,b int)bool{
+ return map_num[ans[a]]>map_num[ans[b]]
+ })
+ return ans[:k]
+}class Solution {
+public:
+ // 小顶堆
+ class mycomparison {
+ public:
+ bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
+ return lhs.second > rhs.second;
+ }
+ };
+ vector<int> topKFrequent(vector<int>& nums, int k) {
+ // 要统计元素出现频率
+ unordered_map<int, int> map; // map<nums[i],对应出现的次数>
+ for (int i = 0; i < nums.size(); i++) {
+ map[nums[i]]++;
+ }
+
+ // 对频率排序
+ // 定义一个小顶堆,大小为k
+ priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;
+
+ // 用固定大小为k的小顶堆,扫描所有频率的数值
+ for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it++) {
+ pri_que.push(*it);
+ if (pri_que.size() > k) { // 如果堆的大小大于了K,则队列弹出,保证堆的大小一直为k
+ pri_que.pop();
+ }
+ }
+
+ // 找出前K个高频元素,因为小顶堆先弹出的是最小的,所以倒序来输出到数组
+ vector<int> result(k);
+ for (int i = k - 1; i >= 0; i--) {
+ result[i] = pri_que.top().first;
+ pri_que.pop();
+ }
+ return result;
+ }
+};代码随想录-贪心
+ +假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
+对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
+贪心策略:对于每个孩子,找到能满足他的最小饼干,并分配给他。从胃口最大的孩子开始,从最大的饼干开始。
+func findContentChildren(g []int, s []int) int {
+ sort.Slice(g, func(i, j int) bool {return g[i] > g[j]})
+ sort.Slice(s, func(i, j int) bool {return s[i] > s[j]})
+ leng := len(g)
+ lens := len(s)
+ si := 0
+ gi := 0
+ childsum := 0
+ for{
+ if (si == lens) || (gi == leng){
+ break
+ }
+ if s[si] >= g[gi]{
+ childsum++
+ si++
+ }
+ gi++
+ }
+ return childsum
+}class Solution {
+public:
+ int findContentChildren(vector<int>& g, vector<int>& s) {
+ sort(g.begin(), g.end());
+ sort(s.begin(), s.end());
+ int gindex = 0;
+ int sindex = 0;
+ while(gindex != g.size() && sindex != s.size()){
+ if(s[sindex] >= g[gindex]){
+ gindex += 1;
+ sindex += 1;
+ } else{
+ sindex += 1;
+ }
+ }
+ return gindex;
+ }
+};如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
+例如, [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ,因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
+相反,[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
+子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
+贪心策略:统计整个序列的峰值,但是序列的两个端点不好统计,需要进行特殊判断。
+这里的技巧是结尾直接加上,开头的判断融入到循环内部
+func wiggleMaxLength(nums []int) int {
+ lennums := len(nums)
+ if lennums == 1{
+ return 1
+ } else if lennums == 2{
+ if nums[1] != nums[0]{
+ return 2
+ }
+ return 1
+ } else{
+ result := 1
+ predif := 0
+ for i:=0;i<=lennums-2;i++{
+ curdif := nums[i+1] - nums[i]
+ if (predif <= 0 && curdif > 0) || (predif >= 0 && curdif < 0){
+ result++
+ predif = curdif
+ }
+ }
+ if result == 2 && nums[0] == nums[lennums-1]{
+ return 1
+ }
+ return result
+ }
+}class Solution {
+public:
+ int wiggleMaxLength(vector<int>& nums) {
+ vector<vector<int> > dp(nums.size(), vector<int>(2,1));
+ dp[0][0] = 1;
+ dp[0][1] = 1;
+ for(int i=1;i<nums.size();i++){
+ for(int j=0;j<i;j++){
+ if(nums[j] < nums[i]){
+ dp[i][0] = max(dp[i][0],dp[j][1]+1);
+ }
+ if(nums[j] > nums[i]){
+ dp[i][1] = max(dp[i][1], dp[j][0] + 1);
+ }
+ }
+ }
+ return max(dp[nums.size()-1][0], dp[nums.size()-1][1]);
+ }
+};给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
+判断你是否能够到达最后一个下标。
+贪心策略:跳几步不重要,重要的是跳一次的覆盖范围。只要覆盖的范围能超过最后一个下标即可
+这里的更新注意是遍历的范围变化
+func canJump(nums []int) bool {
+ lennums := len(nums)
+ result := 0
+ for i:=0;i<=result;i++{
+ result = max(result,i+nums[i])
+ if result >= lennums - 1{
+ return true
+ }
+ }
+ return false
+}
+
+func max(a,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ bool canJump(vector<int>& nums) {
+ vector<bool> judge(nums.size(),false);
+ judge[0] = true;
+ for(int i=0;i<nums.size();i++){
+ if(judge[i] == true){
+ for(int j=i;j<=i+nums[i];j++){
+ if(j < nums.size()){
+ judge[j] = true;
+ if(judge[nums.size()-1] == true){
+ return true;
+ }
+ }
+ }
+ }
+ }
+ return judge[nums.size()-1];
+ }
+};给你一个非负整数数组 nums ,你最初位于数组的第一个位置。
+数组中的每个元素代表你在该位置可以跳跃的最大长度。
+你的目标是使用最少的跳跃次数到达数组的最后一个位置。
+假设你总是可以到达数组的最后一个位置。
+贪心策略:记录当前的覆盖范围和下一步的覆盖范围,覆盖范围超过了最后的下标就可以
+代码不会写。。。。
+func jump(nums []int) int {
+ lennums := len(nums)
+ curDistance := 0; // 当前覆盖的最远距离下标
+ ans := 0; // 记录走的最大步数
+ nextDistance := 0; // 下一步覆盖的最远距离下标
+ for i := 0; i < lennums - 1; i++ { // 注意这里是小于nums.size() - 1,这是关键所在
+ nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖的最远距离下标
+ if i == curDistance { // 遇到当前覆盖的最远距离下标
+ curDistance = nextDistance; // 更新当前覆盖的最远距离下标
+ ans++;
+ }
+ }
+ return ans;
+}
+func max(a,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int jump(vector<int>& nums) {
+ int curDistance = 0; // 当前覆盖的最远距离下标
+ int ans = 0; // 记录走的最大步数
+ int nextDistance = 0; // 下一步覆盖的最远距离下标
+ for (int i = 0; i < nums.size() - 1; i++) { // 注意这里是小于nums.size() - 1,这是关键所在
+ nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖的最远距离下标
+ if (i == curDistance) { // 遇到当前覆盖的最远距离下标
+ curDistance = nextDistance; // 更新当前覆盖的最远距离下标
+ ans++;
+ }
+ }
+ return ans;
+ }
+};给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组:
i 并将 nums[i] 替换为 -nums[i] 。重复这个过程恰好 k 次。可以多次选择同一个下标 i 。
以这种方式修改数组后,返回数组 可能的最大和 。
+贪心策略:计数数组中有多少负值,从负值最大的开始向最小的逐渐变为相反数。如果负数都变为正数了,就对最小的正数进行重复改变。
+落实到代码上,对数组进行排序,然后一边计数一边加和即可。
+func largestSumAfterKNegations(nums []int, k int) int {
+ sort.Slice(nums, func(i, j int) bool {return nums[i] < nums[j]})
+
+ minnum := 1000
+ lennum := len(nums)
+ sum := 0
+ for i:=0;i<lennum;i++{
+ if nums[i] < 0{
+ if k != 0{
+ k--
+ nums[i] = -nums[i]
+ }
+ }
+ sum += nums[i]
+ minnum = min(minnum,nums[i])
+ }
+ if k % 2 == 1{
+ sum -= 2 * minnum
+ }
+ return sum
+
+}
+func min(a,b int) int {
+ if a <b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int largestSumAfterKNegations(vector<int>& nums, int k) {
+ int maxsum = 0;
+ sort(nums.begin(),nums.end());
+ for(int i=0;i<nums.size() && k > 0;i++,k--){
+ if(nums[i] < 0){
+ nums[i] = -nums[i];
+ } else{
+ break;
+ }
+ }
+ for(int i=0;i<nums.size();i++){
+ maxsum += nums[i];
+ }
+ if(k == 0 || k % 2 == 0){
+ return maxsum;
+ }
+ int minvalue = nums[0];
+ for(int i=0;i<nums.size();i++){
+ minvalue = min(minvalue, nums[i]);
+ }
+ return maxsum - 2 * minvalue;
+ }
+};在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
贪心策略:首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。每个加油站的剩余量rest[i]为gas[i] - cost[i]。i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,起始位置从i+1算起,再从0计算curSum。
+func canCompleteCircuit(gas []int, cost []int) int {
+ lengas := len(gas)
+ totalgas := 0
+ totalcost := 0
+ start := 0
+ sum := 0
+ for i:=0;i<lengas;i++{
+ totalgas += gas[i]
+ totalcost += cost[i]
+ sum += gas[i] - cost[i]
+ if sum < 0{
+ start = i+1
+ sum = 0
+ }
+ }
+ if totalcost > totalgas{
+ return -1
+ }
+ return start
+}class Solution {
+public:
+ int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
+ int curSum = 0;
+ int totalSum = 0;
+ int start = 0;
+ for (int i = 0; i < gas.size(); i++) {
+ curSum += gas[i] - cost[i];
+ totalSum += gas[i] - cost[i];
+ if (curSum < 0) { // 当前累加rest[i]和 curSum一旦小于0
+ start = i + 1; // 起始位置更新为i+1
+ curSum = 0; // curSum从0开始
+ }
+ }
+ if (totalSum < 0) return -1; // 说明怎么走都不可能跑一圈了
+ return start;
+ }
+};n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
+1 个糖果。请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
+贪心策略:从左到右遍历一遍,从右到左遍历一遍,每一次只看一侧的孩子就可以
+需要注意在右往左遍历的时候不要毁掉左往右遍历好的
+func candy(ratings []int) int {
+ lenratings := len(ratings)
+ result := make([]int,lenratings)
+ for i:=0;i<lenratings-1;i++{
+ if ratings[i+1] > ratings[i]{
+ result[i+1] = result[i] + 1
+ }
+ }
+ for i:=lenratings-1;i>0;i--{
+ if ratings[i-1] > ratings[i] && result[i-1] <= result[i]{
+ result[i-1] = result[i] + 1
+ }
+ }
+ sum := 0
+ for i:=0;i<lenratings;i++{
+ sum += result[i]
+ }
+ return sum + lenratings
+}class Solution {
+public:
+ int candy(vector<int>& ratings) {
+ vector<int> temp(ratings.size(),1);
+ for(int i=0;i<ratings.size();i++){
+ if(i == 0){
+ continue;
+ }
+ if(ratings[i] > ratings[i-1]){
+ temp[i] = temp[i-1] + 1;
+ }
+ }
+ for(int i=ratings.size()-1;i>=0;i--){
+ if(i == ratings.size()-1){
+ continue;
+ }
+ if(ratings[i] > ratings[i+1]){
+ temp[i] = max(temp[i], temp[i+1] + 1);
+ }
+ }
+ int totalsum = 0;
+ for(int i=0;i<temp.size();i++){
+ totalsum += temp[i];
+ }
+ return totalsum;
+ }
+};在柠檬水摊上,每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。
每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付 5 美元。
注意,一开始你手头没有任何零钱。
+给你一个整数数组 bills ,其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零,返回 true ,否则返回 false 。
贪心策略:直接模拟就好了,没有什么意思
+func lemonadeChange(bills []int) bool {
+ bill10 := 0
+ bill5 := 0
+ for i:=0;i<len(bills);i++{
+ if bills[i] == 5{
+ bill5 += 1
+ } else if bills[i] == 10{
+ bill10 += 1
+ if bill5 > 0{
+ bill5 -= 1
+ } else{
+ return false
+ }
+ } else{
+ if bill10 >= 1 && bill5 >= 1{
+ bill5 -= 1
+ bill10 -= 1
+ } else if bill5 >= 3{
+ bill5 -= 3
+ } else{
+ return false
+ }
+ }
+ }
+ return true
+}class Solution {
+public:
+ bool lemonadeChange(vector<int>& bills) {
+ map<int,int> mp;
+ mp[5] = 0;
+ mp[10] = 0;
+ for(int i=0;i<bills.size();i++){
+ if(bills[i] == 5){
+ mp[5] += 1;
+ } else if (bills[i] == 10){
+ if(mp[5] <= 0){
+ return false;
+ }
+ mp[5] -= 1;
+ mp[10] += 1;
+ } else{
+ if(mp[10] >= 1 && mp[5] >= 1){
+ mp[5] -= 1;
+ mp[10] -= 1;
+ } else if(mp[5] >= 3){
+ mp[5] -= 3;
+ } else{
+ return false;
+ }
+ }
+ }
+ return true;
+ }
+};假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
贪心策略:身高一定是从大到小排(身高相同的话则k小的站前面),让高个子在前面。然后只需要按照k为下标重新插入队列就可以了
+func reconstructQueue(people [][]int) [][]int {
+ sort.Slice(
+ people, func(i,j int) bool{
+ if people[i][0] == people[j][0]{
+ return people[i][1] < people[j][1]
+ }
+ return people[i][0] > people[j][0]
+ })
+ result := make([][]int,0)
+ for _,info := range people{
+ result = append(result,info)
+ copy(result[info[1] +1:], result[info[1]:])
+ result[info[1]] = info
+ }
+ return result
+}class Solution {
+public:
+ static bool cmp(const vector<int>& a, const vector<int>& b) {
+ if (a[0] == b[0]) return a[1] < b[1];
+ return a[0] > b[0];
+ }
+ vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
+ sort (people.begin(), people.end(), cmp);
+ vector<vector<int>> que;
+ for (int i = 0; i < people.size(); i++) {
+ int position = people[i][1];
+ que.insert(que.begin() + position, people[i]);
+ }
+ return que;
+ }
+};有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中 points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。
一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart, xend, 且满足 xstart ≤ x ≤ xend, 则该气球会被 引爆。 可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后,可以无限地前进。
给你一个数组 points , 返回引爆所有气球所必须射出的 最小 弓箭数 。
贪心策略:按照最小末尾坐标排序,射出的箭在保证将最末尾的气球引爆的同时最好引爆更多的气球。
+func findMinArrowShots(points [][]int) int {
+ lenpoints := len(points)
+ sort.Slice(
+ points,func(i,j int) bool{
+ if points[i][1] == points[j][1]{
+ return points[i][0] < points[j][0]
+ }
+ return points[i][1] < points[j][1]
+ })
+ count := 0
+ start := 0
+ for start < lenpoints{
+ count += 1
+ arrow := points[start][1]
+ for i:=start;i<lenpoints;i++{
+ start = i+1
+ if points[i][0] <= arrow && points[i][1] >= arrow{
+ continue
+ } else{
+ start -= 1
+ break
+ }
+ }
+ if start == lenpoints{
+ break
+ }
+ }
+ return count
+}class Solution {
+public:
+ static bool cmp(const vector<int>& a, const vector<int>& b){
+ return a[0] < b[0];
+ }
+ int findMinArrowShots(vector<vector<int>>& points) {
+ sort(points.begin(), points.end(), cmp);
+ int result = 1;
+ for(int i=1;i<points.size();i++){
+ if(points[i][0] > points[i-1][1]){
+ result += 1;
+ } else{
+ points[i][1] = min(points[i-1][1], points[i][1]);
+ }
+ }
+ return result;
+ }
+};给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回需要移除区间的最小数量,使剩余区间互不重叠。
贪心策略:与上一道题相同,仍然是对后面的值进行排序,然后从头到尾遍历去除即可。
+func eraseOverlapIntervals(intervals [][]int) int {
+ leni := len(intervals)
+ sort.Slice(
+ intervals,func(i,j int) bool{
+ if intervals[i][1] == intervals[j][1]{
+ return intervals[i][0] < intervals[j][0]
+ }
+ return intervals[i][1] < intervals[j][1]
+ })
+ count := 0
+ min1 := intervals[0][1]
+ for i:=1;i<leni;i++{
+ if intervals[i][0] >= min1{
+ min1 = intervals[i][1]
+ } else{
+ count += 1
+ }
+ }
+ return count
+}class Solution {
+public:
+ static bool cmp(const vector<int>& a, const vector<int>& b){
+ if(a[1] == b[1]){
+ return a[0] < b[0];
+ }
+ return a[1] < b[1];
+ }
+ int eraseOverlapIntervals(vector<vector<int>>& intervals) {
+ int result = 0;
+ sort(intervals.begin(), intervals.end(), cmp);
+ int nowend = intervals[0][1];
+ for(int i=1;i<intervals.size();i++){
+ if(intervals[i][0] < nowend){
+ result += 1;
+ } else{
+ nowend = intervals[i][1];
+ }
+ }
+ return result;
+ }
+};字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
贪心策略:与上一题的贪心策略也是相同的,只是多了一步字母到区间的转换
+注意这道题的区别是看0位置进行排序,因为是一个包括的区间,与前面只看后面1位置不相同
+func partitionLabels(s string) []int {
+ result := make([][]int,26)
+ for i:=0;i<26;i++{
+ result[i] = make([]int,2)
+ result[i][0] = 1000
+ result[i][1] = 1000
+ }
+ s1 := []rune(s)
+ lens := len(s1)
+ for i:=0;i<lens;i++{
+ index := int(s1[i]) - 97
+ if result[index][0] == 1000{
+ result[index][0] = i
+ }
+ result[index][1] = i
+ }
+ sort.Slice(
+ result,func(i,j int)bool{
+ if result[i][0] == result[j][0]{
+ return result[i][1] < result[j][1]
+ }
+ return result[i][0] < result[j][0]
+ })
+ submit := make([]int,0)
+ startmin := result[0][0]
+ endmax := result[0][1]
+ for i:=1;i<26;i++{
+ if result[i][0] > endmax{
+ submit = append(submit,endmax-startmin+1)
+ endmax = result[i][1]
+ startmin = result[i][0]
+ } else{
+ startmin = min(startmin,result[i][0])
+ endmax = max(endmax,result[i][1])
+ }
+ }
+ if startmin != 1000{
+ submit = append(submit,endmax-startmin+1)
+ }
+ return submit
+}
+
+func min(a,b int) int{
+ if a < b{
+ return a
+ }
+ return b
+}
+
+func max(a,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ vector<int> partitionLabels(string s) {
+ int hash[27] = {0};
+ for (int i = 0; i < s.size(); i++) {
+ hash[s[i] - 'a'] = i;
+ }
+ vector<int> result;
+ int left = 0;
+ int right = 0;
+ for (int i = 0; i < s.size(); i++) {
+ right = max(right, hash[s[i] - 'a']);
+ if (i == right) {
+ result.push_back(right - left + 1);
+ left = i + 1;
+ }
+ }
+ return result;
+ }
+};以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
贪心策略:相当于上一道题的简化版
+func merge(intervals [][]int) [][]int {
+ leni := len(intervals)
+ sort.Slice(
+ intervals,func(i,j int) bool {
+ if intervals[i][0] == intervals[j][0]{
+ return intervals[i][1] < intervals[j][1]
+ }
+ return intervals[i][0] < intervals[j][0]
+ })
+ result := make([][]int,0)
+ minstart := intervals[0][0]
+ maxend := intervals[0][1]
+ for i:=1;i<leni;i++{
+ if intervals[i][0] > maxend{
+ temp := []int{minstart,maxend}
+ result = append(result,temp)
+ minstart = intervals[i][0]
+ maxend = intervals[i][1]
+ } else{
+ minstart = min(minstart,intervals[i][0])
+ maxend = max(maxend,intervals[i][1])
+ }
+ }
+ temp := []int{minstart,maxend}
+ result = append(result,temp)
+ return result
+}
+
+func min(a,b int) int{
+ if a < b{
+ return a
+ }
+ return b
+}
+func max(a,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ static bool cmp(const vector<int>& a, const vector<int>& b){
+ if(a[0] == b[0]){
+ return a[1] < b[1];
+ }
+ return a[0] < b[0];
+ }
+ vector<vector<int>> merge(vector<vector<int>>& intervals) {
+ vector<vector<int> > result;
+ sort(intervals.begin(), intervals.end(), cmp);
+ int nowstart = intervals[0][0];
+ int nowend = intervals[0][1];
+ for(int i=1;i<intervals.size();i++){
+ if(intervals[i][0] <= nowend){
+ nowstart = min(nowstart,intervals[i][0]);
+ nowend = max(nowend,intervals[i][1]);
+ } else{
+ result.push_back(vector<int>{nowstart, nowend});
+ nowstart = intervals[i][0];
+ nowend = intervals[i][1];
+ }
+ }
+ result.push_back(vector<int>{nowstart, nowend});
+ return result;
+ }
+};当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
贪心策略:局部最优:遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]–,然后strNum[i]给为9,可以保证这两位变成最大单调递增整数 。
+从前向后遍历的话,遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]减一,但此时如果strNum[i - 1]减一了,可能又小于strNum[i - 2]。
+因此应该从后向前遍历
+func monotoneIncreasingDigits(N int) int {
+ s := strconv.Itoa(N)//将数字转为字符串,方便使用下标
+ ss := []byte(s)//将字符串转为byte数组,方便更改。
+ n := len(ss)
+ if n <= 1 {
+ return N
+ }
+ for i:=n-1 ; i>0; i-- {
+ if ss[i-1] > ss[i] {//前一个大于后一位,前一位减1,后面的全部置为9
+ ss[i-1] -= 1
+ for j := i ; j < n; j++ {//后面的全部置为9
+ ss[j] = '9'
+ }
+ }
+ }
+ res, _ := strconv.Atoi(string(ss))
+ return res
+}class Solution {
+public:
+ int monotoneIncreasingDigits(int n) {
+ string strNum = to_string(n);
+ int flag = strNum.size();
+ for (int i = strNum.size() - 1; i > 0; i--) {
+ if (strNum[i - 1] > strNum[i] ) {
+ flag = i;
+ strNum[i - 1]--;
+ }
+ }
+ for (int i = flag; i < strNum.size(); i++) {
+ strNum[i] = '9';
+ }
+ return stoi(strNum);
+ }
+};给定一个二叉树,我们在树的节点上安装摄像头。
+节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
+计算监控树的所有节点所需的最小摄像头数量。
+局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少!
+在二叉树中如何从低向上推导呢?
+可以使用后序遍历也就是左右中的顺序,这样就可以在回溯的过程中从下到上进行推导了。
+每个节点可能有如下三种状态:
+为了让摄像头数量最少,我们要尽量让叶子节点的父节点安装摄像头,这样才能摄像头的数量最少。
+那么空节点不能是无覆盖的状态,这样叶子节点就要放摄像头了,空节点也不能是有摄像头的状态,这样叶子节点的父节点就没有必要放摄像头了,而是可以把摄像头放在叶子节点的爷爷节点上。
+所以空节点的状态只能是有覆盖,这样就可以在叶子节点的父节点放摄像头了
+后续待补充
+const inf = math.MaxInt64 / 2
+
+func minCameraCover(root *TreeNode) int {
+ var dfs func(*TreeNode) (a, b, c int)
+ dfs = func(node *TreeNode) (a, b, c int) {
+ if node == nil {
+ return inf, 0, 0
+ }
+ lefta, leftb, leftc := dfs(node.Left)
+ righta, rightb, rightc := dfs(node.Right)
+ a = leftc + rightc + 1
+ b = min(a, min(lefta+rightb, righta+leftb))
+ c = min(a, leftb+rightb)
+ return
+ }
+ _, ans, _ := dfs(root)
+ return ans
+}
+
+func min(a, b int) int {
+ if a <= b {
+ return a
+ }
+ return b
+}class Solution {
+private:
+ int result;
+ int traversal(TreeNode* cur) {
+ if (cur == NULL) return 2;
+ int left = traversal(cur->left); // 左
+ int right = traversal(cur->right); // 右
+ if (left == 2 && right == 2) return 0;
+ else if (left == 0 || right == 0) {
+ result++;
+ return 1;
+ } else return 2;
+ }
+public:
+ int minCameraCover(TreeNode* root) {
+ result = 0;
+ if (traversal(root) == 0) { // root 无覆盖
+ result++;
+ }
+ return result;
+ }
+};代码随想录-双指针法
+ +给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
+注意:答案中不可以包含重复的三元组。
+func threeSum(nums []int) [][]int {
+ result := make([][]int, 0)
+ sort.Slice(nums,func(i,j int) bool {return nums[i] < nums[j]})
+ lennums := len(nums)
+ for i :=0;i<lennums;i++ {
+ if i > 0 && nums[i] == nums[i-1]{
+ continue
+ }
+ left := i+1
+ right := lennums-1
+ for left < right{
+ if nums[i] + nums[left] + nums[right] == 0{
+ result = append(result, []int{nums[i],nums[left],nums[right]})
+ for left < right && nums[left] == nums[left+1]{
+ left++
+ }
+ for left < right && nums[right] == nums[right-1]{
+ right--
+ }
+ left++
+ right--
+ } else if nums[i] + nums[left] + nums[right] < 0{
+ left++
+ } else{
+ right--
+ }
+ }
+ }
+ return result
+}class Solution {
+public:
+ vector<vector<int>> threeSum(vector<int>& nums) {
+ vector<vector<int> > result;
+ sort(nums.begin(), nums.end());
+ for(int i=0;i<nums.size();i++){
+ int j = i + 1;
+ int k = nums.size() - 1;
+ if(i != 0 && nums[i] == nums[i-1]){
+ continue;
+ }
+ while(j < k){
+ if(nums[i] + nums[j] + nums[k] == 0){
+ result.push_back(vector<int>{nums[i], nums[j], nums[k]});
+ while(j < k && nums[j] == nums[j+1]){
+ j++;
+ }
+ while(j < k && nums[k] == nums[k-1]){
+ k--;
+ }
+ j++;
+ k--;
+ } else if(nums[i] + nums[j] + nums[k] > 0){
+ k--;
+ } else{
+ j++;
+ }
+ }
+ }
+ return result;
+ }
+};给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
+0 <= a, b, c, d < n,a、b、c 和 d 互不相同,nums[a] + nums[b] + nums[c] + nums[d] == target
+你可以按 任意顺序 返回答案 。
+func fourSum(nums []int, target int) [][]int {
+ sort.Slice(nums,func(a,b int)bool{return nums[a] < nums[b]})
+ lennums := len(nums)
+ result := make([][]int,0)
+ for i:=0;i<=lennums-4;i++{
+ if i > 0 && nums[i] == nums[i-1]{
+ continue
+ }
+ for j:=i;j<lennums;j++{
+ if j < lennums - 1 && nums[j] == nums[j+1]{
+ continue
+ }
+ left := i+1
+ right := j-1
+ for left < right{
+ if nums[i] + nums[j] + nums[left] + nums[right] == target{
+ result = append(result,[]int{nums[i],nums[j],nums[left],nums[right]})
+ for left < right && nums[left] == nums[left+1]{
+ left++
+ }
+ for left < right && nums[right] == nums[right-1]{
+ right--
+ }
+ left++
+ right--
+ } else if nums[i] + nums[j] + nums[left] + nums[right] < target{
+ left++
+ } else{
+ right--
+ }
+ }
+ }
+ }
+
+ return result
+}class Solution {
+public:
+ vector<vector<int>> fourSum(vector<int>& nums, int target) {
+ vector<vector<int> > result;
+ sort(nums.begin(), nums.end());
+ for(int i=0;i<nums.size();i++){
+ if(i > nums.size()-4){
+ break;
+ }
+ if(i > 0 && nums[i] == nums[i-1]){
+ continue;
+ }
+ for(int l=i+3;l<nums.size();l++){
+ if(l < nums.size()-1 && nums[l] == nums[l+1]){
+ continue;
+ }
+ int j = i + 1;
+ int k = l - 1;
+
+ while(j < k){
+ if((long long)nums[i] + nums[j] + nums[k] + nums[l] == (long long)target){
+ result.push_back(vector<int>{nums[i], nums[j], nums[k], nums[l]});
+ while(j < k && nums[j] == nums[j+1]){
+ j++;
+ }
+ while(j < k && nums[k] == nums[k-1]){
+ k--;
+ }
+ j++;
+ k--;
+ } else if((long long)nums[i] + nums[j] + nums[k] + nums[l] > (long long)target){
+ k--;
+ } else{
+ j++;
+ }
+ }
+ }
+ }
+ return result;
+ }
+};在数组:就移除个元素很难么? (opens new window)中,原地移除数组上的元素,我们说到了数组上的元素,不能真正的删除,只能覆盖。
+一些同学可能会写出如下代码(伪代码):
+for (int i = 0; i < array.size(); i++) {
+ if (array[i] == target) {
+ array.erase(i);
+ }
+}这个代码看上去好像是O(n)的时间复杂度,其实是O(n^2)的时间复杂度,因为erase操作也是O(n)的操作。
+所以此时使用双指针法才展现出效率的优势:通过两个指针在一个for循环下完成两个for循环的工作。
+在字符串:这道题目,使用库函数一行代码搞定 (opens new window)中讲解了反转字符串,注意这里强调要原地反转,要不然就失去了题目的意义。
+使用双指针法, 定义两个指针(也可以说是索引下标),一个从字符串前面,一个从字符串后面,两个指针同时向中间移动,并交换元素。 ,时间复杂度是O(n)。
+在替换空格 (opens new window)中介绍使用双指针填充字符串的方法,如果想把这道题目做到极致,就不要只用额外的辅助空间了!
+思路就是首先扩充数组到每个空格替换成"%20"之后的大小。然后双指针从后向前替换空格。
+有同学问了,为什么要从后向前填充,从前向后填充不行么?
+从前向后填充就是O(n^2)的算法了,因为每次添加元素都要将添加元素之后的所有元素向后移动。
+其实很多数组(字符串)填充类的问题,都可以先预先给数组扩容带填充后的大小,然后在从后向前进行操作。
+那么在字符串:花式反转还不够! (opens new window)中,我们使用双指针法,用O(n)的时间复杂度完成字符串删除类的操作,因为题目要删除冗余空格。
+在删除冗余空格的过程中,如果不注意代码效率,很容易写成了O(n^2)的时间复杂度。其实使用双指针法O(n)就可以搞定。
+主要还是大家用erase用的比较随意,一定要注意for循环下用erase的情况,一般可以用双指针写效率更高!
+翻转链表是现场面试,白纸写代码的好题,考察了候选者对链表以及指针的熟悉程度,而且代码也不长,适合在白纸上写。
+在链表:听说过两天反转链表又写不出来了? (opens new window)中,讲如何使用双指针法来翻转链表,只需要改变链表的next指针的指向,直接将链表反转 ,而不用重新定义一个新的链表。
+思路还是很简单的,代码也不长,但是想在白纸上一次性写出bugfree的代码,并不是容易的事情。
+在链表中求环,应该是双指针在链表里最经典的应用,在链表:环找到了,那入口呢? (opens new window)中讲解了如何通过双指针判断是否有环,而且还要找到环的入口。
+使用快慢指针(双指针法),分别定义 fast 和 slow指针,从头结点出发,fast指针每次移动两个节点,slow指针每次移动一个节点,如果 fast 和 slow指针在途中相遇 ,说明这个链表有环。
+那么找到环的入口,其实需要点简单的数学推理,我在文章中把找环的入口清清楚楚的推理的一遍,如果对找环入口不够清楚的同学建议自己看一看链表:环找到了,那入口呢? (opens new window)。
+在哈希表:解决了两数之和,那么能解决三数之和么? (opens new window)中,讲到使用哈希法可以解决1.两数之和的问题
+其实使用双指针也可以解决1.两数之和的问题,只不过1.两数之和求的是两个元素的下标,没法用双指针,如果改成求具体两个元素的数值就可以了,大家可以尝试用双指针做一个leetcode上两数之和的题目,就可以体会到我说的意思了。
+使用了哈希法解决了两数之和,但是哈希法并不使用于三数之和!
+使用哈希法的过程中要把符合条件的三元组放进vector中,然后在去去重,这样是非常费时的,很容易超时,也是三数之和通过率如此之低的根源所在。
+去重的过程不好处理,有很多小细节,如果在面试中很难想到位。
+时间复杂度可以做到O(n^2),但还是比较费时的,因为不好做剪枝操作。
+所以这道题目使用双指针法才是最为合适的,用双指针做这道题目才能就能真正体会到,通过前后两个指针不算向中间逼近,在一个for循环下完成两个for循环的工作。
+只用双指针法时间复杂度为O(n^2),但比哈希法的O(n^2)效率高得多,哈希法在使用两层for循环的时候,能做的剪枝操作很有限。
+在双指针法:一样的道理,能解决四数之和 (opens new window)中,讲到了四数之和,其实思路是一样的,在三数之和的基础上再套一层for循环,依然是使用双指针法。
+对于三数之和使用双指针法就是将原本暴力O(n^3)的解法,降为O(n^2)的解法,四数之和的双指针解法就是将原本暴力O(n^4)的解法,降为O(n^3)的解法。
+同样的道理,五数之和,n数之和都是在这个基础上累加。
+ + +代码随想录-单调栈
+ +给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
+func dailyTemperatures(temperatures []int) []int {
+ l := len(temperatures)
+ result := make([]int,l)
+ stack := make([]int,0)
+ for i:=0;i<l;i++{
+ if len(stack) == 0 || temperatures[i] <= temperatures[stack[len(stack)-1]]{
+ stack = append(stack,i)
+ } else{
+ for len(stack) > 0 && temperatures[i] > temperatures[stack[len(stack)-1]]{
+ result[stack[len(stack)-1]] = i - stack[len(stack)-1]
+ stack = stack[:len(stack)-1]
+ }
+ stack = append(stack,i)
+ }
+ }
+ return result
+}class Solution {
+public:
+ vector<int> dailyTemperatures(vector<int>& temperatures) {
+ stack<int> st;
+ vector<int> result(temperatures.size(),0);
+ for(int i=0;i<temperatures.size();i++){
+ while(!st.empty() && temperatures[st.top()] < temperatures[i]){
+ result[st.top()] = i - st.top();
+ st.pop();
+ }
+ st.push(i);
+ }
+ return result;
+ }
+};nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
+给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
+对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
+返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
+func nextGreaterElement(nums1 []int, nums2 []int) []int {
+ lennums1 := len(nums1)
+ ans := make([]int,lennums1)
+ nummap := make(map[int] int)
+ stack := make([]int,0)
+ for i:=0;i<len(nums2);i++{
+ if len(stack) == 0 || nums2[i] <= stack[len(stack)-1]{
+ stack = append(stack,nums2[i])
+ } else{
+ for len(stack) > 0 && nums2[i] > stack[len(stack)-1]{
+ nummap[stack[len(stack)-1]] = nums2[i]
+ stack = stack[:len(stack)-1]
+ }
+ stack = append(stack,nums2[i])
+ }
+ }
+ for i:=0;i<lennums1;i++{
+ a,ok := nummap[nums1[i]]
+ if ok{
+ ans[i] = a
+ } else{
+ ans[i] = -1
+ }
+ }
+ return ans
+}class Solution {
+public:
+ vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
+ vector<int> result(nums1.size(),-1);
+ stack<int> st;
+ unordered_map<int, int> mp;
+ for(int i=0;i<nums1.size();i++){
+ mp[nums1[i]] = i;
+ }
+ for(int i=0;i<nums2.size();i++){
+ while(!st.empty() && st.top() < nums2[i]){
+ if(mp.find(st.top()) != mp.end()){
+ result[mp[st.top()]] = nums2[i];
+ }
+ st.pop();
+ }
+ st.push(nums2[i]);
+ }
+ return result;
+ }
+};给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。
+数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1 。
+func nextGreaterElements(nums []int) []int {
+ lennums1 := len(nums)
+ for i:=0;i<lennums1-1;i++{
+ nums = append(nums,nums[i])
+ }
+ lennums := len(nums)
+ result := make([]int,lennums)
+ for i:=0;i<lennums;i++{
+ result[i] = -1
+ }
+ stack := make([]int,0)
+ for i:=0;i<lennums;i++{
+ if len(stack) == 0 || nums[i] <= nums[stack[len(stack)-1]]{
+ stack = append(stack,i)
+ } else{
+ for len(stack) > 0 && nums[i] > nums[stack[len(stack)-1]]{
+ result[stack[len(stack)-1]] = nums[i]
+ stack = stack[:len(stack)-1]
+ }
+ stack = append(stack,i)
+ }
+ }
+ return result[:lennums1]
+}class Solution {
+public:
+ vector<int> nextGreaterElements(vector<int>& nums) {
+ vector<int> numsall(nums.size()*2);
+ for(int i=0;i<numsall.size();i++){
+ numsall[i] = nums[i%nums.size()];
+ }
+ stack<int> st;
+ vector<int> result(nums.size(),-1);
+ for(int i=0;i<numsall.size();i++){
+ while(!st.empty() && numsall[st.top()] < numsall[i]){
+ if(result[st.top()%nums.size()] == -1){
+ result[st.top()%nums.size()] = numsall[i];
+ }
+ st.pop();
+ }
+ st.push(i);
+ }
+ return result;
+ }
+};给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
func trap(height []int) int {
+ result := 0
+ lenh := len(height)
+ stack := make([]int,0)
+ stack = append(stack,0)
+ for i:=1;i<lenh;i++{
+ if height[i] < height[stack[len(stack)-1]]{
+ stack = append(stack,i)
+ } else if height[i] == height[stack[len(stack)-1]]{
+ stack[len(stack)-1] = i
+ } else{
+ for len(stack) > 0 && height[i] > height[stack[len(stack)-1]]{
+ mid := stack[len(stack)-1]
+ stack = stack[:len(stack)-1]
+ if len(stack) != 0{
+ h := min(height[stack[len(stack)-1]], height[i]) - height[mid];
+ w := i - stack[len(stack)-1] - 1;
+ result += h * w;
+ }
+ }
+ stack = append(stack,i)
+ }
+ }
+ return result
+}
+
+func min(a,b int) int {
+ if a < b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int trap(vector<int>& height) {
+ stack<int> st;
+ st.push(0);
+ int sum = 0;
+ for (int i = 1; i < height.size(); i++) {
+ while (!st.empty() && height[i] > height[st.top()]) {
+ int mid = st.top();
+ st.pop();
+ if (!st.empty()) {
+ int h = min(height[st.top()], height[i]) - height[mid];
+ int w = i - st.top() - 1;
+ sum += h * w;
+ }
+ }
+ st.push(i);
+ }
+ return sum;
+ }
+};func largestRectangleArea(heights []int) int {
+ maxarea := 0
+ stack := []int{-1}
+ heights=append(heights,0)
+ l := len(heights)
+ for i:=0;i<l;i++{
+ for len(stack)>1 && heights[i] < heights[stack[len(stack)-1]]{
+ cur := stack[len(stack)-1]
+ stack = stack[:len(stack)-1]
+ left := stack[len(stack)-1]
+ h := heights[cur]
+ w := i - left - 1
+ maxarea = max(maxarea,h*w)
+ }
+ stack = append(stack,i)
+ }
+ return maxarea
+}
+
+func max(a,b int) int{
+ if a > b{
+ return a
+ }
+ return b
+}class Solution {
+public:
+ int largestRectangleArea(vector<int>& heights) {
+ stack<int> st;
+ heights.insert(heights.begin(), 0);
+ heights.push_back(0);
+ st.push(0);
+ int sum = 0;
+ for (int i = 1; i < heights.size(); i++) {
+ while (heights[i] < heights[st.top()]) {
+ int mid = st.top();
+ st.pop();
+ int w = i - st.top() - 1;
+ int h = heights[mid];
+ sum = max(sum, w * h);
+ }
+ st.push(i);
+ }
+ return sum;
+ }
+};给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
+返回 滑动窗口中的最大值 。
+func maxSlidingWindow(nums []int, k int) []int {
+ lennum := len(nums)
+ queue := make([]int,0)
+ for i:=0;i<k-1;i++{
+ if len(queue) == 0 || nums[i] < nums[queue[len(queue)-1]]{
+ queue = append(queue,i)
+ } else{
+ for len(queue) > 0 && nums[i] >= nums[queue[len(queue)-1]]{
+ queue = queue[:len(queue)-1]
+ }
+ queue = append(queue,i)
+ }
+ }
+ result := make([]int,0)
+ for i:=k-1;i<lennum;i++{
+ if len(queue) == 0 || nums[i] < nums[queue[len(queue)-1]]{
+ queue = append(queue,i)
+ } else{
+ for len(queue) > 0 && nums[i] >= nums[queue[len(queue)-1]]{
+ queue = queue[:len(queue)-1]
+ }
+ queue = append(queue,i)
+ }
+ result = append(result,nums[queue[0]])
+ if i-(k-1) == queue[0]{
+ queue = queue[1:]
+ }
+ }
+ return result
+}class Solution {
+private:
+class MyQueue { //单调队列(从大到小)
+public:
+ deque<int> que; // 使用deque来实现单调队列
+ // 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
+ // 同时pop之前判断队列当前是否为空。
+ void pop(int value) {
+ if (!que.empty() && value == que.front()) {
+ que.pop_front();
+ }
+ }
+ // 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
+ // 这样就保持了队列里的数值是单调从大到小的了。
+ void push(int value) {
+ while (!que.empty() && value > que.back()) {
+ que.pop_back();
+ }
+ que.push_back(value);
+
+ }
+ // 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
+ int front() {
+ return que.front();
+ }
+};
+public:
+ vector<int> maxSlidingWindow(vector<int>& nums, int k) {
+ MyQueue que;
+ vector<int> result;
+ for (int i = 0; i < k; i++) { // 先将前k的元素放进队列
+ que.push(nums[i]);
+ }
+ result.push_back(que.front()); // result 记录前k的元素的最大值
+ for (int i = k; i < nums.size(); i++) {
+ que.pop(nums[i - k]); // 滑动窗口移除最前面元素
+ que.push(nums[i]); // 滑动窗口前加入最后面的元素
+ result.push_back(que.front()); // 记录对应的最大值
+ }
+ return result;
+ }
+};Leetcode-基本数据结构
+ +给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−2<sup>31</sup>, 2<sup>31 </sup>− 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
+class Solution {
+public:
+ int reverse(int x) {
+ int rev = 0;
+ while (x != 0) {
+ if (rev < INT_MIN / 10 || rev > INT_MAX / 10) {
+ return 0;
+ }
+ int digit = x % 10;
+ x /= 10;
+ rev = rev * 10 + digit;
+ }
+ return rev;
+ }
+};给定整数数组 nums 和整数 k,请返回数组中第 <strong>k</strong> 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
class Solution {
+public:
+ void quicksort(vector<int>& nums, int start, int end, int k){
+ if(start >= end){
+ return;
+ }
+ int x = nums[start];
+ int left = start;
+ int right = end;
+ while(left < right){
+ while(left < right && nums[right] <= x){
+ right--;
+ }
+ nums[left] = nums[right];
+ while(left < right && nums[left] > x){
+ left++;
+ }
+ nums[right] = nums[left];
+ }
+ nums[left] = x;
+ // start left end
+ // k
+ if(k == left + 1){
+ return;
+ } else if(k < left+1){
+ quicksort(nums, start, left-1,k);
+ } else{
+ quicksort(nums,left+1,end,k);
+ }
+ }
+ int findKthLargest(vector<int>& nums, int k) {
+ quicksort(nums, 0, nums.size()-1,k);
+ return nums[k-1];
+ }
+};给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
class Solution {
+public:
+ void quicksort(vector<pair<int,int> >& nums, int start, int end, int k){
+ if(start >= end){
+ return;
+ }
+ pair<int,int> x = nums[start];
+ int left = start;
+ int right = end;
+ while(left < right){
+ while(left < right && nums[right].second <= x.second){
+ right--;
+ }
+ swap(nums[left],nums[right]);
+ while(left < right && nums[left].second > x.second){
+ left++;
+ }
+ swap(nums[left],nums[right]);
+ }
+ nums[left].first = x.first;
+ nums[left].second = x.second;
+ // start left end;
+ if(k == left){
+ return;
+ } else if(k > left){
+ quicksort(nums, left+1, end,k);
+ } else{
+ quicksort(nums, start, left-1,k);
+ }
+
+ }
+ vector<int> topKFrequent(vector<int>& nums, int k) {
+ vector<pair<int, int> > result;
+ unordered_map<int, int> mp;
+ for(int i=0;i<nums.size();i++){
+ mp[nums[i]]++;
+ }
+ for(auto it=mp.begin();it!= mp.end();it++){
+ result.push_back({it->first, it->second});
+ }
+ quicksort(result, 0, result.size()-1,k);
+ vector<int> res;
+ for(int i=0;i<k;i++){
+ res.push_back(result[i].first);
+ }
+ return res;
+ }
+};给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
class Solution {
+public:
+ int longestValidParentheses(string s) {
+ vector<bool> visit(s.size(),false);
+ stack<pair<char,int> > st;
+ for(int i=0;i<s.size();i++){
+ if(st.empty() || s[i] == '(' || (s[i] == ')' && st.top().first == ')')){
+ st.push({s[i],i});
+ continue;
+ }
+ for(int j=st.top().second;j<=i;j++){
+ visit[j] = true;
+ }
+ st.pop();
+ }
+ int maxlength = 0;
+ int index = 0;
+ while(index < visit.size()){
+ int counttemp = 0;
+ while(index < visit.size() && visit[index]){
+ counttemp += 1;
+ index += 1;
+ }
+ maxlength = max(maxlength, counttemp);
+ while(index < visit.size() && !visit[index]){
+ index += 1;
+ }
+ }
+ return maxlength;
+ }
+};给你两个 二维 整数数组 nums1 和 nums2.
nums1[i] = [id<sub>i</sub>, val<sub>i</sub>] 表示编号为 id<sub>i</sub> 的数字对应的值等于 val<sub>i</sub> 。nums2[i] = [id<sub>i</sub>, val<sub>i</sub>] 表示编号为 id<sub>i</sub> 的数字对应的值等于 val<sub>i</sub> 。每个数组都包含 互不相同 的 id ,并按 id 以 递增 顺序排列。
+请你将两个数组合并为一个按 id 以递增顺序排列的数组,并符合下述条件:
+0 。返回结果数组。返回的数组需要按 id 以递增顺序排列。
+class Solution {
+public:
+ static bool cmp(const vector<int> &a, const vector<int> &b){
+ return a[0] < b[0];
+ }
+ vector<vector<int>> mergeArrays(vector<vector<int>>& nums1, vector<vector<int>>& nums2) {
+ unordered_map<int, int> mp;
+ for(int i=0;i<nums1.size();i++){
+ if(mp.find(nums1[i][0]) != mp.end()){
+ mp[nums1[i][0]] += nums1[i][1];
+ } else{
+ mp[nums1[i][0]] = nums1[i][1];
+ }
+ }
+ for(int i=0;i<nums2.size();i++){
+ if(mp.find(nums2[i][0]) != mp.end()){
+ mp[nums2[i][0]] += nums2[i][1];
+ } else{
+ mp[nums2[i][0]] = nums2[i][1];
+ }
+ }
+ vector<vector<int> > result;
+ for(auto it = mp.begin(); it != mp.end();it++){
+ result.push_back(vector<int> {it->first, it->second});
+ }
+ sort(result.begin(), result.end(), cmp);
+ return result;
+ }
+};整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转 ,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
class Solution {
+public:
+ int search(vector<int>& nums, int target) {
+ int n = nums.size();
+ int left = 0;
+ int right = n-1;
+ while(left <= right){
+ int mid = (right - left) / 2 + left;
+ if(nums[mid] == target){
+ return mid;
+ }
+ if(nums[0] <= nums[mid]){
+ if(nums[0] <= target && target < nums[mid]){
+ right = mid - 1;
+ } else{
+ left = mid + 1;
+ }
+ } else{
+ if(nums[mid] < target && target <= nums[n-1]){
+ left = mid + 1;
+ } else{
+ right = mid - 1;
+ }
+ }
+ }
+ return -1;
+ }
+};给定一个 *n * × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在** 原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。**请不要 **使用另一个矩阵来旋转图像。
+class Solution {
+public:
+ void rotate(vector<vector<int>>& matrix) {
+ int n = matrix.size();
+ for(int i=0;i< n / 2;i++){
+ for(int j=0;j<(n+1) / 2;j++){
+ int temp = matrix[i][j];
+ matrix[i][j] = matrix[n-j-1][i];
+ matrix[n-j-1][i] = matrix[n-i-1][n-j-1];
+ matrix[n-i-1][n-j-1] = matrix[j][n-i-1];
+ matrix[j][n-i-1] = temp;
+ }
+ }
+ }
+};给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,**原地**对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
+class Solution {
+public:
+ void sortColors(vector<int>& nums) {
+ int left = 0;
+ for(int i=0;i<nums.size();i++){
+ if(nums[i] == 0){
+ swap(nums[i], nums[left]);
+ left += 1;
+ }
+ }
+ for(int i=left;i<nums.size();i++){
+ if(nums[i] == 1){
+ swap(nums[i], nums[left]);
+ left += 1;
+ }
+ }
+ }
+};给定一个 <em>m</em> x <em>n</em> 的矩阵,如果一个元素为 0 ** ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。**
class Solution {
+public:
+ void setZeroes(vector<vector<int>>& matrix) {
+ int m = matrix.size();
+ int n = matrix[0].size();
+ vector<bool> rowvector(m,false);
+ vector<bool> colvector(n,false);
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(matrix[i][j] == 0){
+ rowvector[i] = true;
+ colvector[j] = true;
+ }
+ }
+ }
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(rowvector[i] == true || colvector[j] == true){
+ matrix[i][j] = 0;
+ }
+ }
+ }
+ return;
+ }
+};给定一个非负整数 numRows, 生成「杨辉三角」的前 *numRows *行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
+class Solution {
+public:
+ vector<vector<int>> generate(int numRows) {
+ vector<vector<int> > result;
+ vector<int> temp;
+ temp.push_back(1);
+ result.push_back(temp);
+ if(numRows == 1){
+ return result;
+ }
+ for(int i=2;i<=numRows;i++){
+ vector<int> t;
+ t.push_back(1);
+ for(int j=1;j<i-1;j++){
+ t.push_back(result[i-2][j-1] + result[i-2][j]);
+ }
+ t.push_back(1);
+ result.push_back(t);
+ }
+ return result;
+ }
+};已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:* 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
7 次,则可以得到 [0,1,2,4,5,6,7]注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
class Solution {
+public:
+ int findMin(vector<int>& nums) {
+ int n = nums.size();
+ int left = 0;
+ int right = n-1;
+ while(left < right){
+ int mid = (right - left) / 2 + left;
+ if(nums[mid] < nums[right]){
+ right = mid;
+ } else {
+ left = mid + 1;
+ }
+ }
+ return nums[left];
+ }
+};给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
+请你将两个数相加,并以相同形式返回一个表示和的链表。
+你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
+class Solution {
+public:
+ ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
+ int cur = 0;
+ ListNode* head = new ListNode(-1);
+ ListNode* l3 = head;
+ while(l1 != NULL || l2 != NULL){
+ int target;
+ if(l1 == NULL){
+ target = l2->val + cur;
+ l2 = l2->next;
+ } else if(l2 == NULL){
+ target = l1->val + cur;
+ l1 = l1->next;
+ } else{
+ target = l1->val + l2->val + cur;
+ l1 = l1->next;
+ l2 = l2->next;
+ }
+ if (target >= 10){
+ cur = 1;
+ target -= 10;
+ } else{
+ cur = 0;
+ }
+ l3->next = new ListNode(target);
+ l3 = l3->next;
+ }
+ if(cur == 1){
+ l3->next = new ListNode(1);
+ }
+ return head->next;
+ }
+};将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
+class Solution {
+public:
+ ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
+ ListNode* dummy = new ListNode(0);
+ ListNode* head = dummy;
+ while(list1 != NULL && list2 != NULL){
+ if(list1->val < list2->val){
+ dummy->next = list1;
+ dummy = dummy->next;
+ list1 = list1->next;
+ } else{
+ dummy->next = list2;
+ dummy = dummy->next;
+ list2 = list2->next;
+ }
+ }
+ if(list1 != NULL){
+ dummy->next = list1;
+ }
+ if(list2 != NULL){
+ dummy->next = list2;
+ }
+ return head->next;
+ }
+};将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:
P A H N
+A P L S I I G
+Y I R之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:"PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数:
+string convert(string s, int numRows);class Solution {
+public:
+ string convert(string s, int numRows) {
+ if(numRows == 1){
+ return s;
+ }
+ vector<queue<char> > vt(numRows);
+ int nowindex = 0;
+ int reverse = false;
+ for(int i=0;i<s.size();i++){
+ vt[nowindex].push(s[i]);
+ if(nowindex == 0 && reverse == true){
+ reverse = false;
+ nowindex += 1;
+ } else if (nowindex == numRows-1 && reverse == false){
+ reverse = true;
+ nowindex -= 1;
+ } else {
+ if(reverse == false){
+ nowindex += 1;
+ } else{
+ nowindex -= 1;
+ }
+ }
+ }
+ string resultstring = "";
+ for(int i=0;i<vt.size();i++){
+ while(!vt[i].empty()){
+ resultstring += vt[i].front();
+ vt[i].pop();
+ }
+ }
+ return resultstring;
+ }
+};请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
0 。必要时更改符号(从步骤 2 开始)。[−2<sup>31</sup>, 2<sup>31 </sup>− 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −2<sup>31</sup> 的整数应该被固定为 −2<sup>31</sup> ,大于 2<sup>31 </sup>− 1 的整数应该被固定为 2<sup>31 </sup>− 1 。注意:
+' ' 。class Solution {
+public:
+ int myAtoi(string s) {
+ int res = 0;
+ bool havenumsign = false;
+ bool negativesign = false;
+ bool fakebigsign = false;
+ for(int i=0;i<s.size();i++){
+ if(s[i] == ' ' && havenumsign == false){
+ continue;
+ }
+ if(s[i] == '-' && havenumsign == false){
+ negativesign = true;
+ havenumsign = true;
+ continue;
+ }
+ if(s[i] == '+' && havenumsign == false){
+ havenumsign = true;
+ continue;
+ }
+ if(s[i] >= '0' && s[i] <= '9'){
+ havenumsign = true;
+ if(res > (INT_MAX - s[i] + '0') / 10){
+ res = INT_MAX;
+ fakebigsign = true;
+ break;
+ }
+ res = res * 10 - '0' + s[i];
+ continue;
+ }
+ if(havenumsign == true){
+ break;
+ }
+ break;
+ }
+ if (negativesign){
+ if(res == INT_MAX && fakebigsign){
+ return INT_MIN;
+ }
+ return -res;
+ }
+ return res;
+ }
+};罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
+I 1
+V 5
+X 10
+L 50
+C 100
+D 500
+M 1000例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。给你一个整数,将其转为罗马数字。
+class Solution
+{
+public:
+ string intToRoman(int num)
+ {
+ pair<int, string> valueSymbols[] = {
+ {1000, "M"},
+ {900, "CM"},
+ {500, "D"},
+ {400, "CD"},
+ {100, "C"},
+ {90, "XC"},
+ {50, "L"},
+ {40, "XL"},
+ {10, "X"},
+ {9, "IX"},
+ {5, "V"},
+ {4, "IV"},
+ {1, "I"},
+ };
+ string roman;
+ for (auto &[value, symbol] : valueSymbols)
+ {
+ while (num >= value)
+ {
+ num -= value;
+ roman += symbol;
+ }
+ if (num == 0)
+ {
+ break;
+ }
+ }
+ return roman;
+ }
+};Leetcode-双指针法
+ +给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
class Solution {
+public:
+ int lengthOfLongestSubstring(string s) {
+ int result = 0;
+ unordered_set<char> st;
+ int left = 0;
+ for(int right=0; right<s.size(); right++){
+ while(st.find(s[right]) != st.end()){
+ st.erase(s[left]);
+ left++;
+ }
+ st.insert(s[right]);
+ result = max(result, right - left + 1);
+ }
+ return result;
+ }
+};给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
class Solution {
+public:
+ double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
+ int m = nums1.size();
+ int n = nums2.size();
+ bool next;
+ int sign = (m + n) / 2;
+ if((m + n) % 2 == 1){
+ next = false;
+ } else{
+ sign -= 1;
+ next = true;
+ }
+ int res1 = 0;
+ int res2 = 0;
+ int globalindex = 0;
+ int nums1index = 0;
+ int nums2index = 0;
+ while(globalindex <= sign){
+ if(nums1index < m && nums2index < n){
+ if(nums1[nums1index] < nums2[nums2index]){
+ res1 = nums1[nums1index];
+ nums1index += 1;
+ } else{
+ res1 = nums2[nums2index];
+ nums2index += 1;
+ }
+ } else if (nums1index < m){
+ res1 = nums1[nums1index];
+ nums1index += 1;
+ } else {
+ res1 = nums2[nums2index];
+ nums2index += 1;
+ }
+ globalindex += 1;
+ }
+ if(next == false){
+ return res1;
+ }
+ if(nums1index < m && nums2index < n){
+ if(nums1[nums1index] < nums2[nums2index]){
+ res2 = nums1[nums1index];
+ } else{
+ res2 = nums2[nums2index];
+ }
+ } else if (nums1index < m){
+ res2 = nums1[nums1index];
+ } else {
+ res2 = nums2[nums2index];
+ }
+ return ((double)res1 + (double)res2) / 2.0;
+ }
+};给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
+class Solution {
+public:
+ string longestPalindrome(string s) {
+ vector<int> result = {0,0};
+ for(int i=0;i<s.size()-1;i++){
+ int left = i;
+ int right = i;
+ while(left >= 0 && right < s.size()){
+ if(s[left] == s[right]){
+ if(result[1] - result[0] < right - left){
+ result[1] = right;
+ result[0] = left;
+ }
+ right += 1;
+ left -= 1;
+ } else{
+ break;
+ }
+ }
+ left = i;
+ right = i+1;
+ while(left >= 0 && right < s.size()){
+ if(s[left] == s[right]){
+ if(result[1] - result[0] < right - left){
+ result[1] = right;
+ result[0] = left;
+ }
+ right += 1;
+ left -= 1;
+ } else{
+ break;
+ }
+ }
+ }
+ return s.substr(result[0], result[1]-result[0] + 1);
+ }
+};给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
+121 是回文,而 123 不是。class Solution {
+public:
+ bool isPalindrome(int x) {
+ string s = to_string(x);
+ int left = 0;
+ int right = s.size() - 1;
+ while(left < right){
+ if(s[left] != s[right]){
+ return false;
+ }
+ left += 1;
+ right -= 1;
+ }
+ return true;
+ }
+};给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
+说明: 你不能倾斜容器。
+class Solution {
+public:
+ int maxArea(vector<int>& height) {
+ int maxarea = 0;
+ int left = 0;
+ int right = height.size() - 1;
+ while(left < right) {
+ if(height[left] < height[right]){
+ maxarea = max(maxarea, (right - left) * height[left]);
+ left += 1;
+ } else{
+ maxarea = max(maxarea, (right - left) * height[right]);
+ right -= 1;
+ }
+ }
+ return maxarea;
+ }
+};给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意: 最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
class Solution {
+public:
+ void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
+ int index = m + n - 1;
+ m -= 1;
+ n -= 1;
+ while(index >= 0){
+ if(m < 0){
+ nums1[index] = nums2[n];
+ n--;
+ } else if (n < 0){
+ nums1[index] = nums1[m];
+ m--;
+ } else{
+ if(nums1[m] > nums2[n]){
+ nums1[index] = nums1[m];
+ m--;
+ } else{
+ nums1[index] = nums2[n];
+ n--;
+ }
+ }
+ index--;
+ }
+ return;
+ }
+};给你一个链表数组,每个链表都已经按升序排列。
+请你将所有链表合并到一个升序链表中,返回合并后的链表。
+class Solution {
+public:
+ ListNode* merge(vector<ListNode*>& lists, int start, int end){
+ if(start > end){
+ return NULL;
+ }
+ if(start == end){
+ return lists[start];
+ }
+ int mid = (end - start) / 2 + start;
+ ListNode* first = merge(lists, start, mid);
+ ListNode* second = merge(lists, mid + 1, end);
+ if(first == NULL){
+ return second;
+ }
+ if(second == NULL){
+ return first;
+ }
+ ListNode* head = new ListNode(0);
+ ListNode* p = head;
+ while(first != NULL && second != NULL){
+ if(first->val < second->val){
+ p->next = first;
+ first = first->next;
+ } else{
+ p->next = second;
+ second = second->next;
+ }
+ p = p->next;
+ }
+ if(first != NULL){
+ p->next = first;
+ } else{
+ p->next = second;
+ }
+ return head->next;
+ }
+ ListNode* mergeKLists(vector<ListNode*>& lists) {
+ return merge(lists, 0, lists.size()-1);
+ }
+};Leetcode-回溯算法
+ +数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的括号组合。
class Solution {
+public:
+ vector<string> result;
+ void backtracking(vector<string> temp, int n, int nowleft, int nowright){
+ if(temp.size() == n * 2){
+ string res = "";
+ for(int i=0;i<temp.size();i++){
+ res += temp[i];
+ }
+ result.push_back(res);
+ return;
+ }
+ if (nowleft < n){
+ temp.push_back("(");
+ backtracking(temp,n,nowleft+1,nowright);
+ temp.pop_back();
+ }
+ if(nowright < n && nowright < nowleft){
+ temp.push_back(")");
+ backtracking(temp,n,nowleft,nowright+1);
+ temp.pop_back();
+ }
+ }
+ vector<string> generateParenthesis(int n) {
+ vector<string> temp;
+ backtracking(temp,n,0,0);
+ return result;
+ }
+};整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
+arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
+arr = [1,2,3] 的下一个排列是 [1,3,2] 。arr = [2,3,1] 的下一个排列是 [3,1,2] 。arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。给你一个整数数组 nums ,找出 nums 的下一个排列。
必须原地修改,只允许使用额外常数空间。
+class Solution {
+public:
+ void nextPermutation(vector<int>& nums) {
+ int n = nums.size();
+ int index = n-1;
+ for(;index>=1;index--){
+ if(nums[index] > nums[index-1]){
+ break;
+ }
+ }
+ if(index != 0){
+ index -= 1;
+ for(int i=n-1;i>=0;i--){
+ if(nums[i] > nums[index]){
+ swap(nums[index], nums[i]);
+ reverse(nums.begin()+index+1,nums.end());
+ return;
+ }
+ }
+ }
+ else{
+ reverse(nums.begin(), nums.end());
+ }
+ }
+};给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
+class Solution {
+public:
+ bool result = false;
+ void DFS(int i, int j, int m, int n,int now, vector<vector<char>>& board,vector<vector<bool> > &visited, string word){
+ if(i < 0 || j < 0 || i >= m || j >= n || visited[i][j] == true || board[i][j] != word[now]){
+ return;
+ }
+ if(now == word.size() - 1){
+ result = true;
+ return;
+ }
+ visited[i][j] = true;
+ DFS(i+1,j,m,n,now+1,board,visited, word);
+ DFS(i-1,j,m,n,now+1,board,visited, word);
+ DFS(i,j+1,m,n,now+1,board,visited, word);
+ DFS(i,j-1,m,n,now+1,board,visited, word);
+ visited[i][j] = false;
+ }
+ bool exist(vector<vector<char>>& board, string word) {
+ int m = board.size();
+ int n = board[0].size();
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ vector<vector<bool> > visited(m, vector<bool>(n, false));
+ DFS(i,j,m,n,0,board,visited, word);
+ if(result){
+ return result;
+ }
+ }
+ }
+ return result;
+ }
+};Leetcode-二叉树
+ +给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
class Solution {
+public:
+ vector<int> result;
+ void inorder(TreeNode* root){
+ if(root == NULL){
+ return;
+ }
+ inorder(root->left);
+ result.push_back(root->val);
+ inorder(root->right);
+ }
+ vector<int> inorderTraversal(TreeNode* root) {
+ inorder(root);
+ return result;
+ }
+};给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
class Solution {
+public:
+ vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
+ vector<vector<int> > result;
+ if(root == NULL){
+ return result;
+ }
+ queue<TreeNode*> q;
+ q.push(root);
+ int sign = 0;
+ while(!q.empty()){
+ int t = q.size();
+ vector<int> temp;
+ for(int i=0;i<t;i++){
+ TreeNode* x = q.front();
+ q.pop();
+ temp.push_back(x->val);
+ if(x->left != NULL){
+ q.push(x->left);
+ }
+ if(x->right != NULL){
+ q.push(x->right);
+ }
+ }
+ if(sign == 1){
+ reverse(temp.begin(), temp.end());
+ }
+ result.push_back(temp);
+ sign = 1 - sign;
+ }
+ return result;
+ }
+};HR面试准备
+您好,我是张兆,就读于中国科学院计算技术研究所,是预计25年夏季毕业的硕士研究生。我本科来自于中南大学计算机学院,是通过推荐免试的方式进入到中科院计算所就读研究生的。我在本科期间获得了国家奖学金和省级优秀毕业生的荣誉称号,同时拿过一些程序设计竞赛、数学建模和英语竞赛的奖项。在研究生期间连续获得了两年的中国科学院大学三好学生。
+在科研经历方面,我一共发表过5篇论文,涉及信息检索、大模型、可视化、数学建模等多个领域。在实习经历方面,我先后尝试过四份实习工作,分别是在商汤科技、MetaApp、微软STCA和蚂蚁集团,主要进行算法相关的研究工程等相关工作,涉及到传统算法、后端开发、自然语言处理、推荐等多种技术领域。除此之外我在其他业余时间参加了一些NLP、大模型或搜索等相关的算法竞赛,参加的所有比赛都拿到了比较好的名次。
+我认为我拥有较强的学习能力,善于学习新事物、适应新环境。对待工作比较踏实认真,团队合作能力强。我的专业知识和实习工作经验,和这个岗位要求也比较相符,希望能够得到一个施展才华的空间。
+我的自我介绍就到这里,谢谢。
+首先听取领导的指示和要求,然后就有关情况进行了解和熟悉,接下来制定一份近期的工作计划并报领导批准,最后根据计划开展工作。
+通过之前的了解,我知道了你们要招聘的这个岗位,主要负责xx方面的内容,需要xx方面的能力(贴合岗位JD),我是xx专业的,有理论知识背景,之前在xx公司作为实习生在xx岗位主要负责xx方面的内容,取得了xx成果,解决了xx问题,跟贵公司要招聘的岗位相似度比较高,然后本人比较擅长xx(个人能力内容),我有信心可以胜任这个岗位。最后,我还拥有xx特色或某方面的经验(个人比较有差异性的优势),应该会比一般的应聘者更适合这个岗位。
+问题八:对这项工作,你有哪些可预见的困难?
+【思路】:①不宜直接说出具体的困难,否则可能令对方怀疑应聘者不行。②可以尝试迂回战术,说出应聘者对困难所持有的态度。
+【参考答案】:工作中出现一些困难是正常的,也是难免的,但是只要有坚韧不拔的毅力、良好的合作精神以及事前周密而充分的准备,任何困难都是可以克服的。
我之前在公司时,领导给我安排了一个从未接手过的任务,写一个品牌宣传文案,我用了一晚上的时间拆解其他人的宣传文案,然后按领导要求的写了出来,当投放出去的时候,获得了XX的效果,通过这次面对困难的经历,我除了收获成绩以外,还收获了如何写品牌宣传文案的底层逻辑。
+你觉得自己在面试中有什么表现好的地方,有什么表现差的地方(这个问题要注意回答,这个问题大概率表明你的评级有弹性空间,后续可能会用来argue薪资)
+你更看重工作那个方面(薪资,发展空间,工作氛围灯)
+(这个问题中,主要要说清楚base地等硬性需求,防止被改base,其他自由发挥)
要表明自己是非常喜欢这份工作,才来公司面试的,如果在入职后是公司这边发现这份工作不适合自己,那希望公司要提出来,自己会去自查后提升能力,或端正态度来好这份工作,如果是自己发现不适合,自己也会自查,找到自己觉得不合适的原因,进行自我完善,我相信我的能力这边匹配JD岗位的话我是不会觉得不合适的。
+你为什么选择我们公司?
+【思路】:①面试官试图从中了解你求职的动机、愿望以及对此项工作的态度。②建议从行业、企业和岗位这三个角度来回答
+【参考答案】:我十分看好贵公司所在的行业,我认为贵公司十分重视人才,而且这项工作很适合我,相信自己一定能做好。
面试官通过这个问题主要想考察你是否对公司和岗位感兴趣,有了解,把你招进来是否具备稳定性,主要突出公司知名度+工作内容+匹配度。
+首先,贵公司在行业中有着xxX的成绩,同时我了解贵公司在XX方向近期有拓展的规划,这部分也是我非常感兴趣的地方。
+其次,该岗位和我的职业规划比较匹配,我理解后续我的工作内容是做XX方向的工作,这部分内容是我后续想尝试的一个方向。
+最后,我认为我目前的能力和该岗位的招聘标准比较契合,之前我做过XXX的工作,相关的工作经验能够在贵司复用,同时也能帮助自己在这一方向完成进一步的能力深造。
+所以我想加入贵公司。
·想测试你来公司面试前有没有做过调查研究,是不是海投;可以从岗位性质或者公司的角度回答。
+【回答公式】
+·万с真能鮒譞蕹餓胪坰卦疫由:发展平台、管理、产品实力、业界口碑
+【机智回答】
+据我了解,贵公司很注重企业文化,特别注重员工个人能力的培养。我想,在.一个学习氛围良好的企业工作,自身将会受到很好的影响,也能做到为公司提供最大化的价值服务。另外,公司岗位性质也是我人比较喜欢的,人们都说兴趣是最好的老师,我想这更有利于自身能力的发挥。
问题六:我我们为什么要录用你?
+【思路】:招聘单位一般会录用这样的招聘者:基本符合条件、对这份工作感兴趣、有足够信心。
+【参考答案】:我符合贵公司的招聘条件,凭我目前掌握的技能、高度的责任感和良好的适应能力以及学习能力,完全能胜任这份工作。我十分希望能为贵公司服务,如果贵公司给我这个机会,我一定能成为贵公司的栋娆贑壞婚梁!
问题十三:你是应届毕业生,缺乏经验,如何胜任这项工作?
+思路】:①如果招聘单位对应届生提出这个问题,说明招聘单位并不在乎“经验”,关键看应聘者怎样回答,②对这个问题的回答最好体现出应聘者的诚恳、机智果敢及敬业。
+【参考答案】:作为应届毕业生,在工作经验方面的确会有所欠缺,因此读书期间我一直利用各种机会在这个行业做兼职。发现实际工作远比书本知识丰富、复杂。但我有较强的责任心、适应能力和学习能力,请贵公司放心,!学校所学及兼职的工作经验使我一定能胜任这个职位。
在来应聘这个岗位之前,我通过XX的方式对行业和岗位进行了一定的了解,同时针对这个岗位,我发现之前的工作/实习经验也有一些可迁移的地方,且我自己是一个具备很强学习能力和思考能力的人,相信我能够在日后快速上手并融入工作,为公司创造价值。
+我认为我的核心竞争力是有0-1搭建账号的丰富经验。我擅长以结果为导向的数据分析、内容选题,个人账号在1个月发布x篇笔记,其中爆款x篇,共获赞万,涨粉1K+个,通过不断参考竞品、优化封面和内容、完善用户画像,提升转化率xx%。根据岗位JD介绍,我深信我能很好的将这些能力迁移到工作中。
+你会如何处理工作中的压力?(压力测试题)6、
+【回答思路】
+这个问题主要是想考察你在面对工作中压力的抗压能力,时决断能力、应变能力怎么样,所以阐述实例时一定要注意要有正向的证明。【机智回答】
+我相信压力是工作中的一部分,并且难以完全避免。关键在于找到压力的来源,并学会如何将其转化为动力。
+个人来说,我处理压力的方式是对压力来源进行详细的拆解和分析。通过对工作进行总结和复盘,我可以更清楚地了解自己的优势和劣势,并利用碎片化的时间来提升自己的短板,从而将压力转变为动力。当我面临一时无法解决源头问题的情况时,我不会过度纠结或困扰自己。相反,我会转移注意力,放松心情,并思结或困扰自己。相反,我会转移注意力,放松心情,并寻求他人的倾诉以缓解压力。与他人交流可以帮助我获得新的思路和解决问题的方向,同时也能得到情感上的支持。总的来说,我认为将压力转化为动力的关键在于积极应对并努力解决问题,在面对无解或困境时保持冷静,并适当转移注意力和寻求他人的帮助。这样的处理方式有助于提升个人的应变能力和团队协作的效果。非常感谢您给我这次机会分享我的经验。
在上一段实习中,我对于自己负责的这个部分已经非常熟悉,同时对于整个组接触到的整个的算法工程的流程也有了一定的认知和了解,Leader对我的能力也有一定的认可,如果继续实习下去可能对于我自身来说就不会有特别大的进步或者学习更大量的东西了,因此在完成手头工作后就离开了上个实习单位。
+问题十七:你最近3~5年的职业规划是什
+么?
+【思路】:①考察应聘者职业规划和他们公司的发展是否匹配。②考察应聘者对未来是否有清晰的规划。【参考答案】:第一阶段:,熟悉业务,提高自己的专业和技能水平,让自己胜任这个岗位。第二阶段:稳定提升,除了做好本职工作,持续学习行业知识,同时对公司各部门有全面的了解。第三阶段:不断学习、积极探索。横向拓宽自己的业务能力,寻求更多的发展机会,为公司带来更大的价值。
(回答公式】
+近期规划(1-3年),适应位+提升岗位技能+积累工作经验远期规划(三到五年),在岗位上独当一面+在行业内立足【机智回答一】
+未来1年,我会尽快适应新环境的工作节奏,熟悉相关业务和流程,并不断提高自己专业上和技能上的水平。
+未来3年,我希望跟随公司的发展,在自己的业务能力和管理水平上再上一个台阶,比如带领一个小团队共同做好项目,用自己的影响力帮助他人。
+未来5年,我会根据环境的变化,工作内容的变化,以及我自身能力的变化,不断进调整。
+【机智回答二)
+未来1年,我会尽快适应新环境的工作节奏,熟悉相关业务和流程,并不断提高自己专业上和技能上的水平。
+未来3年,我希望跟随公司的发展,在自己的业务能力和管理水平上再上一个台阶,比如带领一个小团队共同做好项目,用自己的影响力帮助他人。
+未来5年,我会根据环境的变化,工作内容的变化,以及我自身能力的变化,不断进调整
应届生:
+。我是xx届刚毕业的应届生,目前需要解决的问题就是工作经验不足,面对这个问题,我首先要做的就是尽快了解行业和岗位的发展趋势,尽快熟悉和上手自己的工作,努力提升自己的xxx能力和xxx能力(你求职的岗位所需的能力),在工作中多总结复盘,对于不懂的地方和不熟悉的地方及时反馈寻求帮助,拓宽自己的能力范围和视野。在熟悉自己的工作之后,我不会局限于自己眼前的小事,会针对性提升工作中需要的xx能力,形成自己的方法论以更高效地完成自己的工作,为公司创造更多的价值。在过后的2-3年中,我希望能够在xx岗位上独当一面(你求职的岗位),独立负责xxx项日。
+。职场人:
+首先我要将我的职业规划分为短期和长期两个方面:
+短期规划:刚进入公司首先要做的是熟悉公司的制度和xx岗位(你求职的岗位)的工作流程,尽快融入到公司的业务之中,因为我之前有过xx的工作经验,学到了xx技能和xx技能(你的岗位所需技能),在接下来的工作中我也会精进这些技能,不断提升自己的业务能力。
+长期规划:在接下来的1-2年内,我会不断深耕行业的专业领域,(提升自己的专业能力和岗位所需的能力)未来三年,行业也会不断变化,我会及时关注行业的发展趋势和市场的发展变化,我会根据行业的大环境不断积累岗位知识提升自身的专业水平,能够带领团队完整完成一个项目,为公司承担更多责任。
问题十四:你怎么看待加班?
+【思路】:实际上很多公司问这个问题,并不证明一定要加班,只是想测试你是否愿意为公司奉献。
+【参考答案】:如果是工作需要我会义不容辞加班,我现在单身,没有任何家庭负担,可以全身心投入工作。但同时我也会提高工作效率,减少不必要的加班。
高情商回答话术:
+。注意:回答要给自己留有余地,不要完全拒绝也不要太快接受(回答太积极可能会给自己留下大坑哦)
+(明确自己的态度,拒绝无效加班)首先,有些项目会出现紧急情况需要加班,这点我是可以接受的,有些情况确实是不可抗因素,这种时候需要的话我会积极配合。
+(导致加班的原因+解决方室),其次,如果出现了需要加班的情况,我会分析加班的原因,如果是因为刚入职还没熟悉导致加班,我会及时请教前辈和领导,在空闲时间弥补自己的不足,提高工作效率,做到按时按量完成工作。但是我不会特意为了“表现自己”而加班,我认为高效率完成工作是对自己和公司的负责,高效率的产出才不会浪费时间。
+(打探公司的真实情况,如果“卷加班”是企业文化就赶紧跑路吧!!)既然说到了加班的问题,我想了解一下我这个岗位的架构组成和工作分配,加班频率高吗?一般是什么情况需要加班呢?
问题十五:你为什么转行?
+【思路】:①从行业-转行动机(离开老行业和选择新行业的原因)。②从岗位-新旧岗位(可以从个人兴趣&能力&新旧岗位匹配度等方向说明选择新岗位的原因)。③从规划-未来1-3年的职业规划【参考答案】:行业:政策影响老行业-新行业的优势平时对这个行业关注比较多;岗位:对应聘岗位的认识,以及选择这个岗位的原因。;规划:从短期和长期来说,最后一般都是称为某领域专家or走管理路线。
在过去的工作中,我是做XX行业的XX岗位,但是在工作过程中我发现,这个行业的增长到达了瓶颈,同时我在岗的方向也做到了一定的稳定程度,缺少一些可以下钻的方向,后来接触到了XX行业,发现这个行业具备一定的增长空间,同时在学习了解的过程中,我也发现了我目前岗位和该岗位在工作技能上的可迁移性,认为自己的一些历史经验能够在这个行业做到差异化的应用,同时还能收获到新的思考,所以我选择转澛浰羰両寑线殄。
+我认为自己有很强的责任感和高要求的工作态度,这也得到了前任领导的认可。在工作中,我总是尽职尽责,不轻易放弃,努力追求卓越的工作表现。这一点也得到了团队成员的认可和肯定。同时,我在为人处世方面也被朋友和同事认为很随和。整体而言,我的人际关系良好,能够和不同的人群建立良好的合作关系。
+问题三:谈谈你的优点
+【思路】:①这是面试常见问题,看似简单反而很容易陷入自嗨,最后反而导致HR不满意,这里需要注意的是所回答的点一定要和你应聘的岗位相匹配,一定一定要相匹配!不然这个不匹配的优点在HR看来就不是优点。②回答一定要符合STAR法则。③一定要有例子!!!不然怎么证明这的确是你的优点。
+【参考答案】: 我认为我最大的优点是执行能力强,具体来说就是面对一个任务,只要我确定了目标和实现路径,会立马执行,然后在过程中进行优化迭代。比如在XX时候,领导下发了一个紧急重要并且我完全没有做过的项目,我在做了任务的分析和背景调查后,当天就做出来完成这个目标的To-do list,第二天就马上开始逐一执行,及时根据进度、反馈调整,最后成功在任务前一天提前完成了任务,所以执行力强是我认为自己的优点。同时我觉得对于我应聘的岗位,这个优点可以让我在工作中及时验证用户反馈,帮助团队目标的实现。
回答思路:
+这里主要考察面试者对工作技能的理解程度,说2点即可,最好是展示这些优点是怎么体现出来的。
+参考模板:
+我认为我的优点是执行能力强和多任务并行能力强关于执行能力,对于工作中有明确目标和路径的事情,我都能很快推进项目的落地,比如XX。
+关于多任务并行能力,我在工作中经常承接多个项目,不同的项目我都能按照优先级合理推进项目的落地,比如XX。
问题四:谈谈你的缺点
+【思路】:①不宜说自己没缺点。②不宜把那些明显的优点说成缺点。③不宜说出严重影响所应聘工作的缺点。④不宜说出令人不放心、不舒服的缺点。⑤可以说出一些对于说应聘工作“无关紧要”的缺点,甚至是一些表面看起来是去缺点,从工作的角度看却是优点的缺点。
+【参考答案】:我的缺点在于不是这个专业or行业的,同时工作经验比较少,所具备的理论知识和实践能力有限。但我已经开始在网上学习这方面的知识,包括网上看视频学习,看别人的知识点总结以及看有关xx的书籍。我相信我很快能够具备这方面的知识,并且能很快上手工作,为公司创造更大的效益。
.你觉得自己最大的缺点是什么?
+回答思路:
+这里不要说与面试岗位冲突的缺点,要尽量挑选与岗位弱相关但是可以改进和优化的缺点进行回复,参考模板:
+我认为自己最大的缺点是执行过程中有些完美主义。在推进项目的过程中,我会关注很多细节,在细节方向上不断进行修改,但实际有些事情是已经可以先推进落地来满足业务需求了。所以之后的工作中,我希望自己能够抓住项目核心快速迭代,保证MVP版本优先上线,提升推进的效率,
优点.
+做事有条理:我做事很有计划性,每天都会按要做的事优先级来列个清单,我会把每件事整理得非常有条理。并且我也有很明确的职业规划,大学期间我学习了xxx技能,在学校参加过xxx活动,学到了xxx能力(阐述和岗位相关的技能/能力)
事整理得非常有条理。并且我也有很明确的职业规划,大学期间我学习了xxx技能,在学校参加过xxx活动,学到了xxx能力(阐述和岗位相关的技能/能力)
+时间观念很强:我是一个凡事都要做好计划的人,并且也会根据时间更合理规划。在面试之前我会做好面试准备和路线规划,同时在平时工作中,我也会时刻做好规划,防止不必要的情况发生。
+责任心强:我是一个责任感很强的人。一旦确定了目标,我会用最大的努力去完成,我认为做事情就一定要有始有终,在今后对待工作我也是一样的态度,半途而废这个词不存在在我的字典里。
+沟通能力强:我是个善于沟通的人,在工作的各种场合都会很好的听他人的想法,同时也乐于表达自己的观点,在学校参加过辩论比赛和演讲比赛,在工作中敢于表达自己也是对工作负责的表现。
+缺点
+性格急躁:如果在工作上没能及时的达到转化会焦虑,有一点结果导向。但是这种情绪往往会推进我优化工作流程,直到预期的结果出现。我也在不断学习调整,能够将这种心态更多的转化为动力。
+不懂得拒绝:(比如别人拜托你做不属于你的活)但现在我会努力改进工作处理的优先级顺序,在时间宽松的情况下再去帮忙,这种情况已经很少了。
+不够自信:我性格比较内向,缺乏自信,在一些大的场合会害怕不敢发言,为了解决这个情况,我看了很多的演讲视频,平时会经常锻炼自己的表达能力,也会找身边的朋友同事练习,在不断的尝试之后现在也比较自信了。
问题十八:谈谈你的一次成功经历【思路】:①举一个你最后把握的例子,把来龙去脉说清楚,而不要说了很多却没有重点。②切记夸张,把别人的功劳说成自己的,很多主管为确保要用的人是最合适的,会打电话向你前任主管征询对你的看法及意见。【参考答案】:通过努力,每完成一个工作目标,都是一种成就感。例如,在短短的5天内,完成资质增项并受到了老板的夸奖…
+问题五:谈谈你的一次失败经历
+【思路】:①不宜说自己没有失败的经历②不宜把那些明显的成功说成是失败。③所谈经历的结果应是失败的。④宜说明失败之前自己曾信心百倍、尽心尽力。⑤说明仅仅是外在客观原因导致失败。⑥失败后自己很快振作起来,以更加饱满的热情面对以后的工作。
+【参考答案】:曾经接触过一个客户,原本就有耳闻他们以挑剔出名,所以事前准备功夫做得十分充足,也投入了相当多的时间与精力,最后客户虽然并没有照单全收,但是接受的程度已经出乎我们意料之外了。原以为从此可以合作愉快,却得知客户最后因为预算关系选择了另外一家代理商,之前的努力因而付诸流水。尽管如此,我还是从这次的经验学到很多,如对该产业的了解,整个team的默契也更好了
我平时喜欢一些球类运动,经常约朋友一起打乒乓球和羽毛球等,如果是自己休闲的时候喜欢听一些音乐。
+我认为我是一个积极进取、坚持不懈、具有团队合作精神的人。在上学期间,我始终保持着对学习的热情和好奇心,不断提升自己的专业技能和综合素质。在项目、参加竞赛或者是实习工作中,我面临过很多挑战和困难,不过从来没有放弃过,也因此取得了很多的成绩。同时,我也注重与他人的交流和合作,相信通过共同努力可以实现更好的成果。
+我的家庭比较温馨和睦,我的父亲是初中数学教师,我的母亲是三甲医院的护士,工作都比较稳定,也都准备步入退休生活了。我的父母从小就很注重对我的教育,我的父母同时也是很开明的家长,我们家的沟通是平等友好的。在选择的就业方向与岗位这块,我父母也支持我的自由选择。在未来的职业生涯中,我也将努力工作,回报我的父母,为家庭做出更多的贡献。
+我一般会设立目标,首先是把整个项目的目标拆解成可执行的小目标,然后设置好小目标的完成时间,设置完成后,我会召集团队成员,让大家聊聊对这个项目的想法,之后,整合大家的想法,现场一起把项目再拆一遍,然后让大家领取自己擅长的部分去做,和大家商量一个大概的截止时间。在做的过程中,我会和每一个执行的同事及时沟通,了解情况,完成一个小阶段,我也会组织会议,一起讨论下一步怎么更好的执行,以此流程进行,直到项目完成为止。
+作为一个刚步入社会的新人,熟悉环境、适应环境应该是我的首要任务,我就不对工作环境提出更多的要求了,我只希望能够发挥自己的能力、专长,快速熟悉并独立完成工作。希望上级在我的工作中能多指导、多帮助,这样我也能立即纠正自己的错误,更快地成长和进步,为公司的发展贡献更多的力量。
+对于非原则性问题,就类似于项目研究等方向技术路径之类的,我会服从,并在执行过程中进行完善。然后,在执行上级的要求的同时,我也会找适当的机会给领导提出我的建议,交换一下看法。如果是涉及原则性问题或者涉及公司利益的重大问题,我希望能向更高层领导反映并交流看法。
+Leetcode-动态规划
+ +给定一个包含非负整数的 <em>m</em> x <em>n</em> 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明: 每次只能向下或者向右移动一步。
+class Solution {
+public:
+ int minPathSum(vector<vector<int>>& grid) {
+ int m = grid.size();
+ int n = grid[0].size();
+ vector<vector<int> > dp(m, vector<int>(n,0));
+ dp[0][0] = grid[0][0];
+ for(int i=1;i<m;i++){
+ dp[i][0] = dp[i-1][0] + grid[i][0];
+ }
+ for(int j=1;j<n;j++){
+ dp[0][j] = dp[0][j-1] + grid[0][j];
+ }
+ for(int i=1;i<m;i++){
+ for(int j=1;j<n;j++){
+ dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
+ }
+ }
+ return dp[m-1][n-1];
+ }
+};搜推面试题目准备
+ +FM:作为逻辑回归模型的改进版,拟解决在稀疏数据的场景下模型参数难以训练的问题。并且考虑了特征的二阶交叉,弥补了逻辑回归表达能力差的缺陷。
+优点:
+缺点:
+FFM 是 FM 的改进版,作者引入 field 的概念,把相同性质的特征 (经过 onehot 编码的类别特征) 归于同一个 field,同一特征与属于不同域的特征作交互时,具有不同的隐向量表示。
+FFM 将隐向量进一步细分,每个特征具有多个隐向量 (等于 field 的数目)。模型参数量为 1+n+n(F−1)k , F为 field 数。公式不可化简,复杂度为n^2k ,随着特征数n 平方级增长。
+优点:
+缺点:
+Wide&Deep:一个线性模型与深度模型结合的产物
+
左边(Wide Models)为拆解出来线性模型,右边(Deep Models)为深度模型。未激活的线性模型输出与深度模型输出相加,再进行激活即得到总体模型的输出。
+Wide 部分:Dense Features + Sparse Features(onehot 处理)+ 特征组合
+Deep 部分:Dense Embeddings (Sparse Features 进行 onehot + embedding 处理)
+优点:
+缺点:
+DCN 是基于 Wide&Deep 的改进版,它把 wide 侧的 LR 换成了 cross layer,可显式的构造有限阶特征组合,并且具有较低的复杂度。
+
优点:
+缺点:
+xDeepFM 是 Wide & Deep 的改进版,在此基础上添加了 CIN 层显式的构造有限阶特征组合。
+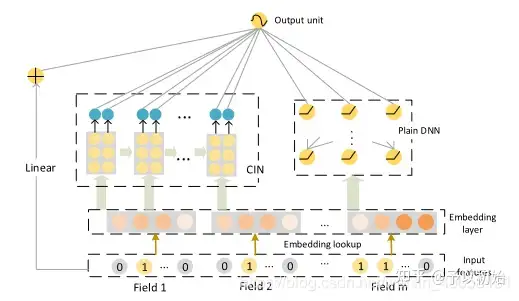
上图为 xDeepFM 的总体结构,有三个分支:Linear(稀疏的01向量作为输入)、DNN(经过embedding的稠密向量作为输入)、CIN(压缩感知层)。
+xDeepFM 如果去掉 CIN 分支,就等同于 Wide & Deep。
+优点:
+使用 vector-wise 的方式,通过特征的元素积来进行特征交互,将一个特征域的元素整体考虑,比 bit-wise 方式更 make sence 一些;
+缺点:
+CIN 层的复杂度通常比较大,它并不具有像 DCN 的 cross layer 那样线性复杂度,它的复杂度通常是平方级的,因为需要计算两个特征矩阵中特征的两两交互,这就给模型上线带来压力。
+FNN 采用的是串行拼接的结合方式,将 DNN 接在 FM 层后方,以减轻全连接层构造隐式特征的工作。
+FNN 并不是端到端的训练方式,而是两阶段的训练方式。阶段一训练一个 FM,阶段二训练一个带嵌入层的 DNN。
+阶段一: 先使用带标签的训练集有监督的训练 FM 模型,训练完成后,会得到每个特征对应的隐向量。若输入特征维度为 n,隐向量维度为 k,则隐向量矩阵 W 的形状就为 [n, k]。
+阶段二: 然后用隐向量矩阵 W 初始化 DNN 的嵌入层,然后再有监督训练 DNN 即可。DNN 的输入包含了 FM 学到的先验知识,可减轻 DNN 的学习压力。
+优点:
+缺点:
+PNN 通过引入特征交互层 Product Layer,显式的对特征进行交互,以提升模型的表达能力。Product Layer层为特征交互层,由 z 和 p 两部分组成,其中 z 为上层的输出结果,p 为上层输出的特征交互结果,低维与高维特征的直接拼接。
+优点:
+缺点:
+DIN:
+Base 模型的做法是将用户点击的商品序列,简单的进行 SUM Pooling,然后将聚合得到的 embedding 向量,作为用户的兴趣表示。
+这种做法的缺陷也很明显,简单的累加无法突出某些商品的重要性。对于与候选商品具有强关联性的 item,应该给予更大的权重,让其在提取用户兴趣时发挥更大的作用。
+DIN 便是采用这种方式,引入 Activation Unit 为每个商品计算一个重要性权重,再 Pooling 得到兴趣表示。模型结构如下:
+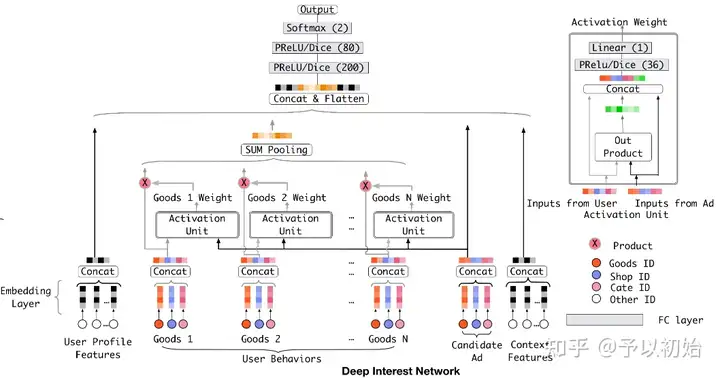
主要关注 Activation Unit 内的权重计算方式,该单元的输入为:用户点击的商品(Inputs from User)、候选商品(Inputs from Ad)。
+优点:
+缺点:
+DIEN:针对行为的时间顺序进行建模,挖掘用户的兴趣及兴趣变化趋势。
+优点:
+缺点:
+DSIN:将行为序列划分为多个 Session,然后针对每个 Session 去挖掘用户的兴趣以及兴趣变化趋势。
+优点:
+缺点:
+LLM强化学习相关学习资料
+ +图解大模型RLHF系列之:人人都能看懂的PPO原理与源码解读:https://zhuanlan.zhihu.com/p/677607581
+原理解析:https://blog.csdn.net/v_JULY_v/article/details/134242910
+KL散度详解:https://blog.csdn.net/Rocky6688/article/details/103470437
+简要版本解析:https://blog.csdn.net/u014386899/article/details/136633074
+代码解读:https://zhuanlan.zhihu.com/p/696044978
+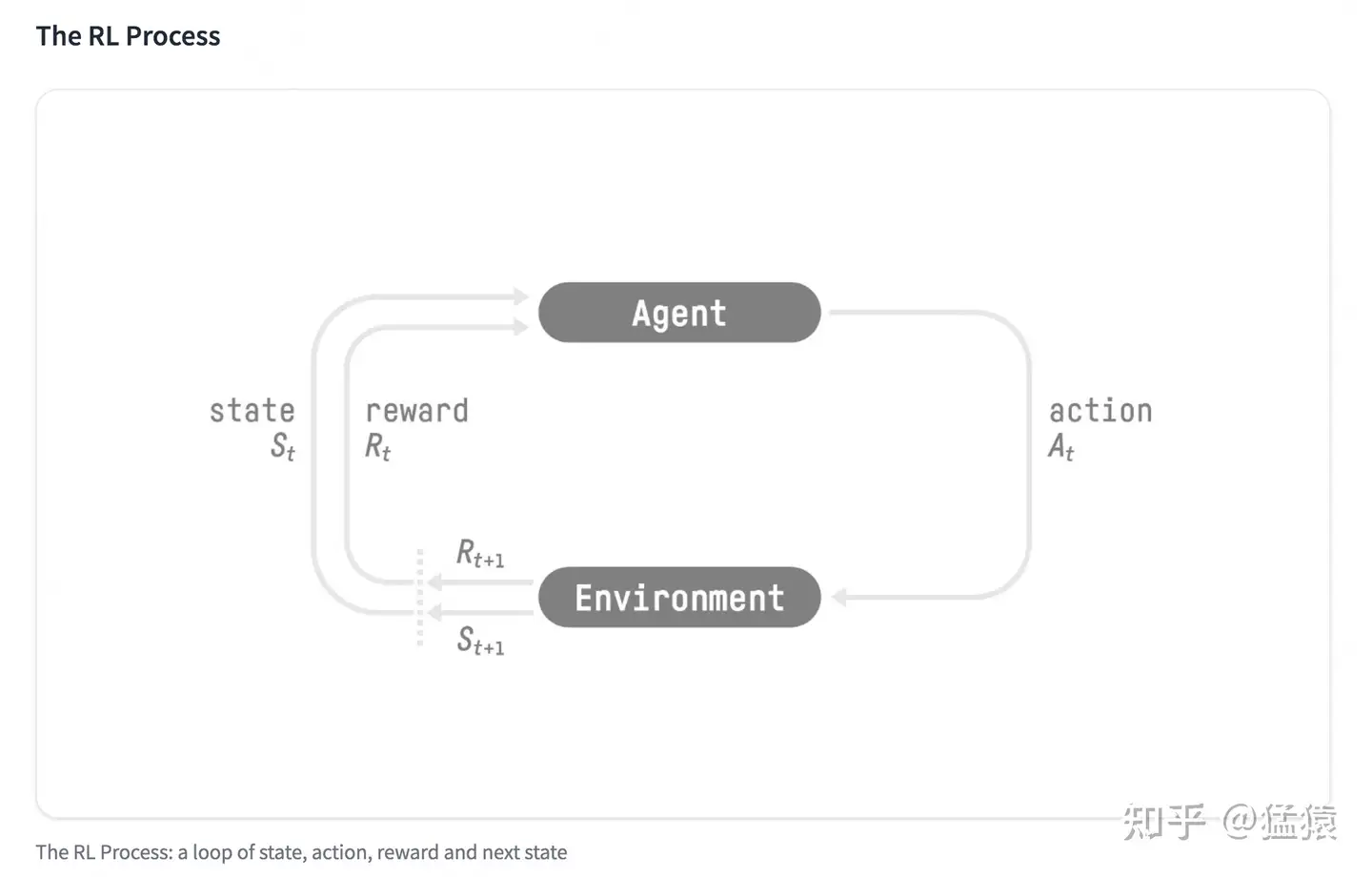
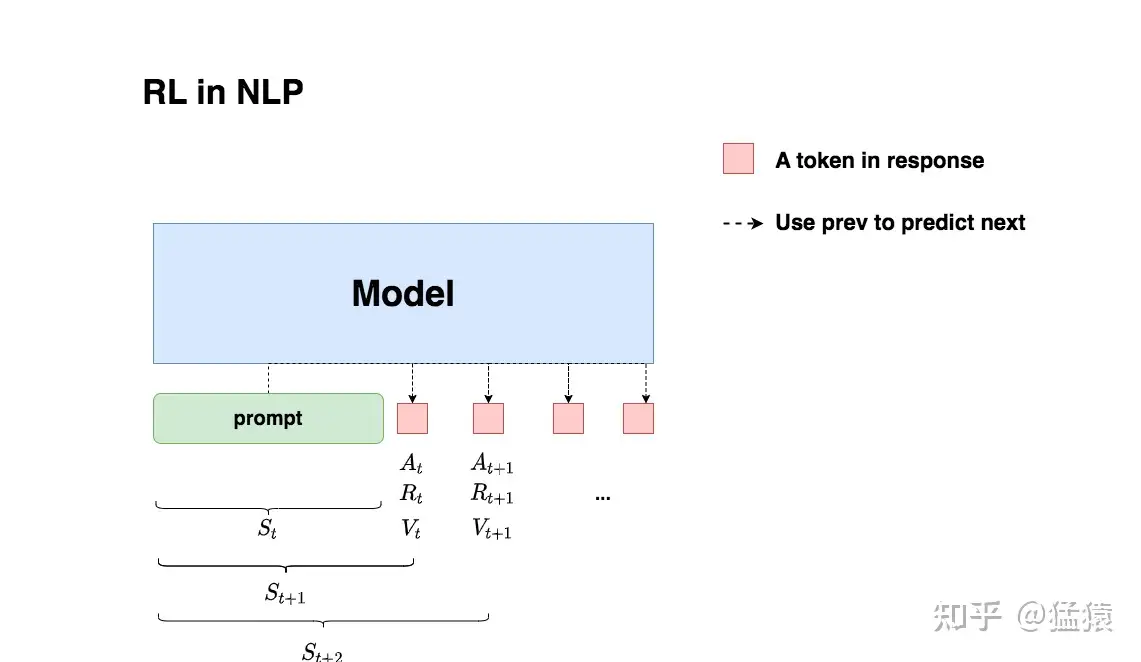
 :模型根据上文,产生一个token
:模型根据上文,产生一个token :即时收益,指语言模型当下产生token
:即时收益,指语言模型当下产生token 的收益
的收益 :实际期望总收益(即时+未来),指对语言模型“当下产生token
:实际期望总收益(即时+未来),指对语言模型“当下产生token  ,一直到整个response生产结束”的后期收益预估。因为当下语言模型还没产出
,一直到整个response生产结束”的后期收益预估。因为当下语言模型还没产出 后的token,所以我们只是对它之后一系列动作的收益做了估计,因而称为“期望总收益”。
后的token,所以我们只是对它之后一系列动作的收益做了估计,因而称为“期望总收益”。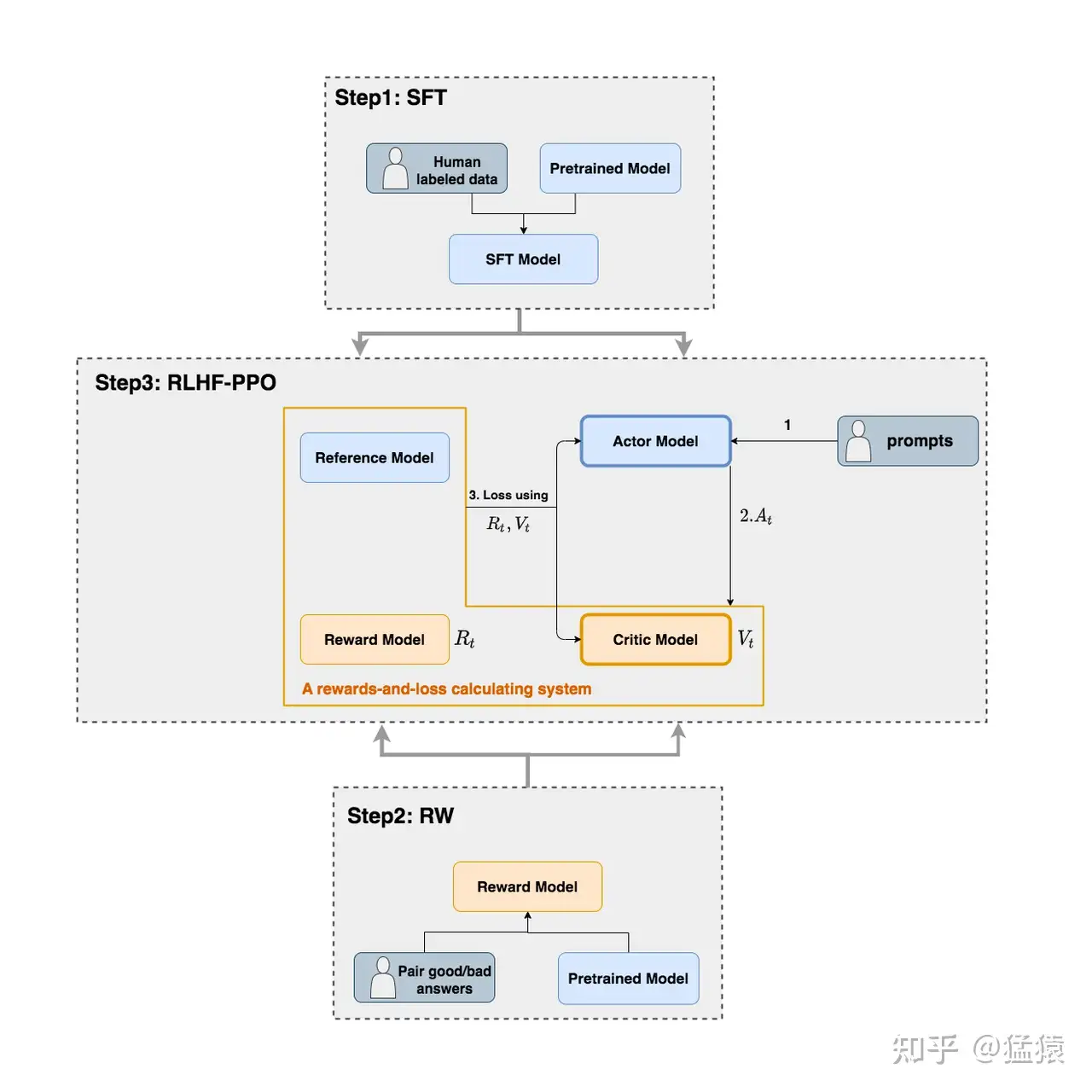
在RLHF-PPO阶段,一共有四个主要模型 ,分别是:
+

Actor/Critic Model在RLHF阶段是需要训练的(图中给这两个模型加了粗边,就是表示这个含义);而Reward/Reference Model是参数冻结的。
+Critic/Reward/Reference Model共同组成了一个“奖励-loss”计算体系(我自己命名的,为了方便理解),我们综合它们的结果计算loss,用于更新Actor和Critic Model
+Actor就是我们想要训练的目标语言模型。我们一般用SFT阶段产出的SFT模型来对它做初始化。
+我们的最终目的是让Actor模型能产生符合人类喜好的response。所以我们的策略是,先喂给Actor一条prompt (这里假设batch_size = 1,所以是1条prompt),让它生成对应的response。然后,我们再将“prompt + response"送入我们的“奖励-loss”计算体系中去算得最后的loss,用于更新actor。
+Reference Model(以下简称Ref模型)一般也用SFT阶段得到的SFT模型做初始化,在训练过程中,它的参数是冻结的。 Ref模型的主要作用是防止Actor”训歪”
+我们希望训练出来的Actor模型既能达到符合人类喜好的目的,又尽量让它和SFT模型不要差异太大 。因此我们使用KL散度来衡量输出分布的相似度
+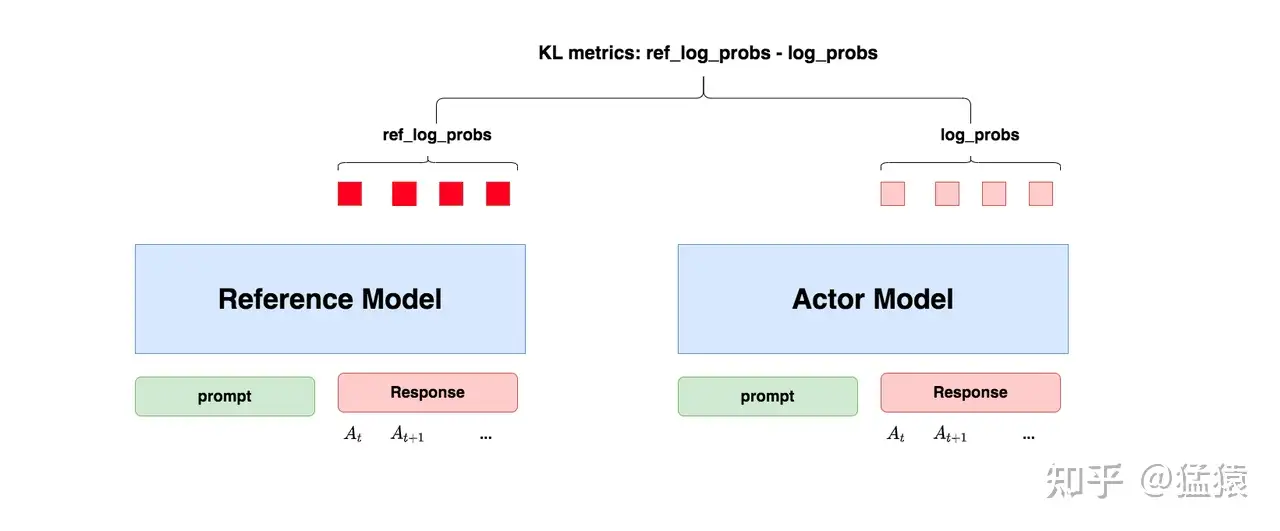
ref_log_probs - log_probs 来衡量,就是KL散度的公式
+Critic Model用于预测期望总收益,和Actor模型一样,它需要做参数更新 。
+在

在RLHF中,我们不仅要训练模型生成符合人类喜好的内容的能力(Actor),也要提升模型对人类喜好量化判断的能力(Critic)
+deepspeed-chat采用了Reward模型作为它的初始化,可以简单理解成,Reward/Critic模型和Actor模型的架构是很相似的(毕竟输入都一样),同时,它在最后一层增加了一个Value Head层,该层是个简单的线形层,用于将原始输出结果映射成单一的
Reward Model用于计算生成token的即时收益,它就是RW阶段所训练的奖励模型,在RLHF过程中,它的参数是冻结的。
+Reward模型是站在上帝视角的。这个上帝视角有两层含义:
+ 已经产生,因此即时收益自然可以立刻算出。
已经产生,因此即时收益自然可以立刻算出。reward是对actor模型进行了某一个action之后的直接打分;而critic则是对这个actor模型的整体预估得分。每次actor模型更新后,critic模型都要对这个新的actor模型重新打分,所以critic模型也要更新参数。critic模型对actor模型的整体预估得分,是根据reward模型的每一次实时打分来预估的。当critic模型的预估得分达到了一定的基准,就代表actor模型训练完成。
+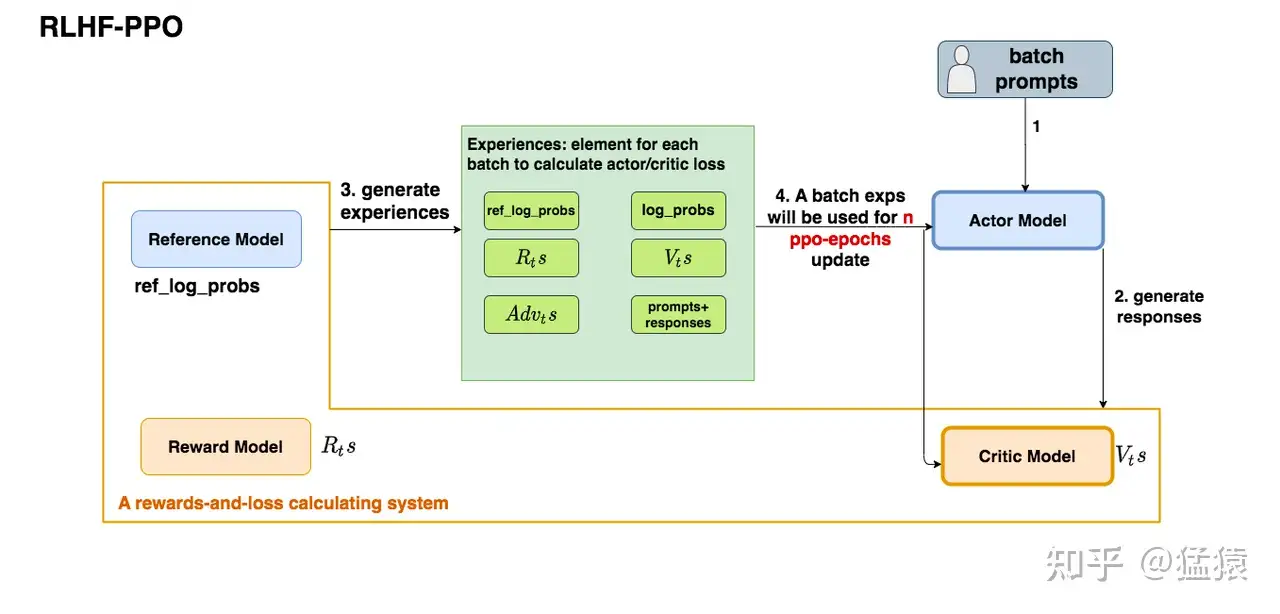
直观设计
+ ,产出token
,产出token  ,概率是
,概率是
 和
和  ,产出对总收益的预测
,产出对总收益的预测
 +
+ 时,意味着Critic对Actor当前采取的动作给了正向反馈,因此我们就需要在训练迭代中提高
时,意味着Critic对Actor当前采取的动作给了正向反馈,因此我们就需要在训练迭代中提高 ,这样就能达到减小loss的作用。
,这样就能达到减小loss的作用。 时,意味着Critic对Actor当前采取的动作给了负向反馈,因此我们就需要在训练迭代中降低
时,意味着Critic对Actor当前采取的动作给了负向反馈,因此我们就需要在训练迭代中降低 ,这样就能到达到减小loss的作用。
,这样就能到达到减小loss的作用。引入优势
+如果Critic对




actor loss =


 时,我们更加关心Actor是否有在Ref的约束下生产token
时,我们更加关心Actor是否有在Ref的约束下生产token
 时,我们不仅关心Actor是否遵从了Ref的约束,也关心真正的即时收益
时,我们不仅关心Actor是否遵从了Ref的约束,也关心真正的即时收益
为什么只有最后一个时刻的


改造优势
+新引入的
对于最后一个时刻




重复使用
+太慢了,所以一个batch的经验值将被用于n次模型更新
+1个batch的经验值被使用ppo_epochs次,在这ppo_epochs中,Actor是不吃任何新数据,不做任何交互的,所以我们只能让Actor“模拟”一下和环境交互的过程,吐出一些新数据出来。
+还是保证新的数据和旧的差不多,还是使用KL散度
+actor loss =
在Actor想通过模拟交互的方式,使用一个batch的经验值更新自己时,它需要收到真正吃到batch的那个时刻的Actor的约束,这样才能在有效利用batch,提升训练速度的基础上,保持训练的稳定。
+设置一个范围,差距太大就不要更新了
+ :Critic对
:Critic对 时刻的总收益的预估,这个总收益包含即时和未来的概念(预估收益)
时刻的总收益的预估,这个总收益包含即时和未来的概念(预估收益) :Reward计算出的即时收益
:Reward计算出的即时收益 ,Critic预测出的
,Critic预测出的 及之后时候的收益的折现,这是比
及之后时候的收益的折现,这是比 更接近
更接近 时刻真值总收益的一个值(实际收益)
时刻真值总收益的一个值(实际收益)第一想法:Critic loss =$ (𝑅_𝑡+ \gamma ∗𝑉_{𝑡+1}-V_t)^2$
+实际收益优化:
预估收益优化:类比于Actor,Critic模型在ppo_epochs的过程中也是不断更新的。所以这个

用老
最终我们就取实际收益和预估收益的MSE做为loss就好,这里注意,计算实际收益时
DPO通过简单的分类目标直接优化最满足偏好的策略,而没有明确的奖励函数或RL
+DPO的本质在于增加了被首选的response相对不被首选的response的对数概率,但它包含了一个动态的、每个示例的重要性权重,以防止设计的概率比让模型的能力退化。
+
IPO相当于在DPO的损失函数上添加了一个正则项,从而可以使得不使用early stopping技巧就可以使模型收敛。
+KTO定义的损失函数只需要将样本标注为"好(good)“或"坏(bad)”,从而使得获取标注样本的成本更低。(就是不需要一对一对标注了)
+CPO在训练期间不需要加载参考策略模型。通过省略内存的参考模型,CPO提高了操作效率,与DPO相比,能够以更低的成本训练更大的模型。
+ORPO整合SFT和DPO,且不需要额外的参考模型
+SimPO 包含两个主要组件:(1)在长度上归一化的奖励,其计算方式是使用策略模型的奖励中所有 token 的平均对数概率;(2)目标奖励差额,用以确保获胜和失败响应之间的奖励差超过这个差额。
+SimPO 不需要参考模型,性能却明显优于 DPO 及其最新变体,且不会显著增加响应长度
+ + +Leetcode-图论
+ +你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [a<sub>i</sub>, b<sub>i</sub>] ,表示如果要学习课程 a<sub>i</sub> 则 必须 先学习课程 b<sub>i</sub> ~ ~ 。
[0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
class Solution {
+public:
+ bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
+ vector<int> totalnum(numCourses,0);
+ vector<vector<int> > matrix(numCourses, vector<int>(0,0));
+ for(int i=0;i<prerequisites.size();i++){
+ totalnum[prerequisites[i][0]] += 1;
+ matrix[prerequisites[i][1]].push_back(prerequisites[i][0]);
+ }
+ bool judge = true;
+ while(judge){
+ judge = false;
+ for(int i=0;i<numCourses;i++){
+ if(totalnum[i] == 0){
+ judge = true;
+ for(int j=0;j<matrix[i].size();j++){
+ totalnum[matrix[i][j]] -= 1;
+ }
+ totalnum[i] = -1;
+ }
+ }
+ }
+ for(int i=0;i<numCourses;i++){
+ if(totalnum[i] != -1){
+ return false;
+ }
+ }
+ return true;
+ }
+};Leetcode-Hot 100
+ +给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 **和为目标值 **target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
+你可以按任意顺序返回答案。
+class Solution {
+public:
+ vector<int> twoSum(vector<int>& nums, int target) {
+ vector<int> result(2,0);
+ map<int,int> mp;
+ for(int i=0;i<nums.size();i++){
+ if(mp.find(target - nums[i]) != mp.end()){
+ result[0] = mp[target - nums[i]];
+ result[1] = i;
+ break;
+ }
+ mp[nums[i]] = i;
+ }
+ return result;
+ }
+};给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
+字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
+class Solution {
+public:
+ vector<vector<string>> groupAnagrams(vector<string>& strs) {
+ vector<vector<string> > result;
+ unordered_map<string, vector<string> > mp;
+ for(int i=0;i<strs.size();i++){
+ string t = strs[i];
+ sort(t.begin(),t.end());
+ mp[t].push_back(strs[i]);
+ }
+ for (auto it = mp.begin();it != mp.end();it++){
+ result.push_back(it->second);
+ }
+ return result;
+ }
+};给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
class Solution {
+public:
+ int longestConsecutive(vector<int>& nums) {
+ unordered_map<int, bool> mp;
+ if(nums.size() == 0){
+ return 0;
+ }
+ for(int i=0;i<nums.size();i++){
+ mp[nums[i]] = true;
+ }
+ int maxcount = 0;
+ for(int i=0;i<nums.size();i++){
+ int tempcount = 0;
+ int num = nums[i];
+ if(mp.find(num-1) != mp.end()){
+ continue;
+ }
+ while(mp.find(num) != mp.end()){
+ num += 1;
+ tempcount += 1;
+ }
+ maxcount = max(maxcount, tempcount);
+ }
+ return maxcount;
+ }
+};给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
+class Solution {
+public:
+ void moveZeroes(vector<int>& nums) {
+ int left = 0;
+ for(int right=0; right < nums.size(); right++){
+ if(nums[right] != 0){
+ nums[left] = nums[right];
+ left += 1;
+ }
+ }
+ while(left < nums.size()){
+ nums[left] = 0;
+ left += 1;
+ }
+ }
+};给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
+说明: 你不能倾斜容器。
+class Solution {
+public:
+ int maxArea(vector<int>& height) {
+ int result = 0;
+ int left = 0;
+ int right = height.size()-1;
+ while(left < right){
+ result = max(result, (right - left) * min(height[left], height[right]));
+ cout << left << " " << right << " " << endl;
+ if(height[left] < height[right]){
+ left += 1;
+ } else{
+ right -= 1;
+ }
+ }
+ return result;
+ }
+};给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意: 答案中不可以包含重复的三元组。
+class Solution {
+public:
+ vector<vector<int>> threeSum(vector<int>& nums) {
+ vector<vector<int>> result;
+ sort(nums.begin(), nums.end());
+ for(int start = 0; start < nums.size()-2;start += 1){
+ if(start > 0 && nums[start] == nums[start - 1]){
+ continue;
+ }
+ int left = start + 1;
+ int right = nums.size() - 1;
+ while(left < right){
+ int res = nums[start] + nums[left] + nums[right];
+ if(res == 0){
+ result.push_back(vector<int> {nums[start], nums[left], nums[right]});
+ while(left < right && nums[right] == nums[right-1]){
+ right -= 1;
+ }
+ while(left < right && nums[left] == nums[left + 1]){
+ left += 1;
+ }
+ left += 1;
+ right -= 1;
+ } else if (res < 0){
+ left += 1;
+ } else{
+ right -= 1;
+ }
+ }
+ }
+ return result;
+ }
+};给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
class Solution {
+public:
+ int trap(vector<int>& height) {
+ int result = 0;
+ int leftMax = 0;
+ int rightMax = 0;
+ int left = 0;
+ int right = height.size() - 1;
+ while(left < right){
+ leftMax = max(leftMax, height[left]);
+ rightMax = max(rightMax, height[right]);
+ if(height[left] < height[right]){
+ result += leftMax - height[left];
+ left += 1;
+ } else{
+ result += rightMax - height[right];
+ right -= 1;
+ }
+ }
+ return result;
+ }
+};给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串 的长度。
class Solution {
+public:
+ int lengthOfLongestSubstring(string s) {
+ int n = s.size();
+ int result = 0;
+ int right = 0;
+ unordered_set<char> st;
+ for(int left = 0;left < n;left++){
+ while(right < n && !st.count(s[right])){
+ st.insert(s[right]);
+ right++;
+ }
+ result = max(result, right - left);
+ st.erase(s[left]);
+ }
+ return result;
+ }
+};给定两个字符串 s 和 p,找到 s 中所有 p 的 **异位词 **的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
**异位词 **指由相同字母重排列形成的字符串(包括相同的字符串)。
+class Solution {
+public:
+ vector<int> findAnagrams(string s, string p) {
+ vector<int> schar(26, 0);
+ for(int i=0;i<p.size();i++){
+ schar[p[i]-'a'] += 1;
+ }
+ vector<int> result;
+ if(p.size() > s.size()){
+ return result;
+ }
+ int left = 0;
+ for(int right = 0;right < s.size();right++){
+ schar[s[right]-'a'] -= 1;
+ if (right < p.size()-1){
+ continue;
+ }
+ bool flag = false;
+ for(int i=0;i<26;i++){
+ if(schar[i] != 0){
+ flag = true;
+ break;
+ }
+ }
+ if(flag == false){
+ result.push_back(left);
+ }
+ schar[s[left]-'a'] += 1;
+ left += 1;
+ }
+ return result;
+ }
+};给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数。
子数组是数组中元素的连续非空序列。
+class Solution {
+public:
+ int subarraySum(vector<int>& nums, int k) {
+ int n = nums.size();
+ vector<int> pre(n+1,0);
+ for(int i=1;i<=n;i++){
+ pre[i] = nums[i-1] + pre[i-1];
+ }
+ for(int i=0;i<=n;i++){
+ cout << pre[i] << " ";
+ }
+ cout << endl;
+ unordered_map<int, int> cnt;
+ int result = 0;
+ for(int i=0; i<=n; i++){
+ if (cnt.contains(pre[i] - k)){
+ result += cnt[pre[i] - k];
+ }
+ cnt[pre[i]] += 1;
+ }
+ return result;
+ }
+};给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 *滑动窗口中的最大值 * 。
+class Solution {
+public:
+ vector<int> maxSlidingWindow(vector<int>& nums, int k) {
+ deque<int> st;
+ vector<int> result;
+ int n = nums.size();
+ for(int i=0;i<n;i++){
+ if(!st.empty() && st.front() <= i-k){
+ st.pop_front();
+ }
+ while(!st.empty() && nums[st.back()] < nums[i]){
+ st.pop_back();
+ }
+ st.push_back(i);
+ if(i >= k-1){
+ result.push_back(nums[st.front()]);
+ }
+ }
+ return result;
+ }
+};给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
+t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。s 中存在这样的子串,我们保证它是唯一的答案。class Solution {
+private:
+ unordered_map<char, int> map_window, map_base;
+ bool check() {
+ for (auto &it : map_base) { // 遍历字符串t的哈希表!!不要遍历错了!!
+ // 只要出现窗口内的某字符数量<字符串t的同一字符数量,则说明“窗口字符串”未覆盖“字符串t”
+ if (map_window[it.first] < it.second) {
+ return false;
+ }
+ }
+ return true;
+ }
+public:
+ string minWindow(string s, string t) {
+ // 初始化固定“字符串t”的字符频率哈希表
+ for (char c : t) {
+ map_base[c]++;
+ }
+ int left = 0;
+ int current_min_length = INT_MAX; // 因为后续下相当于取min,所以这里取MAX
+ int res_start_index = -1;
+ for (int right = 0; right < s.size(); right++) {
+ map_window[s[right]]++; // 更新“当前窗口字符串”的哈希表(right右移,添加字符)
+ while (check()) { // 如果覆盖
+ if (right - left + 1 < current_min_length) { // 窗口大小 < 当前覆盖子串最小长度
+ current_min_length = right - left + 1; // 更新当前覆盖子串的最小长度
+ res_start_index = left; // 记录该覆盖子串的起始索引。最后直接通过起始索引+最小长度来求结果,避免这里重复的拷贝复制
+ }
+ map_window[s[left]]--; // 更新“当前窗口字符串”的哈希表(left右移,删除字符)
+ left++;
+ }
+ }
+ // 别漏了无结果的情况,返回空串
+ return res_start_index == -1 ? "" : s.substr(res_start_index, current_min_length);
+ }
+};给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
**子数组 **是数组中的一个连续部分。
+class Solution {
+public:
+ int maxSubArray(vector<int>& nums) {
+ int result = nums[0];
+ int n = nums.size();
+ vector<int> dp(n, 0);
+ dp[0] = nums[0];
+ for(int i=1;i<n;i++){
+ dp[i] = max(nums[i], nums[i] + dp[i-1]);
+ result = max(result, dp[i]);
+ }
+ return result;
+ }
+};以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [start<sub>i</sub>, end<sub>i</sub>] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
class Solution {
+public:
+ static bool cmp(vector<int> &a, vector<int> &b){
+ if(a[0] == b[0]){
+ return a[1] < b[1];
+ }
+ return a[0] < b[0];
+ }
+ vector<vector<int>> merge(vector<vector<int>>& intervals) {
+ vector<vector<int> > result;
+ sort(intervals.begin(), intervals.end(), cmp);
+ bool now = false;
+ int start = intervals[0][0];
+ int end = intervals[0][1];
+ for(int i=0;i<intervals.size();i++){
+ if(intervals[i][0] > end){
+ result.push_back(vector<int>{start, end});
+ start = intervals[i][0];
+ end = intervals[i][1];
+ } else{
+ start = min(start, intervals[i][0]);
+ end = max(end, intervals[i][1]);
+ }
+ }
+ result.push_back(vector<int>{start, end});
+ return result;
+ }
+};给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
class Solution {
+public:
+ void reverse(vector<int> & nums, int start, int end){
+ while(start < end){
+ int temp = nums[start];
+ nums[start] = nums[end];
+ nums[end] = temp;
+ start += 1;
+ end -= 1;
+ }
+ }
+ void rotate(vector<int>& nums, int k) {
+ k = k % nums.size();
+ reverse(nums,0, nums.size()-1);
+ reverse(nums,0,k-1);
+ reverse(nums,k,nums.size()-1);
+ }
+};给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法, 且在 O(<em>n</em>) 时间复杂度内完成此题。
class Solution {
+public:
+ vector<int> productExceptSelf(vector<int>& nums) {
+ vector<int> pre(nums.size()+1,1);
+ vector<int> back(nums.size()+1,1);
+ for(int i=0;i<nums.size();i++){
+ pre[i+1] = nums[i] * pre[i];
+ }
+ for(int i=nums.size();i>0;i--){
+ back[i-1] = nums[i-1] * back[i];
+ }
+ vector<int> result(nums.size(),0);
+ for(int i=0;i<nums.size()+1;i++){
+ cout << pre[i] << " " << back[i] << endl;
+ }
+ for(int i=0;i<nums.size();i++){
+ result[i] = pre[i] * back[i+1];
+ }
+ return result;
+ }
+};给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
class Solution {
+public:
+ int firstMissingPositive(vector<int>& nums) {
+ int n = nums.size();
+ for(int i=0;i<n;i++){
+ if(nums[i] <= 0){
+ nums[i] = n + 1;
+ }
+ }
+ for(int i=0;i<n;i++){
+ int num = abs(nums[i]);
+ if(num <= n){
+ nums[num-1] = -abs(nums[num-1]);
+ }
+ }
+ for(int i=0;i<n;i++){
+ if(nums[i] > 0){
+ return i+1;
+ }
+ }
+ return n+1;
+ }
+};给定一个 <em>m</em> x <em>n</em> 的矩阵,如果一个元素为0 ,则将其所在行和列的所有元素都设为0 。请使用 原地 算法
class Solution {
+public:
+ void setZeroes(vector<vector<int>>& matrix) {
+ int m = matrix.size();
+ int n = matrix[0].size();
+ bool firstrow = false;
+ bool firstcol = false;
+ for(int i=0;i<m;i++){
+ if(matrix[i][0] == 0){
+ firstcol = true;
+ break;
+ }
+ }
+ for(int j=0;j<n;j++){
+ if(matrix[0][j] == 0){
+ firstrow = true;
+ break;
+ }
+ }
+ for(int i=1;i<m;i++){
+ for(int j=1;j<n;j++){
+ if(matrix[i][j] == 0){
+ matrix[0][j] = 0;
+ matrix[i][0] = 0;
+ }
+ }
+ }
+ for(int i=1;i<m;i++){
+ for(int j=1;j<n;j++){
+ if(matrix[i][0] == 0 || matrix[0][j] == 0){
+ matrix[i][j] = 0;
+ }
+ }
+ }
+ if(firstcol == true){
+ for(int i=0;i<m;i++){
+ matrix[i][0] = 0;
+ }
+ }
+ if(firstrow == true){
+ for(int j=0;j<n;j++){
+ matrix[0][j] = 0;
+ }
+ }
+ }
+};给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
class Solution {
+public:
+ vector<int> spiralOrder(vector<vector<int>>& matrix) {
+ vector<int> result;
+ int m = matrix.size();
+ int n = matrix[0].size();
+ vector<vector<bool> > visit(m, vector<bool>(n, false));
+ vector<vector<int> > directions{
+ {0,1},{1,0},{0,-1},{-1,0}
+ };
+ int xIndex = 0;
+ int yIndex = 0;
+ result.push_back(matrix[xIndex][yIndex]);
+ visit[xIndex][yIndex] = true;
+ while(result.size() != m*n){
+ for(int i=0;i<directions.size();i++){
+ while(xIndex + directions[i][0] >= 0 && xIndex + directions[i][0] < m && yIndex + directions[i][1] >= 0 && yIndex + directions[i][1] < n && visit[xIndex + directions[i][0]][yIndex + directions[i][1]] == false){
+ xIndex = xIndex + directions[i][0];
+ yIndex = yIndex + directions[i][1];
+ result.push_back(matrix[xIndex][yIndex]);
+ visit[xIndex][yIndex] = true;
+ }
+ }
+ }
+ return result;
+ }
+};给定一个 *n * × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在** 原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。**请不要 **使用另一个矩阵来旋转图像。
+class Solution {
+public:
+ void rotate(vector<vector<int>>& matrix) {
+ int n = matrix.size();
+ for(int i=0;i<(n+1)/2;i++){
+ for(int j=0;j<n/2;j++){
+ int temp = matrix[n-j-1][i];
+ matrix[n-j-1][i] = matrix[n-i-1][n-j-1];
+ matrix[n-i-1][n-j-1] = matrix[j][n-i-1];
+ matrix[j][n-i-1] = matrix[i][j];
+ matrix[i][j] = temp;
+ }
+ }
+ }
+};编写一个高效的算法来搜索 <em>m</em> x <em>n</em> 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
class Solution {
+public:
+ bool searchMatrix(vector<vector<int>>& matrix, int target) {
+ int m = matrix.size();
+ int n = matrix[0].size();
+ int x = 0;
+ int y = n-1;
+ while(x < m && y >= 0){
+ if (matrix[x][y] == target){
+ return true;
+ }
+ if(target < matrix[x][y]){
+ y -= 1;
+ }
+ else{
+ x += 1;
+ }
+ }
+ return false;
+ }
+};给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
class Solution {
+public:
+ ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
+ ListNode* p = headA;
+ ListNode* q = headB;
+ while(p != q){
+ if(p == NULL){
+ p = headB;
+ } else{
+ p = p->next;
+ }
+ if(q == NULL){
+ q = headA;
+ } else{
+ q = q->next;
+ }
+ }
+ return p;
+ }
+};给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
class Solution {
+public:
+ ListNode* reverseList(ListNode* head) {
+ ListNode* pre = NULL;
+ while(head != NULL){
+ ListNode* q = head->next;
+ head->next = pre;
+ pre = head;
+ head = q;
+ }
+ return pre;
+ }
+};给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
class Solution {
+public:
+ bool isPalindrome(ListNode* head) {
+ ListNode* pre = NULL;
+ ListNode* slow = head;
+ ListNode* fast = head;
+ bool flag = false;
+ while(fast != NULL){
+ if(fast->next == NULL){
+ fast = fast->next;
+ flag = true;
+ } else{
+ fast = fast->next->next;
+ }
+ ListNode* q = slow->next;
+ slow->next = pre;
+ pre = slow;
+ slow = q;
+ if(flag){
+ pre = pre->next;
+ }
+
+ }
+ while(pre != NULL && slow != NULL){
+ if(pre->val != slow->val){
+ return false;
+ }
+ pre = pre->next;
+ slow = slow->next;
+ }
+ return true;
+
+ }
+};给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 **注意:pos 不作为参数进行传递 ** 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
class Solution {
+public:
+ bool hasCycle(ListNode *head) {
+ if(head == NULL){
+ return false;
+ }
+ ListNode* slow = head;
+ ListNode* fast = head->next;
+ while(fast != NULL && fast->next != NULL){
+ slow = slow->next;
+ fast = fast->next->next;
+ if(slow == fast){
+ return true;
+ }
+ }
+ return false;
+ }
+};给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置( 索引从 0 开始 )。如果 pos 是 -1,则在该链表中没有环。 注意:pos 不作为参数进行传递 ,仅仅是为了标识链表的实际情况。
**不允许修改 **链表。
+class Solution {
+public:
+ ListNode *detectCycle(ListNode *head) {
+ if(head == NULL){
+ return NULL;
+ }
+ ListNode* slow = head;
+ ListNode* fast = head;
+ bool flag = false;
+ while(fast != NULL && fast->next != NULL){
+ slow = slow->next;
+ fast = fast->next->next;
+ if(slow == fast){
+ flag = true;
+ break;
+ }
+ }
+ if(flag == false){
+ return NULL;
+ }
+ fast = head;
+ while(slow != fast){
+ slow = slow->next;
+ fast = fast->next;
+ }
+ return slow;
+ }
+};将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
+class Solution {
+public:
+ ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
+ ListNode* dummy = new ListNode(-1);
+ ListNode* head = dummy;
+ while(list1 != NULL && list2 != NULL){
+ if(list1->val < list2->val){
+ dummy->next = list1;
+ list1 = list1->next;
+ dummy = dummy->next;
+ } else{
+ dummy->next = list2;
+ list2 = list2->next;
+ dummy = dummy->next;
+ }
+ }
+ if(list1 != NULL){
+ dummy->next = list1;
+ } else{
+ dummy->next = list2;
+ }
+ return head->next;
+ }
+};给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
+请你将两个数相加,并以相同形式返回一个表示和的链表。
+你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
+class Solution {
+public:
+ ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
+ ListNode* dummy = new ListNode(-1);
+ ListNode* l3 = dummy;
+ int cur = 0;
+ int sum = 0;
+ while(l1 != NULL || l2 != NULL){
+ if(l1 != NULL && l2 != NULL){
+ sum = l1->val + l2->val + cur;
+ l1 = l1->next;
+ l2 = l2->next;
+ } else if (l1 != NULL){
+ sum = l1->val + cur;
+ l1 = l1->next;
+ } else if(l2 != NULL){
+ sum = l2->val + cur;
+ l2 = l2->next;
+ }
+ if(sum >= 10){
+ sum -= 10;
+ cur = 1;
+ } else{
+ cur = 0;
+ }
+ l3->next = new ListNode(sum);
+ l3 = l3->next;
+ }
+ if (cur == 1){
+ l3->next = new ListNode(1);
+ }
+ return dummy->next;
+ }
+};给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
class Solution {
+public:
+ ListNode* removeNthFromEnd(ListNode* head, int n) {
+ ListNode* dummy = new ListNode(-1);
+ dummy->next = head;
+ ListNode* pre = dummy;;
+ ListNode* slow = head;
+ ListNode* fast = head;
+ while(n--){
+ fast = fast->next;
+ }
+ while(fast != NULL){
+ pre = slow;
+ slow = slow->next;
+ fast = fast->next;
+ }
+ pre->next = pre->next->next;
+ return dummy->next;
+ }
+};给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
+class Solution {
+public:
+ ListNode* reverseList(ListNode* head){
+ ListNode* pre = NULL;
+ while(head != NULL){
+ ListNode* q = head->next;
+ head->next = pre;
+ pre = head;
+ head = q;
+ }
+ return pre;
+ }
+ ListNode* swapPairs(ListNode* head) {
+ ListNode* dummy = new ListNode(-1);
+ ListNode* realhead = dummy;
+ while(head != NULL && head->next != NULL){
+ ListNode* q = head->next->next;
+ head->next->next = NULL;
+ dummy->next = reverseList(head);
+ dummy = dummy->next->next;
+ head = q;
+ }
+ if(head != NULL){
+ dummy->next = head;
+ }
+ return realhead->next;
+ }
+};给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
+class Solution {
+public:
+ ListNode* reverseList(ListNode* head){
+ ListNode* pre = NULL;
+ while(head != NULL){
+ ListNode* q = head->next;
+ head->next = pre;
+ pre = head;
+ head = q;
+ }
+ return pre;
+ }
+ ListNode* reverseKGroup(ListNode* head, int k) {
+ ListNode* dummy = new ListNode(-1);
+ ListNode* realhead = dummy;
+
+ while(1){
+ bool sign = false;
+ ListNode* p = head;
+ ListNode* pre = NULL;
+ for(int i=0;i<k;i++){
+ if(p == NULL){
+ sign = true;
+ break;
+ }
+ pre = p;
+ p = p->next;
+ }
+ if(sign){
+ break;
+ }
+ pre->next = NULL;
+ dummy->next = reverseList(head);
+ for(int i=0;i<k;i++){
+ dummy = dummy->next;
+ }
+ head = p;
+ }
+ if(head != NULL){
+ dummy->next = head;
+ }
+ return realhead->next;
+ }
+};给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝 。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。 **复制链表中的指针都不应指向原链表中的节点 ** 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
+用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示 Node.val 的整数。random_index:随机指针指向的节点索引(范围从 0 到 n-1);如果不指向任何节点,则为 null 。你的代码 只 接受原链表的头节点 head 作为传入参数。
class Solution {
+public:
+ Node* copyRandomList(Node* head) {
+ if(head == NULL){
+ return NULL;
+ }
+ Node* cur = head;
+ unordered_map<Node*, Node*> map;
+ // 3. 复制各节点,并建立 “原节点 -> 新节点” 的 Map 映射
+ while(cur != NULL) {
+ map[cur] = new Node(cur->val);
+ cur = cur->next;
+ }
+ cur = head;
+ // 4. 构建新链表的 next 和 random 指向
+ while(cur != NULL) {
+ map[cur]->next = map[cur->next];
+ map[cur]->random = map[cur->random];
+ cur = cur->next;
+ }
+ // 5. 返回新链表的头节点
+ return map[head];
+ }
+};给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
class Solution {
+public:
+ ListNode* mergesort(ListNode* head){
+ if(head == NULL || head->next == NULL){
+ return head;
+ }
+ ListNode* slow = head;
+ ListNode* fast = head->next;
+ while(fast != NULL && fast->next != NULL){
+ slow = slow->next;
+ fast = fast->next->next;
+ }
+
+ ListNode* right = mergesort(slow->next);
+ if(slow != NULL){
+ slow->next = NULL;
+ }
+ ListNode* left = mergesort(head);
+ ListNode* dummy = new ListNode(-1);
+ ListNode* p = dummy;
+ while(left != NULL || right != NULL){
+ if(left == NULL){
+ p->next = right;
+ right = right->next;
+ } else if(right == NULL){
+ p->next = left;
+ left = left->next;
+ } else{
+ if(left->val < right->val){
+ p->next = left;
+ left = left->next;
+ } else{
+ p->next = right;
+ right = right->next;
+ }
+ }
+ p = p->next;
+ }
+ return dummy->next;
+ }
+ ListNode* sortList(ListNode* head) {
+ return mergesort(head);
+ }
+};给你一个链表数组,每个链表都已经按升序排列。
+请你将所有链表合并到一个升序链表中,返回合并后的链表。
+class Solution {
+public:
+ ListNode* merge(vector<ListNode*>& lists, int start, int end){
+ if(start == end){
+ return lists[start];
+ }
+ int mid = (end - start) / 2 + start;
+ ListNode* left = merge(lists, start, mid);
+ ListNode* right = merge(lists, mid+1, end);
+ ListNode* dummy = new ListNode(-1);
+ ListNode* p = dummy;
+ while(left != NULL || right != NULL){
+ if(left == NULL){
+ dummy->next = right;
+ right = right->next;
+ } else if(right == NULL){
+ dummy->next = left;
+ left = left->next;
+ } else{
+ if(left->val < right -> val){
+ dummy->next = left;
+ left = left->next;
+ } else{
+ dummy->next = right;
+ right = right->next;
+ }
+ }
+ dummy = dummy->next;
+ }
+ return p->next;
+ }
+ ListNode* mergeKLists(vector<ListNode*>& lists) {
+ if(lists.size() == 0){
+ return NULL;
+ }
+ return merge(lists, 0, lists.size()-1);
+ }
+};请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
+实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
struct DLinkedNode {
+ int key, value;
+ DLinkedNode* prev;
+ DLinkedNode* next;
+ DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}
+ DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
+};
+
+class LRUCache {
+private:
+ unordered_map<int, DLinkedNode*> cache;
+ DLinkedNode* head;
+ DLinkedNode* tail;
+ int size;
+ int capacity;
+public:
+ LRUCache(int _capacity): capacity(_capacity), size(0) {
+ // 使用伪头部和伪尾部节点
+ head = new DLinkedNode();
+ tail = new DLinkedNode();
+ head->next = tail;
+ tail->prev = head;
+ }
+
+ int get(int key) {
+ if (!cache.count(key)) {
+ return -1;
+ }
+ // 如果 key 存在,先通过哈希表定位,再移到头部
+ DLinkedNode* node = cache[key];
+ moveToHead(node);
+ return node->value;
+ }
+
+ void put(int key, int value) {
+ if (!cache.count(key)) {
+ // 如果 key 不存在,创建一个新的节点
+ DLinkedNode* node = new DLinkedNode(key, value);
+ // 添加进哈希表
+ cache[key] = node;
+ // 添加至双向链表的头部
+ addToHead(node);
+ ++size;
+ if (size > capacity) {
+ // 如果超出容量,删除双向链表的尾部节点
+ DLinkedNode* removed = removeTail();
+ // 删除哈希表中对应的项
+ cache.erase(removed->key);
+ // 防止内存泄漏
+ delete removed;
+ --size;
+ }
+ }
+ else {
+ // 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
+ DLinkedNode* node = cache[key];
+ node->value = value;
+ moveToHead(node);
+ }
+ }
+ void addToHead(DLinkedNode* node) {
+ node->prev = head;
+ node->next = head->next;
+ head->next->prev = node;
+ head->next = node;
+ }
+
+ void removeNode(DLinkedNode* node) {
+ node->prev->next = node->next;
+ node->next->prev = node->prev;
+ }
+
+ void moveToHead(DLinkedNode* node) {
+ removeNode(node);
+ addToHead(node);
+ }
+
+ DLinkedNode* removeTail() {
+ DLinkedNode* node = tail->prev;
+ removeNode(node);
+ return node;
+ }
+};给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
class Solution {
+public:
+ void inorder(TreeNode* root, vector<int> & result){
+ if(root == NULL){
+ return;
+ }
+ inorder(root->left, result);
+ result.push_back(root->val);
+ inorder(root->right, result);
+ }
+ vector<int> inorderTraversal(TreeNode* root) {
+ vector<int> result;
+ inorder(root, result);
+ return result;
+ }
+};给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
+class Solution {
+public:
+ int max_depth = 0;
+ void DFS(TreeNode* root, int depth){
+ if(root == NULL){
+ max_depth = max(max_depth, depth);
+ return;
+ }
+ DFS(root->left, depth+1);
+ DFS(root->right, depth+1);
+ }
+ int maxDepth(TreeNode* root) {
+ DFS(root,0);
+ return max_depth;
+ }
+};给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
class Solution {
+public:
+ TreeNode* invertTree(TreeNode* root) {
+ if(root == NULL){
+ return NULL;
+ }
+ swap(root->left, root->right);
+ invertTree(root->left);
+ invertTree(root->right);
+ return root;
+ }
+};给你一个二叉树的根节点 root , 检查它是否轴对称。
class Solution {
+public:
+ bool issame(TreeNode* left, TreeNode* right){
+ if(left == NULL && right == NULL){
+ return true;
+ } else if(left == NULL){
+ return false;
+ } else if(right == NULL){
+ return false;
+ } else{
+ if(left->val != right->val){
+ return false;
+ }
+ }
+ return issame(left->right, right->left) && issame(right->right, left->left);
+ }
+ bool isSymmetric(TreeNode* root) {
+ if(root == NULL){
+ return true;
+ }
+ return issame(root->left, root->right);
+ }
+};给你一棵二叉树的根节点,返回该树的 直径 。
+二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
+class Solution {
+public:
+ int maxlength = 0;
+ int DFS(TreeNode* root, int nowlength){
+ if(root == NULL){
+ return 0;
+ }
+ int leftlength = DFS(root->left, nowlength+1);
+ int rightlength = DFS(root->right, nowlength+1);
+ maxlength = max(maxlength, leftlength + rightlength + 1);
+ return max(leftlength, rightlength) + 1;
+ }
+ int diameterOfBinaryTree(TreeNode* root) {
+ DFS(root,0);
+ return maxlength-1;
+ }
+};给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
class Solution {
+public:
+ vector<vector<int>> levelOrder(TreeNode* root) {
+ vector<vector<int>> result;
+ if(root == NULL){
+ return result;
+ }
+ queue<TreeNode* > q;
+ q.push(root);
+ while(!q.empty()){
+ int s = q.size();
+ vector<int> temp;
+ for(int i=0;i<s;i++){
+ TreeNode* t = q.front();
+ q.pop();
+ temp.push_back(t->val);
+ if(t->left != NULL){
+ q.push(t->left);
+ }
+ if(t->right != NULL){
+ q.push(t->right);
+ }
+ }
+ result.push_back(temp);
+ }
+ return result;
+ }
+};给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树。
class Solution {
+public:
+ TreeNode* sortedArrayToBST(vector<int>& nums) {
+ if(nums.size() == 0){
+ return NULL;
+ }
+ int start = 0;
+ int end = nums.size();
+ int mid = (start + end) / 2;
+ vector<int> numsleft;
+ vector<int> numsright;
+ for(int i=start;i<end;i++){
+ if(i < mid){
+ numsleft.push_back(nums[i]);
+ } else if(i > mid){
+ numsright.push_back(nums[i]);
+ }
+ }
+ TreeNode* left = sortedArrayToBST(numsleft);
+ TreeNode* root = new TreeNode(nums[mid]);
+ TreeNode* right = sortedArrayToBST(numsright);
+ root->left = left;
+ root->right = right;
+ return root;
+
+ }
+};给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
+class Solution {
+public:
+ vector<int> result;
+ void inorder(TreeNode* root){
+ if(root == NULL){
+ return;
+ }
+ inorder(root->left);
+ result.push_back(root->val);
+ inorder(root->right);
+ }
+ bool isValidBST(TreeNode* root) {
+ inorder(root);
+ for(int i=0;i<result.size()-1;i++){
+ if(result[i] < result[i+1]){
+ continue;
+ }
+ return false;
+ }
+ return true;
+ }
+};给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
class Solution {
+public:
+ int num = 0;
+ int result = 0;
+ void inorder(TreeNode* root,int k){
+ if(root == NULL){
+ return;
+ }
+ inorder(root->left, k);
+ num += 1;
+ if(num == k){
+ result = root->val;
+ }
+ inorder(root->right, k);
+ }
+
+ int kthSmallest(TreeNode* root, int k) {
+ inorder(root, k);
+ return result;
+ }
+};给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
class Solution {
+public:
+ vector<int> rightSideView(TreeNode* root) {
+ vector<int> result;
+ if(root == NULL){
+ return result;
+ }
+ queue<TreeNode*> q;
+ q.push(root);
+ while(!q.empty()){
+ int s = q.size();
+ for(int i=0;i<s;i++){
+ TreeNode* t = q.front();
+ q.pop();
+ if(t->left != NULL){
+ q.push(t->left);
+ }
+ if(t->right != NULL){
+ q.push(t->right);
+ }
+ if(i == s-1){
+ result.push_back(t->val);
+ }
+ }
+ }
+ return result;
+ }
+};给你二叉树的根结点 root ,请你将它展开为一个单链表:
TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。class Solution {
+public:
+ void flatten(TreeNode* root) {
+ if (root == NULL){
+ return;
+ }
+ flatten(root->left);
+ flatten(root->right);
+ if (root->left != NULL) {
+ auto pre = root->left;
+ while (pre->right != NULL){
+ pre = pre->right;
+ }
+ pre->right = root->right;
+ root->right = root->left;
+ root->left = NULL;
+ }
+ root = root->right;
+ return;
+ }
+};给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的 先序遍历 , inorder 是同一棵树的 中序遍历 ,请构造二叉树并返回其根节点。
class Solution {
+public:
+ TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
+ if(preorder.size() == 0){
+ return NULL;
+ }
+ int val = preorder[0];
+ TreeNode* root = new TreeNode(val);
+ int k;
+ vector<int> leftpreorder, leftinorder, rightpreorder, rightinorder;
+ for(int i=0;i<inorder.size();i++){
+ if(inorder[i] == val){
+ k = i;
+ break;
+ }
+ }
+ for(int i=1;i<preorder.size();i++){
+ if(i <= k){
+ leftpreorder.push_back(preorder[i]);
+ } else{
+ rightpreorder.push_back(preorder[i]);
+ }
+ }
+ for(int i=0;i<inorder.size();i++){
+ if(i < k){
+ leftinorder.push_back(inorder[i]);
+ } else if (i > k){
+ rightinorder.push_back(inorder[i]);
+ }
+ }
+ root->left = buildTree(leftpreorder, leftinorder);
+ root->right = buildTree(rightpreorder, rightinorder);
+ return root;
+ }
+};给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
+class Solution {
+public:
+ int DFS(TreeNode* root, long long targetSum){
+ if(root == NULL){
+ return 0;
+ }
+ int res = 0;
+ if(root->val == targetSum){
+ res += 1;
+ }
+ res += DFS(root->left, targetSum - root->val);
+ res += DFS(root->right, targetSum - root->val);
+ return res;
+ }
+ int pathSum(TreeNode* root, int targetSum) {
+ if(root == NULL){
+ return 0;
+ }
+ int nownum = DFS(root, (long long)targetSum);
+ nownum += pathSum(root->left, targetSum);
+ nownum += pathSum(root->right, targetSum);
+ return nownum;
+ }
+};给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
+百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大( 一个节点也可以是它自己的祖先 )。”
+class Solution {
+public:
+ TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
+ if(root == NULL){
+ return root;
+ }
+ if(root == p || root == q){
+ return root;
+ }
+ TreeNode* left = lowestCommonAncestor(root->left,p,q);
+ TreeNode* right = lowestCommonAncestor(root->right,p,q);
+ if(left != NULL && right != NULL){
+ return root;
+ }
+ if(left == NULL){
+ return right;
+ }
+ return left;
+ }
+};二叉树中的** 路径** 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径** 至少包含一个 **节点,且不一定经过根节点。
+路径和 是路径中各节点值的总和。
+给你一个二叉树的根节点 root ,返回其 最大路径和 。
class Solution {
+private:
+ int maxSum = INT_MIN;
+public:
+
+ int maxGain(TreeNode* node){
+ if(node == NULL){
+ return 0;
+ }
+ int leftGain = max(maxGain(node->left), 0);
+ int rightresult = max(maxGain(node->right), 0);
+ int priceNewpath = node->val + leftGain + rightresult;
+
+ // 更新答案
+ maxSum = max(maxSum , priceNewpath);
+ return node->val + max(leftGain, rightresult);
+ }
+ int maxPathSum(TreeNode* root) {
+ maxGain(root);
+ return maxSum ;
+ }
+};给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
+此外,你可以假设该网格的四条边均被水包围。
+class Solution {
+public:
+ void DFS(vector<vector<char>>& grid, vector<vector<bool> > & visited, int i, int j, int m, int n){
+ if(i < 0 || i >= m || j < 0 || j >= n || visited[i][j] == true || grid[i][j] == '0'){
+ return;
+ }
+ visited[i][j] = true;
+ DFS(grid, visited, i-1, j, m, n);
+ DFS(grid, visited, i+1, j, m, n);
+ DFS(grid, visited, i, j-1, m, n);
+ DFS(grid, visited, i, j+1, m, n);
+ }
+ int numIslands(vector<vector<char>>& grid) {
+ int sum = 0;
+ int m = grid.size();
+ int n = grid[0].size();
+ vector<vector<bool> > visited(m, vector<bool>(n, false));
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(visited[i][j] == false && grid[i][j] == '1'){
+ DFS(grid, visited, i, j, m, n);
+ sum += 1;
+ }
+ }
+ }
+ return sum;
+
+ }
+};在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
0 代表空单元格;1 代表新鲜橘子;2 代表腐烂的橘子。每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
+返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
class Solution {
+public:
+ int orangesRotting(vector<vector<int>>& grid) {
+ int m = grid.size();
+ int n = grid[0].size();
+ vector<vector<bool>> visited(m, vector<bool>(n, false));
+ int minpath = 0;
+ queue<pair<int, int> > q;
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(grid[i][j] == 2){
+ visited[i][j] = true;
+ q.push({i,j});
+ }
+ }
+ }
+ while(!q.empty()){
+ minpath += 1;
+ int s = q.size();
+ for(int i=0;i<s;i++){
+ pair<int, int> p = q.front();
+ q.pop();
+ int pi = p.first;
+ int pj = p.second;
+ if(pi-1 >= 0 && visited[pi-1][pj] == false && grid[pi-1][pj] == 1){
+ visited[pi-1][pj] = true;
+ grid[pi-1][pj] = 2;
+ q.push({pi-1,pj});
+ }
+ if(pj-1 >= 0 && visited[pi][pj-1] == false && grid[pi][pj-1] == 1){
+ visited[pi][pj-1] = true;
+ grid[pi][pj-1] = 2;
+ q.push({pi,pj-1});
+ }
+ if(pi+1 < m && visited[pi+1][pj] == false && grid[pi+1][pj] == 1){
+ visited[pi+1][pj] = true;
+ grid[pi+1][pj] = 2;
+ q.push({pi+1,pj});
+ }
+ if(pj+1 < n && visited[pi][pj+1] == false && grid[pi][pj+1] == 1){
+ visited[pi][pj+1] = true;
+ grid[pi][pj+1] = 2;
+ q.push({pi,pj+1});
+ }
+ }
+ }
+
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(grid[i][j] == 1){
+ return -1;
+ }
+ }
+ }
+ if(minpath == 0){
+ return 0;
+ }
+ return minpath-1;
+ }
+};你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [a<sub>i</sub>, b<sub>i</sub>] ,表示如果要学习课程 a<sub>i</sub> 则 必须 先学习课程 b<sub>i</sub> ~ ~ 。
[0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
class Solution {
+public:
+ bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
+ vector<vector<int> > table(numCourses, vector<int>(0,0));
+ vector<int> judge(numCourses,0);
+ vector<bool> visit(numCourses,false);
+ for(int i=0;i<prerequisites.size();i++){
+ int pre = prerequisites[i][1];
+ int post = prerequisites[i][0];
+ table[pre].push_back(post);
+ judge[post] += 1;
+ }
+
+ while(1){
+ bool modify = false;
+ for(int i=0;i<numCourses;i++){
+ if(visit[i] == false && judge[i] == 0){
+ modify = true;
+ visit[i] = true;
+ for(int j=0;j<table[i].size();j++){
+ judge[table[i][j]] -= 1;
+ }
+ }
+ }
+ if(modify == false){
+ break;
+ }
+ }
+ for(int i=0;i<numCourses;i++){
+ if(judge[i] != 0){
+ return false;
+ }
+ }
+ return true;
+ }
+};Trie (发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
+请你实现 Trie 类:
+Trie() 初始化前缀树对象。void insert(String word) 向前缀树中插入字符串 word 。boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。class Trie {
+private:
+ bool isEnd;
+ Trie* next[26];
+public:
+ Trie() {
+ isEnd = false;
+ memset(next, 0, sizeof(next));
+ }
+
+ void insert(string word) {
+ Trie* node = this;
+ for (char c : word) {
+ if (node->next[c-'a'] == NULL) {
+ node->next[c-'a'] = new Trie();
+ }
+ node = node->next[c-'a'];
+ }
+ node->isEnd = true;
+ }
+
+ bool search(string word) {
+ Trie* node = this;
+ for (char c : word) {
+ node = node->next[c - 'a'];
+ if (node == NULL) {
+ return false;
+ }
+ }
+ return node->isEnd;
+ }
+
+ bool startsWith(string prefix) {
+ Trie* node = this;
+ for (char c : prefix) {
+ node = node->next[c - 'a'];
+ if (node == NULL) {
+ return false;
+ }
+ }
+ return true;
+ }
+};给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
class Solution {
+private:
+ vector<vector<int> > result;
+public:
+ void backtracking(vector<int>& nums, vector<bool>& visited, vector<int>& temp){
+ if(temp.size() == nums.size()){
+ result.push_back(temp);
+ return;
+ }
+ for(int i=0;i<nums.size();i++){
+ if(visited[i] == true){
+ continue;
+ }
+ visited[i] = true;
+ temp.push_back(nums[i]);
+ backtracking(nums, visited, temp);
+ temp.pop_back();
+ visited[i] = false;
+ }
+ }
+ vector<vector<int>> permute(vector<int>& nums) {
+ vector<int> temp;
+ vector<bool> visited(nums.size(), false);
+ backtracking(nums, visited, temp);
+ return result;
+ }
+};给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
+class Solution {
+private:
+ vector<vector<int> > result;
+public:
+ void backtracking(vector<int>& nums, vector<int>& temp, int start){
+ result.push_back(temp);
+ if(start >= nums.size()){
+ return;
+ }
+ for(int i=start;i<nums.size();i++){
+ temp.push_back(nums[i]);
+ backtracking(nums, temp, i+1);
+ temp.pop_back();
+ }
+ }
+ vector<vector<int>> subsets(vector<int>& nums) {
+ vector<int> temp;
+ backtracking(nums, temp, 0);
+ return result;
+ }
+};给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
+class Solution {
+private:
+ vector<string> result;
+ vector<char> temp;
+public:
+ void backtracking(string digits, map<char, vector<char> > &mp, int start){
+ if(start == digits.size()){
+ string t = "";
+ for(int i=0;i<temp.size();i++){
+ t += temp[i];
+ }
+ result.push_back(t);
+ return;
+ }
+ vector<char> now = mp[digits[start]];
+ for(int i=0;i<now.size();i++){
+ temp.push_back(now[i]);
+ backtracking(digits, mp, start+1);
+ temp.pop_back();
+ }
+ }
+ vector<string> letterCombinations(string digits) {
+ if(digits == ""){
+ return result;
+ }
+ map<char, vector<char> > mp;
+ mp['2'] = vector<char>{'a', 'b', 'c'};
+ mp['3'] = vector<char>{'d', 'e', 'f'};
+ mp['4'] = vector<char>{'g', 'h', 'i'};
+ mp['5'] = vector<char>{'j', 'k', 'l'};
+ mp['6'] = vector<char>{'m', 'n', 'o'};
+ mp['7'] = vector<char>{'p', 'q', 'r', 's'};
+ mp['8'] = vector<char>{'t', 'u', 'v'};
+ mp['9'] = vector<char>{'w', 'x', 'y', 'z'};
+ backtracking(digits, mp, 0);
+ return result;
+ }
+};给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
class Solution {
+private:
+ vector<vector<int>> result;
+ vector<int> temp;
+public:
+ void backtracking(vector<int>& candidates, int target, int nowsum, int start){
+ if(nowsum > target){
+ return;
+ }
+ if(nowsum == target){
+ result.push_back(temp);
+ return;
+ }
+ for(int i=start;i<candidates.size();i++){
+ temp.push_back(candidates[i]);
+ backtracking(candidates, target, nowsum+candidates[i], i);
+ temp.pop_back();
+ }
+ }
+ vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
+ backtracking(candidates, target, 0, 0);
+ return result;
+ }
+};数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 **有效的 **括号组合。
class Solution {
+private:
+ vector<string> result;
+ vector<char> temp;
+public:
+ void backtracking(int n, int left){
+ if(temp.size() == 2 * n && left == 0){
+ string res = "";
+ for(int i=0;i<temp.size();i++){
+ res += temp[i];
+ }
+ result.push_back(res);
+ return;
+ }
+ if(temp.size() == 2*n){
+ return;
+ }
+ if(left > n){
+ return;
+ }
+ if(left == 0){
+ temp.push_back('(');
+ backtracking(n, 1);
+ temp.pop_back();
+ } else{
+ temp.push_back('(');
+ backtracking(n, left+1);
+ temp.pop_back();
+ temp.push_back(')');
+ backtracking(n, left-1);
+ temp.pop_back();
+ }
+ }
+ vector<string> generateParenthesis(int n) {
+ backtracking(n,0);
+ return result;
+ }
+};给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
+class Solution {
+private:
+ bool sign = false;
+ string temp = "";
+public:
+ void backtracking(vector<vector<char>>& board, vector<vector<bool> > &visited, string word, int i, int j, int m, int n, int now){
+ if(temp == word){
+ sign = true;
+ return;
+ }
+ if(now >= word.size()){
+ return;
+ }
+ if(i < 0 || i >= m || j < 0 || j >= n){
+ return;
+ }
+ if(visited[i][j] == true){
+ return;
+ }
+ if(board[i][j] != word[now]){
+ return;
+ }
+ visited[i][j] = true;
+ string t = temp;
+ temp += board[i][j];
+ backtracking(board, visited, word, i+1, j, m, n, now+1);
+ backtracking(board, visited, word, i-1, j, m, n, now+1);
+ backtracking(board, visited, word, i, j+1, m, n, now+1);
+ backtracking(board, visited, word, i, j-1, m, n, now+1);
+ temp = t;
+ visited[i][j] = false;
+ }
+ bool exist(vector<vector<char>>& board, string word) {
+ int m = board.size();
+ int n = board[0].size();
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ vector<vector<bool> > visited(m, vector<bool>(n,false));
+ temp = "";
+ backtracking(board, visited, word, i, j, m, n, 0);
+ if(sign == true){
+ return true;
+ }
+ }
+ }
+ return false;
+ }
+};给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
class Solution {
+private:
+ vector<vector<string>> result;
+ vector<string> temp;
+public:
+ bool judge(string t){
+ int start = 0;
+ int end = t.size() - 1;
+ while(start < end){
+ if(t[start] != t[end]){
+ return false;
+ }
+ start += 1;
+ end -= 1;
+ }
+ return true;
+ }
+ void backtracking(string s, int start){
+ if(start == s.size()){
+ result.push_back(temp);
+ return;
+ }
+ for(int i=1; i<=s.size()-start;i++){
+ string t = s.substr(start,i);
+ if(judge(t)){
+ temp.push_back(t);
+ backtracking(s,start+i);
+ temp.pop_back();
+ }
+ }
+ }
+ vector<vector<string> > partition(string s) {
+ backtracking(s,0);
+ return result;
+ }
+};按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
+n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
class Solution {
+private:
+ vector<vector<string>> result;
+public:
+ bool judge(vector<vector<char> > &board, int i, int j, int n){
+ for(int p=0;p<i;p++){
+ if(board[p][j] == 'Q'){
+ return false;
+ }
+ }
+ int l = i-1;
+ int r = j-1;
+ while(l >= 0 && r >= 0){
+ if(board[l][r] == 'Q'){
+ return false;
+ }
+ l--;
+ r--;
+ }
+ l = i-1;
+ r = j+1;
+ while(l >= 0 && r < n){
+ if(board[l][r] == 'Q'){
+ return false;
+ }
+ l--;
+ r++;
+ }
+ return true;
+ }
+ void backtracking(vector<vector<char> > &board, int start, int n){
+ if(start == n){
+ vector<string> vt;
+ for(int i=0;i<n;i++){
+ string temp = "";
+ for(int j=0;j<n;j++){
+ temp += board[i][j];
+ }
+ vt.push_back(temp);
+ }
+ result.push_back(vt);
+ return;
+ }
+ for(int i=0;i<n;i++){
+ board[start][i] = 'Q';
+ if(judge(board,start,i,n)){
+ backtracking(board,start+1,n);
+ }
+ board[start][i] = '.';
+ }
+ }
+ vector<vector<string> > solveNQueens(int n) {
+ vector<vector<char> > board(n, vector<char>(n, '.'));
+ backtracking(board,0,n);
+ return result;
+ }
+};给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
+请必须使用时间复杂度为 O(log n) 的算法。
class Solution {
+public:
+ int searchInsert(vector<int>& nums, int target) {
+ int left = 0;
+ int right = nums.size() - 1;
+ while(left <= right){
+ int mid = (right - left) / 2 + left;
+ if(nums[mid] == target){
+ return mid;
+ } else if (nums[mid] < target){
+ left = mid + 1;
+ } else{
+ right = mid - 1;
+ }
+ }
+ return left;
+ }
+};给你一个满足下述两条属性的 m x n 整数矩阵:
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
class Solution {
+public:
+ bool searchMatrix(vector<vector<int>>& matrix, int target) {
+ int m = matrix.size();
+ int n = matrix[0].size();
+ int i = 0;
+ int j = n - 1;
+ while(i <= m-1 && j >= 0){
+ if(matrix[i][j] == target){
+ return true;
+ } else if(matrix[i][j] < target){
+ i += 1;
+ } else{
+ j -= 1;
+ }
+ }
+ return false;
+ }
+};给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
class Solution {
+public:
+ int lowerbound(vector<int>& nums, int target){
+ int left = 0;
+ int leftBorder = -2;
+ int right = nums.size() - 1;
+ while(left <= right){
+ int mid = (right - left) / 2 + left;
+ if(nums[mid] >= target){
+ right = mid - 1;
+ leftBorder = right;
+ } else{
+ left = mid + 1;
+ }
+ }
+ return leftBorder;
+ }
+ int upperbound(vector<int>& nums, int target){
+ int left = 0;
+ int rightBorder = -2;
+ int right = nums.size() - 1;
+ while(left <= right){
+ int mid = (right - left) / 2 + left;
+ if(nums[mid] > target){
+ right = mid - 1;
+ } else{
+ left = mid + 1;
+ rightBorder = left;
+ }
+ }
+ return rightBorder;
+ }
+ vector<int> searchRange(vector<int>& nums, int target) {
+ int leftBorder = lowerbound(nums, target);
+ int rightBorder = upperbound(nums,target);
+ if (leftBorder == -2 || rightBorder == -2){
+ return vector<int>{-1,-1};
+ }
+ if (rightBorder - leftBorder > 1){
+ return vector<int>{leftBorder + 1, rightBorder - 1};
+ }
+ return vector<int>{-1, -1};
+ }
+};整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转 ,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
class Solution {
+public:
+ int search(vector<int>& nums, int target) {
+ int left = 0;
+ int right = nums.size() - 1;
+ while(left <= right){
+ int mid = (right - left) / 2 + left;
+ if(nums[mid] == target){
+ return mid;
+ }
+ if(nums[0] <= nums[mid]){
+ if(nums[0] <= target && target <= nums[mid]){
+ right = mid - 1;
+ } else{
+ left = mid + 1;
+ }
+ } else{
+ if(nums[mid] <= target && target <= nums[nums.size()-1]){
+ left = mid + 1;
+ } else{
+ right = mid - 1;
+ }
+ }
+
+ }
+ return -1;
+ }
+};已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
4 次,则可以得到 [4,5,6,7,0,1,2]7 次,则可以得到 [0,1,2,4,5,6,7]注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
class Solution {
+public:
+ int findMin(vector<int>& nums) {
+ int left = 0;
+ int right = nums.size() - 1;
+ while(left < right){
+ int mid = (right - left) / 2 + left;
+ if(nums[right] > nums[mid]){
+ right = mid;
+ } else{
+ left = mid + 1;
+ }
+ }
+ return nums[left];
+ }
+};给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
class Solution {
+public:
+ double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
+ int m = nums1.size();
+ int n = nums2.size();
+ bool next;
+ int sign = (m + n) / 2;
+ if((m + n) % 2 == 1){
+ next = false;
+ } else{
+ sign -= 1;
+ next = true;
+ }
+ int res1 = 0;
+ int res2 = 0;
+ int globalindex = 0;
+ int nums1index = 0;
+ int nums2index = 0;
+ while(globalindex <= sign){
+ if(nums1index < m && nums2index < n){
+ if(nums1[nums1index] < nums2[nums2index]){
+ res1 = nums1[nums1index];
+ nums1index += 1;
+ } else{
+ res1 = nums2[nums2index];
+ nums2index += 1;
+ }
+ } else if (nums1index < m){
+ res1 = nums1[nums1index];
+ nums1index += 1;
+ } else {
+ res1 = nums2[nums2index];
+ nums2index += 1;
+ }
+ globalindex += 1;
+ }
+ if(next == false){
+ return res1;
+ }
+ if(nums1index < m && nums2index < n){
+ if(nums1[nums1index] < nums2[nums2index]){
+ res2 = nums1[nums1index];
+ } else{
+ res2 = nums2[nums2index];
+ }
+ } else if (nums1index < m){
+ res2 = nums1[nums1index];
+ } else {
+ res2 = nums2[nums2index];
+ }
+ return ((double)res1 + (double)res2) / 2.0;
+ }
+};给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
+class Solution {
+public:
+ bool isValid(string s) {
+ stack<char> st;
+ for(int i=0;i<s.size();i++){
+ if(s[i] == '(' || s[i] == '[' || s[i] == '{'){
+ st.push(s[i]);
+ } else{
+ if(st.size() == 0){
+ return false;
+ }
+ if(s[i] == ')'){
+ if(st.top() != '('){
+ return false;
+ } else{
+ st.pop();
+ }
+ } else if (s[i] == ']'){
+ if(st.top() != '['){
+ return false;
+ } else{
+ st.pop();
+ }
+ } else if (s[i] == '}'){
+ if(st.top() != '{'){
+ return false;
+ } else{
+ st.pop();
+ }
+ }
+ }
+ }
+ return st.size() == 0;
+ }
+};设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。void push(int val) 将元素val推入堆栈。void pop() 删除堆栈顶部的元素。int top() 获取堆栈顶部的元素。int getMin() 获取堆栈中的最小元素。class MinStack {
+private:
+ stack<int> st1;
+ stack<int> st2;
+public:
+ MinStack() {
+ }
+
+ void push(int val) {
+ st1.push(val);
+ if(st2.empty() || val < st2.top()){
+ st2.push(val);
+ } else{
+ st2.push(st2.top());
+ }
+ }
+
+ void pop() {
+ st1.pop();
+ st2.pop();
+ }
+
+ int top() {
+ return st1.top();
+ }
+
+ int getMin() {
+ return st2.top();
+ }
+};给定一个经过编码的字符串,返回它解码后的字符串。
+编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
+此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
class Solution {
+public:
+ string decodeString(string s) {
+ stack<char> st;
+ for(int i=0;i<s.size();i++){
+ if(s[i] == ']'){
+ vector<char> tempchar;
+ vector<int> tempnum;
+ while(st.top() != '['){
+ tempchar.push_back(st.top());
+ st.pop();
+ }
+ st.pop();
+ while(!st.empty() && st.top() >= '0' && st.top() <= '9'){
+ tempnum.push_back(st.top() - '0');
+ st.pop();
+ }
+ int num = 0;
+ for(int j=tempnum.size()-1;j>=0;j--){
+ num = num * 10 + tempnum[j];
+ }
+ for(int j=0;j<num;j++){
+ for(int k=tempchar.size()-1;k>=0;k--){
+ st.push(tempchar[k]);
+ }
+ }
+ }else{
+ st.push(s[i]);
+ }
+ }
+ string res;
+ while(!st.empty()){
+ res += st.top();
+ st.pop();
+ }
+ reverse(res.begin(), res.end());
+ return res;
+ }
+};给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
class Solution {
+public:
+ vector<int> dailyTemperatures(vector<int>& temperatures) {
+ int n = temperatures.size();
+ vector<int> result(n,0);
+ stack<int> st;
+ for(int i=0;i<temperatures.size();i++){
+ while(!st.empty() && temperatures[st.top()] < temperatures[i]){
+ result[st.top()] = i - st.top();
+ st.pop();
+ }
+ st.push(i);
+ }
+ return result;
+ }
+};给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
+求在该柱状图中,能够勾勒出来的矩形的最大面积。
+class Solution {
+public:
+ int largestRectangleArea(vector<int>& heights) {
+ int result = 0;
+ int n = heights.size();
+ if(n == 1){
+ return heights[0];
+ }
+ vector<int> minLeftIndex(n,0);
+ vector<int> minRightIndex(n,0);
+ minLeftIndex[0] = -1;
+ for(int i=1;i<n;i++){
+ int t = i - 1;
+ while (t >= 0 && heights[t] >= heights[i]){
+ t = minLeftIndex[t];
+ }
+ minLeftIndex[i] = t;
+ }
+ minRightIndex[n-1] = n;
+ for(int i=n-2;i>=0;i--){
+ int t = i + 1;
+ while (t < n && heights[t] >= heights[i]){
+ t = minRightIndex[t];
+ }
+ minRightIndex[i] = t;
+ }
+ for(int i=0;i<n;i++){
+ result = max(result, heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1));
+ }
+ return result;
+ }
+};给定整数数组 nums 和整数 k,请返回数组中第 <strong>k</strong> 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
class Solution {
+public:
+ void quicksort(vector<int>& nums, int i, int j, int k){
+ if(i >= j){
+ return;
+ }
+ int start = i;
+ int end = j;
+ int x = nums[start];
+ while(start < end){
+ while(start < end && nums[end] < x){
+ end--;
+ }
+ nums[start] = nums[end];
+ while(start < end && nums[start] >= x){
+ start++;
+ }
+ nums[end] = nums[start];
+ }
+ nums[start] = x;
+ if(k-1 == start){
+ return;
+ } else if(k-1 < start){
+ quicksort(nums, i, start-1,k);
+ } else{
+ quicksort(nums,start+1,j,k);
+ }
+ }
+ int findKthLargest(vector<int>& nums, int k) {
+ quicksort(nums,0,nums.size()-1,k);
+ return nums[k-1];
+ }
+};给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
class Solution {
+public:
+ static bool cmp(int a, int b){
+ return a > b;
+ }
+ vector<int> topKFrequent(vector<int>& nums, int k) {
+ unordered_map<int, int> mp;
+ for(int i=0;i<nums.size();i++){
+ mp[nums[i]] += 1;
+ }
+ vector<int> temp;
+ for(auto it = mp.begin(); it != mp.end();it++){
+ temp.push_back(it->second);
+ }
+ sort(temp.begin(), temp.end(), cmp);
+ int sign = temp[k-1];
+ vector<int> result;
+ for(auto it = mp.begin(); it != mp.end();it++){
+ if(it->second >= sign){
+ result.push_back(it->first);
+ }
+ }
+ return result;
+ }
+};中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。
+arr = [2,3,4] 的中位数是 3 。arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。实现 MedianFinder 类:
+MedianFinder() 初始化 MedianFinder 对象。void addNum(int num) 将数据流中的整数 num 添加到数据结构中。double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10<sup>-5</sup> 以内的答案将被接受。class MedianFinder {
+public:
+ priority_queue<int, vector<int>, greater<int>> A; // 小顶堆,保存较大的一半
+ priority_queue<int, vector<int>, less<int>> B; // 大顶堆,保存较小的一半
+
+ MedianFinder() {
+
+ }
+ void addNum(int num) {
+ if (A.size() != B.size()) {
+ A.push(num);
+ B.push(A.top());
+ A.pop();
+ } else {
+ B.push(num);
+ A.push(B.top());
+ B.pop();
+ }
+
+ }
+
+ double findMedian() {
+ return A.size() != B.size() ? A.top() : (A.top() + B.top()) / 2.0;
+ }
+};给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
+返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
class Solution {
+public:
+ int maxProfit(vector<int>& prices) {
+ int minprice = INT_MAX, maxprofit = 0;
+ for(int i=0;i<prices.size();i++){
+ maxprofit = max(maxprofit, prices[i] - minprice);
+ minprice = min(prices[i], minprice);
+ }
+ return maxprofit;
+ }
+};给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
class Solution {
+public:
+ bool canJump(vector<int>& nums) {
+ int n = nums.size();
+ int result = 0;
+ for(int i=0;i<nums.size();i++){
+ if (i <= result){
+ result = max(result, i + nums[i]);
+ if(result >= n - 1){
+ return true;
+ }
+ }
+ }
+ return false;
+ }
+};给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
class Solution {
+public:
+ int jump(vector<int>& nums) {
+ int n = nums.size();
+ int result = n+1;
+ vector<int> dp(n+1,n+1);
+ dp[0] = 0;
+ for(int i=1;i<n;i++){
+ for(int j=0;j<i;j++){
+ if(j + nums[j] >= i){
+ dp[i] = min(dp[i], dp[j] + 1);
+ }
+ }
+ }
+ return dp[n-1];
+ }
+};给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。
注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。
返回一个表示每个字符串片段的长度的列表。
+class Solution {
+public:
+ vector<int> partitionLabels(string s) {
+ vector<int> result;
+ int n = s.size();
+ vector<int> alphabet(26,0);
+ for(int i=0;i<s.size();i++){
+ alphabet[s[i] - 'a'] = i;
+ }
+ int start = 0;
+ int end = 0;
+ for(int i=0;i<s.size();i++){
+ end = max(end, alphabet[s[i] - 'a']);
+ if(i == end){
+ result.push_back(end - start + 1);
+ start = end + 1;
+ }
+ }
+ return result;
+ }
+};假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
class Solution {
+public:
+ int climbStairs(int n) {
+ if(n == 1 || n == 2){
+ return n;
+ }
+ vector<int> dp(n+1,0);
+ dp[1] = 1;
+ dp[2] = 2;
+ for(int i=3;i<=n;i++){
+ dp[i] = dp[i-1] + dp[i-2];
+ }
+ return dp[n];
+ }
+};给定一个非负整数 numRows, 生成「杨辉三角」的前 *numRows *行。
class Solution {
+public:
+ vector<vector<int>> generate(int numRows) {
+ vector<vector<int>> result;
+ for(int i=1;i<=numRows;i++){
+ vector<int> temp;
+ for(int j=0;j<i;j++){
+ if(j == 0 || j == i-1){
+ temp.push_back(1);
+ } else{
+ vector<int> last = result[result.size()-1];
+ temp.push_back(last[j-1] + last[j]);
+ }
+ }
+ result.push_back(temp);
+ }
+ return result;
+ }
+};你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统, 如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
+给定一个代表每个房屋存放金额的非负整数数组,计算你 ** 不触动警报装置的情况下 ** ,一夜之内能够偷窃到的最高金额。
+class Solution {
+public:
+ int rob(vector<int>& nums) {
+ int n = nums.size();
+ vector<int> dp(n+1);
+ if(n == 1){
+ return nums[0];
+ }
+ if(n == 2){
+ return max(nums[0], nums[1]);
+ }
+ dp[1] = nums[0];
+ dp[2] = max(nums[0], nums[1]);
+ for(int i=3;i<=n;i++){
+ dp[i] = max(dp[i-1], dp[i-2] + nums[i-1]);
+ }
+ return dp[n];
+ }
+};给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
class Solution {
+public:
+ int numSquares(int n) {
+ vector<int> dp(n+1,n+1);
+ for(int i=1;i<=n;i++){
+ if(i*i < n){
+ dp[i*i] = 1;
+ } else if(i*i == n){
+ return 1;
+ } else{
+ break;
+ }
+ }
+ for(int i=1;i<=n;i++){
+ for(int j=i;j>=1;j--){
+ dp[i] = min(dp[i], dp[i-j]+ dp[j]);
+ }
+ }
+ return dp[n];
+ }
+};给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
+class Solution {
+public:
+ int coinChange(vector<int>& coins, int amount) {
+ vector<int> dp(amount+1,amount+1);
+ dp[0] = 0;
+ for(int i=0;i<coins.size();i++){
+ for(int j=0;j<=amount;j++){
+ if(j >= coins[i]){
+ dp[j] = min(dp[j], dp[j-coins[i]] + 1);
+ }
+
+ }
+ }
+ return dp[amount] == amount+1 ? -1:dp[amount];
+ }
+};给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
注意: 不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
+class Solution {
+public:
+ bool wordBreak(string s, vector<string>& wordDict) {
+ unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
+ vector<bool> dp(s.size()+1,false);
+ dp[0] = true;
+ for(int i=0;i<=s.size();i++){
+ for(int j=0;j<i;j++){
+ string word = s.substr(j,i-j);
+ if(wordSet.find(word) != wordSet.end() && dp[j] == true){
+ dp[i] = true;
+ }
+ }
+ }
+ return dp[s.size()] == true;
+ }
+};给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
**子序列 **是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
class Solution {
+public:
+ int lengthOfLIS(vector<int>& nums) {
+ int n = nums.size();
+ vector<int> dp(n,1);
+ int result = 0;
+ dp[0] = 1;
+ for(int i=0;i<n;i++){
+ for(int j=0;j<i;j++){
+ if(nums[j] < nums[i]){
+ dp[i] = max(dp[i], dp[j] + 1);
+ }
+ }
+ result = max(result, dp[i]);
+ }
+ return result;
+ }
+};给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
+class Solution {
+public:
+ int maxProduct(vector<int>& nums) {
+ double maxF = nums[0], minF = nums[0], ans = nums[0];
+ for (int i = 1; i < nums.size(); ++i) {
+ double mx = maxF, mn = minF;
+ maxF = max(mx * nums[i], max(static_cast<double>(nums[i]), mn * nums[i]));
+ minF = min(mn * nums[i], min(static_cast<double>(nums[i]), mx * nums[i]));
+ ans = max(maxF, ans);
+ }
+ return static_cast<int>(ans);
+ }
+};给你一个 **只包含正整数 **的 **非空 **数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
class Solution {
+public:
+ bool canPartition(vector<int>& nums) {
+ int sum = 0;
+ for(int num : nums){
+ sum += num;
+ }
+ if(sum % 2 == 1){
+ return false;
+ }
+ sum /= 2;
+ vector<bool> dp(sum+1,false);
+ dp[0] = true;
+ for(int i=0;i<nums.size();i++){
+ for(int j=sum;j>=nums[i];j--){
+ dp[j] = dp[j] || dp[j-nums[i]];
+ }
+ }
+ return dp[sum];
+ }
+};给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
class Solution {
+public:
+ int longestValidParentheses(string s) {
+ stack<int> st;
+ int ans = 0;
+ int start = 0;
+ for(int i=0;i<s.size();i++){
+ if(s[i] == '('){
+ st.push(i);
+ } else{
+ if(!st.empty()){
+ st.pop();
+ if (st.empty()) {
+ ans = max(ans, i - start + 1);
+ }
+ else {
+ ans = max(ans, i - st.top());
+ }
+
+ } else{
+ start = i + 1;
+ }
+ }
+ }
+ return ans;
+ }
+};一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
+问总共有多少条不同的路径?
+class Solution {
+public:
+ int uniquePaths(int m, int n) {
+ vector<vector<int> > dp(m+1, vector<int>(n+1,0));
+ for(int i=1;i<=m;i++){
+ for(int j=1;j<=n;j++){
+ if(i == 1 && j == 1){
+ dp[i][j] = 1;
+ } else{
+ dp[i][j] = dp[i-1][j] + dp[i][j-1];
+ }
+
+ }
+ }
+ return dp[m][n];
+ }
+};给定一个包含非负整数的 <em>m</em> x <em>n</em> 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明: 每次只能向下或者向右移动一步。
+class Solution {
+public:
+ int minPathSum(vector<vector<int>>& grid) {
+ int m = grid.size();
+ int n = grid[0].size();
+ vector<vector<int> > dp(m, vector<int>(n,0));
+ for(int i=0;i<m;i++){
+ for(int j=0;j<n;j++){
+ if(i == 0 && j == 0){
+ dp[i][j] = grid[i][j];
+ } else if (i == 0){
+ dp[i][j] = grid[i][j] + dp[i][j-1];
+ } else if (j == 0){
+ dp[i][j] = grid[i][j] + dp[i-1][j];
+ } else{
+ dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
+ }
+ }
+ }
+ return dp[m-1][n-1];
+ }
+};给你一个字符串 s,找到 s 中最长的 回文 子串。
class Solution {
+public:
+ string longestPalindrome(string s) {
+ string result = "";
+ int longresult = 1;
+ result += s[0];
+ int l = s.size();
+ for(int i=0;i<l-1;i++){
+ int start = i;
+ int end = i + 1;
+ while(start >= 0 && end < l && s[start] == s[end]){
+ start--;
+ end++;
+ }
+ start++;
+ end--;
+ if(end-start+1 > longresult){
+ longresult = end-start+1;
+ result = s.substr(start,longresult);
+ }
+ }
+ for(int i=1;i<l-1;i++){
+ int start = i - 1;
+ int end = i + 1;
+ while(start >= 0 && end < l && s[start] == s[end]){
+ start--;
+ end++;
+ }
+ start++;
+ end--;
+ if(end-start+1 > longresult){
+ longresult = end-start+1;
+ result = s.substr(start,longresult);
+ }
+ }
+ return result;
+ }
+};给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
+"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
+class Solution {
+public:
+ int longestCommonSubsequence(string text1, string text2) {
+ int m = text1.size();
+ int n = text2.size();
+ vector<vector<int> > dp(m+1, vector<int>(n+1,0));
+ for(int i=1;i<=m;i++){
+ for(int j=1;j<=n;j++){
+ if(text1[i-1] == text2[j-1]){
+ dp[i][j] = dp[i-1][j-1] + 1;
+ } else{
+ dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
+ }
+ }
+ }
+ return dp[m][n];
+ }
+};给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
+class Solution {
+public:
+ int minDistance(string word1, string word2) {
+ int s1 = word1.size();
+ int s2 = word2.size();
+ vector<vector<int> > dp(s1+1, vector<int>(s2+1,0));
+ for(int i=0;i<=s1;i++){
+ dp[i][0] = i;
+ }
+ for(int j=0;j<=s2;j++){
+ dp[0][j] = j;
+ }
+ for(int i=1;i<=s1;i++){
+ for(int j=1;j<=s2;j++){
+ if(word1[i-1] == word2[j-1]){
+ dp[i][j] = dp[i-1][j-1];
+ } else{
+ dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1])) + 1;
+ }
+ }
+ }
+ return dp[s1][s2];
+ }
+};给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
+class Solution {
+public:
+ int singleNumber(vector<int>& nums) {
+ int ret = 0;
+ for (auto e: nums) ret ^= e;
+ return ret;
+ }
+};给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
+class Solution {
+public:
+ int majorityElement(vector<int>& nums) {
+ int x = 0, votes = 0;
+ for (int num : nums){
+ if (votes == 0) x = num;
+ votes += num == x ? 1 : -1;
+ }
+ return x;
+ }
+};给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,**原地**对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
+class Solution {
+public:
+ void sortColors(vector<int>& nums) {
+ int left = 0;
+ for(int right = 0;right < nums.size();right++){
+ if(nums[right] == 0){
+ swap(nums[left], nums[right]);
+ left += 1;
+ }
+ }
+ left = nums.size() - 1;
+ for(int right = nums.size()-1;right >= 0; right--){
+ if(nums[right] == 2){
+ swap(nums[left], nums[right]);
+ left -= 1;
+ }
+ }
+ }
+};整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
+arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
+arr = [1,2,3] 的下一个排列是 [1,3,2] 。arr = [2,3,1] 的下一个排列是 [3,1,2] 。arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。给你一个整数数组 nums ,找出 nums 的下一个排列。
必须** 原地 **修改,只允许使用额外常数空间。
+class Solution {
+public:
+ void nextPermutation(vector<int>& nums) {
+ int n = nums.size();
+ int sign = -1;
+ for(int i=n-1;i>0;i--){
+ if(nums[i-1] < nums[i]){
+ sign = i-1;
+ break;
+ }
+ }
+ if(sign == -1){
+ reverse(nums.begin(),nums.end());
+ return;
+ }
+ int sign2 = 0;
+ for(int i=n-1;i>0;i--){
+ if(nums[i] > nums[sign]){
+ sign2 = i;
+ break;
+ }
+ }
+ swap(nums[sign], nums[sign2]);
+ reverse(nums.begin()+sign+1,nums.end());
+ return;
+ }
+};给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
class Solution {
+public:
+ int findDuplicate(vector<int>& nums) {
+ int fast = 0, slow = 0;
+ while(true){
+ fast = nums[nums[fast]];
+ slow = nums[slow];
+ if(fast == slow)
+ break;
+ }
+ int finder = 0;
+ while(true){
+ finder = nums[finder];
+ slow = nums[slow];
+ if(slow == finder)
+ break;
+ }
+ return slow;
+ }
+};Leetcode-栈与队列
+ +中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。
+arr = [2,3,4] 的中位数是 3 。arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。实现 MedianFinder 类:
+MedianFinder() 初始化 MedianFinder 对象。void addNum(int num) 将数据流中的整数 num 添加到数据结构中。double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10<sup>-5</sup> 以内的答案将被接受。class MedianFinder {
+public:
+ priority_queue<int, vector<int>, less<int>> queMin;
+ priority_queue<int, vector<int>, greater<int>> queMax;
+
+ MedianFinder() {
+
+ }
+
+ void addNum(int num) {
+ if (queMin.empty() || num <= queMin.top()) {
+ queMin.push(num);
+ if (queMax.size() + 1 < queMin.size()) {
+ queMax.push(queMin.top());
+ queMin.pop();
+ }
+ } else {
+ queMax.push(num);
+ if (queMax.size() > queMin.size()) {
+ queMin.push(queMax.top());
+ queMax.pop();
+ }
+ }
+ }
+
+ double findMedian() {
+ if (queMin.size() > queMax.size()) {
+ return queMin.top();
+ }
+ return (queMin.top() + queMax.top()) / 2.0;
+ }
+};Leetcode-Interview
+ +实现一个算法,确定一个字符串 s 的所有字符是否全都不同。
class Solution {
+public:
+ bool isUnique(string astr) {
+ vector<int> visited(26, false);
+ for(int i=0;i<astr.size();i++){
+ int t = astr[i] - 'a';
+ if(visited[t] == true){
+ return false;
+ }
+ visited[t] = true;
+ }
+ return true;
+ }
+};给定两个由小写字母组成的字符串 s1 和 s2,请编写一个程序,确定其中一个字符串的字符重新排列后,能否变成另一个字符串。
class Solution {
+public:
+ bool CheckPermutation(string s1, string s2) {
+ vector<int> visited(26, 0);
+ for(int i=0;i<s1.size();i++){
+ visited[s1[i] - 'a'] += 1;
+ }
+ for(int i=0;i<s2.size();i++){
+ visited[s2[i] - 'a'] -= 1;
+ }
+ for(int i=0;i<26;i++){
+ if(visited[i] != 0){
+ return false;
+ }
+ }
+ return true;
+ }
+};URL化。编写一种方法,将字符串中的空格全部替换为 %20。假定该字符串尾部有足够的空间存放新增字符,并且知道字符串的“真实”长度。(注:用 Java实现的话,请使用字符数组实现,以便直接在数组上操作。)
class Solution {
+public:
+ string replaceSpaces(string S, int length) {
+ string res = "";
+ for(int i=0;i<length;i++){
+ if(S[i] == ' '){
+ res += "%20";
+ } else{
+ res += S[i];
+ }
+ }
+ return res;
+ }
+};给定一个字符串,编写一个函数判定其是否为某个回文串的排列之一。
+回文串是指正反两个方向都一样的单词或短语。排列是指字母的重新排列。
+回文串不一定是字典当中的单词。
+class Solution {
+public:
+ bool canPermutePalindrome(string s) {
+ set<char> st;
+ for(int i=0;i<s.size();i++){
+ if(st.count(s[i]) == 0){
+ st.insert(s[i]);
+ } else{
+ st.erase(s[i]);
+ }
+ }
+ return st.size() == 1 || st.size() == 0;
+ }
+};字符串有三种编辑操作:插入一个英文字符、删除一个英文字符或者替换一个英文字符。 给定两个字符串,编写一个函数判定它们是否只需要一次(或者零次)编辑。
+class Solution {
+public:
+ bool oneEditAway(string first, string second) {
+ int m = first.size();
+ int n = second.size();
+ vector<vector<int> > dp(m+1, vector<int>(n+1, 0));
+ for(int i=0;i<=m;i++){
+ dp[i][0] = i;
+ }
+ for(int j=0;j<=n;j++){
+ dp[0][j] = j;
+ }
+ for(int i=1;i<=m;i++){
+ for(int j=1;j<=n;j++){
+ if(first[i-1] == second[j-1]){
+ dp[i][j] = dp[i-1][j-1];
+ }else{
+ dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1])) + 1;
+ }
+ }
+ }
+ return dp[m][n] == 0 || dp[m][n] == 1;
+ }
+};字符串压缩。利用字符重复出现的次数,编写一种方法,实现基本的字符串压缩功能。比如,字符串 aabcccccaaa会变为 a2b1c5a3。若“压缩”后的字符串没有变短,则返回原先的字符串。你可以假设字符串中只包含大小写英文字母(a至z)。
class Solution {
+public:
+ string compressString(string S) {
+ if(S.size() == 0){
+ return S;
+ }
+ string res = "";
+ int count = 1;
+ char temp = S[0];
+ for(int i=1;i<S.size();i++){
+ if(S[i] == temp){
+ count += 1;
+ } else{
+ res += temp;
+ string tempcount = "";
+ while(count != 0){
+ tempcount += count%10 + '0';
+ count /= 10;
+ }
+ reverse(tempcount.begin(), tempcount.end());
+ res += tempcount;
+
+ count = 1;
+ temp = S[i];
+ }
+ }
+ res += temp;
+ string tempcount2 = "";
+ while(count != 0){
+ tempcount2 += count%10 + '0';
+ count /= 10;
+ }
+ reverse(tempcount2.begin(), tempcount2.end());
+ res += tempcount2;
+ if(res.size() < S.size()){
+ return res;
+ }
+ return S;
+ }
+};给你一幅由 N × N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。
不占用额外内存空间能否做到?
+class Solution {
+public:
+ void rotate(vector<vector<int>>& matrix) {
+ int n = matrix.size();
+ for(int i=0;i<(n+1)/2;i++){
+ for(int j=0;j<n/2;j++){
+ int temp = matrix[i][j];
+ matrix[i][j] = matrix[n-j-1][i];
+ matrix[n-j-1][i] = matrix[n-i-1][n-j-1];
+ matrix[n-i-1][n-j-1] = matrix[j][n-i-1];
+ matrix[j][n-i-1] = temp;
+ }
+ }
+ }
+};编写一种算法,若M × N矩阵中某个元素为0,则将其所在的行与列清零。
+class Solution {
+public:
+ void setZeroes(vector<vector<int>>& matrix) {
+ int m = matrix.size();
+ int n = matrix[0].size();
+ bool rowflag = false;
+ bool colflag = false;
+ for(int i=0;i<m;i++){
+ if(matrix[i][0] == 0){
+ colflag = true;
+ break;
+ }
+ }
+ for(int j=0;j<n;j++){
+ if(matrix[0][j] == 0){
+ rowflag = true;
+ break;
+ }
+ }
+ for(int i=1;i<m;i++){
+ for(int j=1;j<n;j++){
+ if(matrix[i][j] == 0){
+ matrix[0][j] = 0;
+ matrix[i][0] = 0;
+ }
+ }
+ }
+ for(int i=1;i<m;i++){
+ for(int j=1;j<n;j++){
+ if(matrix[0][j] == 0 || matrix[i][0] == 0){
+ matrix[i][j] = 0;
+ }
+ }
+ }
+ if(rowflag){
+ for(int j=0;j<n;j++){
+ matrix[0][j] = 0;
+ }
+ }
+ if(colflag){
+ for(int i=0;i<m;i++){
+ matrix[i][0] = 0;
+ }
+ }
+ }
+};字符串轮转。给定两个字符串 s1和 s2,请编写代码检查 s2是否为 s1旋转而成(比如,waterbottle是 erbottlewat旋转后的字符串)。
示例1:
+输入:s1 = "waterbottle", s2 = "erbottlewat" + 输出:True +
示例2:
+输入:s1 = "aa", s2 = "aba" + 输出:False +
class Solution {
+public:
+ bool isFlipedString(string s1, string s2) {
+ if(s1.size() != s2.size()){
+ return false;
+ }
+ if(s1 == ""){
+ return true;
+ }
+ int l = s1.size();
+ s1 = s1 + s1;
+ for(int i=0;i<s1.size();i++){
+ if(s1.substr(i,l) == s2){
+ return true;
+ }
+ }
+ return false;
+ }
+};编写代码,移除未排序链表中的重复节点。保留最开始出现的节点。
+class Solution {
+public:
+ ListNode* removeDuplicateNodes(ListNode* head) {
+ ListNode* t = head;
+ ListNode* p = head;
+ if(p == NULL){
+ return p;
+ }
+ set<int> st;
+ st.insert(p->val);
+ while(p->next != NULL){
+ ListNode* q = p->next;
+ if(st.count(q->val) != 0){
+ p->next = p->next->next;
+ } else{
+ p = p->next;
+ st.insert(q->val);
+ }
+ }
+ return t;
+ }
+};实现一种算法,找出单向链表中倒数第 k 个节点。返回该节点的值。
+class Solution {
+public:
+ int kthToLast(ListNode* head, int k) {
+ ListNode* slow = head;
+ ListNode* fast = head;
+ for(int i=0;i<k;i++){
+ fast = fast->next;
+ }
+ while(fast != NULL){
+ slow = slow->next;
+ fast = fast->next;
+ }
+ return slow->val;
+ }
+};若链表中的某个节点,既不是链表头节点,也不是链表尾节点,则称其为该链表的「中间节点」。
+假定已知链表的某一个中间节点,请实现一种算法,将该节点从链表中删除。
+例如,传入节点 c(位于单向链表 a->b->c->d->e->f 中),将其删除后,剩余链表为 a->b->d->e->f
示例:
+输入:节点 5 (位于单向链表 4->5->1->9 中) +输出:不返回任何数据,从链表中删除传入的节点 5,使链表变为 4->1->9 +
class Solution {
+public:
+ void deleteNode(ListNode* node) {
+ *node = *node->next;
+ }
+};给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你不需要 保留 每个分区中各节点的初始相对位置。
+class Solution {
+public:
+ ListNode* partition(ListNode* head, int x) {
+ ListNode* p = head;
+ ListNode* q = head;
+ while(q != NULL){
+ if(q->val < x){
+ swap(p->val,q->val);
+ p = p->next;
+ }
+ q = q->next;
+ }
+ return head;
+ }
+};给定两个用链表表示的整数,每个节点包含一个数位。
+这些数位是反向存放的,也就是个位排在链表首部。
+编写函数对这两个整数求和,并用链表形式返回结果。
+class Solution {
+public:
+ ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
+ ListNode* dummy = new ListNode(-1);
+ ListNode* l3 = dummy;
+ int cnt = 0;
+ int temp = 0;
+ while(l1 != NULL || l2 != NULL){
+ if(l1 == NULL){
+ temp = l2->val + cnt;
+ l2 = l2->next;
+ } else if(l2 == NULL){
+ temp = l1->val + cnt;
+ l1 = l1->next;
+ } else{
+ temp = l1->val + l2->val + cnt;
+ l1 = l1->next;
+ l2 = l2->next;
+ }
+ if(temp >= 10){
+ temp = temp - 10;
+ cnt = 1;
+ } else{
+ cnt = 0;
+ }
+ l3->next = new ListNode(temp);
+ l3 = l3->next;
+ }
+ if(cnt == 1){
+ l3->next = new ListNode(1);
+ }
+ return dummy->next;
+ }
+};编写一个函数,检查输入的链表是否是回文的。
+class Solution {
+public:
+ bool isPalindrome(ListNode* head) {
+ vector<int> result;
+ while(head != NULL){
+ result.push_back(head->val);
+ head = head->next;
+ }
+ int left = 0;
+ int right = result.size()-1;
+ while(left < right){
+ if(result[left] != result[right]){
+ return false;
+ }
+ left++;
+ right--;
+ }
+ return true;
+ }
+};给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
图示两个链表在节点 c1 开始相交**:**
题目数据 保证 整个链式结构中不存在环。
+注意 ,函数返回结果后,链表必须 保持其原始结构 。
+class Solution {
+public:
+ ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
+ ListNode* p = headA;
+ ListNode* q = headB;
+ while(p != q){
+ if(p == NULL){
+ p = headB;
+ } else{
+ p = p->next;
+ }
+ if(q == NULL){
+ q = headA;
+ } else{
+ q = q->next;
+ }
+ }
+ return p;
+ }
+};给定一个链表,如果它是有环链表,实现一个算法返回环路的 开头节点。若环不存在,请返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。 注意:pos 不作为参数进行传递 ,仅仅是为了标识链表的实际情况。
class Solution {
+public:
+ ListNode *detectCycle(ListNode *head) {
+ ListNode* slow = head;
+ ListNode* fast = head;
+ while(fast != NULL && fast->next != NULL){
+ slow = slow->next;
+ fast = fast->next->next;
+ if(slow == fast){
+ break;
+ }
+ }
+ if(fast == NULL || fast->next == NULL){
+ return NULL;
+ }
+ fast = head;
+ while(slow != fast){
+ slow = slow->next;
+ fast = fast->next;
+ }
+ return slow;
+ }
+};三合一。描述如何只用一个数组来实现三个栈。
+你应该实现 push(stackNum, value)、pop(stackNum)、isEmpty(stackNum)、peek(stackNum)方法。stackNum表示栈下标,value表示压入的值。
构造函数会传入一个 stackSize参数,代表每个栈的大小。
class TripleInOne {
+private:
+ vector<int> stackown;
+ vector<int> nowtop;
+public:
+ TripleInOne(int stackSize) {
+ for(int i=0;i<stackSize*3;i++){
+ stackown.push_back(0);
+ }
+ nowtop.push_back(0);
+ nowtop.push_back(1);
+ nowtop.push_back(2);
+ }
+
+ void push(int stackNum, int value) {
+ if(nowtop[stackNum] / 3 == stackown.size() / 3){
+ return;
+ }
+ stackown[nowtop[stackNum]] = value;
+ nowtop[stackNum] += 3;
+ }
+
+ int pop(int stackNum) {
+ if(nowtop[stackNum] == stackNum){
+ return -1;
+ }
+ int t = stackown[nowtop[stackNum]-3];
+ nowtop[stackNum] -= 3;
+ return t;
+ }
+
+ int peek(int stackNum) {
+ if(nowtop[stackNum] == stackNum){
+ return -1;
+ }
+ return stackown[nowtop[stackNum]-3];
+ }
+
+ bool isEmpty(int stackNum) {
+ if(nowtop[stackNum] == stackNum){
+ return true;
+ }
+ return false;
+ }
+};
+
+/**
+ * Your TripleInOne object will be instantiated and called as such:
+ * TripleInOne* obj = new TripleInOne(stackSize);
+ * obj->push(stackNum,value);
+ * int param_2 = obj->pop(stackNum);
+ * int param_3 = obj->peek(stackNum);
+ * bool param_4 = obj->isEmpty(stackNum);
+ */请设计一个栈,除了常规栈支持的pop与push函数以外,还支持min函数,该函数返回栈元素中的最小值。执行push、pop和min操作的时间复杂度必须为O(1)。
+class MinStack {
+private:
+ stack<int> st;
+ stack<int> minst;
+public:
+ /** initialize your data structure here. */
+ MinStack() {
+ minst.push(INT_MAX);
+ }
+
+ void push(int x) {
+ st.push(x);
+ if(x < minst.top()){
+ minst.push(x);
+ }else{
+ minst.push(minst.top());
+ }
+ }
+
+ void pop() {
+ st.pop();
+ minst.pop();
+ }
+
+ int top() {
+ return st.top();
+ }
+
+ int getMin() {
+ return minst.top();
+ }
+};堆盘子。设想有一堆盘子,堆太高可能会倒下来。因此,在现实生活中,盘子堆到一定高度时,我们就会另外堆一堆盘子。请实现数据结构 SetOfStacks,模拟这种行为。SetOfStacks应该由多个栈组成,并且在前一个栈填满时新建一个栈。此外,SetOfStacks.push()和 SetOfStacks.pop()应该与普通栈的操作方法相同(也就是说,pop()返回的值,应该跟只有一个栈时的情况一样)。 进阶:实现一个 popAt(int index)方法,根据指定的子栈,执行pop操作。
当某个栈为空时,应当删除该栈。当栈中没有元素或不存在该栈时,pop,popAt 应返回 -1.
class StackOfPlates {
+private:
+ vector<stack<int> > vt;
+ int capacity;
+public:
+ StackOfPlates(int cap) {
+ capacity = cap;
+ }
+
+ void push(int val) {
+ if (capacity == 0){
+ return;
+ }
+ if(vt.empty()){
+ stack<int> st;
+ st.push(val);
+ vt.push_back(st);
+ return;
+ }
+ int l = vt.size()-1;
+ if(vt[l].size() == capacity){
+ stack<int> st;
+ st.push(val);
+ vt.push_back(st);
+ return;
+ }
+ vt[l].push(val);
+ }
+
+ int pop() {
+ if (capacity == 0 || vt.empty()) {
+ return -1;
+ }
+ int l = vt.size()-1;
+ int t = vt[l].top();
+ vt[l].pop();
+ if(vt[l].empty()){
+ vt.pop_back();
+ }
+ return t;
+ }
+
+ int popAt(int index) {
+ if (capacity == 0 || index >= vt.size()){
+ return -1;
+ }
+ int res = vt[index].top();
+ vt[index].pop();
+ if (vt[index].empty()) {
+ // 如果当前栈空,最后删除当前栈
+ vt.erase(vt.begin() + index);
+ }
+ return res;
+ }
+};实现一个MyQueue类,该类用两个栈来实现一个队列。
+class MyQueue {
+private:
+ stack<int> st1;
+ stack<int> st2;
+public:
+ /** Initialize your data structure here. */
+ MyQueue() {
+
+ }
+
+ /** Push element x to the back of queue. */
+ void push(int x) {
+ while(!st2.empty()){
+ st1.push(st2.top());
+ st2.pop();
+ }
+ st1.push(x);
+ }
+
+ /** Removes the element from in front of queue and returns that element. */
+ int pop() {
+ while(!st1.empty()){
+ st2.push(st1.top());
+ st1.pop();
+ }
+ int t = st2.top();
+ st2.pop();
+ return t;
+ }
+
+ /** Get the front element. */
+ int peek() {
+ while(!st1.empty()){
+ st2.push(st1.top());
+ st1.pop();
+ }
+ return st2.top();
+ }
+
+ /** Returns whether the queue is empty. */
+ bool empty() {
+ return st1.empty() && st2.empty();
+ }
+};栈排序。 编写程序,对栈进行排序使最小元素位于栈顶。最多只能使用一个其他的临时栈存放数据,但不得将元素复制到别的数据结构(如数组)中。该栈支持如下操作:push、pop、peek 和 isEmpty。当栈为空时,peek 返回 -1。
class SortedStack {
+private:
+ stack<int> st1;
+ stack<int> st2;
+public:
+ SortedStack() {
+
+ }
+
+ void push(int val) {
+ while(!st2.empty() && st2.top() > val){
+ st1.push(st2.top());
+ st2.pop();
+ }
+ while(!st1.empty() && st1.top() < val){
+ st2.push(st1.top());
+ st1.pop();
+ }
+ st1.push(val);
+ }
+
+ void pop() {
+ while(!st2.empty()){
+ st1.push(st2.top());
+ st2.pop();
+ }
+ if(st1.size() != 0){
+ st1.pop();
+ }
+ }
+
+ int peek() {
+ while(!st2.empty()){
+ st1.push(st2.top());
+ st2.pop();
+ }
+ if(!st1.empty()){
+ return st1.top();
+ }
+ return -1;
+ }
+
+ bool isEmpty() {
+ return st1.empty() && st2.empty();
+ }
+};动物收容所。有家动物收容所只收容狗与猫,且严格遵守“先进先出”的原则。在收养该收容所的动物时,收养人只能收养所有动物中“最老”(由其进入收容所的时间长短而定)的动物,或者可以挑选猫或狗(同时必须收养此类动物中“最老”的)。换言之,收养人不能自由挑选想收养的对象。请创建适用于这个系统的数据结构,实现各种操作方法,比如 enqueue、dequeueAny、dequeueDog和 dequeueCat。允许使用Java内置的LinkedList数据结构。
enqueue方法有一个 animal参数,animal[0]代表动物编号,animal[1]代表动物种类,其中 0 代表猫,1 代表狗。
dequeue*方法返回一个列表 [动物编号, 动物种类],若没有可以收养的动物,则返回 [-1,-1]。
class AnimalShelf {
+private:
+ queue<int> cats, dogs;
+public:
+ AnimalShelf() {
+
+ }
+
+ void enqueue(vector<int> animal) {
+ int id = animal[0];
+ int type = animal[1];
+ if (type == 1){
+ dogs.push(id);
+ }
+ else{
+ cats.push(id);
+ }
+ }
+
+ vector<int> dequeueAny() {
+ if(cats.empty()){
+ return dequeueDog();
+ }
+ if(dogs.empty()){
+ return dequeueCat();
+ }
+ if(cats.front() < dogs.front()){
+ return dequeueCat();
+ }
+ return dequeueDog();
+ }
+
+ vector<int> dequeueDog() {
+ if(dogs.empty()){
+ return {-1, -1};
+ }
+ int id = dogs.front();
+ dogs.pop();
+ return {id, 1};
+ }
+
+ vector<int> dequeueCat() {
+ if(cats.empty()){
+ return {-1, -1};
+ }
+ int id = cats.front();
+ cats.pop();
+ return {id, 0};
+ }
+};节点间通路。给定有向图,设计一个算法,找出两个节点之间是否存在一条路径。
+class Solution {
+public:
+ bool findWhetherExistsPath(int n, vector<vector<int>>& graph, int start, int target) {
+ if(n == 0){
+ return false;
+ }
+ vector<vector<int> > g(n);
+ for(int i=0;i<graph.size();i++){
+ g[graph[i][0]].push_back(graph[i][1]);
+ }
+ vector<bool> vis(n, false);
+ queue<int> q;
+ q.push(start);
+ vis[start] = true;
+ while(!q.empty()){
+ int cur = q.front();
+ q.pop();
+ for(int i=0;i<g[cur].size();i++){
+ if(g[cur][i] == target){
+ return true;
+ }
+ if(!vis[g[cur][i]] && g[cur][i] != cur){
+ q.push(g[cur][i]);
+ vis[g[cur][i]] = true;
+ }
+ }
+ }
+ return false;
+ }
+};给定一个有序整数数组,元素各不相同且按升序排列,编写一个算法,创建一棵高度最小的二叉搜索树。
+class Solution {
+public:
+ TreeNode* sortedArrayToBST(vector<int>& nums) {
+ if(nums.size() == 0){
+ return NULL;
+ }
+ int mid = nums.size() / 2;
+ TreeNode* root = new TreeNode(nums[mid]);
+ vector<int> templeft;
+ vector<int> tempright;
+ for(int i=0;i<nums.size();i++){
+ if(i < mid){
+ templeft.push_back(nums[i]);
+ } else if(i > mid){
+ tempright.push_back(nums[i]);
+ }
+ }
+ root->left = sortedArrayToBST(templeft);
+ root->right = sortedArrayToBST(tempright);
+ return root;
+ }
+};给定一棵二叉树,设计一个算法,创建含有某一深度上所有节点的链表(比如,若一棵树的深度为 D,则会创建出 D 个链表)。返回一个包含所有深度的链表的数组。
class Solution {
+public:
+ vector<ListNode*> listOfDepth(TreeNode* tree) {
+ vector<ListNode*> vt;
+ queue<TreeNode*> q;
+ if(tree == NULL){
+ return vt;
+ }
+ q.push(tree);
+ while(!q.empty()){
+ int t = q.size();
+ ListNode* n = new ListNode(-1);
+ ListNode* nhead = n;
+ for(int i=0;i<t;i++){
+ TreeNode* a = q.front();
+ q.pop();
+ n->next = new ListNode(a->val);
+ n = n->next;
+ if(a->left != NULL){
+ q.push(a->left);
+ }
+ if(a->right != NULL){
+ q.push(a->right);
+ }
+ }
+ vt.push_back(nhead->next);
+ }
+ return vt;
+ }
+};实现一个函数,检查二叉树是否平衡。在这个问题中,平衡树的定义如下:任意一个节点,其两棵子树的高度差不超过 1。
+class Solution {
+public:
+ int balance(TreeNode* root){
+ if(root == NULL){
+ return 0;
+ }
+ int left = balance(root->left);
+ int right = balance(root->right);
+ return max(left, right) + 1;
+ }
+ bool isBalanced(TreeNode* root) {
+ if(root == NULL){
+ return true;
+ }
+ int left = balance(root->left);
+ int right = balance(root->right);
+ if(abs(left-right) > 1){
+ return false;
+ }
+ return isBalanced(root->left) && isBalanced(root->right);
+ }
+};实现一个函数,检查一棵二叉树是否为二叉搜索树。
+class Solution {
+private:
+ vector<int> result;
+public:
+ void inorder(TreeNode* root){
+ if(root == NULL){
+ return;
+ }
+ inorder(root->left);
+ result.push_back(root->val);
+ inorder(root->right);
+ }
+ bool isValidBST(TreeNode* root) {
+ if(root == NULL){
+ return true;
+ }
+ inorder(root);
+ for(int i=0;i<result.size()-1;i++){
+ if(result[i+1] <= result[i]){
+ return false;
+ }
+ }
+ return true;
+ }
+};设计一个算法,找出二叉搜索树中指定节点的“下一个”节点(也即中序后继)。
+如果指定节点没有对应的“下一个”节点,则返回 null。
class Solution {
+public:
+ TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
+ stack<TreeNode*> st;
+ TreeNode *prev = NULL, *curr = root;
+ while (!st.empty() || curr != NULL) {
+ while (curr != NULL) {
+ st.emplace(curr);
+ curr = curr->left;
+ }
+ curr = st.top();
+ st.pop();
+ if (prev == p) {
+ return curr;
+ }
+ prev = curr;
+ curr = curr->right;
+ }
+ return NULL;
+ }
+};设计并实现一个算法,找出二叉树中某两个节点的第一个共同祖先。不得将其他的节点存储在另外的数据结构中。注意:这不一定是二叉搜索树。
+class Solution {
+public:
+ TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
+ if(root == NULL || root == p || root == q){
+ return root;
+ }
+ TreeNode* left = lowestCommonAncestor(root->left, p, q);
+ TreeNode* right = lowestCommonAncestor(root->right, p, q);
+ if(left != NULL && right != NULL){
+ return root;
+ }
+ if(left == NULL){
+ return right;
+ }
+ return left;
+ }
+};从左向右遍历一个数组,通过不断将其中的元素插入树中可以逐步地生成一棵二叉搜索树。
+给定一个由不同节点组成的二叉搜索树 root,输出所有可能生成此树的数组。
class Solution {
+private:
+ vector<vector<int>> res;
+ vector<int> tmp;
+public:
+ void dfs(deque<TreeNode*> dq){
+ if (dq.empty())
+ {
+ res.push_back(tmp); //得到一种合法序列
+ return;
+ }
+
+ int size = dq.size();
+ while (size -- ) //二叉树的层序遍历
+ {
+ TreeNode* node = dq.front();
+ dq.pop_front();
+
+ tmp.push_back(node->val);
+
+ if (node->left) dq.push_back(node->left); //左右子树入队
+ if (node->right) dq.push_back(node->right);
+
+ dfs(dq);
+
+ if (node->right) dq.pop_back(); //左右子树出队
+ if (node->left) dq.pop_back();
+
+ dq.push_back(node);
+ tmp.pop_back();
+ }
+ }
+
+ vector<vector<int>> BSTSequences(TreeNode* root) {
+ if (root == nullptr) return {{}};
+ deque<TreeNode*> dq;
+ dq.push_back(root);
+ dfs(dq);
+
+ return res;
+ }
+};检查子树。你有两棵非常大的二叉树:T1,有几万个节点;T2,有几万个节点。设计一个算法,判断 T2 是否为 T1 的子树。
+如果 T1 有这么一个节点 n,其子树与 T2 一模一样,则 T2 为 T1 的子树,也就是说,从节点 n 处把树砍断,得到的树与 T2 完全相同。
+class Solution {
+public:
+ bool isSame(TreeNode* t1, TreeNode* t2){
+ if(t1 == NULL && t2 == NULL){
+ return true;
+ }
+ if(t1 == NULL || t2 == NULL){
+ return false;
+ }
+ if(t1->val != t2->val){
+ return false;
+ }
+ return isSame(t1->left, t2->left) && isSame(t1->right, t2->right);
+ }
+ bool checkSubTree(TreeNode* t1, TreeNode* t2) {
+ if(t1 == NULL && t2 == NULL){
+ return true;
+ }
+ if(t1 == NULL || t2 == NULL){
+ return false;
+ }
+ if(t1->val == t2->val && isSame(t1, t2)){
+ return true;
+ }
+ return checkSubTree(t1->left, t2) || checkSubTree(t1->right, t2);
+ }
+};给定一棵二叉树,其中每个节点都含有一个整数数值(该值或正或负)。设计一个算法,打印节点数值总和等于某个给定值的所有路径的数量。注意,路径不一定非得从二叉树的根节点或叶节点开始或结束,但是其方向必须向下(只能从父节点指向子节点方向)。
+class Solution {
+private:
+ int res;
+public:
+ void DFS(TreeNode* root, int sum){
+ if(root == NULL){
+ return;
+ }
+ if(sum == root->val){
+ res += 1;
+ }
+ DFS(root->left, sum-root->val);
+ DFS(root->right, sum-root->val);
+ }
+ void DFS1(TreeNode* root, int sum){
+ if(root == NULL){
+ return;
+ }
+ DFS(root, sum);
+ DFS1(root->left, sum);
+ DFS1(root->right, sum);
+ }
+ int pathSum(TreeNode* root, int sum) {
+ res = 0;
+ DFS1(root, sum);
+ return res;
+ }
+};给定两个整型数字 N 与 M,以及表示比特位置的 i 与 j(i <= j,且从 0 位开始计算)。
编写一种方法,使 M 对应的二进制数字插入 N 对应的二进制数字的第 i ~ j 位区域,不足之处用 0 补齐。具体插入过程如图所示。
N的第 i ~ j位全部置零;M左移 i位,使之对齐上一步中 N置零的位,直接相加即可。class Solution {
+public:
+ int insertBits(int N, int M, int i, int j) {
+ for (int k = i; k <= j; ++ k){
+ //举例说明: (1 << 3) 表示 00001000,取反后得 11110111
+ // N &= (11110111) 表示将 N 的第3位置零了
+ N &= ~(1 << k);
+ }
+ return N + (M << i);
+ }
+};二进制数转字符串。给定一个介于0和1之间的实数(如0.72),类型为double,打印它的二进制表达式。如果该数字无法精确地用32位以内的二进制表示,则打印“ERROR”。
+class Solution {
+public:
+ string printBin(double num) {
+ string res = "0.";
+ while (res.size() <= 32 && num != 0) {
+ num *= 2;
+ int digit = num;
+ res.push_back(digit + '0');
+ num -= digit;
+ }
+ return res.size() <= 32 ? res : "ERROR";
+ }
+};给定一个32位整数 num,你可以将一个数位从0变为1。请编写一个程序,找出你能够获得的最长的一串1的长度。
暴力思路:
+思路优化:
+class Solution {
+public:
+ int reverseBits(int num) {
+ if (~num == 0) return 32;
+ int previous = 0;
+ int current = 0;
+ int length = 0;
+ for (int i = 0; i < 32; i++) {
+ if (num & 1) {
+ current++;
+ } else {
+ previous = current;
+ current = 0;
+ }
+ length = max(length, previous + current + 1);
+ num >>= 1;
+ }
+ return length;
+
+ }
+};下一个数。给定一个正整数,找出与其二进制表达式中1的个数相同且大小最接近的那两个数(一个略大,一个略小)。
+class Solution {
+public:
+ int f(int num) {
+ int lb = num & -num;
+ int r = lb + num;
+ //if(r==0)return 0; 这里是对small没有10的判断,但是也会影响large
+ return (num ^r)/lb >> 2 | r;
+ }
+ vector<int> findClosedNumbers(int num) {
+ if (num == INT_MAX) return {-1,-1};
+ if (num==1)return {2,-1};
+ return {f(num), ~f(~num)}; //large和small
+ }
+};整数转换。编写一个函数,确定需要改变几个位才能将整数A转成整数B。
+不断对 c 进行移位操作,然后检查最低有效位。
+class Solution {
+public:
+ int convertInteger(int A, int B) {
+ int res = 0;
+ for (unsigned c = A ^ B; c != 0; c = c >> 1)
+ res += c & 1; // 数一数 c 中有几个 1
+ return res;
+ }
+};配对交换。编写程序,交换某个整数的奇数位和偶数位,尽量使用较少的指令(也就是说,位0与位1交换,位2与位3交换,以此类推)。
+class Solution {
+public:
+ int exchangeBits(int num) {
+ int pre=1;
+ int res=0;
+ while(pre<=num)
+ {
+ res|=(pre&num)<<1;
+ res|=((pre<<1)&num)>>1;
+ pre<<=2;
+ }
+ return res;
+ }
+};已知一个由像素点组成的单色屏幕,每行均有 w 个像素点,所有像素点初始为 0,左上角位置为 (0,0)。
现将每行的像素点按照「每 32 个像素点」为一组存放在一个 int 中,再依次存入长度为 length 的一维数组中。
我们将在屏幕上绘制一条从点 (x1,y) 到点 (x2,y) 的直线(即像素点修改为 1),请返回绘制过后的数组。
class Solution {
+public:
+ vector<int> drawLine(int length, int w, int x1, int x2, int y) {
+ // 注意直线的坐标
+ // 实际上需要特殊处理的 只有直线所在的那一行
+ // 结果数组从 像素点(0, 0)开始计算
+ int per_row = w / 32;
+ vector<int> res(length, 0);
+ for(int i = x1; i <= x2 && i < length * 32; i++)
+ res[y * per_row + i / 32] |= (1 << 31 - i % 32); // 从左到右,先高后低
+
+ return res;
+ }
+};三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
+class Solution {
+public:
+ int waysToStep(int n) {
+ if(n == 1 || n == 2){
+ return n;
+ }
+ if(n == 3){
+ return 4;
+ }
+ vector<int> dp(n+1, 0);
+ dp[0] = 0;
+ dp[1] = 1;
+ dp[2] = 2;
+ dp[3] = 4;
+ for(int i=4;i<=n;i++){
+ dp[i] = (dp[i-1] + dp[i-2]) % 1000000007 +dp[i-3];
+ dp[i] %= 1000000007;
+ }
+ return dp[n];
+ }
+};设想有个机器人坐在一个网格的左上角,网格 r 行 c 列。机器人只能向下或向右移动,但不能走到一些被禁止的网格(有障碍物)。设计一种算法,寻找机器人从左上角移动到右下角的路径。
+class Solution {
+public:
+ bool DFS(vector<vector<int>>& obstacleGrid, vector<vector<int>>& result, int i, int j, int m, int n){
+ if(obstacleGrid[i][j] == 1){
+ return false;
+ }
+ if(i == m-1 && j == n-1){
+ result.push_back({i,j});
+ return true;
+ }
+ result.push_back({i,j});
+ if(i+1 < m && DFS(obstacleGrid, result, i+1,j,m,n)){
+ return true;
+ }
+ if(j+1 < n && DFS(obstacleGrid, result, i,j+1,m,n)){
+ return true;
+ }
+ result.pop_back();
+ obstacleGrid[i][j] = 1;
+ return false;
+ }
+ vector<vector<int>> pathWithObstacles(vector<vector<int>>& obstacleGrid) {
+ vector<vector<int> > result;
+ int m = obstacleGrid.size();
+ int n = obstacleGrid[0].size();
+ DFS(obstacleGrid, result, 0,0,m,n);
+ return result;
+ }
+};魔术索引。 在数组 A[0...n-1]中,有所谓的魔术索引,满足条件 A[i] = i。给定一个有序整数数组,编写一种方法找出魔术索引,若有的话,在数组A中找出一个魔术索引,如果没有,则返回-1。若有多个魔术索引,返回索引值最小的一个。
class Solution {
+public:
+ int findMagicIndex(vector<int>& nums) {
+ for(int i = 0; i<nums.size(); i++){
+ if(i == nums[i]) return i;
+ }
+ return -1;
+ }
+};幂集。编写一种方法,返回某集合的所有子集。集合中 不包含重复的元素 。
+说明:解集不能包含重复的子集。
+class Solution {
+public:
+ void backtracking(vector<vector<int> > &result, vector<int>& temp, vector<int>& nums, int start){
+ result.push_back(temp);
+ for(int i=start;i<nums.size();i++){
+ temp.push_back(nums[i]);
+ backtracking(result, temp, nums, i+1);
+ temp.pop_back();
+ }
+ }
+ vector<vector<int>> subsets(vector<int>& nums) {
+ vector<vector<int> > result;
+ vector<int> temp;
+ backtracking(result, temp, nums, 0);
+ return result;
+ }
+};递归乘法。 写一个递归函数,不使用 * 运算符, 实现两个正整数的相乘。可以使用加号、减号、位移,但要吝啬一些。
+class Solution {
+public:
+ int multiply(int A, int B) {
+ if(B){//B非0才计算
+ //从0阶(A*(B&1)*2^0)开始,每次算当前阶(A*(B&1)*2^n)的乘法并累加起来,算到B为0为止。
+ if(B&1){//如果B的最后一位是1
+ //把B的阶放到A上去,递归算B的倒数第2位和A的乘法,然后求和+(1*A=A)。
+ return multiply((long long)A<<1,B>>1)+A;
+ }else{
+ //把B的阶放到A上去,递归算B的倒数第2位和A的乘法,然后求和+(0*A=0)。
+ return multiply((long long)A<<1,B>>1);
+ }
+ }
+ // B为0结果当然是0
+ return 0;
+ }
+};在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
+(1) 每次只能移动一个盘子;
+(2) 盘子只能从柱子顶端滑出移到下一根柱子;
+(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
+你需要原地修改栈。
+class Solution {
+public:
+ void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
+ int n = A.size();
+ move(n, A, B, C);
+ }
+ void move(int n, vector<int>& A, vector<int>& B, vector<int>& C){
+ if (n == 1){
+ C.push_back(A.back());
+ A.pop_back();
+ return;
+ }
+
+ move(n-1, A, C, B); // 将A上面n-1个通过C移到B
+ C.push_back(A.back()); // 将A最后一个移到C
+ A.pop_back(); // 这时,A空了
+ move(n-1, B, A, C); // 将B上面n-1个通过空的A移到C
+ }
+};无重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合,字符串每个字符均不相同。
+class Solution {
+public:
+ void backtracking(vector<string> & result, string S, vector<char> &temp, vector<bool> &visited){
+ if(temp.size() == S.size()){
+ string t = "";
+ for(int i=0;i<temp.size();i++){
+ t += temp[i];
+ }
+ result.push_back(t);
+ return;
+ }
+ for(int i=0;i<S.size();i++){
+ if (visited[i] == false){
+ visited[i] = true;
+ temp.push_back(S[i]);
+ backtracking(result, S, temp, visited);
+ temp.pop_back();
+ visited[i] = false;
+ }
+
+ }
+ }
+ vector<string> permutation(string S) {
+ vector<string> result;
+ vector<char> temp;
+ vector<bool> visited(S.size(), false);
+ backtracking(result, S, temp, visited);
+ return result;
+ }
+};有重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合。
+class Solution {
+public:
+ void backtracking(vector<string> & result, string S, vector<char> &temp, vector<bool> &visited){
+ if(temp.size() == S.size()){
+ string t = "";
+ for(int i=0;i<temp.size();i++){
+ t += temp[i];
+ }
+ result.push_back(t);
+ return;
+ }
+ for(int i=0;i<S.size();i++){
+ if(i > 0 && S[i] == S[i-1] && visited[i-1] == false){
+ continue;
+ }
+ if (visited[i] == false){
+ visited[i] = true;
+ temp.push_back(S[i]);
+ backtracking(result, S, temp, visited);
+ temp.pop_back();
+ visited[i] = false;
+ }
+
+ }
+ }
+ vector<string> permutation(string S) {
+ sort(S.begin(), S.end());
+ vector<string> result;
+ vector<char> temp;
+ vector<bool> visited(S.size(), false);
+ backtracking(result, S, temp, visited);
+ return result;
+ }
+};括号。设计一种算法,打印n对括号的所有合法的(例如,开闭一一对应)组合。
+说明:解集不能包含重复的子集。
+class Solution {
+public:
+ void backtracking(vector<string> &result, vector<char> &temp, int nowleft, int n){
+ if(temp.size() == n * 2){
+ if(nowleft == 0){
+ string t = "";
+ for(int i=0;i<temp.size();i++){
+ t += temp[i];
+ }
+ result.push_back(t);
+ }
+ return;
+ }
+ temp.push_back('(');
+ backtracking(result, temp, nowleft+1, n);
+ temp.pop_back();
+ if(nowleft > 0){
+ temp.push_back(')');
+ backtracking(result, temp, nowleft-1, n);
+ temp.pop_back();
+ }
+ }
+ vector<string> generateParenthesis(int n) {
+ vector<string> result;
+ vector<char> temp;
+ backtracking(result, temp, 0, n);
+ return result;
+ }
+};编写函数,实现许多图片编辑软件都支持的「颜色填充」功能。
+待填充的图像用二维数组 image 表示,元素为初始颜色值。初始坐标点的行坐标为 sr 列坐标为 sc。需要填充的新颜色为 newColor 。
「周围区域」是指颜色相同且在上、下、左、右四个方向上存在相连情况的若干元素。
+请用新颜色填充初始坐标点的周围区域,并返回填充后的图像。
+class Solution {
+public:
+ vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor) {
+ int m = image.size();
+ int n = image[0].size();
+ vector<vector<bool> > visited(m, vector<bool>(n, false));
+ queue<pair<int, int> > q;
+ q.push({sr, sc});
+ visited[sr][sc] = true;
+ int sign = image[sr][sc];
+ image[sr][sc] = newColor;
+ vector<vector<int> > direction = {
+ {0,-1},
+ {0,1},
+ {-1,0},
+ {1,0},
+ };
+ while(!q.empty()){
+ pair<int, int> p = q.front();
+ q.pop();
+ for(int i=0;i<direction.size();i++){
+ for(int j=0;j<direction[0].size();j++){
+ int x = p.first + direction[i][0];
+ int y = p.second + direction[i][1];
+ if(x >= 0 && x < m && y >= 0 && y < n && image[x][y] == sign && visited[x][y] == false){
+ q.push({x,y});
+ image[x][y] = newColor;
+ visited[x][y] = true;
+ }
+ }
+ }
+ }
+ return image;
+ }
+};硬币。给定数量不限的硬币,币值为25分、10分、5分和1分,编写代码计算n分有几种表示法。(结果可能会很大,你需要将结果模上1000000007)
+class Solution {
+public:
+ int waysToChange(int n) {
+ vector<int> coins = {25,10,5,1};
+ vector<int> dp(n+1, 0);
+ dp[0] = 1;
+ for(int i=0;i<coins.size();i++){
+ for(int j=coins[i];j<=n;j++){
+ dp[j] = (dp[j] + dp[j-coins[i]]) % 1000000007;
+ }
+ }
+ return dp[n];
+ }
+};设计一种算法,打印 N 皇后在 N × N 棋盘上的各种摆法,其中每个皇后都不同行、不同列,也不在对角线上。这里的“对角线”指的是所有的对角线,不只是平分整个棋盘的那两条对角线。
+class Solution {
+public:
+ bool check(vector<vector<char> > &temp, int nowindex){
+ int m = temp.size();
+ int n = temp[0].size();
+ for(int i=0;i<m-1;i++){
+ if(temp[i][nowindex] == 'Q'){
+ return false;
+ }
+ }
+ int x = m-1-1;
+ int y = nowindex-1;
+ while(x >= 0 && y >= 0){
+ if(temp[x][y] == 'Q'){
+ return false;
+ }
+ x--;
+ y--;
+ }
+ x = m-1-1;
+ y = nowindex+1;
+ while(x >= 0 && y < n){
+ if(temp[x][y] == 'Q'){
+ return false;
+ }
+ x--;
+ y++;
+ }
+ return true;
+ }
+ void backtracking(vector<vector<string> > &result, vector<vector<char> > &temp, int n, int now){
+ if(now == n){
+ vector<string> t;
+ for(int i=0;i<temp.size();i++){
+ string tempstring = "";
+ for(int j=0;j<temp[i].size();j++){
+ tempstring += temp[i][j];
+ }
+ t.push_back(tempstring);
+ }
+ result.push_back(t);
+ return;
+ }
+
+ for(int i=0;i<n;i++){
+ vector<char> vt;
+ for(int j=0;j<n;j++){
+ vt.push_back('.');
+ }
+ vt[i] = 'Q';
+ temp.push_back(vt);
+ if(check(temp, i)){
+ backtracking(result, temp, n, now+1);
+ }
+ temp.pop_back();
+ }
+ }
+ vector<vector<string>> solveNQueens(int n) {
+ vector<vector<string> > result;
+ vector<vector<char> > temp;
+ backtracking(result, temp, n, 0);
+ return result;
+ }
+};堆箱子。给你一堆n个箱子,箱子宽 wi、深 di、高 hi。箱子不能翻转,将箱子堆起来时,下面箱子的宽度、高度和深度必须大于上面的箱子。实现一种方法,搭出最高的一堆箱子。箱堆的高度为每个箱子高度的总和。
+输入使用数组 [wi, di, hi]表示每个箱子。
class Solution {
+public:
+ int pileBox(vector<vector<int>>& box) {
+ sort(box.begin(), box.end());
+ vector<int> dp(box.size(), 0);
+ for (int i = 0; i < box.size(); ++i) {
+ dp[i] = box[i][2];
+ }
+ for (int i = 1; i < box.size(); ++i) {
+ for (int j = 0; j < i; ++j) {
+ if (box[i][0] > box[j][0] && box[i][1] > box[j][1] && box[i][2] > box[j][2])
+ dp[i] = max(dp[i], dp[j] + box[i][2]);
+ }
+ }
+ return *max_element(dp.begin(), dp.end());
+ }
+};给定一个布尔表达式和一个期望的布尔结果 result,布尔表达式由 0 (false)、1 (true)、& (AND)、 | (OR) 和 ^ (XOR) 符号组成。实现一个函数,算出有几种可使该表达式得出 result 值的括号方法。
然后枚举中间断点就行啦
+class Solution {
+public:
+ int countEval(string s, int result) {
+ int n = s.length();
+ vector<vector<vector<int>>> dp(n, vector<vector<int>>(n, vector<int>(2, 0)));
+
+ for (int i=0; i<n; i+=2){
+ int tmp = 0;
+ if (s[i] == '1') tmp = 1;
+ dp[i][i][0] = 1-tmp;
+ dp[i][i][1] = tmp;
+ }
+
+ for (int step=0; step<n; step+=2){
+ for (int i=0; i+step<n; i+=2){
+ for (int j=i+1; j<i+step; j+=2){
+ int left0 = dp[i][j-1][0], left1 = dp[i][j-1][1];
+ int right0 = dp[j+1][i+step][0], right1 = dp[j+1][i+step][1];
+ // cout<<i<<" "<<i+step<<" "<<left0<<" "<<left1<<" "<<right0<<" "<<right1;
+ if (s[j]=='&'){
+ dp[i][i+step][0] += left0*(right0+right1)+left1*right0;
+ dp[i][i+step][1] += left1*right1;
+ }
+ else if (s[j]=='|'){
+ dp[i][i+step][0] += left0*right0;
+ dp[i][i+step][1] += left0*right1 + left1*(right0+right1);
+ }
+ else{//s[j]=='^'
+ dp[i][i+step][0] += left0*right0 + left1*right1;
+ dp[i][i+step][1] += left0*right1 + left1*right0;
+ }
+ // cout<<" dp[i][i+step][0]:"<<dp[i][i+step][0]<<" dp[i][i+step][1]:"<<dp[i][i+step][1]<<endl;
+ }
+ }
+ }
+ return dp[0][n-1][result];
+ }
+};给定两个排序后的数组 A 和 B,其中 A 的末端有足够的缓冲空间容纳 B。 编写一个方法,将 B 合并入 A 并排序。
+初始化 A 和 B 的元素数量分别为 m 和 n 。
+class Solution {
+public:
+ void merge(vector<int>& A, int m, vector<int>& B, int n) {
+ int actualindex = m + n - 1;
+ int Aindex = m - 1;
+ int Bindex = n - 1;
+ while(Aindex >= 0 || Bindex >= 0){
+ if(Aindex < 0){
+ A[actualindex] = B[Bindex];
+ Bindex--;
+ } else if(Bindex < 0){
+ A[actualindex] = A[Aindex];
+ Aindex--;
+ } else{
+ if(A[Aindex] < B[Bindex]){
+ A[actualindex] = B[Bindex];
+ Bindex--;
+ } else{
+ A[actualindex] = A[Aindex];
+ Aindex--;
+ }
+ }
+ actualindex--;
+ }
+ }
+};编写一种方法,对字符串数组进行排序,将所有变位词组合在一起。变位词是指字母相同,但排列不同的字符串。
+class Solution {
+public:
+ vector<vector<string>> groupAnagrams(vector<string>& strs) {
+ unordered_map<string, vector<string> > mp;
+ for(int i=0;i<strs.size();i++){
+ string t = strs[i];
+ sort(t.begin(), t.end());
+ mp[t].push_back(strs[i]);
+ }
+ vector<vector<string> > result;
+ for(auto it = mp.begin(); it != mp.end();it++){
+ result.push_back(it->second);
+ }
+ return result;
+ }
+};搜索旋转数组。给定一个排序后的数组,包含n个整数,但这个数组已被旋转过很多次了,次数不详。请编写代码找出数组中的某个元素,假设数组元素原先是按升序排列的。若有多个相同元素,返回索引值最小的一个。
+class Solution {
+public:
+ int search(vector<int>& arr, int target) {
+ int left = 0;
+ int right = arr.size() - 1;
+ if (right == -1)
+ return -1;
+ while (left < right) { // 循环结束条件left==right
+ int mid = left + (right - left) / 2;
+ if (arr[left] < arr[mid]) { // 如果左值小于中值,说明左边区间升序
+ if (arr[left] <= target && target <= arr[mid]) { // 如果目标在左边的升序区间中,右边界移动到mid
+ right = mid;
+ } else { // 否则目标在右半边,左边界移动到mid+1
+ left = mid + 1;
+ }
+ } else if (arr[left] > arr[mid]) { // 如果左值大于中值,说明左边不是升序,右半边升序
+ if (arr[left] <= target || target <= arr[mid]) { // 如果目标在左边,右边界移动到mid
+ right = mid;
+ } else { // 否则目标在右半边,左边界移动到mid+1
+ left = mid + 1;
+ }
+ } else if (arr[left] == arr[mid]) { // 如果左值等于中值,可能是已经找到了目标,也可能是遇到了重复值
+ if (arr[left] != target) { // 如果左值不等于目标,说明还没找到,需要逐一清理重复值。
+ left++;
+ } else { // 如果左值等于目标,说明已经找到最左边的目标值
+ right = left; // 将右边界移动到left,循环结束
+ }
+ }
+ }
+ return (arr[left] == target) ? left : -1; // 返回left,或者-1
+ }
+};稀疏数组搜索。有个排好序的字符串数组,其中散布着一些空字符串,编写一种方法,找出给定字符串的位置。
+int findString(char** words, int wordsSize, char* s){
+ int left = 0, right = wordsSize-1, mid;
+ while(left<right){
+ mid = (left + right) / 2;
+ if (*words[mid] == NULL) {//如果中间为空,则由二分查找变为线性遍历
+ if(strcmp(words[left],s)) left++;//从左至右扫描
+ else return left;
+ }
+ else if (strcmp(words[mid],s) > 0) right = mid - 1;
+ else if (strcmp(words[mid],s) < 0) left = mid + 1;
+ else return mid;
+ }
+ if (strcmp(words[left],s) == 0) return left;
+ else return -1;
+
+}给定M×N矩阵,每一行、每一列都按升序排列,请编写代码找出某元素。
+class Solution {
+public:
+ bool searchMatrix(vector<vector<int>>& matrix, int target) {
+ int m = matrix.size();
+ if(m == 0){
+ return false;
+ }
+ int n = matrix[0].size();
+ int x = 0;
+ int y = n - 1;
+ while(x < m && y >= 0){
+ if(matrix[x][y] == target){
+ return true;
+ } else if(matrix[x][y] > target){
+ y--;
+ } else{
+ x++;
+ }
+ }
+ return false;
+ }
+};假设你正在读取一串整数。每隔一段时间,你希望能找出数字 x 的秩(小于或等于 x 的值的个数)。请实现数据结构和算法来支持这些操作,也就是说:
+实现 track(int x) 方法,每读入一个数字都会调用该方法;
实现 getRankOfNumber(int x) 方法,返回小于或等于 x 的值的个数。
树状数组的模板题目
+class StreamRank {
+private:
+ int a[50010];
+public:
+ StreamRank() {
+ for (int i=1;i<=50001;++i) a[i]=0;
+ }
+
+ void track(int x) {
+ ++x;
+ for (int i=x;i<=50001;i+=i&(-i)) a[i]++;
+ }
+
+ int getRankOfNumber(int x) {
+ ++x;
+ int sum=0;
+ for (int i=x;i;i-=i&(-i)) sum+=a[i];
+ return sum;
+ }
+};
+
+/**
+ * Your StreamRank object will be instantiated and called as such:
+ * StreamRank* obj = new StreamRank();
+ * obj->track(x);
+ * int param_2 = obj->getRankOfNumber(x);
+ */在一个整数数组中,“峰”是大于或等于相邻整数的元素,相应地,“谷”是小于或等于相邻整数的元素。例如,在数组{5, 8, 4, 2, 3, 4, 6}中,{8, 6}是峰, {5, 2}是谷。现在给定一个整数数组,将该数组按峰与谷的交替顺序排序。
+class Solution {
+public:
+ void wiggleSort(vector<int>& nums) {
+ vector<int> temp=nums;
+ sort(temp.begin(), temp.end());
+ int Left=0, Right=nums.size()-1;
+ int index=0;
+ while(index < nums.size()){
+ nums[index++] = temp[Left++];
+ if(index < nums.size()){
+ nums[index++] = temp[Right--];
+ }
+ }
+ return;
+ }
+};编写一个函数,不用临时变量,直接交换 numbers = [a, b]中 a与 b的值。
设计一个方法,找出任意指定单词在一本书中的出现频率。
+你的实现应该支持如下操作:
+WordsFrequency(book)构造函数,参数为字符串数组构成的一本书get(word)查询指定单词在书中出现的频率给定两条线段(表示为起点 start = {X1, Y1}和终点 end = {X2, Y2}),如果它们有交点,请计算其交点,没有交点则返回空值。
要求浮点型误差不超过 10^-6。若有多个交点(线段重叠)则返回 X 值最小的点,X 坐标相同则返回 Y 值最小的点。
设计一个算法,判断玩家是否赢了井字游戏。输入是一个 N x N 的数组棋盘,由字符" ",“X"和"O"组成,其中字符” "代表一个空位。
+以下是井字游戏的规则:
+如果游戏存在获胜者,就返回该游戏的获胜者使用的字符(“X"或"O”);如果游戏以平局结束,则返回 “Draw”;如果仍会有行动(游戏未结束),则返回 “Pending”。
+设计一个算法,算出 n 阶乘有多少个尾随零。
+给定两个整数数组 a和 b,计算具有最小差绝对值的一对数值(每个数组中取一个值),并返回该对数值的差
编写一个方法,找出两个数字 a和 b中最大的那一个。不得使用if-else或其他比较运算符。
给定一个整数,打印该整数的英文描述。
+请实现整数数字的乘法、减法和除法运算,运算结果均为整数数字,程序中只允许使用加法运算符和逻辑运算符,允许程序中出现正负常数,不允许使用位运算。
+你的实现应该支持如下操作:
+Operations() 构造函数minus(a, b) 减法,返回 a - bmultiply(a, b) 乘法,返回 a * bdivide(a, b) 除法,返回 a / b给定 N 个人的出生年份和死亡年份,第 i 个人的出生年份为 birth[i],死亡年份为 death[i],实现一个方法以计算生存人数最多的年份。
你可以假设所有人都出生于 1900 年至 2000 年(含 1900 和 2000 )之间。如果一个人在某一年的任意时期处于生存状态,那么他应该被纳入那一年的统计中。例如,生于 1908 年、死于 1909 年的人应当被列入 1908 年和 1909 年的计数。
+如果有多个年份生存人数相同且均为最大值,输出其中最小的年份。
+你正在使用一堆木板建造跳水板。有两种类型的木板,其中长度较短的木板长度为 shorter,长度较长的木板长度为 longer。你必须正好使用 k块木板。编写一个方法,生成跳水板所有可能的长度。
返回的长度需要从小到大排列。
+给定两个正方形及一个二维平面。请找出将这两个正方形分割成两半的一条直线。假设正方形顶边和底边与 x 轴平行。
+每个正方形的数据 square包含3个数值,正方形的左下顶点坐标 [X,Y] = [square[0],square[1]],以及正方形的边长 square[2]。所求直线穿过两个正方形会形成4个交点,请返回4个交点形成线段的两端点坐标(两个端点即为4个交点中距离最远的2个点,这2个点所连成的线段一定会穿过另外2个交点)。2个端点坐标 [X<sub>1</sub>,Y<sub>1</sub>]和 [X<sub>2</sub>,Y<sub>2</sub>]的返回格式为 {X<sub>1</sub>,Y<sub>1</sub>,X<sub>2</sub>,Y<sub>2</sub>},要求若 X<sub>1</sub> != X<sub>2</sub>,需保证 X<sub>1</sub> < X<sub>2</sub>,否则需保证 Y<sub>1</sub> <= Y<sub>2</sub>。
若同时有多条直线满足要求,则选择斜率最大的一条计算并返回(与Y轴平行的直线视为斜率无穷大)。
+给定一个二维平面及平面上的 N 个点列表 Points,其中第 i个点的坐标为 Points[i]=[X<sub>i</sub>,Y<sub>i</sub>]。请找出一条直线,其通过的点的数目最多。
设穿过最多点的直线所穿过的全部点编号从小到大排序的列表为 S,你仅需返回 [S[0],S[1]]作为答案,若有多条直线穿过了相同数量的点,则选择 S[0]值较小的直线返回,S[0]相同则选择 S[1]值较小的直线返回。
珠玑妙算游戏(the game of master mind)的玩法如下。
+计算机有4个槽,每个槽放一个球,颜色可能是红色(R)、黄色(Y)、绿色(G)或蓝色(B)。例如,计算机可能有RGGB 4种(槽1为红色,槽2、3为绿色,槽4为蓝色)。作为用户,你试图猜出颜色组合。打个比方,你可能会猜YRGB。要是猜对某个槽的颜色,则算一次“猜中”;要是只猜对颜色但槽位猜错了,则算一次“伪猜中”。注意,“猜中”不能算入“伪猜中”。
+给定一种颜色组合 solution和一个猜测 guess,编写一个方法,返回猜中和伪猜中的次数 answer,其中 answer[0]为猜中的次数,answer[1]为伪猜中的次数。
给定一个整数数组,编写一个函数,找出索引 m和 n,只要将索引区间 [m,n]的元素排好序,整个数组就是有序的。注意:n-m尽量最小,也就是说,找出符合条件的最短序列。函数返回值为 [m,n],若不存在这样的 m和 n(例如整个数组是有序的),请返回 [-1,-1]。
给定一个整数数组,找出总和最大的连续数列,并返回总和。
+你有两个字符串,即 pattern和 value。 pattern字符串由字母 "a"和 "b"组成,用于描述字符串中的模式。例如,字符串 "catcatgocatgo"匹配模式 "aabab"(其中 "cat"是 "a","go"是 "b"),该字符串也匹配像 "a"、"ab"和 "b"这样的模式。但需注意 "a"和 "b"不能同时表示相同的字符串。编写一个方法判断 value字符串是否匹配 pattern字符串。
你有一个用于表示一片土地的整数矩阵 land,该矩阵中每个点的值代表对应地点的海拔高度。若值为0则表示水域。由垂直、水平或对角连接的水域为池塘。池塘的大小是指相连接的水域的个数。编写一个方法来计算矩阵中所有池塘的大小,返回值需要从小到大排序。
在老式手机上,用户通过数字键盘输入,手机将提供与这些数字相匹配的单词列表。每个数字映射到0至4个字母。给定一个数字序列,实现一个算法来返回匹配单词的列表。你会得到一张含有有效单词的列表。映射如下图所示:
+
给定两个整数数组,请交换一对数值(每个数组中取一个数值),使得两个数组所有元素的和相等。
+返回一个数组,第一个元素是第一个数组中要交换的元素,第二个元素是第二个数组中要交换的元素。若有多个答案,返回任意一个均可。若无满足条件的数值,返回空数组。
+一只蚂蚁坐在由白色和黑色方格构成的无限网格上。开始时,网格全白,蚂蚁面向右侧。每行走一步,蚂蚁执行以下操作。
+(1) 如果在白色方格上,则翻转方格的颜色,向右(顺时针)转 90 度,并向前移动一个单位。
+(2) 如果在黑色方格上,则翻转方格的颜色,向左(逆时针方向)转 90 度,并向前移动一个单位。
编写程序来模拟蚂蚁执行的前 K 个动作,并返回最终的网格。
+网格由数组表示,每个元素是一个字符串,代表网格中的一行,黑色方格由 'X' 表示,白色方格由 '_' 表示,蚂蚁所在的位置由 'L', 'U', 'R', 'D' 表示,分别表示蚂蚁 左、上、右、下 的朝向。只需要返回能够包含蚂蚁走过的所有方格的最小矩形。
设计一个算法,找出数组中两数之和为指定值的所有整数对。一个数只能属于一个数对。
+设计和构建一个“最近最少使用”缓存,该缓存会删除最近最少使用的项目。缓存应该从键映射到值(允许你插入和检索特定键对应的值),并在初始化时指定最大容量。当缓存被填满时,它应该删除最近最少使用的项目。
+它应该支持以下操作: 获取数据 get 和 写入数据 put 。
获取数据 get(key) - 如果密钥 (key) 存在于缓存中,则获取密钥的值(总是正数),否则返回 -1。
+写入数据 put(key, value) - 如果密钥不存在,则写入其数据值。当缓存容量达到上限时,它应该在写入新数据之前删除最近最少使用的数据值,从而为新的数据值留出空间。
给定一个包含正整数、加(+)、减(-)、乘(*)、除(/)的算数表达式(括号除外),计算其结果。
+表达式仅包含非负整数,+, - ,*,/ 四种运算符和空格 。 整数除法仅保留整数部分。
设计一个函数把两个数字相加。不得使用 + 或者其他算术运算符。
+数组 nums包含从 0到 n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗?
给定一个放有字母和数字的数组,找到最长的子数组,且包含的字母和数字的个数相同。
+返回该子数组,若存在多个最长子数组,返回左端点下标值最小的子数组。若不存在这样的数组,返回一个空数组。
+编写一个方法,计算从 0 到 n (含 n) 中数字 2 出现的次数。
+每年,政府都会公布一万个最常见的婴儿名字和它们出现的频率,也就是同名婴儿的数量。有些名字有多种拼法,例如,John 和 Jon 本质上是相同的名字,但被当成了两个名字公布出来。给定两个列表,一个是名字及对应的频率,另一个是本质相同的名字对。设计一个算法打印出每个真实名字的实际频率。注意,如果 John 和 Jon 是相同的,并且 Jon 和 Johnny 相同,则 John 与 Johnny 也相同,即它们有传递和对称性。
+在结果列表中,选择** 字典序最小 **的名字作为真实名字。
+有个马戏团正在设计叠罗汉的表演节目,一个人要站在另一人的肩膀上。出于实际和美观的考虑,在上面的人要比下面的人矮一点且轻一点。已知马戏团每个人的身高和体重,请编写代码计算叠罗汉最多能叠几个人。
+有些数的素因子只有 3,5,7,请设计一个算法找出第 k 个数。注意,不是必须有这些素因子,而是必须不包含其他的素因子。例如,前几个数按顺序应该是 1,3,5,7,9,15,21。
+数组中占比超过一半的元素称之为主要元素。给你一个** 整数 **数组,找出其中的主要元素。若没有,返回 -1 。请设计时间复杂度为 O(N) 、空间复杂度为 O(1) 的解决方案。
有个内含单词的超大文本文件,给定任意两个 不同的单词,找出在这个文件中这两个单词的最短距离(相隔单词数)。如果寻找过程在这个文件中会重复多次,而每次寻找的单词不同,你能对此优化吗?
二叉树数据结构 TreeNode可用来表示单向链表(其中 left置空,right为下一个链表节点)。实现一个方法,把二叉搜索树转换为单向链表,要求依然符合二叉搜索树的性质,转换操作应是原址的,也就是在原始的二叉搜索树上直接修改。
返回转换后的单向链表的头节点。
+哦,不!你不小心把一个长篇文章中的空格、标点都删掉了,并且大写也弄成了小写。像句子 "I reset the computer. It still didn’t boot!"已经变成了 "iresetthecomputeritstilldidntboot"。在处理标点符号和大小写之前,你得先把它断成词语。当然了,你有一本厚厚的词典 dictionary,不过,有些词没在词典里。假设文章用 sentence表示,设计一个算法,把文章断开,要求未识别的字符最少,返回未识别的字符数。
设计一个算法,找出数组中最小的k个数。以任意顺序返回这k个数均可。
+给定一组单词 words,编写一个程序,找出其中的最长单词,且该单词由这组单词中的其他单词组合而成。若有多个长度相同的结果,返回其中字典序最小的一项,若没有符合要求的单词则返回空字符串。
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。
+给定一个较长字符串 big和一个包含较短字符串的数组 smalls,设计一个方法,根据 smalls中的每一个较短字符串,对 big进行搜索。输出 smalls中的字符串在 big里出现的所有位置 positions,其中 positions[i]为 smalls[i]出现的所有位置。
假设你有两个数组,一个长一个短,短的元素均不相同。找到长数组中包含短数组所有的元素的最短子数组,其出现顺序无关紧要。
+返回最短子数组的左端点和右端点,如有多个满足条件的子数组,返回左端点最小的一个。若不存在,返回空数组。
+给定一个数组,包含从 1 到 N 所有的整数,但其中缺了两个数字。你能在 O(N) 时间内只用 O(1) 的空间找到它们吗?
+以任意顺序返回这两个数字均可。
+随机产生数字并传递给一个方法。你能否完成这个方法,在每次产生新值时,寻找当前所有值的中间值(中位数)并保存。
+中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。
+例如,
+[2,3,4] 的中位数是 3
+[2,3] 的中位数是 (2 + 3) / 2 = 2.5
+设计一个支持以下两种操作的数据结构:
+给定一个直方图(也称柱状图),假设有人从上面源源不断地倒水,最后直方图能存多少水量?直方图的宽度为 1。
+
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的直方图,在这种情况下,可以接 6 个单位的水(蓝色部分表示水)。
+给定字典中的两个词,长度相等。写一个方法,把一个词转换成另一个词, 但是一次只能改变一个字符。每一步得到的新词都必须能在字典中找到。
+编写一个程序,返回一个可能的转换序列。如有多个可能的转换序列,你可以返回任何一个。
+给定一个方阵,其中每个单元(像素)非黑即白。设计一个算法,找出 4 条边皆为黑色像素的最大子方阵。
+返回一个数组 [r, c, size] ,其中 r, c 分别代表子方阵左上角的行号和列号,size 是子方阵的边长。若有多个满足条件的子方阵,返回 r 最小的,若 r 相同,返回 c 最小的子方阵。若无满足条件的子方阵,返回空数组。
给定一个正整数、负整数和 0 组成的 N × M 矩阵,编写代码找出元素总和最大的子矩阵。
+返回一个数组 [r1, c1, r2, c2],其中 r1, c1 分别代表子矩阵左上角的行号和列号,r2, c2 分别代表右下角的行号和列号。若有多个满足条件的子矩阵,返回任意一个均可。
给定一份单词的清单,设计一个算法,创建由字母组成的面积最大的矩形,其中每一行组成一个单词(自左向右),每一列也组成一个单词(自上而下)。不要求这些单词在清单里连续出现,但要求所有行等长,所有列等高。
+如果有多个面积最大的矩形,输出任意一个均可。一个单词可以重复使用。
+两个(具有不同单词的)文档的交集(intersection)中元素的个数除以并集(union)中元素的个数,就是这两个文档的相似度。例如,{1, 5, 3} 和 {1, 7, 2, 3} 的相似度是 0.4,其中,交集的元素有 2 个,并集的元素有 5 个。给定一系列的长篇文档,每个文档元素各不相同,并与一个 ID 相关联。它们的相似度非常“稀疏”,也就是说任选 2 个文档,相似度都很接近 0。请设计一个算法返回每对文档的 ID 及其相似度。只需输出相似度大于 0 的组合。请忽略空文档。为简单起见,可以假定每个文档由一个含有不同整数的数组表示。
+输入为一个二维数组 docs,docs[i] 表示 id 为 i 的文档。返回一个数组,其中每个元素是一个字符串,代表每对相似度大于 0 的文档,其格式为 {id1},{id2}: {similarity},其中 id1 为两个文档中较小的 id,similarity 为相似度,精确到小数点后 4 位。以任意顺序返回数组均可。
 +
+ 共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2023
+ + + +共计 142 篇文章
+2023
+ + + +共计 142 篇文章
+2023
+ + + +共计 142 篇文章
+2023
+ + + +共计 142 篇文章
+2023
+ + + +共计 142 篇文章
+2023
+ + + +共计 142 篇文章
+2023
+ + + +共计 142 篇文章
+2023
+ + + +共计 142 篇文章
+2023
+ + + +共计 142 篇文章
+2024
+ + + +共计 142 篇文章
+2024
+ + + +共计 142 篇文章
+2024
+ + + +共计 142 篇文章
+2024
+ + + +2023
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2023
+ + + +共计 142 篇文章
+2023
+ + + +共计 142 篇文章
+2023
+ + + +共计 142 篇文章
+2023
+ + + +2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 142 篇文章
+2022
+ + + +共计 9 篇文章
+2023
+ + + +2022
+ + + +共计 129 篇文章
+2024
+ + + +2023
+ + + +共计 129 篇文章
+2022
+ + + +共计 129 篇文章
+2022
+ + + +共计 129 篇文章
+2022
+ + + +共计 129 篇文章
+2022
+ + + +共计 129 篇文章
+2023
+ + + +共计 129 篇文章
+2023
+ + + +共计 129 篇文章
+2023
+ + + +2022
+ + + +共计 129 篇文章
+2022
+ + + +共计 129 篇文章
+2022
+ + + +共计 129 篇文章
+2022
+ + + +共计 129 篇文章
+2022
+ + + +共计 129 篇文章
+2022
+ + + +| \n", + " | Id | \n", + "MSSubClass | \n", + "LotFrontage | \n", + "LotArea | \n", + "OverallQual | \n", + "OverallCond | \n", + "YearBuilt | \n", + "YearRemodAdd | \n", + "MasVnrArea | \n", + "BsmtFinSF1 | \n", + "... | \n", + "WoodDeckSF | \n", + "OpenPorchSF | \n", + "EnclosedPorch | \n", + "3SsnPorch | \n", + "ScreenPorch | \n", + "PoolArea | \n", + "MiscVal | \n", + "MoSold | \n", + "YrSold | \n", + "SalePrice | \n", + "
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1201.000000 | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1452.000000 | \n", + "1460.000000 | \n", + "... | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "1460.000000 | \n", + "
| mean | \n", + "730.500000 | \n", + "56.897260 | \n", + "70.049958 | \n", + "10516.828082 | \n", + "6.099315 | \n", + "5.575342 | \n", + "1971.267808 | \n", + "1984.865753 | \n", + "103.685262 | \n", + "443.639726 | \n", + "... | \n", + "94.244521 | \n", + "46.660274 | \n", + "21.954110 | \n", + "3.409589 | \n", + "15.060959 | \n", + "2.758904 | \n", + "43.489041 | \n", + "6.321918 | \n", + "2007.815753 | \n", + "180921.195890 | \n", + "
| std | \n", + "421.610009 | \n", + "42.300571 | \n", + "24.284752 | \n", + "9981.264932 | \n", + "1.382997 | \n", + "1.112799 | \n", + "30.202904 | \n", + "20.645407 | \n", + "181.066207 | \n", + "456.098091 | \n", + "... | \n", + "125.338794 | \n", + "66.256028 | \n", + "61.119149 | \n", + "29.317331 | \n", + "55.757415 | \n", + "40.177307 | \n", + "496.123024 | \n", + "2.703626 | \n", + "1.328095 | \n", + "79442.502883 | \n", + "
| min | \n", + "1.000000 | \n", + "20.000000 | \n", + "21.000000 | \n", + "1300.000000 | \n", + "1.000000 | \n", + "1.000000 | \n", + "1872.000000 | \n", + "1950.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "... | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "1.000000 | \n", + "2006.000000 | \n", + "34900.000000 | \n", + "
| 25% | \n", + "365.750000 | \n", + "20.000000 | \n", + "59.000000 | \n", + "7553.500000 | \n", + "5.000000 | \n", + "5.000000 | \n", + "1954.000000 | \n", + "1967.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "... | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "5.000000 | \n", + "2007.000000 | \n", + "129975.000000 | \n", + "
| 50% | \n", + "730.500000 | \n", + "50.000000 | \n", + "69.000000 | \n", + "9478.500000 | \n", + "6.000000 | \n", + "5.000000 | \n", + "1973.000000 | \n", + "1994.000000 | \n", + "0.000000 | \n", + "383.500000 | \n", + "... | \n", + "0.000000 | \n", + "25.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "6.000000 | \n", + "2008.000000 | \n", + "163000.000000 | \n", + "
| 75% | \n", + "1095.250000 | \n", + "70.000000 | \n", + "80.000000 | \n", + "11601.500000 | \n", + "7.000000 | \n", + "6.000000 | \n", + "2000.000000 | \n", + "2004.000000 | \n", + "166.000000 | \n", + "712.250000 | \n", + "... | \n", + "168.000000 | \n", + "68.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "0.000000 | \n", + "8.000000 | \n", + "2009.000000 | \n", + "214000.000000 | \n", + "
| max | \n", + "1460.000000 | \n", + "190.000000 | \n", + "313.000000 | \n", + "215245.000000 | \n", + "10.000000 | \n", + "9.000000 | \n", + "2010.000000 | \n", + "2010.000000 | \n", + "1600.000000 | \n", + "5644.000000 | \n", + "... | \n", + "857.000000 | \n", + "547.000000 | \n", + "552.000000 | \n", + "508.000000 | \n", + "480.000000 | \n", + "738.000000 | \n", + "15500.000000 | \n", + "12.000000 | \n", + "2010.000000 | \n", + "755000.000000 | \n", + "
8 rows × 38 columns
\n", + "| \n", + " | Feature | \n", + "Unique_values | \n", + "Percentage of missing values | \n", + "Percentage of values in the biggest category | \n", + "type | \n", + "
|---|---|---|---|---|---|
| 72 | \n", + "PoolQC | \n", + "3 | \n", + "99.520548 | \n", + "99.520548 | \n", + "object | \n", + "
| 74 | \n", + "MiscFeature | \n", + "4 | \n", + "96.301370 | \n", + "96.301370 | \n", + "object | \n", + "
| 6 | \n", + "Alley | \n", + "2 | \n", + "93.767123 | \n", + "93.767123 | \n", + "object | \n", + "
| 73 | \n", + "Fence | \n", + "4 | \n", + "80.753425 | \n", + "80.753425 | \n", + "object | \n", + "
| 57 | \n", + "FireplaceQu | \n", + "5 | \n", + "47.260274 | \n", + "47.260274 | \n", + "object | \n", + "
| 3 | \n", + "LotFrontage | \n", + "110 | \n", + "17.739726 | \n", + "17.739726 | \n", + "float64 | \n", + "
| 63 | \n", + "GarageQual | \n", + "5 | \n", + "5.547945 | \n", + "89.794521 | \n", + "object | \n", + "
| 58 | \n", + "GarageType | \n", + "6 | \n", + "5.547945 | \n", + "59.589041 | \n", + "object | \n", + "
| 60 | \n", + "GarageFinish | \n", + "3 | \n", + "5.547945 | \n", + "41.438356 | \n", + "object | \n", + "
| 64 | \n", + "GarageCond | \n", + "5 | \n", + "5.547945 | \n", + "90.821918 | \n", + "object | \n", + "
' + match_content + '...
'; + } + } + }); + if (resultHTML.indexOf('list-group-item') === -1) { + return $input.addClass('invalid').removeClass('valid'); + } + $input.addClass('valid').removeClass('invalid'); + $result.html(resultHTML); + }); + } + }); + } + + function localSearchReset(searchSelector, resultSelector) { + 'use strict'; + var $input = jQuery(searchSelector); + var $result = jQuery(resultSelector); + + if ($input.length === 0) { + // eslint-disable-next-line no-console + throw Error('No element selected by the searchSelector'); + } + if ($result.length === 0) { + // eslint-disable-next-line no-console + throw Error('No element selected by the resultSelector'); + } + + $input.val('').removeClass('invalid').removeClass('valid'); + $result.html(''); + } + + var modal = jQuery('#modalSearch'); + var searchSelector = '#local-search-input'; + var resultSelector = '#local-search-result'; + modal.on('show.bs.modal', function() { + var path = CONFIG.search_path || '/local-search.xml'; + localSearchFunc(path, searchSelector, resultSelector); + }); + modal.on('shown.bs.modal', function() { + jQuery('#local-search-input').focus(); + }); + modal.on('hidden.bs.modal', function() { + localSearchReset(searchSelector, resultSelector); + }); +})(); diff --git a/js/plugins.js b/js/plugins.js new file mode 100644 index 000000000..2a364b04c --- /dev/null +++ b/js/plugins.js @@ -0,0 +1,164 @@ +/* global Fluid, CONFIG */ + +HTMLElement.prototype.wrap = function(wrapper) { + this.parentNode.insertBefore(wrapper, this); + this.parentNode.removeChild(this); + wrapper.appendChild(this); +}; + +Fluid.plugins = { + + typing: function(text) { + if (!('Typed' in window)) { return; } + + var typed = new window.Typed('#subtitle', { + strings: [ + ' ', + text + ], + cursorChar: CONFIG.typing.cursorChar, + typeSpeed : CONFIG.typing.typeSpeed, + loop : CONFIG.typing.loop + }); + typed.stop(); + var subtitle = document.getElementById('subtitle'); + if (subtitle) { + subtitle.innerText = ''; + } + jQuery(document).ready(function() { + typed.start(); + }); + }, + + fancyBox: function(selector) { + if (!CONFIG.image_zoom.enable || !('fancybox' in jQuery)) { return; } + + jQuery(selector || '.markdown-body :not(a) > img, .markdown-body > img').each(function() { + var $image = jQuery(this); + var imageUrl = $image.attr('data-src') || $image.attr('src') || ''; + if (CONFIG.image_zoom.img_url_replace) { + var rep = CONFIG.image_zoom.img_url_replace; + var r1 = rep[0] || ''; + var r2 = rep[1] || ''; + if (r1) { + if (/^re:/.test(r1)) { + r1 = r1.replace(/^re:/, ''); + var reg = new RegExp(r1, 'gi'); + imageUrl = imageUrl.replace(reg, r2); + } else { + imageUrl = imageUrl.replace(r1, r2); + } + } + } + var $imageWrap = $image.wrap(` + ` + ).parent('a'); + if ($imageWrap.length !== 0) { + if ($image.is('.group-image-container img')) { + $imageWrap.attr('data-fancybox', 'group').attr('rel', 'group'); + } else { + $imageWrap.attr('data-fancybox', 'default').attr('rel', 'default'); + } + + var imageTitle = $image.attr('title') || $image.attr('alt'); + if (imageTitle) { + $imageWrap.attr('title', imageTitle).attr('data-caption', imageTitle); + } + } + }); + + jQuery.fancybox.defaults.hash = false; + jQuery('.fancybox').fancybox({ + loop : true, + helpers: { + overlay: { + locked: false + } + } + }); + }, + + imageCaption: function(selector) { + if (!CONFIG.image_caption.enable) { return; } + + jQuery(selector || `.markdown-body > p > img, .markdown-body > figure > img, + .markdown-body > p > a.fancybox, .markdown-body > figure > a.fancybox`).each(function() { + var $target = jQuery(this); + var $figcaption = $target.next('figcaption'); + if ($figcaption.length !== 0) { + $figcaption.addClass('image-caption'); + } else { + var imageTitle = $target.attr('title') || $target.attr('alt'); + if (imageTitle) { + $target.after(``); + } + } + }); + }, + + codeWidget() { + var enableLang = CONFIG.code_language.enable && CONFIG.code_language.default; + var enableCopy = CONFIG.copy_btn && 'ClipboardJS' in window; + if (!enableLang && !enableCopy) { + return; + } + + function getBgClass(ele) { + return Fluid.utils.getBackgroundLightness(ele) >= 0 ? 'code-widget-light' : 'code-widget-dark'; + } + + var copyTmpl = ''; + copyTmpl += ''; + jQuery('.markdown-body pre').each(function() { + var $pre = jQuery(this); + if ($pre.find('code.mermaid').length > 0) { + return; + } + if ($pre.find('span.line').length > 0) { + return; + } + + var lang = ''; + + if (enableLang) { + lang = CONFIG.code_language.default; + if ($pre[0].children.length > 0 && $pre[0].children[0].classList.length >= 2 && $pre.children().hasClass('hljs')) { + lang = $pre[0].children[0].classList[1]; + } else if ($pre[0].getAttribute('data-language')) { + lang = $pre[0].getAttribute('data-language'); + } else if ($pre.parent().hasClass('sourceCode') && $pre[0].children.length > 0 && $pre[0].children[0].classList.length >= 2) { + lang = $pre[0].children[0].classList[1]; + $pre.parent().addClass('code-wrapper'); + } else if ($pre.parent().hasClass('markdown-body') && $pre[0].classList.length === 0) { + $pre.wrap(''); + } + lang = lang.toUpperCase().replace('NONE', CONFIG.code_language.default); + } + $pre.append(copyTmpl.replace('LANG', lang).replace('code-widget">', + getBgClass($pre[0]) + (enableCopy ? ' code-widget copy-btn" data-clipboard-snippet>' : ' code-widget">'))); + + if (enableCopy) { + var clipboard = new ClipboardJS('.copy-btn', { + target: function(trigger) { + var nodes = trigger.parentNode.childNodes; + for (var i = 0; i < nodes.length; i++) { + if (nodes[i].tagName === 'CODE') { + return nodes[i]; + } + } + } + }); + clipboard.on('success', function(e) { + e.clearSelection(); + e.trigger.innerHTML = e.trigger.innerHTML.replace('icon-copy', 'icon-success'); + setTimeout(function() { + e.trigger.innerHTML = e.trigger.innerHTML.replace('icon-success', 'icon-copy'); + }, 2000); + }); + } + }); + } +}; diff --git a/js/utils.js b/js/utils.js new file mode 100644 index 000000000..d61bc2642 --- /dev/null +++ b/js/utils.js @@ -0,0 +1,245 @@ +/* global Fluid, CONFIG */ + +window.requestAnimationFrame = window.requestAnimationFrame || window.webkitRequestAnimationFrame || window.mozRequestAnimationFrame; + +Fluid.utils = { + + listenScroll: function(callback) { + var dbc = new Debouncer(callback); + window.addEventListener('scroll', dbc, false); + dbc.handleEvent(); + return dbc; + }, + + unlistenScroll: function(callback) { + window.removeEventListener('scroll', callback); + }, + + listenDOMLoaded(callback) { + if (document.readyState !== 'loading') { + callback(); + } else { + document.addEventListener('DOMContentLoaded', function () { + callback(); + }); + } + }, + + scrollToElement: function(target, offset) { + var of = jQuery(target).offset(); + if (of) { + jQuery('html,body').animate({ + scrollTop: of.top + (offset || 0), + easing : 'swing' + }); + } + }, + + elementVisible: function(element, offsetFactor) { + offsetFactor = offsetFactor && offsetFactor >= 0 ? offsetFactor : 0; + var rect = element.getBoundingClientRect(); + const viewportHeight = window.innerHeight || document.documentElement.clientHeight; + return ( + (rect.top >= 0 && rect.top <= viewportHeight * (1 + offsetFactor) + rect.height / 2) || + (rect.bottom >= 0 && rect.bottom <= viewportHeight * (1 + offsetFactor) + rect.height / 2) + ); + }, + + waitElementVisible: function(selectorOrElement, callback, offsetFactor) { + var runningOnBrowser = typeof window !== 'undefined'; + var isBot = (runningOnBrowser && !('onscroll' in window)) + || (typeof navigator !== 'undefined' && /(gle|ing|ro|msn)bot|crawl|spider|yand|duckgo/i.test(navigator.userAgent)); + if (!runningOnBrowser || isBot) { + return; + } + + offsetFactor = offsetFactor && offsetFactor >= 0 ? offsetFactor : 0; + + function waitInViewport(element) { + Fluid.utils.listenDOMLoaded(function() { + if (Fluid.utils.elementVisible(element, offsetFactor)) { + callback(); + return; + } + if ('IntersectionObserver' in window) { + var io = new IntersectionObserver(function(entries, ob) { + if (entries[0].isIntersecting) { + callback(); + ob.disconnect(); + } + }, { + threshold : [0], + rootMargin: (window.innerHeight || document.documentElement.clientHeight) * offsetFactor + 'px' + }); + io.observe(element); + } else { + var wrapper = Fluid.utils.listenScroll(function() { + if (Fluid.utils.elementVisible(element, offsetFactor)) { + Fluid.utils.unlistenScroll(wrapper); + callback(); + } + }); + } + }); + } + + if (typeof selectorOrElement === 'string') { + this.waitElementLoaded(selectorOrElement, function(element) { + waitInViewport(element); + }); + } else { + waitInViewport(selectorOrElement); + } + }, + + waitElementLoaded: function(selector, callback) { + var runningOnBrowser = typeof window !== 'undefined'; + var isBot = (runningOnBrowser && !('onscroll' in window)) + || (typeof navigator !== 'undefined' && /(gle|ing|ro|msn)bot|crawl|spider|yand|duckgo/i.test(navigator.userAgent)); + if (!runningOnBrowser || isBot) { + return; + } + + if ('MutationObserver' in window) { + var mo = new MutationObserver(function(records, ob) { + var ele = document.querySelector(selector); + if (ele) { + callback(ele); + ob.disconnect(); + } + }); + mo.observe(document, { childList: true, subtree: true }); + } else { + Fluid.utils.listenDOMLoaded(function() { + var waitLoop = function() { + var ele = document.querySelector(selector); + if (ele) { + callback(ele); + } else { + setTimeout(waitLoop, 100); + } + }; + waitLoop(); + }); + } + }, + + createScript: function(url, onload) { + var s = document.createElement('script'); + s.setAttribute('src', url); + s.setAttribute('type', 'text/javascript'); + s.setAttribute('charset', 'UTF-8'); + s.async = false; + if (typeof onload === 'function') { + if (window.attachEvent) { + s.onreadystatechange = function() { + var e = s.readyState; + if (e === 'loaded' || e === 'complete') { + s.onreadystatechange = null; + onload(); + } + }; + } else { + s.onload = onload; + } + } + var ss = document.getElementsByTagName('script'); + var e = ss.length > 0 ? ss[ss.length - 1] : document.head || document.documentElement; + e.parentNode.insertBefore(s, e.nextSibling); + }, + + createCssLink: function(url) { + var l = document.createElement('link'); + l.setAttribute('rel', 'stylesheet'); + l.setAttribute('type', 'text/css'); + l.setAttribute('href', url); + var e = document.getElementsByTagName('link')[0] + || document.getElementsByTagName('head')[0] + || document.head || document.documentElement; + e.parentNode.insertBefore(l, e); + }, + + loadComments: function(selector, loadFunc) { + var ele = document.querySelector('#comments[lazyload]'); + if (ele) { + var callback = function() { + loadFunc(); + ele.removeAttribute('lazyload'); + }; + Fluid.utils.waitElementVisible(selector, callback, CONFIG.lazyload.offset_factor); + } else { + loadFunc(); + } + }, + + getBackgroundLightness(selectorOrElement) { + var ele = selectorOrElement; + if (typeof selectorOrElement === 'string') { + ele = document.querySelector(selectorOrElement); + } + var view = ele.ownerDocument.defaultView; + if (!view) { + view = window; + } + var rgbArr = view.getComputedStyle(ele).backgroundColor.replace(/rgba*\(/, '').replace(')', '').split(/,\s*/); + if (rgbArr.length < 3) { + return 0; + } + var colorCast = (0.213 * rgbArr[0]) + (0.715 * rgbArr[1]) + (0.072 * rgbArr[2]); + return colorCast === 0 || colorCast > 255 / 2 ? 1 : -1; + }, + + retry(handler, interval, times) { + if (times <= 0) { + return; + } + var next = function() { + if (--times >= 0 && !handler()) { + setTimeout(next, interval); + } + }; + setTimeout(next, interval); + } + +}; + +/** + * Handles debouncing of events via requestAnimationFrame + * @see http://www.html5rocks.com/en/tutorials/speed/animations/ + * @param {Function} callback The callback to handle whichever event + */ +function Debouncer(callback) { + this.callback = callback; + this.ticking = false; +} + +Debouncer.prototype = { + constructor: Debouncer, + + /** + * dispatches the event to the supplied callback + * @private + */ + update: function() { + this.callback && this.callback(); + this.ticking = false; + }, + + /** + * ensures events don't get stacked + * @private + */ + requestTick: function() { + if (!this.ticking) { + requestAnimationFrame(this.rafCallback || (this.rafCallback = this.update.bind(this))); + this.ticking = true; + } + }, + + /** + * Attach this as the event listeners + */ + handleEvent: function() { + this.requestTick(); + } +}; diff --git a/lib/hbe.js b/lib/hbe.js new file mode 100644 index 000000000..71205dd75 --- /dev/null +++ b/lib/hbe.js @@ -0,0 +1,297 @@ +(() => { + 'use strict'; + + const cryptoObj = window.crypto || window.msCrypto; + const storage = window.localStorage; + + const storageName = 'hexo-blog-encrypt:#' + window.location.pathname; + const keySalt = textToArray('hexo-blog-encrypt的作者们都是大帅比!'); + const ivSalt = textToArray('hexo-blog-encrypt是地表最强Hexo加密插件!'); + +// As we can't detect the wrong password with AES-CBC, +// so adding an empty div and check it when decrption. +const knownPrefix = "中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。
arr = [2,3,4] 的中位数是 3 。arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。实现 MedianFinder 类:
MedianFinder() 初始化 MedianFinder 对象。void addNum(int num) 将数据流中的整数 num 添加到数据结构中。double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10<sup>-5</sup> 以内的答案将被接受。class MedianFinder {public: priority_queue<int, vector<int>, less<int>> queMin; priority_queue<int, vector<int>, greater<int>> queMax; MedianFinder() { } void addNum(int num) { if (queMin.empty() || num <= queMin.top()) { queMin.push(num); if (queMax.size() + 1 < queMin.size()) { queMax.push(queMin.top()); queMin.pop(); } } else { queMax.push(num); if (queMax.size() > queMin.size()) { queMin.push(queMax.top()); queMax.pop(); } } } double findMedian() { if (queMin.size() > queMax.size()) { return queMin.top(); } return (queMin.top() + queMax.top()) / 2.0; }};你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [a<sub>i</sub>, b<sub>i</sub>] ,表示如果要学习课程 a<sub>i</sub> 则 必须 先学习课程 b<sub>i</sub> ~ ~ 。
[0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
class Solution {public: bool canFinish(int numCourses, vector<vector<int>>& prerequisites) { vector<int> totalnum(numCourses,0); vector<vector<int> > matrix(numCourses, vector<int>(0,0)); for(int i=0;i<prerequisites.size();i++){ totalnum[prerequisites[i][0]] += 1; matrix[prerequisites[i][1]].push_back(prerequisites[i][0]); } bool judge = true; while(judge){ judge = false; for(int i=0;i<numCourses;i++){ if(totalnum[i] == 0){ judge = true; for(int j=0;j<matrix[i].size();j++){ totalnum[matrix[i][j]] -= 1; } totalnum[i] = -1; } } } for(int i=0;i<numCourses;i++){ if(totalnum[i] != -1){ return false; } } return true; }};图解大模型RLHF系列之:人人都能看懂的PPO原理与源码解读:https://zhuanlan.zhihu.com/p/677607581
原理解析:https://blog.csdn.net/v_JULY_v/article/details/134242910
KL散度详解:https://blog.csdn.net/Rocky6688/article/details/103470437
简要版本解析:https://blog.csdn.net/u014386899/article/details/136633074
代码解读:https://zhuanlan.zhihu.com/p/696044978



在RLHF-PPO阶段,一共有四个主要模型 ,分别是:
Actor/Critic Model在RLHF阶段是需要训练的(图中给这两个模型加了粗边,就是表示这个含义);而Reward/Reference Model是参数冻结的。
Critic/Reward/Reference Model共同组成了一个“奖励-loss”计算体系(我自己命名的,为了方便理解),我们综合它们的结果计算loss,用于更新Actor和Critic Model
Actor就是我们想要训练的目标语言模型。我们一般用SFT阶段产出的SFT模型来对它做初始化。
我们的最终目的是让Actor模型能产生符合人类喜好的response。所以我们的策略是,先喂给Actor一条prompt (这里假设batch_size = 1,所以是1条prompt),让它生成对应的response。然后,我们再将“prompt + response"送入我们的“奖励-loss”计算体系中去算得最后的loss,用于更新actor。
Reference Model(以下简称Ref模型)一般也用SFT阶段得到的SFT模型做初始化,在训练过程中,它的参数是冻结的。 Ref模型的主要作用是防止Actor”训歪”
我们希望训练出来的Actor模型既能达到符合人类喜好的目的,又尽量让它和SFT模型不要差异太大 。因此我们使用KL散度来衡量输出分布的相似度

ref_log_probs - log_probs 来衡量,就是KL散度的公式Critic Model用于预测期望总收益,和Actor模型一样,它需要做参数更新 。
在时刻,我们给不出客观存在的总收益
,我们只能训练一个模型去预测它。
在RLHF中,我们不仅要训练模型生成符合人类喜好的内容的能力(Actor),也要提升模型对人类喜好量化判断的能力(Critic)
deepspeed-chat采用了Reward模型作为它的初始化,可以简单理解成,Reward/Critic模型和Actor模型的架构是很相似的(毕竟输入都一样),同时,它在最后一层增加了一个Value Head层,该层是个简单的线形层,用于将原始输出结果映射成单一的值。
Reward Model用于计算生成token的即时收益,它就是RW阶段所训练的奖励模型,在RLHF过程中,它的参数是冻结的。
Reward模型是站在上帝视角的。这个上帝视角有两层含义:
reward是对actor模型进行了某一个action之后的直接打分;而critic则是对这个actor模型的整体预估得分。每次actor模型更新后,critic模型都要对这个新的actor模型重新打分,所以critic模型也要更新参数。critic模型对actor模型的整体预估得分,是根据reward模型的每一次实时打分来预估的。当critic模型的预估得分达到了一定的基准,就代表actor模型训练完成。

直观设计
引入优势
如果Critic对的总收益预测为
,但实际执行
后的总收益是
,我们就定义优势为:
,替换上面的
actor loss =
本来是即时收益,但是可以调整一下:(
是最后一个时刻)
为什么只有最后一个时刻的被纳入了考量呢?这是因为在Reward模型训练阶段,就是用这个位置的的
来表示对完整的prompt + response的奖励预测(但不妨碍你理解成是执行完
的即时奖励),然后用这个指标来做模型eval的(但是Reward训练阶段算loss时,还是考虑了response部分所有token输出的reward值)。所以到了RLHF的场景下,其余时刻的即时奖励,我们就用“Actor是否遵循了Ref的约束”来进行评价。
改造优势
新引入的也是一个常量,可将其理解为权衡因子,直觉上看它控制了在计算当前优势时对未来优势的考量。
对于最后一个时刻,它的未来收益
和未来优势
都是0,也就是
,这是可以直接算出来的。而有了
,我们可以通过动态规划的方法,把所有时刻的优势算出来
重复使用
太慢了,所以一个batch的经验值将被用于n次模型更新
1个batch的经验值被使用ppo_epochs次,在这ppo_epochs中,Actor是不吃任何新数据,不做任何交互的,所以我们只能让Actor“模拟”一下和环境交互的过程,吐出一些新数据出来。
还是保证新的数据和旧的差不多,还是使用KL散度
actor loss =
在Actor想通过模拟交互的方式,使用一个batch的经验值更新自己时,它需要收到真正吃到batch的那个时刻的Actor的约束,这样才能在有效利用batch,提升训练速度的基础上,保持训练的稳定。
设置一个范围,差距太大就不要更新了
第一想法:Critic loss =$ (𝑅_𝑡+ \gamma ∗𝑉_{𝑡+1}-V_t)^2$
实际收益优化:
预估收益优化:类比于Actor,Critic模型在ppo_epochs的过程中也是不断更新的。所以这个可以理解成是
,也就是真正吃了batch,参与产出经验的那个时候的Critic产出的收益预测结果。
用老设计了了一个变动范围,然后用这个变动范围去约束新
最终我们就取实际收益和预估收益的MSE做为loss就好,这里注意,计算实际收益时都是老Critic(真正吃了batch的那个)产出的结果,而预估收益是随着ppo_epochs而变动的。
DPO通过简单的分类目标直接优化最满足偏好的策略,而没有明确的奖励函数或RL
DPO的本质在于增加了被首选的response相对不被首选的response的对数概率,但它包含了一个动态的、每个示例的重要性权重,以防止设计的概率比让模型的能力退化。

IPO相当于在DPO的损失函数上添加了一个正则项,从而可以使得不使用early stopping技巧就可以使模型收敛。
KTO定义的损失函数只需要将样本标注为"好(good)“或"坏(bad)”,从而使得获取标注样本的成本更低。(就是不需要一对一对标注了)
CPO在训练期间不需要加载参考策略模型。通过省略内存的参考模型,CPO提高了操作效率,与DPO相比,能够以更低的成本训练更大的模型。
ORPO整合SFT和DPO,且不需要额外的参考模型
SimPO 包含两个主要组件:(1)在长度上归一化的奖励,其计算方式是使用策略模型的奖励中所有 token 的平均对数概率;(2)目标奖励差额,用以确保获胜和失败响应之间的奖励差超过这个差额。
SimPO 不需要参考模型,性能却明显优于 DPO 及其最新变体,且不会显著增加响应长度
]]>给定一个包含非负整数的 <em>m</em> x <em>n</em> 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明: 每次只能向下或者向右移动一步。
class Solution {public: int minPathSum(vector<vector<int>>& grid) { int m = grid.size(); int n = grid[0].size(); vector<vector<int> > dp(m, vector<int>(n,0)); dp[0][0] = grid[0][0]; for(int i=1;i<m;i++){ dp[i][0] = dp[i-1][0] + grid[i][0]; } for(int j=1;j<n;j++){ dp[0][j] = dp[0][j-1] + grid[0][j]; } for(int i=1;i<m;i++){ for(int j=1;j<n;j++){ dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]; } } return dp[m-1][n-1]; }};给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
class Solution {public: vector<int> result; void inorder(TreeNode* root){ if(root == NULL){ return; } inorder(root->left); result.push_back(root->val); inorder(root->right); } vector<int> inorderTraversal(TreeNode* root) { inorder(root); return result; }};给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
class Solution {public: vector<vector<int>> zigzagLevelOrder(TreeNode* root) { vector<vector<int> > result; if(root == NULL){ return result; } queue<TreeNode*> q; q.push(root); int sign = 0; while(!q.empty()){ int t = q.size(); vector<int> temp; for(int i=0;i<t;i++){ TreeNode* x = q.front(); q.pop(); temp.push_back(x->val); if(x->left != NULL){ q.push(x->left); } if(x->right != NULL){ q.push(x->right); } } if(sign == 1){ reverse(temp.begin(), temp.end()); } result.push_back(temp); sign = 1 - sign; } return result; }};数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的括号组合。
class Solution {public: vector<string> result; void backtracking(vector<string> temp, int n, int nowleft, int nowright){ if(temp.size() == n * 2){ string res = ""; for(int i=0;i<temp.size();i++){ res += temp[i]; } result.push_back(res); return; } if (nowleft < n){ temp.push_back("("); backtracking(temp,n,nowleft+1,nowright); temp.pop_back(); } if(nowright < n && nowright < nowleft){ temp.push_back(")"); backtracking(temp,n,nowleft,nowright+1); temp.pop_back(); } } vector<string> generateParenthesis(int n) { vector<string> temp; backtracking(temp,n,0,0); return result; }};整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
arr = [1,2,3] 的下一个排列是 [1,3,2] 。arr = [2,3,1] 的下一个排列是 [3,1,2] 。arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。给你一个整数数组 nums ,找出 nums 的下一个排列。
必须原地修改,只允许使用额外常数空间。
class Solution {public: void nextPermutation(vector<int>& nums) { int n = nums.size(); int index = n-1; for(;index>=1;index--){ if(nums[index] > nums[index-1]){ break; } } if(index != 0){ index -= 1; for(int i=n-1;i>=0;i--){ if(nums[i] > nums[index]){ swap(nums[index], nums[i]); reverse(nums.begin()+index+1,nums.end()); return; } } } else{ reverse(nums.begin(), nums.end()); } }};给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
class Solution {public: bool result = false; void DFS(int i, int j, int m, int n,int now, vector<vector<char>>& board,vector<vector<bool> > &visited, string word){ if(i < 0 || j < 0 || i >= m || j >= n || visited[i][j] == true || board[i][j] != word[now]){ return; } if(now == word.size() - 1){ result = true; return; } visited[i][j] = true; DFS(i+1,j,m,n,now+1,board,visited, word); DFS(i-1,j,m,n,now+1,board,visited, word); DFS(i,j+1,m,n,now+1,board,visited, word); DFS(i,j-1,m,n,now+1,board,visited, word); visited[i][j] = false; } bool exist(vector<vector<char>>& board, string word) { int m = board.size(); int n = board[0].size(); for(int i=0;i<m;i++){ for(int j=0;j<n;j++){ vector<vector<bool> > visited(m, vector<bool>(n, false)); DFS(i,j,m,n,0,board,visited, word); if(result){ return result; } } } return result; }};给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
class Solution {public: int lengthOfLongestSubstring(string s) { int result = 0; unordered_set<char> st; int left = 0; for(int right=0; right<s.size(); right++){ while(st.find(s[right]) != st.end()){ st.erase(s[left]); left++; } st.insert(s[right]); result = max(result, right - left + 1); } return result; }};给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
class Solution {public: double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) { int m = nums1.size(); int n = nums2.size(); bool next; int sign = (m + n) / 2; if((m + n) % 2 == 1){ next = false; } else{ sign -= 1; next = true; } int res1 = 0; int res2 = 0; int globalindex = 0; int nums1index = 0; int nums2index = 0; while(globalindex <= sign){ if(nums1index < m && nums2index < n){ if(nums1[nums1index] < nums2[nums2index]){ res1 = nums1[nums1index]; nums1index += 1; } else{ res1 = nums2[nums2index]; nums2index += 1; } } else if (nums1index < m){ res1 = nums1[nums1index]; nums1index += 1; } else { res1 = nums2[nums2index]; nums2index += 1; } globalindex += 1; } if(next == false){ return res1; } if(nums1index < m && nums2index < n){ if(nums1[nums1index] < nums2[nums2index]){ res2 = nums1[nums1index]; } else{ res2 = nums2[nums2index]; } } else if (nums1index < m){ res2 = nums1[nums1index]; } else { res2 = nums2[nums2index]; } return ((double)res1 + (double)res2) / 2.0; }};给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
class Solution {public: string longestPalindrome(string s) { vector<int> result = {0,0}; for(int i=0;i<s.size()-1;i++){ int left = i; int right = i; while(left >= 0 && right < s.size()){ if(s[left] == s[right]){ if(result[1] - result[0] < right - left){ result[1] = right; result[0] = left; } right += 1; left -= 1; } else{ break; } } left = i; right = i+1; while(left >= 0 && right < s.size()){ if(s[left] == s[right]){ if(result[1] - result[0] < right - left){ result[1] = right; result[0] = left; } right += 1; left -= 1; } else{ break; } } } return s.substr(result[0], result[1]-result[0] + 1); }};给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
121 是回文,而 123 不是。class Solution {public: bool isPalindrome(int x) { string s = to_string(x); int left = 0; int right = s.size() - 1; while(left < right){ if(s[left] != s[right]){ return false; } left += 1; right -= 1; } return true; }};给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明: 你不能倾斜容器。
class Solution {public: int maxArea(vector<int>& height) { int maxarea = 0; int left = 0; int right = height.size() - 1; while(left < right) { if(height[left] < height[right]){ maxarea = max(maxarea, (right - left) * height[left]); left += 1; } else{ maxarea = max(maxarea, (right - left) * height[right]); right -= 1; } } return maxarea; }};给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意: 最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
class Solution {public: void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) { int index = m + n - 1; m -= 1; n -= 1; while(index >= 0){ if(m < 0){ nums1[index] = nums2[n]; n--; } else if (n < 0){ nums1[index] = nums1[m]; m--; } else{ if(nums1[m] > nums2[n]){ nums1[index] = nums1[m]; m--; } else{ nums1[index] = nums2[n]; n--; } } index--; } return; }};给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
class Solution {public: ListNode* merge(vector<ListNode*>& lists, int start, int end){ if(start > end){ return NULL; } if(start == end){ return lists[start]; } int mid = (end - start) / 2 + start; ListNode* first = merge(lists, start, mid); ListNode* second = merge(lists, mid + 1, end); if(first == NULL){ return second; } if(second == NULL){ return first; } ListNode* head = new ListNode(0); ListNode* p = head; while(first != NULL && second != NULL){ if(first->val < second->val){ p->next = first; first = first->next; } else{ p->next = second; second = second->next; } p = p->next; } if(first != NULL){ p->next = first; } else{ p->next = second; } return head->next; } ListNode* mergeKLists(vector<ListNode*>& lists) { return merge(lists, 0, lists.size()-1); }};给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−2<sup>31</sup>, 2<sup>31 </sup>− 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
class Solution {public: int reverse(int x) { int rev = 0; while (x != 0) { if (rev < INT_MIN / 10 || rev > INT_MAX / 10) { return 0; } int digit = x % 10; x /= 10; rev = rev * 10 + digit; } return rev; }};给定整数数组 nums 和整数 k,请返回数组中第 <strong>k</strong> 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
class Solution {public: void quicksort(vector<int>& nums, int start, int end, int k){ if(start >= end){ return; } int x = nums[start]; int left = start; int right = end; while(left < right){ while(left < right && nums[right] <= x){ right--; } nums[left] = nums[right]; while(left < right && nums[left] > x){ left++; } nums[right] = nums[left]; } nums[left] = x; // start left end // k if(k == left + 1){ return; } else if(k < left+1){ quicksort(nums, start, left-1,k); } else{ quicksort(nums,left+1,end,k); } } int findKthLargest(vector<int>& nums, int k) { quicksort(nums, 0, nums.size()-1,k); return nums[k-1]; }};给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
class Solution {public: void quicksort(vector<pair<int,int> >& nums, int start, int end, int k){ if(start >= end){ return; } pair<int,int> x = nums[start]; int left = start; int right = end; while(left < right){ while(left < right && nums[right].second <= x.second){ right--; } swap(nums[left],nums[right]); while(left < right && nums[left].second > x.second){ left++; } swap(nums[left],nums[right]); } nums[left].first = x.first; nums[left].second = x.second; // start left end; if(k == left){ return; } else if(k > left){ quicksort(nums, left+1, end,k); } else{ quicksort(nums, start, left-1,k); } } vector<int> topKFrequent(vector<int>& nums, int k) { vector<pair<int, int> > result; unordered_map<int, int> mp; for(int i=0;i<nums.size();i++){ mp[nums[i]]++; } for(auto it=mp.begin();it!= mp.end();it++){ result.push_back({it->first, it->second}); } quicksort(result, 0, result.size()-1,k); vector<int> res; for(int i=0;i<k;i++){ res.push_back(result[i].first); } return res; }};给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
class Solution {public: int longestValidParentheses(string s) { vector<bool> visit(s.size(),false); stack<pair<char,int> > st; for(int i=0;i<s.size();i++){ if(st.empty() || s[i] == '(' || (s[i] == ')' && st.top().first == ')')){ st.push({s[i],i}); continue; } for(int j=st.top().second;j<=i;j++){ visit[j] = true; } st.pop(); } int maxlength = 0; int index = 0; while(index < visit.size()){ int counttemp = 0; while(index < visit.size() && visit[index]){ counttemp += 1; index += 1; } maxlength = max(maxlength, counttemp); while(index < visit.size() && !visit[index]){ index += 1; } } return maxlength; }};给你两个 二维 整数数组 nums1 和 nums2.
nums1[i] = [id<sub>i</sub>, val<sub>i</sub>] 表示编号为 id<sub>i</sub> 的数字对应的值等于 val<sub>i</sub> 。nums2[i] = [id<sub>i</sub>, val<sub>i</sub>] 表示编号为 id<sub>i</sub> 的数字对应的值等于 val<sub>i</sub> 。每个数组都包含 互不相同 的 id ,并按 id 以 递增 顺序排列。
请你将两个数组合并为一个按 id 以递增顺序排列的数组,并符合下述条件:
0 。返回结果数组。返回的数组需要按 id 以递增顺序排列。
class Solution {public: static bool cmp(const vector<int> &a, const vector<int> &b){ return a[0] < b[0]; } vector<vector<int>> mergeArrays(vector<vector<int>>& nums1, vector<vector<int>>& nums2) { unordered_map<int, int> mp; for(int i=0;i<nums1.size();i++){ if(mp.find(nums1[i][0]) != mp.end()){ mp[nums1[i][0]] += nums1[i][1]; } else{ mp[nums1[i][0]] = nums1[i][1]; } } for(int i=0;i<nums2.size();i++){ if(mp.find(nums2[i][0]) != mp.end()){ mp[nums2[i][0]] += nums2[i][1]; } else{ mp[nums2[i][0]] = nums2[i][1]; } } vector<vector<int> > result; for(auto it = mp.begin(); it != mp.end();it++){ result.push_back(vector<int> {it->first, it->second}); } sort(result.begin(), result.end(), cmp); return result; }};整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转 ,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
class Solution {public: int search(vector<int>& nums, int target) { int n = nums.size(); int left = 0; int right = n-1; while(left <= right){ int mid = (right - left) / 2 + left; if(nums[mid] == target){ return mid; } if(nums[0] <= nums[mid]){ if(nums[0] <= target && target < nums[mid]){ right = mid - 1; } else{ left = mid + 1; } } else{ if(nums[mid] < target && target <= nums[n-1]){ left = mid + 1; } else{ right = mid - 1; } } } return -1; }};给定一个 *n * × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在** 原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。**请不要 **使用另一个矩阵来旋转图像。
class Solution {public: void rotate(vector<vector<int>>& matrix) { int n = matrix.size(); for(int i=0;i< n / 2;i++){ for(int j=0;j<(n+1) / 2;j++){ int temp = matrix[i][j]; matrix[i][j] = matrix[n-j-1][i]; matrix[n-j-1][i] = matrix[n-i-1][n-j-1]; matrix[n-i-1][n-j-1] = matrix[j][n-i-1]; matrix[j][n-i-1] = temp; } } }};给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,**原地**对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
class Solution {public: void sortColors(vector<int>& nums) { int left = 0; for(int i=0;i<nums.size();i++){ if(nums[i] == 0){ swap(nums[i], nums[left]); left += 1; } } for(int i=left;i<nums.size();i++){ if(nums[i] == 1){ swap(nums[i], nums[left]); left += 1; } } }};给定一个 <em>m</em> x <em>n</em> 的矩阵,如果一个元素为 0 ** ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。**
class Solution {public: void setZeroes(vector<vector<int>>& matrix) { int m = matrix.size(); int n = matrix[0].size(); vector<bool> rowvector(m,false); vector<bool> colvector(n,false); for(int i=0;i<m;i++){ for(int j=0;j<n;j++){ if(matrix[i][j] == 0){ rowvector[i] = true; colvector[j] = true; } } } for(int i=0;i<m;i++){ for(int j=0;j<n;j++){ if(rowvector[i] == true || colvector[j] == true){ matrix[i][j] = 0; } } } return; }};给定一个非负整数 numRows, 生成「杨辉三角」的前 *numRows *行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
class Solution {public: vector<vector<int>> generate(int numRows) { vector<vector<int> > result; vector<int> temp; temp.push_back(1); result.push_back(temp); if(numRows == 1){ return result; } for(int i=2;i<=numRows;i++){ vector<int> t; t.push_back(1); for(int j=1;j<i-1;j++){ t.push_back(result[i-2][j-1] + result[i-2][j]); } t.push_back(1); result.push_back(t); } return result; }};已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:* 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
7 次,则可以得到 [0,1,2,4,5,6,7]注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
class Solution {public: int findMin(vector<int>& nums) { int n = nums.size(); int left = 0; int right = n-1; while(left < right){ int mid = (right - left) / 2 + left; if(nums[mid] < nums[right]){ right = mid; } else { left = mid + 1; } } return nums[left]; }};给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
class Solution {public: ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) { int cur = 0; ListNode* head = new ListNode(-1); ListNode* l3 = head; while(l1 != NULL || l2 != NULL){ int target; if(l1 == NULL){ target = l2->val + cur; l2 = l2->next; } else if(l2 == NULL){ target = l1->val + cur; l1 = l1->next; } else{ target = l1->val + l2->val + cur; l1 = l1->next; l2 = l2->next; } if (target >= 10){ cur = 1; target -= 10; } else{ cur = 0; } l3->next = new ListNode(target); l3 = l3->next; } if(cur == 1){ l3->next = new ListNode(1); } return head->next; }};将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
class Solution {public: ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) { ListNode* dummy = new ListNode(0); ListNode* head = dummy; while(list1 != NULL && list2 != NULL){ if(list1->val < list2->val){ dummy->next = list1; dummy = dummy->next; list1 = list1->next; } else{ dummy->next = list2; dummy = dummy->next; list2 = list2->next; } } if(list1 != NULL){ dummy->next = list1; } if(list2 != NULL){ dummy->next = list2; } return head->next; }};将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:
P A H NA P L S I I GY I R之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:"PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数:
string convert(string s, int numRows);class Solution {public: string convert(string s, int numRows) { if(numRows == 1){ return s; } vector<queue<char> > vt(numRows); int nowindex = 0; int reverse = false; for(int i=0;i<s.size();i++){ vt[nowindex].push(s[i]); if(nowindex == 0 && reverse == true){ reverse = false; nowindex += 1; } else if (nowindex == numRows-1 && reverse == false){ reverse = true; nowindex -= 1; } else { if(reverse == false){ nowindex += 1; } else{ nowindex -= 1; } } } string resultstring = ""; for(int i=0;i<vt.size();i++){ while(!vt[i].empty()){ resultstring += vt[i].front(); vt[i].pop(); } } return resultstring; }};请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
0 。必要时更改符号(从步骤 2 开始)。[−2<sup>31</sup>, 2<sup>31 </sup>− 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −2<sup>31</sup> 的整数应该被固定为 −2<sup>31</sup> ,大于 2<sup>31 </sup>− 1 的整数应该被固定为 2<sup>31 </sup>− 1 。注意:
' ' 。class Solution {public: int myAtoi(string s) { int res = 0; bool havenumsign = false; bool negativesign = false; bool fakebigsign = false; for(int i=0;i<s.size();i++){ if(s[i] == ' ' && havenumsign == false){ continue; } if(s[i] == '-' && havenumsign == false){ negativesign = true; havenumsign = true; continue; } if(s[i] == '+' && havenumsign == false){ havenumsign = true; continue; } if(s[i] >= '0' && s[i] <= '9'){ havenumsign = true; if(res > (INT_MAX - s[i] + '0') / 10){ res = INT_MAX; fakebigsign = true; break; } res = res * 10 - '0' + s[i]; continue; } if(havenumsign == true){ break; } break; } if (negativesign){ if(res == INT_MAX && fakebigsign){ return INT_MIN; } return -res; } return res; }};罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值I 1V 5X 10L 50C 100D 500M 1000例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。给你一个整数,将其转为罗马数字。
class Solution{public: string intToRoman(int num) { pair<int, string> valueSymbols[] = { {1000, "M"}, {900, "CM"}, {500, "D"}, {400, "CD"}, {100, "C"}, {90, "XC"}, {50, "L"}, {40, "XL"}, {10, "X"}, {9, "IX"}, {5, "V"}, {4, "IV"}, {1, "I"}, }; string roman; for (auto &[value, symbol] : valueSymbols) { while (num >= value) { num -= value; roman += symbol; } if (num == 0) { break; } } return roman; }};又感冒了(or 发烧?)没什么区别吧,反正现在感冒必发烧。
我还记得上初中的时候,有一次去辽工大打篮球,碰见了有一段时间没有见面的小学同学。他当时问了我一句话:“你还像小时候那样总生病吗?“当时我很奇怪,因为在我的印象里面小学时候生病不算很多。这个小学同学我至今也没有再见过了,也没有联系方式,但是这一次见面我始终都会记得,可能就因为他问了我这一句话吧。
初中我已经不太记得了,但是高中确实一直在生病。几乎每一个月我都要感冒或者发烧一次。尤其是刚刚保送的一个月中,我还记得应该是周四的物理晚自习(当时物理老师给我的印象很恐怖),正好我也在生病,我就把卷子都扔给了我同桌,美美的回去休息了一个晚上,第二天就基本好的差不多了。从那之后我渐渐意识到,生病也并不是纯客观原因,其实自己的情绪、压力等主观因素才是生病的必要条件。
上了大学之后我的感冒的次数就少很多了,但是每次有一些让我非常伤心难过的事情的时候,总会发一次烧。发烧逐渐成为了我宣泄的一个出口。心情难过了,无处抱怨,用较高的体温促使自己休息一下,帮助自己放松心情缓解压力。
前一段刚刚发烧了一次,在床上躺了一天的同时出去吃了一些想吃的,完全没有看电脑。然而短暂的放松过后,自己的任务也并没有随之减轻,还是要一点一点继续推进。虽然发烧可以帮助我休息,但是实际上并没有对我的目标等起到任何的作用,短暂的麻痹过后还是要继续前行。可能我就是这样的人吧,目标很现实,丝毫不敢放松,完成一个目标后开心的同时又向着下一个目标推进,因此我现在过的并不快乐。
如果有一天,我能真正放下一切好好休息一下,才算与自己达成了和解,内心可能才能真正快乐一些?
写的稍微有点丧,心情不太好。
]]>今天看了一些自己博客的文章,发现对外公开的居然全都是刷题或者学习的内容,对于外人来说是不是太枯燥了一些hh。
于是挑了几篇过了很长时间的,或者已经没有隐藏的必要的文章,放出来也可以让其他人对我有更多的了解。
当然没放出来的文章还有很多,没办法很多的内容利益相关,或者写的时候直呼其名,要是公开感觉对其他人不太好,后续我会慢慢调整一下。
这些文章基本都在Life的标签下。
文笔不好,请见谅。
]]>论文:Stance and Sentiment in Tweets
数据集可视化:http://www.saifmohammad.com/WebPages/StanceDataset.htm
Zero-shot数据集
New data released in this submission. Short column descriptions
相关链接:https://github.com/BinLiang-NLP/TPDG
51284条英文Tweet
关于公司的兼并收购的信息,第一个金融领域的数据集
四个标签:
21574条英文Tweet
对三个target(Donald Trump(7953),Joe Biden(7296),Bernie Sanders(6325))的立场
按照8:1:1进行划分
时间:2017年4月
等级:EACL 2017
时间:2020年5月1日
等级:ACL 2020
思想:
时间:2020年10月7日
等级:EMNLP 2020(CCF B)
思想:提出了VAST数据集
同时提出了一个方法解决Zero-shot问题
数据集:VAST
时间:2021年4月
等级:WWW 2021(CCF A)
时间:2021年6月
等级:NAACL 2021(CCF B)
时间:2021年6月
等级:NAACL 2021(CCF B)
思想:使用对抗学习增强zero-shot的立场检测的效果
数据集:Sem-16
时间:2021年8月
等级:ACL 2021(CCF A)
思想:
数据集:自行构建的COVID-19数据集
时间:2021年8月
等级:ACL 2021 Findings (CCF A)
思想:topic在文本中是可以通过图推断出来的
数据集:
时间:2021年09月16日
等级:EMNLP 2021 Findings
思想:
数据集:SemEval 2016
时间:2021年08月
等级:ACL 2021 Findings
思想:
数据集:SemEval-2016、Multi-Target stance datasets
时间:2022年4月
等级:WWW 2022(CCF A)
思想:
时间:2022年5月
等级:ACL 2022 Workshop(WASSA)
思想:从Wikipedia上预先查询到target的相关知识,融合到模型中进行立场检测
数据集:P-Stance、COVID-19-Stance、VAST
时间:2022年6月27日
等级:SIGIR 2022(CCF A)
思想:
数据集:SemEval-2016、UKP
时间:2022年5月
等级:ACL 2022(CCF A)
思想:
图相关
数据集:VAST、SEM-16、WT-WT
时间:2022年7月
等级:NAACL 2022 Findings(CCF B)
思想:虚假新闻的立场检测,一篇综述性质的文章
数据集:没有做实验,只是汇总之前人的数据、方法与结果
时间:2022年7月
等级:SIGIR 2022(CCF A)
思想:
数据集:VAST、SEM-16、WT-WT
时间:2022年10月
等级:COLING 2022
思想:
图相关
时间:2022年12月
等级:EMNLP 2022(CCF B)
思想:在看见过的target的基础之上生成没有看见过的target的数据
数据集:VAST、Sem-16
时间:2022年12月30日
等级:Arxiv
思想:
数据集:P-Stance
时间:2023年2月20日
等级:WWW 2023(CCF A)
思想:
数据集:
时间:2023年3月31日
等级:IEEE Transactions on Computational Social Systems(CCF C)
思想:
数据集:P-Stance,额外找到了作者的关系信息
时间:2023年4月6日
等级:Arxiv
思想:通过思维链的方式,给一个例子帮助ChatGPT进行分析,在多个数据集上达到了SOTA(假)效果
数据集:SEM-16、VAST、P-Stance
时间:2023年4月
等级:WWW 2023 Companion
思想:
时间:2023年4月22日
等级:无
思想:
时间:2023年5月7日
等级:ICWSM Data Challenge
思想:
数据集:COVID数据集
(Contextual information integration for stance detection via cross-attention)
时间:2023年5月25日
等级:SEM2023(Co-located with ACL 2023)
思想:
时间:2023年5月31日
等级:ACL 2023
思想:
数据集:SEM-16、P-Stance、VAST、Tweet-COVID
时间:2023年6月
等级:2023 ACM Transactions on Asian and Low-Resource Language Information Processing(SCI 4区 CCF C)
思想:
数据集:SEM16、VAST、P-stance、自己的数据集(ISD)
时间:2023年6月
等级:ACL 2023 Oral(CCF A)
思想:
数据集:16个benchmark数据集
时间:2023年6月15日
等级:Arxiv
思想:
数据集:x-stance
时间:2023年7月
等级:ACL 2023(CCF A)
思想:第一个中文的Zero-shot数据集
数据集:C-STANCE
时间:2023年7月
等级:ACL 2023(CCF A)
思想:
数据集:SemEval-2016、AM、COVID-19、P-Stance、自己构建的zero-shot数据集
时间:2023年7月
等级:ACL 2023 Findings(CCF A)
思想:与知识蒸馏等相关
数据集:AM、COVID-19、P-Stance
时间:2023年7月
等级:ACL 2023 Findings(CCF A)
思想:将单语言的立场检测迁移到多语言上
也是图相关的工作
数据集:X-Stance-all
时间:2023年7月
等级:ACL 2023 Workshop(WASSA)
思想:使用对比学习增强立场检测系统的鲁棒性
数据集:DebateForum (DF), SemEval2016 (SE) ,ARC, Perspectrum, FNC-1, KSD-Biden, KSD-Trump
时间:2023年7月
等级:ACL 2023(CCF A)
思想:
数据集:VAST
时间:2023年8月31日
等级:Arxiv
思想:
数据集:VAST
时间:2023年9月24日
等级:ICWSM 2024 (CCF B)
思想:
数据集:covid-lies、election2016、phemerumors、semeval2016、wtwt
时间:2023年9月26日
等级:无
思想:
时间:2023年10月
等级:投稿 EMNLP 2023 没中
思想:
数据集:SEM-16、VAST、WT-WT
时间:2023年10月
等级:Arxiv
思想:多个LLM的Agent一起分析文本的各个方面,最后一正一反对立场进行推断,完全的Zero-shot
数据集:Sem-16、WT-WT、VAST
时间:2023年12月
等级:EMNLP 2023(CCF B)
思想:
数据集:VAST
时间:2023年12月
等级:EMNLP 2023(CCF B)
思想:多模态的信息不匹配会造成误解
分别训练图片的立场检测分类器、文本的立场检测分类器,外加一些实体的知识进行识别
数据集:NewsCLIPpings
时间:2023年12月
等级:EMNLP 2023(CCF B)
思想:在文本审核中加入立场检测从而进行自动判断其是否应该被删除
数据集:提出了多语言的Wiki的审核数据集
时间:2023年12月
等级:EMNLP 2023(CCF B)
思想:
数据集:
时间:2023年12月
等级:EMNLP 2023(CCF B)
思想:
数据集:X-Stance、Semeval-2016、R-ita、Czech
时间:2023年12月
等级:EMNLP 2023(CCF B)
思想:文字和图片的多模态立场检测,主要的贡献是数据集
数据集:MMVAX-STANCE
时间:2023年12月
等级:EMNLP 2023(CCF B)
思想:与价值观相关,不算立场检测任务
数据集:非立场检测
时间:2023年12月
等级:EMNLP 2023(CCF B)
思想:补充两种知识增强立场检测的效果
数据集:Sem-16、P-Stance、VAST
时间:2023年12月
等级:EMNLP 2023 Findings
思想:提出了与VAST对标的EZ-Stance数据集
数据集:EZ-Stance
时间:2023年12月
等级:EMNLP 2023 Findings
思想:思维链等zero-shot来增强直接使用大模型进行立场检测的效果
数据集:
时间:2023年12月
等级:EMNLP 2023 Findings
思想:用大模型对立场进行预测,然后输入到Roberta中进行再次预测
数据集:Tweet-Stance、P-Stance
时间:2023年12月
等级:EMNLP 2023 Findings
思想:关注一些情绪倾向
数据集:SemEval、P-Stance、Climate、COVID
时间:2023年12月
等级:EMNLP 2023 Findings
思想:使用大模型对人工编写的新闻的倾向进行判断,不算立场检测
数据集:与立场检测无关
]]>源码解析:PyTorch 源码解读之 DP & DDP:模型并行和分布式训练解析
简单小模型示例:pytorch中分布式训练DDP教程(新手快速入门!)
系列文章:【分布式训练】单机多卡的正确打开方式(一):理论基础
【分布式训练】基于PyTorch进行多GPU分布式模型训练(补充)
较新较详细的教程:torch分布式训练
把模型隔成不同的层,每一层都放到一块GPU上
(1)GPU利用度不够。

如图,阴影部分所表示的时间段里,总有GPU在空转。GPU的数量越多时,空置的比例接近1
(2)中间结果占据大量内存
在做backward计算梯度的过程中,我们需要用到每一层的中间结果z。假设我们的模型有L层,每一层的宽度为d,则对于每块GPU,不考虑其参数本身的存储,额外的空间复杂度为 。从这个复杂度可以看出,随着模型的增大,N,L,d三者的增加可能会平滑掉K增加带来的GPU内存收益。因此,这也是需要优化的地方。
流水线并行的核心思想是: 在模型并行的基础上,进一步引入数据并行的办法,即把原先的数据再划分成若干个batch,送入GPU进行训练 。未划分前的数据,叫 mini-batch 。在mini-batch上再划分的数据,叫 micro-batch 。

其中,第一个下标表示GPU编号,第二个下标表示micro-batch编号。假设我们将mini-batch划分为M个,则流水线并行下,bubble的时间复杂度为: 。Gpipe通过实验证明,当
时,bubble产生的空转时间占比对最终训练时长影响是微小的,可以忽略不计。
将batch切好,并逐一送入GPU的过程,就像一个流水生产线一样(类似于CPU里的流水线),因此也被称为Pipeline Parallelism。
Gpipe采用用时间换空间的方法,几乎不存中间结果,等到backward的时候,再重新算一遍forward
每块GPU上只保存来自上一块的最后一层输入z,其余的中间结果我们算完就废。等到backward的时候再由保存下来的z重新进行forward来算出。
空间复杂度为 。
在实际应用中,流水线并行并不特别流行,主要原因是模型能否均匀切割,影响了整体计算效率,这就需要算法工程师做手调。
数据并行的核心思想是: 在各个GPU上都拷贝一份完整模型,各自吃一份数据,算一份梯度,最后对梯度进行累加来更新整体模型 。理念不复杂,但到了大模型场景, 巨大的存储和GPU间的通讯量, 就是系统设计要考虑的重点了。在本文中,我们将递进介绍三种主流数据并行的实现方式:
一个经典数据并行的过程如下:
DP 基于单机多卡,所有设备都负责计算和训练网络,除此之外, device[0] (并非 GPU 真实标号而是输入参数 device_ids 首位) 还要负责整合梯度,更新参数。从图中我们可以看出,有三个主要过程:
所有卡都并行运算(图中红色),将梯度收集到 device[0](图中浅蓝色)和 device[0] 分享模型参数给其他 GPU(图中绿色)三个主要过程。
更详细的流程如下图所示:

梯度异步更新:Worker并不会实际等到把聚合梯度拿回来,更新完参数W后再做计算。而是直接拿旧的W,吃新的数据,继续第11轮的计算。这样就保证在通讯的时间里,Worker也在马不停蹄做计算,提升计算通讯比。
但是模型收敛的速度不会变快,只是多用了一些数据
受通讯负载不均的影响, DP一般用于单机多卡场景 。
DDP作为一种更通用的解决方案出现了,既能多机,也能单机。DDP首先要解决的就是通讯问题:将Server上的通讯压力均衡转到各个Worker上。实现这一点后,可以进一步去Server,留Worker。
随着大模型的出现,简单的数据并行已经无法满足需求,毕竟一个模型的大小就有可能超过显卡的显存,更不可能将其复制多份。因此需要让每一张卡仅负责模型的一部分计算,承载模型的一小部分。
使用DDP进行分布式训练有以下几个优势:
Scatter Reduce过程:首先将参数分为份,相邻的GPU传递不同的参数,在传递
次之后,可以得到每一份参数的累积(在不同的GPU上)。

All Gather:得到每一份参数的累积之后,再做一次传递,同步到所有的GPU上。

假设有个GPU, 传输总量是
,每一次的通信上限是
,则完成一次通信需要时间
,那么总共需要花费时间
,可以看到通信成本
与GPU数量无关。
DP和DDP的总通讯量相同,但因负载不均的原因,DP需要耗费更多的时间搬运数据,但是DP不一定就比DDP差
DDP采用多进程控制多GPU,共同训练模型,一份代码会被pytorch自动分配到n个进程并在n个GPU上运行。 DDP运用Ring-Reduce通信算法在每个GPU间对梯度进行通讯,交换彼此的梯度,从而获得所有GPU的梯度。对比DP,不需要在进行模型本体的通信,因此可以加速训练。
需要注意以下几点:
如下图所示,共有3个节点(机器),每个节点上有4个GPU,每台机器上起4个进程,每个进程占一块GPU,那么图中一共有12个rank,nproc_per_node=4,nnodes=3,每个节点都有一个对应的node_rank

rank与GPU之间没有必然的对应关系,一个rank可以包含多个GPU;一个GPU也可以为多个rank服务(多进程共享GPU),在torch的分布式训练中习惯默认一个rank对应着一个GPU,因此local_rank可以当作GPU号
torchrun相当于原来的torch.distributed.launch,有一些额外增加的功能:
torchrun命令与 python -m torch.distributed.run命令完全等同,为命令行命令
有一个参数 --use_env在目前版本的torchrun中是不存在的,因此需要做一点处理
--use_env参数旧版本代码:
$ python -m torch.distributed.launch --use-env train_script.pyimport argparseparser = argparse.ArgumentParser()parser.add_argument("--local-rank", type=int)args = parser.parse_args()local_rank = args.local_rank新版本代码:
$ torchrun train_script.pyimport oslocal_rank = int(os.environ["LOCAL_RANK"])| 参数名称 | 含义 | 示例 |
|---|---|---|
| –nnodes | 节点数量,一个节点对应一个主机 | 1或MIN_SIZE:MAX_SIZE(弹性训练) |
| –nproc-per-node | 一个节点中的进程数量,一般一个进程使用一个显卡,故也通常表述为一个节点中显卡的数量 | [auto, cpu, gpu, int] |
| –rdzv-backend | rendezvous 后端 | c10d etcd |
| –rdzv-endpoint | rendezvous 后端地址 | <host>:<port> |
| –rdzv-id | 用户可以指定当前rendezvous的id,所有的node都要使用这同一个id | |
| –rdzv-conf | 希望传入rendezvous的其他参数 | <key1>=<value1> |
| –standalone | 单节点多卡的默认配置,不需要再传入上述的rendezvous参数,默认为C10d TCP 29400(–master-addr等也会失效) | 选项 |
| –max-restarts | worker group重启的最大次数 | |
| –monitor-interval | 检测worker状态的时间间隔(以秒为单位) | |
| –start-method | 创建子进程的方式 | {spawn,fork,forkserver} |
| –role | User-defined role for the workers. | |
| -m | 与python -m相同,将模块当作脚本运行 | 选项 |
| –no-python | 不使用python命令而是直接执行(如果这个文件并不是一个py文件会使用这个) | |
| –run-path | 使用runpy.run_path执行文件 | |
| –log-dir | 日志文件存放目录 | |
| –redirects | 将控制台输出的日志信息重定向到日志目录中的文件 | [-r 3] 将所有worker的标准输出和标准错误进行重定向,[-r 0:1,1:2] 将rank 0的标准输出重定向,将rank 1的标准错误重定向 |
| –tee | 除将日志输出到控制台外也输出到日志文件 | 日志文件流 |
| –node-rank | 多节点分布式训练的时候该节点的Rank | |
| –master-addr | master 节点的 IP 地址,也就是 rank=0 对应的主机地址 | |
| –master-port | master 节点的端口号,用于通信 | |
| –local-addr | 本地节点的IP地址 |
torchrun主要是对多节点作了分布式的优化,从而可以满足容错性和弹性伸缩。如果是单节点就不需要很复杂。
| 名称 | 含义 | 示例 | |
|---|---|---|---|
| LOCAL_RANK | GPU在单节点中的序号 | 0 | 1 |
| RANK | GPU在全部节点的序号 | 0 | 1 |
| GROUP_RANK | worker组的rank | 0 | 0 |
| ROLE_RANK | 相同ROLE的worker的rank | 0 | 1 |
| LOCAL_WORLD_SIZE | 与–nproc-per-node相同 | 2 | 2 |
| WORLD_SIZE | job中worker的总数 | 2 | 2 |
| ROLE_WORLD_SIZE | 相同角色的worker的数量 | 1 | 2 |
| MASTER_ADDR | rank为0的worker的地址 | 127.0.0.1 | 127.0.0.1 |
| MASTER_PORT | rank为0的worker的端口 | 29500 | 29500 |
| TORCHELASTIC_RESTART_COUNT | 最近重启的worker组的数量 | 0 | 0 |
| TORCHELASTIC_MAX_RESTARTS | 配置的最大重启次数 | 0 | 0 |
| TORCHELASTIC_RUN_ID | 与–rdzv-id相同 | none | none |
| PYTHON_EXEC | 执行这个脚本的python的位置 | 没有 | 没有 |
import torchimport torch.nn as nnimport torch.nn.functional as Ffrom torch.utils.data import Dataset, DataLoaderfrom torch.utils.data.distributed import DistributedSamplerfrom torch.nn.parallel import DistributedDataParallelfrom torch.distributed import init_process_group, destroy_process_groupimport osimport timeclass ToyModel(nn.Module): def __init__(self): super(ToyModel, self).__init__() self.net1 = nn.Linear(10, 10) self.relu = nn.ReLU() self.net2 = nn.Linear(10, 5) def forward(self, x): return self.net2(self.relu(self.net1(x)))class MyTrainDataset(Dataset): def __init__(self, size): self.size = size self.data = [(torch.rand(10), 0) for _ in range(size)] def __len__(self): return self.size def __getitem__(self, index): return self.data[index]class Trainer: def __init__( self, model: torch.nn.Module, train_data: DataLoader, optimizer: torch.optim.Optimizer, save_every: int, snapshot_path: str, ) -> None: self.gpu_id = int(os.environ["LOCAL_RANK"]) self.model = model.to(self.gpu_id) self.train_data = train_data self.optimizer = optimizer self.save_every = save_every self.epochs_run = 0 self.snapshot_path = snapshot_path if os.path.exists(snapshot_path): print("Loading snapshot") self._load_snapshot(snapshot_path) self.model = DistributedDataParallel(self.model, device_ids=[self.gpu_id]) def _load_snapshot(self, snapshot_path): loc = f"cuda:{self.gpu_id}" snapshot = torch.load(snapshot_path, map_location=loc) self.model.load_state_dict(snapshot["MODEL_STATE"]) self.epochs_run = snapshot["EPOCHS_RUN"] print(f"Resuming training from snapshot at Epoch {self.epochs_run}") def _run_batch(self, source, targets): self.optimizer.zero_grad() output = self.model(source) # print(output,targets) loss = F.cross_entropy(output, targets) print(f"[GPU{self.gpu_id}] Loss {loss.item()}") loss.backward() self.optimizer.step() def _run_epoch(self, epoch): b_sz = len(next(iter(self.train_data))[0]) print(f"[GPU{self.gpu_id}] Epoch {epoch} | Batchsize: {b_sz} | Steps: {len(self.train_data)}") self.train_data.sampler.set_epoch(epoch) for source, targets in self.train_data: source = source.to(self.gpu_id) targets = targets.to(self.gpu_id) self._run_batch(source, targets) def _save_snapshot(self, epoch): snapshot = { "MODEL_STATE": self.model.module.state_dict(), "EPOCHS_RUN": epoch, } torch.save(snapshot, self.snapshot_path) print(f"Epoch {epoch} | Training snapshot saved at {self.snapshot_path}") def train(self, max_epochs: int): for epoch in range(self.epochs_run, max_epochs): self._run_epoch(epoch) if self.gpu_id == 0 and epoch % self.save_every == 0: self._save_snapshot(epoch) time.sleep(1)def ddp_setup(): init_process_group(backend="nccl") print("Parameters") print(f"LOCAL_RANK:{os.environ['LOCAL_RANK']}") print(f"RANK:{os.environ['RANK']}") print(f"GROUP_RANK:{os.environ['GROUP_RANK']}") print(f"ROLE_RANK:{os.environ['ROLE_RANK']}") print(f"LOCAL_WORLD_SIZE:{os.environ['LOCAL_WORLD_SIZE']}") print(f"WORLD_SIZE:{os.environ['WORLD_SIZE']}") print(f"ROLE_WORLD_SIZE:{os.environ['ROLE_WORLD_SIZE']}") print(f"MASTER_ADDR:{os.environ['MASTER_ADDR']}") print(f"MASTER_PORT:{os.environ['MASTER_PORT']}") print("") torch.cuda.set_device(int(os.environ["LOCAL_RANK"]))def load_train_objs(): train_set = MyTrainDataset(2048) # load your dataset model = ToyModel() optimizer = torch.optim.SGD(model.parameters(), lr=1e-3) return train_set, model, optimizerdef prepare_dataloader(dataset: Dataset, batch_size: int): return DataLoader( dataset, batch_size=batch_size, pin_memory=True, shuffle=False, sampler=DistributedSampler(dataset) )def main(save_every: int, total_epochs: int, batch_size: int, snapshot_path: str = "snapshot.pt"): ddp_setup() dataset, model, optimizer = load_train_objs() train_data = prepare_dataloader(dataset, batch_size) trainer = Trainer(model, train_data, optimizer, save_every, snapshot_path) trainer.train(total_epochs) destroy_process_group()if __name__ == "__main__": import argparse parser = argparse.ArgumentParser(description='simple distributed training job') parser.add_argument('--total_epochs', default=10, type=int, help='Total epochs to train the model') parser.add_argument('--save_every', default=2, type=int, help='How often to save a snapshot') parser.add_argument('--batch_size', default=512, type=int, help='Input batch size on each device (default: 32)') args = parser.parse_args() main(args.save_every, args.total_epochs, args.batch_size)与单卡有几点不同:
init_process_group(backend="nccl"),后端一般选择ncclsampler=DistributedSampler(dataset)self.model = DistributedDataParallel(self.model, device_ids=[self.gpu_id])训练脚本:
torchrun \ --nnodes=1 \ --nproc_per_node=2 \--master-addr=127.0.0.1 \--master-port=29500 \main.pyexport NCCL_DEBUG=infoexport NCCL_SOCKET_IFNAME=bond0export NCCL_IB_DISABLE=1torchrun \ --nnodes=2 \ --nproc_per_node=2 \--master-addr=10.208.58.27 \--master-port=29602 \--node-rank=0 \main.pyexport NCCL_DEBUG=infoexport NCCL_SOCKET_IFNAME=bond0export NCCL_IB_DISABLE=1torchrun \ --nnodes=2 \ --nproc_per_node=1 \--master-addr=10.208.58.27 \--master-port=29602 \--node-rank=1 \main.py注意事项:
测试环境:
master:10.208.58.27 2*V100
ParametersLOCAL_RANK:0RANK:0GROUP_RANK:0ROLE_RANK:0LOCAL_WORLD_SIZE:2WORLD_SIZE:3ROLE_WORLD_SIZE:3MASTER_ADDR:10.208.58.27MASTER_PORT:29602ParametersLOCAL_RANK:1RANK:1GROUP_RANK:0ROLE_RANK:1LOCAL_WORLD_SIZE:2WORLD_SIZE:3ROLE_WORLD_SIZE:3MASTER_ADDR:10.208.58.27MASTER_PORT:29602worker:1*A100
ParametersLOCAL_RANK:0RANK:2GROUP_RANK:1ROLE_RANK:2LOCAL_WORLD_SIZE:1WORLD_SIZE:3ROLE_WORLD_SIZE:3MASTER_ADDR:10.208.58.27MASTER_PORT:29602数据并行中,每个GPU上都复制了一份完整模型,当模型变大时,很容易打爆GPU的显存
存储主要分为两大块:Model States和Residual States
Model States指和模型本身息息相关的,必须存储的内容,具体包括:
Residual States指并非模型必须的,但在训练过程中会额外产生的内容,具体包括:

其中很大的momentum和variance是Adam保存的,首先就优化他们
将optimizer state分成若干份,每块GPU上各自维护一份。这样就减少了相当一部分的显存开销。

得到G是与DP一样的通信,然后还要聚合W
显存和通讯量的情况如下:

把梯度也拆开,每个GPU格子维护一块梯度。

此时,数据并行的整体流程如下:
对梯度做一次 Reduce-Scatter ,保证每个GPU上所维持的那块梯度是聚合梯度。例如对GPU1,它负责维护G1,因此其他的GPU只需要把G1对应位置的梯度发给GPU1做加总就可。

每块GPU用自己对应的O和G去更新相应的W。更新完毕后, 每块GPU维持了一块更新完毕的W 。同理,对W做一次 All-Gather ,将别的GPU算好的W同步到自己这来。单卡通讯量 Φ 。

每块GPU只维持对应的optimizer states,gradients和parameters

到这一步, 我们用1.5倍的通讯开销,换回近120倍的显存 。只要梯度计算和异步更新做的好,通讯时间大部分可以被计算时间隐藏,因此这样的额外通讯开销,也是划算的。
ZeRO是模型并行的形式,数据并行的实质 。
模型并行,是指在forward和backward的过程中,我只需要用自己维护的那块W来计算就行。即 同样的输入X,每块GPU上各算模型的一部分,最后通过某些方式聚合结果 。
对ZeRO来说,它做forward和backward的时候,是需要把各GPU上维护的W聚合起来的,即本质上还是用完整的W进行计算。 它是不同的输入X,完整的参数W,最终再做聚合 。
核心思想是: 显存不够,内存来凑
把要存储的大头卸载(offload)到CPU上,而把计算部分放到GPU上
ZeRO-Offload的做法是:
具体切分如下图:

ZeRO-infinity也是同理,它们在解决的事情都是:找个除GPU之外的地方,存数据。感兴趣的朋友可以深入研究,这里就不展开了。
把模型的参数纵向切开,放到不同的GPU上进行独立计算,然后再做聚合。
假设现在W太大,导致单卡装不下。我们需要把W切开放到不同的卡上,则我们面临三个主要问题:
forward
我们用N来表示GPU的数量。有几块GPU,就把W按行维度切成几份。下图展示了N=2时的切割方式:

W按照行维度切开后,X的维度和它不对齐了,这可怎么做矩阵乘法呢?很简单,再把X“按列切开”就行了,如下图所示:

backward
做完forward,取得预测值Y,进而可计算出损失L,接下来就能做backward了。我们重画一下forward的过程,并在其中加入backward的部分,整体流程图如下:

forward
按列切分权重后,forward计算图如下:

backward

具体模型拆分方式:https://zhuanlan.zhihu.com/p/622212228
在实际应用中,对Transformer类的模型,采用最经典方法是张量模型并行 + 数据并行,并在数据并行中引入ZeRO做显存优化。具体的架构如下:

其中,node表示一台机器, 一般我们在同一台机器的GPU间做张量模型并行。在不同的机器上做数据并行 。图中颜色相同的部分,为一个数据并行组。凭直觉,我们可以知道这么设计大概率和两种并行方式的通讯量有关。具体来说, 它与TP和DP模式下每一层的通讯量有关,也与TP和DP的backward计算方式有关。
]]>干什么事情都没有动力,学习也不知道学什么,玩也不知道去哪,打球也略显尴尬,聊天也不知道找谁,刷剧也没有看下去的动力。
不管了,好久没有刷剧了,先刷一刷比较火的悬疑剧吧
]]>“NoBugVideo”基于Gin Web框架,采用微服务架构,使用Kong集成Consul做服务发现,实现了“抖音”的基本功能,包括视频流的推送、视频投稿、用户的注册与登录,以及社交(用户之间的关注与聊天)与互动(用户对视频点赞及评论)等功能。
项目服务地址:http://124.221.120.88:8000
Github地址:https://github.com/xu-jq/simple-DY
我们团队实现了包括基础功能在内的两大方向:互动方向与 社交方向 ,根据项目考核的4个标准,自评如下:
| 评价项 | 实现情况 |
|---|---|
| 功能实现 | 微服务与其他资源能够正常运行,完全实现文档中定义的全部接口,边界情况处理良好 |
| 代码质量 | 项目结构清晰,包划分合理,代码符合编码规范 |
| 服务性能 | 数据表设置了合理的索引,代码中尽量使用并行处理提高性能 |
| 安全可靠 | 通过GORM框架防止SQL注入,通过JWT进行用户的认证,防止越权 |
| 团队成员 | 主要贡献 |
|---|---|
| @汪辉 | 开发社交模块,搭建Kong集成Consul做服务发现 |
| @许珺琪 | 开发用户互动相关模块包括点赞评论等相关接口、搭建redis服务 |
| @张兆 | 开发用户模块与视频模块相关接口、搭建MySQL、RabbitMQ等服务 |
抖音上线于2016年9月26日,一开始是定位于专注于新生代的音乐创意短视频App,视频时常限制在15s内。年轻人比较爱赶新潮,乐于尝试新鲜事物,通过清晰明确定位在“潮流”“炫酷”“技术流”的方式,抖音吸引了第一批忠实粉丝。当产品功能逐渐完善后,抖音在运营方面开始发力,用户迎来大幅增长。抖音的主力用户群体年龄段上升,已经从早期的18岁到24岁,上升到了25岁到30岁用户。随着用户的快速增长,在内容层面也向着更加主流化、多元化的方向转变。
架构方面比较常见的有三种:
所有的模块打包到一起部署运行,在开发小型项目上有独特优势:易于调试、部署,运维方便。缺点是容错性低,不可靠。只能通过运行更多的服务器水平扩展, 而不同的应用服务对资源的需求不同,且不可持续发展。
面向服务架构是一种设计方法,设计上通常是自上而下的,服务间松散耦合。ESB集成不同协议的服务,做消息的转化、解释、路由从而联通各个服务,解决企业通信问题,服务松耦合、可扩展。缺点是SOA更多的面向企业服务,服务拆分粒度很大,更多的是为了复用。
微服务是去中心化的SOA的扩展,强调服务彻底的组件化,一个组件就是一个产品,服务切分力度更小,设计上更多的是自下而上的。服务间通过轻量级的协议进行通信,并根据服务本身需要独立化部署。从产品视角出发,更多聚焦可扩展性,兼顾可维护性。
综合上述几种服务的对比,我们最终选择了微服务架构,并使用下面的技术栈:
用户模块包括用户注册、用户登录和用户信息三个部分。
POST-/douyin/user/register/新用户注册时提供用户名,密码,昵称即可,用户名需要保证唯一。创建成功后返回用户 id 和权限token。
接口定义:
message douyin_user_register_request{ string username = 1; // 注册用户名,最长32个字符 string password = 2; // 密码,最长32个字符}message douyin_user_register_response{ int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 int64 user_id = 3; // 用户id string token = 4; // 用户鉴权token}POST-/douyin/user/login/通过用户名和密码进行登录,登录成功后返回用户 id 和权限 token
接口定义:
message douyin_user_login_request{ string username = 1; // 登录用户名 string password = 2; // 登录密码}message douyin_user_login_response{ int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 int64 user_id = 3; // 用户id string token = 4; // 用户鉴权token}GET-/douyin/user/获取登录用户的 id、昵称,如果实现社交部分的功能,还会返回关注数和粉丝数。
接口定义:
message douyin_user_request{ int64 user_id = 1; // 用户id string token = 2; // 用户鉴权token}message douyin_user_response{ int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 User user = 3; // 用户信息}视频模块包括包括视频Feed流获取、视频投稿和获取用户投稿列表三个模块
GET-/douyin/feed/不限制登录状态,返回按投稿时间倒序的视频列表,视频数由服务端控制,单次最多30个。
接口定义:
message douyin_feed_request{ int64 latest_time = 1; // 可选参数,限制返回视频的最新投稿时间戳,精确到秒,不填表示当前时间 string token = 2; // 可选参数,登录用户设置}message douyin_feed_response{ int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 repeated Video video_list = 3; // 视频列表 int64 next_time = 4; // 本次返回的视频中,发布最早的时间,作为下次请求时的latest_time}GET-/douyin/publish/list/登录用户的视频发布列表,直接列出用户所有投稿过的视频。
接口定义:
message douyin_publish_list_request{ int64 user_id = 1; // 用户id string token = 2; // 用户鉴权token}message douyin_publish_list_response{ int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 repeated Video video_list = 3; // 用户发布的视频列表}POST-/douyin/publish/action/登录用户选择视频上传。
接口定义:
message douyin_publish_action_request{ string token = 1; // 用户鉴权token bytes data = 2; // 视频数据 string title = 3; // 视频标题}message douyin_publish_action_response{ int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述}POST-/douyin/favorite/action/登录用户对视频进行点赞与取消点赞操作。
接口定义:
message douyin_favorite_action_request { string token = 1; // 用户鉴权token int64 video_id = 2; // 视频id int32 action_type = 3; // 1-点赞,2-取消点赞}message douyin_favorite_action_response { int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述}GET-/douyin/favorite/list/登录用户的所有点赞视频。
接口定义:
message douyin_favorite_list_request { int64 user_id = 1; // 用户id string token = 2; // 用户鉴权token}message douyin_favorite_list_response { int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 repeated Video video_list = 3; // 用户点赞视频列表}POST-/douyin/comment/action/登录用户对视频进行评论。
接口定义:
message douyin_comment_action_request { string token = 1; // 用户鉴权token int64 video_id = 2; // 视频id int32 action_type = 3; // 1-发布评论,2-删除评论 string comment_text = 4; // 用户填写的评论内容,在action_type=1的时候使用 int64 comment_id = 5; // 要删除的评论id,在action_type=2的时候使用}message douyin_comment_action_response { int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 Comment comment = 3; // 评论成功返回评论内容,不需要重新拉取整个列表}GET-/douyin/comment/list/查看视频的所有评论,按发布时间倒序。
接口定义:
message douyin_comment_list_request { string token = 1; // 用户鉴权token int64 video_id = 2; // 视频id}message douyin_comment_list_response { int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 repeated Comment comment_list = 3; // 评论列表}POST-/douyin/relation/action/登录用户对其他用户进行关注或取消关注。实现用户之间的关注关系维护,登录用户能够关注或取关其他用户,同时自己能够看到自己关注过的所有用户列表,以及所有关注自己的用户列表。
接口定义:
message douyin_favorite_list_request { int64 user_id = 1; // 用户id string token = 2; // 用户鉴权token}message douyin_favorite_list_response { int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 repeated Video video_list = 3; // 用户点赞视频列表}GET-/douyin/relatioin/follow/list/登录用户关注的所有用户列表。
message douyin_favorite_list_request { int64 user_id = 1; // 用户id string token = 2; // 用户鉴权token}message douyin_favorite_list_response { int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 repeated Video video_list = 3; // 用户点赞视频列表}GET-/douyin/relation/follower/list/所有关注登录用户的粉丝列表。
message douyin_favorite_list_request { int64 user_id = 1; // 用户id string token = 2; // 用户鉴权token}message douyin_favorite_list_response { int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 repeated Video video_list = 3; // 用户点赞视频列表}GET-/douyin/relation/friend/list/互相关注的用户列表。
message douyin_favorite_list_request { int64 user_id = 1; // 用户id string token = 2; // 用户鉴权token}message douyin_favorite_list_response { int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 repeated Video video_list = 3; // 用户点赞视频列表}客户端通过定时轮询服务端接口查询消息记录
GET-/douyin/message/chat/当前登录用户和其他指定用户的聊天消息记录
message douyin_message_chat_request{ required string token=1;//用户鉴权token required int64 to_user_id=2;//对方用户id required int64 pre_msg_time=3;//上次最新消息的时间}message douyin_message_chat_response { required int:32 status_code=1;//状态码,g-成功,其他值-失败 optional string status._msg=2;//返回状态描述 repeated Message message_list=3;//消息列表}message Message{ required int64 id=1;//消息id required int64 to_user_id=2;//该消息接收者的d required int64 from_user_id=3;//该消息发送者的id required string content=4;//消息内容 optional int64 create_time=5;//消息创建时间}POST-/douyin/message/action/登录用户对消息的相关操作,目前只支持消息发送
message douyin_relation_action_request{ required string token=1;//用户鉴权token required int64 to_user_id=2;//对方用户id required int32 action_type=3;//1-发送消息 required string content=4;//消息内容}message douyin_relation_action_response{ required int32 status._code=1;//状态码,g-成功,其他值-失败 optional string status_msg=2;//返回状态描述}运行流程:
用户注册的逻辑比较简单,请求的参数中只包含用户的用户名与密码,不支持手机注册以及各种验证码操作。因此用户的唯一识别信息为用户名。如果数据库中存在相同的用户名,则认为这个用户已经存在,拒绝注册;否则则允许用户注册,并在数据库中分配给这个用户唯一的id。最后调用JWT生成Token返回响应,作为在Token生效期间的用户的唯一标识符。
用户注册流程:
用户登录请求的参数中只包含用户的用户名与密码,不支持手机登录以及各种验证码操作。因此用户的唯一识别信息为用户名。如果数据库中不存在相同的用户名,则认为这个用户不存在,拒绝登录;否则则允许用户登录,并返回数据库中这个用户的唯一id。同时调用JWT生成Token返回响应,作为在Token生效期间的用户的唯一标识符。
用户登录流程:
用户信息请求的参数包括要请求的用户的id和当前登录的用户的Token。返回的用户信息应该包括用户的名称,用户的关注人数和粉丝人数,以及用户与当前登录用户的关注关系。因此除了调用DY-api.UserInfo获取用户的基本信息之外,还需要调用DY-srv.GetFollowList与DY-srv.GetFollowerList获取用户的关注人和用户的粉丝列表。两个Count数值可以通过查看切片的大小获得,关注关系需要遍历切片进行搜索。
在对不同的服务进行调用的时候采取并行调用的方式,服务全部返回后在api层进行拼接,从而提高效率。
用户信息流程:
获取视频流的请求参数包括视频的最新时间和当前用户的Token信息。如果当前用户在登录的状态下请求视频流,则通过最新时间在数据库中查询前30个视频的信息,包括视频本身的id和作者的id。获得最多30个视频的信息后,创建多个协程(视频数量个数),根据每个id获得视频的其他信息,如作者的详细信息,视频的点赞数量,作者的关注人数等等。在调用不同服务的时候也采用并行调用的方式。最后对返回的全部响应进行组织返回。
如果用户没有登录,则Token信息为空,那么返回的响应中缺少一些交互信息,如当前用户是否已经对当前视频点赞等等。
获取视频流流程:
DY-api.Feed处理请求,准备请求服务
首先请求DY-srv.Feed服务,根据时间戳查询数据库,查询出不超过时间戳的前30个视频,查询后返回视频列表
随后并行请求视频列表中的每一个视频(即最大并发数为30)
对每一个视频,根据前一个服务响应的作者的id并行请求DY-srv.UserInfo、DY-srv.GetFollowList和DY-srv.GetFollowerList,等待全部成功返回后记录Author响应相关的5个字段
对每一个视频,根据视频id并行请求DY-srv.douyinCommentList和DY-srv.douyinLikeVideo,对于每个视频
等待全部的视频返回响应后,构建响应结构体并返回给客户端
获取用户视频发布列表的请求参数包括用户的id和当前用户的Token信息。两者不一定是相同的用户,因为用户在观看视频的同时点击用户头像即可以看到这个视频作者的信息和作者的视频发布列表。
如果当前用户是查看自己的视频发布列表,则通过用户的id在数据库中查询发布的视频的信息。获得最多视频的信息后,创建多个协程(视频数量个数),根据每个id获得视频的其他信息,如视频的点赞数量,作者的关注人数等等。在调用不同服务的时候也采用并行调用的方式。最后对返回的全部响应进行组织返回。
如果Token信息为空,则当前场景是用户查看其他用户的发布视频列表。那么返回的响应中缺少一些交互信息,如当前用户是否已经对当前作者的视频点赞等等。
获取视频发布列表流程:
DY-api.PublishList处理请求,准备请求服务
首先请求DY-srv.PublishList服务,根据id查询数据库,如果id在数据库中不存在,则直接返回错误,然后根据用户id查询发布的视频列表并返回
随后并行请求DY-srv.UserInfo、DY-srv.GetFollowList和DY-srv.GetFollowerList,等待全部成功返回后记录User响应相关的5个字段
对每一个视频,根据视频id并行请求DY-srv.douyinCommentList和DY-srv.douyinLikeVideo,对于每个视频
等待全部的视频返回响应后,构建响应结构体并返回给客户端
视频投稿的请求参数中包括用户的Token,上传的视频流数据以及视频的标题。其中视频流是用户从本地上传得到的,视频的标题是用户自行输入得到的。上传视频必须是在登录的状态下,因此必须包含用户的Token信息。获得参数后,根据Token信息解析出当前用户的id,然后根据用户id判断是否存在这个用户的文件夹。如果不存在文件夹则新建用户文件夹。创建文件夹后将视频流写入这个文件夹下的视频文件,同时调用ffmpeg对视频的封面进行截取从而获得视频的首图。确认视频文件与图片文件都保存在本地后,构建返回的响应,并将上传文件的消息推送到消息队列中,此时消息队列将视频文件和图片文件异步上传到对象存储当中,上传结束后将视频信息写入数据库,在下次请求视频流的过程中就可以请求到这个视频了。
其中使用RabbitMQ进行异步处理,在服务器带宽有限的情况下,上传视频对用户来说基本无感,增加了用户的体验。且上传到对象存储后视频和图片的展示和下载速度也会更快,方便用户查看视频。
视频投稿流程:
点赞操作分为对未点赞的视频点赞以及对已点赞的视频取消点赞。点赞操作接口的请求参数包括,用户token;视频id;操作类型(1–点赞,2–取消点赞)。通过解析用户token可获得用户id。构建一个redis集合,将用户已经点赞的视频将其按照k-v形式存入redis。
2.1.1 对视频点赞
当请求参数操作类型的值为1时,即为点赞操作,点赞操作是要对用户未点赞的视频进行点赞,首先在redis集合中查询该用户是否对此视频点赞过,若点赞过则返回视频已点赞,若未点赞,则将该条点赞记录先插入redis再插入数据库中,最后返回成功的响应码。
2.1.2 对视频取消点赞
当请求参数操作类型的值为2时,即为取消点赞操作,取消点赞操作是要对用户点赞的视频进行取消,首先在redis集合中查询该用户是否对此视频点赞过,若未点赞过则返回视频暂未点赞,若点赞了,则将该条点赞记录先从redis中删除再从数据库中删除,最后返回成功的响应码。
喜欢列表接口的请求参数为用户id和用户token,先根据token验证用户身份与登录状态,若成功,则根据用户id查询用户的喜欢列表,将喜欢列表封装进响应结构体中,返回参数中还需要视频相关信息,通过调用视频服务接口,获取视频相关信息,并封装到响应结构体中,最终将响应结构体返回。
评论操作分为发表评论和删除评论,评论操作接口的请求参数包括用户token,视频id,操作类型(1–发表评论,2–删除评论),评论内容(发表评论时),评论id(删除评论时)。首先根据token验证用户身份与登录状态,若成功,则解析token获取用户id。
2.1.1 发表评论
当操作类型等于1时,表示是发表评论,将对应评论内容,用户id,视频id,添加进数据库,并且将评论列表封装进响应结构体,同时调用社交服务,获取对应的用户信息,将用户信息也封装进响应结构体,最后将其返回。
2.1.2 删除评论
当操作类型等于2时,表示是删除评论,将评论id对应的数据从数据库中删除,并返回删除成功的信息。
评论列表接口的请求参数为视频id和用户token,先根据token验证用户身份与登录状态,若成功,则根据视频id查询视频的评论列表,将评论列表封装进响应结构体中,返回参数中还需要用户相关信息,通过调用社交服务接口,获取用户相关信息,并封装到响应结构体中,最终将响应结构体返回。
社交模块的整体设计如下图:
其中 social-api程序是使用Gin框架搭建的Web服务。主要接受url请求,通过路由绑定handler处理函数,添加授权中间件。social-api部署了多个,并将自己注册在Consule服务上,支持负载均衡,并通过服务发现调用gRPC服务。
social-srv是业务处理代码,主要和MySQL数据库打交道。social-srv可以部署在多个不同服务器上,并将自己注册到Consul上来实现负载均衡,提供被其他服务发现。
详细设计:
关注接口的请求参数为用户ID和被关注的用户ID,先根据token验证用户身份与登录状态,若成功,则向数据库插入数据,同时互相关注的用户会成为朋友,在朋友界面显示朋友列表,并展现最近的一条消息。用户也可以在信息详情页面来查看关注的用户和粉丝。
通过用户ID和朋友ID可以新增一条消息。使用定时调用接口的方式来获取消息。
字段如下:
| 名称 | 类型 | 说明 |
|---|---|---|
id | bigint | 视频唯一id,自增主键 |
author_id | bigint | 视频作者id |
file_name | varchar | 文件名称 |
publish_time | bigint | 发布时间 |
title | varchar | 视频标题 |
索引设置:
| 名称 | 类型 | 说明 |
|---|---|---|
id | bigint | 用户id,自增主键 |
name | varchar | 用户名 |
password | varchar | 用户密码 |
索引设置:
| 名称 | 类型 | 说明 |
|---|---|---|
id | bigint | 评论唯一id,自增主键 |
user_id | bigint | 评论发布者的id |
video_id | bigint | 评论发布位置的视频id |
comment_text | varchar | 评论内容 |
create_time | datetime | 评论创建时间 |
索引设置:
| 名称 | 类型 | 说明 |
|---|---|---|
id | bigint | 关注关系id,自增主键 |
user_id | bigint | 用户id |
follower_id | bigint | 关注的用户id |
索引设置:
| 名称 | 类型 | 说明 |
|---|---|---|
id | bigint | 喜欢关系id,自增主键 |
user_id | bigint | 点赞用户的id |
video_id | bigint | 被点赞的视频id |
索引设置:
| 名称 | 类型 | 说明 |
|---|---|---|
id | bigint | 消息唯一id,自增主键 |
user_id | bigint | 发送消息的用户id |
to_user_id | bigint | 接收消息的用户id |
sent_time | datetime | 消息发送时间 |
content | varchar | 消息内容 |
索引设置:
后端项目总体分为两个大部分:
simple-DY/DY-api/):使用Gin框架来获取用户请求,连接GRPC远程调用服务,最后返回数据。simple-DY/DY-srvs/):GRPC编写的微服务。项目的总体结构如下所示:
├── simple-DY│ ├── db.sql // 数据库初始化文件│ ├── DY-api // web项目│ │ ├── interact-web // 互动模块│ │ ├── social-web // 社交模块│ │ └── video-web // 视频模块│ ├── DY-srvs // service项目│ │ ├── interact-srv // 互动模块│ │ ├── social-srv // 社交模块│ │ └── video-srv // 视频模块│ ├── go.mod│ ├── go.sum│ └── README.md代码结构:
video-web├── api│ ├── base.go│ ├── feed.go│ ├── info.go│ ├── otherapi.go│ ├── publishaction.go│ ├── publishlist.go│ ├── userinfo.go│ ├── userlogin.go│ └── userregister.go├── config│ └── config.go├── config-debug.yaml├── config-pro.yaml├── global│ └── global.go├── initialize│ ├── config.go│ ├── logger.go│ ├── router.go│ ├── srv_conn.go│ └── validator.go├── logs│ └── video-web.log├── main.go├── middlewares│ ├── cors.go│ └── jwt.go├── models│ ├── base.go│ ├── jwt.go│ ├── other.go│ ├── request.go│ └── response.go├── proto│ ├── simpledy_grpc.pb.go│ ├── simpledy.pb.go│ └── simpledy.proto├── README.md└── utils └── consul └── register.go详细说明:
api:编写路由的Handler处理函数config:读取yaml文件时的接收结构体*.yaml:配置文件config-debug.yaml:线下开发使用的配置文件config-pro.yaml: 线上配置文件global:存放全局变量,例如config信息,连接信息等initialize:初始化程序代码config.go:读取配置文件logger.go:日志配置router.go:gin路由srv_conn.go:连接微服务validator.go:翻译器logs:日志文件main.go:主程序入口middlewares:gin的自定义中间件cors.go:跨域中间件jwt.go:JWT中间件models:用户请求参数的结构体proto:编写和生成proto文件README.md:说明文件utils:工具类consul:调用consul api进行服务注册发现等操作代码结构:
.├── config│ └── config.go├── config-debug.yaml├── config-pro.yaml├── global│ └── global.go├── handler│ ├── base.go│ ├── feed.go│ ├── publishaction.go│ ├── publishlist.go│ ├── userinfo.go│ ├── userlogin.go│ ├── userregister.go│ └── videoinfo.go├── initialize│ ├── config.go│ ├── db.go│ ├── handler.go│ └── logger.go├── logs│ └── video-srv.log├── main.go├── models│ ├── base.go│ └── db.go├── proto│ ├── simpledy_grpc.pb.go│ ├── simpledy.pb.go│ └── simpledy.proto├── README.md└── utils ├── backup │ └── backup.go ├── consul │ └── register.go ├── dao │ ├── followdao.go │ ├── userdao.go │ └── videodao.go ├── ffmpeg │ └── extractFirstFrame.go ├── freeport │ └── port.go ├── jwt │ └── token.go ├── md5salt │ └── md5.go ├── oss │ └── upload.go └── rabbitmq ├── base.go ├── consumer.go └── producer.go详细说明:
config:读取yaml文件时的接收结构体*.yaml:配置文件config-debug.yaml:线下开发使用的配置文件config-pro.yaml: 线上配置文件global:存放全局变量,例如config信息,连接信息等handler:主要的逻辑代码,proto的service的实现类initialize:初始化程序代码config.go:读取配置文件db.go:数据库全局连接handler.go:监听客户端连接logger.go:日志配置logs:日志文件main.go:主程序入口models:用户请求参数的结构体proto:编写和生成proto文件README.md:说明文件utils:工具类backup:备份用户上传的视频和图片文件consul:调用consul api进行服务注册发现等操作dao:数据库相关操作ffmpeg:视频首页截图freeport:获取空闲网络端口jwt:鉴权Token的生成与解析md5salt:密码加密存储oss:七牛云对象存储相关操作rabbitmq:消息队列相关操作interact-web├── api│ ├── base.go│ ├── comment.go│ └── like.go├── config│ └── config.go├── global│ └── global.go├── initialize│ ├── config.go│ ├── logger.go│ ├── router.go│ ├── srv_conn.go│ └── validator.go├── main.go├── middlewares│ ├── cors.go│ └── jwt.go├── models│ └── request.go├── proto│ ├── simpledy_grpc.pb.go│ ├── simpledy.pb.go│ └── simpledy.proto├── router│ ├── comment.go│ └── like.go└── utils └── register └── consul └── register.gointeract-srv├── build.sh├── config│ └── config.go├── global│ └── global.go├── handler│ └── interact.go├── initalize│ ├── config.go│ ├── db.go│ ├── logger.go│ ├── rdb.go│ └── srvs_conn.go├── main.go├── model│ ├── base.go│ ├── comment.go│ ├── like.go│ └── video.go├── proto│ ├── simpledy_grpc.pb.go│ ├── simpledy.pb.go│ └── simpledy.proto└── utils ├── addr.go ├── jwt │ └── token.go ├── key │ └── key.go └── register └── consul └── register.gosocial-web├── api│ ├── base.go│ ├── message.go│ └── relation.go├── config│ └── config.go├── config-debug.yaml├── config-pro.yaml├── forms│ ├── message.go│ └── relation.go├── global│ └── global.go├── initialize│ ├── config.go│ ├── logger.go│ ├── router.go│ ├── srv_conn.go│ └── validator.go├── main.go├── middlewares│ ├── cors.go│ └── jwt.go├── models│ └── request.go├── proto│ ├── simpledy_grpc.pb.go│ ├── simpledy.pb.go│ └── simpledy.proto├── router│ ├── message.go│ └── relation.go└── utils ├── addr.go └── register └── consul └── register.gosocial-srv├── build.sh├── config│ └── config.go├── config-debug.yaml├── config-pro.yaml├── global│ └── global.go├── handler│ └── social.go├── initialize│ ├── config.go│ ├── db.go│ └── logger.go├── main.go├── model│ └── base.go└── proto ├── simpledy_grpc.pb.go ├── simpledy.pb.go └── simpledy.proto通过Apifox的自动化测试,构建不同实际使用中可能遇到的情况,对接口进行充分测试。
/douyin/user/register/需要对如下的用例进行测试:
测试结果:
/douyin/user/login/需要对如下的用例进行测试:
测试结果:
/douyin/user/需要对如下的用例进行测试:
测试结果:
/douyin/feed/需要对如下的用例进行测试:
测试结果:
/douyin/publish/list/需要对如下的用例进行测试:
测试结果:
/douyin/publish/action/需要对如下的用例进行测试:
测试结果:
在参加青训营期间,官方提供了全面的课程,涵盖了创作技巧、内容制作、问题分析等多个方面。这些课程不仅提供了实用的知识和技能,还可以让我们更好地理解抖音平台和用户需求。抖音青训营项目还提供了多种资源支持,包括专业导师、团队合作等。这些资源可以帮助我们更好地实践和落地自己的创意。
回顾整个项目的过程,我们团队做了如下总结:
https://www.jianshu.com/p/4e4ff6be6af9
https://www.apifox.cn/apidoc/shared-09d88f32-0b6c-4157-9d07-a36d32d7a75c/api-50707523
https://juejin.cn/post/7174037539345399839
https://blog.csdn.net/cc18868876837/article/details/90672971
]]>首先需要安装Java
sudo apt install openjdk-11-jdk下载安装kafka
wget https://dlcdn.apache.org/kafka/3.4.0/kafka_2.13-3.4.0.tgztar -xzf kafka_2.13-3.4.0.tgzcd kafka_2.13-3.4.0启动zookeeper和kafka:
bin/zookeeper-server-start.sh config/zookeeper.propertiesbin/kafka-server-start.sh config/server.properties使用给定代理地址和配置创建一个同步生产者
// 使用给定代理地址和配置创建一个同步生产者SyncProducer, err := sarama.NewSyncProducer( []string{conn}, config,)config可以自由配置:
config := sarama.NewConfig()// 等待服务器所有副本都保存成功后的响应config.Producer.RequiredAcks = sarama.WaitForAll// 随机的分区类型:返回一个分区器,该分区器每次选择一个随机分区config.Producer.Partitioner = sarama.NewRandomPartitioner// 是否等待成功和失败后的响应config.Producer.Return.Successes = true构建发送的消息:
// 构建发送的消息msg := &sarama.ProducerMessage{ Topic: topic, Key: sarama.StringEncoder(time.Now().String()), Value: sarama.StringEncoder(content),}生产者发送消息:
// SendMessage:该方法是生产者生产给定的消息// 生产成功的时候返回该消息的分区和所在的偏移量// 生产失败的时候返回errorpartition, offset, err := SyncProducer.SendMessage(msg)创建一个消费者的实例
config := sarama.NewConfig()consumer, err := sarama.NewConsumer(c.Node, config)查询这个 topic 有多少分区
partitions, err := consumer.Partitions(c.Topic)每个分区开一个 goroutine 来消费
wg.Add(len(partitions))// 然后每个分区开一个 goroutine 来消费for _, partitionId := range partitions { //不开异步会导致一个消费完才会消费另外一个 go c.consumeByPartition(consumer, c.Topic, partitionId, &wg)}消费
partitionConsumer, err := consumer.ConsumePartition(topic, partitionId, sarama.OffsetNewest)// 然后可以通过partitionConsumer.Messages()打印得到的消息func main() { Conn := "127.0.0.1:9092" topic := "test_log" var wg sync.WaitGroup wg.Add(2) // 消费者 go func() { defer wg.Done() // 初始化consumer var kafkaConsumer = consumer.KafkaConsumer{ Node: []string{Conn}, Topic: topic, } // 消费 go kafkaConsumer.Consume() }() // 生产者 go func() { defer wg.Done() index := 0 for { // 生产者发送消息 _, err := producer.Send(Conn, topic, fmt.Sprintf("lox_%d", index)) if err != nil { log.Print("测试失败:" + err.Error()) return } index++ time.Sleep(1 * time.Second) } }() wg.Wait()}Prometheus 是一款基于时序数据库的开源监控告警系统。Prometheus的基本原理是通过HTTP协议周期性抓取被监控组件的状态,任意组件只要提供对应的HTTP接口就可以接入监控。不需要任何SDK或者其他的集成过程。
wget https://github.com/prometheus/prometheus/releases/download/v2.37.6/prometheus-2.37.6.linux-amd64.tar.gztar xvfz prometheus-2.37.6.linux-amd64.tar.gz cd prometheus-2.37.6.linux-amd64/./prometheus --config.file=prometheus.yml此时打开http://localhost:9090/即可以看到监控界面
package mainimport ( "net/http" "github.com/prometheus/client_golang/prometheus/promhttp")func main() { //提供 /metrics HTTP 端点 http.Handle("/metrics", promhttp.Handler()) //端口号 http.ListenAndServe(":2112", nil)}运行后访问http://localhost:2112/metrics可以看到采集的指标数据
注册自定义应用程序指定指标:
package mainimport ( "net/http" "time" "github.com/prometheus/client_golang/prometheus" "github.com/prometheus/client_golang/prometheus/promauto" "github.com/prometheus/client_golang/prometheus/promhttp")func recordMetrics() { //每2秒,计数器增加1。 go func() { for { opsProcessed.Inc() time.Sleep(2 * time.Second) } }()}// 公开了 myapp_processed_ops_total 计数器var ( opsProcessed = promauto.NewCounter(prometheus.CounterOpts{ Name: "myapp_processed_ops_total", Help: "The total number of processed events", }))func main() { recordMetrics() http.Handle("/metrics", promhttp.Handler()) http.ListenAndServe(":2112", nil)}运行后访问http://localhost:2112/metrics可以看到自定义的指标,每2秒,计数器增加1
可以修改配置文件:prometheus.yml
# my global configglobal: scrape_interval: 15s # Set the scrape interval to every 15 seconds. Default is every 1 minute. evaluation_interval: 15s # Evaluate rules every 15 seconds. The default is every 1 minute. # scrape_timeout is set to the global default (10s).# Alertmanager configurationalerting: alertmanagers: - static_configs: - targets: # - alertmanager:9093# Load rules once and periodically evaluate them according to the global 'evaluation_interval'.rule_files: # - "first_rules.yml" # - "second_rules.yml"# A scrape configuration containing exactly one endpoint to scrape:# Here it's Prometheus itself.scrape_configs: # The job name is added as a label `job=<job_name>` to any timeseries scraped from this config. - job_name: "prometheus" # metrics_path defaults to '/metrics' # scheme defaults to 'http'. static_configs: - targets: ["localhost:2112"]将最后的targets修改成客户端启动的端口即可
]]>Hertz 是字节跳动服务框架团队研发的超大规模的企业级微服务 HTTP 框架,具有高易用性、易扩展、低时延等特点。
官方文档:https://www.cloudwego.io/zh/docs/hertz/
基本使用:
定义路由:
func main() {h := server.Default(server.WithHostPorts("127.0.0.1:50000"))h.GET("/ping", router.Deal)h.Spin()}路由的Handler:
其中与其他框架最大的不同点是将Context分成了两个部分:
两个上下文主要有两点区别:
Copy()方法获取一个协程安全的副本,而 context.Context 本身就是协程安全的。func Deal(c context.Context, ctx *app.RequestContext) {ctx.JSON(consts.StatusOK, utils.H{"message": res})}Thrift是一个 轻量级 、跨语言的远程服务调用框架,最初由 Facebook开发,后面进入 Apache开源项目。它通过自身的 IDL 中间语言 , 并借助代码生成引擎生成各种主流语言的 RPC 服务端 /客户端模板代码。
官方安装:https://thrift.apache.org/docs/BuildingFromSource.html
网上资料:
注意安装的thrift的版本与go的插件版本一定要相同!
安装go插件:
go get github.com/apache/thrift/lib/go/thrift首先安装依赖:
apt install libboost-dev libboost-test-dev libboost-program-options-dev libboost-filesystem-dev libboost-thread-dev libevent-dev automake libtool flex bison pkg-config g++ libssl-dev安装Thrift:
git clone https://github.com/apache/thriftcd thrift./bootstrap.sh./configure --without-qt4 --wihout-qt5makemake install编译使用:
thrift -r --gen go compute.thriftnamespace go computeservice MulRange { string BigRange(1:i64 max)}func Deal(c context.Context, ctx *app.RequestContext) {transportFactory := thrift.NewTTransportFactory()protocolFactory := thrift.NewTBinaryProtocolFactoryConf(nil)addr := "127.0.0.1:9999"cfg := &thrift.TConfiguration{}// 建立和服务器的连接socket,通过socket建立Transportvar transport thrift.TTransporttransport = thrift.NewTSocketConf(addr, cfg)transport, _ = transportFactory.GetTransport(transport)defer transport.Close()// 打开Transport,与服务器进行连接transport.Open()iprot := protocolFactory.GetProtocol(transport)oprot := protocolFactory.GetProtocol(transport)client := compute.NewMulRangeClient(thrift.NewTStandardClient(iprot, oprot))num, _ := client.BigRange(context.Background(), 10)fmt.Println(num)ctx.JSON(consts.StatusOK, utils.H{"message": num})}// 尽量一个struct对应一个servicetype mulrangeThrift struct {}func (m *mulrangeThrift) BigRange(_ context.Context, max int64) (string, error) {result := max + 1253return strconv.FormatInt(result, 10), nil}func main() {// 创建服务器serverTransport, _ := thrift.NewTServerSocket(net.JoinHostPort("127.0.0.1", "9999"))// 创建二进制协议transportFactory := thrift.NewTTransportFactory()protocolFactory := thrift.NewTBinaryProtocolFactoryConf(nil)mulrangeProcessor := compute.NewMulRangeProcessor(new(mulrangeThrift))// 启动服务器server := thrift.NewTSimpleServer4(mulrangeProcessor, serverTransport, transportFactory, protocolFactory)server.Serve()// 退出时停止服务器defer server.Stop()}参考资料:https://juejin.cn/post/6844903622380093447
Thrift是一个 轻量级 、跨语言的远程服务调用框架,最初由 Facebook开发,后面进入 Apache开源项目。它通过自身的 IDL 中间语言 , 并借助代码生成引擎生成各种主流语言的 RPC 服务端 /客户端模板代码。
通过编写 RPC接口 Thrift IDL文件,利用编译生成器自动生成 服务端骨架 (Skeletons)和 客户端桩 (Stubs)。从而省去开发者自定义和 维护接口编解码 、 消息传输 、服务器多线程模型等基础工作。
Handler)即实现类即可。IDL定义好的客户端桩和 服务对象 ,然后就像调用本地对象的方法一样调用远端服务。通过维护 Thrift格式的IDL( 接口描述语言 )文件(注意写好注释),即可作为给 Client使用的接口文档使用,也自动生成接口代码,始终保持代码和文档的一致性。且 Thrift协议可灵活支持接口的 可扩展性 。
因为其来自 Google Protobuf开发团队,所以其 IDL文件风格类似 Google Protobuf,且更加 易读易懂 ;特别是 RPC服务接口的风格就像写一个面向对象的 Class一样简单。
初学者只需参照:thrift.apache.org/,一个多小时就可以理解 Thrift IDL文件的语法使用。
Thrift支持 C++、 Java、Python、PHP、Ruby、Erlang、Perl、Haskell、C#、Cocoa、JavaScript、Node.js、Smalltalk等多种语言,即可生成上述语言的服务器端和 客户端程序 。
对于我们经常使用的 Java、PHP、Python、C++支持良好,虽然对 iOS环境的 Objective-C(Cocoa)支持稍逊,但也完全满足我们的使用要求。
Thrift在很多开源项目中已经被验证是稳定和高效的,例如 Cassandra、Hadoop、HBase等;国外在 Facebook中有广泛使用,国内包括百度、美团小米、和饿了么等公司。
Thrift可以让用户选择客户端与服务端之间传输通信协议的类别,在传输协议上总体划分为 文本 (text)和 二进制 (binary)传输协议。为 节约带宽 , 提高传输效率 ,一般情况下使用二进制类型的传输协议为多数,有时还会使用基于文本类型的协议,这需要根据项目/产品中的实际需求。常用协议有以下几种:
JSON文本的数据编码协议进行数据传输JSON只写的协议,适用于通过脚本语言解析Thrift和Protobuf的最大不同,在于Thrift提供了完整的RPC支持,包含了Server/Client,而Protobuf只包括了stub的生成器和格式定义。
User.thrift
namespace go Samplestruct User { 1:required i32 id; 2:required string name; 3:required string avatar; 4:required string address; 5:required string mobile;}struct UserList { 1:required list<User> userList; 2:required i32 page; 3:required i32 limit;}Service.thrift
include "User.thrift"namespace go Sampletypedef map<string, string> Datastruct Response { 1:required i32 errCode; //错误码 2:required string errMsg; //错误信息 3:required Data data;}//定义服务service Greeter { Response SayHello( 1:required User.User user ) Response GetUser( 1:required i32 uid )}thrift支持引入另一个thrift文件:
include "User.thrift"注意:
include 引入文件的使用,字段必须带文件名前缀:
1:required User.User user不能直接写 User user,这样会提示找不到 User定义。
编译时只编译引用了其他文件的thrift文件即可:
thrift -r --gen go Service.thriftnamespace go Samplenamespace php Sample需要支持多个语言,则需要定义多行。
命名空间或者包名是多层级,使用 .号隔开。例如golang对于 Sample.Model会生成目录 Sample/Model,包名是 Model。
struct User { 1:required i32 id = 0; 2:optional string name;}字段选项 支持 required、optional两种。
一旦一个参数设置为 required,未来就一定不能删除或者改为 optional,否则就会出现版本不兼容问题,老客户端访问新服务会出现参数错误。不确定的情况可以都使用 optional 。
bool:布尔值(true或false)byte:8位有符号整数i16:16位有符号整数i32:32位有符号整数i64:64位有符号整数double:64位浮点数string:使用UTF-8编码编码的文本字符串list<t1>:一系列t1类型的元素组成的有序列表,元素可以重复set<t1>:一些t1类型的元素组成的无序集合,元素唯一不重复map<t1,t2>:key/value对,key唯一typedef map<string, string> Dataenum TweetType { TWEET, RETWEET = 2, DM = 0xa, REPLY}默认从0开始赋值,枚举值可以赋予某个常量,允许常量是十六进制整数。末尾没有逗号。
不支持枚举类嵌套,枚举常量必须是32位正整数。
对于go,会生成 TweetType_开头的常量。
Thrift允许用户定义常量,复杂的类型和结构体可以使用JSON形式表示:
const i32 INT_CONST = 1234const map<string,string> MAP_CONST = {"hello": "world", "goodnight": "moon"}exception BizException { 1:required i32 code 2:required string msg}结构体可以包含其他结构体,但不支持继承结构体。
struct Response { 1:required i32 errCode; //错误码 2:required string errMsg; //错误信息 3:required Data data;}Thrift编译器会根据选择的目标语言为server产生服务接口代码,为client产生桩(stub)代码。
在go里是 interface。service里定义的方法必须由服务端实现。
service Greeter { Response SayHello( 1:required User.User user )}参数是user,返回值是Response类型
服务端主要完成4个部分的工作:
服务端最终要创建这样的一个server
func NewTSimpleServerFactory6(processorFactory TProcessorFactory, serverTransport TServerTransport, inputTransportFactory TTransportFactory, outputTransportFactory TTransportFactory, inputProtocolFactory TProtocolFactory, outputProtocolFactory TProtocolFactory) *TSimpleServer { return &TSimpleServer{ processorFactory: processorFactory, serverTransport: serverTransport, inputTransportFactory: inputTransportFactory, outputTransportFactory: outputTransportFactory, inputProtocolFactory: inputProtocolFactory, outputProtocolFactory: outputProtocolFactory, }}说明:
server := thrift.NewTSimpleServer4(processor, transport, transportFactory, protocolFactory)err = server.Serve()// 定义服务type Greeter struct {}handler := &Greeter{}processor := Sample.NewGreeterProcessor(handler)var transport thrift.TServerTransporttransport, err = thrift.NewTServerSocket(*addr)不同类型可选
//bufferedvar transportFactory thrift.TTransportFactoryif *buffered { transportFactory = thrift.NewTBufferedTransportFactory(8192)} else { transportFactory = thrift.NewTTransportFactory()}//framedif *framed { transportFactory = thrift.NewTFramedTransportFactory(transportFactory)}不同类型可选
var protocolFactory thrift.TProtocolFactoryswitch *protocol {case "compact": protocolFactory = thrift.NewTCompactProtocolFactory()case "simplejson": protocolFactory = thrift.NewTSimpleJSONProtocolFactory()case "json": protocolFactory = thrift.NewTJSONProtocolFactory()case "binary", "": protocolFactory = thrift.NewTBinaryProtocolFactoryDefault()客户端定义好client后直接调用方法即可,如下所示:
client := GetClient()rep, err := client.GetUser(ctx, 100)rep, err := client.SayHello(ctx, &Sample.User{ Name: "thrift", Address: "address", })iprot := protocolFactory.GetProtocol(transport)oprot := protocolFactory.GetProtocol(transport)client := Sample.NewGreeterClient(thrift.NewTStandardClient(iprot, oprot))涉及到protocolFactory与transport
protocolFactory := thrift.NewTBinaryProtocolFactoryDefault()iprot := protocolFactory.GetProtocol(transport)oprot := protocolFactory.GetProtocol(transport)注意要与服务端定义的protocolFactory要一致
创建socket连接:
var transport thrift.TTransportvar err errortransport, err = thrift.NewTSocket(addr)注意要提前进行类型定义,否则后面类型不匹配
定义transportFactory:
transportFactory := thrift.NewTTransportFactory()transport, err = transportFactory.GetTransport(transport)transport.Open()注意transportFactory的类型要与服务端相同
可以添加key同时使用SSL进行Socket连接从而确保安全性
]]>也许今天你很迷茫,不知道应该做一些什么事情
也许今天你很失落,努力了两周的结果是从头再来
也许今天你很懊恼,后悔自己之前的选择不够合适
也许今天你很伤心,并不会有人记得你的生日
但是今天是你的生日呀
在这个并不算很特殊的日子里,也值得你对自己说一声
张兆,生日快乐!
]]>本节课程分为四个部分
课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
数据库是结构化信息或数据的有序集合,一般以电子形式存储在计算机系统中。通常由数据库管理系统 (DBMS) 来控制。在现实中,数据、DBMS 及关联应用一起被称为数据库系统,通常简称为数据库。
查询包含一系列含有最终结果的字段, 紧跟 SELECT关键词。星号(“*”)也可以用来指定查询应当返回查询表所有字段,可选的关键词和子句包括:
FROM子句指定了选择的数据表。FROM子句也可以包含 JOIN 二层子句来为数据表的连接设置规则。WHERE子句后接一个比较谓词以限制返回的行。WHERE子句仅保留返回结果里使得比较谓词的值为True的行。GROUP BY子句用于将若干含有相同值的行合并。 GROUP BY通常与SQL聚合函数连用,或者用于清除数据重复的行。GROUP BY子句要用在 WHERE子句之后。HAVING子句后接一个谓词来过滤从 GROUP BY子句中获得的结果,由于其作用于 GROUP BY子句之上,所以聚合函数也可以放到其谓词中。ORDER BY子句指明将哪个字段用作排序关键字,以及排序顺序(升序/降序),如果无此子句,那么返回结果的顺序不能保证有序。CREATE TABLE default.test_insert_local( `p_date` Date, `id` Int32)ENGINE = MergeTreePARTITION BY p_dateORDER BY idSETTINGS index_granularity = 8192复制代码b. 读写数据库数据
insert into default.test_insert_local values ('2022-01-01', 1);select count() from default.test_insert_local;复制代码a. 数据压缩
【LZ4】
输入:abcde_bcdefgh_abcdefghxxxxxxx输出:abcde_(5,4)fgh_(14,5)fghxxxxxxx复制代码(5,4) 代表向前5个byte,匹配到的内容长度有4,即"bcde"是一个重复
重复项越多或者越长,压缩率就会越高
【Run-length encoding】
输入:WWWWWWWWWWWWBWWWWWWWWWWWWBBBWWWWWWWWWWWWWWWWWWWWWWWWBWWWWWWWWWWWWWW输出:12W1B12W3B24W1B14W复制代码压缩重复的数据
【Delta encoding】
输入:105, 135, 112, 135, 143, 147输出:105(base),30, -23, 23, 8, 4复制代码将数据存储为连续数据之间的差异,而不是直接存储数据本身
b. 数据处理
【查询优化】1.可以选择特定的列做计算而不是读所有列 2.对聚合计算友好
【延迟物化】
【向量化】
for (size_t i = 0; i < 100; ++i) c[i] = a[i] + b[i];复制代码非向量化执行
c[0] = a[0] + b[0]; c[1] = a[1] + b[1];... ... 复制代码如果这时候CPU也可以并行的计算我们写的代码,那么理论上我们的处理速度就会是之前代码的100倍,幸运的是SIMD指令就是完成这样的工作的,用SIMD指令完成这样代码设计和执行就叫做向量化
a.文件组织
b.文件内容
对于表
CREATE TABLE test.test_insert_local( `p_date` Date, `id` Int32)ENGINE = MergeTreePARTITION BY p_dateORDER BY idSETTINGS index_granularity = 8192复制代码它的文件组织
├── 20220101_1_1_0│ ├── checksums.txt│ ├── columns.txt│ ├── count.txt│ ├── data.bin│ ├── data.mrk3│ ├── default_compression_codec.txt│ ├── minmax_p_date.idx│ ├── partition.dat│ ├── primary.idx│ └── versions.txt├── 20220102_2_2_0│ ├── checksums.txt│ ├── columns.txt│ ├── count.txt│ ├── data.bin│ ├── data.mrk3│ ├── default_compression_codec.txt│ ├── minmax_p_date.idx│ ├── partition.dat│ ├── primary.idx│ └── versions.txt├── detached└── format_version.txt复制代码c. part和partition
d. part和column
e. column和index
CREATE TABLE hits_UserID_URL( `UserID` UInt32, `URL` String, `EventTime` DateTime)ENGINE = MergeTreePRIMARY KEY (UserID, URL)ORDER BY (UserID, URL, EventTime)SETTINGS index_granularity = 8192, index_granularity_bytes = 0;复制代码SELECT URL, count(URL) AS CountFROM hits_UserID_URLWHERE UserID = 749927693GROUP BY URLORDER BY Count DESCLIMIT 10复制代码CREATE TABLE test_multi_columns( `p_date` Date, `id` Int32, `map_a` Map(String, Int32))ENGINE = MergeTreePARTITION BY p_dateORDER BY map_a复制代码map中的每个key都是一列
map中的每一列都可以单独的查询
使用方式同普通列,可以做任何计算
大宽表查询
可以建非常多的列查询的时候引擎可以快速选择需要的列,查询的时候引擎可以快速选择需要的列
数据可以通过spark生成clickhouse格式的文件
导入到hdfs上由hive2ch导入工具完成数据导入
数据直接导入到各个物理节点
保证查询可以及时访问已有数据
可以按需加载需要的列
select countDistinct(uid)from user_detialwhere tag_id = 'a' and uid in ( select uid from user_detail wherer tag_id = 'b') 复制代码本节课程主要分为三个方面:
RDBMS(关系型数据库)是目前使用最为广泛的数据库之一,同时也是整个信息化时代的基石。本节课程通过生活中常见的场景向大家介绍RDBMS的作用、发展历程及其核心技术,最后以字节为例,展示了RDBMS的企业级实践。本节课程主要包含以下内容:
RDBMS有相关的数据和材料都非常多,这里主要给大家提供几篇经典论文,从经典的论文中,能够更有效的帮助大家理解RDBMS。
暂时无法在飞书文档外展示此内容
这篇论文是RDBMS的奠基之作,由RDBMS之父E.F.Codd博士于1970年发表。在这篇论文中,E.F.Codd首次提出了用于管理数据的关系模型,并将数据独立于硬件来存储,用户使用一个非过程语言来访问数据。
暂时无法在飞书文档外展示此内容
这本书被称为数据库领域的“红宝书”,由著名的图灵奖获得者,数据库领域专家,Michael Stonebraker撰写。其中介绍了数据库的基本概念,传统的RDBMS以及新的数据库架构等等,是一本非常棒的数据库领域入门文章。
通过抖音红包雨的案例,介绍 RDBMS 中 ACID 的概念:
数据库发展最初过程中,诞生过3种数据模型,最终关系型模型成为了应用最为广泛的数据库模型。
| 网状模型 | 层次模型 | 关系模型 | |
|---|---|---|---|
| 优势 | 能直接描述现实世界 存取效率较高 | 结构简单 查询效率高 可以提供较好的完整性支持 | 实体及实体间的的联系都通过二维表结构表示 可以方便的表示M:N关系 数据访问路径对用户透明 |
| 劣势 | 结构复杂 用户不易使用 访问程序设计复杂 | 无法表示M:N的关系 插入、删除限制多 遍历子节点必须经过父节点 访问程序设计复杂 | 关联查询效率不够高 关系必须规范化 |
在SQL执行过程中,需要经历SQL引擎、存储引擎、以及事务引擎等模块。而其中SQL引擎又分为Parser、Optimizer、Executor几个部分:
SQL引擎包括了:
存储引擎负责了数据的底层存储、管理和访问工作。各大RDBMS存储引擎的设计都有不少的差异,这里选择MySQL的InnoDB存储引擎来向大家做一个介绍:
事务引擎实现了数据库的ACID能力,这里还是以MySQL的InnoDB为例来介绍数据库内部是通过哪些技术来实现ACID:
字节中是国内数据规模最大的互联网公司之一,公司内部有成千上万套RDBMS系统。这一章节还是以红包雨为案例,展示了字节是如何解决大流量、流量突增、高可靠等问题的。
存储系统和数据库系统往往是后端服务的最后一环,提供数据存储、查询能力。本课程会先用模拟案例导入,向学员介绍存储系统、数据库系统的特点,然后解析多个主流产品,最后分享存储和数据库结合新技术演进的方向。本节课程主要包含以下内容:
跟存储 & 数据库系统相关的材料很多,涵盖开源项目、博客、论文等。下面提供部分资料作为参考
static.googleusercontent.com/media/resea…
作为各种开源分布式文件系统的鼻祖,GFS论文里面提到的架构非常经典,值得一学。
本书介绍了很多Linux内核子系统的实现,其中第13章着重讲了单机的文件IO。学习完Linux中的文件IO栈,对单机存储系统会有更深的认识。
通过一个模拟案例,描述了数据是怎么产生,在后端系统里怎么流通,最后怎么写入到存储/数据库系统。
本节课程主要分为四个方面:
课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;
课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;
课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
RPC的概念模型:User、User-Stub、RPC-Runtime、Server-Stub、Server
IDL(Interface Definition Language) 文件
生成代码
编解码(序列化/反序列化)
通信协议
网络通信
编解码层
传输协议层
网络通信层
稳定性
易用性
扩展性
观测性
高性能
相比本地函数调用,RPC调用需要解决的问题
一次 RPC 的完整过程
RPC 带来的问题将由 RPC 框架来解决
数据格式
选型考察点
生成代码和编解码层相互依赖,框架的编解码应当具备扩展任意编解码协议的能力
- LENGTH 字段 32bits,包括数据包剩余部分的字节大小,不包含 LENGTH 自身长度- HEADER MAGIC 字段16bits,值为:0x1000,用于标识 协议版本信息,协议解析的时候可以快速校验- FLAGS 字段 16bits,为预留字段,暂未使用,默认值为 0x0000- SEQUENCE NUMBER 字段 32bits,表示数据包的 seqId,可用于多路复用,最好确保单个连接内递增- HEADER SIZE 字段 16bits,等于头部长度字节数/4,头部长度计算从第14个字节开始计算,一直到 PAYLOAD 前(备注:header 的最大长度为 64K)- PROTOCOL ID 字段 uint8 编码,取值有: - ProtocolIDBinary = 0 - ProtocolIDCompact = 2- NUM TRANSFORMS 字段 uint8 编码,表示 TRANSFORM 个数- TRANSFORM ID 字段 uint8 编码,表示压缩方式 zlib or snappy- INFO ID 字段 uint8 编码,具体取值参考下文,用于传递一些定制的 meta 信息- PAYLOAD 消息内容第一种方式浪费线程(会占用内存和上下文切换开销),第二种方式浪费 CPU 做大量无效工作。而基于 IO 多路复用系统调用实现的 Poll 的意义在于将可读/可写状态通知和实际文件操作分开,并支持多个文件描述符通过一个系统调用监听以提升性能。
网络库的核心功能就是去同时监听大量的文件描述符的状态变化(通过操作系统调用),并对于不同状态变更,高效,安全地进行对应的文件操作。
从某种程度上讲超时、限流和熔断也是一种服务降级的手段 。
请求成功率
长尾请求
开箱即用
周边工具
框架文档 Kitex
自研网络库 Netpoll,背景:
a. 原生库无法感知连接状态
b. 原生库存在 goroutine 暴涨的风险
扩展性:支持多协议,也支持灵活的自定义协议扩展
性能优化,参考 字节跳动 Go RPC 框架 KiteX 性能优化实践
a. 网络优化
b. 编解码优化
合并部署
a. 微服务过微,引入的额外的传输和序列化开销越来越大
b. 将强依赖的服务统计部署,有效减少资源消耗
本节课程主要分为五个方面:
课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
kafka使用场景,业务日志、用户行为数据、Metrics数据
基本概念,Producer、Cluster、Consumer、Topic、Partition
数据迁移、Offset、Partition选主
一条消息从生产到消费是如何处理的,Producer端逻辑、Broker端逻辑、Consumer端逻辑
Kafka在使用中遇到问题
BMQ架构
BMQ各模块是如何工作的,Broker、Proxy、HDFS、MetaStorage
BMQ多机房容灾
RocketMQ使用场景
RocketMQ和Kafka对比
RocketMQ架构介绍,Producer、Broker、Nameserver、Consumer
一条消息从生产到消费是如何处理的,Producer端逻辑、Broker端逻辑、Consumer端逻辑
一些最佳实践的场景,包括数据展示
本节课程主要分为五个方面:
课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
每年春节抖音都会有很多有意思的玩法,如果同学们是字节的后端同学,怎么设计今年春节集卡瓜分20亿的技术方案?
业务流程
技术体量
方案引出
方案一:腾讯字节方案
方案二:Quartz方案——时间轮
资源来源
企业的信息安全体系是非常庞大的,任何一个环节都可能会出现安全风险。其中,黑灰产是安全人员最为关注的一个风险来源,也是历年来导致企业和用户损失最大的因素。
如果某个平台或者业务被黑灰产盯上,可能是因为这个业务存在安全隐患被黑灰产利用,也可能只是被黑灰产当做牟利的垫脚石。对黑灰产的监控和防御,就是要了解他们的意图、手段和行为模式,避免被黑灰产攻击或者利用。
本次可能会给大家简单介绍国内黑灰产的情况,挑选了几种比较经典的黑产作弊手段进行详细分析,希望能帮助大家对黑灰产这个群体有一定的了解,提升各位的安全意识,在日后的工作和生活中,多一些安全角度的思考。
本次课程偏科普性质,但内容不是大家在网络上可以随便看到的,课前可以阅读一些国内黑灰产的调研报告
推荐 Freebuf 黑镜调查系列 ,其中部分内容是讲师参与调查编写,不一定权威,但内容和数据都比较真实
《风控要略 互联网业务反欺诈之路》讲师参与编写
《互联网平台智能风控实战》
《白帽子讲web安全》
《Web安全深度剖析》
《Web安全机器学习入门》
上述几本都是入门级的书,挑一本即可
《 SQL注入攻击与防御》数据库安全进阶
《 linux服务器安全攻防》 主机安全进阶
《互联网企业安全高级指南》
《大型互联网企业安全架构》
]]>Consul 是 HashiCorp 公司推出的开源工具,用于实现分布式系统的服务发现与配置。与其他分布式服务注册与发现的方案,Consul的方案更“一站式”,内置了服务注册与发现框 架、分布一致性协议实现、健康检查、Key/Value存储、多数据中心方案,不再需要依赖其他工具(比如ZooKeeper等)。使用起来也较 为简单。Consul使用Go语言编写,因此具有天然可移植性(支持Linux、windows和Mac OS X);安装包仅包含一个可执行文件,方便部署,与Docker等轻量级容器可无缝配合 。
consul主要由server和client两种组件组成。
server负责核心数据的存储和处理请求,server可以部署多个实例(通常推荐3-5个),server只有一个leader实例,就是主节点,主节点是通过选举产生的,主节点负责数据的写入处理,同时将数据同步至其他server节点
client负责跟server通信,处理转发服务注册、服务发现请求到server节点,client还负责服务的健康检查,client节点可以部署多个实例,甚至每个微服务节点都部署一个client实例。
以开发模式启动consul,同时具备server和client的功能,不需要单独部署server和client
consul健康检查机制制运行在consul client中,会定期的根据服务健康检查配置,去检测服务是否正常,如果服务异常,就将服务的实例标记为不用, 如果恢复了,就标记为可用。
Kong是一款基于OpenResty(Nginx + Lua模块)编写的高可用、易扩展的,由Mashape公司开源的API Gateway项目。Kong是基于NGINX和Apache Cassandra或PostgreSQL构建的,能提供易于使用的RESTful API来操作和配置API管理系统,所以它可以水平扩展多个Kong服务器,通过前置的负载均衡配置把请求均匀地分发到各个Server,来应对大批量的网络请求。
Konga是可以管理Kong的图形界面,带来的一个最大的便利就是可以很好地通过UI观察到现在kong的所有的配置,并且可以对于管理kong节点情况进行查看、监控和预警。
微服务架构是由多个服务端和多个api端组成,客户端发起请求,需要单独的api进行接收和路由转发,然后通过与不同的服务端建立连接从而获得服务。
这个过程中需要在程序中记忆大量的端口,且一旦有节点失效,整个服务都将不可用。
Kong
Consul
api端
服务注册:
registerClient := consul.NewRegistryClient(global.GlobalConfig.Consul.Address, global.GlobalConfig.Consul.Port)err = registerClient.Register(global.GlobalConfig.MainServer.Address, global.GlobalConfig.MainServer.Port, "video-api", []string{"api", "video"})健康检查(注意是HTTP类型的):
check := &api.AgentServiceCheck{HTTP: "http://" + address + ":" + port + "/health",Timeout: "5s",Interval: "5s",DeregisterCriticalServiceAfter: "10s",}连接服务端:
conn, err = grpc.Dial("consul://"+global.GlobalConfig.Consul.Address+":"+global.GlobalConfig.Consul.Port+"/"+name+"?wait=14s",grpc.WithTransportCredentials(insecure.NewCredentials(),),grpc.WithDefaultCallOptions(grpc.MaxCallRecvMsgSize(1024*1024*size),grpc.MaxCallSendMsgSize(1024*1024*size),),grpc.WithDefaultServiceConfig(`{"loadBalancingPolicy": "round_robin"}`),)服务端
注意监听的时候要监听内网地址
lis, err := net.Listen("tcp", global.GlobalConfig.Address.In+":"+port)服务注册:
register_client := consul.NewRegistryClient(global.GlobalConfig.Consul.Address, global.GlobalConfig.Consul.Port)register_client.Register(global.GlobalConfig.Address.Out, port, name, []string{"srv", "video"})健康检查(注意是GRPC类型的):
grpc_health_v1.RegisterHealthServer(s, health.NewServer())check := &api.AgentServiceCheck{GRPC: address + ":" + port,Timeout: "5s",Interval: "5s",DeregisterCriticalServiceAfter: "10s",}连接api端:
s := grpc.NewServer()手把手教你做系统设计之秒杀系统
本节课程主要分为四个方面:
课前部分主要罗列课程中涉及到的中间件和相关背景知识。对于使用到的中间件,同学们需要体验了解概念,安装并正确使用。课中部分会详细讲解系统设计的方法论和秒杀系统实践,帮助同学们入门系统设计。课后部分会做一些总结,梳理核心思想和重点。
高性能系统的通用设计思想
本课程内容主要分为以下4个方面:
微服务架构介绍
微服务架构原理及特征
核心服务治理功能
字节跳动服务治理实践
为了帮助大家更好地预习及理解本节课程,该学员手册列出了课前、课中、及课后这三个阶段所涉及到的专业内容大纲,其中课前部分供同学们提前预习参考,课中部分给出了课程大纲,帮助同学们整理思路,课后部分列出一些扩展性的问题让同学们进一步延伸思考。
系统架构的演进历史
微服务架构的三大要素
微服务架构中的基本概念及组件
服务间通信
服务注册及服务发现
服务发布
流量治理
负载均衡
稳定性治理
单体架构
垂直应用架构
分布式架构
SOA架构
微服务架构
服务治理(本课程内容)
可观测性
安全
服务
实例
实例与进程的关系
常见的实例承载形式
基本问题
简单方案
服务注册发现
微服务流量特征
何为服务发布
服务发布难点
蓝绿部署
灰度发布(金丝雀发布)
流量控制
控制维度
限流
熔断
过载保护
降级
请求重试的意义
请求重试的难点
重试策略
重试效果验证
本节课程主要分为6个方面:
课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
为了帮助同学们更好地理解本课程,我为大家准备了本学员手册。它包含以下几大模块内容:
本课程的包含以下四个方面:
常见软件架构:
一些小问题:
Q:如何给架构下定义?
A:架构,又称软件架构:
Q:架构的重要性?
A:那盖房子来做举例子。
我们都知道,地基对于一栋楼房的主要性,架构对于一个软件的重要性也是类似的:
All in one,所有的东西都在一个进程里,部署在一个机器上。
优点:
缺点:
在单机架构的基础上,将进程部署到多个机器上。
优点:
缺点:
在单机架构基础上,将进程按照某种依据切分开。比如,A 软件和 B 软件的后端原先采用单机架构部署,那就是一个进程部署在多个机器上;如果用垂直应用架构,可以将 A 和 B 的后端拆分为 A、B 两个进程,然后再按照单体模式的思路,部署在多个机器上。
优点:
缺点:
SOA 架构中,服务为一等公民,将进程按照不同的功能单元进行抽象,拆分为『服务』。有了服务之后,SOA 还为服务之间的通信定义了标准,保证各个服务之间通讯体验的一致性。
优点:
缺点:
在 SOA 架构中,ESB 起到了至关重要的作用。但从架构拓扑来看,它更像是一个集中式的模块。有一个 SOA 分布式演进的分支,最终的形态便是微服务。
优点:
缺点:
云计算基础:
云计算架构:
云原生,实际是云原生(计算)的简称,它是云计算发展到现在的一种形态。
云原生技术为组织(公司)在公有云、自由云、混合云等新型的动态环境中,构建和运行可弹性拓展的应用提供了可能。 它的代表技术:
基于虚拟化技术,提供的可以快速扩缩容的能力。可以分为弹性计算资源和弹性存储资源两个方面。
弹性计算资源:
弹性存储资源:
在云原生的大背景下,不论是计算资源还是存储资源,他们都像是服务一样供用户使用。
微服务架构下,服务之间的通讯标准是基于协议而不是 ESB 的。
如何在 HTTP 和 RPC 之间选择?
什么是服务网格?
没有什么是加一层代理解决不了的问题,服务网格相比较于 RPC/HTTP 框架:
基础设施层面:
Q:我们总说,云是弹性的,也就是说,在用户的角度,云提供的资源是无限的。然而,云背后的物理资源是有限的。在企业级后端架构里,云如何解决近乎无限的弹性资源和有限的物理资源之间的矛盾?
Q:闲事的资源就这么空着呢?如何提高资源利用率,提高物理资源的价值转换率?
用户层面:
Q:上了云原生微服务后,服务之间的通信开销较大,应该如何做成本优化?
Q:微服务看起来没有那么美好,抖动导致的运维成本较高,如何解决?
Q:异构的物理环境应该对用户是透明的,如何屏蔽这些细节?
考虑到在线业务的 潮汐性 ,物理资源的用量不是一成不变的。离在线资源并池,可以:
微服务之间的通信成本较高,是否可以:
亲合性部署,通过将微服务调用形态与资源调度系统结合,将一些调用关系紧密、通信量大的服务部署在同一个机器上,并且使用 IPC 代替 RPC 的方式,降低网络通信带来的开销
Q:微服务之间的通信流量为什么需要治理?
Q:都有哪些常用的治理手段?
Q:微服务中心件和服务网格在其中扮演着怎样的角色?
Q:基础设施层往往是个复杂的异构环境,比如,有些机器的 CPU 是英特尔的,而有些是 AMD 的。就算是同一个品牌,也可能是不同代际。如何将这些差异屏蔽掉,使用户尽可能不感知呢?
Q:什么情况下,我们觉得,服务需要扩容了?异构环境会对这个评判标准产生怎样的影响?
如何设计一个根据主机层面的资源信息,实时进行流量调度的系统,打平不同宿主机异构环境的算力差异。
关键点:
设计需求:
注意: 不需要考虑与做蛋糕相关服务的交互
这是构建容错k/v存储系统的一系列实验室中的第一个。这个实验室将实现复制状态机协议Raft。
复制服务通过在多个副本服务器上存储其状态(即数据)的完整副本来实现容错。复制允许服务继续运行,即使某些服务器出现故障(崩溃或网络问题)。挑战在于,故障可能会导致复制副本保存不同的数据副本。
Raft将客户端请求组织成一个序列,称为日志,并确保所有副本服务器都看到相同的日志。每个副本按日志顺序执行客户端请求,并将它们应用于服务状态的本地副本。由于所有活动副本都看到相同的日志内容,因此它们都以相同的顺序执行相同的请求,从而继续具有相同的服务状态。如果服务器出现故障,但稍后恢复,Raft会负责更新其日志。只要有大多数服务器处于活动状态,并且可以相互通信,Raft就会继续运行。如果没有这样的大多数,Raft将会暂时停机,但一旦大多数服务器能够再次通信,Raft就会恢复原来的状态。
在这个实验中,将会把Raft实现为一个Go对象类型,并实现相关的方法,这意味着要在更大的服务中将Raft用作模块。一组Raft实例通过RPC相互通信,以维护复制的日志。Raft接口将支持无限序列的编号命令,也称为日志条目。条目用索引编号进行编号。具有给定索引的日志条目最终会被提交。此时,Raft应该将日志条目发送到更大的服务以供其执行。
您应该遵循扩展的Raft论文中的设计,尤其是图2。您将实现本文中的大部分内容,包括保存持久状态,并在节点发生故障后重新启动后读取该状态。不实现第6节提到的集群成员资格更改。
最具挑战性的部分可能不是实现解决方案,而是调试解决方案。为了帮助解决这一挑战,您可能需要花时间思考如何使实现更易于调试。
我们还提供了一个Raft交互的图表,可以帮助阐明Raft代码如何与上面的层进行交互。
(几年前编写,特别是2D部分已经发生了变化)
Raft 是一种共识算法,旨在轻松理解。它与Paxos的容错和性能相当。不同的是,它被分解成相对独立的子问题,它干净地解决了所有主要部分的实际系统需求。我们希望Raft可供更广泛的受众使用,并且这些更广泛的受众将是能够开发各种更高质量的基于共识的系统。
与所有分布式共识协议一样,细节很难理解。在没有故障的稳定状态下,Raft 的行为易于理解,并且可以直观地解释。例如,从可视化中很容易看出, 假设没有失败,最终将选出Leader,并且最终,发送给Leader的所有操作都将由Follower按照顺序正确执行。但是,当消息延迟,网络分区或者服务故障,细节变得至关重要。特别是,我们可能一遍又一遍地重复许多错误,仅仅是由于阅读论文时的误解或疏忽。这个问题并非Raft所独有。
Raft 的最终指南在 Raft 论文的图 2 中。这个图片指定在Raft服务器之间交换的每个RPC的行为, 给出服务器必须维护的各种不变量,并指定何时应执行某些操作。我们将在本文的其余部分大量讨论图 2。它需要一字不差地遵循。
图 2 定义了每个服务器在各种状态下应该对每个传入的 RPC应该做什么,以及何时发生某些其他事情(例如就像在日志中应用条目是安全的一样)。图 2 非常精确,每一条语句在规范术语中,它应该被视为必须,而不是应该。例如,您可以合理地重置一台服务器的选举计时器,只要您收到或RPC,都表明其他服务器要么认为它是Leader,或者是努力成为Leader。直觉上,这意味着我们不应该干扰。但是,如果您仔细阅读图 2,它会说:如果选举超时过去而没有收到当前Leader的RPC或投票给其他的服务器,则转换为Candidate。
事实证明,区别很重要,因为前一种实现在某些情况下,可能导致活性显著降低。
考虑一个例子。Raft论文在许多地方提到了心跳RPC。具体来说,领导者将偶尔(每个检测信号间隔至少一次)向所有服务器发送 RPC,以防止它们启动新的选举。如果领导者没有要发送到特定对等方的新条目, RPC 不包含任何条目,被视为心跳。
我们的许多学生认为心跳在某种程度上是“特别的”,当服务器收到心跳时,它应该以不同的方式对待它。特别是,许多人会只在收到心跳时重置他们的选举计时器,然后返回成功,而不执行图2中指定的任何检查。这是极其危险的。通过接受 RPC, Follower隐式地告诉Leader他们的日志与Leader匹配并包括参数中包含的内容。收到回复后,领导可能错误地确定某个条目已被复制到大多数服务器,并开始提交它。
许多人遇到的另一个问题是在收到心跳时,他们会截断Follower的记录,然后添加参数中包含的日志条目。这也是不正确的。图 2说明,如果现有条目与新条目冲突(相同的索引但 不同的任期),删除现有条目及其后面的所有条目。
这里的如果至关重要。如果Follower拥有Leader的所有条目,Follower不得截断其日志。必须保留Leader发送的条目之后的任何元素。这是因为我们可能从Leader收到过期的RPC,截断日志将意味着“收回”我们可能已经告诉Leader的我们的日志。
在调试时,Raft通常有四个主要的错误来源: 活锁、不正确或不完整的 RPC 处理程序、未能遵循规则和术语混淆。死锁也是一个常见问题,但它们通常可以通过记录所有锁和解锁来调试,并且弄清楚你正在占有哪些锁且没有释放。
当系统活锁时,系统中的每个节点都在执行一些东西,但总的来说,你的节点没有取得进展。一个活锁场景特别频繁出现:没有领导人被选举出来,或者一个领导者被选举出来后另一个节点马上开始选举,迫使最近当选的领导人立即退位。
出现这种情况的原因有很多:
确保在图 2说明的时候准确重置选举计时器。具体来说,有三种情况:
最后一种情况在不可靠的网络中尤其重要,其中Follower可能有不同的日志,在这些情况下, 只有少量的服务器使得大多数服务器都愿意投票支持。如果每当有人要求您投票给他们时都重置选举计时器,会使日志过时的服务器同样有可能向前迈进
事实上,因为很少的服务器有足够的最新的日志,这些服务器不太可能在足够和平的情况下进行选举。如果您遵循图 2,具有最新日志的服务器不会被过时的服务器选举打断,因此更有可能完成选举并成为Leader。
按照图 2 的说明操作了解何时应开始选举。 特别要注意的是,如果您是Candidate,但选举计时器触发,应该开始另一次选举。这对于避免由于 RPC 延迟或丢弃而导致系统停止非常重要。
在处理传入的 RPC 之前 ,请确保遵循“服务器规则”中的第二条规则。第二条规则规定:如果 RPC 请求或响应包含术语set ,则转换为Follower
例如,如果您已经在当前任期内投票,并且传入的RPC有一个更高的任期号,你应该首先下台并采用他们的任期(从而重置),然后处理RPC,处理的过程中就会进行投票
尽管图 2 准确地说明了每个 RPC 处理程序应该执行的操作, 一些细节仍然很容易被忽略。
如果步骤显示“回复错误”,这意味着您应该立即回复,不要执行任何后续步骤。
如果你得到一个指向日志末尾的RPC,应该像确实有该条目,但该任期不匹配处理这个。
如果领导者没有发送任何条目,RPC处理程序的检查 2 应执行。
#5 是必要的, 并且需要使用最后一个新条目的索引进行计算。 这是因为日志中可能存在与领导者日志不同的条目。因为 #3 规定您只有在有冲突的条目情况下才会截断日志,这些条目不会被删除,如果超出领导发送给您的条目,您可能会应用不正确的条目。
实施“最新日志”检查非常重要。只是检查长度!
虽然 Raft 论文非常明确地说明了如何实现每个 RPC 处理程序,它还留下了许多规则的实现和未指定的不变量。这些列在“服务器规则”中 图 2 右侧的块。虽然其中一些是不言自明的,也有一些需要非常小心地设计,以免违反规则:
如果在执行过程中的任何时候应用特定的日志条目。请务必确保仅由一个实体完成此应用程序。具体来说,您需要有一个专门的 “应用器”,或者锁定这些应用,以便其他一些例程不会同时检测到需要应用条目。
确保定期更新,或更新后进行检查。例如,如果您在发送给同行的同时进行检查,您可能需要等到下一个条目追加到日志中后再应用您刚刚发送并得到确认的条目。
如果领导者发出 RPC,并且被拒绝,但不是因为日志不一致(这只有在我们的任期中才会发生),那么您应该立即下台并且不更新。
领导者不允许更新到上一任期(或就此而言,未来任期)的某个地方。因此特别需要检查。这是因为如果这不是他们目前的任期,Raft 领导者无法确定条目是否实际提交(并且将来永远不会更改)。
一个常见的问题来源是nextIndex和matchIndex之间的区别。特别是,你可能会观察到matchIndex = nextIndex - 1,而干脆不实现matchIndex。这是不安全的。虽然nextIndex和matchIndex通常在同一时间被更新为类似的值(具体来说,nextIndex = matchIndex + 1),但两者的作用完全不同。它通常是相当乐观的(我们分享一切),并且只在消极的反应中向后移动。例如,当一个领导者刚刚当选时,nextIndex被设置为日志末尾的索引指数。在某种程度上,nextIndex是用于性能的–你只需要将这些东西发送给这个对等体。
matchIndex是用于安全的。MatchIndex不能被设置为一个太高的值,因为这可能会导致commitIndex被向前移动得太远。这就是为什么matchIndex被初始化为-1(也就是说,我们不同意任何前缀),并且只在跟随者肯定地确认AppendEntries RPC时才更新。
任期混淆是指服务器被来自旧任期的RPC所迷惑。一般来说,在收到RPC时,这不是一个问题,因为图2中的规则确切地说明了当你看到一个旧任期时你应该做什么。然而,图2一般没有讨论当你收到旧的RPC回复时你应该做什么。根据经验,我们发现到目前为止,最简单的做法是首先记录回复中的任期(它可能比你当前的任期高),然后将当前任期与你在原始RPC中发送的任期进行比较。如果两者不同,就放弃回复并返回。只有当这两个任期相同时,你才应该继续处理回复。
一个相关但不完全相同的问题是,预设你的状态在你发送RPC和你收到回复之间没有变化。这方面的一个很好的例子是,当你收到RPC的响应时,设置matchIndex = nextIndex - 1,或者matchIndex = len(log)。这并不安全,因为这两个值都可能在你发送RPC后被更新。相反,正确的做法是将 matchIndex 更新为你最初在 RPC 中发送的参数中 prevLogIndex + len( entries[]) 。
一个Raft实例必须处理外部事件的到来(Start()调用、AppendEntries和RequestVote RPC以及RPC回复),它必须执行定期任务(选举和心跳)。有许多方法可以构造Raft代码来管理这些活动,下面是一些想法。
rf.mu.Lock() rf.currentTerm += 1 rf.state = Candidate for <each peer> { go func() { rf.mu.Lock() args.Term = rf.currentTerm rf.mu.Unlock() Call("Raft.RequestVote", &args, ...) // handle the reply... } () } rf.mu.Unlock()这个代码在单独的goroutine中发送每个RPC。这是不正确的,因为如果周围的代码是决定成为Candidate,args.Term可能与rf.currentTerm不同。当周围的代码创建goroutine和当goroutine读取rf.currentTerm时可能过去了很多的时间,这台服务器也可能不再是Candidate。一种方法是当外部代码持有锁的时候创建rf.currentTerm的副本从而让goroutine去使用。同样的,在调用之后的回复处理代码重新获取锁后必须重新检查所有相关的假设,例如,它应该检查自从决定成为Candidate后rf.currentTerm没有再次改变。
一种方法是从没有锁的代码开始,然后仔细考虑需要在哪里添加锁以变得正确。另一个更务实的方法从观察开始,如果没有并发性(没有同时执行goroutine)则根本不需要锁。但是当RPC系统创建goroutine以执行RPC处理程序时,以及
因为您需要在单独的goroutine中发送RPC以避免等待,并发性就有了。可以通过识别所有goroutine开始的位置(RPC处理程序、在Make()中创建的后台goroutine,&c),并且在每个goroutine开始的时候获得锁,只有当goroutine
完全完成并返回的时候才释放锁,从而消除并发性。这个锁定协议确保任何重要的事情都不会并行执行;锁确保每个goroutine在其他goroutine执行之前完成,没有并行执行,很难违反规则1、2、3或5。如果每个goroutine的代码正确,在使用锁抑制并发时仍然是正确的。
然而,规则4可能是一个问题。所以下一步是找到代码等待的位置,然后根据需求添加锁释放和重新获取(或goroutine的创建),记得小心重新建立和重新获取后的情况。
框架代码:src/raft/raft.go
测试代码:src/raft/test_test.go,运行go test即可
通过在src/raft/raft.go中增加代码实现Raft,必须遵循下面的接口:
// create a new Raft server instance:rf := Make(peers, me, persister, applyCh)// start agreement on a new log entry:rf.Start(command interface{}) (index, term, isleader)// ask a Raft for its current term, and whether it thinks it is leaderrf.GetState() (term, isLeader)// each time a new entry is committed to the log, each Raft peer// should send an ApplyMsg to the service (or tester).type ApplyMsg服务调用 Make(peers, me, ...)创建一个 Raft peer。peers 参数是所有 Raft peers(包括这一个)的网络标识符数组,用于 RPC。me参数是网络标识符数组中,属于这个peer的网络标识符的下标。Start(command) 要求 Raft 启动处理,将命令追加到日志副本中。Start()应立即返回,无需等待日志追加完成。该服务希望你将每个新的日志条目,封装为 ApplyMsg,发送给Make函数中的 applyCh参数(这是一个channel)。
raft.go包含发送 RPC sendRequestVote()和处理传入 RPC RequestVote()的样例代码。您的 Raft peers 应该使用 labrpc Go 包(源代码在 src/labrpc)交换 RPC。测试代码可以告诉 labrpc 延迟 RPC请求,重新排列它们,并丢弃它们以模拟各种网络故障。Raft 实例必须仅与 RPC 交互;例如,不允许它们使用共享的 Go 变量或文件进行通信。
后续的实验也在此实验上进行构建。
参考翻译:https://zhuanlan.zhihu.com/p/248686289
实现Raft算法中的Leader选举和心跳机制(AppendEntries RPC 且没有日志条目)。确保只有一个Leader被选中,且若无错误该Leader会一直唯一存在,当该Leader下线或发生其他错误导致发出的数据无法被成功接收,则会产生新的Leader来替代。
go test -run 2A 来验证代码的正确性raft.go中添加Figure 2的Leader选举的状态,同时也需要定义一个结构体保留日志条目的信息RequestVoteArgs和 RequestVoteReply结构。修改 Make()以创建一个后台 go 协程,该协程将在一段时间未从其他 peers 那里听到请求投票 RPC 时,发送 RequestVote RPC 来定期启动 Leader 选举。这样,如果已经有一个 Leader,或者自己成为 Leader,其他 peers 就会知道谁是Leader。实现 RequestVote() RPC 函数,以便服务器投票给别人。AppendEntries RPC 结构(尽管您可能还不需要所有参数),并让 Leader 定期发送它们。AppendEntries RPC 函数需要重置选举超时时间,以便其他服务器已当选时,不会以 Leader 的身份继续运行。time.Timer或 time.Ticker,这两个并不好用,容易出错。GetState()。rf.Kill()时,您可以先调用 rf.killed()再检查是否 Kill()。您可能希望在所有循环中执行此功能,以避免已经死亡的 Raft 实例打印令人困惑的信息。go test -run 2A > out,将日志收集到文件中。然后,通过研究 out 文件,可以确定实现中不正确的地方。您可能会喜欢用 util.go中的 Dprintf函数来调试,其可以在不同情况下打开和关闭日志。labgob包会警告您这一点,不要忽略警告。go test -race测试你的代码,并修复它报告的任何问题。输出应该如下面所示:
$ go test -run 2ATest (2A): initial election ... ... Passed -- 3.5 3 58 16840 0Test (2A): election after network failure ... ... Passed -- 5.4 3 118 25269 0Test (2A): multiple elections ... ... Passed -- 7.3 7 624 138014 0PASSok 6.824/raft16.265s$每一个“通过”的测试用例会输出五个数字;他们分别是
首先需要对代码中不完整的结构体进行填充,论文中的Figure 2有的字段一定保留,其他的字段看情况保留
首先定义服务器的状态,用字符串常量表示:
// 定义Peer的状态type State stringconst (Follower State = "follower"Candidate State = "candidate"Leader State = "leader")然后定义Raft结构体:
type Raft struct {mu sync.Mutex // Lock to protect shared access to this peer's statepeers []*labrpc.ClientEnd // RPC end points of all peerspersister *Persister // Object to hold this peer's persisted stateme int // this peer's index into peers[]dead int32 // set by Kill()// Your data here (2A, 2B, 2C).// Look at the paper's Figure 2 for a description of what// state a Raft server must maintain.// 在所有peer上面的持久性的状态// 在对RPC进行响应之后要在稳定存储上更新currentTerm int // this peer 看到的最新的任期号votedFor int // 在当前任期获得选票的Candidate的id(如果没有则为-1)log []LogEntry // 日志信息// 在所有peer上面的变化的状态commitIndex int // 已知的已经被提交的日志条目的最大索引值lastApplied int // 最后被应用到状态机的日志条目索引值(初始化为 0,持续递增)// 在Leader上面的变化的状态// 每一次选举后都要重新进行初始化nextIndex []int // 对于每⼀个服务器,需要发送给他的下⼀个日志条目的索引值(初始化为Leader最后索引值加1)matchIndex []int // 对于每⼀个服务器,已经复制给他的日志的最高索引值// 与时间相关的变量electTimeout int64 // 选举超时时间randomTimeout int64 // 随机时间heartBeatTimeout int64 // 心跳周期// 当前状态state State // 当前Peer所处的状态(Leader、Candidate或Follower)majorityVote int // 成为Leader需要获得的最少票数lastReceive int64}其中多定义了6个变量,3个变量与时间相关,分别表示选举超时时间、随机的时间上限和Leader发送心跳的周期时间
// 与时间相关的变量electTimeout int64 // 选举超时时间randomTimeout int64 // 随机时间heartBeatTimeout int64 // 心跳周期最后3个变量,第1个表示服务器当前所处的状态,第2个表示成为Leader需要获得的最少票数,这个值提前计算出来,最后一个值表示最后一次接收到Leader的心跳信号的时间
// 当前状态state State // 当前Peer所处的状态(Leader、Candidate或Follower)majorityVote int // 成为Leader需要获得的最少票数lastReceive int64 // 最后一次接收到Leader的心跳信号的时间服务器不同状态之间的转换比较频繁,因此可以将这些服务器状态转换的代码提取出来编写成工具函数,方便后续直接调用
// 转为Leaderfunc (rf *Raft) toLeader() {DPrintf("[%d]: convert from [%s] to [%s], term [%d]", rf.me, rf.state, Leader, rf.currentTerm)rf.state = Leader// rf.lastReceive = time.Now().Unix()}// 转为Followerfunc (rf *Raft) toFollower(newTerm int) {DPrintf("[%d]: convert from [%s] to [%s]", rf.me, rf.state, Follower)rf.state = Followerrf.currentTerm = newTermrf.votedFor = -1rf.lastReceive = time.Now().Unix()}// 转为Candidatefunc (rf *Raft) toCandidate() {DPrintf("[%d]: convert from [%s] to [%s]", rf.me, rf.state, Candidate)rf.state = Candidaterf.currentTerm += 1rf.votedFor = rf.me// rf.lastReceive = time.Now().Unix()}然后补充一个预定义的获取服务器状态的方法
// return currentTerm and whether this server// believes it is the leader.func (rf *Raft) GetState() (int, bool) {var term intvar isleader bool// Your code here (2A).rf.mu.Lock()defer rf.mu.Unlock()isleader = falseterm = rf.currentTermif rf.state == Leader {isleader = true}return term, isleader}结构体定义完全按照论文即可,目前不需要其他字段
// example RequestVote RPC arguments structure.// field names must start with capital letters!type RequestVoteArgs struct {// Your data here (2A, 2B).Term int // Candidate的任期号CandidateId int // Candidate的 IdLastLogIndex int // Candidate最后一条日志条目的索引LastLogTerm int // Candidate最后一条日志条目的任期}// example RequestVote RPC reply structure.// field names must start with capital letters!type RequestVoteReply struct {// Your data here (2A).Term int // 当前的任期,接收到了之后Candidate可以更新自己VoteGranted bool // 是否给这个Candidate投票}核心RPC:
// example RequestVote RPC handler.func (rf *Raft) RequestVote(args *RequestVoteArgs, reply *RequestVoteReply) {// Your code here (2A, 2B).// RPC 请求不一定在什么时候应用,因此必须加锁rf.mu.Lock()defer rf.mu.Unlock()DPrintf("[%d]: received vote request from [%d]", rf.me, args.CandidateId)reply.VoteGranted = false// 如果参数的任期号还没有我的大,不投票,直接默认值返回即可if args.Term < rf.currentTerm {// 响应中包含当前自己的任期号reply.Term = rf.currentTermreturn}// 如果参数的任期号比我的大,则我在这个任期内就只能是它的Follower,则更改我的任期号,而且在这个任期内我要投票给它if args.Term > rf.currentTerm {rf.toFollower(args.Term)}reply.Term = rf.currentTerm // 注意这里任期号已经变化了,因此要重新赋值DPrintf("[%d]: status: term [%d], state [%s], vote for [%d]", rf.me, rf.currentTerm, rf.state, rf.votedFor)// 如果参数的任期号和我的相同,则任期号不变,需要通过日志确定是否投票给它// 这里论文要求的 rf.VotedFor == args.CandidateId 不是很明白if rf.votedFor == -1 || rf.votedFor == args.CandidateId {// Todo:判断日志是否至少更新才可以投票rf.votedFor = args.CandidateIdrf.lastReceive = time.Now().Unix() // 更新时间,上面操作相当于与可能的Leader通信过了reply.VoteGranted = trueDPrintf("[%d]: voted to [%d]", rf.me, args.CandidateId)}}核心就是计算返回的reply中的两个值,第一个是是否投票,第二个是当前服务器的任期号。其中任期号一定要小心,可能服务器自己的状态改变后任期号会随之改变,因此一定要及时更新。
if args.Term < rf.currentTerm {// 响应中包含当前自己的任期号reply.Term = rf.currentTermreturn}if args.Term > rf.currentTerm {rf.toFollower(args.Term)}(这个结构不返回,投票的逻辑在下一个结构)
rf.votedFor == -1 承接上面的投票逻辑,把情况2的票投了
rf.VotedFor == args.CandidateId 在后面要加上对于日志的判断,这里仅仅是简单投票给它
if rf.votedFor == -1 || rf.votedFor == args.CandidateId {// Todo:判断日志是否至少更新才可以投票rf.votedFor = args.CandidateIdrf.lastReceive = time.Now().Unix() // 更新时间,上面操作相当于与可能的Leader通信过了reply.VoteGranted = trueDPrintf("[%d]: voted to [%d]", rf.me, args.CandidateId)}在调用的时候,Candidate请求每一台服务器投票给它,如果得到的响应说我的任期号比你还大,也就是上面的情况2,也自动放弃Candidate的地位成为Follower。否则这个Candidate就会得到自己的票。
// 向每一个Peer请求投票func (rf *Raft) requestVoteToPeer(index int, args *RequestVoteArgs, votesSum *int, votesGet *int, cond *sync.Cond) {reply := RequestVoteReply{}ok := rf.sendRequestVote(index, args, &reply)rf.mu.Lock()defer rf.mu.Unlock()defer cond.Broadcast()*votesSum += 1if !ok {return}if reply.Term > rf.currentTerm {rf.toFollower(reply.Term)// } else if reply.VoteGranted && reply.Term == rf.currentTerm {} else if reply.VoteGranted {*votesGet += 1}}结构体定义完全按照论文即可,目前不需要其他字段
type AppendEntriesArgs struct {// Your data here (2A, 2B).Term int // Leader的任期号LeaderId int // Follower可以通过这个LeaderId重定向客户端PrevLogIndex int // 新的日志条目紧随之前的索引值PrevLogTerm int // PrevLogIndex日志条目的任期Entries []LogEntry // 存储的日志条目,如果是心跳包则为空LeaderCommit int // Leader的提交索引}type AppendEntriesReply struct {// Your data here (2A).Term int // 当前的任期,接收到了之后Leader可以更新自己Success bool // Follower包含了匹配上 prevLogIndex 和 prevLogTerm 的日志时为真}这个RPC既作为日志更新的来源,在没有日志携带的时候也作为心跳包用于维持Leader的地位
func (rf *Raft) AppendEntries(args *AppendEntriesArgs, reply *AppendEntriesReply) {// Your code here (2A, 2B).// RPC 请求不一定在什么时候应用,因此必须加锁rf.mu.Lock()defer rf.mu.Unlock()// 更新至少为当前的任期reply.Term = rf.currentTermreply.Success = false// 如果Leader的任期还没有我的大,则直接拒绝请求if args.Term < rf.currentTerm {return}// 如果Leader的任期比我的大,则我转为这个任期的Followerif args.Term >= rf.currentTerm || rf.state == Candidate {rf.toFollower(args.Term)}// 如果Leader的任期和我的相同,则操作日志// Todo:日志操作rf.lastReceive = time.Now().Unix()reply.Term = rf.currentTermreply.Success = true}核心也是计算返回的reply中的两个值,第一个是是否更新成功,第二个是当前服务器的任期号。其中任期号一定要小心,可能服务器自己的状态改变后任期号会随之改变,因此一定要及时更新。
if args.Term < rf.currentTerm {return}// 如果Leader的任期比我的大,则我转为这个任期的Followerif args.Term >= rf.currentTerm || rf.state == Candidate {rf.toFollower(args.Term)}(同时要对我自己的日志进行更新,目前还没有实现)
rf.lastReceive = time.Now().Unix()reply.Term = rf.currentTermreply.Success = true主要是要对服务器的收到Leader的请求的时间进行更新,从而避免Follower转为Candidate,在Leader存在的情况下发起选举
在调用的时候,Leader向其他的每一台服务器发送这个RPC,如果得到的响应说我的任期号比你还大,也就是上面的情况2,也自动放弃Leader的地位成为Follower。
// 向指定的Peer增加日志条目或者发送心跳包func (rf *Raft) appendEntriesToPeer(index int, args *AppendEntriesArgs) {reply := AppendEntriesReply{}if ok := rf.sendAppendEntries(index, args, &reply); ok {rf.mu.Lock()defer rf.mu.Unlock()// Todo:log相关// 如果响应的任期比Leader更大了,说明Leader需要退位成Follower了if reply.Term > rf.currentTerm {rf.toFollower(reply.Term)}}}每一台服务器初始化的时候都是一个Follower,任期号为0
除此之外还要设置选举超时时间,心跳发送时间等
以及根据服务器的数量计算好需要多少张选票才能达成共识
然后直接开始选举
rf.toFollower(0)rf.electTimeout = 200 // 初始化选举超时时间rf.heartBeatTimeout = 100 // 初始化心跳间隔时间rf.randomTimeout = 100 // 设置随机时间的最大范围// 初始化成为Leader需要得到的票数if len(rf.peers)%2 == 0 {rf.majorityVote = len(rf.peers)/2 + 1} else {rf.majorityVote = (len(rf.peers) + 1) / 2}// start ticker goroutine to start electionsgo rf.leaderElection()所有的协程都不设置退出条件,因此内部要么是无限循环,要么是有状态变量等进行控制
选举Leader是一个无限循环,在每一次循环的时候记录当前的时间后进行睡眠(固定时间+随机时间),然后在循环内部进行判断,如果上一次循环到这里的实时时间比上一次接收到心跳包的时间还大,说明在睡眠时间内一直没有接收到心跳包,则认为超时,此时就要放弃自己的Follower身份,转为Candidate开始竞选。
// The ticker go routine starts a new election if this peer hasn't received// heartsbeats recently.func (rf *Raft) leaderElection() {lastElectTime := time.Now().Unix()for !rf.killed() {// Your code here to check if a leader election should// be started and to randomize sleeping time using// time.Sleep().time.Sleep(time.Duration(rf.electTimeout+rand.Int63n(rf.randomTimeout)) * time.Millisecond)rf.mu.Lock()// lastStartTime := startTime// 如果上一次循环到这里的实时时间比上一次接收到心跳包的时间还大,说明在睡眠时间内一直没有接收到心跳包,则认为超时if lastElectTime > rf.lastReceive {//DPrintf("[%d]: current state is [%s].", rf.me, rf.state)if rf.state != Leader {DPrintf("[%d]: is not leader, start election.", rf.me)rf.tryLeader()}}lastElectTime = time.Now().Unix() // 更新“上一次”的时间rf.mu.Unlock()}}然后在 rf.tryLeader()中,首先将服务器的状态转为Candidate,然后构建请求,向其他的peer发送请求投票的RPC,收到响应后对收到的投票进行统计。如果得到了大多数的选票,则这个Candidate可以转为Leader,同时向其他的服务器发送心跳包说明自己已经成为了Leader,其他的peer需要放弃竞选。
func (rf *Raft) tryLeader() {rf.toCandidate()votesSum := 1 // 总共的票的数量votesGet := 1 // 收到的票数,自己首先给自己投票cond := sync.NewCond(&rf.mu) // 条件变量,控制投票结果的返回args := RequestVoteArgs{Term: rf.currentTerm,CandidateId: rf.me,}for i := 0; i < len(rf.peers); i++ {if i != rf.me {go rf.requestVoteToPeer(i, &args, &votesSum, &votesGet, cond)}}// 等待票数统计完毕并判断是否能成为Leadergo func() {rf.mu.Lock()defer rf.mu.Unlock()for votesGet < rf.majorityVote && votesSum < len(rf.peers) && rf.state == Candidate {cond.Wait()}if votesGet >= rf.majorityVote && rf.state == Candidate {rf.toLeader()// 发送心跳包go rf.logReplication()}}()}内部的协程同步使用状态变量控制(虽然不明白为什么使用WaitGroup不可以实现功能)
心跳包发送(或与日志更新一起)是只有Leader才可以发起的动作。
注意定时发起请求即可
// Leader定时发送更新log的请求,同时也作为心跳包func (rf *Raft) logReplication() {for !rf.killed() {rf.mu.Lock()if rf.state == Leader {args := AppendEntriesArgs{Term: rf.currentTerm,LeaderId: rf.me,}for i := 0; i < len(rf.peers); i++ {if i != rf.me {go rf.appendEntriesToPeer(i, &args)}}}rf.mu.Unlock()time.Sleep(time.Duration(rf.heartBeatTimeout) * time.Millisecond)}}目前最快的结果:
Test (2A): initial election ... ... Passed -- 3.0 3 72 18660 0Test (2A): election after network failure ... ... Passed -- 4.9 3 166 31952 0Test (2A): multiple elections ... ... Passed -- 5.3 7 522 111880 0PASSok 6.824/raft 13.335s运行10次后均成功
完善 Leader 和 Follower 的代码,使他们可以追加新的日志条目,并通过 go test -run 2B。
TestBasicAgree2B()。首先实现 Start(),然后按照 Figure 2,实现 RPC 函数 AppendEntries来收发新的日志条目。通过 applyCh发送每一个新提交的日志条目。time.Sleep(10 * time.Millisecond)。如果运行太慢,可能会没法通过接下来的测试。您可以使用 time命令检查您的解决方案使用了多少实时时间和CPU时间。这是典型的输出:
$ time go test -run 2BTest (2B): basic agreement ... ... Passed -- 0.9 3 16 4572 3Test (2B): RPC byte count ... ... Passed -- 1.7 3 48 114536 11Test (2B): agreement after follower reconnects ... ... Passed -- 3.6 3 78 22131 7Test (2B): no agreement if too many followers disconnect ... ... Passed -- 3.8 5 172 40935 3Test (2B): concurrent Start()s ... ... Passed -- 1.1 3 24 7379 6Test (2B): rejoin of partitioned leader ... ... Passed -- 5.1 3 152 37021 4Test (2B): leader backs up quickly over incorrect follower logs ... ... Passed -- 17.2 5 2080 1587388 102Test (2B): RPC counts aren't too high ... ... Passed -- 2.2 3 60 20119 12PASSok 6.824/raft35.557sreal0m35.899suser0m2.556ssys0m1.458s$“ok 6.824/raft 35.557s” 意味着 Go 运行 2B 的测试所用的实时时间为 35.557 秒。“user 0m2.556s” 表示代码运行了 2.556 秒的 CPU 时间,或实际运行(而不是等待或睡眠)所花费的时间。如果测试 2B 使用超过 1 分钟的实时时间,或超过 5 秒的 CPU 时间,则以后的实验可能会遇到麻烦。检查睡眠时间、等待 RPC 超时所花费的时间、没有睡眠或等待地检查条件或channel信息的循环、或发送大量 RPC 的地方。
无论是转为Leader、Follower或者转为Candidate,实际上都可以看成是有一个隐含存在的Leader告诉他们这样做的,因此都要同步更新自己的选举超时时间,防止在有Leader的时候就已经超时,导致Leader的存在时间过短。
// 转为Leaderfunc (rf *Raft) toLeader() {DPrintf("[%d]: convert from [%s] to [%s], term [%d]", rf.me, rf.state, Leader, rf.currentTerm)rf.state = Leaderrf.lastReceive = time.Now().Unix()// 选举为Leader后重新对所有的peer进行初始化for i := 0; i < len(rf.peers); i++ {rf.nextIndex[i] = len(rf.log)rf.matchIndex[i] = -1}}// 转为Followerfunc (rf *Raft) toFollower(newTerm int) {DPrintf("[%d]: convert from [%s] to [%s]", rf.me, rf.state, Follower)rf.state = Followerrf.currentTerm = newTermrf.votedFor = -1rf.lastReceive = time.Now().Unix()}// 转为Candidatefunc (rf *Raft) toCandidate() {DPrintf("[%d]: convert from [%s] to [%s]", rf.me, rf.state, Candidate)rf.state = Candidaterf.currentTerm += 1rf.votedFor = rf.merf.lastReceive = time.Now().Unix()}首先要注意由于论文中的索引是从1开始计算的,而计算机上切片的索引是从0开始算的,因此论文说明的初始化为0的地方都要初始化为-1
nextIndex[]:leader要发送给follower的下一条log entry(各follower不同),follower与leader一致的时候只发最新一条log,有不一致的时候,nextIndex要减,一次发多条log。把不一致的部分都修正过来。
matchIndex[]:已知follower上,从0开始有多少条连续的log entry与leader一致。即: 有多少条log entry已经被成功replicate到follower上了。如果过半数,就可以增加commitIndex, apply到状态机, 答复客户端操作成功了
commitIndex: 已知被提交的最高日志项对应的index。当日志项被提交(committed)了,意味着该日志项已经成功复制到了集群中的多数派server上,属于“集体记忆”了。如果当前的leader宕机再次发生选举,只有拥有完整已提交日志的server才能够获得多数派选票,才能被选举为leader。根据Leader完整性(Leader Completeness),如果一个日志项在某个term被提交了,则该Entry会存在于所有更高term的leader日志中。
lastApplied: 应用(apply)给状态机的最高日志项的index,也就是上层应用“消费”到Raft日志项的最新index。Leader使用nextIndex和matchIndex两个数组来维护集群中其它server的日志状态。
其他结构体字段:
Start函数是raft顶层的服务最开始调用的类似初始化的函数
如果server不是leader则返回false。如果是leader的话,那么将command组装成LogEntry后追加到自己的日志中。此处要同时更新leader自己的matchIndex(由于自己就是Leader,自己肯定与自己一致)和nextIndex(如果自己是Follower,这条日志肯定就不能改了)
func (rf *Raft) Start(command interface{}) (int, int, bool) {index := -1term := -1isLeader := false// Your code here (2B).if !rf.killed() {rf.mu.Lock()defer rf.mu.Unlock()if rf.state == Leader {isLeader = true// 只有是Leader才可以接收日志信息// 添加日志信息rf.log = append(rf.log, LogEntry{Term: rf.currentTerm,Command: command,})index = len(rf.log) - 1term = rf.currentTermrf.matchIndex[rf.me] = index // 已经复制给他的日志的最高索引值rf.nextIndex[rf.me] = index + 1 // 需要发送给他的下⼀个日志条目的索引值}// 论文与代码起始位置索引不同index += 1}return index, term, isLeader}请求投票RPC:新增了最后一个日志项的信息
新增日志RPC:(只有Leader才可能发出)
AppendEntryReply结构体新增了XTerm、XIndex和XLen几个变量用于nextIndex的快速回退。
论文中的nextIndex在AppendEntry RPC返回不匹配后,默认只是回退一个日志项(nextIndex[i]=PrevLogIndex)。如果follower能够返回更多信息,那么leader可以根据这些信息使对应server的nextIndex快速回退,减少AppendEntry RPC通信不匹配的次数,从而加快同步日志的步伐。这几个变量的具体含义:
make()函数中除做一些初始化的工作之外,新增了将已经被提交的日志项返回给上层应用的goroutine
// 初始化日志相关rf.log = make([]LogEntry, 0)rf.commitIndex = -1rf.lastApplied = -1rf.nextIndex = make([]int, len(peers))rf.matchIndex = make([]int, len(peers))rf.applyCh = applyChrf.moreApply = falserf.applyCond = sync.NewCond(&rf.mu)go rf.appMsgApplier()这个新增的goroutine无限循环判断rf.moreApply字段,一旦发现为真,则触发返回的操作,返回新的提交过的日志给上层应用
func (rf *Raft) sendApplyMsg() {rf.moreApply = truerf.applyCond.Broadcast()}func (rf *Raft) appMsgApplier() {for {rf.mu.Lock()// 等待这个字段为真才可以继续for !rf.moreApply {rf.applyCond.Wait()}rf.moreApply = falsecommitIndex := rf.commitIndexlastApplied := rf.lastAppliedentries := rf.logrf.mu.Unlock()// 发送已经提交但是还没有返回的日志字段for i := lastApplied + 1; i <= commitIndex; i++ {msg := ApplyMsg{CommandValid: true,Command: entries[i].Command,CommandIndex: i + 1,}DPrintf("[%d]: apply index %d - 1", rf.me, msg.CommandIndex)rf.applyCh <- msg// 及时加锁更新,否则可能会变化rf.mu.Lock()rf.lastApplied = irf.mu.Unlock()}}}返回给上层应用的情况两种:
在前面选举Leader时,并没有对日志做限制,在这里需要补充日志层面的选举限制
首先要在请求投票的结构体中附带自己最后一条日志的信息
// Candidate最后一条日志的信息lastLogIndex := len(rf.log) - 1lastLogTerm := -1// 如果日志为空需要添加判断if lastLogIndex != -1 {lastLogTerm = rf.log[lastLogIndex].Term}args := RequestVoteArgs{Term: rf.currentTerm,CandidateId: rf.me,LastLogIndex: lastLogIndex,LastLogTerm: lastLogTerm,}然后严格按照论文说明对请求投票的双方进行判断即可:
总体原则:candidate的log是否至少和接受者的log一样新
len(rf.log) ==0args.LastLogTerm > rf.log[len(rf.log)-1].Termargs.LastLogTerm == rf.log[len(rf.log)-1].Term,但是它的日志长度比我长或一样(它先请求我投票,那么我就投票给他吧)args.LastLogIndex >=len(rf.log)-1// 是否没投票或者投给的是这个candidateif rf.votedFor == -1 || rf.votedFor == args.CandidateId {// candidate的log是否至少和接受者的log一样新// 1. 我的log长度为0,那我肯定投票给他了// 2. candidate的最后的log的任期比我的最后的log的任期大// 3. candidate的最后的log的任期和我的最后的log的任期相同,但是它的日志长度比我长if len(rf.log) == 0 || (args.LastLogTerm > rf.log[len(rf.log)-1].Term) ||(args.LastLogTerm == rf.log[len(rf.log)-1].Term && args.LastLogIndex >= len(rf.log)-1) {rf.votedFor = args.CandidateIdrf.lastReceive = time.Now().Unix() // 更新时间,上面操作相当于与可能的Leader通信过了reply.VoteGranted = trueDPrintf("[%d]: voted to [%d]", rf.me, args.CandidateId)}}// 找到日志的同步位置prevLogIndex := rf.nextIndex[index] - 1prevLogTerm := -1if prevLogIndex != -1 {prevLogTerm = rf.log[prevLogIndex].Term}// 找到要发送的日志var entries []LogEntryif len(rf.log)-1 >= rf.nextIndex[index] {entries = rf.log[rf.nextIndex[index]:]}// 补充结构体args := AppendEntriesArgs{Term: rf.currentTerm,LeaderId: rf.me,LeaderCommit: rf.commitIndex,PrevLogIndex: prevLogIndex,PrevLogTerm: prevLogTerm,Entries: entries,}论文的日志匹配性质:
因此只需要判断PrevLogIndex和PrevLogTerm与follower的日志匹配的程度即可,这里只是Leader猜测一下,真正的判断在接收到RPC后完成
在处理AppendEntry RPC的代码中,新增了日志匹配的逻辑。
如果日志在prevLogIndex处不包含term为prevLogTerm的日志项,那么返回false,(需要回退才能找到对应的位置)。
回退的逻辑:
// Reply false if log doesn’t contain an entry at prevLogIndex// whose term matches prevLogTerm (§5.3)if args.PrevLogIndex >= len(rf.log) || (args.PrevLogIndex >= 0 && rf.log[args.PrevLogIndex].Term != args.PrevLogTerm) {reply.Term = rf.currentTerm// 回退reply.XLen = len(rf.log)if args.PrevLogIndex >= 0 && args.PrevLogIndex < len(rf.log) {reply.XTerm = rf.log[args.PrevLogIndex].Termfor i := args.PrevLogIndex; i >= 0; i-- {if rf.log[i].Term == reply.XTerm {reply.XIndex = i} else {break}}}return}此外还要注意prevLogIndex可能为-1,意味着日志全都没有匹配上,或者leader此刻还没有日志,此时接收者就要完全服从。
接下来是PreLogIndex与PrevLogTerm匹配到的情况,还要额外检查新同步过来的日志和已存在的日志是否存在冲突。如果一个已经存在的日志项和新的日志项冲突(相同index但是不同term),那么要删除这个冲突的日志项及其往后的日志。
// If an existing entry conflicts with a new one (same index// but different terms), delete the existing entry and all that// follow it (§5.3)misMatchIndex := -1for i := range args.Entries {if args.PrevLogIndex+1+i >= len(rf.log) || rf.log[args.PrevLogIndex+1+i].Term != args.Entries[i].Term {misMatchIndex = ibreak}}将新的日志项追加到日志中
// Append any new entries not already in the logif misMatchIndex != -1 {rf.log = append(rf.log[:args.PrevLogIndex+1+misMatchIndex], args.Entries[misMatchIndex:]...)}最后根据论文,如果 leaderCommit > commitIndex,说明follower的commitIndex也需要更新。为了防止越界,commitIndex取 min(leaderCommit, index of last new entry)。同时要向上层应用发回响应。
// If leaderCommit > commitIndex, set commitIndex = min(leaderCommit, index of last new entry)if args.LeaderCommit > rf.commitIndex {newEntryIndex := len(rf.log) - 1if args.LeaderCommit >= newEntryIndex {rf.commitIndex = newEntryIndex} else {rf.commitIndex = args.LeaderCommit}DPrintf("[%d]: commit index [%d]", rf.me, rf.commitIndex)rf.sendApplyMsg()}由于RPC在网络中可能乱序或者延迟,我们要确保当前RPC发送时的term、当前接收时的currentTerm以及RPC的reply.term三者一致,丢弃过去term的RPC,避免对当前currentTerm产生错误的影响。
reply.Term == rf.currentTerm && rf.currentTerm == args.Term当reply.Success为true,说明follower包含了匹配prevLogIndex和prevLogTerm的日志项,更新nextIndex[serverTo]和matchIndex[serverTo]。这里只能用prevLogIndex和entries来更新,而不能用nextIndex及len(log),因为后两者可能已经被别的RPC更新了,进而导致数据不一致。
由于matchIndex发生了变化,我们要检查是否更新commitIndex。根据论文,如果存在一个N,这个N大于commitIndex,多数派的matchIndex[i]都大于等于N,并且log[N].term等于currentTerm,那么更新commitIndex为N。这里必须注意,日志提交是有限制的,Raft从不提交过去term的日志项,即使已经复制达到了多数派。如果要更新commitIndex为N,那么N所对应的日志项的term必须是当前currentTerm。
在检查是否更新commitIndex的实现上,我们将matchIndex复制到了matches数组中,通过sort升序排序以方便遍历。然后对matches数组进行遍历,找到大多数都提交的索引位置,随后调用sendApplyMsg(),通知有更多的日志项已经被提交,上层应用可以应用。
if reply.Success {// 更新服务器的状态rf.nextIndex[index] = prevLogIndex + len(entries) + 1rf.matchIndex[index] = prevLogIndex + len(entries)// If there exists an N such that N > commitIndex, a majority of matchIndex[i] ≥ N, and log[N].term == currentTerm:// set commitIndex = Nmatches := make([]int, len(rf.peers))copy(matches, rf.matchIndex)sort.Ints(matches)for i := rf.majorityVote - 1; i >= 0 && matches[i] > rf.commitIndex; i-- {if rf.log[matches[i]].Term == rf.currentTerm {rf.commitIndex = matches[i]DPrintf("[%d]: commit index [%d]", rf.me, rf.commitIndex)rf.sendApplyMsg()break}}}当reply.Success为false,说明follower的日志不包含在prevLogIndex处并匹配prevLogTerm的日志项,要将nextIndex缩减。此处更新不宜采用自减的方式更新,因为RPC可能会重发,正确的方式是 rf.nextIndex[serverTo] = prevLogIndex。
在AppendEntryReply中增加了几个变量,以使nextIndex能够快速回退(back up)。如果接下来要尝试匹配的prevLogIndex比follower当前所拥有的的日志长度(XLen)还要大,那么显然直接从XLen尝试匹配即可。如果接下来要尝试匹配的prevLogIndex在XLen以内,因为我们已经知道了follower的日志从XIndex到当前prevLogIndex的日志项的term都是XTerm,那么我们可以直接在leader侧遍历匹配一遍,而无需多次往返RPC通信。
} else {// In Test (2C): Figure 8 (unreliable), the AppendEntry RPCs are reordered// So rf.nextIndex[index]-- would be wrongrf.nextIndex[index] = prevLogIndex// 如果接下来要尝试匹配的prevLogIndex比follower当前所拥有的的日志长度(XLen)还要大,那么显然直接从XLen尝试匹配即可。if rf.nextIndex[index]-1 >= reply.XLen {rf.nextIndex[index] = reply.XLen} else {// 如果接下来要尝试匹配的prevLogIndex在XLen以内,因为我们已经知道了follower的日志从XIndex到当前prevLogIndex的日志项的term都是XTerm,那么我们可以直接在leader侧遍历匹配一遍,而无需多次往返RPC通信for i := rf.nextIndex[index] - 1; i >= reply.XIndex; i-- {if rf.log[i].Term != reply.XTerm {rf.nextIndex[index] -= 1} else {break}}}}Test (2B): basic agreement ... ... Passed -- 1.3 3 16 4546 3Test (2B): RPC byte count ... ... Passed -- 2.7 3 48 114510 11Test (2B): agreement after follower reconnects ... ... Passed -- 7.1 3 116 31767 8Test (2B): no agreement if too many followers disconnect ... ... Passed -- 4.1 5 160 37664 3Test (2B): concurrent Start()s ... ... Passed -- 1.2 3 12 3466 6Test (2B): rejoin of partitioned leader ... ... Passed -- 5.6 3 166 40233 4Test (2B): leader backs up quickly over incorrect follower logs ... ... Passed -- 34.1 5 2352 2038228 102Test (2B): RPC counts aren't too high ... ... Passed -- 2.5 3 42 12630 12PASSok 6.824/raft 58.652sreal 0m59.353suser 0m1.744ssys 0m1.630s如果基于 Raft 的服务器重新启动,它应该在中断的地方恢复服务。这要求 Raft 在重启后,依旧能确保数据持久化。本文的Figure 2 提到的那些状态应该被持久化。
真正的实现会在每次 persistent state 被修改时写磁盘,并在重新启动后从磁盘读取状态。您不需要使用磁盘,而应该通过 Persister 对象保存和恢复 persistent state (请参阅 persister.go)。调用 Raft.Make()时会提供一个 Persister, 其可能会包含 Raft 最近的 persistent state(也可能没有) 。Raft 应从 Persister 初始化其状态(对应方法 ReadRaftState()),并在每次 president state 更改后使用 Persister 保存(对应方法 SaveRaftState())。
完善 raft.go中的 persist()和 readPerisit()函数,实现保存和读取 persistent state。你可能需要使用 labgob encoder 来编码(或者说序列化)persistent state,让 Persister来存储二进制流。欢迎查看 persist()和 readPerisit()的注释了解更多。labgob很像 go 的 gob,只是会在序列化非导出字段时报错。实现完“ 在每次 persistent state 改变时调用 presist()”后,应通过其余测试。
您可能想优化为一次性保存多条日志。查看论文第7页的顶部到第 8 页顶部(用灰色线标记的地方)。论文没有描述清楚细节,你需要自己多考虑一下。 6.824 Raft 的讲座或许也能提供一些帮助。
您的代码应通过所有 2C 测试:
$ go test -run 2CTest (2C): basic persistence ... ... Passed -- 5.0 3 86 22849 6Test (2C): more persistence ... ... Passed -- 17.6 5 952 218854 16Test (2C): partitioned leader and one follower crash, leader restarts ... ... Passed -- 2.0 3 34 8937 4Test (2C): Figure 8 ... ... Passed -- 31.2 5 580 130675 32Test (2C): unreliable agreement ... ... Passed -- 1.7 5 1044 366392 246Test (2C): Figure 8 (unreliable) ... ... Passed -- 33.6 5 10700 33695245 308Test (2C): churn ... ... Passed -- 16.1 5 8864 44771259 1544Test (2C): unreliable churn ... ... Passed -- 16.5 5 4220 6414632 906PASSok 6.824/raft123.564s$最好能多次运行:for i in {0..10}; do go test; done
就目前情况而言,重新启动的服务器会重放完整的Raft日志,以恢复其状态。然而,对于长期运行的服务来说,永远记住完整的Raft日志是不现实的。相反,您将修改Raft以与持久存储其状态的“快照”的服务协作,此时Raft将丢弃快照之前的日志条目。其结果是持久数据量更少,重启速度更快。然而,现在有可能一个追随者远远落后,以至于领导者放弃了需要追赶的日志条目;然后领导者必须发送快照以及快照时开始的日志。
您的Raft必须提供以下函数 Snapshot(index int, snapshot []byte),服务可以使用其状态的序列化快照调用该函数。
在Lab 2D中,测试代码定期调用 Snapshot()。在Lab 3中,您将编写一个k/v服务器调用 Snapshot();快照将包含k/v对的完整表。服务层对每个对等方(而不仅仅是Leader)调用 Snapshot()。
index参数指示快照中包括的最高日志条目。raft应该在这个参数之前丢弃其日志条目。您需要修改Raft代码以只存储日志尾部。
您需要实现论文中讨论的 InstallSnapshot RPC,该RPC允许raft的Leader告诉落后的Raft服务器用快照替换其状态。您可能需要考虑 InstallSnapshot应该如何与图2中的状态和规则交互。
当Follower的Raft代码接收到 InstallSnapshot RPC时,它可以使用 applyCh将快照发送到 ApplyMsg中的服务。ApplyMsg结构定义已经包含了您需要的字段(并且是测试代码期望的)。请注意,这些快照只会增加服务的状态,而不会导致服务向后移动。
如果服务器崩溃,它必须从持久数据重新启动。您的Raft应该保持Raft状态和相应的快照。使用 persister.SaveStateAndSnapshot(),它对于Raft状态和相应的快照有单独的参数。如果没有快照,则传递nil作为快照参数。
当服务器重新启动时,应用程序层读取持久化快照并恢复其保存状态。
以前,建议您实现一个名为 CondInstallSnapshot的函数,以避免在 applyCh上发送的快照和日志条目需要协调。这个残留的API接口仍然存在,但不希望实现它:相反,我们建议您只需将其返回true。
任务:实现 Snapshot()和 InstallSnapshot RPC,以及对Raft的更改以支持这些(例如,使用修剪日志的操作)。
提示:
Snapshot(index)放弃索引之前的日志,并将X设置为索引。如果一切顺利,您现在应该通过第一个2D测试。InstallSnapshot RPC。InstallSnapshot RPC中发送整个快照。不要实现图13的用于分割快照的偏移机制。AppendEntries RPC中的新条目之前正确发送条目的术语和索引;这可能需要保存和引用最新快照的 lastIncludedTerm/lastIncludedIndex(请考虑是否应持久化)。输出示例:
$ go test -run 2DTest (2D): snapshots basic ... ... Passed -- 11.6 3 176 61716 192Test (2D): install snapshots (disconnect) ... ... Passed -- 64.2 3 878 320610 336Test (2D): install snapshots (disconnect+unreliable) ... ... Passed -- 81.1 3 1059 375850 341Test (2D): install snapshots (crash) ... ... Passed -- 53.5 3 601 256638 339Test (2D): install snapshots (unreliable+crash) ... ... Passed -- 63.5 3 687 288294 336Test (2D): crash and restart all servers ... ... Passed -- 19.5 3 268 81352 58PASSok 6.824/raft 293.456s规则引擎是一种嵌入在应用服务中的组件,可以将灵活多变的业务决策从服务代码中分离出来。通过使用预定义的语义模块来编写业务逻辑规则。在执行时接受数据输入、解释业务规则,并做出决策。规则引擎能大大提高系统的灵活性和扩展性。
在字节跳动,规则引擎已经在风控识别、活动运营、配置下发等场景得到了广泛的应用。开发人员可以将业务逻辑与服务代码解耦,实现灵活、高效的业务策略发布。目前公司内部基于规则引擎的动态决策系统已经承接了千万级别QPS的决策请求。
规则引擎的实现需要在满足大容量、高请求、低延迟的基础上尽可能做到简单易上手。本次课程将会带领大家实现一个简单版的规则引擎。
重点
难点
主要涉及到编译原理的部分
课前必看!!!
本部分是需要大家在上课之前了解的内容,主要是一些基本的概念和原理。
在这门课程之前你可能根本没有听说过规则引擎这个东西,当然也可能是浅浅的大概知道这是个什么东西,或者是个规则引擎方面的资深专家(还没毕业,五年工作经验那种🐶,如果是这样请赶紧找我内推)。都没有关系,这门课包教包会!!!(学不会的下课后可以找我们运营人员联系我一对一教学)
当然,这门课程还是有一定的门槛的,这也就是我为什么要说这么多一定要让你仔细看看这部分的原因。经过实验,课程的内容如果只依赖于课上老师的讲解,只能做到:能听懂,能跟上,来不及思考。要想能够理解掌握这部分内容,能跟别人battle下,再向自己的知识山峰上加那么一块小石头,得好好预习。
开始之前先百度或者Google一下 “规则引擎”简单浏览下哈,📪📪📪另外掘金app上面也有许多不错的文章。可以先浏览看看。
数据结构得学过吧,考多少分?😁
这块的预习目标呢,包括以下几个部分
是的,就这一个要求,其实学完青训营的前几节课就可以达到了
编译原理被誉为"程序员的三大浪漫"之一,足以可见这块知识的深度与广度,我们这次课程也是简单的介绍一下与规则引擎相关的概念。
那么可能会有疑问了,不是讲规则引擎么?为啥还得学编译原理?
规则引擎的本质呢就是我们自己定义一套语法,然后去解析用这套语法写的表达式,然后根据解析的内容执行表达式。这个过程其实就是编译和执行的过程。
因此呢需要自行了解以下的内容
课程之前,大家需要根据项目工程,来完成环境的搭建和Demo的运行
项目地址:
相信大家已经完成了Go环境的搭建,项目工程依赖了hertz框架,如果在之前的课程中完成了项目环境搭建可以直接复用。
项目环境:
项目clone到本地后,可以执行测试脚本来测试环境的可用性。如果有错误欢迎百度和Google解决
git clone https://github.com/qimengxingyuan/young_engine.gitchmod a+x ./setup.sh./setup.sh脚本执行成功,则环境可以支持项目的执行
项目说明:
本项目是一个简单的规则引擎的实现,详细目录可以参考README.md
项目实现时间有限,没有做比较完备的测试,如果在demo执行的过程中出现某些bug或者执行异常可以直接在github提交issue或者修复后提起PR
编译的过程就是 把某种语言的源程序, 在不改变语义的条件下 ,转换成另一种语言程序(目标语言程序)
解释型语言和编译型语言
关于 Java 和 Python .
JVM 和 Python解释器 | 为什么一个叫虚拟机一个叫解释器
把源代码字符串转换为词法单元(Token)的这个过程。
确定的有限自动机 DFA | Deterministic Finite Automaton
确定的有限自动机就是一个状态机,它的状态数量是有限的。该状态机在任何一个状态,基于输入的字符,都能做一个确定的状态转换。
词法分析是识别一个个的单词,而语法分析就是在词法分析的基础上识别出程序的语法结构。这个结构是一个树状结构。这棵树叫做抽象语法树(Abstract Syntax Tree,AST)。树的每个节点(子树)是一个语法单元,这个单元的构成规则就叫“语法”。每个节点还可以有下级节点。
Token -> AST
上下文无关语法 Context-Free Grammar
语言句子无需考虑上下文,就可以判断正确性
...a = 0;...这是一个赋值语句,无论此语句的前后是什么代码,此语句所代表的操作是确定的。即给变量a赋值等于0
编程语言为什么不用人类的语言(自然语言),而是用上下文无关的文法呢? 因为
上下文无关语法G:终结符集合T + 非终结符集合N + 产生式集合P + 起始符号S
G由T、N、S和P组成,由语法G推导出来的所有句子的集合称为G语言!
终结符: 组成串的基本符号。可以理解为词法分析器产生的token集合。比如 + Id ( ) 等
非终结符: 表示token的的集合的语法变量。比如 stmt varDecl 等等
start:blockStmts ; //起始block : '{' blockStmts '}' ; //语句块blockStmts : stmt* ; //语句块中的语句stmt = varDecl | expStmt | returnStmt | block; //语句varDecl : type Id varInitializer? ';' ; //变量声明type : Int | Long ; //类型varInitializer : '=' exp ; //变量初始化expStmt : exp ';' ; //表达式语句returnStmt : Return exp ';' ; //return语句exp : add ; //表达式 add : add '+' mul | mul; //加法表达式mul : mul '*' pri | pri; //乘法表达式pri : IntLiteral | Id | '(' exp ')' ; //基础表达式 产生式:表示形式,S : AB ,就是说S的含义可以用语法AB进行表达
S : ABA : aA | εB : b | bB展开(expand):将P(A->u )应用到符号串vAw中,得到新串vu **w
折叠(reduce):将P(A->uu )应用到符号串vuu w中,得到新串vAw
推导(derivate):符号串u 应用一系列产生式,变成符号串v ,则u =>v:S => ab | b | bb
巴科斯范式
BNF是描述上下文无关理论的一种具体方法,通过BNF可以实现上下文无关文法的具体化、公式化、科学化,是实现代码解析的必要条件。
<expr> ::= <expr> + <term> | <expr> - <term> | <term><term> ::= <term> * <factor> | <term> / <factor> | <factor><factor> ::= ( <expr> ) | NumBNF本质上就是树形分解,分解成一棵抽象语法树
递归下降算法 Recursive Descent Parsing
基本思路就是按照语法规则去匹配 Token 串。比如说,变量声明语句的规则如下:
varDecl : types Id varInitializer? ';' ; //变量声明varInitializer : '=' exp ; //变量初始化exp : add ; //表达式 add : add '+' mul | mul; //加法表达式mul : mul '*' pri | pri; //乘法表达式pri : IntLiteral | Id | '(' exp ')' ; //基础表达式如果写成产生式格式,是下面这样:
varDecl -> types Id varInitializer ';' varInitializer -> '=' exp varInitializer -> εexp -> addadd -> add + muladd -> mulmul -> mul * primul -> pripri -> IntLiteralpri -> Idpri -> ( exp )而基于这个规则做解析的算法如下:
匹配一个数据类型(types)匹配一个标识符(Id),作为变量名称匹配初始化部分(varInitializer),而这会导致下降一层,使用一个新的语法规则: 匹配一个等号 匹配一个表达式(在这个步骤会导致多层下降:exp->add->mul->pri->IntLiteral) 创建一个varInitializer对应的AST节点并返回如果没有成功地匹配初始化部分,则回溯,匹配ε,也就是没有初始化部分。匹配一个分号 创建一个varDecl对应的AST节点并返回int a = 2
课上我们重点讲了规则引擎的设计和实现,结合前面课程的内容课后实现一个在线版本的规则引擎
使用Hertz框架开发一个HTTP服务,服务使用mysql,支持表达式的增删查改和编译执行。
并实现以下接口
请求参数为待执行的表达式和表达式中参数的值,并输出编译结果
实时编译并执行结果,不需要写入DB中
POST api/engine/run{ "exp": "uid == 12345 && did > 0", "params": { "uid": 123456, "did": 0 }}{ "code": 0, "message": "success", "data": { // 执行结果 "result": true }}新增一条表达式到DB中,并返回表达式在DB中的ID
需要检测表达式 是否已经存在 ,如果已经存在,直接返回表达式的ID
需要检测表达式是否合法(编译是否通过) ,如果编译失败,返回错误码 20001和编译错误
POST api/engine/exp/new{ "exp": "uid == 12345 && did > 0",}{ "code": 0, "message": "success", "data": { // 表达式ID "id": 1 }}// 编译失败时{ "code": -1, "message": "compile error: xxxxx", // 编译失败的信息 "data": { // 表达式ID "id": 0 }}查询数据库中所有的表达式
GET api/engine/exp/list{ "code": 0, "message": "success", "data": [ { "id": 1, "exp": "uid > 0" } ]}根据ID删除表达式,表达式不存在时返回错误码 20002 , 和错误信息
删除成功返回被删除的表达式信息
DELETE api/engine/exp/:id// 删除成功时{ "code": 0, "message": "success", "data": { // 表达式ID "id": 1, "exp": "uid > 0" }}// 删除失败时{ "code": -1, "message": "exp id 1 not exist", //查询失败的信息 "data": {}}根据表达式的ID,查询出表达式内容,并编译执行。表达式不存在时返回错误码 20002 , 和错误信息
POST api/engine/exp/run{ "exp_id": 1, "parmas": { "uid": 123456, "did": 0 }}{ "code": 0, "message": "success", "data": { // 执行结果 "result": true }}// 表达式不存在时{ "code": -1, "message": "exp id 1 not exist", //查询失败的信息 "data": {}}日志擦除可能会带来一些问题,论文中的Figure 8 说明了这个问题,因此需要有日志提交条件的额外限制: Leader 在当前任期至少有一条日志被提交
前面的协议中一直是减1操作,因此如果Follower落后过多,通信开销会很大
追赶更快的优化算法:并不按照索引后退,而是按照term后退,然后再扫描相同的位置
此时Follower并不只是拒绝,而是返回前一个term以及这个term开始的索引
重启机器会发生什么?
需要持久化什么信息?我们应该尽量不保存信息,因为需要存入磁盘,开销很大,只需要保留必要的信息
状态机通过apply channel获得一个快照,然后使用它来进行恢复
步骤:
客户端也需要保存Raft的Leader和Follower的信息,可以切换它的通信对象
客户端如果没有接收到服务器的响应会进行重试,而服务器可鞥已经执行过这些操作了,因此需要对这些重复的操作进行检测。
一种实现方法:客户端的每一个操作都带有一个id,通过id对重复的操作进行过滤
模糊定义:多台机器的行为如同单独的一台机器一样
精确定义:
线性一致性:
查看历史操作,即使是并行的程序是否可以在一台机器上执行相同的结果,从而判断是否满足线性一致性。
]]>视频模块包括包括视频Feed流获取、视频投稿和获取用户投稿列表三个模块
不限制登录状态,返回按投稿时间倒序的视频列表,视频数由服务端控制,单次最多30个。
接口定义:
service Feed { rpc Feed (douyin_feed_request) returns (douyin_feed_response) {}}message douyin_feed_request{ int64 latest_time = 1; // 可选参数,限制返回视频的最新投稿时间戳,精确到秒,不填表示当前时间 string token = 2; // 可选参数,登录用户设置}message douyin_feed_response{ int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 repeated Video video_list = 3; // 视频列表 int64 next_time = 4; // 本次返回的视频中,发布最早的时间,作为下次请求时的latest_time}登录用户的视频发布列表,直接列出用户所有投稿过的视频。
接口定义:
service PublishList { rpc PublishList (douyin_publish_list_request) returns (douyin_publish_list_response) {}}message douyin_publish_list_request{ int64 user_id = 1; // 用户id string token = 2; // 用户鉴权token}message douyin_publish_list_response{ int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 repeated Video video_list = 3; // 用户发布的视频列表}登录用户选择视频上传。
接口定义:
service PublishAction { rpc PublishAction (douyin_publish_action_request) returns (douyin_publish_action_response) {}}message douyin_publish_action_request{ string token = 1; // 用户鉴权token bytes data = 2; // 视频数据 string title = 3; // 视频标题}message douyin_publish_action_response{ int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述}返回的状态码(虽然客户端并没有逻辑进行处理):
用户模块包括用户注册、用户登录和用户信息三个部分。
新用户注册时提供用户名,密码,昵称即可,用户名需要保证唯一。创建成功后返回用户 id 和权限token.
接口定义:
service UserRegister { rpc UserRegister (douyin_user_register_request) returns (douyin_user_register_response) {}}message douyin_user_register_request{ string username = 1; // 注册用户名,最长32个字符 string password = 2; // 密码,最长32个字符}message douyin_user_register_response{ int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 int64 user_id = 3; // 用户id string token = 4; // 用户鉴权token}通过用户名和密码进行登录,登录成功后返回用户 id 和权限 token
接口定义:
service UserLogin { rpc UserLogin (douyin_user_login_request) returns (douyin_user_login_response) {}}message douyin_user_login_request{ string username = 1; // 登录用户名 string password = 2; // 登录密码}message douyin_user_login_response{ int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 int64 user_id = 3; // 用户id string token = 4; // 用户鉴权token}获取登录用户的 id、昵称,如果实现社交部分的功能,还会返回关注数和粉丝数。
接口定义:
service UserInfo { rpc UserInfo (douyin_user_request) returns (douyin_user_response) {}}message douyin_user_request{ int64 user_id = 1; // 用户id string token = 2; // 用户鉴权token}message douyin_user_response{ int32 status_code = 1; // 状态码,0-成功,其他值-失败 string status_msg = 2; // 返回状态描述 User user = 3; // 用户信息}返回的状态码(虽然客户端并没有逻辑进行处理):
本节课程主要分为四个方面:
课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
Auto memory management: 自动内存管理
Grabage collction: 垃圾回收
Mutator: 业务线程
Collector: GC 线程
Concurrent GC: 并发 GC
Parallel GC: 并行 GC
Tracing garbage collection: 追踪垃圾回收
Reference counting: 引用计数
Generational GC: 分代 GC
mmap() 系统调用什么是性能优化?
为什么要做性能优化?
性能优化
软件质量
测试驱动
通过清晰的文档告诉用户这一项优化 做了什么 , 没做什么 ,能达到怎样的效果
隔离,优化代码用选项和原先的路径隔离,保证优化未启用时的行为同以前一致
可观测、可灰度、可回滚
自动内存管理:由程序语言的运行时系统管理动态内存
避免手动内存管理,专注于实现业务逻辑
保证内存使用的正确性和 安全性 : double-free problem, use-after-free problem
三个任务
概念
Mutator: 业务线程,分配新对象,修改对象指向关系
Collector: GC 线程,找到存活对象,回收死亡对象的内存空间
Serial GC: 只有一个 collector
Parallel GC: 并行 GC,支持多个 collectors 同时回收的 GC 算法
Concurrent GC: 并发 GC,支持 mutator(s) 和 collector(s) 同时执行的 GC 算法
Collectors 必须感知对象指向关系的改变!
每个对象都有一个与之关联的引用数目
对象存活的条件:当且仅当引用数大于 0
优点
缺点
说明
TCMalloc: TC is short for thread caching
目标:为对象在 heap 上分配内存
提前将内存分块
对象分配:根据对象的大小,选择最合适的块返回
内存缓存
mspan, mcache 和 mcentral 构成了内存管理的多级缓存机制。
可以看到,用于分配对象的函数 mallocgc() 占用 CPU 较高
横轴是对象大小,纵轴是数目,可以看到绝大多数对象都小于 80 B。因此 优化小对象分配是关键 。
if g.ab.end - g.ab.top < size { // Allocate a new allocation buffer}addr := g.ab.topg.ab.top += sizereturn addrtop 指针并返回,快速完成一次对象分配mallocgc() 进行对象分配的方式相比,balanced GC 缩短了对象分配的路径,减少了对象分配执行的指令数目,降低 CPU 使用从 Go runtime 内存管理模块的角度看,一个 allocation buffer 其实是一个大对象。本质上 balanced GC 是 将多次小对象的分配合并成一次大对象的分配 。因此,当 GAB 中哪怕只有一个小对象存活时,Go runtime 也会认为整个大对象(即 GAB)存活。为此,balanced GC 会根据 GC 策略, 将 GAB 中存活的对象移动到另外的 GAB 中 ,从而压缩并清理 GAB 的内存空间,原先的 GAB 空间由于不再有存活对象,可以全部释放,如下图所示。
上图上方是两个 GAB,其中虚线表示 GAB 中对象的分界线。黑色表示 GAB 中存活的对象,白色表示死掉的对象。由于 GAB 中有存活对象,整个 GAB 无法被回收。
Balanced GC 会将 GAB 中存活的对象移动到下面的 GAB 中,这样原先的两个 GABs 就可以被释放,压缩并清理 GAB 的内存空间。
Balanced GC 只负责 noscan 对象的分配和移动,对象的标记和回收依然依赖 Go GC 本身,并和 Go GC 保持兼容。
上图的程序转换成控制流图 (control-flow graph)
定义:将被调用函数的函数体的副本替换到调用位置上,同时重写代码以反映参数的绑定
优点
缺点
函数内联在大多数情况下是正向优化,即多内联,会提升性能
采取一定的策略决定是否内联
Go 内联的限制
字节跳动的优化方案
开销
定义:分析代码中指针的动态作用域,即指针在何处可以被访问
大致思路
优化:未逃逸出当前函数的指针指向的对象可以在栈上分配
总结
注释应该解释代码作用
注释应该解释代码如何做的
注释应该解释代码实现的原因
注释应该解释代码什么情况会出错
公共符号始终要注释
总结
variable
function
package
总结
避免嵌套,保持正常流程清晰
如果两个分支中都包含 return 语句,则可以去除冗余的 else
尽量保持正常代码路径为最小缩进,优先处理错误情况/特殊情况,并尽早返回或继续循环来减少嵌套,增加可读性
总结
简单错误处理
错误的 Wrap 和 Unwrap
错误判定
panic
recover
总结
在满足正确性、可靠性、健壮性、可读性等质量因素的前提下,设法提高程序的效率
性能对比测试代码,可参考 github.com/RaymondCode…
性能调优的核心是性能瓶颈的分析,对于 Go 应用程序,最方便的就是 pprof 工具
搭建课程所需要的开发环境以及安装需要用到的软件。
提前体验一下课程涉及的 HTTP/RPC/ORM 框架
通过阅读 www.cloudwego.io/zh/docs/her… 尝试运行 Hertz 的示例代码(Hertz 框架地址: github.com/cloudwego/h…)
go install github.com/cloudwego/hertz/cmd/hz@latesthz new -module github.com/cloudwego/hertz-examplesgo mod tidygo build -o hertz_demo && ./hertz_demo通过阅读 www.cloudwego.io/zh/docs/kit… 尝试运行 Kitex 的示例代码(KItex 框架地址: github.com/cloudwego/k…)
go install github.com/cloudwego/kitex/tool/cmd/kitex@latestgo install github.com/cloudwego/thriftgo@latestgit clone https://github.com/cloudwego/kitex-examples.githello 目录 cd kitex-examples/hellogo run .go run ./client通过阅读 gorm.cn/docs/#Insta… 尝试运行 Gorm 的示例代码(Gorm 框架地址: github.com/go-gorm/gor…)
go get -u gorm.io/gormgo get -u gorm.io/driver/sqlite直播链接:https://live.juejin.cn/4354/9899243
Gorm是一个已经迭代了10年+的功能强大的ORM框架,在字节内部被广泛使用并且拥有非常丰富的开源扩展。
Kitex是字节内部的Golang微服务RPC框架,具有高性能、强可扩展的主要特点,支持多协议并且拥有丰富的开源扩展。
Hertz是字节内部的HTTP框架,参考了其他开源框架的优势,结合字节跳动内部的需求,具有高易用性、高性能、高扩展性特点。
Gorm拥有丰富的扩展生态,可以使用代码生成工具、分片库方案、手动索引、乐观锁、读写分离、OpenTelemetry 扩展等等
本节课程主要分为四个方面:
属于编程进阶内容,考虑到工程项目的可用性和可靠性,工程实践中经常会用到。
了解Go依赖管理演进的历程,通过课程学习以及课后实践能能够熟练使用go module 管理依赖。
需求模型来源
青训营话题页forum.juejin.cn/youthcamp/p…
需求
组件及技术点
课程链接:
Go可以充分发挥多核的优势,高效运行
线程:内核态,比较重量级
协程:用户态,线程可以跑多个协程,比较轻量
快速打印:
func hello(i int) {println("hello goroutine : " + fmt.Sprint(i))}func HelloGoRoutine() {for i := 0; i < 5; i++ {go func(j int) {hello(j)}(i)}time.Sleep(time.Second)}最后是使用time.sleep进行阻塞,防止在协程未运行结束前主线程先运行结束了。
协程通过通信来共享内存
func CalSquare() {src := make(chan int)dest := make(chan int, 3)go func() {defer close(src)for i := 0; i < 10; i++ {src <- i}}()go func() {defer close(dest)for i := range src {dest <- i * i}}()for i := range dest {//复杂操作println(i)}}var (x int64lock sync.Mutex)func addWithLock() {for i := 0; i < 2000; i++ {lock.Lock()x += 1lock.Unlock()}}func addWithoutLock() {for i := 0; i < 2000; i++ {x += 1}}func Add() {x = 0for i := 0; i < 5; i++ {go addWithoutLock()}time.Sleep(time.Second)println("WithoutLock:", x)x = 0for i := 0; i < 5; i++ {go addWithLock()}time.Sleep(time.Second)println("WithLock:", x)}func ManyGoWait() {var wg sync.WaitGroupwg.Add(5)for i := 0; i < 5; i++ {go func(j int) {defer wg.Done()hello(j)}(i)}wg.Wait()}GOPATH:环境变量,项目代码直接依赖src下的代码,go get下载最新的包到src目录下
Go Vendor:增加vendor文件,存放依赖包的副本,优先从vendor文件里面查找,但是仍然无法控制依赖的版本
Go Module:go.mod:依赖管理基本单元、原生库、单元依赖
func HelloTom() string {return "Tom"}func TestHelloTom(t *testing.T) {output := HelloTom()expectOutput := "Tom"assert.Equal(t, expectOutput, output)}添加–cover参数可以评价测试代码的覆盖率
一些函数对本地的数据库、文件等有强依赖,在测试的同时找到这些依赖要求过高
可以使用Mock进行测试,在函数执行的时候替换成另外一个函数(打桩),从而规避掉对本地其他的强依赖
func ReadFirstLine() string {open, err := os.Open("log")defer open.Close()if err != nil {return ""}scanner := bufio.NewScanner(open)for scanner.Scan() {return scanner.Text()}return ""}func ProcessFirstLine() string {line := ReadFirstLine()destLine := strings.ReplaceAll(line, "11", "00")return destLine}func TestProcessFirstLine(t *testing.T) {firstLine := ProcessFirstLine()assert.Equal(t, "line00", firstLine)}func TestProcessFirstLineWithMock(t *testing.T) {monkey.Patch(ReadFirstLine, func() string {return "line110"})defer monkey.Unpatch(ReadFirstLine)line := ProcessFirstLine()assert.Equal(t, "line000", line)}对函数的运行时间进行测试:go test -bench=.
var ServerIndex [10]intfunc InitServerIndex() {for i := 0; i < 10; i++ {ServerIndex[i] = i+100}}func Select() int {return ServerIndex[rand.Intn(10)]}func FastSelect() int {return ServerIndex[fastrand.Intn(10)]}func BenchmarkSelect(b *testing.B) {InitServerIndex()b.ResetTimer()for i := 0; i < b.N; i++ {Select()}}func BenchmarkSelectParallel(b *testing.B) {InitServerIndex()b.ResetTimer()b.RunParallel(func(pb *testing.PB) {for pb.Next() {Select()}})}func BenchmarkFastSelectParallel(b *testing.B) {InitServerIndex()b.ResetTimer()b.RunParallel(func(pb *testing.PB) {for pb.Next() {FastSelect()}})}需求
分层结构
组件及技术点
具体逻辑见代码
本节课程主要分为四个方面:
课前部分主要罗列课程中涉及到的概念。对于不熟悉的概念,同学们可以提前查询预习;课中部分主要罗列每一部分的关键思路,帮助同学们跟上课程的进度;课后部分是一些问题,帮助同学们在课后梳理本课程的重点。
可以选择安装 VS Code , 或者 Goland ,对于 VS Code,需要安装 Go 插件
go run example/01-hello/main.go 如果正确输出 hello world,则说明环境配置正确空余时间阅读 Go语言圣经(中文版)
课程链接:
package mainimport ("fmt")func main() {fmt.Println("hello world")}注意常量没有类型,会根据使用的上下文自动推断类型
package mainimport ("fmt""math")func main() {var a = "initial"var b, c int = 1, 2var d = truevar e float64f := float32(e)g := a + "foo"fmt.Println(a, b, c, d, e, f) // initial 1 2 true 0 0fmt.Println(g) // initialappleconst s string = "constant"const h = 500000000const i = 3e20 / hfmt.Println(s, h, i, math.Sin(h), math.Sin(i))}package mainimport "fmt"func main() {i := 1for {fmt.Println("loop")break}for j := 7; j < 9; j++ {fmt.Println(j)}for n := 0; n < 5; n++ {if n%2 == 0 {continue}fmt.Println(n)}for i <= 3 {fmt.Println(i)i = i + 1}}package mainimport "fmt"func main() {if 7%2 == 0 {fmt.Println("7 is even")} else {fmt.Println("7 is odd")}if 8%4 == 0 {fmt.Println("8 is divisible by 4")}if num := 9; num < 0 {fmt.Println(num, "is negative")} else if num < 10 {fmt.Println(num, "has 1 digit")} else {fmt.Println(num, "has multiple digits")}}默认不需要添加break
可以使用任意的变量类型
package mainimport ("fmt""time")func main() {a := 2switch a {case 1:fmt.Println("one")case 2:fmt.Println("two")case 3:fmt.Println("three")case 4, 5:fmt.Println("four or five")default:fmt.Println("other")}t := time.Now()switch {case t.Hour() < 12:fmt.Println("It's before noon")default:fmt.Println("It's after noon")}}真实场景下很少用,一般使用切片
package mainimport "fmt"func main() {var a [5]inta[4] = 100fmt.Println("get:", a[2])fmt.Println("len:", len(a))b := [5]int{1, 2, 3, 4, 5}fmt.Println(b)var twoD [2][3]intfor i := 0; i < 2; i++ {for j := 0; j < 3; j++ {twoD[i][j] = i + j}}fmt.Println("2d: ", twoD)}package mainimport "fmt"func main() {s := make([]string, 3)s[0] = "a"s[1] = "b"s[2] = "c"fmt.Println("get:", s[2]) // cfmt.Println("len:", len(s)) // 3s = append(s, "d")s = append(s, "e", "f")fmt.Println(s) // [a b c d e f]c := make([]string, len(s))copy(c, s)fmt.Println(c) // [a b c d e f]fmt.Println(s[2:5]) // [c d e]fmt.Println(s[:5]) // [a b c d e]fmt.Println(s[2:]) // [c d e f]good := []string{"g", "o", "o", "d"}fmt.Println(good) // [g o o d]}实际中使用最频繁,完全无序
package mainimport "fmt"func main() {m := make(map[string]int)m["one"] = 1m["two"] = 2fmt.Println(m) // map[one:1 two:2]fmt.Println(len(m)) // 2fmt.Println(m["one"]) // 1fmt.Println(m["unknow"]) // 0r, ok := m["unknow"]fmt.Println(r, ok) // 0 falsedelete(m, "one")m2 := map[string]int{"one": 1, "two": 2}var m3 = map[string]int{"one": 1, "two": 2}fmt.Println(m2, m3)}package mainimport "fmt"func main() {nums := []int{2, 3, 4}sum := 0for i, num := range nums {sum += numif num == 2 {fmt.Println("index:", i, "num:", num) // index: 0 num: 2}}fmt.Println(sum) // 9m := map[string]string{"a": "A", "b": "B"}for k, v := range m {fmt.Println(k, v) // b 8; a A}for k := range m {fmt.Println("key", k) // key a; key b}}一般返回两个值,第一个值是真正需要的,第二个值是错误信息
package mainimport "fmt"func add(a int, b int) int {return a + b}func add2(a, b int) int {return a + b}func exists(m map[string]string, k string) (v string, ok bool) {v, ok = m[k]return v, ok}func main() {res := add(1, 2)fmt.Println(res) // 3v, ok := exists(map[string]string{"a": "A"}, "a")fmt.Println(v, ok) // A True}对传入的参数进行修改
功能比较有限,不如C++丰富
package mainimport "fmt"func add2(n int) {n += 2}func add2ptr(n *int) {*n += 2}func main() {n := 5add2(n)fmt.Println(n) // 5add2ptr(&n)fmt.Println(n) // 7}传入指针避免传递的开销过大,同时也可以对结构体进行修改
package mainimport "fmt"type user struct {name stringpassword string}func main() {a := user{name: "wang", password: "1024"}b := user{"wang", "1024"}c := user{name: "wang"}c.password = "1024"var d userd.name = "wang"d.password = "1024"fmt.Println(a, b, c, d) // {wang 1024} {wang 1024} {wang 1024} {wang 1024}fmt.Println(checkPassword(a, "haha")) // falsefmt.Println(checkPassword2(&a, "haha")) // false}func checkPassword(u user, password string) bool {return u.password == password}func checkPassword2(u *user, password string) bool {return u.password == password}相当于一个类成员函数
带指针就能对结构体进行修改
package mainimport "fmt"type user struct {name stringpassword string}func (u user) checkPassword(password string) bool {return u.password == password}func (u *user) resetPassword(password string) {u.password = password}func main() {a := user{name: "wang", password: "1024"}a.resetPassword("2048")fmt.Println(a.checkPassword("2048")) // true}package mainimport ("errors""fmt")type user struct {name stringpassword string}func findUser(users []user, name string) (v *user, err error) {for _, u := range users {if u.name == name {return &u, nil}}return nil, errors.New("not found")}func main() {u, err := findUser([]user{{"wang", "1024"}}, "wang")if err != nil {fmt.Println(err)return}fmt.Println(u.name) // wangif u, err := findUser([]user{{"wang", "1024"}}, "li"); err != nil {fmt.Println(err) // not foundreturn} else {fmt.Println(u.name)}}package mainimport ("fmt""strings")func main() {a := "hello"fmt.Println(strings.Contains(a, "ll")) // truefmt.Println(strings.Count(a, "l")) // 2fmt.Println(strings.HasPrefix(a, "he")) // truefmt.Println(strings.HasSuffix(a, "llo")) // truefmt.Println(strings.Index(a, "ll")) // 2fmt.Println(strings.Join([]string{"he", "llo"}, "-")) // he-llofmt.Println(strings.Repeat(a, 2)) // hellohellofmt.Println(strings.Replace(a, "e", "E", -1)) // hEllofmt.Println(strings.Split("a-b-c", "-")) // [a b c]fmt.Println(strings.ToLower(a)) // hellofmt.Println(strings.ToUpper(a)) // HELLOfmt.Println(len(a)) // 5b := "你好"fmt.Println(len(b)) // 6}+和#号可以打印更为详细的信息
package mainimport "fmt"type point struct {x, y int}func main() {s := "hello"n := 123p := point{1, 2}fmt.Println(s, n) // hello 123fmt.Println(p) // {1 2}fmt.Printf("s=%v\n", s) // s=hellofmt.Printf("n=%v\n", n) // n=123fmt.Printf("p=%v\n", p) // p={1 2}fmt.Printf("p=%+v\n", p) // p={x:1 y:2}fmt.Printf("p=%#v\n", p) // p=main.point{x:1, y:2}f := 3.141592653fmt.Println(f) // 3.141592653fmt.Printf("%.2f\n", f) // 3.14}注意结构体要保证大写,小写传参的问题使用反射解决
package mainimport ("encoding/json""fmt")type userInfo struct {Name stringAge int `json:"age"`Hobby []string}func main() {a := userInfo{Name: "wang", Age: 18, Hobby: []string{"Golang", "TypeScript"}}buf, err := json.Marshal(a)if err != nil {panic(err)}fmt.Println(buf) // [123 34 78 97...]fmt.Println(string(buf)) // {"Name":"wang","age":18,"Hobby":["Golang","TypeScript"]}buf, err = json.MarshalIndent(a, "", "\t")if err != nil {panic(err)}fmt.Println(string(buf))var b userInfoerr = json.Unmarshal(buf, &b)if err != nil {panic(err)}fmt.Printf("%#v\n", b) // main.userInfo{Name:"wang", Age:18, Hobby:[]string{"Golang", "TypeScript"}}}package mainimport ("fmt""time")func main() {now := time.Now()fmt.Println(now) // 2022-03-27 18:04:59.433297 +0800 CST m=+0.000087933t := time.Date(2022, 3, 27, 1, 25, 36, 0, time.UTC)t2 := time.Date(2022, 3, 27, 2, 30, 36, 0, time.UTC)fmt.Println(t) // 2022-03-27 01:25:36 +0000 UTCfmt.Println(t.Year(), t.Month(), t.Day(), t.Hour(), t.Minute()) // 2022 March 27 1 25fmt.Println(t.Format("2006-01-02 15:04:05")) // 2022-03-27 01:25:36diff := t2.Sub(t)fmt.Println(diff) // 1h5m0sfmt.Println(diff.Minutes(), diff.Seconds()) // 65 3900t3, err := time.Parse("2006-01-02 15:04:05", "2022-03-27 01:25:36")if err != nil {panic(err)}fmt.Println(t3 == t) // truefmt.Println(now.Unix()) // 1648738080}package mainimport ("fmt""strconv")func main() {f, _ := strconv.ParseFloat("1.234", 64)fmt.Println(f) // 1.234n, _ := strconv.ParseInt("111", 10, 64)fmt.Println(n) // 111n, _ = strconv.ParseInt("0x1000", 0, 64)fmt.Println(n) // 4096n2, _ := strconv.Atoi("123")fmt.Println(n2) // 123n2, err := strconv.Atoi("AAA")fmt.Println(n2, err) // 0 strconv.Atoi: parsing "AAA": invalid syntax}package mainimport ("fmt""os""os/exec")func main() {// go run example/20-env/main.go a b c dfmt.Println(os.Args) // [/var/folders/8p/n34xxfnx38dg8bv_x8l62t_m0000gn/T/go-build3406981276/b001/exe/main a b c d]fmt.Println(os.Getenv("PATH")) // /usr/local/go/bin...fmt.Println(os.Setenv("AA", "BB"))buf, err := exec.Command("grep", "127.0.0.1", "/etc/hosts").CombinedOutput()if err != nil {panic(err)}fmt.Println(string(buf)) // 127.0.0.1 localhost}rand.Seed(time.Now().UnixNano())secretNumber := rand.Intn(maxNum)reader := bufio.NewReader(os.Stdin)input, err := reader.ReadString('\n')input = strings.Trim(input, "\r\n")最终代码:
package mainimport ("bufio""fmt""math/rand""os""strconv""strings""time")func main() {maxNum := 100rand.Seed(time.Now().UnixNano())secretNumber := rand.Intn(maxNum)// fmt.Println("The secret number is ", secretNumber)fmt.Println("Please input your guess")reader := bufio.NewReader(os.Stdin)for {input, err := reader.ReadString('\n')if err != nil {fmt.Println("An error occured while reading input. Please try again", err)continue}input = strings.Trim(input, "\r\n")guess, err := strconv.Atoi(input)if err != nil {fmt.Println("Invalid input. Please enter an integer value")continue}fmt.Println("You guess is", guess)if guess > secretNumber {fmt.Println("Your guess is bigger than the secret number. Please try again")} else if guess < secretNumber {fmt.Println("Your guess is smaller than the secret number. Please try again")} else {fmt.Println("Correct, you Legend!")break}}}抓包:找到翻译网站,提交一个翻译后去控制台抓包,然后copy as cURL,可以将这个请求转到本地进行运行
为了方便,可以将这个请求copy到一些在线将请求转换为Go代码的网站,最终得到可以直接运行的代码,运行代码获得与网页返回相同的结果。
将请求的部分单独提取出来,通过用户的输入进行序列化
解析返回的响应,进行反序列化提取真正需要的部分
返回的响应也使用在线工具转换为go代码,减少工作量
最后通过命令行读入即可
最终代码:
package mainimport ("bytes""encoding/json""fmt""io""log""net/http""os")type DictRequest struct {TransType string `json:"trans_type"`Source string `json:"source"`UserID string `json:"user_id"`}type DictResponse struct {Rc int `json:"rc"`Wiki struct {KnownInLaguages int `json:"known_in_laguages"`Description struct {Source string `json:"source"`Target interface{} `json:"target"`} `json:"description"`ID string `json:"id"`Item struct {Source string `json:"source"`Target string `json:"target"`} `json:"item"`ImageURL string `json:"image_url"`IsSubject string `json:"is_subject"`Sitelink string `json:"sitelink"`} `json:"wiki"`Dictionary struct {Prons struct {EnUs string `json:"en-us"`En string `json:"en"`} `json:"prons"`Explanations []string `json:"explanations"`Synonym []string `json:"synonym"`Antonym []string `json:"antonym"`WqxExample [][]string `json:"wqx_example"`Entry string `json:"entry"`Type string `json:"type"`Related []interface{} `json:"related"`Source string `json:"source"`} `json:"dictionary"`}func query(word string) {client := &http.Client{}request := DictRequest{TransType: "en2zh", Source: word}buf, err := json.Marshal(request)if err != nil {log.Fatal(err)}var data = bytes.NewReader(buf)req, err := http.NewRequest("POST", "https://api.interpreter.caiyunai.com/v1/dict", data)if err != nil {log.Fatal(err)}req.Header.Set("Authority", "api.interpreter.caiyunai.com")req.Header.Set("Accept", "application/json, text/plain, */*")req.Header.Set("Accept-Language", "zh-CN,zh;q=0.9,en-US;q=0.8,en;q=0.7")req.Header.Set("App-Name", "xy")req.Header.Set("Content-Type", "application/json;charset=UTF-8")req.Header.Set("Origin", "https://fanyi.caiyunapp.com")req.Header.Set("Os-Type", "web")req.Header.Set("Referer", "https://fanyi.caiyunapp.com/")req.Header.Set("Sec-Ch-Ua", "\"Not?A_Brand\";v=\"8\", \"Chromium\";v=\"108\", \"Microsoft Edge\";v=\"108\"")req.Header.Set("Sec-Ch-Ua-Mobile", "?0")req.Header.Set("Sec-Ch-Ua-Platform", "\"Windows\"")req.Header.Set("Sec-Fetch-Dest", "empty")req.Header.Set("Sec-Fetch-Mode", "cors")req.Header.Set("Sec-Fetch-Site", "cross-site")req.Header.Set("User-Agent", "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/108.0.0.0 Safari/537.36 Edg/108.0.1462.76")req.Header.Set("X-Authorization", "token:qgemv4jr1y38jyq6vhvi")resp, err := client.Do(req)if err != nil {log.Fatal(err)}defer resp.Body.Close()bodyText, err := io.ReadAll(resp.Body)if err != nil {log.Fatal(err)}if resp.StatusCode != 200 {log.Fatal("bad StatusCode:", resp.StatusCode, "body", string(bodyText))}var dictResponse DictResponseerr = json.Unmarshal(bodyText, &dictResponse)if err != nil {log.Fatal(err)}fmt.Println(word, "UK:", dictResponse.Dictionary.Prons.En, "US:", dictResponse.Dictionary.Prons.EnUs)for _, item := range dictResponse.Dictionary.Explanations {fmt.Println(item)}}func main() {if len(os.Args) != 2 {fmt.Fprintf(os.Stderr, `usage: simpleDict WORDexample: simpleDict hello`)os.Exit(1)}word := os.Args[1]query(word)}正常浏览器访问一个网站,先和对方的网站建立TCP连接,然后正常发起HTTP请求,服务器返回响应
如果设置了代理服务器,浏览器要先和代理服务器建立TCP连接,然后代理服务器再去和真正的网站建立TCP连接,可以分为4个阶段:
实现流程:
nc 127.0.0.1 1080)进行测试curl --socks5 127.0.0.1:1080 -v http://www.qq.com进行测试,但是仅为协商,因此不会成功,但是服务器端会有正确的输出。最终代码:
package mainimport ("bufio""context""encoding/binary""errors""fmt""io""log""net")const socks5Ver = 0x05const cmdBind = 0x01const atypIPV4 = 0x01const atypeHOST = 0x03const atypeIPV6 = 0x04func main() {server, err := net.Listen("tcp", "127.0.0.1:1080")if err != nil {panic(err)}for {client, err := server.Accept()if err != nil {log.Printf("Accept failed %v", err)continue}go process(client)}}func process(conn net.Conn) {defer conn.Close()reader := bufio.NewReader(conn)err := auth(reader, conn)if err != nil {log.Printf("client %v auth failed:%v", conn.RemoteAddr(), err)return}err = connect(reader, conn)if err != nil {log.Printf("client %v auth failed:%v", conn.RemoteAddr(), err)return}}func auth(reader *bufio.Reader, conn net.Conn) (err error) {// +----+----------+----------+// |VER | NMETHODS | METHODS |// +----+----------+----------+// | 1 | 1 | 1 to 255 |// +----+----------+----------+// VER: 协议版本,socks5为0x05// NMETHODS: 支持认证的方法数量// METHODS: 对应NMETHODS,NMETHODS的值为多少,METHODS就有多少个字节。RFC预定义了一些值的含义,内容如下:// X’00’ NO AUTHENTICATION REQUIRED// X’02’ USERNAME/PASSWORDver, err := reader.ReadByte()if err != nil {return fmt.Errorf("read ver failed:%w", err)}if ver != socks5Ver {return fmt.Errorf("not supported ver:%v", ver)}methodSize, err := reader.ReadByte()if err != nil {return fmt.Errorf("read methodSize failed:%w", err)}method := make([]byte, methodSize)_, err = io.ReadFull(reader, method)if err != nil {return fmt.Errorf("read method failed:%w", err)}// +----+--------+// |VER | METHOD |// +----+--------+// | 1 | 1 |// +----+--------+_, err = conn.Write([]byte{socks5Ver, 0x00})if err != nil {return fmt.Errorf("write failed:%w", err)}return nil}func connect(reader *bufio.Reader, conn net.Conn) (err error) {// +----+-----+-------+------+----------+----------+// |VER | CMD | RSV | ATYP | DST.ADDR | DST.PORT |// +----+-----+-------+------+----------+----------+// | 1 | 1 | X'00' | 1 | Variable | 2 |// +----+-----+-------+------+----------+----------+// VER 版本号,socks5的值为0x05// CMD 0x01表示CONNECT请求// RSV 保留字段,值为0x00// ATYP 目标地址类型,DST.ADDR的数据对应这个字段的类型。// 0x01表示IPv4地址,DST.ADDR为4个字节// 0x03表示域名,DST.ADDR是一个可变长度的域名// DST.ADDR 一个可变长度的值// DST.PORT 目标端口,固定2个字节buf := make([]byte, 4)_, err = io.ReadFull(reader, buf)if err != nil {return fmt.Errorf("read header failed:%w", err)}ver, cmd, atyp := buf[0], buf[1], buf[3]if ver != socks5Ver {return fmt.Errorf("not supported ver:%v", ver)}if cmd != cmdBind {return fmt.Errorf("not supported cmd:%v", ver)}addr := ""switch atyp {case atypIPV4:_, err = io.ReadFull(reader, buf)if err != nil {return fmt.Errorf("read atyp failed:%w", err)}addr = fmt.Sprintf("%d.%d.%d.%d", buf[0], buf[1], buf[2], buf[3])case atypeHOST:hostSize, err := reader.ReadByte()if err != nil {return fmt.Errorf("read hostSize failed:%w", err)}host := make([]byte, hostSize)_, err = io.ReadFull(reader, host)if err != nil {return fmt.Errorf("read host failed:%w", err)}addr = string(host)case atypeIPV6:return errors.New("IPv6: no supported yet")default:return errors.New("invalid atyp")}_, err = io.ReadFull(reader, buf[:2])if err != nil {return fmt.Errorf("read port failed:%w", err)}port := binary.BigEndian.Uint16(buf[:2])dest, err := net.Dial("tcp", fmt.Sprintf("%v:%v", addr, port))if err != nil {return fmt.Errorf("dial dst failed:%w", err)}defer dest.Close()log.Println("dial", addr, port)// +----+-----+-------+------+----------+----------+// |VER | REP | RSV | ATYP | BND.ADDR | BND.PORT |// +----+-----+-------+------+----------+----------+// | 1 | 1 | X'00' | 1 | Variable | 2 |// +----+-----+-------+------+----------+----------+// VER socks版本,这里为0x05// REP Relay field,内容取值如下 X’00’ succeeded// RSV 保留字段// ATYPE 地址类型// BND.ADDR 服务绑定的地址// BND.PORT 服务绑定的端口DST.PORT_, err = conn.Write([]byte{0x05, 0x00, 0x00, 0x01, 0, 0, 0, 0, 0, 0})if err != nil {return fmt.Errorf("write failed: %w", err)}ctx, cancel := context.WithCancel(context.Background())defer cancel()go func() {_, _ = io.Copy(dest, reader)cancel()}()go func() {_, _ = io.Copy(conn, dest)cancel()}()<-ctx.Done()return nil}head -c 32 /dev/random | base64sudo visudotar -cvf temp.tar temp.txt temp/tar -xvf temp.tar -C temp/tar cvzf - pic | split -b 10m -d - piccat pic* > pic.tar.gztar xvzf pic.tar.gz| 描述 | 命令 |
|---|---|
| 查看都有什么环境 | conda info --envs |
| 查看当前环境有什么包 | conda list |
| 创建环境 | conda create -n env_name python=version package_names |
| 安装包 | conda install name=version |
| 离线安装包 | conda install --use-local name |
| 导出当前环境 | conda env export > name.yaml |
| 导出base环境需要更换名称 | conda create -n new_name --clone base |
| 复制后导入 | conda env create -f name.yaml |
| 删除环境下的某个包 | conda env remove -n your_env_name package_name |
| 删除环境 | conda env remove --name your_env_name |
| 打包环境 | conda pack -n my_env -o out_name.tar.gz |
| 利用打包的环境复现 | tar -xzf my_env.tar.gz -C my_env && source my_env/bin/activate |
sudo apt updatesudo apt install vimsudo cp /etc/apt/sources.list /etc/apt/sources.list.baksudo vim /etc/apt/sources.listsudo apt updatesudo apt upgradesudo apt install python3-pipsudo mkdir ~/.pipcd ~/.pipsudo vim pip.conf# [global]# index-url=https://mirrors.aliyun.com/pypi/simple/ # https://pypi.org/simplevim ~/.bashrcexport PATH=~/mypath/bin:$PATHsource ~/.bashrc添加%zhangzhao ALL=(ALL:ALL) NOPASSWD: ALL 到最后一行 , 后 ctrl+o, 回车 , ctrl+x 退出
How can I install vscode-server in linux offline
安装说明:https://www.v2fly.org/guide/install.html
脚本下载地址:https://github.com/v2fly/fhs-install-v2ray
执行脚本前首先临时更改hosts,避免github连接不上的情况
参考仓库:https://github.com/521xueweihan/GitHub520
执行脚本下载安装V2ray
bash install-release.sh安装后的文件位置:
installed: /usr/local/bin/v2rayinstalled: /usr/local/share/v2ray/geoip.datinstalled: /usr/local/share/v2ray/geosite.datinstalled: /usr/local/etc/v2ray/config.jsoninstalled: /var/log/v2ray/installed: /var/log/v2ray/access.loginstalled: /var/log/v2ray/error.loginstalled: /etc/systemd/system/v2ray.serviceinstalled: /etc/systemd/system/v2ray@.service按照上面的配置文件路径写入配置文件(可以直接从Windows客户端中copy过来)
V2ray命令:
# 启动V2raysystemctl start v2ray# 检查V2ray状态systemctl status v2ray# 设置V2ray开机自启动systemctl enable v2ray测试:
curl -x socks5://127.0.0.1:10808 https://www.google.com -v下载地址:https://github.com/Dreamacro/clash/releases/tag/v1.12.0
解压并赋予权限:
gzip -d clash-linux-amd64-v1.11.4.gzchmod a+x clash-linux有的代理服务商会直接给出配置文件config.yaml,如果没有,可以将订阅链接直接粘贴在浏览器网址栏,然后搜索,会直接下载下来文件或者展示出配置文件,如果搜索到的是一大堆字符则需要在订阅链接的后面添加 &flag=clash ,然后会下载下来一个文件,将其更名为config.yaml即可
然后替换~/.config/clash下自动生成的config.yaml,删除Country.mmdb文件,然后再次执行 ./clash-linux
即可以使用
释放9090端口后可以通过Web端查看:http://clash.razord.top
(WSL2 git push时候可能会遇到错误,解决方法:将下述代码粘贴到~/.ssh/config文件中)
Host github.comHostname ssh.github.comPort 443安装proxychains从而避免全局代理
apt install proxychains4配置文件:(/etc/proxychains.conf)
# proxychains.conf VER 4.x## HTTP, SOCKS4a, SOCKS5 tunneling proxifier with DNS.# The option below identifies how the ProxyList is treated.# only one option should be uncommented at time,# otherwise the last appearing option will be accepted## dynamic_chain## Dynamic - Each connection will be done via chained proxies# all proxies chained in the order as they appear in the list# at least one proxy must be online to play in chain# (dead proxies are skipped)# otherwise EINTR is returned to the app#strict_chain## Strict - Each connection will be done via chained proxies# all proxies chained in the order as they appear in the list# all proxies must be online to play in chain# otherwise EINTR is returned to the app##round_robin_chain## Round Robin - Each connection will be done via chained proxies# of chain_len length# all proxies chained in the order as they appear in the list# at least one proxy must be online to play in chain# (dead proxies are skipped).# the start of the current proxy chain is the proxy after the last# proxy in the previously invoked proxy chain.# if the end of the proxy chain is reached while looking for proxies# start at the beginning again.# otherwise EINTR is returned to the app# These semantics are not guaranteed in a multithreaded environment.##random_chain## Random - Each connection will be done via random proxy# (or proxy chain, see chain_len) from the list.# this option is good to test your IDS :)# Make sense only if random_chain or round_robin_chain#chain_len = 2# Quiet mode (no output from library)# quiet_mode# Proxy DNS requests - no leak for DNS dataproxy_dns# set the class A subnet number to use for the internal remote DNS mapping# we use the reserved 224.x.x.x range by default,# if the proxified app does a DNS request, we will return an IP from that range.# on further accesses to this ip we will send the saved DNS name to the proxy.# in case some control-freak app checks the returned ip, and denies to # connect, you can use another subnet, e.g. 10.x.x.x or 127.x.x.x.# of course you should make sure that the proxified app does not need# *real* access to this subnet. # i.e. dont use the same subnet then in the localnet section#remote_dns_subnet 127 #remote_dns_subnet 10remote_dns_subnet 224# Some timeouts in millisecondstcp_read_time_out 15000tcp_connect_time_out 8000### Examples for localnet exclusion## localnet ranges will *not* use a proxy to connect.## Exclude connections to 192.168.1.0/24 with port 80# localnet 192.168.1.0:80/255.255.255.0## Exclude connections to 192.168.100.0/24# localnet 192.168.100.0/255.255.255.0## Exclude connections to ANYwhere with port 80# localnet 0.0.0.0:80/0.0.0.0## RFC5735 Loopback address range## if you enable this, you have to make sure remote_dns_subnet is not 127## you'll need to enable it if you want to use an application that ## connects to localhost.# localnet 127.0.0.0/255.0.0.0## RFC1918 Private Address Ranges# localnet 10.0.0.0/255.0.0.0# localnet 172.16.0.0/255.240.0.0# localnet 192.168.0.0/255.255.0.0# ProxyList format# type ip port [user pass]# (values separated by 'tab' or 'blank')## only numeric ipv4 addresses are valid### Examples:## socks5192.168.67.781080lamersecret#http192.168.89.38080justuhidden# socks4192.168.1.491080# http192.168.39.938080### proxy types: http, socks4, socks5# ( auth types supported: "basic"-http "user/pass"-socks )#[ProxyList]# add proxy here ...# meanwile# defaults set to "tor"socks5 127.0.0.1 10808http 127.0.0.1 10809需要走代理的命令在命令开头添加proxychains即可
全局代理:(似乎对软件内部,例如go没有作用)
export http_proxy=http://127.0.0.1:10809export https_proxy=https://127.0.0.1:10809网站说明:https://golang.google.cn/doc/install
wget https://golang.google.cn/dl/go1.19.5.linux-amd64.tar.gz删除旧版本并解压安装包:
rm -rf /usr/local/go && tar -C /usr/local -xzf go1.19.5.linux-amd64.tar.gz编辑配置文件,增加环境变量:
vim ~/.bashrcexport PATH=$PATH:/usr/local/go/binsource ~/.bashrc验证安装:
go version查看配置:
go env修改配置:
go env -w GO111MODULE=ongo env -w GOPROXY=https://goproxy.io,direct拉取私有仓库的包
go env -w GOPRIVATE=gitlab.appshahe.com除配置私有仓库的地址外,还需要将走http或者https的协议转到git协议上
具体命令:
git config --global url."git@gitlab.appshahe.com:".insteadOf "https://gitlab.appshahe.com/"git config --global url."git@gitlab.appshahe.com:".insteadOf "http://gitlab.appshahe.com/"具体的更改会体现在 ~/.gitconfig里面
docker安装直接可以远程访问,不需要任何配置操作
apt install mysql-server运行mysql服务并查看是否正在运行
service mysql startservice mysql status刚开始安装不能使用用户名和密码访问,需要更换为原来的密码验证方式
mysqlALTER USER 'root'@'localhost' IDENTIFIED WITH mysql_native_password BY 'root';FLUSH PRIVILEGES;创建数据库:
CREATE DATABASE simpledy取消bind-address=127.0.0.1
vim /etc/mysql/mysql.conf.d/mysqld.cnf密码生成为随机字符串:
head -c 8 /dev/random | base64创建用户:
CREATE USER 'dymysql'@'%' IDENTIFIED BY 'gxnw21XxRhY';更改密码验证方式:
ALTER USER 'dymysql'@'%' IDENTIFIED WITH mysql_native_password BY 'gxnw21XxRhY';授予用户某个数据库的全部权限:
GRANT ALL PRIVILEGES ON `simpledy`.* TO `dymysql`@`%` WITH GRANT OPTION;撤销某个用户对某个数据库的全部权限:
REVOKE ALL PRIVILEGES, GRANT OPTION FROM 'dymysql';刷新缓存:
FLUSH PRIVILEGES;展示某个用户的权限:
SHOW GRANTS FOR 'dymysql'@'%';查看已有用户以及是否可以远程登录:
select host,user,plugin from mysql.user;docker安装配置成功
apt install redis-server运行并查看是否正在运行
service redis-server startservice redis-server status打开redis配置文件 /etc/redis/redis.conf
找到requirepass,修改即可
默认情况下,Redis 不允许远程连接。只能从127.0.0.1(localhost)连接 Redis 服务器
打开redis配置文件 /etc/redis/redis.conf
注释掉 bind 127.0.0.1 ::1
关闭保护模式 protected-mode no
重启Redis服务:service redis-server restart
(注意WSL的ip要到WSL里面去看)
官网安装脚本:https://www.rabbitmq.com/install-debian.html#apt-cloudsmith
注意修改apt-get为apt,将软件源设置为对应版本(如Ubuntu22.04为jammy)
查看安装状态:
service rabbitmq-server status打开管理界面:
rabbitmq-plugins enable rabbitmq_management通过http://localhost:15672/#/进行查看
默认的guest用户,密码为guest,具有超级管理员权限,无法远程登录
创建用户并设置密码:
add_user root QxdkQeiIUNY管理用户角色:
rabbitmqctl set_user_tags root administrator查看当前的用户及角色:
rabbitmqctl list_users不需要开启远程连接,自动支持
然后进入到管理页面中,对virtual hosts进行设置(相当于数据库中的db)
然后即可使用程序等跑通
apt install ffmpegapt install nginx配置文件:/etc/nginx/nginx.conf
增加mp4支持:
apt install nginx-extrasapt install vsftpd下载protobuf官方的protoc工具(tar.gz版本)
编译安装:
# 安装需要的工具包apt install autoconf automake libtool curl make g++ unzip# 解压安装包tar xvf protobuf-21.12.tar.gz && cd protobuf-21.12# 编译安装./autogen.sh./configuremake && make installldconfig# 验证安装protoc --version安装go语言插件:
go get -u google.golang.org/protobuf/cmd/protoc-gen-gogo get -u google.golang.org/grpc/cmd/protoc-gen-go-grpc将执行文件添加到环境变量中:
export PATH=$PATH:/root/go/bin执行:
protoc --go_out=. video.proto下载地址:https://developer.hashicorp.com/consul/downloads
解压后直接执行即可
核心思想:
root@hecs-296470:/etc/apt/keyrings# cd /etc/apt/keyringsroot@hecs-296470:/etc/apt/keyrings# lsdocker.gpgroot@hecs-296470:/etc/apt/sources.list.d# lsdocker.listroot@hecs-296470:/etc/apt/sources.list.d# cat docker.listdeb [arch=amd64 signed-by=/etc/apt/keyrings/docker.gpg] https://download.docker.com/linux/ubuntu jammy stableroot@hecs-296470:/etc/apt/sources.list.d#apt install docker-ce docker-ce-cli containerd.io docker-buildx-plugin docker-compose-plugin换源:
vim /etc/docker/daemon.json写入源:
{ "registry-mirrors": ["https://hub-mirror.c.163.com","https://ustc-edu-cn.mirror.aliyuncs.com","https://ghcr.io","https://mirror.baidubce.com" ]}重启docker:
systemctl daemon-reloadsystemctl restart docker准备重装编程环境,以Docker为基础,既能开发,又能方便部署,同时不损害原有的其他环境
但是Docker Desktop坑点太多,且占用资源巨大,因此不安装Windows环境下面的Docker,而是在WSL内部安装Docker,VSCode通过SSH方式跨过WSL访问容器。
与上面的Docker安装基本相同,不过注意每一次重启WSL的时候要手动重启Docker,否则无法使用Docker
service docker start由于WSL的ip会总变化,这里准备配桥接模式,我的理解是WSL与主机的地位相同,在内网中都有自己的ip,这样无论是互相访问还是访问外网都没有什么问题。
参考资料:
| 描述 | 命令 |
|---|---|
| 查询容器 | sudo docker ps -a |
| 删除容器 | sudo docker rm 容器ID |
| 查询镜像 | sudo docker images |
| 删除镜像 | sudo docker rmi 镜像ID(要先删除掉容器才能删除掉镜像) |
| 拉取镜像 | sudo docker pull python:3.8.13(去dockerhub上找合适的版本) |
| 根据镜像启动容器并挂载数据 | docker run -v 绝对路径:/mnt --gpus all --shm-size=6g -it python:3.8.13 /bin/bash |
| 启动已经停止的容器 | sudo docker start ID |
| 进入某个容器的终端 | sudo docker exec -it ID /bin/bash |
| 将容器转为镜像并上传到dockerhub-登录 | docker login |
| 将容器转为镜像并上传到dockerhub-提交 | sudo docker commit 容器ID zhangzhao219/仓库名(也是将容器写回到镜像中的操作) |
| 将容器转为镜像并上传到dockerhub-打标签 | sudo docker tag zhangzhao219/仓库名 zhangzhao219/TAG |
| 将容器转为镜像并上传到dockerhub-上传 | sudo docker push zhangzhao219/仓库名:TAG |
| 导出容器到文件 | sudo docker export -o *.tar 容器ID |
| 从文件导入容器(会直接变为镜像) | sudo docker import IR.tar 名称 |
一致性算法,或者说 共识算法 ,让⼀组机器像⼀个整体⼀样工作,即使其中⼀些机器出现故障也能够继续工作。
Raft 是⼀种为了管理复制日志的⼀致性算法。
它将⼀致性算法分解成了几个关键模块:领导人选举、日志复制和安全性。同时它通过更强的⼀致性来 减少状态机的数量 。
总之,对比传统的一致性算法 Paxos,Raft 更清晰易懂,易于实现。
一致性算法允许多台机器作为一个集群协同工作,并且在其中的某几台机器出故障时集群仍然能正常工作。正因为如此,一致性算法在建立可靠的大规模软件系统方面发挥了重要作用。在过去十年中,Paxos 主导了关于一致性算法的讨论:大多数一致性的实现都是基于 Paxos 或受其影响,Paxos 已经成为教授学生关于一致性知识的主要工具。然而尽管很多人一直在努力尝试使 Paxos 更易懂,Paxos 还是太难理解了。此外,Paxos 的架构需要复杂的改变来支持实际系统。
我们开始着手寻找一个新的一致性算法,希望可以为系统开发和教学提供更好的基础。 我们的方法是不寻常的,因为我们的主要目标是可理解性。在该算法的设计中,重要的不仅是如何让算法起作用,还要清晰地知道该算法为什么会起作用。这项工作的结果是一个称为 Raft 的一致性算法。在设计 Raft 时,我们使用了特定的技术来提高它的可理解性,包括:
一项针对 2 所大学共 43 名学生的用户研究表明,Raft 比 Paxos 更容易理解:在学习两种算法后,其中 33 名学生能够更好地回答 Raft 的相关问题。
Raft 在许多方面类似于现有的公式算法,但它有几个新特性:
我们认为 Raft 跟 Paxos 以及其他一致性算法相比是更优的,这不仅体现在教学方面,还体现在工程实现方面。
一致性算法基于复制状态机
一致性算法一般都是在 复制状态机 的背景下实现的。在这种方法下,一组服务器在的状态机计算相同状态的相同副本,即使某些服务器崩溃,它们也可以继续运行。
复制状态机是用来解决分布式系统中的各种容错问题。比如说,具有单个 leader 的大规模的系统,如 GFS,HDFS 和 RAMCloud ,他们通常都使用单独的复制状态机来管理 leader election 和保存 leader 崩溃后重新选举所需的配置信息。像 Chubby 和 ZooKeeper 都是复制状态机。
复制状态机通常都是使用日志复制(log replication)来实现。

如图:每个服务器都保存着一份拥有一系列命令的日志,然后服务器上的状态机会按顺序执行日志中的命令。每一份日志中命令相同并且顺序也相同,因此每个状态机可以处理相同的命令序列。所以状态机是可确定的,每个状态机都执行相同的状态和相同的输出序列。
一致性算法的主要工作就是保证复制日志(replicated log)的一致性 。每台服务器上的一致性模块接收来自客户端的命令,并将这些命令添加到其日志当中。一致性模块与其他服务器上的一致性模块进行通信,以确保每台服务器上最终以相同的顺序包含相同的命令,即使部分服务器崩溃了,这个条件也可以满足。一旦命令被正确复制,每台服务器上的状态机就会按日志顺序处理它们,并将输出返回给客户端。这样就形成了高可用的复制状态机。
适用于实际系统的 一致性算法通常都包含以下几点特征 :
在过去的十年间,Leslie Lamport 的 Paxos 协议 几乎成为一致性的同义词。它是课堂上被教授最多的一致性协议,大多数一致性的实现也是以它为起点。Paxos 首先定义了能在单个决策问题(例如单个复制日志条目)上达成一致性的协议。我们将这个子集称为 single-decree Paxos 。然后 Paxos 组合该协议的多个实例去实现一系列决策,比如日志(multi-Paxos)。Paxos 保证了安全性和活性,它也支持改变集群中的成员,它的安全性也已经被论证了,并且大多数情况下都是高效的。
美中不足的是,Paxos 有两个严重的缺点:
众所周知,Paxos 非常晦涩难懂,除非下了很大的功夫,很少有人能够成功理解它。因此,尽管目前已经有几个尝试希望将 Paxos 解释得通俗易懂一些,而且这些解释都集中在 single-decree Paxos,但是它们还是很难懂。在对 NSDI 2012 参会者的非正式调查中,我们发现很少人会喜欢 Paxos,即使是经验丰富的研究人员。我们自己也一直在跟 Paxos 作斗争,我们也无法完全理解整个 Paxos 协议,直到阅读了几个更简单的描述和自己设计了替代 Paxos 的协议,我们才对 Paxos 有了比较深刻的理解。但这个过程,花了将近一年。我们推测 Paxos 这么晦涩难懂,主要是因为作者选择了 Single-decree Paxos 来作为基础。Single-decree Paxso 非常搞人:它分为两个阶段,但是并没有对这两个阶段进行简单直观的说明,而且这两个阶段也不能分开了单独理解,所以使用者将就很难理解为什么该算法能起作用。Multi-Paxos 的合成规则又增加了许多复杂性。我们相信,对多个决定(日志,并非单个日志条目)达成一致性的总体问题可以用其他更直接和更明显的方式进行分解。
其中一个原因是没有广泛认同的针对 Multi-Paxos 的算法。Lamport 的描述主要是针对 signle-decree Paxos 的,他描述了针对 multi-Paxos 的可能方法,但缺少了很多细节。目前已经有人在尝试具体化和优化 Paxos,但是这些尝试都互不相同并且它们跟 Lamport 描述的也不尽相同。虽然像 Chubby 这样的系统已经实现了类 Paxos 算法,但是他们并没有透露出很多的实现细节。
此外,Paxos 的架构对于构建实际系统来说其实是一个糟糕的设计,这是 single-decree Paxos 分解的另一个结果。举个例子,这对于独立选择地日志条目的集合,然后再将它们合并到顺序日志当中没有任何好处,这只会增加复杂性。围绕日志来设计系统是更加简单和高效的方法,其中新条目按受约束的顺序依次附加。另外一个问题是 Paxos 在其核心使用了 对称对等方法 (尽管它最终表明了这会被用作一种性能优化的弱领导模式)。这在只有一个决策的情况下是有意义的,但是尽管如此,还是很少有实际系统采用了这种方法。如果有一系列的决策需要制定,更简单和更快速的方法应该是首先选择一个 leader,然后由 leader 去协调这些决策。
因此,按照 Paxos 来实现的实际系统往往跟 Paxos 相差很大。几乎所有的实现都是从 Paxos 开始,然后在实现的过程中发现了一系列的难题,在解决难题的过程中,开发出了跟 Paxos 完全不一样的架构。这样既费时又容易出错,而且 Paxos 本身的晦涩难懂又使得问题变得更加严重。Paxos 公式可能是证明其正确性的一个很好的公式,但真正的实现与 Paxos 又相差很大,这证明了它其实没有什么价值。来自 Chubby 作者的评论非常典型:在 Paxos 算法描述和现实实现系统之间有着巨大的鸿沟,如果一直按照 Paxos 算法走下去,最终的系统往往会建立在一个还未被证明的协议之上。
综合上述问题,我们觉得 Paxos 在教学端和系统构建端都没有提供一个良好的基础。考虑到共识性在大规模软件系统中的重要性,我们决定去尝试一下看看能不能设计一个替代 Paxos 并且具有更好特性的共识算法。
Raft 算法就是尝试克服以上缺点,替代 Paxos 的一致性算法。
设计 Raft 的初衷:
在设计 Raft 算法的过程中,很多情况下我们需要在多个备选方案下做出抉择。在这种情况下,我们往往会基于可理解性来进行抉择:
我们意识到这一的分析具有高度的主观性。所以我们采取了两种通用的措施来解决这个问题。
Raft 是一种用来管理第2节中提到的复制日志(replicated log)的算法
Raft算法的关键特性:
Raft算法的简略版:
Raft 选举一个 Leader ,给予管理所有复制日志的权限,由此实现一致性。
Leader 从客户接受指令,写入日志,复制到其他 Backup Server 上,在保证安全性时通知其他 Server 根据日志执行指令更新状态机。
Leader 大大简化了对复制日志的管理。leader 可以自行决定新日志写入位置,数据都从 Leader 流向其他 Server。当 Leader 宕机,从其他 Server 中选举一个新 Leader。
Raft 将一致性问题分解为 三个子问题 :
所有服务器上持久存在的:
(在响应RPCs之前已在稳定存储上进行更新)
| 状态变量 | 说明 |
|---|---|
| currentTerm | 服务器最后⼀次知道的最新的任期号(初始化为 0,持续递增) |
| votedFor | 在当前任期获得选票的候选人的id(如果没有则为 null) |
| log[] | 日志条目集;每⼀个条目包含⼀个用户状态机执行的指令,和收到时的任期号 |
所有服务器上经常变的:
| 状态变量 | 说明 |
|---|---|
| commitIndex | 已知的最大的已经被提交的日志条目的索引值 |
| lastApplied | 最后被应用到状态机的日志条目索引值(初始化为 0,持续递增) |
在leader里面经常改变的:
(选举后重新初始化)
| 状态变量 | 说明 |
|---|---|
| nextIndex[] | 对于每⼀个服务器,需要发送给他的下⼀个日志条目的索引值(初始化为领导人最后索引值加1) |
| matchIndex[] | 对于每⼀个服务器,已经复制给他的日志的最高索引值 |
由 Leader 负责调用来复制日志(5.3);也会用作心跳机制(5.2)
传入参数:
| 状态变量 | 说明 |
|---|---|
| term | Leader的任期号 |
| leaderId | Leader的 id,以便于跟随者重定向请求 |
| prevLogIndex | 新的日志条目紧随之前的索引值 |
| prevLogTerm | prevLogIndex 条目的任期号 |
| entries[] | 准备存储的日志条目(表示心跳时为空;⼀次性发送多个是为了提高效率) |
| leaderCommit | Leader已经提交的日志的索引值 |
返回值:
| 状态变量 | 说明 |
|---|---|
| term | 当前的任期号,用于Leader去更新自己 |
| success | 跟随者包含了匹配上 prevLogIndex 和 prevLogTerm 的日志时为真 |
接收者实现:
false (5.1 节)prevLogIndex 位置处的日志条目的任期号和 prevLogTerm 不匹配,则返回 false (5.3 节)leaderCommit > commitIndex ,令 commitIndex = min(leaderCommit, 新日志条目索引)由候选人调用用来征集选票(5.2 节)
传入参数 :
| 状态变量 | 说明 |
|---|---|
| term | 候选人的任期号 |
| candidateId | 请求选票的候选人的 Id |
| lastLogIndex | 候选人的最后日志条目的索引值 |
| lastLogTerm | 候选人最后日志条目的任期号 |
返回值 :
| 状态变量 | 说明 |
|---|---|
| term | 当前任期号,以便于候选人去更新自己的任期号 |
| voteGranted | 候选人赢得了此张选票时为 true |
接收者实现:
false (5.2 节)votedFor 为 null 或者为 candidateId,并且候选人的日志至少和接受者一样新,那么就给它投票(5.2 节,5.4 节)所有服务器 :
lastApplied 加一,并把 log[lastApplied] 应用到状态机中(5.3 节)currentTerm 等于 T,并切换状态为 Follower(5.1 节)Followers(跟随者)(5.2 节):
Candidates(候选人)(5.2 节):
currentTerm)Leader(领导人):
nextIndex 开始的所有日志条目:nextIndex 和 matchIndexnextIndex 并重试| 特性 | 解释 |
|---|---|
| 选举安全 | 对于一个给定的任期号,最多只会有一个 Leader 被选举出来(5.2 节) |
| Leader 只追加 | Leader 绝对不会删除或者覆盖自己的日志,只会增加(5.3 节) |
| 日志匹配特性 | 如果两个日志在相同的索引位置的日志条目的任期号相同,那么我们就认为这个日志从头到这个索引位置之间全部完全相同(5.3 节) |
| 领导人完全特性 | 如果某个日志条目在某个任期号中已经被提交,那么这个条目必然出现在更大任期号的所有领导人中(5.4 节) |
| 状态机安全特性 | 如果一个 Leader 已经在给定的索引值位置的日志条目应用到状态机中,那么其他任何的服务器在这个索引位置不会提交一个不同的日志(5.4.3 节) |
一个 Raft 集群通常包含 5 个节点,能容忍 2 个节点宕机。
Raft 集群的服务器都处于三个状态之一:

服务器状态。Follower 只响应来自其他服务器的请求。如果 Follower 接收不到消息,那么他就会变成 Candidate 并发起一次选举。获得集群中大多数选票的 Candidate 将成为 Leader。在一个任期内,Leader 保持身份直到自己宕机。
Raft 把时间分割成任意长度的 任期(term) ,用 连续递增整数编号 ,任期开始即选举。Raft 保证一个任期只有一个 Leader。在某些情况下,一次选举无法选出 leader,这个时候这个任期会以没有 leader 而结束。同时一个新的任期(包含一次新的选举)会很快重新开始。

时间被划分成一个个的任期(term),每个任期开始都是一次选举。在选举成功后,领导人会管理整个集群直到任期结束。有时候选举会失败,那么这个任期就会没有领导人而结束。任期之间的切换可以在不同的时间不同的服务器上观察到。
任期编号在 Raft 算法中充当逻辑时钟,每个节点都储存当前任期号, 节点之间通信会交换任期号 ,当一个节点:
节点之间通信使用远程过程调用(RPCs) ,包含两种(第7节还增加了第三种传送快照的):
当节点没有及时的收到 RPC 的响应时,会进行重试,而且节点之间都是以并行的方式发送 RPC 请求,以此来获得更好的性能。
term(任期号)并转为 Candidate,并行向其他节点发送 RV RPC 等待给自己投票。commitIndex。leaderCommit,并放进所有 AE PRCs,其他节点由此得知 Leader 已提交位置,并按日志顺序应用到自己的状态机。
日志由序号标记的条目组成。每个条目都包含创建时的任期号和一个状态机需要执行的指令。一个条目当可以安全的被应用到状态机中去的时候,就认为是可以提交了。
这样 Raft 能维持 日志的一致性 (日志匹配特性):
正常情况下一致性检查不会失败,能一直保持一致。 但是 Leader 在未完全复制日志时宕机会使日志不一致 。例如 Follower 可能没有新 Leader 有的条目,也可能有新 Leader 没有的条目,或者都有,如下图。

当一个领导人成功当选时,跟随者可能是任何情况(a-f)。每一个盒子表示是一个日志条目;里面的数字表示任期号。跟随者可能会缺少一些日志条目(a-b),可能会有一些未被提交的日志条目(c-d),或者两种情况都存在(e-f)。
例如,场景 f 可能会这样发生:f 对应的服务器在任期2的时候是 Leader,它追加了一些日志条目到自己的日志中,一条日志还没提交就宕机了,但是它很快就恢复重启了,然后再在任期3重新被选举为 Leader,又追加了一些日志条目到自己的日志中,在这些任期2和任期3的日志还没有被提交之前,该服务器又宕机了,并且在接下来的几个任期里一直处于宕机状态。
Raft 中处理这种不一致方法是, Leader 强制 Follower 复制自己的日志,即覆盖 Follower 中所有冲突日志 (安全性在5.4)。
Leader 找到最后和 Follower 一致的地方,删除 Follower 之后的冲突日志,发送自己的日志附加给 Follower。这些操作 在 AE RPCs 一致性检查时完成 :
nextIndex,在刚上任时初始化为最新日志索引+1。nextIndex 重试直到成功 ,Follower 删除冲突日志并追加 Leader 日志。日志即保持一致。所以 Leader 无需特殊操作就能恢复一致性 ,Leader 也从不会覆盖删除自己的日志(图3 Leader 只追加特性)。
日志复制机制展示了一致性特征:
目前为止所讨论的机制并不能充分地保证每一个状态机会按相同的顺序执行相同的指令。比如说,一个 follower 可能会进入不可用状态,在此期间,leader 可能提交了若干的日志条目, 然后这个 follower 可能被选举为新的 leader 并且用新的日志条目去覆盖这些日志条目 。这样就会造成不同的状态机执行不同的指令的情况。
故需 增加选举限制 ,保证图 3 中的领导人完整性,即 Leader 一定包含所有已提交日志条目 。
某些一致性算法中需要额外复杂机制把缺少的日志传给 Leader。但是 Raft 保证 Leader 本来就有所有日志,所有日志都是单向从 Leader 传出去。
Raft 在等待投票时,RV PRC 包含 Candidate 的日志信息, 投票人会拒绝日志没有自己新的 Candidate 的投票请求。
投票人 比较最后一条日志的索引值和任期号 :
(本小节是一种错误情况)
前面介绍,一旦当前任期内的某个日志条目以及存储到过半的服务器节点上,Leader 就知道此日志在自己任期已提交。
但 Leader 可能在提交之前崩溃 ,新 Leader 不知道保存在多数节点的的条目是否提交。例如下图,存在多数节点的老日志仍可能被覆盖。

所以 Raft 对日志提交条件增加一个额外限制: Leader 在当前任期至少有一条日志被提交 (即超过半数节点复制),如图 8 中的(e)所示。而©中并没有提交4任期的日志。
所以新上任的 Leader 在接受客户写入命令前先提交一个 no-op(空命令),携带自己任期号的日志复制到多数节点,这样能保证选举限制成立。

假设:
假设任期 T 的 leaderT 在任期内提交了一个日志条目,但是该日志条目没有存在未来某些任期的 leader 中,假设 U 是大于 T 的没有存储该日志条目的最小任期号,处在任期 U 的 leader 称为 leaderU。
反证法论证:
通过 leader 的完整性特性,我们就可以证明状态机安全特性了,即如果某个节点已经将某个给定的索引处的日志条目应用到自己的状态机里了,那么其他的节点就不会在相同的索引处应用一个不同的日志条目。在一个节点应用一个日志条目到自己的状态机中时,它的日志和 leader 的日志从开始到该日志条目都是相同的,并且该日志条目必须被提交。现在考虑一个最小的任期号,在该任期中任意节点应用了一个给定的最小索引上面的日志条目,那么 Log 的完整性特性就会保证该任期之后的所有 leader 将存储相同的日志条目,因此在后面的任期中应用该索引上的日志条目的节点会应用相同的值。所以,状态机安全特性是可以得到保证的。
因为 Raft 要求服务器节点按照日志索引顺序应用日志条目,再加上状态机安全特性,这样就意味着我们可以保证所有的服务器都会按照相同的顺序应用相同的日志条目到自己的状态机中了。
前面都是讨论 Leader 崩溃,Follower和 Candidate 崩溃后的处理方式简单的多,Raft 只需要不断重试发送 RPCs 即可,崩溃重启后再执行 RPC。
Raft 的 RPCs 都是幂等的,重试不会产生问题。如果 Follower 发现 AE RPC 中的日志已经有了,它直接忽略这个请求。
Raft 的要求之一就是 安全性不能依赖时间 :整个系统不能因为某些事件运行的比预期快一点或者慢一点就产生了错误的结果。
但可用性不可避免要依赖时间,最关键在于 Leader 选举,需要满足如下时间要求:
broadcastTime<<electionTimeout<<MTB
到目前为止,我们都假设集群的配置(参与共识算法的服务器节点集合)是固定不变的。但是在实际情况中,我们有时候是需要去改变集群配置的,比如说在服务器崩溃的时候去更换服务器或者是更改副本的数量。尽管可以通过下线整个集群,更新所有配置,然后重启整个集群的方式来实现这个需求,但是这会导致集群在更改过程中是不可用的。另外,如果这个过程中存在一些操作需要人工干预,那么就会有操作失误的风险。为了避免这些问题,我们决定将配置变更自动化并将其纳入到 Raft 的共识算法中来。
为了让配置修改机制安全,在转换的过程中同一个任期里 不能够存在两个 Leader 同时当选 。问题在于, 一次性自动的转换所有服务器是不可能的 ,任何切换方法都是不安全的,所以在转换期间 整个集群可能分裂成两个独立的多数 。

直接从一种配置转到新的配置是十分不安全的,因为各个机器可能在不同时候进行转换。在中间位置 Server1 可以通过自身和 Server2 的选票成为 leader(满足旧配置下收到大多数选票的原则);Server3 可以通过自身和 Server4、Server5 的选票成为 leader(满足新配置线,即集群有 5 个节点的情况下的收到大多数选票的原则);此时整个集群可能在同一任期中出现了两个 leader,这和 Raft 协议是违背的。
为了保证安全性,配置更改必须使用 两阶段方法 。有些系统在第一阶段停掉旧的配置,集群就不能处理客户端请求;然后在第二阶段在启用新的配置。
在 Raft 中,集群先切换到一个过渡性配置,我们称之为 Joint Consensus ( 联合共识 );一旦联合共识被提交,那么系统就切换到新的配置上。
Joint Consensus 是老配置和新配置的结合:
Joint Consensus 允许独立的服务器在不影响安全性的前提下,在不同的时间进行配置转换,还可以让集群在配置转换的过程中依然响应客户端的请求。
集群配置在复制日志中以特殊的日志条目来存储和通信。下图展示了配置转换的过程:
在整个过程中 没有哪个时候让 C-old 和 C-new 同时产生影响 ,保证了安全性。

日志不能无限增长, Snapshotting ( 快照 )是最简单的压缩方法。在快照系统中,整个系统的状态都以快照的形式写入到稳定的持久化存储中,那个时间点之前的日志全部丢弃。
增量压缩 ,例如日志清理或者日志结构合并树也可行,这些方法每次只对一小部分数据进行操作,分散了负载压力。首先,选择一个已经积累的大量已经被删除或者被覆盖对象的区域,然后重写那个区域还活跃的对象,之后释放那个区域。
增量压缩需要增加复杂的机制来实现,而快照总是简单操作整个数据集合,简化了这个问题。日志清除方法需要修改 Raft,但是 状态机可以使用和快照相同的接口实现 LSM tree(日志结构合并树) 。

上图展示了 Raft 中快照的基本思路:
lastIncludedIndex:被快照取代的最后的条目在日志中的索引值(状态机最后应用的日志)lastIncludedTerm:该条目的任期号保留这些数据是为了支持快照后第一个 AE RPC 时的一致性检查,因为这个条目需要前一日志条目的索引值和任期号。
Leader 必须偶尔 通过 RPC 发送快照给一些落后的 Follower 。一般发生于当 Leader 已经删除下一条需要发送给某 Follower 的日志条目的时候。例如一个运行非常缓慢的 Follower 或者新加入集群的服务器(第 6 节),这时让这个 Follower 更新到最新的状态的方式就是通过网络把快照发送给他们。
当 Follower 接收到 IS RPC 时,自己决定对于已经存在的日志该如何处理。
由 Leader 调用,将快照的分块发送给 Follower。Leader 总是按顺序发送分块。
| 参数 | 解释 |
|---|---|
| term | 领导人的任期号 |
| leaderId | 领导人的 Id,以便于跟随者重定向请求 |
| lastIncludedIndex | 快照中包含的最后日志条目的索引值 |
| lastIncludedTerm | 快照中包含的最后日志条目的任期号 |
| offset | 分块在快照中的字节偏移量 |
| data[] | 原始数据 |
| done | 如果这是最后一个分块则为 true |
| 返回结果 | 解释 |
|---|---|
| term | 当前任期号(currentTerm),便于领导人更新自己 |
接收者实现 :
这种快照的方式背离了 Raft 的强 Leader 原则,因为 Follower 可以在 Leader 不知情情况下创建快照,但是这是值得的。Leader 的存在,是为了解决在达成一致性的时候的冲突,创建快照的时候一致性已经达成,不存在冲突了,所以没有 Leader 也是可以的。数据依然是从 Leader 传给 Follower,只是Follower 可以重新组织他们的数据。
而只有 Leader 创建快照,发送给所有的 Follower 的方案有三个问题:
还有两个问题影响快照性能:
这一节将介绍客户端是如何和 Raft 进行交互的,包括:
这些问题对于所有基于一致性的系统都存在,并且 Raft 的解决方案和其他的也差不多。
可选项: Leader 可以通过心跳机制实现租约机制 ,但是这种方法依赖时间来保证安全性(假设时间误差是有界的)。
算法的设计通常以正确性、效率和简洁性为主要目标。虽然这些都是有价值的目标,但我们相信可理解性同样重要。在开发人员将算法转化为实际实现之前,其他任何目标都不能实现,而实际实现将不可避免地偏离和扩展发布的形式。除非开发人员对算法有深刻的理解,并能对算法有直观的认识,否则他们很难在实现中保留算法理想的特性。
在本文中,我们讨论了分布式共识的问题,在这个问题上,一个被广泛接受但难以理解的算法:Paxos,多年来一直让学生和开发人员非常挣扎。我们开发了一种新的算法:Raft,我们已经证明它比 Paxos 更容易理解。我们也相信 Raft 会为系统建设提供更好的基础。将可理解性作为主要设计目标改变了我们处理 Raft 设计的方式。随着设计的进展,我们发现自己反复使用了一些技术,比如分解问题和简化状态空间。这些技术不仅提高了 Raft 的可理解性,而且使我们更容易证实它的正确性。
前面的系统都有单点故障:例如Coordinator、Master等等。因为要避免脑裂问题,因此并不设计成分布式的。
这种在一般情况下是没有问题的,出错的概率很小,即使出错了也可以在很短的时间内恢复回来。
Raft协议就是处理这种类型的问题,不允许单点故障产生,即使产生了也会更快恢复。
客户端访问两台服务器,一台得到了响应,另一台没有得到响应,如果另一台服务器挂掉了最好,但是如果仅仅是网络不通,会造成网络分区的问题,也就是脑裂,导致服务器不一致。因此前面的方案中都使用单点服务器的方式。
处理原则:少数服从多数
客户端的操作需要在大多数服务器都成功,否则一直等待恢复,这样可以实现强一致性
大多数:全部服务器,无论是开机的还是停机的,需要获得一半以上的服务器同意
两种前协议:Paxos和View-stamped replication
步骤:
如果失败,需要选举新的Leader,重试操作
K/V服务器是保留操作表的,为什么还需要日志呢?
最终需要保证日志在所有的服务器上都是相同的
日志条目包括序号、操作和Leader的任期(隐含表示了这个日志条目是哪个Leader追加的)
Follower如果接收不到Leader发送的周期性的心跳信号,就认为Leader挂掉了,开始选举Leader
具体实施:Follower自己有计时器,如果在一段的时间之内既没有接收到新的日志条目,也没有接收到Leader的心跳信号,则认为选举超时,开始进行选举。
此时新的Leader的任期号要大于原来的Leader的任期号,如果此时客户端与旧的Leader进行交互,Leader给新的Leader发送了增加日志的请求,会被拒绝,发送给旧的Leader自己的任期号。旧的Leader发现任期号比自己大,不会再成为Leader。从而避免了脑裂的问题。
挑战:两个Follower几乎同时发起选举,选不出Leader(分裂选举)
因此设置选举超时时间,但是是随机的,如果选不出Leader,经过一段时间后就不会同时开始选举Leader,就可以最终选出Leader了。
到了一年的末尾,伴着客厅的电视声音和窗外若有若无的鞭炮声,还是要写一点总结。
我本想用“高开低走”来对这一年做一个精炼的总结,虽然说目前确实是“低”的状态,可是年初似乎也并没有什么“高”的事情,故这个词语还是不怎么恰当。
回想去年的这个时候,应该是在科一招和两位同学一起跑赛车吧,当时虽然屋子里面很冷,心是火热的,幻想着这样的生活可以一直持续下去。今天屋子里面还是很冷,不同的是心也很冷,目前过的不怎么样,也看不到什么未来。
再回想几年前,已经想不起来什么印象深刻的事情了,可能大多数都是在准备考试吧hh。
现在我自己的状态,或许和2018年初是相同的,又或许是2019年,又或许不同,只是我自己的内心深处偏要找一个相同的历史时刻才能让我自己获得某种慰藉。
我不知道应该写些什么关于今年的事情,写一写可能又写到了感情生活上,而这是我现在最不愿触及的部分之一。
突然想起了五年前看到过的一篇文章,翻出来,最后就用它做一个总结吧:
小时候,过年是头等大事。我们家的人不多,但是和父母一起,准备小零食,准备年夜饭,包饺子,看春晚。年少时的我总觉得,日子一天天过去,没有开端也没有终结。
那时我总以为,过完了今天,明天还是一样的会来,过完了今年,还有明天这个时候的“今年”。可曾经那个心心念念的过年,曾经的那个“今年”,都像天上的云彩和海上的浪花一样,早已不知所踪。
人不能两次踏进同一条河流,也不能,重新过一遍2022。
季节流转,日升月落,星移斗转,世事如白衣苍狗。这一年有多少遗憾和侥幸,有多少悲恼和欣欢,多少披星染雾的启程和多少戴月荷锄的归途。新的一年终将随着初生的太阳喷薄而出,我们如同站在两个世界的边缘,愧疚地送别过去,紧张地等候未来。
我不愿意用一句“新年新气象”,就将过去一年的得失通通扫净,尽管它们终将消失在记忆的犄角旮旯。
新的一年,不是一切归零的重新开局,也不是一成不变的延续。
回头再看看2022,我们有伤感的时候,有无奈的时候,有纠结的时候,也有骄傲的时候。总结过去,才能展望未来。
2023,不是新的开始,而是新的征程。
]]>25道选择题,5道大题(简答题与计算题结合在一起)
非监督学习:不考死记硬背的概念,看一下作业题的例子,比如给一些具体样本分布的图,如果使用KMeans聚类会怎么样,Kmeans的判别界面应该是一个中垂线,两个簇的中垂线,如果不是大小均匀的球体可能KMeans就不适合,如果是有疏有密的,一个椭球形的,是不是考虑基于混合高斯的模型,或者簇是一个不规则的形状,比如是字母S或者C型,甚至有的簇是一个同心圆的,最适合的聚类算法应该是什么样的,可以考虑一下基于密度的聚类是不是可以,基于密度的聚类有没有不适合的情况,包括基于层次聚类会遇到什么问题,结合一些实际的例子请大家分析一下。
降维:PCA每年都考,可能和前面讲K-L变换的知识结合起来,比如PCA为什么要先做零均值的平移,特征值的选择,为什么先做倒序的排序,选排在前面的特征值最大的几个特征值对应的特征向量来构成对应的变换核,基本原理希望掌握。后面的非线性降维,核PCA的主要思想是什么,先升维再降维,基于流形的非线性降维方法,说出一些经典方法的名字就行,不可能考太细。(前面讲了一些降维,这里不可能考大题,可以看看Fisher线性判别怎么做降维,选择最佳投影方向等等)
半监督学习:半监督学习是基于一些假设的,最基本的假设有哪些,不同的半监督算法各自基于什么假设?比如半监督的SVM应该是基于低密度分割的假设,半监督SVM里面有一些比较关键的参数,C1,C2等等,分别表达什么意思,C2很小表达对未标注样本错分的容忍度比较大,很大表示不容忍错分,每一个未标注样本也要分对,但是所有的样本都必须要严格分对这种也可能有问题,过拟合等等,过拟合怎么办呢?可以把模型参数调简单点,怎么让模型参数调简单?不同的模型方法不一样,比如半监督SVM就可以把C2调小一点,或者把C1调小也行,如果是神经网络可以让结构简单一点,层数和节点变少参数就变少,欠拟合怎么办,如何让模型变复杂,除了从模型参数上调,增加数据样本是不是一定有用?
概率图模型每年都会有大题,要么是考贝叶斯球判断条件独立性,或者大题问维特比解码,一般只考前向的推导。
集成学习只考经典的bagging和boosting两种,其他的不考,考的时候从基本原理出发,比如bagging的基本原理是降低方差,但是不能改变偏差,boosting主要是降低偏差,考的时候可能会给实际的例子去判断哪种更适用,比如模型的单个基学习器都是偏差比较高的情况,要把多个集成起来增加学习能力,到底是用boosting还是bagging,如果选择boosting,不同的基学习器的权重是完全一样的吗,谁的权重大,或者是boosting作迭代训练的时候,训练样本每一次的权重在迭代的时候是不是都要改变,为什么要让分错的样本权重更大,分对的样本下一次权重就调小,要知道这些基本的调节权重的原则。
人工神经网络只考基本原理和卷积神经网络,可能让你设计一个人工神经网络的结构,和前面几章的内容有结合,比如线性分类器,非线性分类器,两类分类的,多类分类的,都怎么来设计,能画出大概的结构,写出能用什么(激励?)函数就可以。卷积神经网络主要是考察基本原理,比如为什么卷积神经网络能够进一步降低(深度,参数量?)但是又不会降低性能。可能是基于局部连接和参数重用,池化等等技术,这几个技术的基本的动机是什么,是因为有一些很有判别力的局部模式,他是之前局部出现,并且能够在不同的位置出现,还有有的时候下采样也不会影响这种局部模式的识别。可能会问一些深度神经网络训练的时候遇到一些问题怎么解决,比如说层数很深的时候,会遇到梯度消失、梯度爆炸的问题,遇到问题怎么办呢,激活函数从sigmoid换成relu为什么这样能解决这个问题,比如说使用batch normalization也可以缓解梯度消失的问题,甚至还能带来一些正则化的效果,或者是残差网络的技术,将前层的信息引入进来,可能还带有一些集成学习的思想,把这些基本的原理说清楚。人工神经网络的训练可能也会遇到过拟合,模型的参数可能就过于复杂,除了简化模型的结构之外,还有什么其他的技术,比如是不是可以考虑添加正则化项,正则化也分为L1和L2,L1正则能让系数=0也能做特征选择,L2可以让参数趋向于变小,对整体的影响就变小了,相当于参数变简单了,也能防止过拟合,包括做数据增强,增加训练样本集尽可能让他多样化,也是可以增加模型的泛化能力,还有做梯度下降的时候收敛速度变慢怎么办,陷入局部极值点怎么办,一般是这种实际一些的问题
不考:
势函数、决策树、贝叶斯参数估计、后向算法、马尔科夫随机场、SMO、拉普拉斯平滑
没有证明题,但是会有一点公式推导
EM算法不作为重点考察,最多知道概念是拿来干什么的就行,是对含有隐含变量的模型做优化,不会考很细节的
零碎考点:
判别器有讲过贝叶斯风险,是每年都会考的,感知器算法、朴素贝叶斯、Fisher判别分析,都有可能考到的,K-L变换作特征提取或者后面的PCA,还有像LR,SVM,还有线性回归,另外就是机器学习一般的概念,过拟合、欠拟合应该怎么办,怎么判断模型处于哪种状态,正则的概念,可能放到多种模型中,都要能理解。
降维需要掌握的知识点:PCA是怎么做的,Fisher判别分析要会
Fisher判别分析是要考的但是不考计算,除了两类也要看一下多类的
深度学习有一道大题,偏简答性质的
HMM有计算题,判断独立性是选择题
概率图掌握贝叶斯球就可以,概率的分布表示还是要的
多类LR不需要特别掌握,知道有这回事就行,比如用softmax函数做最后一层就可以
多类分类问题在SVM或者LR可以转化为两两的分类问题,算术题,转成多少个需要知道
支持向量考的挺多的,给一个图,哪些点是支持向量,或者自己画图
偏差方差分解具体的证明不考,但是要知道泛化误差是三部分,会判断模型什么时候偏差比较大,什么时候方差比较大,应该怎么办
高斯判别分析今年没有大题,Fisher判别分析多看看
SVM软间隔硬间隔都会有
一般对线性回归、LR、SVM公式推导方面严一点,比如损失函数是怎么推导来的,极大似然估计是怎么回事,MAP估计是怎么样,这些基本概念需要掌握,SVM的模型推导可能少一些。SVM更多理解margin、支持向量、不同的C的影响等等、核函数,RBF核模型复杂度的参数是核函数的宽度,多项式核模型复杂度还有多项式的项数。
类内类间散度矩阵应该怎么算是要求掌握的,与Fisher是什么关系,但是不会考察具体的数值计算
多类感知器不考,感知器是有的
PCA没有计算,需要知道PCA的计算过程,另外目的和达到的效果也需要知道。首先要减均值,然后再算协方差矩阵作矩阵分解,或者是作SVD分解都可以,测试的过程也一样,目的是去掉各个维度之间的相关性
bagging知道功效和怎么做就行,是多个模型做平均,目的是偏差不变,降低模型的方差,boosting是降低模型的偏差,方差不变
聚类:比如像K均值,GMM,DBSCAN这三类聚类方法需要掌握他的特点,我们什么时候用哪种方法来做,选择题
降维:今年考的不是很多,稍微看一看就行
半监督学习:不会考的特别细,但是半监督学习是基于一些假设的,最基本的假设有哪些,不同的半监督算法各自基于什么假设?
概率图模型一方面考对于有向图模型,判断给定观测到某些节点的情况下,这个变量和那个变量是否独立,可以通过贝叶斯球的方式做,需要记忆贝叶斯球的规则,根据一个图模型把联合分布写出来,HMM要求掌握前向算法求观测概率和利用维特比算法求给定一个观测后最可能的隐含状态的序列
集成学习主要是bagging和boosting,要知道bagging的原理是通过对训练样本进行bootstrap采样,然后训练多个模型,最后对多个模型作平均,得到最后的融合模型。它的好处是可以降低模型的方差,偏差不变。boosting对于Adaboost的过程,比如一开始初始化的时候每个样本的权重相同,经过一轮迭代之后哪些样本的权重会增加,哪些样本的权重会减小,最后模型是怎么融合的,没有计算题,知道Adabooost的过程就可以。对于boosting一般的原理也要知道,每次迭代顺序的把一些模型加进去,最后一些子模型的加权平均是我们最后的集成模型,boosting的好处是降低模型的偏差,方差不变。
深度学习:知道神经元的结构(线性组合+激活函数),一个神经元可以起到一个什么样的作用,神经网络是把神经元组合起来,卷积神经网络为什么要局部连接,为什么要权重共享,这样做的基于对数据的假设是什么,局部连接我们认为是一个模式在一个比较小的范围内,而不是要看全局,权值共享是说不同位置可能都有这样的模式,这样做可以使得模型的参数变少,另外多层感知器很多层并不能带来性能提升,现在的模型采用哪些技术使得训练深度模型成为可能?比如说激活函数,sigmoid容易梯度消失,使用relu使得梯度消失的问题会减弱,这样网络层数可以更深,另外batch normalization会使得我们的训练会和好多因素(学习率、初始化)的要求没有那么高,这样也是一种技术,另外采用预训练网络作初始化也是一种方式,或者核初始化等等,也可以让模型的层数更深。另外Resnet,或者叫skip-connect,通过跳接的方式使得梯度消失的问题能减弱,使得模型可以很深很深甚至上千层。神经网络设计的时候也讲了一些其他的技术。不要求全部掌握,至少知道几点。为什么要用mini-batch的梯度下降,随机的梯度下降,有什么样的好处或者特点等等。
第一章:模式识别和机器学习我们并不是很区分它们,可以看成一个问题的两个方面
第二章:统计判别,主要是讲了错误率最小,错误率最小对应到分类问题等价于后验概率最大,后验概率怎么算需要大家一定掌握,后面也把风险带进来
第三章:判别函数,作判别的时候一种方式可以使用生成式分类器,高斯分布的贝叶斯分类器采用的实际上是生成式分类器,指的是我们的联合分布可以由先验和似然相乘得到,有了联合分布可以从联合分布进行采样从而得到新的数据,也就是我们知道数据的产生过程,因此叫做生成式分类器。朴素贝叶斯,高斯判别分析,概率图模型,HMM都属于生成式分类器。好处是因为我们对数据的产生过程有比较强的假设,如果我们的数据符合这个假设,通常用很少量的数据就能得到很好的模型,或者说收敛的比较快,缺点是如果数据不符合这个假设,模型的性能就很不好。另外是判别式分类器,就是直接对后验概率进行建模,或者是定义一个判别函数,根据判别函数的值判断是哪一个类别。像逻辑斯蒂回归,决策树,SVM,深度学习都是判别式的。
线性判别函数如何将多类分类任务转化成两类分类任务或者是直接用多类分类任务去做。线性判别函数处理的都是线性可分的问题,如果不是线性可分的需要用广义的线性判别函数,或者是分段线性判别函数实现。模式空间和权空间只是一些基本概念。重点掌握Fisher线性判别,协方差矩阵、类内类间,向量等都是怎么定义的,Fisher线性判别的准则是什么,都需要掌握,两类的情况,多类的情况,大家都去想想,感知器算法需要重点掌握,它是线性判别函数,只能在线性可分的时候可以使用,感知器多类也需要大家掌握。
第四章:特征选择是很重要的内容,但是不作为重点考察。特征提取重点掌握K-L变换,比较简单,实际也比较有用,PCA实际上和K-L变换就是一回事。需要知道K-L变换的目的和过程,做了K-L变换之后能达到一个什么样的效果。
第五章:期望风险:在没有见过的数据上的误差,也就是期望风险。结构风险:正则项,L1正则和L2正则,泛化误差的分解,证明过程不要求,结论要知道,用VC维计算泛化误差的上界,基本概念比较多
第六章:线性回归的损失函数,目标函数包括两部分,L1损失或者L2损失,负log似然损失,需要掌握似然是怎么定义的,由负log似然损失怎么推到了L2损失,L2损失的问题是对噪声比较敏感,因为是平方的关系,预测差距比较大的时候损失也比较大,可以采用L1损失,但是是不连续的,因此一般采用Huber损失,实际上是L1损失和L2损失的分段的情况。正则可以是L1正则或者L2正则,目的是为了限制模型的复杂度,L2会使得w的绝对值会缩小,也叫权重缩减,但是一般不为0。L1会为0,可以起到特征选择的作用。然后讲了逻辑斯蒂回归,是一个分类问题,直接计算后验概率,多类分类需要softmax函数,损失也是负log似然,只是称为交叉熵损失,推导的时候都是从负log似然推导过来的。然后生成式分类器,高斯判别分析和朴素贝叶斯,两种分类器的先验是相同的,两类是伯努利分布,多类是多项式分布,两者不同的地方是类条件的定义不一样,高斯是在给定类别的条件下是高斯分布,朴素贝叶斯是独立的,
第七章:SVM,考察的重点,需要掌握线性的SVM,核化的SVM,回归了解一下就行,首先要知道间隔的概念,硬间隔和软间隔的目标函数分别是什么,可以写成损失+正则的情况,合页损失+正则,什么样的样本是支持向量,了解原问题和对偶问题,核化也是很重要的,后面的PCA,包括逻辑斯蒂回归都可以核化,但是模型比较复杂,大家用的比较少,线性核,多项式核的复杂度体现在基数,RBF核的复杂度是核函数的宽度,软间隔的复杂度还有松弛因子C,概念需要掌握
第八章:聚类:重点掌握K均值,GMM,DBSCAN,知道聚类的过程,对什么样的数据比较适合,K均值每一个类的都是高斯,方差相同等等,GMM更宽泛,不球形,DBSCAN不要求每一类的具体形式,找密度最大的作为中心,还可以处理带有噪声的情况。
第九章降维:PCA就是K-L变换,目标是重构误差最小,MDS不作重点考察,非线性降维知道一些常用的非线性降维方法的做法就可以了
第十章半监督学习:重点掌握三种基本假设,半监督学习算法了解就行,想一下每一种算法的背后是基于哪些假设在做
第十一章概率图模型,考试时候主要是考察有向的图模型,无向图模型了解一下就行,给定一个概率图模型,能不能写出概率分布来,根据有向图模型,判断给定观测到某些节点的情况下,这个变量和那个变量是否独立,可以通过贝叶斯球的方式做,需要记忆贝叶斯球的规则,缺失的边实际上也蕴含了独立的关系,HMM要求掌握前向算法求观测概率和利用维特比算法求给定一个观测后最可能的隐含状态的序列。HMM的模型参数学习,全监督的用极大似然估计,隐含状态不知道用EM算法。
第十二章集成学习主要是bagging和boosting,要知道bagging的原理是通过对训练样本进行bootstrap采样,然后训练多个模型,最后对多个模型作平均或者投票,得到最后的融合模型。可以并行训练,它的好处是可以降低模型的方差,偏差不变。基学习器的选择可以选方差比较大的模型。比如随机森林里面选取的决策树就是选层数比较深或者叶子节点比较多的。或者多个神经网络进行。boosting是多个基学习器采用顺序的方式进行训练,不能并行训练,每一个新加入的学习器希望能纠正前面的学习器的一些错误,实现的时候每个基学习器都是一样的,融合的方式是加权平均,权重和每个基学习器是相关的。boosting的好处是降低模型的偏差,方差不变。因此基学习器可以比较简单,决策树就树比较浅。重点考察Adaboost的过程,需要掌握。
第十三章深度学习:知道神经元的结构(多个输入线性组合+激活函数得到输出),与人类神经元比较像,线性回归实际上也可以用一个神经元来表示,相当于激活函数是一个线性的激活函数(恒等映射函数)。逻辑斯蒂回归就相当于一个神经元+sigmoid函数,SVM也可以写成这样的形式。多层叠加就可以实现非常复杂的非线性函数的拟合。80年代层数不深,当时的训练方法有一些问题,sigmoid或者tanh会产生梯度消失的问题,relu可以解决梯度消失,计算简单。梯度消失是梯度传几层就没了,一个原因是激活函数,另外的原因是乘很多次,也会没了。神经网络之间的连接方式:全连接,每一个神经元都和其他的神经元相连。为了简化,图像可以采用卷积神经网络,通常只是局部连接,为什么要局部连接,因为图像里面一些局部的输入就可以判断模式的存在。为什么要权重共享,权值共享是说不同位置可能都有这样的模式,这样做可以使得模型的参数变少,计算量并不会减少。数据不满足这种特点不能使用卷积做。另外多层感知器很多层并不能带来性能提升,现在的模型采用哪些技术使得训练深度模型成为可能?Resnet,或者叫skip-connect,通过跳接的方式使得梯度消失的问题能减弱,使得模型可以很深很深甚至上千层。另外batch normalization相当于做一个标准化,使得输入的范围的差异不至于这么大。相当于在神经网络里面增加了一个层,学习这个层的参数。会使得模型训练更快更稳定,性能更好。dropout使得某些输出是0,不往下传,相当于集成学习的高效的实现方式,主要使用在全连接层里面。另外讲了一些神经网络的训练技巧,基本算法是梯度下降,梯度爆炸就是乘多了很大很大,梯度的计算首先是利用网络结构进行反向传播,批处理梯度下降是所有的样本一起,算一次很慢,一般不采用,随机梯度下降是每一个只选取一个样本,比较快,但是受单个样本的影响比较大。梯度的方向可能是锯齿的形状。通常使用小批量梯度下降,两者取中间。走一步的步长叫做学习率,下降的方法不一定是梯度,因为鞍点可能不动,平滑的区域也不怎么动,因此考虑动量法,进行自适应调整。参数初始化也比较重要。另外关于抗过拟合的问题,每一层的节点很多,模型就非常复杂,需要抗过拟合。及早停止,监控验证集上的误差,正则,数据增广,收集更多的训练样本,但是收集样本需要费用,可以采用一些图像处理的方法。还有dropout。
非线性降维基本掌握流程就行
大题没有画模型结构图
RNN不作为重点考察内容
极大似然:给一个应用场景,写似然的式子,概率分布都写的,无非是取一个log然后对所有的样本求和
SVM二维计算量不大,侧重于概念,考了很多选择题
考试不涉及求矩阵的逆、特征值的具体计算
没有问概念的简答题
选择题重点:过拟合欠拟合、偏差方差、概率图、深度学习等等
MAP的概念需要知道,大题里面没有
LDA需要知道
K-L变换需要掌握过程,能达到什么目的,但是没有数值计算
逻辑斯蒂回归需要知道正则,损失函数的推导,实际上是负log似然,关于似然的计算,这个过程需要大家知道。
极大似然或贝叶斯求参数今年没有
线性回归逻辑斯蒂回归损失函数的推导需要掌握,+正则
Adaboost知道过程就行
核函数表示两个样本的相似度,常用的核函数,比如多项式核,RBF核,还有核函数控制模型复杂度的超参数,就差不多了
DBSCAN具体过程不考,需要知道对哪些数据合适
EM算法不考察
泛化误差不会考具体的公式,知道泛化误差的上界由两部分构成,一部分是和训练误差有关系,另外一部分是模型复杂度(VC维)有关系,是一个正关系还是反关系就行了
贝叶斯估计、高斯分布参数求解不作为大题考试内容,MLE的计算过程希望大家了解,考试可能不考
20道选择题
3道简答题
3道综合应用题
确定性的知识:
命题逻辑:语法和语义,蕴含和形式推演
三种形式推演的系统:
一阶谓词逻辑:与命题逻辑对应复习,不考证明
Logic Programming:一种新的编程的思路
不确定性的知识:
模糊集合之间的运算,交并补、模糊关系、模糊关系的合成,用模糊逻辑表示自然语言
模糊逻辑比一阶谓词逻辑多了模糊谓词、模糊量词和模糊修饰词
深度学习部分:
受限玻尔兹曼机原理理解就可以了
卷积神经网络、循环神经网络用的比较多,对于具体模型来说,要了解模型的原理,为什么采用这种结构就可以
更倾向于概念
不会考公式,梯度下降应该熟练掌握的
综合应用题分三个小问题,每一个是一个方面,各自独立
A*树搜索和图搜索的最优性证明最好是了解一下
简答题是搜索方面的,搜索这些算法相应的原理了解一下就可以了
简答题不是要求证明的,没有证明题
简答题是单个题目
没有考公式推导
野人传教士问题,实际上是考你搜索问题的形式化描述,形式化描述了解的话应该是没问题的
对于GAN,基本概念和原理掌握,考试掌握基本原理就可以了
对于启发式搜索,主要是设计一个合适的启发式函数(可采纳性和一致性),针对实际问题用松弛问题的解来作为启发式函数就可以
综合应用题是神经网络相关
综合应用题有要求画神经网络结构的,说明具体采用的算法
选择题都是一些基本概念
单选30题,每题1分
多选15题,每题1分
简答3题,每题5分
计算3题,每题10分
设计1题,每题10分
]]>通过提供故障容错性的虚拟机,我们实现了一个商业化的企业级系统,建立在复制一个主虚拟机的执行过程到另一个服务器上的备份虚拟机的基础上。系统很容易使用,同时保证了应用的性能仅有少于10%的降低。另外,为了让主VM和二级VM的执行活动保持一致,对于几个实际的应用而言,需要的数据带宽少于20Mbit/s,这也允许实现更长距离的故障容错的可能性。一种容易使用,在故障后自动恢复备份的商业化系统,在复制VM执行之前需要额外的组件。我们已经设计并且实现了这些额外的组件,并且解决了在支持VM运行企业级应用的时候,遇到的许多实际问题。
一个实现故障容忍服务器的常见方法是主备机制,主服务器失败的同时另外一个备份服务器立即进行接管,此时对于外部客户端而言,故障就相当于被隐藏了起来,并且不会造成数据丢失。因此在任何时间,备份服务器的状态必须和主服务器几乎保持一致,在备份服务器上复制状态的一种方法是将主服务器的所有状态,包括CPU、memory、IO设备,连续地送给备份服务器。然而,这种发送状态的方法,尤其是涉及到内存中的变更,其需要的带宽非常大。
另一种可以用更少带宽复制服务器的方法类似于状态机。这种思路是将服务器建模为确定性的状态机,他们从相同的初始状态开始,并且确保以相同的顺序接收相同的输入请求,这样就能保持同步。因为大多数服务器或服务有一些不确定性的操作,因此必须使用额外的协调机制来确保主备同步。然而,需要保持主备一致性的额外信息数目,远远少于正在变更的主服务器上状态(主要是内存更新)的数目。
实现协调机制来确保物理服务器的确定性操作是困难的,尤其随着处理器频率增长。反之,一个运行在管理程序(hypervisor)上的VM,是一个实现状态机方法的很好的平台。 一个VM可以被当作一个定义好的状态机,它的操作是机器被虚拟化的操作(包括它所有的设备) 。和物理服务器一样,VM有相同的非确定性操作(例如读取时钟或发送中断),因此为了保持同步,额外的信息必须被发送给备份服务器。管理程序(hypervisor)有VM的全权控制权利,包括处理所有输入,因此它能够获得所有与主VM上的非确定性操作有关的必要信息,并且能正确地重放这些操作。
因此,这个状态机方法可以通过商业化软件上的VM来实现,它不需要硬件更改,允许在最新的微处理器上立刻实现故障容错。另外,状态机方法需要的低带宽允许了主备服务器能更好地进行物理分隔。例如,被复制的VM可以运行在横跨一个学校的物理机器上,相比于运行在同一建筑内的VM而言,可以提供更多的可靠性。
我们在VMware vSphere 4.0平台上使用主备机制实现了故障容忍的VMs,VMware vSphere实现了一个完整的x86虚拟机,所以我们自动地能够为任何x86操作系统和应用提供故障容忍。这种允许我们记录一个主服务器执行,并确保备份服务器一致执行的基础技术是确定性重放。VMware vSphere Fault Tolerance(FT)是基于确定性重放(Deterministic Replay) 的,但是为了建立一个完整的故障容忍系统,还增加了必要的额外协议和功能。除了提供硬件故障容忍,我们的系统在一次失败后,通过在局部集群中任何可接受的服务器上开始一个新的备份虚拟机,进行自动地存储备份。目前确定性重放和VMare FT的产品版本只支持单处理器的VMs。多处理器VM的操作记录和重放还在开发中,因为每个共享内存的操作都是一个非确定性的操作,因此还有重要的性能问题待解决。
Bressoud和Schneider描述了一个针对HP PA-RISC平台的故障容忍VMs的原型实现。我们的方法是相似的,但是出于性能原因,以及在调查了许多可替代设计后,我们已经做了一些基础性的改变。另外,为了建立一个完整的系统,而这个系统是有效的并且能够被正在运行企业级应用的客户使用,我们已经设计并实现了系统中许多额外的组件,可以处理许多实际问题。与大多数其他实际系统讨论的类似, 我们只尝试应付fail-stop的故障 ,这是一种服务器故障,可以在故障服务器造成一次不正确的外部可见行为之前被检测。( Hades注:fail-stop故障指的是,如果某些东西出现故障,只是单纯的停止运行,而不是运算出错误结果。比如电源线、服务器风扇导致CPU过热停止运行、网络等故障 )

图1展示了我们系统在故障容忍VMs的基本步骤。对于一个给定的VM,我们希望提供故障容忍(主VM),我们在一个完全不同的物理机器上运行一个备份VM,保持和主VM同步并且执行一致,虽然存在短时间的滞后。我们说这两个VMs是虚拟的步调一致。VMs的虚拟磁盘是在一个共享存储中的(例如一个Fibre Channel或者iSCSI磁盘阵列),因此可以接受主备服务器的输入和输出。(我们将在4.1节中讨论带有分隔的非共享虚拟磁盘的主备VM的设计)只有主VM会说明它在网络中的存在,因此所有网络输入都会来到主VM上。相似地,所有其他输入(例如键盘和鼠标)也只会来到主VM上。
所有主VM接收到的输入都会通过名为logging channel的网络连接,被发送到备份VM上。对于几个工作负载而言,主要的输入途径是网络和磁盘。为了保证备份VM和主VM使用相同的方式执行非确定性操作,下面2.1节讨论的额外的信息也需要发送。最终备份VM总是执行和主VM一致的操作。然而,备份VM的输出会被管理程序扔掉,因此只有主VM产生实际输出,并被返回给客户端。和2.2节中描述的一样,为了确保主VM失败后没有数据丢失,主备VM遵循一个具体的协议,包括备份VM明确的确认信息。
为了检测主或备份虚拟机是否失败,我们的系统既使用相关服务器间的心跳机制,同时也监测 logging channel 上的流量。另外,我们我们必须确保只有主或备份VM执行操作,即使存在脑裂(split brain)的场景(在这种场景中主备服务器互相之间会失去通信)。
正如我们已经提到的,复制服务器(或者VM)的操作可以被建模为确定性状态机的复制。如果两个确定性的状态机以相同的初始状态开始,并且以相同的顺序提供确切的输入,它们将经历相同的状态序列并且产生相同的输出。一个虚拟机有很宽泛的输入,包括到来的网络包,磁盘读,以及来自键盘和鼠标的输入。非确定性事件(例如虚拟中断)和非确定性操作(例如处理器的时钟周期计数器)也会影响虚拟机的状态。这显示了对于正在运行任何操作系统和工作负载的任何虚拟机而言,复制执行有 三个挑战 :
另外,许多在x86处理器上的复杂操作还未被定义,因此会引起非确定性以及副作用。捕获这些未定义的操作并且重放它们产生相同的状态是一个额外的挑战。
针对在VMare vSphere平台上的x86虚拟机,VMware确定性地重放恰好提供了这个功能。确定性重放记录了 VM 的输入以及与 VM执行相关的所有可能的不确定性的日志条目流,这些条目会被写入日志文件。在读取日志文件中的条目后,VM 操作会被精确地重放。 对于非确定性操作,为了允许操作以相同的状态变化和输出再现,需要记录足够的信息。 对于非确定性事件,例如定时器或 IO 完成中断,事件发生的确切指令也会被记录下来。 在重播期间,事件被传递在指令流中的同一位置。 VMware 确定性重放采用各种技术,实现了高效的事件记录和事件传递机制,包括使用AMD和英特尔联合开发的硬件性能计数器。
Bressoud 和 Schneider提到将VM执行切分成不同的epoch,其中非确定性事件,例如中断仅在一个epoch结束时传递。 epoch的概念似乎被用作批处理机制,因为在它发生的确切指令处单独传递每个中断的成本太高。然而,我们的事件传递机制足够高效,以至于 VMware确定性重放不需要使用epochs。 每次中断在发生时被记录,并且在重放时有效地传递到适当的指令处。
对于 VMware FT而言,我们使用确定性重放来生成必要的日志条目来记录主VM的执行情况,但是不是将日志条目写入磁盘,而是通过日志通道将它们发送到备份VM。备份 VM 实时重放日志条目,因此与主 VM 的执行保持一致。 然而,我们必须在日志通道中使用严格的 FT 协议以增强日志条目,从而确保我们实现故障容忍。 我们的基本要求如下:
输出要求 :如果备份VM在主VM发生故障后接管,那么备份VM将继续以一种与主虚拟机发送到外部世界的所有输出完全一致的方式执行。
请注意,在发生故障转移后(即备份 VM 需要在主VM故障后接管),备份VM开始执行的方式可能与主 VM 相当不同,因为在执行期间发生了许多非确定性事件。但是,只要备份VM满足输出要求,在故障转移到备份 VM期间 没有外部可见状态或数据的丢失 ,客户端将注意到他们的服务没有中断或不一致。
可以通过延迟任何外部输出(通常是网络数据包)直到备份VM 已收到重放的所有信息来确保输出要求,这些信息允许它至少执行到该输出操作的点。一个必要条件是备份 VM 必须接收到输出操作之前生成的所有日志条目。这些日志条目将允许它执行到最后一个日志条目的点。但是,假设失败是在主VM执行输出操作后立即发生。备份 VM 必须知道它必须继续重播到输出操作点,并且到那时只能“上线”(停止重播并作为主VM接管,如2.3 节所述)。如果备份将在输出操作之前的最后一个日志条目点上线,一些非确定性事件(例如计时器传递给 VM 的中断)可能会在执行输出操作之前改变其执行路径。
给定上述的限制,强制满足输入要求的最容易的方式是在每个输出操作时创建一个特殊的日志条目。然后,输出要求一定被下面特殊的规则限制:
输出规则 :主VM可能不发送一个输出到外部世界,直到备份VM已收到并确认与产生输出的操作相关的日志条目。
如果备份 VM 已收到所有日志条目,包括生成输出操作的日志条目,然后备份 VM 将能够准确地重现主 VM在输出点的状态,所以如果主VM死了, 备份将正确地达到一个与输出一致的状态 。相反,如果备份VM在没有收到所有必要的日志条目的情况下接管,那么它的状态可能会 迅速分歧 ,以至于与主服务器的输出不一致。输出规则在某些方面类似于 [11] 中描述的方法,其中“外部同步” IO 实际上可以被缓存,只要它在下一次外部通信之前确实被写入磁盘了。
请注意,输出规则没有说明关于停止主VM执行的任何事。我们只需要延迟输出发送,但 VM 本身可以继续执行。由于操作系统通过异步中断来指示完成,因此可以执行非阻塞的网络和磁盘输出,VM可以轻松地继续执行并且不一定会立即受到输出延迟的影响。相比之下,以前的工作 [3, 9] 通常必须在执行输出之前完全停止主VM,直到备份 VM 已确认来自主 VM 的所有必要信息。

作为一个例子,我们在图2中展示了 FT 协议的需求。该图显示了一个主VM和备份VM上的事件时间线。从主线到备份线的箭头表示日志条目的传输,从备份线路到主线路的箭头表示确认。有关异步事件、输入和输出操作的信息必须作为日志条目发送到备份VM并确认。如图所示,到外部世界的输出被延迟,直到主VM收到来自备份 VM 的确认,它已经收到与输出操作相关的日志条目。鉴于遵循输出规则,备份VM将能够以这样一种状态接管,即与主VM最后的输出一致。
我们不能保证一旦出现故障转移情况,所有输出都准确地产生一次。当主VM打算发送输出时, 没有使用两阶段提交事务 ,备份VM无法确定主VM是在发送它的最后一个输出之前还是之后立即崩溃。 幸运的是,网络基础设施(包括常用的TCP)旨在处理丢失的数据包和相同(重复)的数据包 。 请注意传入到主VM的数据包也可能在其故障的期间丢失,因此不会被传递给备份VM。 但是,传入的数据包可能会由于与服务器故障无关的任何原因被丢弃,因此网络基础设施、操作系统和应用程序都被写入,以确保他们可以弥补丢失的数据包。
如上所述,如果另一个 VM 出现故障,主备VMs必须快速响应。如果备份VM出现故障,主VM将上线,即离开记录模式(因此停止发送条目到日志通道)并开始正常执行。如果主VM失败,备份VM应该同样上线(go live),但过程更为复杂。由于其执行的滞后,备份 VM 可能会有许多它已收到并确认,但尚未消耗的日志条目,因为备份 VM 尚未达到执行的适当点。 备份VM必须继续重放日志条目,直到它消耗了最后一个日志条目 。此时,备份 VM 将停止重放模式并开始作为正常VM执行。本质上备份VM被提升为主VM(现在缺少备份VM)。由于它不再是备份 VM,当操作系统执行输出操作时,新的主VM现在将向外部世界生产输出。在过渡到正常模式期间,可能会有一些特定设备的操作需要允许正确地发送输出。特别是, 出于联网目的,VMware FT 自动在网络上通告新的主VM的MAC 地址,以便物理网络交换机知道新的主 VM 所在的服务器 。此外,新提升的主VM可能需要重做一些磁盘 IO(如第 3.4 节所述)。
有许多可能的方法来尝试检测主备VMs的故障。VMware FT在运行容错VMs的服务器之间使用 UDP心跳 ,来检测服务器何时崩溃。此外,VMware FT 监控日志流量,包括从主到备的发送以及从备到主的确认。因为定时器中断,日志流量应该是有规律的,并且永远不会停止。因此,在日志条目或确认流中的中断可能表明VM故障。如果心跳或记录流量已停止超过特定超时时间(大约几秒钟),就可能发生故障了。
但是,任何此类故障检测方法都容易受到脑裂(split brain)问题的影响 。如果备份服务器停止接收来自主服务器的心跳,这可能表明主服务器出现故障,或者可能只是意味着所有仍在运行的服务器之间的网络连接丢失。如果备份VM随后上线,而主VM也仍然在运行,对于与VM通信的客户端而言可能会有数据损坏以及其他问题。因此,我们必须确保当检测到故障时,主VM和备份VM只有一个在线。为了避免脑裂问题,我们利用共享存储,来存储VM的虚拟磁盘。 当任一主或备份VM想要上线时,它会在共享存储中执行一个原子性的测试设置操作 。 如果操作成功,VM 被允许上线。 如果操作失败,那么另一个 VM 一定已经上线,所以当前虚拟机实际上停止了自己(“自杀”)。 如果尝试执行此原子操作时,VM 无法访问共享存储,然后它只是等待,直到可以访问。 注意如果由于存储网络上的某些故障而无法访问共享存储时,那么虚拟机可能无法做有用的工作,因为虚拟磁盘在同样的共享存储中,因此,为了解决脑裂问题而使用共享存储不会引入任何额外的不可接受性。( Hades注:使用共享存储这种解决方案本身使得主备又得以通信了,只不过是通过信号量,而非socket。 )
这个设计的一个最终方面是一旦故障发生并且一个VM已经上线,VMware FT自动地通过在另一个主机上开始一个新的备份VM,来恢复备份。虽然这个过程不能覆盖过去大部分的工作,但是对于故障容忍的VM有用,它是基础,需要仔细设计。
第二节描述了我们基础的设计以及FT协议。然而,为了创建一个有用的、健壮的以及自动化的系统,有许多其他组件必须设计实现。
一个必须被设计的最大的额外组件是这种机制,即 启动一个拥有和主VM状态一样的备份VM 。当故障发生后重启一个备份VM时,这个机制也将变得很有用。因此,这个机制一定可用于一个处于任意状态的正在运行中的主VM。此外,我们希望该机制不会显著地中断主VM的执行,因为这会影响 VM 的任何当前客户端。
对于 VMware FT而言,我们调整了VMware vSphere上现有的 VMotion 功能。 VMware VMotion [10] 允许以最少中断的方式,将正在运行的 VM 从一台服务器迁移到另一台服务器,VM的暂停时间通常不到一秒钟。我们创建了一个VMotion的修改形式,可在远程服务器上创建准确的 VM 运行副本,但不会破坏本地服务器的虚拟机。也就是说,我们修改后的 FT VMotion 将VM克隆到远程主机上而不是迁移它。 FT VMotion还设置了一个日志记录通道,并导致源VM作为主VM进入日志记录模式,而目的VM 作为备份进入重放模式。像平常的VMotion一样,FT VMotion 通常会中断主VM的执行不到一秒。因此,启用 FT在正在运行的 VM 上是一个简单的、无中断的操作。
启动备份 VM 的另一个方面是选择一个运行它的服务器。容错 VM 在服务器集群中运行,可以访问共享存储,因此所有 VM通常可以运行在集群上的任何服务器中。这种灵活性允许VMware vSphere恢复FT冗余,即使一个或多个服务器失效。 VMware vSphere 实现了一种集群服务,用于维护管理以及资源信息 。 当发生故障并且主VM 现在需要一个新的备份 VM 来重新建立冗余时,主 VM 通知集群服务它需要一个新的备份。 集群服务基于资源利用率以及其他约束,决定运行备份VM最好的服务器,并调用 FT VMotion 以创建新的备份 VM。 结果是 VMware FT通常可以在几分钟内重新建立VM冗余,在一个故障容忍VM的执行上,所有这些都没有任何明显的中断。

在管理日志通道上的流量时,有许多有趣的实现细节。在我们的实现中,管理程序为主备 VM 的日志记录条目维持了一个大的 缓冲区 。当主 VM 执行时,它生成日志条目到缓冲区中,类似地,备份VM从它的日志缓冲区中消耗日志条目。主日志缓冲区的内容会被尽快刷新到日志记录通道,这些日志条目一到日志通道,就会被读取到备份的日志缓冲区。备份每次从网络上读取一些日志条目到它的日志缓冲区时,都会发送确认返回给主VM。这些确认允许 VMware FT 确定一个被输入规则延迟的输出何时可以被发送。图3说明了这个过程。
如果备份 VM 在需要读取下一个日志条目时,遇到空的日志缓冲区,它将停止执行直到有新的日志条目可用。由于备份 VM 是不与外部通信的,此暂停不会影响任何VM 的客户端。同样地,当主VM需要写入一个日志条目时,如果主VM遇到一个完整的日志缓冲区,它必须停止执行,直到可以刷新日志条目。这种执行的停止是一种自然的流控制机制,当主VM生产日志条目太快了,它会减慢主VM。但是,此暂停可能会影响VM的客户端,因为主 VM 将完全停止并且无响应,直到它可以记录其条目并继续执行。因此,我们的实现必须设计为尽量减少主日志缓冲区填满的可能性。
主日志缓冲区可能填满的原因之一是备份 VM 执行速度太慢,因此消耗日志条目太慢。 一般来说,备份VM必须能够以与正在记录执行的主VM大致相同的速度重放执行 。幸运的是,在 VMware 确定性重放中,记录和重放的开销大致相同。然而,如果由于其他VMs,托管备份 VM 的服务器负载很重(因此过度使用资源),备份VM 可能无法获得足够的 CPU 和内存资源,来与主 VM 一样快地执行,尽管备份管理程序的VM调度器已经尽了最大努力。
如果日志缓冲区填满,除了避免意外暂停,还有另一个原因是我们不希望滞后变得太大。如果主VM出现故障,备份VM必须通过重放它在上线和开始与外部世界交流之前已经确认的所有日志条目来“赶上”。完成重放的时间基本上是失败点的执行延迟时间,所以 备份上线的时间大约等于故障检测时间加上当前执行时差 。因此,我们不希望执行滞后时间太大(超过一秒),因为这将显著地增加故障转移时间。
因此,我们有一个额外的机制减慢主VM,以防止备份 VM 获取太滞后了。在我们的发送和确认日志条目的协议中,我们发送附加信息来确定主备VM之间的实时执行滞后。通常执行滞后小于 100 毫秒。 如果备份 VM 有一个显著的执行滞后(例如,超过 1 秒),VMware FT 通过通知调度程序给它稍微少一点的CPU(最初只是百分之几)来减慢主 VM 。我们使用一个缓慢的反馈循环,这将尝试逐步确定适当的 CPU 限制,将允许主备 VM同步执行。如果备份 VM 继续滞后,我们继续逐步降低主VM的 CPU 限制。反之,如果备份VM赶上,我们逐渐增加主VM的 CPU 限制,直到备份虚拟机恢复轻微的滞后。
请注意,主VM的这种减速很少见,通常只在系统处于低压力时发生。第 5 节的所有性能编号包括任何此类放缓的成本。
另一个实际问题是处理各种控制操作,它们可以应用于主 VM 。例如,如果主VM明确关闭电源,备份 VM 也应该停止,而不是尝试上线。 再举一个例子,任何主VM上的资源管理更改(例如增加 CPU 份额)应该 也适用于备份。 对于此类操作,为了影响备份进行合适的操作,特殊的控制条目通过日志通道从主发送到备份。
一般来说,VM 上的大部分操作都应该仅在主 VM 上初始化。 VMware FT 然后发送任何必要的控制条目以造成备份VM上适当的更改。 唯一可以独立在主VM和备份VM上完成的操作是 VMotion。 那即,主VM和备份VM可以独立被 VMotioned到其他主机。 请注意,VMware FT 确保两个 VM 都不会移动到另一个 VM 所在的服务器,因为这种场景将不再提供故障容忍。
主VM的VMotion增加了比普通VM更多的复杂性,因为备份VM一定会与源主VM失去连接以及在适当的时间重连。备份VM的VMotion有一个相似的问题,但是只增加了一个额外的复杂性。对于一个正常的VMotion而言,我们需要当VMotion上最后的切换发生时,所有的磁盘IO停止(或完成)。对于一个主VM而言,这种停顿是容易应付的,通过等待直到物理IO完成并将这些完成信息发送给VM。然而,对于一个备份VM而言,没有容易的方式来使得所有IO在任何需要的时刻完成,因为备用VM必须重放主VM的执行过程,并在相同的执行点完成IO。主VM可能正运行在一个工作负载上,在正常执行过程中总是有磁盘IO。VMware FT有一个独一无二的方法来解决这个问题。当一个备份VM是在VMotion最后的切换点时,它需要通过日志通道来告知主VM临时停止所有IO。备份VM的IO将自然地被停止在一个单独的执行点,因为它需要重放主VM的停止操作的过程。
有许多与磁盘IO相关的微小的实现问题。首先,假设磁盘操作是非阻塞的,因此访问相同磁盘位置的并行、同时执行的磁盘操作将引起非确定性。此外,我们的磁盘 IO 实现使用DMA 直接from/to虚拟机的内存,所以同时访问相同内存页的磁盘操作也可能导致不确定性。我们的解决方案是 经常检测任何此类 IO 竞争 (很少见),以及强制此类竞争磁盘操作在主备VM上按顺序执行。
第二,通过 VM 中的应用程序(或操作系统)时,磁盘操作与内存访问也会存在竞争,因为磁盘操作通过 DMA 直接访问 VM 的内存。例如,如果一个VM 中的应用程序/操作系统正在读取内存块,同时对该块进行磁盘读取。( Hades注:这里的意思应该是,该块内存作为DMA操作的目的地址。 )这个情况也不太可能发生,但如果它发生,我们必须检测它并处理它。一种解决方案是临时设置页保护,在作为磁盘操作目标的页面上。如果VM 碰巧访问一个页,同时该页面也是磁盘操作的目标,页保护将导致一个陷阱( Hades注:trap,陷入系统调用 ),VM将暂停直到磁盘操作完成。 因为改变页上的MMU 保护是一项昂贵的操作,所以我们选择使用 弹跳缓冲区(Bounce Buffer) 代替 。bounce buffer是临时缓冲区,与正在被磁盘操作访问的内存大小相同。磁盘读取操作被修改为读取指定数据到bounce buffer,并在在IO完成时将数据复制到内存中。相似地,对于磁盘写操作,首先将要发送的数据复制到bounce buffer,磁盘写入修改为向bounce buffer写入数据。bounce buffer的使用会减慢磁盘操作,但我们还没有看到它会导致任何明显的性能损失。( Hades注:bounce buffer存在的意义是在内存访问这个操作之前加了一个拦截器,其最本质的意义是为了supervisor监控DMA操作,使得数据从bounce buffer拷贝到到内存和系统中断这两个步骤,能够同时在backup VM上被复制, 否则网卡直接将网络数据包DMA到Primary虚机中这个操作是无法通过log channel进行复制的 。 )
第三,有一些与故障发生并且备份VM接管时,主VM未完成的磁盘 IO 相关的问题。对于新上线的主VM,没有办法确定磁盘IO是有问题的还是成功完成了。另外,由于磁盘IO没有从外部发布到备用VM上,而是通过主备传递,因此对于继续运行的新上任的主VM来说,将没有明确的IO完成信息,最终将导致VM上的操作系统开始中止或者重调度程序。我们能够发送一个错误完成,表示每个IO失败,因为即使IO成功完成了,它可以接受返回一个错误。然而,操作系统可能不能对这些来自本地磁盘的错误有很好的响应。反之,我们在备份VM上线的过程中,重新发送这些悬挂着的IO。因为我们已经限制了所有的竞争和所有的直接指定内存和磁盘的IO,这些磁盘操作可以被重新发送,即使它们已经成功完成了(即他们是幂等的)。
VMware vSphere针对VM网络提供了很多性能优化。一些优化是基于管理程序(supervisor) 异步更新虚拟机的网络设备状态 。例如,当VM正在执行时,接收缓冲区可以由管理程序直接更新。不幸的是这些对 VM 状态的 异步更新会增加不确定性 。除非我们可以保证所有更新都发生在主备指令流上的同一点,否则备份VM的执行可能与主VM的执行不同。
对于FT而言,网络仿真代码的最大变化是禁用异步网络优化。异步更新带有传入数据包的VM环形缓冲区的代码已被修改,以强制管理程序捕获到操作系统,它可以在其中记录更新然后将它们应用到 VM。同样,异步地将数据包从传输队列中拉出也被修改了,取而代之的是通过管理程序traps来完成传输(如下所述)。
网络设备异步更新的消除结合第 2.2 节中描述的发送数据包的延迟带来了一些网络性能的挑战。我们采取了两种方法在运行 FT 时提高 VM 的网络性能。第一,我们实施了集群优化以减少 VM 的陷阱和中断。当 VM 以足够的比特率流式传输数据时,管理程序可以对每组数据包做一个传输trap,在最好的情况下零trap,因为它可以传输所接收新数据包的一部分数据包。同样地,通过仅对于一组数据包发布中断,管理程序可以将接收包的中断数量减少。
我们对网络的第二个性能优化涉及 减少传输数据包的延迟 。如前所述,管理程序必须延迟所有发送的包直到它得到备份VM对于某些日志条目的确认。减少发送延迟的关键在于减少发送/接收备份VM信息的所需时间。我们的主要优化包括 保证收发信息在无需任何线程上下文切换的情形下就可以被执行 。VMware vSphere管理程序允许函数被注册到TCP栈中,只要TCP数据被接收到了,函数就会被一个延期执行的上下文调用(和Linux中的tasklet类似)。这允许我们快速处理备份VM上任何即将到来的日志消息,以及主VM接收的任何确认消息,而不需要任何线程上下文的切换。另外,当主VM有一个包要寄出去时,我们强制一次相关输出日志条目的日志刷出(正如2.2节中所描述的),通过调度一个延迟执行的上下文来执行这次刷出。
在我们VMware FT的实现中,我们已经探索了许多有趣的替代设计。在这节中,我们探索一些替代设计。
在我们默认的设计中,主备VM共享相同的虚拟磁盘。因此,如果一次故障转移发生,共享磁盘的内容自然是正确、可接受的。必要地,对于主备VM来说,共享磁盘被认为是外部的,因此任何共享磁盘的写入被认为是一次与外部世界的沟通。因此,只有主VM做这种实际的磁盘写入,并且为了遵循输出规则,这种写入必须被延迟。

对于主备VM而言,一种可替代的选择是分隔的虚拟磁盘。在这种设计中,备份VM要执行所有虚拟磁盘的写入操作。而且这样做的话自然要保持它的虚拟磁盘内容与主VM虚拟磁盘内容一致。图4阐述了这种配置。在非共享磁盘的情况下,虚拟磁盘必须被认为是每个VM的内部状态。因此,依据输出规则, 主VM的磁盘写入不必延迟 。在共享存储不能被主备VM接受的情况下,非共享的设计是相当有用的。这种情况可能是由于共享存储不可接受或者太昂贵,或者由于运行主备VM的服务器相隔太远(“长距离FT”)。非共享设计的一个缺点是在首次启动故障容错时,虚拟磁盘的两个复制必须以相同的方式进行显示同步。另外,发生故障后磁盘 可能会不同步 ,因此当在一次失败后备份VM重启的时候,他们必须再显式地同步。FT VMotion必须不止同步主备VM的运行状态,还要同步他们的磁盘状态。
在这种非共享磁盘的配置中,他们也能应付脑裂场景。在这种场景中,系统能够 使用一些其他的外部决策者 ,例如所有服务器可以沟通的一个第三方服务。如果服务器是超过两个节点的集群的一部分,这个系统能够基于集群关系使用一种majority算法。在这个例子中,一个VM能够被允许上线,如果它正在一个服务器上运行,这个服务器是包含大多数原始节点的正在通信的子集群的一部分。
在我们默认的设计中,备份的VM从不会从它自己的虚拟磁盘上读取(无论共享还是非共享)。 因为磁盘读取被认为是一个输入 ,它是自然地通过日志通道将磁盘读取的结果发送到备份VM上。
一种替代的设计是 让备份VM执行磁盘读取 ,因此消除了磁盘读取的日志。对于大多数时候都做磁盘读取的工作负载而言,这种方法可以很好地降低日志通道上的流量。然而,这种方法有很多小问题。它可能会减慢备份VM的执行速度,因为备份VM必须执行所有的磁盘读取,当到达VM执行中主VM已经完成的位置时,如果备份上的磁盘读取还没完成就必须等待。
同样地, 为了处理失败的磁盘读取操作,必须做一些额外的工作 。如果一个主VM的磁盘读取成功了,但是相应的备份VM磁盘读取失败了,备份VM的磁盘读取必须重试直到成功。因为备份VM必须获得和主VM一样的数据到内存中。相反地,如果一个主VM的磁盘读取失败了,目标内存的内容必须通过日志通道发送给备份服务器,因此内存的内容将被破坏,不能被备份VM成功的磁盘读取复制。
最后,如果这种磁盘读取被用于共享磁盘配置的话,还有一个小问题。如果主VM做了一次对具体磁盘位置的读取,然后紧跟相同磁盘位置的写入,然后这个磁盘写必须被延迟到备份VM已经执行了第一次磁盘读取。这种依赖可以被检测和正确处理,但是需要增加实现上额外的复杂性。
在5.1节中,对于实际的应用而言,我们给出一些性能结果以表示在备份VM上执行磁盘读取会造成一些轻微的吞吐量减少(1-4%),因此在日志通道的带宽被限制的情况下,在备份VM上执行磁盘读取可能是有用的。
在这节中,我们做了一次VMware FT性能的基础评估,针对许多应用负载以及网络基准。为了得到这些结果,我们在一样的服务器上运行主备VM,每个都带9个Intel Xeon 2.8Ghz CPUs and 8Gbytes of RAM。服务器间通过10 Gbit/s的交换机连接,但是在所有的例子中都能看到被使用的网络带宽远远少于1Gbit/s。从一个通过标准的4Gbit/s的光纤通道网络连接的EMC Clariion中,服务器可以连接他们的共享虚拟磁盘。客户端通过1 Gbit/s的网络来驱动一些连接服务器的工作负载。
我们评估性能结果的应用如下所示。SPECJbb2005是工业标准的Java应用基准,非常耗费CPU和内存,但是IO非常少。Kernel Compile是一种运行Linux核编译的工作负载。由于许多编译过程的创建和毁灭,这个工作负载做很多磁盘读取和写入,是非常耗费CPU和MMU的。Oracle Swingbench是被Swingbench OLTP工作负载(在线事务处理)驱动的一个Oracle 11g的数据库。这个工作负载做连续的磁盘和网络IO,有80个同时在线的数据库会话。MS-SQL DVD Store是一种工作负载,运行了一个Microsoft SQL Server 2005的数据库,有60个同时在线的客户端。

表 1 列出了基本的性能结果。对于每个应用程序,第二列给出了应用程序的性能比例,运行服务器工作负载的虚拟机上启用和未启用FT的情况。性能比小于 1 表示带FT的工作负载更慢。显然,这些有代表性的工作负载上启用FT 的开销小于10%。 SPECJbb2005 完全受计算限制,没有空闲时间,但其表现性能良好,因为它具有最小的除定时器中断以外的不确定性事件。另一个工作负载做磁盘 IO 有一些空闲时间,所以一些FT 开销可能被 FT虚拟机的空闲时间更少的真实情况隐藏。然而,一般的结论是VMware FT 能够支持故障容忍VM,并且具备相当低的性能开销。
在表的第三列中,我们给出了当应用程序正在运行时,在日志通道上发送数据的平均带宽。对于这些应用程序,日志带宽相当合理,1 Gbit/s的网络就能满足 。事实上,低带宽要求表明多个 FT 工作负载可以共享相同的 1 Gbit/s网络,同时没有任何负面的性能影响。
对于运行常见操作系统的 VM,例如Linux 和 Windows,我们发现当操作系统空闲时,通常的日志记录带宽为 0.5-1.5 Mbits/sec。"空闲"带宽主要是记录定时器中断发送的结果。对于具有活动中工作负载的 VM而言,日志带宽由网络和必须发送到备份的磁盘输入主导—网络收到的数据包和从磁盘读取的磁盘块。因此,对于非常高的网络接收或者磁盘读取带宽的应用而言,日志带宽高于表1中的测量值。对于这类应用而言,日志通道的带宽可能是瓶颈,特别是日志通道还有其他使用时。
对于许多实际应用程序而言, 日志记录所需的带宽相对较低,这使得基于重放的故障容忍对于使用非共享磁盘的长距离配置非常有吸引力 。对于远距离配置而言,其主备VM可能相隔1-100公里,光纤可以轻松地支持延迟小于 10 毫秒的100-1000 Mbit/s带宽。对于表 1 中的应用而言,主备之间的额外往返延迟,可能会导致网络和磁盘输出最多延迟 20 毫秒。远距离配置仅适用于这类应用程序:他的客户端可以容忍每个请求的额外延迟。
对于两个最占用磁盘空间的应用程序,我们测量了在备份 VM上执行磁盘读取(如第 4.2 节所述)与通过日志记录通道发送磁盘读取数据相比,对于性能的影响。对于 Oracle Swingbench来说,在备份VM上执行磁盘读取时的吞吐量降低约 4%;对于 MS-SQL DVD 存储,吞吐量约降低 1%。同时,Oracle Swingbench的日志带宽从 12 Mbits/sec 降低到 3 Mbits/sec,MS-SQL DVD 存储从 18 Mbits/sec 降低到 8 Mbits/sec。显然,对于具有更大磁盘读取带宽的应用程序,带宽可能会节省很多。如第 4.2 节所述,预计在备份 VM 上执行磁盘读取时,性能可能会更差。但是,对于日志通道的带宽是有限的(例如,远程配置)情况下,在备份 VM 上执行磁盘读取可能有用。
出于多种原因。网络基准测试对我们的系统来说非常具有挑战性。第一,高速网络会有一个非常高的中断率,这需要以非常高的速度记录和重放异步事件。 第二,以高速率接收数据包的基准将导致高速率的日志流量,因为所有这些数据包必须通过日志通道发送到备份。第三,发送数据包的基准测试将受制于输出规则,延迟网络数据包的发送直到已收到来自备份VM的确认。 此延迟会增加对客户端测量的延迟。这种延迟还可能会降低到客户端的网络带宽,因为网络协议(如 TCP)由于往返延迟增加,可能不得不降低网络传输速率。

表 2 给出了我们通过标准的netperf 基准测试,多次测量的结果。在所有这些测量中,客户端 VM 和主 VM 通过 1 Gbit/s 网络连接。前两行给出了主备主机间通过1 Gbit/s 的日志通道连接时,发送和接收的性能。第三行和第四行给出当主备服务器通过10 Gbit/s的日志通道连接时,发送和接收的性能,不仅带宽更高,延迟也低于 1 Gbit/s。作为一个粗略的测量,在1 Gbit/s 网络连接的管理程序之间, ping 时间约为 150 微秒,而对于 10 Gbit/s 连接,ping时间大约需要 90 微秒。
未启用 FT 时,主 VM 对于接收和发送,可以实现接近 (940 Mbit/s) 1 Gbit/s 的线路传输速率。当为接收工作负载启用 FT 时,日志记录带宽非常大,因为所有传入的网络数据包必须在日志通道上发送。因此,日志记录通道可能成为瓶颈,正如1 Gbit/s 日志网络的结果。对于 10 Gbit/s 的日志网络,影响则小了很多。当为上传工作负载启用 FT 时,上传数据包的数据不会记录,但仍必须记录网络中断。日志带宽要低得多,因此可实现的网络上传带宽高于网络接收带宽。 总的来说,我们看到 FT 在非常高的上传和接收速率情况下,可以显著地限制网络带宽,但仍然可以实现很高的速率 。
我们在VMware vSphere 中设计并实施了一个高效完整的系统(FT) ,用于为服务器上运行的虚拟机提供容错。我们的设计基于复制主VM中的执行,再通过另一台主机上的备份VM执行VMware确定性重放。如果运行主 VM的服务器出现故障,备份 VM 能立即接管且不会中断或丢失数据。
总体而言,在商业硬件上运行VMware FT时,故障容错VM的性能非常出色,并且对于某些典型应用程序,其开销低于 10%。大多数 VMware FT 的性能成本来自于使用 VMware 确定性重放来保持主备VM同步。因此,VMware FT 的低开销源自 VMware 确定性重放的效率。此外,保持主备同步所需的日志带宽非常小,通常小于 20 Mbit/s。因为日志带宽在大多数情况下很小,主备相隔很长的距离(1-100公里)似乎也是可行的实施配置。因此,VMware FT 可用于这种场景:可以防止整个站点发生故障的灾难。值得注意的是,日志流通常是可压缩的,因此简单的压缩技术可以显著地减少日志带宽,虽然有少量额外的 CPU 开销。
我们对 VMware FT 的结果表明, 一个高效的故障容错VM的实现可以建立在确定性重放的基础上 。 这样的系统可以透明地为运行任何操作系统和应用的虚拟机提供容错能力,仅会带来极小的开销 。然而,对客户有用的故障容错VM系统而言,它必须还具有强大、易于使用和高度自动化的特点。一个可用的系统除了复制虚拟机执行之外,还需要许多其他组件。特别是VMware FT 故障后自动地恢复冗余,通过在本地集群中找到合适的服务器并在其上创建一个新的备份VM。通过解决所有必要的问题,我们已经展示了一个在客户的数据中心可用于实际应用的系统。
通过确定性重放实现容错的权衡之一是当前确定性重放仅针对单处理器VM 。然而,单处理器虚拟机足够应付各种各样的工作负载,特别是因为物理处理器不断变得更加强大。此外,许多工作负载可以通过使用许多单处理器的虚拟机来扩展,而不是通过使用一个更大的多处理器虚拟机来扩展。多处理器 VM 的高性能重放是一种活跃的研究领域,并且可以潜在地被微处理器中的一些额外硬件支持。一个有趣的方向可能是扩展事务内存模型以促进多处理器重放。
将来,我们也有兴趣扩展我们的系统处理部分硬件故障。通过部分硬件故障,我们的意思是服务器上功能或冗余的部分丢失,不会导致损坏或丢失数据。一个例子是到 VM所有网络连接的丢失,或在物理服务器中备用电源丢失。如果在运行主 VM 的服务器上发生部分硬件故障,在许多情况下(但不是all) 故障转移到备份 VM 将是有利的。这样的故障转移对于关键VM而言,可以立即恢复完整服务,并确保虚拟机从可能不可靠的服务器上快速地移走。
我们希望复制方案可以处理的故障:
如果发生了故障,主机器真的挂掉了吗?
在分布式系统中,没有办法区分网络分区和机器故障的区别,因此很有可能主机器并没有挂掉,有一些客户端还能访问主机器,但是从机器和主机器之间的网络有问题,无法互相访问到,所以从机器认为主机器已经挂掉了。因此不能有两个主机器同时存在的情况,也就是脑裂问题。
如何保持主从同步?
如果主机器挂了,从机器要从主机器挂掉的地方直接开始,这就意味着从机器的状态与主机器的状态相同,都是最新的。从客户端的角度感知不到这种变化。
非常困难:
两种方法都是目前流行的方法,状态转移的缺点是如果一个操作生成了很多状态,这个传输的数据量非常大,因此如果只发送操作过去就很轻松。
应用级别:文件追加写入,需要在应用程序上进行修改
机器级别:寄存器指令级别的复制,只有x86指令,不涉及应用程序方面的更改,可以使用虚拟机实现,从而不用再硬件级别上实现。
利用虚拟化技术,使得复制操作对应用程序是透明的,应用程序认为仅有一台服务器,并且也同时提供了很强的一致性。
虚拟机监控器(hypervisor):在实际硬件上运行,虚拟出多个虚拟的硬件
任何我们看到的外部事件实际上都经过了hypervisor,例如一个外部中断,hypervisor会先观察到并决定什么时候传递给虚拟机
多个hypervisor之间通过logging channel进行通信,从而进行操作的精确复制
storage server可以对谁当主机器进行仲裁
如果主机器和从机器不能相互通信,但是都能看到storage server,两台机器都会进行test-and-set操作,比较早的那一个就会成为主机器。
目标:多台虚拟机对外表现为单一的机器
问题:差异来源导致两台机器表现不一样
非确定性指令:
确定性指令不需要通过logging channel进行通信
中断发生后,会传递给从机器中断发生的前一个指令号,但是从机器并不会马上去执行,而是缓存下来,等到下一条中断指令传递过来之后,再执行前一条指令。这样会落后一条指令
在机器启动之前会遍历全部的指令,确保浏览到全部的非确定性指令,不会直接执行,而会交给hypervisor进行控制。hypervisor执行的时候会额外记录下这些指令操作后的对应结果。传递的时候会同时对结果进行传递,这样从机器不需要真正去执行,直接修改结果就可以。
指令级别的复制会付出性能的代价
论文的实验表明带宽会降低大概30%左右,由于主机器接收来自客户端的输入,然后传递给从机器,这个过程中主机器必须等待,才能将响应传递给客户端。
因此状态机复制的方法并不常用的原因之一是性能会下降。
]]>参考资料(感谢Alex!这篇论文翻译得非常有质量!)
Google GFS文件系统是一个面向大规模数据密集型应用的、可伸缩的分布式文件系统。GFS运行在廉价的普遍硬件设备上,但是依然了提供容错机制,为大量客户提供了高性能的服务。
GFS的设计目标与许多传统的分布式文件系统有很多相同之处,不过还是以我们对自己的应用的负载情况和技术环境的分析为基础进行设计,和早期的分布式文件系统有明显的不同。
GFS完全满足了我们对存储的需求。GFS作为存储平台已经被广泛的部署在Google内部,存储我们的服务产生和处理的数据,同时还用于那些需要大规模数据集的研究和开发工作。目前为止,最大的一个集群利用数千台机器的数千个硬盘,提供了数百TB的存储空间,同时为数百个客户机服务。
在本论文中,我们展示能够支持分布式应用的文件系统接口扩展,讨论我们设计的许多方面,最后列出了小规模性能测试以及真实生产系统中性能的相关数据。
GFS与传统的分布式文件系统有着很多相同的设计目标,比如,性能、可伸缩性、可靠性以及可用性。但是,我们的设计还基于我们对我们自己的应用的负载情况和技术环境的观察的影响,和早期文件系统的假设都有明显的不同。
所以我们重新审视了传统文件系统在设计上的折衷选择,衍生出了完全不同的设计思路。
首先,组件失效被认为是常态事件,而不是意外事件。GFS组件的数量和质量导致在任何给定时间内都有可能发生某些组件无法工作,且某些组件无法从它们目前的失效状态中恢复。因此,持续的监控、错误侦测、容错以及自动恢复的机制必须集成在GFS中。
其次,我们的文件非常巨大,GB的文件非常普遍。当我们经常需要处理快速增长的、并且由数亿个对象构成的、数以TB的数据集时,采用管理数亿个KB大小的小文件的方式是非常不明智的。因此,设计的假设条件和参数,比如I/O操作和Block的尺寸等都需要重新考虑。
第三,绝大部分文件的修改是采用在文件尾部追加数据,而不是覆盖原有数据的方式。一旦写完之后,对文件的操作就只有读,而且通常是按顺序读。对于这种针对海量文件的访问模式,客户端对数据块缓存是没有意义的,数据的追加操作是性能优化和原子性保证的主要考量因素。
第四,应用程序和文件系统API的协同设计提高了整个系统的灵活性。比如,我们放松了对GFS一致性模型的要求,这样就减轻了文件系统对应用程序的苛刻要求,大大简化了GFS的设计。我们引入了原子性的记录追加操作,从而保证多个客户端能够同时进行追加操作,不需要额外的同步操作来保证数据的一致性。
GFS提供了一套类似传统文件系统的API接口函数,虽然并不是严格按照POSIX等标准API的形式实现的。文件以分层目录的形式组织,用路径名来标识。支持常用的操作如创建新文件、删除文件、打开文件、关闭文件、读和写文件。
另外,GFS提供了快照和记录追加操作。快照以很低的成本创建一个文件或者目录树的拷贝。记录追加操作允许多个客户端同时对一个文件进行数据追加操作,同时保证每个客户端的追加操作都是原子性的。多个客户端可以在不需要额外的同步锁定的情况下,同时对一个文件追加数据。这些类型的文件对于构建大型分布应用是非常重要的。
一个GFS集群包含一个单独的Master节点 (alex注:这里的一个单独的Master节点的含义是GFS系统中只存在一个逻辑上的Master组件。后面还会提到Master节点复制,因此,为了理解方便,我们把Master节点视为一个逻辑上的概念,一个逻辑的Master节点包括两台物理主机,即两台Master服务器)、 和多台Chunk服务器,并且同时被多个客户端访问。Chunk服务器和客户端也可以放在同一台机器上。
GFS存储的文件都被分割成固定大小的Chunk。在Chunk创建的时候,Master服务器会给每个Chunk分配一个唯一不变的64位的Chunk标识。Chunk服务器把Chunk以linux文件的形式保存在本地硬盘上,并且根据指定的Chunk标识和字节范围来读写块数据。出于可靠性的考虑,每个块都会复制到多个块服务器上,默认是3份。
Master节点管理所有的文件系统元数据。这些元数据包括名字空间、访问控制信息、文件和Chunk的映射信息、以及当前Chunk的位置信息。Master节点还管理着系统范围内的活动,比如,Chunk租用管理、孤儿Chunk的回收、以及Chunk在Chunk服务器之间的迁移。Master节点使用心跳信息周期地和每个Chunk服务器通讯,发送指令到各个Chunk服务器并接收Chunk服务器的状态信息。
GFS客户端代码以库的形式链接到客户程序里。客户端代码实现了GFS文件系统的API接口函数、应用程序与Master节点和Chunk服务器通讯、以及对数据进行读写操作。客户端和Master节点的通信只获取元数据,所有的数据操作都是由客户端直接和Chunk服务器进行交互的。
无论是客户端还是Chunk服务器都不需要缓存文件数据。客户端缓存数据几乎没有什么用处,因为大部分程序要么以流的方式读取一个巨大文件,要么工作集太大根本无法被缓存。无需考虑缓存相关的问题也简化了客户端和整个系统的设计和实现。(不过,客户端会缓存元数据。)Chunk服务器不需要缓存文件数据的原因是,Chunk以本地文件的方式保存,Linux操作系统的文件系统缓存会把经常访问的数据缓存在内存中。
单一的Master节点可以通过全局的信息精确定位Chunk的位置以及进行复制决策。不过我们必须减少对Master节点的读写,避免Master节点成为系统的瓶颈。客户端并不通过Master节点读写文件数据。而是向Master节点询问它应该联系的Chunk服务器。客户端将这些元数据信息缓存一段时间,后续的操作将直接和Chunk服务器进行数据读写操作。
一次简单读取的流程:首先,客户端把文件名和程序指定的字节偏移,根据固定的Chunk大小,转换成文件的Chunk索引。然后,它把文件名和Chunk索引发送给Master节点。Master节点将相应的Chunk标识和副本的位置信息发还给客户端。客户端用文件名和Chunk索引作为key缓存这些信息。之后客户端发送请求到其中的一个(一般是最近的)副本处。请求信息包含了Chunk的标识和字节范围。在对这个Chunk的后续读取操作中,客户端不必再和Master节点通讯了,除非缓存的元数据信息过期或者文件被重新打开。实际上,客户端通常会在一次请求中查询多个Chunk信息,Master节点的回应也可能包含了紧跟着这些被请求的Chunk后面的Chunk的信息。在实际应用中,这些额外的信息避免了客户端和Master节点未来可能会发生的几次通讯。
Chunk的大小是关键的设计参数之一。我们选择了64MB,远远大于一般文件系统的Block size。每个Chunk的副本都以普通Linux文件的形式保存在Chunk服务器上,只有在需要的时候才扩大。惰性空间分配策略避免了因内部碎片造成的空间浪费,内部碎片或许是对选择这么大的Chunk尺寸最具争议的一点。
选择较大的Chunk尺寸有几个重要的优点。首先,它减少了客户端和Master节点通讯的需求,一次和Master节点的通信就可以获取Chunk的位置信息,之后就可以对同一个Chunk进行多次的读写操作。即使是小规模的随机读取,客户端可以轻松的缓存一个数TB的工作数据集所有的Chunk位置信息。其次,采用较大的Chunk尺寸,客户端能够对一个块进行多次操作,这样就可以通过与Chunk服务器保持较长时间的TCP连接来减少网络负载。第三,选用较大的Chunk尺寸减少了Master节点需要保存的元数据的数量。
另一方面,即使配合惰性空间分配,采用较大的Chunk尺寸也有其缺陷。小文件包含较少的Chunk,甚至只有一个Chunk。当有许多的客户端对同一个小文件进行多次的访问时,存储这些Chunk的Chunk服务器就会变成热点。在实际应用中,热点不是主要问题。
然而,当我们第一次把GFS用于批处理队列系统的时候,热点的问题还是产生了:一个可执行文件在GFS上保存为single-chunk文件,之后这个可执行文件在数百台机器上同时启动。存放这个可执行文件的几个Chunk服务器被数百个客户端的并发请求访问导致系统局部过载。我们通过将这个文件复制更多份,并错开批处理队列系统程序的启动时间的方法解决了这个问题。一个可能的长效解决方案是,在这种的情况下,允许客户端从其它客户端读取数据。
Master服务器(alex注:注意逻辑的Master节点和物理的Master服务器的区别。后续我们谈的是每个Master服务器的行为,如存储、内存等等,因此我们将全部使用物理名称)存储3种主要类型的元数据,包括:文件和Chunk的命名空间、文件和Chunk的对应关系、每个Chunk副本的存放地点。所有的元数据都保存在Master服务器的内存中。前两种类型的元数据(命名空间、文件和Chunk的对应关系)同时也会以记录变更日志的方式记录在操作系统的系统日志文件中,日志文件存储在本地磁盘上,同时日志会被复制到其它的远程Master服务器上。采用保存变更日志的方式,我们能够简单可靠的更新Master服务器的状态,并且不用担心Master服务器崩溃导致数据不一致的风险。Master服务器不会持久保存Chunk位置信息。Master服务器在启动时,或者有新的Chunk服务器加入时,向各个Chunk服务器轮询它们所存储的Chunk的信息。
因为元数据保存在内存中,所以Master服务器可以在后台简单而高效的周期性扫描自己保存的全部状态信息。这种周期性的状态扫描也用于实现Chunk垃圾收集、在Chunk服务器失效的时重新复制数据、通过Chunk的迁移实现跨Chunk服务器的负载均衡以及磁盘使用状况统计等功能。
将元数据全部保存在内存中的方法的问题:Chunk的数量以及整个系统的承载能力都受限于Master服务器所拥有的内存大小。但是在实际应用中,这并不是一个严重的问题。Master服务器只需要不到64个字节的元数据就能够管理一个64MB的Chunk。每个文件的在命名空间中的数据大小通常在64字节以下,因为保存的文件名是用前缀压缩算法压缩过的。
即便是需要支持更大的文件系统,为Master服务器增加额外内存的费用是很少的,增强了系统的简洁性、可靠性、高性能和灵活性。
Master服务器并不保存持久化保存哪个Chunk服务器存有指定Chunk的副本的信息。Master服务器只是在启动的时候轮询Chunk服务器以获取这些信息。Master服务器能够保证它持有的信息始终是最新的,因为它控制了所有的Chunk位置的分配,而且通过周期性的心跳信息监控Chunk服务器的状态。
最初设计时,我们试图把Chunk的位置信息持久的保存在Master服务器上,但是后来我们发现在启动的时候轮询Chunk服务器,之后定期轮询更新的方式更简单。这种设计简化了在有Chunk服务器加入集群、离开集群、更名、失效、以及重启的时候,Master服务器和Chunk服务器数据同步的问题。
可以从另外一个角度去理解这个设计决策:只有Chunk服务器才能最终确定一个Chunk是否在它的硬盘上。我们从没有考虑过在Master服务器上维护一个这些信息的全局视图,因为Chunk服务器的错误可能会导致Chunk自动消失(比如,硬盘损坏了或者无法访问了),亦或者操作人员可能会重命名一个Chunk服务器。
操作日志包含了关键的元数据变更历史记录。这对GFS非常重要。这不仅仅是因为操作日志是元数据唯一的持久化存储记录,它也作为判断同步操作顺序的逻辑时间基线 (alex注:也就是通过逻辑日志的序号作为操作发生的逻辑时间,类似于事务系统中的LSN) 。文件和Chunk,连同它们的版本,都由它们创建的逻辑时间唯一的、永久的标识。
操作日志非常重要,我们必须确保日志文件的完整,确保只有在元数据的变化被持久化后,日志才对客户端是可见的。否则,即使Chunk本身没有出现任何问题,我们仍有可能丢失整个文件系统,或者丢失客户端最近的操作。所以,我们会把日志复制到多台远程机器,并且只有把相应的日志记录写入到本地以及远程机器的硬盘后,才会响应客户端的操作请求。Master服务器会收集多个日志记录后批量处理,以减少写入磁盘和复制对系统整体性能的影响。
Master服务器在恢复时,通过重演操作日志把文件系统恢复到最近的状态。为了缩短Master启动的时间,我们必须使日志足够小 (alex注:即重演系统操作的日志量尽量的少)。 Master服务器在日志增长到一定量时对系统状态做一次Checkpoint (alex注:Checkpoint是一种行为,一种对数据库状态作一次快照的行为), 将所有的状态数据写入一个Checkpoint文件 (alex注:并删除之前的日志文件)。 在灾难恢复的时候,Master服务器就通过从磁盘上读取这个Checkpoint文件,以及重演Checkpoint之后的有限个日志文件就能够恢复系统。Checkpoint文件以压缩B-树形势的数据结构存储,可以直接映射到内存,在用于命名空间查询时无需额外的解析。这大大提高了恢复速度,增强了可用性。
由于创建一个Checkpoint文件需要一定的时间,所以Master服务器的内部状态被组织为一种格式,这种格式要确保在Checkpoint过程中不会阻塞正在进行的修改操作。Master服务器使用独立的线程切换到新的日志文件和创建新的Checkpoint文件。新的Checkpoint文件包括切换前所有的修改。对于一个包含数百万个文件的集群,创建一个Checkpoint文件需要1分钟左右的时间。创建完成后,Checkpoint文件会被写入在本地和远程的硬盘里。
Master服务器恢复只需要最新的Checkpoint文件和后续的日志文件。旧的Checkpoint文件和日志文件可以被删除,但是为了应对灾难性的故障 (alex注:catastrophes,数据备份相关文档中经常会遇到这个词,表示一种超出预期范围的灾难性事件), 我们通常会多保存一些历史文件。Checkpoint失败不会对正确性产生任何影响,因为恢复功能的代码可以检测并跳过没有完成的Checkpoint文件。
GFS支持一个宽松的一致性模型,这个模型能够很好的支撑我们的高度分布的应用,同时还保持了相对简单且容易实现的优点。本节我们讨论GFS的一致性的保障机制,以及对应用程序的意义。我们也着重描述了GFS如何管理这些一致性保障机制。
文件命名空间的修改(例如,文件创建)是原子性的。它们仅由Master节点的控制:命名空间锁提供了原子性和正确性的保障;Master节点的操作日志定义了这些操作在全局的顺序。
数据修改后文件region (alex注:region这个词用中文非常难以表达,我认为应该是修改操作所涉及的文件中的某个范围) 的状态取决于操作的类型、成功与否、以及是否同步修改。如果所有客户端,无论从哪个副本读取,读到的数据都一样,那么我们认为文件region是“一致的”;如果对文件的数据修改之后,region是一致的,并且客户端能够看到写入操作全部的内容,那么这个region是“已定义的”。当一个数据修改操作成功执行,并且没有受到同时执行的其它写入操作的干扰,那么影响的region就是已定义的(隐含了一致性):所有的客户端都可以看到写入的内容。并行修改操作成功完成之后,region处于一致的、未定义的状态:所有的客户端看到同样的数据,但是无法读到任何一次写入操作写入的数据。通常情况下,文件region内包含了来自多个修改操作的、混杂的数据片段。失败的修改操作导致一个region处于不一致状态(同时也是未定义的):不同的客户在不同的时间会看到不同的数据。
数据修改操作分为写入或者记录追加两种。写入操作把数据写在应用程序指定的文件偏移位置上。即使有多个修改操作并行执行时,记录追加操作至少可以把数据原子性的追加到文件中一次,但是偏移位置是由GFS选择的 (alex注:这句话有点费解,其含义是所有的追加写入都会成功,但是有可能被执行了多次,而且每次追加的文件偏移量由GFS自己计算) 。(相比而言,通常说的追加操作写的偏移位置是文件的尾部。)GFS返回给客户端一个偏移量,表示了包含了写入记录的、已定义的region的起点。另外,GFS可能会在文件中间插入填充数据或者重复记录。这些数据占据的文件region被认定是不一致的,这些数据通常比用户数据小的多。
经过了一系列的成功的修改操作之后,GFS确保被修改的文件region是已定义的,并且包含最后一次修改操作写入的数据。GFS通过以下措施确保上述行为:(a) 对Chunk的所有副本的修改操作顺序一致(3.1章),(b)使用Chunk的版本号来检测副本是否因为它所在的Chunk服务器宕机(4.5章)而错过了修改操作而导致其失效。失效的副本不会再进行任何修改操作,Master服务器也不再返回这个Chunk副本的位置信息给客户端。它们会被垃圾收集系统尽快回收。
由于Chunk位置信息会被客户端缓存,所以在信息刷新前,客户端有可能从一个失效的副本读取了数据。在缓存的超时时间和文件下一次被打开的时间之间存在一个时间窗,文件再次被打开后会清除缓存中与该文件有关的所有Chunk位置信息。而且,由于我们的文件大多数都是只进行追加操作的,所以,一个失效的副本通常返回一个提前结束的Chunk而不是过期的数据。当一个Reader (alex注:本文中将用到两个专有名词,Reader和Writer,分别表示执行GFS读取和写入操作的程序) 重新尝试并联络Master服务器时,它就会立刻得到最新的Chunk位置信息。
即使在修改操作成功执行很长时间之后,组件的失效也可能损坏或者删除数据。GFS通过Master服务器和所有Chunk服务器的定期“握手”来找到失效的Chunk服务器,并且使用Checksum来校验数据是否损坏(5.2章)。一旦发现问题,数据要尽快利用有效的副本进行恢复(4.3章)。只有当一个Chunk的所有副本在GFS检测到错误并采取应对措施之前全部丢失,这个Chunk才会不可逆转的丢失。在一般情况下GFS的反应时间 (alex注:指Master节点检测到错误并采取应对措施) 是几分钟。即使在这种情况下,Chunk也只是不可用了,而不是损坏了:应用程序会收到明确的错误信息而不是损坏的数据。
使用GFS的应用程序可以利用一些简单技术实现这个宽松的一致性模型,这些技术也用来实现一些其它的目标功能,包括:尽量采用追加写入而不是覆盖,Checkpoint,自验证的写入操作,自标识的记录。
在实际应用中,我们所有的应用程序对文件的写入操作都是尽量采用数据追加方式,而不是覆盖方式。一种典型的应用,应用程序从头到尾写入数据,生成了一个文件。写入所有数据之后,应用程序自动将文件改名为一个永久保存的文件名,或者周期性的作Checkpoint,记录成功写入了多少数据。Checkpoint文件可以包含程序级别的校验和。Readers仅校验并处理上个Checkpoint之后产生的文件region,这些文件region的状态一定是已定义的。这个方法满足了我们一致性和并发处理的要求。追加写入比随机位置写入更加有效率,对应用程序的失败处理更具有弹性。Checkpoint可以让Writer以渐进的方式重新开始,并且可以防止Reader处理已经被成功写入,但是从应用程序的角度来看还并未完成的数据。
我们再来分析另一种典型的应用。许多应用程序并行的追加数据到同一个文件,比如进行结果的合并或者是一个生产者-消费者队列。记录追加方式的“至少一次追加”的特性保证了Writer的输出。Readers使用下面的方法来处理偶然性的填充数据和重复内容。Writers在每条写入的记录中都包含了额外的信息,例如Checksum,用来验证它的有效性。Reader可以利用Checksum识别和抛弃额外的填充数据和记录片段。如果应用不能容忍偶尔的重复内容(比如,如果这些重复数据触发了非幂等操作),可以用记录的唯一标识符来过滤它们,这些唯一标识符通常用于命名程序中处理的实体对象,例如web文档。这些记录I/O功能 (alex注:These functionalities for record I/O) (除了剔除重复数据)都包含在我们的程序共享的库中,并且适用于Google内部的其它的文件接口实现。所以,相同序列的记录,加上一些偶尔出现的重复数据,都被分发到Reader了。
我们在设计这个系统时,一个重要的原则是最小化所有操作和Master节点的交互。带着这样的设计理念,我们现在描述一下客户机、Master服务器和Chunk服务器如何进行交互,以实现数据修改操作、原子的记录追加操作以及快照功能。
(alex注:lease是数据库中的一个术语)
变更是一个会改变Chunk内容或者元数据的操作,比如写入操作或者记录追加操作。变更操作会在Chunk的所有副本上执行。我们使用租约(lease)机制来保持多个副本间变更顺序的一致性。Master节点为Chunk的一个副本建立一个租约,我们把这个副本叫做主Chunk。主Chunk对Chunk的所有更改操作进行序列化。所有的副本都遵从这个序列进行修改操作。因此,修改操作全局的顺序首先由Master节点选择的租约的顺序决定,然后由租约中主Chunk分配的序列号决定。
设计租约机制的目的是为了最小化Master节点的管理负担。租约的初始超时设置为60秒。不过,只要Chunk被修改了,主Chunk就可以申请更长的租期,通常会得到Master节点的确认并收到租约延长的时间。这些租约延长请求和批准的信息通常都是附加在Master节点和Chunk服务器之间的心跳消息中来传递。有时Master节点会试图提前取消租约(例如,Master节点想取消在一个已经被改名的文件上的修改操作)。即使Master节点和主Chunk失去联系,它仍然可以安全地在旧的租约到期后和另外一个Chunk副本签订新的租约。
在图中,依据步骤编号,展现写入操作的控制流程。
如果应用程序一次写入的数据量很大,或者数据跨越了多个Chunk,GFS客户机代码会把它们分成多个写操作。这些操作都遵循前面描述的控制流程,但是可能会被其它客户机上同时进行的操作打断或者覆盖。因此,共享的文件region的尾部可能包含来自不同客户机的数据片段,尽管如此,由于这些分解后的写入操作在所有的副本上都以相同的顺序执行完成,Chunk的所有副本都是一致的。这使文件region处于2.7节描述的一致的、但是未定义的状态。
为了提高网络效率,我们采取了把数据流和控制流分开的措施。在控制流从客户机到主Chunk、然后再到所有二级副本的同时,数据以管道的方式,顺序的沿着一个精心选择的Chunk服务器链推送。我们的目标是充分利用每台机器的带宽,避免网络瓶颈和高延时的连接,最小化推送所有数据的延时。
为了充分利用每台机器的带宽,数据沿着一个Chunk服务器链顺序的推送,而不是以其它拓扑形式分散推送(例如,树型拓扑结构)。线性推送模式下,每台机器所有的出口带宽都用于以最快的速度传输数据,而不是在多个接受者之间分配带宽。
为了尽可能的避免出现网络瓶颈和高延迟的链接(eg,inter-switch最有可能出现类似问题),每台机器都尽量的在网络拓扑中选择一台还没有接收到数据的、离自己最近的机器作为目标推送数据。假设客户机把数据从Chunk服务器S1推送到S4。它把数据推送到最近的Chunk服务器S1。S1把数据推送到S2,因为S2和S4中最接近的机器是S2。同样的,S2把数据传递给S3和S4之间更近的机器,依次类推推送下去。我们的网络拓扑非常简单,通过IP地址就可以计算出节点的“距离”。
最后,我们利用基于TCP连接的、管道式数据推送方式来最小化延迟。Chunk服务器接收到数据后,马上开始向前推送。管道方式的数据推送对我们帮助很大,因为我们采用全双工的交换网络。接收到数据后立刻向前推送不会降低接收的速度。在没有网络拥塞的情况下,传送B字节的数据到R个副本的理想时间是 B/T+RL ,T是网络的吞吐量,L是在两台机器数据传输的延迟。通常情况下,我们的网络连接速度是100Mbps(T),L将远小于1ms。因此,1MB的数据在理想情况下80ms左右就能分发出去。
GFS提供了一种原子的数据追加操作–记录追加。传统方式的写入操作,客户程序会指定数据写入的偏移量。对同一个region的并行写入操作不是串行的:region尾部可能会包含多个不同客户机写入的数据片段。使用记录追加,客户机只需要指定要写入的数据。GFS保证至少有一次原子的写入操作成功执行(即写入一个顺序的byte流),写入的数据追加到GFS指定的偏移位置上,之后GFS返回这个偏移量给客户机。这类似于在Unix操作系统编程环境中,对以O_APPEND模式打开的文件,多个并发写操作在没有竞态条件时的行为。
记录追加在我们的分布应用中非常频繁的使用,在这些分布式应用中,通常有很多的客户机并行地对同一个文件追加写入数据。如果我们采用传统方式的文件写入操作,客户机需要额外的复杂、昂贵的同步机制,例如使用一个分布式的锁管理器。在我们的工作中,这样的文件通常用于多个生产者/单一消费者的队列系统,或者是合并了来自多个客户机的数据的结果文件。
记录追加是一种修改操作,它也遵循3.1节描述的控制流程,除了在主Chunk有些额外的控制逻辑。客户机把数据推送给文件最后一个Chunk的所有副本,之后发送请求给主Chunk。主Chunk会检查这次记录追加操作是否会使Chunk超过最大尺寸(64MB)。如果超过了最大尺寸,主Chunk首先将当前Chunk填充到最大尺寸,之后通知所有二级副本做同样的操作,然后回复客户机要求其对下一个Chunk重新进行记录追加操作。(记录追加的数据大小严格控制在Chunk最大尺寸的1/4,这样即使在最坏情况下,数据碎片的数量仍然在可控的范围。)通常情况下追加的记录不超过Chunk的最大尺寸,主Chunk把数据追加到自己的副本内,然后通知二级副本把数据写在跟主Chunk一样的位置上,最后回复客户机操作成功。
如果记录追加操作在任何一个副本上失败了,客户端就需要重新进行操作。重新进行记录追加的结果是,同一个Chunk的不同副本可能包含不同的数据–重复包含一个记录全部或者部分的数据。GFS并不保证Chunk的所有副本在字节级别是完全一致的。它只保证数据作为一个整体原子的被至少写入一次。这个特性可以通过简单观察推导出来:如果操作成功执行,数据一定已经写入到Chunk的所有副本的相同偏移位置上。这之后,所有的副本至少都到了记录尾部的长度,任何后续的记录都会追加到更大的偏移地址,或者是不同的Chunk上,即使其它的Chunk副本被Master节点选为了主Chunk。就我们的一致性保障模型而言,记录追加操作成功写入数据的region是已定义的(因此也是一致的),反之则是不一致的(因此也就是未定义的)。正如我们在2.7.2节讨论的,我们的程序可以处理不一致的区域。
(alex注:这一节非常难以理解,总的来说依次讲述了什么是快照、快照使用的COW技术、快照如何不干扰当前操作)
快照操作几乎可以瞬间完成对一个文件或者目录树(“源”)做一个拷贝,并且几乎不会对正在进行的其它操作造成任何干扰。我们的用户可以使用快照迅速的创建一个巨大的数据集的分支拷贝(而且经常是递归的拷贝拷贝),或者是在做实验性的数据操作之前,使用快照操作备份当前状态,这样之后就可以轻松的提交或者回滚到备份时的状态。
就像AFS (alex注:AFS,即Andrew File System,一种分布式文件系统), 我们用标准的copy-on-write技术实现快照。当Master节点收到一个快照请求,它首先取消作快照的文件的所有Chunk的租约。这个措施保证了后续对这些Chunk的写操作都必须与Master交互交互以找到租约持有者。这就给Master节点一个率先创建Chunk的新拷贝的机会。
租约取消或者过期之后,Master节点把这个操作以日志的方式记录到硬盘上。然后,Master节点通过复制源文件或者目录的元数据的方式,把这条日志记录的变化反映到保存在内存的状态中。新创建的快照文件和源文件指向完全相同的Chunk地址。
在快照操作之后,当客户机第一次想写入数据到Chunk C,它首先会发送一个请求到Master节点查询当前的租约持有者。Master节点注意到Chunke C的引用计数超过了1 (alex注:不太明白为什么会大于1.难道是Snapshot没有释放引用计数?) 。Master节点不会马上回复客户机的请求,而是选择一个新的Chunk句柄C 。之后,Master节点要求每个拥有Chunk C当前副本的Chunk服务器创建一个叫做C的新Chunk。通过在源Chunk所在Chunk服务器上创建新的Chunk,我们确保数据在本地而不是通过网络复制(我们的硬盘比我们的100Mb以太网大约快3倍)。从这点来讲,请求的处理方式和任何其它Chunk没什么不同:Master节点确保新Chunk C`的一个副本拥有租约,之后回复客户机,客户机得到回复后就可以正常的写这个Chunk,而不必理会它是从一个已存在的Chunk克隆出来的。
Master节点执行所有的名称空间操作。此外,它还管理着整个系统里所有Chunk的副本:它决定Chunk的存储位置,创建新Chunk和它的副本,协调各种各样的系统活动以保证Chunk被完全复制,在所有的Chunk服务器之间的进行负载均衡,回收不再使用的存储空间。
Master节点的很多操作会花费很长的时间:比如,快照操作必须取消Chunk服务器上快照所涉及的所有的Chunk的租约。我们不希望在这些操作的运行时,延缓了其它的Master节点的操作。因此,我们允许多个操作同时进行,使用名称空间的region上的锁来保证执行的正确顺序。
不同于许多传统文件系统,GFS没有针对每个目录实现能够列出目录下所有文件的数据结构。GFS也不支持文件或者目录的链接(即Unix术语中的硬链接或者符号链接)。在逻辑上,GFS的名称空间就是一个全路径和元数据映射关系的查找表。利用前缀压缩,这个表可以高效的存储在内存中。在存储名称空间的树型结构上,每个节点(绝对路径的文件名或绝对路径的目录名)都有一个关联的读写锁。
每个Master节点的操作在开始之前都要获得一系列的锁。通常情况下,如果一个操作涉及/d1/d2/…/dn/leaf,那么操作首先要获得目录/d1,/d1/d2,…,/d1/d2/…/dn的读锁,以及/d1/d2/…/dn/leaf的读写锁。注意,根据操作的不同,leaf可以是一个文件,也可以是一个目录。
我们演示一下在/home/user被快照到/save/user的时候,锁机制如何防止创建文件/home/user/foo。快照操作获取/home和/save的读取锁,以及/home/user和/save/user的写入锁。文件创建操作获得/home和/home/user的读取锁,以及/home/user/foo的写入锁。这两个操作要顺序执行,因为它们试图获取的/home/user的锁是相互冲突。文件创建操作不需要获取父目录的写入锁,因为这里没有”目录”,或者类似inode等用来禁止修改的数据结构。文件名的读取锁足以防止父目录被删除。
采用这种锁方案的优点是支持对同一目录的并行操作。比如,可以在同一个目录下同时创建多个文件:每一个操作都获取一个目录名的上的读取锁和文件名上的写入锁。目录名的读取锁足以的防止目录被删除、改名以及被快照。文件名的写入锁序列化文件创建操作,确保不会多次创建同名的文件。
因为名称空间可能有很多节点,读写锁采用惰性分配策略,在不再使用的时候立刻被删除。同样,锁的获取也要依据一个全局一致的顺序来避免死锁:首先按名称空间的层次排序,在同一个层次内按字典顺序排序。
GFS集群是高度分布的多层布局结构,而不是平面结构。典型的拓扑结构是有数百个Chunk服务器安装在许多机架上。Chunk服务器被来自同一或者不同机架上的数百个客户机轮流访问。不同机架上的两台机器间的通讯可能跨越一个或多个网络交换机。另外,机架的出入带宽可能比机架内所有机器加和在一起的带宽要小。多层分布架构对数据的灵活性、可靠性以及可用性方面提出特有的挑战。
Chunk副本位置选择的策略服务两大目标:最大化数据可靠性和可用性,最大化网络带宽利用率。为了实现这两个目的,仅仅是在多台机器上分别存储这些副本是不够的,这只能预防硬盘损坏或者机器失效带来的影响,以及最大化每台机器的网络带宽利用率。我们必须在多个机架间分布储存Chunk的副本。这保证Chunk的一些副本在整个机架被破坏或掉线(比如,共享资源,如电源或者网络交换机造成的问题)的情况下依然存在且保持可用状态。这还意味着在网络流量方面,尤其是针对Chunk的读操作,能够有效利用多个机架的整合带宽。另一方面,写操作必须和多个机架上的设备进行网络通信,但是这个代价是我们愿意付出的。
Chunk的副本有三个用途:Chunk创建,重新复制和重新负载均衡。
当Master节点创建一个Chunk时,它会选择在哪里放置初始的空的副本。Master节点会考虑几个因素。(1)我们希望在低于平均硬盘使用率的Chunk服务器上存储新的副本。这样的做法最终能够平衡Chunk服务器之间的硬盘使用率。(2)我们希望限制在每个Chunk服务器上”最近”的Chunk创建操作的次数。虽然创建操作本身是廉价的,但是创建操作也意味着随之会有大量的写入数据的操作,因为Chunk在Writer真正写入数据的时候才被创建,而在我们的”追加一次,读取多次”的工作模式下,Chunk一旦写入成功之后就会变为只读的了。(3)如上所述,我们希望把Chunk的副本分布在多个机架之间。
当Chunk的有效副本数量少于用户指定的复制因数的时候,Master节点会重新复制它。这可能是由几个原因引起的:一个Chunk服务器不可用了,Chunk服务器报告它所存储的一个副本损坏了,Chunk服务器的一个磁盘因为错误不可用了,或者Chunk副本的复制因数提高了。每个需要被重新复制的Chunk都会根据几个因素进行排序。一个因素是Chunk现有副本数量和复制因数相差多少。例如,丢失两个副本的Chunk比丢失一个副本的Chunk有更高的优先级。另外,我们优先重新复制活跃(live)文件的Chunk而不是最近刚被删除的文件的Chunk(查看4.4节)。最后,为了最小化失效的Chunk对正在运行的应用程序的影响,我们提高会阻塞客户机程序处理流程的Chunk的优先级。
Master节点选择优先级最高的Chunk,然后命令某个Chunk服务器直接从可用的副本”克隆”一个副本出来。选择新副本的位置的策略和创建时类似:平衡硬盘使用率、限制同一台Chunk服务器上的正在进行的克隆操作的数量、在机架间分布副本。为了防止克隆产生的网络流量大大超过客户机的流量,Master节点对整个集群和每个Chunk服务器上的同时进行的克隆操作的数量都进行了限制。另外,Chunk服务器通过调节它对源Chunk服务器读请求的频率来限制它用于克隆操作的带宽。
最后,Master服务器周期性地对副本进行重新负载均衡:它检查当前的副本分布情况,然后移动副本以便更好的利用硬盘空间、更有效的进行负载均衡。而且在这个过程中,Master服务器逐渐的填满一个新的Chunk服务器,而不是在短时间内用新的Chunk填满它,以至于过载。新副本的存储位置选择策略和上面讨论的相同。另外,Master节点必须选择哪个副本要被移走。通常情况,Master节点移走那些剩余空间低于平均值的Chunk服务器上的副本,从而平衡系统整体的硬盘使用率。
GFS在文件删除后不会立刻回收可用的物理空间。GFS空间回收采用惰性的策略,只在文件和Chunk级的常规垃圾收集时进行。我们发现这个方法使系统更简单、更可靠。
当一个文件被应用程序删除时,Master节点像对待其它修改操作一样,立刻把删除操作以日志的方式记录下来。但是,Master节点并不马上回收资源,而是把文件名改为一个包含删除时间戳的、隐藏的名字。当Master节点对文件系统命名空间做常规扫描的时候,它会删除所有三天前的隐藏文件(这个时间间隔是可以设置的)。直到文件被真正删除,它们仍旧可以用新的特殊的名字读取,也可以通过把隐藏文件改名为正常显示的文件名的方式“反删除”。当隐藏文件被从名称空间中删除,Master服务器内存中保存的这个文件的相关元数据才会被删除。这也有效的切断了文件和它包含的所有Chunk的连接 (alex注:原文是This effectively severs its links to all its chunks) 。
在对Chunk名字空间做类似的常规扫描时,Master节点找到孤儿Chunk(不被任何文件包含的Chunk)并删除它们的元数据。Chunk服务器在和Master节点交互的心跳信息中,报告它拥有的Chunk子集的信息,Master节点回复Chunk服务器哪些Chunk在Master节点保存的元数据中已经不存在了。Chunk服务器可以任意删除这些Chunk的副本。
虽然分布式垃圾回收在编程语言领域是一个需要复杂的方案才能解决的难题,但是在GFS系统中是非常简单的。我们可以轻易的得到Chunk的所有引用:它们都只存储在Master服务器上的文件到块的映射表中。我们也可以很轻易的得到所有Chunk的副本:它们都以Linux文件的形式存储在Chunk服务器的指定目录下。所有Master节点不能识别的副本都是”垃圾”。
垃圾回收在空间回收方面相比直接删除有几个优势。首先,对于组件失效是常态的大规模分布式系统,垃圾回收方式简单可靠。Chunk可能在某些Chunk服务器创建成功,某些Chunk服务器上创建失败,失败的副本处于无法被Master节点识别的状态。副本删除消息可能丢失,Master节点必须重新发送失败的删除消息,包括自身的和Chunk服务器的 (alex注:自身的指删除metadata的消息) 。垃圾回收提供了一致的、可靠的清除无用副本的方法。第二,垃圾回收把存储空间的回收操作合并到Master节点规律性的后台活动中,比如,例行扫描和与Chunk服务器握手等。因此,操作被批量的执行,开销会被分散。另外,垃圾回收在Master节点相对空闲的时候完成。这样Master节点就可以给那些需要快速反应的客户机请求提供更快捷的响应。第三,延缓存储空间回收为意外的、不可逆转的删除操作提供了安全保障。
根据我们的使用经验,延迟回收空间的主要问题是,延迟回收会阻碍用户调优存储空间的使用,特别是当存储空间比较紧缺的时候。当应用程序重复创建和删除临时文件时,释放的存储空间不能马上重用。我们通过显式的再次删除一个已经被删除的文件的方式加速空间回收的速度。我们允许用户为命名空间的不同部分设定不同的复制和回收策略。例如,用户可以指定某些目录树下面的文件不做复制,删除的文件被即时的、不可恢复的从文件系统移除。
当Chunk服务器失效时,Chunk的副本有可能因错失了一些修改操作而过期失效。Master节点保存了每个Chunk的版本号,用来区分当前的副本和过期副本。
无论何时,只要Master节点和Chunk签订一个新的租约,它就增加Chunk的版本号,然后通知最新的副本。Master节点和这些副本都把新的版本号记录在它们持久化存储的状态信息中。这个动作发生在任何客户机得到通知以前,因此也是对这个Chunk开始写之前。如果某个副本所在的Chunk服务器正好处于失效状态,那么副本的版本号就不会被增加。Master节点在这个Chunk服务器重新启动,并且向Master节点报告它拥有的Chunk的集合以及相应的版本号的时候,就会检测出它包含过期的Chunk。如果Master节点看到一个比它记录的版本号更高的版本号,Master节点会认为它和Chunk服务器签订租约的操作失败了,因此会选择更高的版本号作为当前的版本号。
Master节点在例行的垃圾回收过程中移除所有的过期失效副本。在此之前,Master节点在回复客户机的Chunk信息请求的时候,简单的认为那些过期的块根本就不存在。另外一重保障措施是,Master节点在通知客户机哪个Chunk服务器持有租约、或者指示Chunk服务器从哪个Chunk服务器进行克隆时,消息中都附带了Chunk的版本号。客户机或者Chunk服务器在执行操作时都会验证版本号以确保总是访问当前版本的数据。
我们在设计GFS时遇到的最大挑战之一是如何处理频繁发生的组件失效。组件的数量和质量让这些问题出现的频率远远超过一般系统意外发生的频率:我们不能完全依赖机器的稳定性,也不能完全相信硬盘的可靠性。组件的失效可能造成系统不可用,更糟糕的是,还可能产生不完整的数据。我们讨论我们如何面对这些挑战,以及当组件失效不可避免的发生时,用GFS自带工具诊断系统故障。
在GFS集群的数百个服务器之中,在任何给定的时间必定会有些服务器是不可用的。我们使用两条简单但是有效的策略保证整个系统的高可用性:快速恢复和复制。
不管Master服务器和Chunk服务器是如何关闭的,它们都被设计为可以在数秒钟内恢复它们的状态并重新启动。事实上,我们并不区分正常关闭和异常关闭;通常,我们通过直接kill掉进程来关闭服务器。客户机和其它的服务器会感觉到系统有点颠簸 (alex注:a minor hiccup) ,正在发出的请求会超时,需要重新连接到重启后的服务器,然后重试这个请求。
正如之前讨论的,每个Chunk都被复制到不同机架上的不同的Chunk服务器上。用户可以为文件命名空间的不同部分设定不同的复制级别。缺省是3。当有Chunk服务器离线了,或者通过Chksum校验(参考5.2节)发现了已经损坏的数据,Master节点通过克隆已有的副本保证每个Chunk都被完整复制 (alex注:即每个Chunk都有复制因子制定的个数个副本,缺省是3)。 虽然Chunk复制策略对我们非常有效,但是我们也在寻找其它形式的跨服务器的冗余解决方案,比如使用奇偶校验、或者Erasure codes (alex注:Erasure codes用来解决链接层中不相关的错误,以及网络拥塞和buffer限制造成的丢包错误) 来解决我们日益增长的只读存储需求。我们的系统主要的工作负载是追加方式的写入和读取操作,很少有随机的写入操作,因此,我们认为在我们这个高度解耦合的系统架构下实现这些复杂的冗余方案很有挑战性,但并非不可实现。
为了保证Master服务器的可靠性,Master服务器的状态也要复制。Master服务器所有的操作日志和checkpoint文件都被复制到多台机器上。对Master服务器状态的修改操作能够提交成功的前提是,操作日志写入到Master服务器的备节点和本机的磁盘。简单说来,一个Master服务进程负责所有的修改操作,包括后台的服务,比如垃圾回收等改变系统内部状态活动。当它失效的时候,几乎可以立刻重新启动。如果Master进程所在的机器或者磁盘失效了,处于GFS系统外部的监控进程会在其它的存有完整操作日志的机器上启动一个新的Master进程。客户端使用规范的名字访问Master(比如gfs-test)节点,这个名字类似DNS别名,因此也就可以在Master进程转到别的机器上执行时,通过更改别名的实际指向访问新的Master节点。
此外,GFS中还有些“影子”Master服务器,这些“影子”服务器在“主”Master服务器宕机的时候提供文件系统的只读访问。它们是影子,而不是镜像,所以它们的数据可能比“主”Master服务器更新要慢,通常是不到1秒。对于那些不经常改变的文件、或者那些允许获取的数据有少量过期的应用程序,“影子”Master服务器能够提高读取的效率。事实上,因为文件内容是从Chunk服务器上读取的,因此,应用程序不会发现过期的文件内容。在这个短暂的时间窗内,过期的可能是文件的元数据,比如目录的内容或者访问控制信息。
“影子”Master服务器为了保持自身状态是最新的,它会读取一份当前正在进行的操作的日志副本,并且依照和主Master服务器完全相同的顺序来更改内部的数据结构。和主Master服务器一样,“影子”Master服务器在启动的时候也会从Chunk服务器轮询数据(之后定期拉数据),数据中包括了Chunk副本的位置信息;“影子”Master服务器也会定期和Chunk服务器“握手”来确定它们的状态。在主Master服务器因创建和删除副本导致副本位置信息更新时,“影子”Master服务器才和主Master服务器通信来更新自身状态。
每个Chunk服务器都使用Checksum来检查保存的数据是否损坏。考虑到一个GFS集群通常都有好几百台机器、几千块硬盘,磁盘损坏导致数据在读写过程中损坏或者丢失是非常常见的(第7节讲了一个原因)。我们可以通过别的Chunk副本来解决数据损坏问题,但是跨越Chunk服务器比较副本来检查数据是否损坏很不实际。另外,GFS允许有歧义的副本存在:GFS修改操作的语义,特别是早先讨论过的原子纪录追加的操作,并不保证副本完全相同 (alex注:副本不是byte-wise完全一致的) 。因此,每个Chunk服务器必须独立维护Checksum来校验自己的副本的完整性。
我们把每个Chunk都分成64KB大小的块。每个块都对应一个32位的Checksum。和其它元数据一样,Checksum与其它的用户数据是分开的,并且保存在内存和硬盘上,同时也记录操作日志。
对于读操作来说,在把数据返回给客户端或者其它的Chunk服务器之前,Chunk服务器会校验读取操作涉及的范围内的块的Checksum。因此Chunk服务器不会把错误数据传递到其它的机器上。如果发生某个块的Checksum不正确,Chunk服务器返回给请求者一个错误信息,并且通知Master服务器这个错误。作为回应,请求者应当从其它副本读取数据,Master服务器也会从其它副本克隆数据进行恢复。当一个新的副本就绪后,Master服务器通知副本错误的Chunk服务器删掉错误的副本。
Checksum对读操作的性能影响很小,可以基于几个原因来分析一下。因为大部分的读操作都至少要读取几个块,而我们只需要读取一小部分额外的相关数据进行校验。GFS客户端代码通过每次把读取操作都对齐在Checksum block的边界上,进一步减少了这些额外的读取操作的负面影响。另外,在Chunk服务器上,Chunksum的查找和比较不需要I/O操作,Checksum的计算可以和I/O操作同时进行。
Checksum的计算针对在Chunk尾部的追加写入操作作了高度优化(与之对应的是覆盖现有数据的写入操作),因为这类操作在我们的工作中占了很大比例。我们只增量更新最后一个不完整的块的Checksum,并且用所有的追加来的新Checksum块来计算新的Checksum。即使是最后一个不完整的Checksum块已经损坏了,而且我们不能够马上检查出来,由于新的Checksum和已有数据不吻合,在下次对这个块进行读取操作的时候,会检查出数据已经损坏了。
相比之下,如果写操作覆盖已经存在的一个范围内的Chunk,我们必须读取和校验被覆盖的第一个和最后一个块,然后再执行写操作;操作完成之后再重新计算和写入新的Checksum。如果我们不校验第一个和最后一个被写的块,那么新的Checksum可能会隐藏没有被覆盖区域内的数据错误。
在Chunk服务器空闲的时候,它会扫描和校验每个不活动的Chunk的内容。这使得我们能够发现很少被读取的Chunk是否完整。一旦发现有Chunk的数据损坏,Master可以创建一个新的、正确的副本,然后把损坏的副本删除掉。这个机制也避免了非活动的、已损坏的Chunk欺骗Master节点,使Master节点认为它们已经有了足够多的副本了。
详尽的、深入细节的诊断日志,在问题隔离、调试、以及性能分析等方面给我们带来无法估量的帮助,同时也只需要很小的开销。没有日志的帮助,我们很难理解短暂的、不重复的机器之间的消息交互。GFS的服务器会产生大量的日志,记录了大量关键的事件(比如,Chunk服务器启动和关闭)以及所有的RPC的请求和回复。这些诊断日志可以随意删除,对系统的正确运行不造成任何影响。然而,我们在存储空间允许的情况下会尽量的保存这些日志。
RPC日志包含了网络上发生的所有请求和响应的详细记录,但是不包括读写的文件数据。通过匹配请求与回应,以及收集不同机器上的RPC日志记录,我们可以重演所有的消息交互来诊断问题。日志还用来跟踪负载测试和性能分析。
日志对性能的影响很小(远小于它带来的好处),因为这些日志的写入方式是顺序的、异步的。最近发生的事件日志保存在内存中,可用于持续不断的在线监控。
在建造和部署GFS的过程中,我们经历了各种各样的问题,有些是操作上的,有些是技术上的。
起初,GFS被设想为我们的生产系统的后端文件系统。随着时间推移,在GFS的使用中逐步的增加了对研究和开发任务的支持。我们开始增加一些小的功能,比如权限和配额,到了现在,GFS已经初步支持了这些功能。虽然我们生产系统是严格受控的,但是用户层却不总是这样的。需要更多的基础架构来防止用户间的相互干扰。
我们最大的问题是磁盘以及和Linux相关的问题。很多磁盘都声称它们支持某个范围内的Linux IDE硬盘驱动程序,但是实际应用中反映出来的情况却不是这样,它们只支持最新的驱动。因为协议版本很接近,所以大部分磁盘都可以用,但是偶尔也会有由于协议不匹配,导致驱动和内核对于驱动器的状态判断失误。这会导致数据因为内核中的问题意外的被破坏了。这个问题促使我们使用Checksum来校验数据,同时我们也修改内核来处理这些因为协议不匹配带来的问题。
较早的时候,我们在使用Linux 2.2内核时遇到了些问题,主要是fsync()的效率问题。它的效率与文件的大小而不是文件修改部分的大小有关。这在我们的操作日志文件过大时给出了难题,尤其是在我们尚未实现Checkpoint的时候。我们费了很大的力气用同步写来解决这个问题,但是最后还是移植到了Linux2.4内核上。
另一个和Linux相关的问题是单个读写锁的问题,也就是说,在某一个地址空间的任意一个线程都必须在从磁盘page in(读锁)的时候先hold住,或者在mmap()调用(写锁)的时候改写地址空间。我们发现即使我们的系统负载很轻的情况下也会有偶尔的超时,我们花费了很多的精力去查找资源的瓶颈或者硬件的问题。最后我们终于发现这个单个锁在磁盘线程交换以前映射的数据到磁盘的时候,锁住了当前的网络线程,阻止它把新数据映射到内存。由于我们的性能主要受限于网络接口,而不是内存copy的带宽,因此,我们用pread()替代mmap(),用了一个额外的copy动作来解决这个问题。
尽管偶尔还是有其它的问题,Linux的开放源代码还是使我们能够快速探究和理解系统的行为。在适当的时候,我们会改进内核并且和公开源码组织共享这些改动。
Google文件系统展示了一个使用普通硬件支持大规模数据处理的系统的特质。虽然一些设计要点都是针对我们的特殊的需要定制的,但是还是有很多特性适用于类似规模的和成本的数据处理任务。
首先,我们根据我们当前的和可预期的将来的应用规模和技术环境来评估传统的文件系统的特性。我们的评估结果将我们引导到一个使用完全不同于传统的设计思路上。根据我们的设计思路,我们认为组件失效是常态而不是异常,针对采用追加方式(有可能是并发追加)写入、然后再读取(通常序列化读取)的大文件进行优化,以及扩展标准文件系统接口、放松接口限制来改进整个系统。
我们系统通过持续监控,复制关键数据,快速和自动恢复提供灾难冗余。Chunk复制使得我们可以对Chunk服务器的失效进行容错。高频率的组件失效要求系统具备在线修复机制,能够周期性的、透明的修复损坏的数据,也能够第一时间重新建立丢失的副本。此外,我们使用Checksum在磁盘或者IDE子系统级别检测数据损坏,在这样磁盘数量惊人的大系统中,损坏率是相当高的。
我们的设计保证了在有大量的并发读写操作时能够提供很高的合计吞吐量。我们通过分离控制流和数据流来实现这个目标,控制流在Master服务器处理,而数据流在Chunk服务器和客户端处理。当一般的操作涉及到Master服务器时,由于GFS选择的Chunk尺寸较大 (alex注:从而减小了元数据的大小), 以及通过Chunk Lease将控制权限移交给主副本,这些措施将Master服务器的负担降到最低。这使得一个简单、中心的Master不会成为成为瓶颈。我们相信我们对网络协议栈的优化可以提升当前对于每客户端的写入吞吐量限制。
GFS成功的实现了我们对存储的需求,在Google内部,无论是作为研究和开发的存储平台,还是作为生产系统的数据处理平台,都得到了广泛的应用。它是我们持续创新和处理整个WEB范围内的难题的一个重要工具。
存储系统是容错系统的基础构件
如果可以建立一个持久的存储系统,应用程序不需要特殊对自己的状态进行保存,因为存储系统已经存好了,从而简化了应用程序的设计。
因此存储系统本身必须有很高的容错性能,设计这个并不容易。
因此形成了一个环,主要矛盾是一致性和性能之间的矛盾
理想情况下的一致性:分布式系统与单机系统在表现上完全相同
然而在实际情况下很难实现
两个线程和
为同一个变量写入了不同的值,此时有两个线程
和
读取。
此时读取的值应该是
或
中的任意一个,而
的值应该与
相同,才是我们希望看到的结果。
解决故障一般是通过使用复制数据到其他机器上的方式。
一个很烂的服务器之间复制数据的方案:客户端写入数据的时候,同时向两个服务器写入数据,不需要服务器之间同步。
此时两个线程和
为同一个变量写入了不同的值,两个线程
和
读取不一定读出什么。
相当于一个分布式系统的案例研究,包括了高性能、复制和容错、一致性等等主题
GFS是第一个在上千台计算机上构建的分布式系统,后续的HDFS等都受到了GFS的启发。
两个非标准做法:
关键属性
如果中间过程有错误,客户端一般会重试,希望下一次可以正常运行(也就是最少一次)
这可能会造成在一个磁盘中有两份数据的拷贝。会有id和checksum协助控制不会将相同的数据读取两次。
一个服务器暂时挂掉了,导致版本号没有更新,同时一个客户端的版本号也是一个老版本号,结果正好匹配到了这个刚刚挂掉的服务器,最终导致读取的数据和期望的不同。
通过租约机制确保只会存在一个primary服务器,不会产生“脑裂”现象
获得强一致性?更新所有的除primary外的其他服务器或者全部都不更新,GFS没有实现这个。
]]>How do Go channels work? How does Go make sure they are synchronized between the many possible goroutines?
https://golang.org/src/runtime/chan.go
At a high level, a chan is a struct holding a buffer and a lock. Sending on a channel involves acquiring the lock, waiting (perhaps releasing the CPU) until some thread is receiving, and handing off the message. Receiving involves acquiring the lock and waiting for a sender. You could implement your own channels with Go sync.Mutex and sync.Cond.
在一个进程中并行运行多个线程
线程原语:开启线程、退出线程(隐式)、停止线程(挂在一边不懂)、恢复线程
支持并发
数量可以不考虑,按照需求创建线程即可
channels和condition variables
分配条件变量并且和锁关联,不满足条件进入睡眠状态,并释放关联的锁。
在goroutine运行的最后唤醒睡眠状态的线程,重新进行判断
package mainimport "sync"import "time"import "math/rand"func main() {rand.Seed(time.Now().UnixNano())count := 0finished := 0var mu sync.Mutexcond := sync.NewCond(&mu)for i := 0; i < 10; i++ {go func() {vote := requestVote()mu.Lock()defer mu.Unlock()if vote {count++}finished++cond.Broadcast()}()}mu.Lock()for count < 5 && finished != 10 {cond.Wait()}if count >= 5 {println("received 5+ votes!")} else {println("lost")}mu.Unlock()}func requestVote() bool {time.Sleep(time.Duration(rand.Intn(100)) * time.Millisecond)return rand.Int() % 2 == 0}package mainimport "time"import "math/rand"func main() {rand.Seed(time.Now().UnixNano())count := 0ch := make(chan bool)for i := 0; i < 10; i++ {go func() {ch <- requestVote()}()}for i := 0; i < 10; i++ {v := <-chif v {count += 1}}if count >= 5 {println("received 5+ votes!")} else {println("lost")}}func requestVote() bool {time.Sleep(time.Duration(rand.Intn(100)) * time.Millisecond)return rand.Int()%2 == 0}package mainimport ("fmt""sync")//// Several solutions to the crawler exercise from the Go tutorial// https://tour.golang.org/concurrency/10////// Serial crawler//func Serial(url string, fetcher Fetcher, fetched map[string]bool) {if fetched[url] {return}fetched[url] = trueurls, err := fetcher.Fetch(url)if err != nil {return}for _, u := range urls {Serial(u, fetcher, fetched)}return}//// Concurrent crawler with shared state and Mutex//type fetchState struct {mu sync.Mutexfetched map[string]bool}func ConcurrentMutex(url string, fetcher Fetcher, f *fetchState) {f.mu.Lock()already := f.fetched[url]f.fetched[url] = truef.mu.Unlock()if already {return}urls, err := fetcher.Fetch(url)if err != nil {return}var done sync.WaitGroupfor _, u := range urls {done.Add(1)go func(u string) {defer done.Done()ConcurrentMutex(u, fetcher, f)}(u)}done.Wait()return}func makeState() *fetchState {f := &fetchState{}f.fetched = make(map[string]bool)return f}//// Concurrent crawler with channels//func worker(url string, ch chan []string, fetcher Fetcher) {urls, err := fetcher.Fetch(url)if err != nil {ch <- []string{}} else {ch <- urls}}func coordinator(ch chan []string, fetcher Fetcher) {n := 1fetched := make(map[string]bool)for urls := range ch {for _, u := range urls {if fetched[u] == false {fetched[u] = truen += 1go worker(u, ch, fetcher)}}n -= 1if n == 0 {break}}}func ConcurrentChannel(url string, fetcher Fetcher) {ch := make(chan []string)go func() {ch <- []string{url}}()coordinator(ch, fetcher)}//// main//func main() {fmt.Printf("=== Serial===\n")Serial("http://golang.org/", fetcher, make(map[string]bool))fmt.Printf("=== ConcurrentMutex ===\n")ConcurrentMutex("http://golang.org/", fetcher, makeState())fmt.Printf("=== ConcurrentChannel ===\n")ConcurrentChannel("http://golang.org/", fetcher)}//// Fetcher//type Fetcher interface {// Fetch returns a slice of URLs found on the page.Fetch(url string) (urls []string, err error)}// fakeFetcher is Fetcher that returns canned results.type fakeFetcher map[string]*fakeResulttype fakeResult struct {body stringurls []string}func (f fakeFetcher) Fetch(url string) ([]string, error) {if res, ok := f[url]; ok {fmt.Printf("found: %s\n", url)return res.urls, nil}fmt.Printf("missing: %s\n", url)return nil, fmt.Errorf("not found: %s", url)}// fetcher is a populated fakeFetcher.var fetcher = fakeFetcher{"http://golang.org/": &fakeResult{"The Go Programming Language",[]string{"http://golang.org/pkg/","http://golang.org/cmd/",},},"http://golang.org/pkg/": &fakeResult{"Packages",[]string{"http://golang.org/","http://golang.org/cmd/","http://golang.org/pkg/fmt/","http://golang.org/pkg/os/",},},"http://golang.org/pkg/fmt/": &fakeResult{"Package fmt",[]string{"http://golang.org/","http://golang.org/pkg/",},},"http://golang.org/pkg/os/": &fakeResult{"Package os",[]string{"http://golang.org/","http://golang.org/pkg/",},},}RPC:在客户端上调用在服务器端实现的函数-传递参数并返回结果
实际过程:
package mainimport ("fmt""log""net""net/rpc""sync")//// Common RPC request/reply definitions//type PutArgs struct {Key stringValue string}type PutReply struct {}type GetArgs struct {Key string}type GetReply struct {Value string}//// Client//func connect() *rpc.Client {client, err := rpc.Dial("tcp", ":1234")if err != nil {log.Fatal("dialing:", err)}return client}func get(key string) string {client := connect()args := GetArgs{"subject"}reply := GetReply{}err := client.Call("KV.Get", &args, &reply)if err != nil {log.Fatal("error:", err)}client.Close()return reply.Value}func put(key string, val string) {client := connect()args := PutArgs{"subject", "6.824"}reply := PutReply{}err := client.Call("KV.Put", &args, &reply)if err != nil {log.Fatal("error:", err)}client.Close()}//// Server//type KV struct {mu sync.Mutexdata map[string]string}func server() {kv := new(KV)kv.data = map[string]string{}rpcs := rpc.NewServer()rpcs.Register(kv)l, e := net.Listen("tcp", ":1234")if e != nil {log.Fatal("listen error:", e)}go func() {for {conn, err := l.Accept()if err == nil {go rpcs.ServeConn(conn)} else {break}}l.Close()}()}func (kv *KV) Get(args *GetArgs, reply *GetReply) error {kv.mu.Lock()defer kv.mu.Unlock()reply.Value = kv.data[args.Key]return nil}func (kv *KV) Put(args *PutArgs, reply *PutReply) error {kv.mu.Lock()defer kv.mu.Unlock()kv.data[args.Key] = args.Valuereturn nil}//// main//func main() {server()put("subject", "6.824")fmt.Printf("Put(subject, 6.824) done\n")fmt.Printf("get(subject) -> %s\n", get("subject"))}构建一个MapReduce系统
在 src/main/mrsequential.go 中提供了串行的mapreduce程序,在单进程里面直接顺序执行Map操作和Reduce操作
同时提供了一些MapReduce的应用程序:
mrapps/wc.go:WordCount程序
mrapps/indexer.go:text-indexer
按照如下的方式运行串行的mapreduce程序:
cd src/maingo build -race -buildmode=plugin ../mrapps/wc.gorm mr-out*go run -race mrsequential.go wc.so pg*.txtmore mr-out-0输出的文件中是对文件的WordCount结果
Go是静态编译型语言,在编译时就将所有引用的包(库)全部加载打包到最终的可执行程序(或库文件)中,因此并不能在运行时动态加载其他共享库。Go Plugin提供了这样一种方式,能够让你在运行时动态加载外部功能。
type Plugin即Golang加载的插件,与之有关的两个方法:
因此这一行命令将 wc.go文件编译成了一个插件 wc.so(默认文件名),从而可以插入到MapReduce主程序中运行。
// The map function is called once for each file of input. The first// argument is the name of the input file, and the second is the// file's complete contents. You should ignore the input file name,// and look only at the contents argument. The return value is a slice// of key/value pairs.func Map(filename string, contents string) []mr.KeyValue {// function to detect word separators.ff := func(r rune) bool { return !unicode.IsLetter(r) }// split contents into an array of words.words := strings.FieldsFunc(contents, ff)kva := []mr.KeyValue{}for _, w := range words {kv := mr.KeyValue{w, "1"}kva = append(kva, kv)}return kva}对每一个传进来的字符串,通过 strings.FieldsFunc函数找到字符串的分割点,分割成单独的单词,构造成KeyValue结构体并合并成切片返回
// The reduce function is called once for each key generated by the// map tasks, with a list of all the values created for that key by// any map task.func Reduce(key string, values []string) string {// return the number of occurrences of this word.return strconv.Itoa(len(values))}直接以字符串的形式返回values的长度
// load the application Map and Reduce functions// from a plugin file, e.g. ../mrapps/wc.sofunc loadPlugin(filename string) (func(string, string) []mr.KeyValue, func(string, []string) string) {p, err := plugin.Open(filename)if err != nil {log.Fatalf("cannot load plugin %v", filename)}xmapf, err := p.Lookup("Map")if err != nil {log.Fatalf("cannot find Map in %v", filename)}mapf := xmapf.(func(string, string) []mr.KeyValue)xreducef, err := p.Lookup("Reduce")if err != nil {log.Fatalf("cannot find Reduce in %v", filename)}reducef := xreducef.(func(string, []string) string)return mapf, reducef}从编译好的*.so文件中查找Map函数和Reduce函数,通过函数的返回值类型进行类型推断,最终返回两个函数通过主函数里面的变量进行接收
mapf, reducef := loadPlugin(os.Args[1]) //// read each input file,// pass it to Map,// accumulate the intermediate Map output.//intermediate := []mr.KeyValue{}for _, filename := range os.Args[2:] {file, err := os.Open(filename)if err != nil {log.Fatalf("cannot open %v", filename)}content, err := ioutil.ReadAll(file)if err != nil {log.Fatalf("cannot read %v", filename)}file.Close()kva := mapf(filename, string(content))intermediate = append(intermediate, kva...)}pg-*.txt会匹配到所有满足条件的文件,将文件逐个打开,读取文件内容,通过Map函数处理成中间数据格式,存入中间变量intermediate
对中间变量的切片按照键的字典序进行排序
sort.Sort(ByKey(intermediate))// for sorting by key.func (a ByKey) Len() int { return len(a) }func (a ByKey) Swap(i, j int) { a[i], a[j] = a[j], a[i] }func (a ByKey) Less(i, j int) bool { return a[i].Key < a[j].Key }这里是通过实现Sort的接口实现了自定义排序
//// call Reduce on each distinct key in intermediate[],// and print the result to mr-out-0.//i := 0for i < len(intermediate) {j := i + 1for j < len(intermediate) && intermediate[j].Key == intermediate[i].Key {j++}values := []string{}for k := i; k < j; k++ {values = append(values, intermediate[k].Value)}output := reducef(intermediate[i].Key, values)// this is the correct format for each line of Reduce output.fmt.Fprintf(ofile, "%v %v\n", intermediate[i].Key, output)i = j}由于已经排好顺序了,从左到右遍历一遍就可以统计每一个键出现的数量,然后输出到文件即可。
实现一个分布式MapReduce,由coordinator和worker两个程序组成。
coordinator进程只有一个,worker进程有一个或多个并行执行。
worker进程将通过RPC与coordinator进程进行通信。每个worker进程将向coordinator进程请求任务,从一个或多个文件中读取任务的输入,执行任务,并将任务的输出写入一个或更多个文件。
coordinator进程应该注意到一个worker进程是否没有在合理的时间内完成其任务(10秒),并将相同的任务交给另一个worker进程。
coordinator和worker的“main”函数在 main/mrcordinator.go和 main/mrworker.go中
实现应该在 mr/coordinator.go、mr/worker.go和 mr/rpc.go中。
测试运行:
go build -race -buildmode=plugin ../mrapps/wc.gorm mr-out*go run -race mrcoordinator.go pg-*.txtgo run -race mrworker.go wc.sogo run -race mrworker.go wc.so测试脚本:
bash test-mr.sh待补充的代码提供了一个RPC的示例
启动Worker后,会调用CallExample()函数
// example function to show how to make an RPC call to the coordinator.//// the RPC argument and reply types are defined in rpc.go.func CallExample() {// declare an argument structure.args := ExampleArgs{}// fill in the argument(s).args.X = 99// declare a reply structure.reply := ExampleReply{}// send the RPC request, wait for the reply.// the "Coordinator.Example" tells the// receiving server that we'd like to call// the Example() method of struct Coordinator.ok := call("Coordinator.Example", &args, &reply)if ok {// reply.Y should be 100.fmt.Printf("reply.Y %v\n", reply.Y)} else {fmt.Printf("call failed!\n")}}函数构建了RPC的结构体,然后调用call函数并接收响应
在这里体现了RPC的核心思想:在这里看起来就是调用的本地函数call,但是实际上call内部是与coordinator进行通信,然后在远程得到返回值后返回给reply结构体,因此为“远程过程调用”
call函数:
// send an RPC request to the coordinator, wait for the response.// usually returns true.// returns false if something goes wrong.func call(rpcname string, args interface{}, reply interface{}) bool {// c, err := rpc.DialHTTP("tcp", "127.0.0.1"+":1234")sockname := coordinatorSock()c, err := rpc.DialHTTP("unix", sockname)if err != nil {log.Fatal("dialing:", err)}defer c.Close()err = c.Call(rpcname, args, reply)if err == nil {return true}fmt.Println(err)return false}注意coordinatorSock()方法,会获取一个临时文件,通信是通过这个临时文件进行的。
在coordinator.go内部,RPC指定的方法"Coordinator.Example":
// an example RPC handler.//// the RPC argument and reply types are defined in rpc.go.func (c *Coordinator) Example(args *ExampleArgs, reply *ExampleReply) error {reply.Y = args.X + 1return nil}因此返回的结构体中reply.Y的值就为100
在启动Worker前要先启动Coordinator,启动后首先创建一个Coordinator结构:
// create a Coordinator.// main/mrcoordinator.go calls this function.// nReduce is the number of reduce tasks to use.func MakeCoordinator(files []string, nReduce int) *Coordinator {c := Coordinator{}// Your code here.c.server()return &c}其中调用server方法,监听Worker的RPC:
// start a thread that listens for RPCs from worker.gofunc (c *Coordinator) server() {rpc.Register(c)rpc.HandleHTTP()//l, e := net.Listen("tcp", ":1234")sockname := coordinatorSock()os.Remove(sockname)l, e := net.Listen("unix", sockname)if e != nil {log.Fatal("listen error:", e)}go http.Serve(l, nil)}Coordinator会不断检测Done方法的返回值,一旦为true,Coordinator就会退出:
// main/mrcoordinator.go calls Done() periodically to find out// if the entire job has finished.func (c *Coordinator) Done() bool {ret := false// Your code here.return ret}首先考虑简单一些,不考虑并行、容错处理等,先把整个的流程跑通。
首先跑通Map流程
Coordinator的数据结构:
type Coordinator struct {// Your definitions here.MapTask []MapTaskInformation // Map任务列表ReduceTask []ReduceTaskInformation // Reduce任务列表}内部有两个切片,分别对应Map的任务列表和Reduce的任务列表。
两个任务列表是在Coordinator启动的时候就设置好:
// create a Coordinator.// main/mrcoordinator.go calls this function.// nReduce is the number of reduce tasks to use.func MakeCoordinator(files []string, nReduce int) *Coordinator {mapTaskSlice := []MapTaskInformation{}for id, fileName := range files {mapTaskSlice = append(mapTaskSlice, MapTaskInformation{Id: id + 1,State: 0,NReduce: nReduce,OriginFileName: fileName,IntermediateFileName: "mr-" + strconv.Itoa(id+1) + "-",})}reduceTaskSlice := []ReduceTaskInformation{}for i := 0; i < nReduce; i++ {reduceTaskSlice = append(reduceTaskSlice, ReduceTaskInformation{Id: i + 1,State: 0,OriginFileName: "mr-0-" + strconv.Itoa(i+1),OutputFileName: "mr-" + strconv.Itoa(i+1),})}c := Coordinator{MapTask: mapTaskSlice,ReduceTask: reduceTaskSlice,}// Your code here.c.server()return &c}其中为Map和Reduce暂时设计的数据结构:
type MapTaskInformation struct {Id int // 任务唯一编码State int // 0表示未开始,1表示正在进行,2表示已经完成NReduce int // 分成Reduce任务的数量OriginFileName string // 原始文件名称IntermediateFileName string // Map任务完成后的文件名称(中间文件)}type ReduceTaskInformation struct {Id int // 任务唯一编码State int // 0表示未开始,1表示正在进行,2表示已经完成OriginFileName string // Reduce的初始文件名称(中间文件)OutputFileName string // Reduce任务完成后的最终文件名称}Worker启动时,通过RPC向Coordinator要一个任务
// main/mrworker.go calls this function.func Worker(mapf func(string, string) []KeyValue,reducef func(string, []string) string) {args := TaskInformation{}reply := TaskInformation{}ok := call("Coordinator.AsssignTask", &args, &reply)Coordinator会遍历自己内部的所有任务列表,找到第一个还没有完成的任务分配给这个Worker:
// 分配任务func (c *Coordinator) AsssignTask(args *TaskInformation, reply *TaskInformation) error {isMapfinished := true//遍历所有的Map任务信息,将未开始的分配给这个节点for i, mapTask := range c.MapTask {if mapTask.State == 0 {isMapfinished = falsereply.Id = mapTask.Idreply.TaskType = "map"reply.InputFileName = mapTask.OriginFileNamereply.OutputFileName = mapTask.IntermediateFileNamereply.NReduce = mapTask.NReducec.MapTask[i].State = 1return nil} else if mapTask.State == 1 {isMapfinished = false}}// 如果所有的Map任务都完成了,就遍历Reduce任务if isMapfinished {for _, reduceTask := range c.ReduceTask {if reduceTask.State == 0 {return nil}}}return nil}Worker接收到任务后使用插件中的Map函数进行处理,并将成功完成任务的消息通过RPC的方式返回给Coordinator
if ok {fmt.Println("Call Success!")if reply.TaskType == "map" {fmt.Printf("Map Task!\n")intermediate := []KeyValue{}file, err := os.Open(reply.InputFileName)if err != nil {log.Fatalf("cannot open %v", reply.InputFileName)}content, err := io.ReadAll(file)if err != nil {log.Fatalf("cannot read %v", reply.InputFileName)}file.Close()kva := mapf(reply.InputFileName, string(content))intermediate = append(intermediate, kva...)// 排序sort.Sort(ByKey(intermediate))fmt.Println(intermediate)args = replycall("Coordinator.TaskFinish", &args, &reply)Coordinator接收消息,将自己内部的任务状态修改,后续就不会再将这个任务分配给Worker了。
// 接收任务已经完成的信息func (c *Coordinator) TaskFinish(args *TaskInformation, reply *TaskInformation) error {if args.TaskType == "map" {c.MapTask[args.Id-1].State = 2} else if args.TaskType == "reduce" {c.ReduceTask[args.Id-1].State = 2}return nil}问题:
首先在Worker的主函数增加一层循环,从而使Worker不断请求任务,由Coordinator按需分配
首先要构造中间文件,也就是map结束后的文件需要存起来,然后才能用reduce去处理
// 循环创建NReduce个文件准备保存encoderList := make([]*json.Encoder, 0)for i := 0; i < reply.NReduce; i++ {fileName := reply.OutputFileName + strconv.FormatInt(int64(i+1), 10)tempFile, err := os.Create(fileName)if err != nil {log.Fatalf("cannot create %v", fileName)}defer tempFile.Close()encoderList = append(encoderList, json.NewEncoder(tempFile))}for i, v := range intermediate {encoderList[ihash(v.Key)%reply.NReduce].Encode(&intermediate[i])}map在保存的时候要直接分成NReduce的文件,文件的内容是由哈希函数对键进行映射后得到的,保证键大致平均分到NReduce个节点上
保存文件的时候使用的是json的格式,保存的过程有些慢,需要对整个map的结果全部遍历一遍,后续可以考虑并行处理?
Reduce内容:
} else if reply.TaskType == "reduce" {ofile, _ := os.Create(reply.OutputFileName)fmt.Printf("Reduce Task!\n")kva := make([]KeyValue, 0)for p := 1; p <= 8; p++ {filename := strings.Replace(reply.InputFileName, "*", strconv.FormatInt(int64(p), 10), 1)fmt.Println(filename)file, err := os.Open(filename)if err != nil {log.Fatalf("cannot open %v", filename)}dec := json.NewDecoder(file)for {var kv KeyValueif err := dec.Decode(&kv); err != nil {break}kva = append(kva, kv)}}// 排序sort.Sort(ByKey(kva))//// call Reduce on each distinct key in intermediate[],// and print the result to mr-out-0.//i := 0for i < len(kva) {j := i + 1for j < len(kva) && kva[j].Key == kva[i].Key {j++}values := []string{}for k := i; k < j; k++ {values = append(values, kva[k].Value)}output := reducef(kva[i].Key, values)// this is the correct format for each line of Reduce output.fmt.Fprintf(ofile, "%v %v\n", kva[i].Key, output)i = j}循环读取map保存下来的内容,这里写死了,后面需要调整。
读取内容后汇总并排序,排序后直接使用串行的Reduce代码即可
对于Coordinator,将Reduce的内容添加进去即可:
// 如果所有的Map任务都完成了,就遍历Reduce任务if isMapfinished {for i, reduceTask := range c.ReduceTask {if reduceTask.State == 0 {reply.Id = reduceTask.Idreply.TaskType = "reduce"reply.InputFileName = reduceTask.OriginFileNamereply.OutputFileName = reduceTask.OutputFileNamemu.Lock()c.ReduceTask[i].State = 1mu.Unlock()return nil}}}Reduce结束后需要告知主Coordinator在无限循环的Done(),返回True让其退出:
// main/mrcoordinator.go calls Done() periodically to find out// if the entire job has finished.func (c *Coordinator) Done() bool {ret := truemu.Lock()// Your code here.for _, v := range c.ReduceTask {if v.State != 2 {ret = falsebreak}}mu.Unlock()return ret}中间添加了锁,但是添加的有些问题,后面需要调整。
到这里的代码除了异常处理外已经都能测试通过了,只不过是有data race问题
问题:
首先将Coordinator对于任务的数据结构更改,内部维护三个双向链表,分别表示未开始的任务,正在进行的任务和已经结束的任务,链表外面使用map的数据结构,从而支持快速查找。在生成任务的时候自动赋值一个全局唯一的id。
数据结构中要包括全部的信息,主要变化部分是对输入和输出的信息,将Map的输入、输出和Reduce的输出都在初始化的时候直接写在结构体中,避免后续进行多次判断和修改。
结构体:
// Coordinator存储的主要信息,包括Map和Reduce两部分任务的信息以及工作节点的信息type Coordinator struct {UniqueIdSlice []*list.Element // 通过任务Id找到任务信息的切片,相当于一个MapMapTaskNum int // map任务总数量ReduceTaskNum int // reduce任务总数量WorkerNum int // 目前正在工作的节点数量MapTask // Map任务信息链表ReduceTask // Reduce任务信息链表WorkerInformation // Worker的信息}// Map任务信息链表,包括三个链表,分别表示未开始、正在进行和已经完成的任务type MapTask struct {MapListReady *list.List // 未开始的Map任务MapListRunning *list.List // 正在进行的Map任务MapListComplete *list.List // 已经完成的Map任务}// Reduce任务信息链表,包括三个链表,分别表示未开始、正在进行和已经完成的任务type ReduceTask struct {ReduceListReady *list.List // 未开始的Reduce任务ReduceListRunning *list.List // 正在进行的Reduce任务ReduceListComplete *list.List // 已经完成的Reduce任务}// Map任务具体信息type MapTaskInformation struct {Id int // 任务唯一编码OriginFileName string // 原始文件名称IntermediateFileName []string // Map任务完成后中间文件列表}// Reduce任务具体信息type ReduceTaskInformation struct {Id int // 任务唯一编码IntermediateFileName []string // Reduce的初始中间文件列表(从Map处获得)OutputFileName string // Reduce任务完成后的最终文件名称}Worker中分为几个步骤:
主程序如下:
// main/mrworker.go 调用的函数func Worker(mapf func(string, string) []KeyValue, reducef func(string, []string) string) {// 1. 告知Coordinator自己已经上线args := WorkerArgs{TaskType: "None"}reply := WorkerReply{TaskType: "None"}call("Coordinator.WorkerOnline", &args, &reply)// 无限循环向Coordinator请求任务for {// 2. 向Coordinator请求任务args = WorkerArgs{TaskType: "None"}reply = WorkerReply{TaskType: "None"}ok := call("Coordinator.AsssignTask", &args, &reply)if ok {fmt.Println("Call Success!")if reply.TaskType == "map" {fmt.Printf("Map Task!\n")// 读取文件,调用map函数进行处理intermediate := []KeyValue{}file, err := os.Open(reply.MapInput)if err != nil {log.Fatalf("cannot open %v", reply.MapInput)}content, err := io.ReadAll(file)if err != nil {log.Fatalf("cannot read %v", reply.MapInput)}file.Close()kva := mapf(reply.MapInput, string(content))intermediate = append(intermediate, kva...)// 循环创建NReduce个文件准备保存encoderList := make([]*json.Encoder, 0)for _, fileName := range reply.MapOutput {tempFile, err := os.Create(fileName)if err != nil {log.Fatalf("cannot create %v", fileName)}defer tempFile.Close()encoderList = append(encoderList, json.NewEncoder(tempFile))}// 将map后的结果存入文件中(最费时间)for i, v := range intermediate {encoderList[ihash(v.Key)%len(reply.MapOutput)].Encode(&intermediate[i])}// 3. 向Coordinator返回自己的Map任务已经完成args.TaskType = "map"args.Taskid = reply.Idcall("Coordinator.TaskFinish", &args, &reply)} else if reply.TaskType == "reduce" {fmt.Printf("Reduce Task!\n")// 创建输出文件ofile, _ := os.Create(reply.ReduceOutput)// 遍历输入文件,汇总Map产生的所有结果kva := make([]KeyValue, 0)for _, filename := range reply.ReduceInput {// fmt.Println(filename)file, err := os.Open(filename)if err != nil {log.Fatalf("cannot open %v", filename)}dec := json.NewDecoder(file)for {var kv KeyValueif err := dec.Decode(&kv); err != nil {break}kva = append(kva, kv)}}// 排序sort.Sort(ByKey(kva))// 在已经排好序的键值对上进行统计,并写入到文件中i := 0for i < len(kva) {j := i + 1for j < len(kva) && kva[j].Key == kva[i].Key {j++}values := []string{}for k := i; k < j; k++ {values = append(values, kva[k].Value)}output := reducef(kva[i].Key, values)fmt.Fprintf(ofile, "%v %v\n", kva[i].Key, output)i = j}// 4. 向Coordinator返回自己的Reduce任务已经完成args.Taskid = reply.Idargs.TaskType = "reduce"call("Coordinator.TaskFinish", &args, &reply)} else if reply.TaskType == "finish" {// 5. 向Coordinator返回自己退出的消息call("Coordinator.WorkerFinish", &args, &reply)fmt.Printf("Bye!\n")return}} else {fmt.Printf("Call failed!\n")}// 间隔1秒请求一次time.Sleep(time.Second)}}其中将RPC的发送和接收的结构体更改的更为合理:
// Worker向Coordinator传递的信息type WorkerArgs struct {Id int // Worker的唯一IDTaskid int // 任务全局唯一IDTaskType string // 任务类型}// Coordinator向Worker传递的信息type WorkerReply struct {Id int // 任务idTaskType string // 任务类型MapInput string // Map任务的输入MapOutput []string // Map任务的输出ReduceInput []string // Reduce任务的输入ReduceOutput string // Reduce任务的输出}// Worker告知Coordinator自己上线了func (c *Coordinator) WorkerOnline(args *WorkerArgs, reply *WorkerReply) error {mu.Lock()if c.WorkerNum == -1 {c.WorkerNum = 0}c.WorkerNum += 1mu.Unlock()return nil}这里暂时比较简单,后续需要进行处理,以进行异常处理
// Worker向Coordinator请求任务func (c *Coordinator) AsssignTask(args *WorkerArgs, reply *WorkerReply) error {mu.Lock()// 首先查看map任务是否已经全部完成,如果全部完成了就去完成Reduce任务,如果也全部完成了就发送Worker可以退出的消息// 判断方式:通过完成链表的节点数量与初始化时侯计算的数量是否相同if c.MapListComplete.Len() != c.MapTaskNum {// 分配map任务if c.MapListReady.Len() == 0 {// 没有没开始的Map任务reply.TaskType = "waiting"} else {// 将一个未完成的任务从未开始的链表中取出,插入到正在进行的链表里面e := c.MapListReady.Front()c.MapListReady.Remove(e)c.MapListRunning.PushBack(e)// 构建返回消息,告知Worker这个任务的信息reply.TaskType = "map"value := e.Value.(MapTaskInformation)reply.Id = value.Idreply.MapInput = value.OriginFileNamereply.MapOutput = value.IntermediateFileName}} else if c.ReduceListComplete.Len() != c.ReduceTaskNum {// 分配reduce任务if c.ReduceListReady.Len() == 0 {// 没有没开始的Reduce任务reply.TaskType = "waiting"} else {// 将一个未完成的任务从未开始的链表中取出,插入到正在进行的链表里面e := c.ReduceListReady.Front()c.ReduceListReady.Remove(e)c.ReduceListRunning.PushBack(e)// 构建返回消息,告知Worker这个任务的信息reply.TaskType = "reduce"value := e.Value.(ReduceTaskInformation)reply.Id = value.Idreply.ReduceInput = value.IntermediateFileNamereply.ReduceOutput = value.OutputFileName}} else {//告知Worker已经没有任务了,可以退出了reply.TaskType = "finish"}mu.Unlock()return nil}收到请求后操作全局链表,构建消息并返回即可
// Worker告知Coordinator刚才分配的任务已经完成func (c *Coordinator) TaskFinish(args *WorkerArgs, reply *WorkerReply) error {mu.Lock()// 将节点从正在进行的链表中取出,插入到已经完成的链表中if args.TaskType == "map" {// 操作节点e := c.UniqueIdSlice[args.Taskid]c.MapListRunning.Remove(e)c.MapListComplete.PushBack(e)// 如果是Map任务,需要将产生的nReduce个中间文件分配给Reduce节点for _, file := range e.Value.(MapTaskInformation).IntermediateFileName {// 计算是哪个Reduce节点reduceTaskNum, err := strconv.Atoi(strings.Split(file, "-")[2])if err != nil {log.Fatalf("cannot parseInt %v", file)}// 将产生的nReduce个中间文件分配给Reduce节点(需要重新构建节点)value := c.UniqueIdSlice[reduceTaskNum].ValuetempSlice := append(value.(ReduceTaskInformation).IntermediateFileName, file)c.UniqueIdSlice[reduceTaskNum].Value = ReduceTaskInformation{Id: value.(ReduceTaskInformation).Id,IntermediateFileName: tempSlice,OutputFileName: value.(ReduceTaskInformation).OutputFileName,}}} else if args.TaskType == "reduce" {// 操作节点e := c.ReduceListRunning.Remove(c.UniqueIdSlice[args.Taskid])c.ReduceListComplete.PushBack(e)}mu.Unlock()return nil}对于Map任务需要传递Map输出,Reduce输入的文件信息,将结构体填充完整
// Worker告知Coordinator自己退出了func (c *Coordinator) WorkerFinish(args *WorkerArgs, reply *WorkerReply) error {mu.Lock()// 退出时将Coordinator内部存储的Worker数量-1c.WorkerNum -= 1mu.Unlock()return nil}将全局的WorkerNum减去1,后续需要进行处理。
经测试,除异常检测完已经都能顺利pass,多次运行的结果也完全相同
有一个小问题是它的脚本给的超时时间不够,调大一些后才能顺利运行,后续可以进行更改。
原文与异常处理相关的部分:
The coordinator should notice if a worker hasn’t completed its task in a reasonable amount of time (for this lab, use ten seconds), and give the same task to a different worker.
The best you can do is have the coordinator wait for some amount of time, and then give up and re-issue the task to a different worker. For this lab, have the coordinator wait for ten seconds; after that the coordinator should assume the worker has died (of course, it might not have).
To test crash recovery, you can use the mrapps/crash.go application plugin. It randomly exits in the Map and Reduce functions.
可以先查看crash.go,看看是如何模拟线程崩溃的:
func maybeCrash() {max := big.NewInt(1000)rr, _ := crand.Int(crand.Reader, max)if rr.Int64() < 330 {// crash!os.Exit(1)} else if rr.Int64() < 660 {// delay for a while.maxms := big.NewInt(10 * 1000)ms, _ := crand.Int(crand.Reader, maxms)time.Sleep(time.Duration(ms.Int64()) * time.Millisecond)}}阅读代码,可以发现这个设置是有1/3的概率直接崩溃掉,有2/3的概率线程睡眠不到10s,模拟的环境还是比较简单的。
实现:
Worker部分:
Worker上线后,由Coordinator为其分配一个ID,随后在Worker的每一个rpc请求中都带有这个ID
WorkerID := reply.WorkerIDWorker上线后每5秒发送心跳信号给Coordinator,表明自己在线
// 心跳信号go func() {for {args := WorkerArgs{TaskType: "None"}args.Id = WorkerIDreply := WorkerReply{TaskType: "None"}time.Sleep(time.Second * 5)call("Coordinator.WorkerAlive", &args, &reply)}}()Coordinator部分:
维护一个切片结构体,索引表示Worker的ID,结构体内部包括任务ID和上一次心跳信号的时间
type HeartBeat struct {WorkID intTime int64}var WorkerList []HeartBeat接收到Worker上线的RPC后,记录当前的时间戳,记录任务ID为-1,即表示这个索引ID已经分配给Worker了
// 分配任务ID并记录时间WorkerList = append(WorkerList, HeartBeat{WorkID: -1,Time: time.Now().Unix(),})reply.WorkerID = len(WorkerList)接收心跳信号后更新切片结构体
// Coordinator接收心跳信号func (c *Coordinator) WorkerAlive(args *WorkerArgs, reply *WorkerReply) error {mu.Lock()WorkerList[args.Id-1].Time = time.Now().Unix()fmt.Printf("接收到%d心跳信号\n", args.Id-1)mu.Unlock()return nil}分配任务后在切片结构体内更新任务ID信息
WorkerList[args.Id-1].WorkID = value.Id开启协程每10秒检查切片结构体的时间戳,如果时间戳与当前时间间隔大于10秒,将任务的状态更改为未完成,重新分配。
// Worker信息存储WorkerList = make([]HeartBeat, 0)// 每间隔10秒进行验证go func() {for {time.Sleep(10 * time.Second)mu.Lock()for i := 0; i < len(WorkerList); i++ {if WorkerList[i].WorkID != -1 && time.Now().Unix()-WorkerList[i].Time > 10 {fmt.Printf("%d心跳信号过期\n", i)e2 := *(c.UniqueIdSlice[WorkerList[i].WorkID])// 这里不太懂为什么要这样写if WorkerList[i].WorkID < c.MapTaskNum {c.MapListRunning.Remove(&e2)c.MapListReady.PushBack(e2.Value)} else {c.ReduceListRunning.Remove(&e2)c.ReduceListReady.PushBack(e2.Value)}c.WorkerNum -= 1WorkerList[i].WorkID = -1}}mu.Unlock()}}()至此,可以单独通过全部的test,但是仍然存在一些问题
总之基本功能已经没有什么问题了,以后有时间再进行重构。
]]>(WordCount)
map(String key, String value):// key: document name// value: document contents for each word w in value: EmitIntermediate(w, "1");reduce(String key, Iterator values):// key: a word// values: a list of counts int result = 0; for each v in values: result += ParseInt(v); Emit(AsString(result));map函数输出每个单词和计数的数量,reduce汇总其中某个特定单词的数量并输出。
<target, source>键值对,reduce函数对目标URL汇总source并输出如上图所示,map的过程是在多机器上调用的,其中分配的过程是自动化的,共分配了个节点进行。reduce过程是通过用户指定的节点数量,通过某种方法(如计算哈希值等)分配
台机器进行。
其中有一个master节点,这个节点负责将任务进行分配,有些机器进行map操作,有些机器进行reduce操作等。
被分配到map任务的节点读取输入,将处理好的内容写入缓存,周期性的存入硬盘。存入时直接分为部分,并将数据存放的位置告知master
当一个节点被master通知要进行reduce时,通过RPC的方式从硬盘中读取数据到缓存中,进行处理并排序,保证相同的key出现在相同的位置
最终输出的时的文件,但是并不需要用户进行手动合并,因为这些文件通常是作为下一阶段的输入。
对于每一个map任务或者reduce任务,都要保存任务的状态(已经完成或者未完成)以及工作节点的信息
对于每一个完成后的map任务,还要保存完成后的中间数据的位置和大小等信息
机器太多了肯定有的机器会失效
Worker失效:Master会定期ping每一个Worker,如果没有得到响应,将这个节点标记为失效
Master失效:Master的数据要经常备份,且由于只有一个Master,不太可能失效(因为被保护好了?),因此如果Master失效了会终止整个任务
故障时处理的机制:用户提供的Map和Reduce操作是输入确定性函数时,分布式的计算要保证任何情况下的输出都要一致没有错误.
使用map和reduce的原子提交特点来实现。map和reduce操作都写入临时文件中,完成操作后通知Master节点。如果Master节点被通知了另外一次,则直接忽略掉。reduce操作结束后将临时文件重命名为最终输出的文件,重命名操作也是原子性,最终只会有一个符合条件的文件名。
尽量存储在本地的硬盘中,通过GFS把每个文件按64MB一个块,并在不同的机器上存储三份冗余的数据。
理想情况下和
都应该比物理节点数量大得多,在每台机器都执行大量的不同任务能够提高集群的动态的负载均衡能力,并且能够加快故障恢复的速度。
在我们的具体实现中对和
的取值有一定的限制,因为master必须执行
)次调度,并且在内存中保存
个状态(一个字节一个状态)
值通常由用户指定,实际使用中选择合适的
值,以使得每一个独立任务都是处理大约
到
的输入数据
MapReduce的合适执行比例:,
,使用
台机器节点
在运算过程中,如果有一台机器花了很长的时间才完成最后几个Map或Reduce任务,会导致MapReduce操作总的执行时间超过预期。
当一个MapReduce操作接近完成的时候,master会调度备用任务进程来一起执行最后的任务,谁完成了整个任务都算完成。
在具体的实现上,对上面描述的简单mapreduce过程可以进行优化
MapReduce的成功取决于采用MapReduce库能够在不到半个小时时间内写出一个简单的程序,这个简单的程序能够在上千台机器的组成的集群上做大规模并发处理,极大的加快了开发和原形设计的周期。另外,采用MapReduce库,可以让完全没有分布式和/或并行系统开发经验的程序员很容易的利用大量的资源,开发出分布式和/或并行处理的应用。
MapReduce的成功有几个方面:
从MapReduce开发过程中也学到了不少东西。
判断系统是否正常工作非常困难,例如两台机器间的网络挂掉,两边都认为对方挂掉了,因此对外提供了两份服务。
课程不关注应用程序,只关注基础设施,也就是支撑这些应用程序正确工作的部分。
关注的三个方面:存储、计算和通信
抽象:分布式系统的抽象与单机系统的抽象基本相同
容错机制
一致性:分布式系统与单机的行为相同
性能:不同类型的一致性和容错机制与性能相关
实现细节:如何实现并发、远程过程调用等等
在Google早期的数据中心,有一个搜索引擎,需要构建万维网的倒排索引,允许用户上网查询。
在这个过程中处理TB级别的数据需要耗费几个小时。
为每一个应用都编写一个这种系统很困难,因此提出了MapReduce,使得构建不同应用的分布式程序比较轻松
不过这些应用必须要能分成map和reduce两个部分,然后放到MapReduce框架下运行,不需要再关注其他细节(如容错机制等等)
主要的网络通信在于传输map产生的中间文件给reduce使用
如果一个机器在一定的时间内没有对Coordinator作出响应,就认为这个机器已经挂掉了,因此Coordinator会重新安排其他机器重启它的任务。
map和reduce任务可能会运行两次,例如Coordinator认为这个机器挂掉了,把它的任务分配给别人了,但是实际上这个机器并没有挂掉。最终使用重命名操作的原子性确保只存储一个结果。
Coordinator会挂掉吗?挂掉了整个任务就都要重新跑了,一般不会挂掉。
一些机器可能会运行很慢从而拖累整个任务的进程。当整个任务快要结束的时候,会复制任务到其他的空闲节点上一起做,谁先做完取谁的。
]]>监督学习:贝叶斯分类器、支持向量机、Logistic回归、决策树、线性回归、最大熵、CRF
无监督学习:主成分分析、K-Means、高斯混合聚类、层次聚类
线性分类方法:感知机、线性鉴别分析、最小距离分类器
非线性分类方法:决策树、最近邻、集成学习、核SVM
线性分类器最佳准则:感知准则函数、支持向量机、Fisher准则
生成式模型:朴素贝叶斯、隐马尔可夫模型、高斯混合模型
判别式模型:支持向量机、线性分类器、神经网络、线性判别分析
Logistic回归使用最大似然估计
回归问题和分类问题的区别:前者预测函数值为连续值,后者为离散值
最小二乘回归方法的等效回归方法:线性均值和正态误差的最大似然回归
正则化的回归分析,可以避免过拟合
假如使用一个较复杂的回归模型来拟合样本数据,使用岭回归,调试正则化参数λ,来降低模型复杂度。若λ较大时,偏差增大,方差减小
在线性回归中使用正则项,你发现解的不少coefficient都是0,这个正则项可能是L0-norm或L1-norm
LR模型的损失函数是交叉熵
在Logistic Regression 中,如果同时加入L1和L2范数,可以做特征选择,并在一定程度上防止过拟合
逻辑斯蒂回归没有利用回归的思想
二项式分布的共轭分布是Beta分布
多项式分布的共轭分布是Dirichlet分布
朴素贝叶斯分类器的特点是假设样本各维属性独立
最大似然估计没有考虑先验分布
对于正态密度的贝叶斯分类器,各类协方差矩阵相同时,决策函数为线性决策函数
下面关于贝叶斯分类器描述错误:是基于后验概率,推导出先验概率
朴素贝叶斯模型属于生成式模型
贝叶斯分类器参数估计的准则:最大高斯后验、最大beta后验、极大似然
错误:以贝叶斯估计的角度来看朴素贝叶斯时,其没有估计联合概率
以下模型中属于贝叶斯网络的有( BD )
A.马尔可夫随机场
B.隐马尔可夫模型
C.条件随机场
D.朴素贝叶斯分类器
支持向量机属于判别式模型
SVM的原理:最大间隔分类
SVM的算法性能取决于:核函数的选择、核函数的参数、软间隔参数C
支持向量机的对偶问题是凸二次优化
支撑向量:最大间隔支撑面上的向量
避免直接的复杂非线性变换,采用线性手段实现非线性学习的方法是:核函数方法
软间隔SVM的阈值趋于无穷:只要最佳分类超平面存在,它就能将所有数据全部正确分类
核函数并不是把特征映射到的空间维度越高越好
如果SVM模型欠拟合, 以下方法哪些可以改进模型:增大惩罚参数C的值,增大核系数(gamma参数)
密度聚类方法充分考虑了样本间的密度可达关系
混合高斯聚类使用了EM算法
k-means算法初始值不同,最终结果可能不同
k-means不适合处理非凸型数据
以下可用于聚类性能测量的评估方法:Jaccard系数、FM指数、Rand指数、DB指数
主成分分析方法是一种降维方法
PCA在做降维处理时,优先选取中心化样本的协方差矩阵的最大特征值对应特征向量
可以用于特征降维的:SVD、PCA和LDA
不可以用于特征降维的:蒙特卡洛方法
特征降维带来的好处:节省数据通信开销、节省数据存储资源、加快模型计算速度
关于决策树节点划分指标描述正确的是信息增益越大越好
决策树不受数据归一化影响,SVM、神经网络、Logistic回归都会受影响
增加决策树的深度可能导致随机森林模型过拟合数据
我们想在大数据集上训练决策树, 为了使用较少时间, 我们可以减少树的深度,减少树的数量
Bootstrap数据:有放回地从总共N个样本中抽样n个样本
集成学习中基分类器多样,差异大,学习效率通常越好,每个基分类器的正确率的最低要求50%以上
Bagging方法的特点:构造训练集时采用Bootstraping的方式
Boosting方法的特点:预测结果时,分类器的比重不同
随机森林方法属于Bagging方法
Adaboost算法:
Adaboost方法中,需要迭代调整的两个重要参数是:样本权重和分类器权重
以下关于深度网络训练的说法正确的:
在训练神经网络时,如果出现训练error过高,增加训练数据不能大幅度降低训练error
Tanh可以导致梯度消失
ReLU在神经网络中引入了非线性
关于CNN,Pooling层用于减少图片的空间分辨率
卷积神经网络可以有多个卷积核,可以不同大小
GRU和LSTM的说法正确的是:GRU的参数比LSTM的参数少
与普通反向传播不同的是,BPTT会在每个时间步长内叠加所有对应权重的梯度
在RNN中,梯度裁剪可以较好地处理梯度爆炸问题
循环神经网络有反馈连接并常被用来处理序列数据
数据增强会增加模型的欠拟合风险
过拟合现象中训练样本的测试误差最小,测试样本的正确识别率却很低
过拟合:训练误差小,测试误差大
容易引起过拟合:SVM算法中使用高斯核代替线性核
不容易引起过拟合:增加训练集量、减少神经网络隐藏层节点数、删除稀疏的特征
神经网络处理过拟合:Dropout、Batch Normalization、regularization
在HMM中,如果已知观察序列和产生观察序列的状态序列,那么可用极大似然估计直接进行参数估计
解决隐马模型中预测问题的算法是维特比算法
K-NN最近邻方法在什么情况下效果好:样本较少但典型性较好
以下可行的最近邻分类的加速方案:分层搜索和训练样本缩减
线性鉴别分析:找到一个投影方向,使得类内距离最小,类间距离最大
KL散度是根据类概率密度构造的可分性判据
最大似然估计没有考虑先验分布
多层感知机方法中,可用作神经元的非线性激活函数:logistic 函数
在有限支撑集上,均匀分布的熵最大
已知均值和方差,高斯分布的熵最大
受限玻尔兹曼机属于概率图模型
余弦距离会侧重考虑向量的方向
除了EM算法,梯度下降也可求混合高斯模型的参数
下列哪个不属于常用的文本分类的特征选择算法(D)
A. 卡方检验值
B. 互信息
C. 信息增益
D. 主成分分析
解决样本类别不平衡的手段:欠采样、过采样、使用focal loss
对于k折交叉验证, 以下对k的说法正确的是:
A.k越大, 不一定越好, 选择大的k会加大评估时间
B.选择更大的k, 就会有更小的bias ,因为训练集更加接近总数据集
C.在选择k时, 要最小化数据集之间的方差
下列选项中,关于KNN算法说法不正确的是(D)
A.能找出与待测样本相近的K个样本
B.可以使用欧氏距离度量相似度
C.实现过程相对简单,但是可解释性不强
D.效率很高
73.关于特征预处理,下列说法中错误的是(B )
A.包含标准化和归一化
B.标准化在任何场景下受异常值的影响都很小
C.归一化利用了样本中的最大值和最小值
D.标准化实际上是将数据在样本的标准差上做了等比例的缩放操作
交叉验证不能够提升模型的准确率
76.EM算法(Expectation Maximization Algorithm)是机器学习领域的一个经典算法,下面关于EM算法的说法中不正确的有:(A)
A.EM算法属于一种分类算法
B.EM算法可用于隐马尔科夫模型的参数估计
C.EM算法可以分为E-step和M-step两步
D.EM算法可用于从不完整的数据中计算最大似然估计
将一个k分类问题分解成一对一问题时总共需要k(k-1)/2个分类器
在有限支撑集上,下面分布中熵最大的是均匀分布
在机器学习中,当模型的参数量大于样本量时参数估计使用梯度下降法
A. GRU通过output gate控制memory;
B. LSTM对memory不做控制,直接传递给下一个unit
C. GRU不对上一时刻的信息做任何控制;
D. GRU的参数比LSTM的参数少;
以下哪些算法, 可以用神经网络去构造( BD )
A.KNN
B.Logistic回归
C.决策树
D.最小二乘估计
给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近,异类样例的投影点尽可能远离;
在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来判断新样本的类别。
答案:SVM是一个分类算法,它的目标为确定一个分类超平面,从而将不同类别的数据分隔开达到分类的目标。
当训练数据线性可分时,通过硬间隔最大化,学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机;
当训练数据近似线性可分时,通过软间隔最大化,也学习一个线性的分类器,即线性支持向量机,又称为软间隔支持向量机;
当训练数据线性不可分时,通过使用核技巧及软间隔最大化,学习非线性支持向量机。
给定训练集,SVM最优决策边界由支持向量决定。
当增加噪声时,那么该噪声有极高的可能是含噪声训练集的一个支持向量,这意味着决策边界需要变。
不引入非线性激活函数的情况下,不管神经网络有多少层其输出都是输入的线性组合,与没有隐藏层的效果相当
在实际问题中,我们使用的样本通常是多维数据,每一维对应一个特征,这些特征的量纲和数量级都是不一样的
这时需要对数据进行标准化处理,试所有的特征具有同样的尺度
如果单用线性函数作为激活函数,无论多少层的神经网络会退化成一个线性回归,不能处理非线性分类任务。
如果学习率太低,每次下降的很慢,使得迭代次数非常多。
如果学习率太高,在后面迭代时会出现震荡现象,在最小值附近来回波动。
前面层上的梯度是来自于后面层上梯度的乘积。当存在过多的层次时,且激活函数的梯度小于1时,就会使前面层的梯度变得很小,更新速度过慢,导致梯度消失。
一种解决方案是使用Relu激活函数替换sigmoid,relu函数的梯度不会随着x的增大而变小,sigmoid在x取值较大时梯度趋近于0。
对3个32×32的特征图进行卷积层操作,卷积核10个5×5,Stride是1,pad为2,输出特征图的尺度是多少?卷积层的参数是多少?写出公式和结果。
输出尺度:(N+2P-F)/stride+1
卷积层的参数:(F×F×n+1)×N
答案:输出尺度( 32+2×2-5)/1+1 = 32
卷积层的参数 (5×5×3+1)×10=760
随机森林是Bagging算法的一个扩展变体,以决策树为基学习器构建Bagging集成,
Bagging在选择划分属性时需要考察结点的所有属性,而随机森林只需随机地考察一个属性子集
所以随机森林比决策树Bagging训练速度更快,泛化能力越强。
L1范数为向量各个元素绝对值之和可以使权值稀疏,方便特征提取。
L2 范数为向量各个元素平方和的1/2次方可以防止过拟合,提升模型的泛化能力。
基于L1范数的特征选择:不能直接设置最终选择特征的个数k;通过设置正则化系数λ来隐式控制k;
λ值越大,模型越关注稀疏性,得到的非零系数个数越少;
反之,非零稀疏个数越多;
可以设置一个选择特征个数的上限,通过设置不同λ值,得到满足要求的特征。
从有条件极值问题的角度来看,L1范数相当于将模型界空间限制在了L1-ball上,目标函数的等高线有很大的概率与坐标轴和边相交,这样的解具有稀疏性。
根据给定的训练集,其中
,要求寻找
上的决策函数
。
泛化误差 = 偏差+方差+噪声
偏差:度量了学习算法的期望预测与真实结果的偏离程度,刻画了学习算法本身的拟合能力
方差:度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响
噪声:表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即刻画了学习问题本身的难度
过拟合是指模型对于训练数据拟合呈过当的情况,反映到评估指标上,就是模型在训练集上的表现很好,但在测试集和新数据上的表现较差。
欠拟合是模型在训练和预测时表现都不好的情况。
降低过拟合:
降低欠拟合:
K均值算法缺点:例如受初值和离群点的影响每次的结果不稳定、结果通常不是全局最优而是局部最优解、无法很好地解决数据簇分布差别比较大的情况、不太适用于离散分类等。
K均值聚类的优点:主要体现在对于大数据集,K均值聚类算法相对是高效的,计算复杂度是 O(NKt) 接近于线性,其中N是数据对象的数目,K是聚类的簇数,t 是迭代的轮数。
调优方法:数据归一化,离群点预处理,采用核函数,合理选择K值。
优点:
缺点:
在较大学习率设置下Relu可能会出现大量神经元死亡问题。后面神经元方向传播梯度为正,且学习率较大,Relu的梯度为1,梯度下降此时会导致该神经元的参数为负值,可能之后不会再被激活,造成神经元死亡。
生成模型估计的是联合概率分布,然后求出条件概率分布P(Y|X)作为预测的模型,即生成模型:P(Y|X)= P(X,Y)/ P(X)。
生成方法关心的是给定输入x产生输出y的生成关系。
判别模型估计的是条件概率分布,有数据直接学得决策函数P(X)或者条件概率分布P(Y|X)作为预测的模型。
判别式方法关心的是给定输入X,应该预测什么样的输出Y
不同之处:
相同之处:
根据最大熵模型, 推导出x概率密度函数是一个常函数,所以最大熵分布为均匀分布。
根据最大熵模型推导出x概率密度函数是一个高斯分布 。
写出概率图模型联合分布的因子分解式
无向图看团,有向图看条件概率
贝叶斯网络计算概率
前向算法
后向算法
维特比解码
Kmeans:
层次聚类自底向上:初始每一个点为一类,逐步合并更新中心即可,注意更新的时候要使用原始的点重新进行计算
贝叶斯最小错误分类
贝叶斯最小风险
抛一枚硬币问题,观察数据情况是:一枚硬币包括正反两面,共抛了30次,其中12次是正面,18次是反面。采用Maximum Likelihood方法,估计正面出
现的概率和反面出现的概率。
在机器学习中常常采用基于数据驱动的方法进行图像分类。所谓基于数据驱动的方法,就是给计算机很多数据,然后实现学习算法,让计算机学习到每个类的外形的方法。基于这种方法的完整流程如下
[
人工智能的三大主义:行为主义、联结主义、符号主义
图灵测试是做什么的?给几个论断,哪些是哪些不是?
图灵测试:一个人(C)在完全不接触对方(A和B)的情况下,和对方进行一系列的问答,如果在相当长时间内,他无法根据这些问题判断对方是人(B)还是计算机(A),那么,就认为该计算机具有同人相当的智能(即计算机是能思维的)。
g(x)为从根节点到x节点的代价总和
h(x)为从x节点到目标节点的估计代价总和
代价一致搜索 f(x) = g(x)
贪婪搜索 f(x) = h(x)
A*搜索 f(x) = g(x) + h(x)
蚁群优化算法和粒子群优化算法是群体智能优化算法的两个代表,请从蚁群优化算法和粒子群优化算法中任选一个阐述其基本原理、算法过程及适用范围。
基本原理:
粒子群优化算法中的每个粒子模拟一只鸟,代表待求解问题搜索解空间中的一个潜在解,“飞行信息”包括粒子当前的位置和速度两个状态量。每个粒子都可以获得其邻域内其它个体的信息,对所经过的位置进行评价,并根据这些信息和位置速度更新规则,改变自身的两个状态量,随着这一过程的不断进行,粒子群最终能够找到问题的近似最优解。
算法过程:
适用范围:适用于求解连续解空间的优化问题
基本原理:
蚁群算法是一种用来寻找优化路径的概率型算法。用蚂蚁的行走路径表示待优化问题的可行解,整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多,随着时间的推进,较短的路径上累积的信息素浓度逐渐增高,选择该路径的蚂蚁个数也愈来愈多。最终,整个蚂蚁会在正反馈的作用下集中到最佳的路径上,此时对应的便是待优化问题的最优解。
算法过程:
其中表示边
上的信息素浓度,
是根据距离定义的启发信息,
和
反映了信息素与启发信息的相对重要性
其中: 为常数,
表示第
只蚂蚁在本轮迭代中走过的路径,
为路径长度,
为小于1的常数,反映信息素挥发速度
适用范围:适用于求解离散解空间的优化问题,适用于在图上寻找最优路径
A*树搜索的最优性条件
A*图搜索的最优性条件
传教士和野人问题通常描述如下:三个传教士和三个野人在河的一边,还有一条能载一个人或者两个人的船,找到一个方法让所有的人都渡到河的另一岸,要求在任何地方野人数都不能多于传教士的人数(可以只有野人没有传教士)。
(1) 精确地形式化该问题,只描述确保该问题有解所必须的特性,画出该问题的完全状态图
(2) 用一个合适的算法实现和最优地求解该问题,检查重复状态是个好主意吗?
采用先深搜索、先广搜索以及图搜索都可以,注意检查重复状态,重复状态的检测避免程序陷入死循环。
(3) 这个问题的状态空间如此简单,你认为为什么人们求解他却很困难?
虽然状态空间比较简单,但是要检测重复状态是一个困难:另外,在当前状态选取下一个合法状态,要能够不漏举所有合法状态也存在困难,当在某个状态无下一个合法状态时,需要回溯,这些都使得人为求解它变得困难
已知知识库里包含如下的句子:
请用归结原理证明该知识库蕴含如下的句子:$\neg A \land \neg B $
Forward chain 证明7<3+9
kb中所有句子都为definite子句,请构造一种真值指派使得kb中所有子句为真
将所有的原子命题指派为True即可。
归结原理及证明:
设计一个可靠但不完备的规则
描述语义蕴含、的作用
设计A*启发式函数来使归结次数最少
构想一个A启发式函数,使得A归结结果为最优,并证明
h(n)为集合中的最短子句的长度
胜者为王,败者为寇
不到长城非好汉,到了长城就是好汉;两个句子是否语义等价,并证明
成绩好的人都很刻苦,刻苦的人,一定成绩好;两个句子是否语义等价,并证明
理发师只给不给自己理发的人理发
将如下的一阶谓词逻辑的句子转化为合取范式:(不需要包含存在量词)
构造一个一阶谓词逻辑的知识库和句子
,使得
的归结过程永远不会停止。
(刻画模糊量词、模糊修饰词等)
很少有成绩好的学生特别贪玩
很少有成绩好的学生特别喜欢玩游戏
普通编程的步骤:了解问题-收集条件-寻找解决方法-编程解决-将问题数据化-用程序运行数据-debug
逻辑编程的步骤:了解问题-收集条件-不寻找解决方法-将条件写进KB-将问题转换为fact-问query-寻找错误的事实
C :- A,B 如果AB,则implyC(definite 子句)
[E | L]:将list拆解成第一个是E,后面的剩下
trace 和 notrace是debug的过程
DFS+backward chaining
不教程序怎么算,只列出事实
Prolog缺点:
谱方法:在谱空间中定义卷积:
空间方法:在向量空间中定义卷积
谱方法是空间方法的特例
聚合,更新是什么?
图神经网络的框架:聚合邻居节点的信息从而更新中心节点的表示
GraphSAGE:从每个结点开始随机游走,采样个结点,不用临近度指标判断。然后通过聚合函数进行参数共享
图卷积网络(GCN):通过归一化的拉普拉斯矩阵从不固定数量的邻居结点中聚合信息,通过特征变换共享参数
证明感知机不能表示异或逻辑
异或的逻辑为:
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
两个变量的感知机模型为
代入上面的异或逻辑:
因此感知机不能表示异或逻辑
设计用于异或问题的二层感知机
(以下简答题目答案来源于shmily)
描述BP算法
BP算法由正向传播与反向传播两个过程组成。正向传播时,输入由输入层经过隐藏层到输出层;反向传播时,输出结果与真实结果通过损失函数计算误差,误差信号再沿相反方向传播至输入层,获得各层各单元的误差信号(梯度),并将其作为修正权值的依据。通过梯度下降算法更新权值,使得网络的整体误差迭代减小。
试论述在深度神经网络中BP算法遇到的困难,并说明为什么会出现“梯度消失”问题
当网络变深时,BP算法会遇到梯度消失或者梯度爆炸的现象,此时浅层的神经元几乎接受不到来自输出层的误差信号或者误差太大,无法更新其参数或参数剧烈波动。
根据链式求导法则,浅层参数的梯度来源于深层参数梯度的乘积。由于中间梯度矩阵的范数可能远小于1,再加上许多激活函数的导数小于1,随着传播层数的增多,误差信号反向传播的过程中以指数形式衰减,当传播到浅层时便出现了梯度消失现象。
简述对抗式生成网络(GAN)的基本原理及其学习算法
GAN的思想来源于博弈论当中的均衡理论,其由生成器G与判别器D构成。生成器G希望生成更接近于真实分布的数据,判别器则希望尽可能分辨所给数据是由生成器生成的还是从真实分布中采样的。
GAN的学习算法交替地更新判别器D与生成器G:
首先训练判别器D,
接着训练生成器G,
重复进行以上各步骤直至收敛。
描述ResNet(ResNet的原理和结构图)
ResNet由如下多个Residual Block堆叠构成
残差网络容易优化恒等式函数,学习优化残差映射比原始映射更加容易,随着网络加深,网络至少不会变得更差,有效地缓解了梯度消失等现象;此外,残差连接隐式地扩展了模型的特征空间,可以看作一种模型集成。
利用RNN构建一个翻译器
采用编码器-解码器结构,二者都是RNN网络,示意图如下:
其中,编码器RNN接受输入(原文token) ,并通过RNN结构编码隐藏状态
。编码器编码完成后所有隐藏状态聚合为背景向量
。
解码器的RNN同样编码隐藏状态,并将编码的隐藏状态
映射到预测结果
,计算
与
间的损失来完成模型的训练
预测时,通过自回归与束搜索的方式得到翻译序列。
多臂赌博机:
一台赌博机有多个摇臂,每个摇臂摇出的奖励大小不确定,玩家希望摇固定次数的臂所获得的期望累积奖励最大
优化目标:期望累计奖励最大化
探索和利用的关系:
策略:
马尔可夫状态过程的要素:
奖励假设:最终目标是通过最大化累积的Reward实现的
策略学习方法:
博弈的要素
剪刀石头布:所有玩家的收益之和为0-零和博弈
最佳应对:针对局中人2的策略t,若局中人1用策略s产生的收益大于或等于其任何其他策略,则称策略s是局中人1对局中人2的策略t的最佳应对
纳什均衡:如果一个局势下,每个局中人的策略都是相对其他局中人当前策略的最佳应对,则称该局势是一个纳什均衡
帕累托最优:对于一组策略选择(局势)若不存在其他策略选择使所有参与者得到至少和目前一样高的回报,且至少一个参与者会得到严格较高的回报,则这组策略选择为帕累托最优。(“不可能再改善某些人的境况,而不使任何其他人受损。”)
社会最优:使参与者的回报之和最大的策略选择,社会最优的结果一定也是帕累托最优的结果
应用案例:
讨价的对象是双方对商品估价之差
maxmin策略:最大化自己最坏情况时的效用
minmax策略:最小化对手的最大效用
零和博弈情况下:
匹配市场:
市场结清价格:给定买方报价的情况下,如果卖方的某种价格使得对应的买方偏好图中存在完全匹配,则称卖方的这组价格为市场结清价格。市场结清价格总是存在,且使得买卖双方总效用最优。
议价权:
不稳定边:对于结局中未参与配对的边,如果边的两个端点获得的收益之和小于1,则称这条边为不稳定边,不稳定边的存在意味着其两个端点可以通过改变报价而改变结局
稳定结局:如果一个结局中不存在不稳定边,则称该结局为稳定结局
纳什议价解:
均衡结局:给定一个结局,如果结局中的任意一个参与配对的边都满足纳什议价解的条件,则称该结局是均衡结局
均衡结局一定是稳定结局
画一个图,什么什么路径,上课那种,阻断、D分离
后门准则:Z满足关于(X,Y)的后门准则
模式识别:利用计算机对物理对象进行分类,在错误概率最小的条件下,使识别的结果尽量与客观物体相符合
在特征空间和解释空间之间找到一种映射关系:
机器学习:利用大量的训练数据,获得产生数据的模式或预测
什么是线性判别函数?
统计模式识别中用以对模式进行分类的一种最简单的判别函数称为线性判别函数。线性判别函数的一般形式是,其中
是特征向量的增广形式,
是权重系数。根据
的取值进行分类,这个函数在几何上一般表现为直线(高维空间的超平面),所以称之为线性判别函数。
为什么需要非线性判别函数?
对于复杂的实际应用,线性分类器往往无法满足要求,不同类别的样本之间并不总是线性可分的,比如著名的异或问题,这就需要寻找能够实现非线性分类的判别函数分类器。
多类情况:
权重分量数量计算:,
为
的维度,
为多项式次数。
多类情况增广向量不需要变为负数,要求这个类别的比其他的类别都要大,否则这个类别+样本,其他的类别-样本
H-K算法可以发现类别不可分的情况
期望风险:机器学习算法的目标就是降低式所示的期望泛化误差(这个数据量被称为风险),选择期望风险最小的模型。
经验风险:用训练集的分布代替真实情况下的数据分布,最小化训练集上的期望损失
结构风险:在经验风险最小化的基础上再引入参数的正则化来限制模型能力,使其不要过度地最小化经验风险
简述偏差方差分解及其推导过程,并说明偏差、方差和噪声三部分的内在含义
过拟合:当学习器把训练样本学的“太好”了的时候,很可能已经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质,在训练集上效果好。但是在测试集上效果差,这样就会导致模型的泛化性能下降。
欠拟合:模型尚未学习到数据的真实结构。在训练集和验证集上的性能都很差。
如何判断一个模型处在过拟合状态还是欠拟合状态?
给出3种减轻模型过拟合的方法:
过拟合:
欠拟合:
假设某研究者在 ImageNet 数据上使用线性支持向量机 Linear SVM 来做文本分类的任务,请说明在如下情况下分别如何操作才能得到更好的结果, 并说明原因。
如果使用SVM做二分类问题得到如下结果,分别应该采取什么措施以取得更好的结果?并说明原因。
如果使用逻辑回归算法做二分类问题得到如下结果,分别应该采取什么措施以取得更好的结果?并说明理由。
2018-2019
2021-2022
径向基函数(RBF)gamma和C的影响:
最小化VC维h等价于最大化间隔,使分类器的复杂度小!
简述SVM算法的原理
K均值:CE
密度:AF
高斯混合:BD
Kmeans:Kmeans的判别界面应该是簇的中垂线
K-Means与GMM
K-Means
GMM
层次聚类:最小距离层次聚类可以做同心圆相关聚类
DBSCAN
PCA的优化目标:
平滑假设:如果高密度区域中两个点距离较近, 那么对应的输出
也应该接近
聚类假设:如果两个点在同一个簇,那么它们很有可能属于同一个类别
流形假设:输入空间由所有数据点所在的多个低维流形构成,位于同一流形上的数据点具有相同的标签,流形上距离近的点的标签相似
自我训练算法:假设输出的高度置信的预测是正确的
协同训练:假设特征可分裂,
或
单独对于训练一个好的分类器是充分的,
和
在给定类别后是条件独立的
生成式模型:假设所有数据(带标签&不带标签)都由一个潜在的模型生成(GMM,HMM,朴素贝叶斯)
半监督支持向量机:假设来自不同类别的无标记数据之间会被较大的间隔隔开
基于干扰的半监督:基于连续性假设:考虑对输入稍加改变,得到其增广表示
,模型对
的预测和对原始数据点的预测
相似。
基于图的半监督学习:假设在所有数据点(标注数据和无标注数据)定义一个相似性图,相似的数据点之间存在边,边的权重表示两个数据点之间的相似程度,相似图中“紧密”连接的点趋向于有相同的标签
贝叶斯球:
降低模型的方差,偏差不变
原理:通过对训练样本进行bootstrap采样(有放回的随机采样),然后训练多个模型,最后对多个模型作平均,得到最后的融合模型。
Bagging适合对偏差低、方差高的模型进行融合,如决策树、神经网络等
降低模型的偏差,方差不变
原理:每次迭代顺序的把一些模型加进去,最后一些子模型的加权平均是我们最后的集成模型
Adaboost:在弱学习器失败的样本上,学习第二个弱学习器
开始初始化的时候每个样本的权重相同
分对的样本,其权重除以,权重减小
分错的样本,其权重乘以,权重增大
最后对模型进行加权融合
Adaboost 原理:先从初始训练集训练出一个学习器,再根据基学习器的表现来对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续得到更多的关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直到基学习器达到事先指定的值T,最终将这T个基学习器进行加权结合。
Adaboost 损失函数:使用指数损失函数
Adaboost算法流程:
为什么AdaBoost经常可以在训练误差为0后继续训练还可能带来测试误差的持续下降?
在训练误差下降到接近0的时候,更多的训练,会增加分类器的分类margin,这个过程也能够防止测试误差的上升,随着Margin的变大,测试误差会逐渐收敛。
AdaBoost优缺点:
优点:实现快速简单、灵活、通用性高
缺点:AdaBoost性能取决于数据和弱学习器,如果弱分类器过于复杂,可能会产生过拟合情况,如果弱分类器太弱有可能造成欠拟合,还容易收到均匀噪声的影响。
Sigmoid函数:
在早期的神经网络中较为普遍,逐渐被更简单的ReLU函数取代
容易导致梯度消失问题:
Tanh函数:形状和sigmoid函数的形状很像,但tanh函数在坐标系的原点上对称:使用tanh激活函数收敛会更快,减轻消失梯度的现象
ReLU函数:
梯度爆炸:梯度值超出范围:无穷大值
对学习率敏感
梯度消失:梯度值趋近0
无论如何选择学习率,训练都没有进展
只有顶层训练有效,底层训练基本无效,使网络更深可能并没有更好
模型的深度增加,梯度会逐渐消失:
其他技巧:
FIFO:先淘汰缓存中最早添加的记录
LFU:淘汰缓存中访问频率最低的记录,需要维护一个访问频率的表
LRU:最近最少使用,认为如果数据最近被访问过,那么将来被访问的概率也会更高。维护一个队列,如果一条记录被访问,则移动到队列尾端,这样保证队首一定是最近最少访问的数据
package lruimport "container/list"// LRU cache 结构体type Cache struct {maxBytes int64 // 允许使用的最大内存nbytes int64 // 当前已使用的内存ll *list.List // cache链表cache map[string]*list.Element // 查找键值对的字典OnEvicted func(key string, value Value) // 某条记录被移除时的回调函数}// 双向链表节点的数据类型// 主要目的是为了删除节点后能从字典中删除该键值对type entry struct {key stringvalue Value}// 值的类型可以是任意的,定义一个空接口,实现Len()方法返回值的占用空间大小// Len the number of cache entriesfunc (c *Cache) Len() int {return c.ll.Len()}type Value interface {Len() int // 包含一个方法返回值占用的内存大小}// 工厂模式,返回实例化的cachefunc New(maxBytes int64, onEvicted func(string, Value)) *Cache {return &Cache{maxBytes: maxBytes,ll: list.New(),cache: make(map[string]*list.Element),OnEvicted: onEvicted,}}// 查找功能,在字典中进行查找,然后移动到队尾(Front)func (c *Cache) Get(key string) (value Value, ok bool) {if ele, ok := c.cache[key]; ok {c.ll.MoveToFront(ele)kv := ele.Value.(*entry)return kv.value, true}return}// LRU删除策略:从队首(Back)拿到节点,然后将其删除func (c *Cache) RemoveOldest() {ele := c.ll.Back()if ele != nil {c.ll.Remove(ele)kv := ele.Value.(*entry)delete(c.cache, kv.key)c.nbytes -= int64(len(kv.key)) + int64(kv.value.Len()) // 更新当前已经使用的内存if c.OnEvicted != nil {c.OnEvicted(kv.key, kv.value)}}}// 新增节点/修改节点func (c *Cache) Add(key string, value Value) {// 如果在链表中找到则将其更新,同时更新占用的空间大小等,并移动到队列尾端if ele, ok := c.cache[key]; ok {c.ll.MoveToFront(ele)kv := ele.Value.(*entry)c.nbytes += int64(value.Len()) - int64(kv.value.Len())kv.value = value} else { // 如果找不到则直接插入ele := c.ll.PushFront(&entry{key, value})c.cache[key] = elec.nbytes += int64(len(key)) + int64(value.Len())}// 如果占用空间超过了链表的最大空间,则删除掉队首的节点for c.maxBytes != 0 && c.maxBytes < c.nbytes {c.RemoveOldest()}}多个协程(goroutine)同时读写同一个变量,在并发度较高的情况下,会发生冲突。确保一次只有一个协程(goroutine)可以访问该变量以避免冲突,这称之为 互斥,互斥锁可以解决这个问题。
当一个协程调用了 Lock() 方法时,其他协程被阻塞了,直到 Unlock()调用将锁释放。因此被包裹部分的代码就能够避免冲突,实现互斥。
抽象了一个只读数据结构 ByteView 用来表示缓存值:
package geecache// 只读数据结构用来表示缓存值type ByteView struct {b []byte}// 返回缓存值的长度func (v ByteView) Len() int {return len(v.b)}// 返回拷贝从而防止这个值被外部操作修改func (v ByteView) ByteSlice() []byte {return cloneBytes(v.b)}// 将数据作为一个字符串进行返回func (v ByteView) String() string {return string(v.b)}func cloneBytes(b []byte) []byte {c := make([]byte, len(b))copy(c, b)return c}为 lru.Cache 添加并发特性(加锁):
package geecacheimport ("Go-Projects/GeeCache/lru""sync")type cache struct {mu sync.Mutexlru *lru.CachecacheBytes int64}func (c *cache) add(key string, value ByteView) {c.mu.Lock()defer c.mu.Unlock()// 延迟初始化if c.lru == nil {c.lru = lru.New(c.cacheBytes, nil)}c.lru.Add(key, value)}func (c *cache) get(key string) (value ByteView, ok bool) {c.mu.Lock()defer c.mu.Unlock()if c.lru == nil {return}if v, ok := c.lru.Get(key); ok {return v.(ByteView), ok}return}Group 是 GeeCache 最核心的数据结构,负责与用户的交互,并且控制缓存值存储和获取的流程。
在缓存不存在时,调用这个函数,得到源数据:
type Getter interface {Get(key string) ([]byte, error)}// 定义函数类型 GetterFunc,并实现 Getter 接口的 Get 方法type GetterFunc func(key string) ([]byte, error)func (f GetterFunc) Get(key string) ([]byte, error) {return f(key)}核心Group:
// 缓存的命名空间type Group struct {name string // 每个Group拥有一个唯一的名称getter Getter // 缓存未命中时的回溯mainCache cache // 并发缓存}var (mu sync.RWMutexgroups = make(map[string]*Group))// 创建Group实例,并且将group的名称存在全局变量中func NewGroup(name string, cacheBytes int64, getter Getter) *Group {if getter == nil {panic("nil Getter")}mu.Lock()defer mu.Unlock()g := &Group{name: name,getter: getter,mainCache: cache{cacheBytes: cacheBytes},}groups[name] = greturn g}// 获取指定的groupfunc GetGroup(name string) *Group {mu.RLock()g := groups[name]mu.RUnlock()return g}Group的Get方法,完成对缓存的查找以及未命中后的回调操作
// 找到缓存值func (g *Group) Get(key string) (ByteView, error) {// 如果没有键则报错if key == "" {return ByteView{}, fmt.Errorf("key is required")}// 从 mainCache 中查找缓存,如果存在则返回缓存值if v, ok := g.mainCache.get(key); ok {log.Println("[GeeCache] hit")return v, nil}return g.load(key)}// 缓存不存在,则调用 load 方法func (g *Group) load(key string) (value ByteView, err error) {return g.getLocally(key)}// getLocally 调用用户回调函数 g.getter.Get() 获取源数据,并且将源数据添加到缓存 mainCache 中func (g *Group) getLocally(key string) (ByteView, error) {bytes, err := g.getter.Get(key)if err != nil {return ByteView{}, err}value := ByteView{b: cloneBytes(bytes)}g.populateCache(key, value)return value, nil}func (g *Group) populateCache(key string, value ByteView) {g.mainCache.add(key, value)}分布式缓存需要实现节点间通信,建立基于 HTTP 的通信机制是比较常见和简单的做法。如果一个节点启动了 HTTP 服务,那么这个节点就可以被其他节点访问。
承载节点间 HTTP 通信的核心数据结构:
package geecacheconst defaultBasePath = "/_geecache/"type HTTPPool struct {self string // 记录自己的地址,包括主机名/IP 和端口basePath string // 节点间通讯地址的前缀}// 返回HTTP实例func NewHTTPPool(self string) *HTTPPool {return &HTTPPool{self: self,basePath: defaultBasePath,}}实现最为核心的 ServeHTTP 方法:
// 使用服务器登录func (p *HTTPPool) Log(format string, v ...interface{}) {log.Printf("[Server %s] %s", p.self, fmt.Sprintf(format, v...))}// 处理HTTP请求func (p *HTTPPool) ServeHTTP(w http.ResponseWriter, r *http.Request) {// 判断访问路径的前缀是否是 basePath,不是返回错误if !strings.HasPrefix(r.URL.Path, p.basePath) {panic("HTTPPool serving unexpected path: " + r.URL.Path)}p.Log("%s %s", r.Method, r.URL.Path)// /<basepath>/<groupname>/<key> requiredparts := strings.SplitN(r.URL.Path[len(p.basePath):], "/", 2)if len(parts) != 2 {http.Error(w, "bad request", http.StatusBadRequest)return}groupName := parts[0]key := parts[1]// 通过 groupname 得到 group 实例,再使用 group.Get(key) 获取缓存数据group := GetGroup(groupName)if group == nil {http.Error(w, "no such group: "+groupName, http.StatusNotFound)return}view, err := group.Get(key)if err != nil {http.Error(w, err.Error(), http.StatusInternalServerError)return}w.Header().Set("Content-Type", "application/octet-stream")// 将缓存值作为 httpResponse 的 body 返回w.Write(view.ByteSlice())}一致性哈希算法将 key 映射到 2^32 的空间中,将这个数字首尾相连,形成一个环
package consistenthashimport ("hash/crc32""sort""strconv")// 定义了函数类型 Hash,采取依赖注入的方式,允许用于替换成自定义的 Hash 函数type Hash func(data []byte) uint32// 一致性哈希算法的主数据结构type Map struct {hash Hashreplicas int // 虚拟节点倍数keys []int // 哈希环hashMap map[int]string // 虚拟节点与真实节点的映射表}// 允许自定义虚拟节点倍数和 Hash 函数func New(replicas int, fn Hash) *Map {m := &Map{replicas: replicas,hash: fn,hashMap: make(map[int]string),}if m.hash == nil {m.hash = crc32.ChecksumIEEE}return m}// 实现添加真实节点/机器的 Add() 方法func (m *Map) Add(keys ...string) {for _, key := range keys {for i := 0; i < m.replicas; i++ {hash := int(m.hash([]byte(strconv.Itoa(i) + key)))m.keys = append(m.keys, hash)m.hashMap[hash] = key}}sort.Ints(m.keys)}// 实现选择节点的 Get() 方法func (m *Map) Get(key string) string {if len(m.keys) == 0 {return ""}hash := int(m.hash([]byte(key))) // 计算 key 的哈希值// 顺时针找到第一个匹配的虚拟节点的下标 idxidx := sort.Search(len(m.keys), func(i int) bool {return m.keys[i] >= hash})return m.hashMap[m.keys[idx%len(m.keys)]]}抽象 PeerPicker
package geecache// PeerPicker 的 PickPeer() 方法用于根据传入的 key 选择相应节点 PeerGettertype PeerPicker interface {PickPeer(key string) (peer PeerGetter, ok bool)}// 接口 PeerGetter 的 Get() 方法用于从对应 group 查找缓存值type PeerGetter interface {Get(group string, key string) ([]byte, error)}节点选择与 HTTP 客户端
const (defaultBasePath = "/_geecache/"defaultReplicas = 50)type HTTPPool struct {self string // 记录自己的地址,包括主机名/IP 和端口basePath string // 节点间通讯地址的前缀mu sync.Mutex // 锁peers *consistenthash.Map // 新增成员变量 peers,类型是一致性哈希算法的 Map,用来根据具体的 key 选择节点httpGetters map[string]*httpGetter // 映射远程节点与对应的 httpGetter}// 实现 PeerGetter 接口type httpGetter struct {baseURL string}// 使用 http.Get() 方式获取返回值,并转换为 []bytes 类型func (h *httpGetter) Get(group string, key string) ([]byte, error) {u := fmt.Sprintf("%v%v/%v",h.baseURL,url.QueryEscape(group),url.QueryEscape(key),)res, err := http.Get(u)if err != nil {return nil, err}defer res.Body.Close()if res.StatusCode != http.StatusOK {return nil, fmt.Errorf("server returned: %v", res.Status)}bytes, err := ioutil.ReadAll(res.Body)if err != nil {return nil, fmt.Errorf("reading response body: %v", err)}return bytes, nil}实现 PeerPicker 接口
// Set() 方法实例化了一致性哈希算法,并且添加了传入的节点,为每一个节点创建了一个 HTTP 客户端 httpGetterfunc (p *HTTPPool) Set(peers ...string) {p.mu.Lock()defer p.mu.Unlock()p.peers = consistenthash.New(defaultReplicas, nil)p.peers.Add(peers...)p.httpGetters = make(map[string]*httpGetter, len(peers))for _, peer := range peers {p.httpGetters[peer] = &httpGetter{baseURL: peer + p.basePath}}}// PickerPeer() 包装了一致性哈希算法的 Get() 方法,根据具体的 key,选择节点,返回节点对应的 HTTP 客户端func (p *HTTPPool) PickPeer(key string) (PeerGetter, bool) {p.mu.Lock()defer p.mu.Unlock()if peer := p.peers.Get(key); peer != "" && peer != p.self {p.Log("Pick peer %s", peer)return p.httpGetters[peer], true}return nil, false}修改主方法
// 将 实现了 PeerPicker 接口的 HTTPPool 注入到 Group 中func (g *Group) RegisterPeers(peers PeerPicker) {if g.peers != nil {panic("RegisterPeerPicker called more than once")}g.peers = peers}// 使用实现了 PeerGetter 接口的 httpGetter 从访问远程节点,获取缓存值func (g *Group) getFromPeer(peer PeerGetter, key string) (ByteView, error) {bytes, err := peer.Get(g.name, key)if err != nil {return ByteView{}, err}return ByteView{b: bytes}, nil}// 缓存不存在,则调用 load 方法// 若非本机节点,则调用 getFromPeer() 从远程获取。若是本机节点或失败,则回退到 getLocally()func (g *Group) load(key string) (value ByteView, err error) {if g.peers != nil {if peer, ok := g.peers.PickPeer(key); ok {if value, err = g.getFromPeer(peer, key); err == nil {return value, nil}log.Println("[GeeCache] Failed to get from peer", err)}}return g.getLocally(key)}并发了 N 个请求,假设对数据库的访问没有做任何限制的,很可能向数据库也发起 N 次请求,容易导致缓存击穿和穿透。针对相同的 key,如何做到只向远端节点发起一次请求呢?
实现了一个名为 singleflight 的 package 来解决这个问题
package singleflightimport "sync"// call 代表正在进行中,或已经结束的请求。使用 sync.WaitGroup 锁避免重入type call struct {wg sync.WaitGroupval interface{}err error}// Group 是 singleflight 的主数据结构,管理不同 key 的请求(call)type Group struct {mu sync.Mutex // protects mm map[string]*call}实现 Do 方法
// 针对相同的 key,无论 Do 被调用多少次,函数 fn 都只会被调用一次,等待 fn 调用结束了,返回返回值或错误。func (g *Group) Do(key string, fn func() (interface{}, error)) (interface{}, error) {g.mu.Lock()if g.m == nil {g.m = make(map[string]*call)}if c, ok := g.m[key]; ok {g.mu.Unlock()c.wg.Wait() // 如果请求正在进行中,则等待return c.val, c.err // 请求结束,返回结果}c := new(call)c.wg.Add(1) // 发起请求前加锁g.m[key] = c // 添加到 g.m,表明 key 已经有对应的请求在处理g.mu.Unlock()c.val, c.err = fn() // 调用 fn,发起请求c.wg.Done() // 请求结束g.mu.Lock()delete(g.m, key) // 更新 g.mg.mu.Unlock()return c.val, c.err // 返回结果}目标:学习从环境状态到行为的映射(即策略),智能体选择能够获得环境最大奖赏的行为,使得外部环境对学习系统在某种意义下的评价为最佳。
区别于监督学习:监督学习是从标注中学习;强化学习是从交互中学习
评价性反馈
指导性反馈
试错搜索和延迟奖励,用于判断某一问题是否适用于强化学习求解。
利用和探索之间的矛盾
主体:智能体和环境-状态、行为和奖励
要素:
一台赌博机有多个摇臂 ,每个摇臂摇出的奖励(reward)大小不确定 ,玩家希望摇固定次数的臂所获得的期望累积奖励最大
行为:摇哪个臂
奖励:每次摇臂获得的奖金
表示第
轮的行为,
表示第
轮获得的奖励
第轮采取行为
的期望奖励为:
假如摇臂次, 那么按照什么策略摇臂,才能使期望累积奖励最大呢?
当已知时, 每次都选择
最大的
(贪心策略)
但是一般情况下,对于玩家而言是未知的或具有不确定性,玩家在第
轮时只能依赖于当时对
的估值
进行选择,此时,贪心策略是在第
轮 选择
最大的
利用:
探索:
每步选择在“利用”和“探索”中二选一
如何平衡“利用”和“探索” 是关键
贪心策略形式化地表示为:,当有多个行为的
同时为最大时,随机选择一个
贪心策略:
根据历史观测样本的均值对进行估计
约定:
行为估值时,一个行为被选择了次后的估值记为
,该估值方式需要记录
个奖励值
行为的初始估值
乐观初值法:Optimistic Initial Values
贝尔曼方程定义了状态估值函数的依赖关系
求解贝尔曼最优性方程寻找最优策略的局限性
集群智能:众多无智能的个体,通过相互之间的简单合作所表现出来的智能行为
博弈:具备一定智能的理性个体,按照某种机制行动,在群体层面体现出的智能
众包:设计合适的机制,激励个体参与,从而实现单个个体不具备的社会智能
分布式 、 自组织的(自然/人造)系统表现出的一种群体智能
集群智能系统一般由一群简单的智能体构成,智能体按照简单的规则彼此进行局部交互,智能体也可以环境交互
灵感通常来自生物系统(蚁群、鸟群、兽群、粒子群)
特点:
一种解空间搜索方法,适用于在图上寻找最优路径
算法形式化:
TSP问题蚁群算法流程
蚁群大小:一般情况下,蚁群中的蚂蚁个数不超过TSP图中节点的个数
终止条件:
思想:局部随机搜索+自增强
缺点:
是一种随机优化方法,通过粒子群在解空间中进行搜索,寻找最优解(适应度最大的解)
粒子速度更新公式:
算法终止条件:
速度更新参数:又称加速度参数,用来控制粒子当前最优位置和粒子群当前最优位置
对粒子飞行速度的影响
惯性权重:速度冲量导致微粒按照先前速度方向继续移动。提出一个惯性权重来控制先前微粒速度的影响
优点:
缺点:和其它演化计算算法类似,不保证收敛到全局最优解
import numpy as npdef cal(x): return x*x*x-5*x*x-2*x+3x_min = -2x_max = 5p_num = 1000g_best_max = 1g_best_max_i = 0g_best_min = 1g_best_min_i = 0x_MAX = (x_max - x_min) * np.random.random_sample((p_num,)) + x_minv_MAX = (x_max - x_min) * np.random.random_sample((p_num,)) + x_minx_MIN = (x_max - x_min) * np.random.random_sample((p_num,)) + x_minv_MIN = (x_max - x_min) * np.random.random_sample((p_num,)) + x_minp_best_max = np.ones_like(x_MAX)p_best_min = np.ones_like(x_MAX)for i in range(1,10000): f_max = cal(x_MAX) f_min = cal(x_MIN) t_max = cal(p_best_max) t_min = cal(p_best_min) p_best_max = np.where(t_max > f_max, p_best_max, x_MAX) p_best_min = np.where(t_min < f_min, p_best_min, x_MIN) if np.max(f_max) > g_best_max: g_best_max = np.max(f_max) g_best_max_i = x_MAX[np.argmax(f_max)] if np.min(f_min) < g_best_min: g_best_min = np.min(f_min) g_best_min_i = x_MIN[np.argmin(f_min)] v_MAX = v_MAX + (p_best_max - x_MAX) + (g_best_max - x_MAX) x_MAX = x_MAX + v_MAX x_MAX = np.where(x_MAX > x_max,x_max,x_MAX) x_MAX = np.where(x_MAX < x_min,x_min,x_MAX) v_MIN = v_MIN + (p_best_min - x_MIN) + (g_best_min - x_MIN) x_MIN = x_MIN + v_MIN x_MIN = np.where(x_MIN > x_max,x_max,x_MIN) x_MIN = np.where(x_MIN < x_min,x_min,x_MIN)print(g_best_max_i)print(g_best_min_i)net/http库以及 http.Handler接口路由(router)独立出来,方便之后增强。上下文(Context),封装 Request 和 Response ,提供对 JSON、HTML 等返回类型的支持。Logger中间件,能够记录请求到响应所花费的时间,Go语言内置了 net/http库,封装了HTTP网络编程的基础的接口,使用这个库:
package mainimport ("fmt""net/http")func main() {// 设置两个路由http.HandleFunc("/", indexHandler)http.HandleFunc("/hello", helloHandler)// 启动Web服务,在9999端口进行监听,处理所有的HTTP请求的实例http.ListenAndServe("localhost:9999", nil)// 最后的nil即为实现框架的入口}// 根路由func indexHandler(w http.ResponseWriter, req *http.Request) {fmt.Fprintf(w, "URL.Path=%q\n", req.URL.Path)}// hello路由func helloHandler(w http.ResponseWriter, req *http.Request) {for k, v := range req.Header {fmt.Fprintf(w, "Header[%q] = %q\n", k, v)}}使用curl进行测试:
> curl http://localhost:9999/URL.Path="/"> curl http://localhost:9999/helloHeader["User-Agent"] = ["curl/7.68.0"]Header["Accept"] = ["*/*"]其中代码的nil就是一个接口,需要实现方法 ServeHTTP ,也就是说,只要传入任何实现了 ServerHTTP 接口的实例,所有的HTTP请求,就都交给了该实例处理了。
拦截一下请求进行尝试
package mainimport ("fmt""net/http")// 定义一个空结构体,因为后面实现的是一个方法,比如在一个结构体的基础上进行实现type Engine struct{}// 实现ServeHTTP方法func (engine *Engine) ServeHTTP(w http.ResponseWriter, req *http.Request) {switch req.URL.Path {case "/":fmt.Fprintf(w, "URL.Path=%q\n", req.URL.Path)case "/hello":for k, v := range req.Header {fmt.Fprintf(w, "Header[%q] = %q\n", k, v)}default:fmt.Fprintf(w, "404 NOT FOUND: %s\n", req.URL)}}func main() {engine := &Engine{}// 多设置一个路由http.HandleFunc("/hi", indexHandler)// 启动Web服务,在9999端口进行监听,处理所有的HTTP请求的实例http.ListenAndServe("localhost:9999", engine)// 最后的nil即为实现框架的入口}// 根路由func indexHandler(w http.ResponseWriter, req *http.Request) {fmt.Fprintf(w, "URL.Path=%q\n", req.URL.Path)}测试:
> curl http://localhost:9999/helloHeader["User-Agent"] = ["curl/7.68.0"]Header["Accept"] = ["*/*"]> curl http://localhost:9999/URL.Path="/"> curl http://localhost:9999/hi404 NOT FOUND: /hi因此就将所有的HTTP请求转向了自己的处理逻辑,代码的运行结果与之前的是一致的。
我们拦截了所有的HTTP请求,拥有了统一的控制入口。在这里我们可以自由定义路由映射的规则,也可以统一添加一些处理逻辑,例如日志、异常处理等。
因此就可以从这里入手完成这个Web框架,最终的代码结构是这样的
.├── gee│ └── gee.go└── main.gomain.go:
使用 New()创建 gee 的实例,使用 GET()方法添加路由,最后使用 Run()启动Web服务。
package mainimport ("Go-Projects/Gee/gee""fmt""net/http")func main() {r := gee.New()r.Get("/", func(w http.ResponseWriter, req *http.Request) {fmt.Fprintf(w, "URL.Path=%q\n", req.URL.Path)})r.Get("/hello", func(w http.ResponseWriter, req *http.Request) {for k, v := range req.Header {fmt.Fprintf(w, "Header[%q] = %q\n", k, v)}})r.Run("localhost:9999")}gee.go
package geeimport ("fmt""net/http")// 定义一个普遍使用的函数类型,避免后面再次定义type HandlerFunc func(http.ResponseWriter, *http.Request)// 定义路由表type Engine struct {router map[string]HandlerFunc}// 工厂模式的构造方法,返回一个实例func New() *Engine {return &Engine{router: make(map[string]HandlerFunc),}}// 将路由添加到路由表中func (engine *Engine) addRoute(method, pattern string, handler HandlerFunc) {key := method + "-" + patternengine.router[key] = handler}// 实现GET方法func (engine *Engine) GET(pattern string, handler HandlerFunc) {engine.addRoute("GET", pattern, handler)}// 实现POST方法func (engine *Engine) POST(pattern string, handler HandlerFunc) {engine.addRoute("POST", pattern, handler)}// 实现Run方法func (engine *Engine) Run(addr string) (err error) {return http.ListenAndServe(addr, engine)}// 完成统一的控制入口方法ServeHTTPfunc (engine *Engine) ServeHTTP(w http.ResponseWriter, req *http.Request) {key := req.Method + "-" + req.URL.Pathif handler, ok := engine.router[key]; ok {handler(w, req)} else {fmt.Fprintf(w, "404 NOT FOUND: %s\n", req.URL)}}测试后的效果和之前完全相同。
整个 Gee框架的原型已经出来了。实现了路由映射表,提供了用户注册静态路由的方法,包装了启动服务的函数。
最终调用的效果:
package mainimport ("Go-Projects/Gee/gee""net/http")func main() {r := gee.New()r.GET("/", func(c *gee.Context) {c.HTML(http.StatusOK, "<h1>Hello Gee</h1>")})r.GET("/hello", func(c *gee.Context) {c.String(http.StatusOK, "hello %s, you're at %s\n", c.Query("name"), c.Path)})r.POST("/login", func(c *gee.Context) {c.JSON(http.StatusOK, gee.H{"username": c.PostForm("username"),"password": c.PostForm("password"),})})r.Run("localhost:9999")}Handler的参数变成成了 gee.Context,提供了查询Query/PostForm参数的功能。gee.Context封装了 HTML/String/JSON函数,能够快速构造HTTP响应。*http.Request,构造响应 http.ResponseWriter。但是这两个对象提供的接口粒度太细,比如我们要构造一个完整的响应,需要考虑消息头(Header)和消息体(Body),而 Header 包含了状态码(StatusCode),消息类型(ContentType)等几乎每次请求都需要设置的信息。因此,如果不进行有效的封装,那么框架的用户将需要写大量重复,繁杂的代码,而且容易出错。针对常用场景,能够高效地构造出 HTTP 响应是一个好的框架必须考虑的点。*http.Request和 http.ResponseWriter的方法,简化相关接口的调用,只是设计 Context 的原因之一。对于框架来说,还需要支撑额外的功能。例如,将来解析动态路由 /hello/:name,参数 :name的值放在哪呢?再比如,框架需要支持中间件,那中间件产生的信息放在哪呢?Context 随着每一个请求的出现而产生,请求的结束而销毁,和当前请求强相关的信息都应由 Context 承载。因此,设计 Context 结构,扩展性和复杂性留在了内部,而对外简化了接口。路由的处理函数,以及将要实现的中间件,参数都统一使用 Context 实例, Context 就像一次会话的百宝箱,可以找到任何东西。context.go
package geeimport ("encoding/json""fmt""net/http")// 给map[string]interface{}起了一个别名gee.H,构建JSON数据时,显得更简洁。type H map[string]interface{}type Context struct {// 原始的两个参数Writer http.ResponseWriterReq *http.Request// 请求信息Path stringMethod string// 响应信息StatusCode int}// 创建一个Context实例func newContext(w http.ResponseWriter, req *http.Request) *Context {return &Context{Writer: w,Req: req,Path: req.URL.Path,Method: req.Method,}}// 根据key返回用户输入的value,属于POST方法的工具func (c *Context) PostForm(key string) string {return c.Req.FormValue(key)}// 根据key返回用户输入的value,属于GET方法的工具func (c *Context) Query(key string) string {return c.Req.URL.Query().Get(key)}// 写入状态码并更改Context的状态码func (c *Context) Status(code int) {c.StatusCode = codec.Writer.WriteHeader(code)}// 帮助下面的方法快速构造响应func (c *Context) SetHeader(key, value string) {c.Writer.Header().Set(key, value)}// 构造字符串类型的响应func (c *Context) String(code int, format string, values ...interface{}) {c.SetHeader("Content-Type", "text/plain")c.Status(code)c.Writer.Write([]byte(fmt.Sprintf(format, values...)))}// 构造JSON类型的响应func (c *Context) JSON(code int, obj interface{}) {c.SetHeader("Content-Type", "application/json")c.Status(code)encoder := json.NewEncoder(c.Writer) // 流数据构造jsonif err := encoder.Encode(obj); err != nil {http.Error(c.Writer, err.Error(), 500)}}// 构造data类型的响应func (c *Context) Data(code int, data []byte) {c.Status(code)c.Writer.Write(data)}// 构造HTML类型的响应func (c *Context) HTML(code int, html string) {c.SetHeader("Content-Type", "text/html")c.Status(code)c.Writer.Write([]byte(html))}将和路由相关的方法和结构提取出来,放到了一个新的文件中 router.go,方便我下一次对 router 的功能进行增强,
package geeimport ("log""net/http")type router struct {handlers map[string]HandlerFunc}func newRouter() *router {return &router{handlers: make(map[string]HandlerFunc),}}// 将路由添加到路由表中func (r *router) addRoute(method, pattern string, handler HandlerFunc) {log.Printf("Route %4s - %s", method, pattern)key := method + "-" + patternr.handlers[key] = handler}// 路由处理func (r *router) handle(c *Context) {key := c.Method + "-" + c.Pathif handler, ok := r.handlers[key]; ok {handler(c)} else {c.String(http.StatusNotFound, "404 NOT FOUND: %s\n", c.Path)}}调整主框架入口gee.go
package geeimport ("net/http")// 定义一个普遍使用的函数类型,避免后面再次定义type HandlerFunc func(*Context)// 定义路由表type Engine struct {router *router}// 工厂模式的构造方法,返回一个实例func New() *Engine {return &Engine{router: newRouter(),}}// 实现GET方法func (engine *Engine) GET(pattern string, handler HandlerFunc) {engine.router.addRoute("GET", pattern, handler)}// 实现POST方法func (engine *Engine) POST(pattern string, handler HandlerFunc) {engine.router.addRoute("POST", pattern, handler)}// 实现Run方法func (engine *Engine) Run(addr string) (err error) {return http.ListenAndServe(addr, engine)}// 完成统一的控制入口方法ServeHTTPfunc (engine *Engine) ServeHTTP(w http.ResponseWriter, req *http.Request) {c := newContext(w, req)engine.router.handle(c)}测试代码
启动程序后:
2022/11/21 21:05:40 Route GET - /2022/11/21 21:05:40 Route GET - /hello2022/11/21 21:05:40 Route POST - /login> curl -i http://localhost:9999/HTTP/1.1 200 OKContent-Type: text/htmlDate: Mon, 21 Nov 2022 13:05:47 GMTContent-Length: 19<h1>Hello Gee</h1>> curl "http://localhost:9999/hello?name=geektutu"hello geektutu, you're at /hello> curl "http://localhost:9999/login" -X POST -d 'username=geektutu&password=1234'{"password":"1234","username":"geektutu"}> curl "http://localhost:9999/xxx"404 NOT FOUND: /xxx之前,我们用了一个非常简单的 map结构存储了路由表,使用 map存储键值对,索引非常高效,但是有一个弊端,键值对的存储的方式,只能用来索引静态路由。那如果我们想支持类似于 /hello/:name这样的动态路由怎么办呢?
实现动态路由最常用的数据结构,被称为前缀树(Trie树),每一个节点的所有的子节点都拥有相同的前缀。这种结构非常适用于路由匹配。
首先设计树节点上应该存储哪些信息
type node struct {pattern string // 待匹配路由,例如 /p/:langpart string // 路由中的一部分,例如 :langchildren []*node // 子节点,例如 [doc, tutorial, intro]isWild bool // 是否精确匹配,part 含有 : 或 * 时为true}将匹配的逻辑,包装为一个辅助函数:
// 查找第一个匹配的节点,用于插入func (n *node) matchChild(part string) *node {for _, child := range n.children {if child.part == part || n.isWild {return child}}return nil}// 查找全部匹配的节点,用于查找func (n *node) matchChildren(part string) []*node {nodes := make([]*node, 0)for _, child := range n.children {if child.part == part || n.isWild {nodes = append(nodes, child)}}return nodes}实现节点的递归插入和查找
// 插入节点func (n *node) insert(pattern string, parts []string, height int) {// 到达高度了就停止if len(parts) == height {n.pattern = patternreturn}part := parts[height] // 获取当前的规则child := n.matchChild(part) // 尝试用当前的规则进行匹配// 如果没有匹配成功,就新建一个节点,并加入到当前节点的孩子们中去if child == nil {child = &node{part: part,isWild: part[0] == ':' || part[0] == '*',}n.children = append(n.children, child)}// 递归进行插入child.insert(pattern, parts, height+1)}// 查询节点func (n *node) search(parts []string, height int) *node {if len(parts) == height || strings.HasPrefix(n.part, "*") {if n.pattern == "" {return nil}return n}part := parts[height] // 获取当前的规则children := n.matchChildren(part) // 尝试用当前的规则进行匹配// 遍历所有当前匹配的节点进行递归匹配for _, child := range children {result := child.search(parts, height+1)if result != nil {return result}}return nil}使用 roots 来存储每种请求方式的Trie 树根节点。使用 handlers 存储每种请求方式的 HandlerFunc 。getRoute 函数中解析了 :和 *两种匹配符的参数,返回一个 map 。
// 将字符串解析成一个切片func parsePattern(pattern string) []string {vs := strings.Split(pattern, "/")parts := make([]string, 0)for _, item := range vs {if item != "" {parts = append(parts, item)if item[0] == '*' {break}}}return parts}// 将路由添加到路由表中func (r *router) addRoute(method, pattern string, handler HandlerFunc) {parts := parsePattern(pattern)key := method + "-" + pattern// 先看看是不是Get或者Post方法_, ok := r.roots[method]if !ok {r.roots[method] = &node{}}r.roots[method].insert(pattern, parts, 0)r.handlers[key] = handler}// 从路由表中查找路由func (r *router) getRoute(method, path string) (*node, map[string]string) {searchParts := parsePattern(path)params := make(map[string]string)root, ok := r.roots[method]if !ok {return nil, nil}n := root.search(searchParts, 0)if n != nil {parts := parsePattern(n.pattern)for index, part := range parts {if part[0] == ':' {params[part[1:]] = searchParts[index]}if part[0] == '*' && len(part) > 1 {params[part[1:]] = strings.Join(searchParts[index:], "/")break}}return n, params}return nil, nil}对 Context 对象增加一个属性和方法,来提供对路由参数的访问。我们将解析后的参数存储到 Params中
更改路由处理的方法
// 路由处理func (r *router) handle(c *Context) {n, params := r.getRoute(c.Method, c.Path)if n != nil {c.Params = paramskey := c.Method + "-" + n.patternr.handlers[key](c)} else {c.String(http.StatusNotFound, "404 NOT FOUND: %s\n", c.Path)}}测试:
> curl "http://localhost:9999/hello/geektutu"hello geektutu, you're at /hello/geektutu> curl "http://localhost:9999/assets/css/geektutu.css"{"filepath":"css/geektutu.css"}真实的业务场景中,往往某一组路由需要相似的处理。例如:
/post开头的路由匿名可访问。/admin开头的路由需要鉴权。/api开头的路由是 RESTful 接口,可以对接第三方平台,需要三方平台鉴权。一个 Group 对象需要具备哪些属性呢?
首先是前缀(prefix),比如 /,或者 /api;
要支持分组嵌套,那么需要知道当前分组的父亲(parent)是谁;
中间件是应用在分组上的,那还需要存储应用在该分组上的中间件(middlewares)。
还需要有访问 Router的能力
// 分组路由type RouterGroup struct {prefix stringmiddlewares []HandlerFuncparent *RouterGroupengine *Engine}将 Engine作为最顶层的分组,也就是说 Engine拥有 RouterGroup所有的能力。
// 扩展Enginetype Engine struct {*RouterGrouprouter *routergroups []*RouterGroup}更改下面的其他Engine方法即可
// 工厂模式的构造方法,返回一个实例func New() *Engine {engine := &Engine{router: newRouter(),}engine.RouterGroup = &RouterGroup{engine: engine,}engine.groups = []*RouterGroup{engine.RouterGroup}return engine}增加一个Group的方法,创建一个新的RouterGroup
// 创建一个新的RouterGroupfunc (group *RouterGroup) Group(prefix string) *RouterGroup {engine := group.enginenewGroup := &RouterGroup{prefix: group.prefix + prefix,parent: group,engine: engine,}engine.groups = append(engine.groups, newGroup)return newGroup}后面的Get方法和Post方法就都换成RouterGroup的方法就可以了
测试:
> curl "http://localhost:9999/v1/hello?name=geektutu"hello geektutu, you're at /v1/hello> curl "http://localhost:9999/v2/hello/geektutu"hello geektutu, you're at /v2/hello/geektutu> curl "http://localhost:9999/index"<h1>Index Page</h1>中间件(middlewares),简单说,就是非业务的技术类组件。Web 框架本身不可能去理解所有的业务,因而不可能实现所有的功能。因此,框架需要有一个插口,允许用户自己定义功能,嵌入到框架中,仿佛这个功能是框架原生支持的一样。因此,对中间件而言,需要考虑2个比较关键的点:
Gee 的中间件的定义与路由映射的 Handler 一致,处理的输入是 Context对象。插入点是框架接收到请求初始化 Context对象后,允许用户使用自己定义的中间件做一些额外的处理,例如记录日志等,以及对 Context进行二次加工。另外通过调用 (*Context).Next()函数,中间件可等待用户自己定义的 Handler处理结束后,再做一些额外的操作,例如计算本次处理所用时间等。即 Gee 的中间件支持用户在请求被处理的前后,做一些额外的操作。举个例子,我们希望最终能够支持如下定义的中间件,c.Next()表示等待执行其他的中间件或用户的 Handler:
package geeimport ("log""time")func Logger() HandlerFunc {return func(c *Context) {t := time.Now() // 开始计时c.Next() // 等待用户自己的Handler处理结束log.Printf("[%d] %s in %v", c.StatusCode, c.Req.RequestURI, time.Since(t)) // 打印时间}}中间件是应用在 RouterGroup上的,应用在最顶层的 Group,相当于作用于全局,所有的请求都会被中间件处理。
给 Context添加了2个参数,定义了 Next方法:
func (c *Context) Next() {c.index++s := len(c.handlers)for ; c.index < s; c.index++ {c.handlers[c.index](c)}}index是记录当前执行到第几个中间件,当在中间件中调用 Next方法时,控制权交给了下一个中间件,直到调用到最后一个中间件,然后再从后往前,调用每个中间件在 Next方法之后定义的部分。
定义 Use函数,将中间件应用到某个 Group 。
func (group *RouterGroup) Use(middlewares ...HandlerFunc) {group.middlewares = append(group.middlewares, middlewares...)}ServeHTTP 函数也有变化,当我们接收到一个具体请求时,要判断该请求适用于哪些中间件,在这里我们简单通过 URL 的前缀来判断。得到中间件列表后,赋值给 c.handlers。
// 完成统一的控制入口方法ServeHTTPfunc (engine *Engine) ServeHTTP(w http.ResponseWriter, req *http.Request) {var middlewares []HandlerFuncfor _, group := range engine.groups {if strings.HasPrefix(req.URL.Path, group.prefix) {middlewares = append(middlewares, group.middlewares...)}}c := newContext(w, req)c.handlers = middlewaresengine.router.handle(c)}handle 函数中,将从路由匹配得到的 Handler 添加到 c.handlers列表中,执行 c.Next()。
// 路由处理func (r *router) handle(c *Context) {n, params := r.getRoute(c.Method, c.Path)if n != nil {key := c.Method + "-" + n.patternc.Params = paramsc.handlers = append(c.handlers, r.handlers[key])} else {c.handlers = append(c.handlers, func(c *Context) {c.String(http.StatusNotFound, "404 NOT FOUND: %s\n", c.Path)})}c.Next()}测试:
> go run Go-Projects/Gee2022/11/22 15:45:00 Route GET - /2022/11/22 15:45:00 Route GET - /v2/hello/:name>2022/11/22 15:45:11 [200] / in 3µs>2022/11/22 15:45:25 [500] /v2/hello/geektutu in 39.4µs for group v22022/11/22 15:45:25 [500] /v2/hello/geektutu in 77.6µs> curl http://localhost:9999/<h1>Hello Gee</h1>> curl http://localhost:9999/v2/hello/geektutu{"message":"Internal Server Error"}Web 框架如何支持服务端渲染的场景
解析请求的地址,映射到服务器上文件的真实地址:
// 解析请求的地址,映射到服务器上文件的真实地址func (group *RouterGroup) createStaticHandler(relativePath string, fs http.FileSystem) HandlerFunc {absolutePath := path.Join(group.prefix, relativePath)fileServer := http.StripPrefix(absolutePath, http.FileServer(fs))return func(c *Context) {file := c.Param("filepath")// Check if file exists and/or if we have permission to access itif _, err := fs.Open(file); err != nil {c.Status(http.StatusNotFound)return}fileServer.ServeHTTP(c.Writer, c.Req)}}func (group *RouterGroup) Static(relativePath string, root string) {handler := group.createStaticHandler(relativePath, http.Dir(root))urlPattern := path.Join(relativePath, "/*filepath")// Register GET handlersgroup.GET(urlPattern, handler)}HTML 模板渲染
// 扩展Enginetype Engine struct {*RouterGrouprouter *routergroups []*RouterGrouphtmlTemplates *template.Template // 模板渲染funcMap template.FuncMap // 模板渲染}func (engine *Engine) SetFuncMap(funcMap template.FuncMap) {engine.funcMap = funcMap}func (engine *Engine) LoadHTMLGlob(pattern string) {engine.htmlTemplates = template.Must(template.New("").Funcs(engine.funcMap).ParseGlob(pattern))}对原来的 (*Context).HTML()方法做了些小修改,使之支持根据模板文件名选择模板进行渲染。
// 构造HTML类型的响应func (c *Context) HTML(code int, name string, data interface{}) {c.SetHeader("Content-Type", "text/html")c.Status(code)if err := c.engine.htmlTemplates.ExecuteTemplate(c.Writer, name, data); err != nil {c.Fail(500, err.Error())}}进行测试:
package mainimport ("Go-Projects/Gee/gee""fmt""html/template""net/http""time")type student struct {Name stringAge int8}func FormatAsDate(t time.Time) string {year, month, day := t.Date()return fmt.Sprintf("%d-%02d-%02d", year, month, day)}func main() {r := gee.New()r.Use(gee.Logger())r.SetFuncMap(template.FuncMap{"FormatAsDate": FormatAsDate,})r.LoadHTMLGlob("Gee/templates/*")r.Static("/assets", "./static")stu1 := &student{Name: "Geektutu", Age: 20}stu2 := &student{Name: "Jack", Age: 22}r.GET("/", func(c *gee.Context) {c.HTML(http.StatusOK, "css.tmpl", nil)})r.GET("/students", func(c *gee.Context) {c.HTML(http.StatusOK, "arr.tmpl", gee.H{"title": "gee","stuArr": [2]*student{stu1, stu2},})})r.GET("/date", func(c *gee.Context) {c.HTML(http.StatusOK, "custom_func.tmpl", gee.H{"title": "gee","now": time.Date(2019, 8, 17, 0, 0, 0, 0, time.UTC),})})r.Run("localhost:9999")}错误处理也可以作为一个中间件,增强 gee 框架的能力
package geeimport ("fmt""log""net/http""runtime""strings")// print stack trace for debugfunc trace(message string) string {var pcs [32]uintptrn := runtime.Callers(3, pcs[:]) // skip first 3 callervar str strings.Builderstr.WriteString(message + "\nTraceback:")for _, pc := range pcs[:n] {fn := runtime.FuncForPC(pc)file, line := fn.FileLine(pc)str.WriteString(fmt.Sprintf("\n\t%s:%d", file, line))}return str.String()}func Recovery() HandlerFunc {return func(c *Context) {defer func() {if err := recover(); err != nil {message := fmt.Sprintf("%s", err)log.Printf("%s\n\n", trace(message))c.Fail(http.StatusInternalServerError, "Internal Server Error")}}()c.Next()}}用户注册、用户登录、显示在线用户列表、群聊(广播)、点对点聊天、离线留言
package mainimport "fmt"// 定义两个变量,一个表示用户ID,一个表示用户密码var userId intvar userPwd stringfunc main() {// 接收用户的选择var key int// 判断是否还能继续显示菜单var loop = true// 循环展示菜单for loop {fmt.Println("---------------欢迎登录多人聊天系统---------------")fmt.Println("--------------- 1 登录聊天室")fmt.Println("--------------- 2 注册用户")fmt.Println("--------------- 3 退出系统")fmt.Println("请选择(1-3):")fmt.Scanln(&key)switch key {case 1:fmt.Println("登录聊天室")loop = falsecase 2:fmt.Println("注册用户")case 3:fmt.Println("退出系统")loop = falsedefault:fmt.Println("输入有误,请重新输入")}}if key == 1 {fmt.Println("请输入用户ID")fmt.Scanln(&userId)fmt.Println("请输入用户密码")fmt.Scanln(&userPwd)// 先把登录的函数写在另外一个文件err := login(userId, userPwd)if err != nil {fmt.Println("登录失败")} else {fmt.Println("登录成功")}} else if key == 2 {fmt.Println("进行用户注册的逻辑")}}登录逻辑的判断首先写在另外的文件中,后续再进行修改
package mainimport "fmt"func login(userId int, userPwd string) (err error) {fmt.Printf("userId=%d, userPed=%s\n", userId, userPwd)return nil}注意这种在同一个包下引用函数的方式需要在src文件夹之外进行编译,然后手动运行
重点是如何发送包以及如何对包进行校验,同时要保证多线程
要对发送的消息进行序列化等操作,首先定义好处理这些数据的结构体
package message// 确定消息类型const (LoginMesType = "LoginMes"LoginResMesType = "LoginResMes")type Message struct {Type string `json:"type"` // 消息类型Data string `json:"data"` // 消息内容}// 定义两个消息,后面需要再增加type LoginMes struct {UserId int `json:"userId"` // 用户IdUserPwd string `json:"userPwd"` // 用户密码UserName string `json:"userName"` // 用户名}type LoginResMes struct {Code int `json:"code"` // 返回的状态码 500 表示用户未注册,200 表示成功Error string `json:"error"` // 返回错误信息}客户端发送消息(消息的长度)
package mainimport ("Go-Projects/Mass-Communication-System/common/message""encoding/binary""encoding/json""fmt""net")func login(userId int, userPwd string) (err error) {// fmt.Printf("userId=%d, userPed=%s\n", userId, userPwd)// return nil// 连接到服务器端conn, err := net.Dial("tcp", "localhost:8889")if err != nil {fmt.Println("net.Dial err=", err)return}defer conn.Close()// 准备通过conn发送消息给服务var mes message.Messagemes.Type = message.LoginMesType// 创建一个LoginMes结构体var loginMes message.LoginMesloginMes.UserId = userIdloginMes.UserPwd = userPwd// 将loginMes序列化data, err := json.Marshal(loginMes)if err != nil {fmt.Println("json Marshal err=", err)return}mes.Data = string(data)// 将mes进行序列化data, err = json.Marshal(mes)if err != nil {fmt.Println("json Marshal err=", err)return}// data为发送的消息// 先把data的长度发送给服务器var pkgLen = uint32(len(data))var buf [4]bytebinary.BigEndian.PutUint32(buf[0:4], pkgLen)// 发送长度n, err := conn.Write(buf[:4])if n != 4 || err != nil {fmt.Println("conn.Write err=", err)return}fmt.Println("客户端发送的消息长度为", len(data))fmt.Println("客户端发送的消息内容为", string(data))return}服务器端接收消息
package mainimport ("fmt""net")func process(conn net.Conn) {// 延时关闭连接defer conn.Close()// 读取客户端发送的信息for {buf := make([]byte, 1024*4)fmt.Println("等待读取客户端发送的数据.....")n, err := conn.Read(buf[:4])if n != 4 || err != nil {fmt.Println("conn.Read err=", err)return}fmt.Println("读到的长度为", buf[:4])}}func main() {fmt.Println("服务器在8889端口监听.....")listen, err := net.Listen("tcp", "localhost:8889")defer listen.Close()if err != nil {fmt.Println("net.Listen err=", err)return}// 一旦监听成功,等待客户端连接服务器for {fmt.Println("等待客户端连接服务器.....")conn, err := listen.Accept()if err != nil {fmt.Println("listen.Accept err=", err)}// 一旦连接成功,则启动一个协程和客户端保持通讯go process(conn)}}将服务器端的消息接收封装成一个函数
func readPkg(conn net.Conn) (mes message.Message, err error) {buf := make([]byte, 1024*4)fmt.Println("等待读取客户端发送的数据.....")_, err = conn.Read(buf[:4])if err != nil {fmt.Println("conn.Read err=", err)return}// fmt.Println("读到的长度为", buf[:4])// 转换为一个uint32类型var pkgLen = binary.BigEndian.Uint32(buf[0:4])// 发送长度n, err := conn.Read(buf[:pkgLen])if n != int(pkgLen) || err != nil {fmt.Println("conn.Read err=", err)return}// 把pkgLen反序列化成messageerr = json.Unmarshal(buf[:pkgLen], &mes)if err != nil {fmt.Println("json.Unmarshal err=", err)return}return}客户端发送消息
// 发送消息本身_, err = conn.Write(data)if err != nil {fmt.Println("conn.Write err=", err)return}服务器端封装一个发送消息的函数
func writePkg(conn net.Conn, data []byte) (err error) {// 先发送一个长度var pkgLen = uint32(len(data))var buf [4]bytebinary.BigEndian.PutUint32(buf[0:4], pkgLen)// 发送长度_, err = conn.Write(buf[:4])if err != nil {fmt.Println("conn.Write err=", err)return}//发送data本身n, err := conn.Write(data)if n != int(pkgLen) || err != nil {fmt.Println("conn.Write err=", err)return}return}将这种请求通用化,为后面的其他消息做准备
// 编写serverProcessLogin函数,专门处理登录的请求func serverProcessLogin(conn net.Conn, mes *message.Message) (err error) {// 从mes中取出data,并反序列化var loginMes message.LoginMeserr = json.Unmarshal([]byte(mes.Data), &loginMes)if err != nil {fmt.Println("json.Unmarshal error, err=", err)return}// 先声明一个resMesvar resMes message.MessageresMes.Type = message.LoginResMesType// 声明一个LoginResMesvar loginResMes message.LoginResMes// 如果用户的id为100,密码为123456,认为合法,否则不合法if loginMes.UserId == 100 && loginMes.UserPwd == "123456" {//合法loginResMes.Code = 200} else {//不合法loginResMes.Code = 500loginResMes.Error = "该用户不存在,请注册再使用..."}// 将loginResMes序列化data, err := json.Marshal(loginResMes)if err != nil {fmt.Println("json.Marshal error, err=", err)return}// 将data赋值给resMesresMes.Data = string(data)// 对resMes进行序列化,准备发送data, err = json.Marshal(resMes)if err != nil {fmt.Println("json.Marshal error, err=", err)return}// 发送data,封装到writePkg函数err = writePkg(conn, data)return}// 根据客户端发送消息种类不同,决定调用哪个函数来实现func serverProcessMes(conn net.Conn, mes *message.Message) (err error) {switch mes.Type {case message.LoginMesType:// 处理登录的逻辑err = serverProcessLogin(conn, mes)case message.RegisterMesType:// 处理注册的逻辑default:fmt.Println("消息类型不存在,无法处理")}return}客户端对消息进行处理
// 处理服务器端返回的消息mes, err = readPkg(conn)if err != nil {fmt.Println("readPkg(conn) error, err=", err)return}// 将mes的data部分反序列化var loginResMes message.LoginResMeserr = json.Unmarshal([]byte(mes.Data), &loginResMes)if loginResMes.Code == 200 {fmt.Println("登录成功")} else if loginResMes.Code == 500 {fmt.Println(loginResMes.Error)}改进主要是将前面编写的函数封装进方法之中,减少不同函数之间参数的传递,通过结构体直接调用即可
客户端的改进增加了一个与服务器端保持联系的函数
// 和服务器端保持通讯func serverProcessMes(conn net.Conn) {tf := &utils.Transfer{Conn: conn,}for {fmt.Println("客户端正在等待读取服务器发送的消息")mes, err := tf.ReadPkg()if err != nil {fmt.Println("tf.ReadPkg err=", err)return}// 如果读取到消息,下一步进行处理fmt.Println(mes)}}MVC开发模式,增加models,从而从数据库中进行读取和接收,验证用户的有效性
models层
package modelimport ("Go-Projects/Mass-Communication-System/common/message""encoding/json""fmt""github.com/gomodule/redigo/redis")// 使用工厂模式创建一个UserDao的实例func NewUserDao(pool *redis.Pool) (userDao *UserDao) {userDao = &UserDao{pool: pool,}return}// 在服务器启动后初始化一个userDao实例var (MyUserDao *UserDao)// 定义一个userDao的结构体type UserDao struct {pool *redis.Pool}// 根据用户id返回user实例func (ud *UserDao) getUserById(conn redis.Conn, id int) (user *User, err error) {res, err := redis.String(conn.Do("HGET", "users", id))if err != nil {if err == redis.ErrNil {err = ERROR_USER_NOTEXISTS}return}user = &User{}// 把res反序列化成User实例err = json.Unmarshal([]byte(res), user)if err != nil {fmt.Println("json.Unmarshal err=", err)return}return}// 完成登录的校验func (ud *UserDao) Login(userId int, userPwd string) (user *User, err error) {conn := ud.pool.Get()defer conn.Close()user, err = ud.getUserById(conn, userId)if err != nil {return}if user.UserPwd != userPwd {err = ERROR_USER_PWDreturn}return}// 注册func (ud *UserDao) Register(user *message.User) (err error) {conn := ud.pool.Get()defer conn.Close()_, err = ud.getUserById(conn, user.UserId)if err == nil {err = ERROR_USER_EXISTSreturn}// 说明该用户还没有注册过,则可以完成注册data, err := json.Marshal(user)if err != nil {return}_, err = conn.Do("HSET", "users", user.UserId, string(data))if err != nil {fmt.Println("保存注册用户错误,err=", err)return}return}处理注册的请求
// 编写ServerProcessRegister函数,专门处理注册的请求func (u *UserProcess) ServerProcessRegister(mes *message.Message) (err error) {// 从mes中取出data,并反序列化var registerMes message.RegisterMeserr = json.Unmarshal([]byte(mes.Data), ®isterMes)if err != nil {fmt.Println("json.Unmarshal error, err=", err)return}// 先声明一个resMesvar resMes message.MessageresMes.Type = message.RegisterResMesType// 声明一个RegisterResMesvar registerResMes message.RegisterResMeserr = model.MyUserDao.Register(®isterMes.User)if err != nil {if err == model.ERROR_USER_EXISTS {registerResMes.Code = 505registerResMes.Error = err.Error()} else {registerResMes.Code = 506registerResMes.Error = "注册发生未知错误"}} else {registerResMes.Code = 200}// 将loginResMes序列化data, err := json.Marshal(registerResMes)if err != nil {fmt.Println("json.Marshal error, err=", err)return}// 将data赋值给resMesresMes.Data = string(data)// 对resMes进行序列化,准备发送data, err = json.Marshal(resMes)if err != nil {fmt.Println("json.Marshal error, err=", err)return}// 发送data,封装到writePkg函数tf := &utils.Transfer{Conn: u.Conn,}err = tf.WritePkg(data)return}完成对当前在线用户的增删改查
package process2import "fmt"// 在服务器端实例只有一个,在很多的地方都会使用到var (userMgr *UserMgr)type UserMgr struct {onlineUsers map[int]*UserProcess}// 完成对userMgr初始化工作func init() {userMgr = &UserMgr{onlineUsers: make(map[int]*UserProcess, 1024),}}// 完成对onlineUsers的增删改查func (um *UserMgr) AddOnlineUser(up *UserProcess) {um.onlineUsers[up.UserId] = up}func (um *UserMgr) DelOnlineUser(userId int) {delete(um.onlineUsers, userId)}func (um *UserMgr) GetAllOnlineUser() map[int]*UserProcess {return um.onlineUsers}func (um *UserMgr) GetOnlineUserById(userId int) (up *UserProcess, err error) {up, ok := um.onlineUsers[userId]if !ok {err = fmt.Errorf("用户%d不存在", userId)return}return}显示当前在线用户列表
// 因为用户登录成功,要将用户放入全局变量中以返回列表u.UserId = loginMes.UserIduserMgr.AddOnlineUser(u)// 将当前在线用户的id放入到loginResMes.UsersIdsfor id := range userMgr.onlineUsers {loginResMes.UsersIds = append(loginResMes.UsersIds, id)}fmt.Println(user, "登录成功")// 显示当前在线用户列表fmt.Println("当前在线用户列表如下:")for _, v := range loginResMes.UsersIds {fmt.Println("用户id,\t", v)}服务器端对用户列表进行处理
// 通知所有用户在线func (u *UserProcess) NotifyOthersOnlineUser(userId int) {for id, up := range userMgr.onlineUsers {if id == userId {continue}up.NotifyMeOnline(userId)}}func (u *UserProcess) NotifyMeOnline(userId int) {var mes message.Messagemes.Type = message.NotifyUserStatusMesTypevar notifyUserStatusMes message.NotifyUserStatusMesnotifyUserStatusMes.UserId = userIdnotifyUserStatusMes.Status = message.UserOnlinedata, err := json.Marshal(notifyUserStatusMes)if err != nil {fmt.Println("json.Marshal err=", err)return}mes.Data = string(data)data, err = json.Marshal(mes)if err != nil {fmt.Println("json.Marshal err=", err)return}tf := &utils.Transfer{Conn: u.Conn,}err = tf.WritePkg(data)if err != nil {fmt.Println("NotifyMeOnline err=", err)}}客户端对用户列表进行处理
package processimport ("Go-Projects/Mass-Communication-System/common/message""fmt")// 客户端要维护的mapvar onlineUsers map[int]*message.User = make(map[int]*message.User, 10)// 在客户端显示当前在线的用户func outputOnlineUser() {fmt.Println("当前在线用户列表")for id, user := range onlineUsers {fmt.Println(id, user)}}// 处理返回的NotifyUserStatusMesfunc updateUserStatus(notifyUserStatusMes *message.NotifyUserStatusMes) {user, ok := onlineUsers[notifyUserStatusMes.UserId]if !ok {user = &message.User{UserId: notifyUserStatusMes.UserId,}}user.UserStatus = notifyUserStatusMes.StatusonlineUsers[notifyUserStatusMes.UserId] = useroutputOnlineUser()}客户端显示用户列表
// 显示当前在线用户列表fmt.Println("当前在线用户列表如下:")for _, v := range loginResMes.UsersIds {fmt.Println("用户id,\t", v)user := &message.User{UserId: v,UserStatus: message.UserOnline,}onlineUsers[v] = user}直接调用前面写好的就行,代码很少了
package processimport ("Go-Projects/Mass-Communication-System/client/utils""Go-Projects/Mass-Communication-System/common/message""encoding/json""fmt")type SmsProecss struct {}func (sp *SmsProecss) SendGroupSms(content string) (err error) {var mes message.Messagemes.Type = message.SmsMesTypevar smsMes message.SmsMessmsMes.Content = contentsmsMes.UserId = CurUser.UserIdsmsMes.UserStatus = CurUser.UserStatusdata, err := json.Marshal(smsMes)if err != nil {fmt.Println("json.Marshal err=", err)return}mes.Data = string(data)data, err = json.Marshal(mes)if err != nil {fmt.Println("json.Marshal err=", err)return}tf := &utils.Transfer{Conn: CurUser.Conn,}err = tf.WritePkg(data)if err != nil {fmt.Println("tf.WritePkg err=", err)return}return}也是和上面的差不多
package process2import ("Go-Projects/Mass-Communication-System/common/message""Go-Projects/Mass-Communication-System/server/utils""encoding/json""fmt""net")type SmsProecss struct {}func (sp *SmsProecss) SendGroupSms(mes *message.Message) (err error) {var smsMes message.SmsMeserr = json.Unmarshal([]byte(mes.Data), &smsMes)if err != nil {fmt.Println("json.Unmarshal err=", err)return}data, err := json.Marshal(mes)if err != nil {fmt.Println("json.Marshal err=", err)return}for id, up := range userMgr.onlineUsers {if id == smsMes.UserId {continue}sp.SendMesToEachOnlineUser(data, up.Conn)}return}func (sp *SmsProecss) SendMesToEachOnlineUser(data []byte, conn net.Conn) (err error) {tf := &utils.Transfer{Conn: conn,}err = tf.WritePkg(data)if err != nil {fmt.Println("tf.WritePkg err=", err)return}return}考试主要涉及概念上的问题,可能没有特别复杂的计算的内容
倒排索引基本结构:
对每个词项t,记录所有包含t的文档列表。每篇文档用一个唯一的docID来表示,通常是正整数,如1,2,3…
为什么要用倒排索引:
当用户发起查询时(假设查询为一个关键词),搜索引擎会扫描索引库中的所有文档,找出所有包含关键词的文档,这样依次从文档中去查找是否含有关键词的方法叫做正向索引 。
为了增加效率, 搜索引擎会把正向索引变为倒排索引即把“文档→单词”的形式变为“单词→文档”的形式 。
倒排索引是实现“单词-文档矩阵”的一种具体存储形式,通过倒排索引,可以根据单词快速获取包含这个单词的文档列表。
布尔查询的处理优化:
问题:什么是倒排索引?为什么说倒排索引能加快检索的速度?假设“信息”、“检索”在倒排索引中是两个独立的term,试说明检索短语“信息检索”的基本流程。
答案:倒排索引指的是从词项到文档的一种索引结构。由于它直接可以从查询词定位到文档,所以能够大大加快检索的速度。检索短语“信息检索”的基本流程:从词典中分别查找到“信息”和“检索”这两个词,分别返回它们的倒排记录表,然后求这两个表的交集,在求交集时要考虑它们在文档中的位置相对关系。
词条 :一段文本中有效词的子序列,其中每个子序列称为一个词条。
词条类 :相同词条构成的集合。
词项 :一个词项指的是在信息检索系统词典中所包含的某个可能经过归一化处理的词条类。(词项集合和词条集合可以完全不同,比如可以采用某一个分类体系中的类别标签作为词项。当然,在实际的信息检索系统中,词项往往和词条密切相关)
注意:①文档-词项关联矩阵只包含01②要按字典序进行排序
在构建索引时,每次解析一篇文档,因此对于每个词项而言,其倒排记录表不到最后一篇文档都是不完整的。
如果每个 (termID, docID)对占用 8个字节, 那么处理大规模语料需要大量的空间。
一般内存的容量比较小,没有办法将前面产生的倒排记录表全部放在内存中,需要在磁盘上存储中间结果。
一种减少寻道操作的排序:Blocked sort-based Indexing
将所有记录划分为每个大小约为10M的块,收集每一块的倒排记录,排序,将倒排索引写入硬盘,最后将不同的分块合并为一个大的倒排索引。
内存式单遍扫描索引构建算法:Single-pass in-memory indexing
关键思想:
term-termID的映射)在扫描文档的同时,直接在内存中维护一个不断更新的倒排索引
因此对每个块生成一个完整的倒排索引,这些独立的索引最后合并成一个大索引
最终合并词典的过程中,需要进行词项字符串的比较,因为此时没有全局词典提供词项-整数ID的映射。
BSBI算法:在分块索引阶段,BSBI算法维护一个全局Term (String) – Termid (int) 的映射表,局部索引为Termid及其倒排记录表,仍然按词典顺序排序。
SPIMI算法:分块索引阶段与BSBI算法不同在于建立局部词典和索引,无需全局词典。在合并阶段,将局部索引两两合并,最后产生全局词典建立Term – Termid的映射。
使用文本预处理步骤可以大大减小系统所需要存储的倒排记录表的数目,从而提高索引构建和检索的速度
有损压缩:丢弃一些信息-很多常用的预处理步骤可以看成是有损压缩
无损压缩:所有信息都保留-索引压缩中通常都使用无损压缩
定长数组方式下的词典存储:每个词项需要20(字符串)+4(词频)+4(指向倒排索引表的指针)=28个字节。
将整部词典看成单一字符串:4(词频)+4(指向倒排索引表的指针)+3(指向字符串的指针,按照实际大小决定,例如8*400000个位置需要$log_2(8 * 400000)< 24 $位来表示)+8(每个字符串平均需要8个字节)=19个字节
按块存储,假设块大小k=4,此时每4个词项只需要保留1个词项指针,但是同时需要增加4个字节(比较短,1个字节就可以)来表示每个词项的长度,因此每4个词项需要3+4=7B,比之前的节省了12-7=5B
前端编码:每个块当中 (k = 4)会有公共前缀,可以采用前端编码方式继续压缩
如果使用词干还原,由于将同一词汇的不同形式还原到词根,因此前端编码的压缩效果有限
倒排记录表的压缩:两种经典编码VB和γ编码(注意对gap进行编码,第一个id,后面都是gap)
可变字节(VB)码:设定一个专用位 (高位) c作为延续位(continuation bit),如果间隔表示少于7比特,那么c置1,将间隔编入一个
字节的后7位中;否则将高7位放入当前字节中,并将c置0,剩下的位数采用同样的方法进行处理,最后一个字节的c置1(表
示结束)
编码:
通道模型:
若有包含个词条的大文本语料,则
,
是词频。(一元先验概率)
通道模型概率-计算错误概率:混淆“矩阵”(计算一个字符变为另一个字符的概率如何)
轮排索引:(主要思想:让星号出现在词汇的末尾)
轮排索引的查找过程:
相对于通常的B-树,轮排索引(轮排树)的空间要大4倍以上 (经验值)
k-gram索引:枚举一个词项中所有连读的k个字符构成k-gram(在首尾添加k-1个首尾符号)
k-gram索引 vs. 轮排索引
tf-idf词频及log词频
TF是词项t的词项频率,是与文档相关的一个量,可以认为是文档内代表度的一个量,也可以认为是一种局部信息。
IDF是反映词项t的信息量的一个指标,是一种全局性指标,反应的是词项在全局的区别性,可视为一种词项全局信息量的指标。
向量空间模型基本思想:把查询和文本表示成向量(早期表示成TF-IDF权重)
向量空间模型的不同实现方案(不用背表,但是有很多情况,要看好题)(比如有时候idf不用算):
注意:看好题目,不说对数、归一化什么的就不要做
主要是BM25模型的基本概念,IDF是怎么计算的,以及它的基本假设,伯努利分布
BIM的基本假设,BM25的二重泊松分布,考虑了哪些因素,如长度归一等等。
以往的向量空间模型是将query和文档使用向量表示然后计算其内容相似性来进行相关性估计的,而概率检索模型是一种直接对用户需求进行相关性的建模方法,一个query进来,将所有的文档分为两类-相关文档、不相关文档,这样就转为了一个相关性的分类问题。
对于某个文档来说,
表示该文档属于相关文档的概率,则
表示该文档属于不相关文档的概率,如果query属于相关文档的概率大于不相关文档
,则认为这个文档是与用户查询相关的。
使用贝叶斯公式转换一下,则在搜索排序过程中不需要真正的分类,只需要保证相关性由高到底排序即可,所以只需要降序即可,
这样就最终转为计算的值即可。
为了能够使得上述两个计算因子可行,二元独立模型做出了两个假设
类似于布尔模型中的文档表示方法,一篇文档在由特征(或者单词)进行表示的时候,以特征(或者单词)出现和不出现两种情况来表示,不考虑词频等其他因素。
指文档里出现的单词之间没有任何关联,任意一个单词在文档的分布概率不依赖于其他单词是否出现。因为词汇之间没有关联,所以可以将文档概率转换为单词概率的乘积。
上述提到的文档D表示为,用
来表示第
个单词在相关文档出现的概率,则在已知相关文档集合的情况下,观察到D的概率为:
同理在不相关文档中出现的概率为
可以推导出:
设文档统计量如下:
| 相关文档 | 不相关文档 | 文档数量 | |
|---|---|---|---|
| 文档数量 |
则可以得出(加1平滑):,
因此最终的公式为:
其代表的含义是:对于同时出现在用户查询Q和文档D中的单词,累加每个单词的估值,其和就是文档D和查询的相关性度量。
在不确定哪些文档是相关的,哪些文档是不相关的的时候,可以给公式的估算因子直接赋予固定值,则该公式将会退化为IDF因子。
优点:BIM模型建立在数学基础上,理论性较强
缺点:
BM25模型计算公式其实融合了4个考虑因素:IDF因子,文档长度因子,文档词频和查询词频。并对3个自由调节因子进行权值的调整。
IDF因子:设BIM模型中的相关文档数量为0,则退化为
查询权重:,考虑查询词频
TF权重(基于二重泊松分布):,考虑文档中词频和文档长度
最终形式为三项相乘
例题:
优点:
缺点:
问题:BM25和向量空间模型(VSM)为何需要长度归一?语言模型为何需要平滑处理?两个问题之间有何联系?
答案:由于长文挡中词项反复出现的可能性大,包含更多的不同词项,所以词项频率和词汇量可能更大。这显然是不公平的。长度归一化,可以使长文档和短文档的向量中的权重都处于同一数量级。平滑处理是为了解决数据稀疏引起的0概率问题。两者都是常见的数据预处理方法,提高了数据质量,为了保证模型的鲁棒性。
流行的是基于多项式分布,对于生成模型的计算有零概率的问题,需要进行平滑,基本概念要知道
指标计算,如正确率召回率等等,F1,未插值的AP
题目:什么是非插值的MAP?为什么说它在引入序的作用的同时考虑了召回率?
答案:单个查询的非插值MAP指的是所有相关文档(不论是否在结果出现,若不出现就假定出现在无穷远处)在结果出现位置上的正确率的算术平均值。系统的非插值MAP是所有查询上的非插值AP的算术平均值。从非插值AP的定义看,一方面,如果出现在结果中的相关文档越多,求和结果也越大,那么非插值AP值也越大。另一方面,如果相关文档在结果中出现位置越靠前,那么非插值AP值也越大。因此,可以认为非插值MAP同时考底了召回率和序的作用。
Bpref:在相关性判断不完全的情况下,计算在进行了相关性判断的文档集合中,在判断到相关文档前,需要判断的不相关文档的篇数。相关性判断完全的情况下,利用Bpref和MAP进行评价的结果很一致,但是相关性判断不完全的情况下,Bpref更鲁棒。
NDCG:每个文档不仅仅只有相关和不相关两种情况,而是有相关度级别,比如0,1,2,3。我们可以假设,对于返回结果:相关度级别越高的结果越多越好,相关度级别越高的结果越靠前越好
优点:
缺点:
考试基本不涉及
相关反馈的本质是将检索返回的文档的相关性判定(不同的判定来源:人工或非人工)作为返回信息,希望提升检索效果(召回率和正确率)
反馈信息的来源:显式(用户点击)、隐式(用户行为等)、伪相关反馈(返回的前几个结果算相关)
Rocchio算法
查询扩展的最初含义是对查询进行扩充,近年来越来越向查询重构偏移,即现在的查询扩展是指对原有查询进行修改。
通过在查询中加入同义或者相关的词项来提高检索结果。
相关词项的来源: 人工编辑的同义词词典、自动构造的同义词词典、查询日志等等。
查询扩展和相关反馈对检索效果的提升是非常有用的经验性的方法
问题:什么是伪相关反馈?为什么说有时候伪相关反馈会降低某个查询的检索效果?
答案:伪相关反馈指的是系统对上次返回的检索结采进行“伪”判定(比如假设前几个结果是相关的),然后根据这个结果进行反馈。伪相关反馈依赖于上次检索的结果,那么在上次检索结果不可靠情况下,假设成立的可能性很小,此时就进行伪相关反馈反而可能降低后一次检索的效果。
注意:负权重要记为0,同时也要进行排序
问题:文本分类当中,什么是宏平均?什么是微平均?为什么说微平均计算时易受大类影响?
答案:宏平均指的是在每个类别上分类效果的平均值,也即将每个类别看成一个单位。而微平均是将所有类别看成一个类别后求到的效果值,即将每篇文档看成一个单位。由于微平均将文档看成单位,而大类文档数目较多,因此它在计算时易受大类影响。
使用log将乘积计算变为求和计算
最大似然估计(零概率的情况下怎么进行加一平滑)
计算每个类的中心向量(所有文档向量的算术平均)
将每篇测试文档分到离它最近的那个中心向量
Rocchio分类器是要训练的
kNN分类决策取决于k个邻居类中的多数类
类别之间的分类面是分段线性的
kNN分类器几乎不需要训练
但是像kNN这种非线性学习方法在某些情况下也会产生一个线性分类器
SVM分线性SVM和非线性SVM,SVM本身是一个线性决策,但是核函数可以是线性或非线性的
算法本身是转化成一个线性公式,但是最终得到的是一个非线性的决策面,只不过把样本投射到高维空间里面
问题:总结SVM中处理线性不可分数据的方法,给出其基本原理。
问题:什么是核函数?它的作用是什么?为什么核函数的引入常常称为核技巧?
答案:核函数是满足若干性质的相似度计算函数。它的主要作用是计算两个对象的相似度,具体地说,它可以基于原始空间上的点来定义映射后空间上的内积函数。核函数避免知道空间映射的具体函数形式,能够直接基于核函数进行映射后的对象相似度计算,所以它的引入常常称为核技巧。
对于像Rocchio和NB一样的线性方法来说,对于非线性问题它们的偏差就比较大
像kNN一样的非线性方法的偏差较小,方差较大
如果拥有的训练数据非常少,而又要训练出一个基于监督学习的分类器,应该采用具有高偏差的分类器,在这种情况下NB能取得较好的结果,诸如kNN的低偏差模型大概是不可取的。
现有检索排序算法存在哪些问题,怎么改进?
很多传统的IR权重计算机制中都包含了基本指标的非线性缩放过程(比如词项频率或idf 的对数权重计算)。目前为止,机器学习非常擅长特征线性组合(或者其他类似的受限模型)中的权重优化,但是并不擅长基本指标的非线性缩放。这个领域仍然需要人工的特征工程方法。
给定训练样例集合,每个样例表示为三元组,相关或者不相关
从上述样例中学习权重,使得学到的评分接近训练集中的相关性判定结果。
设置评分函数是两个因子的线性组合:查询和文档的向量空间相似度评分和查询词项在文档中存在的最小窗口宽度
相关记为1,不相关记为0,我们的目标是寻找一个评分函数,该函数能够组合特征因子的值,并尽量接近0或1,希望该函数的结果尽量与训练集上的结果保持一致
为什么将IR排序问题看成一个序回归问题?
方法:
词项表示:通过分析文档集来自动生成同义词库-基于共现的同义词库
词嵌入:得到每个词的低维密集向量表示
Neural IR 模型分类
Representation based(基于表示学习的模型):学习文本的分布式表示,在高维空间匹配
Matching function(基于交互匹配的模型):文本之间先进行交互匹配,再对匹配信号进行融合
Combination of both: 既考虑 Representation 又考虑 Matching function
BERT在检索应用中的特点:
问题:简述BERT的基本结构?如何预训练一个BERT(涉及什么任务)?
BERT的基本结构:
BERT的训练任务有两类:
Google次高竞标价格拍卖机制:
bid:每个广告商为每次点击给出的最大投标价格
CTR:一旦被显示后被点击的比率
ad rank=bid × CTR:这种做法可以在广告商愿意支付的价钱和广告的相关度高低之间进行平衡。
排名第1的C,需要支付的价格是它的下一位的
排名第2的B,需要支付的价格是它的下一位的
这样做避免了“保底”行为的产生,可以使收益更大化。
采集器必须做到
锚文本是人为创建的超链接,可以理解为质量认证的信号。
邻接表:一个节点的邻居集合,可以视为一个结点(URL)所有指向它的页面的集合
假设每个URL由一个整数表示,对于40亿页的网站,每个结点需要32位甚至64位,存储开销非常大
BV算法可以降低到平均3位
压缩中使用到的属性:
BV算法主要思想:由于模板的缘故,一个节点的邻接列表类似于字典顺序中的7个先前的URL之一,根据这7个中的之一表示邻接表,否则重新编码。
BV算法的主要优势
起源 : 引用分析
特点:
PageRank背后的假设:
PageRank的计算:迭代法计算
如果存在循环通路,需要虚拟一个结点,或者以一定的概率选取一个其他结点到达
每个网页计算两个值:
计算方法:
,其中
是所有链接到
的页面
,其中
是所有页面
链接到的页面
实际计算过程:
PageRank算法是Google提出的一个链接分析的算法,它可以根据节点之间的链接关系计算出每个节点的重要性,反映的是“越多越重要的节点指向该节点则该节点越重要”这个事实。
HITS是IBM提出的另一种链接分析算法,它根据节点之间的链接关系对每个节点计算出两个值:权威度(authority值)和导航度(hub值).
相同点:两者都是基于链接分析的排序算法,并且在算法中两者都利用了特征向量作为理论基础和收敛性依据。
不同点:网页的PageRank是一种静态评分,与查询主题无关,可以事先算好,因此适合于大型搜索引擎;HITS算法的计算与查询主题相关,检索之后再进行计算,因此不适合于大型搜索引擎。
]]>主要是用于表示一个客户的信息,包含结构体以及在其他地方如果调用它的工厂模式的方法
package modelimport "fmt"// 定义Customer结构体,表示一个客户信息type Customer struct {Id intName stringGender stringAge intPhone stringEmail string}// 工厂模式返回Customer的结构体,在CustomerService里面使用// 感觉就是新建一个Customer的实例func NewCustomer(id int, name string, gender string, age int, phone string, email string) *Customer {return &Customer{Id: id,Name: name,Gender: gender,Age: age,Phone: phone,Email: email,}}func (cu *Customer) GetInfo() string {return fmt.Sprintf("%v\t%v\t%v\t%v\t%v\t%v", cu.Id, cu.Name, cu.Gender, cu.Age, cu.Phone, cu.Email)}以及如果我们要返回一个客户的信息,操作也是在Customer的实例上进行的,因此后面的方法也要写在这个结构体的下面
完成对Customer结构体的操作的代码在CustomerService里面,定义另外一个结构体,里面包含一个切片,存储全部实例化的Customer
// 完成对Customer的操作,包括增删改查type CustomerService struct {// 存储当前的客户Customers []model.Customer// 声明一个字段,表示当前切片含有多少个客户CustomerNum int}主菜单:
func (cv *CustomerView) MainMenu() {for {var username, password stringfmt.Print("请输入用户名:")fmt.Scanln(&username)fmt.Print("请输入密码:")fmt.Scanln(&password)if cv.login(username, password) {break} else {fmt.Println("用户名或密码错误!")}}// 显示主菜单for cv.loop {fmt.Println("\n---------------------客户信息管理软件---------------------")fmt.Println(" 1 添加客户")fmt.Println(" 2 修改客户")fmt.Println(" 3 删除客户")fmt.Println(" 4 客户列表")fmt.Println(" 5 退 出")fmt.Print("请选择(1-5):")// 接收用户的输入fmt.Scanln(&cv.key)// 对用户的输入进行判断switch cv.key {case "1":cv.addCustomer()case "2":cv.changeCustomer()case "3":cv.deleteCustomer()case "4":cv.showCustomer()case "5":cv.exit()default:fmt.Println("请输入正确的选项------")}}}主菜单里面有的变量是需要定义在结构体中的
type CustomerView struct {key string // 接收用户输入loop bool // 表示是否循环的显示主菜单username string // 用户的用户名password string // 用户的密码customerService *service.CustomerService // 获取用户服务}同时也编写一个工厂模式的方法,方便main.go文件进行调用
func NewCustomerView() *CustomerView {return &CustomerView{key: "",loop: true,username: "admin",password: "password",customerService: service.NewCustomerService(),}}main.go:
package mainimport ("Go-Projects/Customer-Management-System/view")func main() {view.NewCustomerView().MainMenu()}要注意,全部的功能实现细节都应该是在customerService里面进行编写的,customerView.go 文件只负责调用,并对返回的结果进行判断等。
首先要对CustomerService进行初始化,也是相当于工厂模式了
// 初始化CustomerServicefunc NewCustomerService() *CustomerService {customerService := &CustomerService{} // 初始化customerService.CustomerNum = 0return customerService}func (cv *CustomerView) showCustomer() {if cv.customerService.CustomerNum == 0 {fmt.Println("没有客户!")return}fmt.Println("\n-------------------------客户列表-------------------------")fmt.Println("编号\t姓名\t性别\t年龄\t电话\t电子邮件")for _, eachCustomer := range cv.customerService.ShowCustomerSlice() {fmt.Println(eachCustomer.GetInfo())}}func (cs *CustomerService) ShowCustomerSlice() []model.Customer {return cs.Customers}对切片增加一个客户的实例,然后将记录的数量+1
func (cv *CustomerView) addCustomer() {id := cv.customerService.CustomerNum + 1var name, gender, phone, email stringvar age intfmt.Print("请输入姓名:")fmt.Scanln(&name)fmt.Print("请输入性别:")fmt.Scanln(&gender)fmt.Print("请输入年龄:")fmt.Scanln(&age)fmt.Print("请输入电话:")fmt.Scanln(&phone)fmt.Print("请输入电子邮件:")fmt.Scanln(&email)if cv.customerService.AddCustomer(*model.NewCustomer(id, name, gender, age, phone, email)) {fmt.Println("-------------------------添加成功-------------------------")} else {fmt.Println("-------------------------添加失败-------------------------")}}func (cs *CustomerService) AddCustomer(customer model.Customer) bool {cs.Customers = append(cs.Customers, customer)cs.CustomerNum += 1return true}根据客户的ID寻找客户在切片中的位置,然后将它删除即可。
func (cv *CustomerView) changeCustomer() {var id intfmt.Print("请输入修改的ID号:")fmt.Scanln(&id)if cv.customerService.ChangeCustomer(id) {fmt.Println("-------------------------修改成功-------------------------")} else {fmt.Println("-------------------------添加失败-------------------------")}}func (cs *CustomerService) DeleteCustomer(id int) bool {for index, cus := range cs.Customers {if cus.Id == id {cs.Customers = append(cs.Customers[:index], cs.Customers[index+1:]...)cs.CustomerNum -= 1return true}}return false}根据客户的ID寻找客户在切片中的位置,然后修改需要修改的字段即可。
func (cv *CustomerView) changeCustomer() {var id intfmt.Print("请输入修改的ID号:")fmt.Scanln(&id)if cv.customerService.ChangeCustomer(id) {fmt.Println("-------------------------修改成功-------------------------")} else {fmt.Println("-------------------------添加失败-------------------------")}}func (cs *CustomerService) ChangeCustomer(id int) bool {reader := bufio.NewReader(os.Stdin) // 标准输入输出for index, cus := range cs.Customers {if cus.Id == id {fmt.Printf("请输入修改的姓名(%v):", cus.Name)name, _ := reader.ReadString('\n')name = strings.TrimSpace(name)if len(name) != 0 {cs.Customers[index].Name = name}fmt.Printf("请输入修改的性别(%v):", cus.Gender)gender, _ := reader.ReadString('\n')gender = strings.TrimSpace(gender)if len(gender) != 0 {cs.Customers[index].Gender = gender}fmt.Printf("请输入修改的年龄(%v):", cus.Age)age, _ := reader.ReadString('\n')age = strings.TrimSpace(age)if len(age) != 0 {t, _ := strconv.ParseInt(age, 10, 64)cs.Customers[index].Age = int(t)}fmt.Printf("请输入修改的电话(%v):", cus.Phone)phone, _ := reader.ReadString('\n')phone = strings.TrimSpace(phone)if len(phone) != 0 {cs.Customers[index].Phone = phone}fmt.Printf("请输入修改的电子邮件(%v):", cus.Email)email, _ := reader.ReadString('\n')email = strings.TrimSpace(email)if len(email) != 0 {cs.Customers[index].Email = email}return true}}return false}修改的时候回车表示对这个字段不修改,因此要调一个reader的包来完成这个工作,自己无法作出这种判断。
.
├── Customer-Management-System
│ ├── main
│ │ └── main.go
│ ├── model
│ │ └── customer.go
│ ├── service
│ │ └── customerService.go
│ └── view
│ └── customerView.go
main.go
package mainimport ("Go-Projects/Customer-Management-System/view")func main() {view.NewCustomerView().MainMenu()}customer.go
package modelimport "fmt"// 定义Customer结构体,表示一个客户信息type Customer struct {Id intName stringGender stringAge intPhone stringEmail string}// 工厂模式返回Customer的结构体,在CustomerService里面使用// 感觉就是新建一个Customer的实例func NewCustomer(id int, name string, gender string, age int, phone string, email string) *Customer {return &Customer{Id: id,Name: name,Gender: gender,Age: age,Phone: phone,Email: email,}}func (cu *Customer) GetInfo() string {return fmt.Sprintf("%v\t%v\t%v\t%v\t%v\t%v", cu.Id, cu.Name, cu.Gender, cu.Age, cu.Phone, cu.Email)}customerService.go
package serviceimport ("Go-Projects/Customer-Management-System/model""bufio""fmt""os""strconv""strings")// 完成对Customer的操作,包括增删改查type CustomerService struct {// 存储当前的客户Customers []model.Customer// 声明一个字段,表示当前切片含有多少个客户CustomerNum int}// 初始化CustomerServicefunc NewCustomerService() *CustomerService {customerService := &CustomerService{} // 初始化customerService.CustomerNum = 0return customerService}func (cs *CustomerService) ShowCustomerSlice() []model.Customer {return cs.Customers}func (cs *CustomerService) AddCustomer(customer model.Customer) bool {cs.Customers = append(cs.Customers, customer)cs.CustomerNum += 1return true}func (cs *CustomerService) DeleteCustomer(id int) bool {for index, cus := range cs.Customers {if cus.Id == id {cs.Customers = append(cs.Customers[:index], cs.Customers[index+1:]...)cs.CustomerNum -= 1return true}}return false}func (cs *CustomerService) ChangeCustomer(id int) bool {reader := bufio.NewReader(os.Stdin) // 标准输入输出for index, cus := range cs.Customers {if cus.Id == id {fmt.Printf("请输入修改的姓名(%v):", cus.Name)name, _ := reader.ReadString('\n')name = strings.TrimSpace(name)if len(name) != 0 {cs.Customers[index].Name = name}fmt.Printf("请输入修改的性别(%v):", cus.Gender)gender, _ := reader.ReadString('\n')gender = strings.TrimSpace(gender)if len(gender) != 0 {cs.Customers[index].Gender = gender}fmt.Printf("请输入修改的年龄(%v):", cus.Age)age, _ := reader.ReadString('\n')age = strings.TrimSpace(age)if len(age) != 0 {t, _ := strconv.ParseInt(age, 10, 64)cs.Customers[index].Age = int(t)}fmt.Printf("请输入修改的电话(%v):", cus.Phone)phone, _ := reader.ReadString('\n')phone = strings.TrimSpace(phone)if len(phone) != 0 {cs.Customers[index].Phone = phone}fmt.Printf("请输入修改的电子邮件(%v):", cus.Email)email, _ := reader.ReadString('\n')email = strings.TrimSpace(email)if len(email) != 0 {cs.Customers[index].Email = email}return true}}return false}customerView.go
package viewimport ("Go-Projects/Customer-Management-System/model""Go-Projects/Customer-Management-System/service""fmt")type CustomerView struct {key string // 接收用户输入loop bool // 表示是否循环的显示主菜单username string // 用户的用户名password string // 用户的密码customerService *service.CustomerService // 获取用户服务}func NewCustomerView() *CustomerView {return &CustomerView{key: "",loop: true,username: "admin",password: "password",customerService: service.NewCustomerService(),}}func (cv *CustomerView) login(username, password string) bool {if username == cv.username && password == cv.password {return true}return false}func (cv *CustomerView) addCustomer() {id := cv.customerService.CustomerNum + 1var name, gender, phone, email stringvar age intfmt.Print("请输入姓名:")fmt.Scanln(&name)fmt.Print("请输入性别:")fmt.Scanln(&gender)fmt.Print("请输入年龄:")fmt.Scanln(&age)fmt.Print("请输入电话:")fmt.Scanln(&phone)fmt.Print("请输入电子邮件:")fmt.Scanln(&email)if cv.customerService.AddCustomer(*model.NewCustomer(id, name, gender, age, phone, email)) {fmt.Println("-------------------------添加成功-------------------------")} else {fmt.Println("-------------------------添加失败-------------------------")}}func (cv *CustomerView) changeCustomer() {var id intfmt.Print("请输入修改的ID号:")fmt.Scanln(&id)if cv.customerService.ChangeCustomer(id) {fmt.Println("-------------------------修改成功-------------------------")} else {fmt.Println("-------------------------添加失败-------------------------")}}func (cv *CustomerView) deleteCustomer() {var id intfmt.Print("请输入删除的ID号:")fmt.Scanln(&id)if cv.customerService.DeleteCustomer(id) {fmt.Println("-------------------------删除成功-------------------------")} else {fmt.Println("-------------------------删除失败-------------------------")}}func (cv *CustomerView) showCustomer() {if cv.customerService.CustomerNum == 0 {fmt.Println("没有客户!")return}fmt.Println("\n-------------------------客户列表-------------------------")fmt.Println("编号\t姓名\t性别\t年龄\t电话\t电子邮件")for _, eachCustomer := range cv.customerService.ShowCustomerSlice() {fmt.Println(eachCustomer.GetInfo())}}func (cv *CustomerView) exit() {var choice bytefor {fmt.Print("确定退出?(y/n):")fmt.Scanf("%c\n", &choice)if choice == 'y' {cv.loop = falsebreak} else if choice == 'n' {break} else {fmt.Println("输入有误!!请重新输入")}}}func (cv *CustomerView) MainMenu() {for {var username, password stringfmt.Print("请输入用户名:")fmt.Scanln(&username)fmt.Print("请输入密码:")fmt.Scanln(&password)if cv.login(username, password) {break} else {fmt.Println("用户名或密码错误!")}}// 显示主菜单for cv.loop {fmt.Println("\n---------------------客户信息管理软件---------------------")fmt.Println(" 1 添加客户")fmt.Println(" 2 修改客户")fmt.Println(" 3 删除客户")fmt.Println(" 4 客户列表")fmt.Println(" 5 退 出")fmt.Print("请选择(1-5):")// 接收用户的输入fmt.Scanln(&cv.key)// 对用户的输入进行判断switch cv.key {case "1":cv.addCustomer()case "2":cv.changeCustomer()case "3":cv.deleteCustomer()case "4":cv.showCustomer()case "5":cv.exit()default:fmt.Println("请输入正确的选项------")}}}func main() {// 声明一个变量保存用户的输入key := ""// 声明一个变量,控制是否退出for循环loop := true// 显示主菜单for loop {fmt.Println("---------------------家庭收支记账软件---------------------")fmt.Println(" 1 收支明细")fmt.Println(" 2 登记收入")fmt.Println(" 3 登记输出")fmt.Println(" 4 退出软件")fmt.Print("请选择(1-4):")// 接收用户的输入fmt.Scanln(&key)// 对用户的输入进行判断switch key {case "1":fmt.Println("---------------------当前收支明细记录---------------------")case "2":case "3":fmt.Println("登记支出------")case "4":loop = falsedefault:fmt.Println("请输入正确的选项------")}}fmt.Println("-------------------退出家庭收支记账软件-------------------")}没啥有意思的,基础编程,效果如下:
case "1":fmt.Println("---------------------当前收支明细记录---------------------")fmt.Println(details)case "2":fmt.Println("-------------------------登记收入-------------------------")fmt.Print("本次收入金额:")fmt.Scanln(&money)fmt.Print("本次收入说明:")fmt.Scanln(¬e)balance += moneydetails += fmt.Sprintf("收 入\t%v\t%v\t%v\n", balance, money, note)fmt.Println("收入登记成功!")其中明细是用字符串拼接实现的,实际中应该是要操作数据库的
case "3":fmt.Println("-------------------------登记支出-------------------------")fmt.Print("本次支出金额:")fmt.Scanln(&money)if money > balance {fmt.Println("余额的金额不足!")break} else if money <= 0 {fmt.Println("支出金额应为正数!")}fmt.Print("本次支出说明:")fmt.Scanln(¬e)balance -= moneydetails += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", balance+money, money, balance, note)fmt.Println("支出登记成功!")注意支出的金额要小于账户余额,也要注意收入和支出的时候用户输入的数字需要为正数。
case "4":var choice bytefor {fmt.Print("确定退出?(y/n):")fmt.Scanf("%c\n", &choice)if choice == 'y' {loop = falsebreak} else if choice == 'n' {break} else {fmt.Println("输入有误!!请重新输入")}}注意scanf字符的时候与C语言是差不多的,需要考虑回车符号
// 判断当前是否有输入或者输出的记录flag := false也没啥好说的,加个标志位,有记录的时候将这个标志位改掉就可以了
将上面的面向过程的代码修改成面向对象的代码
主要思想:将记账软件的功能封装到结构体中,然后调用这个结构体的方法完成功能。
// 定义结构体type FamilyAccount struct {// 声明一个变量保存用户的输入key string// 声明一个变量,控制是否退出for循环loop bool// 定义账户的初始值balance float64// 定义每次收支的金额和说明money float64note string// 收支的详情使用字符串来记录// 当有记录时对这个字符串进行拼接details string// 判断当前是否有输入或者输出的记录flag bool}注意定义结构体的时候不能进行初始化
// 编写一个工厂模式的构造方法,返回结构体的指针func NewFamilyAcount() *FamilyAccount {return &FamilyAccount{key: "",loop: true,balance: 10000.0,money: 0.0,note: "",details: "收 支\t收支前账户余额\t收支金额\t收支后账户余额\t说 明\n",flag: false,}}注意如果结构体是私有的是一定要有的,公开的也可以有,以后就要记得一定要有这样的一个方法
简单改造一下面向过程的代码即可完成面向对象的效果
将显示明细写成一个方法
func (fa *FamilyAccount) showDetails() {if !fa.flag {fmt.Println("当前没有任何收支记录!")} else {fmt.Println("---------------------当前收支明细记录---------------------")fmt.Println(fa.details)}}将登记收入写成一个方法
func (fa *FamilyAccount) income() {fmt.Println("-------------------------登记收入-------------------------")fmt.Print("本次收入金额:")fmt.Scanln(&fa.money)// 收入金额不能是负数if fa.money <= 0 {fmt.Println("收入金额应为正数!")return}fmt.Print("本次收入说明:")fmt.Scanln(&fa.note)fa.balance += fa.moneyfa.details += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", fa.balance-fa.money, fa.money, fa.balance, fa.note)fmt.Println("收入登记成功!")fa.flag = true}将登记支出写成一个方法
func (fa *FamilyAccount) pay() {fmt.Println("-------------------------登记支出-------------------------")fmt.Print("本次支出金额:")fmt.Scanln(&fa.money)if fa.money > fa.balance {fmt.Println("余额的金额不足!")return} else if fa.money <= 0 {fmt.Println("支出金额应为正数!")}fmt.Print("本次支出说明:")fmt.Scanln(&fa.note)fa.balance -= fa.moneyfa.details += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", fa.balance+fa.money, fa.money, fa.balance, fa.note)fmt.Println("支出登记成功!")fa.flag = true}将退出系统写成一个方法
func (fa *FamilyAccount) exit() {var choice bytefor {fmt.Print("确定退出?(y/n):")fmt.Scanf("%c\n", &choice)if choice == 'y' {fa.loop = falsebreak} else if choice == 'n' {break} else {fmt.Println("输入有误!!请重新输入")}}}显示主菜单
func (fa *FamilyAccount) MainMenu() {// 显示主菜单for fa.loop {fmt.Println("\n---------------------家庭收支记账软件---------------------")fmt.Println(" 1 收支明细")fmt.Println(" 2 登记收入")fmt.Println(" 3 登记输出")fmt.Println(" 4 退出软件")fmt.Print("请选择(1-4):")// 接收用户的输入fmt.Scanln(&fa.key)// 对用户的输入进行判断switch fa.key {case "1":fa.showDetails()case "2":fa.income()case "3":fa.pay()case "4":fa.exit()default:fmt.Println("请输入正确的选项------")}}}func main() {utils.NewFamilyAcount().MainMenu()}添加一个用户登录的功能,即只有将用户名和密码输入正确后才能打开软件,否则无法看到主界面
实现:在显示菜单之前增加一个无限循环要求用户输入用户名和密码,只有输入正确才能退出循环
for {var username, password stringfmt.Print("请输入用户名:")fmt.Scanln(&username)fmt.Print("请输入密码:")fmt.Scanln(&password)if fa.login(username, password) {break} else {fmt.Println("用户名或密码错误!")}}用户登录的方法
func (fa *FamilyAccount) login(username string, password string) bool {if (username == fa.username) && (password == fa.password) {return true}return false}package mainimport "fmt"func main() {// 声明一个变量保存用户的输入key := ""// 声明一个变量,控制是否退出for循环loop := true// 定义账户的初始值balance := 10000.0// 定义每次收支的金额和说明var money float64var note string// 收支的详情使用字符串来记录// 当有记录时对这个字符串进行拼接details := "收 支\t收支前账户余额\t收支金额\t收支后账户余额\t说 明\n"// 判断当前是否有输入或者输出的记录flag := false// 显示主菜单for loop {fmt.Println("\n---------------------家庭收支记账软件---------------------")fmt.Println(" 1 收支明细")fmt.Println(" 2 登记收入")fmt.Println(" 3 登记输出")fmt.Println(" 4 退出软件")fmt.Print("请选择(1-4):")// 接收用户的输入fmt.Scanln(&key)// 对用户的输入进行判断switch key {case "1":if !flag {fmt.Println("当前没有任何收支记录!")} else {fmt.Println("---------------------当前收支明细记录---------------------")fmt.Println(details)}case "2":fmt.Println("-------------------------登记收入-------------------------")fmt.Print("本次收入金额:")fmt.Scanln(&money)// 收入金额不能是负数if money <= 0 {fmt.Println("收入金额应为正数!")break}fmt.Print("本次收入说明:")fmt.Scanln(¬e)balance += moneydetails += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", balance-money, money, balance, note)fmt.Println("收入登记成功!")flag = truecase "3":fmt.Println("-------------------------登记支出-------------------------")fmt.Print("本次支出金额:")fmt.Scanln(&money)if money > balance {fmt.Println("余额的金额不足!")break} else if money <= 0 {fmt.Println("支出金额应为正数!")}fmt.Print("本次支出说明:")fmt.Scanln(¬e)balance -= moneydetails += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", balance+money, money, balance, note)fmt.Println("支出登记成功!")flag = truecase "4":var choice bytefor {fmt.Print("确定退出?(y/n):")fmt.Scanf("%c\n", &choice)if choice == 'y' {loop = falsebreak} else if choice == 'n' {break} else {fmt.Println("输入有误!!请重新输入")}}default:fmt.Println("请输入正确的选项------")}}fmt.Println("-------------------退出家庭收支记账软件-------------------")}.
├── Family-Ledger
│ ├── main
│ │ └── main.go
│ └── utils
│ └── familyAccount.go
main.go
package mainimport ("Go-Projects/Family-Ledger/utils")func main() {utils.NewFamilyAcount().MainMenu()}familyAccount.go
package utilsimport "fmt"// 定义结构体type FamilyAccount struct {// 用户名和密码username stringpassword string// 声明一个变量保存用户的输入key string// 声明一个变量,控制是否退出for循环loop bool// 定义账户的初始值balance float64// 定义每次收支的金额和说明money float64note string// 收支的详情使用字符串来记录// 当有记录时对这个字符串进行拼接details string// 判断当前是否有输入或者输出的记录flag bool}// 编写一个工厂模式的构造方法,返回结构体的指针func NewFamilyAcount() *FamilyAccount {return &FamilyAccount{username: "admin",password: "password",key: "",loop: true,balance: 10000.0,money: 0.0,note: "",details: "收 支\t收支前账户余额\t收支金额\t收支后账户余额\t说 明\n",flag: false,}}// 给结构体绑定相应的方法// 将显示明细写成一个方法func (fa *FamilyAccount) showDetails() {if !fa.flag {fmt.Println("当前没有任何收支记录!")} else {fmt.Println("---------------------当前收支明细记录---------------------")fmt.Println(fa.details)}}// 将登记收入写成一个方法func (fa *FamilyAccount) income() {fmt.Println("-------------------------登记收入-------------------------")fmt.Print("本次收入金额:")fmt.Scanln(&fa.money)// 收入金额不能是负数if fa.money <= 0 {fmt.Println("收入金额应为正数!")return}fmt.Print("本次收入说明:")fmt.Scanln(&fa.note)fa.balance += fa.moneyfa.details += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", fa.balance-fa.money, fa.money, fa.balance, fa.note)fmt.Println("收入登记成功!")fa.flag = true}// 将登记支出写成一个方法func (fa *FamilyAccount) pay() {fmt.Println("-------------------------登记支出-------------------------")fmt.Print("本次支出金额:")fmt.Scanln(&fa.money)if fa.money > fa.balance {fmt.Println("余额的金额不足!")return} else if fa.money <= 0 {fmt.Println("支出金额应为正数!")}fmt.Print("本次支出说明:")fmt.Scanln(&fa.note)fa.balance -= fa.moneyfa.details += fmt.Sprintf("收 入\t%v\t%v\t%v\t%v\n", fa.balance+fa.money, fa.money, fa.balance, fa.note)fmt.Println("支出登记成功!")fa.flag = true}// 将退出系统写成一个方法func (fa *FamilyAccount) exit() {var choice bytefor {fmt.Print("确定退出?(y/n):")fmt.Scanf("%c\n", &choice)if choice == 'y' {fa.loop = falsebreak} else if choice == 'n' {break} else {fmt.Println("输入有误!!请重新输入")}}}// 用户登录的功能func (fa *FamilyAccount) login(username string, password string) bool {if (username == fa.username) && (password == fa.password) {return true}return false}// 显示主菜单func (fa *FamilyAccount) MainMenu() {for {var username, password stringfmt.Print("请输入用户名:")fmt.Scanln(&username)fmt.Print("请输入密码:")fmt.Scanln(&password)if fa.login(username, password) {break} else {fmt.Println("用户名或密码错误!")}}// 显示主菜单for fa.loop {fmt.Println("\n---------------------家庭收支记账软件---------------------")fmt.Println(" 1 收支明细")fmt.Println(" 2 登记收入")fmt.Println(" 3 登记输出")fmt.Println(" 4 退出软件")fmt.Print("请选择(1-4):")// 接收用户的输入fmt.Scanln(&fa.key)// 对用户的输入进行判断switch fa.key {case "1":fa.showDetails()case "2":fa.income()case "3":fa.pay()case "4":fa.exit()default:fmt.Println("请输入正确的选项------")}}}链接无处不在
为什么我们对链接分析感兴趣?
链接分析对目前为止的完全基于文本的IR任务进行了补充
Web可以看成一个有向图
对锚文本构建索引
PageRank背后的假设
Google炸弹:指由于人为恶意构造锚文本而导致的结果很差的搜索。用户群体有意创建链接误导搜索引擎
锚文本索引:将从指向文档D的链接的锚文本(也可能包含锚文本附近的文本)包含在D的索引中
有时会产生低于期望的效果,例如:垃圾邮件过滤应用全然失败
可以根据锚页面网站的权威性对锚文本进行加权
链接服务器:低成本地获取所有链接信息
Boldi and Vigna:基本目标-维护内存中的节点邻接表
邻接表压缩中利用到的属性:
间隔编码
给出整数x,y,z 的已排序列表,用 x y-x z-y 来对 x,y,z 进行表示
使用编码来压缩整数
BV算法的主要优势
引用分析:科技文献中的引用分析
另一个应用:引用频率可以用度量一篇文档的影响度
更好的度量方法:对不同网页来的引用频率进行加权
原始PageRank的一个不足:图中存在一个循环通路,每次迭代,该循环通路中的每个节点的 PageRank不断增加,但是它们并不指出去,即不将PageRank分配给其他节点!
改进的PageRank公式:随机冲浪或随机游走(Random Walk)模型
每个网页计算两个值:
Hub:作为目录型或导航型网页的权重
Authority:作为权威型网页的权重
一个网页被越重要的导航型网页指向越多,那么它的Authority越大;
一个网页指向的高重要度权威型网页越多,那么它的Hub越大。
HITS算法也是收敛的,也可以通过迭代的方式计算。
HITS算法的实际计算过程
PageRank vs. HITS
网页的PageRank 与查询主题无关,可以事先算好,因此适合于大型搜索引擎的应用。
HITS算法的计算与查询主题相关,检索之后再进行计算,因此,不适合于大型搜索引擎。
]]>基本的采集过程
上述简单采集器的问题:
采集器必须做到
任意一个采集器应该做到:
待采集URL池:
基本的采集架构
URL规范化
内容重复判别
分布式采集
分布式采集器
待采集URL池 : 主要考虑两点
采集器陷阱
搜索是Web上使用最多的应用之一
没有搜索引擎,Web甚至无法运转
兴趣聚合:具有相同兴趣的人,即使所处地理位置分散,也可以通过Web找到对方。
搜索引擎是实现兴趣聚合的关键事物
在Web上,搜索不仅仅是一个好的特点
Web是一个充满噪声数据且组织失调的集合体→大量的重复需要检测
用户可以(某种意义上)无控制和无限制地发布内容→大量作弊内容需要检测
传统广告:品牌广告、直接营销、
传统广告的不足:
互联网广告的优点:
互联网广告的主要形式:图片广告、文本广告、搜索广告、网页广告、
第一代搜索广告:Goto
第二代搜索广告:Google
如何对广告排序?
Web查询“长尾”现象:基于AOL查询频次的统计、基于查询频次的流量统计
长尾效应的解释
近似重复的检测:采用编辑距离指标计算页面之间的相似度
将每篇文档表示成一个shingle 集合
每个shingle 是一个基于词语的 n-gram
使用shingle 来计算文档之间的语法相似度
两个文档的相似度定义为它们的shingle 集合的Jaccard距离
每篇文档的shingle的个数非常大
为提高效率,接下来我们使用文档的梗概来表示文档,它由文档的shingle集合中精巧挑选出的子集构成
高效的近似重复检测:局部敏感哈希或排序
]]>什么是“数理逻辑”?
一个算法,以任何作为输入,输出的都是正确答案
输入:
输出答案:该查询在此知识库上的正确答案
如果有上面的算法,那么所有难题都能得到解决
如果有这样的一种“终极算法”,首先要将自然语言表达的知识库和查询表示成形式语言表达的知识库和查询,然后通过自动的知识推理,得到形式语言表达的答案
解决如下问题:
研究形式化定义的sentences之间的关系
左侧是语义的蕴含关系(逻辑推导),,从知识库出发一定正确的知识
右侧是语法的演绎关系(形式推演),,通过算法可以从知识库推出的
如果左侧的是右侧的子集,说明正确的结论都在算法推导的里面,那么说明这个算法是完备的,但是有一些结论可能算法计算出来是错误的
如果右侧的是左侧的子集,说明算法推出来的结论都是正确的,因此算法是可靠的,但是有可能有一些正确的结论算法算不出来
如果兼具完备性和可靠性,那么证明这个算法是正确的。
如果在
的条件下是
true,那么称是句子
的一个
model,句子的所有model的集合是
KB指的是一些句子的集合
:在任意的条件下(一个真值指派)只要
成立,
一定成立,称为
KB蕴含
因此与
完全等价(当且仅当)(
,
是不可满足的)
命题是一种声明,要么是真的,要么是假的,不存在第三种可能
命题逻辑通常不考虑时间
原子命题指的是最小的命题,用大写字母表达
文字是原子命题,或者是原子命题的否
一个句子是一个原子句或者复杂句
一个原子句表示为:
复杂句有五种表示形式,与复杂句之间的真值表:
| false | false | true | false | false | true | true |
| false | true | true | false | true | true | false |
| true | false | false | false | true | false | false |
| true | true | false | true | true | true | true |
连接词和集合之间的联系:
两个句子是逻辑等价的-两个句子的model相同: 当且仅当
且
定理:
KB: 满足命题逻辑语法的sentence的集合
假设:这组sentence中,一共有n个原子命题
真值指派(truth assignment):对每个原子名字赋值
一共有种真值指派,其中:使得KB中的每个sentence都为真的真值指派,就是KB的model
在此基础上,在命题逻辑中,我们可以明确的定义
蕴含,不是连接词:描述的是蕴含的一种关系,有了知识表示后,额外推出其他的知识
命题逻辑里面的连接词,用于知识表示(实际上是可以替代的,但是引入这个符号进行知识表示比较方便)
推出:,通过算法可以从知识库推出的
共有两套规则(11条规则和归结原理)
11条形式推演规则:(不需要背诵)
形式可推演性:A在命题逻辑中由形式可推演的,记作
,当且仅当
能由(有限次使用)命题逻辑的形式推演规则生成
句子可以通过规则
从KB中得出,记作
可靠性:任意时刻当时,
同时成立,那么说
是可靠的
完备性:任意时刻当时,
同时成立,那么说
是完备的
合取范式:子句(文字和析取符号)的合取形式,子句内部是没有合取的(CNF)转换为合取范式是多项式时间复杂度的
归结原理:互补文字可以互相消去(但是每一次只能消去一对)
归结原理是既可靠又完备的
证明:若,
当且仅当
,其中
仅使用归结法则获得新子句
使用上述证明来证明知识库可以推出某个子句
在研究可靠性与完备性问题时,应当把语法层面的知识理解为Groundtruth
因此可靠性可以大概表述为:语义上推演得到的知识在语法上正确。因此要证明归结原理的可靠性,即证明
使用真值表进行证明即可
完备性可以大概表述为:如果语法上能够推理得到的,那么语义上正确。
即证明:如果,则
RC(S):对S内部的全部子句进行归结后的集合。
完备性证明
等价于
永假,等价于
是不可满足的。
等价于
可以归结出空子句,即RC(S)包含空子句
则只需要证明:如果是不可满足的,则RC(S)包含空子句
等价于证明逆否命题:如果RC(S)不包含空子句,则是可满足的
证明:针对S中的原子命题,我们构造如下的model:
首先,因为RC(S)中不包含空集,即RC(S)中不包含永假的子句。
从到
, 顺序指派
的真值:
如果RC(S)中包含一个子句,此子句包含,且此子句的其它文字都已经被指派为False(在之前的步骤中进行的)或不包含其它文字,则把
指派为False;否则,把
指派为True
我们用反证法证明:这个真值指派使得RC(S)中的子句都为真。
假设,在此过程的第i步,我们这样来指派使得某个子句C为False,且假设这是首次出现False的子句;此时,子句C只能是如下两种形式之一:
或者
显然,如果RC(S)中只包含以上两个子句之一,子句C是不会在此真值指派中为False的。因此, RC(S)此时应该同时包含了以上两个子句。
以上两个子句显然是满足归结条件的,也就是说,它归结后的子句也应该在RC(S)中;同时,该子句已经被指派为False了;这与我们之前的假设矛盾。
因此这个真值指派使得RC(S)中的子句都为真,进而S是可满足的。
可以转换为搜索问题,如何使用A*搜索实现呢?
以限制知识库里面的句子形式为代价,获得时间复杂度上的提升
上述提到的归结原理具有完备性,这是很好的性质,对于许多现实世界的应用,如果添加一些限制,可以实现更高效的推理。为了换取更好的inference的时间效率,缩小命题逻辑的表达范围,得到适用于Horn Form的Modus Ponens规则,是另外一种形式的归结原理。
KB为Definite clause的合取形式:
Definite clause: 每一个句子有且只有一个文字是正文字的析取形式
只有两种形式:①原子命题②命题的合取另外一个命题
Horn clause: 每一个句子最多一个文字是正文字的析取形式
PPT例子:KB是全部句子的情况下是否能推出Q
前向推理:从条件出发去推结论
前向推理是数据驱动的,可能推出一些结论与我们要推出的结论是无关的
后向推理:从结论返回推出条件
后向推理是目的驱动的,找为了推出这个结论所需要的条件,因此通常情况下后向推理比前向推理好,但是也存在某种情况前向推理比后向推理好
(全连接神经网络)
证明是可靠的,即证明
通过真值表进行证明即可
证明是完备的:
若,
。此时,
中仅包含definite子句,
仅使用Modus Ponens规则,且
是一个正文字
证明:RC(KB)是KB中原始的句子和通过Modus Ponens推出的句子的全部集合
(如果一个正文字在中,就设为True,不在就设置为False)
反证:若此时为False,那么:必存在一个definite子句,在
下为False。
若该子句为 也就是说,在m中,
均为True,且
为False。根据1中的定义,
,又根据Modus Ponens规则,
根据1中的定义,在
中,
为True。推出矛盾。
若该子句为,在
下为
为False,则
,矛盾
命题逻辑的缺点:能表达的东西比较有限。
命题逻辑假设世界上都是事实(fact),一阶谓词逻辑认为世界上还包括对象、关系和函数等等。
基本元素:
简单句:或
或常量或变量
嵌套函数会造成很大的问题。命题逻辑的算法一定会停止(decidable可判定的),但是由于嵌套函数的存在,谓词逻辑只是半可判定的。
复杂句:使用连接词对简单句进行连接构成复杂句
在谓词逻辑中,要将每一个符号指派到现实世界中,将常量转化为对象、将谓词转化为关系、将函数符号转化为真正的函数
量词与变量是对应的,有变量一定要有量词来量化
全称量词:变量所有实例的合取形式
错误的形式:
存在量词:变量所有实例的析取形式
错误的形式:
量词的属性关系
两种量词之间可以相互转换
全称实例化:实例化全称量词蕴含的每一个实例
注意在实例化的过程中,第n次循环只能嵌套n次函数
因此算法可能不会停止,为semi-decidable的
存在实例化:赋予一个新的常量符号
去掉存在量词和存在量词修饰的变量,使得句子里面的每一个变量都是全称量词修饰的变量,且为合取范式
合一算子:替换后等价的替换方式(只能将常量赋值给变量)
归结原理:
尤其注意要赋值
归结原理既完备又可靠,证明比较复杂不讲
可能有很多的归结策略,选择哪种方式进行归结呢?
没有一种归结策略适用于全部情况
广度优先策略:扩展所有可能的情况然后归结
优点:
缺点:
广度优先对大问题的归结容易产生组合爆炸,但对小问题却仍是一种比较好的归结策略。
常用的归结策略可分为两大类:
删除法主要想法是:把子句集中无用的子句删除掉,这就会缩小搜索范围,减少比较次数,从而提高归结效率。
删除纯文字:
重言式删除法:
限制策略要慎重,防止可以得到空子句但是限制后就得不到空子句了
支持集策略:每一次参加归结的两个亲本子句中,至少应该有一个是由目标公式的否定所得到的子句或它们的后裔。(就是别自己本身进行归结,带上一起归结)
支持集策略是完备的,即当子句集为不可满足时,则由支持集策略一定能够归结出一个空子句。
单文字子句策略:每次参加归结的两个亲本子句中至少有一个子句是单文字子句
采用单文字子句策略,归结式包含的文字数将少于其非单文字亲本子句中的文字数,这将有利于向空子句的方向发展,因此会有较高的归结效率。
单文字子句策略是不完备的,即当子句集为不可满足时,用这种策略不一定能归结出空子句。原因: 没有可用的单文字字句
祖先过滤策略:满足以下两个条件中的任意一个就可进行归结:
祖先过滤策略是完备的
GMP的可靠性证明:将量词去掉变量替换为,使用命题逻辑的Modus Ponens证明即可
同样有前向推理和后向推理,同样是半可判定的
但是,如果仅包含一阶谓词的definite子句且没有函数,那么是decidable的(也叫Datalog)
清晰的概念:对象是否属于这个概念是明确的。
模糊性的概念:对象从属的界限是模糊的,随判断人的思维而定
取得精确数据不可能或很困难,也没有必要获取精确数据
要使计算机能够模仿人脑,对复杂系统进行识别和判断,出路何在?
1965年扎德(Zadeh)教授开创了对“模糊数学”的研究。他认为数学是可以模糊的,主张从精度方面“后退”一步。他提出用隶属函数使模糊概念数学化。
设是给定论域,
是把任意
映射为
上某个实值的函数,即
,则称
为定义在
上的一个隶属函数,由
(对所有
)所构成的集合
称为
上的一个模糊集,
称为
对
的隶属度。
模糊集完全是由隶属函数
来刻画的,
把
中的每一个元素
都映射为
上的一个值
的值表示
隶属于
的程度,其值越大,表示
隶属于
的程度越高。当
仅取
和
时,模糊集
便退化为一个普通集合。
模糊性:事件发生的程度,而不是一个事件是否发生
随机性:描述事件发生的不确定性,即一个事件发生与否
离散且为有限论域的表示方法
设论域为离散论域,则其模糊集可表示为:
为了能够表示出论域中的元素与其隶属度之间的对应关系,扎德引入了一种模糊集的表示方式:先为论域中的每个元素都标上其隶属度,然后再用“+”号把它们连接起来,即,其中
为
对
的隶属度;“
”不是相除关系,只是一个记号;“+”也不是算术意义上的加,只是一个连接符号。
连续论域的表示方法:如果论域是连续的,则其模糊集可用一个实函数来表示。
设分别是
上的两个模糊集,对任意
,都有
成立,则称
等于
,记为
设分别是
上的两个模糊集,对任意
,都有
成立,则称
包含
,记为
设分别是
上的两个模糊集,则
、
分别称为
与
的并集、交集,它们的隶属函数分别为:
设为
上的模糊集,称
为
的补集,其隶属函数为:
两个模糊集之间的运算实际上就是逐点对隶属函数作相应的运算
经典集合的关系:
笛卡尔积:设与
是两个普通集合,
与
的笛卡尔乘积为
从到
的关系
:
上的一个子集,即
,记为
对于中的元素
,若
,则称
与
有关系
;若
,则称
与
没有关系
模糊集合的关系:在二元关系上定义隶属度函数
设是
上的模糊集,则称
为的笛卡尔乘积,它是
上的一个模糊集
在上的一个
元模糊关系
是指以
为论域的一个模糊集,记为
设与
分别是
与
上的两个模糊关系,则
与
的合成是从
到
的一个模糊关系,记为
。其隶属函数为
,其中其中,
和
分别表示取最小和取最大
模糊逻辑:定义模糊谓词、模糊量词、模糊修饰语等
模糊谓词:设,
为模糊谓词,即U中的一个模糊关系,则模糊命题可表示为
,其中的模糊谓词
可以是大、小、年轻、年老、冷、暖、长、短等。
模糊量词:模糊逻辑中使用的模糊量词,如极少、很少、几个、少数、多数、大多数、几乎所有等。
模糊修饰语:
设是模糊修饰语,
是变量,
是模糊谓词,则模糊命题可表示为为
,模糊修饰语也称为程度词,常用的程度词有“很”、“非常”、“有些”、“绝对”等。
模糊修饰语的四种主要运算:
演化计算(Evolutionary Computation, EC):
典型代表:
演化计算:一种模拟自然界生物进化过程与机制进行问题求解的自组织、自适应的随机搜索技术。
演化规则:“物竞天择、适者生存”
演化操作:繁殖(Reproduction)、变异(Mutation)、竞争(Competition)、选择(Selection)
遗传算法的基本思想是从初始种群出发,采用优胜劣汰、适者生存的自然法则选择个体,并通过杂交、变异来产生新一代种群,如此逐代进化,直到满足目标为止
基本概念:
遗传算法主要由染色体编码、初始种群设定、适应度函数设定、遗传操作设计等几大部分所组成,
算法基本步骤:
二进制编码是将原问题的结构变换为染色体的位串结构。假设某一参数的取值范围是。用长度为
的二进制编码串来表示该参数,将
等分成
个子部分,记每一个等分的长度为
优点:易于理解和实现,可表示的模式数最多
缺点:海明悬崖。当算法从7改进到8时,就必须改变所有的位
要求两个连续整数的编码之间只能有一个码位不同,其余码位都是完全相同的。有效地解决了海明悬崖问题。
基本原理:
个体染色体编码串中的基因值取自一个无数值含义,而只有代码含义的符号集。
适应度函数是一个用于对个体的适应性进行度量的函数。个体的适应度值越大,它被遗传到下一代种群中的概率越大
常用的适应度函数
选择(selection)操作:根据选择概率按某种策略从当前种群中挑选出一定数目的个体,使它们能够有更多的机会被遗传到下一代中
交叉(crossover)操作:按照某种方式对选择的父代个体的染色体的部分基因进行交配重组,从而形成新的个体。
二进制交叉:二进制编码情况下所采用的交叉操作
实值交叉:在实数编码情况下所采用的交叉操作,主要包括离散交叉和算术交叉
变异(Mutation)操作:对选中个体的染色体中的某些基因进行变动,以形成新的个体。遗传算法中的变异操作增加了算法的局部随机搜索能力,从而可以维持种群的多样性。
精英主义 (Elitism)
仅仅从产生的子代中选择基因去构造新的种群可能会丢失掉上一代种群中的很多信息。也就是说当利用交叉和变异产生新的一代时,我们有很大的可能把在某个中间步骤中得到的最优解丢失。
使用精英主义(Elitism)方法,在每一次产生新的一代时,我们首先把当前最优解原封不动的复制到新的一代中,其他步骤不变。这样任何时刻产生的一个最优解都可以存活到遗传算法结束。
一直都没弄明白,也没下决心去弄明白。昨天感觉基本上差不多了,整理一下,再加深一下印象。
给你两个字符串 haystack和 needle,请你在 haystack字符串中找出 needle字符串的第一个匹配项的下标(下标从 0开始)。如果 needle不是 haystack的一部分,则返回 -1 。
AC代码:
func strStr(haystack string, needle string) int { needlelen := len(needle) haystacklen := len(haystack) next := make([]int,needlelen) next[0] = 0 j := 0 for i:=1;i<needlelen;i++{ for j > 0 && needle[i] != needle[j]{ j = next[j-1] } if needle[i] == needle[j]{ j++ } next[i] = j } j = 0 for i:=0;i<haystacklen;i++{ for j > 0 && needle[j] != haystack[i]{ j = next[j-1] } if needle[j] == haystack[i]{ j++ } if j == needlelen{ return i-j+1; } } return -1}判断一个字符串(模式串)是不是另外一个字符串(文本串)的子串,怎么做?
最容易想到的:暴力匹配。
比如有下面的两个字符串:
abacac和 ac
开始肯定是第一个 a开始和 ac进行匹配,匹配失败了,然后从 b再开始匹配。最坏情况,每一个都要判断到匹配字符串的最后一个字符,两层循环,时间复杂度很容易想到就是。
但是事实上,如果从人工匹配的角度来看,我们都知道 b不可能匹配成功,让你用肉眼匹配,傻子才会去看 b。但是计算机程序为了全部判断还是要去尝试一下。
那么怎么把这种无效的匹配让开呢?直观上可能想到,我判断第一个能不能匹配上不就行了,应该能降低时间复杂度?
那么再举一个例子:aaaaaaaaaa和 ab,时间复杂度一样是。
所以不仅仅要看第一个,看第一个也无法完全抹去无效的匹配。这时候需要一种高效的匹配算法,核心思想就是在匹配的过程中要记录,匹配失败后从第一个可能成功的地方开始即可,不要做无效工作。
因此就有了超难理解的KMP算法以及各种比KMP还要复杂的算法。这里就先好好的讲一下KMP,希望以后可以真正理解,抬手就来。
前缀表:记录下标 i之前(包括 i)的字符串中,有多大长度的相同前缀后缀。
前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串 。
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串 。
啥意思?举例子就好了
| 模式串下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 字符串 | a | b | c | d | a | b | c | a | b | c | d | a | b |
| 前缀表 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | 6 |
怎么算的?
下标为 0,字符串为 a,前缀为空(因为不包含最后一个字符,因此字符就没了),后缀为空(因为不包含第一个字符,因此字符就没了),因此相同前缀后缀长度为0(因为都是空串)
下标为 1,字符串为 ab,前缀为 a,后缀为 b,因此相同前缀后缀长度为 0
下标为 2,字符串为 abc,前缀为 ab,后缀为 bc,因此相同前缀后缀长度为 0
下标为 3,字符串为 abcd,前缀为 abc,后缀为 bcd,因此相同前缀后缀长度为 0
下标为 4,字符串为 abcda,前缀为 abcd,后缀为 bcda,因此相同前缀后缀长度为 1,也就是 a
下标为 5,字符串为 abcdab,前缀为 abcda,后缀为 bcdab,因此相同前缀后缀长度为 2,也就是 ab
下标为 6,字符串为 abcdabc,前缀为 abcdab,后缀为 bcdabc,因此相同前缀后缀长度为 3,也就是 abc
下标为 7,字符串为 abcdabca,前缀为 abcdabc,后缀为 bcdabca,因此相同前缀后缀长度为 1,也就是 a
…
下标为 12,字符串为 abcdabcabcdab,前缀为 abcdabcabcda,后缀为 bcdabcabcdab,因此相同前缀后缀长度为 6,也就是 abcdab
人工计算还是挺好算的,用眼睛看看简单算算就行了。网上有些资料是从 -1开始,然后右移一位,我认为不好理解,不如保留前缀表的本意
所以算来算去,前缀表有什么用处呢?
前缀表可以帮助我们在匹配不成功的时候找到前面最佳的重新开始的位置,从而保证我们只遍历文本串一次就能判断模式串与文本串是否匹配。(废话)
先举例:后面的 i指文本串的下标,j指模式串的下标。(文本串下标保证递增,绝对不回退)
| 文本串下标 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 字符串 | a | c | b | a | b | a |
| 模式串下标 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 字符串 | a | c | b | a | c |
| 前缀表 | 0 | 0 | 0 | 1 | 2 |
开始匹配,i和 j匹配的很顺利,转眼就到了 i=j=4,然后发现糟了,匹配不上了,现在 j要回退,找到重新开始匹配的位置。
j退到哪里呢?因为 j是没有匹配上的,而 j-1如果有意义(j≠0),一定是能匹配上的!(为什么?因为只有匹配上了 j才会移动,j移动过的位置一定是之前匹配好了的)
那么 j-1是匹配上的又说明了什么呢?说明对于 0~j-1的字符串,如果有相同的前缀后缀,一定也是能和i-1匹配的上的,因此就不需要回退超过前缀的位置!
还是上面的例子,模式串的 j-1前缀表的值是 1,说明 j-1位置的 a在模式串的前面也出现过,就是模式串 0位置的 a。由于 j-1是和 i-1匹配上了的,因此 j=0和 i-1也是匹配上了的,不需要再去看模式串 0的位置,只需要看0的后一个位置 1和 i是否能匹配上就好了!
流程步骤:
i和 j匹配不上了,隐含条件是 i-1和 j-1是可以匹配的j-1后缀的相同长度的前缀长度,也就是 next[j-1]的值j到 next[j-1]的位置,隐含了这一步将相同长度的前缀绕过然后 j=next[j-1]后就去判断 j和 i是不是相同就好了,很不幸的是,还是不相同,i指向的是 b,j指向的是 c。
那么没办法,留着这个前缀也无法匹配了,只好再次回退,这一退就退到 j=0了,但是还是不相等。
j=0就没有办法再次回退了,只好 i++,舍弃这一个部分的文本串,开始新的文本串。
到这里应该明白了前缀表的作用了,字面上很难理解,跟着流程走一遍就明白它的思想了,确实精妙
所以在已知 next数组的前提下,这个字符串匹配的代码就很简单了。虽然简单,但是结构一点都不可以修改,循环和顺序都是精心设计的。
j = 0for i:=0;i<haystacklen;i++{ for j > 0 && needle[j] != haystack[i]{ // 匹配不上就一直回退,j=0说明真的匹配不上了,跳出来i++ j = next[j-1] } // j=0也会跳到这里尝试一下 if needle[j] == haystack[i]{ // 匹配上的就能j++去看模式串的下一个字符了,然后进入下一个循环i++,判断文本串的下一个字符能不能和模式串的这个字符匹配上 j++ }}还有一个问题,next数组怎么求?
next数组首先要明确一点,next数组是针对模式串而言的,与文本串半毛钱关系没有
| 模式串下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 字符串 | a | b | a | a | b | a | e |
| 前缀表 | 0 | 0 | 1 | 1 | 2 | 3 | 0 |
其实思想和匹配是相同的,不同的地方在于上面的是用模式串和文本串进行匹配,这里是用自己和自己进行匹配,匹配的过程中看看能匹配上多少,就能得出 next数组的数值了
next[0]=0,初始化毫无争议,因为空串一定是0
指针 i同样一直向前,指针 j会进行回退,因为 next[0]确定了,因此直接初始化i=1
最开始,j指向的是 0的位置,就在这里等着到底哪个 i能和我这个可爱的 j匹配上
到了 i=2,匹配上了!这时候 j不满足了,是不是 i+1也能和 j+1匹配上呢?所以就 j++,尝试匹配下一个
要是匹配不上了怎么办呢?比如 j=3,i=6匹配不上了,也隐含了条件,就是 j=2是能和 i-1匹配上的(要是匹配不上j也不可能不等于0)
那么j=2时候的相同长度的前后缀在哪里呢?因为如果相同也不需要去看了,所以更新j=next[j-1]就可以了,和上面的字符串的匹配思想是完全相同的。
如果还是匹配不上,那么j只好乖乖变为0,等待着下一个能匹配上的将j+1了
代码如下:
next[0] = 0 // 初始化j := 0 // j指向首位for i:=1;i<needlelen;i++{ // 遍历模式串,不回退 for j > 0 && needle[i] != needle[j]{ j = next[j-1] // 匹配不上了,绕过已知的相同长度的前后缀,直到变为j=0的初始状态 } // 如果j=0还是有一次判断的机会的 if needle[i] == needle[j]{ // 匹配上了将j解放出来,+1再试试 j++ } next[i] = j // 赋值next数组}设 n为文本串长度,m为模式串长度
在匹配的过程中,根据前缀表不断调整匹配的位置,如果没有一个字符能匹配的上,时间复杂度就是文本串的指针从头移到尾,也就是
如果能匹配上一些字符,回退的次数也不可能超过 n次。因此时间复杂度是
生成 next数组,不会比匹配的时间复杂度高(因为如果模式串比文本串还要长,根本就不需要匹配了)
所以从平方级别的时间复杂度直接降到了线性的时间复杂度。
看过很多遍,应该也曾经懂过,就是从来没有整理过,因此可能也没有真正懂过。
希望这次能真真正正懂了,后面忘记了再来看看这篇文章,希望能快一些想起来。
]]>ANN到DL的技术发展
DL在AI的成功应用
语音识别
2009年, Hinton把深层神经网络介绍给做语音识别的学者们。2010年,语音识别就产生了巨大突破。本质上是把传统的混合高斯模型(GMM)替换成了
深度神经网络(DNN)模型,但相对识别错误率一下降低20%多,这个改进幅度超过了过去很多年的总和。这里的关键是把原来模型中通过 GMM 建模的手工特征换成了通过 DNN 进行更加复杂的特征学习。
在此之后,在深度学习框架下,人们还在不断利用更好的模型和更多的训练数据进一步改进结果。现在语音识别已经真正变得比较成熟,并且被广泛商用,目前所有的商用语音识别算法没有一个不是基于深度学习的。
计算视觉:通过组合低层特征形成更加抽象的高层特征
DL在图像识别
Yann LeCun早在1989年就开始了卷积神经网络的研究,取得了在一些小规模(手写字)的图像识别的成果,但在像素丰富的图片上迟迟没有突破,直到2012年Hinton和他学生在ImageNet上的突破,使识别精度提高了一大步;截至2015年最好的模型ResNet
2012年 Google Brain 用 16000 个 CPU 核的计算平台训练 10 亿神经元的深度网络,无外界干涉下自动识别了“Cat”
2014年香港中文大学教授汤晓鸥研究组DeepID的深度学习模型,在 LFW 数据库上获得了99.15%的识别率,人用肉眼在LFW上的识别率为97.52%,深度学习在学术研究层面上已经超过了人用肉眼的识别 。
自然语言处理
词向量表示学习
词向量是指通过对大量文本的无监督学习,根据前后文自动学习到每个词的紧凑向量表达,包括NNML 、 Word2Vector 、预训练模型等。
预训练模型:ELMo、 GPT和BERT 等,全线提升自然语言领域的多项任务的Baseline
递归神经网络 RNN:文本的各个词之间是有顺序的,RNN能更好的挖掘和利用这个性质,在自然语言各个领域都在尝试进行中。 已经有BPTT 、 LSTM等。
神经网络模型学习框架
损失函数:
平方损失:
交叉熵损失:,
单个神经元模型:
单个神经元模型:
多层感知机
卷积网络
核函数网络:单隐层神经网络、非线性体现在径向基核函数
自组织映射
RBM
递归网络
深度前馈网络
常见的结构:
递归神经网络
常见的结构:
生成对抗网络(GAN)
两个网络博弈:G(Generator)和D(Discriminator)
深度强化学习
强化学习:学习目标:策略概率
值函数网络:Deep Q-Learning
策略网络:Deep Policy Network
含有数据输入层、1个以上隐藏层、 1个输出层;各层神经元全连接,同一层神经元之间无连接。
多层感知机的运算:
激活函数(包括硬门限阈值函数),是导致网络运算非线性的直接原因。
学习问题:
学习目标:调整神经元连接权重值,使得平均误差能量最小。
两种方法:批量学习和在线学习。
目标:最小化损失函数
批量学习(Batch Learning)
在线学习(Online Learning):sample by sample 调整权值
缺点:学习过程随机、不稳定。
两个方向的信号流、两个方向的函数运算
函数信号:计算输出函数信号
误差信号:计算梯度向量
数据前馈运算
梯度反馈运算
BP 算法小结
激活函数
异或问题
改善性能的试探法
函数逼近
卷积层:卷积层具有局部连接和权重共享特点。
一维、二维卷积
卷积层的输出尺度
卷积层的参数个数
子采样层:每个通道,通过下采样,缩减尺度。
典型实例:LeNet-5
四种基本递归结构
通用逼近定理:如果网络具有充分多的隐藏神经元,任意的非线性动态系统可以由递归神经网络以期望的精度来逼近,对于状态空间的紧致性没有限制。
计算能力
Recurrent 网络
RNN分回合训练
RNN连续训练
RNN长期依赖
RNN扩展的递归结构
深层结构:神经网络 + 深层结构 + 优化 + 计算资源 + 人工智能应用
梯度消失:解决梯度消失
视觉识别
自然语言处理
生成对抗模型原理
生成器(Generator):尽可能去学习真实样本的分布,迷惑鉴别器。
鉴别器(Discriminator):尽可能的正确判断输入数据是来自真实数据还是来自生成器。
损失函数:
训练过程:生成器与鉴别器交替训练,互相提升各自的生成能力和鉴别能力,最终寻找二者之间的一个纳什均衡。
马尔科夫决策过程:
智能体环境交互-智能体的目标是最大化将来的期望累积奖励
背景
知识图谱的概念最早出现于Google公司的知识图谱项目,体现在使用Google搜索引擎时,出现于搜索结果右侧的相关知识展示。
截止到2016 年底,Google知识图谱中的知识数量已经达到了600亿条,关于1500个类别的5.7亿个实体,以及它们之间的3.5万种关系。
实体、关系和事实:
狭义知识图谱
狭义知识图谱:具有图结构的三元组知识库。
节点:实体。 边:事实(由头实体指向尾实体)。 边的类型:关系。
链接预测、三元组分类:知识图谱上的链接预测
分布式知识表示方法分类:
最简单的神经网络-神经元
激活函数:主要作用是引入非线性,增强网络的表示能力。
最简单的多层神经网络-多层感知机
Softmax归一化是在使用神经网络进行分类时常用的方法,对于分类问题,通常需要给出可能属于每一个类别的概率,即需要输出介于 0 和 1 之间,且加和为 1
参数的学习
正则化
卷积神经网络
循环神经网络
Neural IR 模型分类
Representation based:学习文本的分布式表示 在高维空间匹配
Matching function:文本之间先进行交互匹配,再对匹配信号进行融合
Combination of both: 既考虑 Representation 又考虑 Matching function
DSSM:Deep Structured Semantic Models
word hashing: Bag of letter trigrams representation
模型:DNN学习查询,文本的语义表示, cosine相似度作为匹配评分
MatchPyramid:
考虑各种层次的匹配信号,包括单词层次、短语层次以及句子层次等等;
在图像领域,基于 CNN 特征提取的图像金字塔被证明是有效的
DRMM:相比普通的文本匹配任务,检索任务更需要关注相关性匹配
通过显式地对精确匹配信号,查询词重要度以及多样匹配要求进行建模,得到的模型更加适合于检索任务。
DRMM是第一个在 TREC 数据集能够取得比传统检索模型更好效果的基于 DNN 模型
DRMM的设计思路在一定程度上借鉴了传统的 TF-IDF
K-NRM:使用kernel pooling 技术提取多层次的软匹配 (soft match)特征
PACRR:通过将具有不同大小(k= lg 卷积核的卷积层作用于查询与文档间的单词-单词相似度矩阵,来对 k gram 匹配信息进行建模。
DUET:Representation与Matching function 的方法是互补的
SNRM:监督学习得到文本稀疏表示,解决效率问题
NPRF:将反馈文档视为原始查询的扩充表示,通过增强与查询相关的信息匹配信号获得更好的交互矩阵
总结与展望
基于BERT的检索模型
稠密向量检索模型
直接改变了原有第一阶段的检索模式,通过BERT等预训练语言模型,将查询和文档都映射到语义空间中,编码成单个稠密向量表示,用ANN 算法来进行检索。在一定程度上缓解了词汇不匹配问题,并将检索阶段的匹配效果推到了一个新的台阶
模型框架:一般采用双塔结构对查询和文档单独地编码得到二者独立的表达,从而使文档可以进行离线索引。
RepBERT:平均词项表示作为文档的单个向量
ANCE:利用k-1的模型来检索得到top-n文档并随机采样负样本,每隔一段时间都需要对训练数据中的负样本进行更新,因此该方法的训练代价较大。
RocketQA:与ANCE相比,做了额外的denoised操作;
TCT-ColBERT:通过蒸馏技术,将ColBERT的强建模能力蒸馏到类似于RepBERT这样的双塔架构上去
Condenser:为了将更完整的序列信息压缩到CLS 位置上
DAR:通过插值、扰动的方式在文档表示层面进行数据增强
JPQ:除了直接采用乘积量化(Product Quantization, PQ )方法来压缩向量外,将乘积量化后的文档d†表示用于模型训练,通过排序排序训练目标来优化 PQ 的聚类中心表示
]]>卷积神经网络在欧式数据(图像、文本、声音和视频等)上获得了巨大的成功,广泛应用于图像分类、目标检测、机器翻译等
卷积神经网络可以学习局部小结构,使用局部的卷积核,然后形成多维的模式
卷积如何迁移到非欧空间上去?
卷积是在函数和函数
上的数学运算,从而得到函数
连续形式:
离散形式:
在图上定义卷积的方法:
谱方法:在谱空间中定义卷积:
空间方法:在向量空间中定义卷积
定义一个图(结点、边、邻接矩阵)
图上的每个结点上都有
维的特征,因此
是结点的特征矩阵,每一列是结点的一个信号
图的拉普拉斯算子:,其中
归一化的拉普拉斯算子:
图的傅里叶变换:
的正交特征向量是
,对应的非负特征值是
,可以对拉普拉斯矩阵进行分解:
对于一个信号的图傅里叶变换为
两个信号的卷积的傅里叶变换是两个信号的傅里叶变换的逐点相乘,卷积核就是
图卷积神经网络:
缺点:
ChebyNet:参数化-将参数的数量从n降为K
优点:
Graph wavelet neural network:图小波神经网络
将傅里叶基换为小波基:稀疏、局部化、计算代价低
方法类比卷积:
GraphSAGE:从每个结点开始随机游走,采样个结点,不用临近度指标判断。然后通过聚合函数进行参数共享
图卷积网络(GCN):通过归一化的拉普拉斯矩阵从不固定数量的邻居结点中聚合信息,通过特征变换共享参数
GAT:Graph Attention Network:通过注意力机制学习聚合矩阵
MoNet:空间方法的一般意义框架:所有的空间方法都是定义多个核函数,来测量目标结点和其他结点之间的相似度
谱方法是空间方法的特例
图粗化:将结点进行聚类,每一类作为一个超级结点
结点选择:学习一个评价标准去挑选比较重要的结点
图神经网络在结点分类、链接预测、图分类上取得了巨大的成功,但是图神经网络的设计大多基于直觉、启发式方法或者实验试错,缺少对于图神经网络的理论理解。
]]>桑克(R.Shank)“一台计算机若不会学习,就不能说它具有智能。”
机器学习更强调面向算法,而统计学更偏重于面向模型。换而言之,机器学习强调算法的结果要好,所以机器学习很关注损失函数。而统计学要先扔出来一大堆模型假设,然后站在模型上面通过严格的数学推导做出结果。
统计机器学习:是基于数据构建概率统计模型并运用模型对数据进行预测分析的一门学科。
机器学习的学习过程:
机器学习的特点:
机器学习方法分类:
自监督学习是自主监督学习。它提取并使用自然可用的相关上下文和嵌入式元数据作为监督信号。
输入训练样本,目标是损失函数期望风险最小化
期望风险最小化:
经验风险最小化:(导致过拟合)
结构风险最小化:
怎么样在测试数据上预测得好?
两方面:
正则项:在原来的经验损失函数中添加一个惩罚项,不鼓励复杂的模型
偏差-方差分解:expected loss=bias2+variance+noise
偏差:度量了模型的期望预测和真实结果的偏离程度
方差:刻画了数据扰动所造成的影响
噪声:与f相互独立,刻画了问题的难易程度
由正则化参数控制的偏差和方差对模型复杂性的依赖性说明:
大的值将权重参数拉至零导致较大偏差,较小的
值允许对噪声进行微调,从而导致较大的方差
对模型复杂度问题的深刻理解:
图结构:有向无环图
结点:一个或一组随机变量
边:随机变量之间的单向、直接影响
联合概率分布分解形式:,其中,
为
所有父结点构成的集合
条件独立性 D-分离准则(D-separation criterion):判断贝叶斯网络结点之间的条件独立性。
贝叶斯网络的全局马尔科夫性:给定结点集合A,B,C,若A到B中结点的所有无向路径都是被C阻塞的(blocked),则称A和B被C D-分离(D-separated),即A和B关于C条件独立。
若一条无向路径包含结点x满足以下条件之一,则称其是阻塞的:
贝叶斯网络的局部马尔科夫性:
图结构:无向图
结点:一个或一组随机变量。
边:随机变量之间的相互依赖(非“因果关系”)。
团:对于图中的结点子集,若其中任意两个节点之间都有连边,则称该结点子集为一个团(clique)。
极大团:若在团中加入其他任意一个结点都不再形成团,则称该团为极大团(maximal clique)。
分解形式:
其中, 为团集合,
为团
对应的变量集合,
为定义在团
上的非负势函数,
是归一化因子
条件独立性:
马尔可夫随机场的全局马尔科夫性:给定结点集合A,B,C,若从A中的结点到B中结点必须经过C中的结点,则称A和B被C分离,即A和B关于C条件独立。
局部马尔科夫性:给定某变量的马尔可夫毯(邻接变量),则该变量条件独立于其他变量。
成对马尔科夫性:给定其他所有变量,两个非相邻变量条件独立。 if
基本定义
推断:已知联合概率分布 ,估计
,其中
是集合
的子集。
是问题变量,
是证据变量。
学习:从观测数据 中学习联合概率分布
,寻找最符合观测数据的概率图模型。
推断:已知联合概率分布 ,估计
,其中
枚举 : 假设 有
个变量,每个变量的取值个数的期望是
,则时间复杂度为
推断的核心问题 : 如何高效地计算边际分布
推断方法
精确推断:计算或
的精确值。
变量消去(variable elimination)
思路:利用图模型的紧凑概率分布形式来削减计算量。
优点:简单直观,代数上的消去对应图中结点的消去。
缺点:针对不同证据变量会造成大量冗余计算。
信念传播(belief propagation)
思路:将变量消去过程中产生的中间结果视为可复用的消息,避免重复计算。
消息传递仅在邻接变量之间发生,与边的方向性无关。
树结构:有向树=无向树
树结构上的消息传递:
消息计算公式:
边际分布:
二次扫描算法:
近似推断:在较低的时间复杂度下获得原问题的近似解。通过采样一组服从特定分布的样本,来近似原始分布,适用范围更广,操作性更强。
前向采样(forward sampling)
思路:依据贝叶斯网络的(条件)概率直接采样。采样后,进行需要的概率统计。
缺点:对于小概率事件采样困难,可能经过很多次采样也无法获得足够多的样本
仅适用于贝叶斯网络,不适用于马尔可夫随机场。
吉布斯采样(Gibbs sampling)
思路:直接依照条件概率采样。
马尔可夫毯的性质:
优点:
隐马尔可夫模型是关于时序的概率模型,是最简单的动态贝叶斯网络模型。
状态变量 表示第
时刻的系统状态,观测变量
表示第
时刻的观测值。
观测变量仅依赖于当前时刻的状态变量,当前状态仅依赖于前一时刻的状态。状态集合 ,观测值集合
联合概率:
状态转移矩阵,其中
表示
时刻处于状态
的条件下,
时刻转移到状态
的概率
观测概率矩阵,其中
表示
时刻处于状态
的条件下观测到
的概率
初始状态概率向量 ,其中
表示系统初始状态为
的概率。
生成过程:
给定 ,生成观测序列
三个基本问题
条件随机场(Conditional Random Field) 是给定随机变量的条件下,随机变量
的马尔可夫随机场。
是
中的随机变量构成的无向图,图中每个变量在给定
的条件下都满足马尔可夫性:
线性链条件随机场(linear-chain CRF)是随机变量为线性链时的条件随机场
是观测序列。
是标记序列(或称状态序列 ),在给定
的条件下,
的条件分布
构成条件随机场。
怎样更鲁棒的匹配用户搜索意图?
查询扩展/Query expansion:
文档扩展/Document expansion:
使用锚文本/anchor text可以通过提供人工创作的同义词(即锚文本)来解决此问题,但不适用于新的或不太受欢迎的网页(注:链接稀疏,锚文本少)或无超链接的语料
基于查询日志的查询扩展
不考虑上下文语境的查询扩展可能会导致问题
从查询日志学习考虑上下文语境的查询重写:识别同一用户基于同一信息需求的多次查询请求
自动同义词库生成
表示词项之间的关系
使用词项的标准符号编码,每个词项都是一个维度
不同的词项没有内在的相似性
基于分布式相似度的表示:用相邻词项的意义来表示一个词项
解决方案:低维向量
基本思想: 将“大部分的”重要信息存储在一个维度固定的低维向量中 - 即“密集向量”
传统方法:潜在语义索引/分析
使用奇异值分解(Singular Value Decomposition,SVD)–或只是随机映射(random projection)以找到低维基向量或正交向量
词项的意义由向量表示:为每个词类构建一个密集向量,该向量应当能够准确的预测其上下文词项
学习神经词嵌入:基本思路
思路:直接基于预测能力学习低维词向量
Word2Vec包含一组算法预测每个词的上下文(或者反过来)
神经网络的优化:(求导的)链式法则
Word2vec里的线性关系
Word2vec的向量表示非常善于对相似性和相似性的维度编码!
仅通过在嵌入空间中进行向量减法就可以很好地解决类比测试相似度的问题
Dual Embedding Space Model (DESM)
一种简单的利用词嵌入的检索模型
文档由其词项嵌入的中心向量表示
查询-文档相似度:查询词向量与文档向量的平均相似度
DESM 是一个弱排序模型,但是具有发现微妙相似性/关联性的能力
]]>数组是一个由固定长度的特定类型元素组成的序列,一个数组可以由零个或多个元素组成。因为数组的长度是固定的,因此在Go语言中很少直接使用数组。
一个nil值的slice的长度和容量都是0,但是也有非nil值的slice的长度和容量也是0
如果你需要测试一个slice是否是空的,使用len(s) == 0来判断,而不应该用s == nil来判断。
一个slice可以用来模拟一个stack
最初给定的空slice对应一个空的stack,然后可以使用append函数将新的值压入stack:
stack = append(stack, v) // push vstack的顶部位置对应slice的最后一个元素:
top := stack[len(stack)-1] // top of stack通过收缩stack可以弹出栈顶的元素
stack = stack[:len(stack)-1] // pop要删除slice中间的某个元素并保存原有的元素顺序,可以通过内置的copy函数将后面的子slice向前依次移动一位完成:
func remove(slice []int, i int) []int { copy(slice[i:], slice[i+1:]) return slice[:len(slice)-1]}func main() { s := []int{5, 6, 7, 8, 9} fmt.Println(remove(s, 2)) // "[5 6 8 9]"}如果删除元素后不用保持原来顺序的话,我们可以简单的用最后一个元素覆盖被删除的元素:
func remove(slice []int, i int) []int { slice[i] = slice[len(slice)-1] return slice[:len(slice)-1]}func main() { s := []int{5, 6, 7, 8, 9} fmt.Println(remove(s, 2)) // "[5 6 9 8]}type Movie struct { Title string Year int `json:"released"` Color bool `json:"color,omitempty"` Actors []string}var movies = []Movie{ {Title: "Casablanca", Year: 1942, Color: false, Actors: []string{"Humphrey Bogart", "Ingrid Bergman"}}, {Title: "Cool Hand Luke", Year: 1967, Color: true, Actors: []string{"Paul Newman"}}, {Title: "Bullitt", Year: 1968, Color: true, Actors: []string{"Steve McQueen", "Jacqueline Bisset"}}, // ...}这样的数据结构特别适合JSON格式,并且在两者之间相互转换也很容易。将一个Go语言中类似movies的结构体slice转为JSON的过程叫编组(marshaling)。编组通过调用json.Marshal函数完成:
data, err := json.Marshal(movies)if err != nil { log.Fatalf("JSON marshaling failed: %s", err)}fmt.Printf("%s\n", data)另一个json.MarshalIndent函数将产生整齐缩进的输出。该函数有两个额外的字符串参数用于表示每一行输出的前缀和每一个层级的缩进:
data, err := json.MarshalIndent(movies, "", " ")if err != nil { log.Fatalf("JSON marshaling failed: %s", err)}fmt.Printf("%s\n", data)编码的逆操作是解码,对应将JSON数据解码为Go语言的数据结构,Go语言中一般叫unmarshaling,通过json.Unmarshal函数完成。
var titles []struct{ Title string }if err := json.Unmarshal(data, &titles); err != nil { log.Fatalf("JSON unmarshaling failed: %s", err)}fmt.Println(titles) // "[{Casablanca} {Cool Hand Luke} {Bullitt}]"var形式的声明语句往往是用于需要显式指定变量类型的地方,或者因为变量稍后会被重新赋值而初始值无关紧要的地方。
简短变量声明语句中必须至少要声明一个新的变量
如果用“var x int”声明语句声明一个x变量,那么&x表达式(取x变量的内存地址)将产生一个指向该整数变量的指针,指针对应的数据类型是 *int,指针被称之为“指向int类型的指针”。
指针是实现标准库中flag包的关键技术,它使用命令行参数来设置对应变量的值,而这些对应命令行标志参数的变量可能会零散分布在整个程序中。
// Echo4 prints its command-line arguments.package mainimport ( "flag" "fmt" "strings")var n = flag.Bool("n", false, "omit trailing newline")var sep = flag.String("s", " ", "separator")func main() { flag.Parse() fmt.Print(strings.Join(flag.Args(), *sep)) if !*n { fmt.Println() }}程序中的 sep和 n变量分别是指向对应命令行标志参数变量的指针,因此必须用 *sep和 *n形式的指针语法间接引用它们。
另一个创建变量的方法是调用内建的new函数。表达式new(T)将创建一个T类型的匿名变量,初始化为T类型的零值,然后返回变量地址,返回的指针类型为 *T。
p := new(int) // p, *int 类型, 指向匿名的 int 变量fmt.Println(*p) // "0"*p = 2 // 设置 int 匿名变量的值为 2fmt.Println(*p) // "2"下面的两个newInt函数有着相同的行为:
func newInt() *int { return new(int)}func newInt() *int { var dummy int return &dummy}变量的生命周期指的是在程序运行期间变量有效存在的时间段。对于在包一级声明的变量来说,它们的生命周期和整个程序的运行周期是一致的。而相比之下,局部变量的生命周期则是动态的:每次从创建一个新变量的声明语句开始,直到该变量不再被引用为止,然后变量的存储空间可能被回收。函数的参数变量和返回值变量都是局部变量。它们在函数每次被调用的时候创建。
一个类型声明语句创建了一个新的类型名称,和现有类型具有相同的底层结构。新命名的类型提供了一个方法,用来分隔不同概念的类型,这样即使它们底层类型相同也是不兼容的。
type 类型名字 底层类型在Go语言中,一个简单的规则是:如果一个名字是大写字母开头的,那么该名字是导出的
Unicode字符rune类型是和int32等价的类型,通常用于表示一个Unicode码点。这两个名称可以互换使用。
标准库中有四个包对字符串处理尤为重要:bytes、strings、strconv和unicode包。strings包提供了许多如字符串的查询、替换、比较、截断、拆分和合并等功能。
bytes包也提供了很多类似功能的函数,但是针对和字符串有着相同结构的[]byte类型。因为字符串是只读的,因此逐步构建字符串会导致很多分配和复制。在这种情况下,使用bytes.Buffer类型将会更有效,稍后我们将展示。
strconv包提供了布尔型、整型数、浮点数和对应字符串的相互转换,还提供了双引号转义相关的转换。
unicode包提供了IsDigit、IsLetter、IsUpper和IsLower等类似功能,它们用于给字符分类。每个函数有一个单一的rune类型的参数,然后返回一个布尔值。而像ToUpper和ToLower之类的转换函数将用于rune字符的大小写转换。所有的这些函数都是遵循Unicode标准定义的字母、数字等分类规范。strings包也有类似的函数,它们是ToUpper和ToLower,将原始字符串的每个字符都做相应的转换,然后返回新的字符串。
将一个整数转为字符串,一种方法是用fmt.Sprintf返回一个格式化的字符串;另一个方法是用strconv.Itoa(“整数到ASCII”)
如果要将一个字符串解析为整数,可以使用strconv包的Atoi或ParseInt函数,还有用于解析无符号整数的ParseUint函数
常量声明可以使用iota常量生成器初始化,它用于生成一组以相似规则初始化的常量,但是不用每行都写一遍初始化表达式。在一个const声明语句中,在第一个声明的常量所在的行,iota将会被置为0,然后在每一个有常量声明的行加一。
type Weekday intconst ( Sunday Weekday = iota Monday Tuesday Wednesday Thursday Friday Saturday)os 包以跨平台的方式,提供了一些与操作系统交互的函数和变量。程序的命令行参数可从 os 包的 Args 变量获取;os 包外部使用 os.Args 访问该变量。
os.Args 的第一个元素:os.Args[0],是命令本身的名字;其它的元素则是程序启动时传给它的参数。
package mainimport ("fmt""os")func main() {var s, sep stringfor i := 1; i < len(os.Args); i++ {s += sep + os.Args[i]sep = " "}fmt.Println(s)}> go run main.go 4 2 5 4 14 2 5 4 1for 循环的另一种形式,在某种数据类型的区间(range)上遍历
func main() {var s, sep stringfor _, j := range os.Args[1:] {s += sep + jsep = " "}fmt.Println(s)}使用 strings 包的 Join 函数:
func main() {fmt.Println(strings.Join(os.Args[1:], " "))}// Dup1 prints the text of each line that appears more than// once in the standard input, preceded by its count.package mainimport ("bufio""fmt""os")func main() {counts := make(map[string]int)input := bufio.NewScanner(os.Stdin)for input.Scan() {counts[input.Text()]++}// NOTE: ignoring potential errors from input.Err()for line, n := range counts {if n > 1 {fmt.Printf("%d\t%s\n", n, line)}}}> abc> abc> def> efd> efd2 abc2 efdPrintf的多种转换形式:
%d 十进制整数%x, %o, %b 十六进制,八进制,二进制整数。%f, %g, %e 浮点数: 3.141593 3.141592653589793 3.141593e+00%t 布尔:true或false%c 字符(rune) (Unicode码点)%s 字符串%q 带双引号的字符串"abc"或带单引号的字符'c'%v 变量的自然形式(natural format)%T 变量的类型%% 字面上的百分号标志(无操作数)以 ln 结尾的格式化函数,则遵循 Println 的方式,以跟 %v 差不多的方式格式化参数,并在最后添加一个换行符。
第二个版本,可以接收文件并判断重复行
// Dup2 prints the count and text of lines that appear more than once// in the input. It reads from stdin or from a list of named files.package mainimport ("bufio""fmt""os")func main() {counts := make(map[string]int)files := os.Args[1:]if len(files) == 0 {countLines(os.Stdin, counts)} else {for _, arg := range files {f, err := os.Open(arg)if err != nil {fmt.Fprintf(os.Stderr, "dup2: %v\n", err)continue}countLines(f, counts)f.Close()}}for line, n := range counts {if n > 1 {fmt.Printf("%d\t%s\n", n, line)}}}func countLines(f *os.File, counts map[string]int) {input := bufio.NewScanner(f)for input.Scan() {counts[input.Text()]++}// NOTE: ignoring potential errors from input.Err()}map 是一个由 make 函数创建的数据结构的引用。map 作为参数传递给某函数时,该函数接收这个引用的一份拷贝(copy,或译为副本),被调用函数对 map 底层数据结构的任何修改,调用者函数都可以通过持有的 map 引用看到。
package mainimport ("fmt""os""strings")func main() {counts := make(map[string]int)for _, filename := range os.Args[1:] {data, err := os.ReadFile(filename)if err != nil {fmt.Fprintf(os.Stderr, "dup3: %v\n", err)continue}for _, line := range strings.Split(string(data), "\n") {counts[line]++}}for line, n := range counts {if n > 1 {fmt.Printf("%d\t%s\n", n, line)}}}引入了 ReadFile 函数(来自于 os包),其读取指定文件的全部内容,strings.Split 函数把字符串分割成子串的切片。
// Lissajous generates GIF animations of random Lissajous figures.package mainimport ("image""image/color""image/gif""io""math""math/rand""os""time")var palette = []color.Color{color.White, color.Black}const (whiteIndex = 0 // first color in paletteblackIndex = 1 // next color in palette)func main() {// The sequence of images is deterministic unless we seed// the pseudo-random number generator using the current time.// Thanks to Randall McPherson for pointing out the omission.rand.Seed(time.Now().UTC().UnixNano())lissajous(os.Stdout)}func lissajous(out io.Writer) {const (cycles = 5 // number of complete x oscillator revolutionsres = 0.001 // angular resolutionsize = 100 // image canvas covers [-size..+size]nframes = 64 // number of animation framesdelay = 8 // delay between frames in 10ms units)freq := rand.Float64() * 3.0 // relative frequency of y oscillatoranim := gif.GIF{LoopCount: nframes}phase := 0.0 // phase differencefor i := 0; i < nframes; i++ {rect := image.Rect(0, 0, 2*size+1, 2*size+1)img := image.NewPaletted(rect, palette)for t := 0.0; t < cycles*2*math.Pi; t += res {x := math.Sin(t)y := math.Sin(t*freq + phase)img.SetColorIndex(size+int(x*size+0.5), size+int(y*size+0.5),blackIndex)}phase += 0.1anim.Delay = append(anim.Delay, delay)anim.Image = append(anim.Image, img)}gif.EncodeAll(out, &anim) // NOTE: ignoring encoding errors}// Fetch prints the content found at a URL.package mainimport ("fmt""io""net/http""os")func main() {for _, url := range os.Args[1:] {resp, err := http.Get(url)if err != nil {fmt.Fprintf(os.Stderr, "fetch: %v\n", err)os.Exit(1)}b, err := io.ReadAll(resp.Body)resp.Body.Close()if err != nil {fmt.Fprintf(os.Stderr, "fetch: reading %s: %v\n", url, err)os.Exit(1)}fmt.Printf("%s", b)}}改进:
避免申请缓冲区、url参数没有 http:// 前缀、打印出HTTP协议的状态码
// Fetch prints the content found at a URL.package mainimport ("fmt""io""net/http""os""strings")func main() {for _, url := range os.Args[1:] {if !strings.HasPrefix(url, "http://") {url = "http://" + url}resp, err := http.Get(url)if err != nil {fmt.Fprintf(os.Stderr, "fetch: %v\n", err)os.Exit(1)}_, err = io.Copy(os.Stdout, resp.Body)if err != nil {fmt.Fprintf(os.Stderr, "fetch: reading %s: %v\n", url, err)os.Exit(1)}fmt.Println(resp.Status)resp.Body.Close()}}// Fetchall fetches URLs in parallel and reports their times and sizes.package mainimport ("fmt""io""net/http""os""time")func main() {start := time.Now()ch := make(chan string)for _, url := range os.Args[1:] {go fetch(url, ch) // start a goroutine}for range os.Args[1:] {fmt.Println(<-ch) // receive from channel ch}fmt.Printf("%.2fs elapsed\n", time.Since(start).Seconds())}func fetch(url string, ch chan<- string) {start := time.Now()resp, err := http.Get(url)if err != nil {ch <- fmt.Sprint(err) // send to channel chreturn}nbytes, err := io.Copy(io.Discard, resp.Body)resp.Body.Close() // don't leak resourcesif err != nil {ch <- fmt.Sprintf("while reading %s: %v", url, err)return}secs := time.Since(start).Seconds()ch <- fmt.Sprintf("%.2fs %7d %s", secs, nbytes, url)}goroutine是一种函数的并发执行方式,而channel是用来在goroutine之间进行参数传递。main函数本身也运行在一个goroutine中,而go function则表示创建一个新的goroutine,并在这个新的goroutine中执行这个函数。
// Server1 is a minimal "echo" server.package mainimport ( "fmt" "log" "net/http")func main() { http.HandleFunc("/", handler) // each request calls handler log.Fatal(http.ListenAndServe("localhost:8000", nil))}// handler echoes the Path component of the request URL r.func handler(w http.ResponseWriter, r *http.Request) { fmt.Fprintf(w, "URL.Path = %q\n", r.URL.Path)}为访问的url添加某种状态。比如,下面这个版本输出了同样的内容,但是会对请求的次数进行计算
// Server2 is a minimal "echo" and counter server.package mainimport ("fmt""log""net/http""sync")var mu sync.Mutexvar count intfunc main() {http.HandleFunc("/", handler)http.HandleFunc("/count", counter)log.Fatal(http.ListenAndServe("localhost:8000", nil))}// handler echoes the Path component of the requested URL.func handler(w http.ResponseWriter, r *http.Request) {mu.Lock()count++mu.Unlock()fmt.Fprintf(w, "URL.Path = %q\n", r.URL.Path)}// counter echoes the number of calls so far.func counter(w http.ResponseWriter, r *http.Request) {mu.Lock()fmt.Fprintf(w, "Count %d\n", count)mu.Unlock()}handler函数会把请求的http头和请求的form数据都打印出来,这样可以使检查和调试这个服务更为方便
// handler echoes the HTTP request.func handler(w http.ResponseWriter, r *http.Request) { fmt.Fprintf(w, "%s %s %s\n", r.Method, r.URL, r.Proto) for k, v := range r.Header { fmt.Fprintf(w, "Header[%q] = %q\n", k, v) } fmt.Fprintf(w, "Host = %q\n", r.Host) fmt.Fprintf(w, "RemoteAddr = %q\n", r.RemoteAddr) if err := r.ParseForm(); err != nil { log.Print(err) } for k, v := range r.Form { fmt.Fprintf(w, "Form[%q] = %q\n", k, v) }}面向文本分类的决策树
决策树的学习
学习一个序列的特征测试,典型的做法是由上到下的贪心搜索,每一步选择具有最高信息收益的未使用特征
叶节点标记:yes/no 类别标记,或连续值
如果有个特征,决策树的节点数量上限是
(太大了,会有计算开支等方面的问题)
我们可以通过在每个节点上递归选择最佳拆分特征,以贪心的方式创建树
属性选择基本思想:(理想情况下)一个好的特征能够把所有样本划分成“全部正样本”和“全部负样本”两个子集
利用信息论:
信息熵(Entropy):考虑每个节点的类分解
信息增益
对每个节点,我们选择使信息增益最大的特征f
数值特征 (例如tf-idf):通常使用二元的切分 (f < t), t怎样确定?
穷尽式(搜索):评估观察值之间的每个分割点的信息增益。
分箱(Discretize into bins)
(树的构建)什么时候停止?
宏平均:计算每个类别的性能指标,然后取平均值
微平均:收集所有类别的决策(分类)结果,计算列联表,评价
判别式 (discriminative) 分类方法: Logistic Regression (逻辑回归) 与 Support vector machines (支持向量机)
Ensemble 方法
随机森林 (Random Forests)
从原始数据集重复采样(bootstrap采样),在采样数据上构建K个树,p=特征数量
原则:我们希望在不同的学习器(learner)之间进行投票,因此我们不希望这些模型过于相似。这两个标准确保了各个树的多样性
优点:
缺点:
Boosted Decision Trees (BDT, 增强决策树)
随机森林(RF) vs 增强树(BDT)
]]>信息量(信息增益量)定义:,
信息量性质:概率越小的状态,信息量越大
信息熵定义:信息量在全部数值域上的概率平均值
微分熵性质:平移不变、尺度变化,且可以是负值
当根据不完整的信息作为依据进行推断时,应该由满足分布限制条件的具有最大熵的概率分布推得。
最大微分熵问题:
已知均值和方差,高斯分布的微分熵最大
条件信息量:
条件熵:
联合熵:
互信息:信息熵与条件熵的差:
互信息性质:非负性、对称性、不变性
相对熵是衡量两个分布的平均信息差异
相对熵和互信息之间的关系:
最大熵模型:最大化 , 求取类别后验概率分布
, 用于分类、预测等
最大互信息模型: 最大化 ; 最大化
最小互信息模型:最小化 ; 最小化
, 独立分析
Go 语言表现力强,且简单明了。 它在设计时考虑了惯用语言,这使程序员能够高效地编写高效且可靠的代码。 以 Go 语言编写的程序可以在 Unix 系统上运行,例如 Linux 和 macOS,还有 Windows。 Go 语言之所以值得注意,部分原因在于它独特的并发机制,使得编写可同时利用多个内核的程序非常容易。 它主要是一种强化静态类型的语言,这意味着变量类型在编译时是已知的。 不过,它确实具有一些动态类型化功能。
下面是 Go 编程语言的基本原理优势:
如果不想在本地安装 Go,可以使用 Go Playground。 Go Playground 是一款 Web 服务,可在浏览器中运行 Go 应用程序。
本地安装包下载地址
wget https://go.dev/dl/go1.19.1.linux-amd64.tar.gz // 版本号可能改变提取本地安装包
sudo tar -C /usr/local -xzf go1.19.1.linux-amd64.tar.gz编辑配置文件,添加到环境变量:
vim ~/.bashrcexport PATH=$PATH:/usr/local/go/binsource ~/.bashrc确认是否已经安装好:
go versiongo version go1.19.1 linux/amd64Go 在组织项目文件方面与其他编程语言不同。 首先,Go 是在工作区的概念下工作的。 工作区就是应用程序源代码所在的位置。 所有 Go 项目共享同一个工作区。 不过,从版本 1.11 开始,Go 已开始更改此方法。 你尚且不必担心,因为我们将在下一个模块中介绍工作区。 现在,Go 工作区位于 $HOME/go,但如果需要,可以为所有项目设置其他位置。
若要将工作区设置为其他位置,可以使用 $GOPATH 环境变量。 在处理更复杂的项目时,此环境变量有助于避免将来出现问题。
export GOPATH=/mnt/d/Programming_Design/Go每个 Go 工作区都包含三个基本文件夹:
例如,工作站文件夹结构树可能与下面的示例类似:
bin/ hello coolapppkg/ github.com/gorilla/ mux.asrc/ github.com/golang/example/ .git/ hello/ hello.go在安装插件之前要先更改go的源
The "gopls" command is not available. Run "go install -v golang.org/x/tools/gopls@latest" to install.然后点击上边的窗口的install All,即可完成插件的安装
文件夹组织形式:
package mainimport "fmt"func main() {fmt.Println("Hello World!")}运行:
go run main.goHello World!只生成二进制文件但是不运行:
go build main.go我们在 package main 语句中告诉 Go,我们将要创建的应用是一个可执行程序(可以运行的文件)。 我们的“Hello World!”应用是 main 包的一部分。
包是一组常用的源代码文件。 每个可执行应用都具有此第一行,即使项目或文件具有不同的名称。
import 语句使你的程序可以访问其他包中的其他代码。 在本例中,fmt 为标准库包。
你需要此 import 语句,因为你将在此程序的稍后部分使用此包中的函数将消息打印到屏幕上。 可以在程序中包含你想要或需要的任意数量的 import 语句。 但是,Go 在这方面是惯用的。 如果导入包,但不使用包中的相应函数,应用将不会进行编译。 Visual Studio Code 的一大功能是,当你保存文件时,它会自动删除程序中未使用的导入。
VSCode 是自动帮助我们删除的,但是和Python什么的不一样,如果多了冗余的包程序是无法运行的。
# command-line-arguments./main.go:4:8: imported and not used: "math"func 语句是用于声明函数的保留字。 第一个函数名为“main”,因为它是程序的起始点。 整个 package main 中只能有一个 main() 函数(在第一行中定义的那个)。 在 main() 函数中,你调用了 fmt 包中的 Println 函数。 你发送了你希望在屏幕上看到的文本消息。
var firstName string // 声明单一变量var secondName, lastName string // 如果多个变量的类型相同,可以用逗号分隔一起声明多个变量var age int// 也可以在一个括号内批量声明变量var (thirdName, fourthName stringsecondage int)(VSCode会自动进行格式化,完全不用担心格式的问题)
可以在声明的时候直接对变量进行初始化,会自动对变量的类型进行推断,不用显式指定类型
var ( firstName string = "John" lastName string = "Doe" age int = 32)等价于下面的写法:
var ( firstName, lastName, age = "John", "Doe", 32)package mainimport "fmt"func main() {firstName, lastName := "John", "Doe"age := 32fmt.Println(firstName, lastName, age)}John Doe 32请注意,在定义变量名称后,需要在此处加入一个冒号等于号 (:=) 和相应的值。 使用冒号等于号时, 要声明的变量必须是新变量 。 如果使用冒号等于号并已经声明该变量,将不会对程序进行编译。
用于声明常量的关键字是 const
const HTTPStatusOK = 200const (StatusOK = 0StatusConnectionReset = 1StatusOtherError = 2)常量和变量之间既有相似之处,也有一些重要差异。 例如,你可以在不使用常量的情况下声明常量。 你不会收到错误消息。 不能使用冒号等于号来声明常量。 如果采用这种方式,Go 会发出警告。
在 Go 中,当你(在函数内部)声明一个变量但不使用它时,Go 会抛出错误,而不是像某些其他编程语言一样抛出警告。
一般来说,定义整数类型的关键字是 int。 但 Go 还提供了 int8、int16、int32 和 int64 类型,其大小分别为 8、16、32 或 64 位的整数。 使用 32 位操作系统时,如果只是使用 int,则大小通常为 32 位。 在 64 位系统上,int 大小通常为 64 位。 但是,此行为可能因计算机而不同。 可以使用 uint。 但是,只有在出于某种原因需要将值表示为无符号数字的情况下,才使用此类型。 此外,Go 还提供 uint8、uint16、uint32 和 uint64 类型。
var integer8 int8 = 127var integer16 int16 = 32767var integer32 int32 = 2147483647var integer64 int64 = 9223372036854775807不能进行隐式转换,如果两个变量的类型不同,需要进行强制转换,否则编译不能通过。
Go 提供两种浮点数大小的数据类型:float32 和 float64。 如果需要存储较大的数字,则可以使用这些类型,这些类型无法适应前面提到的任何一个整数类型。 这两种类型的区别是它们可以容纳的最大位数。
var float32 float32 = 2147483647var float64 float64 = 9223372036854775807fmt.Println(float32, float64)可以使用 math 包中提供的 math.MaxFloat32 和 math.MaxFloat64 常量来查找这两种类型的限制。
package mainimport ("fmt""math")func main() {fmt.Println(math.MaxFloat32, math.MaxFloat64)}3.4028234663852886e+38 1.7976931348623157e+308布尔类型仅可能有两个值:true 和 false。 你可以使用关键字 bool 声明布尔类型。 Go 不同于其他编程语言,在 Go 中,你不能将布尔类型隐式转换为 0 或 1。
var featureFlag bool = true最后,让我们看一下编程语言中最常见的数据类型:string。 在 Go 中,关键字 string 用于表示字符串数据类型。 若要初始化字符串变量,你需要在双引号(")中定义值。 单引号(')用于单个字符(以及 runes,正如我们在上一节所述)。
var firstName string = "John"lastName := "Doe"fmt.Println(firstName, lastName)John Doe到目前为止,几乎每次声明变量时,都使用值对其进行了初始化。 但与在其他编程语言中不同的是,在 Go 中,如果你不对变量初始化,所有数据类型都有默认值。 此功能非常方便,因为在使用之前,你无需检查变量是否已初始化。
下面列出了我们目前浏览过类型的几个默认值:
int 类型的 0(及其所有子类型,如 int64)float32 和 float64 类型的 +0.000000e+000bool 类型的 falsestring 类型的空值Go 中隐式强制转换不起作用。 接下来,需要显式强制转换。 Go 提供了将一种数据类型转换为另一种数据类型的一些本机方法。
一种方法是对每个类型使用内置函数,如下所示:
var integer16 int16 = 127var integer32 int32 = 32767fmt.Println(int32(integer16) + integer32)Go 的另一种转换方法是使用 strconv 包。 将 string 与 int
package mainimport ("fmt""strconv")func main() {i, _ := strconv.Atoi("-42")s := strconv.Itoa(-42)fmt.Println(i, s)}-42 -42有一个下划线 (_) 用作变量的名称。 在 Go 中(或Python中),这意味着我们不会使用该变量的值,而是要将其忽略。
在 Go 中,函数允许你将一组可以从应用程序的其他部分调用的语句组合在一起。 你可以使用函数来组织代码并使其更易于阅读,而不是创建包含许多语句的程序。 更具可读性的代码也更易于维护。
与之交互的函数是 main() 函数。 Go 中的所有可执行程序都具有此函数,因为它是程序的起点。 你的程序中只能有一个 main() 函数。
package mainimport ("fmt""os""strconv")func main() {number1, _ := strconv.Atoi(os.Args[1])number2, _ := strconv.Atoi(os.Args[2])fmt.Println("Sum:", number1+number2)}os.Args 变量包含传递给程序的每个命令行参数。 由于这些值的类型为 string,因此需要将它们转换为 int 以进行求和。
> go run main.go 3 5Sum: 8使用 func 关键字来定义函数,然后为其指定名称。 在命名后,指定函数的参数列表。 你可以指定零个或多个参数。 你还可以定义函数的返回类型,该函数也可以是零个或多个。 (我们将在下一节中讨论如何返回多个值)。在定义所有这些值之后,你可以编写函数的正文内容。
package mainimport ("fmt""os""strconv")func main() {sum := sum(os.Args[1], os.Args[2])fmt.Println("Sum:", sum)}func sum(number1 string, number2 string) int {int1, _ := strconv.Atoi(number1)int2, _ := strconv.Atoi(number2)return int1 + int2}此代码创建一个名为 sum 的函数,该函数采用两个 string 参数,并将它们强制转换为 int,然后返回求和所得的结果。 定义返回类型时,函数需要返回该类型的值。
在 Go 中,你还可以为函数的返回值设置名称,将其当作一个变量。
func sum(number1 string, number2 string) (result int) {int1, _ := strconv.Atoi(number1)int2, _ := strconv.Atoi(number2)result = int1 + int2return}package mainimport ("fmt""os""strconv")func main() {sum, mul := calc(os.Args[1], os.Args[2])fmt.Println("Sum:", sum)fmt.Println("Mul:", mul)}func calc(number1 string, number2 string) (sum int, mul int) {int1, _ := strconv.Atoi(number1)int2, _ := strconv.Atoi(number2)sum = int1 + int2mul = int1 * int2return}> go run main.go 3 5Sum: 8Mul: 15将值传递给函数时,该函数中的每个更改都不会影响调用方。 Go 是“按值传递”编程语言。 每次向函数传递值时,Go 都会使用该值并创建本地副本(内存中的新变量)。 在函数中对该变量所做的更改都不会影响你向函数发送的更改。
指针是包含另一个变量的内存地址的变量。 当你发送指向某个函数的指针时,不会传递值,而是传递地址内存。 因此,对该变量所做的每个更改都会影响调用方。
在 Go 中,有两个运算符可用于处理指针:
& 运算符使用其后对象的地址。* 运算符取消引用指针。 也就是说,你可以前往指针中包含的地址访问其中的对象。package mainimport "fmt"func main() {firstName := "John"updateName(&firstName)fmt.Println(firstName)}func updateName(name *string) {*name = "David"}首先要做的就是修改函数的签名,以指明你要接收指针。 为此,请将参数类型从 string 更改为 *string。 (后者仍是字符串,但现在它是指向字符串 的 指针。)然后,将新值分配给该变量时,需要在该变量的左侧添加星号 (*) 以暂停该变量的值。 调用 updateName 函数时,系统不会发送值,而是发送变量的内存地址。 这就是前面的代码在变量左侧带有 & 符号的原因。
Go 包与其他编程语言中的库或模块类似。 你可以打包代码,并在其他位置重复使用它。 包的源代码可以分布在多个 .go 文件中。 到目前为止,我们已编写 main 包,并对其他本地包进行了一些引用。
你可能注意到,在 Go 中,甚至最直接的程序都是包的一部分。 通常情况下,默认包是 main 包,即目前为止一直使用的包。 如果程序是 main 包的一部分,Go 会生成二进制文件。 运行该文件时,它将调用 main() 函数。
换句话说,当你使用 main 包时,程序将生成独立的可执行文件。 但当程序非是 main 包的一部分时,Go 不会生成二进制文件。 它生成包存档文件(扩展名为“.a”的文件)。
在 Go 中,包名称需遵循约定。 包使用其导入路径的最后一部分作为名称。 例如,Go 标准库包含名为 math/cmplx 的包,该包提供用于处理复数的有用代码。 此包的导入路径为 math/cmplx,导入包的方式如下所示:
import "math/cmplx"在名为 calculator 的目录中 创建名为 sum.go 的文件。 树目录应如下列目录所示:
用包的名称初始化 sum.go 文件:
package calculator你现在可以开始编写包的函数和变量。 不同于其他编程语言,Go 不会提供 public 或 private 关键字,以指示是否可以从包的内外部调用变量或函数。 但 Go 须遵循以下两个简单规则:
接下来,让我们将以下代码添加到我们要创建的计算器包:
package calculatorvar logMessage = "[LOG]"// Version of the calculatorvar Version = "1.0"func internalSum(number int) int { return number - 1}// Sum two integer numbersfunc Sum(number1, number2 int) int { return number1 + number2}让我们看一下该代码中的一些事项:
logMessage 变量。Version 变量。 建议你添加注释来描述此变量的用途。 (此描述适用于包的任何用户。)internalSum 函数。Sum 函数。 建议你添加注释来描述此函数的用途。若要确认一切正常,可在 calculator 目录中运行 go build 命令。 如果执行此操作,请注意系统不会生成可执行的二进制文件。
你已将计算器功能放入包中。 现在可以将包放到模块中。 Go 模块通常包含可提供相关功能的包。 包的模块还指定了 Go 运行你组合在一起的代码所需的上下文。 此上下文信息包括编写代码时所用的 Go 版本。
此外,模块还有助于其他开发人员引用代码的特定版本,并更轻松地处理依赖项。 另一个优点是,我们的程序源代码无需严格存在于 $GOPATH/src 目录中。 如果释放该限制,则可以更方便地在其他项目中同时使用不同包版本。
(下面与教程不同,自己探索出了一个可用不报错的方法)
VSCode GOPATH设置:"go.gopath": "/mnt/d/Programming_Design/Go"
首先设置 go env -w GO111MODULE=on
如果 helloworld要引用 calculator,则文件夹的组织形式如下:
在 $GOPATH/src/calculator创建 go.mod文件,其中文件第一行与文件夹同名
module calculatorgo 1.19在 $GOPATH/src/helloworld创建 go.mod文件,其中文件第一行与文件夹同名,下面要写好版本号和包的路径
module helloworldgo 1.19require "calculator" v1.0.0replace "calculator" => "../calculator"然后可以导入这个包并运行主文件
package mainimport ("calculator""fmt")func main() {total := calculator.Sum(3, 5)fmt.Println(total)fmt.Println("Version: ", calculator.Version)}8Version: 1.0有时,程序需要引用其他开发人员编写的包。
测试后不是很明白,基本上是在主文件和 .mod文件中写入包的名称和版本即可。然后根据控制台的输出将包安装好即可使用
main.go:
package mainimport ("calculator""fmt""rsc.io/quote")func main() {total := calculator.Sum(3, 5)fmt.Println(total)fmt.Println("Version: ", calculator.Version)fmt.Println(quote.Hello())}go.mod:
module helloworldgo 1.19require (calculator v1.0.0rsc.io/quote v1.5.2)require (golang.org/x/text v0.0.0-20170915032832-14c0d48ead0c // indirectrsc.io/sampler v1.3.0 // indirect)replace calculator => ../calculator输出:
8Version: 1.0Ahoy, world!与其他编程语言不同的是,在 Go 中,你不需要在条件中使用括号。 else 子句可选。 但是,大括号仍然是必需的。 此外,为了减少行,Go 不支持三元 if 语句,因此每次都需要编写完整的 if 语句。
package mainimport "fmt"func givemeanumber() int {return -1}func main() {if num := givemeanumber(); num < 0 {fmt.Println(num, "is negative")} else if num < 10 {fmt.Println(num, "has only one digit")} else {fmt.Println(num, "has multiple digits")}}其中,有一个在 Go 中常见的约定进行高效编程的方式 if num := givemeanumber(); num < 0,同时接收函数的返回值,但是不重复进行接收,然后使用到if语句中进行判断。当然这个 num变量在 if的外部是无法使用的。
像其他编程语言一样,Go 支持 switch 语句。 可以使用 switch 语句来避免链接多个 if 语句。 使用 switch 语句,就不需维护和读取包含多个 if 语句的代码。 这些语句还可以让复杂的条件更易于构造。 请参阅以下部分的 switch 语句。
普通的switch语句:
package mainimport ("fmt""math/rand""time")func main() {sec := time.Now().Unix()rand.Seed(sec)i := rand.Int31n(10)switch i {case 0:fmt.Print("zero...")case 1:fmt.Print("one...")case 2:fmt.Print("two...")default:fmt.Print("no match...")}fmt.Println("ok")}有时,多个表达式仅与一个 case 语句匹配。 在 Go 中,如果希望 case 语句包含多个表达式,请使用逗号 (,) 来分隔表达式。 此方法可避免代码重复。
package mainimport "fmt"func location(city string) (string, string) {var region stringvar continent stringswitch city {case "Delhi", "Hyderabad", "Mumbai", "Chennai", "Kochi":region, continent = "India", "Asia"case "Lafayette", "Louisville", "Boulder":region, continent = "Colorado", "USA"case "Irvine", "Los Angeles", "San Diego":region, continent = "California", "USA"default:region, continent = "Unknown", "Unknown"}return region, continent}func main() {region, continent := location("Irvine")fmt.Printf("John works in %s, %s\n", region, continent)}John works in California, USA在 case 语句的表达式中包含的值对应于 switch 语句验证的变量的数据类型。
switch 还可以调用函数。 在该函数中,可以针对可能的返回值编写 case 语句。
第一种是在switch上调用函数,对返回值进行判断
package mainimport ("fmt""time")func main() {switch time.Now().Weekday().String() {case "Monday", "Tuesday", "Wednesday", "Thursday", "Friday":fmt.Println("It's time to learn some Go.")default:fmt.Println("It's weekend, time to rest!")}fmt.Println(time.Now().Weekday().String())}It's time to learn some Go.Wednesday第二种是在case上调用函数
package mainimport ("fmt""regexp")func main() {var email = regexp.MustCompile(`^[^@]+@[^@.]+\.[^@.]+`)var phone = regexp.MustCompile(`^[(]?[0-9][0-9][0-9][). \-]*[0-9][0-9][0-9][.\-]?[0-9][0-9][0-9][0-9]`)contact := "foo@bar.com"switch {case email.MatchString(contact):fmt.Println(contact, "is an email")case phone.MatchString(contact):fmt.Println(contact, "is a phone number")default:fmt.Println(contact, "is not recognized")}}foo@bar.com is an email上面的 switch 语句中省略了条件,就像在 if 语句中那样。 此模式类似于比较 true 值,就像强制 switch 语句一直运行一样。
一个条件 switch 块比一长串的 if 和 else if 语句更易于维护。
在某些编程语言中,你会在每个 case 语句末尾写一个 break 关键字。 但在 Go 中,当逻辑进入某个 case 时,它会退出 switch 块,除非你显式停止它。 若要使逻辑进入到下一个紧邻的 case,请使用 fallthrough 关键字。
package mainimport ("fmt")func main() {switch num := 15; {case num < 50:fmt.Printf("%d is less than 50\n", num)fallthroughcase num > 100:fmt.Printf("%d is greater than 100\n", num)fallthroughcase num < 200:fmt.Printf("%d is less than 200\n", num)}}15 is less than 5015 is greater than 10015 is less than 200请注意,由于 num 为 15(小于 50),因此它与第一个 case 匹配。 但是,num 不大于 100。 由于第一个 case 语句包含 fallthrough 关键字,因此逻辑会立即转到下一个 case 语句,而不会对该 case 进行验证。 因此,在使用 fallthrough 关键字时必须谨慎。 该代码产生的行为可能不是你想要的。
另一个常用控制流是循环。 Go 只使用一个循环构造,即 for 循环。 但是,你可以通过多种方式表示循环。
package mainimport ("fmt")func main() {sum := 0for i := 1; i <= 100; i++ {sum += i}fmt.Println("sum of 1..100 is", sum)}sum of 1..100 is 5050package mainimport ("fmt""math/rand""time")func main() {var num int64rand.Seed(time.Now().Unix())for num != 5 {num = rand.Int63n(15)fmt.Println(num)}}只要 num 变量保存的值与 5 不同,程序就会输出一个随机数。
可以在 Go 中编写的另一种循环模式是无限循环。 在这种情况下,你不编写条件表达式,也不编写预处理语句或后处理语句, 而是采取退出循环的方式进行编写。 否则,逻辑永远都不会退出。 若要使逻辑退出循环,请使用 break 关键字。
package mainimport ("fmt""math/rand""time")func main() {var num int32sec := time.Now().Unix()rand.Seed(sec)for {fmt.Print("Writing inside the loop...")if num = rand.Int31n(10); num == 5 {fmt.Println("finish!")break}fmt.Println(num)}}在 Go 中,可以使用 continue 关键字跳过循环的当前迭代。 例如,可以使用此关键字在循环继续之前运行验证。 也可以在编写无限循环并需要等待资源变得可用时使用它。
package mainimport "fmt"func main() {sum := 0for num := 1; num <= 100; num++ {if num%5 == 0 {continue}sum += num}fmt.Println("The sum of 1 to 100, but excluding numbers divisible by 5, is", sum)}The sum of 1 to 100, but excluding numbers divisible by 5, is 4000在 Go 中,defer 语句会推迟函数(包括任何参数)的运行,直到包含 defer 语句的函数完成。 通常情况下,当你想要避免忘记任务(例如关闭文件或运行清理进程)时,可以推迟某个函数的运行。
可以根据需要推迟任意多个函数。 defer 语句按逆序运行,先运行最后一个,最后运行第一个。
package mainimport "fmt"func main() {for i := 1; i <= 4; i++ {defer fmt.Println("deferred", -i)fmt.Println("regular", i)}}regular 1regular 2regular 3regular 4deferred -4deferred -3deferred -2deferred -1在此示例中,请注意,每次推迟 fmt.Println("deferred", -i) 时,都会存储 i 的值,并会将其运行任务添加到队列中。 在 main() 函数输出完 regular 值后,所有推迟的调用都会运行。 这就是你看到输出采用逆序(后进先出)的原因。
defer 函数的一个典型用例是在使用完文件后将其关闭。
package mainimport ("fmt""io""os")func main() {newfile, error := os.Create("learnGo.txt")if error != nil {fmt.Println("Error: Could not create file.")return}defer newfile.Close()if _, error = io.WriteString(newfile, "Learning Go!"); error != nil {fmt.Println("Error: Could not write to file.")return}newfile.Sync()}创建或打开某个文件后,可以推迟 .Close() 函数的执行,以免在你完成后忘记关闭该文件。
运行时错误会使 Go 程序崩溃,例如尝试通过使用超出范围的索引或取消引用 nil 指针来访问数组。 你也可以强制程序崩溃。
内置 panic() 函数可以停止 Go 程序中的正常控制流。 当你使用 panic 调用时,任何延迟的函数调用都将正常运行。 进程会在堆栈中继续,直到所有函数都返回。 然后,程序会崩溃并记录日志消息。 此消息包含错误信息和堆栈跟踪,有助于诊断问题的根本原因。
调用 panic() 函数时,可以添加任何值作为参数。 通常,你会发送一条错误消息,说明为什么会进入紧急状态。
例如,下面的代码将 panic 和 defer 函数组合在一起。 尝试运行此代码以了解控制流的中断。 请注意,清理过程仍会运行。
package mainimport "fmt"func highlow(high int, low int) {if high < low {fmt.Println("Panic!")panic("highlow() low greater than high")}defer fmt.Println("Deferred: highlow(", high, ",", low, ")")fmt.Println("Call: highlow(", high, ",", low, ")")highlow(high, low+1)}func main() {highlow(2, 0)fmt.Println("Program finished successfully!")}Call: highlow( 2 , 0 )Call: highlow( 2 , 1 )Call: highlow( 2 , 2 )Panic!Deferred: highlow( 2 , 2 )Deferred: highlow( 2 , 1 )Deferred: highlow( 2 , 0 )panic: highlow() low greater than highgoroutine 1 [running]:main.highlow(0x4b8018?, 0xc000012018?) /mnt/d/Programming_Design/Go/src/helloworld/main.go:8 +0x285main.highlow(0x2, 0x2) /mnt/d/Programming_Design/Go/src/helloworld/main.go:13 +0x211main.highlow(0x2, 0x1) /mnt/d/Programming_Design/Go/src/helloworld/main.go:13 +0x211main.highlow(0x2, 0x0) /mnt/d/Programming_Design/Go/src/helloworld/main.go:13 +0x211main.main() /mnt/d/Programming_Design/Go/src/helloworld/main.go:17 +0x25exit status 2下面是运行代码时会发生的情况:
highlow() 函数中的高值和低值。low 的值大于 high 的值,则程序会崩溃。 会显示“Panic!”消息。 此时,控制流中断,所有推迟的函数都开始输出“Deferred...”消息。Program finished successfully!”消息。有时,你可能想要避免程序崩溃,改为在内部报告错误。 或者,你可能想要先清理混乱情况,然后再让程序崩溃。 例如,你可能想要关闭与某个资源的连接,以免出现更多问题。
Go 提供内置 recover() 函数,让你可以在程序崩溃之后重新获得控制权。 你只会在你同时调用 defer 的函数中调用 recover。 如果调用 recover() 函数,则在正常运行的情况下,它会返回 nil,没有任何其他作用。
尝试修改前面的代码中的 main 函数,以添加对 recover() 的调用,如下所示:
package mainimport "fmt"func highlow(high int, low int) {if high < low {fmt.Println("Panic!")panic("highlow() low greater than high")}defer fmt.Println("Deferred: highlow(", high, ",", low, ")")fmt.Println("Call: highlow(", high, ",", low, ")")highlow(high, low+1)}func main() {defer func() {handler := recover()if handler != nil {fmt.Println("main(): recover", handler)}}()highlow(2, 0)fmt.Println("Program finished successfully!")}Call: highlow( 2 , 0 )Call: highlow( 2 , 1 )Call: highlow( 2 , 2 )Panic!Deferred: highlow( 2 , 2 )Deferred: highlow( 2 , 1 )Deferred: highlow( 2 , 0 )main(): recover highlow() low greater than high在 main() 函数中,你会将一个可以调用 recover() 函数的匿名函数推迟。 当程序处于紧急状态时,对 recover() 的调用无法返回 nil。 你可以在此处执行一些操作来清理混乱,但在本例中,你只是简单地输出一些内容。
panic 和 recover 函数的组合是 Go 处理异常的惯用方式。 其他编程语言使用 try/catch 块。 Go 首选此处所述的方法。
首先,编写一个用于输出数字(1 到 100)的程序,其中有以下变化:
Fizz。Buzz。FizzBuzz。尝试使用 switch 语句。
package mainimport ( "fmt" "strconv")func fizzbuzz(num int) string { switch { case num%15 == 0: return "FizzBuzz" case num%3 == 0: return "Fizz" case num%5 == 0: return "Buzz" } return strconv.Itoa(num)}func main() { for num := 1; num <= 100; num++ { fmt.Println(fizzbuzz(num)) }}编写一个程序来查找小于 20 的所有质数。 质数是大于 1 的任意数字,只能被它自己和 1 整除。 “整除”表示经过除法运算后没有余数。 与大多数编程语言一样,Go 还提供了一种方法来检查除法运算是否产生余数。 我们可以使用模数 %(百分号)运算符。
在本练习中,你将更新一个名为 findprimes 的函数,以检查数值是否为质数。 该函数有一个整数参数,并返回一个布尔值。 函数通过检查是否有余数来测试输入数字是否为质数。 如果数字为质数,则该函数返回 true。
package mainimport "fmt"func findprimes(number int) bool {for i := 2; i < number; i++ {if number%i == 0 {return false}}if number > 1 {return true} else {return false}}func main() {fmt.Println("Prime numbers less than 20:")for number := 1; number < 20; number++ {if findprimes(number) {fmt.Printf("%v ", number)}}fmt.Println()}Prime numbers less than 20:2 3 5 7 11 13 17 19编写一个要求用户输入一个数字的程序。 在开始时使用以下代码片段:
此程序要求用户输入一个数字,然后将其输出。 修改示例代码,使之符合以下要求:
0 is neither negative nor positive”。 继续要求用户输入数字。You entered: X”(其中的 X 为输入的数字)。 继续要求用户输入数字。package mainimport "fmt"func main() {val := 0for {fmt.Print("Enter number: ")fmt.Scanf("%d", &val)if val < 0 {panic("Negative!")} else if val == 0 {fmt.Println("0 is neither negative nor positive")} else {fmt.Printf("You entered: %d\n", val)}}}Go 中的数组是一种特定类型且长度固定的数据结构。 它们可具有零个或多个元素,你必须在声明或初始化它们时定义大小。 此外,它们一旦创建,就无法调整大小。 鉴于这些原因,数组在 Go 程序中并不常用,但它们是切片和映射的基础。
要在 Go 中声明数组,必须定义其元素的数据类型以及该数组可容纳的元素数目。 然后,可采用下标表示法访问数组中的每个元素,其中第一个元素是 0,最后一个元素是数组长度减去 1(长度 - 1)。
package mainimport "fmt"func main() {var a [3]inta[1] = 10fmt.Println(a[0])fmt.Println(a[1])fmt.Println(a[len(a)-1])}0100已声明的数组访问其元素时不会遇到错误。 默认情况下,Go 会用默认数据类型初始化每个元素。 这样的话,int 的默认值为零。 不过,你可为特定位置分配值。 这就是为什么你会看到 a[1] = 10。 你可采用上述表示法来访问该元素。 另请注意,为了打印出第一个元素,我们使用了 a[0]。 为了打印出最后一个元素,我们使用了 a[len(a)-1]。 len 函数是 Go 中的内置函数,用于获取数组、切片或映射中的元素数。
声明数组时,还可使用非默认值来初始化数组。
package mainimport "fmt"func main() {cities := [5]string{"New York", "Paris", "Berlin", "Madrid"}fmt.Println("Cities:", cities)}Cities: [New York Paris Berlin Madrid ]如果你不知道你将需要多少个位置,但知道你将具有多少数据,那么还有一种声明和初始化数组的方法是使用省略号 (...)
package mainimport "fmt"func main() {cities := [...]string{"New York", "Paris", "Berlin", "Madrid"}fmt.Println("Cities:", cities)}另一种有趣的数组初始化方法是使用省略号并仅为最新的位置指定值。
package mainimport "fmt"func main() {numbers := [...]int{99: -1}fmt.Println("First Position:", numbers[0])fmt.Println("Last Position:", numbers[99])fmt.Println("Length:", len(numbers))}First Position: 0Last Position: -1Length: 100注意数组的长度是 100,因为你为第 99 个位置指定了一个值。
如果需要处理复杂数据结构,请记住 Go 支持多维数组。
package mainimport "fmt"func main() {var twoD [3][5]intfor i := 0; i < 3; i++ {for j := 0; j < 5; j++ {twoD[i][j] = (i + 1) * (j + 1)}fmt.Println("Row", i, twoD[i])}fmt.Println("\nAll at once:", twoD)}Row 0 [1 2 3 4 5]Row 1 [2 4 6 8 10]Row 2 [3 6 9 12 15]All at once: [[1 2 3 4 5] [2 4 6 8 10] [3 6 9 12 15]]与数组一样,切片也是 Go 中的一种数据类型,它表示一系列类型相同的元素。 不过,与数组更重要的区别是切片的大小是动态的,不是固定的。
切片是数组或另一个切片之上的数据结构。 我们将源数组或切片称为基础数组。 通过切片,可访问整个基础数组,也可仅访问部分元素。
切片只有 3 个组件:
array[0]。要声明切片,可采用与声明数组相同的方式操作。
package mainimport "fmt"func main() {months := []string{"January", "February", "March", "April", "May", "June", "July", "August", "September", "October", "November", "December"}fmt.Println(months)fmt.Println("Length:", len(months))fmt.Println("Capacity:", cap(months))}[January February March April May June July August September October November December]Length: 12Capacity: 12Go 支持切片运算符 s[i:p],其中:
s 表示数组。i 表示指向要添加到新切片的基础数组(或另一个切片)的第一个元素的指针。 变量 i 对应于数组 array[i] 中索引位置 i 处的元素。 请记住,此元素不一定是基础数组的第一个元素 array[0]。p 表示创建新切片时要使用的基础数组中的元素数目。 变量 p 对应于可用于新切片的基础数组中的最后一个元素。 可在位置 array[i+1] 找到基础数组中位置 p 处的元素。 请注意,此元素不一定是基础数组的最后一个元素 array[len(array)-1]。package mainimport "fmt"func main() {months := []string{"January", "February", "March", "April", "May", "June", "July", "August", "September", "October", "November", "December"}quarter1 := months[0:3]quarter2 := months[3:6]quarter3 := months[6:9]quarter4 := months[9:12]fmt.Println(quarter1, len(quarter1), cap(quarter1))fmt.Println(quarter2, len(quarter2), cap(quarter2))fmt.Println(quarter3, len(quarter3), cap(quarter3))fmt.Println(quarter4, len(quarter4), cap(quarter4))}[January February March] 3 12[April May June] 3 9[July August September] 3 6[October November December] 3 3注意,切片的长度不变,但容量不同。 我们来了解 quarter2 切片。 声明此切片时,你指出希望切片从位置编号 3 开始,最后一个元素位于位置编号 6。 切片长度为 3 个元素,但容量为 9,原因是基础数组有更多元素或位置可供使用,但对切片而言不可见。
切片容量仅指出切片可扩展的程度。 因此可从 quarter2 创建扩展切片
package mainimport "fmt"func main() {months := []string{"January", "February", "March", "April", "May", "June", "July", "August", "September", "October", "November", "December"}quarter2 := months[3:6]quarter2Extended := quarter2[:4]fmt.Println(quarter2, len(quarter2), cap(quarter2))fmt.Println(quarter2Extended, len(quarter2Extended), cap(quarter2Extended))}[April May June] 3 9[April May June July] 4 9切片与数组之间有何不同? 第一个区别是切片的大小不是固定的,而是动态的。 创建切片后,可向其添加更多元素,这样切片就会扩展。
Go 提供了内置函数 append(slice, element),便于你向切片添加元素。 将要修改的切片和要追加的元素作为值发送给该函数。 然后,append 函数会返回一个新的切片,将其存储在变量中。 对于要更改的切片,变量可能相同。
package mainimport "fmt"func main() {var numbers []intfor i := 0; i < 10; i++ {numbers = append(numbers, i)fmt.Printf("%d\tcap=%d\t%v\n", i, cap(numbers), numbers)}}0 cap=1 [0]1 cap=2 [0 1]2 cap=4 [0 1 2]3 cap=4 [0 1 2 3]4 cap=8 [0 1 2 3 4]5 cap=8 [0 1 2 3 4 5]6 cap=8 [0 1 2 3 4 5 6]7 cap=8 [0 1 2 3 4 5 6 7]8 cap=16 [0 1 2 3 4 5 6 7 8]9 cap=16 [0 1 2 3 4 5 6 7 8 9]当切片容量不足以容纳更多元素时,Go 的容量将翻倍。 它将新建一个具有新容量的基础数组。 无需执行任何操作即可使容量增加。 Go 会自动扩充容量。
Go 没有内置函数用于从切片中删除元素。 可使用上述切片运算符 s[i:p] 来新建一个仅包含所需元素的切片。
package mainimport "fmt"func main() {letters := []string{"A", "B", "C", "D", "E"}remove := 2if remove < len(letters) {fmt.Println("Before", letters, "Remove ", letters[remove])letters = append(letters[:remove], letters[remove+1:]...)fmt.Println("After", letters)}}Before [A B C D E] Remove CAfter [A B D E]Go 具有内置函数 copy(dst, src []Type) 用于创建切片的副本。
更改切片中的元素时,基础数组将随之更改。
package mainimport "fmt"func main() {letters := []string{"A", "B", "C", "D", "E"}fmt.Println("Before", letters)slice1 := letters[0:2]slice2 := letters[1:4]slice1[1] = "Z"fmt.Println("After", letters)fmt.Println("Slice2", slice2)}Before [A B C D E]After [A Z C D E]Slice2 [Z C D]创建副本则不会产生影响
package mainimport "fmt"func main() {letters := []string{"A", "B", "C", "D", "E"}fmt.Println("Before", letters)slice1 := letters[0:2]slice2 := make([]string, 3)copy(slice2, letters[1:4])slice1[1] = "Z"fmt.Println("After", letters)fmt.Println("Slice2", slice2)}Before [A B C D E]After [A Z C D E]Slice2 [B C D]Go 中的映射是一个哈希表,是键值对的集合。 映射中所有的键都必须具有相同的类型,它们的值也是如此。 不过,可对键和值使用不同的类型。 例如,键可以是数字,值可以是字符串。 若要访问映射中的特定项,可引用该项的键。
若要声明映射,需要使用 map 关键字。 然后,定义键和值类型,如下所示:map[T]T。
package mainimport "fmt"func main() {studentsAge := map[string]int{"john": 32,"bob": 31,}fmt.Println(studentsAge)}map[bob:31 john:32]如果不想使用项来初始化映射,可使用内置函数 make() 在上一部分创建切片。
要添加项,无需像对切片一样使用内置函数。 映射更加简单。 你只需定义键和值即可。 如果没有键值对,则该项会添加到映射中。
package mainimport "fmt"func main() {studentsAge := make(map[string]int)studentsAge["john"] = 32studentsAge["bob"] = 31fmt.Println(studentsAge)}若要访问映射中的项,可使用常用的下标表示法 m[key]
在映射中使用下标表示法时,即使映射中没有键,你也总会获得默认值的响应。
package mainimport "fmt"func main() {studentsAge := make(map[string]int)studentsAge["john"] = 32studentsAge["bob"] = 31fmt.Println("Bob's age is", studentsAge["bob"])fmt.Println("Christy's age is", studentsAge["christy"])}Bob's age is 31Christy's age is 0在很多情况下,访问映射中没有的项时 Go 不会返回错误,这是正常的。 但有时需要知道某个项是否存在。 在 Go 中,映射的下标表示法可生成两个值。 第一个是项的值。 第二个是指示键是否存在的布尔型标志。
package mainimport "fmt"func main() {studentsAge := make(map[string]int)studentsAge["john"] = 32studentsAge["bob"] = 31age, exist := studentsAge["christy"]if exist {fmt.Println("Christy's age is", age)} else {fmt.Println("Christy's age couldn't be found")}}Christy's age couldn't be found若要从映射中删除项,请使用内置函数 delete()。
package mainimport "fmt"func main() {studentsAge := make(map[string]int)studentsAge["john"] = 32studentsAge["bob"] = 31delete(studentsAge, "bob")delete(studentsAge, "christy")fmt.Println(studentsAge)}map[john:32]如果你尝试删除不存在的项,Go 不会执行 panic
最后,让我们看看如何在映射中进行循环来以编程方式访问其所有的项。 为此,可使用基于范围的循环
package mainimport ("fmt")func main() {studentsAge := make(map[string]int)studentsAge["john"] = 32studentsAge["bob"] = 31for name, age := range studentsAge {fmt.Printf("%s\t%d\n", name, age)}}john 32bob 31range 会首先生成项的键,然后再生成该项的值。 可使用 _ 变量忽略其中任何一个
有时,你需要在一个结构中表示字段的集合。在 Go 中,可使用结构将可能构成记录的不同字段组合在一起。Go 中的结构也是一种数据结构,它可包含零个或多个任意类型的字段,并将它们表示为单个实体。
若要声明结构,需要使用 struct 关键字,还要使用希望新的数据类型具有的字段及其类型的列表。
若要访问结构的各个字段,可使用点表示法 (.) 做到这一点
可使用 & 运算符生成指向结构的指针以修改结构中的项
package mainimport "fmt"type Employee struct {ID intFirstName stringLastName stringAddress string}func main() {employee := Employee{LastName: "Doe", FirstName: "John"}fmt.Println(employee)employeeCopy := &employeeemployeeCopy.FirstName = "David"fmt.Println(employee)}{0 John Doe }{0 David Doe }通过 Go 中的结构,可将某结构嵌入到另一结构中。
package mainimport "fmt"type Person struct {ID intFirstName stringLastName stringAddress string}type Employee struct {PersonManagerID int}type Contractor struct {PersonCompanyID int}func main() {employee := Employee{Person: Person{FirstName: "John",},}employee.LastName = "Doe"employee.ManagerID = 2fmt.Println(employee)}{{0 John Doe } 2}最后,可使用结构来对 JSON 中的数据进行编码和解码。 Go 对 JSON 格式提供很好的支持,该格式已包含在标准库包中。
你还可执行一些操作,例如重命名结构中字段的名称。 例如,假设你不希望 JSON 输出显示 FirstName 而只显示 name,或者忽略空字段, 可使用如下例所示的字段标记:
然后,若要将结构编码为 JSON,请使用 json.Marshal 函数。 若要将 JSON 字符串解码为数据结构,请使用 json.Unmarshal 函数。 下例将所有内容组合在一起,将员工数组编码为 JSON,并将输出解码为新的变量:
package mainimport ("encoding/json""fmt")type Person struct {ID intFirstName string `json:"name"`LastName stringAddress string `json:"address,omitempty"`}type Employee struct {PersonManagerID int}type Contractor struct {PersonCompanyID int}func main() {employees := []Employee{{Person: Person{LastName: "Doe", FirstName: "John",},},{Person: Person{LastName: "Campbell", FirstName: "David",},},}data, _ := json.Marshal(employees)fmt.Printf("%s\n", data)var decoded []Employeejson.Unmarshal(data, &decoded)fmt.Printf("%v\n", decoded)}[{"ID":0,"name":"John","LastName":"Doe","ManagerID":0},{"ID":0,"name":"David","LastName":"Campbell","ManagerID":0}][{{0 John Doe } 0} {{0 David Campbell } 0}]在这第一个挑战中,你将编写一个程序来计算某个数字的斐波纳契数列。 这是在学习新语言时要编码的一个典型的编程练习。 你将编写一个函数,它返回一个包含按斐波纳契数列排列的所有数字的切片,而这些数字是通过根据用户输入的大于 2 的数字计算得到的。 让我们假设小于 2 的数字会导致错误,并返回一个 nil 切片。
请记住,斐波那契数列是一个数字列表,其中每个数字是前两个斐波那契数字之和。 例如,数字 6 的序列是 1,1,2,3,5,8,数字 7 的序列是 1,1,2,3,5,8,13,数字 8 的序列是 1,1,2,3,5,8,13,21,以此类推。
package mainimport "fmt"func fibonacci(n int) []int {if n < 2 {return make([]int, 0)}nums := make([]int, n)nums[0], nums[1] = 1, 1for i := 2; i < n; i++ {nums[i] = nums[i-1] + nums[i-2]}return nums}func main() {var num intfmt.Print("What's the Fibonacci sequence you want? ")fmt.Scanln(&num)fmt.Println("The Fibonacci sequence is:", fibonacci(num))}编写一个程序来转换罗马数字(例如将 MCLX 转换成 1,160)。 使用映射加载要用于将字符串字符转换为数字的基本罗马数字。 例如,M 将是映射中的键,其值将为 1000。 使用以下字符串字符映射表列表:
M => 1000D => 500C => 100L => 50X => 10V => 5I => 1如果用户输入的字母与上述列表中的不同,则打印一个错误。
请记住在有些情况下,较小的数字会排在较大的数字前面,因此不能仅仅将数字相加。 例如,数字 MCM 应打印为 1,900。
package mainimport ("fmt")func romanToArabic(numeral string) int {romanMap := map[rune]int{'M': 1000,'D': 500,'C': 100,'L': 50,'X': 10,'V': 5,'I': 1,}arabicVals := make([]int, len(numeral)+1)for index, digit := range numeral {if val, present := romanMap[digit]; present {arabicVals[index] = val} else {fmt.Printf("Error: The roman numeral %s has a bad digit: %c\n", numeral, digit)return 0}}total := 0for index := 0; index < len(numeral); index++ {if arabicVals[index] < arabicVals[index+1] {arabicVals[index] = -arabicVals[index]}total += arabicVals[index]}return total}func main() {fmt.Println("MCLX is", romanToArabic("MCLX"))fmt.Println("MCMXCIX is ", romanToArabic("MCMXCIX"))fmt.Println("MCMZ is", romanToArabic("MCMZ"))}编写程序时,需要考虑程序失败的各种方式,并且需要管理失败。 无需让用户看到冗长而混乱的堆栈跟踪错误。 让他们看到有关错误的有意义的信息更好。 正如你所看到的,Go 具有 panic 和 recover 之类的内置函数来管理程序中的异常或意外行为。 但错误是已知的失败,你的程序应该可以处理它们。
Go 的错误处理方法只是一种只需要 if 和 return 语句的控制流机制。 例如,在调用函数以从 employee 对象获取信息时,可能需要了解该员工是否存在。 Go 处理此类预期错误的一贯方法如下所示:
employee, err := getInformation(1000)if err != nil { // Something is wrong. Do something.}注意 getInformation 函数返回了 employee 结构,还返回了错误作为第二个值。 该错误可能为 nil。 如果错误为 nil,则表示成功。 如果错误不是 nil,则表示失败。 非 nil 错误附带一条错误消息,你可以打印该错误消息,也可以记录该消息(更可取)。
当函数返回错误时,该错误通常是最后一个返回值。 正如上一部分所介绍的那样,调用方负责检查是否存在错误并处理错误。
你可能还需要在传播错误之前添加更多信息。 为此,可以使用 fmt.Errorf() 函数,该函数与我们之前看到的函数类似,但它返回一个错误。 例如,你可以向错误添加更多上下文,但仍返回原始错误,如下所示:
func getInformation(id int) (*Employee, error) { employee, err := apiCallEmployee(1000) if err != nil { return nil, fmt.Errorf("got an error when getting the employee information: %v", err) } return employee, nil}另一种策略是在错误为暂时性错误时运行重试逻辑。 例如,可以使用重试策略调用函数三次并等待两秒钟
func getInformation(id int) (*Employee, error) { for tries := 0; tries < 3; tries++ { employee, err := apiCallEmployee(1000) if err == nil { return employee, nil } fmt.Println("Server is not responding, retrying ...") time.Sleep(time.Second * 2) } return nil, fmt.Errorf("server has failed to respond to get the employee information")}有时错误消息数会增加,你需要维持秩序。 或者,你可能需要为要重用的常见错误消息创建一个库。 在 Go 中,你可以使用 errors.New() 函数创建错误并在若干部分中重复使用这些错误,如下所示:
var ErrNotFound = errors.New("Employee not found!")func getInformation(id int) (*Employee, error) { if id != 1001 { return nil, ErrNotFound } employee := Employee{LastName: "Doe", FirstName: "John"} return &employee, nil}最后,如果你具有错误变量,则在处理调用方函数中的错误时可以更具体。 errors.Is() 函数允许你比较获得的错误的类型
employee, err := getInformation(1000)if errors.Is(err, ErrNotFound) { fmt.Printf("NOT FOUND: %v\n", err)} else { fmt.Print(employee)}在 Go 中处理错误时,请记住下面一些推荐做法:
日志在程序中发挥着重要作用,因为它们是在出现问题时你可以检查的信息源。 通常,发生错误时,最终用户只会看到一条消息,指示程序出现问题。 从开发人员的角度来看,我们需要简单错误消息以外的更多信息。 这主要是因为我们想要再现该问题以编写适当的修补程序。
log 包对于初学者,Go 提供了一个用于处理日志的简单标准包。 可以像使用 fmt 包一样使用此包。 该标准包不提供日志级别,且不允许为每个包配置单独的记录器。 如果需要编写更复杂的日志记录配置,可以使用记录框架执行此操作。
package mainimport ("log")func main() {log.Print("Hey, I'm a log!")}2022/10/05 15:37:16 Hey, I'm a log!默认情况下,log.Print() 函数将日期和时间添加为日志消息的前缀。 你可以通过使用 fmt.Print() 获得相同的行为,但使用 log 包还能执行其他操作,例如将日志发送到文件。 稍后我们将详细介绍 log 包功能。
你可以使用 log.Fatal() 函数记录错误并结束程序,就像使用 os.Exit(1) 一样。
package mainimport ("fmt""log")func main() {log.Fatal("Hey, I'm an error log!")fmt.Print("Can you see me?")}2022/10/05 15:38:56 Hey, I'm an error log!exit status 1使用 log.Panic() 函数时会出现类似行为,但是还会获取错误堆栈跟踪。
另一重要函数是 log.SetPrefix()。 可使用它向程序的日志消息添加前缀。
package mainimport ("log")func main() {log.SetPrefix("main(): ")log.Print("Hey, I'm a log!")log.Fatal("Hey, I'm an error log!")}main(): 2022/10/05 15:40:36 Hey, I'm a log!main(): 2022/10/05 15:40:36 Hey, I'm an error log!exit status 1除了将日志打印到控制台之外,你可能还希望将日志发送到文件,以便稍后或实时处理这些日志。
package mainimport ("log""os")func main() {file, err := os.OpenFile("info.log", os.O_CREATE|os.O_APPEND|os.O_WRONLY, 0644)if err != nil {log.Fatal(err)}defer file.Close()log.SetOutput(file)log.Print("Hey, I'm a log!")}最后,可能有 log 包中的函数不足以处理问题的情况。 你可能会发现,使用记录框架而不编写自己的库很有用。 Go 的几个记录框架有 Logrus、zerolog、zap 和 Apex。
面向对象编程 (OOP) 是一种广受欢迎的编程模式,大部分编程语言都支持(至少部分支持)。 Go 是其中一种语言,但它并不完全支持所有 OOP 原则。
Go 中的方法是一种特殊类型的函数,但存在一个简单的区别:你必须在函数名称之前加入一个额外的参数。 此附加参数称为 接收方 。
如你希望分组函数并将其绑定到自定义类型,则方法非常有用。 Go 中的这一方法类似于在其他编程语言中创建类,因为它允许你实现面向对象编程 (OOP) 模型中的某些功能,例如嵌入、重载和封装。
到目前为止,你仅将结构用作可在 Go 中创建的另一种自定义类型。 在此模块中你将了解到,通过添加方法你可以将行为添加到你所创建的结构中。
在声明方法之前,必须先创建结构。 假设你想要创建一个几何包,并决定创建一个名为 triangle 的三角形结构作为此程序包的一个组成部分。 然后,你需要使用一种方法来计算此三角形的周长。 你可以在 Go 中将其表示为:
type triangle struct {size int}func (t triangle) perimeter() int {return t.size * 3}结构看起来像普通结构,但 perimeter() 函数在函数名称之前有一个类型 triangle 的额外参数。 也就是说,在使用结构时,你可以按如下方式调用函数:
func main() {t := triangle{3}fmt.Println("Perimeter:", t.perimeter())}如果尝试按平常的方式调用 perimeter() 函数,则此函数将无法正常工作,因为此函数的签名表明它需要接收方。 正因如此,调用此方法的唯一方式是先声明一个结构,获取此方法的访问权限。 这也意味着,只要此方法属于不同的结构,你甚至可以为其指定相同的名称。 例如,你可以使用 perimeter() 函数声明一个 square 结构,具体如下所示:
package mainimport "fmt"type triangle struct {size int}type square struct {size int}func (t triangle) perimeter() int {return t.size * 3}func (s square) perimeter() int {return s.size * 4}func main() {t := triangle{3}s := square{4}fmt.Println("Perimeter (triangle):", t.perimeter())fmt.Println("Perimeter (square):", s.perimeter())}Perimeter (triangle): 9Perimeter (square): 16通过对 perimeter() 函数的两次调用,编译器将根据接收方类型来确定要调用的函数。 这有助于在各程序包之间保持函数的一致性和名称的简短,并避免将包名称作为前缀。
有时,方法需要更新变量,或者,如果参数太大,则可能需要避免复制它。 在遇到此类情况时,你需要使用指针传递变量的地址。 在之前的模块中,当我们在讨论指针时提到,每次在 Go 中调用函数时,Go 都会复制每个参数值以便使用。
如果你需要更新方法中的接收方变量,也会执行相同的行为。 例如,假设你要创建一个新方法以使三角形的大小增加一倍。 你需要在接收方变量中使用指针,具体如下所示:
func (t *triangle) doubleSize() {t.size *= 2}如果方法仅可访问接收方的信息,则不需要在接收方变量中使用指针。 但是,依据 Go 的约定,如果结构的任何方法具有指针接收方,则此结构的所有方法都必须具有指针接收方,即使某个方法不需要也是如此。
方法的一个关键方面在于,需要为任何类型定义方法,而不只是针对自定义类型(如结构)进行定义。 但是,你不能通过属于其他包的类型来定义结构。 因此,不能在基本类型(如 string)上创建方法。
尽管如此,你仍然可以利用一点技巧,基于基本类型创建自定义类型,然后将其用作基本类型。 例如,假设你要创建一个方法,以将字符串从小写字母转换为大写字母。 你可以按如下所示写入方法:
package mainimport ("fmt""strings")type upperstring stringfunc (s upperstring) Upper() string {return strings.ToUpper(string(s))}func main() {s := upperstring("Learning Go!")fmt.Println(s)fmt.Println(s.Upper())}在之前的模块中,您已了解到可以在一个结构中使用属性,并将同一属性嵌入另一个结构中。 也就是说,可以重用来自一个结构的属性,以避免出现重复并保持代码库的一致性。 类似的观点也适用于方法。 即使接收方不同,也可以调用已嵌入结构的方法。
例如,假设你想要创建一个带有逻辑的新三角形结构,以加入颜色。 此外,你还希望继续使用之前声明的三角形结构。 然后,你可以初始化 coloredTriangle 结构,并从 triangle 结构调用 perimeter() 方法(甚至访问其字段)
package mainimport "fmt"type triangle struct {size int}type coloredTriangle struct {trianglecolor string}func (t triangle) perimeter() int {return t.size * 3}func main() {t := coloredTriangle{triangle{3}, "blue"}fmt.Println("Size:", t.size)fmt.Println("Perimeter", t.perimeter())}Size: 3Perimeter 9让我们回到之前讨论过的 triangle 示例。 如果要在 coloredTriangle 结构中更改 perimeter() 方法的实现,会发生什么情况? 不能存在两个同名的函数。 但是,因为方法需要额外参数(接收方),所以,你可以使用一个同名的方法,只要此方法专门用于要使用的接收方即可。 这就是重载方法的方式。
如果你仍需要从 triangle 结构调用 perimeter() 方法,则可通过对其进行显示访问来执行此操作
package mainimport "fmt"type triangle struct {size int}type coloredTriangle struct {trianglecolor string}func (t coloredTriangle) perimeter() int {return t.size * 3 * 2}func (t triangle) perimeter() int {return t.size * 3}func main() {t := coloredTriangle{triangle{3}, "blue"}fmt.Println("Size:", t.size)fmt.Println("Perimeter (colored)", t.perimeter())fmt.Println("Perimeter (normal)", t.triangle.perimeter())}“封装”表示对象的发送方(客户端)无法访问某个方法。 通常,在其他编程语言中,你会将 private 或 public 关键字放在方法名称之前。 在 Go 中,只需使用大写标识符,即可公开方法,使用非大写的标识符将方法设为私有方法。
Go 中的封装仅在程序包之间有效。 换句话说,你只能隐藏来自其他程序包的实现详细信息,而不能隐藏程序包本身。
package geometrytype Triangle struct {size int}func (t *Triangle) doubleSize() {t.size *= 2}func (t *Triangle) SetSize(size int) {t.size = size}func (t *Triangle) Perimeter() int {t.doubleSize()return t.size * 3}package mainimport ("fmt""geometry")func main() {t := geometry.Triangle{}t.SetSize(3)fmt.Println("Perimeter", t.Perimeter())}Go 中的接口是一种用于表示其他类型的行为的数据类型。 接口类似于对象应满足的蓝图或协定。 在你使用接口时,你的基本代码将变得更加灵活、适应性更强,因为你编写的代码未绑定到特定的实现。 因此,你可以快速扩展程序的功能。
与其他编程语言中的接口不同,Go 中的接口是满足隐式实现的。 Go 并不提供用于实现接口的关键字,因此,如果你之前使用的是其他编程语言中的接口,但不熟悉 Go,那么此概念可能会造成混淆。
Go 中的接口是一种抽象类型,只包括具体类型必须拥有或实现的方法。 正因如此,我们说接口类似于蓝图。
假设你希望在几何包中创建一个接口来指示形状必须实现的方法。 你可以按如下所示定义接口:
type Shape interface { Perimeter() float64 Area() float64}Shape 接口表示你想要考虑 Shape 的任何类型都需要同时具有 Perimeter() 和 Area() 方法。 例如,在创建 Square 结构时,它必须实现两种方法,而不是仅实现一种。 另外,请注意接口不包含这些方法的实现细节(例如,用于计算某个形状的周长和面积)。 接口仅表示一种协定。 三角形、圆圈和正方形等形状有不同的计算面积和周长方式。
正如上文所讨论的内容,你没有用于实现接口的关键字。 当 Go 中的接口具有接口所需的所有方法时,则满足按类型的隐式实现。
让我们创建一个 Square 结构,此结构具有 Shape 接口中的两个方法
type Square struct {size float64}func (s Square) Area() float64 {return s.size * s.size}func (s Square) Perimeter() float64 {return s.size * 4}请注意 Square 结构的方法签名与 Shape 接口的签名的匹配方式。
func main() {var s Shape = Square{3}fmt.Printf("%T\n", s)fmt.Println("Area: ", s.Area())fmt.Println("Perimeter:", s.Perimeter())}main.SquareArea: 9Perimeter: 12此时,无论你是否使用接口,都没有任何区别。 接下来,让我们创建另一种类型,如 Circle,然后进行相同的操作:
package mainimport ("fmt""math")type Shape interface {Perimeter() float64Area() float64}type Square struct {size float64}func (s Square) Area() float64 {return s.size * s.size}func (s Square) Perimeter() float64 {return s.size * 4}type Circle struct {radius float64}func (c Circle) Area() float64 {return math.Pi * c.radius * c.radius}func (c Circle) Perimeter() float64 {return 2 * math.Pi * c.radius}func printInformation(s Shape) {fmt.Printf("%T\n", s)fmt.Println("Area: ", s.Area())fmt.Println("Perimeter:", s.Perimeter())fmt.Println()}func main() {var s Shape = Square{3}printInformation(s)c := Circle{6}printInformation(c)}main.SquareArea: 9Perimeter: 12main.CircleArea: 113.09733552923255Perimeter: 37.69911184307752使用接口的优点在于,对于 Shape的每个新类型或实现,printInformation 函数都不需要更改。 正如之前所述,当你使用接口时,代码会变得更灵活、更容易扩展。
假设你具有以下代码,并且希望通过编写负责处理某些数据的 Writer 方法的自定义实现来扩展其功能。
通过使用以下代码,你可以创建一个程序,此程序使用 GitHub API 从 Microsoft 获取三个存储库:
package mainimport ("fmt""io""net/http""os")func main() {resp, err := http.Get("https://api.github.com/users/microsoft/repos?page=15&per_page=5")if err != nil {fmt.Println("Error:", err)os.Exit(1)}io.Copy(os.Stdout, resp.Body)}改写后:
package mainimport ("encoding/json""fmt""io""net/http""os")type GitHubResponse []struct {FullName string `json:"full_name"`}type customWriter struct{}func (w customWriter) Write(p []byte) (n int, err error) {var resp GitHubResponsejson.Unmarshal(p, &resp)for _, r := range resp {fmt.Println(r.FullName)}return len(p), nil}func main() {resp, err := http.Get("https://api.github.com/users/microsoft/repos?page=15&per_page=5")if err != nil {fmt.Println("Error:", err)os.Exit(1)}writer := customWriter{}io.Copy(writer, resp.Body)}最后,我们一起来探讨接口的另一种用例,如果你要创建服务器 API,你可能会发现此用例非常实用。 编写 Web 服务器的常用方式是使用 net/http 程序包中的 http.Handler 接口
package mainimport ("fmt""log""net/http")// 创建 float32 类型的自定义类型,然后编写 String() 方法的自定义实现type dollars float32func (d dollars) String() string {return fmt.Sprintf("$%.2f", d)}// 写入 http.Handler 可使用的 ServeHTTP 方法的实现。type database map[string]dollars// 通过使用 database 类型作为接收方来写入 ServeHTTP 方法。func (db database) ServeHTTP(w http.ResponseWriter, req *http.Request) {for item, price := range db {fmt.Fprintf(w, "%s: %s\n", item, price)}}// 在 main() 函数中,我们将 database 类型实例化,并使用一些值对其进行初始化。 我们使用 http.ListenAndServe 函数启动了 HTTP 服务器,在其中定义了服务器地址,包括要使用的端口和实现 ServerHTTP 方法自定义版本的 db 对象。func main() {db := database{"Go T-Shirt": 25, "Go Jacket": 55}log.Fatal(http.ListenAndServe("localhost:8000", db))}编写一个程序,此程序使用自定义程序包来管理在线商店的帐户。 你的挑战包括以下四个要素:
Account 的自定义类型,此类型包含帐户所有者的名字和姓氏。 此类型还必须加入 ChangeName 的功能。Employee 的自定义类型,此类型包含用于将贷方数额存储为类型 float64 并嵌入 Account 对象的变量。 类型还必须包含 AddCredits、RemoveCredits 和 CheckCredits 的功能。 你需要展示你可以通过 Employee 对象更改帐户名称。Account 对象,以便按包含名字和姓氏的格式打印 Employee 名称。package mainimport ("errors""fmt")type Account struct {firstname stringlastname string}func (a *Account) ChangeName(afterfirstname string) {a.firstname = afterfirstname}type Employee struct {Accountcredit float64}func (e Employee) String() string {return fmt.Sprintf("Firstname:%s,Lastname:%s,Credit:%.2f\n", e.firstname, e.lastname, e.credit)}func CreateEmployee(firstname, lastname string, credit float64) (*Employee, error) {return &Employee{Account{firstname, lastname}, credit}, nil}func (e *Employee) AddCredits(amount float64) (float64, error) {if amount > 0.0 {e.credit += amountreturn e.credit, nil}return 0.0, errors.New("invalid amount")}func (e *Employee) RemoveCredits(amount float64) (float64, error) {if e.credit-amount < 0 {return 0.0, errors.New("too much")}if amount < 0 {return 0.0, errors.New("invalid amount")}e.credit -= amountreturn e.credit, nil}func (e Employee) CheckCredits() float64 {return e.credit}func main() {bruce, _ := CreateEmployee("Bruce", "Lee", 500)fmt.Println(bruce.CheckCredits())credits, err := bruce.AddCredits(250)if err != nil {fmt.Println("Error:", err)} else {fmt.Println("New Credits Balance = ", credits)}_, err = bruce.RemoveCredits(2500)if err != nil {fmt.Println("Can't withdraw or overdrawn!", err)}bruce.ChangeName("Mark")fmt.Println(bruce)}并发是独立活动的组合,就像 Web 服务器虽然同时处理多个用户请求,但它是自主运行的。 并发在当今的许多程序中都存在。 Web 服务器就是一个例子,但你也能看到,在批量处理大量数据时也需要使用并发。
Go 有两种编写并发程序的样式。 一种是在其他语言中通过线程实现的传统样式。
通常,编写并发程序时最大的问题是在进程之间共享数据。 Go 采用不同于其他编程语言的通信方式,因为 Go 是通过 channel 来回传递数据的。 这意味着只有一个活动 (goroutine) 有权访问数据,设计上不存在争用条件。 学完本模块中的 goroutine 和 channel 之后,你将更好地理解 Go 的并发方法。
可以使用下面的标语来概括 Go 的方法:“不是通过共享内存通信,而是通过通信共享内存。”
goroutine 是轻量线程中的并发活动,而不是在操作系统中进行的传统活动。 假设你有一个写入输出的程序和另一个计算两个数字相加的函数。 一个并发程序可以有数个 goroutine 同时调用这两个函数。
我们可以说,程序执行的第一个 goroutine 是 main() 函数。 如果要创建其他 goroutine,则必须在调用该函数之前使用 go 关键字
func main(){ login() go launch()}许多程序喜欢使用匿名函数来创建 goroutine
func main(){ login() go func() { launch() }()}由于我们只想将重点放在并发部分,因此我们使用现有程序来检查 API 终结点是否响应。
串行程序:
package mainimport ("fmt""net/http""time")func main() {start := time.Now()apis := []string{"https://management.azure.com","https://dev.azure.com","https://api.github.com","https://outlook.office.com/","https://api.somewhereintheinternet.com/","https://graph.microsoft.com",}for _, api := range apis {_, err := http.Get(api)if err != nil {fmt.Printf("ERROR: %s is down!\n", api)continue}fmt.Printf("SUCCESS: %s is up and running!\n", api)}elapsed := time.Since(start)fmt.Printf("Done! It took %v seconds!\n", elapsed.Seconds())}SUCCESS: https://management.azure.com is up and running!SUCCESS: https://dev.azure.com is up and running!SUCCESS: https://api.github.com is up and running!SUCCESS: https://outlook.office.com/ is up and running!ERROR: https://api.somewhereintheinternet.com/ is down!SUCCESS: https://graph.microsoft.com is up and running!Done! It took 5.163787068 seconds!同时检查所有站点?我们需要并发运行的代码部分是向站点进行 HTTP 调用的部分。 换句话说,我们需要为程序要检查的每个 API 创建一个 goroutine。为了创建 goroutine,我们需要在调用函数前使用 go 关键字。
首先创建一个新函数:
func checkAPI(api string) { _, err := http.Get(api) if err != nil { fmt.Printf("ERROR: %s is down!\n", api) return } fmt.Printf("SUCCESS: %s is up and running!\n", api)}修改 main() 函数中的代码,为每个 API 创建一个 goroutine
for _, api := range apis {go checkAPI(api)}Done! It took 3.42e-05 seconds!即使看起来 checkAPI 函数没有运行,它实际上是在运行。 它只是没有时间完成。
添加 time.Sleep(3 * time.Second)
ERROR: https://api.somewhereintheinternet.com/ is down!SUCCESS: https://api.github.com is up and running!SUCCESS: https://management.azure.com is up and running!SUCCESS: https://dev.azure.com is up and running!SUCCESS: https://outlook.office.com/ is up and running!SUCCESS: https://graph.microsoft.com is up and running!Done! It took 3.001536063 seconds!Go 中的 channel 是 goroutine 之间的通信机制。 这就是为什么我们之前说过 Go 实现并发的方式是:“不是通过共享内存通信,而是通过通信共享内存。”需要将值从一个 goroutine 发送到另一个时,可以使用通道。
由于 channel 是发送和接收数据的通信机制,因此它也有类型之分。 这意味着你只能发送 channel 支持的数据类型。 除使用关键字 chan 作为 channel 的数据类型外,还需指定将通过 channel 传递的数据类型,如 int 类型。
每次声明一个 channel 或希望在函数中指定一个 channel 作为参数时,都需要使用 chan <type>,如 chan int。 要创建 channel,需使用内置的 make() 函数,如下所示:
ch := make(chan int)一个 channel 可以执行两项操作:发送数据和接收数据。 若要指定 channel 具有的操作类型,需要使用 channel 运算符 <-。 此外,在 channel 中发送数据和接收数据属于阻止操作。
如果希望 channel 仅发送数据,则必须在 channel 之后使用 <- 运算符。 如果希望 channel 接收数据,则必须在 channel 之前使用 <- 运算符
ch <- x // sends (or write) x through channel chx = <-ch // x receives (or reads) data sent to the channel ch<-ch // receives data, but the result is discarded可在 channel 中执行的另一项操作是关闭 channel
close(ch)关闭 channel 时,你希望数据将不再在该 channel 中发送。 如果试图将数据发送到已关闭的 channel,则程序将发生严重错误。 如果试图通过已关闭的 channel 接收数据,则可以读取发送的所有数据。 随后的每次“读取”都将返回一个零值。
使用 channel 来删除睡眠功能并稍做清理:
package mainimport ("fmt""net/http""time")// 通过 channel 发送该消息,而不是在 checkAPI 函数中打印结果func checkAPI(api string, ch chan string) {_, err := http.Get(api)if err != nil {ch <- fmt.Sprintf("ERROR: %s is down!\n", api)return}ch <- fmt.Sprintf("SUCCESS: %s is up and running!\n", api)}func main() {// 创建channelch := make(chan string)start := time.Now()apis := []string{"https://management.azure.com","https://dev.azure.com","https://api.github.com","https://outlook.office.com/","https://api.somewhereintheinternet.com/","https://graph.microsoft.com",}for _, api := range apis {go checkAPI(api, ch)}fmt.Print(<-ch)elapsed := time.Since(start)fmt.Printf("Done! It took %v seconds!\n", elapsed.Seconds())}ERROR: https://api.somewhereintheinternet.com/ is down!Done! It took 0.088759104 seconds!但是事实上并没有实现功能
使用 make() 函数创建 channel 时,会创建一个无缓冲 channel,这是默认行为。 无缓冲 channel 会阻止发送操作,直到有人准备好接收数据。 这就是为什么我们之前说发送和接收都属于阻止操作。 这也是上面的程序在收到第一条消息后立即停止的原因。
我们可以说 fmt.Print(<-ch) 会阻止程序,因为它从 channel 读取,并等待一些数据到达。 一旦有任何数据到达,它就会继续下一行,然后程序完成。
其他 goroutine 发生了什么? 它们仍在运行,但都没有在侦听。 而且,由于程序提前完成,一些 goroutine 无法发送数据。
读取数据和接收数据都属于阻止操作
要解决此问题,只需更改循环的代码,然后只接收确定要发送的数据
package mainimport ("fmt""net/http""time")// 通过 channel 发送该消息,而不是在 checkAPI 函数中打印结果func checkAPI(api string, ch chan string) {_, err := http.Get(api)if err != nil {ch <- fmt.Sprintf("ERROR: %s is down!\n", api)return}ch <- fmt.Sprintf("SUCCESS: %s is up and running!\n", api)}func main() {// 创建channelch := make(chan string)start := time.Now()apis := []string{"https://management.azure.com","https://dev.azure.com","https://api.github.com","https://outlook.office.com/","https://api.somewhereintheinternet.com/","https://graph.microsoft.com",}for _, api := range apis {go checkAPI(api, ch)}for i := 0; i < len(apis); i++ {fmt.Print(<-ch)}elapsed := time.Since(start)fmt.Printf("Done! It took %v seconds!\n", elapsed.Seconds())}ERROR: https://api.somewhereintheinternet.com/ is down!SUCCESS: https://api.github.com is up and running!SUCCESS: https://management.azure.com is up and running!SUCCESS: https://graph.microsoft.com is up and running!SUCCESS: https://dev.azure.com is up and running!SUCCESS: https://outlook.office.com/ is up and running!Done! It took 1.029620196 seconds!无缓冲 channel 在同步发送和接收操作。 即使使用并发,通信也是同步的。
默认情况下 channel 是无缓冲行为。 这意味着只有存在接收操作时,它们才接受发送操作。 否则,程序将永久被阻止等待。
有时需要在 goroutine 之间进行此类同步。 但是,有时你可能只需要实现并发,而不需要限制 goroutine 之间的通信方式。
有缓冲 channel 在不阻止程序的情况下发送和接收数据,因为有缓冲 channel 的行为类似于队列。 创建 channel 时,可以限制此队列的大小
package mainimport ("fmt")func send(ch chan string, message string) {ch <- message}func main() {size := 4ch := make(chan string, size)send(ch, "one")send(ch, "two")send(ch, "three")send(ch, "four")fmt.Println("All data sent to the channel ...")for i := 0; i < size; i++ {fmt.Println(<-ch)}fmt.Println("Done!")}All data sent to the channel ...onetwothreefourDone!channel 与 goroutine 有着紧密的联系。 如果没有另一个 goroutine 从 channel 接收数据,则整个程序可能会永久处于被阻止状态。
func main() { size := 2 ch := make(chan string, size) send(ch, "one") send(ch, "two") go send(ch, "three") go send(ch, "four") fmt.Println("All data sent to the channel ...") for i := 0; i < 4; i++ { fmt.Println(<-ch) } fmt.Println("Done!")}现在,你可能想知道何时使用这两种类型。 这完全取决于你希望 goroutine 之间的通信如何进行。 无缓冲 channel 同步通信。 它们保证每次发送数据时,程序都会被阻止,直到有人从 channel 中读取数据。
相反,有缓冲 channel 将发送和接收操作解耦。 它们不会阻止程序,但你必须小心使用,因为可能最终会导致死锁(如前文所述)。 使用无缓冲 channel 时,可以控制可并发运行的 goroutine 的数量。 例如,你可能要对 API 进行调用,并且想要控制每秒执行的调用次数。 否则,你可能会被阻止。
Go 中 channel 的一个有趣特性是,在使用 channel 作为函数的参数时,可以指定 channel 是要发送数据还是接收数据。 随着程序的增长,可能会使用大量的函数,这时候,最好记录每个 channel 的意图,以便正确使用它们。 或者,你要编写一个库,并希望将 channel 公开为只读,以保持数据一致性。
要定义 channel 的方向,可以使用与读取或接收数据时类似的方式进行定义。 但是你在函数参数中声明 channel 时执行此操作。 将 channel 类型定义为函数中的参数的语法如下所示:
chan<- int // it's a channel to only send data<-chan int // it's a channel to only receive data通过仅接收的 channel 发送数据时,在编译程序时会出现错误。
让我们使用以下程序作为两个函数的示例,一个函数用于读取数据,另一个函数用于发送数据:
package mainimport "fmt"func send(ch chan<- string, message string) { fmt.Printf("Sending: %#v\n", message) ch <- message}func read(ch <-chan string) { fmt.Printf("Receiving: %#v\n", <-ch)}func main() { ch := make(chan string, 1) send(ch, "Hello World!") read(ch)}运行程序时,将看到以下输出:
Sending: "Hello World!"Receiving: "Hello World!"程序阐明每个函数中每个 channel 的意图。 如果试图使用一个 channel 在一个仅用于接收数据的 channel 中发送数据,将会出现编译错误。 例如,尝试执行如下所示的操作:
func read(ch <-chan string) { fmt.Printf("Receiving: %#v\n", <-ch) ch <- "Bye!"}运行程序时,将看到以下错误:
# command-line-arguments./main.go:12:5: invalid operation: ch <- "Bye!" (send to receive-only type <-chan string)编译错误总比误用 channel 好。
最后,让我们讨论一个关于如何在使用 select 关键字的同时与多个 channel 交互的简短主题。 有时,在使用多个 channel 时,需要等待事件发生。 例如,当程序正在处理的数据中出现异常时,可以包含一些逻辑来取消操作。
select 语句的工作方式类似于 switch 语句,但它适用于 channel。 它会阻止程序的执行,直到它收到要处理的事件。 如果它收到多个事件,则会随机选择一个。
select 语句的一个重要方面是,它在处理事件后完成执行。 如果要等待更多事件发生,则可能需要使用循环。
package mainimport ("fmt""time")func process(ch chan string) {time.Sleep(3 * time.Second)ch <- "Done processing!"}func replicate(ch chan string) {time.Sleep(1 * time.Second)ch <- "Done replicating!"}func main() {ch1 := make(chan string)ch2 := make(chan string)go process(ch1)go replicate(ch2)for i := 0; i < 2; i++ {select {case process := <-ch1:fmt.Println(process)case replicate := <-ch2:fmt.Println(replicate)}}}Done replicating!Done processing!请注意,replicate 函数先完成。 这就是你在终端中先看到其输出的原因。 main 函数存在一个循环,因为 select 语句在收到事件后立即结束,但我们仍在等待 process 函数完成。
实现并发的改进版本。 完成此操作需要几秒钟的时间(不超过 15 秒),应使用有缓冲 channel。
package mainimport ("fmt""math/rand""time")func fib(number float64, ch chan string) {x, y := 1.0, 1.0for i := 0; i < int(number); i++ {x, y = y, x+y}r := rand.Intn(3)time.Sleep(time.Duration(r) * time.Second)ch <- fmt.Sprintf("Fib(%v): %v\n", number, x)}func main() {ch := make(chan string, 15)start := time.Now()for i := 1; i < 15; i++ {go fib(float64(i), ch)}for i := 1; i < 15; i++ {fmt.Printf(<-ch)}elapsed := time.Since(start)fmt.Printf("Done! It took %v seconds!\n", elapsed.Seconds())}编写一个新版本以计算斐波纳契数,直到用户使用 fmt.Scanf() 函数在终端中输入 quit。 如果用户按 Enter,则应计算新的斐波纳契数。
使用两个无缓冲 channel:一个用于计算斐波纳契数,另一个用于等待用户的“退出”消息。 你需要使用 select 语句。
package mainimport ("fmt""time")var quit = make(chan bool)func fib(c chan int) {x, y := 1, 1for {select {case c <- x:x, y = y, x+ycase <-quit:fmt.Println("Done calculating Fibonacci!")return}}}func main() {start := time.Now()command := ""data := make(chan int)go fib(data)for {num := <-datafmt.Println(num)fmt.Scanf("%s", &command)if command == "quit" {quit <- truebreak}}time.Sleep(1 * time.Second)elapsed := time.Since(start)fmt.Printf("Done! It took %v seconds!\n", elapsed.Seconds())}线性可分情况下,不仅要区分开,而且要使得区分间隔最大
最优超平面)是使得两类的分类间隔(Margin)最大的超平面,即每类中离超平面最近的样本到超平面的距离最大。距离这个最优超平面最近的样本被称为支持向量。
求解最优超平面就相当于,在上述约束条件下,求2/||W||的最大值 ,即以下损失函数最小值
二次优化问题可以采用Lagrange方法求解
非线性可分情况下的处理
广义最优分类面方法:在线性不可分的情况下,就是某些训练样本不能满足约束条件,因此可以在条件中增加一个松弛项ζ(发音Zeta,也称
引入Soft Margin,软边界),变换约束条件。
变换到高维空间的支持向量机
为什么要使间隔最大化?
SVM用于支持多类问题:结构化SVM
权重学习主要方法:
给定训练样例集合,每个样例表示为三元组<q, d, R(d,q)>
从上述样例中学习权重,使得学到的评分接近训练集中的相关性判定结果。
评分函数是两个因子的线性组合:
我们的一个因子取决于查询词项在文档中的词袋统计量,另一个因子取决于邻近度权重
基于机器学习的检索结果排序
将IR排序问题看成序回归
对于同一查询,文档之间可以按照相对得分排序即可,并不一定要求每篇文档有一个全局的绝对得分。因此,只需要一个排序,而不要得到相关度的绝对得分,问题空间可以减小。
排序SVM的构建
排序学习算法现在一般分为以下三类
虽然近年来基于深度学习和大规模预训练语言模型的方法已成功应用于IR,排序学习仍然是一种整合不同文本特征的有效方法。
]]>机器学习算法的有效性和计算复杂度是敏感于数据的特征表达和维度。
特征降维的意义:
数据压缩:简化数据表示,加快数据通信传输、节省存储资源、…
学习算法效率:
特征选择:从D个特征中选择d个,来表达模式
特征提取:采用特征变换的方法,生成d个新的特征
特征选择问题:从D维特征中选择d维(d<D)特征子集
特征选择的处理过程:
特征子集生成问题:D维特征中,选择d维(d<D)特征子集,子集个数为
基于距离的可分性判据:
通常依赖于类内类间的距离度量,前提是数据具有类别标签。可分性评估是在选择的特征子集维度上计算数据统计量。
距离的可分性判据的特点:
基于概率分布的可分性判据:从类别概率密度的角度,讨论两个类别的交叠程度
常见的概率距离准则:
熵可分性判据:
Filter 方法:
不依赖于学习算法(如分类器)的结果,直接由数据构建评估函数,对选择的特征子集进行评估。
通常方法:根据特征评价准则进行评估,选择最优的特征子集。
评价准则:距离准则、概率可分、熵可分准则。
优点:计算复杂度低,效率高。
缺点:选择的特征之间存在冗余信息。
Wrapper 方法:
原理:通过学习算法(如分类器),对选择的特征子集进行评估。
优点:选择的特征可以支持学习算法。
缺点:算法的计算复杂度高。
Embedded 方法:
原理:特征选择过程在学习算法中完成,目标是完成学习过程。
特点:不是专门的特征选择过程
缺点:计算复杂度高。
优点:
不同的应用问题会有不同的特征提取研究问题
特征提取目标:学习变换矩阵
给定 , 通过某种降维准则, 学习变换矩阵
两种降维表示途径:
目标函数:均方误差最小原则(求最优重构子空间)
s.t.
最小误差等价于最大投影
求解目标函数:
特征值的意义:样本在w方向的投影平均值(或和)最大
PCA算法流程:
PCA能保证类别区分的有效性,LDA特征的优点:类内最小、类间最大。
特征方向的提取:
LLE方法是一种流形学习,保持样本间的局部线性关系,整体实现非线性映射。
基本思想:通过矩阵分解,进行数据降维;分解后的矩阵为非负矩阵
不同的目标函数情况:
常设查询(Standing Queries)
从检索到文本分类:假设某用户有一个经常关注的信息需求,用户会经常输入这个查询来寻找关于这个主题的新内容,关注于浏览新内容,此时排序问题变成了一个分类问题(相关 vs. 不相关)
需要构建分类函数
专家分类一般都是准确的
当数据规模不大、标注者人数较少时,分类一致
当数据规模变大,人工分类困难且代价昂贵
新闻机构,情报机构等使用的一个技术,广泛部署于政府和企业
供应商提供“ IDE”来编写此类规则,商业系统具有复杂的查询语言
如果领域专家花时间精心完善规则,则准确性会很高,但是建立和维护这些规则非常昂贵
监督学习分类器可以使用各种特征
仅使用词项特征,使用文本中的所有词项
最简单的特征选择方法:
更聪明的特征选择方法:卡方(chi-square)等
朴素贝叶斯分类的目标是寻找具有最大后验概率的类别
对数计算:通过取对数将原来的乘积计算变成求和计算
参数估计:极大似然估计
避免零概率:加一平滑
朴素贝叶斯对于训练集的大小和测试文档的大小而言是线性的,在某种意义上是最优的。
分类结果的评价:评估必须在独立于训练数据的测试数据上完成
评价指标:正确率(Precision),召回率(Recall),F1,分类准确率r/n ,其中 n 是所有测试文档的数量,r是正确分类的测试文档数量
训练集包含一系列文档,每篇都标记着它的类别
在向量空间分类中,该集合对应着空间中一系列标记的点或向量。
利用Rocchio方法进行向量空间分类
基本思想:计算每个类的中心向量(所有文档向量的算术平均),将每篇测试文档分到离它最近的那个中心向量
Rocchio简单地将每个类别表示成其中心向量,分类基于文档向量到原型的相似度或聚类来进行,并不保证分类结果与训练集一致,即得到分类器后,不能保证训练集中的文档能否正确分类。
很多情况下,Rocchio的效果不如朴素贝叶斯:Rocchio算法不能正确处理非凸、多模式类别问题
将每篇测试文档分给训练集中离它最近的那篇文档所属的类别。
线性分类器计算特征值的一个线性加权和
很多常用的文本分类器都是线性分类器:朴素贝叶斯、Rocchio、logistic回归、线性SVM等等
不同的方法选择超平面的策略不同,造成了在测试文档分类性能的巨大差异
不能通过更强大的非线性分类器来获得更好的分类性能
不存在某个学习方法对于任何分类问题都最优
kNN高方差低偏差,而朴素贝叶斯分类器低方差高偏差
单标签问题:类别之间互斥,每篇文档属于且仅属于某一个类
多标签分类问题:一篇文档可以属于0、1或更多个类,针对某个类的决策并不影响其他类别上的决策
对于给定的分类问题,要考虑很多因素从而选择合适的分类器算法。
]]>计算广告是指借助大数据的分析建模,使得广告能够覆盖广泛区域和实现消费者的多跨度精准曝光,让同一份广告尽可能接触到更多有效的流量和更多对广告感兴趣的人,从而用同样低的成本,让广告的效果尽可能更好,使产品和服务获得更多商业上的成功。
如何协调广告主、平台和消费者三方之间的利益
在线投放引擎:
分布式计算平台:
流式计算平台:
合约广告:包括CPT广告和定向广告。CPT广告指的是按照时间成本计算,广告主以固定的价格买断一段时间内的广告位来展示自己的广告;定向广告指的是广告主选择自己要投放的兴趣标签,然后算法为其匹配相应的受众人群并进行广告投放。
竞价广告:采用“价高者得”的方案来决策每次展示哪个广告,使得媒体主可以实时对不同广告进行比价,从而最大化收益。
程序化交易广告:广告主可以实时地在每一次广告展示中选择自己的目标受众,并且参与竞价。
根据用户或商品属性以及页面上下文属性从广告索引中检索符合投放条件的候选广告。
布尔表达式召回:根据广告主设置的定向标签组合成布尔表达式。
向量检索召回:通过传统的Word2Vec方式获取广告的向量表示,然后通过相似度计算对受众人群进行召回;或者通过深度学习模型获取广告的向量表示。
基于TDM(深度树匹配模型)的召回:基于深度学习的大规模推荐系统算法框架。
目前的找回策略大多是多路召回与权重检索相结合。
为用户侧特征和广告侧特征构建不同的塔,在经过多层全连接后,计算相似度并进行广告检索。
广泛应用于搜索、推荐等领域的召回和排序问题中。
对广告召回模块送来的广告候选集计算值,并按照所得值的大小倒排序。
点击率预估:向用户投放一个广告,然后预测用户点击广告的概率
特征处理:特征交叉组合、连续值特征的处理、点击率平滑、向量化表示
常见模型:
在广告竞拍机制中,广告的实际曝光量取决于广告的流量覆盖大小和在竞争广告中的相对竞争力水平,其中前者取决于广告的人群定向(匹配对应特征的用户数量)、广告素材尺寸(匹配的广告位)以及投放时段、预算等设置项;影响后者的因素主要有出价、广告质量、以及对用户体验的控制策略等。
序列数据建模:
为什么不使用标准的神经网络?
RNN的特点:
一般来说,RNN每一时间的输入和输出是不一样的
序列学习:对于序列数据是将序列项依次传入,每个序列项再对应不同的输出
时序展开:在RNN中每一个时间步骤用到的参数都是一样的
RNN可看作权值共享的多层、前向网络,训练权值约束的前向网络
Back Propagation Through Time:前向传播和反向传播
示例:
语言模型
新序列采样
字符级别的语言模型
序列生成
训练长序列 (100 time steps) RNN中,梯度很容易膨胀或消散
即使好的初始化,也难以检测当前目标输出对很多步之前的输入的依赖关系
GRU
LSTM:
解决了RNN长期(like hundreds of time steps)记忆的问题
LSTM是一个存储单元,使用logistic和linear单元执行乘法运算
记忆单元:存储RNN的长期信息
LSTM vs GRU
GRU是更加简单的模型,更容易创建一个更大的网络,而且它只有两个门,在计算性上也运行得更快,可以扩大模型的规模。
LSTM更加强大和灵活,有三个门而不是两个。
双向循环神经网络(Bidirectional RNN)
深层循环神经网络(Deep RNNs)
机器翻译
图片说明
使用集束搜索(Beam search algorithm)而不使用贪心搜索
改进集束搜索(Refinements to Beam Search),序列长度归一化
注意力模型
]]>考虑查询q: [aircraft] . . .
某篇文档 d 包含“plane”, 但是不包含 “aircraft”
显然对于查询q,一个简单的IR系统不会返回文档d,即使d是和q最相关的文档
提高召回率的方法:
局部(local)方法:对用户查询进行局部的即时的分析
全局(Global)方法: 进行一次性的全局分析(比如分析整个文档集)来产生同/近义词词典
关于相关反馈和查询扩展:
相关反馈的本质是将检索返回的文档的相关性判定(不同的判定来源:人工或非人工)作为返回信息,希望提升检索效果(召回率和正确率)。
相关反馈常常用于查询扩展,所以提到相关反馈往往默认为有查询扩展
而查询扩展的最初含义是对查询进行扩充,近年来越来越向查询重构偏移,即现在的查询扩展是指对原有查询进行修改。
相关反馈的基本思想
显式相关反馈:用户显式参加交互过程
隐式相关反馈:系统跟踪用户的行为来推测返回文档的相关性,从而进行反馈。
伪相关反馈或盲相关反馈:没有用户参与,系统直接假设返回文档的前k篇是相关的,然后进行反馈。
相关反馈中的核心概念:矩心
矩心是一系列点的中心
Rocchio算法是向量空间模型中相关反馈的实现方式
相关反馈中的假设:
假设 A1: 对于某初始查询,用户知道在文档集中使用哪些词项来表达
假设A2: 相关文档中出现的词项类似 (因此,可以基于相关反馈,从一篇相关文档跳到另一篇相关文档)
相关反馈的评价:
基于存留文档集(residual collection):用户没有判断的文档集
一轮相关反馈往往非常有用,相对一轮相关反馈,两轮相关反馈效果的提高有限。
用户相关反馈存在的问题:
隐式相关反馈
通过观察用户对当前检索结果采取的行为来给出对检索结果的相关性判定。
判定不一定很准确,但是省却了用户的显式参与过程。
用户行为种类:鼠标键盘动作和用户眼球动作
隐式相关反馈小结:
优点:
缺点:
伪相关反馈
伪相关反馈对于真实相关反馈的人工部分进行自动化
伪相关反馈算法:对于用户查询返回有序的检索结果,假定前 k 篇文档是相关的进行相关反馈 (如 Rocchio)
优点:
缺点:
相关反馈小结:
查询扩展是另一种提高召回率的方法
使用 “全局查询扩展” 来指那些 “查询重构(query reformulation)的全局方法”
在全局查询扩展中,查询基于一些全局的资源(同义词或近义词)进行修改,这些资源是与查询无关的
查询扩展的方法
交互式查询扩展 (Interactive QE):用户通常很懒,用户提交的扩展词项并不一定有用
基于词项相似度的查询扩展:
基于候选词和原始查询词项共现 (co-occurrences)的查询扩展
查询扩展的优点:
使用外部资源进行查询扩展(External QE)
选择性查询扩展(Selective QE)
搜索引擎中的查询扩展主要依赖的资源:查询日志
]]>四年相识、三年相恋、抵不过些许距离。
并没有表现得太过于悲伤,甚至都没有留下眼泪。可能是因为从日常的点点滴滴中已经知道这个结果了,最后的两三个月完全就是在硬撑着,我一厢情愿地在努力,但是她的心里早就已经有了答案。
相识的第一天,2018年9月24日,中秋节。两个人走进教室,拿出简历,面试。面试后一起下楼,简单的说了第一句打招呼的话语,分开。那是第一次见面,内心里有一种悸动,真的似乎有点喜欢。此时的我,刚刚经历了高考的失利,急于在这个看起来与我的能力并不匹配的学校中证明我自己。去竞选班干部,去参加各种学生组织,去认识更多的人,同时也不再压抑内心的感情,积极去找寻自己的爱情。当初对爱情只是懵懂,被拒绝了一次,拒绝了别人一次,有点怕了。有时候我也毫不掩饰我对她的喜欢,去车站接,送奶茶,约出来走走等等。就这样默默暗恋了一年。
第二年的中秋节,2019年9月13日,我终于鼓起勇气,约出来转到了湖大再转回来,说出了压在心底一年的话。这样就收获了我的初恋。当时的我,并不优秀,对未来一片迷茫,不知道四年大学毕业后要去到哪里。“我们在一无所有的情况下选择去尝试”,我同时也坚定了要共度一生的想法,想要给她今后一个更好的生活,于是我努力学习,从一个将将摸到保研边的中等生,逐渐变成了一个强者,拿下了很好的成绩排名,拿到了学校里面的绝大部分奖项,拿到了国家奖学金,成功保研。因为有了动力,一切都变得理所应当,再苦再累真的值得。
我们之间的感情没有那么多的激情燃烧,更多的是平淡。我尽量在她需要我的时候出现在她的身边,平时四周转一转,一起去图书馆学习,感冒了送她去医院,脚伤了每天接送,中午晚上点好饭送到身边。我很享受这种平淡的生活,因为我已经认准了她,什么东西都不能减少我对她的爱。我也认为她是和我一样性格的人,有自己的个性,有上进心进取心,不安于现状希望改变。就这样过了两年的美好时光,我们走入了大四的毕业季。
大四开始的我,松弛了下来,暂时与紧张的学习生活说了再见,开始无底线的放松。而她却要每天准备考研,还有两节课要上。而且由于搬校区的缘故,我见到她并不是很容易了。在这期间有了一些她不怎么讲话的迹象,甚至在我离开长沙和她吃的最后一顿饭上也是心不在焉。我把它归结为考研焦虑,并没有太过在意。也还是因为我对这段感情太有信心了吧,我相信时间距离都不是问题,我们只要努力把自己变得更好,总有一天会克服种种困难生活在一起衣食无忧。这也导致了大四下学期去实习的时候有点忽略了对她的关心,感觉是因为都忙,说的话也变少了。这种下了分手的种子。
6月正式本科毕业,2022年6月21日,突然的完全不理我,突然的提出分手,我直接崩溃掉。原来她并没有任何的信心,只是我自己自作多情罢了。原来这半年我基本不知道任何有关她的生活,我不知道她实习的工作怎么样,不知道她去面试了教师岗位,不知道她成功考上教师编制。我终于发现了这个问题,但是事实上已经晚了。虽然这一次分手我用回忆挽回,但是并没有打消她的念头,也并没有增加很多她对我的爱。而且由于距离,也阻隔了表达爱的方式。就好像“inception”一样,动了念头就很难再忘记掉了。
然后是短短四天的青岛旅行,差不多一年以来的首次见面。尤其是最后一天的晚上,最后一次吃饭基本上全程都在看手机。虽然是在修朋友圈的照片,但是我当然也是有一点点不高兴的。从上次几乎分手后我就十分在乎她的感受,但是我从来都没有勇气当面问出这些话语。这样过了两个月,我不断询问她的感受,不断讲给她我现在的想法。然而一切都是没有作用的。不爱了真的就不爱了。2022年9月24日,正式分手。我拼了命的想要挽回,我真的放不下,也不可能放得下三年的感情,换回来的仅仅是“不甜”、“不爱了”如此冰冷的字眼。我也并没有像我想象中的那么悲伤绝望,甚至一滴眼泪都没有落下。也许是因为早已经知道了这个结果吧。但是还是一夜没有睡着觉,真的无法接受这个冰冷的事实。
人,真的是会变的,会根据环境而变化。上大学的时候我们周围什么都没有,只有彼此。而步入社会,找到了稳定的工作,接触了各种各样的有趣的人,就会重新审视自己之前的生活,自己之前爱过的人。“我想换人了”“我倾向于比较条件,你的条件不如我”“及时止损”如此冰冷的话语,真的很难相信是从她的聊天框里面弹出来的。或许她发现自己面前存在着无数种可能性,为什么还要等着可能一年仅能见几次面,至少还要等上三年的远方的人呢?总之她不再怀念我们共度的三年时光了,毅然放手投入了新生活的怀抱,只能留下我在这里独自悲伤。
所以什么是爱情?我这几天不断在问自己这个问题。我一直认为爱情是一份承诺,是能克服重重困难一起走下去的勇气。现在我觉得这个想法确实太过于理想化了。可能我自己是这种想法,但是我不能要求别人有完全相同的想法。女孩子可能需要的并不是这种承诺,也不愿意有勇气,更愿意的是就在此时此刻,能有一个人在身边照顾她,关心她,两个人在一起的样子才是爱情。爱情也不可能没有物质需求,如果没有面包,只有爱情 ,那么这段爱情能撑到什么时候呢?如果能有一个人在身边照顾她,不愁吃穿,稳定工作,未来立刻触手可及,有人会不希望过上这种生活吗?可能以前觉得,两个人向着一个目标而努力,最终实现了理想,爱情自然修成了正果。但是如果不努力就能得到爱情,还努力做什么呢?为什么还要体验那种拼搏痛苦的生活,为什么不能躺在现实中直接享受呢?我这个人,对待每一件事情都很认真,对待每一个人也很认真,过于认真就过于理想化,理想化的目标,我能坚持但是并不能保证别人也坚持。世界是很残酷的,人也是很残酷的,坚持初心的人真的很少。
我的第一段恋爱之旅就这样结束了。我不恨她,她没有什么错误,也从来没有对我做出过任何的承诺,也没有做任何对不起我的事情。只能说,我们的爱情观确实不一致。好的恋爱让我们都成长了很多,学会更好地爱自己、爱他人。如果我还能有下一段爱情,我会更加谨慎地做出选择,没有结果,或者是短期内看不到结果的爱情,我宁愿不要,也不会去轻易去做出承诺,即使我知道我的承诺我一定坚持。
我不能这样悲伤下去,我要抬头向前看。虽然可能以后都不会有合适的人,合适的爱情,但,还是要过好每一天,珍惜自己现在的生活。最近纠结于这段感情,对父母疏远了一些,但其实他们才是这个世界上真的真的无条件爱我的人,我又有什么理由不爱他们呢?
放下过去,原谅自己,弥补过错,重新开始。
]]>聚类是无监督机器学习问题
影响聚类结果的因素:
样本-样本:(向量相似性)
样本-集合:
到集合最远点距离:
到集合最近点距离:
到集合平均点距离:
集合为平面:
集合为圆:
集合-集合:(类间距离)
集合间最远点距离:
集合间最近点距离:
集合间所有点平均距离:
集合表征点间距离(如平均值):
集合内样本间距离(类内距离):
聚类性能的外部指标指通过已知类簇划分,对聚类结果进行评价;判别同类别样本对标签一致与否,避免相同类簇划分,不同标签名称导致的不一致。
Jaccard系数、FM系数和Rand系数
聚类性能的内部指标:没有已知的类簇划分进行参考,通过聚类具有的类内相似和类间相异的特点进行评价。
DB指数:,越小越好
Dunn指数:,越大越好
基本思想:逐一比较单个样本与类簇的相似性,有相似类则归类,无相似类则建立新类。
优点:一种简单的,快速算法
相似性的关键度量:类别相似性:样本—类簇(样本—集合)。
缺点:所有样本过滤一遍后才知道类别总数,而先出现的样本不能找到(后出现的)合适类别
改进算法:采用两个阶段,类别确定、分类。
两阶段序贯方法:
缺点:以上两种方法依赖于阈值
改进方法:弱化阈值作用,采用两个阈值,形成灰色带。
双阈值序贯方法
三种算法缺点:
增强算法
增强处理1:对类别集合进行合并操作
增强处理2:对样本类别重置
基本思想:
聚类嵌套定义:和
是样本集
上的两种聚类划分,如果
中所有的类簇都是
中类簇的子集,则称
嵌套在
内,记作
层次聚类策略:类簇之间(依据相似性)不断合并、或不断的分化, 直到满足聚类停止条件。
自底向上/归并算法:
第次迭代:计算所有两个类簇的相似性,归并最相似的两个类簇,更新类别划分
缺点:没有归并的类簇间相似性,被重复计算
基于矩阵的归并算法
利用矩阵记录类簇间的相似性
优点:不必重新计算“没有合并的类簇间”的相似性
分化算法:过程与归并相反
第次迭代:在所有类簇的所有划分中,计算所有两个类簇相似性,选择最不相似的类簇集合划分,更新类别划分
缺点:没有划分的类簇间相似性,被重复计算
如何确定聚类个数?
Kmeans:将样本分给最近的类心,然后重新调整类心;通过多次迭代,逐步进行类别划分。
最优准则:最小化误差平方和,
,
是第
个类簇的样本。
一般方法:最近类心原则,批量划分后修正类心
改进方法:单个划分最优原则,单个划分后修正类心
]]>不排序的问题严重性
排序的重要性:
倒排索引中的词项频率存储
两种常见的评分累加算法:
以词项为单位(term-at-a-time, TAAT),首先获得词项t的posting list,然后累加得分
以文档为单位的计算,首先获得包含查询词的所有文档,将这些文档按照静态评分排序,然后依次累加得分
精确top K检索及其加速办法:
目标:从文档集的所有文档中找出K个离查询最近的文档
步骤:对每个文档评分(余弦相似度),按照评分高低排序,选出前K个结果
加速方法:
快速计算余弦:不考虑查询词项的权重
堆法N中选K:不对所有文档进行排序,只需要挑出最高的K个结果
提前终止计算:得到了top K结果,不需要再进行后续计算
精确topK检索的问题:仍然无法避免大量文档参与计算
非精确topK检索:非精确topK的结果如果和精确topK的结果相似度相差不大,应该也能让用户满意
找一个文档集合A,K<|A|<<N,利用A中的top K结果代替整个文档集的top K结果
方法一:索引去除
从查询词的角度:只考虑那些包含高idf查询词项的文档
从文档的角度:只考虑那些包含多个查询词项的文档
仅考虑高idf词项、仅考虑包含多个词项的文档
方法二:胜者表
对每个词项t,预先计算出其倒排记录表中权重最高的r篇文档,如果采用tfidf机制,即tf最高的r篇
方法三:静态质量得分排序方式
为每篇文档赋予一个与查询无关的[0,1]之间的值,记为g(d),例如Pagerank
最终文档排名基于g(d)和相关度的线性组合
目标是找net-score最高的top K文档
方法四:影响度(Impact)排序
提前结束法:
遍历倒排记录表时,可以在如下情况之一发生时停止:
将词项按照idf排序:
方法五: 簇剪枝
随机选 篇文档作为先导者,对于其他文档,计算和它最近的先导者
非docID的倒排记录表排序方法
与查询无关的一种反映结果好坏程度的指标
以文档为单位(Document-at-a-time)的处理、以词项为单位(Term-at-a-time)的处理方式
WAND(Weak AND) 评分算法
多层次索引基本思路:
时间序列是按时间顺序索引(或列出或图示)的一系列数据点。组成时间序列的数据由相对确定的时间戳组成。
对时间序列的分析基于以下假设:数据文件中标签的数据值表示以等间隔时间进行的连续测量值。假设数据存在相关性,然后通过建模找到对应的相关性,并利用它预测未来的数据走向。
可以从变量角度将这些问题归纳为单变量时间序列和多变量时间序列
可以从预测目标角度将这些问题归纳为单步预测和多步预测
单变量时间序列仅具有单个时间相关变量,所以仅受时间因素的影响。这类问题重点在于分析数据的变化特点,受相关性、趋势性、周期性和循环性等因素的影响。
多变量时间序列具有多个时间相关变量,除了受时间因素的影响,还受其他变量的影响。需要考虑更多的因素,挑战也更大。
单步预测问题比较基础,仅在训练集的时间基础上添加一个时间单位便可以作为测试集
多步预测问题比较复杂,是在训练集的时间基础上添加多个时间单位作为测试集
交叉验证的时候为了保留时间相关性,需要采用滚动交叉验证的方式:
加权平均:离当前时间点越近的数据的重要性越高
指数平滑:将每个时间单位的权重按照指数级进行衰减(指数平滑像是拥有无限记忆且权值呈指数级递减的移动平均法)
趋势性:在很长一段时间内呈现的数据持续上升或持续下降的变动
周期性:在一段时间序列内重复出现的波动,是各种因素综合影响的结果。
相关性:在某一段序列往往存在正相关或负相关,前后时间点会有很大的关联
随机性:除了上述三种模式外的随机扰动
历史平移:直接将历史记录作为特征
窗口统计:从多个序列单位中提取特征
序列熵特征:描述序列的确定性和不确定性
还有时间特征与统计特征
传统的时序模型:ARIMA(差分自回归滑动平均模型)
树模型:对时间序列进行平稳性调整
深度学习模型
回归问题:
根据给定的训练集,其中
(预测的结果
是连续函数值)
要求寻找上的决策函数
性能评价:
均方误差:
泛化误差可分解为偏差、方差和噪声之和
线性回归原理:使用线性函数来预测数据的分布
目标函数:最小误差平方和
求解:
正态分布假设的似然函数
误差服从正态分布:
似然函数:,可以转换为对数的形式
高斯误差的最大似然估计=最小二乘估计
优化学习:梯度下降方法
正态分布的先验似然函数:
最大后验估计目标函数:,
高斯分布的最大后验估计 = 正则化最小二乘估计
正则化最小二乘估计解:,
正则项解决过拟合问题
线性基函数回归
线性回归:
扩展的非线性回归:
基函数形式:多项式函数、高斯分布函数、sigmoid类型的函数、tanh类型的函数
多项式回归:
正则项对Bias和Variance的影响
参数估计
最小二乘估计是无偏估计
正则化最小二乘估计是有偏估计
使得参数估计更加稳定
相当于增加正则项
相当于加入白噪声
]]>计算机视觉需要应用大量的图像数据
卷积神经网络是一种特殊的深层神经网络模型
20世纪60年代,Hubel和Wiesel研究猫脑皮层
局部连接
局部感知野:图像的空间联系也是局部的像素联系较为紧密,而距离较远的像素相关性则较弱,减少了需要训练的权值数目
参数共享:图像的一部分的统计特性与其他部分是一样的。在输入的不同位置检测同一种特征具有平移不变性
一维、二维、三维卷积
其中三维卷积:假设输入数据的大小为a1×a2×a3,过滤器大小为f,即过滤器维度为f×f×f。三维卷积最终的输出为(a1−f+1)×(a2−f+1)×(a3−f+1)。
多卷积核:
边缘检测示例:卷积运算是输入图像与过滤器(也叫核)进行的运算,得到输出图像。卷积核与图像对应的位置相乘求和得到一个新值。
假定要识别图像中的特定曲线,也就是说,对这种曲线有很高的输出,对其他形状则输出很低,这也就像是神经元的激活。
Padding:边缘不填充
卷积步长:卷积中的步幅是另一个构建卷积神经网络的基本操作
输入与输出的尺寸关系:
单层卷积网络:每一个卷积核的输出对应一个实数b(偏差),然后在进行激活函数的非线性转换得到输出
Pooling池化:
通过卷积获得了特征之后,下一步利用这些特征去做分类。
池化层中没有需要学习的参数,所以通常不把池化层当做独立的一层来看。
池化层是一般不会设置padding,即一般padding为0。
fitter为2,stride为2是最常见的参数设置,尺寸图像缩小为原来的一半。
卷积时用的尺寸计算公式同样适用于池化层。
CNN基本结构:卷积层和子采样层
卷积神经网络是一个多层的神经网络
CNN训练过程
监督训练:Bp算法
向前传播
反向传播
卷积网络的核心思想:将局部感受野、权值共享以及时间或空间亚采样这三种结构思想结合起来获得了某种程度的位移、尺度、形变不变性。
层间联系和空域信息的紧密关系,使其适于图像处理和理解:图像和网络的拓扑结构能很好的吻合
避免了显式的特征抽取,而隐式地从训练数据中进行学习:特征提取和模式分类同时进行,并同时在训练中产生;权重共享可以减少网络的训练参数,使神经网络结构变得更简单,适应性更强。
CNN的改进:
Rectified linear function:加速收敛和稀疏化
dropout:将隐层节点以一定概率清0
局部对比归一
非线性变换、池化
残差网络(Residual Networks(ResNets))
评价什么?
使用相同的文档集合,相同的查询主题集合,相同的评价指标,对不同的检索系统进行比较。
评价指标:某个或某几个可衡量、可比较的值
评价过程:设计上保证公平、合理
IR中评价的难点:相关性(Relevance)是一个主观概念,文档相关性依赖于查询(数据标记工作量庞大)
召回率(Recall):返回的相关结果数占实际相关结果总数的比率
正确率(Precision):返回的结果中真正相关结果的比率
虽然Precision和Recall都很重要,但是不同的应用、不用的用户可能会对两者的要求不一样。
问题①:召回率难以计算:
对于大规模语料集合,列举每个查询的所有相关文档是不可能的事情,因此,这种情况几乎不可能准确地计算召回率可以采用Pooling方法,或者不考虑召回
缓冲池(Pooling)方法:对多个检索系统的Top k个结果组成的集合(并集)进行人工标注,标注出的相关文档集合作为整个相关文档集合。这种做法被验证是可行的(可以比较不同系统的相对效果),在TREC会议中被广泛采用。
问题②:两个指标需要融成一个指标,或者只采用单一指标
F值(F-measure):召回率R和正确率P的调和平均值
Fβ:表示召回率的重要程度是正确率的β(>=0)倍,β>1更重视召回率, β<1更重视正确率
E(Effectiveness)值:召回率R和正确率P的加权平均值,b>1表示更重视P
精确率是所有判定中正确的比率,一般不使用这一评价指标
问题③:两个指标都是基于(无序)集合进行计算,并没有考虑(排)序的作用
R-Precision:检索结果中,在所有相关文档总数位置上的准确率,如某个查询的相关文档总数为80,则计算检索结果中在前80篇文档的正确率。
正确率-召回率 曲线:检索结果以排序方式排列,用户不可能马上看到全部文档,因此,在用户观察的过程中,正确率和召回率在不断变化。
在上面的曲线对应的系统结果更好,也就是线下的面积(AUC)
P-R 曲线的插值问题:利用存在的召回率点对不存在的召回率点进行插值
优点:
缺点:单个查询的P-R曲线虽然直观,但是难以明确表示两个查询的检索结果的优劣
基于P-R曲线的单一指标:P-R曲线上P=R的那个点(Break Point)
平均正确率(Average Precision, AP):对不同召回率点上的正确率进行平均
不考虑召回率的指标:
Precision@N:在第N个位置上的正确率,对于搜索引擎,大量统计数据表明,大部分搜索引擎用户只关注前一、两页的结果,
平均的求法:
MAP(Mean AP):对所有查询的AP求宏平均
整个IR系统的P-R曲线:
在每个召回率点上,对所有的查询在此点上的正确率进行算术平均,得到系统在该点上的正确率的平均值。
两个检索系统可以通过P-R曲线进行比较。位置在上面的曲线代表的系统性能占优。
MRR(Mean Reciprocal Rank): 对于某些IR系统(如问答系统或主页发现系统),只关心第一个标准答案返回的位置(Rank),越前越好,这个位置的倒数称为RR,对问题集合求平均,则得到MRR
Bpref:在相关性判断不完全的情况下,计算在进行了相关性判断的文档集合中,在判断到相关文档前,需要判断的不相关文档的篇数。
相关性判断完全的情况下,利用Bpref和MAP进行评价的结果很一致,但是相关性判断不完全的情况下,Bpref更鲁棒
GMAP:几何平均值
NDCG:对于返回结果,相关度级别越高的结果越多越好,相关度级别越高的结果越靠前越好。
优点:
缺点:
现有评价体系远没有达到完美程度
TREC
总目标:支持在信息检索领域的基础研究,提供对大规模文本检索方法的评估办法
用户:产品的使用者
数据收集方为了推广产品同时持续维护和改善用户体验需要对由用户操作而产生的数据进行挖掘,以期从中发现群体乃至个体的行为偏好,形成数据层面上的所谓画像。
用于商业分析和数据挖掘的用户画像。基于给定的数据对用户属性及行为进行描述,然后提取用户的个性化指标,再以此分析可能存在的群体共性,并落地应用到各种业务场景中。
核心就是给用户打标签,用来分析社会属性、社会习惯、生活习惯、消费行为。
通过分析一个用户的特征来展示标签分类方式:
标签获取方式也可以看作特征获取方式
事实类:直接来自原始数据,比如性别、年龄、会员等级。也可以进行简单统计,比如用户行为次数、消费总额。
规则类:由运营人员和数据人员经过共同协商设定。例如,地域属性、家庭类型、年龄层等。所用技术知识:数理统计类,如基础统计、数值分层、概率分布、均值分析、方差分析等。
模型类:经过机器学习和深度学习等模型处理后,二次加工生成的洞察性标签。比如预测用户状态、预测用户信用分、划分兴趣人群和对评论文本进行分类。特点:综合程度高、复杂,依托数学建模,多种算法组合。
LSA:非概率主题模型,与词向量有关,主要用于文档的话题分析。其核心思想是通过矩阵分解的方式发现文档和词之间基于话题的语义关系。
具体:将文档集表示为词-文档矩阵,对矩阵进行SVD(奇异值分解),从而得到话题向量以及文档在话题向量的表示。
举例:2020腾讯广告大赛,首先构造用户点击的广告素材id序列(creative_id),然后进行TF-IDF计算,最后经过SVD得到结果。
(代码与书中不同,未验证)
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer# 稀疏特征降维 TruncatedSVDfrom sklearn.decomposition import TruncatedSVDfrom sklearn.pipeline import Pipeline# 提取用户点击序列docs = data_df.groupby(['user_id'])['creative_id'].agg(lambda x:"".join(x)).reset_index()['creative_id']# tf-idftfd = TfidfVectorizer()svd = TruncatedSVD(n_components=100, n_iter=50, random_state=2020)PLSA:PLSA(概率潜在语义分析)模型是为了克服LSA模型潜在存在的一些缺点而提出的。通过一个生成模型来为LSA赋予概率意义上的解释。该模型假设每一篇文档都包含一系列可能的潜在话题,文档中的每一个词都不是凭空产生的,而是在潜在话题的指引下通过一定的概率生成的。
LDA:LDA(潜在狄利克雷分布)是一种概率主题模型,与词向量无关,可以将文档集中的每篇文档的主题以概率分布的形式给出。通过分析一批文档集,抽取出他们的主题分布,就可以根据主题进行聚类或分类。同时,它是一种典型的词袋模型,即一篇文档由一组相互独立的词构成,词和词之间没有先后顺序。
word2Vec:可调用gensim包,参数:窗口大小、模型类型选择、生成词向量长度
对于Skip-Gram和CBOW:
DeepWalk
对于Word2Vec的衍生Item2Vec以及更多图嵌入方法,比如LINE、Node2Vec和SDNE
特点:
参考资料:《机器学习算法竞赛实战》整理 | 八、实战案例:Elo Merchant Category Recommendation
Imagine being hungry in an unfamiliar part of town and getting restaurant recommendations served up, based on your personal preferences, at just the right moment. The recommendation comes with an attached discount from your credit card provider for a local place around the corner!
Right now, Elo, one of the largest payment brands in Brazil, has built partnerships with merchants in order to offer promotions or discounts to cardholders. But do these promotions work for either the consumer or the merchant? Do customers enjoy their experience? Do merchants see repeat business? Personalization is key.
Elo has built machine learning models to understand the most important aspects and preferences in their customers’ lifecycle, from food to shopping. But so far none of them is specifically tailored for an individual or profile. This is where you come in.
In this competition, Kagglers will develop algorithms to identify and serve the most relevant opportunities to individuals, by uncovering signal in customer loyalty. Your input will improve customers’ lives and help Elo reduce unwanted campaigns, to create the right experience for customers.
train.csv 训练数据集,包括 first_active_month,card_id,feature_1,feature_2,feature_3,target字段test.csv 测试数据集,包括 first_active_month,card_id,feature_1,feature_2,feature_3字段first_active_month表示的是信用卡产生第一笔交易的时间,feature是信用卡类型的脱敏特征。最后一列 target是要预测的数值
historical_transactions.csv 信用卡在给定商家的历史交易记录,文件比较大,基本都是一些脱敏的特征
merchants.csv所有商家的附加信息
new_merchant_transactions.csv two months’ worth of data for each card_id containing ALL purchases that card_id made at merchant_ids that were not visited in the historical data .(每张信用卡在新商家的购物数据)
评价指标使用RMSE
一直想学,前面看过觉得太难,这回一定要坚持看完!
分析数据进而抽象出建模目标和方案。自行利用主办方提供的数据构造训练集与测试集。
EDA(探索性数据分析),Exploratory Data Analysis。在大致了解问题建模方式后,需结合对赛题背景业务的理解去看数据长什么样子、数据是否和描述相符、包含哪些信息等。首先需要对数据有清晰认知,主要是宽表中各个字段的取值含义、范围和数据结构等。然后更深层次地结合标签分析特征的分布状态、训练集与测试集的同分布情况、特征之间的业务关联以及隐含信息表征等。
Feature Engineering。特征决定机器学习预测效果上限,算法不断逼近这个上限。最费时的模块。
选模型、调参数
找找队友,看看Code
从直观上梳理问题,分析问题可解的方法、赛题背景等
业务理解:从个人生活的直观角度对业务进行分析
数据理解:在问题建模阶段,只需对数据做基本的分析。可以将数据理解分为数据基础层和数据描述层两个部分。主办方提供的原始数据质量良莠不齐,往往需要对原始数据进行清洗、加工和计算等处理。
分类指标:
错误率:分类错误的样本数占样本总数的比例
精度:分类正确的样本数占样本总数的比例
精度=1-错误率
查准率P反映真实情况与预测结果都为正例的样例在预测结果为正例的样例中的占比
查全率R反映真实情况与预测结果都为正例的样例在真实情况为正例的样例中的占比
(查准率与查全率是一对矛盾的度量,一般来讲,查准率高时,查全率偏低;查全率高时,查准率偏低)
,在查准率与查全率之间取得一个平衡
# 构建一个计算准确率、召回率和F1-score的评价代码y_train = np.array([1,0,1,0,1,0,1,0,1,1])y_pred = np.array([1,1,1,1,0,0,0,0,1,0])precision = precision_score(y_train,y_pred) #准确率recall = recall_score(y_train,y_pred) #召回率f1 = f1_score(y_train,y_pred) #f1度量print(precision,recall,f1)0.6 0.5 0.5454545454545454先根据学习器的预测结果对样例进行排序,按此顺序逐个把样例作为正例进行预测,每次计算出“真正例率”(True Positive Rate,简称TPR)和“假正例率”(False Positive Rate,简称FPR),分别以他们为纵、横轴作图,就得到了ROC曲线。
,真正例率TPR反映真正例在实际情况为正例的样例中的占比
,假正例率FPR反映假正例在实际情况为反例的样例中的占比
ROC曲线对正负样本的数量和分布不敏感。
AUC定义为ROC下方的面积,在互联网的搜索、推荐和广告的排序业务中都极为常见。AUC作为一个数值,其值越大就代表分类器的效果越好。
值得一提的还有AUC的排序特性。相对于准确率、召回率等指标,AUC指标本身和模型预测的概率绝对值无关,它只关注样本间的排序效果,因此特别适合用作排序相关问题建模的评价指标。AUC是一个概率值,我们随机挑选一个正样本与一个负样本,由当前分类算法根据计算出的分数将这个正样本排在负样本前面的概率就是AUC值。
为什么AUC与模型预测的分数值无关是个很好的特性?假设采用的是准确率等指标,而模型预测的分数是个概率值,那么必须选择一个阈值来决定把哪些样本预测为1,哪些预测为0。阈值的选择不同,准确率的值就会不同。而AUC可以直接使用模型预测分数本身,参考的是相对顺序。在竞赛中,省去了参赛者试探阈值的麻烦。
对数损失可用于评价分类器的概率输出。对数损失通过惩罚错误的分类来实现对分类器的准确度的量化。最小化对数损失基本等价于最大化分类器的准确度。为了计算对数损失,分类器必须提供概率结果,即把输入样本喂入模型后,预测得到每个类别的概率值(0~1),而不只是预测最可能的类别。
AUC与对数损失的区别
对数损失主要评价模型预测的概率是否足够准确,更关注和观察数据的吻合程度;AUC评价的则是模型把正样本排列到前面的能力。两者侧重不同,故应用不同。对于广告CTR问题,如果考虑广告排序效果,则可以选择AUC,这样不会受极端值影响。此外,对数损失反映了评价偏差,更偏向于将样本数量多的那类划分准确。由于使用AUC或对数损失可以避免把预测概率转换成类别的麻烦,在各种数据竞赛的分类问题中,AUC和对数损失基本是最常见的模型评价指标。
回归指标:
MAE不是二阶连续可微的,其二阶导数总为0。
MSE的量纲与数据标签不一致,为了保证量纲的一致性,通常需要对均方误差进行开方(均方根误差RMSE)
平均绝对误差MAE与均方误差MSE的区别
均方误差对误差(真实值-预测值)取了平方,若误差>1,则均方误差会进一步增大误差。如果数据中存在异常点,那误差值就会很大,而误差的平方则会远大于误差的绝对值。因此,相对于使用平均绝对误差计算损失,使用均方误差的模型会赋予异常点更大的权重。简而言之,均方误差对异常值更加敏感。
为什么在XGBoost里通常选择Huber损失替换MAE?
由于MAE不是连续可导的(0处不可导),所以需要使用可导目标函数来逼近平均绝对误差。而对于均方误差MSE,梯度又会随着损失的减小而减小,使预测结果更加精确。在这种情况下,Huber损失就非常有用,它会由于梯度的减小而落在最小值附近。比起均方误差MSE,Huber损失对异常点更加健壮。因此,Huber损失结合了MAE和MSE的优点。但是Huber损失可能需要我们不断调整超参数delta。
MAPE与MAE一样,不存在二阶导数。但不用于MAE,平均绝对百分比误差MAPE除了考虑预测值与真实值的误差,还考虑了误差与真实值之间的比例。因此真实值越大,误差会越小。
主办方提供的数据往往令人脑壳疼,主要是以下四个原因:
问题1:在数据量非常大的情况下,为了降低成本,如何提高模型的训练速度?
问题2:针对正负样本分布不均衡的问题,如何通过数据采样解决这类问题?
思考:在什么场景下需要处理样本的不均衡问题?
由于需要数据集对模型的效果进行线下验证,所以需要考虑如何对数据进行划分,构建合适的线下验证集。针对不同类型的问题,需要不同的线下验证方式。
书中将这些问题大致分为强时序性与弱时序性两类,然后以此确定线下验证方式。
定义:先将总数据集D划分为k个大小相似的互斥子集,每个子集都尽可能保持数据分布的一致性(即从D中分层采样得到)。然后每次用K-1个子集的并集作为训练集,余下的自己作为测试集。这样可以获得K组训练/测试集,从而可进行k次训练和测试,最终返回这k个测试结果的均值。
注意:
以下为交叉验证代码,其中参数NFOLDS用来控制折数**(未实际验证)**
from sklearn.model_selection import KFoldNFOLDS = 5 #五折交叉验证folds = KFold (n_split = NFOLDS,shuffle=True,random_state=2021)#random_state只要是一个固定的值就可以了,不一定是2021for trn_idx,val_idx in folds.split(X_train,y_train):train_df,train_label = X_train.iloc[trn_idx, :],y_train[trn_idx]valid_df,valid_label = X_train.iloc[val_idx, :],y_train[val_idx]参数random_state默认设置为None,这意为着每次进行KFold(…, shuffle=True)时,打散都是不同的。
为了保证结果的可重复性(在相同的平台上),应该给random_state设定一个固定的值。
如何确保自己准备好竞赛使用的算法模型?如何为数据集选择最合适的算法?如何定义可用于算法模型的特征变量?数据探索可以帮助回答以上三点。
一般而言,数据探索可以分为三个部分:
赛前数据探索,主要包含分析思路、分析方法和明确目的。
在实际竞赛中,最好使用多种探索思路和方法来探索每个变量并比较结果。在完全理解数据集后,就可以进入数据预处理阶段和特征提取阶段了,以便根据所期望的业务结果转换数据集。此步骤的目标是确信数据集已准备好应用于机器学习算法。
数据探索的分析主要采用以下方法:
可以检查每个变量的分布,定义一些丢失值,最终找到替换它们的可能方法。
在竞赛中跳过数据探索阶段可能会导致数据倾斜、出现异常值和过多的缺失值,产生以下糟糕结果:
数据探索阶段必须要明确:
数据探索最基本的步骤之一是获取对数据的基本描述,通过获取对数据的基本描述从而获得对数据的基本感觉。以下方法有助于我们认识数据:
DataFrame.describe():查看数据的基本分布,具体是对每列数据进行统计,统计值包含频次、均值、方差、最小值、分位数、最大值等。DataFrame.head(n):可以直接加载数据集的前n行,n默认为5DataFrame.shape:得到数据集的行列情况DataFrame.info():可以快速获得对数据集的简单描述,比如每个变量的类型、数据集的大小和缺失值情况。下面通过一段代码展示nunique和缺失值的情况:
stats = []for col in train.columns: stats.append((col, train[col].nunique(), train[col].isnull().sum() * 100 / train.shape[0], train[col].value_counts(normalize=True, dropna=False).values[0] * 100, train[col].dtype))stats_df = pd.DataFrame(stats, columns=['Feature', 'Unique_values', 'Percentage of missing values', 'Percentage of values in the biggest category', 'type'])stats_df.sort_values('Percentage of missing values', ascending=False)[:10]上图展示了经过上述代码生成的数据基本信息,我们从中找到特殊变量进行细致分析,这里选择nunique值低和缺失值多的变量进行观察。一般而言,nunique为1是不具备任何意义的,表示所有值都一样,不存在区分性,需要进行删除。可以发现有些变量的缺失值很多,比如缺失比例达到95%以上,我们可以考虑将其删除。
用柱状图的形式可以更加直观地展示变量的缺失值分布情况,以下为变量缺失值可视化图的具体生成代码:
missing = train.isnull().sum()missing = missing[missing > 0]missing.sort_values(inplace=True)missing.plot.bar()单变量可以分为标签、连续型和类别型
标签是最重要的变量,首先应当观察标签的分布情况。对于房屋价格预测,其标签SalePrice为连续型变量。
通过可视化的方式观察SalePrice的分布情况
sns.distplot(train['SalePrice'], color='b', bins=100, hist_kws={'alpha': 0.4})可见,SalePrice呈偏离正态分布,属于向右倾斜类型,存在峰值状态,一些异常值在500000以上。我们最终会想办法去掉这些异常值,得出能够让算法模型很好学习的、符合正态分布的变量。
下面对SalePrice进行对数转换,并生成可视化图
sns.distplot(np.log(train['SalePrice']), color='b', bins=100, hist_kws={'alpha': 0.4})可以看出 ,对数转换后的标签的分布为正态分布形式,比较适合算法模型学习。
类似于标签的查看方式,这里主要使用直方图这种可视化方式观察值的分布、每个值出现的频率等。以下为连续型变量的分布可视化的生成代码:
df_num = train.select_dtypes(include = ['float64', 'int64'])df_num.hist(figsize=(16, 20), bins=50, xlabelsize=8, ylabelsize=8)实际中要对全部的变量进行查看,分析每一个变量的分布情况。
接着进行更加科学的分析,首先是相关性分析。相关性分析只能比较数值间特征,所以对于字母或字符串特征,需要先进行编码,并将其转换为数值,然后再看有什么关联。在实际竞赛中,相关性分析可以很好地过滤掉与标签没有直接关系的特征。
正相关和负相关
在搭建或训练模型时,如果同时使用这两个特征,可能其中一个会是多余的。我们应尽量消除冗余特征,因为它会使训练时间变长,同时影响其他优势
以下代码为生成有关SalePrice的相似性矩阵图
corrmat = train.corr()f, ax = plt.subplots(figsize=(20, 9))sns.heatmap(corrmat, vmax=0.8, square=True)从生成的相似性矩阵中,可以找出与房价相关性最强的变量,其中OverallQual(总评价)、GarageCars(车库)、TotalBsmtSF(地下室面积)、GrLivArea(生活面积)等特征与SalePrice呈正相关
从相似性矩阵中,我们还能发现变量之间的关系,如何利用相似性矩阵进行分析就成为了关键
数据探索的目的是为了帮助我们了解数据并且构建有效特征。
比如,我们找到了与标签有着强相关的特征,那么就可以围绕着这个强相关特征进行一系列的扩展,具体可以进行交叉组合,比如强相关加弱相关、强相关加强相关等组合,挖掘更高维度的潜在信息。
首先,观察类别型变量的基本分布情况,即观察每个属性的频次。根据频次,我们不仅可以发现热点属性和极少出现的属性,还可以进一步分析出现这些情况的原因,比如淘宝网的女性用户多于男性,主要是因为平台在服饰和美妆业务方面拥有强大的影响力。这是从业务角度考虑,自然也有可能是数据采样的原因。
对部分类别变量的分布进行可视化展示
df_not_num = train.select_dtypes(include = ['O'])fig, axes = plt.subplots(round(len(df_not_num.columns) / 3), 3, figsize=(12, 30))for i, ax in enumerate(fig.axes): if i < len(df_not_num.columns): ax.set_xticklabels(ax.xaxis.get_majorticklabels(), rotation=45) sns.countplot(x=df_not_num.columns[i], alpha=0.7, data=df_not_num, ax=ax)fig.tight_layout()单变量分析太过于单一,不足以挖掘变量之间的内在联系,获取更加细粒度的信息,所以有必要进行多变量分析。分析特征变量与特征变量之间的关系有助于构建更好的特征,同时降低构建冗余特征的概率值。
此处选用本赛题中需要特别关注的特征变量进行分析
从相似性矩阵中,我们已知房屋评价与SalePrice呈正相关。进一步扩展分析,通过可视化来考虑房屋评价和房屋位置是否存在某种联系。
plt.style.use('seaborn-white')type_cluster = train.groupby(['Neighborhood','OverallQual']).size()type_cluster.unstack().plot(kind='bar',stacked=True, colormap= 'PuBu', figsize=(13,11), grid=False)plt.xlabel('OverallQual', fontsize=16)plt.show()上图为不同房屋位置的评价分布条状图,我们可发现颜色越深代表评价越高。NoRidge、NridgHt和StoneBr都有不错的评价
再进一步看看不同位置房屋的SalePrice
var = 'Neighborhood'data = pd.concat([train['SalePrice'], train[var]], axis=1)f, ax = plt.subplots(figsize=(26, 12))fig = sns.boxplot(x=var, y="SalePrice", data=data)高评价位置对应高SalePrice,说明房屋位置评价与房屋售价有比较强的相关性。除了通过这样的分析证明原始特征与SalePrice强相关外,还可以通过分析来构建新的特征。
既然房屋位置和房屋评价的组合能够出现更高售价的房屋,那么我们可以构造这两个类别特征的交叉组合特征来进行更细致的描述,也可以构造这个组合特征下的房屋均价等。
学习曲线是机器学习中被广泛使用的效果评估工具,能够反映训练集和验证集在训练迭代中的分数变化情况,帮助我们快速了解模型的学习效果。我们可以通过学习曲线来观察模型是否过拟合,通过判断拟合程度来确定如何改进模型
学习曲线广泛应用于机器学习中的模型评估,模型会随着训练迭代逐步学习(优化其内部参数),例如神经网络模型。这时用于评估学习的指标可能会最大化(分类准确率)或者最小化(回归误差),这也意味着得分越高(低)表示学习到的信息越多(少)。
以下是学习曲线图中观察到的一些常见形状
欠拟合是指模型无法学习到训练集中数据所展现的信息,这里可以通过训练损失的学习曲线来确定是否发生欠拟合。在通常情况下,欠拟合学习曲线可能是一条平坦的线或者有着相对较高的损失,也就表明该模型根本无法学习训练集
过拟合是指模型对训练集学习得很好,包括统计噪声或训练集中的随机波动。过拟合的问题在于,模型对于训练数据的专业化程度越高,对新数据的泛化能力就越差,这会导致泛化误差增加。泛化误差的增加可以通过模型在验证集上的表现来衡量。如果模型的容量超出了问题所需的容量,而灵活性又过多,则会经常发生这种情况。如果模型训练时间过长,也会发生过拟合。
通过模型训练可以得到特征重要性。对于树模型(如LightGBM和XGBoost),通过计算特征的信息增益或分裂次数得到特征的重要性得分。对于模型LR和SVM,则是使用特征系数作为特征重要性得分,例如LR(逻辑回归),每个特征各对应一个特征系数w,w越大,那么改特征对模型预测结果的影响就会越大,就可以认为该特征越重要。我们假定特征性得分和特征系数w都是在衡量特征在模型中的重要性,都可以起到特征选择的作用。
误差分析是通过模型预测结果来发现问题的关键。
一般而言,回归问题中看预测结果的分布,分类问题中看混淆矩阵等。
在真实问题中,误差分析会更加细致。比如,在进行一个用户违约预估的二分类任务中,验证集结果中有200个错误分类样本,进一步分析发现有70%的错误分类样本是由于大量特征缺失而导致的误判,这时就需要调整,既可以通过挖掘更多能够描述这些误判样本的特征信息帮助增强模型的预测能力,还可以在模型训练中赋予这些误判样本更高的权重。
尽量得到标准、干净、连续的数据,供数据统计、数据挖掘等使用,视情况尝试对缺失值进行处理,比如是否要填充,填充什么。此外,有些竞赛提供的数据集以及对应的存储方式可能使得需要占用超过参赛者本身硬件条件的内存,故有必要进行一定的内存优化,这也有助于在有限的内存空间对更大的数据集进行操作。
除了XGBoost和LightGBM等算法在训练时可以直接处理缺失值以外,其他很多例如LR、DNN、CNN、RNN等都并不能对缺失值进行直接处理。故而在数据准备阶段,要比构建算法阶段花更多时间,因为像填补缺失值这样的操作需要细致处理。
首先,需找到缺失值表现形式。除了None、NA和NaN外,还有例如-1或-999来填充的缺失值。还有一种看上去像缺失值,但实际上有实际意义的业务,此时需特殊对待。例如没有填“婚姻状态”的用户可能是对自己隐私比较敏感,应为其单独设为一个分类;没有“驾龄”可能是没有车,为其填充0比较合适。
数据缺失可以分为类别特征的缺失和数值特征的缺失两种。
填充方法总结如下:
实际数据中可能会发现某个或某些字段(特征)根据某个变量(如时间序列问题中的时间)排序后,经观察存在一些数值远高于或低于其一定范围内的其他数值。还有些不合理的存在,这些都可以视作异常值,他们可能会给算法性能带来负面影响。
首先,找到异常值,总结了两种方法:
离散型异常值(离散属性定义范围以外的所有值均为异常值)、知识型异常值(如大学生脱发情况:从无)等,都可以当做类别缺失值来处理。
数据集太大而自己的硬件条件有限就有可能会因为内存不够导致代码出现memory error,介绍Python的内存回收机制和数值类型优化这两种有助于优化内存的常见方法。
我们可以用np.iinfo类来确认每一个int型子类型的最大值和最小值
import numpy as npnp.iinfo(np.int8).minnp.iinfo(np.int8).max无量纲化指的是将不同规格的数据转换到同一规格。常见无量纲化方法有标准化和区间缩放法。标准化的前提是特征值服从正态分布,标准化后,特征值服从标准正态分布。区间缩放法利用了边界信息,将特征的取值区间缩放到某个特定的范围,例如[0,1]
单特征转换是构建一些模型(如线性回归、KNN、神经网络)的关键,对于决策树相关模型并无影响。还有些纯粹的工程原因,即在进行回归预测时,对目标取对数处理,不仅可以缩小数据范围,而且压缩变量尺度使数据更平稳。
然而,数据要求不仅是通过参数化方法施加的。如果特征没有被规范化,例如当一个特征的分布位于0附近且范围不超过(-1,1),而另一个特征的分布范围在数十万数量级时,会导致分布于0附近的特征变得完全无用。
扩展:cbox-cox变换,一种自动寻找最佳正态分布变换函数的方法。
log变换可以将倾斜数据变得接近正态分布。
离散化后的特征对异常数据有很强的健壮性,更便于探索数据的相关性。常用的离散化分为无监督和有监督两种。
无监督的离散化分桶操作可以将连续变量离散化,同时使数据平滑,即降低噪声的影响。一般分为等频和等距两种分桶方式。
有监督的离散化对目标有很好的区分能力,常用的是使用树模型返回叶子节点来进行离散化。如在GBDT+LR经典模型中,就是先使用GBDT来将连续值转化为离散值。具体方法:用训练集中的所有连续值和标签输出来训练LightGBM,共训练两棵决策树,第一棵有4个叶子节点,第二棵树有3个叶子节点。如果某一个样本落在第一棵树的第三个叶子节点上,落在第二棵树的第一个叶子节点上,那么它的编码就是0010100,一共7个离散特征,其中会有两个取值为1的位置,分别对应每棵树中样本落点的位置。最终我们会获得num_trees*num_leaves维特征。
在实际数据中,特征并不总是数值,还有可能是类别。对于离散型的类别特征进行编码,一般分为两种情况:自然数编码(特征有意义)和独热(one-hot)编码(特征无意义)。
自然数编码:一列有意义的类别特征(即有顺序关系)可以使用自然数进行编码,利用自然数的大小关系可以保留其顺序关系。以下是两种自然数编码的常用方式:
①调用sklearn中函数:
from sklearn import preprocessingfrom f in columns:le = preprocessing.LableEncoder()le.fit(data[f})②自定义实现(速度快)
for f in columns:data[f] = data[f].fillna(-999)data[f] = data[f].map(dict(zip(data[f].unique(),range(0,data[f].nunique()))))独热编码:当类别特征没有意义(即无顺序关系)时,需要使用独热编码。例如,红>蓝>绿不代表任何东西,进行独热编码后,每个特征的取值对应一维特征,最后得到一个样本数×类别数大小的0~1矩阵。可直接调用sklearn中API进行生成(或者是使用哑变量的方式)
不规则特征可能包含样本的很多信息,比如身份证号,各段表示不同的信息。一般不会提供这种比较敏感的信息。
机器学习模型很难识别复杂的模式,特别是很难学习到不同特征组合交叉的信息,所以我们可以基于对数据集的直觉分析和业务理解创建一些特征来帮助模型有效学习。下面我们将介绍结构化数据的特征提取方式。
(结构化数据由明确定义的数据类型组成,非结构化数据由音频、视频和图片等不容易搜索的数据组成。)
类别特征又可以称为离散特征,除了每个类别属性的特定含义外,还可以构造连续型的统计特征,以挖掘更多有价值的信息,比如构造目标编码、count、nunique和ratio等特征。另外,也可以通过类别特征间的交叉组合构造更加细粒度的特征。
目标编码可以理解为用目标变量(标签)的统计量对类别特征进行编码,即根据目标变量进行有监督的特征构造。如果是分类问题,可以统计目标均值、中位数和最值。目标编码的方式可以很好地替代类别特征,或者作为新特征。
使用目标变量时,非常重要的一点是不能泄露任何验证集的信息。所有基于目标编码的特征都应该在训练集上计算,测试集则由完整的训练集来构造。更严格一点,我们在统计训练集的特征时,需要采用K折交叉统计法构造目标编码特征,从而最大限度地防止信息泄露。如用五折交叉统计构造特征时,我们将样本划分为五份,对于其中每一份数据,我们都将用另外四份来计算每个类别取值对应目标变量的频次、比例或者均值,简单来说就是未知的数据(一份)在已知的数据(四份)里面取特征。
目标编码方法对于基数较低的类别特征通常很有效,但对于基数较高的类别特征,可能会有过拟合的风险。因为会存在一些类别出现频次非常低,统计出来的结果不具有代表性。一般会加入平滑性来降低过拟合风险。在处置妥当的情况下,无论是线性模型,还是非线性模型,目标编程都是最佳的编码方式和特征构造方式。
count:计数特征,用于统计类别特征的出现频次
nunique和ratio常常会涉及多个类别特征的联合构造。例如在广告点击率预测问题中,对于用户ID和广告ID,使用nunique可以反映用户对广告的兴趣宽度,也就是统计用户ID看过几种广告ID;使用ratio可以反映用户对某类广告的偏好程度,即统计用户ID点击某类广告ID的频次占用户点击所有广告ID频次的比例。
交叉组合能够描述更细粒度的内容。对类别特征进行交叉组合在竞赛中是一项非常重要的工作,这样可以进行很好的非线性特征拟合。如用户年龄和用户性别可以组合成“年龄_性别”这样的新特征。一般我们可以对两个类别或三个类别特征进行组合,也称作二阶组合或三阶组合。简单来讲,就是对两个类别特征进行笛卡尔积的操作,产生新的类别特征。
并非所有组合都是需要考虑的,我们会从两个方面进行分析。
这里所说的数值特征,我们认为是连续的。数值特征的大小是有意义的,通常不需要处理就可以直接“喂”给模型进行训练。除了之前对数值特征进行各种变换外,还存在一些其他常见的数值特征构造方式。
在实际数据中,通常给出的时间特征是时间戳属性,所以首先需要将其分离成多个维度,比如年月日小时分钟秒钟。如果你的数据源来自于不同的地理数据源,还需要利用时区将数据标准化。除了分离出来的基本时间特征外,还可以构造时间差特征,即计算出各个样本的时间与未来某一个时间的数值差距,这样这个差距是UTC的时间差,从而将时间特征转换为连续值,比如用户首次行为日期与用户注册日期的时间差、用户当前行为与用户上次行为的时间差等。
在竞赛中,可能会遇到某一列特征中每行都包含多个属性的情况,这就是多值特征。例如广告大赛中的兴趣类目,其中包含5个兴趣特征组,每个兴趣特征组都包含若干个兴趣ID。对于多值特征,通常可以进行稀疏化或者向量化的处理,这种操作一般出现在自然语言处理中,比如文本分词后使用TF-IDF(词频-逆文档频率)、LDA(隐含狄利克雷分布)、NMF(非负矩阵分解)等方式进行处理,这里则可以将多值特征看作文本分词后的结果,然后做相同的处理。
对多值特征最基本的处理办法是完全展开,即把这列特征所包含的n个属性展开成n维稀疏矩阵。使用sklearn中的CountVectorizer函数,可以方便地将多值特征展开,只考虑每个属性在这个特征的出现频次。
还有一种情况,比如在广告算法大赛中,需要根据用户的历史点击行为预测用户的属性标签。这时候用户的点击序列尤为重要,当我们构造好用户对应的历史点击序列后,除了使用上述的TF-IDF等方法外,还可以提取点击序列中商品或广告的嵌入表示,比如用Word2Vec、DeepWalk等方法获取embedding向量表示。因为要提取用户单个特征,所以可以对序列中的嵌入向量进行聚合统计,这种方法本质上是假设用户点击过的商品或广告等同重要,是一种比较粗糙的处理方式。我们可以引入时间衰减因素,或者使用序列模型,如RNN、LSTN、GRU,套用NLP的方法进行求解。
当我们添加新特征时,需要验证它是否确实能够提高模型预测的准确度,以确定不是加入了无用的特征,因为这样只会增加算法运算的复杂度,这时候就要通过特征选择算法自动选择出特征集中的最优子集,帮助模型提供更好的性能。特征选择算法用于从数据中识别并删除不需要、不相关以及冗余特征。这些特征可能会降低模型的准确度和性能,特征选择的方法主要有先验的特征关联性分析以及后验的特征重要性分析。、
特征关联性分析是使用统计量来为特征之间的相关性进行评分。特征按照分数进行排序,要么保留,要么从数据集中删除。关联性分析方法通常是针对单变量的,并独立考虑特征或者因变量。常见的特征关联性分析方法有皮尔逊相关系数、卡方检验、互信息法和信息增益等。这些方法速度快、使用方便,但是忽略了特征之间的关系,以及特征和模型之间的关系。
不仅可以衡量变量之间的线性相关性,解决共线变量问题,还可以衡量特征与标签的相关性。共线变量是指变量之间存在高度相关关系,这会降低模型的学习可用性,可解释性以及测试集的泛化性能。但这三个特性都是我们想增加的,所以删除共线变量是一个有价值的步骤。我们将为删除共线变量建立一个基本的阈值(根据想要保留的特征数量决定)。
下面代码用于解决特征与标签不具有相关性的问题,根据皮尔逊相关系数的计算提取top300的相似特征:
def feature_select_pearson(train,features):featureSelect = features[:]#进行皮尔逊相关性计算corr=[]for feat in featureSelect:corr.append(abs(train[[feat,'target']].fillna(0).corr().values[0][1]))se = pd.Series(corr,index=featureSelect).sort_values(ascending=False)feature_select = se[:300}.index.tolist()#返回特征选择后的训练集return train[feature_select]用于检验特征变量与因变量的相关性。对于分类问题,一般假设与标签独立的特征为无关特征,而卡方检验恰好可以进行独立性检验,所以使用与特征选择。如果检验结果是某个特征与标签独立,则可以去除该特征。
互信息是对一个联合分布中两个变量之间相互影响关系的度量,也可以用于评价两个变量之间的相关性。互信息法之所以能够用于特征选择,可以从两个角度进行解释:基于KL散度和基于信息增益。互信息越大说明两个变量相关性越高。
但是想把互信息直接用于特征选择其实不太方便,由于:
在实际竞赛中,经常用到的一种特征选择方法是基于树模型评估特征的重要性分数。特征的重要性分数越高,说明特征在模型中被用来构建决策树的次数越多。这里我们以XGBoost为例来介绍树模型评估特征重要性的三种计算方法(weight、gain和cover)。(LightGBM也可以返回特征重要性)
params ={'max_depth':10,'subsample':1,'verbose_eval':True,'seed':12,'objective':'binary:logistic'}xgtrain = xgb.DMatrix(x,label=y)bst = xgb.train(params,xgtrain,numm_boost_round=10)importance = bst.get_score(fmap='',importance_type='weight')importance =bst.get_score(fmap='',importance_type='gain')importance = bst.get_score(fmap='',importance_type='cover')技巧:虽然特征重要性可以帮助我们快速分析特征在模型训练过程中的重要性,但不能将其当做绝对的参考依据。一般而言,只要特征不会导致过拟合,我们就可以选择重要性高的特征进行分析和扩展,对于重要性低的特征,可以考虑将之从特征集中移除,然后观察线下效果,再做进一步判断。
可以将一组特征的选择视作一个搜索问题,在这个问题中,通过准备、评估不同的组合并对这些组合进行比较,从而找出最优的特征子集,搜索过程可以是系统性的,比如最佳优先搜索;也可以是随机的,比如随机爬山算法,或者启发式方法,比如通过向前和向后搜索来添加和删除特征(类似前剪枝和后剪枝算法)。这种方法比较耗时。
from sklearn.feature_selection import RFEfrom sklearn.linear_model import LogisticRegression#递归消除特征法,返回特征选择后的数据#参数estimator为基模型#参数n_feature_to_select 为选择的特征个数RFE(estimator=LogisticRegression(),n_features_to_select=2).fit_transform(data,target)技巧:在使用封装方法进行特征选择时,用全量数据训练并不是最明智的选择。应先对大数据进行采样,再对小数据使用封装方法
以上三种特征选择方法按需使用或组合使用,建议优先考虑特征重要性,其次是特征关联性。
此外还有null importance。其思想:将构建好的特征和正确的标签喂给树模型得到一个特征重要性分数,再将特征和打乱后的标签喂给树模型得到一个特征重要性分数,然后对比两个分数,如果前者没有超过后者,那么这个特征就是一个无用的特征。
参考资料 :《机器学习算法竞赛实战》整理 | 五、模型训练
Lasso回归是对普通的线性回归采用L1正则化进行优化,通过惩罚或限制估计值的绝对值之和,可以使某些系数为零,从而达到特征稀疏化和特征选择的效果。当我们需要一些自动的特征、变量选择,或者处理高度相关的预测因素时,很方便。
from sklearn.linear_model import Lassolasso_model = Lasso(alpha = 0.1, normalize = True)只保留不相关的特征,其他为0,可能会导致信息损失
Ridge回归是对普通的线性回归采用L2正则化进行优化,对特征的权重系数设置了惩罚项。
from sklearn.linear_model import Ridgeridge_model = Ridge(alpha = 0.05, normalize = True)不会减少特征数量,不利于特征缩减。
两者合并:Elastic Net Regression
本节将介绍竞赛中常见的树模型,这些模型简单易用,能够带来高收益。
可将树模型分为随机森林(Random Forest, RF)和梯度提升树(GBDT), 这两者最大的差异是前者并行、后者串行。在梯度提升树部分我们将介绍如今竞赛中大火的三种树模型: XGBoost、 LightGBM 和CatBoost。能够灵活运用这三种模型是竞赛中的必备技能。接下来将详细介绍各种树模型的数学形式、优缺点、使用细节和应用场景。
随机森林就是通过集成学习的思想将多个决策树集成在一起,各个决策树之间没有任何关联。随机森林算法对多个决策树的结果进行投票得到最终结果,也是最简单的bagging思想 。
随机森林的优点:
很多缺点都是相对而言的:
from sklearn.ensemble import RandomForestClassifierrf = RandomForestClassifier(max_ features=' auto', oob_ score=True, random state=1, n_ jobs=-1)梯度提升树(GBDT)是基于Boosting改进而得的,在Boosting算法中,一系列基学习器都需要串行生成,每次学习一棵树,学习目标是上棵树的残差。和AdaBoost 一样,梯度提升树也是基于梯度下降函数。梯度提升树算法已被证明是Boosting算法集合中最成熟的算法之一,它的特点是估计方差增加,对数据中的噪声更敏感(这两个问题都可以通过使用子采样来减弱),以及由于非并行操作而导致计算成本显著,因此要比随机森林慢很多。
梯度提升树是XGBoost、LightGBM和CatBoost的基础。
import xgboost as xgbparams = {'eta': 0.01, ' max depth': 11, 'objective': 'reg:linear', 'eval_ metric': 'rmse' }dtrain = xgb.DMatrix(data=X_train, label=y_train)dtest = xgb.DMatrix(data=X_valid, label=y_valid)watchlist = [(train.data, 'train'), (valid_data, 'valid_ data')]model=xgb. train(params, train_data,num_boost_round=20000,evals=watchlist,early_stopping_rounds=200,verbose_eval=500)y_pred = model. predict(xgb .DMatrix(X_test), ntree_limit=model.best_ntree_limit)LightGBM是微软的一个团队在Github上开发的一个开源项目,高性能的LightGBM算法具有分布式和可以快速处理大量数据的特点。LightGBM虽然基于决策树和XGBoost而生,但它还遵循其他不同的策略。
XGBoost使用决策树对一个变量进行拆分,并在该变量上探索不同的切割点(按级别划分的树生长策略),而LightGBM则专注于按叶子节点进行拆分,以便获得更好的拟合(这是按叶划分的树生长策略)。这使得LightGBM能够快速获得很好的数据拟合,并生成能够替代XGBoost的解决方案。从算法上讲,XGBoost将决策树所进行的分割结构作为一个图来计算,使用广度优先搜索(BFS),而LightGBM使用的是深度优先搜索(DFS)。
主要特点
import lightgbm as lgbparams = {'num_leaves': 54, 'objective': 'regression', 'max_depth': 18,'learning_rate': 0.01, 'boosting': 'gbdt', 'metric': 'rmse', 'lambda_11': 0.1}model = lgb.LGBMRegressor(**params, n_estimators = 20000, nthread = 4, n_jobs = -1)model.fit(x_train, y_train, eval_set=[(X_train, y_train), (X_valid, y_valid)], eval_metric='rmse', verbose=1000, early_stopping_rounds=200)y_pred= model.predict(X_test, num_iteration=model.best_iteration_)CatBoost是由俄罗斯搜索引擎Yandex在2017年7月开源的一个GBM算法,它最强大的点是能够采用将独热编码和平均编码混合的策略来处理类别特征。
CatBoost用来对类别特征进行编码的方法并不是新方法,是均值编码,该方法已经成为一种特征工程方法,被广泛应用于各种数据科学竞赛中,如Kaggle。
均值编码,也称为似然编码、影响编码或目标编码,可将标签转换为基于它们的数字,并与目标变量相关联。如果是回归问题,则基于级别典型的平均目标值转换标签;如果是分类问题,则仅给定标签的目标分类概率(目标概率取决于每个类别值)。均值编码可能看起来只是一个简单而聪明的特征工程技巧,但实际上它也有副作用,主要是过拟合,因为会把目标信息带入预测中。
主要特点
from catboost import CatBoostRegressorparams = {'learning_rate': 0.02, 'depth': 13,'bootstrap_type': 'Bernoulli', 'od_type': 'Iter', 'od_wait': 50, 'random_seed': 11}model = CatBoostRegressor(iterations=20000, eval_metric='RMSE', **params)model.fit(X_train, y_train, eval_set=(X_valid, y_valid), cat_features=[], use_best_model=True, verbose=False)y_pred = model.predict(X_test)每类树模型都其与众不同的地方,接下来将从决策树的生长策略、梯度偏差、类别特征处理和参数对比四个方面深入理解这些树模型,帮助参赛者更好地将它们应用到竞赛中。
XGBoost,LightGBM 和 CatBoost是三个非常核心的树模型,本节将对它们进行分析,因为三者之间有着千丝万缕的关系,只有厘清其中的关系,才能更好地运用这三个模型。
随着拥有数据量的增加,神经网络战胜传统机器学习模型的可能性也会加大。
#接第5章实战案例代码,构造训练集和测试集x_train = data[:ntrain][all_cols]x_test = data[ntrain:][all_cols]#对售价进行log处理y_train = np.log1p(data[data.SalePrice.notnull()]['SalePrice'].values)XGBoost:使用比较常规的五折交叉验证
import xgboost as xgbfrom sklearn.model_selection import KFoldkf = KFold(n_splits=5,shuffle=True,random_state=2020)for i,(train_index,valid_index)in enumerate(kf.split(x_train,y_train)): trn_x,trn_y,val_x,val_y = x_train.iloc[train_index],y_train[train_index],x_train.iloc[valid_index],y_train[valid_index] params ={'eta':0.01,'max_depth':11,'objective':'reg:linear','eval_metric':'mae'} dtrain = xgb.DMatrix(data=trn_x,label=trn_y) dtest = xgb.DMatrix(data=val_x,label=val_y) watchlist =[(dtrain,'train'),(dtest,'valid_data')] model=xgb.train(params,dtrain,num_boost_round=20000,evals=watchlist,early_stopping_rounds=200,verbose_eval=500)多层感知机:要确保数据中没有缺失值,并且要对数据进行归一化处理。
from sklearn. model_selection import train_test_splitfrom sklearn.preprocessing import StandardScalerx_train = x_train. fillna(0)x_train = StandardScaler(). fit_transform(x_train)trn_x, val_x, trny, val_y = train_test_split(x_train, y_train, random_state=2020)def create_mlp(shape): x_input = Input((shape, )) X = Dropout(0.2)(BatchNormalization()( Dense(256, activation=' relu')(X_input))) X = Dropout(0.2)(BatchNormalization()(Dense(128, activation=' relu')(X))) X = Dropout(0.2)(BatchNormalization()(Dense(64, activation=' relu')(X))) X = Dense(1)(X) model = Model(inputs=X_input, outputs=X) model. compile(optimizer=' adam', loss=' mse', metrics=[' mae']) return modelmlp_model = create_mlp(trn_x. shape[1])mlp_model.fit(x=trn_x, y=trn_y, validation_data=(val_x, val_y), epochs=30, batch_size=16)本章将向大家介绍在算法竞赛中提分的关键步骤,这也是最后阶段的惯用方法,即模型融合(或者集成学习),通过结合不同子模型的长处进行模型融合,当然这是在理想状态下。
本章主要分为构建多样性、训练过程融合和训练结果融合三部分。
模型融合常常是竞赛取得胜利的关键,相比之下具有差异性的模型融合往往能给结果带来很大提升。了解的模型融合方法越多,最后取胜的概率就会越高。
本章从这三个部分介绍不同模型融合方法的应用场景,同时给出使用技巧和应用代码。
介绍三种模型融合中构建多样性的方式,分别是特征多样性、样本多样性和模型多样性。其中多样性是指子模型之间存在着差异,可以通过降低子模型融合的同质性来构建多样性,好的多样性有助于模型融合效果的提升。
构建多个有差异的特征集并分别建立模型,可使特征存在于不同的超空间(hyperspace),从而建立的多个模型有不同的泛化误差,最终模型融合时可以起到互补的效果。在竞赛中,队友之间的特征集往往是不一样的,在分数差异不大的情况下,直接进行模型融合基本会获得不错的收益。
另外,像随机森林中的max_features,XGBoost中的colsample_bytree 和LightGBM中的feature_fraction都是用来对训练集中的特征进行采样的,其实本质上就是构建特征的多样性。
样本多样性也是竞赛中常见的一种模型融合方式,这里的多样性主要来自不同的样本集。
具体做法是将数据集切分成多份,然后分别建立模型。我们知道很多树模型在训练的时候会进行采样(sampling),主要目的是防止过拟合,从而提升预测的准确性。
有时候将数据集切分成多份并不是随机进行的,而是根据具体的赛题数据进行切分,需要考虑如何切分可以构建最大限度的数据差异性,并用切分后的数据分别训练模型。
例如,在天池“全球城市计算AI挑战赛”中,竞赛训练集包含从2019年1月1日到1月25日共25天的地铁刷卡数据记录,要求预测1月26日每个地铁站点每十分钟的平均出入客流量(2019年1月26日是周六)。显然,工作日和周末的客流量分布具有很大差异,这时会面临一个问题,若只保留周末的数据进行训练,则会浪费掉很多数据;若一周的数据全部保留,则会对工作日的数据产生一定影响。这时候就可以尝试构建两组有差异性的样本分别训练模型,即整体数据保留为一组,周末数据为一组。当然,模型融合后的分数会有很大提升。
不同模型对数据的表达能力是不同的,比如FM能够学习到特征之间的交叉信息,并且记忆性较强;树模型可以很好地处理连续特征和离散特征(如LightGBM 和CatBoost),并且对异常值也具有很好的健壮性。把这两类在数据假设、表征能力方面有差异的模型融合起来肯定会达到一定的效果。
对于竞赛而言,传统的树模型(XGBoost,LightGBM、CatBoost)和神经网络都需要尝试一遍,然后将尝试过的模型作为具有差异性的模型融合在一起。
还有很多其他构建多样性的方法,比如训练目标多样性、参数多样性和损失函数选择的多样性等,这些都能产生非常好的效果。
模型融合的方式有两种,第一种是训练过程融合,比如我们了解到的随机森林和XGBoost,基于这两种模型在训练中构造多个决策树进行融合,这里的多个决策树可以看作多个弱学习器。其中随机森林通过Bagging的方式进行融合,XGBoost通过Boosting的方式进行融合。
Bagging的思想很简单,即从训练集中有放回地取出数据(Bootstrapping),这些数据构成样本集,这也保证了训练集的规模不变,然后用样本集训练弱分类器。重复上述过程多次,取平均值或者采用投票机制得到模型融合的最终结果。
当在不同的样本集上训练模型时,Bagging通过减小误差之间的差来减少分类器的方差,因此Bagging可以降低过拟合的风险。Bagging算法的效率在于训练数据的不同,各模型之间存在着很大的差异,并且在加权融合的过程中可以使训练数据的错误相互抵消。
Boosting的思想其实并不难理解,首先训练一个弱分类器,并把这个弱分类器分错类的样本记录下来,同时给予这个弱分类器一定的权重;然后建立一个新的弱分类器,新的弱分类器基于前面记录的错误样本进行训练,同样,我们也给予这个分类器一个权重。重复上面的过程,直到弱分类器的性能达到某一指标,例如当再建立的新弱分类器并不会使准确率显著提升时,就停止选代。最后,把这些弱分类器各自乘上相应的权重并全部加起来,就得到了最后的强分类器。其实,基于Boosting的算法是比较多的,有Adaboost、LightGBM、XGBoost和CatBoost等。
模型融合的第二种方式是训练结果融合,主要分为加权法、Stacking和Blending,这些方法都可以有效地提高模型的整体预测能力,在竞赛中也是参赛者必须要掌握的方法。
加权法对于一系列任务(比如分类和回归)和评价指标(如AUC,MSE 或 Logloss)都是很有效的,比如我们有10个算法模型并都预测到了结果,直接对这10个结果取平均值或者给予每个算法不同的权重,即得到了融合结果。加权法通常还能减少过拟合,因为每个模型的结果可能存在一定的噪声,加权法能够平滑噪声,提高模型的泛化性。
分类问题:对于分类问题,需要注意不同分类器的输出结果范围一致,因为输出的预测结果可以是0/1值,也可以是介于0和1之间的概率。另外,投票法(Voting)也是一种特殊的加权法。
回归问题:对于回归问题,使用加权法会非常简单。这里主要介绍算术平均和几何平均。
算术平均:基于算术平均数的集成方法在算法中是用得最多的,因为它不仅简单,而且基本每次使用该算法都有较大概率能获得很好的效果。
几何平均:根据很多参赛选手的分享,基于几何平均数的加权法在算法中使用得还不是很多,但在实际情况中,有时候基于几何平均数的模型融合效果要稍好于基于算术平均数的效果。
一般推荐问题中的主要任务是对推荐结果进行排序,常见的评价指标有mAP(mean Average Precision),NDCG(Normalized Discounted Cumulative Gain),MRR(Mean Reciprocal Rank)和AUC,这里主要介绍MRR和AUC。
MRR:给定推荐结果q,如果q在推荐序列中的位置是r,那么MRR(q)就是1/r。可以看出,如果向用户推荐的产品在推荐序列中命中,那么命中的位置越靠前,得分也就越高。显然,排序结果在前在后的重要性是不一样的,因此我们不仅要进行加权融合,还需要让结果偏向小值。这时候就要对结果进行转换,然后再用加权法进行融合,一般而言使用的转换方式是log变换。
其基本思路如下:首先,输人三个预测结果文件,每个预测结果文件都包含M条记录,每条记录各对应N个预测结果,最终输出三个预测结果文件的整合结果。统计三个预测结果文件中记录的所有推荐商品(共N个商品)出现的位置,例如商品A,在第一份文件中的推荐位置是1,在第二个文件的推荐位置是3,在第三个文件中未出现,此时我们计算商品A的得分为log1+log3+log(N+1),此处我们用N+1来表示未出现,即在N个推荐商品中是找不到商品A的,所以只能是N+1。对每条记录中的商品按计算得分由小到大排序,取前N个作为这条记录的最终推荐结果。
AUC:作为排序指标,一般使用排序均值的融合思路,使用相对顺序来代替原先的概率值。很多以AUC为指标的比赛均取得了非常不错的成绩。使用过程如下:对每个分类器中分类的概率进行排序,然后用每个样本排序之后得到的排名值(rank)作为新的结果。对每个分类器的排名值求算术平均值作为最终结果。
使用加权法进行融合虽然简单,但需要人工来确定权重,因此可以考虑更加智能的方式,通过新的模型来学习每个分类器的权重。这里我们假设有两层分类器,如果在第一层中某个特定的基分类器错误地学习了特征空间的某个区域,则这种错误的学习行为可能会被第二层分类器检测到,这与其他分类器的学习行为一样,可以纠正不恰当的训练。上述过程便是Stacking融合的基本思想。
这里需要注意两点:第一,构建的新模型一般是简单模型,比如逻辑回归这样的线性模型;第二,使用多个模型进行Stacking融合会有比较好的结果。
Stacking融合使用基模型的预测结果作为第二层模型的输入。然而,我们不能简单地使用完整的训练集数据来训练基模型,这会产生基分类器在预测时就已经“看到”测试集的风险,因此在提供预测结果时出现过度拟合问题。所以我们应该使用Out-of-Fold的方式进行预测,也就是通过K折交叉验证的方式来预测结果。这里我们将Stacking融合分为训练阶段和测试阶段两部分,将并以流程图的形式展示每部分的具体操作。如图6.2所示为训练阶段。
特征加权的线性堆叠,可参考相应论文“Feature-Weighted Linear Stacking two layer stacking",其实就是对传统的Stacking融合方法在深度上进行扩展。通过传统的Stacking融合方法得到概率值,再将此值与基础特征集进行拼接,重新组成新的特征集,进行新一轮训练。
不同于Stacking融合使用K折交叉验证方式得到预测结果,Blending融合是建立一个Holdout集,将不相交的数据集用于不同层的训练,这样可以在很大程度上降低过拟合的风险。
假设构造两层Blending,训练集等分为两部分(train_one和train_two),测试集为test。第一层用train_one训练多个模型,将train_two和test的预测结果合并到原始特征集合中,作为第二层的特征集。第二层用train_two的特征集和标签训练新的模型,然后对test预测得到最终的融合结果。
以stacking为例。选择ExtraTreesRegressor、RandomForestRegressor、Ridge、Lasso作为基学习器,Ridge为最终分类器。
依然采用5折交叉验证
kf = KFold(n_splits=5, shuffle=True, random_state=2020)然后构建一个sklearn中模型的功能类,初始化参数然后训练和预测。这段代码可复用性很高,建议完善、储存。
class SklearnWrapper(object): def __init__(self, clf, seed=0, params=None): params['random_state'] = seed self.clf = clf(**params) def train(self, x_train, y_train): self.clf.fit(x_train, y_train) def predict(self, x): return self.clf.predict(x)封装交叉验证函数。可复用性也很高。
def get_oof(clf): oof_train = np.zeros((x_train.shape[0],)) oof_test = np.zeros((x_test.shape[0],)) oof_test_skf = np.empty((5, x_test.shape[0])) for i, (train_index, valid_index) in enumerate(kf.split(x_train, y_train)): trn_x, trn_y, val_x, val_y = x_train.iloc[train_index], y_train[train_index],\ x_train.iloc[valid_index], y_train[valid_index] clf.train(trn_x, trn_y) oof_train[valid_index] = clf.predict(val_x) oof_test_skf[i, :] = clf.predict(x_test) oof_test[:] = oof_test_skf.mean(axis=0) return oof_train.reshape(-1, 1), oof_test.reshape(-1, 1)预测四个模型的验证集结果和测试集结果。并辅助最后一步的stacking融合操作:
et_params = { 'n_estimators': 100, 'max_features': 0.5, 'max_depth': 12, 'min_samples_leaf': 2,}rf_params = { 'n_estimators': 100, 'max_features': 0.2, 'max_depth': 12, 'min_samples_leaf': 2,}rd_params={'alpha': 10}ls_params={ 'alpha': 0.005}et = SklearnWrapper(clf=ExtraTreesRegressor, seed=2020, params=et_params)rf = SklearnWrapper(clf=RandomForestRegressor, seed=2020, params=rf_params)rd = SklearnWrapper(clf=Ridge, seed=2020, params=rd_params)ls = SklearnWrapper(clf=Lasso, seed=2020, params=ls_params)et_oof_train, et_oof_test = get_oof(et)rf_oof_train, rf_oof_test = get_oof(rf)rd_oof_train, rd_oof_test = get_oof(rd)ls_oof_train, ls_oof_test = get_oof(ls)最后就是stacking部分,使用ridge模型。
def stack_model(oof_1, oof_2, oof_3, oof_4, predictions_1, predictions_2, predictions_3, predictions_4, y): train_stack = np.hstack([oof_1, oof_2, oof_3, oof_4]) test_stack = np.hstack([predictions_1, predictions_2, predictions_3, predictions_4]) oof = np.zeros((train_stack.shape[0],)) predictions = np.zeros((test_stack.shape[0],)) scores = [] for fold_, (trn_idx, val_idx) in enumerate(kf.split(train_stack, y)): trn_data, trn_y = train_stack[trn_idx], y[trn_idx] val_data, val_y = train_stack[val_idx], y[val_idx] clf = Ridge(random_state=2020) clf.fit(trn_data, trn_y) oof[val_idx] = clf.predict(val_data) predictions += clf.predict(test_stack) / 5 score_single = sqrt(mean_squared_error(val_y, oof[val_idx])) scores.append(score_single) print(f'{fold_+1}/{5}', score_single) print('mean: ',np.mean(scores)) return oof, predictionsoof_stack , predictions_stack = stack_model(et_oof_train, rf_oof_train, rd_oof_train, ls_oof_train, et_oof_test, rf_oof_test, rd_oof_test,ls_oof_test, y_train)实际运行后发现,基分类器的分类效果差别很大,且最终融合后的模型效果确实要比基分类器的模型效果好很多。
]]>特征选择和提取是模式识别中的一个关键问题,前面讨论分类器设计的时候,一直假定已给出了特征向量维数确定的样本集,其中各样本的每一维都是该样本的一个特征;这些特征的选择是很重要的,它强烈地影响到分类器的设计及其性能;假若对不同的类别,这些特征的差别很大,则比较容易设计出具有较好性能的分类器。
例如,描述人可以用好多特征,如肤色,体重,身高等,但是如果要判断软件工程师,显然编程这个特征比较有判别性;如果要判断是不是篮球员,则体重、身高有很强的判别性。
特征选择和提取是构造模式识别系统时的一个重要课题。在很多实际问题中,往往不容易找到那些最重要的特征,或受客观条件的限制,不能对它们进行有效的测量;因此在测量时,由于人们心理上的作用,只要条件许可总希望把特征取得多一些;另外,由于客观上的需要,为了突出某些有用信息,抑制无用信息,有意加上一些比值、指数或对数等组合计算特征;如果将数目很多的测量值不做分析,全部直接用作分类特征,不但耗时,而且会影响到分类的效果,产生“特征维数灾难”问题。
为了设计出效果好的分类器,通常需要对原始的测量值集合进行分析,经过选择或变换处理,组成有效的识别特征;在保证一定分类精度的前提下,减少特征维数,即进行“降维”处理,使分类器实现快速、准确和高效的分类。为达到上述目的,关键是所提供的识别特征应具有很好的可分性,使分类器容易判别。为此,需对特征进行选择:
特征选择和提取这一任务应在设计分类器之前进行;
所谓特征选择,就是从个度量值集合
中,按某一准则选取出供分类用的子集,作为降维(
维,
)的分类特征;
所谓特征提取,就是使通过某种变换,产生
个特征
,作为新的分类特征(或称为二次特征);
其目的都是为了在尽可能保留识别信息的前提下,降低特征空间的维数,以达到有效的分类效果。
距离和散布矩阵:
类内距离:维空间中同一类内各模式样本点集
,其内部各点的均方距离为
,其中
类内散布矩阵:考虑一类内模式点集,其类内散布矩阵为:
,其中
对属于同一类的模式样本,类内散布矩阵表示各样本点围绕其均值周围的散布情况。
在考虑有两个以上的类别,如集合时,类间距离对类别的可分性起着重要作用,此时应计算
为简化起见,常用两类样本各自质心间的距离作为类间距离,并假设两类样本出现的概率相等,则
其中和
为两类模式样本集各自的均值向量,
和
为
和
的第
个分量,
为维数。
两类模式的类间散布矩阵:
对三个以上的类别,类间散布矩阵常写成,其中,
为多类模式(如共有
类)分布的总体均值向量,即
多类情况的类内散布矩阵可写成各类的类内散布矩阵的先验概率的加权和,即,其中
是第
类的协方差矩阵。
有时,用多类模式总体分布的散布矩阵来反映其可分性,即:,其中
为多类模式分布的总体均值向量。
,即总体散布矩阵是各类类内散布矩阵与类间散布矩阵之和。
设有个可用作分类的测量值,为了在不降低(或尽量不降低)分类精度的前提下,减小特征空间的维数以减少计算量,需从中直接选出
个作为分类的特征。
从个测量值中选出
个特征,一共有
种可能的选法,需寻找一种简便的可分性准则,间接判断每一种子集的优劣。
对于独立特征的选择准则:类别可分性准则应具有这样的特点,即不同类别模式特征的均值向量之间的距离应最大,而属于同一类的模式特征,其方差之和应最小。假设各原始特征测量值是统计独立的,此时,只需对训练样本的个测量值独立地进行分析,从中选出
个最好的作为分类特征即可。
对于 和
两类训练样本,假设其均值向量为
和
,
维方向的分量为
和
,方差为
和
,定义可分性准则函数
,则
为正值。
值越大,表示测度值的第
个分量对分离
和
类越有效。将
按大小排队, 选出最大的
个对应测度值作为分类特征,即达到特征选择的目的。
上述基于距离测度的可分性准则,其适用范围与模式特征的分布有关。假若类概率密度函数不是或不近似正态分布,均值和方差就不足以用来估计类别的可分性,此时该准则函数不完全适用。
一般特征的散布矩阵准则:
直观上,类间离散度越大且类内离散度越小,则可分性越好。因此,可推导出散布矩阵准则采用如下形式:
其中, 是矩阵
的特征值。使
或
最大的子集可作为选择的分类特征。
前面讨论的特征选择是在一定准则下,从个特征中选出
个来反映原有模式。这种简单删掉某
个特征的做法并不十分理想,因为一般来说,原来的
个数据各自在不同程度上反映了识别对象的某些特征,简单地删去某些特征可能会丢失较多的有用信息。如果将原来的特征做正交变换,获得的每个数据都是原来
个数据的线性组合,然后从新的数据中选出少数几个,使其尽可能多地反映各类模式之间的差异,而这些特征间又尽可能相互独立,则比单纯的选择方法更灵活、更有效。
K-L变换就是一种适用于任意概率密度函数的正交变换。
离散的有限K-L展开式的形式:
设一连续的随机实函数,则
可用已知的正交函数集
的线性组合来展开,即:
。式中,
为展开式的随机系数,
为一连续的正交函数,它应满足:
,其中
为
的共轭复数式。
将上式写成离散的正交函数形式,使连续随机函数和连续正交函数
在区间
内被等间隔采样为
个离散点,即:
,
写成向量形式:,
将展开式写成离散形式:,其中
为展开式中随机系数的向量形式
,
为
维矩阵,
其中,每一列为正交函数集中的一个函数,小括号内的序号为正交函数的采样点次序。因此,
实质上是由
向量组成的正交变换矩阵,
它将变换成
。
对各个模式类别,正交函数都是相同的,但其展开系数向量则因类别的不同模式分布而异。
K-L展开式的根本性质是将随机向量展开为另一组正交向量
的线性和,且其展开式系数
(即系数向量
的各个分量)具有不同的性质。
正交向量集的确定:
设随机向量的总体自相关矩阵为
,则
,要求系数向量
的各个不同分量应统计独立,则应使
,其中
为对角形矩阵,其互相关成分均为0
因为是实对称矩阵,其不同特征值对应的特征向量应正交,即:
K-L展开式系数的计算步骤:
K-L展开式用于特征选择相当于一种线性变换。若从个特征向量中取出
个组成变换矩阵
,即
,此时
是一个
维矩阵,
是
维向量,经过
变换,即得到降维为
的新向量。
从K-L展开式的性质和按最小均方差的准则来选择特征,应使。由于
,故应使
。基于这一条件,在将整体模式进行K-L变换之前,应先将其均值作为新坐标轴的原点,采用协方差矩阵
或自相关矩阵
来计算特征值。如果
,则只能得到“次最佳”的结果。
将K-L展开式系数(亦即变换后的特征)用
表示,写成向量形式:
,此时变换矩阵
用
个特征向量组成。为使误差最小,不采用的特征向量,其对应的特征值应尽可能小。因此,将特征值按大小次序标号,即
。若首先采用前面的
个特征向量,便可使变换误差最小。此时的变换矩阵为
,
K-L变换是在均方误差最小的意义下获得数据压缩(降维)的最佳变换,且不受模式分布的限制。对于一种类别的模式特征提取,它不存在特征分类问题,只是实现用低维的个特征来表示原来高维的
个特征,使其误差最小,亦即使其整个模式分布结构尽可能保持不变。
通过K-L变换能获得互不相关的新特征。若采用较大特征值对应的特征向量组成变换矩阵,则能对应地保留原模式中方差最大的特征成分,所以K-L变换起到了减小相关性、突出差异性的效果。在此情况下,K-L变换也称为主成分变换(PCA变换)。
需要指出的是,采用K-L变换作为模式分类的特征提取时,要特别注意保留不同类别的模式分类鉴别信息,仅单纯考虑尽可能代表原来模式的主成分,有时并不一定有利于分类的鉴别。
]]>并查集(union-find, 或disjoint set)可以动态地连通两个点,并且可以非常快速地判断两个点是否连通。假设存在n个节点,我们先将所有节点的父亲标为自己;每次要连接节点i和j时,我们可以将i的父亲标为j;每次要查询两个节点是否相连时,我们可以查找i和j的祖先是否最终为同一个人。
在无向图找出一条边,移除它之后该图能够成为一棵树(即无向无环图)。如果有多个解,返回在原数组中位置最靠后的那条边。
class Solution {public: int Find(vector<int>& parent, int index) { if (parent[index] != index) { parent[index] = Find(parent, parent[index]); } return parent[index]; } void Union(vector<int>& parent, int index1, int index2) { parent[Find(parent, index1)] = Find(parent, index2); } vector<int> findRedundantConnection(vector<vector<int>>& edges) { int n = edges.size(); vector<int> parent(n + 1); for (int i = 1; i <= n; ++i) { parent[i] = i; } for (auto& edge: edges) { int node1 = edge[0], node2 = edge[1]; if (Find(parent, node1) != Find(parent, node2)) { Union(parent, node1, node2); } else { return edge; } } return vector<int>{}; }};分析:在一棵树中,边的数量比节点的数量少1。如果一棵树有n个节点,则这棵树有n−1条边。这道题中的图在树的基础上多了一条附加的边,因此边的数量也是n。树是一个连通且无环的无向图,在树中多了一条附加的边之后就会出现环,因此附加的边即为导致环出现的边。可以通过并查集寻找附加的边。初始时,每个节点都属于不同的连通分量。遍历每一条边,判断这条边连接的两个顶点是否属于相同的连通分量。如果两个顶点属于不同的连通分量,则说明在遍历到当前的边之前,这两个顶点之间不连通,因此当前的边不会导致环出现,合并这两个顶点的连通分量。如果两个顶点属于相同的连通分量,则说明在遍历到当前的边之前,这两个顶点之间已经连通,因此当前的边导致环出现,为附加的边,将当前的边作为答案返回。
错误:不知道怎么使用并查集
请你设计并实现一个满足 LRU (最近最少使用) 缓存约束的数据结构。
class LRUCache {public: //定义双链表 struct Node{ int key,value; Node* left ,*right; Node(int _key,int _value): key(_key),value(_value),left(NULL),right(NULL){} }*L,*R;//双链表的最左和最右节点,不存贮值。 int n; unordered_map<int,Node*>hash; void remove(Node* p) { p->right->left = p->left; p->left->right = p->right; } void insert(Node *p) { p->right = L->right; p->left = L; L->right->left = p; L->right = p; } LRUCache(int capacity) { n = capacity; L = new Node(-1,-1),R = new Node(-1,-1); L->right = R; R->left = L; } int get(int key) { if(hash.count(key) == 0) return -1; //不存在关键字 key auto p = hash[key]; remove(p); insert(p);//将当前节点放在双链表的第一位 return p->value; } void put(int key, int value) { if(hash.count(key)) //如果key存在,则修改对应的value { auto p = hash[key]; p->value = value; remove(p); insert(p); } else { if(hash.size() == n) //如果缓存已满,则删除双链表最右侧的节点 { auto p = R->left; remove(p); hash.erase(p->key); //更新哈希表 delete p; //释放内存 } //否则,插入(key, value) auto p = new Node(key,value); hash[key] = p; insert(p); } }};分析:采用一个链表 list<pair<int, int>>来储存信息的 key和 value,链表的链接顺序即为最近使用的新旧顺序,最新的信息在链表头节点。同时我们需要一个嵌套着链表的迭代器的 unordered_map<int, list<pair<int, int>>::iterator>进行快速搜索,存迭代器的原因是方便调用链表的 splice函数来直接更新查找成功(cash hit)时的信息,即把迭代器对应的节点移动为链表的头节点。
错误:不明白
付费题目
设计一个插入、删除和随机取值均为时间复杂度的数据结构
class RandomizedSet {private: vector<int> nums; unordered_map<int, int> indices;public: RandomizedSet() { srand((unsigned)time(NULL)); } bool insert(int val) { if (indices.count(val)) { return false; } int index = nums.size(); nums.emplace_back(val); indices[val] = index; return true; } bool remove(int val) { if (!indices.count(val)) { return false; } int index = indices[val]; int last = nums.back(); nums[index] = last; indices[last] = index; nums.pop_back(); indices.erase(val); return true; } int getRandom() { return nums[rand()%nums.size()]; }};分析:变长数组 + 哈希表可以实现
错误:随机数不太会,剩下的自己实现了
设计一个increaseKey,decreaseKey,getMaxKey,getMinKey 均为时间复杂度的数据结构。
class AllOne { list<pair<unordered_set<string>, int>> lst; unordered_map<string, list<pair<unordered_set<string>, int>>::iterator> nodes;public: AllOne() {} void inc(string key) { if (nodes.count(key)) { auto cur = nodes[key], nxt = next(cur); if (nxt == lst.end() || nxt->second > cur->second + 1) { unordered_set<string> s({key}); nodes[key] = lst.emplace(nxt, s, cur->second + 1); } else { nxt->first.emplace(key); nodes[key] = nxt; } cur->first.erase(key); if (cur->first.empty()) { lst.erase(cur); } } else { // key 不在链表中 if (lst.empty() || lst.begin()->second > 1) { unordered_set<string> s({key}); lst.emplace_front(s, 1); } else { lst.begin()->first.emplace(key); } nodes[key] = lst.begin(); } } void dec(string key) { auto cur = nodes[key]; if (cur->second == 1) { // key 仅出现一次,将其移出 nodes nodes.erase(key); } else { auto pre = prev(cur); if (cur == lst.begin() || pre->second < cur->second - 1) { unordered_set<string> s({key}); nodes[key] = lst.emplace(cur, s, cur->second - 1); } else { pre->first.emplace(key); nodes[key] = pre; } } cur->first.erase(key); if (cur->first.empty()) { lst.erase(cur); } } string getMaxKey() { return lst.empty() ? "" : *lst.rbegin()->first.begin(); } string getMinKey() { return lst.empty() ? "" : *lst.begin()->first.begin(); }};分析:双向链表+哈希表
错误:好难
付费题目
基本上都是要自己写数据结构的题目,应该也不是很常见了。
]]>二分图算法也称为染色法,是一种广度优先搜索。如果可以用两种颜色对图中的节点进行着色,并且保证相邻的节点颜色不同,那么图为二分。
判断一个图是不是二分图
class Solution {private: static constexpr int UNCOLORED = 0; static constexpr int RED = 1; static constexpr int GREEN = 2; vector<int> color;public: bool isBipartite(vector<vector<int>>& graph) { int n = graph.size(); vector<int> color(n, UNCOLORED); for (int i = 0; i < n; ++i) { if (color[i] == UNCOLORED) { queue<int> q; q.push(i); color[i] = RED; while (!q.empty()) { int node = q.front(); int cNei = (color[node] == RED ? GREEN : RED); q.pop(); for (int neighbor: graph[node]) { if (color[neighbor] == UNCOLORED) { q.push(neighbor); color[neighbor] = cNei; } else if (color[neighbor] != cNei) { return false; } } } } } return true; }};分析:广度优先遍历,需要判断
错误:想简单了
拓扑排序(topological sort)是一种常见的,对有向无环图排序的算法。给定有向无环图中的N个节点,我们把它们排序成一个线性序列;若原图中节点i指向节点j,则排序结果中i一定在j之前。拓扑排序的结果不是唯一的,只要满足以上条件即可。
给定N个课程和这些课程的前置必修课,求可以一次性上完所有课的顺序。
class Solution {public: vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) { vector<int> result; vector<int> indegree(numCourses,0); vector<vector<int>> graph(numCourses,vector<int>(numCourses,0)); int m = prerequisites.size(); for(int i=0;i<m;++i){ graph[prerequisites[i][1]][prerequisites[i][0]] = 1; ++indegree[prerequisites[i][0]]; } while(1){ if(result.size() == numCourses){ return result; } int sign = 0; for(int i=0;i<numCourses;++i){ if(indegree[i] == 0){ indegree[i] = -1; result.push_back(i); sign = 1; for(int j=0;j<numCourses;++j){ if(graph[i][j] == 1){ graph[i][j] = 0; --indegree[j]; } } } } if(sign == 0){ break; } } result.clear(); return result; }};分析:经典拓扑排序
错误:有一点小错误,基本一遍AC
付费题目
付费题目
经典的节点最短距离问题
class Solution {public: int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) { // 先构建图 vector<vector<pair<int, int>>> graph(n); for (vector<int>& edge : edges) { int s = edge[0]; int e = edge[1]; int cnt = edge[2]; graph[s].emplace_back(e, cnt); graph[e].emplace_back(s, cnt); } // 保持一个从起点到当前点的距离 unordered_map<int, int> distances; distances[0] = 0; for (int i = 1; i < n; ++i) { distances[i] = maxMoves + 1; } // 点到点的“额外扩展距离”,最大是cnt // 二维变一维 int<<32 + int unordered_map<long, int> extras; // 结果记录 int res = 0; // 从起点到改点的距离的小顶堆 priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int, int>>> q; q.push({0, 0}); while (!q.empty()) { int dist = q.top().first; int curr = q.top().second; q.pop(); // 忽略更大的距离 if (dist > distances[curr]) { continue; } distances[curr] = dist; ++res; for (auto& pair : graph[curr]) { int next = pair.first; int cnt = pair.second; // 这里取最小的距离, 取(cnt和 maxMoves-dist)的最小值 extras[((long)curr << 32) + next] = min(cnt, maxMoves - dist); // 计算基于当前点到下一个结点的距离,额外走一步,如果找到更小,则插入队列里 int dist2 = dist + cnt + 1; if (dist2 < distances[next]) { q.emplace(dist2, next); distances[next] = dist2; } } } // 最后加上“额外扩展距离” for (vector<int>& edge : edges) { int s = edge[0]; int e = edge[1]; res += min(edge[2], extras[((long)s<< 32) +e] + extras[((long)e<<32) +s]); } return res; }};各种高级用法,还比较简单,但是应该不是很常见
]]>统计语言模型(Statistical Language Modeling,SLM)
SLM广泛使用于语音识别和统计机器翻译领域,利用概率统计理论研究语言。
规则方法:词、句、篇章的生成比如满足某些规则,不满足该规则就不应存在。
统计方法:任何语言片断都有存在的可能,只是可能性大小不同
对于n-gram,n越大,则模型越复杂,估计的参数(即估计的概率)也越多。当然,当数据量足够大的情况下,模型阶数越高越对片段概率的计算也越准确。
理论上说,在数据充足的情况下,利用更多的历史高阶的模型更准确,但是总计算量也越大
数据规模总是有限的,即用于训练模型参数的语料存在稀疏性 (Data Sparseness ,即某参数在训练语料中没有出现问题。
数据稀疏性导致零概率问题,但是训练集上不出现的事件并不代表在新的语料上不出现。
SLM的一个重要工作就是进行平滑重新分配概率,即使没出现的事件也会赋予一个概率。
总体分布&抽样
文档的模型风格实际上是某种总体分布
(待评分)文档和查询都是该总体分布下的一个抽样样本实例
根据文档,估计文档的模型,即求出该总体分布(一般假设某种总体分布,然后求出其参数),然后计算该总体分布下抽样出查询的概率
查询似然模型(Query Likelihood Model)
文本生成的多项式模型
数据平滑的一般形式
其它SLMIR 模型
基于翻译模型的IR模型:
基本的QLM模型不能解决词语失配(word mismatch)问题,即查询中的用词和文档中的用词不一致
翻译概率P(qi|wj)在计算时可以将词项之间的关系融入。
KL距离(相对熵)模型
统计语言建模IR模型优缺点
优点:
缺点:数据稀疏性,需要参数估计
SLMIR vs. VSM :
共性:
不同:
基于统计建模的IR模型 : 假设
给定一个二叉树,找出其最大深度。
class Solution {public: static int DFS(TreeNode* &root,int sum){ if(root == nullptr){ return sum; } return max(DFS(root->left,sum+1),DFS(root->right,sum+1)); } int maxDepth(TreeNode* root) { return DFS(root,0); }};分析:递归计算最大高度即可
错误:开始递归写的有问题,变成引用传参了,后面改对后调通。
给定一个二叉树,判断它是否是高度平衡的二叉树。
class Solution {public: static int DFS(TreeNode* &root){ if(root == nullptr){ return 0; } int left = DFS(root->left); int right = DFS(root->right); if(left == -1 || right == -1 || abs(left - right) > 1){ return -1; } return max(left,right)+1; } bool isBalanced(TreeNode* root) { return DFS(root) != -1; }};分析:解法类似于求树的最大深度,但有两个不同的地方:一是我们需要先处理子树的深度再进行比较,二是如果我们在处理子树时发现其已经不平衡了,则可以返回一个-1,使得所有其长辈节点可以避免多余的判断
错误:思路不对,看了解析
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
class Solution {public: static int DFS(TreeNode* &root,int &maxsum){ if(root == nullptr){ return 0; } int left = DFS(root->left,maxsum); int right = DFS(root->right,maxsum); maxsum = max(maxsum,left+right+1); return max(left,right)+1; } int diameterOfBinaryTree(TreeNode* root) { int maxsum = 0; int a = DFS(root,maxsum); return maxsum-1; }};分析:还是递归,要留两个变量进行记录
错误:没看解析调通,但是自己想的挺艰难的。
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
class Solution {public: static long long DFS(TreeNode* &root, long long sum){ if(root == nullptr){ return 0; } long long count; if(root->val == sum){ count = 1; } else{ count = 0; } return count + DFS(root->left,sum-root->val) + DFS(root->right,sum-root->val); } int pathSum(TreeNode* root, int targetSum) { if(root == nullptr){ return 0; } return DFS(root,targetSum)+pathSum(root->left,targetSum)+pathSum(root->right,targetSum); }};分析:递归每个节点时,需要分情况考虑:(1)如果选取该节点加入路径,则之后必须继续加入连续节点,或停止加入节点(2)如果不选取该节点加入路径,则对其左右节点进行重新进行考虑。因此一个方便的方法是我们创建一个辅函数,专门用来计算连续加入节点的路径。
错误:两层的递归有点做不了
给你一个二叉树的根节点 root , 检查它是否轴对称。
class Solution {public: static bool DFS(TreeNode* &left,TreeNode* &right){ if(left == nullptr && right != nullptr){ return false; } if(left != nullptr && right == nullptr){ return false; } if(left == nullptr && right == nullptr){ return true; } if(left->val != right->val){ return false; } return DFS(left->left,right->right) && DFS(left->right,right->left); } bool isSymmetric(TreeNode* root) { if(root == nullptr){ return true; } return DFS(root->left,root->right); }};分析:判断一个树是否对称等价于判断左右子树是否对称。笔者一般习惯将判断两个子树是否相等或对称类型的题的解法叫做“四步法”:(1)如果两个子树都为空指针,则它们相等或对称(2)如果两个子树只有一个为空指针,则它们不相等或不对称(3)如果两个子树根节点的值不相等,则它们不相等或不对称(4)根据相等或对称要求,进行递归处理。
错误:不明白
给出二叉树的根节点 root,树上每个节点都有一个不同的值。如果节点值在 to_delete 中出现,我们就把该节点从树上删去,最后得到一个森林(一些不相交的树构成的集合)。返回森林中的每棵树。你可以按任意顺序组织答案。
class Solution {public: void DFS(TreeNode* &root, vector<int>& to_delete,vector<TreeNode*>& result){ if(root == nullptr){ return; } DFS(root->left,to_delete,result); DFS(root->right,to_delete,result); auto it = find(to_delete.begin(),to_delete.end(),root->val); if(it != to_delete.end()){ if(root->left != nullptr){ result.push_back(root->left); } if(root->right != nullptr){ result.push_back(root->right); } root->left = nullptr; root->right = nullptr; root = nullptr; } return; } vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) { vector<TreeNode*> result; DFS(root,to_delete,result); if(root != nullptr){ result.push_back(root); } return result; }};分析:遍历,然后置为空指针就好
错误:开始的判断条件不太够,后来自己调通。
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10<sup>-5</sup> 以内的答案可以被接受。
class Solution {public: vector<double> averageOfLevels(TreeNode* root) { vector<double> result; queue<TreeNode*> q; q.push(root); while(!q.empty()){ int num = 0; double sum = 0.0; int nowsize = q.size(); while(nowsize--){ TreeNode* t = q.front(); q.pop(); num += 1; sum += t->val; if(t->left != nullptr){ q.push(t->left); } if(t->right != nullptr){ q.push(t->right); } } result.push_back(sum/num); } return result; }};分析:层序遍历即可
一遍AC
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的 先序遍历 , inorder 是同一棵树的 中序遍历 ,请构造二叉树并返回其根节点。
class Solution {private: unordered_map<int, int> index;public: TreeNode* myBuildTree(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) { if (preorder_left > preorder_right) { return nullptr; } // 前序遍历中的第一个节点就是根节点 int preorder_root = preorder_left; // 在中序遍历中定位根节点 int inorder_root = index[preorder[preorder_root]]; // 先把根节点建立出来 TreeNode* root = new TreeNode(preorder[preorder_root]); // 得到左子树中的节点数目 int size_left_subtree = inorder_root - inorder_left; // 递归地构造左子树,并连接到根节点 // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素 root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1); // 递归地构造右子树,并连接到根节点 // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素 root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right); return root; } TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) { int n = preorder.size(); // 构造哈希映射,帮助我们快速定位根节点 for (int i = 0; i < n; ++i) { index[inorder[i]] = i; } return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1); }};分析:很老的题,好好判断,数据结构设计对即可
错误:太久远了忘记怎么判断了
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
class Solution {public: static void dfs(TreeNode* &root,vector<int> &result){ if(root == nullptr){ return; } result.push_back(root->val); dfs(root->left,result); dfs(root->right,result); } vector<int> preorderTraversal(TreeNode* root) { vector<int> result; dfs(root,result); return result; }};分析:递归遍历即可
一遍AC
给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。 请在不改变其结构的情况下,恢复这棵树。
class Solution {public: void inorder(TreeNode* root, TreeNode*& mistake1, TreeNode*& mistake2, TreeNode*& prev) { if (!root) { return; } if (root->left) { inorder(root->left, mistake1, mistake2, prev); } if (prev && root->val < prev->val) { if (!mistake1) { mistake1 = prev; mistake2 = root; } else { mistake2 = root; } cout << mistake1->val; cout << mistake2->val; } prev = root; if (root->right) { inorder(root->right, mistake1, mistake2, prev); } } void recoverTree(TreeNode* root) { TreeNode *mistake1 = nullptr, *mistake2 = nullptr, *prev = nullptr; inorder(root, mistake1, mistake2, prev); if (mistake1 && mistake2) { int temp = mistake1->val; mistake1->val = mistake2->val; mistake2->val = temp; } }};分析:我们可以使用中序遍历这个二叉查找树,同时设置一个prev 指针,记录当前节点中序遍历时的前节点。如果当前节点大于prev 节点的值,说明需要调整次序。有一个技巧是如果遍历整个序列过程中只出现了一次次序错误,说明就是这两个相邻节点需要被交换;如果出现了两次次序错误,那就需要交换这两个节点。
错误:没有思路
给你二叉搜索树的根节点 root ,同时给定最小边界 low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在 [low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
class Solution {public: TreeNode* trimBST(TreeNode* root, int low, int high) { if(root == nullptr){ return root; } if(root->val > high){ return trimBST(root->left,low,high); } if(root->val < low){ return trimBST(root->right,low,high); } root->left = trimBST(root->left, low, high); root->right = trimBST(root->right, low, high); return root; }};分析:利用二叉查找树的大小关系递归进行树的处理。
错误:看了解析
尝试建立一个字典树,支持快速插入单词、查找单词、查找单词前缀的功能。
class Trie {private: vector<Trie*> children; bool isEnd; Trie* searchPrefix(string prefix) { Trie* node = this; for (char ch : prefix) { ch -= 'a'; if (node->children[ch] == nullptr) { return nullptr; } node = node->children[ch]; } return node; }public: Trie() : children(26), isEnd(false) {} void insert(string word) { Trie* node = this; for (char ch : word) { ch -= 'a'; if (node->children[ch] == nullptr) { node->children[ch] = new Trie(); } node = node->children[ch]; } node->isEnd = true; } bool search(string word) { Trie* node = this->searchPrefix(word); return node != nullptr && node->isEnd; } bool startsWith(string prefix) { return this->searchPrefix(prefix) != nullptr; }};分析:字典树的典型实现方法
错误:没做过,尝试理解
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
class Solution {public: TreeNode* invertTree(TreeNode* root) { if(root == nullptr){ return nullptr; } TreeNode* left = invertTree(root->left); TreeNode* right = invertTree(root->right); root->left = right; root->right = left; return root; }};分析:递归反转即可
错误:翻转值是不对的,需要反转结点
给你两棵二叉树: root1 和 root2 。想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。返回合并后的二叉树。
class Solution {public: TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) { if (t1 == nullptr) { return t2; } if (t2 == nullptr) { return t1; } auto merged = new TreeNode(t1->val + t2->val); merged->left = mergeTrees(t1->left, t2->left); merged->right = mergeTrees(t1->right, t2->right); return merged; }};分析:递归处理即可
错误:自己尝试的方法有问题,不太明白错在哪
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
class Solution {public: static bool check(TreeNode* root, TreeNode* subRoot){ if(root == nullptr && subRoot == nullptr){ return true; } if(root == nullptr && subRoot != nullptr){ return false; } if(root != nullptr && subRoot == nullptr){ return false; } if(root->val != subRoot->val){ return false; } return check(root->left,subRoot->left) && check(root->right,subRoot->right); } static bool DFS(TreeNode* root, TreeNode* subRoot){ if(root == nullptr){ return false; } return check(root,subRoot) || DFS(root->left,subRoot) || DFS(root->right,subRoot); } bool isSubtree(TreeNode* root, TreeNode* subRoot) { bool judge = DFS(root,subRoot); return judge; }};分析:递归判断即可
错误:自己写了前半部分,看了一眼后写了后半部分
给定二叉树的根节点 root ,返回所有左叶子之和。
class Solution {public: bool isLeafNode(TreeNode* node) { return !node->left && !node->right; } int dfs(TreeNode* node) { int ans = 0; if (node->left) { ans += isLeafNode(node->left) ? node->left->val : dfs(node->left); } if (node->right && !isLeafNode(node->right)) { ans += dfs(node->right); } return ans; } int sumOfLeftLeaves(TreeNode* root) { return dfs(root); }};分析:递归判断结点
错误:没有思路
给定一个二叉树的 根节点 root,请找出该二叉树的最底层最左边节点的值。
class Solution {public: int findBottomLeftValue(TreeNode* root) { queue<TreeNode*> q; q.push(root); int result = root->val; while(!q.empty()){ int tempsize = q.size(); int sign = 0; while(tempsize--){ TreeNode* t = q.front(); q.pop(); if(sign == 0){ result = t->val; sign = 1; } if(t->left != nullptr){ q.push(t->left); } if(t->right != nullptr){ q.push(t->right); } } } return result; }};分析:广度优先遍历即可
一遍AC
给出二叉搜索树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
class Solution {public: void DFS(TreeNode* root,int &sum){ if(root == nullptr){ return; } DFS(root->right,sum); root->val = root->val + sum; sum = root->val; DFS(root->left,sum); return; } TreeNode* convertBST(TreeNode* root) { int sum = 0; DFS(root,sum); return root; }};分析:反向的中序遍历
错误:开始顺序弄反,后面修正了
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
class Solution {public: vector<TreeNode*> getPath(TreeNode* root, TreeNode* target) { vector<TreeNode*> path; TreeNode* node = root; while (node != target) { path.push_back(node); if (target->val < node->val) { node = node->left; } else { node = node->right; } } path.push_back(node); return path; } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { vector<TreeNode*> path_p = getPath(root, p); vector<TreeNode*> path_q = getPath(root, q); TreeNode* ancestor; for (int i = 0; i < path_p.size() && i < path_q.size(); ++i) { if (path_p[i] == path_q[i]) { ancestor = path_p[i]; } else { break; } } return ancestor; }};分析:从根节点开始遍历;如果当前节点就是p,那么成功地找到了节点;如果当前节点的值大于p的值,说明p应该在当前节点的左子树,因此将当前节点移动到它的左子节点;如果当前节点的值小于p的值,说明p应该在当前节点的右子树,因此将当前节点移动到它的右子节点。对于节点q同理。在寻找节点的过程中,我们可以顺便记录经过的节点,这样就得到了从根节点到被寻找节点的路径。
错误:没有思路
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
class Solution {public: void DFS(TreeNode* &root,vector<int>& result){ if(root == nullptr){ return; } DFS(root->left,result); result.push_back(root->val); DFS(root->right,result); } int getMinimumDifference(TreeNode* root) { vector<int> result; DFS(root,result); int minval = 100000; for(int i=0;i<result.size()-1;++i){ if(result[i+1]-result[i] < minval){ minval = result[i+1]-result[i]; } } return minval; }};分析:中序遍历存在数组内部,然后遍历判断即可
一遍AC
给定两个整数数组,preorder 和 postorder ,其中 preorder 是一个具有 无重复 值的二叉树的前序遍历,postorder 是同一棵树的后序遍历,重构并返回二叉树。
class Solution { int preIdx = 0, postIdx = 0;public: TreeNode* constructFromPrePost(vector<int>& preorder, vector<int>& postorder) { TreeNode *node = new TreeNode(preorder[preIdx++]); if(node->val != postorder[postIdx]){ node->left = constructFromPrePost(preorder, postorder); } if(node->val != postorder[postIdx]){ node->right = constructFromPrePost(preorder, postorder); } postIdx++; return node; }};分析:利用前序遍历来构建Tree,然后通过后续遍历来检验当前树是否构建完毕 。
错误:思路不对
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
class Solution {public: TreeNode* DFS(vector<int>& inorder, int inleft,int inright,vector<int>& postorder,int postleft,int postright){ if(inleft > inright){ return nullptr; } TreeNode* root = new TreeNode(postorder[postright]); int k; for(k=inleft;k<=inright;++k){ if(inorder[k] == postorder[postright]){ break; } } int rightsize = inright - k; root->left = DFS(inorder,inleft,k-1,postorder,postleft,postright-rightsize-1); root->right = DFS(inorder,k+1,inright,postorder,postright-rightsize,postright-1); return root; } TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) { int n = inorder.size(); TreeNode* root = DFS(inorder,0,n-1,postorder,0,n-1); return root; }};分析:与前面的题目相同
一遍AC
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
class Solution {public: static void dfs(TreeNode* &root,vector<int> &result){ if(root == nullptr){ return; } dfs(root->left,result); result.push_back(root->val); dfs(root->right,result); } vector<int> inorderTraversal(TreeNode* root) { vector<int> result; dfs(root,result); return result; }};分析:普通递归
一遍AC
给你一棵二叉树的根节点 root ,返回其节点值的后序遍历。
class Solution {public: static void dfs(TreeNode* &root,vector<int> &result){ if(root == nullptr){ return; } dfs(root->left,result); dfs(root->right,result); result.push_back(root->val); } vector<int> postorderTraversal(TreeNode* root) { vector<int> result; dfs(root,result); return result; }};分析:普通递归
一遍AC
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
class Solution {public: TreeNode* ans; bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) { if (root == nullptr) return false; bool lson = dfs(root->left, p, q); bool rson = dfs(root->right, p, q); if ((lson && rson) || ((root->val == p->val || root->val == q->val) && (lson || rson))) { ans = root; } return lson || rson || (root->val == p->val || root->val == q->val); } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { dfs(root, p, q); return ans; }};分析:不太明白
错误:不太明白
给定一个单链表的头节点 head ,其中的元素 按升序排序 ,将其转换为高度平衡的二叉搜索树。
class Solution {public: ListNode* getMedian(ListNode* left, ListNode* right) { ListNode* fast = left; ListNode* slow = left; while (fast != right && fast->next != right) { fast = fast->next; fast = fast->next; slow = slow->next; } return slow; } TreeNode* buildTree(ListNode* left, ListNode* right) { if (left == right) { return nullptr; } ListNode* mid = getMedian(left, right); TreeNode* root = new TreeNode(mid->val); root->left = buildTree(left, mid); root->right = buildTree(mid->next, right); return root; } TreeNode* sortedListToBST(ListNode* head) { return buildTree(head, nullptr); }};分析:每一次找中位数,然后递归构造两边就可以了
错误:以为要调整平衡,没有思路
给你一棵二叉搜索树的 root ,请你 按中序遍历 将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
class Solution {public: void inorder(TreeNode *node, vector<int> &res) { if (node == nullptr) { return; } inorder(node->left, res); res.push_back(node->val); inorder(node->right, res); } TreeNode* increasingBST(TreeNode* root) { vector<int> res; inorder(root, res); TreeNode *dummyNode = new TreeNode(-1); TreeNode *currNode = dummyNode; for (int value : res) { currNode->right = new TreeNode(value); currNode = currNode->right; } return dummyNode->right; }};分析:遍历建树就可以,注意不要在函数中建树,原因没明白
错误:在函数中建树不行
给定一个二叉搜索树 root 和一个目标结果 k,如果二叉搜索树中存在两个元素且它们的和等于给定的目标结果,则返回 true。
class Solution {public: void DFS(TreeNode* root,vector<int> &result){ if(root == nullptr){ return; } DFS(root->left,result); result.push_back(root->val); DFS(root->right,result); return; } bool findTarget(TreeNode* root, int k) { vector<int> result; DFS(root,result); int left = 0; int right = result.size()-1; while(left < right){ if(result[left] + result[right] == k){ return true; } else if(result[left] + result[right] < k){ ++left; } else{ --right; } } return false; } };分析:读出来二分就可以了
一遍AC
给定一个二叉搜索树的根节点root和一个值key,删除二叉搜索树中的key对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
class Solution {public: TreeNode* deleteNode(TreeNode* root, int key) { if (root == nullptr) { return nullptr; } if (root->val > key) { root->left = deleteNode(root->left, key); return root; } if (root->val < key) { root->right = deleteNode(root->right, key); return root; } if (root->val == key) { if (!root->left && !root->right) { return nullptr; } if (!root->right) { return root->left; } if (!root->left) { return root->right; } TreeNode *successor = root->right; while (successor->left) { successor = successor->left; } root->right = deleteNode(root->right, successor->val); successor->right = root->right; successor->left = root->left; return successor; } return root; }};分析:解析
错误:不明白应该怎么调整
看起来树的题目并没有特别复杂的。主要的难度在于递归的思路,想明白后就简单了。另外就是各种边界条件的判断,也要多想多练。
]]>个数组成的有序数组, 称为一个
维向量
向量空间:所有分量为实数的维向量构成的集合
称为一个
维向量空间,又称线性空间。
超平面表达式:
线性判别函数表达式:
线性函数刻画了样本到超平面的距离
相似性测度:
常用的统计量:
分类问题
线性分类问题
线性决策的多分类问题:
类问题,需要至少预先训练多少个二分类器?
需要训练好个分类器(所有可能的分类器),然后采用二叉树比对测试。
根据最大相似性决定类别。
基本知识:
感知机结构
感知机学习准则:目标:最小化错分样本的误差代价。
代价函数(错分样本的误差函数):(只统计错分的样本,是错分的样本到超平面的距离之和)
的含义:错分样本到分类超平面误差距离的总和
感知机优化:Batch Perception和Online Perception
误差修正基本规则:
基本思想:求线性变换,使得样本集${x_i}
{y_i} $后,类别间距大,类内间距小。
目标函数:(
)
样本投影后的类别间距离: ; 其中,
表示第
类样本投影后的均值
样本投影后的类别内距离:投影后的各类样本方差
计算:
基本思想:假设likelihood ratio的对数为线性判别函数
两类问题:
,
学习目标:
标签 类,
越大,
越小,标签
类,
越大,
越小。
非线性问题:对于线性不可分数据,采用非线性决策的方法
线性扩展的思想:线性扩展模型,核函数方法
非线性的思想:最近邻、决策树、神经网络、集成学习
决策问题一定是一个二判决问题
样本根据问题一定可以分成两部分,两部分之间没有交集,两部分的并集包括所有的情况
决策树的目标:在树结构上,根据节点的判断,搜索类别。
树结构的优点:可以不必测试所有特征和区域。
设属性的可能离散取值个数为
属性上出现的样本特征值个数为
方法:每个特征上的样本特征值作为候选问题,属性产生的候选问题数为
无论特征值是连续还是离散,确定每个属性所产生的候选问题,候选的问题总数为
非纯度(Impurity Measure)需要满足两条性质:
非纯度的熵度量(C4.5):
非纯度的基尼度量(CART):
划分目标:选择最大减少类别非纯度的问题作为划分节点。
基于非纯度变化量的三个指标:
信息增益(熵度量):,
是问题
导致的决策划分数目
倾向于选择划分集合个数
多的节点。区间划分的越细,区间内纯度越高,极端情况每个区间只有一个样本,则熵为0。
增益率(信息增益与数据集关于问题
的熵值之比)
,
增益率改善信息增益:对划分集合个数
少的属性有所偏好,
越小则
越小
基尼指数(基尼度量):
节点类别设置:叶子节点纯度达到预设阈值后,停止划分,并对叶子节点进行类别设置。(按概率最大的类别设定)
决策树生成过程
从顶向下(不断增加一个节点)
ID3 决策树:属性特征作为结点问题,划分选择实际是特征选择过程,最大化信息增益作为划分选择依据
C4.5 决策树:属性特征作为结点问题,划分选择实际是特征选择过程,最大化信息增益率作为划分选择依据
CART 决策树:属性特征离散值作为结点问题,本质是二叉树,最小化基尼指数作为划分选择依据
连续值二叉决策树
ID3、C4.5决策树剪枝
泛化性能评估法
原理:将样本分类为离之最近的样本类别
类判别函数:
决策规则:
最近邻分类隐含的决策边界是非线性的
原理:将样本分给个近邻中类别样本个数最多的类
为
的
个近邻中属于
的样本数
判别函数:
决策规则:
误差讨论
近邻法的缺点:
原理:将样本分成不相交的子集,基于子集的搜索
规则1-找最近子集:如果到
的距离 > 当前最近子集距离
,则
被忽略。
规则2-找最近样本:如果到
的距离>已存在的最近点,则样本
被忽略。
k 近邻快速搜索推广:子集搜索过程与最近邻一致,样本搜索时,存有
个最近距离值。
原理:通过剪掉边界样本(错误分类样本),缩减样本规模
剪辑规则:两分剪辑近邻法
原理:去掉中心附近样本,保留错误样本,在剪辑基础上进行压缩
基本思想:分类中通常被正确分类的样本,较少支持决策,将常分误的样本保留。
压缩规则:
原理:对于与各类别相似度较低的样本,不做判断
优点:在样本压缩时,给可是可非的样本机会。
原理:不同的分类器对样本有不同的鉴别力;综合优势,使错误率最小。
问题描述:已知一组训练分类器,分类器的类别后验为,其中
为索引类别,
为索引分类器.
目标是对进行分类,求
概率分布相似性的计算:
Geometric Average Rule
Arithmetic Average Rule
Majority Voting Rule
Bagging:通过随机采样,训练分类器,保证分类器的差异。从训练集中不断随机抽取样本构造分类器,分类时通过投票进行类别判断。
随机森林:多决策树的Bagging;决策树随机属性选择;从训练集中不断随机构造决策树分类器,分类时通过投票进行类别判断。
随机森林较一般Bagging效果好
Boosting原理:一系列弱分类器,在不同子集上学习,得到增强分类器。
AdaBoost加权分类器
AdaBoost 目标函数
两个核心思想
KKT:任何目标函数有解的充要条件
一个原始问题总有它的对偶问题
对于特殊的凸优化来说,原始问题的对偶问题是
,两个函数的极值相等,也就是最优解是相等的
如果原始问题和它的对偶问题都满足KKT条件,对于条件好的凸优化,可以构造与
的关系,从而将不好求解的原始问题转化为好求的对偶问题
目标:找到最大间隔分类超平面(类别集合到分类超平面的最小距离最大化)
函数间隔:给定的训练数据集和超平面
几何间隔:给定的训练数据集和超平面
最大几何间隔等价的问题:
函数间隔的取值并不影响最优化问题的解。
支撑向量(SV):支撑最小距离最大化的样本
支撑超平面:通过支持向量,平行于分类面的超平面
间隔:支撑向量到分类面的距离
支持向量机学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。
根据KKT条件成立求解
避免直接求非线性映射,由核函数替代内积运算
硬间隔SVM
软间隔SVM
]]>(单)链表是由节点和指针构成的数据结构,每个节点存有一个值,和一个指向下一个节点的指针,因此很多链表问题可以用递归来处理。不同于数组,链表并不能直接获取任意节点的值,必须要通过指针找到该节点后才能获取其值。同理,在未遍历到链表结尾时,我们也无法知道链表的长度,除非依赖其他数据结构储存长度。
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
class Solution {public: ListNode* reverseList(ListNode* head) { ListNode* p = nullptr; ListNode* q = head; while(q){ ListNode* r = q->next; q->next = p; p = q; q = r; } return p; }};分析:两种方式,迭代法和递归法反转链表。
错误:算法忘记了,稍稍看了一眼后明白了
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
class Solution {public: ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) { ListNode* result = new ListNode(-1); ListNode* head = result; while(list1 != nullptr && list2 != nullptr){ if(list1->val > list2->val){ head->next = list2; list2 = list2->next; } else{ head->next = list1; list1 = list1->next; } head = head->next; } if(list1 != nullptr){ head->next = list1; } else{ head->next = list2; } return result->next; }};分析:按照顺序一点一点合并即可,前面设置一个头结点,后面把它扔掉返回。
错误:链表操作忘记了
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
class Solution {public: ListNode* swapPairs(ListNode* head) { ListNode* pre = new ListNode(-1); pre->next = head; head = pre; while(pre->next != nullptr && pre->next->next != nullptr){ ListNode* p = pre->next; ListNode* q = p->next; pre->next = q; p->next = q->next; q->next = p; pre = p; } return head->next; }};分析:链表操作
错误:已经不熟练了,不知道什么时候加结点什么的。
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
class Solution {public: ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) { if(headA == nullptr || headB == nullptr){ return nullptr; } ListNode* pa = headA; ListNode* pb = headB; while(pa != pb){ if(pa == nullptr){ pa = headB; pb = pb->next; } else if(pb == nullptr){ pb = headA; pa = pa->next; } else{ pa = pa->next; pb = pb->next; } } return pa; }};分析:当链表headA和headB都不为空时,创建两个指针pA和pB,初始时分别指向两个链表的头节点headA和headB,然后将两个指针依次遍历两个链表的每个节点。具体做法如下:每步操作需要同时更新指针pA和pB。如果指针pA不为空,则将指针pA移到下一个节点;如果指针 pB不为空,则将指针pB移到下一个节点。如果指针pA为空,则将指针pA移到链表headB的头节点;如果指针pB为空,则将指针pB移到链表headA的头节点。当指针pA和pB指向同一个节点或者都为空时,返回它们指向的节点或者null。
错误:不会做
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
class Solution {public: bool isPalindrome(ListNode* head) { vector<int> vt; while(head != nullptr){ vt.push_back(head->val); head = head->next; } int n = vt.size(); for(int i=0;i<n/2;++i){ if(vt[i] != vt[n-i-1]){ return false; } } return true; }};分析:复制到数组中判断
一遍AC
给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。
class Solution {public: ListNode* deleteDuplicates(ListNode* head) { ListNode* p = head; if(p == nullptr){ return nullptr; } while(p->next != nullptr){ ListNode* q = p->next; if(p->val == q->val){ p->next = q->next; q = p->next; } else{ q = q->next; p = p->next; } } return head; }};分析:遍历判断即可
错误:没有考虑链表中没有结点的情况。
给定单链表的头节点 head ,将所有索引为奇数的节点和索引为偶数的节点分别组合在一起,然后返回重新排序的列表。
class Solution {public: ListNode* oddEvenList(ListNode* head) { if(head == nullptr){ return head; } ListNode* odd = head; ListNode* even = head->next; ListNode* evenhead = even; while(even != nullptr && even->next != nullptr){ odd->next = even->next; even->next = even->next->next; odd = odd->next; even = even->next; } odd->next = evenhead; return head; }};分析:单独存储奇偶结点即可。
错误:还是不熟练
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
class Solution {public: ListNode* removeNthFromEnd(ListNode* head, int n) { ListNode* p = head; int sum = 0; while(p != nullptr){ ++sum; p = p->next; } p = head; int num = sum - n; if(num == 0){ return head->next; } ListNode* pre = new ListNode(-1); pre->next = p; for(int i=0;i<num;++i){ pre = p; p = p->next; } pre->next = p->next; return head; }};分析:先数一遍一共有多少个结点,然后再遍历一遍删掉即可。
一遍AC
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
class Solution {public: ListNode* sortList(ListNode* head) { if(head == nullptr){ return head; } vector<int> result; ListNode* p = head; while(head != nullptr){ result.push_back(head->val); head = head->next; } sort(result.begin(),result.end()); head = p; int index = 0; while(head != nullptr){ head->val = result[index++]; head = head->next; } return p; }};分析:可以用一些比较高大上的链表排序方法,也可以耍赖,直接读入数组中排序即可。
一遍AC
链表不难,就是太容易忘记了,后面要经常复习。
]]>向量空间模型的优缺点
优点:
缺点:
检索系统中,给定查询,计算每个文档的相关度
检索系统对用户查询的理解是非确定的(uncertain),对返回结果的猜测也是非确定的
而概率理论为非确定推理提供了坚实的理论基础,可以计算文档和查询相关的可能性
概率检索模型是通过概率的方法将查询和文档联系起来
定义3个随机变量R、Q、D:相关度R={0,1},查询Q可以是q1,q2,…中的一个查询,文档D可以是d1,d2,…中的一篇文档,则可以通过计算条件概率P(R=1|Q=q,D=d)来度量文档和查询的相关度。
概率排序原理(PRP):
回归分析:回归分析是处理变量之间相关关系的一种工具,回归的结果可以用于预测或者分类
一元线性回归:根据观测点,拟合出一条直线,使得某种损失 (如离差平方和)最小
Logistic回归是一种非线性回归,可以转化成线性回归来实现。
基本思想:为了求Q和D相关的概率P(R=1|Q,D),通过定义多个特征函数fi(Q,D),认为P(R=1|Q,D)是这些函数的组合。
求解和使用过程:通过训练集合拟和得到相应系数 ,对于新的文档,代入公式计算得到概率P
优缺点:
二值独立概率模型
BIM模型通过贝叶斯公式对所求条件概率P(R=1|Q,D)展开进行计算,是一种生成式(generative)模型
对每个Q定义排序(Ranking)函数RSV(Q,D)
其中,P(D|R=1)、P(D|R=0)分别表示在相关和不相关情况下生成文档D的概率。Ranking函数显然是随着P(R=1|D)的增长而增长。
两种常用的文档生成的总体分布:多元贝努利分布和多项式分布
BIM中P(D|R=1)或P(D|R=0)的计算:类比M次独立试验
BIM模型公式的推导:pi qi参数的计算,RSJ权重
BIM计算过程:目标是求排序函数P(D|R=1)/P(D|R=0)
优点:
缺点:
二重泊松分布
泊松分布是一个经典的随机分布:分布公式参数:均值 λ,分布形式随参数取值变化
关于文本中词频分布的一个经典结论:在高质量精英文档集(Elite Set)中:均值较高,接近正态分布;在整个语料中:均值低,接近指数分布
优点:
缺点:
BM25被视为现实应用中最好的IR模型之一。即便现在基于BERT预训练语言模型的方法可以获得更好的效果,仍然需要使用BM25进行无监督过滤来保证检索精度。
]]>联结主义学派:又称仿生学派或生理学派
核心:智能的本质是联接机制。
原理:神经网络及神经网络间的连接机制和学习算法
生物神经元
神经元特性
工作状态
结构的可塑性:神经元之间的柔性连接:突触的信息传递特性是可变的——学习记忆的基础
从生物学结构到数学模型
人工神经元
,
为激活函数,
为组合函数
组合函数:
权重和:
➡
径向距离:
激活函数
生物系统中的学习:
ANN的学习规则:能量最小
对人工神经网络,需要确定合适的能量定义;可以使用数学上的优化技术来发现如何改变神经元间的联接权重。
两个主要问题:结构和学习方法
ANN结构
ANN的学习方法:通过神经网络所在环境的模拟过程,调整网络中的自由参数。
学习策略:Error Correction:最小化实际输出与期望输出之间的误差,属于监督学习。
感知机实质上是一种神经元模型
阈值激活函数:
判别规则:
输入空间中
单层感知机学习:用现在的权重进行分类,如果分类正确,权重不改变;如果分类错误,用分类错误的样本调整权重
感知机收敛定理:若训练数据集是线性可分的,则感知机模型收敛。
感知机存在的问题:如果存在噪声,或样本不是线性可分的,不会收敛。(例如不能处理异或操作),且泛化性比较差。
多层感知机:三层可以学习全部连续的函数,四层就可以学习全部的函数。层间神经元全连接,层内神经元不连接。
学习方法:反向传播
全局误差度量:(最小平方误差)
权值更新规则采用梯度下降的方法:
误差反向传播:
实际应用中要对数据进行归一化,并且选择合适的学习率
优点:
缺点:
多层感知机解决了一般性学习问题,并且与生物系统相联系。
层数增加使用BP算法会存在梯度消失的问题:在后面的几层,误差反向传播后可能变得非常小,权重不太好更新。
采用sigmoid函数,多个相乘使得传递过来的残差会越来越小。
时代背景:数据爆炸、计算性能提升
传统机器学习解决问题的思路:
使用深度学习去自动学习特征!
人脑视觉机理
为什么使用深度学习?
深层 vs 浅层神经网络
BP算法的问题:
Deep learning训练:
自下向上的非监督学习(greedy layer-wise training)
自顶向下的监督学习
对输入的结构建模:建立产生输入的生成式模型,调整参数使得生成式模型的概率最大。
学习过程:无标签数据,用非监督学习学习特征
利用人工神经网络本身的层次结构特点
自动编码器就是一种尽可能复现输入信号的神经网络。
为了实现这种复现,自动编码器就必须捕捉可以代表输入数据的最重要的因素
网络结构
自动编码器可以只训练单组参数,不需要关心另一半的参数。
Deep结构——逐层训练
监督学习
两隐层自编码网络MNIST手写数字识别:
训练一个包含两个隐含层的栈式自编码网络,用来进行MNIST手写数字分类
栈式自编码器神经网络
Hopfield Network
结构:
Hopfield网络按动力学方式运行,其工作过程为状态的演化过程,即从初始状态按能量减小的方向进行演化,直到达到稳定状态。稳定状态即为网络的输出。
二值随机神经元(Bernoulli variables):以一定的概率产生1
波尔兹曼机(Boltzmann Machine):
BM基本原理:
缺点:网络结构复杂、训练代价大、局部极小
受限波尔兹曼机(Restricted Boltzmann Machines):
Deep Belief Networks:
Deep Boltzmann Machines:
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。注意: 若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t互为字母异位词。
class Solution {public: bool isAnagram(string s, string t) { sort(s.begin(),s.end()); sort(t.begin(),t.end()); if(s == t){ return true; } return false; }};分析:哈希表或者直接排序
一遍AC
给定两个字符串 s 和 t ,判断它们是否是同构的。如果 s 中的字符可以按某种映射关系替换得到 t ,那么这两个字符串是同构的。每个出现的字符都应当映射到另一个字符,同时不改变字符的顺序。不同字符不能映射到同一个字符上,相同字符只能映射到同一个字符上,字符可以映射到自己本身。
class Solution {public: bool isIsomorphic(string s, string t) { unordered_map<char,char> mp1; unordered_map<char,char> mp2; for(int i=0;i<s.size();++i){ if(mp1.find(s[i]) == mp1.cend()){ mp1[s[i]] = t[i]; } if(mp2.find(t[i]) == mp2.cend()){ mp2[t[i]] = s[i]; } if(mp1[s[i]] != t[i] || mp2[t[i]] != s[i]){ return false; } } return true; }};分析:通过字典比较即可
错误:开始想用统计的方法去做,后面用字符字典的方式也有一些小错误,应该是比较两遍的。
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。回文字符串 是正着读和倒过来读一样的字符串。子字符串 是字符串中的由连续字符组成的一个序列。具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
class Solution {public: int countSubstrings(string s) { int countsum = 0; int n = s.size(); for(int i=0;i<n;++i){ countsum += 1; int leftindex = i-1; int rightindex = i+1; while(leftindex >= 0 && rightindex < n && s[leftindex] == s[rightindex]){ ++countsum; --leftindex; ++rightindex; } } for(int i=0;i<n-1;++i){ if(s[i] == s[i+1]){ ++countsum; int leftindex = i-1; int rightindex = i+2; while(leftindex >= 0 && rightindex < n && s[leftindex] == s[rightindex]){ ++countsum; --leftindex; ++rightindex; } } } return countsum; }};分析:遍历扩展即可,注意分两种情况讨论一下
一遍AC
给定一个字符串 s,统计并返回具有相同数量 0 和 1 的非空(连续)子字符串的数量,并且这些子字符串中的所有 0 和所有 1 都是成组连续的。重复出现(不同位置)的子串也要统计它们出现的次数。
class Solution {public: int countBinarySubstrings(string s) { int n = s.size(); int countsum = 0; for(int i=0;i<n-1;++i){ if(s[i] != s[i+1]){ ++countsum; int leftindex = i-1; int rightindex = i+2; while(leftindex >= 0 && rightindex < n && s[leftindex] == s[leftindex+1] && s[rightindex] == s[rightindex-1]){ ++countsum; --leftindex; ++rightindex; } } } return countsum; }};分析:和上一道题目相同,甚至只考虑一种情况就可以了,比上一道题目还要简单一点。
一遍AC
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。整数除法仅保留整数部分。
class Solution {public: int calculate(string s) { vector<int> stk; char preSign = '+'; int num = 0; int n = s.length(); for (int i = 0; i < n; ++i) { if (isdigit(s[i])) { num = num * 10 + int(s[i] - '0'); } if (!isdigit(s[i]) && s[i] != ' ' || i == n - 1) { switch (preSign) { case '+': stk.push_back(num); break; case '-': stk.push_back(-num); break; case '*': stk.back() *= num; break; default: stk.back() /= num; } preSign = s[i]; num = 0; } } return accumulate(stk.begin(), stk.end(), 0); }};分析:栈和字符串的应用
错误:最后的运算顺序有问题,没有能自己实现。
给你两个字符串 haystack和 needle,请你在 haystack字符串中找出 needle字符串的第一个匹配项的下标(下标从 0开始)。如果 needle不是 haystack的一部分,则返回 -1。
class Solution {public: int strStr(string haystack, string needle) { int m = haystack.size(); int n = needle.size(); for(int i=0;i<m-n+1;++i){ if(haystack.substr(i,n) == needle){ return i; } } return -1; }};分析:可以使用KMP算法,但是不会,简单一点就直接字符串匹配即可。
一遍AC
给定一个包含大写字母和小写字母的字符串 s ,返回通过这些字母构造成的最长的回文串。在构造过程中,请注意区分大小写 。比如 "Aa" 不能当做一个回文字符串。
class Solution {public: int longestPalindrome(string s) { unordered_map<char,int> mp; int n = s.size(); for(int i=0;i<s.size();++i){ if(mp.find(s[i]) == mp.cend()){ mp[s[i]] = 1; } else{ ++mp[s[i]]; } } int ans = 0; int sign = 0; for(auto it : mp){ if(it.second % 2 == 0){ ans += it.second; } else{ if(sign == 0){ ans += it.second; sign = 1; } else{ ans = ans + it.second / 2 * 2; } } } return ans; }};分析:统计数数即可
一遍AC
给定一个字符串 s ,请你找出其中不含有重复字符的最长子串的长度。
class Solution {public: int lengthOfLongestSubstring(string s) { map<char,int> mp; int n = s.size(); int right = 0; int maxlen = 0; int left = 0; while(left < n){ while(right < n && (mp.find(s[right]) == mp.cend() || mp[s[right]] == 0)){ ++mp[s[right]]; ++right; } maxlen = max(maxlen,right-left); --mp[s[left]]; ++left; } return maxlen; }};分析:滑动窗口经典算法
错误:与或非的括号忘记添加了
付费题目
给你一个字符串 s,找到 s 中最长的回文子串。
class Solution {public: string longestPalindrome(string s) { int countsum = 1; string result = s.substr(0,1); int n = s.size(); for(int i=0;i<n;++i){ int temp = 1; int leftindex = i-1; int rightindex = i+1; while(leftindex >= 0 && rightindex < n && s[leftindex] == s[rightindex]){ temp += 2; --leftindex; ++rightindex; } if(temp > countsum){ countsum = temp; result = s.substr(leftindex+1,rightindex-1-(leftindex+1)+1); } } for(int i=0;i<n-1;++i){ if(s[i] == s[i+1]){ int temp = 2; int leftindex = i-1; int rightindex = i+2; while(leftindex >= 0 && rightindex < n && s[leftindex] == s[rightindex]){ temp += 2; --leftindex; ++rightindex; } if(temp > countsum){ countsum = temp; result = s.substr(leftindex+1,rightindex-1-(leftindex+1)+1); } } } return result; }};分析:还是这种题,都第三道了
错误:开始有些索引没考虑好错了一些,后来调通了。
字符串还可以,主要是熟悉一下字符串的处理过程,其余的知识点其他的数据结构中都有。
]]>布尔检索的优点:
布尔检索的不足:
在布尔检索中,需要大量技巧来生成一个可以获得合适规模结果的查询
排序式检索会对查询和文档的匹配程度进行排序,即给出一个查询和文档匹配评分
自由文本查询:与布尔查询不同,在排序式检索应用中,用户查询通常都是一个或几个关键字
排序式检索可以解决返回结果过少或过多的问题,可以把相关的结果排在前面
希望文档集中相关度高的文档排名高于相关度低的文档:对每个查询-文档对赋一个[0, 1]之间的分值,度量了文档和查询的匹配程度
Jaccard系数:计算两个集合重合度的常用方法,也就是计算查询文档之间的词项重合度——交集/并集
Jaccard系数的不足:
查询-文档匹配评分计算:
从单词项查询(查询只包含一个词项)开始,若该词项不出现在文档当中,该文档得分应该为0,该词项在文档中出现越多,则得分越高。
即为词项频率 (term frequency,TF)评分
词袋(Bag of words)模型:不考虑词在文档中出现的顺序
利用tf来计算文档评分的方法:采用原始的tf值(raw tf)
但是原始tf不太合适:某个词项在A文档中出现十次,即tf = 10,在B文档中tf = 1,那么A比B更相关,但是相关度不会相差10倍。
替代原始tf的方法:对数词频
罕见词项比常见词所蕴含的信息更多
考虑查询中某个词项,它在整个文档集中非常罕见,但是某篇包含该词项的文档很可能相关,因此需要提高权重
常见词项的信息量不如罕见词,一篇包含该词项的文档当然比不包含该词项的文档的相关度要高,但是,这些词对于相关度而言并不是非常强的指示词。
文档频率(Document frequency, df):出现词项的文档数目
idf 权重
是出现词项
的文档数目
是和词项
的信息量成反比的一个值
于是可以定义词项t的idf权重(逆文档频率):,其中
是文档集中文档的数目
是反映词项
的信息量的一个指标,是一种全局性指标,反应的是词项在全局的区别性。
对于单词项查询,idf对文档排序没有任何影响,idf 会影响至少包含2个词项的查询的文档排序结果
词项的tf-idf权重是tf权重和idf权重的乘积:,
tf-idf权重:
二值-tfidf矩阵
文档表示成向量:每篇文档表示成一个基于tfidf权重的实值向量 ∈ R|V|。有一个|V|维实值空间,空间的每一维都对应词项,文档都是该空间下的一个点或者向量。
查询看成向量:
向量空间下相似度:利用余弦相似度
文档长度归一化:一个向量可以通过除以它的长度进行归一化处理(防止长度影响)
问题:
余弦归一化倾向于短文档,即对短文档产生的归一化因子太大,而平均而言对长文档产生的归一化因子太小,因此余弦归一化对长文档的惩罚过重,实际上长文档中虽然词频较高,但也会包含较多的信息。
可以先找到一个支点(pivot,平衡点),然后通过这个支点对余弦归一化操作进行线性调整。因此短文档的相似度降低,而长文档的相似度增大,可以去除原来余弦归一化偏向短文档的问题
回转归一化:基本思想是旋转归一化曲线,使得两条曲线尽量重合
向量空间模型小结:
模式识别系统的主要作用:判别各个模式(也称样本)所属的类别
模式分类若可用任一个线性函数来划分,则这些模式就称为线性可分的,否则就是非线性可分的。
一旦线性函数的系数被确定,这些函数就可用作模式分类的基础。
对一个两类问题的判别,就是将模式划分成
和
两类
这两类可以通过一个直线方程来划分
若,则
,若
,则
称为决策面/判别界面方程**(判别函数和判别界面是否等于0要注意)**
用判别函数进行模式分类依赖的两个因素:
一个维线性判别函数的一般形式:
权向量(参数向量):
维线性判别函数也可以表示为
增广模式向量:,增广权向量:
多类情况1:用线性判别函数将属于类的模式与不属于
类的模式分开,称为
两分法,即把
类多类问题分成
个两类问题,因此共有
个判别函数。会存在分类失败的问题:
多类情况2:采用每对划分,即 两分法,此时一个判别界面只能分开两种类别,但不能把它与其余所有的界面分开。
判别函数为,若
,则
因此要分开类模式,共需
个判别函数。也会存在不确定区域,即分类失败。
多类情况1和多类情况2的比较
多类情况3:没有不确定区域的 两分法
,此时,对
类情况应有
个判别函数。
线性判别函数简单,容易实现,而非线性判别函数复杂,不容易实现。
若能将非线性判别函数转换为线性判别函数,则有利于模式分类的实现。
设有一个训练用的模式集,在模式空间
中线性不可分,但在模式空间
中线性可分,其中
的各个分量是
的单值实函数,
的维数
高于
的维数
,即若取
,则分类界面在
中是线性的,在
中是非线性的,此时只要将模式
进行非线性变换,使之变换后得到维数更高的模式
,就可以用线性判别函数来进行分类。
一个非线性判别函数可如下表示:,其中
是模式
的单值实函数。
若定义成广义形式:
此时有:。其中
非线性判别函数已被变换成广义线性,因此只讨论线性判别函数不会失去一般性意义。
当是模式
的二次多项式函数时:
式中各项的组成应包含的各个分量的二次项、一次项和常数项,其中平方项
个,二次项
个,一次项
个,常数项1个,其总项数为:
若是模式
的
次多项式函数,总项数为
也就是说,可以使用一个二次判别函数进行分类的地方,也可以使用一个分段线性判别函数来逼近这个二次曲线。
可以采用最小距离分类的方法,只有在类别密集地分布在其均值附近时才有效。
对于各类交错分布的情况,若再用每类一个均值代表点产生最小距离分类器,就会产生很明显的错误率。在这种情况下,可以运用聚类方法将一些类分解成若干个子类,再用最小距离分类。
模式空间:
对一个线性方程,它在三维空间
中是一个平面方程式,
是方程的系数。
把向量作为该平面的法线向量,则该线性方程决定的平面通过原点且与
垂直
若是二维的增广向量,
为非增广的权向量,它与直线AB垂直
模式空间即为增广向量决定的平面或非增广向量决定的直线。
权空间:
若将方程绘在权向量
的三维空间中,则
为方程的系数
问题描述:
Fisher判别方法所要解决的基本问题:如何根据实际情况找到一条最好的、最易于分类的投影线。
从维空间到一维空间的一般数学变换方法:
假设有一集合包含
个
维样本
,其中
个属于
类的样本记为子集
,
个属于
类的样本记为子集
,若对
的分量做线性组合可得标量:
,这样便得到
个一维样本
组成的集合,并可分为两个子集
和
。
实际上,的值是无关紧要的,它仅是
乘上一个比例因子,重要的是选择
的方向。
的方向不同,将使样本投影后的可分离程度不同,从而直接影响分类效果。因此,上述寻找最佳投影方向的问题,在数学上就是寻找最好的变换向量
的问题。
Fisher准则函数中的基本参量:
在维
空间:
各类样本的均值向量
样本类内离散度矩阵:
总样本类内离散度矩阵:(对称半正定矩阵)
样本类间离散度矩阵:(对称半正定矩阵)
在一维空间:
各类样本的均值:
样本类内离散度:
总样本类内离散度:
我们希望投影后,在一维空间中各类样本尽可能分得开些,即希望两类均值之差越大越好,同时希望各类样本内部尽量密集,即希望类内离散度越小越好。
Fisher准则函数:将其推导为
的显函数:
然后使用Lagrange乘数法求解,最终解得
事实上,Fisher的降维就相当于找一个线性判别函数。投影后的是
变化得来的,就相当于线性判别。
多类情形:
类间散度矩阵与两类情形略有不同:原来度量的是两个均值点的散列情况,现在度量的是每类均值点相对于样本中心的散列情况
推导可得:
一旦判别函数的形式确定下来,不管它是线性的还是非线性的,剩下的问题就是如何确定它的系数。在模式识别中,系数确定的一个主要方法就是通过对已知样本的训练和学习来得到。感知器算法就是通过训练样本模式的迭代和学习,产生线性(或广义线性)可分的模式判别函数。
基本思想:采用感知器算法能通过对训练模式样本集的“学习”得到判别函数的系数。不需要对各类别中模式的统计性质做任何假设,因此称为确定性的方法。
感知器作为人工神经网络中最基本的单元,由多个输入和一个输出组成。
已知两个训练模式集分别属于类和
类,权向量的初始值为
,可任意取值。
若,若
第次的训练步骤为:
若,则分类器对第
个模式
做了错误分类,此时应校正权向量,使得
,其中
为一个校正增量。
若,则分类器对第
个模式
做了错误分类,此时应校正权向量,使得
,其中
为一个校正增量。
若以上情况不符合,则表明该模式样本在第次中分类正确,因此权向量不变
感知器算法的收敛性:只要模式类别是线性可分的,就可以在有限的迭代步数里求出权向量。
采用多类情况3,将感知器算法推广到多类模式。
多类情况3:对类模式存在
个判别函数
,若
, 则
设有种模式类别
,若在训练过程的第
次迭代时,一个属于
类的模式样本
送入分类器,则应先计算出
个判别函数:
。若
的条件成立,则权向量不变,即
若其中第个权向量使得
,则相应的权向量应做调整,即
其中是一个正常数。权向量的初始值
可视情况任意选择。
这里的分类算法都是通过模式样本来确定判别函数的系数,但一个分类器的判断性能最终要受并未用于训练的那些未知样本来检验。要使一个分类器设计完善,必须采用有代表性的训练数据,它能够合理反映模式数据的整体。
要获得一个判别性能好的线性分类器,直观上训练样本越多越好,但实际上能收集到的样本数目会受到客观条件的限制,且过多的训练样本在训练阶段会使计算机需要较长的运算时间。一般来说,合适的样本数目可如下估计:若是模式的维数,令
,则通常选用的训练样本数目约为
的10~20倍。
感知器算法的解与初值的选择和迭代过程中误分类点的选择顺序有关。
设函数 是向量
的函数, 则
的梯度定义为
从导出
的一般关系式
,
是一个正的比例因子(步长)
梯度是一个向量,它的最重要性质就是指出了函数在其自变量增加时最大增长率的方向。负梯度指出
的最陡下降方向,利用这个性质可以设计一个迭代方案来寻找函数的最小值。
定义一个对错误分类敏感的准则函数。先任选一个初始权向量
,计算准则函数
的梯度,然后从
出发,在最陡方向(梯度方向)上移动某一距离得到下一个权向量
C值的选择是很重要的。若C值太小,则收敛太慢;若C值太大,则搜索可能过头,引起发散。
设取准则函数为:
则对
的微分式:
,其中
则由梯度法中和
的关系有:
其中是训练模式样本,
是指第
次迭代。
若模式是线性可分的,选择合适的准则函数,算法就能给出解。若模式不是线性可分的,算法的结果就会来回摆动,得不到收敛。
感知器算法只是当被分模式可用一个特定的判别界面分开时才收敛,在不可分情况下,只要计算程序不终止,它就始终不收敛。即使在模式可分的情况下,也很难事先算出达到收敛时所需要的迭代次数。这样,在模式分类过程中,有时候会出现一次又一次迭代却不见收敛的情况,白白浪费时间。为此需要知道:发生迟迟不见收敛的情况时,到底是由于收敛速度过慢造成的呢,还是由于所给的训练样本集不是线性可分造成的呢?
最小平方误差(LMSE)算法,除了对可分模式是收敛的以外,对于类别不可分的情况也能指出来。
求两类问题的解相当于求一组线性不等式的解,因此,若给出分别属于和
的两个模式样本的训练样本集,即可求出其权向量
的解。
设两类模式的训练样本总数为,写成增广形式,则有不等式组
H-K算法:
模式类别可分性的判别:
当不等式组有解时,该算法对
收敛,可求得解
。
固定增量算法与LMSE算法的比较:
用势函数的概念来确定判别函数和划分类别界面
基本思想:
模式分类的判别函数可由分布在模式空间中的许多样本向量的势函数产生。任意一个样本所产生的势函数以
表征,则判别函数
可由势函数序列
来构成,序列中的这些势函数相应于在训练过程中输入机器的训练模式样本
。在训练状态,模式样本逐个输入分类器,分类器就连续计算相应的势函数,在第
步迭代时的积累位势决定于在该步前所有的单独势函数的累加。以
表示积累位势函数,若加入的训练样本
是错误分类,则积累函数需要修改,若是正确分类,则不变。
从势函数可以看出,积累位势起着判别函数的作用:
由于一个模式样本的错误分类可造成积累位势在训练时的变化,因此势函数算法提供了确定和
两类判别函数的迭代过程。
判别函数表达式:取,则有
选择势函数的条件:一般来说,若两个维向量
和
的函数
同时满足下列三个条件,则可作为势函数。
第一类势函数:可用对称的有限多项式展开:
,
在模式定义域内为正交函数集。
将这类势函数代入判别函数:,其中
因此,积累位势可写成,
可用迭代式求得。
第二类势函数:选择双变量和
的对称函数作为势函数,即
,并且它可展开成无穷级数。
例如:
,
是正常数
用第二类势函数,当训练样本维数和数目都较高时,需要计算和存储的指数项较多。
因为势函数由许多新项组成,因此有很强的分类能力。
决策树,或称多级分类器,是模式识别中进行分类的一种有效方法,对于多类或多峰分布问题,这种方法尤为方便。利用树分类器可以把一个复杂的多类别分类问题,转化为若干个简单的分类问题来解决。它不是企图用一种算法、一个决策规则去把多个类别一次分开,而是采用分级的形式,使分类问题逐步得到解决。
一般来讲,一个决策树由一个根节点,一组非终止节点
和一些终止节点
组成,可对
标以各种类别标签,有时不同的终止节点上可以出现相同的类别标签。
如果用表示决策树,则一个决策树
对应于特征空间的一种划分,它把特征空间分成若干个区域,在每个区域中,某类的样本占优势,因此可以标出该类样本的类别标签。
决策树的一种简单形式是二叉树,它是指除叶结点外,树的每个节点仅分为两个分支,即每个非终止节点都有且仅有两个子节点
和
。
二叉树结构分类器可以把一个复杂的多类别分类问题转化为多级多个两类问题来解决,在每个非终止节点都把样本集分成左右两个子集。分成的每一部分仍然可能包含多个类别的样本,可以把每一部分再分成两个子集,如此下去,直至分成的每一部分只包含同一类别的样本,或某一类样本占优势为止。
二叉树结构分类器概念简单、直观、便于解释,而且在各个节点上可以选择不同的特征和采用不同的决策规则,因此设计方法灵活多样,便于利用先验知识来获得一个较好的分类器。
在设计一个决策树时,主要应解决以下几个问题:
把一个多类别分类问题转化为两类问题的形式是多种多样的,因此,对应的二叉树的结构也是各不相同的。通常的目的是要找一个最优的决策树。一个性能良好的决策树结构应该具有小的错误率和低的决策代价。但是由于很难把错误率的解析表达式和树的结构联系起来,而且在每个节点上所采用的决策规则也仅仅是在该节点上所采用的特征观测值的函数,因此,即使每个节点上的性能都达到最优,也不能说整个决策树的性能达到最优。在实际问题中,人们往往提出其它一些优化准则,例如极小化整个树的节点数目,或从根节点到叶结点的最大路经长度,或从根节点到叶结点的平均路经长度等,然后采用动态规划的方法,力争设计出能满足某种准则的“最优”决策树。
]]>搜索问题是对原问题的建模
搜索问题的构成:状态空间➡后继函数(状态转化为另一个状态,采取的动作,付出的代价)➡初始状态和目标测试
解是一个行动序列,将初始状态转换成目标状态
例1:罗马尼亚旅行:
解:从Arad到Bucharest的最短路径
例2:吃豆子游戏
状态空间包含了环境中的每一个细节:Agent,Ghost,大的豆子和小的豆子
搜索状态只保留行动需要的细节:
对于走到终点来说:
对于吃掉所有豆子来说:
状态数量计算:
例3:三个传教士和三个野人
状态空间:{(M, C, B)},表示河左岸的传教士数量、野人数量和船目前的方位
后继函数:{P01, P10, P02, P20, P11, Q01, Q10, Q02, Q20, Q11},P表示现在是从左岸到右岸,后面两个数字表示船上的传教士数量和野人数量
初始状态:(3, 3, 1)
目标状态:(0, 0, 0)
状态空间图:搜索问题的数学表示,在状态空间图中,每个状态只出现一次
搜索树:
状态空间图的每一个结点表示每一个状态
搜索树的每一个结点不表示状态,而是从初始状态到这个状态的一个路径(因此要尽量少构建搜索树的结点)
基于搜索树的搜索:
搜索算法特性:
所有搜索算法都是相同的,除了对边缘的处理策略
结合DFS的空间优势与BFS的时间优势
深度优先按照层数进行约束,不要搜索到层
通常绝大多数的节点都在底层,所以上层的节点生成多次影响不是很大
代价一致搜索(Uniform Cost Search):将之前的走过的路径的代价进行一个累加,然后寻找其代价最低的路径。
可以看成代价敏感搜索的一种实现。
启发策略:估计一个状态到目标距离的函数,问题给予算法的额外信息,为特定搜索问题而设计。
策略:扩展你认为最接近目标状态的节点
启发式:对每个状态估计到最近目标的距离(曼哈顿距离或者欧氏距离),只使用启发函数来评价节点
通常情况下最佳优先使你直接(或很快)到达目标,最坏情况类似DFS
结合代价一致搜索和贪婪搜索
重点搜索评价函数:
表示路径的代价,或者称为后向的代价
表示前方距离目标的距离,或者称为前向的代价
A* 搜索将两个代价进行组合
A* 搜索结束条件是目标出列的时候,而不是目标入列的时候,因为目标入列的时候可能路径并不是最优的。
A*搜索不一定是最优的,启发函数要好好选择
启发函数是可采纳的,那么
,其中
是到最近目标的真实耗散。(例如曼哈顿距离)
前提:启发函数是可采纳的,那么A* 树搜索是最优的。
对于解决难的搜索问题,大部分工作就是想出可采纳的启发函数。通常可采纳启发函数是松弛问题的解的耗散
A*图搜索与树搜索的区别在于图搜索不允许访问相同结点
图搜索中,如果启发函数是一致的,A* 搜索是最优的。
一致的:启发函数不仅仅要是可采纳的,同时在每一个局部的位置也要合理。
也就是:如果沿路径的节点估计耗散值单调递增,即
,那么A*图搜索具备最优性。
通常,天然的可采纳启发函数是倾向于一致的,特别是从松弛问题中获得的启发函数
树搜索在边缘集合中保留未探索的替代路径(确保完备性)
局部搜索: 改进单一选项直到不能再改善为止
爬山法搜索
模拟退火搜索:避免局部极大(允许向山下移动)
遗传算法——自然选择
词典是指存储词项词汇表的数据结构:作用:存储词项以及定位词项
词项词汇表指的是具体数据,而词典指的是数据结构
采用定长数组的词典结构对每个词项需要存储文档频率和指向倒排记录表的指针
词项定位(查词典):在词典中查找给定关键字
用于词项定位的数据结构:主要是哈希表和树
有些IR系统用哈希表,有些系统用树结构
采用哈希表或树的准则:
哈希函数:输入词项,输出正整数(通常是地址)
树
树可以支持前缀查找(相当于对词典再建一层索引)
最简单的树结构:二叉树,搜索速度略低于哈希表方式,时间复杂度为, 其中
是词汇表大小,即所有词项的数目
且仅仅对平衡树成立,使二叉树重新保持平衡开销很大
B-树:每个内部节点的子节点数目在之间,其中
为合适的正整数
通配查询:包含通配符的查询
mon*: 找出所有包含以mon开头的词项的文档
如果采用B-树词典结构,那么实现起来非常容易,只需要返回区间mon ≤ t < moo上的词项t
*mon: 找出所有包含以mon结尾的词项的文档
将所有的词项倒转过来,然后基于它们建一棵附加的树,返回区间nom ≤ t < non上的词项t
词项中间的*号处理:mnchen
轮排索引:(主要思想:让星号出现在词汇的末尾)
轮排索引的查找过程:
相对于通常的B-树,轮排索引(轮排树)的空间要大4倍以上 (经验值)
k-gram索引:枚举一个词项中所有连读的k个字符构成k-gram
k-gram存在两个倒排索引:
k-gram索引 vs. 轮排索引
涉及的任务:拼写错误检测和拼写错误矫正(并不是先后的关系)
错误种类:非词汇错误(纠正的时候不需要考虑上下文)和真实词汇错误(纠正的时候需要考虑上下文)
两个主要用途
非词汇拼写错误检测:词典中不存在的词均视为错误
非词汇拼写错误矫正:
词独立法:
采用拼写噪声通道模型:通过贝叶斯定理求解:
正确拼写为,错误拼写为
,则
可以通过文档进行估计
产生候选词的方法:
语言模型
若有包含个词条的大文本语料,则
,
是词频。(一元先验概率)
通道模型概率-计算错误概率:混淆“矩阵”(计算一个字符变为另一个字符的概率如何)
然后可以计算噪声通道模型
计算的过程中可以添加加一概率平滑:上述混淆矩阵的例子很难避免某种操作样本数为0,要避免这种概率为0的情况
真实词汇错误的纠正通常需要考虑上下文
上下文敏感法:
真实词汇拼写矫正的噪声通道:二元语言模型,将一元模型与二元模型插值
通道模型的改进:
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
class Solution {public: vector<int> findDisappearedNumbers(vector<int>& nums) { int n = nums.size(); vector<bool> vt(n+1,false); for(int i=0;i<n;++i){ vt[nums[i]] = true; } vector<int> result; for(int i=1;i<=n;++i){ if(vt[i] == false){ result.push_back(i); } } return result; }};分析:扫一遍确认一下,再扫一遍找出结果。
一遍AC
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像原地顺时针旋转 90 度。
class Solution {public: void rotate(vector<vector<int>>& matrix) { int temp = 0, n = matrix.size()-1; for (int i = 0; i <= n / 2; ++i) { for (int j = i; j < n - i; ++j) { temp = matrix[j][n-i]; matrix[j][n-i] = matrix[i][j]; matrix[i][j] = matrix[n-j][i]; matrix[n-j][i] = matrix[n-i][n-j]; matrix[n-i][n-j] = temp; } } }};分析:转转转
错误:没想到原地旋转的思路。
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:每行的元素从左到右升序排列,每列的元素从上到下升序排列。
class Solution {public: bool searchMatrix(vector<vector<int>>& matrix, int target) { int m = matrix.size(); int n = matrix[0].size(); int x = 0; int y = n-1; while(x >= 0 && x < m && y >= 0 && y < n){ if(matrix[x][y] == target){ return true; } else if(target < matrix[x][y]){ y -= 1; } else{ x += 1; } } return false; }};分析:从右上角开始查找,若当前值大于待搜索值,我们向左移动一位;若当前值小于待搜索值,我们向下移动一位。如果最终移动到左下角时仍不等于待搜索值,则说明待搜索值不存在于矩阵中。
错误:找到思路后一遍AC
给定一个长度为 n 的整数数组 arr ,它表示在 [0, n - 1] 范围内的整数的排列。我们将 arr 分割成若干 块 (即分区),并对每个块单独排序。将它们连接起来后,使得连接的结果和按升序排序后的原数组相同。返回数组能分成的最多块数量。
class Solution {public: int maxChunksToSorted(vector<int>& arr) { int n = arr.size(); int result = 0; int maxnum = 0; for(int i=0;i<n;++i){ maxnum = max(maxnum,arr[i]); if(maxnum == i){ ++result; } } return result; }};分析:从左往右遍历,同时记录当前的最大值,每当当前最大值等于数组位置时,我们可以多一次分割。
错误:看了思路后实现的
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty)
class MyQueue { stack<int> st1; stack<int> st2;public: MyQueue() { } void push(int x) { st1.push(x); } int pop() { while(!st1.empty()){ st2.push(st1.top()); st1.pop(); } int a = st2.top(); st2.pop(); while(!st2.empty()){ st1.push(st2.top()); st2.pop(); } return a; } int peek() { while(!st1.empty()){ st2.push(st1.top()); st1.pop(); } int a = st2.top(); while(!st2.empty()){ st1.push(st2.top()); st2.pop(); } return a; } bool empty() { return st1.empty(); }};分析:比较简单,也没有算法
错误:全局变量没定义好,返回值漏掉了,调通了。
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
class MinStack { stack<int> s1; stack<int> mins;public: MinStack() { } void push(int val) { if(mins.empty() || val <= mins.top()){ mins.push(val); } s1.push(val); } void pop() { int a = s1.top(); s1.pop(); if(mins.top() == a){ mins.pop(); } } int top() { return s1.top(); } int getMin() { return mins.top(); }};分析:可以额外建立一个新栈,栈顶表示原栈里所有值的最小值。每当在原栈里插入一个数字时,若该数字小于等于新栈栈顶,则表示这个数字在原栈里是最小值,我们将其同时插入新栈内。每当从原栈里取出一个数字时,若该数字等于新栈栈顶,则表示这个数是原栈里的最小值之一,我们同时取出新栈栈顶的值。
错误:没有思路
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
class Solution {public: bool isValid(string s) { stack<char> st; int n = s.size(); for(int i=0;i<n;++i){ if(s[i] == '(' || s[i] == '{' || s[i] == '['){ st.push(s[i]); } else{ if(st.empty()){ return false; } else if(st.top() == '[' && s[i] == ']'){ st.pop(); } else if(st.top() == '(' && s[i] == ')'){ st.pop(); } else if(st.top() == '{' && s[i] == '}'){ st.pop(); } else{ return false; } } } if(st.empty()){ return true; } return false; }};分析:用栈进行匹配即可
错误:没有考虑只有一个左括号的情况,改正后调通了
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
class Solution {public: vector<int> dailyTemperatures(vector<int>& temperatures) { int n = temperatures.size(); vector<int> answer(n); stack<int> s; for(int i=0;i<n;++i){ while (!s.empty()) { int pre_index = s.top(); if (temperatures[i] <= temperatures[pre_index]) { break; } s.pop(); answer[pre_index] = i - pre_index; } s.push(i); } return answer; }};分析:我们可以维持一个单调递减的栈,表示每天的温度;为了方便计算天数差,我们这里存放位置(即日期)而非温度本身。我们从左向右遍历温度数组,对于每个日期p,如果p的温度比栈顶存储位置q的温度高,则我们取出q,并记录q需要等待的天数为p-q;我们重复这一过程,直到p的温度小于等于栈顶存储位置的温度(或空栈)时,我们将p插入栈顶,然后考虑下一天。在这个过程中,栈内数组永远保持单调递减,避免了使用排序进行比较。最后若栈内剩余一些日期,则说明它们之后都没有出现更暖和的日期。
错误:感觉并不是非常理解。
给你一个链表数组,每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中,返回合并后的链表。
class Solution {public: struct Comp{ bool operator()(ListNode* l1,ListNode* l2){ return l1->val > l2->val; } }; ListNode* mergeKLists(vector<ListNode*>& lists) { if(lists.empty()){ return nullptr; } priority_queue<ListNode*,vector<ListNode*>,Comp> q; for(ListNode* list:lists){ if(list){ q.push(list); } } ListNode* dummy = new ListNode(0), *cur = dummy; while (!q.empty()) { cur->next = q.top(); q.pop(); cur = cur->next; if (cur->next) { q.push(cur->next); } } return dummy->next; }};分析:即把所有的链表存储在一个优先队列中,每次提取所有链表头部节点值最小的那个节点,直到所有链表都被提取完为止。
错误:优先队列不是很熟悉
给定建筑物的起止位置和高度,返回建筑物轮廓(天际线)的拐点。
Hard难度,想不太明白,暂时不做了
分析:使用优先队列储存每个建筑物的高度和右端(这里使用pair,其默认比较函数是先比较第一个值,如果相等则再比较第二个值),从而获取目前会拔高天际线、且妨碍到前一个建筑物(的右端端点)的下一个建筑物。
错误:没有思路
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。
class Solution {public: vector<int> maxSlidingWindow(vector<int>& nums, int k) { vector<int> result; deque<int> dq; int n = nums.size(); for(int i=0;i<n;++i){ if(!dq.empty() && nums[i] > nums[dq.back()]){ while(!dq.empty() && nums[dq.back()] < nums[i]){ dq.pop_back(); } } dq.push_back(i); if(i >= k-1){ result.push_back(nums[dq.front()]); if(nums[i-k+1] == nums[dq.front()]){ dq.pop_front(); } } } return result; }};分析:利用双端队列进行操作:每当向右移动时,把窗口左端的值从队列左端剔除,把队列右边小于窗口右端的值全部剔除。这样双端队列的最左端永远是当前窗口内的最大值。
错误:理解了思路后调通了。
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出和为目标值 target的那两个整数,并返回它们的数组下标。
class Solution {public: vector<int> twoSum(vector<int>& nums, int target) { vector<int> result; unordered_map<int, int> hash; int n = nums.size(); for(int i=0;i<n;++i){ if(hash.count(target - nums[i])){ result.push_back(hash[target - nums[i]]); result.push_back(i); break; } hash[nums[i]] = i; } return result; }};分析:利用哈希表存储遍历过的值以及它们的位置,每次遍历到位置i 的时候,查找哈希表里是否存在target - nums[i],若存在,则说明这两个值的和为target。
一遍AC
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
class Solution {public: int longestConsecutive(vector<int>& nums) { unordered_set<int> hash; for(const int & num:nums){ hash.insert(num); } int ans = 0; while(!hash.empty()){ int cnt = *(hash.begin()); hash.erase(cnt); int pre = cnt - 1; int next = cnt + 1; while(!hash.empty() && hash.count(pre)){ hash.erase(pre); --pre; } while(!hash.empty() && hash.count(next)){ hash.erase(next); ++next; } ans = max(ans,next-pre-1); } return ans; }};分析:把所有数字放到一个哈希表,然后不断地从哈希表中任意取一个值,并删除掉其之前之后的所有连续数字,然后更新目前的最长连续序列长度。重复这一过程,我们就可以找到所有的连续数字序列。
错误:看了思路后实现了
给你一个数组 points ,其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
class Solution {public: int maxPoints(vector<vector<int>>& points) { unordered_map<double, int> hash; // <斜率, 点个数> int max_count = 0, same = 1, same_y = 1; for (int i = 0; i < points.size(); ++i) { same = 1, same_y = 1; for (int j = i + 1; j < points.size(); ++j) { if (points[i][1] == points[j][1]) { ++same_y; if (points[i][0] == points[j][0]) { ++same; } } else { double dx = points[i][0] - points[j][0], dy = points[i][1] - points[j][1]; ++hash[dx/dy]; } } max_count = max(max_count, same_y); for (auto item : hash) { max_count = max(max_count, same + item.second); } hash.clear(); } return max_count; }};分析:对于每个点,我们对其它点建立哈希表,统计同一斜率的点一共有多少个。这里利用的原理是,一条线可以由一个点和斜率而唯一确定。另外也要考虑斜率不存在和重复坐标的情况。
错误:好麻烦先算了
给你一份航线列表 tickets ,其中 tickets[i] = [from<sub>i</sub>, to<sub>i</sub>] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。
class Solution {public: vector<string> findItinerary(vector<vector<string>>& tickets) { vector<string> ans; if (tickets.empty()) { return ans; } unordered_map<string, multiset<string>> hash; for (const auto & ticket: tickets) { hash[ticket[0]].insert(ticket[1]); } stack<string> s; s.push("JFK"); while (!s.empty()) { string next = s.top(); if (hash[next].empty()) { ans.push_back(next); s.pop(); } else { s.push(*hash[next].begin()); hash[next].erase(hash[next].begin()); } } reverse(ans.begin(), ans.end()); return ans; }};分析:本题可以先用哈希表记录起止机场,其中键是起始机场,值是一个多重集合,表示对应的终止机场。因为一个人可能坐过重复的线路,所以我们需要使用多重集合储存重复值。储存完成之后,我们可以利用栈来恢复从终点到起点飞行的顺序,再将结果逆序得到从起点到终点的顺序。
错误:多重集合的第一道题,也是唯一一道题,不是很明白
设计一个数据结构,使得其能够快速查询给定数组中,任意两个位置间所有数字的和。
class NumArray { vector<int> frontsum;public: NumArray(vector<int>& nums) { for(int i=0;i<nums.size();++i){ if(i == 0){ frontsum.push_back(nums[i]); } else{ frontsum.push_back(nums[i] + frontsum[i-1]); } } } int sumRange(int left, int right) { if(left == 0){ return frontsum[right]; } return frontsum[right] - frontsum[left-1]; }};分析:前缀和即可
一遍AC
设计一个数据结构,使得其能够快速查询给定矩阵中,任意两个位置包围的长方形中所有数字的和。
class NumMatrix { vector<vector<int>> frontmatrix;public: NumMatrix(vector<vector<int>>& matrix) { int m = matrix.size(); int n = matrix[0].size(); for(int i=0;i<m;++i){ vector<int> temp; for(int j=0;j<n;++j){ if(i == 0 && j == 0){ temp.push_back(matrix[i][j]); } else if(i == 0){ temp.push_back(matrix[i][j] + temp[j-1]); } else if(j == 0){ temp.push_back(matrix[i][j] + frontmatrix[i-1][j]); } else{ temp.push_back(matrix[i][j] + frontmatrix[i-1][j] + temp[j-1] - frontmatrix[i-1][j-1]); } } frontmatrix.push_back(temp); } } int sumRegion(int row1, int col1, int row2, int col2) { if(row1 == 0 && col1 == 0){ return frontmatrix[row2][col2]; } else if(row1 == 0){ return frontmatrix[row2][col2]-frontmatrix[row2][col1-1]; } else if(col1 == 0){ return frontmatrix[row2][col2]-frontmatrix[row1-1][col2]; } return frontmatrix[row2][col2]-frontmatrix[row2][col1-1]-frontmatrix[row1-1][col2]+frontmatrix[row1-1][col1-1]; }};分析:二维上的前缀和(积分图)即可
一遍AC
给你一个整数数组 nums 和一个整数 k ,请你统计并返回该数组中和为 k 的连续子数组的个数。
class Solution {public: int subarraySum(vector<int>& nums, int k) { int count = 0, psum = 0; unordered_map<int, int> hashmap; hashmap[0] = 1; // 初始化很重要 for (int i: nums) { psum += i; count += hashmap[psum-k]; ++hashmap[psum]; } return count; }};分析:本题同样是利用前缀和,不同的是这里我们使用一个哈希表 hashmap,其键是前缀和,而值是该前缀和出现的次数。在我们遍历到位置i 时,假设当前的前缀和是 psum ,那么 hashmap[psum-k]即为以当前位置结尾、满足条件的区间个数。
错误:直接使用前缀和会超时,然而这个短代码挺难理解的样子。
在 MATLAB 中,有一个非常有用的函数 reshape ,它可以将一个 m x n 矩阵重塑为另一个大小不同(r x c)的新矩阵,但保留其原始数据。给你一个由二维数组 mat 表示的 m x n 矩阵,以及两个正整数 r 和 c ,分别表示想要的重构的矩阵的行数和列数。重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序填充。如果具有给定参数的 reshape 操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
class Solution {public: vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) { int m = mat.size(); int n = mat[0].size(); if(m*n != r*c){ return mat; } int rowindex = 0; int colindex = 0; vector<vector<int>> result(r,vector<int>(c)); for(int i=0;i<r;++i){ for(int j=0;j<c;++j){ result[i][j] = mat[rowindex][colindex]; ++colindex; if(colindex == n){ ++rowindex; colindex = 0; } } } return result; }};分析:很简单的小题,没有任何难度。
一遍AC
用两个队列实现一个栈
class MyStack { queue<int> q1; queue<int> q2;public: MyStack() { } void push(int x) { q1.push(x); return; } int pop() { while(q1.size() != 1){ q2.push(q1.front()); q1.pop(); } int a = q1.front(); q1.pop(); while(!q2.empty()){ q1.push(q2.front()); q2.pop(); } return a; } int top() { while(q1.size() != 1){ q2.push(q1.front()); q1.pop(); } int a = q1.front(); q2.push(q1.front()); q1.pop(); while(!q2.empty()){ q1.push(q2.front()); q2.pop(); } return a; } bool empty() { return q1.empty(); }};分析:也是很简单的题,倒腾倒腾数字就行了
一遍AC
给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的下一个更大元素 。
class Solution {public: vector<int> nextGreaterElements(vector<int>& nums) { int n = nums.size(); stack<int> st; vector<int> result(n,-1); for(int i=0;i<2*n-1;++i){ while(!st.empty() && nums[i%n] > nums[st.top()]){ result[st.top()] = nums[i%n]; st.pop(); } st.push(i%n); } return result; }};分析:使用单调栈解决本题。单调栈中保存的是下标,从栈底到栈顶的下标在数组 nums中对应的值是单调不升的。每次我们移动到数组中的一个新的位置 i,我们就将当前单调栈中所有对应值小于 nums[i]的下标弹出单调栈,这些值的下一个更大元素即为 nums[i]。随后我们将位置 i入栈。
错误:没有想到单调栈,看了一下思路后自己实现的。
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
class Solution {public: bool containsDuplicate(vector<int>& nums) { unordered_map<int,int> mp; int n = nums.size(); for(int i=0;i<n;++i){ if(mp.find(nums[i]) == mp.end()){ mp[nums[i]] = 1; } else{ return true; } } return false; }};分析:非常简单的哈希表,没什么难度
错误:下标和数字插入看的不太对
给定一个非空且只包含非负数的整数数组 nums,数组的度的定义是指数组里任一元素出现频数的最大值。你的任务是在 nums 中找到与 nums 拥有相同大小的度的最短连续子数组,返回其长度。
class Solution {public: int findShortestSubArray(vector<int>& nums) { unordered_map<int,vector<int>> mp; int n = nums.size(); for(int i=0;i<n;++i){ if(mp.find(nums[i]) == mp.end()){ mp[nums[i]].push_back(i); mp[nums[i]].push_back(i); mp[nums[i]].push_back(1); } else{ if(i < mp[nums[i]][0]){ mp[nums[i]][0] = i; } if(i > mp[nums[i]][1]){ mp[nums[i]][1] = i; } ++mp[nums[i]][2]; } } int maxnum = 0; int result = n+1; for(auto it = mp.cbegin();it != mp.cend();++it){ if(it->second[2] > maxnum){ maxnum = it->second[2]; result = it->second[1]-it->second[0]+1; } else if (it->second[2] == maxnum){ result = min(result,it->second[1]-it->second[0]+1); } } return result; }};分析:比较简单的数据结构应用题
错误:语法问题,还有下标数字问题,后面自己调通
和谐数组是指一个数组里元素的最大值和最小值之间的差别 正好是 1 。现在,给你一个整数数组 nums ,请你在所有可能的子序列中找到最长的和谐子序列的长度。数组的子序列是一个由数组派生出来的序列,它可以通过删除一些元素或不删除元素、且不改变其余元素的顺序而得到。
class Solution {public: int findLHS(vector<int>& nums) { int n = nums.size(); int ans = 0; unordered_map<int,int> mp; for(int i=0;i<n;++i){ if(mp.find(nums[i]) == mp.end()){ mp[nums[i]] = 1; } else{ ++mp[nums[i]]; } } for(auto it = mp.cbegin();it != mp.cend();++it){ if(mp.find(it->first-1) != mp.end()){ ans = max(ans,it->second + mp[it->first-1]); } if(mp.find(it->first+1) != mp.end()){ ans = max(ans,it->second + mp[it->first+1]); } } return ans; }};分析:看起来挺像动态规划,实际上并不是,统计一下就好了
错误:还是map迭代器不太熟练,后面调通。
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
class Solution {public: int findDuplicate(vector<int>& nums) { int n = nums.size(); int len = nums.length; for (int num : nums) { int idx = Math.abs(num); if (nums[idx] < 0) { return idx; } nums[idx] = -nums[idx]; } return len; }};分析:考虑到数组元素值的范围是 [1,n],但数组长度为 n+1,那么很显然在遍历数组的时候,我们将数组的值变为其对应的负数,那么再次遇到负数就得到了答案。
错误:上面不是最优解,没有想到最优解
超级丑数 是一个正整数,并满足其所有质因数都出现在质数数组 primes 中。给你一个整数 n 和一个整数数组 primes ,返回第 n 个 超级丑数 。题目数据保证第 n 个 超级丑数 在 32-bit 带符号整数范围内。
class Solution {public: int nthSuperUglyNumber(int n, vector<int>& primes) { vector<long> dp(n + 1); int m = primes.size(); vector<int> pointers(m, 0); vector<long> nums(m, 1); for (int i = 1; i <= n; i++) { long minNum = INT_MAX; for (int j = 0; j < m; j++) { minNum = min(minNum, nums[j]); } dp[i] = minNum; for (int j = 0; j < m; j++) { if (nums[j] == minNum) { pointers[j]++; nums[j] = dp[pointers[j]] * primes[j]; } } } return dp[n]; }};分析:动态规划,没有思路
错误:没有思路
给定两个大小相等的数组 nums1 和 nums2,nums1 相对于 nums 的优势可以用满足 nums1[i] > nums2[i] 的索引 i 的数目来描述。返回 nums1 的任意排列,使其相对于 nums2 的优势最大化。
class Solution {public: vector<int> advantageCount(vector<int>& nums1, vector<int>& nums2) { sort(nums1.begin(),nums1.end()); vector<pair<int,int>> vt; for(int i=0;i<nums2.size();i++){ vt.push_back(make_pair(nums2[i],i)); } sort(vt.begin(),vt.end()); vector<int> ans(nums2.size()); int l1=0,r1=nums1.size()-1,l2=0,r2=nums2.size()-1; while(r2>=0){ if(nums1[r1]>vt[r2].first){ ans[vt[r2].second]=nums1[r1]; r1--; } else{ ans[vt[r2].second]=nums1[l1]; l1++; } r2--; } return ans; }};分析:田忌赛马,能打就打,打不过让最菜的送人头。
错误:没思路
线段树先算了
数据结构是最最基础的算法,没有合适的数据结构就不可能有高效的算法。普通的数据结构掌握的还不错,但是有一些比较高级的数据结构练的比较少,掌握的不太好。今后要注重这些比较高级的数据结构,并尽量去在实际中应用。
]]>统计学(statistics)是用以收集数据,分析数据和由数据得出结论的一组概念、原则和方法。
给定观测值,判断其属于类
还是类
,作出某次判断时的错误率是:
最小化误差概率条件下,若,则
;若
,则
,
两类模式集的分类:
目的:要确定是属于
类还是
类,要看
是来自于
类的概率大还是来自
类的概率大。
根据概率判别规则,若,则
;若
,则
,
由贝叶斯定理,后验概率可由类别
的先验概率
和
的条件概率密度
来计算,即:
,其中
也称为似然函数。
与概率判别规则结合,则若,则
;若
,则
,
不等式转换一下:
若,则
;
若,则
;
其中,称为似然比,
称为似然比的判决阈值
此判别称为贝叶斯判别。
贝叶斯判别的推广:
可以通过引入一个更一般的损失函数来替代误差概率
特征是多维向量时,假设各个特征之间相互独立
当考虑到对于某一类的错误判决要比对另一类的判决更为关键时,就需要把最小错误概率的贝叶斯判别做一些修正,提出条件平均风险
对类问题,如果观察样本被判定属于
类,则条件平均风险
为将本应属于
类的模式判别成属于
类的是非代价。
若,即判别正确,得分,
可以取负值或零,表示不失分。
若,即判别错误,失分,
应取正值。
意义:
分类器对每一个模式有
种可能的类别可供选择,若对每一个
计算出全部类别的平均风险值
,并且将
指定为是具有最小风险值的那一类,则这种分类器称为最小平均条件风险分类器。
按贝叶斯公式,最小平均条件风险可写成:
可以舍去公共项,则可以简化为:
也是贝叶斯分类器,只是它的判别方法不是按错误概率最小作为标准,而是按平均条件风险作为标准。
举例若:
当分类器将判别为
时:
当分类器将判别为
时:
若,则
被判定为属于
,
此时:
即:
通常,因此
当时,
左边为似然比:,右边为阈值
因此两类模式的贝叶斯判别条件为:
通常,当判别正确时,不失分,可选常数
判别错误时,可选常数
此时:
对于类情况来说,若仍按判对失分为0,判错失分为1记,则
贝叶斯最小错误判别是计算得到某个类别的概率,而最小风险判别是计算得到某个类别后存在风险的概率。两者正好相反。
出发点:当已知或者有理由设想类概率密度函数是多变量的正态分布时,贝叶斯分类器可以导出一些简单的判别函数。由于正态密度函数易于分析,且对许多重要的实际应用又是一种合适的模型,因此受到很大的重视。
种模式类别的多变量正态类密度函数:(参考数学推导)
其中,每一类模式的分布密度都完全被其均值向量和协方差矩阵
所规定
当协方差矩阵的全部非对角线上的元素都为零时,多变量正态类密度函数可简化为个单变量正态类密度函数的乘积,即
个单变量为互相独立的。
已知类别的判别函数可写成如下形式:
可以取自然对数的形式以方便计算:
代入正态类密度函数,可以得到:
去掉与无关的项,最终可以得到:
即为正态分布模式的贝叶斯判别函数。
因此判别函数是一个超二次曲面,对于正态分布模式的贝叶斯分类器,两个模式类别之间用一个二次判别界面分开,就可以求得最优的分类效果。
两类模式的正态分布:表示为
,
表示为
,
和
两类的判别函数对应为:
判别界面是
的二次型方程,即
和
两类模式可用二次判别界面分开。
当是二维时,判别界面为二次曲线,如椭圆,圆,抛物线或双曲线等
,
因为对称矩阵,上式可简化为:
,
由此可导出类别和
间的判别界面为:
判别界面为的线性函数,为一超平面。
当是二维时,判别界面为一直线
决策边界的特征:
贝叶斯分类规则是基于统计概念的。如果只有少数模式样本,一般较难获得最优的结果。
defBayesian(data,label,P): if data.shape[0] != label.shape[0]: # 如果数据和标签的数量不相同 print('Error!') sys.exit() M = data[0].shape[0] # 获取数据的维度 data_list = [[],[]] # 将不同类别的数据分开存储 data_list[0] = np.array([data[i] for i inrange(len(label)) if label[i] ==0]) data_list[1] = np.array([data[i] for i inrange(len(label)) if label[i] ==1]) # 计算均值向量 m0 = np.sum(data_list[0],axis=0) / data_list[0].shape[0] m1 = np.sum(data_list[1],axis=0) / data_list[1].shape[0] # 计算协方差矩阵 C0 = np.sum(np.array([np.dot((data_list[0][i] - m0).reshape(-1,1), \ (data_list[0][i] - m0).reshape(1,-1)) for i inrange(data_list[0].shape[0])]),axis=0) / data_list[0].shape[0] C1 = np.sum(np.array([np.dot((data_list[1][i] - m1).reshape(-1,1),\ (data_list[1][i] - m1).reshape(1,-1)) for i inrange(data_list[1].shape[0])]),axis=0) / data_list[1].shape[0] return np.dot(m0-m1,np.linalg.inv(C0)),np.log(P[0]) - np.log(P[1]) +0.5* (np.dot(np.dot(m1.reshape(1,-1),\ np.linalg.inv(C0)),m1.reshape(-1,1)) - np.dot(np.dot(m0.reshape(1,-1),np.linalg.inv(C0)),m0.reshape(-1,1)))在贝叶斯分类器中,构造分类器需要知道类概率密度函数,如果按先验知识已知其分布,则只需知道分布的参数即可。(例如:类概率密度是正态分布,它完全由其均值向量和协方差矩阵所确定)。
对均值向量和协方差矩阵的估计即为贝叶斯分类器中的一种参数估计问题。
参数估计的两种方式:
设模式的类概率密度函数为,则其均值向量定义为:
,其中
若以样本的平均值作为均值向量的近似值,则均值估计量为
,其中
为样本的数目
协方差矩阵,
其中的每个元素
其中,和
分别为
和
的第
和
个分量。
协方差矩阵写成向量形式为:,(后面这样算更简单一点)
协方差矩阵的估计量(当时)为:
假设已经计算了个样本的均值估计量,若再加上一个样本,其新的估计量
为:
其中为从
个样本计算得到的估计量。迭代的第一步应取
协方差矩阵估计量的迭代运算与上述相似:
将概率密度函数的参数估计量看成是随机变量,它可以是纯量、向量或矩阵。按这些估计量统计特性的先验知识,可以先粗略地预选出它们的密度函数。通过训练模式样本集
,利用贝叶斯公式设计一个迭代运算过程求出参数的后验概率密度
。当后验概率密度函数中的随机变量
的确定性提高时,可获得较准确的估计量。
按位异或:x ^ 0s = x, x ^ 1s = ~x, x ^ x = 0
按位与:x & 0s = 0, x & 1s = x, x & x = x
按位或:x | 0s = x, x | 1s = 1s, x | x = x
n & (n - 1)可以去除 n的位级表示中最低的那一位,例如对于二进制表示 11110100,减去 1得到 11110011,这两个数按位与得到 11110000。
n & (-n)可以得到n的位级表示中最低的那一位,例如对于二进制表示 11110100,取负得到 00001100,这两个数按位与得到 00000100。
给定两个十进制数字,求它们二进制表示的汉明距离(Hamming distance,即不同位的个数)。
class Solution {public: int hammingDistance(int x, int y) { int diff = x ^ y; int ans = 0; while(diff){ ans += diff & 1; diff >>= 1; } return ans; }};分析:将x和y按位异或,则不同的位置为1,相同的位置为0。然后将得到的结果与1进行与操作,为0说明是0,为1说明是1,就计数了1。然后将这个结果逐步右移就可以看出下一位了。
错误:第一道题不太熟悉。
颠倒给定的 32 位无符号整数的二进制位
class Solution {public: uint32_t reverseBits(uint32_t n) { uint32_t ans = 0; for(int i=0;i<32;++i){ ans <<= 1; ans += n & 1; n >>= 1; } return ans; }};分析:摆出一个0,然后左移,逐步加上n右移的数字。
错误:不太明白左右移这种东西
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
class Solution {public: int singleNumber(vector<int>& nums) { int ret = 0; for (auto e: nums) ret ^= e; return ret; }};分析:一个数字和 0进行按位异或会得到本身,一个数字和本身进行按位异或会得到0。因此在数组内部进行循环,两次的元素出现了一定会变为0,最后剩下的一个就是这个数字本身。
错误:不熟练
给定一个整数,判断它是否是4 的次方。
class Solution {public: bool isPowerOfFour(int n) { return n > 0 && !(n & (n - 1)) && (n & 1431655765); }};分析:首先我们考虑一个数字是不是2 的(整数)次方:如果一个数字n 是2 的整数次方,那么它的二进制一定是0…010…0 这样的形式;考虑到n - 1 的二进制是0…001…1,这两个数求按位与的结果一定是0。因此如果n & (n - 1) 为0,那么这个数是2 的次方。如果这个数也是4 的次方,那二进制表示中1 的位置必须为奇数位。我们可以把n 和二进制的10101…101(即十进制下的1431655765)做按位与,如果结果不为0,那么说明这个数是4的次方。
错误:不理解
给你一个字符串数组 words ,找出并返回 length(words[i]) * length(words[j]) 的最大值,并且这两个单词不含有公共字母。如果不存在这样的两个单词,返回 0 。
class Solution {public: int maxProduct(vector<string>& words) { unordered_map<int, int> hash; int ans = 0; for (const string & word : words) { int mask = 0, size = word.size(); for (const char & c : word) { mask |= 1 << (c - 'a'); } hash[mask] = max(hash[mask], size); for (const auto& [h_mask, h_len]: hash) { if (!(mask & h_mask)) { ans = max(ans, size * h_len); } } } return ans; }};分析:怎样快速判断两个字母串是否含有重复数字呢?可以为每个字母串建立一个长度为26的二进制数字,每个位置表示是否存在该字母。如果两个字母串含有重复数字,那它们的二进制表示的按位与不为0。
错误:看了思路后自己实现的。
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
class Solution {public: vector<int> countBits(int n) { vector<int> ans(n+1,0); for (int i = 1; i <= num; ++i){ dp[i] = i & 1? dp[i-1] + 1: dp[i>>1]; } return ans; }};分析:本题可以利用动态规划和位运算进行快速的求解。定义一个数组dp,其中dp[i] 表示数字i的二进制含有1 的个数。对于第i 个数字,如果它二进制的最后一位为1,那么它含有1 的个数
则为dp[i-1] + 1;如果它二进制的最后一位为0,那么它含有1 的个数和其算术右移结果相同,即dp[i>>1]。
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
class Solution {public: int missingNumber(vector<int>& nums) { int n = nums.size(); int total = n * (n + 1) / 2; int arrSum = 0; for (int i = 0; i < n; i++) { arrSum += nums[i]; } return total - arrSum; }};分析:高斯求和后相减即可
给定一个正整数,检查它的二进制表示是否总是 0、1 交替出现:换句话说,就是二进制表示中相邻两位的数字永不相同。
class Solution {public: bool hasAlternatingBits(int n) { int pre = 0; int sign = 0; while(n){ int ans = n & 1; if(sign == 1){ if(pre == ans){ return false; } } pre = ans; sign = 1; n >>= 1; } return true; }};分析:存储并判断即可
错误:有一点小问题,很快调通
给你一个整数 num ,输出它的补数。
class Solution {public: int findComplement(int num) { uint t = 1u << 31; while (! (t & num)) { num |= t; t >>= 1; } return ~num; }};分析:前边补1,然后就可以直接取反了
错误:没有思路
给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
class Solution {public: vector<int> singleNumber(vector<int>& nums) { map<int,int> mp; for(int i=0;i<nums.size();++i){ ++mp[nums[i]]; } vector<int> result; for(const auto &[a,b] : mp){ if(b == 1){ result.push_back(a); } } return result; }};分析:哈希表算了。。。
一遍AC
这东西和计组挺相关的,面试中应该不会怎么考察这种数学题,但不失为一种运算加速的好办法。
]]>利用辗转相除法求得两个数的最大公因数,将两个数相乘再除以最大公因数即可得到最小公倍数
int gcd(int a, int b) { return b == 0 ? a : gcd(b, a% b);}int lcm(int a, int b) { return a * b / gcd(a, b);}进一步也可以通过扩展欧几里得算法在求得 a和 b最大公因数的同时,也得到它们的系数 x和 y,从而使 ax + by = gcd(a, b)
int xGCD(int a, int b, int &x, int &y) { if (!b) { x = 1, y = 0; return a; } int x1, y1, gcd = xGCD(b, a % b, x1, y1); x = y1, y = x1 - (a / b) * y1; return gcd;}给定整数 n ,返回所有小于非负整数 n 的质数的数量 。
class Solution {public: int countPrimes(int n) { if(n <= 2){ return 0; } vector<bool> nums(n,true); for(int i=2;i<n;++i){ if(nums[i] == true){ for(int j=2*i;j<n;j += i){ nums[j] = false; } } } return accumulate(nums.begin(),nums.end(),0) - 2; }};分析:使用埃拉托斯特尼筛法即可。
错误:有点忘记算法了。
给定一个整数 num,将其转化为7进制,并以字符串形式输出。
class Solution {public: string convertToBase7(int num) { int sign = 0; if(num < 0){ num = -num; sign = 1; } if(num == 0){ return "0"; } string result = ""; while(num/7){ char c = num%7 + '0'; result = c + result; num /= 7; } if(num != 0){ char b = '0' + num; result = b + result; } if(sign == 1){ return '-' + result; } return result; }};分析:直接进制转换就行,注意进制转换的时候用十进制进行过渡比较方便。
错误:磕磕绊绊调通了。
给定一个整数 n ,返回 n! 结果中尾随零的数量。
class Solution {public: int trailingZeroes(int n) { return n == 0? 0: n / 5 + trailingZeroes(n / 5); }};分析:每个尾部的0由2*5 = 10而来,因此我们可以把阶乘的每一个元素拆成质数相乘,统计有多少个2和5。明显的,质因子2的数量远多于质因子5的数量,因此我们可以只统计阶乘结果里有多少个质因子5。
错误:没想到这么好的思路
给定两个字符串形式的非负整数 num1 和 num2 ,计算它们的和并同样以字符串形式返回。
class Solution {public: string addStrings(string num1, string num2) { int n1 = num1.size(); int n2 = num2.size(); --n1; --n2; string result = ""; int cnt = 0; while(n1 >= 0 && n2 >= 0){ int temp = num1[n1] - '0' + num2[n2] - '0' + cnt; if(temp >= 10){ cnt = 1; } else{ cnt = 0; } char c = temp%10 + '0'; result = c + result; --n1; --n2; } while(n1 >= 0){ int temp = num1[n1] - '0' + cnt; if(temp >= 10){ cnt = 1; } else{ cnt = 0; } char c = temp%10 + '0'; result = c + result; --n1; } while(n2 >= 0){ int temp = num2[n2] - '0' + cnt; if(temp >= 10){ cnt = 1; } else{ cnt = 0; } char c = temp%10 + '0'; result = c + result; --n2; } if(cnt == 1){ return '1' + result; } return result; }};分析:大数相加,没什么新的东西
一遍AC
给定一个整数,写一个函数来判断它是否是 3 的幂次方。如果是,返回 true ;否则,返回 false
class Solution {public: bool isPowerOfThree(int n) { if(n == 1){ return true; } for(long long i=3;i<INT_MAX;i*=3){ if(i == n){ return true; } } return false; }};分析:比较简单,有更好的解法,需要数学能力
错误:n=1没有考虑
给定一个数组,要求实现两个指令函数。第一个函数“shuffle”可以随机打乱这个数组,第二个函数“reset”可以恢复原来的顺序。
class Solution {public: Solution(vector<int>& nums) { this->nums = nums; this->original.resize(nums.size()); copy(nums.begin(), nums.end(), original.begin()); } vector<int> reset() { copy(original.begin(), original.end(), nums.begin()); return nums; } vector<int> shuffle() { if (nums.empty()) return {}; vector<int> shuffled(nums); int n = nums.size(); for (int i = n - 1; i >= 0; --i) { swap(shuffled[i], shuffled[rand() % (i + 1)]); } // 正向洗牌: // for (int i = 0; i < n; ++i) { // int pos = rand() % (n - i); // swap(shuffled[i], shuffled[i+pos]); // } return shuffled; }private: vector<int> nums; vector<int> original;};分析:经典的Fisher-Yates洗牌算法,原理是通过随机交换位置来实现随机打乱,有正向和反向两种写法
错误:类什么的还是不太会写
给定一个数组,数组每个位置的值表示该位置的权重,要求按照权重的概率去随机采样。
class Solution { vector<int> W;public: Solution(vector<int>& w) { partial_sum(w.begin(), w.end(), back_inserter(W)); } int pickIndex() { int pos = rand() % W.back(); return upper_bound(W.begin(), W.end(), pos) - W.begin(); }};分析:我们可以先使用 partial_sum求前缀和(即到每个位置为止之前所有数字的和),这个结果对于正整数数组是单调递增的。每当需要采样时,我们可以先随机产生一个数字,然后使用二分法查找其在前缀和中的位置,以模拟加权采样的过程。
错误:没思路
给你一个单链表,随机选择链表的一个节点,并返回相应的节点值。每个节点被选中的概率一样 。
class Solution { vector<int> arr;public: Solution(ListNode* head) { while (head) { arr.emplace_back(head->val); head = head->next; } } int getRandom() { return arr[rand() % arr.size()]; }};分析:用一个数组记录链表中的所有结点值,然后随机输出即可。
错误:思路简单就是不会写
给你一个整数 columnNumber ,返回它在 Excel 表中相对应的列名称。
class Solution {public: string convertToTitle(int columnNumber) { string ans; while (columnNumber > 0) { int a0 = (columnNumber - 1) % 26 + 1; ans += a0 - 1 + 'A'; columnNumber = (columnNumber - a0) / 26; } reverse(ans.begin(), ans.end()); return ans; }};分析:进制转换的变形题
错误:减法操作没想好
给你两个二进制字符串,返回它们的和(用二进制表示)。
class Solution {public: string addBinary(string a, string b) { int a_size = a.size(); int b_size = b.size(); --a_size; --b_size; int cnt = 0; int sign; string result = ""; while(a_size >= 0 && b_size >= 0){ sign = a[a_size] - '0' + b[b_size] - '0' + cnt; if(sign == 0){ result = "0" + result; cnt = 0; } else if(sign == 1){ result = "1" + result; cnt = 0; } else if(sign == 2){ result = "0" + result; cnt = 1; } else if(sign == 3){ result = "1" + result; cnt = 1; } --a_size; --b_size; } while(a_size >= 0){ sign = a[a_size] - '0' + cnt; if(sign == 0){ result = "0" + result; cnt = 0; } else if(sign == 1){ result = "1" + result; cnt = 0; } else if(sign == 2){ result = "0" + result; cnt = 1; } else if(sign == 3){ result = "1" + result; cnt = 1; } --a_size; } while(b_size >= 0){ sign = b[b_size] - '0' + cnt; if(sign == 0){ result = "0" + result; cnt = 0; } else if(sign == 1){ result = "1" + result; cnt = 0; } else if(sign == 2){ result = "0" + result; cnt = 1; } else if(sign == 3){ result = "1" + result; cnt = 1; } --b_size; } if(cnt == 1){ result = "1" + result; } return result; }};分析:还是大数加法
错误:忘记了,应该没什么错误
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
class Solution {public: vector<int> productExceptSelf(vector<int>& nums) { int n = nums.size(); vector<int> left(n); vector<int> right(n); int start = 1; left[0] = start; for(int i=1;i<n;++i){ left[i] = start * nums[i-1]; start = left[i]; } int end = 1; right[n-1] = end; for(int i=n-2;i>=0;--i){ right[i] = end * nums[i+1]; end = right[i]; } vector<int> result(n); for(int i=0;i<n;++i){ result[i] = left[i] * right[i]; } return result; }};分析:前缀积+后缀积
错误:看了一下思路,后面自己想通了实现了
给你一个长度为 n 的整数数组 nums ,返回使所有数组元素相等需要的最少移动数。在一步操作中,你可以使数组中的一个元素加 1 或者减 1 。
class Solution {public: int minMoves2(vector<int>& nums) { int n = nums.size(); sort(nums.begin(),nums.end()); int num = nums[n/2]; int sum2 = 0; for(int i=0;i<n;++i){ if(nums[i] > num){ sum2 += nums[i] - num; } else{ sum2 += num - nums[i]; } } return sum2; }};分析:如果仅仅考虑最大的数字和最小的数字,那么这个数字一定在这两个数字中间,去除掉后这个数字也一定在次大的和次小的数字之间。因此是中位数
错误:思路不对,开始想成平均数了
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
class Solution {public: int majorityElement(vector<int>& nums) { int candidate = -1; int count = 0; for (int num : nums) { if (num == candidate) ++count; else if (--count < 0) { candidate = num; count = 1; } } return candidate; }};分析:Boyer-Moore 算法:维护一个候选众数 candidate 和它出现的次数 count。初始时 candidate 可以为任意值,count 为 0;我们遍历数组 nums 中的所有元素,对于每个元素 x,在判断 x 之前,如果 count 的值为 0,我们先将 x 的值赋予 candidate,随后我们判断 x:如果 x 与 candidate 相等,那么计数器 count 的值增加 1;如果 x 与 candidate 不等,那么计数器 count 的值减少 1。在遍历完成后,candidate 即为整个数组的众数。
错误:算法想的不太好,没有想到最优的解法。
给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数,试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数。
class Solution {public: int rand10() { int row, col, idx; do { row = rand7(); col = rand7(); idx = col + (row - 1) * 7; } while (idx > 40); return 1 + (idx - 1) % 10; }};分析:调用两次rand7(),找到一些等概率的数字,然后拒绝掉另外的数字。
错误:想当然认为是直接乘法了。
编写一个算法来判断一个数 n 是不是快乐数。
class Solution {public: bool isHappy(int n) { int sum = 6; while(sum--){ string s = to_string(n); int t = 0; for(int i=0;i<s.size();++i){ t += (s[i] - '0') * (s[i] - '0'); } if(t == 1){ return true; } n = t; } return false; }};分析:看看会不会跳出循环
一遍AC,但是解法不够好,后面要用更好的方法进行尝试。
数学问题需要有数学基础,一般面试中应该用的比较少,有些问题还是挺有意思的。
]]>顾名思义,分治问题由“分”(divide)和“治”(conquer)两部分组成,通过把原问题分为子问题,再将子问题进行处理合并,从而实现对原问题的求解。我们在排序章节展示的归并排序就是典型的分治问题,其中“分”即为把大数组平均分成两个小数组,通过递归实现,最终我们会得到多个长度为1的子数组;“治”即为把已经排好序的两个小数组合成为一个排好序的大数组,从长度为1 的子数组开始,最终合成一个大数组。
给定一个只包含加、减和乘法的数学表达式,求通过加括号可以得到多少种不同的结果
class Solution {public: vector<int> diffWaysToCompute(string expression) { vector<int> ways; for(int i=0;i<expression.size();++i){ char c = expression[i]; if(c == '+' || c == '-' || c == '*'){ vector<int> left = diffWaysToCompute(expression.substr(0,i)); vector<int> right = diffWaysToCompute(expression.substr(i+1)); for(const int &l : left){ for(const int &r : right){ if(c == '+'){ ways.push_back(l+r); } else if(c == '-'){ ways.push_back(l-r); } else{ ways.push_back(l*r); } } } } } if (ways.empty()){ ways.push_back(stoi(expression)); } return ways; }};分析:利用分治思想,我们可以把加括号转化为,对于每个运算符号,先执行处理两侧的数学表达式,再处理此运算符号。注意边界情况,即字符串内无运算符号,只有数字。
错误:想不通的
class Solution {public: vector<int> beautifulArray(int n) { vector<int> ans; if(n==1){ ans.push_back(1); return ans; } int odd_num=(n+1)/2; int even_num=n/2; vector<int> left_arry=beautifulArray(odd_num); vector<int> right_arry=beautifulArray(even_num); //将左侧数组映射为奇数 for(auto &val:left_arry){ ans.push_back(val*2-1); } //将右侧数组映射为偶数 for(auto &val:right_arry){ ans.push_back(val*2); } return ans; }};分析:不懂
错误:不懂
class Solution {public: int maxCoins(vector<int>& nums) { int n = nums.size(); vector<vector<int>> rec(n + 2, vector<int>(n + 2)); vector<int> val(n + 2); val[0] = val[n + 1] = 1; for (int i = 1; i <= n; i++) { val[i] = nums[i - 1]; } for (int i = n - 1; i >= 0; i--) { for (int j = i + 2; j <= n + 1; j++) { for (int k = i + 1; k < j; k++) { int sum = val[i] * val[k] * val[j]; sum += rec[i][k] + rec[k][j]; rec[i][j] = max(rec[i][j], sum); } } } return rec[0][n + 1]; }};分析:不懂
错误:不懂
不懂不懂不懂啊啊啊啊啊
]]>举例:将长编码串用短编码串来代替:111111111111111111➡18个1
为什么要压缩?
为什么在IR中需要压缩?
IR中压缩的两个基本要求:无损压缩和随机访问
压缩的一个基本问题:对齐,即建立不同压缩单元之间的分界标识
有损压缩:丢弃一些信息-很多常用的预处理步骤可以看成是有损压缩
无损压缩:所有信息都保留-索引压缩中通常都使用无损压缩
词典压缩中词典的大小即词汇表的大小是关键
词汇表大小会随着文档集的大小增长而增长,没有办法估计数量。
存在一个经验规律可以进行估计:
Heaps定律:,其中
是词汇表大小,
是文档集的大小。参数
和
的一个经典取值是:
及
Heaps定律在对数空间下是线性的。
在容许拼写错误或者对拼写错误自动纠错的情况下,Heaps定律的效果如何?
倒排记录表压缩中词项的分布情况是关键
我们还需要知道在文档集中有多少高频词项和低频词项
Zipf定律:第常见的词项的频率
和
成正比
是语料中词项频率:词项
在所有文档中出现的次数
实际统计中可以发现拟合度并不是很高,但是可以发现高频词项很少,低频罕见词项很多。
一般而言,相对于倒排记录表,词典所占空间较小。但是我们想将词典放入内存,另外满足一些特定领域特定应用的需要,如手机、机
载计算机上的应用或要求快速启动等需求。因此,压缩词典也很重要。
定长数组方式下的词典存储:每个词项需要20(字符串)+4(词频)+4(指向倒排索引表的指针)=28个字节。
不足之处:
将整部词典看成单一字符串:4(词频)+4(指向倒排索引表的指针)+3(指向字符串的指针,按照实际大小决定,例如8*400000个位置需要$log_2(8 * 400000)< 24 $位来表示)+8(每个字符串平均需要8个字节)=19个字节
按块存储,假设块大小k=4,此时每4个词项只需要保留1个词项指针,但是同时需要增加4个字节(比较短,1个字节就可以)来表示每个词项的长度,因此每4个词项需要3+4=7B,比之前的节省了12-7=5B
但是不采用块存储方式下的词项查找是典型的二叉查找,而采用块存储方式下的词项查找需要进行顺序查找,块如果太大会影响效率。
每个块当中,会有公共前缀,可以采用前端编码方式继续压缩。
哪些前缀应该用于前端编码?需要在哪些方面有所权衡?
倒排记录表空间远大于词典,压缩关键是对每条倒排记录进行压缩
关键思想:存储 docID间隔而不是 docID本身
设计一个变长编码(variable length encoding):可变长编码对于小间隔采用短编码而对于长间隔采用长编码
可变字节(VB)码:设定一个专用位 (高位) c作为延续位(continuation bit),如果间隔表示少于7比特,那么c置1,将间隔编入一个
字节的后7位中;否则将高7位放入当前字节中,并将c置0,剩下的位数采用同样的方法进行处理,最后一个字节的c置1(表
示结束)
一元码:将n表示成n个1和最后一个0
基于位的编码:
编码:(不考虑0)
偏移部分是比特位,长度部分需要
比特位,因此全部编码需要
比特位。
组变长整数编码:
Simple9编码:每块4字节,前4位标识块内结构,剩余28位存储若干个数字,每个数字占用相同的位数。
]]>语料通常很大,而服务器内存通常相对较小,因此需要在内存有限的情况下的索引构建策略。
词项:一个语料中不同的词的数量
词条:一个语料中所有词的数量(包括重复的)
在构建索引时,每次解析一篇文档,因此对于每个词项而言,其倒排记录表不到最后一篇文档都是不完整的。
如果每个 (termID, docID)对占用 8个字节, 那么处理大规模语料需要大量的空间。
一般内存的容量比较小,没有办法将前面产生的倒排记录表全部放在内存中,需要在磁盘上存储中间结果。
内存的典型配置是几G ~ 几十G的内存或上百G或1-2T
磁盘空间通常有几T(小型服务器)或10T以上(磁盘阵列)
硬盘空间更大,但是在内存中访问数据会比从硬盘访问数据快很多(大概10倍以上的差距)
硬盘寻道时间是闲置时间:磁头在定位时不发生数据传输(假设使用的是机械硬盘)
因此一个大(连续)块的传输会比多个小块(非连续)的传输速度快
硬盘 I/O是基于块的:读写时是整块进行的。块大小:8KB到256KB不等
不能在硬盘上对倒排索引表进行排序,因为寻道的时间很慢,导致排序的时间也很慢。
一种减少寻道操作的排序:Blocked sort-based Indexing
将所有记录划分为每个大小约为10M的块,收集每一块的倒排记录,排序,将倒排索引写入硬盘,最后将不同的分块合并为一个大的倒排索引。
关键决策:块的大小-块越大,最后的合并操作就越少
合并的过程中需要在磁盘中同时保存数据的两份拷贝(合并前与正在合并),因此磁盘空间要足够大。
词项字符串的占用空间比较大,因此维护一个全局词典来将字符串映射到唯一的全局ID
合并的过程中,将每一个小块的一点点数据放入内存中进行排序,排序好了就放在写缓冲区中,写缓冲区满了就写回硬盘,直到排序完成。
可以将两两合并的方式优化为多项合并(multi-way merge):
termid的优先级队列(priority queue),每次迭代从队列中选取一个最小的未处理 termidtermid的倒排记录,并写入磁盘。BSBI算法的问题:
term映射成 termID。实际上倒排记录表可以直接采用 (term,docID)方式而不是(termID,docID)方式,但是此时中间文件(即待合并的倒排记录表)将会变得很大(字符串比整型数空间消耗更大)内存式单遍扫描索引构建算法:Single-pass in-memory indexing
关键思想:
term-termID的映射)在扫描文档的同时,直接在内存中维护一个不断更新的倒排索引
因此对每个块生成一个完整的倒排索引,这些独立的索引最后合并成一个大索引
最终合并词典的过程中,需要进行词项字符串的比较,因为此时没有全局词典提供词项-整数ID的映射。
BSBI算法:在分块索引阶段,BSBI算法维护一个全局Term (String) – Termid (int) 的映射表,局部索引为Termid及其倒排记录表,仍然按词典顺序排序。
SPIMI算法:分块索引阶段与BSBI算法不同在于建立局部词典和索引,无需全局词典。在合并阶段,将局部索引两两合并,最后产生全局词典建立Term – Termid的映射。
实际中文档会增加、删除和修改,因此词典和倒排记录表必须要动态更新。
最简单的方法:主索引(Main index)+辅助索引(Auxiliary index)
删除的处理:
问题:
辅助索引方式: 每次合并都需要处理每个倒排记录,索引构建时间为,其中
是所有倒排记录的个数
对数合并(Logarithmic merge):
对数合并算法能够缓解(随时间增长)索引合并的开销 → 用户并不感觉到响应时间上有明显延迟。
因此每次两两合并中两个索引的大小相同
索引数目的上界为 ,因此查询处理时需要合并
个索引,因此每个倒排记录需要合并
次,则索引构建时间为
,时间复杂度相比较辅助索引方式小了一个数量级。
某地全年365天,晴朗265天,非晴朗100天。判断明天天气如何?
令,
,则:
,
,因此
,明天晴天的概率更大。
令,
,
,
,
,
,
今天有晚霞,判断明天天气如何? 即计算,
今天没有晚霞,判断明天天气如何? 即计算,
利用贝叶斯决策原理:
和
的联合概率:
因此可以求得,则在前一天有晚霞的条件下晴天的概率要大于不是晴天的概率。
贝叶斯公式:
因此
贝叶斯决策:
基于观察特征、类别的贝叶斯公式:
也就是:
因此,即
如果存在,
两个变量进行决策,即计算
,则可以转换为计算
,
更改为比值的形式:
可以定义类别相似性函数
分母都是相同的,因此可以将转化为
概率有很多都是的形式,因此可以将
转化为
,将乘积的形式转换为和的形式。
对于两变量决策问题来说,可以计算决策边界,绘制后可以直观看出边界的形状,可能是直线也可能是曲线,这样实现了贝叶斯决策方法。
采用了“属性条件独立性假设”
关键问题:由训练样本学习类别条件概率和类别先验概率和
包括
的
个属性和
的
个类别,加上
,共有
个概率分布需要统计。
类别先验概率
类别概率密度 ,
对于来说,若
是离散的变量,则
,其中
表示
中在第
个属性上取值为
的样本组成的集合。
若是连续的变量,则
(由某一概率分布估计类别概率)
拉普拉斯平滑:避免因训练集样本不充分而导致概率估计值为零。
平滑后:,
为类别数;
,
为
的可能取值个数。
若是连续的变量,则
(设置其为正态分布的概率密度)
多维正态分布的概率密度:
在每个维度上都是正态分布:
贝叶斯学习将公式化简为对数的形式:
不同的高斯参数情况:
:均为正态分布(当各个类别先验相等时,退化为最小距离分类器,退化为垂直平分面)
:各类分布都相同
什么是人工智能?
“人工智能就是让机器来完成那些如果由人来做则需要智能的事情的科学”;
“人工智能就是研究如何使计算机去做只有人才能做的智能工作”
“人工智能是研究使计算机来模拟人的某些思维过程和智能行为 (如学习、推理、思考、规划等)的学科 ”
图灵测试思考的问题:
我们研究的是弱人工智能
对人工智能的期望
人工智能创新发展引领新一轮产业变革之势,推动人类社会进入智能化时代,人工智能成为世界各国竞相战略布局的新高地,我国人工智能综合实力不断提升。
机器学习是一门人工智能的科学
“机器学习是一门人工智能的科学,该领域的主要研究对象是人工智能,特别是如何在经验学习中改善具体算法的性能 。 Langley(1996)“
“机器学习是对能通过经验自动改进的计算机算法的研究 。 Tom Mitchell (1997)“
“机器学习是用数据或以往的经验,以此优化计算机程序的性能标准”。 Alpaydin (2004)
机器学习发展时期
推理期➡知识期➡学科形成➡蓬勃发展期
应用领域
机器学习研究意义
机器学习的一般过程
x到输出 y的映射,训练数据会有标签 y,分为回归问题和分类问题。x到输出 y的映射,不会提供标签,但是会给一个反馈表示目前的选择有多好。机器学习流程:
动态规划和其它遍历算法(如深/广度优先搜索)都是将原问题拆成多个子问题然后求解,他们之间最本质的区别是,动态规划保存子问题的解,避免重复计算。解决动态规划问题的关键是找到状态转移方程,这样我们可以通过计算和储存子问题的解来求解最终问题。同时也可以对动态规划进行空间压缩,起到节省空间消耗的效果。
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
class Solution {public: int climbStairs(int n) { vector<int> num(n+1); if(n <= 2){ return n; } else{ num[1] = 1; num[2] = 2; for(int i=3;i<=n;++i){ num[i] = num[i-1] + num[i-2]; } } return num[n]; }};分析:num[i]表示在第 i阶的方法数,则到达第 i阶的方法是到达第 i-1阶的方法和到达第 i-2阶的方法数之和。因此 num[i] = num[i-1] + num[i-2]。判断边界条件即可。
一遍AC
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统, 如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。给定一个代表每个房屋存放金额的非负整数数组,计算你不触动警报装置的情况下,一夜之内能够偷窃到的最高金额。
class Solution {public: int rob(vector<int>& nums) { int n = nums.size(); vector<int> dp(n+1); if(n == 1){ return nums[0]; } else if(n == 2){ return max(nums[0],nums[1]); } dp[1] = nums[0]; dp[2] = max(nums[0],nums[1]); for(int i=3;i<=n;++i){ dp[i] = max(dp[i-1],dp[i-2] + nums[i-1]); } return dp[n]; }};分析:定义一个数组 dp,dp[i]表示抢劫到第i个房子时,可以抢劫的最大数量。我们考虑 dp[i],此时可以抢劫的最大数量有两种可能,一种是我们选择不抢劫这个房子,此时累计的金额即为 dp[i-1];另一种是我们选择抢劫这个房子,那么此前累计的最大金额只能是 dp[i-2]。因此本题的状态转移方程为 dp[i] = max(dp[i-1],nums[i-1] + dp[i-2])。然后判断边界条件即可。
一遍AC
给定一个数组,求这个数组中连续且等差的子数组一共有多少个
class Solution {public: int numberOfArithmeticSlices(vector<int>& nums) { int n = nums.size(); if(n == 1 || n == 2){ return 0; } vector<int>dp(n+1); dp[0] = 0; dp[1] = 0; dp[2] = 0; for(int i=2;i < n;++i){ if(nums[i] - nums[i-1] == nums[i-1] - nums[i-2]){ dp[i+1] = dp[i] + 1; } } return accumulate(dp.begin(),dp.end(),0); }};分析:这道题略微特殊,因为要求是等差数列,可以很自然的想到子数组必定满足 num[i] - num[i-1] = num[i-1] - num[i-2]。然而由于我们对于 dp数组的定义通常为以 i结尾的,满足某些条件的子数组数量,而等差子数组可以在任意一个位置终结,因此此题在最后需要对 dp数组求和。
错误:最开始写的时候越界了
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
class Solution {public: int minPathSum(vector<vector<int>>& grid) { int m = grid.size(); int n = grid[0].size(); vector<vector<int>> dp(m,vector<int>(n,0)); dp[0][0] = grid[0][0]; for(int i=1;i<m;++i){ dp[i][0] = dp[i-1][0] + grid[i][0]; } for(int j=1;j<n;++j){ dp[0][j] = dp[0][j-1] + grid[0][j]; } for(int i=1;i<m;++i){ for(int j=1;j<n;++j){ dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j]; } } return dp[m-1][n-1]; }};分析:定义一个同样是二维的 dp数组,其中 dp[i][j]表示从左上角开始到 (i, j)位置的最优路径的数字和。因为每次只能向下或者向右移动,我们可以很容易得到状态转移方程 dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j],其中 grid表示原数组。
错误:注意区间,开多大的 dp数组以及怎么进行状态转移,不要把自己转蒙。
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。两个相邻元素间的距离为 1 。
class Solution {public: vector<vector<int>> updateMatrix(vector<vector<int>>& mat) { int m = mat.size(); int n = mat[0].size(); vector<vector<int>> dp(m,vector<int>(n,0)); if(mat[0][0] == 0){ dp[0][0] = 0; } else{ dp[0][0] = 10002; } for(int i=1;i<m;++i){ if(mat[i][0] == 0){ dp[i][0] = 0; } else{ dp[i][0] = dp[i-1][0] + 1; } } for(int j=1;j<n;++j){ if(mat[0][j] == 0){ dp[0][j] = 0; } else{ dp[0][j] = dp[0][j-1] + 1; } } for(int i=1;i<m;++i){ for(int j=1;j<n;++j){ if(mat[i][j] == 0){ dp[i][j] = 0; } else{ dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + 1; } } } for(int i=m-2;i>=0;--i){ if(mat[i][n-1] == 0){ dp[i][n-1] = 0; } else{ dp[i][n-1] = min(dp[i][n-1],dp[i+1][n-1] + 1); } } for(int j=n-2;j>=0;--j){ if(mat[m-1][j] == 0){ dp[m-1][j] = 0; } else{ dp[m-1][j] = min(dp[m-1][j],dp[m-1][j+1] + 1); } } for(int i=m-2;i>=0;--i){ for(int j=n-2;j>=0;--j){ if(mat[i][j] != 0){ dp[i][j] = min(dp[i][j],min(dp[i+1][j],dp[i][j+1])+1); } } } return dp; }};分析:从左上到右下进行一次动态搜索,再从右下到左上进行一次动态搜索。两次动态搜索即可完成四个方向上的查找。
错误:看了一下题解的思路,还是有点不敢想。另外要细心,注意越界!!!
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
class Solution {public: int maximalSquare(vector<vector<char>>& matrix) { int m = matrix.size(); int n = matrix[0].size(); vector<vector<int>> dp(m+1,vector<int>(n+1,0)); int maxside = 0; for(int i=1;i<=m;++i){ for(int j=1;j<=n;++j){ if(matrix[i-1][j-1] == '1'){ dp[i][j] = min(dp[i-1][j-1],min(dp[i][j-1],dp[i-1][j])) + 1; } maxside = max(maxside,dp[i][j]); } } return maxside * maxside; }};分析:dp[i][j]表示以 (i, j)为右下角的全由 1构成的最大正方形边长。
错误:状态转移方程没有想太好。
对于分割类型题,动态规划的状态转移方程通常并不依赖相邻的位置,而是依赖于满足分割条件的位置。
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
class Solution {public: int numSquares(int n) { vector<int> dp(n+1,100000000); dp[0] = 0; for(int i=1;i<=n;++i){ for(int j=1;j*j<=i;++j){ dp[i] = min(dp[i],dp[i-j*j]+1); } } return dp[n]; }};分析:dp[i]表示数字 i最少可以由几个完全平方数相加构成。
错误:没有思路
输入是一个由数字组成的字符串,输出是满足条件的解码方式总数。
class Solution {public: int numDecodings(string s) { int n = s.size(); if(s[0] == '0'){ return 0; } if(n == 1){ return 1; } vector<int>dp(n+1,1); int prev = s[0] - '0'; for(int i=2;i<=n;++i){ int cur = s[i-1] - '0'; if((prev == 0 || prev > 2) && cur == 0){ return 0; } if((prev == 1) || (prev == 2 && cur < 7)){ if(cur){ dp[i] = dp[i-1] + dp[i-2]; } else{ dp[i] = dp[i-2]; } } else{ dp[i] = dp[i-1]; } prev = cur; } return dp[n]; }};分析:dp[i]表示以当前第i个位置上的数字为结尾的表示方法总数。dp[i]取决于两个数字,当前的数字和前一个数字。如果当前数字是 0,而前一个数字不是 1或者 2,说明这两个数字不可能构成字符,因此直接返回 0。如果前一个数字是 1,当前的数字是什么都行,或者前一个数字是 2,而当前的数字是 0-6的某一个数,说明这两个能构成一种组合。同时如果当前的数字不是 0,那么这个数字自己也能构成一种。如果前一个数字是其他,说明不能和当前的数字产生关系了,就只能是当前的数字自己了。
错误:不明白
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s
class Solution {public: bool wordBreak(string s, vector<string>& wordDict) { int n = s.size(); vector<bool> dp(n+1,false); dp[0] = true; for(int i=1;i<=n;++i){ for(const string & word : wordDict){ int len = word.size(); if(i >= len && s.substr(i-len,len) == word){ dp[i] = dp[i] || dp[i-len]; } } } return dp[n]; }};分析:类似于完全平方数分割问题,这道题的分割条件由集合内的字符串决定,因此在考虑每个分割位置时,需要遍历字符串集合,以确定当前位置是否可以成功分割。注意对于位置0,需要初始化值为真。
对于子序列问题,第一种动态规划方法是,定义一个 dp数组,其中 dp[i]表示以 i结尾的子序列的性质。在处理好每个位置后,统计一遍各个位置的结果即可得到题目要求的结果。第二种动态规划方法是,定义一个 dp数组,其中 dp[i]表示到位置 i为止的子序列的性质,并不必须以 i结尾。这样 dp数组的最后一位结果即为题目所求,不需要再对每个位置进行统计。
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
class Solution {public: int lengthOfLIS(vector<int>& nums) { int n = nums.size(); vector<int> dp(n+1,1); dp[0] = 0; for(int i=1;i<=n;++i){ for(int j=0;j<i;j++){ if(nums[i-1] > nums[j]){ dp[i] = max(dp[i],dp[j+1]+1); } } } return *max_element(dp.begin(),dp.end()); }};分析: dp[i]表示以 i结尾的子序列的性质。简单动态规划即可。
错误:下标指代不清,初始化应该全部为1
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列,返回 0 。
class Solution {public: int longestCommonSubsequence(string text1, string text2) { int m = text1.size(); int n = text2.size(); vector<vector<int>> dp(m+1,vector<int>(n+1,0)); for(int i=1;i<=m;++i){ for(int j=1;j<=n;++j){ if(text1[i-1] == text2[j-1]){ dp[i][j] = dp[i-1][j-1] + 1; } else{ dp[i][j] = max(dp[i][j-1],dp[i-1][j]); } } } return dp[m][n]; }};分析:建立一个二维数组 dp,其中 dp[i][j]表示到第一个字符串位置 i为止、到第二个字符串位置 j为止、最长的公共子序列长度。
错误:没想到是二维的动态规划。
给定一个正整数数组,求是否可以把这个数组分成和相等的两部分。
class Solution {public: bool canPartition(vector<int>& nums) { int n = nums.size(); int sum = accumulate(nums.begin(),nums.end(),0); if(sum % 2 == 1){ return false; } sum /= 2; vector<vector<int>> dp(n+1,vector<int>(sum+1,false)); dp[0][0] = true; for(int i=1;i<=n;++i){ for(int j=0;j<=sum;++j){ if(j < nums[i-1]){ dp[i][j] = dp[i-1][j]; } else{ dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i-1]]; } } } return dp[n][sum]; }};分析:背包问题,价值是一半,背包容量没有限制。比较重要的是 dp[0][0] =true,后续的判断都是从这个 true继承过来的。
错误:思路不够完善
给你一个二进制字符串数组 strs 和两个整数 m 和 n ,请你找出并返回 strs 的最大子集的长度,该子集中最多有 m 个 0 和 n 个 1
class Solution {public: static vector<int> getzerosandones(string &str){ vector<int> result(2); int n = str.size(); for(int i=0;i<n;++i){ if(str[i] == '0'){ ++result[0]; } else{ ++result[1]; } } return result; } int findMaxForm(vector<string>& strs, int m, int n) { int l = strs.size(); vector<vector<vector<int>>> dp(l+1,vector<vector<int>>(m+1,vector<int>(n+1,0))); for(int i=1;i<=l;++i){ vector<int> && zerosones = getzerosandones(strs[i-1]); int zero = zerosones[0]; int one = zerosones[1]; for(int j=0;j<=m;++j){ for(int k=0;k<=n;++k){ dp[i][j][k] = dp[i-1][j][k]; if(j >= zero && k >= one){ dp[i][j][k] = max(dp[i][j][k],dp[i-1][j-zero][k-one]+1); } } } } return dp[l][m][n]; }};分析:三维的背包问题,要同时考虑两个背包的容量。
错误:还是不理解
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1 ,可以认为每种硬币的数量是无限的。
class Solution {public: int coinChange(vector<int>& coins, int amount) { int n = coins.size(); vector<vector<int>> dp(n+1,vector<int>(amount+1,amount+1)); dp[0][0] = 0; for(int i=0;i<=amount;++i){ for(int j=1;j<=n;++j){ if(coins[j-1] <= i){ dp[j][i] = min(dp[j-1][i],dp[j][i-coins[j-1]]+1); } else{ dp[j][i] = dp[j-1][i]; } } } return dp[n][amount] == amount+1 ? -1 : dp[n][amount]; }};分析:完全背包问题。
错误:就是不理解
给定两个字符串,已知你可以删除、替换和插入任意字符串的任意字符,求最少编辑几步可以将两个字符串变成相同。
class Solution {public: int minDistance(string word1, string word2) { int m = word1.size(); int n = word2.size(); vector<vector<int>> dp(m+1,vector<int>(n+1,0)); for(int i=0;i<=m;++i){ dp[i][0] = i; } for(int j=0;j<=n;++j){ dp[0][j] = j; } for(int i=1;i<=m;++i){ for(int j=1;j<=n;++j){ if(word1[i-1] == word2[j-1]){ dp[i][j] = dp[i-1][j-1]; } else{ dp[i][j] = min(dp[i-1][j-1],min(dp[i][j-1],dp[i-1][j])) + 1; } } } return dp[m][n]; }};分析:使用一个二维数组 dp[i][j],表示将第一个字符串到位置 i为止,和第二个字符串到位置 j为止,最多需要几步编辑。当第 i位和第 j位对应的字符相同时,dp[i][j]等于 dp[i-1][j-1];当二者对应的字符不同时,修改的消耗是 dp[i-1][j-1]+1,插入 i位置/删除 j位置的消耗是 dp[i][j-1] + 1,插入 j位置/删除 i位置的消耗是 dp[i-1][j] + 1。
错误:初始化没有做好。
给定一个字母A,已知你可以每次选择复制全部字符,或者粘贴之前复制的字符,求最少需要几次操作可以把字符串延展到指定长度。
class Solution {public: int minSteps(int n) { vector<int> dp(n+1,0); for(int i=2;i<=n;++i){ dp[i] = i; for(int j=2;j * j <= i;++j){ if(i % j == 0){ dp[i] = dp[j] + dp[i/j]; break; } } } return dp[n]; }};分析:我们使用一个一维数组dp,其中位置i表示延展到长度i的最少操作次数。对于每个位置j,如果j可以被i整除,那么长度i就可以由长度j操作得到,其操作次数等价于把一个长度为1的A延展到长度为i/j。因此我们可以得到递推公式dp[i] = dp[j] + dp[i/j]
错误:还是不会想。
给定一个字符串和一个正则表达式,求该字符串是否可以被匹配。
class Solution {public: bool isMatch(string s, string p) { int m = s.size(); int n = p.size(); vector<vector<bool>> dp(m+1,vector<bool>(n+1,false)); dp[0][0] = true; for(int i=1;i<=n;++i){ if(p[i-1] == '*'){ dp[0][i] = dp[0][i-2]; } } for(int i=1;i<=m;++i){ for(int j=1;j<=n;++j){ if(p[j-1] == '.'){ dp[i][j] = dp[i-1][j-1]; } else if (p[j-1] != '*') { dp[i][j] = dp[i-1][j-1] && p[j-1] == s[i-1]; } else if (p[j-2] != s[i-1] && p[j-2] != '.') { dp[i][j] = dp[i][j-2]; } else { dp[i][j] = dp[i][j-1] || dp[i-1][j] || dp[i][j-2]; } } } return dp[m][n]; }};分析:使用一个二维数组 dp,其中 dp[i][j]表示以 i截止的字符串是否可以被以 j截止的正则表达式匹配。
错误:没有思路
给定一段时间内每天某只股票的固定价格,已知你只可以买卖各一次,求最大的收益。
class Solution {public: int maxProfit(vector<int>& prices) { int sell = 0, buy = INT_MIN; for (int i = 0; i < prices.size(); ++i) { buy = max(buy, -prices[i]); sell = max(sell, buy + prices[i]); } return sell; }};分析:遍历一次就行,记录一下最小的价格,然后遍历到每个价格的时候看看是不是比这个价格更大就行了。
错误:简单的问题也不会想了。。。
给定一段时间内每天某只股票的固定价格,已知你只可以买卖各 k次,且每次只能拥有一支股票,求最大的收益。
给定一段时间内每天某只股票的固定价格,已知每次卖出之后必须冷却一天,且每次只能拥有一支股票,求最大的收益。
class Solution {public: int maxProfit(vector<int>& prices) { int n = prices.size(); if(n == 0){ return 0; } vector<int> buy(n),sell(n),s1(n),s2(n); s1[0] = buy[0] = -prices[0]; sell[0] = s2[0] = 0; for(int i=1;i<n;++i){ buy[i] = s2[i-1] - prices[i]; s1[i] = max(buy[i-1],s1[i-1]); sell[i] = max(buy[i-1],s1[i-1]) + prices[i]; s2[i] = max(s2[i-1],sell[i-1]); } return max(sell[n-1],s2[n-1]); }};分析:状态机求解
错误:完全不懂
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
class Solution {public: int rob(vector<int>& nums) { int n = nums.size(); if(n == 1){ return nums[0]; } else if(n == 2){ return max(nums[0],nums[1]); } vector<int> dp(n+1); int answer_a; dp[0] = dp[1] = dp[2] = nums[0]; for(int i=3;i<n;++i){ dp[i] = max(dp[i-1],dp[i-2] + nums[i-1]); } answer_a = dp[n-1]; dp[0] = dp[1] = 0; dp[2] = nums[1]; for(int i=3;i<=n;++i){ dp[i] = max(dp[i-1],dp[i-2] + nums[i-1]); } return max(answer_a,dp[n]); }};分析:分两种情况进行讨论,选第一个和不选第一个。
错误:看了一下思路,最后调通了
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
class Solution {public: int maxSubArray(vector<int>& nums) { int n = nums.size(); vector<int> dp(n+1); dp[0] = -20000; for(int i=1;i<=n;++i){ dp[i] = max(nums[i-1],dp[i-1] + nums[i-1]); } return *max_element(dp.begin(),dp.end()); }};分析:dp数组记录以当前位置为结尾的子数组的最大和,因此后面再加一位有两种可能,一是和这个一起,二是自己一组。最后取最大的部分即可。
错误:开始没想太懂,后来自己调通了。
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
class Solution {public: int integerBreak(int n) { vector<int> dp(n+1); for(int i=2;i<=n;++i){ for(int j=1;j<i;++j){ dp[i] = max(dp[i],max(j*(i-j),j*dp[i-j])); } } return dp[n]; }};分析:对于正整数n,当n≥2时,可以拆分成至少两个正整数的和。令x是拆分出的第一个正整数,则剩下的部分是n-x,n−x可以不继续拆分,或者继续拆分成至少两个正整数的和。每个正整数对应的最大乘积取决于比它小的正整数对应的最大乘积。
错误:分割问题还是没有什么思路
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的 最小步数 。每步可以删除任意一个字符串中的一个字符。
class Solution {public: int minDistance(string word1, string word2) { int m = word1.size(); int n = word2.size(); vector<vector<int>> dp(m+1,vector<int>(n+1,0)); for(int i=0;i<=m;++i){ dp[i][0] = i; } for(int i=0;i<=n;++i){ dp[0][i] = i; } for(int i=1;i<=m;++i){ for(int j=1;j<=n;++j){ if(word1[i-1] == word2[j-1]){ dp[i][j] = dp[i-1][j-1]; } else{ dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + 1; } } } return dp[m][n]; }};分析:不相等的时候看两边的字符串,相等的时候看前一位
错误:字符相等的时候有些没想明白,后来调通了
给出 n 个数对。 在每一个数对中,第一个数字总是比第二个数字小。现在,我们定义一种跟随关系,当且仅当 b < c 时,数对 (c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。给定一个数对集合,找出能够形成的最长数对链的长度。你不需要用到所有的数对,你可以以任何顺序选择其中的一些数对来构造。
class Solution {public: static bool cmp(vector<int> &a,vector<int> &b){ return a[0] < b[0]; } int findLongestChain(vector<vector<int>>& pairs) { int n = pairs.size(); sort(pairs.begin(),pairs.end(),cmp); vector<int> dp(n+1,1); for(int i=1;i<=n;++i){ for(int j=0;j<i-1;++j){ if(pairs[i-1][0] > pairs[j][1]){ dp[i] = max(dp[i],dp[j+1]+1); } } } return dp[n]; }};分析:排序后进行动态规划即可
错误:排序有问题。
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。给你一个整数数组 nums ,返回 nums 中作为摆动序列的最长子序列的长度 。
class Solution {public: int wiggleMaxLength(vector<int>& nums) { int n = nums.size(); if(n == 1 || (n == 2 && nums[0] != nums[1])){ return n; } if(n == 2 && nums[0] == nums[1]){ return 1; } vector<int> up(n),down(n); up[0] = down[0] = 1; for(int i=1;i<n;++i){ if(nums[i] > nums[i-1]){ up[i] = max(up[i-1],down[i-1] + 1); down[i] = down[i-1]; } else if(nums[i] < nums[i-1]){ up[i] = up[i-1]; down[i] = max(down[i-1],up[i-1] + 1); } else{ up[i] = up[i-1]; down[i] = down[i-1]; } } return max(up[n-1],down[n-1]); }};分析:每当我们选择一个元素作为摆动序列的一部分时,这个元素要么是上升的,要么是下降的,这取决于前一个元素的大小。那么列出状态表达式为:up[i]表示以前 i个元素中的某一个为结尾的最长的「上升摆动序列」的长度。down[i]表示以前i个元素中的某一个为结尾的最长的「下降摆动序列」的长度。
错误:没有思路
class Solution {public: int findTargetSumWays(vector<int>& nums, int target) { int sum = 0; for (int& num : nums) { sum += num; } int diff = sum - target; if (diff < 0 || diff % 2 != 0) { return 0; } int n = nums.size(), neg = diff / 2; vector<vector<int>> dp(n + 1, vector<int>(neg + 1)); dp[0][0] = 1; for (int i = 1; i <= n; i++) { int num = nums[i - 1]; for (int j = 0; j <= neg; j++) { dp[i][j] = dp[i - 1][j]; if (j >= num) { dp[i][j] += dp[i - 1][j - num]; } } } return dp[n][neg]; }};分析:转化为0-1背包问题
错误:背包问题一直都不怎么理解,就先这样,后续再补充。
给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。返回获得利润的最大值。
class Solution {public: int maxProfit(vector<int>& prices, int fee) { int n = prices.size(); vector<vector<int>> dp(n, vector<int>(2)); dp[0][0] = 0, dp[0][1] = -prices[0]; for (int i = 1; i < n; ++i) { dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee); dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]); } return dp[n - 1][0]; }};分析:股票问题的变形,比较类似于状态机,不是很能想得到
错误:股票问题后面也要再做一做
动态规划比较有难度,一是状态转移方程的写法,二是在实现状态转移中的各种细节。以后对于动态规划还要勤加练习,多练习思考方法。
]]>首先讲授人工智能基础知识,进而分三个专题(联结主义、符号主义、行为主义)介绍人工智能的新进展。
智能:个体适应环境并能在不同环境中实现其目标的能力。
蕴含众多方面的能力
人工智能:
机械智能 ➡ 理性思考 ➡ 数理逻辑 ➡ 计算思维
萌芽期
孕育期(文艺复兴以来)
形成期(1956年-1961年)
发展期(60年代)
寒冬期(60年代末到70年代初)
艰难前行(70年代)
走向工业(80年代)
今天
Can Machine Think?
图灵测试:一个人(C)在完全不接触对方(A和B)的情况下,和对方进行一系列的问答,如果在相当长时间内,他无法根据这些问题判断对方是人(B)还是计算机(A),那么,就认为该计算机具有同人相当的智能(即计算机是能思维的)。
质疑:
图灵预言:到2000年,机器可以做到5分钟内以30%的可能性让普通人分辨不出其是机器还是人。
图灵测试案例
达特茅斯会议:1956年在达特茅斯学院发起
发起人
会议成就
并且出现了人工智能三大学派:
衍生出:逻辑、专家系统、知识库
衍生出:人工神经网络、认知科学、类脑计算
衍生出:控制论、多智能体、强化学习等
三大层次
四大问题
弱人工智能
强人工智能
人工智能恐慌
人工智能实现了会怎样?
人工智能伦理
“准人”水平的人工智能:手写识别、物体识别、语音识别、自然语言处理、词义消歧、机器翻译
“过人”水平的人工智能:游戏、双陆棋、国际象棋、桥牌、填词、拼字、七巧板、自动驾驶、智力竞赛问答、OCR字符识别
“许多尖端的人工智能由于应用广泛,已经不再被称为人工智能。因为,人们一旦觉得某些东西非常有用并广泛使用,就不再称之为人工智能了。”
人工智能是国家战略:2017年,国务院印发了《新一代人工智能发展规划》,人工智能成为国家战略,大数据在人工智能中将扮演越来越重要的角色。
人工智能经过60余年的发展取得了长足进步,近年来呈现出爆发之势,但总体上还处于初级阶段,通用智能之路任重道远。
]]>模式识别的目的:利用计算机对物理对象进行分类,在错误概率最小的条件下,使识别的结果尽量与客观物体相符合。
模式识别的数学化:Y= F(X),X的定义域取自特征集,Y的值域为类别的标号集,F是模式识别的判别方法。
机器学习:研究如何构造理论、算法和计算机系统,让机器通过从数据中学习后可以进行分类和识别事物、推理决策、预测未来等工作。
在特征空间和解释空间之间找到一种映射关系,这种映射也称之为假说。
c个类别的集合表示为Ω,称为解释空间。机器学习的目标:针对某类任务 T,用 P衡量性能,根据经验 E来学习和自我完善,提高性能。
假说的两种获得方法:
数据聚类
统计分类
结构模式识别
神经网络
监督学习
无监督学习
半监督学习
强化学习
集成学习
深度学习
元学习
多任务学习
多标记学习
对抗学习
模式识别系统与机器学习系统构成对比


在传送带上用光学传感器件对鱼按品种分类
深度优先搜索和广度优先搜索是两种最常见的优先搜索方法,它们被广泛地运用在图和树等结构中进行搜索。
岛屿是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直的四个方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。岛屿的面积是岛上值为 1 的单元格的数目。计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
class Solution {public: static int DFS(vector<vector<int>> & grid,int x,int y,int m,int n){ if(x < 0 || x >= m || y < 0 || y >= n || grid[x][y] == 0){ return 0; } grid[x][y] = 0; return 1 + DFS(grid,x+1,y,m,n) + DFS(grid,x-1,y,m,n) + DFS(grid,x,y+1,m,n) + DFS(grid,x,y-1,m,n); } int maxAreaOfIsland(vector<vector<int>>& grid) { int m = grid.size(); int n = grid[0].size(); int maxarea = 0; for(int i=0;i<m;++i){ for(int j=0;j<n;++j){ if(grid[i][j] == 1){ maxarea = max(maxarea,DFS(grid,i,j,m,n)); } } } return maxarea; }};分析:标准的DFS,重点要判断是否越界以及返回值的处理。
错误:基本思路是正确的,返回值的处理有问题,以及想的有些复杂。
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。返回矩阵中 省份 的数量。
class Solution {public: static void DFS(vector<vector<int>>& isConnected, vector<bool>& visit,int x,int n){ if(x < 0 || x >= n || visit[x] == true){ return; } visit[x] = true; for(int i=0;i<n;i++){ if(isConnected[x][i] == 1){ DFS(isConnected,visit,i,n); } } return; } int findCircleNum(vector<vector<int>>& isConnected) { int n = isConnected.size(); int sumCount = 0; vector<bool> visit(n); fill(visit.begin(),visit.end(),false); for(int i=0;i<n;i++){ if(visit[i] == false){ DFS(isConnected,visit,i,n); ++sumCount; } } return sumCount; }};分析:还是比较基本的DFS,只不过是一个一维的DFS,比较简单
错误:开始的思路有一些偏差,后面纠正过来没什么问题了。
有一个 m × n 的矩形岛屿,与太平洋和大西洋相邻。 太平洋”处于大陆的左边界和上边界,而“大西洋”处于大陆的右边界和下边界。这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights , heights[r][c] 表示坐标 (r, c) 上单元格高于海平面的高度 。岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。返回网格坐标 result 的 2D 列表 ,其中 result[i] = [r<sub>i</sub>, c<sub>i</sub>] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。
class Solution {public: static void DFS(vector<vector<int>>& heights,vector<vector<bool>>& Ocean,int x,int y,int m,int n){ Ocean[x][y] = true; if(x+1 < m && Ocean[x+1][y] == false && heights[x+1][y] >= heights[x][y]){ DFS(heights,Ocean,x+1,y,m,n); } if(x-1 >= 0 && Ocean[x-1][y] == false && heights[x-1][y] >= heights[x][y]){ DFS(heights,Ocean,x-1,y,m,n); } if(y+1 < n && Ocean[x][y+1] == false && heights[x][y+1] >= heights[x][y]){ DFS(heights,Ocean,x,y+1,m,n); } if(y-1 >= 0 && Ocean[x][y-1] == false && heights[x][y-1] >= heights[x][y]){ DFS(heights,Ocean,x,y-1,m,n); } return; } vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) { int m = heights.size(); int n = heights[0].size(); vector<vector<bool>> pOcean(m,vector<bool>(n,false)); vector<vector<bool>> aOcean(m,vector<bool>(n,false)); for(int i=0;i<m;++i){ if(pOcean[i][0] == false){ DFS(heights,pOcean,i,0,m,n); } if(aOcean[i][n-1] == false){ DFS(heights,aOcean,i,n-1,m,n); } } for(int i=0;i<n;++i){ if(pOcean[0][i] == false){ DFS(heights,pOcean,0,i,m,n); } if(aOcean[m-1][i] == false){ DFS(heights,aOcean,m-1,i,m,n); } } vector<vector<int>> result; for(int i=0;i<m;++i){ for(int j=0;j<n;++j){ if(pOcean[i][j] == true && aOcean[i][j] == true){ result.push_back(vector<int>{i,j}); } } } return result; }};分析:仍然是比较普通的DFS,不过只要对周围的一圈进行DFS就足够了,不需要全部遍历。
错误:细节问题,写的时候一定好好检查 m和 n有没有用反。
给定一个不含重复数字的数组 nums ,返回其所有可能的全排列。
class Solution {public: static void backtracking(vector<int>& nums,int level,vector<vector<int>>&result){ if(level == nums.size()-1){ result.push_back(nums); return; } for(int i=level;i<nums.size();i++){ swap(nums[i],nums[level]); backtracking(nums,level+1,result); swap(nums[i],nums[level]); } } vector<vector<int>> permute(vector<int>& nums) { vector<vector<int>> result; backtracking(nums,0,result); return result; }};分析:对于每一个当前位置 i,我们可以将其于之后的任意位置交换,然后继续处理位置 i+1,直到处理到最后一位。为了防止我们每此遍历时都要新建一个子数组储存位置 i之前已经交换好的数字,我们可以利用回溯法,只对原数组进行修改,在递归完成后再修改回来。
错误:学习一下回溯法的基本框架。
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
class Solution {public: static void backtracking(vector<vector<int>> &result,vector<int> &temp,int n,int level,int k){ if(temp.size() == k){ result.push_back(temp); return; } for(int i=level+1;i<=n;++i){ temp.push_back(i); backtracking(result,temp,n,i,k); temp.pop_back(); } } vector<vector<int>> combine(int n, int k) { vector<vector<int>> result; vector<int> temp; backtracking(result,temp,n,0,k); return result; }};分析:类似于排列问题,也可以进行回溯。排列回溯的是交换的位置,而组合回溯的是是否把当前的数字加入结果中。
错误:需要有一个记录状态的数值,要不然就变成全排列了。
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
class Solution {public: static void backtracking(vector<vector<char>>& board, string &word,int x,int y,int m,int n,vector<vector<bool>> &visited,bool &find,int level){ if(x < 0 || x >= m || y < 0 || y >= n){ return; } if(visited[x][y] == true || word[level] != board[x][y] || find == true){ return; } if(level == word.size() - 1){ find = true; return; } visited[x][y] = true; backtracking(board,word,x+1,y,m,n,visited,find,level+1); backtracking(board,word,x-1,y,m,n,visited,find,level+1); backtracking(board,word,x,y+1,m,n,visited,find,level+1); backtracking(board,word,x,y-1,m,n,visited,find,level+1); visited[x][y] = false; return; } bool exist(vector<vector<char>>& board, string word) { int m = board.size(); int n = board[0].size(); vector<vector<bool>> visited(m, vector<bool>(n, false)); bool find = false; for(int i=0;i<m;++i){ for(int j=0;j<n;++j){ backtracking(board,word,i,j,m,n,visited,find,0); } } return find; }};分析:典型回溯题,判断条件需要多一些
错误1:回溯法不要有返回值,都使用引用传参
错误2:判断条件:①是否越界②访问过③不匹配④已经确定对的了
n皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数 n ,返回所有不同的n皇后问题的解决方案。
class Solution {public: void backtracking(vector<vector<string>> & result,vector<string> tempresult,vector<bool> &column,vector<bool> &ldiag,vector<bool> &rdiag,int n,int level){ if(level == n){ result.push_back(tempresult); return; } for(int i=0;i<n;++i){ if (column[i] || ldiag[n-level+i-1] || rdiag[level+i]) { continue; } tempresult[level][i] = 'Q'; column[i] = ldiag[n-level+i-1] = rdiag[level+i] = true; backtracking(result,tempresult,column,ldiag,rdiag,n,level+1); column[i] = ldiag[n-level+i-1] = rdiag[level+i] = false; tempresult[level][i] = '.'; } return; } vector<vector<string>> solveNQueens(int n) { vector<vector<string>> result; string tempstring = ""; for(int i=0;i<n;i++){ tempstring += "."; } vector<string> tempresult(n,tempstring); vector<bool> column(n,false); vector<bool> ldiag(2*n-1,false); vector<bool> rdiag(2*n-1,false); backtracking(result,tempresult,column,ldiag,rdiag,n,0); return result; }};分析:最典型的回溯法之一。类似于在矩阵中寻找字符串,本题也是通过修改状态矩阵来进行回溯。不同的是,我们需要对每一行、列、左斜、右斜建立访问数组,来记录它们是否存在皇后。本题需要判断满足条件的结果中每一行或列有且仅有一个皇后。这是因为我们一共只有 n行和 n列。所以如果我们通过对每一行遍历来插入皇后,我们就不需要对行建立访问数组了。
错误:再理解吧。
在给定的二维二进制数组 A 中,存在两座岛。(岛是由四面相连的 1 形成的一个最大组。)现在,我们可以将 0 变为 1,以使两座岛连接起来,变成一座岛。返回必须翻转的 0 的最小数目。(可以保证答案至少是 1 。)
class Solution {public: static void DFS(vector<vector<int>>& grid,queue<pair<int,int>> &points,int x,int y,int n){ if(x < 0 || x >= n || y < 0 || y >= n || grid[x][y] == 2){ return; } if(grid[x][y] == 0){ points.push({x,y}); return; } grid[x][y] = 2; DFS(grid,points,x+1,y,n); DFS(grid,points,x-1,y,n); DFS(grid,points,x,y+1,n); DFS(grid,points,x,y-1,n); return; } int shortestBridge(vector<vector<int>>& grid) { int n = grid.size(); queue<pair<int,int>> points; bool find = false; for(int i=0;i<n;++i){ if(find == true){ break; } for(int j=0;j<n;++j){ if(grid[i][j] == 1){ find = true; DFS(grid,points,i,j,n); break; } } } int level = 0; vector<vector<int>> d = {{0,1},{0,-1},{1,0},{-1,0}}; while(!points.empty()){ ++level; int n_points = points.size(); while(n_points--){ auto [r,c] = points.front(); grid[r][c] = 2; points.pop(); for(int k=0;k<4;k++){ int x = r + d[k][0]; int y = c + d[k][1]; if(x >= 0 && y >= 0 && x < n && y < n){ if(grid[x][y] == 1){ return level; } else if(grid[x][y] == 0){ grid[x][y] = 2; points.push({x,y}); } } } } } return 0; }};分析:先通过任意搜索方法找到其中一个岛屿,然后利用广度优先搜索,查找其与另一个岛屿的最短距离
错误:BFS好久没有练习了,也是生疏了。
给定一个起始字符串和一个终止字符串,以及一个单词表,求是否可以将起始字符串每次改一个字符,直到改成终止字符串,且所有中间的修改过程表示的字符串都可以在单词表里找到。若存在,输出需要修改次数最少的所有更改方式。
class Solution {public: vector<vector<string>> findLadders(string beginWord, string endWord, vector<string> &wordList) { vector<vector<string>> res; // 因为需要快速判断扩展出的单词是否在 wordList 里,因此需要将 wordList 存入哈希表,这里命名为「字典」 unordered_set<string> dict = {wordList.begin(), wordList.end()}; // 修改以后看一下,如果根本就不在 dict 里面,跳过 if (dict.find(endWord) == dict.end()) { return res; } // 特殊用例处理 dict.erase(beginWord); // 第 1 步:广度优先搜索建图 // 记录扩展出的单词是在第几次扩展的时候得到的,key:单词,value:在广度优先搜索的第几层 unordered_map<string, int> steps = {{beginWord, 0}}; // 记录了单词是从哪些单词扩展而来,key:单词,value:单词列表,这些单词可以变换到 key ,它们是一对多关系 unordered_map<string, set<string>> from = {{beginWord, {}}}; int step = 0; bool found = false; queue<string> q = queue<string>{{beginWord}}; int wordLen = beginWord.length(); while (!q.empty()) { step++; int size = q.size(); for (int i = 0; i < size; i++) { const string currWord = move(q.front()); string nextWord = currWord; q.pop(); // 将每一位替换成 26 个小写英文字母 for (int j = 0; j < wordLen; ++j) { const char origin = nextWord[j]; for (char c = 'a'; c <= 'z'; ++c) { nextWord[j] = c; if (steps[nextWord] == step) { from[nextWord].insert(currWord); } if (dict.find(nextWord) == dict.end()) { continue; } // 如果从一个单词扩展出来的单词以前遍历过,距离一定更远,为了避免搜索到已经遍历到,且距离更远的单词,需要将它从 dict 中删除 dict.erase(nextWord); // 这一层扩展出的单词进入队列 q.push(nextWord); // 记录 nextWord 从 currWord 而来 from[nextWord].insert(currWord); // 记录 nextWord 的 step steps[nextWord] = step; if (nextWord == endWord) { found = true; } } nextWord[j] = origin; } } if (found) { break; } } // 第 2 步:回溯找到所有解,从 endWord 恢复到 beginWord ,所以每次尝试操作 path 列表的头部 if (found) { vector<string> Path = {endWord}; backtrack(res, endWord, from, Path); } return res; } void backtrack(vector<vector<string>> &res, const string &Node, unordered_map<string, set<string>> &from, vector<string> &path) { if (from[Node].empty()) { res.push_back({path.rbegin(), path.rend()}); return; } for (const string &Parent: from[Node]) { path.push_back(Parent); backtrack(res, Parent, from, path); path.pop_back(); } }};分析:比较复杂的BFS+回溯法
错误:太复杂暂时还理解不了,慢慢来吧。。。
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
class Solution {public: static void DFS(vector<vector<char>>& board,int x,int y,int m,int n){ if(x < 0 || y < 0 || x >= m || y >= n){ return; } if(board[x][y] == 'X' || board[x][y] == 'A'){ return; } board[x][y] = 'A'; DFS(board,x+1,y,m,n); DFS(board,x-1,y,m,n); DFS(board,x,y-1,m,n); DFS(board,x,y+1,m,n); return; } void solve(vector<vector<char>>& board) { int m = board.size(); int n = board[0].size(); for(int i=0;i<m;++i){ DFS(board,i,0,m,n); DFS(board,i,n-1,m,n); } for(int i=0;i<n;++i){ DFS(board,0,i,m,n); DFS(board,m-1,i,m,n); } for(int i=0;i<m;++i){ for(int j=0;j<n;++j){ if(board[i][j] == 'A'){ board[i][j] = 'O'; } else{ board[i][j] = 'X'; } } } return; }};分析:也是比较普通的DFS,注意记录是否访问过即可。
一遍AC
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
class Solution {public: static void DFS(TreeNode* &root,vector<string> &paths,string temp){ if(root != nullptr){ temp += to_string(root->val); if(root->left == nullptr && root->right == nullptr){ paths.push_back(temp); return; } else{ temp += "->"; DFS(root->left,paths,temp); DFS(root->right,paths,temp); } } } vector<string> binaryTreePaths(TreeNode* root) { vector<string> paths; DFS(root,paths,""); return paths; }};分析:使用深度优先搜索。在深度优先搜索遍历二叉树时,我们需要考虑当前的节点以及它的孩子节点。如果当前节点不是叶子节点,则在当前的路径末尾添加该节点,并继续递归遍历该节点的每一个孩子节点。如果当前节点是叶子节点,则在当前路径末尾添加该节点后我们就得到了一条从根节点到叶子节点的路径,将该路径加入到答案即可。如此,当遍历完整棵二叉树以后我们就得到了所有从根节点到叶子节点的路径。
错误:陷入回溯法的坑了。
给定一个可包含重复数字的序列 nums ,按任意顺序返回所有不重复的全排列。
class Solution {public: static void backtracking(vector<int>& nums,vector<vector<int>> &result,int level){ if(level == nums.size() - 1){ result.push_back(nums); return; } set<int> st; for(int i=level;i<nums.size();++i){ if(st.find(nums[i]) == st.end()){ st.insert(nums[i]); swap(nums[level],nums[i]); backtracking(nums,result,level+1); swap(nums[level],nums[i]); } } return; } vector<vector<int>> permuteUnique(vector<int>& nums) { vector<vector<int>> result; backtracking(nums,result,0); return result; }};分析:与全排列基本相同,添加一个set用于记录曾经交换过的数字,如果这个数字曾经交换过就不换了
错误:看了网上的思路。
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次 。
class Solution {public: static void backtracking(vector<int>& candidates,vector<vector<int>> &result,vector<int> &path,vector<bool> &used,int level,int sum,int target){ if(sum > target){ return; } else if(sum == target){ result.push_back(path); return; } else{ for(int i=level;i<candidates.size() && sum + candidates[i] <= target;++i){ if(i > 0 && candidates[i] == candidates[i-1] && used[i - 1] == false){ continue; } sum += candidates[i]; path.push_back(candidates[i]); used[i] = true; backtracking(candidates,result,path,used,i+1,sum,target); used[i] = false; sum -= candidates[i]; path.pop_back(); } } } vector<vector<int>> combinationSum2(vector<int>& candidates, int target) { vector<vector<int>> result; vector<int> path; vector<bool> used(candidates.size(),false); sort(candidates.begin(),candidates.end()); backtracking(candidates,result,path,used,0,0,target); return result; }};分析:还是组合数,但是数字内部有重复的,因此需要对同一树层上的“使用过”进行去重。
错误:没什么思路。
编写一个程序,通过填充空格来解决数独问题。
class Solution {public: static bool isValid(int i,int j,char k,vector<vector<char>>& board){ set<char> st; for(int x=0;x<9;x++){ st.insert(board[i][x]); st.insert(board[x][j]); } int p = i / 3; int q = j / 3; for(int x = p*3;x < p*3+3;++x){ for(int y = q * 3;y < q*3+3;++y){ st.insert(board[x][y]); } } if(st.find(k) == st.end()){ return true; } return false; } static bool backtracking(vector<vector<char>>& board){ for(int i=0;i<9;++i){ for(int j=0;j<9;++j){ if(board[i][j] != '.'){ continue; } for(char k = '1';k <= '9';++k){ if(isValid(i,j,k,board)){ board[i][j] = k; if(backtracking(board) == true){ return true; } board[i][j] = '.'; } } return false; } } return true; } void solveSudoku(vector<vector<char>>& board) { bool judge = backtracking(board); return; }};分析:二维的回溯问题,说白了就是去尝试填充每一个数字,合理就填上,不合理就删掉之前填充的重新进行尝试。
错误:看题解。
给你一棵包含 n 个节点的树,标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表(每一个边都是一对标签),其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。可选择树中任何一个节点作为根。当选择节点 x 作为根节点时,设结果树的高度为 h 。在所有可能的树中,具有最小高度的树(即,min(h))被称为 最小高度树 。请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。
class Solution {public: vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) { int m = edges.size(); vector<int> result; if(m == 0){ result.push_back(0); return result; } vector<int> degree(n,0); vector<vector<int>> tree(n); for(int i=0;i<m;++i){ ++degree[edges[i][0]]; ++degree[edges[i][1]]; tree[edges[i][0]].push_back(edges[i][1]); tree[edges[i][1]].push_back(edges[i][0]); } queue<int> q; for(int i=0;i<n;++i){ if(degree[i] == 1){ q.push(i); } } while(!q.empty()){ int size = q.size(); result.clear(); for(int i=0;i<size;++i){ int top = q.front(); result.push_back(top); q.pop(); --degree[top]; for(int j=0;j<tree[top].size();++j){ --degree[tree[top][j]]; if(degree[tree[top][j]] == 1){ q.push(tree[top][j]); } } } } return result; }};分析:拓扑排序的思想,从多端同时BFS到中心点,直到到达最后一层,输出这一层的结点即为最小的高度。
错误:看了思路后自己实现,注意判断边界条件。
深度优先、广度优先和回溯法,理解的还是并不是非常深入,今后还要多加练习。
]]>信息检索应用例子的共同特征:
给定需求或者是对象,从信息库中找出与之最匹配的信息或对象。
数据形式是无固定结构的自由文本(谷歌搜索)或者结构化数据(京东商品)
信息检索与其他的学科关系密切,包括自然语言处理、数据挖掘和机器学习。
信息检索技术广泛应用于搜索、推荐、挖掘、舆情分析、情报处理和内容安全。
从信息规模上分类,信息检索可以分为:
现在提到信息检索,通常会首先想到Web搜索,但是除此之外还有很多其它的搜索应用,如电子邮件搜索、笔记本电脑(桌面)搜索、知识库搜索、法律文献搜索等。
本课程主要关注文本检索,因为文本检索是最早的检索应用,也仍然是目前最主要的应用,且文本检索理论可以用于其他领域。
信息检索与数据库的区别主要在于数据的区别,信息检索关注的是非结构化的数据,而数据库关注的是结构化的数据。
数据库常常支持范围或者精确匹配查询。
非结构化数据通常指自由文本,允许关键词加上操作符号的查询和更复杂的概念性查询,经典的检索模型一般都针对自由文本进行处理。
文档集(Collection): 由固定数目的文档组成
目标:返回与用户需求相关的文档并辅助用户来完成某项任务
相关性(Relevance):主观的概念,反映对象的匹配程度不同,应用相关性不同。
检索效果的评价:准确率和召回率(准确率是自己的,召回率才是真正的)
布尔检索:针对布尔查询的检索,布尔查询是指利用 AND,OR或者 NOT操作符将词项连接起来的查询。
需求:莎士比亚的哪部剧本包含Brutus及Caesar但是不包含Calpurnia
将需求表示为布尔表达式: Brutus AND Caesar AND NOT Calpurnia
从头到尾扫描所有剧本,对每部剧本判断它是否包含Brutus AND Caesar ,同时又不包含Calpurnia
暴力方法的优点:①实现简单②很容易支持文档动态变化
暴力方法的不足:
关联矩阵:
| Antony and Cleopatra | Julius Caesar | The Tempest | Hamlet | Othello | Macbeth | |
|---|---|---|---|---|---|---|
| Antony | 1 | 1 | 0 | 0 | 0 | 1 |
| Brutus | 1 | 1 | 0 | 1 | 0 | 0 |
| Caesar | 1 | 1 | 0 | 1 | 1 | 1 |
| Calpurnia | 0 | 1 | 0 | 0 | 0 | 0 |
| Cleopatra | 1 | 0 | 0 | 0 | 0 | 0 |
| mercy | 1 | 0 | 1 | 1 | 1 | 1 |
| worser | 1 | 0 | 1 | 1 | 1 | 0 |
行表示单词,列表示文本,若文本中包含这个单词,则记录为1,反之记录为0
使用关联矩阵进行查询的时候,即将关联矩阵有关单词的行向量取出来后进行按位与或非操作即可。
但是这种词项-文档的关联矩阵将非常大,由于是 one-hot存储,矩阵高度稀疏,需要更好的表示方式,因此有了倒排索引。
对每个词项 t,记录所有包含 t的文档列表,每篇文档用一个唯一的 docID来表示,通常是正整数。
词典 ➡ 倒排记录(Posting)
Brutus ➡ 1 2 4 11 31 45 173
Calpurnia ➡ 1 2 4 5 6 16 57 132
Caesar ➡2 31 54 101
倒排索引的存储通常采用变长表方式
文本预处理:
构建词条序列:<词条,docID> 类型的二元组
按词项排序:每个词项按 docID排序
某个词项在单篇文档中的多次出现会被合并
拆分成词典和倒排记录表两部分
每个词项出现的文档数目(doc.frequency, DF)会被加入
最终构成倒排索引:
对于布尔查询来说,对倒排记录表进行操作即可。
每个倒排记录表都有一个定位指针,两个指针同时从前往后扫描, 每次比较当前指针对应倒排记录,然后移动某个或两个指针。合并时间为两个表长之和的线性时间。时间复杂度为 O(m+n)
这也是倒排记录表按照 docID排序的关键原因!
查询处理中存在处理的顺序问题:n个词项的 AND我们希望查询的次数越少越好,因此要按照表从小到大(即 df从小到大)的顺序进行处理,每次从最小的开始合并(这样可以尽量提前结束合并)
按照直接加和的方式对 Or的 df进行估计。
每个布尔表达式都能转换成(合取范式)
获得每个词项的 df
通过将词项的 df相加,估计每个 OR表达式对应的倒排记录表的大小
按照上述估计从小到大依次处理每个 OR表达式
构建简单,是构建信息检索系统的一种最简单方式
排序自然都有C++的STL搞定了,但是在实际中仍然需要这些排序算法,一方面夯实基础,另一方面有一些题目是从这些排序算法中引申出来的,掌握这些排序算法对于做题也会有很大的帮助。
int main(void){ vector<int> nums = {1,3,5,7,2,6,4,8,9,2,8,7,6,0,3,5,9,4,1,0}; vector<int> temp(nums.size()); sort(nums.begin(), nums.end()); quick_sort(nums, 0, nums.size()); print(nums); merge_sort(nums, 0, nums.size(), temp); print(nums); insertion_sort(nums, nums.size()); print(nums); bubble_sort(nums, nums.size()); print(nums); selection_sort(nums, nums.size()); print(nums); return 0;}void quick_sort(vector<int> &nums,int left,int right){ int l = left; int r = right; if(left+1 >= right){ return; } int k = nums[left]; while(left+1 < right){ while(left+1 < right && nums[right-1] >= k){ --right; } nums[left] = nums[right-1]; while(left+1 < right && nums[left] < k){ ++left; } nums[right-1] = nums[left]; } nums[left] = k; quick_sort(nums,l,left); quick_sort(nums,left+1,r);}错误:while内部的 left < right的条件没有加,导致内部会出问题,而且也是要+1的
void merge_sort(vector<int> &nums,int left,int right,vector<int> &temp){ if(left + 1 >= right){ return; } int mid = (right - left) / 2 + left; merge_sort(nums,left,mid,temp); merge_sort(nums,mid,right,temp); int p = left; int q = mid; int i = left; while(p < mid && q < right){ if(nums[p] <= nums[q]){ temp[i++] = nums[p++]; } else{ temp[i++] = nums[q++]; } } while(p < mid){ temp[i++] = nums[p++]; } while(q < right){ temp[i++] = nums[q++]; } for(int j=left;j<right;++j){ nums[j] = temp[j]; }}错误:应该是 left + 1 >= right,只剩下一个数字后就应该返回了。
void insertion_sort(vector<int> &nums,int n){ for(int i=1;i<n;i++){ int a = i; while(a - 1 >= 0 && nums[a] < nums[a-1]){ swap(nums[a],nums[a-1]); --a; } } return;}void bubble_sort(vector<int> &nums,int n){ for(int i=0;i<n-1;i++){ for(int j=0;j<n-i-1;j++){ if(nums[j] > nums[j+1]){ swap(nums[j],nums[j+1]); } } } return;}void selection_sort(vector<int> &nums,int n){ for(int i=0;i<n;i++){ int minnum = nums[i]; int minindex = i; for(int j=i+1;j<n;j++){ if(nums[j] < minnum){ minnum = nums[j]; minindex = j; } } swap(nums[i],nums[minindex]); } return;}在一个未排序的数组中,找到第 k大的数字
class Solution {public: static void quick_selection(vector<int> &nums,int left,int right,int k){ int l = left; int r = right; int k2 = nums[left]; if(left + 1 > right){ return; } while(left+1 < right){ while(left+1 < right && nums[right-1] < k2){ --right; } nums[left] = nums[right-1]; while(left+1 < right && nums[left] >= k2){ ++left; } nums[right-1] = nums[left]; } nums[left] = k2; if(k <= left){ quick_selection(nums,l,left,k); } else{ quick_selection(nums,left+1,r,k); } return; } int findKthLargest(vector<int>& nums, int k) { quick_selection(nums,0,nums.size(),k-1); return nums[k-1]; }};分析:与快速排序相同的思路,但是不需要对没有用的一侧进行快速排序,只需要对k在的区间一侧进行快速排序即可。
错误:开始快速排序有问题,然后k的值想不清楚造成错误。
class Solution {public: static bool cmp(pair<int,int> &a,pair<int,int> &b){ return a.first > b.first; } vector<int> topKFrequent(vector<int>& nums, int k) { map<int,int> mp1,mp2; for(auto i : nums){ ++mp1[i]; } vector<pair<int,int>> pr; vector<int> result; for(auto i = mp1.cbegin();i != mp1.cend();++i){ pr.push_back(make_pair(i->second,i->first)); } sort(pr.begin(),pr.end(),cmp); for(auto i = pr.cbegin();i != pr.cend();++i){ if(k != 0){ result.push_back(i->second); } else{ break; } k--; } return result; }};分析:也是比较简单的一道题,通过这道题可以复习一下各种 STL数据结构,总也不用生疏了。
错误:STL有一些生疏,调了一段时间才调好。
给定一个字符串 s ,根据字符出现的频率对其进行降序排序。一个字符出现的频率是它出现在字符串中的次数。返回已排序的字符串。
class Solution {public: static bool cmp(pair<char,int> &a,pair<char,int> &b){ return a.second > b.second; } string frequencySort(string s) { string result = ""; map<char,int> mp; for(auto i : s){ mp[i] += 1; } vector<pair<char,int>> pr; for(auto i = mp.cbegin();i != mp.cend();i++){ pr.push_back(make_pair(i->first,i->second)); } sort(pr.begin(),pr.end(),cmp); for(auto i = pr.cbegin();i != pr.cend();i++){ for(int j=0;j<i->second;j++){ result += i->first; } } return result; }};分析:桶排序的变形题,没有什么新意,还是数据结构
一遍AC
void sortColors(vector<int>& nums) { int n = nums.size(); int p0 = 0; int p1 = 0; for(int i=0;i<n;++i){ if(nums[i] == 1){ swap(nums[i],nums[p1]); ++p1; } else if(nums[i] == 0){ swap(nums[i],nums[p0]); if(p0 < p1){ swap(nums[i],nums[p1]); } ++p0; ++p1; } }}分析:荷兰国旗问题,双指针一次遍历就可以得到三个数字的排序。
错误:想复杂了。
排序算法基本都可以写,就是变形的题目还是有些不太熟练。还是要多多练习。
]]>二分查找也常被称为二分法或者折半查找,每次查找时通过将待查找区间分成两部分并只取一部分继续查找,将查找的复杂度大大减少。
二分查找也可以看作双指针的一种特殊情况,但我们一般会将二者区分。双指针类型的题,指针通常是一步一步移动的,而在二分查找里,指针每次移动半个区间长度。
因为我们初始化 right = nums.length - 1,所以决定了我们的「搜索区间」是 [left, right],所以决定了 while (left <= right),同时也决定了 left = mid+1 和 right = mid-1,因为我们只需找到一个 target 的索引即可,所以当 nums[mid] == target 时可以立即返回。
因为我们初始化 right = nums.length,所以决定了我们的「搜索区间」是 [left, right),所以决定了 while (left < right),同时也决定了 left = mid + 1 和 right = mid,因为我们需找到 target 的最左侧索引,所以当 nums[mid] == target 时不要立即返回,而要收紧右侧边界以锁定左侧边界。
因为我们初始化 right = nums.length,所以决定了我们的「搜索区间」是 [left, right),所以决定了 while (left < right),同时也决定了 left = mid + 1 和 right = mid,因为我们需找到 target 的最右侧索引,所以当 nums[mid] == target 时不要立即返回,而要收紧左侧边界以锁定右侧边界,又因为收紧左侧边界时必须 left = mid + 1,所以最后无论返回 left 还是 right,必须减一。
给定一个非负整数,求它的开方,向下取整。
class Solution {public: int mySqrt(int x) { long long left = 0; long long right = sqrt(x) + 1; while(left <= right){ long long mid = (right - left) / 2 + left; if(mid * mid < x){ left = mid + 1; } else if(mid * mid > x){ right = mid - 1; } else{ return mid; } } return left - 1; }};思路很简单,主要是细节问题,已经整理了笔记。
给定一个增序的整数数组和一个值,查找该值第一次和最后一次出现的位置。
class Solution {public: vector<int> searchRange(vector<int>& nums, int target) { vector<int> result; int n = nums.size(); if (n == 0){ return vector<int>{-1, -1}; } int left = 0; int right = n; while(left < right){ int mid = (right - left) / 2 + left; if(nums[mid] >= target){ right = mid; } else if(nums[mid] < target){ left = mid + 1; } } if(right >= n || nums[right] != target){ return vector<int>{-1, -1}; } else{ result.push_back(right); } left = 0; right = n; while(left < right){ int mid = (right - left) / 2 + left; if(nums[mid] > target){ right = mid; } else if(nums[mid] <= target){ left = mid + 1; } } result.push_back(left - 1); return result; }};分析:也是最基础的二分查找,实现了 upper_bound和 lower_bound两个函数。
错误:判断的时候忘记判断是否越界。
一个原本增序的数组被首尾相连后按某个位置断开(如[1,2,2,3,4,5] - [2,3,4,5,1,2],在第一位和第二位断开),我们称其为旋转数组。给定一个值,判断这个值是否存在于这个旋转数组中。
class Solution {public: bool search(vector<int>& nums, int target) { int n = nums.size(); int left = 0; int right = n; while(left < right){ int mid = (right - left) / 2 + left; if(nums[mid] == target){ return true; } else if(nums[mid] < nums[right-1]){ // 说明右端是排好序的 if(target >= nums[mid] && target <= nums[right-1]){ left = mid + 1; } else{ right = mid; } } else if(nums[mid] > nums[right-1]){ // 说明左端是排好序的 if(target <= nums[mid] && target >= nums[left]){ right = mid; } else{ left = mid + 1; } } else{ --right; } } return false; }};分析:旋转数组是一类经典题目,需要抓住旋转后二分会有一个区间是单调的性质进行判断,从而对所查找的数字进行区间的锁定。
错误:条件考虑不全面,没有对旋转数组充分理解。
寻找旋转排序数组中的最小值
class Solution {public: int findMin(vector<int>& nums) { int n = nums.size(); int left = 0; int right = n; int minnum = 10000; while(left < right){ int mid = (right - left) / 2 + left; if(nums[mid] > nums[left]){ // 左边一定有序 minnum = min(minnum,nums[left]); left = mid + 1; } else if(nums[mid] < nums[left]){ // 右边一定有序 minnum = min(minnum,nums[mid]); right = mid; } else{ minnum = min(minnum,nums[mid]); ++left; } } return minnum; }};分析:比查找还要稍稍简单一点,只需要想好最小值可能出现的位置即可。
错误:相等的时候没有判断,会导致漏掉元素。
给你一个仅由整数组成的有序数组,其中每个元素都会出现两次,唯有一个数只会出现一次。请你找出并返回只出现一次的那个数。
class Solution {public: int singleNonDuplicate(vector<int>& nums) { int n = nums.size(); int left = 0; int right = n; if(nums.size()==1){ return nums[0]; } while(left < right){ int mid = (right - left) / 2 + left; if(mid % 2 == 0){ if(nums[mid] == nums[mid+1]){ left = mid + 2; } else{ right = mid; } } else{ if(nums[mid] == nums[mid-1]){ left = mid + 1; } else{ right = mid; } } } return nums[left]; }};分析:如果mid是偶数,则比较nums[mid]和nums[mid+1]是否相等;如果mid是奇数,则比较nums[mid−1]和nums[mid]是否相等。
错误:感觉需要判断很多条件?其实不用,只需要考虑长度为1的数组,然后根据下标寻找规律就可以。
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数 。
分析:二分的解法太难了。。后续补充吧
错误:没有思路。。。
二分查找是非常好的降低时间复杂度的方法之一,整体的思想不是很难,但是细节的部分需要多多注意。当然也有难题,还要多练习。
]]>双指针主要用于遍历数组,两个指针指向不同的元素,从而协同完成任务。也可以延伸到多个数组的多个指针。
若两个指针指向同一数组,遍历方向相同且不会相交,则也称为滑动窗口(两个指针包围的区域即为当前的窗口),经常用于区间搜索。
若两个指针指向同一数组,但是遍历方向相反,则可以用来进行搜索,待搜索的数组往往是排好序的。
在一个增序的整数数组里找到两个数,使它们的和为给定值。已知有且只有一对解。
class Solution {public: vector<int> twoSum(vector<int>& numbers, int target) { vector<int> result; int left = 0; int right = numbers.size() - 1; while(left < right){ if(numbers[left] + numbers[right] < target){ ++left; } else if(numbers[left] + numbers[right] > target){ --right; } else{ result.push_back(left+1); result.push_back(right+1); break; } } return result; }};分析:左右两个指针分别进行移动,加和小了就把左边的指针往右移动一下,加和大了就把右边的指针往左移动一下。这道题比较特殊,限定了一定有答案而且答案只会有一个,因此不需要添加任何其他的额外条件。
错误:没看清下标的表示方式,直接输出数组下标了。
给定两个有序数组,把两个数组合并为一个。
class Solution {public: void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) { if(n == 0){ return; } if(m == 0){ nums1 = nums2; return; } int mi = m - 1; int ni = n - 1; int numIndex = m+n-1; while(numIndex >= 0){ if(mi >= 0 && ni >= 0){ if(nums1[mi] > nums2[ni]){ swap(nums1[mi],nums1[numIndex]); --mi; } else{ swap(nums2[ni],nums1[numIndex]); --ni; } } else if(mi == -1){ while(ni != -1){ nums1[numIndex] = nums2[ni]; --ni; --numIndex; } break; } --numIndex; } }};分析:从后边开始安排数字,填充0的空位
错误:挺简单的一道题,首先是刚开始没有想到非常好的解法,看了答案后双指针又有一些问题。。真的是生疏了。
给定一个链表,如果有环路,找出环路的开始点。
class Solution {public: ListNode *detectCycle(ListNode *head) { ListNode* slow = head; ListNode* fast = head; do{ if(fast == nullptr || fast->next == nullptr){ return nullptr; } slow = slow->next; fast = fast->next->next; }while(slow != fast); fast = head; while(slow != fast){ slow = slow->next; fast = fast->next; } return fast; }};分析:有一个通用的解法——快慢指针(Floyd判圈法)。给定两个指针,分别命名为slow和fast,起始位置在链表的开头。每次fast前进两步,slow前进一步。如果fast可以走到尽头,那么说明没有环路;如果fast可以无限走下去,那么说明一定有环路,且一定存在一个时刻slow 和fast 相遇。当slow和fast第一次相遇时,我们将fast重新移动到链表开头,并让slow和fast每次都前进一步。当slow和fast第二次相遇时,相遇的节点即为环路的开始点。
错误:算法忘记了,没有思路。
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 ""
class Solution {public: string minWindow(string s, string t) { size_t s_size = s.size(); size_t t_size = t.size(); map<char,int> mp1; for(size_t i=0;i<t_size;i++){ if(mp1.count(t[i])){ mp1[t[i]] += 1; } else{ mp1[t[i]] = 1; } } int left = 0,cnt = 0,min_l = 0,min_size = s_size+1; for(int r=0;r<s_size;++r){ if(mp1.count(s[r])){ --mp1[s[r]]; if(mp1[s[r]] >= 0){ ++cnt; } while(cnt == t_size){ if(r - left + 1 < min_size){ min_size = r - left + 1; min_l = left; } if(mp1.count(s[left]) && ++mp1[s[left]] > 0){ --cnt; } ++left; } } } return min_size > s_size ? "" : s.substr(min_l,min_size); }};分析:滑动窗口典型题目
首先对子字符串进行计数,记录是否出现,以及出现的次数。然后采取滑动窗口的策略,两个指针都从左开始滑动,以右指针为基准构成外侧的大循环。右指针滑动的过程中,对之前的计数进行更改,滑动到了一个字符就减小1。等到0的时候,说明右指针滑动过了的字符串一定包含子字符串的全部字符,然后将左指针向右滑动来减小这个字符串的长度。左指针碰到了某个子字符串内部的字符,就会将计数+1,从而不满足这个字符串包含整个子字符串的要求,因此重新开始移动右字符串,以尝试再次包含整个子字符串。
错误:算法忘记了,没有思路。
给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a^2 + b^2 = c 。
class Solution {public: bool judgeSquareSum(int c) { long long left = 0; long long right = sqrt(c); while(left <= right){ if(left * left + right * right < c){ ++left; } else if(left * left + right * right > c){ --right; } else{ return true; } } return false; }};分析:仍然是双指针的问题,多了一点点细节问题。
错误:left = right,right的范围考虑的不太好。
给你一个字符串 s,最多可以从中删除一个字符。请你判断 s是否能成为回文字符串:如果能,返回 true ;否则,返回 false 。
class Solution {public: bool judge(string &s,int left,int right){ while(left <= right){ if(s[left] == s[right]){ ++left; --right; } else{ return false; } } return true; } bool validPalindrome(string s) { size_t s_size = s.size(); int left = 0; int right = s_size - 1; while(left <= right){ if(s[left] == s[right]){ ++left; --right; } else{ return judge(s,left+1,right) || judge(s,left,right-1); } } return true; }};分析:双指针移动就好
错误:没有考虑到删除一个字符后有两种情况,应该共同考虑而不是仅仅使用某一种情况进行判断。
给你一个字符串 s 和一个字符串数组 dictionary ,找出并返回 dictionary 中最长的字符串,该字符串可以通过删除 s 中的某些字符得到。如果答案不止一个,返回长度最长且字母序最小的字符串。如果答案不存在,则返回空字符串。
class Solution {public: static bool cmp(string &a,string &b){ if(a.size() != b.size()){ return a.size() > b.size(); } return a < b; } string findLongestWord(string s, vector<string>& dictionary) { sort(dictionary.begin(),dictionary.end(),cmp); size_t s_size = s.size(); for(auto t : dictionary){ size_t t_size = t.size(); int si = 0,ti = 0; while(si != s_size){ if(s[si] == t[ti]){ ++ti; } ++si; if(ti == t_size){ return t; } } } return ""; }};分析:先排序,然后双指针进行移动匹配,如果子字符串的指针移动到字符串的末尾了,说明已经匹配成功了,可以直接输出这个字符串。如果原始的字符串的指针移动到末尾了,说明没有匹配成功,因此转为匹配下一个字符串。
错误:题目要求的排序条件没有看好,返回了长度比较短的字符串。
给定一个字符串 s,找出至多包含 k个不同字符的最长子串 T
分析:还是滑动窗口的策略,以右边指针为基准,滑动一下就记录一下最长的长度,滑动到不满足条件了,就将左边的指针收回来,收到满足条件了就继续放右边的指针去滑动。
class Solution {public: int lengthOfLongestSubstringKDistinct(string s, int k) { size_t s_size - s.size(); map<char,int> mp; int maxlen = 0; int l = 0; for(int r=0;r<s_size;r++){ if(mp.size() <= k){ ++mp[s[r]]; } while(mp.size() > k){ if(--mp[s[l]] == 0){ mp.erase(s[l]); } l++; } maxlen = max(maxlen,r-l+1); } return maxlen; }};错误:会员题,无法提交。
双指针的题目还可以,感觉重要的是判断条件。滑动窗口的题目比较困难,可能也是做的题目比较少。后面还需要加强练习。
]]>贪心算法或贪心思想采用贪心的策略,保证每次操作都是局部最优的,从而使最后得到的结果是全局最优的。
有一群孩子和一堆饼干,每个孩子有一个饥饿度,每个饼干都有一个大小。每个孩子只能吃一个饼干,且只有饼干的大小不小于孩子的饥饿度时,这个孩子才能吃饱。求解最多有多少孩子可以吃饱。
class Solution {public: int findContentChildren(vector<int>& g, vector<int>& s) { sort(g.begin(),g.end()); sort(s.begin(),s.end()); int childrenCount = 0; for(size_t i = 0;i<s.size() && childrenCount < g.size();i++){ if(s[i] >= g[childrenCount]){ ++childrenCount; } } return childrenCount; }};分析:用最小大小的饼干 (s)去满足最小饥饿度的孩子 (g),一直满足到饥饿度最大的孩子,相当于双指针的移动。
贪心策略是给剩余孩子里最小饥饿度的孩子分配最小的能饱腹的饼干。
错误:忘记检查g是否越界,可能发生所有饼干都能满足所有孩子,然而饼干还剩着的情况。下标运算一定要确认是否越界。
一群孩子站成一排,每一个孩子有自己的评分。现在需要给这些孩子发糖果,规则是如果一个孩子的评分比自己身旁的一个孩子要高,那么这个孩子就必须得到比身旁孩子更多的糖果;所有孩子至少要有一个糖果。求解最少需要多少个糖果。
class Solution {public: int candy(vector<int>& ratings) { vector<int> candyNum(ratings.size(),1); for(size_t i = 0;i<ratings.size()-1;++i){ if(ratings[i+1] > ratings[i] && candyNum[i+1] <= candyNum[i]){ candyNum[i+1] = candyNum[i] + 1; } } for(size_t i = ratings.size()-1;i>0;--i){ if(ratings[i-1] > ratings[i] && candyNum[i-1] <= candyNum[i]){ candyNum[i-1] = candyNum[i] + 1; } } return accumulate(candyNum.cbegin(),candyNum.cend(),0); }};分析:首先至少有一个糖果分配好,然后从左向右扫一遍,如果右边的孩子评分高,则右边孩子的糖果=左边孩子的糖果+1,再从右往左扫一遍,如果左边的孩子评分高,则左边孩子的糖果=右边孩子的糖果+1。最后求和即可。
贪心策略:在每次遍历中,只考虑并更新相邻一侧的大小关系
错误:没有更新为相邻孩子+1,而是仅仅加了1,考虑不够完整。
给定一个区间的集合 intervals ,返回 需要移除区间的最小数量,使剩余区间互不重叠。
class Solution {public: static bool cmp(vector<int> &a,vector<int> &b){ return a[1] < b[1]; } int eraseOverlapIntervals(vector<vector<int>>& intervals) { sort(intervals.begin(),intervals.end(),cmp); int intervalsCount = 1; int searchBack = intervals[0][1]; size_t n = intervals.size(); for(size_t i=0;i<n;++i){ if (intervals[i][0] >= searchBack){ intervalsCount += 1; searchBack = intervals[i][1]; } } return n - intervalsCount; }};分析:假设第一个区间是 k,k的左边没有任何区间,因此使用其他任何一个区间,只要右端点小于 k的右端点就可以了。而且右端点向左移动,比 k更优。因此首个区间就是所有可以选择的区间中右端点最小的那个区间 。后面只要去寻找其中与首个区间不重合并且右端点最小的区间即可。
贪心策略:优先保留结尾小且不相交的区间
错误1:没想明白右端点的问题
错误2:函数要加 static(但是不太明白)
错误3:使用引用传参,防止拷贝浪费时间
建议:一些比如数组大小的数字提前计算出来,避免反复计算。
有一个很长的花坛,一部分地块种植了花,另一部分却没有。花不能种植在相邻的地块上。 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 表示没种植花,1 表示种植了花。另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?能则返回 true ,不能则返回 false。
class Solution {public: bool canPlaceFlowers(vector<int>& flowerbed, int n) { int flowerCount = 0; size_t m = flowerbed.size(); if(m == 1){ if(flowerbed[0] == 0){ return true; } else if (flowerbed[0] == 1 && n == 1){ return false; } } if(flowerbed[0] == 0 && flowerbed[1] == 0){ flowerbed[0] = 1; flowerCount += 1; } if(flowerbed[m-1] == 0 && flowerbed[m-2] == 0){ flowerbed[m-1] = 1; flowerCount += 1; } for(size_t i=1;i<m-1;i++){ if(flowerbed[i] == 0 && flowerbed[i-1] == 0 && flowerbed[i+1] == 0){ flowerbed[i] = 1; flowerCount += 1; } } return flowerCount >= n; }};分析:遍历即可,尤其注意开头部分和结尾部分。
错误:最后没有考虑等于条件也为 true
建议:判断太多,有更为简洁的解法,大致思路是计算相邻的 1之间能种多少个 0。
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,不知道具体位置,但是知道一个位置的范围。一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,射进了气球的位置范围后,该气球就会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。给你一个数组 points , 返回引爆所有气球所必须射出的最小弓箭数 。
class Solution {public: static bool cmp(vector<int> &a,vector<int> &b){ return a[1] < b[1]; } int findMinArrowShots(vector<vector<int>>& points) { sort(points.begin(),points.end(),cmp); int n = points.size(); int arrowCount = 1; int endPoint = points[0][1]; for(size_t i=0;i<n;i++){ if(points[i][0] > endPoint){ ++arrowCount; endPoint = points[i][1]; } } return arrowCount; }};分析:拿第一个气球来说,要是想射爆,最佳的方法就是射最右侧的位置,这样能射到的其他的气球数量也会增加,以此类推,构成贪心算法。
一遍AC
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
class Solution {public: vector<int> partitionLabels(string s) { vector<int> last(26,-1); for(int i = s.size() - 1;i >= 0;i--){ if(last[s[i] - 'a'] == -1){ last[s[i] - 'a'] = i; } } vector<int> result; int start = 0; int end = 0; for(int i=0;i<s.size();i++){ end = max(end,last[s[i] - 'a']); if(i == end){ result.push_back(end - start + 1); start = i + 1; } } return result; }};分析:首先得到字符出现的最后的下标位置,然后重新遍历字符串,得到每个字符最后出现的位置。一旦前面的所有字符都出现完了,就算一个区间。
上述做法使用贪心的思想寻找每个片段可能的最小结束下标,因此可以保证每个片段的长度一定是符合要求的最短长度,如果取更短的片段,则一定会出现同一个字母出现在多个片段中的情况。由于每次取的片段都是符合要求的最短的片段,因此得到的片段数也是最多的。
错误:思路有问题,没有做对
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。在每一天,你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买,然后在同一天出售。返回你能获得的最大利润 。
class Solution {public: int maxProfit(vector<int>& prices) { int stockSum = 0; for(size_t i=0;i<prices.size()-1;i++){ if(prices[i+1] > prices[i]){ stockSum = stockSum+prices[i+1]-prices[i]; } } return stockSum; }};分析:什么都不限制,涨了就卖就完事了,比较简单。贪心策略就是只要价格上涨就直接出售。
一遍AC
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面正好有 ki个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
class Solution {public: static bool cmp(vector<int> &a,vector<int> &b){ if(a[0] != b[0]){ return a[0] < b[0]; } return a[1] > b[1]; } vector<vector<int>> reconstructQueue(vector<vector<int>>& people) { vector<vector<int>> result(people.size()); sort(people.begin(),people.end(),cmp); for(size_t i=0;i<people.size();++i){ int pos = people[i][1]; for(size_t j=0;j<result.size();j++){ if(result[j].empty()){ pos--; } if(pos == -1){ result[j] = people[i]; break; } } } return result; }};分析:将人员从低往高先排列,然后一个个进行插入。插入的人只会对后面的人有影响,因为后面的人的身高都会大于等于他。而对已经插入的人没有影响。因此插入的时候给后面的人要留出空位置,以便后面的人插入进去。如果身高相同,就去比较 ki。 ki更小一点的,说明这个人在靠前一点,也就是最小的 ki前面是不会有相同身高的人的,由于相同身高也会算在内,因此要先插入大 ki。
错误:思路有问题,没有做对
给你一个长度为 n 的整数数组 nums ,请你判断在最多改变 1 个元素的情况下,该数组能否变成一个非递减数列。
class Solution {public: bool checkPossibility(vector<int>& nums) { int count = 0; for (int i = 1; i < nums.size(); i++) { if (nums[i] < nums[i - 1]) { if(i == 1 || nums[i] >= nums[i - 2]){ nums[i - 1] = nums[i]; } else{ nums[i] = nums[i - 1]; } ++count; } } return count <= 1; }};分析:要多种情况一起考虑。。。。
错误:思路有问题,没有做对。另外不要去改 i+1啊。。判断什么修改什么好吧,要不就乱套了。
贪心算法确实是比较好理解的,但是怎么贪心?什么时候贪心?这些问题都要去详细认真的思考,真正出题的时候不会如此直白,要多练多想。
]]>总的来说,这里确实是一群学霸。首先可以拿我室友来说,早上7点起床,晚上11点左右睡觉,几乎每时每刻都在看论文做实验,甚至在看比赛的过程中间也会去看论文。他的目标就是要发文章,发一篇顶会文章,因此现在在努力完成这个目标。之后的方向他还没有想好,可能出国或者找音频算法相关的工作。其次是图书馆的同学们,才开学没有几天,图书馆就已经爆满了。大家都是思维缜密且有计划的人,昨天一窝蜂去抢机房,抢各种台式电脑去选课,选过课后去找相关的书籍,这在之前都是我的标准操作,在这里却被其他人不断模仿甚至比我做的更好。我有一种压力感,同时也有一种恐惧。
我的内心真的很脆弱。感觉其他人都还很适应的,我表面上也是这样,但是内心里已经稍稍有点崩溃了。我不禁回想我本科阶段,如果我高考真的考的好了,去了一些顶级985的学校,那么我是会坚持住学下去拼下去,还是会基本上崩溃掉,完全没有任何的竞争实力了呢?或许去了中南大学,并不是考的不好,而是帮我减轻了同龄人的压力。现在研究生的阶段,我是真真正正感受到了同龄人的压力。这么多优秀的人当中,我又能排到一个什么水平?如果真的在各个方面都比不上别人,我会不会崩溃呢?这些都是我现在所担心的。
其实换个角度来想,我没有必要去和任何人去比较。大家的人生道路都是不一样的,也无所谓好与不好,只是适不适合,以及过的是否开心罢了。对于我现在来说,虽然我知道不要去和其他人比较,总有人比你更强,比你过的更好。但是我还是时不时会看看想想别人现在在做什么,看看别人取得的成就,想想自己有没有可能赶得上甚至超过。这样就造成了现在每一天都非常不开心,学习也没有什么动力,学到后面甚至有一点混时间的感觉。这种想法困扰了我很长的一段时间,目前仍然在困扰着我。
我现在能做的,就是找准自己的目标,制定好计划,坚定不移地实施下去。至于我脆弱的内心,慢慢调解吧。没有人能帮助我,最后能靠得住的只有我自己。
]]>iostream定义了用于读写流的基本类型
fstream定义了读写命名文件的类型
sstream定义了读写内存 string对象的类型
用法都是完全相同的,得益于继承机制
流的状态:
auto old_state = cin.rdstate(); // 获取流的当前状态cin.clear(); // 将所有条件状态复位,将流的状态置为有效cin.setstate(old_state); // 根据给定的标志位对流进行复位输出缓冲:每个输出流都管理一个缓冲区,保存程序读写的数据。
控制输出缓冲:
cout << "hi!" << endl; // 多输出一个换行符,然后刷新缓冲区cout << "hi!" << flush; // 输出后直接刷新缓冲区cout << "hi!" << ends; // 多输出一个空字符,然后刷新缓冲区cout << unitbuf; // 所有输出操作后都立即刷新缓冲区cout << nounitbuf; // 回到正常的缓冲方式关联输入和输出流:如果某一个输入流和输出流关联,则从输入流读取的操作会对这个输出流进行刷新。
标准库将 cout和 cin关联在一起
cin.tie(&cerr); // 将cin和cerr关联在一起ifstream in("infile");ofstream output("outfile");string s;while(getline(in,s)){ output << s << endl;}return 0;显式打开或者关闭文件流:
ofstream output; // 空文件流对象output.open("outfile"); // 调用open进行关联output.close(); // 关闭文件流文件模式:
ofstream output("outfile");这种方式其实隐含了以输出模式打开文件并进行截断,显式控制如下:
ofstream output("outfile",ofstream::out | ofstream::trunc);为了保留之前的文件内容,需要显式指定 app模式
ofstream output("outfile",ofstream::out | ofstream::app);ifstream in("infile");ofstream output("outfile",ofstream::out | ofstream::app);string s;while(getline(in,s)){ string a,b,c; istringstream s1(s); ostringstream s2; s1 >> a; s2 << a; s1 >> b; s2 << b; s1 >> c; s2 << c; cout << s2.str() << endl;}return 0;一个容器就是一些特定类型对象的集合,顺序容器为程序员提供了控制元素存储和访问顺序的能力。
vector是可变大小数组,支持快速随机访问。但是在尾部之外的位置插入或者删除元素可能很慢。
deque是双端队列,支持快速随机访问,在头尾部插入或者删除元素的速度很快。
list是双向链表,只支持双向顺序访问,在 list中任意位置进行插入/删除的速度都很快
forward_list是单向链表,只支持单向顺序访问,在链表中任意位置进行插入/删除的速度都很快
array是固定大小的数组,支持快速随机访问,不能添加或者删除元素
string是与 vector相似的容器,专门用于保存字符,随机访问快,在尾部插入/删除的速度很快
顺序容器几乎可以保存任意类型的元素
各种迭代器:
auto it1 = a.begin(); // list<string>::iteratorauto it2 = a.rbegin(); // list<string>::reverse_iteratorauto it3 = a.cbegin(); // list<string>::const_iteratorauto it4 = a.crbegin(); // list<string>::const_reverse_iterator元素的拷贝初始化:
list<string> a = {"Milton","SHakespeare","Austen"};list<string> a2(a);array具有固定的大小,并且可以进行拷贝
array<int,10> ia1 = {0,1,2,3,4,5,6,7,8,9};array<int,10> ia2 = ia1;使用 assign对不同但相容的类型进行赋值
list<string> names;vector<const char*> oldstyle;names.assign(oldstyle.cbegin(),oldstyle.cend());添加元素三种方法:push_front(),insert(),push_back()
新标准对应了三种直接构造元素的方法:emplace_front()、emplace()、emplace_back()
更安全的访问元素的方法:svec.at(0)
改变容器大小并使用某个元素填充更大的部分:ilist.resize(15,-1)
管理容量的成员函数:
c.capacity(); // 不重新分配内存空间的话最多能保存多少元素c.reserve(n); // 分配至少能容纳n个元素的内存空间c.shrink_to_fit() // 请求将capacity()减小为size()一样的大小数值转换:
int i = 42;string s = to_string(i);double d = stod(s);cout << s << " " << d << endl;42 42对于容器的其他操作,并没有通过定义成员函数的方式实现,而是定义一套泛型算法,实现了一些算法的公共接口。
在容器中对值进行查找使用 find,返回查找元素的指针的位置
auto result = find(vec.cbegin(),vec.cend(),val)返回元素在容器中出现的次数:
vector<int> a;int temp;for(int i=0;i<10;i++){ cin >> temp; a.push_back(temp);}cin >> temp;auto result = count(a.cbegin(),a.cend(),temp);cout << result << endl;泛型算法本身不会执行容器的操作,只会运行于迭代器之上,执行迭代器的操作。
因此泛型算法永远不会改变底层容器的大小。
元素求和:
vector<int> a{1,2,3,4,5,6,7,8};int sum = accumulate(a.cbegin(),a.cend(),0);cout << sum << endl;36可以推广到字符串中用来连接字符串:
vector<int> a{1,2,3,4,5,6,7,8};vector<string> b{"df","fsfds","rte"};string sum = accumulate(b.cbegin(),b.cend(),string(""));cout << sum << endl;dffsfdsrte确定两个序列中保存的值是否相同(假定第二个序列至少与第一个序列一样长)
vector<int> a{1,2,3,4,5,6,7,8};vector<string> b{"df","fsfds","rte"};vector<string> c{"df","fsfds","rte","fdsf"};auto sum = equal(b.cbegin(),b.cend(),c.cbegin());cout << sum << endl;1使用 fill和 fill_n填充元素:
vector<int> a{1,2,3,4,5,6,7,8};fill(a.begin(),a.end(),0);for(auto i : a){ cout << i << " ";}cout << endl;fill_n(a.begin(),a.size(),1);for(auto i : a){ cout << i << " ";}cout << endl;0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1算法是不会检查写操作的,泛型算法也不能更改容器的大小。因此需要自行检查容器是否越界等问题。
安全的方式:插入迭代器
vector<int> a{1,2,3,4,5,6,7,8};vector<string> b{"df","fsfds","rte"};vector<string> c{"df","fsfds","rte","fdsf"};fill_n(back_inserter(a),10,1);for(auto i : a){ cout << i << " ";}cout << endl;1 2 3 4 5 6 7 8 1 1 1 1 1 1 1 1 1 1将 a1的内容拷贝到 a2:copy(begin(a1),end(a1),a2)
对元素进行排序去重:
vector<string> d{"the","quick","red","fox","jumps","over","the","slow","red","turtle"};sort(d.begin(),d.end()); // 排序auto end_unique = unique(d.begin(),d.end()); // 将重复的移到末尾,并同时返回最后一个不重复的元素的后一位置d.erase(end_unique,d.end()); // 使用容器操作删除重复的元素(因为泛型算法无法改变容器大小)for(auto i : d){ cout << i << " ";}cout << endl;fox jumps over quick red slow the turtlelambda表达式:
一个 lambda表达式表示一个可调用的代码单元,可以理解为一个未命名的内联函数。
auto f = []{return 42;};cout << f() << endl;42int a = 0, b = 1;auto f6 = [&a, &b]{ return a + b; };cout << f6() << endl;1lambda表达式还有其他的一些用法。
插入迭代器:
back_inserter:创建一个使用 push_back的迭代器
front_inserter:创建一个使用 push_front的迭代器
inserter:创建一个使用 insert的迭代器
list<int> lst = {1,2,3,4};list<int> lst2 = {5,6};list<int> lst3 = {9,10,11};list<int> lst4 = {12};copy(lst.cbegin(),lst.cend(),front_inserter(lst2));for(auto i : lst2){ cout << i << " ";}cout << endl;copy(lst.cbegin(),lst.cend(),inserter(lst3,lst3.begin()));for(auto i : lst3){ cout << i << " ";}cout << endl;copy(lst.cbegin(),lst.cend(),back_inserter(lst4));for(auto i : lst4){ cout << i << " ";}cout << endl;4 3 2 1 5 6 1 2 3 4 9 10 11 12 1 2 3 4流迭代器:
istream_iterator<int> in(cin),eof;cout << accumulate(in,eof,0) << endl;> 2 1 4 5 6 7 8 942ostream_iterator<int> out(cout," ");for(int i=0;i<10;i++){ out = i;}cout << endl;0 1 2 3 4 5 6 7 8 9反向迭代器:
vector<int> vi{1,2,3,4,5,6,7,8,9,10};for(auto i = vi.crbegin();i != vi.crend();i++){ cout << *i << " ";}cout << endl;10 9 8 7 6 5 4 3 2 1要注意反向迭代器真的是反的。。。比如下面的例子:
string line = "first,middle,end";auto rcomma = find(line.crbegin(),line.crend(),',');cout << string(line.crbegin(),rcomma) << endl;cout << string(rcomma.base(),line.cend()) << endl;dneend关联容器中的元素是按关键字来保存和访问的,而顺序容器中的元素是按它们在容器中的位置来顺序保存和访问的。
map是关键字-值对的结合
map<string,size_t> word_count;string word;while(cin >> word){ ++word_count[word];}for(const auto &w : word_count){ cout << w.first << " " << w.second << endl;}> a b c d e d b ca 1b 2c 2d 2e 1关联容器的元素都是根据关键字存储的,因此不支持位置相关的操作。
multimap和 multiset允许相同关键字:
vector<int> vi{1,2,3,4,5,5,4,3,2,1};set<int> iset(vi.cbegin(),vi.cend());multiset<int> miset(vi.cbegin(),vi.cend());cout << iset.size() << " " << miset.size() << endl;关联容器的迭代器:
vector<int> vi{1,2,3,4,5,5,4,3,2,1};set<int> iset(vi.cbegin(),vi.cend());for(auto set_it = iset.cbegin();set_it != iset.cend();set_it++){ cout << *set_it << " ";}cout << endl;1 2 3 4 5插入元素:
iset.insert(8);查找元素的下标操作:
c[k]; // 如果没有会添加,并对值进行初始化c.at(k); // 如果没有会抛出异常访问元素:find和 count
在 multimap中查找元素:
multimap<string,int> mi{make_pair("as",1),make_pair("as",2),make_pair("ab",2),make_pair("ac",2),make_pair("ac",5)};for(auto pos = mi.equal_range("as");pos.first != pos.second;++pos.first){ cout << pos.first->second << " ";}cout << endl;根据转换规则对文件内容进行转换:
转换规则:
brb be right backk okay?y whyr areu youpic picturethk thanks!l8r later文件内容:
where r uy dont u send me a pic k thk l8r转换代码:
// 实际的转换工作,生成转换文本const string & transform(const string &s, const map<string,string> &m){ auto map_it = m.find(s); if (map_it != m.cend()){ return map_it->second; } else{ return s; }}// 读入给定文件,建立转换映射map<string,string> buildMap(ifstream &map_file){ map<string,string> trans_map; string key,value; // 读取第一个单词存入key,剩余内容存入value while(map_file >> key && getline(map_file,value)){ if(value.size() > 1){ trans_map[key] = value.substr(1); } else{ throw runtime_error("No rule for " + key); } } return trans_map;}int main(void){ ifstream map_file("rules"); ifstream input("text"); auto trans_map = buildMap(map_file); // 保存转换规则 string text; // 保存输入中的每一行 while(getline(input,text)){ istringstream stream(text); // 读取每个单词 string word; bool firstword = true; // 控制是否打印空格 while(stream >> word){ if(firstword){ firstword = false; } else{ cout << " "; } cout << transform(word,trans_map); } cout << endl; } return 0;}输出:
where are youwhy dont you send me a pictureokay? thanks! later无序容器:不适用比较运算符来组织元素,而是使用哈希函数组织元素。
一般情况下的性能要比有序容器更好,但是不能按照顺序输出。
前面都是静态对象,由程序自动分配内存并销毁。而动态对象需要被显式进行释放。
动态内存需要显式进行分配和释放,因此很容易忘记释放导致一些问题。因此定义了两种智能指针来管理这些动态对象,自动进行释放。
shared_ptr<string> p1; // 指向string的shared_ptrshared_ptr<list<int>> p2; // 指向int的list的shared_ptr默认初始化的智能指针中保存着一个空指针。
最安全的分配和使用动态内存的方式是调用 make_shared的标准库函数。
shared_ptr<int> p3 = make_shared<int>(42);shared_ptr<string> p4 = make_shared<string>(10,'9');shared_ptr<int> p5 = make_shared<int>();shared_ptr会自动记录有多少个其他 shared_ptr指向相同的对象,如果没有了,会自动销毁所管理的对象并自动释放相关联的内存。
离开作用域也会被销毁。如果返回这个指针,也不会被销毁(就是挺智能的)
直接管理内存:使用 new和 delete
int *pi = new int;string *ps = new string(10,'9');const string *pcs = new const string;delete pi;delete ps;delete pcs;delete不会抛出任何异常,尽管可能已经释放过了,甚至有可能都不是指针也会释放,会造成一些问题。
delete还可能会造成空悬指针,因此这个 delete只提供了有限的保护。
不要混用智能指针和普通指针,不要使用 get初始化另一个智能指针或者赋值。
unique_ptr“拥有”它所指向的对象,某个时刻只能由一个 unique_ptr指向一个给定对象。销毁指针就一起销毁了。
weak_ptr指向一个 shared_ptr管理的对象,不会改变 shared_ptr的计数,计数为 0后会自动释放。
使用 new分配一个 int数组:
int *p = new int[42];实际上并没有得到一个数组类型的对象,而是得到一个数据元素类型的指针。
动态分配并初始化数组:
int *pia3 = new int[10]{0,1,2,3,4,5,6,7,8,9};动态分配的数组的大小可以为0,会返回一个类似于尾后迭代器的指针。
释放动态数组:delete [] p
智能指针管理动态数组:
unique_ptr<int[]> up(new int[10]);for(size_t i = 0;i != 10;++i){ up[i] = i;}up.release();allocator将内存分配和对象构造分离开来,提供一种类型感知的内存分配方法。
int n = 5;allocator<string> alloc;auto const p = alloc.allocate(n);这个 allocator为5个 string分配了内存
在内存中构造对象:
auto q = p;alloc.construct(q++,"hi");cout << *p << endl;hi在一个给定文件中查询单词,最终返回单词在文件中出现的次数及其所在行的列表。
]]>大一学过C语言,当时学的不是很好,但是后面接触到算法竞赛的时候就慢慢补上来了,而且增加了一些C++特性以及STL标准模板库,也靠着半吊子C++拿了一些小奖,但是确实没有系统的学过C++。总之听说C++比较难,这次准备半系统性的学习一下。之前会的东西就做做题简单过一下,不会的重点看,尤其是指针和面向对象方面。希望以后能更加得心应手地使用C++,也为后面求职打打基础。
std::cout << "/*";std::cout << "*/";std::cout << /* "*/" *.;std::cout << /* "*/" /* "/*" */;前两行没问题,注释只有一边,编译运行顺利通过
第三行注释全,但是字符串不全,缺少右边的",编译运行不能通过
第四行两边分别有两组注释,且中间的字符串是全的,因此编译运行顺利通过
int sum = 0,value = 0;while(std::cin >> value){ sum += value;}std::cout << sum << std::endl;读取数量不定的整数,将其加和。
std::cin属于一种 istream对象,将其作为条件时是检测流的状态,遇到文件结束符或者无效输入时会变为无效,从而退出循环。
在Ubuntu中输入 Ctrl+D来输入一个文件结束符。
定义好的头文件:
#ifndef SALESITEM_H// we're here only if SALESITEM_H has not yet been defined #define SALESITEM_H// Definition of Sales_item class and related functions goes here#include <iostream>#include <string>class Sales_item {// these declarations are explained section 7.2.1, p. 270 // and in chapter 14, pages 557, 558, 561friend std::istream& operator>>(std::istream&, Sales_item&);friend std::ostream& operator<<(std::ostream&, const Sales_item&);friend bool operator<(const Sales_item&, const Sales_item&);friend bool operator==(const Sales_item&, const Sales_item&);public: // constructors are explained in section 7.1.4, pages 262 - 265 // default constructor needed to initialize members of built-in type Sales_item() = default; Sales_item(const std::string &book): bookNo(book) { } Sales_item(std::istream &is) { is >> *this; }public: // operations on Sales_item objects // member binary operator: left-hand operand bound to implicit this pointer Sales_item& operator+=(const Sales_item&); // operations on Sales_item objects std::string isbn() const { return bookNo; } double avg_price() const;// private members as beforeprivate: std::string bookNo; // implicitly initialized to the empty string unsigned units_sold = 0; // explicitly initialized double revenue = 0.0;};// used in chapter 10inlinebool compareIsbn(const Sales_item &lhs, const Sales_item &rhs) { return lhs.isbn() == rhs.isbn(); }// nonmember binary operator: must declare a parameter for each operandSales_item operator+(const Sales_item&, const Sales_item&);inline bool operator==(const Sales_item &lhs, const Sales_item &rhs){ // must be made a friend of Sales_item return lhs.units_sold == rhs.units_sold && lhs.revenue == rhs.revenue && lhs.isbn() == rhs.isbn();}inline bool operator!=(const Sales_item &lhs, const Sales_item &rhs){ return !(lhs == rhs); // != defined in terms of operator==}// assumes that both objects refer to the same ISBNSales_item& Sales_item::operator+=(const Sales_item& rhs) { units_sold += rhs.units_sold; revenue += rhs.revenue; return *this;}// assumes that both objects refer to the same ISBNSales_item operator+(const Sales_item& lhs, const Sales_item& rhs) { Sales_item ret(lhs); // copy (|lhs|) into a local object that we'll return ret += rhs; // add in the contents of (|rhs|) return ret; // return (|ret|) by value}std::istream& operator>>(std::istream& in, Sales_item& s){ double price; in >> s.bookNo >> s.units_sold >> price; // check that the inputs succeeded if (in) s.revenue = s.units_sold * price; else s = Sales_item(); // input failed: reset object to default state return in;}std::ostream& operator<<(std::ostream& out, const Sales_item& s){ out << s.isbn() << " " << s.units_sold << " " << s.revenue << " " << s.avg_price(); return out;}double Sales_item::avg_price() const{ if (units_sold) return revenue/units_sold; else return 0;}#endif暂时不用怎么管,先试着使用:
Sales_item book; // 创建一个对象std::cin >> book;std::cout << book << std::endl;return 0;0-201-70353-x 4 24.99> 0-201-70353-x 4 99.96 24.99Sales_item book1,book2; // 创建一个对象std::cin >> book1 >> book2;std::cout << book1+book2 << std::endl;return 0;0-201-70353-x 3 20.000-201-70353-x 2 25.00> 0-201-70353-x 5 110 22Sales_item book1,book2; // 创建一个对象std::cin >> book1 >> book2;if(book1.isbn() == book2.isbn()){ std::cout << book1+book2 << std::endl;}else{ std::cerr << "Error!" << std::endl;}return 0;0-201-70353-x 3 20.000-201-70343-x 2 25.00> Error!#include <bits/stdc++.h>#include "Sales_item.h"int main(void){ Sales_item total; if(std::cin >> total){ // 读取第一条数据,确保有数据可以处理 Sales_item trans; while(std::cin >> trans){ if(total.isbn() == trans.isbn()){ total += trans; } else{ std::cout << total << std::endl; total = trans; } } std::cout << total << std::endl; // 打印最后一本书 } else{ std::cerr << "No data!" << std::endl; } return 0;}0-201-70353-X 4 24.990-201-82470-1 4 45.390-201-88954-4 2 15.00 0-201-88954-4 5 12.00 0-201-88954-4 7 12.00 0-201-88954-4 2 12.00 0-399-82477-1 2 45.390-399-82477-1 3 45.390-201-78345-X 3 20.000-201-78345-X 2 25.00> 0-201-70353-X 4 99.96 24.990-201-82470-1 4 181.56 45.390-201-88954-4 16 198 12.3750-399-82477-1 5 226.95 45.390-201-78345-X 5 110 22这个程序的局限性在于,必须是连号的输入,不连号的输入就失效了。
当然这个时候学到的还不多,后面会将这个程序继续完善。
整型可以分为带符号类型和无符号类型(在前面添加 unsigned)
选择类型的原则:
创建变量时赋予其一个初始值(赋值指的是将对象的当前值用一个新值来替代,含义不同)
初始化的4种方式:
int a = 0;int a = {0};int a{0}; // 列表初始化int a(0);变量声明:“一个文件如果想使用别处定义的名字,必须包含对那个名字的声明”
与定义的区别在于不赋初值
extern int i;
如:
int a = 0;int main(void){ std::cout << a << std::endl; int a = 1; std::cout << a << std::endl; std::cout << ::a << std::endl; // 显式指定访问全局变量 return 0;}010相当于为对象起一个另外的名字,通过 &符号来定义
int ival = 1024;int &refVal = ival;引用必须初始化,因为引用需要和它的初始化对象一起绑定在一起,不能重新绑定到其他对象。
定义引用之后,对其进行的所有操作都是在它的绑定对象上进行的
refVal = 12;std::cout << refVal << std::endl;12引用本身不是一个对象,不能定义引用的引用
如下面的方式,实际上是绑定到了该引用对应的绑定对象上:
int &refVal2 = refVal;std::cout << refVal2 << std::endl;12引用的类型要与绑定的对象严格匹配
引用不能绑定到字面值上
指针也实现了对其他对象的间接访问,但是指针本身也是一个对象,通过 *符号来定义
&int ival = 42;int *p = &ival;指针的类型也要与它所指向的对象严格匹配
*来访问这个对象int ival = 42;int *p = &ival;std::cout << *p << std::endl;42符号的多重含义:
int i = 42;int &r = i; // &随类型名出现,是声明的一部分,r是一个引用int *p; // *随类型名出现,是声明的一部分,p是一个指针p = &i; // &出现在表达式中,是一个取地址符*p = i; // *出现在表达式中,是一个解引用符int &r2 = *p; // r2是一个引用,*是一个解引用符std::cout << i << std::endl << r << std::endl << *p << std::endl << r2 << std::endl;42424242空指针:int *p1 = nullptr
建议:初始化所有的指针
指针与引用不同,是可以赋值的。赋值的时候永远改变的是等号左侧的对象。
void*指针,可以用于存放任意类型对象的地址
double obj = 3.14;double *pd = &obj;void *pv = &obj;pv = pd;std::cout << *pv << std::endl;error: ‘void*’ is not a pointer-to-object typevoid*指针只能与其他指针作比较,作为函数的输入和输出,或者赋值给另外一个 void*指针。
甚至连访问对象都不可以
指向指针的指针
int ival = 1024;int *pi = &ival;int **ppi = πstd::cout << ival << std::endl;std::cout << *pi << std::endl;std::cout << **ppi << std::endl;102410241024指向指针的引用
int i = 42;int *p;int *&r = p;r = &i; // p = &i;std::cout << i << std::endl;std::cout << *r << std::endl;std::cout << *p << std::endl;424242阅读定义要从右往左,离变量名最近的符号对变量类型有最直接的影响
最近的是 &,因此 r是一个引用
然后是 *,说明 r引用的是一个指针
const对象一旦创建,值不可以再改变,因此在创建的时候必须初始化
const int a = 45;
只能在 const类型的对象上执行不改变其内容的操作
可以添加extern关键字,使const变量在文件间共享
extern const int bufSize = fcn(); // file.cpp定义并初始化了这个常量,可以被其他文件访问extern const int bufSize; // file.h 和上面的变量是同一个,只是一个声明,说明定义会在其他地方出现const的引用是对常量的引用,不能改变引用的值,引用的时候也要添加 const限定符
const int ci = 1024;const int &r1 = ci;初始化常量引用时可以使用任意的表达式,只要表达式的结果能转化成引用的类型即可
int i = 42;const int &r1 = i;const int &r2 = 42;const int &r3 = r1 * 2;std::cout << r1 << std::endl;std::cout << r2 << std::endl;std::cout << r3 << std::endl;i = 56;std::cout << r1 << std::endl;std::cout << r2 << std::endl;std::cout << r3 << std::endl;424284564284因此,对 const的引用可以并非一个 const的对象,不能通过这种引用改变被引用的对象的值,但是可以通过其他方式改变这个对象的值
指向常量的指针也不能用于改变其所指对象的值,且指向常量的指针所指的对象也不一定是一个常量
const double pi = 3.14;const double *cptr = &pistd::cout << *cptr << std::endl;double dval = 3.14;cptr = &dval;std::cout << *cptr << std::endl;3.143.14const指针:将指针本身定义为常量,也就是指针所指的地址不变
int errNumb = 0;int *const curErr = &errNumb; // curErr将一直指向errNumb,不能改变const double pi = 3.14159;const double *const pip = &pi // 一个指向常量对象的常量指针*curErr = 56;std::cout << errNumb << std::endl;56指针所指的地址不变,但是如果指向的不是常量,还是可以改变指向的值的
顶层 const可以表示任意的对象是一个常量,底层 const与复合类型有关,指的是下一层对象是常量。
常量表达式:值不会改变且在编译过程就能得到计算结果的表达式
将变量声明为 constexpr来由编译器验证是否为一个常量表达式:constexpr int limit = mf + 1;
在 constexpr中如果声明了一个指针,那么一定是常量指针,即顶层 const
类型别名的两种定义方式:
typedef double wages;using wages = double;如果别名是一个复合类型,不能仅仅将其替换进行理解。
auto类型:将类型交给编译器自己去分析,一般会忽略掉顶层 const,如果需要保留要加 const auto进行推断
decltype类型指示符:通过表达式的类型推断出要定义的变量的类型
const int a = 0,b = 0;decltype(a+b) x = 0;std::cout << x << std::endl;0如果希望得到引用类型,可以添加两层括号,即 decltype((a+b))
struct Sales_data{ std::string bookNo; unsigned units_sold = 0; double revenue = 0.0;};读取单价和数量,输出总价格
Sales_item book; // 创建一个对象std::cin >> book;std::cout << book << std::endl;return 0;0-201-70353-x 4 24.99> 0-201-70353-x 4 99.96 24.99头文件:包含只能被定义一起的实体
通过头文件保护符来确保不允许重复包含:
#ifndef SALES_DATA_H#define SALES_DATA_H#include <string>struct Sales_data{ std::string bookNo; unsigned units_sold = 0; double revenue = 0.0;};#endifusing声明:使用命名空间中的成员
using std::cin;头文件不应包含 using声明
string s1;string s2(s1); // string s2 = s1;string s3("value"); // string s3 = "value";string s4(10,'c');cout << s1 << endl;cout << s2 << endl;cout << s3 << endl;cout << s4 << endl;valuecccccccccc初始化分为直接初始化和拷贝初始化,有 =的为拷贝初始化,一般只用于单个初始值的情况下
输入输出与对整数等的操作相同
使用getline读入一整行(可以带空格)
string line;while(getline(cin,line)){ cout << line << endl;}return 0;> fds fdsfdsf dsffds fdsfdsf dsf> dsfdsfdsfds fdsfds dsfdsfdsfds fdsfdsstring.size()返回的是无符号整形数,不要去负数值混用
字面值不为字符串,不能将字面值相加,只能将字符串相加,如 "df"+"fdsfs"是不合法的
基于范围的 for语句:遍历给定序列中的每一个元素
string str("some string");for (auto c : str){ cout << c;}cout << endl;some string如果要改变字符,需要使用引用类型:
string str("some string");for (auto &c : str){ c = toupper(c);}cout << str << endl;SOME STRINGvector属于一个类模板,模板不是类或者函数,但是可以看作编译器生成类或函数编写的一份说明,编译器根据模板创建类或函数的过程称为实例化。
vector<int> ivec;vector<int> ivec2(ivec);vector<int> ivec3 = ivec;vector<string> articles{"a","an","the"};vector<string> svec(10,"hi");for(auto i : svec){ cout << i << " ";}cout << endl;hi hi hi hi hi hi hi hi hi hi值初始化:只初始化 vector的大小,不赋值具体数值 vector<int> i(10)
vector在设计上事先指定容量是不好的做法,比较适合运行时再添加具体的值
循环内部如果包含向 vector添加元素的语句,不能使用范围 for循环
不能用下标形式添加元素,也就是下标操作只能对确知已经存在的元素进行
vector<int> vi = {1,2,4,5,7,8,9,5,6,4};for(auto it1 = vi.begin();it1 != vi.end();it1++){ *it1 *= 2;}for(auto it2 = vi.cbegin();it2 != vi.cend();it2++){ cout << *it2 << " ";}cout << endl;2 4 8 10 14 16 18 10 12 8int a2[] = {0,1,2};int a3[5] = {1,2,4}; // 多余的初始化成默认值char a4[8] = "Daniel"; // 至少是7,要有一个空字符for (auto i: a3){ cout << i << " ";}cout << endl;for (auto i: a4){ cout << i << " ";}cout << endl;1 2 4 0 0 D a n i e l数组不允许拷贝和赋值
复杂的数组声明:
int *ptrs[10]; // 含有10个整型指针的数组int arr[10];int (*Parray)[10] = &arr; // Parray指向一个含有10个整数的数组int (&arrRef)[10] = arr; // arrRef引用一个含有10个整数的数组int *(&arry)[10] = ptrs; // arry是数组的引用,该数组含有10个指针使用数组的时候编译器一般将其转化为指针
string nums[] = {"one","two","three"};string *p = &nums[0]; // p指向nums的第1个元素string *p2 = nums // 等价于上面的语句使用 auto推断时会返回一个指针,但是只用 decltype推断的时候会返回数组
利用指针对数组可以起到迭代器的效果
int ia[] = {1,2,3,4,5,6,7,8,9};int *beg = begin(ia); // 指向ia的第一个元素int *last = end(ia); // 指向ia的最后一个元素的下一个位置for(auto it = beg;it != last;it++){ cout << *it << " ";}cout << endl;string转化为C风格字符串
string s("Hello World!");const char *str = s.c_str();cout << *str << endl;使用数组初始化vector
int int_arr[] = {0,1,2,3,4,5};vector<int> ivec(begin(int_arr),end(int_arr));for(auto it : ivec){ cout << it << " ";}cout << endl;0 1 2 3 4 5int ia[3][4] = {{1,2,3,4},{5,6,7,8},{9,10,11,12}};int (*p)[4] = ia; // p指向含有4个整数的数组p = &ia[2]; // p 指向ia的尾元素for(auto p = ia;p != ia+3;++p){ for(auto q = *p;q != *p+4;q++){ cout << *q << " "; }}cout << endl;for(auto p = begin(ia);p != end(ia);++p){ for(auto q = begin(*p);q != end(*p);q++){ cout << *q << " "; }}cout << endl;通俗的讲,左值就是能够出现在赋值符号左面的东西,而右值就是那些可以出现在赋值符号右面的东西.
左值:指表达式结束后依然存在的持久对象,可以取地址,具名变量或对象
右值:表达式结束后就不再存在的临时对象,不可以取地址,没有名字。
当一个对象被用作右值的时候,使用的是对象的值(内容);当一个对象被用作左值的时候,用的是对象的身份(在内存中的位置)
m%n的符号与 m相同
强制类型转换:
int i = 52;int j = 9;double slope = static_cast<double>(j) / i;cout << slope << endl;0.173077switch语句:
int a;while(cin >> a){ switch(a){ case 0: cout << '1' << endl;break; case 1: cout << '2' << endl;break; case 2: cout << '3' << endl;break; case 3: cout << '4' << endl;break; case 4: cout << '5' << endl;break; case 5: cout << '6' << endl;break; case 6: cout << '7' << endl;break; case 7: cout << '8' << endl;break; case 8: cout << '9' << endl;break; case 9: cout << '0' << endl;break; default: cout << 'N' << endl;break; }}> 01> 90> 45Ntry语句块和异常处理:
throw语句抛出异常:
int a = 1;throw runtime_error("fdsdfds");terminate called after throwing an instance of 'std::runtime_error' what(): fdsdfdsAbortedcatch语句捕捉异常:
double m, n;cin >> m >> n;try { if (n == 0) throw - 1; //抛出整型异常 else if (m == 0) throw - 1.0; //拋出 double 型异常 else cout << m / n << endl;}catch (double d) { cout << "catch (double)" << d << endl;}catch (...) { cout << "catch (...)" << endl;}> 0 6catch (double)-1> 6 0catch (...)局部静态对象:程序第一次经过时被初始化,直到程序终止时才被销毁。
int count_calls(){ static int ctr = -1; return ++ctr;}int main(void){ for(int i = 0;i != 10; ++i){ cout << count_calls() << " "; } cout << endl; return 0;}0 1 2 3 4 5 6 7 8 9函数声明(函数原型):在使用函数之前对函数的名字进行声明
函数声明可以忽略形参的名字,也可以加上形参的名字。
函数声明最好写在头文件中
分离式编译:编译和链接多个源文件
指针形参:
void reset(int *ip){ *ip = 0;}int main(void){ int i = 42; reset(&i); cout << i << endl; return 0;}0传引用参数:
void reset(int &i){ i = 0;}int main(void){ int i = 42; reset(i); cout << i << endl; return 0;}0尽量使用引用形式从而避免拷贝
还可以通过引用形式返回一些额外信息。因为函数只能返回一个返回值,但是如果某个值是引用的形式传到函数中的,也会保留下修改后的值。
不修改的变量尽量使用常量引用
数组形参:
void Print(const int i[]){ cout << i[0] << endl;}void Print(const int *i){ cout << i[0] << endl;}void Print(const int i[10]){ cout << i[0] << endl;}int main(void){ int i = 5; int j[2] = {6,7}; Print(&i); Print(j);}56数组不能直接进行传递,直接作为指针的形式传递,因此丢掉了数组大小的信息
可以使用指针的形式进行提示,也可以传入一个表示数组大小的参数。
void print(const int *beg,const int *end){ while(beg != end){ cout << *beg++ << " "; }}void print(const int i[] ,size_t size){ for(size_t a=0;a<size;a++){ cout << i[a] << " "; }}int main(void){ int i[10] = {6,7,5,4,7,8,9,6,5,4}; print(begin(i),end(i)); cout << endl; return 0;}6 7 5 4 7 8 9 6 5 4数组引用形参:(缺点是只能作用于大小固定的数组)
void print(int (&arr)[10]){ for(auto elem : arr){ cout << elem << " "; }}含有可变形参的函数:
void error_msg(initializer_list<string> il){ for(auto beg = il.begin();beg != il.end();++beg){ cout << *beg << " "; } cout << endl;}int main(void){ error_msg({"a","b"}); error_msg({"a","b","c"});}a b a b c函数返回时不要返回局部对象的引用或指针
调用一个返回引用的函数会得到左值
char &get_val(string &str,string::size_type ix){ return str[ix];}int main(void){ string s("a value"); cout << s << endl; get_val(s,0) = 'A'; cout << s << endl; return 0;}a valueA value返回值也可以是一个花括号包围起来的列表
定义相同名称的函数,但是形参列表不同,可能是数量上的不同,也可能是类型上的不同。使得函数调用的时候根据不同的形参列表自动判断指定哪一个函数。
顶层 const不影响传入的参数
在不同的作用域中无法重载函数,会覆盖掉
默认实参:在函数的声明中给一个默认值,调用时可以覆盖掉,也可以不写以使用默认值。
内联函数:将函数在调用点展开,但是编译器不一定支持
constexpr函数:能用于常量表达式的函数,函数的返回值和所有形参的类型都要是字面值类型,函数体中有且只有一条 return语句。
assert表达式:用于调试的时候对程序进行检查 assert(s == "dfdsf");如果不满足条件程序会中断退出。
完全不明白。。。没有示例程序看不懂
成员函数是类定义的一部分,通过特定的对象来调用。非成员函数就是普通的函数。
成员函数的声明必须在类的内部,定义可以在类的内部或者外部。非成员函数的声明和定义都在类的外部。
构造函数:控制对象的初始化过程
访问控制与封装:
定义在public说明符后的成员在整个程序内可被访问,public成员定义类的接口。
定义在private说明符之后的成员可以被类的成员函数访问,但是不能被使用该类的代码访问,private部分封装了类的实现细节。
使用class和struct定义类的区别在于默认的访问权限不同,struct默认访问权限都是public的
友元:令其他类或成员成为访问它的非公有成员。但是友元只算一个权限控制,在类外一样要进行声明。
上述代码:
#include <bits/stdc++.h>using std::string;using std::vector;using std::cin;using std::cout;using std::endl;using std::begin;using std::end;using std::runtime_error;using std::initializer_list;using std::istream;using std::ostream;class Sales_data{friend Sales_data add(const Sales_data&,const Sales_data&);friend std::ostream &print(std::ostream&,const Sales_data&);friend std::istream &read(std::istream&,Sales_data&);public: // 构造函数 Sales_data() = default; // 默认构造函数 // 构造函数初始值列表 Sales_data(const std::string &s):bookNo(s){ } Sales_data(const std::string &s,unsigned n,double p):bookNo(s),units_sold(n),revenue(p*n){ } Sales_data(std::istream &); // 常量成员函数 std::string isbn() const { return bookNo; } Sales_data &combine(const Sales_data&);private: double avg_price() const; std::string bookNo; unsigned units_sold = 0; double revenue = 0.0;};Sales_data add(const Sales_data&,const Sales_data&);std::ostream &print(std::ostream&,const Sales_data&);std::istream &read(std::istream&,Sales_data&);// 在类的外部定义成员函数double Sales_data::avg_price() const { if(units_sold){ return revenue / units_sold; } else{ return 0; }}// 定义一个返回this对象的函数Sales_data& Sales_data::combine(const Sales_data &rhs){ units_sold += rhs.units_sold; revenue += rhs.revenue; return *this;}// 类相关的非成员函数istream &read(istream &is, Sales_data &item){ double price = 0; is >> item.bookNo >> item.units_sold >> price; item.revenue = price * item.units_sold; return is;}ostream &print(ostream &os,const Sales_data &item){ os << item.isbn() << " " << item.units_sold << " " << item.revenue << " " << item.avg_price(); return os;}Sales_data add(const Sales_data &lhs,const Sales_data &rhs){ Sales_data sum = lhs; sum.combine(rhs); return sum;}// 在类的外部定义构造函数Sales_data::Sales_data(std::istream &is){ read(is,*this);}int main(void){ return 0;}inline写在类内或者类外,一般写在类外const里面也可以变化class Screen{ public: typedef std::string::size_type pos; // 定义类型的成员 Screen() = default; Screen(pos ht,pos wd,char c): height(ht), width(wd),contents(ht*wd,c){ } char get() const { return contents[cursor]; // 隐式内联函数 }; inline char get(pos ht,pos wd) const; // 显式内联函数 Screen &move(pos r, pos c); // 后面设置为内联函数 size_t some_member() const; Screen &set(char); Screen &set(pos,pos,char); Screen &display(std::ostream &os){ do_display(os); return *this; } const Screen &display(std::ostream &os) const { do_display(os); return *this; } private: pos cursor = 0; pos height = 0,width = 0; std::string contents; mutable size_t access_ctr = 0; void do_display(std::ostream &os) const { os << contents; }};inline Screen &Screen::move(pos r,pos c){ pos row = r * width; cursor = row + c; return *this;}char Screen::get(pos r,pos c) const { pos row = r * width; return contents[row + c];}size_t Screen::some_member() const{ ++access_ctr; return access_ctr;}inline Screen &Screen::set(char c){ contents[cursor] = c; return *this;}inline Screen &Screen::set(pos r,pos col,char ch){ contents[r*width+col] = ch; return *this;}// 类数据成员的初始值class Window_mgr{ private: std::vector<Screen> screens{Screen(24,80,' ')};};int main(void){ Screen myscreen; char ch = myscreen.get(); cout << myscreen.some_member() << endl; ch = myscreen.get(0,0); cout << myscreen.some_member() << endl; myscreen.move(4,0); myscreen.set('#'); cout << myscreen.get() << endl; Screen myScreen(5,3,'!'); const Screen blank(5,3,'?'); myScreen.set(2,1,'#').display(cout); cout << endl; blank.display(cout); cout << endl; return 0;}12#!!!!!!!#!!!!!!!???????????????类之间的友元关系:不存在传递性
class Screen{ friend class Window_mgr;// 类数据成员的初始值class Window_mgr{ public: using ScreenIndex = std::vector<Screen>::size_type; void clear(ScreenIndex); private: std::vector<Screen> screens{Screen(24,80,' ')};};void Window_mgr::clear(ScreenIndex i){ Screen &s = screens[i]; s.contents = string(s.height * s.width, ' ');}class Screen{ friend class Window_mgr; public: typedef std::string::size_type pos; // 定义类型的成员 Screen() = default; Screen(pos ht,pos wd,char c): height(ht), width(wd),contents(ht*wd,c){ } char get() const { return contents[cursor]; // 隐式内联函数 }; inline char get(pos ht,pos wd) const; // 显式内联函数 Screen &move(pos r, pos c); // 后面设置为内联函数 size_t some_member() const; Screen &set(char); Screen &set(pos,pos,char); Screen &display(std::ostream &os){ do_display(os); return *this; } const Screen &display(std::ostream &os) const { do_display(os); return *this; } private: pos cursor = 0; pos height = 0,width = 0; std::string contents; mutable size_t access_ctr = 0; void do_display(std::ostream &os) const { os << contents; }};inline Screen &Screen::move(pos r,pos c){ pos row = r * width; cursor = row + c; return *this;}char Screen::get(pos r,pos c) const { pos row = r * width; return contents[row + c];}size_t Screen::some_member() const{ ++access_ctr; return access_ctr;}inline Screen &Screen::set(char c){ contents[cursor] = c; return *this;}inline Screen &Screen::set(pos r,pos col,char ch){ contents[r*width+col] = ch; return *this;}// 类数据成员的初始值class Window_mgr{ public: using ScreenIndex = std::vector<Screen>::size_type; void clear(ScreenIndex); ScreenIndex addScreen(const Screen&); private: std::vector<Screen> screens{Screen(24,80,' ')};};void Window_mgr::clear(ScreenIndex i){ Screen &s = screens[i]; s.contents = string(s.height * s.width, ' ');}Window_mgr::ScreenIndex Window_mgr::addScreen(const Screen &s){ screens.push_back(s); return screens.size() - 1;}int main(void){ Screen myscreen; char ch = myscreen.get(); cout << myscreen.some_member() << endl; ch = myscreen.get(0,0); cout << myscreen.some_member() << endl; myscreen.move(4,0); myscreen.set('#'); cout << myscreen.get() << endl; Screen myScreen(5,3,'!'); const Screen blank(5,3,'?'); myScreen.set(2,1,'#').display(cout); cout << endl; blank.display(cout); cout << endl; return 0;}构造函数初始值列表:定义变量的时候习惯对其立即进行初始化,有时初始化的值是必不可少的,且要注意成员初始化的顺序。
委托构造函数:使用它所属类的其他构造函数执行它自己的初始化过程
默认构造函数
类类型转换
聚合类:就是比较简单的结构体
字面值常量类
类的静态成员存在于任何对象之外,对象中不包含任何与静态数据成员有关的数据
]]>首先从二维入手,然后扩展到三维以及更高的维度(从特殊到一般),然后找出普遍的规律,再进行验证(从一般到特殊)
官方文档应该是最权威的,首先看官方文档是怎么说明的,然后查找一些资料,看看其他人是怎么理解的,最后总结出自己的一套规律
import numpy as np感受一个ndarray,最简单的方法就是打印ndarray的shape。
官方文档里面是这样写的:
the dimensions of the array. This is a tuple of integers indicating the size of the array in each dimension. For a matrix with n rows and m columns, shape will be (n,m). The length of the shape tuple is therefore the number of axes, ndim.
只列举了矩阵的例子,尝试一下:
a1 = np.arange(15).reshape(3, 5)print(a1,'\n',a1.shape,'\n',a1.ndim)输出结果:
[[ 0 1 2 3 4] [ 5 6 7 8 9] [10 11 12 13 14]] (3, 5) 2简单推断:最开始有2个方括号,因此矩阵是2维的,且第1个方括号内部有3个“2级方括号”,每一个“2级方括号”内部都有5个元素,因此这个shape可能是从外向里数的。
尝试1维ndarray:
a2 = np.arange(15)print(a2,'\n',a2.shape,'\n',a2.ndim)输出结果:
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14] (15,) 1尝试3维ndarray:
a3 = np.arange(24).reshape(3,2,4)print(a3,'\n',a3.shape,'\n',a3.ndim)输出结果:
[[[ 0 1 2 3] [ 4 5 6 7]] [[ 8 9 10 11] [12 13 14 15]] [[16 17 18 19] [20 21 22 23]]] (3, 2, 4) 3尝试4维ndarray:
a4 = np.arange(24).reshape(3,2,1,4)print(a4,'\n',a4.shape,'\n',a4.ndim)输出结果:
[[[[ 0 1 2 3]] [[ 4 5 6 7]]] [[[ 8 9 10 11]] [[12 13 14 15]]] [[[16 17 18 19]] [[20 21 22 23]]]] (3, 2, 1, 4) 4因此可以得出结论:对于给定的ndarray,判断ndim就是计数最前面有多少个相连的方括号,判断shape就是从外向内看,每一层分别有多少个“元素”。
也可以看出,数组超过4维后,肉眼就有些难以区分了。
索引就是取数组中的某些元素,官方文档有下面的举例:
>>> a = np.arange(30).reshape(2, 3, 5)>>> aarray([[[ 0, 1, 2, 3, 4], [ 5, 6, 7, 8, 9], [10, 11, 12, 13, 14]], [[15, 16, 17, 18, 19], [20, 21, 22, 23, 24], [25, 26, 27, 28, 29]]])>>> a[0, 2, :]array([10, 11, 12, 13, 14])>>> a[0, :, 3]array([ 3, 8, 13])索引操作是与shape相对应的。如上述例子,a[0]即为取数组的第1个维度(2)的第1个元素,这样原来3维的数组就降到了2维;a[0, :]就是在a[0]的基础上取数组的第2个维度(3)的全部元素,数组的维度不变,还是2维;a[0, :, 3]就是在a[0, :]的基础上取数组的第3个维度(5)的第4个元素,即可得出上面的结果。
索引操作后的维度与索引的数量以及是否有“:”相关。如果索引的数量与ndim相同,则最后取出来的是一个数。如果数量不同或者有“:”(数量不同可以看成在后面补“:”),则最终取得的数组的维度与“:”对应的原数组的维度相同。
以numpy.sum为例:
官方文档:
Axis or axes along which a sum is performed. The default, axis=None, will sum all of the elements of the input array. If axis is negative it counts from the last to the first axis.
If axis is a tuple of ints, a sum is performed on all of the axes specified in the tuple instead of a single axis or all the axes as before.
以三维数组为例:
print('origin')print(a3,a3.shape)print('axis=0')print(a3.sum(axis=0),a3.sum(axis=0).shape)print('axis=1')print(a3.sum(axis=1),a3.sum(axis=1).shape)print('axis=2')print(a3.sum(axis=2),a3.sum(axis=2).shape)print('axis=(0,1)')print(a3.sum(axis=(0,1)),a3.sum(axis=(0,1)).shape)print('axis=(1,2)')print(a3.sum(axis=(1,2)),a3.sum(axis=(1,2)).shape)print('axis=(0,2)')print(a3.sum(axis=(0,2)),a3.sum(axis=(0,2)).shape)print('axis=(0,1,2)')print(a3.sum(axis=(0,1,2)),a3.sum(axis=(0,1,2)).shape)origin[[[ 0 1 2 3] [ 4 5 6 7]] [[ 8 9 10 11] [12 13 14 15]] [[16 17 18 19] [20 21 22 23]]] (3, 2, 4)axis=0[[24 27 30 33] [36 39 42 45]] (2, 4)axis=1[[ 4 6 8 10] [20 22 24 26] [36 38 40 42]] (3, 4)axis=2[[ 6 22] [38 54] [70 86]] (3, 2)axis=(0,1)[60 66 72 78] (4,)axis=(1,2)[ 28 92 156] (3,)axis=(0,2)[114 162] (2,)axis=(0,1,2)276 ()axis为多少,就是在这个维度上进行操作,最终的结果就是这个维度消失
不要从行列什么的去思考怎么变化,直接从shape的角度入手。设置axis为多少,这个维度就没有了!比如原来是(3,2,4)的维度,要是axis=0,第一个维度就没有了,加和得到的矩阵就是(2,4)。
如果希望保留维度,可以增加keepdims=True的选项,这样被操作的维度就会变为1而不是直接消失。
print('axis=(0,1)')print(a3.sum(axis=(0,1),keepdims=True),a3.sum(axis=(0,1),keepdims=True).shape)axis=(0,1)[[[60 66 72 78]]] (1, 1, 4)这样想应该会比较好理解,尤其是对于更高维的数组来说,行列的概念基本失效,从shape的角度思考会好。
另外一个比较常用的操作是np.concatenate,可以将数组进行合并,在数据处理或者神经网络中很常用。
在np.concatenate上检验一下对于axis的理解:
ta = np.arange(24).reshape(3,2,4)tb = np.arange(24,36).reshape(3,1,4)print(ta,ta.shape)print(tb,tb.shape)[[[ 0 1 2 3] [ 4 5 6 7]] [[ 8 9 10 11] [12 13 14 15]] [[16 17 18 19] [20 21 22 23]]] (3, 2, 4)[[[24 25 26 27]] [[28 29 30 31]] [[32 33 34 35]]] (3, 1, 4)两者合并,第2个维度不相同,应该是可以合并的,合并后的shape应该为(3,3,4)
print(np.concatenate((ta,tb),axis=1),np.concatenate((ta,tb),axis=1).shape)[[[ 0 1 2 3] [ 4 5 6 7] [24 25 26 27]] [[ 8 9 10 11] [12 13 14 15] [28 29 30 31]] [[16 17 18 19] [20 21 22 23] [32 33 34 35]]] (3, 3, 4)np.concatenate除了在待合并的axis上之外,必须具有相同的shape
之前的结论也得到了验证。
我们处在三维空间中,二维和三维是比较直观的,可以在脑海中想象出来。因此我们会觉得axis的设计有些反直觉。以后应该从shape的角度去看待axis的设计思想,首先理解上比较直观,其次在更高维度的数组上也能合理的进行操作。不要去思考数组实际中应该是个什么样子,直接观察axis就足够了。
In the third course of the Machine Learning Specialization, you will:
• Use unsupervised learning techniques for unsupervised learning: including clustering and anomaly detection.
• Build recommender systems with a collaborative filtering approach and a content-based deep learning method.
• Build a deep reinforcement learning model.
The Machine Learning Specialization is a foundational online program created in collaboration between DeepLearning.AI and Stanford Online. In this beginner-friendly program, you will learn the fundamentals of machine learning and how to use these techniques to build real-world AI applications.
This Specialization is taught by Andrew Ng, an AI visionary who has led critical research at Stanford University and groundbreaking work at Google Brain, Baidu, and Landing.AI to advance the AI field.
This 3-course Specialization is an updated and expanded version of Andrew’s pioneering Machine Learning course, rated 4.9 out of 5 and taken by over 4.8 million learners since it launched in 2012.
It provides a broad introduction to modern machine learning, including supervised learning (multiple linear regression, logistic regression, neural networks, and decision trees), unsupervised learning (clustering, dimensionality reduction, recommender systems), and some of the best practices used in Silicon Valley for artificial intelligence and machine learning innovation (evaluating and tuning models, taking a data-centric approach to improving performance, and more.)
By the end of this Specialization, you will have mastered key concepts and gained the practical know-how to quickly and powerfully apply machine learning to challenging real-world problems. If you’re looking to break into AI or build a career in machine learning, the new Machine Learning Specialization is the best place to start.
无监督学习是在没有标签的数据中自动寻找某些规律
聚类任务是典型的无监督学习任务,通过某些特征将相似的人或事物自动归为一类
无监督学习任务还有异常检测(找出一些不寻常的数据)和维度降低(使用更少的数字对数据进行压缩)
聚类是一种典型的无监督学习算法,不定义标签,让算法自己去寻找数据中有趣的特征
聚类可以在下面几个方面得到应用:
K-means聚类步骤:
如何决定聚类的数量?Elbow method
多种聚类数量都尝试一下,找到“肘点”,也就是增加聚类数量后代价函数也不能明显减小的点
如何随机初始化最初的类别中心点?
已经拥有一些数据,增加一条数据,判断其是否符合已有的数据的特征,如果不符合则为异常数据
正态分布:
异常检测:,计算点的
是否满足大于预先定义的阈值
实际应用中,可以找一些有标记的异常点,指导算法选取合适的阈值
在某种类别(异常)的数据量很少的情况下,且异常的种类较多,特征无法很好区分出来的时候,使用异常检测算法比较好。
场景:很多用户对电影进行打分,分数从0-5,如何向用户推荐合适的电影?
设用户的数量为,电影的数量为
,
如果用户对电影
进行了打分,那么
,反之
。
表示用户
对电影
打分的分数(0-5)
表示电影的特征数量(如浪漫程度、武打程度等等),则用户
对应的特征向量为
表示的是用户
打分的电影数目
预测用户对电影
的打分:
代价函数:
对所有用户来说,,
是定值,忽略不计
前面是有特征,通过类似于线性回归的方式可以进行预测,但是如果没有特征应该怎么做呢?
已知,预测
代价函数:
将两个代价函数结合到一起:
如果评分是二值化的,则类似于线性回归与逻辑回归的区别:
如果一个人没有对任何电影进行评分,则选取其他所有人的评分平均值作为他的评分。
协同过滤算法的局限性:
协同过滤算法是基于用户的评分,根据比较相似的评分情况来进行推荐
基于内容的过滤算法是基于用户和物品的特征来寻找比较合适的匹配对
设用户对应的特征是
,电影
对应的特征是
比较两个特征之间相似度的方法是点乘,但是两者的维度不同,因此要对输入的特征增加几层神经网络,使其输出相同,再进行点乘。
通过神经网络后,是
的32维向量,
是
的32维向量,
代价函数为::
检索和排序策略:
强化学习不告诉应该怎么做,而是只告诉做什么,如果做的好有奖励,做的不好有惩罚,从而让算法自动向着奖赏最多的方向优化,最终学习出最好的结果。
目前的状态、动作、奖励、下一个状态,下一个状态的动作
每一个时间步后,会有一个权重,最终的返回值(Return)是权重
与奖励
的乘积
一般来说,权重按照幂的方式变化,如第一步是,第二步是
,第
步是
。
措施指的是在状态
应该采取什么样的动作
强化学习的目标就是找到合适的措施从而最大化返回的奖励(Return)
马尔可夫决策过程:未来只取决于现在所处的位置,与之前是怎么到达现在这个位置的无关。
状态-动作方程:表示从状态
开始进行动作
,然后后面采取最优化的动作
因此,可以得出两个结论:
贝尔曼方程:
在更为复杂的环境下,状态之间的转移可能并不是确定的,有一定的几率到达其他的状态
因此得到的返回奖励实际上是期望的返回奖励,即
状态空间可能是连续的,对于月球车来说,有方向(前后左右和旋转)和速度两种变量,因此
训练神经网络:输入是,输出目的是找到最合适的动作
使得
最大。其中,神经网络的最后一层输出的神经元数量可以修改为
的数量,就可以对所有可能情况的
进行同时训练。
训练步骤:
-贪心策略:在DQN的第一步中,以
的概率随意选取,以
的概率选取能使
最大化的
mini-batch:在只选取一部分进行训练
soft update:步骤中,并不直接修改,而是使用权重对新旧参数进行组合
In the second course of the Machine Learning Specialization, you will:
• Build and train a neural network with TensorFlow to perform multi-class classification
• Apply best practices for machine learning development so that your models generalize to data and tasks in the real world
• Build and use decision trees and tree ensemble methods, including random forests and boosted trees
The Machine Learning Specialization is a foundational online program created in collaboration between DeepLearning.AI and Stanford Online. In this beginner-friendly program, you will learn the fundamentals of machine learning and how to use these techniques to build real-world AI applications.
This Specialization is taught by Andrew Ng, an AI visionary who has led critical research at Stanford University and groundbreaking work at Google Brain, Baidu, and Landing.AI to advance the AI field.
This 3-course Specialization is an updated and expanded version of Andrew’s pioneering Machine Learning course, rated 4.9 out of 5 and taken by over 4.8 million learners since it launched in 2012.
It provides a broad introduction to modern machine learning, including supervised learning (multiple linear regression, logistic regression, neural networks, and decision trees), unsupervised learning (clustering, dimensionality reduction, recommender systems), and some of the best practices used in Silicon Valley for artificial intelligence and machine learning innovation (evaluating and tuning models, taking a data-centric approach to improving performance, and more.)
By the end of this Specialization, you will have mastered key theoretical concepts and gained the practical know-how to quickly and powerfully apply machine learning to challenging real-world problems. If you’re looking to break into AI or build a career in machine learning, the new Machine Learning Specialization is the best place to start.
生物神经元:通过树突接收到来自不同地方的输入,然后通过轴突将神经冲动传递出去。
但是目前对于人脑的运作方式了解的还不是很透彻。
model = Sequential( [ tf.keras.Input(shape=(400,)), #specify input size tf.keras.layers.Dense(25, activation='sigmoid'), tf.keras.layers.Dense(15, activation='sigmoid'), tf.keras.layers.Dense(1, activation='sigmoid') ], name = "my_model" )model.compile( loss=tf.keras.losses.BinaryCrossentropy(), optimizer=tf.keras.optimizers.Adam(0.001),)model.fit( X,y, epochs=20)prediction = model.predict(X[0].reshape(1,400)) # a zeroprint(f" predicting a zero: {prediction}")prediction = model.predict(X[500].reshape(1,400)) # a oneprint(f" predicting a one: {prediction}")def my_dense_v(A_in, W, b, g): """ Computes dense layer Args: A_in (ndarray (m,n)) : Data, m examples, n features each W (ndarray (n,j)) : Weight matrix, n features per unit, j units b (ndarray (1,j)) : bias vector, j units g activation function (e.g. sigmoid, relu..) Returns A_out (ndarray (m,j)) : m examples, j units """ z = np.matmul(A_in,W)+b A_out = g(z) return(A_out)def my_sequential_v(X, W1, b1, W2, b2, W3, b3): A1 = my_dense_v(X, W1, b1, sigmoid) A2 = my_dense_v(A1, W2, b2, sigmoid) A3 = my_dense_v(A2, W3, b3, sigmoid) return(A3)Prediction = my_sequential_v(X, W1_tmp, b1_tmp, W2_tmp, b2_tmp, W3_tmp, b3_tmp )Prediction.shape人工智能(AI)可以分为两种,ANI和AGI:
ANI指在某一特定领域应用的人工智能,目前已经取得了很好的效果;
AGI指通用人工智能,人工智能可以做任何人类可以做到的事情。
鉴于对人脑的了解还不够,如果通过模拟人脑的方式达到通用人工智能比较困难。
不过目前有一些进展,让通用人工智能看到了一点点希望。
如果不使用激活函数,那么不管多么复杂的神经网络都会退化成线性回归方法可以实现的效果。
Sigmoid激活函数:
ReLU激活函数:
如何选择输出层的激活函数:
隐藏层中大多数使用ReLU激活函数而非Sigmoid激活函数
多类别分类是指输出不止两种情况的分类问题,如对手写数字进行分类,输出的类别会有10个
可以使用Softmax回归算法:
损失函数:,也就是
多标签分类:可以看成很多多类别分类问题,也可以使用一个神经网络预测所有的类别
Adam优化方法:自动调节学习率
如果梯度下降的方向一直是同一方向则增大学习率,让算法运行更快
如果梯度下降的方向一直在波动,则减小学习率。
如果发现训练好的模型在预测上存在很大的问题,可以从以下几个方面入手查找原因:
训练时对训练集进行划分,可以划分为训练集和测试集,如果希望使用交叉验证的方式,可以划分为训练集、验证集和测试集。通过测试集的表型评估模型的效果。模型的选择上,可以从多项式的次数从低到高依次进行选择,找出测试集误差最小的模型。
更大规模的神经网络的偏差往往更小
如果恰当选择正则化参数,更大规模的神经网络的表现比小规模的神经网络表现更好
欠拟合:函数对于训练集的拟合效果不好——高偏差(high bias)
过拟合:函数对于训练集的拟合效果好,对于测试集的效果不好——高方差(high variance)
避免过拟合的方法:
正则项参数对模型的影响
学习曲线:
评价分类(尤其针对分布不平衡的数据)
熵(Entropy)
信息增益
如果一个决策结点有三个可选项,可以通过独热编码的方式将其转换为多个二分类形式。
如果变量是连续的数值,可以计算从那里开始划分的信息增益最高,从而转化为判断大小于的二分类形式。
决策树解决回归问题,则将熵替换为节点上数据的方差进行计算。
随机森林:
XGBoost:采样训练数据的时候更倾向于采样前面的树中被分类错误的数据
决策树更适用于结构化的数据,快速,但是不适用于其他类似于图片文本等的数据
神经网络适用于所有类型的数据,运行可能稍慢一些,可以迁移学习,更适合将不同的神经网络结合到一起。
This course offers a brief introduction to the multivariate calculus required to build many common machine learning techniques. We start at the very beginning with a refresher on the “rise over run” formulation of a slope, before converting this to the formal definition of the gradient of a function. We then start to build up a set of tools for making calculus easier and faster. Next, we learn how to calculate vectors that point up hill on multidimensional surfaces and even put this into action using an interactive game. We take a look at how we can use calculus to build approximations to functions, as well as helping us to quantify how accurate we should expect those approximations to be. We also spend some time talking about where calculus comes up in the training of neural networks, before finally showing you how it is applied in linear regression models. This course is intended to offer an intuitive understanding of calculus, as well as the language necessary to look concepts up yourselves when you get stuck. Hopefully, without going into too much detail, you’ll still come away with the confidence to dive into some more focused machine learning courses in future.
函数是从输入到输出的映射,选择函数来建模世界的过程是伟大天才的科学目的,微积分只是对这些函数如何相对于它们的输入变量如何变化的研究。
对于线性函数而言,斜率(梯度、gradient)=‘rise over run’,也就是任意取两点,方向的距离与
方向的距离之比即为梯度。
对于梯度一直在变化的函数来说,设函数为,任意取两点
和
,
即,
导数的求和法则:
幂函数求导法则:令,则
不连续(discontinuity)的函数,例如,在
处没有定义,导数
在
处也没有定义.
例如这种函数,
,这种类型的函数与导数始终相等,因此有两个特点:
三角函数:
导数乘积法则:令,则
求导的链式法则:若,且
,则
偏导数求导法则:
偏导数仍然遵循导数的求导法则
设函数,它的雅可比行列式为
这样给予一组的值,可以快速得出函数在该点指向此函数最陡斜率方向的向量。
设函数,则它的雅可比行列式为
对雅可比行列式再求一次偏导数,构成的二阶偏导数矩阵为海森矩阵
设函数,它的雅可比行列式为
,则海森矩阵为
雅可比行列式求得的值为0的情况下,首先求海森矩阵的行列式,如果行列式为正数,说明目前的点是一个极值点;然后看海森矩阵的第一个数字,如果第一个数字是正数,说明目前在极小值点,否则在极大值点;如果海森矩阵的行列式为负,说明目前的点是一个鞍点。
最简单的神经网络:,其中,
表示活动,
表示权重,
表示偏差,
表示激活函数
输入可能不仅仅是一个,设输入的神经元有个,则
输出可能也不仅仅是一个,设输出的神经元有个,总体的神经网络表示为:
可以简化表示为:
如果神经网络不止一层,则可以表示为:
神经网络(分类任务)的损失函数为
泰勒展开式是对一个复杂函数的简化估计函数
(麦克劳林形式,需要知道零点)
泰勒形式:
(泰勒形式,知道任意一点
即可)
(零阶泰勒展开)
(一阶泰勒展开-雅可比行列式)
(二阶泰勒展开-海森矩阵)
迭代求解方程的近似根:
这种方法会存在一些问题,如果选取的点比较靠近函数的拐点,会得不到正确的结果,或者得到的结果并不是与选取的点最接近的。
如何使用梯度找到多元函数的最大值或者最小值
函数的梯度:,即为函数值增加最快的方向
如果希望找到最大值,将梯度与它的单位向量相乘,则
梯度下降:
计算函数在某些约束下的最大值或者最小值
,
为拉格朗日乘子
即:
设函数,
计算平方误差:
求解使得误差最小:
则可以解得:
Formula Sheet: Sheet summarising all the formulae covered in this course.
吴恩达的机器学习课程终于更新了!!!想当初应该是大二的时候,看了吴恩达的课程,对机器学习有了初步的了解。当时听的不是很明白,英语看不太懂,一些给了充分提示的代码也写不太好,也就是入了一个门而已。这次有一些时间,正好捡一捡机器学习的基础知识,推一推那些一直在调包的数学公式。注重记录!
In the first course of the Machine Learning Specialization, you will:
• Build machine learning models in Python using popular machine learning libraries NumPy and scikit-learn.
• Build and train supervised machine learning models for prediction and binary classification tasks, including linear regression and logistic regression
The Machine Learning Specialization is a foundational online program created in collaboration between DeepLearning.AI and Stanford Online. In this beginner-friendly program, you will learn the fundamentals of machine learning and how to use these techniques to build real-world AI applications.
This Specialization is taught by Andrew Ng, an AI visionary who has led critical research at Stanford University and groundbreaking work at Google Brain, Baidu, and Landing.AI to advance the AI field.
This 3-course Specialization is an updated and expanded version of Andrew’s pioneering Machine Learning course, rated 4.9 out of 5 and taken by over 4.8 million learners since it launched in 2012.
It provides a broad introduction to modern machine learning, including supervised learning (multiple linear regression, logistic regression, neural networks, and decision trees), unsupervised learning (clustering, dimensionality reduction, recommender systems), and some of the best practices used in Silicon Valley for artificial intelligence and machine learning innovation (evaluating and tuning models, taking a data-centric approach to improving performance, and more.)
By the end of this Specialization, you will have mastered key concepts and gained the practical know-how to quickly and powerfully apply machine learning to challenging real-world problems. If you’re looking to break into AI or build a career in machine learning, the new Machine Learning Specialization is the best place to start.
监督学习是学习从输入到输出标签
的一个函数映射,主要特征是给予算法示例去学习,也就是从被给予的正确答案中学习。
监督学习的基本类型有两种:回归和分类
回归任务是在大量的数值空间中,对某一个具体数值进行预测
分类任务是在给定的数值空间中(如0和1),对某一个具体数据进行预测
表示输入的变量或者特征
表示输出的实际目标变量,
表示预测的变量
表示训练样本总数
表示一个训练样本,
表示第
个训练样本
线性回归的机器学习模型可以表示为:
度量预测值与实际目标值之间的差异
线性回归中使用的平方损失函数:,将机器学习模型代入,则表示为
目标就是要找出最合适的和
,使得
最小
使用梯度下降算法:
,
,
为学习率
梯度下降在更新的时候需要同时更新和
,因此在计算的过程中,首先要计算
和
,然后再相减,保证同步更新。
具体计算:
学习率的选择:
如果学习率过小,梯度下降算法运行会比较慢
如果学习率过大,梯度下降算法可能运行过头,最终导致算法不能收敛
如果使用固定的学习率,梯度下降算法运行到局部最小值后不会再变化。因为到达局部最小值的附近后,梯度下降的每一步会变得更小,更新的值也会逐渐变小。
通过损失值随着迭代次数的变化可以看出一些错误:
将学习率调整足够小,损失值在每一次迭代的过程中都会减小
表示第
个特征,
表示特征的数量
表示第
个训练样本的全部特征,
表示第
个训练样本中的第
个特征
令,
,则
可以通过Numpy的向量化进行计算
当具有不同的值范围的不同特征时,可能会导致梯度下降算法运行较慢
需要对不同的特征重新缩放到相同或相似的范围
均值归一化:,可以缩放到
的范围内
Z-score归一化:
sigmoid函数:
逻辑回归:,用概率的形式表达:
不同的决策边界:
逻辑回归损失函数:
简化写法:
欠拟合:函数对于训练集的拟合效果不好——高偏差(high bias)
过拟合:函数对于训练集的拟合效果好,对于测试集的效果不好——高方差(high variance)
避免过拟合的方法:
通过将损失函数加上特别大的常数与某一参数的乘积,使得这个参数在优化的过程中变得非常小
例如回归问题:
由于不知道哪些特征是比较重要的,哪些特征不重要,因此加上参数平方求和的正则项,让优化算法自行选择。
对于线性回归来说:
进一步推导:
因此正则项的加入实际上相当于将参数略微减小
青岛的五天旅行结束了,251天后的初次见面,美好的时光总是短暂。
回家后心里一直不太舒服,一直在胡思乱想,想着想着有时还偷偷抹抹眼泪。父母也是真的了解我,虽然并没有表现出什么,一直在不断追问我怎么了。当然就算有明确的原因也不会说,对爸妈只能是报喜不报忧,何况我现在也不知道我为什么这样。
可能是不舍得吧,分开了251天,再次见面的时间只有短短的五天,下一次见面还不知道什么时候。
可能是由于毕业季的几乎分手吧,可能现在自己的信心没有那么足了。
可能是对自己未来的迷茫吧,本科取得了不错的成绩,研究生一切从头开始,不知该从何做起。
这一段时间,对我影响最大的就是那一次的几乎分手。女孩子真的需要陪伴,异地太久了,感情是真的会变淡的。而且之前并没有很明确的聊过未来的规划。可能随口的一句“杭州南京”,就成为了一道跨不过去的坎。
我出生在东北的一个小城,从小的梦想就是要走出去,给我自己,甚至给我的下一代创造一个更好的生活环境。高二那年清华暑校遇到全国的优秀学生,发现不同地区顶尖学生之间的差异居然也有如此之大,更加坚定了我走出去的决心。我也很庆幸在高考失利的情况下能选到一个好专业,在房价居高不下的大环境下,至少目前来看毕业后的薪资还是非常有竞争力的。
我很开心可以遇到我的女朋友,我们在一无所有的情况下愿意去尝试。我也从此有了另外的一个前进动力,从高考失利和大一的挫折中走了出来,拿下了年级排名和无数的竞赛奖项、荣誉称号,成功保研。保研的时候也没有选择华师大,想着自己应该获得更好的学历,以后赚更多的钱,才能和她一起有更好的生活。我按照我的道路一步一步在走。
然而由于我早去北京的提前异地,我们之间的沟通就少了许多。地理上的距离造成了心的距离,找到了一个很好的教师编职位后,她便产生了分手的想法。整个过程我甚至都是毫不知情的状态。虽然靠着一条时间轴挽回,但是我需要对自己做一个深刻的反思。我自认为我的爱没有变,但是异地半年多,确实很难将爱表达出来,同时也忽略了她的感受,我们之间的交流变得更少,最终导致了单方面无吵架的分手。
能有一个爱人时刻陪伴在身边,确实是一件非常美好的事情。才分开两天,五天的回忆一波一波涌上心头,真的很难受。想起她忘记带伞的时候,只能躲在小店内等待雨停,却无法等到一个送伞的我。异地恋真的难熬。然而这还不到一年的时间。最少需要三年才能奔现,要是找一份更高薪的工作,甚至需要五年的时间,我才能在合肥站稳脚跟,真正地和她在一起。“所以你就选定我了是嘛”“是的”“为什么呢”“。。。”是啊,为什么呢,我回答不上来。后来我也认真考虑了很久,我是一个纯理性思维的人,这一次我选择听从我的心。我相信我三年前的选择,不管是现在,三年后,三十年后,我还会作出同样的选择。
我是一个很坚定的人,我作出了选择,就会坚定的走下去。这几年我会尽全力维护这一段感情,改正掉我之前的错误,尽量多见面,尽量提升自己以后拿到更好的薪资,尽量多关心,多询问她的感受。三年前我还是一个懵懂无知的学生,我不知道三年后,甚至五年后我会成为什么样的人,但是我的爱是永远不变的。
如果她熬不住了,我会坦然接受。因为我知道,我才是那个最对不起她的人。长三角省会城市工作稳定,我又何德何能拴住她数年的时间,忍受着屏幕那边可有可无的关心,忍受着几个月甚至半年才有的一次短短几天的见面。
我真的希望最终我们可以幸福地走到一起。
为你,千千万万遍。
]]>总是觉得自己数学有一点差,可能是因为上大学学习的时候题目做的比较少,我的脑子又不太灵光,因此一直不能很好的理解数学相关的一些公式、定理等,平时编程的时候尽量找简单的方法绕开复杂的数学公式。假期有时间了,试一下帝国理工的线性代数课程,注重记录,注重理解。这也是第一次看没有中文字幕的全英文课。加油!
In this course on Linear Algebra we look at what linear algebra is and how it relates to vectors and matrices. Then we look through what vectors and matrices are and how to work with them, including the knotty problem of eigenvalues and eigenvectors, and how to use these to solve problems. Finally we look at how to use these to do fun things with datasets - like how to rotate images of faces and how to extract eigenvectors to look at how the Pagerank algorithm works.
Since we’re aiming at data-driven applications, we’ll be implementing some of these ideas in code, not just on pencil and paper. Towards the end of the course, you’ll write code blocks and encounter Jupyter notebooks in Python, but don’t worry, these will be quite short, focussed on the concepts, and will guide you through if you’ve not coded before.
At the end of this course you will have an intuitive understanding of vectors and matrices that will help you bridge the gap into linear algebra problems, and how to apply these concepts to machine learning.
Linear algebra is a mathematical system for manipulating vectors in the spaces described by vectors.
Linear algebra is linear, because it just takes input values, and multiplies them by constants, everything is linear.
Linear algebra is algebra, that is it’s a notation describing mathematical objects and a system of manipulating those notations.
How vectors are transformed by matrices is the heart of linear algebra.
在计算机科学中,向量被认为是描述一个物体的属性的集合。
向量有两种操作:向量与向量之间的加法,以及向量与标量之间的乘法。
向量与向量之间的加法满足结合律(associativity)。
向量与标量之间的乘法,要将标量与向量中的每一个属性相乘
如果不以坐标系的角度去观察向量,那么一个向量由两个属性构成:向量的方向和向量的模长
向量的模长指的是向量各组成成分的平方和开根号
向量的点乘指的是向量对应位置的数值相乘之和,满足交换律(commutative)
同时满足向量的加法分配律(distributive over addition),即
向量与标量相乘满足结合律和交换律,即
向量模长与点乘之间的关系:向量自身的点乘与模长的平方相等,即
向量的余弦定理:
向量投影(projection):
到
上的投影标量(scalar projection)=
到
上的投影向量(vector projection)= scalar projection *
单位向量 =
向量投影是一个标量,但是,如果需要投影向量的方向,直接与被投影的单位向量相乘即可。
两个不共线的向量可以确定一个坐标系(coordinate system)。要描述一个向量,首先要定义一个坐标系,决定坐标系的是基向量。
基向量是维的向量集合,需要满足3个条件:
虽然并不要求基向量正交,但是如果它们正交,会为解决数学问题带来很大的方便。
如果二维的基向量互相垂直,转换坐标系只需将向量投影到转换后的基向量,计算数值即可。
设原始坐标系,
,转换后的基向量
,
首先验证与
是否垂直,
然后将待转换的向量,对
的投影为
,这个投影除以
的模长
,即
在
方向的投影为2个
长度。同理,即
在
方向的投影为0.5个
长度。
从而得出,最终计算得
。
找到一个合适的坐标系,帮助我们解决数学问题,是非常重要的。
矩阵与向量相乘,相当于将向量转换到不同的坐标系。
矩阵的乘法满足结合律,但是不满足交换律.
如,相当于将
转换到了
如,相当于将
转换到了
通过矩阵的转换实际上可以看作不同转换向量之间的和。
如果我们对做这个矩阵的变换,则可以推导:
.
单位矩阵(identity matrix)不对向量做任何变换
设单位矩阵,
,
为待求根,
根据逆矩阵的定义,
因此,即
。
通过初等行变换求解逆矩阵:。
对于二维矩阵来说,它的逆矩阵是
,
。
二维行列式(determinant):
行列式为0的矩阵,维度不满足当前矩阵的维度,因此在矩阵操作前要首先检查行列式。
矩阵的转置:,正交矩阵
,则
,且正交矩阵的行列式为-1或1。
设,
,则
则是由
中的某一行与
中的某一列相乘求和后填充的矩阵。
如,
因此,
即为爱因斯坦求和约定的表示法。
设原始坐标系,
,现在有另外一个坐标系,坐标系在原始坐标系下基向量表示为
,
。
如果将坐标系下的向量
转换到原始坐标系中,则为
。
反之,将原始坐标系中的向量转换到坐标系下,则
。
如果基向量是正交的,可以使用投影来实现坐标系的转换:
设原始坐标系,
,现在有另外一个坐标系,坐标系在原始坐标系下基向量表示为
,
。
则将坐标系下的向量
转换到原始坐标系中,通过投影实现:
,
,因此在原始坐标系下的向量为
。
正交的基向量会给我们解决问题带来很多的方便,需要一种方法将基向量转换为正交的基向量。
设原始的维基向量为
,
对特征向量的直观感受:在进行变换的时候方向仍然保持不变的向量。
,
为特征向量,
为特征值。
求特征值,即的行列式为0
对角矩阵(diagonal matrix)会使矩阵的乘法变得更加容易,
因此可以通过特征值与特征向量的转换,将矩阵转化为对角矩阵,然后求矩阵的幂。
设特征向量,特征值的对角矩阵
,
矩阵,
# GRADED FUNCTIONimport numpy as np# Our function will go through the matrix replacing each row in order turning it into echelon form.# If at any point it fails because it can't put a 1 in the leading diagonal,# we will return the value True, otherwise, we will return False.# There is no need to edit this function.def isSingular(A) : B = np.array(A, dtype=np.float_) # Make B as a copy of A, since we're going to alter it's values. try: fixRowZero(B) fixRowOne(B) fixRowTwo(B) fixRowThree(B) except MatrixIsSingular: return True return False# This next line defines our error flag. For when things go wrong if the matrix is singular.# There is no need to edit this line.class MatrixIsSingular(Exception): pass# For Row Zero, all we require is the first element is equal to 1.# We'll divide the row by the value of A[0, 0].# This will get us in trouble though if A[0, 0] equals 0, so first we'll test for that,# and if this is true, we'll add one of the lower rows to the first one before the division.# We'll repeat the test going down each lower row until we can do the division.# There is no need to edit this function.def fixRowZero(A) : if A[0,0] == 0 : A[0] = A[0] + A[1] if A[0,0] == 0 : A[0] = A[0] + A[2] if A[0,0] == 0 : A[0] = A[0] + A[3] if A[0,0] == 0 : raise MatrixIsSingular() A[0] = A[0] / A[0,0] return A# First we'll set the sub-diagonal elements to zero, i.e. A[1,0].# Next we want the diagonal element to be equal to one.# We'll divide the row by the value of A[1, 1].# Again, we need to test if this is zero.# If so, we'll add a lower row and repeat setting the sub-diagonal elements to zero.# There is no need to edit this function.def fixRowOne(A) : A[1] = A[1] - A[1,0] * A[0] if A[1,1] == 0 : A[1] = A[1] + A[2] A[1] = A[1] - A[1,0] * A[0] if A[1,1] == 0 : A[1] = A[1] + A[3] A[1] = A[1] - A[1,0] * A[0] if A[1,1] == 0 : raise MatrixIsSingular() A[1] = A[1] / A[1,1] return A# This is the first function that you should complete.# Follow the instructions inside the function at each comment.def fixRowTwo(A) : # Insert code below to set the sub-diagonal elements of row two to zero (there are two of them). A[2] = A[2] - A[2,0] * A[0] A[2] = A[2] - A[2,1] * A[1] # Next we'll test that the diagonal element is not zero. if A[2,2] == 0 : # Insert code below that adds a lower row to row 2. A[2] = A[2] + A[3] # Now repeat your code which sets the sub-diagonal elements to zero. A[2] = A[2] - A[2,0] * A[0] A[2] = A[2] - A[2,1] * A[1] if A[2,2] == 0 : raise MatrixIsSingular() # Finally set the diagonal element to one by dividing the whole row by that element. A[2] = A[2] / A[2,2] return A# You should also complete this function# Follow the instructions inside the function at each comment.def fixRowThree(A) : # Insert code below to set the sub-diagonal elements of row three to zero. A[3] = A[3] - A[3,0] * A[0] A[3] = A[3] - A[3,1] * A[1] A[3] = A[3] - A[3,2] * A[2] # Complete the if statement to test if the diagonal element is zero. if A[3,3] == 0: raise MatrixIsSingular() # Transform the row to set the diagonal element to one. A[3] = A[3] / A[3,3] return AA = np.array([ [2, 0, 0, 0], [0, 3, 0, 0], [0, 0, 4, 4], [0, 0, 5, 5] ], dtype=np.float_)isSingular(A)A = np.array([ [0, 7, -5, 3], [2, 8, 0, 4], [3, 12, 0, 5], [1, 3, 1, 3] ], dtype=np.float_)isSingular(A)fixRowZero(A)fixRowOne(A)fixRowTwo(A)fixRowThree(A)# GRADED FUNCTIONimport numpy as npimport numpy.linalg as laverySmallNumber = 1e-14 # That's 1×10⁻¹⁴ = 0.00000000000001# Our first function will perform the Gram-Schmidt procedure for 4 basis vectors.# We'll take this list of vectors as the columns of a matrix, A.# We'll then go through the vectors one at a time and set them to be orthogonal# to all the vectors that came before it. Before normalising.# Follow the instructions inside the function at each comment.# You will be told where to add code to complete the function.def gsBasis4(A) : B = np.array(A, dtype=np.float_) # Make B as a copy of A, since we're going to alter it's values. # The zeroth column is easy, since it has no other vectors to make it normal to. # All that needs to be done is to normalise it. I.e. divide by its modulus, or norm. B[:, 0] = B[:, 0] / la.norm(B[:, 0]) # For the first column, we need to subtract any overlap with our new zeroth vector. B[:, 1] = B[:, 1] - B[:, 1] @ B[:, 0] * B[:, 0] # If there's anything left after that subtraction, then B[:, 1] is linearly independant of B[:, 0] # If this is the case, we can normalise it. Otherwise we'll set that vector to zero. if la.norm(B[:, 1]) > verySmallNumber : B[:, 1] = B[:, 1] / la.norm(B[:, 1]) else : B[:, 1] = np.zeros_like(B[:, 1]) # Now we need to repeat the process for column 2. # Insert two lines of code, the first to subtract the overlap with the zeroth vector, # and the second to subtract the overlap with the first. B[:, 2] = B[:, 2] - B[:, 2] @ B[:, 0] * B[:, 0] B[:, 2] = B[:, 2] - B[:, 2] @ B[:, 1] * B[:, 1] # Again we'll need to normalise our new vector. # Copy and adapt the normalisation fragment from above to column 2. if la.norm(B[:, 2]) > verySmallNumber : B[:, 2] = B[:, 2] / la.norm(B[:, 2]) else : B[:, 2] = np.zeros_like(B[:, 2]) # Finally, column three: # Insert code to subtract the overlap with the first three vectors. B[:, 3] = B[:, 3] - B[:, 3] @ B[:, 0] * B[:, 0] B[:, 3] = B[:, 3] - B[:, 3] @ B[:, 1] * B[:, 1] B[:, 3] = B[:, 3] - B[:, 3] @ B[:, 2] * B[:, 2] # Now normalise if possible if la.norm(B[:, 3]) > verySmallNumber : B[:, 3] = B[:, 3] / la.norm(B[:, 3]) else : B[:, 3] = np.zeros_like(B[:, 3]) # Finally, we return the result: return B# The second part of this exercise will generalise the procedure.# Previously, we could only have four vectors, and there was a lot of repeating in the code.# We'll use a for-loop here to iterate the process for each vector.def gsBasis(A) : B = np.array(A, dtype=np.float_) # Make B as a copy of A, since we're going to alter it's values. # Loop over all vectors, starting with zero, label them with i for i in range(B.shape[1]) : # Inside that loop, loop over all previous vectors, j, to subtract. for j in range(i) : # Complete the code to subtract the overlap with previous vectors. # you'll need the current vector B[:, i] and a previous vector B[:, j] B[:, i] = B[:, i] - B[:, i] @ B[:, j] * B[:, j] # Next insert code to do the normalisation test for B[:, i] if la.norm(B[:, i]) > verySmallNumber : B[:, i] = B[:, i] / la.norm(B[:, i]) else : B[:, i] = np.zeros_like(B[:, i]) # Finally, we return the result: return B# This function uses the Gram-schmidt process to calculate the dimension# spanned by a list of vectors.# Since each vector is normalised to one, or is zero,# the sum of all the norms will be the dimension.def dimensions(A) : return np.sum(la.norm(gsBasis(A), axis=0))V = np.array([[1,0,2,6], [0,1,8,2], [2,8,3,1], [1,-6,2,3]], dtype=np.float_)gsBasis4(V)# Once you've done Gram-Schmidt once,# doing it again should give you the same result. Test this:U = gsBasis4(V)gsBasis4(U)# Try the general function too.gsBasis(V)# See what happens for non-square matricesA = np.array([[3,2,3], [2,5,-1], [2,4,8], [12,2,1]], dtype=np.float_)gsBasis(A)dimensions(A)B = np.array([[6,2,1,7,5], [2,8,5,-4,1], [1,-6,3,2,8]], dtype=np.float_)gsBasis(B)dimensions(B)# Now let's see what happens when we have one vector that is a linear combination of the others.C = np.array([[1,0,2], [0,1,-3], [1,0,2]], dtype=np.float_)gsBasis(C)dimensions(C)# PACKAGE# Run this cell first once to load the dependancies.import numpy as npfrom numpy.linalg import norm, invfrom numpy import transposefrom readonly.bearNecessities import *# GRADED FUNCTION# You should edit this cell.# In this function, you will return the transformation matrix T,# having built it out of an orthonormal basis set E that you create from Bear's Basis# and a transformation matrix in the mirror's coordinates TE.def build_reflection_matrix(bearBasis) : # The parameter bearBasis is a 2×2 matrix that is passed to the function. # Use the gsBasis function on bearBasis to get the mirror's orthonormal basis. E = gsBasis(bearBasis) # Write a matrix in component form that performs the mirror's reflection in the mirror's basis. # Recall, the mirror operates by negating the last component of a vector. # Replace a,b,c,d with appropriate values TE = np.array([[1, 0], [0, -1]]) # Combine the matrices E and TE to produce your transformation matrix. T = E @ TE @ inv(E) # Finally, we return the result. There is no need to change this line. return T# First load Pyplot, a graph plotting library.%matplotlib inlineimport matplotlib.pyplot as plt# This is the matrix of Bear's basis vectors.# (When you've done the exercise once, see what happns when you change Bear's basis.)bearBasis = np.array( [[1, -1], [1.5, 2]])# This line uses your code to build a transformation matrix for us to use.T = build_reflection_matrix(bearBasis)# Bear is drawn as a set of polygons, the vertices of which are placed as a matrix list of column vectors.# We have three of these non-square matrix lists: bear_white_fur, bear_black_fur, and bear_face.# We'll make new lists of vertices by applying the T matrix you've calculated.reflected_bear_white_fur = T @ bear_white_furreflected_bear_black_fur = T @ bear_black_furreflected_bear_face = T @ bear_face# This next line runs a code to set up the graphics environment.ax = draw_mirror(bearBasis)# We'll first plot Bear, his white fur, his black fur, and his face.ax.fill(bear_white_fur[0], bear_white_fur[1], color=bear_white, zorder=1)ax.fill(bear_black_fur[0], bear_black_fur[1], color=bear_black, zorder=2)ax.plot(bear_face[0], bear_face[1], color=bear_white, zorder=3)# Next we'll plot Bear's reflection.ax.fill(reflected_bear_white_fur[0], reflected_bear_white_fur[1], color=bear_white, zorder=1)ax.fill(reflected_bear_black_fur[0], reflected_bear_black_fur[1], color=bear_black, zorder=2)ax.plot(reflected_bear_face[0], reflected_bear_face[1], color=bear_white, zorder=3);# PACKAGE# Here are the imports again, just in case you need them.# There is no need to edit or submit this cell.import numpy as npimport numpy.linalg as lafrom readonly.PageRankFunctions import *np.set_printoptions(suppress=True)# GRADED FUNCTION# Complete this function to provide the PageRank for an arbitrarily sized internet.# I.e. the principal eigenvector of the damped system, using the power iteration method.# (Normalisation doesn't matter here)# The functions inputs are the linkMatrix, and d the damping parameter - as defined in this worksheet.# (The damping parameter, d, will be set by the function - no need to set this yourself.)def pageRank(linkMatrix, d) : n = linkMatrix.shape[0] M = d * linkMatrix + (1-d)/n * np.ones([n, n]) r = 100 * np.ones(n) / n lastR = r r = M @ r i = 0 while la.norm(lastR - r) > 0.01 : lastR = r r = M @ r i += 1 return r# Use the following function to generate internets of different sizes.generate_internet(5)# Test your PageRank method against the built in "eig" method.# You should see yours is a lot faster for large internetsL = generate_internet(10)pageRank(L, 1)# Do note, this is calculating the eigenvalues of the link matrix, L,# without any damping. It may give different results that your pageRank function.# If you wish, you could modify this cell to include damping.# (There is no credit for this though)eVals, eVecs = la.eig(L) # Gets the eigenvalues and vectorsorder = np.absolute(eVals).argsort()[::-1] # Orders them by their eigenvalueseVals = eVals[order]eVecs = eVecs[:,order]r = eVecs[:, 0]100 * np.real(r / np.sum(r))# You may wish to view the PageRank graphically.# This code will draw a bar chart, for each (numbered) website on the generated internet,# The height of each bar will be the score in the PageRank.# Run this code to see the PageRank for each internet you generate.# Hopefully you should see what you might expect# - there are a few clusters of important websites, but most on the internet are rubbish!%pylab notebookr = pageRank(generate_internet(100), 0.9)plt.bar(arange(r.shape[0]), r);Formula Sheet: Sheet summarising all the formulae covered in this course.
理论上的防疫政策:低风险地区提前三天向酒店等报备,第一天和第三天两次核酸。
实际:基本只看“青岛一码通”的绿码和7天内核酸阴性报告(有的地方可能要48小时核酸阴性报告)
具体措施:
| 日期 | 计划 | 备注 |
|---|---|---|
| Day0 | 晚上到达青岛,做核酸、住酒店 | 可以去旁边的丽达生活超市买一些水和吃的 |
| Day1上午 | 信号山公园、栈桥 | |
| Day1中午 | 王姐烧烤午餐 | |
| Day1下午 | 小青岛公园、鲁迅公园、小鱼山公园、青岛第一海水浴场、八大关风景区 | |
| Day1晚上 | 台东步行街小吃晚餐、回酒店 | 可以去大商场买一点点吃的和水果等 |
| Day2上午 | 小麦岛公园 | |
| Day2中午 | 船歌鱼水饺午餐 | |
| Day2下午 | 燕儿岛公园、奥帆中心、情人坝、五四广场、海天云上艺术中心 | 看天气,太热了就先去海天云上艺术中心 |
| Day2晚上 | 探海岛海鲜自助(探鲜岛海鲜自助餐厅)晚餐、栈桥附近的夜景、回酒店 | |
| Day3上午 | 去崂山风景区 | |
| Day3中午 | 吃一些提前买的面包等,景区内应该也有一些吃的 | |
| Day3下午 | 崂山风景区、回市区 | |
| Day3晚上 | 前海沿晚餐、回酒店 | |
| Day4 | 返程 |
备注:
交通方式:酒店——信号山公园,公交前往,37分钟,步行680米
预约:已经预约好 7月24日 6:00-20:30,包括收费5元的旋转观景楼
时间:1个小时左右
简介:信号山公园位于青岛市中心,因曾在山顶建有为船只引航的信号台而得名。信号山海拔98米,山顶三幢红顶蘑菇楼尤为显眼,其中较高的一幢是旋转观景楼,在这里你可以360度俯看青岛“红瓦绿树,碧海蓝天”的景色。进入景区大门,南坡上有踏浪观景台,就在连心桥下面一点,是拍摄南边德国古堡式建筑迎宾馆的好位置。连心桥上一把把红色爱心造型的锁挂在绿色栏杆上,情侣们可以在此买一把同心锁把彼此的山盟海誓锁在信号山上,据说手拉手走过连心桥可以得到祝福,单身的话自个儿的左手拉右手一样很好!再往前,可以看看五龙潭喷泉等景点,周围四条小龙围着中间一条大龙,与信号山又叫五龙山对应,因为山周边有龙江路、龙华路、龙口路、龙山路、伏龙路五条带“龙”字的路而得此别名。最后到达山顶的旋转观景楼,登上楼上观景台观景,一幢幢掩映在绿树中红瓦黄墙的德式建筑令人惊叹。往西南看,近处有绿色钟楼屋顶的基督教堂在一片红屋顶中非常出挑。



交通方式:步行,共3公里左右
预约:小鱼山公园开放时间08:00-17:00,网上找不到预约入口
时间:2-3小时
简介:小青岛故称为“琴岛”,是青岛湾内的一座小岛,青岛这个城市的名称就来源于它。小青岛与陆地之间有长长的海堤相接,岛上矗立着德国人建于1898年的灯塔,是青岛的标志之一。小青岛面积很小,岛上绿树成荫,岛的四周礁石环绕,海水清澈、蔚蓝,岛上常能见到来垂钓的游客。坐在礁石上吹吹海风,赤脚踩踩海水,看看四周青岛湾边林立的高楼和红顶的小洋房,仿佛置身于海上花园。每当夕阳西下时景色尤其美,阳光把整个海湾都镀成了金色。小青岛的南侧有一尊姿态优美的琴女雕像,雕像周围是花坛,种植着五颜六色的鲜花。岛的较高处有当年德国人建造的灯塔,整个岛的海拔也不高,才17米,走到灯塔脚下不需要爬多少路。灯塔通体洁白,由大理石构筑,是海上过往船只进出胶州湾的重要航标。每当夜幕降临,灯塔与岛上的灯光倒映在海面上,像一匹飘动的彩绸,形成青岛的一大胜景“琴屿飘灯”,在这里拍摄夜景很不错。鲁迅公园是青岛市内一处对外开放的临海公园,海边有大片的红褐色礁石,景色很特别,常有不少新人在此拍摄婚纱照。沿着海边步道慢慢走、听听海浪拍壁之声,或是走上岩石高处的亭子远眺大海,很是惬意。公园的东部紧邻青岛海底世界,再往东走是第一海水浴场,沿途风光很美。小鱼山公园是青岛佳风景眺望点之一,一是因为它位于市中心,是青岛离海近的一座山,地理位置;二是因为它的海拔仅60米,爬山不累,登到山顶能看到“红瓦绿树,碧海蓝天”具青岛代表性的景色。
交通方式:步行,毗邻青岛第一海水浴场
景区图:
预约:无需预约,内部场馆单独售票,营业时间:9:00-17:00;换票时间:9:00-15:00
时间:2小时
简介:八大关是青岛市区南部相交错的十几条马路的总称,它们大多取名于我国知名关隘的名称。这里环境清幽,春季有碧桃盛开、夏季有紫薇盛放,秋季可见银杏红枫夹道,还坐落着许多各国风格的别墅,是摄影胜地。在这里,你可以进入欧洲古堡风格的“花石楼”参观、登上楼顶遥望大海,或者外观开国元帅住过的日式洋楼“元帅楼”、流传着唯美爱情故事的丹麦建筑“公主楼”等经典别墅,让你仿佛身处欧洲的某个角落。
交通方式:地铁,24分钟,步行248m
预约:无需预约
时间:晚上
简介:“朝观壁画夜赏灯,购物休闲在台东”,台东步行街是青岛有名的街区,街内有国内外知名的沃尔玛、万达广场、百信鞋业、利群集团、苏宁电器、三联家电、亚泰电器、新华书店、医保城等各类业态的企业245家。步行街两侧的21座楼6万余平方米的墙面为统一彩绘,精心绘制了色彩斑斓、造型生动的大型壁画,形成了独特的彩色画廊,这是大型的手工彩绘一条街。台东三路经过精心的景观设置,夜景迷人。这里还有男士、女士特色广场,营造出优美的购物和休闲环境,使市民在购物消费的同时,还享受着文化特色的盛宴。
美食推荐(有人排队多的肯定好吃):



交通方式:地铁+公交(打车)(或公交),58分钟,步行1.2公里
预约:无需预约
时间:1-2小时
简介:小麦岛公园位于崂山区麦岛路西50米,小麦岛属环形岛屿,有大片平坦宽广的绿化草地,远处就是湛蓝的海水,可在这里眺望到遥远的海岸线,一派海滨美景,非常适宜拍照。
就在小麦岛公园的公交站旁边,逛后吃午餐。
重点菜:鲅鱼、墨鱼、三鲜、虾仁水饺,海菜凉粉


交通方式:公交34分钟,步行883米
预约:无需预约
时间:1-3小时
简介:燕儿岛山公园位于山东省青岛市南部,处在浮山湾东端,是一个突出海中的岬角。园内环境优美,集生态、景观、文化、健身、休闲等为一体,是市民休闲锻炼、观光游玩的好地方。公园里的海滨栈道是一大亮点,木栈道与阶梯相连,一边是大海,一边是峭壁,峭壁底下鲜花盛开,在这里拍照仿佛置身于美丽的垦丁,有着独特的韵味。登上阶梯高处的平台放眼望去,可以将整个大海纳入眼帘,景色十分迷人。
交通方式:步行,直线距离2公里左右
预约:无需预约,奥帆中心其他景点待确定
时间:2-3小时
简介:青岛奥帆中心景区位于青岛市浮山湾畔,与青岛市标志性景点——五四广场近海相望,总占地面积约45公顷,是2008年北京第29届奥运会奥帆赛和第13届残奥会帆船比赛举办场地,奥帆中心景区依山面海,景色宜人,是全国唯一“国家滨海旅游休闲示范区”。青岛被誉为“帆船之都”,作为最能体现青岛城市特色和展示城市形象的景区,奥帆中心景区内不仅有飞帆渺渺的优雅,有青岛十大旧景代表燕岛秋潮,有青岛新时代景观鸥翔彩虹,更有众多惊险刺激的娱乐体验,是游客来青必看的景点。
交通方式:公交或地铁,20分钟
预约:已经预约好 7月25日 9:00-20:00,80F+81F联票
时间:没查到。。。
简介:海天中心城市观光厅是山东省超高层垂直建筑之上的高空观光平台。在这里,向西可揽胜八大关老城区红瓦绿树,向东承接新城区璀璨繁华,360°俯瞰壮美海景、山景、城景,全方位感受身处"天空之城"的独特体验。其内部设置的透明观景区、沉浸式体验区、多媒体展示区与空中水吧等多个功能空间,将内部游览体验与外部自然景观融为一体。站在369米之上的城市观光厅,可以看尽因海而生、向海而兴的魅力青岛在时间长河中的风貌变迁与发展动线。随着观光者的漫步,不同姿态的青岛都将尽收眼底。
回青岛站附近吃晚餐,美团可以订座,顺便可以游览栈桥附近的夜景。


交通方式:地铁接公交
预约:已经预约好 7月26日 6:00-12:00太清,12:01-17:30 华严和仰口
时间:一天
路线:大河东检票——第三站下车游览太清宫、太清索道——索道往返——走到垭口乘坐公交618路前往华严(或仰口)——景区游览车到仰口(或华严)——原路返回大河东(或者直接从仰口出去)
这个位置暂定,美团可以排队
重点菜:蒜蓉粉丝虾、手锤茄子卷饼



南京大学今年养了一个大鱼塘,就拿我们专业来说,65人的小专业前三名都通过了南大的初审。当时接到了南大的邮件激动坏了,然而南大先搞了一波笔试。。。
我实在是太菜了,有一半的题里面的名词都没听说过。。。所以就挂了,也没有然后了。
面试后就结束了,几周后公布了优营名单,一共三四百入营的,优营给了不到二百个,承诺优营一定录取。
北航最后拿到了候补,一共500个入营的,过了机试有400左右,优营给了110多个,候补给了100个。不过整个夏令营的阶段都没有北航的同学参与,而看去年的录取名单基本都是北航的。。不知道是什么原因
入营有五百左右,给了三百的优营,要自己联系老师,8月底联系不到的认为放弃优营资格。
入营只有200左右,大多数给了优营,但是是唯一一个没有后续的学校,没人说过优营有什么用接下来干什么。。。
吐槽吐槽!!!!中山真的是太烦人了,就算过了也真心不想去。
入营资格要一个一个电话确认,还没开始夏令营就开了三场会,一个面试环境检查会,一个笔试环境检查会,一个面试分组抽签会。更为奇葩的双机位要求:两个机位互相能看见,次机位看清电脑屏幕,主机位能看到脑袋+肩膀且能看到双手???你来教教我咋能主机位看到双手???我双手举起来编程吗???更为奇葩的机试监考,要共享屏幕到腾讯会议中。好家伙总共五百多人参加机试你找了五百多个研究生坐五百多个电脑前面开五百多个腾讯会议盯着我们???面试环境检查会都已经查看完了承诺书,正式面试还要再看一遍???程序无比繁琐,而且充斥着学校对学生的满满的不信任感!
五百多人给了300优营和100候补,还承诺优营一定录取,还说不搞预推免了。祝愿中山被鸽穿!
中科院计算所本来是没有入营的(意料之中),看QQ群里面的报名号有六千多人报名,入营名单发了400多。但是实验室秘书有一天早上打电话过来希望我能去北京参加机试面试,难得的机会就过去了。在报名后和入营名单公布之前会在QQ群里面让选意向导师,实际上就是意向实验室,才会有实验室秘书联系你,所以要多关注群消息。
面试结束当天晚上就打来了电话并发送了拟录取的邮件。一个月后在官网公布了拟录取的名单,入营的优营与没入营的优营(比如我)各占一半,总共给了200优营,承诺一定录取。其中查了一下,网数实验室面试38进12。
共计 11 篇文章
+2022
+ + + +共计 24 篇文章
+2024
+ + + +2022
+ + + +共计 24 篇文章
+2022
+ + + +共计 24 篇文章
+2022
+ + + +共计 35 篇文章
+2023
+ + + +共计 35 篇文章
+2023
+ + + +共计 35 篇文章
+2023
+ + + +2022
+ + + +共计 35 篇文章
+2022
+ + + +共计 21 篇文章
+2023
+ + + +共计 21 篇文章
+2023
+ + + +共计 24 篇文章
+2024
+ + + +2022
+ + + +共计 24 篇文章
+2022
+ + + +共计 24 篇文章
+2022
+ + + +共计 5 篇文章
+2022
+ + + +共计 7 篇文章
+2023
+ + + +2022
+ + + +共计 8 篇文章
+2023
+ + + +2022
+ + + +共计 18 篇文章
+2023
+ + + +2022
+ + + +共计 18 篇文章
+2022
+ + + +共计 20 篇文章
+2022
+ + + +共计 20 篇文章
+2022
+ + + +共计 22 篇文章
+2024
+ + + +2022
+ + + +共计 22 篇文章
+2022
+ + + +共计 22 篇文章
+2022
+ + + +共计 22 篇文章
+2022
+ + + +共计 22 篇文章
+2022
+ + + +共计 22 篇文章
+2022
+ + + +共计 7 篇文章
+2022
+ + + +共计 49 篇文章
+2022
+ + + +共计 49 篇文章
+2022
+ + + +共计 49 篇文章
+2022
+ + + +共计 49 篇文章
+2022
+ + + +共计 49 篇文章
+2022
+ + + +共计 5 篇文章
+2022
+ + + +共计 14 篇文章
+2024
+ + + +2023
+ + + +2022
+ + + +共计 14 篇文章
+2022
+ + + +共计 1 篇文章
+2022
+ + + +共计 48 篇文章
+2022
+ + + +共计 48 篇文章
+2022
+ + + +共计 48 篇文章
+2022
+ + + +共计 48 篇文章
+2022
+ + + +共计 48 篇文章
+2022
+ + + +