第十三部分 强化学习(Reinforcement Learning)和控制(Control) 这一章我们就要学习强化学习(reinforcement learning)和适应性控制(adaptive control)了。
在监督学习(supervised learning)中,我们已经见过的一些算法,输出的标签类 $y$ 都是在训练集中已经存在的。这种情况下,对于每个输入特征 $x$ ,都有一个对应的标签作为明确的“正确答案(right answer)”。与之相反,在很多的连续判断(sequential decisions making)和控制(control)的问题中,很难提供这样的明确的显示监督(explicit supervision)给学习算法。例如,假设咱们制作了一个四条腿的机器人,然后要编程让它能走路,而我们并不知道怎么去采取“正确”的动作来进行四条腿的行走,所以就不能给他提供一个明确的监督学习算法来进行模仿。
在强化学习(reinforcement learning)的框架下,我们就并不提供监督学习中那种具体的动作方法,而是只给出一个奖励函数(reward function),这个函数会告知学习程序(learning agent) 什么时候的动作是好的,什么时候的是不好的。在四腿机器人这个样例中,奖励函数会在机器人有进步的时候给出正面回馈,即奖励,而有退步或者摔倒的时候给出负面回馈,可以理解成惩罚。接下来随着时间的推移,学习算法就会解决如何选择正确动作以得到最大奖励。
强化学习(Reinforcement learning,下文中缩写为 RL)已经成功用于多种场景了,例如无人直升机的自主飞行,机器人用腿来运动,手机的网络选择,市场营销策略筛选,工厂控制,高效率的网页索引等等。我们对强化学习的探索,要先从马尔可夫决策过程(Markov decision processes,缩写为 MDP) 开始,这个概念给出了强化学习问题的常见形式。
1 马尔可夫决策过程(Markov decision processes) 一个马尔可夫决策过程(Markov decision process)由一个元组(tuple) $(S, A, {P_{sa}}, \gamma, R)$ 组成,其中元素分别为:
$S$ 是一个状态 集合(a set of states)。(例如,在无人直升机飞行的案例中,$S$ 就可以是直升机所有的位置和方向的集合。)
$A$ 是一个动作 集合(a set of actions)。(例如,还以无人直升机为例,$A$ 就可以是遥控器上面能够操作的所有动作方向。)
$P_{sa}$ 为状态转移概率(state transition probabilities)。对于每个状态 $s \in S$ 和动作 $a \in A$ , $P_{sa}$ 是在状态空间上的一个分布(a distribution over the state space)。后面会再详细讲解,不过简单来说, $P_{sa}$ 给出的是在状态 $s$ 下进行一个动作 $a$ 而要转移到的状态的分布。
$\gamma \in [0, 1)$ 叫做折扣因子(discount factor)。
$R : S × A → R$ 就是奖励函数(reward function)。 (奖励函数也可以写成仅对状态 $S$ 的函数,这样就可以写成 $R : S → R$ 。)
马尔可夫决策过程(MDP)的动力学(dynamics)过程如下所示:于某个起始状态 $s_0$ 启动,然后选择某个动作 $a_0 \in A$ 来执行 MDP 过程。根据所选的动作会有对应的结果,MDP 的状态则转移到某个后继状态(successor state),表示为 $s_1$ ,根据 $s_1 \sim P_{s_0a_0}$ 得到。然后再选择另外一个动作 $a_1$ ,接下来又有对应这个动作的状态转移,状态则为 $s_2 \sim P_{s_1a_1}$ 。接下来再选择一个动作 $a_2$ ,就这样进行下去。如果将这个过程绘制出来的话,结果如下所示:
$$
s_0\xrightarrow{a_0}s_1\xrightarrow{a_1}s_2\xrightarrow{a_2}s_3\xrightarrow{a_3}\dots
$$
通过序列中的所有状态 $s_0, s_1, \dots$ 和对应的动作 $a_0, a_1,\dots$ ,你就能得到总奖励值,即总收益函数(total payoff)为
$$
R(s_0,a_0) + \gamma R(s_1,a_1) + \gamma^2 R(s_2,a_2) + \dots
$$
如果把奖励函数作为仅与状态相关的函数,那么这个值就简化成了
$$
R(s_0) + \gamma R(s_1) + \gamma^2 R(s_2) + \dots
$$
多数情况下,我们都用后面这种仅为状态的函数$R(s)$这种形式,虽然扩展到对应状态-动作两个变量的函数 $R(s,a)$ 也并不难。
强化学习的目标就是找到的一组动作,能使得总收益函数(total payoff)的期望值最大:
$$
E[R(s_0) + \gamma R(s_1) + \gamma^2 R(s_2) + \dots]
$$
注意,在时间步长(timestep) $t$ 上的奖励函数(reward)通过一个参数(factor)$\gamma^t$ 而进行了缩减(discounted)。 因此,要使得期望最大化,就需要尽可能早积累符号为正的奖励(positive rewards),而尽量推迟负面奖励(negative rewards,即惩罚)的出现。在经济方面的应用中,其中的 $R(·)$ 就是盈利金额(amount of money made),$\gamma$ 也可以理解为利润率(interest rate)的表征,这样有自然的解释(natural interpretation),例如今天的一美元就比明天的一美元有更多价值。
有一种策略(policy), 是使用任意函数 $\pi : S → A$ ,从状态(states)到动作(actions)进行映射(mapping)。如果在状态 $s$ ,采取动作 $a = \pi(s)$ ,就可以说正在执行(executing) 某种策略(policy) $\pi$ 。然后还可以针对策略函数(policy)$\pi$ 来定义一个值函数(value function):
$$
V^\pi(s)=E[R(s_0) + \gamma R(s_1) + \gamma^2 R(s_2) + \dots | s_0=s,\pi]
$$
$V^\pi(s)$ 就是从状态 $s$ 开始,根据 $\pi^1$ 给出的动作来积累的部分奖励函数(discounted rewards)的期望总和(expected sum)。
1 实际上这里我们用 $\pi$ 这个记号来表示,严格来说不太正确,因为 $\pi$ 并不是一个随机变量,不过在文献里面这样表示很多,已经成了某种事实上的标准了。
给定一个固定的策略函数(policy) $\pi$ ,则对应的值函数 $V^\pi$ 满足贝尔曼等式(Bellman equations):
$$
V^\pi(s)=R(s)+\gamma \sum_{s'\in S}P_{s\pi(s)}(s')V^\pi(s')
$$
这也就意味着,从状态 $s$ 开始的这个部分奖励(discounted rewards)的期望总和(expected sum) $V^\pi(s)$ 由两部分组成:首先是在状态 $s$ 时候当时立即获得的奖励函数值 $R(s)$ ,也就是上面式子的第一项;另一个就是第二项,即后续的部分奖励函数值(discounted rewards)的期望总和(expected sum)。对第二项进行更深入的探索,就能发现这个求和项(summation term)可以写成 $E_{s'\sim P_{s\pi(s)}} [V^\pi(s')]$ 的形式。这种形式也就是从状态 $s'$ 开始的这个部分奖励(discounted rewards)的期望总和(expected sum) $V^\pi(s')$ ,此处的 $s'$ 是根据 $P_{s\pi(s)}$ 分布的,在 MDP 过程中从状态 $s$ 采取第一个动作 $\pi(s)$ 之后,确定了这个分布所在的空间。因此,上面的第二项实际上也就是给出了在 MDP 过程中第一步之后的部分奖励(discounted rewards)的期望总和(expected sum)。
贝尔曼等式(Bellman’s equations)可以有效地解出 $V^\pi$ 。尤其是在一个有限状态的 MDP 过程中,即 $(|S| < \infty)$ ,我们可以把每个状态 $s$ 对应的 $V^\pi (s)$ 的方程写出来。这样就得到了一系列的 $|S |$ 个线性方程,有 $|S |$ 个变量(也就是对应每个状态的未知的 $V^\pi(s)$ ),这些 $V^\pi(s)$ 都很容易解出来。
然后可以定义出最优值函数(optimal value function)
$$
V^*(s)=\max_\pi V^\pi(s)\qquad(1)
$$
换一种说法,这个值也就是能用任意一种策略函数(policy)来获得的,最佳的可能部分奖励(discounted rewards)的期望总和(expected sum)。另外对于最优值函数(optimal value function),也有一个版本的贝尔曼等式(Bellman’s equations):
$$
V^(s)=R(s)+\max_{a\in A}\gamma\sum_{s'\in S}P_{sa}(s')V^ (s')\qquad(2)
$$
上面这个等式中的第一项,还是跟之前一样的,还是即时奖励函数值。第二项是在采取了动作 $a$ 之后的所有动作 $a$ 的部分奖励(discounted rewards)的未来期望总和(expected future sum)的最大值。要确保理解这个等式,并且要明白为什么这个等式有意义。
译者注:抱歉,这里的这个 discounted rewards 弄得我不知道怎么翻译才顺,意思表达得很狗,非常抱歉。
另外还定义了一个策略函数(policy) $\pi^* : S → A$ ,如下所示
$$
\pi^(s)=arg\max_{a\in A}\sum_{s'\in S}P_{sa}(s')V^ (s')\qquad(3)
$$
注意,这里的 $\pi^*(s)$ 给出的动作 $a$ 实现了上面等式$(2)$当中能够使 “max” 项取到最大值。
事实上,对于每个状态 $s$ 和每个策略函数(policy)$\pi$,我们都可以得出:
$$
V^(s)=V^{\pi^ }(s)\ge V^\pi(s)
$$
上面的第一个等式关系表明,在任何状态 $s$ 下,对应策略函数(policy) $V^{\pi^}$的值函数(value function)$\pi^ $ 等于最优值函数 $V^$。右边的不等式则表明,$\pi^ $ 的值至少也等于任意其他策略函数的值。也就是说,上面在等式$(3)$当中定义的这个 $\pi^*$ 就是最佳策略函数(optimal policy)。
注意,这个 $\pi^$ 有一个有趣的特性,它是所有状态 $s$ 下的最佳策略。具体来讲,并不是说只是从某些状态 $s$ 开始的MDP过程才使得这个$\pi^ $是对应这些状态的最佳策略,而如果从某些别的状态 $s'$ 开始就有其他的最佳策略。而是对于所有的状态 $s$ ,都是同样的一个策略函数 $\pi^$ 能够使得等式$(1)$中的项目取得最大值。这也就意味着无论 MDP 过程的初始状态(initial state)如何,都可以使用同样的策略函数 $\pi^ $。
2 值迭代(Value iteration)和策略迭代(policy iteration) 现在我们要讲两种算法,都能很有效地解决有限状态的马尔可夫决策过程问题(finite-state MDPs)。目前为止,我们只考虑有限状态和动作空间的马尔可夫决策过程,也就是状态和动作的个数都是有限的,即$|S| < \infty, |A| < \infty$。
第一种算法,值迭代(value iteration), 过程如下所述:
对每个状态 $s$ , 初始化 $V (s) := 0$ .
重复直到收敛 {
对每个状态,更新规则$V(s):=R(s)+\max_{a\in A}\gamma\sum_{s'}P_{sa}(s')V(s')$
}
这个算法可以理解成,利用贝尔曼等式(Bellman Equations)$(2)$重复更新估计值函数(estimated value function)。
在上面的算法的内部循环体中,有两种进行更新的方法。首先,我们可以为每一个状态 $s$ 计算新的值 $V(s)$ ,然后用新的值覆盖掉所有的旧值。这也叫做同步更新(synchronous update)。 在这种情况下,此算法可以看做是实现(implementing)了一个“贝尔曼备份运算符(Bellman backup operator)”,这个运算符接收值函数(value function)的当前估计(current estimate),然后映射到一个新的估计值(estimate)。(更多细节参考作业题目中的内容。)另外一种方法,即我们可以使用异步更新(asynchronous updates)。 使用这种方法,就可以按照某种次序来遍历(loop over)所有的状态,然后每次更新其中一个的值。
无论是同步还是异步的更新,都能发现最终值迭代(value iteration)会使 $V$ 收敛到 $V^$ 。找到了 $V^ $ 之后,就可以利用等式$(3)$来找到最佳策略(optimal policy)。
除了值迭代(value iteration)之外,还有另外一种标准算法可以用来在马尔可夫决策过程(MDP)中寻找一个最佳策略(optimal policy)。这个策略迭代(policy iteration) 算法如下所述:
随机初始化 $\pi$ 。
重复直到收敛{
$(a)$ 令 $V := V^\pi$ .
$(b)$ 对每个状态 $s$ ,令 $\pi(s):=arg\max_{a\in A}\sum_{s'}P_{sa}(s')V(s')$
}
因此,在循环体内部就重复计算对于当前策略(current policy)的值函数(value function),然后使用当前的值函数(value function)来更新策略函数(policy)。(在步骤 $(b)$ 中找到的策略 $\pi$ 也被称为对应 $V$ 的贪心策略(greedy with respect to V) )注意,步骤 $(a)$ 可以通过解贝尔曼等式(Bellman’s equation)来实现,之前已经说过了,在固定策略(fixed policy)的情况下,这个等式只是一系列有 $|S|$ 个变量(variables)的 $|S|$ 个线性方程(linear equations)。
在上面的算法迭代了某个最大迭代次数之后,$V$ 将会收敛到 $V^$,而 $\pi$ 会收敛到 $\pi^ $。
值迭代(value iteration)和策略迭代(policy iteration)都是解决马尔可夫决策过程(MDPs)问题的标准算法, 而且目前对于这两个算法哪个更好,还没有一个统一的一致意见。对小规模的 MDPs 来说,策略迭代(policy iteration)通常非常快,迭代很少的次数就能瘦脸。然而,对有大规模状态空间的 MDPs,确切求解 $V^\pi$ 就要涉及到求解一个非常大的线性方程组系统,可能非常困难。对于这种问题,就可以更倾向于选择值迭代(value iteration)。因此,在实际使用中,值迭代(value iteration)通常比策略迭代(policy iteration)更加常用。
3 学习一个马尔可夫决策过程模型(Learning a model for an MDP) 目前为止,我们已经讲了 MDPs,以及用于 MDPs 的一些算法,这都是基于一个假设,即状态转移概率(state transition probabilities)以及奖励函数(rewards)都是已知的。在很多现实问题中,却未必知道这两样,而是必须从数据中对其进行估计。(通常 $S,A 和 \gamma$ 都是知道的。)
例如,加入对倒立摆问题(inverted pendulum problem,参考习题集 $4$ ),在 MDP 中进行了一系列的试验,过程如下所示:
$$
\begin{aligned}
&s_0^{(1)}\xrightarrow{a_0^{(1)}}s_1^{(1)}\xrightarrow{a_1^{(1)}}s_2^{(1)}\xrightarrow{a_2^{(1)}}s_3^{(1)}\xrightarrow{a_3^{(1)}}\dots \\
&s_0^{(2)}\xrightarrow{a_0^{(2)}}s_1^{(2)}\xrightarrow{a_1^{(2)}}s_2^{(2)}\xrightarrow{a_2^{(2)}}s_3^{(2)}\xrightarrow{a_3^{(2)}}\dots \\
&\cdots
\end{aligned}
$$
其中 $s_i^{(j)}$ 表示的是第 $j$ 次试验中第 $i$ 次的状态,而 $a_i^{(j)}$ 是该状态下的对应动作。在实践中,每个试验都会运行到 MDP 过程停止(例如在倒立摆问题(inverted pendulum problem)中杆落下(pole falls)),或者会运行到某个很大但有限的一个数的时间步长(timesteps)。
有了在 MDP 中一系列试验得到的“经验”,就可以对状态转移概率(state transition probabilities)推导出最大似然估计(maximum likelihood estimates)了:
$$
P_{sa}(s')= \frac{在状态 s 执行动作 a 而到达状态 s' 的次数}{在状态 s 执行动作 a 的次数}\qquad(4)
$$
或者,如果上面这个比例出现了$“0/0”$的情况,对应的情况就是在状态 $s$ 之前没进行过任何动作 $a$ ,这样就可以简单估计 $P_{sa}(s')$ 为 $1/|S|$ 。(也就是说把 $P_{sa}$ 估计为在所有状态上的均匀分布(uniform distribution)。)
注意,如果在 MDP 过程中我们能获得更多经验信息(观察更多次数),就能利用新经验来更新估计的状态转移概率(estimated state transition probabilities),这样很有效率。具体来说,如果我们保存下来等式$(4)$中的分子(numerator)和分母(denominator)的计数(counts),那么观察到更多的试验的时候,就可以很简单地累积(accumulating)这些计数数值。计算这些数值的比例,就能够给出对 $P_{sa}$ 的估计。
利用类似的程序(procedure),如果奖励函数(reward) $R$ 未知,我们也可以选择在状态 $s$ 下的期望即时奖励函数(expected immediate reward) $R(s)$ 来当做是在状态 $s$ 观测到的平均奖励函数(average reward)。
学习了一个 MDP 模型之后,我们可以使用值迭代(value iteration)或者策略迭代(policy iteration),利用估计的状态转移概率(transition probabilities)和奖励函数,来去求解这个 MDP 问题。例如,结合模型学习(model learning)和值迭代(value iteration),就可以在未知状态转移概率(state transition probabilities)的情况下对 MDP 进行学习,下面就是一种可行的算法:
随机初始化 $\pi$ 。
重复 {
$(a)$ 在 MDP 中执行 $\pi$ 作为若干次试验(trials)。
$(b)$ 利用上面在 MDP 积累的经验(accumulated experience),更新对 $P_{sa}$ 的估计(如果可以的话也对奖励函数 $R$ 进行更新)。
$(c)$ 利用估计的状态转移概率(estimated state transition probabilities)和奖励函数
(rewards),应用值迭代(value iteration),得到一个新的估计值函数(estimated value function) $V$ 。
$(d)$ 更新 $\pi$ 为与 $V$ 对应的贪婪策略(greedy policy)。
}
我们注意到,对于这个特定的算法,有一种简单的优化方法(optimization),可以让该算法运行得更快。具体来说,在上面算法的内部循环中,使用了值迭代(value iteration),如果初始化迭代的时候不令 $V = 0$ 启动,而是使用算法中上一次迭代找到的解来初始化,这样就有了一个更好的迭代起点,能让算法更快收敛。
4 连续状态的马尔可夫决策过程(Continuous state MDPs) 目前为止,我们关注的都是有限个状态(a finite number of states)的马尔可夫决策过程(MDPs)。接下来我们要讲的就是有无限个状态(an infinite number of states)的情况下的算法。例如,对于一辆车,我们可以将其状态表示为 $(x, y, \theta, \dot x,\dot y,\dot\theta)$ ,其中包括位置(position) $(x, y)$ ,方向(orientation)$\theta$, 在 $x$ 和 $y$ 方向的速度分量 $\dot x$ 和 $\dot y$ ,以及角速度(angular velocity)$\dot\theta$。这样,$S = R^6$ 就是一个无限的状态集合,因为一辆车的位置和方向的个数是有无限可能$^2$。与此相似,在习题集 $4$ 中看到的倒立摆问题(inverted pendulum)中,状态也有$(x,\theta,\dot x,\dot\theta)$,其中的 $\theta$ 是杆的角度。在直升机飞行的三维空间中,状态的形式则为$(x,y,x,\phi,\theta,\psi,\dot x,\dot y,\dot z,\dot\phi,\dot\theta,\dot\psi)$,其中包含了滚动角(roll)$\phi$,俯仰角(pitch)$\theta$,以及偏航角(yaw)$\psi$,这几个角度确定了直升机在三维空间中的运动方向。在本节中,我们考虑状态空间为 $S = R^n$ 的情况,并描述此种情况下解决 MDPs 的方法。
2 从理论上讲,$\theta$ 是一个方向(orientation),所以更应当把 $\theta$ 的取值空间写为 $\theta \in [\pi, \pi)$ ,而不是写为实数集合 $\theta \in R$ ;不过在我们讨论的问题中,这种区别不要紧。
解决连续状态 MDP 问题最简单的方法可能就是将状态空间(state space)离散化(discretize),然后再使用之前讲过的算法,比如值迭代(value iteration)或者策略迭代(policy iteration)来求解。
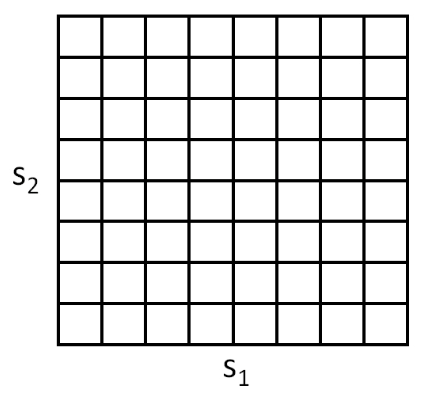
例如,假设我们有一个二维状态空间$(s_1,s_2)$,就可以用下面的网格(grid)来将这个状态空间离散化:
如上图所示,每个网格单元(grid cell)表示的都是一个独立的离散状态 $\overline s$ 。这样就可以把一个连续状态 MDP 用一个离散状态的 $(\overline S, A, {P_{\overline sa}}, \gamma, R)$ 来进行逼近,其中的$\overline S$ 是离散状态集合,而${P_{\overline sa}}$ 是此离散状态上的状态转移概率(state transition probabilities),其他项目同理。然后就可以使用值迭代(value iteration)或者策略迭代(policy iteration)来求解出离散状态的 MDP $(\overline S, A, {P_{\overline sa}}, \gamma, R)$ 的 $V^(\overline s)$ 和 $\pi^ (\overline s)$。当真实系统是某种连续值的状态 $s \in S$ ,而有需要选择某个动作来执行,就可以计算对应的离散化的状态 $\overline s$ ,然后执行对应的动作 $\pi^*(\overline s)$ 。
这种离散化方法(discretization approach)可以解决很多问题。然而,也有两个缺陷(downsides)。首先,这种方法使用了对 $V^$ 和 $\pi^ $ 相当粗糙的表征方法。具体来说,这种方法中假设了在每个离散间隔(discretization intervals)中的值函数(value function)都是一个常数值(也就是说,值函数是在每个网格单元中分段的常数。)。
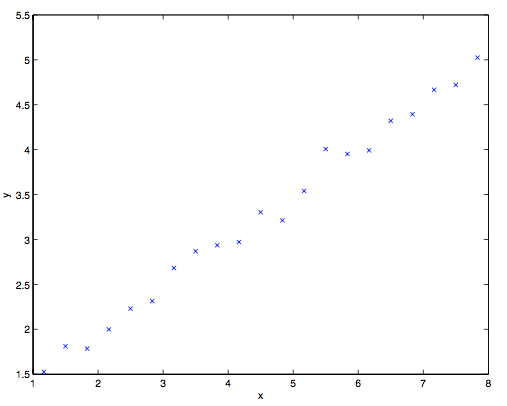
要更好理解这样表征的的局限性,可以考虑对下面这一数据集进行函数拟合的监督学习问题:
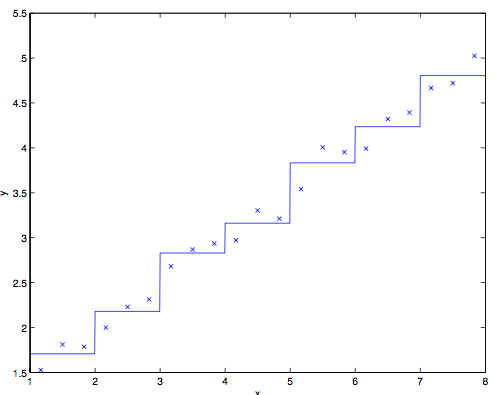
很明显,上面这个数据适合使用线性回归。然而,如果我们对 $x$ 轴进行离散化,那么在每个离散间隔中使用分段常数表示,对同样的数据进行拟合,得到的曲线则如下所示:
这种分段常数表示,对于很多的光滑函数,都不能算好。这会导致输入值缺乏平滑(little smoothing over the inputs),而且在不同的望各单元中间也没有进行扩展(generalization)。使用这种表示方法,我们还需要一种非常精细的离散化过程(也就是网格单元要非常小),才能得到一个比较好的近似估计。
第二个缺陷可以称之为维度的诅咒(curse of dimensionality)。 设 $S = R^n$ ,然后我们队每个 $n$ 维度状态离散成 $k$ 个值。这样总共的离散状态的个数就是 kn。在状态空间 $n$ 的维度中,这个值会呈指数级增长,对于大规模问题就不好缩放了。例如,对于一个 $10$ 维的状态,如果我们把每个状态变量离散化成为 $100$ 个值,那么就会有 $100^{10} = 10^{20}$ 个离散状态,这个维度太大了,远远超过了当前桌面电脑能应付的能力之外。
根据经验法则(rule of thumb),离散化通常非常适合用于 $1$ 维和 $2$ 维的问题(而且有着简单和易于快速实现的优势)。对于 $4$ 维状态的问题,如果使用一点小聪明,仔细挑选离散化方法,有时候效果也不错。如果你超级聪明,并且还得有点幸运,甚至也有可能将离散化方法使用于 $6$ 维问题。不过在更高维度的问题中,就更是极其难以使用这种方法了。
4.2 值函数近似(Value function approximation) 现在我们来讲另外一种方法,能用于在连续状态的 MDPs 问题中找出策略,这种方法也就是直接对进行近似 $V^*$ ,而不使用离散化。这个方法就叫做值函数近似(value function approximation),在很多强化学习的问题中都有成功的应用。
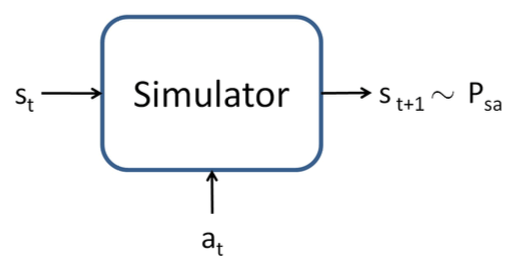
4.2.1 使用一个模型或模拟器(Using a model or simulator) 要开发一个值函数近似算法,我们要假设已经有一个对于 MDP 的模型, 或者模拟器。 简单来看,一个模拟器就是一个黑箱子(black-box),接收输入的任意(连续值的)状态 $s_t$ 和动作 $a_t$ ,然后输出下一个状态 $s_{t+1}$ ,这个新状态是根据状态转移概率(state transition probabilities) $P_{s_ta_t}$ 取样(sampled)得来:
有很多种方法来获取这样的一个模型。其中一个方法就是使用物理模拟(physics simulation)。 例如,在习题集 $4$ 中倒立摆模拟器,就是使用物理定律,给定当前时间 $t$ 和采取的动作 $a$ ,假设制导系统的所有参数,比如杆的长度、质量等等,来模拟计算在 $t+1$ 时刻杆所处的位置和方向。另外也可以使用现成的物理模拟软件包,这些软件包将一个机械系统的完整物理描述作为输入,当前状态 $s_t$ 和动作 $a_t$ ,然后计算出未来几分之一秒的系统状态 $s_{t+1}$ 。$^3$
3 开放动力引擎(Open Dynamics Engine,http://www.ode.com)就是一个开源物理模拟器,可以用来模拟例如倒立摆这样的系统,在强化学习研究领域中,已经相当流行了。
另外一个获取模型的方法,就是从 MDP 中收集的数据来学习生成一个。例如,加入我们在一个 MDP 过程中重复进行了 $m$ 次试验(trials), 每一次试验的时间步长(time steps)为 $T$ 。这可以用如下方式实现,首先是随机选择动作,然后执行某些特定策略(specific policy),或者也可以用其他方法选择动作。接下来就能够观测到 $m$ 个状态序列,如下所示:
$$
\begin{aligned}
&s_0^{(1)}\xrightarrow{a_0^{(1)}}s_1^{(1)}\xrightarrow{a_1^{(1)}}s_2^{(1)}\xrightarrow{a_2^{(1)}}\dots\xrightarrow{a_{T-1}^{(1)}}s_T^{(1)} \\
&s_0^{(2)}\xrightarrow{a_0^{(2)}}s_1^{(2)}\xrightarrow{a_1^{(2)}}s_2^{(2)}\xrightarrow{a_2^{(2)}}\dots\xrightarrow{a_{T-1}^{(2)}}s_T^{(2)} \\
&\cdots \\
&s_0^{(m)}\xrightarrow{a_0^{(m)}}s_1^{(m)}\xrightarrow{a_1^{(m)}}s_2^{(m)}\xrightarrow{a_2^{(m)}}\dots\xrightarrow{a_{T-1}^{(m)}}s_T^{(m)}
\end{aligned}
$$
然后就可以使用学习算法,作为一个关于 $s_t$ 和 $a_t$ 的函数来预测 $s_{t+1}$ 。
例如,对于线性模型的学习,可以选择下面的形式:
$$
s_{t+1}=As_t+Ba_t\qquad(5)
$$
然后使用类似线性回归(linear regression)之类的算法。上面的式子中,模型的参数是两个矩阵 $A$ 和 $B$ ,然后可以使用在 $m$ 次试验中收集的数据来进行估计,选择:
$$
arg\min_{A,B}\sum_{i=1}^m\sum_{t=0}^{T-1}||s_{t+1}^{(i)}-(As_t^{(i)}+Ba_t^{(i)})||^2
$$
(这对应着对参数(parameters)的最大似然估计(maximum likelihood estimate)。)
通过学习得到 $A$ 和 $B$ 之后,一种选择就是构建一个确定性 模型(deterministic model),在此模型中,给定一个输入 $s_t$ 和 $a_t$ ,输出的则是固定的 $s_{t+1}$ 。具体来说,也就是根据上面的等式$(5)$来计算 $s_{t+1}$ 。或者用另外一种办法,就是建立一个随机 模型(stochastic model),在这个模型中,输出的 $s_{t+1}$ 是关于输入值的一个随机函数,以如下方式建模:
$$
s_{t+1}=As_t+Ba_t+\epsilon_t
$$
上面式子中的 $\epsilon_t$ 是噪音项(noise term),通常使用一个正态分布来建模,即 $\epsilon_t\sim N (0, \Sigma)$ 。(协方差矩阵(covariance matrix) $\Sigma$ 也可以从数据中直接估计出来。)
这里,我们把下一个状态 $s_{t+1}$ 写成了当前状态和动作的一个线性函数;不过当然也有非线性函数的可能。比如我们学习一个模型 $s_{t+1} = A\phi_s(s_t) + B\phi_a(a_t)$ ,其中的 $\phi_s$ 和 $\phi_a$ 就可以使某些映射了状态和动作的非线性特征。另外,我们也可以使用非线性的学习算法,例如局部加权线性回归(locally weighted linear regression)进行学习,来将 $s_{t+1}$ 作为关于 $s_t$ 和 $a_t$ 的函数进行估计。 这些方法也可以用于建立确定性的(deterministic)或者随机的(stochastic)MDP 模拟器。
4.2.2 拟合值迭代(Fitted value iteration) 接下来我们要讲的是拟合值迭代算法(fitted value iteration algorithm), 作为对一个连续状态 MDP 中值函数的近似。在这部分钟,我们假设学习问题有一个连续的状态空间 $S = R^n$ ,而动作空间 $A$ 则是小规模的离散空间。$^4$
4 在实践中,大多数的 MDPs 问题中,动作空间都要远远比状态空间小得多。例如,一辆汽车可能有 $6$ 维的状态空间,但是动作空间则只有 $2$ 维,即转向和速度控制;倒立的摆有 $4$ 维状态空间,而只有 $1$ 维的动作空间;一架直升机有 $12$ 维状态空间,只有 $4$ 维的动作空间。所以对动作空间进行离散化,相比对状态空间进行离散化,遇到的问题通常会少得多。
回忆一下值迭代(value iteration),其中我们使用的更新规则如下所示:
$$
\begin{aligned}
V(s) &:= R(s)+\gamma\max_a \int_{s'}P_{sa}(s')V(s')ds' \qquad&(6)\\
&= R(s)+\gamma\max_a E_{s'\sim P_{sa}}[V(s')]\qquad&(7)
\end{aligned}
$$
(在第二节当中,我们把值迭代的更新规则写成了求和(summation)的形式:$V(s) := R(s)+\gamma\max_a\sum_{s'}P_{sa}(s')V(s')$而没有像刚刚上面这样写成在状态上进行积分的形式;这里采用积分的形式来写,是为了表达我们现在面对的是连续状态的情况,而不再是离散状态。)
拟合值迭代(fitted value iteration)的主要思想就是,在一个有限的状态样本 $s^{(1)}, ... s^{(m)}$ 上,近似执行这一步骤。具体来说,要用一种监督学习算法(supervised learning algorithm),比如下面选择的就是线性回归算法(linear regression),以此来对值函数(value function)进行近似,这个值函数可以使关于状态的线性或者非线性函数:
$$
V(s)=\theta^T\phi(s)
$$
上面的式子中,$\phi$ 是对状态的某种适当特征映射(appropriate feature mapping)。对于有限个 $m$ 状态的样本中的每一个状态 $s$ ,拟合值迭代算法将要首先计算一个量 $y^{(i)}$ ,这个量可以用 $R(s)+\gamma\max_aE_{s'\sim P_{sa}}[V(s')]$ 来近似(根据等式$(7)$的右侧部分)。然后使用一个监督学习算法,通过逼近 $R(s) + \gamma\max_a E_{s'\sim P_{sa}}[V (s')]$ 来得到$V(s)$(或者也可以说是通过逼近到 $y^{(i)}$ 来获取 $V(s)$ )。
具体来说,算法如下所示:
从 $S$ 中随机取样 $m$ 个状态 $s^{(1)}, s^{(2)}, . . . s^{(m)}\in S$ 。
初始化 $\theta := 0$ .
重复 {
对 $i = 1, ... , m$ {
对每一个动作 $a \in A$ {
取样 $s_1',... , s_k'\sim P_{s^{(i)}a}$ (使用一个 MDP 模型)
设$q(a)=\frac 1k\sum_{j=1}^kR(s^{(i)})+\gamma V(s_j')$
// 因此, $q(a)$ 是对$R(s)^{(i)}+\gamma E_{s'\sim P_{sa}}[V(s')]$的估计。
}
设$y^{(i)} = \max_a q(a)$.
// 因此, $y^{(i)}$ 是对$R(s^{(i)})+\gamma\max_aE_{s'\sim P_{sa}}[V(s')]$的估计。
}
// 在原始的值迭代算法(original value iteration algorithm)中,(离散状态的情况 )
// 是根据 $V(s^{(i)}) := y^{(i)}$ 来对值函数(value function)进行更新。
// 而在这里的这个算法中,我们需要的让二者近似相等,即 $V(s^{(i)}) \approx y^{(i)}$ ,
// 这可以通过使用监督学习算法(线性回归)来实现。
设 $\theta := arg\min_\theta \frac 12\sum_{i=1}^m(\theta^T\phi(s^{(i)})-y^{(i)})^2$
}
以上,我们就写出了一个拟合值迭代算法(fitted value iteration),其中使用线性回归作为算法(linear regression),使 $V (s^{(i)})$ 逼近 $y^{(i)}$ 。这个步骤完全类似在标准监督学习问题(回归问题)中面对 $m$ 个训练集 $(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})$ ,而要利用学习得到从$x$ 到 $y$ 的映射函数的情况;唯一区别无非是这里的 $s$ 扮演了当时 $x$ 的角色。虽然我们上面描述的算法是线性回归,很显然其他的回归算法(例如局部加权线性回归)也都可以使用。
与离散状态集合上进行的的值迭代(value iteration)不同,拟合值迭代(fitted value iteration)并不一定总会收敛(converge)。然而,在实践中,通常都还是能收敛的(或者近似收敛),而且能解决大多数问题。另外还要注意,如果我们使用一个 MDP 的确定性模拟器/模型的话,就可以对拟合值迭代进行简化,设置算法中的 $k = 1$ 。这是因为等式$(7)$当中的期望值成为了对确定性分布(deterministic distribution)的期望,所以一个简单样本(single example)就足够计算该期望了。否则的话,在上面的算法中,就还要取样出 $k$ 个样本,然后取平均值,来作为对期望值的近似(参考在算法伪代码中的 $q(a)$ 的定义)。
最后,拟合值迭代输出的 $V$ ,也就是对 $V^*$ 的一个近似。这同时隐含着对策略函数(policy)的定义。 具体来说,当我们的系统处于某个状态 $s$ 的时候,需要选择一个动作,我们可能会选择的动作为:
$$
arg\max_a E_{s'\sim P_{sa}}[V(s')]\qquad(8)
$$
这个计算/近似的过程很类似拟合值迭代算法的内部循环体,其中对于每一个动作,我们取样 $s_1',...,s_k'\sim P_{sa}$ 来获得近似期望值(expectation)。(当然,如果模拟器是确定性的,就可以设 $k = 1$ 。)
在实际中,通常也有其他方法来实现近似这个步骤。例如,一种很常用的情况就是如果模拟器的形式为 $s_{t+1} = f(s_t,a_t) + \epsilon_t$ ,其中的 $f$ 是某种关于状态 $s$ 的确定性函数(例如 $f(s_t,a_t) = As_t + Ba_t$ ),而 $\epsilon$ 是均值为 $0$ 的高斯分布的噪音。在这种情况下,可以通过下面的方法来挑选动作:
$$
arg\max_a V(f(s,a))
$$
也就是说,这里只是设置 $\epsilon_t = 0$ (即忽略了模拟器中的噪音项),然后设 $k = 1$ 。同样地,这也可以通过在等式$(8)$中使用下面的近似而推出:
$$
\begin{aligned}
E_{s'}[V(s')] &\approx V(E_{s'}[s']) &(9) \\
&= V(f(s,a)) &(10)
\end{aligned}
$$
这里的期望是关于随机分布 $s'\sim P_{sa}$ 的。所以只要噪音项目 $\epsilon_t$ 很小,这样的近似通常也是合理的。
然而,对于那些不适用于这些近似的问题,就必须使用模型,取样 $k|A|$ 个状态,以便对上面的期望值进行近似,当然这在计算上的开销就很大了。