This team (me and @oswidan97) work was developed as assignment for Analysis & Design of Algorithms Course Fall 2018 offering at CCE department, Faculty of Engineering, Alexandria University
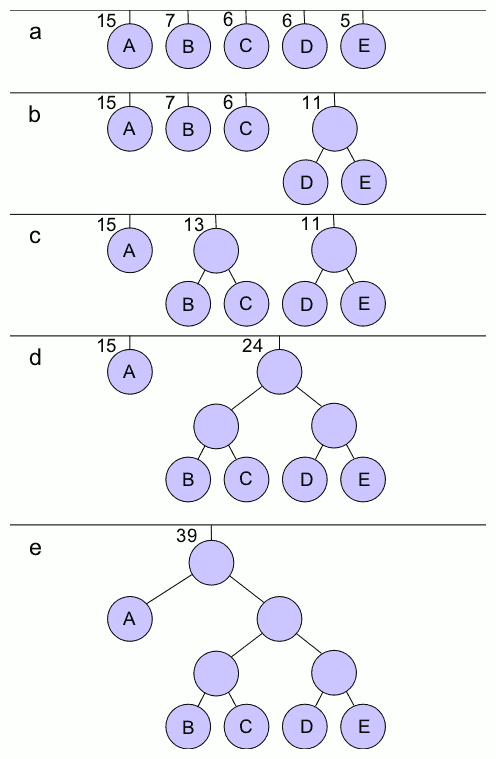
We use Huffman's algorithm to construct a tree that is used for data compression. We assume that each character has an associated weight equal to the number of times the character occurs in a file, When compressing a file we'll need to calculate these weights.
Huffman's algorithm assumes that we're building a single tree from a group (or forest) of trees. Initially, all the trees have a single node with a character and the character's weight. Trees are combined by picking two trees, and making a new tree from the two trees. This decreases the number of trees by one at each step since two trees are combined into one tree.
-
Begin with a forest of trees. All trees are one node, with the weight of the tree equal to the weight of the character in the node. Characters that occur most frequently have the highest weights. Characters that occur least frequently have the smallest weights. Repeat this step until there is only one tree.
-
Choose two trees with the smallest weights, call these trees T1 and T2. Create a new tree whose root has a weight equal to the sum of the weights T1 + T2 and whose left subtree is T1 and whose right subtree is T2.
-
The single tree left after the previous step is an optimal encoding tree.
There are two parts to an implementation: a compression program and an un-compression/decompression program. You need both to have a useful compression utility. We'll assume these are separate programs, but they share many classes, functions, modules, code or whatever unit-of-programming you're using.
- We'll call the program that reads a regular file and produces a compressed file the compression or huffing program.
- The program that does the reverse, producing a regular file from a compressed file, will be called the uncompression or un-huffing program.
- Two unordered maps, one for the character and coding pairs and another for the character and the frequency or number of times repeated.
- One priority queue to apply the minimum heap minimum extraction property in the tree construction algorithm.
You must store some initial information in the compressed file that will be used by the uncompression/un-huffing program (the tree basically). There are several alternatives for storing the tree:
-
Store the character counts at the beginning of the file. You can store counts for every character, or counts for the non-zero characters. If you do the latter, you must include some method for indicating the character, e.g., store character/count pairs.
-
You could use a "standard" character frequency, e.g., for any English language text you could assume weights/frequencies for every character and use these in constructing the tree for both compression and uncompression.
-
You can store the tree at the beginning of the file. One method for doing this is to do a pre-order traversal, writing each node visited. You must differentiate leaf nodes from internal/non-leaf nodes. One way to do this is write a single bit for each node, say 1 for leaf and 0 for non-leaf. For leaf nodes, you will also need to write the character stored. For non-leaf nodes there's no information that needs to be written, just the bit that indicates there's an internal node.
When you write output the operating system typically buffers the output for efficiency. This means output is actually written to disk when some internal buffer is full, not every time you write to a stream in a program. Operating systems also typically require that disk files have sizes that are multiples of some architecture/operating system specific unit, e.g., a byte or word. On many systems all file sizes are multiples of 8 or 16 bits so that it isn't possible to have a 122 bit file.
In any case, when you write 3 bits, then 2 bits, then 10 bits, all the bits are eventually written, but you cannot be sure precisely when they're written during the execution of your program. Also, because of buffering, if all output is done in eight-bit chunks and your program writes exactly 61 bits explicitly, then 3 extra bits will be written so that the number of bits written is a multiple of eight.
Our decompressing/un-huff program must have some mechanism to account for these extra or "padding" bits since these bits do not represent compressed information. So, we check if the size of the bits string is multiple of 8 or not by checking the modulo of 8. Using that modulo value we can calculate the number of bits that need to be padded and handle them correctly.
Finally, we added a pseudo EOF character, and we chose it out of the ASCII table in the human readable range so we are not limiting the user to not use any ASCII characters.
1. Huffman coding, from WikiWorld
2. Thomas H. Cormen, Charles E. Leiserson, Ronald L.Rivest, Clifford Stein “Introduction to Algorithms 3rd Edition - Thomas H. Cormen, Charles E. Leiserson, R”
3. Weiss, Mark Allen. “Data structures and algorithm analysis in Java." Addison-Wesley Long-man Publishing Co., Inc., 1998.