Multigrid
Multigrid is a general class of algorithms to solve partial differential equations, elliptic and parabolic ones such as Poisson's equation for self-gravity and diffusion-like equations in particular. Among many variants of Multigrid solvers, Athena++ adopts a simple geometric Multigrid using cell-centered discretization. To learn practical usage with self-gravity, see Self-Gravity with Multigrid.
- Currently only self-gravity is implemented.
- No external library is required.
- It works both with and without mesh refinement.
- It works with any number of parallization and
MeshBlocks. - OpenMP support is poorly tested.
- Currently it works only in 3D Cartesian coordinates.
- Each cell size must be cubic and mesh spacing must be uniform.
- The
MeshBlocksize must be power of 2 and same in all the directions. - The root grid size does not have to be power of 2, but the code is most efficient if so.
- (Up to) Second-order accurate.
- Currently incompatible with some modules including shearing box.
Because Multigrid inherently involves global operations across MeshBlocks, the Multigrid solver consists of two components: MultigridDriver which contains global properties and controls the progress of the solver, and Multigrid which contains actual data. Roughly speaking, MultigridDriver corresponds to Mesh, while Multigrid corresponds to MeshBlock. This design is similar to FFT.
Although currently only self-gravity solver is implemented, the Multigrid solver is extensible to other physical processes. In order to achieve maximum flexibility, the actual solver is implemented as derived classes of MultigridDriver and Multigrid. While the base classes implement operations and data common to all physics, the derived classes implement operations and data specific to each physical process. For example, MGGravityDriver and MGGravity classes are implemented for self-gravity. Also, as the Multigrid solver has more complicated communication patterns than the MHD part, the MGBoundaryValues class is separately implemented for processing boundaries and communications.
The solver works as follows. When MultigridDriver::Solve (a pure virtual function) is called, it loads the source function data (e.g. the density distribution for self-gavity) from MeshBlock to Multigrid objects. Then it sets up the data on the Multigrid hierarchy and runs the algorithm on it. Once the solution is obtained, it returns the data (e.g. the gravitational potential for self-gravity) to MeshBlock. Then the solution can be used in the integrator to update physical quantities. In the present implementation, Athena++ calls MultigridDriver::Solve at every subsycle so that the solution can be used in the time integrator without algorithmic complication and loss of the time accuracy.
The implemented algorithms are based on U. Trottenberg, C. W. Osterlee and A. Schuller, Multigrid, 2000, Academic Press. This is a good, comprehensive and practical textbook. If you want to learn Multigrid and/or implement something on it, I highly recommend this textbook.
The computational cost of Multigrid is O(N3) in 3D with N cells in each dimension, as long as operations in active cells are dominant. However, if there is constant cost per each communication message, and if it is not negligible, then Multigrid behaves O(N3 log N). Roughly speaking, Multigrid behaves like O(N3) when the number of processes is not so large, and it becomes O(N3 log N) with a larger number of processes. Usually, for self-gravity, Multigrid is faster than FFT which is intrinsically O(N3 log N), although it depends on physics and required accuracy. Also it should be noted that Multigrid is more compatible with various boundary conditions.
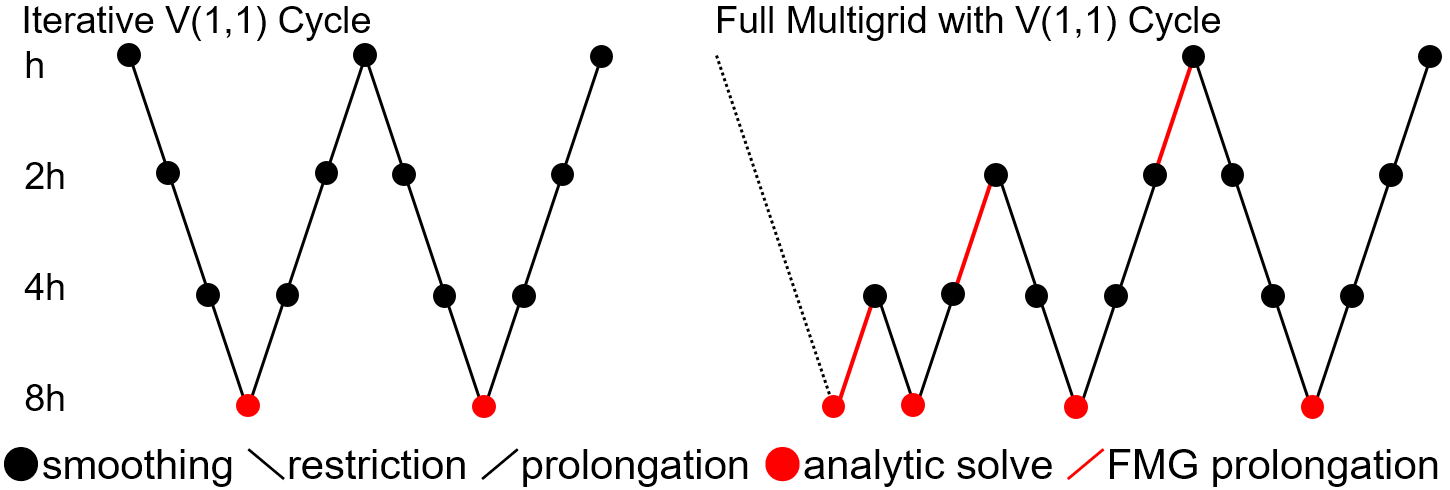
Currently two cycle modes are provided. One is MGI (MultiGrid Iteration) mode, which uses standard V-cycle iterations (left in the figure, one "V" shape corresponds to one iteration). In this mode, the solver starts from the finest level, and applies smoothing operations on each level by reducing the resolution (restriction). When it reaches the coarsest level, it calculates the solution on that level either analytically or numerically (anyway the cost is small), and then goes back the hierarchy to the finer levels (prolongation), applying smoothing operations on each level. Once it reaches the finest level, the defect (also called residual or error) is measured, and it repeats the process until the required accuracy is achieved or the convergence stalls. Each sweep typically reduces the defect by a factor of 7-10 depending on physics and grid structures. This mode requires a good initial guess to achieve fast and robust convergence. Currently the solution from the previous timestep is used but it is not always good enough.
The other is FMG (Full MultiGrid) mode (right in the figure). In this mode, the solver stars from the coarsest level. On the coarsest level, the solution can be easily obtained either analytically or numerically. Then the solver interpolates the coarse grid solution to the finer grid, and uses it as an initial guess for the finer level. This FMG prolongation requires higher order interpolation than the prolongation in the normal V-cycle explained above. Then, it applies V-cycle once to improve the solution. It goes down to the finer levels applying the FMG prolongation and V-cycle on each level. Once it reaches the finest level, the defect is measured, and additional V-cycles are applied until the required accuracy is achieved or the convergence stalls. In general, this mode is superior to the MGI mode (i.e. faster and more robust), because it does not require any initial guess and it usually achieves reasonably good convergence even in the first sweep.
During restriction processes toward coarser levels, each MeshBlock is reduced to a single cell at some point. Then all the Multigrid data in MeshBlocks are collected and packed in to the "root Multigrid" object, in which one cell corresponds to one MeshBlock. Then the algorithm is applied on this root Multigrid. And when the algorithm comes back to this level, the prolongated data are transferred from the root Multigrid to the Multigrid object in each MeshBlock. Operations on the MeshBlock levels are parallelized using TaskList, but operations on the root Multigrid are not parallelized because the computational costs are very small and communication overhead is significant there.
Currently, our restriction algorithm is simple volume-weighted average, prologantion is tri-linear interpolation which is second-order accurate, and FMG prolongation is tri-cubic interpolation. Overall, the solution should be second-order accurate as long as it is sufficiently converged.
In the basic Multigrid algorithm, only the defect is restricted to and prolongated from the coarser levels. When the problem is non-linear and/or mesh refinement is in use, however, the whole system must be properly propagated to the coarser levels. This method is called Full Approximation Scheme (FAS). Our Multigrid solver supports FAS, and it is automatically enabled when mesh refinement is enabled. For non-linear problems, FAS should be enabled in the derived class.
The smoothing operation (and defect calculation) depends on physics, and currently the Red-Black Gauss-Seidel smoother is implemented for self-gravity. While the number of smoother application on each level can be adjusted, the current default is 1 time on each level both for downward and upward operations, which is the so-called V(1,1) method.
When mesh refinement (either adaptive or static) is in use, some additional considerations are needed. First, FAS explained above is automatically enabled. Also, a proper interpolation is needed to fill ghost cells at level boundaries. For this purpose, we use the mass-conservation formula (Feng et al. 2018, Journal of Computational Physics, 352, 463) for self-gravity, which does not produce any fake mass at level boundaries. In their paper, two second-order variants are proposed (Figure 4, Δ stencil and Π stencil), but as far as tested the Π stencil works much better because it does not use extrapolation while the other does. Note that this implementation of the mass-conservation formula (I think flux conservation is more appropriate) depends on physics as specific discretization is needed for each physics. Also, this mass-conservation discretization is used only in the smoothing operation and defect calculation. For level boundaries needed for prolongation, normal tri-linear (tri-cubic for FMG prolongation) interpolation is used, as suggested in the paper.
With mesh refinement, some regions are locally refined. To go up and down the multigrid higherarchy, at some point we need to remove and generate locally refined grids. Our implementation of Multigrid with mesh refinement is slightly different from what is suggested in Trottenberg et al.. The implementation of the V-cycle proposed in the textbook first removes the locally refined regions. However, this causes poor load balancing as the number of MeshBlocks changes. Instead, we first restrict all the MeshBlocks coherently keeping the load balancing as much as possible, and we start removing locally refined regions only beyond the level where each MeshBlock is restricted to a single cell. This is the same timing where the data is transferred from MeshBlocks to the root grid, and operations in the root grid are not parallelized. Locally refined data are stored in Octets which contains 2x2x2 cells, and manipulation of MeshBlocks is performed using these Octets. For details, please refer to the method paper (in preparation).
Convergence is slightly slower and more iterations are needed with mesh refinement, because level boundaries inevitably produce noises. This is partially because the resolution is not uniform there and the interpolation is not perfect, but also because it is impossible to satisfy the red-black iteration order; a coarser cell always interacts with both red and black finer cells, while half of finer cells interact with coarser cells of the same color. Still, one V-cycle iteration can reduce the defect by a factor of 5-7.
Boundary conditions are of crucial importance, as elliptic problems are boundary condition problems. While they depend on physics, some common boundary conditions are built-in, including periodic, zero-fixed and zero-gradient, as well as isolated boundary conditions using multipole expansion (up to quadrapole or hexadecapole). Also, users can implement user-defined boundary conditions. For details, please refer to each physics module. Note that, when all the boundaries are periodic or zero-gradient (more generally, any boundary function that does not fix absolute values), the average of the source must be subtracted in order to fix the zero point. This can be done by enabling the subtract average flag, but this is done automatically for periodic and zero-gradient boundaries.
Implementing user-defined boundary conditions for Multigrid is a bit tricky, even for simple fixed (Dirichlet) boundary conditions. Because the Multigrid solver applies boundary conditions on levels with different resolution, the cell-centered position shifts as the resolution changes. Therefore, fixing cell-centered values in ghost cells does not work. Instead, we need to fix the values on the surface of the active zone. Currently, such boundary conditions are implemented by calculating cell-centered values in ghost cells by extrapolation from the first active cells and the surface fixed values (see mgbval_multipole.cpp or mgbval_zerofixed.cpp).
In addition, boundary functions have to be aware of whether FAS is in use or not as boundary conditions are applied on every level. Without FAS, appropriate boundary conditions for the residual equation are needed, which can be zero-fixed. For FAS, the physical boundary conditions for the original equation but for the lower resolution are needed. Currently the code does not handle this automatically except for the built-in boundary conditions. Users must define the consistent boundary conditions for all the multigrid levels. The most straightforward option is using the physical boundary conditions with FAS enabled, although FAS is slightly more expensive than the basic multigrid algorithm.
While you can set different boundary conditions for the multigrid and hydrodynamics, there are some limitations. When you want to use periodic boundary conditions, you have to use periodic for both multigrid and hydrodynamics because currently they share the same neighbor structure.
Both in the MGI and FMG modes, the convergence threshold must be specified in terms of the volume-weighted root-mean-square of the defect. In FMG, it anyway performs the first FMG sweep regardless of the specified threshold. When a very small (or zero) threshold is specified, the solver continues iterations until the convergence saturates and significantly slows down. This threshold must be specified according to your problem. Practically it is not necessary to apply iterations until the convergence saturates.
One FMG sweep is actually quite good and it can already achieve the error close enough to the truncation error compared to the analytic solution, and the error is already second-order accurate. However, the defect is not very small at this point yet. There remain high-frequency noises originating from the red-black iteration pattern, which is particularly prominent at level boundaries with mesh refinement. Therefore it is recommended to apply further V-cycle iterations at least a few times to smooth out the high-frequency noies and decrease the defect, although the error measured against the analytic solution does not necessarily decrease significantly. This is because the numerical solution does not converge to the analytic solution which is defined with inifinite resolution, but to the exact discretized solution with the given resolution.