Run:

>>> python Hangman.py

Run and show flow graph:

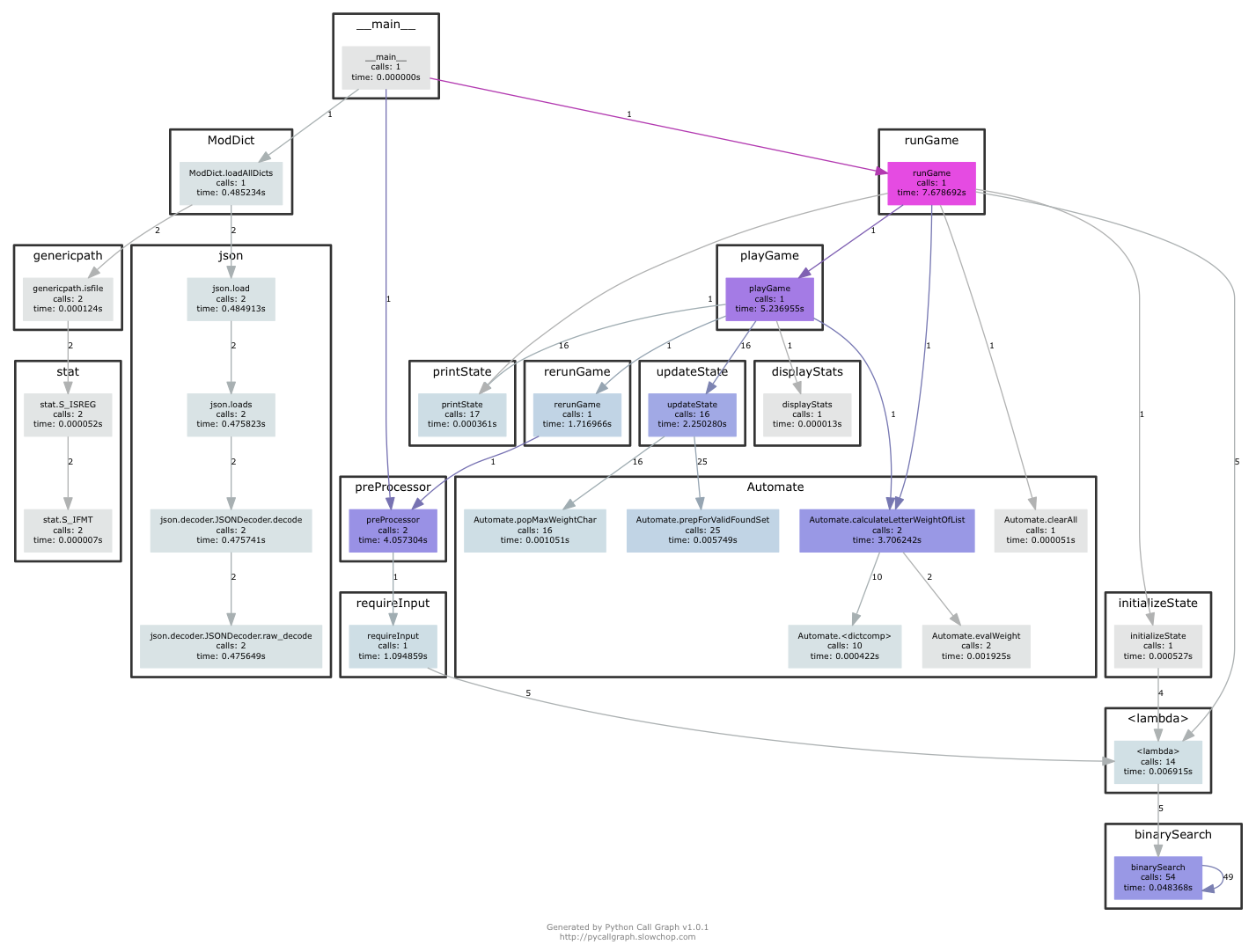
>>> pycallgraph graphviz —- ./Hangman.py

How the algorithm works (Overview):

There are two things that we keep track of in this algorithm: letter frequency and word frequency. If you choose to have the word generator randomly select words for the program to solve, there is no need to main word frequency list since every word has equal probability of being chosen. This is however not the case if a human decides to provide an input. You start out with list of possible words you can have for the blanks and keep finding the letter frequency of that list and then extract the letter with the highest probability as our next guess. (A priority queue-like structure is used to order the probabilities). You keep doing this process until you have either reduced your list size to a single word, which means you’ve found the word, or there are only two letters left to be guessed for the word and the input was inputted by the human. In the latter case, you maintain word frequency of the left-over list and pick the highest probabilistic word. The algorithm is based on a probabilistic model of letter and word frequencies combined. We also keep track of fill factor that keeps track of how filled is the word in the letters we have guessed.

It is important to note that there is no randomness in the answer on the same input and that smaller words are harder to predict. For example, "on" and "of" differ by only 1 letter and if that letter doesn't appear in the rest of the sentence and these are the only two letter words that start with "o" then it's just a guessing game with a probability of 50% for each event.

Note: The input dictionary is not a valid English dictionary. It contains words that are not actually real words.

You can keep playing the game as many times you wish and see in the generated flow graph the processes and time each function went through.

Feel free to point out any bugs/improve it.

Probability of Success on 1,000,000 Commonly Used Sentences:

>>> python TestAverage.py
Tests Done: 1000000/1000000
Average: 98.5602%

Probability of Success on 1,000,000 Randomly Generated Input (Extreme Cases):

>>> python TestAverage.py
Tests Done: 1000000/1000000
Average: 92.5692%

Sample Input

1 : Generate input for me
2 : Enter custom input
Type 'out' to exit program
--> 1
Generated Input: pardy stoutheartedly valetudinarians cusp portion
_____ ______________ _______________ ____ _______

Guess: e
_____ ______e___e___ ___e___________ ____ _______

Guess: s
_____ s_____e___e___ ___e__________s __s_ _______

Guess: y
____y s_____e___e__y ___e__________s __s_ _______

Guess: u
____y s__u__e___e__y ___e_u________s _us_ _______

Guess: t
____y st_ut_e__te__y ___etu________s _us_ ___t___

Guess: v
____y st_ut_e__te__y v__etu________s _us_ ___t___

Guess: r
__r_y st_ut_e_rte__y v__etu____r___s _us_ __rt___

Guess: o
__r_y stout_e_rte__y v__etu____r___s _us_ _ort_o_

Guess: p
p_r_y stout_e_rte__y v__etu____r___s _usp port_o_

Guess: n
p_r_y stout_e_rte__y v__etu__n_r__ns _usp port_on

Guess: l
p_r_y stout_e_rte_ly v_letu__n_r__ns _usp port_on

Guess: i
p_r_y stout_e_rte_ly v_letu_in_ri_ns _usp portion

Guess: h
p_r_y stouthe_rte_ly v_letu_in_ri_ns _usp portion

Guess: d
p_rdy stouthe_rtedly v_letudin_ri_ns _usp portion

Guess: c
p_rdy stouthe_rtedly v_letudin_ri_ns cusp portion

Guess: a
pardy stoutheartedly valetudinarians cusp portion

ALL COMPLETED! SOLVED!

TRIES LEFT: 3 out of 3

Flow Diagram for input above: