The HeLO-System

HeLO (Hell Let Loose Elo Score) is a system designed by me to rank competitive teams playing the realistic multiplayer World War Two combined arms first person shooter Hell Let Loose. I'll give you a short introduction of how and why I created this. The official website with statistics and other stuff that uses this system can be found here.

• The HeLO-System
  • What is an Elo System?
  • What Factors influence the HeLO Score?
  • Calculating the Probability of a Victory
  • Calculating the new HeLO Score
  • Guessing the HeLO Score of a new Team
  • Full Example
  • What if more than one team plays together?
• Project Overview
  • Current State (deprecated)
  • Planned Features

What is an Elo System?

The Elo rating system is a method to calculate the relative skill levels of players in zero-sum games such as chess. It is named after its creator Arpad Elo, a Hungarian-American physics professor. If you have ever played chess online or in a competitive tournament you might be familiar with the concept. If not, you can read more about the system on Wikipedia.

What Factors influence the HeLO Score?

In contrast to chess where you can either win, lose or draw, HLL offers additional outcomes determined by the amount of controlled cap points per team at the end of the match.

There are three main factors influencing the HeLO-Score of a team: To summarize, there are three main factors:

• the game result
• the number of players
• the match type (competitive or regular)

Calculating the Probability of a Victory

Let's dive a little bit deeper into the maths. Based on the current score of each team, we need to know the probabilty of winning, which can be calculated by the following integral (don't worry, I will strongly simplify it):

$$ P(D) \hspace{1mm} = \hspace{1mm} \frac{1}{\sigma \sqrt{2\pi}} \hspace{1mm} \int_{-\infty}^D e^{-\frac{t^2}{2\sigma^2}} dt $$

D is the difference between the scores of team 1 and team 2. The standard deviation is set to $\sigma \hspace{1mm} = \hspace{1mm} 200 \sqrt{2}$ and the mean is 0. As promised, the integral mentioned above simplifies to:

$$ P(D) \hspace{1mm} = \hspace{1mm} \frac{\mathrm{erf}(\frac{D}{400})+1}{2} $$

where erf(x) is the Gaussian error function. That's basically it. Let's have a look at a small example. Team A (734) plays against team B (579). The difference is: D = 734 - 579 = 155. Now we just have to insert the numbers in the equation ... and P(D) = 0.708. What does this mean? It means that Team A will win the game with a probability of 70.8%. The probabilty of Team B winning is the counter-probability: 1 - P(D) = 0.292.
Side information: In case the difference D should be greater than 400, the system will take 400 as the maximum. Otherwise, the score gain or loss would be either too significant or absolutely irrelevant.

Calculating the new HeLO Score

For that I copied the formula from chess, but adjusted a few factors (as mentioned earlier):

$$ H^\prime_\mathrm{n} \hspace{1mm} = \hspace{1mm} H_\mathrm{n} \hspace{1mm} + \hspace{1mm} k(S_\mathrm{n} \hspace{1mm} - \hspace{1mm} P_\mathrm{n}(D)) $$

$H^\prime_\mathrm{n}$ is the current. HeLO score Let's have a closer look on $k$:

$$k \hspace{1mm} = \hspace{1mm} ac (log_{a} \frac{N}{50} \hspace{1mm} + \hspace{1mm} 1)$$

• a: The "Number of Games" factor. The default factor for the number of matches/games played is 40. If a team played more than 30 games, this factor changes to 20. It hasn't been mentioned yet, since its only purpose is to accelerate the settling process in order to calculate a reliable score faster.
• c: The "Competitive" factor. Off seasonal time is during Christmas and New Year's eve, easter time and during the summer (1st of July until 31st of August).
  • friendly match (off seasonal): c = 0.5
  • friendly match (on seasonal): c = 0.8
  • competitve match: c = 1
  • competitve match (extra sweaty): c = 1.2
• N: The "Number of Players" factor. Why is it logarithmic? For me it was not an option to scale the number of players linearly, because it is a huge difference of missing a full squad in a 50v50 game and missing a squad in a 25v25 game. Therefore, this factor decreases even heavier the more players are missing. Fun fact: there have to be at least 3 players on each side. Otherwise the logarithm will be negative (and that is something we don't want to happen).

$S_\mathrm{n}$ are the points your team holds at the end of the game normalized to 5.

Guessing the HeLO Score of a new Team

New teams start with a HeLO score of 600. To be honest, there will be exceptions to this. In order to reduce the "settling time", I will guess the strength of a team and give them a score between 550 and 650. The affected team will be informed about that.

Full Example

Let's have a look at a realistic example. Team A (746) plays a competitive match (extra sweaty) against Team B (613). They play with 45 players on each side. Team A played more than 30 games, but Team B is relatively new on scene (played less than 30 games). Team B (everyone sympathizes for the underdog) wins with a score of 5-0.

1. Calculate the difference: D = 746 - 613 = 133
2. Calculate the probability of winning for Team A: P(121) = 0.681
3. Calculate the probability of winning for Team B: 1 - P(121) = 0.319
4. New HeLO score for Team A:

$$ H^\prime_\mathrm{A} \hspace{1mm} = \hspace{1mm} 746 \hspace{1mm} + \hspace{1mm} 20 \hspace{1mm}\cdot \hspace{1mm} 1.2 \hspace{1mm}\cdot \hspace{1mm} (log_{20} \frac{45}{50} \hspace{1mm} + \hspace{1mm} 1) (\frac{0}{5} \hspace{1mm} - \hspace{1mm} 0.681) \hspace{1mm} \approx \hspace{1mm} 730 $$

5. New HeLO score for Team B:

$$ H^\prime_\mathrm{B} \hspace{1mm} = \hspace{1mm} 613 \hspace{1mm} + \hspace{1mm} 40 \hspace{1mm}\cdot \hspace{1mm} 1.2 \hspace{1mm} \cdot \hspace{1mm}(log_{40} \frac{45}{50} \hspace{1mm} + \hspace{1mm} 1) (\frac{5}{5} \hspace{1mm} - \hspace{1mm} 0.319) \hspace{1mm} \approx \hspace{1mm} 645 $$

So Team A loses 16 score points while Team B gains 32 score points for beating a better team.

What if more than one team plays together?

This is called a cooperation. Cooperations can consist of teams fielding an equal amount of players, e.g. 25 each, or a different amount of players, e.g. 15 and 35. We have multiple options here. The most intuitive one is to assign the score changes of that specific game according to the player distributions. This is done by weighing the average. If the easier and less accurate option is used, the player distributions are ignored. The normal average is computed and score changes are shared equally among the participants of the cooperation. This will be used in case no player distributions are given. Check this out:

$$ \overline{x} \hspace{1mm} = \hspace{1mm} \sum_{i=1}^{n}w_i x_i $$

where the $w_i$ are the player fielded by a team normalized to the total number of players. $x_i$ is then the score of the corresponding team. First good thing about this is that we can calculate the new score of this specific cooperation with the average as it was the score of a "normal" team. And second, we can assign the gain/loss of this game to the teams in the same manner.

Project Overview

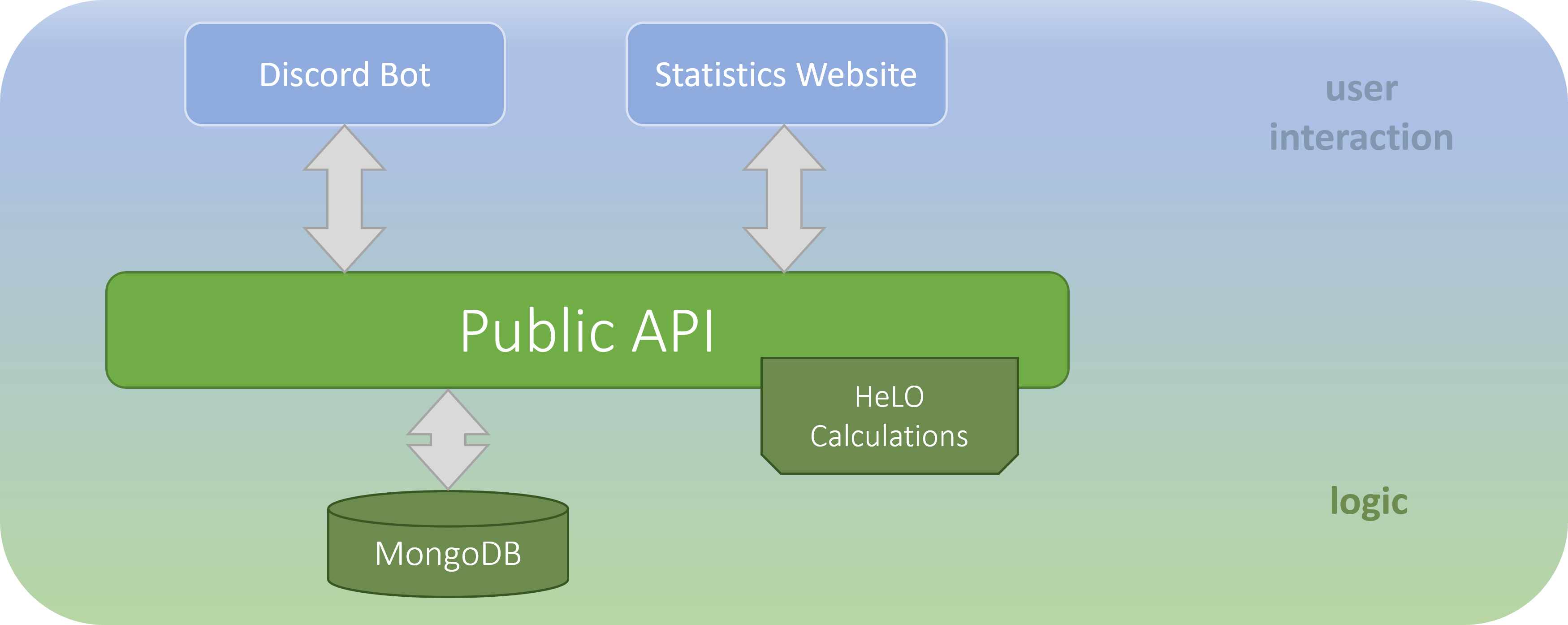
The HeLO-System has become more than just a hobby. I have created a whole project from it. Here is an overview:

Current State (deprecated)

At the moment there is a downloadable and executable desktop application. The main window looks like this:

Originally, the intention was to grant every team manager Superuser permissions, which are necessary to report game results. Additionally, users that do not have these permissions can request the scores of all teams. There is also some kind of security implemented (e.g. Superusers must authenticate themselves). I'll keep this section small, because I am currently working on major improvements (see "Planned Features"). Soon, all of this will be much better and easier to use.

Planned Features

The following features are either planned or already partially implemented:

• REST API replacing the downloadable client (see: https://github.com/HeLO-System/HeLO-Server)
• Discord Bot with various quality of life features (including easy reporting of game results, request of scores and statistics, simulation mode, betting system, ...)

The Discord Bot's development branch (not public atm) currently runs on my Raspberry Pi and there are not a lot of security mechanism (therefore not public). But you can use the Bot on the HeLO-Discord: https://discord.gg/dmtcbrV7t5, feel free to join and stress test him.
There are already 67 teams registered in the HeLO-System. The Discord has more than 590 members. I had no idea that the project would be so well received and I am genuinely thankful for it.