This package implements Bayesian annealed sequential importance sampling (BASIS), a Sequential Monte Carlo sampling technique described by Wu2017. In particular, it implements the special case with a maximum chain length of one (l_max = 1). Sequential Monte Carlo methods stand out against MCMC or HMC methods as they are able to estimate the model evidence (also called marginal likelihood) which can be used to objectively compare models of varying complexity. We combine the algorithm by Wu2017 with an optional tuning method for the proposal scaling factor beta, as described by Minson2013. The sample function can perform parameter inference and model selection on any valid PyMC2-model object.
The easiest way to install the latest release version of bayesianfridge is via pip:
pip install bayesianfridge
Alternatively, a zipped version can be downloaded here. The module is installed by calling python setup.py install.
The latest development version of bayesianfridge can be installed from the master branch using pip (requires git):
pip install git+https://github.com/christophmark/bayesianfridge
Alternatively, use this zipped version or clone the repository.
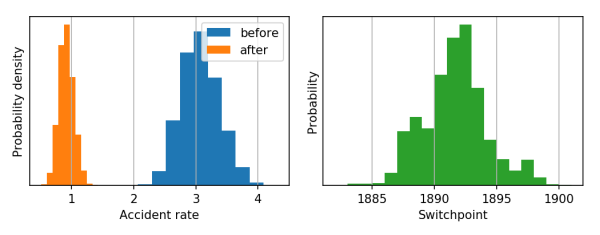
The following code provides a minimal example of an analysis carried out using bayesloop. The data here consists of the number of coal mining disasters in the UK per year from 1851 to 1962 (see this article for further information). This example is also discussed in the official PyMC2 documentation.
import numpy as np
import pymc
from bayesianfridge import sample
import matplotlib.pyplot as plt
data = np.array([5, 4, 1, 0, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6, 3, 3, 5, 4, 5, 3, 1, 4,
4, 1, 5, 5, 3, 4, 2, 5, 2, 2, 3, 4, 2, 1, 3, 2, 2, 1, 1, 1, 1, 3, 0,
0, 1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0,
0, 2, 1, 0, 0, 0, 1, 1, 0, 2, 3, 3, 1, 1, 2, 1, 1, 1, 1, 2, 3, 3, 0,
0, 0, 1, 4, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0])
# Probabilistic model
switchpoint = pymc.DiscreteUniform('switchpoint', lower=0, upper=110)
early_mean = pymc.Exponential('early_mean', beta=1.)
late_mean = pymc.Exponential('late_mean', beta=1.)
@pymc.deterministic
def rate(s=switchpoint, e=early_mean, l=late_mean):
out = np.empty(len(data))
out[:s] = e
out[s:] = l
return out
obs = pymc.Poisson('disasters', mu=rate, value=data, observed=True)
model = pymc.Model([switchpoint, early_mean, late_mean, obs])
# Inference
samples, marglike = sample(model, 10000)
# Plotting
m1 = samples['early_mean']
t = samples['switchpoint'] + 1852
m2 = samples['late_mean']
plt.figure()
plt.subplot2grid((1, 2), (0, 0))
plt.hist(m1, facecolor='C0', label='before')
plt.hist(m2, facecolor='C1', label='after')
plt.xlabel('Accident rate')
plt.ylabel('Probability density')
plt.yticks([])
plt.grid()
plt.legend()
plt.subplot2grid((1, 2), (0, 1))
plt.hist(t, bins=range(int(min(t)), int(max(t)) + 1, 1), facecolor='C2')
plt.xlabel('Switchpoint')
plt.ylabel('Probability')
plt.yticks([])
plt.grid()