Technica 2022 Tech+Research: Course Assistant

This repository contains materials for UMD's Technica 2022 Tech+Research "course assistant" project, supported by Amazon AWS. The event was held October 14-16, 2022.

Have you ever wondered how courses get scheduled? Each course needs to be assigned to a suitably large classroom at a time its instructor finds acceptable. Unfortunately, not all classrooms are big enough for all courses, and not all instructors' (and students') most-preferred times will be available. How can we meet our minimum goal (schedule all classes) and maximize our constituents' preferences, even as we have thousands of students, dozens or hundreds of courses, and dozens of rooms? This is a real problem for UMD CS!

This research project will explore one approach to solving this problem. Student researchers will develop solutions to the problem and scientifically evaluate them both analytically and empirically. The mentors will teach the participants about cutting-edge automated reasoning technology based on SMT -- "SAT modulo theories" -- solvers, which can be used as the basis for a solution, and which are seeing increasing use in industry, particularly at Amazon. With this technology you can specify constraints on your solution, and the solver will automatically find it. But it takes some skill to encode a solution amenable to SMT -- the mentors will help the students develop this skill.

Target Outcomes:

• Learn about automated reasoning technology and how to use it.
• Try designing a computer science research project!

Assumed Background:

• Programming experience, preferably in Python.
• Some experience with data analysis algorithms, like sorting algorithms.

If you don't have this background, then please pair up wth someone in your group who does. And always feel free to ask for help from your mentors -- we intend for this to be a collaborative activity!

---

Table of Contents

• Setup
• Background Reading
  • Review of Logical Operators
  • SAT & SMT
  • Solving Puzzles with SMT
    • Rabbits and Chickens
    • Cats and Dogs
    • Sudoku
  • Proving Theorems with SMT
  • Additional Resources
• Project: An Automated Assistant for Course Management

---

Setup

Clone this repository:

git clone https://github.com/khieta/technica-2022

We assume that you have a Python 3 installation available. You can check if this is the case by running python3, which should open a Python session.

For this project, you will need to install the Z3 SMT solver and its Python bindings. Open a terminal, and from the command line run:

pip3 install z3-solver

Now to check that everything was correctly installed, start a Python session and run:

from z3 import *

You can copy and paste the code examples below into this session.

If any of the steps above fail, please ask a mentor for help.

---

Background Reading

Review of Logical Operators

First, we'll do a quick review of some useful logical operators.

• And(x, y) (x && y) is true iff x and y are true.
• Or(x, y) (x || y) is true iff x or y are true.
• Not(x) (!x) is true iff x is false.
• Implies(x, y) (x ==> y) is true iff x is true implies that y is true.

It is common to write truth tables to describe the behavior of these operators. We show the tables for And, Or, and Implies below. Do these tables make sense? The rule for Implies is a little tricky. Ask a mentor or group member if you're stuck.

And	Or	Implies
a b a && b true true true true false false false true false false false false	a b a || b true true true true false true false true true false false false	a b a ==> b true true true true false false false true true false false true

SAT & SMT

Say that we want to find a satisfying assignment for (a || !b) && (!a || c), i.e., values for a, b, and c that make the expression true. One way to do this is by trying all possible values of a, b, and c. There are 2^3 = 8 possible choices of a, b, and c -- can you list them?

In general, for n variables, there will be 2^n possible assignments, so the approach of "trying everything" is not efficient for large n. In fact, this is the SAT ("satisfiability") problem, which is NP-complete, meaning that it is "one of the hardest problems to which solutions can be verified quickly". But this difficult problem is exactly what tools like the Z3 SMT solver! Here's how we can solve the problem using the Z3:

a = Bool('a')
b = Bool('b')
c = Bool('c')

s = Solver()
s.add(Or(a, Not(b))) # a || !b
s.add(Or(Not(a), c)) # !a || c
s.check() # do these equations have a solution?
s.model() # get the solution

# Output: [b = False, a = False, c = False]

The output says that the formula (a || !b) && (!a || c) will be true when a, b, and c are all false.

But what if we want a different solution?

In this case, we can add an additional constraint that says that we don't want the solution where a, b, and c are all false.

s.add(Not(And(Not(a), Not(b), Not(c))))
s.check()
s.model()

# Output: [b = False, c = True]

This output says that the formula (a || !b) && (!a || c) will be true when b is false and c is true (it doesn't matter what a is).

Let's try adding one more constraint:

s.add(And(Not(a), b))
s.check()

# Output: unsat

The output unsat means unsatisfiable. The solver is telling us that there is no possible choice of a, b, c that makes the current constraints true.

Z3 can find solutions to more than just SAT problems -- it is an SMT solver. SMT stands for SAT modulo theories; it generalizes SAT to formulas involving integers, strings, arrays, and so on. For example, we can use Z3 to find a solution for the system of equations {3x - 2y = 1, y - x = 1}.

x, y = Ints('x y')
solve(3 * x - 2 * y == 1, y - x == 1)

# Output: [x = 3, y = 4]

Note: solve is shorthand for the check and model we were using above.

Solving Puzzles with SMT

SMT solvers are useful for more than finding solutions to a random set of equations -- you just have to know how to encode your problem in a form that the SMT solver understands. Here are three examples of puzzles that an SMT solver can solve. Next time you're working on a puzzle, ask yourself whether it could be solved using SMT.

Rabbits and Chickens

Uncle Henry has 48 rabbits and chickens. He knows his rabbits and chickens have 108 legs, but does not know the exact number of rabbits and chickens. Can you help him? How many rabbits and chickens does Uncle Henry have?

# Create 2 integer variables
rabbit, chicken = Ints('rabbit chicken')
s = Solver()
s.add(rabbit + chicken == 48) # 48 animals
s.add(4 * rabbit + 2 * chicken == 108) # 108 legs
s.check() # solve the constraints
s.model() # get the solution

Cats and Dogs

Say that you want to spend exactly 100 dollars to buy exactly 100 animals. Dogs cost 15 dollars, cats cost 1 dollar, and mice cost 25 cents each. You have to buy at least one of each. How many of each should you buy?

# Solution from <https://ericpony.github.io/z3py-tutorial/guide-examples.htm>

# Create 3 integer variables
dog, cat, mouse = Ints('dog cat mouse')

solve(dog >= 1,                   # at least one dog
      cat >= 1,                   # at least one cat
      mouse >= 1,                 # at least one mouse
      dog + cat + mouse == 100,   # 100 animals total
      # We have 100 dollars (10000 cents):
      #   dogs cost 15 dollars (1500 cents), 
      #   cats cost 1 dollar (100 cents), and 
      #   mice cost 25 cents 
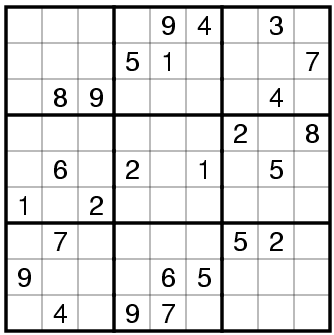
      1500 * dog + 100 * cat + 25 * mouse == 10000)

Sudoku

Sudoku is a puzzle where the goal is to insert numbers in boxes to satisfy the following condition: each row, column, and 3x3 box must contain the digits 1 through 9 exactly once.

The program in sudoku.py finds the solution for the puzzle shown below. You can run it with python3 sudoku.py.

Proving Theorems with SMT

Often, SMT solvers are not used to find a solution, but to prove that no solution exists. For instance, say that we want to prove the mathematical fact y > 0 ==> x + y > x. To do this, we can ask the SMT solver if it ever the case that this is not true.

x, y = Ints('x y')
solve(Not(Implies(y > 0, x + y > x)))

# Output: no solution

The output here says that it is never not the case that y > 0 ==> x + y > x (a double negative). In other words: this formula is true for any choice of x and y!

Additional Resources

• Programming Z3 (Tutorial)
• Z3 API in Python (Tutorial)
• Z3 GitHub (includes links to various papers and presentations)
• If you'd like to know how SMT solvers are used in the "real world", we recommend the materials for the University of Washington's CSE 507: Computer-Aided Reasoning for Software

---

Project: An Automated Assistant for Course Management

Develop a class-to-room scheduler for your favorite University:

• Input: List of classes, with sizes
• Input: Available rooms, with sizes
• Output: A schedule of classes to rooms

Assume that there are 8 one-hour time slots in a school day, each class is one hour, and the schedule is the same for every day.

We've provided a basic solution in basic-scheduler.py, now it's up to you to turn this into a research project! Here are some questions you might try to answer:

• Is the current solution good? Does it give a useful schedule? Why or why not?
• How can you modify the solution to support the case where:
  • Classes and rooms are unavailable for certain time slots
  • Rooms should be close to the class' teacher's office
  • Some classes are Tu/Th, and some are Mo/We/Fr
  • Small classes should be in small classrooms (don't put a 15 person seminar in a lecture hall)
  • Different classes have different durations
  • Some classes can't overlap
  • ...
• How can you empirically evaluate your solution? A couple ideas:
  • How would you implement the scheduler without an SMT solver? Would it be harder/easier to write? How would it compare in terms of performance?
  • Try your solution on inputs of varying sizes -- how does performance scale with problem size?