-
Notifications
You must be signed in to change notification settings - Fork 19
week 10.10 16.10
Numpy tutorial iPython, also see previous week (WildML)
-
Image data preprocessing: In Machine Learning, it is a very common practice to always perform normalization of your input features. In particular, it is important to center your data by subtracting the mean from every feature.
In the case of images, this corresponds to computing a mean image across the training images and subtracting that mean image from every image to get images where the pixels range from approximately [-127 … 127].
Further common preprocessing is to scale each input feature so that its values range from [-1, 1].
Of these, zero mean centering is arguably more important but we will have to wait for its justification until we understand the dynamics of gradient descent. -
Multiclass Support Vector Machine loss Li=∑j≠yimax(0,sj−syi+Δ) In summary, the SVM loss function wants the score of the correct class yi to be larger than the incorrect class scores by at least by Δ (delta). If this is not the case, we will accumulate loss.
W not unique (linear dependencies) -> extend the loss function with a regularization penalty R(W) The most common regularization penalty is the L2 norm that discourages large weights through an elementwise quadratic penalty over all parameters: R(W)=∑k∑lW2k,l penalizing large weights tends to improve generalization, because it means that no input dimension can have a very large influence on the scores all by itself (no overfitting).
The full Multiclass Support Vector Machine loss, which is made up of two components: the data loss (which is the average loss Li over all examples) and the regularization loss
- other loss function: Softmax:
fj(z)=ezj/∑kezk : takes a vector of arbitrary real-valued scores (in z) and squashes it to a vector of values between zero and one that sum to one.
- practical: add exponent C to softmax formula for numerical stability
-
The numerical gradient is very simple to compute using the finite difference approximation, but the downside is that it is approximate (since we have to pick a small value of h, while the true gradient is defined as the limit as h goes to zero), and that it is very computationally expensive to compute.
The second way to compute the gradient is analytically using Calculus, which allows us to derive a direct formula for the gradient (no approximations) that is also very fast to compute. However, unlike the numerical gradient it can be more error prone to implement.
That's why in practice it is very common to compute the analytic gradient and compare it to the numerical gradient to check the correctness of your implementation. This is called a gradient check. -
Mini-batch gradient descent. In large-scale applications (such as the ILSVRC challenge), the training data can have on order of millions of examples. Hence, it seems wasteful to compute the full loss function over the entire training set in order to perform only a single parameter update.
A very common approach to addressing this challenge is to compute the gradient over batches of the training data. For example, in current state of the art ConvNets, a typical batch contains 256 examples from the entire training set of 1.2 million. We use powers of 2 for batch size in practice because many vectorized operation implementations work faster when their inputs are sized in powers of 2.This batch is then used to perform a parameter update:
# Vanilla Minibatch Gradient Descent
while True:
data_batch = sample_training_data(data, 256) # sample 256 examples
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += - step_size * weights_grad # perform parameter update
-> find gradient of f (=> the derivative on each variable tells you the sensitivity of the whole expression on its value.) Backpropagation can thus be thought of as gates communicating to each other (through the gradient signal) whether they want their outputs to increase or decrease (and how strongly), so as to make the final output value higher.
# say f= z(x+y), or f=q*z where q=(x+y)
# -> df/dz = q, df/dq= z, dq/dx = dq/dy =1
# -> df/dx= df/dq * dq/dx = z * 1
Tthe intuition behind the operations that backpropagation performs during the backward pass in order to compute the gradients on the inputs:
- Sum operation distributes gradients equally to all its inputs.
- Max operation routes the gradient to the higher input.
- Multiply gate takes the input activations, swaps them and multiplies by its gradient.
Unintuitive effects and their consequences. Notice that if one of the inputs to the multiply gate is very small and the other is very big, then the multiply gate will do something slightly unintuitive: it will assign a relatively huge gradient to the small input and a tiny gradient to the large input. Note that in linear classifiers where the weights are dot producted wTxi (multiplied) with the inputs, this implies that the scale of the data has an effect on the magnitude of the gradient for the weights. For example, if you multiplied all input data examples xi by 1000 during preprocessing, then the gradient on the weights will be 1000 times larger, and you’d have to lower the learning rate by that factor to compensate. This is why preprocessing matters a lot, sometimes in subtle ways! And having intuitive understanding for how the gradients flow can help you debug some of these cases.
In practice: decompose your expressions into stages such that you can differentiate every stage independently (the stages will be matrix vector multiplies, or max operations, or sum operations, etc.) and then backprop through the variables one step at a time.
Different activation functions:
-
sigmoid:
-
*Sigmoids saturate and kill gradients*. when the neuron’s activation saturates at either tail of 0 or 1, the gradient at these regions is almost zero. Therefore, if the local gradient is very small, it will effectively “kill” the gradient and almost no signal will flow through the neuron to its weights and recursively to its data. Additionally, one must pay extra caution to prevent saturation. If the initial weights are too large then most neurons would become saturated and the network will barely learn. -
*Sigmoid outputs are not zero-centered*. This is undesirable since neurons in later layers of processing in a Neural Network (more on this soon) would be receiving data that is not zero-centered. This has implications on the dynamics during gradient descent, and could introduce undesirable zig-zagging dynamics in the gradient updates for the weights. This is an inconvenience but it has less severe consequences compared to the saturated activation problem above after averaging over all training.
-
-
tanh: Like the sigmoid neuron, its activations saturate, but unlike the sigmoid neuron its output is zero-centered. Therefore, in practice the tanh non-linearity is always preferred to the sigmoid nonlinearity. Also note that the tanh neuron is simply a scaled sigmoid neuron, in particular the following holds: tanh(x)=2σ(2x)−1.
-
ReLU: max(0,x) -> inexpensive, fast, but can lead to 'dead' neurons if learning rate too high.
-
Maxout neuron -> generalized version of ReLU, no neuron dying, but 2x the amount of parameters per neuron.
=> TLDR: “What neuron type should I use?” Use the ReLU non-linearity, be careful with your learning rates and possibly monitor the fraction of “dead” units in a network. If this concerns you, give Leaky ReLU or Maxout a try. Never use sigmoid. Try tanh, but expect it to work worse than ReLU/Maxout.
Dimensions of Weight matrix:
- rows = # neurons in that layer.
- columns = # neurons in the layer before eg output, 1 neuron, with last hidden layer 5 neurons -> W_last = [1x5]
# forward-pass of a 3-layer neural network:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid)
x = np.random.randn(3, 1) # random input vector of three numbers (3x1)
h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer activations (4x1)
h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1)
out = np.dot(W3, h2) + b3 # output neuron (1x1)
In the above code, W1,W2,W3,b1,b2,b3 are the learnable parameters of the network.
The variable x could hold an entire batch of training data (where each input example would be a column of x) and then all examples would be efficiently evaluated in parallel.
The final Neural Network layer usually doesn’t have an activation function (e.g. it represents a (real-valued) class score in a classification setting). (-> SoftMax)
The forward pass of one fully-connected layer corresponds to one matrix multiplication followed by a bias offset and an activation function.
- The fact that deeper networks can work better than a single-hidden-layer networks is an empirical observation, despite the fact that their mathematical representational power is equal. * In practice it is often the case that 3-layer neural networks will outperform 2-layer nets, but going even deeper (4,5,6-layer) rarely helps much more. This is in stark contrast to Convolutional Networks, where depth has been found to be an extremely important component for a good recognition system (e.g. on order of 10 learnable layers). One argument for this observation is that images contain hierarchical structure, so several layers of processing make intuitive sense for this data domain.
- preventing overfitting: it seems that smaller neural networks can be preferred if the data is not complex enough to prevent overfitting. In practice, it is always better to use L2 regularization, dropout, input noise etc to control overfitting instead of the number of neurons. you should use as big of a neural network as your computational budget allows, and use other regularization techniques to control overfitting. In practice, what you find is that if you train a small network the final loss can display a good amount of variance - in some cases you get lucky and converge to a good place but in some cases you get trapped in one of the bad minima. On the other hand, if you train a large network you’ll start to find many different solutions, but the variance in the final achieved loss will be much smaller.
-
mean subtraction:
X -= np.mean(X) -
normalization: if different input features have different scales (or units), but they should be of approximately equal importance to the learning algorithm. (for images, already -256<256, so not really necessary.
- One way is to divide each dimension by its standard deviation, once it has been zero-centered:
X /= np.std(X, axis = 0) - Another form of this preprocessing normalizes each dimension so that the min and max along the dimension is -1 and 1 respectively.
- One way is to divide each dimension by its standard deviation, once it has been zero-centered:
- reduce dimensionality: by using SVD and only keeping the top eigenvectors, we can discard lots of unimportant information (Principal Component Analysys (PCA))
# Assume input data matrix X of size [N x D]
X -= np.mean(X, axis = 0) # zero-center the data (important)
cov = np.dot(X.T, X) / X.shape[0] # get the data covariance matrix
U,S,V = np.linalg.svd(cov)
Xrot = np.dot(X, U) # decorrelate the data
Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced becomes [N x 100]
After this operation, we would have reduced the original dataset of size [N x D] to one of size [N x 100]. It is very often the case that you can get very good performance by training linear classifiers or neural networks on the PCA-reduced datasets, obtaining savings in both space and time. However, SVD computation can be quite expensive.
Common pitfall. An important point to make about the preprocessing is that any preprocessing statistics (e.g. the data mean) must only be computed on the training data, and then applied to the validation / test data. E.g. computing the mean and subtracting it from every image across the entire dataset and then splitting the data into train/val/test splits would be a mistake.
Instead, the mean must be computed only over the training data and then subtracted equally from all splits (train/val/test).
- Weights: there is no source of asymmetry between neurons if their weights are initialized to be the same -> we still want the weights to be very close to zero, but as we have argued above, not identically zero. Thenthey will compute distinct updates (backprop) and integrate themselves as diverse parts of the full network. Also normalize to account for nb of inputs:
w = np.random.randn(n) * sqrt(2.0/n)
-
Biases: initialize the biases to be zero, since the asymmetry breaking is provided by the small random numbers in the weights.
-
Batch Normalization: alleviates a lot of headaches with properly initializing neural networks by explicitly forcing the activations throughout a network to take on a unit gaussian distribution at the beginning of the training. Applying this technique usually amounts to insert the BatchNorm layer immediately after fully connected layers (or convolutional layers, as we’ll soon see), and before non-linearities. In practice networks that use Batch Normalization are significantly more robust to bad initialization.
- L2 regularization:
W += -lambda * W, with \lambda the regularization strength - L1 regularization: L1 regularization has the intriguing property that it leads the weight vectors to become sparse during optimization. \TODO: combine with SVD to minimize amount of parameters?
- max norm: prevent explosion
- dropout: extremely effective, simple; during training, only keep a neuron active with some probability p (a hyperparameter), or set it to zero otherwise. dropout paper
-> It is most common to use a single, global L2 regularization strength that is cross-validated. It is also common to combine this with dropout applied after all layers. The value of p=0.5 is a reasonable default, but this can be tuned on validation data.
- Softmax
- Hierarchical Softmax: tree structure of classes; Softmax classifier is trained at every node of the tree to disambiguate between the left and right branch. The structure of the tree strongly impacts the performance and is generally problem-dependent.
- The recommended preprocessing is to center the data to have mean of zero, and normalize its scale to [-1, 1] along each feature
- Initialize the weights by drawing them from a gaussian distribution with standard deviation of 2/n‾‾‾√
, where n is the number of inputs to the neuron. E.g. in numpy:
w = np.random.randn(n) * sqrt(2.0/n). - Use L2 regularization and dropout (the inverted version)
- Use batch normalization
- We discussed different tasks you might want to perform in practice, and the most common loss functions for each task
- use df(x)/dx=[f(x+h)−f(x−h)]/2h; check for relative error, div by max(abs1, abs2), double prec,
- few data points for check, careful step size h (1e-5?),
- regularization vs data loss (check that data loss is ok by setting regularization strength to 0
- turn dropout off.
- softmax loss = -ln(class probab). eg 10 classes-> -ln(1/10)=2.302;
- more regularization -> more loss (reg. loss increases);
- try to overfit on tiny subset
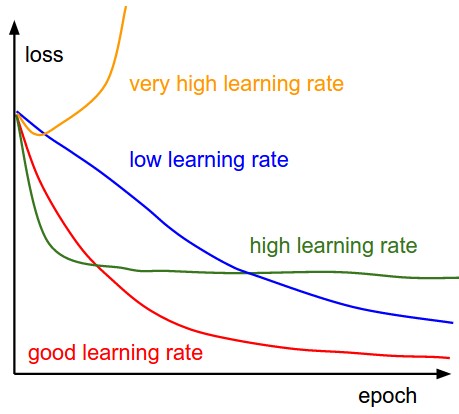
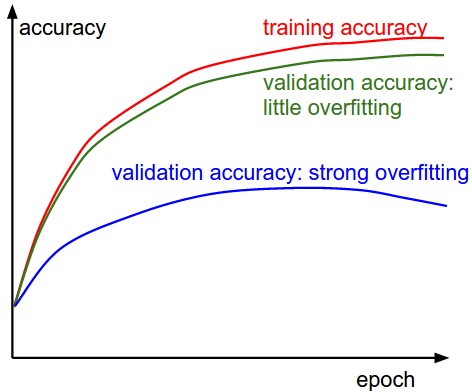
The x-axis of the plots below are always in units of epochs (epoch= every example has been seen once) keep track of:
- loss: curve shape -> learning rate; 'noise' -> batch size; plot in log scale?
- training vs validation set -> overfitting? If so, more regularization (stronger L2 weight penalty, more dropout, etc.) or collect more data.
- ratio weight/updates: update=gradient*learning rate. Should be around 1e-3 -> modify learning rate
# assume parameter vector W and its gradient vector dW
param_scale = np.linalg.norm(W.ravel())
update = -learning_rate*dW # simple SGD update
update_scale = np.linalg.norm(update.ravel())
W += update # the actual update
print update_scale / param_scale # want ~1e-3
- visualize
- momentum: update velocity, integrate it instead of directly the position (x)
v = mu * v - learning_rate * dx # integrate velocity
x += v # integrate position
- dynamic learning rate:
- Reduce the learning rate by some factor every few epochs (eg by a half every 5 epochs, or reduce whenever the validation error stops improving.)
- adaptive per parameter: Adagrad, RMSprop
cache = decay_rate * cache + (1 - decay_rate) * dx**2 ## decay_rate: typical values are [0.9, 0.99, 0.999].
x += - learning_rate * dx / (np.sqrt(cache) + eps) # eps: typically 1e-4 to 1e-8 avoids division by zero
- Hyperparameter optimization
- learning rate and decay schedule -> log scale
learning_rate = 10 ** uniform(-6, 1) - regularization strength
- dropout: usually in uniform interval eg
ropout = uniform(0,1)generally: also random search < grid search, maybe better parameters outside of specified range?, first broad, then finer model ensembles: several models, take average (eg different initializations, top 10 hyperparameters, checkpoints of a model (diff. points during training), extra percent or two of performance is to maintain a second copy of the network’s weights in memory that maintains an exponentially decaying sum of previous weights during training -> smoothing gets closer to minimum)
- learning rate and decay schedule -> log scale
- Gradient check your implementation with a small batch of data and be aware of the pitfalls. -As a sanity check, make sure your initial loss is reasonable, and that you can achieve 100% training accuracy on a very small portion of the data
- During training, monitor the loss, the training/validation accuracy, and if you’re feeling fancier, the magnitude of updates in relation to parameter values (it should be ~1e-3), and when dealing with ConvNets, the first-layer weights.
- The two recommended updates to use are either SGD+Nesterov Momentum or Adam.
- Decay your learning rate over the period of the training. For example, halve the learning rate after a fixed number of epochs, or whenever the validation accuracy tops off.
- Search for good hyperparameters with random search (not grid search). Stage your search from coarse (wide hyperparameter ranges, training only for 1-5 epochs), to fine (narrower rangers, training for many more epochs)
- Form model ensembles for extra performance