Fresh off of the production release of my first iOS app, Puff, I realized that I wanted to challenge myself to put something together that had a "bit more going on" to it than just a password manager. After all, Puff was a great project, but I want to build something that was a bit fancier... maybe with more computatation? ... or logic?
Well, it turned out that the previous weekend I had been reviewing graph algorithms to prep for interview season 😤 and that's when it hit me! Let's make a graph! And even better, let's visualize it and allow the user be able to interact with it!
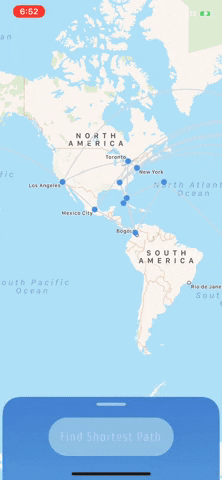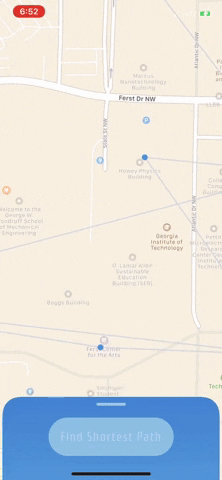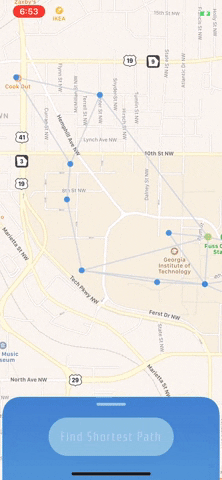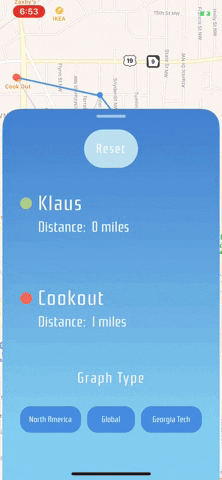
But wait– there's more!...I had also learned that week in my intro to AI course that there are some pretty cool algorithms to optimize graph traversals. So, let's implement one of these algorithms to visualize one of these traversals to show the user the shortest path between the points on the map of data we will present (heeello MapKit 👀)
So at a high level, this was the plan:
• Implement a Graph 🤓
• Implement the A*Star Algorithm to find the shortest path between vertices 😱
• Create a map of data using Apple's MapKit 🗺
• Connect our graph with our map 👉👈
• Allow our users to interact with our map 🥳
• And voila! Now that's a project! ...and did I mention I wanted to cook 👨🍳 this up in under a week 💪
First thing first was learning everything I could about graphs. I watched videos, read articles, read some code, and most importantly– diagrammed! 👨🎨
I eventually got comfortable enough tracing through AStar that I was ready to start studying and planning out an implementation in Swift. While I'm not going to go super into depth with AStar, I'll say that it is very similar to a breadth-first graph traversal. The key difference is how the algorithm decides which node to visit next. It makes this important decision using a heuristic. Let's paraphrase from good 'ole Wikipedia:
A heuristic is any approach to problem solving that employs a practical method, not guaranteed to be optimal, perfect, or rational, but instead sufficient for reaching an immediate goal.
Sooooo, what will our heuristic be? I decided that, considering we are searching for a goal vertex given a start vertex, let's calculate for each vertex we are considering visiting the distance between it and the goal vertex. This distance is purely the displacement between the potential vertex we are considering visiting and the goal vertex.
At a high level, graphs are collections of nodes that have edges that connect to other nodes. The result is a web of vertices (nodes) that can represent some pretty cool things. A famous example of their use includes the way Google Maps works. Basically, think of all the intersections in the world being represented by nodes (heads up! I'm gonna start calling these vertices 👌🏼) with all the roads connecting those intersections representing the edges that connect vertices (which are the intersections!).
So we need to create a Vertex object, an Edge object, and our overarching Graph object.
The Vertex object was pretty simple. The key property will be used for the name of a vertex we will later create. So, if we have a vertex object representing Atlanta 🐍, then we can set key = 'Atlanta'.
In the Vertex intializer, we create a set that will contain th vertex's edges. So, adding to the city example, if we want to connect Atlanta with other cities like New York and Los Angeles, then we use an edge to connect Atlanta with New York and add that edge to our atlantaVertex's set of edges.
Cool, so let's make our Edge so we can actually start connecting our vertices. Each edge has an anchor representing the vertex it is tied to. So if we add an edge from an atlantaVertex to a newYorkVertex, then this edge's anchor would be the atlantaVertex. An Edge also has a length property which is what will later compute. In our case, this will be the distance from one point on Earth to another. But, remember how I said graphs could represent lots of types of relationships (besides just distance)? Welp, if we were building a social media app, we could set a property like this to some computed value representing the degree of connection between two people.
So we got `vertices` and we got `edges`, let's get this information into our central `Graph` object. A `graph` will have a canvas which will be an array of all of our `vertices`. It
will also have an `isDirected` property that is a `boolean`. I added this because I read a great graph implementation and liked the idea of building that functionality into my graph. A
directed graph is a graph where edges connecting vertices are a "one way street". When we connected our `atlantaVertex` to our `newyorkVertex`, we could either decide to make an edge connecting the `newYorkVertex` back to the `atlantaVertex` or just keep the edge only going from `ATL -> NYC`. If we made the extra edge from `NYC -> ATL` then we can move back and forth between them. If we didn't add that edge then we can only go from `ATL -> NYC'
IF you notice we also have methods to add Vertex's and Edge's to our graph! You can check them out in the Graph.swift file.
By the time I got started on actually writing the code to implement the algorithm, I was pretty comfortable with it since I knew its flow (since I worked out so many examples) and understood some of the pseudocode for it I found online.
But after finishing, I couldn't help but ask: will this even work?
While I didn't doubt A*Star, I was a bit curious, and apprehensive, if it worked work together seamlesslessy with my graph implementation.
So to be sure, I wanted to write up some tests before I moved any further. I figured that trying to connect the graph with a view would be pointless if the graph didn't work right to begin with. This brings to the next part of the project which was a bit unexpected but totally awesome! 😎
Until now, I had never written tests for much of the code I wrote. I thought this would be a great opportunity to build some testing skills for my SWE toolbox 🧰.
Here is an example of a test case I wrote for a medium sized graph:
Andddd... I ran the test and it passed! 🥳 Even though I had some confirmation that it worked, I spent awhile writing some more tests and adjusting little things before trying to visualize the graph.
This part was probably my favorite part of the project. Since it was time to connect my graph with a map of the world, I needed to add some stuff to my Vertex object. Since each vertex would be a point on Earth 🌍, it needed to have a coordinates property. I decided to make a protocol that I could conform my general Vertex class to for the purpose of my specific implementation.
protocol Positionable {
var coordinates: CLLocationCoordinate2D { get set }
}
To keep my Vertex class even cleaner, I wanted to conform to Positionable in an extension. I noticed this is a pretty common pattern in Swift development. But, as I was kindly reminded by XCode: 🚨Extensions must not contain stored properties. So this is a bit of an aside but I found a really cool work around after researching some things for a while. The idea is to essentially declare the property you want stored and make it a computed property instead. This is then done in an extension through taking advantage of some memory addresses that will be created for the new property. Here is the code that got the job done:
Honestly, the work around adds a bit of code you could exclude if you just did like:
class Vertex: Positionable {
// regular Vertex stuff
coordinates = CLLocationCoordinate2D()
}
But I just thought the work-around was creative enough to have some fun with and include.
Our Vertex also needed to be able to calculate a heuristic (Vertex's h property) so I conformed Vertex to another protocol Heuristable in another extension of Vertex
I placed these protocols and corresponding extensions in the // LocationVertexImplementation.swift file so take a look 👀 if interested!
I also made some protocols to fine tune the Graph class use with Vertex's with coordinates and searching with A*Star. You can check them out at the bottom of the Graph.swift file.
Getting the map set up reminded be a good bit of implementing a UITableView. There were a few delegate methods you needed to conform to and you then were good to go.
I had to do a few things to render the vertices in the graph on the mapView. To render the blue dots for each vertex in the graph, I subclassed MKAnnotationView to create CircleAnnotationand then added CAShapeLayer to my custom class. I used UIBezierPath to create a perfect circle to represent each location on the map.
To render the edges, I added a MKGeodesicPolyline as an overlay on the mapView from each vertex to each of its neighbors.
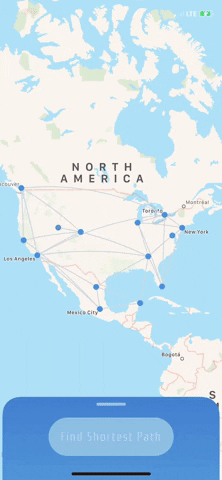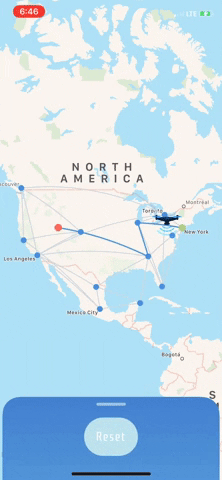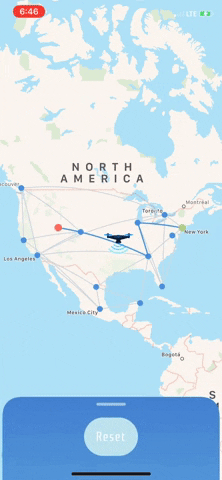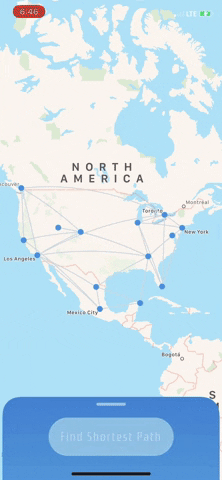
Since running the algorithm to get the the shortest path returned a list of vertices, I then iterated over that path adding blue MKGeodesicPolylines.
I found an awesome tutorial for the animated drone that moves across the map when you find the shortest path. I think it was a great addition that makes the app feel more fun and playful.
Like in my last project, I used some more awesome lottie animations!
There were defintely a few hiccups along the way. Some of the most challenging included selecting annotations on the map and properly resetting them after the user taps them or the Reset button. There was lot of logic going into how to manage what was allowed to be pressed and when should it be.
I also had issues with my custom annotations rendering when they were scrolled out and back into view. In fact, there is one small bug 🐛 where if the user selects a annotation and scrolls it out and back into view, it sometime doesn't show it back in its selected state. Even weirder, sometimes it renders another annotation as selected. I had a work around I used to solve this but it wasn't 100% and was pretty messy. From the reading I did, it seems that MKMapView doesn't save the order of annotations laid onto it so when it re-adds them after they scroll back into the view, it can give the effect of them being scrambled.
Reflecting, this project really tested me, both mentally and physically. When I set out to do it, I told myself I would give myself only a few days to finish it. I wanted to work quickly both to avoid dragging the project on into the future (since school is only getting busier 😫) and to simulate completing a complicated project on a short deadline.
As the hours ticked by and I pushed through, it did become harder and harder to write code of the same quality as I had when I started the project. But I think this is pretty understandable. After all, by Monday, I had two consecutive all-nighters. Healthy? No! Productive? Well, the result is pretty cool... 😎 I will say One black sheep of the project was the layout. It got the point where it was quicker to layout the app for the iPhone X (my iPhone I was developing it on) then think about a more universal layout. I think this is ok since I don't think this is an app for the App Store but I figured I would add this.
Anyone that does want to see it in XCode can use the simulator for the iPhone X for the best results.
But after a few sleepless nights, a lot of whiteboarding, a bunch of Apple docs, a few clutch answers on Stack, and a lot of insant coffee ☕️ (we didn't have time to let anything brew!) I was done 💯
S/O to the internet for holding it down as always 🙏🏻💯
These were some of the most useful resources!
🔥Geodesic Polylines for MapView
🔥MapKit: Annotations and Shape Rendering
🔥MapKit Beginner’s Guide: Polylines, Polygons, and Callouts
👀 Peep my resume and contact info here 😃