Optimal Hard Threshold for Matrix Denoising

---

Off-the-shelf method for determining the optimal singular value truncation (hard threshold) for matrix denoising.

The method gives the optimal location both in the case of the konwn or unknown noise level.

Example

---

Reproduce the example

---

Create some data:

import numpy as np
import scipy as sci
import matplotlib.pyplot as plt 

t = np.arange(-2,2, 0.01)

Utrue = np.array(( [np.cos(17*t) * np.exp(-t**2) , np.sin(11*t)] )).T
Strue = np.array(( [2, 0], [0, .5] ))
Vtrue = np.array(( [np.sin(5*t) * np.exp(-t**2) , np.cos(13*t)] )).T

# construct image
X = Utrue.dot(Strue).dot(Vtrue.T)

# define the noise level and add
sigma = 0.5
X_noisy = X + sigma * np.random.standard_normal(X.shape)

Compute the singular value decompositionn (SVD):

U,s,Vh = np.linalg.svd(X_noisy, full_matrices=False)

Determine optimal hard threshold and reconstruct image

k = optht(X_noisy, sv=s, sigma=None)
X_denoised = (U[:, xrange(k)] * s[xrange(k)] ).dot( Vh[xrange(k),:])

Plot the results:

plt.subplot(131)
plt.imshow(X, cmap = 'gray', interpolation = 'bicubic')
plt.title('Original image', fontsize=30)
plt.axis('off')

plt.subplot(132)
plt.imshow(X_noisy, cmap = 'gray', interpolation = 'bicubic')
plt.title('Noisy image, sigma=%s'%sigma, fontsize=30)
plt.axis('off')

plt.subplot(133)
plt.imshow(X_denoised, cmap = 'gray', interpolation = 'bicubic')
rmseSVD = np.sqrt(np.sum( ( X - X_denoised )**2 ) /  np.sum(X**2))
plt.title('Denoised image,  nrmse=%s '%np.round(rmseSVD,2), fontsize=30)
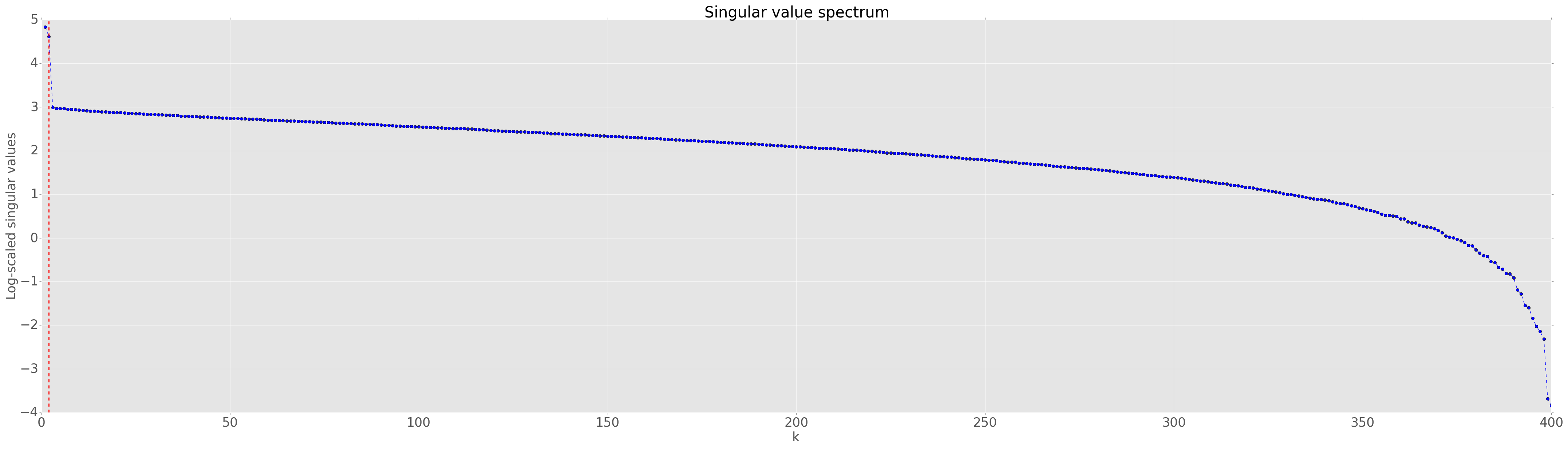
plt.axis('off')

Plot the singular value spectrum:

plt.plot( (np.arange(1,s.shape[0]+1)), np.log(s), c='b', marker='o', linestyle='--')
plt.xlabel('k', fontsize=25)
plt.ylabel('Log-scaled singular values', fontsize=25)
plt.tick_params(axis='x', labelsize=25) 
plt.tick_params(axis='y', labelsize=25) 
plt.title('Singular value spectrum', fontsize=30)
plt.axvline(k, c='r', linewidth=2, linestyle='--')

Notes

---

Code is adapted from Matan Gavish and David Donoho, see [1].

References

---

[1] Gavish, Matan, and David L. Donoho. "The optimal hard threshold for singular values is 4/sqrt(3)" IEEE Transactions on Information Theory 60.8 (2014): 5040-5053.
http://arxiv.org/abs/1305.5870