-
Notifications
You must be signed in to change notification settings - Fork 121
BCILAB documentation
Open Source Matlab Toolbox for Brain-Computer Interface research.
Download the code from ftp://sccn.ucsd.edu/pub/bcilab.
Extract the file to some folder that is not your EEGLAB folder. Start MATLAB (2008a+ required for the GUI), and reset you path to default settings by clicking File / Set Path / Default, and then Save. If you have misc toolboxes in your path, you run the risk of creating unexpected errors (due to name conflicts), but you can add your directories back later once you know what outputs to expect. Enter in MATLAB's command line:
cd your/path/to/bcilab; bcilabYou should now be getting a menu in the upper left corner of the screen. For BCI newcomers, it is highly recommended to watch the BCI introduction video (from the EEGLAB workshop 2010) before diving into the GUI. It is found at: http://thesciencenetwork.org/programs/12th-eeglab-workshop/eeg-classification-and-cross-validation-using-the-bcilab-toolbox-overview Once you are familiar with the BCI principles, please follow the extended practicum slides from ftp://sccn.ucsd.edu/pub/bcilab to get familiar with the GUI. The rest of this page gives a more in-depth background on the toolbox use, organization, and especially on working with the script and plugin interfaces.
Important notes: The data sets that the practicum slides refer to were only distributed for use in workshops; instead, we now have alternative data sets packaged with the toolbox. The tutorials are essentially the same, except for the different files to use (and different marker names). The updated file names are userdata/tutorial/imag_movements/calib/DanielS001R01.dat for imagined movements training, userdata/tutorial/imag_movements/feedback/DanielS001R01.dat for testing, and userdata/tutorial/flanker_task/12-08-001_ERN.vhdr for the error perception data set. The second difference are the marker types that need to be specified: they are {'StimulusCode_2','StimulusCode_3'} instead of {'S 1','S 2'} for imagined movements, and { {'S101','S102'},{'S201','S202'} } instead of {'S 11',{'S 12','S 13'} } for the error perception. Also, the feedback session in the imag_movements1 directory contains no labels - therefore it is not possible to apply a model to it and get error rates ("Apply model to data"). Real-time playback is possible, however. The slides will be updated at the next opportunity to reflect these changes.
You need at least ~2.5gb of free memory to be able to run all tutorials. If you have Windows Vista and many gadgets etc. installed, you may run into memory issues under 32-bit Windows, as the data sets are quite large.
BCILAB is a MATLAB toolbox and EEGLAB plugin for the design, prototyping, testing, experimentation with, and evaluation of Brain-Computer Interfaces (BCIs), and other systems in the same computational framework. The toolbox has been developed by C. Kothe at the Swartz Center, inspired by the preceding PhyPA BCI toolbox created by C. Kothe and T. Zander at the Chair for Human-Machine Systems, Berlin Institute of Technology.
A Brain-Computer Interface is, most generally, a system which receives biosignals measured from a person and which predicts from these (in real time) some aspect of the person's cognitive state.
The most important case is the clinical BCI, developed for tetraplegic or locked-in patients (who have lost some or all their muscular control) in order to control devices [orig-def], such as wheelchairs or spellers. [wheelchair/speller] In these, the input is the Electroencephalogram (EEG) or some other direct measure of brain activity, and the output is taken as a control signal. In the most commonplace settings, control is exerted by means of imagining limb movements which are translated into movements of a virtual cursor ("motor imagery BCI"), or by attending to letters in an on-screen letter matrix in which rows and columns are flashed at random ("P300 speller"). Various other designs have been proposed, such as spellers controlled by attending to directional sound cues. [audiospeller]
Besides the clinical context, BCI technology can be used to control Human-Computer interfaces via brain activity alone -- in principle allowing for hands-free operation [HCII]. An even more practically relevant use case is the assessment of aspects of user state "in the background", i.e., without requiring voluntary control commands by the operator. Instead, a spectrum of user state can be passively tracked, such as the level of arousal, the level of some aspect of cognitive load, the probability of being surprised, or of perceiving some event as an error, and so on. [Tan/Halo, us/Error] The idea is that this kind of information, when made accessible to applications, can allow for a better (e.g., higher-bandwidth) Human-Computer Interaction, perhaps approaching that of Human-to-Human interaction. [BCI+HCI] For example, if software in a multi-screen workplace can determine which of the information it presented was likely missed by an operator, it could subsequently re-display that information, potentially preventing costly user errors.
Lastly, since BCI technology comes with an ability to derive latent information from highly complex and noisy brain-/biosignals, it can be applied as a science tool, for the purposes of pattern recognitition and analysis, structure and novelty discovery, and other data analysis tasks. Here, the analysis tools would be used on previously recorded data sets, just like any other tool in EEGLAB. This approach is quite new to the EEG field, but is becoming a staple of fMRI analysis, there often called multivariate pattern analysis (MVPA). [ref] This methodology allows to integrate multiple weak information sources (such as multiple channels of EEG) to derive strong statistical statements from them and guide the search for (or validate) scientific hypotheses.
BCILAB aims at facilitating and accelerating research in these areas, and supplies tools that simplify all aspects of Brain-Computer Interface research, from design to field testing, and from clinical applications to the general HCI context. We hope that BCILAB is useful for students, experimental scientists, engineers and developers alike. For these reasons, the toolbox offers multiple different interfaces which link to the same backend functionality, including a GUI, scripting support (MATLAB-based), APIs for real-time processing, and a variety of extension component interfaces. MATLAB programming is not strictly necessary, as most BCILAB features can be accessed from the GUI, although it is required for batch scripting and custom extensions. The strength of MATLAB-based software lies in its resources for leading-edge scientific computing, as well as in the good support for rapid prototyping, but BCI systems developed in it can be used for real-time out-of-lab experimentation, and can in principle be deployed without the need for a MATLAB license. However, due to the complexity and overhead of the MATLAB environment, the system is best used as a research platform, and not as a product development environment -- end-user software is ideally re-implemented in a compiled language, after a suitable approach has been identified and extensively tested. The process of identifying and testing an approach involves more than just computation, but also data exploration and investigation - an area which is helped by the deep integration with the EEGLAB platform. In the future, this integration will be further strengthened, bringing rich statistical learning and signal processing into routine EEG analysis workflows.
Brain-Computer Interfacing is fundamentally an inference problem: the task is to infer, from observed data (for example, a person's EEG), the value or distribution of some latent variable (e.g., the person's movement intent), usually in real time. This inferential step, however, cannot be done without additional information about the relation between the two regimes. Depending on assumptions imposed, different approaches follow (e.g., relying on oscillatory idle processes of the brain, or on slow-changing cortical potentials), but the bulk of the required information are highly person-specific details, which are themselves hard to obtain (e.g., rooted in physiology and functional allocation within the brain). Obtaining this information amounts to a second inference problem - inferring the optimal parameter settings of the BCI on the basis of data at hand. The (by far) most relevant data to compute these parameters is example data: simultaneous recordings of both the biosignals (such as EEG) serving as source data, as well as the variables to be predicted (= estimated) from them (e.g., level of user workload). From these data, a predictive model can be computed (encompassing the individualized parameters), which can then make new predictions based on raw data. A highly recommended introduction to the principles and concrete technology behind BCIs is given in the EEGLAB Workshop 2010 Talk and associated Slides. [ref]
Standard analyses. As the optimal learned parameters vary with cap montage, time of day, medication and various other factors, the best results are obtained by recording example data (usually called training data, or calibration data) immediately before the experiment in which the system is put to the test; thus, a typical BCI experiment consists of at least two subsequent sessions: the "training" session and the "test" session. Both can be set up as standard psychological experiments, where in the training session the variable to be predicted must be known (via instructions and/or stimuli in the experimental design), so that a predictive model can be computed from it. In the test session, these quantities will be predicted by the BCI. The prediction can be done in real time ("online analysis"), and can be made accessible to the user/subject, thus forming a closed-loop system, or in a post-hoc analysis of the recorded data ("offline analysis").
Advanced analyses. Accurate predictions are harder to obtain if the test session is recorded with a different cap montage or on a different day than the training session, but the ability to use BCIs without the need for a per-session calibration is critical for many HCI use cases. Therefore, research is ongoing to improve this session-to-session transfer, e.g., by integrating multiple calibration data sets across persons, sessions and/or tasks to learn predictive models that generalize well across these boundaries. For example, a joint predictive model may be computed from the pooled data of a multi-subject study, and its performance with no (or minimal) individualization can be evaluated in a subsequent study with different subjects. In future iterations, BCILAB will add facilities to streamline this type of analysis, as well. At this point, it requires advanced MATLAB programming.
Cross-validation analysis. The simplest experimental settings are studies comprising a single session per subject (e.g., a standard psychological experiment). BCI performance on this type of data can be assessed via cross-validation, a mode of analysis in which a recording is partitioned into multiple sections (e.g., k=10), and all but one are used to learn a predictive model, which is then applied on the held-out section (where its outputs are compared to the expected/known value of the latent variable to obtain accuracy scores). This procedure is repeated with each section held out once (and training being done on the remaining sections).
Neuroscience questions. Under some considerations, the internal structure of predictive models learned from data can be investigated and yield insights. For example, the relative weighting of different sensor channels, time points, brain territories, spectrum portions, etc. can give insight into the underlying processes that relate to a particular aspect of cognitive state. Thus, BCI technology may be applied to answer questions about the most likely expression of certain underlying brain processes. These applications are, however, only in their infancy.
Most of BCILAB's functionality is contained in (plugin) components, of which there are five types. Most plugin types reside in their own directory and are automatically identified and loaded by BCILAB.
Signal Processing. Signal processing components are implemented as single MATLAB functions that translate input signals into output signals; they can be adaptive or static, linear or non-linear, causal or non-causal, they can operate both in real time or offline, and on continuous or epoched data -- thus they can implement arbitrary processing, as long as the inputs and outputs are both signals. Signals are represented as extended EEGLAB datasets. The majority of signal processing components serve to filter the input signals (e.g., spatially, spectrally, or in time), thereby discarding unwanted information and "amplifying" information of interest, i.e., improving the signal/noise ratio of the data. Other filters may implement more specialized processing, such re-representing the data in a more interpretable basis (ICA, sparse reconstruction, or the Fourier transform). [picture] Most signal processing components reside in code/filters and some are in code/dataset_editing.
Feature Extraction. Feature extraction components take off where signal processing ends; they accept epoched or continuous signals and output sequences of feature vectors, thereby transforming segments of data into some abstract domain (referred to as the feature space). Feature extraction often simplifies the data and can drastically reduce its dimensionality. The processing may be static or adaptive, and, if adaptive, it frequently uses information about the value of the variables to be predicted (called supervised learning). Typical algorithm choices are certain simple mathematical transformations (e.g., PCA, wavelet decomposition, etc), or in other cases, the data is transformed into a space which is more amenable to interpretation and robust association (e.g., if it is neurophysiologically meaningful). [picture] Feature extraction functions are frequently contained in the BCI Paradigm components that use them.
Machine Learning. Machine learning components come in two parts, one to learn a predictive model from some data, and the other to apply a previously learned model to data, in order to make predictions. The learning function ultimately summarizes the data (the pre-processed example data gathered in the calibration session), for example its structure (in what is known as unsupervised learning) or the relationship between observed and latent variables (in supervised learning) under some implementation-specific assumptions. It learns from a set of feature vectors as produced by the feature extraction stage, as well as usually their associated target values (i.e., desired predictions, if known by the design of the calibration experiment) and produces a MATLAB structure which encodes the learned model. The prediction function takes that model and a set of feature vectors and outputs the estimated target value for each vector. Target values are often referred to as labels in the machine learning literature. All machine learning components reside in code/machine_learning.
BCI Paradigms. BCI paradigm components are MATLAB functions that tie together all stages of a BCI approach, including any signal processing, feature extraction, machine learning functions, as well as their default parameters or allowed parameter ranges. They do not nececssarily need to be implemented in terms of these stages, however; they can do completely arbitrary processing of their input datasets. Thus, BCI paradigms codify the entire computational approach, including learning of a model from a dataset (or collection of datasets), as well as prediction, given a dataset or given real-time data. In addition, they may support visualization of their learned models. Most BCI paradigms are heavily customizable implementations of common standard BCI approaches. These components reside in code/paradigms.
Online Plugins. Online plugins are MATLAB functions that link certain hardware and drivers to BCILAB's processing facilities. There are three types of online plugins: Input plugins, which receive data from a source and provide it to BCILAB, output plugins, which receive processed data from BCILAB and output the result over some interface, and input/output ("processing") plugins, which handle both input and output via some interface, and do the intermediate processing through BCILAB.
Framework. In addition to the plugins, there is common low-level infrastructure which makes various functionality available to the plugins, such as distributed cluster computation, disk caching of intermediate results, or a platform-independent file interface. Lastly, the toolbox has high-level facilities that offer functionality on top of the plugins. These handle the design and customization of BCI approaches, the learning, offline/online application, evalution and visualization of predictive models, as well as the user and application programming interfaces to these (i.e., the GUI, script language, as well as the processing API).
GUI. The graphical user interface of BCILAB supports almost all functionality provided by the toolbox, and reflects all parameters of every plugin. As most of the BCI paradigms have reasonable default parameters, working BCI systems can be set up with very little customization -- but if necessary, every setting can be changed through the GUI. Offline analysis, including prototyping, performance analysis and visualization, as well as online processing can be done via the GUI. The GUI functions reside in code/gui.
Scripting. The scripting system gives access to all functionality of BCILAB. It consists of an offline scripting language (learning and application / evaluation of predictive models, visualization) and an online scripting language (feeding chunks of raw data into BCILAB, and getting results out of BCILAB in real time). The respective facilities reside in code/offline_analysis, code/online_analysis, with additional tools in code/dataset_editing.
Plugins. The plugin authoring interface consists of the utilities and contracts provided to implement BCILAB plugins, see also the plugin authoring guides for more information. Since all plugin types (except for feature extraction) need to be accessible from the GUI, a subsystem for the GUI-friendly declaration of function arguments is provided in code/arguments, used by all of these plugins. For the definition of signal processing plugins, a (trivial) contract needs to be followed by the user, supported by two functions in code/expressions. Machine learning functions, BCI paradigms, and online plugins have specific interface contracts, as well, and additional helper tools exist to simplify the definition of the respective functionality, found in code/helpers.
The toolbox core is structured into several layers and groups of related functions, which will be explained from bottom to top in the following. [picture]
Dependencies. BCILAB ships with a set of externally maintained dependencies. Some of these had been minimally modified; see the respective readme file in each sub-directory for details. Dependencies are automatically loaded, and added to the MATLAB path by BCILAB's startup script (controlled by marker files env_add.m / env_exec.m in the respective dependency folders).
Miscellaneous functions. BCILAB contains several groups of miscellaneous functions. This includes convenience keywords (code/keywords -- note: the capital-letter keywords should currently not be used), useful additions to the MATLAB language (code/misc), as well as "query" functions to tell different BCILAB data structures apart (code/queries).
Helpers. Helper functions (code/helpers) implement compact stand-alone functionality and can be used without the rest of the toolbox (though they may depend on other helpers, and possibly some keywords). Among others, distributed computation, data fingerprinting, function memoization, directory traversing, as well as a few useful MATLAB hacks are provided.
Utility functions. Utility functions (code/utils) are more complex and interwoven functions than helpers; as their functionality is strongly tied to the toolbox architecture, they are only useful to BCILAB experts. Some core functionality used by the GUI functions, etc., is implemented in these (such as cross-validation and parameter search).
Argument sub-system. BCILAB contains a sub-system of functions (code/arguments) to declare function arguments in a way that allows these functions to be displayed in a GUI. Among others, they allow to auto-generate dialog windows for user functions, or display their parameters in a property grid widget. All plugins (except for feature extractors) use the argument sub-system to declare their arguments.
Expression sub-system. A small sub-system for the construction of algebraic expressions (code/expressions), their manipulation (in the style of Mathematica) and their lazy evaluation is included with BCILAB. Signal processing plugins follow are contract that makes them compatible with this framework, which allows the BCILAB framework functions to do heavy manipulation of user-defined signal processing chains (e.g., reordering, caching of intermediate results, or piecewise online execution).
Input/Output functions. Functions to load/save data sets in a variety of formats (containing time series data, such as EEG), as well as generic MATLAB variables. Found in code/io.
Dataset editing plugins. Dataset editing (code/dataset_editing) functions are Signal Processing plugins which do not primarily transform the signal contents but rather the meta-data of the data sets (e.g. marker annotations, channel names, etc.). Their use in scripts is occasionally necessary (concatenating datasets, changing event markers, etc.)
Signal Processing plugins. Signal processing plugins (code/filters) transform data sets, and particularly the signals stored in them. See Functionality:Signal Processing. These functions are only rarely invoked directly by users -- instead, they are used as part of a data processing pipeline, which is configured via BCILAB's high-level prototyping tools and then executed by high-level processing tools. A special signal processing plugin, which sits on top of all the others, is flt_pipeline; this function allows to apply any subset of signal processing functions in sequence (with automatic ordering).
Machine Learning plugins. Like signal processing plugins, these functions (code/machine_learning) are rarely invoked directly (although they can be used without the rest of BCILAB, as long as the respective dependencies are properly loaded). Instead, they are used as part of a processing pipeline, configured and executed via GUI, scripts and/or programming APIs. A special machine learning plugin is ml_train/ml_predict; these functions dispatch to one of the user-supplied signal processing functions.
BCI Paradigm plugins. BCI paradigms (code/paradigms) make use of signal processing, machine learning, feature extraction and dataset editing functions, and are therefore a layer above these other plugins. These functions are exclusively ran by the framework, and not by the user. A special paradigm function is para_dataflow, which allows to set up a sequence of signal processing steps, feature extraction and machine learning as a processing chain; most (but not all) other paradigms use para_dataflow with appropriate parameters to implement such a three-stage design.
Offline analysis tools. BCILAB currently contains four core functions for offline (i.e., post-hoc) analysis of recorded data (code/offline_analysis). The most important function is bci_train, which learns ("trains") predictive models from user-supplied calibration datasets, estimates their likely predictive performance (online / real time) on new data, and can also search for optimal parameters within certain ranges. The function bci_predict applies predictive models to previously recorded data sets to obtain cognitive state estimates. Models can also be visualized, using bci_visualize. The function bci_preproc is a specialty function which allows to partially pre-process previously recorded data according to some BCI paradigm or predictive model, in order to analyze and explore the result in EEGLAB or other tools. These functions make use of BCI paradigms (customizing them, running them, etc).
Online analysis facilities. Online analysis (code/online_analysis) involves receiving raw signal chunks in real time from external sources, feeding them through a (previously loaded) predictive model, and obtaining the output estimates for the most recent signal time point. This is handled by a small language of scriptable functions, onl_newstream / onl_append / onl_clear to manage streams of raw data (create, update, clear), onl_newpredictor / onl_predict to load and invoke predictive models on raw data streams, and optionally onl_simulate to test the online processing pipeline on a previously loaded dataset. These functions can not only be used in user scripts, but they are also the basis which is used to implement online plugins.
Online processing plugins. These user-defined functions (code/online_plugins) allow to link external hard/software to BCILAB for the purpose of real-time data processing. They are implemented in terms of online analysis facilities (which in turn invoke BCI paradigms, which invoke machine learning, signal processing, and feature extraction functions, etc.).
Graphical User Interface. The GUI (code/gui) functions sit on top of all other facilities. It is organized into IO, offline analysis (with approach design, model learning & evaluation, visualization, and model testing), and online analysis (loading of predictive models, real-time input / output via certain supported interfaces).
Environment support. The environment functions (code/environment) bring up the BCILAB environment from the MATLAB command line (env_startup), load its dependencies, and set any global variables (such as default directories for data, etc.). The function env_showmenu opens the BCILAB main menu, and some others manage directory / file name translation and error handling.
Data structures. The main data structure used by the toolbox is the data set, which is an extension of the EEGLAB data set format (->REF). A data set encapsulates a multi-channel time series, together with meta-data. The time series data may come from different types of sensors (such as EEG, EMG, EOG), but has a uniform sampling rate. EEGLAB's standard meta-data involves time information (e.g., sampling rate), channel information (e.g., channel labels), dataset information (e.g., subject name), event marker information (e.g., event types & latencies), possibly epoch information, internal bookkeeping data, as well as some domain-specific data (e.g., a decomposition into independent components). BCILAB adds the tracking field (for internal tracking), as well as the target field as a field of EEGLAB's epoch sub-structure. The target field is critical, as it stores information about the cognitive state to be predicted for a given segment of sensor data. In future iterations, BCILAB will standardize the format of dataset collections (possibly adopting EEGLAB's STUDY data structure). Additional data structures include the predictive models learned by BCI paradigm plugins as well as machine learning plugins - these are, however, largely user-defined (except for another tracking field that is automatically added to model structures).
Top-level directories. The resources directory contains resource files (e.g., channel locations), as well as user-supplied approaches, workspaces, documentation, and test cases. The userscripts directory contains user-written scripts.The userdata directory contains data as needed by user scripts, but preferably not entire studies (as this makes copying the BCILAB folder tedious). The root folder contains the startup scripts, as well as the bcilab configuration file.
The standard data flow inside BCILAB is best explained by working backwards from the outputs to the inputs. The desired output of any BCI is a real-time measure of an aspect of a person's cognitive state: this may be a real number (e.g., an index of the user's working-memory load), a categorial value (e.g., the most likely type of movement imagined), a probability (e.g., the probability of being surprised), or a probability distribution (e.g., the area of the person's auditory attention focus).
The computation of this value is periodically scheduled by a running online (output) plugin of the toolbox (e.g. in a loop or via a timer) or a script, and then forwarded by it to an external destination. This code requests an estimate from the online prediction function of the toolbox (onl_predict), part of the online analysis interface, which in turn obtains the most recent data from any input data streams to which it has been linked and then pipes the new data through the signal processing of the (loaded) predictive model to pre-process it. The input data streams used by onl_predict are usually updated independently, e.g., scheduled by some other online plugin interfacing to an external source (and updated via the function onl_append).
While sending the data through the signal processing chain, onl_predict distinguishes between stateful, stateless and epoch-based signal processing plugins, and passes appropriate signal portions to each of the functions. Additional parameters to these functions are held in the predictive model, and can be defined by the signal processing function. Once up-to-date pre-processed data is available, onl_predict takes the most recent segment of the processed data and delegates any further calculation to the prediction function of its loaded predictive model.
This model's prediction function then maps the data segment onto the output value. The implemented mapping is completely up to the respective BCI paradigm, but most paradigms use para_dataflow to send the input data through a feature extraction plugin, followed by a machine learning plugin. The feature extraction function takes the data segment and maps it onto a feature vector (which can be viewed as a point in a high-dimensional space). This feature vector is then sent through the prediction function of the respective machine learning plugin and mapped onto the final output value (both stages depending on parameters previously learned from calibration data).
[picture: processing?]
More generally, the recording of user-specific calibration data, learning of predictive models from them, and application of these models in online processing is also a part of the data flow. Details of the learning process can be involved, but in most (current) designs, the raw data is sent through the same sequence of processing stages as online, whereas each stage has access to the desired outputs (the target labels, if available) and may adapt itself based on this information before passing the data on. Also, because typically the entire recording is available by the time the learning is done, its processing does not have to be causal. Any additional piece of information on which the outputs depend (e.g., MR images when doing advanced source localization) are also part of the data flow of BCILAB.
System Requirements. BCILAB requires MATLAB 2008a+ (with support back to MATLAB 7.1 in the works for the non-GUI parts), and a Windows / Linux / Mac computer with at least 1GB of memory. For fast online processing or advanced offline analysis, a 1 GHz processor or faster is required, and multiple cores are recommended. As a very important consideration, the MATLAB path should be pristine, i.e. it ideally contains only MATLAB toolboxes and as little extra material as possible, since clutter in the path can lead to unexpected errors (this can be achieved by clicking File / Set Path ... / Default, and then Save). Also, the BCILAB directory itself should NOT be added to the path.
Obtaining the code. Current BCILAB releases (including betas) can be downloaded from ftp://sccn.ucsd.edu/pub/bcilab. The packages contain a single directory and can be unpacked in any place (however, if BCILAB is placed inside an EEGLAB folder, special considerations apply, as the toolbox is then loaded in plugin mode -- for now, it is better to run BCILAB in standalone mode).
Setup and Startup. The toolbox is loaded by moving into the BCILAB directory (via the MATLAB command cd your/path/to/bcilab, or the directory picker in MATLAB's GUI, and then entering startup at the command line. If the command line is not visible, it can be enabled via Desktop / Command Window. The startup script automatically loads all dependency modules (including EEGLAB), and uses the variables specified in the file bcilab_config.m as default configuration parameters. These parameters can be changed to customize the BCILAB setup - see code/environment/env_startup for a description of the configuration parameters. In particular, the directory in which studies are located (the 'data' directory) may be adapted.
For a GUI walkthrough with example data, see the extended Practicum slides at ftp://sccn.ucsd.edu/pub/bcilab. The GUI tools are split into data sources, offline analysis and online analyis. The data sources menu allows to select recordings for further analysis. Offline analysis allows to design computational approaches (specializations of standard or user-defined BCI paradigms), learn predictive models from recordings (according to a previously defined computational approach), evaluate their estimated performances, and visualize aspects of their structure. The online analysis menu allows to load predictive models for real-time use, and link external sources (such as EEG amplifiers) and destinations (such as stimulus presentation software) with loaded predictive models for online processing.
Naming things. Most of the steps that are offered by the GUI produce some data item (e.g., a model, a dataset, or a result), and in general these data items are assigned names and stored as variables in the MATLAB workspace. The MATLAB workspace is a collection of objects of various types, and it can be viewed by checking, in the MATLAB menu, the item Desktop / Workspace. The default names proposed by BCILAB for storing things are lastmodel, lastresult, lastdata, etc., but custom names can be given. When a subsequent processing step depends on an item of one of these types, the one called 'last***' (if any) is usually proposed by BCILAB as the default choice.
Saving things. All data items produced in a BCILAB session can be saved for later reuse. The easiest way is to save the entire workspace (note to EEGLAB experts: BCILAB usually only keeps references to datasets in its workspace, which take up very little space), but various GUI dialogs include a dedicated "Save" button to save a computational approach, a model, etc. These items are by default stored in subdiretories of resources. Things can also be saved and loaded with MATLABs load and save commands; type help load or help save in the command line for details.
Writing scripts in BCILAB is relatively straight-forward and rarely requires more than 3-10 lines of code for standard analyses. It allows to automate entire workflows (e.g., load a dataset, define an approach, learn a model from the data and estimate performances, visualize model properties, save the model for later use or load a model for real-time use, connect to an EEG amplifier, connect to a simulus presentation software, run), which is essential for reproducibility and can greatly boosts productivity, especially in batch analyses. Most importantly, it allows to do custom dataset formatting (see also EEGLAB scripting wiki), and to define custom analysis modules that fit seamlessly into the BCILAB pipeline.
It is highly recommended to first proceed through the GUI example (REF) before going through the scripting guide, to get an quick initial overview of the provided functionality. We also strongly recommend working through the MATLAB "Getting Started" help file, which contains invaluable knowledge, of which the essentials can be picked up in as little as an hour. It is accessible from the main menu via Help / Product Help / MATLAB / Getting Started.
A basic script is a sequence of commands that operate on the contents of the MATLAB workspace, may invoke built-in or user-defined functions, and/or interact with any hardware connected to the computer. Commands may create or overwrite (or, if desired, remove) variables, such as data sets, models, results, data streams, or other MATLAB data structures (arrays, etc.). Whenever MATLAB is first started, BCILAB must be loaded by entering the appropriate directory, and then invoking the startup command in it. This is best done in the MATLAB command line (in a script it would lead to the toolbox being reloaded whenever the script is executed).
% old BCILAB
cd your/path/to/bcilab
startup% new BCILAB
cd your/path/to/bcilab
bcilabA new script is created by selecting File / New... / Script in the MATLAB main menu (not the BCILAB menu), and then saving it under some name via File / Save As.... Scripts are by default saved in the current folder, which is set to your/path/to/bcilab/userscripts after BCILAB has been loaded. It is good practice to prefix script names (e.g., with 'do_') to avoid name conflicts with functions used by the toolbox or other MATLAB code. The same lines that can be written in a script can also be entered in the MATLAB command line to get instant feedback. Running a script is in fact equivalent to typing its contents into the command line.
The first step in any analysis would be to learn a predictive model from calibration data, and to estimate/evaluate its accuracy. The standard function to load datasets from disk is io_loadset, which takes a file path and some optional arguments. The file path can be an operating system specific path, such as 'C:\Projects\bcilab-0.9\userdata\test\imag.vhdr' on a particular Windows installation, or a platform-independent path, such as 'bcilab:/userdata/test/imag.vhdr' (where bcilab:/ refers to the BCILAB base directory). It is generally recommended to use the platform-independent version, as the same script is then almost guaranteed to work on different machines, installations and operating systems. Other base directories include data:/, temp:/ and store:/. The defaults for these directories can be set in the file bcilab_config.m. The result shall be stored in the variable 'mytrainset'.
mytrainset = io_loadset('bcilab:/userdata/test/imag.set')Note: if this dataset is not in your distribution, you may download it here and put it in the userdata folder of BCILAB
A data set, as loaded by io_loadset holds some biosignal, which may or may not include additional annotations, such as event markers. Datasets to be used for calibrating predictive models typically require that event markers are present to indicate the type of user state that is expected (in accordance with the experimental design) at certain time points. The learned model would then likely produce a corresponding output when fed this or a similar piece of raw data (note that the output is usually not the exact marker id used, but more flexible). As the entire data processing must take place inside BCILAB (or else it could not reproduce the results online / on new data), the data to start with should always be continuous (i.e. not epoched).
The loaded dataset contains the EEG of a person who was imagining different types of hand movements for 20 minutes. A stimulus presentation software presented an instruction every 7.5 seconds, which was either the letter "L" or "R", and the user was instructed to imagine either a certain left-hand movement or a right-hand movement. The goal in the subsequent analysis is to learn from these data (and the respective stimulus event markers) how to estimate the type of hand movement that the user is imagining from his raw EEG. This knowledge will be distilled into a predictive model, which can then be applied to datasets (giving a time course) or in real time (e.g., to control a cursor).
The most important distinction (and possible stumbling block) between EEGLAB's functions at the signal level and BCILAB's is that the former ones immediately compute and return the requested result (i.e., they evaluate "eagerly"), whereas BCILAB's functions by default only return a data structure that can subsequently be evaluated (by the user or by the BCILAB framework) to get that result (i.e., they evaluate "lazily"). This data structure (an "expression") only captures what has to be done in order to get the result. Only when the contents of a result are to be manually processed or inspected by the user script, it is necessary evaluate it -- in other cases, BCILAB makes sure that it data that it actually needs is obtained fast as possible (e.g., it may skip an intermediate step if it knows the outcome already, or it may store intermediate results to disk for later retrieval). The function which turns an expression into a value (e.g. a dataset) is called exp_eval. For example, the previous result can be obtained by the command: mytrainsetnew = exp_eval(mytrainset) which then assigns the corresponding EEGLAB dataset to the variable mytrainsetnew.
The next step is to specify the computational approach that should be used to learn a predictive model, and thereby, which assumptions should be made while learning that model. For example, one might assume that the relevant contents of the raw signal (for the purpose of making the desired estimates) are primarily its oscillatory properties, which is usually the case if neural idle rhythms correlate to the cognitive state of interest. Alternatively, one might assume that certain slow-changing cortical potentials relate to the user state of interest in a way that can be exploited for predicting that user state. These assumptions are expressed in the chosen algorithms and their parameters.
A convenient way to specify an approach is to reuse one that is known to work under similar conditions, and to customize it as necessary. BCILAB contains a collection of "reference" approaches, many of which have been used in many different scenarios, and most of which are customizable beyond recognition. These are called "BCI paradigms" in BCILAB. In addition, the user can save their own approaches (i.e., customizations of these paradigms) and use these as starting points for later designs, or define their own paradigms. Customization of an approach in many cases comes down to setting particular parameters, such as the set of sensors to be used, or the frequency bands of interest, but it may also involve replacing particular components (e.g. exchange one type of machine learning component by another one) and their parameters.
In the following, a new approach will be designed based on the CSP (Common Spatial Patterns) paradigm (file paradigms/para_csp), with one of its default parameters replaced by a new value. CSP is a fast and powerful method for learning and exploiting spatial patterns in the expression of oscillatory processes in the brain (in the context of imagined movements, these processes are an effect of Event-Related Synchronization / Desynchronization, ERD/ERS). As there may be many different types of event markers in the data set, it is necessary to specify which ones indicate that a left/hand movement imagination happens in their proximity.
In this case, the process of interest takes place after each stimulus event 'S 1' (for left) and 'S 2' (for right), respectively. Note: there are 2 spaces between the S and the number. These are standard marker types assigned by BrainProducts recording software, indicating Stimulus Type #1 and Stimulus Type #2. The parameter that needs to be changed to accomodate for this is called EventTypes, and it belongs to the EpochExtraction group of parameters (as it controls which segments / epochs of the data are extracted for further processing), which in turn is part of the SignalProcessing group of parameters (as this processing is implemented as a signal processing module in BCILAB). In the GUI's approach review panel, the respective parameter is found in SignalProcessing / EpochExtraction / EventTypes.
% old BCILAB
myapproach = {'CSP', 'SignalProcessing',{'EpochExtraction',{'EventTypes',{'S 1','S 2'} }} }% new BCILAB
myapproach = 'CSP'The following material assumes basic familiarity with the MATLAB language (and its data structures, such as cell arrays); these can be read up in the MATLAB help. A BCILAB convention is that a list of parameter assignments should be expressed as {'name1',value1, 'name2', value2, ...} - also called name-value pairs. In the previous assignment, {'S 1','S 2'} is a list of marker names, and {'EventTypes',{'S 1','S 2'} } is a list of parameter assignments (here for one parameter). The expression 'SignalProcessing',{'EpochExtraction',{'EventTypes',{'S 1','S 2'} }} is another parameter specification, here specifying the group of parameters that is to be assigned to the SignalProcessing parameter of the BCI paradigm.
Finally, approaches are declared as a cell array that has the paradigm name (here 'CSP') as its first entry, followed by parameter assignments. Thus, approach declarations are always of the form approachname = {'paradigmname', 'param1',value1, 'param2', value2, ...}. The main parameters of this paradigm itself are SignalProcessing, FeatureExtraction, MachineLearning, and all others are sub-parameters of these. All parameters have defaults, which apply if not explicitly overridden. The approach review panel in the GUI (see GUI walkthrough) gives an good overview of the complete hierarchy of parameters for any paradigm and approach, as well as their default values.
It is possible to specify parameters with short forms (for experts), which can be found in the respective functions. For example, code/paradigms/para_dataflow.m defines both the 'SignalProcessing' argument as well as its 'flt' alias. MATLAB provides a search tool (in the bottom-left corner under Start / Find Files...), which can be used to search for such aliases in the code directory (and sub-directories). The short form for the previous command is:
% old BCILAB
myapproach = {'CSP','flt',{'epoch',{'events',{'S 1','S 2'} }} }Predictive models are learned via the function bci_train, which expects the data, as well as the approach to be used as arguments. This function does not learn just a predictive model given an approach and calibration data, but it also produces (by default) an estimate of the performance of the model when making new predictions (on future data). Therefore, it returns two results, which are here assigned to the variables loss and model. Loss is the so-called "loss estimate" for the model. Here, it is the mis-classification rate (a.k.a. error rate), which is an estimate of the fraction of trials (in this case: movement imagination events) that it will likely mis-classify.
%old BCILAB
[loss,model] = bci_train({'data',mytrainset, 'approach',myapproach})%new BCILAB
[trainloss,model,laststats] = bci_train('Data',mytrainset,'Approach',myapproach,'TargetMarkers',{'S 1','S 2'})If there are only two possible outcomes (e.g. 0=Left / 1=Right) and both appear with equal chance, deciding by throwing a coin will have a mis-classification rate of 50% (0.5), which gives the chance level in this situation. A loss estimate of 0 would mean that all events are correctly classified. However, due to the high variability of the EEG, errors made by the subject when executing the task, artifacts, etc., perfect classification is almost never attained. This statistic is obtained via cross-validation (ref), a procedure in which the original data set is repeatedly split into training and test sets. Additional statistics (such as the loss estimate for every split, the confusion matrix, etc.), can be obtained by invoking the bci_train function with three output arguments instead:
%old BCILAB
[loss,model,stats] = bci_train({'data',mytrainset, 'approach',myapproach})The variable model in both cases contains the learned predictive model, which is a data structure which specifies both the algorithms to be used for online processing, as well as the parameters to be used in these algorithms. It can be saved to disk for later use (by entering save model), or it can be directly loaded into one of the online plugins. The training function supports additional arguments to control the type of loss metric to use (e.g., mean-square error), the cross-validation partitioning scheme, etc. Type doc bci_train to get additional information on these parameters (reference table at the very end). By typing stats or stats.fieldname, different aspects of the statistics can be investigated (depending on the field name chosen). MATLAB also provides a graphical array editor which can be used to explore data structures such as stats; it can be invoked with the command openvar stats.
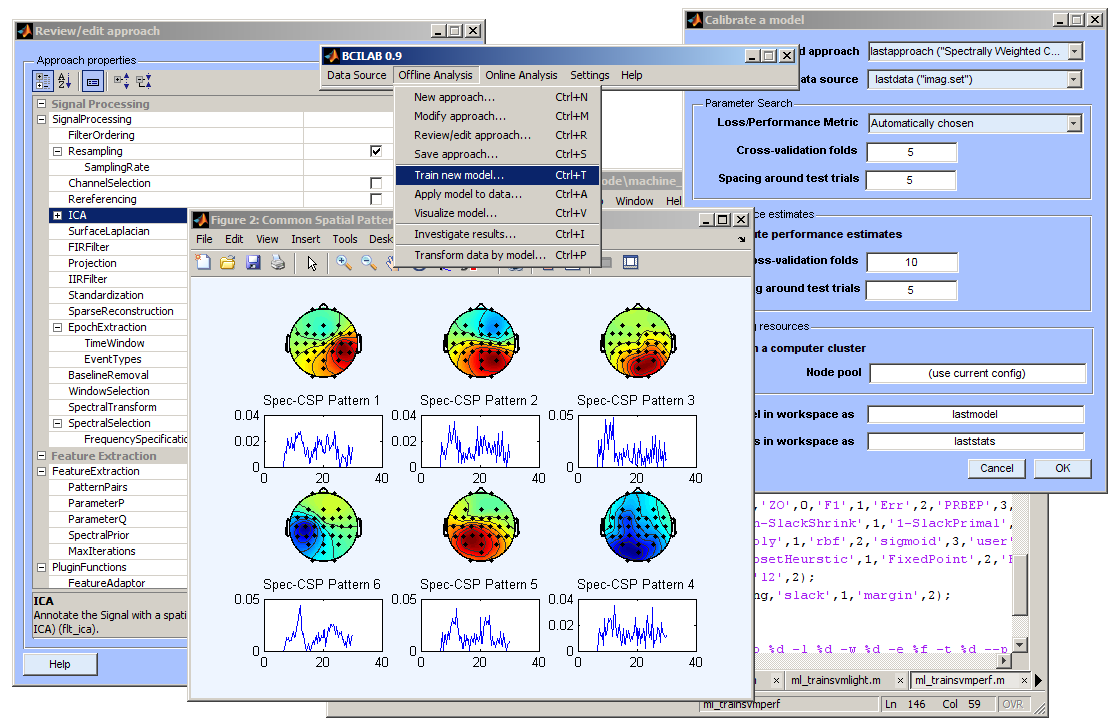
The structure of predictive models can be visualized. Depending on the BCI paradigm used, this may involve different types of visualizations to present the respective parameters. For example, the CSP model learned consists of six sets of parameters that can be interpreted as per-channel weights, and thus, as topographic maps. In the case of CSP, the 6 maps are rows of a matrix, and the columns of its inverse matrix happen to be more interpretable (akin to mixing and unmixing matrices in ICA); therefore, the inverse maps are being displayed by default. [picture] In addition, this model also contains the overall weighting of these six maps, which is however not separately displayed. Other possible visualizations involve per-frequency weighting, per-timepoint weighting, weights per cortical area, etc. The following command brings up a visualization:
bci_visualize(model)Predictive models, once learned, represent the structure of the data set on which they were learned. Applying the model to this data set to obtain performance estimates yields results which are practically meaningless (roughly comparable to circular reasoning). For this reason, bci_train uses cross-validation to arrive at performance estimates from a single data set. However, applying a model to new ("unseen") data is a valid case of offline analysis. The following code loads a second dataset from the same person and day, and then applies the previously learned model to it, obtaining predictions. This second data set was recorded under the same type of experimental paradigm as the first one, so that event markers are available which encode the types and time points of presented stimuli throughout the recording. Following the same procedure as the during calibration, the actual cognitive state labels are known for each trial -- bci_predict optionally returns this information in its fourth output. Given the known labels and the model's predictions, it is possible to compute the discrepancy between the two in the form of a loss measure, returned in the second output, here assigned to the variable testloss. By default, a loss measure is chosen which is compatible with both the type of target variable and prediction variable (categorical, continuous, etc.). Additional parameters of bci_predict allow to change this default, though.
testset = io_loadset('bcilab:/userdata/test/imag2.set');
[predictions,testloss,teststats,targets] = bci_predict(model,testset);The same could also have been written in one line:
[predictions,loss,teststats,targets] = bci_predict(model,io_loadset('bcilab:/userdata/test/imag2.set'));The following lines print a part of this information in human-readable form:
disp(['training mis-classification rate: ' num2str(loss*100,3) '%']);
disp(['test mis-classification rate: ' num2str(testloss*100,3) '%']);
disp([' predicted classes: ',num2str(round(predictions{2}*predictions{3})')]);
disp([' true classes : ',num2str(round(targets)')]);The test mis-classification rate is usually worse than the training mis-classification rate, as many conditions are likely to have changed between the two sessions, and some of these might affect the model's outputs. It is possible to factor out large quantities of these session-specific details, either by means of fairly strong regularizing (or simplifying) assumptions in the learning approach, or by using far larger quantities of training data, e.g., spanning many different sessions. Overly strong regularization may constrain the expressive power of the model (i.e., what types of structure it can capture) to an extent that it fails to capture much of what is characteristic in the data at hand, thus leading to worse training and test performances. Overly lax regularization in turn tends to result in the model learning the peculiarities of the specific data sample used for training (which is of course a random draw out of an infinitely large pool of possible alternative recordings), which in turn also leads to poor performance. This phenomenon is called overfitting. Therefore, a good tradeoff must be chosen, and ideally, the remaining modeling assumptions should be in good agreement with reality, as far as that is possible. Also, it is generally a good idea to choose a computational approach that allows to incorporate as much information about the person (and task) as possible. The current version of BCILAB offers relatively little in this particular direction, but future versions will add more support.
An important trade-off when analyzing data is that of accuracy versus computational expense. The toolbox contains several BCI paradigms that can be applied in roughly the same circumstances, but primarily differ in terms of their simplicity, computation time, and attainable performance. For oscillatory processes, these are log-BP, CSP, and Spec-CSP (in increasing complexity), as well as DAL_Hifreq. The following code performs the same analysis as the basic scripting example, but uses the Spec-CSP (spectrally weighted common spatial patterns) instead of the CSP approach (which is, essentially, a more advaned feature extraction component which is sandwiched between the signal processing and machine learning stages).
trainset = io_loadset('bcilab:/userdata/test/imag.set');
approach = {'SpecCSP','flt',{'epoch',{'events',{'S 1','S 2'} }} }
[loss,model,stats] = bci_train({'data',trainset,'approach',approach})
bci_visualize(model)Spec-CSP learns not just optimized spatial (i.e. topographic) weights, but also optimized spectral weights. As both sets of parameters are updated repeatedly in alternation, this takes significantly longer than CSP alone, but with the added benefit of learning individualized frequency bands that exhibit the oscillatory processes of interest (whereas CSP uses "a priori" fixed bands).
In some cases, BCI paradigms have parameters that are not known precisely for a given person (although some reasonable defaults usually exist). Though it is always possible to try several settings for these parameters and taking the one that gives the best results, the resulting loss estimates are systematically biased, and cannot be reported in a publication (for the same reason that multiple hypothesis tests require a correction). The correct way to calculate loss estimates in the presence of a parameter search is to run the entire search procedure itself inside one large cross-validation (i.e., partition the data set into k sections, take all but one section for training and compare all possible parameters on it, each time computing loss estimates via a nested cross-validation within these k-1 sections, and then testing the best model on the held-out section). This procedure is called a nested cross-validation and is natively supported by BCILAB. It is conducted by specifying values for unknown parameters in a special way, using a so-called "search clause", which lists all possibilities to be compared. After loading a data set,
trainset = io_loadset('bcilab:/userdata/test/imag.set')a typical CSP approach may be specified with an additional custom parameter -- the number of CSP patterns to compute (this is the number of columns in the CSP visualization, and controls the simplicity of the model), which is part of the 'FeatureExtraction' (or short, 'fex') parameter group of the approach, and is called patterns. The below code sets it to 3 (also the default value).
approach = {'CSP', 'flt',{'epoch',{'events',{'S 1','S 2'} }}, 'fex',{'patterns',3} }Common choices of this parameter are 2,3, or 4, and it is not known in advance which one to use. Therefore, one may alternatively specify the parameter as to be searched, using a search clause:
approach = {'CSP', 'flt',{'epoch',{'events',{'S 1','S 2'} }}, 'fex',{'patterns',search(2,3,4)} }If this approach is now applied by BCILAB, using the same code as before, the computation takes significantly longer, but with the added benefit that the resulting accuracy of the model may well be better than before, as this parameter is now individualized.
[loss,model,stats] = bci_train({'data',trainset,'approach',approach})It is also possible to specify multiple parameters to be searched at the same time, though this will increase the running time of bci_train combinatorially. Some paradigms and, especially, machine learning components have parameters that are by default specified as a search range.
While the previous examples operated exclusively on oscillatory processes, another relevant type of brain process is slow cortical potentials (SCPs), i.e. changes in the cortical voltage distribution throughout some time period. The characteristic feature of these SCPs is their structure within a time window, which is usually locked to certain events (then called event-related potentials, or ERPs). For this reason, the applications of many SCP-based BCIs are constrained to situations where such event information is available in real time. One example are human-computer interfaces which occasionally exhibit erroneous or unexpected behavior, triggering a characteristic brain response that can be detected. The following script learns a predictive model for the detection of such error responses.
First, a calibration data set is loaded. The recorded data contained periods in which expected (normal) events happened (tagged in the data set with the marker S 11), as well as periods in which various types of error events happened (some tagged with S 12 and others tagged with S 13). Also, a list of marker types is created, which contains the marker for expected events as its first entry, and a sub-list of markers (identifying unexpected events) as its second entry).
traindata = io_loadset('bcilab:/userdata/test/errors.set')
mrks = {'S 11',{'S 12' 'S 13'} }Then, a computational approach is specified. A standard BCI paradigm for use with slow cortical potentials is para_windowmeans, which, however requires some knowledge about the expected time course of the responses. Instead, a newer approach is being used, called in BCILAB the Dual-Augmented Lagrange method. The only information that needs to be specified for this approach is the list of relevant event types and the time window around these event markers that is of interest (i.e. which assumed to be holding information about the cognitive state of interest, here: whether the user was perceiving an expected or erroneous event). In addition, it is important to use a low sampling rate in order to keep the complexity of the learned model low.
approach = {'DAL_Lofreq', 'SignalProcessing',{'EpochExtraction',{'EventTypes',mrks, 'TimeWindow',[0 0.8]}, 'Resampling',30} }Finally, a model is being learned. It can subsequently be used for the real-time estimation of whether the user is perceiving an event as being erroneous or not. The paradigm contains one parameter which is by default set to a search range; for this reason, the computation will a relatively long time.
[loss,model,stats] = bci_train({'data',traindata,'approach',approach})A faster to compute, but more involved to specify, way to achieve comparable precision is via the WindowMeans paradigm (this is the "classical" approach to handle SCPs). Here, it is necessary to specify the time window of interest relative to an event (as before), but also sub-windows within that time segment, within which the signal's average shall be computed for further processing. As these are slow-changing potentials, this is a way of reducing the dimensionality / complexity of the data without losing significant information, and selecting the portions of the data that are likely relevant. The resulting values for each event are concatenated into a feature vector (#time windows * #channels) and then picked up by the machine learning stage. First, the time segments within the window are defined (in seconds relative to the event, here 0.25s to 0.3s, 0.3s to 0.35s, etc.), as well as the event types.
wnds = [0.25 0.3; 0.3 0.35; 0.35 0.4; 0.4 0.45; 0.45 0.5; 0.5 0.55; 0.55 0.6]
mrks = {'S 11',{'S 12' 'S 13'} }
traindata = io_loadset('bcilab:/userdata/test/errors.set')Then, an approach is defined, based on WindowMeans, with custom epoch extraction and spectral selection specified. The seven sub-windows are specified via the 'TimeWindows' parameter that is part of the 'FeatureExtraction' group of parameters (see also the documentation of paradigms/para_windowmeans, or its review/edit panel in the GUI).
approach = {'Windowmeans', 'SignalProcessing',{'EpochExtraction',{'TimeWindow',[0 0.8], 'EventTypes',mrks}, ...
'SpectralSelection',[0.1 15]}, 'FeatureExtraction',{'TimeWindows',wnds} }A shorter form for the previous definition, using the short-hand names, is:
approach = {'Windowmeans', 'flt',{'epoch',{'TimeWindow',[0 0.8],'EventTypes',mrks},'spectrum',[0.1 15]},'fex',{'wnds',wnds} }Note to experts: If all parameters in a parameter list are specified (as here in for the EpochExtraction), then it is often possible to specify these parameters not by their name but by their position in the parameter list of the function that processes them; in other words, the order determines which value gets associated with what parameter. The following line of code specifies the same approach as before, but the parameters in the 'epoch' list are specified by position, instead. The order is as in the review/edit panel in the GUI (under EpochExtraction), but the canonical reference is the argument declaration in the respective function, here dataset_editing/set_makepos.m.
approach = {'Windowmeans', 'flt',{'epoch',{[0 0.8],mrks},'spectrum',[0.1 15]},'fex',{'wnds',wnds} }Finally, the model is learned and visualized. The visualization now yields a different output than for CSP; displayed are the weights (relevances) for each channel and time window, displayed as #windows topographic maps.
[loss,model,stats] = bci_train({'data',traindata,'approach',approach})
bci_visualize(model)A core part of modern BCI approaches is the component which does statistical learning based on the calibration data. A good introduction to the underlying problem and the surrounding mathematical setting is given in the EEGLAB Workshop 2010 talk and slides. It is this part which handles most of the individualization and optimization of predictive performance. In almost all cases, this component can be swapped out against a great variety of drop-in replacements, using different sets of underlying assumptions, or having a different performance/computation tradeoff, and is therefore a major opportunity for customization. In the previous example, the default machine learning component is a special type of Linear Discriminant Analysis (LDA) classifier. The standard LDA tends to break down as the number of dimensions (independent variables) approaches the number of data points (trials), leading to degraded performance (this problem is called the "curse of dimensionality" in statistics). The WindowMeans paradigm uses by default a regularized variant of LDA which is robust against this situation, by restricting (or regularizing) the problem to the point that it can be solved with the given amount of data. The root problem with LDA is that, given enough degrees of freedom, spurious correlations between variables will be learned (originating from the small sample size), and regularization overcomes this by dampening these parameters towards zero.
An alternative assumption that can be used in classifiers is that only a sparse subset the features (and thus feature space dimensions) is actually carrying information about the variable to be estimated. Thus, all but a small set of learned parameters will be dampened towards zero, which is a very powerful tool if the assumption is true for the underling data. The most practical sparse classifier offered by the toolbox is sparse logistic regression, which learns a sparse linear model. There are two different implementations in the toolbox: first, the variational Bayesian approach (using automatic relevance determination), which is fast and very effective, but occasionally prone to numerical problems, illustrated below:
approach = {'Windowmeans', ...
'SignalProcessing',{'EpochExtraction',{'TimeWindow',[0 0.8], 'EventTypes',mrks}, 'SpectralSelection',[0.1 15]}, ...
'FeatureExtraction',{'TimeWindows',wnds}, ...
'MachineLearning',{'Learner',{'logreg',1,'variant','vb-ard'} }}
[loss,model,stats] = bci_train({'data',traindata,'approach',approach})Given the ERP data fed into this classifier (where each feature corresponds to an averaged signal value within some channel and time window), the assumption translates into a model that uses as few of these time windows as possible, also seen in the visualization:
bci_visualize(model)An alternative approach uses not the Bayesian method, but instead the regularization approach using the l1 norm. Here, a parameter search over a set of possible values for the regularization parameter is used (which takes far longer, unless a cluster is being used for the computation).
approach = {'Windowmeans', ...
'SignalProcessing',{'EpochExtraction',{'TimeWindow',[0 0.8], 'EventTypes',mrks}, 'SpectralSelection',[0.1 15]}, ...
'FeatureExtraction',{'TimeWindows',wnds}, ...
'MachineLearning',{'Learner',{'logreg',search(2.^(-6:2:10)),'variant','l1'} }}
[loss,model,stats] = bci_train({'data',traindata,'approach',approach})Editing data sets for use with BCILAB. The most frequent problem when preparing data for use with BCILAB is to ensure that there exist markers (in the calibration data sets) that indicate the time points at which information about the subject's cognitive state is available. These markers are the main tool in BCILAB to encode this type of information. In many cases, the stimulus presentation software can be configured to emit events of appropriate types into the data stream, and in other cases, they can be added via the EEGLAB GUI or ad hoc EEGLAB-style script code (editing the data set structure). In addition to these tools, BCILAB provides functions to split and concatenate continuous data sets, and to merge, sort or subset epoched data sets. Below are a few examples.
part1 = io_loadset('data:/recordings/file1.raw');
part2 = io_loadset('data:/recordings/file2.raw');
part3 = io_loadset('data:/recordings/file3.raw');
combined = set_concat(part1,part2,part3);
from_10_to_1000_seconds = set_selinterval(combined,[10 1000]);Inserting events into a data set. An important and frequent editing task is the insertion of an array of markers into one or multiple intervals of the data set, especially when a standard machine learning toolchain is used. The reason is that most machine learning components are trial-based, i.e., if there is significant variability within a particular condition (of cognitive state), its different aspects need to be captured by specific trials. Therefore, it makes sense to cover prolonged calibration periods that have no intrinsic trial structure with an array of markers (e.g., placed at random, or in regular intervals), whose density depends on the computational work that the user is willing to invest (up to one marker per sample). Another case is when the exact timing of an event is not known (only an approximate interval), or when it cannot be guaranteed that the BCI will be queried (online) at a precise event-related time point, but rather only within some short interval after an event, for example. There, the interval in question (often relative to a particular event) can be covered with markers to make sure that all data that is potentially of interest is captured by the model. In the following are a few examples.
raw = io_loadset('data:/recordings/file1.raw');
% insert 100 markers of type 'test' into an interval between 200s and 1500s into the data set, using random placement
edited = set_insert_markers(raw,'segment',{200 1500},'event','test','count',100)
% insert 10 markers per second into an interval, using equidistant placement
edited = set_insert_markers(raw,'segment',{200 1500},'event','test','count',10,'counting','persecond','placement','equidistant')
% insert 10 markers of type 'test' into intervals that begin 1 second before each event of type 'X' and end 5 seconds after the respective event
edited = set_insert_markers(raw,'segment',{'X' -1 5},'event','test','count',10)
% insert 10 markers of type 'test' into intervals that begin 1 second after each event of type 'X' and end 5 seconds after the subsequent event of type 'Y' (if there are no other events in between)
edited = set_insert_markers(raw,'segment',{'X' 1 5 'Y'},'event','test','count',10)
% insert 10 markers of type 'test' into intervals that begin 1 second after each event of type 'X' and end 5 seconds after the subsequent event of type 'Y' (if there are no events other than, possibly, 'A' or 'B' in between)
edited = set_insert_markers(raw,'segment',{'X' 1 {'A','B'} 5 'Y'},'event','test','count',10)Once a model has been learned, it can be used to estimate certain aspects of a user's cognitive state on raw continuous data. This can happen in real time within a live experimentation environment, in a real-time simulation using a previously recorded data, in a pseudo-online analysis, and for the purpose of annotating a dataset with BCI estimates.
The simplest use case is the augmentation of a previously recorded data set with additional channels that hold the estimates of a predictive model. The following code illustrates this use case. First, a calibration data set is loaded, a computational approach is defined, and finally, a predictive model is computed.
approach = {'CSP','flt',{'epoch',{'events',{'S 1','S 2'} }} }
[loss,model] = bci_train({'data',io_loadset('bcilab:/userdata/test/imag.set'), 'approach',approach})Then, another data set is loaded (for which perhaps some information about the user's cognitive state shall be deduced from the EEG), and the predictive model is applied to it, yielding additional channel which hold its outputs (in this case, the probabilities for either the left-hand movement imagination or the right-hand movement imagination).The function bci_annotate supports additional options, such as the rate at which predictions should be made (possibly saving time).
dataset = io_loadset('bcilab:/userdata/test/imag2.set')
dataset = bci_annotate(model,dataset)Now, the time course of this channel (and its relationship to the rest of the data) can be investigated using standard EEGLAB tools.
pop_eegplot(dataset)
pop_saveset(dataset)A more elaborate way to obtain BCI outputs for a data set is the so-called pseudo-online analysis. Here, the user has more control over the exact time points (within the data set) at which predictions should be made, which can save time over the annotation of an entire dataset. The following code demonstrates how to obtain the BCI's output at particular time points (here: 3.5s after each occurrence of a particular marker), which is one of the main use cases for onl_simulate.
approach = {'CSP','flt',{'epoch',{'events',{'S 1','S 2'} }} }
[loss,model] = bci_train({'data',io_loadset('bcilab:/userdata/test/imag.set'), 'approach',approach})
newdata = io_loadset('bcilab:/userdata/test/imag2.set')
[predictions,latencies] = onl_simulate(newdata,model,'markers',{'S 1','S 2'},'offset',3.5)The real-time behavior of a previously learned predictive model can be simulated via the functions run_readdataset (which plays back a data set in the background, creating and updating a buffer variable named by default 'laststream'), and run_writevisualization (which reads by default from the laststream variable, invokes its specified predictive model, and calls the given visualization function / code with the result, all in the background).
approach = {'CSP','flt',{'epoch',{'events',{'S 1','S 2'} }} }
[loss,model] = bci_train({'data',io_loadset('bcilab:/userdata/test/imag.set'), 'approach',approach})
newdata = io_loadset('bcilab:/userdata/test/imag2.set')
run_readdataset('Dataset',newdata);
run_writevisualization('Model',model, 'VisFunction','bar(y)');Using BCILAB's real-time processing tools within some experimentation environment comes down to using online plugins which communicate with that interface. There are three categories of online plugins: Input plugins, which read from external sources in the background, output plugins which write to external destinations in the background, and processing plugins, which read from an external source, send data through BCILAB's processing pipeline, and write the results back to an external destination (which is usually in the same framework as the source). The processing plugins do usually not run in the background, but block until terminated by the user. At present, solid support exists for reading from BioSemi amplifier and DataRiver (as well as from files for simulations), processing within the DataRiver environment, as well as writing data to either a MATLAB-based visualization function, or directly to an EEGLAB dataset file.
Reading data from BioSemi devices (tested on Windows/Linux, hopefully working on Mac, as well) is done using the function run_readbiosemi, as demonstrated below:
calib = io_loadset('bcilab:/userdata/test/imag.set');
approach = {'CSP','flt',{'epoch',{'events',{'S 1','S 2'} }} }
[loss,model] = bci_train({'data',calib, 'approach',approach})
run_readbiosemi('UpdateFrequency',20,'SamplingRate',256);
run_writevisualization('Model',model, 'VisFunction','bar(y)');Reading data from DataRiver in the background (which in turns allows to use a variety of lab hardware for data acquisition, transport, synchronization, and storage) is done via the function run_readdatariver. The following code assumes that some model calibration code as above was executed, and that an acquisition device was set up in the DataRiver GUI to produce a stream named C:/tmp/DataRiver. As DataRiver does not (yet) supply its own meta-data (e.g., channel names), these are supplied in form of either an EEGLAB data set with appropriate fields (e.g., srate, chanlocs), or a cell array of name-value pairs, defining these fields.
run_readdatariver('UpdateFrequency',20, 'DiskStream','C:/tmp/DataRiver', 'InputMetadata',calib);
run_writevisualization('Model',model, 'VisFunction','bar(y)');Processing can also be done within DataRiver (in lock-step between input and output), using run_pipedatariver, as shown below:
run_pipedatariver('Model',model, 'InputStream','C:/tmp/DataRiver', 'OutputStream','C:/tmp/BCI', ...
'InputMetadata',calib, 'OutputSamplingRate',25);Raw data can also be written to a .set file (possibly in parallel to being processed), using the function run_writedataset, as below:
run_readbiosemi('UpdateFrequency',20,'SamplingRate',256);
run_writedataset('FileName','C:\Recordings\Myset.set');Support is planned for BCI2000 (untested code available) and OpenViBE environments, as well as BrainProducts and g.Tec amplifiers (and possibly others, depending on hardware availability).
Using the online processing language of BCILAB (onl_* functions), it is very easy to connect to further external systems using custom script code. The general concept of an online script is a loop which reads a chunk of data from some source (formatted as a numeric array with #Channels x #Samples entries), sends it to the BCILAB processing chain, queries a processed output from BCILAB (which is usually a number or a row vector, depending on the type of the provided/requested prediction), and forwards that output to some destination. In addition, the input stream(s) must have been opened beforehand (which is the place to declare meta-data such as channel names and sampling rate), and a predictive model must have been loaded. The following code demonstrates this concept (requesting a row vector of per-class probabilities from BCILAB, by calling onl_predict with the format set to 'distribution'):
onl_newstream('mystream','srate',200,'chanlocs',{'C3','Cz','C4'});
onl_newpredictor('mypredictor',model);
while 1
mychunk = get_new_samples_from_some_device();
onl_append('mystream',mychunk);
myestimate = onl_predict('mypredictor');
send_to_some_destination(myestimate);
endWhen creating a new stream, any kind of meta-data can be assigned in the form of name-value pairs (ideally adhering to the EEGLAB dataset / field name formats where appropriate). The only required data is the sampling rate and channel names. When a new predictor is loaded, the list of channels used by the predictor (determined according to the original calibration data set(s)) is matched against the channels held by the currently existing streams, and the appropriate source stream is chosen automatically. However, if there are multiple concurrent streams with the same channel names, the stream name(s) to consider can be specified in onl_newpredictor to avoid ambiguities.
In many cases, other tasks should be run on the same machine in parallel to doing real-time processing. In these cases, it is usually necessary to conserve CPU resources by using the pause function in between loop cycles. An example implementation is as follows. The variable next shall hold the time, in seconds, when the next output should be produced. At the end of each loop, a pause command is introduced which waits until the appropriate amount of time has elapsed.
output_rate = 25; % desired output sampling rate, in Hz
t = tic;
next = 0;
while 1
mychunk = get_new_samples_from_some_device();
onl_append('mystream',mychunk);
myestimate = onl_predict('mypredictor','distribution');
send_to_some_destination(myestimate);
next = next + 1/output_rate;
pause(next - toc(t));
endSome devices do not support polling of new data since the last request, but instead block until new data has arrived. The following example shows how to handle a source which produces sample-by-sample data; it is also an example of how to use the stream's clock (dictated by the source device, instead of the local timer).
input_srate = 256;
output_srate = 25;
t = 0;
while 1
sample = wait_for_sample_from_device();
onl_append('mystream',sample);
t = t + 1/input_srate;
if t > 1/output_srate
myestimate = onl_predict('mypredictor','distribution');
send_to_some_destination(myestimate);
t = t - 1/output_srate;
end
endFeeding individual samples into a BCI stream can be inefficient, especially at very high sampling rates. To maximize the performance of online code, it can be good idea to collect samples into a block which is then fed into the BCI at once. The following code illustrates this variant.
buffer = {};
t = 0;
while 1
sample = wait_for_sample_from_device();
buffer{end+1} = sample;
t = t + 1/input_srate;
if t > 1/output_srate
block = [buffer{:}];
onl_append('mystream',block);
myestimate = onl_predict('mypredictor','distribution');
send_to_some_destination(myestimate);
buffer = {};
t = t - 1/output_srate;
end
endIt is possible to process multiple concurrent streams with the same predictor (although at present no predefined BCI paradigms exist which allow to calibrate such a predictor); in this case, it becomes important to ensure that the relative timing of the input streams is properly matched (especially if the relative timing is accounted for by the predictor). By default, it is assumed that the first sample of each stream is recorded at exactly the same time, and the time points of all other samples are calculated based on the respective sampling rates. If this is not the case, the xmin field can be specified for each stream to define the correct times (in seconds, and in some arbitrary time domain which must, however, be the same for all streams in question), or, alternatively, it is possible to pass a time stamp that marks the time of the last supplied sample with each (or some) of the onl_append calls, again in seconds and in some arbitrary time domain. As these may be prone to jitter, BCILAB takes into account the last few time stamps (their number can be specified in onl_newstream).
BCILAB has been created from the ground up for easy extensibility. This means that new plugins can be written as simple MATLAB functions, often requiring just a few lines of code. The interface that these functions should adhere to in order to be compatible with all others is generally quite simple, yet at the same time non-constraining. It is therefore possible to implement just about any type of brain-computer interface for use within the toolbox. Only minimal knowledge of the BCILAB system is required - in fact, it is possible to create useful plugins without even knowing how a Brain-Computer Interface works. Given an entry barrier this low, BCILAB is one of the easiest to extend BCI research environments.
BCILAB has been created from the ground up for easy extensibility. This means that new plugins can be written as simple MATLAB functions, often requiring just a few lines of code. The interface that these functions should adhere to in order to be compatible with all others is generally quite simple, yet at the same time non-constraining. It is therefore possible to implement just about any type of brain-computer interface for use within the toolbox. Only minimal knowledge of the BCILAB system is required - in fact, it is possible to create useful plugins without even knowing how a Brain-Computer Interface works. Given an entry barrier this low, BCILAB is one of the first BCI research environments that can be meaningfully extended by its users.
Readers who are not yet familiar with writing MATLAB functions are referred to MATLAB's function help, accessible via Help / MATLAB / Getting Started / Prgramming / Scripts-and-Functions / Functions. Creating a plugin boils down to creating a new .m file in an appropriate directory, and using the same type of file name prefix as used by the other files in that directory, as listed in the following table:
Signal processing: code/filters/flt_*.m Dataset editing: code/dataset_editing/set_*.m Machine learning: code/machine_learning/ml_train*.m and ml_predict*.m BCI paradigms: code/paradigms/para_*.m Online plugins: code/online_plugins/*/run_read*.m or run_write*.m or run_pipe*.m
Each type of plugin function has a different set of required input and output arguments. These carry the data that is always passed by BCILAB, or that is always expected in return by BCILAB. In addition to these, a plugin can have any number of optional input arguments which the plugin user may or may not specify, if desired. The reason for making all other parameters optional (by default) is that any plugin should ideally be usable without the user having to specify parameters first. For example, if a sampling rate converter is invoked without a target sampling rate, it will simply return the input signal unmodified.
Because most plugins have at least one or two optional parameters, and some have dozens (such as independent component analysis or some machine learning tools), every plugin function needs solid and convenient support for handling optional parameters. In addition, every plugin will be displayed by BCILAB's graphical user interface in one place or another. This can be a dialog window that let users review/change optional parameters, or it can be entries in a graphical property table (such as the Review/edit approach panel in the main GUI). For these reasons, the input arguments of every plugin are declared using a descriptive mini-language within MATLAB, which allows to specify every argument's name, position in the argument list, default value, type constraints (if any), a human-readable name and optional help text, as well as some optional features. The functions that form this mini-language begin with the prefix arg and are found in code/arguments.
In addition to custom argument declarations, some types of plugins can declare special properties (properties of the plugin), such as the human-readable name, a description text, etc. This is done via the function declare_properties.
In the following, the various plugin categories are introduced, going from the simple to the complex. It is thus recommended to read through the sections in order. Complete example code for plugins of each type is given. In addition, the functions in the previously mentioned directories are all open source, and can be used for reference and modified as desired.
Online processing plugins are very similar to online processing scripts (see section "Writing online processing scripts" for the processing basics), except that they are functions which declare their arguments in a form that is compatible with BCILAB. The function code/online_plugins/Examples/run_pipetcpip.m is a complete online plugin, and will be analyzed in detail in the following.
The function declaration line for online plugins usually looks like the following (no return values, and no input arguments except for varargin). The portion run_pipe indicates to BCILAB that this is a pipelining online plugin, which reads, in a loop, a block of data from some source, pipes the data through BCILAB, and then forwards the result to some destination. The other two types of BCILAB plugins are input plugins (which read from a source in the background) and output plugins (which write to a destination in the background). The first line is called (in MATLAB) the "H1 header"; this is the executive summary of the function, also displayed by the built-in help and doc commands when run on directories.
function run_pipetcpip(varargin)
% Run BCILAB's real-time engine as a processing node via TCP/IP
% run_pipetcpip(Arguments...)
Following the declaration comes a section which explains what the function does. This is the core documentation of the function.
%
% This plugin reads raw data from some source host/port and writes predictions to some output
% host/port. This example code is implemented using MATLAB's Instrument Control Toolbox.
%
% The example plugin reads raw signal data from some TCP/IP server, formatted as one
% sample per line (and each line containing a space-separated list of floating-point values, in
% string format). For simplicity, the sampling rate and channel names of the input data stream are
% not communicated over the TCP link, and are therefore to be manually specified in user parameters.
% The plugin processes the incoming data and produces outputs at a fixed rate, which are forwarded
% to some destination TCP server. The output sampling rate is usually much lower than the raw-data
% rate (e.g. matching the screen refresh rate), and the output data form can be specified in an
% optional parameter. The message format is one line per output, as space-separated list of
% floating-point values.
%The next comment lines list the input (and output) arguments and their meaning, if any. This material will be displayed when typing help run_pipetcpip or doc run_pipetcpip in the command line, and it is therefore critical that the parameter names and descriptions match the actual usage. Although not always the case throughout the toolbox, it shall be adhered to for all new code. The format for parameter names should ideally be CamelCase, and parameter names should be reasonably informative (as they are displayed to users in the GUI); if there are precedents for some parameters in other functions, please use the same names to reduce the amount of terminology that the users need to deal with. Also, please make sure that all parameters have reasonable defaults.
% InputHost : hostname (or IP string) of the source machine (default: '127.0.0.1')
%
% InputPort : listening port of the source service (default: 12345)
%
% InputMetadata : Meta-data of the input stream. This is a struct or cell array of name-value
% pairs with meta-data fields to use. The mandatory fields are 'srate' and
% 'chanlocs', where chanlocs is either a channel locations struct array, or a cell
% array of channel names, or the number of channels (in which case a cell array of
% the form {'A1','A2', ..., 'A32','B1', ...} is created). Optionally, the field
% 'datasource' can be set to point to a dataset on disk or in a MATLAB workspace
% variable.
%
% Model : a file, struct or workspace variable name that contains a predictive model, as
% previously computed by bci_train (default: 'lastmodel')
%
% OutputHost : hostname (or IP string) of the destination machine (default: '127.0.0.1')
%
% OutputPort : listening port of the destination service (default: 12346)
%
% OutputSamplingRate : rate, in Hz, at which the output stream shall be sampled (default: 20)
% make sure that this rate is low enough so that BCILAB can process in real
% time (otherwise it would lag)
%
% OutputFormat : format of the data sent to the output stream, can be one of the following:
% 'expectation': the expected value (= posterior mean) of the outputs; can be
% multi-dimensional but is usually 1d (default) this mode is
% appropriate for simple applications that expect a smooth control
% signal, or for applications that expect a regression output
% 'distribution' : parameters of the output distribution; for discrete
% distributions, this is one probability value for each target
% (adding up to 1) this mode is appropriate for more advanced
% applications that use the full output distribution (e.g., for
% decision-theoretical processing) (default)
% 'mode' : the most likely output value (currently only supported for discrete
% distributions) this mode is appropriate for simple applications that
% take a non-probabilistic classifier decision (e.g., as from a Support
% Vector Machine)The remaining lines contain a command-line usage example and authorship notice.
% Example:
% run_pipetcpip('Model','lastmodel', 'InputPort',2050, 'OuputHost','192.168.1.10','OutputPort',...
% 2051, 'InputMetadata',{'srate',256,'chanlocs',{'C3','Cz','C4'} })
%
% Christian Kothe, Swartz Center for Computational Neuroscience, UCSD
% 2011-01-18The comment block is followed by a declaration of a property -- here: the human-readable name of the plugin -- which is displayed in the GUI menu, and thus mandatory.
% declare the name of this component (shown in the menu)
declare_properties('name','TCP (Instrument Control Toolbox)');Next, the function arguments are formally declared; this is initiated with the following line (the ... indicate that the statement continues in the next line).
arg_define(varargin, ...A list of formal argument declarations follows (this is an advanced alternative to the usual declaration of function arguments in the function declaration line), where each argument is declared by the function arg(). See also help arg_define and help arg The first element in the arg() declaration is the list of names of the current argument to be declared (each can have multiple names). In particular, the first name is the one that is used throughout the function's code (thus, it can be short, and may be in any naming scheme), and the second name (if any) is the human-readable name, which is displayed in GUIs, and in the preceding help text. Any other names are optional, and useful for legacy support/compatibility. The following elements are all optional, but are used in most cases. The next element is the default value (here the string '127.0.0.1'). The default value determines the MATLAB type of the argument, if not otherwise specified (the MATLAB type controls the type of widget that is used in GUIs to display/manipulate the argument). The next element (here: []) is the range constraint on the argument, if any (it allows to restrict the permitted range of the argument). The next element is the help text of the argument. This is split into an executive summary (which must be at most 60 characters), analogous to the H1 line in the function's help, and, following the full stop, any additional help text. If this argument is shown in a dialog (click Online Analysis / Process data within... / TCP (Instrument Control Toolbox) in the BCILAB main menu to see how the function under discussion is rendered), the executive summary will be shown next to the edit field, and the remaining help will be displayed as tool tip if the user hovers the mouse over the edit field.
arg({'in_hostname','InputHost'}, '127.0.0.1', [],'Source TCP hostname. Can be a computer name, URL, or IP address.'), ...The next argument has a default that is a number; therefore, an error message will pop up if the user types in a non-numeric string in the edit field.
arg({'in_port','InputPort'}, 12345, [],'Source TCP port. Depends on the source application, usually > 1024.'), ...The follwing argument (InputMetadata) is special; it lists an empty default, but uses a function as its range constraint (and is declared via arg_sub instead of arg). The result is that whatever arguments that other function declares, will be "sub-arguments" of InputMetadata; they will be displayed as subordinate arguments in a GUI panel or spliced into the argument list in a GUI dialog. To pass the sub-arguments of this parameter in the command line, a cell array containing name-value pairs is used where the value for InputMetadata would be expected (see also code example). A struct with subfields for the respective parameters can also be passed. InputMetadata allows to specify the list of meta-data fields of the online stream (i.e., srate, chanlocs, etc.), but can also be used to refer to some existing data set from which the meta-data shall be taken (e.g., from the calibration set).
arg_sub({'in_metadata','InputMetadata'},{},@utl_parse_metadata, 'Meta-data of the input stream. These are fields as they appear in EEGLAB data sets; only sampling rate and channel labels are mandatory.'), ...The next argument, Model, holds a string (default: 'lastmodel') that refers to the name of the predictive model to be used; an appropriately-named variable is expected to exist in the workspace by the time this function is executed. Following the help text, the type of the argument is changed from 'char' (string) to 'expression', which indicates that any MATLAB expression can be used in this place, and will be evaluated by the GUI (e.g., 'load(mydetector.mat)')).
arg({'pred_model','Model'}, 'lastmodel', [], 'Predictive model. As obtained via bci_train or the Model Calibration dialog.','type','expression'), ...The following three arguments are a string, a number, and another number.
arg({'out_hostname','OutputHost'}, '127.0.0.1',[],'Destination TCP hostname. Can be a computer name, URL, or IP address.'), ...
arg({'out_port','OutputPort'}, 12346, [],'Destination TCP port. Depends on the destination application, usually > 1024.'), ...
arg({'out_srate','OutputSamplingRate'}, 20,[],'Output sampling rate. This is the rate at which estimate should be computed. If this value is too high, the BCI will start to lag behind.'), ...The last argument, OutputFormat, has a string as its default, but lists a cell array of strings as its type constraint. Since the possible input strings are thereby constrained, the parameter is editable via a pull-down menu in any GUI that is rendered for this plugin. The trailing ");" terminates the arg_define( clause.
arg({'out_format','OutputFormat'}, 'distribution',{'expectation','distribution','mode'},'Format of the produced output values. Can be the expected value (posterior mean) of the target variable, or the distribution over possible target values (probabilities for each outcome, or parametric distribution), or the mode (most likely value) of the target variable.'));An important caveat holds for the first name of each argument: if any function with the same name exists in MATLAB's path, this is very likely to lead to errors in current MATLAB versions (up to 7.10). For this reason, attempt to use names that are unlikely to clash with functions that people might have in their path (e.g., use underscores, or use the CamelCase parameters as the sole declared name.
Following the argument declarations, the actual function code begins. First, the meta-data is turned into a struct with fields srate, chanlocs, etc., using a convenience function specifically for online plugins (other plugins use the same function). This function allows to pass both a listing of meta-data fields, such as srate, chanlocs, etc., manually, or allows to specify them in a GUI, but it also allows to pass an entire data set for the parameter from which the relevant meta-data fields shall be taken.
meta = utl_parse_metadata(in_metadata);Then, a new online stream is opened and a new predictor is loaded, nearly identical to online script example.
% set up BCILAB stream
onl_newstream('stream_tcpip','srate',meta.srate,'chanlocs',meta.chanlocs);
% load the given predictor
onl_newpredictor('predictor_tcpip',pred_model,'stream_tcpip');Next, the actual TCP/IP connections are established. For simplicity, the Instrument Control Toolbox is used here, but an alternative would have been Java code as used in the (unrelated) function hlp_worker.
% connect to source
src = tcpip(in_hostname,in_port);
fopen(src);
% connect to destination
dst = tcpip(out_hostname,out_port);
fopen(out);Finally, the online processing loop is entered, which uses essentially the same pattern as the previous one-sample-at-a-time online scripting example. However, the sample is obtained using the appropriate TCP interface code, and the estimate (here called result) is sent to a destination using the appropriate TCP code, as well (and custom message formatting).
t = 0; % current stream clock
while 1
% get a sample and append it to the BCILAB stream
sample = str2num(fgetl(src))';
onl_append('stream_tcpip',sample);
t = t + 1/meta.srate;
% if it is time to produce an output sample...
if t > 1/out_srate
t = t - 1/out_srate;
% compute the output
result = onl_predict('predictor_tcpip',out_format);
% and send a message
fprintf(dst,'%s/n',sprintf('%.3f ',result));
end
endAn entirely different form of online plugin are those that read or write their data in the background - i.e., any other code, including other data acquisition, processing or sending code (even certain offline analysis scripts) can be run in parallel to it. This is only easy to implement for data sources which do not block the calling function when no samples are available (possible for TCP, but too complicated with MATLAB's Instrument Control Toolbox to serve as example). The BioSemi input plugin (code/online_plugins/BioSemi/run_readbiosemi.m) is a simple example of such a source, and will be analyzed in detail in the following.
First, the plugin function is defined, and input arguments are documented.
function run_readbiosemi(varargin)
% Receive real-time data from BioSemi.
%
% This plugin connects to a BioSemi ActiveTwo amplifier (Mk1 or Mk2), using the BioSemi USB driver.
% It was tested on Linux and Window, but it may be necessary to recompile the driver interface for
% your platform (esp. on Linux); see the readme files in dependencies/BioSemi-2010-11-19 for this.
%
% The meta-data (channel names and order) is pre-defined by the amplifier, but it is possible to
% read only a subset of the provided data (for efficiency), using the ChannelRange and SamplingRate
% parameters.
%
% In:
% MatlabStream : name of the stream to create in the MATLAB environment (default: 'laststream')
%
% ChannelRange : numeric vector of channel indices that should be recorded (referring to the
% default BioSemi channel order); default: 3:131
%
% SamplingRate : sampling rate for the amplifier, in Hz (default: 256)
%
% UpdateFrequency : update frequency, in Hz (default: 25)
%
% Example:
% run_readbiosemi('UpdateFrequency',30, 'SamplingRate',512);
%
% Christian Kothe, Swartz Center for Computational Neuroscience, UCSD
% 2010-11-19Then, the name of the plugin is declared
declare_properties('name','BioSemi amplifier');and the arguments are parsed. If the output of arg_define is captured in a variable (as below), the declared arguments will be returned as subfields of this variable. The arguments are comparable to the input arguments of the previously shown plugin, with the exception of the MatlabStream argument. This argument allows the user to specify the name of the stream variable which will be created in the workspace, and be updated in the background. This makes it possible to launch other plugins later which periodically read from this variable (perhaps also in the background).
opts = arg_define(varargin, ...
arg({'new_stream','MatlabStream'}, 'laststream',[],'New Stream to create. This is the name of the stream within the MATLAB environment.'), ...
arg({'channel_range','ChannelRange'}, 3:128+3,[],'Reduced channel range. Allows to specify a sub-range of the default BioSemi channels.'), ...
arg({'sample_rate','SamplingRate'}, 256,[],'Sampling rate. In Hz.'), ...
arg({'update_freq','UpdateFrequency'},10,[],'Update frequency. New data is polled at this rate, in Hz.'));Then, a connection to the amplifier is established
conn = bs_open;and an online stream with meta-data is created (like in the previous plugin case).
onl_newstream(opts.new_stream,'srate',opts.sample_rate,'chanlocs',conn.channels(opts.channel_range),'xmin',toc(uint64(0)));;With stream and connection having been set up, the background acquisition is initiated via the function onl_read_background. This function expects the name of the stream variable to write to, a function which will be periodically called to obtain blocks of new samples, and the rate at which the stream variable should be updated. The function which reads a block is here given as @()read_block(conn,opts), which is an inline definition of an unnamed function (a.k.a. lambda function) with no arguments (empty brackets), whose only statement is read_block(conn,opts). The return value of that statement is taken as the return value of the newly defined function.
onl_read_background(new_stream,@()read_block(conn,opts),update_freq);The actual work is done in the read_block sub-function, which takes two arguments - a handle to the BioSemi amplifier, and the options structure that was originally created by arg_define.
function block = read_block(conn,opts)
block = bs_read(conn);
if ~isempty(block)
block = block(opts.channel_range,1:double(bshandle.srate)/opts.sample_rate:end); endThis function fetches a new block from the amplifier connection, sub-samples it (poorly) for performance reasons, and returns the result. The background processing will be automatically terminated if this function throws an error, or if the stream that should be updated is deleted or replaced.
Background output plugins are programmed in a very similar way to input plugins. In the following, the function code/online_plugins/TCP/run_writetcp.m will be analyzed in detail, which sends processed BCI outputs to a remote machine via TCP (this time using Java code from within MATLAB).
First, the function is declared as usual, and parameters are documented (not shown).
function run_writetcp(varargin)Then, the mandatory GUI name of the function is declared.
declare_properties('name','TCP');Next, the parameters of this function are introduced. This holds no surprises - note, however, that the Model parameter has its type set to 'expression', which means that, if a string is passed, it will be evaluated (against what is defined in the MATLAB workspace), and otherwise, any data structure passed for this argument is taken as-is. Thus, both the name of a model in the workspace can be passed here (or entered in the respective GUI edit field), as well as the actual data structure itself (e.g. in script code). In addition, it is possible to type an expression which, e.g., loads the model from disk in the GUI dialogs. The message format is also an expression, which allows to define formatting functions in the GUI, using MATLAB code (but does not rule out passing function handles directly from scripts or the command line).
arg_define(varargin, ...
arg({'pred_model','Model'}, 'lastmodel', [], 'Predictive model. As obtained via bci_train or the Model Calibration dialog.','type','expression'), ...
arg({'in_stream','SourceStream'}, 'laststream',[],'Input Matlab stream. This is the stream that shall be analyzed and processed.'), ...
arg({'out_hostname','OutputHost'}, '127.0.0.1',[],'Destination TCP hostname. Can be a computer name, URL, or IP address.'), ...
arg({'out_port','OutputPort'}, 12346, [],'Destination TCP port. Depends on the destination application, usually > 1024.'), ...
arg({'out_form','OutputForm'},'distribution',{'expectation','distribution','mode'},'Output form. Can be the expected value (posterior mean) of the target variable, or the distribution over possible target values (probabilities for each outcome, or parametric distribution), or the mode (most likely value) of the target variable.'), ...
arg({'msg_format','MessageFormat'},'@(D)[sprintf(''%.3f '',D) ''/n'']',[],'Message Format. Either a formatting function (Data to string) or an fprintf-style format string (in quotes).','shape','row','type','expression'), ...
arg({'update_freq','UpdateFrequency'},10,[],'Update frequency. This is the rate at which the graphics are updated.'), ...
arg({'pred_name','PredictorName'}, 'lastpredictor',[],'Name of new predictor. This is the workspace variable name under which a predictor will be created.'), ...
arg({'conn_timeout','ConnTimeout'},15,[],'Connection timeout. If the remote machine is unreachable for at least this many seconds, the connection is dropped and processing is ended.'));In the following, some special input handling is done, which allows to pass standard formatting strings (e.g. '%0.3f %0.3f /n') in place of a formatting function (for convenience).laststream
if ischar(msg_format)
msg_format = @(D) sprintf(msg_format,D); endNext, the TCP connection is established using Java code (see Java documentation of Socket and DataOutputStream), is configured, and a so-called Java Stream is obtained, which allows to send formatted data over the connection.
conn = Socket(out_hostname, out_port);
conn.setTcpNoDelay(1);
conn.setSoTimeout(round(1000*conn_timeout));
strm = DataOutputStream(conn.getOutputStream());Finally, a background writer job is started, which periodically processes data and calls the the send_message function to send the result to some remote device. The function onl_write_background loads the predictor, connects it to a stream, and launches a timer which periodically processes data and calls the message sending function. As before, the message-sending function is declared here as an in-line unnamed function (or lambda function), which takes one parameter (y, which is the BCI output) and determines its result by calling send_message with that parameter and a few others that were obtained before.
onl_write_background(@(y)send_message(y,conn,strm,msg_format),in_stream,pred_model,out_form,update_freq,0,pred_name);The message sending function is implemented as follows:
function send_message(y,conn,strm,formatter)
strm.writeBytes(formatter(y));
strm.flush();Any data processing step that can be described as taking a signal as input (plus optional parameters) and producing another signal as output can be implemented in BCILAB as a signal processing plugin, and can subsequently be used with other plugins and parts of the toolbox for brain-computer interfacing, cognitive monitoring, etc.. All signal processing plugins are single MATLAB functions (found in the code/filters directory, starting with flt_) that follow a simple contract of only a few lines.
Types of signal processing plugins. Just like EEGLAB, BCILAB supports two signals formats - continuous signals and epoched signals. Accordingly, there are two broad groups of signal processing plugins: those, which operate on continuous signals, and those which operate on epoched signals. While epoched signals are usually processed each epoch by itself (i.e., not moving information across epochs), continuous signals are often not just processed each sample by itself - instead, there are three distinct sub-types of signal processors (including those whose emitted samples depend on more than one source sample, e.g., spectral filters). According to whether emitted samples depend on source samples that lie in the future or not, these signal processing plugins are called in BCILAB non-causal/stateful (taking information from the future) or causal/stateful (taking samples exclusively from the present and past samples). Finally, plugins which process strictly each sample by itself are called stateless. All four types of signal processing functions will be illustrated with examples in the following.
Features of signal processing plugins. Signal processing plugins can be applied either to full pre-recorded data sets (i.e. very long signals), or they can be applied incrementally to blocks of data as they become available "online" from some acquisition device, often using the same code path in both cases. In some cases, however, some data structures may be pre-computed for more efficient online processing (e.g., computing an efficient filter kernel from some given frequency specification), so the parameters used to apply some processing step offline (e.g., the convenient filter frequency specs) may be different from the parameters used to achieve the same effect in real time (e.g., the efficient filter kernel). The solution used in BCILAB is to automatically annotate every data set with a formal description of how to replicate the entire processing (that generated the data set) both offline, and online - i.e., there are two different annotations stored with each data set. A plugin (when called with some parameters) may then specify an alternative set of parameters used to achieve the same effect in real time instead of offline.
Integration into a processing pipeline. Like in other plugins, input arguments are declared in a way that allows GUI dialogs and/or panels to be generated. Since signal processing is usually one (subordinate) step in a larger pipeline, the arguments of signal processing functions are mostly displayed in large parameter tables, also called property grids (see the Review/Edit approach panel in the BCILAB main menu), where the user can configure an entire approach at once. It is, however, also possible to apply a signal processing function individually to an EEGLAB dataset, just like in standard EEGLAB scripting on the command line or from an analysis script (e.g., for artifact rejection, exploratory filtering, etc.). A special feature of BCILAB is that the user typically does not need to care about the order in which to apply signal processing functions when they are run inside the BCILAB pipeline. To make this possible, each plugin specifies a set of ordering relationships, i.e., its preferences as to when it should be applied w.r.t. other filters (explained later).
These plugins operate on epoched signals, that is, signals which are split into segments of data (of uniform length). A standard example of epoch-based processing is the FFT filter; it transforms each given epoch from the time domain into the frequency domain. A full-fledged version of this is supplied as standard filter named flt_fourier, but a simpler example (here called flt_fft) will be worked out in the following. To be able to test the function, create a file called flt_fft.m in the directory code/filters and paste the following code sections into it. A usage example will be shown later.
The function declaration of any epoched signal processor has a single return value, namely the output signal. The input is always declared as varargin.
function signal = flt_fft(varargin)
% Apply an FFT to each epoch of an epoched signal (Example code).
The rest of the documentation follows, explaining the parameters. This function takes a single optional parameter, LogPower.
% Signal = flt_fft(Signal, LogPower)
%
% This is example code to transform a signal into the frequency domain. A
% fully-featured version of this is flt_fourier.
%
% In:
% Signal : Epoched data set to be processed
%
% LogPower : whether to take the logarithm of the power (instead of the raw power) (default: false)
%
% Out:
% Signal : processed data set
%
% Christian Kothe, Swartz Center for Computational Neuroscience, UCSD
% 2011-01-19Any signal processing plugin uses the following line as its prologue. The line allows exp_beginfun to record the used input parameters (among others, to be able to annotate the resulting data set after processing, but also to be able to look up the result from a cache without having to do the computation in the first place, in case the same computation had been run already at some earlier time). If the plugin is designed for pure offline analysis and thus should give an error when applied in an online processing setting, use 'offline' instead of 'filter' in the prologue line.
if ~exp_beginfun('filter') return; endNext, the properties of the filter are being declared, including the GUI name (here: EpochedFFT), and its ordering relationships w.r.t. other filter stages in the toolbox. There are four types of possible ordering relationships: follows, precedes, cannot_follow and cannot_precede. The first two are 'soft' preferences - for example, if the data is resampled (using flt_resample), it is generally a good idea to run any heavy-duty processing after that (e.g. flt_reconstruct), since it will be faster. The latter two are 'hard' constraints - for example, a continuous-data filter (such as flt_iir) cannot be run after the signal has been converted to epochs (via set_makepos. A special type of ordering relationship is 'depends', which means that the filter requires that some other filter has been run on the data in a previous step - for example, an epoched filter like the one being defined here cannot be run on non-epoched data; therefore, it depends on set_makepos. Depends implies cannot_precede. These relationships are by default transitive; i.e., if C follows B and B follows A, C will follow A, if possible (even if B was not used). Spectral filters such as the one being defined here are most useful when applied to properly spatially filtered data, and on properly temporally filtered data; therefore, this filter follows by default after both flt_project and flt_window. Any such relationship can be overridden by the user (except for the hard constraints) both in the command line and in the GUI, and also when defining a new paradigm.
Finally, a special property that a filter may or may not have is that any channel that it outputs depends only on the data of the channel with the same name in the input signal. This is true, for example, for most spectral and temporal filters (e.g. the output channel 'C3' is computed on the raw data of 'C3', and nothing else), but it is false for most spatial filters (such as the surface laplacian or ICA). This property is optional, but makes the filter easier to handle in online settings, as it allows the toolbox to resolve which channels of raw data any given predictive model actually depends on - so it can automatically identify the correct streams to use as data sources when a new predictor is loaded for online use, or it can give meaningful error messages when a required channel is not present in any of the source streams being recorded.
declare_properties('name','EpochedFFT', 'depends','set_makepos', 'follows',{'flt_project','flt_window'}, 'independent_channels',true);Now, argument declaration of the filter begins, using the function arg_define. In normal usage, the first input is always the varargin of the function.
arg_define(varargin,...... and the first argument being declared is generally called 'signal' (and carries the input signal). It is usually being declared via arg_norep instead of arg, which denotes that the parameter is not reported in user interfaces (the user is supposed to specify the optional parameters there, rather than the actual signal data).
arg_norep({'signal','Signal'}), ...The second argument is optional, and it allows to toggle whether the logarithm of the spectral power density should be taken, or not (default: no). See also the online plugin authoring guide (or enter doc arg_define in the MATLAB command line) for a documentation on the argument declaration format.
arg({'do_logpower','LogPower'}, false, [], 'Compute log-power. Taking the logarithm of the power in each frequency band is easier to handle for simple statistical classifiers, such as LDA.'));Following these declarations, the actual signal processing implementation begins. In the case of an FFT filter, this is relatively simple and equals exactly the type of code that would be required for an EEGLAB plugin.
% apply FFT and cut mirror half of the resulting samples
tmp = fft(signal.data,[],2);
tmp = tmp(:,1:signal.pnts/2,:);
% take signal power or log(power)
if do_logpower
signal.data = log(abs(tmp));
else
signal.data = abs(tmp);
endAny signal processing function is concluded by an epilogue using the function exp_endfun. This is the place where alternative parameters for the online processing case could be specified (example later). The function serves to incorporate any annotations into the resulting data, and may also cache the result on disk or in memory (if the toolbox is configured appropriately).
exp_endfun;Testing the function from the GUI. The function is now ready to be used from the graphical user interface. As the function transforms the raw signal of each channel into the frequency domain (within some epoch window), a possible use case might be as pre-processing for some multi-band spectral classification. As testing data for this, the imagined movements dataset in userdata/test/imag.set will be used. It contains the marker 'S 1' whenever a symbol was presented which instructed the subject to imagine a movement of her left hand, and the marker 'S 2' whenever, she was instructed to imagine a movement of her right hand; in total, there are approx. 80 such trials per condition in the recording.
Computational approach / calibration stage. For learning, the raw data will be resampled to 100 Hz, and a surface laplacian with 8 neighbors around each electrode will be computed (yielding a spatially filtered signal). Then, epochs will be extracted following 0.5s after each stimulus marker (to account for the delayed reaction of the subject) and spanning 3s until 3.5s after the respective stimulus. Each epoch will be labelled according to the type of marker from which it was derived. Then, each epoch will be transformed into the frequency domain via FFT (using the new plugin). ThenNext, spectral power features are being extracted for each epoch; specifically, the spectral power in a set of frequency windows (6-15 Hz, 15-30 Hz, 6-30 Hz) will be averaged for each channel (yielding 3x #channels = 96 features per epoch). A non-linear classifier will be learned on the resulting data using regularized quadratic discriminant analysis.
Computational approach / prediction stage. During online processing, the incoming data will be resampled to 100Hz, a surface laplacian with 8 neighbor electrodes will be derived for each channel, and the most recent 3s of the incoming data will be transformed into the spectral domain (using the new plugin). From these data, spectral power features will be computed as described before, and the resulting features will be classified using the previously learned quadratic classifier.
Evaluation approach. The performance of the newly defined method will be evaluated offline using 10x blockwise cross-validation, where 5 trials around any test trial will be excluded from the training set, using mis-classification rate as the loss measure.
Instructions. Follow the steps from the extended practicum (ftp) to load the toolbox and the data, but stop at the point where Common Spatial Patterns would be selected as the BCI paradigm to use. Select instead the Windowed Means (para_windowmeans) paradigm, and click "Refine". Use [0.5 3.5] as the epoch time window, and choose {'S 1','S 2'} as event marker types (note: there are 2 spaces between the S and the respective digit). Choose [] as the frequency-domain selection. The time windows are more difficult to specify, as the unit of measure is seconds (in time), rather than Hz (in frequency): use [2 5; 5 10; 2 10]. Choose qda as the classifier, and click OK. In the next screen, uncheck the checkbox labeled SpectralSelection, and check instead EpochedFFT. Click OK to finalize the approach, type in a descriptive name for the approach (e.g., Multi-band QDA) and click "Save on disk..." if you like to re-use what was just defined at a later time. Choose a file name, click Ok, and also click OK in the Save approach dialog.
Click Offline Analysis / Train new model..., and click ok. Wait for the Review Results dialog to pop up.
Stateless signal processing plugins operate on continuous signals, produce one output sample for every input sample, and each output sample Y(t) depends only on the respective input sample X(t). Thus, they cannot implement any spectral or temporal filtering; instead, they are restricted to spatial filtering operations on the data (such as channel selection, re-referencing, linear projection or decomposition, surface laplacian, non-linear reconstruction, etc.). They are called "stateless", because there is no information that must be maintained after having processed any sample, in order to process the next sample.
One of the simplest examples for stateless signal processors is the channel selector - a filter which allows to select a subset of channels from a data set. In the following, the standard function code/filters/flt_selchans.m will be analyzed.
First, the function's signature is defined. The only return value of any stateless signal processor is its output signal. The input arguments are always declared as varargin.
function signal = flt_selchans(varargin)
% Selects a subset of channels from the given data set.
% Signal = flt_selchans(Signal, Channels)Next, the inputs and outputs are documented. In almost all BCILAB plugins, these arguments can be passed either in order of appearance, i.e., flt_selchans(mysignal,{'C3','C4','Cz'}) or in the form of name-value pairs (in any order), using the names listed in the documentation, i.e., flt_selchans('Signal',mysignal,'Channels',{'C3','C4','Cz'}). This is enabled by using arg_define to specify the function's input arguments. A mixture of the two modes, i.e. passing the first n arguments in order of appearance, followed by some of the remaining arguments passed as name-value pairs is usually not allowed, unless the function explicitly accounts for it (enter doc arg_define for more information). For any type of signal processor, it is, however, generally disallowed. Since arguments often have multiple names, these alternative names may be used to specify arguments when calling a function, e.g. flt_selchans('signal',sysignal,'channels',{'C3','C4','Cz'}) uses the lower-case versions of these parameters, as declared later in the code.
% In:
% Signal : Data set
%
% Channels : vector of channel indices or cell array of channel names to retain
%
% Out:
% Signal : EEGLAB data set restricted to the supplied channels (that were found in the original set)Next, the standard prologue line for all filters is invoked (see epoched plugins for additional details).
if ~exp_beginfun('filter') return; endThen, the properties of the function are being declared; the properties must always be declared before the function arguments. Here, the GUI name, and certain ordering preferences are specified. Recall that if no ordering relationships are declared, the function will not show up by itself in any of the standard paradigms (but only in custom paradigms which explicitly make use of (and know when/where to apply) the filter in question). The channel selection prefers to precede any surface laplacian, ICA decomposition and Re-Referencing (as it serves to remove missing or broken channels which should not affect any of those operations). Not every possibly reasonable ordering relationship has to be written down explicitly, as these are transitive (e.g. whatever prefers to follow flt_laplace also follows flt_selchans).
declare_properties('name',{'ChannelSelection','channels'}, 'precedes',{'flt_laplace','flt_ica','flt_reref'});Next, the two arguments of the function and their defaults are being declared. The second argument, 'channels', has an empty default value, but should be a cell array of strings (namely the channel labels to be retained). To specify this, the type and shape properties of the argument are explicitly defined.
arg_define(varargin, ...
arg_norep({'signal','Signal'}), ...
arg({'channels','Channels'}, [], [], 'Cell array of channel names to retain.','type','cellstr','shape','row'));Finally, the actual signal processing code follows. Here, the EEGLAB function pop_select is being used to select the channels from signal (and produce the appropriate return value). If you use EEGLAB functions extensively, you may have to benchmark (and perhaps optimize) their online performance, as they will be called many times a second - thus, use them with care. However, if you implement certain operations such as channel selection manually, please make sure that you update meta-data accordingly, as well (this makes up the majority of code); for example, pop_select does not just update the signal.data field, but also its chanlocs, ica matrices, etc. Otherwise, some subtle bugs may be introduced into later processing stages that depend on these meta-data.
signal = pop_select(signal,'channel',set_chanid(signal,channels),'sort',0);Any filter is concluded with the epilogue function, exp_endfun (see the epoch signal processor example for more details).
exp_endfun;In the following, a special type of spatial filter, which demonstrates how to use signal meta-data to implement complex processing, will serve as an advanced example. The function flt_selvolume (code/filters/flt_selvolume.m) assumes that the input signal has an associated ICA decomposition in its meta-data, and in addition, that equivalent dipole coordinates for every independent component have been fitted and that their corresponding anatomical structure labels have already been looked up (also stored in the signal meta-data). Thus, this filter depends on set_fit_dipoles to fit the dipoles (using the dipfit plugin to EEGLAB) and look up the anatomical labels (using Talairach), which in turn depends on flt_ica to compute the ICA decomposition (e.g., using Infomax or AMICA).
First, the function signature is defined as below. For any stateless filter, there must be exactly one output argument (the name is arbitrary, but using the same name as the input signal is convenient). The input arguments are always declared as varargin.
function signal = flt_selvolume(varargin)
% Select independent components according to what brain volumes they are in.Next, the input arguments are declared.
% In:
% Signal : input data set, assumed to have an associated IC decomposition
%
% Hemisphere : Cell array of hemisphere names to retain (or empty to retain all) (default: {})
%
% Lobe : Cell array of lobe names to retain (or empty to retain all) (default: {})
%
% Gyrus : Cell array of gyrus names to retain (or empty to retain all) (default: {})
%
% TransformData : Return the result as data (instead of as IC decomposition).
%
% Out:
% Signal : input data set restricted to dipoles which lie in the respective areas
%
% Notes:
% Requires that set_fit_dipoles (and flt_ica) have been run before.Then, the standard prologue line for signal processing functions follows (see also epoch-based filters).
if ~exp_beginfun('filter') return; endNext, the plugin's GUI name is declared, and some ordering relationships w.r.t. other filters are expressed. In this example, the function depends on set_fit_dipoles, and prefers to precedes set_makepos (among others, for efficiency reasons - as this is a data reduction step, and because the code has not been written to handle epoched data).
declare_properties('name','VolumeSelection', 'depends','set_fit_dipoles', 'precedes','set_makepos');Then, the function's arguments are being declared. As for the epoched plugins, the first input must be named 'signal', and be treated by the function as the method's input signal; all other inputs are optional (see also: epoched signal processors).
arg_define(varargin, ...
arg_norep({'signal','Signal'}), ...The subsequent three arguments of the function are of a rare (though useful) type. The range is a cell array of strings, which is interpreted as a set of possible strings that the value can take on. However, the default value is not one of the strings in the range - instead it is a logical value. If the default value is either a logical value or a cell array of strings (while the range is also a cell array of strings), the type of the argument is inferred to be a subset of the strings specified in range. In other words, the value is a cell array of strings, each of which must be listed in the range; if the value is true or false, it is translated to either the full set (range) or the empty set ({}). In the GUI, arguments of this type are displayed as an array of checkboxes - one for each string in range, or a multi-select list.
The first such argument allows to specify from which hemispheres of the brain ICs should be retained. By default, all hemispheres are checked.
arg({'sel_hemi','Hemisphere'},true, {'Left Cerebrum','Right Cerebrum','Left Cerebellum','Right Cerebellum','Left Brainstem','Right Brainstem','Inter-Hemispheric'}, 'Hemispheres to retain. Restrict ICs to those that fall in the specified hemispheres.'),...The second and third argument (not shown here for brevity) are similar, but allow to specify the lobes and gyri to retain. The fourth argument is a typical boolean argument, letting the user specify whether the output should be channel data with a reduced ICA annotation, or directly the reduced IC data itself.
arg({'do_transform','TransformData','transform'},false,[],'Transform the data rather than annotate. By default, ICA decompositions are maintained as annotations to the data set, but several algorithms operate by default on the raw data, and are unaware of these annotations.'),...The last argument is invisible to the user, and has no default value assigned (i.e., the argument will not be present in the function's workspace unless manually assigned). Generally, the default value is being assigned to an argument when no value for it was passed to the function, and there are two default values with special behavior: unassigned, meaning that the argument does not show up in the function workspace when not overridden with a value, and mandatory, meaning that a value must be passed for the respective argument, or else an error message is being generated. If no default is specified (such as for the initial 'signal' argument), it defaults to []. In this function, retain_ics allows to bypass the (computationally costly) logic of the function which determines what ICs should be retain.
arg_norep('retain_ics', unassigned));If that variable does not exist in the workspace, it needs to be computed (which is the regular case). The following code analyzes the .dipfit.model sub-structure of the signal (which is being filled in by set_fit_dipoles), and in particular checks, for each independent component of the data, whether a volume around its equivalent dipole coordinates in the brain contains any of the labels that were checked in the three selection arguments. If so, it is retained, otherwise, it is discarded. This test is done separately for each of the three criteria (i.e., not being in any of the checked hemispheres leads to a component being discarded, but not being in any of the checked lobes, as well).
if ~exist('retain_ics','var')
retain_ics = true(1,length(signal.dipfit.model));
% for each IC...
for ic=1:length(retain_ics)
% for each of the three partitions...
for partition = {sel_hemi,sel_lobe,sel_gyrus}
% for each of the checked labels in the partition...
for checked_label = partition{1}
% if this label shows up in any chunk of the labels for the given IC, we're okay
if any(~cellfun('isempty',strfind(signal.dipfit.model(ic).labels,checked_label{1})))
continue; end
end
% if, for any of the three partitions, none of the checked labels shows up in the IC's
% labels, then the IC is dropped
retain_ics(ic) = false;
break;
end
end
endNext, the actual signal processing code follows (which is essentially component-based rejection). This code is always executed, regardless of whether retain_ics was passed or computed (above) on demand.
signal.icaweights = signal.icaweights(retain_ics,:);
signal.dipfit.model = signal.dipfit.model(retain_ics);
if ~isempty(signal.icaact)
signal.icaact = signal.icaact(retain_ics,:,:); endThe previous changes to the signal only affected the meta-data, and not the signal time series itself. Thus, the processing step will be ignored by any subsequent processing step that ignores these meta-data and operates only on the raw signal. Ideally, all filters were advanced enough to take care of the meta-data that is relevant to them, however, for rapid prototyping (and some simple filtering), this is often not the case - thus, it is desirable to be able to replace the actual sensor-space signal by its independent component decomposition (restricted to those components that are associated with desired brain territories). If the optional parameter do_transform (a.k.a. TransformData) is enabled, the following code will do that. To avoid any inconsistencies, all subtle meta-data that related to the original raw signal is scrubbed.
if do_transform
signal.data = (signal.icaweights*signal.icasphere)*signal.data(signal.icachansind,:);
signal.chanlocs = struct('labels',cellfun(@num2str,num2cell(1:signal.nbchan,1),'UniformOutput',false));
signal.icaweights = [];
signal.icasphere = [];
signal.icawinv = [];
signal.icachansind = [];
signal.dipfit = [];
endFinally, the function epilogue follows, concluding the plugin code. In this example, a special remark is passed to exp_endfun - the fact that to replicate this processing step in real time, the name-value pair 'retain_ics',retain_ics should be appended to the parameters that are passed to the function (in addition to those that were passed by the user during the present invocation). The value of retain_ics that matches the three selection criteria has been pre-computed above, so a computational shortcut (using this value) can be taken if the function is later invoked in real time.
exp_endfun('append_online',{'retain_ics',retain_ics});For example, if this function was called as:
NEWEEG = flt_selvolume(EEG,{'Left Cerebrum'},{'Frontal Lobe','Claustrum'},true)... then, NEWEEG will have two annotations: first, the expression that were used to compute it in the first place (offline):
flt_selvolume(EEG,{'Left Cerebrum'},{'Frontal Lobe','Claustrum'},true)and second, the expression that may be used to replicate the same processing (efficiently) on real-time data, which will skip the "if ~exist('retain_ics') ..." part:
flt_selvolume(EEG,{'Left Cerebrum'},{'Frontal Lobe','Claustrum'},true,'retain_ics',[false,false,false,true,false,...])Stateful plugins differ from stateless ones in that they carry some state over from one sample to the next. In particular, as real-time data needs to be processed one chunk at a time, the plugin functions must be run on one chunk at a time, as well - and, for a given data stream, produce the same collective results as if invoked on the entire recorded data set. Therefore, the function must be able to carry over some state from one of its invocations to the next. This feature is the only difference between stateful and stateless filters. A simple analog is found in MATLAB's built-in function filter(), which has the ability to return state (in a second output value) after it processed a piece of signal, and can accept this state value (as an additional input parameter) when called the next time on a continuation of the signal. Likewise, all stateful filters in BCILAB have a mandatory additional output (a state value) and must be able to take an additional input (again, a state value).
A simple example of a stateful filter is the IIR (Infinite Impulse Response) filter. It is one of the most versatile frequency filters in BCILAB as long as the desired filter function can be expressed as a series of bandpass, bandstop, highpass, and lowpass filters. The following example will analyze the function code/filters/flt_iir.m in detail, which uses the Signal Processing toolbox to implement
is functionality.
First, the function signature is defined. In any stateful function, there are generally two outputs, the first being the output signal, and the second being the state after having consumed the input signal. The input arguments are always specified as varargin. The documentation of parameters is omitted here.
function [signal,state] = flt_iir(varargin)
% Filter a continuous data set by a digital IIR lowpass/highpass/bandpass/bandstop filter.Next, the mandatory filter prologue line follows; it looks the same in all filters.
if ~exp_beginfun('filter') return; endThen, the plugin properties are being declared. Here, the GUI name shall be IIRFilter. Some ordering relationships are declared: The filter prefers to follow flt_fir (because the signal will be more well-behaved after that stage than before it, which is helpful in preventing numeric inaccuracies). Second, the filter can not follow set_makepos, because it can only be (reasonably) applied to continuous data. The filter treats each channel independently.
declare_properties('name','IIRFilter', 'follows','flt_fir', 'cannot_follow','set_makepos', 'independent_channels',true);Next, the definition of the function's input arguments begins...
arg_define(varargin, ...The first argument is, as always, the signal, and it must always be named 'signal'. It is not reported to user interfaces.
arg_norep({'signal','Signal'}), ...The following argument is the frequency specification (default: []), and two multi-option parameters (displayed as pulldown menues in GUIs).
arg({'f','Frequencies'}, [], [], 'Frequency specification of the filter. For a low/high-pass filter, this is: [transition-start, transition-end], in Hz and for a band-pass/stop filter, this is: [low-transition-start, low-transition-end, hi-transition-start, hi-transition-end], in Hz.'), ...
arg({'fmode','Mode'}, 'bandpass', {'bandpass','highpass','lowpass','bandstop'}, 'Filtering mode. Determines how the Frequencies parameter is interpreted.'), ...
arg({'ftype','Type'},'butterworth', {'butterworth','chebychev1','chebychev2','elliptic'}, 'Filter type. Butterworth has a flat response overall but a slow/gentle rolloff. Chebychev Type I has a steep rolloff, but strong passband ripples. Chebychev Type II has a flat passband response, but a slower rolloff than Type I. The elliptic filter has the steepest rolloff (or lowest latency at comparable steepness) but passband rippling.'), ...The remaining two user arguments are numeric, but have a special kind of range value, encoded as an unnamed function (a few standard forms of such range functions are supported by arg; please consult the documentation for an overview).
arg({'atten','Attenuation'}, 50, @(x)0<x<=180, 'Minimum signal attenuation in the stop band. In db.'),...
arg({'ripple','Ripple'}, 0.5, @(x)0<=x<=60, 'Maximum peak-to-peak ripple in pass band. In db.'), ...The last argument is for internal purposes: it is the optional state input argument, not visible in user interface, and by default unassigned. The state argument should always be the last listed one (users may want to specify parameters in order of appearance, which is less transparent if there are internal parameters in between), and it must be called state (as the online system generally passes the state under this name).
arg_norep({'state','State'},unassigned));Next, the actual code begins. If no state was passed (the variable is not assigned, i.e. does not exist), it must be generated. The state object encapsulates the filter design, as well - thus, this is also the place where the filter is designed according to the specified parameters. If a plugin depends on a Mathworks toolbox, it is good practice to generate informative error messages, as below.
if ~exist('state','var')
if ~exist('dfilt','file')
error('You need the Signal Processing toolbox to make use of IIR filters in BCILAB.'); endNext, the long forms of some values are being transcribed into short forms. The function hlp_rewrite is a convenient way to unify multiple possibly syntaxes (it works for any value type).
fmode = hlp_rewrite(fmode,'bandpass','bp','highpass','hp','lowpass','lp','bandstop','bs');
ftype = hlp_rewrite(ftype,'butterworth','butt','chebychev1','cheb1','chebychev2','cheb2','elliptic','ellip');Then, the filter order is being computed. This generally involves a function like buttord, ellipord, etc., and the order of frequency band edges depends on the filtering mode (band-pass, band-stop, etc.). Note that most signal processing plugins will not attempt to support every possible filter design, and thus be somewhat simpler. The label variable is for convenience in the subsequent section.
f = [2*f/signal.srate 0 0];
switch fmode
case 'bp'
[Wp,Ws,label] = deal(f([2,3]),f([1,4]),{});
case 'bs'
[Wp,Ws,label] = deal(f([1,4]),f([2,3]),{'stop'});
case 'lp'
[Wp,Ws,label] = deal(f(1),f(2),{'low'});
case 'hp'
[Wp,Ws,label] = deal(f(2),f(1),{'high'});
end
[n,Wn] = feval([ftype 'ord'],Wp,Ws,ripple,atten);Next, the filter coefficients are designed (depending on order and specs). The Z-P-K form is best used with the (very convenient) dfilt object.
switch ftype
case 'butt'
[z,p,k] = butter(n,Wn,label{:});
case 'cheb1'
[z,p,k] = cheby1(n,ripple,Wn,label{:});
case 'cheb2'
[z,p,k] = cheby2(n,atten,Wn,label{:});
case 'ellip'
[z,p,k] = ellip(n,ripple,atten,Wn,label{:});
end
[sos,g] = zp2sos(z,p,k);
state = dfilt.df2sos(sos,g);As dfilt objects will not by default memorize their state across invocations, this needs to be enabled manually:
set(state,'PersistentMemory',true);Finally, in case the state was already passed as an argument, this type of filter design pre-computation has already been performed, and nothing needs to be done. However, dfilt objects in particular have handle semantics, i.e., writing y = x and modifying y also modifies x, unless y is turned into a genuine copy. To avoid accidentally manipulating the function's parameters, the state is being copied, if it was passed. Accidentally modifying handle parameters can lead to extremely hard-to-find bugs, as BCILAB tracks its filter arguments in various data structures, annotations, and caches.
else
state = copy(state);
endThen, the actual signal processing is being performed, by calling the filter() function for dfilt objects. This updates the state (which subsequently being returned as the second output).
signal.data = filter(state,double(signal.data),2);The plugin definition is concluded by the standard filter epilogue line.
exp_endfun;Generally, any adaptive signal processing method can be implemented as a stateful filter. A typical adaptive statistical filter is flt_standardize, which standardizes the signal in a moving window. In many cases, however, such fine-grained sample-by-sample updating is not necessary, and it can be very costly to do the update computations incrementally, so that real time operation would not be possible. As an alternative, a filter may also be adapted on the calibration data set "en block", and then be used with its adapted parameters held fixed in an online setting. Currently, there is no such example in the toolbox, but, for instance, independent component analysis could be implemented as such a filter (see code/filters/flt_ica.m). In this case, the decomposition would be computed if ICA is applied to a calibration dataset, and the resulting processed data set would be annotated with an additional parameter for online use, which holds the computed decomposition. If re-run in real time with this additional parameter, the data would only be transformed by the decomposition, without updating the composition dynamically. Another example would be artifact rejection functions, which often first need to learn the statistics of the data from the calibration set, but then can use a fixed criterion for online processing.
Machine learning is a field of theoretical computer science with large overlaps with statistical learning theory, probability theory, optimization and decision theory, and diverse other fields. The theory is still in rapid development and still quite fragmented, however, the interface through which machine learning methods interact with their data is consistent and mature (perhaps as a side effect of the computer science background). This interface is closely reflected in the machine learning plugin interface adopted by BCILAB.
The role of machine learning in brain-computer interfacing is to learn the central person-specific (and/or montage/session/task-specific) properties of the data, and to exploit that learned information for producing optimized, robustified and individualized outputs. Machine learning operates by convention on abstract representations of data (usually a set of feature vectors, or equivalently, of distinct points in a high-dimensional space) rather than signals, and therefore requires that the raw signals have been mapped into some appropriate representation in a prior step (this task is often handled by signal processing and/or feature extraction components). In addition, since machine learning usually operates on a set of items (feature vectors), the recorded signals must necessarily be chopped up into a set of trials, as well. This is the reason why epoching (segmentation) of data plays such a central role in BCI signal processing, and also why an experimental design that naturally gives rise to trials plays a critical role for the calibration session.
Given such appropriate data, machine learning methods can learn (estimate/derive) parameters, which are collectively called a model of the data. Given such a model, and similar (but new) data, they can make inferences about and output predictions with those data (using the previously learned information). The most common situation in BCIs is that the training data contains not just readily observable information (i.e., representations of measured biosignals), but also information that the system should learn to predict, namely information on the latent or hidden (hard to observe) cognitive state of the person that gave rise to (aspects of) the measured signals. Thus, the method receives both a feature vector and a so-called "label" (or target value) for each trial, and should learn the relationships between the two, condense them into a model, and use that model to predict the label for future feature vectors. This is called supervised learning (the "supervisor" is supplying the labels by virtue of the experiment design that was used to produce the training data). If the label indexes cognitive state and the feature vectors are derived from bio-signals, the system is set up to learn how to predict cognitive state from these bio-signals.
In the simplest (and most common) use case, information about the cognitive state of interest is not available during the practical use of a BCI (which is why the BCI is necessary in the first place), but only during the (artificially set up) calibration session. Following this constraint, the majority of learning can be done in a single step, after the entire calibration session has been recorded, yielding a model. This model can then be held fixed and be used to make predictions (from newly recorded data) throughout any subsequent use of the BCI.
In more advanced scenarios, the model could also be updated during use of the system (for example, to track changes in the statistical properties of the data), which is called (semi-supervised) online learning, or adaptation. It is also conceivable (though rare) that the outputs of the model should be available throughout the calibration phase, for example, if the user wants to interact with the system while it is learning to interpret his/her commands (called co-adaptive learning). Further, an existing model can also be updated (perhaps efficiently) given an additional newly recorded calibration set, then called incremental learning. Finally, as any type of information can in principle be used to enhance the performance of a model (given an appropriate algorithm), multiple pools of calibration data, e.g., from other persons, other tasks, other sessions, etc., can be exploited. This is a form of multi-task learning (though currently in its very infancy).
The interface of a machine learning plugin largely depends on the type of outputs that it should be able to make, and in some special cases on additional properties of the training data. Any machine learning plugin consists of two MATLAB functions, one for learning a model (given training data), and one for making predictions given a model. Both are placed in code/machine_learning/, and one is called ml_train.m, the other is called ml_predict.m. is usually the acronym for the method (e.g. SVM, GMM, LDA, etc.). The learning function always receives a set of feature vectors (trials) as its first input, optionally a set of target values (one per trial) as its second input, plus further optional user parameters, and always has one output (the model structure). The prediction function always receives a set of feature vectors (trials) as input and has one output, the set of predictions (one per trial). Machine learning functions are not expected to support all possible output formats; instead, they should support what the method can naturally handle, without unnecessary restrictions. Since the performance estimates that BCILAB can compute for a given method are depending on the format of the method's outputs, different formats allow for different types of performance (or more correctly, loss) measures and prohibit others. Thus, not every possible loss measure can be used with every possible algorithm -- for example, mis-classification rate is inappropriate for regression outputs, and mean-square error is inappropriate for classification outputs.
Classification. The most common type of output is the discrete target label, i.e., a set of cognitive state classes is assumed (e.g., surprised and not surprised), and the BCI should output which class holds true for the user (at any given time). This case is called classification. Here, the targets are passed as a vector of numbers (one number for each class, but not necessarily consecutive integers). The simplest possible output is a vector of the most probable target value per trial. The preferred output is fully probabilistic, and is a cell array which contains a set of discrete probability distributions (one per trial). Each distribution describes the probability that each of the possible outcomes was the true one for the given trial. The formats are specified more precisely in the function code/machine_learning/ml_predict.m. Generally, each method should be able to handle the multi-class case, i.e., more than 2 classes (possibly using the provided voting utilities internally).
Regression. In regression, the space of possible outputs is continuous, i.e., both the target values and the prediction values are real numbers (for example, the degree of cognitive workload). Accordingly, the target argument passed to the learning function are a vector of real numbers (one per trial), and the output produced by the prediction function is, in the simple case, a vector of real numbers (one point estimate per trial, for example a maximum-likelihood or maximum-a-posteriori estimate). In the advanced case, the output is a univariate statistical distribution per trial (returned as a specially formatted cell array, see ml_predict for more details), preferably using standard distributions of the Statistics toolbox.
Multivariate regression. In multivariate regression, the target values and prediction values are vectors, and accordingly, the target argument passed to the learning function is a matrix (one row per trial), as is the output of the prediction function (one row per trial). In the advanced case, the output is a multivariate distribution per trial (returned as a specially formatted cell array, see ml_predict), in most cases of Gaussian type (though custom distribution functions are possible).
Structured prediction. It is theoretically possible to use arbitrary data types for target values (both in learning and prediction); these are passed as a cell array (one element per trial, both in the targets argument passed to the learning function, and in the output of the prediction function).
Uncertain targets. It is in principle possible to learn from incomplete knowledge about the target values (e.g., from a discrete probability distribution over possible target values for a given trial in a calibration dataset, or from a multivariate distribution in the case of regression with uncertain training data). In this case, the set of target values passed to the learning function will themselves be in the previously mentioned distribution formats (see code/machine_learning/ml_train.m).
Weighted trials. Especially in complex machine learning settings, where a learning function is used in a larger framework (for example meta-learning, Adaboost, multiple-model ICA) the inputs to the learning function may have an associated weight (determining the influence of each trial on the model). Many standard learning functions, especially those based on statistics, optimization and probabilistic inference, can be extended to supported weighted trials (though only few of them are), and are therefore applicable in the weighted learning setting. If a method can easily support weighted trials, it is worth considering the implementation.
In the following, the SVM plugin (code/machine_learning/ml_trainsvm.m & ml_predictsvm.m) will be analyzed and explained in detail. Support vector machines are some of the most frequently used machine learning methods both for classification and regression, and have proven to be useful in BCI settings, as well (see also documentation of the method).
First, the learning function is defined, beginning with the function signature. In general, the only output is the learned model (whose format is left to the implementation), and the inputs are always declared as varargin.
function model = ml_trainsvm(varargin)
% Learn a predictive model by Support Vector Machines.
% Model = ml_trainsvm(Trials, Targets, Cost, Options...)Following the function's description (omitted), the input parameters are documented. As for any other plugin, the names of input arguments should match the names that are displayed in the GUI, and those that can be used in name-value pairs. When called from a script or the command line, this function allows to pass the first three parameters (Trials, Targets and Cost) as positional arguments (i.e., in order of appearance), where all remaining parameters must be passed via name-value pairs. Alternatively, all parameters (including the first three) can be passed via name-value pairs. Especially for machine learning, it is good practice to include full references in the documentation (these are being referred to in the omitted description).
% In:
% Trials : training data, as in ml_train
%
% Targets : target variable, as in ml_train
%
% Cost : regularization parameter, reasonable range: 2.^(-5:2:15), greater is stronger
% default: 1
%
% Options : optional name-value pairs to control the training details:
% 'variant': one of several SVM variants
% 'dual' : L2-regularized L2-loss support vector classification (dual), usually preferred (default)
% 'primal' : L2-regularized L2-loss support vector classification (primal), can be faster than dual
% 'crammer' : Crammer and Singer approach to multi-class support vector classification,
% as alternative to the voted classification employed in the other variants
% 'sparse' : L1-regularized L2-loss support vector classification, gives sparse results but
% will likely not be better unless the solution is truly sparse.
% 'l1loss' : L2-regularized L1-loss support vector classification (dual), rarely needed
% 'native' : native MATLAB implementation (using CVX); equivalent to 'dual', but slower
%
% 'kernel': one of several kernel types:
% * 'linear': Linear
% * 'rbf': Gaussian / radial basis functions (default)
% * 'laplace': Laplacian
% * 'poly': Polynomial
% * 'cauchy': Cauchy
%
% 'gamma': scaling parameter of the kernel (for regularization), default: 1
% reasonable range: 2.^(-16:2:4)
%
% 'degree': degree of the polynomial kernel, if used (default: 3)
%
% 'eps' : desired accuracy (default: [], meaning LIBLINEAR's default)
%
% 'bias' : include a bias variable (default: 1)
%
% 'scaling': pre-scaling of the data (see hlp_findscaling for options) (default: 'std')
%
% 'verbose' : verbosity level (default: 0)
%
% Out:
% Model : a predictive model;
% classes indicates the class labels which the model predicts
% sc_info is the scaling info
%
% Examples:
% model = ml_trainsvm(trials,labels,1): learn a linear SVM model
%
% See also:
% ml_predictsvm()
%
% References:
% [1] P. S. Bradley and O. L. Mangasarian. "Massive data discrimination via linear support vector machines."
% Optimization Methods and Software, 13:1-10, 2000.
% [2] R.-E. Fan, K.-W. Chang, C.-J. Hsieh, X.-R. Wang, and C.-J. Lin. "LIBLINEAR: A library for large linear classification"
% Journal of Machine Learning Research 9(2008), 1871-1874.
%
% Christian Kothe, Swartz Center for Computational Neuroscience, UCSD
% 2010-04-04Next, the definition of function arguments begins. The function arg_define allows for a special first parameter to describe how many of the arguments can be passed as positional arguments (i.e., by passing values in order of appearance); here, either 0 or 3 parameters can be passed positionally (as described earlier). Currently, only values of the form [0 x] are allowed, but more flexibility may be added in the future.
arg_define([0 3],varargin, ...For any supervised learning function, the first two parameters must be called 'trials' and 'targets', and should not be reported in user interfaces, as follows:
arg_norep('trials'), ...
arg_norep('targets'), ...The 'Cost' parameter has a special default value, which is being recognized by the BCILAB machine learning framework as denoting a range of possible values, out of which the optimal one should be determined via parameter search. Whenever a parameter in a plugin function defaults to search(...) or is specified by the user as search(...), the framework will try all possibilities and take the one which yields the best performance in a cross-validation. As this process can be extremely costly (computationally), such expressions should only be used as defaults when it is absolutely necessary to search over them - the user usually knows better how much time he/she wants to invest in learning a classifier. In the case of support vector machines, this is called the regularization parameter, and searching for it via cross-validation is a core ingredient of the algorithm.
arg({'cost','Cost'}, search(2.^(-5:2:15)), [], 'Regularization parameter. Reasonable range: 2.^(-5:2:15), greater is stronger.'), ...The next two parameters are standard multi-option strings.
arg({'variant','Variant'}, 'dual', {'dual','primal','crammer','sparse','l1loss','native'}, 'Variant to use. Dual and primal are l2-regularized l2-loss support vector classification, dual usually preferred but primal can be faster. Crammer is a special approach to multi-class problems. Sparse assumes that the result should be sparse, l1loss uses a rarely used loss function, native is a native MATLAB implementation, if the binary fails to work.'), ...
arg({'kernel','Kernel'}, 'rbf', {'linear','rbf','laplace','poly','cauchy'}, 'Kernel type. Linear, or Non-linear kernel types: Radial Basis Functions (general-purpose), Laplace (sparse), Polynomial (rarely preferred), and Cauchy (slightly experimental).','cat','Core Parameters'), ...The following parameter is another search parameter; if multiple parameters need to be searched, BCILAB will try all possible combinations (implying combinatorial running time). In some cases it is practical for the user to just make an educated guess and learn a model with it - if it performs sufficiently well, no costly search optimization will be necessary. However -- when searching manually for optimal parameters (or methods, in fact), treat the results with extreme care, since the manual search procedure is prone to producing systematically biased (towards the positive) results, if the results are noisy (which they are). Automatic parameter search does not have this bias (which is why it is so expensive to compute).
arg({'gammap','KernelScale','gamma'}, search(2.^(-16:2:4)), [], 'Scaling of the kernel functions. Should match the size of structures in the data. A reasonable range is 2.^(-16:2:4).','cat','Core Parameters'), ...Five misc parameters follow, of which the first is type-constrained to be an integer. It can be very helpful to constrain argument types as much as is reasonable (to prevent mis-use), but using integers tends to lead to extremely hard-to-find bugs. The reason is that integer arithmetic in MATLAB is so counter-intuitive that one might consider it broken: most operations involving one or more integers produce integer-valued results (even if real numbers are also involved).
arg({'polydegree','PolyDegree','degree'}, uint32(3), [], 'Degree of the polynomial kernel, if chosen.','cat','Core Parameters'), ...
arg({'epsi','Epsilon','eps'}, [], [], 'Tolerated solution accuracy. If unspecified, the default of the library (LIBLINEAR) will be taken.'), ...
arg({'bias','Bias'}, true, [], 'Include a bias term.'), ...
arg({'scaling','Scaling'}, 'std', {'none','center','std','minmax','whiten'}, 'Pre-scaling of the data. For the regulariation to work best, the features should either be naturally scaled well, or be artificially scaled.'), ...
arg({'verbose','Verbose'}, false, [], 'Whether to show diagnostic output.'));Next, the actual implementation of the method begins. To make the function usable without running it inside the machine learning framework of bcilab, it should be checked for any parameter defaulting to search(...) whether the search was actually expanded by the framework. If not (the function was called by itself), the parameter must be replaced by an educated guess, as below (except if the subsequent code can handle the search() format itself).
if is_search(cost)
cost = 1; end
if is_search(gammap)
gammap = 1; endMost functions that are used for classification will contain a line similar to the following. Since target values are not necessarily 0,1,2,3 but can be anything (e.g. -3.4), the unique target values must be obtained.
classes = unique(targets);Most machine learning plugins will make use of an external library, among others for performance reasons (in the case of this plugin, the library LIBLINEAR is used to perform the actual work), and the remaining code only adapts the parameter format appropriately. Dependencies should generally be placed in the directory "dependencies", as they can then be automatically loaded (or compiled, or downloaded) when the BCILAB toolbox is started (see dependencies.README therein for a brief guide). As binary code tends to fail on all but one platform, external dependencies are notoriously flaky when used in a cross-platform environment such as BCILAB. To guarantee stability nevertheless, it is good practice to provide native MATLAB fallback code for the remaining platforms (which would typically be slower, but would at least run), or to use a library which ships with pre-compiled binaries for all three platforms (Windows, Linux, Mac). In some cases (see dependencies/CStrAinBP*/fast_setdiff.m), an elaborate auto-compile script can be packaged with the library to compile it transparently on demand - this is, however, very tough, as the code needs to work with both modern versions of GCC (on Linux, very strict), mcc (on Win64, very low-end), and a variety of others.
The following code is the native MATLAB version. Here, it requires different parameters, as the behavior is not identical to the LIBLINEAR version (a function should behave identical across all platforms on which it runs, for a given parameter combination).
if strcmp(variant,'native')
% MATLAB versionThe following code section is a good example of code which supports only two classes, and which is (transparently) adapted to the multi-class case using the voting tools provided by BCILAB. It applies nearly unmodified to almost any other machine learning function which only supports binary classification. The follwing case calls the function with identical arguments, but chops up the trials and targets such that each call only involves two classes. During prediction, these two-class models are then combined via voting.
if length(classes) > 2
% in this case we use the voter...
model = ml_trainvote(trials,targets,@ml_trainsvmlinear,@ml_predictsvmlinear,cost,varargin{:});
return;
endA key consideration in many machine learning methods (especially regularized ones) is to scale and center the data appropriately. If in doubt, always add these two lines. It is also possible to perform very customized scaling as a tool in a regularized framework, for certain types of algorithms (e.g. if the natural scale / importance of features is known and can be used). Recall that the scaling parameter was a declared as a user parameter (defaulting to 'std').
% scale the data
sc_info = hlp_findscaling(trials,scaling);
trials = hlp_applyscaling(trials,sc_info);The following two lines map the data into a kernel space. This is a way to use linear methods to perform non-linear classification, but can be computationally quite costly if there are many trials involved (unless the more advanced "kernel trick" is used, which is, however, only applicable to certain types of methods). Kernelization yields remarkably powerful non-linear methods when used with strong and robust linear methods as a starting point. The three last parameters are all user-accessible.
basis = trials;
trials = utl_kernelize(trials,basis,kernel,gammap,polydegree);Many of the methods that support only two classes also require that the target values are {0,1} or {-1,+1}; forgetting this can lead to very hard-to-find bugs.
% remap targets
targets(targets == classes(1)) = -1;
targets(targets == classes(2)) = +1;Next, the actual machine learning code follows. This section solves a non-linear (but convex) optimization problem, using the CVX toolbox. CVX is very well supported across all platforms (and reasonably recent MATLAB versions), and is used extensively for fallback code throughout BCILAB. Because a large fraction of (efficiently solvable) machine learning problems can be formulated as such optimization problems, CVX is one of the methods of choice to implement fallbacks (or to prototype new algorithms). The problem formulation can be copied almost unmodified from any paper describing support vector machines.
[n,f] = size(trials);
cvx_begin
variables w(f) b xi(n)
minimize 1/2*sum(w.*w) + cost*sum(xi)
subject to
targets.*(trials*w + b) >= 1 - xi;
xi >= 0;
cvx_endFinally, the model (result) structure is built from the computed parameters.
model = struct('w',w,'b',b);The remaining code section does approx. the same computation, but using the LIBLINEAR library; it is therefore omitted here.
else
...
endThe learning function is concluded by storing the remaining variables in the model structure (whatever is needed to be able to make predictions).
model.sc_info = sc_info;
model.classes = classes;
model.variant = variant;
model.basis = basis;
model.kernel = kernel;
model.gammap = gammap;
model.degree = polydegree;The prediction function is usually much more compact than the training function (and most prediction functions for different methods look very similar). The prediction function here is called ml_predictsvm.m. The function signature is essentially identical across all machine learning plugins:
function pred = ml_predictsvm(trials, model)
% Prediction function for the Support Vector Machine.
% Prediction = ml_predictsvmlinear(Trials, Model)
%
% In:
% Trials : the data a matrix, as in ml_predict
%
% Model : predictive model as produced by ml_trainsvmlinear
%
% Out:
% Prediction : discrete probability distribution, formatted as
% {'disc' [NxC] [Cx1]}, with element #2 being the per-class probability and
% element #3 the original target values per class
% thus, the expected target values are Prediction{2}*Prediction{3}As the training function made use of ml_trainvote, the following boilerplate code is necessary:
if isfield(model,'voted')
pred = ml_predictvote(trials,model);
elseThe remaining code will operate in a two-class regime, if that was necessary for training. First, if the data was scaled during training, it must be scaled here, as well (which requires the previously learned scaling parameters to be part of the model). Likewise, if the data was kernelized in the learning function, it must be kernelized here, as well (which requires, among others, the original data points as basis vectors).
trials = hlp_applyscaling(trials,model.sc_info);
trials = utl_kernelize(trials,model.basis,model.kernel,model.gammap,model.degree);Here, a distinction is made according to which code path was chosen during learning. In both cases, the most likely class label (in {0,1,2,...}) is estimated for the trials. These predictive maps are usually very compact, as they need to be very fast.
if strcmp(model.variant,'native')
% MATLAB implementation
class = trials*model.w + model.b > 0;
else
% LIBLINEAR implementation
class = llpredict(zeros(size(trials,1),1),sparse(double(trials)),model);
endFinally, the class indices are translated into a discrete probability distribution. Even if a function does not support probabilistic outputs (SVMs do not natively handle probabilities, unless a "trick" is used), it is a good idea to generate such a distribution (then containing only 0's and one 1), since almost all higher-level evaluation code is being tested extensively with this format, and less extensively with the more primitive class labels (as basically no method actually outputs it).
probs = zeros(length(model.classes),length(class));
probs(length(model.classes)*(0:length(class)-1)'+ class + 1) = 1;
pred = {'disc', probs', model.classes};
endIn the following, a few code snippets from selected functions will be analzed to illustrate noteworthy points for the creation of machine learning plugins.
Weighted learners. The function ml_traingauss is an example for a function that optionally supports weights for every trial. To unify code in such functions, weights (which are packaged with trials) can be extracted in the following way from the parameters:
% obtain weights
if iscell(targets)
[targets,weights] = deal(targets{:});
else
weights = ones(size(targets,1),1);
endMatrix-shaped features. A special-purpose format for trial data are feature matrices instead of feature vectors. This may be practical for to impose certain types of groupwise sparsity assumptions. For example, the function ml_traindal supports row-sparse, column-sparse and low-rank regularization on the respective feature spaces. The code in the function is a good example of handling shape parameters appropriately, even if features are passed in vectorized form.
Built-in cross-validation. Some external machine learning tools support built-in parameter search (via cross-validation) on the trials passed to them. In many cases, this is orders of magnitude faster as if computed using the search() expressions. Thus, any such feature should be exploited to find parameters efficiently -- however, most such methods implement randomized cross-validation, which is not the ideal choice in BCI situations (since the trials come from signals, nearby trials are not statistically independent, but tend to be similar to each other so that any parameters learned with randomized CV may easily be biased towards overfitting). The function ml_trainhkl allows to pass a vector of possible regularization values, which are internally searched (using blockwise CV).
Randomized algorithms. Some algorithms are intrinsically randomized (e.g. certain clustering methods). These methods tend to give non-reproducible results (which is catastrophic in science, but also for mundane test cases). Therefore, the random seed used by these methods should first be backed up, replaced by a fixed (or user-accessible) value, and finally be restored. The restoration should be bulletproof, if possible (and in particular, should even execute if the user presses Ctrl+C), which is only possible since MATLAB 2008a. See the following code (from ml_traingmm) for how to support this robustly.
% back up the rand state
oldstate = rand('state');
c = onCleanup(@() rand('state',oldstate));
rand('seed',1337)... randomized code
% recover the rand state
if exist('oldstate','var')
rand('state',oldstate); endUsing command-line tools. Many high-end machine learning packages support only command line interfaces, and constructing GUIs that expose every possible command line parameter in a human-readable form can be very tedious to write. See ml_trainsvmperf for an example of how to expose expressive parameter names and values to the user, but internally construct a command line from them, using argument declarations, hlp_rewrite, and sprintf.