Merge Sort

Why is this important?

This workshop is important because:

Merge sort is the first fast, powerful sorting algorithm that you will encounter in the wilds of the real world (it's baked into Safari and Firefox!). It uses an extremely efficient application of the 'Divide and Conquer' concept to sort lists of elements. It's also a great chance to practice recursion.

What are the objectives?

After this workshop, developers will be able to:

• explain three steps to create a recursive algorithm.
• describe the merge sort algorithm and a merge algorithm.
• write a pseudocode version of merge sort and a JavaScript version of merge sort.
• determine the runtime (in big-O() notation) for merge sort.

Where should we be now?

Before this workshop, developers should already be able to:

• iterate through an array using a for loop, forEach, or other iterators.
• describe the purpose of big-O() notation.

Recursion

With factorial! The notation n! (pronounced "n factorial") is defined for whole numbers greater than or equal to 0 -- it means the result of multiplying n * (n-1) * (n-2) * ... * 3 * 2 * 1. You can probably think of an iterative way to write this with a for loop, but a recursive version can give us a little insight into recursion. Here's some code to define a recursive factorial function:

function factorial(n):
  if (n === 0 || n === 1){
    return n;
  }
  else {
    return n * factorial(n-1);
  }

Let's use this example to illustrate the three steps of a recursive algorithm:

1. Define base case(s) - make special case or cases to handle the simplest possible inputs without recursion. The base cases above are where n is 1 or 0. By definition, 0! and 1! are both just 1.
2. Make recursive call(s) - recursively solve smaller subproblems to help find the answer to the main problem. In the example above, factorial(n-1) is a call to solve the subproblem of (n-1)!.
3. Phrase overall answer in terms of subproblem answer(s) - combine subproblem answers (the result of recursive calls) with any extra processing needed to pull out the final answer. In the example, multiplying the subproblem answer factorial(n-1) by n gives the final result.

###Check for Understanding

Here's pseudocode for calculating the Fibonacci sequence:

fibonacci(n) {
   if n == 1 or n == 0
      return 1
   else
      return fibonacci(n-1) + fibonacci(n-2)
}

1. What base case(s) are covered?
2. What recursive subproblem(s) are solved?
3. What processing turns the answers from the subproblem(s) into an answer for the overall problem?

Want something a little less obvious? Think about the same three questions for this binary search pseudocode:

binarySearch(array, target, low, high) {
  if (low > high)
     return -1;

  int mid = (low + high)/2;

  if (array[mid] == target)
     return mid;
  else if (array[mid] < target)
     return binarySearch(array, target, mid+1, high);
  else // last possibility: a[mid] > target
     return binarySearch(array, target, low, mid-1);
}

Merge Sort

Take a look at this video. Can you see how merge sort works?

Merge sort works on the basic principal of divide and conquer - dividing your list into sub-lists (recursively) until your sub-lists are of length one or zero. Once your sub-lists are at that size, you merge with a neighboring sub-list. When you merge them, you merge them in sorted order.

There are usually TWO algorithms that work together to accomplish a merge sort:

• A merging algorithm that takes two sorted arrays and combined them into one large sorted array pushing the lowest to highest valued elements. The merge algorithm is not recursive.

• A merge sort algorithm that takes an array, splits it into two halves, recursively merge sorts both halves, and finally uses the merge algorithm to put them back together into one sorted array.

Note: iterative merge sort is possible, but it's much harder. Please work on a recursive version!

Make your own merge sort implementation!

Goal: Write a merge function and a mergeSort function to implement recursive merge sort as described above.

1. Start with the recursive mergeSort -- assume you have a working merge function. Consider:

• What base case(s) do you need for mergeSort?
• What smaller subproblems can you solve recursively?
• How will you go from the solutions for subproblems, to a solution for the overall problem?

1. Next, tackle merge. This isn't recursive, but edge cases can make it tricky!

Recursion Trees

When dealing with recursion, we often use a tree structure to make an educated guess about Big O runtime. Here's one for factorial:

Each node in the tree represents a subproblem. The root node is the original problem. Base cases are the leaves - the nodes at the bottom of the tree that don't have any children.

Once we have our tree, the total runtime can be calculated by summing up the work required for every node. We can do this by finding the total work at each level of the tree, then summing up the levels of the tree. If the work at each level is the same, this can be simplified to multiplying the work at each level by the number of levels in the tree.

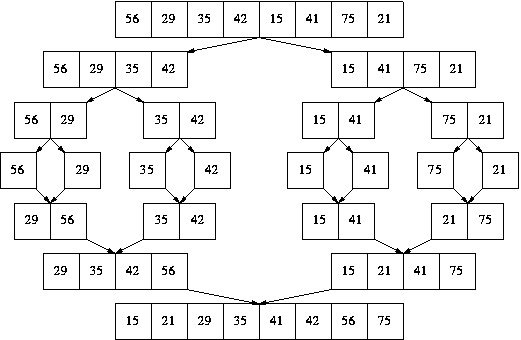
Here's a merge sort recursion tree:

The number of levels is log₂n, and the work required at each level adds up to O(n). Recursion trees aren't foolproof - this is a "hand wavey" way to show that the Big O runtime of merge sort is O(n log(n)). Since the work at each level is very, very similar, the recursion tree gives us the correct big O for merge sort!

Additional Resources

• Merge sort on wikipedia
• Calculating Big O for recursion from MIT
• Graphical comparison of sorting algorithms