This repo contains the ClustAssess R package, which provides a set of tools for evaluating clustering robustness.
To assess clustering robustness, the proportion of ambiguously clustered pairs (PAC) [1] uses a consensus clustering. The rate of element co-clustering is recorded across various numbers of clusters, k. The lower the PAC, the stabler the clustering for that k.
ClustAssess uses a heirarchical clustering as base for the consensus clustering, and an optimized Rcpp [2] implementation to compute the PAC values. To calculate PAC, we write:
cc_res = consensus_cluster(your_data, n_reps=50, k_max=20, p_sample=0.8, p_feature=0.8)
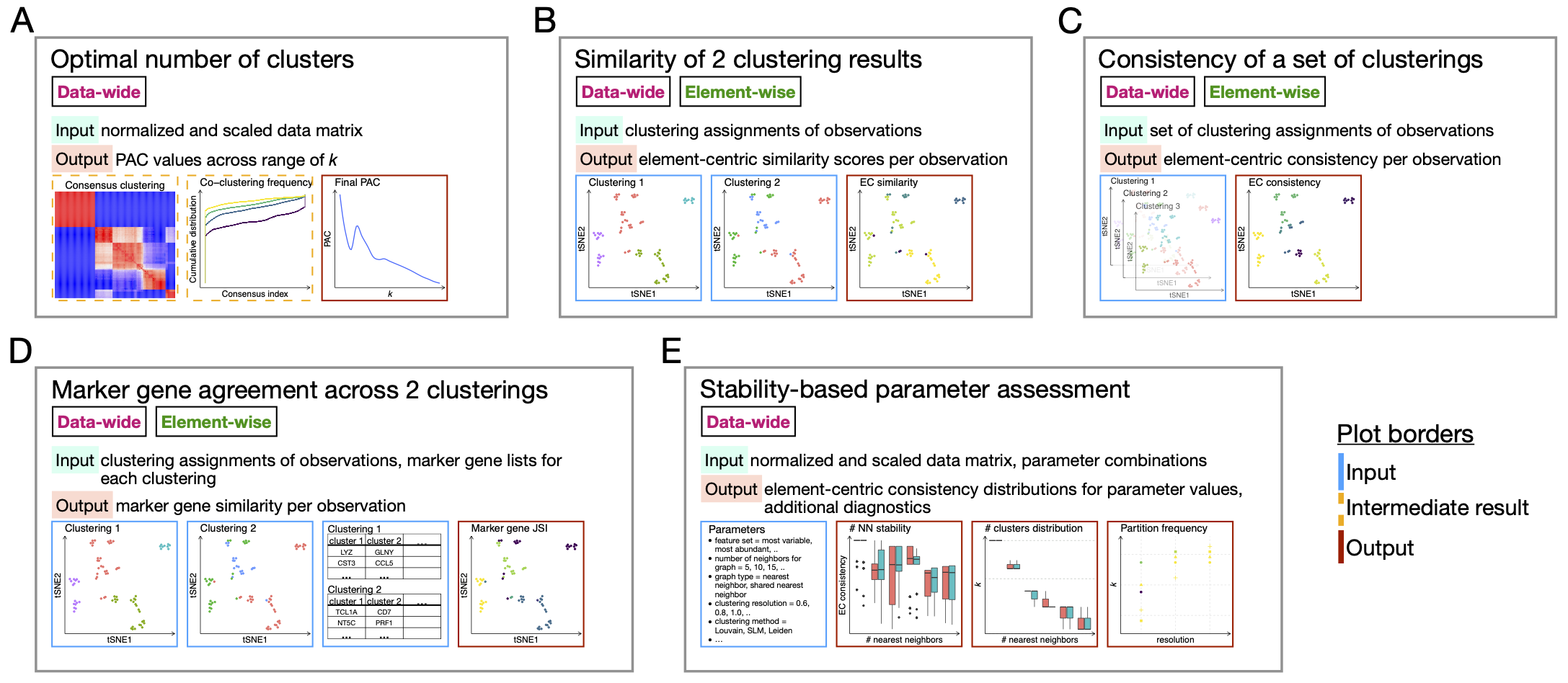
It is important that the PAC has converged before using it to assess your data;
the pac_convergence function can be used to visualize the PAC curves across
iterations:
As the curves have evened out, we surmize that PAC has converged in this case.
If the PAC has not converged, increase the n_reps value.
If the dataset contains >1000 elements, we recommend calculating a geometric sketch [3] of your data of size <1000, and running PAC on that sketch.
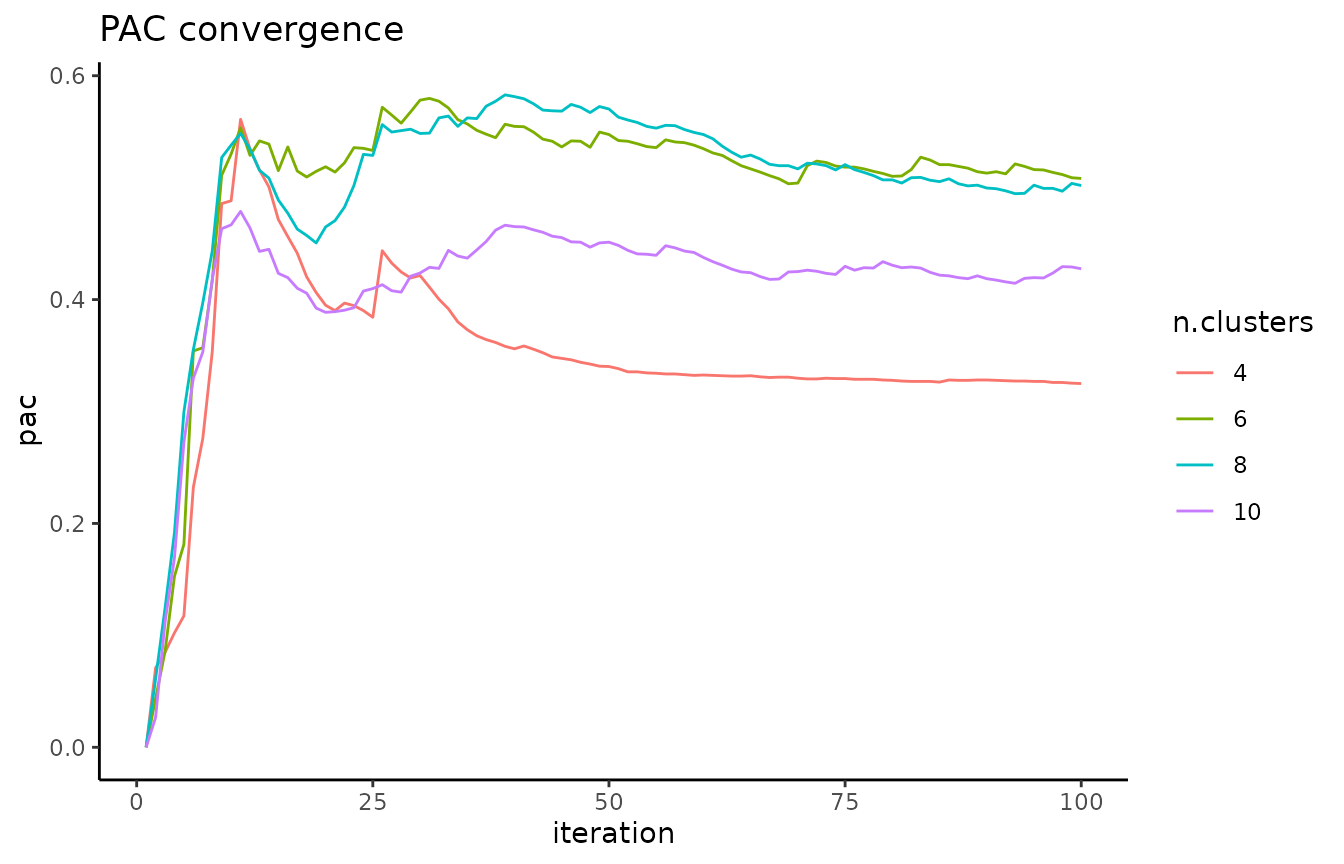
A local minimum in the PAC landscape, as visualized below using the
pac_landscape function, can be interpreted as an optimal k for the dataset:
Element-centric similarity (ECS) [4] is a per-observation measure of clustering similarity. Briefly, ECS is obtained by constructing a cluster-induced element graph, and subsequently calculating the stationary probability distribution of a random walk with restarts (also known as a personalized Pagerank) over the elements.
In addition to providing per-element information on clustering agreement, ECS avoids several pitfalls associated with other measures of clustering similarity (refer to [4] for more detail).
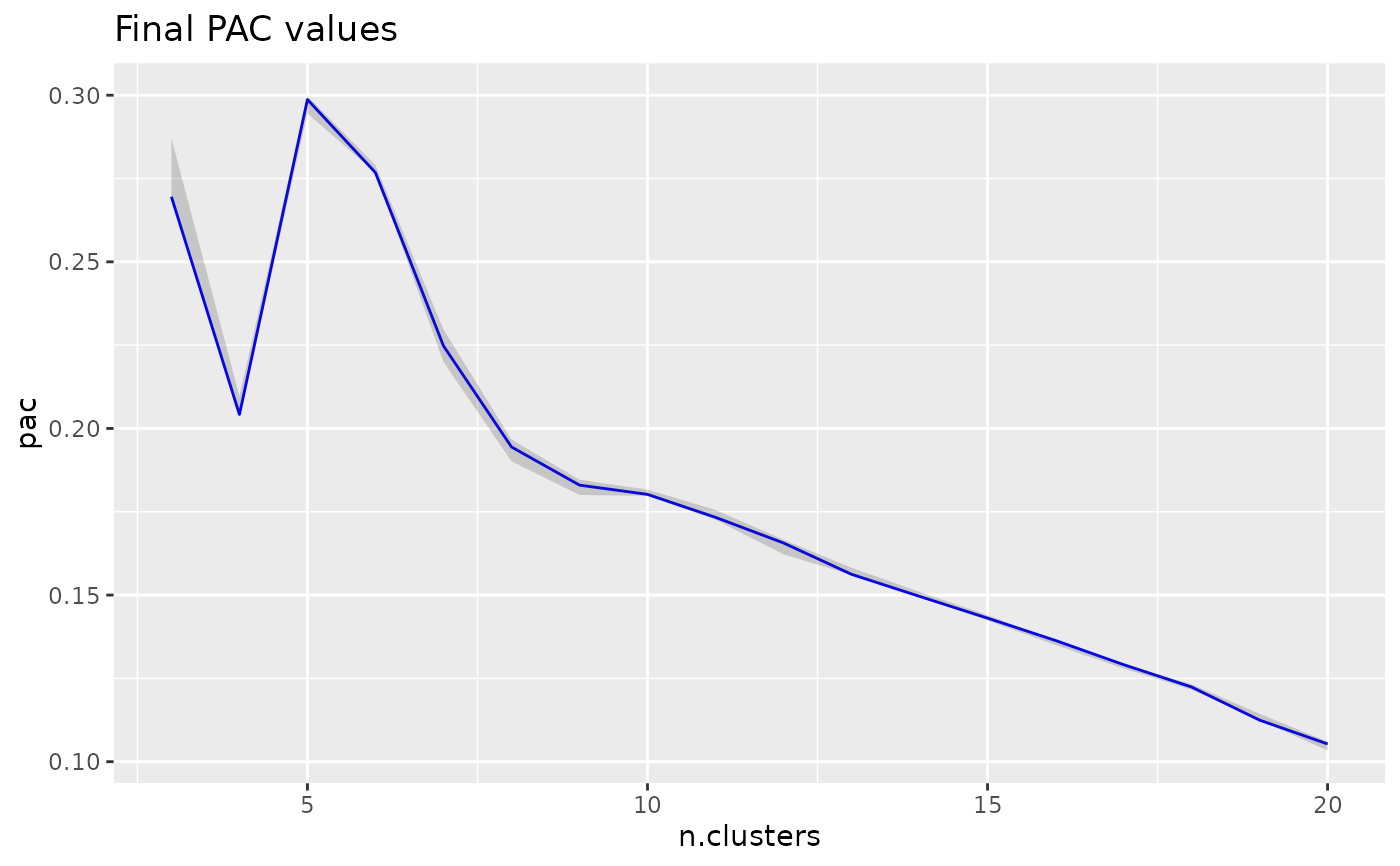
To compare two clusterings with ECS, we use the element_sim_elscore function:
ecs = element_sim_elscore(clustering_result1, clustering_result2, alpha=0.9)
where 1-alpha is the restart probability of the random walk. We can
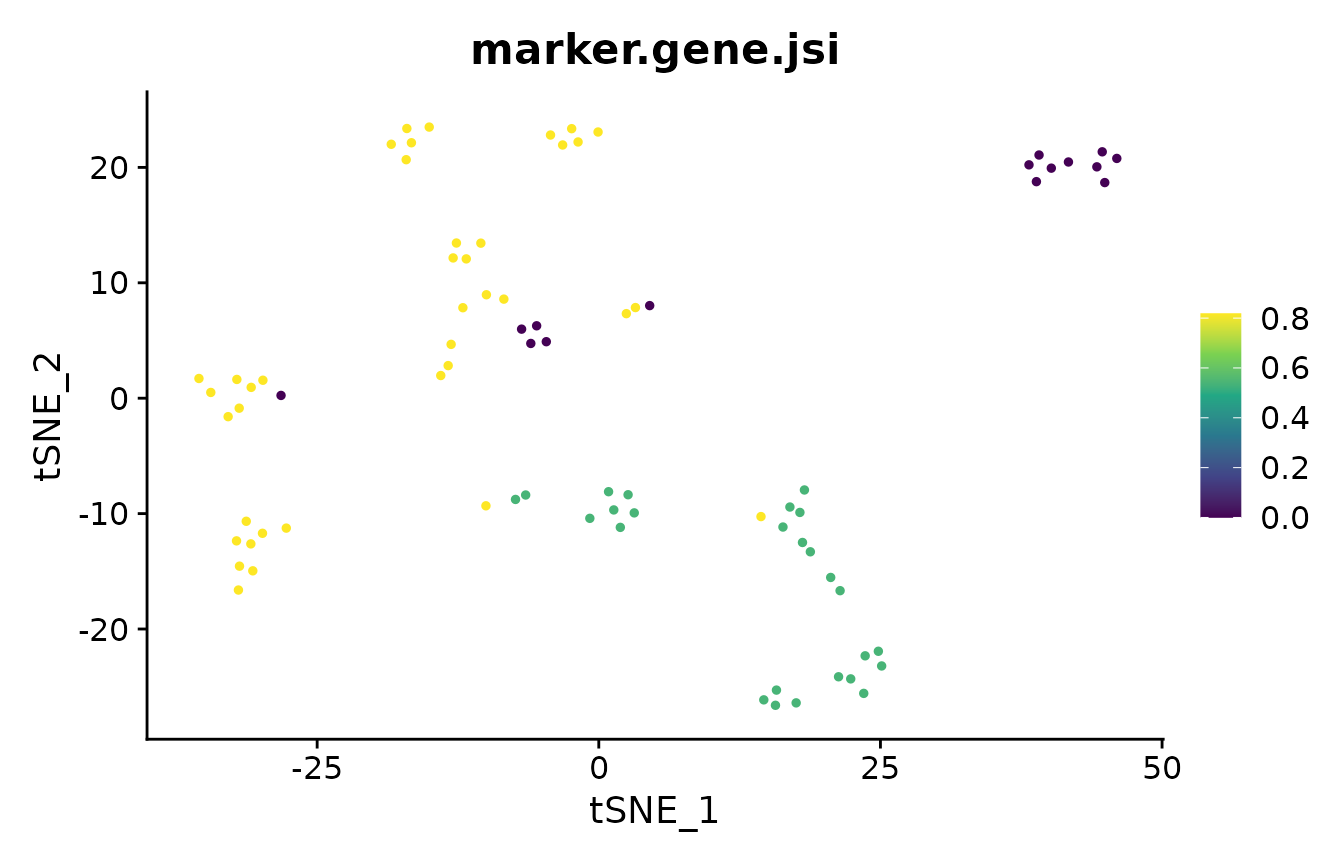
subsequently visualize the ECS on a PCA of the data:
In addition to flat disjoint clusterings (like the result of k-means for
example), ClustAssess can also compare overlapping clusterings and hierarchical
clusterings; refer to the comparing-soft-and-hierarchical vignette for more
detail.
Besides comparing two clusterings with element_sim_elscore, ClustAssess
also enables computing the per-element consistency (aka frustration) between a
set of clusterings with the element_consistency function, and comparing a set
of clusterings with a ground truth partitioning of elements with the
element_agreement function.
In the analysis of single-cell RNA-seq data, cluster marker genes are typically
used to infer the cell type of clusters. However, two different clustering
results may lead to two different sets of markers for the cells. The
marker_overlap function allows the comparison of two sets of markers. The
output can be either as the number of common marker genes per cell, or as
Jaccard similarity (size of intersect divided by size of union) per cell.
The most common clustering pipeline for single-cell data consists of
constructing a nearest-neighbor graph of the cells, followed by community
detection to obtain the clustering. This pipeline is available in multiple
single-cell toolkits, including Seurat, Monocle v3, and SCANPY.
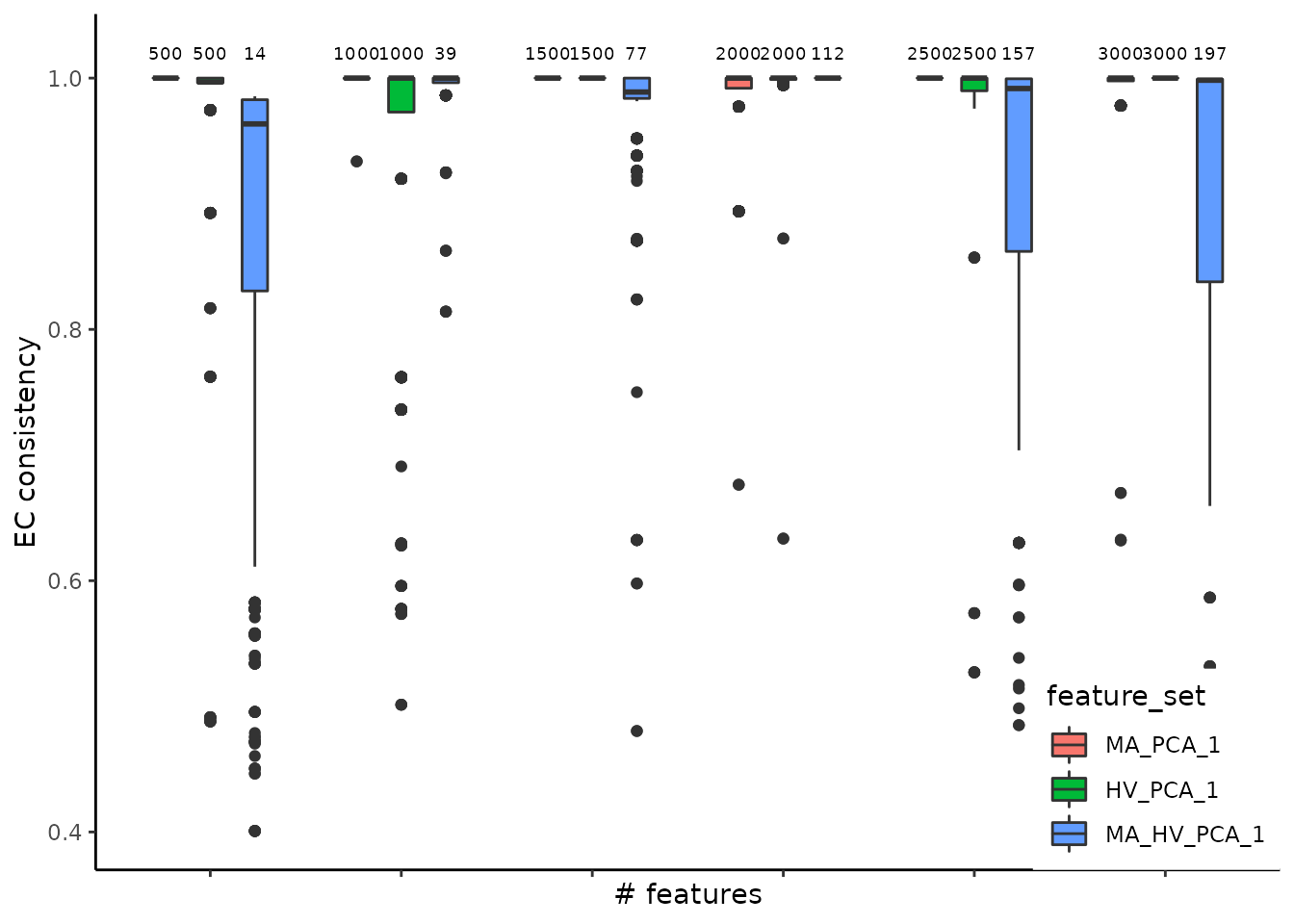
ClustAssess provides several methods to assess the stability of parameter
choices that influence the final clustering, for example to evaluate feature
sets, we use get_feature_stability_object, and plot the results with
plot_feature_stability_boxplot:
where the higher element-centric consistency (ECC) indicates more stable clustering results across random seeds. For more details, please see this vignette.
If your dataset is large, the runtime for the tools described above may be prohibitive. In these cases, we recommend subsampling your data using geometric sketching [3]. In R, the subsampling can be done via reticulate:
geosketch <- reticulate::import('geosketch')
assuming data.embed contains a dimensionality reduction of your data, you can then call:
sketch.indices <- geosketch$gs(data.embed, sketch.size, one_indexed = TRUE)
and use the resulting indices for your subsample. For PAC, subsampling to <1000 cells should help, and for ECS and data assessment functions, <5000 cells may be appropriate (and parallelization can further help reduce the runtime).
ClustAssess can be installed from CRAN:
install.packages("ClustAssess")
or from github using remotes:
remotes::install_github("Core-Bioinformatics/ClustAssess")
The following packages are required for ClustAssess:
- ggplot2
- dplyr
- fastcluster
- rlang
- Matrix
- igraph
- magrittr
- Rcpp
- methods
- stats
- foreach
- doParallel
- irlba
- progress
- reshape2
- stringr
- uwot
- gtable
To use all stability-based assessment methods, and run all examples and vignettes, the following packages are also needed:
- knitr
- rmarkdown
- e1071
- dbscan
- dendextend
- Seurat
- readr
- patchwork
If you have used ClustAssess in your work, please cite Shahsavari et al. 2022:
Shahsavari, A., Munteanu, A., & Mohorianu, I. (2022). ClustAssess: Tools for Assessing the Robustness of Single-Cell Clustering. bioRxiv. https://doi.org/10.1101/2022.01.31.478592
or in BibTex:
@ARTICLE{clustassess,
title = "ClustAssess: Tools for Assessing the Robustness of Single-Cell Clustering",
author = "Shahsavari, Arash and Munteanu, Andi and Mohorianu, Irina",
journal = "bioRxiv",
year = 2022,
url = "https://doi.org/10.1101/2022.01.31.478592",
language = "en"
}
[1] Șenbabaoğlu, Y., Michailidis, G., & Li, J. Z. (2014). Critical limitations of consensus clustering in class discovery. Scientific reports, 4(1), 1-13. https://doi.org/10.1038/srep06207
[2] Eddelbuettel, D., & Balamuta, J. J. (2018). Extending R with C++: A brief introduction to Rcpp. The American Statistician, 72(1), 28-36. https://doi.org/10.1080/00031305.2017.1375990
[3] Hie, B., Cho, H., DeMeo, B., Bryson, B., & Berger, B. (2019). Geometric sketching compactly summarizes the single-cell transcriptomic landscape. Cell systems, 8(6), 483-493. https://doi.org/10.1016/j.cels.2019.05.003
[4] Gates, A. J., Wood, I. B., Hetrick, W. P., & Ahn, Y. Y. (2019). Element-centric clustering comparison unifies overlaps and hierarchy. Scientific reports, 9(1), 1-13. https://doi.org/10.1038/s41598-019-44892-y